Página 50

Parte 2

4. Adição algébrica com radicais

Acompanhe duas fórmas de efetuar a adição algébrica com radicais.

1ª fórma

Substituímos as raízes por seus valores e fazemos os cálculos indicados. Por exemplo:

\sqrt{49} + \sqrt{16}

= 7 + 4 = 11

\sqrt[3]{8} ‒ \sqrt[4]{16}

= 2 ‒ 2 = 0

‒ 5 \sqrt[3]{0, 125} + 2 \sqrt{1, 69}

= ‒5 ⋅ 0,5 + 2 ⋅ 1,3 = ‒2,5 + 2,6 = 0,1

2ª fórma

Se houver vários radicais iguais, podemos colocá-los em evidência. Por exemplo:

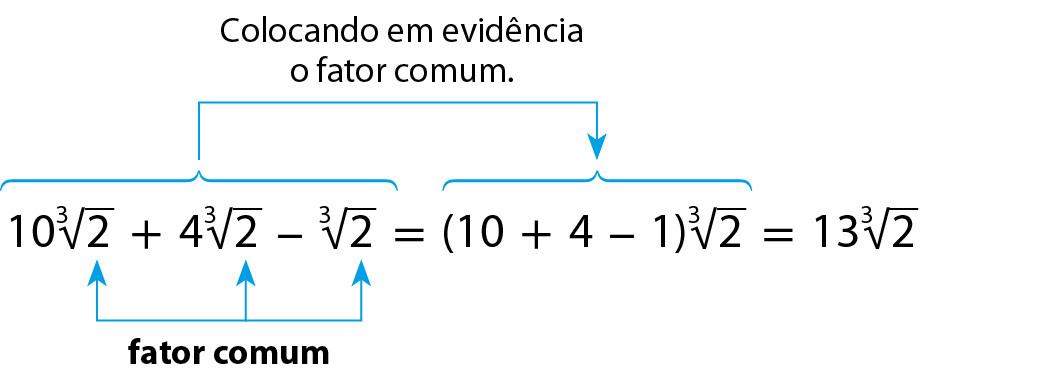
Esquema. 10 vezes raiz cubica de 2, mais 4 vezes raiz cubica de 2, menos raiz cubica de 2, igual a, entre parênteses, 10 mais 4 menos 1, vezes raiz cubica de 2, igual a 13 vezes raiz cubica de 2. Setas azul apontando para os fatores raiz cúbica de 2 da expressão antes do primeiro sinal de igual com a indicação fator comum. Chave horizontal destacando a expressão antes do primeiro sinal de igual e chave horizontal destacando a expressão depois do primeiro sinal de igual. Da primeira para a segunda chave seta azul com a indicação Colocando em evidência o fator comum.

Ilustração. Menina de cabelo comprido castanho, camiseta amarela e saia roxa. Ela fala: Isso me lembra da propriedade distributiva.

3 \sqrt{5} + 2 \sqrt{7} - 5 \sqrt{5} + \sqrt{7} + 4 \sqrt{7}

(3 - 5) \sqrt{5} + (2 + 1 + 4) \sqrt{7}

- 2 \sqrt{5} + 7 \sqrt{7}

A expressão

‒ 2 \sqrt{5} + 7 \sqrt{7}

não pode mais ser reduzida, porque seus termos não têm radicais iguais. Mas é possível encontrar um valor aproximado para ela.

Como

\sqrt{5} ≃ 2, 2

\sqrt{7} ≃ 2, 6

, temos:

‒ 2 \sqrt{5} + 7 \sqrt{7} ≃ ‒ 2 \cdot 2, 2 + 7 \cdot 2, 6

‒ 2 \sqrt{5} + 7 \sqrt{7} ≃ 13, 8

\sqrt{18} + \sqrt{50} = \sqrt{2 \cdot 3^{2}} + \sqrt{2 \cdot 5^{2}} = 3 \sqrt{2} + 5 \sqrt{2} = 8 \sqrt{2}

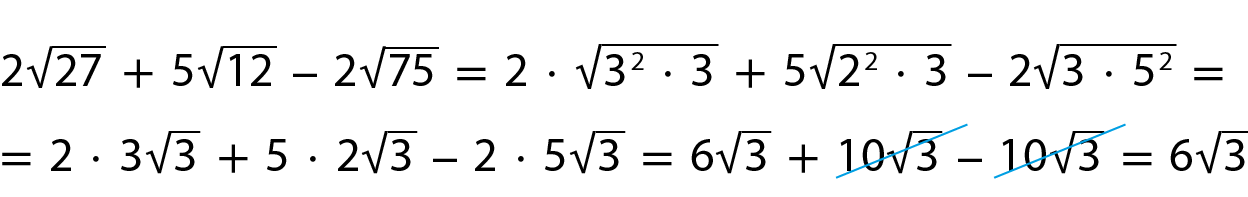
2 vezes raiz quadrada de 27, mais 5 vezes raiz quadrada de 12, menos 2 vezes raiz quadrada de 75, igual a, 2 vezes raiz quadrada de 3 ao quadrado vezes 3, mais 5 vezes raiz quadrada de 2 ao quadrado vezes 3, menos 2 vezes raiz quadrada de 3 vezes 5 ao quadrado, igual a, 2 vezes 3 vezes raiz quadrada de 3, mais 5 vezes 2 vezes raiz quadrada de 3 menos 2 vezes 5 vezes raiz quadrada de 3, igual a, 6 vezes raiz quadrada de 3, mais 10 vezes raiz quadrada de 3 menos 10 vezes raiz quadrada de 3, igual a 6 raiz quadrada de 3.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

21 Calcule.

\sqrt{25} + \sqrt[3]{27} + \sqrt[4]{81}

\sqrt[3]{‒ 64} + \sqrt{64} + \sqrt[6]{64}

2 \sqrt{4, 41} ‒ 3 \sqrt{2, 56}

5 \sqrt{1, 44} + 3 \sqrt[3]{0, 343}

22 Efetue.

3 \sqrt{5} + \sqrt{5} ‒ 6 \sqrt{5}

4 \sqrt{2} + 6 \sqrt{3} ‒ 2 \sqrt{2} + 9 \sqrt{3}

2 \sqrt[5]{3} ‒ 2 \sqrt{3} + 3 \sqrt{3} + 3 \sqrt[5]{3}

3 + \sqrt{2} + 7 ‒ 5 \sqrt{2}

Página 51

23 Reduza os radicais a uma expressão na fórma

a \sqrt{b}

, com a e b inteiros.

\sqrt{20} + \sqrt{45}

4 \sqrt{63} ‒ \sqrt{7}

\sqrt{50} + \sqrt{98} ‒ \sqrt{72}

\sqrt{12} + \sqrt{75} + \sqrt{108}

24 Determine a medida do perímetro das figuras, cujas medidas dos lados são dadas em uma mesma unidade de medida de comprimento.

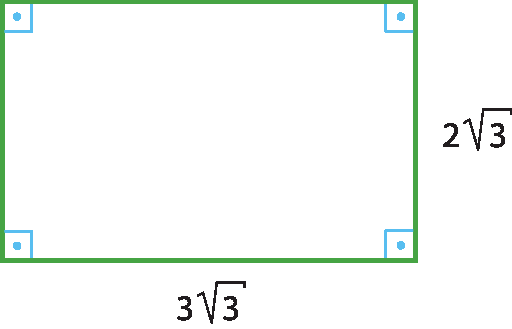
Ilustração. Retângulo com medidas: 2, raiz quadrada de 3 por 3, raiz quadrada de 3.

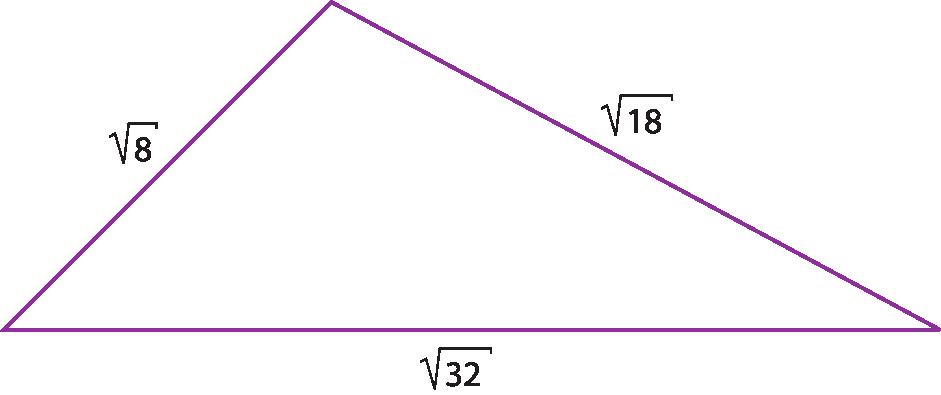
Ilustração. Triângulo com as medidas: raiz quadrada de 8 por raiz quadrada de 18 por raiz quadrada de 32

25 Ao efetuar

\sqrt[3]{\frac{15}{343} + \sqrt{\frac{3}{7} ‒ \frac{5}{49}}}

, qual é o valor obtido?

\frac{\sqrt[3]{211}}{7}

\frac{\sqrt[3]{211}}{49}

\frac{211}{343}

\frac{19}{350}

5. Multiplicação e divisão com radicais

Multiplicação com radicais

Para multiplicar radicais de mesmo índice, aplicamos a 3ª propriedade dos radicais:

\sqrt[n]{a \cdot b} = \sqrt[n]{a} \cdot \sqrt[n]{b}

sendo n um número natural não nulo e a e b números reais positivos.

Portanto, para multiplicar radicais de mesmo índice, mantemos o índice e multiplicamos os radicandos, simplificando, sempre que possível, o resultado obtido.

Acompanhe alguns exemplos.

\sqrt[4]{2} \cdot \sqrt[4]{8} = \sqrt[4]{2 \cdot 8} = \sqrt[4]{16} = \sqrt[4]{2^{4}} = 2

‒ 5 \sqrt{3} \cdot 3 \sqrt{2} = (‒ 5 \cdot 3) \sqrt{3 \cdot 2} = ‒ 15 \sqrt{6}

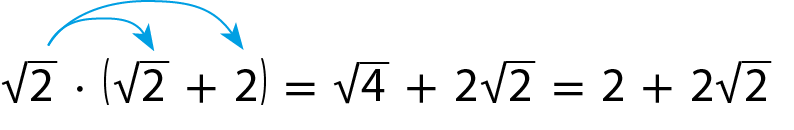
Esquema. Raiz quadrada de 2, vezes, entre parenteses, raiz quadrada de 2 mais 2, igual a, raiz quadrada de 4 mais 2, raiz quadrada de 2, igual a, 2 mais 2, raiz quadrada de 2.
Na expressão há duas setas azuis saindo do primeiro raiz de 2 e chegando no segundo raiz de 2 e no primeiro 2.

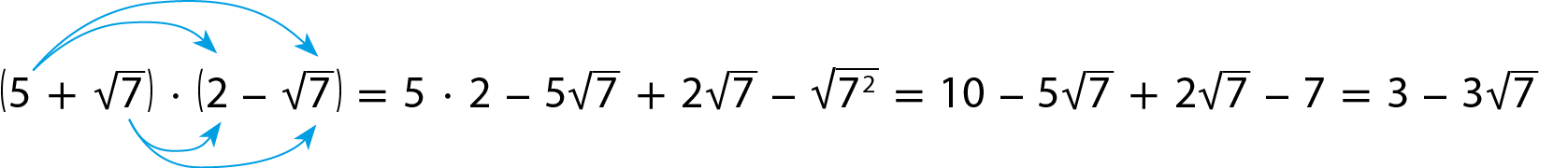
Esquema. entre parenteses, 5 mais raiz quadrada de 7, vezes, entre parenteses, 2 menos raiz quadrada de 7, igual a, 5 vezes 2 menos 5, raiz quadrada de 7, mais 2, raiz quadrada de 7, menos raiz quadrada de 7 ao quadrado, igual a, 10 menos 5, raiz quadrada de 7, mais 2, raiz quadrada de 7 menos 7, igual a 3 menos 3, raiz quadrada de 7. Na expressão há duas setas azuis saindo do primeiro 5 e chegando no primeiro 2 e no segundo raiz de 7. Também há duas setas azuis saindo do primeiro raiz de 7 e chegando no primeiro 2 e no segundo raiz de 7.

Página 52

Se os índices dos radicais forem diferentes, antes da multiplicação reduzimos esses radicais a um mesmo índice. Observe, por exemplo, como fazemos a redução dos radicais

\sqrt[3]{2^{2}}

\sqrt[4]{3}

a um mesmo índice.

Esquema. raiz cubica de 2 ao quadrado, igual a, 2 elevado a 2 terços, igual a, 2 elevado a 8, 12 avos, igual a, raiz 12 de 2 elevado a 8. raiz quarta de 3, igual a, 3 elevado a 1 quarto, igual a, 3 elevado a 3, 12 avos, igual a, raiz 12 de 3 elevado ao cubo. Seta azul apontando para um reticulado que destaca 2 elevado a 2 terços e 3 elevado a 1 quarto com a indicação: Escrevemos os radicais na forma de potência. Seta azul apontando para um reticulado que destaca 2 elevado a 8, 12 avos e 3 elevado a 3, 12 avos com a indicação: Determinamos, no expoente, frações equivalentes de mesmo denominador. Seta azul apontando para um reticulado que destaca raiz 12 de 2 elevado a 8 e raiz 12 de 3 elevado ao cubo com indicação: Escrevemos as potências na forma de radical.

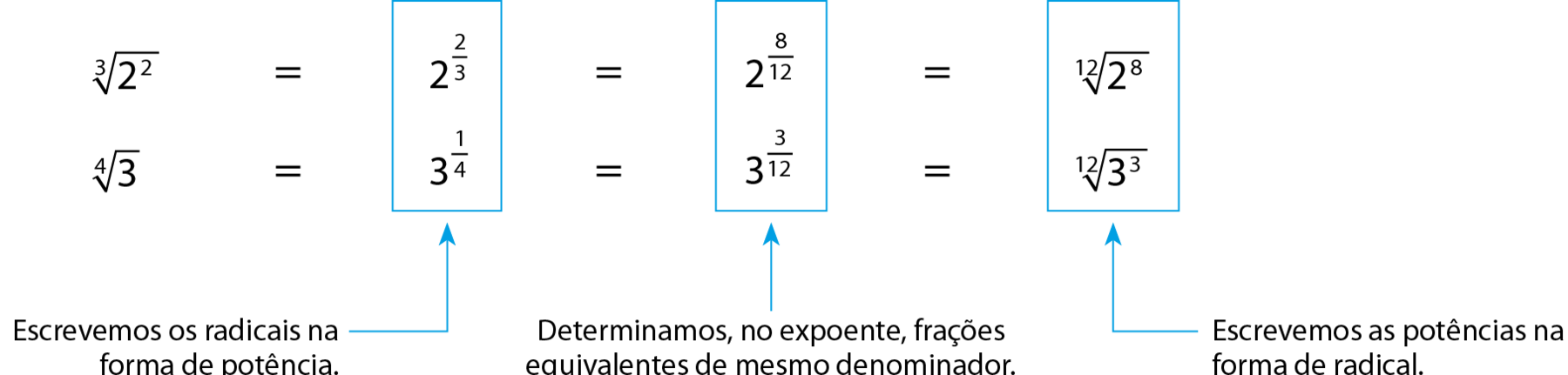
Então, multiplicando esses dois radicais, obtemos:

\sqrt[3]{2^{2}} \cdot \sqrt[4]{3} = \sqrt[12]{2^{8}} \cdot \sqrt[12]{3^{3}} = \sqrt[12]{2^{8} \cdot 3^{3}} = \sqrt[12]{6912}

Observe que, no desenvolvimento apresentado, os números considerados são positivos. Mas também poderíamos ter números negativos, caso o índice do radical seja ímpar. Por exemplo:

\sqrt[3]{‒ 5} \cdot \sqrt[3]{0, 2} = \sqrt[3]{(‒ 5) \cdot 0, 2} = \sqrt[3]{‒ 1} = ‒ 1

\sqrt[3]{‒ 27} \cdot \sqrt[3]{‒ 8} = \sqrt[3]{(‒ 27) \cdot (‒ 8)} = \sqrt[3]{216} = 6

Divisão com radicais

Para dividir radicais de mesmo índice, aplicamos a 4ª propriedade dos radicais:

\sqrt[n]{\frac{a}{b}} = \frac{\sqrt[n]{a}}{\sqrt[n]{b}}

sendo n um número natural não nulo e a e b números reais positivos (note que b ≠ 0).

Logo, para dividir radicais de mesmo índice, conservamos o índice e dividimos os radicandos, simplificando o resultado obtido, sempre que possível.

Acompanhe alguns exemplos.

\sqrt[3]{20} : \sqrt[3]{10} = \sqrt[3]{20 : 10} = \sqrt[3]{2}

\sqrt{28} : \sqrt{7} = \sqrt{28 : 7} = \sqrt{4} = 2

30 \sqrt{15} : 5 \sqrt{3} = (30 : 5) \sqrt{15 : 3} = 6 \sqrt{5}

(12 \sqrt{6} - 2 \sqrt{3}) : (5 \sqrt{2}) = 12 \sqrt{6} : 5 \sqrt{2} - 2 \sqrt{3} : 5 \sqrt{2} = \frac{12}{5} \sqrt{3} - \frac{2}{5} \sqrt{\frac{3}{2}}

Página 53

Se os índices dos radicais forem diferentes, antes da divisão reduzimos esses radicais a um mesmo índice. Por exemplo:

\sqrt{\frac{8}{3}} : \sqrt[3]{\frac{8}{3}} = \sqrt[6]{{(\frac{8}{3})}^{3}} : \sqrt[6]{{(\frac{8}{3})}^{2}} = \sqrt[6]{\frac{8}{3}}

\sqrt[3]{4} : \sqrt[4]{2} = \sqrt[12]{4^{4}} : \sqrt[12]{2^{3}} = \sqrt[12]{2^{8} : 2^{3}} = \sqrt[12]{2^{5}}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

26 Efetue as multiplicações.

\sqrt[3]{5} \cdot \sqrt[3]{6}

\sqrt{2} \cdot \sqrt{8}

\sqrt{2} \cdot \sqrt{6} \cdot \sqrt{3}

\sqrt{5} \cdot \sqrt{10}

\sqrt[3]{4} \cdot \sqrt[3]{6}

\sqrt{2} \cdot \sqrt[3]{5}

27 Aplicando a propriedade distributiva, calcule:

\sqrt{5} \cdot (1 + \sqrt{5})

(3 \sqrt{2} ‒ 2) \cdot (\sqrt{2} + 3)

(\sqrt{3} + 2) \cdot (2 \sqrt{3})

28 Calcule as medidas da área e do perímetro das figuras, cujas medidas são dadas em uma mesma unidade de medida de comprimento.

Ilustração. Retângulo com as medidas: 1 mais raiz quadrada de 2 por raiz quadrada de 3.

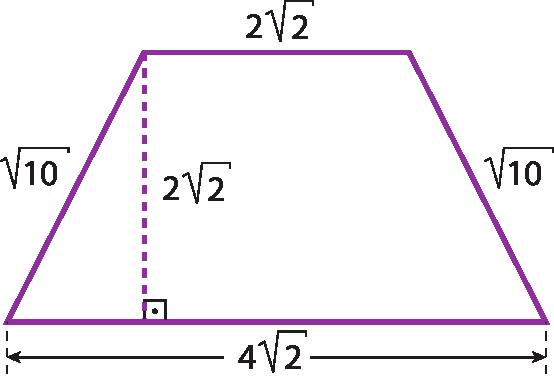
Ilustração. Trapézio com as medidas: raiz quadrada de 10, 4 raiz quadrada de 2, raiz quadrada de 10, 2, raiz quadrada de 2. Altura: 2, raiz quadrada de 2.

29 Efetue as divisões.

\sqrt{12} : \sqrt{3}

\sqrt{50} : \sqrt{2}

12 \sqrt[3]{‒ 6} : 3 \sqrt[3]{2}

\sqrt[3]{6} : \sqrt{3}

30 Calcule o valor das expressões.

(\sqrt{18} + \sqrt{98} + \sqrt{200}) : (2 \sqrt{2} + \sqrt{8})

(\sqrt{150} ‒ \sqrt{24}) : (2 \sqrt{8} ‒ 3 \sqrt{2})

(10 \sqrt{27} + 10 \sqrt{3}) : 10 \sqrt{3}

(20 \sqrt{10} + 10 \sqrt{18}) : 2 \sqrt{2}

31 (ú é cê é) Se p = 3 +

\sqrt{2}

e q = 2 ‒

\sqrt{2}

, então p ⋅ q ‒ p é igual a:

a) 1 ‒

2 \sqrt{2}

b) 1 ‒

\sqrt{2}

c) 1 +

\sqrt{2}

d) 1 +

2 \sqrt{2}

32 (Fuvest-São Paulo) Se a =

\sqrt{2}

e b =

\sqrt[4]{2}

, então o valor de a ⋅ b é:

\sqrt[4]{8}

\sqrt[4]{4}

\sqrt{8}

\sqrt{4}

\sqrt[8]{4}

Hora de criar – Reúna-se com um colega e façam o que se pede.

a) Calculem:

•

(\sqrt{201} + \sqrt{199}) \cdot (\sqrt{201} ‒ \sqrt{199})

•

(\sqrt{31,4} + \sqrt{29,4}) \cdot (\sqrt{31,4} ‒ \sqrt{29,4})

•

(\sqrt{89} + \sqrt{82}) \cdot (\sqrt{89} ‒ \sqrt{82})

b) Cada um de vocês pensa em dois números positivos e substitui as figuras △ e ◇ na expressão

(\sqrt{△} + \sqrt{◇}) \cdot (\sqrt{△} ‒ \sqrt{◇})

para que o outro faça o cálculo. Discutam os resultados obtidos e elaborem uma regra para o resultado dêsse tipo de expressão.

Página 54

6. Potenciação e radiciação com radicais

Potenciação

Observe o cálculo a seguir.

{(\sqrt[5]{3})}^{4} = \sqrt[5]{3} \cdot \sqrt[5]{3} \cdot \sqrt[5]{3} \cdot \sqrt[5]{3} = \sqrt[5]{3 \cdot 3 \cdot 3 \cdot 3} = \sqrt[5]{3^{4}}

Então:

{(\sqrt[5]{3})}^{4} = \sqrt[5]{3^{4}}

Para potenciação com radicais, basta elevar o radicando à potência indicada. Observe como podemos fazer para simplificar algumas expressões.

{(\sqrt{2})}^{3} = \sqrt{2^{3}} = \sqrt{2^{2} \cdot 2} = 2 \sqrt{2}

{(\sqrt[3]{9})}^{2} = {(\sqrt[3]{3^{2}})}^{2} = \sqrt[3]{{(3^{2})}^{2}} = \sqrt[3]{3^{4}} = \sqrt[3]{3^{3} \cdot 3} = 3 \sqrt[3]{3}

{(4 \sqrt{5})}^{3} = 4^{3} \cdot \sqrt{5^{3}} = 64 \cdot \sqrt{5^{2} \cdot 5} = 64 \cdot 5 \sqrt{5} = 320 \sqrt{5}

{(\sqrt{2} + \sqrt{3})}^{2} = {(\sqrt{2})}^{2} + 2 \cdot \sqrt{2} \cdot \sqrt{3} + {(\sqrt{3})}^{2} = 2 + 2 \sqrt{6} + 3 = 5 + 2 \sqrt{6}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

34 Calcule:

{(\sqrt{15})}^{2}

{(\sqrt[3]{3})}^{3}

{(3 \sqrt{7})}^{2}

{(3 \sqrt[4]{3})}^{4}

{(\sqrt{10})}^{3}

{(2 \sqrt[3]{3})}^{4}

35 Efetue:

{(\sqrt{7} + \sqrt{3})}^{2}

{(3 ‒ \sqrt{7})}^{2}

36 Qual é o valor da expressão A = x ⁴ + x ² + 2, para x =

‒ \sqrt{3}

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Bruno tem 30 cubos cujas arestas medem

2 \sqrt{7}

centímetros.

Ilustração. Menino de cabelo castanho e camiseta vermelha. Ele está sentado no chão de pernas cruzadas na frente de 30 cubos pequenos. Ao lado, gato marrom.

a) Quantos desses cubos ele deve usar para formar o maior cubo possível?

b) Calcule a medida do volume do cubo formado.

Radiciação com radicais

Observe como podemos proceder para simplificar as expressões a seguir e reduzi-las a um radical, utilizando os conceitos estudados.

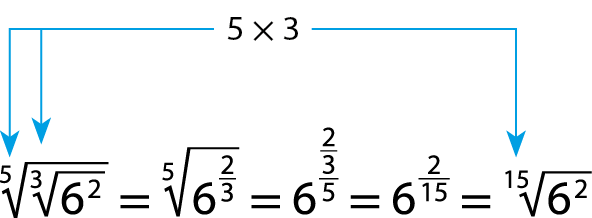
Esquema. raiz quinta de, raiz cubica de 6 ao quadrado, igual a, raiz quinta de 6 elevado 2 terços, igual a, 6 elevado a 2 terços sobre 5, igual a, 6 elevado a 2, 15 avos, igual a, raiz 15 de 6 ao quadrado. Acima do primeiro termo duas setas azuis apontado para o índice 5 e o índice 3 elas indicam a multiplicação 5 vezes 3 e apontam para o índice 15 do último termo da expressão.

Página 55

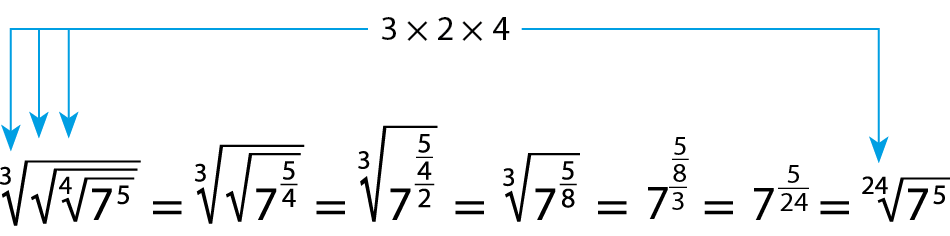
Esquema. raiz cubica de, raiz quadrada de, raiz quarta de 7 elevado a 5, igual, raiz cubica de raiz quadrada de 7 elevado a 5 quartos, igual, raiz cubica de 7 elevado a 5 quartos sobre 2, igual, raiz cubica de 7 elevado a 5 oitavos, igual, 7 elevado a 5 oitavos sobre 3, igual, 7 elevado a 5, 24 avos, igual a raiz 24 de 7 elevado a 5. Acima do primeiro termo três setas azuis apontado para o índice 3, o índice 2 e o índice 4 elas indicam a multiplicação 3 vezes 2 vezes 4 e apontam para o índice 24 do último termo da expressão.

Para extrair a raiz de um radical, devemos multiplicar os índices desses radicais e conservar o radicando, simplificando o radical obtido sempre que possível (considerando o radicando um número real positivo e os índices números naturais não nulos).

Acompanhe outros exemplos.

\sqrt{\sqrt[3]{7}} = \sqrt[2 \cdot 3]{7} = \sqrt[6]{7}

\sqrt{\sqrt[3]{\sqrt{5^{2}}}} = \sqrt[2 \cdot 3 \cdot 2]{5^{2}} = \sqrt[12]{5^{2}} = \sqrt[6]{5}

\sqrt[4]{\sqrt{2 \sqrt[3]{5}}} = \sqrt[4]{\sqrt{\sqrt[3]{2^{3} \cdot 5}}} = \sqrt[4 \cdot 2 \cdot 3]{8 \cdot 5} = \sqrt[24]{40}

\sqrt[4]{2 \sqrt{\sqrt[3]{5}}} = \sqrt[4]{2 \sqrt[2 \cdot 3]{5}} = \sqrt[4]{2 \sqrt[6]{5}}

\sqrt[4]{\sqrt[6]{2^{6} \cdot 5}} = \sqrt[4 \cdot 6]{64 \cdot 5} = \sqrt[24]{320}

\sqrt[4]{2^{2} \sqrt[3]{2^{3} \sqrt{2^{4}}}} = \sqrt[4]{2^{2} \sqrt[3]{\sqrt{2^{6} \cdot 2^{4}}}}

\sqrt[4]{2^{2} \sqrt[3 \cdot 2]{2^{10}}} = \sqrt[4]{2^{2} \sqrt[6]{2^{10}}}

\sqrt[4]{\sqrt[6]{2^{12} \cdot 2^{10}}} = \sqrt[24]{2^{22}} = \sqrt[12]{2^{11}}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

37 Reduza estas expressões a um único radical e simplifique-as, se possível.

\sqrt{\sqrt{10}}

\sqrt[3]{\sqrt{3}}

\sqrt{\sqrt{\sqrt{2}}}

\sqrt[3]{\sqrt[3]{\sqrt{3}}}

\sqrt[6]{\sqrt{5^{3}}}

\sqrt[3]{2 \sqrt{2^{4}}}

\sqrt{\sqrt{15^{4}}}

\sqrt[4]{3 \sqrt{5}}

38 Verifique qual das sentenças a seguir é falsa.

\sqrt[3]{\sqrt{11}} = \sqrt[6]{11}

\sqrt[2]{\sqrt[3]{2}} = \sqrt[5]{2}

\sqrt{\sqrt{\sqrt{1024}}} = \sqrt[4]{2^{5}}

\sqrt[3]{\sqrt{81}} = \sqrt[3]{3^{2}}

Racionalização de denominadores

Considere o quociente de 2 por

\sqrt{3}

. Ele pode ser indicado por

\frac{2}{\sqrt{3}}

Um quociente não se altera quando multiplicamos o dividendo e o divisor por um mesmo número não nulo. Observe, por exemplo, o que acontece quando multiplicamos o numerador e o denominador da fração

\frac{2}{\sqrt{3}}

por

\sqrt{3}

\frac{2}{\sqrt{3}} = \frac{2 \cdot \sqrt{3}}{\sqrt{3} \cdot \sqrt{3}} = \frac{2 \sqrt{3}}{{(\sqrt{3})}^{2}} = \frac{2 \sqrt{3}}{3}

Com essa multiplicação, obtemos uma expressão com denominador racional. Esse procedimento é chamado de racionalização de denominadores.

É conveniente efetuar cálculos com radicais quando eles não estão no denominador. Por isso, quando necessário, racionalizamos o denominador de uma expressão fracionária.

Página 56

Acompanhe outros exemplos.

a) Vamos racionalizar o denominador da expressão

\frac{2}{3 \sqrt{2}}

Multiplicando os dois termos dessa expressão por

\sqrt{2}

, obtemos:

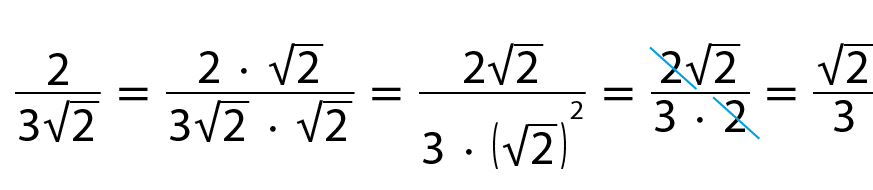
fração, numerador 2, denominador 3, raiz quadrada de 2, igual, fração, numerador 2 vezes raiz quadrada de 2, denominador 3, raiz quadrada de 2 vezes raiz quadrada de 2, igual, fração, numerador 2, raiz quadrada de 2, denominador 3 vezes raiz quadrada de 2 ao quadrado, igual, fração, numerador 2 (com risco azul), raiz quadrada de 2, denominador 3 vezes 2 (com risco azul), igual, fração, numerador raiz quadrada de 2, denominador 3

b) Vamos racionalizar o denominador da expressão

\frac{2}{\sqrt[5]{7^{2}}}

Para multiplicar os dois termos da expressão, convém escolher um número que, multiplicado por

\sqrt[5]{7^{2}}

, resulte em

\sqrt[5]{7^{5}}

, isto é, em 7. Esse número é o quociente

\sqrt[5]{7^{5}} : \sqrt[5]{7^{2}} = \sqrt[5]{7^{3}}

Portanto, multiplicando os dois termos da expressão por

\sqrt[5]{7^{3}}

, obtemos:

\frac{2}{\sqrt[5]{7^{2}}} = \frac{2 \cdot \sqrt[5]{7^{3}}}{\sqrt[5]{7^{2}} \cdot \sqrt[5]{7^{3}}} = \frac{2 \cdot \sqrt[5]{7^{3}}}{\sqrt[5]{7^{2} \cdot 7^{3}}} = \frac{2 \cdot \sqrt[5]{7^{3}}}{\sqrt[5]{7^{5}}} = \frac{2 \sqrt[5]{7^{3}}}{7} = \frac{2 \sqrt[5]{343}}{7}

c) Vamos racionalizar o denominador da expressão

\frac{1}{\sqrt{7} ‒ \sqrt{3}}

Nesse caso, convém aplicar o produto notável (a + b) ⋅ (a ‒ b) = a² ‒ b² Multiplicando os dois termos da expressão por

\sqrt{7} + \sqrt{3}

, obtemos:

\frac{1}{\sqrt{7} - \sqrt{3}} = \frac{1 \cdot (\sqrt{7} + \sqrt{3})}{(\sqrt{7} - \sqrt{3}) \cdot (\sqrt{7} + \sqrt{3})}

\frac{\sqrt{7} + \sqrt{3}}{{(\sqrt{7})}^{2} ‒ {(\sqrt{3})}^{2}} = \frac{\sqrt{7} + \sqrt{3}}{7 - 3} = \frac{\sqrt{7} + \sqrt{3}}{4}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

39 Qual é um número pelo qual devemos multiplicar os dois termos da expressão

\frac{15}{4 \sqrt{3}}

para obter uma expressão cujo denominador seja um número racional?

40 Para racionalizar o denominador da expressão

\frac{10}{\sqrt[3]{5}}

, podemos multiplicar seus dois termos por qual radical?

41 Racionalize o denominador das expressões a seguir.

\frac{6}{\sqrt{3}}

\frac{1}{\sqrt{2}}

\frac{2}{3 \sqrt{5}}

\frac{3}{2 \sqrt{3}}

\frac{5}{\sqrt[3]{5}}

\frac{4}{\sqrt[8]{2^{5}}}

42 Sabendo que

\sqrt{5}

com três casas decimais é 2,236, calcule o quociente

\frac{3}{\sqrt{5}}

a) substituindo

\sqrt{5}

por 2,236;

b) racionalizando o denominador e, depois, substituindo

\sqrt{5}

por 2,236.

43 Sabendo que

\sqrt{10}

com três casas decimais é 3,162, calcule da maneira mais conveniente o quociente

\frac{2}{\sqrt{10} ‒ 3}

44 Sabendo que a medida da área da região retangular a seguir é 10 centímetros quadrados, calcule o valor de x.

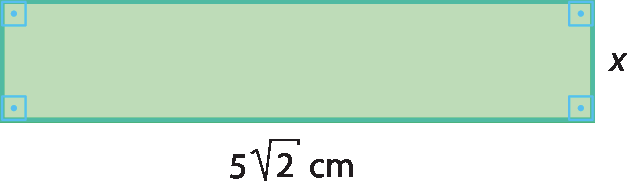
Ilustração. Retângulo com as medidas: 5, raiz quadrada de 2 centímetros por x.

45 Demonstre que o inverso de

\sqrt{2} ‒ 1

\sqrt{2} + 1

Página 57

TRABALHANDO A INFORMAÇÃO

Construindo e interpretando gráfico de linha

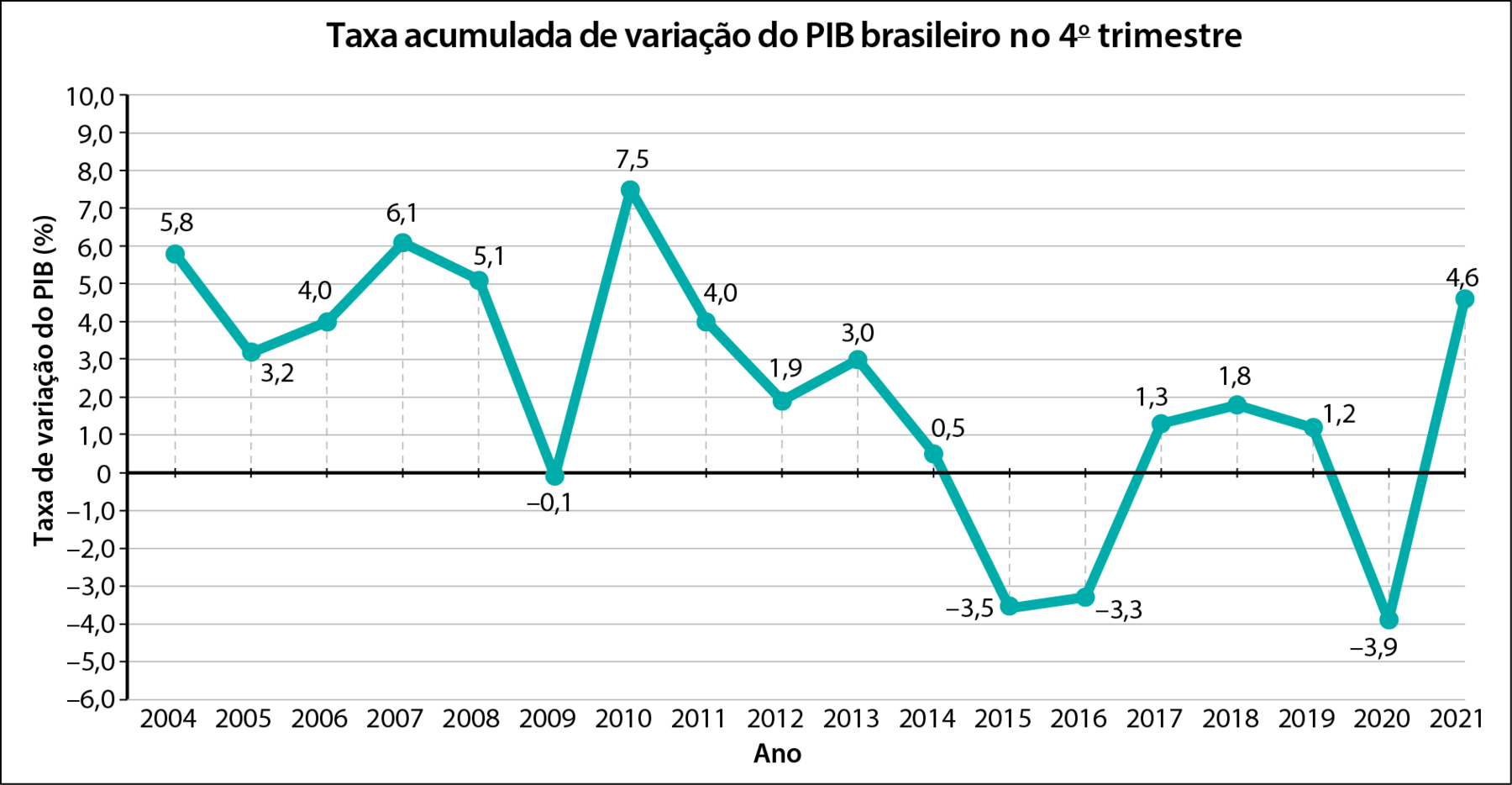
Observe a tabela a seguir, que mostra a taxa acumulada de variação do Produto Interno Bruto (Píbi) brasileiro, em porcentagem, de 2004 a 2021, no 4º trimestre de cada ano.

Taxa acumulada de variação do PIB no 4º trimestre (em %)
Ano	PIB
2004	5,8
2005	3,2
2006	4,0
2007	6,1
2008	5,1
2009	−0,1
2010	7,5
2011	4,0
2012	1,9
2013	3,0
2014	0,5
2015	−3,5
2016	−3,3
2017	1,3
2018	1,8
2019	1,2
2020	−3,9
2021	4,6

Dados obtidos em: í bê gê É. Disponível em: https://oeds.link/4LsKpzjulho 2022.

O gráfico que melhor comunica a variação de valores no decorrer do tempo é o gráfico de linha. Já estudamos a construção de um gráfico de linha com base em um gráfico de colunas. Lá, construímos um gráfico de colunas usando os valores da tabela. Nesse gráfico, antes de apagar as colunas, marcamos o ponto médio do lado superior do retângulo de cada coluna e traçamos uma linha de segmentos consecutivos cujas extremidades são esses pontos assinalados.

Porém podemos construir o gráfico de linha sem passar pelo de colunas; basta traçar os eixos vertical e horizontal com as respectivas escalas e localizar os pontos dados pelas coordenadas (ano, Píbi), por exemplo (2004; 5,8), (2005; 3,2) etcétera É como se reduzíssemos as colunas a linhas verticais tracejadas e destacássemos o “ponto de cima”.

Nesse gráfico de linha, os únicos pontos confiáveis são os das extremidades dos segmentos; os outros só compõem o segmento que indica se, naquele intervalo de tempo, há acréscimo, constância ou decréscimo do Píbi. Observe.

Gráfico em linha. Taxa acumulada de variação do PIB brasileiro no 4º trimestre. Eixo x, ano de 2004 a 2021. Eixo y, Taxa de variação do PIB (%) de menos 6,0 a 10,0. Os dados são: 2004: 5,8. 2005: 3,2. 2006: 4,0.2007: 6,1.2008: 5,1.2009: menos 0,1. 2010: 7,5.2011: 4,0.2012: 1,9. 2013: 3,0.2014: 0,5.2015: menos 3,5.2016: menos 3,3. 2017: 1,3.2018: 1,8.2019: 1,2.2020: menos 3,9.2021: 4,6. — Dados obtidos em: í bê gê É. Disponível em: https://oeds.link/4LsKpz. Acesso em: 24 julho 2022.

Página 58

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

1 Com base no gráfico anterior, responda.

a) Em que ano o índice percentual foi maior? Em que ano ele foi menor?

b) Há algum ano em que o Píbi não cresceu nem diminuiu? Qual?

c) Usando as mesmas unidades, reconstrua o gráfico em papel vegetal e considere apenas os pontos de ano par. Depois, sobreponha-o ao gráfico anterior e escreva as diferenças que você observa entre os dois gráficos.

2 Considere a tabela a seguir.

Taxa acumulada de variação do PIB brasileiro per capita (em %)
Ano	PIB
2000	2,9
2001	0
2002	1,7
2003	−0,2
2004	4,4
2005	2,0
2006	2,8
2007	4,9
2008	4,0
2009	−1,2
2010	6,5
2011	3,0
2012	1,0
2013	2,1
2014	−0,4
2015	−4,6
2016	−4,4

Dados obtidos em: í bê gê É. Contas Nacionais Trimestrais. Rio de Janeiro: í bê gê É, outubro/dezembro 2016. Disponível em: https://oeds.link/s4peK1. Acesso em: 26 maio 2022.

a) Em que ano o índice percentual foi maior? Em que ano esse índice foi menor?

b) Há algum ano em que o Píbi não cresceu nem diminuiu? Qual?

c) Construa o gráfico de linha com os dados da tabela.

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Em 1995, Dave Wineland e Chris Monroe construíram o primeiro transmissor do tamanho de um átomo, ou seja, 1 milhão de vezes menor do que 1 milímetro. Use o prefixo do SI mais adequado para expressar essa medida em metro.

2 “Quando o Sol se for – Na fase gigante vermelha, daqui a 5 bilhões de anos, o diâmetro do Sol engolirá a atual órbita da Terra. Já quando virar uma anã branca, o Sol deve ficar com um diâmetro parecido com o do nosso planeta – cêrca de 1 centésimo do diâmetro que a estrela tem hoje.”

Fonte: ALMANAQUE Abril 2015. São Paulo: Abril, 2015. página 173.

Pesquise as medidas dos diâmetros da Terra e do Sol e verifique se a informação dêsse texto tem coerência.

3 Ontem, o celular de Andréa tinha 1,2 giga báite disponível para armazenamento quando Caio lhe enviou vários vídeos que fez durante a apresentação de uma banda. Eles tinham 21,5 mégabáites, .33450 quilobáites, 318 mégabáites, 104 mégabáites, .43500 quilobáites, 99,5 mégabáites e 110,55 mégabáites.

a) O celular de Andréa tinha capacidade para receber todos os vídeos enviados por Caio?

b) Caso a resposta ao item anterior seja afirmativa, quantos mégabáites o celular dela ainda poderia receber?

Página 59

4 No caderno, complete a tabela com as medidas das distâncias médias dos planetas do Sistema Solar ao Sol e com as medidas dos respectivos diâmetros.

Distância média ao Sol dos planetas do Sistema Solar
Planeta	Medida da distância média ao Sol em ua	Medida da distância média ao Sol em km	Medida do diâmetro em ano-luz	Medida do diâmetro em km
Mercúrio	0,4			4,8 ⋅ 103
Vênus		1,08 ⋅ 108		1,2 ⋅ 104
Terra	1	1,5 ⋅ 108	1,35 ⋅ 10−9
Marte	1,5		7,16 ⋅ 10−10
Júpiter		7,8 ⋅ 108		1,43 ⋅ 105
Saturno	9,5			1,2 ⋅ 105
Urano	19,1			5,1 ⋅ 104
Netuno		4,5 ⋅ 109	5,16 ⋅ 10−9

Dados obtidos em: PLANETÁRIO ú éfe ésse cê. Disponível em: https://oeds.link/8swgxy. Acesso em: 23 mar. 2022.

5 Use uma régua para traçar uma reta numérica e, com o auxílio de um compasso, represente nela os números

\sqrt{5}

\sqrt{6}

(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)

6 Com régua e compasso, represente o número

\sqrt{13}

na reta numérica.

7 Com régua e compasso, represente o número

\sqrt{17}

em uma reta numérica.

8 Considere o paralelepípedo a seguir.

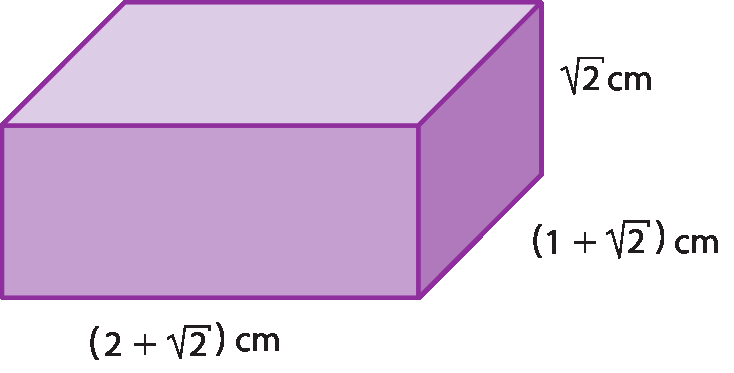
Ilustração. Representação de um paralelepípedo roxo com as indicações das medidas. Medida de comprimento: abre parêntese, 2 mais raiz de 2, fecha parêntese, centímetros. Medida da largura: abre parêntese, 1 mais raiz de 2, fecha parêntese, centímetros. Medida a altura: raiz de 2 centímetros.

Determine:

a) a soma das medidas de todas as arestas do paralelepípedo;

b) a soma das medidas das áreas das faces laterais;

c) a medida do volume dêsse paralelepípedo.

9 O passo de um robô mede exatamente

50 \sqrt{3}

centímetros. Quantos passos ele deverá dar para percorrer

18, 5 \sqrt{3}

métros?

10 Racionalize o denominador de cada uma das expressões a seguir.

\frac{8}{\sqrt{2}}

\frac{10}{\sqrt{3} ‒ 1}

\frac{5 + 3 \sqrt{5}}{\sqrt{5}}

Por volta dos anos 1800, a expressão

\frac{26 \cdot \sqrt{146}}{100}

foi usada como um valor aproximado do número π. Usando uma calculadora simples, verifique até que casa decimal a expressão dada coincide com o valor de π conhecido atualmente: π = 3,1415927reticências

Página 60

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 O disco rígido, popularmente conhecido como agá dê, é a parte do computador no qual se armazenam dados. Em 2022, o agá dê de maior capacidade poderia armazenar 120 petabytes de dados. Qual é o armazenamento dêsse agá dê em byte?

a) 120 ⋅ 2elevado a 30

b) 120 ⋅ 2elevado a 50

c) 120 ⋅ 10elevado a 15

d) 120 ⋅ 10elevado a 50

2 Qual é a raiz reduzida da expressão

5^{\frac{3}{4}} \cdot {(\sqrt[3]{5})}^{\frac{5}{2}}

\sqrt[12]{5^{19}}

\sqrt[19]{5^{12}}

\sqrt[12]{5^{5}}

\sqrt[12]{5^{8}}

3 Ao simplificar a expressão a seguir em um só radical, obtemos:

\frac{b \cdot \sqrt[9]{a^{6}}}{\sqrt[6]{c^{14}}}

\sqrt[3]{\frac{a^{3} b}{c^{12}}}

\sqrt[]{\frac{a^{6} b^{2}}{c^{5}}}

\sqrt[3]{\frac{a^{6} b}{c^{14}}}

\sqrt[3]{\frac{a^{2} b^{3}}{c^{7}}}

4 Qual é a medida do perímetro do quadrilátero da figura a seguir?

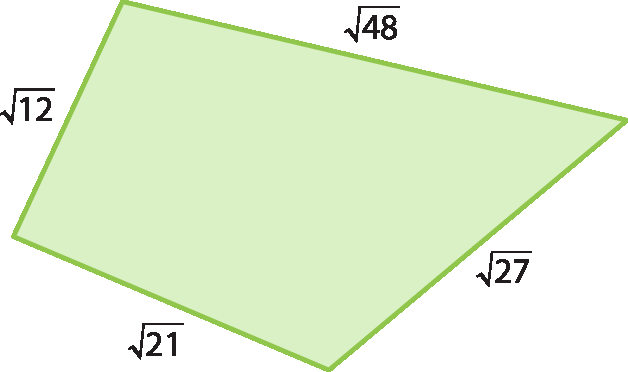
Ilustração. Quadrilátero com as medidas: raiz quadrada de 12, raiz quadrada de 48, raiz quadrada de 27 e raiz quadrada de 21.

16 \sqrt{3}

\sqrt{3} (29 + \sqrt{7})

\sqrt{3} (9 + \sqrt{7})

27 + 3 \sqrt{7}

5 Se a =

\sqrt[4]{3}

e b =

\sqrt[6]{2}

, então a ⋅ b é igual a:

\sqrt[12]{31}

\sqrt[12]{108}

\sqrt[6]{108}

\sqrt[24]{108}

6 A área de um retângulo mede

\sqrt{1550}

centímetros quadrados e a altura,

\sqrt{62}

centímetros. A medida da base dêsse retângulo é igual a:

a) 25 centímetros.

b) 5 centímetros.

\sqrt{15}

centímetros.

\sqrt{40}

centímetros.

7 Qual é a medida do volume do cubo da figura a seguir?

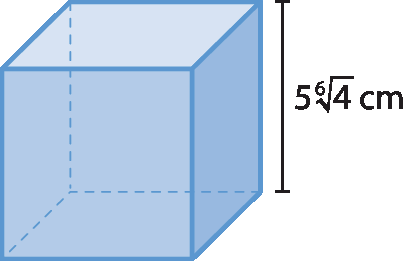
a) 125 centímetros cúbicos

125 \sqrt[3]{4}

centímetros cúbicos

c) 250 centímetros cúbicos

250 \sqrt[3]{4}

centímetros cúbicos

8 Assinale a alternativa que contém a fórma simplificada da expressão

\sqrt{9 - \sqrt{34 + \sqrt[3]{8}}}

a) 3

\sqrt{15}

c) 4

\sqrt{3}

9 Racionalizando o denominador da expressão a seguir, obtemos a expressão de qual das alternativas?

\frac{\sqrt{12}}{\sqrt{5} + \sqrt{3}}

\frac{\sqrt{60} + 6}{2}

\frac{\sqrt{60} ‒ 6}{8}

\sqrt{15} ‒ 3

\sqrt{30} ‒ 3

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.

a) Descreva como você transforma a medida de um comprimento dada em ano-luz para uma medida aproximada dada em quilômetro.

b) Que relação podemos estabelecer entre um radical e uma potência?

c) Descreva a estratégia que você utiliza para efetuar a multiplicação e a divisão de radicais com um mesmo índice.

d) Descreva a estratégia que você utiliza para efetuar a multiplicação e a divisão de radicais com índices diferentes.

e) Como você explicaria a um colega no que consiste o processo de racionalização do denominador de uma fração com denominador irracional?