Página 91

CAPÍTULO 4 Proporcionalidade em Geometria

Fotografia em preto e branco. Vista do interior de estação composta por colunas nas laterais. O teto é arcado com blocos retangulares. Dando uma ideia de profundidade e infinito. — Estação de trem em Washington D.C., Estados Unidos. (Fotografia de 2012.)

Paralelas e transversais, cruzando em feixes, compõem um cenário harmonioso nas construções humanas. E a perspectiva oferece aos nossos olhos a ideia de proporcionalidade e uma representação de infinitude.

Observe, leia e responda no caderno.

a) Se o número do calçado de uma criança com idade de 1 ano é 20, então, é verdade que, quando essa criança tiver o dobro da idade, usará calçado cujo número é o dobro de 20?

b) De acordo com sua resposta ao item a, você entende que há proporcionalidade entre as grandezas idade e comprimento do pé?

c) Converse com um colega e elaborem uma lista com três pares de grandezas em que há proporcionalidade e três pares em que não há proporcionalidade.

Página 92

1. Razão entre dois segmentos de reta

Neste capítulo, vamos retomar o conceito de razão entre dois números e o conceito de razão entre grandezas de mesma natureza, estudados anteriormente.

Considere as situações a seguir.

Situação 1

Ilustração. Quatro meninos em pé à frente de uma piscina com raias vermelhas.

Em um campeonato de natação, na prova de 50 metros nado livre, Leo precisou dar 48 braçadas para atravessar a piscina, enquanto Márcio deu 56 braçadas.

A razão entre o número de braçadas de Leo e o número de braçadas de Márcio é dada por:

\frac{48}{56} = \frac{6}{7}

Isso significa que 6 braçadas de Leo equivalem a 7 braçadas de Márcio.

Ilustração. Homem de cabelo castanho e agasalho verde. Ao lado, homem mais baixo de cabelo preto e agasalho laranja.

Considerando que Leo meça 1,80 métro de altura e Márcio meça 1,71 métro, a razão entre as medidas de suas alturas é:

\frac{m e d i d a d a a l t u r a d e L e o}{m e d i d a d a a l t u r a d e M á r c i o} = \frac{1, 80 m}{1, 71 m} = \frac{180}{171} = \frac{20}{19}

•

A idade de uma criança e sua altura estão sempre à mesma razão?

Agora, vamos analisar outras duas situações que tratam de razão entre dois segmentos.

Situação 2

Observe os segmentos de reta a seguir.

Ilustração. Segmento de reta AB , 4 centímetros. Ilustração. Segmento de reta CD , 5 centímetros.

A razão entre eles é dada pela razão entre suas medidas:

\frac{A B}{C D} = \frac{4 c m}{5 c m} = \frac{4}{5}

A razão entre dois segmentos de reta é a razão entre suas medidas tomadas em uma mesma unidade.

Situação 3

Considere os segmentos

\overline{A B}, \overline{C D}, \overline{E F}

\overline{G H}

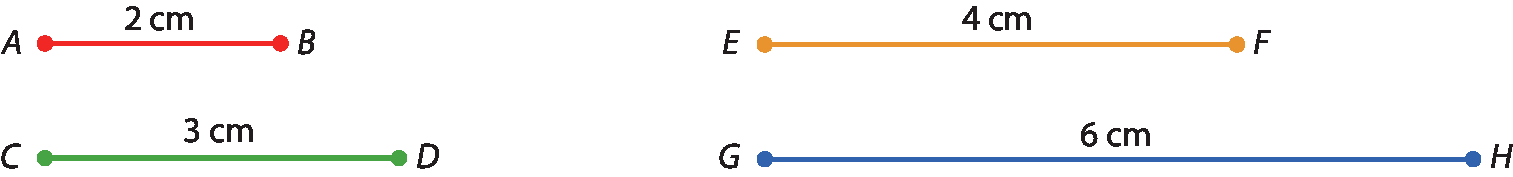
Ilustração. Segmento de reta AB, medindo 2 centímetros. Segmento de reta CD, medindo 3 centímetros. Segmento de reta EF, medindo 4 centímetros. Segmento de reta GH, medindo 6 centímetros.

Página 93

Vamos calcular as razões:

\frac{A B}{C D} = \frac{2}{3}

\frac{E F}{G H} = \frac{4}{6} = \frac{2}{3}

Como as razões são iguais,

\overline{A B}, \overline{C D}, \overline{E F} e \overline{G H},

nessa ordem, são proporcionais, isto é:

\frac{A B}{C D} = \frac{E F}{G H}

\frac{2}{3} = \frac{4}{6}

Dizemos que quatro segmentos,

\overline{A B}, \overline{C D}, \overline{E F} e \overline{G H},

nessa ordem, são segmentos proporcionais quando suas medidas, tomadas na mesma unidade, formam uma proporção, isto é, quando

\frac{A B}{C D} = \frac{E F}{G H}

De acordo com o conceito de segmentos proporcionais, resolvemos problemas como o seguinte.

Para fazer uma tela mosquiteiro com moldura retangular cujas medidas dos comprimentos dos lados estão na razão 3 : 2 (lemos: “três para dois”), Zildo tem uma ripa que mede 5 métros de comprimento.

Que medidas devem ter os pedaços da ripa serrados por Zildo, sem haver sobra?

Vamos representar essas medidas por x e y.

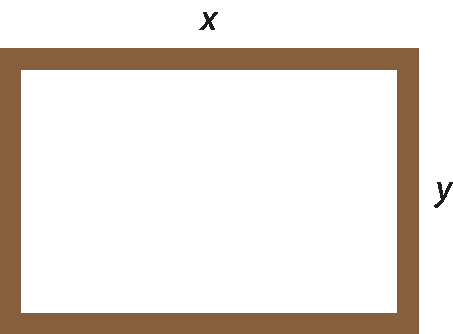
Ilustração. Tela retangular medindo x por y.

Assim, podemos escrever:

\frac{x}{y} = \frac{3}{2}

ou x =

\frac{3 y}{2}

2x + 2y = 5

Substituindo x por

\frac{3 y}{2}

em 2x + 2y = 5, temos:

2 ⋅

\frac{3 y}{2}

+ 2y = 5

3y + 2y = 5

y = 1

Logo: x =

\frac{3 \cdot 1}{2}

= 1,5

Portanto, a ripa deve ser serrada em pedaços de 1 metro e 1,5 metro.

A proporcionalidade entre segmentos é muito usada em Geometria e na vida prática. Por exemplo, para fazer a ampliação de uma fotografia, é necessário que os lados da fotografia ampliada sejam, respectivamente, proporcionais aos lados da fotografia original.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Observe a figura.

Ilustração. Segmento de reta AD com pontos B, C entre A e D. A medida de AB é 3 centímetros, de BC é 3,5 centímetros, e de CD é 4 centímetros.

Considerando as medidas indicadas, determine a razão entre:

\overline{A B} e \overline{C D}

;

\overline{A C} e \overline{A D}

;

\overline{A B} e \overline{B D}

;

\overline{B C} e \overline{A D}

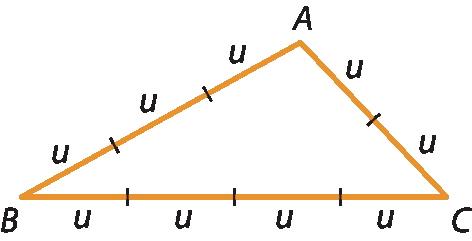
2 No triângulo a seguir, determine a razão entre:

\overline{A B} e \overline{B C}

;

\overline{A C} e \overline{A B}

;

\overline{B C} e \overline{A B}

Ilustração. Triângulo ABC. O lado AB está dividido em 3 partes iguais, o lado BC está dividido em 4 partes iguais, e o lado CA está dividido em 2 partes iguais, sendo cada parte indicada por u.

Página 94

3 Sendo

\overline{A B}

um segmento de medida x, calcule essa medida nos seguintes casos:

\frac{A B}{5} = \frac{14}{10}

\frac{3, 4}{A B} = \frac{12}{18}

\frac{0, 9}{0, 5} = \frac{A B}{3, 5}

\frac{2, 4}{3, 2} = \frac{1, 5}{A B}

4 (púqui-Minas Gerais) Se o ponto ême divide um segmento

\overline{A B}

de 18 centímetros na razão

\frac{2}{7}

, as medidas de

\overline{A M}

\overline{M B}

são, respectivamente, em centímetros:

a) 4 e 14.

b) 7 e 11.

c) 8 e 10.

d) 10 e 8.

e) 14 e 4.

5 Uma fotografia foi impressa no tamanho 10 × 15 (lemos: “10 por 15”), ou seja, um lado mede 10 centímetros e o outro, 15 centímetros. Para ampliá-la de modo que o lado menor tenha 13 centímetros, qual deve ser a medida do lado maior?

6 Os segmentos

\overline{A B}, \overline{M N}, \overline{C D} e \overline{P Q}

formam, nessa ordem, uma proporção. Calcule a medida de

\overline{C D}

\overline{P Q}

sabendo que A bê = 12 centímetros, MN = 15 centímetros e CD + PQ = 45 centímetros.

7 Considere dois triângulos: o triângulo ABC, cujo lado

\overline{A B}

mede 20 centímetros e a altura

\overline{C H}

relativa a esse lado mede 18 centímetros; e o triângulo MNP, cujo lado

\overline{M N}

mede 30 centímetros e a altura

\overline{P G}

relativa a esse lado mede x centímetros.

\frac{A B}{M N} = \frac{C H}{P G}

, determine:

a) o valor de x ;

b) a medida da área do triângulo ême êne pê.

8 O perímetro de um quadrilátero a bê cê dê mede 63 centímetros. As medidas dos lados

\overline{A B}, \overline{B C}, \overline{C D}

\overline{A D}

formam, nessa ordem, uma proporção. Se A bê = 12 centímetros e bê cê = 15 centímetros, quais são as medidas dos outros dois lados désse quadrilátero?

9 Hélio tem um terreno retangular cujas medidas das dimensões estão na razão 2 para 3. O perímetro dêsse terreno mede .1500 métros. Responda às questões no caderno.

a) Quais são as medidas das dimensões dêsse terreno?

b) Qual é a medida da área dêsse terreno?

Ilustração. Homem de chapéu e camisa vermelha está com o braço esticado em direção a uma casa amarela de telhado vermelho sobre área gramada.

PARA SABER MAIS

Uma razão de ouro

Estudando o pentágono regular estrelado, os gregos descobriram, mais de 500 anos antes de Cristo, um número irracional determinado pelas razões entre os segmentos dêsse pentágono.

Na figura a seguir, por exemplo, temos:

\frac{A C}{A J} = \frac{A J}{A F} = \frac{2}{\sqrt{5} ‒ 1} ≃ 1, 618

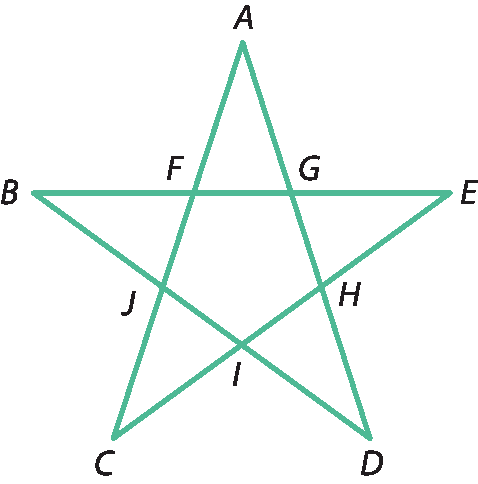
Ilustração. Estrela de 5 pontas ABCDE formando os triângulos: AFG, EGH, DIH, CIJ e BFJ. No centro, pentágono FGHIJ.

cêrca de .2000 anos depois, esse número, que já vimos representado pela letra grega fi (ϕ) e que tem infinitas casas decimais sem período, passou a ser chamado de número áureo ou número de ouro.

Observando a natureza, a arquitetura, algumas razões entre medidas do corpo humano etcétera, encontramos razões que se aproximam do número de ouro.

Página 95

Observe o exemplo do girassol.

A estrutura central do girassol é formada por um grande número de pequenas sementes dispostas em espirais, algumas no sentido horário e outras no sentido anti-horário.

Fotografia. Miolo de um girassol de cor amarelo com sementes formando um círculo. Parte está virada para um lado e parte para outro lado.

A razão é dada por:

\frac{número de espirais no sentido horário}{número de espirais no sentido anti-horário}

Chamamos de retângulo áureo ou retângulo de ouro todo retângulo cuja razão entre as medidas dos lados maior e menor é o número de ouro (≃ 1,618).

Para todo retângulo áureo, vale a seguinte propriedade: se dele retirarmos o maior quadrado possível, o retângulo restante também será um retângulo áureo, isto é, a proporção entre os lados se manterá.

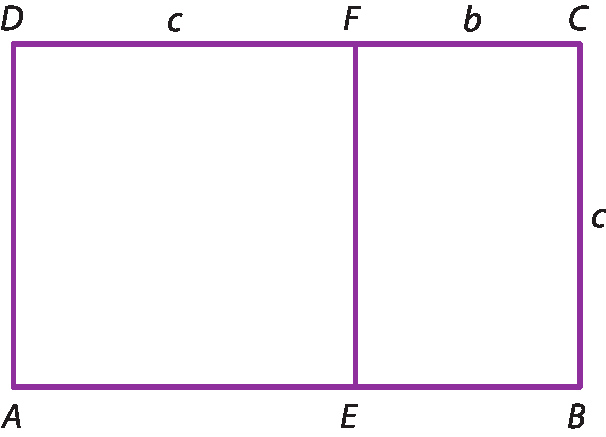
Ilustração. Retângulo ABCD. Em DC, ponto F, Em AB ponto E na mesma direção que o ponto F . Na vertical, AD paralelo EF paralelo BC c minúsculo entre DF, b minúsculo entre FC; c minúsculo entre BC.

Retirando do retângulo a bê cê dê o quadrado á é éfe dê (maior possível), obtemos o retângulo é bê cê éfe de modo que:

\frac{c + b}{c} = \frac{c}{b}

Considerando c = 1 em

\frac{c + b}{c}

, temos:

\frac{1 + b}{1} = \frac{1}{b}

ou b 2 + b ‒ 1 = 0

Chegamos a uma equação do 2º grau cuja resolução será estudada no capítulo 7.

Resolvendo essa equação, obtemos

\frac{\sqrt{5} ‒ 1}{2}

como um dos valores de b; logo:

\frac{1}{b} = \frac{2}{\sqrt{5} ‒ 1} ≃ 1, 618

Página 96

Agora é com você!

FAÇA A ATIVIDADE NO CADERNO

Observe os passos a seguir e construa retângulos áureos de duas maneiras diferentes.

1ª maneira: com dobradura

• Copie, em uma folha de papel em branco, o retângulo a bê cê dê (figura 1).

• Recorte o retângulo e, com dobradura, obtenha o quadrado á é éfe dê (figura 2).

• Recorte o quadrado (figura 3) e obtenha um novo retângulo áureo (figura 4).

Ilustração. Figura 1. Retângulo amarelo ABCD.

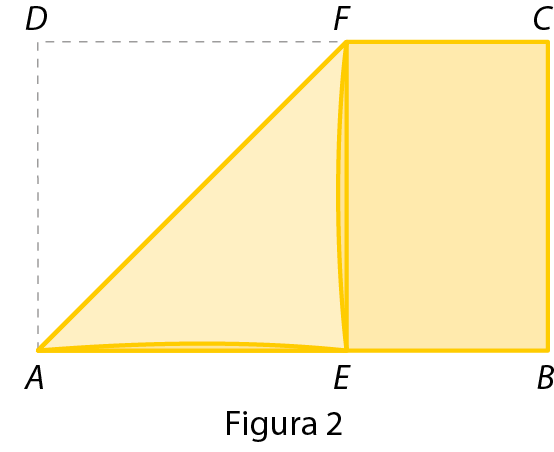
Ilustração. Figura 2. Do retângulo amarelo ABCD, uma dobradura foi feita do vértice D em direção ao lado AB. O segmento EF divide o retângulo, formando o triângulo AEF, e o retângulo BCFE.

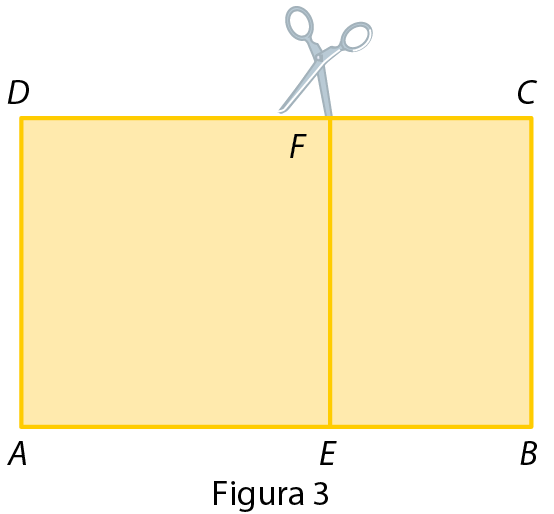
Ilustração. Figura 3. Retângulo amarelo ABCD, com segmento EF destacado. Uma Tesoura indica o recorte no segmento EF.

Ilustração. Figura 4. Retângulo amarelo BCEF.

(Use tesoura com ponta arredondada e a manuseie com cuidado!)

2ª maneira: com régua e esquadro

• Copie novamente, em uma folha de papel em branco, o retângulo a bê cê dê (figura 1).

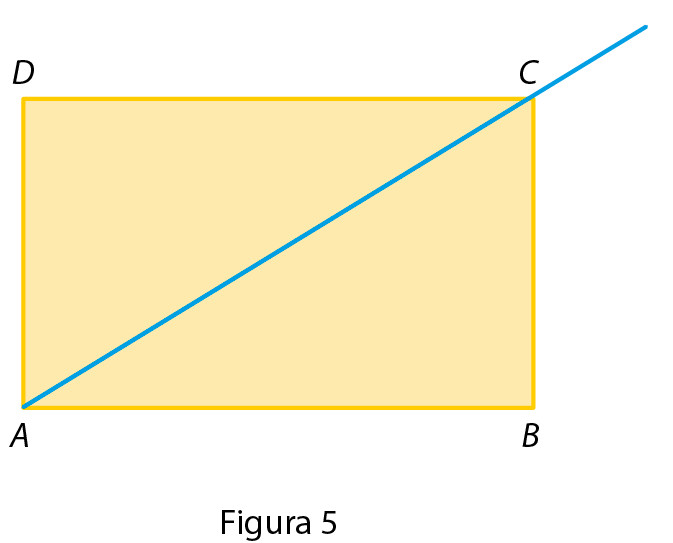
• Trace, com o auxílio de uma régua, uma semirreta com origem em a que passe por C (figura 5).

\overline{A C}

é uma diagonal do retângulo.

• Com o auxílio de um esquadro, trace retas perpendiculares ao lado

\overline{A B}

(ou à reta-suporte) e determine outros retângulos áureos (figura 6).

Ilustração. Figura 5. Retângulo amarelo ABCD com semirreta azul de origem em A que passa pela diagonal AC.

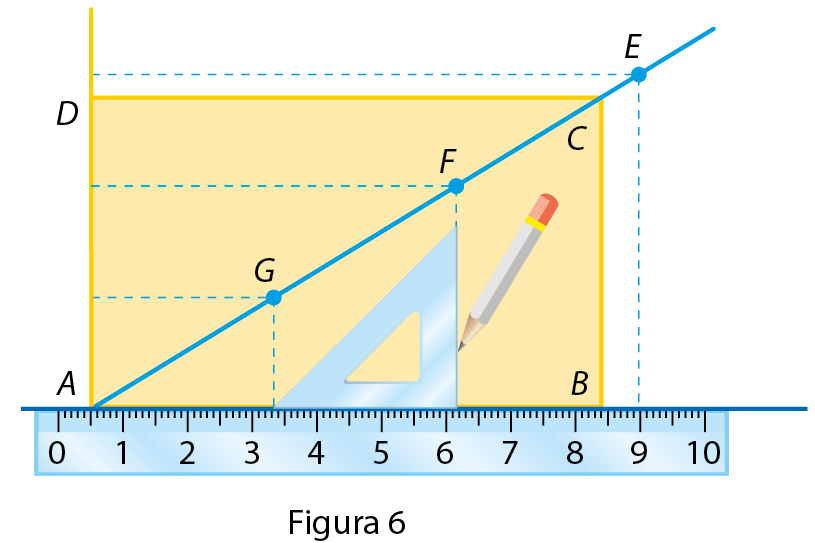
Ilustração. Figura 6. Retângulo amarelo ABCD. Na horizontal AB, uma régua graduada de 0 até 10. Na diagonal AC, os pontos A, G, F, C, E, nessa ordem. Do ponto G, uma linha tracejada horizontal até o lado AD, e uma linha tracejada vertical até o lado AB. Do ponto F, uma linha tracejada horizontal até o lado AD, e uma linha tracejada vertical até o lado AB. Do ponto E, uma linha tracejada horizontal até o lado AD, e uma linha tracejada vertical até o lado AB. Esquadro, com o canto reto, apoiado na linha horizontal, desliza do ponto G para o ponto F. Um lápis indica o traço vertical a ser feito de F até a linha horizontal. vertical.

(A imagem não respeita as proporções reais entre os objetos.)

Com os retângulos áureos que construiu, descubra se uma folha de papel de formato a4 (21 centímetros por 29,7 centímetros) e uma de formato carta (21,59 centímetros por 27,94 centímetros) são retângulos áureos.

Página 97

2. Feixe de retas paralelas

Um conjunto de três ou mais retas paralelas de um plano (como as retas a, b, c e d da figura 1) chama-se feixe de retas paralelas.

Uma reta que corta um feixe de retas paralelas (como a reta t) é chamada de reta transversal.

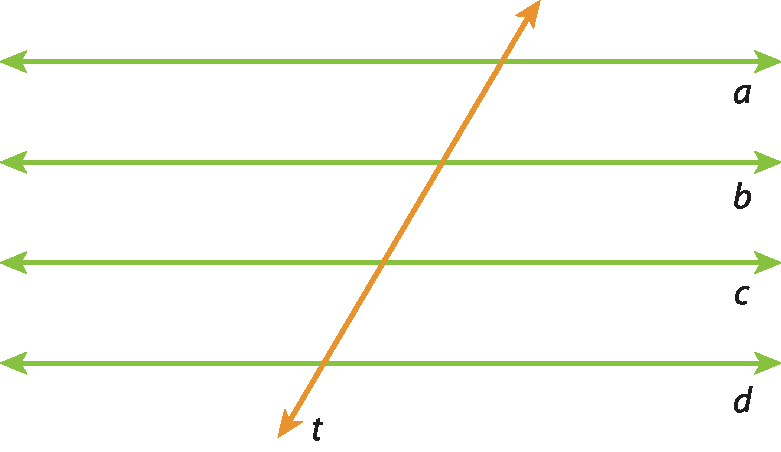
Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e d. Reta transversal t, que corta as 4 retas paralelas .

Figura 1

Considere a figura 2, com a ⫽ b ⫽ c, em que as retas s e t são transversais e

\overline{A B} ≅ \overline{B C} .

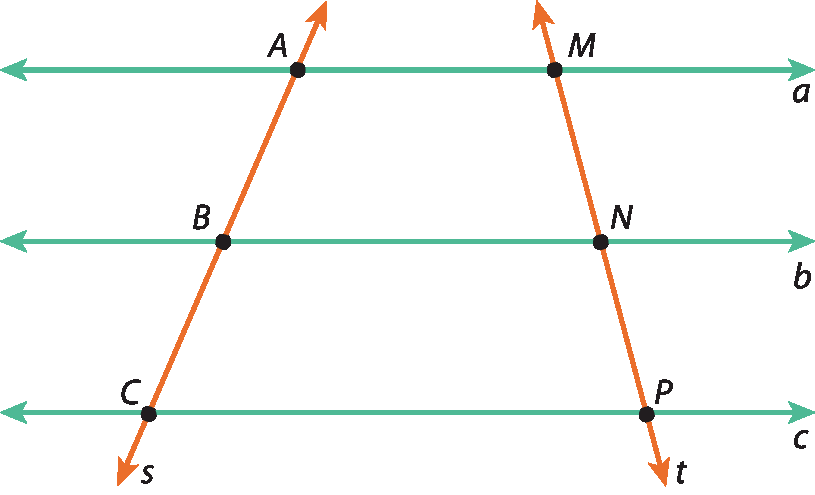
Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e retas transversais s e t, inclinadas para dentro. À esquerda, reta transversal s: corta a reta c no ponto C: corta a reta b no ponto B: corta a reta a no ponto A. À direita, reta transversal t: corta a reta c no ponto P: corta a reta b no ponto N; corta a reta a no ponto M.

Figura 2

Queremos provar que

\overline{M N} ≅ \overline{N P} .

• Demonstração

Por M traçamos

\overline{M R}

⫽ s. Com isso, obtemos o paralelogramo ABRM, com

\overline{A B} ≅ \overline{M R}

Por N traçamos

\overline{N S}

⫽ s. Assim, obtemos o paralelogramo bê cê ésse êne, em que

\overline{B C} ≅ \overline{N S}

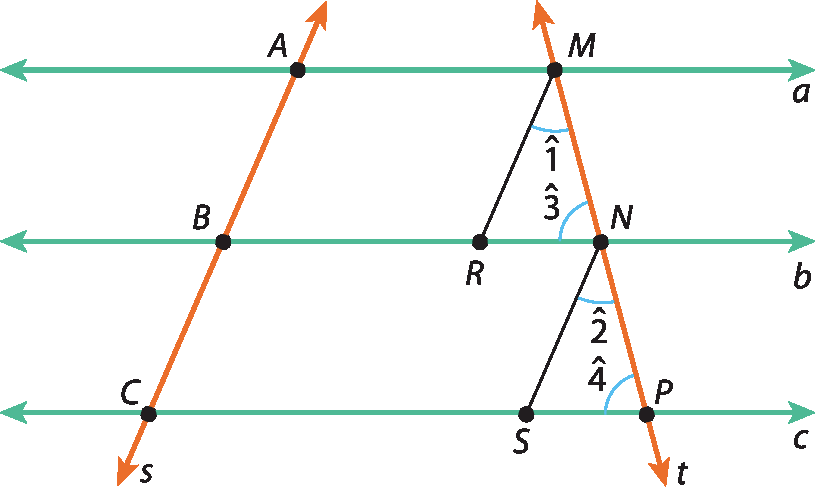
Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e duas retas transversais inclinadas para dentro s e t . À esquerda, reta transversal s: corta a reta c no ponto C; corta a reta b no ponto B; corta a reta a no ponto A. À direita, reta transversal t: corta a reta c no ponto P: corta a reta b no ponto N; corta a reta a no ponto M. À esquerda da reta transversal t: ponto R pertencente a reta b , forma segmento RM; abertura entre a reta transversal t e segmento RM forma ângulo 1, com vértice em M; abertura entre á esquerda da reta transversal t e reta b, forma ângulo 3; ponto S pertencente a reta c , forma segmento SN, abertura entre a reta transversal t e segmento SN forma ângulo 2, com vértice em N; abertura a esquerda, entre a reta transversal t e reta c forma ângulo 4.

, temos

\overline{M R} ≅ \overline{N S},

pois

\overline{A B} ≅ \overline{B C} .

Comparando os triângulos ême érre êne e êne ésse pê, temos:

•

\overline{M R} ≅ \overline{N S}

(já provado)

•

\hat{1} ≅ \hat{2}

(ângulos correspondentes em retas paralelas)

•

\hat{3} ≅ \hat{4}

(ângulos correspondentes em retas paralelas)

Assim, pelo caso lado-ângulo-ângulo opostoo , os triângulos ême érre êne e êne ésse pê são congruentes. Como

\overline{M N} e \overline{N P}

são lados correspondentes em triângulos congruentes, então

\overline{M N} ≅ \overline{N P} .

Se um feixe de retas paralelas determina segmentos congruentes sobre uma reta transversal, então esse feixe determina segmentos congruentes sobre qualquer outra reta transversal.

Página 98

3. Teorema de Tales

Considere a figura a seguir, em que a, b e c formam um feixe de retas paralelas e as retas s e t são transversais.

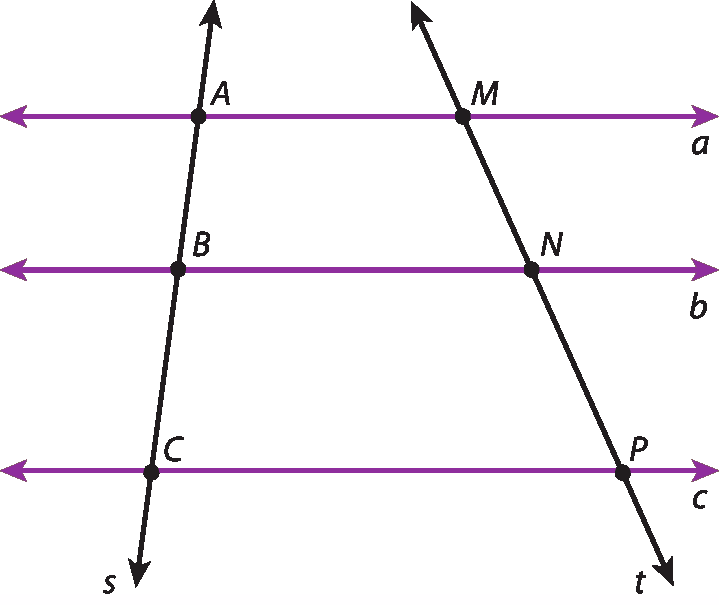
Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e duas retas transversais inclinadas para dentro. À esquerda, reta transversal s: corta a reta c no ponto C: corta a rea b no ponto B: corta a reta a no ponto A. À direita, reta transversal t: corta a reta c no ponto P: corta a reta b no ponto N; corta a reta a no ponto M.

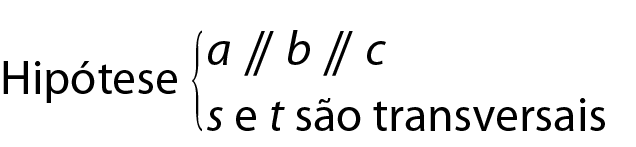
Esquema. Hipótese: a reta a é paralela à reta b, que é paralela à reta c; e retas s e t são transversais.

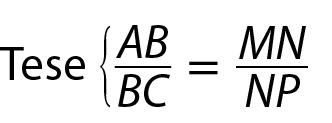
Fração: numerador AB, denominador BC, igual , fração: numerador MN, denominador NP.

Queremos provar que

\overline{A B}

\overline{B C}

\overline{M N}

\overline{N P}

, nessa ordem, são segmentos proporcionais.

• Demonstração

Admitindo que exista um segmento de medida u que caiba x vezes em

\overline{A B}

e y vezes em

\overline{B C},

com x e y sendo números inteiros, temos: AB = xu e BC = yu.

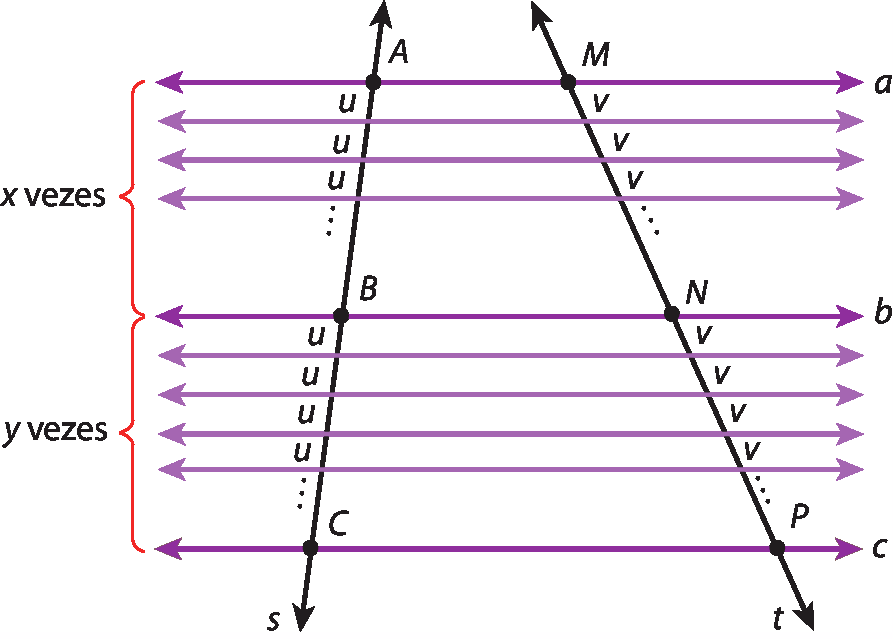
'Feixe de retas paralelas formada por 10 retas paralelas horizontais e duas retas transversais inclinadas para dentro, s à esquerda e t à direita. De cima para baixo: reta horizontal a, 3 retas paralelas abaixo, com distância u, marcado na reta transversal s e distância v marcado na reta transversal t; abaixo do u três pontinhos e abaixo do v três pontinhos; distância; reta horizontal b, 4 retas paralelas abaixo com distância de u, marcado na reta transversal s e distância v marcado na reta transversal t; abaixo do u três pontinhos e abaixo do v três pontinhos; distância ; reta horizontal c; à esquerda, reta transversal s: corta a reta c no ponto C: corta a reta b no ponto B: corta a reta a no ponto A. À direita, reta transversal t: corta a reta c no ponto P: corta a reta b no ponto N; corta a reta a no ponto M. Do lado esquerdo da reta transversal s, uma chave que vai da reta a até a reta b, indica x vezes. Do lado esquerdo da reta transversal s, uma chave que vai da reta b até a reta c, indica y vezes.'

Logo:

\frac{A B}{B C} = \frac{x u}{y u}

\frac{A B}{B C} = \frac{x}{y}

Traçando pelos pontos de divisão de

\overline{A B} e \overline{B C}

retas paralelas ao feixe, elas dividirão

\overline{M N}

\overline{N P}

em segmentos congruentes. Indicando por v a medida desses segmentos (com v ≠ 0), temos MN = xv e NP = yv e, portanto:

\frac{M N}{N P} = \frac{x v}{y v}

\frac{M N}{N P} = \frac{x}{y}

Comparando as igualdades

, temos:

\frac{A B}{B C} = \frac{M N}{N P}

Com base nessa demonstração, podemos enunciar o teorema de Tales:

Um feixe de retas paralelas determina sobre duas transversais segmentos proporcionais.

Com o auxílio do teorema de Tales, vamos calcular, como exemplo, o valor de x desta figura, sendo a ⫽ b ⫽ c.

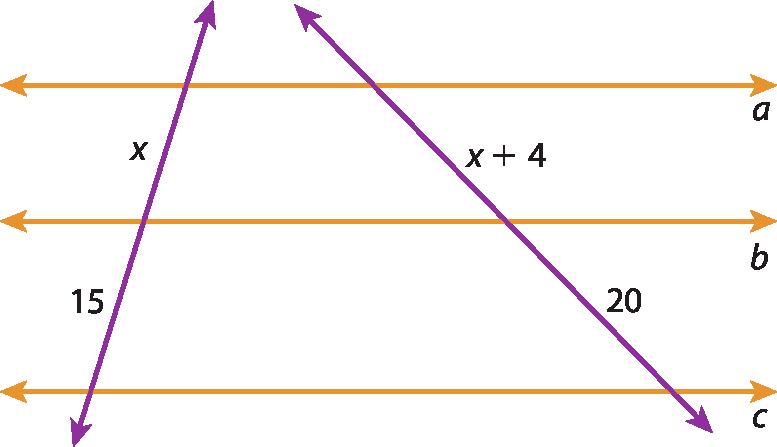
Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e duas retas transversais inclinadas para dentro. Segmento de reta de medida x, marcado na reta transversal da esquerda, entre retas a e b; Segmento de reta de medida 15, marcado na reta transversal da esquerda, entre retas b e c; Segmento de reta de medida x mais 4, marcado na reta transversal da direita, entre retas a e b; segmento de reta de medida 20, marcado na reta transversal da direita entre retas b e c.

\frac{x}{15} = \frac{x + 4}{20}

20x = 15(x + 4)

Resolvendo a equação, obtemos: x = 12

Página 99

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

10 Sendo a ⫽ b ⫽ c, calcule o valor de x.

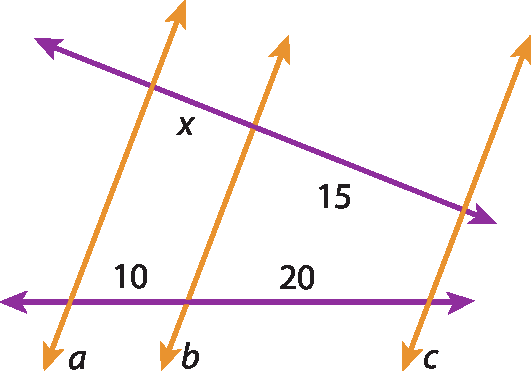
Ilustração. Retas paralelas inclinadas, da esquerda para direita, a, b, c e duas retas transversais, uma horizontal e outra acima inclinada para baixo. Segmento de reta de medida x, marcado na reta transversal acima, entre retas a e b; segmento de reta de medida 15, marcado na reta transversal acima, entre retas b e c; segmento de reta de medida 10, marcado na reta transversal horizontal, entre retas a e b; segmento de reta de medida 20, marcado na reta transversal horizontal, entre retas b e c.

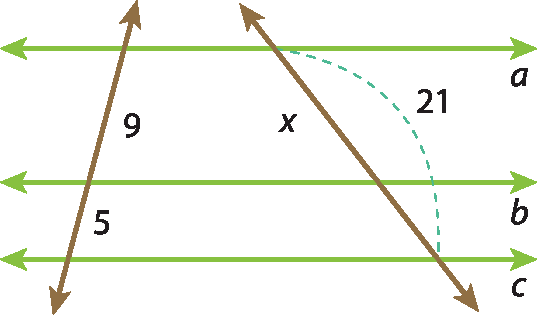
Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e duas retas transversais inclinadas para dentro. Segmento de reta de medida 9, marcado na reta transversal da esquerda, entre retas a e b; Segmento de reta de medida 5, marcado na reta transversal da esquerda, entre retas b e c; Segmento de reta de medida x, marcado na reta transversal da direita, entre retas a e b; Segmento de reta de medida 21, marcado na reta transversal da direita entre retas a e c.

Ilustração. Retas paralelas horizontais, de cima para baixo, a, b, c e duas retas transversais inclinadas para dentro. Segmento de reta de medida 12, marcado na reta transversal da esquerda, entre retas a e b; Segmento de reta de medida 33, marcado na reta transversal da esquerda, entre retas a e c; Segmento de reta de medida 8, marcado na reta transversal da direita, entre retas a e b; Segmento de reta de medida x, marcado na reta transversal da direita entre retas a e c.

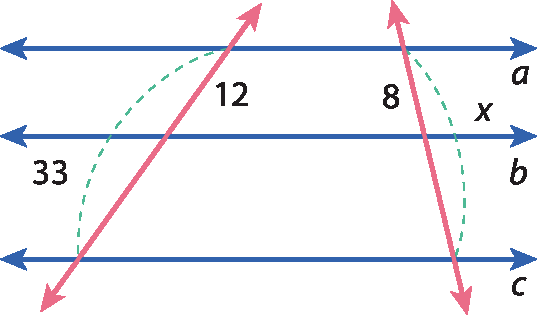
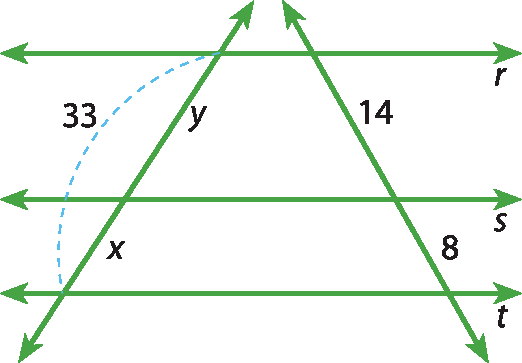
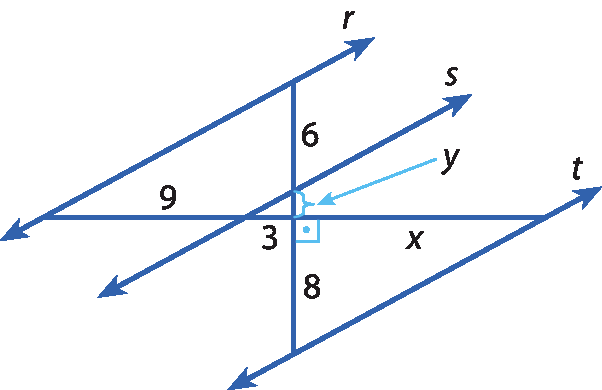
11 Determine os valores de x e de y nos seguintes feixes de paralelas:

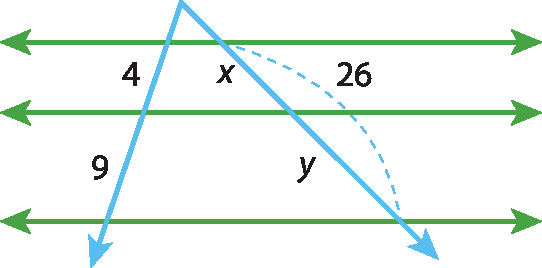
Ilustração. 3 retas paralelas horizontais e 2 retas transversais inclinadas que se encontram num ponto acima da primeira reta horizontal. De cima para baixo: segmento de reta de medida 4, marcado na reta transversal da esquerda, entre a primeira e segunda reta;
segmento de reta de medida 9, marcado na reta transversal da esquerda, entre a segunda e terceira reta; segmento de reta de medida x, marcado na reta transversal da direita, entre a primeira e segunda reta; segmento de reta de medida y, marcado na reta transversal da direita, entre a segunda e terceira reta; segmento de reta de medida 26, marcado na reta transversal da direita entre a primeira e terceira reta.

12 Três retas paralelas determinam sobre uma transversal segmentos medindo 4,2 centímetros e 5,4 centímetros. Calcule a medida do maior segmento que o feixe determina sobre outra transversal, sabendo que o segmento menor mede 6,3 centímetros.

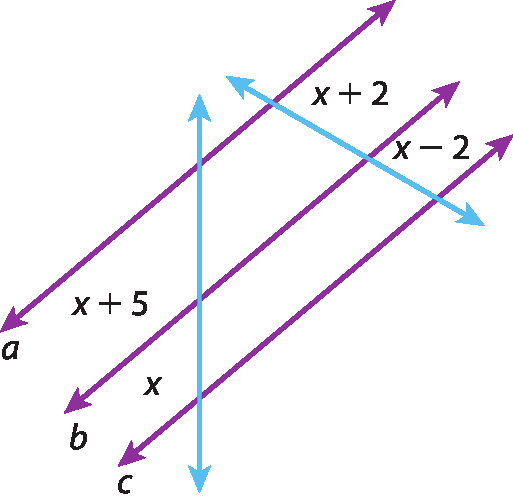
13 Sendo a ⫽ b ⫽ c, calcule o valor de x aplicando o teorema de Tales.

Ilustração. Retas paralelas inclinadas, de cima para baixo, a, b, c e duas retas transversais inclinadas para dentro. Segmento de reta de medida x mais 5, marcado na reta transversal da esquerda, entre retas a e b; Segmento de reta de medida x, marcado na reta transversal da esquerda, entre retas b e c; Segmento de reta de medida x mais 2, marcado na reta transversal da direita, entre retas a e b; Segmento de reta de medida x menos 2, marcado na reta transversal da direita entre retas b e c.

14 A figura a seguir representa um terreno com frente para duas alamedas. A frente para a alameda das Magnólias mede 90 métros, e a frente para a alameda dos Jasmins, 135 métros.

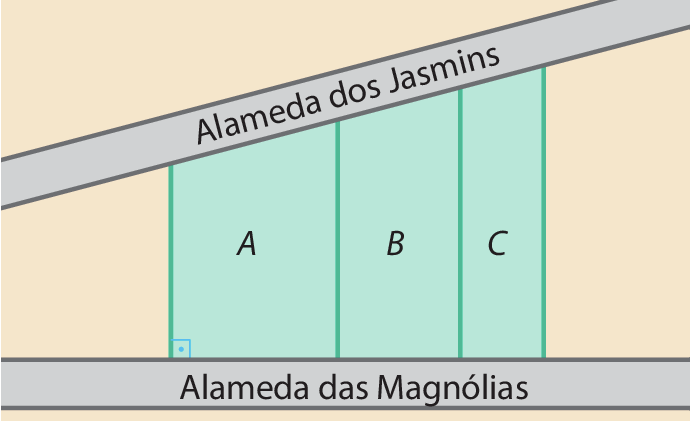
Ilustração. Acima, inclinado, Alameda dos Jasmins. Abaixo, na horizontal, Alameda das Magnólias. Entre as Alamedas, trapézios retângulos de tamanhos diferentes: A, B e C.

O proprietário do terreno resolveu dividi-lo em três lotes menores, traçando sobre ele duas paralelas perpendiculares à alameda das Magnólias. O terreno a ficou com 40 métros de frente para essa alameda, e o terreno B, com 30 métros de frente para a mesma alameda. Com base nessas informações, responda.

a) Quanto mede a frente do terreno C para a alameda das Magnólias?

b) Quanto medem as frentes dos três terrenos para a alameda dos Jasmins?

PARA SABER MAIS

Um pouco da história de Tales

Para tratar de semelhança, é imprescindível retomar os estudos do filósofo e matemático grego Tales de Mileto (cêrca de 624 a 547 antes de Cristo), cujo nome está associado ao seguinte teorema:

Se um feixe de retas paralelas é intersectado por duas retas transversais, então os segmentos determinados pelas retas paralelas sobre as transversais são proporcionais.

Página 100

Esse teorema, que provém diretamente da ideia de semelhança entre triângulos, que você estudará no capítulo 5, é conhecido como teorema de Tales.

Sabe-se pouco a respeito da vida e da obra de Tales. Acredita-se que ele tenha sido o primeiro filósofo e geômetra da Grécia conhecido e o primeiro de seus sábios. Acredita-se também que tenha sido o criador da Geometria demonstrativa.

Gravura em preto e branco. Homem de cabelo enrolado, barba e tecido sobre os ombros. — Gravura de Tales de Mileto produzida no século dezenove.

Nenhum escrito de Tales chegou até nós, o que dificulta determinar precisamente suas ideias e suas descobertas matemáticas. Muito do que sabemos a respeito dele vem do chamado Sumário eudemiano, escrito pelo matemático, filósofo e comentarista grego Proclus (411 a 485 Depois de Cristo).

Essa obra é um breve resumo do desenvolvimento da Geometria grega desde os primeiros tempos até a época de Euclides e é, ainda hoje, o principal registro histórico do início dessa ciência na Grécia.

Muitos dos conhecimentos de Tales resultaram de viagens que ele empreendeu, especialmente ao Egito. Tales morou por um tempo no Egito, onde teria aprendido Geometria com os sacerdotes egípcios e, também, aplicado a semelhança de triângulos.

Segundo o Sumário eudemiano, Tales introduziu a Geometria na Grécia após essas viagens. Utilizando metodologias gerais e empíricas, o filósofo grego descobriu muitas proposições, algumas delas envolvendo semelhança.

Além de Proclus, outras fontes fazem menção a Tales. O grego Eudemo de Rodes (350‑290 antes de Cristo), primeiro grande historiador da Matemática, por exemplo, afirma que Tales mediu a distância de uma torre a um navio.

Hierônimo, um discípulo de Aristóteles (384 a 322 antes de Cristo), afirmou que Tales teria medido a altura da grande pirâmide de Quéops, no Egito, por meio da observação e da comparação da própria sombra com a sombra da pirâmide. Tales teria chegado à conclusão de que, quando sua sombra tivesse o mesmo comprimento de sua altura, a sombra da pirâmide teria o mesmo comprimento da altura dela.

O matemático e filósofo grego Plutarco (cêrca de 46 a 119 Depois de Cristo) também o menciona em sua obra, ao dizer que Tales mediu a altura da pirâmide fincando verticalmente uma vara no chão e comparando as razões entre os dois triângulos formados.

Fotografia. Vista frontal de três pirâmides de cor marrom em chão de areia. — Pirâmides de Gizé no Egito. (Fotografia de 2021.)

Com base nesses relatos, percebemos que as ideias de proporcionalidade e de semelhança, em particular entre triângulos, estão estreitamente associadas ao nome de Tales. Adicionando a isso a grande importância que a Arquitetura e a Agrimensura tiveram no Egito antigo, bem como o fato de ele ter sido o fundador da Geometria demonstrativa na Grécia e quem primeiro organizou a Matemática dedutiva, é razoável a hipótese de que a primeira sistematização da Geometria tenha ocorrido na época de Tales.

Página 101

Consequências do teorema de Tales

1ª consequência

Observe os triângulos á bê cê sobre os quais foram traçadas as retas r (qualquer) e s, que passa pelo vértice A; ambas as retas são paralelas à reta

\overset{\leftrightarrow}{B C}

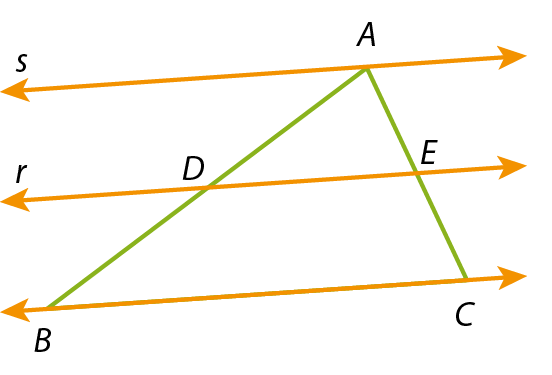
Ilustração: triângulo escaleno ABC, nele destacam-se três reta paralelas: reta BC, reta r que passa pelos pontos D e E, sendo D pertencente ao lado AB e E pertencente ao lado AC, reta s passando pelo vértice A.

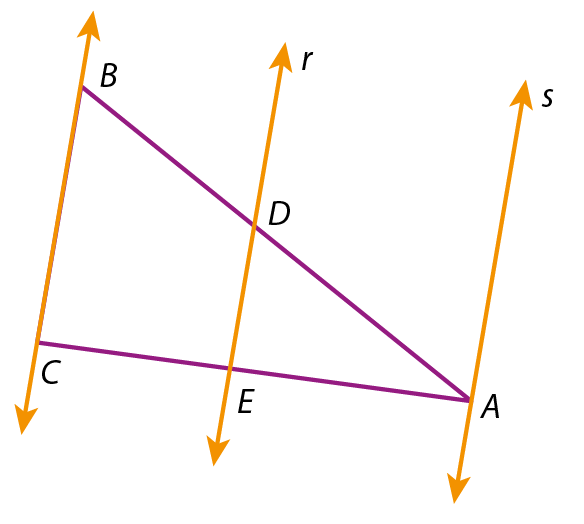
Ilustração: Triângulo escaleno ABC, com lado BC á esquerda. Ponto D no lado AB; Na mesma direção, ponto E no lado AC; Reta passa pelos vértices B e C, paralelo, reta r que passa pelos pontos D e E, paralelo, reta s, passa pelo vértice A.

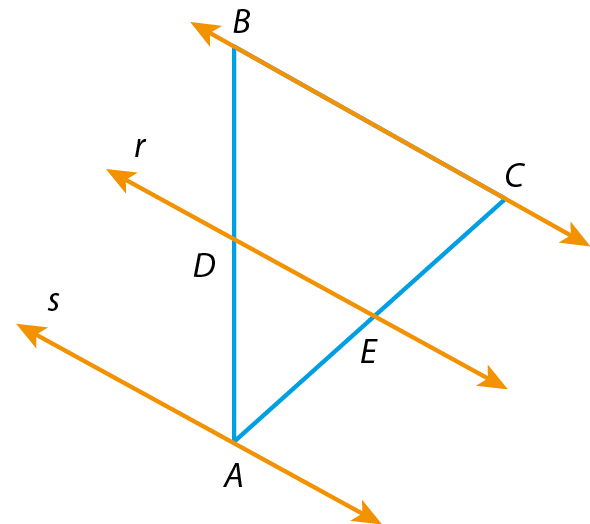
Ilustração: Triângulo escaleno ABC, com lado BC acima e a direita. Ponto D no lado AB; Na mesma direção, ponto E no lado AC; Reta passa pelos vértices B e C, paralelo, reta r que passa pelos pontos D e E, paralelo, reta s, passa pelo vértice A.

Pelo teorema de Tales, nos três casos, temos:

\frac{A D}{D B} = \frac{A E}{E C}

Podemos expressar essa consequência do teorema de Tales do seguinte modo:

Quando uma reta paralela a um lado de um triângulo intersecta os outros lados em dois pontos distintos, ela determina sobre esses lados segmentos proporcionais.

Observe que a recíproca dêsse teorema é verdadeira: se no triângulo á bê cê vale a relação

\frac{A D}{D B} = \frac{A E}{E C},

então

\overline{D E} ⫽ \overline{B C}

Ilustração: Triângulo escaleno ABC, com lado BC na horizontal. Ponto D no lado AB; Na mesma direção, ponto E no lado AC; Segmento DE, paralelo lado BC

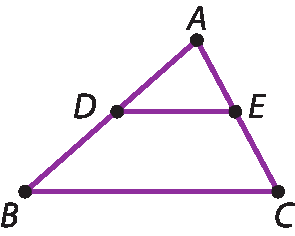
Acompanhe um exemplo de aplicação dessa propriedade.

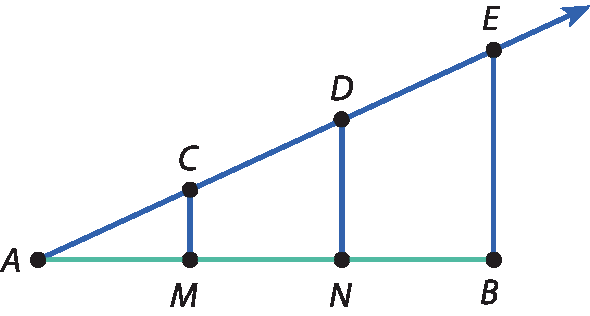
Vamos dividir o segmento

\overline{A B}

em três partes iguais.

Pelo ponto A, traçamos uma semirreta oblíqua a

\overline{A B}

sobre a qual, a partir de a, marcamos os pontos C, D e ê, de modo que á cê = CD = dê ê, e traçamos o segmento

\overline{B E} .

Pelos pontos C e D, com o auxílio de uma régua e de um esquadro, traçamos paralelas a

\overline{B E} .

Como á cê = CD = dê ê, então ei ém = MN = NB.

Ilustração: Segmento horizontal AB, com pontos M e N; Semirreta inclinada para cima AE, com pontos C, D; Segmentos MC, paralelo ao segmento ND, paralelo ao segmento BE

Página 102

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

15 Calcule o valor de x nas figuras a seguir.

\overline{D E} ⫽ \overline{B C}

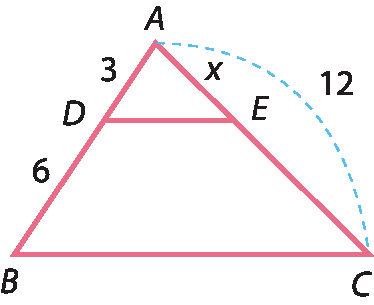
Ilustração: Triângulo escaleno ABC, com lado BC na horizontal. Ponto D pertencente ao lado AB; Ponto E pertencente ao lado AC; Segmento DE, paralelo lado BC Medidas dos segmentos: AD, 3; DB, 6; AE, x e AC, 12

\overline{D E} ⫽ \overline{B C}

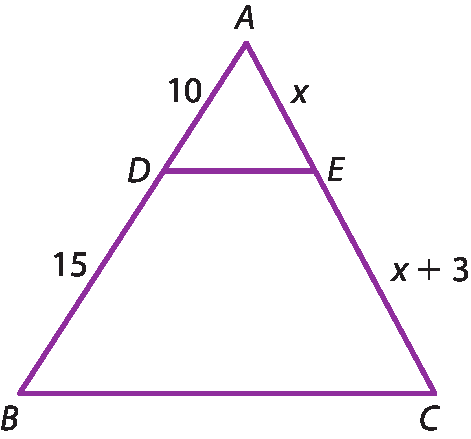
16 Verifique, em cada caso, se o segmento

\overline{N M}

é paralelo ao lado

\overline{G F}

do triângulo. Justifique sua resposta.

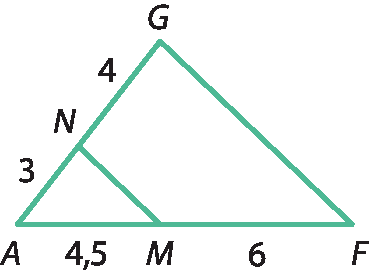
Ilustração: Triângulo escaleno AFG, com lado AF na horizontal. Ponto M pertencente ao lado AF; Ponto N pertencente ao lado AG; Segmento MN, paralelo lado FG; Medidas dos segmentos: AM, 4,5; MF, 6; AN, 3; NG, 4.

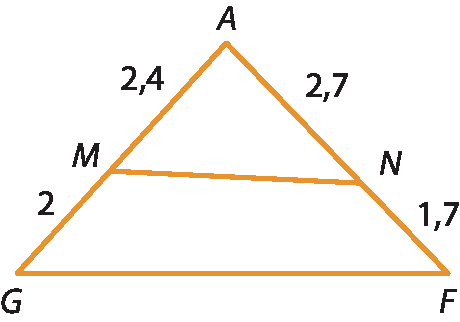
Ilustração: Triângulo escaleno AGF, com lado GF na horizontal. Ponto M pertencente ao lado AG; Ponto N pertencente ao lado AF; Segmento MN, paralelo lado GF; Medidas dos segmentos: AM, 2,4; MF, 2; AN, 2,7; NF, 1,7.

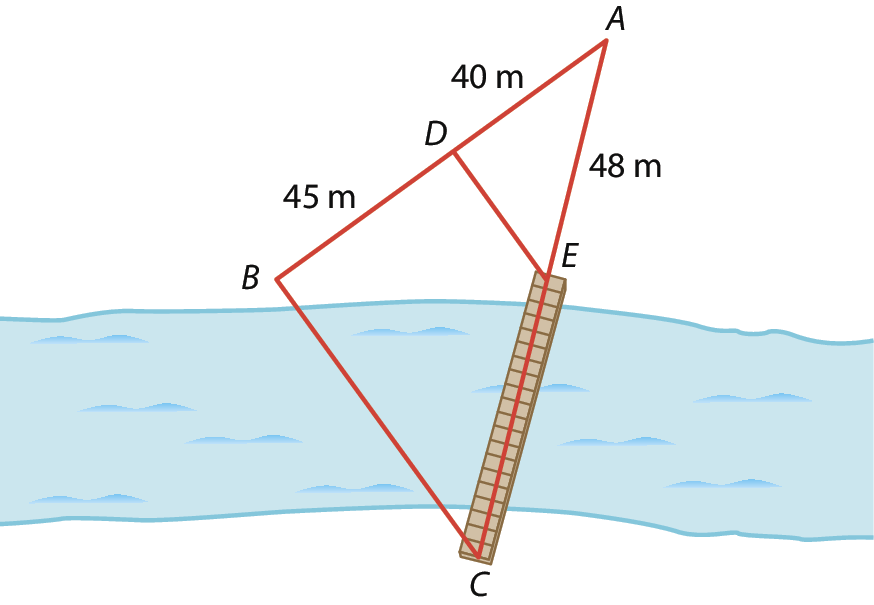
17 Para calcular a medida do comprimento da ponte a ser construída, um engenheiro elaborou o esquema a seguir, em que o segmento

\overline{C E}

representa a ponte. Sabe-se que

\overline{D E}

⫽

\overline{B C} .

Calcule a medida do comprimento dessa ponte.

Ilustração. Ponte CE sobre um rio e figura que lembra um triângulo A ,B C, passa sobre a ponte. Lado AC, com CE medida da ponte, e EA medindo 48 metros. Lado AB, com AD medindo 40 metros e DB, medindo 45 metros. Lado BC paralelo a DE.

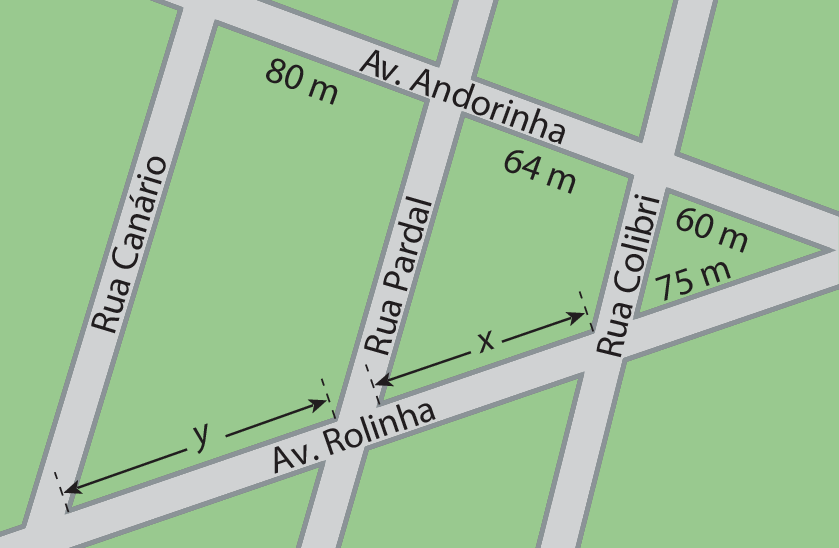
18 Na planta a seguir, as ruas Colibri, Pardal e Canário são paralelas. Determine as medidas das distâncias x e y.

Ilustração: mapas de ruas que lembram um triângulo cortado por duas retas paralelas. Da esquerda para direita. Rua Canário, paralela a Rua Pardal, paralela, a Rua Colibri. Rua Canário lembra o lado do triângulo. Av Rolinha, lembra a base do triângulo, cruza a rua Colibri e a Rua Pardal e se encontra com a Rua Canário á esquerda e com a Av. Andorinha á direita; Av Andorinha, lembra o outro lado do triângulo, cruza com a Rua Colibri, com a Rua Pardal, e se encontra com a rua Canário à esquerda e com a Av. Rolinha á direita; Pela Av Rolinha, distância: entre as ruas Pardal e Canário é y; entre as ruas Colibri e Pardal é x; entre o cruzamento das avenidas e a rua Colibri é 75 metros. Pela Av. Andorinha, distância: entre ruas Pardal e Canário é 80 metros; entre as ruas Colibri e Pardal é 64 metros, entre o cruzamento das avenidas e a rua Colibri é 60 metros.

19 É hora de fazer o retrato da turma, e todos querem aparecer. Ana, a primeira menina da esquerda, está a 3 metros da câmera; Bete, a última da direita, está a 3,6 metros. Nessa disposição, todas as meninas ficam enquadradas, mas os meninos, não.

Ilustração. Nove jovens de camiseta branca e calça azul estão abraçados lado a lado. À frente deles, um homem tira uma foto

Então, o fotógrafo pediu a todos que se afastassem, mantendo a mesma posição na fila, de modo que Ana ficasse distante 4,5 metros. Observe o esquema.

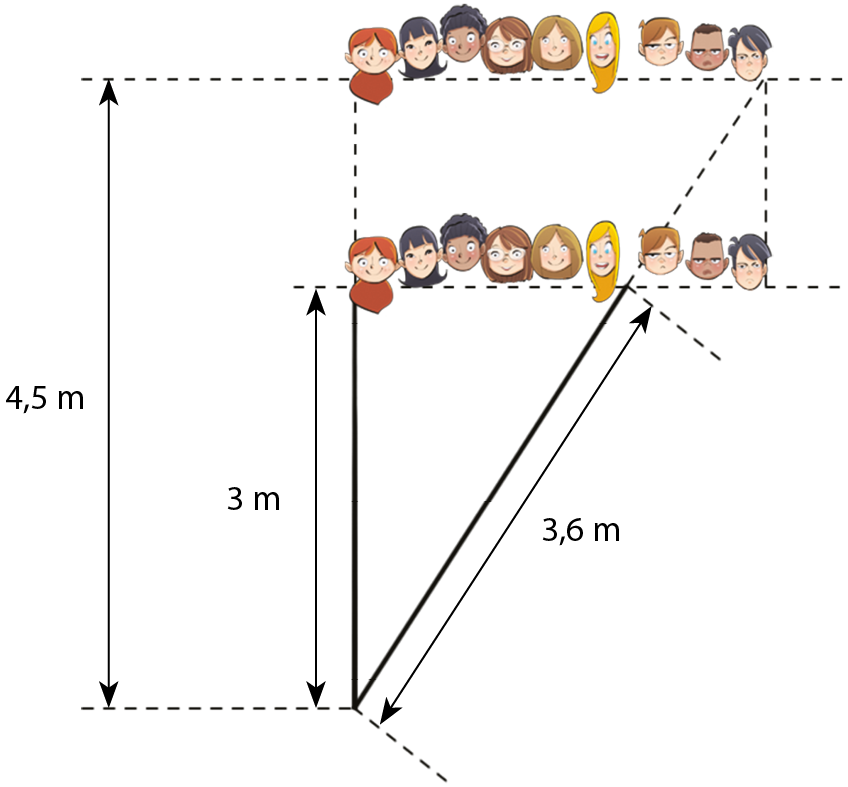
Esquema. Duas fileiras de 9 rostos de jovens, distam de um ponto em comum. Desse ponto até a primeira fileira, 3 metros. Desse ponto até a segunda fileira, 4,5 metros. Desse ponto até a antepenúltima pessoa da primeira fileira, 3,6 metros. Há uma linha desse ponto até a última pessoa da segunda fileira.

Sabendo que essa câmera fotográfica mantém uma boa resolução até 5,5 metros, a imagem do menino da direita ficará prejudicada?

Página 103

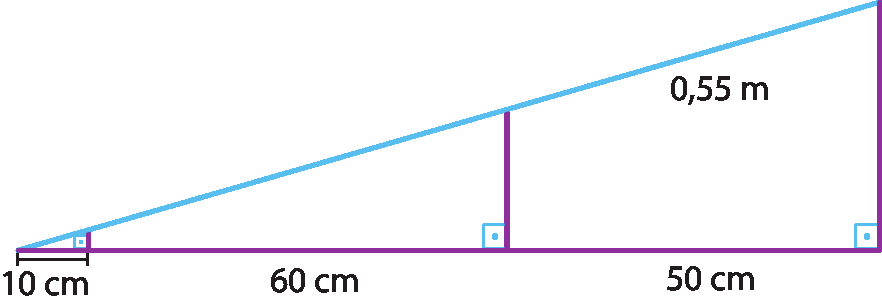
20 O proprietário de uma loja, preocupado em oferecer a seus clientes um acesso mais seguro e confortável, vai construir uma rampa ao lado dos degraus da escada da entrada da loja.

Para a construção dessa rampa, deverão ser instaladas três vigas de sustentação: uma a 10 centímetros do início, outra a 60 centímetros da primeira e a terceira a 50 centímetros desta última. Observando o esboço feito pelo dono da loja, determine o comprimento, em metro, da rampa que está destacada em azul.

Ilustração: triângulo retângulo, com ângulo reto inferior á direita, dividido por dois segmentos de retas paralelos ao lado direito. Do vértice da esquerda até a primeira paralela, 10 centímetros, na horizontal; Dessa paralela até a outra paralela , á direita e na horizontal, distância de 60 centímetros; E , dessa paralela até o lado paralelo do triângulo, na horizontal, distância de 50 centímetro. Acima, no lado inclinado do triângulo distância de 0,55 metros entre o lado direito do triângulo até a paralela á sua esquerda.

Hora de criar – Em dupla, cada um cria um problema sobre aplicação do teorema de Tales. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi‑los.

Pense mais um poucoreticências

FAÇA AS ATIVIDADES NO CADERNO

Reúna-se com um colega e façam o que se pede.

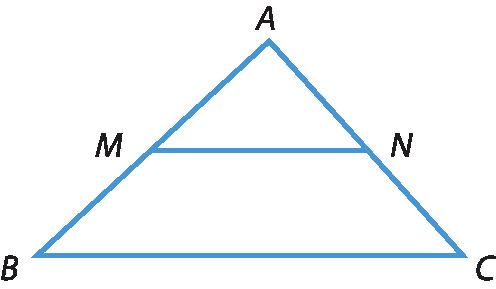
1 Em um triângulo á bê cê, foi traçado um segmento paralelo ao lado

\overline{B C}

pelo ponto M, ponto médio de

\overline{A B} .

Esse segmento tem o outro extremo no lado

\overline{A C},

no ponto N.

Provem que N é ponto médio de

\overline{A C} .

Ilustração: Triângulo ABC, com base BC. Segmento MN, paralelo lado BC, em que o ponto M pertence a AB e o ponto N pertence a AC.

2 Aprendam a dividir um segmento qualquer em 5 partes iguais sem usar a escala da régua.

No caderno, façam os seguintes passos:

• tracem um segmento

\overline{A B}

e uma semirreta

\vec{A C},

de modo que B não pertença à reta

\overset{\leftrightarrow}{A C};

• com um compasso, marquem os pontos P1, P2, P3, P4 e P5 em

\vec{A C},

de maneira que AP1 = P1P2 = P2P3 = P3P4 = P4P5 ;

• tracem a reta

\overset{\leftrightarrow}{P_{5} B};

• com o esquadro deslizando ao lado da régua, tracem, por P4, P3, P2 e P1, paralelas a

\overset{\leftrightarrow}{P_{5} B}

que cortem

\overline{A B}

nos pontos Q 4, Q 3, Q 2, Q 1;

• verifiquem com o compasso que AQ1 = Q 1Q 2 = Q 2Q 3 = Q 3Q 4 = Q 4B.

(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)

3 Justifiquem a construção realizada na atividade anterior.

PARA SABER MAIS

Rumo ao teorema das bissetrizes dos ângulos internos de um triângulo

Vamos provar o seguinte teorema:

Duas retas paralelas cortadas por uma transversal determinam ângulos alternos internos congruentes.

Esquema. Hipótese: reta r paralela à reta s. Reta t é transversal. Ângulos a e b são ângulos alternos internos. Tese: ângulo a é congruente ao ângulo b.

Página 104

• Demonstração

Construção auxiliar: pelo ponto M, ponto médio de

\overline{A B},

traçamos o segmento

\overline{P Q},

perpendicular às retas r e s.

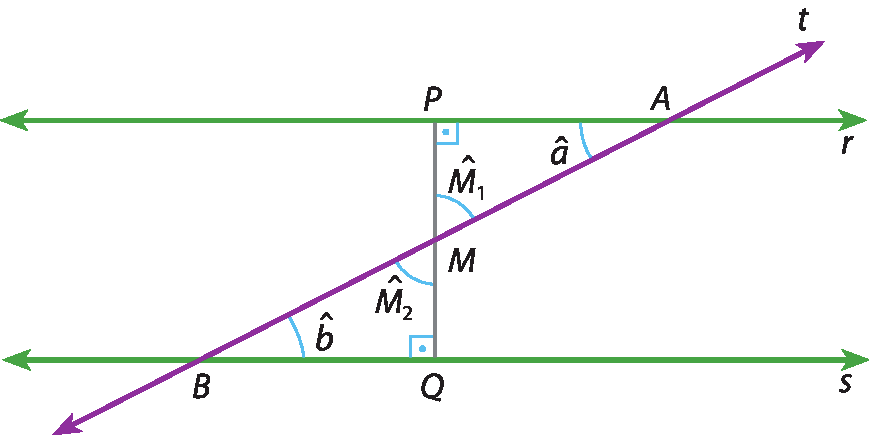
Ilustração. Duas retas paralelas de baixo para cima s e r. e uma reta transversal t. A reta transversal t, corta a reta s, no ponto B: Abertura, para cima, á direita, entre reta s e a reta transversal t forma ângulo b; Arco azul indica ângulo b; A reta transversal t, corta a reta r, no ponto A: Abertura, para baixo, á esquerda, entre reta r e a reta transversal t forma ângulo a; Arco azul indica ângulo a. Ponto M , divide segmento AB em duas parte iguais. Perpendicular que passa pelo ponto M , determina o ponto Q na reta s e ponto P na reta r. Abertura entre perpendicular e reta transversal t : para baixo , á esquerda, forma o ângulo M2 e; para cima , á direita, forma a ângulo M1. arco azul indica cada um desses ângulos.

Comparando os triângulos á ême pê e bê ême quê, temos:

\overline{A M} ≅ \overline{M B}

(M é ponto médio)

{\hat{M}}_{1} ≅ {\hat{M}}_{2}

(ângulos opostos pelo vértice)

\hat{P} ≅ \hat{Q}

(ângulos retos)

Logo, pelo caso lado-ângulo-ângulo opostoo , os triângulos á ême pê e bê ême quê são congruentes. Portanto,

\hat{a} ≅ \hat{b},

pois são ângulos correspondentes em triângulos congruentes.

Agora é com você!

FAÇA A ATIVIDADE NO CADERNO

Observe a figura, em que:

•

\overline{A D}

é bissetriz do ângulo

B \hat{A} C

do triângulo á bê cê;

•

\overset{\leftrightarrow}{C E}

⫽

\overset{\leftrightarrow}{A D}

;

•

m (B \hat{A} C) = 82 °

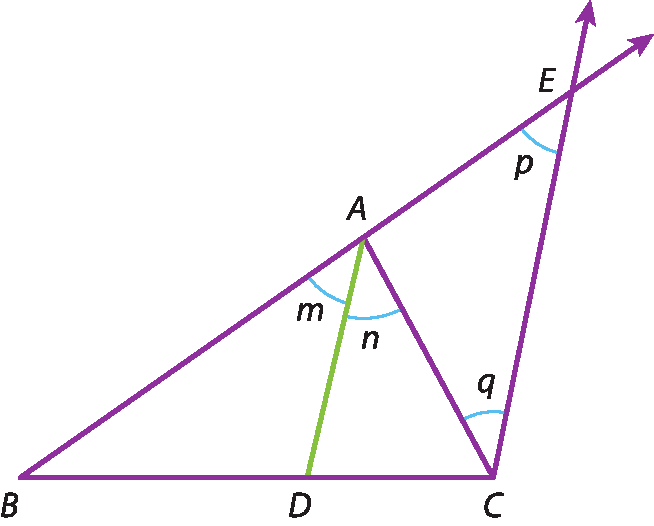
'Ilustração. Segmento de reta BC na horizontal, semirreta BE cruza com semirreta CE no ponto E. Ponto A , pertence ao segmento BE. Segmento de reta une ponto A com ponto C, formando triângulo ABC, e o triângulo ACE. Ponto D pertence ao segmento BC. Segmento de reta une ponto A com ponto D. Abertura entre o lado AB e o segmento AD forma o ângulo m; Abertura entre o lado AC e o segmento AD forma o ângulo n; Abertura do lado AC e CE forma Ângulo q; Abertura entre os lados CE e EA forma o ângulo p.'

a) Calcule o valor de m, n, p e q.

b) Mostre que o triângulo á cê ê é isósceles.

2ª consequência

Considere o triângulo á bê cê e a bissetriz

\overline{A D}

relativa ao ângulo

\hat{A} .

Traçamos pelo vértice C uma semirreta paralela a

\overline{A D},

que cruza a semirreta

\vec{B A}

em um ponto que chamamos de ê.

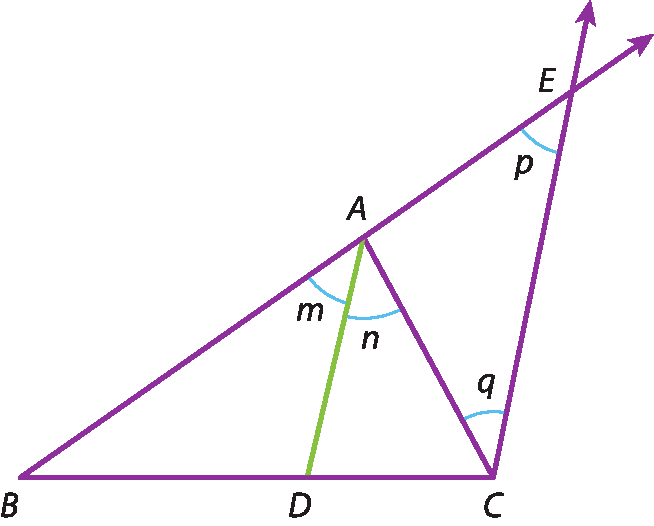
Pelo teorema de Tales, temos:

\frac{B D}{D C} = \frac{A B}{A E}

\frac{B D}{A B} = \frac{D C}{A E}

Página 105

Dessa maneira:

• p = m (medidas de ângulos correspondentes em retas paralelas)

• m = n (

\overline{A D}

é bissetriz)

• n = q (medidas de ângulos alternos internos em retas paralelas)

Concluímos, então, que p = q.

Logo, o triângulo CAE é isósceles. Portanto,

\overline{A C} ≅ \overline{A E} .

Substituindo A Ê por á cê em

\frac{B D}{A B} = \frac{D C}{A E},

temos:

\frac{B D}{A B} = \frac{D C}{A C}

A bissetriz de um ângulo interno de um triângulo divide o lado oposto em segmentos proporcionais aos lados adjacentes.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

22 Calcule x nos triângulos, sabendo que

\overline{A D}

é bissetriz relativa ao ângulo

\hat{A} .

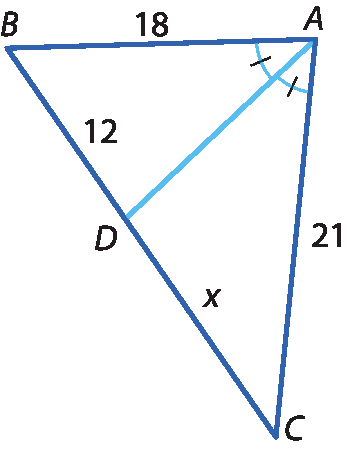
Ilustração. Triângulo ABC. lado AB, 18; lado AC, 21; ponto D pertence ao lado BC; segmento de reta une pontos AD; AD é bissetriz; segmento de reta BD, 12; segmento de reta DC, x.

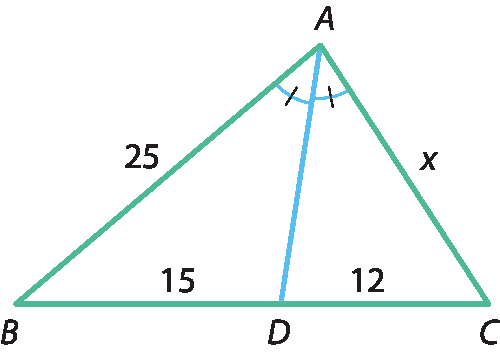
Ilustração. Triângulo ABC. lado AB, 25; lado AC, x; ponto D pertence ao lado BC; segmento de reta une pontos AD; AD é bissetriz; segmento de reta BD, 15; segmento de reta DC, 12.

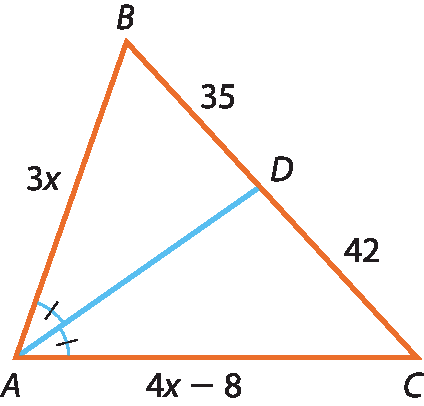
Ilustração. Triângulo ABC. lado AB, 3x; lado AC, 4x-8; ponto D pertence ao lado BC; segmento de reta une pontos AD; AD é bissetriz; segmento de reta BD, 35; segmento de reta DC, 42.

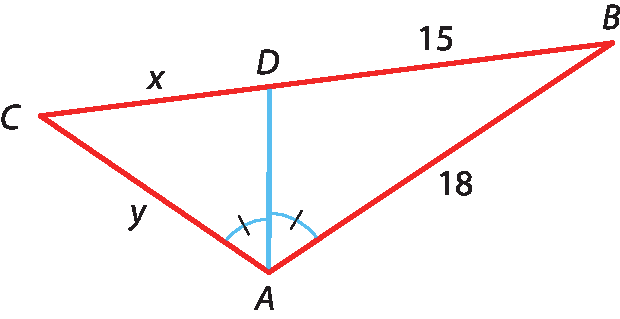
23 Calcule x e y nos triângulos, sabendo que

\overline{A D}

é bissetriz relativa ao ângulo

\hat{A}

a) x + y = 55

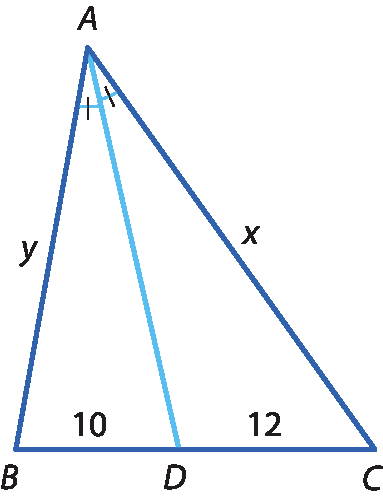
Ilustração. Triângulo ABC. lado AB, y; lado AC, x; ponto D pertence ao lado BC; segmento de reta une pontos AD; AD é bissetriz; segmento de reta BD, 10; segmento de reta DC, 12.

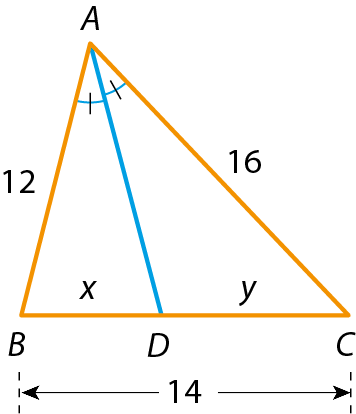
Ilustração. Triângulo ABC. lado AB, 12; lado AC, 16; lado BC, 14; ponto D pertence ao lado BC; segmento de reta une pontos AD; AD é bissetriz; segmento de reta BD, x; segmento de reta DC, y.

c) x + y = 22

Ilustração. Triângulo ABC. lado AB, 18; lado AC, y; ponto D pertence ao lado BC; segmento de reta une pontos AD; AD é bissetriz; segmento de reta BD, 15; segmento de reta DC, x.

24 Com o auxílio de uma régua, construa um triângulo á bê cê, em que A bê = 4,8 centímetros, á cê = 7,2 centímetros e bê cê = 8 centímetros. Usando régua e compasso, trace a bissetriz

\overline{A D} .

Calcule BD e DC e, depois, verifique os valores obtidos, medindo com a régua a figura construída.

(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)

25 Considere um triângulo á bê cê. A bissetriz

\overline{A D}

determina sobre

\overline{B C}

dois segmentos,

\overline{B D}

\overline{D C},

de medidas 2 centímetros e 2,4 centímetros, respectivamente. Sabendo que A bê = 5 centímetros, determine á cê .

Página 106

TRABALHANDO A INFORMAÇÃO

Ícone do Tema Contemporâneo Transversal: CIDADANIA E CIVISMO.

Cartograma do Índice de Vulnerabilidade Social (í vê ésse)

No dicionário, o verbete cartograma é definido como:

Ilustração. Folha de papel com as informações: Cartograma. Substantivo masculino. Quadro ou mapa em que se representa graficamente, por meio de linhas e figuras, a ocorrência quantitativa ou a intensidade de diversos fenômenos (índices de natalidade, distribuição de populações etcétera.) — Fonte: HOUAISS, A.; VILLAR, M. S. (edição). Cartograma. In: Dicionário Houaiss da Língua Portuguesa. Rio de Janeiro: Objetiva, 2009.

Com a produção de informações cada vez mais crescente e diversificada, a alfabetização de uma pessoa não está mais restrita a textos. Atualmente, é necessário nos alfabetizarmos em linguagens diversas. A alfabetização cartográfica, por exemplo, aprender a ler e interpretar mapas, como os cartogramas, também é muito importante.

Vamos analisar o tema vulnerabilidade social por meio da comparação de cartogramas elaborados pelo Instituto de Pesquisa Econômica Aplicada (ipéa) com dados do í bê gê É de 2000 e de 2010.

O Índice de Vulnerabilidade Social (í vê ésse)

[reticências] O Índice de Vulnerabilidade Social (í vê ésse), construído a partir de indicadores do Atlas do Desenvolvimento Humano (ADH) no Brasil, procura dar destaque a diferentes situações indicativas de exclusão e vulnerabilidade social no território brasileiro, em uma perspectiva que vai além da identificação da pobreza entendida apenas como insuficiência de recursos monetários. [reticências]

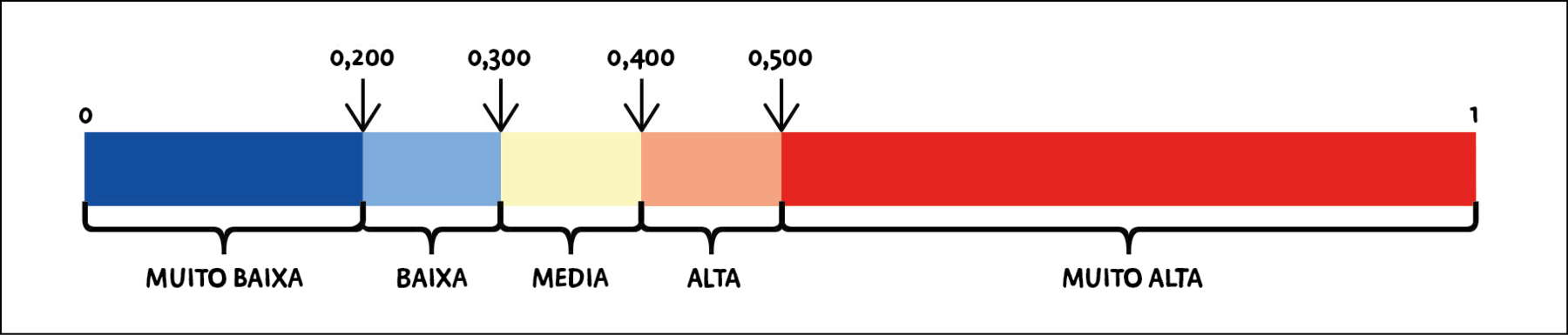
Como ler o í vê ésse

O í vê ésse é um índice que varia entre 0 e 1. Quanto mais próximo a 1, maior é a vulnerabilidade social de um município. [reticências]

Ilustração. Barra colorida que vai de 0 a 1 aponta o IVS, Índice de Vulnerabilidade Social. Azul escuro, de 0 a 0,200, indica: muito baixa. Azul claro, de 0,200 a 0,300, indica: baixa. Amarelo, de 0,300 a 0,400, indica: média. Laranja, de 0,400 a 0,500, indica: alta. Vermelha, de 0,500 a 1, indica: muito alta.

Como é construído o í vê ésse

O í vê ésse é o resultado da média aritmética dos subíndices: í vê ésse Infraestrutura Urbana [saneamento básico e mobilidade urbana], í vê ésse Capital Humano [saúde e educação] e í vê ésse Renda e Trabalho [renda domiciliar per capita, desocupação de adultos, trabalho infantil], cada um deles entra no cálculo do í vê ésse final com o mesmo peso. [reticências]

O í vê ésse no Brasil

Em 2000, o Brasil apresentava í vê ésse igual a 0,446. Este valor indica que o país encontrava-se na faixa da alta vulnerabilidade social. Passados dez anos, a vulnerabilidade social é reduzida a 0,326, trazendo o país para a faixa do médio í vê ésse, em um avanço equivalente a 27% em direção a níveis mais baixos de vulnerabilidade social [reticências].

Fonte: Instituto de Pesquisa Econômica Aplicada. Atlas da vulnerabilidade social nos municípios brasileiros. Brasília, Distrito Federal: ipéa, 2015. Disponível em: https://oeds.link/UeDIog. Acesso em: 28 março 2022.

Página 107

Observe a seguir os cartogramas que mostram a distribuição espacial do Índice de Vulnerabilidade Social (í vê ésse) para os municípios brasileiros nos anos de 2000 e 2010.

Vulnerabilidade social de acordo com o í vê ésse (2000)

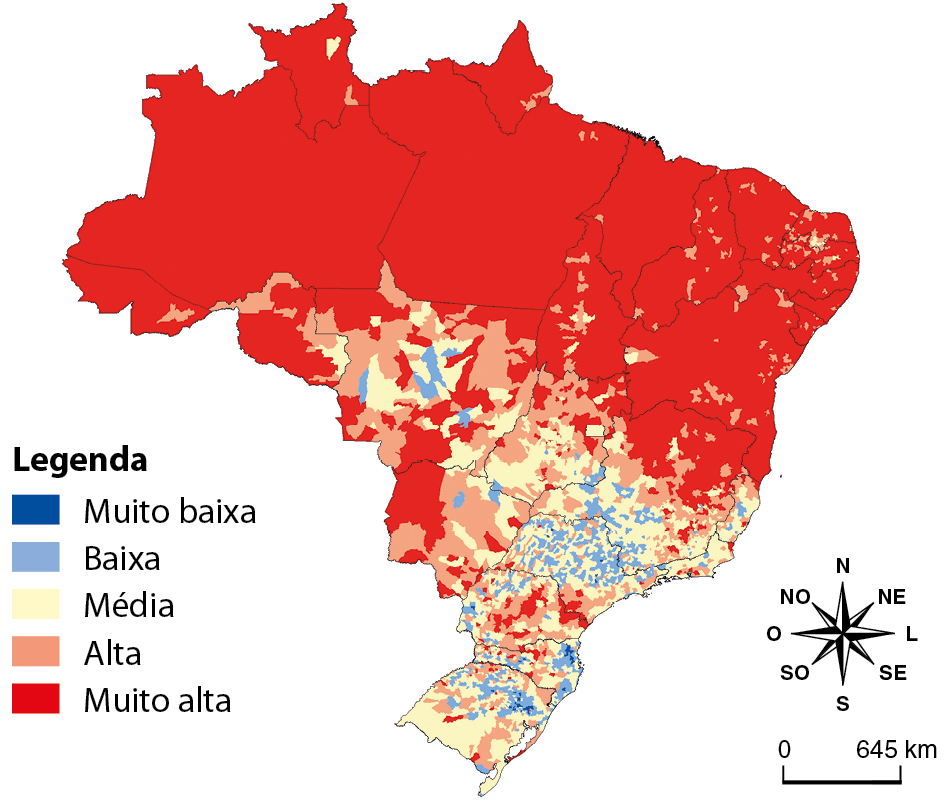
Mapa. O mapa mostra o Brasil e a legenda indica as seguintes informações: azul escuro, muito baixa: predomina em pequena parte do sudeste e sul. Azul claro, baixa: predomina em pequena parte do centro-oeste, sudeste e sul. Amarelo, baixa: predomina em pequena parte do centro-oeste, sudeste e sul. Laranja, alta: predomina em parte do centro-oeste, sudeste, sul e pequenas áreas do nordeste. Vermelha, muito alta: predomina em grande parte do norte, nordeste, centro-oeste e pequena parte do sudeste. No canto inferior direito, rosa dos ventos e escala de 0 a 645 quilômetros. — Fonte: Instituto de Pesquisa Econômica Aplicada. Atlas da vulnerabilidade social nos municípios brasileiros. Brasília, Distrito Federal: ipéa, 2015. Disponível em: https://oeds.link/UeDIog. Acesso em: 28 março 2022.

Vulnerabilidade social de acordo com o í vê ésse (2010)

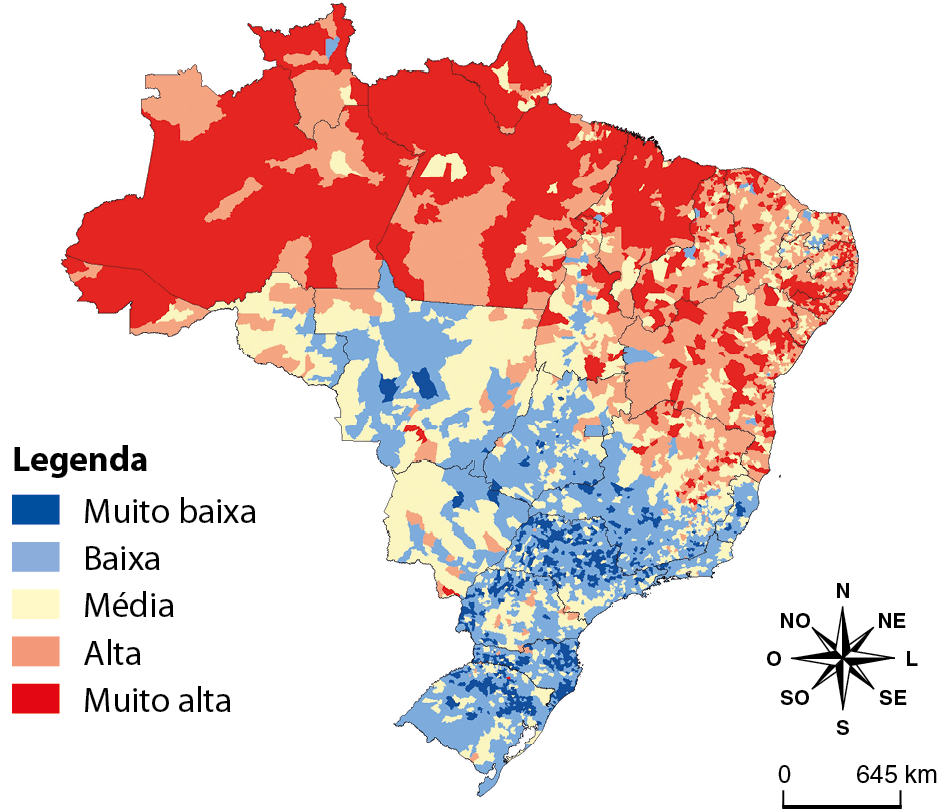
Mapa. O mapa mostra o Brasil e a legenda indica as seguintes informações: azul escuro, muito baixa: predomina em pequena parte do sul, sudeste e centro-oeste. Azul claro, baixa: predomina em grande parte do centro-oeste, sudeste e sul. Amarelo, baixa: predomina em pequena parte do centro-oeste, sudeste, sul e nordeste. Laranja, alta: predomina em parte do norte e nordeste. Vermelha, muito alta: predomina em grande parte do norte e nordeste. No canto inferior direito, rosa dos ventos e escala de 0 a 645 quilômetros. — Fonte: Instituto de Pesquisa Econômica Aplicada. Atlas da vulnerabilidade social nos municípios brasileiros. Brasília, Distrito Federal: ipéa, 2015. Disponível em: https://oeds.link/UeDIog. Acesso em: 28 março 2022.

Agora quem trabalha é você!

FAÇA A ATIVIDADE NO CADERNO

Observe os dois cartogramas, analise com atenção suas legendas e identifique pela cor a situação de cada região. Em seguida, identifique a localização aproximada do município em que você vive em cada cartograma.

a) Em que situação ele se classificava em 2000? E em 2010?

b) Atualmente, quais são os maiores problemas do município em que você vive que podem fazer com que o índice de vulnerabilidade social aumente?

Discuta com os colegas o que poderia ser feito para resolver os problemas relacionados a situações de vulnerabilidade social no município em que vocês vivem.

Página 108

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Sendo r ⫽ s ⫽ t, calcule x e y.

lustração. Retas paralelas horizontais, de cima para baixo, r, s, t e duas retas transversais inclinadas para dentro. Segmento de reta de medida y, marcado na reta transversal da esquerda, entre retas r e s; Segmento de reta de medida x, marcado na reta transversal da esquerda, entre retas s e t; Arco pontinhado azul indica a medida 33, entre as retas r e t. Segmento de reta de medida 14, marcado na reta transversal da direita, entre retas r e s; Segmento de reta de medida 8, marcado na reta transversal da direita entre retas s e t.

Ilustração. Retas paralelas inclinadas, de cima para baixo, r, s, t e duas retas transversais perpendiculares entre si. Segmento de reta de medida 6, marcado na reta perpendicular vertical, entre retas r e s; Segmento de reta de medida y, marcado na reta perpendicular vertical, entre retas s e a perpendicular horizontal; Segmento de reta de medida 8 , marcado na reta perpendicular vertical, entre a retas perpendicular horizontal e t; Segmento de reta de medida 9, marcado na reta perpendicular horizontal, entre retas r e s; Segmento de reta de medida 3, marcado na reta perpendicular horizontal, entre retas s e a perpendicular vertical. Segmento de reta de medida x, marcado na reta perpendicular horizontal, entre as retas perpendicular vertical e t.

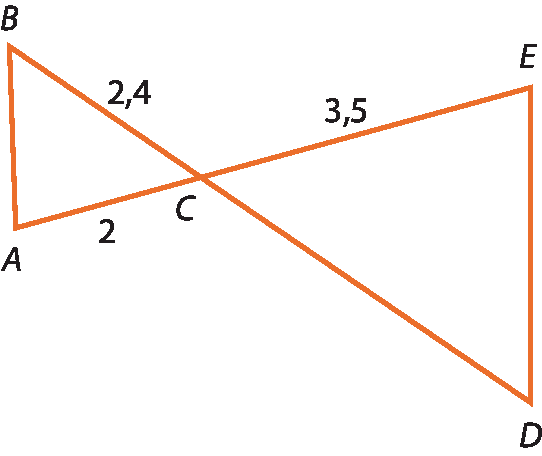
2 Calcule a medida de

\overline{B D}

na figura, sabendo que

\overline{A B} ⫽ \overline{D E} .

Ilustração. Triângulo ABC, unido com triângulo CDE pelo vértice C. lado BC, 2,4; lado AC, 2; lado CE, 3,5 lado AB paralelo lado DE.

3 Calcule a medida da altura

\overline{C H},

relativa ao lado

\overline{A B}

do triângulo ABC, sabendo que

\overline{M N} ⫽ \overline{A B} .

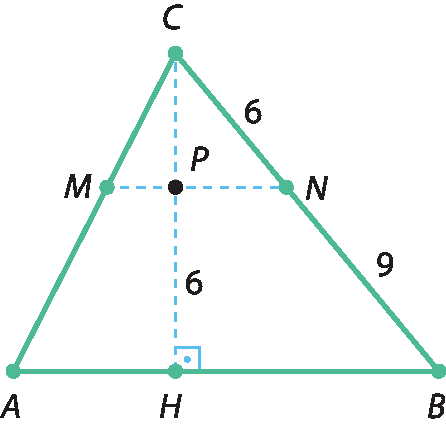
Ilustração. Triângulo ABC. ponto M, pertence ao lado AC; ponto N, pertence ao lado BC; ponto H pertence ao lado AB; ponto P, é o encontro dos segmentos perpendiculares CH e MN; segmento CN, 6; segmento NB, 9; segmento PH, 6.

4 Construa um segmento de 11 centímetros e divida-o em quatro partes iguais sem usar a escala da régua.

5 As medidas dos lados de um △ABC são: A bê = 21 centímetros, á cê = 18 centímetros e BC = 26 centímetros. Calcule as medidas dos segmentos determinados no lado

\overline{B C}

pela bissetriz relativa ao ângulo

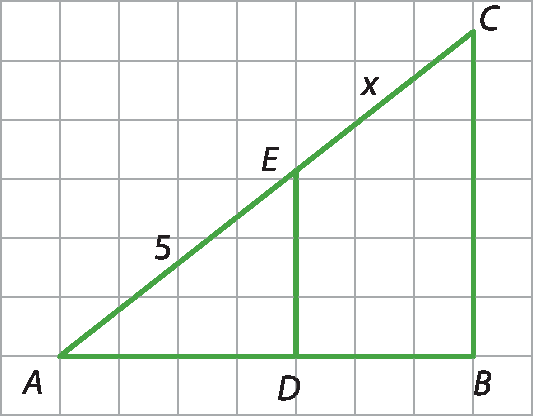
\hat{A} .

6 Na figura,

\overline{D E} ⫽ \overline{B C} .

Considerando o lado do quadradinho do quadriculado como unidade de medida, calcule o valor de x.

Ilustração. Triângulo ABC, na malha quadriculada. lado AB, horizontal, medindo 7 quadradinhos; distância do vértice A até o ponto D, 4 quadradinhos; distância do ponto D até o vértice B, 3 quadradinhos; ponto E pertence ao lado AC; segmentos de reta DE paralelo ao lado BC; segmento de reta AE, 5; segmento de reta EC, x.

7 A bissetriz relativa ao ângulo

\hat{A}

do △á bê cê determina sobre o lado

\overline{B C}

segmentos de 15 centímetros e 20 centímetros. Sabendo que a medida do perímetro do △á bê cê é 84 centímetros, calcule as medidas dos lados dêsse triângulo.

8 (unicâmpi-São Paulo) A figura mostra um segmento

\overline{A D}

dividido em três partes: A bê = 2 centímetros, BC = 3 centímetros e CD = 5 centímetros. O segmento

\overline{A D ʹ}

mede 13 centímetros, e as retas

\overset{\leftrightarrow}{B B ʹ}

\overset{\leftrightarrow}{C C ʹ}

são paralelas a

\overset{\leftrightarrow}{D D ʹ} .

Determine as medidas dos segmentos

\overline{A B ʹ},

\overline{B ʹ C ʹ},

\overline{C ʹ D ʹ} .

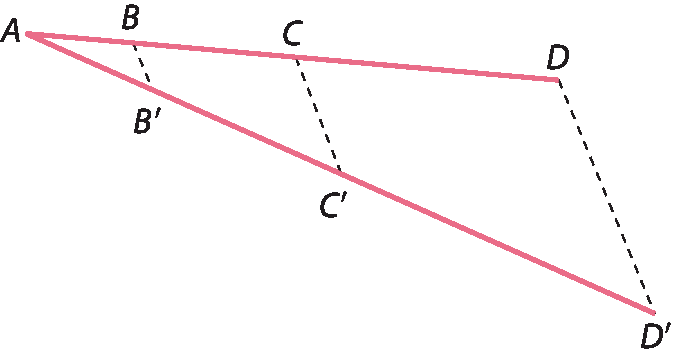
Ilustração. Segmentos de reta AD e AD linha, formam um triângulo ADD linha. Pontos B e C pertencem ao segmento de reta AD. Pontos B linha e C linha pertencem ao segmento de reta AD linha. Os segmentos de reta BB linha, CC linha e DD linha estão destacados com pontilhados e são paralelos.

9 No triângulo,

\overline{D E} ⫽ \overline{B C} .

Calcule o valor de x.

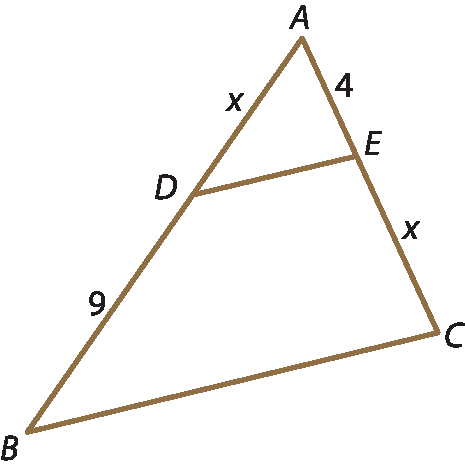
Ilustração: Triângulo ABC. ponto D pertencente ao lado AB; ponto E pertencente ao lado AC; segmento DE, paralelo lado BC; Medidas dos segmentos: AE, 4; EC, x; AD, x; DB, 9.

10 Construa um triângulo á bê cê de modo que A bê = 4,2 centímetros, á cê  = 5,6 centímetros e BC = 7 centímetros. Trace a bissetriz relativa ao ângulo

\hat{A} .

Chame de D o ponto de encontro dessa bissetriz com

\overline{B C} .

Determine as medidas de

\overline{B D}

\overline{D C} .

Em seguida, meça esses segmentos com a régua e compare os valores encontrados com as respectivas medidas obtidas pelo cálculo.

Página 109

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 As medidas dos lados de um quadro retangular estão na razão 7 para 5. Se o perímetro do quadro mede 432 centímetros, quais são as medidas de suas dimensões?

a) 77 centímetros e 108 centímetros

b) 90 centímetros e 126 centímetros

c) 100 centímetros e 140 centímetros

d) 180 centímetros e 252 centímetros

2 Na figura a seguir, as retas horizontais são paralelas e BP = PD. Qual é a medida de

\overline{A C} ?

Ilustração. 3 retas paralelas horizontais e duas retas transversais . A segunda reta paralela horizontal e as duas retas transversais se encontram no ponto P; De cima para baixo: A reta transversal inclinada da esquerda superior para direita inferior cruza com a primeira reta paralela no ponto A e com a terceira reta paralela no ponto C; A reta transversal inclinada da esquerda inferior para direita superior cruza a primeira reta paralela no ponto B e a terceira reta paralela no ponto C. Segmento A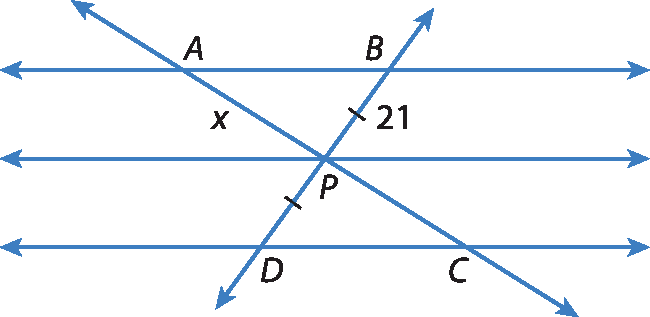P, x; Segmento BP 21; Segmentos BP=PD.

a) 21

b) 42

c) x

d) 2x

3 Se as retas r, s e t da figura a seguir são paralelas, qual é o valor de x?

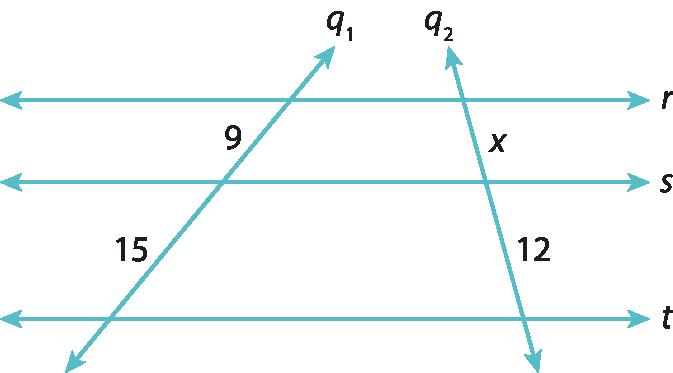
Ilustração. Retas paralelas horizontais, de cima para baixo, r, s, t e duas retas transversais, q1 e q2, inclinadas para dentro. Segmento de reta de medida 9, marcado na reta transversal da esquerda, q1, entre retas r e s. Segmento de reta de medida 15, marcado na reta transversal da esquerda, q1, entre retas s e t. Segmento de reta de medida x, marcado na reta transversal da direita, q2, entre retas r e s. Segmento de reta de medida 12, marcado na reta transversal da direita, q2, entre retas s e t.

a) 6,0

b) 7,2

c) 8,0

d) 12,0

4 No triângulo da figura a seguir, foi traçado um segmento paralelo à base, que mede 4 centímetros de comprimento. Qual é a medida do perímetro do triângulo menor gerado?

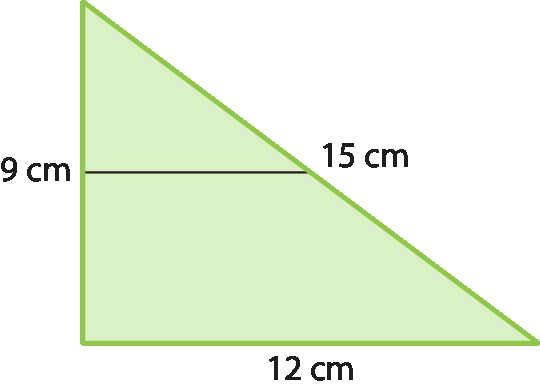
lustração. Triângulo retângulo. Cateto, na posição vertical, mede 9 centímetros. Cateto, na posição horizontal, mede 12 centímetros. Hipotenusa mede 15 centímetros. Segmento paralelo ao cateto na posição horizontal une cateto na posição vertical à hipotenusa.

a) 3 centímetros

b) 5 centímetros

c) 8 centímetros

d) 12 centímetros

5 Na figura a seguir, as retas r, s e t são paralelas? Qual é a medida da distância entre as retas r e t?

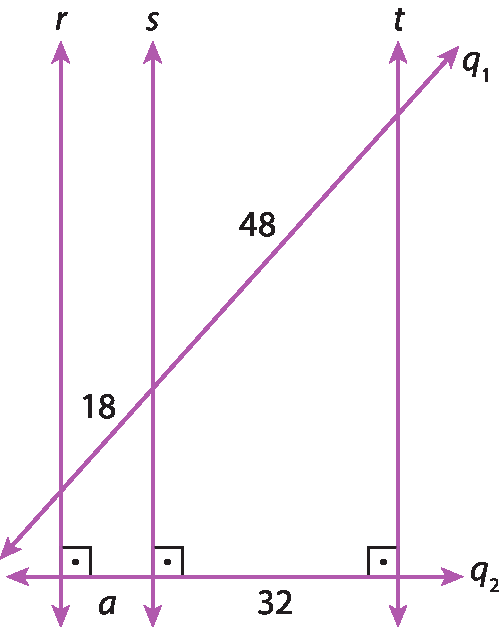
Ilustração. Retas paralelas verticais, da esquerda para direita, r, s, t e duas retas transversais, uma horizontal perpendicular as retas paralelas, q2, e outra inclinada da esquerda inferior para direita superior, q1. Segmento de reta de medida 18, marcado na reta q1, entre retas r e s. Segmento de reta de medida 48, marcado na reta q1, entre retas s e t. Segmento de reta de medida a, marcado na reta q2,entre retas r e s. Segmento de reta de medida 32, marcado na reta q2 entre retas s e t.

a) Sim; 12.

b) Sim; 44.

c) Não; 12.

d) Sim; 66.

6 Uma pessoa avista uma árvore e um poste alinhados nas condições da imagem.

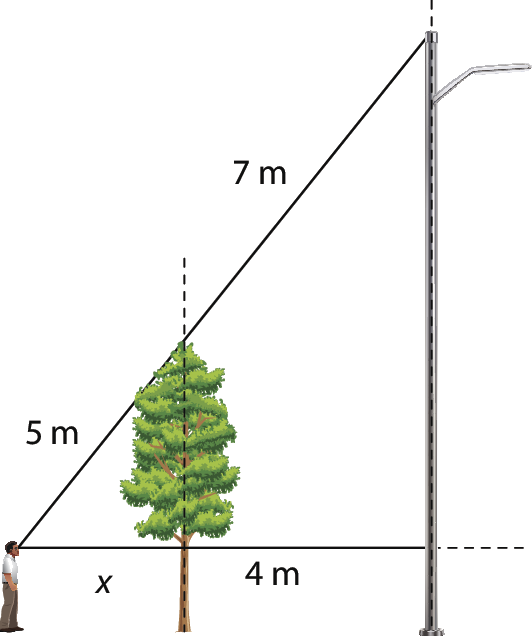
Ilustração. Pessoa, da altura da sua visão parte uma linha horizontal e uma linha inclinada para cima . A frente, em linha reta horizontal, uma árvore e mais a frente um poste. A linha inclinada tangência a ponta superior da árvore e do poste. Uma linha pontinhada vertical passa pela árvore e outra pelo poste; As linhas verticais são paralelas. Distância x, marcado na linha horizontal , entre a pessoa e a árvore,; Distância 4 metros, marcado na linha horizontal, entre a árvore e o poste; Distância 5 metros , marcado na linha inclinada , entre a pessoa e a árvore; Distância 7 metros, marcado na linha inclinada, entre a árvore e o poste.

Qual é a medida aproximada da distância entre a pessoa e o poste?

a) 3 métros

b) 5 métros

c) 7 métros

d) 8 métros

7 Na figura a seguir, x e y são, respectivamente, iguais a:

a) 7 e 42.

b) 10 e 30.

c) 16 e 28.

d) 22 e 22.

Ilustração. Triângulo de base medindo 42 e lados medindo x e 32. A bissetriz do ângulo oposto à base divide a base em dois segmentos, medindo 14 e y.

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.

a) Em que situação quatro segmentos de medidas A bê, CD, ê éfe e GH são proporcionais?

b) Quais são as hipóteses, ou seja, que situações geométricas devem ocorrer para que a aplicação do teorema de Tales seja válida?

c) Como você explicaria para um colega como aplicar o teorema de Tales?

d) Quais são as consequências do teorema de Tales?