
CAPÍTULO 5 Semelhança


Os tapetes são uma herança cultural para muitos povos do norte da África e do Oriente Médio. Apesar de hoje terem uso mais decorativo, para os berberes, povos seminômades do norte da África, os tapetes originalmente serviam de proteção contra o frio, cobrindo não só o chão das casas, mas também o corpo nas noites mais frias.
Compostos de padrões geométricos variados, esses tapetes, tradicionalmente tecidos à mão por mulheres, comunicam a identidade cultural desses povos por meio de combinações de diferentes figuras geométricas em padrões que contam histórias com temas variados, como fertilidade, riqueza, liberdade e natureza.
Observe, leia e responda no caderno.
a) Que figuras geométricas você identifica nos tapetes da fotografia? Você consegue identificar transformações geométricas de algumas dessas figuras? Que transformações?
b) Utilizando transformações geométricas de alguns polígonos, represente um padrão geométrico inspirado nos tapetes da fotografia.
c) Identifique alguns pares de polígonos congruentes no seu padrão geométrico. Para isso, verifique se todos os seus lados correspondentes são congruentes e se seus ângulos correspondentes são congruentes.
d) Pesquise a importância de preservar e respeitar as tradições culturais de um povo.
1. Figuras semelhantes
Quando uma imagem é formada em uma tela de televisão, de cinema, de celular etcétera, o tamanho dessa imagem geralmente é diferente do tamanho da imagem original, no entanto, a fórma é mantida.
Assim, dizemos que a imagem que aparece na tela é semelhante à original.
Além de cópias em tamanho original, as fotocopiadoras podem ampliar ou reduzir determinada imagem; nesse caso, também se mantém a fórma do original.
Para obter uma ampliação de, por exemplo, 50%, devemos programar essa máquina para fazer uma cópia de 150%, pois a ampliação deverá ser igual ao original (100%) aumentado de 50%. Se quisermos uma redução de 25%, devemos programar a máquina para 75%, que corresponde ao original (100%) diminuído de 25%.
Fotografia original

Fotografia ampliada (150% em relação à original)

Fotografia reduzida (75% em relação à original)


Figuras semelhantes são aquelas que têm a mesma fórma, mas não necessariamente o mesmo tamanho.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Em uma fotografia, a medida da altura de João corresponde a 10 centímetros. Qual deve ser a porcentagem que devemos programar em uma fotocopiadora para que a medida da altura de João em uma cópia ampliada seja de 12 centímetros?
2. Semelhança de polígonos
O uso de papel quadriculado pode auxiliar o trabalho de ampliação ou de redução de figuras. Acompanhe, por exemplo, como foi obtida a ampliação em 100% do polígono a bê cê dê, que resultou no polígono A'B'C'D'.
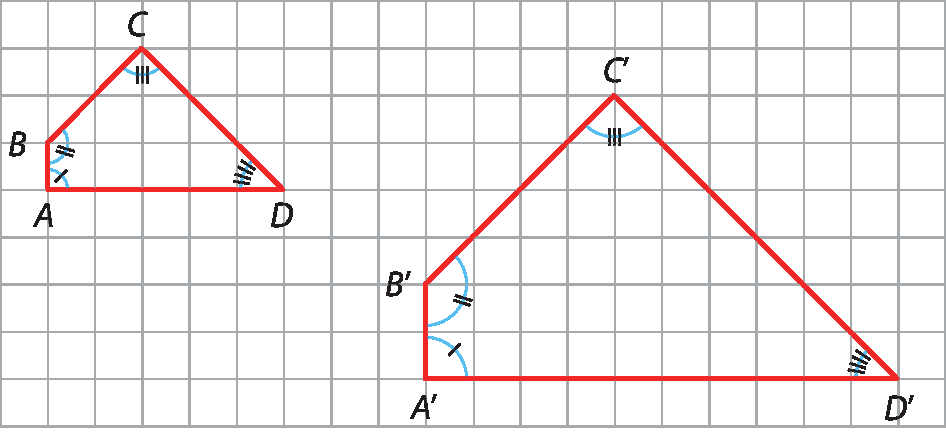
Os pares de ângulos
Ângulo A e ângulo A'.,
Ângulo B e ângulo B'.,
Ângulo C e ângulo C'.,
Ângulo D e ângulo D'.são chamados de ângulos correspondentes. Observe que eles são congruentes, ou seja:
Os pares de lados
Segmento AB e segmento A'B'.,
Segmento BC e segmento B'C'.,
Segmento CD e segmento C'D'.,
Segmento DA e segmento D'A'.são chamados de lados correspondentes. Observe que eles têm medidas de comprimento proporcionais, pois:

Assim, concluímos que o polígono A'B'C'D' é semelhante ao polígono a bê cê dê e indicamos por:
a bê cê dê ∼ á linha bê linha cê linha dê linha
Como qualquer lado do polígono ampliado (A'B'C'D' ) tem por medida o dobro da medida do lado correspondente no polígono original (a bê cê dê), dizemos que a razão de semelhança entre o polígono ampliado e o polígono original é 2. Isso significa que qualquer lado do polígono A'B'C'D' tem por medida o dobro da medida do lado correspondente no polígono a bê cê dê.
Dois polígonos são semelhantes quando os lados correspondentes têm medidas de comprimento proporcionais e os ângulos correspondentes são congruentes.
Agora, vamos reduzir o polígono á bê cê dê é em 50%, obtendo o polígono A'B'C'D'E'. Acompanhe.
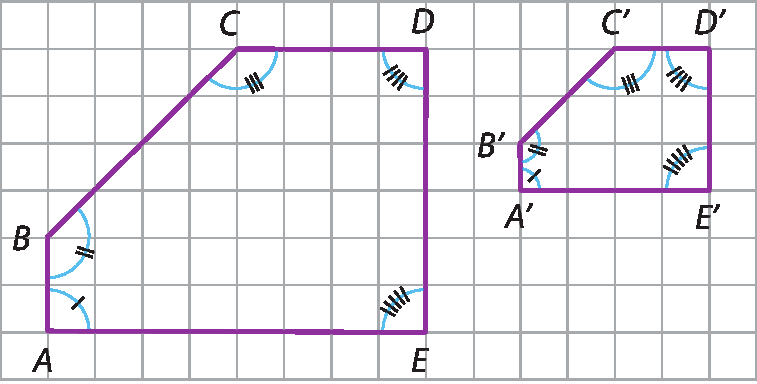
A medida de qualquer lado do polígono á linha bê linha cê linha dê linha é linha tem metade da medida do lado correspondente no polígono á bê cê dê é. Nesse caso, dizemos que a razão de semelhança entre o polígono reduzido (á linha bê linha cê linha dê linha é linha ) e o polígono original (á bê cê dê é) é
Fração. 1 sobre 2.. Então:
Observe agora o par de polígonos.
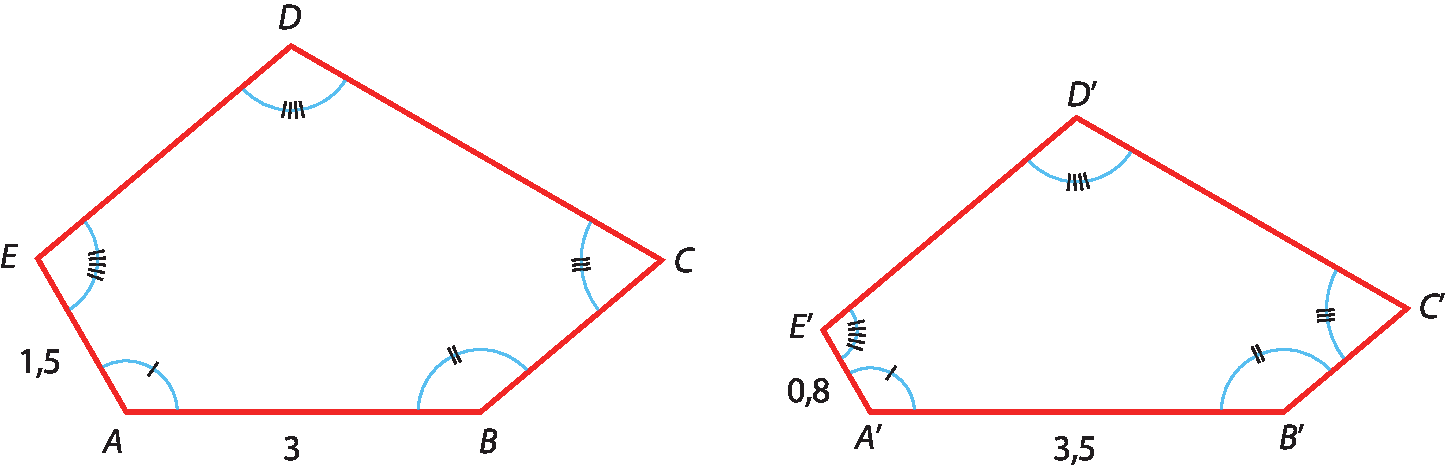
Esses polígonos têm os ângulos correspondentes congruentes, mas seus lados correspondentes não têm medidas de comprimento proporcionais. Logo, eles não são semelhantes.
Observe estes outros polígonos.
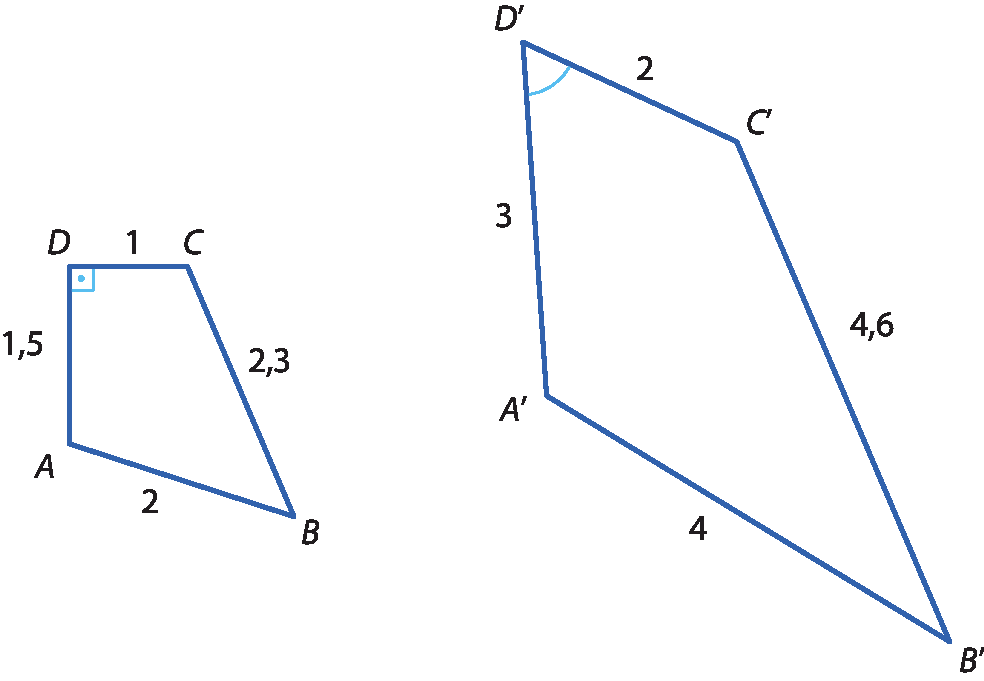
Esses polígonos têm os lados correspondentes com medidas de comprimento proporcionais, mas seus ângulos correspondentes não são congruentes. Logo, eles não são semelhantes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
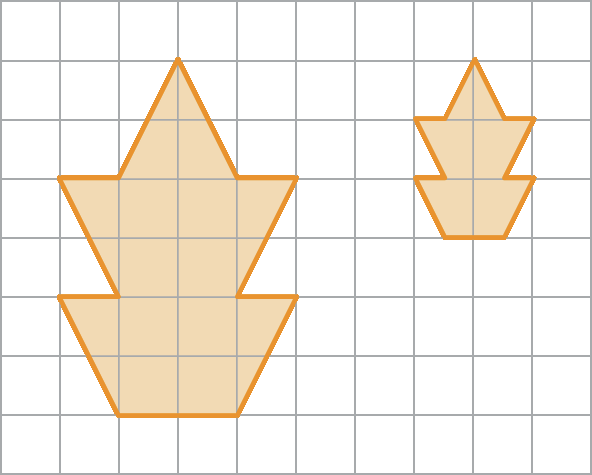
1 Qual é a razão de semelhança entre a figura reduzida (à direita) e a figura original (à esquerda) na ilustração a seguir?
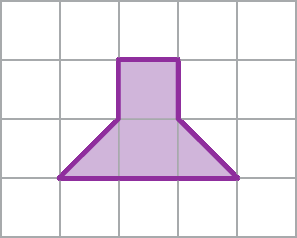
2 Em um papel quadriculado, amplie esta figura na razão
Fração 3 sobre 1..
3 Os lados correspondentes de dois polígonos têm medidas de comprimento proporcionais. Podemos dizer que eles são semelhantes? Por quê?
4 Com uma régua, meça a base e a altura dos retângulos a seguir e, com o auxílio de um transferidor, meça os ângulos de ambos.

a) Qual é a razão entre a medida da base do retângulo vermelho e a medida da base do retângulo verde?
b) Qual é a razão entre a medida da altura do retângulo vermelho e a medida da altura do retângulo verde?
c) Esses retângulos são semelhantes? Por quê?
Versão adaptada acessível
4. Construa um retângulo ABCD de base medindo 4 centímetros e altura medindo 2 centímetros e um retângulo EFGH de base medindo 6 centímetros e altura medindo 3 centímetros. Depois, responda:
a) Qual é a razão entre a medida da base do retângulo ABCD e a medida da base do retângulo EFGH?
b) Qual é a razão entre a medida da altura do retângulo ABCD e a medida da altura do retângulo EFGH?
c) Esses retângulos são semelhantes? Por quê?
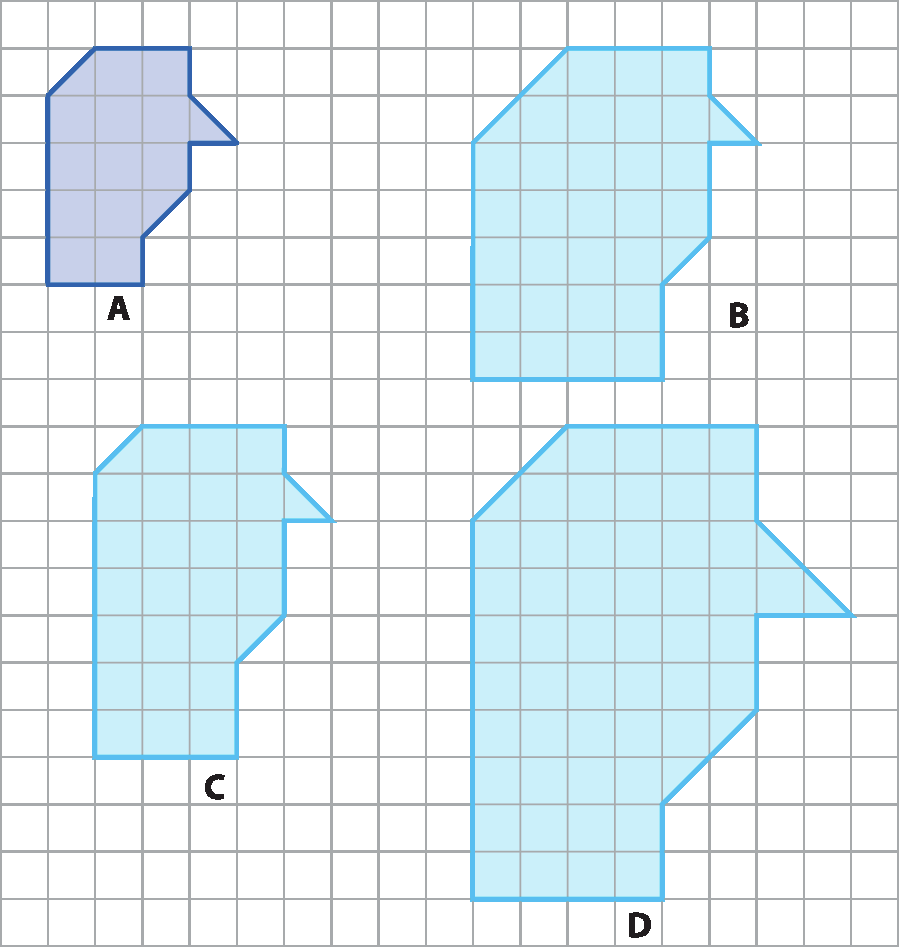
5 Indique a figura semelhante à figura A.
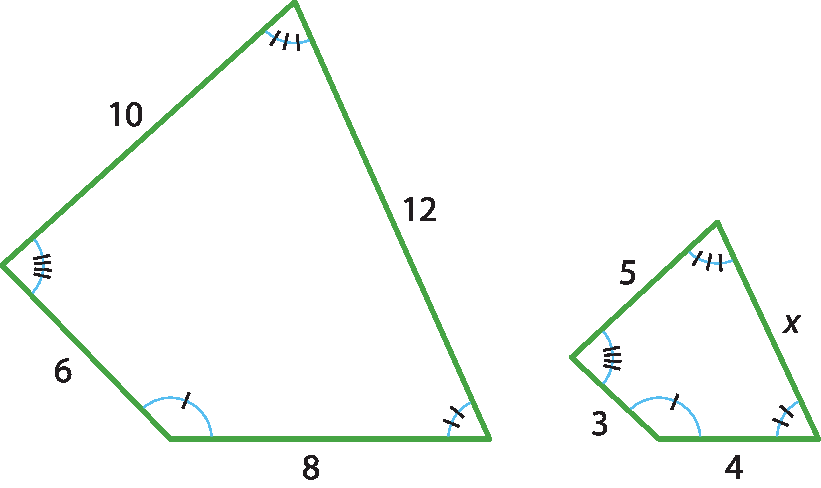
6 Sabendo que os polígonos a seguir são semelhantes, calcule x.
7 Considere os triângulos semelhantes á bê cê e á linha bê linha cê linha.
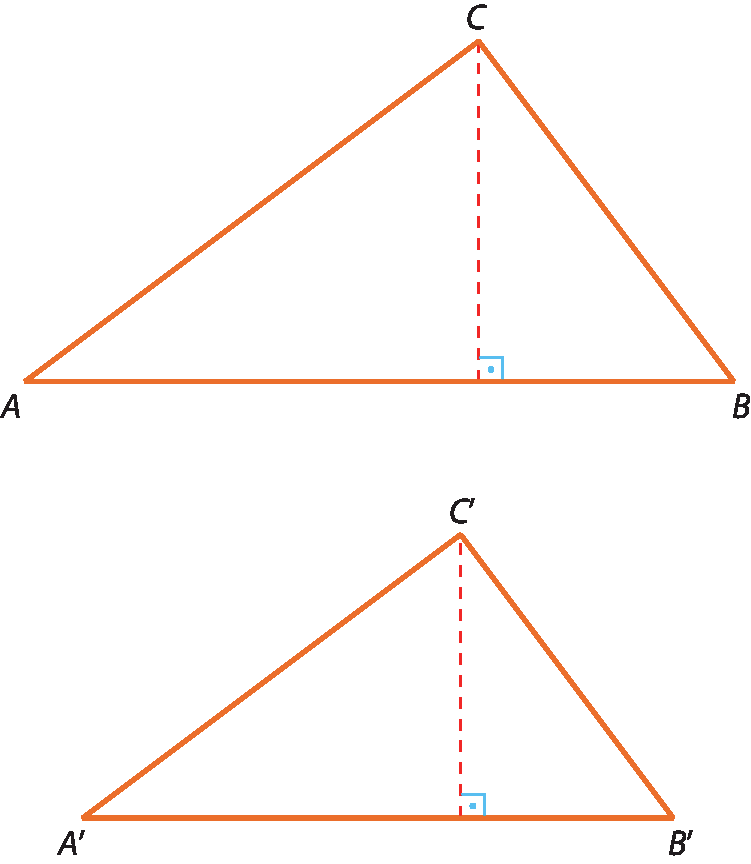
Com uma régua, determine a medida do comprimento dos lados e a medida das alturas relativas a
Segmento AB e segmento A'B'.Considerando as razões, sempre do triângulo á bê cê para o triângulo á linha bê linha cê linha, responda às perguntas.
a) Qual é a razão entre as medidas de dois lados correspondentes?
b) Qual é a razão entre as medidas de duas alturas relativas a lados correspondentes?
c) Qual é a razão entre as medidas dos perímetros?
d) Qual é a razão entre as medidas das áreas?
Versão adaptada acessível
7. Considere um triângulo ABC de base medindo 4 centímetros e altura medindo 2 centímetros e um triângulo DEF de base medindo 8 centímetros e altura medindo 4 centímetros. Depois, responda:
a) Qual é a razão entre as medidas de dois lados correspondentes?
b) Qual é a razão entre as medidas de duas alturas relativas a lados correspondentes?
c) Qual é a razão entre as medidas dos perímetros?
d) Qual é a razão entre as medidas das áreas?
8 Marcos desenhou um triângulo retângulo em um papel quadriculado. O papel tem quadradinhos medindo 1 centímetro por 1 centímetro de lado, e Marcos usou 12 vezes a medida do lado para a medida da base e 8 vezes a medida do lado para a medida da altura.
Pedro também desenhou um triângulo retângulo com medida da base igual a 12 vezes a medida do lado do quadradinho e medida da altura igual a 8 vezes a medida do lado do quadradinho, mas em um papel quadriculado com quadradinhos medindo 0,5 centímetro por 0,5 centímetro.
Considere que os triângulos desenhados por Marcos e Pedro são semelhantes.
a) Qual é a razão de semelhança entre as medidas dos lados do triângulo de Marcos e as medidas dos lados do triângulo de Pedro?
b) Qual é a razão de semelhança entre a medida do perímetro do triângulo de Marcos e a medida do perímetro do triângulo de Pedro?
c) Qual é a razão de semelhança entre a medida da área do triângulo de Marcos e a medida da área do triângulo de Pedro?
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Um grupo de amigos fez uma viagem para Recife (Pernambuco).
Lá, tiraram muitas fotografias, que foram impressas no tamanho 10 centímetros por 15 centímetros.
A fotografia do monumento Tortura Nunca Mais, construído em memória das pessoas torturadas e desaparecidas durante o período da ditadura civil-militar (1964 a 1985), ficou excelente. Resolveram, então, fazer uma cópia ampliada para cada um, no tamanho 20 centímetros por 30 centímetros.

Na fotografia original, o monumento mede 7,2 centímetros de largura.
Qual é a medida, em centímetro, da largura do monumento na cópia ampliada?
PARA SABER MAIS
Construindo figuras semelhantes por homotetia
A homotetia é um exemplo de transformação geométrica que preserva a fórma da figura original, mas não necessariamente seu tamanho, que pode ser ampliado ou reduzido. dêsse modo, a figura original e a figura obtida são semelhantes. Essas figuras são chamadas de figuras homotéticas.
Acompanhe como ampliar o pentágono á bê cê dê é, na razão 1,5, por homotetia.
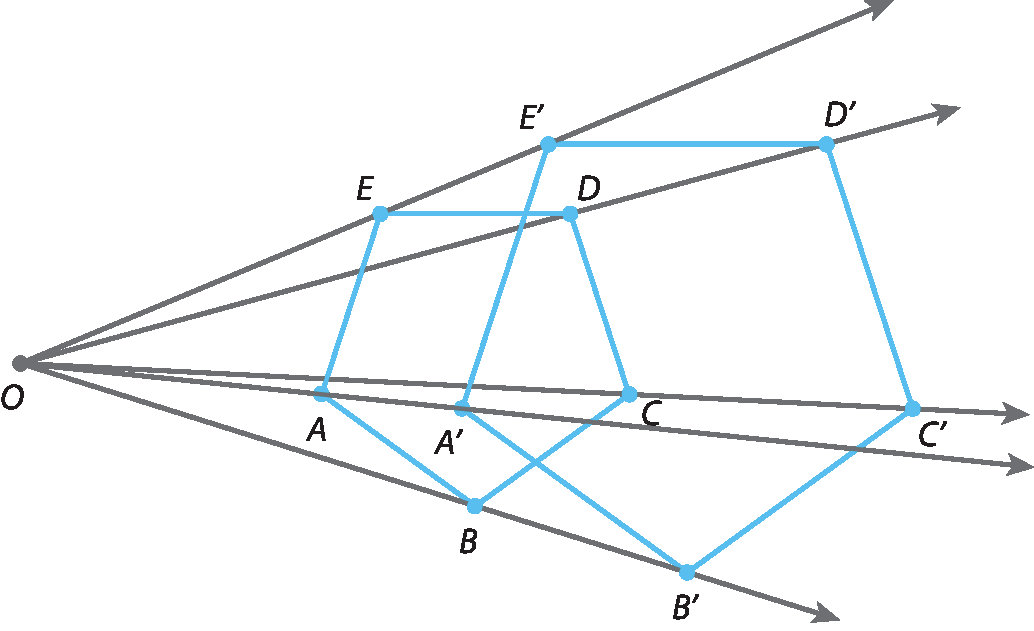
• Fixamos um ponto óh (centro de homotetia).
• Traçamos, a partir do ponto óh, semirretas que passam pelos vértices do pentágono á bê cê dê é.
• Fazendo ó, á linha = 1,5 ⋅ ó á, ó, bê linha = 1,5 ⋅ ó bê, e assim por diante, determinamos os vértices do pentágono ampliado á linha bê linha cê linha dê linha é linha.
O pentágono á linha bê linha cê linha dê linha é linha é semelhante ao pentágono á bê cê dê é na razão de semelhança 1,5.
Observe outros exemplos de figuras homotéticas.
a) A figura original foi invertida por homotetia de centro óh e razão ‒1.
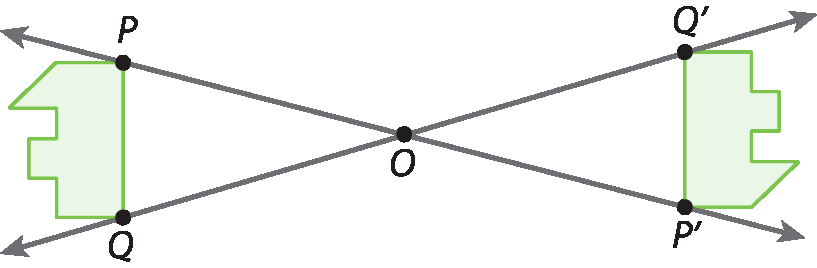
Nesse caso, as figuras são congruentes, ou seja, têm ângulos correspondentes de mesmas medidas e lados correspondentes de mesmas medidas.
Note que figuras congruentes também são semelhantes.
b) A figura original foi reduzida por homotetia de centro óh e razão
Fração. 1 sobre 2.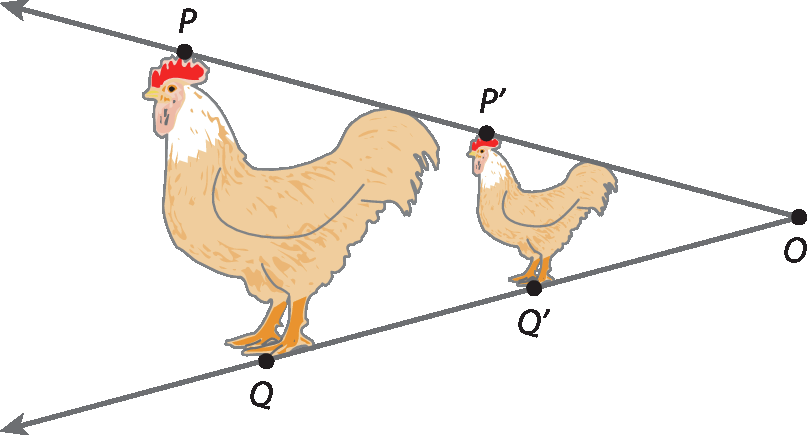
c) Por meio da homotetia, podemos formar uma sequência de figuras homotéticas. A figura conhecida como floco de neve de córh é criada com um padrão de triângulos equiláteros que pode ser obtido pela combinação das transformações geométricas de translação, rotação e homotetia.
Note que os triângulos que compõem o floco de neve de córh são semelhantes, ou seja, têm todos a mesma fórma, mas não necessariamente o mesmo tamanho.

Essa figura, formada por repetições de um padrão, é um exemplo de fractal.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Desenhe um triângulo retângulo isósceles. Fixe um ponto óh e, por homotetia de centro óh, construa o triângulo homotético ao que você desenhou aplicando a razão:
a) 2
b)
Fração menos 1 sobre 2.2 Utilizando algumas das figuras geométricas presentes na fotografia da abertura deste capítulo, escolha um tema e crie um desenho aplicando os conceitos de semelhança e homotetia.
3. Semelhança de triângulos
Dizemos que, para dois triângulos serem semelhantes, deve ser possível estabelecer uma correspondência entre as medidas dos lados por proporcionalidade e entre os ângulos, por congruência.
Considere os triângulos á bê cê e dê ê éfe a seguir.
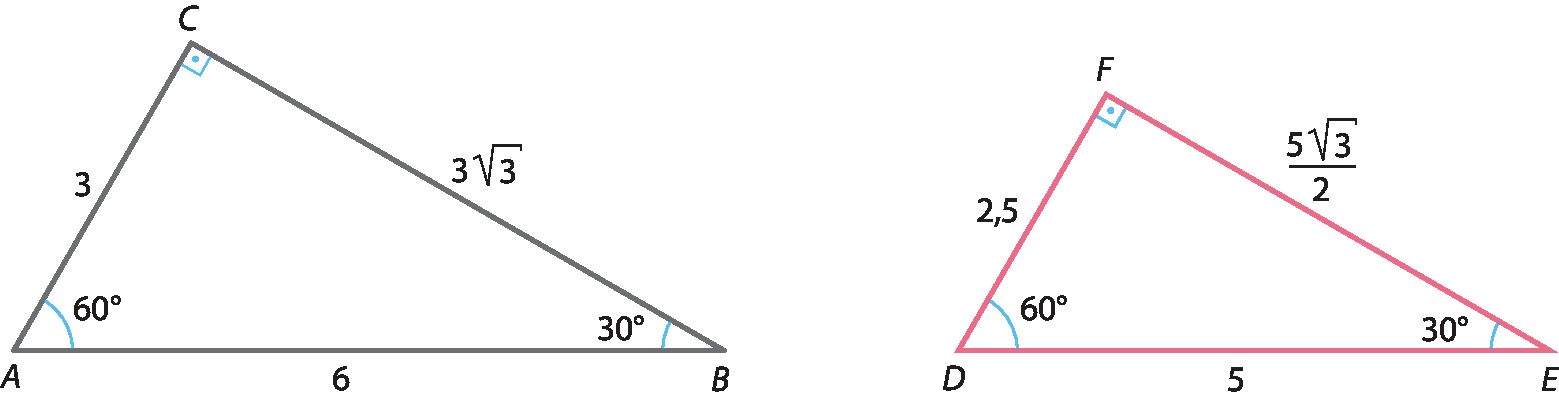
Esses triângulos são semelhantes, pois:
• os ângulos correspondentes são congruentes;
• os lados correspondentes têm medidas de comprimento proporcionais.
Observações
▶ Para saber quais lados se correspondem, observamos os ângulos opostos a eles. Assim:
• o lado
Segmento AB.corresponde ao lado
Segmento DE.pois são opostos a ângulos congruentes (
Ângulo C é congruente ao ângulo F.);
• o lado
Segmento AC.corresponde ao lado
Segmento DF.pois são opostos a ângulos congruentes (
Ângulo B é congruente ao ângulo E.);
• o lado
Segmento BC.corresponde ao lado
Segmento EF.pois são opostos a ângulos congruentes (
Ângulo A é congruente ao ângulo D.).
▶ Se dois triângulos são semelhantes e a razão de semelhança é k, então:
• a razão entre duas medidas de altura correspondentes é k ;
• a razão entre duas medidas de comprimento de medianas correspondentes é k ;
• a razão entre duas medidas de comprimento de bissetrizes correspondentes é k ;
• a razão entre as medidas de seus perímetros é k ;
• a razão entre as medidas de suas áreas é k².
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
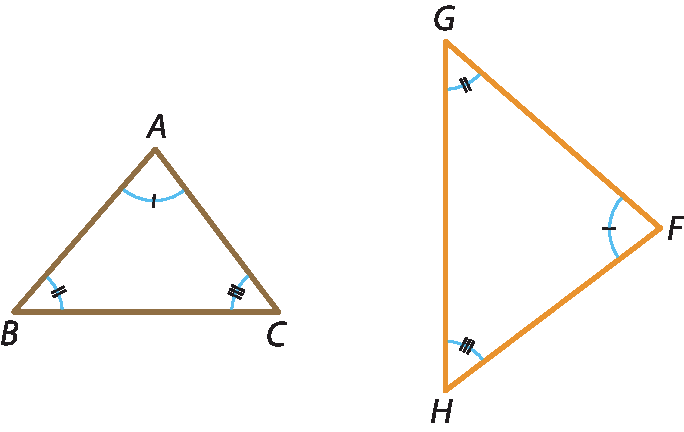
9 Indique quais são os lados correspondentes nestes triângulos semelhantes.
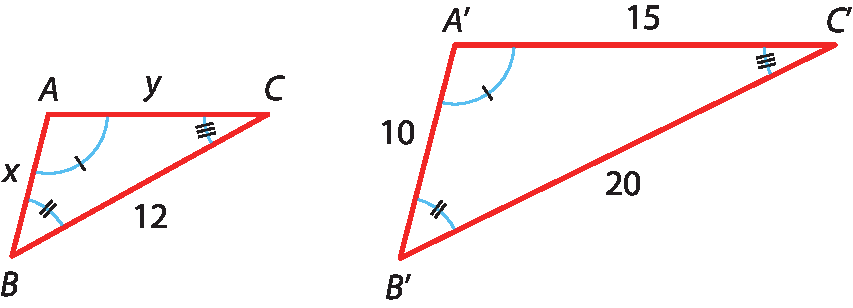
10 Considere o seguinte par de triângulos semelhantes e determine os valores de x e de y.
11 Sabendo que △á bê cê ∼ △ême êne pê, calcule a medida da mediana
Segmento MS.do △ême êne pê.
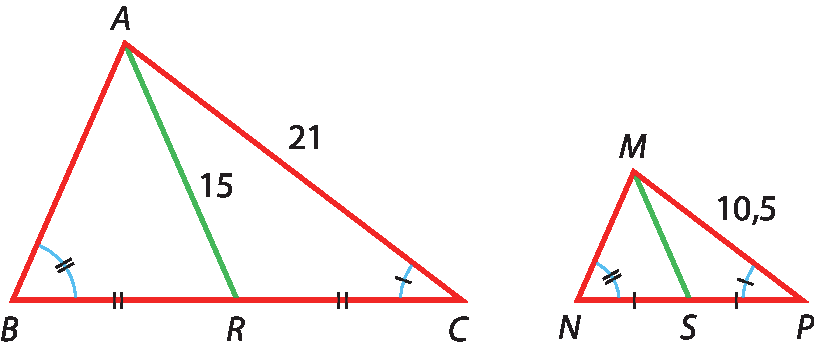
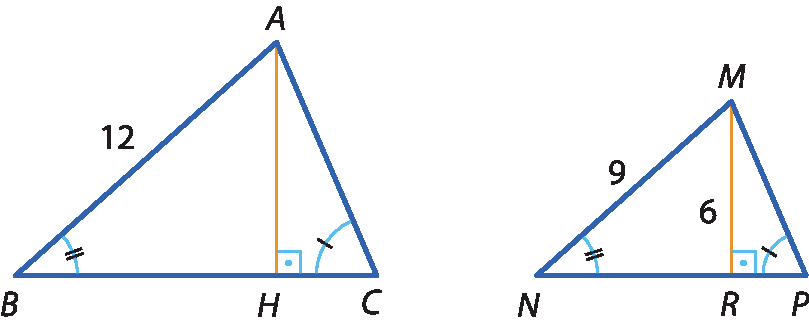
12 Sabendo que △á bê cê ∼ △ême êne pê, calcule a medida da altura
Segmento AH.do △á bê cê.
13 Construa com régua e compasso um triângulo escaleno qualquer. Depois, construa um triângulo semelhante a esse na razão de semelhança 3 e outro na razão de semelhança
Fração. Três quartos..
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)
14

Os lados de um triângulo medem 12,0 centímetros, 18,0 centímetros e 20,4 centímetros. O maior lado de um triângulo semelhante ao primeiro mede 15,3 centímetros.
a) Qual é a medida do perímetro do segundo triângulo?
b) Com o auxílio de uma calculadora, determine a medida aproximada da área do segundo triângulo, sabendo que a medida da área do primeiro é de aproximadamente 107,2 centímetros quadrados.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Na figura,
Segmento BD é paralelo ao segmento CE.e
Ângulo AEB é congruente ao ângulo AFC.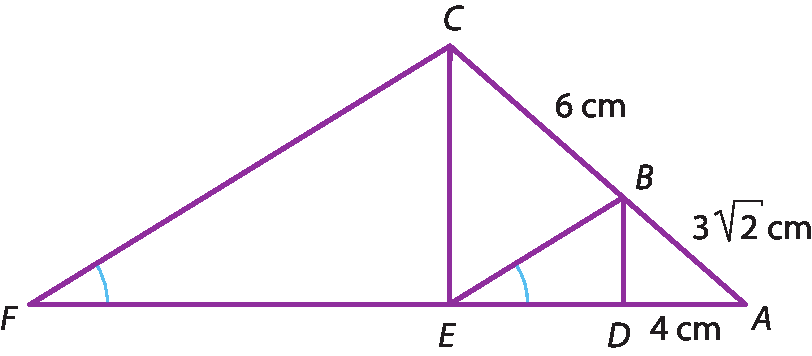
Determine a medida, em centímetro, de
Segmento AF.
Teorema fundamental da semelhança
Toda reta paralela a um lado de um triângulo que cruza os outros lados em dois pontos distintos determina um triângulo semelhante ao primeiro.
Observe a figura a seguir, em que
Segmento DE.⫽
Segmento BC.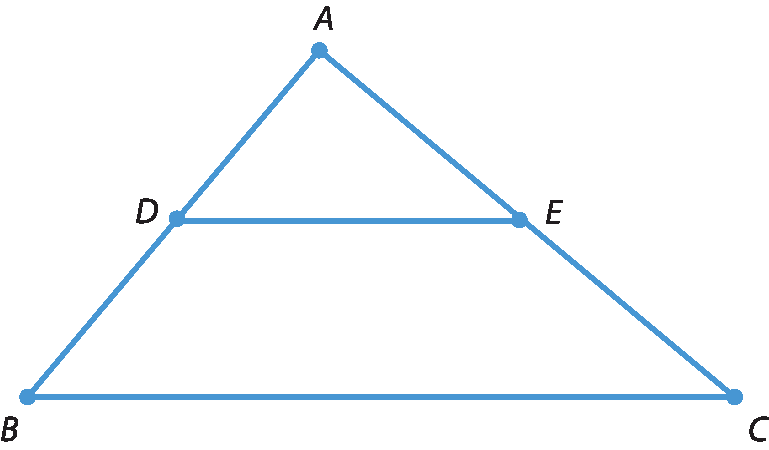
Vamos provar que os triângulos á dê é e á bê cê são semelhantes.
Para a demonstração formal de um teorema, indicaremos, como em outras vezes, a hipótese (proposição aceita como verdadeira) e a tese (proposição cuja verdade se quer provar).
Hipótese:
Segmento DE paralelo ao segmento BC.Tese: △ADE ∼ △ABC
• Demonstração Construção auxiliar: traçamos, por ê,
Segmento EF paralelo ao segmento AB..
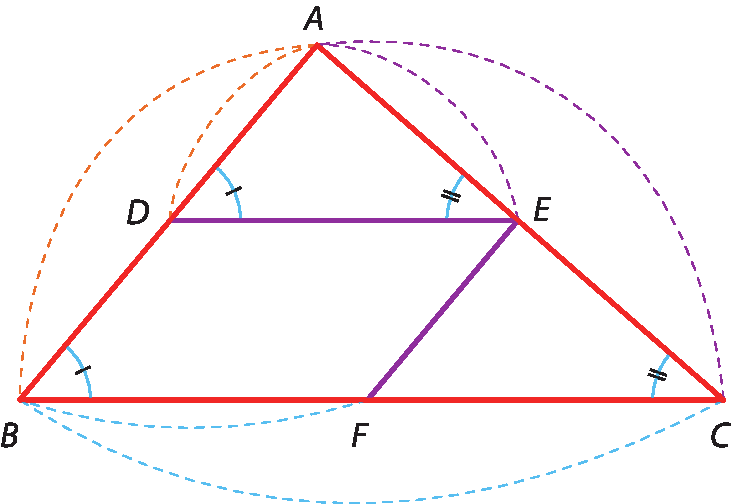
Analise atentamente os passos a seguir para acompanhar a demonstração.

(por hipótese)

(pelo teorema de Tales)

(ângulo comum)

(ângulos correspondentes em retas paralelas)

(ângulos correspondentes em retas paralelas)

(pelo teorema de Tales)

(lados opostos de um paralelogramo)

(de

e

)

(de

e

)

△á dê é ∼ △á bê cê (de

,

,

e

) Note que os lados correspondentes dos dois triângulos têm medidas de comprimento proporcionais e os ângulos correspondentes são congruentes. Portanto, á dê é e á bê cê são triângulos semelhantes, como queríamos demonstrar.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
15 Os prolongamentos dos lados não paralelos do trapézio a bê cê dê encontram-se em um ponto ê. Determine:
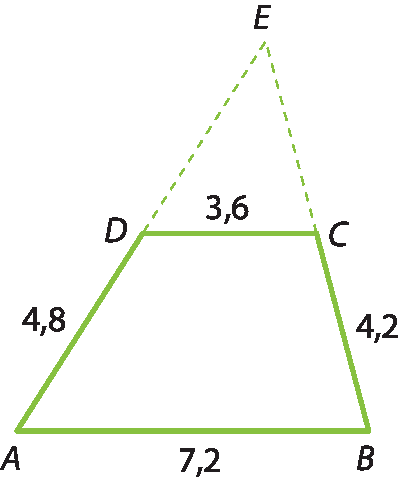
a) a medida de
Segmento AE.
b) a medida de
Segmento CE.
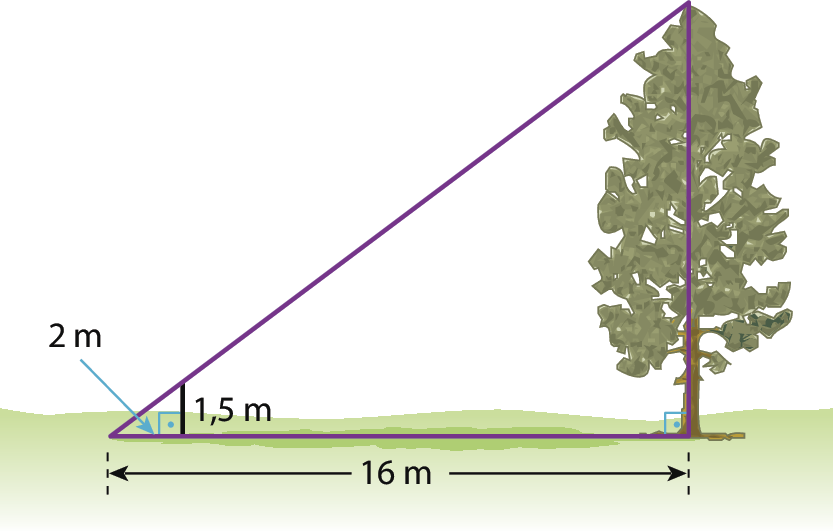
16 Para medir a altura de um pinheiro, Elza pegou um bastão medindo 1,5 métro de altura e posicionou-o verticalmente não muito longe do pinheiro. Ela verificou que o bastão projetava uma sombra medindo 2 métros de comprimento. Então, no mesmo instante, ela mediu o comprimento da sombra projetada pelo pinheiro, igual a 16 métros. Considerando as medidas obtidas por Elza, qual é a medida da altura dessa árvore?
17 Determine o valor de x e de y em cada caso.
a)
Segmento MN é paralelo ao segmento BC.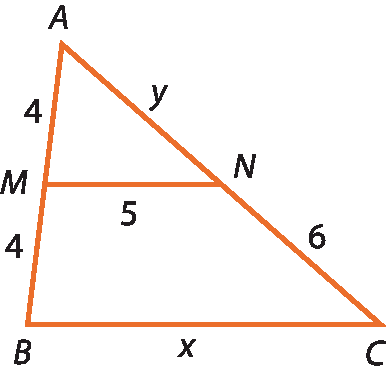
b)
Segmento MN é paralelo ao segmento BC.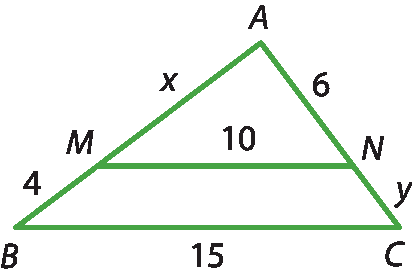
c)
Segmento EB é paralelo ao segmento DC.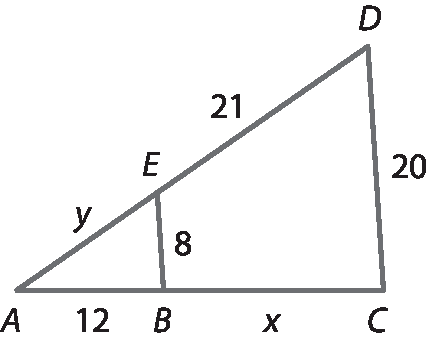
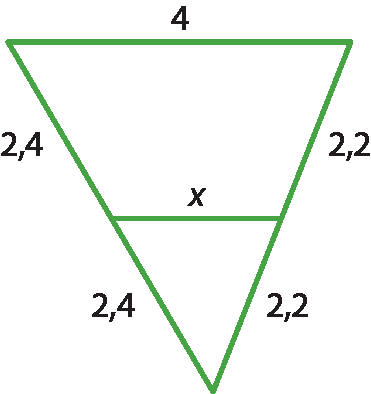
18 Calcule x nos seguintes triângulos:
a)
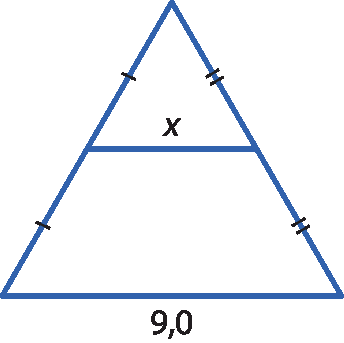
b)
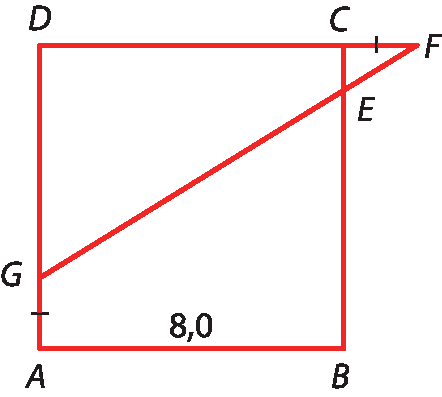
19 Na figura, a bê cê dê é um quadrado e cê éfe = á gê = 2,0.
Calcule cê é.
20 (unirrio-Rio de Janeiro) Numa cidade do interior, à noite, surgiu um objeto voador não identificado, em fórma de disco, que estacionou a 50 métros do solo, aproximadamente. Um helicóptero do Exército, situado a aproximadamente 30 métros acima do objeto, iluminou-o com um holofote, conforme mostra a figura a seguir.
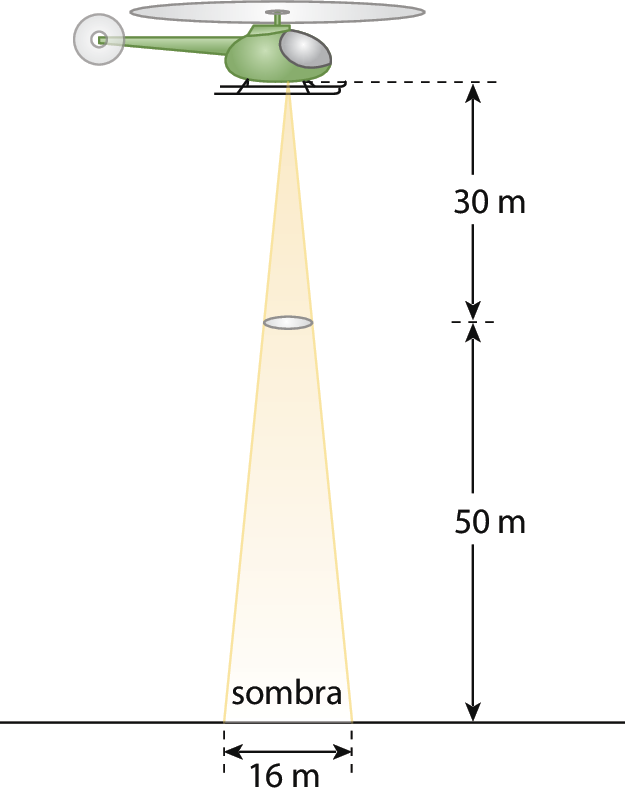
Sendo assim, pode-se afirmar que o raio do disco voador mede, em métros, aproximadamente:
a) 3,0.
b) 3,5.
c) 4,0.
d) 4,5.
e) 5,0.
21

Hora de criar – Em dupla com um colega, criem um fluxograma para determinar se dois triângulos são semelhantes. Em seguida, desenhem em seus cadernos dois triângulos semelhantes cada um. Troquem de caderno e, seguindo o passo a passo do fluxograma criado por vocês, verifiquem se os triângulos desenhados pelo colega são, de fato, semelhantes. Destroquem de caderno para a correção.
Casos de semelhança de triângulos

Caso ângulo-ângulo (á á)
Se dois triângulos têm dois ângulos correspondentes respectivamente congruentes, esses triângulos são semelhantes.
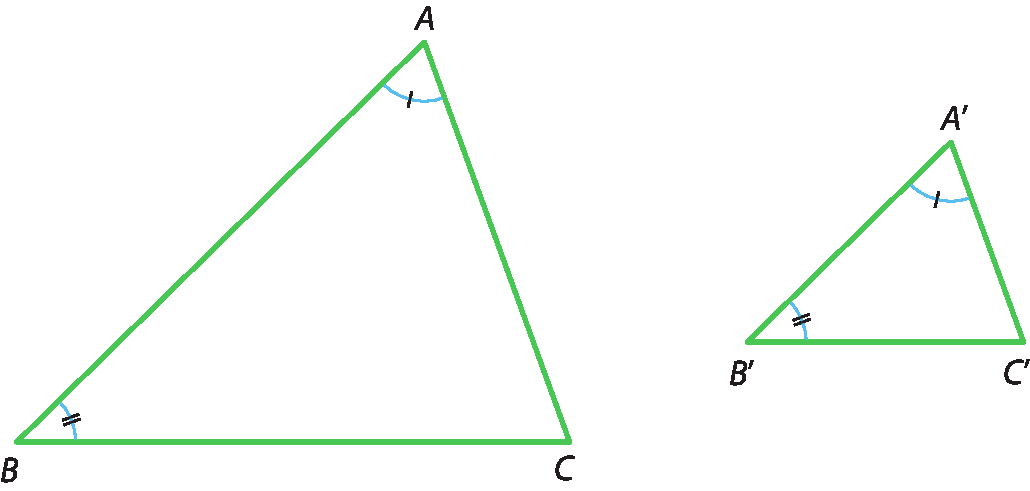
Hipótese:
Ângulo A é congruente ao ângulo A' e ângulo B é congruente ao ângulo B'.Tese: △ABC ∼ △A'B'C'
• Demonstração Considerando que AB > A'B', vamos marcar sobre
Segmento AB.um ponto D, tal que
Segmento AD congruente ao segmento A'B'.Por D, traçamos
Segmento DE paralelo ao segmento BC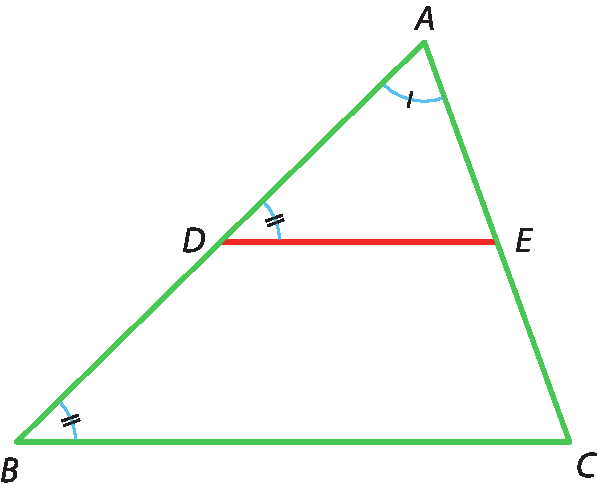
Assim, temos:

(ângulos correspondentes em retas paralelas)

(por hipótese)

(por construção)

(pois
Ângulo B congruente ao ângulo B'.e
Ângulo D é congruente ao ângulo B.) Logo, de

,

e

sabemos que os triângulos á dê é e á linha bê linha cê linha são congruentes pelo caso ângulo-lado-ângulo (á éle á ), já que esses dois triângulos têm dois ângulos e o lado adjacente a esses ângulos respectivamente congruentes. Pelo teorema fundamental da semelhança, △á bê cê ∼ △á dê é. Se △á bê cê ∼ △á dê é e △á dê é
congruente△á'bit'centésimo', então △á bê cê ∼ △á'bit'centésimo', como queríamos provar.

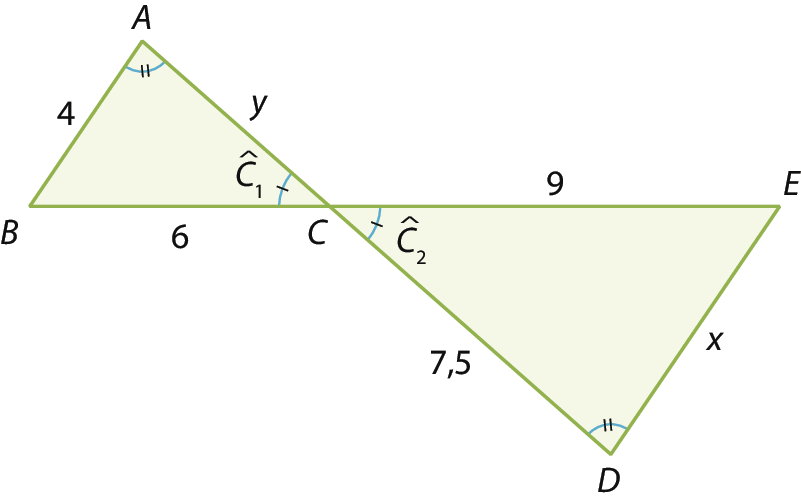
Nesses triângulos, temos:
•
Ângulo A congruente ao ângulo D.(ângulos correspondentes formados por duas retas paralelas e uma transversal)
•
Ângulo C1 é congruente ao ângulo C2.(ângulos opostos pelo vértice)
Portanto, os triângulos á bê cê e Dê ê cê são semelhantes pelo caso á á.
Assim, os lados correspondentes têm medidas de comprimento proporcionais:

Portanto, os valores de x e de y são, respectivamente, 6 e 5.
Caso lado-ângulo-lado (éle á éle)
Se dois triângulos têm dois lados correspondentes com medidas de comprimento proporcionais, e os ângulos compreendidos por esses lados são congruentes, então esses triângulos são semelhantes.
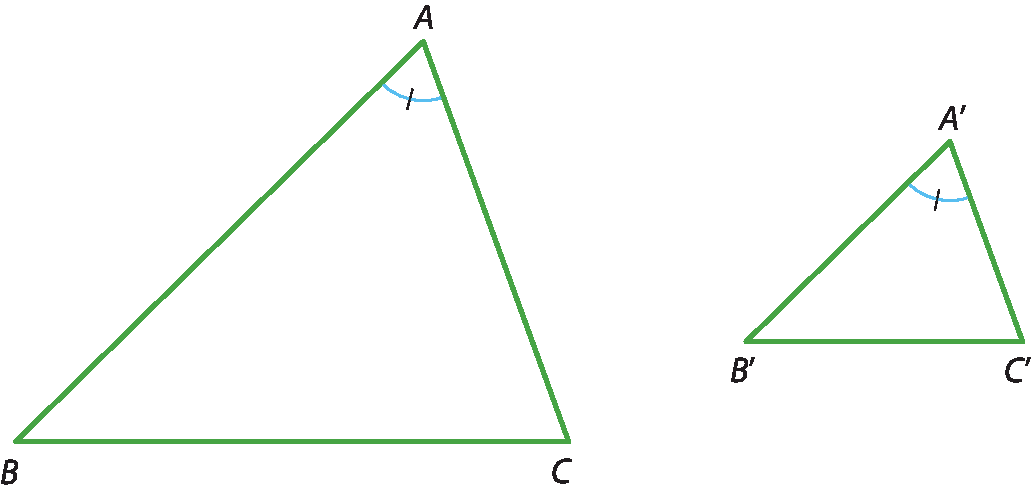
Hipótese:
AB está para A'B' assim como AC está para A'C' e o ângulo A é congruente ao ângulo A'.Tese: △ABC ∼ △A'B'C'
• Demonstração Considerando que A bê > A'B', vamos marcar sobre
Segmento AB.um ponto D, tal que
Segmento AD congruente ao segmento A'B'.Por D, traçamos
Segmento DE paralelo ao segmento BC. Pelo teorema fundamental da semelhança, △á bê cê ∼ △á dê é.
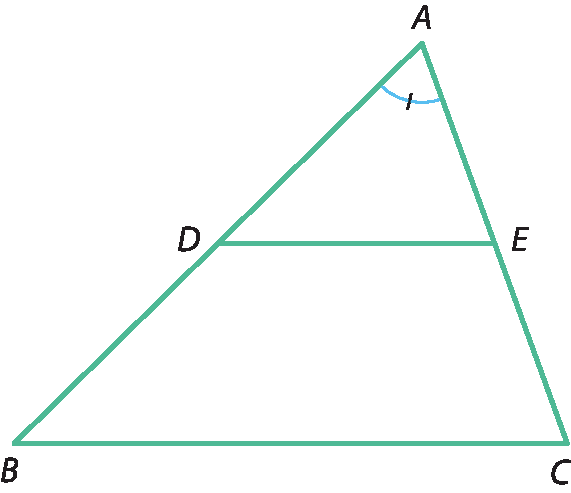
Vamos mostrar, pelo caso lado ângulo lado de congruência de triângulos, que △á dê é ≅ △á'bit'centésimo'. Já sabemos que
Segmento AD congruente ao segmento A'B'.(por construção) e que
Ângulo A congruente ao ângulo A'.(por hipótese). Resta provar que
Segmento AE congruente ao segmento A'C'.Do teorema fundamental da semelhança (△á bê cê ∼ △á dê é), podemos escrever
AB está para AD assim como AC está para AE.ou, ainda,
AB está para A'B' assim como AC está para AE., pois
Segmento AD congruente ao segmento A'B'.Comparando
AB está para A'B' assim como AC está para AE.com
AB está para A'B' assim como AC está para A'C'.(hipótese), temos:
Segmento AE congruente ao segmento A'C'.Então:
Segmento AD congruente ao segmento A'B', Ângulo A congruente ao ângulo A'.e
Segmento AE é congruente ao segmento A'C'.Logo: △á dê é
congruente△á'bit'centésimo' (pelo caso lado ângulo lado de congruência de triângulos). Se △á bê cê ∼ △á dê é e △á dê é
congruente△á'bit'centésimo', então △á bê cê ∼ △á'bit'centésimo', como queríamos provar.

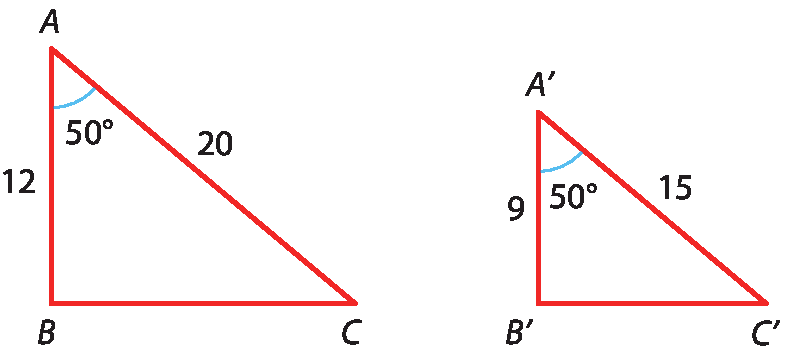
Nesses triângulos, temos:
•
Ângulo A congruente ao ângulo A'.(dado)
•
AB está para A'B' assim como AC está para A'C'., pois
12 está para 9 assim como 20 está para 15.Portanto, os triângulos á bê cê e á'bit'centésimo' são semelhantes pelo caso lado ângulo lado.
Caso lado-lado-lado (éle éle éle)
Se dois triângulos têm os três lados correspondentes com medidas de comprimento proporcionais, então esses triângulos são semelhantes.
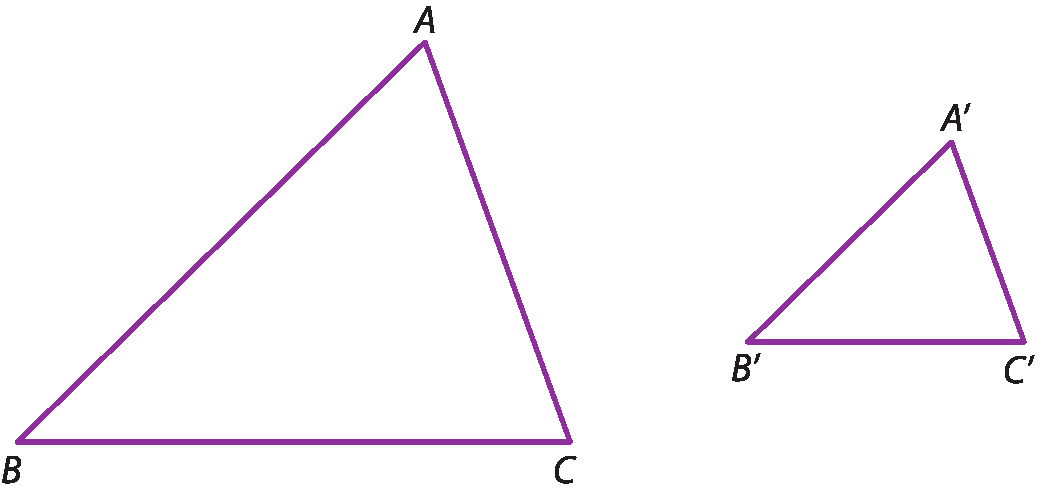
Hipótese:
AB está A'B' assim como AC está para A'C' assim como BC está para B'C'.Tese: △ABC ∼ △A'B'C'
• Demonstração Considerando que A bê > á'bit', vamos marcar sobre
Segmento AB.um ponto D, tal que
Segmento AD é congruente ao segmento A'B'.Por D, traçamos
Segmento DE paralelo ao segmento BC.. Pelo teorema fundamental da semelhança, temos △á dê é ∼ △á bê cê.
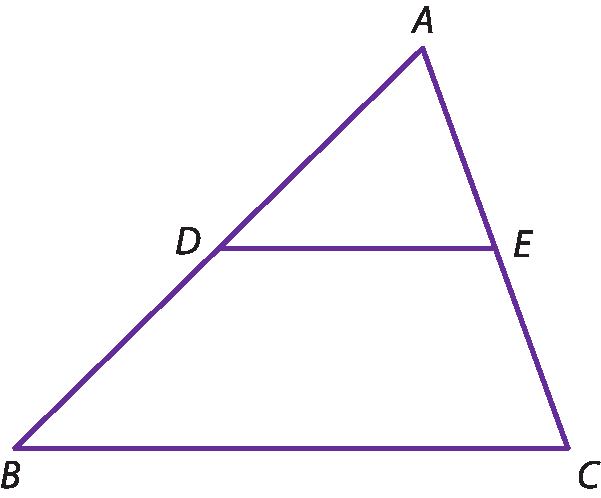
Vamos mostrar, pelo caso lado lado lado de congruência de triângulos, que △á dê é ≅ △á'bit'centésimo'. Como sabemos que
Segmento AD congruente ao segmento A'B'.(por construção), resta provar que
Segmento AE congruente ao segmento A'C'.e que
Segmento DE congruente ao segmento B'C'.
Do teorema fundamental da semelhança (△á bê cê ∼ △á dê é ), podemos escrever:
•
AB está para AD assim como AC está para AE.ou, ainda,
AB está para A'B' assim como AC está para AE., pois
Segmento AD é congruente ao segmento A'B'.Comparando
AB está para A'B' assim como AC está para AE.com
AB está A'B' assim como AC está para A'C'.(hipótese), temos:
Segmento AE congruente ao segmento A'C'.•
AB está para AD assim como BC está para DE.ou, ainda,
AB está para A'B' assim como BC está para DE.pois
Segmento AD é congruente ao segmento A'B'.Comparando
AB está para A'B' assim como BC está para DE.com
AB está para A'B' assim como BC está para B'C'.(hipótese), temos:
Segmento DE é congruente ao segmento B'C'.Então,
Ângulo D congruente ao ângulo B'.,
Segmento AE é congruente ao segmento A'C'.e
Segmento DE é congruente ao segmento B'C'.. Logo: △á dê é ≅ △á'bit'centésimo' (pelo caso lado lado lado) Se △á bê cê ∼ △á dê é e △á dê é ≅ △á'bit'centésimo', então △á bê cê ∼ △á'bit'centésimo', como queríamos provar.

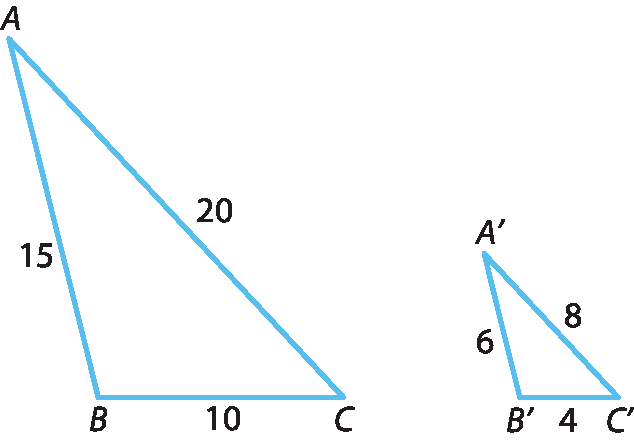
Nesses triângulos, os lados correspondentes têm medidas de comprimento proporcionais.
, pois
15 está para 6 assim como 10 está para 4 assim como 20 está para 8Portanto, os triângulos á bê cê e á linha bê linha cê linha são semelhantes pelo caso lado lado lado.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
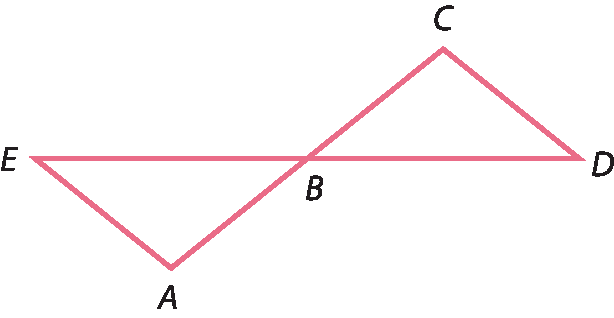
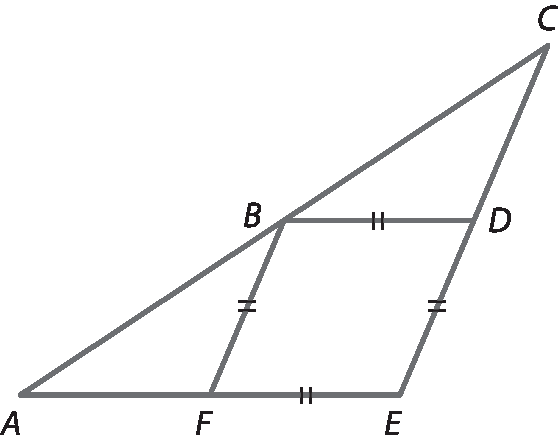
22 Prove que o △á bê é e o △cê bê dê são semelhantes, sabendo que
Segmento AE.⫽
Segmento CD.Para facilitar a visualização, refaça o desenho marcando os ângulos congruentes ou mudando a posição de um dos triângulos.
23 Calcule x e y em cada caso.
a)
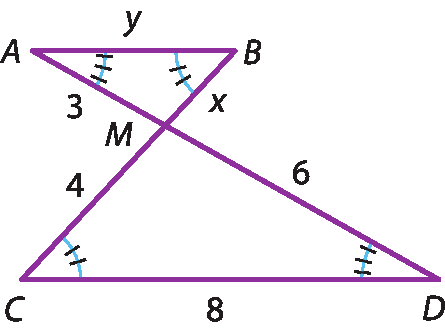
b)
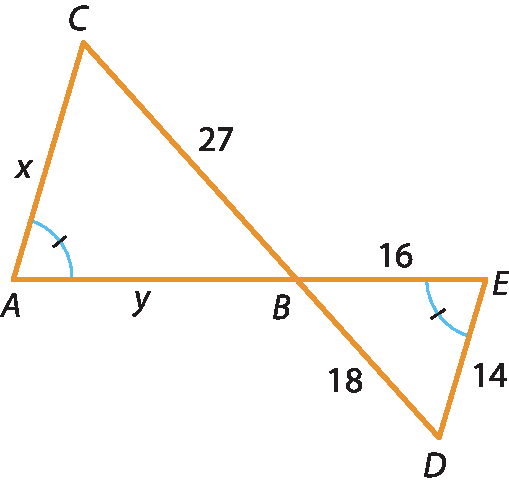
c)
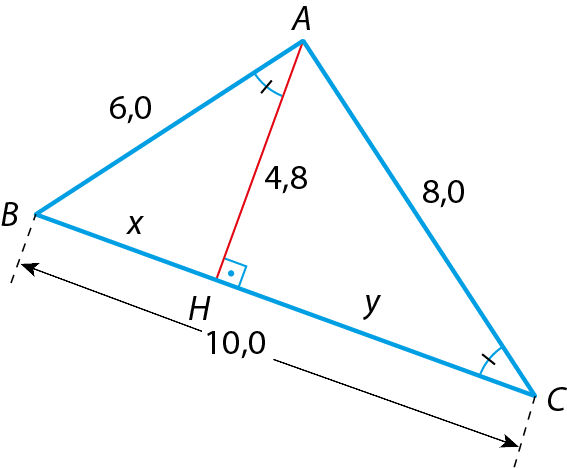
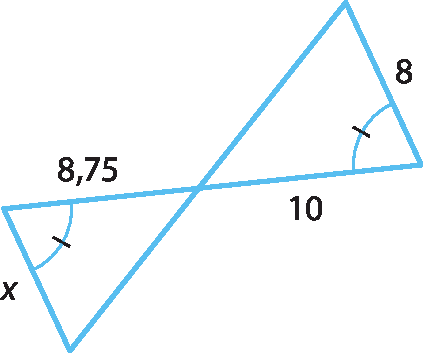
24 Identifique os triângulos semelhantes e calcule o valor de x.
a)
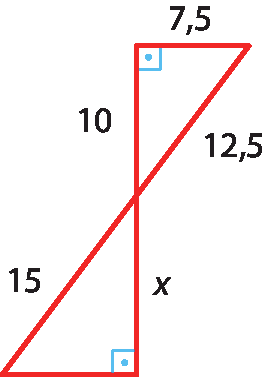
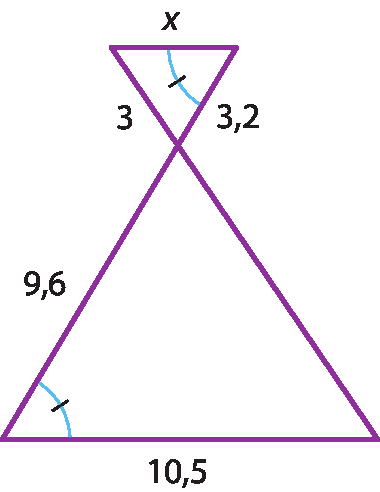
b)
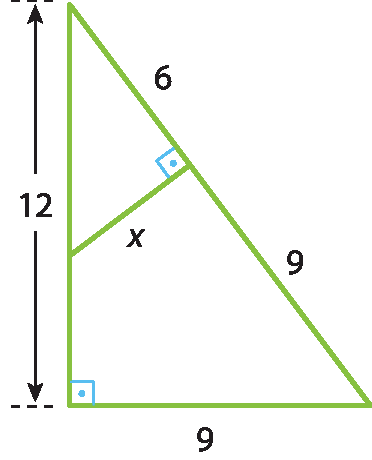
c)
d)
25 Mostre que os triângulos indicados são semelhantes e calcule o valor de x.
a) △á bê cê e △á dê bê
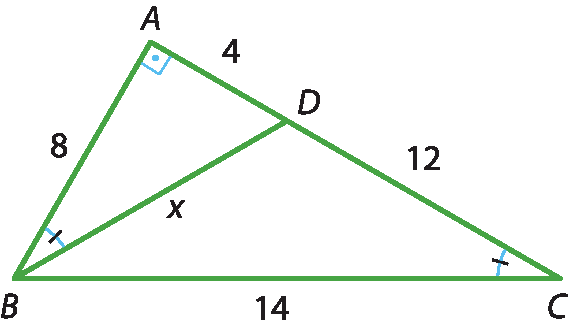
b) △á dê bê e △cê dê á
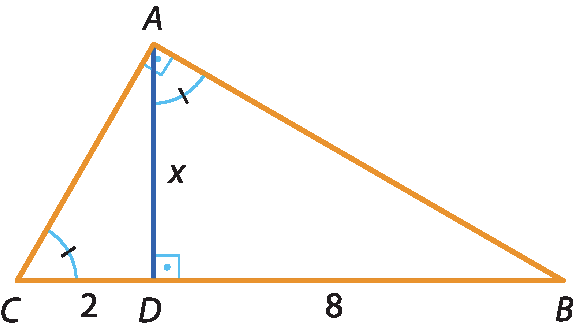
26 Verifique quais triângulos são semelhantes, sabendo que
Segmento AE paralelo ao segmento BD, segmento CE paralelo ao segmento BFe que F é o ponto médio de
Segmento AE.. Entre os pares de triângulos semelhantes, quais são triângulos congruentes?
27

Hora de criar – Em duplas, com o auxílio de régua e transferidor, construam dois triângulos semelhantes cada um, utilizando um dos três casos de semelhança de triângulos. Troquem de caderno e verifiquem a semelhança entre os triângulos construídos pelo colega aplicando um caso de semelhança diferente do utilizado para a construção das figuras. Destroquem de caderno para a correção.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
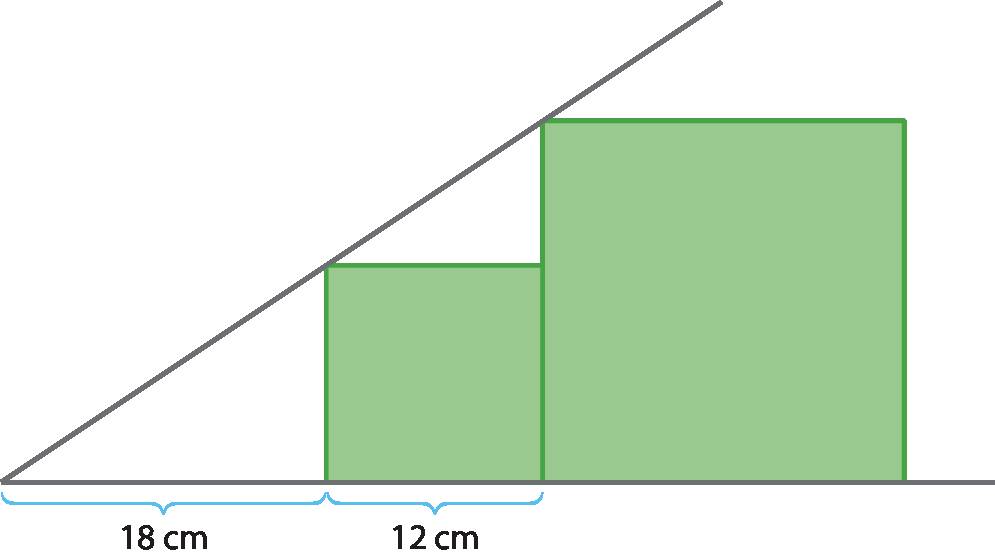
Observe os dois quadrados da figura e determine a medida do perímetro e a medida da área do quadrado maior.
PARA SABER MAIS
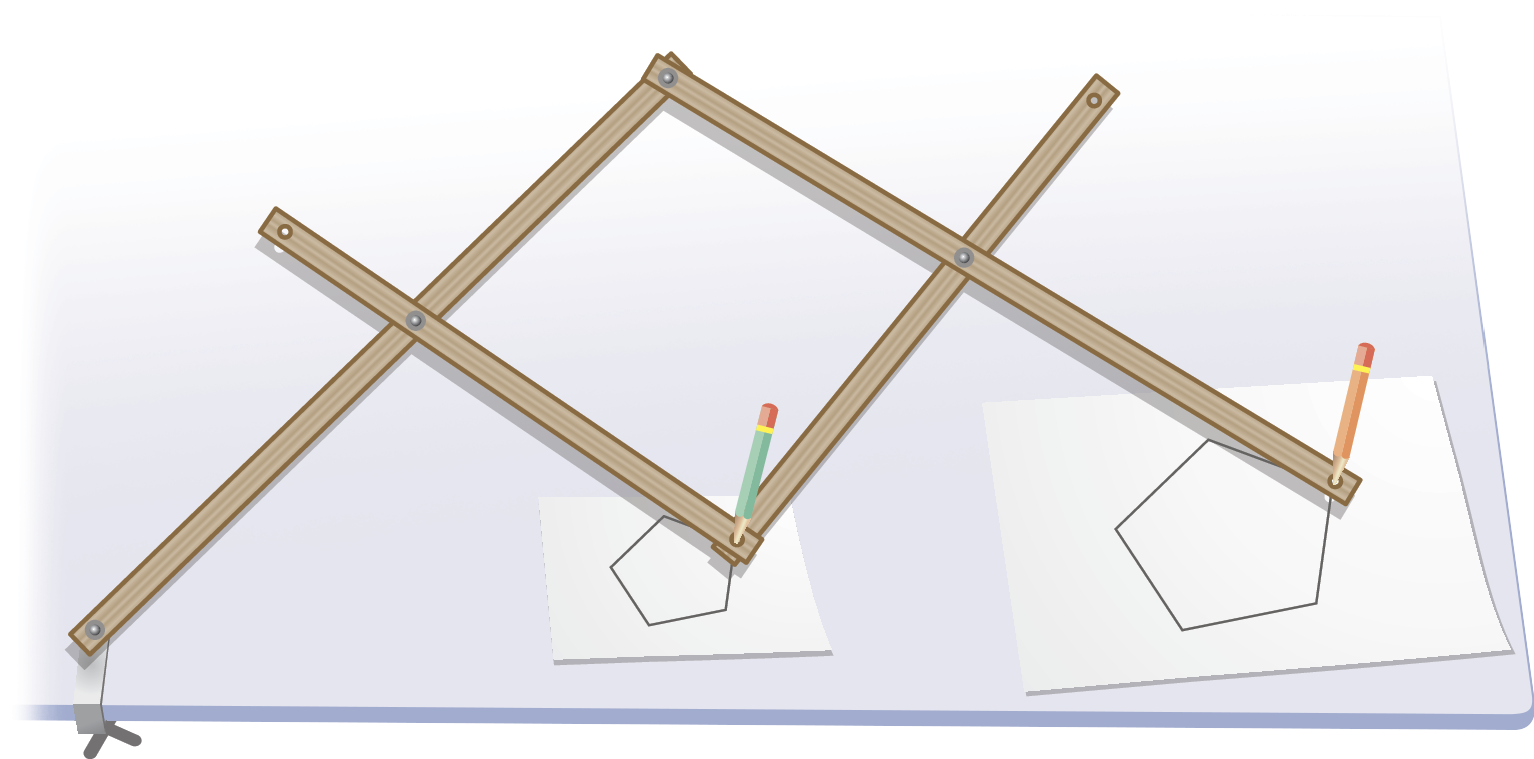
Construindo um pantógrafo
Pantógrafo é um aparelho usado para ampliar ou reduzir figuras em determinada razão. Esse aparelho foi desenvolvido no século dezessete e vem sendo utilizado por artistas para auxiliar na cópia de desenhos em escala ampliada ou reduzida.

Para construí-lo, você vai precisar de:
• 4 ripas de madeira pequenas com as mesmas medidas de comprimento, perfuradas nas extremidades e no centro (peça ajuda a um adulto para evitar acidentes ao perfurar as ripas);

• 2 lápis;
• 3 parafusos com porcas, com medidas de diâmetro compatíveis com os furos nas ripas de madeira.
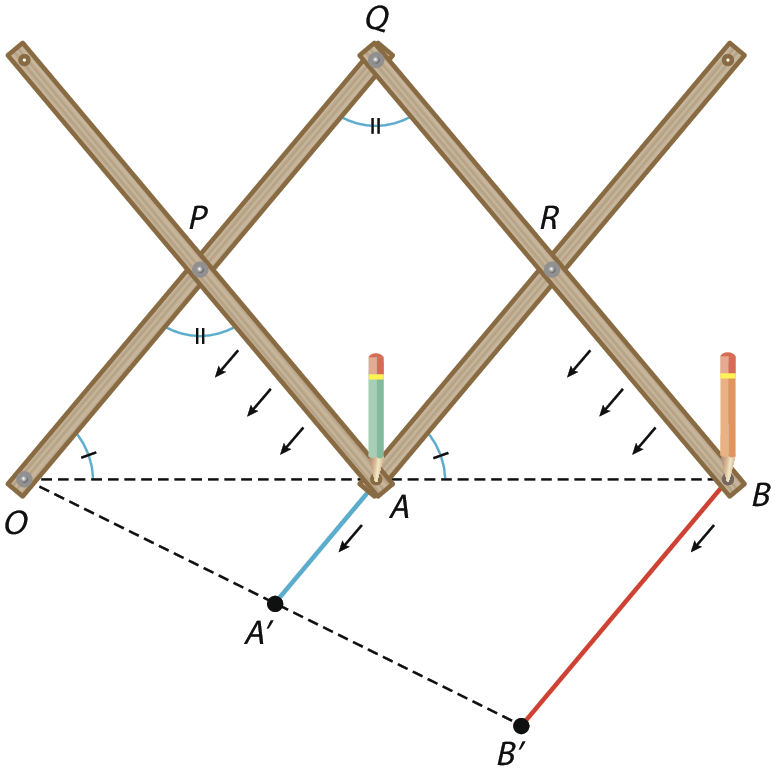
Com os materiais indicados, vamos montar o pantógrafo, conectando as ripas de madeira com os parafusos e as porcas de modo que as junções fiquem móveis; assim, as partes do pantógrafo podem se movimentar umas em relação às outras. Observe o esquema a seguir.
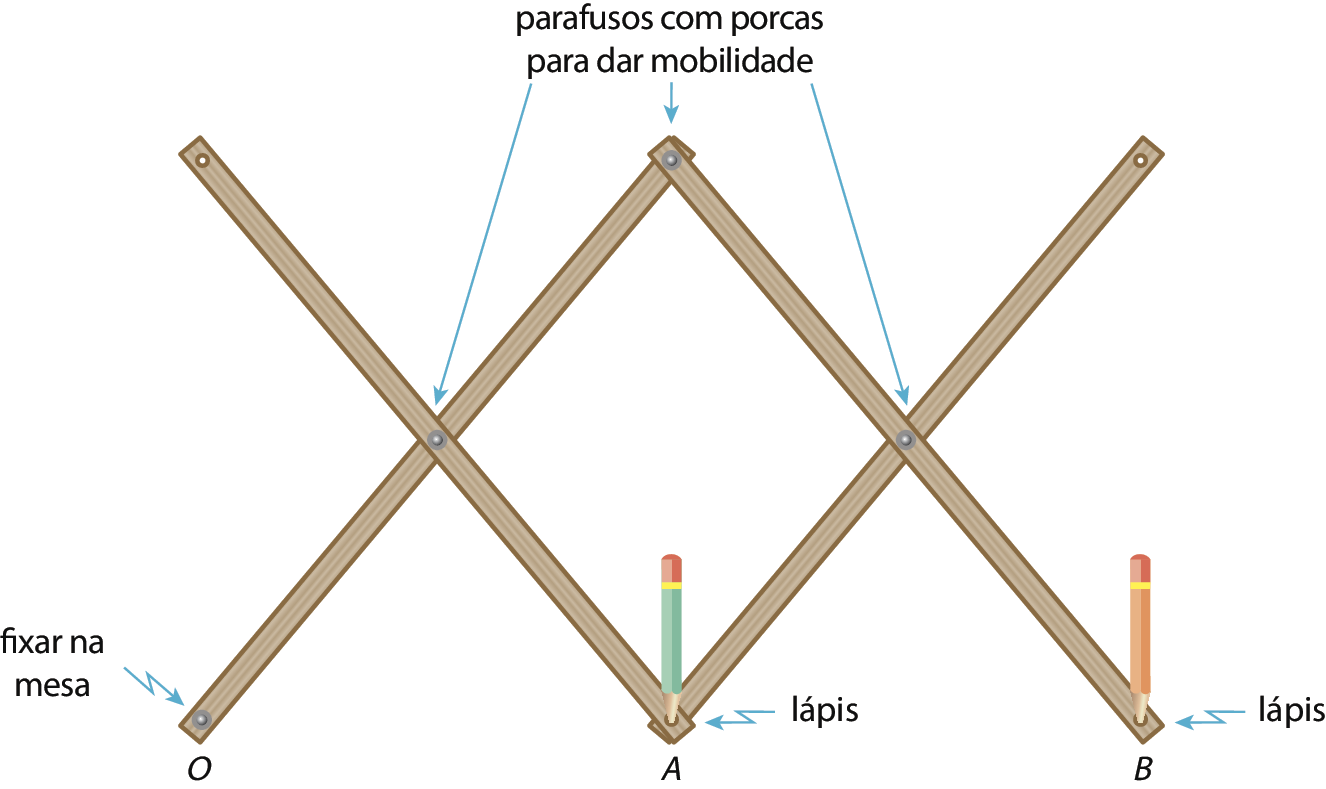
Para utilizar o pantógrafo, fixamos um ponto óh sobre uma superfície plana, como uma mesa, e colocamos cada um dos lápis nos pontos a e B indicados no esquema. Quando movemos o lápis em a, contornando a imagem original que queremos ampliar, o lápis em B também se move, desenhando uma nova imagem semelhante à original, mas ampliada. Para reduzir uma imagem, devemos colocá-la sob o lápis no ponto B. Assim, quando movemos o lápis contornando a imagem original em B, o lápis em a também se move, desenhando uma nova imagem semelhante à original, mas agora reduzida.
Observe na figura a seguir que os triângulos ó pê á e ó quê bê são semelhantes e a razão de semelhança é
OQ está para OP assim como 2 está para 1.. Assim, quando você traçar com o lápis em a um segmento
Segmento AA'.o lápis em B traçará um segmento
Segmento BB'.com o dobro da medida de comprimento. É assim que uma imagem qualquer é ampliada com um pantógrafo.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 O pantógrafo também pode ser utilizado para a ampliação de mapas. Use o pantógrafo que você construiu para ampliar o contorno do mapa do Brasil, de acordo com a razão de semelhança k = 2. Não se esqueça de dar título ao mapa, de inserir legenda e rosa dos ventos (para indicar a orientação geográfica) e de corrigir a escala cartográfica de acordo com a ampliação.
Fuso horário civil (2018)
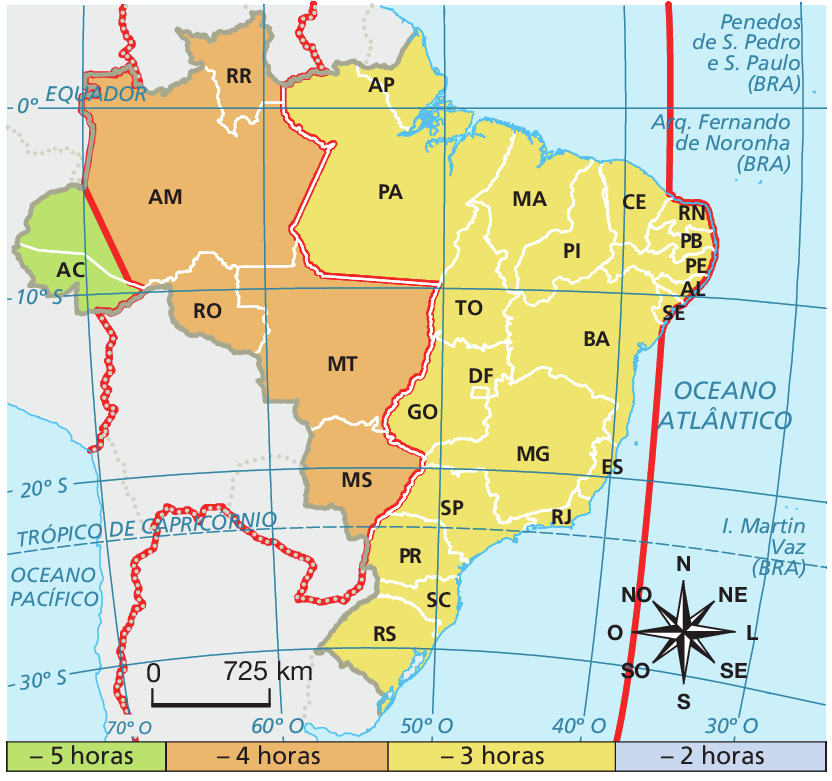
2 Se a razão de semelhança fosse
K é igual a um meio., como seria o novo mapa desenhado? Desenhe o contorno dêsse novo mapa utilizando seu pantógrafo.
Observação
▶ Perfurando as ripas em várias posições, você poderá montar e desmontar o pantógrafo, obtendo outras razões de semelhança.
Por exemplo, se as ripas forem perfuradas em três partes iguais, você poderá triplicar as medidas lineares de uma figura ou reduzi-las a um terço.
TRABALHANDO A INFORMAÇÃO

Um gráfico chamado pirâmide etária
Os gráficos são muito comuns em Matemática e em Física. No entanto, outras ciências, como a Geografia, também fazem uso dêsse importante instrumento de análise de informações. Particularmente, o gráfico conhecido como pirâmide etária é frequente no estudo da distribuição da população de acordo com a idade e o sexo.
Observe a tabela a seguir com dados do Censo realizado pelo Instituto Brasileiro de Geografia e Estatística (í bê gê É) em 2010.
|
Grupo etário* |
Homens (em porcentagem) |
Mulheres (em porcentagem) |
|---|---|---|
|
0 – 4 |
5,0 |
4,8 |
|
5 – 9 |
5,3 |
5,1 |
|
10 – 14 |
5,6 |
5,4 |
|
15 – 19 |
5,2 |
5,1 |
|
20 – 24 |
4,9 |
4,9 |
|
25 – 29 |
4,6 |
4,7 |
|
30 – 34 |
4,1 |
4,1 |
|
35 – 39 |
3,4 |
3,4 |
|
40 – 44 |
3,0 |
2,8 |
|
45 – 49 |
2,4 |
2,3 |
|
50 – 54 |
2,0 |
1,9 |
|
55 – 59 |
1,5 |
1,5 |
|
60 – 64 |
1,1 |
1,1 |
|
65 – 69 |
0,9 |
0,8 |
|
70 – 74 |
0,6 |
0,6 |
|
75 – 79 |
0,4 |
0,4 |
|
80 – 84 |
0,2 |
0,3 |
|
85 – 89 |
0,1 |
0,1 |
|
90 – 94 |
0,0 |
0,1 |
|
95 – 99 |
0,0 |
0,0 |
|
100 anos ou mais |
0,0 |
0,0 |
Dados obtidos em: INSTITUTO BRASILEIRO DE GEOGRAFIA E ESTATÍSTICA. Censo 2010. Disponível em: https://oeds.link/K1z03e. Acesso em: 5 abril 2022.
*Intervalo de idade, em anos, no qual o indivíduo se enquadra no momento da pesquisa.
Os geógrafos costumam representar essas informações em uma pirâmide etária como esta.
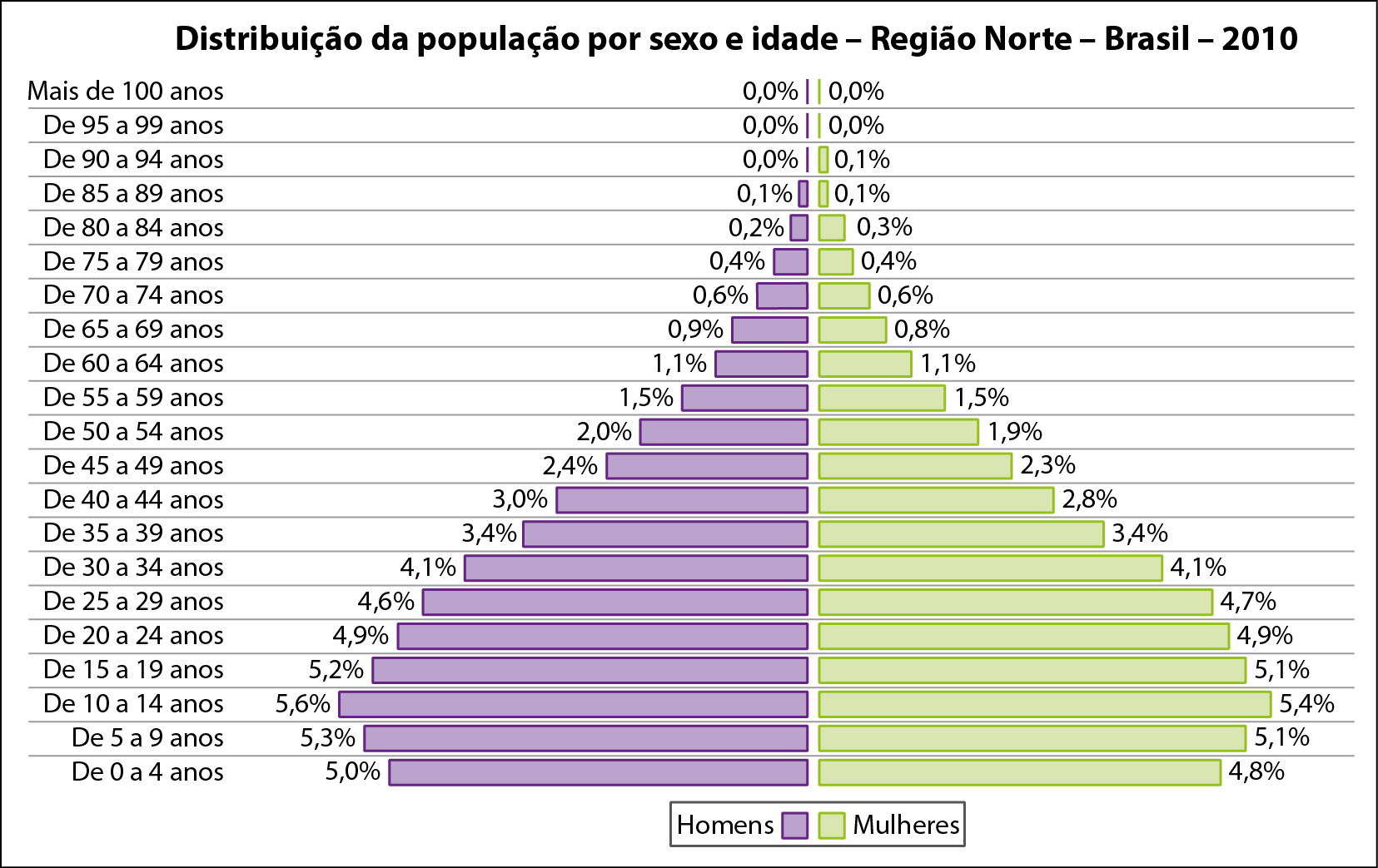
Por meio dêsse gráfico, fica fácil saber que a maioria da população pesquisada (60,6%) é constituída por crianças, adolescentes e jovens de até 29 anos. Com base nesse gráfico, também é possível traçar um perfil da população, por sexo e por grupo etário, o que contribui na elaboração de projetos que atendam às suas necessidades, visto que esses dados indicam aos governos quanto e em que setores – educação, esporte e lazer, saúde etcétera – se deve investir.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Observe a pirâmide etária relativa à projeção da população do Brasil para 2060.
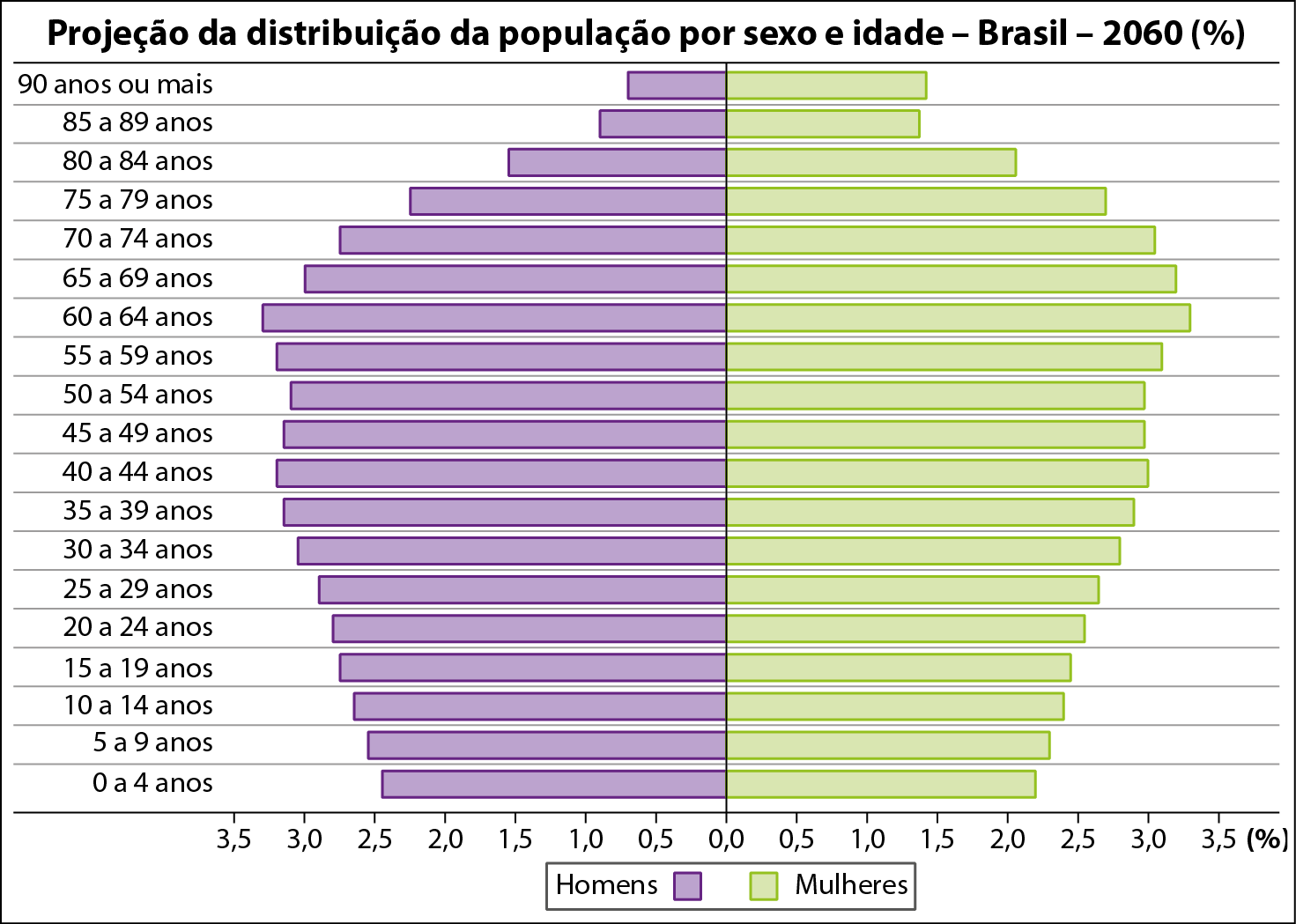
a) A maior parte dessa população também é constituída por crianças, adolescentes e jovens?
b) Em relação aos dias de hoje, os futuros governos do Brasil deverão destinar à terceira idade uma parte maior ou menor de seu orçamento? Por quê?
c) Pesquise previdência social e previdência privada. A mudança prevista no perfil da população brasileira afetará a atual situação previdenciária brasileira? Por quê?
2 Agora, observe a pirâmide etária relativa à população da região Sul do Brasil em 2010.
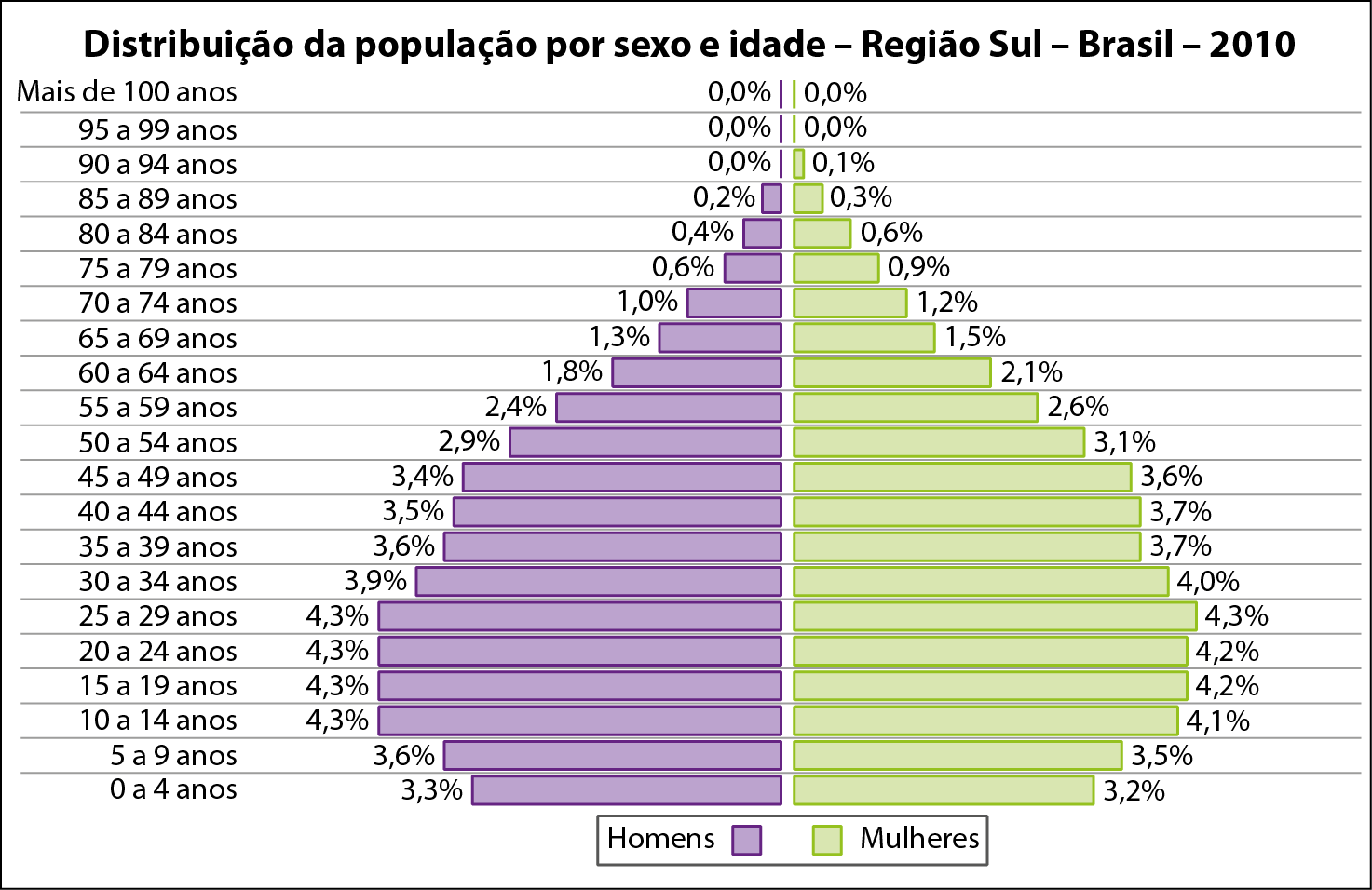
Que diferenças você observa nessa pirâmide em relação à da região Norte?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Classifique cada sentença a seguir em verdadeira ou falsa e justifique as falsas.
a) Todos os triângulos congruentes são semelhantes.
b) Todos os triângulos semelhantes são congruentes.
c) Dois triângulos isósceles que têm os ângulos do vértice congruentes são semelhantes.
2 (Covest-Pernambuco) A figura a seguir representa um rio cujas margens são retas paralelas.
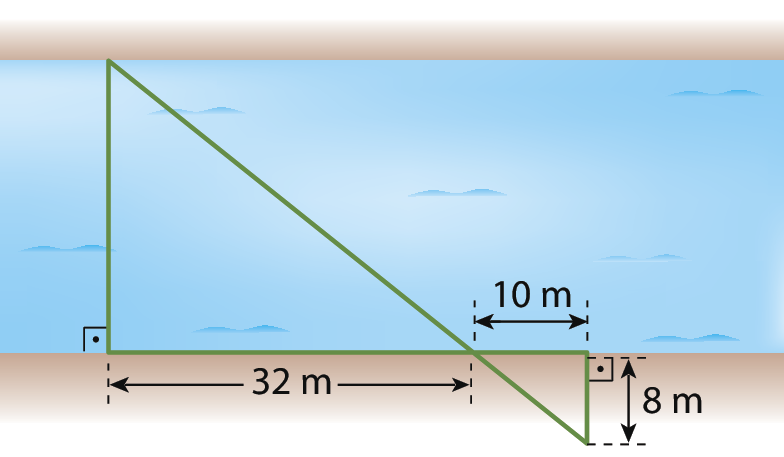
Qual é o inteiro mais próximo da largura do rio, medida em metro?
3 (enêm) A sombra de uma pessoa que mede 1,80 métro de altura mede 60 centímetros. No mesmo momento, a seu lado, a sombra projetada de um poste mede 2,00 métros. Se, mais tarde, a sombra do poste diminuir 50 centímetros, a sombra da pessoa passará a medir:
a) 30 centímetros.
b) 45 centímetros.
c) 50 centímetros.
d) 80 centímetros.
e) 90 centímetros.
4 Os lados
Segmentos AB e ACde um triângulo medem, respectivamente, 35 centímetros e 42 centímetros. No lado
Segmento AB.distante 10 centímetros de a, marca-se um ponto D. Por D, traça-se uma paralela a
Segmento BC.que encontra
Segmento AC.no ponto ê.
a) Construa uma figura que represente a situação.
b) Determine as medidas de
Segmento AE e EC.5 O esquema a seguir representa a relação entre quatro estradas.
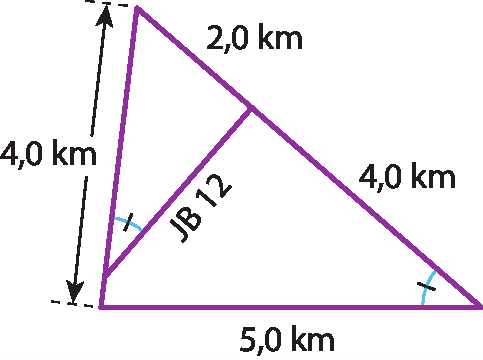
Determine a medida do comprimento da estrada JB 12.
6 Os lados de um triângulo medem 15 centímetros, 20 centímetros e 25 centímetros. Calcule as medidas aproximadas dos lados de um triângulo semelhante a ele que tenha perímetro medindo aproximadamente 45 centímetros.
7 Observe no esquema a seguir o procedimento usado por Marcelo para determinar a medida da distância entre as árvores a e B próximas do lago.
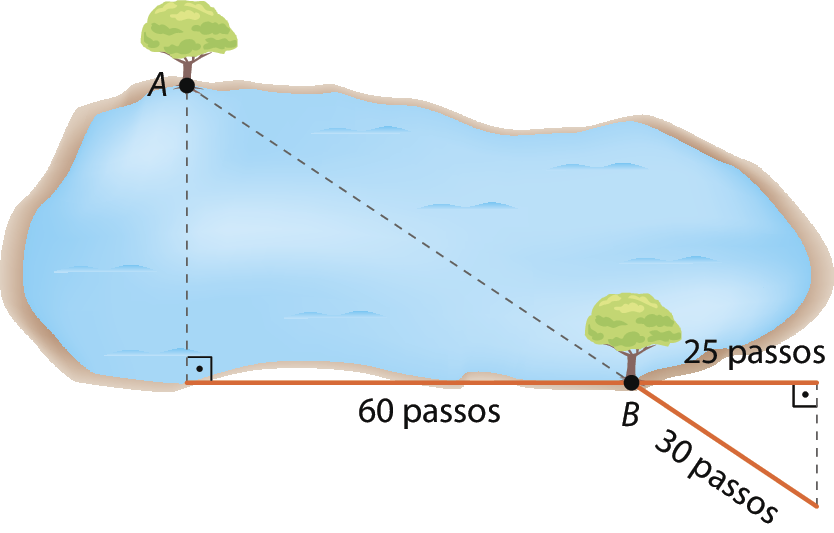
Sabendo que a medida do comprimento do passo de Marcelo é de 75 centímetros, determine a medida da distância entre essas árvores, em metro.
8 As medidas dos perímetros de dois triângulos semelhantes são 48 centímetros e 60 centímetros. As medidas das áreas deles são, respectivamente, 96 centímetros quadrados e 150 centímetros quadrados. O maior lado do triângulo maior mede 25 centímetros. Determine a medida do maior lado do triângulo menor.
9 Uma pessoa sobe uma rampa que mede 4,0 métros de altura na parte mais alta. Após caminhar 12,3 métros sobre a rampa, ela nota que está a 1,5 métro de altura em relação ao solo. Calcule quantos metros a pessoa ainda deve caminhar para atingir o ponto mais alto da rampa.
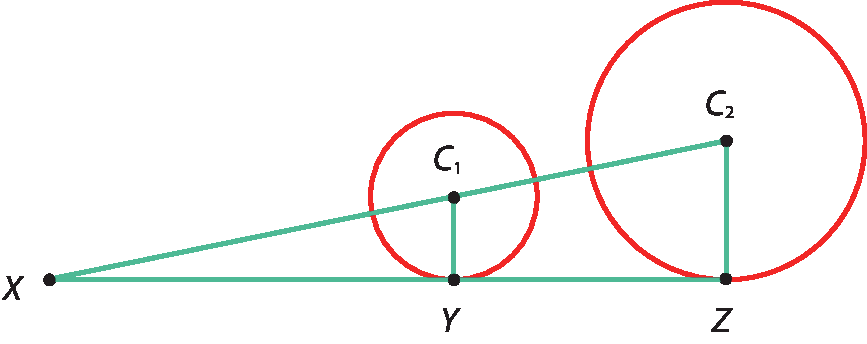
10 Na figura, o raio da circunferência menor mede 6 centímetros e o da maior mede 10 centímetros. Se XC1 = 30 centímetros e
Segmento YC1 paralelo ao segmento ZC2, determine a medida do comprimento do segmento
Segmento C1C2
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Um arquiteto desenhou um pequeno esboço de um ambiente a ser decorado e, em seguida, reproduziu o desenho ampliando-o na razão 1:5 para inserir mais detalhes. A figura a seguir mostra o primeiro esboço feito pelo arquiteto.
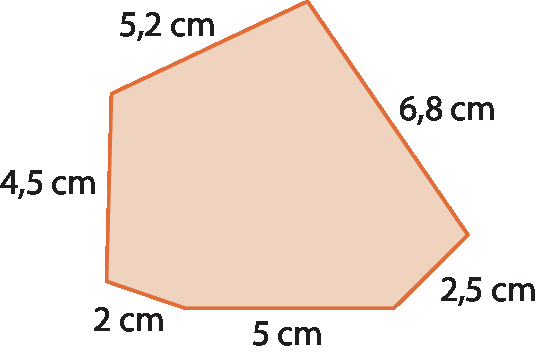
Com base nesse esboço, qual é a medida do perímetro do ambiente a ser decorado no desenho ampliado?
a) 26 centímetros
b) 105 centímetros
c) 52 centímetros
d) 130 centímetros
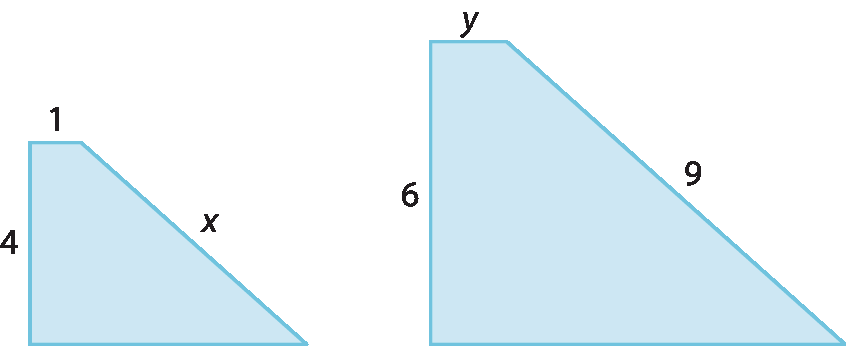
2 Para que os polígonos a seguir sejam semelhantes, os valores de x e de y devem ser, respectivamente:
a) 6 e
Três meios..
b)
27 meios.e
Três meios..
c) 6 e
Dois terços..
d) 3 e 2.
3 Para que os triângulos a seguir sejam semelhantes, os valores de a e b devem ser iguais, respectivamente, a:
a) 15 e 25.
b) 9 e 15.
c) 12 e 20.
d) 9 e 25.
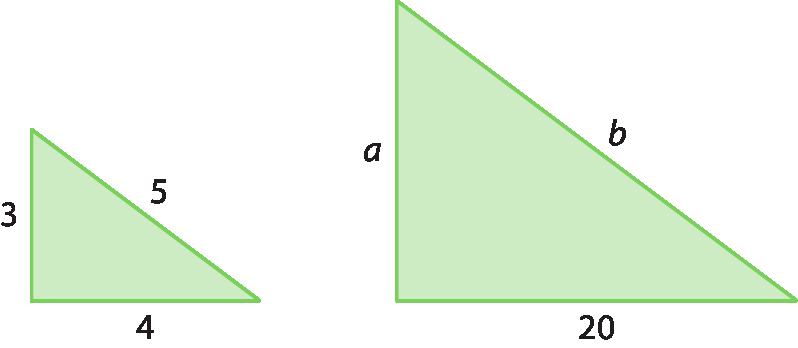
4 Os triângulos a seguir são semelhantes?
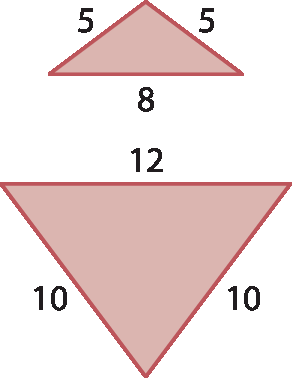
a) Sim, pois
Oito quintos igual a doze décimos..
b) Sim, pois
Oito quintos diferente de dez doze avos..
c) Não, pois
Oito quintos diferente de doze décimos..
d) Não, pois
Oito quintos diferente de dez doze avos..
5 O quadrilátero a seguir foi obtido ao traçar um segmento de reta cortando dois lados de um triângulo e paralelo ao terceiro lado. Qual é a medida aproximada de x?
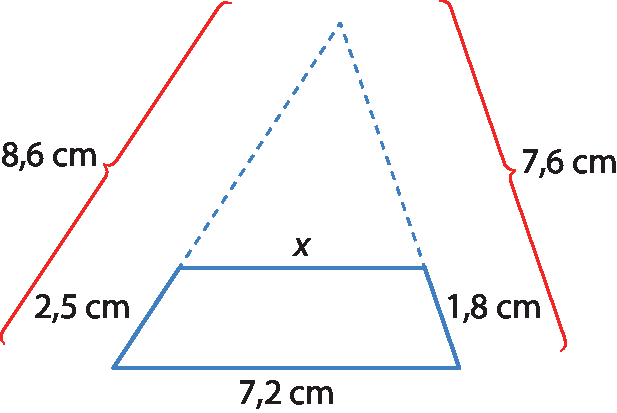
a) 4,9 centímetros
b) 5,1 centímetros
c) 6,1 centímetros
d) 7,3 centímetros
6 O triângulo á bê cê é obtusângulo, A bê = x centímetro e os ângulos internos com vértices em a e em B são congruentes. Considerando um triângulo dê ê éfe tal que dê éfe = 3x centímetros, cujos ângulos com vértice em D e em F são congruentes entre si e, ainda, congruentes aos dois ângulos agudos do triângulo á bê cê, então, os triângulos á bê cê e dê ê éfe são:
a) congruentes (pelo caso ângulo-lado-ângulo).
b) congruentes (pelo caso lado-ângulo-ângulo opostoo).
c) semelhantes (pelo caso lado ângulo lado).
d) semelhantes (pelo caso ângulo ângulo).
7 Para que dois triângulos sejam semelhantes pelo caso lado lado lado, é preciso que eles tenham:
a) lados correspondentes congruentes.
b) lados correspondentes com medidas de comprimento proporcionais.
c) ângulos correspondentes com medidas proporcionais.
d) ângulos correspondentes congruentes.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões.
a) Quais são as condições para que dois polígonos sejam considerados semelhantes?
b) Descreva cada um dos casos de semelhança de triângulos que você estudou.

Gire o seu dispositivo para a posição vertical
DIVERSIFICANDO
Câmara escura de orifício
A câmara escura de orifício, precursora das câmeras fotográficas modernas, é um dispositivo óptico muito simples, pois fórma imagens apenas com a focalização dos raios de luz ao atravessarem um pequeno orifício. Ela pode ser feita com uma caixa ou uma lata qualquer, desde que suas paredes internas sejam opacas e escuras. De um lado, deve ter um pequeno orifício e, na parte oposta, uma folha de papel branca.
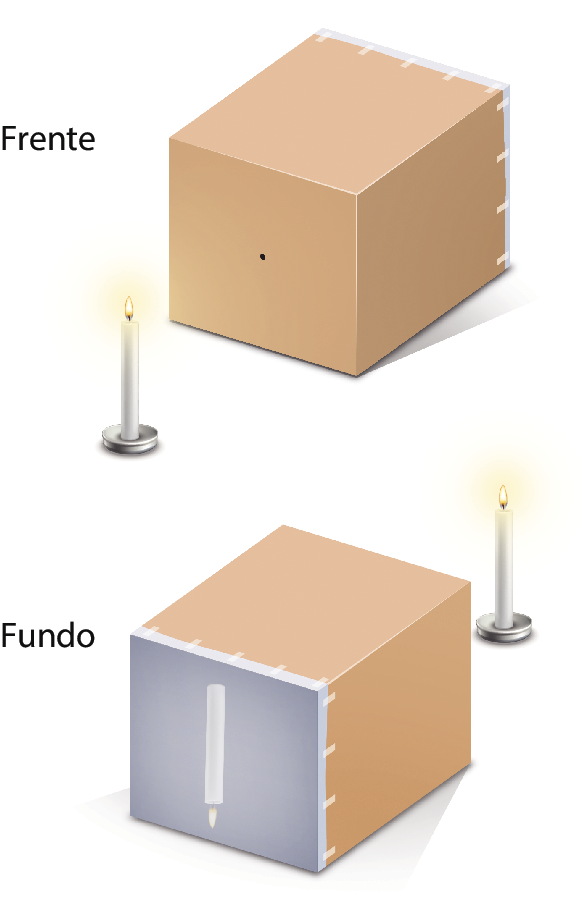
(Representação esquemática. As imagens não respeitam as proporções reais entre os objetos.)
Quando apontamos o orifício da câmara escura para um objeto iluminado, observamos a projeção da imagem invertida dêsse objeto sobre o papel. Isso ocorre em virtude de uma importante propriedade da luz, que é a de se propagar em linha reta. Observe o esquema a seguir.
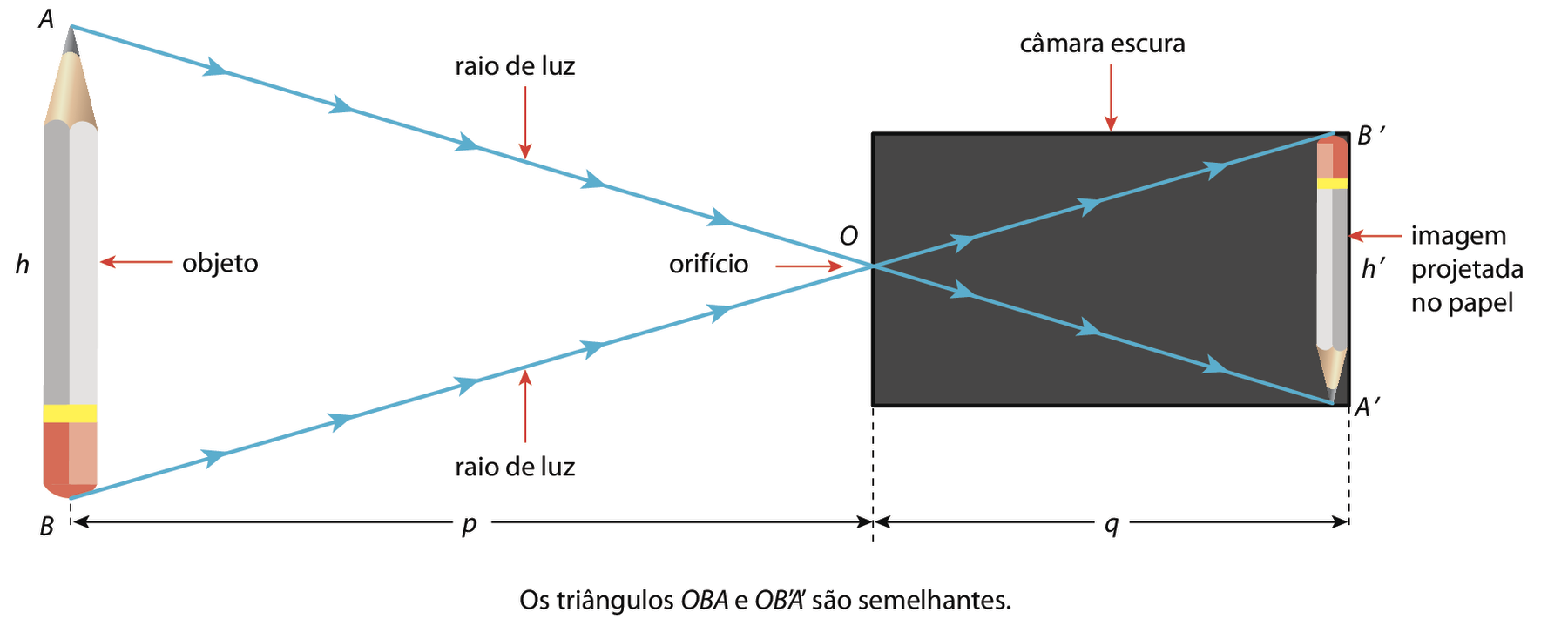
Nesse esquema, h é a medida da altura do objeto, h' é a medida da altura da imagem projetada e da caixa também, p é a medida da distância do objeto até o orifício e q é a medida da distância da imagem até o orifício. Os triângulos ó á bê e OA'bit' são semelhantes, pois os ângulos correspondentes são congruentes:
Ângulo AOB congruente ao ângulo A'OB'. Ângulo ABO congruente ao ângulo A'B'O.e
Ângulo BAO congruente ao ângulo B'A'O.Portanto, por semelhança, h ⋅ q = p ⋅ h'.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Originalmente desenvolvida como um instrumento científico e muito utilizada na Antiguidade para observações astronômicas, a câmara escura se tornou popular entre os artistas do século dezesseis como um instrumento para auxiliar na criação de pinturas e facilitar o desenho em perspectiva. Explique como a câmera escura poderia auxiliar um artista na criação de uma pintura.
2 Felipe usou uma caixa de formato cúbico, com aresta medindo 20 centímetros de comprimento, para fazer uma câmara escura e retratar um quadro pendurado na parede de sua casa. Qual é a medida mínima da distância que esse quadro, de 50 centímetros por 50 centímetros, deve ficar do orifício da câmara para aparecer por inteiro no papel?