Página 146

CAPÍTULO 7 Equações do 2º grau

Fotografia. Vista de alto de um ringue de boxe com dois lutadores e um juiz. Ao lado do ringue, duas pessoas assistem a luta. No ringue, à esquerda, homem branco, usando regata vermelha e shorts vermelho. À direita, homem branco, usando regata azul e shorts azul. Ambos usam luvas de boxe. Ao lado deles, homem negro, usando camisa branca, calça preta e gravata borboleta observa os lutadores. — Anthony Joshua enfrenta Carlos Takam em luta de boxe realizada no Reino Unido. (Fotografia de 2020.)

Observe a fotografia e responda às questões no caderno.

a) Pesquise o boxe amador nas Olimpíadas: em qual ano foi introduzido, obrigatoriedade do uso do capacete, categorias dos boxes masculino e feminino.

b) Além do boxe, você conhece outros esportes nos quais os atletas ficam sobre tablados?

c) Pesquise as medidas oficiais dos tablados de alguns dos esportes que você mencionou no item b.

Oficialmente, o tablado de um ringue de boxe deve ser quadrado, com medida dos lados variável de 4,9 métros a 7,0 métros, além de uma borda mínima de 0,6 métro.

Se uma academia de esportes dispõe de uma superfície quadrada de 36 métros quadrados para construir um ringue de boxe, o construtor pode resolver uma equação do 2º grau para determinar a medida dos lados dêsse ringue. Reúna-se a um colega para pensarem em uma estratégia de resolução dêsse problema, que será retomado neste capítulo.

Página 147

1. Equações do 2º grau com uma incógnita

Considere a situação a seguir.

Fotografia. Vista de uma piscina retangular. Nas laterais, espreguiçadeiras, guarda sóis e coqueiros.

O engenheiro Vítor recebeu uma encomenda para a construção de uma piscina retangular, com duas exigências:

1ª) comprimento medindo 10 métros a mais que a largura;

2ª) área medindo 144 métros quadrados.

Para determinar as medidas da largura e do comprimento dessa piscina, Vítor representou a da largura por x, e a do comprimento por x + 10.

Ilustração. Homem branco, de cabelo preto, camisa rosa e calça preta. Ele está sentado em uma cadeira de frente para uma mesa, com uma folha de papel com um retângulo desenhado nela. Sobre a mesa, há uma luminária acesa.

Como a medida da área de um retângulo é o produto das medidas da largura e do comprimento, ele escreveu:

x ⋅ (x + 10) = 144 ou x elevado a 2 + 10x menos 144 = 0

Observe que a equação obtida, xelevado a 2 + 10x menos 144 = 0, tem uma só incógnita (x), cujo maior expoente é 2. Ela é um exemplo de equação do 2º grau com uma incógnita.

Toda equação do 2º grau com uma incógnita pode ser reduzida à seguinte fórma:

Fórmula. Equação de segundo grau. a vezes x ao quadrado, mais b vezes x, mais c é igual a 0 (com a diferente de 0). Sobre a fórmula, há uma chave e uma seta, indicando que a fórmula representa a forma reduzida de uma equação de segundo grau.

Os números reais a, b e c são os coeficientes da equação do 2º grau, sendo:

• a o coeficiente do quadrado da incógnita (coeficiente de xelevado a 2);

• b o coeficiente da incógnita (coeficiente de x);

• c o termo independente da incógnita.

Nos exemplos a seguir, as equações do 2º grau estão escritas na fórma reduzida, e destacamos seus coeficientes a, b e c.

a) Na equação 5xelevado a 2 menos 6x +

\frac{1}{5}

= 0, a = 5, b = menos 6 e c =

\frac{1}{5}

b) Na equação menos 0,4xelevado a 2 + 9x = 0, a = menos 0,4, b = 9 e c = 0

c) Na equação

\frac{x^{2}}{2}

menos 10 = 0, a =

\frac{1}{2}

, b = 0 e c = menos10

d) Na equação

‒ \frac{\sqrt{5}}{5}

x 2 = 0, a =

‒ \frac{\sqrt{5}}{5}

, b = 0 e c = 0

Ilustração. Menino branco, de cabelo castanho e camiseta vermelha. Ele fala: A equação 0 vezes x elevado ao quadrado, mais 3 vezes x, menos 8 é igual a zero, em que a é igual a zero, equivale a 3 vezes x, menos 8 igual a zero. Então, 0 vezes x elevado ao quadrado, mais 3 vezes x, menos 8 é igual a 0 não é uma equação do 2º grau.

Página 148

Uma equação do 2º grau é considerada completa quando os coeficientes b e c são diferentes de zero, e é incompleta quando b = 0 ou c = 0, ou, ainda, b = 0 e c = 0.

Observe que, nos exemplos anteriores, o item a apresenta uma equação completa, e os itens b, c e d apresentam equações incompletas do 2º grau.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Verifique quais das equações a seguir são do 2º grau e identifique os coeficientes a, b e c.

a) 8x elevado a 2 + 17x + 4 = 0

b) 3x menos 5 = 0

c) 0x elevado a 2 + 10x menos 8 = 0

d) menos

\frac{y^{2}}{5}

menos 25 = 0

e) 4yelevado a 2 menos 5y = 0

f) menos9 + x elevado a 2 = 0

2 Escreva as equações do 2º grau a seguir na fórma reduzida e classifique-as em c (completa) ou em ih (incompleta).

a) 2x elevado a 2 menos 5x = menos2

b) x elevado a 2 + 6x = 2x + 3

c) y elevado a 2 = 8y

d) menos5x elevado a 2 = 30x + 40

e) 3x ⋅ (x menos 2) = 2 ⋅ (2x menos 1)

f) (x + 4) ⋅ (x menos 4) = 5x menos 16

3 Dados os coeficientes a, b e c, escreva no caderno as equações do 2º grau correspondentes.

a) a = 5; b = menos7; c = 0

b) a = menos1; b = 3; c = menos4

c) a = 2; b = 0; c = 4

d) a = menos

\frac{1}{2}

; b =

\frac{5}{7}

; c =

\sqrt{2}

4 Para que valor de n a equação

(5n + 2)x elevado a 2 menos 4nx + n = 0 não é do 2º grau?

5 Determine no caderno os valores de m na equação (m + 3)x elevado a 2 menos (2m menos 1)x + m + 4 = 0 de modo que ela:

a) não seja do 2º grau em x ;

b) seja do 2º grau em x ;

c) seja do 2º grau em x e seja completa;

d) seja do 2º grau em x e seja incompleta.

6 Considere esta figura.

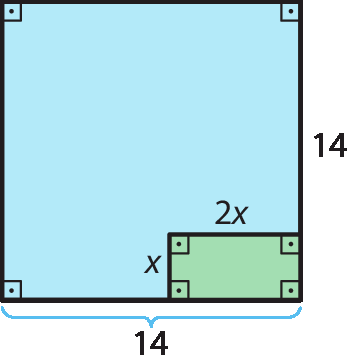
Ilustração. Quadrado azul, cujo lado mede 14. Dentro deste quadrado, no canto inferior direito, retângulo verde cujos lados medem x e 2 vezes x.

a) Determine a medida da área da parte azul.

b) Calcule no caderno o valor de x quando a área da parte azul medir 124.

7 A figura a seguir representa uma caixa em fórma de paralelepípedo.

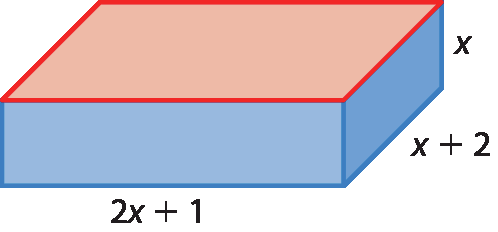
Ilustração. Paralelepípedo cujas medidas são: 2 vezes x, mais 1 (largura), x (altura) e x mais 2 (profundidade). As faces laterais são azuis e a face superior é vermelha.

a) Determine a expressão da soma das medidas das áreas das faces laterais.

b) Determine a expressão da medida da área da face destacada em vermelho.

c) Se a soma das medidas das áreas das faces laterais, em unidade de área, for 880, determine a equação correspondente em relação a x.

Ícone de Atividade em dupla ou em grupo.

Reúna-se com um colega e façam o que se pede.

Na figura, estão indicadas as medidas das áreas, em uma mesma unidade de medida, de três retângulos adjacentes. O retângulo vermelho é um quadrado.

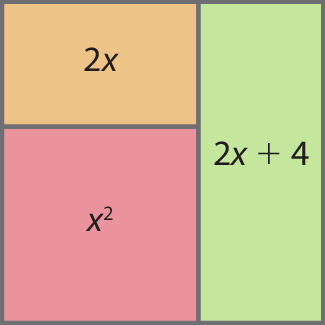
Ilustração. Quadrado maior composto por um quadrado e dois retângulos dentro. Um retângulo laranja, com área igual a 2 vezes x. Um retângulo verde, com área igual a 2 vezes x, mais 4. Quadrado rosa, com área igual a x ao quadrado

a) Escrevam no caderno as medidas dos lados desses retângulos.

b) Escrevam no caderno uma expressão da medida da área do quadrilátero, que é a reunião dos três retângulos.

c) Classifiquem o quadrilátero citado no item b.

Página 149

9 Sendo x um número desconhecido, vamos representar com símbolos a sentença:

Esquema. O quadrado de um número, x elevado ao quadrado, mais o seu triplo, 3 vezes x, é igual a 18.

Na fórma reduzida, escrevemos xelevado a 2 + 3x menos 18 = 0.

Seguindo esse modelo, represente o número desconhecido por x e escreva no caderno a equação do 2º grau na fórma reduzida que corresponde a cada sentença a seguir.

a) O quadrado de um número adicionado ao dobro dêsse número é igual a 99.

b) O triplo do quadrado de um número menos o próprio número é igual a 30.

c) Um número é igual ao quadrado dêsse próprio número menos 42.

d) Três quintos do quadrado de um número é igual a esse número menos 40.

10 Hora de criar – Elabore um problema que possa ser resolvido por meio da equação xelevado a 2 + x + 5 = 0.

Raízes de uma equação do 2º grau

Voltando ao problema da construção da piscina (página 147), podemos obter, por tentativa, o valor de x da medida da largura.

Ilustração. Retângulo azul, cujos lados medem x mais 10 e x.

Vamos recordar que Vítor desenhou a figura e chegou à equação x ⋅ (x + 10) = 144.

Atribuindo a x, por exemplo:

• o número 10, o valor do 1º membro da equação é:

10 ⋅ (10 + 10) = 200, maior do que o 2º membro (200 > 144)

• o número 7, o valor do 1º membro da equação é:

7 ⋅ (7 + 10) = 119, menor do que o 2º membro (119 < 144)

• o número 8, o valor do 1º membro da equação é:

8 ⋅ (8 + 10) = 144, igual ao 2º membro (144 = 144)

Ao substituir x por 8 na equação x ⋅ (x + 10) = 144, ou na sua equivalente xelevado a 2 + 10x menos 144 = 0, obtemos uma sentença verdadeira. Observe.

8 ⋅ (8 + 10) = 144 ou 8elevado a 2 + 10 ⋅ 8 menos 144 = 0

Portanto, uma solução para a situação é a largura da piscina medir 8 metros, e o comprimento, 18 metros.

lustração. Homem branco, de cabelo castanho e camisa bege. Ele fala: Quando substituímos a incógnita de uma equação por um número e encontramos uma sentença verdadeira, dizemos que esse número é raiz da equação. Se a equação for do segundo grau, ela pode ter até duas raízes reais diferentes.

Página 150

Acompanhe alguns exemplos.

a) Vamos verificar se os números menos3, menos2, 2 e 6 são raízes da equação x elevado a 2 + x menos 6 = 0.

• Para x = menos3, obtemos:

(menos3)elevado a 2 + (menos3) menos 6 = 0

9 menos 3 menos 6 = 0

9 menos 9 = 0 (verdadeira)

Logo, menos3 é raiz da equação.

• Para x = menos2, obtemos:

(menos2)elevado a 2 + (menos2) menos 6 = 0

4 menos 2 menos 6 = 0

4 menos 8 = 0 (falsa)

Logo, menos2 não é raiz da equação.

• Para x = 2, obtemos:

2elevado a 2 + 2 menos 6 = 0

4 + 2 menos 6 = 0

6 menos 6 = 0 (verdadeira)

Logo, 2 é raiz da equação.

• Para x = 6, obtemos:

6elevado a 2 + 6 menos 6 = 0

36 + 6 menos 6 = 0

36 = 0 (falsa)

Logo, 6 não é raiz da equação.

b) Vamos determinar o valor de m na equação (3m menos 1) ⋅ xelevado a 2 menos (m + 8) ⋅ x + 10 = 0 de modo que uma de suas raízes seja 2. Como 2 deve ser raiz da equação, consideramos verdadeira a sentença:

(3m menos 1) ⋅ 2elevado a 2 menos (m + 8) ⋅ 2 + 10 = 0

Assim, obtemos: (3m menos 1) ⋅ 4 menos (m + 8) ⋅ 2 + 10 = 0 12m menos 4 menos 2m menos 16 + 10 = 0 10m menos 10 = 0 ⇒

\frac{10 m}{10} = \frac{10}{10}

⇒ m = 1

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

11 Observe o diálogo entre Júlia e Dora.

Ilustração. Duas meninas estão de frente para uma mesa, em que nela está um livro aberto sob uma das mãos de uma delas e um lápis está a frente da outra. À esquerda, Dora, menina negra, de cabelo preto e blusa verde. Ela diz: Júlia, como é possível provar que o número 7 não é uma das raízes da equação x elevado ao quadrado, menos 3 vezes x, mais 4, que é igual a 0? Ao lado de Dora está Júlia, menina branca, de cabelo ruivo, touca e casaco rosa. Ela diz: É muito fácil, Dora. É só…

Complete a resposta de Júlia para Dora.

12 Verifique, entre os números 2, menos5, 9 e 10, quais são raízes da equação xelevado a 2 menos 11x + 18 = 0.

13 Verifique se o número 5 é raiz de cada equação a seguir.

a) xelevado a 2 + 6x = 0

b) 2xelevado a 2 menos 10x = 0

c) 3xelevado a 2 menos 75 = 0

d) xelevado a 2 menos 7x + 10 = 0

14 Dois dos números menos10,

‒ \sqrt{10}

\sqrt{10}

e 10 são raízes da equação xelevado a 2 menos 10 = 0. Quais são eles?

15 Calcule o valor de q de modo que menos1 seja raiz da equação (3q menos 2) ⋅ xelevado a 2 + (2q menos 1) ⋅ x + 5 = 0.

16 Calcule no caderno o valor de:

a) p na equação 3xelevado a 2 menos 14x + 2p = 0 para que uma das raízes seja 4;

b) k na equação (k menos 3)xelevado a 2 menos (k + 4)x + 6 = 0 para que uma das raízes seja 0.

Página 151

2. Resolvendo equações do 2º grau

Vamos estudar a resolução de equações do 2º grau, considerando que as raízes, quando existirem, pertencerão ao conjunto dos números reais.

Equações do 2º grau incompletas

Quando ax 2 + c = 0

Vamos aprender a resolver equações do 2º grau do tipo axelevado a 2 + bx + c = 0, com a ≠ 0 e b = 0.

Considere, por exemplo, a equação xelevado a 2 ‒ 64 = 0. Ela é uma equação do 2º grau incompleta, com b = 0. Adicionando 64 a ambos os membros da equação, obtemos:

xelevado a 2 ‒ 64 + 64 = 0 + 64

xelevado a 2 = 64

Agora, encontramos os números que, elevados ao quadrado, resultem em 64.

x =

‒ \sqrt{64}

ou x =

\sqrt{64}

, ou seja, x = ‒8 ou x = 8

Logo, as raízes da equação são: x 1 = ‒8 e x 2 = 8.

Ilustração. Mulher branca, de cabelo ruivo e camiseta roxa. Ela fala: Quando uma equação do segundo grau do tipo a vezes x elevado ao quadrado, mais c, é igual a zero, com a diferente de 0 e c diferente de 0, admitir raízes reais, elas serão opostas.

Acompanhe outros exemplos.

a) Resolver a equação x elevado a 2 menos 1 = 8,61.

x elevado a 2 menos 1 = 8,61

x elevado a 2 = 8,61 + 1

xelevado a 2 = 9,61

x = ±

\sqrt{9, 61}

x = ±3,1

Logo, as raízes são x 1 = ‒3,1 e x 2 = 3,1.

b) Resolver a equação x elevado a 2 + 9 = 0. x elevado a 2 + 9 = 0 x elevado a 2 = ‒9

Como não existe número real que elevado ao quadrado resulte em ‒9, essa equação não tem raiz real.

Observações

▶ Usamos o símbolo ± (lemos: “mais ou menos”) para representar que algo pode assumir dois valores opostos. Por exemplo, escrevemos x = ±7 para indicar que x = ‒7 ou x = 7.

▶ As equações do 2º grau do tipo ax elevado a 2 + c = 0 apresentam sempre duas raízes reais opostas ou não têm raízes reais.

▶ As equações do 2º grau do tipo ax elevado a 2 = 0 têm sempre duas raízes reais iguais a zero.

Página 152

Quando ax elevado a 2 + bx = 0

Vamos aprender a resolver equações do 2º grau do tipo ax elevado a 2 + bx + c = 0, com a ≠ 0 e c = 0.

Considere a equação 5x elevado a 2 + 6x = 0. Ela é uma equação do 2º grau incompleta, com c = 0. Colocando x em evidência, obtemos: x ⋅ (5x + 6) = 0.

Como o produto dos fatores x e 5x + 6 é zero, pelo menos um deles é zero. Assim:

x = 0 ou 5x + 6 = 0

Resolvendo a equação 5x + 6 = 0, encontramos x =

‒ \frac{6}{5}

Logo, as raízes da equação são x₁ = 0 e x₂ =

‒ \frac{6}{5}

lustração. Menina negra, de cabelo preso, comprido e castanho e camiseta rosa. Ela fala: Toda equação do segundo grau do tipo a vezes x elevado ao quadrado, mais b vezes x, que é igual a 0, com a diferente de 0 e b diferente de 0, tem sempre duas raízes diferentes, sendo uma delas igual a zero.

Acompanhe outros exemplos.

a) Vamos resolver a equação 4y elevado a 2 + 2y = 0.

Colocando 2y em evidência, obtemos: 2y ⋅ (2y + 1) = 0

Como o produto dos fatores 2y e 2y + 1 é zero, pelo menos um deles é zero. Assim:

2y = 0 ou 2y + 1 = 0

Resolvendo essas equações, encontramos, respectivamente, y = 0 e y =

‒ \frac{1}{2}

Logo, as raízes da equação são y₁ = 0 e y₂ =

‒ \frac{1}{2}

b) Vamos determinar as raízes da equação ‒5z 2 ‒ 0,2z = 0.

Colocando z em evidência, obtemos: z ⋅ (‒5z ‒ 0,2) = 0

Como o produto dos fatores z e ‒5z ‒ 0,2 é zero, pelo menos um deles é zero. Assim:

z = 0 ou ‒5z ‒ 0,2 = 0

Resolvendo a equação ‒5z ‒ 0,2 = 0, encontramos z = ‒0,04.

Logo, as raízes da equação são z₁ = 0 e z₂ = ‒0,04.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

17 Escreva no caderno as equações a seguir na forma reduzida. Depois, resolva-as.

a) (3y ‒ 4) ⋅ (3y + 1) = 14 ‒ 9y

b) (m + 5) ⋅ (m ‒ 4) = m + 16

18 Que valores de x são raízes destas equações?

a) x 2 ‒ 100 = 0

b) 4x 2 = 81

c) (2x ‒ 1) ⋅ (x + 2) = 3x ‒ 7x 2

• O que podemos afirmar sobre as raízes dessas equações?

Determine mentalmente as raízes reais das equações a seguir.

‒ \frac{7 x^{2}}{3} = 0

x^{2} = \frac{9}{4}

c) ‒4x 2 + 2 = 2

d) 2x 2 = 1

20 Pensei em um número, elevei-o ao quadrado, subtraí 60 e obtive 840. Se pensei em um número negativo, qual é esse número?

Página 153

21 Resolva as equações a seguir no caderno.

a) 3x 2 + 15x = 0

b) 2y 2 ‒

\frac{y}{3}

= 0

c) 9 ⋅ (2n ‒ 5) ⋅ (n + 2) = 0

\frac{2 x ‒ 3}{x ‒ 6} = \frac{3 x ‒ 1}{x ‒ 2}

(x ≠ 6 e x ≠ 2)

22 Encontre as soluções das equações e, em seguida, responda à questão.

a) 5x 2 + 12x = 0

b) ‒3y 2 = 6y

\sqrt{3} x^{2}

+ x = 0

d) (m + 3) ⋅ (m ‒ 6) = ‒18

• O que essas equações têm em comum?

Hora de criar – Elabore um problema que seja resolvido por uma equação do 2º grau em que uma de suas soluções seja igual a zero. Em seguida, troque com um colega para que um resolva o problema do outro. Depois, confiram as resoluções.

24 Calcule no caderno o valor de p na equação x 2 ‒ 6x + p + 5 = 0 de modo que uma das raízes seja nula.

25 O dobro do quadrado de um número negativo adicionado ao triplo dele é igual a zero. Determine no caderno esse número.

26 Se do quadrado da idade de Luísa subtrairmos o dobro da idade dela, obteremos 10 vezes a idade de Lúcia, a irmã gêmea de Luísa. Qual é a idade de Luísa?

27 Hora de criar – Elabore no caderno um problema que possa ser resolvido por uma equação do 2º grau que tenha duas raízes reais e iguais.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Descubra o valor de x no quadrado mágico e determine o valor da soma das colunas, das linhas e das diagonais.

Lembre-se de que a soma das colunas, das linhas e das diagonais em um quadrado mágico é sempre a mesma.

Ilustração. Quadrado mágico. 9 números organizados em três linhas e três colunas. Primeira linha, primeira coluna: 2 vezes x elevado ao quadrado, menos 20. Primeira linha, segunda coluna: 3. Primeira linha, terceira coluna: x ao quadrado menos 1. Segunda linha, primeira coluna: 3 vezes x, menos 1. Segunda linha, segunda coluna: 2 vezes x, mais 2. Segunda linha, terceira coluna: 7 Terceira linha, primeira coluna: 5 Terceira linha, segunda coluna: fração; numerador: x ao quadrado; denominador: 2; fim da fração, mais 9 Terceira linha, terceira coluna: 2 vezes x.

Equações do 2º grau completas

Vamos aplicar o que foi estudado sobre fatoração e produtos notáveis para resolver algumas equações do 2º grau completas.

Quando o primeiro membro é um trinômio quadrado perfeito

Considere, por exemplo, a equação x 2 ‒ 12x + 36 = 0, que é uma equação do 2º grau completa.

Observe que o 1º membro dessa equação é um trinômio quadrado perfeito.

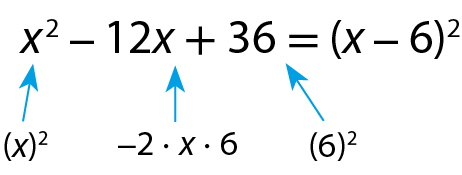
Esquema. x elevado ao quadrado, menos 12 vezes x, mais 36, que é igual a x menos 6 (entre parênteses) ao quadrado. Em que x elevado ao quadrado corresponde a x (entre parênteses) ao quadrado. Menos 12 vezes x corresponde a menos 2 vezes x, vezes 6. E 36 corresponde a 6 (entre parênteses) elevado a 2.

Assim, podemos escrever (x ‒ 6)2 = 0.

Como uma potência é nula somente se a base for zero, então, devemos ter:

x ‒ 6 = 0, ou seja, x = 6

Portanto, a equação tem duas raízes reais iguais a 6.

Ilustração. Mulher negra, de cabelo crespo, faixa verde na cabeça e camiseta roxa. Ela fala: Toda equação do segundo grau que pode ser reduzida à forma m vezes x, mais n (entre parênteses) elevado ao quadrado é igual a zero, com m e n reais, m diferente de 0, tem duas raízes reais e iguais.

Página 154

Voltemos ao problema da abertura deste capítulo, em que a academia de esportes dispõe de 36 métros quadrados para a construção do ringue de boxe, e o construtor precisa determinar a medida dos lados do tablado quadrado, que varia de 4,9 métros a 7,0 métros mais a borda de 0,6 métro.

Representando a medida do lado do ringue por x, a medida da área será representada por (x + 0,6)2.

Então, podemos escrever a equação (x + 0,6)2 = 36.

Resolvendo-a, obtemos:

x + 0,6 =

\pm \sqrt{36}

x = ‒0,6 ± 6

x1 = 5,4 e x2 = ‒6,6

Como a medida é positiva, o ringue dessa academia deve ter 5,4 metros de lado.

Ilustração. Menina negra, de cabelo castanho e camiseta amarela e colar azul. Ela diz: Pelas medidas oficiais, qual é a medida da área máxima do tablado de um ringue de boxe? E a mínima?

Acompanhe outros exemplos de resolução de equações.

a) y 2 + 2 ⋅

\sqrt{2}

⋅ y + 2 = 0 y 2 ‒ 2 ⋅ y ⋅

\sqrt{2} + {(\sqrt{2})}^{2}

= 0

{(y ‒ \sqrt{2})}^{2}

= 0 y ‒

\sqrt{2}

= 0 y =

\sqrt{2}

Duas raízes reais iguais a

\sqrt{2}

b) 4x 2 ‒ 12 ⋅ x + 9 = 0

(2x)2 ‒ 2 ⋅ 2x ⋅ 3 + 32 = 0

(2x ‒ 3)2 = 0

2x ‒ 3 = 0

x =

\frac{3}{2}

Duas raízes reais iguais a

\frac{3}{2}

\frac{z^{2}}{4}

‒ z + 1 = 0

\frac{z^{2}}{4}

{(\frac{z}{2})}^{2} ‒ 2 (\frac{z}{2})

⋅ 1 + 1elevado a 2 = 0

{(\frac{z}{2} ‒ 1)}^{2}

= 0

\frac{z}{2}

‒ 1 = 0 z = 2

Duas raízes reais iguais a 2.

Quando o 1º membro não é um trinômio quadrado perfeito

As raízes positivas de equações do 2º grau já eram determinadas pelos babilônios por volta do ano 1800 antes de Cristo Eles utilizavam seus conhecimentos de Geometria para representar a equação algébrica e, assim, resolvê-la.

Fotografia. Tábua babilônica de cor marrom com linhas e cheia de inscrições. — Tábua babilônica BM 13901 (1800 antes de Cristo). Nessa tábua há 24 problemas que envolvem equações do 2º grau.

Essa representação consistia em duas etapas: primeiro, traçavam uma figura cuja medida da área representasse o 1º membro da equação; depois, completavam a figura de modo a formar uma região quadrada. Com isso, eles conseguiam encontrar uma equação equivalente à equação inicial cujo 1º membro fosse um trinômio quadrado perfeito.

Esse método, conhecido como método de completar quadrados, também era usado pelos matemáticos árabes e hindus.

Acompanhe, por exemplo, como resolver a equação x elevado a 2 + 4x ‒ 21 = 0 aplicando esse método.

Observe que o 1º membro dessa equação não é um trinômio quadrado perfeito, mas é possível transformá-lo em um.

Página 155

Primeiro, isolamos os termos algébricos no 1º membro da equação:

x 2 + 4x ‒ 21 + 21 = 0 + 21

x 2 + 4x = 21

Em seguida, representamos os termos algébricos como figuras geométricas. Podemos, por exemplo, considerar três figuras:

• um quadrado com lado de medida x, que tem medida da área igual a x elevado a 2.

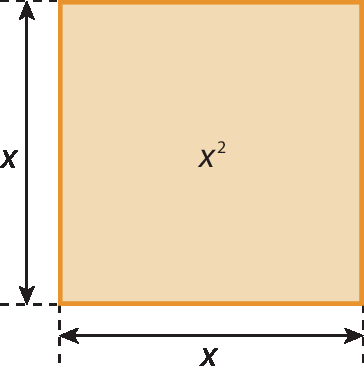
Ilustração. Quadrado laranja cujo lado mede x e a área é igual a x ao quadrado.

• dois retângulos com um lado de medida x e o outro de medida 2. Cada retângulo tem medida da área igual a 2x.

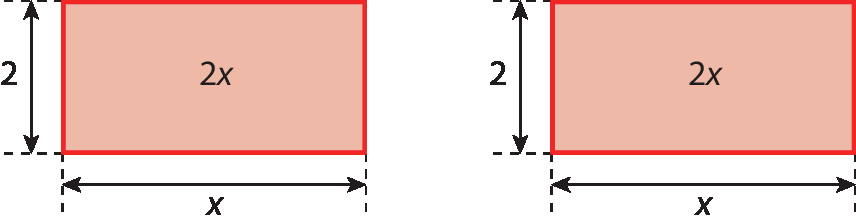
Ilustração. Dois retângulos vermelhos, lado a lado, cujas medidas dos lados são x e 2, e a medida de área é igual a 2 vezes x.

Dispomos os retângulos de modo que um dos lados de medida x de cada retângulo coincida com um dos lados do quadrado (figura 1). Depois, completamos a figura com um quadrado cuja medida do lado é 2. Assim, obtemos um quadrado maior (figura 2), formado pelas quatro figuras geométricas.

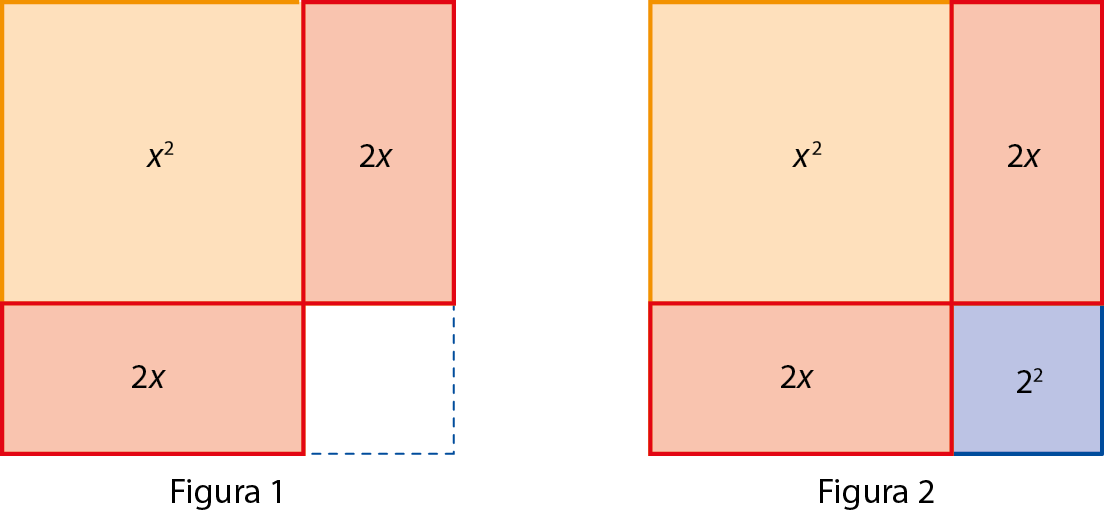
lustrações. À esquerda, figura 1, composta por um quadrado e dois retângulos iguais. Para completar um quadrado maior, há um quadrado branco, pontilhado. O quadrado interno é laranja, e sua área é x ao quadrado. Os retângulos menores são vermelhos, suas áreas são iguais a 2 vezes x. À direita, figura 2, composta por dois retângulos iguais e dois quadrados diferentes. O quadrado maior é laranja, e sua área é x ao quadrado. O quadrado menor é azul, e sua área mede 2 ao quadrado. Os retângulos menores são vermelhos, suas áreas são iguais a 2 vezes x.

Dessa fórma, para representar algebricamente a medida da área do quadrado da figura 2, devemos adicionar 2elevado a 2 a ambos os membros da equação:

x elevado a 2 + 4x + 2elevado a 2 = 21 + 2elevado a 2

Observe que a expressão do 1º membro dessa equação é um trinômio quadrado perfeito.

Fatorando esse trinômio, obtemos:

x elevado a 2 + 4x + 2elevado a 2 = (x + 2)elevado a 2

Assim, obtemos a seguinte equação do 2º grau:

(x + 2)elevado a 2 = 25

Consideramos x + 2 positivo porque é a medida do lado de um quadrado. Assim:

x + 2 = 5

x = 3

Logo, uma raiz da equação x elevado a 2 + 4x ‒ 21 = 0 é 3.

Ilustração. Homem branco, de cabelo ruivo e camisa vermelha. Ele fala: Observe que a outra raiz da equação x elevado ao quadrado, mais 4 vezes x, menos 21, igual a zero, é x igual a menos 7.

Página 156

Vamos acompanhar alguns exemplos.

Exemplo 1

Para resolver a equação x elevado a 2 ‒ 12x ‒ 13 = 0, primeiro fazemos x elevado a 2 ‒ 12x = 13. Em seguida, fazemos as representações geométricas:

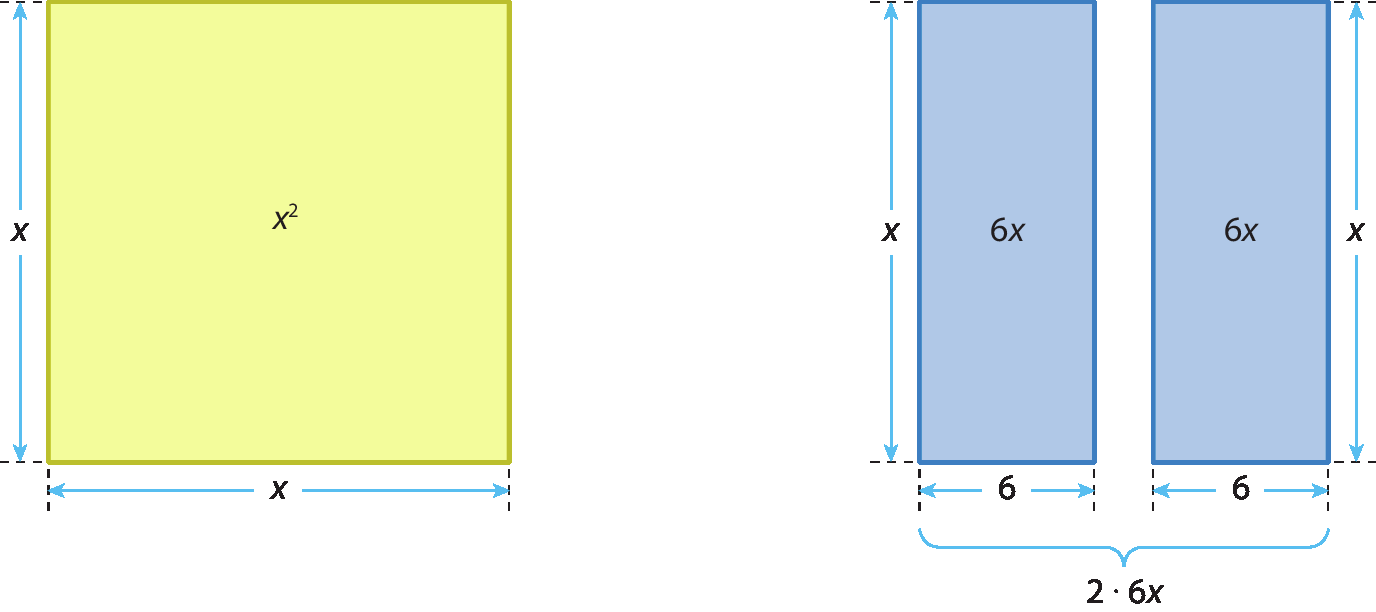
Ilustrações. À esquerda, quadrado amarelo cujos lados medem x, e a área x elevado ao quadrado. À direita, dois retângulos verticais azuis idênticos, cujos lados medem 6 e x. As áreas são iguais a 6 vezes x. Abaixo, um esquema mostra que a medida total dos dois retângulos é 2 vezes 6 vezes x.

Do quadrado de lado x, devemos tirar os dois retângulos de lados 6 e x.

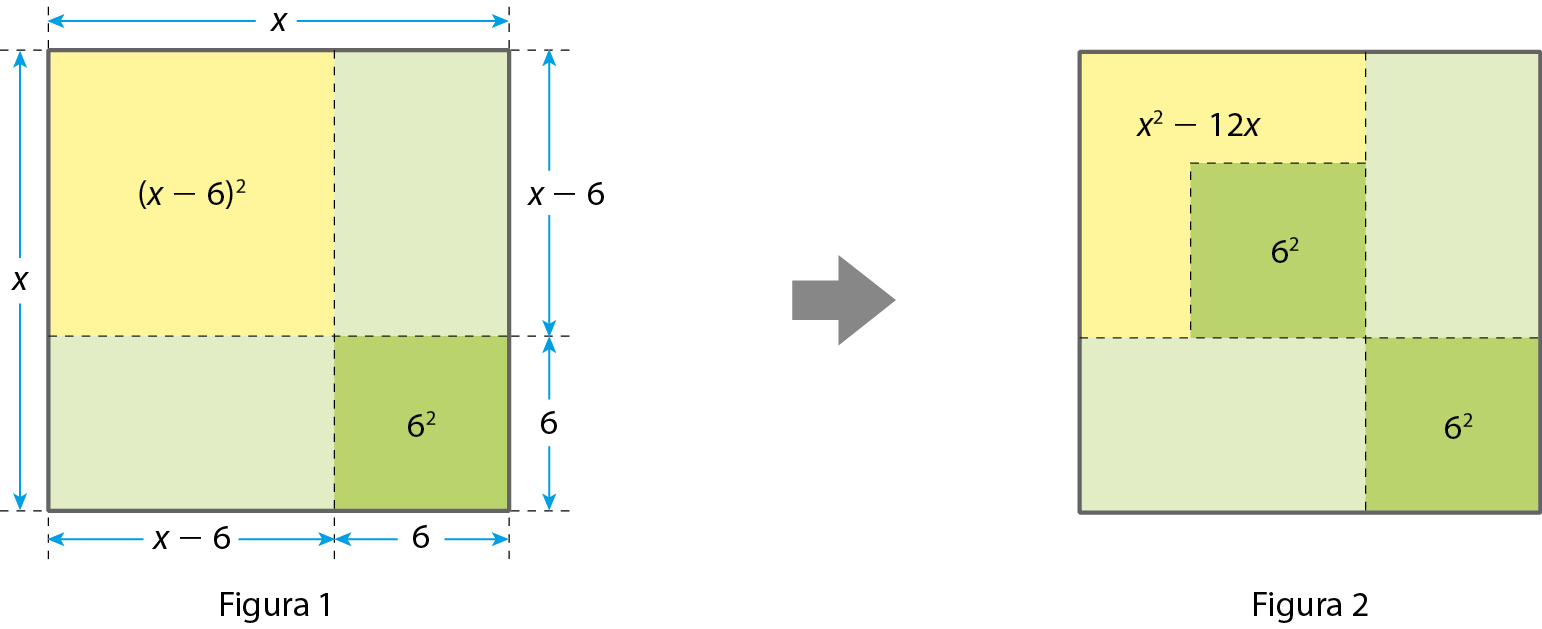
Ilustração. Figura 1, composta por quadrado amarelo, com área igual a (abre parênteses) x menos 6 (fecha parênteses) elevado ao quadrado. Ao lado, retângulo verde claro vertical, com lado maior medindo x menos 6. Abaixo do quadrado amarelo, retângulo verde claro horizontal, cujo lado maior mede x menos 6. Ao lado, quadrado verde cujo lado mede 6 e a área é igual a 6 ao quadrado. Seta para direita. Figura 2, composta da mesma forma que a anterior. A diferença entre as imagens é que, dentro do quadrado amarelo, no canto inferior direito, há um quadrado verde de área 6 elevado ao quadrado. Desta forma, o quadrado amarelo transformou-se em uma figura de 6 lados, com área igual a x ao quadrado, menos 12 vezes x.

Observe que, na figura 1, há um quadrado de lado 6 que deve ser tirado duas vezes, o que nos leva à figura 2.

O que sobra é só a parte amarela. Note, na figura 2, que, para completar o quadrado de lado x ‒ 6, devemos acrescentar um quadrado de lado 6. Isso equivale a dizer que, para obter um trinômio quadrado perfeito, devemos adicionar 62 no primeiro membro. E, para manter a igualdade, adicionar 62 no segundo membro.

x elevado a 2 ‒ 12x + 6elevado a 2 = 13 + 6elevado a 2

x elevado a 2 ‒ 12x + 36 = 13 + 36

(x ‒ 6)elevado a 2 = 49

(x ‒ 6) é positivo, pois é medida do lado de um quadrado. Assim: x ‒ 6 = 7, ou seja, x = 13.

Caso estivéssemos resolvendo a equação sem o uso de figuras, prosseguiríamos assim:

x ‒ 6 = \pm \sqrt{49}

x ‒ 6 = ±7

• Para x ‒ 6 = 7, obtemos x1 = 13.

• Para x ‒ 6 = ‒7, obtemos x₂ = ‒1.

Página 157

Exemplo 2

Vamos determinar as raízes da equação 4y elevado a 2 + 8y + 3 = 0.

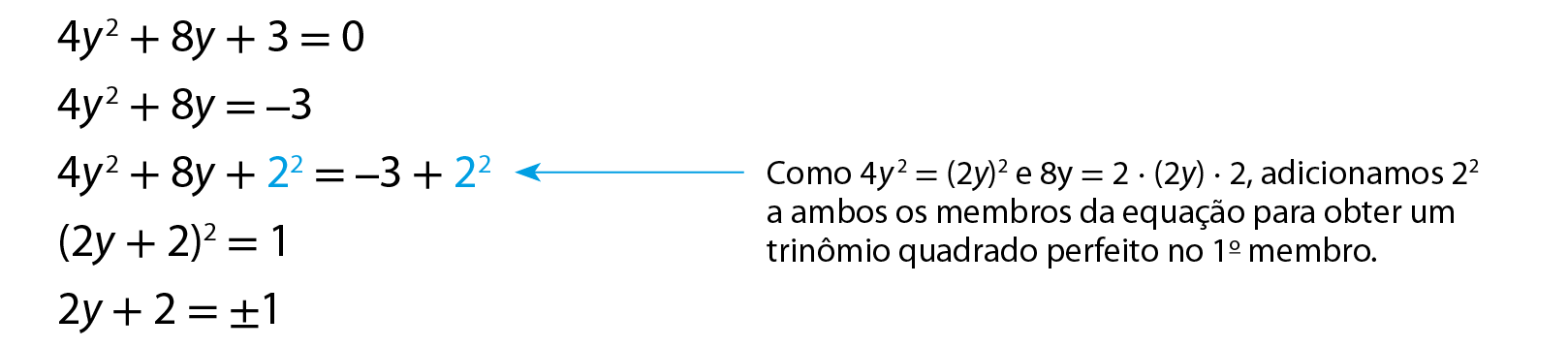
Esquema. 4 y ao quadrado, mais 8 y, mais 3, é igual a zero. Abaixo: 4 y ao quadrado, mais 8 y, é igual a menos 3. Abaixo: 4 y ao quadrado, mais 8 y, mais 2 ao quadrado, é igual a menos 3, mais 2 ao quadrado. Desta equação, uma seta indica que: Como 4 y ao quadrado é igual a, abre parêntese, 2 y, fecha parênteses, ao quadrado, e 8 y é igual a 2 vezes, abre parêntese, 2 y, fecha parêntese, vezes 2, adicionamos 2 ao quadrado a ambos os membros da equação para obter um trinômio quadrado perfeito no primeiro membro. Abaixo da equação: abre parêntese, 2 y mais 2, fecha parêntese, ao quadrado, é igual a 1. Abaixo: 2 y mais 2, é igual a mais ou menos 1.

• Para 2y + 2 = ‒1, obtemos y =

‒ \frac{3}{2}

• Para 2y + 2 = 1, obtemos y =

‒ \frac{1}{2}

Logo, as raízes da equação são

y_{1} = ‒ \frac{3}{2}

y_{2} = ‒ \frac{1}{2}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

28 Resolva no caderno cada uma das equações a seguir.

a) x elevado a 2 ‒ 14x + 49 = 0

b) 4x elevado a 2 ‒ 20x + 25 = 0

c) 4y elevado a 2 = 4y ‒ 1

d) p elevado a 2 + 6p = 16p ‒ 25

29 Nesta figura, das partes quadradas coloridas com verde, a maior tem área medindo x elevado a 2. A soma das medidas das áreas dos retângulos lilases é 8x. Determine a medida da área do quadrado menor.

Ilustração. Figura dividida em dois quadrados verdes e dois retângulos roxos. No canto superior esquerdo, quadrado verde menor. No canto superior direito, retângulo roxo. No canto inferior esquerdo, retângulo roxo, e no canto inferior direito, quadrado verde maior

30 Resolva no caderno as equações a seguir usando o método de completar quadrados.

a) x elevado a 2 + 10x + 24 = 0

b) y elevado a 2 ‒ 4y + 3 = 0

c) n elevado a 2 + 4n ‒ 12 = 0

d) r elevado a 2 ‒ 2r ‒ 3 = 0

31 Determine os valores reais de x que verificam as equações a seguir.

a) 4x elevado a 2 ‒ 12x + 5 = 0

b) 9y elevado a 2 ‒ 3y ‒ 2 = 0

c) 2n elevado a 2 + 7n + 6 = 0

d) 3x elevado a 2 + 8x ‒ 3 = 0

32 Considere três números naturais e consecutivos. O produto dos dois maiores é igual a 10 vezes o menor mais 10 unidades. Calcule no caderno a média aritmética desses três números.

33 Daqui a 6 anos, a idade de Daniela será igual ao quadrado da idade dela há 6 anos. Indique a idade atual de Daniela por x para resolver as questões que se seguem.

a) Construa no caderno um quadro com as idades de Daniela: hoje, 6 anos atrás e daqui a 6 anos.

b) Que equação traduz a situação do problema?

c) Qual é a idade atual de Daniela?

Hora de criar – Troque com um colega um problema, criado por vocês, que possa ser resolvido por uma equação do 2º grau que tenha duas raízes reais e iguais. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Leia e resolva o problema.

Um prédio é abastecido por duas caixas-d’água em fórma de cubo. A maior tem arestas internas medindo 1 métro a mais que a menor.

Conversando com uma moradora do prédio sobre a capacidade das caixas-d’água, o síndico disse:

— A diferença entre as capacidades das duas caixas é .91000 litros.

Qual é a medida, em metro, das arestas de cada uma dessas caixas-d’água?

Ilustração. Mulher branca, de cabelo ruivo, blusa vermelha e saia. Ela segura a coleira de um cachorro marrom. À frente dela, homem branco, de óculos, camisa azul clara e calça. Eles conversam

Página 158

3. A fórmula resolutiva de uma equação do 2º grau

Clique no play e acompanhe a reprodução do Áudio.

Transcrição do áudio

A fórmula é de Bhaskara?

Duração: 5:37min. Página: 158.

>> [Locutor] A fórmula é de Bhaskara?

Som de música indiana ao fundo.

>> [Narrador] Você provavelmente já ouviu falar na fórmula de Bhaskara. [Tom de questionamento] Mas você sabe quem foi Bhaskara e qual sua relação com a fórmula para a resolução das equações de segundo grau?

>> [Narrador] Para entendermos quem foi Bhaskara, vamos falar um pouco sobre a história da Matemática na Índia.

>> [Narrador] Indícios arqueológicos apontam para a existência de uma civilização de alta cultura na Índia já na época das construções das pirâmides egípcias, mas não há registros matemáticos nesse período.

>> [Narrador] Um dos textos matemáticos indianos mais antigos conhecido foi escrito por Aryabhata, no século VI depois de Cristo. Ele escreveu um pequeno texto em versos, com 123 estrofes, contendo regras de cálculo a serem utilizadas na Astronomia e na Matemática de medição. Os principais destaques dessa obra são o uso do sistema decimal e a presença de uma das primeiras tabelas de seno.

>> [Narrador] No século seguinte, Brahmagupta trabalhou sistematicamente em soluções gerais para equações quadráticas, inclusive as que envolvem situações com raízes negativas e nulas.

>> [Narrador] No final do século IX, início do século X, o matemático Sridhara escreveu trabalhos em que demonstra regras matemáticas, sem provas, descrevendo operações aritméticas e aplicações, ampliando o trabalho de Aryabhata.

>> [Narrador] Bhaskara atribui a ele a criação da regra para equações quadráticas que permite duas soluções para uma única equação.

>> [Narrador] Bhaskara Akaria, ou simplesmente Bhaskara, como o conhecemos, viveu no século XII e foi um nome importante tanto na Astronomia como na Matemática.

>> [Narrador] Em um de seus dois livros, o Vija-Ganita, Bhaskara apresentou a solução de diversas equações, em especial, as equações indeterminadas (equações com infinitas soluções), todas aplicadas à Astronomia ou a problemas comerciais.

>> [Narrador] É importante destacar que, naquela época, as soluções das equações eram dadas sempre em formato de texto, como em uma receita.

>> [Narrador] Para se resolver uma equação de segundo grau, a regra sugerida por Sridhara e citada por Bhaskara, foi: “Multiplique ambos os termos da equação pelo coeficiente do quadrado e some a eles um número igual ao quadrado do coeficiente original da incógnita. A solução desejada é a raiz quadrada disso”.

>> [Narrador] Um exemplo de problema descrito por Bhaskara: “A raiz quadrada da metade do número de abelhas de um enxame voou rumo a um jasmineiro, enquanto 8/9 do enxame permaneceu atrás. Uma abelha fêmea ficou voando em torno de um macho que se encontrava preso numa flor de lótus para a qual foi atraído por seu doce odor. Diga-me, adorável mulher, qual é o número de abelhas?”.

>> [Narrador] Na notação atual, a resolução seria: Vamos representar o número de abelhas do enxame por “2x²”. A metade desse número é x², logo, a raiz quadrada dessa metade é x, e 8/9 do número de abelhas do enxame é 16/9 de x². Portanto, a situação escrita no enunciado é representada pela equação: x mais 16/9 de x² mais 2 é igual a 2x².

>> [Narrador] Após reduzir ao mesmo denominador os dois termos da equação e simplificar, a equação transforma-se em: 18x² é igual a 16x² mais 9x mais 18, ou 2x² menos 9x menos 18 é igual a 0, e a única solução positiva é 6. Havia apenas 6 abelhas.

>> [Narrador] Sabemos que problemas envolvendo equações de segundo grau não eram novidade para os matemáticos indianos. Os primeiros registros [de equações desse tipo] datam de 1700 anos antes de Cristo, na Mesopotâmia.

>> [Narrador] Os matemáticos gregos, por volta de 500 anos antes de Cristo, resolviam equações desse tipo com o auxílio de métodos geométricos, assim como os árabes, que utilizavam o método de completar quadrados, já no século IV depois de Cristo.

>> [Narrador] A grande contribuição dos matemáticos indianos para essa área foi a resolução de equações baseada na extração de raízes quadradas.

>> [Narrador] Esse método foi posteriormente aprimorado por François Viète, já no século XVII, culminando na fórmula que conhecemos hoje. Aparentemente, o Brasil é o único país a atribuir a fórmula de resolução da equação de segundo grau ao matemático Bhaskara.

Som de música indiana.

Vinheta.

Créditos

Todos os áudios inseridos nesse conteúdo são da Free Sound.

Assim como os árabes, os matemáticos indianos – entre eles Bhaskara – também se interessavam pelas equações do 2º grau. Embora não aplicassem exatamente as fórmulas que conhecemos hoje, o processo de resolução dessas equações com base em regras, usado por eles, era bastante próximo dos procedimentos atuais.

Vamos agora generalizar o método de completar quadrados obtendo uma fórmula para resolver equações do 2º grau.

Considere a equação completa do 2º grau ax 2 + bx + c = 0, com coeficientes reais a, b e c, e a ≠ 0.

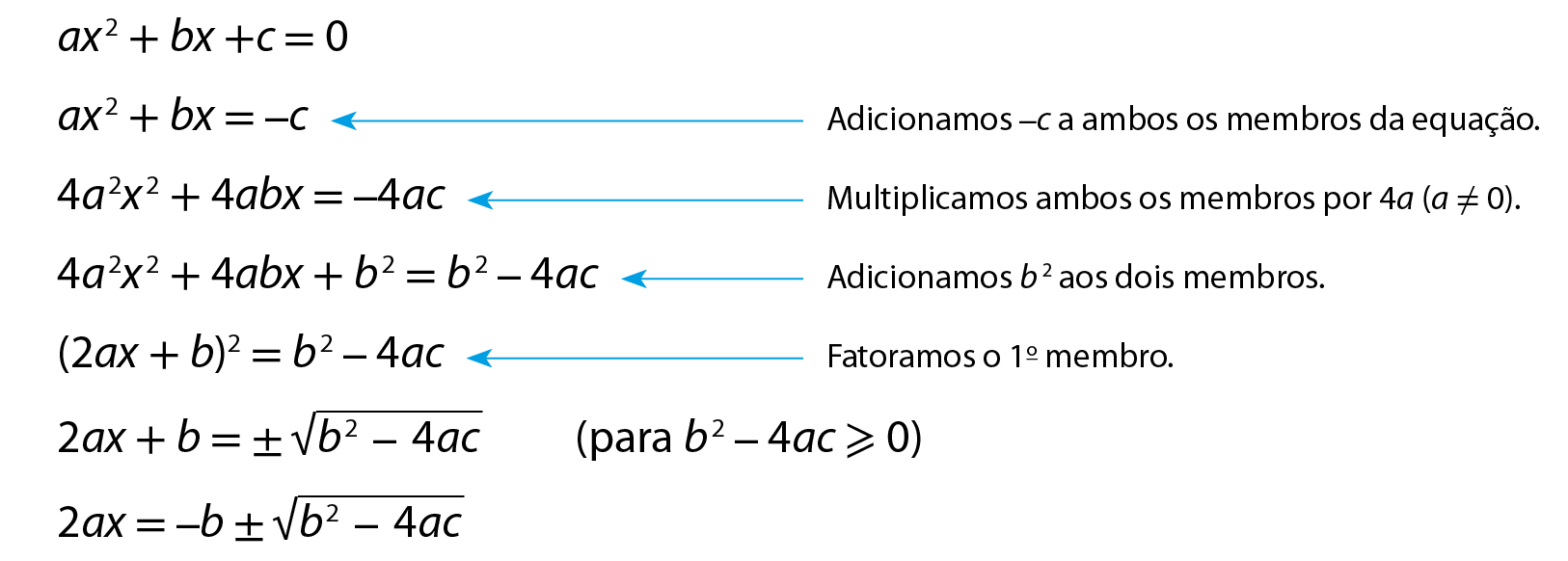
Esquema. a x elevado ao quadrado, mais b x, mais c, é igual a zero. Abaixo: a x elevado ao quadrado, mais b x, é igual a menos c. Uma seta ligada a essa equação diz: Adicionamos menos c a ambos os membros da equação. Abaixo da equação: 4 a ao quadrado x ao quadrado, mais 4 a b x, é igual a menos 4 a c. Uma seta ligada a essa equação diz: Multiplicamos ambos os membros por 4 a, sendo a diferente de zero. Abaixo da equação: 4 a ao quadrado x ao quadrado, mais 4 a b x, mais b ao quadrado, é igual à, b ao quadrado, menos 4 a c. Uma seta ligada a essa equação diz: Adicionamos b ao quadrado aos dois membros. Abaixo da equação: abre parêntese, 2 a x, mais b, fecha parêntese, ao quadrado, é igual à, b ao quadrado, menos 4 a c. Uma seta ligada a essa equação diz: Fatoramos o primeiro membro. Abaixo da equação: 2 a x, mais b, é igual a mais ou menos raiz quadrada de b ao quadrado, menos 4 a c, fim da raiz. Um texto, entre parênteses, ligado a essa equação diz: para b ao quadrado, menos 4 a c, maior que ou igual a zero. Abaixo da equação: 2 a x, é igual a menos b mais ou menos raiz quadrada de b elevado ao quadrado, menos 4 a c, fim da raiz.

Isolando x, obtemos a fórmula resolutiva:

x = \frac{‒ b \pm \sqrt{b^{2} ‒ 4 a c}}{2 a}

Na fórmula resolutiva, a expressão b2 ‒ 4ac é chamada de discriminante da equação, que geralmente é representado pela letra grega Δ (lemos: “delta”). Então:

Δ = b2 ‒ 4ac

dêsse modo, se Δ ⩾ 0, podemos escrever a fórmula resolutiva da seguinte maneira:

x = \frac{‒ b \pm \sqrt{Δ}}{2 a}

Observação

▶ Quando Δ < 0, a equação não admite raízes reais.

Acompanhe um exemplo.

Vamos calcular a medida da altura do triângulo a seguir, cuja área a mede 10,5 centímetros quadrados.

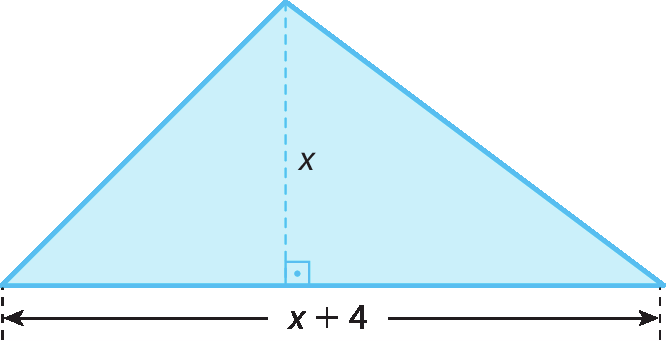
Ilustração. Triângulo com medida do lado maior x mais 4. Uma reta vertical pontilhada, que indica a altura do triângulo, forma um ângulo de 90 graus em relação ao lado maior e mede x.

A = \frac{medida da base \times medida da altura}{2}

10, 5 = \frac{(x + 4) x}{2} = \frac{x (x + 4)}{2}

Página 159

2 \cdot \frac{x (x + 4)}{2} = 2 \cdot 10, 5

x(x + 4) = 2 ⋅ 10,5

x elevado a 2 + 4x = 21

x elevado a 2 + 4x ‒ 21 = 0

Nessa equação, a = 1, b = 4 e c = ‒21.

Resolvendo a equação, obtemos:

Δ = b elevado a 2 ‒ 4ac

Δ = 42 ‒ 4 ⋅ 1 ⋅ (‒21) = 16 + 84 = 100

x = \frac{‒ b \pm \sqrt{Δ}}{2 a}

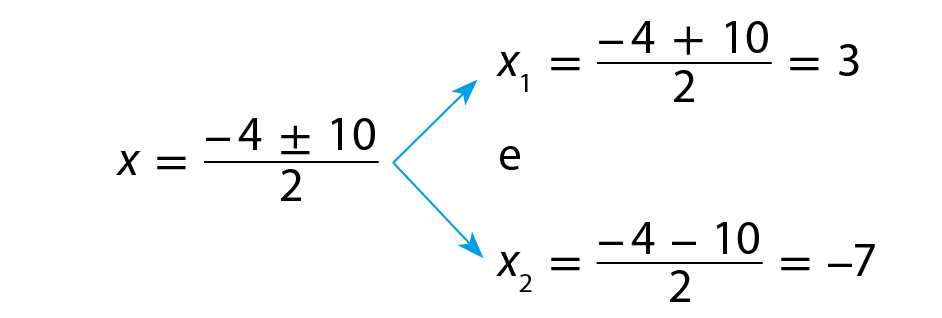
Esquema. x é igual a fração; numerador: menos 4 mais ou menos 10; denominador: 2; fim da fração. Uma seta indica que a raiz x1 é igual a fração; numerador: menos 4 mais 10; denominador: 2; fim da fração, que é igual a 3. Outra seta indica que a raiz x2 é igual a fração; numerador: menos 4 menos 10; denominador: 2; fim da fração, que é igual a menos sete.

As raízes da equação são x₁ = 3 e x₂ = ‒7.

Como x representa a medida de comprimento, a raiz ‒7 não é solução. Logo, x = 3.

Observação

▶ Substituindo cada um dos valores encontrados na equação x elevado a 2 + 4x ‒ 21 = 0, obtemos igualdades numéricas verdadeiras. Por exemplo, para x = ‒7, obtemos:

(‒7)2 + 4 ⋅ (‒7) ‒ 21 = 0

49 ‒ 28 ‒ 21 = 0

49 ‒ 49 = 0 (verdadeira)

Acompanhe outros exemplos de resolução de equações.

a) x elevado a 2 + 8x + 16 = 0

Indicamos: a = 1, b = 8 e c = 16

Δ = b elevado a 2 ‒ 4ac

Δ = (8)2 ‒ 4 ⋅ (1) ⋅ (16)

Δ = 64 ‒ 64 = 0

Como Δ = 0, a equação tem duas raízes reais e iguais dadas por

x = \frac{‒ b}{2 a}

. Então:

x₁ = x₂ =

\frac{‒ (+ 8)}{2} = ‒ 4

b) 3x2 ‒ 2x + 1 = 0 Indicamos: a = 3, b = ‒2 e c = 1 Δ = b 2 ‒ 4ac Δ = (‒2)2 ‒ 4 ⋅ (3) ⋅ (1) Δ = 4 ‒ 12 Δ = ‒8 < 0

Como os números negativos não têm raiz quadrada real, dizemos que a equação não admite raízes reais.

c) 4x 2 ‒ 12x + 7 = 0

Indicamos: a = 4, b = ‒12 e c = 7

Δ = b 2 ‒ 4ac ⇒ Δ = (‒12)2 ‒ 4 ⋅ (4) ⋅ (7) = 144 ‒ 112 = 32

\sqrt{Δ} = \sqrt{32} = \sqrt{2^{5}} = 4 \sqrt{2}

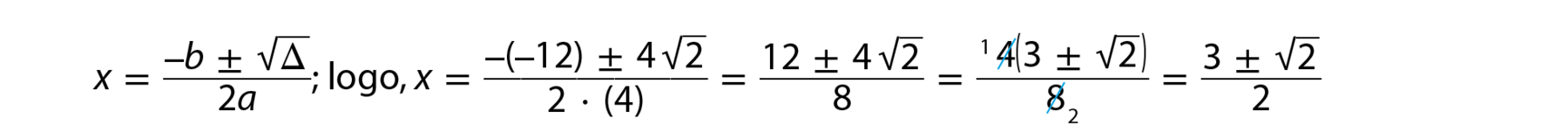
Portanto, as raízes são

x_{1} = \frac{3 ‒ \sqrt{2}}{2} e x_{2} = \frac{3 + \sqrt{2}}{2}

Página 160

PARA SABER MAIS

Número de ouro

No texto Uma razão de ouro, na seção Para saber mais do capítulo 4 (página 95), percebemos que, se retirarmos o maior quadrado possível de um retângulo áureo, o retângulo restante também será um retângulo áureo, isto é, a proporção entre os lados se manterá.

Observe a figura a seguir.

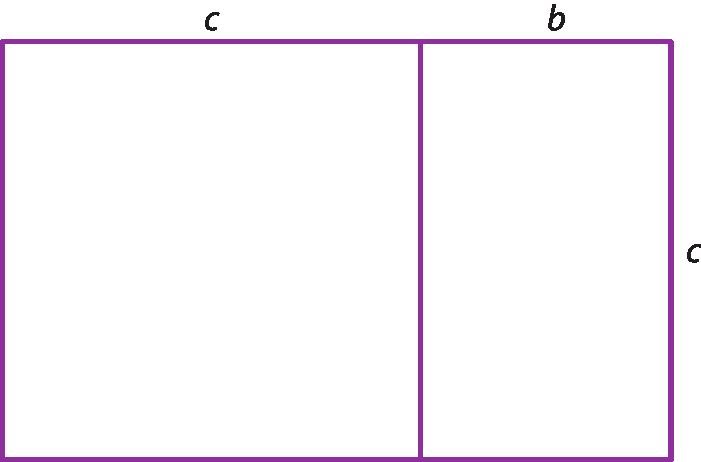
Ilustração. Retângulo dividido na vertical em um quadrado (à esquerda) e outro retângulo menor (à direita). A medida do lado quadrado é c. O retângulo tem medidas b (lado menor) e c (lado maior).

\frac{medida largura}{m e d i d a d a a l t u r a} = \frac{c + b}{c} = \frac{c}{b}

Fazendo c = 1, obtemos:

\frac{1 + b}{1} = \frac{1}{b}

b 2 + b ‒ 1 = 0

Agora, podemos resolver a equação do 2º grau obtida. Os coeficientes são 1, 1 e ‒1.

Δ = 12 ‒ 4 ⋅ 1 ⋅ (‒1) = 1 + 4 = 5

\sqrt{Δ} = \sqrt{5}

b = \frac{‒ 1 \pm \sqrt{5}}{2}

Como a medida do lado é positiva, então

b = \frac{\sqrt{5} ‒ 1}{2}

Logo, o número de ouro, que fascinou os matemáticos gregos, instrumentou arquitetos do Partenon (templo da deusa Atena) e inspirou mestres da pintura, como Leonardo Da Vinti, é dado por:

\frac{medida da largura}{medida da a l t u r a} = \frac{1 + b}{1} = 1 + \frac{\sqrt{5} ‒ 1}{2} ≃ 1, 618

A partir de um quadrado, podemos construir um retângulo áureo com régua e compasso. Observe.

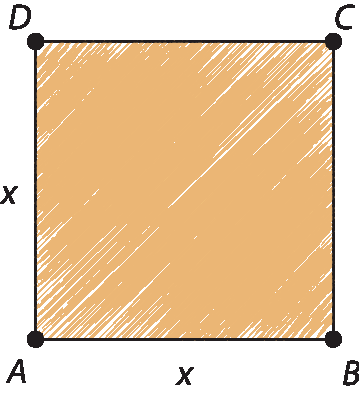
Ilustração. Quadrado ABCD cujo lado mede x. — Construir um quadrado de lado x.

Construir um quadrado de lado x.

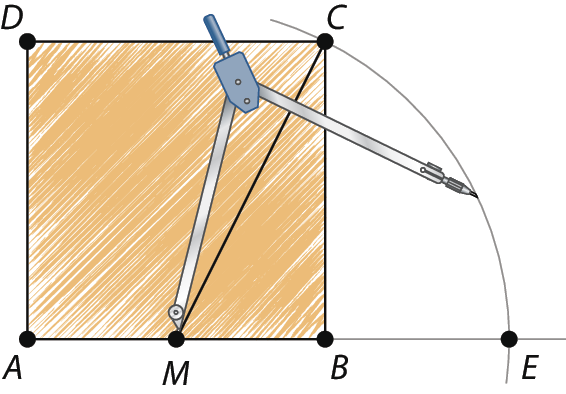
Ilustração. Quadrado ABCD. De C, reta diagonal até o ponto M, ponto médio de AB. Compasso aberto em M vai até ponto E (externo ao quadrado) e traça arco CE

Obter o ponto M, médio de

\overline{A B} .

Com centro M e raio MC, traçar arco obtendo o ponto E em

\overset{\leftrightarrow}{A B} .

Página 161

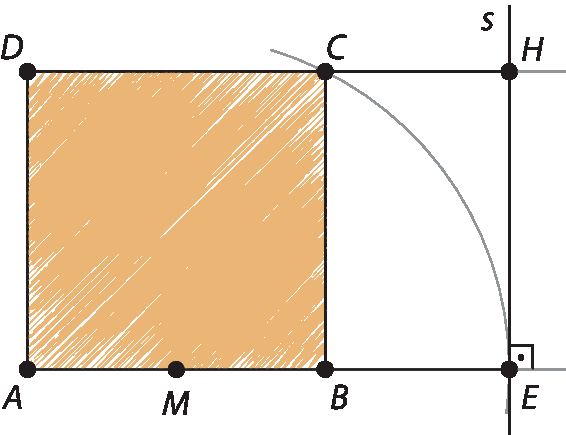
Ilustração. Quadrado ABCD. Ponto M entre AB. Arco CE traçado. Ponto E sobre reta AB e ponto H sobre reta DC. Reta s sobre H e E.

Por E, traçar a reta s, perpendicular a

\overset{\leftrightarrow}{A B}

. Na intersecção de

\overset{\leftrightarrow}{D C}

com s, indicar o ponto H.

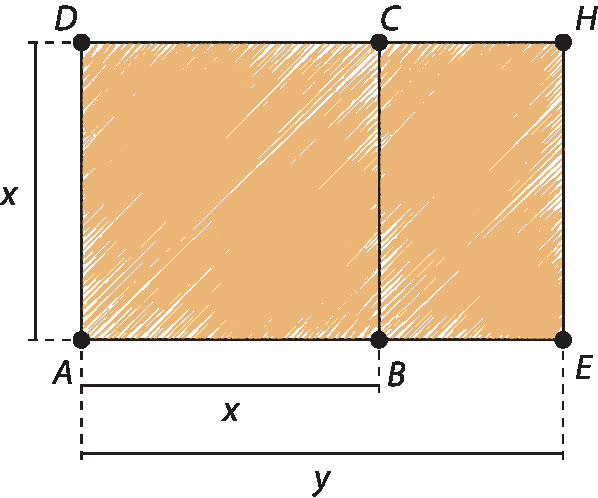
Ilustração. Quadrado ABCD com medida x por x. Ao lado, retângulo CBHE. medida de A até E é y.

O retângulo á é agá dê é um retângulo áureo.

\frac{A E}{A B} = \frac{E H}{B E} = \frac{1 + \sqrt{5}}{2} ≃ 1, 618

Agora é com você!

FAÇA A ATIVIDADE NO CADERNO

Seguindo o procedimento anterior, construa um retângulo áureo a partir de um quadrado de lado medindo 6 centímetros. Depois, com a régua, obtenha as medidas A Ê e bê ê.

Com essas medidas, verifique que

\frac{A E}{A B} = \frac{E H}{B E} ≃ 1,618 .

(Ao usar o compasso, atenção para não se machucar com a ponta-sêca!)

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

35 Encontre as raízes reais das equações.

a) 3x 2 ‒ 7x + 4 = 0

b) 2m 2 ‒ m ‒ 6 = 0

c) ‒x 2 + 3x + 10 = 0

d) y 2 + 8y ‒ 4 = 0

e) 9y 2 ‒ 12y + 4 = 0

f) 5x 2 + 3x + 5 = 0

36 Escreva no caderno as equações a seguir na fórma reduzida e resolva-as.

a) x(x + 3) = 5x + 15

\frac{3 y + 1}{2} = \frac{y^{2} ‒ 1}{3}

c) (x + 4)2 = 9x + 22

d) (x ‒ 1)2 + 3x = x + 26

e) (x + 4) ⋅ (x ‒ 1) = 5x + 20

37 Na figura, a bê cê dê é um quadrado. As partes lilases também são quadrados.

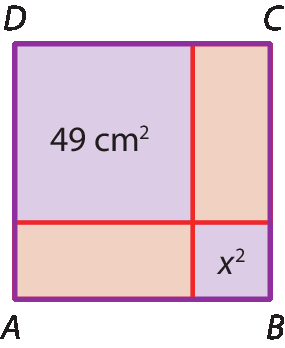
Ilustração. Figura ABCD. Composta por dois quadrados roxos e dois retângulos rosas. No canto superior esquerdo, quadrado (maior) de área 49 centímetros quadrados. Do lado direito, retângulo vertical. No canto inferior direito, quadrado (menor) de área x ao quadrado. Do lado esquerdo, retângulo horizontal.

a) Escreva no caderno a expressão que representa a medida da área da figura.

b) Sabendo que a área do quadrado a bê cê dê mede 100 centímetros quadrados, determine a medida do lado do menor quadrado dessa figura.

38 Escreva no caderno a equação do 2º grau que expressa as descrições a seguir.

a) A metade da soma de um número com o seu quadrado é igual a 210.

b) O quadrado de um número aumentado de seus

\frac{3}{5}

é igual a 28.

• Encontre as raízes reais das equações dos itens a e b.

39 A diferença entre a terça parte do quadrado de um número e o próprio número é 60. Qual é o triplo dêsse número?

40 Uma folha quadrada de cartolina mede x centímetro de lado. Recorta-se dessa folha um retângulo que mede x centímetro de comprimento e 15 centímetros de largura. A parte que restou da folha é um retângulo de área medindo .1750 centímetros quadrados. Encontre a medida da área da folha de cartolina.

Página 162

41 A base de um retângulo mede 5 métros a mais que sua altura. A área do retângulo mede 300 métros quadrados. Calcule no caderno a medida do perímetro dêsse retângulo.

42 Sabemos que o número de diagonais de um polígono convexo é determinado pela fórmula

d = \frac{n \cdot (n ‒ 3)}{2}

, na qual d é o número de diagonais e n, o número de lados do polígono. Assim, escreva no caderno o nome do polígono que tem 35 diagonais.

43 Considere a figura composta de retângulos.

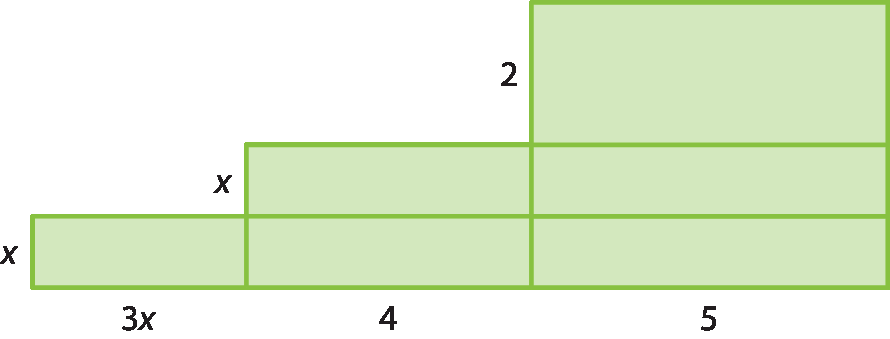
Ilustração. Figura composta por três retângulos verdes na parte inferior com lados de medidas: x e 3 x; x e 4; e x e 5. Acima, dois retângulos verdes com lados medindo x e 4, e x e 5. Na parte superior, à direita, retângulo verde com lados de medidas 2 e 5.

a) Qual é a expressão que representa a medida da área dessa figura?

b) Se a medida da área for 31, qual será a equação correspondente?

c) Quais são as raízes da equação encontrada?

d) Qual dessas raízes será solução, se a área medir 31?

44 Considere a figura.

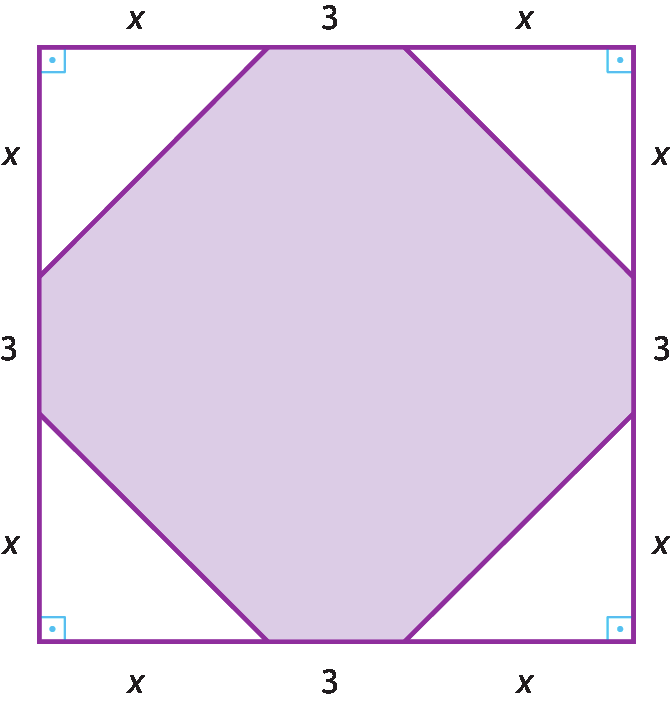
Ilustração. Quadrado, cujos lados medem x mais 3, mais x. Dentro do quadrado, há um octógono roxo, em que quatro lados coincidem com a medida 3 do quadrado, e os outros quatro lados são hipotenusas dos quatro triângulos retângulos de catetos medindo x.

a) Determine a expressão que representa a medida da área lilás da figura.

b) Indique o valor de x para que essa área meça 119.

45 Contornando-se um quadrado com uma faixa de 2 centímetros de largura, obtém-se um novo quadrado medindo 56,25 centímetros quadrados de área. Qual é a medida do lado do primeiro quadrado?

46 (Vunéspi) Corta-se um pedaço de arame de 12 decímetros em duas partes e constrói-se, com cada uma delas, um quadrado. Se a soma das medidas das áreas é 5 decímetros quadrados, determine a que distância de uma das extremidades do arame foi feito o corte.

47 Para que valor de x o triângulo a seguir tem 95 centímetros quadrados de medida de área?

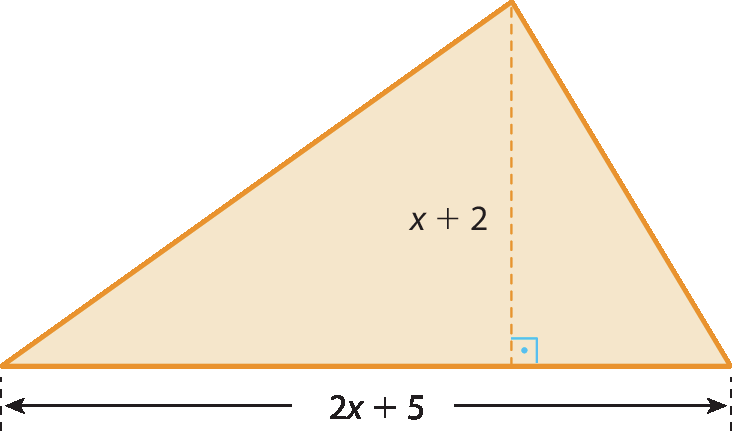
Ilustração. Triângulo com base medindo 2 x mais 5, e altura (relativa a essa base) medindo x mais 2.

48 Sueli gosta de inventar problemas de Matemática para suas amigas. Certo dia, ela escreveu um problema em uma folha de papel e entregou-o para Marlene resolver.

Ilustração. Caderno espiral com texto escrito: O dobro do quadrado de certo número subtraído do quádruplo desse número e adicionado a 13 é igual a 10. Determine uma equação que represente essa situação.

Resolva o problema que Sueli inventou.

49 Considere as equações do exercício 35. Para cada item de a a ê, calcule no caderno as seis razões possíveis entre os coeficientes das equações. Depois, calcule:

a) a soma das raízes e compare-a com as razões obtidas;

b) o produto das raízes e compare-o com as razões obtidas.

• Há alguma relação entre o oposto da soma das raízes e alguma das razões obtidas?

• Há alguma relação entre o produto das raízes e alguma das razões obtidas?

Hora de criar – Troque com um colega um problema, criado individualmente por vocês, que se possa resolver por uma equação do 2º grau. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Página 163

4. Estudando as raízes de uma equação do 2º grau

Analisando a fórmula resolutiva das equações do 2º grau, podemos verificar se uma equação tem ou não raízes reais e obter uma relação entre os coeficientes dessa equação e suas raízes.

• Uma equação do 2º grau admite duas raízes reais e diferentes se, e somente se, Δ > 0. Nesse caso, as raízes são dadas por:

x_{1} = \frac{‒ b + \sqrt{Δ}}{2 a}

x_{2} = \frac{‒ b ‒ \sqrt{Δ}}{2 a}

• Uma equação do 2º grau admite duas raízes reais e iguais se, e somente se, Δ = 0. Nesse caso, as raízes são dadas por:

x_{1} = x_{2} = \frac{‒ b}{2 a}

• Uma equação do 2º grau não admite raízes reais se, e somente se, Δ < 0.

Acompanhe a resolução dos exemplos a seguir.

a) Observe como Gláucia determinou o valor de k para que a equação x2 ‒ 8x + k = 0 tenha duas raízes reais e diferentes.

Ilustração. Menina de cabelo castanho, camisa branca e calça jeans ao lado de um quadro de giz. Ao lado da menina, homem branco de cabelo castanho, camiseta amarela, calça jeans e jaleco. Ela fala para ele: Como queremos que a equação do segundo grau tenha duas raízes reais e diferentes, escrevemos a condição delta maior que 0. No quadro de giz, as informações: Temos: Primeira linha: a é igual a 1, b é igual a menos 8 e c é igual a k. Segunda linha: b ao quadrado, menos 4 a c, é maior que 0. Terceira linha: (abre parênteses) menos 8 (fecha parênteses) ao quadrado, menos 4 vezes (abre parênteses) 1 (fecha parênteses), vezes (abre parênteses) k (fecha parênteses), é maior que 0. Quarta linha: 64 menos 4 k é maior que 0. Quinta linha: menos 4 k é maior que menos 64. Sexta linha: 4 k sobre menos 4, é menor que, 64 sobre menos 4. Sétima linha: k é menor que 16.

Observação

▶ Podemos substituir valores possíveis de k na equação para verificar se o valor de Δ é positivo. Observe.

• Para k = 0, obtemos: x 2 ‒ 8x = 0 Δ = 64 ‒ 4 ⋅ 1 ⋅ 0 Δ = 64 > 0

• Para k = 16, obtemos: x 2 ‒ 8x + 16 = 0 Δ = 64 ‒ 4 ⋅ 1 ⋅ 16 Δ = 0

• Para k = 20, obtemos: x 2 ‒ 8x + 20 = 0 Δ = 64 ‒ 4 ⋅ 1 ⋅ 20 Δ = ‒16 < 0

Esse procedimento não resolve a questão proposta e serve apenas para verificar valores particulares.

Página 164

b) Vamos determinar o valor de n para que a equação x 2 ‒ 5x + n = 0 tenha duas raízes reais e iguais.

Como queremos que a equação do 2º grau admita duas raízes reais e iguais, devemos impor a condição Δ = 0.

Assim: a = 1, b = ‒5 e c = n

Δ = b2 ‒ 4ac = 0

(‒5)2 ‒ 4 ⋅ (1) ⋅ (n) = 0

25 ‒ 4n = 0

4n = 25

n = \frac{25}{4}

c) Vamos determinar o valor de m na equação 3x 2 ‒ 7x + 2m = 0 para que não existam raízes reais.

Como queremos que a equação do 2º grau não admita raízes reais, devemos impor a condição Δ < 0.

Assim: a = 3, b = ‒7 e c = 2m

Δ = b2 ‒ 4ac < 0

(‒7)2 ‒ 4 ⋅ (3) ⋅ (2m) < 0

49 ‒ 24m < 0

24m > 49

m > \frac{49}{24}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

51 Dada a equação 2x 2 + 3x + p = 0, determine no caderno:

a) o valor de p para que as raízes sejam reais e iguais;

b) as raízes para o valor de p encontrado no item anterior;

c) o valor de p para que uma das raízes seja igual a zero;

d) o valor de p para que uma das raízes seja 2;

e) o valor de p para que a equação não admita raízes reais.

52 Para que valores de k a equação

2x 2 + 4x + 5k = 0 tem raízes reais e diferentes?

53 Determine no caderno o valor de k na equação x 2 ‒ kx + 9 = 0 para que as raízes sejam reais e iguais.

54 Determine no caderno o valor de p na equação x 2 ‒ ( p + 5)x + 36 = 0 para que as raízes sejam reais e iguais.

55 Considere a equação 9x 2 + 12x + 2m = 0. Para que valores de m essa equação:

a) não admite raízes reais?

b) tem duas raízes reais e iguais?

c) tem duas raízes reais e diferentes?

d) tem o número 0,2 como raiz?

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Considere o exercício 55.

Ilustração. Menino negro, de cabelo crespo preto, óculos de grau e camiseta verde e amarela. Ele escreve em um caderno sobre uma mesa. Sobre a mesa, além do caderno está uma caneta, uma borracha e um estojo.
Ele pensa: 9 x ao quadrado, mais 12 x, mais 2 m é igual a zero. Se m é igual a 2,5…? Se m é igual a 1,8…?

O que podemos concluir sobre as raízes da equação:

• quando m = 2,5?

• quando m = 1,8?

Página 165

Relações de Girard

No início do século dezessete, houve grande interesse pelos estudos matemáticos em toda a Europa Ocidental. Muitas pesquisas foram feitas para encontrar soluções às diversas equações e estabelecer relações entre seus coeficientes e suas raízes. Porém, esses estudos eram limitados porque os matemáticos da época não consideravam as raízes negativas.

Em 1629, foi publicado o livro Invention nouvelle en l’algèbre (Novas invenções em álgebra), do francês Albert Girard (1595 a 1632). Nesse livro, Girard demonstra as relações que há entre as raízes e os coeficientes de uma equação, admitindo a existência das raízes negativas.

Vamos acompanhar, agora, como aplicar essas relações em uma equação do 2º grau.

Consideremos a equação do 2º grau ax 2 + bx + c = 0, sendo x₁ e x₂ suas raízes.

Vamos estabelecer as relações de Girard entre essas raízes e os coeficientes a, b e c dessa equação.

Sabemos que:

x_{1} = \frac{‒ b + \sqrt{Δ}}{2 a}

x_{2} = \frac{‒ b ‒ \sqrt{Δ}}{2 a}

(com Δ ⩾ 0)

1ª relação: soma das raízes

Considerando S a soma das raízes de uma equação do 2º grau, podemos verificar que

S = \frac{‒ b}{a}

De fato:

x_{1} + x_{2} = \frac{‒ b + \sqrt{Δ}}{2 a} + \frac{‒ b ‒ \sqrt{Δ}}{2 a} = \frac{‒ b + \sqrt{Δ} ‒ b ‒ \sqrt{Δ}}{2 a} = \frac{‒ 2 b}{2 a} = \frac{‒ b}{a}

Então:

x_{1} + x_{2} = \frac{‒ b}{a} o u S = \frac{‒ b}{a}

2ª relação: produto das raízes

Indicando por P o produto das raízes de uma equação do 2º grau, podemos verificar que P =

\frac{c}{a}

De fato:

x_{1} \cdot x_{2} = (\frac{‒ b + \sqrt{Δ}}{2 a}) \cdot (\frac{‒ b ‒ \sqrt{Δ}}{2 a}) = \frac{{(‒ b)}^{2} ‒ {(\sqrt{Δ})}^{2}}{4 a^{2}} = \frac{b^{2} ‒ Δ}{4 a^{2}} =

Esquema. Continuação da linha anterior... é igual a fração; numerador: b ao quadrado menos (abre parênteses) b ao quadrado, menos 4 a c (fecha parênteses); denominador: 4 a ao quadrado; fim da fração, é igual a fração; numerador: b ao quadrado (cortado) menos b ao quadrado (cortado), mais 4 a c; denominador: 4 a ao quadrado; fim da fração, é igual a fração; numerador: 4 a c; denominador: 4 a ao quadrado; fim da fração, que é igual a fração; numerador: c; denominador: a; fim da fração.

Então:

x_{1} \cdot x_{2} = \frac{c}{a} o u P = \frac{c}{a}

Página 166

• Exemplos

a) Vamos determinar a soma e o produto das raízes da equação 3x 2 ‒ 7x + 2 = 0. Os coeficientes da equação são: a = 3, b = ‒7 e c = 2. Usando a relação

S = x_{1} + x_{2} = ‒ \frac{b}{a}

para encontrar a soma das raízes, consideramos:

S = x_{1} + x_{2} = ‒ \frac{b}{a} = \frac{‒ (‒ 7)}{3} = \frac{7}{3}

Usando a relação

P = x_{1} \cdot x_{2} = \frac{c}{a}

para encontrar o produto das raízes, consideramos:

P = x_{1} \cdot x_{2} = \frac{c}{a} = \frac{2}{3}

Portanto, a soma das raízes é

\frac{7}{3}

e o produto é

\frac{2}{3}

Ilustração. Mulher branca, de cabelo castanho, camisa rosa e colete azul.Ela fala: Para verificar a validade das respostas encontradas, podemos calcular as raízes da equação e comprovar se a soma e o produto são iguais aos valores indicados

b) Vamos determinar o valor de k, com k ≠ 0, na equação kx 2 ‒ 22x + 20 = 0 para que a soma das raízes seja

\frac{11}{3}

. Assim: a = k, b = ‒22 e c = 20

Esquema. x 1 mais x 2 é igual 11 sobre 3. Uma chave mostra que x 1 mais x 2 corresponde à fração menos b sobre a, que é igual a 11 sobre 3.

\frac{‒ (‒ 22)}{k} = \frac{11}{3}

\frac{22}{k} = \frac{11}{3}

11k = 66

\frac{11 k}{11} = \frac{66}{11}

Portanto, k = 6.

c) Vamos determinar o valor de p, com p ≠ 0, na equação px 2 ‒ 5x + (p ‒ 5) = 0 para que o produto das raízes seja

\frac{1}{6}

. Assim: a = p, b = ‒5 e c = p ‒ 5

Esquema. x 1 vezes x 2 é igual 1 sobre 6. Uma chave mostra que x 1 vezes x 2 corresponde à fração c sobre a, que é igual a 1 sobre 6.

\frac{p ‒ 5}{p} = \frac{1}{6}

6 ⋅ (p ‒ 5) = p 6p ‒ 30 = p 5p = 30

Portanto, p = 6.

d) Vamos calcular o valor de k na equação x 2 ‒ 12x + k = 0 para que uma das raízes seja o dobro da outra. Indicando as raízes dessa equação por m e n, obtemos:

\{\begin{cases} m + n = \frac{‒ b}{a} = \frac{‒ (‒ 12)}{1} = 12 \\ m \cdot n = \frac{c}{a} = \frac{k}{1} = k \end{cases}

\{\begin{cases} m + n = 12 \\ m \cdot n = k \end{cases}

De acordo com a condição do problema, m = 2n. Primeiro, vamos resolver o sistema:

\{\begin{cases} m + n = 12 \\ m = 2 n \end{cases}

Página 167

Substituindo m por 2n na equação m + n = 12, obtemos:

2n + n = 12

n = 4

Como m = 2n e n = 4, então: m = 8.

Mas k = m ⋅ n, então: k = 8 ⋅ 4 = 32.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

56 Considere x1 e x2 as raízes da equação x 2 ‒ 6x + 5 = 0. Sem resolver a equação, determine no caderno o que se pede em cada item.

a) x1 + x2

b) x1 ⋅ x2

57 Em cada caso, determine no caderno a soma S e o produto P das raízes das equações e calcule as raízes.

a) x 2 ‒ 8x + 15 = 0

b) x 2 + 2x ‒ 3 = 0

c) 5x 2 + 21x + 4 = 0

d) x 2 + 7x + 12 = 0

e) 3x 2 ‒ 6x = 0

f) x 2 ‒ 144 = 0

58 Se m e n são raízes da equação x 2 ‒ 9x + 20 = 0, determine no caderno o valor da expressão mn(m + n).

59 Determine no caderno o valor de m na equação 4x 2 ‒ (m ‒ 2) ⋅ x + 3 = 0 para que a soma das raízes seja

\frac{3}{4}

60 Calcule no caderno o valor de m na equação (m + 10) ⋅ x 2 + 21x + 5 = 0 para que a soma das raízes seja

‒ \frac{7}{6}

61 Determine no caderno o valor de p na equação 6x 2 ‒ 11x + ( p ‒ 1) = 0 para que o produto das raízes seja

\frac{2}{3}

62 Calcule no caderno o valor de p na equação x 2 ‒ 8x + 2p = 0 para que uma das raízes seja o triplo da outra.

63 A professora Neusa fez vários cartões com exercícios para sortear na aula de Matemática. Felipe pegou este cartão:

Ilustração. Folha de papel com o texto: Qual é o resultado da operação alfa vezes beta menos (abre parênteses) alfa mais beta (fecha parênteses), se alfa e beta são as raízes da equação 2 vezes x elevado ao quadrado, menos 2 vezes x menos 24 é igual a 0?

Felipe acertou a questão. Que resposta ele deu?

Composição de uma equação do 2º grau

Conhecidas as relações de Girard, é possível determinar uma equação do 2º grau quando são dadas suas raízes. É o que vamos estudar a seguir.

Considere a equação do 2º grau ax 2 + bx + c = 0.

Dividindo todos os termos por a, sendo a ≠ 0, obtemos:

\frac{a x^{2}}{a} + \frac{b x}{a} + \frac{c}{a} = \frac{0}{a}

x^{2} + \frac{b x}{a} + \frac{c}{a} = 0

De acordo com as relações de Girard, obtemos:

\frac{‒ b}{a} = S

\frac{b}{a} = ‒ S

\frac{c}{a} = P

Substituindo

\frac{b}{a}

por ‒S e

\frac{c}{a}

por P, em

x^{2} + \frac{b x}{a} + \frac{c}{a} = 0

, obtemos:

x 2 ‒ Sx + P = 0

Página 168

Observe alguns exemplos de composição de equações do 2º grau a partir de suas raízes.

a) Vamos determinar uma equação do 2º grau cujas raízes sejam 3 e ‒8.

Inicialmente, vamos calcular a soma S das raízes.

S = x1 + x2

S = 3 + (‒8)

S = ‒5

Agora, vamos calcular o produto P das raízes.

P = x1 ⋅ x2

P = 3 ⋅ (‒8)

P = ‒24

Substituindo S por ‒5 e P por ‒24 em x 2 ‒ Sx + P = 0, obtemos:

x 2 ‒ Sx + P = 0

x 2 ‒ (‒5) ⋅ x + (‒24) = 0

x 2 + 5x ‒ 24 = 0

Logo, x 2 + 5x ‒ 24 = 0 é a equação procurada.

b) Vamos determinar uma equação do 2º grau de coeficientes inteiros cujas raízes sejam 2 e

\frac{3}{5}

S = x1 + x2

S = 2 + \frac{3}{5} = \frac{13}{5}

P = x1 ⋅ x2

P = 2 \cdot \frac{3}{5} = \frac{6}{5}

x 2 ‒ Sx + P = 0

x^{2} ‒ \frac{13}{5} x + \frac{6}{5} = 0

Como os coeficientes devem ser inteiros, então: 5x 2 ‒ 13x + 6 = 0

Logo, a equação procurada é 5x 2 ‒ 13x + 6 = 0.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

64 Escreva no caderno uma equação do 2º grau de coeficientes inteiros em que as raízes sejam:

a) x1 = ‒8 e x2 = 5;

b) x1 = 2 e x2 =

\frac{4}{5}

;

c) x1 = ‒3 e x2 = ‒

\frac{1}{2}

;

d) x1 =

\frac{1}{3}

e x2 = ‒

\frac{2}{5}

65 Escreva no caderno uma equação do 2º grau em que a soma das raízes seja 35 e o produto, 300.

Em seguida, calcule as raízes dessa equação.

66 Determine no caderno, por meio de uma equação do 2º grau, dois números tais que a soma e o produto sejam, respectivamente:

a) 2 e ‒120;

b) 0,2 e ‒1,2.

Hora de criar – Troque com um colega um problema, criado individualmente por vocês, sobre soma e produto de raízes de uma equação do 2º grau. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Página 169

TRABALHANDO A INFORMAÇÃO

A leitura de um mapa, anamorfose geográfica

Quando representamos as superfícies de um país em áreas proporcionais a determinada quantidade, dizemos que construímos uma anamorfose geográfica.

Brasil – População por regiões (2020)

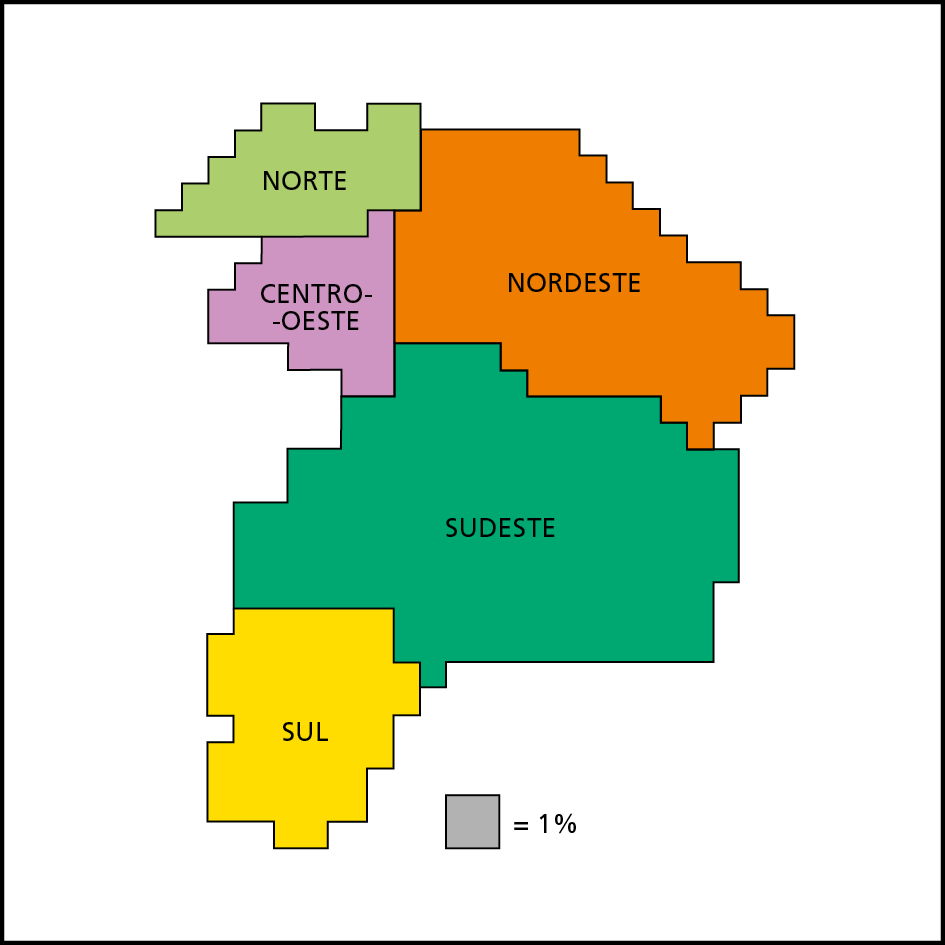
Mapa anamórfico. Título: Brasil, População por regiões (em 2020). O mapa mostra as regiões do Brasil composto por figuras coloridas de tamanhos diferentes e formato poligonal. Uma legenda indica que cada quadradinho de área corresponde a 1 por cento. Da maior para a menor região: Verde: Sudeste. Laranja: Nordeste. Amarelo: Sul. Verde claro: Norte. Roxo: Centro-Oeste. — Elaborado a partir de: FERREIRA, G. M. L. Atlas geográfico: espaço mundial. São Paulo: Moderna, 2013. página 14.

Note, no mapa, uma anamorfose geográfica da população do Brasil, por regiões, que é um tipo de cartograma. Observe que o quadradinho cinza indicado na legenda equivale a 1% da população brasileira. A superfície referente ao total da população vale 100%, mas não há preocupação com a precisão, pois o objetivo é comunicar visualmente informações gerais sobre a proporção entre as partes entre si e em relação ao todo.

Podemos quadricular essa representação e estimar quantos quadradinhos de 1% tem cada região.

Brasil – População por regiões (2020)

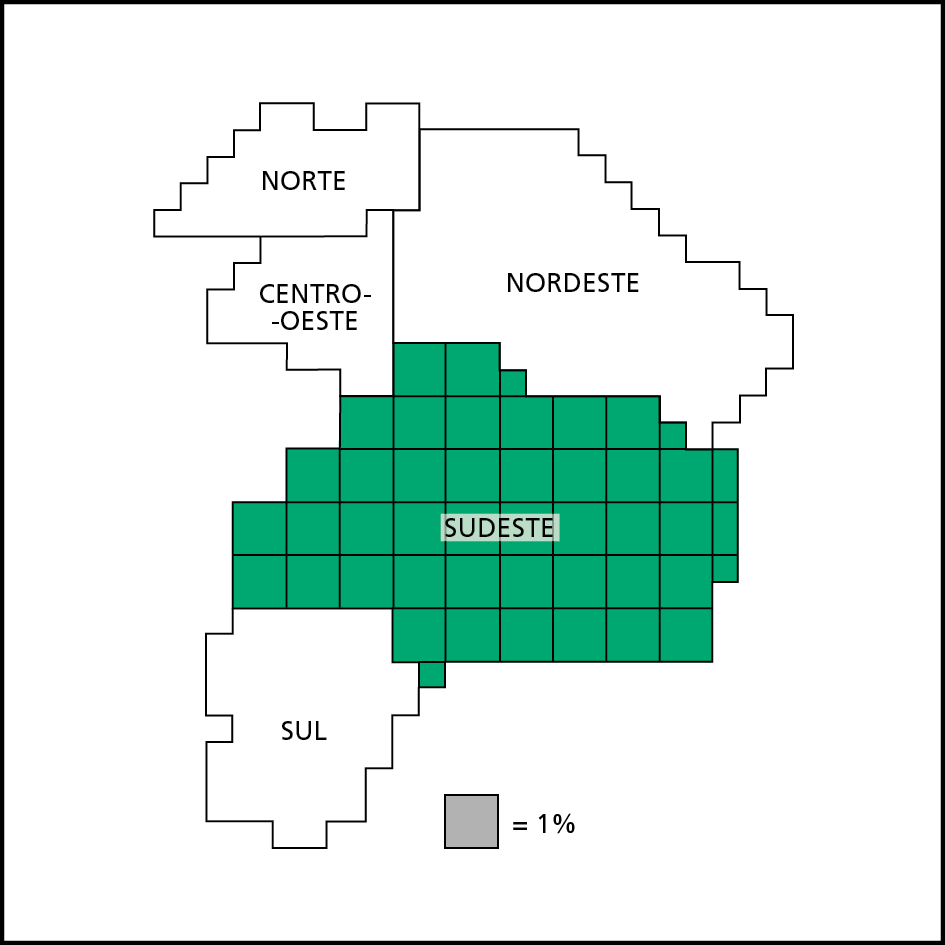
Sabendo que, em 2020, o Brasil tinha aproximadamente ..212000000 de habitantes, aplicamos a porcentagem de cada região e calculamos a respectiva população. Nesse mapa, a região Sudeste tem aproximadamente 42 quadradinhos, ou seja, sua população em 2020 correspondia a, aproximadamente, 42% de ..212000000 de habitantes.

População ≃ 0,42 ⋅ ..212000000

População ≃ ..89040000

Mapa. Região Sudeste. Mapa colorido, composto pelos estados da região sudeste do Brasil e as bandeiras de cada estado. Região em vermelho: estado de Minas Gerais e uma bandeira branca, com um triângulo vermelho ao centro, e os contorno do triângulo com as palavras LIBERTAS QUAE SERA TAMEN. Região em laranja: estado de São Paulo e uma bandeira com listras pretas e brancas, e um retângulo vermelho na parte superior esquerda contendo um círculo branco e, dentro dele, um mapa do Brasil em azul. Região em roxo: estado do Rio de Janeiro e uma bandeira dividida em quatro retângulos, 2 brancos e 2 azuis claro, com um brasão no centro da bandeira. Região em verde: estado do Espírito Santo e uma bandeira composta por três faixas horizontais, azul, branca e rosa (de cima para baixo), e a frase ao centro da faixa branca, TRABALHA E CONFIA.

Página 170

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

1 Sabemos qual era a população aproximada do Sudeste. Agora, copie o mapa da população e termine de quadriculá-lo. Em seguida, estime quantos quadradinhos de 1% tem cada região e calcule a população aproximada de cada uma delas nessa data.

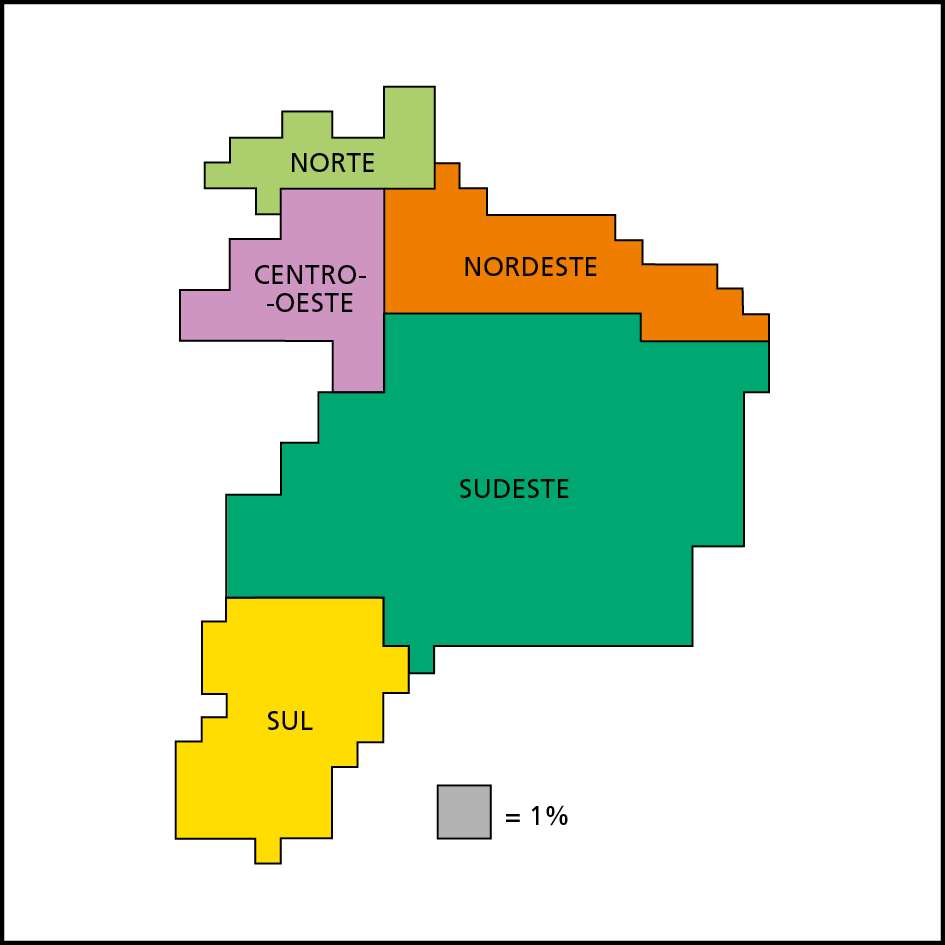
2 Copie no caderno o mapa do Píbi por regiões do Brasil, de 2019, e quadricule-o. Em seguida, estime quantos quadradinhos de 1% tem cada região e calcule quanto falta para a soma das porcentagens das regiões atingir 100%.

Brasil – PIB por regiões (2019)

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Determine no caderno o valor de k na equação (k + 5)x 2 + (k ‒ 1)x + k = 0 de modo que ela seja do 2º grau.

2 Escreva no caderno as equações a seguir na fórma reduzida e encontre as respectivas raízes.

a) (1 ‒ x) ⋅ (5 + 2x) = 5

b) (3y ‒ 5) ⋅ ( y ‒ 5) + y 2 = 0

c) (‒2x ‒ 1) ⋅ (x ‒ 2) = 3x + 5x 2

d) 5x 2 + 7 = 2x 2 ‒ 5

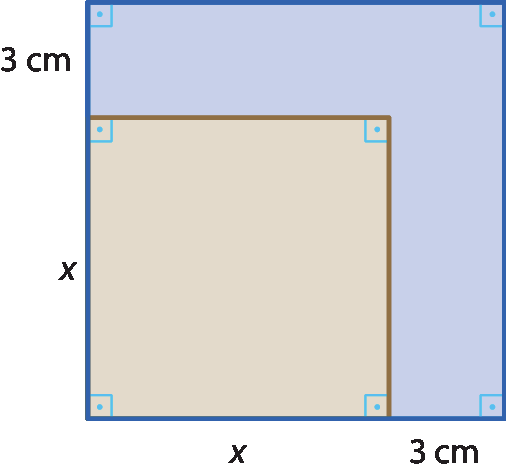
3 Na figura, qual deve ser o valor de x para que a área pintada de azul meça 57 centímetros quadrados?

Ilustração. Quadrado azul. Dentro, no canto inferior esquerdo, quadrado cujo lado mede x. A distância do quadrado de dentro para a extremidade do quadrado azul é 3 centímetros.

4 Dada a equação x 2 ‒ (m ‒ 5) ⋅ x + (1 ‒ m) = 0, determine m no caderno, de modo que:

a) uma das raízes seja nula;

b) as raízes sejam opostas.

5 A soma das medidas das áreas de três terrenos quadrados de mesmo tamanho é igual à medida da área de um campo de futebol que mede 80 métros por 60 métros.

Ilustração. Vista superior de três terrenos quadrados lado a lado. Em cada terreno há grama verde e algumas árvores.

a) Escreva no caderno a equação que corresponde a essa situação.

b) Quais são as raízes dessa equação?

c) Qual dessas raízes representa a medida do lado de cada terreno quadrado?

Página 171

6 Determine no caderno os números reais que são soluções da equação x 2 + 10x = 11x.

7 Observe as figuras.

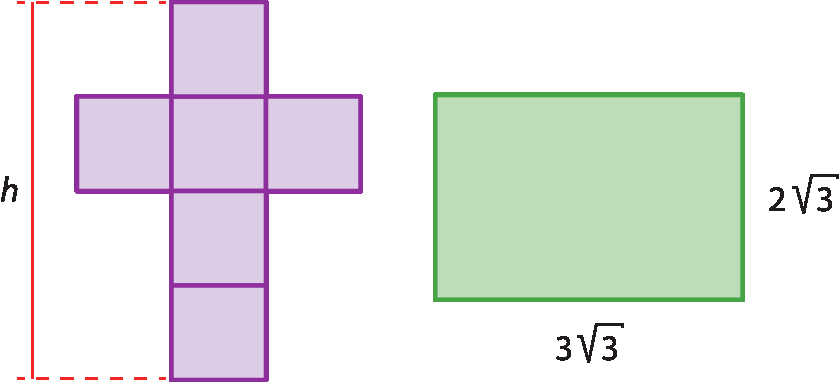
Ilustrações. À esquerda, figura lilás, composta por seis retângulos: quatro na vertical e um em cada lado do segundo retângulo (de baixo pra cima). A altura da figura mede h. À direita, retângulo verde, cujos lados medem 3 raiz quadrada de 3, e 2 raiz quadrada de 3.

A medida da área da figura lilás, composta de retângulos, é igual à medida da área do retângulo verde. Qual é a medida da altura da figura lilás?

8 Determine no caderno o valor de k na equação kx 2 ‒ 16x + 5 = 0 para que:

a) uma das raízes seja 3;

b) uma das raízes seja

\frac{1}{2}

;

c) as raízes sejam reais e distintas;

d) a soma das raízes seja

\frac{4}{3}

9 (ú cê ésse-Rio Grande do Sul) Se uma das raízes da equação

2x 2 ‒ 3px + 40 = 0 é 8, então o valor de p é:

a) 5.

\frac{13}{3}

c) 7.

d) ‒5.

e) ‒7.

10 (unifór-Ceará) Uma das soluções da equação

\frac{2 x^{2} + x}{11} = 2 x + 1

é um número inteiro múltiplo de:

a) 2.

b) 3.

c) 5.

d) 7.

e) 11.

11 (Fuvésti-São Paulo) Sejam x1 e x2 as raízes da equação 10x 2 + 33x ‒ 9 = 0. O número inteiro mais próximo do número 5 ⋅ x1 ⋅ x2 + 2 ⋅ (x1 + x2) é:

a) ‒33.

b) ‒10.

c) ‒7.

d) 10.

e) 33.

12 (ulbra-Rio Grande do Sul) o valor ou os valores de B na equação x 2 ‒ Bx + 4 = 0 para que o discriminante seja igual a 65 é (são):

a) 0.

b) 9.

c) ‒9.

d) ‒9 ou 9.

e) 16.

13 (úfes) O valor de k para que a soma das raízes da equação (k ‒ 3)x 2 ‒ 4kx + 1 = 0 seja igual ao seu produto é:

\frac{1}{2}

\frac{1}{3}

\frac{1}{4}

\frac{2}{3}

\frac{3}{4}

14 (púqui-Minas Gerais) O quociente da divisão de 72 por um número negativo é o dobro dêsse número. A metade dêsse número é:

a) ‒3.

b) ‒4.

c) ‒5.

d) ‒6.

e) ‒7.

15 (Vunéspi) Se aumentarmos em 3 centímetros o lado de um quadrado, sua área aumentará 27 centímetros quadrados. A partir desses dados, podemos dizer que o lado do quadrado mede, em centímetro:

a) 3.

b) 4.

c) 5.

d) 6.

e) 7.

16 Ao compor uma equação do 2º grau, Fernanda, por engano, escreveu:

x 2 ‒ Px + S = 0

Resolveu a equação corretamente e encontrou as raízes 1 e 5. Se Fernanda tivesse usado corretamente as relações de Girard para compor sua equação, quais seriam as raízes?

17 (éfe gê vê-São Paulo) Se a soma das raízes da equação kx 2 + 3x ‒ 4 = 0 é 10, podemos afirmar que o produto das raízes é:

\frac{40}{3}

‒ \frac{40}{3}

\frac{80}{3}

‒ \frac{80}{3}

‒ \frac{3}{10}

18 (unifór-Ceará) Um estudante resolve uma equação do tipo x 2 + bx + c = 0 e, enganando-se no valor de c, obtém as raízes 8 e 2. Um colega seu, resolvendo a mesma equação, engana-se no valor de b e obtém as raízes ‒9 e ‒1. Resolvendo-se a equação correta, quanto se obtém somando o triplo da menor raiz com a outra?

Página 172

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Qual das equações a seguir não é de 2º grau?

a) (x ‒ 2)(x ‒3) = 0

b) x2 ‒ 2x + 4 = 0

c) x + 2x ‒ 3 = 0

d) (x + 2)2 = 0

2 Quais são os valores dos coeficientes a, b e c na equação 2x2 + 3 = 0, respectivamente?

a) 2, 1 e 3.

b) 2, 0 e 3.

c) 2, 2 e 2.

d) 1, 2 e 3.

3 Complete a frase: “Uma equação de 2º grau é

quando

coeficientes

de zero”.

a) incompleta; todos os; são diferentes.

b) completa; um dos; é diferente.

c) completa; dois dos; são diferentes.

d) completa; todos os; são diferentes.

4 Um retângulo tem lados medindo x e 3x. Qual é a fórma reduzida da equação de segundo grau da medida da área (a) do retângulo?

a) 3xelevado a 2 ‒ a = 0

b) 3x + x = a

c) 3xelevado a 2 = a

d) 3x + x ‒ a = 0

5 Quais são as raízes da equação de 2º grau xelevado a 2 ‒ 2x = 0?

a) 2 e ‒2.

b) 2 e 0.

c) 2 e 4.

d) 4 e ‒4.

6 Qual dessas equações tem como raiz o número 7?

a) xelevado a 2 + 4x ‒ 2 = 0

b) 4xelevado a 2 ‒ 2 = 0

c) ‒2xelevado a 2 + 4x = 0

d) xelevado a 2 ‒3x ‒ 28 = 0

7 Quais são as raízes reais da equação de 2º grau xelevado a 2 + 4 = 0?

a) A equação não possui raízes reais.

b) 2 e ‒2.

c) 2 e 0.

d) 1 e ‒2.

8 Qual é o valor de Δ para a equação de 2º grau 2xelevado a 2 ‒ 4x + 2 = 0?

a) 8

b) 2

c) 0

d) 4

9 Um quadrado de área medindo 49 centímetros quadrados tem lado que mede x. Qual é o valor de x?

a) 6 centímetros.

b) 7 centímetros.

c) 8 centímetros.

d) 9 centímetros.

10 Um retângulo de área medindo 200 métros quadrados tem seus lados de modo que a medida do comprimento do maior é duas vezes a do comprimento do menor. Quanto mede o comprimento do maior lado do retângulo?

a) 25 métros.

b) 15 métros.

c) 10 métros.

d) 20 métros.

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.

a) Qual é a fórma geral de uma equação de 2º grau?

b) Qual é a fórmula resolutiva da equação do 2º grau dada por seus coeficientes da fórma reduzida?

c) O que se pode dizer dos coeficientes de uma equação de 2º grau que apresenta somente uma raiz diferente de zero?

d) Em que caso as raízes de uma equação de 2º grau são números reais opostos?

e) Quais são as razões entre os coeficientes a, b e c da equação reduzida do 2º grau que fornecem, respectivamente, a soma e o produto das raízes dessa equação?

f) É possível determinar a expressão de uma equação do 2º grau conhecidas suas raízes? Explique.