
CAPÍTULO 9 Razões trigonométricas nos triângulos retângulos

Observe, leia e responda no caderno.
a) Na região em que você mora, há algum teleférico? Mesmo que não haja, você conhece algum teleférico brasileiro? Sabe qual é a inclinação de seus cabos?
b) E você conhece algum parque com tirolesa? Pesquise essa prática esportiva originária da região do Tirol, na Áustria. Escolha uma tirolesa que achar mais interessante e informe qual é a inclinação dessa tirolesa.
c) Observe escadas fixas (na sua escola ou residência). Os degraus têm altura de mesma medida e piso de mesma medida? A inclinação deve ser igual em todos os degraus?
Durante os 30 minutos do passeio, os passageiros dentro das cabines suspensas percorrem 7 quilômetros entre nuvens e paredões das montanhas e se elevam, com inclinações que medem até 37graus, à altitude que mede .1279 métros.
Nesse percurso, é possível observar a chamada Estrada do Céu (Tongtian Highway) serpenteando a montanha com seus 11 quilômetros e 99 curvas.
1. Primeiras razões trigonométricas
A figura a seguir mostra o esquema de uma represa. A ponte, representada pelo segmento
AB, pode ser medida com uma trena de maneira que
medida do segmento AB= 164 métros.
•

Observando o esquema indicado na figura, como poderíamos determinar a medida BC na realidade? E a medida á cê ?
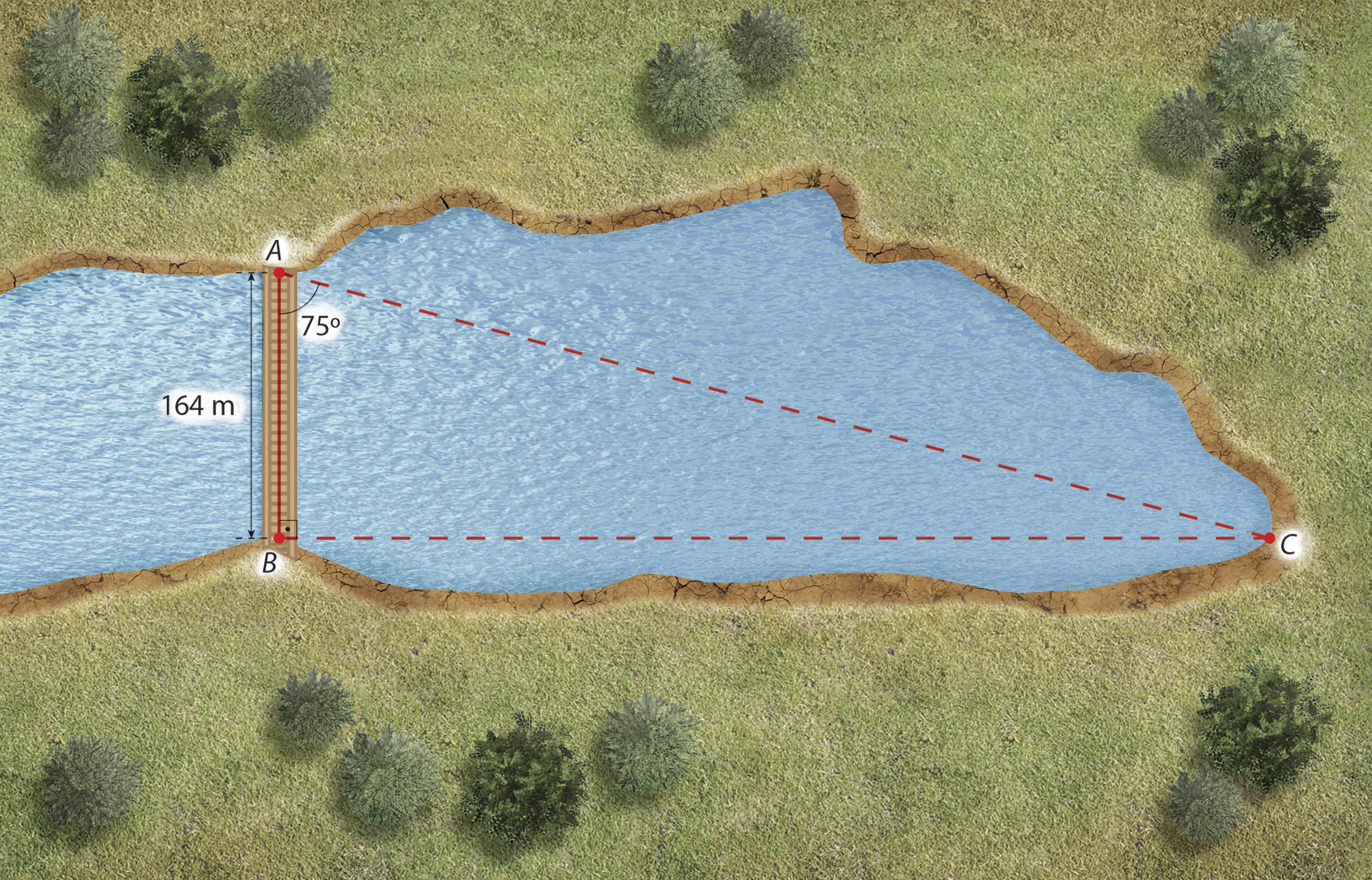
Já o ângulo
BACpode ser medido diretamente usando um teodolito (instrumento de precisão usado para medir ângulos horizontais e verticais):
medida do ângulo BAC= 75graus.
Existem, contudo, muitas situações em que não é possível medir diretamente um ângulo ou a distância entre dois pontos. Um exemplo é a medida da distância entre os pontos a (localizado em um extremo da ponte) e C (localizado na margem oposta da represa) da figura anterior.
Procurando resolver problemas dessa natureza, os matemáticos estabeleceram importantes relações entre as medidas dos ângulos e as medidas dos lados de um triângulo. A área da Matemática que estuda essas relações é chamada de Trigonometria.
A palavra trigonometria, de origem grega, significa “medida de triângulos”. Embora não tenhamos informações precisas sobre a origem dos estudos trigonométricos, há registros de sua aplicação por babilônios e antigos egípcios, especialmente na Agrimensura e na Astronomia.
Sabe-se que a Trigonometria era usada, por exemplo, para determinar medidas de distâncias que não podiam ser realizadas com instrumentos, como aquelas entre os planetas. Para tais cálculos, eram aplicadas relações entre as medidas dos lados e as medidas dos ângulos de um triângulo.
Neste capítulo, estudaremos as razões trigonométricas seno, cosseno e tangente de um ângulo agudo.
Seno de um ângulo agudo
Considere a figura a seguir.
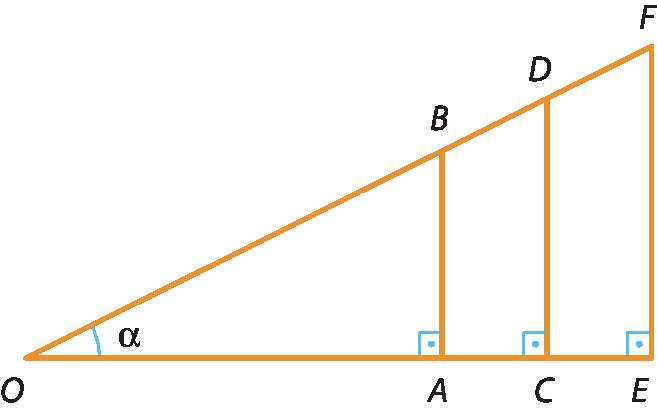
Os triângulos retângulos ó á bê, ó cê dê e ó é éfe são semelhantes pelo caso ângulo ângulo, pois têm em comum o ângulo de medida α (também chamado de ângulo α) e um ângulo reto.
Como os triângulos ó á bê e ó cê dê são semelhantes e os lados correspondentes são proporcionais, podemos escrever:
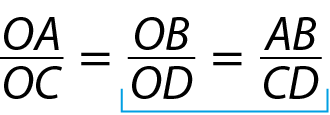
Os triângulos ó á bê e ó é éfe são semelhantes; portanto, as medidas dos lados correspondentes são proporcionais:

Observe as duas proporções que foram destacadas:
Proporção. Fração; numerador OB, denominador OD. É igual à: Fração; numerador AB, denominador CD.e
Proporção. Fração; numerador OB, denominador OF. É igual à: Fração; numerador AB, denominador EF.Da propriedade fundamental das proporções, podemos escrever:
e
Proporção. Fração; numerador EF, denominador OF. É igual à: Fração; numerador AB, denominador OB.Assim, obtemos:
Proporção. Fração; numerador AB, denominador OB. É igual à: Fração; numerador CD, denominador OD. É igual à: Fração; numerador EF, denominador OF.=
Fração; numerador medida do cateto oposto à alfa, denominador medida da hipotenusaHá infinitos outros triângulos retângulos que têm como ângulo interno o ângulo α e que, por isso, também são semelhantes aos triângulos ó á bê, ó cê dê e ó é éfe.
Para todos esses triângulos retângulos, a razão entre a medida do cateto oposto ao ângulo α e a medida da hipotenusa, em uma mesma unidade, é constante. Chamamos essa razão constante de seno do ângulo α e a indicamos por sen α.
Seno de um ângulo agudo de um triângulo retângulo é a razão entre a medida do cateto oposto a esse ângulo e a medida da hipotenusa.
Considerando qualquer um desses triângulos:
Acompanhe um exemplo.
No triângulo MNP, vamos calcular o seno do ângulo interno
P, que mede 25graus.
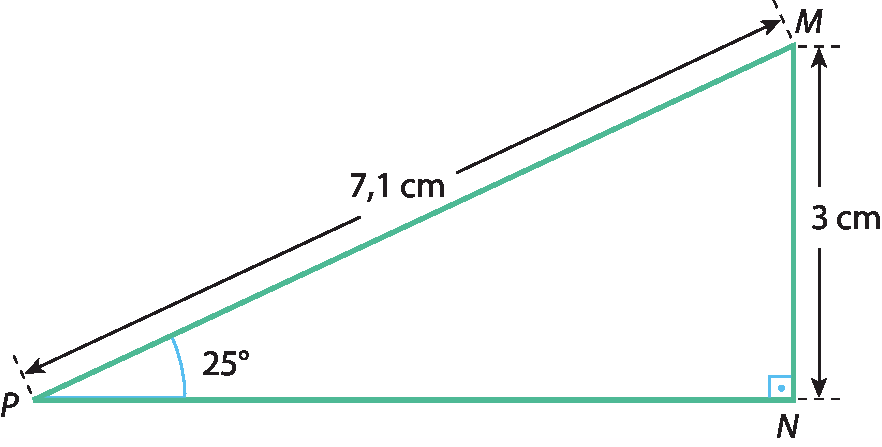
seno de 25graus ≃ 0,42
Clique no play e acompanhe as informações do vídeo.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Construa um triângulo retângulo com um dos ângulos internos medindo 30graus. Com uma régua, determine as medidas aproximadas, em milímetro, do cateto oposto ao ângulo de 30graus e da hipotenusa.
a) Qual é a razão entre a medida do cateto oposto ao ângulo de 30graus e a medida da hipotenusa dêsse triângulo?
b) Indique o valor do seno de 30graus.
2 Construa um triângulo á bê cê, retângulo em
ângulo Bem que
medida do ângulo C= 40graus e á cê = 10 centímetros. Com uma régua obtenha, em milímetro, a medida aproximada do cateto
AB.
Qual é o valor, aproximado com uma casa decimal, do seno de 40graus?
3 O valor do seno de um ângulo varia de acordo com as medidas dos lados do triângulo ou de acordo com a medida do ângulo?
Cosseno e tangente de um ângulo agudo
Considere novamente os triângulos retângulos ó á bê, ó cê dê e ó é éfe.
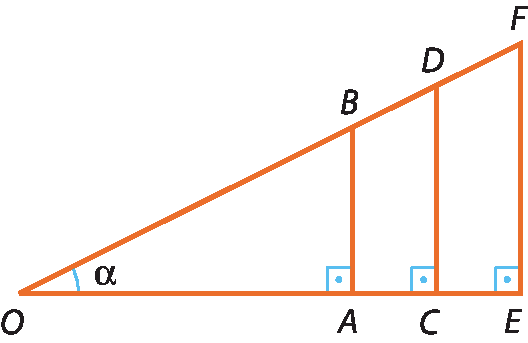
Como já observamos, esses triângulos são semelhantes.
De modo análogo ao que fizemos para a razão seno, dessa semelhança, obtemos:
=
Fração; numerador medida do cateto adjacente à alfa, denominador medida da hipotenusaChamamos essa razão constante de cosseno do ângulo α e a indicamos por cos α.
Cosseno de um ângulo agudo de um triângulo retângulo é a razão entre a medida do cateto adjacente a esse ângulo e a medida da hipotenusa.
Para qualquer um desses triângulos:
Da mesma semelhança, também obtemos:
Chamamos essa razão constante de tangente do ângulo α e a indicamos por tg α.
Tangente de um ângulo agudo de um triângulo retângulo é a razão entre a medida do cateto oposto e a medida do cateto adjacente a esse ângulo.
Considerando qualquer dos triângulos da figura anterior, obtemos:
Acompanhe alguns exemplos.
a) No triângulo érre ésse tê, vamos calcular o cosseno do ângulo interno
R, que mede 42graus.
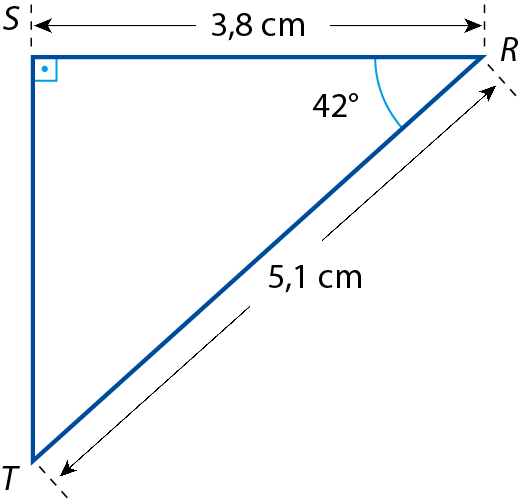
cosseno de 42graus =
medida do cateto adjacente ao ângulo R sobre medida da hipotenusa.cosseno de 42graus ≃ 0,74
b) Vamos calcular a tangente do ângulo interno
Bdo triângulo á bê cê.
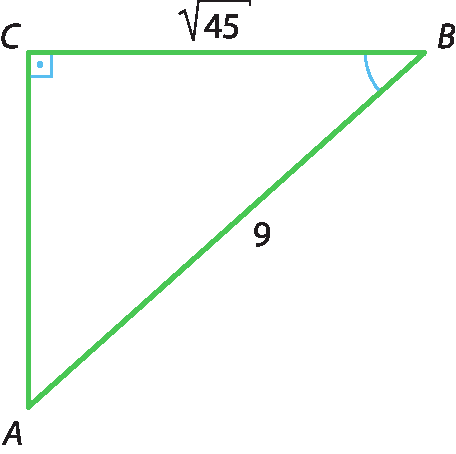
Inicialmente, aplicamos o teorema de Pitágoras para calcular a medida do segmento á cê :
(AC )elevado a 2 + (BC )elevado a 2 = (AB )elevado a 2
(AC )elevado a 2 + (BC )elevado a 2 = (AB )elevado a 2
(AC )elevado a 2 +
abre parênteses, raiz quadrada de 45, fecha parênteses, elevado ao quadrado.= 9elevado a 2
(AC )elevado a 2 + 45 = 81
(AC )elevado a 2 = 36
AC = 6
Portanto:
tangente do ângulo B é igual à duas vezes raiz quadrada de 5 sobre 5.Observações
▶ O seno e o cosseno de um ângulo agudo de um triângulo retângulo são números reais positivos menores que 1.
▶ A tangente de um ângulo agudo de um triângulo retângulo é um número real positivo.
▶ Outras razões trigonométricas serão estudadas no Ensino Médio.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
4 Construa um triângulo retângulo com um dos ângulos internos medindo 45graus. Com uma régua, determine as medidas aproximadas, em centímetro, dos catetos e da hipotenusa.
a) Qual é o valor aproximado da razão entre a medida do cateto adjacente ao ângulo de 45grause a medida da hipotenusa dêsse triângulo?
b) Qual é o valor aproximado de cosseno de 45graus?
c) Qual é o valor da razão entre a medida do cateto oposto ao ângulo de 45graus e a medida do cateto adjacente ao ângulo de 45graus?
d) Qual é o valor de tangente de 45graus?
5

Considere o triângulo retângulo a seguir e, usando uma calculadora, obtenha, com aproximação de duas casas decimais:
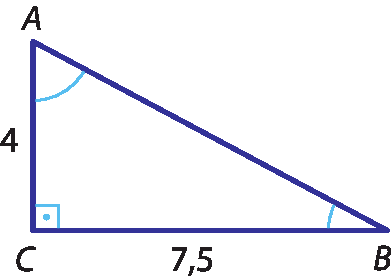
a) medida de
segmento AB;
b) cosseno de
ângulo B;
c) tangente de
ângulo B;
d) cosseno de
ângulo A;
e) tangente de
ângulo A.
6 Um brinquedo tem uma rampa medindo 64 centímetros de comprimento, por meio da qual se desloca um carrinho. A parte mais alta da rampa está a 12 centímetros da horizontal que passa pela parte mais baixa.
a) Faça uma figura representando essa situação.
b) Calcule o seno do ângulo que a rampa fórma com a horizontal.
7 Considere um papel retangular de medidas 15,6 centímetros de comprimento por 7,2 centímetros de largura. Traça-se uma das diagonais dêsse retângulo. Qual é a tangente do ângulo que a diagonal fórma com o lado maior do papel? E a tangente do ângulo que a diagonal fórma com o lado menor?
8 Justifique a afirmação: “O seno e o cosseno de um ângulo agudo são números reais positivos menores que 1”.
9 No triângulo retângulo MQR, determine:
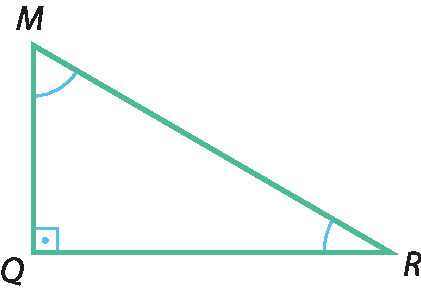
a) as medidas aproximadas dos lados (use uma régua);
b) as medidas dos ângulos agudos (use um transferidor);
c) seno de
ângulo M;
d) cosseno de
ângulo M;
e) tangente de
ângulo M.
10 Desenhe um triângulo retângulo ABC de modo que
medida do ângulo B= 36graus. Determine, com duas casas decimais, o valor aproximado de cada razão.
a) seno de
ângulo Bb) cosseno de
ângulo Bc) tangente de
ângulo B11 A tampa retangular de uma caixa de madeira mede 32 centímetros de comprimento por 24 centímetros de largura. Entre dois cantos diagonalmente opostos da tampa, prende-se um fio esticado. Qual é o cosseno do ângulo
Aque o fio fórma com o lado maior da tampa?
12 Considerando o triângulo MNP, determine, com duas casas decimais, o que se pede a seguir.
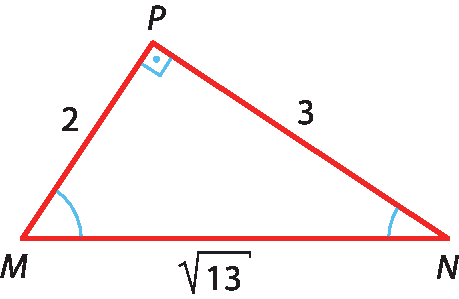
a) seno de
ângulo M
b) cosseno de
ângulo N
c) tangente de
ângulo M
d) cosseno de
ângulo M
e) tangente de
ângulo N
f ) seno de
ângulo N
13 (Etec-São Paulo) O acesso a um edifício é feito por uma escada de dois degraus, sendo que cada um mede 16 centímetros de altura. Para atender a portadores de necessidades especiais, foi construída uma rampa.
Respeitando a legislação em vigor, a rampa deve formar, com o solo, um ângulo de 6graus, conforme mostrado na figura.
Dados:
• seno de 6graus = 0,10
• cosseno de 6graus = 0,99
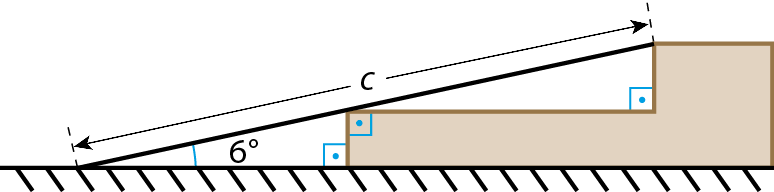
A medida c do comprimento da rampa é, em metro, igual a:
a) 1,8.
b) 2,0.
c) 2,4.
d) 2,9.
e) 3,2.
14

Reúna-se com três colegas e façam o que se pede.
a) Cada um constrói um triângulo á bê cê, retângulo em a, e passa ao colega, que medirá os seus lados e ângulos.
b) Com base nas medidas obtidas no item a, calculem o valor de cada uma das expressões:
• seno de
ângulo B‒ cosseno de
ângulo C
• seno de
ângulo C‒ cosseno de
ângulo B
• tangente de
ângulo B· tangente de
ângulo C
•
A fração seno do ângulo B sobre cosseno do ângulo B fim da fração, menos tangente do ângulo B.
•
seno do ângulo C sobre cosseno do ângulo C fim da fração, menos tangente do ângulo C
c) Analisem os valores obtidos em cada expressão do item b e respondam às questões:
• O que ocorre com o seno de um ângulo e com o cosseno do seu complementar?
• O que ocorre com as tangentes de um ângulo e de seu complementar?
• O que ocorre com a razão entre o seno e o cosseno de um ângulo agudo e com a tangente dêsse ângulo?
15

Hora de criar – Troque com um colega um problema, criado individualmente por vocês, sobre seno, cosseno ou tangente. O problema pode se referir à necessidade de obter a medida de certa altura ou profundidade cuja situação seja representada por um triângulo retângulo. Forneça dados tais como a medida do ângulo sob o qual a altura/profundidade seja vista, e/ou a medida do afastamento (cateto) e/ou a medida da hipotenusa do triângulo. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
2. Quadro de razões trigonométricas
As razões trigonométricas são aplicadas na resolução de uma grande variedade de problemas. Para facilitar, reproduzimos mais adiante um quadro dos valores aproximados do seno, do cosseno e da tangente dos ângulos de 1grau a 89graus.
Atribui-se ao astrônomo grego Hiparco de Niceia (180 a 125 antes de Cristo) o estabelecimento das bases da Trigonometria, e deve-se a ele a construção dos primeiros quadros de razões trigonométricas.
Mais tarde, Cláudio Ptolomeu (85 a 165 Depois de Cristo), astrônomo, matemático e geógrafo grego, ampliou o trabalho de Hiparco com sua obra Sintaxe matemática, na qual apresenta um trabalho sobre Trigonometria.
Os árabes traduziram os treze livros que compunham a obra de Ptolomeu e a intitularam Almagesto, que em árabe significa “o maior”.
Atualmente, muitas calculadoras fornecem os valores das razões trigonométricas.
Acompanhe como calculamos o seno, o cosseno e a tangente do ângulo de 45graus usando uma calculadora científica como a da fotografia a seguir:
• seno de 45graus:

• cosseno de 45graus:

• tangente de 45graus:


Muitas calculadoras científicas são importadas. Nelas, a tecla

representa o seno, a tecla

representa o cosseno, e a tecla

, a tangente.

|
Ângulo |
Seno |
Cosseno |
Tangente |
|---|---|---|---|
|
1° |
0,0175 |
0,9998 |
0,0175 |
|
2° |
0,0349 |
0,9994 |
0,0349 |
|
3° |
0,0523 |
0,9986 |
0,0524 |
|
4° |
0,0698 |
0,9976 |
0,0699 |
|
5° |
0,0872 |
0,9962 |
0,0875 |
|
6° |
0,1045 |
0,9945 |
0,1051 |
|
7° |
0,1219 |
0,9925 |
0,1228 |
|
8° |
0,1392 |
0,9903 |
0,1405 |
|
9° |
0,1564 |
0,9877 |
0,1584 |
|
10° |
0,1736 |
0,9848 |
0,1763 |
|
11° |
0,1908 |
0,9816 |
0,1944 |
|
12° |
0,2079 |
0,9781 |
0,2126 |
|
13° |
0,2250 |
0,9744 |
0,2309 |
|
14° |
0,2419 |
0,9703 |
0,2493 |
|
15° |
0,2588 |
0,9659 |
0,2679 |
|
16° |
0,2756 |
0,9613 |
0,2867 |
|
17° |
0,2924 |
0,9563 |
0,3057 |
|
18° |
0,3090 |
0,9511 |
0,3249 |
|
19° |
0,3256 |
0,9455 |
0,3443 |
|
20° |
0,3420 |
0,9397 |
0,3640 |
|
21° |
0,3584 |
0,9336 |
0,3839 |
|
22° |
0,3746 |
0,9272 |
0,4040 |
|
23° |
0,3907 |
0,9205 |
0,4245 |
|
24° |
0,4067 |
0,9135 |
0,4452 |
|
25° |
0,4226 |
0,9063 |
0,4663 |
|
26° |
0,4384 |
0,8988 |
0,4877 |
|
27° |
0,4540 |
0,8910 |
0,5095 |
|
28° |
0,4695 |
0,8829 |
0,5317 |
|
29° |
0,4848 |
0,8746 |
0,5543 |
|
30° |
0,5000 |
0,8660 |
0,5774 |
|
31° |
0,5150 |
0,8572 |
0,6009 |
|
32° |
0,5299 |
0,8480 |
0,6249 |
|
33° |
0,5446 |
0,8387 |
0,6494 |
|
34° |
0,5592 |
0,8290 |
0,6745 |
|
35° |
0,5736 |
0,8192 |
0,7002 |
|
36° |
0,5878 |
0,8090 |
0,7265 |
|
37° |
0,6018 |
0,7986 |
0,7536 |
|
38° |
0,6157 |
0,7880 |
0,7813 |
|
39° |
0,6293 |
0,7771 |
0,8098 |
|
40° |
0,6428 |
0,7660 |
0,8391 |
|
41° |
0,6561 |
0,7547 |
0,8693 |
|
42° |
0,6691 |
0,7431 |
0,9004 |
|
43° |
0,6820 |
0,7314 |
0,9325 |
|
44° |
0,6947 |
0,7193 |
0,9657 |
|
45° |
0,7071 |
0,7071 |
1,0000 |
|
46° |
0,7193 |
0,6947 |
1,0355 |
|
47° |
0,7314 |
0,6820 |
1,0724 |
|
48° |
0,7431 |
0,6691 |
1,1106 |
|
49° |
0,7547 |
0,6561 |
1,1504 |
|
50° |
0,7660 |
0,6428 |
1,1918 |
|
51° |
0,7771 |
0,6293 |
1,2349 |
|
52° |
0,7880 |
0,6157 |
1,2799 |
|
53° |
0,7986 |
0,6018 |
1,3270 |
|
54° |
0,8090 |
0,5878 |
1,3764 |
|
55° |
0,8192 |
0,5736 |
1,4281 |
|
56° |
0,8290 |
0,5592 |
1,4826 |
|
57° |
0,8387 |
0,5446 |
1,5399 |
|
58° |
0,8480 |
0,5299 |
1,6003 |
|
59° |
0,8572 |
0,5150 |
1,6643 |
|
60° |
0,8660 |
0,5000 |
1,7321 |
|
61° |
0,8746 |
0,4848 |
1,8040 |
|
62° |
0,8829 |
0,4695 |
1,8807 |
|
63° |
0,8910 |
0,4540 |
1,9626 |
|
64° |
0,8988 |
0,4384 |
2,0503 |
|
65° |
0,9063 |
0,4226 |
2,1445 |
|
66° |
0,9135 |
0,4067 |
2,2460 |
|
67° |
0,9205 |
0,3907 |
2,3559 |
|
68° |
0,9272 |
0,3746 |
2,4751 |
|
69° |
0,9336 |
0,3584 |
2,6051 |
|
70° |
0,9397 |
0,3420 |
2,7475 |
|
71° |
0,9455 |
0,3256 |
2,9042 |
|
72° |
0,9511 |
0,3090 |
3,0777 |
|
73° |
0,9563 |
0,2924 |
3,2709 |
|
74° |
0,9613 |
0,2756 |
3,4874 |
|
75° |
0,9659 |
0,2588 |
3,7321 |
|
76° |
0,9703 |
0,2419 |
4,0108 |
|
77° |
0,9744 |
0,2250 |
4,3315 |
|
78° |
0,9781 |
0,2079 |
4,7046 |
|
79° |
0,9816 |
0,1908 |
5,1446 |
|
80° |
0,9848 |
0,1736 |
5,6713 |
|
81° |
0,9877 |
0,1564 |
6,3138 |
|
82° |
0,9903 |
0,1392 |
7,1154 |
|
83° |
0,9925 |
0,1219 |
8,1443 |
|
84° |
0,9945 |
0,1045 |
9,5144 |
|
85° |
0,9962 |
0,0872 |
11,4301 |
|
86° |
0,9976 |
0,0698 |
14,3007 |
|
87° |
0,9986 |
0,0523 |
19,0811 |
|
88° |
0,9994 |
0,0349 |
28,6363 |
|
89° |
0,9998 |
0,0175 |
57,2900 |
Observe alguns exemplos de utilização do quadro de razões trigonométricas. É importante lembrar que os valores dêsse quadro são aproximações para as razões trigonométricas.
a) Vamos procurar no quadro o seno de 35graus e a tangente de 35graus.
|
Ângulo |
Seno |
Cosseno |
Tangente |
|---|---|---|---|
|
34° |
0,5592 |
0,8290 |
0,6745 |
|
35° |
0,5736 |
0,8192 |
0,7002 |
|
36° |
0,5878 |
0,8090 |
0,7265 |
Na coluna ângulo, procuramos 35graus.
Na coluna seno e na linha 35graus, encontramos 0,5736 e, na coluna tangente e na linha 35graus, encontramos 0,7002.
Portanto, seno de 35graus = 0,5736 e tangente de 35graus = 0,7002.
b) Vamos procurar no quadro a medida do ângulo que tem cosseno 0,4695.
|
Ângulo |
Seno |
Cosseno |
Tangente |
|---|---|---|---|
|
61° |
0,8746 |
0,4848 |
1,8040 |
|
62° |
0,8829 |
0,4695 |
1,8807 |
|
63° |
0,8910 |
0,4540 |
1,9626 |
Na coluna cosseno, procuramos o número 0,4695.
Na coluna ângulo e na linha cujo cosseno é igual a 0,4695, encontramos 62graus.
Portanto, cosseno de 62graus = 0,4695.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
16 Consulte o quadro de razões trigonométricas para encontrar o valor indicado em cada item.
a) seno de 54graus
b) cosseno de 36graus
c) tangente de 12graus
d) seno de 56graus
e) cosseno de 75graus
f) tangente de 89graus
17 Em cada item, determine x utilizando o quadro de razões trigonométricas.
a) seno de x = 0,4695
b) cosseno de x = 0,7771
c) tangente de x = 0,2867
d) seno de x = 0,9135
e) cosseno de x = 0,1908
f ) tangente de x = 9,5144
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO
1 Consultando o quadro de razões trigonométricas e sem usar transferidor, determine em cada caso a medida aproximada do ângulo
A.
a)
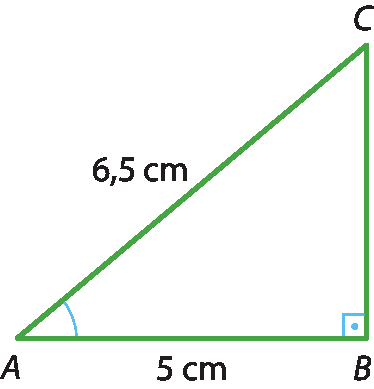
b)
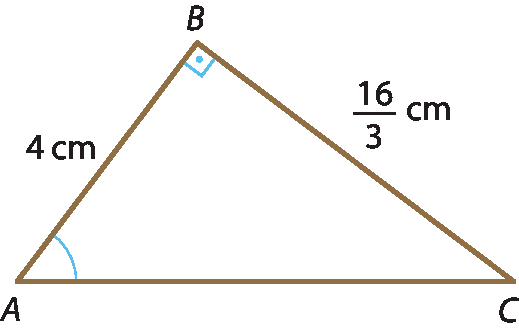
c)
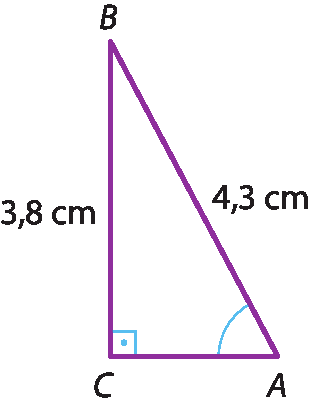
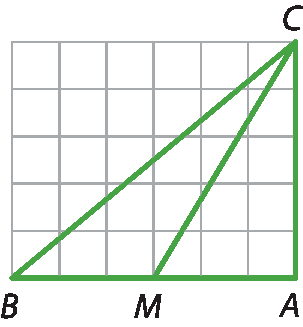
2 Determine, consultando o quadro de razões trigonométricas e sem usar transferidor, as medidas aproximadas, em grau, dos ângulos
ABC, BMCe
BCM.
PARA SABER MAIS
Ângulos da cidade maravilhosa
Na abertura do capítulo, pudemos observar o maior teleférico do mundo, que fica na montanha Tianmen, na China.
No Brasil, o trajeto do bondinho do Pão de Açúcar, no Rio de Janeiro, tem duas etapas. Na primeira etapa, da subida da praia Vermelha para o morro da Urca, a extensão do cabo mede 575 metros e eleva-se da altitude próxima de 0 até 220 metros. Com esses dados, podemos obter a medida aproximada α do ângulo que o cabo fórma com a horizontal. Observe o esquema.
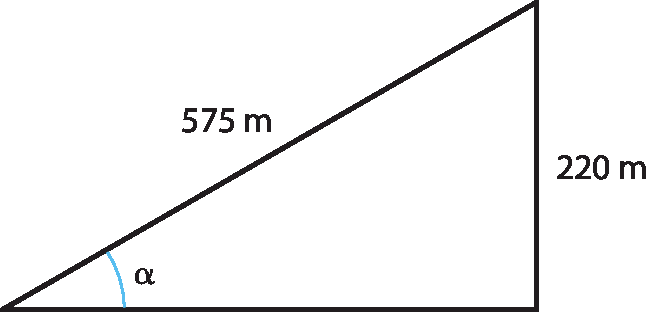

Calculando o seno de α, obtemos:
Seno de alfa é igual a 220 sobre 575, é aproximadamente igual a 0,38.Consultando o quadro de razões trigonométricas, encontramos α ≃ 22graus.
Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
Na segunda etapa do trajeto, do morro da Urca ao morro Pão de Açúcar, com extensão que mede 750 métros, o bondinho eleva-se a uma altitude que mede 396 métros. Calcule a medida aproximada β do ângulo de inclinação do cabo do teleférico dessa etapa. Lembre-se de descontar a altitude do morro da Urca.
3. Resolução de problemas que envolvem triângulos retângulos
Observe algumas situações envolvendo triângulos retângulos em que podemos aplicar as razões trigonométricas estudadas.
Situação 1
Uma pessoa observa o ponto mais alto de uma árvore sob um ângulo de 20graus em relação à horizontal, conforme a situação representada na figura. Vamos calcular a medida da altura dessa árvore.

Do triângulo retângulo representado na figura, obtemos:
• a medida do cateto adjacente ao ângulo de 20graus: 30 métros;
• a medida do cateto oposto ao ângulo de 20graus: x.
Como conhecemos a medida do cateto adjacente e queremos determinar a medida do cateto oposto ao ângulo de 20graus, vamos aplicar a razão trigonométrica definida por esses dois lados do triângulo, isto é, a tangente. Usando o valor aproximado com duas casas decimais, obtemos tangente de 20graus = 0,36.
x = 10,8
Para determinar a medida da altura da árvore, precisamos adicionar a altura dos olhos da pessoa que a observa, que é 1,80 métro: x + 1,80 = 10,8 + 1,80 = 12,60.
Portanto, a medida da altura dessa árvore é 12,60 métros.
Situação 2
Os bombeiros são chamados para tirar um gato de cima de uma árvore. Eles apoiam na árvore uma escada, formando com o chão um ângulo de 68graus, cuja base dista 1,4 métro do tronco. Qual é a medida do comprimento aproximado dessa escada?

Do triângulo retângulo da figura, obtemos:
• a medida da distância da base da escada ao tronco (cateto adjacente ao ângulo de 68graus): 1,4 métro;
• a medida do comprimento da escada (hipotenusa): x.
Como conhecemos a medida do cateto adjacente e queremos determinar a medida da hipotenusa, vamos aplicar a razão trigonométrica definida por esses dois lados do triângulo, isto é, o cosseno. Usando o valor aproximado com duas casas decimais, obtemos cos 68graus = 0,37.
O comprimento da escada mede aproximadamente 3,8 metros.

• Se uma escada fosse apoiada à distância de 1,4 métro de uma árvore e, assim, formasse um ângulo de 60graus com o solo, o comprimento dessa escada seria maior ou menor do que 3,8 métros?
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
18 Retome o esquema da represa (apresentado na página 198) e calcule a medida da distância aproximada do ponto A ao ponto C.
19 Usando valores das razões trigonométricas com duas casas decimais, calcule o valor aproximado de x no triângulo retângulo á bê cê a seguir.
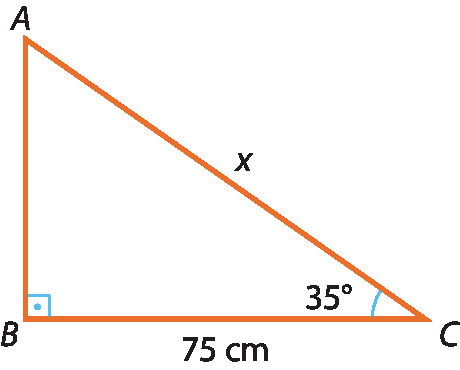
20 Para determinar a medida aproximada da largura de um rio, André mediu com um teodolito o ângulo indicado na figura a seguir.
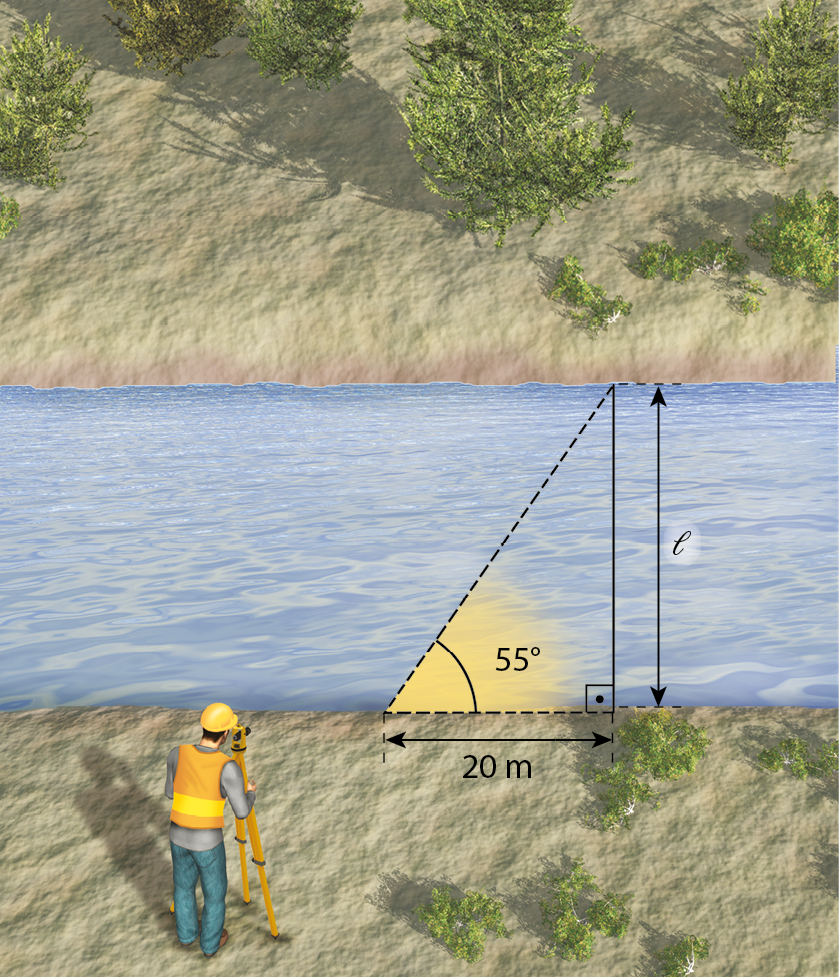
Qual é a medida aproximada, em metro, da largura do rio?
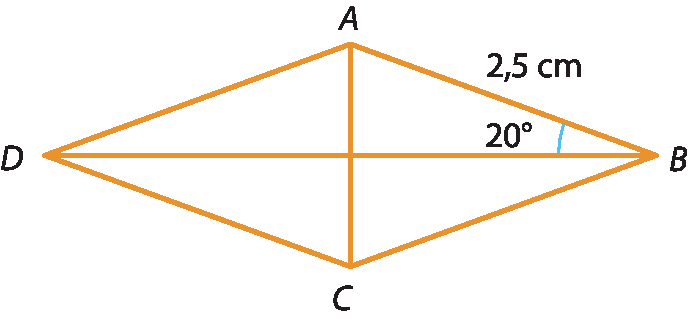
21 Para o losango a bê cê dê, determine:
a) a medida aproximada da diagonal maior;
b) a medida aproximada da diagonal menor;
c) a medida aproximada da área do losango.
22 Considere o triângulo retângulo á bê cê e faça o que se pede.
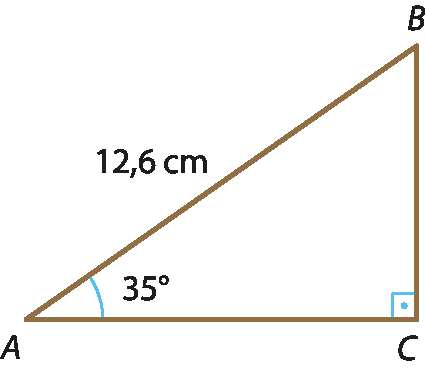
a) Qual é a medida do ângulo
B?
b) Calcule a medida aproximada do cateto
segmento BCc) Determine a medida aproximada da área dêsse triângulo.
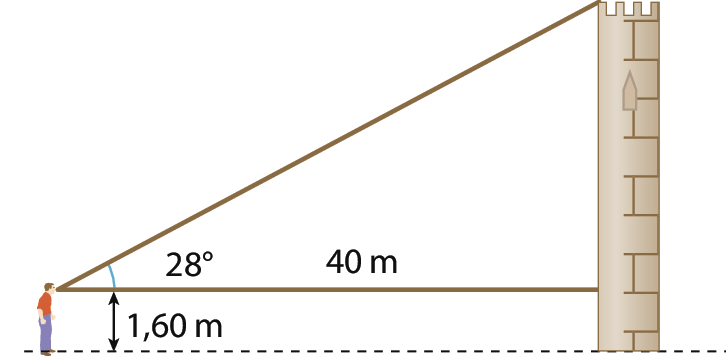
23 Um observador vê o ponto mais alto de uma torre sob um ângulo de 28°, conforme a figura a seguir. Calcule a medida aproximada da altura dessa torre.
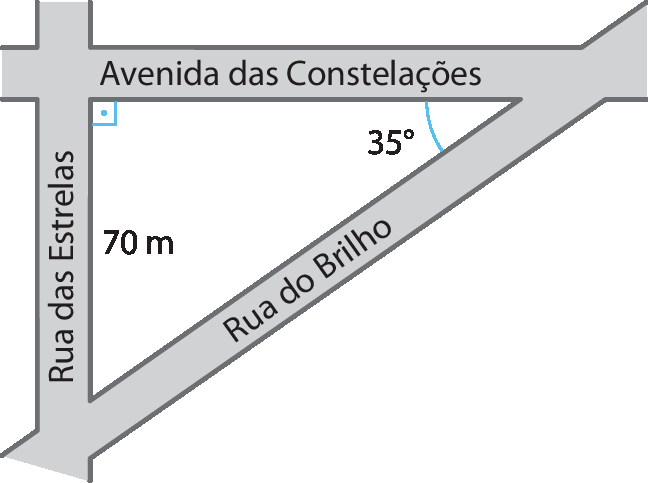
24 Observando a representação a seguir, calcule quanto mede, aproximadamente, o trecho da avenida das Constelações entre a rua do Brilho e a rua das Estrelas.
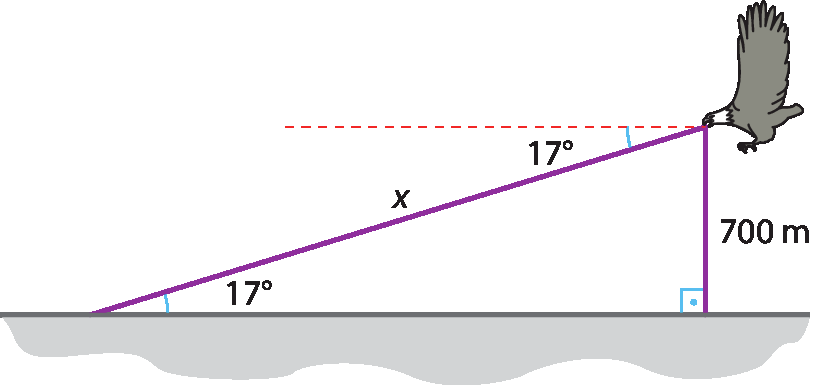
25 Um gavião, a 700 métros de altura, avista uma presa no chão; faz uma descida de 17graus em relação à horizontal e consegue capturá-la. Quanto o gavião percorreu para capturar essa presa?
26


Reúna-se com um colega e façam o que se pede.
a) Cada um escolhe cinco medidas de 1grau a 89grauspara que o outro calcule, usando o quadro de razões trigonométricas e uma calculadora, a soma dos quadrados do seno e do cosseno de cada uma das medidas escolhidas.
b) Arredondando os resultados obtidos no item anterior, qual é o valor do quadrado do seno de um ângulo mais o quadrado do cosseno do mesmo ângulo?
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO
1 Considerando que a figura á bê cê dê é é um pentágono regular e H é o ponto médio da diagonal
ACcalcule:
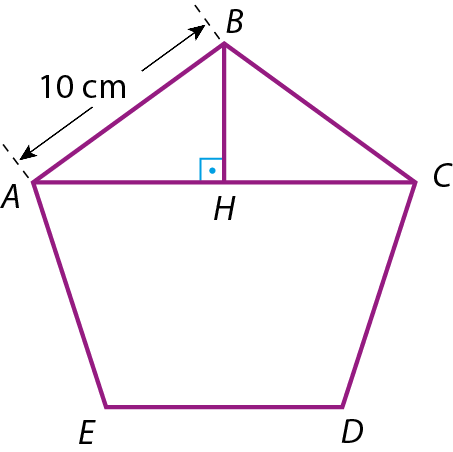
a)
medida do ângulo ABCe
medida do ângulo ABH
b) as medidas aproximadas de
segmento AH segmento ACe
de segmento AD

2 No início do capítulo 8 aprendemos que o emblema da sociedade secreta formada pelos pitagóricos era um pentagrama.
a) No pentágono regular á bê cê dê é, podemos perceber que suas diagonais formam o pentagrama. Sendo A bê = 10 centímetros, calcule a razão
Fração. AC sobre AB..
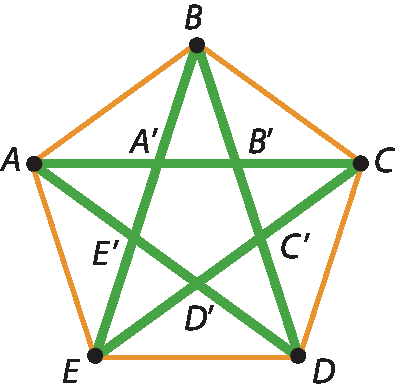
b) Tendo por base o pentágono á bê cê dê é do item a, também podemos obter o pentagrama, se prolongarmos os seus lados.

Considerando o pentagrama da figura 1, calcule:
• AJ
• JE
•
JE sobre AJc) Na figura 1, podemos traçar
segmento FG segmento GH segmento HI,
segmento IJe
segmento JFe obter um novo pentágono regular.
Dessa maneira, calcule: JF, JH e
Fração. JH sobre JF..
d) Copie a figura 1 e siga estes passos:
• trace o pentágono éfe gê agá í jota ;
• prolongue os lados do pentágono éfe gê agá í jota para obter um pentagrama;
• trace as diagonais do pentágono A’B ’C ’D ’E’ para obter um pentagrama.
e)

Reúna-se com um colega e façam o que se pede. As razões
AC sobre AB. JE sobre AJ. JH sobre JF.são iguais a um mesmo número irracional, conhecido como número de ouro, do qual vocês já obtiveram um valor aproximado. Pesquisem informações a respeito dêsse número e façam um resumo de sua pesquisa.
PARA SABER MAIS
O teodolito
Instrumento de medição de ângulos, o teodolito é usado geralmente por agrimensoresglossário e construtores para calcular medidas de grandes distâncias ou de alturas inacessíveis. Para efetuar as medições com esse instrumento, o profissional utiliza-se do conceito de tangente de um ângulo agudo.

Vamos aprender a construir um teodolito?
• Construção de um teodolito “caseiro”
Material
• papelão grosso (10 centímetros por 15 centímetros);
• barbante (medindo cêrca de 20 centímetros);
• um canudo de papel;
• um peso (moeda ou argola de metal);
• imagem (cópia xerográfica) de um transferidor de 180graus;
• fita adesiva;
• cola.
Como construir
• Com a fita adesiva, prenda o canudo em uma das bordas de 15 centímetros do papelão.
• Cole a imagem do transferidor logo abaixo do canudo.
• Prenda o peso em uma das extremidades do barbante.
• Com cuidado, faça um pequeno furo, transpassando o papelão bem no encontro da linha de fé do transferidor (linha 0grau/180graus) com a linha perpendicular que marca 90graus.
• Passe por esse furo a outra extremidade do barbante, deixando o restante no mesmo lado em que está a imagem do transferidor e dê um nó bem firme.
Como fazer a medição
Agora, vamos experimentar o instrumento para cálculos de medida de grandes alturas. Para isso, necessitamos de uma trena (ou de uma fita métrica ou de um metro articulado).
• Afaste-se de um poste de iluminação, meça sua distância (d) até ele e anote (corresponde ao cateto adjacente).
• Olhe pelo orifício do canudo até enxergar o topo do poste (que corresponde ao cateto oposto).
• Segure o barbante com o peso na posição em que ele parou.

• Anote a medida do ângulo determinado pelo barbante (na posição horizontal, o ângulo marcado mede 90graus).
• Procure, no quadro de razões trigonométricas, a tangente do seu ângulo de visão, cuja medida é 90graus menos o valor anotado. Essa tangente é a razão entre h e d, em que h é a diferença entre a medida da altura do poste (H ) e a do olho do observador.
Faça os cálculos e determine H, que é a medida da altura do poste. Não se esqueça de que H é igual à medida h adicionada à altura dos olhos do observador.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Paulo usa um teodolito “caseiro” para calcular a medida da altura de uma torre. O ângulo de visão de Paulo ao topo dela é de 45graus, ele está a 3,5 métros dela e seus olhos estão a 1,25 métro do chão. Qual é a altura da torre?
2 Ainda treinando o uso de seu teodolito, Paulo observou o topo de um poste de 7 métros, sob um ângulo de visão de 15graus. Qual é a distância aproximada de Paulo até o poste?
4. Razões trigonométricas dos ângulos de 45graus, 30graus e 60graus
Estudamos que os valores das razões seno, cosseno e tangente podem ser encontrados no quadro de razões trigonométricas ou obtidos com uma calculadora científica.
Mas os valores encontrados dessas duas maneiras não são valores exatos, exceto os valores para seno de 30º, cosseno de 60º e tangente de 45º.
No entanto, os valores exatos das razões seno, cosseno e tangente dos ângulos de 30graus, 45graus e 60graus são facilmente calculados, como verificaremos a seguir.
Razões trigonométricas do ângulo de 45graus
Considere o quadrado a bê cê dê. Aplicando o teorema de Pitágoras no triângulo á bê cê, obtemos:
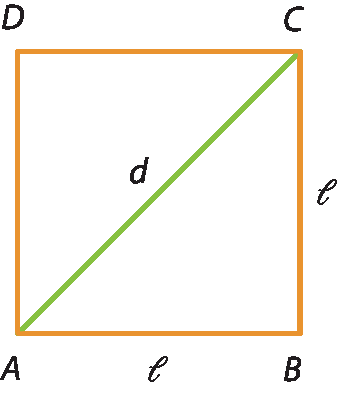
(AB )elevado a 2 + (BC )elevado a 2 = (AC )elevado a 2
𝓁elevado a 2 + 𝓁elevado a 2 = d elevado a 2
𝓁
raiz quadrada de 2= d ou d = 𝓁
raiz quadrada de 2A diagonal
ACmede 𝓁
raiz quadrada de 2.
Destacando o triângulo ABC, obtemos:
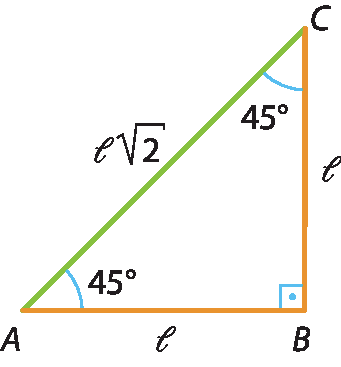

Razões trigonométricas do ângulo de 30graus
Considere agora o triângulo equilátero á bê cê, com lado de medida 𝓁.
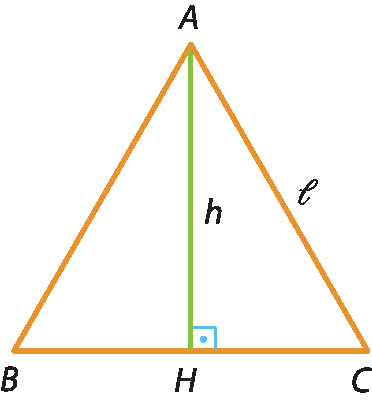
Já sabemos que a altura
AHdo triângulo mede
h igual a fração de numerador l raiz quadrada de 3, e denominador 2.Destacando do triângulo á bê cê o triângulo á agá cê, obtemos:
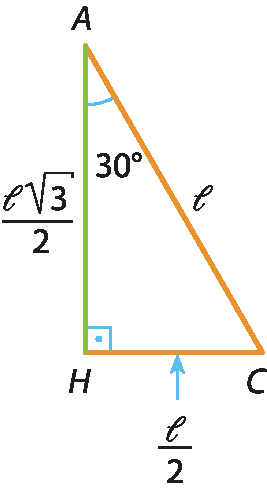

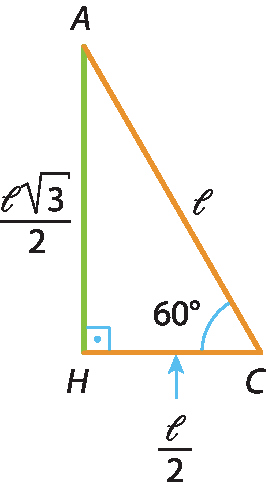
Razões trigonométricas do ângulo de 60graus
Destacando novamente o triângulo á agá cê da figura anterior, obtemos:
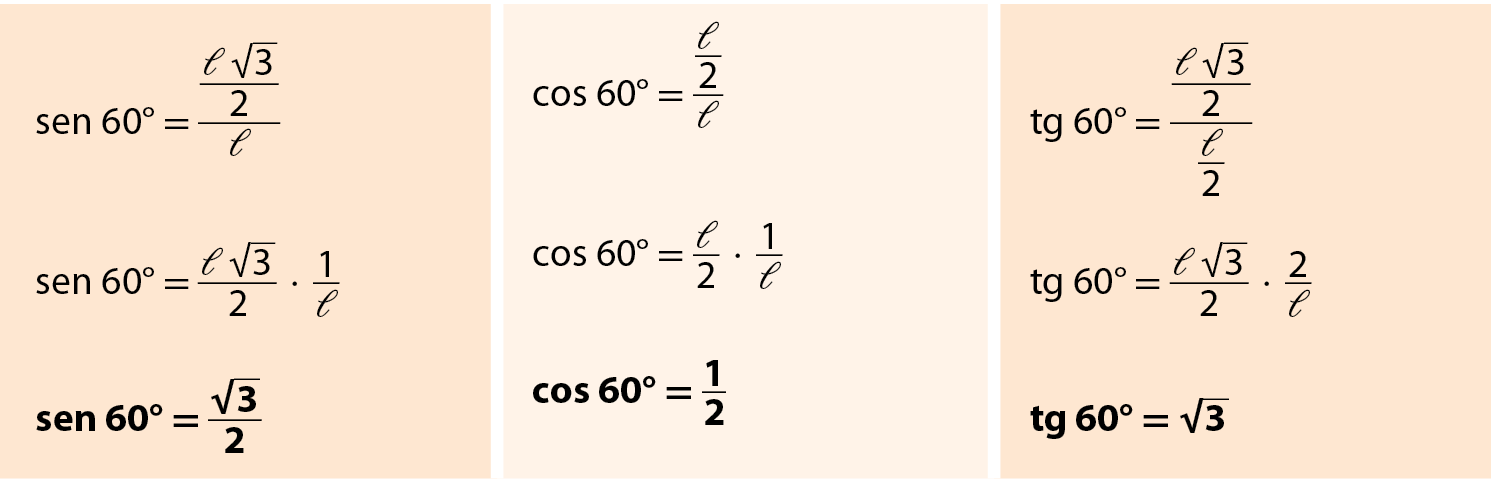
Agora, vamos organizar em um quadro todos os valores obtidos:
|
Ângulo |
Seno |
Cosseno |
Tangente |
|---|---|---|---|
|
30° |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
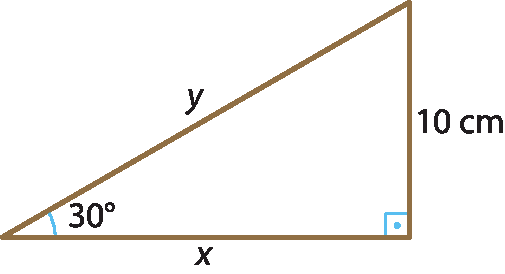
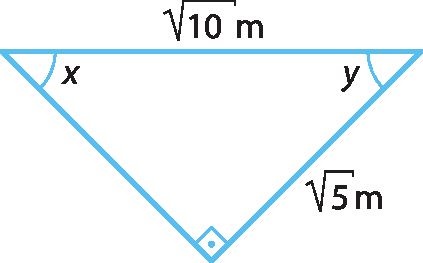
27 Usando as razões trigonométricas, calcule o valor de x e de y nos triângulos retângulos.
a)
b)
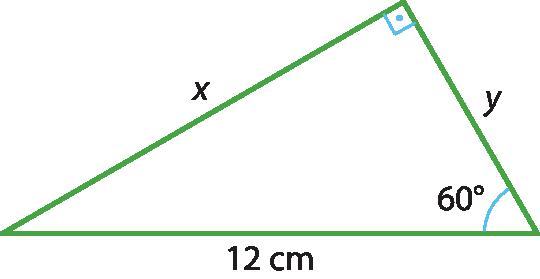
c)
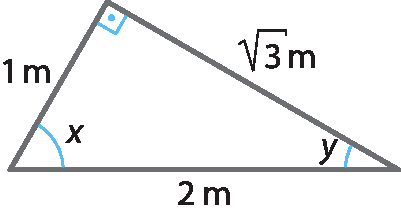
d)
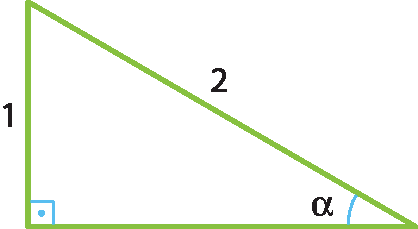
28 (ú éfe vê-Minas Gerais) O cosseno do ângulo α, assinalado na figura a seguir, é:
a)
[a] Fração. 1 meio..
b)
[b] Fração. 2 sobre raiz quadrada de 3..
c)
[c] Fração. 2 raiz quadrada de 3, sobre 3..
d)
raiz quadrada 3 sobre 2.
e)
raiz quadrada de 3 sobre 3.
29 O lado não perpendicular às bases de um trapézio retângulo fórma com a base maior um ângulo de 45graus. Considerando que as bases medem 12 centímetros e 9 centímetros, determine:
a) a medida da altura;
b) a medida do lado não perpendicular às bases.
30 Construa um losango em que uma das diagonais meça 12 centímetros e forme com um dos lados um ângulo de 30graus. Determine:
a) a medida da outra diagonal;
b) a medida do lado do losango.
31 Um poste cilíndrico cujo diâmetro da base mede 0,40 métro projeta uma sombra de 5,6 métros no momento em que os raios solares determinam um ângulo de 45graus com a vertical.
a) Quanto mede a altura dêsse poste?
b) Para o cálculo do item a, foi preciso usar a medida 0,40 métro?
32 Uma das alturas de um triângulo equilátero mede
2 raiz quadrada de 3, centímetrosDetermine a medida do lado dêsse triângulo.
33 Em um trapézio isósceles, os lados não paralelos formam com a base maior ângulos de 60°. Se as bases medem 28 centímetros e 20 centímetros, então:
a) qual é a medida do perímetro do trapézio?
b) qual é a medida da área do trapézio?
34 (uquisal-Bahia) Na figura a seguir, tem-se um trapézio isósceles cujos lados têm as medidas indicadas.
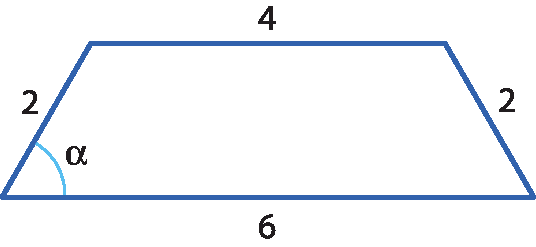
A medida do ângulo assinalado é:
a) 60graus.
b) 45graus.
c) 30graus.
d) 22graus30minutos.
e) 15graus.
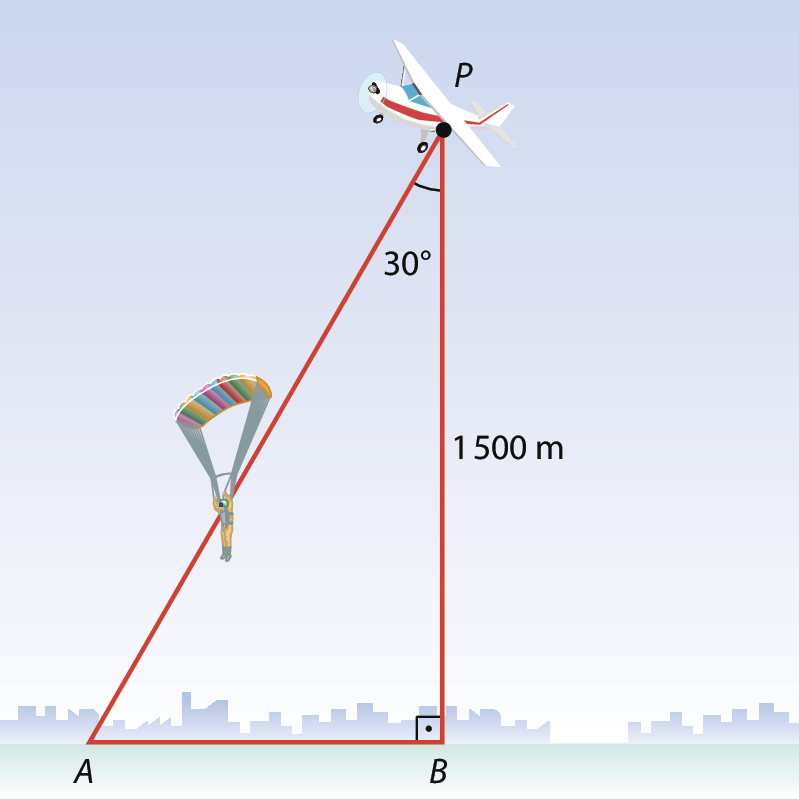
35 Um paraquedista salta de um avião que voa a .1500 métros de altura. Devido à velocidade do avião e à ação do vento, o paraquedista faz um percurso aproximado conforme indica o segmento
PA. A que medida de distância do ponto B o paraquedista cai?
TRABALHANDO A INFORMAÇÃO



Gráficos com distorção
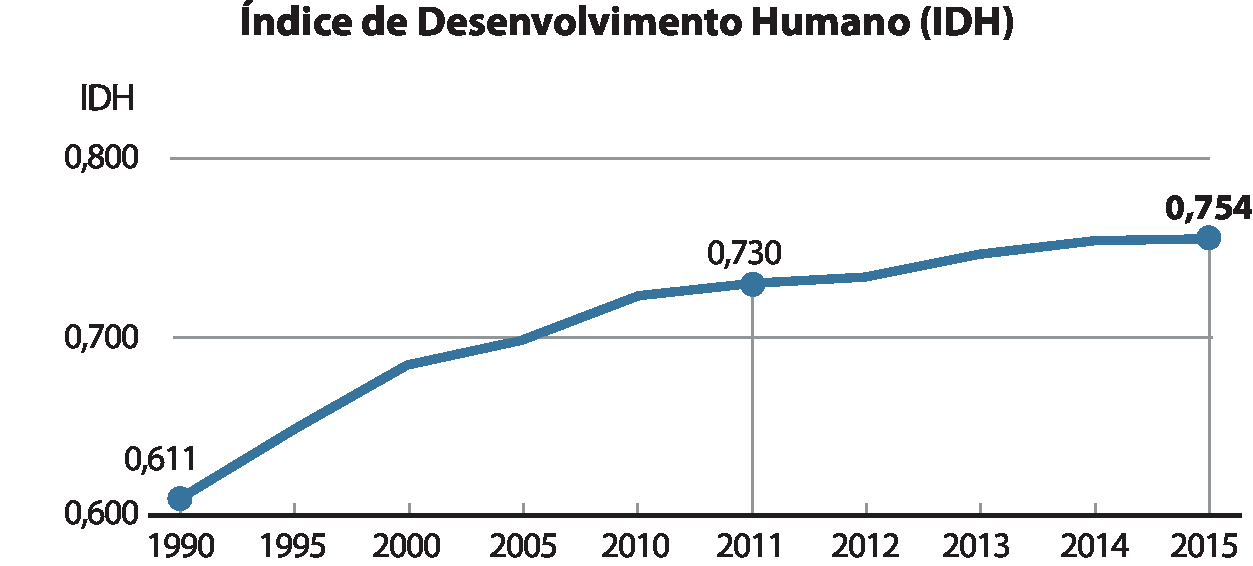
Pela primeira vez na série histórica, em 2017, o Brasil ficou estagnado (79ª posição) no Índice de Desenvolvimento Humano, com o indicador de 0,754.
O Índice de Desenvolvimento Humano (í dê agá) é uma medida composta de indicadores de três dimensões do desenvolvimento humano: longevidade, educação e renda. Ele varia de 0 a 1; quanto mais próximo de 1, maior o desenvolvimento humano. São quatro classificações: baixo, médio, alto e muito alto.
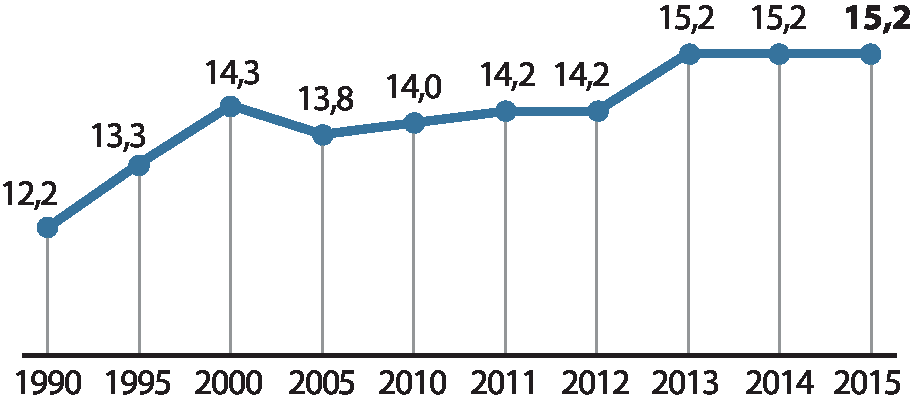
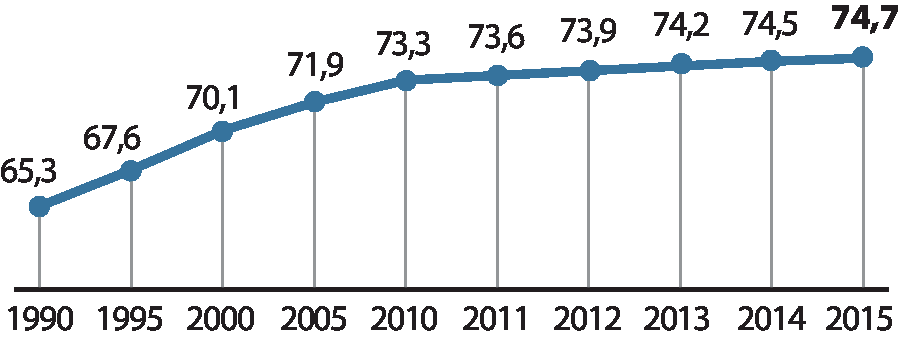
O Relatório de Desenvolvimento Humano 2016 da ônu (Organização das Nações Unidas) mostra que, em 2015, o Brasil apresentou uma discreta melhora em relação a 2014 em alguns aspectos, como: expectativa de vida (de 74,5 para 74,7 anos) e média de anos de estudo (de 7,7 para 7,8 anos). Porém, o país estagnou na marca de 15,2 anos na expectativa de anos de estudo.
Podemos ler essa situação nos gráficos a seguir. Porém, para essa leitura, observe atentamente estes gráficos.
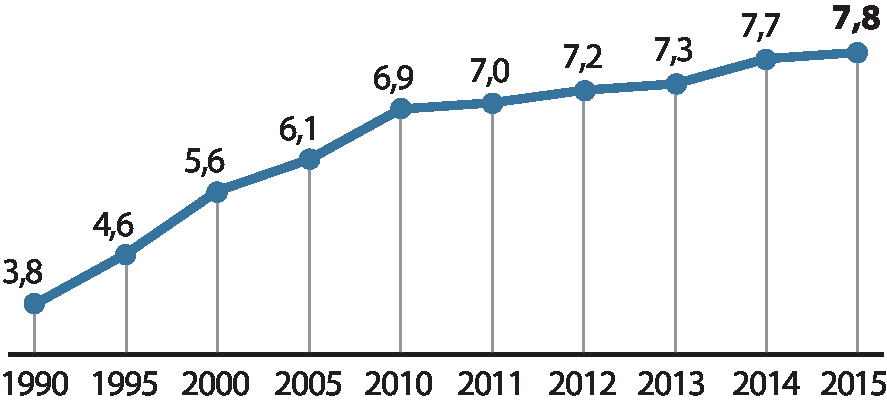
1. Expectativa de anos de estudo
2. Expectativa de vida ao nascer
3. Média de anos de estudo
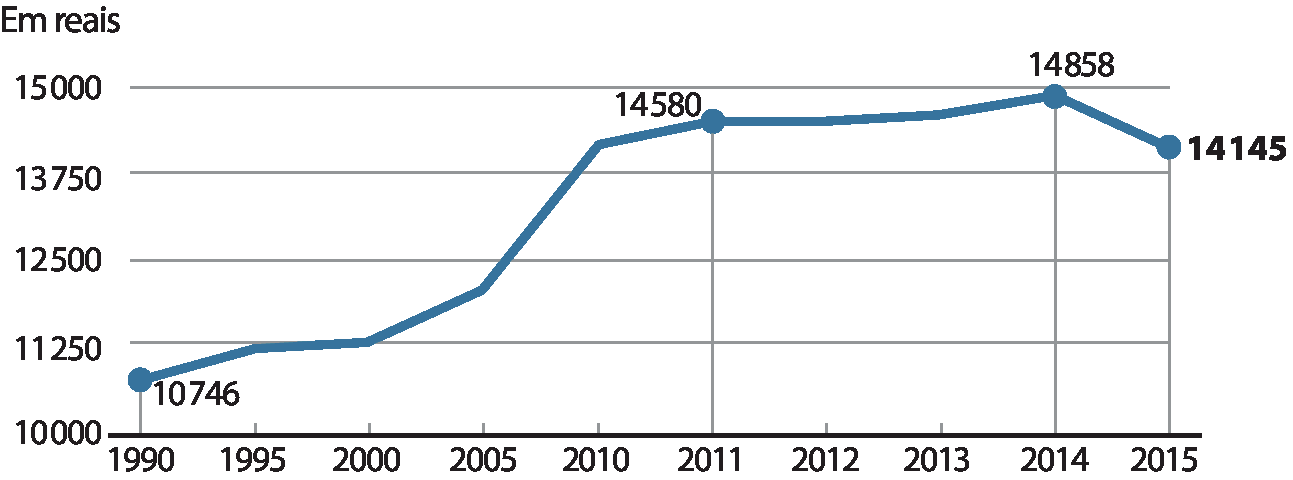
4. Renda Nacional Bruta per cápita (PPS)
Os quatro gráficos anteriores podem ser resumidos no gráfico a seguir.
Agora quem trabalha é você!
FAÇA AS ATIVIDADES NO CADERNO
1 Em um gráfico de linha que preserva a escala nos eixos, isto é, em que a unidade é uniforme em cada eixo, ao caminhar da esquerda para a direita, a maior inclinação da linha indica maior variação na grandeza do eixo vertical. Identifique, em cada um dos quatro primeiros gráficos, o período em que houve a maior evolução.
2 Refaça os gráficos dados com espaçamentos horizontais iguais para períodos de tempo iguais, por exemplo, 1 centímetro para cada ano. Responda novamente à atividade 1. As suas respostas são as mesmas? Por quê?
3 Em sua opinião, os gráficos de linha divulgados na mídia (jornais, revistas, internet, tê vê etcétera) devem aplicar unidades uniformes nos eixos?
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1

Construa um triângulo retângulo em que um dos ângulos meça 55graus. Meça os lados dêsse triângulo, em milímetro. Calcule as razões trigonométricas dêsse ângulo, com uma casa decimal. Confira os resultados consultando o quadro de razões trigonométricas ou uma calculadora.
2 Nos triângulos, determine o valor de x :
a)
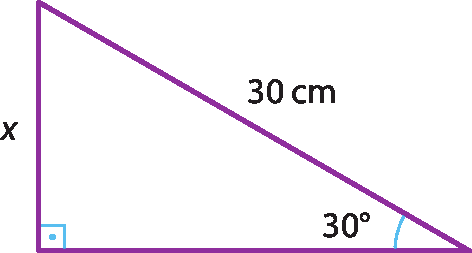
b)
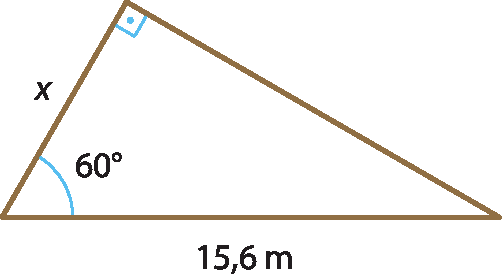
c)
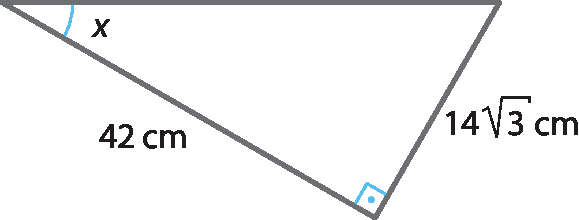
3 (Unopar-Paraná) Se um cateto e a hipotenusa de um triângulo retângulo medem a e 3a, respectivamente, então o cosseno do ângulo oposto ao menor lado é:
a)
raiz quadrada de 10 sobre 10.
b)
2 raiz quadrada de 2 sobre 3.
c)
um terço.
d)
raiz quadrada de 2 sobre 3.
e)
2 raiz quadrada de 2.
4 Os ângulos da base de um triângulo isósceles medem 50graus. Calcule a medida aproximada dos lados congruentes, sabendo que a altura em relação à base mede 20 centímetros.
5 A figura a seguir representa um canudinho biodegradável dentro de um copo cuja altura mede 15 centímetros.
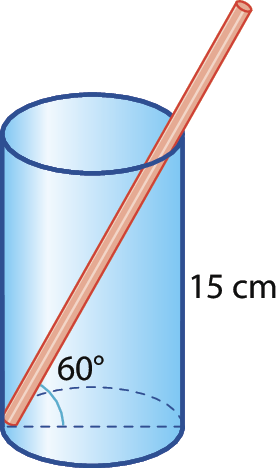
Calcule a medida aproximada do comprimento dêsse canudinho, sabendo que 8 centímetros dele estão fóra do copo.
(Dado:
raiz quadrada de 3= 1,73.)
6 Uma escada medindo 2,80 métros de comprimento e 0,65 métro de largura está apoiada no topo de um muro, formando com ele um ângulo de 60graus. Qual é a medida da altura do muro?
7 Regina tem um terreno no formato de um trapézio, conforme mostra a figura. Quantos metros quadrados de muro, aproximadamente, serão necessários para cercar esse terreno, se o muro tiver 1,80 métro de altura? Calcule, se possível, a medida do volume dêsse muro.
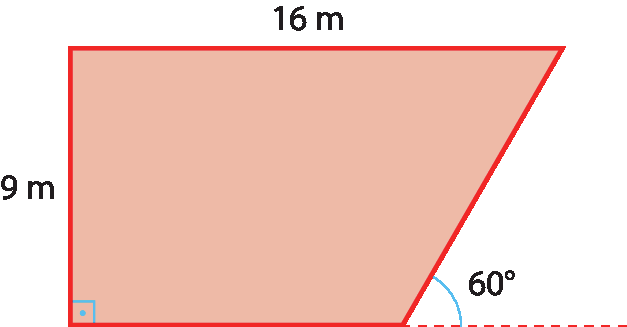
8 (uquisal-Bahia) Na figura a seguir tem-se o triângulo á bê cê, cujos ângulos internos têm as medidas indicadas.
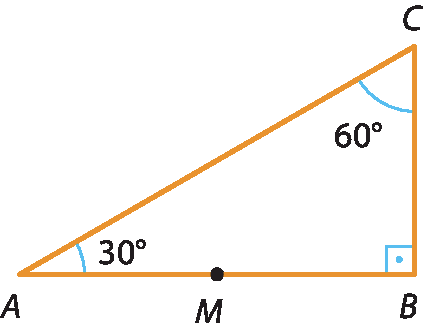
Se M é ponto médio de
ABe AC = 10 centímetros, qual é a medida do segmento
AM?
9 Rosana mediu a largura de um rio fixando um ponto A em uma das margens e um ponto B na margem oposta, de modo que
ABficasse perpendicular às margens dêsse rio. Do ponto a, caminhou 40 métros perpendicularmente a
ABe marcou um ponto C. Mediu o ângulo
BCAobtendo 30graus. Assim, ela pôde determinar a medida da largura do rio.
(Dado:
raiz quadrada de 3= 1,73.)
a) Determine a medida dessa largura, expressa na fórma
a raiz quadrada de b.
b) Determine a medida aproximada dessa largura.
10 De uma folha de cartolina, foi recortado um triângulo isósceles cujo ângulo do vértice mede 120graus. Cada um dos lados congruentes do triângulo mede 40 centímetros. Qual é a medida da área do triângulo recortado?
11 Uma escada rolante une dois andares de uma loja. Sabendo que o comprimento dessa escada mede 10 métros e tem inclinação de 30graus, a medida de sua altura, em metro, fica entre quais números pares consecutivos?
12 (Mackenzie-São Paulo) Na figura,
ABé paralelo a
segmento CD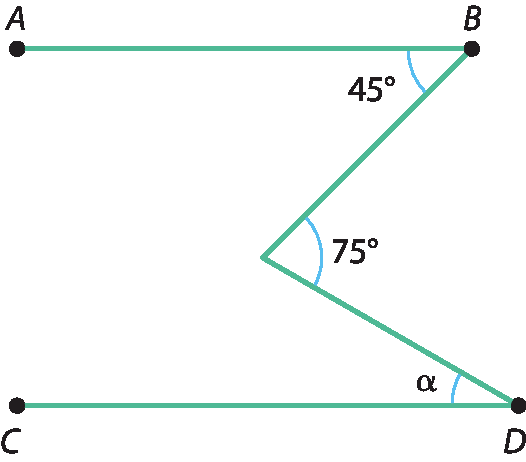
O valor de seno de α é:
a)
raiz quadrada de 2 sobre 2.
b)
raiz quadrada de 3 sobre 2.
c)
1 sobre 2.
d) 1.
e) 0.
13 Dois prédios, A e B, estão situados em um mesmo plano. Da base do prédio A, avista-se o topo do prédio B sob um ângulo de 45graus com a horizontal, e da base do prédio B avista-se o topo do prédio A sob um ângulo de 60graus com a horizontal. Se a medida da distância entre A e B é 34,6 métros, determine as medidas das alturas do prédio A e do prédio B.
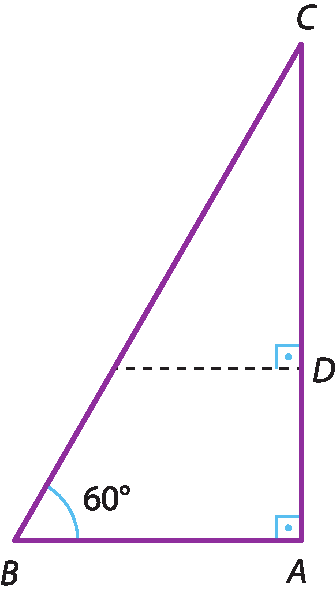
14 Considere o triângulo á bê cê da figura.
Sabendo que A bê = 750 métros e á dê = 620 métros, determine a medida DC.
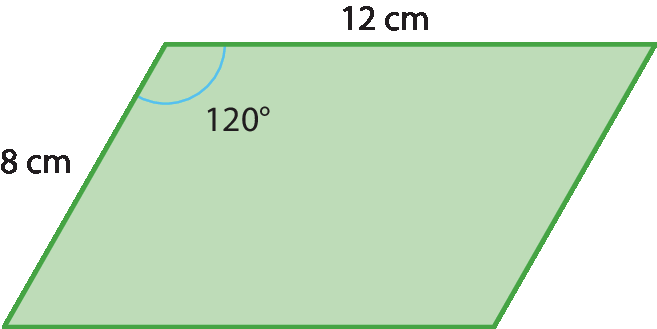
15 Um paralelogramo tem lados de medida 8 centímetros e 12 centímetros, e um de seus ângulos internos mede 120graus. Calcule a medida da sua área.
16 Um avião de acrobacias levanta voo formando um ângulo de 50graus em relação à pista. Calcule a que altura o avião estará do solo após percorrer 3,5 quilômetros em linha reta. (Dado: seno de 50graus = 0,76.)
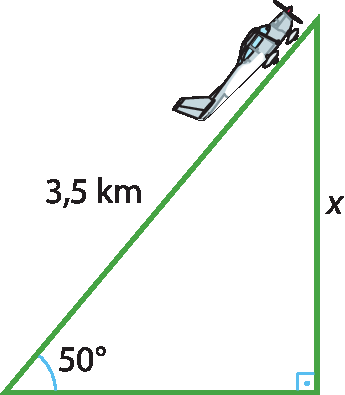
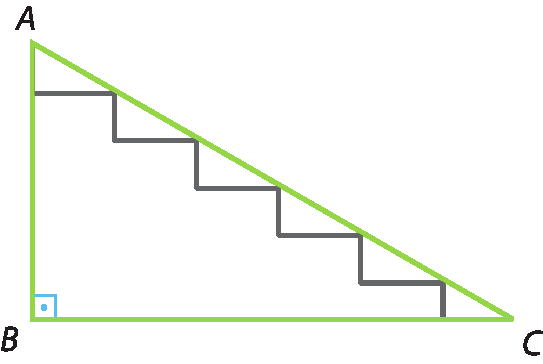
17 (Vunéspi-São Paulo) A figura representa o perfil de uma escada cujos degraus têm todos a mesma extensão, além de mesma altura. Se A bê = 2 métros e
ângulo BCAmede 30graus, qual é a medida da extensão de cada degrau?
18 Qual é a medida da área do triângulo a seguir?
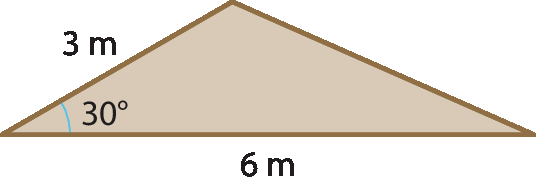
a) 4 métros quadrados
b) 4,5 métros quadrados
c) 5 métros quadrados
d) 5,5 métros quadrados
19 Um automóvel parte de a e segue, em uma direção que forma com a reta
ACum ângulo de 30graus, com velocidade média de 50 quilômetros por hora. Após 3 horas de percurso, qual será a medida da distância que o automóvel estará da reta
AC?
a) 75 quilômetros
b)
[b] Medida. 75 raiz de 3 quilômetros.c)
[c] Medida. 50 raiz de 3 quilômetros..
d)
[d] Medida. 75 raiz de 2 quilômetros.VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 O seno de um ângulo pode ser calculado em um triângulo retângulo pela razão, nessa ordem, entre as medidas:
a) do cateto oposto ao ângulo e da hipotenusa.
b) do cateto adjacente ao ângulo e da hipotenusa.
c) do cateto oposto ao ângulo e do cateto adjacente ao ângulo.
d) da hipotenusa e do cateto oposto ao ângulo.
2 Sabendo que, em um triângulo retângulo, a hipotenusa mede 13 centímetros e o cateto adjacente a um ângulo mede 5 centímetros, qual é o valor do seno dêsse ângulo?
a)
[a] Fração. 5 sobre 13.b)
[b] Fração. 13 sobre 5.c)
[c] Fração. 5 sobre 12.d)
[d] Fração. 12 sobre 13.3 A tangente de um ângulo agudo de medida α é uma relação entre as medidas do seno e do cosseno dêsse ângulo. Essa relação é:
a)
[a] Fração. seno de alfa sobre cosseno de alfa.b)
[b] Fração. cosseno de alfa sobre seno de alfa.c) seno de α · cosseno de α
d) seno de² α + cosseno de² α
4 Qual é a medida x do cateto adjacente ao ângulo de 38graus?
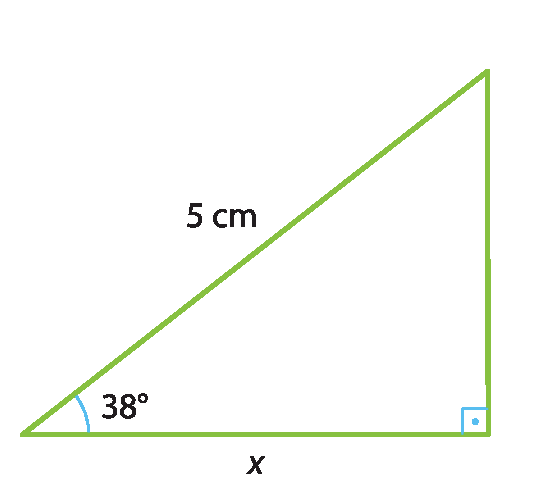
a) 6,34 centímetros
b) 3,94 centímetros
c) 0,158 centímetro
d) Não é possível determinar.
5 Qual é, aproximadamente, a medida do ângulo agudo indicado na imagem?
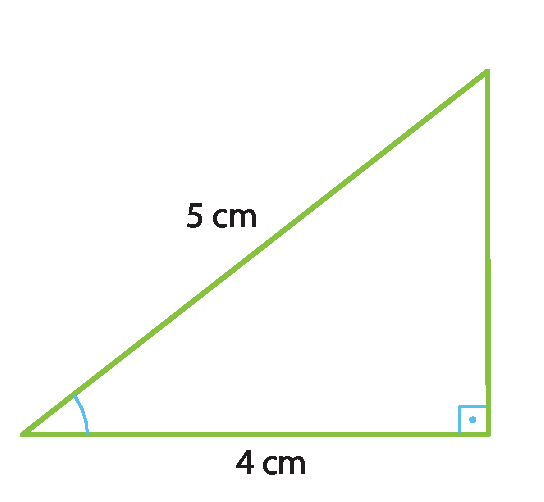
a) 53graus
b) 37graus
c) 51graus
d) 45graus
6 Qual é a diferença entre os valores do seno do ângulo de 30graus e do cosseno do ângulo de 60graus?
a) 1
b) 0,5
c) 0,25
d) 0
7 Qual é a medida do ângulo agudo de um triângulo retângulo com hipotenusa medindo 2 centímetros e cateto oposto medindo 1 centímetro?
a) 60graus
b) 45graus
c) 30graus
d) 15graus
8 Qual é o valor da tangente do menor ângulo do triângulo a seguir, formado pela diagonal de um retângulo de lados medindo 10 métros e 5 métros?
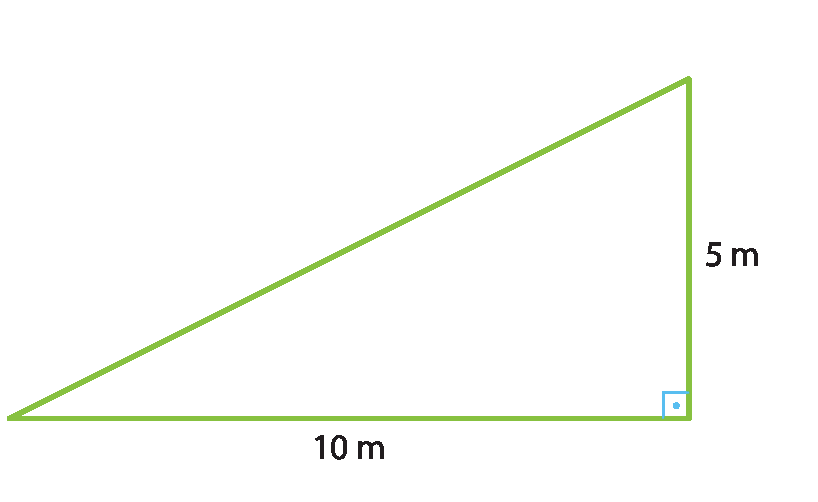
a) 2
b) 0,3
c) 0,5
d) 0,8
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) Quais são as três razões trigonométricas que você estudou neste capítulo?
b) Qual é o instrumento de precisão usado para medir ângulos horizontais e verticais que você conheceu neste capítulo?
c) Quais são as razões do seno, do cosseno e da tangente dadas pelas medidas á cê e bê cê dos catetos e A bê da hipotenusa de um triângulo retângulo em
ângulo C?
d) Verifique a relação
tangente de alfa é igual a seno de alfa sobre cosseno de alfacom os valores do seno, do cosseno e da tangente do ângulo de 30graus.
Glossário
- Agrimensor
- : profissional legalmente habilitado para medir e demarcar terras ou propriedades rurais.
- Voltar para o texto