CAPÍTULO 10 Estudo das funções

Observe a fotografia e responda às questões no caderno.
a) Você conhece algum esporte em que os atletas fazem giros no ar?
b) Represente, em uma folha quadriculada, a trajetória do giro com a motocicleta realizada por Travis Pastrana desde o momento em que começa a subir na rampa para saltar até o momento em que chega à outra rampa.
c) Uma atividade como essa, em que o corpo é projetado no espaço com ou sem motocicleta, pode ser realizada pelas pessoas sem conhecimento das técnicas próprias, sem preparo com instrutores, sem treinamento evolutivo e sem os elementos necessários para a sua segurança?
Travis Pastrana é um atleta que compete em várias modalidades, como Supercross, Motocross, Freestyle e corridas de rally. Na fotografia, está registrada uma sequência de momentos em que ele realiza uma de suas acrobacias em um movimento que pode ser associado ao lançamento oblíquo.
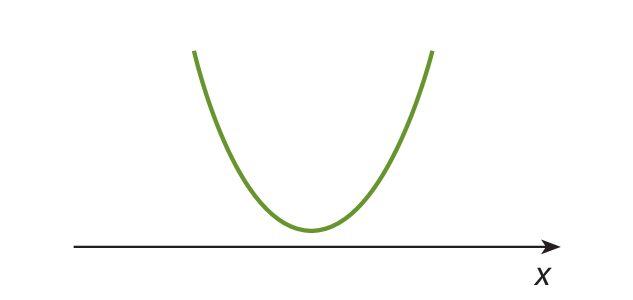
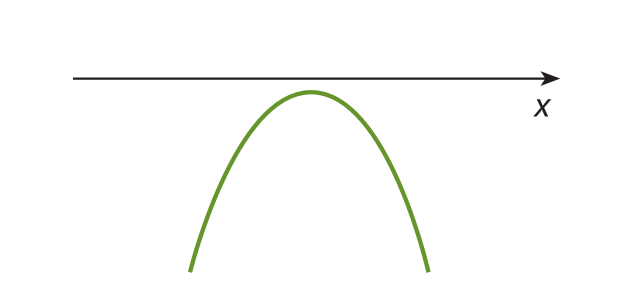
Nesse tipo de lançamento, desprezada a resistência do ar, sob a ação de seu peso, um corpo fica sujeito à aceleração da gravidade, e sua trajetória em relação à Terra é uma parábola.
O estudo dêsse fenômeno envolve dois movimentos:
• horizontal, descrito por uma função polinomial do 1º grau;
• vertical, descrito por uma função polinomial do 2º grau.
1. Conceito de função
Acompanhe as situações a seguir.
Situação 1
Uma empresa de tê vê a cabo cobra de seus assinantes uma mensalidade de R$ 195,00cento e noventa e cinco reais e mais R$ 9,00nove reais por programa extra comprado. dêsse modo, o valor a ser pago (preço) no final de cada mês depende do número de programas extras adquiridos pelo assinante.
Vamos organizar um quadro que mostra a relação entre o número de programas extras comprados e o total a ser pago.

|
Número de programas extras |
Preço (em real) |
|---|---|
|
0 |
195 + 0 ⋅ 9 |
|
1 |
195 + 1 ⋅ 9 |
|
2 |
195 + 2 ⋅ 9 |
|
3 |
195 + 3 ⋅ 9 |
|
4 |
195 + 4 ⋅ 9 |
Indicando por x o número de programas extras comprados e por y o preço a pagar, podemos relacionar essas duas grandezas por meio da sentença:
y = 195 + x · 9 ou y = 195 + 9x
Note que, a cada valor atribuído para x, obtemos um único valor para y; por exemplo:
• para x = 0, obtemos:
y = 195 + 9 · 0 = 195 + 0 = 195
Isso significa que, quando não se compra programa extra, o preço é R$ 195,00cento e noventa e cinco reais.
• para x = 1, obtemos:
y = 195 + 9 · 1 = 195 + 9 = 204
Ou seja, com a compra de 1 programa extra, o preço é R$ 204,00duzentos e quatro reais.
• para x = 2, obtemos:
y = 195 + 9 · 2 = 195 + 18 = 213
Ou seja, com a compra de 2 programas extras, o preço é R$ 213,00duzentos e treze reais.
Nesse caso, podemos dizer que o preço a pagar ( y) é obtido em função do número de programas extras comprados (x).
Dizemos que a grandeza y é função da grandeza x se há entre elas uma correspondência tal que, para cada valor de x, exista um único valor de y.
Na função que relaciona o número de programas extras comprados (x) e o preço a pagar (y), escrevemos a sentença y = 195 + 9x. Nesse caso, x e y são chamadas de variáveis, e a sentença y = 195 + 9x é chamada de lei da função.
Em geral, dizemos que y é uma função de x por y = f (x) (lemos: “y é igual a f de x ”). Então, para o caso em que a lei da função é y = 195 + 9x, podemos escrever f (x) = 195 + 9x.
Situação 2
Paulo é vendedor de assinaturas de revistas, e seu salário varia conforme o número de assinaturas que ele vende no mês. Ele recebe um valor fixo de R$ 1.800,00mil oitocentos reais, e uma comissão de R$ 40,00quarenta reais para cada assinatura vendida. Considere a relação entre o número de assinaturas vendidas e o salário de Paulo indicada no quadro.

|
Número de assinaturas vendidas |
Salário de Paulo (em real) |
|---|---|
|
0 |
1.800 + 0 ⋅ 40 = 1.800 |
|
1 |
1.800 + 1 ⋅ 40 = 1.840 |
|
2 |
1.800 + 2 ⋅ 40 = 1.880 |
|
3 |
1.800 + 3 ⋅ 40 = 1.920 |
|
4 |
1.800 + 4 ⋅ 40 = 1.960 |
|
5 |
1.800 + 5 ⋅ 40 = 2.000 |
Nesse caso, podemos escrever a função:
f (décima) = .1800 + x · 40 ou f (décima) = .1800 + 40x
Observe que f abre parênteses décimafecha parênteses representa o salário de Paulo, e x, o número de assinaturas vendidas por ele.
Com essas informações, podemos responder, por exemplo, às questões a seguir.

a) Se Paulo vender 59 assinaturas em um mês, qual será seu salário? Nesse caso, substituímos x por 59 na lei da função f (décima) = .1800,00 + 40x ; desta maneira:
f (59) = .1800 + 40 · 59
f (59) = .1800 + .2360
f (59) = .4160
Logo, se vender 59 assinaturas, Paulo receberá R$ 4.160,00quatro mil cento e sessenta reais de salário.
Observe que f (59) corresponde ao salário de Paulo quando x for igual a 59.
•

Analisando os valores de f abre parênteses décimafecha parênteses, apresentados no quadro, é correto afirmar que f (60) < f (61)? E é verdade que, se x < y, fabre parênteses décimafecha parênteses < f abre parênteses yfecha parênteses?
b) Se o salário ao final do mês foi de R$ 3.600,00três mil seiscentos reais, quantas assinaturas Paulo vendeu? Agora, substituímos fabre parênteses décimafecha parênteses por .3600 e encontramos o valor de x correspondente.
.3600 = .1800 + 40x
‒ 40x = .1800 ‒ .3600
40x = .1800
x = 45
Portanto, se Paulo receber R$ 3.600,00três mil seiscentos reais de salário, ele vendeu 45 assinaturas.
Situação 3
José tem um sítio e pratica agricultura de subsistência. Para proteger durante a noite suas galinhas de outros animais, ele resolveu construir um galinheiro retangular com 16 metros de tela e aproveitou um muro já existente como um dos lados.
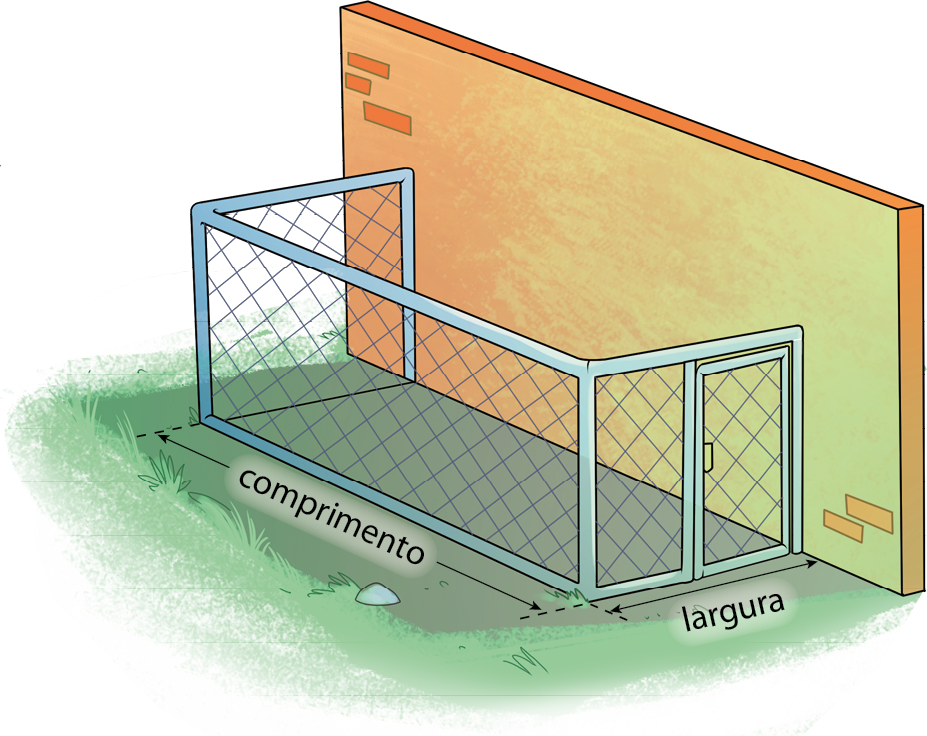
Observe que a soma das medidas de duas larguras com a de um comprimento resulta em 16 metros. Assim, se José construir um galinheiro medindo 3 metros de largura, o comprimento medirá 10 metros.
16 ‒ 2 · 3 = 10, pois 2 · 3 + 10 = 16
Considere outros possíveis valores para as medidas do galinheiro, em metro, como indicados no quadro:
|
Medida da largura (m) |
Medida do comprimento (m) |
|---|---|
|
1 |
16 − 2 ⋅ 1 = 14 |
|
2 |
16 − 2 ⋅ 2 = 12 |
|
3,5 |
16 − 2 ⋅ 3,5 = 9 |
|
5 |
16 − 2 ⋅ 5 = 6 |
|
6,4 |
16 − 2 ⋅ 6,4 = 3,2 |
Note que a medida y do comprimento é dada em função da medida x da largura e que ambos se relacionam de acordo com a lei y = 16 ‒ 2x, ou seja, para essa situação, podemos considerar a função f dada por f (décima) = 16 ‒ 2x, em que x assume valores entre 0 e 8.
Com essas informações, podemos responder às questões a seguir.

a) Para José construir um galinheiro medindo 7,5 metros de comprimento, qual será a medida da largura?
Basta substituir f abre parênteses décimafecha parênteses por 7,5 e encontramos o valor de x correspondente.
7,5 = 16 ‒ 2x
2x = 16 ‒ 7,5
2x = 8,5
x = 4,25
Portanto, para o galinheiro medir 7,5 metros de comprimento, a largura deverá medir 4,25 metros.
b) Se José quiser construir um galinheiro quadrado, qual será a medida da largura? Nesse caso, a medida x da largura deverá ser igual à do comprimento f abre parênteses décimafecha parênteses. Assim, substituímos fabre parênteses décimafecha parênteses por x na lei f (décima) = 16 ‒ 2x, obtendo: x = 16 ‒ 2x 3x = 16
x é igual a fração numerador: 16; denominador: 3.Logo, se José construir um galinheiro quadrado, ele medirá
16 terçosmetros de largura.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
1 Responda oralmente às questões.
Em certa loja, uma camiseta custa R$ 40,00quarenta reais a unidade, não importando a quantidade que se compre.
a) Na compra de duas camisetas, qual será o valor pago? E na compra de 10 camisetas?
b) Para cada quantidade comprada dessa camiseta, o preço associado é único?
c) A relação entre a quantidade de camisetas compradas e o preço a ser pago é uma função?
d) Determine o preço pago (y) como uma função do número de camisetas compradas (x).
2 Responda no caderno às questões a seguir.
a) Considerando a relação que associa uma mãe a cada filho, podemos dizer que essa relação é uma função?
b) Considerando a relação que associa cada filho à sua mãe biológica, podemos dizer que essa relação é uma função?
3 Em um estacionamento, são cobradas as seguintes tarifas:
• pela 1ª hora: R$ 15,00quinze reais;
• pela 2ª hora e seguintes: R$ 4,00quatro reais por hora.
Se x representa o número de horas que um carro permaneceu no estacionamento e y, o valor a ser pago, qual é a lei da função que fornece y em função de x?
4 Uma máquina produz 8 litros de sorvete a cada 10 minutos. Assim, a produção p depende da quantidade t de minutos que a máquina funciona.
Escreva a lei dessa função, que fornece p em função de t.
5 Faça o que se pede.
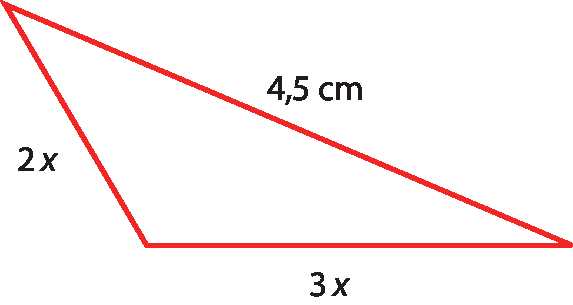
a) Represente a medida do comprimento y, em centímetro, em função de x, na figura a seguir.

b) Determine a medida do perímetro y, em centímetro, em função de x, nos polígonos a seguir.

6 Considerando a função f cuja lei é f (x) = 4x + 9, determine os valores indicados em cada item.
a) f (2)
b)
f de meio
c) f (‒2)
d) f (‒0,3)
e)
f de raiz quadrada de 2.
7 A diagonal maior de um losango mede 12 centímetros.
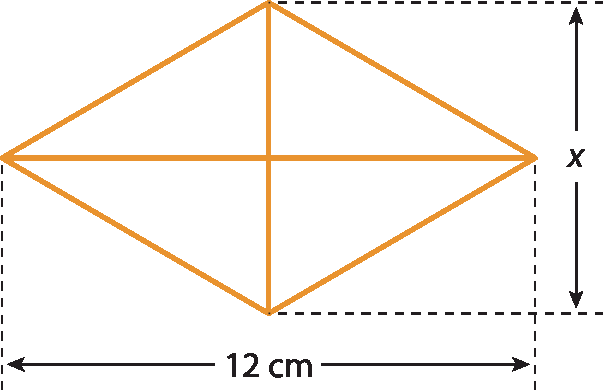
a) Represente a medida da área dêsse losango em função da medida da diagonal menor.
b) Calcule a medida da área dêsse losango quando a diagonal menor medir 7 centímetros.
c) Quanto deve medir a diagonal menor para que a área dêsse losango meça 45 centímetros quadrados?
8

Reúna-se com um colega para resolverem a atividade a seguir.
Certo fabricante de pirulitos tem uma despesa diária fixa de R$ 27,00vinte e sete reais mais R$ 0,30zero reais e trinta centavos por pirulito produzido. Ele vende cada pirulito por R$ 1,20um reais e vinte centavos.
a) Represente o custo diário c em função da quantidade n de pirulitos produzidos.
b) Se em um dia ele vender 200 pirulitos, terá lucro ou prejuízo? De quanto?
c) Qual é o número mínimo de pirulitos que esse fabricante deverá vender por dia para ter lucro?
d) Para esse fabricante ter um lucro de R$ 45,00quarenta e cinco reais, quantos pirulitos deverá vender?
e) Quantos pirulitos ele deve vender por dia útil para que, no fim de um mês com 22 dias úteis, lucre 6 salários mínimos?
f) Expliquem para outra dupla como vocês chegaram às respostas das questões.
9 A produção de uma fábrica onde trabalham 121 funcionários é dada por
y é igual a 50 vezes a raiz quadrada de x., em que y representa a quantidade, em tonelada, de certo produto fabricado mensalmente e x representa o número de funcionários.
a) Calcule no caderno quantas toneladas a mais serão produzidas, em um mês, com a contratação de 48 novos funcionários.
b) Se o número de funcionários fosse quadruplicado, a produção também seria quadruplicada? A variação do número de funcionários é proporcional à variação da produção?
10 Represente no caderno um retângulo medindo 10 centímetros de comprimento e a largura medindo x centímetro a menos.
a) Construa um quadro colocando na primeira linha os valores 1, 2, 3, 4 e 5 para x e, na segunda linha, a medida da área (a) do retângulo.
b) Pode-se atribuir a x um valor igual a 10 ou maior que 10? Justifique sua resposta.
c) Escreva uma dupla desigualdade, do tipo a < x < b, para indicar os valores reais que x pode assumir.
11

Hora de criar – Troque com um colega um problema sobre a lei de uma função, criado individualmente por vocês. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Observe o mapa.
MAPA POLÍTICO BRASILEIRO
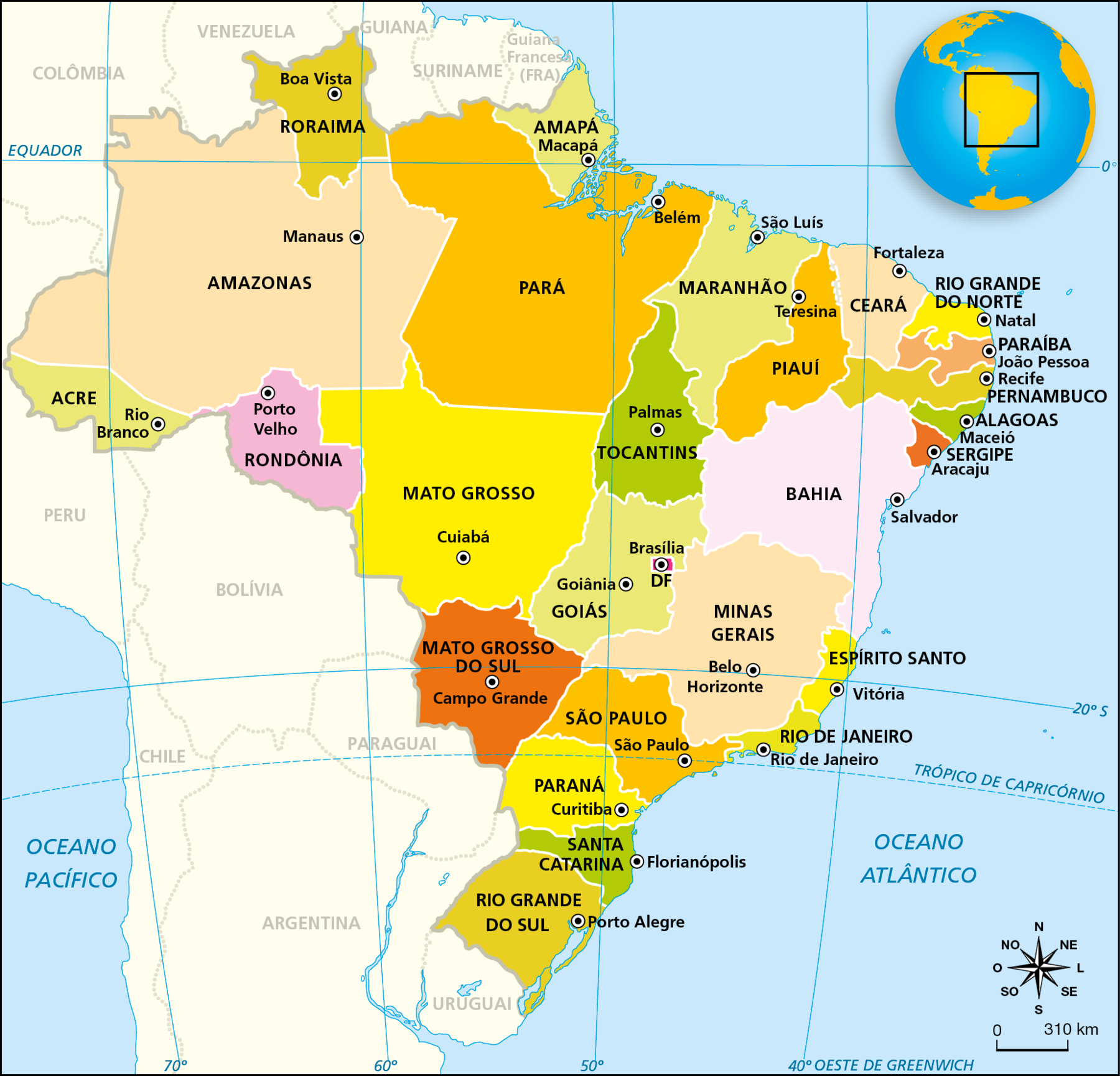
Considerando a escala indicada no mapa, resolva as questões a seguir no caderno.
a) Escreva a lei da função que fornece a medida da distância real y, em quilômetro, entre duas cidades do mapa em função da medida da distância x, em centímetro, medida no mapa.
b) Use uma régua para medir a distância entre São Paulo e Florianópolis em linha reta. Em seguida, calcule a distância real aproximada entre essas duas cidades.
c) Qual capital está a .1800 quilômetros de Brasília?
d) Um pequeno avião tem autonomia de voo igual a .1350 quilômetros. Se ele partisse de Belo Horizonte, a quais das cidades destacadas no mapa ele conseguiria chegar sem precisar reabastecer?
Versão adaptada acessível
Pense mais um pouco…
Um mapa do Brasil foi construído em uma escala de modo que cada centímetro, no mapa, corresponde à 310 quilômetros na realidade.
a) Escreva a lei da função que fornece a medida da distância real y, em quilômetro, entre duas cidades do mapa em função da medida da distância x, em centímetro, medida no mapa.
b) Sabendo, que neste mapa, a distância em linha reta entre São Paulo e Florianópolis é de aproximadamente 1,6 centímetro, qual é a distância aproximada entre essas capitais?
c) Uma capital que esteja a .1800 quilômetros de distância de Brasília, deve estar a que distância no mapa?
d) Um pequeno avião tem autonomia de voo igual a .1350 quilômetros. Se ele partisse de Belo Horizonte, a quais cidades poderia chegar?
i) Cidades que estão em um raio de medida menor que 4,4 centímetros, no mapa.
ii) Cidades que estão em um raio de medida igual a 4,4 centímetros, no mapa.
iii) Cidades que estão em um raio de medida maior que 4,4 centímetros, no mapa.
PARA SABER MAIS
Função, um longo caminho na história da Matemática
Não sabemos exatamente quando o conceito de função foi usado pela primeira vez. Sabe-se que os babilônios, cêrca de 2000 antes de Cristo, construíram quadros sexagesimais de quadrados e de raízes quadradas, as quais podem ser consideradas quadros de funções.
Antigos registros mesopotâmicos sobre lunaçõesglossário representavam, por meio de quadros, a relação entre as fases da Lua e o período de tempo solar. Os babilônios valorizavam esses quadros, pois eles estabeleciam uma correspondência de valores. Eram utilizados não somente para obter as informações que continham, mas também para avaliar os resultados correspondentes a valores intermediários, calculados por meio de aproximações por segmentos de reta.
O emprego das aproximações na Antiguidade significa a aplicação de uma relação funcional elementar, pois é uma simples proporcionalidade e constituiu o primeiro passo rumo ao desenvolvimento posterior de noções mais gerais de função.
Novas contribuições, ainda implícitas, para o desenvolvimento do conceito de função surgiram muito depois, no final da Idade Média, como as do matemático francês Nicole Oresme (1323 a 1382).
As ideias mais explícitas de função parecem ter surgido por meio de René Decárte (1596 a 1650), matemático e filósofo francês que adotou equações em x e em y para introduzir uma relação de dependência entre quantidades variáveis, de modo a possibilitar o cálculo de valores de uma delas por meio do valor da outra.

Foi a partir dos trabalhos do físico e matemático inglês Isaac Newton (1642 a 1727) e do matemático alemão Gottfried Wilhelm von Leibniz (1646 a 1716) que a palavra função, na sua fórma latina equivalente, parece ter sido introduzida. Eles fizeram as primeiras contribuições efetivas para o desenvolvimento dêsse conceito.
Por volta de 1718, o matemático suíço Johann Bernoulli (1667‑1748) chegou a considerar uma função como uma expressão qualquer, formada de uma variável e algumas constantes. Usou várias notações para uma função de x, sendo fx a mais próxima da que usamos hoje.
O suíço Leonhard Euler (1707 a 1783), um dos maiores matemáticos de sua época, também trabalhou com funções e introduziu a notação fabre parênteses décimafecha parênteses, hoje padronizada.
Posteriormente, outros matemáticos, como Joseph-Louis Lagrange (1736‑1813), Jean-Baptiste furriê (1768‑1830) e Johann Dirichlet (1805 a 1859), contribuíram significativamente para o desenvolvimento do conceito de função.
A teoria dos conjuntos, criada pelo matemático alemão Georg Cantor (1845‑1918), ampliou o conceito de função até chegar à definição conhecida atualmente.
Esse relato nos leva a concluir que os conceitos matemáticos são construídos e evoluem segundo as necessidades históricas e as conjunturas favoráveis nas mais diversas civilizações.
Gráfico de uma função
Considere a função f dada pela lei y = x + 1, em que x representa um número inteiro qualquer. Vamos construir seu gráfico.
Para isso, atribuímos valores inteiros a x e calculamos os valores de y, determinando os pares ordenados correspondentes. Esses dados foram organizados no quadro com alguns pontos do gráfico de f.
Quadro com alguns pontos do gráfico de f
|
x |
y = x + 1 |
(x, y) |
|---|---|---|
|
−2 |
y = −2 + 1 = −1 |
(−2, −1) |
|
−1 |
y = −1 + 1 = 0 |
(−1, 0) |
|
0 |
y = 0 + 1 = 1 |
(0, 1) |
|
1 |
y = 1 + 1 = 2 |
(1, 2) |
|
3 |
y = 3 + 1 = 4 |
(3, 4) |
Para representar graficamente essa função, vamos marcar, em um plano cartesiano, os pontos determinados por esses pares ordenados. Os pontos marcados são apenas alguns dos pontos do gráfico dessa função, pois existem infinitos pares ordenados (x, y) que satisfazem a lei y = x + 1, sendo x um número inteiro.
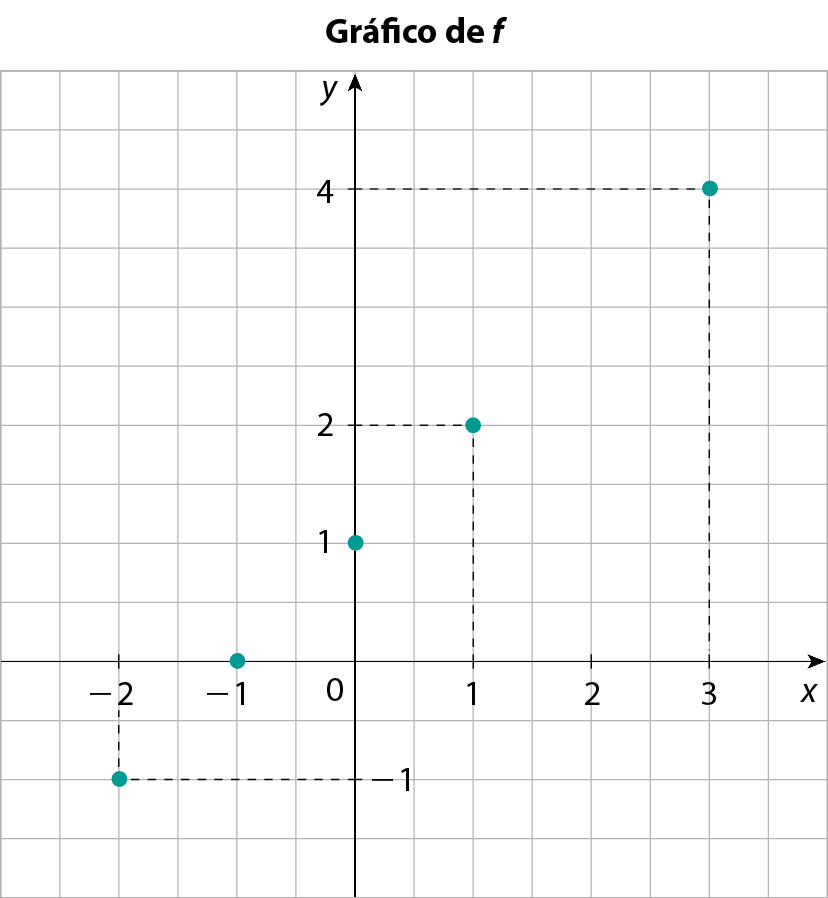

Considere agora uma função g dada pela mesma lei da função f, y = x + 1, porém com x representando um número racional qualquer.
Como todo número inteiro é também um número racional, todos os pontos do gráfico de f também são pontos do gráfico de g. Além desses pontos, podemos obter outros. Acompanhe:
Quadro com alguns pontos do gráfico de g
|
x |
y = x + 1 |
(x, y) |
|---|---|---|
|
−0,5 |
y = −0,5 + 1 = 0,5 |
(−0,5; 0,5) |
|
0,5 |
y = 0,5 + 1 = 1,5 |
(0,5; 1,5) |
|
|
= + = |
() |
|
2,3 |
y = 2,3 + 1 = 3,3 |
(2,3; 3,3) |
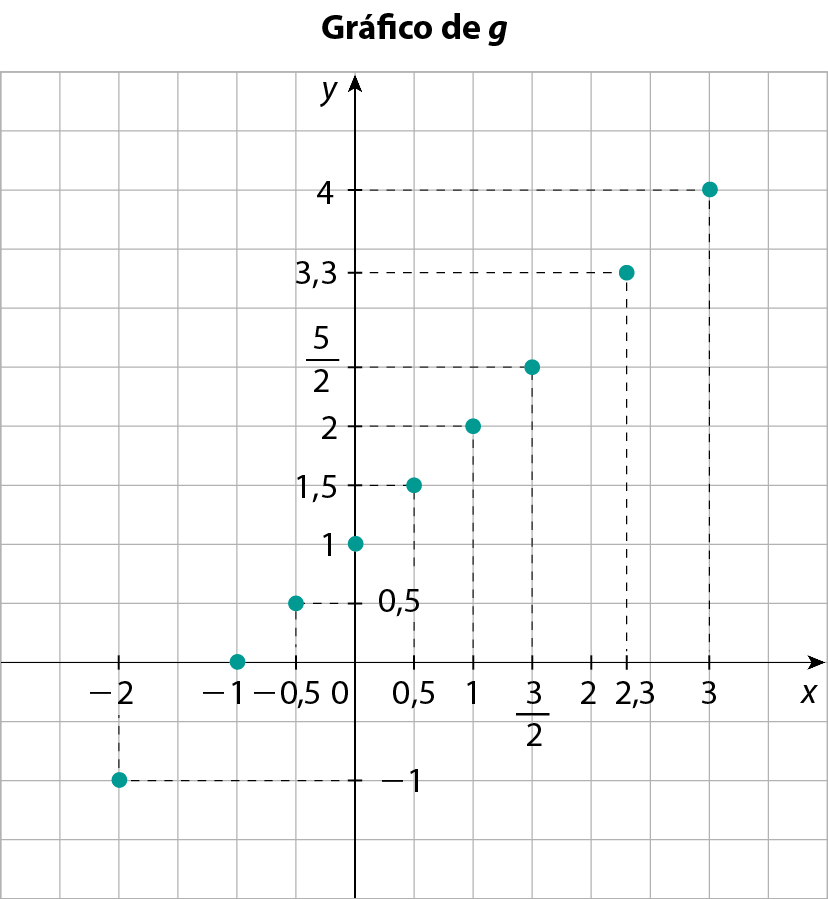
Também nesse caso não foram marcados todos os pontos do gráfico de g, pois existem infinitos pares ordenados (x, y ), sendo x um número racional, que satisfazem a lei y = x + 1.

Observação
▶ O termo infinitos não significa todos, por isso não podemos traçar a reta que passa pelos pontos obtidos no gráfico da função g.
▶ Em um ponto (x, y), dizemos que x corresponde à abscissa e y, à ordenada do ponto.
Agora, vamos considerar uma função h dada pela mesma lei da função f, y = x + 1, porém com x representando um número real qualquer.
Os pontos obtidos para os gráficos das funções f e g também são pontos do gráfico de h, pois os números inteiros e os números racionais são números reais. Além desses pontos, devemos considerar aqueles cujos pares ordenados (x, y) satisfazem a lei y = x + 1, sendo x um número irracional, como x =
raiz quadrada de 2, ou seja,
Ponto de abscissa raiz quadrada de 2 e ordenada raiz quadrada de dois, mais um..

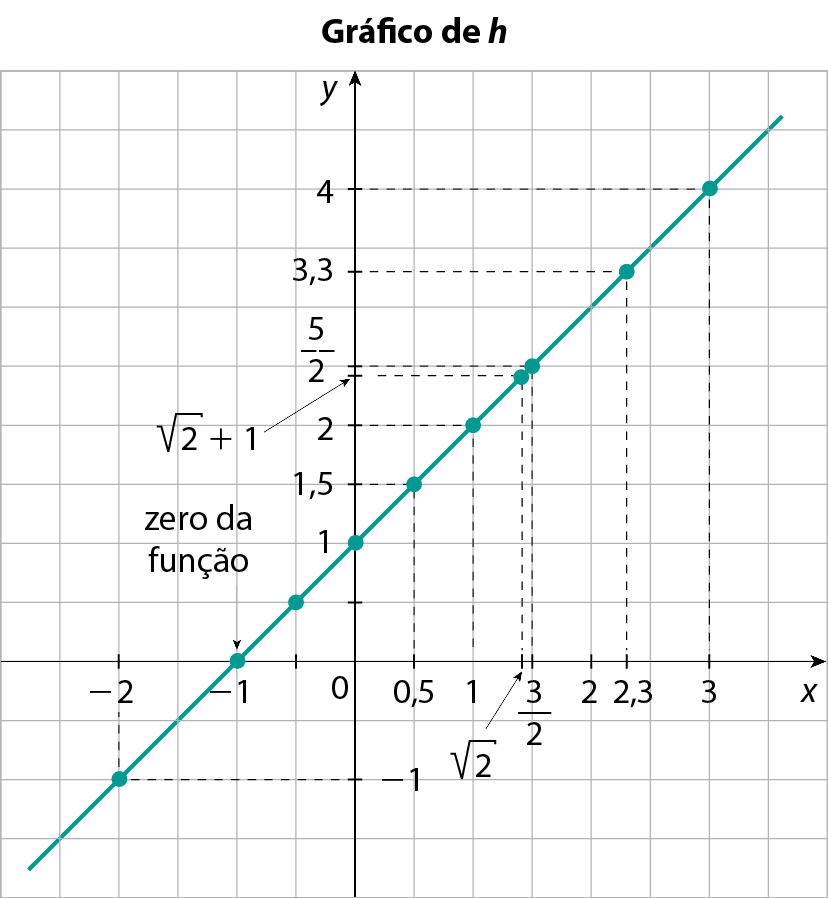
Zero de uma função
No gráfico anterior, observe que a abscissa do ponto que tem y = 0 é x = ‒1. Esse valor de x é chamado de zero da função.
Zero da função é todo valor de x para o qual y é igual a zero, ou seja, é a abscissa do ponto onde o gráfico da função cruza o eixo x.
dêsse modo, para calcular o zero da função do nosso exemplo, cuja lei é y = x + 1, basta resolver a equação x + 1 = 0. Assim, obtemos x = ‒1.
Acompanhe estes outros exemplos em que obtemos o zero da função dada pela lei:
a) y = 4x + 9 Basta atribuir a y o valor zero: 0 = 4x + 9 ou 4x + 9 = 0. 4x = ‒9 ⇒ x =
fração numerador: menos 9; denominador: 4ou x = ‒2,25 O zero da função dada por y = 4x + 9 é x = ‒2,25.
b) y = xelevado a 2 ‒ 121 Basta atribuir a y o valor zero: 0 = xelevado a 2 ‒ 121 ou xelevado a 2 ‒ 121 = 0. xelevado a 2 = 121 ⇒ x = 11 ou x = ‒11 Os zeros da função dada por y = xelevado a 2 ‒ 121 são x = 11 e x = ‒11.
Como reconhecer o gráfico de uma função

Já vimos que, quando y é função de x, para cada valor de x existe um único valor de y.
dêsse modo, em um gráfico de função, para cada abscissa haverá somente um ponto correspondente no gráfico. Podemos verificar isso geometricamente, traçando retas perpendiculares ao eixo x.
Acompanhe alguns exemplos.
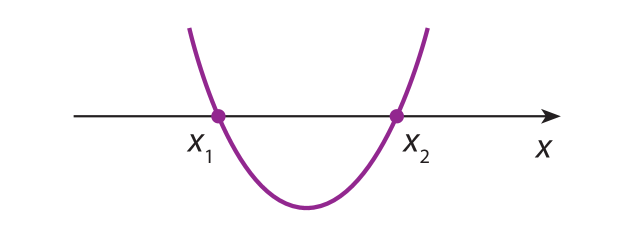
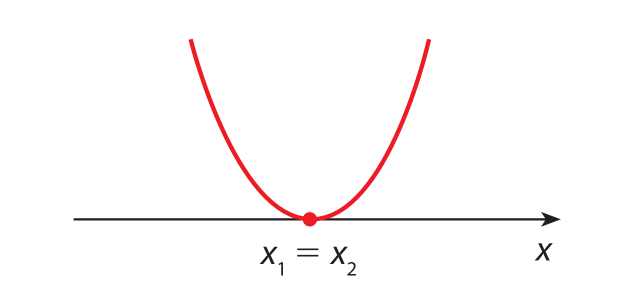
a)
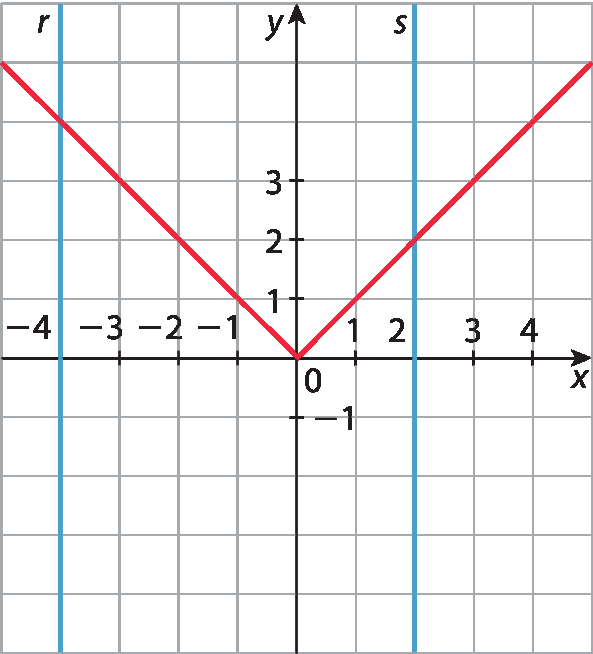
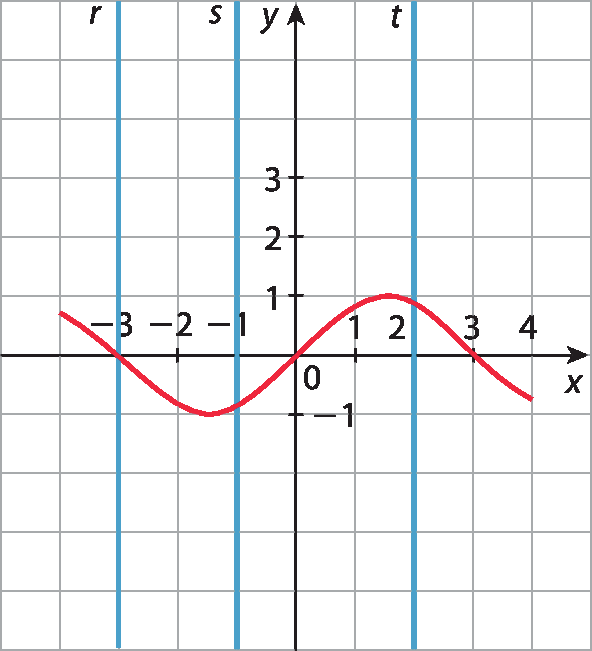
Em ambos os casos, qualquer reta perpendicular ao eixo dos x intersectará os gráficos em um único ponto. Logo, cada um desses gráficos representa uma função, pois, para qualquer valor de x, obtemos um único valor de y correspondente.
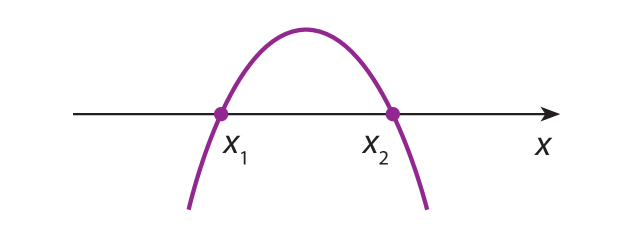
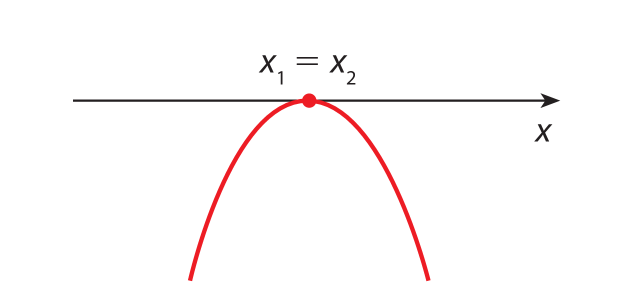
b)
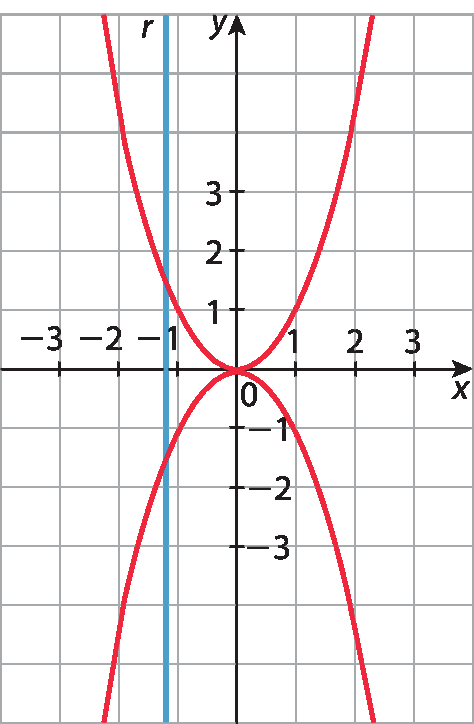
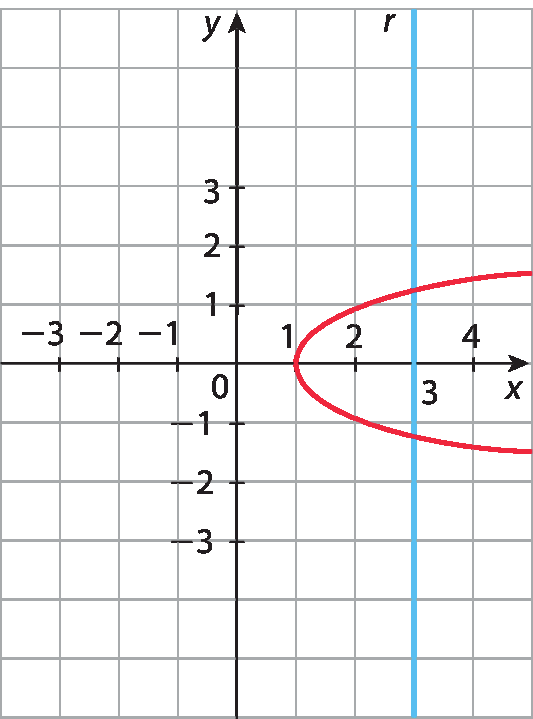
Observe, em cada caso, que existe uma reta r, perpendicular ao eixo x, que intersecta os gráficos em dois pontos com ordenadas ( y ) diferentes. Então, esses gráficos não representam função, pois existe valor de x com dois valores de y correspondentes.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
12 Considere a função dada pela lei y = ‒x + 1. Construa, em uma folha de papel quadriculado, o gráfico dessa função, sendo:
a) x um número inteiro qualquer;
b) x um número real qualquer.
13 Um automóvel percorre uma estrada à velocidade constante de 80 quilômetros por hora.
a) Indicando por x a medida do tempo transcorrido (em hora) e por y a medida da distância percorrida (em quilômetro), organize um quadro com os seguintes valores para x: 0, 1, 2, 3, 4 e 5. Em seguida, escreva a lei da função que fornece y em relação a x.
b) A variável x pode assumir qualquer número real, por exemplo, um número negativo?
c) O gráfico dessa função é uma reta ou uma semirreta?
d) Represente, em uma folha de papel quadriculado, o gráfico correspondente.
14 Determine no caderno o zero das funções representadas nos gráficos a seguir.
a)
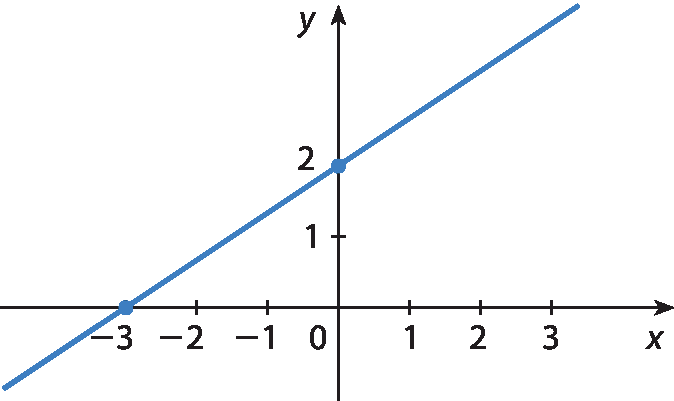
b)
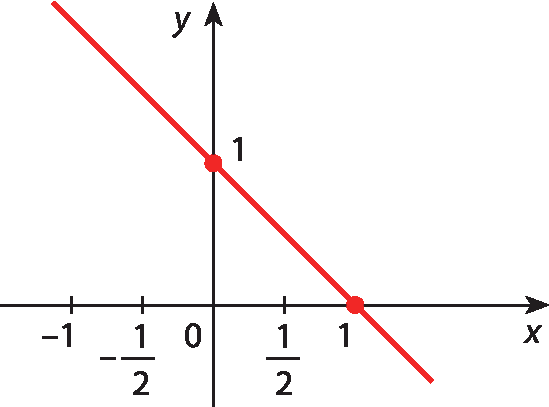
15 Determine no caderno o zero das funções dadas por:
a) y = x + 3
b) y = ‒3xelevado a 2 + 6
c) y = 3x + 18
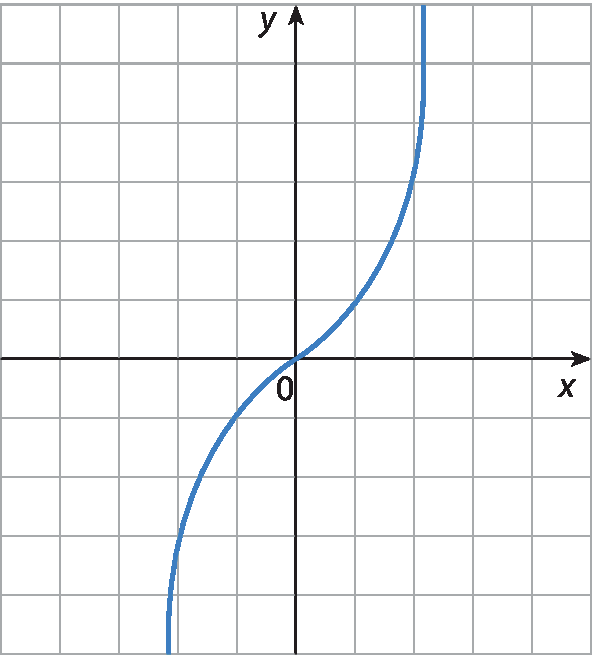
16 Observe os gráficos a seguir e identifique aqueles que representam funções. Justifique sua resposta.
a)
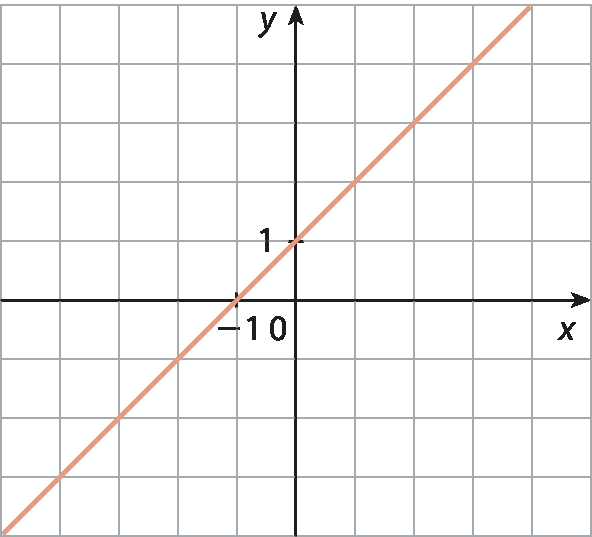
b)
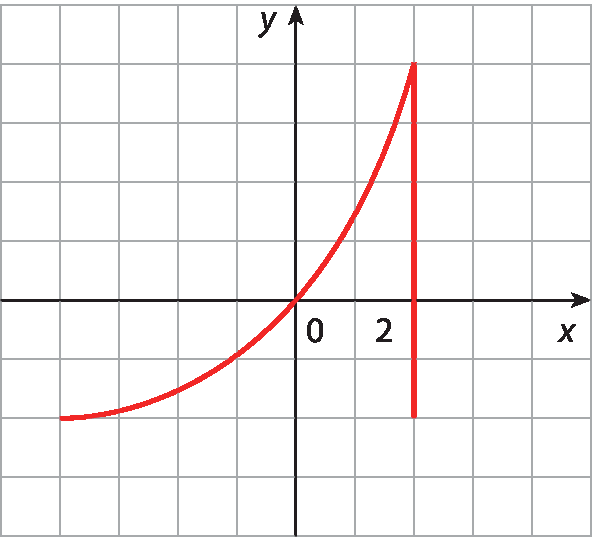
c)
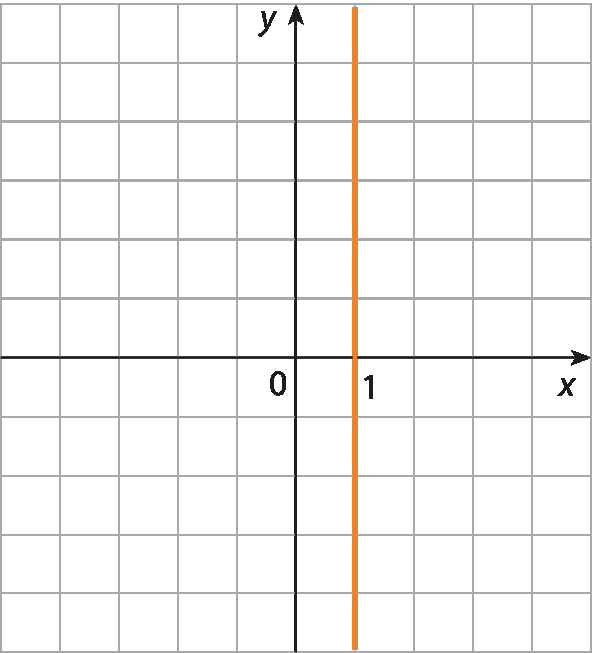
d)
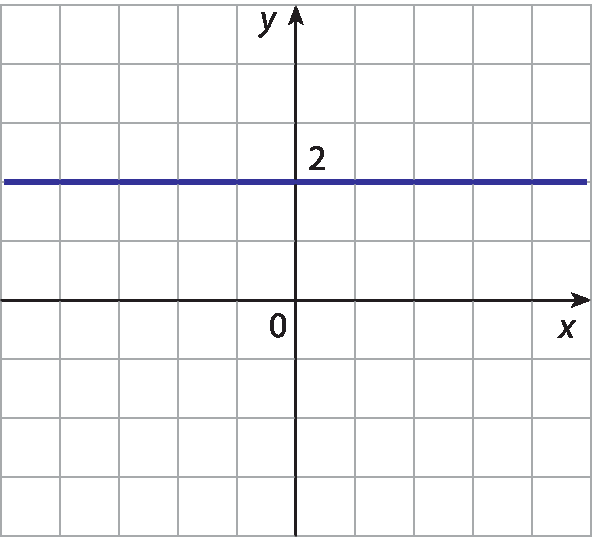
e)
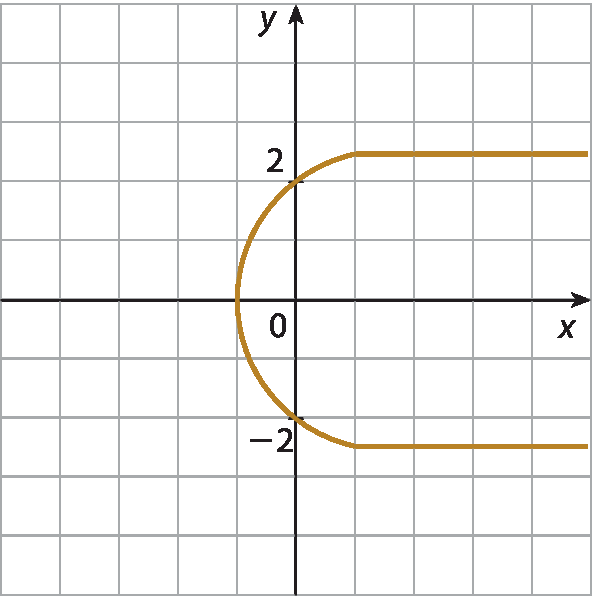
f)
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Sabendo que o preço de uma revista em quadrinhos é 16 reais, faça o que se pede.
a) Construa um quadro que apresente o preço de 0, 1, 2, 3, 4, 5 e 6 exemplares dessa revista.
b) Represente em um plano cartesiano os pares ordenados (x, y) do quadro, colocando no eixo x o número de revistas e no eixo y o preço a pagar.
c) É possível comprar 4,5 revistas? E
raiz quadrada de 3.revistas? Justifique sua resposta.
d) Você pode traçar uma reta por esses pontos para representar o gráfico? Por quê?
2. Função polinomial do 1º grau
Considere o pentágono da figura a seguir.
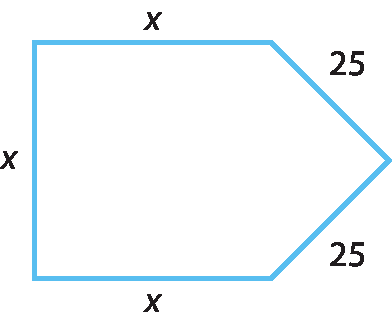
Nele, as medidas são dadas em centímetro. A medida do perímetro dêsse polígono depende dos valores que forem atribuídos a x. Indicando a medida do perímetro por y, obtemos:
y = 3x + 50
A função definida pela lei y = 3x + 50 é um exemplo de função polinomial do 1º grau.
Uma função polinomial do 1º grau é toda função dada por uma lei de formação do tipo y = ax + b, sendo os coeficientes a e b números reais e a ≠ 0, e é definida para todo x real.
Observe outros exemplos de funções polinomiais do 1º grau, dos quais destacamos os valores de a e b.
a) y = 2x ‒ 1, sendo a = 2 e b = ‒1.
b)
y igual a menos 3 meios de x, mais 5.sendo
a igual a fração; menos 3 meios.e b = 5.
c) y = ‒5x, sendo a = ‒5 e b = 0. Em casos como este, nos quais b = 0, chamamos a função polinomial do 1º grau de função linear.
d)
y igual a x sobre 2.sendo
a é igual a fração um meio.e b = 0.

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
17 Identifique as leis que representam funções polinomiais do 1º grau.
a) y = x + 3
b) y = ‒5x + 1
c) y = x2 ‒ 3x
d) y = ‒ 4x
e) y = x2 ‒ 5x + 6
f) y = 2 ‒ x
18 Dados a e b, escreva a lei de cada função polinomial do 1º grau, em que y = ax + b.
a) a = 2 e b = ‒1
b)
a igual a fração de um meio.e b = 0
c)
a igual a raiz quadrada de 2 e b igual a fração; menos um meio.
d)
a é igual a fração; menos um terço e b é igual a fração; menos um terço.
19 Dada a função definida pela lei fabre parênteses décimafecha parênteses = 5x ‒ 4 com x real, determine:
a) f (‒1)
b) f
de menos 3 quintos
c) o valor de x para que se tenha f abre parênteses décimafecha parênteses = 6;
d) o valor de x para que se tenha f abre parênteses décimafecha parênteses = 0.
20 Considere o retângulo:

Determine:
a) a medida do perímetro y em função de x ;
b) a medida do perímetro para x = 12,5 metros;
c) o valor de x para y = 90 metros.
21 Considerando um quadrado cujo lado mede x centímetros, determine:
a) a medida do perímetro em função de x;
b) a medida do perímetro para x = 10.
22 A lei que fornece a medida da temperatura tê, em grau céucius, de ebulição da água de acordo com a medida da altitude h, em metro, é: T = 100 ‒ 0,001h.
Responda no caderno às questões a seguir.
a) Qual é a medida da temperatura de ebulição da água a .2400 métros de altitude?
b) Qual é a medida da temperatura de ebulição da água ao nível do mar?
23 Uma caixa-d’água de .1000 litros de capacidade é alimentada por um registro que, totalmente aberto, despeja 25 litros de água a cada 3 minutos.
a) Considerando que a caixa-d’água esteja vazia, em quanto tempo ela ficará cheia depois que o registro for totalmente aberto?
b) Se o registro permanecer totalmente aberto por 15 minutos, quantos litros de água serão despejados na caixa-d’água durante esse tempo?
c) Faça um quadro indicando a medida do volume de água que haverá na caixa-d’água de 15 em 15 minutos até ela ficar cheia.
d) Qual é a lei da função que representa a medida do volume de água v em função da medida do tempo t do registro totalmente aberto?
Gráfico de uma função polinomial do 1º grau
O gráfico de uma função polinomial do 1º grau é uma reta não perpendicular ao eixo x.
Acompanhe os exemplos a seguir.
a) Vamos representar graficamente a função polinomial do 1º grau definida pela lei y = 2x + 1.
Quadro com alguns pontos do gráfico da função
|
x |
y = 2x + 1 |
(x, y) |
|---|---|---|
|
−1 |
−1 |
(−1, −1) |
|
0 |
1 |
(0, 1) |
|
1 |
3 |
(1, 3) |
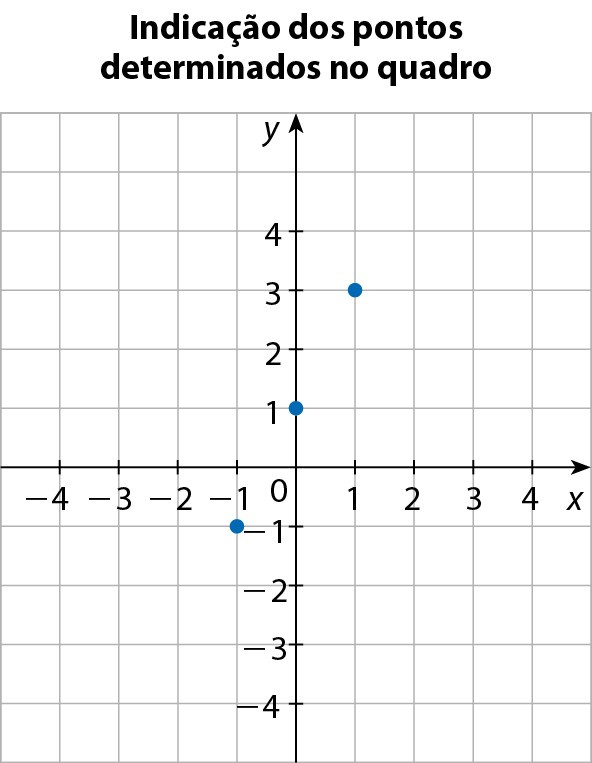
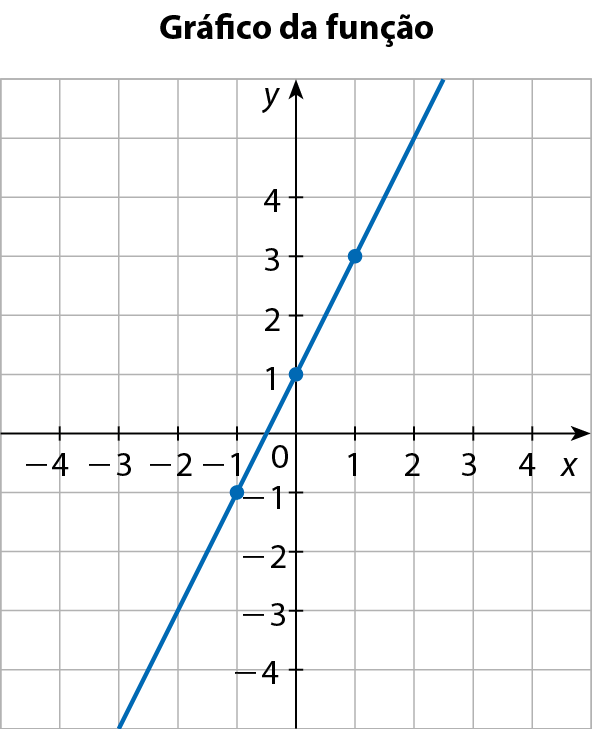
Como uma reta pode ser determinada por dois pontos distintos, então, para construir o gráfico de uma função polinomial do 1º grau, é suficiente representar dois pontos no plano cartesiano e traçar a reta que passa por esses pontos.
b) Vamos representar graficamente a função polinomial do 1º grau definida pela lei y = ‒2x.
Quadro com dois pontos do gráfico da função
|
x |
y = −2x |
(x, y) |
|---|---|---|
|
0 |
0 |
(0, 0) |
|
1 |
−2 |
(1, −2) |
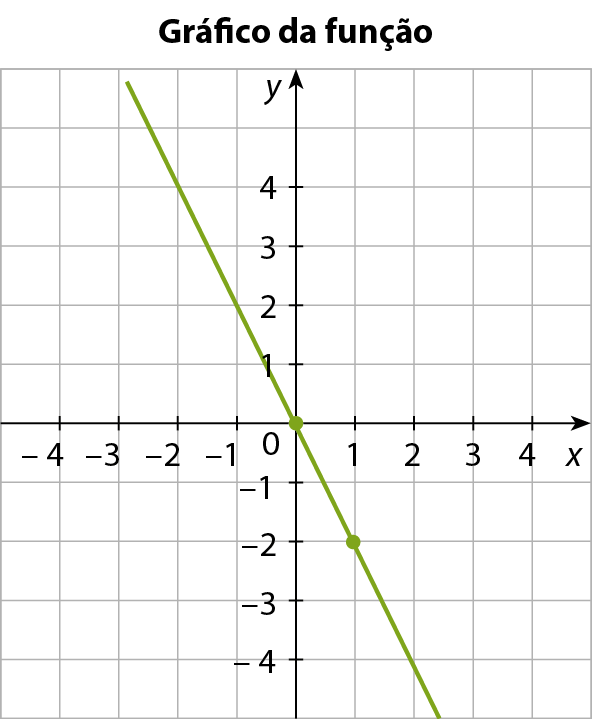

EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
24 Observe o gráfico de uma função para responder no caderno às questões.
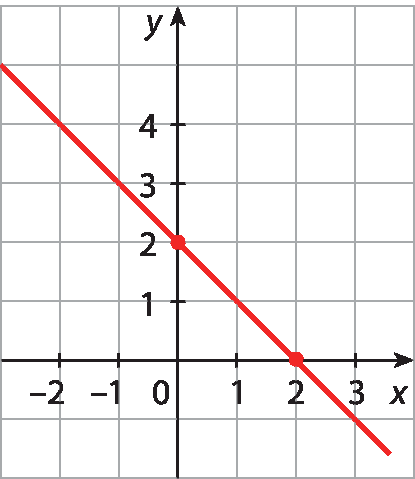
a) Qual é o valor de y quando x = 2?
b) Para que valor de x obtemos y = 4?
25 O par ordenado (2, 8) representa um ponto do gráfico de uma função polinomial do 1º grau do tipo y = ax.
a) Determine o valor de a da lei dessa função.
b) Determine o valor de y para x = 3,5.
c) Dê o valor de x para y = 0.
d) Represente graficamente essa função. Utilize uma folha de papel quadriculado para representar o plano cartesiano.
26 Considere a função polinomial do 1º grau definida pela lei y = x ‒ 3.
a) Represente graficamente essa função.
b) Qual é a abscissa do ponto em que a reta corta o eixo x ?
c) Qual é a ordenada do ponto em que a reta corta o eixo y ?
27 O gráfico a seguir mostra a variação da medida do volume de álcool em função da medida de sua massa.
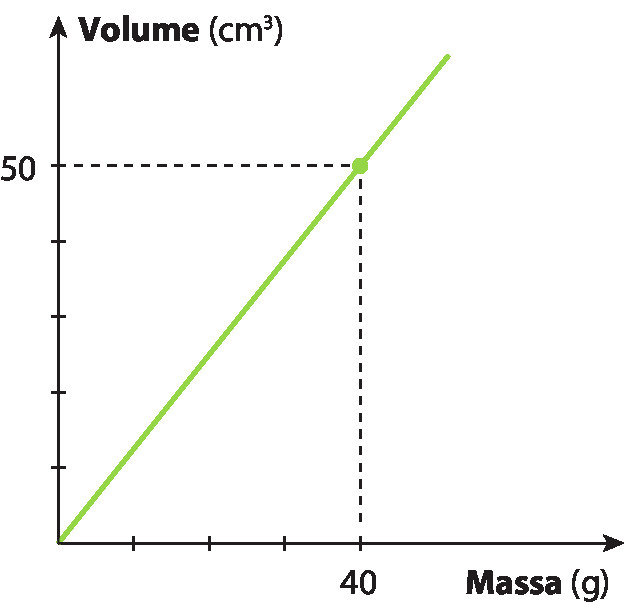
Determine no caderno:
a) a lei da função;
b) a massa (em grama) de 30 centímetros cúbicos de álcool.
28 Usando uma folha de papel quadriculado, represente graficamente, em um mesmo plano cartesiano, as funções polinomiais do 1º grau dadas pelas leis: f abre parênteses décimafecha parênteses = 3x + 1 e gabre parênteses décimafecha parênteses = ‒2x + 6.
Em seguida, responda às questões.:
a) Para que valor de x obtemos f abre parênteses décimafecha parênteses = 0?
b) Qual é a abscissa do ponto onde o gráfico da função g corta o eixo x ?
c) Qual é a ordenada do ponto onde o gráfico da função f corta o eixo y ?
d) Para que valor de x obtemos f abre parênteses décimafecha parênteses = g abre parênteses décimafecha parênteses?
29 No papel quadriculado, construa o gráfico, em um mesmo plano cartesiano, das funções polinomiais do 1º grau dadas pelas leis: hidrogênioabre parênteses décimafecha parênteses = ‒3x + 1 e primeiraabre parênteses décimafecha parênteses = ‒3x + 6.
Em seguida, responda às questões.
a) Quais são as coordenadas do ponto em que o gráfico de h corta o eixo x ? E o eixo y ?
b) Quais são as coordenadas do ponto em que o gráfico de i corta o eixo x? E o eixo y?
c) Os gráficos de h e de ih têm ponto comum?
d) Para que valor de x obtemos hidrogênioabre parênteses décimafecha parênteses = primeiraabre parênteses décimafecha parênteses?
Pense mais um poucoreticências
FAÇA AS ATIVIDADES NO CADERNO
1 Em uma folha de papel quadriculado e em um mesmo plano cartesiano para cada item, construa os gráficos das funções:
a) y = ‒0,5x + 3 e y = 0,5x + 3
b) y = ‒x + 3 e y = x + 3
c) y = ‒2x + 3 e y = 2x + 3
d) y = ‒3x + 3 e y = 3x + 3
2 Observando os gráficos das funções y = ax + b do exercício anterior, responda às questões.
a) Quando a > 0, ao aumentar o valor atribuído a x, também aumenta (cresce) o valor de y? Se tivesse que classificar essas funções polinomiais do 1º grau com a > 0 entre função crescente ou função decrescente, por qual delas você optaria?
b) Quando a < 0, ao aumentar o valor atribuído a x, também aumenta (cresce) o valor de y? Se tivesse que classificar essas funções polinomiais de 1º grau com a < 0 como função crescente ou função decrescente, por qual delas você optaria?
3

Hora de criar – Escreva duas leis de função polinomial do 1º grau y = ax + b, nas quais os valores de a sejam opostos. Troque-as com um colega. Depois que cada um construir os gráficos das funções dadas pelo colega, discutam e identifiquem em qual dos esboços a seguir a inclinação da reta mais se aproxima dos gráficos em que a > 0 e em qual deles a inclinação mais se aproxima dos gráficos em que a < 0.
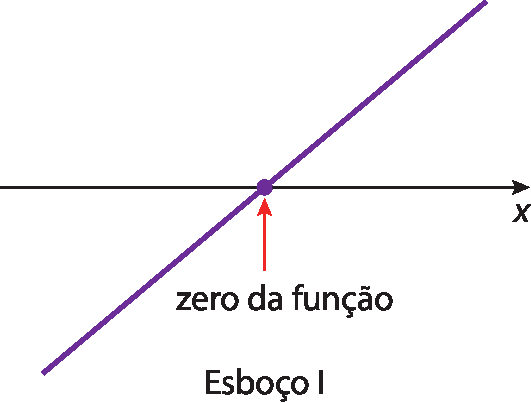
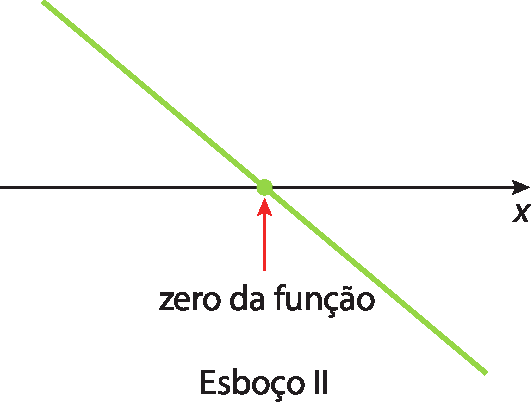
Variação de uma função polinomial do 1º grau
Observe os gráficos das funções y = 2x + 2 e y = ‒3x + 1, em que x pode ser qualquer número real.
Quadro com alguns pontos do gráfico de y = 2x + 2
|
x |
y |
Par ordenado |
|---|---|---|
|
0 |
2 |
(0, 2) |
|
−1 |
0 |
(−1, 0) |
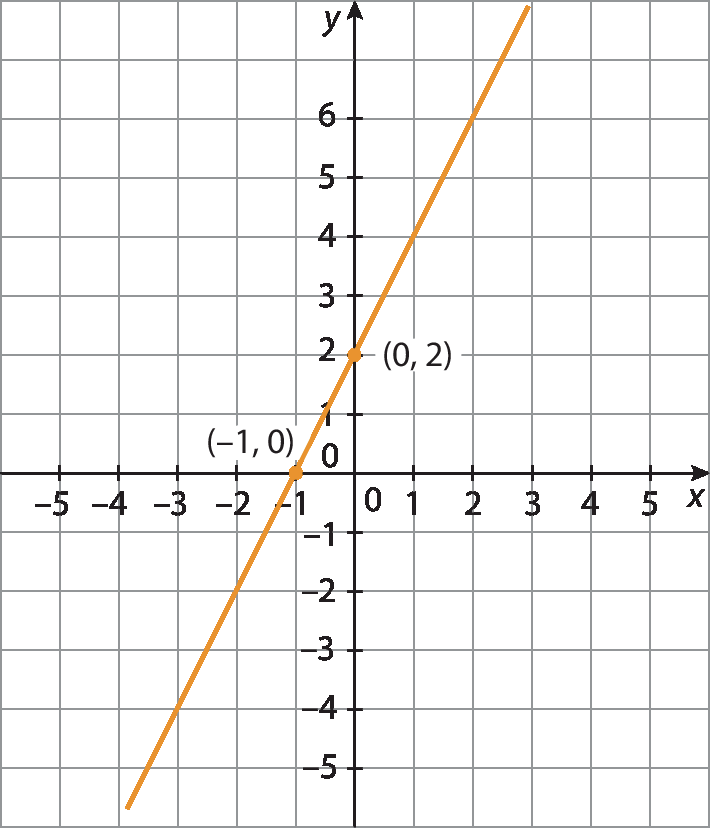
Quadro com alguns pontos do gráfico de y = ‒3x + 1
|
x |
y |
Par ordenado |
|---|---|---|
|
0 |
1 |
(0, 1) |
|
2 |
−5 |
(2, −5) |
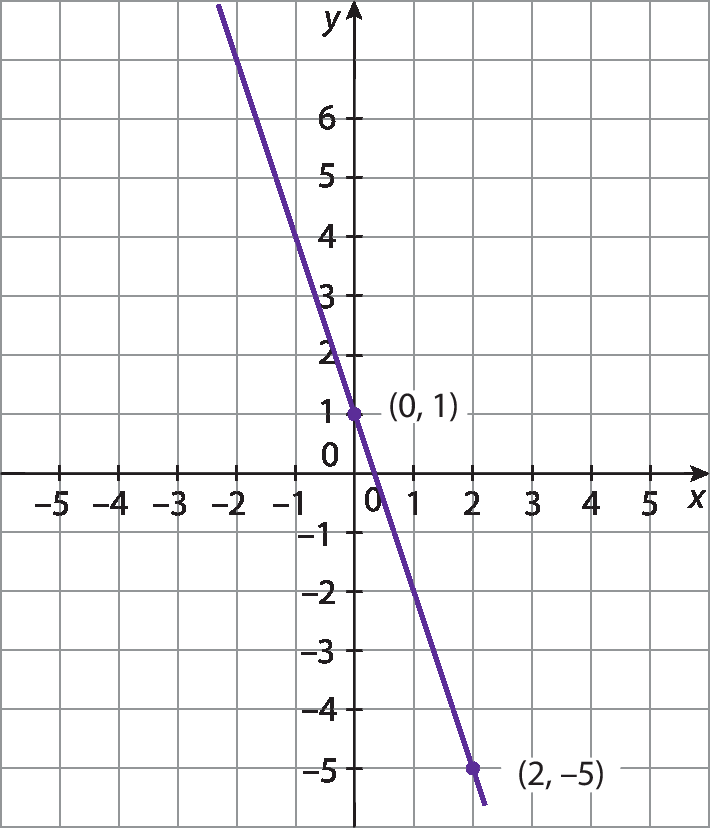
De modo geral, verificamos:
• uma função polinomial do 1º grau y = ax + b é crescente quando o coeficiente a é maior que zero (a > 0);
• uma função polinomial do 1º grau y = ax + b é decrescente quando o coeficiente a é menor que zero (a < 0).
Acompanhe mais exemplos.
a)
f de x é igual a menos fração numerador: x; denominador: 5.é decrescente, pois a < 0.
b)
g de z é igual a raiz quadrada de 3z é crescente, pois a > 0.
Observação
▶ Existem funções que não são crescentes nem decrescentes. Por exemplo:
a) hidrogênioabre parênteses yfecha parênteses = ‒10
b) páginaabre parênteses kfecha parênteses = π
Funções como essas são chamadas de constantes, e seu gráfico é uma reta paralela ao eixo x.
PARA SABER MAIS
Uso do computador: retas
Na internet, existem softwares de geometria dinâmica gratuitos que apresentam muitas ferramentas, entre elas uma que nos auxilia no estudo das funções. É possível, por exemplo, construir o gráfico de qualquer função digitando a lei correspondente no campo “Entrada” na tela inicial e, em seguida, teclando “Enter”.
Por meio dêsse recurso, podemos estudar o que acontece com o gráfico de funções do tipo f (x) = ax + b à medida que os coeficientes a e b variam.
1. Ao digitar f (x) = ax + b e teclar “Enter” no campo “Entrada” da tela inicial do software, aparecerá uma janela.
2. Clicando em “Criar Controles Deslizantes”, aparecerão os controles deslizantes correspondentes aos coeficientes a e b de f (x) = ax + b, além do gráfico para a = 1 e b = 1.
3. É possível movimentar os cursores dos controles deslizantes para variar os valores dos coeficientes a e b.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Considere os gráficos das funções f abre parênteses décimafecha parênteses = x, g abre parênteses décimafecha parênteses = x + 2 e hidrogênioabre parênteses décimafecha parênteses = x ‒ 3.
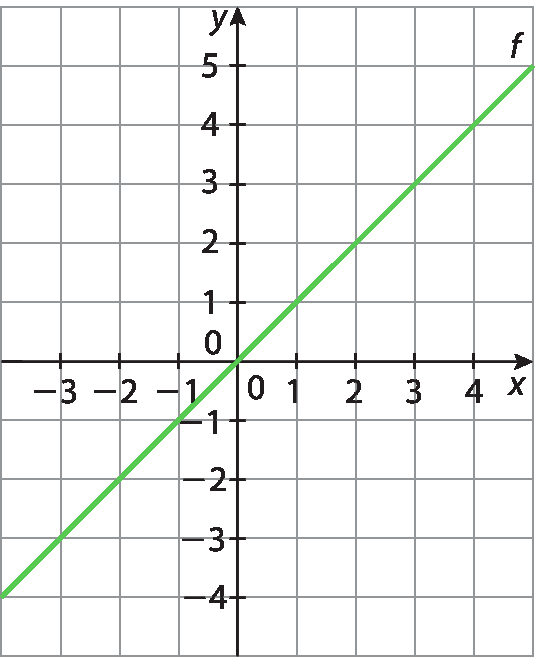
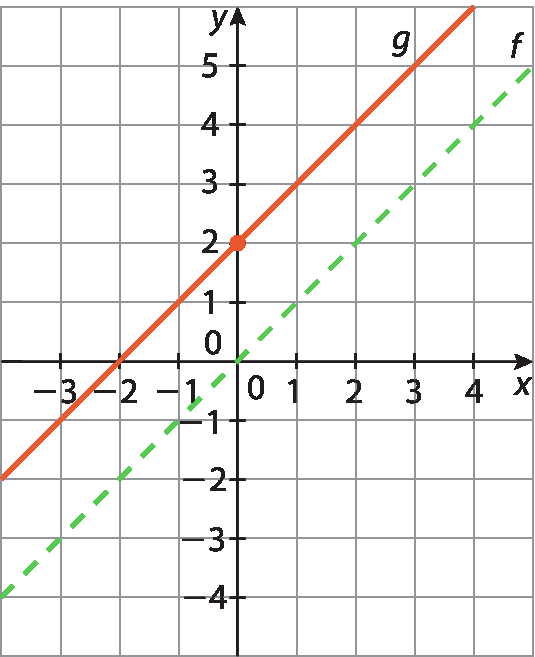
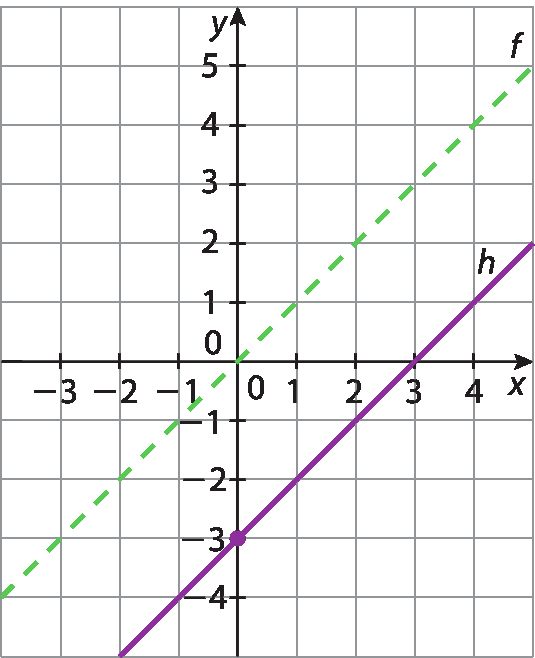
Agora, responda: como seria o gráfico das funções páginaabre parênteses décimafecha parênteses = ‒x, queabre parênteses décimafecha parênteses = ‒x + 4 e t abre parênteses décimafecha parênteses = ‒x ‒ 5?
Se for possível, construa esses gráficos usando um software de geometria dinâmica e confira suas respostas.
2 Imagine o que acontece se modificarmos o coeficiente a. Qual é o papel do coeficiente a no gráfico de f abre parênteses décimafecha parênteses = ax + b?
3 Imagine se modificarmos o coeficiente b. Em seguida, responda às questões.
a) Qual é o papel do coeficiente b no gráfico de f abre parênteses décimafecha parênteses = ax + b?
b) Podemos associar esse coeficiente à ordenada de um ponto. Que ponto é esse?
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
30 Classifique cada função em crescente ou decrescente.
a) f abre parênteses décimafecha parênteses = ‒2x + 3
b) g abre parênteses décimafecha parênteses = 7x + 1
c) hidrogênioabre parênteses décimafecha parênteses = x
d) medida doabre parênteses décimafecha parênteses =
menos fração numerador: x; denominador: 3.
e) norteabre parênteses décimafecha parênteses = 5 ‒ x
f) página (décima) =
raiz quadrada de 2.+ 6x
g) que (décima) = πx
h) r (décima) = ‒5 + 0,001x
31 Responda às questões sobre função polinomial do 1º grau.
a) A função cujo gráfico passa pelos pontos (‒3, 4) e (0, 0) é crescente ou decrescente?
b) A função cujo gráfico passa pelos pontos (‒3, ‒4) e (0, 0) é crescente ou decrescente?
Estudo do sinal de uma função polinomial do 1º grau

Acompanhe dois exemplos.
a) Vamos estudar o sinal da função dada pela lei: y = 2x ‒ 4.
Podemos fazer esse estudo por meio do esboço do gráfico da função. Para isso, calculamos o valor de x para o qual essa função se anula.
Para y = 0, obtemos:
2x ‒ 4 = 0, ou seja, x = 2.
Logo, essa função se anula quando x = 2.
Observando ainda que na lei dessa função y = 2x ‒ 4, a = 2, portanto a > 0, podemos esboçar o gráfico e fazer o estudo do sinal.
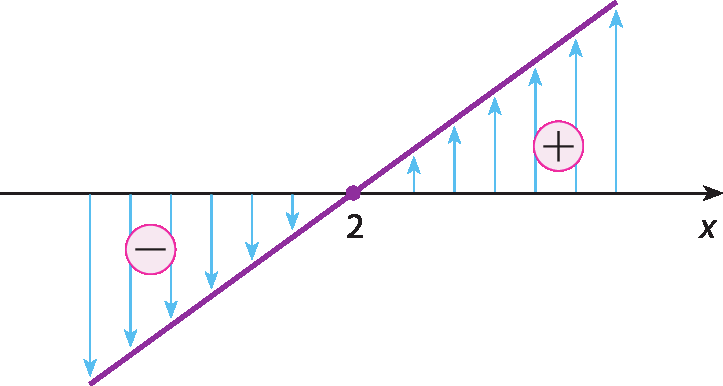
Estudo do sinal
• Para x = 2, ponto do eixo x, obtemos: y = 0
• Para x > 2, pontos acima do eixo x, obtemos: y > 0
• Para x < 2, pontos abaixo do eixo x, obtemos: y < 0
b) Vamos estudar o sinal da função dada pela lei: y = ‒2x + 4.
Inicialmente, vamos calcular o valor de x para o qual essa função se anula. Para y = 0, obtemos:
‒2x + 4 = 0, ou seja, x = 2.
Logo, essa função se anula quando x = 2.
Observando ainda que em y = ‒2x + 4, a = ‒2, portanto a < 0, podemos esboçar o gráfico e fazer o estudo do sinal.
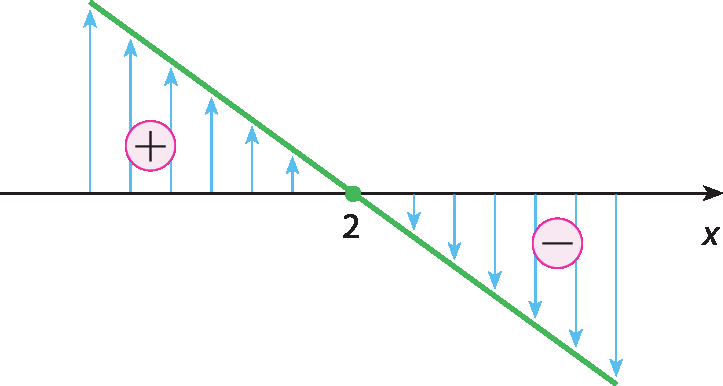
Estudo do sinal
• Para x = 2, ponto do eixo x, obtemos: y = 0
• Para x > 2, pontos abaixo do eixo x, obtemos: y < 0
• Para x < 2, pontos acima do eixo x, obtemos: y > 0
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
32 Considere o seguinte gráfico de uma função polinomial do 1º grau.
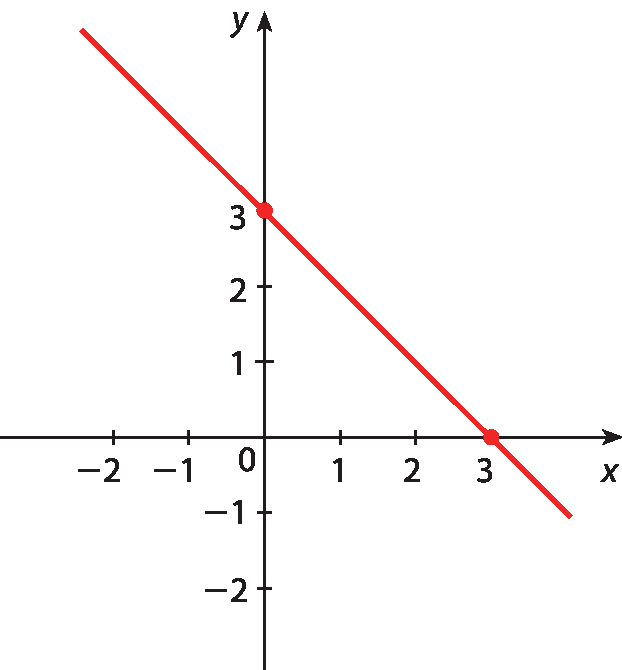
Responda:
a) Para que valor de x obtemos y = 0?
b) Para que valores de x obtemos y > 0?
c) Para que valores de x obtemos y < 0?
33 Estude o sinal das funções polinomiais do 1º grau.
a) y = 2x ‒ 8
b) y = ‒3x + 6
c) y = 2x ‒ 5
d) y = ‒2x ‒ 1
34 Considere a função polinomial do 1º grau definida por y = ax + b. Sabe-se que a > 0 e que o ponto determinado pelo par (5, 0) pertence ao gráfico dessa função. Determine o sinal de y em cada caso.
a) x = ‒2
b) x = 0
c) x = 4,99
d) x = 5,01
e) x = 10
35 Hora de criar – Crie uma função polinomial do 1º grau de modo que:
• o zero dessa função seja 2;
• o gráfico para x > 2 esteja acima do eixo das abscissas, ou seja, y > 0.
Quantas funções assim existem?
PARA SABER MAIS
Proporcionalidade na função linear
Vamos analisar a função linear dada pela lei y = 2x.
|
x |
y |
|---|---|
|
−1 |
−2 |
|
0 |
0 |
|
1 |
2 |
|
2 |
4 |
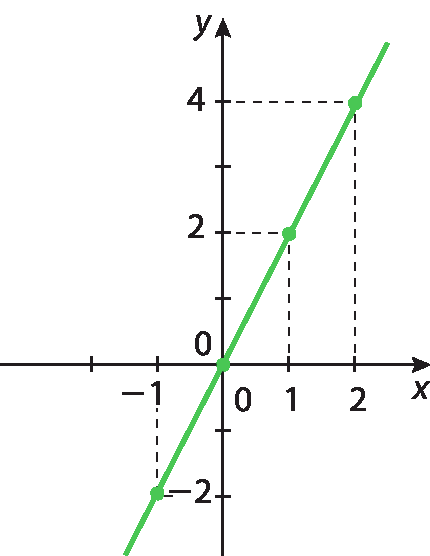
Se há proporcionalidade direta entre os valores reais de x e y, existe uma função linear que relaciona as variáveis x e y, ou seja, uma função cuja lei pode ser escrita na fórma y = ax, com a real, a ≠ 0, x e y reais. Reciprocamente, se as variáveis x e y estão relacionadas por uma função linear, então x e y são diretamente proporcionais.
Outras funções apresentam proporcionalidade inversa, e algumas não apresentam proporcionalidade direta nem inversa entre os valores de x e de y. Acompanhe alguns exemplos.
a) y =
fração numerador: 1; denominador: x.|
x |
y |
|---|---|
|
1 |
1 |
|
2 |
|
|
3 |
|
|
4 |
|
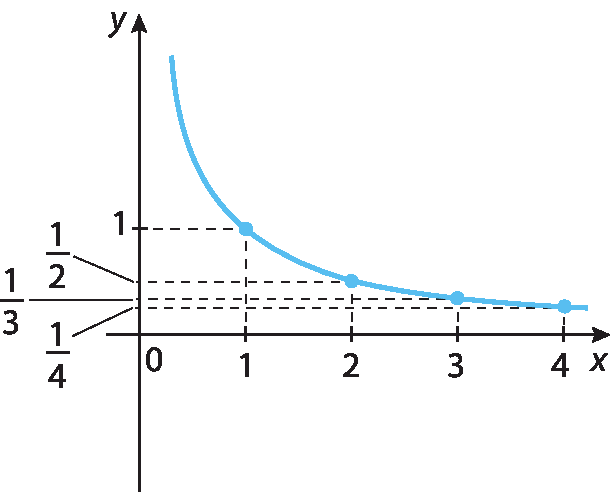
b) y = 2x ‒ 1
|
x |
y |
|---|---|
|
−1 |
−3 |
|
0 |
−1 |
|
1 |
1 |
|
2 |
3 |
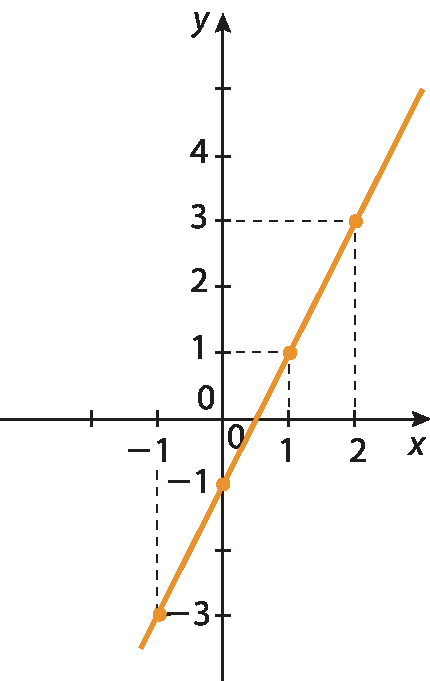
Agora é com você!
FAÇA A ATIVIDADE NO CADERNO
Um automóvel percorre certa distância com velocidade constante de 50 quilômetros por hora.
a) Qual é a lei da função que relaciona a distância percorrida (y), em quilômetro, e o tempo (x), em hora?
b) Considerando que a velocidade é constante, as grandezas distância percorrida e tempo são diretamente proporcionais, inversamente proporcionais ou não são proporcionais? Por quê?
3. Função polinomial do 2º grau

Gustavo e Nicole estudam as possibilidades de uso do quintal de sua casa para a construção de um terraço com piscina ladeada por um gramado cuja medida da área eles precisam decidir. Nicole fez o croqui e Gustavo representou algebricamente a medida da área do gramado em função de x, com as medidas indicadas em metro. Observe:
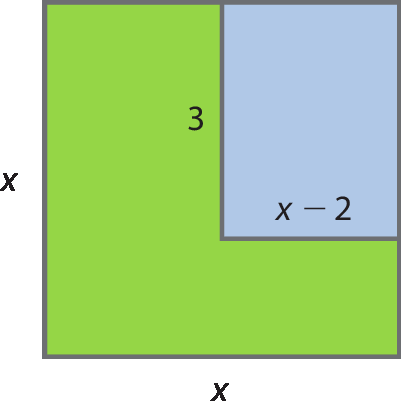
A medida da área do quadrado é: x2
A medida da área da piscina, representada pelo retângulo azul, é: 3(x ‒ 2)
Então, a medida da área do gramado é: x 2 ‒ 3(x ‒ 2), ou seja, x 2 ‒ 3x + 6
Indicando essa medida de área por y, obtemos: y = x 2 ‒ 3x + 6.
A função definida pela lei y = x2 ‒ 3x + 6 é um exemplo de função polinomial do 2º grau (ou função quadrática).
Uma função polinomial do 2º grau é uma função dada por uma lei de formação do tipo y = ax 2 + bx + c, com a, b e c números reais e a ≠ 0, e é definida para todo x real.
•

Considerando f abre parênteses décimafecha parênteses = x 2 ‒ 3x + 6 e os valores f (0), f (1) e f (2), é possível afirmar que o gráfico de fabre parênteses décimafecha parêntesesé uma reta?
Observe outros exemplos de funções polinomiais do 2º grau, em que destacamos os valores de a, b e c.
a) y = x2 ‒ 5x + 4, sendo a = 1, b = ‒5 e c = 4
b) y = 2x 2 + 5x ‒ 2, sendo a = 2, b = 5 e c = ‒2
c) y = x 2 ‒ 9, sendo a = 1, b = 0 e c = ‒9
d) y = ‒3x 2 + 2x, sendo a = ‒3, b = 2 e c = 0
e) y = x 2, sendo a = 1, b = 0 e c = 0
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
36 Na situação inicial desta página, se Gustavo e Nicole reservarem para o terraço (incluindo a piscina) um quadrado de lado medindo 8 métros, quantos metros quadrados de gramado eles deverão comprar?
37 Sendo f abre parênteses décimafecha parênteses = x 2 ‒ 5x + 6, determine:
a) f (0), f (2), f (3) e f (4);
b) os valores de x de modo que f abre parênteses décimafecha parênteses seja 0;
c) os valores de x de modo que f abre parênteses décimafecha parênteses seja 20.
38 Expresse a medida da área y de cada polígono em função de x.
a)
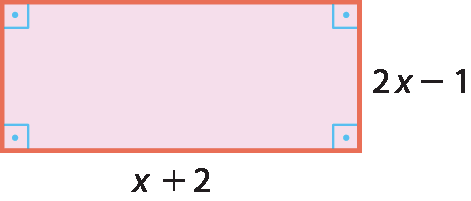
b)
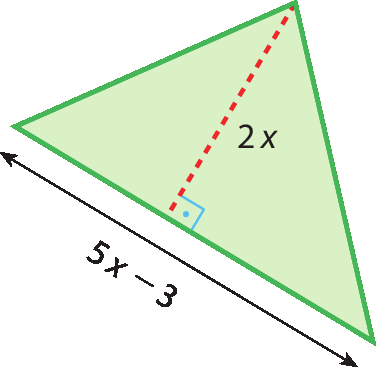
39 Sendo f (x) = x 2 + 3x, determine o que se pede em cada item.
a) f (0)
b) Os valores de x para que y = 0.
c) f (2);
d) Os valores de x para que y = 10.
40 Sendo f abre parênteses décimafecha parênteses = 2x 2 + 5, determine no caderno:
a) o valor de f
de raiz quadrada de 3;
b) os valores de x para que f (x) = 21.
41 Expresse na fórma y = ax 2 + bx + c a medida do volume do paralelepípedo.
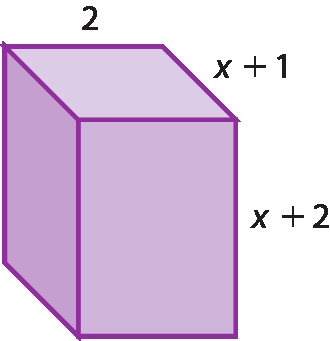
Gráfico de uma função polinomial do 2º grau
O gráfico de uma função polinomial do 2º grau é uma curva chamada parábola.

Para construir o gráfico de uma função dêsse tipo, procedemos como no caso da função polinomial do 1º grau:
• Atribuímos valores a x e obtemos os correspondentes valores de y.
• Organizamos os dados obtidos em um quadro com os pares ordenados.
• Localizamos esses pontos no plano cartesiano.
• Se o conjunto de pontos localizados possibilitar que se perceba a linha que passa por eles, traçamos essa linha. Caso contrário, devemos obter e localizar mais pontos do gráfico.
Acompanhe alguns exemplos.
a) Vamos representar graficamente a função polinomial do 2º grau definida pela lei: y = x 2 ‒ 2x ‒ 3
Para x = ‒2, obtemos: y = (‒2)2 ‒ 2 · (‒2) ‒ 3 = 4 + 4 ‒ 3 = 5
Para x = ‒1, obtemos: y = (‒1)2 ‒ 2 · (‒1) ‒ 3 = 1 + 2 ‒ 3 = 0
Para x = 0, obtemos: y = (0)2 ‒ 2 · (0) ‒ 3 = ‒3
Para x = 1, obtemos: y = (1)2 ‒ 2 · (1) ‒ 3 = 1 ‒ 2 ‒ 3 = ‒4
Para x = 2, obtemos: y = (2)2 ‒ 2 · (2) ‒ 3 = 4 ‒ 4 ‒ 3 = ‒3
Para x = 3, obtemos: y = (3)2 ‒ 2 · (3) ‒ 3 = 9 ‒ 6 ‒ 3 = 0
Para x = 4, obtemos: y = (4)2 ‒ 2 · (4) ‒ 3 = 16 ‒ 8 ‒ 3 = 5
|
x |
y = x2 − 2x − 3 |
(x, y) |
|---|---|---|
|
−2 |
5 |
(−2, 5) |
|
−1 |
0 |
(−1, 0) |
|
0 |
−3 |
(0, −3) |
|
1 |
−4 |
(1, −4) |
|
2 |
−3 |
(2, −3) |
|
3 |
0 |
(3, 0) |
|
4 |
5 |
(4, 5) |
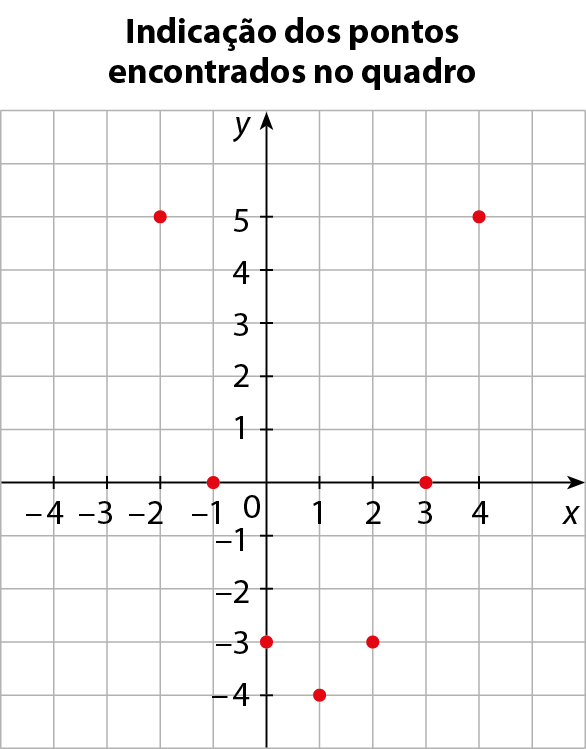
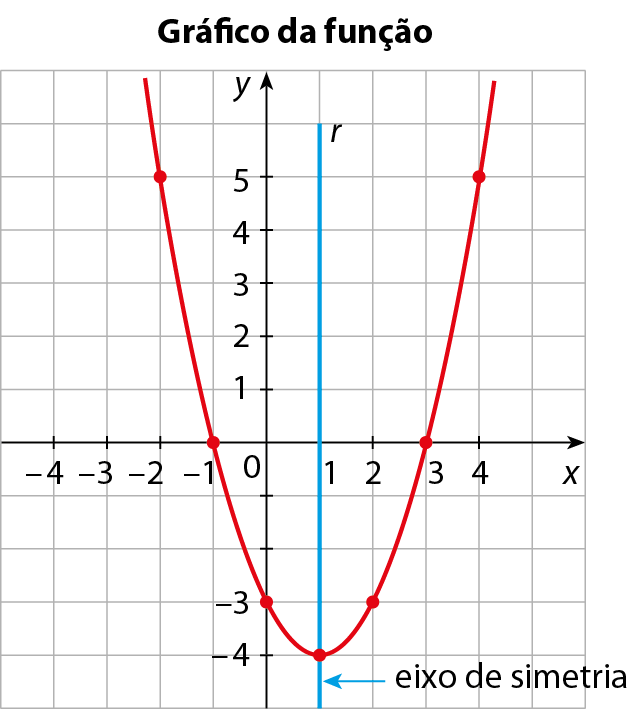
b) Vamos representar graficamente a função polinomial do 2º grau definida pela lei: y = ‒x 2 + 4x ‒ 3
Para x = 0, obtemos: y = ‒(0)2 + 4 · (0) ‒ 3 = 0 + 0 ‒ 3 = ‒3
Para x = 1, obtemos: y = ‒(1)2 + 4 · (1) ‒ 3 = ‒1 + 4 ‒ 3 = 0
Para x = 2, obtemos: y = ‒(2)2 + 4 · (2) ‒ 3 = ‒4 + 8 ‒ 3 = 1
Para x = 3, obtemos: y = ‒(3)2 + 4 · (3) ‒ 3 = ‒9 + 12 ‒ 3 = 0
Para x = 4, obtemos: y = ‒(4)2 + 4 · (4) ‒ 3 = ‒16 +16 ‒ 3 = ‒3
|
x |
y = −x2 + 4x − 3 |
(x, y) |
|---|---|---|
|
0 |
−3 |
(0, −3) |
|
1 |
0 |
(1, 0) |
|
2 |
1 |
(2, 1) |
|
3 |
0 |
(3, 0) |
|
4 |
−3 |
(4, −3) |
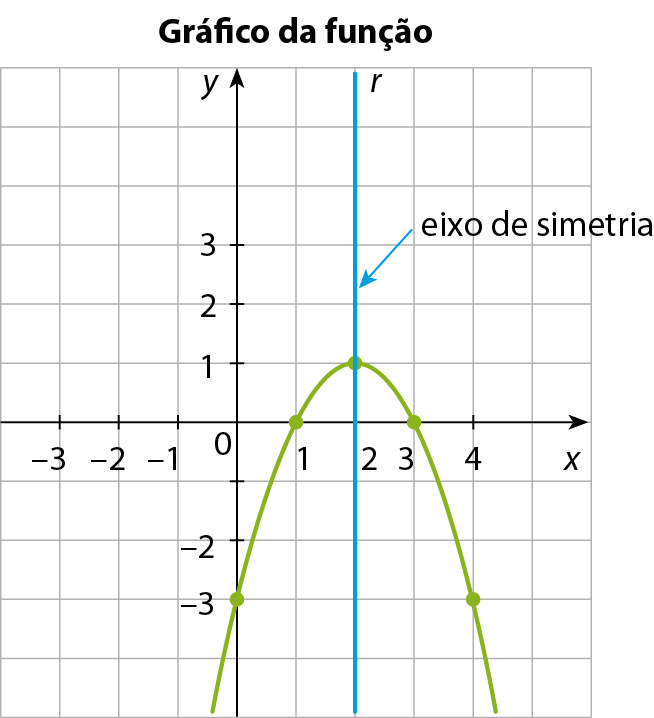
Concavidade da parábola
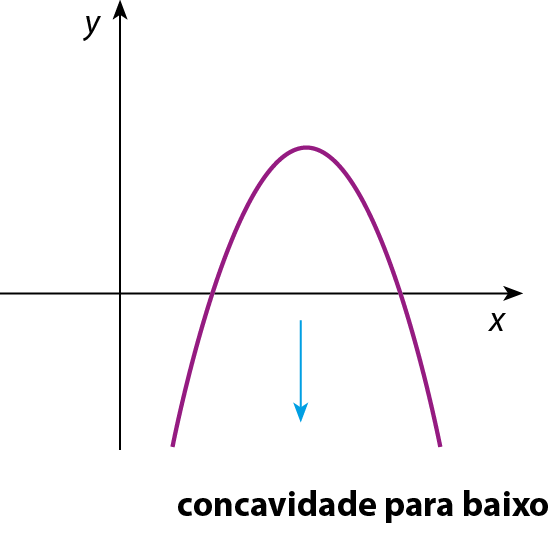
Conforme observamos nos gráficos dos dois exemplos anteriores, a parábola pode ter a concavidade voltada para cima ou para baixo.
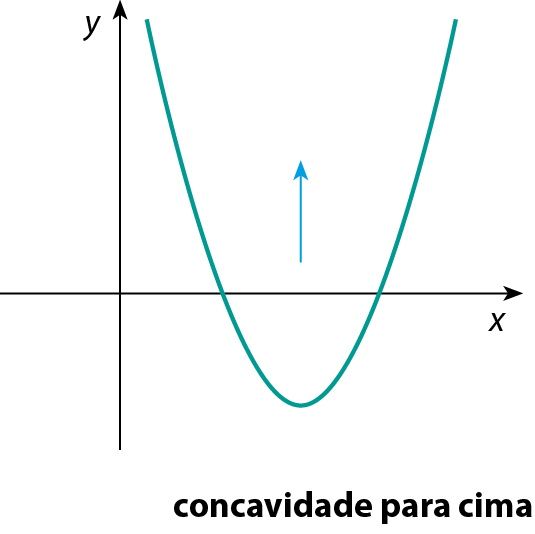
No primeiro exemplo ( y = x 2 ‒ 2x ‒ 3), o coeficiente a é positivo, e a parábola tem a concavidade voltada para cima.
No segundo exemplo ( y = ‒x 2 + 4x ‒ 3), o coeficiente a é negativo, e a parábola tem a concavidade voltada para baixo.

Vértice da parábola
Toda parábola tem um eixo de simetria e um vértice (V ).
Observe os exemplos.
a) p(x) = ‒x2 + 4x ‒ 2
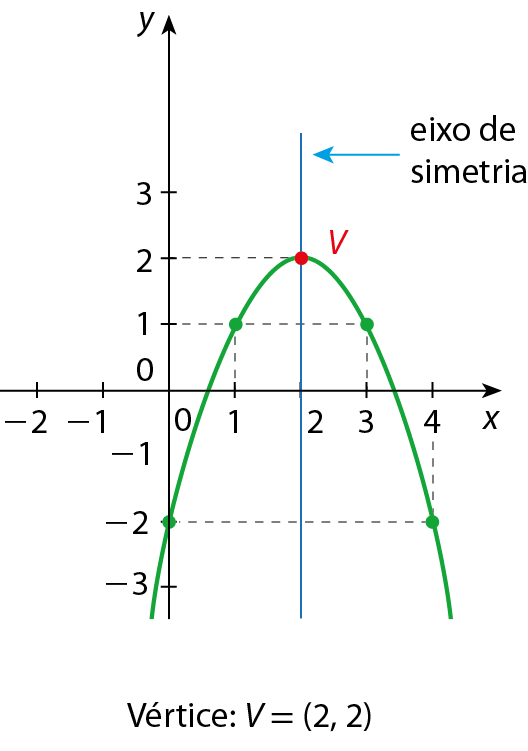
b) q(x) = x2 + 2x ‒ 1
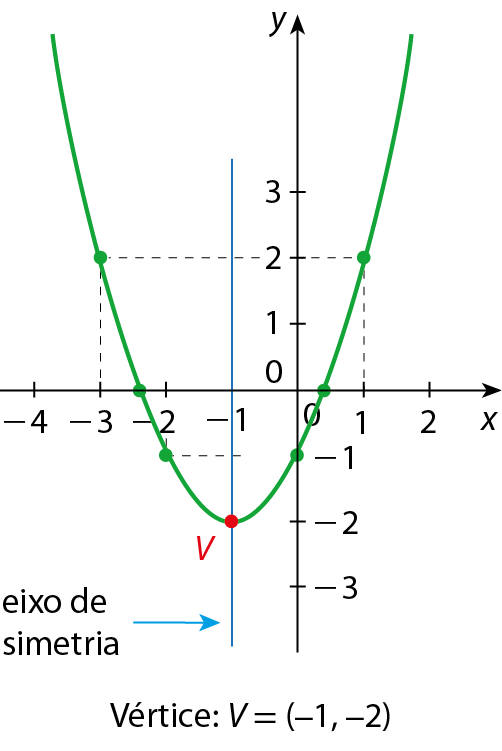
O vértice da parábola é o ponto de intersecção da parábola com seu eixo de simetria.
Observações
▶ O vértice de uma parábola corresponde ao ponto de máximo dessa parábola quando ela tem concavidade voltada para baixo e corresponde ao ponto de mínimo dessa parábola quando ela tem concavidade voltada para cima.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
42 Considere a parábola indicada no plano cartesiano.
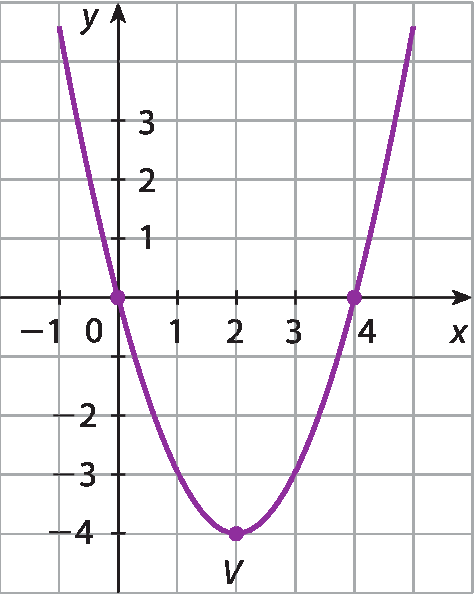
a) Qual é o sinal do coeficiente a ?
b) Quais são as coordenadas do vértice da parábola?
c) Para quais valores de x se obtém y = 0?
d) Identifique o ponto de intersecção entre o eixo x e o eixo de simetria da parábola.
43 As medidas, em centímetro, das diagonais de um losango são expressas por (x + 2) e (2x + 4). Determine no caderno:
a) a medida da área y dêsse losango em função de x ;
b) para que valor de x esse losango tem área medindo 25 centímetros.
44 O gráfico de cada uma das funções a seguir é uma parábola. Determine no caderno os casos em que a parábola tem concavidade voltada para cima.
a) y = 2x 2 ‒ 3x + 1
b) y = ‒x 2 + 4x ‒ 4
c) y = ‒3x 2 + x ‒ 4
d) y = x 2 + 5x
e) y = x 2
f) y = ‒x 2 + 9
45 Considere a parábola a indicada no plano cartesiano.
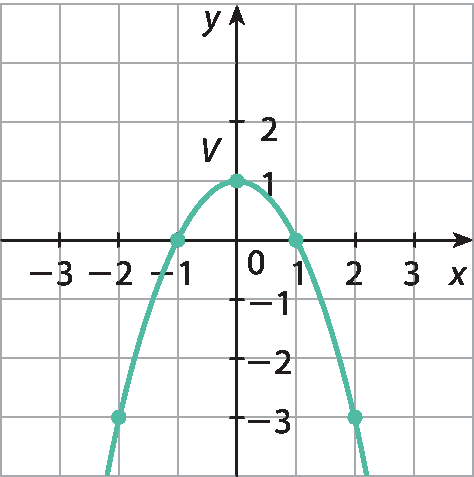
Determine no caderno:
a) x quando y = ‒3;
b) x quando y = 2;
c) y quando x = 2;
d) f (1);
e) as coordenadas do vértice.
46 Determine no caderno os valores de p na função definida pela lei y = (p ‒ 3)x 2 ‒ 5x ‒ 24 para que a parábola tenha a concavidade voltada para cima.
47 Determine no caderno os valores de p na função definida pela lei y = (2p + 1)x 2 ‒ 2x + 1 para que a parábola tenha a concavidade voltada para baixo.
48 Uma função polinomial do 2º grau é definida pela lei:
y = (m + 2)x 2 + (m + 3)x + m + 4
Responda no caderno às questões a seguir.
a) Para que valores reais de ême o gráfico dessa função tem concavidade voltada para baixo?
b) Para que valores reais de m o gráfico dessa função passa pelo ponto (0, 0)?
Zeros de uma função polinomial do 2º grau
Antes de fazer o esboço de uma parábola, devemos determinar os zeros da função e identificar sua concavidade.
Acompanhe um exemplo. Vamos determinar os zeros da função dada pela lei y = x elevado a 2 ‒ 3x ‒ 10.
x elevado a 2 ‒ 3x ‒ 10 = 0 (a = 1, b = ‒3 e c = ‒10)
Δ = b elevado a 2 ‒ 4ac
Δ = (‒3)elevado a 2 ‒ 4 · 1 · (‒10) = 9 + 40 = 49

= 7
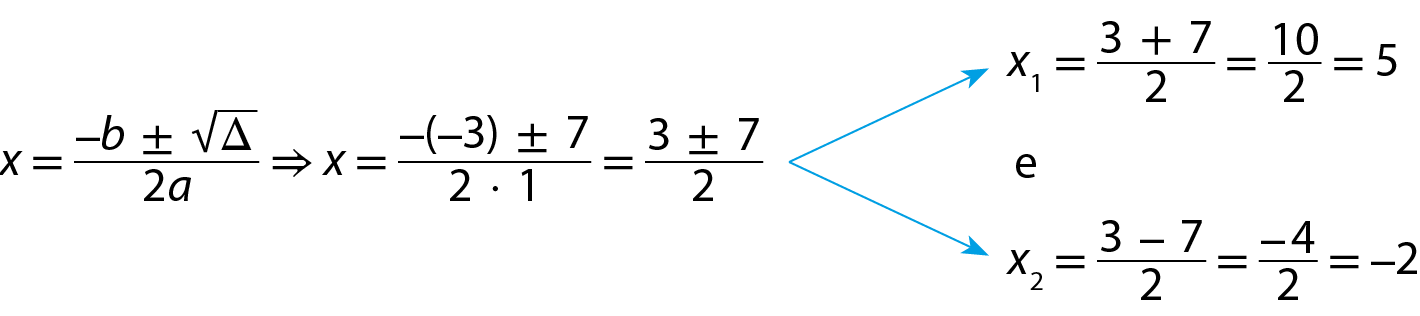
Portanto, os zeros da função são ‒2 e 5.
Como a > 0, a parábola tem a concavidade voltada para cima. dêsse modo, podemos fazer o esboço do gráfico da função dada pela lei y = x2 ‒ 3x ‒ 10.
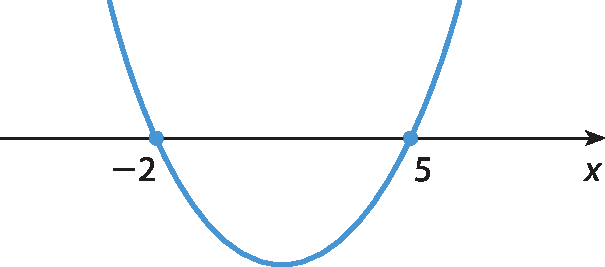
Considere estes outros exemplos.
a) y = ‒2x elevado a 2 + 5x ‒ 2 ‒2x elevado a 2 + 5x ‒ 2 = 0 Δ = b elevado a 2 ‒ 4ac Δ = (5)elevado a 2 ‒ 4 · (‒2) · (‒2) = 9
raiz quadrada de delta.= 3
x é igual a fração numerador: menos b, mais ou menos raiz quadrada de delta; denominador: 2 vezes a; fim da fração.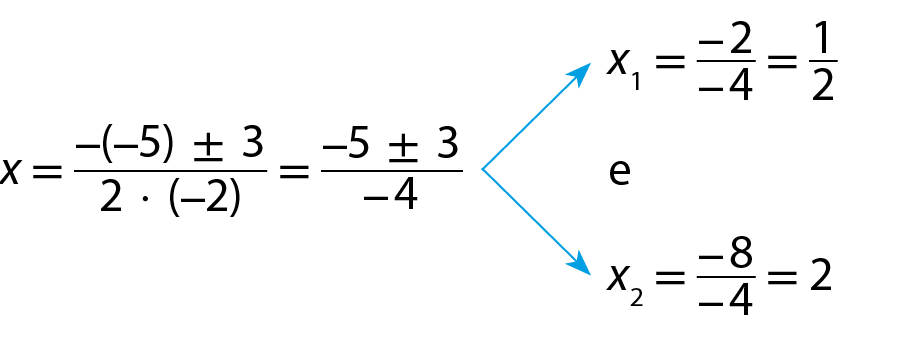
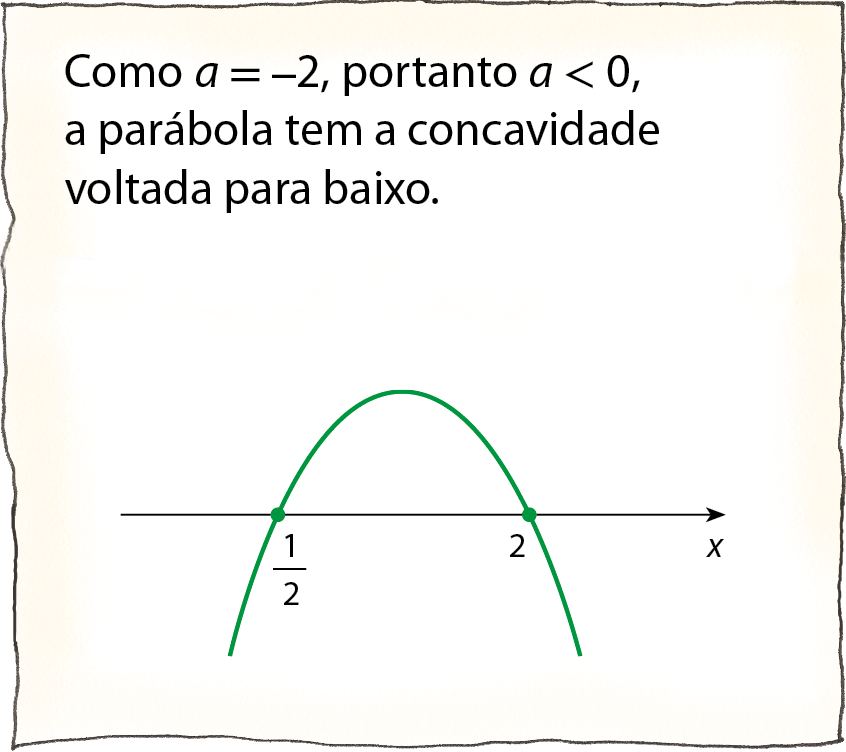
b) y = 4x elevado a 2 ‒ 4x + 1 4x elevado a 2 ‒ 4x + 1 = 0 Como o 1º membro dessa equação é um trinômio quadrado perfeito, podemos escrever: (2x ‒ 1)elevado a 2 = 0 Assim, obtemos: 2x ‒ 1 = 0 x =
fração um meio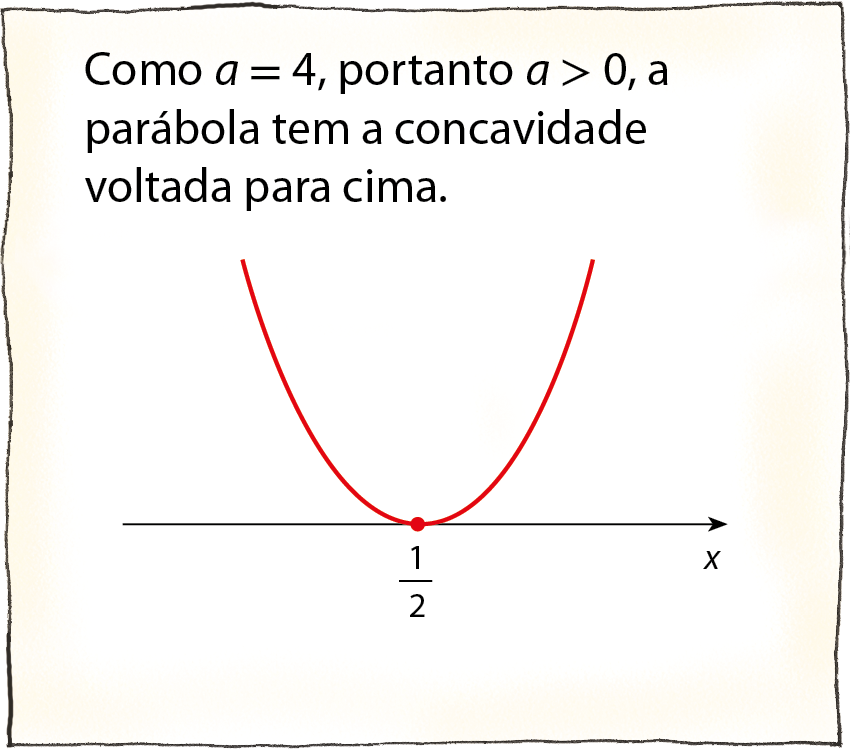
c) y = ‒3x elevado a 2 + 2x ‒ 1 ‒3x elevado a 2 + 2x ‒ 1 = 0 Δ = b elevado a 2 ‒ 4ac Δ = (2)elevado a 2 ‒ 4 · (‒3) · (‒1) Δ = 4 ‒ 12 = ‒8 Como Δ < 0, a equação não tem raízes reais. Portanto, a parábola não corta o eixo x.

No esboço do gráfico de uma função quadrática, podem ocorrer os seguintes casos:
|
a > 0 |
a < 0 |
|
|---|---|---|
|
Δ > 0 |
|
|
|
Δ = 0 |
|
|
|
Δ < 0 |
|
|
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
49 Determine no caderno os zeros (se existentes) das funções quadráticas e faça um esboço do gráfico de cada uma.
a) y = x elevado a 2 ‒ 6x + 8
b) y = x elevado a 2 + 2
c) y = ‒x elevado a 2 + 4x
d) y = x elevado a 2 ‒ 6x + 9
e) y = ‒9x elevado a 2 + 12x ‒ 4
f) y = 2x elevado a 2 ‒ 2x + 1
50 A trajetória de um projétil lançado obliquamente por um canhão, em um local plano e horizontal, é dada por parte do gráfico da função cuja lei é:
Se as medidas das distâncias horizontal e vertical, em relação ao canhão, são dadas em quilômetro e representadas, respectivamente por x e y, determine a quantos quilômetros do canhão o projétil caiu.
Coordenadas do vértice da parábola
Observe o gráfico correspondente à função y = x 2 ‒ 2x ‒3.
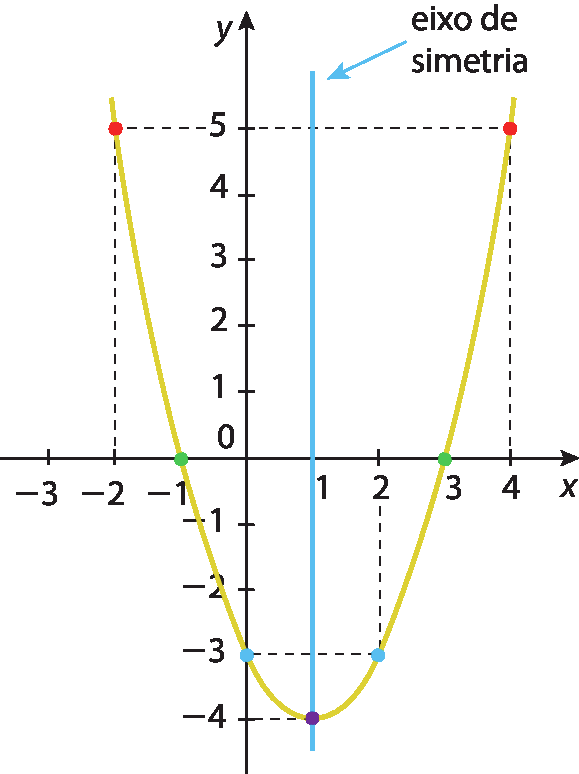
Note que a abscissa do vértice da parábola (x = 1) corresponde à metade da soma das abscissas dos pontos que são simétricos em relação ao eixo de simetria da parábola. Assim, considerando os pares de pontos destacados no gráfico, obtemos:
Fração numerador: menos 1 mais 3; denominador: 2; fim da fração; é igual a fração; numerador: 2; denominador: 2; fim da fração, que é igual a 1.
Substituindo x por 1 em y = x 2 ‒ 2x ‒3 e efetuando os cálculos, obtemos a ordenada do vértice:
y = (1)elevado a 2 ‒ 2(1) ‒ 3 = 1 ‒ 2 ‒ 3 = ‒ 4
De modo geral, podemos relacionar a abscissa do vértice da parábola (xv ) que representa a função quadrática dada por fabre parênteses décimafecha parênteses = ax 2 + bx + c aos coeficientes a e b.
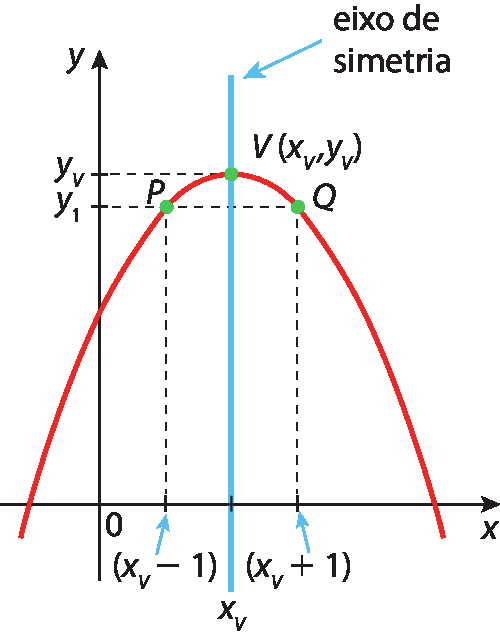

Por causa da simetria do gráfico, observe, por exemplo, que as abscissas (xV ‒ 1) e (xV + 1) estão a uma mesma distância de xV e que f (xV ‒ 1) = f (xV + 1) = y1. Dessa fórma, obtemos:
a(xV ‒ 1)elevado a 2 + b(xV ‒ 1) + c = a(xV + 1)elevado a 2 + b(xV + 1) + c
a[(xV)elevado a 2 ‒ 2xV · 1 + 1] + b (xV ‒ 1) + c = a[(xV)elevado a 2 + 2xV · 1 + 1] + b(xV + 1) + c
a(xV)elevado a 2 ‒ 2axV + a + bxV ‒ b + c = a(xV)elevado a 2 + 2axV + a + bxV + b + c
‒2axV ‒ b = 2axV + b
‒4axV = 2b
xV =
fração numerador: 2 b; denominador: menos 4 a., ou seja:
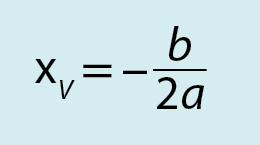

Como exemplo, vamos determinar as coordenadas do vértice da parábola das funções quadráticas dadas por:
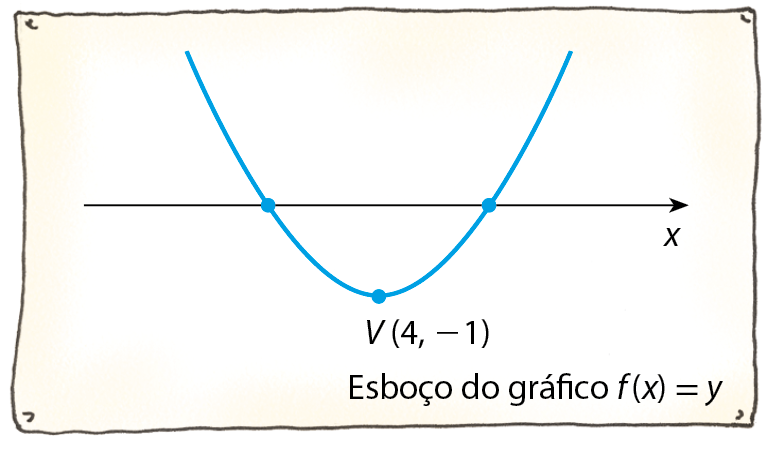
a) y = x elevado a 2 ‒ 8x + 15
• Abscissa do vértice:
• Ordenada do vértice:
Substituindo x por 4 na lei da função, obtemos:
yV = (4)elevado a 2 ‒ 8 · (4) + 15 = 16 ‒ 32 + 15 = ‒1
Logo, o vértice da parábola é V (4, ‒1).
Note que a > 0 e Δ = 4 > 0.
b) y = 2x elevado a 2 ‒ 3x + 2
• Abscissa do vértice:
x v é igual a fração; numerador: menos b; denominador: 2 a; fim da fração, é igual a fração numerador: menos abre parênteses menos 3 fecha parênteses; denominador: 2 vezes abre parênteses 2 fecha parênteses; fim da fração, é igual a fração 3 quartos.• Ordenada do vértice:
y v é igual a 2 vezes abre parênteses fração 3 quartos fecha parênteses, elevado ao quadrado, menos 3 vezes abre parênteses fração 3 quartos fecha parênteses, mais 2, é igual a 2 vezes abre parênteses fração numerador: 9; denominador: 16 fecha parênteses; menos fração 9 quartos; fim da fração, mais 2, é igual a fração numerador: 18; denominador: 16; fim da fração, menos fração 9 quartos; fim da fração, mais 2, é igual a Fração numerador: 18; denominador: 16; fim da fração, menos fração numerador: 36; denominador: 16; fim da fração, mais fração numerador: 32; denominador: 16; fim da fração, que é igual a fração numerador: 14; denominador: 16; fim da fração, que é igual a fração, 7 oitavos.Portanto, o vértice da parábola é
V de coordenadas fração 3 quartos; e fração 7 oitavos..
Note que a > 0 e Δ = ‒7 < 0.
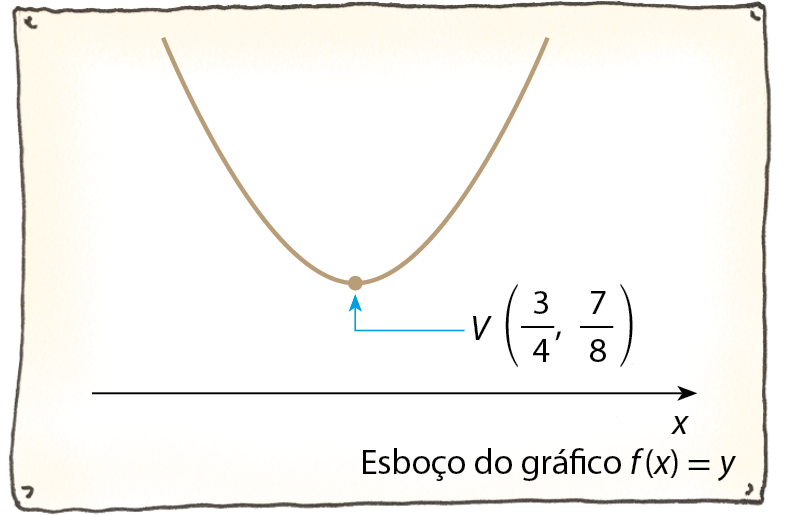
Valor máximo e valor mínimo de uma função polinomial do 2º grau
Considere as funções polinomiais do 2º grau cujos gráficos estão representados a seguir.
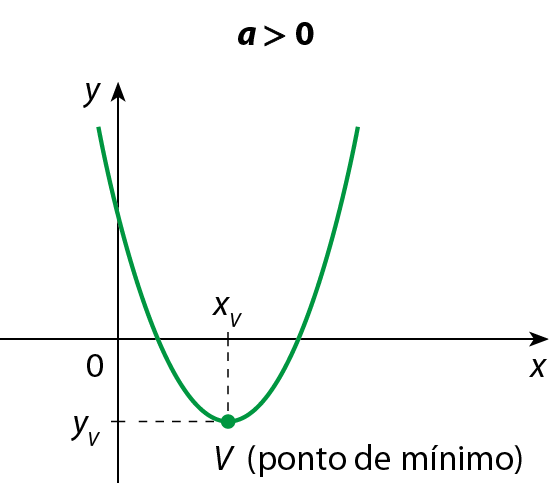
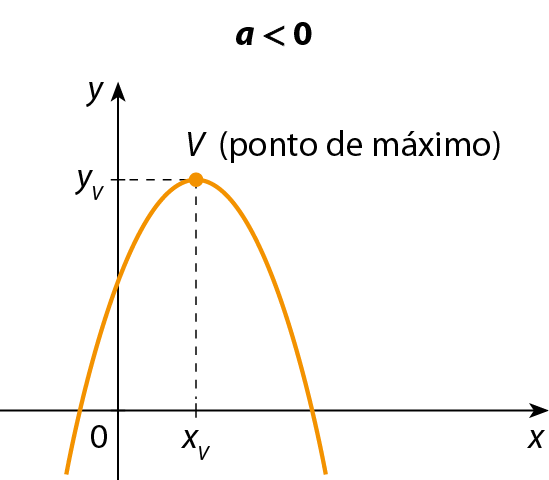
Examinando esses gráficos, podemos dizer que:
• se a > 0, o vértice é o ponto da parábola que tem ordenada mínima. Nesse caso, o vértice é chamado ponto de mínimo, e a ordenada do vértice, valor mínimo da função;
• se a < 0, o vértice é o ponto da parábola que tem ordenada máxima. Nesse caso, o vértice é chamado ponto de máximo, e a ordenada do vértice, valor máximo da função.
Acompanhe dois exemplos.
a) Para que valor de x o valor de y = ‒2x elevado a 2 + 6x + 1 é máximo?
O ponto de máximo de uma função polinomial do 2º grau com a < 0 é o vértice V. Como queremos o valor de x, devemos calcular xV.
Logo, y tem valor máximo para x = 1,5.
b) Vamos determinar o valor mínimo da função dada pela lei y = x elevado a 2 ‒ 10x + 24.
O valor mínimo de uma função polinomial do 2º grau com a > 0 é dado pela ordenada yV do vértice da parábola. Primeiro, calculamos xV:
Agora, calculamos yV , substituindo x por 5 na lei da função: yV = 5elevado a 2 ‒ 10 · 5 + 24 = 25 ‒ 50 + 24 = ‒1 Logo, o valor mínimo dessa função ocorre quando y = ‒1.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
51 Determine no caderno as coordenadas do vértice da parábola em cada caso.
a) y = ‒x elevado a 2 ‒ 8x + 16
b) y = 2x elevado a 2 + 6x
c) y = x elevado a 2 ‒ 16
52 O ponto de vértice da parábola definida pela lei da função y = 3x elevado a 2 ‒ px + 2q é dado por V (2, 1). Determine no caderno os valores reais de p e q.
53 Verifique se a função tem ponto de máximo ou de mínimo.
a) y = 4x elevado a 2 ‒ 9x + 2
b) y = x elevado a 2 + 3x ‒ 70
c) y = ‒x elevado a 2 + 14x ‒ 24
d) y = 5x elevado a 2 ‒ 6x
e) y = ‒3x elevado a 2 + 9x
f) y = ‒2x elevado a 2 ‒ 50
54 Para cada lei da função, calcule no caderno o x correspondente ao valor mínimo.
a) y = 3x elevado a 2 ‒ 4x + 1
b) y = x elevado a 2 + 12x + 11
55 Para cada lei da função, calcule no caderno o x correspondente ao valor máximo.
a) y = ‒2x elevado a 2 + 11x ‒ 5
b) y = ‒2x elevado a 2 + 25x ‒ 150
56 Calcule no caderno o valor máximo da função dada pela lei y = ‒x elevado a 2 + 11x ‒ 18.
57 Calcule no caderno o valor mínimo da função dada pela lei y = x elevado a 2 ‒ 6x + 8.
58 Fernando demarcou uma região retangular de 100 métros de medida do perímetro em um terreno para construir uma casa.
Calcule no caderno as dimensões dessa região para que Fernando aproveite a maior medida de área possível.
59 O custo C, em real, de um produto é dado por centésimaabre parênteses décimafecha parênteses = x elevado a 2 ‒ 80x + .3000, sendo x a quantidade de unidades produzidas.
a) Qual deve ser a quantidade de unidades para que o custo seja mínimo?
b) Qual é o valor dêsse custo mínimo?
Construção do gráfico de uma função polinomial do 2º grau

• Determinamos as coordenadas do vértice V ;
• atribuímos a x valores próximos de décimoV e calculamos os correspondentes valores de y ;
• construímos um quadro com os pontos determinados;
• marcamos, no plano cartesiano, os pontos obtidos;
• considerando o sentido da concavidade dada pelo sinal de a, traçamos o gráfico (a parábola).
Acompanhe alguns exemplos.
a) y = x elevado a 2 ‒ 4x + 3
• Coordenadas do vértice:
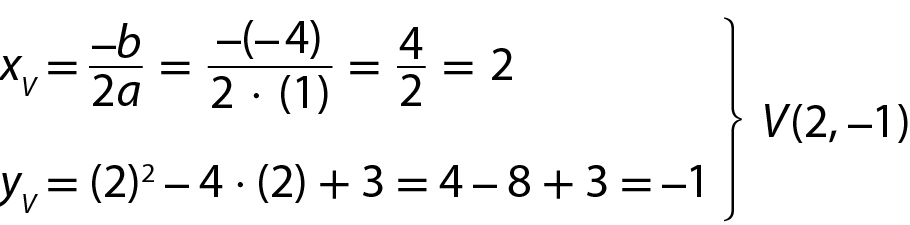
Portanto, V(2, ‒1) é o vértice da parábola.
Vamos atribuir a x valores próximos de xV.

Para x = 0, obtemos: y = (0)elevado a 2 ‒ 4 · (0) + 3 = 0 ‒ 0 + 3 = 3
Para x = 1, obtemos: y = (1)elevado a 2 ‒ 4 · (1) + 3 = 1 ‒ 4 + 3 = 0
Para x = 3, obtemos: y = (3)elevado a 2 ‒ 4 · (3) + 3 = 9 ‒ 12 + 3 = 0
Para x = 4, obtemos: y = (4)elevado a 2 ‒ 4 · (4) + 3 = 16 ‒ 16 + 3 = 3
|
x |
y = x2 − 4x + 3 |
(x, y) |
|
|---|---|---|---|
|
0 |
3 |
(0, 3) |
|
|
1 |
0 |
(1, 0) |
|
|
2 |
−1 |
(2, −1) |
V |
|
3 |
0 |
(3, 0) |
|
|
4 |
3 |
(4, 3) |

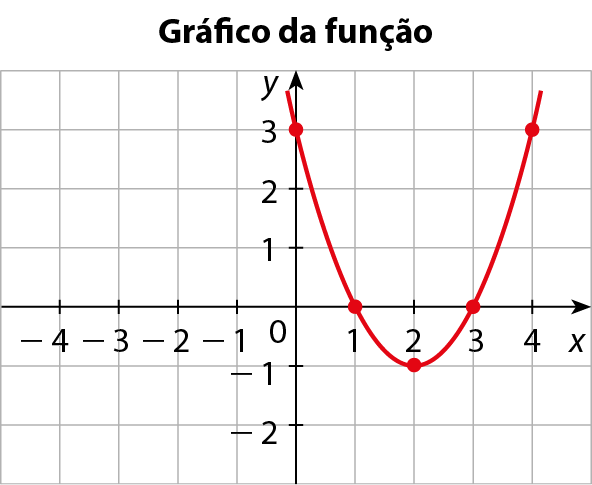
b) y = ‒x elevado a 2 + 4x ‒ 4
• Coordenadas do vértice:
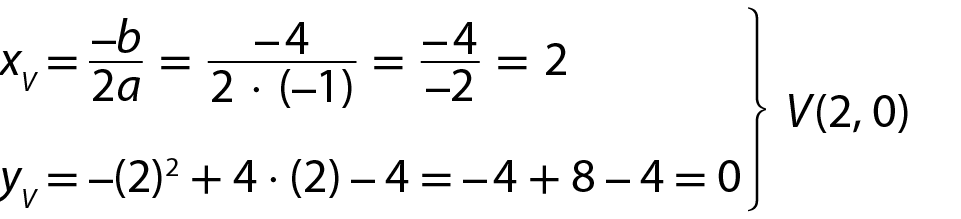
Note que a < 0; então, a concavidade é voltada para baixo.
|
x |
y = −x2 + 4x − 4 |
(x, y) |
|
|---|---|---|---|
|
0 |
−4 |
(0, −4) |
|
|
1 |
−1 |
(1, −1) |
|
|
2 |
0 |
(2, 0) |
V |
|
3 |
−1 |
(3, −1) |
|
|
4 |
−4 |
(4, −4) |
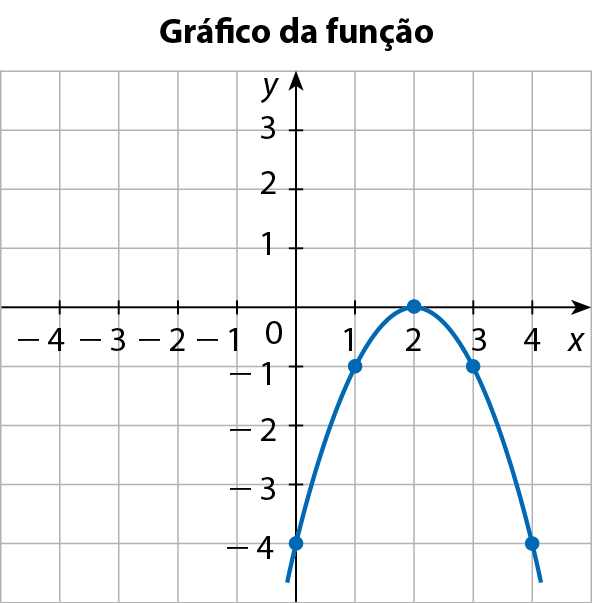
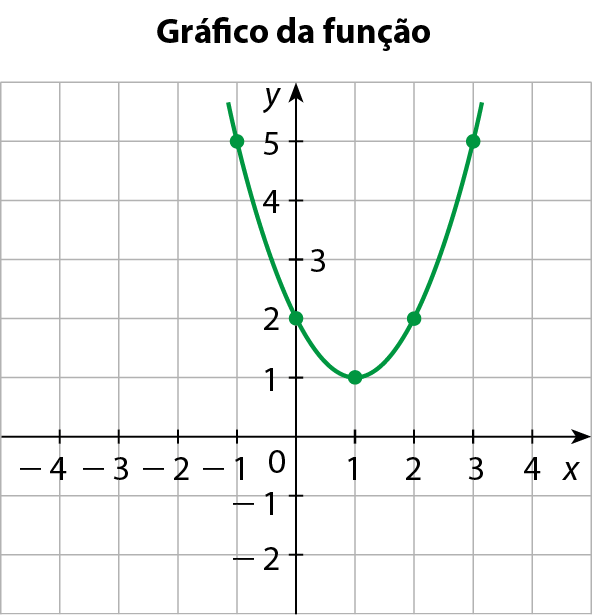
c) y = x elevado a 2 ‒ 2x + 2
• Coordenadas do vértice:
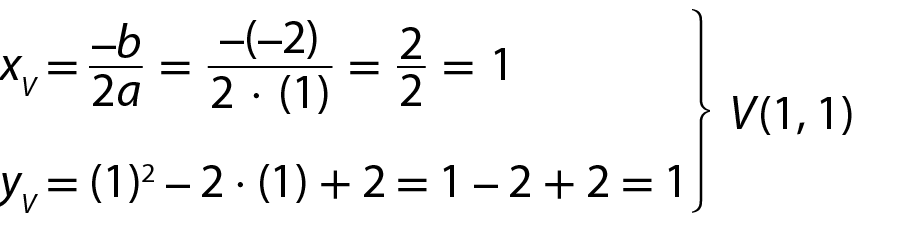
Note que a > 0; então, a concavidade é voltada para cima.
|
x |
y = x2 − 2x + 2 |
(x, y) |
|
|---|---|---|---|
|
−1 |
5 |
(−1, 5) |
|
|
0 |
2 |
(0, 2) |
|
|
1 |
1 |
(1, 1) |
V |
|
2 |
2 |
(2, 2) |
|
|
3 |
5 |
(3, 5) |
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
60 Construa o gráfico das funções quadráticas em uma folha de papel quadriculado.
a) y = x elevado a 2 + 2x ‒ 8
b) y = ‒x elevado a 2 + 6x ‒ 5
c) y = 3x elevado a 2 ‒12x + 9
d) y = ‒x elevado a 2 + x + 1
e) y = ‒x elevado a 2
f) y = x elevado a 2 ‒ x + 2
61 Em uma folha de papel quadriculado e em um mesmo plano cartesiano, construa os gráficos das funções dadas pelas leis y = x elevado a 2 ‒ 4 e y = ‒x elevado a 2 + 4 e determine os pontos de intersecção desses dois gráficos.
62

Reúna-se com um colega para fazerem esta atividade.
Usando uma folha de papel quadriculado, construam, para cada item, em um mesmo plano cartesiano, os gráficos das funções dadas pelas seguintes leis:
a) fabre parênteses décimafecha parênteses = x elevado a 2, gabre parênteses décimafecha parênteses = x elevado a 2 + 1 e hidrogênioabre parênteses décimafecha parênteses = x elevado a 2 ‒ 1
b) fabre parênteses décimafecha parênteses = x elevado a 2 e gabre parênteses décimafecha parênteses = ‒x elevado a 2
c) fabre parênteses décimafecha parênteses = x elevado a 2, gabre parênteses décimafecha parênteses = 2x elevado a 2 e hidrogênioabre parênteses décimafecha parênteses = 4x elevado a 2
Comparando os gráficos em cada plano cartesiano, o que vocês podem observar?
PARA SABER MAIS
Uso do computador: parábolas
Com o auxílio de um software de geometria dinâmica, é possível estudar o que acontece com o gráfico de funções do tipo f(décima) = ax elevado a 2 + bx + c à medida que os coeficientes a, b e c variam.
1. Ao digitar fabre parênteses décimafecha parênteses = ax elevado a 2 + bx + c e teclar “Enter” no campo “Entrada” na tela inicial, aparecerá uma janela.
2. Clicando em “Criar Controles Deslizantes” na tela inicial, aparecerão os controles deslizantes correspondentes aos coeficientes a, b e c de fabre parênteses décimafecha parênteses = ax elevado a 2 + bx + c, além do gráfico para a = 1, b = 1 e c = 1.
3. É possível movimentar os cursores dos controles deslizantes para variar os valores dos coeficientes a, b e c .
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Imagine se modificarmos o coeficiente a. Em seguida, responda às questões a seguir.
a) O que acontece quando o valor absoluto de a aumenta?
b) O que acontece quando o valor absoluto de a diminui?
2 Imagine o que acontece se modificarmos o coeficiente c. Em seguida, responda às questões a seguir.
a) Qual é o papel do coeficiente c no gráfico de f abre parênteses décimafecha parênteses = ax elevado a 2 + bx + c?
b) Podemos associar esse coeficiente à ordenada de um ponto. Que ponto é esse?
3 Construa o gráfico de algumas funções quadráticas do tipo f abre parênteses décimafecha parênteses = ax elevado a 2 + c. Depois, responda às questões a seguir.
a) Em que ponto cada parábola traçada intersecta o eixo y?
b) Qual é o eixo de simetria de cada parábola traçada?
Estudo do sinal de uma função polinomial do 2º grau
Estudar o sinal de uma função polinomial do 2º grau é determinar os valores reais de x que tornam a função positiva (y > 0), negativa (y < 0) ou nula (y = 0). Para isso, é necessário determinar, quando houver, os zeros da função (valores de x que anulam a função), observar o sentido da concavidade (para cima ou para baixo) e esboçar seu gráfico.
Agora, acompanhe alguns exemplos do estudo do sinal de funções polinomiais do 2º grau.
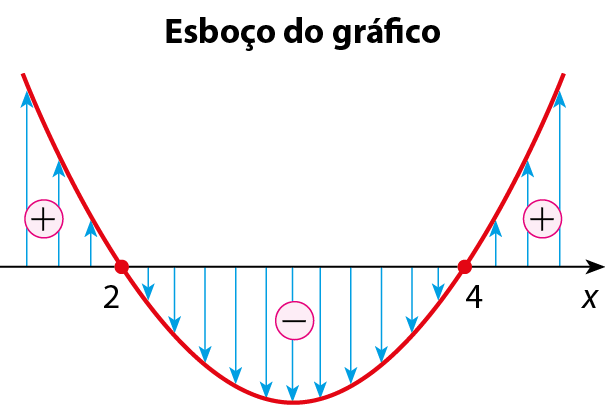
a) Vamos estudar o sinal da função dada pela lei y = x elevado a 2 ‒ 6x + 8. Como a = 1 > 0, a parábola tem concavidade voltada para cima. Zeros da função x elevado a 2 ‒ 6x + 8 = 0 (a = 1 > 0, b = ‒6, c = 8) Δ = (‒6)2 ‒ 4 · 1 · 8 = 4
Raiz quadrada de delta, igual a raiz quadrada de 4, que é igual a 2.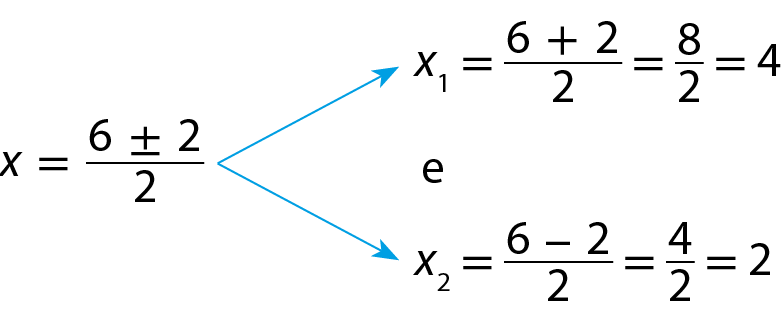
Estudo do sinal
• Para x < 2 ou x > 4, obtemos: y > 0; pontos acima do eixo x.
• Para x = 2 ou x = 4, obtemos: y = 0; pontos do eixo x.
• Para 2 < x < 4, obtemos: y < 0; pontos abaixo do eixo x.
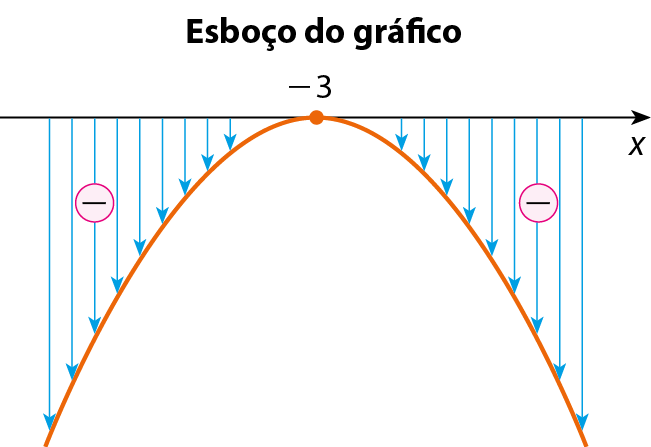
b) Vamos estudar o sinal da função dada pela lei y = ‒x 2 ‒ 6x ‒ 9. Como a = ‒1 < 0, a parábola tem concavidade voltada para baixo. Zeros da função ‒x elevado a 2 ‒ 6x ‒ 9 = 0 (a = ‒1 < 0, b = ‒6, c = ‒9) Δ = (‒6)elevado a 2 ‒ 4 · (‒1) · (‒9) = 0
Raiz quadrada de delta, é igual a raiz quadrada de 0, que é igual a 0. x é igual a fração numerador: menos abre parênteses menos 6 fecha parênteses; denominador: 2 vezes abre parênteses menos 1 fecha parênteses; é igual a fração numerador: 6; denominador: menos 2; que é igual a menos 3.Estudo do sinal
• Para x ≠ ‒3, obtemos: y < 0; pontos abaixo do eixo x.
• Para x = ‒3, obtemos: y = 0; ponto do eixo x.
• Não existe valor real de x que torne y > 0.
c) Vamos estudar o sinal da função dada pela lei y = x elevado a 2 ‒ 3x + 3. Como a = 1 > 0, a parábola tem concavidade voltada para cima. Zeros da função x elevado a 2 ‒ 3x + 3 = 0 (a = 1 > 0, b = ‒3, c = 3) Δ = (‒3)elevado a 2 ‒ 4 · 1 · 3 = ‒3 A função não tem zeros reais. Estudo do sinal A função nunca se anula e não existe valor de x real que a torne negativa, ou seja, para qualquer x real, a função sempre é positiva.
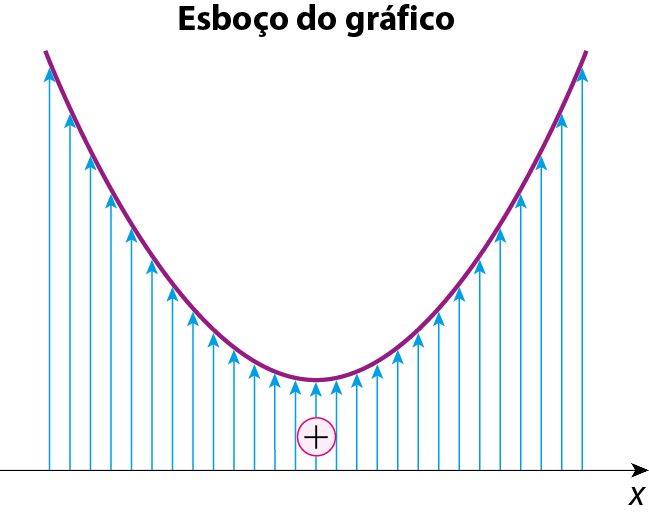
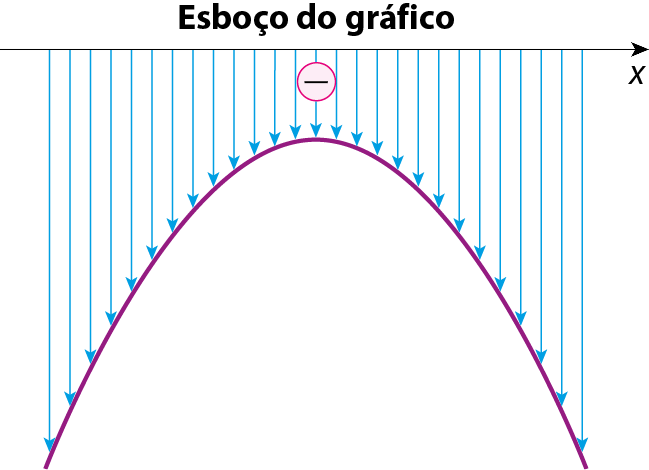
d) Vamos estudar o sinal da função dada pela lei y = ‒x elevado a 2 + 3x ‒ 3. Como a = ‒1 < 0, a parábola tem concavidade voltada para baixo. Zeros da função ‒x elevado a 2 + 3x ‒ 3 = 0 (a = ‒1 < 0, b = 3, c = ‒3) Δ = 32 ‒ 4 · (‒1) · (‒3) = ‒3 A função não tem zeros reais. Estudo do sinal A função nunca se anula e não existe valor de x real que a torne positiva, ou seja, para cada x real, a função sempre é negativa.
EXERCÍCIO PROPOSTO
FAÇA AS ATIVIDADES NO CADERNO
63 Faça o estudo do sinal das funções dadas pelas leis:
a) y = x elevado a 2 ‒ 3x + 2
b) y = 6x elevado a 2 ‒ 5x + 1
c) y = ‒2x elevado a 2 ‒ 5x + 3
d) y = x elevado a 2 + 8x + 16
e) y = ‒x elevado a 2 + 12x ‒ 36
f) y = 3x elevado a 2 ‒ 2x + 1
PARA SABER MAIS
Sistema de equações do 2º grau
Na linguagem matemática, as situações que relacionam dados por meio de uma igualdade são expressas por uma equação. Duas ou mais equações, com incógnitas em comum, constituem um sistema de equações. Se pelo menos uma delas é do 2º grau, obtemos um sistema de equações do 2º grau.
Considere a situação a seguir.
Hoje, a soma das idades de um tio e de seu sobrinho é 38 anos. Sabendo que daqui a 2 anos a idade do tio será igual ao quadrado da idade do sobrinho, calcule a idade de cada um hoje.

Para calcular as idades, vamos chamar de x a idade do tio e de y a idade do sobrinho. Com os dados fornecidos, podemos montar o seguinte sistema:
Isolando x na equação x + y = 38, obtemos:
x = 38 ‒ y
Substituindo x por 38 ‒ y na equação x + 2 = ( y + 2)elevado a 2, obtemos:
x + 2 = ( y + 2)elevado a 2
38 ‒ y + 2 = y elevado a 2 + 4y + 4
‒y elevado a 2 ‒ y ‒ 4y + 38 + 2 ‒ 4 = 0
‒y elevado a 2 ‒ 5y + 36 = 0
y elevado a 2 + 5y ‒ 36 = 0
Resolvendo essa equação na incógnita y, obtemos:
Δ = b elevado a 2 ‒ 4ac = 5elevado a 2 ‒ 4 · 1 · (‒36) = 25 + 144 = 169

Como não pode haver idade negativa, então y = 4.
Portanto, o sobrinho tem 4 anos.
Substituindo y por 4 na equação x = 38 ‒ y, encontramos a idade do tio.
x = 38 ‒ y = 38 ‒ 4 = 34
Logo, hoje o sobrinho tem 4 anos e o tio, 34 anos.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Determine no caderno dois números positivos a e b de modo que a + b = 2 e a elevado a 2 + b elevado a 2 =
fração 5 meios.2 A diferença entre dois números é 3. A soma de seus quadrados é 17. Qual é o maior desses números?
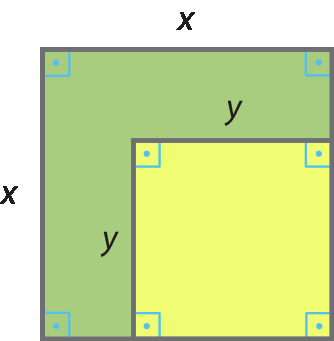
3 Na figura, a área verde mede 51 centímetros quadrados, e a diferença entre as medidas dos lados dos quadrados é 3 centímetros. Calcule no caderno a medida da área amarela.
TRABALHANDO A INFORMAÇÃO

O envelhecimento populacional
O artigo 3º da lei 10.741 estabelece que é obrigação de todos, inclusive do Estado, garantir aos idosos (pessoas com 60 anos ou mais) a efetivação do direito à vida, à saúde, à alimentação e, entre outros, à dignidade.
Em 1950, o total de brasileiros idosos era maior do que 2,6 milhões e correspondia a cêrca de 4,9% da população naquele ano. Já em 2020, o total de brasileiros idosos era de quase 30 milhões, cêrca de 14% da população brasileira. Esses dados evidenciam o envelhecimento populacional, que pode ser analisado, também, por meio do índice de envelhecimento (í ê). Esse índice é a razão entre o número de pessoas idosas e o número de jovens (crianças e adolescentes até 14 anos). A população é considerada idosa quando o í ê é maior do que 1.
Alguns meios de comunicação expressam a preocupação de que o envelhecimento populacional comprometa o crescimento econômico, pois a população em idade ativa diminui em relação à população total, como indica o gráfico a seguir.
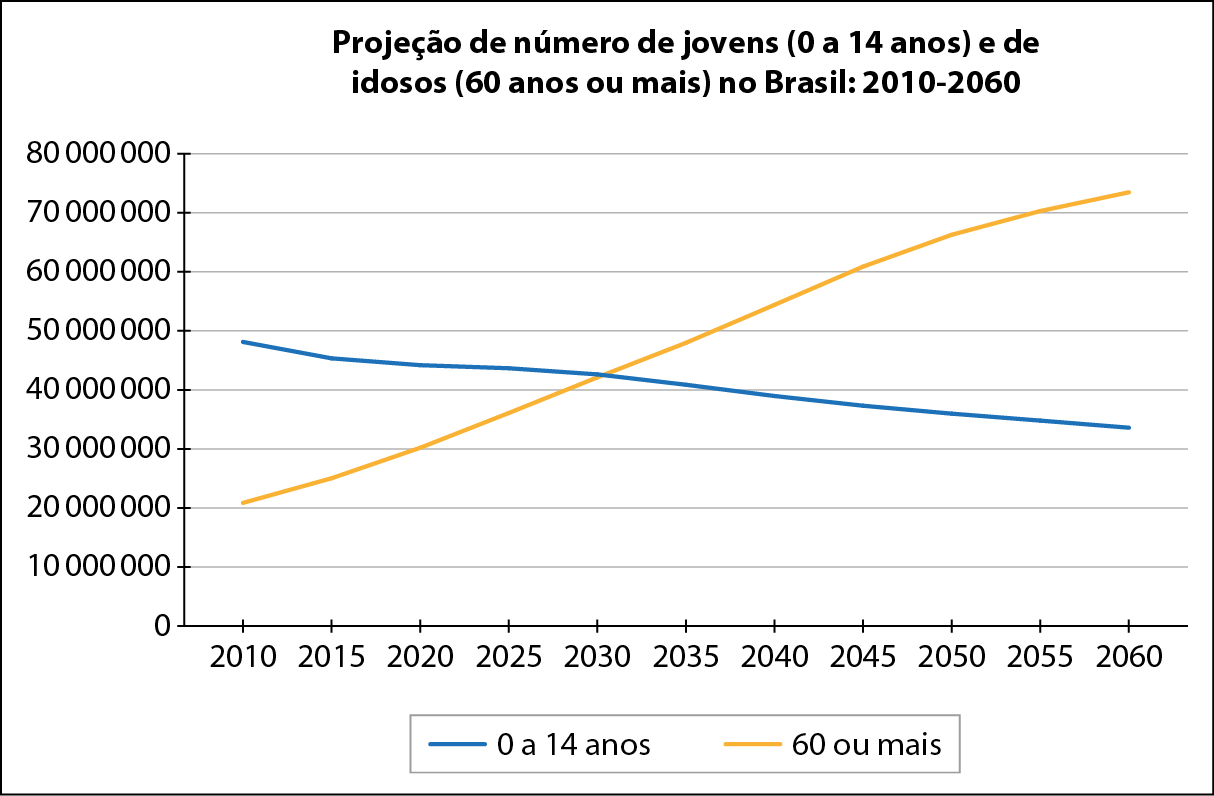
Apesar da preocupação em relação à diminuição da população em idade ativa, há outros fatores que podem ser considerados, como o comportamento dessa população. A inserção da mulher no mercado de trabalho, por exemplo, possibilitou que a população ocupada passasse de 32% em 1950 para 45,3% em 2010.
Agora quem trabalha é você!
FAÇA A ATIVIDADE NO CADERNO

Reúna-se em um grupo e façam o que se pede.
a) Determinem uma função polinomial do 1º grau, fabre parênteses décimafecha parênteses, que indique, aproximadamente, a projeção de número de jovens de 2010 a 2060. Depois, determinem uma função polinomial do 1º grau, gabre parênteses décimafecha parênteses, que aproxime a projeção do número de idosos nesse mesmo período. Considere que x = 0 corresponde ao ano 2010; x = 1, ao ano 2015; x = 2, ao ano 2020; e assim sucessivamente até x = 10, correspondendo ao ano 2060.
b) Em que ano, aproximadamente, o índice de envelhecimento (í ê) será maior do que 1 de acordo com essas projeções?
c) Na opinião de vocês, qual é a importância da participação das mulheres no mercado de trabalho, considerando o envelhecimento populacional?
d) Qual é a importância da projeção do envelhecimento populacional em relação às políticas públicas que garantem os direitos dos idosos?
e) Pesquisem informações sobre envelhecimento saudável e, depois, com base na projeção do envelhecimento populacional, discutam como vocês poderiam se preparar para envelhecer de maneira saudável.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Logo depois da formatura, a família de Juliana resolveu comemorar em uma pizzaria. Ao se despedirem, todos os familiares deram apertos de mão. Juliana calculou que o total de cumprimentos foi 78. Sabendo que, quando uma pessoa cumprimenta outra, esta outra também está cumprimentando-a, portanto, conta-se como um só cumprimento, quantas pessoas estavam participando dessa comemoração?

EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
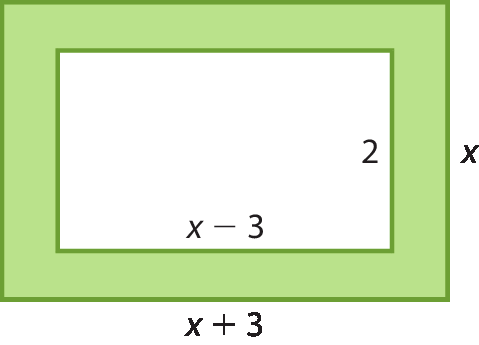
1 Considerando a figura, expresse a medida da área y da região verde em função de x.
2 Considerando a função dada pela lei
, calcule no caderno:
3 Uma função é dada pela lei f (x) = 10x + 10. Calcule no caderno f (10) ‒ f (0).
4 Observe este gráfico da função polinomial f do 1º grau:
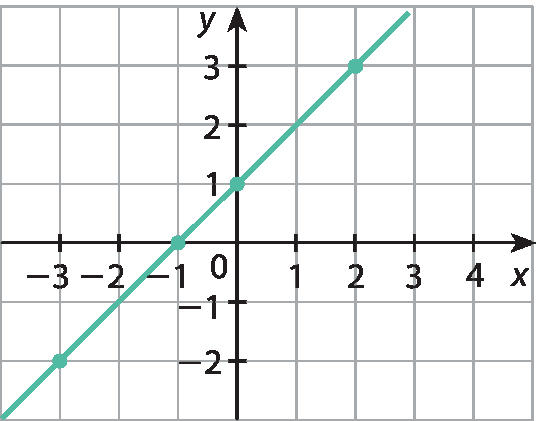
Determine no caderno o que se pede em cada item.
a) f (‒3)
b) f (0)
c) O valor de x para y = 3.
d) O zero da função.
• Agora, responda: o gráfico passa pelo ponto (10, 11)?
5 Considere a função polinomial do 1º grau dada pela lei y = 7x ‒ 4.
a) Determine no caderno o zero da função.
b) Construa, em uma folha de papel quadriculado, o gráfico dessa função.
c) Para que valor de x se obtém f abre parênteses décimafecha parênteses = 2?
d) Para que valores de x se obtém y > 0?
6 Dadas as funções f abre parênteses décimafecha parênteses = 2x ‒ 6 e g abre parênteses décimafecha parênteses = ‒3x + 6, determine no caderno os valores reais de x de acordo com o que se pede em cada item.
a) f abre parênteses décimafecha parênteses > 0
b) g abre parênteses décimafecha parênteses > 0
c) f abre parênteses décimafecha parênteses = g abre parênteses décimafecha parênteses
d) f abre parênteses décimafecha parênteses > g abre parênteses décimafecha parênteses
7 O gráfico da função dada pela lei y = 6x + p passa pelo ponto (1, 11). Determine no caderno para que valores reais de x se obtém:
a) y = 23
b) y < 0
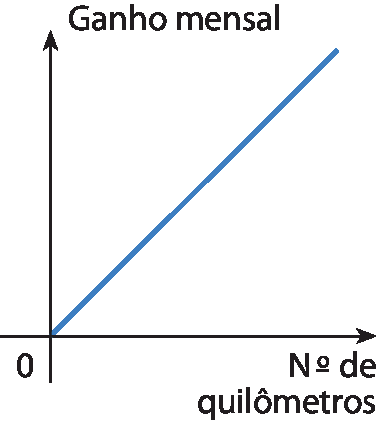
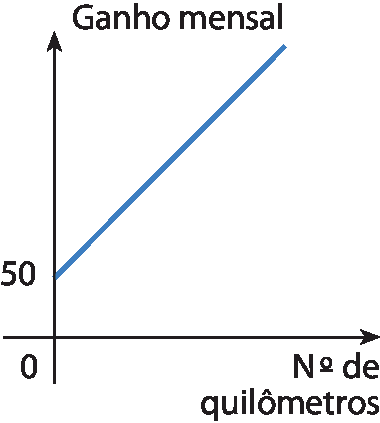
8 (saréspi) Um motoboy, para fazer entregas ou retirar documentos de escritórios espalhados pela cidade de São Paulo, recebe R$ 3,00três reais por quilômetro rodado. Suponhamos que ele passe a receber, mensalmente, um auxílio fixo de R$ 50,00cinquenta reais. O gráfico que representa o seu ganho mensal, em reais, em função dos quilômetros rodados é:
a)
b)
c)
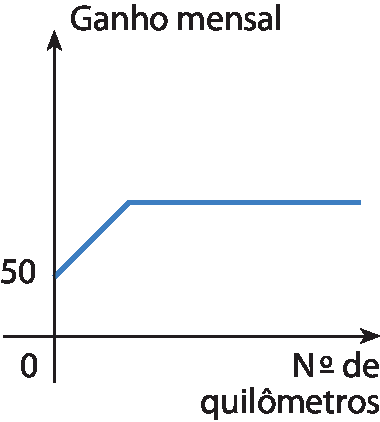
d)
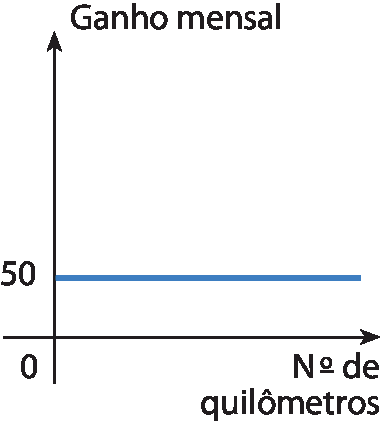
9 (unifór-Ceará) A função f do 1º grau é definida por f (x) = ‒3x + k. O valor de k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é:
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
10 Considere a função definida pela lei
y = x 2 ‒ 2x + 1.
a) Determine no caderno o(s) zero(s) dessa função.
b) Construa, em uma folha de papel quadriculado, o gráfico da função.
c) Para que valores de x obtemos y = 1?
d) Para que valores de x obtemos y > 0?
11 A medida da temperatura, em grau Celsius, no interior de uma câmara frigorífica é dada por uma função cuja lei é y = t 2 ‒ 7t + c, em que t indica a medida de tempo após a câmara ser ligada até atingir a temperatura mínima e y indica a medida da temperatura.
a) Sabendo que para t = 0 a temperatura mede 10 graus Célsius, calcule no caderno o valor de c.
b) Qual é a lei da função?
c) Calcule o valor de t para que a medida da temperatura seja a mínima possível.
12 (uquisal-Bahia) A parábola de equação y = 2x elevado a 2 ‒ 3x + 1 corta o eixo das abscissas nos pontos:
a) (0, 0) e (3, 0).
b) (0, 1) e (0, 2).
c) (0, 1) e
Par ordenado: 0, fração um meio..
d) (1, 0) e
Par ordenado: fração um meio, 0..
e) (2, 0) e (1, 0).
13 O custo (C ) de certo produto é obtido pela função definida pela lei centésimaabre parênteses décimafecha parênteses = x elevado a 2 ‒ 50x + 2, em que x representa a quantidade do produto. Calcule no caderno o valor de x para que o custo dêsse produto seja mínimo.
14 (púqui-Minas Gerais) O valor máximo da função f (x) = ‒x elevado a 2 + 2x + 2 é:
a) 2.
b) 3.
c) 4.
d) 5.
e) 6.
15 Em um experimento, um objeto é solto do alto de um prédio e cai, em queda livre, em direção ao chão. A medida de sua altura y em relação ao solo, x segundos após o lançamento, é dada por y = ‒16x 2 + 256. Quantos segundos após o lançamento o objeto atingirá o chão?
a) 2 segundos
b) 4 segundos
c) 6 segundos
d) 8 segundos
e) 16 segundos
16 (u éfe érre gê ésse-Rio Grande do Sul) Uma bola colocada no chão é chutada para o alto, percorrendo uma trajetória descrita por y = ‒2x elevado a 2 + 12x, em que y é a medida da altura dada em metro. A altura máxima atingida pela bola mede:
a) 36 métros.
b) 18 métros.
c) 12 métros.
d) 6 métros.
e) 3 métros.
17 Um engenheiro vai projetar uma piscina em fórma de paralelepípedo retângulo, cujas dimensões internas, em metro, são expressas por x, (20 ‒ x) e 2. Qual é a maior medida de volume que essa piscina poderá ter, em metro cúbico?
18 (ê ésse pê ême-São Paulo) A estrutura do lucro de uma pequena empresa pode ser estudada através da equação y = ‒x2 + 120x ‒ .2000, sendo y o lucro em real quando a empresa vende x unidades. Com base nisso, pode-se afirmar que:
a) o lucro é máximo quando x = 60.
b) o lucro é máximo quando x = .1600.
c) o lucro é máximo quando x = 20 ou x = 100.
d) o lucro é máximo quando x > .2000.
e) o lucro é máximo quando x < 20 ou x > 100.
19 O lucro (L) de uma empresa para certo produto é obtido pela função definida pela lei L = ‒2xelevado a 2 + .2000x ‒ 100, em que x representa a quantidade do produto. Calcule no caderno para quantas unidades se obtém o lucro máximo possível.
20 (éfespSão Paulo) Considere a função quadrática f (x) = (m + 1)x elevado a 2 ‒ 5x + 5.
a) Para que valores de m o gráfico da função tem concavidade voltada para baixo?
b) Para que valor de m o gráfico da função tangencia o eixo das abscissas?
21 Estude o sinal das funções quadráticas.
a) y = ‒3x elevado a 2 ‒ 5x + 2
b) y = 9x elevado a 2 ‒ 12x + 4
c) y = 4x elevado a 2 ‒ 2x + 3
d) y = 2x elevado a 2 ‒ 6x
22 Assinale a alternativa que indica quando o vértice da parábola que representa a função quadrática y = ax elevado a 2 + bx + c será um ponto do eixo das abscissas.
a) a = 0
b) Δ < 0
c) Δ = 0
d) Δ > 0
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Quais são os valores de y para x igual a 0, 1, 2 e 3 na função dada pela lei y = 14 ‒ 2x, respectivamente?
a) 8; 10; 12; 14.
b) 14; 12; 10; 8.
c) 12; 10; 8; 6.
d) 12; 12; 12; 12.
2 João trabalha com venda de planos de celular. Seu salário mensal é composto de um valor fixo de R$ 2.500,00dois mil quinhentos reais e de R$ 12,00doze reais por plano vendido. Qual é a equação que ele deve usar para calcular seu salário (S) em um mês em que vender uma quantidade v de planos?
a) v = 12 + .2500S
b) S = 12 + .2500v
c) v = .2500 + 12S
d) S = .2500 + 12v
3 Qual deve ser o valor de x para que y seja igual a 47 na função dada pela lei y = 20 + 3x?
a) 7
b) 9
c) 8
d) 10
4 Qual é a equação de 2º grau que dá a medida da área (a) de um retângulo de lados que medem x e x + 3?
a) A = x² + 3x
b) A = 3x²
c) A = x² + 3x²
d) A = 3x² + x
5 Qual é o zero da função dada pela lei y = 3x + 2?
a) 2
b)
Fração menos 3 meios.c)
Fração menos 3 meios.d) 3
6 Qual é a lei da função que relaciona as variáveis x e y no gráfico a seguir?
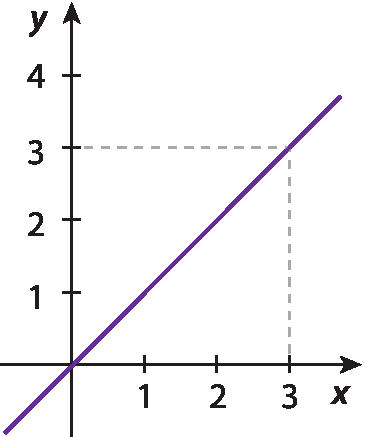
a) y =
Fração; x sobre 2.b) y = 3x
c) y = 2x
d) y = x
7 Quais são os zeros da função polinomial do 2º grau dada pela lei y = ‒2xelevado a 2 + 5x ‒ 2?
a)
Fração um meioe 2
b)
Fração menos um meioe 2
c)
Fração um meioe ‒2
d)
Fração menos um meioe ‒2
8 qual é o zero ou quais são os zeros da função polinomial do 2º grau dada pela lei y = (4x ‒ 1)elevado a 2?
a)
Fração um meiob)
Fração um meioe
Fração um quartoc)
Fração um quartod)
Fração menos um quartoe
Fração um quarto9 Assinale a alternativa que completa a frase corretamente: “O gráfico da função dada pela lei y = x2 ‒ 5x + 6 é uma parábola voltada para

e cruza o eixo x

vez ou vezes”.
a) baixo; uma.
b) baixo; duas.
c) cima; duas.
d) cima; uma.
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir:
a) Qual é a definição de função?
b) O que é uma função polinomial de 1º grau? E de 2º grau?
c) Como são os gráficos das funções polinomiais de 1º e 2º grau, respectivamente?
d) Como você explicaria a um colega um procedimento para verificar se um gráfico cartesiano representa uma função?
e) Dada uma função polinomial do 2º grau pela lei y = axelevado a 2 + bx + c, qual condição deve haver para que o vértice do gráfico seja um ponto de mínimo? E como as suas coordenadas podem ser obtidas?
DIVERSIFICANDO
Clique no play e acompanhe a reprodução do Áudio.
Transcrição do áudio
Animação gráfica
Duração: 7:54min. Página: 261.
>> [Locutor] Animação gráfica
>> [Joaquim] Olá! Eu sou o Joaquim.
>> [Diana] Eu sou a Diana!
>> [Joaquim] Neste podcast, vamos conversar um pouco sobre uma profissão que está bastante ligada à criatividade e à tecnologia: a de designer de animação.
Música eletrônica.
>> [Diana] Mas, antes de começarmos, aqui vai uma curiosidade: [tom de questionamento] você sabia que a palavra “animação” vem do verbo “animar”, que significa “dar vida a algo”?
>> [Joaquim] Pois é exatamente isso que faz o designer de animação, ou animador gráfico, como esse profissional também é conhecido. Ele dá vida a personagens e cenários, criando filmes de animação, como aqueles que vemos na televisão e no cinema.
>> [Diana] [Tom de interesse] Eu sempre tive curiosidade de saber como essas animações são feitas, Joaquim! Então, fui pesquisar sobre o assunto e descobri que há animações com técnicas 2D e 3D. [Tom de questionamento] Você sabia que a técnica de animação 2D já era conhecida no século XIX? Esse tipo de animação é aquele em que o cenário e os personagens são representados por figuras planas, com duas dimensões, comprimento e largura. Já nas animações 3D, como o próprio nome indica, os desenhos têm três dimensões: comprimento, largura e altura. Por isso, eles se assemelham mais ao mundo [tom enfático] real!
>> [Joaquim] Também fiz algumas pesquisas, Diana, e vi que, no início, nas animações 2D, os desenhos eram feitos todos a mão; cada cena de um filme era desenhada uma a uma. Hoje em dia, os desenhos podem ser criados e animados com o auxílio de softwares, tudo no computador, tanto para fazer animações 2D como animações 3D.
>> [Diana] [Tom de confirmação de raciocínio] É verdade!
>> [Joaquim] Para entender como as animações eram feitas a mão, podemos pensar naquela técnica de desenhar uma ação cena a cena nas folhas de um bloco de papel e depois folhear as páginas rapidamente, criando a ilusão de movimento contínuo, um desenho animado.
>> [Diana] [Tom de confirmação de raciocínio] Isso mesmo! [Tom explicativo] Por exemplo, se quisermos animar um personagem levantando um dos braços, no primeiro desenho, ele deve aparecer com os braços abaixados. Nas folhas seguintes, a cada novo desenho o braço deve ser levantado um pouco mais do que no desenho anterior, até chegar ao último desenho, em que o personagem estará com um dos braços totalmente levantado.
>> [Joaquim] [Tom de brincalhão] Nossa, que trabalhão, hein, Diana! E olha que, nesse exemplo, só falamos de uma cena, com apenas um personagem fazendo um movimento bem simples. [Tom enfático] Imagine o que seria animar uma história inteira com vários personagens, muitos movimentos e diversos cenários!
>> [Diana] Hoje em dia, existem diversos recursos digitais com técnicas mais sofisticadas para fazer a animação das cenas, o que torna o processo muito mais rápido. Atualmente, o designer de animação digital pode contar com softwares específicos para a modelagem de personagens e cenários, em que modelos matemáticos são utilizados na construção dos objetos digitais.
>> [Joaquim] [Tom de descoberta] Que interessante, Diana! [Tom de questionamento] Mas onde exatamente a Matemática é aplicada na criação de animações?
>> [Diana] [Tom enfático] Em praticamente tudo, Joaquim! [Tom explicativo] Para fazer o esboço de um personagem, por exemplo, conectam-se pontos, linhas retas e curvas. São também utilizadas figuras geométricas planas e não planas como referência para alguns desenhos. Para dar movimento a um personagem ou determinar a posição de um objeto em um cenário, são utilizadas coordenadas cartesianas. Como a animação é do tipo 3D, cada elemento é construído considerando três eixos cartesianos: um relacionado ao comprimento do objeto, que chamamos de eixo x; outro à largura, o eixo y; e outro à altura, o eixo z. Para o esboço de um personagem em três dimensões, o animador gráfico precisa pensar nas diferentes vistas do personagem: frontal, lateral, superior e inferior, por exemplo. No software, cada uma dessas vistas está relacionada a pares de eixos: as vistas superior e inferior ficam no plano limitado pelos eixos x e y, ou plano horizontal; as vistas laterais, pelos eixos y e z, ou plano lateral; e a vista frontal, pelos eixos x e z, ou plano vertical.
>> [Joaquim] [Tom de confirmação do raciocínio] Certo. [Tom explicativo] Então, o personagem é desenhado em um sistema de coordenadas cartesiano, e cada ponto do seu contorno é dado por um par de coordenadas. Assim, é possível determinar a posição do personagem, as medidas de suas dimensões e o espaço que ele ocupa. E, com esses eixos, também dá para fazer a rotação da imagem. [Tom de questionamento] E para fazer cada parte do corpo do personagem se movimentar ao mesmo tempo e de forma independente?
>> [Diana] [Tom explicativo] Para realizar a animação completa desse personagem, são traçados eixos secundários em cada parte do corpo que será movimentada de forma independente. Para cada um desses eixos, o designer de animação define os diferentes pares de coordenadas que determinarão o movimento de cada parte do corpo do personagem, considerando pelo menos dois instantes ou duas posições diferentes.
>> [Joaquim] É preciso bastante atenção na hora de conceber a imagem de um personagem e planejar os movimentos que ele vai fazer. [Tom enfático] E ainda tem a criação dos cenários, não é?
>> [Diana] [Tom de confirmação do raciocínio] Exatamente! E, para que uma cena pareça real, é necessário pensar em alguns itens importantes, como a iluminação desejada para a cena, as sombras dos objetos e também a profundidade.
>> [Joaquim] Para dar a ideia de profundidade, imagino que os profissionais elaborem desenhos em perspectiva.
>> [Diana] [Tom de confirmação do raciocínio] Isso mesmo! O desenho em perspectiva representa objetos tridimensionais em uma superfície bidimensional, dando a ideia de profundidade e fazendo com que eles tenham uma aparência mais realista.
>> [Joaquim] [Tom enfático] É muito interessante como esses conceitos matemáticos também podem ajudar na descrição do mundo ao nosso redor, não é?
>> [Diana] [Tom de confirmação do raciocínio] Sem dúvida!
>> [Joaquim] [Tom explicativo] É importante destacar que o trabalho do designer de animação não se restringe apenas ao desenho e à animação dos personagens e cenários. Ele pode também criar roteiros e contar histórias, descrevendo as cenas que imaginou.
>> [Diana] [Tom de questionamento] Como será que é o mercado de trabalho nessa área?
>> [Joaquim] [Tom explicativo] Eu pesquisei sobre isso e posso dizer que, hoje em dia, com as novas tecnologias e o uso cada vez mais frequente de mídias e plataformas digitais, a atuação do profissional que trabalha com animação gráfica não se restringe somente à criação de filmes de animação. Ele também pode atuar na produção de videoclipes, videoaulas, webseries, na animação de games e em campanhas publicitárias, por exemplo.
>> [Diana] O mercado de trabalho tem se ampliado com as novas tecnologias.
>> [Joaquim] [Tom de confirmação do raciocínio] Sim, hoje, esses profissionais são contratados por emissoras de TV, produtoras de conteúdo para a internet, agências de publicidade, indústrias de jogos, estúdios de animação e empresas do setor educacional, entre outras!
>> [Diana] Para quem quer trabalhar nessa área, existem desde cursos técnicos [tom enfático] até cursos de graduação em diferentes universidades.
>> [Joaquim] [Tom animado] Muito legal conhecer mais sobre essa profissão! [Tom empolgado] É isso aí, pessoal! Espero que tenham curtido o nosso podcast.
>> [Diana] [Tom empolgado] Até a próxima, então!
>> [Joaquim] Até!
Música eletrônica.
Créditos
O áudio inserido neste conteúdo é da Free Sound.
Vistas ortogonais
Em um jogo, apresenta-se dois tipos de cartas.
Tipo 1: cartas com a representação de uma figura tridimensional.
Tipo 2: cartas com a representação de vistas dessa figura.
O objetivo do jogo é de que os jogadores associem as vistas ortogonais à figura tridimensional.
Observe os exemplos de cartas que compõe esse jogo:
Exemplo 1

Exemplo 2
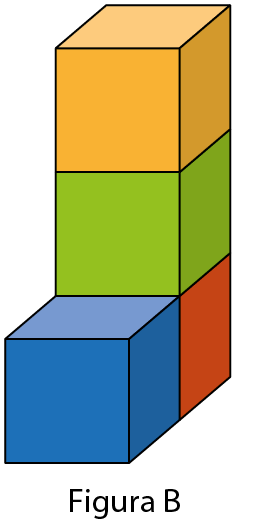
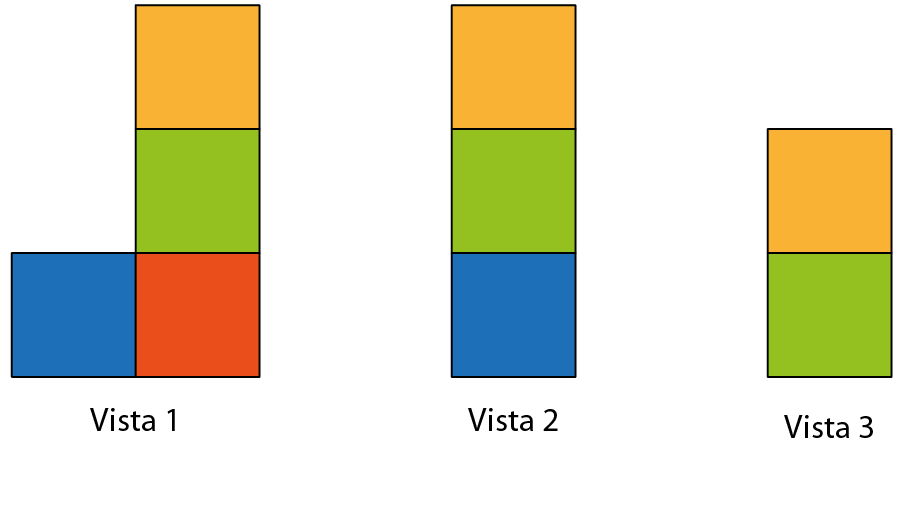
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO

Reúnam-se em grupos e façam o que se pede em cada item.
a) Que figuras geométricas planas podem ser associadas às vistas ortogonais de um objeto com:
• formato de cubo?
• formato de cilindro reto?
• formato de pirâmide quadrangular?
b) Escolham alguns objetos que lembram figuras geométricas planas e produzam cartas contendo vistas ortogonais desses objetos.
c) Elaborem as regras de um jogo em que esses objetos e as cartas sejam utilizados. Lembrem-se de definir um objetivo para o jogo e de explicar como jogar, dando exemplos.
d) Apresentem o jogo aos demais colegas da turma. Depois, joguem o jogo.
Glossário
- Lunação
- : período de tempo entre duas luas novas consecutivas.
- Voltar para o texto