ORIENTAÇÕES ESPECÍFICAS
Parte 1
O livro do 9º ano é composto de doze capítulos em que se desenvolvem as cinco Unidades Temáticas propostas pela Bê êne cê cê: Números, Álgebra, Geometria, Grandezas e medidas e Probabilidade e estatística, intercaladas e, sempre que possível, integradas, exploradas no corpo do texto explicativo e nas atividades.
A seguir, apresentamos sugestões de cronogramas para trabalhar com esses conteúdos em bimestre, trimestre e semestre com base nas organizações dos capítulos.
|
Capítulos |
Conteúdos |
Habilidades e competências da BNCC |
|||
|---|---|---|---|---|---|
|
1º semestre |
1º trimestre |
1º bimestre |
Capítulo 1 – Números reais |
• Números racionais, números irracionais e números reais; |
Habilidades: |
|
Capítulo 2 – Operações com números reais |
• Cálculo com potências de expoentes naturais e inteiros negativos; |
Habilidades: |
|||
|
Capítulo 3 – Grandezas proporcionais |
• Determinação da razão entre duas grandezas de espécies diferentes; |
Habilidades: |
|||
|
2º bimestre |
Capítulo 4 – Proporcionalidade em Geometria |
• Determinação da razão entre dois segmentos de reta; |
Habilidades: |
||
|
1º semestre |
2º trimestre |
2º bimestre |
Capítulo 5 – Semelhança |
• Resolução de problemas envolvendo relações de proporcionalidade, ampliação e redução de figuras; |
Habilidades: |
|
2º semestre |
Capítulo 6 – Um pouco mais sobre Estatística |
• Escolha do gráfico mais adequado para apresentar determinado conjunto de dados, destacando a análise de medidas estatísticas de tendência central; |
Habilidades: |
||
|
3º bimestre |
Capítulo 7 – Equações do |
• Resolução de problemas que envolvem relações de proporcionalidade que podem ser representados por uma equação polinomial do 2º grau; |
Habilidades: |
||
|
Capítulo 8 – Triângulo retângulo |
• Resolução de problemas que envolvam semelhança de triângulos e triângulos retângulos; |
Habilidades: |
|||
|
3º trimestre |
Capítulo 9 – Razões trigonométricas nos triângulos retângulos |
• Aplicação da semelhança de triângulos para obtenção das razões trigonométricas em um triângulo retângulo; |
Habilidades: |
|
2º semestre |
3º trimestre |
4º bimestre |
Capítulo 10 – Estudo das funções |
• Conceituação e reconhecimento de função como relação de dependência unívoca entre duas grandezas; |
Habilidades: |
|
Capítulo 11 – Circunferência, arcos e relações métricas |
• Reconhecimento e determinação do número irracional π; |
Habilidades: |
|||
|
Capítulo 12 – Polígonos regulares e áreas |
• Resolução de problemas envolvendo números reais em cálculo de medida de áreas e volume; |
Habilidades: |
Considerações iniciais
Cada capítulo aborda objetos de conhecimento, entendidos como conteúdos, conceitos, processos, com a intenção de desenvolver as habilidades relacionadas a eles. Esses conhecimentos são articulados, retomados e ampliados a fim de proporcionar sua apropriação pelos estudantes, considerando a aprendizagem um processo contínuo e integrado.
Os conteúdos matemáticos são desenvolvidos de modo que as habilidades, as Unidades Temáticas, as competências e outras áreas do conhecimento se articulem e se relacionem, e são tratados na perspectiva das aprendizagens dos anos anteriores e posteriores. Assim, no livro do 9º ano do Ensino Fundamental, levamos em conta os objetivos de aprendizagem para o 8º ano, conforme proposto na Bê êne cê cê, visando preparar os estudantes para se apropriar dos conhecimentos previstos para o Ensino Médio.
A seguir, são feitas orientações didáticas sobre cada capítulo e o que se pretende que os estudantes desenvolvam neles.
Capítulo 1 — Números reais
• Objetivos do capítulo e justificativas
• Retomar os números racionais e reconhecer a ampliação dos conjuntos numéricos.
• Identificar e determinar dízimas periódicas.
• Identificar números quadrados perfeitos.
• Calcular raiz quadrada exata de um número racional não negativo.
• Calcular raiz quadrada com aproximação decimal.
• Reconhecer números irracionais e números reais.
• Verificar experimentalmente o teorema de Pitágoras.
• Localizar números irracionais na reta real.
• Resolver e elaborar problemas de contagem envolvendo números reais.
• Calcular porcentagens sucessivas.
• Analisar dados de pesquisa amostral.
A ampliação do trabalho com conjuntos numéricos tem como objetivo fazer com que os estudantes desenvolvam o pensamento numérico, compreendendo as características dos números pertencentes a cada conjunto numérico. O trabalho com as outras Unidades Temáticas se faz necessário para que esse pensamento seja ampliado e aprofundado. Assim, contribui-se para o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2, 3 e 5.
O trabalho com o cálculo de raiz quadrada de números perfeitos e por aproximação contribui para a compreensão de diferentes conteúdos que serão estudados, como o cálculo da raiz quadrada de equações do 2º grau. O uso da calculadora é uma importante ferramenta para esse processo. dêsse modo, é favorecido o desenvolvimento das competências gerais 2, 4 e 5 e das competências específicas 2, 3 e 5.
Na seção Para Saber Mais, exploramos a sequência de Fibonacci e o número de ouro, que também é trabalhado na página de Abertura, relacionado a outras áreas de conhecimento. Assim, é favorecido o trabalho com as competências gerais 1 e 3 e as competências específicas 1 e 6.
Na seção Trabalhando a informação exploramos dados estatísticos sobre a violência contra a mulher. A escola, como centro de convívio e de formação cidadã, tem responsabilidade nas propostas de mudança, visando uma sociedade mais justa, democrática e inclusiva. Esse trabalho está alinhado e favorece o desenvolvimento das competências gerais 8, 9 e 10 e das competências específicas 4, 7 e 8.
• Habilidades trabalhadas no capítulo
(ê éfe zero nove ême ah zero um) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).
(ê éfe zero nove ême ah zero dois) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica.
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.
(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.
Neste capítulo, são desenvolvidos objetos de conhecimento da Unidade Temática Números. Nos conteúdos e nas atividades propostos, foram consideradas as aprendizagens dos anos anteriores, em especial do 8º ano (ê éfe zero oito ême ah zero três), relativas aos conjuntos numéricos estudados.
Esse é um momento de ampliação dos conhecimentos desenvolvidos sobre números para apresentar os números irracionais e o conjunto dos números reais, na perspectiva de que a continuidade dêsse processo leve os estudantes à apropriação da noção de número real. Para isso, apresentam-se conceitos e atividades que os conduzem nessa aprendizagem, favorecendo o trabalho com as habilidades (ê éfe zero nove ême ah zero dois) e (ê éfe zero nove ême ah zero quatro).
Ao ampliar os conhecimentos que eles já têm sobre os números, espera-se prepará-los para a apropriação de outros tipos de número e para a ampliação dos conjuntos numéricos que serão estudados no Ensino Médio, como os números complexos.
Ainda na Unidade Temática Números, desenvolvem-se atividades que envolvem cálculos com radiciação, favorecendo o desenvolvimento da habilidade (ê éfe zero nove ême ah zero três).
Promove-se a articulação com a Unidade Temática Geometria ao apresentar uma verificação experimental do teorema de Pitágoras e aplicando esse teorema na localização de números irracionais dados por raízes quadradas não exatas na reta real e na construção da espiral de Teodoro, Pitágoras ou ainstain, contribuindo para o desenvolvimento das habilidades (ê éfe zero nove ême ah zero um).
A conexão com a Unidade Temática Probabilidade e estatística ocorre em atividade na qual se explora as informações relacionadas a uma pesquisa estatística amostral com margem de erro, o que contribui para o desenvolvimento da habilidade (ê éfe zero nove ême ah dois um).
• Comentários e resoluções
Apresentamos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.
Exercícios propostos
1. a) É possível, 3 + 7 = 10; 10 é um número natural.
1. b) Não é possível realizar essa operação apenas com números naturais, pois 235 é maior que 5. dêssemodo, o resultado dessa operação é um número inteiro não natural.
1. c) É possível, 0 ‒ 0 = 0; 0 é um número natural.
1. d) É possível, pois 7 ‒ 0 = 7, que é um número natural.
1. e) Como 3 é menor que 7, a divisão de 3 por 7 é um número racional menor que um inteiro. Portanto, não é um número natural.
1. f) É possível, pois 3 · 7 = 21, que é um número natural.
1. g) A divisão de 8 por 3 não é exata. Portanto, o resultado não é um número natural.
1. h) Como 10 é maior que 7, a divisão de 7 por 10 é um número racional menor que um inteiro. Portanto, não é um número natural.
12. a) 9 : 66 = 0,13636reticências A calculadora pode ter arredondado o último algarismo visível para 4.
12. b)
9 dividido por 66, igual a, 9 sobre 66, igual a, fração de numerador 9 dividido por 3, e de denominador 66 dividido por 3, igual a, 3 sobre 22.13.
0,36 igual a, 36 sobre 100, igual a, fração de numerador 36 dividido por 4, e de denominador 100 dividido por 4, igual a, 9 sobre 2514. a) x = 3,444reticências ⇒ 10x = 34,444reticências
Assim:
10x ‒ x = 34,444... ‒ 3,444... ⇒ 9x = 31 ⇒
10x menos x, igual a, dízima periódica 34,444.. de período 4, menos, dízima periódica, 3,444... de período 4, implica, 9x igual a 31, implica, x igual a 31 nonos.14. b) x = ‒ 12,555reticências ⇒ 10x = ‒125,555reticências
Assim:
10x ‒ x = ‒125,555reticências ‒ (‒12,555reticências) ⇒
14. c) x = 0,454545reticências ⇒ 100x = 45,454545reticências
Assim:
100x ‒ x = 45,454545reticências ‒ 0,454545reticências ⇒ 99x = 45 ⇒
14. d) x = ‒0,31222reticências ⇒ 100x = ‒ 31,222reticências ⇒
⇒ .1000x = ‒312,222reticências
Assim:
⇒ .1000x ‒ 100x = ‒312,222reticências ‒ (‒31,222reticências) ⇒
15. a) x = 0,333reticências ⇒ 10x = 3,333reticências
Assim:
10x ‒ x = 3,333reticências ‒ 0,333reticências ⇒ 9x = 3 ⇒
Portanto, 0,333reticências =
um terço.
Como
0,2 igual a 2 sobre 10, temos:
0,2 + 0,333reticências
2 sobre 10, fim da fração, mais, um terço, igual a, fração de numerador 3 vezes 2, mais 10 vezes 1, e de denominador 30, igual a, fração de numerador 6 mais 10 e de denominador 30, igual a=
2 sobre 10, fim da fração, mais, um terço, igual a, fração de numerador 3 vezes 2, mais 10 vezes 1, e de denominador 30, igual a, fração de numerador 6 mais 10 e de denominador 30, igual a15. b) x = 0,277reticências ⇒ 10x = 2,777reticências
Assim:
10x ‒ x = 2,777reticências ‒ 0,277reticências ⇒ 9x = 2,5
Como
2,5 igual a 25 sobre 10, temos:
Portanto, 0,277reticências
5 sobre 18.
y = 2,333reticências ⇒ 10y = 23,333reticências
Assim:
10y ‒ y = 23,333reticências ‒ 2,333reticências ⇒ 9y = 21 ⇒
Portanto, 2,333reticências
igual a, 7 sobre 3. Logo:
0,277 + 2,333reticências =
15. c) x = 0,388reticências ⇒ 10x = 3,888reticências
Assim:
10x ‒ x = 3,888reticências ‒ 0,388reticências ⇒ 9x = 3,5
Como
3,5 igual a 35 sobre 10, temos:
Portanto, 0,388reticências
35 sobre 90.
y = 1,4555reticências ⇒ 100y = 145,555reticências ⇒
⇒ .1000y = .1455,555reticências
Assim:
.1000y ‒ 100y = .1455,555reticências ‒ 145,555reticências ⇒
Portanto, 1,4555reticências
igual a, 131 sobre 90. Logo:
0,388 + 1,4555reticências =
35, 90 avos, mais 131, 90 avos, igual a 166 sobre 90, igual a, fração de numerador 166 dividido por 2, e de denominador 90 dividido por 2, igual a, 83 sobre 4515. d) x = 1,888reticências ⇒ 10x = 18,888reticências
Assim:
10x ‒ x = 18,888reticências ‒ 1,888reticências ⇒ 9x = 17 ⇒
x igual a 17 sobre 9Portanto, 1,888reticências
igual a 17 sobre 9.
Assim:
17. Para cada item dêsse exercício há diversas respostas possíveis. Incentive os estudantes a compartilhar suas respostas e organize-as na lousa para que eles percebam as diferentes possibilidades.
18. a) Como Márcio retirou os números 6, 4 e 2, nessa ordem, o número formado é 6,42.
18. b) Como sobraram as bolas com os números 1, 3, 5 e 7, o maior número a ser formado é 7,53. E o menor número é 1,35.
20. a) A decomposição é 225 = 32 · 52; 225 é um quadrado perfeito, pois 225 = (3 · 5)2.

20. b) A decomposição é 360 = 23 · 32 · 5; então, 360 não é um quadrado perfeito.

20. c) A decomposição é 441 = 32 · 72; 441 é um quadrado perfeito, pois 441 = (3 · 7)2.

20. d) A decomposição é 480 = 25 · 3 · 5; então, 480 não é um quadrado perfeito.

20. e) A decomposição é 576 = 26 · 32; 576 é um quadrado perfeito, pois 576 = (23 · 3)2.

20. f) A decomposição é 784 = 24 · 72; 784 é um quadrado perfeito, pois 784 = (22 · 7)2.

21. Como 144 = 24 · 32 = (22 · 3)2 = 122; então, em cada linha do novo quadrado há 12 quadradinhos.

25. a)
raiz quadrada de 0,64, igual a, 0,8, pois:
0,82 = 0, 64
25. b)
raiz quadrada de 2 elevado a 10, fim do expoente, vezes, 3 elevado ao quadrado, fim da raiz= 25 · 3, pois:
(25 · 3)2 = (25)2 · 32 = 210 · 32
26. a) 256 = 28 = (24 )2 = 162; então,
raiz quadrada de 256 igual a 16.

26. b) 196 = 22 ·72 = (2 · 7)2 = 142; então,
raiz quadrada de 196 igual a 14.

26. c) 484 = 22 · 112 = (2 · 11)2 = 222; então,
raiz quadrada de 484 igual a 22.

26. d) 729 = 36 = (33 )2 = 272; então,
raiz quadrada de 729 igual a 27.

26. e) .1600 = 26 · 52 = (23)2 · 52 = (23 · 5)2 = 402; então,
raiz quadrada de 1.600 igual a 40= 40.
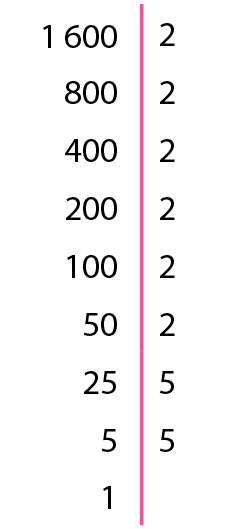
26. f) .1024 = 210 = (25)2 = 322; então,
raiz quadrada de 1.024 igual a 32.
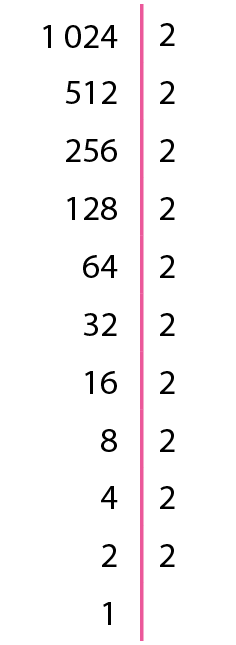
28. Seja h a medida da altura dêsse sólido. Então, a medida da área lateral total é dada por: 4 · (a · h) = 4ah = 162.
A medida da área de todas as faces é dada por:
2 · (a · a) + 4ah = 2a2 + 4ah = 202,5
Assim, para determinar a medida a, vamos construir um sistema de equações.
Substituindo h por
162 sobre 4ana segunda equação, temos:
Como 81 = 92 e 4 = 22, então:
a elevado ao quadrado, igual a, 81 sobre 4, igual a, fração de numerador 9 elevado ao quadrado, e de denominador 2 elevado ao quadrado, implica, a igual a, 9 sobre 2, igual a, 4,5Portanto, a medida do lado da base é 4,5 cm.
Outra maneira de resolver é considerar que a diferença entre a medida da área total e a medida da área lateral é a medida da área das bases (superior e inferior), ou seja, 2 · (a2 ) = 202,5 ‒ 162. Portanto:
29. a) Como 25 = 52 e 576 = 26 · 32 = (23 · 3)2 = 242; então:
raiz quadrada de 25 sobre 576, igual a, raiz quadrada da fração de numerador 5 elevado ao quadrado, e de denominador 24 elevado ao quadrado, igual a, 5 sobre 24
29. b) Como 0,01 =
0,01 igual a 1 sobre 100e 100 = 22 · 52 = (2 · 5)2 = 102; então:
raiz quadrada de 0,01, igual a, raiz quadrada de 1 sobre 100, igual a, raiz quadrada da fração de numerador 1 elevado ao quadrado, e de denominador 10 elevado ao quadrado, igual a, 1 sobre 10, igual a, 0,1.
29. c) Como 64 = 26 = (23 )2 = 82 e .1225 = 52 · 72 = (5 · 7)2 = 352;
então:
Raiz quadrada de 64 sobre 1225 é igual a raiz quadrada de oito ao quadrado sobre 35 ao quadrado é igual a 8 sobre 35
29. d) Como
19,36 igual a 1.936 sobre 100e .1936 = 24 · 112 = (22)2 · 112 = = (4 · 11)2 = 442; então:
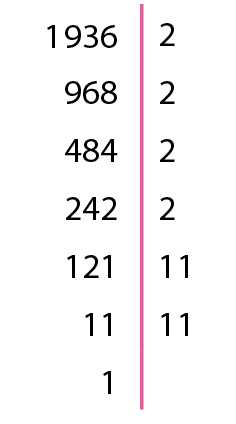
30. A área total dos retângulos de papel vermelho mede .1200 centímetros quadrados, pois 2 · (20 · 30) = .1200. Então, a área total da pipa mede .6400 centímetros quadrados, pois:
.2500 + 3 · 900 + .1200 = .2500 + .2700 + .1200 = .6400 Como .6400 = 28 · 52 = (24)2 · 52 = (24 · 5)2, então o lado da pipa mede 80 cm.
31. a) A medida da área de cada lajota é .1200 centímetros quadrados (40 · 30 = .1200). Como são 10.oitocentas lajotas, a área total que elas ocupam, que corresponde à área do salão, tem medida .1296 métros quadrados.
.10800 · .1200 = ..12960000
..12960000 centímetros quadrados = (..12960000 : .10000) métros quadrados =.1296 métros quadrados
31. b) Como é um salão quadrado de área medindo .1296 métros quadrados, seu lado mede 36 m.
33. O número 640 está compreendido entre os números quadrados perfeitos 625 e 676.
625 < 640 < 676
Assim, para obter o número quadrado perfeito 625, devemos subtrair 15 de 640 (640 ‒ 15 = 625).
dêsse modo,
Raiz quadrada de 640deve estar compreendida entre
Raiz quadrada de 625 e raiz quadrada de 676..
Como
raiz quadrada de 625 igual a 25e
raiz quadrada de 676 igual a 26, temos:
Portanto, 25 é a raiz quadrada aproximada por falta, a menos de uma unidade, do número 640.
34. Alguns anos quadrados perfeitos foram 1600 (402 = .1600) e 1849 (432 =.1849). O século vinte compreende os anos entre 1901 e 2000, sendo o único quadrado perfeito nesse intervalo o número 1936 (442 = .1936). O século vinte e um compreende os anos entre 2001 e 2100, assim, o único número quadrado perfeito nesse intervalo é .2025(452 = .2025). O próximo número quadrado perfeito é .2116 (462 = .2116). O ano 2116 estará no século vinte e dois.
36. O número 3 está compreendido entre os números quadrados perfeitos 1 e 4 (1 < 3 < 4).
dêsse modo,
raiz quadrada de 3deve estar compreendida entre
raiz quadrada de 1e
raiz quadrada de 4.
Como
raiz quadrada de 1 igual a 1e
raiz quadrada de 4 igual a 2, temos:
1 menor que raiz quadrada de 3, menor que 2Como 1,72 = 2,89 e 1,82 = 3,24; então:
2,89 < 3 < 3,24 ⇒
raiz quadrada de 2,89 menor que raiz quadrada de 3, menor que raiz quadrada de 3,24, implica, 1,7 menor que, raiz quadrada de 3, menor que, 1,8Portanto, 1,7 pode ser considerado uma raiz quadrada aproximada do número 3.
37. Como 3,872 = 14,9769 e 3,882 = 15,0544; então:
14,9769 < 15 < 15,0544 ⇒
raiz quadrada de 14,9769, menor que, raiz quadrada de 15, menor que, raiz quadrada de 15,0544,⇒
implica, raiz quadrada de 3,87 elevado ao quadrado, menor que, raiz quadrada de 15, menor que, raiz quadrada de 3,88 elevado ao quadrado, implica, 3,87, menor que, raiz quadrada de 15, menor que, 3,88Portanto, 3,87 se aproxima mais de
Raiz quadrada de 15.
38. Como 162 = 256 e 172 = 289, então:
Para uma aproximação mais precisa, um número com uma casa decimal, vamos começar testando 16,2.
(16,2)2 = 262,44 < 265
Então, vamos testar o próximo número, 16,3.
(16,3)2 = 265,69 > 265. Assim, a raiz quadrada aproximada, com uma casa decimal, do número 265 é 16,2 (
Raiz quadrada de 265, aproximadamente igual, 16 vírgula 2).
39. a)
Raiz quadrada de 572, aproximadamente igual a 23 vírgula 9Como 232 = 529 e 242 = 576, então:
Para uma aproximação mais precisa, um número com uma casa decimal, vamos começar testando 23,9.
(23,9)2 = 571,21 < 572
Então: 571,21 < 572 < 576 ⇒ 23,9 <
Raiz quadrada de 572< 24
39. b)
raiz quadrada de 28,19 aproximadamente igual a 5,3≃ 5,3
Como 52 = 25 e 62 = 36, então:
Para uma aproximação que seja um número com uma casa decimal, vamos começar testando 5,3.
(5,3)2 = 28, 09 < 28,19
Então, vamos testar o próximo número, 5,4.
(5,4)² = 29,16 > 28,19
Assim, a raiz quadrada aproximada, com uma casa decimal, do número 28,19 é 5,3 (
Raiz quadrada de 28 vírgula 19≃ 5,3).
39. c)
raiz quadrada de 42,55 aproximadamente igual a 6,5Como 62 = 36 e 72 = 49, então: 36 < 42,55 < 49 ⇒
6 menor que raiz quadrada de 42 vírgula 55, menor que 7Para uma aproximação que seja um número com uma casa decimal, vamos começar testando 6,5.
(6,5)2 = 42,25 < 42,55
Então, vamos testar o próximo número, 6,6.
(6,6)2 = 43,56 > 42,55
Assim, a raiz quadrada aproximada, com uma casa decimal, do número 42,55 é 6,5 (
abre parênteses, raiz quadrada de 42,55, aproximadamente igual a, 6,5, fecha parênteses.).
39. d)
raiz quadrada de 12,6, aproximadamente igual a 3,5Como 32 = 9 e 42 = 16, então:
Para uma aproximação que seja um número com uma casa decimal, vamos começar testando 3,5.
(3,5)2 = 12,25 < 12,6
Então, vamos testar o próximo número, 3,6.
(3,6)² = 12,96 > 12,6
Assim, a raiz quadrada aproximada, com uma casa decimal, do número 12,6 é 3,5 (
Raiz quadrada de 12 vírgula 6, aproximadamente igual a 3 vírgula 5).
40. a)
raiz quadrada de 88, aproximadamente igual a 9,3840. b)
raiz quadrada de 8.800, aproximadamente igual a 93,8140. c)
raiz quadrada de 6.000.000, aproximadamente igual a, 2.449,9940. d)
raiz quadrada de 6, aproximadamente igual a, 2,4540. e)
raiz quadrada de 1.000, aproximadamente igual a, 31,6240. f)
raiz quadrada de 100.000, aproximadamente igual a, 316,2341. a) Como 202 = 400 e 212 = 441, então 400 < 410 < 441. Logo,
20, menor que, raiz quadrada de 410, menor que, 21.
Como queremos encontrar a raiz quadrada aproximada com duas casas decimais, vamos continuar testando 20,2.
(20,2)2 = 408,04 < 410
Então, vamos testar o próximo número, 20,3.
(20,3)2 = 412,09 > 410
Com duas casas decimais, agora vamos testar 20,25.
(20,25)2 = 410,0625 > 410
Então, vamos testar o número 20,24.
(20,24)2 = 409,6576 < 410
Assim, a raiz quadrada aproximada do número 410, com duas casas decimais, é 20,24.
41. b) Como 412 = .1681 e 422 = .1764, então:
.1681 < .1715 < .1764
Logo,
41 menor que, raiz quadrada de 1.715, menor que 42.
Como queremos encontrar a raiz quadrada aproximada com duas casas decimais, vamos continuar testando 41,4.
(41,4)2 = .1713,96 < .1715
Então, vamos testar o próximo número, 41,5.
(41,5)2 = .1722,25 > .1715
Com duas casas decimais, agora vamos testar 41,41.
(41,41)2 = .1714,7881 < .1715
Então, vamos testar o número 41,42.
(41,42)2 = .1715,6164 > .1715
Assim, a raiz quadrada aproximada do número .1715, com duas casas decimais, é 41,41.
41. c) Como 442 = .1936 e 452 = .2025, então:
.1936 < .1999 < .2025
Logo,
44 menor que, raiz quadrada de 1.999, menor que, 45..
Como queremos encontrar a raiz quadrada aproximada com duas casas decimais, vamos continuar testando 44,7.
(44,7)2 = .1998,09 < .1999
Então, vamos testar o próximo número, 44,8.
(44,8)2 = .2007,04 > .1999
Com duas casas decimais, agora vamos testar 44,71.
(44,71)2 = .1998,9841 < .1999
Então, vamos testar o número 44,72.
(44,72)2 = .1999,8784 > .1999
Assim, a raiz quadrada aproximada do número .1999, com duas casas decimais, é 44,71.
41. d) Como 592 = .3481 e 602 = .3600, então:
.3481 < .3500 < .3600
Logo,
59 menor que, raiz quadrada de 3.500, menor que, 60.
Como queremos encontrar a raiz quadrada aproximada com duas casas decimais, vamos continuar testando 59,1.
(59,1)2 = .3492,81 < .3500
Então, vamos testar o próximo número, 59,2.
(59,2)2 = .3504,64 > .3500
Com duas casas decimais, agora vamos testar 59,16.
(59,16)2 = .3499,9056 < .3500
Então, vamos testar o número 59,17.
(59,17)2 = .3501,0889 > .3500
Assim, a raiz quadrada aproximada do número .3500, com duas casas decimais, é 59,16.
42. a)
raiz quadrada de 410, aproximadamente igual, a 20,2484567342. b)
raiz quadrada de 1.715, aproximadamente igual a, 41,4125584842. c)
raiz quadrada de 1.999, aproximadamente igual a, 44,7101778142. d)
raiz quadrada de 3.500, aproximadamente igual a, 59,1607978343. Como o triângulo da figura tem catetos medindo 1, sua hipotenusa mede
a igual a raiz quadrada de 2, pois:
Como m está à esquerda da origem, então:
m igual a menos a, igual a, menos, raiz quadrada de 2.45. a) As medidas dos catetos são 1 e 4; então, pelo teorema de Pitágoras:
x2 = 12 + 42 ⇒ x2 = 1 + 16 = 17 ⇒
x igual a raiz quadrada de 1745. b) Como não existe nenhum número racional x tal que x2 = 17, então
raiz quadrada de 17é um número irracional.
45. c) Como
raiz quadrada de 17é um número irracional, ele tem infinitas casas decimais em sua representação decimal; porém, usando uma calculadora, aparecerá no visor um número limitado de casas decimais, conforme o espaço disponível. Representando esse número na fórma decimal aproximada, com duas casas decimais, temos 4,12 (
abre parênteses, raiz quadrada de 17, aproximadamente igual a, 4,12, fecha parênteses.).
46. O triângulo ó á bê é retângulo com catetos medindo 3 e 1; portanto, sua hipotenusa
segmento A Omede h.
h2 = 32 + 12 ⇒ h2 = 9 + 1 = 10 ⇒
h é igual a raiz quadrada de 1047. a) O lado de medida x corresponde à hipotenusa de um triângulo retângulo com catetos medindo 2 métros e 3 métros. Assim, pelo teorema de Pitágoras:
x2 = 22 + 32 ⇒ x2 = 4 + 9 = 13 ⇒
x é igual a raiz quadrada de 13Portanto, a medida do comprimento da rampa do escorregador é
raiz quadrada de 13métros.
47. b) Utilizando uma calculadora ou um método de aproximação, é possível obter
Raiz quadrada de 13≃ 3,61, ou
raiz quadrada de 13≃ 3,6. Portanto:
3,61 métros = (3,61 · 100) centímetros = 361 centímetros
Ou 3,6 m = 360 centímetros.
Assim, a medida do comprimento do escorregador pode ser aproximada para 361 centímetros ou para 360 centímetros.
Pense mais um poucoreticências
Página 13
a)
a igual a fração de numerador 3 mais 7 e denominador 2, igual a, 10 sobre 2, igual a 5.b)
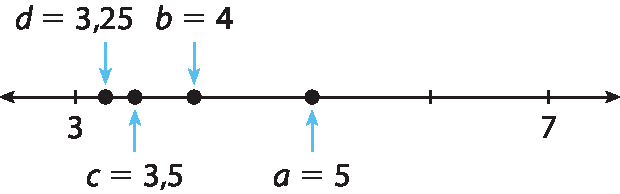
c) Sim, pois, 3 < 4 < 5 < 7; 3,5 está entre 3 e 4; 3,25 está entre 3 e 3,5.
d) Sim, observe os primeiros casos:
Espera-se que os estudantes percebam que é possível continuar essa sequência de divisão infinitamente.
e) Espera-se que os estudantes respondam que existem infinitos números racionais entre 3 e 7, assim como existem também infinitos números racionais entre dois números racionais distintos quaisquer.
Página 17
a)
1 mais 1 sobre 2, igual a, fração de numerador 2 mais 1, e de denominador 2, igual a, 3 sobre 2b)
1 mais, fração de numerador 1, e de denominador 1 mais 1 sobre 2, igual a, 1 mais, fração de numerador 1, e de denominador 3 sobre 2, igual a, 1 mais 2 terços, igual a, fração de numerador 3 mais 2, e de denominador 3, igual a, 5 terços.c)
1 mais, fração de numerador 1 e de denominador 1 mais, fração de numerador 1 e de denominador 1 mais 1 sobre 2, igual a, 1 mais fração de numerador 1, e de denominador 5 sobre 3, igual a, 1 mais 3 quintos, igual a, fração de numerador 5 mais 3, e de denominador 5, igual a, 8 quintosSeguindo o padrão, a quarta expressão é:
Para saber mais
Página 18
1. 1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13
Ao efetuar essas adições, espera-se que os estudantes percebam que a soma de dois números consecutivos é igual ao próximo número da sequência.
2. 8 + 13 = 21; 13 + 21 = 34; 21 + 34 = 55; 34 + 55 = 89
Os próximos números da sequência são 21, 34, 55 e 89.
3.
1 sobre 1, aproximadamente igual a 1,000; 2 sobre 1, aproximadamente igual a 2,000; 3 sobre 2, aproximadamente igual a, 1,500; 5 sobre 3, aproximadamente igual a, 1,667; 8 sobre 5, aproximadamente igual a, 1,600; 13 sobre 8, aproximadamente igual a, 1,625; 21 sobre 13, aproximadamente igual a, 1,615; 34 sobre 21, aproximadamente igual a, 1,619; 55 sobre 34, aproximadamente igual a, 1,618; 89 sobre 55, aproximadamente igual a, dizima periódica 1,618 de período 18.;
Espera-se que os estudantes percebam que essas razões se aproximam do número áureo.
Páginas 34 e 35
1. Com a construção da espiral é possível perceber que, de fato,
raiz quadrada de 9 igual a 3..
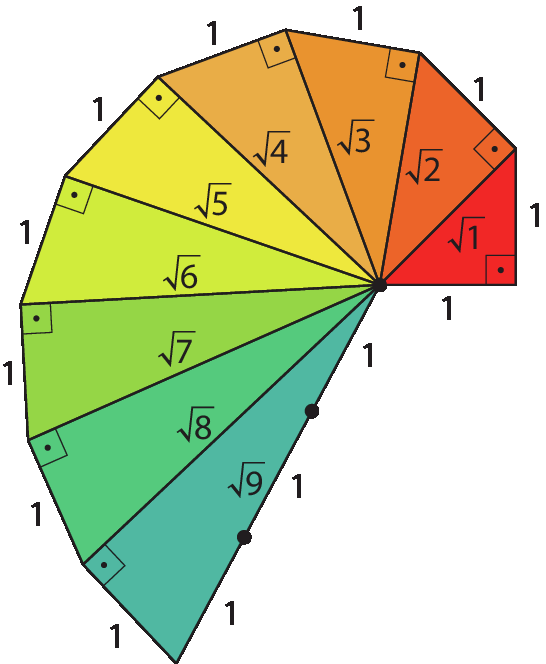
2. Espera-se que os estudantes transportem as medidas encontradas na atividade 1 para localizar na reta numérica os números pedidos.
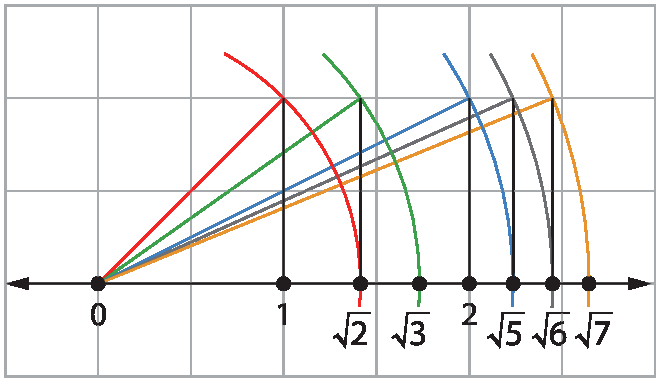
Exercícios complementares
1. a) Falsa, ‒1 não é natural.
1. b) Falsa,
um meionão é um número inteiro.
1. c) Verdadeira.
1. d) Verdadeira.
2.
x igual a dízima periódica 1,4 de período 4, implica, 10x igual a, dízima periódica 14, 4 de período 4Assim:
10x menos x, igual a, dízima periódica 14,4 de período 4, menos dízima periódica 1,4 de período 4, implica
Assim:
10 y menos y, igual a, dízima periódica 7,7 de período 7, menos, dízima periódica 0,7 de período 7, implica, 9y igual a 7, implica y igual 7 nonosEntão:
Portanto:
Então, A : B = 1.
3. a) 2,555reticências + 0, 222reticências = 2 + (0,555reticências + 0,222reticências) = = 2 + 0,777reticências = 2,777reticências
dízima periódica 2,7 de período 73. b) Primeiro vamos determinar as frações equivalentes às dízimas periódicas 2,555reticências e 0,222reticências .
x = 2,555reticências ⇒ 10x = 25,555reticências
Assim:
10x ‒ x = 25,555reticências ‒ 2,555reticências ⇒ 9x = 23 ⇒ x =
fração 23 sobre 9y = 0,222reticências ⇒ 10y = 2,222reticências
Assim:
10y ‒ y = 2,222reticências ‒ 0,222reticências ⇒
9y igual a 2, implica, y igual a 2 sobre 9.Portanto:
(2,555reticências) · (0,222reticências) =
23 nonos, vezes, 2 nonos, igual a, fração de numerador 23 vezes 2, e de denominador 9 vezes 9, igual a 46 sobre 814. Como (2,2)2 = 2,2 · 2,2 = 4,84; então:
5. Como x = 28 · 52 = (24 )2 · 52 = (24 · 5)2; então:
= 24 · 5 = 16 · 5 = 80
6. 25 · 34 · 53 · 7 = 25 · 2 · 17 · 53 · 7 = 26 · 17 · 52 · 5 · 7 = = (23)2 · 52 · 5 · 7 · 17 =
abre parênteses, 2 elevado ao cubo, vezes 5 elevado ao quadrado, vezes 7, vezes 17, fecha parênteses, elevado ao quadrado, é quadrado perfeito
Então, multiplicar por 595, ou seja, 5 · 7 · 17, é o menor número possível que, multiplicado por 25 · 34 · 53 · 7, resulta em um número natural que é quadrado perfeito.
(23 · 5)2 · (5 · 7 · 17) · (5 · 7 · 17) = (23 · 5)2 · (5 · 7 · 17)2 = = (23 · 5 · 5 · 7 · 17)2 =
abre parênteses, 2 elevado ao cubo, vezes 5, vezes 5, vezes 7, vezes 17, fecha parênteses, elevado ao quadrado, é quadrado perfeito7. A · B = (33 · 5 · 7) · (3 · 5 · 7) = 34 · 52 · 72 ⇒
= 32 · 5 · 7 = 9 · 5 · 7 = 315
8. Como a medida da área é 231,04 métros quadrados e o terreno tem formato de um quadrado, seu lado mede 15,2 métros.
A = ℓ2 = 231,04 ⇒
4 · ℓ = 4 · 15,2 = 60,8
Então, a medida do perímetro é 60,8 m.
9. x = 5,888reticências ⇒ 10x = 58,888reticências
Assim:
10x ‒ x = 58,888reticências ‒ 5,888reticências ⇒ 9x = 53 ⇒
x igual a 53 sobre 9.Portanto:
Considerando as opções do enunciado, temos:
reticências
Alternativa b.
10. a) Pelo teorema de Pitágoras, sendo h a medida da hipotenusa:
h2 = 122 + 52 ⇒ h2 = 144 + 25 = 169 ⇒ h =
Raiz quadrada de 169= 13 A hipotenusa mede 13 centímetros.
10. b) A medida é um número natural; portanto, também é racional.
11. a) Pelo teorema de Pitágoras, se h é a medida da hipotenusa do triângulo, temos:
h2 = 62 + 22 ⇒ h2 = 36 + 4 = 40 ⇒ h =
Raiz quadrada de 40A hipotenusa mede
raiz quadrada de 40centímetros.
11. b) É irracional, pois não existe nenhum número racional x, tal que x2 = 40.
11. c) Como 62 = 36 e 72 = 49 , então:
36 < 40 < 49 ⇒ 6 <
Raiz quadrada de 40< 7
Para uma aproximação com uma casa decimal, considerando que 6,32 = 39,69 e 6,42 = 40,96, então:
39,69 < 40 < 40,96
Portanto,
Raiz quadrada de 40≃ 6,3.
A medida da hipotenusa é aproximadamente 6,3 centímetros.
12. O valor de a é o mesmo da medida da hipotenusa do triângulo, com catetos de medidas 5 e 1. Portanto:
a2 = 52 + 12 ⇒ a2 = 25 + 1 = 26 ⇒ a =
Raiz quadrada de 2613. Como 29 = 25 + 4 ⇒
abre parêntese, raiz quadrada de 29, fecha parêntese, elevado ao quadrado= 52 + 22, então
Raiz quadrada de 29é a medida da hipotenusa de um triângulo retângulo com catetos medindo 5 e 2.
Como 5 = 1 + 4 ⇒
Abre parêntese, raiz quadrada de 5, fecha parêntese, elevado ao quadrado= 12 + 22, então
Raiz quadrada de 5é a medida da hipotenusa de um triângulo retângulo com catetos medindo 1 e 2.
Transpondo as medidas das hipotenusas para a reta numérica, temos:
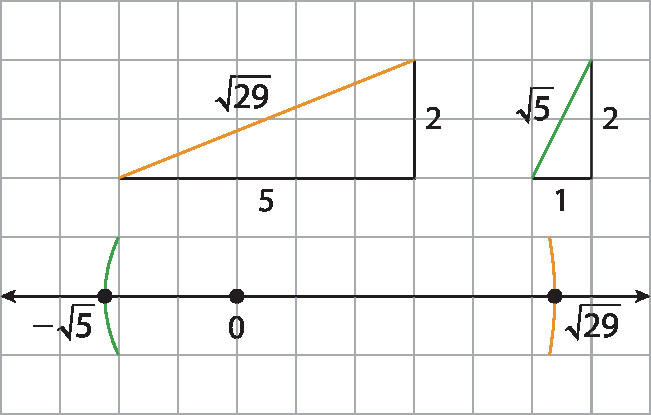
14. A altura do poste é um cateto de um triângulo retângulo com o outro cateto medindo 3 métros e a hipotenusa medindo 6 métros. Portanto, se c é a medida do cateto desconhecido, temos:
c2 + 32 = 62 ⇒ c2 + 9 = 36 ⇒ c2 = 36 ‒ 9 = 27 ⇒
c igual a raiz quadrada de 27Como 52 = 25 e 62 = 36, então: 25 < 27 < 36 ⇒
5 menor que raiz quadrada de 27 menor que 6< 6
Como (5,1)2 = 26,01 e (5,2)2 = 27,04, temos:
26,01 < 27 < 27,04 ⇒5,1 <
Raiz quadrada de 27< 5,2
Utilizando uma calculadora, verificamos que:
Verificando
1. a) 350 : 8 = 43,75; 43,75 não é um número natural, pois tem parte decimal. Então, 350 : 8 + 34 também não tem como resultado um número natural
(350 : 8 + 34 = 77,75).
1. b) 352 : 8 menos 90 : 2 = 44 ‒ 45 = ‒ 1
‒1 não é um número natural.
1. c) 456 : 5 + 88 : 10 = 91,2 + 8,8 = 100
100 é um número natural; portanto, esta é a alternativa correta.
1. d) 456 : 6 menos 88 = 57 ‒ 88 = ‒ 31
‒31 não é um número natural.
2.
x igual a dízima periódica 15,623 de período 623, implica, 1.000 x igual a, dízima periódica 15.623,623 de período 623. Assim: 1.000 x menos x, igual a, dízima periódica 15.623,623 de período 623 menos dízima periódica 15,623 de período 623, implica, 999x igual a, 15.608, implica, x igual a 15.608 sobre 999.Assim:
Alternativa b.
3. a) Incorreta. menos3, por exemplo, é um número inteiro, mas não é natural.
3. b) Correta. Se um número é racional, ele não pode ser irracional, e vice-versa.
3. c) Incorreta. Todo número inteiro é racional
abre parêntese, x igual a x sobre 1, fecha parênteses..
3. d) Incorreta.
raiz quadrada de 2, por exemplo, é um número real, mas não é racional.
4. a) .1764 = 22 · 32 · 72 = (2 · 3 · 7)2 (quadrado perfeito).
4. b) .1225 = 52 · 72 = (5 · 7)2 (quadrado perfeito).
4. c) 882 = 2 · 32 · 72 = (3 · 7)2 · 2 (não é quadrado perfeito).
4. d) .1296 = 24 · 34 = (22 · 32)2 (quadrado perfeito).
5. Vamos determinar um valor com uma casa decimal para
raiz quadrada de 42.
Como 36 = 62 e 49 = 72, então:
36 < 42 < 49 ⇒ 6 <
Raiz quadrada de 42< 7
Como 40,96 = 6,42 e 42,25 = 6,52, então:
40,96 < 42 < 42,25 ⇒ 6,4 <
Raiz quadrada de 42< 6,5
Alternativa a.
6. Como 342 = .1156 e 352 = .1225, então:
.1156 < .1185 < .1225 ⇒
Alternativa b.
7. Como a área mede 18,49 métros quadrados, o lado do quadrado mede 4,3 métros, pois
raiz quadrada de 18,49. Assim, o perímetro mede 17,2 métros, pois 4,3 · 4 = 17,2.
Alternativa b.
8. A diagonal do retângulo é equivalente à hipotenusa de um triângulo cujos catetos são a base e a altura do retângulo. Assim, pelo teorema de Pitágoras, sendo H a medida da diagonal, temos:
H2 = 42 + 62 ⇒ H2 = 16 + 36 = 52 ⇒
H igual a raiz quadrada de 52Portanto, a diagonal dêsse retângulo mede
raiz quadrada de 52, fim da raiz, centímetroscentímetros. O número
raiz quadrada de 52, fim da raiz, centímetrosé irracional.
Alternativa d.
9. No triângulo retângulo:
= x2 + 12 ⇒ 23 = x2 + 1 ⇒ x2 = 23 menos 1 = 22 ⇒ x =
Raiz quadrada de 22Alternativa c.
10. Pelo teorema de Pitágoras, a medida h da hipotenusa é tal que:
h2 = 82 + 62 ⇒ h2 = 64 + 36 = 100 ⇒
h igual a raiz quadrada de 100, igual a 10Portanto, a hipotenusa mede 10 centímetros.
Alternativa b.
Capítulo 2 — Operações com números reais
• Objetivos do capítulo e justificativas
• Compreender o surgimento dos números irracionais, reconhecê-los e utilizá-los na resolução de problemas.
• Representar geometricamente números irracionais usando régua e compasso.
• Explorar potências de 10 e a notação científica.
• Reconhecer e empregar unidades usadas para expressar medidas muito grandes ou muito pequenas.
• Empregar unidades de medida utilizadas na informática.
• Resolver problemas envolvendo cálculos com potências de expoentes inteiros.
• Determinar potências com expoente fracionário.
• Efetuar cálculos com números reais.
• Estudar e aplicar as propriedades de radicais.
• Simplificar radicais.
• Efetuar operações envolvendo radicais.
• Racionalizar expressões contendo radicais no denominador.
• Resolver e elaborar problemas com números reais envolvendo diferentes operações.
• Construir e interpretar gráfico de linha.
Neste capítulo, ampliamos o trabalho com números reais com o foco nas operações de potenciação e radiciação. Inicialmente, exploramos as potências de 10 e a notação científica, com situações que envolvem medidas muito grandes ou muito pequenas, além das unidades de medida relacionadas à informática. A compreensão do conceito de número irracional é favorecida por meio de situações variadas que ampliam o conhecimento já construído sobre números irracionais e, assim, consolidam a aprendizagem dos números reais. Assim, contribui-se para a compreensão numérica e o letramento matemático dos estudantes, além do desenvolvimento das competências gerais 1, 2 e 4 e das competências específicas 1, 2, 3 e 6.
O trabalho com as operações de potenciação e radiciação mobilizam aspectos das competências específicas 2, 3 e 5, pois contribuem para o desenvolvimento de ferramentas matemáticas na resolução de problemas das diferentes Unidades Temáticas.
Na seção Trabalhando a informação os estudantes devem analisar dados em um gráfico de linhas, o que contribui para o desenvolvimento das competências gerais 2 e 4 e das competências específicas 4, 6 e 7.
O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diferentes atividades a serem realizadas em grupos, pois possibilitam aos estudantes exercitar habilidades socioemocionais ao trabalharem com a diversidade de aprendizagem entre os colegas, interagindo de fórma cooperativa.
• Habilidades trabalhadas no capítulo
(ê éfe zero nove ême ah zero um) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).
(ê éfe zero nove ême ah zero dois) Reconhecer um número irracional como um número real cuja representação decimal é infinita e não periódica, e estimar a localização de alguns deles na reta numérica.
(ê éfe zero nove ême ah zero três) Efetuar cálculos com números reais, inclusive potências com expoentes fracionários.
(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.