Página cinquenta e cinco

Parte 4

• Suíça:

\frac{0, 957}{0, 955} = \frac{10}{s} \Rightarrow 0, 957 s = 9, 55 \Rightarrow s = \frac{9, 55}{0, 957} ≃ 9, 98

;

• Irlanda:

\frac{0, 957}{0, 955} = \frac{10}{i} \Rightarrow 0, 957 s = 9, 55 \Rightarrow s = \frac{9, 55}{0, 957} ≃ 9, 98

;

• Chade:

\frac{0, 957}{0, 398} = \frac{10}{c} \Rightarrow 0, 957 s = 3, 98 \Rightarrow s = \frac{3, 98}{0, 957} ≃ 4, 16

;

• República Centro-Africana:

\frac{0, 957}{0, 397} = \frac{10}{s}

\Rightarrow 0, 957 s = 3, 97 \Rightarrow s = \frac{3, 97}{0, 957} ≃ 4, 15

;

• Níger:

\frac{0, 957}{0, 394} = \frac{10}{s} \Rightarrow 0, 957 s = 3, 94 \Rightarrow s = \frac{3, 94}{0, 957} ≃ 4, 12

A seguir, um exemplo de gráfico.

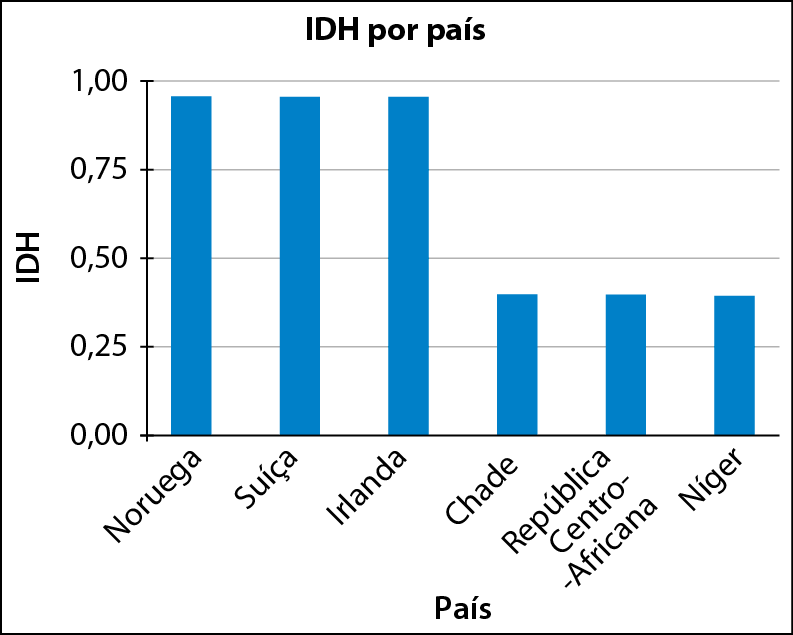
Gráfico de barras verticais. Título: IDH por país. Eixo horizontal: país. Eixo vertical , IDH com escala de 0,00 a 1,00. Os dados são: Noruega: 0,957. Suíça: 0,955. Irlanda: 0,955. Chade: 0,398. República Centro‑Africana: 0,397. Níger: 0,394.

Dados obtidos em: HUMAN DEVELOPMENT REPORTS. HDR 2020 Tables and Dashboards. Disponível em: https://oeds.link/10rJjS. Acesso em: 30 junho 2022.

Exercícios complementares

1. a)

Velocidade média = \frac{225 km}{2,5 h} = 90 k m / h

1. b)

\frac{90 km}{h} = \frac{270 km}{t} \Rightarrow t = 3 h

1. c)

\frac{259}{14} = 18, 5

Portanto, 18,5 quilômetros por litro.

2. Como a densidade demográfica é calculada por

\frac{número de habitantes}{medida da área} = \frac{27 000 \cdot 10^{3}}{844 453} ≃

≃ 0,03197 · 103 = 31,97 ≃ 32

Portanto, aproximadamente 32 habitantes por quilômetro quadrado.

Número de frangos	Quantidade de ração (kg)
1.200	90
2.000	x

As grandezas são diretamente proporcionais, assim:

\frac{1 200}{2 000} = \frac{90}{x}

⇒ .1200x = .180000 ⇒ 12x = .1800 ⇒ x = 150

Portanto, 150 quilogramas.

Área (m²)	Tempo (h)
5.100	6
11.900	x

As grandezas área e tempo são diretamente proporcionais, assim:

\frac{5 100}{11 900} = \frac{6}{x} \Rightarrow 5 100 x = 71 400 \Rightarrow x = \frac{71 400}{5 100} = 14

Portanto, são 14 horas.

Tempo de trabalho por dia (h)	Quantidade de trabalhadores	Tempo (dias)
8	3	15
9	2	x

As grandezas quantidade de trabalhadores e tempo de trabalho por dia são inversamente proporcionais à quantidade de dias necessários para realizar o mesmo serviço (meio muro), assim:

\frac{15}{x} = \frac{2}{3} \cdot \frac{9}{8} \Rightarrow \frac{15}{x} = \frac{18}{24}

⇒ 18x = 360 ⇒ x = 20

Portanto, o muro foi construído em 35 dias (20 + 15 = 35).

Quantidade de latinhas	Tempo (h)
1	3
x	24

As grandezas são diretamente proporcionais, então:

\frac{1}{x} = \frac{3}{24} \Rightarrow 3 x = 24 \Rightarrow x = \frac{24}{3} \Rightarrow x = 8

Portanto, 8 latinhas.

Massa de papel (kg)	Quantidade de livros	Quantidade de páginas
6.510	5.000	280
x	4.000	240

As grandezas são diretamente proporcionais, assim:

\frac{6 510}{x} = \frac{5 000}{4 000} \cdot \frac{280}{240} \Rightarrow \frac{6 510}{x} = \frac{1 400 000}{960 000} \Rightarrow

⇒ .1400x = ..6249600 ⇒ x =

\frac{62 496}{14}

= .4464

Portanto, .4464 quilogramas de papel.

Página cinquenta e seis

8. Chamando as idades do pai de x, do 1º filho de y e do 2º filho de z. Então, pela proporção,

\frac{x}{27} = \frac{y}{14} = \frac{z}{11} = r

; portanto, x = 27r, y = 14r e z = 11r. Como x + y + z = 104, temos:

27r + 14r + 11r = 104 ⇒ 52r = 104 ⇒

r = \frac{104}{52} = 2

Desta maneira, com r = 2, então: x = 27r ⇒ x = 27 · 2 = 54, y = 14r ⇒ x = 14 · 2 = 28 e z = 11r ⇒ x = 11 · 2 = 22

Alternativa a.

\frac{x}{4}

= 4y = r

Sendo x = 4r e

y = \frac{1}{4} r

, como x + y = 204, então:

4 r + \frac{r}{4} = 204

Fazendo a adição de frações com denominadores comuns:

16r + r = 816 ⇒ 17r = 816 ⇒ r = 48

Como x = 4r, então o menor valor será y, pois:

y = \frac{1}{4} r \Rightarrow y = \frac{r}{4} \Rightarrow y = \frac{48}{4} \Rightarrow y = 12

Alternativa b.

10. Se a proporcionalidade direta se mantém para o total da população, então, temos:

\frac{7 500}{3 000} = \frac{21 000}{x}

⇒ 75x = 210 · .3000 = .630000 ⇒

⇒

x = \frac{630 000}{75} \Rightarrow x = 8 400

Portanto, .8400 pessoas.

11.

Número de campos	Quantidade de pessoas
18	1.000.000
1	x

São grandezas diretamente proporcionais, então:

\frac{18}{1} = \frac{1 000 000}{x}

⇒ 18x = ..1000000 ⇒

x = \frac{1 000 000}{18} ≃ 55 556

Portanto, aproximadamente .55556 pessoas.

12.

Quantidade de páginas	Quantidade de linhas	Quantidade de letras por linha
6	45	80
x	30	40

\frac{6}{x} = \frac{30}{45} \cdot \frac{40}{80} \Rightarrow \frac{6}{x} = \frac{1 200}{3 600}

⇒ 36 · 6 = 12x ⇒

⇒ 12x = 216 ⇒ x = 18

Portanto, o texto ocupará 18 páginas.

Alternativa c.

13.

Massa dos fios (kg)	Comprimento da fazenda (m)	Largura da fazenda (cm)
4	14	80
x	350	120

As grandezas são todas diretamente proporcionais. Então:

\frac{4}{x} = \frac{14}{350} \cdot \frac{80}{120} \Rightarrow \frac{4}{x} = \frac{1 120}{42 000} \Rightarrow 112 \cdot x = 4 \cdot 4 200 \Rightarrow

\Rightarrow 112 x = 16 800 \Rightarrow x = \frac{16 800}{112} \Rightarrow x = 150

Portanto, 150 quilogramas.

Alternativa b.

Verificando

4. Os valores são tais que se formam as proporções:

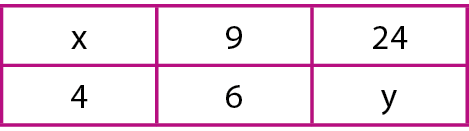
Quadro de duas linhas e três colunas. Linha 1: x; 9; 24. Linha 2: 4; 6; y.

\frac{x}{4} = \frac{9}{6} \Rightarrow 6 x = 36 \Rightarrow x = \frac{36}{60} \Rightarrow x = 6

\frac{24}{y} = \frac{9}{6} \Rightarrow 9 y = 144 \Rightarrow y = \frac{144}{9} \Rightarrow y = 16

Alternativa d.

5. Como são inversamente proporcionais, então 3A = 2B = r. Assim,

A = \frac{r}{3}

B = \frac{r}{2}

. Tomando A + B = 120, temos:

\frac{r}{3} + \frac{r}{2} = 120

. Colocando em denominador comum e adicionando as frações, obtemos:

\frac{2 r + 3 r}{6} = \frac{720}{6}

⇒ 5r = 720 ⇒

r = \frac{720}{5}

⇒ r = 144

Então,

A = \frac{144}{3} = 48

B = \frac{144}{2} = 72

Alternativa a.

Quantidade de máquinas	Tempo (h)
14	6
24	x

Como são grandezas inversamente proporcionais, temos:

\frac{6}{x} = \frac{24}{14} \Rightarrow 24 x = 84 \Rightarrow x = \frac{84}{24} \Rightarrow x = 3, 5

Portanto, 3,5 horas ou 3 horas e 30 minutos.

Alternativa b.

Página cinquenta e sete

Quantidade de páginas	Tempo (min)
20	45
300	x

Como são grandezas diretamente proporcionais, temos:

\frac{45}{x} = \frac{20}{300} \Rightarrow 20 x = 13 500 \Rightarrow x = \frac{1 350}{2} \Rightarrow x = 675

O tempo é de 675 minutos; então, convertendo para horas:

675 : 60 = 11,25

Portanto, 11 horas e

\frac{1}{4}

de hora, ou seja, 11 horas 15 minutos.

Alternativa a.

Quantidade de pintores	Tempo (dias)	Quantidade de corredores
3	2	5
x	5	6

A grandeza quantidade de corredores é diretamente proporcional à quantidade de pintores, porém, o tempo é inversamente proporcional à quantidade de pintores, assim:

\frac{3}{x} = \frac{5}{2} \cdot \frac{5}{36}

 ⇒ 

\frac{3}{x} = \frac{25}{72}

⇒ ⇒ 25x = 216 ⇒ x =

\frac{216}{25}

⇒ x = 8,64

Como a quantidade de pintores tem de ser um número natural, será o próximo natural maior que x; portanto, 9 pintores.

Alternativa c.

Distância percorrida (km)	Tempo de viagem (dias)	Número de horas pedaladas por dia
450	9	4
x	5	6

Como as grandezas são todas diretamente proporcionais, temos:

\frac{450}{x} = \frac{9}{5} \cdot \frac{4}{6} \Rightarrow \frac{450}{x} = \frac{36}{30} \Rightarrow 36 x = 13 500 \Rightarrow

\Rightarrow x = \frac{13 500}{36} \Rightarrow x = 375

Portanto, 375 quilômetros.

Alternativa d.

Capítulo 4 — Proporcionalidade em Geometria

• Objetivos do capítulo e justificativas

• Determinar a razão entre dois segmentos de reta.

• Resolver problemas envolvendo razões entre duas grandezas.

• Resolver problemas envolvendo cálculos com números reais.

• Reconhecer e construir retângulos áureos.

• Apresentar o teorema de Tales.

• Aplicar o teorema de Tales e propriedades que decorrem dele.

• Resolver problemas envolvendo segmentos proporcionais.

• Demonstrar e aplicar relações entre ângulos formados por retas paralelas cortadas por uma transversal.

• Resolver e elaborar problemas que aplicam as relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

• Resolver problemas envolvendo porcentagens e análise de cartograma.

Neste capítulo, ampliamos as noções de razão e de proporção ligadas à Geometria. As atividades buscam inicialmente familiarizar os estudantes com o assunto e depois aplicar os resultados estudados (por exemplo, o teorema de Tales) em situações contextualizadas. O estudo dêsse conjunto de conceitos e procedimentos amplia o repertório de ferramentas para a resolução de diferentes problemas do mundo físico e de diferentes áreas do conhecimento. dêsse modo, contribui-se para o desenvolvimento das competências específicas 3 e 4 e das competências gerais 2 e 4.

O trabalho com a análise de cartograma explora a temática Índice de Vulnerabilidade Social (í vê ésse). A atividade proposta requer que os estudantes pesquisem e listem os cinco maiores problemas atuais do município em que vivem, que influenciam na qualidade de vida dos munícipes. dêsse modo, é favorecido o trabalho com as competências gerais 9 e 10 e com a competência específica 8.

A Abertura usa como motivação uma imagem em que é possível fazer uma associação de retas paralelas e transversais em elementos de construções humanas, ressaltando a noção de proporcionalidade. Assim, as competências específicas 6 e 7 são favorecidas.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah zero um) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).

(ê éfe zero nove ême ah um zero) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal.

(EF09MA14) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.

O foco deste capítulo é a Unidade Temática Geometria, ampliando-se o trabalho feito com proporcionalidade no capítulo anterior para o campo da Geometria. Esse estudo envolve também demonstrar e aplicar relações simples entre ângulos formados por retas paralelas cortadas por uma transversal, explorando demonstrações feitas no 8º ano (ê éfe zero oito ême ah um quatro), e resolução de problemas de aplicação das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes, favorecendo o desenvolvimento das habilidades (EF09MA1), (EF09M10) e (ê éfe zero nove ême ah um quatro).

Página cinquenta e oito

Na articulação com a Unidade Temática Probabilidade e estatística, utiliza-se a leitura de texto e cartogramas, contribuindo para o trabalho com a habilidade (ê éfe zero nove ême ah dois dois), e com a Unidade Temática Álgebra, exploram-se situações que envolvem razões e relações de proporcionalidade. Além desses conteúdos, abordam-se em seções especiais cálculos com números reais e porcentagens, articulando-se com a Unidade Temática Números.

• Comentários e resoluções

Apresentamos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Exercícios propostos

3. a)

A B = \frac{5 \cdot 14}{10} = \frac{70}{10} = 7

3. b)

A B = \frac{18 \cdot 3, 4}{12} = \frac{61, 2}{12} = 5, 1

3. c)

A B = \frac{3, 5 \cdot 0, 9}{0, 5} = \frac{3, 15}{0, 5} = 6, 3

3. d)

A B = \frac{3, 2 \cdot 1, 5}{2, 4} = \frac{4, 8}{2, 4} = 2

4. O segmento

\bar{A B}

é composto de dois segmentos consecutivos,

\bar{A M}

\bar{M B}

de fórma que A bê = AM + MB = 18. Desse modo, temos a relação MB = 18 ‒ AM. Como os segmentos respeitam a razão de

\frac{2}{7}

, temos:

\frac{A M}{M B} = \frac{A M}{18 - A M} = \frac{2}{7}

Assim: 7AM = 2 · (18 ‒ AM) ⇒ 7AM = 36 ‒ 2AM ⇒

⇒ 9AM = 36 ⇒ AM = 4

Logo, MB = 18 ‒ 4 = 14.

Alternativa a.

5. Sendo x a medida do maior lado da ampliação, temos a relação proporcional

\frac{10}{15} = \frac{13}{x}

; então:

x = \frac{15 \cdot 13}{10} = \frac{195}{10} = 19, 5

Portanto, o lado maior medirá 19,5 centímetros.

6. Temos a proporção

\frac{A B}{M N} = \frac{C D}{P Q}

. Como CD + PQ = 45, CD = 45 ‒ PQ; logo,

\frac{12}{15} = \frac{45 - P Q}{P Q}

. Então:

12PQ = 15 · (45 ‒ PQ) ⇒ 12PQ = 675 ‒ 15PQ ⇒ 27PQ = 675 ⇒

⇒

P Q = \frac{675}{27} = 25

Assim: CD = 45 ‒ PQ = 45 ‒ 25 ⇒ CD = 20

Portanto, a medida de

\bar{P Q}

é 25 centímetros e a de

\bar{C D}

é 20 centímetros.

7. a) Pela proporção, temos:

\frac{A B}{M N} = \frac{C H}{P G} \Rightarrow \frac{20}{30} = \frac{18}{x} \Rightarrow x = \frac{30 \cdot 18}{20} = \frac{540}{20} = 27

Portanto, x = 27 centímetros.

7. b) A medida da área do triângulo MNP pode ser calculada por:

\frac{A B \cdot x}{2} = \frac{30 \cdot 27}{2} = \frac{810}{2} = 405

Portanto, a área mede 405 centímetros quadrados.

10. a) Pelo teorema de Tales:

\frac{10}{20} = \frac{x}{15} \Rightarrow x = \frac{15 \cdot 10}{20} = \frac{150}{20} = \frac{15}{2} \Rightarrow x = 7, 5

10. b) Pelo teorema de Tales:

\frac{9}{5} = \frac{x}{21 - x}

⇒ 5x = 9(21 ‒ x) ⇒ ⇒ 5x = 189 ‒ 9x ⇒ 14x = 189 ⇒ x =

\frac{189}{14}

⇒ x = 13,5

10. c) Pelo teorema de Tales:

\frac{12}{21} = \frac{8}{x - 8}

⇒ 12(x ‒ 8) = 8 · 21 ⇒ 12x ‒ 96 = 168 ⇒

⇒ 12x = 264 ⇒ x =

\frac{264}{12}

⇒ x = 22

11. Como x + y = 26, tem-se y = 26 ‒ x. Pelo teorema de Tales:

\frac{4}{9} = \frac{x}{26 - x}

⇒ 9x = 4(26 ‒ x) ⇒ 9x = 104 ‒ 4x ⇒ 13x = 104 ⇒ x =

\frac{104}{13}

⇒ x = 8

Então, y = 18, pois 26 ‒ 8 = 18.

13. Pelo teorema de Tales:

\frac{x + 5}{x} = \frac{x + 2}{x - 2}

⇒ (x + 5)(x – 2) =

= x (x + 2) ⇒ x² + 5x – 2x – 10 = x2 + 2x ⇒ 3x – 10 = 2x ⇒ 3x – 2x = 10 ⇒ x =10

14. a) O terreno para a alameda das Magnólias mede, ao todo, 90 métros; portanto, sendo C a medida procurada, temos: 40 + 30 + C = 90 ⇒ C = 20

Portanto, a frente do terreno mede 20 métros.

14. b) Pelo teorema de Tales, o terreno a mede:

\frac{90}{40} = \frac{135}{A} \Rightarrow A = \frac{135 \cdot 40}{90} \Rightarrow A = \frac{5 400}{90}

⇒ A = 60

O terreno B mede:

\frac{90}{30} = \frac{135}{B} \Rightarrow B = \frac{135 \cdot 30}{90} = \frac{4 050}{90} \Rightarrow B = 45

O terreno C mede:

\frac{90}{20} = \frac{135}{C} \Rightarrow C = \frac{135 \cdot 20}{90} = \frac{2 7000}{90} \Rightarrow C = 30

Portanto, as medidas das frentes dos terrenos na alameda dos Jasmins são as seguintes: terreno a, 60 métros; terreno B, 45 métros; terreno C, 30 métros.

15. a) Pela consequência do teorema de Tales:

\frac{9}{3} = \frac{12}{x} \Rightarrow x = \frac{12 \cdot 3}{9} = \frac{12 \cdot 1}{3} = \frac{4 \cdot 1}{1} \Rightarrow x = 4

15. b) Pela consequência do teorema de Tales:

\frac{15}{10} = \frac{x + 3}{x}

⇒ 15x = 10(x + 3) ⇒ 15x = 10x + 30 ⇒ ⇒ 5x = 30 ⇒ x =

\frac{30}{5}

⇒ x = 6

16. a) Para que o segmento

\bar{N M}

seja paralelo ao segmento

\bar{G F}

, precisamos verificar a validade da igualdade da consequência do teorema de Tales; portanto:

\frac{3}{4} = \frac{4, 5}{6}

⇒ 3 · 6 = 4 · 4,5 ⇒ 18 = 18

É verdade, portanto

\bar{N M} // \bar{G F}

Página cinquenta e nove

16. b) Verificando da mesma maneira do item a:

\frac{2, 4}{2} = \frac{2, 7}{1, 7}

⇒ 2,4 · 1,7 = 2,7 · 2 ⇒ 4,08 = 5,4

É falso, então, é possível concluir que o segmento

\bar{N M}

não é paralelo a

\bar{F G}

17. Pela consequência do teorema de Tales:

\frac{45}{40} = \frac{C E}{48} \Rightarrow C E = \frac{45 \cdot 48}{40} = \frac{2 160}{40} \Rightarrow C E = 54

O comprimento da ponte mede 54 metros.

18. Como as ruas Pardal, Canário e Colibri são paralelas, pela consequência do teorema de Tales:

\frac{60}{64} = \frac{75}{x} \Rightarrow x = \frac{75 \cdot 64}{60} = \frac{4 800}{60} \Rightarrow x = 80

Assim, temos também:

\frac{64}{80} = \frac{x}{y} \Rightarrow \frac{64}{80} = \frac{80}{y} \Rightarrow

⇒ y =

\frac{80 \cdot 80}{64} = \frac{6 400}{64}

⇒ y = 100

Portanto, as medidas procuradas são x = 80 métros e y = 100 métros.

19. Podemos observar que a nova fileira é paralela à antiga, a uma distância de 1,5 métro (4,5 ‒ 3 = 1,5). A distância do último menino da direita deve ser menor do que 5,5 metros para que sua imagem não fique prejudicada na foto. Sendo x a distância do menino na nova fileira, pela consequência do teorema de Tales:

\frac{3}{1, 5} = \frac{3, 6}{x} \Rightarrow x = \frac{3, 6 \cdot 1, 5}{3} = \frac{5, 4}{3} \Rightarrow x = 1, 8

Logo, a distância até a câmera é de 5,4 métros (1,8 + 3,6 = 5,4); portanto, a imagem não será prejudicada, pois o menino está dentro do limite para uma boa resolução.

20. Note que as vigas que sustentam a rampa são perpendiculares ao chão, portanto são paralelas entre si. Sendo x a distância do início da rampa até a segunda viga, pela consequência do teorema de Tales:

\frac{(10 + 60)}{50} = \frac{x}{55} \Rightarrow x = \frac{70 \cdot 55}{50} = \frac{3 850}{50} \Rightarrow x = 77

Como 77 centímetros = 0,77 métros, a medida total da rampa é 1,32 métro, (0,77 + 0,55 = 1,32).

22. a) Pela relação de proporcionalidade:

\frac{12}{18} = \frac{x}{21} \Rightarrow x = \frac{12 \cdot 21}{18} = \frac{252}{18} \Rightarrow x = 14

22. b) Pela relação de proporcionalidade:

\frac{15}{25} = \frac{12}{x} \Rightarrow x = \frac{12 \cdot 5}{3} = \frac{60}{3} \Rightarrow x = 20

22. c) Pela relação de proporcionalidade:

\frac{35}{3 x} = \frac{42}{4 x - 8}

⇒ 35 · (4x ‒ 8) = 42 · 3x ⇒

⇒ 140x ‒ 280 = 126x ⇒ 14x = 280 ⇒ x = 20

23. a) Como x + y = 55 ⇒ x = 55 ‒ y; assim, pela relação de proporcionalidade:

\frac{10}{y} = \frac{12}{x} \Rightarrow \frac{10}{y} = \frac{12}{55 - y} \Rightarrow 12 y = 550 - 10 y \Rightarrow

\Rightarrow 22 y = 550 \Rightarrow y = \frac{550}{22} \Rightarrow y = 25

Então, x = 30, pois 55 ‒ 25 = 30.

23. b) Como x + y = 14 ⇒ x = 14 ‒ y; assim, pela relação de proporcionalidade:

\frac{14 - y}{12} = \frac{y}{16}

⇒ 12y = 16 · (14 ‒ y) = 224 ‒ 16y ⇒

\Rightarrow 28 y = 224 \Rightarrow y = \frac{224}{28} \Rightarrow y = 8

Então, x = 14 ‒ 8 = 6.

23. c) Como x + y = 22 ⇒ x = 22 ‒ y; assim, pela relação de proporcionalidade:

\frac{x}{y} = \frac{15}{18}

⇒ 18 · (22 ‒ y) = 15y ⇒ 396 ‒ 18y = 15y ⇒

⇒ 33y = 396 ⇒ y = 12

Então, x = 22 ‒ 12 = 10.

25. Pela relação de proporcionalidade:

\frac{D C}{A C} = \frac{B D}{A B} \Rightarrow \frac{2, 4}{x} = \frac{2}{5} \Rightarrow x = \frac{2, 4 \cdot 5}{2} = \frac{12}{2} \Rightarrow x = 6

Então, AC = 6 centímetros.

Exercícios complementares

1. a) Pelo teorema de Tales:

\frac{33}{x} = \frac{22}{8}

⇒ 8 · (3 · 11) = (11 · 2) · x ⇒

⇒ 8 · 3 = 2 · x ⇒ x = 4 · 3 ⇒ x = 12

Também:

\frac{33}{y} = \frac{22}{14}

⇒ 2 y = 3 · 14 ⇒ y = 3 · 7 ⇒ y = 21

1. b) Temos que:

\frac{9}{3} = \frac{6}{y}

Assim, y = 2.

Além disso:

\frac{12}{x} = \frac{8}{8}

Portanto, x = 12.

2. O segmento

\bar{B D}

é composto por

\bar{B C}

\bar{C D}

, ou seja, BD = = 2,4 + CD. Pelo teorema de Tales, temos:

\frac{2, 4}{C D} = \frac{2}{3, 5} \Rightarrow C D = \frac{2, 4 \cdot 3, 5}{2} = \frac{8, 4}{2} \Rightarrow C D = 4, 2

Portanto: BD = 2,4 + 4,2 = 6,6

3. Os segmentos

\bar{B C}

\bar{H C}

são transversais aos segmentos paralelos

\bar{M N}

\bar{A B}

. O segmento

\bar{C H}

é composto por

\bar{C P}

\bar{P H}

, logo CH = CP + 6. Pelo teorema de Tales:

\frac{15}{6} = \frac{C P + 6}{C P}

⇒ 15CP = 6(CP + 6) ⇒ 9CP = 36 ⇒

C P = \frac{36}{9} = 4

Assim, CH = 4 + 6 = 10.

Página sessenta

5. O segmento

\bar{A D}

é a bissetriz do ângulo

\hat{A}

em relação ao lado

\bar{B C}

. O lado

\bar{B C}

é composto pelos segmentos

\bar{B D}

\bar{D C}

; logo, BC = BD + DC = 26 ⇒ DC = 26 ‒ BD. Pela relação de proporcionalidade:

\frac{B D}{A B} = \frac{D C}{A C}

⇒ 18BD = 21 · (26 ‒ BD) = 546 ‒ 21BD ⇒ 39BD = 546 ⇒ BD = 14

Assim, DC = 26 ‒ 14 = 12. Portanto, os segmentos medem 14 centímetros e 12 centímetros.

7. O perímetro do triângulo á bê cê mede 84 centímetros; portanto: á cê + A bê + (20 + 15) = 84 ⇒ á cê = 49 ‒ A bê

Pela relação de proporcionalidade:

\frac{D C}{A C} = \frac{D B}{A B} \Rightarrow \frac{15}{49 - A B} = \frac{20}{A B} \Rightarrow 15 A B = 20 (49 - A B)

⇒ ⇒ 15AB = 980 ‒ 20AB ⇒ 35AB = 980 ⇒ AB =

\frac{980}{35}

= 28

Logo: AC = 49 ‒ 28 = 21

Portanto, AC = 21 centímetros, AB = 28 centímetros e BC = 35 centímetros.

8. O segmento

\bar{A D}

mede 10 centímetros. Pelo teorema de Tales:

\frac{A D'}{C' D'} = \frac{A D}{C D} \Rightarrow \frac{13}{C' D'} = \frac{10}{5} \Rightarrow C' D' = \frac{13}{2} = 6, 5

Pelo mesmo argumento:

\frac{A D'}{B' C'} = \frac{A D}{B C} \Rightarrow \frac{13}{B' C'} = \frac{10}{3}

⇒

B ’ C ’ = \frac{13 \cdot 3}{10} = 1, 3 \cdot 3 \Rightarrow B ’ C ’ = 3, 9

Por fim:

\frac{A D'}{A' B'} = \frac{A D}{A B} \Rightarrow \frac{13}{A' B'} = \frac{10}{2} \Rightarrow

⇒

A ’ B ’ = \frac{13}{5} = \frac{26}{10} \Rightarrow A ’ B ’ = 2, 6

Portanto, as medidas são: cê linha dê linha = 6,5 centímetros, bê linha cê linha = 3,9 centímetros e á linha bê linha = 2,6 centímetros.

9. Pelo teorema de Tales, temos:

\frac{x}{9} = \frac{4}{x} \Rightarrow x^{2} = 36

Como 36 = 62 e 36 = (‒6)2, então

x = \sqrt{36} = \pm 6

. Por se tratar de medida, então x = 6.

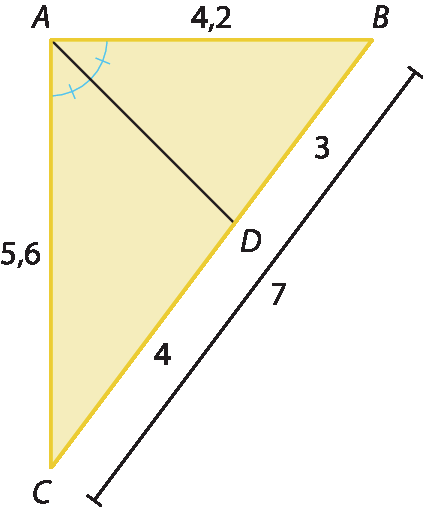
10. O segmento

\bar{A D}

é a bissetriz do triângulo em relação ao ângulo

\hat{A}

em relação ao lado

\bar{B C}

. O lado

\bar{B C}

é composto pelos segmentos

\bar{B D}

\bar{D C}

; logo, BC = BD + DC = 7 ⇒ DC = 7 ‒ BD. Pela relação de proporcionalidade, temos:

\frac{B D}{A B} = \frac{D C}{A C} \Rightarrow \frac{B D}{4, 2} = \frac{7 - B D}{5, 6}

⇒ 5,6BD = 4,2(7 ‒ BD) ⇒

⇒ 5,6BD = 29,4 ‒ 4,2BD ⇒ 9,8BD = 29,4 ⇒ BD = 3

Assim, DC = 7 ‒ 3 = 4. Portanto, a medida do segmento

\bar{B D}

é 3 centímetros e do

\bar{D C}

é 4 centímetros.

Ilustração. Triângulo ABC. Segmento AD que divide o ângulo A em dois ângulos de mesma medida.. As medidas são: AC: 5,6. AB: 4,2. CD: 4. DB: 3. BC: 7.

Verificando

1. Considere x a medida do maior lado do retângulo e y a medida do menor lado. O perímetro mede 432 centímetros; logo: 2x + 2y = 432

Portanto, y = 216 ‒ x. Assim, temos:

\frac{7}{5} = \frac{x}{216 - x}

⇒ 5x = .1512 ‒ 7x ⇒ 12x = .1512 ⇒ x = 126

Portanto: y = 216 ‒ 126 = 90

Alternativa b.

2. Os triângulos APB e DPC são congruentes pois os segmentos

\bar{B P}

\bar{D P}

\bar{A B}

\bar{D C}

são congruentes. Além disso, o ângulo

\hat{P}

é oposto pelo vértice em ambos os triângulos. Assim,

\bar{A P}

é congruente a

\bar{P C}

. Portanto, AC = 2x.

Alternativa d.

3. Pelo teorema de Tales:

\frac{9}{15} = \frac{x}{12} \Rightarrow x = \frac{9 \cdot 12}{15} = \frac{9 \cdot 4}{5} \Rightarrow x = 7, 2

Alternativa b.

4. A razão entre a medida da base do triângulo maior e a medida da base do triângulo menor é

\frac{12}{4} = 3

. Sendo x a medida do maior lado do menor triângulo, temos:

3 = \frac{15}{x} \Rightarrow x = \frac{15}{3} = 5

Sendo y a medida do menor lado do triângulo menor, temos:

3 = \frac{9}{y} \Rightarrow y = \frac{9}{3} = 3

Assim, a medida do perímetro do triângulo menor é 12 centímetros, pois 3 + 4 + 5 = 12.

Alternativa d.

5. As retas são paralelas, pois elas são perpendiculares à reta

q_{2}

; assim, pelo teorema de Tales, temos:

\frac{48}{18} = \frac{32}{a} \Rightarrow a = \frac{18 \cdot 32}{48} \Rightarrow a = \frac{3 \cdot 32}{8}

= 3 · 4 ⇒ a = 12

Portanto, a distância entre as retas r e t mede 44 (12 + 32 = 44).

Alternativa b.

6. Pelo teorema de Tales, temos:

\frac{7}{5} = \frac{4}{x} \Rightarrow x = 4 \cdot \frac{5}{7} = \frac{20}{7} \Rightarrow x ≃ 2, 86

Então, a medida da distância é dada, em metro, por:

2,86 + 4 = 6,86 ≃ 7

Alternativa c.

7. Pela base do triângulo, 14 + y = 42 ⇒ y = 28. Pela relação de proporcionalidade da bissetriz, temos:

\frac{14}{x} = \frac{28}{32}

⇒ (14 · 2) · x = 32 · 14 ⇒ 2x = 32 ⇒ x = 16

Alternativa c.