Página sessenta e um

Parte 5

Capítulo 5 ‒ Semelhança

• Objetivos do capítulo e justificativas

• Resolver problemas envolvendo relações de proporcionalidade.

• Identificar e efetuar ampliação e redução de figuras.

• Resolver problemas envolvendo cálculos com números reais.

• Desenvolver a noção de figuras semelhantes.

• Determinar a razão de semelhança entre dois polígonos semelhantes.

• Aplicar as relações entre ângulos formados por retas paralelas cortadas por uma transversal.

• Reconhecer polígonos semelhantes, em particular triângulos semelhantes.

• Construir figuras semelhantes por homotetia.

• Definir semelhança entre triângulos.

• Estudar e aplicar os casos de semelhança de triângulos.

• Resolver problemas envolvendo semelhança de triângulos.

• Interpretar pirâmides etárias.

Apresentamos neste capítulo o conceito de semelhança entre figuras e, em particular, a semelhança entre polígonos, ampliando o estudo sobre proporcionalidade; são apresentadas atividades em que os estudantes precisam exercitar a curiosidade intelectual, o espírito de investigação, aplicar métodos lógico-dedutivos para demonstrar propriedades e argumentar sobre a validade deles. Assim, promovemos o trabalho com as competências gerais 2 e 4 e com as competências específicas 2 e 3.

O trabalho com triângulos semelhantes é fundamental para o desenvolvimento dos assuntos dos próximos capítulos, como razões métricas e trigonométricas em um triângulo retângulo, favorecendo o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2 e 3.

A abertura apresenta como motivação uma amostra da cultura berbere por meio da arte de seus tapetes com motivos geométricos, contribuindo para o trabalho com a competência geral 3.

O trabalho com homotetia e com o pantógrafo, propostos na seção Para saber mais favorece o desenvolvimento das competências específicas 5 e 6.

Na seção Trabalhando a informação exploramos a leitura da pirâmide etária. A resolução dos itens b e c da atividade 1, favorecem o trabalho com o Tema Contemporâneo Transversal processo de envelhecimento, respeito e valorização do idoso, com as competências específicas 7 e 8 e com as competências gerais 9 e 10.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah zero cinco) Resolver e elaborar problemas que envolvam porcentagens, com a ideia de aplicação de percentuais sucessivos e a determinação das taxas percentuais, preferencialmente com o uso de tecnologias digitais, no contexto da educação financeira.

(ê éfe zero nove ême ah zero oito) Resolver e elaborar problemas que envolvam relações de proporcionalidade direta e inversa entre duas ou mais grandezas, inclusive escalas, divisão em partes proporcionais e taxa de variação, em contextos socioculturais, ambientais e de outras áreas.

(ê éfe zero nove ême ah um zero) Demonstrar relações simples entre os ângulos formados por retas paralelas cortadas por uma transversal.

(ê éfe zero nove ême ah um dois) Reconhecer as condições necessárias e suficientes para que dois triângulos sejam semelhantes.

(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.

Situações que desenvolvem a proporcionalidade são o foco deste capítulo, que trata de semelhança e suas aplicações na Unidade Temática Geometria e que amplia e aprofunda os conhecimentos abordados no capítulo anterior. Os conteúdos são desenvolvidos visando a dar suporte e garantir a continuidade dos estudos em Matemática para temas que serão trabalhados no Ensino Médio, como a Trigonometria, favorecendo o desenvolvimento das habilidades (ê éfe zero nove ême ah zero oito) e (ê éfe zero nove ême ah um zero). O trabalho com semelhança de triângulos se relaciona com a habilidade (ê éfe zero nove ême ah um dois).

A articulação com as Unidades Temáticas Números e Álgebra é feita, respectivamente, com a presença de cálculos com números reais e porcentagens e com relações de proporcionalidade.

Além disso, promove-se ainda a articulação com a Unidade Temática Probabilidade e estatística na seção Trabalhando a informação, que explora pirâmides etárias e promove o desenvolvimento das (ê éfe zero nove ême ah zero cinco) e (ê éfe zero nove ême ah dois dois), ampliando o trabalho com gráficos dos anos anteriores, em especial o do 8º ano (ê éfe zero oito ême ah dois sete).

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Exercícios propostos

1. Para determinar a razão de semelhança, primeiro vamos identificar os vértices da figura original e da figura reduzida.

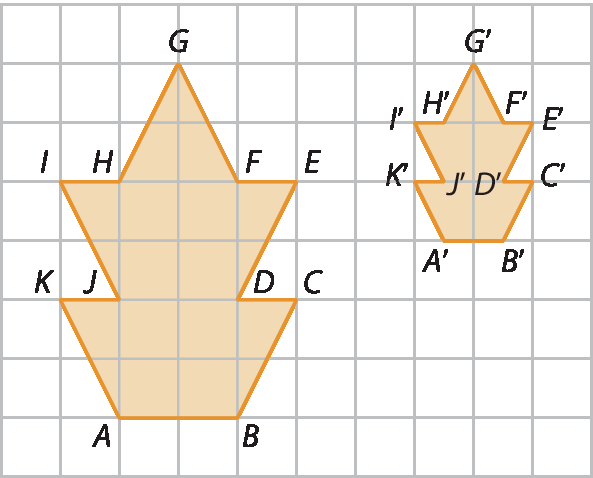
Ilustração. Esquema. Triângulos retângulos coloridos dispostos em espiral. O primeiro triângulo retângulo tem os catetos medindo 1 e a hipotenusa, medindo raiz quadrada de 2. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 3. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 4. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 5. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 6. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 7. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 8. Sobre essa hipotenusa é construído outro triângulo retângulo de altura 1, cuja hipotenusa mede raiz quadrada de 9. Essa última hipotenusa está dividida em três partes iguais de medida 1 cada uma delas.

Página sessenta e dois

A razão de semelhança é dada por:

\frac{A' B'}{A B} = \frac{B' C'}{B C} = \frac{C' D'}{C D} = \frac{D' E'}{D E} = \frac{E' F'}{E F} = \frac{F' G'}{F G} = \frac{G' H'}{G H}

\frac{H' I'}{H I} = \frac{I' J'}{I J} = \frac{J' L'}{J L} = \frac{L' A'}{L A} = \frac{1}{2}

Note que:

\frac{A' B'}{A B} = \frac{1}{2}

\frac{E' F'}{E F} = \frac{\frac{1}{2}}{1} = \frac{1}{2}

\frac{J' L'}{J L} = \frac{\frac{1}{2}}{1} = \frac{1}{2}

3. Não. Para dois polígonos serem semelhantes, eles devem ter lados correspondentes de medidas de comprimento proporcionais e ângulos correspondentes congruentes. Como não foi mencionado que os ângulos correspondentes são congruentes, não é possível afirmar que os polígonos são semelhantes.

4. a) Sendo

b_{1} = 6

centímetros a medida da base do retângulo em verde e

b_{2} = 4

centímetros a medida da base do retângulo em vermelho, para a razão entre a medida da base do retângulo vermelho e a medida da base do retângulo verde, temos:

\frac{b_{2}}{b_{1}} = \frac{4}{6} = \frac{4 : 2}{6 : 2} = \frac{2}{3}

4. b) Sendo

h_{1} = 1, 5

centímetro a medida da altura do retângulo em verde e

h_{2} = 1, 0

centímetro a medida da altura do retângulo em vermelho, para a razão entre a medida da altura do retângulo vermelho e a medida da altura do retângulo verde, temos:

\frac{h_{2}}{h_{1}} = \frac{1, 0}{1, 5} = \frac{1, 0 \cdot 2}{1, 5 \cdot 2} = \frac{2}{3}

4. c) Sim, os retângulos são semelhantes porque seus lados correspondentes têm medidas de comprimento proporcionais e os ângulos correspondentes são congruentes. Todos os ângulos medem 90graus.

6. Como os polígonos são semelhantes, seus lados correspondentes possuem medidas proporcionais. Assim:

\frac{8}{4} = \frac{6}{3} = \frac{10}{5} = \frac{12}{x}

. Verificamos que o numerador é o dôbro do denominador de cada fração. Portanto, x = 6.

7. a) As medidas do comprimento dos lados do triângulo á bê cê são A bê = 6 centímetros; BC = 3,6 centímetros; cê á = 4,8 centímetros.

As medidas do comprimento dos lados do triângulo á linha bê linha cê linha são á linha bê linha = 5 centímetros; B'C' = 3 centímetros; C'A' = 4 centímetros.

Assim, a razão entre as medidas de dois lados correspondentes é:

\frac{A B}{A' B'} = \frac{6}{5} = 1, 2

\frac{B C}{B' C'} = \frac{3, 6}{3} = 1, 2

\frac{C A}{C' A'} = \frac{4, 8}{4} = 1, 2

7. b) A medida da altura relativa a

\bar{A B}

é h = 3 centímetros. A medida da altura relativa a

\bar{A' B'} é h'

= 2,5 centímetros.

Assim, a razão entre as medidas de duas alturas relativas a lados correspondentes é:

\frac{h}{h'} = \frac{3}{2, 5} = 1, 2

7. c) A medida do perímetro do triângulo á bê cê é dada pela adição das medidas de seus lados.

6 + 3,6 + 4,8 = 14,4

A medida do perímetro do triângulo á linha bê linha cê linha é dada pela adição das medidas de seus lados.

5 + 3 + 4 = 12

Logo, a razão entre as medidas dos perímetros é:

\frac{14, 4}{12} = \frac{14, 4 : 4}{12 : 4} = \frac{3, 6 : 3}{3 : 3} = 1, 2

7. d) A medida da área do triângulo á bê cê é dada por:

\frac{A B \cdot h}{2} = \frac{6 \cdot 3}{2} = \frac{18}{2} = 9

A medida da área do triângulo á linha bê linha cê linha é dada por:

\frac{A ’ B ’ \cdot h ’}{2} = \frac{5 \cdot 2, 5}{2} = \frac{12,5}{2} = 6, 5

Logo, a razão entre as medidas das áreas é:

\frac{9}{6, 25} = \frac{9 : 3}{6, 25 : 3} = 1, 44

8. Como os triângulos são semelhantes, os lados correspondentes têm medidas de comprimento proporcionais. Assim, a razão de semelhança entre as medidas dos lados correspondentes dos dois triângulos é dada por:

\frac{8}{4} = \frac{12}{6} = \frac{2}{1}

8. b) A razão entre as medidas do perímetro dos triângulos é

\frac{2}{1}

, pois é igual à razão de semelhança.

Página sessenta e três

8. c) A área do triângulo de Marcos mede 48 centímetros quadrados.

\frac{12 · 8}{2} = 48

A área do triângulo de Pedro mede 12 centímetros quadrados.

\frac{6 · 4}{2} = 12

Assim, a razão entre a medida da área do triângulo de Marcos e a medida da área do triângulo de Pedro é:

\frac{48}{12} = \frac{4}{1}

10. Como os triângulos são semelhantes, as medidas dos lados correspondentes são proporcionais. Assim, considerando os ângulos correspondentes de medidas iguais, identificamos os lados correspondentes e determinamos os valores de x e de y.

\frac{12}{20} = \frac{y}{15} = \frac{x}{10}

Para y, temos:

\frac{12}{20} = \frac{y}{15}

⇒ 20 y = 15 ⋅ 12 ⇒ y =

\frac{180}{20}

⇒ y = 9

Para x, temos:

\frac{12}{20} = \frac{x}{10}

⇒ 20x = 10 ⋅ 12 ⇒ x =

\frac{120}{20}

⇒ x = 6

11. Como os triângulos são semelhantes, as medidas dos lados correspondentes são proporcionais; portanto, as medidas das medianas

\bar{A R}

\bar{M S}

também devem ser proporcionais.

\frac{15}{M S} = \frac{21}{10, 5}

⇒ 21 ⋅ ême ésse = 15 ⋅ 10,5 ⇒ ême ésse =

\frac{157, 5}{21}

⇒

⇒ MS = 7,5

12. Como os triângulos são semelhantes, as medidas dos lados correspondentes são proporcionais; portanto, as medidas das alturas

\bar{A H}

\bar{M R}

também devem ser proporcionais.

\frac{12}{9} = \frac{A H}{6}

⇒ 9 ⋅ á agá = 12 ⋅ 6 ⇒ á agá =

\frac{72}{9}

⇒ á agá = 8

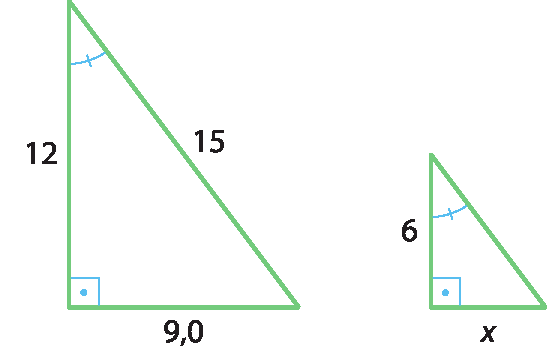
14. a) Para determinar a medida do perímetro é necessário calcular as medidas de comprimento dos dois lados desconhecidos do segundo triângulo (a e b). Como os triângulos são semelhantes, os lados correspondentes são proporcionais. Assim:

\frac{12, 0}{a} = \frac{18, 0}{b} = \frac{20, 4}{15, 3}

Para a, temos:

\frac{12, 0}{a} = \frac{20, 4}{15, 3}

⇒ 20,4 ⋅ a = 12,0 ⋅ 15,3 ⇒

⇒ a =

\frac{183, 6}{20, 4}

⇒ a = 9,0

Para b, temos:

\frac{18, 0}{b} = \frac{20, 4}{15, 3}

⇒ 20,4 ⋅ b = 18,0 ⋅ 15,3 ⇒

\Rightarrow b = \frac{275, 4}{20, 4} \Rightarrow b = 13, 5

Portanto, o perímetro do segundo triângulo mede 37,8 centímetros.

13,5 + 9,0 + 15,3 = 37,8

14. b) Sabemos que, se a razão de semelhança entre dois triângulos é k, a razão entre as medidas de suas áreas é k². Para a razão de semelhança k, temos:

k = \frac{20, 4}{15, 3} \Rightarrow k ≃ 1, 333333

Assim, k² ≃ 1,777777.

Portanto, a área do segundo triângulo mede aproximadamente 60,3 centímetros quadrados, pois:

k^{2} = \frac{107, 2}{x} \Rightarrow 1, 777777 = \frac{107, 2}{x}

⇒ x =

\frac{107, 2}{1,777777}

⇒ x ≃ 60,3

15. a) Aplicando o teorema fundamental da semelhança, considerando os triângulos semelhantes á bê é e dê cê é, temos:

\frac{A E}{D E}

\frac{7, 2}{3, 6}

⇒

\frac{A E}{(A E - 4, 8)}

\frac{7, 2}{3, 6}

⇒

⇒ AE ⋅ 3,6 = (AE ‒ 4,8) ⋅ 7,2 ⇒ 3,6AE = 7,2AE ‒ 34, 56 ⇒

⇒ 7,2AE ‒ 3,6AE = 34,56 ⇒ 3,6AE = 34,56 ⇒

⇒ A Ê =

\frac{34,56}{3, 6}

⇒ A Ê = 9,6

15. b) Procedendo de maneira análoga, temos:

\frac{B E}{C E} = \frac{7, 2}{3, 6} \Rightarrow \frac{(C E + 4, 2)}{C E} = \frac{7, 2}{3, 6} \Rightarrow

⇒ (cê é + 4,2) ⋅ 3,6 = cê é ⋅ 7,2 ⇒ 3,6cê é + 15,12 = 7,2cê é ⇒

⇒ 7,2cê é ‒ 3,6cê é = 15,12 ⇒ 3,6cê é = 15,12 ⇒

⇒ cê é =

\frac{15,12}{3, 6}

⇒ cê é = 4,2

17. a)

\frac{y}{y + 6} = \frac{4}{4 + 4}

⇒ 8 ⋅ y = 4 ⋅ (y + 6) ⇒ 8y = 4y + 24 ⇒

⇒ 8y ‒ 4y = 24 ⇒ 4y = 24 ⇒ y =

\frac{24}{4}

⇒ y = 6

\frac{5}{x} = \frac{4}{4 + 4}

⇒ 4x = 8 ⋅ 5 ⇒ 4x = 40 ⇒

x = \frac{40}{4}

⇒ x = 10

Página sessenta e quatro

17. b)

\frac{x}{x + 4} = \frac{10}{15}

⇒ 15x = 10 ⋅ (x + 4) ⇒ 15x = 10x + 40 ⇒ ⇒ 15x ‒ 10x = 40 ⇒ 5x = 40 ⇒ x =

\frac{40}{5}

⇒ x = 8

\frac{6}{6 + y} = \frac{10}{15}

⇒ 10 ⋅ (6 + y) = 6 ⋅ 15 ⇒ 60 + 10y = 90 ⇒ ⇒ 10y = 30 ⇒ y =

\frac{30}{10}

⇒ y = 3

17. c)

\frac{12}{12 + x} = \frac{8}{20}

⇒ 8 ⋅ (12 + x) = 12 ⋅ 20 ⇒ 96 + 8x = 240 ⇒ ⇒ 8x = 144 ⇒ x =

\frac{144}{8}

⇒ x = 18

\frac{y}{y + 21} = \frac{8}{20}

⇒ 20y = 8 ⋅ (y + 21) ⇒ 20y = 8y + 168 ⇒ ⇒ 12y = 168 ⇒ y =

\frac{168}{12}

⇒ y = 14

18. a)

\frac{x}{4} = \frac{2, 4}{2, 4 + 2, 4}

⇒ 4,8x = 4 ⋅ 2,4 ⇒ x =

\frac{9, 6}{4, 8}

⇒ x = 2

18. b) Como o segmento de medida x divide os dois lados do triângulo maior ao meio, podemos concluir que os lados do triângulo menor têm metade da medida dos lados correspondentes do triângulo maior, ou seja, os dois triângulos são semelhantes. A razão de semelhança entre o triângulo menor e o triângulo maior é

\frac{1}{2}

. Assim:

\frac{x}{9, 0} = \frac{1}{2} \Rightarrow 2 x = 9, 0 \Rightarrow x = \frac{9, 0}{2} \Rightarrow x = 4, 5

21. A seguir, apresentamos um exemplo de fluxograma.

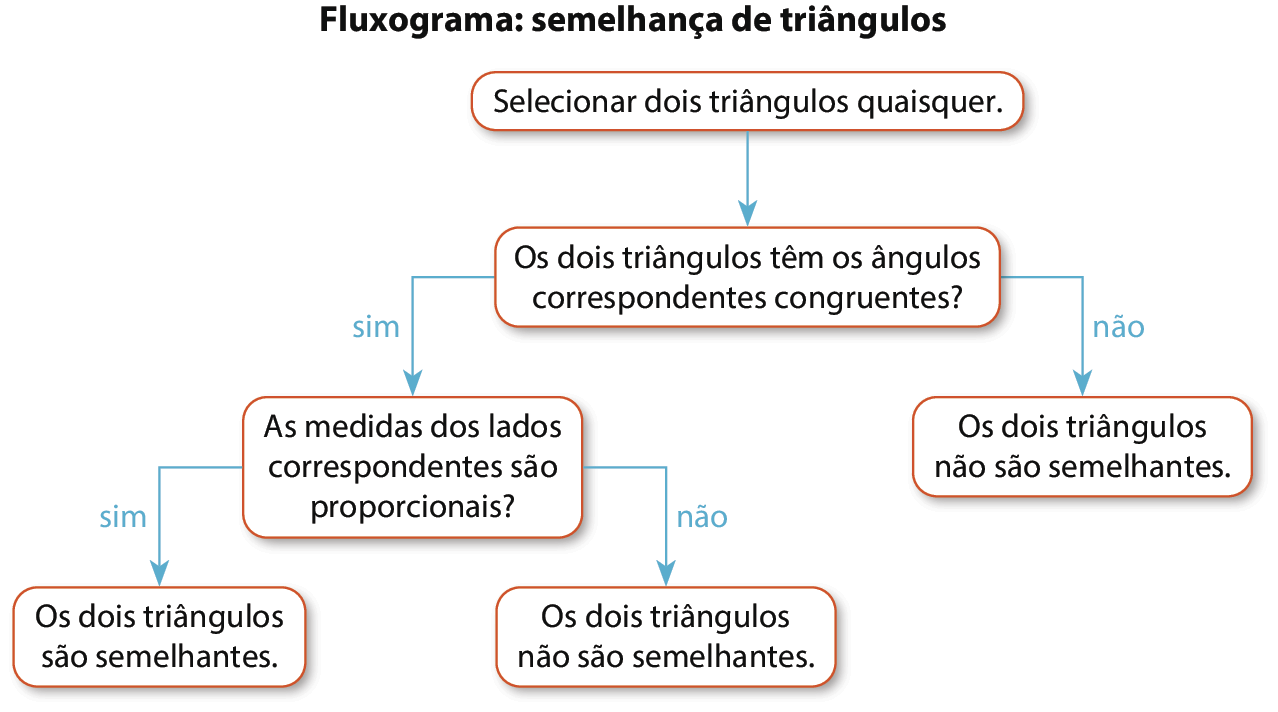
Fluxograma. A figura é um fluxograma com 6 caixas legendadas ligadas por setas. Em cada etapa, as setas apontam para a frente para uma caixa. Aqui, o fluxograma é descrito como listas nas quais os próximos passos possíveis são listados abaixo de cada legenda da caixa. 1. Selecionar dois triângulos quaisquer. a. Avança para Os dois triângulos têm os ângulos correspondentes congruentes? 2. Os dois triângulos têm os ângulos correspondentes congruentes? a. Se sim, as medidas dos lados correspondentes são proporcionais? a1. Se sim, os dois triângulos são semelhantes. a2. Se não, os dois triângulos não são semelhantes. b. Se não, os dois triângulos não são semelhantes.

Observe um exemplo de triângulos semelhantes.

Ilustração. Triângulo ABC escaleno O lado AC mede 2,5; o lado AB mede 6 e o lado BC mede 4. Ao lado, triângulo escaleno A linha B linha C linha. O lado A linha C linha mede 5, o lado A linha B linha mede 12, e lado B linha C linha mede 8. O ângulo A é congruente ao ângulo A linha, o ângulo B é congruente ao ângulo B linha e o ângulo C é congruente ao ângulo C linha.

Esses triângulos são semelhantes, pois os ângulos correspondentes são congruentes e as medidas dos lados correspondentes são proporcionais.

23. a) Vamos refazer o desenho reposicionando os triângulos.

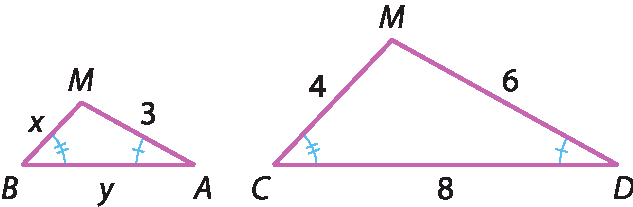
Ilustração. Triângulo escaleno ABM. O lado AB mede y, o lado BM mede x e o lado AM mede 3. Ao lado. triângulo escaleno CDM. O lado CD mede 8, o lado CM mede 4 e o lado DM mede 6. O ângulo B é congruente ao ângulo C, o ângulo A é congruente ao ângulo D.

Observe que os triângulos são semelhantes pelo caso ângulo ângulo. Assim, temos:

\frac{B M}{C M} = \frac{M A}{M D} = \frac{B A}{C D} \Rightarrow \frac{x}{4} = \frac{3}{6} = \frac{y}{8}

Então:

\frac{x}{4} = \frac{3}{6}

⇒ 6x = 12 ⇒ x = 2

\frac{3}{6} = \frac{y}{8}

⇒ 6y = 24 ⇒ y = 4

23. b) Vamos refazer o desenho reposicionando os triângulos.

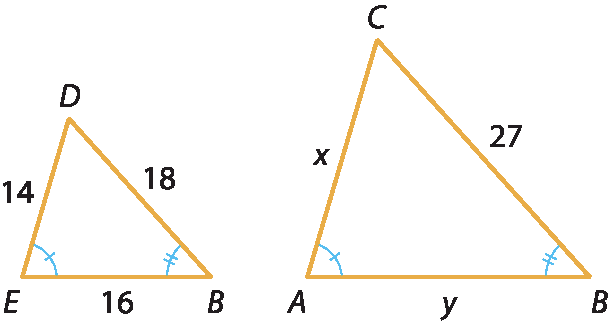
Ilustração. Triângulo escaleno BDE. O lado BD mede 18, o lado BE mede 16 e o lado DE mede 14. Ao lado, triângulo escaleno ABC, o lado AB mede y, o lado BC mede 27 e o lado AC mede x. O ângulo E é congruente ao ângulo A e o ângulo B é congruente ao ângulo B.

Os triângulos são semelhantes pelo caso ângulo ângulo. Assim, temos:

\frac{A C}{E D} = \frac{A B}{E B} = \frac{C B}{D B} \Rightarrow \frac{x}{14} = \frac{y}{16} = \frac{27}{18}

Então:

\frac{x}{14} = \frac{27}{18}

⇒ 18x = 378 ⇒ x = 21

\frac{y}{16} = \frac{27}{18}

⇒ 18y = 432 ⇒ y = 24

23. c) Vamos refazer o desenho reposicionando os triângulos.

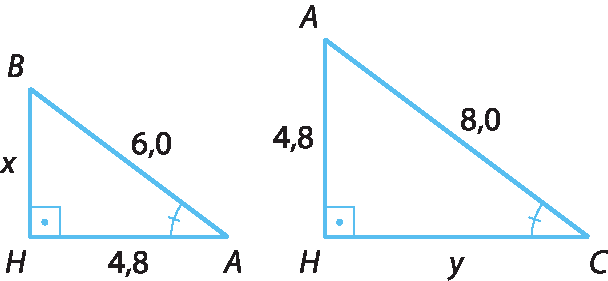
Ilustração. Triângulo retângulo ABH, retângulo em H, o lado AB mede 6,0; o lado AH mede 4,8 e o lado BH mede x. Ao lado, triângulo retângulo ACH, retângulo em H, o lado AC mede 8,0; o lado AH mede 4,8 e o lado CH mede y. O ângulo HAB é congruente ao ângulo HCA.

Observe que esses triângulos são semelhantes pelo caso ângulo ângulo. Assim, temos:

\frac{B H}{A H} = \frac{B A}{A C} = \frac{H A}{H C} \Rightarrow \frac{x}{4, 8} = \frac{6, 0}{8, 0} = \frac{4, 8}{y}

Então:

\frac{x}{4, 8} = \frac{6, 0}{8, 0}

⇒ 8,0x = 28,8 ⇒ x = 3,6

\frac{6, 0}{8, 0} = \frac{4, 8}{y}

⇒ 6,0y = 38,4 ⇒ y = 6,4

Página sessenta e cinco

24. a) Vamos refazer o desenho mudando a posição dos triângulos.

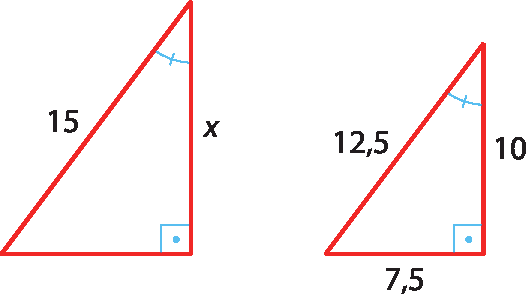
Ilustração. Triângulo retângulo, cuja hipotenusa mede 15 e um cateto mede x Ao lado, triângulo retângulo cuja hipotenusa mede 12,5, cateto correspondente ao cateto do outro triângulo mede 10; e o outro cateto mede 7,5.

Como os triângulos são semelhantes pelo caso ângulo ângulo, temos:

\frac{15}{12, 5} = \frac{x}{10}

⇒ 12,5x = 150 ⇒ x = 12

24. b) Vamos refazer o desenho mudando a posição dos triângulos.

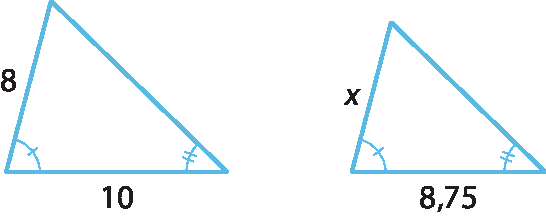
Ilustração. Triângulo cuja base mede 10, lado da esquerda mede 8, ângulos da base estão destacados. Ao lado, triângulo cuja base mede 8,75, lado da esquerda mede x, ângulos da base estão destacados.

Como os triângulos são semelhantes pelo caso ângulo ângulo, temos:

\frac{8}{x} = \frac{10}{8, 75}

⇒ 10x = 70 ⇒ x = 7

24. c) Vamos refazer o desenho mudando a posição dos triângulos.

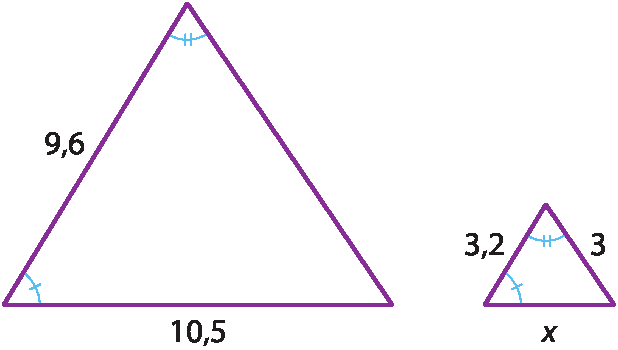
Ilustração. Triângulo cuja base mede 10,5 e o lado da esquerda mede 9,6, ângulo formado pela base e o lado da esquerda está destacado, ângulo oposto à base está destacado. Ao lado, triângulo cuja base mede x, o lado da esquerda mede 3,2 e o lado da direita mede 3. Ângulo formado pela base e o lado da esquerda está destacado, ângulo oposto à base está destacado.

Como os triângulos são semelhantes pelo caso ângulo ângulo, temos:

\frac{9, 6}{3, 2} = \frac{10, 5}{x}

⇒ 9,6x = 33,6 ⇒ x = 3,5

24. d) Vamos refazer o desenho mudando a posição dos triângulos.

Ilustração. Triângulo retângulo de catetos de medida 12 e 9,0, e hipotenusa de medida 15. Ao lado, triângulo retângulo de catetos medindo 6 e x.

Como os triângulos são semelhantes pelo caso ângulo ângulo, temos:

\frac{12}{6} = \frac{9}{x}

⇒ 12x = 54 ⇒ x = 4,5

25. a) Vamos refazer o desenho separando os dois triângulos.

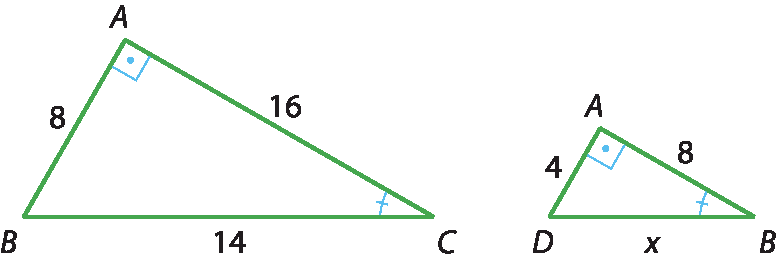
Ilustração. Triângulo retângulo ABC, retângulo em A, o cateto AB mede 8, o cateto AC mede 16 e a hipotenusa BC mede 14. Ao lado, triângulo retângulo ADB, retângulo em A, o cateto AD mede 4, o cateto AB mede 8 e a hipotenusa DB mede x. Ângulo ACB congruente ao ângulo ABD.

Observe que os dois triângulos têm dois lados correspondentes de medidas de comprimento proporcionais, e que os ângulos compreendidos por esses lados são congruentes (

\hat{A}

= 90graus). Então, pelo caso lado ângulo lado, esses triângulos são semelhantes. Assim, temos:

\frac{B A}{D A} = \frac{A C}{A B} = \frac{B C}{D B} \Rightarrow \frac{8}{4} = \frac{16}{8} = \frac{14}{x} \Rightarrow \frac{8}{4} = \frac{14}{x}

⇒

⇒ 8x = 56 ⇒ x = 7

25. b) Vamos refazer o desenho separando os dois triângulos.

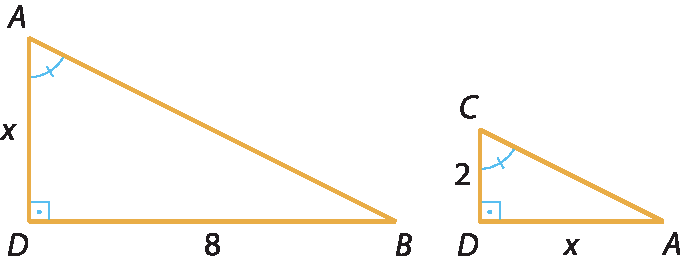
Ilustração. Triângulo retângulo ABD retângulo em D, cateto AD mede x, cateto DB mede 8. Ao lado, triângulo retângulo CDA, retângulo em D, cateto CD mede 2, cateto DA mede x. ângulo DAB congruente ao ângulo DCA.

Note que

B \hat{A} D ≃ A \hat{C} D

B \hat{A} D ≃ A \hat{C} D

Logo, pelo caso ângulo ângulo, concluímos que △á dê bê ~ △cê dê á.

\frac{A D}{C D} = \frac{D B}{D A} \Rightarrow \frac{x}{2} = \frac{8}{x}

⇒ x2 = 16 ⇒ x = ±

\sqrt{16}

⇒

⇒ x = +4 ou x = ‒4

Como uma medida de comprimento não deve ser negativa, nesse caso, x = 4.

26.

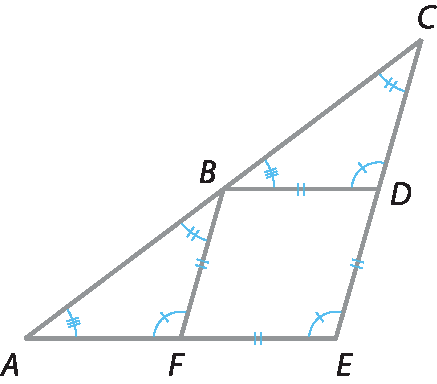
Ilustração. Triângulo ACE. Ponto D sobre o lado CE, ponto F sobre o lado AE, ponto B sobre lado AC, formando o quadrado BDEF. Destaque dos ângulos no triângulo BCD e dos ângulos no triângulo ABF.

Como

\bar{A E} // \bar{B D}

, verificamos que

F \hat{A} B ≃ D \hat{B} C

F \hat{B} A ≃ D \hat{C} B

. Analogamente,

B \hat{D} C ≃ A \hat{E} C

. E como

\bar{B F} // \bar{C E}

, verificamos que

A \hat{F} B ≃ A \hat{E} C

. Portanto:

á cê ê ~

á bê éfe,

á cê ê ~

BCD,

BCD ~

á bê éfe. Como F é o ponto médio de

\bar{A E}

, então á éfe = éfe ê = BD. Logo,

BCD ≅

á bê éfe.

27. Apresentamos um exemplo de triângulos semelhantes.

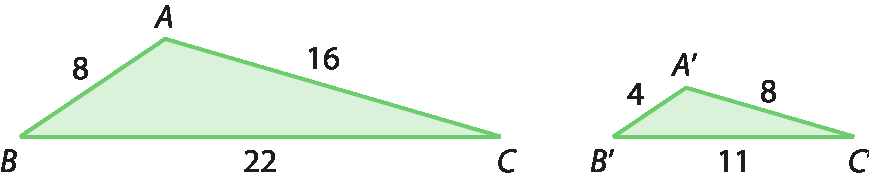
Ilustração. Triângulo ABC. Medidas AB: 8. AC: 16. BC: 22. Ao lado, triângulo A linha, B linha C linha com medidas: A linha B linha: 4. A linha C linha: 8. B linha C linha: 11.

Como os três lados correspondentes têm medidas de comprimento proporcionais, podemos concluir, pelo caso LLL, que os dois triângulos são semelhantes.

\frac{8}{4} = \frac{16}{8} = \frac{22}{11} = 2

Página sessenta e seis

Pense mais um pouco

Página 118

Os triângulos á cê ê e ABD são semelhantes. Portanto:

\frac{A C}{A B} = \frac{6 + 3 \sqrt{2}}{3 \sqrt{2}} = \frac{(6 + 3 \sqrt{2}) \cdot 3 \sqrt{2}}{3 \sqrt{2} \cdot 3 \sqrt{2}} = \frac{18 \sqrt{2} + 9 \cdot 2}{9 \cdot 2}

\frac{18 \sqrt{2} + 18}{18} = 1 + \sqrt{2}

Assim:

\frac{E A}{D A} = \frac{E D + 4}{4} = 1 + \sqrt{2} \Rightarrow E D + 4 = 4 \cdot (1 + \sqrt{2})

⇒

E D = 4 + 4 \sqrt{2} - 4 \Rightarrow E D = 4 \sqrt{2}

Os triângulos ABE e ACF são semelhantes. Portanto:

\frac{A F}{A E} = \frac{A C}{A B} \Rightarrow \frac{A F}{4 + E D} = \frac{6 + 3 \sqrt{2}}{3 \sqrt{2}}

⇒

\frac{A F}{4 + 4 \sqrt{2}} = \frac{6 + 3 \sqrt{2}}{3 \sqrt{2}} \Rightarrow

⇒

A F \cdot 3 \sqrt{2} = (6 + 3 \sqrt{2}) \cdot (4 + 4 \sqrt{2}) \Rightarrow

⇒

A F \cdot 3 \sqrt{2} = 24 + 24 \sqrt{2} + 12 \sqrt{2} + 12 \cdot 2 \Rightarrow

⇒

A F \cdot 3 \sqrt{2} = 48 + 36 \sqrt{2} \Rightarrow A F = \frac{48 + 36 \sqrt{2}}{3 \sqrt{2}} \Rightarrow

⇒

A F = \frac{(48 + 36 \sqrt{2}) \cdot 3 \sqrt{2}}{3 \sqrt{2} \cdot 3 \sqrt{2}} \Rightarrow

⇒

A F = \frac{144 \sqrt{2} + 108 \cdot 2}{9 \cdot 2} \Rightarrow

⇒

A F = \frac{144 \sqrt{2} + 216}{18} \Rightarrow A F = 8 \sqrt{2} + 12

Logo,

\bar{A F}

mede

(8 \sqrt{2} + 12) cm

Para saber mais

Página 126 e 127

1. O mapa construído deve ter as medidas com o dôbro das medidas do mapa original. O segmento que representa a escala no mapa original indica uma distância de 725 quilômetros na realidade; assim, no mapa ampliado, um segmento de mesma medida de comprimento representará uma distância de 362,5 quilômetros na realidade.

2. Nesse caso, o mapa será reduzido, e as medidas do novo mapa devem ter a metade das medidas do mapa original.

Trabalhando a informação

Páginas 128 e 129

1. a) Não, a maior parte é formada por adultos de 60 a 64 anos.

1. b) Maior, pois a população vai envelhecer, tendo a maior parte formada por idosos.

1. c) Resposta pessoal. Uma possível resposta é que sim, a mudança prevista no perfil da população brasileira afetará a atual situação previdenciária brasileira, pois haveria menos pessoas contribuindo e mais usuários utilizando esses recursos.

2. Resposta pessoal. Uma possível resposta é que as diferenças se concentram principalmente na distribuição do número de jovens (no Norte é maior) e no número de adultos (no Sul é maior). Além disso, existem mais pessoas idosas no Sul.

Exercícios complementares

1. a) Verdadeira, pois triângulos congruentes têm ângulos correspondentes de medidas iguais e lados correspondentes de medidas iguais; logo a razão de semelhança é 1.

1. b) Falsa, pois triângulos semelhantes podem ter as medidas de seus lados correspondentes proporcionais, mas apresentarem razão de semelhança diferente de 1, então, nesse caso, as medidas dos lados correspondentes são diferentes; portanto esses triângulos são semelhantes, mas não são congruentes.

1. c) Verdadeira, basta observar o caso LAL de semelhança de triângulos.

2. Seja d a medida da largura do rio; como as margens são paralelas, podemos obter dois triângulos semelhantes.

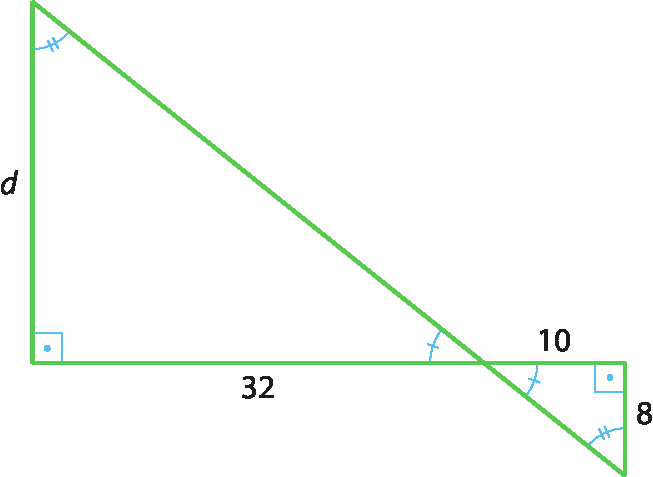
Ilustração. Triângulo retângulo de catetos com medida d e 32. Prolongando o cateto de emedida 32, triângulo retângulo com cateto de medida 10, e o outro cateto de medida 8. Os dois trângulos tem um ângulo oposto pelo vértice.

Logo:

\frac{d}{8} = \frac{32}{10}

⇒ 10d = 32 ⋅ 8 ⇒ d = 25,6

Portanto, o inteiro mais próximo é 26.

3. A medida da altura h do poste, em centímetro, é dada por:

\frac{180}{60} = \frac{h}{200}

⇒ 200 ⋅ 180 = 60h ⇒ h =

\frac{36 000}{60}

⇒ h = 600

Então, a nova medida S do comprimento da sombra da pessoa, em centímetro, será dada por:

\frac{180}{S} = \frac{600}{150}

⇒ 150 ⋅ 180 = 600S ⇒ S =

\frac{27 000}{600}

⇒ S = 45

Portanto, o comprimento da sombra da pessoa passará a medir 45 centímetros.

Alternativa b.

5. Vamos refazer o desenho separando os dois triângulos.

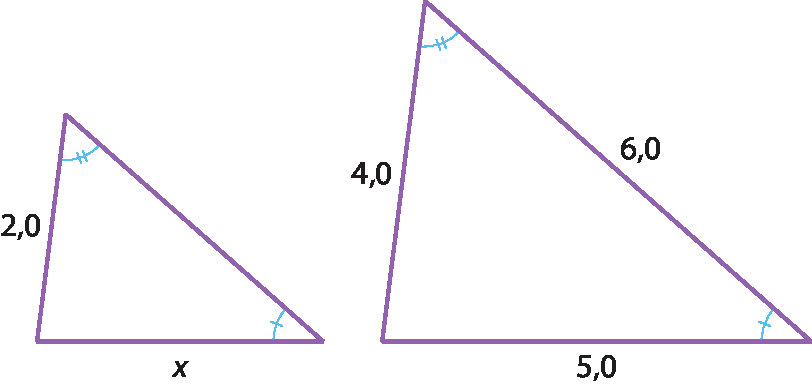
Ilustração. Triângulo com lados de medidas 2,0 e x. Ao lado, triângulo semelhante com lados de medidas 4,0; 5,0 e 6,0

Sendo x a medida do comprimento da estrada jóta bê 12, em quilômetro, temos:

\frac{2, 0}{x} = \frac{4, 0}{5, 0}

⇒ 4,0 ⋅ x = 2,0 ⋅ 5,0 ⇒ x = 2,5

Página sessenta e sete

Portanto, a medida do comprimento da estrada jóta bê 12 é 2,5 quilômetros.

6. Como os triângulos são semelhantes:

\frac{15}{a} = \frac{20}{b} = \frac{25}{c} ≃ \frac{60}{45}

Então:

\frac{15}{a} ≃ \frac{60}{45} \Rightarrow a ≃ 11

\frac{20}{b} ≃ \frac{60}{45} \Rightarrow b ≃ 15

\frac{25}{c} ≃ \frac{60}{45} \Rightarrow c ≃ 19

Portanto, os lados do triângulo medem aproximadamente 11 centímetros, 15 centímetros e 19 centímetros.

7. Os triângulos representados na figura são semelhantes pelo caso AA. Assim, sendo d a medida da distância entre as árvores A e B, em passos, temos:

\frac{d}{30} = \frac{60}{25}

⇒ 25d = 60 ⋅ 30 ⇒ d = 72

Como a medida do comprimento do passo de Marcelo é 75 centímetros = 0,75 métro, a distância entre as árvores mede 54 métros.

72 ⋅ 0,75 = 54

8. Seja k a razão de semelhança:

k = \frac{48}{60} = \frac{4}{5}

Portanto:

\frac{4}{5} = \frac{x}{25}

⇒ 5x = 4 ⋅ 25 ⇒ x = 20

O maior lado do triângulo menor mede 20 centímetros.

9. Podemos representar o problema pelo esquema a seguir.

Ilustração. Triângulo retângulo ABC, retângulo em B. Lado BC mede 4,0 metros. Ponto D sobre cateto AB, ponto E sobre hipotenusa AC., formando o triângulo retângulo ADE, retângulo em D, cateto DE mede 1,5 metro e hipotenusa AE mede 12,3 metros. Segmento EC mede x.

Os triângulos á bê cê e á dê é são semelhantes pelo caso ângulo ângulo. Portanto:

\frac{12, 3}{12, 3 + x} = \frac{1, 5}{4, 0}

⇒ 1,5 ⋅ (12,3 + x) = 12,3 ⋅ 4,0 ⇒

⇒ 18,45 + 1,5x = 49,2 ⇒ 1,5x = 30,75 ⇒ x = 20,5

Portanto, a pessoa ainda deve caminhar 20,5 métros.

10. Como há dois ângulos correspondentes congruentes nos dois triângulos, eles são semelhantes pelo caso ângulo ângulo. Assim:

\frac{30}{(30 + a)} = \frac{6}{10}

⇒ 180 + 6a = 300 ⇒ 6a = 120 ⇒ a = 20

Portanto, o segmento

\bar{C_{1} C_{2}}

mede 20 centímetros.

Verificando

1. Como a ampliação foi feita na razão 1 para 5 e a medida do perímetro do ambiente no esboço é 26 centímetros, sendo x a medida do perímetro do ambiente a ser decorado, em centímetro, temos:

\frac{26}{x} = \frac{1}{5}

⇒ x = 130

Alternativa d.

2. Para que os polígonos sejam semelhantes, seus lados correspondentes devem ser proporcionais e os ângulos correspondentes, congruentes. Assim:

\frac{4}{6} = \frac{1}{y} = \frac{x}{9}

Logo:

\frac{4}{6} = \frac{1}{y} \Rightarrow 4 y = 6 \Rightarrow y = \frac{6}{4} = \frac{3}{2}

\frac{4}{6} = \frac{x}{9} \Rightarrow 6 x = 36 \Rightarrow x = \frac{36}{6} \Rightarrow x = 6

Alternativa a.

3. Para os triângulos serem semelhantes, seus lados correspondentes devem ser proporcionais. Assim:

\frac{3}{a} = \frac{4}{20} = \frac{5}{b}

Logo:

\frac{3}{a} = \frac{4}{20}

⇒ 4a = 60 ⇒ a = 15

\frac{4}{20} = \frac{5}{b}

⇒ 4b = 100 ⇒ b = 25

Alternativa a.

4. Para serem semelhantes, além de os ângulos correspondentes serem congruentes, os triângulos precisam ter os lados correspondentes proporcionais; nesse caso, eles não têm.

\frac{12}{8} = \frac{6}{4} = \frac{3}{2} \neq \frac{10}{5} = \frac{2}{1}

Ou seja:

\frac{8}{5}

≠

\frac{12}{10}

Alternativa c.

\frac{8, 6}{8, 6 ‒ 2, 5} = \frac{7, 2}{x}

⇒ 8,6x = 7,2 ⋅ 6,1 ⇒ x =

\frac{43, 92}{8, 6}

⇒

⇒ x ≃ 5,1

Alternativa b.

6. Os triângulos são semelhantes pelo caso ângulo ângulo, pois têm dois pares de ângulos correspondentes respectivamente congruentes.

Alternativa d.

7. Para que dois triângulos sejam semelhantes pelo caso lado lado lado, seus lados correspondentes devem ter medidas de comprimento proporcionais.

Alternativa b.

Diversificando

2. Vamos construir um esquema da câmara escura de orifício construída por Felipe.

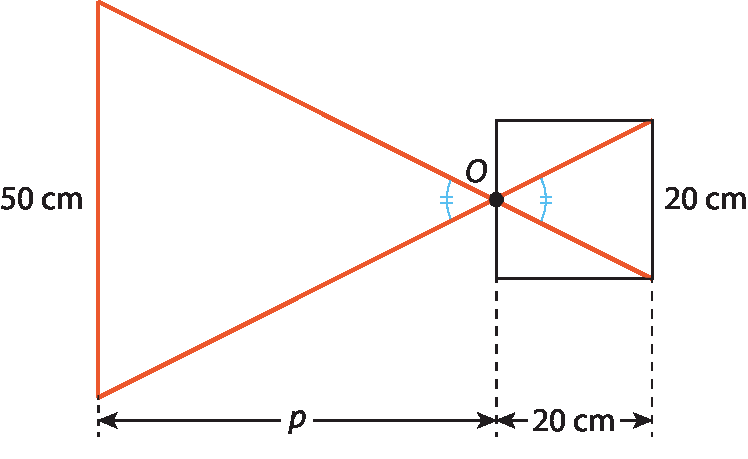
Ilustração. Quadrado de lado 20 centímetros. Ponto O no centro do lado esquerdo do quadrado. Segmento de reta com extremidade no vértice superior direito do quadrado, passa pelo ponto O. Segmento de reta com extremidade no vértice inferior direito do quadrado, passa pelo ponto O. Os dois segmentos que passam por O são lados de um triângulo cuja base mede 50 centímetros. Essa base é paralela ao lado esquerdo do quadrado. A distância entre um vértice da base do triângulo e o vértice inferior esquerdo do quadrado mede p.

Página sessenta e oito

Considerando os triângulos congruentes do esquema, obtemos:

\frac{50}{20} = \frac{p}{20} \Rightarrow 20 p = 20 \cdot 50 \Rightarrow p = 50

Portanto, o quadro deve ficar a no mínimo 50 centímetros do orifício da câmara para aparecer projetado no papel por inteiro.

Capítulo 6 ‒ Um pouco mais sobre Estatística

• Objetivos do capítulo e justificativas

• Reconhecer e determinar medidas estatísticas: média, moda, mediana e desvio médio.

• Resolver e elaborar problemas envolvendo medidas estatísticas.

• Analisar tabelas e gráfico pictórico.

• Analisar a escolha do gráfico mais adequado para apresentar determinado conjunto de dados.

• Efetuar cálculo de probabilidade.

• Resolver problemas envolvendo cálculo de porcentagens.

Este capítulo retoma e amplia assuntos tratados no campo da Estatística ao longo dos anos anteriores. Trabalha as medidas de tendência central (média, moda e mediana) e apresenta o desvio médio absoluto, uma medida de dispersão. Esses conceitos contribuem para que os estudantes desenvolvam habilidades para interpretar e analisar dados em uma variedade de contexto, além de contribuir para o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2, 3, 4 e 6.

O cálculo de probabilidades de eventos dependentes e independentes é explorado na seção Para saber mais com a temática jogos, favorecendo o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2, 3, 4 e 6.

O trabalho com juro composto contribui para a formação cidadã dos estudantes e contribui para o trabalho com o Tema Contemporâneo Transversal educação financeira. Ao explorar o uso de planilhas eletrônicas, contribui-se para o desenvolvimento das competências gerais 5 e 6 e das competências específicas 5 e 7.

O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois permitem aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação as atividades propostas.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah dois zero) Reconhecer, em experimentos aleatórios, eventos independentes e dependentes e calcular a probabilidade de sua ocorrência, nos dois casos.

(ê éfe zero nove ême ah dois três) Planejar e executar pesquisa amostral envolvendo tema da realidade social e comunicar os resultados por meio de relatório contendo avaliação de medidas de tendência central e da amplitude, tabelas e gráficos adequados, construídos com o apoio de planilhas eletrônicas.

Este capítulo amplia e aprofunda os conhecimentos sobre as medidas estatísticas tratadas no 8º ano (ê éfe zero oito ême ah dois cinco), assunto relativo à Unidade Temática Probabilidade e estatística, que favorece o desenvolvimento das habilidades (ê éfe zero nove ême ah dois dois) e (ê éfe zero nove ême ah dois três).

Os conhecimentos trabalhados neste capítulo constituem subsídios para a compreensão da continuidade dos estudos de Estatística no Ensino Médio.

Além disso, ainda nessa Unidade Temática, trabalha-se o cálculo de probabilidade na seção Para saber mais, ampliando conhecimentos desenvolvidos no 8º ano (ê éfe zero oito ême ah dois dois) e contribuindo para o trabalho com a habilidade (ê éfe zero nove ême ah dois zero).

Promove-se também a articulação com a Unidade Temática Números ao apresentar o cálculo de juros compostos envolvendo taxas percentuais, favorecendo o desenvolvimento da habilidade (ê éfe zero nove ême ah zero cinco).

• Comentários e resoluções

Exercícios propostos

1. A média aritmética é:

\frac{5 \cdot 0 + 15 \cdot 1 + 10 \cdot 2 + 15 \cdot 3 + 5 \cdot 4}{5 + 15 + 10 + 15 + 5}

\frac{0 + 15 + 20 + 45 + 20}{50} = \frac{100}{50} = 2

Como a maior frequência (15) ocorre para dois números de irmãos, concluímos que a amostra tem duas modas: 1 irmão e 3 irmãos. Escrevendo o rol de 50 termos, os termos centrais seriam o 25º (último da primeira metade dos dados) e o 26º (primeiro da segunda metade dos dados). Como há 20 dados (5 + 15 = 20) sobre o número de irmãos menor do que 2 e 30 dados (5 + 15 + 10 = 30) sobre o número de irmãos menor do que 3, conclui-se que, tanto o 25º quanto o 26º termos do rol, são iguais a 2. Logo a mediana é:

\frac{2 + 2}{2} = 2

Alternativa a.

2. a)

\frac{7, 0 + 5, 5 + 4, 0 + 6, 0 + 8, 5}{5} = \frac{31}{5} = 6, 2

2. b) Em ordem crescente, as notas dos estudantes foram 4,0 < 5,5 < 6,0 < 7,0 < 8,5; portanto, a nota mediana é a nota central da sucessão, ou seja, 6,0. Como todas as notas têm frequência 1, o conjunto de dados não tem moda.

2. c) Apenas 3 estudantes.

4,0 < 6,2; 5,5 < 6,2; 6,0 < 6,2