Página sessenta e nove

Parte 6

4. A média aritmética é:

\frac{4 \cdot 1 + 1 \cdot 2 + 2 \cdot 4 + 2 \cdot 5 + 1 \cdot 6}{4 + 1 + 2 + 2 + 1}

\frac{4 + 2 + 8 + 10 + 6}{10} = \frac{30}{10} = 3

Escrevendo o rol de 10 termos, os termos centrais seriam o 5º e o 6º: [1, 1, 1, 1, 2, 4, 4, 5, 5, 6]

Logo, a mediana é:

\frac{2 + 4}{2} = 3

A moda é 1, pois ocorre com a maior frequência (4).

Alternativa b.

6. a) Entre as 24 notas de cada um, verifica-se que:

• a nota mais frequente de Caio, com 6 ocorrências, é 7,5;

• a nota mais frequente de Cauê, com 8 ocorrências, é 7,5.

6. b) Como todas as 4 notas de Caio em Língua Portuguesa foram iguais a 7,0, esse conjunto de dados não tem moda. Como todas as 6 notas de Cauê no 3º bimestre foram iguais a 7,5, esse conjunto de dados também não tem moda.

6. c) Caio:

\frac{9, 5 + 9, 5}{2} = 9, 5

e Cauê:

\frac{7, 5 + 8, 0}{2} = 7, 75

6. d) Caio só tem uma nota abaixo da média, a nota 5,5 em Inglês, mas como nessa disciplina sua média foi 6,125, Caio não foi reprovado.

\frac{6, 0 + 5, 5 + 6, 5 + 6, 5}{4} = \frac{24, 5}{4}

= 6,125

Cauê tem notas abaixo da média em todas as disciplinas, exceto Ciências, mas suas médias foram as seguintes:

Língua Portuguesa:

\frac{5, 0 + 7, 5 + 7, 5 + 9, 0}{4} = \frac{29, 0}{4} = 7, 25

Inglês:

\frac{4, 5 + 6, 0 + 7, 5 + 6, 0}{4} = \frac{24, 0}{4} = 6, 0

História:

\frac{5, 5 + 7, 0 + 7, 5 + 8, 5}{4} = \frac{28, 5}{4} = 7, 125

Geografia:

\frac{5, 0 + 8, 0 + 7, 5 + 9, 0}{4} = \frac{29, 5}{4} = 7, 375

Matemática:

\frac{5, 5 + 8, 0 + 7, 5 + 8, 0}{4} = \frac{29, 0}{4} = 7, 25

Portanto, Cauê também não foi reprovado em nenhuma disciplina.

6. e) Em Geografia, a média de Caio foi:

\frac{8, 0 + 7, 5 + 8, 0 + 7, 5}{4} = \frac{31, 0}{4} = 7, 75

Assim, para o desvio médio absoluto das notas de Caio em Geografia, temos:

\frac{|8, 0 - 7, 75| + |7, 5 - 7, 75| + |8, 0 - 7, 75| + |7, 5 - 7, 75|}{4}

\frac{0, 25 + 0, 25 + 0, 25 + 0, 25}{4} = 0, 25

Para o desvio médio absoluto das notas de Cauê em Geografia, temos:

\frac{|5, 0 ‒ 7, 375| + |8, 0 ‒ 7, 375| + |7, 5 ‒ 7, 375| + |9, 0 ‒ 7, 375|}{4}

\frac{2, 375 + 0, 625 + 0, 125 + 1, 625}{4} = \frac{4, 75}{4} = 1, 1875

A média das notas de Caio no 1º bimestre é:

\frac{7, 0 + 6, 0 + 7, 5 + 8, 0 + 7, 5 + 9, 5}{6} = \frac{45, 5}{6} ≃ 7, 6

A média das notas de Cauê no 1º bimestre é:

\frac{5, 0 + 4, 5 + 5, 5 + 5, 0 + 6, 0 + 5, 5}{6} = \frac{31, 5}{6} = 5, 25

Então, para o desvio médio absoluto das notas de Caio no 1º bimestre, temos:

\frac{|7, 0 ‒ 7, 6| + |6, 0 ‒ 7, 6| + |7, 5 ‒ 7, 6| + |8, 0 ‒ 7, 6| + |7, 5 ‒ 7, 6| + |9, 5 ‒ 7, 6|}{6}

\frac{0, 6 + 1, 6 + 0, 1 + 0, 4 + 0, 1 + 1, 9}{6} = \frac{4, 7}{6} ≃ 0, 8

Para o desvio médio absoluto das notas de Cauê no 1º bimestre, temos:

\frac{|5, 0 ‒ 5, 25| + |4, 5 ‒ 5, 25| + |5, 5 ‒ 5, 25| + |5, 0 ‒ 5, 25| + |6, 0 ‒ 5, 25| + |5, 5 ‒ 5, 25|}{6}

= \frac{0, 25 + 0, 75 + 0, 25 + 0, 25 + 0, 75 + 0, 25}{6} = \frac{2, 5}{6} ≃ 0, 4

Página setenta

6. f) Como a regularidade é maior quando o desvio médio absoluto é menor, em Geografia, o mais regular foi Caio. No 3º bimestre, o mais regular foi Cauê.

6. g) A média das notas de Caio em Língua Portuguesa é:

\frac{7, 0 + 7, 0 + 7, 0 + 7, 0}{4} = \frac{28, 0}{4} = 7, 0

A média das notas de Cauê em Língua Portuguesa é:

\frac{5, 0 + 7, 5 + 7, 5 + 9, 0}{4} = \frac{29, 0}{4} = 7, 25

Então, para o desvio médio absoluto das notas de Caio em Língua Portuguesa, temos:

\frac{|7, 0 - 7, 0| + |7, 0 - 7, 0| + |7, 0 - 7, 0| + |7, 0 - 7, 0|}{4}

\frac{0 + 0 + 0 + 0}{4} = 0

Para o desvio médio absoluto das notas de Cauê em Língua Portuguesa, temos:

\frac{|5, 0 - 7, 25| + |7, 5 - 7, 25| + |7, 5 - 7, 25| + |9, 0 - 7, 25|}{4}

\frac{2, 25 + 0, 25 + 0, 25 + 1, 75}{4}

\frac{4, 5}{4} = 1, 125

6. h) A média das notas de Caio no 3º bimestre é:

\frac{7, 0 + 6, 5 + 8, 0 + 8, 0 + 7, 0 + 10}{6} = \frac{46, 5}{6} = 7, 75

A média das notas de Cauê no 3º bimestre é:

\frac{7, 5 + 7, 5 + 7, 5 + 7, 5 + 7, 5 + 7, 5}{6} = \frac{45, 0}{6} = 7, 5

Então, para o desvio médio absoluto das notas de Caio no 3º bimestre, temos:

\frac{|7, 0 - 7, 75| + |6, 5 - 7, 75| + |8, 0 - 7, 75| + |8, 0 - 7, 75| + |7, 0 - 7, 75| + |10 - 7, 75|}{6}

\frac{0, 75 + 1, 25 + 0, 25 + 0, 25 + 0, 75 + 2, 25}{6}

\frac{5, 5}{6} ≃ 0, 9 =

Para o desvio médio absoluto das notas de Cauê no 3º bimestre, temos:

\frac{|7, 5 ‒ 7, 5| + |7, 5 ‒ 7, 5| + |7, 5 ‒ 7, 5| + |7, 5 ‒ 7, 5| + |7, 5 ‒ 7, 5| + |7, 5 ‒ 7, 5|}{6} = \frac{0}{6} = 0

Trabalhando a informação

Páginas 142 e 143

Mês	Juro composto (jc)	Juro simples (js)	jc − js
Janeiro	50	50	0
Fevereiro	105	100	5
Março	165,5	150	15,5
Abril	232,05	200	32,05
Maio	305,255	250	55,255
Junho	385,7805	300	85,7805
Julho	474,35855	350	124,35855
Agosto	571,794405	400	171,794405
Setembro	678,9738455	450	228,9738455
Outubro	796,87123005	500	296,87123005
Novembro	926,558353055	550	376,558353055
Dezembro	1.069,2141883605	600	469,2141883605

Note que a diferença entre os juros composto e simples também aumenta cada vez mais.

2. Em 4 meses a dívida atinge o valor de R$ 2.073,60dois mil setenta e três reais e sessenta centavos, pois:

.1000 · (1 + 20%)4 = .1000 · (1 + 0,2)4 = .1000 · (1,2)4 = .1000 · 2,0736 = .2073,6

Exercícios complementares

1. Como dentre as 30 notas, apenas 9 são maiores do que 6,5, a probabilidade é

\frac{9}{30}

Alternativa b.

Página setenta e um

2. a) A nota 6,0 é a de maior frequência, com 5 ocorrências.

2. b)

\frac{6, 0 + 6, 0}{2} = 6, 0

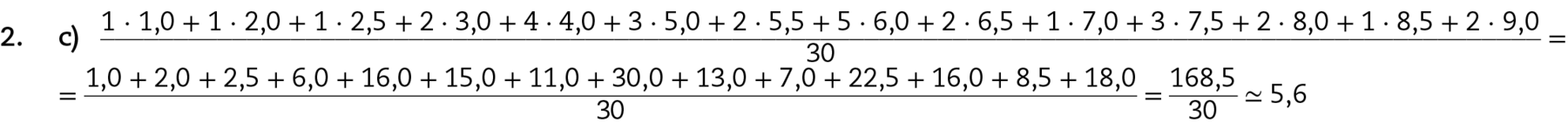
fração de numerador 1 vezes 1,0, mais 1 vezes 2,0 mais 1 vezes 2,5 mais 2 vezes 3,0, mais 4 vezes 4,0, mais 3 vezes 5,0 mais 2 vezes 5,5 mais 5 vezes 6,0 mais 2 vezes 6,5 mais 1 vezes 7,0 mais 3 vezes 7,5 mais 2 vezes 8,0 mais 1 vezes 8,5 mais 2 vezes 9,0, igual a fração de numerador: 1,0 mais 2,0 mais 2,5 mais 6,0 mais 16,0 mais 15,0 mais 11,0 mais 30,0, mais 13,0 mais 7,0 mais 22,5 mais 16,0 mais 8,5 mais 18,0, e de denominador: 30, igual a, 168,5 sobre 30, aproximadamente igual a 5,6

3. Respostas pessoais.

4. Resposta pessoal.

Andar	Número de pessoas no elevador
Térreo	4 − 0 = 4
1º andar	4 + 4 − 3 = 5
2º andar	5 + 1 − 1 = 5
3º andar	5 + 2 − 2 = 5
4º andar	5 + 2 − 0 = 7
5º andar	7 + 2 − 6 = 3

Portanto, a moda é 5.

Alternativa d.

Verificando

\frac{23 + 25 + 25 + 28 + 31 + 24 + 32 + 32 + 27 + 23}{10} = \frac{270}{10} = 27

Alternativa c.

2. A velocidade de maior frequência é 58, com 3 ocorrências.

Alternativa a.

3. Escrevendo o rol com os 10 dados do quadro e destacando as informações centrais, temos:

[23, 47, 48, 49, 72, 72, 74, 84, 271, 650]

Portanto, a mediana é:

\frac{72 + 72}{2} = 72

Alternativa b.

4. A média é:

\frac{15 \cdot 15 + 3 \cdot 16 + 2 \cdot 14}{20} = \frac{225 + 48 + 28}{20}

\frac{301}{20} = 15, 05

Portanto, o desvio médio é:

\frac{15 \cdot |15 - 15, 05| + 3 \cdot |16 - 15, 05| + 2 \cdot |14 - 15, 05|}{20}

\frac{0, 75 + 2, 85 + 2, 10}{20} = \frac{5, 70}{20} = 0, 285

Alternativa d.

5. Foram entrevistadas quinhentas e três pessoas (239 + 132 + 132 = 503). Portanto, a mediana das notas está na posição 252 quando as notas são organizadas em ordem crescente. Nessa organização, perceba que as primeiras duzentas e trinta e nove notas são 1, e as notas das posições 240 até 371 são 2. Portanto, a mediana é 2.

Alternativa c.

6. De acordo com o gráfico, a peça de roupa mais vendida pela loja é a camiseta, com 5 ocorrências; esse é o dado com maior frequência. Então, a peça mais vendida representa o conceito de moda.

Alternativa c.

7. Uma vez verificado o resultado do primeiro lançamento do dado, haverá uma em 6 possibilidades para o resultado do segundo lançamento. Portanto, a probabilidade é de

\frac{1}{6}

Alternativa b.

Página setenta e dois

8. Uma vez verificado o resultado do primeiro lançamento da moeda, haverá 1 em 2 possibilidades para o resultado do segundo lançamento. Portanto, a probabilidade é

\frac{1}{2}

= 0,5 = 50%.

Alternativa a.

9. A alternativa correta mais frequente é a c, com 3 ocorrências, sem contar a resposta deste teste. Porém, a resposta é pessoal, pois depende das respostas dadas pelos estudantes para os testes anteriores.

Capítulo 7 ‒ Equações do 2º grau

• Objetivos do capítulo e justificativas

• Reconhecer uma equação polinomial do 2º grau com uma incógnita.

• Identificar e determinar as raízes reais de uma equação do 2º grau com uma incógnita, quando existirem.

• Utilizar as propriedades da igualdade, na construção de procedimentos para resolver equações do 2º grau por meio de fatorações, pelo método de completar quadrados e pelo uso da fórmula resolutiva.

• Discutir o significado das raízes de uma equação do 2º grau em confronto com a situação proposta.

• Resolver problemas que envolvem relações de proporcionalidade que podem ser representados por uma equação polinomial do 2º grau.

• Resolver problemas envolvendo volume de cubo e equação do 2º grau.

• Resolver e elaborar problemas que podem ser representados por equações polinomiais do 2º grau.

• Ler e analisar mapas anamórficos.

Ampliamos o estudo de equações polinomiais sistematizando o tratamento de uma equação do 2º grau com uma incógnita, analisando procedimentos variados de resolução de equações do 2º grau incompletas ou completas e suas aplicações na resolução de problemas, o que favorece o trabalho com as competências gerais 2 e 4 e com as competências específicas 1 e 4. O desenvolvimento dos temas permitirá aos estudantes desenvolver habilidades necessárias ao estudo das funções polinomiais do 2º grau.

Na seção Trabalhando a informação propomos uma atividade sobre a leitura de um cartograma. Atividades como a desta seção estimulam nos estudantes um olhar e uma ação que transcendem o campo da Matemática e contribuem para o desenvolvimento da competência geral 1 e das competências específicas 6 e 7.

O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois permitem aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação as atividades propostas.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah zero um) Reconhecer que, uma vez fixada uma unidade de comprimento, existem segmentos de reta cujo comprimento não é expresso por número racional (como as medidas de diagonais de um polígono e alturas de um triângulo, quando se toma a medida de cada lado como unidade).

(ê éfe zero nove ême ah zero quatro) Resolver e elaborar problemas com números reais, inclusive em notação científica, envolvendo diferentes operações.

(ê éfe zero nove ême ah zero oito) Resolver e elaborar problemas que envolvam relações de proporcionalidade direta e inversa entre duas ou mais grandezas, inclusive escalas, divisão em partes proporcionais e taxa de variação, em contextos socioculturais, ambientais e de outras áreas.

(ê éfe zero nove ême ah zero nove) Compreender os processos de fatoração de expressões algébricas, com base em suas relações com os produtos notáveis, para resolver e elaborar problemas que possam ser representados por equações polinomiais do 2º grau.

(ê éfe zero nove ême ah dois dois) Escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central.

Este capítulo tem foco em objetos de conhecimento da Unidade Temática Álgebra e amplia o estudo das equações, visando a preparar os alunos para a continuidade de estudos de Álgebra neste volume, no capítulo 10, e para os estudos do Ensino Médio.

Os conteúdos e as atividades propostos exploram tipos variados de equações do 2º grau e sistemas do 2º grau, com base nos conhecimentos construídos no 8º ano (ê éfe zero oito ême ah zero oito e ê éfe zero oito ême ah zero nove) e contribuem para o desenvolvimento da habilidade (ê éfe zero nove ême ah zero nove).

Neste capítulo, explora-se a Unidade Temática Geometria quando são utilizadas figuras geométricas para contextualizar os conceitos algébricos e a Unidade Temática Grandezas e medidas quando se utiliza o cálculo de área e de volume nesses mesmos contextos em diversos momentos, como na seção Pense mais um poucoreticências, que contribui para o trabalho com as habilidades (ê éfe zero nove ême ah zero um) e (ê éfe zero nove ême ah zero quatro).

Além disso, a articulação com a Unidade Temática Números e Probabilidade e estatística é promovida na seção Trabalhando a informação, que envolve cálculo de porcentagem na leitura e análise de cartogramas, contribuindo para o desenvolvimento das habilidades (ê éfe zero nove ême ah zero oito) e (ê éfe zero nove ême ah dois dois).

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Abertura

1. a) É interessante abordar em sala de aula que, mesmo nos esportes em que há variações de medidas, como o muái tái, as dimensões são iguais, e o ringue é quadrado.

b) Resposta pessoal. Possível resposta: Judô, ême ême á, muái tái.

Página setenta e três

Exercícios propostos

1. Durante a resolução dêsse exercício em sala de aula, deixe que os estudantes falem o que pensam ser a resposta correta para cada item. Assim pode-se diagnosticar eventuais dificuldades na leitura das equações e na interpretação das operações entre coeficientes e incógnitas.

1. a) Na equação 8x2 + 17x + 4 = 0, o maior expoente da incógnita x é 2, então a equação é do 2º grau. Os coeficientes são: a = 8 (coeficiente de x²); b = 17 (coeficiente de x); c = 4 (termo independente da equação).

1. b) Em equações como essa, pode acontecer de os estudantes acharem que o expoente de x é zero, pelo fato de x não aparecer elevado a nenhum número. Em casos como esse, o expoente da incógnita x é 1. Essa é uma equação do 1º grau.

1. c) O maior expoente da incógnita x é 2, mas essa incógnita é anulada porque seu coeficiente a é igual a 0. Então: 0 + 10x ‒ 8 = 0 ⇒ 10x ‒ 8 = 0

Portanto, essa é uma equação do 1º grau.

1. d) O maior expoente da incógnita y é 2, então a equação é do 2º grau. Os coeficientes são: a = ‒

\frac{1}{5}

(coeficiente de y²); b = 0 (coeficiente de x, que, não aparece na equação); e c = ‒25 (termo independente da equação).

1. e) O maior expoente da incógnita y é 2; então, a equação é do 2º grau. Os coeficientes são: a = 4 (coeficiente de y²); b = ‒ 5 (coeficiente de x); c = 0 (termo independente da equação).

1. f) O maior expoente da incógnita x é 2; então, a equação é do 2º grau. Os coeficientes são: a = 1 (coeficiente de x²); b = 0 (coeficiente de x, que, não aparece na equação); c = ‒ 9 (termo independente da equação).

2. a) 2x² ‒ 5x = ‒2 ⇒ 2x² ‒ 5x + 2 = ‒2 + 2 ⇒ 2x² ‒ 5x + 2 = 0

A equação é completa, pois a ≠ 0, b ≠ 0 e c ≠ 0.

2. b) x² + 6x = 2x + 3 ⇒ x² + 6x ‒ 2x ‒ 3 = 2x + 3 ‒ 2x ‒ 3 ⇒ x² + 6x ‒ 2x ‒ 3 = 0 ⇒ x² + 4x ‒ 3 = 0

A equação é completa, pois a ≠ 0, b ≠ 0 e c ≠ 0.

2. c) y² = 8y ⇒ y² ‒ 8y = 8y ‒ 8y ⇒ y² ‒ 8y = 0

A equação é incompleta, pois a ≠ 0, b ≠ 0 e c = 0.

2. d) ‒5x² = 30x + 40 ⇒ ‒ 5x² ‒ 30x ‒ 40 =

= 30x + 40 ‒ 30x ‒ 40 ⇒ ‒5x² ‒ 30x ‒ 40 = 0

A equação é completa, pois a ≠ 0, b ≠ 0 e c ≠ 0.

2. e) 3x ⋅ (x ‒ 2) = 2 ⋅ (2x ‒ 1) ⇒ 3x² ‒ 6x = 4x ‒ 2 ⇒

⇒ 3x² ‒ 6x ‒ 4x + 2 = 4x ‒ 2 ‒ 4x + 2 ⇒

⇒ 3x² ‒10x + 2 = 0

A equação é completa, pois a ≠ 0, b ≠ 0 e c ≠ 0.

2. f) (x + 4) ⋅ (x ‒ 4) = 5x ‒ 16 ⇒ x² ‒ 4x +4x ‒16 = 5x ‒ 16 ⇒ x² ‒ 4x + 4x ‒16 ‒5x + 16 = 5x ‒ 16 ‒ 5x + 16 ⇒ x² ‒ 4x + 4x ‒ 16 ‒ 5x + 16 = 0 ⇒ x² ‒ 5x = 0

A equação é incompleta, pois a ≠ 0, b ≠ 0 e c = 0.

4. A condição para que uma equação seja do 2º grau é que o coeficiente a seja diferente de zero. Assim, para que a equação (5n + 2)x² ‒ 4nx + n = 0 não seja do 2º grau, n deve ser igual a

‒ \frac{2}{5}

, pois:

(5n + 2) = 0 ⇒ 5n = ‒2 ⇒ n =

‒ \frac{2}{5}

5. a) Para que a equação não seja do 2º grau, então o coeficiente a tem que ser igual a zero.

Assim: (m + 3) = 0 ⇒ m = ‒3

5. b) Para que a equação seja do 2º grau, o coeficiente a tem que ser diferente de zero.

Então: (m + 3) ≠ 0 ⇒ m ≠ ‒3

5. c) Para que a equação seja do 2º grau, observamos no item b que m ≠ ‒ 3. Para que seja completa, então o coeficiente b e o termo independente devem ser diferente de zero. Para o coeficiente b ser diferente de zero, m deve ser diferente de

\frac{1}{2}

, pois:

(2m ‒ 1) ≠ 0 ⇒ 2m ≠ 1 ⇒ m ≠

\frac{1}{2}

Para o termo independente ser diferente de zero, então (m + 4) ≠ 0 ⇒ m ≠ ‒4. Portanto, para que a equação seja do 2º grau e completa, m ≠ ‒ 3, m ≠

\frac{1}{2}

e m ≠ ‒4.

5. d) Para que seja do 2º grau, sabemos pelo item b que m tem que ser diferente de ‒3. Agora, para que seja incompleta, o coeficiente b ou o coeficiente c tem que ser igual a zero. Então, ou m =

\frac{1}{2}

(p o i s (2 m ‒ 1) = 0 \Rightarrow 2 m = 1 \Rightarrow m = \frac{1}{2})

, ou m = ‒4 (pois (m + 4) = 0 ⇒ m = ‒4).

6. a) A medida da área da região em azul é dada pela diferença entre a medida da área de um quadrado de lados 14 e de um retângulo de lados 2x e x, ou seja, um quadrado de medida de área 196 (14 ⋅ 14 = 196) e retângulo de medida de área 2x² (2x ⋅ x = 2x²). Assim, a medida da área da parte azul será dada por a = 196 ‒ 2x².

6. b) Quando a medida da área da parte azul for 124, então x = 6. Substituindo a por 124 em a = 196 ‒ 2x², obtemos:

124 = 196 ‒ 2x² ⇒ 2x² = 196 ‒ 124 ⇒

⇒ 2x² = 72 ⇒ x² =

\frac{72}{2}

⇒ x² = 36 ⇒ x = 6

7. a)

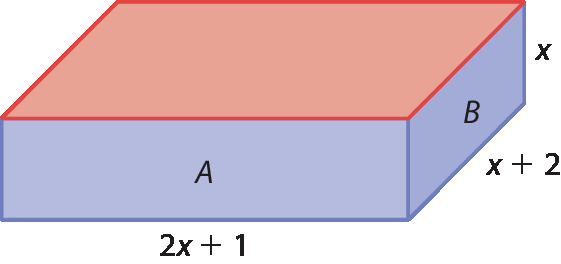
Ilustração. Bloco retangular com 3 faces visíveis, a face superior vermelha e as faces laterais azuis. Em uma das faces laterais cota A e na outra cota B. A medida do comprimento da face com cota A está indicada por 2x mais 1. A medida do comprimento da face com cota B está indicada por x mais 2 e a medida da altura da face com cota B está indicada pela letra x.

As faces laterais são compostas por duas regiões retangulares, como a indicada na figura por a, de medida de área 2x² + x, pois (2x + 1) ⋅ x = 2x² + x; e de duas regiões retangulares, como a indicada na figura por B, de medida de área x² + 2x, pois (x + 2) ⋅ x = x² + 2x. Então, a expressão da soma das medidas das áreas das faces laterais será dada por 6x² + 6x.

2 ⋅ (2x² + x) + 2 ⋅ (x² + 2x) = 4x² + 2x + 2x² + 4x = 6x² + 6x

Página setenta e quatro

7. b) Auxilie os estudantes a encontrar a medida das dimensões do retângulo destacado em vermelho. Se necessário, utilize planificações. Se ocorrer como o esperado, eles perceberão que a face destacada em vermelho é um retângulo de base de medida dada por 2x + 1 e altura de medida dada por x + 2. Assim, a expressão da medida da área da face destacada em vermelho é 2x² + 5x + 2.

(2x + 1) ⋅ (x + 2) = 2x² + 4x + 1x + 2 = 2x² + 5x + 2

7. c) Pelo item a, a expressão da soma das medidas das áreas das faces laterais é dada por 6x² + 6x; portanto, a equação correspondente em relação a x será:

6x² + 6x ‒ 880 = 0

6x² + 6x = 880 ⇒ 6x² + 6x ‒ 880 = 880 ‒ 880 ⇒

⇒ 6x² + 6x ‒ 880 = 0

8. a) Neste exercício, incentive os estudantes a pensarem nas medidas das áreas de cada retângulo como a multiplicação da medida da base pela medida da altura, bem como a observarem que os lados adjacentes devem ter medidas expressas pelas mesmas incógnitas, se for o caso. Ao observar o quadrado cuja medida de área é expressa por x², espera-se que eles cheguem à conclusão de que a base e a altura têm medidas expressas, por x, pois x ⋅ x = x². Assim, conclui-se que a base do retângulo alaranjado também mede x; então, sua altura tem medida 2, pois sua área é dada por a = 2 ⋅ x = 2x. Logo, a altura do retângulo verde tem medida expressa por x + 2. Assim, a base do retângulo verde deve ter medida igual a 2, pois 2 ⋅ (x + 2) = 2x + 4.

8. b) A_{quadrilátero} = (x + 2) ⋅ (2 + x) ⇒

⇒ A_{quadrilátero} = 2x + x² + 4 + 2x ⇒

⇒ A_{quadrilátero} = x² + 4x + 4

A medida da área do quadrilátero também pode ser determinada pela adição das medidas das áreas das figuras que o compõem.

A_{quadrilátero} = 2x + x² + 2x + 4 = x² + 4x + 4

8. c) O quadrilátero é um quadrado.

9. Auxilie os estudantes a pensarem as relações entre os símbolos matemáticos e as sentenças, reforçando a necessidade de uma boa interpretação de texto para minimizar erros. Em casos como “Um número é igual ao quadrado dêsse próprio númeroreticências”, talvez seja importante mencionar regras gramaticais de análise sintática.

9. a) O quadrado de um número (x²) adicionado (+) ao dôbro dêsse número (2x) é igual a (=) 99. Na fórma reduzida x² + 2x ‒ 99 = 0

9. b) O triplo do quadrado de um número menos o próprio número (‒x) é igual a (=) 30. Na fórma reduzida 3x² ‒ x ‒ 30 = 0

9. c) Um número (x) é igual (=) ao quadrado dêsse próprio número (x²) menos (‒) 42. Na fórma reduzida x² ‒ x ‒ 42 = 0

9. d) Três quintos do quadrado de um número é igual a esse número (x) menos (‒) 40. Na fórma reduzida

\frac{3}{5}

x² ‒ x + 40 = 0

12. Para x = 2, temos:

2² ‒ 11 ∙ 2 + 18 = 0 ⇒ 4 ‒ 22 + 18 = 0 ⇒ ‒18 + 18 = 0

Para x = ‒5, temos:

(‒5)² ‒ 11 ∙ 5 + 18 = 0 ⇒ 25 ‒ 55 + 18 = 0 ⇒ ‒30 + 18 = 0

Para x = 9, temos:

9² ‒ 11 ⋅ 9 + 18 = 0 ⇒ 81 ‒ 99 + 18 = 0 ⇒ ‒ 18 + 18 = 0

Para x = 10, temos:

10² ‒ 11 ⋅ 10 + 18 = 0 ⇒ 100 ‒ 110 + 18 = ‒10 + 18 = 0

As raízes da equação x² ‒ 11x + 18 = 0 são x = 2 e x = 9.

13. a) 5² + 6 ⋅ 5 = 0 ⇒ 25 + 30 = 0

Então 5 não é raiz da equação.

13. b) 2 ⋅ 5² ‒ 10 ⋅ 5 = 0 ⇒ 50 ‒ 50 = 0

Então 5 é raiz da equação.

13. c) 3 ⋅ 5² ‒ 75 = 0 ⇒ 75 ‒ 75 = 0

Então 5 é raiz da equação.

13. d) 5² ‒ 7 ⋅ 5 +10 = 0 ⇒ 25 ‒ 35 + 10 = 0 ⇒ 10 ‒ 10 = 0

Então 5 é raiz da equação.

14. Espera-se que os estudantes percebam que, como a incógnita x está elevada ao quadrado, não é possível que os números 10 ou ‒10 sejam as raízes, restando, então, os números

\sqrt{10}

e ‒

\sqrt{10}

15. Lembre aos estudantes que, se ‒1 é raiz da equação, então (3q ‒ 2) ⋅ (‒1)² + (2q ‒ 1) ⋅ (‒1) + 5 = 0 é uma sentença verdadeira. Podemos resolver a equação do 1º grau em q para descobrir seu valor. Assim:

(3q ‒ 2) ⋅ (‒1)² + (2q ‒ 1) ⋅ (‒1) + 5 = 0 ⇒

⇒ 3q ‒2 ‒2q + 1 + 5 = 0 ⇒ q + 4 = 0 ⇒ q = ‒ 4

16. a) Para que uma das raízes seja 4, temos que 3 ⋅ 4² ‒ 14 ⋅ 4 + 2p = 0 é uma sentença verdadeira. Então:

3 ⋅ 4² ‒ 14 ⋅ 4 + 2p = 0 ⇒ 48 ‒ 56 + 2p = 0 ⇒

⇒ 2p = +8 ⇒ p = 8 : 2 ⇒ p = 4

16. b) Para que uma das raízes seja 0, então a sentença a seguir teria que ser verdadeira, o que não acontece.

(k ‒ 3) ⋅ 0² ‒ (k + 4) ⋅ 0 + 6 = 0 ⇒ 0 + 0 + 6 = 0

Portanto, não é possível determinar k.

17. a) Encontrando a fórma reduzida:

(3y ‒ 4) ⋅ (3y + 1) = 14 ‒ 9y ⇒

⇒ 9y² + 3y ‒ 12y ‒ 4 = 14 ‒ 9y ⇒ 9y² ‒ 9y ‒ 4 = 14 ‒ 9y ⇒

⇒ 9y² ‒ 9y ‒ 4 ‒ 14 + 9y = 0 ⇒ 9y² + 0y ‒ 18 = 0 ⇒

⇒ y² ‒ 2 = 0

Resolvendo a equação:

y² ‒ 2 = 0 ⇒ y² = +2 ⇒ y = ±

\sqrt{2}

Então: y₁ = ‒

\sqrt{2}

e y₂ =

\sqrt{2}

17. b) Encontrando a fórma reduzida:

(m + 5) ⋅ (m ‒ 4) = m + 16 ⇒

⇒ m² ‒ 4m + 5m ‒ 20 = m + 16 ⇒

⇒ m² + m ‒ 20 = m + 16 ⇒ m² + m ‒ 20 ‒ m ‒ 16 = 0 ⇒

⇒ m² + 0m ‒ 36 = 0 ⇒ m² ‒ 36 = 0

Resolvendo a equação:

m² ‒ 36 = 0 ⇒ m² = 36 ⇒ m = ±

\sqrt{36}

Então: m₁ = ‒6 e m₂ = 6.

Página setenta e cinco

18. a) Explique aos estudantes o significado de “verificar a equação”. Ajude-os a fazer a relação: se um número verifica uma equação, esse número torna a equação verdadeira: portanto, esse número é a raiz da equação.

x² ‒ 100 = 0 ⇒ x² = 100 ⇒ x = ±

\sqrt{100}

Portanto: x = + 10 ou x = ‒10

18. b)

4 x ² = 81 \Rightarrow x ² = \frac{81}{4} \Rightarrow x = \frac{\pm \sqrt{81}}{\pm \sqrt{4}}

Portanto:

x = + \frac{9}{2} o u x = ‒ \frac{9}{2}

18. c) (2x ‒ 1) ⋅ (x + 2) = 3x ‒ 7x² ⇒ 2x² + 4x ‒ x ‒ 2 = 3x ‒ 7x² ⇒ 2x² + 3x ‒ 2 = 3x ‒ 7x² ⇒ 2x² + 3x ‒ 2 ‒ 3x + 7x² = 0 ⇒ 9x² + 0x ‒ 2 = 0 ⇒ 9x² ‒ 2 = 0 ⇒ 9x² = 2 ⇒

\Rightarrow x ² = \frac{2}{9} \Rightarrow x = \pm \sqrt{\frac{2}{9}}

Portanto:

x = + \frac{\sqrt{2}}{3} e x = ‒ \frac{\sqrt{2}}{3}

As raízes de cada equação deste exercício são opostas. Talvez os estudantes relatem algo do tipo “são números iguais, mas com os sinais trocados”, atente aos termos usados e corrija-os, quando necessário.

19. a) A equação é do tipo ax² = 0; então, x₁ = x₂ = 0.

19. b) A equação é do tipo x² = c; então,

x = \pm \sqrt{c}

. Assim:

x_{1} = \frac{3}{2} e x_{2} = ‒ \frac{3}{2}

19. c) A equação é do tipo ax² = 0, pois ax² + c = c ⇒ ax² = 0; então,

x_{1} = x_{2} = 0

19. d) A equação é do tipo ax² = c; então,

x = \pm \sqrt{\frac{c}{a}}

. Assim:

x_{1} = \frac{\sqrt{2}}{2} e x_{2} = - \frac{\sqrt{2}}{2}

20. Traduzindo a sentença para a linguagem simbólica, obtemos x² ‒ 60 = 840, que na fórma reduzida é a equação x² ‒ 900 = 0 (x² ‒ 60 ‒ 840 = 0 ⇒ x² ‒ 900 = 0).

Resolvendo a equação, chegamos a

x_{1} = 30 e x_{2}

= ‒30. Como o número pensado é negativo, então o número é ‒30.

21. a) Colocando 3x em evidência na equação:

3x² + 15x = 0 ⇒ 3x ⋅ (x + 5) = 0

Como o produto dos fatores 3x e (x + 5) é zero, ao menos um deles é zero. Assim, 3x = 0 ou x + 5 = 0. Resolvendo essas equações, encontramos, respectivamente, x = 0 ou x = ‒5. Logo, as raízes são

x_{1} = 0

x_{2} = ‒ 5

21. b) Colocando y em evidência na equação:

2 y^{2} ‒ \frac{y}{3} = 0 \Rightarrow y \cdot (2 y ‒ \frac{1}{3}) = 0

Como o produto dos fatores y e

(2 y ‒ \frac{1}{3})

é zero, ao menos um deles é zero. Assim:

y = 0 o u 2 y ‒ \frac{1}{3} = 0

Resolvendo essas equações, encontramos, respectivamente,

y = 0 o u y = \frac{1}{6}

. Logo, as raízes são y₁ = 0 e

y_{2} = \frac{1}{6} .

21. c) O produto dos fatores 9, (2n ‒ 5) e (n + 2) é zero. Assim:

2n ‒ 5 = 0 ou n + 2 = 0

Resolvendo essas equações, encontramos, respectivamente,

n = \frac{5}{2}

ou n = ‒2. Logo, as raízes são

n_{1} = \frac{5}{2} e n_{2} = ‒ 2

21. d) (2x ‒ 3) ⋅ (x ‒ 2) = (x ‒ 6) ⋅ (3x ‒ 1) ⇒

⇒ 2x² ‒ 4x ‒ 3x + 6 = 3x² ‒ x ‒ 18x + 6 ⇒

⇒ 2x² ‒ 7x + 6 = 3x² ‒ 19x + 6 ⇒

⇒ 2x² ‒ 7x = 3x² ‒ 19x ⇒ 2x² ‒ 7x ‒ 3x² + 19x = 0 ⇒

⇒‒x² + 12x = 0 ⇒ x² ‒ 12x = 0

Colocando x em evidência na equação, obtemos: x ⋅ (x ‒ 12) = 0. Assim, um dos fatores tem de ser igual a zero. Resolvendo essas equações, encontramos, respectivamente, x = 0 ou x = 12. Logo, as raízes são

x_{1} = 0 e x_{2} = 12

22. Todas as equações deste exercício, na fórma reduzida, têm o coeficiente c = 0; portanto, uma de suas raízes igual a zero.

22. a) Resolvendo a equação 5x2 + 12x = 0 e colocando x em evidência, obtemos: x ⋅ (5x + 12) = 0. Como o produto dos fatores x e (5x + 12) é igual a zero, pelo menos um deles é zero. Assim, x = 0 ou 5x + 12 = 0. Resolvendo essas equações, encontramos, respectivamente, x = 0 e

x = \frac{- 12}{5}

22. b) Resolvendo a equação ‒3y2 ‒ 6y = 0 e colocando ‒3y em evidência, obtemos: ‒3y ⋅ (y + 2) = 0. Como o produto dos fatores ‒3y e (y + 2) é igual a zero, pelo menos um deles é zero. Assim, ‒3y = 0 ou y + 2 = 0. Resolvendo essas equações, encontramos, respectivamente, y = 0 e y = ‒2.

22. c) Resolvendo a equação

\sqrt{3} x ² + x = 0

e colocando x em evidência, obtemos: x ⋅ (

\sqrt{3} x + 1

) = 0. Como o produto dos fatores x e (

\sqrt{3} x + 1

) é igual a zero, pelo menos um deles é zero. Assim, x = 0 ou (

\sqrt{3} x

+ 1) = 0. Resolvendo essas equações, encontramos, respectivamente, x = 0 e

x = - \frac{\sqrt{3}}{3}

22. d) Aplicando a propriedade distributiva e colocando a equação na fórma reduzida, obtemos: m2 ‒ 3m = 0.

(m + 3) ⋅ (m ‒ 6) = ‒18 ⇒ m2 ‒ 6m + 3m ‒ 18 = ‒ 18 ⇒

⇒ m2 ‒ 3m = 0

Colocando m em evidência, obtemos: m ⋅ (m ‒ 3) = 0. Assim, m = 0 ou m ‒ 3 = 0. Resolvendo essas equações, encontramos, respectivamente, m = 0 e m = 3.

23. Esse exercício é uma boa oportunidade de retomar alguns exercícios resolvidos anteriormente (exercícios 19, 21 e 22) e analisar e traçar suas similaridades e diferenças. Durante a elaboração do problema, auxilie os estudantes na investigação e formalização de ideias com perguntas como: “O que faz uma equação ter uma das raízes igual a zero? Que tipos de problemas/sentenças podem levar a uma equação dêsse tipo?”