Página setenta e seis

Parte 7

24. Se 0 é uma raiz, então, substituindo x por 0 em x² ‒ 6x + p + 5 = 0, obtemos: p + 5 = 0

Então: p + 5 = 0 ⇒ p = ‒ 5

25. O dôbro do quadrado de um número negativo adicionado (+) ao triplo dele é igual a zero (= 0). Assim, obtemos a equação: 2x² + 3x = 0. Colocando x em evidência, obtemos: x ⋅ (2x + 3) = 0. Como o produto dos fatores é igual a zero, então pelo menos um dos fatores é igual a zero. Assim, x = 0 ou 2x + 3 = 0 ⇒ x = ‒

\frac{3}{2}

. Logo, o número é ‒

\frac{3}{2}

26. Se do quadrado da idade de Luísa (x²) subtrairmos o dôbro da idade dela (‒2x), obteremos 10 vezes a idade de Lúcia, a irmã gêmea de Luísa (por serem gêmeas, elas têm a mesma idade, 10x).

x² ‒ 2 ⋅ x = 10 ⋅ x ⇒ x² ‒ 2x ‒ 10x = 0 ⇒

⇒ x² ‒ 12x = 0 ⇒ x ⋅ (x ‒ 12) = 0

Como o produto dos fatores é igual a zero, então pelo menos um dos fatores é igual a zero. Assim, x = 0 ou x ‒ 12 = 0 ⇒ x = 12. Logo, Luísa tem 12 anos.

28. a) A equação x² ‒ 14x + 49 = 0 pode ser escrita como x² ‒ 2 ⋅ x ⋅ 7 + 7² = 0. Temos, então, um quadrado perfeito (x ‒ 7)² = 0. Resolvendo, obtemos (x ‒ 7) = 0 ⇒ x = 7. Logo, as raízes são x1 = x2 = 7.

28. b) A equação 4x² ‒ 20x + 25 = 0 pode ser escrita como (2x)² ‒ 2 ⋅ 2x ⋅ 5 + 5² = 0. Temos, então, um quadrado perfeito (2x ‒ 5)² = 0. Resolvendo, obtemos (2x ‒ 5) = 0 ⇒

x = \frac{5}{2}

. Logo, as raízes são

x_{1} = x_{2} = \frac{5}{2}

28. c) A equação 4y² = 4y ‒ 1, na fórma reduzida, é 4y² ‒ 4y + 1 = 0. Essa equação pode ser escrita como (2y)² ‒ 2 ⋅ 2y ⋅ 1 + 1² = 0. Temos, então, um quadrado perfeito (2y ‒ 1)² = 0. Resolvendo, obtemos (2y ‒ 1) = 0 ⇒

y = \frac{1}{2}

. Logo, as raízes são

y_{1} = y_{2} = \frac{1}{2}

28. d) A equação p² + 6p = 16p ‒ 25, na fórma reduzida, é p² ‒ 10p + 25 = 0. Essa equação pode ser escrita como (p)² ‒ 2 ⋅ p ⋅ 5 + 5² = 0. Há, então, um quadrado perfeito (p ‒ 5)² = 0. Resolvendo, obtemos (p ‒ 5) = 0 ⇒ p = 5. Logo, as raízes são p1 = p2 = 5.

29.

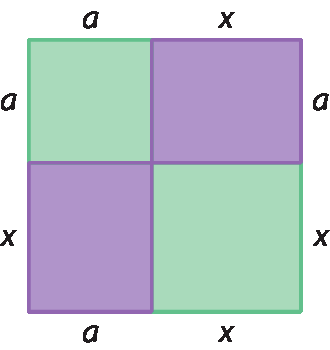
Ilustração. Quadrado dividido em 4 partes, sendo a primeira parte um quadrado verde de lado a, a segunda um retângulo lilás de altura x e base a; a terceira: um retângulo lilás de altura a e base x; e a quarta parte, um quadrado verde de lado x.

Se a maior área quadrada tem medida x², então seus lados podem ter medidas x. Por isso, um dos lados dos dois retângulos lilases também tem medida de comprimento igual a x, pois eles são coincidentes. Como a soma das medidas das áreas dos retângulos lilases é 8x, e as medidas dos lados dos retângulos lilases são iguais, então: ax + ax = 8x ⇒ 2ax = 8x ⇒ ax = 4x ⇒ a = 4

Assim, a área do quadrado verde menor mede 16 (4 ⋅ 4 = 16).

30. a) Em x² + 10x + 24 = 0, como x² = (x)² e 10x = 2 . 5 ⋅ x, vamos adicionar 52 a ambos os membros para completar o quadrado perfeito.

2x2 + 10x = ‒24 ⇒ x2 + 2 · 5 ⋅ x + 52 = ‒ 24 + 52 ⇒

⇒ x² + 10x + 25 = 1 ⇒ (x + 5)2 = 1 ⇒ (x + 5) = ±

\sqrt{1}

⇒

⇒ (x + 5) = ± 1 ⇒x = ±1 ‒ 5

Logo, as raízes são x1 = ‒ 4 e x2 = ‒6.

30. b) Em y² ‒ 4y + 3 = 0, como y² = (y)² e ‒4y = 2 · (‒2) ⋅ y, vamos adicionar (‒2)² a ambos os membros para completar o quadrado perfeito.

y² ‒ 4y = ‒3 ⇒ y² + 2 · (‒2) ⋅ y + (‒2)² = ‒3 + (‒2)² ⇒

⇒ y² ‒ 4y + 4 = 1 ⇒ (y ‒ 2)² = 1 ⇒ (y ‒ 2) = ±

\sqrt{1}

⇒

⇒ (y ‒ 2) = ± 1 ⇒ y = ±1 + 2

Logo, as raízes são y1 = 1 e y2 = 3.

30. c) Em n² + 4n ‒ 12 = 0, como n² = (n)² e 4n = 2 . 2 ⋅ n, vamos adicionar 2² a ambos os membros para completar o quadrado perfeito.

n² + 4n = 12 ⇒ n² + 2 . 2 ⋅ n + 2² = 12 + 2² ⇒

⇒ n² + 4n + 4 = 16 ⇒ (n + 2)² = 16 ⇒

⇒ (n + 2) = ±

\sqrt{16}

⇒ (n + 2) = ± 4 ⇒ n = ±4 ‒ 2

Logo, as raízes são n = ‒6 e n = 2.

30. d) Em r² ‒ 2r ‒ 3 = 0, como r² = (r)² e ‒2r = 2 . (‒1) ⋅ r, vamos adicionar (‒1)² a ambos os membros para completar o quadrado perfeito.

r² ‒ 2r = + 3 ⇒ r² + 2 ⋅ (‒1) ⋅ r + (‒1)² = 3 + (‒1)² ⇒

⇒ r² ‒ 2r + 1 = 4 ⇒ (r ‒ 1)² = 4 ⇒ (r ‒ 1) = ±

\sqrt{4}

⇒

⇒ (r ‒ 1) = ± 2 ⇒ r = ±2 + 1

Logo, as raízes são r1 = ‒1 e r2 = 3.

31. a) Vamos adicionar (‒3)² a ambos os membros para completar o quadrado perfeito. Assim:

4x² ‒ 12x + 5 = 0 ⇒ 4x² + 2 ⋅ (‒3) ⋅ 2x + (‒3)² = ‒5 + (‒3)² ⇒

⇒ (2x ‒ 3)² = 4 ⇒ (2x ‒ 3) = ±

\sqrt{4}

⇒ (2x ‒ 3) = ±2 ⇒

⇒

x = \frac{1}{2}

Logo, os valores reais de x que verificam a equação são

x_{1} = \frac{1}{2} e x_{2} = \frac{5}{2}

31. b) Para ajudar os estudantes a visualizar qual é o termo a ser adicionado, incentive-os a pensar que 2 ⋅ (3y) ∙ k = 6x ⋅ k, e pergunte a eles: “Qual é o número k que devemos multiplicar por 6x para que ele se torne ‒3x?” Espera-se que percebam que 6x é o dôbro de 3x; portanto, é necessário dividir por 2. Como ele é negativo, então k =

\frac{‒ 1}{2}

. Vamos adicionar

{(\frac{‒ 1}{2})}^{2}

a ambos os membros para completar o quadrado perfeito. Assim, obtemos:

9y2 ‒ 3y ‒ 2 = 0 ⇒

\Rightarrow 9 y^{2} + 2 \cdot (\frac{‒ 1}{2}) \cdot 3 y + {(\frac{‒ 1}{2})}^{2} = 2 + {(\frac{‒ 1}{2})}^{2} \Rightarrow

\Rightarrow {(3 y ‒ \frac{1}{2})}^{2} = \frac{9}{4} \Rightarrow 3 y ‒ \frac{1}{2} = \pm \sqrt{\frac{9}{4}} \Rightarrow

\Rightarrow 3 y ‒ \frac{1}{2} = \pm \frac{3}{2} \Rightarrow y = \frac{2}{3} o u y = ‒ \frac{1}{3}

Página setenta e sete

Logo, os valores reais de x que verificam a equação são

y_{1} = ‒ \frac{1}{3} e y_{2} = \frac{2}{3}

31. c) Para ajudar os estudantes a visualizar qual é o termo a ser adicionado, incentive-os a pensar que 2 ⋅ (

\sqrt{2}

n) ⋅ k = 2

\sqrt{2} n

⋅ k, e pergunte a eles: “Qual é o número k que devemos multiplicar por 2

\sqrt{2} n

para que ele se torne 7n?”

2 \sqrt{2} n \cdot k = 7 n \Rightarrow k = \frac{7}{2 \sqrt{2}} \cdot \frac{2 \sqrt{2}}{2 \sqrt{2}} = \frac{7 \cdot 2 \sqrt{2}}{8} k = \frac{7 \sqrt{2}}{4}

Note que

2 n^{2} = {(\sqrt{2} n)}^{2}

Então, vamos adicionar

{(\frac{7 \sqrt{2}}{4})}^{2}

a ambos os membros para completar o quadrado perfeito. Assim, obtemos:

2n² + 7n + 6 = 0 ⇒

2 n ² + 2 \cdot (\frac{7 \sqrt{2}}{4}) \cdot \sqrt{2} n + {(\frac{7 \sqrt{2}}{4})}^{2} =

= ‒ 6 + {(\frac{7 \sqrt{2}}{4})}^{2} \Rightarrow {(\sqrt{2} n + \frac{7 \sqrt{2}}{4})}^{2} = ‒ 6 + \frac{49}{8} \Rightarrow

\Rightarrow {(\sqrt{2} n + \frac{7 \sqrt{2}}{4})}^{2} = \frac{1}{8} \Rightarrow \sqrt{2} n + \frac{7 \sqrt{2}}{4} = \pm \sqrt{\frac{1}{8}} \Rightarrow

\Rightarrow \sqrt{2} n + \frac{7 \sqrt{2}}{4} = \pm \frac{1}{2 \sqrt{2}} \Rightarrow

\Rightarrow \frac{\sqrt{2} n}{\sqrt{2}} + \frac{7 \sqrt{2}}{4 \cdot \sqrt{2}} = \pm \frac{1}{2 \sqrt{2} \cdot \sqrt{2}} \Rightarrow

\Rightarrow n + \frac{7}{4} = \pm \frac{1}{4} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} n_{1} = ‒ \frac{1}{4} ‒ \frac{7}{4} = ‒ 2 \\ n_{2} = \frac{1}{4} ‒ \frac{7}{4} = ‒ \frac{3}{2} \end{array}

31. d) Vamos multiplicar a equação por 3 para obter: 9x² + 24x ‒ 9 = 0. Em seguida, vamos adicionar 4² a ambos os membros para completar o quadrado perfeito. Assim, obtemos:

9x² + 24x ‒ 9 = 0 ⇒ (3x)² + 2 ⋅ 3x ⋅ 4 + 4² = 9 + 4² ⇒

⇒ (3x + 4)² = 25 ⇒ (3x + 4) =

\pm \sqrt{25}

⇒

⇒ (3x + 4) = ± 5 ⇒ 3x = ±5 ‒ 4 ⇒

x = \frac{\pm 5 ‒ 4}{3}

Logo, os valores reais de x que verificam a equação são

x_{1} = ‒ 3 e x_{2} = \frac{1}{3}

32. Considerando x, x + 1 e x + 2, obtemos:

(x + 1) ⋅ (x + 2) = 10 ⋅ x + 10

Então:

(x + 1) ⋅ (x + 2) = 10 ⋅ (x + 1) ⇒

⇒ (x + 2) = 10 ⇒

⇒ x = 8

Assim, os números são 8, 9 e 10, pois:

x = 8

x + 1 = 9

x + 2 = 10

Portanto, a média aritmética é igual a 9, pois:

(8 + 9 + 10) : 3 = 27 : 3 = 9

35. a) Na equação 3x² ‒ 7x + 4 = 0, a = 3, b = ‒ 7 e c = 4. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒7)² ‒ 4 ⋅ 3 ⋅ 4 = 49 ‒ 48 = 1

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{– (– 7) ± 1}{2 \cdot 3} = \frac{7 ± 1}{6}

Portanto, as raízes são

x_{1} = 1 e x_{2} = \frac{4}{3}

35. b) Na equação 2m² ‒ m ‒ 6 = 0, a = 2, b = ‒ 1 e c = ‒6. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒1)² ‒ 4 ⋅ 2 ⋅ (‒6) = 1 + 48 = 49

\sqrt{Δ} = \sqrt{49} = 7

m = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow m = \frac{– (– 1) ± 7}{2 \cdot 2} = \frac{1 ± 7}{4}

Portanto, as raízes são

m_{1} = \frac{‒ 3}{2} e m_{2} = 2

35. c) Na equação ‒x² + 3x + 10 = 0, a = ‒1, b = 3 e c = 10. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = 3² ‒ 4 ⋅ (‒1) ⋅ 10 = 9 + 40 = 49

\sqrt{Δ} = \sqrt{49} = 7

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{‒ 3 \pm 7}{2 \cdot (‒ 1)} = \frac{‒ 3 \pm 7}{‒ 2}

Portanto, as raízes são

x_{1} = ‒ 2 e x_{2} = 5

35. d) Na equação y² + 8y ‒ 4 = 0, a = 1, b = 8 e c = ‒ 4. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = 8² ‒ 4 ⋅ 1 ⋅ (‒4) = 64 + 16 = 80

\sqrt{Δ} = \sqrt{80} = \sqrt{2^{4} \cdot 5} = 4 \sqrt{5}

y = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow y = \frac{‒ 8 \pm 4 \sqrt{5}}{2 \cdot 1} = \frac{‒ 8 \pm 4 \sqrt{5}}{2}

Portanto, as raízes são

y_{1} = ‒ 4 + 2 \sqrt{5}

y_{2} = ‒ 4 ‒ 2 \sqrt{5}

35. e) Na equação 9y² ‒ 12y + 4 = 0, a = 9, b = ‒12 e c = 4. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒12)² ‒ 4 ⋅ 9 ⋅ 4 = 144 ‒ 144 = 0

\sqrt{Δ}

= 0

y = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow y = \frac{– (– 12) ± 0}{2 \cdot 9} = \frac{12}{18} = \frac{2}{3}

Portanto, as raízes são

y_{1} = y_{2} = \frac{2}{3} .

35. f) Na equação 5x² + 3x + 5 = 0, a = 5, b = 3 e c = 5. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = 3² ‒ 4 ⋅ 5 ⋅ 5 = 9 ‒ 100 = ‒91

\sqrt{Δ} = \sqrt{– 91}

Não existem raízes reais para 5x² + 3x + 5 = 0.

36. a) x(x + 3) = 5x + 15 ⇒ x² + 3x = 5x + 15 ⇒

⇒ x² + 3x ‒ 5x ‒ 15 = 0 ⇒ x² ‒ 2x ‒ 15 = 0

Nessa equação, a = 1, b = ‒ 2 e c = ‒15.

Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒2)² ‒ 4 ⋅ 1 ⋅ (‒15) = 4 + 60 = 64

\sqrt{Δ} = \sqrt{64} = 8

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{‒ (‒ 2) \pm 8}{2 \cdot 1} = \frac{2 \pm 8}{2}

Portanto, as raízes são

x_{1} = ‒ 3 e x_{2} = 5

Página setenta e oito

36. b)

\frac{3 y + 1}{2} = \frac{y^{2} ‒ 1}{3}

⇒ 9y + 3 = 2y² ‒ 2 ⇒

⇒ 2y² ‒ 2 ‒ 9y ‒ 3 = 0 ⇒ 2y² ‒ 9y ‒5 = 0

Na equação, a = 2, b = ‒9 e c = ‒5.

Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒9)² ‒ 4 ⋅ 2 ⋅ (‒5) = 81 + 40 = 121

\sqrt{Δ} = \sqrt{121} = 11

y = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow y = \frac{‒ (‒ 9) \pm 11}{2 \cdot 2} = \frac{9 \pm 11}{4}

Portanto, as raízes são

y_{1} = \frac{‒ 1}{2} e y_{2} = 5

36. c) (x + 4)² = 9x + 22 ⇒ x² + 8x + 16 = 9x + 22 ⇒

⇒ x² + 8x + 16 ‒ 9x ‒ 22 = 0 ⇒ x² ‒ x ‒ 6 = 0

Nessa equação, a = 1, b = ‒ 1 e c = ‒6.

Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒1)² ‒ 4 ⋅ 1 ⋅ (‒6) = 1 + 24 = 25

\sqrt{Δ} = \sqrt{25} = 5

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{‒ (‒ 1) \pm 5}{2 \cdot 1} = \frac{1 \pm 5}{2}

Portanto, as raízes são

x_{1} = ‒ 2 e x_{2} = 3

36. d) (x ‒ 1)² + 3x = x + 26 ⇒ x² ‒ 2x + 1 + 3x = x + 26 ⇒ x² ‒ 2x + 1 + 3x ‒ x ‒ 26 = 0 ⇒ x² + (‒25) = 0

Resolvendo a equação, obtemos:

x² = 25 ⇒ x =

\pm \sqrt{25}

⇒ x = ± 5

Portanto, as raízes são x1 = ‒5 e x2 = 5.

36. e) (x + 4) ⋅ (x ‒ 1) = 5x + 20 ⇒ x² ‒ x + 4x ‒ 4 = 5x + 20 ⇒ x² ‒ x + 4x ‒ 4 ‒ 5x ‒ 20 = 0 ⇒ x² ‒ 2x ‒ 24 = 0

Nessa equação, a = 1, b = ‒ 2 e c = ‒ 24.

Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = (‒2)² ‒ 4 ⋅ 1 ⋅ (‒24) = 4 + 96 = 100

\sqrt{Δ} = \sqrt{100} = 10

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{‒ (‒ 2) \pm 10}{2 \cdot 1} = \frac{2 \pm 10}{2}

Portanto, as raízes são

x_{1} = ‒ 4 e x_{2} = 6

37. a) Como as partes lilases são quadrados, os lados do quadrado de medida de área igual a 49 cm² medem 7 cm (7 ⋅ 7 = 49). Os lados do quadrado de medida de área igual a x² medem x.

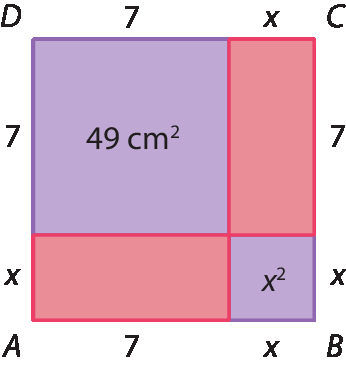
Ilustração. Quadrado ABCD, dividido em 4 partes. Sendo: um quadrado roxo de vértice D, de lado 7, cuja área mede 49 centímetros quadrados; um retângulo vermelho de vértice A medindo x de altura e 7 de base; um retângulo vermelho de vértice C medindo x de base e 7 de altura; e quadrado roxo de vértice B, de lado x, cuja área mede x elevado ao quadrado.

Podemos representar a medida da área dos retângulos vermelhos por 7x. Assim, a medida da área total da figura será a soma das medidas das áreas.

x² + 7x + 7x + 49 = x² + 14x + 49

37. b) x² + 14x + 49 = 100 ⇒ x² + 14x + 49 ‒ 100 = 0 ⇒

⇒ x² + 14x ‒ 51 = 0

Nessa equação, a = 1, b = 14 e c = ‒51. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = 14² ‒ 4 ⋅ 1 ⋅ (‒51) = 196 + 204 = 400

\sqrt{Δ} = \sqrt{400} = 20

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{– 14 \pm 20}{2 \cdot 1} = \frac{– 14 \pm 20}{2}

Portanto, as raízes da equação são

x_{1} = ‒ 17

x_{2} = 3

. Contudo x = ‒17 não convém para o problema, pois a medida x deve ser dada por um número positivo. Logo, x = 3 é a resposta válida para esse problema. Assim, a medida do lado do menor quadrado é 3 centímetros.

38. a) Pode ser que os estudantes confundam “a metade da soma de um número com o seu quadrado...” com “a metade de um número adicionada ao seu quadrado”. Fique atento a isso e reforce que é necessária a leitura atenta do problema:

A equação do 2º grau que representa a descrição “A metade da soma de um número com o seu quadrado é igual a 210.” é:

\frac{x + x^{2}}{2} = 210

Na fórma reduzida, obtemos:

\frac{x + x^{2}}{2}

= 210 ⇒ x² + x = 420 ⇒ x² + x ‒ 420 = 0

Nessa equação, a = 1, b = 1 e c = ‒ 420. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = 1² ‒ 4 ⋅ 1 ⋅ (‒420) = .1681

\sqrt{Δ} = \sqrt{1 681} = 41

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{– 1 \pm 41}{2 \cdot 1} = \frac{– 1 \pm 41}{2}

Portanto, as raízes da equação são

x_{1} = ‒ 21

x_{2} = 20

38. b) A equação do 2º grau que representa a descrição “O quadrado de um número aumentado de seus

\frac{3}{5}

é igual a 28.” é:

x ² + \frac{3}{5} x = 28

Colocando-a na fórma reduzida e multiplicando-a por 5, obtemos:

(x ² + \frac{3}{5} x ‒ 28) \cdot 5

= 0 ⋅ 5 ⇒ 5x² + 3x ‒ 140 = 0

Nessa equação, a = 5, b = 3 e c = ‒ 140. Assim, obtemos:

Δ = b2 ‒ 4ac ⇒ Δ = 3² ‒ 4 ⋅ 5 ⋅ (‒140) = .2809

\sqrt{Δ} = \sqrt{2 809} = 53

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{– 3 \pm 53}{2 \cdot 5} = \frac{– 3 \pm 53}{10}

Portanto, as raízes da equação são

x_{1} = 5

x_{2} = ‒ \frac{28}{5}

Página setenta e nove

39. Da leitura do problema, obtemos a equação:

\frac{x^{2}}{3} ‒ x = 60

Colocando-a na fórma reduzida e, multiplicando-a por 3, temos x² ‒ 3x ‒ 180 = 0.

Resolvendo a equação, a = 1, b = ‒3 e c = ‒180.

Δ = b2 ‒ 4ac ⇒ Δ = (‒3)² ‒ 4 ⋅ 1 ⋅ (‒180) = 9 + 720 = 729

\sqrt{Δ} = \sqrt{729} = 27

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{– (– 3) ± 27}{2 \cdot 1} = \frac{3 ± 27}{2}

Portanto, as raízes da equação são

x_{1} = 15

x_{2} = ‒ 12

O triplo desses números será 45 e ‒36; pois 3 ⋅ 15 = 45 e 3 ⋅ (‒12) = ‒ 36.

40. A medida da área do retângulo recortado é dada por 15x (A = 15 ⋅ x). Assim, a medida da área restante, após o recorte, pode ser dada pela expressão x² ‒ 15x = .1750. Na equação na fórma reduzida, temos:

x² ‒ 15x ‒ .1750 = 0.

Nessa equação, a = 1, b = ‒15 e c = ‒ .1750. Assim:

Δ = b2 ‒ 4ac ⇒ Δ = (‒15)² ‒ 4 ⋅ 1 ⋅ (‒.1750) = .7225

\sqrt{Δ} = \sqrt{7 225} = 85

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow x = \frac{– (– 15) \pm 85}{2 \cdot 1} = \frac{15 \pm 85}{2}

Portanto, as raízes da equação são

x_{1} = 50

x_{2} = ‒ 35

. Como se trata de uma medida de comprimento, ela não pode ser dada por um número negativo. Então, vamos considerar apenas a raiz

x_{1} = 50

. Assim, a área da folha de cartolina mede .2500 centímetros quadrados (50 ⋅ 50 = .2500).

41. Se a altura mede x, o comprimento mede x + 5. Então a medida da área será x · (x + 5) e a medida do perímetro será 2 · x + 2 · (x + 5) = 2x + 2x + 10 = 4x + 10.

Portanto: x · (x + 5) = 300 ⇒ x2 + 5x ‒ 300 = 0

Δ = 52 ‒ 4 · (‒300) = .1225

x = \frac{‒ 5 \pm \sqrt{1 225}}{2} = \frac{‒ 5 \pm 35}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{30}{2} = 15 \\ x_{2} = ‒ \frac{40}{2} = ‒ 20 \end{array}

O resultado negativo não convém, pois x se trata de uma medida de comprimento. Então, a medida do perímetro será 70 métros, pois 4 ⋅15 +10 = 60 + 10 = 70.

42.

35 = \frac{n \cdot (n ‒ 3)}{2}

⇒ 70 = n2 ‒ 3n ⇒ n2 ‒ 3n ‒ 70 = 0

Δ = (‒3)2 ‒ 4 · (‒70) = 289

n = \frac{‒ (‒ 3) \pm \sqrt{289}}{2} = \frac{3 \pm 17}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} n_{1} = \frac{20}{2} = 10 \\ n_{2} = ‒ \frac{14}{2} = ‒ 7 \end{array}

Como não há polígono com número negativo de lados, então podemos concluir que esse polígono tem 10 lados. O polígono é um decágono.

43. a) Separando a figura em três colunas, para representar a medida da área temos a seguinte expressão:

x · 3x + (x + x) · 4 + (x + x + 2) · 5 =

= 3x2 + 2x · 4 + (2x + 2) · 5 = 3x2 + 8x + 10x + 10 =

= 3x2 + 18x + 10

43. b) A equação será 3x2 +18x ‒ 21 = 0, pois:

3x2 + 18x +10 = 31 ⇒ 3x2 + 18x ‒ 21 = 0

43. c) 3x2 + 18x ‒ 21 = 0

Δ = 182 ‒ 4 · 3 · (‒21) = 324 + 252 = 576

x = \frac{‒ 18 \pm \sqrt{576}}{2 \cdot 3} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{‒ 18 ‒ 24}{6} = ‒ \frac{42}{6} = ‒ 7 \\ x_{2} = \frac{‒ 18 + 24}{6} = \frac{6}{6} = 1 \end{array}

43. d) Se a área medir 31,1 será solução da equação, mas ‒ 7 não, pois é negativo.

44. a)

{(2 x + 3)}^{2} ‒ 4 \cdot \frac{x^{2}}{2}

= 4x2 + 12x + 9 ‒ 2x2 = 2x2 + 12x + 9

44. b) 2x2 + 12x + 9 = 119 ⇒ 2x2 + 12x ‒ 110 = 0 ⇒ ⇒ x2 + 6x ‒ 55 = 0

Δ = 62 ‒ 4 · (‒55) = 36 + 220 ⇒ Δ = 256

x = \frac{‒ 6 \pm \sqrt{256}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{‒ 6 + 16}{2} = \frac{10}{2} = 5 \\ x_{2} = \frac{‒ 6 ‒ 16}{2} = ‒ \frac{22}{2} = ‒ 11 \end{array}

Portanto, x = 5.

45. Contornando um quadrado de lado medindo x com um faixa medindo 2 centímetros, então o lado do quadrado final terá lado medindo x + 4. Logo, a medida de sua área será dada por (x + 4)2. Assim:

(x + 4)2 = 56,25 ⇒

\sqrt{{(x + 4)}^{2}} = \sqrt{56, 25}

⇒ x + 4 = 7, 5 ⇒ x = 3,5

Portanto, o lado do primeiro quadrado mede 3,5 centímetros.

46. Os quadrados construídos têm lados medindo x e y. Assim, a soma das medidas dos perímetros deve ter a medida do comprimento do arame, ou seja, 4x + 4y = 12 ⇒ x + y = 3 ⇒ y = 3 ‒ x. Da relação entre as medidas das áreas, temos:

x2 + y2 = 5 ⇒ x2 + (3 ‒ x)2 = 5 ⇒ x2 + 9 ‒ 6x + x2 = 5 ⇒ 2x2 ‒ 6x + 4 = 0 ⇒ x2 ‒ 3x + 2 = 0

Δ = (‒3)2 ‒ 4 · 2 = 9 ‒ 8 = 1

x = \frac{‒ (‒ 3) \pm \sqrt{1}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{3 + 1}{2} = \frac{4}{2} = 2 \\ x_{2} = \frac{3 ‒ 1}{2} = \frac{2}{2} = 1 \end{array}

Então, os quadrados têm lados medindo 1 decímetro e 2 decímetros. Portanto, os perímetros medem 4 e 8, sendo necessário cortar o arame a 4 decímetros ou 8 decímetros de uma das extremidades.

47. A medida da área pode ser calculada por:

\frac{(2 x + 5) \cdot (x + 2)}{2} = \frac{2 x^{2} + 5 x + 4 x + 10}{2} = \frac{2 x^{2} + 9 x + 10}{2}

Então, como a área mede 95 centímetros quadrados, temos:

\frac{2 x^{2} + 9 x + 10}{2}

 = 95 ⇒ 2x2 + 9x + 10 = 190 ⇒

⇒ 2x2 + 9x ‒ 180 = 0

Δ = 92 ‒ 4 ⋅ 2 ⋅ (‒180) = 81 + .1440 ⇒ Δ = .1521

Página oitenta

x = \frac{‒ (9) \pm \sqrt{1 521}}{2 \cdot 2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{‒ 9 + 39}{4} = \frac{30}{4} = 7, 5 \\ x_{2} = \frac{‒ 9 ‒ 39}{4} = ‒ \frac{48}{4} = ‒ 12 \end{array}

Então, como as medidas de comprimento não podem ter valores negativos, o valor de x deve ser igual a 7,5.

48. Sendo x o número procurado, então a equação será: 2x2 ‒ 4x + 13 = 10 ⇒ 2x2 ‒ 4x + 3 = 0

Δ = (‒4)2 ‒ 4 · 2 · 3 = 16 ‒ 24 = ‒8 < 0

Portanto, não existe número real que satisfaça.

51. a) Nessa equação, a = 2 , b = 3 e c = p.

É necessário que Δ = 0, então:

Δ = 32 ‒ 4 · 2 · p ⇒ Δ = 9 ‒ 8 p ⇒ 9 ‒ 8 p = 0 ⇒ p =

\frac{9}{8}

51. b)

x = \frac{‒ b \pm \sqrt{Δ}}{2 a} \Rightarrow \frac{– 3 \pm 0}{2 \cdot 2} = – \frac{3}{4}

51. c)

x = \frac{‒ 3 \pm \sqrt{9 ‒ 8 p}}{2 \cdot 2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} \frac{‒ 3 + \sqrt{9 ‒ 8 p}}{4} = 0 \Rightarrow ‒ 3 + \sqrt{9 ‒ 8 p} = 0 \Rightarrow \sqrt{9 ‒ 8 p} = 3 \\ \frac{‒ 3 ‒ \sqrt{9 ‒ 8 p}}{4} = 0 \Rightarrow ‒ 3 ‒ \sqrt{9 ‒ 8 p} = 0 \Rightarrow \sqrt{9 ‒ 8 p} = ‒ 3 (impossível) \end{array}

{(\sqrt{9 ‒ 8 p})}^{2}

= 9 ⇒ 9 ‒ 8 p = 9 ⇒ ‒8 p = 0 ⇒ p = 0

51. d)

x = \frac{‒ 3 \pm \sqrt{9 ‒ 8 p}}{2 \cdot 2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} \frac{‒ 3 + \sqrt{9 ‒ 8 p}}{4} = 2 \Rightarrow ‒ 3 + \sqrt{9 ‒ 8 p} = 8 \Rightarrow \sqrt{9 ‒ 8 p} = 11 \\ \frac{‒ 3 ‒ \sqrt{9 ‒ 8 p}}{4} = 2 \Rightarrow ‒ 3 ‒ \sqrt{9 ‒ 8 p} = 8 \Rightarrow \sqrt{9 ‒ 8 p} = ‒ 11 (impossível) \end{array}

{(\sqrt{9 ‒ 8 p})}^{2} = 11^{2} \Rightarrow 9 ‒ 8 p = 121 \Rightarrow ‒ 8 p = 112 \Rightarrow p = ‒ \frac{112}{8} = ‒ 14

51. e) Δ < 0 ⇒ 9 ‒ 8p < 0 ⇒ ‒8p < ‒9 ⇒ p >

\frac{9}{8}

52. Nessa equação, a = 2, b = 4 e c = 5k. Então, para Δ > 0, temos: 42 ‒ 4 · 2 · 5k > 0 ⇒ 16 ‒ 40k > 0 ⇒ ⇒ ‒40k > ‒16 ⇒ k <

\frac{2}{5}

53. Nessa equação, a = 1, b = ‒k e c = 9. Então, para Δ = 0, temos: (‒k)2 ‒ 4 · 9 = 0 ⇒ k2 = 36 ⇒

k = \pm \sqrt{36}

= ±6

Então, k = 6 ou k = ‒6.

54. Nessa equação, a = 1, b = ‒(p + 5) e c = 36. Então:

Δ = 0 ⇒ Δ = [‒(p + 5)]2 ‒ 4 ⋅ 1 · 36 = 0 ⇒ (p + 5)2 ‒ 144 = 0 ⇒ (p + 5)2 = 144 ⇒

{(p + 5)}^{2} = 12^{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} p + 5 = ‒ 12 \Rightarrow p = ‒ 17 \\ p + 5 = 12 \Rightarrow p = 7 \end{array}

55. a) Nessa equação, a = 9 , b = 12 e c = 2m.

Para Δ < 0, temos: (12)2 ‒ 4 · 9 · 2m < 0 ⇒ 144 ‒ 72m < 0 ⇒ 72 (2 ‒ m) < 0 ⇒ 2 ‒ m < 0 ⇒ 2 < m ⇒ m > 2

55. b) Para Δ = 0, temos: 72 · (2 ‒ m) = 0 ⇒ 2 ‒ m = 0 ⇒ m = 2

55. c) Para Δ > 0, temos: 72 · (2 ‒ m) > 0 ⇒ 2 ‒ m > 0 ⇒ ‒m > ‒2 ⇒ m < 2

55. d) Como Δ = 72 · (2 ‒ m), temos:

x = \frac{‒ 12 \pm \sqrt{72 \cdot (2 ‒ m)}}{2 \cdot 9}

Portanto, as raízes são:

x_{1} = \frac{‒ 12 + \sqrt{72 \cdot (2 ‒ m)}}{18} = 0, 2

⇒

\Rightarrow ‒ 12 + \sqrt{72 \cdot (2 ‒ m)} = 3, 6 \Rightarrow \sqrt{72 \cdot (2 ‒ m)} = 15, 6

x_{2} = \frac{‒ 12 ‒ \sqrt{72 \cdot (2 ‒ m)}}{18} = 0, 2

\Rightarrow ‒ 12 ‒ \sqrt{72 \cdot (2 ‒ m)} = 3, 6 \Rightarrow ‒ \sqrt{72 \cdot (2 ‒ m)} = 15, 6

⇒ 72 · (2 ‒ m) = 15,62 ⇒

⇒ 72 · (2 ‒ m) = 243,36 ⇒ 2 ‒ m = 3,38 ⇒ m = ‒1,38

Página oitenta e um

56. a) Como

S = ‒ \frac{b}{a}

, temos:

x_{1} + x_{2} = ‒ \frac{‒ 6}{1} = 6 .

56. b) Como

P = \frac{c}{a}

, temos:

x_{1} \cdot x_{2} = \frac{5}{1} = 5 .

57.

	a	b	c	S = $- \frac{b}{a}$	P = $\frac{c}{a}$	x1	x2
Item a	1	− 8	15	$menos divisão de abre parênteses menos 8 fecha parênteses sobre 1$ = 8	$divisão de 15 sobre 1$ = 15	3	5
Item b	1	2	− 3	$menos divisão de 2 sobre 1$ = −2	$divisão de abre parênteses menos 3 fecha parênteses sobre 1$ = −3	− 3	1
Item c	5	21	4	$menos divisão de 21 sobre 5$ = −4,2	$divisão de 4 sobre 5$ = 0,8	− 4	$menos divisão de 1 sobre 5$ 0,2.
Item d	1	7	12	$menos divisão de 7 sobre 1$ = −7	$divisão de 12 sobre 1$ = 12	− 3	− 4
Item e	3	− 6	0	$menos divisão de abre parênteses menos 6 fecha parênteses sobre 3$ = 2	$divisão de 0 sobre 3$ = 0	0	2
Item f	1	0	− 144	$menos divisão de 0 sobre 1$ = 0	$divisão de abre parênteses menos 144 fecha parênteses sobre 1$ = −144	−12	−12

58. Como a = 1, b = ‒9 e c = 20, então:

mn (m + n) = P · S =

\frac{c}{a} \cdot (‒ \frac{b}{a}) = \frac{20}{1} \cdot (‒ \frac{‒ 9}{1})

⇒ mn (m + n) = 180

59.

S = ‒ \frac{b}{a} \Rightarrow ‒ \frac{‒ (m ‒ 2)}{4} = \frac{3}{4}

⇒ m ‒ 2 = 3 ⇒ m = 5

60.

S = ‒ \frac{b}{a} \Rightarrow ‒ \frac{21}{(m + 10)} = ‒ \frac{7}{6} \Rightarrow \frac{3}{m + 10} = \frac{1}{6}

⇒ m + 10 = 18 ⇒ m = 8

61.

P = \frac{c}{a} \Rightarrow \frac{2}{3} = \frac{p ‒ 1}{6} \Rightarrow 2 = \frac{p ‒ 1}{2}

⇒ p ‒ 1 = 4 ⇒ p = 5

62. Se

x_{1} = r

, então

x_{2} = 3 r

, então:

S = r + 3r = 4r e P = r · 3r = 3r2

Portanto:

4 r = ‒ \frac{‒ 8}{1} \Rightarrow 4 r = 8 \Rightarrow r = 2

Assim, obtemos:

3 r^{2} = \frac{2 p}{1}

⇒ 3 · 22 ‒ 1 = 2 p ⇒ p = 3 · 2 = 6

64. a) Considerando x2 ‒ Sx + P = 0, obtemos:

S = ‒8 + 5 = ‒3 e P = 5 · (‒8) = ‒40; então: x2 + 3x ‒ 40 = 0

64. b)

S = 2 + \frac{4}{5} = 2, 8

P = 2 \cdot (\frac{4}{5}) = 1, 6

; então:

x2 ‒ 2,8x + 1,6 = 0 ⇒ 5x2 ‒ 14x + 8 = 0

64. c)

S = ‒ 3 + (‒ \frac{1}{2}) = ‒ 3, 5

P = ‒ 3 \cdot (‒ \frac{1}{2}) = 1, 5

; então:

x2 + 3,5x + 1,5 = 0 ⇒ 2x2 + 7x + 3 = 0

64. d)

S = \frac{1}{3} ‒ \frac{2}{5} = \frac{5 ‒ 6}{15} = ‒ \frac{1}{15}

P = \frac{1}{3} \cdot (‒ \frac{2}{5}) = ‒ \frac{2}{15}

então:

x^{2} + \frac{1}{15} x ‒ \frac{2}{15}

= 0 ⇒ 15x2 + x ‒ 2 = 0

65. x2 ‒ Sx + P = 0; então, x2 ‒ 35x + 300 = 0

Portanto,

x_{1} = 15

x_{2} = 20

(15 + 20 = 35 e 15 · 20 = 300).

66. a) x2 ‒ 2x ‒ 120 = 0

Δ = (‒2)2 ‒ 4 · (‒120) = 4 + 480 ⇒ Δ = 484

x = \frac{‒ (‒ 2) \pm \sqrt{484}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{2 + 22}{2} = 12 \\ x_{2} = \frac{2 ‒ 22}{2} = ‒ 10 \end{array}

Página oitenta e dois

66. b) x2 ‒ 0,2x ‒ 1,2 = 0

Δ = (‒0,2)2 ‒ 4 · (‒1,2) = 0,04 + 4,8 ⇒ Δ = 4,84

x = \frac{‒ (‒ 0, 2) \pm \sqrt{4, 84}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{0, 2 + 2, 2}{2} = 1, 2 \\ x_{2} = \frac{0, 2 ‒ 2, 2}{2} = ‒ 1 \end{array}

Pense mais um pouco

Página 157

Pelos dados do problema, se a caixa-d’água menor tem a medida da aresta representada por x, a caixa-d’água maior terá medida da aresta representada por (x + 1). A diferença entre a capacidade das caixas-d’água é .91000 litros, ou seja, 91 métros cúbicos (1 métro cúbico = .1000 litros). A equação que descreve essa situação é (x + 1)3 ‒ x3 = 91. Aplicando a propriedade do cubo da soma, obtemos:

x3 + 3 ⋅ x² ⋅ 1 + 3 ⋅ x ⋅ 1² + 13 ‒ x3 = 91 ⇒ 3x² + 3x + 1 = 91 ⇒

⇒ 3x² + 3x = 90

Dividindo, membro a membro, por 3, obtemos a equação x² + x = 30. Essa equação pode ser escrita como:

x ² + 2 \cdot x \cdot \frac{1}{2} = 30

Adicionando

{(\frac{1}{2})}^{2}

a cada membro para completar o quadrado perfeito, obtemos:

x ² + 2 \cdot x \cdot \frac{1}{2} + {(\frac{1}{2})}^{2} = 30 + {(\frac{1}{2})}^{2} \Rightarrow {(x + \frac{1}{2})}^{2} = 30 + {(\frac{1}{4})}^{} \Rightarrow

\Rightarrow {(x + \frac{1}{2})}^{2} = \frac{121}{4} \Rightarrow x + \frac{1}{2} = \pm \sqrt{\frac{121}{4}} \Rightarrow x + \frac{1}{2} = \pm \frac{11}{2} \Rightarrow

x = \pm \frac{11}{2} ‒ \frac{1}{2}

Portanto, x = 5 ou x = ‒6.

Concluímos que x = 5 é a solução da equação, pois medidas de comprimento não podem ter valores negativos. Então, as medidas das arestas das caixas-d'água são 5 metros e 6 metros (x = 5 e x + 1 = 6).

Exercícios complementares

1. Como a ≠ 0 ⇒ k + 5 ≠ 0 ⇒ k ≠ ‒5.

2. a) 5 ‒ 5x + 2x ‒ 2x2 = 5 ⇒ 2x2 + 3x = 0 ⇒ x (2x + 3) = 0

Portanto, as raízes da equação são

x_{1} = 0 e x_{2} = ‒ \frac{3}{2}

2. b) 3y2 ‒ 5y ‒ 15y + 25 + y2 = 0 ⇒ 4y2 ‒ 20y + 25 = 0

Δ = (‒20)2 ‒ 4 · 4 · 25 ⇒ Δ = 0

y = \frac{‒ (‒ 20) \pm \sqrt{0}}{2 \cdot 4} = \frac{20}{8} \Rightarrow y = \frac{5}{2}

2. c) ‒2x2 ‒ x + 4x + 2 = 3x + 5x2 ⇒ 7x2 ‒ 2 = 0 ⇒

\Rightarrow x^{2} = \frac{2}{7} \Rightarrow x = \pm \sqrt{\frac{2}{7}}

2. d) 3x2 + 12 = 0 ⇒

x = \pm \sqrt{‒ \frac{12}{3}}

(não há raiz real)

3. A medida da área da parte pintada de azul é dada por:

(x + 3)2 ‒ x2 = x2 + 6x + 9 ‒ x2 = 6x + 9

6x + 9 = 57 ⇒ x = 8

Então, o valor de x deve ser 8 centímetros.

4. a) Nessa equação, b = ‒(m ‒ 5) e c = 1 ‒ m, então:

c = 0 ⇒ 1 ‒ m = 0 ⇒ m = 1

4. b) b = 0 ⇒ m ‒ 5 = 0 ⇒ m = 5

5. a) Sendo x a medida do lado do quadrado, então 3x2 é a medida da área dos três terrenos; portanto, 3x2 = .4800.

5. b) 3x2 = .4800 ⇒ x2 = .1600 ⇒ x = ±40

Portanto, as raízes da equação são

x_{1} = 40 e x_{2} = ‒ 40

5. c) A medida não pode ser negativa; então,

x_{1} = 40

é a raiz que representa a medida do lado de cada terreno quadrado.

6. x2 + 10x = 11x ⇒ x2 ‒ x = 0 ⇒ x · (x ‒ 1) = 0

Portanto: x = 0 ou x ‒ 1 = 0 ⇒ x = 1

7. A figura lilás é formada por 6 quadrados de lados medindo

\frac{h}{4}

; então, sua medida de área é:

6 \cdot {(\frac{h}{4})}^{2}

A medida da área do retângulo verde é:

(2 \sqrt{3}) \cdot (3 \sqrt{3})

= 6 · 3 = 18

Então:

6 \cdot {(\frac{h}{4})}^{2} = 18 \Rightarrow {(\frac{h}{4})}^{2} = 3 \Rightarrow \frac{h}{4} = \sqrt{3} \Rightarrow h = 4 \sqrt{3}

8. a) Nessa equação, a = k, b = ‒16 , c = 5, então:

Δ = (‒16)2 ‒ 4 · k · 5 ⇒ Δ = 256 ‒ 20k

x = \frac{16 \pm \sqrt{256 ‒ 20 k}}{2 k} \Rightarrow \frac{16 \pm \sqrt{256 ‒ 20 k}}{2 k} = 3 \Rightarrow

\Rightarrow 16 \pm \sqrt{256 ‒ 20 k} = 3 \cdot 2 k \Rightarrow \pm \sqrt{256 ‒ 20 k} = 3 \cdot 2 k ‒ 16

⇒

{(\pm \sqrt{256 ‒ 20 k})}^{2}

= (3 · 2k ‒ 16)2 ⇒ 256 ‒ 20k = (6k ‒ 16)2 ⇒

⇒ 256 ‒ 20k = 36k2 ‒ 2 · 6k · (16) + 162 ⇒

⇒ 256 ‒ 20k = 36k2 ‒ 192k + 256 ⇒

⇒ 36k2 ‒ 172k = 0 ⇒ 9k 2 ‒ 43k = 0 ⇒

⇒ k(9k ‒ 43) = 0

Portanto, k = 0 ou 9k ‒ 43 = 0 ⇒

k = \frac{43}{9}

Como para k = a = 0 a equação não é de 2º grau, então

k = \frac{43}{9}

8. b)

\frac{16 \pm \sqrt{256 ‒ 20 k}}{2 k} = \frac{1}{2} \Rightarrow \frac{16 \pm \sqrt{256 ‒ 20 k}}{k}

= 1 ⇒

\Rightarrow 16 \pm \sqrt{256 ‒ 20 k} = k ‒ 16 \Rightarrow

⇒ 256 ‒ 20k = k2 ‒ 32k + 256 ⇒

⇒ k2 ‒ 12k = 0 ⇒ k · (k ‒ 12) = 0

Portanto: k = 0 ou k ‒12 = 0 ⇒ k = 12

Então, k = 12.

8. c) Como Δ = 256 ‒ 20k ⇒ Δ > 0, então:

256 ‒ 20k > 0 ⇒ 256 > 20k

Portanto: 12,8 > k ⇒ k < 12,8 ⇒

k < \frac{64}{5}

8. d) A soma das raízes é:

‒ \frac{b}{a} = ‒ \frac{‒ 16}{k} = \frac{16}{k} = \frac{4}{3}

Portanto: k = 4 · 3 = 12

9. Como 8 é raiz, temos:

2 · 82 ‒ 3p · 8 + 40 = 0 ⇒ 128 ‒ 24p + 40 = 0 ⇒

⇒ 168 ‒ 24p = 0 ⇒

p = \frac{168}{24} = 7

Alternativa c.