Página oitenta e três

Parte 8

10.

\frac{2 x^{2} + x}{11}

= 2x +1 ⇒ 2x2 + x = (2x +1) ⋅ 11 ⇒

⇒ 2x2 + x = 22x +11 ⇒ 2x2 ‒ 21x ‒11 = 0

Δ = (‒21)2 ‒ 4 · 2 · (‒11) = 441 + 88 ⇒ Δ = 529

x = \frac{‒ (‒ 21) \pm \sqrt{529}}{2 \cdot 2} \Rightarrow

⇒ 

x = \frac{21 \pm 23}{4} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x = \frac{21 + 23}{4} = \frac{44}{4} = 11 \\ x = \frac{21 - 23}{4} = ‒ 0,5 \end{array}

O número inteiro 11 é múltiplo de 1 e de 11.

Alternativa ê.

12. Δ = b2 ‒ 4 · a · c = (‒B)2 ‒ 4 · 4 = B2 ‒ 16 ⇒ Δ = 65

B2 ‒16 = 65 ⇒ B2 = 81 ⇒ B = ±

\sqrt{81}

Portanto: B = 9 ou B = ‒9

Alternativa d.

13.

x_{1} + x_{2} = x_{1} \cdot x_{2}

‒ \frac{b}{a} = \frac{c}{a} \Rightarrow ‒ b = c

Como b = ‒4k e c = 1, então ‒(‒4k ) = 1 ⇒ k =

\frac{1}{4}

Alternativa c.

14. 72 : x = 2x ⇒ 72 = 2x2 ⇒ x2 = 36 ⇒ x = ±

\sqrt{36}

Como x < 0, x = ‒6. Então, a metade do número é ‒3, pois ‒6 : 2 = ‒3.

Alternativa a.

16. P = 5 ⋅ 1 = 5 e S = 1 + 5 = 6; então:

x2 ‒ 5x + 6 = 0

Resolvendo corretamente,

S = ‒ \frac{b}{a} = 5

e P = 6, então as raízes são 2 e 3 (2 + 3 = 5 e 2 · 3 = 6).

17. Soma:

‒ \frac{b}{a} = ‒ \frac{3}{k} = 10 \Rightarrow k = ‒ \frac{3}{10} = ‒ 0, 3

Produto:

\frac{c}{a} = ‒ \frac{4}{‒ 0, 3} = \frac{40}{3}

Alternativa a.

18. 8 + 2 = ‒b ⇒ b = ‒10

Com o valor de c correto, o produto é:

\frac{c}{a}

= (‒9) ⋅ (‒1) ⇒

\frac{c}{1}

= 9 ⇒ c = 9

Então, as raízes de x2 ‒ 10x + 9 = 0 são 9 e 1. A soma pedida é 12, pois 3 ⋅ 1 + 9 = 3 + 9 = 12.

Verificando

1. x + 2x ‒ 3 = 0 não tem nenhum termo de grau 2.

Alternativa c.

2. Como ax2 + bx + c = 0, então a = 2, c = 3 e b = 0.

Alternativa b.

3. Uma equação do 2º grau com b ≠ 0 e c ≠ 0 é dita completa.

Alternativa d.

4. A = x · 3x ⇒

⇒ A = 3x2 ⇒ 3x2 ‒ A = 0

Alternativa a.

5. x2 ‒ 2x = 0 ⇒ Δ = (‒2)2 ‒ 4 · 1 · 0 = 4 ⇒

x = \frac{‒ (‒ 2) \pm \sqrt{4}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} \frac{2 + 2}{2} = 2 \\ \frac{2 ‒ 2}{2} = 0 \end{array}

Alternativa b.

6. a) x = 7 em x2 + 4x ‒ 2 ⇒ 72 + 4 · 7 ‒ 2 = 49 + 28 ‒ 2 ≠ 0

6. b) x = 7 em x2 ‒ 2 ⇒ 72 ‒ 2 = 49 ‒ 2 ≠ 0

6. c) x = 7 em ‒2x2 + 4x ⇒ ‒2 · 72 + 4 · 7 = ‒2 · 49 + 28 ≠ 0

6. d) x = 7 em x2 ‒ 3x ‒ 28 ⇒ 72 ‒ 3 · 7 ‒ 28 = 49 ‒ 21 ‒ 28 = 0

Alternativa d.

7. x2 + 4 = 0

Δ = 02 ‒ 4 · 4 = ‒16

Então, como Δ < 0, a equação não possui raízes reais.

Alternativa a.

8. 2x² ‒ 4x + 2 = 0

Δ = (‒4)2 ‒ 4 · 2 · 2 = 16 ‒16 ⇒ Δ = 0

Alternativa c.

9. Temos que a = x2 = 49 ⇒

x = \pm \sqrt{49}

⇒ x = ±7. Como x é uma medida de comprimento, não pode ser negativo, então, temos que x = 7 centímetros.

Alternativa b.

10. A = x · (2x) = 200 ⇒ 2x2 = 200 ⇒ x2 = 100 ⇒ x = ±10

Como é a medida do lado, então 10 métros é a medida do menor lado e 20 métros é a medida do maior lado (2 ⋅ 10 = 20).

Alternativa d.

Capítulo 8 ‒ Triângulo retângulo

• Objetivos do capítulo e justificativas

• Reconhecer os elementos de um triângulo retângulo.

• Conhecer o teorema de Pitágoras, verificar demonstrações e algumas aplicações.

• Resolver problemas que envolvam semelhança de triângulos e triângulos retângulos.

• Demonstrar as relações métricas em um triângulo retângulo.

• Apresentar algoritmo para a construção de um quadrado com régua e compasso.

• Determinar a distância entre dois pontos no plano cartesiano e das coordenadas do ponto médio de um segmento de reta.

• Explorar a representação gráfica de um relevo.

Neste capítulo, retomamos e ampliamos o estudo dos triângulos retângulos, tratando das relações métricas em um triângulo retângulo, com destaque para o teorema de Pitágoras e suas aplicações. Além disso, exploramos a medida da distância entre dois pontos no plano cartesiano e a representação gráfica de um relevo, que pode ser associada com as vistas ortogonais de um sólido geométrico, favorecendo o trabalho com as competências específicas 2, 3 e 6 e com as competências gerais 2 e 4.

Página oitenta e quatro

Nesta abertura, apresentamos um monumento construído em homenagem a Pitágoras, que faz menção à figura de um triângulo retângulo, para posteriormente apresentarmos um pouco sobre a História da Matemática, contribuindo para o desenvolvimento da competência específica 1 e da competência geral 1.

O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois permitem aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação as atividades propostas.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah um três) Demonstrar relações métricas do triângulo retângulo, entre elas o teorema de Pitágoras, utilizando, inclusive, a semelhança de triângulos.

(ê éfe zero nove ême ah um quatro) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

(ê éfe zero nove ême ah um seis) Determinar o ponto médio de um segmento de reta e a distância entre dois pontos quaisquer, dadas as coordenadas dêsses pontos no plano cartesiano, sem o uso de fórmulas, e utilizar esse conhecimento para calcular, por exemplo, medidas de perímetros e áreas de figuras planas construídas no plano.

(ê éfe zero nove ême ah um sete) Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.

Este capítulo tem foco na Unidade Temática Geometria, tratando do estudo do triângulo retângulo, aprofundando o teorema de Pitágoras, sua demonstração e variadas aplicações, assim como apresenta outras relações métricas existentes nesse triângulo desenvolvendo-se, assim, as habilidades (ê éfe zero nove ême ah um três), (ê éfe zero nove ême ah um quatro) e (EF09MA16) e estabelecendo relações com as Unidades Temáticas Álgebra e Grandezas e medidas.

Além disso, aspectos da habilidade (ê éfe zero nove ême ah um sete) também são trabalhados em uma atividade que propõe o estudo de vistas ortogonais em um contexto de representação de relevos.

O trabalho com este capítulo visa também a embasar estudos que serão tratados no Ensino Médio.

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Abertura

a) O monumento lembra um triângulo retângulo pois, pode-se associar um ângulo reto formado entre a estátua e a base.

Exercícios propostos

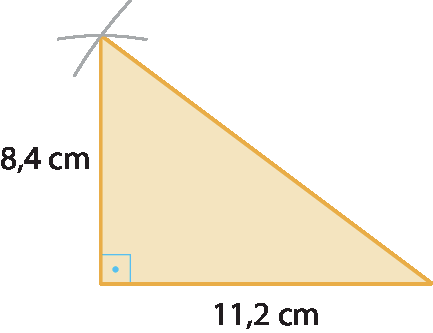
Ilustração. Triângulo retângulo com catetos medindo: 8,4 centímetros, 11,2 centímetros.

1. a) Resposta esperada: ao utilizar uma régua, é esperado que o estudante encontre a medida de comprimento de 14 centímetros, aproximadamente.

1. b) 142 = 8,42 + 11,22 ⇒ 196 = 70,56 + 125,44 ⇒ 196 = 196

Então, sim; a medida da hipotenusa ao quadrado é igual à soma dos quadrados das medidas dos catetos.

2. Construindo os triângulos, obtemos:

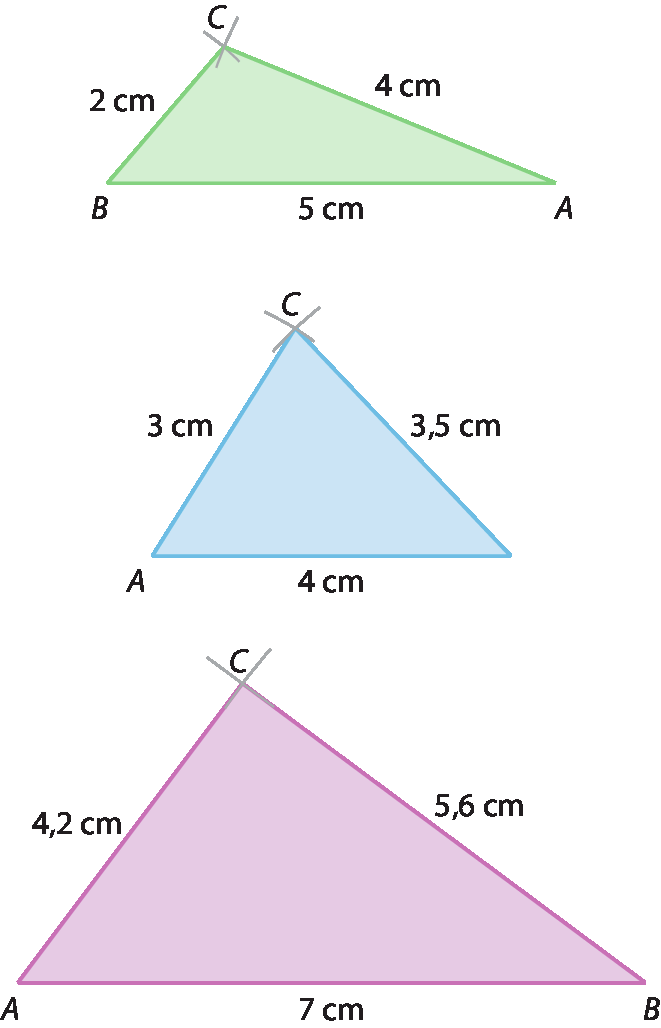
Ilustração. Triângulo escaleno ABC com lados AB medindo 5 centímetros, BC medindo 2 centímetros, AC medindo 4 centímetros.
Ilustração. Triângulo escaleno com vértices A e C indicados. AC mede 3 centímetros, o lado oposto ao vértice C mede 4 centímetros, e o lado oposto ao vértice A mede 3,5 centímetros.
Ilustração. Triângulo escalenos ABC com lados: AB medindo 7 centímetros, BC medindo 5,6 centímetros, AC medindo 4,2 centímetros.

2. a) 1º triângulo: obtusângulo, pois um dos ângulos é maior que 90graus; 2º triângulo: acutângulo, pois todos os ângulos são menores que 90graus; 3º triângulo: retângulo, pois um ângulo

(\hat{C})

tem medida 90graus.

2. b) 1º triângulo: 5² > 2² + 4², pois 25 > 4 + 16; 2º triângulo: 4² < 3² + 3,5², pois 16 < 9 + 12,25; 3º triângulo: 7² = 4,2² + 5,6², pois 49 = 17,64 + 31,36

3. a) 15² = 12² + x² ⇒ 225 = 144 + x² ⇒ 81 = x² ⇒ x = 9

3. b) x2 + x2 = 102 ⇒ 2x2 = 100 ⇒ x2 = 50 ⇒ x =

5 \sqrt{2}

3. c) x2 + (

5 \sqrt{3}

)2 = 142 ⇒ x2 + 75 = 196 ⇒ x2 = 121 ⇒ x = 11

3. d) x2 + (

\sqrt{7}

)2 = (x + 1)2 ⇒ x2 + 7 = x2 + 2x + 1 ⇒ 2x = 6 ⇒ ⇒ x = 3

4. Como o quadrado a bê cê dê tem medida de área 11 centímetros quadrados, seu lado tem medida

\sqrt{11}

centímetros (pois (

\sqrt{11}

)2 = 11). O lado do quadrado dê é éfe gê tem medida 5 centímetros, pois sua área mede 25 centímetros quadrados (

\sqrt{25}

= ±5, considerando-se o valor positivo para a medida do lado).

4. a) Então, a área do triângulo cê dê é mede 2,5

\sqrt{11}

centímetros quadrados, pois:

\frac{\sqrt{11} \cdot 5}{2} = \frac{5 \sqrt{11}}{2} = 2, 5 \sqrt{11}

Página oitenta e cinco

4. b) A hipotenusa mede x = 6 centímetros, pois: x2 = (

\sqrt{11}

)2 + 52 ⇒ ⇒ x2 = 11 + 25 = 36 ⇒ x = 6

5. O lado oposto ao ângulo reto é a hipotenusa que mede x = 24 centímetros, pois: x2 = 122 + (

12 \sqrt{3}

)2 ⇒ x2 = 144 + 144 · 3 ⇒ x2 = 144 · 4 ⇒ x = 12 · 2 ⇒ x = 24

6. a) A hipotenusa do triângulo retângulo cujos catetos medem 9 e 12 tem medida y = 15, pois:

y2 = 92 + 122 ⇒ y2 = 225 ⇒ y = 15

Assim, aplicando o teorema de Pitágoras no outro triângulo retângulo da figura, obtemos:

\frac{16 x^{2}}{9} = 225 + 175 \Rightarrow \frac{16 x^{2}}{9} = 400 \Rightarrow x ² = 225 \Rightarrow x = 15

6. b) x2 + (x + 2)2 = (x + 4)2 ⇒ x2 + x2 + 4x + 4 = x2 + 8x + 16 ⇒ x2 ‒ 4x ‒ 12 = 0

Δ = (‒4)2 ‒ 4 ⋅ 1 ⋅ (‒12) ⇒ Δ = 64

x = \frac{‒ (‒ 4) \pm \sqrt{64}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{4 + 8}{2} \Rightarrow x_{1} = 6 \\ x_{2} = \frac{4 ‒ 8}{2} \Rightarrow x_{2} = ‒ 2 \end{array}

Portanto, x = 6, pois a medida do lado deve ser um valor positivo.

6. c) Por se tratar de um trapézio isósceles, é possível considerar a base maior da maneira apresentada na figura a seguir.

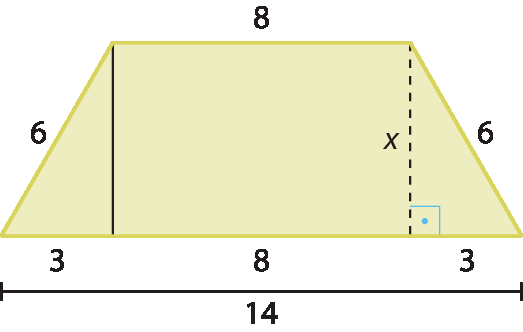
Ilustração. Trapézio isósceles. A base menor mede 8. Estão traçadas as duas alturas, formando um triângulo retângulo de cada lado, cada hipotenusa mede 6, e cada cateto menor mede 3, e a altura do trapézio (cateto maior) mede x. A medida total da base maior é 14.

Portanto: x² + 3² = 6² ⇒ x2 = 27 ⇒

x = 3 \sqrt{3}

6. d) Falta a medida de comprimento de um dos catetos para ser possível calcular o valor de “x”.

7. Podemos representar o losango da seguinte maneira:

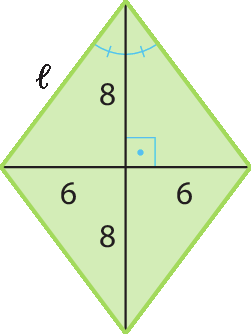
Ilustração. Losango com lado L. As diagonais estão traçadas, cada metade da diagonal maior mede 8, e cada metade da diagonal menor mede 6.

7. a) ℓ2 = 62 + 82 = 36 + 64 ⇒ ℓ2 = 100 ⇒ ℓ = 10

Portanto, 10 centímetros.

7. b)

A = \frac{d \cdot D}{2} \Rightarrow A = \frac{12 \cdot 16}{2}

= 12 · 8 ⇒ A = 96

Portanto, 96 centímetros quadrados.

7. c) Não. A medida do ângulo não foi utilizada para resolver a atividade.

8. Esboço possível:

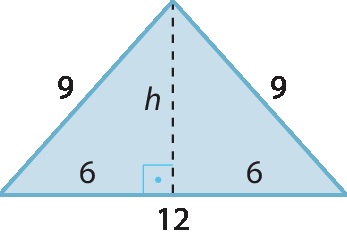
Ilustração. Triângulo isósceles, cujos lados congruentes medem 9. Está traçada a altura h em relação a base, dividindo a base em duas partes de medida igual a 6 cada uma; a base mede 12.

Portanto: h2 + 62 = 92 ⇒ h2 + 36 = 81 ⇒ h2 = 45 ⇒ h =

3 \sqrt{5}

A altura mede

3 \sqrt{5}

centímetros.

9. Traçando a altura do trapézio (de medida h), a partir do vértice superior direito, a base maior se divide em duas partes desiguais: uma medindo 12 (a mesma medida da base menor) e outra parte medindo 8 (a diferença 20 ‒ 12 = 8). Portanto, obtém-se um triângulo retângulo cuja hipotenusa é o lado oblíquo e, assim:

h2 + 82 = 102 ⇒ h2 + 64 = 100 ⇒ h2 = 100 ‒ 64 = 36 ⇒ h = 6

O lado perpendicular às bases tem a mesma medida h e, portanto, o perímetro do trapézio mede 48 métros (6 + 20 + 10 + 12 = 48). Para cercá-lo com 6 voltas, são necessários 288 métros de arame, pois: 6 ⋅ 48 = 288

10. Escrevendo a relação entre as medidas dos lados:

x2 + (x + 3)2 = (

3 \sqrt{5}

)2 ⇒ x2 + x2 + 6 + 9 = 9 · 5 ⇒

⇒ 2x2 + 6x ‒ 36 = 0 ⇒ x2 + 3x ‒ 18 = 0

Resolvendo a equação: Δ = 32 ‒ 4 ⋅ 1 ⋅ (‒18) ⇒ Δ = 81

Calculando os valores de x:

x = \frac{‒ 3 \pm \sqrt{81}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{‒ 3 + 9}{2} \Rightarrow x_{1} = 3 \\ x_{2} = \frac{-3 ‒ 9}{2} \Rightarrow x_{2} = ‒ 6 \end{array}

Como não pode ser negativo, logo um lado mede 3 métros e o outro 6 métros (pois x = 3 e x + 3 = 3 + 3 = 6).

11. O bambu e o solo formam um triângulo retângulo, sendo x a medida da hipotenusa, que é o pedaço quebrado do bambu. Então:

x2 = 4,82 + 3,62 = 23,04 + 12,96 ⇒ x2 = 36 ⇒ x = 6

Portanto, a altura do bambu é 10,8 métros, pois: 6 + 4,8 = 10,8

12. A diagonal da placa tem medida d ≃ 5,38 métros, pois, das informações do enunciado, obtemos: d2 = 22 + 52 = 4 + 25 ⇒ d =

\sqrt{29}

⇒ d ≃ 5,38

13. A figura mostra dois tamanhos de ripa diagonal, que formam triângulos retângulos. Em cada um dos triângulos menores, os catetos medem 1,2 métro e 0,5 métro e, chamando a medida da hipotenusa de d, então d = 1,3 métro, pois:

d2 = 1,22 + 0,52 = 1,44 + 0,25 ⇒ d 2 = 1,69 ⇒ d = 1,3

Em cada um dos triângulos maiores, os catetos medem 3,6 métros e 1,5 métro; portanto, se a medida da hipotenusa é D, então D = 3,9 métros, pois:

D2 = 1,52 + 3,62 = 2,25 + 12,96 ⇒ D2 = 15,21 ⇒ D = 3,9

Portanto, para construir as outras partes são necessários 10,4 métros de madeira, pois:

1,3 + 1,3 + 3,9 + 3,9 = 10,4

14. Percorreria 500 quilômetros, pois, sendo d a medida procurada, temos:

d2 = 3002 + 4002 ⇒ d2 = .90000 +.160000 ⇒

\Rightarrow d = \sqrt{250 000} \Rightarrow d = 500

15. Resposta pessoal. Um exemplo de problema é: um artesão precisa cortar um barbante na exata medida do perímetro de uma janela em formato de um triângulo retângulo. Sabendo que os catetos dêsse triângulo medem 2 metros, qual deve ser a medida do comprimento do barbante cortado? Resolução: d2 = 22 + 22 ⇒ d2 = 8 ⇒

d = 2 \sqrt{2}

⇒ d ≃ 2,8. Assim, o comprimento do barbante deve medir 6,8 métros, pois 2 + 2 + 2,8 = 6,8.

Página oitenta e seis

16. a) A diagonal do quadrado fórma com dois de seus lados um triângulo retângulo. Então, ela mede

15 \sqrt{2}

centímetros, pois:

d2 = 152 + 152 ⇒ d2 = 2 ⋅ 152 ⇒ d =

\sqrt{2}

⋅ 15 ⇒ d =

15 \sqrt{2}

16. b) A área mede 450 centímetros quadrados, pois:

A = 15 \sqrt{2} \cdot 15 \sqrt{2}

⇒ A = 225 ⋅ 2 = 450

17. Sabendo que

d = ℓ \sqrt{2}

, no caso do quadrado a bê cê dê,

d = 2, 5 \sqrt{2}

. Então, o lado do quadrado á cê êne ême mede

2, 5 \sqrt{2}

centímetros e sua área mede 12,5 centímetros quadrados, pois:

2, 5 \sqrt{2} \cdot 2, 5 \sqrt{2}

= 12,5

18. O posicionamento descrito dos quadrados é mostrado na figura a seguir:

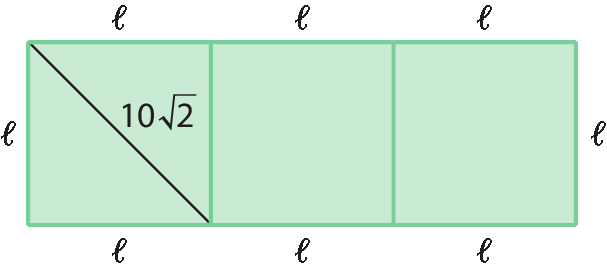
Ilustração. Três quadrados lado a lado, formando um retângulo. A medida de cada lado dos quadrados é L. Diagonal em um dos quadrados medindo 10 vezes raiz quadrada de 2.

Como

d = ℓ \sqrt{2} \Rightarrow 10 \sqrt{2}

ℓ \sqrt{2}

⇒ ℓ = 10. O perímetro do retângulo mede 8ℓ. Portanto, o perímetro mede 80 centímetros (10 ⋅ 8 = 80).

19. A diagonal do cubo, de medida D, é hipotenusa de um triângulo retângulo com catetos medindo 3 e a diagonal de medida d da face quadrada do cubo.

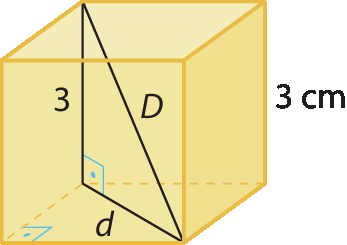
Ilustração. Cubo de aresta medindo 3 centímetros. Triângulo retângulo em que a hipotenusa é a diagonal D do cubo, um dos catetos é a aresta do cubo que mede 3, e o outro cateto é a diagonal d da face.

Então: d2 = 32 + 32 ⇒ d2 = 18

Portanto: D2 = 32 + d2 ⇒ D2 = 9 + 18 ⇒ D2 = 27 ⇒ D =

3 \sqrt{3}

Logo, a diagonal do cubo mede

3 \sqrt{3}

centímetros.

20. Como

h = \frac{ℓ \sqrt{3}}{2}

, nesse caso h =

\frac{3 \sqrt{3}}{2}

centímetros.

21.

h = \frac{ℓ \sqrt{3}}{2} \Rightarrow 12 \sqrt{3} = \frac{ℓ \sqrt{3}}{2} \Rightarrow 12 = \frac{ℓ}{2} \Rightarrow ℓ = 24

Então, a medida da área, em centímetros quadrados, é dada por:

A = \frac{ℓ \cdot h}{2} = \frac{24 \cdot 12 \sqrt{3}}{2} \Rightarrow A = 144 \sqrt{3}

22. O lado do triângulo mede 16 centímetros, pois 48 : 3 = 16.

h = \frac{16 \sqrt{3}}{2} \Rightarrow h = 8 \sqrt{3}

Logo, a altura mede

8 \sqrt{3}

centímetros.

23. Calculando a medida da diagonal do quadrado, obtemos:

d2 = 252 + 252 ⇒ d2 = 2 · 252 ⇒ d =

25 \sqrt{2}

Então, essa é a medida do lado do triângulo e, portanto:

h = \frac{ℓ \cdot \sqrt{3}}{2} \Rightarrow h = \frac{25 \sqrt{2} \cdot \sqrt{3}}{2} \Rightarrow h = \frac{25 \sqrt{6}}{2}

24. O lado do triângulo mede 3 centímetros, pois 1,5 + 1,5 = 3. Sua altura mede 1,5

\sqrt{3}

centímetros, pois

h = \frac{3 \sqrt{3}}{2} = 1, 5 \sqrt{3}

. Portanto, sua área, em centímetros quadrados, é dada por:

A = \frac{3 · 1, 5 \sqrt{3}}{2} = \frac{4, 5}{2} \sqrt{3} \Rightarrow A = 2, 25 \sqrt{3}

25. a) Falsa, pois o ponto P não pertence à reta r.

25. b) Verdadeira, pois

\bar{C' D'}

corresponde à projeção ortogonal de

\bar{C D}

sobre

\bar{A B}

25. c) Verdadeira, pois

\bar{N' N}

é perpendicular a s.

25. d) Verdadeira, pois

\bar{M' N'}

corresponde à projeção ortogonal de MN sobre

\bar{M N}

26. a) A projeção ortogonal de

\bar{A B}

sobre

\bar{B C}

\bar{B H}

. A projeção ortogonal de

\bar{A C}

sobre

\bar{B C}

\bar{H C}

26. b) A projeção ortogonal de

\bar{A B}

sobre

\bar{B C}

\bar{B M}

. A projeção ortogonal de

\bar{A C}

sobre

\bar{B C}

\bar{C M}

27. a) OD2 = OM2 + MD2 ⇒ OD2 = (

\sqrt{2}

)2 + 12 = 2 + 1 ⇒ OD =

\sqrt{3}

Então o perímetro mede:

1 + \sqrt{2} + \sqrt{3}

27. b) A área mede 3 centímetros quadrados, pois:

{(\sqrt{3})}^{2} = 3

28. a) 162 = 12,8 ⋅ x ⇒ 256 = 12,8x ⇒ x = 20

28. b) x2 = 5 ⋅ 20 ⇒ x2 = 100 ⇒ x = 10

28. c) 122 = 9x ⇒ 32 · 42 = 32 · x ⇒ x = 16

29.

{(2 \sqrt{7})}^{2}

+ b2 = 82 ⇒ 28 + b2 = 64 ⇒ b2 = 36 ⇒ b = 6

62 = 8 m ⇒ 22 · 32 = 23 · m ⇒ 32 = 2 · m ⇒ m = 4,5

n = 8 ‒ 4,5 ⇒ n = 3,5

8 h = 6 ⋅

2 \sqrt{7} \Rightarrow h = \frac{12 \sqrt{7}}{8} \Rightarrow h = \frac{3 \sqrt{7}}{2}

30. Das informações do enunciado, m = 3,2 centímetros e n = 1,8 centímetros. Aplicando as relações métricas, obtemos:

h2 = m · n ⇒ h2 = 1,8 ⋅ 3,2 ⇒ h2 = 5,76 ⇒ h = 2,4

a2 = h2 + n2 ⇒ a2 = 2,42 + 1,82 ⇒ a2 = 5,76 + 3,24 = 9 ⇒ a = 3

c = m + n = 3,2 + 1,8 ⇒ c = 5

a2 + b2 = c2 ⇒ 32 + b2 = 52 ⇒ b2 = 25 ‒ 9 = 16 ⇒ b = 4

31. A figura MNPQ é um losango e seu lado de medida x é hipotenusa de um triângulo retângulo com catetos de medida 3 centímetros e 4 centímetros, pois é metade da medida dos lados. Então, x2 = 32 + 42 ⇒ x = 5. O perímetro da figura MNPQ mede 20 centímetros, pois 4 ⋅ 5 = 20.

Alternativa a.

32. a) Os triângulos QPR e QRH são semelhantes, pois têm ângulo Q em comum e os ângulos

Q \hat{R} P

Q \hat{H} R

são retos. Então:

\frac{r}{p} = \frac{p}{x} \Rightarrow p^{2} = r x

32. b) Os triângulos MPN e MNH são semelhantes, pois os ângulos no vértice M são comuns e

M \hat{H} N ≅ M \hat{N} P

(são ambos retos). De fórma análoga, MPN e NPH são semelhantes, pois o ângulo P é comum e

P \hat{H} N ≅ P \hat{N} M

(são retos). Por isso, MPN ≅ MNH ≅ NPH e então:

\frac{x}{a} = \frac{b}{x} \Rightarrow x = a b

33. Sendo h a medida da altura, e a a medida da hipotenusa: a2 = 152 + 202 = 225 + 400 ⇒ a2 = 625 ⇒ a = 25

Pela relação: b · c = a · h ⇒ 15 ⋅ 20 = 25 · h ⇒

\Rightarrow h = \frac{(3 \cdot 5) \cdot (4 \cdot 5)}{5 \cdot 5} = 3 \cdot 4 \Rightarrow h = 12

34. Sendo a a medida da hipotenusa, e h a altura relativa a ela, a área, em centímetros quadrados, é calculada por:

\frac{a \cdot h}{2}

= 36 ⇒ a · h = 72

35. x ⋅ ( x + 2) =

{(\sqrt{3})}^{2}

⇒ x2 + 2x ‒ 3 = 0

Resolvendo a equação: Δ = 22 ‒ 4 ⋅ 1 ⋅ (‒3) ⇒ Δ = 4 + 12 = 16

x = \frac{‒ 2 \pm \sqrt{16}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{‒ 2 + 4}{2} = 1 \\ x_{2} = \frac{‒ 2 ‒ 4}{2} = ‒ 3 \end{array}

Página oitenta e sete

Como não pode ser negativo, x = 1 centímetro; assim, o diâmetro mede 4 centímetros, pois: 1 + 1 + 2 = 4

36. Resposta pessoal. Um exemplo de problema é: Um cateto de um triângulo retângulo mede 12 centímetros, e a hipotenusa dêsse triângulo mede 20 centímetros. Qual é a medida do comprimento da projeção deste cateto sobre a hipotenusa dêsse triângulo? Resolução:

b2 = a · n ⇒ 122 = 20 ⋅ n ⇒ n =

\frac{(4 \cdot 3) \cdot 12^{2}}{4 \cdot 5} \Rightarrow n = \frac{432}{5}

⇒ n = 7,2

Então, 7,2 centímetros.

37. a)

E T = \sqrt{{(105 ‒ 0)}^{2} + {(34 ‒ 0)}^{2}}

⇒

E T = \sqrt{11 025 + 1 156} \Rightarrow E T ≃ 110, 4

37. b)

E Q = \sqrt{{(52, 5 ‒ 0)}^{2} + {(68 ‒ 0)}^{2}}

⇒

E Q = \sqrt{2 756, 25 + 4 624} \Rightarrow E Q ≃ 85, 9

37. c)

P C = \sqrt{{(52, 5 ‒ 11)}^{2} + {(34 ‒ 34)}^{2}} \Rightarrow

\Rightarrow P C = \sqrt{{(52, 5 ‒ 11)}^{2}} \Rightarrow P C = 52, 5 ‒ 11 = 41, 5

37. d)

C T = \sqrt{{(105 ‒ 52, 5)}^{2} + {(34 ‒ 34)}^{2}} \Rightarrow

\Rightarrow C T = \sqrt{{(105 ‒ 52, 5)}^{2}} \Rightarrow C T = 105 ‒ 52, 5 = 52, 5

37. e)

C Q = \sqrt{{(52, 5 - 52, 5)}^{2} + {(68 - 34)}^{2}} \Rightarrow

\Rightarrow C Q = \sqrt{{(68 - 34)}^{2}} \Rightarrow C Q = 68 - 34 \Rightarrow C Q = 34

38. Representando no plano cartesiano, obtemos:

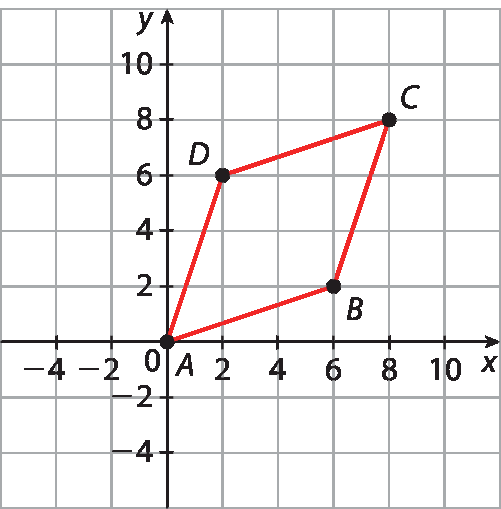
Ilustração. Malha quadriculada com plano cartesiano. Eixo x, com escala de menos 4 a 10, de duas em duas unidades. Eixo y, com escala de menos 4 a 10, de duas em duas unidades. Losango ABCD com vértices A (0, 0). B (6, 2). C (8, 8). D (2, 6).

38. a)

A C = \sqrt{{(8 - 0)}^{2} + {(8 - 0)}^{2}} \Rightarrow A C = \sqrt{2 \cdot 8^{2}} \Rightarrow

\Rightarrow A C = 8 \sqrt{2}

B D = \sqrt{{(2 - 6)}^{2} + {(6 - 2)}^{2}} \Rightarrow B D = \sqrt{2 \cdot 4^{2}} \Rightarrow

\Rightarrow B D = 4 \sqrt{2}

38. b)

B A = \sqrt{{(6 - 0)}^{2} + {(2 - 0)}^{2}} \Rightarrow B A = \sqrt{36 + 4} = \sqrt{40}

⇒

B A = 2 \sqrt{10}

39. Os pontos no plano cartesiano são: a(3, 2), B(6, 4), C(‒4, 5), D (6, ‒4), ê(‒5, ‒4). Logo:

A B = \sqrt{{(6 - 3)}^{2} + {(4 - 2)}^{2}} \Rightarrow A B = \sqrt{3^{2} + 2^{2}} \Rightarrow A B = \sqrt{13}

A C = \sqrt{{(- 4 - 3)}^{2} + {(5 - 2)}^{2}} \Rightarrow A C = \sqrt{7^{2} + 3^{2}} \Rightarrow A C = \sqrt{58}

A D = \sqrt{{(6 - 3)}^{2} + {(- 4 - 2)}^{2}} \Rightarrow A D = \sqrt{3^{2} + 6^{2}} \Rightarrow A D = 3 \sqrt{5}

A E = \sqrt{{(‒ 5 - 3)}^{2} + {(- 4 - 2)}^{2}} \Rightarrow A E = \sqrt{8^{2} + 6^{2}} \Rightarrow A E = 10

B C = \sqrt{{(‒ 4 - 6)}^{2} + {(5 - 4)}^{2}} \Rightarrow B C = \sqrt{10^{2} + 1^{2}} \Rightarrow B C = \sqrt{101}

B D = \sqrt{{(6 - 6)}^{2} + {(- 4 - 4)}^{2}} \Rightarrow B D = \sqrt{8^{2}} \Rightarrow B D = 8

B E = \sqrt{{(‒ 5 - 6)}^{2} + {(- 4 - 4)}^{2}} \Rightarrow B E = \sqrt{11^{2} + 8^{2}} \Rightarrow B E = \sqrt{185}

C D = \sqrt{{(6 - (- 4))}^{2} + {(- 4 - 5)}^{2}} \Rightarrow C D = \sqrt{10^{2} + 9^{2}} \Rightarrow C D = \sqrt{181}

C E = \sqrt{{(- 5 - (‒ 4))}^{2} + {(‒ 4 - 5)}^{2}} \Rightarrow C E = \sqrt{1^{2} + 9^{2}} \Rightarrow C E = \sqrt{82}

D E = \sqrt{{(- 5 - 6)}^{2} + {(- 4 - (- 4))}^{2}} \Rightarrow D E = \sqrt{11^{2}} \Rightarrow D E = 11

Para saber mais

Páginas 179 e 180

1. Resposta pessoal. Uma sugestão de resolução é dada a seguir:

Se um dos catetos mede 15 centímetros, temos:

x + (x + 2) = 15 ou x ⋅ (x + 2) = 15

• x + (x + 2) = 15 ⇒ 2x = 13 ⇒ x = 6,5

Como x é um número inteiro, esse valor não pode ser considerado.

• x ⋅ (x + 2) = 15 ⇒ x2 + 2x ‒ 15 = 0

Resolvendo a equação: Δ = 22 ‒ 4 ⋅ 1 ⋅ (‒15) ⇒ Δ = 64

x = \frac{- 2 \pm \sqrt{64}}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x_{1} = \frac{- 2 + 8}{2} = 3 \\ x_{2} = \frac{- 2 - 8}{2} = - 5 \end{array}

Portanto, x = 3, pois não existe medida de comprimento negativa. Assim, o outro cateto mede 8, pois 3 + (3 + 2) = 8 e a hipotenusa medirá h; logo:

h2 = 82 + 152 = 64 + 225 ⇒ h2 = 289 ⇒ h = 17

Além disso, tomando o triângulo retângulo cujos catetos medem 3 centímetros e 4 centímetros e cuja hipotenusa mede 5 centímetros como referência, temos outro triângulo retângulo com catetos medindo 15 centímetros e 20 centímetros e hipotenusa medindo 25 centímetros.

2. Como os dois triângulos são semelhantes, temos:

\frac{5}{35} = \frac{3}{a} = \frac{4}{b}

, então:

\frac{5}{35} = \frac{3}{a} \Rightarrow a = 21

\frac{5}{35} = \frac{4}{b}

⇒ b = 28

Assim, concluímos que o perímetro mede 84 centímetros, pois 35 + 28 + 21 = 84, e a área tem medida 294 centímetros quadrados, pois:

\frac{28 \cdot 21}{2}

= 14 · 21 = 294

3. O perímetro do triângulo de lados medindo 3 centímetros, 4 centímetros e 5 centímetros mede 12 centímetros (3 + 4 + 5 = 12). Como os triângulos são semelhantes, obtemos:

\frac{12}{108} = \frac{3}{a} = \frac{4}{b} = \frac{5}{c}

Então:

\frac{12}{108} = \frac{3}{a}

⇒ a = 27;

\frac{12}{108} = \frac{4}{b}

⇒ b = 36;

\frac{12}{108} = \frac{5}{c}

⇒ c = 45

4. Resposta pessoal. Um exemplo de quadro:

x	x + 2	x + (x + 2)	x ⋅ (x + 2)	x ⋅ (x + 2) +2
3	5	8	15	17
4	6	10	24	26
5	7	12	35	37
6	8	14	48	50
7	9	16	63	65

Página oitenta e oito

Pense mais um pouco...

Página 179

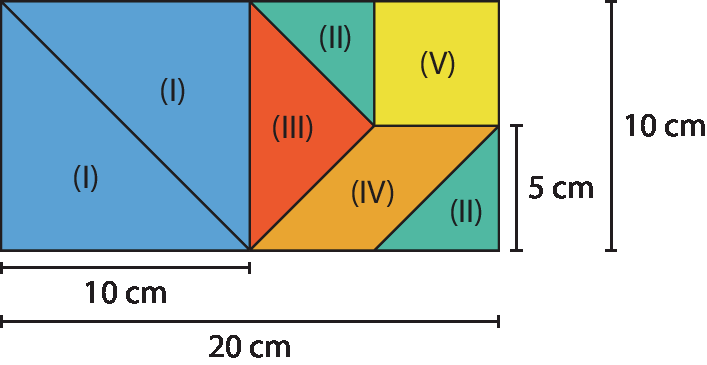
Ilustração. Retângulo dividido ao meio de modo a formar dois quadrados. O retângulo tem base medindo 20 centímetros e altura medindo 10 centímetros. O quadrado da esquerda tem lado de medida 10 centímetros, e está dividido pela diagonal em dois triângulos nomeados de (I) e (I); o quadrado da direita está dividido em 5 polígonos, sendo: um triângulo isósceles cuja base é o lado vertical da esquerda do quadrado e os dois lados congruentes correspondem a metade da diagonal do quadrado, está nomeado de (III); um quadrado cujo lado mede a metade do lado do quadrado maior, e está posicionado no canto direito, e nomeado de (V); abaixo dele há um triângulo retângulo cujos catetos medem 5 centímetros e estão sobre o lado do quadrado maior e está nomeado de (II); um paralelogramo cujo lado maior corresponde a hipotenusa do triângulo (II) e o lado menor corresponde ao lado do quadrado (V); e um triângulo retângulo cuja hipotenusa é o lado do triângulo (III) e um dos catetos corresponde ao lado do quadrado (V).

(um) Sendo x a medida da hipotenusa do triângulo maior (azul), seus catetos medem 10 centímetros e então: x2 = 102 + 102 = 100 + 100 ⇒ x2 = 200 ⇒

x = \sqrt{200} \Rightarrow x = 100 \sqrt{2}

Então, a medida do perímetro desta peça é 34,1 centímetros, pois:

10 + 10 + 14 = 34,1

(dois) No triângulo menor (verde), sendo y a medida da hipotenusa, seus catetos medem 5 centímetros e, então: y2 = 52 + 52 = 25 + 25 ⇒ y2 = 50 ⇒ y =

\sqrt{50} = 5 \sqrt{2}

⇒ y ≃ 7,05

Então, o perímetro desta peça mede 17,05 centímetros, pois:

5 + 5 + 7,05 = 17,05

(três) No triângulo médio (vermelho), os lados tem medidas 10 centímetros e y = 7,05 centímetros. Portanto, o perímetro mede 24,1 centímetros, pois: 10 + 7,05 + 7,05 = 24,1

(quatro) Para o paralelogramo (laranja), seus lados medem 5 centímetros e y = 7,05 centímetros; então, o perímetro desta peça mede 24,1 centímetros, pois: 5 + 5 + 7,05 + 7,05 = 24,1

(cinco) O perímetro do quadrado mede 20 centímetros, pois seu lado mede 5 centímetros.

Página 182

A área de cada um dos triângulos internos ao quadrado a bê cê dê é

\frac{a · b}{2}

, pois eles são triângulos retângulos. Assim, a área total dos 4 triângulos é

4 · \frac{a b}{2} = 2 a b .

Portanto, temos que a área do quadrado a bê cê dê é igual a área do quadrado ê éfe gê agá mais a área dos 4 triângulos juntos. Logo, considerando as medidas de cada figura, temos:

AABCD = A_EFGH + 4 ⋅ Atriângulo ⇒ a2 + b2 = AEFGH + 2ab ⇒

⇒ AEFGH = a2 ‒ 2ab + b2 ⇒ AEFGH = (a ‒ b)2

Página 183

Cada um dos triângulos construídos tem área de medida x2 centímetros quadrados, pois:

\frac{x \cdot 2 x}{2} = \frac{2 x^{2}}{2}

= x2

Então, 20 deles têm área total 20x2 centímetros quadrados (pois x2 · 20 = 20x2). Um quadrado com essa área tem lado de medida

2 x \sqrt{5}

centímetros, pois:

\sqrt{20 x^{2}} = \sqrt{20} \cdot x = 2 \sqrt{5} \cdot x = 2 x \sqrt{5}

Trabalhando a informação

Páginas 188 e 189

1. Segundo o gráfico, o Pão de Açúcar é representado pela parte menor em laranja-escuro, com o maior valor no eixo vertical (medida da altitude em metros). A altura aproximada dele mede 380 metros. O morro da Urca é representado pela imagem amarela à direita do Pão de Açúcar, totalizando cêrca de 210 metros de altura.

2. Ao observar as figuras, podemos perceber que o rádio 1 tem alça superior e nenhum botão na lateral, não sendo possível ter a vista lateral I nem a vista superior F, o que faz com que as alternativas b e d não sejam as corretas. O rádio 3 não tem acessórios superiores e tem um só botão lateral pequeno, não sendo possível que sua vista lateral seja o K e, assim, a alternativa a não está correta. Portanto, a alternativa correta é a c, como de fato se pode relacionar as figuras às respectivas vistas laterais e superiores.

Exercícios complementares

1. A distância de medida x é a medida da hipotenusa, e os catetos medem 120 métros (12 ⋅ 10 = 120) e 160 métros (16 ⋅ 10 = 160), portanto: x2 = 1202 + 1602 ⇒ x2 = .14400 + .25600 ⇒ x = ±

\sqrt{40 000}

⇒ x = +200 ou x = ‒200 (x = ‒200 não convém). Logo, a distância mede 200 métros.

2. Traçamos uma perpendicular passando pelo ponto a, e sendo d igual a A bê:

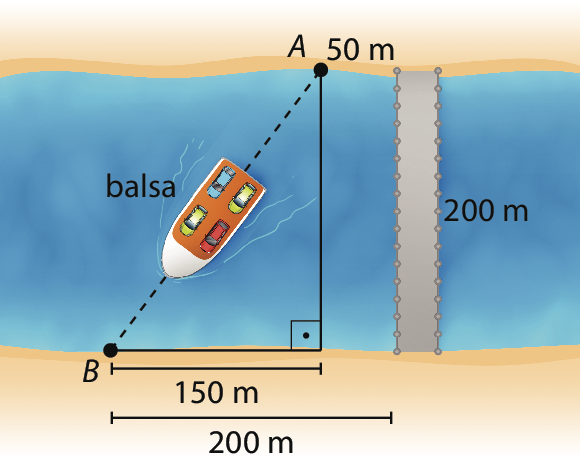
Ilustração. Rio com uma ponte de 200 metros. À esquerda, ponto A com distância de 50 metros da ponte. Na outra margem ponto B com distância de 200 metros da ponte. O segmento que liga o ponto A ao ponto B é a hipotenusa de um triângulo retângulo, nele há uma balsa dentro do rio. A medida do cateto que sai do vértice B é 150 metros.

2. a) d2 = 2002 + 1502 ⇒ d2 = .40000 + .22500 ⇒

⇒

d = \pm \sqrt{62 500}

⇒ d = 250 ou d = ‒250

Portanto, 7,05 (d = ‒250 não convém).

Logo, a distância tem medida 250 métros.

2. b) Considerando a relação

velocidade =

\frac{espa ç o}{tempo}

, temos:

v = \frac{250 m}{5 min} = \frac{\frac{250}{1 000} km}{\frac{5}{60} h}

⇒

v = \frac{\frac{25}{10}}{\frac{5}{6}} = \frac{25}{10} \cdot \frac{6}{5} = \frac{5 \cdot 5 \cdot 2 \cdot 3}{2 \cdot 5 \cdot 5} \Rightarrow v = 3

Portanto, 3 quilômetros por hora.

3. Seja x a medida do lado perpendicular ao de medida 2. Então:

32 = x2 + 22 ⇒ 9 = x2 + 4 ⇒ 9 ‒ 4 = x2 ⇒ x2 = 5 ⇒ x =

\sqrt{5}

x = ‒ \sqrt{5}

Como

x = ‒ \sqrt{5}

não convém,

x = \sqrt{5}

. Então:

y2 = x2 + 82 ⇒

y^{2} = {(\sqrt{5})}^{2}

+ 82 ⇒ y2 = 5 + 64 ⇒

y = \sqrt{69}

4. Traçamos o polígono ABCD conforme as informações do enunciado:

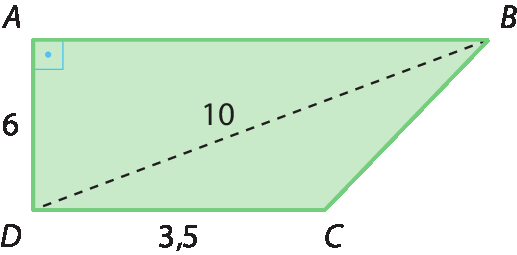
Ilustração. Trapézio retângulo ABCD. Diagonal tracejada BD com medida 10. A medida AD é 6 e CD: 3,5

4. a) A base maior é

\bar{A B}

e, também, é cateto de um triângulo retângulo; portanto, seja x sua medida, então: 102 = x2 + 62 ⇒ 100 = x2 + 36 ⇒

x = \sqrt{64}

⇒ x = 8

A medida é de 8 centímetros.

4. b) O lado oblíquo é

\bar{B C}

, cuja medida é y. Construindo a altura cê agá, perpendicular à A bê, de modo que cê agá = á dê = 6 e bê agá = A bê ‒ á agá = A bê ‒ cedê ⇒ bê agá = 8 ‒ 3,5 = = 4,5. Então: bê cê2 = cê agá2 + bê agá2 ⇒ y2 = 62 + 4,52 = 36 + 20,25 ⇒ y =

\sqrt{56, 25}

⇒ y = 7,5

Logo, a medida é 7,5 centímetros.

Página oitenta e nove

4. c) A medida é 25 centímetros, pois: 6 + 8 + 7,5 + 3,5 = 25

4. d)

A = \frac{(B + b) · h}{2} = \frac{(8 + 3, 5) · 6}{2} = 34, 5

Então, a medida de área é 34,5 centímetros quadrados.

5. A configuração das latas é tal que a altura da pilha mede 2r + h, sendo h a medida da altura do triângulo equilátero ABC de lado ℓ de medida 10r.

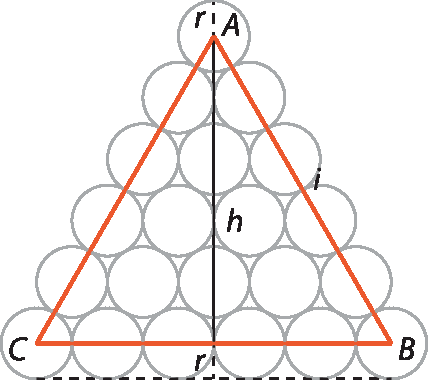
Ilustração. Pilha de circunferências dispostas de forma triangular, de modo que a base tem 6 circunferências em que a primeira circunferência tem o ponto C no centro, e a última tem o ponto B no centro, acima 5 circunferências, acima 4 circunferências, acima 3 circunferências, acima 2 circunferências, acima 1 circunferência que contem o ponto A no centro da circunferência. Triângulo equilátero ABC, com a altura h em relação ao lado CB. As circunferências tem raio r.

Como o raio mede r = 4,5 centímetros, o lado mede ℓ = 45 centímetros; a medida da altura do triângulo equilátero é:

h = \frac{ℓ \sqrt{3}}{2}

⇒

h = \frac{45 \sqrt{3}}{2}

Portanto, a altura da pilha tem medida

(\frac{45 \sqrt{3}}{2} + 9)

centímetros, pois: 

\frac{45 \sqrt{3}}{2} + 2 r = \frac{45 \sqrt{3}}{2} + 2 \cdot 4, 5 = \frac{45 \sqrt{3}}{2} + 9

6. Pelas informações do enunciado, sendo h a medida da altura, então: 152 =

h^{2} + {(\frac{24}{2})}^{2}

⇒ 225 = h2 + 144 ⇒ h2 = 81 ⇒

h = \pm \sqrt{81}

⇒ h = +9 ou h = ‒9

Como o valor negativo não convém, então, h mede 9 centímetros; logo:

A = \frac{b \cdot h}{2} = \frac{24 \cdot 9}{2}

= 12 · 9 = 108

Portanto sua área mede 108 centímetros quadrados.

7. O maior lápis que cabe nesse estojo é o de medida igual à da diagonal d; portanto: d2 = 152 + 122 = 225 + 144 ⇒

d = \pm \sqrt{369}

≃ ±19,2

Como o valor negativo não convém, então d = 19,2 centímetros.

Como 19,2 > 18, é possível colocar o lápis no estojo, se ele for colocado na diagonal.

8. Desenhando os triângulos separadamente e rotacionando para alinhar os ângulos:

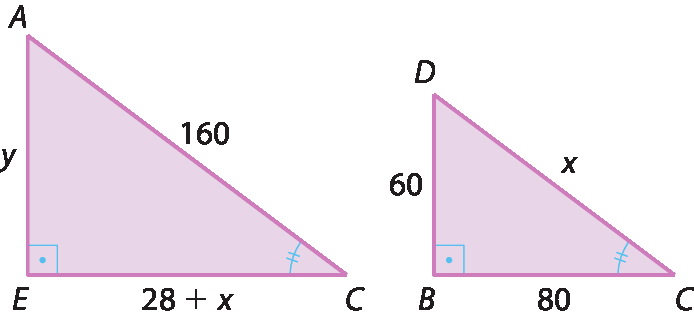
Ilustração. Triângulo retângulo ACE, retângulo em E; com cateto AE de medida y.; hipotenusa AC de medida 160; e cateto CE de medida 28 mais x. Ao lado, triângulo retângulo DCB, retângulo em B; com cateto BC de medida 80; hipotenusa CD de medida x e cateto BD de medida 60.

8. a) CD = x, então x2 = 602 + 802 ⇒ x2 = .3600 + .6400 ⇒ ⇒ x = ±

\sqrt{10 000}

⇒ x = 100 ou x = ‒100, como esse não convém , logo: CD = 100 métros; EC = 28 + x = 28 + 100 = 128, portanto EC = 128 métros; AE = y, então 1602 = y2 + 1282 ⇒ .25600 = y2 + .16834 ⇒ y = ±

\sqrt{9 216}

= ±96. Como o valor negativo não convém, AE = 96 métros.

8. b)

A_{A C E} = \frac{E C \cdot A E}{2} = \frac{128 \cdot 96}{2}

= 64 · 96 = .6144. Então a área de á cê ê mede .6144 métros quadrados;

A_{B C D} = \frac{B C \cdot B D}{2} = \frac{80 \cdot 60}{2}

= 40 · 60 = .2400

Então, a área de bê cê dê mede .2400 métros quadrados.

8. c) AABDE = AACE ‒ ABCE = .6144 ‒ .2400 = .3744, então a área de ABDE é .3744 métros quadrados

9. Se o perímetro mede 60 centímetros e os quatro lados têm a mesma medida, então seu lado mede 15 centímetros (60 : 4 = 15). Metade da diagonal menor, com medida x, é um dos catetos de um triângulo retângulo formado por um lado do losango (mede 15 centímetros) e metade da diagonal maior (ou seja, medindo 13 centímetros). Portanto: 152 = x2 + 132 ⇒ 225 = x2 + 169 ⇒ x2 = 56 ⇒

x = \pm \sqrt{2^{2} · 14}

⇒

x = 2 \sqrt{14}

x = ‒ 2 \sqrt{14}

(não convém)

Logo,

x = 2 \sqrt{14}

Portanto, a diagonal mede

4 \sqrt{14}

centímetros

(2 \sqrt{14} \cdot 2 = 4 \sqrt{14})

10. A área pode ser calculada por: (x + 1) ⋅ (x ‒ 2) = 18 ⇒ ⇒ x2 ‒ 2x + x ‒ 2 = 18 ⇒ x2 ‒ x ‒ 20 = 0 ⇒ x = 5 ou x = ‒4 (não convém)

Logo, x = 5. Aplicando o teorema de Pitágoras:

d2 = 62 + 32 = 36 + 9 ⇒

d = \pm \sqrt{45} = \pm \sqrt{3^{2} \cdot 5} \Rightarrow d = 3 \sqrt{5}

d = ‒ 3 \sqrt{5}

(não convém)

Logo,

d = 3 \sqrt{5}

centímetros.

11. Construímos a figura conforme a descrição do enunciado:

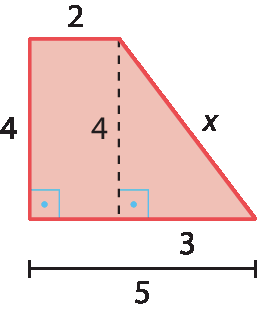
Ilustração. Trapézio retângulo cuja altura mede 4, a base menor mede 2 e a base maior mede 5. O trapézio está dividido em um retângulo e um triângulo retângulo, a hipotenusa do triângulo mede x e corresponde ao lado inclinado do trapézio; o cateto horizontal mede 3.

x2 = 42 + 32 = 16 + 9 ⇒ x = ±

\sqrt{25}

⇒ ⇒ x = 5 ou x = ‒5 ( não convém)

Logo, x = 5.

Então, o perímetro mede 16, pois:

4 + 5 + 5 + 2 = 16

Alternativa d.

12. Aplicando o teorema de Pitágoras: a2 = 42 + 32 ⇒ a2 = = 16 + 9 ⇒

a = \pm \sqrt{25}

⇒ a = 5 ou a = ‒5 (não convém)

Logo, a = 5. Usando as relações métricas: 32 = m ⋅ 5 ⇒

m = \frac{9}{5} e 42 = n \cdot 5 \Rightarrow n = \frac{16}{5}

. Então:

L = 25 \cdot m \cdot n \Rightarrow L = 25 \cdot \frac{9}{5} \cdot \frac{16}{5} = 144

Alternativa d.

13. Chamando ℓ a medida dos lados desconhecidos congruentes:

{(3 \sqrt{3})}^{2}

= ℓ2 + ℓ2 ⇒ 27 = 2ℓ2 ⇒

ℓ = \pm \sqrt{\frac{27}{2}}

⇒

ℓ = \sqrt{\frac{27}{2}} o u ℓ = - \sqrt{\frac{27}{2}}

(não convém)

Logo,

ℓ = \sqrt{\frac{27}{2}}

. Assim, a área é dada por:

{(\sqrt{\frac{27}{2}})}^{2} + \frac{{(\sqrt{\frac{27}{2}})}^{2}}{2} = \frac{27}{2} + \frac{\frac{27}{2}}{2} = \frac{27}{2} + \frac{27}{4}

= 13,5 + 6,75 = 20,25

Então, a área tem medida 20, 25

u^{2}

14. (x + 2)2 = x2 + (x ‒ 2)2 ⇒ x2 + 4x + 4 = x2 + x2 ‒ 4x + 4 ⇒ x2 ‒ 8x = 0 ⇒ x = 8 ou x = 0 (não convém)

Logo, x = 8.

x + 2 é a medida da hipotenusa. Logo, como x = 8 centímetros, a hipotenusa mede 10 centímetros.

Alternativa c.

Página noventa

15. Conforme as informações do enunciado, se a medida de um dos catetos é x, então: x2 = 122 + 92 ⇒ x2 = 144 + 81 ⇒

x = \pm \sqrt{225}

⇒ x = 15 ou x = ‒15 (não convém)

Logo, x = 15 centímetros. Seja y a medida do outro cateto:

\frac{y}{15} = \frac{12}{9}

⇒ 9 y = 180 ⇒ y = 20

Então, o outro cateto mede 20 centímetros.

16. Seja h a altura relativa à hipotenusa, e m a medida da projeção do cateto sobre a hipotenusa. Então:

1^{2} = h^{2} + {(\frac{\sqrt{5}}{5})}^{2} \Rightarrow 1 = h^{2} + \frac{5}{25} \Rightarrow h = \pm \sqrt{\frac{20}{25}} \Rightarrow

\Rightarrow h = \sqrt{\frac{20}{25}} o u h = ‒ \sqrt{\frac{20}{25}}

(não convém)

Logo,

h = \sqrt{\frac{20}{25}}

. Assim, temos que:

h^{2} = m \cdot n \Rightarrow \sqrt{(\frac{\sqrt{5}}{5})} = m \cdot \frac{\sqrt{5}}{5} \Rightarrow

\Rightarrow \frac{20}{25} = \frac{\sqrt{5} m}{5} \Rightarrow m = \frac{4 \sqrt{5}}{5}

Portanto, a medida da hipotenusa é

\sqrt{5}

centímetros, pois:

\frac{4 \sqrt{5}}{5} + \frac{1 \sqrt{5}}{5} = \frac{5 \sqrt{5}}{5} = \sqrt{5}

17. BC2 = 12,82 + 9, 62 ⇒ BC2 = 163,84 + 92,16 ⇒

⇒ BC = ±

\sqrt{256}

⇒ BC = 16 ou BC = ‒16 (não convém)

Logo, BC = 16.

12,82 = BD · 16 ⇒ BD = 10,24

9, 62 = DC · 16 ⇒ 92,16 = 16DC ⇒ DC = 5,76

h · 16 = 12,8 · 9,6 ⇒ 16h = 122,88 ⇒ h = 7,68

Percurso A → D →B → A → C → P mede 46 quilômetros, pois:

7,68 + 10,24 + 12,8 + 9,6 + 5,76 ‒ 0,08 = 46

18. 15 · h = 12 · 9 ⇒ 15h = 108 ⇒ h = 7,2

Alternativa b.

19. Seja m e n as projeções dos catetos. Então:

m ‒ n = 7 ⇒ m = 7 + n

Pela relação h2 = m · n, obtemos: m · n = 144 ⇒ ⇒ (7 + n) · n = 144 ⇒ 7n + n2 ‒144 = 0 ⇒ n2 + 7n ‒ 144 = 0 ⇒ ⇒ n = 9 ou n = ‒16 (não convém)

Logo, n = 9 e, assim, temos: m = 7 + 9 = 16. Então:

a = m + n ⇒ a = 16 + 9 = 25

Alternativa d.

20.

A = \frac{(x + 1) \cdot x}{2}

= 6 ⇒ x2 + x ‒ 12 = 0 ⇒ x = 3 ou x = ‒4 Como x = ‒4 não convém, logo x = 3.

P = 3 + (3 + 2) + (3 + 1) = 12

Alternativa d.

21. A situação descrita pode ser ilustrada pela figura a seguir:

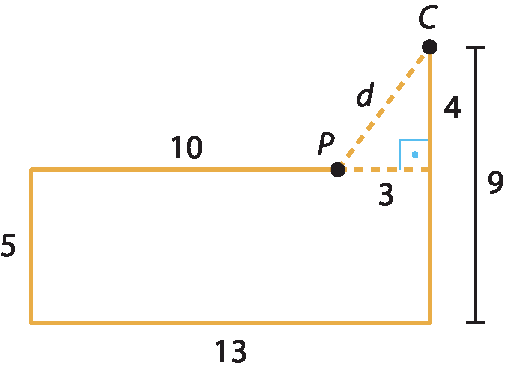
Ilustração. Retângulo de base de medida 13 e altura de medida 5. No lado oposto à base há um ponto P, à esquerda do ponto P, medida 10, à direita de P, medida 3, a partir do ponto P há um triângulo retângulo de base 3 e altura 4, cuja hipotenusa PC mede d. A distância do ponto C à base do retângulo é igual a 9.

Então: d2 = 42 + 32 ⇒ d2 = 16 + 9 ⇒

d = \pm \sqrt{25}

⇒ d = 5 ou d = ‒5 (não convém)

Logo, d = 5 quilômetros.

Portanto 5 quilômetros a noroeste.

Alternativa ê.

22. A distância inicial entre o bloco e a base da elevação tem medida d. Então: 3,92 = 1,52 + d2 ⇒ 15,21 = 2,25 + d2 ⇒

d = \pm \sqrt{12, 96}

⇒ d = ‒3,6 (não convém)

Logo, d = 3,6 métros.

Após o deslocamento, fórma-se um triângulo retângulo de hipotenusa medindo 2,5 métros, pois 3,9 ‒ 1,4 = 2,5.

Então, a distância final entre os blocos é b.

Logo: 2,52 = 1,52 + b2 ⇒ 6,25 = 2,25 + b2 ⇒

b = \pm \sqrt{4}

⇒ b = 2 ou b = ‒2 (não convém)

Logo, b = 2.

Portanto, x = 3,6 ‒ 2,0 = 1,6.

Alternativa c.

Verificando

1. A medida x é tal que: 52 = 32 + x2 ⇒ 25 = 9 + x2 ⇒

⇒ 25 ‒ 9 = x2 ⇒ 16 = x2 ⇒

x = \pm \sqrt{16}

⇒ x = 4 ou x = ‒4

Como x = ‒4 não convém, logo x = 4.

Alternativa b.

3. 302 = x2 + y2

Então, para x = 18 e y = 24, temos:

302 = 182 + 242 ⇒ 900 = 324 + 576 ⇒ 900 = 900 (verdade).

Alternativa c.

4. x2 = 32 + 42 ⇒ x2 = 9 + 16 ⇒ x2 = 25 ⇒

x = \pm \sqrt{25}

⇒

⇒ x = 5 ou x = ‒5 (não convém)

Logo x = 5 métros.

Alternativa a.

5. É possível resolver aplicando a semelhança de triângulos:

\frac{3, 6}{7, 2} = \frac{6}{x}

⇒ 3,6x = 43,2 ⇒ x = 12

Alternativa c.

6. d2 = 82 + 62 = 64 + 36 ⇒

d = \pm \sqrt{100}

⇒ d = 10 ou d = ‒10. Como d = ‒10 (não convém); logo, d = 10.

Alternativa d

7. d2 = 102 + 102 ⇒ d2 = 100 + 100 ⇒ d = ±

\sqrt{200} = \pm \sqrt{10^{2} \cdot 2}

⇒ ⇒

d = + 10 \sqrt{2}

d = ‒ 10 \sqrt{2}

(não convém)

Logo,

d = 10 \sqrt{2}

Alternativa a.

8. A diagonal mede d, pois: d2 = 52 + 52 ⇒ d2 = 25 + 25 ⇒

d = \pm \sqrt{50} = \pm \sqrt{5^{2} \cdot 2}

⇒

d = + 5 \sqrt{2}

d = ‒ 5 \sqrt{2}

(não convém); logo,

d = 5 \sqrt{2}

. Então, a área de um quadrado de lado medindo

5 \sqrt{2}

centímetros mede 50 centímetros quadrados, pois:

A = 5 \sqrt{2} \cdot 5 \sqrt{2} = 25 \sqrt{4}

= 25 ⋅ 2 = 50

Alternativa b.

Organizando

a) Dois lados perpendiculares (catetos) e um lado (hipotenusa) que se opõe ao ângulo reto.

b) O teorema de Pitágoras enuncia que a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.

c) São triângulos retângulos (com um ângulo medindo 90 graus) cujas medidas de seus lados, catetos e hipotenusas, são dadas por números inteiros positivos.