Página noventa e oito

Parte 10

19. c) 5x ‒ 4 = 6 ⇒ 5x = 6 + 4 ⇒

x = \frac{10}{5}

⇒ x = 2

19. d) 5x ‒ 4 = 0 ⇒ 5x = 4 ⇒

x = \frac{4}{5}

20. a) y = x + 35 + x + 35 ⇒ y = 2x + 70

20. b) y = 2 · 12,5 + 70 = 25 + 70 = 95

20. c) 2x + 70 = 90 ⇒ 2x = 90 ‒ 70 ⇒

x = \frac{20}{2}

⇒ x = 10

21. a) y = 4 · 10 = 40 ⇒ y = 4x

21. b) y = 4 · 10 = 40

22. a) T = 100 ‒ 0,001 · .2400 = 100 ‒ 2,4 = 97,6; portanto, 97,6 graus Célsius.

22. b) T = 100 ‒ 0,001 · 0 = 100 ‒ 0 = 100; portanto, 100 graus Célsius.

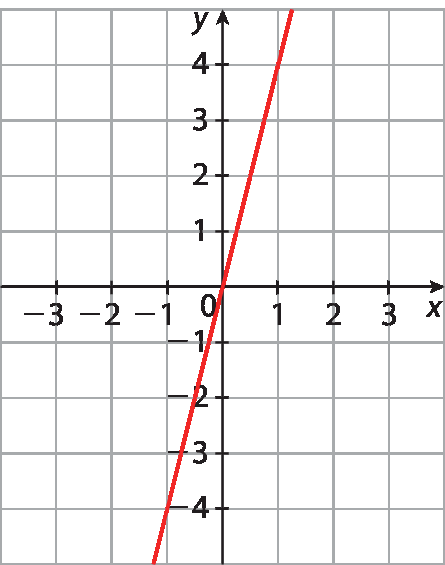
24. a) Observando que a reta contém o ponto (2, 0), conclui-se que: y = 0

24. b) Observando que a reta contém o ponto (‒2, 4), conclui-se que: x = ‒2

25. a) 8 = a · 2 ⇒ a = 4

25. b) y = 4 · 3,5 = 14

25. c) 0 = 4 · x ⇒ x = 0

25. d)

Ilustração. Reta representada em um plano cartesiano. A reta passa pela origem do plano e pelo ponto de abscissa 1 e ordenada 4

26. a)

x	−1	0	1	3
y = x − 3	−1 − 3 = −4	0 − 3 = −3	1− 3 = −2	3 − 3 = 0
(x; y)	(−1; −4)	(0; −3)	(1; −2)	(3; 0)

Ilustração. Plano cartesiano em malha quadriculada. Eixo x com escala de menos 2 a 4 e eixo y com escala de menos 4 a 2. Reta que passa pelos pontos (menos 1, menos 4), (0, menos 3), (1, menos 2) e (3, 0)

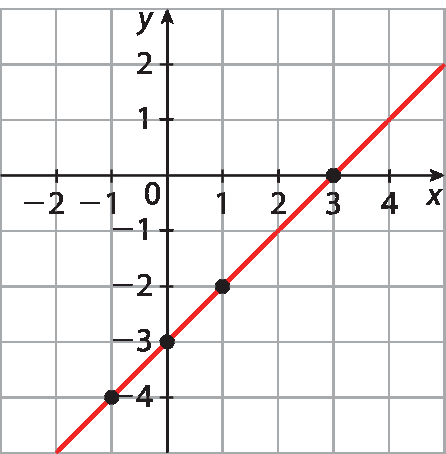
26. b) 0 = x ‒ 3 ⇒ x = 3

26. c) y = 0 ‒ 3 = ‒3

27. a)

y = \frac{50}{40} x

⇒ y = 1,25x

27. b) 30 = 1,25x ⇒

x = \frac{30}{1, 25} = 24

28.

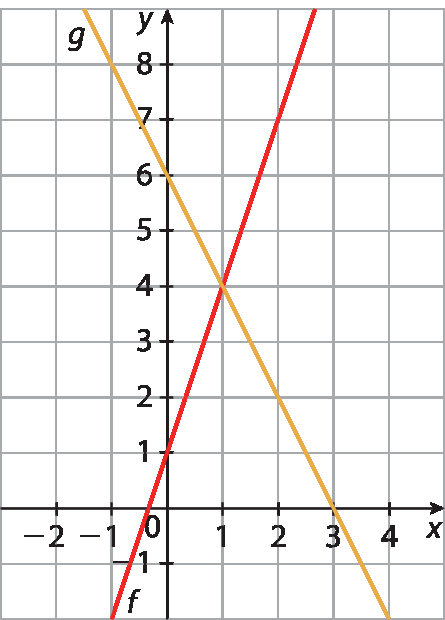
Ilustração. Plano cartesiano em malha quadriculada. Eixo x com escala de menos 2 a 4, e eixo y com escala de menos 1 a 8. Reta g que passa pelos pontos (0, 6) e (3, 0) e reta f que passa pelos pontos (0, 1) e (2, 7). As duas retas se cruzam no ponto (1, 4)

28. a) f(décima) = 0 ⇒ 3x + 1 = 0 ⇒ 3x = ‒1 ⇒

x = ‒ \frac{1}{3}

28. b) 0 = ‒2 · x + 6 = 0 + 6 = 6

28. c) f(0) = 3 · 0 + 1 = 0 + 1 = 1

28. d) f(décima) = g (décima) ⇒ 3x + 1 = ‒2x + 6 ⇒ 3x + 2x = 6 ‒ 1 ⇒

⇒ 5x = 5 ⇒ x = 1

29.

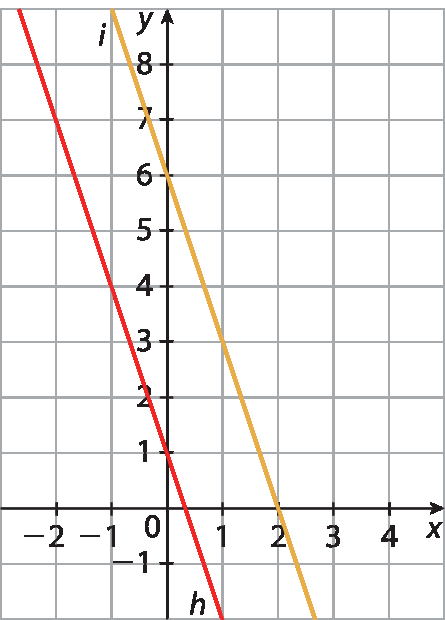
Ilustração. Plano cartesiano em malha quadriculada. Eixo x com escala de menos 2 a 4, e eixo y com escala de menos 1 a 8. Reta i que passa pelos pontos (2, 0) e (0, 6), e reta h paralela à reta i que passa pelo ponto (0, 1)

29. a) Corte no eixo x: hidrogênio(décima) = 0 ⇒ ‒3x +1 = 0 ⇒ ‒3x = ‒1 ⇒

\Rightarrow x = \frac{‒ 1}{‒ 3} \Rightarrow x = \frac{1}{3}

Corte no eixo y: h(0) = ‒3 · 0 + 1 = 0 + 1 = 1

29. b) Corte no eixo x: primeira(décima) = 0 ⇒ ‒3x + 6 = 0 ⇒ ‒3x = ‒6 ⇒ ⇒

x = \frac{‒ 6}{‒ 3} \Rightarrow x = 2

Corte no eixo y: i(0) = ‒2 · 0 + 6 = 0 + 6 = 6

29. c) Não, pois são representados por retas paralelas.

29. d) Nenhum, pois o conjunto solução da equação hidrogênio(décima) = primeira(décima) é o conjunto vazio.

32. a) Observando, pelo gráfico, que a função contém o ponto (3, 0) conclui-se que: x = 3

32. b) Observando que a função é decrescente, conclui-se que: y > 0 ⇒ x < 3

32. c) Novamente, observando que a função é decrescente, conclui-se que: y < 0 ⇒ x > 3

33. Apresentamos aqui o cálculo das raízes e os esboços de cada item. As respostas encontram-se na página 239 deste Manual.

Página noventa e nove

33. a) 2x ‒ 8 = 0 ⇒ 2x = 8 ⇒

x = \frac{8}{2}

⇒ x = 4

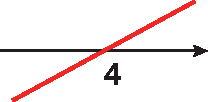
Ilustração. Reta crescente cortando um eixo horizontal no ponto correspondente ao número 4

33. b) ‒3x + 6 = 0 ⇒ ‒3x = ‒6 ⇒

x = \frac{‒ 6}{‒ 3}

⇒ x = 2

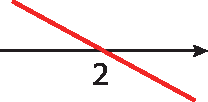
Ilustração. Reta numérica com o número 2. Reta decrescente que passa pelo ponto que representa o número 2.

33. c) 2x ‒ 5 = 0 ⇒ 2x = 5 ⇒

x = \frac{5}{2}

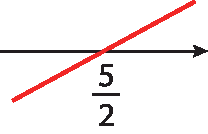
Ilustração. Reta numérica com o número 5 meios. Reta crescente que passa pelo ponto que representa o número 5 meios.

33. d) ‒2x ‒ 1 = 0 ⇒ ‒1 = 2x ⇒

‒ \frac{1}{2}

= x

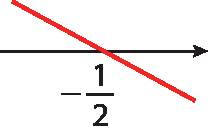
Ilustração. Reta numérica com o número menos 1 sobre 2. Reta decrescente que passa pelo ponto que representa o número menos 1 sobre 2.

34. De acordo com as informações, um esboço do gráfico dessa função é:

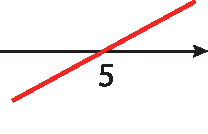
Ilustração. Reta crescente cortando um eixo horizontal no ponto correspondente ao número 5

Então:

34. a) Como ‒2 < 5, tem-se que: y < 0

34. b) Como 0 < 5, tem-se que: y < 0

34. c) Como 4,99 < 5, tem-se que: y < 0

34. d) Como 5,01 > 5, tem-se que: y > 0

34. e) Como 10 < 5, tem-se que: y > 0

36. Com x = 8 tem-se: x2 ‒ 3x + 6 = 82 ‒ 3 · 8 + 6 = 64 ‒ 24 + 6 = 46; portanto, deverão comprar 46 métros quadrados.

37. a) f(0) = 02 ‒ 5 · 0 + 6 = 0 ‒ 0 + 6 = 6

f(2) = 22 ‒ 5 · 2 + 6 = 4 ‒ 10 + 6 = 0

f(3) = 32 ‒ 5 · 3 + 6 = 9 ‒ 15 + 6 = 0

f(4) = 42 ‒ 5 · 4 + 6 = 16 ‒ 20 + 6 = 2

37. b) Pelos resultados do item anterior, quando x = 2 ou quando x = 3.

37. c) x2 ‒ 5x + 6 = 20 ⇒ x2 ‒ 5x + 6 ‒ 20 = 0 ⇒ x2 ‒ 5x ‒ 14 = 0

Δ = (‒5)2 + (‒4) · 1 · (‒14) = 25 + 56 = 81 ⇒

\Rightarrow x = \frac{‒ (‒ 5) \pm \sqrt{81}}{2 \cdot 1} =

= \frac{+ 5 \pm 9}{2} \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x = \frac{14}{2} = 7 \\ x = \frac{‒ 4}{2} = ‒ 2 \end{array}

38. a) y =(x + 2)(2x ‒ 1) = 2x 2 ‒ x + 4 ‒ 2 = 2x 2 + 3x ‒ 2

38. b)

y = \frac{2 x (5 x - 3)}{2}

= x(5x ‒ 3) = 5x2 ‒ 3x

39. a) f(0) = 02 + 3 · 0 = 0 + 0 = 0

39. b) x2 + 3x = 0 ⇒

\Rightarrow x (x + 3) = 0 \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{l} x = 0 \\ x + 3 = 0 \Rightarrow x = ‒ 3 \end{array}

39. c) f(2) = 22 + 3 · 2 = 4 + 6 = 10

39. d) x2 + 3x = 10 ⇒ x2 + 3x − 10 = 0

Δ = 32 ‒ 4 · 1 · (−10) = 9 + 40 = 49 ⇒

\Rightarrow x = \frac{‒ 3 \pm \sqrt{49}}{2 · 1} = \frac{‒ 3 \pm 7}{2} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{4}{2} = 2 \\ x = \frac{‒ 10}{2} = ‒ 5 \end{array}

40. a)

f (\sqrt{3}) = 2 \cdot {(\sqrt{3})}^{2} + 5

= 2 · 3 + 5 = 6 + 5 = 11

40. b) 2x2 + 5 = 21 ⇒ 2x2 = 21 ‒ 5 ⇒ 2x2 = 16 ⇒

x^{2} = \frac{16}{2}

⇒

\Rightarrow x^{2} = 8 \Rightarrow x = \pm \sqrt{8} \Rightarrow x = \pm 2 \sqrt{2}

41. y = 2(x + 1)(x + 2) = 2(x2 + 2x + x + 2) = 2(x 2 + 3x + 2) = = 2x 2 + 6x + 4

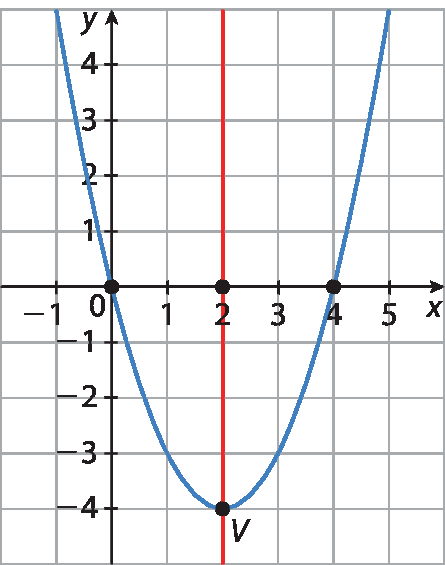
42. a) Observando que a parábola tem sua concavidade voltada para cima, conclui-se que a > 0.

42. b) A abscissa do vértice é xV = 2; a ordenada do vértice é yV = ‒ 4. Portanto, o vértice da parábola é o ponto (2, ‒ 4).

42. c) Observando que a parábola contém os pontos (0, 0) e (4, 0), conclui-se que x = 0 ou x = 4.

42. d) Representando o eixo de simetria da parábola, temos que ele intercepta o eixo das abscissas no ponto (2, 0).

Ilustração. Plano cartesiano em malha quadriculada. Eixo x com escala de menos 1 a 5, e eixo y com escala de menos 4 a 4. Parábola com concavidade voltada para cima que passa pelos pontos (0, 0) e (4, 0) e eixo de simetria da parábola que passa pelo vértice V (2, menos 4) e pelos ponto (2, 0)

43. a)

y = \frac{(2 x + 4) (x + 2)}{2} = \frac{2 (x + 2) (x + 2)}{2} = (x + 2)^{2} \Rightarrow

⇒ y = x2 + 4x + 4

43. b) x2 + 4x + 4 = 25 ⇒ x2 + 4x ‒ 21 = 0

Δ = 42 ‒4 · 1 · (‒21) = 16 + 84 = 100 ⇒

\Rightarrow x = \frac{‒ 4 \pm \sqrt{100}}{2 \cdot 1} = \frac{‒ 4 \pm 10}{2} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{6}{2} = 3 \\ x = \frac{‒ 14}{2} = ‒ 7 \end{array}

Então, como x > 0, tem-se que x = 3.

44. a) Com a = 2 > 0, a concavidade da parábola é voltada para cima.

44. b) Com a = ‒ 1 < 0, a concavidade da parábola é voltada para baixo.

44. c) Com a = ‒ 3 < 0, a concavidade da parábola é voltada para baixo.

44. d) Com a = 1 > 0, a concavidade da parábola é voltada para cima.

Página cem

44. e) Com a = 1 > 0, a concavidade da parábola é voltada para cima.

44. f) Com a = ‒ 1 < 0, a concavidade da parábola é voltada para baixo.

45. a) Observando que a parábola contém (‒2, ‒3) e (2, ‒3), conclui-se que x = ‒2 e x = 2.

45. b) Observando que (0, 1) é o vértice da parábola, conclui-se que y ⩽ 1 para todo valor de x; portanto, não existe x tal que y = 2.

45. c) Observando que a parábola contém o ponto (2, ‒3), conclui-se que y = ‒3.

45. d) Observando que a parábola contém o ponto (1, 0), conclui-se que f(1) = 0.

45. e) A ordenada do vértice é yv = 1. Portanto, o vértice da parábola é o ponto (0, 1).

46. p ‒ 3 > 0 ⇒ p > 3

47. 2 p + 1 < 0 ⇒ 2 p < ‒1 ⇒

p < ‒ \frac{1}{2}

48. a) m + 2 < 0 ⇒ m < ‒2

48. b) 0 = (m + 2) · 02 + (m + 3) · 0 + m + 4 ⇒ 0 = 0 + 0 + m + 4 ⇒ ‒4 = m

49. a) Δ = (‒6)2 ‒ 4 · 1 · 8 = 36 + 32 = 4 ⇒

\Rightarrow x = \frac{‒ (‒ 6) \pm \sqrt{4}}{2 \cdot 1} = \frac{+ 6 \pm 2}{2} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{8}{2} = 4 \\ x = \frac{4}{2} = 2 \end{array}

49. b) Como Δ = 02 ‒ 4 · 1 · 3 = 0 ‒ 12 = ‒12 < 0, conclui-se que não existem raízes reais.

49. c) Δ = 42 ‒ 4 · (‒1) · 0 = 16 + 0 = 16 ⇒

\Rightarrow x = \frac{‒ 4 \pm \sqrt{16}}{2 \cdot (‒ 1)} = \frac{‒ 4 \pm 4}{‒ 2} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{0}{‒ 2} = 0 \\ x = \frac{‒ 8}{‒ 2} = 4 \end{array}

49. d) Δ = (‒6)2 ‒ 4 · 1 · 9 = 36 ‒ 36 = 0 ⇒

\Rightarrow x = \frac{‒ (‒ 6) \pm \sqrt{0}}{2 \cdot 1} = \frac{+ 6 \pm 0}{2} = \frac{6}{3} = 3

49. e) Δ = 122 ‒ 4 · (‒9) · (‒4) = 144 ‒144 = 0 ⇒

\Rightarrow x = \frac{‒ 12 \pm \sqrt{0}}{2 \cdot (‒ 9)} = \frac{‒ 12 + 0}{‒ 18} = \frac{2}{3}

49. f) Como Δ = (‒2)2 ‒ 4 · 2 · 1 = 4 ‒ 8 = ‒ 4 < 0, conclui-se que não existem raízes reais.

50. Com y = 0, tem-se:

\frac{‒ x^{2}}{32} + \frac{x}{8} = 0 \Rightarrow 32 \cdot \frac{‒ x^{2}}{32} + 32 \cdot \frac{x}{8}

= = 32 · 0 ⇒ ‒x2 + 4x = 0 ⇒

‒ x (x ‒ 4) = 0 \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{l} x = 0 \\ x ‒ 4 = 0 \Rightarrow x = 4 \end{array}

Como a distância é positiva, conclui-se que seu valor é 4 quilômetros, pois 4 ‒ 0 = 4.

51. a)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ (‒ 8)}{2 \cdot (‒ 1)} = \frac{8}{‒ 2} = ‒ 4

yv = ‒(‒ 4)2 ‒ 8 · (‒ 4) + 16 = ‒16 + 32 + 16 = 32

51. b)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 6}{2 \cdot 2} = \frac{‒ 6}{4} = ‒ \frac{3}{2}

y_{v} = 2 {(‒ \frac{3}{2})}^{2} + 6 \cdot (‒ \frac{3}{2}) = \frac{9}{2} ‒ 9 = ‒ \frac{9}{2}

51. c)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 0}{2 · 1} = 0

yv = 02 ‒ 16 = ‒16

52. a = 3, b = ‒ p e c = 2q, então:

x_{v} = \frac{‒ b}{2 a} \Rightarrow 2 = \frac{‒ (‒ p)}{2 · 3} \Rightarrow 2 = \frac{p}{6} \Rightarrow

p = 12

yv = 3 · 22 ‒ 12 · 2 + 2q = 1 ⇒ 12 ‒ 24 + 2q = 1 ⇒

⇒ 2q = 1 + 12 ⇒ q =

\frac{13}{2}

53. a) Como a = 4 > 0, a concavidade da parábola é voltada para cima; logo, a função possui ponto de mínimo.

53. b) Como a = 1 > 0, a concavidade da parábola é voltada para cima; logo, a função possui ponto de mínimo.

53. c) Como a = ‒ 1 < 0, a concavidade da parábola é voltada para baixo; logo, a função possui ponto de máximo.

53. d) Como a = 5 > 0, a concavidade da parábola é voltada para cima; logo, a função possui ponto de mínimo.

53. e) Como a = ‒ 3 < 0, a concavidade da parábola é voltada para baixo; logo, a função possui ponto de máximo.

53. f) Como a = ‒ 2 < 0, a concavidade da parábola é voltada para baixo; logo, a função possui ponto de máximo.

54. a)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ (‒ 4)}{2 · 3} = \frac{4}{6} = \frac{2}{3}

54. b)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 12}{2 \cdot 1} = ‒ 6

55. a)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 11}{2 · (- 2)} = \frac{11}{4}

55. b)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 25}{2 \cdot (‒ 2)} = \frac{25}{4}

56.

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 11}{2 · (‒ 1)} = \frac{11}{2}

y_{v} = ‒ {(\frac{11}{2})}^{2} + 11 \cdot (\frac{11}{2}) ‒ 18 = ‒ \frac{121}{4} + \frac{121}{2} ‒ 18 =

= \frac{‒ 121 + 242 - 72}{4} = \frac{49}{4}

57.

x_{v} = \frac{‒ b}{2 a} = \frac{‒ (‒ 6)}{2 · 1} = 3

yv = 32 ‒ 6 · 3 + 8 = 9 ‒ 18 + 8 = ‒1

Página cento e um

58. Sendo x a medida, em metros, de dois dos lados do retângulo, tem-se que o outro lado mede (50 ‒ x). Assim, a área do retângulo fica expressa em métro quadrado pela função: y = x(50 ‒ x) = ‒x2 + 50x. Então, um dos lados do retângulo mede 25 métros, pois

x_{v} = \frac{‒ b}{2 a} = \frac{‒ 50}{2 · (‒ 1)} = 25

; e o outro mede 25 métros, pois 50 ‒ 25 = 25.

59. a)

x_{v} = \frac{‒ b}{2 a} = \frac{‒ (‒ 80)}{2 \cdot 1} = 40

Portanto, 40 unidades do produto.

59. b) y = 402 ‒ 80 · 40 + .3000 = .1600 ‒ .3200 + .3000 = .1400

Portanto, R$ 1.400,00mil quatrocentos reais.

60. a) O vértice é (‒1; ‒9), pois:

x_{v} = ‒ \frac{b}{2 a} = ‒ \frac{2}{2} = ‒ 1

e y = x2 + 2x ‒ 8 para x = ‒1, temos yv = (‒1)2 + 2 · (‒1) ‒ 8 = = 1 ‒ 2 ‒ 8 ⇒ y = ‒9. Como a = 1 > 0, a concavidade está voltada para cima. Encontrando pontos de referência e traçando o gráfico:

x	−4	−2	−1	0	2
y	(−4)2 + 2(−4) − 8 = 16 − 8 − 8 = 0	(−2)2 + 2(−2) − 8 = 4 − 4 − 8 = −8	−9	02 + 2 ⋅ (0) − 8 = −8	(2)2 + 2(2) − 8 = 4 + 4 − 8 = 0
(x; y)	(−4; 0)	(−2; −8)	(−1; −9)	(0; −8)	(2; 0)

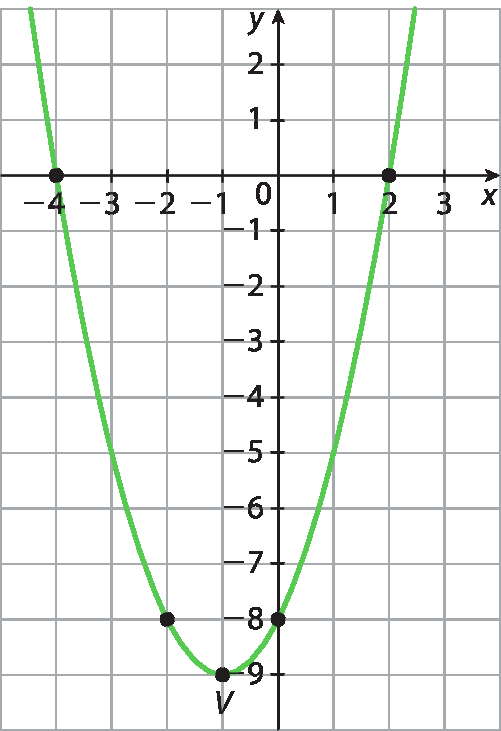
Ilustração. Parábola com a concavidade voltada para cima representada em um plano cartesiano. A parábola intersecta o eixo x nos pontos (menos 4, zero) e (2, zero), passa pelos pontos (menos 2, menos 8) e (zero, menos 8) e tem vértice no ponto (menos 1, menos 9).

60. b) O vértice é (3; 4), pois:

x_{v} = ‒ \frac{b}{2 a} = ‒ \frac{6}{2 · (‒ 1)} = 3

e y = ‒x2 + 6x ‒ 5 para x = 3, temos yv = ‒32 + 6 · 3 ‒ 5 = ‒9 + 18 ‒ 5 ⇒ yv = 4. Como a = ‒1 < 0, a concavidade está voltada para baixo. Encontrando pontos de referência e traçando o gráfico:

x	1	2	3	4	5
y	−12 + 6 ⋅ 1 − 5 = −1 + 6 − 5 = 0	−22 + 6 ⋅ 2 − 5 = −4 + 12 − 5 = 3	4	−42 + 6 ⋅ 4 − 5 = −16 + 24 − 5 = 3	−52 + 6 ⋅ 5 − 5 = −25 + 30 − 5 = 0

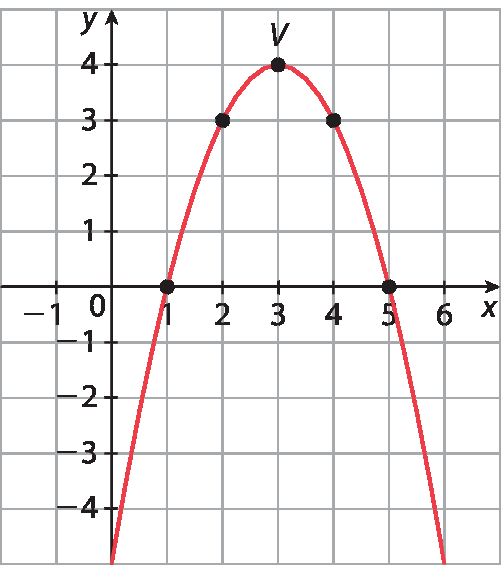
Plano cartesiano com malha quadriculada. Eixo x com escala de menos 1 a 5, e eixo y com escala de menos 4 a 4. Parábola com concavidade voltada para baixo, que passa pelos seguintes pontos destacados (1, 0); (2, 3); V(3, 4); (4, 3); (5, 0)

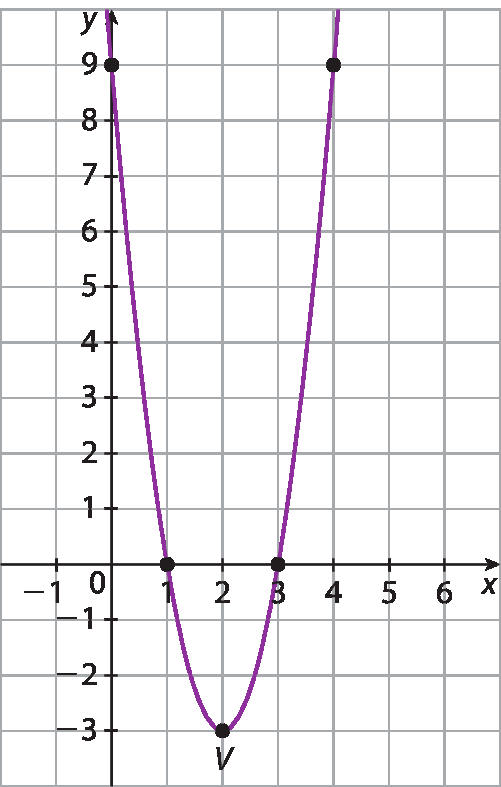
60. c) O vértice é (2; ‒3), pois:

x_{v} = ‒ \frac{b}{2 a} = ‒ \frac{‒ 12}{2 · (3)} = 2

e y = 3x2 ‒ 12x + 9 para x = 2 é y = 3 · 22 ‒ 12 · 2 + 9 = 12 ‒ 24 + 9 ⇒ y = ‒3. Como a = 3 > 0, a concavidade está voltada para cima. Encontrando pontos de referência e traçando o gráfico:

x	0	1	2	3	4
y	3 ⋅ 02 − 12 ⋅ 0 + 9 = 9	3 ⋅ 12 − 12 ⋅ 1 + 9 = 3 − 12 + 9 = 0	−3	3 ⋅ 32 − 12 ⋅ 3 + 9 = 27 − 36 + 9 = 0	3 ⋅ 42 −12 ⋅ 4 + 9 = 48 − 48 + 9 = 9
(x; y )	(0; 9)	(1; 0)	(2; −3)	(3; 0)	(4; 9)

Plano cartesiano em malha quadriculada. Eixo x com escala de menos 1 a 6, e eixo y com escala de menos 3 a 9. Parábola com concavidade voltada para cima, que passa pelos seguintes pontos (0, 9); (1, 0); V(2, menos 3); (3, 0); (4, 9)

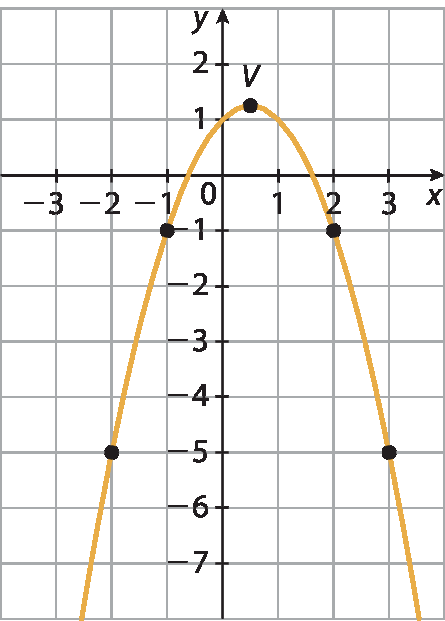
60. d) O vértice é

(\frac{1}{2}; \frac{5}{4})

, pois:

x_{v} = ‒ \frac{b}{2 a} = ‒ \frac{1}{2 \cdot (‒ 1)} = \frac{1}{2}

e y = ‒x2 + x + 1 para

x = \frac{1}{2}

y_{v} = ‒ {(\frac{1}{2})}^{2} + \frac{1}{2} + 1

= =

‒ \frac{1}{4} + \frac{1}{2} + 1 = \frac{5}{4} = 1, 25

. Como a = ‒1 < 0, a concavidade está voltada para baixo. Encontrando pontos de referência e traçando o gráfico:

x	−2	−1	$divisão de 1 sobre 2$	2	3
y	− (−2)2 − 2 + 1 = −4 − 2 + 1 = −5	− (−1)2 − 1 + 1 = −1	$divisão de 5 sobre 4$	−22 + 2 + 1 = −4 + 2 + 1 = −1	−32 + 3 +1 = −9 + 3 + 1 = −5
(x; y)	(−2; −5)	(−1; −1)	( $divisão de 1 sobre 2$ ; $divisão de 5 sobre 4$ )	(2; −1)	(3; −5)

Página cento e dois

Ilustração. Parábola com a concavidade voltada para baixo representada em um plano cartesiano. Ela passa pelos pontos (menos 2, menos 5), menos 1, menos 1), (2, menos 1) e (3, menos 5). O vértice da parábola está indicado pela letra V

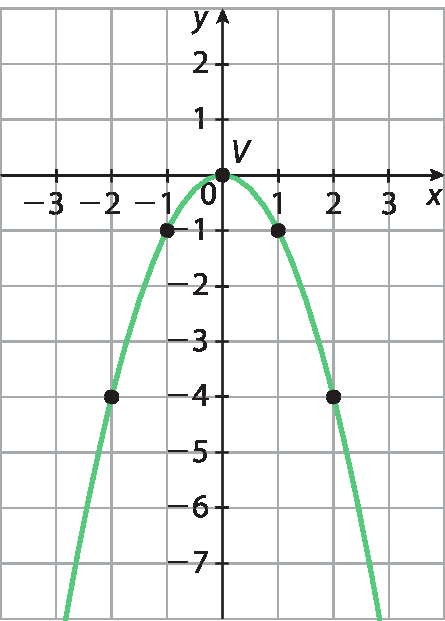
60. e) O vértice é (0; 0), pois

x_{v} = ‒ \frac{b}{2 a} = ‒ \frac{0}{2 \cdot (‒ 1)} = 0

e y = ‒x2 para x = 0 é yv = ‒(0)2 = 0. Como a = ‒1 < 0, a concavidade está voltada para baixo. Encontrando pontos de referência e traçando o gráfico:

x	−2	−1	0	1	2
y	− (−2)2 = −4	− (−1)2 = −1	0	−12 = −1	−22 = − 4
(x; y)	(−2; −4)	(−1; −1)	(0; 0)	(1; −1)	(2; −4)

Plano cartesiano em malha quadriculada. Eixo x com escala de menos 3 a 3, e eixo y com escala de menos 7 a 2. Parábola com concavidade voltada para baixo e que passa pelos seguintes pontos: (menos 2; menos 4); (menos 1; menos 1); V(zero, zero); (1, menos 1); (2, menos 4)

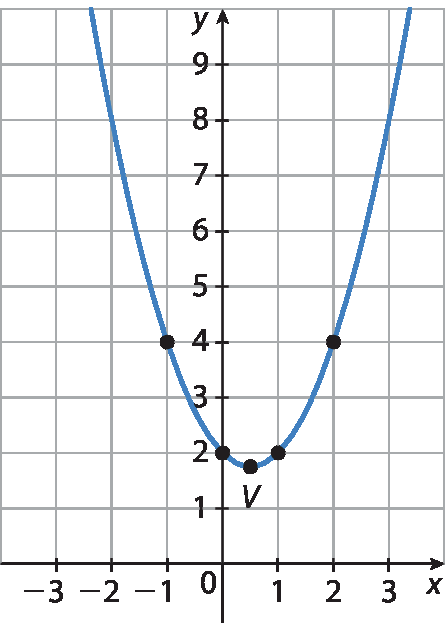
60. f) O vértice é

(\frac{1}{2}; \frac{7}{4})

, pois

x_{v} = - \frac{b}{2 a} = - \frac{- 1}{2 \cdot (1)} = \frac{1}{2}

e y = x2 ‒ x + 2 para

x = \frac{1}{2} é y_{v} = {(\frac{1}{2})}^{2} - \frac{1}{2} + 2 =

\frac{1}{4} - \frac{1}{2} + 2 = \frac{7}{4} = 1, 75

. Como a = 1 > 0, a concavidade está voltada para cima. Encontrando pontos de referência e traçando o gráfico:

x	−1	0	$divisão de 1 sobre 2$	1	2
y	(−1)2 − (−1) + 2 = 4	02 − 0 + 2 = 2	$divisão de 7 sobre 4$	(1)2 −1 + 2 = 2	22 − 2 + 2 = 4
(x; y )	(−1; 4)	(0; 2)	( $divisão de 1 sobre 2$ ; $divisão de 7 sobre 4$ )	(1; 2)	(2; 4)

Plano cartesiano em malha quadriculada. Eixo x com escala de menos 3 a 3, e eixo y com escala de zero a 9. Parábola com concavidade voltada para cima e que passa pelos seguintes pontos: (menos 1, 4); (zero, 2); V(1 sobre 2; 7 sobre 4); (1, 2); (2, 4)

61. Para y = x2 ‒ 4:

O vértice é (0; ‒4), pois

x_{v} = - \frac{b}{2 a} = - \frac{0}{2 \cdot (1)} = 0

e y = x2 ‒ 4 para x = 0 é yv = 0 ‒ 4 = ‒4 . Como a = 1 > 0, a concavidade está voltada para cima. Encontrando pontos de referência:

x	−2	−1	0	1	2
y	(−2)2 − 4 = 4 − 4 = 0	(−1)2 − 4 = 1 − 4 = −3	−4	12 − 4 = 1 − 4 = −3	22 − 4 = 4 − 4 = 0
(x; y )	(−2; 0)	(−1; −3)	(0; −4)	(1; −3)	(2; 0)

Para y = ‒x2 + 4:

O vértice é (0; 4), pois

x_{v} = - \frac{b}{2 a} = - \frac{0}{2 \cdot (- 1)} = 0

e y = ‒x2 + 4 para x = 0 é yv = 02 + 4 = 4. Como a = ‒1 < 0, a concavidade está voltada para baixo. Encontrando pontos de referência:

x	−2	−1	0	1	2
y	− (−2)2 + 4 = −4 + 4 = 0	− (−1)2 + 4 = −1 + 4 = 3	4	−12 + 4 = −1+ 4 = 3	−22 + 4 = −4 + 4 = 0
(x; y)	(−2; 0)	(−1; 3)	(0; 4)	(1; 3)	(2; 0)

Os pontos de intersecção são os pontos em comum aos dois gráficos, ou seja, (‒2; 0) e (2; 0). Traçando os dois gráficos no mesmo plano cartesiano:

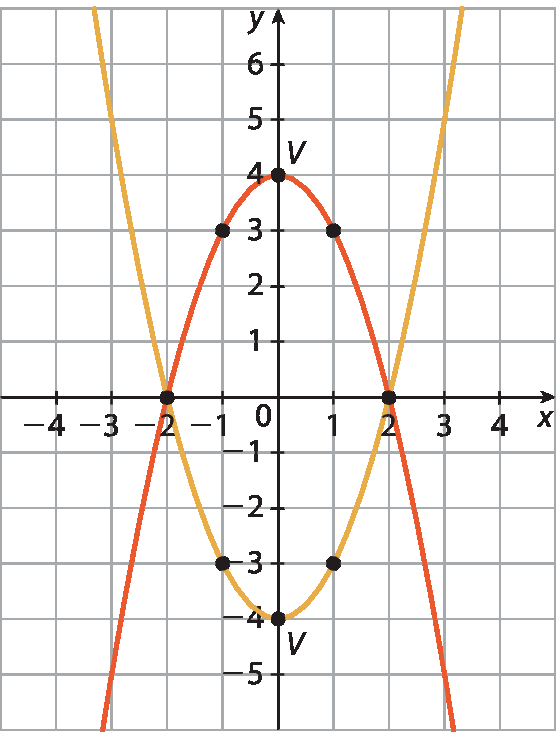
Plano cartesiano em malha quadriculada. Eixo x com escala de menos 4 a 4, e eixo y com escala de menos 5 a 6. Parábola com concavidade voltada para baixo e que passa pelos seguintes pontos: (menos 2; zero); (menos 1; 3); V(zero, 4); (1, 3); (2, zero); e parábola com concavidade voltada para cima e que passa pelos pontos: (menos 2, zero); (menos 1, menos 3); V(zero, menos 4); (1, menos 3), (2, zero).

Página cento e três

62. a) Para f(décima) = x2, temos que o vértice é (0; 0),

pois

x_{v} = - \frac{b}{2 a} = - \frac{0}{2 \cdot (1)} = 0

e y = x2 para x = 0 é yv = 02 = 0. Como a = 1 > 0, a concavidade está voltada para cima, assim como todas as parábolas dêsse item. Encontrando pontos de referência para f(décima):

x	−2	−1	0	1	2
y	(−2)2 = 4	(−1)2 = 1	0	12 = 1	22 = 4
(x; y)	(−2; 4)	(−1; 1)	(0; 0)	(1; 1)	(2; 4)

Os gráficos de g(décima) e de hidrogênio(décima) são obtidos, respectivamente, pela translação vertical de uma unidade para cima e de uma unidade para baixo do gráfico de f(décima).

Traçando os gráficos no mesmo plano cartesiano, obtemos a curva em azul representando f(décima), a laranja representando hidrogênio(décima) e a verde representando g(décima):

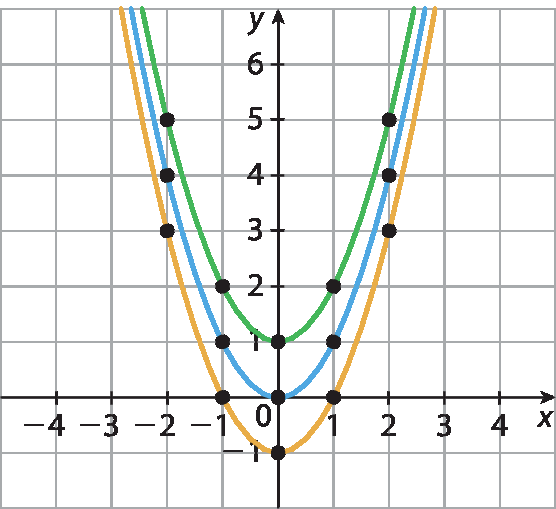
Plano cartesiano em malha quadriculada. Eixo x, com escala de menos 4 a 4. Eixo y, com escala de menos 1 a 6. Três parábolas com concavidade voltada para cima, sendo uma parábola a representação da função f de x igual a x elevado ao quadrado, a outra parábola é uma translação vertical uma unidade para baixo do gráfico de f de x, e a outra parábola uma translação vertical uma unidade para cima, do gráfico de f de x.

62. b) Com base nos pontos do gráfico de f(décima) = x2 que obtivemos no item anterior.

Para g(décima) = ‒x2, ocorre mudança no sinal dos valores de f(décima) para cada x, ou seja, g(décima) é uma reflexão de f(décima) em relação ao eixo x. Assim, obtemos:

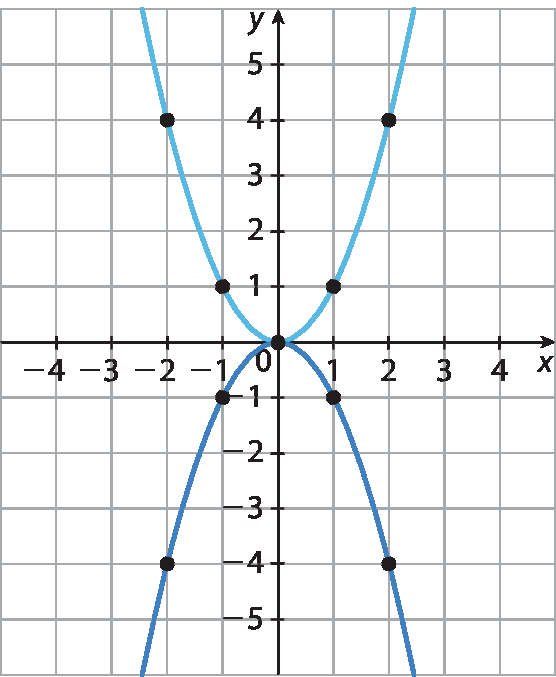
Plano cartesiano em malha quadriculada. Eixo x, com escala de menos 4 a 4. Eixo y, com escala de menos 5 a 5. Parábola com concavidade voltada para cima que passa pelos pontos (menos 2, 4); (menos 1, 1), V(zero, zero), (1, 1); (2, 4) e parábola com concavidade voltada para baixo, simétrica a primeira parábola em relação ao eixo x.

62. c) Para f(décima) = x2, já obtivemos o gráfico nos itens anteriores:

Para g(décima) = 2x2, cada g(décima) é o dôbro de f(décima) para cada x.

Para hidrogênio(décima) = 4x2, cada hidrogênio(décima) é o quadruplo de f(décima) para cada x.

Traçando os gráficos no mesmo plano, é possível perceber que as parábolas têm o mesmo vértice e a concavidade para cima:

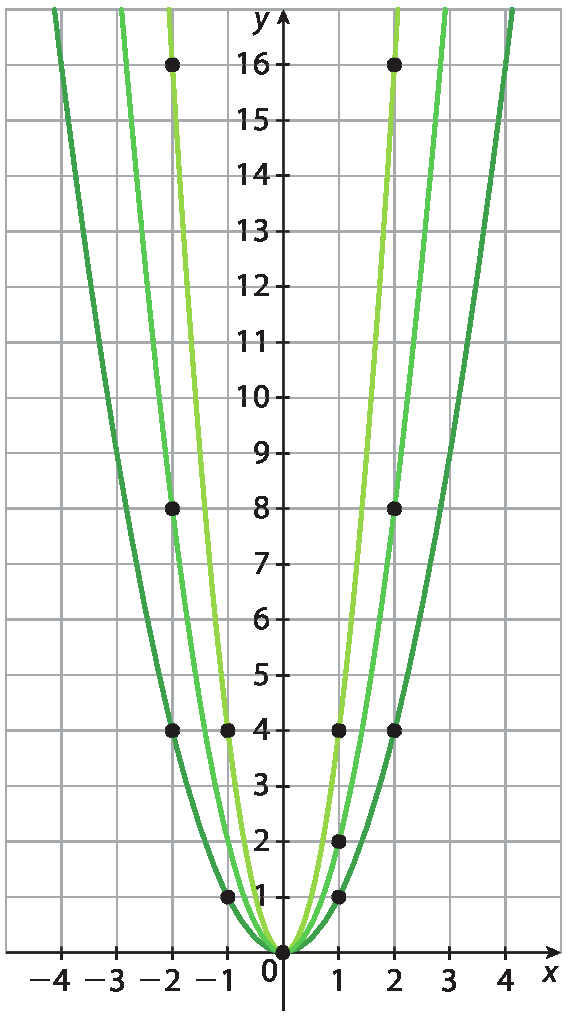
Ilustração. Eixo x com escala de menos 4 a 4, e eixo y com escala de zero a 16. Três parábolas com concavidade voltada para cima, e todas com o vértice no ponto (zero, zero). Uma parábola passa pelos pontos: (menos 2, 4); (menos 1, 1), (zero, zero); (1, 1); (2, 4); a outra parábola passa por (menos 2, 8); (zero, zero); (1, 2); (2, 8), e a outra parábola passa pelos pontos (menos 2, 16); (menos 1, 4); (zero, zero), (1, 4); (2, 16).

63. a) Δ = (‒3)2 ‒ 4 · 1 · 2 = 9 ‒ 8 = 1 ⇒

\Rightarrow x = \frac{‒ (‒ 3) \pm \sqrt{1}}{2 \cdot 1} =

= \frac{+ 3 \pm 1}{2} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{4}{2} = 2 \\ x = \frac{2}{2} = 1 \end{array}

Como a = 1 > 0, obtemos:

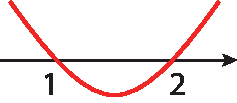
Ilustração. Reta numérica com os pontos que representam 1 e 2, e parábola com concavidade voltada para cima e que passa por esses pontos. Os pontos são raizes da função.

Portanto, para x < 1 ou x > 2: y > 0; para x = 1 ou x = 2, temos y = 0; e para 1 < x < 2, temos y < 0.

63. b) Δ =(‒5)2 ‒ 4 · 6 · 1 = 25 ‒ 24 = 1 ⇒

x = \frac{1}{3}

x = \frac{1}{2}

Como a = 6 > 0, obtemos:

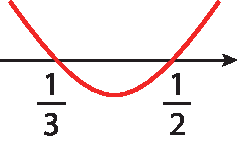
Ilustração. Reta numérica com os pontos que representam 1 terço e 1 sobre 2, e parábola com concavidade voltada para cima que passa por esses pontos. Os pontos são raízes da função.

Portanto, para

x < \frac{1}{3}

x > \frac{1}{2}

, temos y > 0;

x = \frac{1}{3}

ou para

x = \frac{1}{2}

, temos y = 0 e para

\frac{1}{3} < x < \frac{1}{2}

, temos y < 0.

63. c) Δ = (‒5)2 ‒ 4 · (‒2) · 3 = 25 + 24 = 49 ⇒ x = ‒3 ou

x = \frac{1}{2}

Como a = ‒2 < 0, obtemos:

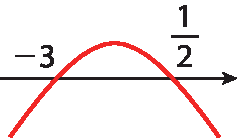
Ilustração. Reta numérica com os pontos que representam menos 3 e 1 sobre 2, e parábola com concavidade voltada para baixo que passa por esses pontos. Os pontos são raízes da função.

Portanto, para ‒3 <

x < \frac{1}{2}

, temos y > 0; para x = ‒3 ou

x = \frac{1}{2}

, temos y = 0; e para x < ‒3 ou

x > \frac{1}{2}

, temos y < 0.

Página cento e quatro

63. d) Δ = 82 ‒ 4 ·1 · 16 = 64 ‒ 64 = 0 ⇒ x = ‒4

Como a = 1 > 0, obtemos:

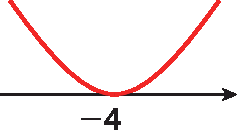
Ilustração. Reta numérica com o ponto que representa menos 4, e parábola com concavidade voltada para cima e que tem o vértice nesse ponto.

Portanto, para x ≠ ‒4, temos y > 0; e para x = ‒4, temos y = 0.

63. e) Δ = 122 ‒ 4 · (‒1) · (‒36) = 144 ‒144 = 0 ⇒ x = 6

Como a = ‒1 < 0, obtemos:

Ilustração. Reta numérica com o ponto que representa 6, e parábola com concavidade voltada para baixo e que tem o vértice nesse ponto.

Portanto, para x = 6, temos y = 0; e para x ≠ 6: y < 0.

63. f) Δ = (‒2)2 ‒ 4 · 3 · 1 = 4 ‒ 12 = ‒8 < 0

Assim, não há raízes reais e como a = 3 > 0.

Ilustração. Reta numérica e parábola com concavidade voltada para cima, acima da reta numérica.

Portanto, para qualquer x real a função é sempre positiva.

Pense mais um pouco

Página 231

Quantidade de exemplares	x	0	1	2	3	4	5	6
Preço total	y	0	16	32	48	64	80	96

Gráfico. Eixo x com escala de 0 a 10., de 2 em 2 unidades. Eixo y com escala de 0 a 160, de 20 em 20 unidades. Pontos alinhados: (1, 16); (2, 32), (3, 48), (4, 64, (5, 80), (6, 96), (7, 112), (8, 128), (9, 144), (10, 160)

Página 235

1. Construindo cada gráfico com base na pesquisa de pares ordenados:

1. a)

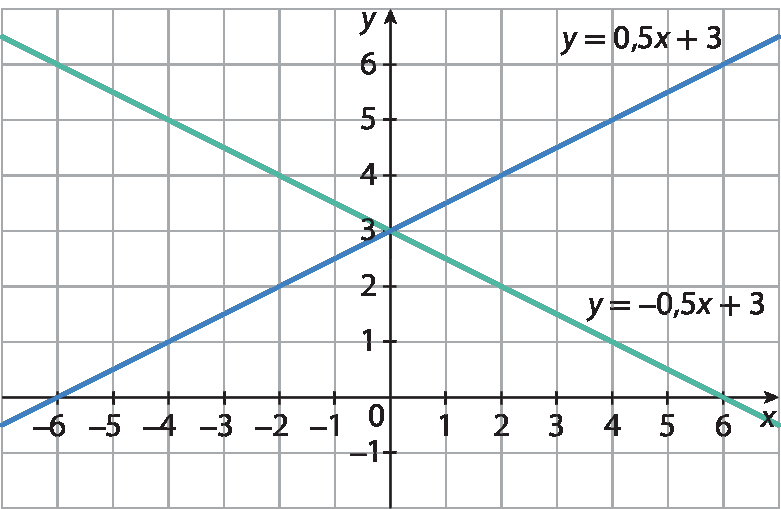
Plano cartesiano em malha quadriculada. Eixo x com escala de menos 6 a 6, eixo y com escala de menos 1 a 6. Reta crescente que representa a função y igual a 0,5x mais 3, que passa pelos pontos (menos 6, zero) e (0, 3); reta decrescente que representa a função y igual a menos 0,5x mais 3, que passa pelos pontos (0, 3) e (6, 0)

1. b)

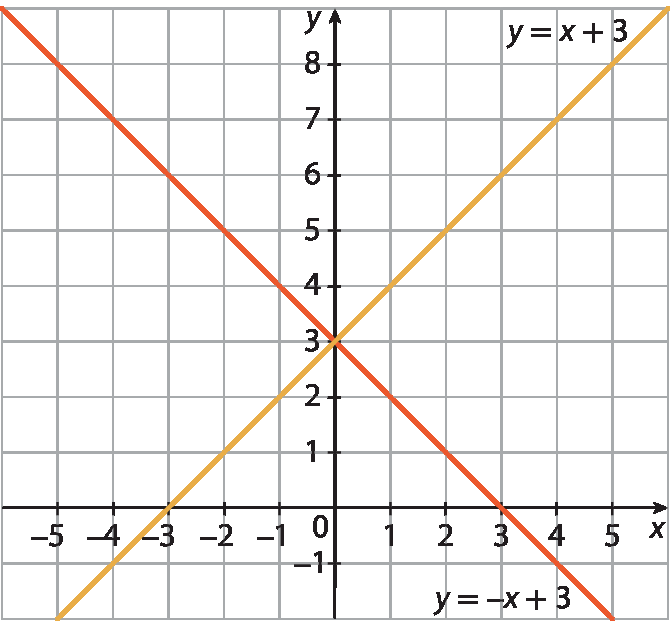
Plano cartesiano em malha quadriculada. Eixo x com escala de menos 5 a 5, eixo y com escala de menos 1 a 8. Reta crescente que representa a função y igual a x mais 3, que passa pelos pontos (menos 3, zero) e (0, 3); reta decrescente que representa a função y igual a menos x mais 3, que passa pelos pontos (0, 3) e (3, 0)

1. c)

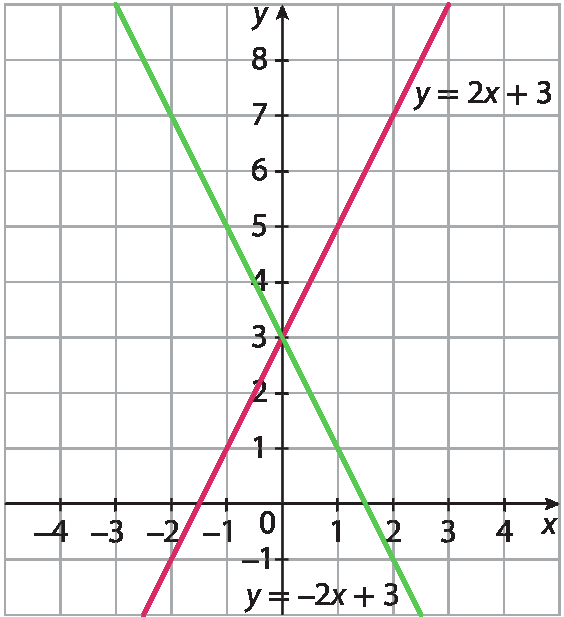
Plano cartesiano em malha quadriculada. Eixo x com escala de menos 4 a 4, eixo y com escala de menos 1 a 8. Reta crescente que representa a função y igual a 2x mais 3, que passa pelos pontos (menos 3 sobre 2, zero) e (0, 3); reta decrescente que representa a função y igual a menos 2x mais 3, que passa pelos pontos (0, 3) e (3 sobre 2, 0)

1. d)

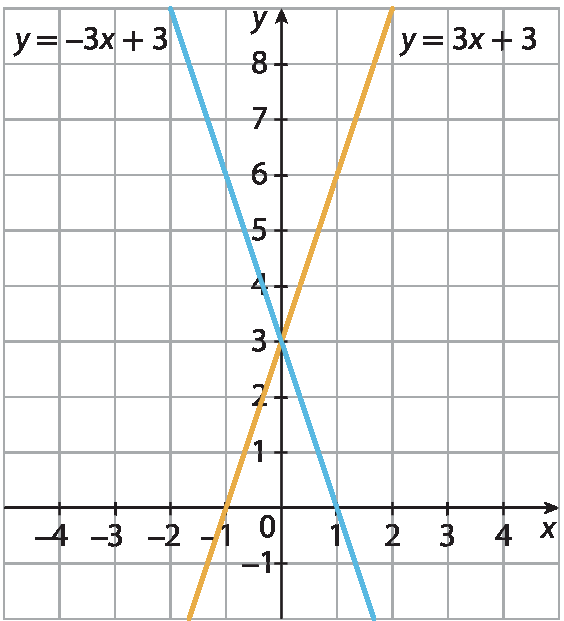
Para saber mais

Página 237

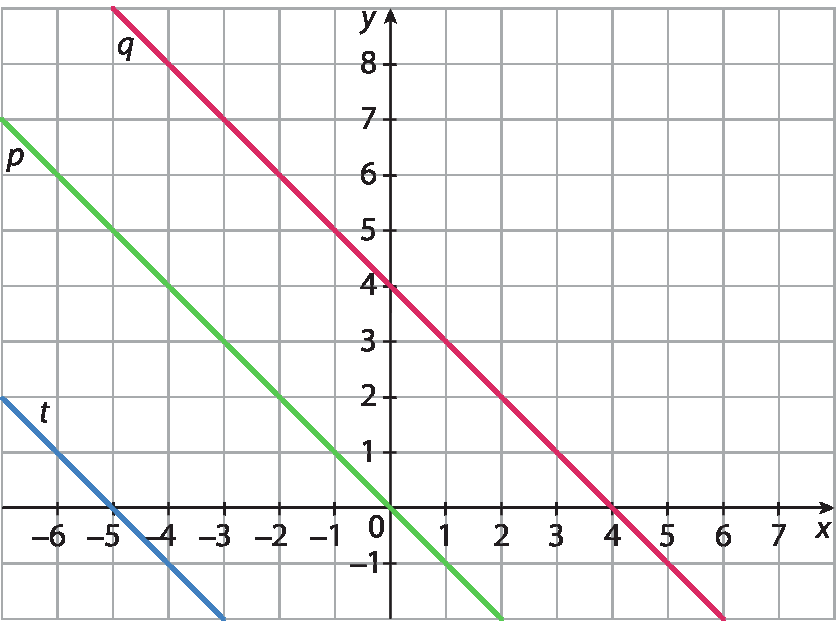
1. Gráficos esperados:

Plano cartesiano em malha quadriculada. Eixo x com escala de menos 6 a 7, eixo y com escala de menos 1 a 8. Reta q decrescente que passa pelos pontos (0, 4) e (4, 0); Reta p paralela a reta q, que passa pelo ponto (zero zero), e reta t paralela a reta p que passa pelo ponto (menos 5, zero)

Página cento e cinco

Página 256

1. De a + b = 2, tem-se: b = 2 ‒ a. Substituindo b por (2 ‒ a) na equação

a^{2} + b^{2} = \frac{5}{2}

, tem-se:

a^{2} + (2 ‒ a)^{2} = \frac{5}{2}

⇒

⇒ a2

+ 4 - 4 a + a^{2} - \frac{5}{2} = 0 \Rightarrow 2 a^{2} - 4 a + \frac{3}{2} = 0

Δ = 42 ‒ 4 · 2 ·

\frac{3}{2}

= 16 ‒ 12 = 4 ⇒

\Rightarrow a = \frac{‒ (‒ 4) \pm \sqrt{4}}{2 \cdot 2} = \frac{+ 4 \pm 2}{4} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} a = \frac{6}{4} = 1, 5 \\ a = \frac{2}{4} = 0, 5 \end{array}

Se a = 1,5, então b = 2 ‒ 1,5 = 0,5. Se a = 0,5, então b = 2 ‒ 0,5 = 1,5.

2. Sendo a e b, com a > b, os números procurados, de a ‒ b = 3, tem-se: a = 3 + b. Substituindo a por (3 + b) na equação a2 + b2 = 17, tem-se:

(3 + b)2 + b2 = 17 ⇒ 9 + 6b + b2 + b2 ‒ 17 = 0 ⇒

⇒ 2b2 + 6b ‒ 8 = 0

Δ = 62 ‒ 4 · 2 · (‒8) = 36 + 64 = 100 ⇒

\Rightarrow b = \frac{‒ 6 \pm \sqrt{100}}{2 \cdot 2} = \frac{‒ 6 \pm 10}{4} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} b = \frac{4}{4} = 1 \\ b = \frac{‒ 16}{4} = ‒ 4 \end{array}

Se b = 1, então a = 3 + 1 = 4. Se b = 0,5, então a = 3 + (‒4) = ‒1. Portanto, o maior número é 4 ou ‒1.

\{\begin{cases} x^{2} - y^{2} = 51 \\ x - y = 3 \end{cases}

Isolando x na primeira equação:

\{\begin{cases} x - y = 3 \\ x = 3 + y \end{cases}

Substituindo x por (3 + y) na equação x2 ‒ y2 = 51, tem-se: (3 + y)3 ‒ y2 = 51 ⇒ 9 + 6y + y2 ‒ y2 = 51 ⇒ 6y = 51 ‒ 9 ⇒ y = 7

Portanto, a área do quadrado amarelo mede 49 centímetros quadrados pois 72 = 49.

Exercícios complementares

1. y = (x + 3)· x ‒ (x ‒ 3) · 2 ⇒ y = x2 + 3x ‒ 2x + 6 ⇒

⇒ y = x2 + x + 6

2. Como

f (15) = \frac{3 \cdot 15}{5} - \frac{7}{4} = 9 - \frac{7}{4} = \frac{36 - 7}{4} = \frac{29}{4}

f (10) = \frac{3 \cdot 10}{5} - \frac{7}{4} = 6 - \frac{7}{4} = \frac{24 - 7}{4} = \frac{17}{4}

, temos:

\frac{f (15) - f (10)}{15 - 10} = \frac{\frac{29}{4} - \frac{17}{4}}{5} = \frac{\frac{12}{4}}{5} = \frac{3}{5}

3. Como f(10) = 10 · 10 + 10 = 100 + 10 = 110 e f(0) = 10 · 0 + 10 = 0 + 10 = 10, temos: f(10) ‒ f(0) = 110 ‒ 10 = 100

4. a) Observando que a reta contém o ponto (‒3, ‒2), conclui-se que f(‒3) = ‒2.

4. b) Observando que a reta contém o ponto (0, 1), conclui-se que f(0) = 1.

4. c) Observando que a reta contém o ponto (2, 3), conclui-se que x = 2.

4. d) Observando que a reta contém o ponto (‒1, 0), conclui-se que x = ‒1.

• Como a lei da função é f(x) = x + 1 e f(10) = 10 + 1 = 11, conclui-se que o gráfico contém o ponto (10, 11).

5. a) 7x ‒ 4 = 0 ⇒ 7x = 4 ⇒ x =

\frac{4}{7}

5. b) Pelo item anterior, a reta passa pelo ponto

(\frac{4}{7}; 0)

e pelo ponto (0; ‒4), pois: x = 0 ⇒ y = 7x ‒ 4 ⇒ y = ‒4

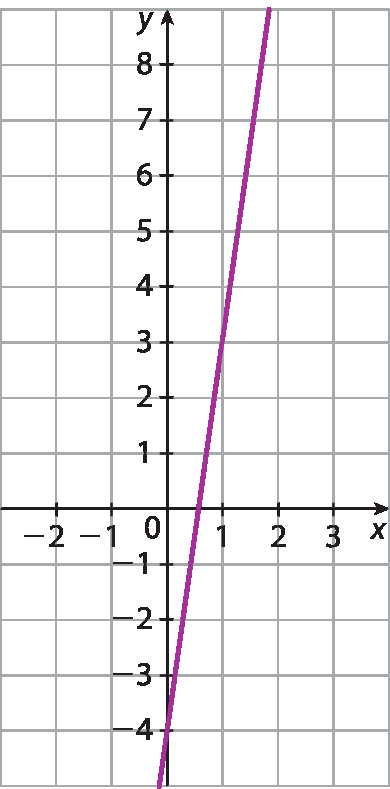
Plano cartesiano em malha quadriculada. Eixo x com escala de menos 2 a 3, eixo y com escala de menos 4 a 8. Reta crescente que passa pelos pontos (zero, menos 4) e (4 sobre 7, zero)

5. c) 7x ‒ 4 = 2 ⇒ 7x = 2 + 4 ⇒

x = \frac{6}{7}

5. d) 7x ‒ 4 > 0 ⇒ 7x > 4 ⇒

x > \frac{4}{7}

6. a) f(x) > 0 ⇒ 2x ‒ 6 > 0 ⇒ 2x > 6 ⇒

x > \frac{6}{2}

⇒ x > 3

6. b) g(x) > 0 ⇒ ‒3x + 6 > 0 ⇒ ‒3x > ‒6 ⇒ 3x < 6 ⇒

x < \frac{6}{3}

⇒ x < 2

6. c) f(x) = g(x) ⇒ 2x ‒ 6 = ‒3x + 6 ⇒ 2x + 3x = 6 + 6 ⇒ 5x = 12 ⇒

x = \frac{12}{5}

6. d) f(x) > g(x) ⇒ 2x ‒ 6 > ‒3x + 6 ⇒ 2x + 3x > 6 + 6 ⇒ ⇒ 5x > 12 ⇒

x > \frac{12}{5}

7. Com x = 1 e y = 11, tem-se: 11 = 6 · 1+ p ⇒ 11 ‒ 6 = p ⇒ 5 = p

7. a) Com y = 23, tem-se: 6x + 5 = 23 ⇒ 6x = 23 ‒ 5 ⇒ ⇒

x = \frac{18}{6}

⇒ x = 3

7. b) Com y < 0, tem-se: 6x + 5 < 0 ⇒ 6x < ‒5 ⇒

x < ‒ \frac{5}{6}

8. Como a expressão do ganho mensal em função do número de quilômetros rodados, em reais, é f(x) = 3x + 50, com x ⩾ 0, o gráfico assume a fórma de uma semirreta. Como f(0) = 50, o gráfico deve conter o ponto (0, 50). E, como a > 0, a semirreta tem inclinação crescente. Alternativa b.

9. Se a função contém o ponto (0, 5), então:

f(0) = ‒3 · 0 + k = 5 ⇒ k = 5.

Alternativa ê.

Página cento e seis

10. a) Δ = (‒2)2 ‒ 4 · 1 · 1 = 4 ‒ 4 = 0 ⇒

x = \frac{‒ (‒ 2) \pm \sqrt{0}}{2 \cdot 1} = \frac{+ 2 \pm 0}{2}

Logo, x = 1.

10. b) Pelo item anterior, a parábola contém (1; 0), e esse é o vértice da função. Encontrando outros pontos e traçando o gráfico:

x	−1	0	2	3
y = x2 − 2	(−1)2 − 2(−1) + 1 = 1 + 2 + 1 = 4	02 − 2 ⋅ (0) + 1 = 1	(2)2 − 2 ⋅ (2) + 1 = 4 − 4 + 1 = 1	(3)2 − 2 ⋅ (3) + 1 = 9 − 6 + 1 = 4
(x; y)	(−1; 4)	(0; 1)	(2;1)	(3; 4)

Plano cartesiano em malha quadriculada. Eixo x com escala de menos 4 a 4, e eixo y com escala de menos 2, a 6. Parábola com concavidade voltada para cima, que passa pelos pontos: (menos 1, 4), (0, 1), V(1, 0), (2, 1), (3, 4)

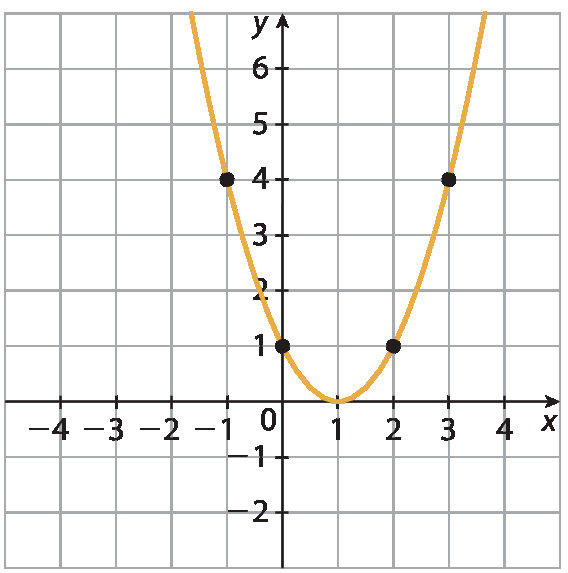
10. c) x2 ‒ 2x + 1 = 1 ⇒ x2 ‒ 2x = 0 ⇒

\Rightarrow x (x ‒ 2) = 0 \begin{array}{l} ↗ \\ ↘ \end{array} \begin{array}{l} x = 0 \\ x ‒ 2 = 0 \Rightarrow x = 2 \end{array}

10. d) Observando que a parábola tem concavidade voltada para cima e tangencia o eixo das abscissas no ponto (1, 0), conclui-se que y > 0 implica x ≠ 1.

11. a) 10 = 02 ‒ 7 · 0 + c ⇒ c = 10

11. b) Substituindo c por 10 na expressão da função, temos:

y = t2 ‒ 7t + 10

11. c)

t = \frac{- b}{2 a} = \frac{- (- 7)}{2 \cdot 1} = 3, 5

; portanto, 3,5 minutos.

12. Com y = 0, tem-se: 2x2 ‒ 3x + 1 = 0

Δ = (‒3)2 ‒ 4 · 2 · 1 = 9 ‒ 8 = 1

x = \frac{‒ (- 3) \pm \sqrt{1}}{2 \cdot 2} = \frac{+ 3 \pm 1}{4} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{4}{4} = 1 \\ x = \frac{2}{4} = \frac{1}{2} \end{array}

Alternativa d.

13.

x_{V} = \frac{- b}{2 a} = \frac{- (- 50)}{2 \cdot 1} = 25

; portanto, x = 25.

14.

x_{V} = \frac{- b}{2 a} = \frac{- 2}{2 \cdot (- 1)} = 1

e yv = f(1) = ‒12 + 2 · 1 + 2 = = ‒1 + 2 + 2 = 3

Alternativa b.

15. Com y = 0 em y = ‒16x² + 256, tem-se: ‒16x2 + 256 = 0 ⇒ 16x2 = 256 ⇒ x2 = 16 ⇒ x = ±4

E como t > 0, conclui-se que t = 4 s.

Alternativa b.

16.

x_{V} = \frac{- b}{2 a} = \frac{- 12}{2 \cdot (- 2)} = 3

e yv = f(3) = ‒2 · 32 + 12 · 3 = = ‒18 + 36 = 18

Alternativa b.

17. A função que expressa o volume da piscina é:

y = 2 · x · (20 ‒ x) = ‒2x2 + 40x

Assim:

x_{V} = \frac{- b}{2 a} = \frac{- 40}{2 \cdot (- 2)} = 10

e yv = f(10) = ‒2 · 102 + + 40 · 10 = ‒200 + 400 = 200

Portanto, 200 métros cúbicos.

18. O lucro é máximo quando:

x = \frac{- b}{2 a} = \frac{- 120}{2 \cdot (- 1)} = 60

Alternativa a.

19.

x_{V} = \frac{- b}{2 a} = \frac{- 2 000}{2 \cdot (- 2)} = 500

; portanto, 500 unidades.

20. a) m + 1 < 0 ⇒ m < ‒1

20. b) Com Δ = 0, tem-se: (‒5)2 ‒ 4 · (m + 1) · 5 = 0 ⇒ 25 ‒ 20m ‒ 20 = 0 ⇒ 5 = 20m ⇒

\frac{5}{20} = m \Rightarrow \frac{1}{4} = m

22. Quando o discriminante é igual a zero, a parábola tem apenas uma raiz, o que significa que ela tangencia o eixo das abcissas em um ponto.

Alternativa c.

Verificando

1. y = f(0) = 14 ‒ 2 · 0 = 14 ‒ 0 = 14

y = f(1) = 14 ‒ 2 · 1 = 14 ‒ 2 = 12

y = f(2) = 14 ‒ 2 · 2 = 14 ‒ 4 = 10

y = f(3) = 14 ‒ 2 · 3 = 14 ‒ 6 = 8

Alternativa b.

2. Sem o valor fixo, os rendimentos extras de João são expressos, em reais, por: 12 · v

Então, acrescentando o valor fixo, tem-se a função:

S = .2500 + 12 · v

Alternativa d.

3. Com y = 47, tem-se: 20 + 3x = 47 ⇒ 3x = 47 ‒ 20 ⇒

x = \frac{27}{3} \Rightarrow x = 9

Alternativa b.

4. A = x(x + 3) = x2 + 3x.

Alternativa a.

5. Alternativa c, pois: 3x + 2 = 0 ⇒ 3x = ‒2 ⇒

x = ‒ \frac{2}{3}

6. Observando que o gráfico é uma reta que contém os pontos de coordenadas (0, 0) e (3, 3), conclui-se que y = x.

Alternativa d.

7. Com y = 0, tem-se: Δ = 52 ‒ 4 · (‒2) · (‒2) = 25 ‒ 16 = 9

x = \frac{‒ 5 \pm \sqrt{9}}{2 \cdot (‒ 2)} = \frac{+ 5 \pm 3}{‒ 4} \begin{array}{c} ↗ \\ ↘ \end{array} \begin{array}{c} x = \frac{8}{- 4} = ‒ 2 \\ x = \frac{‒ 2}{‒ 4} = \frac{1}{2} \end{array}

Alternativa d.

8. (4x ‒ 1)2 = 0 ⇒ 4x ‒ 1 = 0 ⇒ 4x = 0 + 1 ⇒ x =

\frac{1}{4}

9. É uma parábola voltada para cima, pois: a = 1 > 0

Cruza o eixo x duas vezes, pois: Δ = (‒5)2 ‒ 4 · 1 · 6 = = 25 ‒ 24 = 1 > 0