Página CVII

Parte 11

Capítulo 11 – Circunferência, arcos e relações métricas

• Objetivos do capítulo e justificativas

• Reconhecer e determinar o número irracional π.

• Resolver problemas envolvendo a razão entre duas grandezas.

• Determinar o comprimento de uma circunferência e aplicar esse conceito na resolução de problemas.

• Relacionar arcos de circunferência e ângulos centrais.

• Determinar o comprimento de arcos de circunferência e de sua medida angular.

• Resolver problemas envolvendo relações de proporcionalidade no cálculo da medida de arcos.

• Reconhecer e aplicar as propriedades entre arcos e cordas de uma circunferência e das relações métricas em uma circunferência.

• Analisar gráfico com semicoroa circular.

• Resolver problemas envolvendo porcentagens e determinação de ângulos de setores circulares.

• Comunicar resultados de pesquisa por meio de tabela e gráfico.

Neste capítulo, tratamos da circunferência e da determinação da medida de seu comprimento, das medidas de arcos e relações métricas em uma circunferência. O conceito de proporcionalidade, frequente no desenvolvimento de vários conteúdos abordados ao longo do Ensino Fundamental e já estudado neste volume, também é utilizado para determinar a medida de arcos de circunferência. Os tópicos abordados contribuem para a ampliação e a consolidação de ferramentas que contribuem para o desenvolvimento do pensamento geométrico. Assim, contribui-se para o desenvolvimento do raciocínio lógico, do espírito de investigação e a capacidade de produzir argumentos. As atividades propostas relacionam as Unidades Temáticas Álgebra e Geometria e propõem diferentes construções geométricas. Assim, o trabalho realizado favorece o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2, 3 e 5.

Além disso, ampliamos o trabalho com gráficos explorando os formados por semicoroas circulares, contribuindo para o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2, 3 e 4.

O desenvolvimento das competências gerais 9 e 10 e da competência específica 8 é favorecido com as diferentes propostas de atividades a serem realizadas em grupos, pois possibilitam aos estudantes que exercitem diferentes habilidades socioemocionais ao trabalharem com colegas que podem ou não ter dificuldades ou facilidades em relação às atividades propostas.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah um um) Resolver problemas por meio do estabelecimento de relações entre arcos, ângulos centrais e ângulos inscritos na circunferência, fazendo uso, inclusive, de softwares de geometria dinâmica.

(ê éfe zero nove ême ah dois três) Planejar e executar pesquisa amostral envolvendo tema da realidade social e comunicar os resultados por meio de relatório contendo avaliação de medidas de tendência central e da amplitude, tabelas e gráficos adequados, construídos com o apoio de planilhas eletrônicas.

Neste capítulo, serão aprofundados os estudos relativos à Unidade Temática Geometria envolvendo relações com arcos de circunferência, contribuindo para o desenvolvimento da habilidade (ê éfe zero nove ême ah um um).

A Unidade Temática Números também está presente com atividades que abordam o reconhecimento do número irracional π e cálculo de porcentagens na seção Trabalhando a informação. A conexão com a Unidade Temática Álgebra se concretiza por meio da resolução de problemas que envolvem a razão entre duas grandezas e a noção de proporcionalidade.

Com a Unidade Temática Probabilidade e estatística, a conexão se dá por meio da seção Trabalhando a informação, que trata da análise de gráficos associados a semicoroas circulares, favorecendo o desenvolvimento da habilidade (ê éfe zero nove ême ah dois três).

• Comentários e resoluções

Apresentaremos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Abertura

b) Pela simetria da figura, a altura da ponte corresponde à metade do diâmetro da circunferência formada. Portanto, a medida do diâmetro da circunferência é o dôbro da medida da altura da ponte, que é de 15 m. Assim, a circunferência mede 30 métros (15 ⋅ 2 = 30).

c) Resposta dependente da pesquisa dos estudantes. Alguns exemplos que se pode apresentar são “Círculos em um círculo” (candinsqui), máqui Niterói (Niemáier), “Homem vitruviano” (da vinti), abóbadas de igrejas em geral e objetos mais prosaicos do dia a dia, como tampas de bueiros, quadras esportivas, padrões em parapeitos e similares.

Exercícios propostos

1. Se cada pedalada corresponde a uma volta completa da roda, após quinhentas peladas o ciclista percorreu uma distância equivalente a quinhentas vezes o comprimento C da roda. Isto é, 500 ⋅ C. Como a roda pode ser associada a uma circunferência de raio de medida 25 centímetros, seu comprimento é dado por: C = 2πr = 2 ⋅ 3,14 ⋅ 25 = 157

E, como 157 centímetros = 1,57 métros, a distância total foi de 785 métros, pois 500 ⋅ 1,57 = 785.

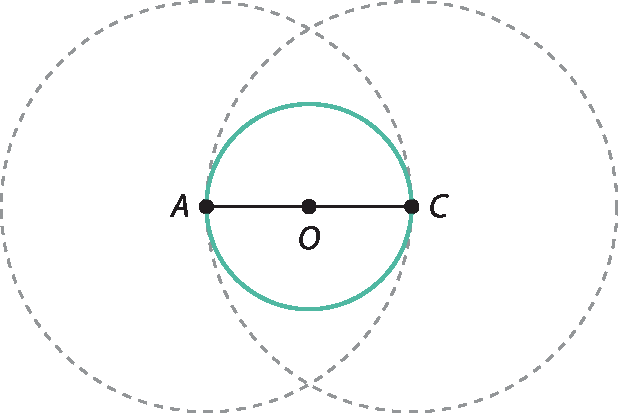
2. A figura proposta pode ser construída utilizando régua e compasso: seja O o centro da circunferência. Primeiro, marca-se um diâmetro qualquer

\bar{A C}

. Em seguida, traçam-se duas circunferências utilizando o compasso, uma com a ponta-seca em a e outra com a ponta seca em C, ambas com a mesma abertura de medida á cê .

Página CVIII

Ilustração. Circunferência de centro O e diâmetro horizontal AC. Circunferência tracejada de centro C e raio AC. Circunferência tracejada de centro A e raio AC.

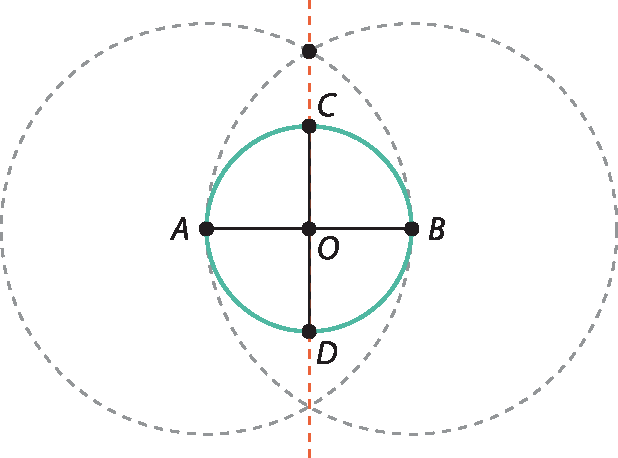
A reta passando por óh e pela intersecção dêsses dois círculos é perpendicular a

\overset{\leftrightarrow}{A B}

, e sua intersecção com a circunferência determina um diâmetro

\bar{B D}

perpendicular a

\bar{A B}

O quadrado a bê cê dê assim determinado decompõe-se em quatro triângulos retângulos isósceles congruentes, cujos lados perpendiculares medem a mesma medida r do raio.

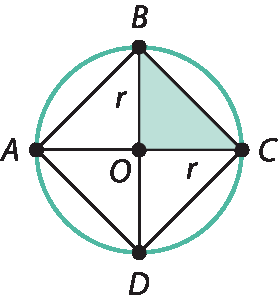
Ilustração. Circunferência de centro O e diâmetros horizontal AC e vertical BD, quadrado ACDB. Raio r OC e raio r OB. O triângulo OBC está pintado de verde.

Assim, A bê = bê cê = CD = á dê. Mas, pelo teorema de Pitágoras: r2 + r2 = BC2 ⇒ 2r2 = BC2 ⇒ BC =

\sqrt{2 r^{2}}

\sqrt{2}

r. Logo, o perímetro do quadrado mede 5,64 r, pois: AB + BC + CD + AD = 4 ⋅

\sqrt{2}

⋅ r = 4 ⋅ 1,41 ⋅ r = 5,64r

Por outro lado, o comprimento da circunferência é dado por 6,28r, pois 2πr = 2 ⋅ 3,14 ⋅ r = 6,28r. A diferença entre este comprimento e o perímetro do quadrado é, portanto, 0,64r, pois: 6,28r ‒ 5,64r = 0,64r

4. Se ℓ é o comprimento do diâmetro em centímetros, organizamos o seguinte quadro, por meio da regra de três:

Polegadas	Centímetros
1	2,5
$divisão de 3 sobre 4$	ℓ

Obtemos a seguinte proporção:

\frac{1}{\frac{3}{4}} = \frac{2, 5}{ℓ} \Rightarrow \frac{4}{3} = \frac{2, 5}{ℓ} \Rightarrow

\Rightarrow4 ℓ = 3 \cdot 2, 5 \Rightarrow ℓ = \frac{3 \cdot 2, 5}{4} = 1, 875

Assim, a medida equivale a 1,875 centímetro.

6. A circunferência total da praça mede 370,52 métros, pois: C = πd = 3,14 ⋅ 118 = 370,52. Logo, se Ari percorreu 192,52 métros, Edu percorreu 178 métros (370,52 ‒ 192,52 = 178), uma distância menor do que a percorrida por Ari. Portanto, Ari é mais rápido.

7. Se adicionarmos as distâncias percorridas por Teca e Lia, obteremos o comprimento total da circunferência da praça. Portanto, C = 376,8 métros, pois: 180 + 196,8 = 376,8. Se r é a medida do raio da praça, C = 2πr. Logo:

r = \frac{C}{2} = \frac{376, 8}{2 \cdot 3, 14} = \frac{376, 8}{6, 28}

= 60

Portanto, o raio mede aproximadamente 60 métros.

8. A largura da pista é a diferença R ‒ r entre os raios de medida R da circunferência externa e de medida r da interna. Como a circunferência externa é a maior, temos 2πR = .1500. Portanto,

R = \frac{1 500}{2 π} = \frac{1 500}{6, 28} ≃ 238, 85

, comprimento de cêrca de 238,85 métros. Analogamente, r ≃ 191,08 métros. Portanto, a largura é de, aproximadamente, 47,77 métros, pois: 238,85 ‒ 191,08 = 47,77

10. Resposta pessoal. Problemas envolvendo circuitos circulares, como pistas de corrida, ou a distância percorrida ao longo de um movimento orbital, são algumas possibilidades.

11. Nesse caso, conhecendo α = 40graus e r = 12 centímetros, temos a proporção: 

\frac{2 π r}{ℓ} = \frac{360}{40} \Rightarrow \frac{2 π \cdot 12}{ℓ} = \frac{360}{40} \Rightarrow \frac{24 π}{ℓ} = 9 \Rightarrow

\Rightarrow 9 ℓ = 24 π \Rightarrow ℓ ≃ \frac{8 \cdot 3, 14}{3} ≃ 8, 37

Assim, o arco mede aproximadamente 8,4 centímetros.

12. Diâmetros perpendiculares dividem a circunferência em quatro arcos de mesmo comprimento, cada um deles com ângulo central reto.

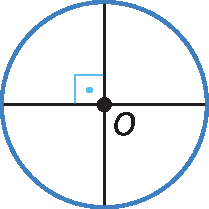
Ilustração. Circunferência de centro O com dois diâmetros perpendiculares destacados.

Assim, o comprimento ℓ dos arcos correspondentes respeita à seguinte razão:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 3}{ℓ} = \frac{360}{90} \Rightarrow \frac{6 π}{ℓ} =

4 \Rightarrow ℓ ≃ \frac{3 \cdot 3, 14}{2} ≃ 4, 71

Portanto, cêrca de 4,71 centímetros.

13. a) Se a circunferência é dividida em 12 arcos congruentes (ou seja, de mesmo comprimento), o comprimento total é determinado multiplicando-se o comprimento de um dêsses arcos por 12. Ou seja, 36π centímetros, pois: 12 ⋅ 3π = 36π

13. b) Pelo item a, o comprimento da circunferência é de 36π cm. Portanto, o raio de medida r satisfaz 2πr = 36π. Dividindo-se ambos os lados da equação por 2π, segue r = 18 centímetros.

14. O raio da circunferência mede r = 1,8 centímetro. Assim, para o arco

\overset{⌢}{A B}

, o ângulo central mede α = 30graus, e o comprimento ℓ correspondente satisfaz à proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow

\Rightarrow \frac{2 π \cdot 1, 8}{ℓ} = \frac{360}{30} \Rightarrow \frac{2 π \cdot 1, 8}{ℓ} = 12 \Rightarrow \frac{1, 8 π}{ℓ} = 6 \Rightarrow ℓ ≃ 0, 9

Portanto, o arco

\overset{⌢}{A B}

mede 0,9 centímetro.

Página CIX

Para o arco

\overset{⌢}{B C}

, o ângulo central mede α = 45graus, e o comprimento ℓ correspondente satisfaz à proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 1, 8}{ℓ} = \frac{360}{45} \Rightarrow \frac{2 π \cdot 1, 8}{ℓ} = 8 \Rightarrow

\Rightarrow \frac{1, 8 π}{ℓ} = 4 \Rightarrow ℓ ≃ 1, 4

Então,

\overset{⌢}{B C}

mede cêrca de 1,4 centímetro.

Para o arco

\overset{⌢}{C D}

, o ângulo central mede α = 60graus, e o comprimento ℓ correspondente satisfaz à proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 1, 8}{ℓ} = \frac{360}{60} \Rightarrow \frac{2 π \cdot 1, 8}{ℓ} = 6 \Rightarrow

\Rightarrow \frac{1, 8 π}{ℓ} = 3 \Rightarrow ℓ ≃ 1, 9

Então,

\overset{⌢}{C D}

mede cêrca de 1,9 centímetro.

15. Medindo os três raios dos arcos representados:

R_{1}

R_{2}

R_{3}

, obtemos, aproximadamente: 12,7 centímetros, 9,3 centímetros e 6,3 centímetros. A linha é formada por arcos com ângulo central de medida 180°; portanto, seu comprimento será 

\frac{2 π R_{1}}{2}

+ \frac{2 π R_{2}}{2} + \frac{2 π R_{3}}{2} = π (R_{1} + R_{2} + R_{3})

Como 1,3 + 0,9 + 0,65 = 2,85, o comprimento procurado é aproximadamente 8,95 centímetros, pois: 3,14 ⋅ 2,85 = 8,949

16. Se óh é o centro da circunferência, e a e B são os pontos nos quais o diâmetro toca a circunferência, a figura resultante tem como perímetro a soma da medida do arco

\overset{⌢}{A B}

com a medida do segmento

\bar{A B} :

Ilustração. Circunferência de centro O e diâmetro horizontal BA, BO mede 4 centímetros, OA mede 4 centímetros. A metade da circunferência abaixo do diâmetro está tracejada.

A medida do arco

\overset{⌢}{A B}

é metade do comprimento da circunferência. Ou seja, 12,56 centímetros, pois: 2πr ∶ 2 = πr ≃ 3,14 ⋅ 4 = 12,56. Além disso,

\bar{A B}

é um diâmetro e, portanto, tem comprimento 8 centímetros. Portanto, o perímetro da figura é aproximadamente 20,56 centímetros, pois: 12,56 + 8 = 20,56

17. Dados o raio r = 6 centímetros e o comprimento ℓ = 6,28 centímetros do arco, temos a proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 6}{6, 28} = \frac{360}{α}

⇒ ⇒ 12πα = 360 ⋅ 6,28 ⇒

α = \frac{360 \cdot 6, 28}{12 π} ≃ \frac{360 \cdot 6, 28}{12 \cdot 3, 14}

= =

\frac{(30 \cdot 12) \cdot (2 \cdot 3, 14)}{12 \cdot 3, 14}

⇒ α ≃ 30 ⋅ 2 = 60

Portanto, a medida aproximada do ângulo é 60graus.

18. Dados o raio r = 15 centímetros e o comprimento ℓ = 9,42 centímetros do arco, temos a proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 15}{9, 42} = \frac{360}{α}

⇒ ⇒ 30πα = 360 ⋅ 9,42 ⇒

α = \frac{360 \cdot 9, 42}{30 π} ≃ \frac{360 \cdot 9, 42}{30 \cdot 3, 14}

\frac{(30 \cdot 12) \cdot (3 \cdot 3, 14)}{30 \cdot 3, 14}

⇒ α ≃ 12 ⋅ 3 = 36

Portanto, a medida aproximada do ângulo é 36graus.

19. Dados o raio r = 18 centímetros e o ângulo α = 40graus, temos a proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 18}{ℓ} = \frac{360}{40} \Rightarrow \frac{36 π}{ℓ} = 9

⇒

\Rightarrow 9 ℓ = 36 π \Rightarrow ℓ = \frac{36 π}{9} = 4 π \Rightarrow ℓ ≃ 4 \cdot 3, 14 = 12, 56

Portanto, o arco tem medida aproximada de 12,56 centímetros.

20. Pela figura, identificamos o arco descrito pelo pêndulo como o arco de ângulo de medida α = 20graus de uma circunferência de raio de medida r = 30 centímetros. Assim, temos a proporção:

\frac{2 π r}{ℓ} = \frac{360 °}{α} \Rightarrow \frac{2 π \cdot 30}{ℓ} = \frac{360}{20} \Rightarrow \frac{60 π}{ℓ} = 18

⇒

18 ℓ = 60 π \Rightarrow ℓ = \frac{60 π}{18} = \frac{6 \cdot 10 \cdot π}{6 \cdot 3} = \frac{10 \cdot π}{3}

⇒

ℓ ≃ \frac{10 \cdot 3, 14}{3} ≃ 10, 5

Então, o peso percorreu um percurso de medida aproximada de 10,5 centímetros.

21. Dados o raio de medida r = 10 centímetros e o comprimento ℓ = 7,85 centímetros do arco, temos a proporção:

\frac{2 π r}{ℓ} = \frac{360}{α}

⇒

\Rightarrow \frac{2 π \cdot 10}{7, 85} = \frac{360}{α} \Rightarrow 20 π α = 360 \cdot 7, 85 \Rightarrow

⇒

α = \frac{360 \cdot 7, 85}{20 π} = \frac{(20 \cdot 18) \cdot 7, 85}{20 π} = \frac{18 \cdot 7, 85}{π} \Rightarrow

⇒

α ≃ \frac{18 \cdot 7, 85}{3, 14} = \frac{18 \cdot (2, 5 \cdot 3, 14)}{3, 14} = 18 \cdot 2, 5 \Rightarrow α ≃ 45

Logo, a medida do arco é 45graus.

24. a) Pela figura, os arcos

\overset{⌢}{A B}

\overset{⌢}{C D}

têm ângulo interno de mesma medida. Logo, têm o mesmo comprimento. Portanto, pela 1ª propriedade, as cordas subentendidas por eles são congruentes. Assim, cedê = A bê = 1,2 centímetros.

24. b) O ângulo BÔC se decompõe nos ângulos adjacentes

A \hat{O} B

A \hat{O} D

C \hat{O} D

. Mas

A \hat{O} B

C \hat{O} D

são congruentes. Logo, medida do(

C \hat{O} D

) = medida do(

A \hat{O} B

) = 45graus. Por fim, como a medida medida do(

A \hat{O} D

) = 65° é dada, temos: medida do(

B \hat{O} C

) = 45graus + 65graus + 45graus ⇒ ⇒ medida do(

B \hat{O} C

) = 155graus

25. Esboçando a situação descrita, temos:

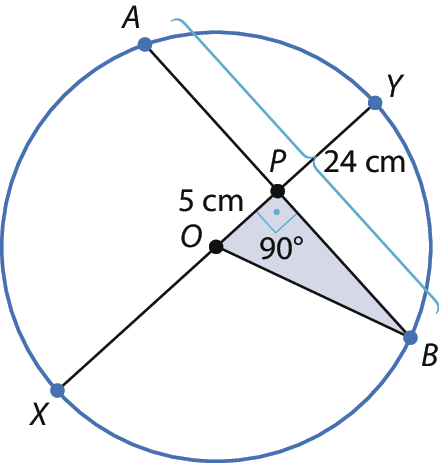
Ilustração. Circunferência de centro O e diâmetro XY, corda AB que corta XY no ponto P. AB mede 24 centímetros, OP mede 5 centímetros. Triângulo retângulo OPB destacado.

Pela 2ª propriedade, á pê = bê pê. Logo, cada um deles tem medida igual à metade de A bê = 24 centímetros. Ou seja, á pê = bê pê = 12 centímetros. Como o triângulo BPO é retângulo, com catetos

\bar{B P}

\bar{O P}

, cuja hipotenusa

\bar{O B}

é um raio da circunferência, temos: bê pê² + ó pê² = ó bê² ⇒ 12² + 5² = ó bê² ⇒ ⇒ OB² = 144 + 25 = 169 ⇒ OB = 13.

Portanto, o raio da circunferência mede 13 centímetros.

Página CX

28. Dados o raio r = 40 centímetros e o ângulo α = 80graus, temos a proporção:

\frac{2 π r}{ℓ} = \frac{360}{α} \Rightarrow \frac{2 π \cdot 40}{ℓ} = \frac{360}{80} \Rightarrow \frac{80 π}{ℓ} = \frac{9 \cdot 40}{2 \cdot 40}

⇒ ⇒

\frac{80 π}{ℓ} = \frac{9}{2} \Rightarrow 9 ℓ = 160 π \Rightarrow ℓ = \frac{160 π}{9} ≃ \frac{160 \cdot 3, 14}{9}

⇒ ℓ ≃ 55,8

Portanto, o comprimento do arco mede aproximadamente 55,8 centímetros.

29. Pelo teorema de Pitágoras, a hipotenusa desse triângulo retângulo mede 6 centímetros, pois:

\sqrt{{(\sqrt{20})}^{2} + 4^{2}} = \sqrt{20 + 16} = \sqrt{36}

= 6. Essa hipotenusa é um diâmetro da circunferência que circunscreve o triângulo. Logo, o raio dessa circunferência mede 3 centímetros. Como a mediana relativa à hipotenusa é um raio da circunferência que circunscreve o triângulo. Assim, essa mediana mede 3 centímetros.

30. A mediana relativa à hipotenusa é um raio da circunferência que circunscreve o triângulo. Assim, o raio dessa circunferência mede 4 centímetros. Como a hipotenusa do triângulo é um diâmetro do círculo que o circunscreve, sua medida é 8 centímetros. Como um dos catetos mede

\sqrt{15}

centímetros, pelo teorema de Pitágoras, o outro cateto mede 7 cm, pois:

\sqrt{8^{2} ‒ {(\sqrt{15})}^{2}} = \sqrt{64 ‒ 15} = \sqrt{49} = 7

31. A mediana relativa à hipotenusa é um raio da circunferência que circunscreve o triângulo. Assim, o raio dessa circunferência mede r = 12 centímetros. O comprimento da circunferência é 75,36 centímetros, pois: C = 2πr ≃ 2 ⋅ 3,14 ⋅ 12 ≃ 75,36

33. a) Recordando que um triângulo inscrito em uma semicircunferência (e, portanto, em uma circunferência) é retângulo, o triângulo á bê cê é retângulo, com medida do

(A \hat{C} B)

= 90graus. Como a soma das medidas dos ângulos internos de um triângulo é 180°, temos: medida do

(B \hat{A} C)

+ + medida do

(A \hat{B} C)

+ medida do

(A \hat{C} B)

= 180graus ⇒ 30° + medida do

(A \hat{B} C)

+ 90graus = 180graus ⇒ ⇒ medida do

(A \hat{B} C)

+ 120graus = 180graus ⇒ medida do

(A \hat{B} C)

= 180graus ‒ 120graus ⇒ ⇒ medida do

(A \hat{B} C)

= 60graus. Agora, como

\bar{O B}

\bar{O C}

são ambos raios da circunferência, o triângulo OBC é isósceles. Portanto, os ângulos

B \hat{C} O

O \hat{B} C

são congruentes. Mas medida do

(O \hat{B} C)

= medida do

(A \hat{B} C)

. Logo, medida do

(B \hat{C} O)

= medida do

(O \hat{B} C)

= medida do

(A \hat{B} C)

= = 60graus. Como a soma das medidas dos ângulos internos de um triângulo é 180graus, no triângulo OBC temos: medida do

(B \hat{O} C)

+ medida do

(B \hat{C} O)

+ medida do

(O \hat{B} C)

= 180graus ⇒ medida do

(B \hat{O} C)

+ 60graus + + 60graus = 180graus ⇒ medida do

(B \hat{O} C)

= 60graus. Por fim, como O está sobre o segmento

\bar{A B}

A \hat{O} C

B \hat{O} C

juntos formam um ângulo raso. Portanto: medida do

(A \hat{O} C)

+ medida do

(B \hat{O} C)

= 180graus ⇒ medida do

(A \hat{O} C)

+ 60graus = = 180graus ⇒ medida do

(A \hat{O} C)

= 120graus

33. b)

\bar{O B}

\bar{O C}

são raios da circunferência. Portanto, OB = OC = 3 centímetros. Como os três ângulos internos do triângulo AOC medem 60graus, ele é equilátero. Portanto,

\bar{B C}

também mede 3 centímetros. Agora,

\bar{A B}

é um diâmetro da circunferência. Portanto, mede o dôbro do raio, isto é, 6 centímetros. Por fim, como o triângulo ACB é reto, temos:

medida do(AC)2 + medida do(BC)² = medida do(AB)² ⇒ medida do(AC)2 + 32 = 62 ⇒

⇒ medida do(AC)2 + 9 = 36 ⇒ medida do(AC)2 = 27 ⇒ medida do(AC) =

\sqrt{27} = \sqrt{9 \cdot 3} = \sqrt{9} \cdot \sqrt{3} = 3 \sqrt{3}

Logo,

\bar{A C}

mede

3 \sqrt{3}

centímetros.

33. c)

Triângulo	Ângulos	Lados
ABC	Retângulo, pois o ângulo AĈB é reto.	Escaleno, pois todos os seus lados possuem medidas distintas.
AOC	Obtusângulo, pois o ângulo AÔC tem medida maior do que 90°.	Isósceles, pois AO = OC.
OBC	Acutângulo, pois seus três ângulos medem 60°.	Equilátero, pois seus três lados são congruentes.

34. Pela 1ª relação métrica:

34. a) 6 ⋅ 9 = 3 ⋅ x ⇒ x = 2 ⋅ 9 ⇒ x = 18

34. b) x ⋅ (x + 1) = 2 ⋅ 10 ⇒ x² + x = 20 ⇒ x² + x ‒ 20 = 0 ⇒ ⇒ (x ‒ 4) ⋅ (x + 5) = 0

Portanto, x = 4 ou x = ‒5. Como medidas não podem ser negativas, x = 4.

34. c) x ⋅ (2x) = 3 ⋅ (4x) ⇒ 2x² = 12x ⇒ 2x² ‒ 12x = 0 ⇒ ⇒ 2x ⋅ (x ‒ 6) = 0

Portanto, x = 0 ou x = 6. Como x é uma medida não nula, x = 6.

34. d) Supondo que óh é o centro da circunferência, o raio mede 8. Portanto, a corda passando pelo ponto O mostrada na figura é dividida pela outra corda em um segmento de medida 2 e outro de medida 14 (16 ‒ 2 = 14). Portanto: 4 ⋅ x = 2 ⋅ 14 ⇒ 4x = 28 ⇒ x = 7

35. Chamando P ao ponto de interseção do diâmetro

\bar{C D}

com a base

\bar{A B}

, que também é uma corda, temos pê á ⋅ PB = PC ⋅ PD. Como são dados pê á = PB = 6 cm e PD = 4 centímetros, temos: 6 ⋅ 6 = PC ⋅ 4 ⇒ 4 ⋅ PC = 36 ⇒ PC = 9

Como

\bar{A B}

é a base e

\bar{P C}

é a altura do triângulo ABC, sua área é dada por: 

\frac{1}{2} A B \cdot P C = \frac{1}{2} \cdot 12 \cdot 9 = 54

A área mede 54 centímetros quadrados.

36. A 1ª relação métrica implica pê á ⋅ PC = PB ⋅ PD. Utilizando passos como unidade de medida, temos pê á = 30, PD = 20 e PB = 72. Assim: 30 ⋅ PC = 72 ⋅ 20 ⇒ PC = 48

Portanto, 48 passos.

37. Pela 2ª propriedade, o diâmetro bissecta a corda em dois segmentos de 3 centímetros cada. Se o raio da circunferência mede r, o diâmetro é dividido pela corda em um segmento de medida r + 4 e outro de medida r ‒ 4. Assim, pela 1ª relação métrica: (r + 4) ⋅ (r ‒ 4) = 3 ⋅ 3 ⇒ r² ‒ 16 = 9 ⇒ ⇒ r² = 25. Como a área do círculo é dada por πr², ela mede 25π centímetros quadrados.

38. Pela 2ª relação métrica:

38. a) 3 ⋅ x = 4 ⋅ 12 ⇒ x = 4 ⋅ 4 = 16

38. b) 12 ⋅ (x + 3 + 12) = 9 ⋅ (27 + 9) ⇒ 12 ⋅ (x + 15) = 9 ⋅ 36 ⇒ 12x + 180 = 324 ⇒ 12x = 324 ‒ 180 ⇒ 12x = 144 ⇒ x = 12

38. c) x ⋅ (x + x + 4) = 8 ⋅ (8 + 22) ⇒ x ⋅ (2x + 4) = 8 ⋅ 30 ⇒ ⇒ 2x² + 4x = 240 ⇒ 2x² + 4x ‒ 240 = 0 ⇒ 2 ⋅ (x² + 2x ‒ 120) = 0 ⇒ 2 ⋅ (x ‒ 10) ⋅ (x + 12) = 0

Portanto, x = 10 ou x = ‒12. Como medidas não podem ser negativas, x = 10.

Página CXI

39. As estradas cortam o canteiro circular como dois segmentos secantes à circunferência que o delimita. Na primeira estrada, a parte externa mede 50 métros, e o segmento secante mede 144 métros (50 + 94 = 144). Já na éle pê-132, a parte externa mede 48 métros, e o segmento secante mede 48 métros + x. Pela 2ª relação métrica: 48 ⋅ (48 + x) = 50 ⋅ 144 ⇒ .2304 + 48x = .7200 ⇒ 48x = .4896 ⇒ x = 102

40. Pela 3ª propriedade métrica:

40. a) x² = 4 ⋅ (21 + 4) ⇒ x² = 4 ⋅ 25 ⇒ x² = 100 ⇒ x = ± 10

Como x é um número positivo, x = 10.

40. b) 9² = x ⋅ (8x + x) ⇒ 81 = x ⋅ (9x) ⇒ 81 = 9x² ⇒ x² = 9 ⇒ x = ±3

Como x é um número positivo, x = 3.

Exercícios complementares

2. A volta completa dada pelo ponteiro pode ser associada a uma circunferência de raio r = 9 centímetros. Portanto, tem comprimento C = 18π centímetros, pois 2πr = 2 ⋅ π ⋅ 9 = 18π. Como o ponteiro é o dos minutos, em 20 minutos, que é um terço de hora, ele terá percorrido um terço desse comprimento. Ou seja, 6π centímetros (pois 18π ∶ 3 = 6π).

4. Pela 1ª relação métrica, MC ⋅ MD = ême á ⋅ MB. Substituindo as medidas indicadas na figura: 2x ⋅ (x + 3) = (2x + 3) ⋅ (x + 1) ⇒ 2x² + 6x = 2x² + 2x + 3x + 3 ⇒ 6x = 5x + 3 ⇒ x = 3

Em particular, MA = 9 centímetros, pois AM = 2x + 3 = 6 + 3 = 9; MB = 4 centímetros, pois MB = x + 1 = 3 + 1 = 4.

Logo: AB = MA + MB = 9 centímetros + 4 centímetros = 13 centímetros

Alternativa e.

5. Pela 1ª relação métrica, pê á ⋅ PB = PC ⋅ PD. Como P é ponto médio do raio, pê á = r ∶ 2 = 4 ∶ 2 = 2. Como

\bar{A B}

é um diâmetro: A bê = 2r ⇒ pê á + PB = 2 ⋅ 4 ⇒ 2 + PB = 8 ⇒ PB = 6 Por fim, pelo enunciado, PC = 2 ⋅ PD. Logo, substituindo todas as informações: 2 ⋅ 6 = (2 ⋅ PD) ⋅ PD ⇒ 12 = 2 ⋅ PD² ⇒ PD² = 6

Como PD é um número positivo,

P D = \sqrt{6}

Por fim: CD = PC + PD = 2 ⋅ PD + PD = 3 ⋅ PD =

3 \sqrt{6}

Alternativa b.

6. Pela 1ª relação métrica aplicada à corda

\bar{A B}

, que também é lado do quadrado, e à outra corda mostrada na figura: x ⋅ x = 3 ⋅ 8 ⇒ x² = 24. Como A bê = 2x, a medida da área do quadrado é dada por A bê² = (2x)² = 2²x² = 4x² = 4 ⋅ (24) = 96. Então, a medida da área é 96 centímetros quadrados.

7. Se r é a medida do raio da circunferência, a intersecção do diâmetro pela corda o divide em um segmento de medida r + 2,5 e outro de medida r ‒ 2,5. O de medida r + 2,5 é o maior deles. Portanto, r + 2,5 = 7 ou, ainda, r = 7 ‒ 2,5 = 4,5.

Logo, 4,5 centímetros.

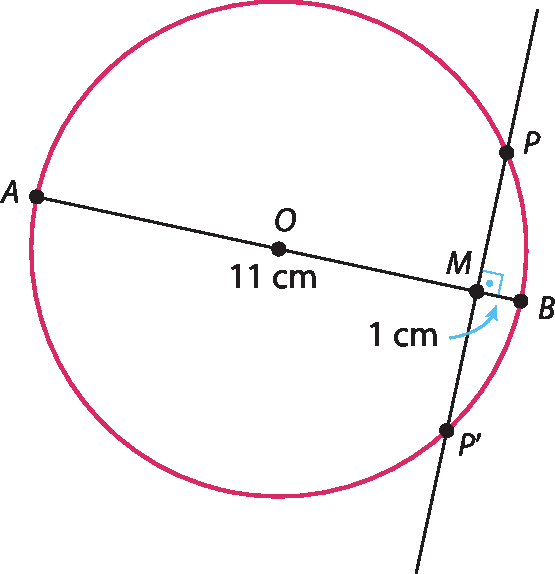
8. Fazendo a construção indicada, percebemos que a perpendicular a

\bar{A B}

pelo ponto M intercepta a circunferência no ponto P e, também, em pê linha. Como

\bar{A B}

é um diâmetro, temos MP = Mpê linha. Além disso, a 1ª relação métrica implica: MP ⋅ Mpê linha = ême á ⋅ MB ⇒ MP ⋅ MP = 11 ⋅ 1 ⇒ MP² = 11. Logo, como a medida deve ser positiva, PM = MP =

\sqrt{11}

; assim, o segmento

\bar{P M}

é a representação geométrica do número

\sqrt{11}

Ilustração. Circunferência de centro O e diâmetros AB medindo 11 centímetros. Reta secante PP linha. O diâmetro AB e a reta PP linha se cruzam no ponto M. a distância de M a B é 1 centímetro.

9. Da figura, podemos afirmar que os triângulos á agá é e dê gê é são semelhantes. Assim:

\frac{A E}{D E} = \frac{H E}{G E} \Rightarrow \frac{9, 5}{6} = \frac{H E}{5, 7} \Rightarrow H E = 9, 025

Assim, a altura procurada mede 9,025 centímetros.

Verificando

1. Conhecendo o comprimento C = 31,4 quilômetros da pista, o raio de medida r é tal que: C = 2πr.

Assim: r =

\frac{C}{2 π} = \frac{31, 4}{2 π}

≃ \frac{31, 4}{2 \cdot 3, 14} \Rightarrow r ≃ 5

Alternativa d.

2. Sabendo que aro é o jargão automotivo para o diâmetro d, temos d = aro 17 = 17 ⋅ aro 1 = 17 ⋅ 2,54 = 43,18. O comprimento correspondente é 135,6 centímetros, pois:

C = πd ≃ 3,14 ⋅ 43,18 ≃ 135,6

Alternativa c.

3. Dados o raio r = 4,5 métros e o ângulo central de medida α = 45graus, o comprimento ℓ do arco correspondente satisfaz à proporção:

\frac{2 π r}{ℓ}

\frac{360}{α}

⇒

\frac{2 π \cdot 4, 5}{ℓ}

\frac{360}{45}

⇒

\frac{9 π}{ℓ}

= 8 ⇒ 8ℓ = 9π ⇒ ℓ =

\frac{9 π}{8}

≃

\frac{9 \cdot 3, 14}{8}

⇒ ℓ ≃ 3,53

Alternativa c.

4. Quando um triângulo retângulo é inscrito em uma circunferência, sua hipotenusa é um diâmetro dessa circunferência. Portanto, sua medida é 30 centímetros (d = 2r = 2 ⋅ 15 = 30).

Alternativa a.

5. Pela 1ª relação métrica, temos:

(2x) ⋅ 5 = 3 ⋅ 8 ⇒ 10x = 24 ⇒ x = 2,4

Alternativa b.

6. Pela 3ª relação métrica: 5 ⋅ (5 + x) = 12² ⇒ 25 + 5x = 144 ⇒ ⇒ 5x = 144 ‒ 25 ⇒ 5x = 119 ⇒ x = 23,8

Portanto, o comprimento de uma circunferência que tenha x como medida de raio é:

C = 2πx ≃ 2 ⋅ 3,14 ⋅ 23,8 ≃ 149,46

Alternativa d.

7. Pela 2ª relação métrica: 7 ⋅ (7 + x) = 6 ⋅ (6 + 9) ⇒ 49 + 7x = = 6 ⋅ 15 ⇒ 49 + 7x = 90 ⇒ 7x = 90 ‒ 49 ⇒ 7x = 41 ⇒

x = \frac{41}{7}

A área de um quadrado que tenha x como medida de lado é:

x^{2} = {(\frac{41}{7})}^{2} = \frac{1 681}{49}

≃ 34,31

Alternativa c.

Página CXII

8. No gráfico de semicoroa circular, 100% correspondem a 180graus. Portanto, 50%, que é metade de 100%, correspondem à metade de 180graus, que é 90graus

Alternativa a.

Organizando

a) O valor constante da razão entre o comprimento de uma circunferência e seu diâmetro é o número π (lê-se “pi”), um número irracional que vale aproximadamente 3,14.

b) Uma das propriedades é o diâmetro. Pelo item a, vemos que a relação é C = πd, em que C é o comprimento da circunferência. A outra propriedade é o raio, que é, por definição, metade do diâmetro. Como, equivalentemente, o diâmetro é o dôbro do raio, temos:

C = πd = π ⋅ (2r) = 2πr.

Capítulo 12 – Polígonos regulares e áreas

• Objetivos do capítulo e justificativas

• Reconhecer e utilizar os elementos e as relações métricas nos polígonos regulares.

• Aplicar o teorema de Pitágoras na determinação de elementos de polígonos regulares inscritos em uma circunferência.

• Resolver e elaborar problemas de aplicação do teorema de Pitágoras envolvendo polígonos regulares.

• Descrever algoritmo por escrito e por meio de fluxograma para a construção de um polígono regular.

• Relacionar arcos de uma circunferência e ângulos centrais de polígonos regulares inscritos nessa circunferência.

• Resolver problemas envolvendo área de um polígono regular, números reais, cálculo de áreas e volumes, relações de proporcionalidade no cálculo da área de um setor circular, área de um círculo, de uma coroa circular e de um setor circular.

• Analisar gráficos com elementos que induzem a erros de leitura e de interpretação.

Neste capítulo, ampliamos o trabalho sobre polígonos regulares e seus elementos ao apresentar as relações métricas entre elementos de um polígono regular e a circunferência a que ele está inscrito. Desenvolvemos o estudo de polígonos regulares com o uso da linguagem algébrica e questões de construção geométrica de figuras. Tratamos da medida da área de um polígono regular, de um círculo e de suas partes; e da medida do volume de alguns sólidos geométricos, relacionando as Unidades Temáticas Geometria e Grandezas e medidas e contribuindo para a consolidação da noção de número, a aplicação de noções geométricas e a construção do pensamento algébrico. Assim, o trabalho realizado favorece o desenvolvimento das competências gerais 2 e 4 e das competências específicas 2, 3 e 5.

O contexto da abertura deste capítulo possibilita desenvolver o Tema Contemporâneo Transversal educação para valorização do multiculturalismo nas matrizes históricas e culturais brasileiras, pois os estudantes podem pesquisar e debater sobre o carimbó que é uma manifestação artística que pode representar o multiculturalismo brasileiro, visto que reúne elementos de diferentes culturas, contribuindo para o trabalho com a competência geral 3.

Na seção Trabalhando a informação exploramos a leitura de gráficos, com destaque para elementos que possam induzir a erros de leitura, o que contribui com a competência geral 4 e as competências específicas 4 e 5.

• Habilidades trabalhadas no capítulo

(ê éfe zero nove ême ah um quatro) Resolver e elaborar problemas de aplicação do teorema de Pitágoras ou das relações de proporcionalidade envolvendo retas paralelas cortadas por secantes.

(ê éfe zero nove ême ah um cinco) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um polígono regular cuja medida do lado é conhecida, utilizando régua e compasso, como também softwares.

(ê éfe zero nove ême ah um sete) Reconhecer vistas ortogonais de figuras espaciais e aplicar esse conhecimento para desenhar objetos em perspectiva.

(ê éfe zero nove ême ah um nove) Resolver e elaborar problemas que envolvam medidas de volumes de prismas e de cilindros retos, inclusive com uso de expressões de cálculo, em situações cotidianas.

(ê éfe zero nove ême ah dois um) Analisar e identificar, em gráficos divulgados pela mídia, os elementos que podem induzir, à vezes propositadamente, erros de leitura, como escalas inapropriadas, legendas não explicitadas corretamente, omissão de informações importantes (fontes e datas), entre outros.

Os conhecimentos abordados neste capítulo referem-se à Unidade Temática Geometria, ampliando o estudo dos polígonos regulares iniciado no livro do 8º ano (ê éfe zero oito ême ah um seis).

Além disso, o capítulo desenvolve assuntos vinculados à Unidade Temática Grandezas e medidas, oportunidade para que seja ampliado o trabalho com medidas de área (com a área de polígono regular e área de partes de um círculo) e medidas de volume, de modo a consolidar e aprofundar os conhecimentos construídos em anos anteriores, em especial no 8º ano (ê éfe zero oito ême ah um nove e ê éfe zero oito ême ah dois um), contribuindo para o desenvolvimento das habilidades (ê éfe zero nove ême ah um quatro), (ê éfe zero nove ême ah um cinco), (ê éfe zero nove ême ah um sete) e (ê éfe zero nove ême ah um nove).

As conexões com as demais Unidades Temáticas estão presentes nas diversas atividades propostas no capítulo. A relação com a Unidade Temática Números se dá nos cálculos com números reais utilizados na determinação de volumes de prisma e de cone; a conexão com a Unidade Temática Álgebra aparece ao utilizar relações de proporcionalidade no cálculo da área de um setor circular; e a articulação com a Unidade Temática Probabilidade e estatística ocorre na seção Trabalhando a informação, favorecendo o desenvolvimento das habilidades (ê éfe zero nove ême ah um um) e (ê éfe zero nove ême ah dois um).

Página CXIII

• Comentários e resoluções

Apresentamos a seguir as resoluções de alguns exercícios e atividades propostos neste capítulo. As resoluções que não constam nesta parte específica estão nas Orientações didáticas que acompanham as reproduções das páginas do livro do estudante.

Exercícios propostos

1. a) Tomando a relação para quadrados inscritos na circunferência:

ℓ = r \sqrt{2} \Rightarrow ℓ = 3 \sqrt{2}

. Usando aproximação:

\sqrt{2} ≃ 1, 4, ℓ ≃ 3 \cdot 1, 4 \Rightarrow ℓ ≃ 4, 2

1. b) Tomando a relação para quadrados inscritos na circunferência:

a = \frac{r \sqrt{2}}{2} \Rightarrow a = \frac{3 \sqrt{2}}{2}

2. Como a =

6 \sqrt[]{2}

a = \frac{r \sqrt{2}}{2}

, então:

\frac{r \sqrt{2}}{2} = 6 \sqrt[]{2} \Rightarrow r \sqrt{2} = 12 \sqrt{2}

⇒

\Rightarrow r = \frac{12 \sqrt{2}}{\sqrt{2}} \Rightarrow r = 12

Portanto, a diagonal do quadrado, que é o dôbro do raio, mede 24 centímetros, pois 12 ⋅ 2 = 24.

3. Como a diagonal do quadrado inscrito mede

d = 5 \sqrt{2}

centímetros; a medida do raio do círculo que o circunscreve é

\frac{d}{2}

, ou seja

r = 2, 5 \sqrt{2}

A medida do apótema é dada por:

a = \frac{r \sqrt{2}}{2} \Rightarrow a = \frac{(2, 5 \sqrt{2}) \cdot \sqrt{2}}{2} \Rightarrow a = \frac{2, 5 \cdot 2}{2} \Rightarrow a = 2, 5

4. A medida do raio da circunferência é metade da medida do lado do quadrado circunscrito:

r = \frac{ℓ}{2} \Rightarrow r = 4

4. a)

ℓ = r \sqrt{2} \Rightarrow ℓ = 4 \sqrt{2}

, então

4 \sqrt{2}

centímetros

4. b) d = 2 ⋅ r ⇒ d = 2 ⋅ 4 cm = 8 centímetros

5. Seja

p_{1}

a medida do perímetro do quadrado circunscrito,

p_{2}

a medida do perímetro do quadrado inscrito,

a_{2}

a medida do apótema do quadrado inscrito. Como

p_{1} = 4 \cdot ℓ e ℓ = 2 r

(raio da circunferência),

p_{1} = 4 \cdot 2 r

8 \cdot r \cdot p_{2} = 4 \cdot (2 \cdot a_{2})

, tomando:

a_{2} = \frac{r \sqrt{2}}{2} \Rightarrow p_{2} = \frac{8 \cdot r \sqrt{2}}{2}

⇒ ⇒

p_{2} = 4 r \sqrt{2} \Rightarrow p_{1} ‒ p_{2} = 8 r ‒ 4 r \sqrt{2} \Rightarrow p_{1} ‒ p_{2} = (8 ‒ 4 \sqrt{2}) r

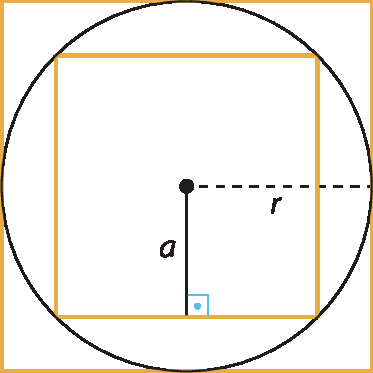
Ilustração Circunferência de raio r, com um quadrado inscrito de apótema a, e um quadrado circunscrito.

6. a) A medida do lado do quadrado maior é igual à medida da diagonal do quadrado menor (d). Pelo teorema de Pitágoras: d2 = 102 + 102 ⇒ d2 = 200 ⇒ d =

10 \sqrt{2}

O lado do quadrado maior mede

10 \sqrt{2}

centímetros.

6. b) A medida da faixa vermelha é dada pela adição da medida do perímetro do quadrado maior com a medida do perímetro do quadrado menor:

p_{m e n o r} = 4 ℓ \Rightarrow p_{m e n o r} = 40. p_{m a i o r} = 4 ℓ \Rightarrow 40 \sqrt{2}

Então, a faixa vermelha tem medida (40 +

40 \sqrt{2}

) centímetros, pois: pmenor + pmaior = (40 +

40 \sqrt{2}

) centímetros

6. c) Obtemos a medida da área dos quatro triângulos subtraindo a medida da área do quadrado menor da medida da área do quadrado maior. Sejam A1 a medida da área do quadrado maior e A2 a medida da área do quadrado menor.

A_{1} = {(10 \sqrt{2})}^{2} \Rightarrow A_{1} = 100 \cdot 2 \Rightarrow A_{1} = 200

A_{2} = 10^{2} \Rightarrow A_{2} = 100

Então,

A_{1} ‒ A_{2} = 100

, a medida da área dos triângulos é 100 centímetros quadrados.

7. Como o lado do quadrado mede 60 cm e seus lados são tangentes à circunferência, a medida do diâmetro da circunferência se relaciona com a medida do lado do quadrado: d = 60 ⇒ r = 60 : 2 = 30

Como ℓ = r ⇒ ℓ = 30, o lado mede 30 centímetros. Então:

a = \frac{r \sqrt{3}}{2} \Rightarrow a = \frac{30 \sqrt{3}}{2} \Rightarrow a = 15 \sqrt{3}

Assim, a medida da área do hexágono é:

A = 6 \frac{ℓ \cdot a}{2}

⇒

A = 6 \cdot \frac{30 \cdot 15 \sqrt{3}}{2}

⇒

A = 1 350 \sqrt{3}

Então, a área mede

1 350 \sqrt{3}

centímetros quadrados.

8. a) ℓ = r ⇒ ℓ = 3,2 centímetros

8. b) Seja 2p a medida do perímetro e ℓ a medida do lado do hexágono regular: 2p = 6 ⋅ ℓ ⇒ 2 p = 19,2

Então, o perímetro mede 19,2 centímetros.

8. c)

a = \frac{r \sqrt{3}}{2} \Rightarrow a = \frac{3, 2 \sqrt{3}}{2} \Rightarrow a = 1, 6 \sqrt{3}

Então, o apótema mede

1, 6 \sqrt{3}

centímetros.

9. Dado:

a = 9 \sqrt{3}

, como

a = \frac{r \sqrt{3}}{2}

, então:

\frac{r \sqrt{3}}{2} = 9 \sqrt{3}

⇒

\Rightarrow r \sqrt{3} = 18 \sqrt{3} \Rightarrow r = 18

O lado de medida ℓ do quadrado será dado por:

ℓ = r \sqrt{2} \Rightarrow ℓ = 18 \sqrt{2}

Portanto, tem medida

18 \sqrt{2}

centímetros.

10. Considere o esquema a seguir.

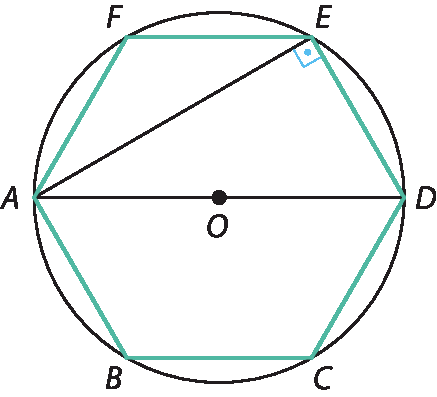
Ilustração. Circunferência de centro O e diâmetro AD com hexágono regular ABCDEF inscrito.

\bar{A E}

é a menor diagonal, então mede

12 \sqrt{3}

centímetros. Também dê ê = r e AD = 2r. Pelo Teorema de Pitágoras: (A Ê)2 = (dê ê)2 + + (á dê)2 ⇒

{(12 \sqrt{3})}^{2}

= r2 + (2r)2 ⇒ 432 = 3r2 ⇒ r2 = 144 ⇒ r = 12

Encontremos o perímetro 2p, sabendo que ℓ = r, temos: 2p = 6ℓ ⇒ 2p = 6 ⋅ 12 ⇒ 2p = 72

Então, o perímetro mede 72 centímetros.