Página cento e catorze

Parte 12

11. O triângulo inscrito é equilátero: d = 10 e r = 5. Pelo teorema de Pitágoras, com ℓ medida do lado do triângulo inscrito: d² = ℓ² + r² ⇒10² = ℓ² + 5² ⇒100 ‒ 25 = ℓ² ⇒ 75 =

ℓ ² \Rightarrow ℓ = 5 \sqrt{3}

Portanto,

5 \sqrt{3}

centímetros.

12. Seja ℓ a medida do lado do hexágono e q a medida do lado do quadrado, ℓ = r = 5 ⇒ q = 2r ⇒ q = 10 ⇒ 2p = 4ℓ ⇒ 2p = 40

Logo, o perímetro mede 40 centímetros.

14. a)

ℓ = r \sqrt{3} \Rightarrow ℓ = 3 \sqrt{3}

14. b)

a = \frac{r}{2} \Rightarrow a = \frac{3}{2} \Rightarrow a = 1, 5

Logo, o apótema mede 1,5 centímetro.

15. a)

a = \frac{r}{2} = \sqrt{12} \Rightarrow r = 2 \sqrt{12} \Rightarrow ℓ = r \sqrt{3} \Rightarrow

\Rightarrow ℓ = 2 \sqrt{12} \cdot \sqrt{3} \Rightarrow ℓ = 2 \sqrt{36} \Rightarrow ℓ = 12

Portanto, 12 centímetros.

15. b)

h = \frac{ℓ \sqrt{3}}{2} \Rightarrow h = \frac{12 \sqrt{3}}{2} \Rightarrow h = 6 \sqrt{3}

Portanto,

6 \sqrt{3}

centímetros.

16. a)

a = \frac{r}{2} \Rightarrow a = 4

Apótema mede 4 centímetros.

16. b) r + a = 4 + 8 = 12

Soma é 12 centímetros.

16. c)

ℓ = r \sqrt{3} \Rightarrow ℓ = 8 \sqrt{3} \Rightarrow h = \frac{ℓ \sqrt{3}}{2} \Rightarrow h = \frac{8 \sqrt{3} \cdot \sqrt{3}}{2}

⇒ h = 12

Altura mede 12 centímetros.

16. d) Como foi observado em b e c: h = r + a, então, sim.

18.

a_{1}

: apótema do quadrado;

a_{2}

: apótema do triângulo

a_{1} = 3, 5 \sqrt{2} = \frac{r \sqrt{2}}{2} \Rightarrow r \sqrt{2} = 7 \sqrt{2} \Rightarrow r = 7

a_{2} = \frac{r}{2} = 3, 5

Então, o apótema do triângulo mede 3,5 centímetros.

19.

ℓ_{1}

: medida do lado do quadrado;

ℓ_{2}

: medida do lado do hexágono

Como

ℓ_{1} = 15 \sqrt{3}, t e m o s : r \sqrt{3} = 15 \sqrt{3} \Rightarrow r = 15

Como

ℓ_{2} = r \Rightarrow ℓ_{2} = 15, o l a d o m e d e 15

centímetros.

21. ℓ = 20 = r. Como

a = \frac{r \sqrt{3}}{2} \Rightarrow a = \frac{20 \sqrt{3}}{2} \Rightarrow a = 10 \sqrt{3}

e também 2p = 6 ⋅ 20 ⇒ 2p = 120. Então p = 60. Usando a relação: A = p ⋅ a ⇒

A = 60 \cdot 10 \sqrt{3}

⇒

A = 600 \sqrt{3}

, então o apótema mede

10 \sqrt{3}

centímetros e a área mede

600 \sqrt{3}

centímetros quadrados.

22. Primeiro, achar o semiperímetro, sendo n o número de lados e ℓ a medida do lado do pentágono: 2p = n ⋅ ℓ

\Rightarrow p = \frac{5 \cdot 20}{2} \Rightarrow p = 50

Agora, calculando a medida ac do ângulo central, temos:

a_{c} = \frac{360 °}{n} \Rightarrow = a_{c} = \frac{360 °}{5} \Rightarrow = a_{c}

= 72graus

Para calcular a medida do apótema usaremos a tangente da metade da medida do ângulo central: tangente de 36graus =

\frac{cateto oposto}{cateto adjacente}

⇒

0, 73 = \frac{10}{a} \Rightarrow a = \frac{10}{0, 73} \Rightarrow a ≃ 13, 7

Finalmente: A = p ⋅ a ⇒ A = 50 ⋅ 13,7 ⇒ A ≃ 685

Portanto, a área mede aproximadamente 685 centímetros quadrados.

23. Eneágono regular tem 9 lados de mesma medida. Para descobrirmos a área pedida, encontraremos o semiperímetro e o apótema, pois: Área = p ⋅ a. Assim:

a_{c} = \frac{360 °}{9}

= 40graus, então usaremos o cosseno de 20graus, que é metade de ac: cosseno de 20graus

= \frac{a}{r} \Rightarrow 0, 93 = \frac{a}{18}

⇒ a = 16,74. Para encontrar ℓ, usaremos a relação seno: sen 20° =

\frac{\frac{ℓ}{2}}{r}

⇒

0, 34 = \frac{\frac{ℓ}{2}}{r} \Rightarrow \frac{ℓ}{2} = 6, 12 \Rightarrow ℓ = 12, 24

Agora, encontraremos o semiperímetro:

2p = 9ℓ ⇒ 2p = 2 ⋅ 12,24 ⇒ p = 55,08

Finalmente: A = p ⋅ a ⇒ A = 55,08 ⋅ 16,74 ⇒ A ≃ 922,04

Portanto, a área mede cêrca de 922 centímetros quadrados.

24. Como o diâmetro mede 3,6 centímetros, o raio mede 1,8 centímetros (3,6 : 2 = 1,8). A área será dada por A = p ⋅ a, com

p = \frac{3 ℓ}{2}

. Encontremos, então, a medida do lado:

ℓ = r \sqrt{3}

⇒ ⇒

ℓ = 1, 8 \sqrt{3} \Rightarrow p = \frac{3 ℓ}{2} \Rightarrow p = \frac{3 \cdot 1, 8 \sqrt{3}}{2} \Rightarrow p = 2, 7 \sqrt{3}

Também:

a = \frac{r}{2} \Rightarrow a = \frac{1, 8}{2} \Rightarrow a = 0, 9

Então:

A = p \cdot a \Rightarrow A = 2, 7 \sqrt{3} \cdot 0, 9 \Rightarrow A = 2, 43 \sqrt{3}

Portanto, a área tem medida de

2, 43 \sqrt{3}

centímetros quadrados.

25.

ℓ = r \sqrt{2} \Rightarrow ℓ = 3 \sqrt{2}

A medida da área da base mede 18 centímetros quadrados, pois é dada por:

A_{b} = ℓ_{2} \Rightarrow A_{b} = {(3 \sqrt{2})}^{2} \Rightarrow A_{b} = 18

A medida da área da superfície lateral é 72 centímetros quadrados, pois é dada por: Asl = 4 ⋅ Ab ⇒ Asl = 4 ⋅ 18 ⇒ A_sl = 72

26. a) Octógono de lado medindo 5 centímetros: Área = p ⋅ a.

Assim:

a_{c} = \frac{360 °}{8}

= 45graus, então, usaremos a tangente de 22,5graus, que é metade de ac: tangente de 22,5graus =

\frac{\frac{ℓ}{2}}{a}

⇒ 0,41

= \frac{\frac{5}{2}}{a} \Rightarrow 0, 41 a = \frac{5}{2} \Rightarrow a ≃ 6, 0975

Agora, encontraremos o semiperímetro: 2p = 8 ⋅ ℓ ⇒ 2p = 8 ⋅ 5 ⇒ p = 20. Finalmente:

A_{o} = p \cdot a \Rightarrow A_{o}

= 20 ⋅ 6,0975 ⇒

A_{o}

≃ 121,95.

Decágono (10 lados) com lado medindo 5 cm. Como Área = p ⋅ a. Assim:

a_{c} = \frac{360 °}{10}

= 36graus

Então, usaremos a tangente de 18graus, que é metade de ac: tangente de 18graus

= \frac{\frac{ℓ}{2}}{a} \Rightarrow 0, 32 = \frac{\frac{5}{2}}{a} \Rightarrow 0, 32 a = \frac{5}{2} \Rightarrow a ≃ 7, 8125

Página cento e quinze

Agora, encontraremos a medida do semiperímetro: 2p = 10 ⋅ ℓ ⇒ 2p = 10 ⋅ 5 ⇒ p = 25

Finalmente:

Au = p ⋅ a ⇒ Au = 25 ⋅ 7,8125 ⇒ Au ≃ 195,31

Triângulo de lado medindo 20 centímetros:

Área = \frac{medida de base \cdot medida de altura}{2}

Sendo medida da base = 20 e medida da altura = h dada pela relação de tangente da metade do ângulo do triângulo. O triângulo equilátero tem seus ângulos de medidas iguais a 60°; então, usaremos a tangente de 30graus, que é metade de ac:

tangente de 30graus

= \frac{\frac{ℓ}{2}}{a} \Rightarrow 0, 58 = \frac{10}{a} \Rightarrow 0, 58 a = 10 \Rightarrow a ≃ 17, 2414

Finalmente:

A_{t} = \frac{medida da base \cdot medida da altura}{2}

⇒

A_{t} = \frac{20 \cdot 17, 2414}{2} \Rightarrow A_{t} ≃ 172, 41

Hexágono com lado medindo 10 centímetros: Área = p ⋅ a

Assim:

a = \frac{r \sqrt{3}}{2}, c o m ℓ = r \Rightarrow a = \frac{r \sqrt{3}}{2} \Rightarrow a = \frac{10 \sqrt{3}}{2}

⇒ ⇒ a = 8,65

Agora, encontraremos a medida do semiperímetro:

2p = 6 ⋅ ℓ ⇒ 2p = 6 ⋅ 10 ⇒ p = 30

Finalmente:

Ah = p ⋅ a ⇒ Ah = 30 ⋅ 8,65 centímetros quadrados ⇒ Ah ≃ 259,5 centímetros quadrados

Pentágono com lado de medida 15 centímetros: Área = p ⋅ a

Assim:

a_{c} = \frac{360 °}{5}

= 72graus

Então, usaremos a tangente de 36graus, que é metade de

a_{c} : t g 36 ° = \frac{\frac{ℓ}{2}}{a} \Rightarrow 0, 73 = \frac{\frac{15}{2}}{a}

⇒ 0,73 a = 7,5 ⇒ a = 10,274 Agora, encontraremos a medida do semiperímetro:

2p = 5 ⋅ ℓ ⇒ 2p = 5 ⋅ 15 ⇒ p = 37,5

Finalmente:

Ap = p ⋅ a ⇒ Ap = 37,5 ⋅ 10,274 ⇒ Ap ≃ 385,28

Portanto, o gráfico de colunas com esses dados é:

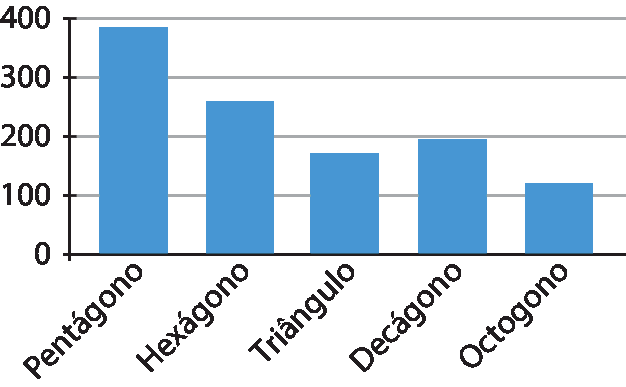
Gráfico de colunas. Eixo horizontal, polígonos. Eixo vertical, escala de 0 a 400, de 100 em 100. Os dados são: pentágono: aproximadamente 400. Hexágono: aproximadamente 250. Triângulo: aproximadamente 190. Decágono: aproximadamente 200. Octógono: aproximadamente 110. — Dados obtidos pelo estudante

26. b) Área média =

\frac{soma das medidas das áreas}{5}

⇒

⇒ Área média =

\frac{385, 28 + 259, 50 + 172, 41 + 195, 31 + 121, 95}{5}

\frac{1 134, 45}{5}

⇒

⇒ Área média = 226,89

Portanto, a medida da área média é 226,89 centímetros quadrados.

28. Acírculo = p ⋅ r2 = 16p ⇒ r2 = 16 ⇒ r = 4

Então, o diâmetro mede 8 centímetros.

Alternativa b.

29.

A = \frac{A C \cdot A B}{2}

. Se

\bar{A B}

é diâmetro, sua medida é o dôbro da medida do raio. Logo A bê = 10 centímetros. Vamos encontrar a medida á cê usando o Teorema de Pitágoras: (á cê )2 + (bê cê)2 = = (A bê)2 ⇒ (á cê )2 + 62 = 102 ⇒ (á cê )² = 100 ‒ 36 ⇒ (á cê )² = 64 ⇒ ⇒ á cê = 8 Então:

A = \frac{A C \cdot A B}{2} \Rightarrow A = \frac{6 \cdot 8}{2} \Rightarrow A = 24

Alternativa a.

30. Como os três triângulos internos tem dois dos lados medindo r = 1, então esses três triângulos são isósceles e seus terceiros lados são congruentes. Logo, o triângulo é equilátero. Basta encontrarmos a medida de um dos lados. Como a = b = g, então

a = b = g = \frac{360 °}{3} =

120graus. Podemos descobrir usando o seno de 60graus, com cateto oposto igual à metade do lado do triângulo inscrito e a hipotenusa igual ao raio: seno de 60graus

= \frac{\frac{ℓ}{2}}{1}

Consultando o quadro de relações trigonométricas:

\frac{\sqrt{3}}{2} = \frac{ℓ}{2} \Rightarrow ℓ = \sqrt{3}

Alternativa ê.

32. Considerando os dois círculos de mesmo diâmetro de medida 6 centímetros, o raio mede r = 3 centímetros; logo:

Área total = 2 ⋅ Área do círculo = 2 ⋅ (p ⋅ r2) ⇒

⇒ Área total = 2 ⋅ 3,14 ⋅ 3² ⇒ Área total = 56,52

Então, a área total mede 56,52 centímetros².

33. A parte verde é formada pela circunferência menor subtraindo-se a área de 4 semicircunferências de diâmetro igual ao raio da circunferência menor. Então, as medidas de: diâmetro da circunferência maior = 4 cm ⇒ r1 = 2 centímetros e também diâmetro da circunferência maior = 4 centímetros ⇒ r1 = 2 centímetros. Assim: área da circunferência maior = π ⋅ r2 = 3,14 ⋅ 22 = 12,56. Agora, encontraremos a área da parte branca: para a medida da área das quatro semicircunferências menores As, então:

A_{s} = 4 \cdot \frac{π \cdot r_{2}^{2}}{2}

= 4 \cdot \frac{3, 14 \cdot 1^{2}}{2} \Rightarrow A_{s} = 4 \cdot 1, 57 = 6, 28

Então, área da parte verde (At) mede 6,28 centímetros quadrados, pois é dada por: At = 12,56 ‒ 6,28 = 6,28.

Página cento e dezesseis

34. Considerando separadamente os quadradinhos onde aparece verde, é possível notar que há:

Ilustração. Quadrado com um quarto de circunferência verde e o restante do quadrado laranja.

• 4 partes como essa. Note que 4 partes como essa formam uma circunferência de raio de medida r = 3 centímetros.

Ilustração. Quadrado com um quarto de circunferência vermelho e o restante do quadrado verde.

• 4 partes como essa. Note que 4 partes como essa são formadas pela área de um quadrado de lado 6 subtraindo-se a área de uma circunferência inscrita de raio 3 centímetros.

Como Área do círculo = p ⋅ r2 ⇒ Área do círculo = = 3,14 ⋅ 32 = 28,26 e também Área do quadrado = ℓ2 ⇒ Área do quadrado = 62 = 36.

Então: Área do círculo = 28, 26 + (36 ‒ 28, 26) ⇒

⇒ Área do círculo = 36

A área mede 36 centímetros quadrados.

35. A área pintada de roxo é igual à medida da área de um hexágono (Ah) inscrito subtraída da medida da área do triângulo inscrito (At). Para a área do hexágono: ℓ = r e

a = \frac{r \sqrt{3}}{2} \Rightarrow p = 6 \cdot ℓ = 6 r \Rightarrow A_{h} = p \cdot a \Rightarrow A_{h} = 6 r \cdot \frac{r \sqrt{3}}{2}

⇒ ⇒

A_{h} = \frac{3 r^{2} \sqrt{3}}{2}

Para a área do triângulo:

ℓ = r \sqrt{3} \Rightarrow a \frac{r \sqrt{3} \cdot \frac{3 r}{2}}{2} \Rightarrow

h = r + a \Rightarrow h = \frac{3 r}{2} \Rightarrow A_{t} = \frac{ℓ \cdot h}{2} \Rightarrow A_{t} = \frac{3 \cdot r^{2} \sqrt{3}}{4}

Assim: Área roxa

= \frac{3 r^{2} \sqrt{3}}{2} ‒ \frac{3 \cdot r^{2 \sqrt{3}}}{4} \Rightarrow

⇒ Área roxa

= \frac{3 r^{2} \sqrt{3}}{4}

Então, a medida da área roxa é

\frac{3 r^{2} \sqrt{3}}{4} u^{2}

36. a)

a_{c} = \frac{360 º}{12}

⇒ ac = 30graus

36. b) Usando a relação cosseno para calcular o apótema (cateto adjacente ao ângulo de 15graus). A hipotenusa tem medida igual à do raio.

cos 15graus

= \frac{a}{10} \Rightarrow 0, 97 = \frac{a}{10} \Rightarrow a = 9, 7

Usando a relação seno para calcular a medida do lado (cateto oposto ao ângulo de 15graus). A hipotenusa tem medida igual ao raio.

s e n 15 ° = \frac{\frac{ℓ}{2}}{10} \Rightarrow 0, 26 = \frac{ℓ}{20} \Rightarrow ℓ = 5, 2

Portanto, o apótema mede 9,7 centímetros e o lado mede 5,2 centímetros.

36. c) C = 2 ⋅ p ⋅ r ⇒ C = 2 ⋅ 3,14 ⋅ 10 ⇒ C = 62,8; 2p = 12 ⋅ ℓ ⇒ 2p =12 ⋅ 5,20 ⇒ 2p = 62,4

Então, a diferença é de 0,4 centímetro, pois: C ‒ 2p = 62,8 ‒ 62, 4 = 0,4

36. d) A = p ⋅ a

p é metade da medida do perímetro; logo, p = 31,2 centímetros.

A = 31,2 ⋅ 9,70 ⇒ A = 302,64

A área mede 302,64 centímetros quadrados.

37. Como a medida Acoroa circular = p (R² ‒ r²) e aproximando p ≃ 3,14.

37. a) p (R2 ‒ r2 ) = p (32 ‒ 22 ) = p (9 ‒ 4) = 5p

Portanto:

Acoroa circular = 15,7 centímetros quadrados

37. b)

\frac{π (5^{2} - 1^{2})}{2} = \frac{π (25 - 1)}{2} = \frac{24 π}{2}

Portanto, a área mede 37,68 centímetros quadrados.

38. Acoroa circular = p (R2 ‒ r2 ) = p (6² ‒ 2²) = p (36 ‒ 4) = 32p

Portanto:

Acoroa circular = 100, 48 centímetros quadrados

41. a) Encontraremos, primeiro, a fração

\frac{1}{x}

que esse arco representa no arco da circunferência:

C_{s e t o r} = \frac{2 π r}{x} \Rightarrow 10 p = \frac{2 π \cdot 15}{x} \Rightarrow x = 3

Logo, o arco, e portanto o ângulo, dêsse setor representa

\frac{1}{3}

da circunferência: ac =

\frac{360 º}{3}

= 120graus

41. b) Sendo Asetor circular a medida procurada:

\frac{π \cdot r^{2}}{A_{s e t o r c i r c u l a r}} = \frac{360 °}{α} \Rightarrow \frac{π \cdot 15^{2}}{A_{s e t o r c i r c u l a r}} = \frac{360 °}{120 °} \Rightarrow

⇒ 3 ⋅ Asetor circular = 225π ⇒ Asetor circular = 75π

Portanto, 75π centímetros².

42. Ao triplicar o raio r de uma circunferência, obtemos 3r. Então, a medida de sua área será:

A3r = π(3r)² ⇒ A3r = 9 ⋅ πr2

Como Ar = πr2, então A3r = 9 ⋅ Ar

Como Cr = 2 ⋅ π ⋅ r, temos: C3r = 2 ⋅ π ⋅ (3r) ⇒ C3r = 3 ⋅ 2πr ⇒ ⇒ C3r = 3 ⋅ Cr

Alternativa c.

43. • Figura 1:

Acoroa circular = π(R2 ‒ r2) ⇒ A = π(52 ‒ 32) = 16 ⋅ π ⇒ A1 ≃ 50,24

• Figura 2: A2 = Acírculo – Atriângulo e considerando r = 3 centímetros e altura h do triângulo como h = 4,85 centímetros, então:

A_{2} = π \cdot 3^{2} ‒ \frac{2 \cdot 4, 82}{2} \Rightarrow A_{2} = 9 π ‒ 4, 82 \Rightarrow A_{2} ≃ 23, 44

• Figura 3:

A_{3} = A_{c í r c u l o} ‒ A_{s e t o r c i r c u l a r}

Assim:

A_{c í r c u l o} = π \cdot 3^{2} = 9 π

⇒

A_{c í r c u l o} = 28, 26 e \frac{π \cdot r^{2}}{A_{s e t o r c i r c u l a r}}

\frac{360 °}{α} \Rightarrow \frac{π \cdot 3^{2}}{A_{s e t o r c i r c u l a r}} = \frac{360 °}{60 °}

⇒

A_{s e t o r c i r c u l a r} = \frac{9 π}{6}

⇒ ⇒

A_{s e t o r c i r c u l a r} = 4, 71

Logo:

A_{3} = 28, 26 ‒ 4, 71 = 23, 55

• Figura 4:

A_{4} = A_{q u a d r a d o} ‒ A_{c í r c u l o}

⇒

A_{4} = 6^{2} ‒ π \cdot 2^{2} \Rightarrow A_{4} = 23, 44

Página cento e dezessete

Então, as medidas são: figura 1: 50,24 centímetros quadrados, figura 2: 23,44 centímetros quadrados; figura 3: 23,55 centímetros quadrados e figura 4: 23,44 centímetros quadrados. As figuras 2 e 4 são equivalentes, pois têm a mesma medida de área.

45. A área que o cavalo não conseguirá alcançar será dada pela área de um quarto de quadrado subtraída da área do setor circular de raio medindo 40 metros e ângulo de medida 90graus. Logo, a medida da área sendo a, então:

A = 50^{2} ‒ \frac{π \cdot 40^{2}}{4}

⇒ A = .2500 ‒ 400p ⇒ A ≃ .2500 ‒ .1256 ⇒ ⇒ A = .1244

Alternativa a.

46. A medida do volume do recipiente cilíndrico é 942 centímetros cúbicos (pois π ⋅ 52 ⋅ 12 ≃ 3,14 ⋅ 25 ⋅ 12 = 942).

Assim, o cone tem medida de volume igual a um terço de 942 centímetros cúbicos; portanto, 314 centímetros cúbicos.

47. A medida do volume do grão é cerca de 0,16 centímetros cúbicos, pois 0,4 ⋅ 0,4 ⋅ 1 = 0,16, enquanto o depósito tem medida de volume .160000 centímetros quadrados, pois 40 ⋅ 40 ⋅ 100 = .160000. Dessa maneira, cabem ..1000000 grãos, pois .160000 : 0,16 = ..1000000. Alternativa d.

48. O triângulo da base é isósceles, pois tem dois lados de mesma medida 5 centímetros. Portanto, a altura do triângulo é cateto de um triângulo retângulo que tem um dos lados congruentes como hipotenusa e metade da base do triângulo isósceles como o outro cateto, então, tem medida 3 centímetros (pois 6 : 2 = 3). Dessa maneira, a medida h de sua altura é 4 centímetros, pois:

h^{2} + 3^{2} = 5^{2} \Rightarrow h = h^{2} + 3^{2} = 5^{2} \Rightarrow h = \sqrt{25 - 9} = 4

Então, o volume dessa peça é 144centímetros cúbicos, pois:

\frac{6 \cdot 4}{2} \cdot 12 = 3 \cdot 4 \cdot 12 = 144

Logo, a menor quantidade de madeira necessária é quando não há sobras, para produzir 10 peças são necessários .1440 centímetros cúbicos (144 ⋅ 10 = .1440).

49. a) Como a fórma do cesto pode ser associada a um cilindro com r = 21 centímetros e h = 45 centímetros, a medida de sua área de superfície pode ser calculada por:

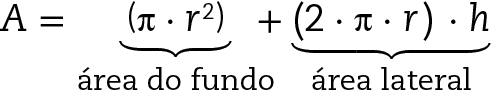
A igual a abre parênteses pi vezes r elevado ao quadrado, fecha parênteses, mais, abre parênteses, 2 vezes pi vezes r, fecha parênteses, vezes h, sendo abre parênteses pi vezes r elevado ao quadrado, fecha parênteses, área do fundo; e abre parênteses, 2 vezes pi vezes r, fecha parênteses, vezes h, área lateral

, então A = πr ⋅(r + 2h) = = 3,14 ⋅ 21 (21 + 2 ⋅ 45) = 65,94 ⋅ 111 = .7319,34

Portanto, a área é aproximadamente .7319 centímetros quadrados.

49. b) O volume será: (π r2) ⋅ h = 3,14 ⋅ 212 ⋅ 45 = 3,14 ⋅ 441 ⋅ 45 = = .62313,3.

Portanto, o volume mede aproximadamente .62313 centímetros cúbicos.

Pense mais um poucoreticências

Página 293

Note que apenas as figuras dos itens c e d podem ser sobrepostas de modo que partes verdes de uma e partes brancas de outra fiquem sobrepostas, pintando assim toda a região interna da circunferência maior. A medida da área verde em c e d são iguais e valem a metade da área da circunferência maior, de raio r = 3. Logo, a medida da área verde é, em centímetro quadrado:

\frac{π \cdot r^{2}}{2} = \frac{π \cdot 3^{2}}{2} = \frac{9 π}{2}

Página 294

As áreas procuradas são formadas por coroas circulares concêntricas. Sendo

A_{n}

a medida da área da coroa, contando a posição n de fora para dentro do alvo, em cada cor:

• Área da parte verde: usando a relação Acoroa círcular = π(R2 ‒ r2) e Acírculo = π ⋅ r2 (para o círculo verde interno), teremos:

A_{1} = π (70^{2} ‒ 60^{2}) \Rightarrow A_{1} = 4 082

A_{2} = π (50^{2} ‒ 40^{2}) \Rightarrow A_{2} = 2 826

A_{3} = π (30^{2} ‒ 20^{2}) \Rightarrow A_{3} = 1 570

A_{4} = 10^{2} π \Rightarrow A_{4} = 314

Então, a área verde total mede .8792 centímetros quadrados (.4082 + + .2826 + .1570 + 314).

• Área da parte amarela:

A_{1} = π (80^{2} ‒ 70^{2}) \Rightarrow A_{1} = 4 710

A_{2} = π (60^{2} ‒ 50^{2}) \Rightarrow A_{2} = 3 454

A_{3} = π (40^{2} ‒ 30^{2}) \Rightarrow A_{3} = 2 198

A_{4} = π (20^{2} ‒ 10^{2}) \Rightarrow A_{4} = 942

Então, a área amarela total mede .11304 centímetros quadrados (.4710 + .3454 + .2198 + 942).

Para saber mais

Página 292

Resposta pessoal a depender do número n de lados escolhidos pelos estudantes. Nas duas atividades espera-se que os estudantes obtenham polígonos congruentes.

Trabalhando a informação

Páginas 296 e 297

b) Basta fazer: 19,7 : 18, 4 = 1,07 = 1 + 0,07 = 100% + 7% Então, o emprego menos qualificado era 7 por cento maior que o emprego mais qualificado

Exercícios complementares

1. A medida do raio da circunferência é 8 centímetros, pois

ℓ = r \sqrt{2} =

8 \sqrt[]{2} \Rightarrow r = 8

. Então, o apótema mede

4 \sqrt{2}

centímetros pois: a =

\frac{r \sqrt{2}}{2} \Rightarrow a = \frac{8 \sqrt{2}}{2} \Rightarrow a = 4 \sqrt{2}

2. No hexágono regular inscrito na circunferência, temos ℓ = r. Como o perímetro 2p = 42 métros, então ℓ = 7 métros, pois 2p = 6 ⋅ ℓ ⇒ 42 = 6ℓ ⇒ ℓ = 7. Logo, r = 7 centímetros.

No quadrado inscrito,

ℓ = r \sqrt{2}

; assim:

ℓ = r \sqrt{2} ⇒ ℓ = 7 \sqrt{2}

2p = 4 ⋅ ℓ ⇒

2 p = 28 \sqrt{2}

A medida do perímetro é

28 \sqrt{2}

métros.

3. bê á = á éfe e bê dê = dê éfe pois os arcos são congruentes. Se r =

7 \sqrt{2}

, sabendo que os lados de um hexágono regular inscrito na circunferência mede

ℓ = r = 7 \sqrt{2}

centímetros, então

B A = A F = 7 \sqrt{2}

centímetros.

Para descobrir DF, podemos traçar um triângulo dê ê éfe, isósceles com ângulo tal que m(

D \hat{E} F

) = 120graus (ângulos internos de um hexágono regular).

Usando a relação de seno de 60graus, que é metade do ângulo

D \hat{E} F

, temos:

s e n 60 º = \frac{\frac{m (D F)}{2}}{m (E F)} \Rightarrow \frac{\sqrt{3}}{2} = \frac{\frac{m (D F)}{2}}{7 \sqrt{2}} \Rightarrow m (D F) = 7 \sqrt{2} \cdot \sqrt{3}

Página cento e dezoito

Perímetro de ABDF:

2 p = 2 \cdot 7 \sqrt{2} + 2 \cdot 7 \sqrt{2} \sqrt{3} \Rightarrow 2 p = 14 \sqrt{2} (1 + \sqrt{3})

Então, a medida do perímetro é

14 \sqrt{2} (1 + \sqrt{3})

centímetros.

4. Como, em um triângulo equilátero inscrito,

ℓ = r \sqrt{3}

, e bê cê =

4 \sqrt{3}

, então r = 4. Como A bê é lado de um hexágono regular, onde ℓ = r, conclui-se que ℓ = 4, ou seja

A B = 4

. Como á dê é lado de um quadrado inscrito, onde ℓ =

r \sqrt{2}

, conclui-se que

ℓ = 4 \sqrt{2}

, ou seja:

A D = 4 \sqrt{2}

5. Note que DB = á cê = medida do raio do círculo. Esta medida é dada por A bê + A Ê, como A bê = DC, então: DB = DC + A Ê ⇒ DB = 8 + 2 = 10

Portanto, 10 centímetros.

6. a) Como CB =

4 \sqrt{2}

e medida do

(C \hat{O} B)

= 90graus, podemos descobrir ó bê = ó cê usando a relação dos senos, em que o cateto oposto é a metade da medida CB e a hipotenusa é o raio: sen 45graus =

\frac{2 \sqrt{2}}{r} \Rightarrow \frac{\sqrt{2}}{2} = \frac{2 \sqrt{2}}{r} \Rightarrow r = 4

Portanto, 4 centímetros.

6. b) Como medida do

(B \hat{O} A)

= 60graus e á ó = ó bê = r, então o triângulo é equilátero. Logo: A bê = á ó = ó bê = r = 4

Portanto, 4 centímetros.

6. c) Usando a relação de seno de 60graus, que é metade do ângulo de 120graus:

sen 60graus

= \frac{\frac{D C}{2}}{r} \Rightarrow \frac{\sqrt{3}}{2} = \frac{\frac{D C}{2}}{4} \Rightarrow D C = 4 \sqrt{3}

Então, a medida é

4 \sqrt{3}

centímetros.

8. A medida do lado de um quadrado inscrito é dada por

ℓ = r \sqrt{2}

, e como r =

\sqrt{2}

, então

ℓ = \sqrt{2} \cdot \sqrt{2} = 2

A medida do perímetro do quadrado inscrito é 8 centímetros por que é dada por 2p1 = 4ℓ ⇒ 2p = 8.

A medida do lado do quadrado circunscrito é dada por ℓ = ême(diâmetro do círculo), então

ℓ = 2 \sqrt{2}

A medida do perímetro do quadrado circunscrito é dada por 2p2 = 4ℓ ⇒ 2p =

8 \sqrt{2}

. A diferença entre as medidas dos perímetros é

8 (\sqrt{2} - 1) cm

, pois é dada por:

8 \sqrt{2} - 8 = 8 (\sqrt{2} - 1)

9. O lado do hexágono mede 12 centímetros.

Podemos encontrar a medida do raio do círculo fazendo:

r = \frac{\sqrt{3}}{2} ℓ \Rightarrow r = \frac{\sqrt{3}}{2} \cdot 12 \Rightarrow r = 6 \sqrt{3}

A medida da área do círculo é 108π centímetros quadrados, pois é dada por: Ac = π ⋅ r2 = π ⋅

{(6 \sqrt{3})}^{2}

⇒ Ac = 108π

10. a) Podemos estimar a medida da área azul escura da seguinte maneira:

A ≃ 4 \cdot \frac{π \cdot r^{2}}{2}

, com r ≃ 1 centímetro, então A ≃ 6 centímetros quadrados, pois:

A = 4 \cdot \frac{π \cdot 1^{2}}{2} \Rightarrow A ≃ 6

10. b) Como = π ⋅ r2 ⇒ 6 = r2π ⇒ r2 ≃ 1,91 ⇒ r ≃ 1,38

Portanto, o círculo terá raio medindo 1,38 centímetro.

11. Em vermelho, temos

\frac{3}{6}

de uma coroa circular com raios tais que R = 2 e r = 1; e também

\frac{3}{6}

de um círculo de raio medindo r = 1.

Como, para as coroas circulares, temos:

Acc = π(R2 ‒ r2 ) = π(22 ‒ 12) ⇒ m(Acc) = 3π

Então:

\frac{3}{6}

⋅ 3π = 1,5π ≃ 4,71

A medida da área do círculo é: Ac = π ⋅ r2 = π ⋅ 12 ⇒ Ac = π

Então:

\frac{3}{6}

⋅ π ≃ 1,57.

Adicionando as medidas das áreas: At = 4,71 + 1,57 = 6,28

A medida total da área procurada é de aproximadamente 6,28 centímetros quadrados.

12. a) Na “largura” da folha que mede 18 centímetros conseguimos desenhar 3 círculos de diâmetro medindo 6 centímetros. No comprimento da folha que mede 12 centímetros conseguiremos desenhar 2 círculos de diâmetro medindo 6 centímetros. Portanto, 6 círculos: 3 ⋅ 2 = 6.

12. b) A medida da área do papel é 216 centímetros quadrados, pois 12 ⋅ 18 = = 216. A medida de área dos círculos é 169,56 centímetros quadrados, pois 6 ⋅ (π ⋅ 33) ≃ 6 ⋅ 3,14 ⋅ 9 = 169,56.

A medida de área que sobra depois de os círculos serem recortados é 46,44 centímetros quadrados, pois 216 ‒ 169,56 = 46,44.

13. A medida da área da placa é 80 centímetros quadrados, pois:

2 \sqrt{10}

= (2 ⋅ 4) ⋅ 10 = = 80. Os círculos, por serem tangentes aos lados da placa e tangentes entre si, têm raio medindo r =

\sqrt{10}

. Então, a área circular recortada é cêrca de 63 centímetros quadrados, pois:

2 \cdot (π \cdot {(\sqrt{10})}^{2})

≃ 2 ⋅ 3,14 ⋅ 10 = 62,8

Então, a área desperdiçada tem medida aproximada de 17 centímetros quadrados (80 ‒ 63 = 17).

14. a) Como a circunferência tangencia o lado da caixa quadrada, o diâmetro da circunferência tem a mesma medida que o lado da caixa, ou seja 3,6 centímetros. Logo, o raio mede 1,8 centímetro (3,6 : 2 = 1,8).

14. b) V = 3,62 ⋅ 20 = 12,96 ⋅ 20 Então, V = 259,2 centímetros quadrados.

14. c) V = π ⋅ r2 ⋅ h ≃ 3,14 ⋅ 1,82 ⋅ 20 ≃ 3,14 ⋅ 3,24 ⋅ 20 Então, V ≃ 203,5 centímetros cúbicos.

15. Em um hexágono regular inscrito, temos ℓ = r. Como r = 5 centímetros, então ℓ = 5 centímetros. Usando a fórmula para calcular a medida do apótema do hexágono inscrito:

a = \frac{r \sqrt{3}}{2}

⇒ ⇒

a = \frac{5 \sqrt{3}}{2}

O lado mede 5 centímetros e o apótema mede

\frac{5 \sqrt{3}}{2}

centímetros.

Verificando

1. Em um quadrado inscrito,

ℓ = r \sqrt{2}

, então se r = 12 centímetros,

ℓ = 12 \sqrt{2}

centímetros. A medida da área do quadrado será:

A = ℓ^{2} = {(12 \sqrt{2})}^{2} \Rightarrow A = 288

Alternativa b.

2. O comprimento da circunferência é 157 métros, então o raio mede 25 centímetros, pois: C = 2 ⋅ π ⋅ r ⇒ 157 = 2 ⋅ 3,14 ⋅ r ⇒ r = 25

Em um triângulo equilátero inscrito, temos

a = \frac{r}{2}

, como o raio mede r = 25 métros, então:

a = \frac{25}{2} \Rightarrow a = 12, 5

Alternativa c.

Página cento e dezenove

3. Se a medida de área do círculo é 113,04 métros quadrados, então:

A_{c í r c u l o} = π \cdot r^{2} = 113, 5 \Rightarrow r^{2} = \frac{113, 5}{3, 14} \Rightarrow r^{2} ≃ 36 \Rightarrow r ≃ 6

Alternativa a.

4. O lado de um hexágono regular é dado pela relação: ℓ = r; já o apótema de um triângulo regular é dado por:

a = \frac{r}{2}

Logo, a diferença entre a medida do lado do hexágono e a medida do apótema de um triângulo, ambos na mesma circunferência, em que o raio é o mesmo, é dada por:

r - \frac{r}{2} = \frac{2 r}{2} - \frac{r}{2} = \frac{r}{2}

Alternativa b.

5. Acoroa circular = π (R2 ‒ r2) = π(52 ‒ 32) = π(25 ‒ 9)

Então: Acoroa circular = 16π ≃ 16 ⋅ 3,14 = 50,24

Alternativa c.

6. A medida da área de qualquer polígono regular é dada por a = p ⋅ a. E a relação entre as medidas do apótema e do lado de um hexágono regular é dada por

a = \frac{r \sqrt{3}}{2}

e também ℓ = r. Assim, o semiperímetro necessário para a fórmula da área será dado por: 2p = 6ℓ ⇒ 2p = 6r ⇒ p = 3r

Substituindo, obtemos:

A = p \cdot a = 3 r \cdot \frac{r \sqrt{3}}{2} = \frac{3 r^{2} \sqrt{3}}{2}

Alternativa a.

7. Primeiramente, obtemos a medida da área da base. Para isso, precisamos da medida do lado desse quadrado inscrito em uma circunferência. Sabemos que

ℓ = r \sqrt{2}

, como r = 4 centímetros, então

ℓ = 4 \sqrt{2}

centímetros. Assim:

V = \frac{1}{3} \cdot A_{b a s e} \cdot h

Sendo h = medida da altura, que nesse caso vale 9 métros, temos:

V = \frac{1}{3} \cdot {(4 \sqrt{2})}^{2} \cdot 9 \Rightarrow V = 96

Alternativa d.

V = \frac{1}{3}

⋅ área da base ⋅ altura

A medida da base é 2302 = .52900 e a medida da altura é 146.

Assim:

V = \frac{1}{3}

⋅ área da base ⋅ altura ⇒

⇒

V = \frac{1}{3}

⋅ .52900 ⋅ 146 ⇒ V ≃ ..2574466,6

Logo, o volume é de aproximadamente 2,5 milhões de metros cúbicos.

Alternativa d.

9. A medida do volume do cone é dada por: V =

\frac{1}{3}

⋅ π ⋅ r2 ⋅ h

Com r = 3 centímetros e h = 10 centímetros.

Então,

V ≃ \frac{1}{3} \cdot 3, 14 \cdot 3^{2} \cdot 10 ≃ \frac{1}{3} \cdot 282, 6 \Rightarrow V ≃ 94, 2

Alternativa b.

Sugestão de avaliação diagnóstica

Atividade 1

(ê éfe zero oito ême ah zero um) Efetuar cálculos com potências de expoentes inteiros e aplicar esse conhecimento na representação de números em notação científica.

Devido ao movimento dos planetas, a distância entre eles está sempre variando. A menor distância entre a Terra e Marte é de 5,4 ⋅ 1010 métros. Sabendo que a luz percorre cerca de 3 ⋅ 108 metros a cada segundo, quanto tempo ela leva para percorrer a distância entre a Terra e Marte?

a) 180 segundos.

b) 18 minutos.

c) 180 minutos.

d) .1800 segundos.

Resposta: Alternativa a.

Resolução e comentários

Esta atividade avalia se o estudante compreende a notação científica e consegue operar com potências de expoentes inteiros. Para resolver o problema eles precisam determinar quantas vezes a medida da distância percorrida pela luz em 1 segundo (3 ⋅ 108 metros) cabe na medida da distância entre os dois planetas (5,4 ⋅1010 metros), ou seja, devem efetuar a divisão:

\frac{5, 4 \cdot 10^{10}}{3 \cdot 10^{8}} = \frac{5, 4}{3} \cdot \frac{10^{10}}{10^{8}} = 1, 8 \cdot 10^{2} = 180

Um erro comum nesse tipo de cálculo é tentar dividir os expoentes.

A vantagem do uso da notação científica para resolver a atividade pode ser discutida com os estudantes, pois, caso eles preferissem transformar os números em sua fórma convencional e realizar a divisão, é fácil perceber que a grande quantidade de algarismos pode levar a erros de contagem.

\frac{54 000 000 000}{300 000 000} = 180

Atividade 2

(ê éfe zero oito ême ah zero dois) Resolver e elaborar problemas usando a relação entre potenciação e radiciação, para representar uma raiz como potência de expoente fracionário.

A Alometria é uma área da Biologia que estuda o crescimento de partes dos seres vivos. As relações alométricas, em geral, envolvem potências de expoentes fracionários. Por exemplo, considere que a medida da área das asas, em metro quadrado, de determinada ave é dada por:

Aasas = 0,1 ⋅

m^{{\frac{2}{3}}^{}}

Nessa relação, m é a medida da massa da ave.

Então, se uma ave tem massa de medida 8 quilogramas, qual é a medida da área de suas asas?

Resposta: A área das asas mede 0,4 métros quadrados.

Resolução e comentários

Na resolução desta atividade, os estudantes devem compreender a relação entre as potências de expoentes fracionários e as raízes, assim como operar com os valores obtidos. Ao substituir a medida da massa na expressão dada, conclui-se que a área das asas da ave mede 0,4 métros quadrados.

Página cento e vinte

A_{a s a s} = 0, 1 \cdot 8^{{\frac{2}{3}}^{}}

A_{a s a s} = 0, 1 \cdot \sqrt[3]{8^{2}}

Aasas = 0,1 ⋅ 4

Aasas = 0,4

Ao realizar o cálculo da raiz cúbica, espera-se que os estudantes reconheçam que a ordem em que o cálculo é efetuado não importa, pois, se calcularem primeiro a raiz cúbica de 8, obtendo 2, e elevarem o resultado ao quadrado, obterão 4; se realizarem primeiro a potenciação 8², eles devem obter

\sqrt[3]{64}

, que também resulta em 4.

Atividade 3

(ê éfe zero oito ême ah zero três) Resolver e elaborar problemas de contagem cuja resolução envolva a aplicação do princípio multiplicativo.

O estacionamento de uma loja dispõe de 4 vagas para os clientes estacionarem seus carros. Se dois clientes chegarem sucessivamente e escolherem uma vaga cada um, de quantos modos diferentes eles podem ocupar as vagas do estacionamento?

Ilustração. Quatro vagas na parte inferior e um carro vermelho acima na horizontal.

Resposta: 12 modos diferentes.

Resolução e comentários

O problema apresentado envolve o uso do princípio multiplicativo da contagem. Nesse caso, espera-se que os estudantes reconheçam que o primeiro cliente tem 4 opções de escolha para a vaga que quer ocupar e que, qualquer que seja a vaga ocupada pelo primeiro cliente, para o próximo cliente existirão apenas 3 vagas disponíveis, de modo que o total de possibilidades de escolha das duas vagas é igual a 12 (4 ⋅ 3 = 12). Um erro comum que pode ser cometido pelos estudantes é aplicar um raciocínio aditivo, pois podem ter dificuldades em aplicar o princípio multiplicativo. Para auxiliá-los, ao realizar a correção da atividade, mostre todas as combinações possíveis, nesse caso, apenas 12.

Ilustração. Doze combinações de 4 vagas com dois carros. 1ª combinação: carro vermelho na primeira vaga e carro cinza na segunda vaga. 2ª combinação: carro vermelho na primeira vaga e carro cinza na terceira vaga. 3ª combinação: carro vermelho na primeira vaga e carro cinza na quarta vaga. 4ª combinação: carro vermelho na segunda vaga e carro cinza na terceira vaga. 5ª combinação: carro vermelho na segunda vaga e carro cinza na quarta vaga. 6ª combinação: carro vermelho na terceira vaga e carro cinza na quarta vaga. 7ª combinação: carro vermelho na segunda vaga e carro cinza na primeira vaga. 8ª combinação: carro vermelho na terceira vaga e carro cinza na primeira vaga. 9ª combinação: carro vermelho na quarta vaga e carro cinza na primeira vaga. 10ª combinação: carro vermelho na terceira vaga e carro cinza na segunda vaga. 11ª combinação: carro vermelho na quarta vaga e carro cinza na segunda vaga. 12ª combinação: carro vermelho na quarta vaga e carro cinza na terceira vaga.

Na primeira fileira horizontal, o carro vermelho ocupa a primeira vaga à esquerda, deixando 3 opções para o carro branco, ou seja, para cada opção para o carro vermelho (4 possibilidades ao todo), há 3 opções disponíveis para o carro branco. Assim, a necessidade de aplicação do raciocínio multiplicativo é evidente na situação proposta.

Atividade 4

(ê éfe zero oito ême ah zero quatro) Resolver e elaborar problemas, envolvendo cálculo de porcentagens, incluindo o uso de tecnologias digitais.

Cláudia realizou o seguinte cálculo em sua calculadora:

200 ∶ 250 = 0,8

Com base nesse cálculo, complete corretamente o enunciado do problema a seguir.

Laura foi a uma loja comprar um forno elétrico cujo preço era R$ 250,00duzentos e cinquenta reais, mas como nesse dia a loja fez uma promoção, o preço baixou para R$ 200,00duzentos reais. A fim de calcular o valor do desconto, Laura dividiu _____ por ____ obtendo ____. Isso significa que o preço atual corresponde a ____% do valor original, de modo que o desconto foi de ___%.

Resposta: 200; 250; 0,8 ; 80; 20.

Resolução e comentários

Quando os estudantes se deparam com esse tipo de problema, eles precisam mobilizar os conhecimentos sobre o significado das operações efetuadas dentro de um contexto. Com isso, esta atividade possibilita avaliar tanto a compreensão do processo de cálculo de porcentagem, como também a habilidade de interpretar e relacionar as informações entre si. O cálculo 200 : 250 representa a razão entre o valor atual e o valor original, ou seja, a fração do preço pago por Laura, 80% do preço original. Portanto, o desconto oferecido equivale a 20% (100% ‒ 80% = 20%).

Atividade 5

(ê éfe zero oito ême ah zero cinco) Reconhecer e utilizar procedimentos para a obtenção de uma fração geratriz para uma dízima periódica.

Gustavo fez uma divisão na calculadora e o resultado mostrado no visor foi 1,878787reticências

Obtenha um possível dividendo e um possível divisor digitados por Gustavo na calculadora.

Resposta: Um possível dividendo é 186 e um possível divisor é 99.

Resolução e comentários

Para responder a esta atividade é necessário compreender que obter os termos da divisão que resultaram em 1,878787reticências equivale a obter a fração geratriz de uma dízima periódica e aplicar o procedimento estudado para resolver o problema. Um modo de resolver o problema é identificar a dízima periódica como x e, depois, multiplicar ambos os lados da igualdade por 100, para, em seguida, subtrair membro a membro os valores obtidos.

x = 1,878787reticências

100x = 187,878787reticências

Subtraindo membro a membro, obtemos:

99x = 186

x = \frac{186}{99}

Ao discutir a resolução da atividade com os estudantes é importante verificar se eles compreendem que a potência de dez pela qual a igualdade inicial é multiplicada depende do número de casas decimais que a dízima deve ser deslocada de modo a repetir os mesmos algarismos na mesma sequência. No caso da dízima 1,878787reticências, se ela for multiplicada por 10, obtemos 18,787878reticências; assim, a subtração do valor original não tornaria a parte decimal nula. Portanto, ao multiplicar pela potência de 10 seguinte (10² = 100), a dízima torna-se 187,878787reticências

Página cento e vinte e um

Atividade 6

(ê éfe zero oito ême ah zero seis) Resolver e elaborar problemas que envolvam cálculo do valor numérico de expressões algébricas, utilizando as propriedades das operações.

Considere uma sequência numérica cuja lei de formação é dada pela expressão 3x ‒ 8, em que x representa a posição de cada um dos termos. Por exemplo, x vale 1 para o primeiro termo, x vale 2 para o segundo termo, e assim por diante. Calcule a diferença entre um termo qualquer e seu antecessor nessa sequência numérica.

Resposta: A diferença é 3.

Resolução e comentários

Para responder a esta atividade, os estudantes devem calcular o valor numérico da expressão algébrica 3x ‒ 8 para dois valores consecutivos de x e, depois, obter a diferença entre eles. É provável que escolham dois valores consecutivos de x para os quais o valor 3x ‒ 8 seja positivo.

Por exemplo, para x = 3, temos: 3 ⋅ 3 ‒ 8 = 1

Para x = 4, temos: 3 ⋅ 4 ‒ 8 = 4

Portanto, a diferença é igual a 3, pois 4 ‒ 1 = 3.

É possível que, durante a correção da atividade, os estudantes questionem o motivo pelo qual a diferença é sempre igual a 3, independente da escolha dos valores para x. Um modo de justificar o resultado é chamar a atenção para o fato de que ‒8 é um valor constante, de modo que a variação de um termo para outro consecutivo provém da multiplicação de x por 3; como a diferença entre os valores escolhidos para x é 1 unidade, ao ser multiplicada por 3, essa diferença resulta em 3 ⋅ 1 = 3.

Atividade 7

(ê éfe zero oito ême ah zero sete) Associar uma equação linear de 1º grau com duas incógnitas a uma reta no plano cartesiano.

Complete o quadro a seguir com o valor de y associado a cada valor de x, de acordo com a expressão y = 2x ‒ 3. Em seguida, localize os pontos (x, y) no plano cartesiano.

x	y = 2x − 3
−1
0
1,5
4

Resposta:

x	y = 2x − 3
−1	y = 2 ⋅ (−1) − 3 = − 5
0	y = 2 ⋅ (0) − 3 = − 3
1,5	y = 2 ⋅ (1,5) − 3 = 0
4	y = 2 ⋅ (4) − 3 = 5

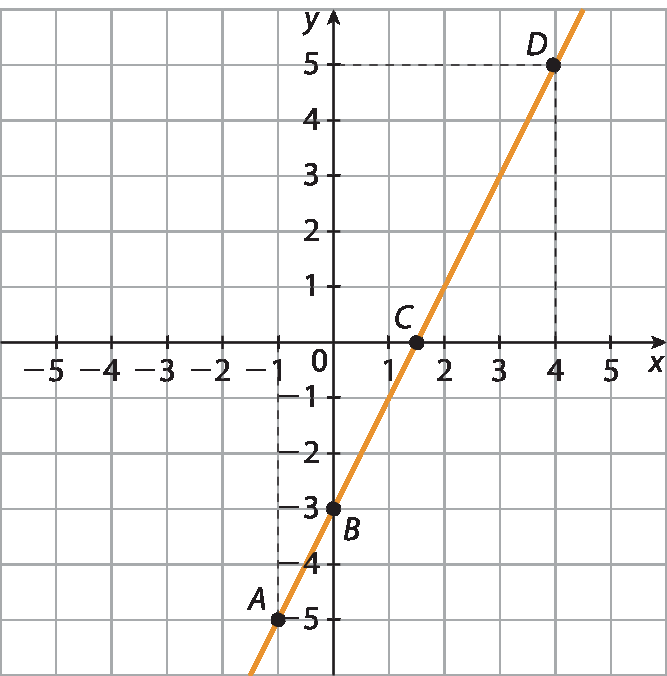
Ilustração. Plano cartesiano em malha quadriculada. Eixo x com escala de menos 5 a 5, e eixo y com escala de menos 5 a 5. Reta que passa pelos pontos A(menos 1, menos 5), B (0, menos 3), C(1,5, 0) e D(4, 5)

Resolução e comentários

O objetivo desta atividade é verificar se os estudantes conseguem calcular o valor numérico de uma expressão algébrica que depende de uma incógnita, obtendo, assim, os pares (x, y) no plano cartesiano. É esperado que os estudantes sejam capazes de verificar os resultados obtidos pela observação dos pontos do gráfico, os quais devem estar alinhados. A localização dos pontos (0, ‒3) e (1,5; 0), correspondentes à intersecção do gráfico com os eixos y e x, respectivamente, podem trazer maior dificuldade para alguns estudantes. Sugira que eles considerem as coordenadas x e y como deslocamentos sequenciais a partir da origem (0, 0). Por exemplo, para localizar o ponto (0, ‒3) desloca-se “0 unidade” ao longo do eixo x, ou seja, não há deslocamento; em seguida, desloca-se 3 unidades para baixo, ao longo do eixo y. No caso do ponto (1,5; 0), desloca-se, a partir da origem, 1,5 unidade para a direita; depois, “0 unidade” ao longo do eixo y, ou seja, não há deslocamento vertical. A vantagem de pensar nas coordenadas como deslocamentos é que, por não haver intersecção de linhas a partir das coordenadas do ponto, a ocorrência de erros torna-se menos provável.

Atividade 8

(ê éfe zero oito ême ah zero oito) Resolver e elaborar problemas relacionados ao seu contexto próximo, que possam ser representados por sistemas de equações de 1º grau com duas incógnitas e interpretá-los, utilizando, inclusive, o plano cartesiano como recurso.

Em um jogo de basquete uma equipe fez um total de 47 pontos entre arremessos de 2 pontos e de 3 pontos, em um total de 20 arremessos. Quantos arremessos de 2 pontos e quantos de 3 pontos a equipe conseguiu?

Resposta: 13 arremessos de 2 pontos e 7 arremessos de 3 pontos.

Resolução e comentários

A resolução de sistemas de duas equações com duas incógnitas traz algumas dificuldades para os estudantes, como a interpretação e a tradução dos dados do problema para a linguagem algébrica e o uso de um método de resolução que envolve a manipulação de expressões algébricas. É possível que alguns estudantes abordem o problema por meio de quadros ou outro mecanismo que possibilite controlar a variação conjunta das respostas de acordo com as tentativas realizadas. Por exemplo, eles podem raciocinar que como os arremessos de 2 pontos resultam sempre em um total par, a quantidade de arremessos de 3 pontos tem de ser uma quantidade ímpar para que seja possível chegar a 47 pontos. Além disso, é necessário controlar a quantidade de arremessos, que deve ser igual a 20. A partir daí, eles podem fazer tentativas, como mostra o quadro a seguir.

Página cento e vinte e dois

Número de arremessos de 3 pontos	Número de arremessos de 2 pontos	Total de pontos
1	19	1 ⋅ 3 + 19 ⋅ 2 = 41
3	17	3 ⋅ 3 + 17 ⋅ 2 = 43
5	15	5 ⋅ 3 + 15 ⋅ 2 = 45

A cada acréscimo de duas unidades na quantidade de arremessos de 3 pontos, os pontos obtidos aumentam duas unidades; assim, para chegar a 47 pontos deve-se aumentar 2 pontos, chegando ao valor esperado. Portanto, foram 7 arremessos de 3 pontos e 13 arremessos de 2 pontos. Entretanto, é mais provável que a maioria dos estudantes utilize a tradução do problema para equações e, depois, aplique um dos métodos estudados (método da adição, método da substituição etc). Para isso, eles podem nomear a quantidade de arremessos de 2 pontos de x e os arremessos de 3 pontos de y; assim, como o total de arremessos é igual a 20, conclui-se que x + y = 20. Em seguida, a pontuação obtida em arremessos de 2 pontos é igual ao número dêsses arremessos que foram convertidos multiplicado por 2, ou seja, 2x. Raciocínio similar possibilita concluir que o número de pontos obtidos com arremessos de 3 pontos é igual a 3y e, então, o total de pontos é igual à soma dêsses valores: 2x + 3y = 47. Resolvendo o sistema de equações pelo método da substituição, temos:

y = 20 ‒ x ⇒ 2x + 3(20 ‒ x) = 47 ⇒ 2x + 60 ‒ 3x = 47 ⇒ x = 13

Portanto: y = 7

Atividade 9

(ê éfe zero oito ême ah zero nove) Resolver e elaborar, com e sem uso de tecnologias, problemas que possam ser representados por equações polinomiais de 2º grau do tipo ax² = b.

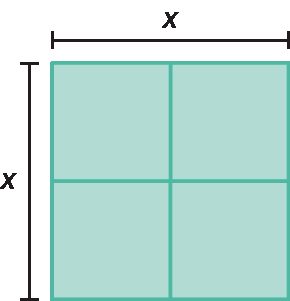
Quantos metros mede o lado de um terreno de 196 métros quadrados de área formado por 4 quadrados menores congruentes, como mostra a figura?

Ilustração. Quadrado com lado de medida x dividido em quatro partes iguais, cada parte tem a forma de um quadrado.

Resposta: 14 metros.

Resolução e comentários

Esta atividade avalia a habilidade dos estudantes de traduzir um problema envolvendo a área de um quadrado em uma equação de 2º grau incompleta, resolvê-la e selecionar a resposta que se adapta ao contexto do problema. Um modo de resolver o problema é considerar que a medida da área de cada um dos quadrados é dada por x². Como eles são em quatro, a medida da área total é dada por 4x². Igualando a expressão para a medida da área total do terreno ao valor dado no enunciado, temos: 4x² = 196

Para resolver a equação, pode-se aplicar o princípio multiplicativo das igualdades e multiplicar os dois membros da equação por

\frac{1}{4}

, ou seja:

\frac{1}{4} \cdot 4 x^{2} = 196 \cdot \frac{1}{4} \Rightarrow x^{2} = 49 \Rightarrow x = \pm 7

O problema envolve a medida da área de um terreno; portanto, a solução x = ‒ 7 é desconsiderada. Como o lado do terreno mede 2x, a resposta é 14 metros.

Outra possibilidade é que os estudantes considerem a medida 2x para o lado do terreno e façam (2x)² = 196, obtendo 4x² = 196, como na estratégia anterior.

Atividade 10

(ê éfe zero oito ême ah um zero) Identificar a regularidade de uma sequência numérica ou figural não recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números ou as figuras seguintes.

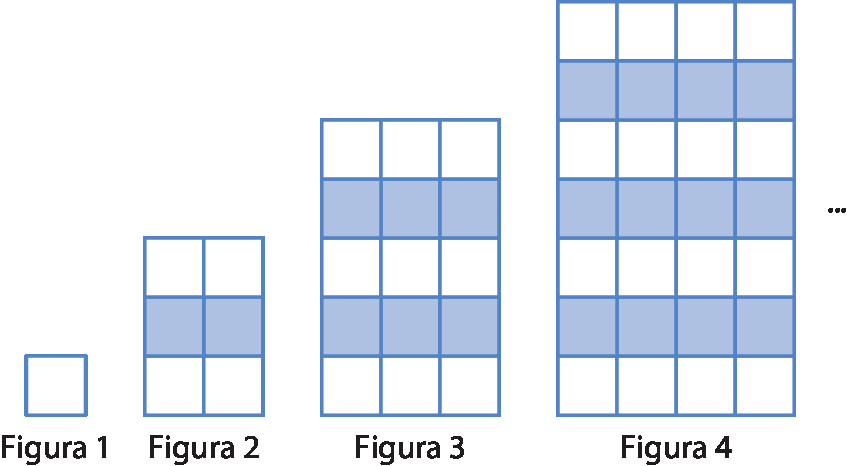
Obtenha o número de quadradinhos azuis da 20ª figura da sequência ilustrada a seguir.

Ilustração. figura 1. Quadrado branco. Figura 2. Quadriculado de 2 colunas por 3 linhas, sendo que os quadradinhos da segunda linha são azuis. Figura 3. Cinco fileiras de 3 quadrados cada intercaladas em branco e azul. Figura 4. Seis fileiras de 4 quadrados cada intercaladas em branco e azul.

Resposta: 380 quadradinhos azuis.

Resolução e comentários

Para responder a esta atividade, os estudantes precisam reconhecer a regularidade que envolve o número de fileiras com quadradinhos azuis em cada figura e, também, a quantidade dêsses quadradinhos em cada uma dessas fileiras. É possível que eles organizem as informações de um modo similar ao mostrado no quadro a seguir.

Número da figura	Número de fileiras de quadradinhos azuis	Número de quadradinhos azuis em cada fileira	Total de quadradinhos azuis
2	1	2	1 · 2 = 2
3	2	3	2 · 3 = 6
4	3	4	3 · 4 = 6

Com base nos dados organizados dessa ou de outra fórma similar, os estudantes podem reconhecer que para uma figura de número n há (n ‒ 1) fileiras com n quadradinhos azuis em cada uma. Assim, na 20ª figura, haverá 380 quadradinhos azuis (19 ⋅ 20 = 380).

Atividade 11

(ê éfe zero oito ême ah um um) Identificar a regularidade de uma sequência numérica recursiva e construir um algoritmo por meio de um fluxograma que permita indicar os números seguintes.

As figuras a seguir foram construídas desenhando-se segmentos de reta de acordo com uma regularidade. Indique a alternativa que representa a regularidade que possibilita obter um termo da sequência recursiva a partir do segundo termo.

Página cento e vinte e três

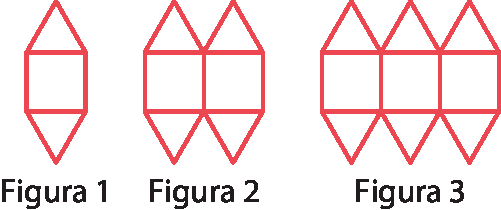
Ilustração. Figura 1. Quadrado com um triângulo equilátero cuja base é o lado de cima do quadrado e o vértice oposto à base está para cima e um triângulo equilátero cuja base é o lado debaixo do quadrado, e o vértice oposto a base está para baixo. Figura 2: É a figura 1 reproduzida duas vezes, uma ao lado da outra, com um lado do quadrado em comum. Figura 3. É a figura 1 reproduzida três vezes, uma tangente a outra pelo lado do quadrado.

a) Multiplicar por 2 o termo anterior.

b) Adicionar 7 unidades ao termo anterior.

c) Multiplicar por 7 o termo anterior e, depois, subtrair 1.

d) Elevar ao quadrado o termo anterior e subtrair 1.

Resposta: Alternativa b.

Resolução e comentários

Espera-se que os estudantes reconheçam que , ao construir cada nova figura, apenas 7 novos segmentos são acrescentados. Apesar da sequência ser expressa por meio de recursividade, também seria possível obter uma lei de formação não recursiva de seus termos.

Número da figura	Número de triângulos	Número de segmentos verticais	Total de segmentos
1	2	2	(2 ⋅ 3) + 2 = 8
2	4	3	(4 ⋅ 3) + 3 = 15
3	6	4	(6 ⋅ 3) + 4 = 22
n	2n	n + 1	(2n ⋅ 3) + (n + 1) = 7n + 1

Portanto, a lei de formação para a enésima figura é dada por 7n + 1.

Atividade 12

(ê éfe zero oito ême ah um dois) Identificar a natureza da variação de duas grandezas, diretamente, inversamente proporcionais ou não proporcionais, expressando a relação existente por meio de sentença algébrica e representá-la no plano cartesiano.

Um automóvel gastou 35 litros de combustível para fazer uma viagem de 280 quilômetros. Considerando o mesmo consumo de combustível, quantos quilômetros ele percorrerá dispondo de 28 litros?

Resposta: 224 quilômetros

Resolução e comentários

Para resolver esta atividade, os estudantes precisam compreender que a relação entre as duas grandezas é de proporcionalidade direta, pois, ao diminuir a quantidade de combustível, a distância percorrida pelo veículo diminuirá de modo proporcional. Assim, a medida da distância (d) está relacionada à medida do volume de combustível (V) por um fator constante k, tal que:

d = k ⋅ V

Substituindo os valores de d por 280 e o de V por 35, obtém-se:

k \cdot 35 = 280 \Rightarrow k = \frac{280}{35} = 8

Assim, podemos substituir a constante k por seu valor numérico 8.

d = 8 ⋅ V

Observe que o valor obtido para a constante k corresponde à quantidade de quilômetros percorridos por litro de combustível, denominado coeficiente de proporcionalidade, pois estabelece a relação entre as duas grandezas. Assim, para determinar a distância percorrida com 28 litros de combustível, basta substituir V por seu valor numérico 28.

d = 8 ⋅ 28 = 224

Portanto, o veículo percorrerá 224 quilômetros.

Durante a correção da atividade com os estudantes, enfatize a importância de compreender o significado da relação observada entre as grandezas nessa situação. O uso de métodos práticos, como a regra de três, tende a tornar a resolução mecanizada e desprovida de significado, fazendo com que, por vezes, um erro cometido não seja percebido, pois a compreensão da situação foi prejudicada pela execução de procedimentos de cálculo sem o acompanhamento da necessária reflexão.

Atividade 13

(ê éfe zero oito ême ah um três) Resolver e elaborar problemas que envolvam grandezas diretamente ou inversamente proporcionais, por meio de estratégias variadas.

Quatro torneiras iguais enchem um reservatório em 6 horas. Se for retirada uma torneira, em quanto tempo as torneiras restantes realizam a mesma tarefa?

Resposta: 8 horas.

Resolução e comentários

O objetivo desta atividade é avaliar a habilidade do estudante em identificar a relação de proporcionalidade envolvida no problema e o emprego de estratégias que possibilitem chegar à sua solução. Um modo é reconhecer que a relação entre as grandezas número de torneiras n e tempo t é de proporcionalidade inversa e, assim, o produto delas é um valor constante k.

n ⋅ t = k

Substituindo os valores n = 4 e t = 6 na relação, obtém-se k = 24.

O tempo t, em hora, em que 3 torneiras preenchem o reservatório será dado por:

3 ⋅ t = k ⇒ 3 ⋅ t = 24 ⇒ t = 8

Ainda que os estudantes não tenham se apropriado da relação existente entre duas grandezas inversamente proporcionais, eles podem resolver o problema de outras maneiras. Por exemplo, se 4 torneiras enchem o reservatório em 6 horas, então, em uma hora, as mesmas 4 torneiras encherão

\frac{1}{6}

dele. Então, cada uma das 4 torneiras terá sido responsável por preencher, em uma hora,

\frac{1}{4}

dessa fração, ou seja,

\frac{1}{4} \cdot \frac{1}{6} = \frac{1}{24}

do reservatório. Como essas 24 partes do reservatório serão preenchidas por 3 torneiras, essas torneiras restantes realizam a mesma tarefa em 8 horas (24 : 3 = 8).

Atividade 14

(ê éfe zero oito ême ah um quatro) Demonstrar propriedades de quadriláteros por meio da identificação da congruência de triângulos.

Página cento e vinte e quatro

Um paralelogramo é um quadrilátero cujos lados opostos são paralelos. Com base nessa informação, foi realizada a demonstração de que os lados opostos de um paralelogramo são congruentes. Acompanhe a demonstração e, depois, indique a alternativa que completa corretamente as etapas que faltam.

Considerando um paralelogramo ABCD, traça-se a diagonal

\bar{B D}

Como os lados

\bar{A B}

\bar{C D}

são paralelos e cortados pela reta transversal que passa por

\bar{B D}

, pode-se concluir que x = z, pois eles são ângulos __________________.

Assim, y = w, pois formam um par de ângulos _______________.

O lado

\bar{B D}

é comum aos triângulos á bê dê e cê dê bê.

Comparando os triângulos á bê dê e cê dê bê, eles são congruentes, devido ao critério _____ de congruência de triângulos.

Conclui-se, portanto, que A bê = ___ e á dê = __.

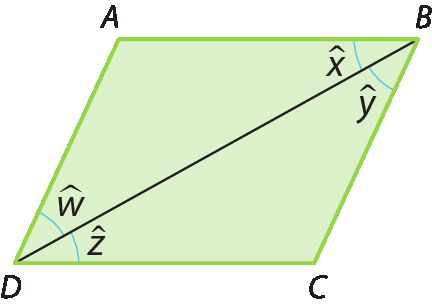
Ilustração. Paralelogramo ABCD. Diagonal BD divide o ângulo B nos ângulos x e y e ângulo D nos ângulos w e z.

a) alternos internos; alternos internos; ângulo-lado-ângulo; CD; BC

b) correspondentes; correspondentes; lado ângulo lado; CD; BC

c) alternos internos; alternos internos; lado lado lado; CD; BC

d) opostos pelo vértice; opostos pelo vértice; lado ângulo lado; CD; BC

Resposta: Alternativa a.

Resolução e comentários

Para responder a esta atividade, os estudantes devem acompanhar a sequência de passos da demonstração e, com base nas informações apresentadas, selecionar a alternativa que dê significado ao encadeamento das etapas. As duas primeiras respostas exigem que os estudantes identifiquem a nomenclatura dos ângulos, no caso, cada um dos pares são alternos internos; depois, o critério de congruência associado à situação é o ângulo-lado-ângulo, pois o lado comum

\bar{B D}

está entre os dois ângulos

\hat{x}

\hat{w}

que são respectivamente congruentes a

\hat{z}

\hat{y}

. Ao final da demonstração, eles devem reconhecer que AB = CD e AD = BC, ou seja, os lados opostos de um paralelogramo são congruentes.

Atividade 15

(ê éfe zero oito ême ah um cinco) Construir, utilizando instrumentos de desenho ou softwares de geometria dinâmica, mediatriz, bissetriz, ângulos de 90graus, 60graus, 45graus e 30graus e polígonos regulares.

(ê éfe zero oito ême ah um seis) Descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um hexágono regular de qualquer área, a partir da medida do ângulo central e da utilização de esquadros e compasso.

O fluxograma a seguir mostra como construir um hexágono regular a partir da medida de seu raio. Associe cada bloco de instrução numerado de 1 a 4 a cada uma das 4 etapas da construção: a, B, C e D.

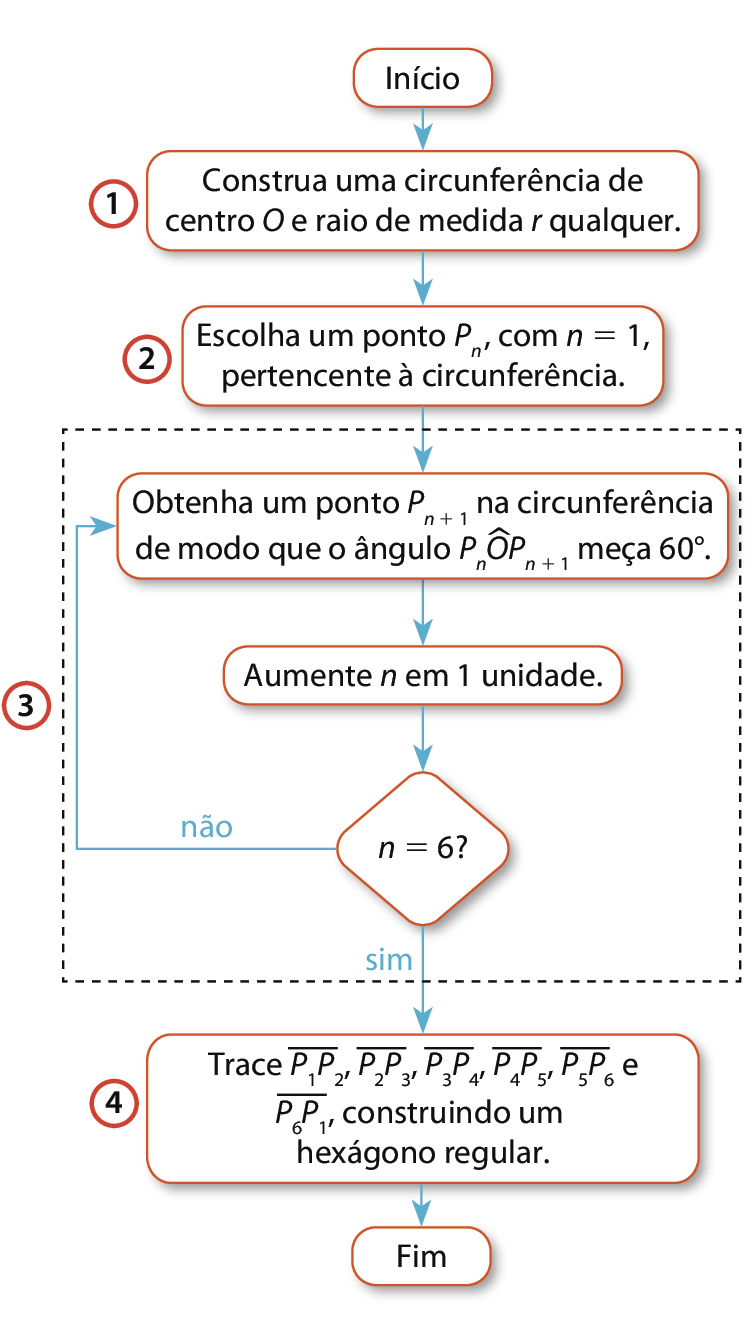
Fluxograma. A figura é um fluxograma com 8 caixas legendadas ligadas por setas. Em cada etapa, as setas apontam para a frente para uma caixa. Aqui, o fluxograma é descrito como listas nas quais os próximos passos possíveis são listados abaixo de cada legenda da caixa. Caixa 1: início. a. avança para caixa 2. Caixa 2: Construa uma circunferência de centro O e raio de medida r qualquer. a. avança para caixa 3. Caixa 3: Escolha um ponto Pn, com n igual a 1, pertencente à circunferência. a. avança para caixa 4. Caixa 4: Obtenha um ponto Pn + 1 circunferência de modo que o ângulo PnOPn mais 1 meça 60 graus. a. avança para caixa 5. Caixa 5: Aumente n em uma unidade. a. avança para caixa 6. Caixa 6: n = 6? a) Se não. Retorne para caixa 4 b) Se sim. Avança para caixa 7. Caixa 7: Trace segmentos P1P2, P2P3, P3P4, P4P5, P5P6 e P6P1, construindo um hexágono regular. a) avança para caixa 8. Caixa 8: Fim. A caixa 2 está indicado por 1; a caixa 3 está indicado por 2, as caixas 4, 5 e 6 estão contornadas por um retângulo tracejados e indicada por 3; a caixa 7 está indicada por 4.

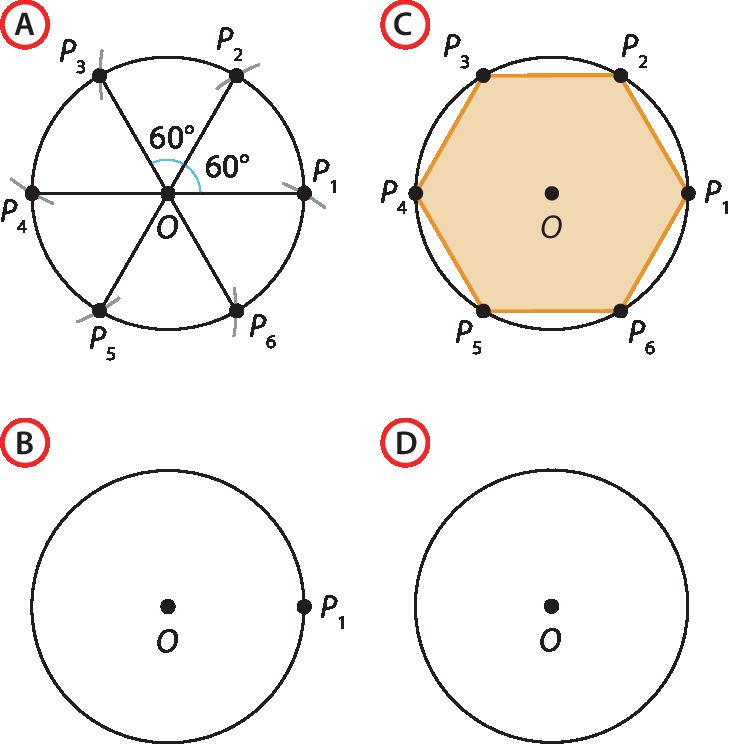
Ilustração. Circunferência com centro O dividida em 6 partes iguais, de modo que fiquem traçados os diâmetros P1P4, P2P5 e P3P6. Os ângulos P1OP2 e P2OP3 estão destacados e medem 60 graus. Ilustração. Circunferência com centro O e P1 sobre a circunferência. Ilustração. Circunferência com centro O dividida em 6 partes iguais e nomeadas de P1 a P6. Hexágono regular P1P2P3P4P5P6 inscrito na circunferência Ilustração. Circunferência com centro O.

Resposta: 1 ‒ D, 2 ‒ B, 3 ‒ A, 4 ‒ C.

Resolução e comentários

Com esta atividade é possível verificar a habilidade dos estudantes em reconhecer as diferentes etapas de um fluxograma que mostra como construir um hexágono regular. Espera-se que os estudantes compreendam que o algoritmo sugere que se construa uma circunferência e, para obter os vértices do hexágono, eles devem manter o mesmo espaçamento entre os pontos, o que pode ser obtido fazendo 360graus : 6 = 60graus. Assim, são construídos ângulos consecutivos de 60graus de modo a obter todos os 6 vértices, daí a presença do bloco de tomada de decisão, que tem por objetivo indicar quando o procedimento de construção dos ângulos deve ser encerrado.

Nos anos posteriores, os estudantes aprenderão que em um hexágono regular a medida do lado é igual à do raio da circunferência em que ele está inscrito, de modo que outro modo de fazer a construção seria marcar um ponto inicial na circunferência e, o compasso com abertura igual à medida do raio, fazer marcas sucessivas sobre a circunferência, obtendo os 6 vértices.

Página cento e vinte e cinco

Atividade 16

(ê éfe zero oito ême ah um sete) Aplicar os conceitos de mediatriz e bissetriz como lugares geométricos na resolução de problemas.

Leia as situações descritas a seguir.

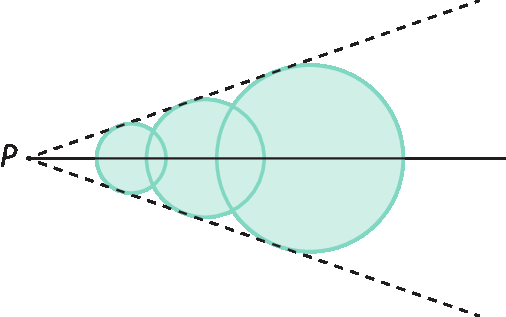
Ana quer desenhar uma sequência de circunferências decorativas que tocam cada uma das duas linhas tracejadas em um único ponto, como mostra a figura a seguir. Ela quer obter a linha que parte do ponto P e contém os centros das circunferências.

Ilustração. semirreta horizontal com ponto P na origem. Acima e abaixo, diagonal tracejada saindo do ponto P. Entre as linhas, três círculos secantes, de modo que cada um seja tangente as diagonais traçadas.

Murilo quer encontrar o ponto no mapa que está à mesma distância dos municípios paraibanos de Campina Grande, Barra de Santa Rosa e Boa Vista.

Municípios paraibanos de Campina Grande, Barra de Santa Rosa e Boa Vista

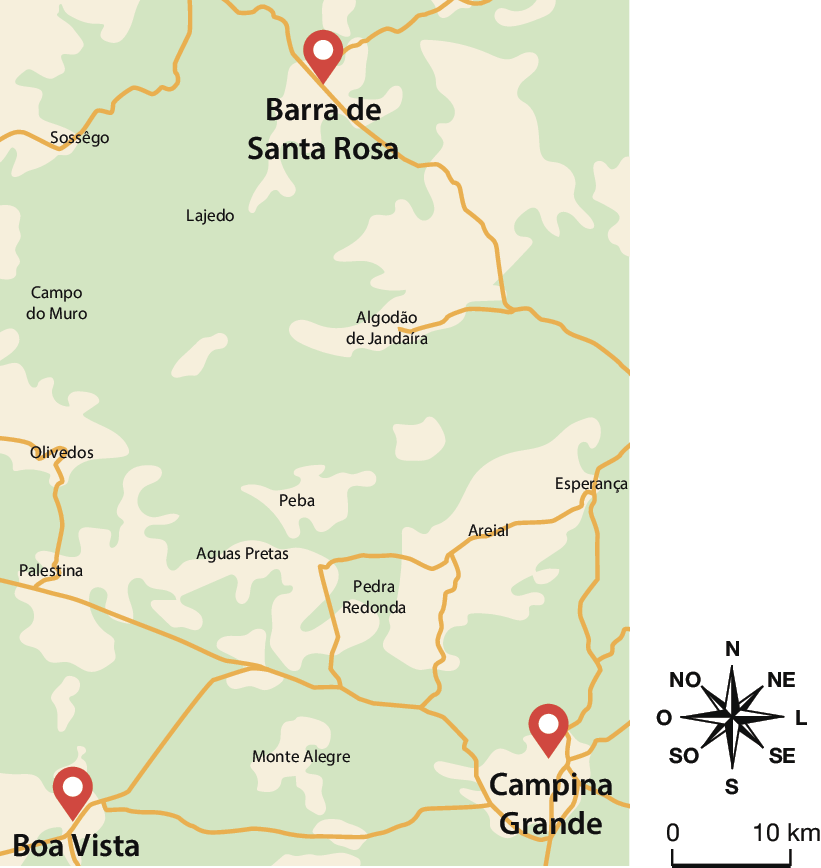
Mapa elaborado com base em: FERREIRA, Graça Maria Lemos. Atlas geográfico: espaço mundial. quinta edição revisada e atual. São Paulo: Moderna, 2019.

As construções geométricas que devem ser utilizadas para que Ana e Murilo resolvam seus problemas, são, respectivamente:

a) mediatriz e bissetriz.

b) mediatriz e mediatriz.

c) bissetriz e bissetriz.

d) bissetriz e mediatriz.

Resposta: Alternativa d.

Resolução e comentários

Esta atividade avalia se os estudantes compreendem as propriedades que caracterizam a bissetriz de um ângulo e a mediatriz de um segmento, para que eles associem as situações-problema apresentadas ao uso de cada uma dessas construções geométricas. Como cada ponto da bissetriz está à mesma distância dos lados do ângulo bissectado, essa construção possibilita a obtenção da com linha que contém os centros das circunferências de Ana. No caso do problema de Murilo, como cada ponto da reta mediatriz de um segmento é equidistante das suas extremidades (os pontos correspondentes a cada município), a intersecção das mediatrizes de dois segmentos, por exemplo, Boa Vista ‒ Campina Grande e Boa Vista ‒ Barra de Santa Rosa, estará equidistante dos 3 pontos. É importante observar se o fato de ambas as construções, bissetriz e mediatriz, envolverem a ideia de equidistância não causa confusão de seus significados, pois em uma delas a equidistância é em relação a duas retas concorrentes (a bissetriz) e na outra a equidistância é em relação a pontos (a mediatriz).

Atividade 17

(ê éfe zero oito ême ah um oito) Reconhecer e construir figuras obtidas por composições de transformações geométricas (translação, reflexão e rotação), com o uso de instrumentos de desenho ou de softwares de geometria dinâmica.

Na figura a seguir é possível observar a reflexão do triângulo á bê cê em relação ao eixo y , obtendo-se o triângulo a linha bê linha cê linha, o qual, por sua vez, também sofre reflexão em relação ao eixo x, resultando no triângulo á duas linhas, bê duas linhas, cê duas linhas.

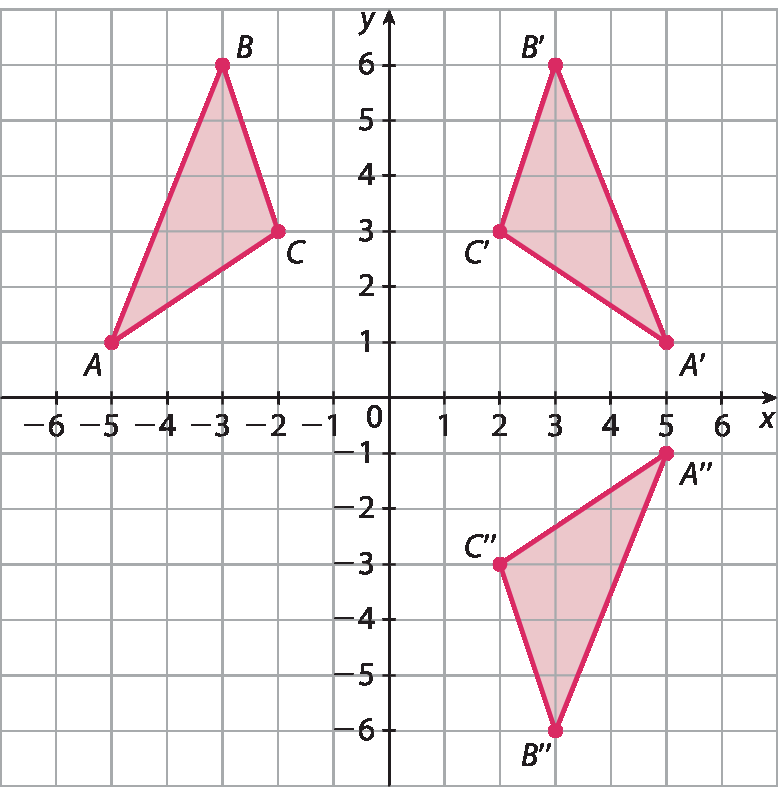
Ilustração. Plano cartesiano em malha quadriculada. Eixo x, com escala de menos 6 a 6. Eixo y, com escala de menos 6 a 6. Triângulo ABC de vértices A (menos 5, 1), B (menos 3, 6) e C (menos 2, 3). Triângulo A linha, B linha, C linha, de vértices A linha (5, 1), B linha (3, 6) e C linha (2, 3). Triângulo A duas linhas, B duas linhas, C duas linhas, de vértices A duas linhas (5, menos 1), B duas linhas (3, menos 6) e C três linhas (2, menos 3).

A transformação que poderia substituir as duas reflexões levando ABC em A”B”C” é:

a) uma reflexão de á bê cê em relação à mediatriz do lado

\bar{B C} .

b) uma translação que leva á bê cê diretamente a A”B”C”.

c) uma rotação de 180graus em relação ao ponto (0, 0).

d) uma rotação de 90graus no sentido horário em relação ao ponto a.

Resposta: Alternativa c.

Resolução e comentários

Para responder a esta atividade, os estudantes devem compreender diferentes transformações geométricas para relacionar a figura final e a figura inicial, de modo a reconhecer qual foi a transformação equivalente a duas reflexões em relação aos eixos coordenados. Espera-se que eles verifiquem que a translação pode ser entendida como um “deslizamento” ao longo de uma direção, em que a orientação da figura não é alterada. Por esse motivo, não é possível que o ponto C, ao ser transladado (cê duas linhas) fique à esquerda de á duas linhas e bê duas linhas. A reflexão mencionada na alternativa a também não levaria o triângulo á bê cê à posição ocupada por á duas linhas, bê duas linhas, cê duas linhas, de modo que restam as alternativas que consideram uma rotação em torno de um centro. Como os estudantes estudaram o conceito de giro de 180graus, espera-se que eles reconheçam que essa é a alternativa correta.

Página cento e vinte e seis

Atividade 18

(ê éfe zero oito ême ah um nove) Resolver e elaborar problemas que envolvam medidas de área de figuras geométricas, utilizando expressões de cálculo de área (quadriláteros, triângulos e círculos), em situações como determinar medida de terrenos.

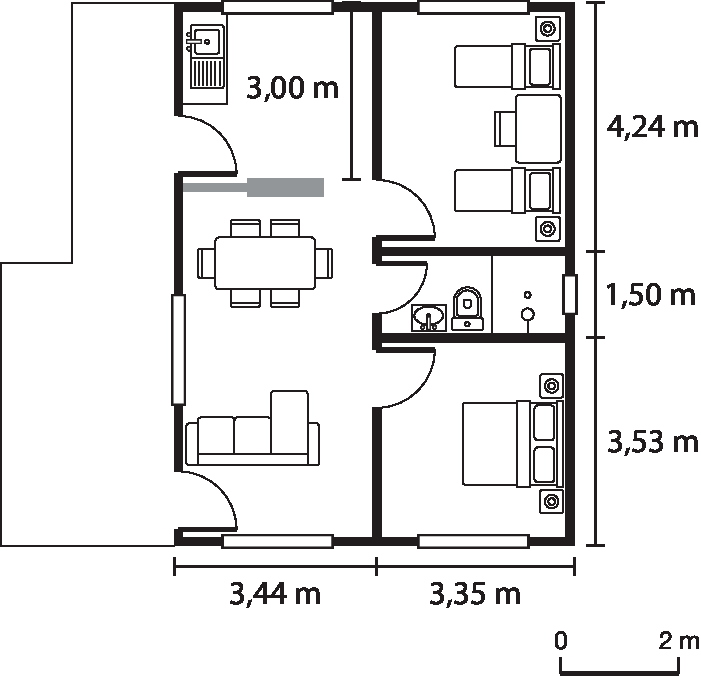
Ilustração. Planta de uma casa. Acima à esquerda, cozinha com largura de 3 metros e dormitório à direita com largura de 4,24 metros. À direita, abaixo, banheiro com largura de 1,5 metros e abaixo dormitório com largura de 3,35 metros e comprimento de 3,53 metros. À esquerda. sala com comprimento 3,44 metros, a sala está abaixo da cozinha.

Qual alternativa apresenta a melhor aproximação para a medida da área da sala da casa representada na planta baixa? Desconsidere a espessura das paredes.

a) 17 métros quadrados

b) 22 métros quadrados

c) 32 métros quadrados

d) 40 métros quadrados

Resposta: Alternativa b.

Resolução e comentários

A situação apresentada na atividade envolve o cálculo da medida da área de um cômodo de uma residência em uma planta baixa, em que o estudante tem de interpretar os dados fornecidos a fim de obter uma medida desconhecida e realizar o cálculo corretamente. É importante abordar questões dêsse tipo para que os estudantes reconheçam que, em situações reais, nem sempre todas as medidas são fornecidas diretamente, e que algumas delas devem ser obtidas a partir de outras. No caso desta atividade, para calcular a medida da área é preciso conhecer a medida do comprimento total da sala, mas a figura mostra apenas uma parte, que corresponde, em metro, a 3,53 + 1,50 = 5,03. A parte que falta pode ser obtida calculando a diferença 4,24 ‒ 3,00 = 1,24 e adicionando-a ao valor parcial obtido anteriormente: 5,03 + 1,24 = 6,27. Assim, a área da sala mede aproximadamente 21,57 métros quadrados (6,27 ⋅ 3,44 ≃ 21,57). Portanto, a alternativa b é a que apresenta o valor mais próximo de 21,57 métros quadrados.

Atividade 19

(ê éfe zero oito ême ah dois zero) Reconhecer a relação entre um litro e um decímetro cúbico e a relação entre litro e metro cúbico, para resolver problemas de cálculo de capacidade de recipientes.

Uma cisterna, inicialmente vazia, tem formato de bloco retangular e suas medidas, em decímetro, estão indicadas na figura a seguir.

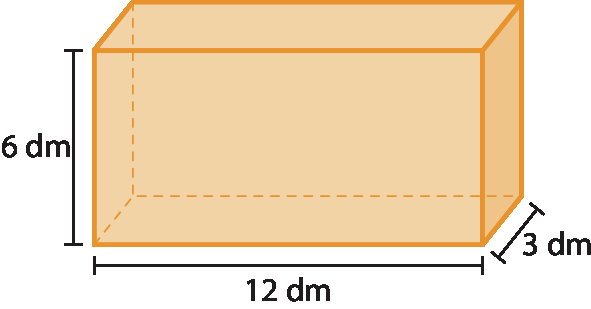
Ilustração. Bloco retangular com as medidas: 6 decímetros de altura, 12 decímetros de comprimento e 3 decímetros de largura.

Se, nessa cisterna, uma torneira despeja 8 litros de água a cada minuto, em quanto tempo a cisterna ficará cheia?

Resposta: 27 minutos.

Resolução e comentários

Para resolver a atividade os estudantes devem saber como obter a medida do volume de um bloco retangular e conhecer a relação de conversão entre a unidade de medida de volume; 1 decímetros cúbicos = 1 litros. Como as medidas da cisterna estão em decímetro, ao multiplicar as medidas de comprimento, largura e altura, o resultado será em decímetro cúbico. Assim: 6 ⋅ 12 ⋅ 3 = 216.

Como a torneira tem vazão de 8 litros por minuto, para determinar o tempo necessário para encher a cisterna vazia, basta fazer 216 : 8 = 27. Portanto, a cisterna ficará cheia em 27 minutos.

Atividade 20

(ê éfe zero oito ême ah dois um) Resolver e elaborar problemas que envolvam o cálculo do volume de recipiente cujo formato é o de um bloco retangular.

Em alguns países de clima seco, os habitantes utilizam a superfície de uma laje de formato retangular sobre a residência para coletar e armazenar a água da chuva. Se essa laje tiver 5 métros de comprimento por 3 métros de largura e recolher água da chuva até a altura de 8 centímetros, quantos litros de água serão coletados?

Resposta: .1200 litros.

Resolução e comentários

Nesta atividade, os estudantes devem calcular a medida da capacidade de um recipiente com formato de um bloco retangular, em metro cúbico, e converter essa medida em litro, atribuindo, assim, significado à quantidade calculada de água coletada da chuva. Antes de iniciar o cálculo, é importante que eles reconheçam a necessidade de converter a medida 8 cm para metro, ou seja, 0,08 métro. Como a medida do volume, em métro cúbico, é 1,2 métro³ ( 5 ⋅ 3 ⋅ 0,08 = 1,2), com base na relação 1 métro³ = .1000 litros, pode-se concluir que serão coletados .1200 litros de água. Ao discutir a resolução da atividade com os estudantes, comente que em uma área relativamente pequena de uma residência é possível coletar uma quantidade significativa de água, o que possibilita que eles percebam o potencial para a coleta de água em áreas maiores. Para contextualizar as informações, comente que, de acordo com os meteorologistas, se no período de uma hora a água da chuva atingir de 0,5 centímetro a 6 centímetros de altura, a chuva é considerada forte, o que corresponde aos dados dessa atividade.

Atividade 21

(ê éfe zero oito ême ah dois dois) Calcular a probabilidade de eventos, com base na construção do espaço amostral, utilizando o princípio multiplicativo, e reconhecer que a soma das probabilidades de todos os elementos do espaço amostral é igual a 1.

Em uma loja de chocolates, se o cliente gasta pelo menos R$ 30,00trinta reais em compras, ele ganha uma caixa que contém 4 bombons com recheios de morango, coco, cereja e abacaxi. O cliente, então, diz quais são seus dois sabores preferidos, em ordem de preferência, e pega, ao acaso, 2 bombons da caixa, um de cada vez; se os bombons sorteados forem os de sua preferência, nessa ordem, ele ganha outra caixa de bombons. Qual é a probabilidade de o cliente ganhar a segunda caixa de bombons?

Página cento e vinte e sete

Resposta:

\frac{1}{12}

Resolução e comentários

Para responder a esta atividade, os estudantes podem construir o espaço amostral indicando as possíveis escolhas de dois sabores (1º sabor preferido, 2º sabor preferido) e, em seguida, indicar a probabilidade por meio da fração correspondente.

Resultados possíveis: {(morango, coco), (morango, cereja), (morango, abacaxi), (coco, morango), (coco, cereja), (coco, abacaxi), (cereja, morango), (cereja, coco), (cereja, abacaxi), (abacaxi, morango), (abacaxi, coco), (abacaxi, cereja)}.

Como há 12 diferentes possibilidades e somente 1 delas corresponde àquela do cliente, a probabilidade é igual a

\frac{1}{12}

. Outra maneira para a determinação da quantidade de elementos do espaço amostral é aplicar o princípio multiplicativo. Existem 4 possíveis escolhas para o 1º sabor preferido e somente 3 outras opções para o 2º sabor, de modo que o total de elementos é 4 ⋅ 3 = 12.

Atividade 22

(ê éfe zero oito ême ah dois três) Avaliar a adequação de diferentes tipos de gráficos para representar um conjunto de dados de uma pesquisa.

Considere as três diferentes situações em que os dados foram coletados e, em seguida, serão apresentados na fórma de um gráfico.

um Acompanhamento mensal do número de vagas de trabalho oferecidas em um município.

dois Valores percentuais dos tipos de doenças que mais causam internações em um hospital.

três Quantidade de estudantes de uma turma que preferem cada tipo de gênero musical.

O gráfico mais adequado para representar os dados dessas situações são, respectivamente:

a) gráfico de barras verticais; gráfico de setores; gráfico de linha.

b) gráfico de barras verticais; gráfico de linha; gráfico de setores.

c) gráfico de linha; gráfico de setores; gráfico de barras verticais.

d) gráfico de linha; gráfico de barras verticais; gráfico de setores.

Resposta: Alternativa c.

Resolução e comentários

Apesar de não haver a obrigatoriedade do uso de cada tipo de gráfico em determinadas situações, é possível reconhecer a adequação de cada um deles para a representação dos dados. A situação um apresenta dados em uma sequência temporal, para a qual é importante reconhecer as tendências em cada período ao qual os dados se referem; assim, o gráfico de linha é a escolha que possibilita realçar os indicativos de crescimento, decrescimento ou estabilidade da variação de acordo com a inclinação dos segmentos que compõem o gráfico. Na situação dois é importante que o gráfico favoreça não apenas os valores percentuais, mas também cada um dos valores em relação ao todo e, nesse caso, o gráfico de setores é o mais adequado.

Atividade 23

(ê éfe zero oito ême ah dois quatro) Classificar as frequências de uma variável contínua de uma pesquisa em classes, de modo que resumam os dados de maneira adequada para a tomada de decisões.

Uma pesquisa sobre o consumo médio de água nos últimos 12 meses, em metro cúbico, realizada com vinte e duas residências de um mesmo bairro apresentou os seguintes resultados.

12,3

25,6

21,2

20,4

34,3

26,6

14,5

17,9

30,1

16,5

12,4

15,3

20,8

28,0

24,7

13,8

19,9

17,6

16,7

28,6

16,3

34,5

O gráfico a seguir indica a frequência absoluta de consumo, o qual foi dividido em 5 faixas. Complete o gráfico com os dados que faltam.

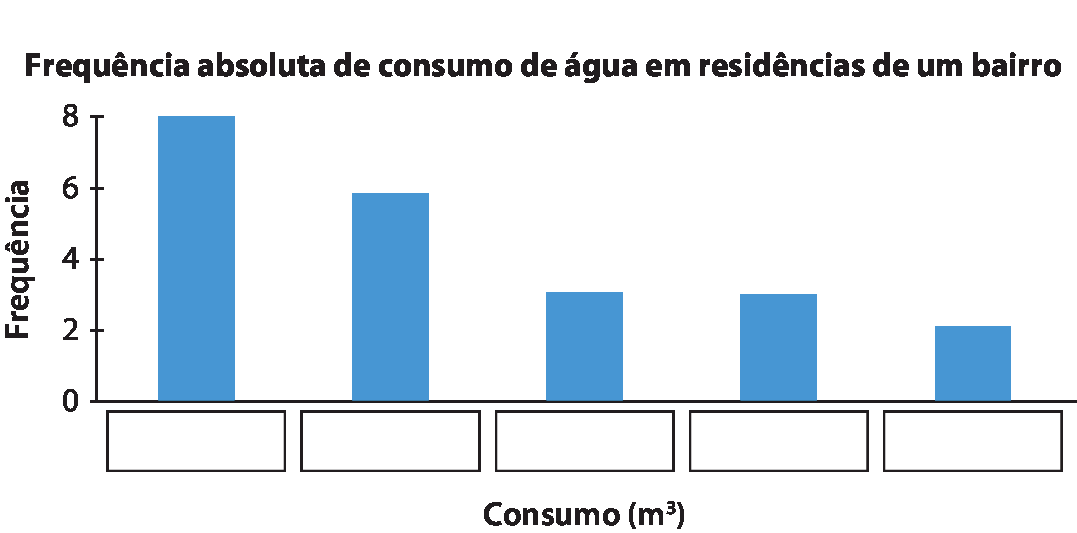
Gráfico. Frequência absoluta de consumo de água em residências de um bairro. Eixo x, consumo (em metros cúbicos) com 5 barras verticais e espaços para resposta. Eixo y, frequência de 0 a 8. Frequência da barra maior para a menor: 8, 6, 3, 3, 2. — Dados fictícios.

Resposta: 12,0 – 16,9; 17,0 – 21,9; 22,0 – 26,9; 27,0 – 31,9; ≥ 32,0

Resolução e comentários

Nesta atividade é avaliada a habilidade dos estudantes em agrupar dados contínuos em uma quantidade adequada de categorias de modo que não haja um grande número de categorias que dificultem a compreensão do panorama geral mostrado pelos dados nem em quantidade muito pequena que agrupe um excesso de dados em uma mesma categoria. Não há um critério adotado universalmente para essa escolha, mas uma possibilidade é tomar a amplitude total, no caso, 34,5 ‒ 12,3 = 22,2, e obter o valor inteiro mais próximo da raiz quadrada da amplitude, no caso, aproximadamente 5. Assim, agrupam-se os dados em 5 categorias. Os intervalos correspondentes poderiam ser:

Consumo (m³)	Frequência
12,0 – 16,9	8
17,0 – 21,9	6
22,0 – 26,9	3
27,0 – 31,9	3
≥ 32,0	2

Ao verificar as respostas dos estudantes, observe se eles realizaram a contagem dos elementos corretamente, adicionando as frequências absolutas e conferindo se a amplitude de cada uma das categorias é igual à amplitude das demais.

Atividade 24

(ê éfe zero oito ême ah dois cinco) Obter os valores de medidas de tendência central de uma pesquisa estatística (média, moda e mediana) com a compreensão de seus significados e relacioná-los com a dispersão de dados, indicada pela amplitude.

Página cento e vinte e oito

Uma equipe de futebol quer contratar um atacante e, para isso, analisou o número de gols que cada um fez ao longo das últimas oito partidas.

Jogador	Gols em cada uma das últimas oito partidas
João	0	2	1	3	3	1	4	2
Ricardo	1	1	0	5	4	3	0	2

Com base nesses dados é possível concluir que:

a) os dois jogadores têm a mesma média de gols por jogo, mas o desempenho de João é mais regular do que o de Ricardo, cujo número de gols marcados tem maior oscilação. b) a média de gols de João é maior do que a de Ricardo e, por esse motivo, seu desempenho pode ser considerado o melhor entre os dois. c) a média de gols de Ricardo é maior do que a de João e, por esse motivo, seu desempenho pode ser considerado o melhor entre os dois.

d) os dois jogadores têm a mesma média de gols por jogo, mas o desempenho de Ricardo é mais regular do que o de João, cujo número de gols marcados oscilou mais ao longo das partidas.

e) não é possível calcular a média de gols dos jogadores porque cada um deles tem jogos nos quais não marcaram gols.

Resposta: Alternativa a.

Resolução e comentários

Esta atividade avalia a compreensão dos estudantes sobre o cálculo da média aritmética e a interpretação informal de dados que mostram a mesma média aritmética, mas diferentes variações dos dados. É esperado que os estudantes calculem corretamente a média aritmética e, ao se depararem com o mesmo valor, analisem o conjunto de dados em cada caso e observem que o número de gols de João está mais bem distribuído ao longo dos jogos do que os de Ricardo, que concentra muitos gols em poucas partidas. Apesar de os estudantes não estudarem as fórmulas para o cálculo de indicadores de variabilidade, é possível que eles reconheçam a maior variabilidade de Ricardo com base em uma rápida inspeção dos números. Ao discutir a resolução da atividade com os estudantes, sugira que eles desenhem uma reta numérica para cada um dos jogadores e marquem nela 16 pontos correspondentes aos gols que cada jogador marcou nas últimas partidas, para que percebam visualmente a maior dispersão dos pontos no caso de Ricardo.

Atividade 25

(ê éfe zero oito ême ah dois seis) Selecionar razões, de diferentes naturezas (física, ética ou econômica), que justificam a realização de pesquisas amostrais e não censitárias, e reconhecer que a seleção da amostra pode ser feita de diferentes maneiras (amostra casual simples, sistemática e estratificada).

Analise as situações descritas a seguir.

um A Polícia Rodoviária quer saber se os veículos que trafegam sentido litoral na rodovia estão com todos os itens de segurança em condições satisfatórias.

dois Pesquisa para atualizar os dados dos moradores de um condomínio de prédios.

três Pesquisa sobre a idade do público de um show de música realizado em um estádio de futebol.

O tipo mais adequado de pesquisa a ser adotado para cada situação apresentada é, respectivamente:

a) censitária; censitária; amostral.

b) amostral; amostral; censitária.

c) amostral; censitária; amostral.

d) censitária; amostral; censitárias.

Resposta: Alternativa c.

Resolução e comentários

Espera-se que os estudantes reconheçam que, em alguns casos, apesar de sua realização não ser impossível, uma pesquisa censitária pode ser dispendiosa em termos de recursos e tempo; assim, a melhor opção é uma pesquisa amostral. No caso da situação um, uma abordagem policial para verificar todos os carros que trafegam em uma rodovia exigiria a interrupção de todo o tráfego; portanto, a pesquisa amostral é mais adequada. No caso da situação dois, a atualização de dados cadastrais pressupõe a coleta de informações sobre todos os moradores do condomínio, de modo que deve ser realizada uma pesquisa censitária. No caso da situação três, o fato de haver milhares de pessoas em um show de música torna a escolha de uma amostra do público presente a melhor.