Página 9

CAPÍTULO 1 Números reais

Fotografia. Vista frontal do Partenon, construção grega em ruínas com colunas cilíndricas e degraus. Céu azul sem nuvens. — O Partenon, em Atenas, Grécia. (Fotografia de 2019.)

Ícone do Tema Contemporâneo Transversal: MULTICULTURALISMO.

Será que a estrutura espiral das conchas de moluscos, o Partenon em Atenas, na Grécia, as pirâmides em Gizé, no Egito, e a obra Mona Lisa, de Leonardo da Vinci, têm algum elemento em comum?

Muitos afirmam que essas e outras obras de arte ou de arquitetura apresentam, em suas composições, segmentos cujas medidas a e b, com a > b, estão à razão:

\frac{a}{b} = \frac{a + b}{a}

Dizemos que as razões dessa proporção são a razão áurea, cujo valor numérico é representado pela letra grega ϕ (fi), o número de ouro. Para que isso ocorra, a e b devem ser tais que:

b = \frac{a (\sqrt{5} ‒ 1)}{2}

Observe a fotografia e responda às questões no caderno.

a) Para a = 1, qual deve ser o valor de b para que estejam à razão áurea?

b) Com os valores de a e de b considerados no item anterior, determine uma aproximação para o número ϕ.

c) Pesquise sobre o número de ouro e debata com os colegas sobre a razão áurea representar um padrão de beleza.

Respostas e comentários

a) b ≃ 0,618033

b) ϕ ≃ 1,62

c) Resposta pessoal.

Capítulo 1 – Números reais

Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.

Este capítulo retoma e amplia a evolução da ideia de número ao longo da história e sua aplicação para atender às necessidades do ser humano no que se refere à sua organização social e à compreensão dos fenômenos da natureza. dêsse modo, o capítulo revisa os números racionais e apresenta os números irracionais e o conjunto dos números reais; trata da reta real e da localização de números irracionais nela com o auxílio de triângulos retângulos e do teorema de Pitágoras; resgata a noção de quadrados perfeitos e explora cálculos com raízes quadradas de números racionais não negativos (exatas e com aproximação). Além disso, o capítulo também explora o cálculo de porcentagens sucessivas.

O tema motivador da abertura do capítulo é o número de ouro, que será explorado no desenvolvimento do capítulo no contexto da sequência de Fibonacci.

Ao trabalhar com a abertura deste capítulo, contribui-se para o desenvolvimento da competência geral 3 e para uma reflexão sobre o Tema Contemporâneo Transversal diversidade cultural.

Sugestão de leitura

Para ampliar o trabalho com esse tema, sugerimos:

NETO, P. R. S.; SILVEIRA, M. R. A.; MELO, L. A. S. Os aspectos “ver e ver-como” e o número de ouro na perspectiva wittgensteiniana da linguagem. Revista Eletrônica de Educação Matemática, volume 15, número 1, página 1 a 18, 2019. Disponível em: https://oeds.link/AA7gcG. Acesso em: 13 junho 2022.

Nesse artigo, os autores apresentam a perspectiva wittgensteiniana acerca das expressões ver e ver-como, com foco voltado para o ensino e a aprendizagem da Matemática, destacando o conceito de número de ouro, na perspectiva da linguagem, por meio de um breve histórico e sua constituição como objeto matemático propriamente dito, além de suas aplicações em outros ramos do conhecimento.

Página 10

1. A história dos números

Desde a invenção da escrita, há cêrca de 4 mil anos, o ser humano começou a usar símbolos para representar quantidades como resultado da contagem de objetos: quantidade de aves que criava, de peixes que pescava, de cereais que colhia etcétera

Os babilônios, por exemplo, muitos séculos antes de Cristo, empregavam símbolos em fórma de cunhaglossário para representar números:

Fotografia. Tábua de argila da civilização babilônica, retangular, com linhas e inscrições. — Tábua de argila da civilização babilônica, do período entre 1900 antes de Cristo e 1600 antes de Cristo Universidade Columbia, Nova York, Estados Unidos.

• Uma cunha “em pé” (

) representava o número 1 e podia ser repetida até nove vezes.

• Uma cunha “deitada” (

) representava o número 10 e podia ser repetida até cinco vezes.

Esses símbolos eram talhados em tábuas de argila, como a da fotografia.

Outros povos, como os egípcios e os romanos, tinham seus próprios símbolos e suas próprias regras para registrar quantidades.

Atualmente, a maioria dos povos adota o sistema de numeração decimal, composto de dez símbolos (0, 1, 2, 3, 4, 5, 6, 7, 8 e 9), denominados algarismos indo-arábicos.

Números naturais

Números naturais são aqueles que expressam o resultado de uma contagem.

O conjunto dos números naturais, representado por

Símbolo. Letra N, com um traço vertical a lado esquerdo da letra. Representa o conjunto dos números naturais.

, pode ser indicado por:

= {0, 1, 2, 3, 4, 5, ...}

Com os números naturais, efetuamos qualquer adição ou multiplicação. As subtrações, no entanto, só serão possíveis quando o minuendo for maior ou igual ao subtraendo, e as divisões, quando o dividendo for múltiplo do divisor.

São exemplos de operações impossíveis de ser realizadas só com números naturais:

a) a subtração 6 ‒ 7 (não há número natural que adicionado a 7 resulte 6);

b) a divisão exata 8 : 5 (não há número natural que multiplicado por 5 resulte 8).

Os números naturais não são suficientes para representar todas as situações do dia a dia. Com eles, não é possível representar, por exemplo, temperaturas abaixo de zero grau Celsius nem a medida do comprimento do nosso palmo em metro.

Para atender a situações como essas, foram criados outros conjuntos numéricos, que estudaremos ao longo deste capítulo.

Respostas e comentários

1. A história dos números

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro.

Este tópico retoma e possibilita aos estudantes ampliar a compreensão dos números naturais, inteiros e racionais, preparando-os para o estudo dos números irracionais e, ainda, para associar os números reais ao conjunto que envolve todos esses números, além de poderem compreender a ideia de reta real. Assim, eles desenvolvem as habilidades (ê éfe zero nove ême ah zero três) e (ê éfe zero nove ême ah zero quatro).

Números naturais

Inicie o trabalho com esse tópico, propondo aos estudantes atividades em grupo que os motivem a mobilizar seus conhecimentos acerca dos números naturais e das características do sistema de numeração decimal. Eles podem:

• elencar as características do sistema de numeração decimal;

• dizer onde ele surgiu, como foi difundido e o motivo de sua prevalência em relação aos demais sistemas das civilizações antigas;

• dizer qual é o uso de um número natural;

• caracterizar o conjunto dos números naturais;

• discutir as limitações das operações com números naturais; entre outras tarefas.

Em seguida, cada grupo apresenta suas conclusões aos demais. No final, faça um encerramento do tema com os estudantes, em uma roda de conversa.

Página 11

Números inteiros

Os números inteiros são números relativos (positivos ou negativos) criados pelo ser humano, em decorrência de necessidades impostas pelo comércio e de situações cotidianas que exigiram a representação de quantidades em relação ao referencial zero.

Acompanhe exemplos em que recorremos aos números inteiros.

a) Nos termômetros, para indicar temperaturas abaixo de zero grau Celsius (números negativos) ou acima de zero grau Celsius (números positivos). O referencial é 0 grau cê.

Fotografia. Pessoa correndo em pista de corrida. À direita, relógio digital marcando menos 2 graus Celsius. — Pessoa em pista de corrida em Curitiba, Paraná. (Fotografia de 2021.)

b) Para descrever o saldo de gols de times em um campeonato de futebol, podemos utilizar os números inteiros positivos para indicar os gols realizados, e os inteiros negativos, para os gols sofridos.

Saldo de gols de alguns times do campeonato de futebol da escola
	Gols realizados	Gols sofridos	Saldo de gols
Time A	3	−4	−1
Time B	2	−1	1
Time C	5	−3	2
Time D	6	−6	0

Fonte: anotações realizadas pelo professor de Educação Física.

O conjunto dos números inteiros, representado por

Símbolo. Letra Z, com traço diagonal ao lado do traço do meio da letra. Representa o conjunto dos números inteiros.

, pode ser indicado por:

= {reticências, ‒3, ‒2, ‒1, 0, +1, +2, +3, reticências}

Os símbolos + e ‒ à esquerda dos números passam a indicar a posição que eles ocupam em relação ao zero, quando organizados em ordem crescente ou decrescente: os números menores do que zero são negativos, e os maiores do que zero, positivos. O número zero não é positivo nem negativo.

Os números inteiros não negativos (0, +1, +2, +3, reticências) são associados aos números naturais, tanto na ordenação como nas operações, então, esses números passarão a ser indicados simplesmente por 0, 1, 2, 3, 4, reticências

Por esse motivo, podemos dizer que qualquer número natural é um número inteiro:

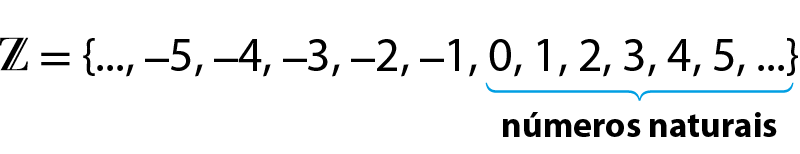
Esquema. Letra Z, que representa o conjunto dos números inteiros, é igual a: abre chave, reticências, menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3, 4, 5, reticências, fecha chave. A parte dos elementos: 0, 1, 2, 3, 4, 5, reticências, está destacada, com a indicação de que esses números fazem parte do conjunto dos números naturais.

Com a criação do conjunto dos números inteiros, tornou-se possível efetuar subtrações em que o minuendo é menor do que o subtraendo. Por exemplo: (6 ‒ 7 = ‒1) e (0 ‒ 3 = ‒3).

Os números inteiros, no entanto, não são suficientes para representar o resultado de qualquer divisão. Por exemplo: (10 : 3) e [(‒5) : 7].

Respostas e comentários

Números inteiros

Antes de começar o trabalho com esse tópico, peça aos estudantes que listem exemplos de utilização de números positivos e de números negativos, retomando o que são os números inteiros. Podem surgir, por exemplo: nos painéis de elevadores, para registrar saldo de pontos em competições esportivas, altitude de montes e profundidades (considerando o nível do mar como referência e valores inteiros das medidas), gols marcados e gols sofridos por um time em uma partida de futebol, entre outros.

O trabalho com os números inteiros pode ser semelhante ao sugerido com os números naturais. Proponha aos estudantes que caracterizem o conjunto dos números inteiros antes da leitura do texto desta página. Retome as ideias de antecessor e de sucessor, de oposto e de módulo de um número inteiro, além da inclusão dos números naturais no conjunto dos números inteiros.

Sugira também que conversem sobre as limitações das operações com os números inteiros, retomando a potenciação com expoente inteiro negativo.

Página 12

Números racionais

Considere os números a seguir.

1,25

0,777reticências

‒13

‒0,75

Eles são exemplos de números racionais, pois podem ser escritos na fórma de fração

\frac{a}{b}

com um número inteiro no numerador e um número inteiro não nulo no denominador. Observe.

1,25 =

\frac{5}{4}

0,777reticências =

\frac{7}{9}

‒13 = ‒

\frac{13}{1}

‒0,75 = ‒

\frac{3}{4}

Com os números racionais, podemos representar o resultado da divisão de quaisquer dois números inteiros, com o divisor não nulo. O conjunto dos números racionais, representado por

Letra Q, que representa o conjunto dos números racionais.

, pode ser indicado por:

= \{\frac{a}{b}, c o m a e b inteiros e b \neq 0\}

Observe o quadro a seguir, com alguns exemplos de números racionais.

	Número natural	Número inteiro	Número racional
3	✓	✓	✓
−8		✓	✓
$divisão de 1 sobre 3$			✓
−0,7555...			✓

Agora, note como podemos representar alguns números racionais na reta numérica.

Ilustração. Reta numérica com os pontos a seguir, da esquerda para a direita: menos 1, fração menos 3 quartos; fração menos meio. Duas unidades à direita, os pontos: 0, fração 1 quinto. Quatro unidades à direita, o ponto, 1. Três unidades à direita: o ponto: fração 8 quintos. Duas unidades à direita, o ponto: 2.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Identifique, entre as operações a seguir, quais não podem ser realizadas apenas com números naturais.

a) 3 + 7

b) 5 ‒ 235

c) 0 ‒ 0

d) 7 ‒ 0

e) 3 : 7

f) 3 ⋅ 7

g) 8 : 3

h) 7 : 10

2 Responda às questões a seguir.

a) Por que é impossível efetuar a divisão exata 7 : 3 dispondo apenas de números naturais?

b) E 3 ‒ 7? Por que é impossível efetuá-la, considerando apenas os naturais?

3 Enquanto um avião sobrevoa a uma altitude de medida igual a 5,8 quilômetros, um submarino está a uma profundidade medindo 0,24 quilômetro.

a) Represente essas medidas com números relativos e explique qual foi o referencial utilizado.

b) Os números que aparecem no enunciado (5,8 e 0,24) são números racionais? Eles estão escritos na fórma de fração?

Respostas e comentários

1. Alternativas b, ê, g, h.

2. a) Porque não há número natural que multiplicado por 3 dê 7.

2. b) Porque não há número natural que adicionado a 7 dê 3.

3. a) +5,8 quilômetros; ‒0,24 quilômetro; nível do mar.

3. b) Sim; não, eles estão escritos na fórma decimal.

Números racionais

Explore a necessidade dos números racionais em situações de medição. Proponha na lousa uma ampliação do quadro apresentado. Peça aos estudantes que digam alguns números e depois falem se eles são números racionais.

Desenhe na lousa uma reta numérica e proponha a localização de números naturais, números inteiros negativos e números racionais na fórma de fração. Se julgar necessário, mostre alguns exemplos antes de pedir aos estudantes que façam atividades sobre esse conteúdo.

Exercícios propostos

Para resolver os exercícios 1 e 2, os estudantes podem se reunir em duplas. A troca de ideias favorece o levantamento de hipóteses e a argumentação, bem como o desenvolvimento das competências gerais 7 e 9. Socialize as respostas, validando-as com os estudantes.

Esses dois exercícios abordam as limitações matemáticas das subtrações e da divisão com números naturais e, assim, mostram que essas operações só serão sempre possíveis com a ampliação dos conjuntos numéricos. Converse com os estudantes sobre alguns exemplos cotidianos em que os números naturais não podem ser aplicados.

As operações apresentadas nos itens b, ê, g e h do exercício 1 não podem ser realizadas apenas utilizando o conjunto dos números naturais.

Acompanhe a resolução do exercício 3:

a) Utilizando como referência o nível do mar, obtemos: +5,8 quilômetros e ‒0,24 quilômetro.

b) 5,8 e 0,24 são números racionais escritos na fórma decimal.

Página 13

4 Entre os números a seguir, quais são inteiros?

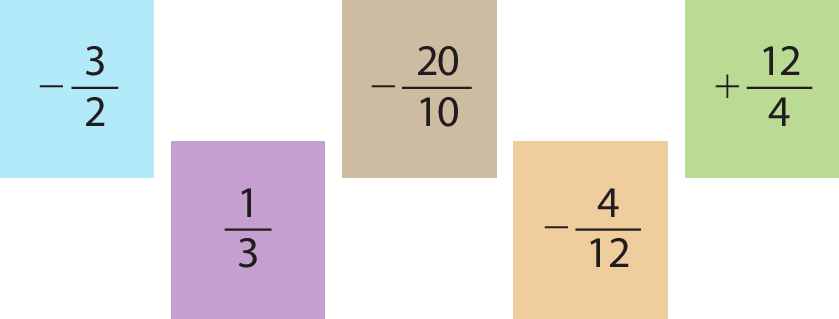
Ilustração. Cartões coloridos com os números: Fração menos 3 meios. Fração 1 terço. Fração menos 20 décimos. Fração menos 4 12 avos. Fração mais 12 quartos.

5 Identifique as sentenças falsas e justifique com um exemplo.

a) Todo número natural é inteiro.

b) Todo número inteiro é racional.

c) Todo número natural é racional.

d) Todo número que pode ser escrito na fórma de fração de inteiros, com denominador não nulo, é racional.

e) Todo número natural é um número inteiro positivo.

f) Todo número inteiro é natural.

g) Todo número racional é inteiro.

Reúna-se com um colega e respondam quantos números inteiros existem:

a) entre dois números inteiros consecutivos;

b) entre 1 e 9, entre ‒1 e 1, entre ‒9 e 9;

c) entre 0 e 10, entre 0 e 100, entre 0 e ..1000000.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e façam o que se pede.

a) Calculem os números racionais:

• a, que é a média aritmética de 3 e 7;

• b, que é a média aritmética de 3 e a ;

• c, que é a média aritmética de 3 e b;

• d, que é a média aritmética de 3 e c.

b) Representem os números racionais 3, a, b, c, d e 7 em uma mesma reta numérica.

c) As médias aritméticas de dois números obtidas no item a estão entre esses dois números?

d) É possível calcular os números ê, f, g, h, reticências, que sejam as médias aritméticas, respectivamente, de 3 e d, de 3 e ê, de 3 e f, de 3 e g, e assim por diante?

e) Considerando os itens anteriores, use sua percepção para dizer quantos números racionais existem entre 3 e 7 e quantos números racionais existem entre dois números racionais distintos quaisquer.

Representações dos números racionais

Com essa breve retomada sobre a necessidade de ampliar os conjuntos numéricos, podemos constatar que os algarismos indo-arábicos servem para representar todos os números que constituem esses conjuntos.

Notamos, também, que há mais de uma representação possível para todos os números racionais: a fracionária e a decimal.

No quadro a seguir, há algumas representações fracionárias e decimais de alguns números racionais.

Número racional	Algumas representações
−2	$menos divisão de 18 sobre 9$	−2,0
$divisão de 1 sobre 4$	$divisão de 4 sobre 16$	0,25
$divisão de 4 sobre 11$	$divisão de 8 sobre 22$	0,3636…

Número racional	Algumas representações
−5,3	$menos divisão de 53 sobre 10$	−5,300
$divisão de 32 sobre 15$	$2 divisão de 2 sobre 15$	2,1333…
6	$divisão de 12 sobre 2$	6,000

Respostas e comentários

‒ \frac{20}{10}

+ \frac{12}{4}

5. a) Verdadeira.

5. b) Verdadeira.

5. c) Verdadeira.

5. d) Verdadeira.

5. e) Falsa, pois zero não é um número inteiro positivo.

5. f) Falsa, pois, por exemplo, ‒1 não é um número natural.

5. g) Falsa, pois, por exemplo, 0,5 não é número inteiro.

6. a) Nenhum.

6. b) 7; 1; 17.

6. c) 9; 99; .999999.

Pense mais um poucoreticências:

a) 5; 4; 3,5; 3,25.

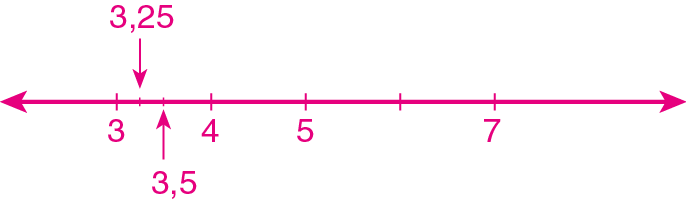
Ilustração. Reta numérica com os pontos, da esquerda da direita: 3; 3,25; 3,5; 4; 5 e 7.

c) Sim.

d) Espera-se que os estudantes respondam afirmativamente.

e) Espera-se que os estudantes respondam que existem infinitos números racionais.

Exercícios propostos

Antes de resolver o exercício 4, se necessário, retome a definição de número inteiro. Nesse exercício, os estudantes devem dividir o numerador pelo denominador de cada fração para descobrir se o número é inteiro ou não. Os números inteiros dentre os apresentados são

‒ \frac{20}{10}

+ \frac{12}{4}

Aproveite o exercício 5 para explorar a noção de contraexemplo, esclarecendo que é útil para corroborar a falsidade das sentenças, mas não serve como prova das sentenças verdadeiras.

No exercício 6, destaque o que há de diferentre entre as expressões “de 1 a 9” e “entre 1 e 9”:

• de 1 a 9, incluem-se o 1 e o 9: 1, 2, 3, 4, 5, 6, 7, 8 e 9;

• entre 1 e 9, excluem-se o 1 e o 9: 2, 3, 4, 5, 6, 7 e 8.

Pense mais um poucoreticências

Essa seção pretende retomar o conceito de média aritmética para tratar de um conceito fundamental no estudo dos conjuntos numéricos: o conjunto dos números racionais é um conjunto denso.

As resoluções dessa seção estão no início deste Manual, nas orientações específicas do capítulo 1.

Representações dos números racionais

Explore as diferentes representações de um número racional e a conversão de uma fórma para a outra: a fórma de fração e a fórmadecimal. Se julgar adequado, retome a fórma percentual, associada a frações centesimais.

Página 14

Muitos números racionais podem ser representados por uma fração decimal, isto é, de denominador 10, 100, .1000 etcétera, como os números a seguir.

Esquema. Quatro números racionais e suas respectivas representações por frações decimais. Número: menos 2, é igual à fração menos 20 décimos. Número: fração 1 quarto, é igual à fração 25 centésimos. Número: menos 5,3, é igual à fração menos 53 décimos. Número: 6,000, é igual à fração 6 mil milésimos. Todas as frações com denominador 10, 100 ou 1000 estão identificadas por: frações decimais.

Já os números

\frac{4}{11}

\frac{32}{15}

não podem ser representados por uma fração decimal. No entanto, eles podem ser escritos na fórma decimal.

Note que, nas representações 0,3636reticências e 2,1333reticências, as reticências indicam infinitas casas decimais e periódicas. Por exemplo: em 0,3636reticências, as reticências indicam que 36, chamado de período, continua se repetindo indefinidamente. Já em 2,1333reticências, temos uma representação decimal periódica de período 3.

A representação decimal periódica recebe o nome de dízima periódica.

Uma dízima periódica pode ser escrita abreviadamente, colocando-se um traço sobre o período. Note a representação abreviada de algumas dízimas periódicas.

a) 2,555reticências =

2, \overline{5}

b) ‒0,1313reticências =

‒ 0, \overline{13}

c) 1,2777reticências =

1, 2 \overline{7}

d) 0,21888reticências =

0, 21 \overline{8}

e) ‒ 8,612612reticências =

‒ 8, \overline{612}

f) 4,0979797reticências =

4, 0 \overline{97}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

7 Escreva no caderno a representação decimal das frações a seguir.

\frac{35}{10}

\frac{28}{100}

‒ \frac{7}{100}

‒ \frac{321}{10000}

\frac{542}{100}

\frac{12}{1000}

8 Observando os resultados do exercício anterior, estabeleça a relação existente entre a quantidade de zeros do denominador de uma fração decimal e a quantidade de casas após a vírgula na representação decimal dessa fração.

9 Represente no caderno cada fração na fórma decimal.

\frac{2}{5}

\frac{5}{6}

\frac{11}{3}

‒ \frac{45}{8}

‒ \frac{11}{90}

\frac{52}{25}

10 Adicionando os dois números de cada item, obtemos outro número na fórma de dízima periódica. Determine em cada caso essa dízima periódica na fórma abreviada.

a) 2,444reticências e 5,111reticências

b) 2,5 e 3,222reticências

Usando uma calculadora, faça o que se pede.

a) Escreva no caderno o número que aparece no visor após digitar estas teclas:

Ilustração. Teclas de uma calculadora: 3, 3, sinal de divisão, 9, sinal de igual.

b) Reserve esse resultado na memória aditiva, digitando a tecla

Ilustração. Tecla: M mais, que representa a memória aditiva.

c) Escreva no caderno o número que aparece no visor após digitar estas teclas:

Ilustração. Teclas de uma calculador: 1, 5, sinal de divisão, 9, sinal de igual.

d) Para subtrair o resultado do item c do resultado do item a, basta digitar as teclas

Ilustração. Tecla: M menos, que representa a memória subtrativa.

da memória subtrativa e

, que recupera o último resultado da memória. Escreva no caderno o número que aparece no visor.

e) Efetue

\frac{20}{9} ‒ \frac{47}{9}

e, em seguida, com uma calculadora, confira o resultado.

f) Calcule o valor da expressão:

5,222reticências ‒ 2,222reticências

Respostas e comentários

7. a) 3,5

7. b) 0,28

7. c) ‒0,07

7. d) ‒0,0321

7. e) 5,42

7. f) 0,012

8. A quantidade de zeros no denominador de uma fração decimal é igual à quantidade de casas após a vírgula na representação decimal dessa fração.

9. a) 0,4

9. b) 0,8333reticências

9. c) 3,666reticências

9. d) ‒5,625

9. e) ‒0,1222reticências

9. f) 2,08

10. a)

7, \overline{5}

10. b)

5, 7 \overline{2}

11. Oriente os estudantes a, antes de iniciar o item ê, limpar a memória da calculadora, digitando a tecla êmi sí.

11. a) 3,66666reticências

11. c) 1,66666reticências

11. d) 2

11. e) ‒3

11. f) 3

Exercícios propostos

Os exercícios 7 e 8 articulam-se para levar os estudantes a elaborar, com suas palavras, um regra prática para escrever frações decimais na fórma decimal.

Para resolver o exercício 9, é suficiente efetuar a divisão entre o numerador e o denominador de cada fração, obtendo-se um número decimal. Se necessário, sugira aos estudantes que confiram as respostas utilizando uma calculadora.

No exercício 10, os estudantes devem perceber que, no item a, obterão a dízima periódica 7,55555reticências, pois em 2,444reticências haverá sempre 4 na parte decimal, indefinidamente, e em 5,111reticências haverá sempre 1, levando a parte decimal da soma desses dois números a ser sempre 5, indefinidamente. E, no item b, obterão a dízima periódica 5,7222reticências pois 2,5 é um número decimal com 5 na parte decimal, e em 3,222reticências haverá sempre 2 na parte decimal, indefinidamente.

No exercício 11, usamos a calculadora para explorar a dízima periódica. No item ê, incentive os estudantes a efetuar a subtração das frações e, depois que obtiverem o resultado na fórma de fração, registrá-lo como um número decimal efetuando a divisão. No item f, destaque que a parte decimal de ambos os números é sempre igual a 2 e, por isso, se anulam na subtração proposta.

Página 15

Da fórma decimal para a fórma de fração

Já trabalhamos com a transformação de um número escrito na fórma de fração para a fórma decimal. Para isso, basta efetuar o algoritmo da divisão, como neste exemplo.

\frac{1}{5} = 1 : 5 = 0, 2

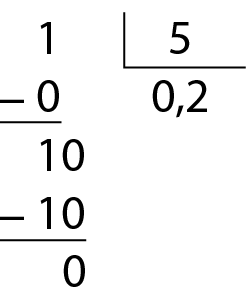
Algoritmo da divisão com chave. Dividendo: 1. Divisor, na chave: 5. Abaixo do dividendo, menos 0; um traço, e abaixo, o número 10; abaixo, o número menos 10; um traço e abaixo, o resto da divisão: 0. Abaixo do número 5, que está na chave, o quociente 0,2.

Agora, vamos acompanhar como transformar um número na fórma decimal para a fórma de fração.

1º caso: Quando o número tem finitas casas decimais, sua leitura fornece uma boa indicação de como expressá-lo na fórma de fração.

Observe alguns exemplos.

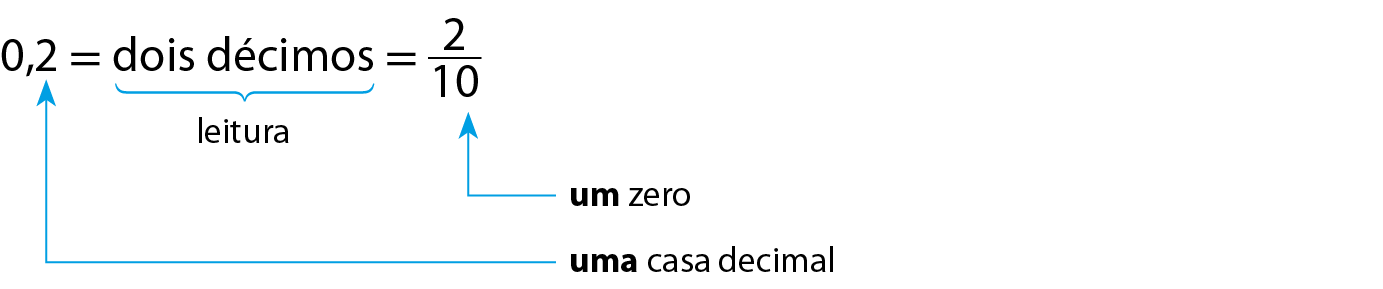
0,2, que é igual a dois décimos, que é igual a Fração; numerador: 2; denominador: 10. De 0,2, uma seta indica que há uma casa decimal. De dois décimos, uma chave indica como se lê o número. Da fração dois décimos, uma seta indica que há um zero acompanhando o 1 no denominador, formando o número 10.

5,325, que é igual a: cinco inteiros, trezentos e vinte e cinco milésimos, que é igual ao número misto: 5, fração; numerador: 325; denominador: 1000; fim da fração. De 5,325, uma seta indica que há três casas decimais. De cinco inteiros, trezentos e vinte e cinco e cinco milésimos, uma chave indica como se lê o número. De 5, Fração; numerador: 325; denominador: 1000; fim da fração, uma seta indica que há três zeros acompanhando o 1 no denominador, formando o número 1000.

2º caso: Quando o número tem infinitas casas decimais, como o número 0,55555reticências, procedemos do seguinte modo.

• Primeiro, chamamos o número 0,55555reticências de x, obtendo a igualdade:

x = 0,55555reticências (um)

• Em seguida, multiplicamos os dois membros por 10, chegando a uma nova igualdade:

10x = 5,5555reticências (dois)

• E, finalmente, subtraímos (um) de (dois), membro a membro, obtendo:

10x ‒ x = 5,555reticências ‒ 0,555reticências

9x = 5

\frac{9 x}{9} = \frac{5}{9}

x = \frac{5}{9}

Logo: 0,55555reticências =

\frac{5}{9}

Ilustração. Homem branco, de cabelo ruivo e camisa vermelha. Ele fala: Note que, ao multiplicar 0,55555 reticências por 10, a vírgula se deslocou uma casa para a direita do primeiro período. Assim, a parte decimal permaneceu a mesma.

Nesse caso, os dois membros da primeira igualdade foram multiplicados por 10. De modo geral, eles devem ser multiplicados por uma potência de 10 conveniente (10, 100, .1000, reticências) a fim de se deslocar a vírgula para a direita do primeiro período.

Respostas e comentários

Da fórma decimal para a fórma de fração

Como sugestão, organize os estudantes em duplas para trabalhar com esse tópico. Algumas duplas podem fazer a leitura do 1º caso, enquanto outras leem o 2º caso. Depois, sorteie um estudante do grupo de duplas que trabalhou com um dos casos, e outro do grupo do outro caso para irem à lousa explicar o que foi discutido em sua dupla. Nesse momento, as demais duplas que exploraram o caso apresentado podem ajudar o colega em sua explicação.

Em seguida, proponha a cada dupla atividades relativas ao caso que não foi trabalhado, para determinarem a fórma de fração de números racionais dados na fórma decimal pelo processo explicado na lousa.

Página 16

Acompanhe outro exemplo, com o número 2,373737reticências

• Chamando 2,373737reticências de x, obtemos a igualdade x = 2,373737reticências

• Multiplicando os dois membros dessa igualdade por 100, obtemos uma nova igualdade:

100x = 237,3737reticências

Ilustração. Mulher branca, de cabelo vermelho e camiseta roxa. Ela diz: Note que, ao multiplicar 2,373737 reticências por 100, a vírgula se deslocou duas casas para a direita do primeiro período. Assim, a parte decimal permaneceu a mesma.

• Subtraindo a primeira igualdade da segunda, membro a membro, temos:

100x ‒ x = 237,3737reticências ‒ 2,3737reticências

99x = 235

\frac{99 x}{99} = \frac{235}{99}

x = \frac{235}{99}

Ilustração. Menino branco, de cabelo preto e camiseta verde. Ele diz: A fração irredutível que gera uma dízima periódica é chamada de fração geratriz (palavra grifada).

Logo: 2,3737reticências =

\frac{235}{99}

Agora, acompanhe o caso da dízima composta 6,8424242reticências com um algarismo (8) após a vírgula, além do período 42.

• A partir da igualdade x = 6,8424242reticências, devemos obter duas outras igualdades em que, no segundo membro, as partes decimais sejam iguais. Dessa maneira, na subtração de uma pela outra, essas partes decimais se anulam.

• Como há um algarismo (8) após a vírgula que não faz parte do período, multiplicamos ambos os membros por 10 e, depois, por .1000:

10x = 68,424242... e .1000x = .6842,424242...

• Subtraindo a primeira igualdade da segunda, membro a membro, temos:

1000 x menos 10 x, igual, seis mil oitocentos e quarenta e dois vírgula quarenta e dois quarenta e dois quarenta e dois reticências, menos, 68 vírgula quarenta e dois quarenta e dois quarenta e dois reticências. Uma seta indica que as partes decimais são iguais e se anulam. x é igual à Fração; numerador: 6774; denominador: 990. Uma seta indica que podemos simplificar a fração dividindo por 6 o numerador e o denominador. x é igual a Fração; numerador: 1129; denominador: 165. Uma seta indica que a fração da igualdade é a fração geratriz.

Portanto, temos: 6,8424242reticências =

\frac{1129}{165}

Respostas e comentários

Da fórma decimal para a fórma de fração

Reproduza os dois exemplos na lousa, explorando os passos com os estudantes. Peça a eles que antecipem o que deve ser feito em cada exemplo e por quê. A justificativa do processo mostra o grau de entendimento que os estudantes têm do procedimento.

Caso algum estudante ainda apresente dúvidas, mostre-lhe outros exemplos na lousa. É importante que esse tipo de transformação seja bem compreendido pelos estudantes.

Página 17

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

Em uma calculadora, digite as teclas mostradas a seguir e escreva no caderno o resultado.

Ilustração. Teclas: 9, sinal de divisão, 6, 6, sinal de igual.

a) Para o último algarismo do número que aparece no visor, sua calculadora faz algum arredondamento?

b) Represente o número obtido na fórma de fração irredutível.

13 Escreva no caderno as frações irredutíveis que representam: o número 0,36, o número 0,04 e a adição 0,36 + 0,04.

14 Expresse os números a seguir na fórma de fração.

a) 3,444reticências

‒ 12, \overline{5}

0, \overline{45}

d) ‒0,31222reticências

15 Determine a fração irredutível que representa o valor de cada expressão a seguir.

0, 2 + 0, \overline{3}

0, 2 \overline{7} + 2, \overline{3}

0, 3 \overline{8} + 1, 4 \overline{5}

1, \overline{8} \cdot \frac{2}{17}

16 Dividindo um número x por um número y, obtém-se 2,555reticências Determine no caderno o valor de x e de y, sabendo que eles são números primos entre si.

17 Hora de criar – Escreva o número 7 como:

a) a soma de dois números racionais na fórma de fração;

b) a diferença de dois números racionais na fórma decimal, cada um com duas casas decimais;

c) a soma de duas dízimas periódicas.

18 Em uma caixa, há sete bolas numeradas de 1 a 7. Márcio retira três bolas consecutivas, sem recolocá-las na caixa, para representar um número a. O número retirado na primeira bola representará as unidades de a; o número da segunda bola representará os décimos de a; e o da terceira bola, os centésimos.

Ilustração. Menino branco, cabelo preto e roupa amarela em pé segurando três bolas numeradas: 2, 6 e 4. Ao lado, menina branca, de cabelo castanho claro, de camiseta amarela. Ela está sentada na carteira com uma caixa com bolinhas numeradas: 1, 3, 5, 7 sobre a mesa.

a) Márcio retirou os números 6, 4 e 2, nessa ordem. Qual é o número A formado nesse caso? Indique-o por uma fração irredutível.

b) Se, em seguida, Márcio retirar mais três bolas, qual é o maior número A possível que poderá ser formado com a retirada dessas bolas? E o menor?

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Observe as expressões a seguir.

1 + \frac{1}{2}

1 + \frac{1}{1 + \frac{1}{2}}

1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{2}}}

Calcule no caderno o valor das expressões dadas e, seguindo o padrão, escreva a quarta expressão e calcule seu valor.

Respostas e comentários

12. 0,13636reticências

12. a) A resposta depende da calculadora utilizada.

12. b)

\frac{3}{22}

13.

\frac{9}{25}; \frac{1}{25}; \frac{2}{5}

14. a)

\frac{31}{9}

14. b)

‒ \frac{113}{9}

14. c)

\frac{5}{11}

14. d)

‒ \frac{281}{900}

15. a)

\frac{8}{15}

15. b)

\frac{47}{18}

15. c)

\frac{83}{45}

15. d)

\frac{2}{9}

16. x = 23 e y = 9.

17. Respostas possíveis:

17. a)

\frac{13}{2} + \frac{1}{2}

;

17. b) 9,42 ‒ 2,42;

17. c)

4, \overline{8} + 2, \overline{1}

18. a) 6,42;

\frac{321}{50}

18. b) 7,53; 1,35.

Pense mais um pouco...:

\frac{3}{2}

\frac{5}{3}

\frac{8}{5}

1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{2}}}} = \frac{13}{8}

Exercícios propostos

As resoluções dos exercícios 12 a 15 e dos exercícios 17 e 18 estão no início deste Manual, nas orientações específicas do capítulo 1.

No exercício 16, comente com os estudantes o significado de números primos entre si: aqueles cujo máximo divisor comum é 1, ou seja, não há fatores primos comuns a esse grupo de números. Segue uma possível resolução dêsse exercício:

Note que, se

\frac{x}{y}

= 2,555reticências, então

\frac{x}{y}

é uma geratriz da dízima 2,555reticências .

Além disso, como x e y são primos entre si, a fração

\frac{x}{y}

é irredutível, ou seja, não pode ser simplificada.

Assim, para determinar x e y, precisamos determinar a fração geratriz irredutível dessa dízima. Fazendo 2,555reticências = a, obtemos:

a = 2,555...

10a = 25,555...

10a ‒ a = 25,555... ‒ 2,555...

9a = 23

a =

\frac{23}{9}

\frac{23}{9}

é uma fração irredutível.

Logo, x = 23 e y = 9.

Pense mais um poucoreticências

A seção tem um aspecto interessante e lúdico que pode ser explorado: o número de ouro (1,618033reticências) e a sequência de Fibonacci. A sequência de expressões dada converge para o número de ouro. Apresente também aos estudantes a sequência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, reticências) e mostre-lhes que o valor de cada expressão é uma fração cujo numerador e denominador são números consecutivos dessa sequência:

\frac{3}{2}, \frac{5}{3}, \frac{8}{5}, \frac{13}{8},

reticências

Sugestão de leitura

Para ampliar o trabalho, sugerimos:

LIVIO, M. Razão áurea. Rio de Janeiro/São Paulo: Record, 2007.

Nesse livro, o autor propõe uma jornada pela Arte e a Arquitetura, Botânica e Biologia, Física e Matemática. Ele relata curiosidades sobre uma série de personalidades fixadas no número ϕ, como os pitagóricos – defensores da tese em que a proporção áurea revelaria segredos dos deuses – Johannes Kepler, que considerava o número de ouro um dos maiores tesouros da Geometria, e Leonardo Fibonacci de Pisa, criador da sequência que leva seu nome.

Página 18

PARA SABER MAIS

O problema dos coelhos de Fibonacci e o número áureo

Leonardo de Pisa (cêrca de 1170-1240), conhecido como Fibonacci, publicou, em 1202, o famoso livro Liber Abaci (Livro do ábaco), em que explicou a notação indo-arábica que usamos hoje.

No capítulo XII, ele propôs o seguinte problema, que originou a sequência de Fibonacci:

Ilustração. Tira de papel com o texto: Um homem pôs um par de coelhos em um lugar cercado de todos os lados por um muro. Quantos pares de coelhos podem ser gerados a partir desse par em um ano se, supostamente, todo mês cada par dá à luz um novo par, que é fértil a partir do segundo mês?

O que nos interessa apresentar aqui é a sequência de Fibonacci. Por isso, vamos apenas iniciar a resolução dos primeiros passos do problema.

Observe a figura na qual um coelho grande representa um par de coelhos maduros (férteis) e um coelho pequeno representa um par de coelhos jovens (que não procriam).

• Vamos começar com um par de coelhos jovens.

• Esse par amadurece durante o 1º mês.

• Após o 1º mês, o 1º par dá à luz outro par, assim ficamos com 2 pares.

• Após o 2º mês, o par maduro dá à luz outro par jovem, enquanto o par de filhotes amadurece. Assim ficam 3 pares.

• Após o 3º mês, cada um dos 2 pares maduros dá à luz outro par, e o par de filhotes amadurece. Temos agora 5 pares.

• Após o 4º mês, cada um dos 3 pares maduros dá à luz outro par, e os 2 pares de filhotes crescem. Agora temos 8 pares.

• Após o 5º mês, temos 1 par de filhotes de cada um dos 5 pares adultos, mais 3 pares crescendo. Total: 13 pares.

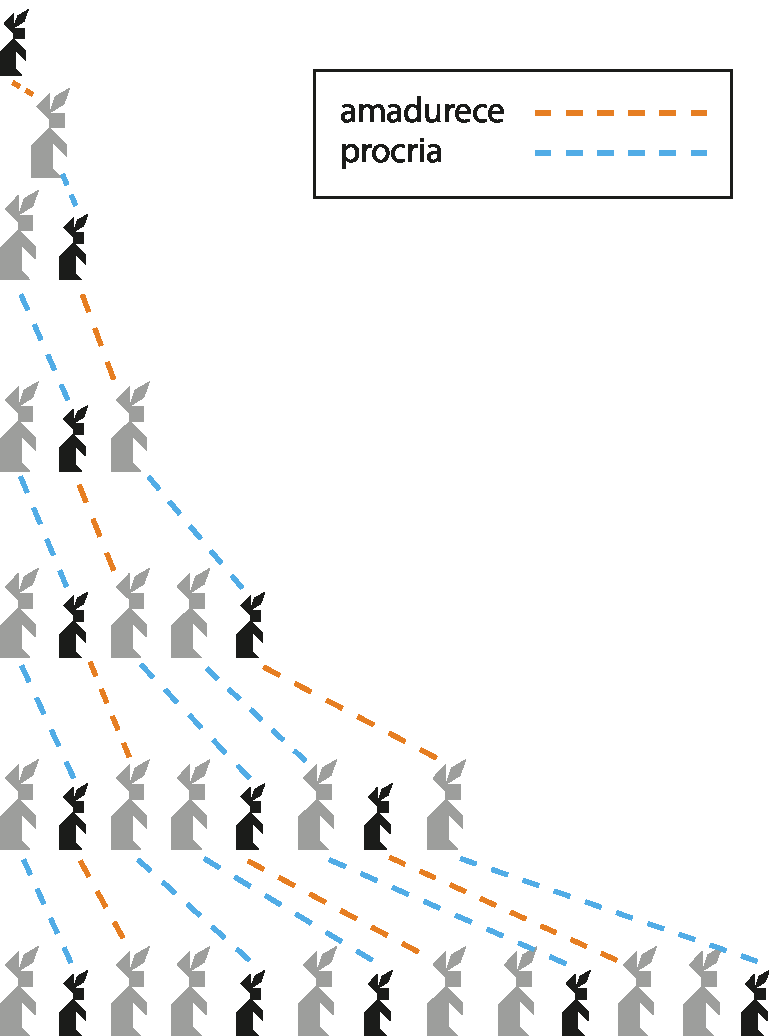
Esquema. Reprodução de coelhos em cinco meses. De cima para baixo: 1 coelho pequeno. Abaixo, 1 coelho grande (coelho pequeno maduro). Abaixo, no primeiro mês: 1 coelho grande procria 1 coelho pequeno; total de 2 coelhos: 1 grande, 1 pequeno. Abaixo, segundo mês: 1 coelho maduro procria 1 coelho pequeno; 1 coelho pequeno amadurece para 1 coelho grande; total de 3 coelhos: 2 grandes, 1 pequeno. Abaixo, terceiro mês: 2 coelhos grandes procriam 2 coelhos pequenos; 1 coelho pequeno amadurece para 1 coelho grande; total de 5 coelhos: 3 grandes e 2 pequenos. Abaixo, quarto mês: 3 coelhos grandes procriam 3 coelhos pequenos; 2 coelhos pequenos amadurecem para 2 coelhos grandes; total de 8 coelhos: 5 grandes, 3 pequenos. Abaixo, quinto mês: 5 coelhos grandes procriam 5 coelhos pequenos; 3 coelhos pequenos amadurecem para 3 coelhos grandes; total de 13 coelhos: 8 grandes, 5 pequenos.

Podemos, então, observar a sequência de números de Fibonacci: 1, 1, 2, 3, 5, 8, 13, reticências

Dados obtidos em: LIVIO, Mario. Razão áurea. 3. ed. Rio de Janeiro: Record, 2008. p. 116.

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

1 Compare a soma de dois números consecutivos da sequência com o número seguinte.

2 Quais são os próximos quatro números da sequência?

3 Com os onze números (n1, n2, n3, n4, reticências) da sequência agora conhecidos, calcule a razão de um número pelo termo anterior com aproximação até a terceira casa após a vírgula. Consulte a abertura do capítulo e diga de qual número os quocientes obtidos se aproximam.

Respostas e comentários

1. Espera-se que os estudantes percebam que a soma é igual ao próximo número da sequência.

2. Espera-se que os estudantes obtenham 21, 34, 55 e 89.

\frac{n_{2}}{n_{1}}

= 1,000;

\frac{n_{3}}{n_{2}}

= 2,000;

\frac{n_{4}}{n_{3}}

= 1,500;

\frac{n_{5}}{n_{4}}

= 1,667;

\frac{n_{6}}{n_{5}}

= 1,600;

\frac{n_{7}}{n_{6}}

= 1,625;

\frac{n_{8}}{n_{7}}

= 1,615;

\frac{n_{9}}{n_{8}}

= 1,619;

\frac{n_{10}}{n_{9}}

= 1,618;

\frac{n_{11}}{n_{10}}

= 1,618. Aproximam-se do número áureo.

Para saber mais

Para trabalhar com essa seção, organize os estudantes em grupos e peça-lhes que leiam o texto e escrevam um pequeno comentário sobre o que entenderam em relação à reprodução dos coelhos. Ao final, em uma roda de conversa, peça a eles que compartilhem suas conclusões.

Essa seção explora a sequência de Fibonacci.

Agora é com você!

As resoluções das atividades 1 a 3 estão no início deste Manual, nas orientações específicas do capítulo 1.

A atividade 3 propicia aos estudantes relacionar a sequência ao número de ouro, ampliando o trabalho da seção anterior Pense mais um poucoreticências .

Se julgar conveniente, peça previamente aos estudantes que pesquisem sobre a sequência de Fibonacci e suas aplicações, o que poderá contribuir para o desenvolvimento dessa seção na sala de aula.

Sugestões de leitura

Para enriquecer o trabalho com essa seção, sugerimos:

BELUSSI, G. M. et alponto Número de ouro. Disponível em: https://oeds.link/2g2vfc. Acesso em: 13 junho 2022.

SILVA, A. L. A sequência da natureza e a matemática de Fibonacci. Jornal Biosferas. Disponível em: https://oeds.link/cy3xNh. Acesso em: 13 junho 2022.

Essas duas sugestões de leitura tratam da sequência de Fibonacci, razão áurea e número de ouro.

Página 19

TRABALHANDO A INFORMAÇÃO

Pesquisa amostral e estimativas

Ícone do Tema Contemporâneo Transversal: CIDADANIA E CIVISMO.

Violência contra mulheres

A violência contra as mulheres se manifesta de diversas fórmas. De fato, o próprio conceito definido na Convenção de Belém do Pará (1994) aponta para esta amplitude, definindo violência contra as mulheres como “qualquer ação ou conduta, baseada no gênero, que cause morte, dano ou sofrimento físico, sexual ou psicológico à mulher, tanto no âmbito público como no privado” (Artigo 1º). Além das violações aos direitos das mulheres e a sua integridade física e psicológica, a violência impacta também no desenvolvimento social e econômico de um país.

SUBSECRETARIA DE POLÍTICAS PÚBLICAS PARA MULHERES. Violência contra a mulher. Mato Grosso do Sul, [2021?]. Disponível em: https://oeds.link/MF1MKA. Acesso em: 2 abril 2022.

Em 2021, o Instituto DataSenado, em parceria com o Observatório da Mulher contra a Violência, realizou uma pesquisa, com 3 mil brasileiras de 16 anos ou mais, denominada “Violência doméstica e familiar contra a mulher – 2021”.

Para 71% das entrevistadas, o Brasil é um país muito machista, e 68% conhecem uma ou mais mulheres vítimas de violência doméstica ou familiar, enquanto 27% declaram já ter sofrido algum tipo de agressão por um homem.

Note, nas tabelas a seguir, outros dados sobre essa pesquisa.

Tabela 1: De forma geral, você acha que as mulheres são tratadas com respeito no Brasil?
	Amostra observada	População estimada
Sim	130	3.422.511
Às vezes	1.280	37.719.799
Não	1.574	49.490.883
Não sei/Prefiro não responder	16	581.707
Total	3.000	91.214.900

Fonte: BRASIL. Senado Federal. Violência doméstica e familiar contra a mulher, Brasília, Distrito Federal: Senado Federal, 2021. Disponível em: https://oeds.link/qWeDZi. Acesso em: 2 abril 2022.

Tabela 2: Alguma amiga, familiar ou conhecida já sofreu algum tipo de violência doméstica ou familiar?
	Amostra observada	População estimada
Sim, mais de uma	1.638	45.041.306
Sim, conheço uma	533	17.279.570
Não conheço	813	28.464.935
Não sei/Prefiro não responder	16	429.089
Total	3.000	91.214.900

Fonte: BRASIL. Senado Federal. Violência doméstica e familiar contra a mulher, Brasília, Distrito Federal: Senado Federal, 2021. Disponível em: https://oeds.link/qWeDZi. Acesso em: 2 abril 2022.

Respostas e comentários

Trabalhando a informação

Habilidade da BNCC: ê éfe zero nove ême ah dois dois.

Ao propor aos estudantes atividades em que eles devem escolher e construir o gráfico mais adequado (colunas, setores, linhas), com ou sem uso de planilhas eletrônicas, para apresentar um determinado conjunto de dados, destacando aspectos como as medidas de tendência central, esta seção favorece o desenvolvimento da habilidade (ê éfe zero nove ême ah dois dois).

A seção trata de pesquisa amostral e estimativas com o tema “Violência contra mulheres”.

Para explorar o Tema Contemporâneo Transversal educação em direitos humanos, os estudantes podem pesquisar e conversar sobre o tema e, para isso, podem ser incentivados a responder perguntas como: O que é preciso mudar na sociedade para que os casos de violência contra as mulheres acabem? Por que as mulheres, mesmo com suas importantes conquistas, ainda são vítimas de assédio sexual, atos de violência doméstica física e/ou psicológica, feminicídio? Como romper o modelo estrutural que coloca as mulheres em posições de inferioridade e situações de opressão?

As reflexões que devem ser feitas para mudar essa situação são muitas, mas o descondicionamento desses pilares deve começar na educação dos estudantes.

Uma sugestão é formar grupos com estudantes e profissionais da escola que trabalhem sistematicamente o tema, promovendo discussões e questionamentos sobre as causas da violência contra as mulheres, procurando envolver todos e desconstruir ideias preconcebidas, que vão contra qualquer ideia de humanismo e de justiça. Podem ser discutidas outras questões com a finalidade de promover a educação inclusiva e solidária, combatendo todo tipo de bullying, mas, neste contexto. A escola, como centro de convívio e de formação cidadã, tem responsabilidade nas propostas de mudança visando a uma sociedade mais justa, democrática e inclusiva. Esse trabalho está alinhado e favorece o desenvolvimento das competências gerais 8, 9 e 10.

Página 20

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

1 O que diz a Convenção de Belém do Pará (1994) sobre o que caracteriza a violência contra as mulheres?

2 Segundo a pesquisa, que percentual das entrevistadas consideram o Brasil um país machista?

3 De acordo com os dados, é possível dizer que as entrevistadas acham que as mulheres são tratadas com respeito no Brasil? Justifique sua resposta.

4 A maioria das entrevistadas conhece alguma mulher que já sofreu alguma violência? Justifique sua resposta.

5 Nas tabelas, foram identificadas a amostra observada e a população estimada. A amostra corresponde ao número de entrevistadas e, com base nesses valores e análises estatísticas, estimou-se a população feminina brasileira com 16 anos ou mais, correspondente a cada resposta.

Ilustração. Mulher negra, de óculos, cabelo preto, faixa roxa na cabeça, e blusa escura com detalhes amarelos. Ela fala: Observe, nas tabelas, que a população estimada para uma mesma quantidade de respostas tem valores diferentes.

A partir de uma pesquisa por amostragem é possível estimar a população correspondente. Para isso, são feitas análises estatísticas dos resultados, estabelecendo margens de erro e um índice de confiança de todo o resultado.

No caso dos dados apresentados na pesquisa “Violência doméstica e familiar contra a mulher – 2021”, o índice de confiança é 95%, e cada grupo de dados apresenta uma margem de erro.

Note que, para as duas perguntas apresentadas nas tabelas, 16 pessoas responderam não sei/prefiro não responder. Mas a estimativa para a população correspondente não foi a mesma. Isso ocorreu porque a margem de erro foi diferente para cada conjunto de dados. Qual foi a população estimada para cada um desses casos?

6 Considerando as 16 pessoas, em qual caso a população foi estimada para um valor maior e em qual caso foi estimada para um valor menor?

7 Você já tomou conhecimento de alguma pesquisa que apresente margem de erro? Converse com o professor e os colegas sobre essas pesquisas.

8 Considerando a temática apresentada pela pesquisa, procure outras informações sobre o assunto e converse com os colegas e o professor sobre ações que entidades governamentais podem fazer para conscientizar a população sobre esse tipo de violência.

Em grupos, elaborem cartazes de conscientização sobre a violência contra as mulheres. Com a permissão da escola e de outros estabelecimentos que frequentam, colem esses cartazes em lugares de grande visibilidade.

Respostas e comentários

1. Qualquer ação ou conduta, baseada no gênero, que cause morte, dano ou sofrimento físico, sexual ou psicológico à mulher, tanto no âmbito público como no privado.

2. 71%

3. Não, pois mais da metade das entrevistas (uma.quinhentas e setenta e quatro) responderam que não.

4. Sim, pois duas.cento e setenta e uma entrevistadas (que correspondem a cêrca de 72% das entrevistadas) responderam que conhecem pelo menos uma mulher que sofreu violência.

5. Tabela 1: quinhentas e oitenta e uma.setecentas e sete mulheres; tabela 2: quatrocentas e vinte e nove.089 mulheres.

6. Observando o conjunto de dados é possível perceber que, para esse grupo de 16 pessoas, os dados da tabela 1 foram arredondados para um valor maior, e os da tabela 2, para um valor menor. Após estudarem o capítulo 3 é possível retornar a esta questão e perceber que, se os valores fossem proporcionais, ou seja, se não fossem consideradas as margens de erro, o valor seria de aproximadamente quatrocentas e oitenta e seis.quatrocentas e oitenta mulheres (16 ⋅ ..91214900 : .3000 ≃ .486480).

7. Espera-se que os estudantes respondam que em pesquisas eleitorais é comum o uso do termo margem de erro.

8. Resposta pessoal.

9. Resposta pessoal.

Agora quem trabalha é você!

Essas atividades podem ser realizadas de maneira coletiva; utilize‑as para direcionar uma roda de conversa com os estudantes e incentive-os a debater o assunto, pesquisar e apresentar outros dados sobre o tema que fundamentem os argumentos que apresentarem.

Página 21

2. Números quadrados perfeitos

Se um número natural é a segunda potência de outro número natural, ele é chamado de quadrado perfeito. Então, um quadrado perfeito pode ser escrito como quadrado de outro número natural.

Observe alguns exemplos.

a) 4 é quadrado perfeito, pois 4 = 2elevado a 2.

b) 81 é quadrado perfeito, pois 81 = 9elevado a 2.

O número 32 não é quadrado perfeito, pois ele não é quadrado de nenhum número natural. Observe que 32 está entre dois quadrados perfeitos:

25 < 32 < 36,

em que 25 = 5elevado a 2, 36 = 6elevado a 2, e entre 5 e 6 não há nenhum número natural.

Assim, para produzir quadrados perfeitos, basta escolher um número natural e elevá-lo ao quadrado. Por exemplo, 12 é um número natural; então, 12elevado a 2 = 144, que é um quadrado perfeito.

Observe o que acontece quando decompomos 12 e 144 em fatores primos.

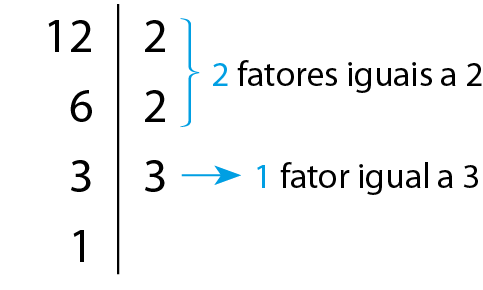
Fatoração do número 12. Do lado esquerdo, abaixo do número 12, os números 6, 3 e 1. Do lado direito, um traço vertical. Ao lado dele, os números: 2, 2 e 3. Ou seja, 2 fatores iguais a 2 e um fator igual a 3.

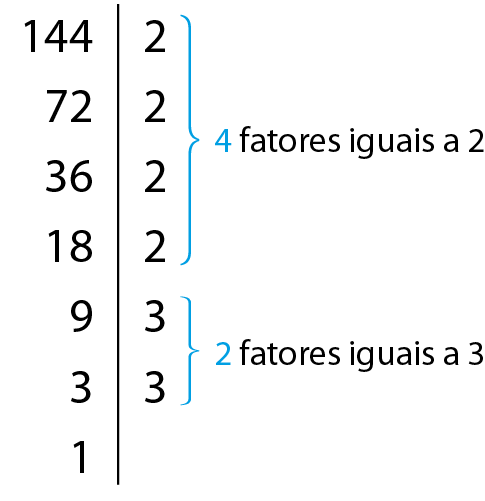
Fatoração do número 144. Do lado esquerdo, abaixo do número 144, os números 72, 36, 18, 9, 3 e 1. Do lado direito, um traço vertical. Ao lado dele, os números: 2, 2, 2, 2, 3 e 3. Ou seja, 4 fatores iguais a 2 e dois fatores iguais a 3.

Observe que 144 tem o dobro de fatores primos de 12:

• 12 tem 2 fatores iguais a 2 e 1 fator igual a 3;

• 144 tem 4 fatores iguais a 2 e 2 fatores iguais a 3.

Podemos verificar se um número é quadrado perfeito decompondo-o em fatores primos e verificando se a quantidade de cada um desses fatores é par.

Ilustração. Garota branca, de cabelo claro e comprido, blusa azul. Ela pergunta: O número 324 é quadrado perfeito?

Ilustração. Homem negro, cabelo curto e castanho, camisa vermelha. Ele fala: Vamos verificar. Decompondo 324 em fatores primos, temos.

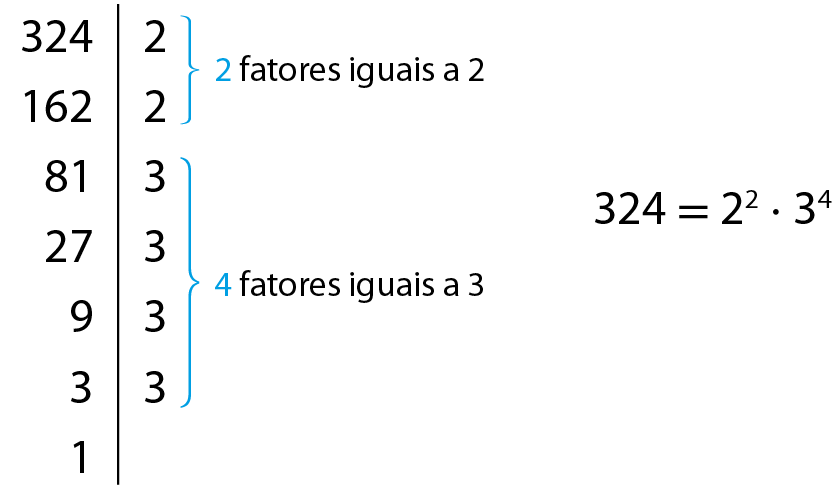
Esquema. Decomposição na vertical. Abaixo do número 324, os números 162, 81, 27, 9, 3 e 1. Do lado direito, um traço vertical. Ao lado dele, os números: 2, 2, 3, 3, 3, 3 e 3. Ou seja, 2 fatores iguais a 2 e 4 fatores iguais a 3, resultando na decomposição: 324 é igual a 2 elevado ao quadrado vezes 3 elevado a 4.

Note que todos os expoentes dos fatores são pares. Então, 324 é um quadrado perfeito.

Respostas e comentários

2. Números quadrados perfeitos

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro.

Retome com os estudantes a noção de quadrado perfeito e a fatoração de números naturais. Para decidir se um número é ou não quadrado perfeito, eles devem compreender que o algarismo das unidades do número pode dar pistas. Ressalte que:

1elevado a 2 = 1 6elevado a 2 = 36

2elevado a 2 = 4 7elevado a 2 = 49

3elevado a 2 = 9 8elevado a 2 = 64

4elevado a 2 = 16 9elevado a 2 = 81

5elevado a 2 = 25 10elevado a 2 = 100

Assim, um número quadrado perfeito só pode terminar em 1, 4, 9, 6, 5 e zero. Os quadrados perfeitos que terminam em:

• 1 são obtidos apenas com bases terminadas em 1 ou 9 (1elevado a 2 = 1 e 9elevado a 2 = 81);

• 4, apenas com bases terminadas em 2 ou 8 (2elevado a 2 = 4 e 8elevado a 2 = 64);

• 5, apenas com bases terminadas em 5 (5elevado a 2 = 25);

• 6, apenas com bases terminadas em 4 ou 6 (4elevado a 2 = 16 e 6elevado a 2 = 36);

• 9, apenas com bases terminadas em 3 ou 7 (3elevado a 2 = 9 e 7elevado a 2 = 49);

• 0, além do próprio zero, são potências de base 10 e de expoente par: 100 = 10elevado a 2, .10000 = (100)elevado a 2 etcétera, ou são produtos de quadrados perfeitos por essas potências de base 10: 900 = 9 · 100;

.160000 = 16 · .10000 etcétera

Também é importante reconhecerem os quadrados perfeitos de 1 a 100: 1, 4, 9, 16, 25, 36, 49, 64, 81 e 100. A identificação de quadrados perfeitos ou dos mais próximos de um número natural dado é a base para o cálculo de raízes quadradas.

Página 22

Acompanhe como podemos encontrar o número que gerou o quadrado perfeito 324:

324 = 22 ⋅ 34 = 22 ⋅ (32)2 = (2 ⋅ 32)2 = 182

Então, podemos dizer que 324 é quadrado perfeito, porque existe o número natural 18, que, elevado ao quadrado, resulta 324.

Ilustração. Garoto branco, de cabelo castanho, óculos e camiseta branca e azul. Ele pergunta: E o número 72, é quadrado perfeito?

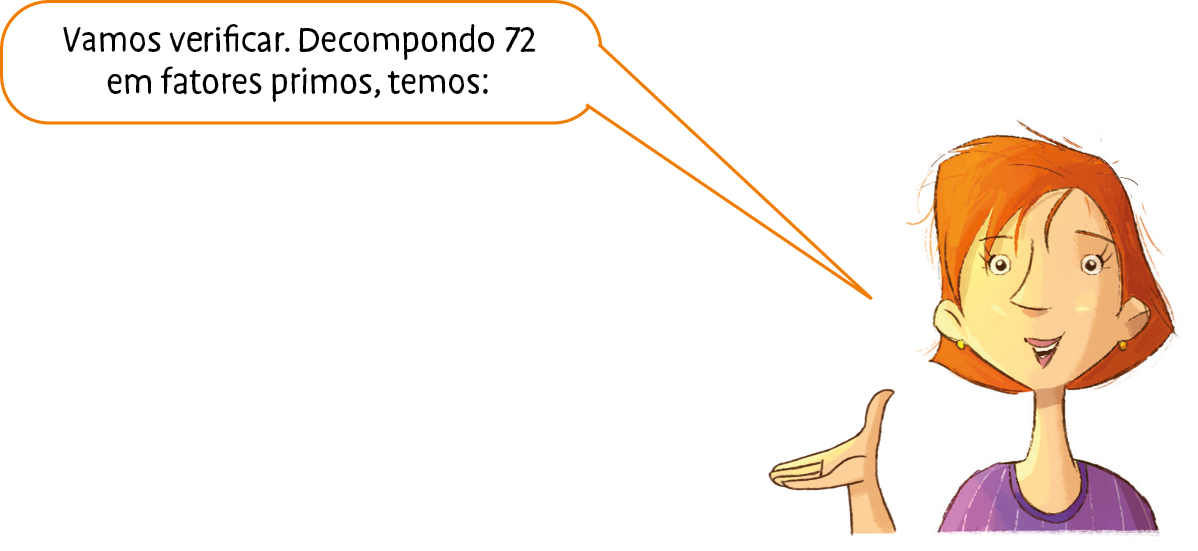
Ilustração. Mulher branca, de cabelo ruivo e camiseta roxa. Ela diz: Vamos verificar. Decompondo o número 72 em fatores primos, temos:

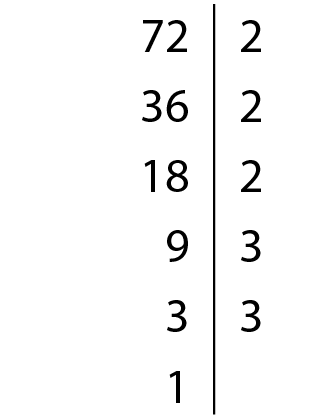
Esquema. Decomposição na vertical. Do lado esquerdo, abaixo do número 72, os números 36, 18, 9, 3 e 1. Do lado direito, um traço vertical. Ao lado dele, os números: 2, 2, 2, 3 e 3. Ou seja, 3 fatores iguais a 2 e dois fatores iguais a 3, resultando na decomposição: 72 é igual a 2 elevado ao cubo (expoente ímpar) vezes 3 elevado ao quadrado.

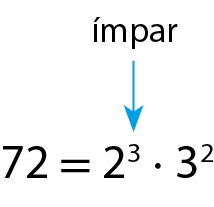
72 é igual a 2 elevado ao cubo (expoente ímpar) vezes 3 elevado ao quadrado.

Note que 72 tem um número ímpar de fatores iguais a 2. Então, 72 não é um quadrado perfeito.

Podemos representar geometricamente um número quadrado perfeito. Por exemplo, com 36 quadradinhos iguais é possível formar um quadrado maior, porque 36 é um número quadrado perfeito.

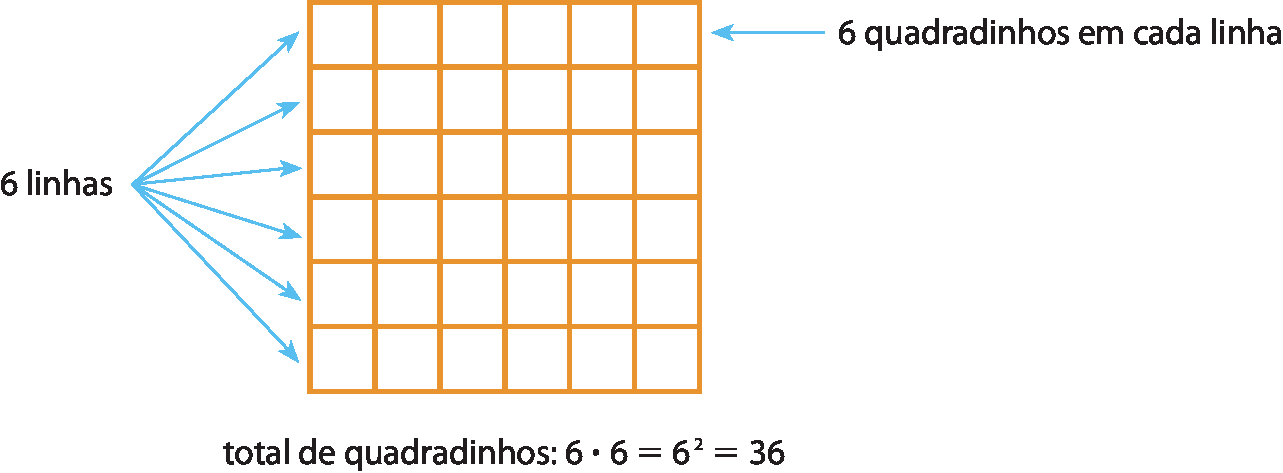
Ilustração. Quadrado dividido em 6 linhas e 6 colunas (6 quadradinhos em cada linha). Total de quadradinhos calculado por: 6 vezes 6 é igual a 6 elevado ao quadrado, que é igual a 36.

Note que, com 8 quadradinhos iguais, não é possível formar um quadrado maior, pois 8 não é quadrado perfeito.

Ilustração. Fileira horizontal com 8 quadradinhos.

Ilustração. Duas fileiras horizontais com 4 quadradinhos cada, resultando em 8 quadradinhos.

Ilustração. Duas fileiras com 3 quadradinhos cada e uma fileira com dois quadradinhos, resultando em 8 quadradinhos.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

19 Determine os quadrados perfeitos entre 100 e 200.

20 Efetuando a decomposição em fatores primos, verifique entre os números a seguir quais são quadrados perfeitos.

a) 225

b) 360

c) 441

d) 480

e) 576

f) 784

21 Com 144 quadradinhos iguais e justapostos, Fernando pode construir um quadrado maior. Quantos quadradinhos há em cada linha dêsse novo quadrado?

Respostas e comentários

19. 121, 144, 169 e 196.

20. Alternativas a, c, ê, f.

21. 12 quadradinhos.

Números quadrados perfeitos

Explore com os estudantes a decomposição em fatores primos como mais um processo de reconhecimento de quadrados perfeitos, principalmente para números maiores que 100.

A associação de um número quadrado perfeito com a possibilidade de obter um quadrado com a mesma quantidade de quadradinhos dá significado ao aprendizado dêsse tema. Forneça malhas quadriculadas e peça aos estudantes que representem os quadrados perfeitos de 1 a 100 pelo respectivo quadrado que pode ser formado.

Exercícios propostos

No exercício 19, para determinar os quadrados perfeitos entre 100 e 200, podem-se determinar as seguintes potências:

112 = 121

122 = 144

132 = 169

142 = 196

Que representam os quadrados perfeitos solicitados.

No exercício 20, temos:

a) 225 = 32 · 52

b) 360 = 23 · 32 · 5

c) 441 = 32 · 72

d) 480 = 25 · 3 · 5

e) 576 = 26 · 32

f) 784 = 24 · 72

O exercício 21, ao propor aos estudantes que imaginem uma figura e apliquem a reversibilidade da potenciação, antecipa o cálculo da raiz quadrada.

Acompanhe uma resolução dêsse exercício:

Como os quadradinhos devem formar um quadrado maior, os lados devem ter a mesma quantidade de quadradinhos. Logo, procuramos um número que elevado ao quadrado resulte em 144. Esse número é o 12.

Portanto, em cada linha dêsse novo quadrado deve haver 12 quadradinhos.

Uma ampliação dessa atividade pode ser feita ao perguntar aos estudantes quantos quadradinhos há em cada coluna dêsse quadrado maior. Eles devem concluir que há 12 quadradinhos em cada coluna.

Página 23

22 Com quantos quadradinhos iguais posso construir um quadrado maior que tenha 8 quadradinhos justapostos em cada linha?

Reúna-se com um colega e leiam o texto a seguir. Vamos usar três algarismos iguais para formar alguns números. A única operação que pode ser utilizada é a potenciação. Ao usar três algarismos iguais a 1, obtemos os números:

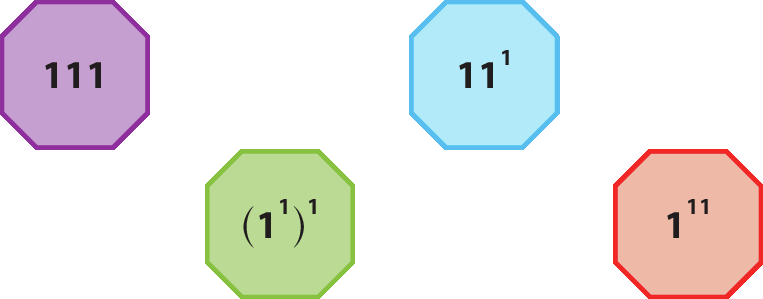
Ilustração. Fichas octogonais com os números: 111. Onze elevado a 1. Abre parêntese 1 elevado a 1 fecha parêntese, elevado a 1. Um elevado a 11.

É fácil verificar que o maior desses números é 111, pois (1elevado a 1)elevado a 1 = 1elevado a 1 = 1; 11elevado a 1 = 11 e 1elevado a 11 = 1.

Com três algarismos iguais a 2, obtemos os números:

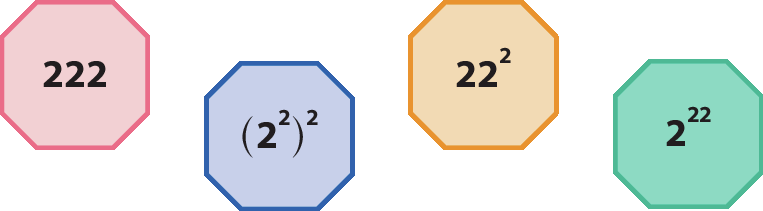
Ilustração. Fichas octogonais com os números: 222. Abre parêntese 2 elevado a 2 fecha parênteses elevado a 2. Vinte e dois elevado a 2. E 2 elevado a 22.

Agora, respondam às questões a seguir no caderno.

a) Qual é o maior desses números?

b) Quais destes números são quadrados perfeitos: 2elevado a 22, (2elevado a 2)elevado a 2 ou 22elevado a 2? Justifiquem a resposta.

Hora de criar – Troque com um colega um problema, criado por vocês, sobre quadrados perfeitos. Depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

3. Raiz quadrada de números racionais não negativos

Quando calculamos o quadrado de um número natural, estamos determinando um número quadrado perfeito. Por exemplo:

15elevado a 2 = 225

Nesse caso, podemos dizer:

• 225 é o quadrado de 15;

• 15 é a raiz quadrada de 225, que indicamos da seguinte maneira:

15 = \sqrt{225}

Isso ocorre com qualquer número racional não negativo. Observe alguns exemplos.

Esquema. Fração; dois quintos (entre parênteses) elevado a dois; é igual à fração 4 25 avos. Uma seta indica que: a fração 4 25 avos é o quadrado da fração 2 quintos. Outra seta indica que: a fração 2 quintos é a raiz quadrada da fração 4 25 avos, isto é, a raiz quadrada da fração 4 25 avos é igual à fração 2 quintos.

\sqrt{1, 44}

= 1,2, pois (1,2)elevado a 2 = 1,44

c) 13elevado a 2 = 169; então, 13 =

\sqrt{169}

Da mesma maneira que representamos os números quadrados perfeitos pela quantidade de quadradinhos que formam um quadrado maior, também podemos relacionar o quadrado de um número racional não negativo à medida da área de uma região quadrada cujo lado tem a medida representada por esse número (em determinada unidade de medida de comprimento).

Respostas e comentários

22. 64 quadradinhos.

23. a) 2elevado a 22 = ..4194304

23. b) Todos, pois 2elevado a 22 = (2elevado a 11)elevado a 2, (2elevado a 2)elevado a 2 = 2elevado a 4 e 22elevado a 2 já está na fórma de quadrado perfeito.

24. Resposta pessoal.

Exercícios propostos

No exercício 22, como cada linha do novo quadrado deverá ter 8 quadradinhos, devemos elevar o número 8 ao quadrado para obter a quantidade de quadradinhos que formam o novo quadrado.

Como 8elevado a 2 = 64, o novo quadrado terá 64 quadradinhos.

No exercício 23, os números apresentados são 222, (2elevado a 2)elevado a 2 = 4elevado a 2 = 16, 22elevado a 2 = 484 e 2elevado a 22 = ..4194304. Destes, o maior é 2elevado a 22.

Proponha aos estudantes outros grupos de números: 333, 33elevado a 3, (3elevado a 3)elevado a 3 e 3elevado a 33.

Nesse caso, nenhum deles é quadrado perfeito porque não é possível expressá-los por uma potência de expoente 2:

• 333 termina em 3; logo, não é quadrado perfeito.

• 33elevado a 3 = (3 · 11)elevado a 3 não pode ser expresso por potência de expoente 2.

• (3elevado a 3)elevado a 3 = 3elevado a 9 = 3elevado a 8 · 3 não pode ser expresso por potência de expoente 2 por causa do fator 3.

• 3elevado a 33 = 3elevado a 3 vezes 11 não pode ser expresso por potência de expoente 2.

3. Raiz quadrada de números racionais não negativos

Habilidades da Bê êne cê cê: EF09MA03 e EF09MA04.

Estendemos a relação de potências de expoente 2 com a formação de quadrados para bases racionais positivas, associando agora à noção de área do quadrado e, dessa maneira, ampliamos o desenvolvimento das habilidades (ê éfe zero nove ême ah zero três) e (ê éfe zero nove ême ah zero quatro) para, depois, estender sua aplicação a qualquer número real positivo.

Inicialmente, retome com os estudantes o cálculo de raízes quadradas exatas de números inteiros não negativos, usando como base o que foi visto anteriormente sobre os quadrados perfeitos. Por exemplo:

• 144 é um quadrado perfeito porque 12elevado a 2 = 144; então, podemos dizer que a raiz quadrada de 144 é 12, isto é, o número que elevado ao quadrado resulta em 144 é o 12.

• 200 não é um quadrado perfeito (200 = 2 · 100, e 2 não é quadrado perfeito). Isso significa que não há número natural que elevado ao quadrado resulta em 200, ou seja, 200 não tem raiz quadrada exata.

• 400 é quadrado perfeito, pois é 4 · 100, ou seja, pode ser expresso por (2 · 10)elevado a 2. Isso significa que o número 20 elevado ao quadrado resulta em 400; então, podemos dizer que a raiz quadrada de 400 é 20, isto é, o número que elevado ao quadrado resulta em 400 é o 20.

Página 24

Observação

▶ No estudo que faremos, vamos sempre nos referir à medida da área da região poligonal simplesmente por medida da área do polígono. Por exemplo, a medida da área de uma região quadrada será denominada área do quadrado.

Acompanhe as situações a seguir.

Situação 1

Uma região quadrada com área medindo 144 métros² tem o lado com 12 métros de medida de comprimento, pois 12elevado a 2 = 144.

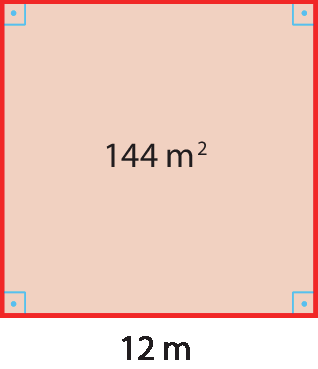
Ilustração. Quadrado de lado medindo 12 metros. Dentro, indicação da área total, medindo 144 metros quadrados.

Então,

12 = \sqrt{144}

Assim, para encontrar a medida ℓ do lado de um quadrado, sabendo que a medida de sua área é A, basta encontrar a raiz quadrada de A.

ℓ = \sqrt{A}, p o i s ℓ^{2} = A

Situação 2

A área de uma plantação, que tem o formato de um quadrado, mede 256 métros quadrados. Para determinar a medida do lado do terreno dessa plantação, temos de calcular

\sqrt{256}

, pois ℓ2 = 256.

Como o número ℓ gera o quadrado perfeito 256, ele pode ser calculado ao decompor 256 em fatores primos. Assim, podemos escrever:

Fotografia. Vista do alto de plantação em formato quadrado em área gramada verde.

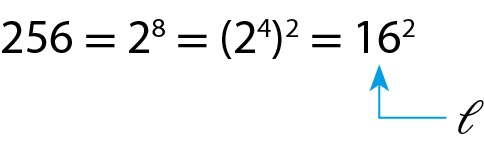
Esquema. 256 é igual a 2 elevado a 8, que é igual a: 2 elevado a 4 (entre parênteses) e elevado ao quadrado, que é igual a 16 ao quadrado. Do número 16, uma seta indica a letra l, que indica a medida do lado do quadrado.

Portanto, o lado do terreno dessa plantação mede 16 métros.

Cálculo da raiz quadrada pela decomposição em fatores primos

Vimos que, para identificar um número quadrado perfeito, verificamos se ele tem uma quantidade par de cada um de seus fatores primos.

Isso também nos possibilita encontrar o número que gerou o quadrado perfeito. Esse número gerador é a raiz quadrada do quadrado perfeito dado.

Acompanhe um exemplo.

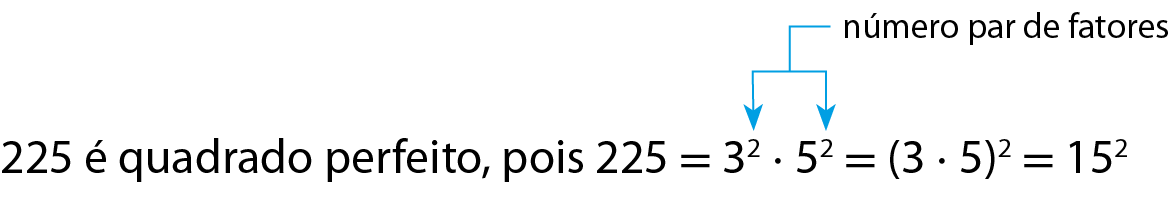
Esquema. 225 é quadrado perfeito, pois: 225 é igual a três ao quadrado vezes 5 ao quadrado, que é igual a 3 vezes 5 (entre parênteses) elevado ao quadrado, que é igual a 15 ao quadrado. Nos números três ao quadrado e 5 ao quadrado, uma seta indica que o expoente representa um número par de fatores que se repetem.

Então, 225 = 15elevado a 2 e, portanto,

15 = \sqrt{225}

Esse procedimento constitui um meio de determinar a raiz quadrada de um número quadrado perfeito.

Respostas e comentários

Raiz quadrada de números racionais não negativos

Para o cálculo de raiz quadrada, podemos usar o procedimento de situar o número dado entre quadrados perfeitos terminados em zero (para facilitar) e descobrir que números poderiam ser as raízes. Calculando o quadrado dessas possíveis raízes, comprovamos qual é o número procurado. Por exemplo:

• Qual é a raiz quadrada de 576? O problema se resume a procurar um número que elevado ao quadrado resulte em 576.

Vamos situar o 576 entre dois quadrados perfeitos (terminados em zeros para facilitar):

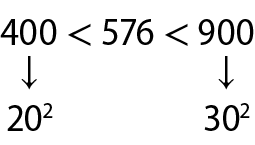
Esquema. 400 é menor que 576 que é menor que 900. 400 corresponde a 20 ao quadrado. 900 corresponde a 30 ao quadrado.

Então, se a raiz quadrada de 576 for exata, ela é um número entre 20 e 30. Mas como 576 tem final 6, as únicas possibilidades de isso ocorrer seriam potências cujas bases tivessem final 4 ou 6, isto é, haveria as possibilidades 24 ou 26. Como 400 é mais próximo de 576, testamos primeiro o 24 : 24 · 24 = 576. Podemos concluir que 24 elevado ao quadrado resulta em 576, isto é, a raiz quadrada de 576 é 24.

Comente com os estudantes que, caso a raiz quadrada procurada seja de um número racional positivo expresso na fórma de fração, podemos trabalhar com o numerador e o denominador separadamente para depois montar a fração que será a raiz quadrada procurada. Se esse número racional estiver expresso na fórma decimal, fazemos sua representação na fórma de fração e seguimos o que já foi exposto.

Página 25

Agora, para dar mais um exemplo, vamos determinar

\sqrt{576}

. Ao decompor 576 em fatores primos, obtemos:

576 = 2elevado a 2 ⋅ 3elevado a 2 = (2elevado a 3 ⋅ 3elevado a 1)elevado a 2 = 24elevado a 2

Como 576 = 24elevado a 2, concluímos que

\sqrt{576}

= 24.

Observe que 24, decomposto em fatores primos (24 = 2elevado a 3 ⋅ 3elevado a 1), apresenta metade dos fatores primos de 576.

Assim, de modo prático, podemos dizer que, para extrair a raiz quadrada de números quadrados perfeitos, primeiro decompomos o número em fatores primos; em seguida, dividimos cada expoente por 2; e, finalmente, efetuamos a multiplicação obtida.

Ilustração. Homem branco, de cabelo ruivo e camiseta vermelha. Ele diz: Dizemos “extrair a raiz quadrada” porque, nesse
procedimento, é como se extraíssemos do radical as bases das potências com expoente dois.

Ilustração. Menina negra, cabelo castanho e blusa amarela. Ela fala: E para calcular a raiz quadrada de números fracionários?

Ilustração. Homem branco, de cabelo ruivo e camiseta vermelha. Ele diz: Nesse caso, decompomos o numerador e o denominador em fatores primos e, em seguida, calculamos a raiz quadrada de cada um deles.

Observe mais alguns exemplos.

\sqrt{\frac{36}{625}} = \sqrt{\frac{2^{2} \cdot 3^{2}}{5^{4}}} = \frac{2 \cdot 3}{5^{2}} = \frac{6}{25}

\sqrt{12, 96} = \sqrt{\frac{1296}{100}} = \sqrt{\frac{2^{4} \cdot 3^{4}}{2^{2} \cdot 5^{2}}} = \frac{2^{2} \cdot 3^{2}}{2 \cdot 5} = \frac{4 \cdot 9}{10} = \frac{36}{10} = 3, 6

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

25 Justifique cada igualdade a seguir.

\sqrt{0,64}

= 0,8

\sqrt{2^{10} \cdot 3^{2}}

= 25 ⋅ 3

26 Extraia a raiz quadrada de cada número a seguir pela decomposição em fatores primos.

a) 256

b) 196

c) 484

d) 729

e) .1600

f) .1024

27 (unirrio-Rio de Janeiro) O valor de

\sqrt{15 ‒ \sqrt{32 + \sqrt{25 ‒ \sqrt{81}}}}

é:

a) 1.

b) 2.

c) 3.

d) 4.

e) 5.

28 Um paliteiro de base quadrada tem o formato da figura a seguir. Sabendo que a soma das medidas das áreas das faces laterais do paliteiro é igual a 162 centímetros² e que a área de todas as faces mede 202,5 centímetros², determine a medida a do lado da base dêsse paliteiro.

Ilustração. Bloco retangular com medida de lado da base quadrada igual à a, e um pequeno orifício na parte superior.

Respostas e comentários

25. a) (0,8)2 = 0,64

25. b) (25 ⋅ 3)2 = 210 ⋅ 32

26. a) 16

26. b) 14

26. c) 22

26. d) 27

26. e) 40

26. f) 32

27. Alternativa c.

28. a = 4,5 centímetros

Cálculo da raiz quadrada pela decomposição em fatores primos

Apresente o procedimento da decomposição em fatores primos como outro modo de determinar as raízes quadradas exatas de números racionais envolvidos.

Seguem alguns exemplos:

•

\sqrt{\frac{1}{25}} = ?

Note que 1 = 12 e 25 = 52. Assim, concluímos que

\frac{1}{25} = {(\frac{1}{5})}^{2}

. Logo:

\sqrt{\frac{1}{25}} = \frac{1}{5}

•

\sqrt{0, 2116} = ?

Como o número racional está na fórma decimal, vamos expressá-lo na fórma de fração:

0, 2116 = \frac{2 116}{10 000}

Agora, precisamos procurar o número que elevado ao quadrado resulta em

\frac{2 116}{10 000}

Sabemos que .10000 = (100)elevado a 2. Então, precisamos decompor o número .2116 em fatores primos e expressá-lo com uma potência de expoente 2, se possível.

.2116 = 4 · 529 = 4 · 23 · 23 =

= 2elevado a 2 · 23elevado a 2 = (2 · 23)elevado a 2 = 46elevado a 2

Utilizando a calculadora, pode-se verificar que:

46 · 46 = .2116

Assim, concluímos que

\frac{2116}{10000} = {(\frac{46}{100})}^{2}

; logo:

\sqrt{0,2116} = \sqrt{\frac{2116}{10000}}

= \frac{46}{100} = 0, 46

Fazendo a verificação:

0,46 · 0,46 = 0,2116

Exercícios propostos

O exercício 27 pode ser feito em duplas, pois a troca de experiências aumenta o repertório de estratégias dos estudantes. Comente que devem resolver primeiro as raízes quadradas. Assim, devem começar por

\sqrt{81}

\sqrt{15 - \sqrt{32 + \sqrt{25 - \sqrt{81}}}} = \sqrt{15 - \sqrt{32 + \sqrt{25 - 9}}} = \sqrt{15 - \sqrt{32 + \sqrt{16}}} =

= \sqrt{15 - \sqrt{32 + 4}} = \sqrt{15 - \sqrt{36}} = \sqrt{15 - 6} = \sqrt{9} = 3

(alternativa c).

As resoluções dos exercícios 25, 26 e 28 estão no início deste Manual, nas orientações específicas do capítulo 1.

Página 26

29 Usando a decomposição em fatores primos, calcule a raiz quadrada de:

\frac{25}{576}

;

b) 0,01;

\frac{64}{1225}

;

d) 19,36.

30 Ivan vai construir uma pipa colorida no formato de um quadrado. Para isso, ele recortou um quadrado de papel azul com área medindo .2500 centímetros quadrados, três quadrados de papel amarelo de área medindo 900 centímetros quadrados cada um e dois retângulos de papel vermelho de lados medindo 20 centímetros por 30 centímetros. Qual será a medida do lado dessa pipa?

Ilustração. Quadrado composto por quadrado grande azul, três quadrados amarelos menores e dois retângulos vermelhos pequenos.

31 O piso de um salão no formato de um quadrado é coberto com .10800 lajotas retangulares de lados medindo 40 centímetros por 30 centímetros. Determine no caderno:

a) a medida da área do salão;

b) as dimensões do salão.

Raiz quadrada aproximada

Os números quadrados perfeitos têm como raiz quadrada um número natural que, elevado ao quadrado, reproduz o número dado.

Observe o que acontece quando queremos extrair a raiz quadrada de um número que não é quadrado perfeito. Para exemplificar, vamos calcular a raiz quadrada do número 31.

O número 31 está compreendido entre os números quadrados perfeitos 25 e 36.

25 < 31 < 36

Então,

\sqrt{31}

deve estar compreendida entre

\sqrt{25}

\sqrt{36}

\sqrt{25} < \sqrt{31} < \sqrt{36}

Como

\sqrt{25}

= 5 e

\sqrt{36}

= 6, temos:

5 < \sqrt{31} < 6

Dizemos, então, que:

• 5 é a raiz quadrada aproximada por falta, a menos de uma unidade, do número 31;

• 6 é a raiz quadrada aproximada por excesso, a menos de uma unidade, do número 31.

Em geral, considera-se raiz quadrada aproximada de um número não quadrado perfeito a raiz quadrada aproximada por falta, a menos de uma unidade. Indica-se que 5 é a raiz quadrada aproximada por falta de 31, escrevendo-se:

\sqrt{31} ≃ 5

(Lemos: “a raiz quadrada do número trinta e um é aproximadamente igual a cinco”.)

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

32 Considerando o número 110, responda.

a) Entre quais números quadrados perfeitos ele está compreendido?

b) A raiz quadrada dêsse número está compreendida entre quais números naturais?

c) Qual é a raiz quadrada por falta, a menos de uma unidade?

Respostas e comentários

29. a)

\frac{5}{24}

29. b) 0,1

29. c)

\frac{8}{35}

29. d) 4,4

30. 80 centímetros

31. a) .1296 métros quadrados

31. b) 36 métros por 36 métros

32. a) 100 e 121.

32. b) 10 e 11.

32. c) 10

Exercícios propostos

As resoluções dos exercícios 29 a 31 estão no início deste Manual, nas orientações específicas do capítulo 1.

Raiz quadrada aproximada

Nesse tópico, apresentamos o cálculo aproximado de uma raiz quadrada, por falta ou por excesso, a menos de uma unidade. Isso ocorre quando queremos calcular a raiz quadrada aproximada de um número que não é quadrado perfeito.

Amplie o trabalho apresentando outros exemplos na lousa, além do dado no livro.

Exercícios propostos

A seguir, apresentamos uma resolução do exercício 32:

a) O número 110 está compreendido entre os números quadrados perfeitos 100 (102) e 121 (112).

b) Como a raiz quadrada de 110 deve estar entre dois números naturais, ela deve estar entre a raiz quadrada dos quadrados perfeitos 100 e 121. Logo, a raiz de 110 está entre 10 e 11.

c) Pelo item b, temos que a raiz quadrada de 110 por falta, a menos de uma unidade, é 10.

Página 27

33 Qual é o menor número natural que devemos subtrair de 640 para obter um número quadrado perfeito? E qual é a raiz quadrada aproximada de 640 por falta, a menos de uma unidade?

34 No século vinte, qual foi o único ano representado por um número quadrado perfeito? E no século vinte e um, qual será o ano?

35 Faça estimativas para obter o valor aproximado de:

\sqrt{51}

b) 50 ⋅

\sqrt{51}

c) 200 ⋅

\sqrt{51}

Como você pode comprovar os resultados que obteve?

Raiz quadrada com aproximação decimal

A seguir, vamos aprender a calcular a raiz quadrada de um número que não é quadrado perfeito com aproximação decimal.

Como exemplo, vamos considerar o número 2. Qual é o número racional que, elevado ao quadrado, resulta 2? Observe.

1 não pode ser, pois 12 = 1

2 não pode ser, pois 22 = 4

Dessa maneira,

\sqrt{2}

é um número compreendido entre 1 e 2

(1 < \sqrt{2} < 2)

Ilustração. Reta numérica com os pontos: 1, raiz quadrada de 2 e 2. Do ponto raiz quadrada de 2 parte uma seta indicando que 1 é menor que raiz quadrada de 2, que é menor que 2.

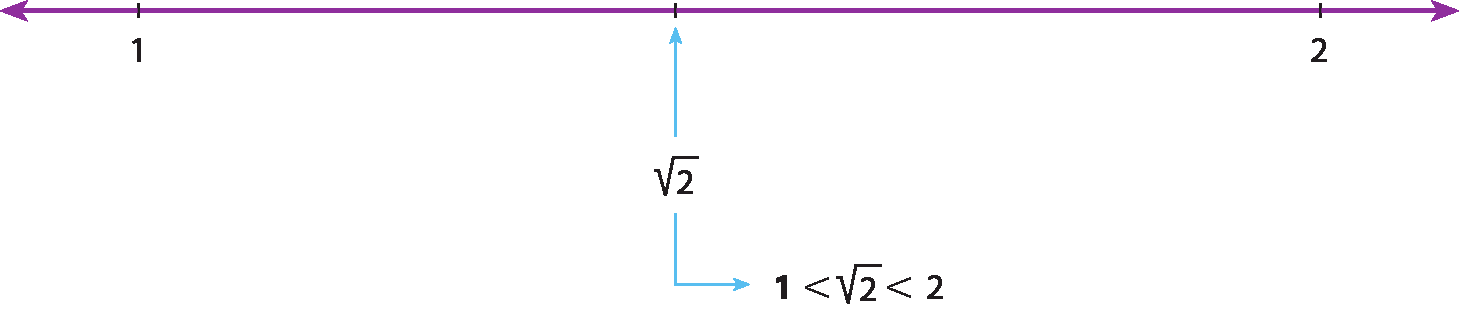
Como não existe nenhum número inteiro cujo quadrado dê 2, dizemos que 1 é a raiz quadrada aproximada do número 2.

Vamos procurar um número com uma casa decimal cujo quadrado seja mais próximo de 2.

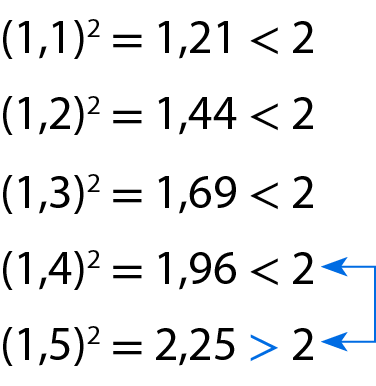
Esquema. 1,1 ao quadrado, é igual a 1,21, que é menor que 2. 1,2 ao quadrado, é igual a 1,44, que é menor que 2. 1,3 ao quadrado, é igual a 1,69, que é menor que 2. 1,4 ao quadrado, é igual a 1,96, que é menor que 2. 1,5 ao quadrado, é igual a 2,25, que é maior que 2. Duas setas indicam que o número 2 está entre 1,4 ao quadrado e 1,5 ao quadrado.

Como também não existe número com uma casa decimal cujo quadrado seja igual a 2, concluímos que

\sqrt{2}

é um número compreendido entre 1,4 e 1,5.

Ilustração. Reta numérica com os pontos: 1, 1,4, raiz quadrada de 2, 1,5 e 2. Do ponto entre os números 1,4 e 1,5, lugar estimado da raiz quadrada de 2, parte uma seta indicando que 1,4 é menor que raiz quadrada de 2, que é menor que 1,5.

Nesse caso, dizemos que a raiz quadrada aproximada do número 2 com uma casa decimal é igual a 1,4 e escrevemos

\sqrt{2}

≃ 1,4.

Respostas e comentários

33. 15; 25.

34. 1936; 2025.

35. a) 7

35. b) 350

35. c) .1400

35. Resposta possível: usando uma calculadora.

Exercícios propostos

As resoluções dos exercícios 33 e 34 estão no início deste Manual, nas orientações específicas do capítulo 1.

O exercício 35, além do uso da calculadora, tem como objetivo o experimento da estimativa.

Apresentar métodos diferentes para fazer cálculos ou resolver problemas é uma estratégia enriquecedora.

Acompanhe uma resolução:

\sqrt{51}

≃ ?

6 · 6 = 36

7 · 7 = 49

8 · 8 = 64

Logo, a

\sqrt{51}

é aproximadamente 7.

b) 50 ·

\sqrt{51}

≃ ?

Pelo item a, obtemos

\sqrt{51}

≃ 7.

Então:

50 ·

\sqrt{51}

≃ 50 · 7

50 ·

\sqrt{51}

≃ 350

c) 200 ·

\sqrt{51}

≃ ?

Pelo item a, obtemos

\sqrt{51}

≃ 7.

200 ·

\sqrt{51}

≃ 200 · 7

200 ·

\sqrt{51}

≃ .1400

• Podemos comprovar os resultados utilizando uma calculadora.

Página 28

Vamos tentar uma aproximação melhor, com duas casas decimais, para

\sqrt{2}

(1,41)2 = 1,9881 < 2

(1,42)2 = 2,0164 > 2

Logo,

\sqrt{2}

é um número compreendido entre 1,41 e 1,42.

Ilustração. Reta numérica com os pontos: 1, 1,4, raiz quadrada de 2 (1,4 menor que raiz quadrada de 2 menor que 1,42), 142 e 2. Setas indicam que raiz quadrada de 2 está localizada, na reta numérica, entre 1,41 e 1,42.

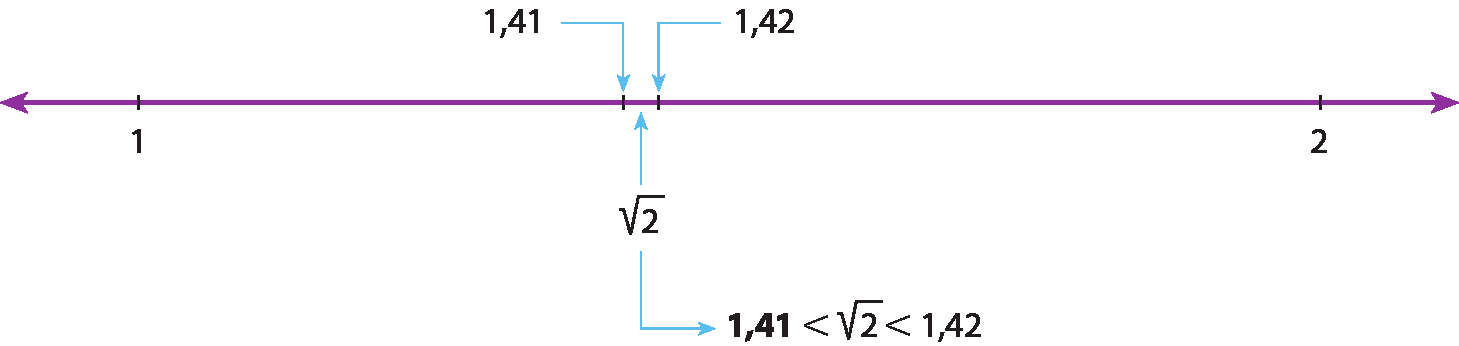
Então, podemos dizer que a raiz quadrada aproximada do número 2 com duas casas decimais é igual a 1,41 e escrevemos

\sqrt{2}

≃ 1,41.

Se prosseguirmos, encontraremos a raiz quadrada aproximada de 2 com quantas casas decimais desejarmos, sem, entretanto, encontrar um número decimal cujo quadrado resulte 2.

Acompanhe outros exemplos.

a) Calcule a raiz quadrada do número 58 com duas casas decimais.

Esquema. Sete ao quadrado é igual a 49, que é menor que 58. Oito ao quadrado é igual a 64, que é maior que 58. Uma chave indica que 7 é menor que raiz quadrada de 58, que é menor que 8.

7 é a raiz quadrada aproximada de 58.

Esquema. 7,1 ao quadrado é igual a 50,41, que é menor que 58. 7,2 ao quadrado é igual a 51,84, que é menor que 58. 7,5 ao quadrado é igual a 56,25, que é menor que 58. 7,6 ao quadrado é igual a 57,76, que é menor que 58. 7,7 ao quadrado é igual a 59,29, que é maior que 58. Uma chave indica que 7,6 é menor que raiz quadrada de 58, que é menor que 7,7.

7,6 é a raiz quadrada aproximada com uma casa decimal do número 58.

Esquema. 7,61 ao quadrado é igual a 57,9121, que é menor que 58. 7,62 ao quadrado é igual a 58,0644, que é maior que 58. Uma chave indica que 7,61 é menor que raiz quadrada de 58, que é menor que 7,62.

Assim, a raiz quadrada de 58 com duas casas decimais é 7,61. Escrevemos

\sqrt{58}

≃ 7,61.

b) Calcule a raiz quadrada do número 7,2 com uma casa decimal.

O número 7,2 está compreendido entre os quadrados perfeitos 4 e 9. Então:

\sqrt{4} < \sqrt{7, 2} < \sqrt{9}

, ou seja,

2 < \sqrt{7, 2} < 3

A raiz quadrada de 7,2 é um número compreendido entre 2 e 3.

Vamos começar testando 2,5.

(2,5)2 = 6,25 < 7,2

(2,6)2 = 6,76 < 7,2

(2,7)2 = 7,29 > 7,2

Assim, a raiz quadrada do número 7,2 com uma casa decimal é 2,6. Escrevemos

\sqrt{7, 2}

≃ 2,6.

Respostas e comentários

Raiz quadrada com aproximação decimal

Nesse tópico também vamos trabalhar com cálculo de raiz quadrada de um número que não é quadrado perfeito. Porém, aqui, a aproximação é decimal.

Reproduza os exemplos na lousa, destacando as etapas com os estudantes. Verifique se eles compreendem os passos de cada etapa.

Amplie o trabalho apresentando-lhes outros exemplos. Depois, peça a alguns estudantes que mostrem na lousa o procedimento que utilizaram. Incentive o uso de estratégias próprias e a descrição do processo.

Página 29

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

36 Verifique se 1,7 pode ser considerado uma raiz quadrada aproximada de 3.

37 Entre os números 3,87 e 3,88, qual deles se aproxima mais de

\sqrt{15}

38 Qual é o número com uma casa decimal que representa a raiz quadrada aproximada de 265?

39 Calcule a raiz quadrada aproximada com uma casa decimal de:

a) 572

b) 28,19

c) 42,55

d) 12,6

Com uma calculadora, encontre a raiz quadrada aproximada com duas casas decimais de:

\sqrt{88}

\sqrt{8 800}

\sqrt{6 000 000}

\sqrt{6}

\sqrt{1 000}

\sqrt{100 000}

Com uma calculadora, mas sem usar a tecla

, encontre a raiz quadrada aproximada com duas casas decimais:

\sqrt{410}

\sqrt{1 715}

\sqrt{1 999}

\sqrt{3 500}

Agora, usando a tecla

da calculadora, determine as raízes quadradas do exercício anterior e verifique se os resultados obtidos nele estão de acordo com os novos resultados.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Sabendo que 2732 = .74529, calcule:

\sqrt{745,29}

\sqrt{7 452 900}

4. Os números reais

Considere o número 0,101112reticências

Observando a formação dêsse número, vamos supor que podemos dar continuidade à sua parte decimal do seguinte modo: 0,10111213reticências; 0,1011121314reticências; e assim por diante.

Como a representação decimal dêsse número tem infinitas casas decimais e não é periódica, ele não pode ser escrito na fórma de fração; logo, esse número não é racional.

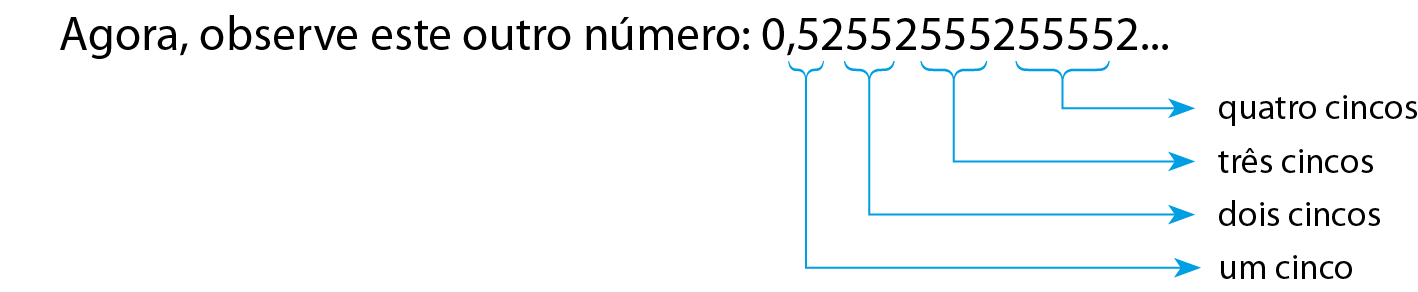
Esquema. Agora, observe este outro número:
Número real 0,52552555255552 reticências. Setas, da esquerda para a direita, indicam que o 5 se repete uma vez, depois duas vezes, depois três vezes, depois quatro vezes.

Imagine que, para continuar escrevendo esse número, devemos acrescentar sempre um algarismo 5 aos grupos de 5 separados por 2:

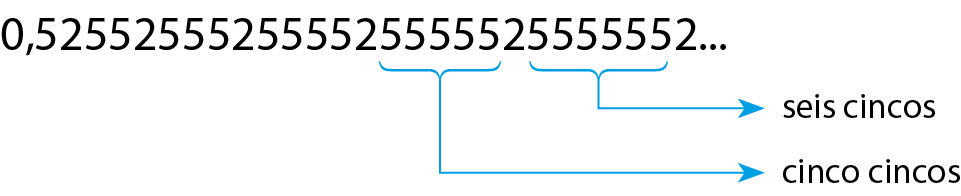
Esquema. Número real 0,525525552555525555525555552 reticências. Setas, da esquerda para a direita, indicam que o 5 se repete cinco vezes, depois seis vezes.

Respostas e comentários

36. Sim.

37. 3,87

38. 16,2

39. a) 23,9

39. b) 5,3

39. c) 6,5

39. d) 3,5

40. a) 9,38

40. b) 93,81

40. c) .2449,49

40. d) 2,45

40. e) 31,62

40. f) 316,23

41. a) 20,24

41. b) 41,41

41. c) 44,71

41. d) 59,16

42. Espera-se que os resultados estejam de acordo.

Pense mais um poucoreticências:

a) 27,3

b) .2730

Exercícios propostos

Com esses exercícios, espera-se que os estudantes mobilizem os conhecimentos construídos acerca de raiz quadrada aproximada. Socialize as diferentes estratégias que surgirem.

Os exercícios 41 e 42 propõem o uso da calculadora como instrumento de pesquisa e de validação de resultados.

As resoluções dos exercícios 36 a 42 estão no início deste Manual, nas orientações específicas do capítulo 1.

Pense mais um poucoreticências

Nesta seção, incentive os estudantes a obter o resultado apenas com base na observação da igualdade informada, sem efetuar outros cálculos. Espera-se que eles percebam que:

• como 745,29 =

\frac{74 529}{100}

\sqrt{74 529} = 273

, obtemos:

\sqrt{745,29} = \frac{273}{10} = 27, 3

• como ..7452900 = .74529 · 100 e

\sqrt{74529} = 273

, obtemos:

\sqrt{7 452 900} = 273 \cdot 10 = 2 730

4. Os números reais

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah zero dois, ê éfe zero nove ême ah zero três e ê éfe zero nove ême ah zero quatro.

Neste tópico, iniciamos a apresentação dos números irracionais, por meio da análise da fórma decimal de números com vírgula que não sejam dízimas periódicas. Os estudantes poderão ampliar a compreensão do conjunto dos números reais como a união do conjunto dos números racionais com o dos números irracionais. Assim, desenvolvem-se as habilidades (ê éfe zero nove ême ah zero dois) e (EF09MA03).

Página 30

A representação dêsse número também não é decimal exata nem periódica. Portanto, esse número não pode ser escrito na fórma de fração. Logo, não é um número racional.

Com esses exemplos, percebemos que existem números que não são representados por uma fórma decimal exata (com um número finito de casas decimais) nem por uma dízima periódica. Portanto, não podem ser escritos na fórma de fração, isto é, na fórma

\frac{a}{b}

com a e b inteiros e b ≠ 0; logo, não são números racionais. Esse tipo de número é chamado de número irracional.

•

Dê exemplos de outros números irracionais indicando uma regra de formação.

Agora, observe a representação decimal dos números

\sqrt{2}

\sqrt{3}

com aproximação de sete casas decimais.

\sqrt{2} ≃ 1, 4142136

\sqrt{3} ≃ 1, 7320508

Por maior que seja o número de casas decimais usadas para representar esses números, nunca vamos encontrar para eles uma representação decimal exata ou periódica. Portanto, não há frações que os representem. Por isso, dizemos que

\sqrt{2}

\sqrt{3}

são números irracionais. Também é irracional toda raiz quadrada de um número natural que não seja quadrado perfeito, assim como toda raiz quadrada de fração positiva irredutível cujos numerador e denominador não sejam quadrados perfeitos.

Além do número π, que conhecemos do cálculo do comprimento da circunferência, e do número ϕ, explorado na abertura deste capítulo, são irracionais raízes cúbicas, quartas, quintas etcétera cujos radicandos não podem ser escritos como potências de expoentes respectivamente iguais a três, a quatro, a cinco etcétera Por exemplo, são irracionais os números:

\sqrt{5}, \sqrt{6}, \sqrt{8}, \sqrt{\frac{3}{10}}, \sqrt[3]{2}, \sqrt[5]{9}

A união do conjunto dos números racionais com o conjunto dos números irracionais fórma um novo conjunto chamado conjunto dos números reais, representado por

Letra R, que representa o conjunto dos números reais.

5. Reta real

Já vimos como representar números inteiros em uma reta.

Ilustração. Reta real com os pontos, nessa ordem: menos 5, menos 4, menos 3, menos 2, menos 1, 0, 1, 2, 3 e 4.

Da mesma maneira, vimos como representar números racionais em uma reta. Na reta a seguir, representamos alguns números racionais.

Ilustração. Reta real com os pontos, nessa ordem: menos 1, menos 0,5, 0, fração 1 oitavo; fração 1 quarto; fração um meio; 1 e 1,5.

Respostas e comentários

Exemplos de números:

• 2,001002003004005reticências

• ‒5,9799799979999799997reticências

Os números reais

Ressalte aos estudantes que o conjunto dos números reais é composto por todos os números racionais e por todos os números irracionais. Por isso, não há número racional que não seja número real, assim como não há número irracional que não seja número real; então todo número real ou é um número racional ou é um número irracional.

Aproveite a atividade proposta para ser realizada oralmente para que os estudantes percebam o número irracional como um número real cuja representação decimal é infinita e não periódica, favorecendo o desenvolvimento da habilidade (ê éfe zero nove ême ah zero dois).

Para ampliar esse assunto, trabalhe com os estudantes questões como:

• Cite um número inteiro que seja real e outro que não seja número real. Espera-se que os estudantes percebam que qualquer número inteiro será um número real e que não há número inteiro que não seja também número real.

• Cite um número real que não seja inteiro. Neste caso, espera-se que os estudantes percebam que há “muitos” números reais que não são inteiros. Podem considerar qualquer número racional não inteiro (como 0,5) ou qualquer número irracional (como

\sqrt{5}

• Cite um número real que não seja inteiro nem racional. Neste caso, os estudantes devem perceber que somente os números irracionais satisfazem essa condição.

• Cite um número real que não seja racional, mas seja inteiro. Espera‑se que eles percebam que não existe um número real nessas condições, pois todo número inteiro é também número racional.

Página 31

Como sabemos, é impossível representar todos eles, pois, entre dois números racionais, existe uma infinidade de outros números racionais. Mesmo que isso fosse possível, os pontos que representariam esses números não seriam suficientes para cobrir toda a reta numérica. Faltariam ainda os pontos correspondentes aos números irracionais para completá-la.

A representação de todos os números racionais e irracionais, isto é, dos números reais, preenche a reta numérica. A essa reta chamamos de reta real.

Vamos representar na reta real o número irracional

\sqrt{2}

Já vimos que

\sqrt{2}

é um número que está entre 1,4 e 1,5; logo, sua localização aproximada na reta real é:

Ilustração. Reta numérica com os pontos menos 2, menos 1, 0, 1, 1,4, raiz quadrada de 2, 1,5, 2. Setas indicam que a raiz quadrada de 2 é um número que está entre 1,4 e 1,5.

Assim, sabendo a aproximação decimal de uma raiz quadrada não exata, podemos determinar sua posição aproximada na reta real.

Observação

▶ Qualquer ponto da reta real tem um único número real correspondente, e todo número real tem um único ponto correspondente na reta.

Localização de alguns números irracionais na reta real

O teorema que estudaremos a seguir vai nos ajudar a determinar a posição de

\sqrt{2}

e de outros números irracionais na reta real.

Você já sabe que o triângulo retângulo é aquele que tem um ângulo interno reto. O maior lado dêsse triângulo é chamado de hipotenusa, e os demais, de catetos.

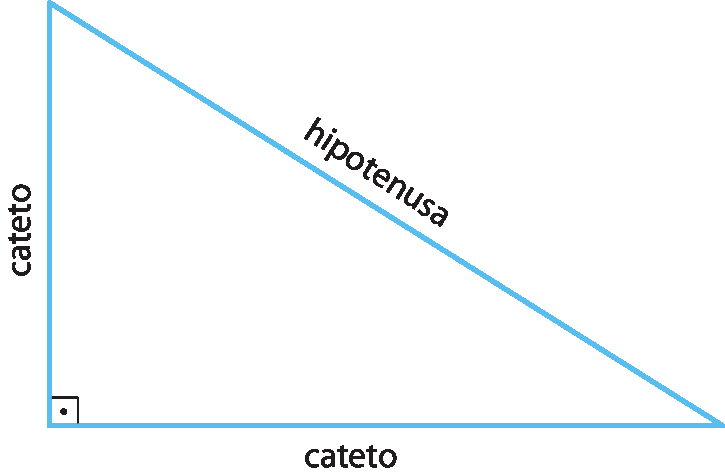
Ilustração. Triângulo retângulo. Dois lados do ângulo reto: catetos. Lado oposto ao ângulo reto: hipotenusa.

Os triângulos retângulos têm uma propriedade muito especial: com quadrados construídos sobre os catetos, sempre é possível construir quadrado sobre a hipotenusa.

Respostas e comentários

5. Reta real

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah zero um, ê éfe zero nove ême ah zero dois e ê éfe zero nove ême ah zero três.

A completude da reta real deve ser compreendida pelos estudantes, a fim de que desenvolvam a habilidades (ê éfe zero nove ême ah zero um), (ê éfe zero nove ême ah zero dois) e (ê éfe zero nove ême ah zero três). Trace uma reta numérica na lousa e pergunte: “Associando cada número natural a pontos dessa reta, sobram pontos dela sem associação?”. Espera-se que os estudantes percebam que sim, pois há os números inteiros negativos que também podem ser associados a pontos da reta numérica e não estão contemplados no conjunto dos números naturais.

Localize alguns números inteiros negativos na reta numérica desenhada e pergunte: “Associando cada número inteiro (o zero, os positivos e os negativos) a pontos dessa reta, sobram pontos sem associação?”. Nesse caso, eles podem perceber que sim, ao recordar que também associamos os números racionais não inteiros (como 1,5 e ‒0,5) a pontos da reta numérica e esses números não estão contemplados no conjunto dos números inteiros.

Localize, então, alguns números racionais não inteiros (na fórma de fração e na fórma decimal) para os estudantes perceberem que a reta numérica não estava completa e pergunte: “E agora, associando cada número racional (inteiros e não inteiros) a pontos dessa reta, sobram pontos sem associação?”. Como sabem da existência dos números irracionais (como o caso de

\sqrt{2}

), devem intuir que esses números têm pontos da reta numérica associados a eles.

Comente que os “buracos” na reta numérica, ao considerar apenas os números racionais, são totalmente preenchidos quando consideramos também os números irracionais. Por isso, essa reta numérica completa será chamada de reta real.

Isso ficará mais evidente quando os estudantes verificarem a localização dos números irracionais dados por raízes quadradas não exatas de números racionais positivos.

Página 32

Na primeira figura a seguir, temos um quadrado (pintado de roxo) sobre um cateto e outro quadrado (pintado de verde) sobre outro cateto. Vamos decompô-los de modo conveniente para formar um quadrado sobre a hipotenusa. Observe.

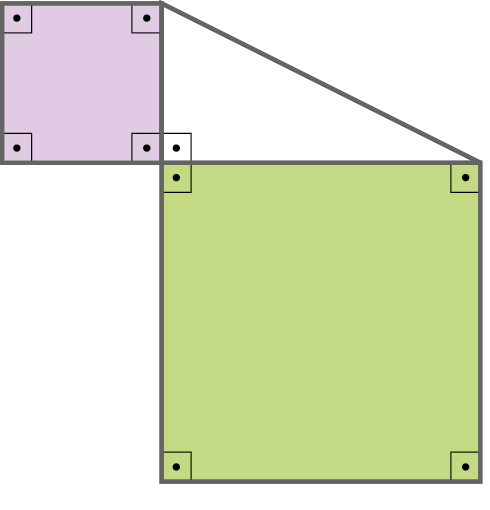
Esquema. Ilustração de um quadrado grande verde e um quadrado roxo pequeno no canto superior esquerdo do quadrado verde. O lado de cima do quadrado verde e o lado direito do quadrado roxo formam um triângulo retângulo.

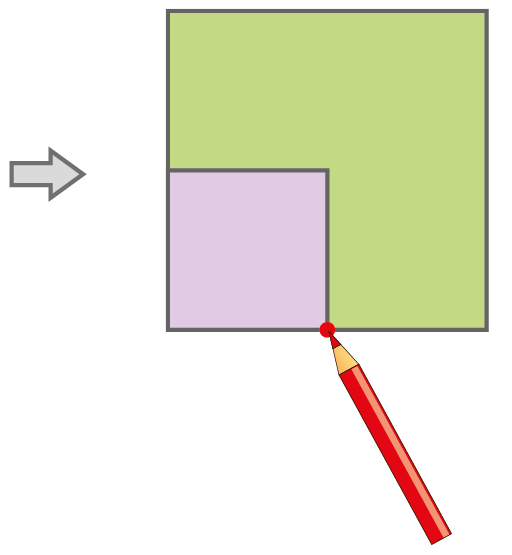
Seta para: quadrado grande verde com o quadrado roxo interno ao quadrado verde, no canto inferior esquerdo. Há um lápis na ponta do quadrado roxo, indicando a marcação deste ponto.

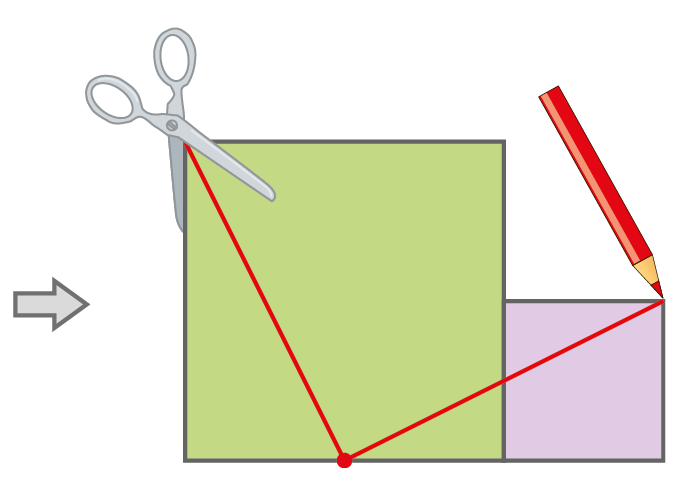
Seta para: quadrado grande verde com duas retas diagonais traçadas a partir do ponto marcado anteriormente e uma tesoura sobre a reta. À direita, no canto inferior direito, externo ao quadrado verde, o quadrado roxo e um lápis no canto superior direito, marcando este ponto.

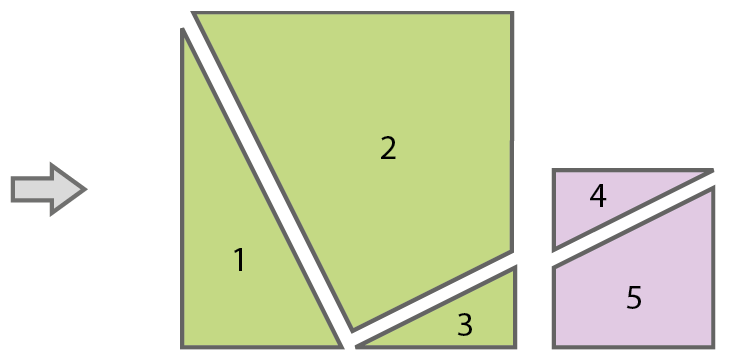
Seta para quadrado verde dividido em dois triângulos, 1 e 3 e um quadrilátero, 2. Ao lado, quadrado roxo dividido em um triângulo, 4 e um quadrilátero, 5.

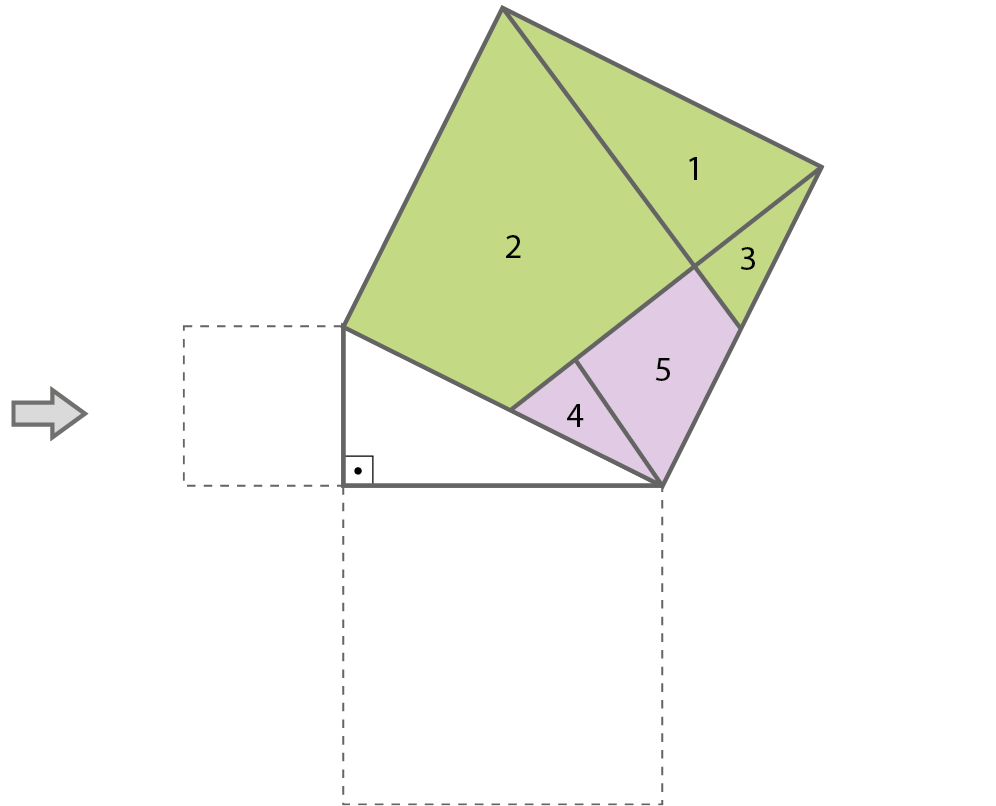
Seta para: Quadrado montado com as peças 1, 2, 3, 4 e 5. Na parte inferior, um triângulo retângulo e a linha tracejada dos quadrados na posição inicial.

Note que a medida da área do quadrado formado sobre a hipotenusa é igual à soma das medidas das áreas dos quadrados construídos sobre os catetos.

Fórmula. Teorema de Pitágoras. a ao quadrado é igual a b ao quadrado mais c ao quadrado. De a, parte uma seta indicando que essa é a medida da área do quadrado construído sobre a hipotenusa. De b e c partem duas setas indicando que indicam a medida da área de cada quadrado construído sobre os catetos.

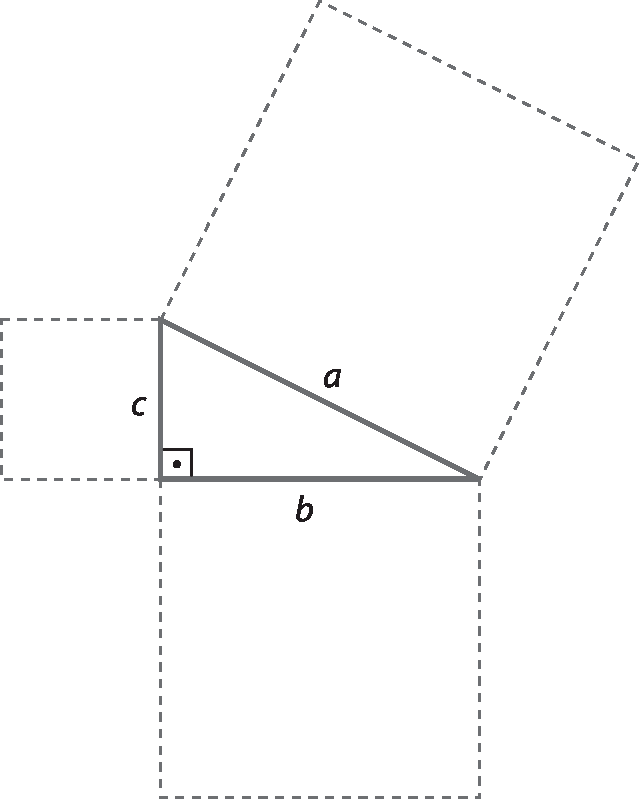
Então, ao indicar por c e b as medidas dos catetos e por a a medida da hipotenusa, podemos escrever:

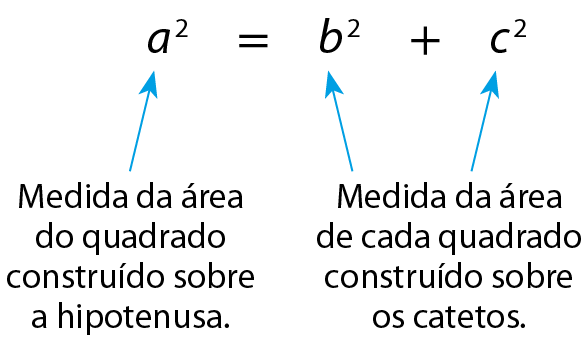
Essa relação, chamada de teorema de Pitágoras, vale para qualquer triângulo retângulo e será usada para determinar a posição de alguns números irracionais na reta real.

Respostas e comentários

Localização de alguns números irracionais na reta real

Apresentamos de maneira informal e lúdica o teorema de Pitágoras.

Providencie modelos das peças que montam o quadrado sobre a hipotenusa. Reúna os estudantes em duplas e proponha a atividade antes de mostrar a solução apresentada no livro do estudante. Destaque os elementos de um triângulo retângulo:

• ângulo interno reto com lados chamados de catetos;

• o lado maior, oposto ao ângulo reto, é a hipotenusa.

Depois de concluírem a montagem do quadrado sobre a hipotenusa, combine com os estudantes que o triângulo retângulo usado para o “quebra-cabeça” tem cateto menor medindo c, cateto maior medindo b e hipotenusa medindo a. Então, pergunte:

• Quanto mede o lado do quadrado roxo, colocado sobre o cateto menor? E o lado do quadrado verde, sobre o outro cateto?

Espera-se que os estudantes identifiquem a medida do lado de cada quadrado com a respectiva medida do cateto onde foram colocados. Assim, o quadrado roxo tem lado de medida c (e área de medida c2), e o quadrado verde tem lado de medida b (e área de medida b2).

• Quanto mede o lado do quadrado montado sobre a hipotenusa?

Os estudantes devem identificar que o lado dêsse quadrado tem mesma medida que a hipotenusa do triângulo, ou seja, mede a e tem área de medida a2.

• O que podemos dizer sobre a medida da área do quadrado montado sobre a hipotenusa?

Espera-se que eles percebam que, como esse quadrado foi montado com peças dos quadrados roxo e verde, a medida da área do quadrado maior deve ser a soma das medidas das áreas dos quadrados roxo e verde, ou seja: b2 + c2 = a2.

Página 33

Por exemplo, se quisermos representar

\sqrt{2}

na reta real, construímos um triângulo retângulo com a hipotenusa medindo

\sqrt{2}

. Observe.

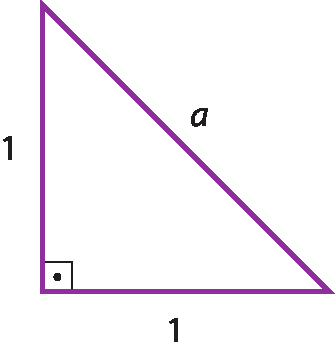
Ilustração. Triângulo retângulo com catetos iguais, de medida 1, e hipotenusa medindo a.

aelevado a 2 = belevado a 2 + celevado a 2

aelevado a 2 = 1elevado a 2 + 1elevado a 2

aelevado a 2 = 1 + 1

aelevado a 2 = 2

O valor procurado é um número positivo que, elevado ao quadrado, resulta 2. Esse número é

\sqrt{2}

. Logo: a =

\sqrt{2}

Então, para representar

\sqrt{2}

na reta, basta construir um triângulo retângulo de catetos medindo uma unidade e transferir a medida da hipotenusa para a reta. Acompanhe.

1. Por a, traçamos

\overline{B A} ⟂ r

, tal que bê á = 1. Também marcamos o ponto óh na reta r, tal que ó á = 1.

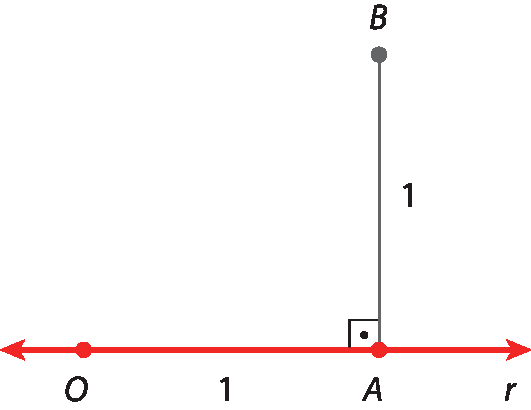
Ilustração. Reta r, que passa pelo segmento O A de medida 1. Segmento de reta A B, de medida 1, perpendicular à reta r.

2. Unimos óh com B e obtemos ó bê =

\sqrt{2}

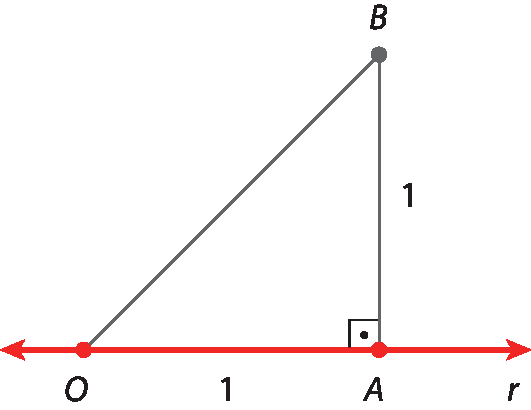
Ilustração. Reta r, que passa pelo segmento O A de medida 1. Segmento de reta A B, de medida 1, perpendicular à reta r. Segmento de reta O B.

3. Com centro em óh e abertura ó bê, marcamos o ponto C.

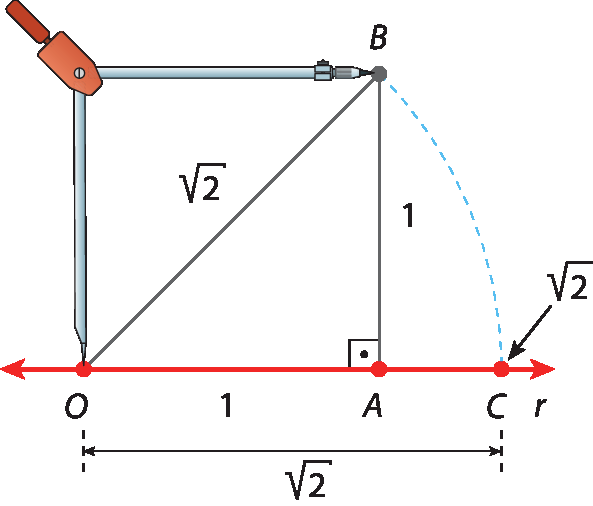
Ilustração. Reta r, que passa pelo segmento O A de medida 1. Segmento de reta A B, de medida 1, perpendicular à reta r. Segmento de reta O B, de medida raiz quadrada de 2, com um compasso aberto marcando essa medida. Um arco BC é tracejado. A medida do segmento O C é indicada por raiz quadrada de 2.

(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)

Agora, vamos representar

\sqrt{3}

na reta numérica. Para isso, podemos construir, por exemplo, um triângulo retângulo de catetos

\sqrt{2}

e 1. A hipotenusa medirá

\sqrt{3}

unidades de comprimento.

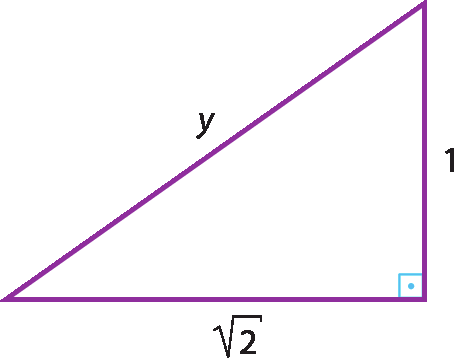
Ilustração. Triângulo retângulo com cateto menor medindo 1, cateto maior medindo raiz quadrada de 2 e hipotenusa medindo y.

y elevado a 2 =

{(\sqrt{2})}^{2}

+ 12

y elevado a 2 = 3

y =

\sqrt{3}

Aproveitando o segmento que representa

\sqrt{2}

, construímos na reta numérica o segmento que mede

\sqrt{3}

Ilustração. Menina branca, cabelo castanho e camisa roxa. Ela fala: Como eu faço para encontrar menos raiz quadrada de 3 na reta?

Ilustração. Homem de cabelo ruivo e camisa vermelha. Ele diz: Basta transportar sobre a reta para a esquerda, a partir do zero, o segmento que mede raiz quadrada de 3.

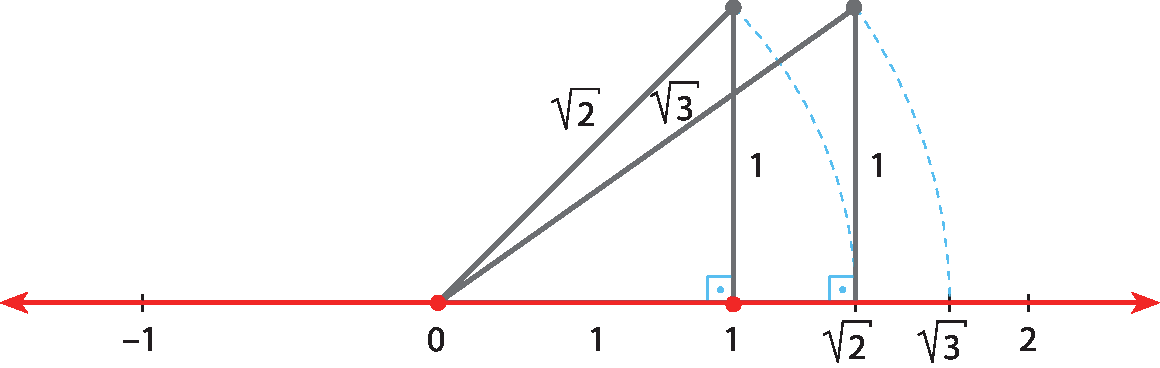
Ilustração. Reta numérica com os pontos, nessa ordem: menos 1, 0, 1, raiz quadrada de 2, raiz quadrada de 3 e 2. Um triângulo retângulo de hipotenusa raiz quadrada de 2 e catetos de medida 1 é formado sobre os pontos 0 e 1 da reta. Um segundo triângulo retângulo de hipotenusa raiz quadrada de 3 é formado sobre os pontos 0 e raiz quadrada de 2 da reta.

Na calculadora, obtemos

\sqrt{3} ≃ 1, 73

. Repare que

\sqrt{3}

fica entre 2 e o ponto médio do segmento de extremos 1 e 2.

Respostas e comentários

Localização de alguns números irracionais na reta real

Se julgar necessário, relembre a construção de uma reta perpendicular a uma reta dada passando por um ponto dessa reta. Depois, reproduza na lousa a construção do segmento de medida

\sqrt{2}

, pedindo aos estudantes que justifiquem cada passo. Por exemplo, pergunte o que garante que o terceiro lado do triângulo mede

\sqrt{2}

, quando tomamos 1 como medida dos dois lados perpendiculares dêsse triângulo. Espera-se que os estudantes citem a relação trabalhada anteriormente, conhecida como teorema de Pitágoras.

Página 34

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

43 Escreva o número irracional que está representado na reta pela letra m.

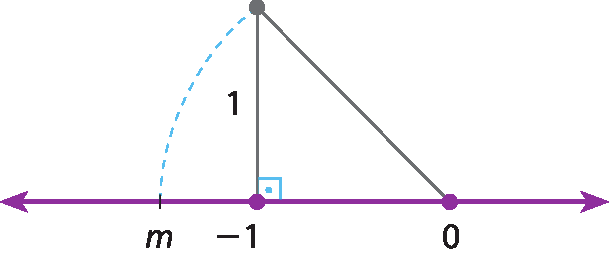
Ilustração. Reta com os pontos: m. menos 1, 0. Triângulo retângulo formado por cateto, de 0 até menos 1, e outro cateto, segmento vertical, medindo 1. Um arco é tracejado do topo do triângulo para m.

44 Construa, com auxílio de régua e compasso, um triângulo retângulo com um cateto de duas unidades de comprimento sobre uma reta numérica e outro cateto de uma unidade de comprimento. Determine a medida da hipotenusa dêsse triângulo e localize na reta numérica o número que expressa a medida da hipotenusa dêsse triângulo.

45 Considere o triângulo retângulo a seguir, cujas medidas dos lados estão indicadas em uma mesma unidade de comprimento.

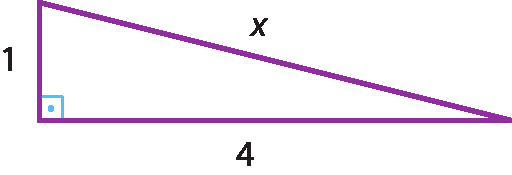
Ilustração. Triângulo retângulo de catetos medindo 1 e 4, e hipotenusa medindo x.

a) Determine o valor de x.

b) Esse número é racional ou irracional?

Usando uma calculadora, represente esse número na fórma decimal aproximada, com duas casas decimais.

46 Na figura a seguir, foi representado o número

\sqrt{10}

na reta numérica. Explique por que essa construção está correta.

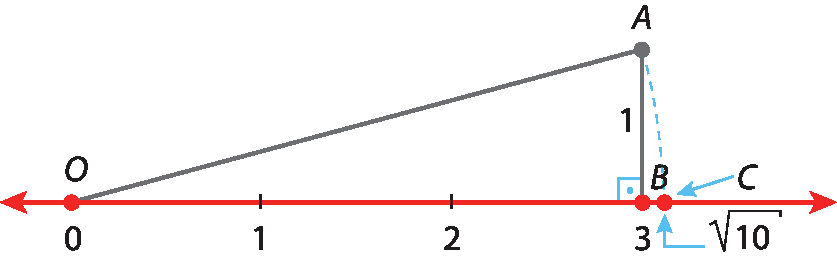
Ilustração. Reta com os pontos: 0 (ponto O), 1, 2 e 3 (ponto B). Triângulo retângulo OAB em que o vértice A tem altura 1. Reta tracejada do ponto A até o ponto C, localizado do lado direito do ponto B. O ponto C vale raiz quadrada de 10.

47 A figura a seguir representa um escorregador cujo comprimento, em metro, foi indicado por x.

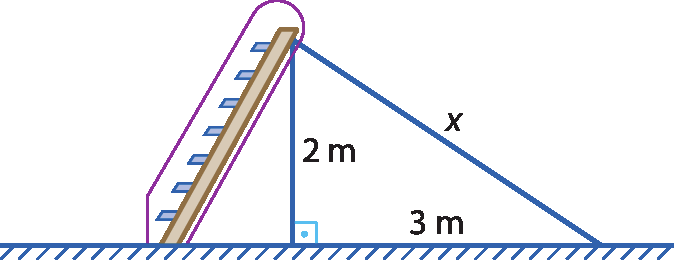
Ilustração. Escorregador cuja altura da escada (altura máxima do escorregador) é igual a 2 metros e cuja distância do início ao fim do escorregador mede 3 metros, que são os catetos de um triângulo retângulo cuja hipotenusa, x, é o comprimento do escorregador.

a) Qual é o número irracional que representa o comprimento dêsse escorregador?

b) Qual é o comprimento aproximado dêsse escorregador em centímetro?

48 Com régua e compasso, trace em seu caderno um segmento de

\sqrt{20}

u e outro de

\sqrt{27} u,

sendo u  =  2 centímetros. Construa um retângulo que tenha essas medidas. Construa outro retângulo que tenha por medidas

2 \sqrt{5}

u e

3 \sqrt{3}

u. Por sobreposição, compare as medidas das áreas dos retângulos encontrados e os produtos

\sqrt{20}

⋅

\sqrt{27}

2 \sqrt{5}

⋅

3 \sqrt{3}

(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)

PARA SABER MAIS

Espiral de Teodoro, Pitágoras ou ainstain

Uma das mais famosas espirais, construída com triângulos retângulos, é conhecida pelos nomes de três grandes personalidades: Teodoro de Cirene, Pitágoras e Álbert Ainstén.

Sua construção tem início com um triângulo retângulo isósceles com catetos de uma unidade, prossegue com outros triângulos retângulos que têm um cateto de uma unidade e outro cateto com a medida da hipotenusa do triângulo anterior. Com ela, obtemos segmentos de medidas iguais a

\sqrt{2}

\sqrt{3}

\sqrt{4}

= 2,

\sqrt{5}

\sqrt{6}

, reticências

Observe como fica a construção de uma dessas espirais até

\sqrt{17}

Ilustração. Esquema. Triângulos coloridos dispostos em espiral. Do centro para a parte externa, a medida da hipotenusa de cada triângulo é: raiz quadrada de 1, raiz quadrada de 2, raiz quadrada de 3, raiz quadrada de 4, raiz quadrada de 5, raiz quadrada de 6, raiz quadrada de 7, raiz quadrada de 8, raiz quadrada de 9, raiz quadrada de 10, raiz quadrada de 11, raiz quadrada de 12, raiz quadrada de 13, raiz quadrada de 14, raiz quadrada de 15, raiz quadrada de 16, raiz quadrada de 17. Todos os triângulos possuem um cateto igual a 1.

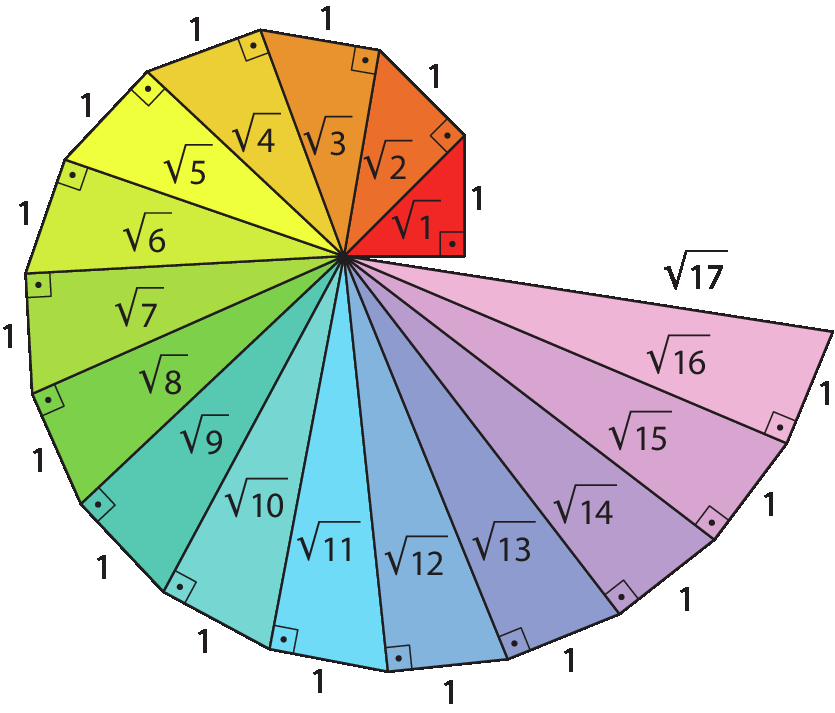
Respostas e comentários

43.

‒ \sqrt{2}

44.

\sqrt{5}

; construção de figura.

45. a)

\sqrt{17}

45. b) Irracional.

45. c) 4,12

46. Resposta pessoal.

47. a)

\sqrt{13}

47. b) 361 centímetros

48. Construção de figura; os produtos são iguais.

Exercícios propostos

As resoluções dos exercícios 43 e dos exercícios 45 a 47 estão no início deste Manual, nas orientações específicas do capítulo 1.

No exercício 44, como a medida x da hipotenusa é dada por x2 = 22 + 11 = 5, obtemos x =

\sqrt{5}

. Uma possível figura para o exercício 44:

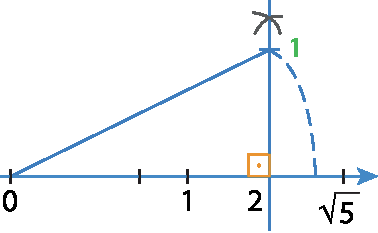
Semirreta horizontal com pontos 0, 1, 2 e raiz quadrada de 5. Reta vertical sobre 2. Reta diagonal de 0 até topo da reta vertical. Linha curvada à direita para reta horizontal.

Para o exercício 48:

Para cada caso a seguir, as medidas usadas são proporcionais, mas não há relação de proporcionalidade entre as diferentes ilustrações, devido ao espaço para representá-las.

• Construção de

\sqrt{20}

unidades:

Triângulo retângulo de catetos medindo 4 unidades e 2 unidades, e hipotenusa medindo

\sqrt{20}

unidades;

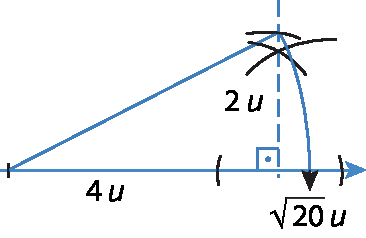
• Construção de

\sqrt{27}

unidades:

Triângulo retângulo de catetos medindo 5 unidades e umaunidade, hipotenusa medindo

\sqrt{26}

unidades; triângulo retângulo de catetos medindo

\sqrt{26}

unidades e umaunidade, hipotenusa medindo

\sqrt{27}

unidades.

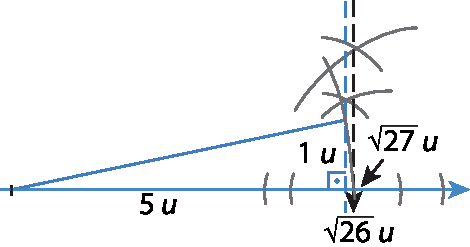
Ilustração. Construção de triângulo retângulo de catetos medindo 5u e 1u, e hipotenusa medindo raiz quadrada de 27u.

• Retângulo de lados medindo

\sqrt{20}

unidades por

\sqrt{27}

unidades (transportando com o compasso as medidas construídas anteriormente):

Ilustração. Retângulo de lados medindo raiz quadrada de 20, vezes u e raiz quadrada de 27, vezes u, correspondentes às hipotenusas dos triângulos retângulos construídos anteriormente.

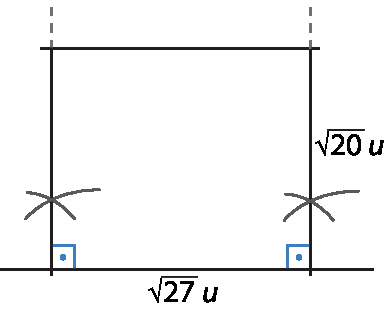
• Construção de

\sqrt{3}

unidades:

Triângulo retângulo de catetos medindo umaunidade e umaunidade; triângulo retângulo de catetos medindo

\sqrt{2}

unidades e umaunidade:

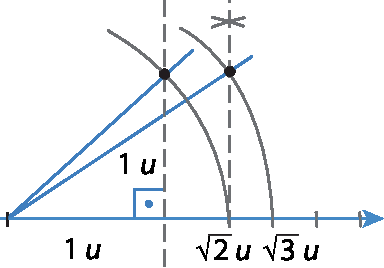
• Construção de

\sqrt{5}

unidades: análoga ao exercício 44.

• Retângulo de lados medindo

2 \sqrt{5}

unidades por

3 \sqrt{3}

unidades (por meio do transporte com o compasso das medidas

\sqrt{5}

\sqrt{3}

realizadas anteriormente):

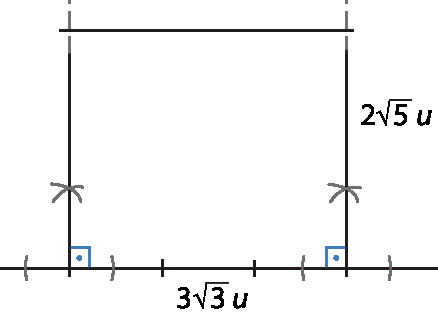
Ilustração. Reta horizontal com duas retas verticais e uma horizontal acima formando retângulo. As medidas dos lados do retângulo são: 3 vezes a raiz quadrada de 3, vezes u, e 2 vezes a raiz quadrada de 5, vezes u.

Página 35

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)

1 Com régua e esquadro, construa uma espiral como a da página anterior até obter

\sqrt{9}

. Depois, confira se essa medida se iguala de fato a 3 unidades usadas por você.

2 Construa uma reta numérica no caderno considerando a mesma medida unitária do cateto dos triângulos para a medida de distância entre 0 e 1. Depois, localize nessa reta os seguintes números:

\sqrt{2}, \sqrt{3}, \sqrt{5}

\sqrt{7}

Explique ao professor e aos colegas como você pensou para localizar cada um desses números na reta numérica.

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

1 Identifique as sentenças falsas e dê um exemplo para justificá-las.

a) Todo número inteiro é natural.

b) Todo número racional é inteiro.

c) Todo número racional é real.

d) Todo número irracional é real.

2 Considere

A = \frac{2}{3} ‒ 1, \overline{4} e B = ‒ 0, 777

reticências Determine em seu caderno A : B.

3 Dadas as dízimas periódicas 2,555reticências e 0,222reticências, determine:

a) a soma delas, escrevendo o resultado na fórma abreviada;

b) o produto delas, escrevendo o resultado na fórma de fração.

4 Justifique em seu caderno por que

\sqrt{4,84}

= 2,2.

5 Sendo x = 2elevado a 8 ⋅ 5elevado a 2, calcule a raiz quadrada de x.

6 Qual é o menor número pelo qual devemos multiplicar 2elevado a 5 ⋅ 34 ⋅ 5elevado a 3 ⋅ 7 para obter um número natural que seja quadrado perfeito?

7 Sendo a = 

3^{3}

 ⋅ 5 ⋅ 7 e B = 3 ⋅ 5 ⋅ 7, calcule a raiz quadrada de a ⋅ B.

8 Um terreno tem o formato de um quadrado, e a medida da sua área é igual a 231,04 métros quadrados. Calcule a medida do perímetro dêsse terreno.

9 O valor de

\sqrt{5, 888 ...}

é aproximadamente igual a:

a) 2,4

b) 2,4333reticências

c) 2,8

d) 2,8333reticências

10 Os catetos de um triângulo retângulo medem 12 centímetros e 5 centímetros.

a) Calcule a medida da hipotenusa.

b) Essa medida é um número racional ou irracional?

11 Os catetos de um triângulo retângulo medem 6 centímetros e 2 centímetros.

a) Calcule a medida da hipotenusa.

b) Essa medida é um número racional ou irracional?

c) Determine a medida da hipotenusa com uma casa decimal.

12 Que número irracional está representado na reta pela letra a?

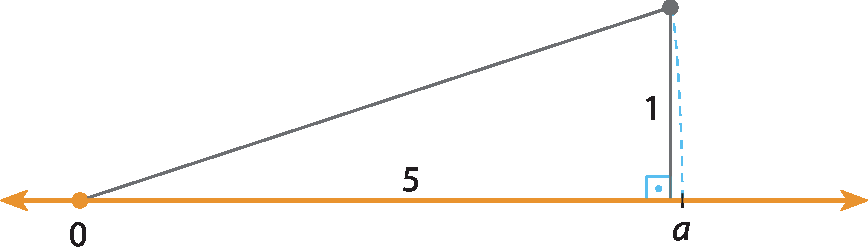
Ilustração. Triângulo retângulo de catetos 1 e 5, sendo que o cateto de comprimento 5 está sobre uma reta. Reta tracejada liga extremidade de altura 1 ao ponto a na reta, à direita do ângulo reto.

13 Em seu caderno, represente na reta real os números

\sqrt{29}

e menos

\sqrt{5}

14 Para calcular a altura de um poste, Alexandre encostou nele uma escada de 6 métros de comprimento, de modo que ela ficou apoiada no chão a 3 métros do poste. Qual é a medida aproximada da altura dêsse poste?

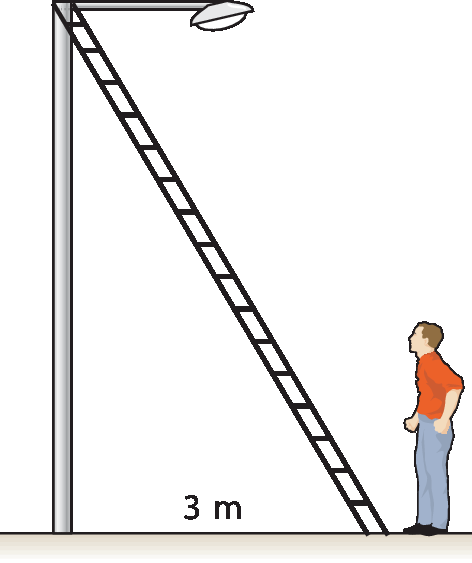
Ilustração. Poste de luz. À direita, homem em pé com uma escada à sua frente até topo do poste, formando um triângulo retângulo. A distância entre a base da escada e a base do poste é de 3 metros.

Respostas e comentários

Para saber mais:

1. Construção de figura.

2. Espera-se que os estudantes transportem as medidas encontradas na atividade 1 para localizar os números pedidos na reta numérica.

Exercícios complementares:

1. a) Falsa, menos1 não é natural.

1. b) Falsa,

\frac{1}{2}

não é número inteiro.

1. c) Verdadeira.

1. d) Verdadeira.

2. a : B = 1

3. a)

2, \overline{7}

3. b)

\frac{46}{81}

4. (2,2)elevado a 2 = 4,84

5. 80

6. 595

7. 315

8. 60,8 métros

9. Alternativa b.

10. a) 13 centímetros

10. b) Racional.

11. a)

\sqrt{40}

centímetros.

11. b) Irracional.

11. c) 6,3 centímetros.

12. a =

\sqrt{26}

13. Construção de figura.

14. 5,2 métros.

Para saber mais

Observe a seguir uma possível figura para a atividade 1 do Agora é com você!:

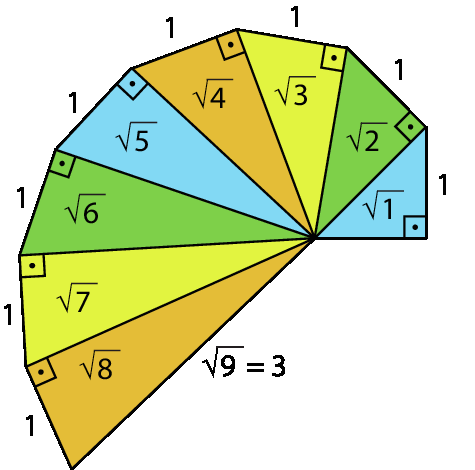
Na atividade 2, espera-se que os estudantes, para localizar os números pedidos na reta numérica, transportem as medidas obtidas na atividade 1.

Exercícios complementares

Este bloco de exercícios explora os principais conceitos estudados no capítulo. Espera-se que os estudantes mobilizem os conhecimentos construídos, percebendo se ainda têm alguma dificuldade.

As resoluções dos exercícios 1 a 14 estão no início deste Manual, nas orientações específicas do capítulo 1.

Página 36

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Entre as sentenças matemáticas indicadas a seguir, qual delas terá como resultado um número natural?

a) 350 : 8 + 34

b) 352 : 8 ‒ 90 : 2

c) 456 : 5 + 88 : 10

d) 456 : 6 ‒ 88

2 Qual é a fração geratriz da dízima periódica 15,623623reticências?

\frac{15 623}{999}

\frac{15 608}{999}

\frac{15 623}{99}

\frac{623}{999}

3 Se um número for:

a) inteiro, então ele é natural.

b) racional, então ele não pode ser irracional.

c) irracional, então ele pode ser inteiro.

d) real, então ele é racional.

4 Qual dos números a seguir não é um quadrado perfeito?

a) .1764

b) .1225

c) 882

d) .1296

5 Sobre o valor de

\sqrt{42}

, podemos afirmar que está entre:

a) 6,4 e 6,5.

b) 6,5 e 6,6.

c) 6,6 e 6,7.

d) 6,8 e 6,9.

6 A raiz quadrada de .1185 está entre:

a) 25 e 26.

b) 34 e 35.

c) 118 e 119.

d) 592 e 593.

7 Um dos quartos de um apartamento tem formato quadrado de área medindo 18,49 métros quadrados. Qual é a medida do perímetro dêsse quarto?

a) 18,8 métros

b) 17,2 métros

c) 9,4 métros

d) 4,3 métros

8 A medida da diagonal de um retângulo de base medindo 4 centímetros e altura medindo 6 centímetros é um número:

a) natural.

b) inteiro.

c) racional.

d) irracional.

9 Considerando as medidas indicadas na figura, em centímetro, o valor de x é:

Ilustração. Reta com pontos 0 e x. Acima da reta, projeção de um triângulo retângulo, cujos catetos são o segmento de 0 a x, e o cateto 1. Hipotenusa com medida raiz quadrada de 23.

a) 1 centímetro.

b) 22 centímetros.

\sqrt{22}

centímetros.

\sqrt{24}

centímetros.

10 Um triângulo retângulo tem catetos medindo 6 centímetros e 8 centímetros. Qual é a medida da hipotenusa dêsse triângulo?

a) 7 centímetros

b) 10 centímetros

c) 14 centímetros

d) 50 centímetros

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.

a) Quais são os conjuntos numéricos estudados no capítulo? Dê um exemplo de um número pertencente a cada conjunto.

b) O que é uma dízima periódica?

c) Explique como determinar a fração geratriz da dízima periódica de 0,666reticências

d) O que é um número quadrado perfeito?

e) Como você explicaria para um colega como encontrar a raiz quadrada aproximada de um número?

f) Que estratégia você utiliza para encontrar a posição da raiz quadrada de um número natural na reta real? Descreva-a.

g) Copie o diagrama a seguir no caderno. Depois, relacione os conjuntos dos números naturais, inteiros, racionais, irracionais e reais neste diagrama.

Ilustração. Modelo. Retângulo dividido em duas partes. Partes esquerda maior com dois pontos de interrogação e quadrado com um ponto de interrogação com três pontos de interrogação abaixo. À direita, dois pontos de interrogação.

Respostas e comentários

1. Alternativa c.

2. Alternativa b.

3. Alternativa b.

4. Alternativa c.

5. Alternativa a.

6. Alternativa b.

7. Alternativa b.

8. Alternativa d.

9. Alternativa c.

10. Alternativa b.

a) Natural: 2; Inteiro: –5; Racional: 0,23; Irracional:

\sqrt{3}

; Real:

\sqrt{4}

b) É a representação decimal periódica de um número.

c) Inicialmente, associa-se:

x = 0,666reticências (um)

Depois, multiplica-se esse valor por 10:

10x = 6,666reticências (dois)

Em seguida, deve-se subtrair (um) de (dois), membro a membro:

10x ‒ x = 6,666reticências ‒ 0,666reticências

9x = 6

x =

\frac{6}{9}

\frac{2}{3}

d) É um número natural que é a segunda potência de algum número natural.

e) Resposta pessoal. Espera-se que os estudantes situem a raiz quadrada do número entre as raízes quadradas dos dois quadrados perfeitos mais próximos.

f) Resposta pessoal. Espera-se que os estudantes considerem o cálculo da hipotenusa a partir do teorema de Pitágoras em triângulos retângulos.

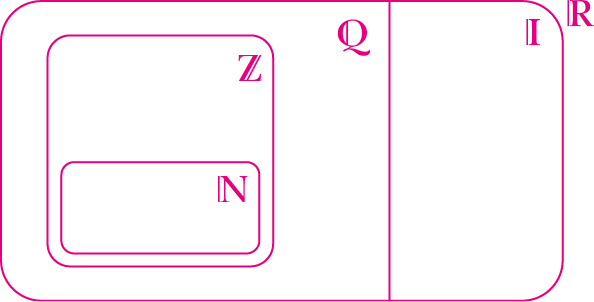
Ilustração. Modelo. Retângulo R, representando o conjunto dos números reais, dividido em duas partes. Parte esquerda maior Q, representando o conjunto dos números racionais, com quadrado Z interno, representando o conjunto dos números inteiros e um e retângulo horizontal N, interno ao quadrado Z, representando o conjunto dos números naturais. Parte direita menor, com retângulo I, representando o conjunto dos números irracionais.

Verificando

Esses exercícios são mais uma oportunidade para o estudante consolidar o entendimento do conteúdo estudado neste capítulo.

As resoluções dos testes 1 a 10 estão no início deste Manual, nas orientações específicas do capítulo 1.

Organizando

Incentive os estudantes a organizar o aprendizado no caderno, fazendo resumos, mapas conceituais ou aplicando destaques em conceitos importantes.

As questões propostas têm como objetivo possibilitar aos estudantes que retomem os conteúdos aprendidos no capítulo e reflitam sobre algumas temáticas.

Página 37

DIVERSIFICANDO

Jogo do enfileirando

Número de participantes: 2 a 4 jogadores.

Material:

• Vinte cartões numerados confeccionados com os números: 0, 2, 6, 7, 9, ‒8, ‒7, ‒4, ‒3, ‒1,

\frac{1}{2}, \frac{1}{3}, \frac{2}{3}, \frac{7}{8}, \frac{3}{8}, \sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{16}, \sqrt{25}

• Quatro cartas de ação: uma de “ordem crescente”; uma de “ordem decrescente”; uma de “adição dos números”; e uma de “multiplicação dos números”.

• Dois saquinhos não transparentes: um para guardar os cartões numerados, outro para guardar as cartas de ação.

• Papel e lápis para resolver as operações.

Regras:

• Sem olhar os números, cada jogador pega cinco cartões numerados de dentro do saquinho.

• Depois, um dos jogadores tira uma carta de ação e a coloca em cima da mesa para que todos a conheçam e façam o que ela indica. Por exemplo, se sair a carta “ordem crescente”, cada jogador colocará em ordem crescente os cartões que pegou. Suponha que um dos jogadores tenha os cartões

2, ‒ 3, \sqrt{2}, \frac{1}{2}

e 9; ele deverá colocá-los nesta disposição:

‒ 3, \frac{1}{2}, \sqrt{2}

, 2 e 9. Então, anota-se o nome de quem terminou a tarefa em primeiro lugar e retira-se outra carta.

• Para os cálculos com

\sqrt{2}

\sqrt{3}

, devem ser usados os valores aproximados 1,4 e 1,7, respectivamente. Exemplo:

2 + (‒ 3) + \sqrt{2} + \frac{1}{2} + 9 = 9, 9

• Vence o jogo aquele que ganhar o maior número de rodadas, isto é, concluir mais vezes as tarefas antes dos outros colegas. Caso nenhum jogador consiga executar as tarefas, reinicia-se o jogo.

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

1 Observe a ilustração e responda à questão. Quem ganhou esta rodada? Justifique.

Ilustração. Ao redor de uma mesa, à esquerda, menina branca, de cabelo ruivo, faixa azul no cabelo e camiseta branca. À frente dela, sobre a mesa, fichas com os números: menos 3, 2, raiz quadrada de 25, 7 e 9. À direita, menino branco, de cabelo preto e camiseta branca com detalhes azuis. À frente dele, sobre a mesa, fichas com os números: menos 1, menos 4, fração; um meio; fim da fração, raiz quadrada de 2 e 6. Sobre a mesa, à frente, há uma placa que diz: Ordem Crescente; ao fundo, há dois saquinhos azuis.

Formem grupos de 3 ou 4 integrantes, modifiquem uma regra do jogo e troquem com outro grupo. Antes de jogar com a nova regra, escolham um representante para explicar a regra nova do outro grupo.

Respostas e comentários

1. A pessoa da esquerda, pois colocou os cinco números na ordem certa, como pedia a carta de ação.

Diversificando

Observe uma variação do jogo proposta nesta seção. No material, mudamos as cartas de ação, que passam a ser: “quadrado da soma”, “soma dos quadrados”, “multiplicação dos números” e “adição dos números”. Nas regras, alteramos a quantidade de cartões numerados que cada jogador deve pegar: em vez de quatro, inicialmente cada jogador pega apenas dois cartões numerados.

Um dos objetivos dessa variação do jogo é levar os estudantes a perceber o que há de diferente entre quadrado de uma soma (a + b)elevado a 2 e soma de dois quadrados (aelevado a 2 + belevado a 2).

Agora é com você!

Na atividade 2, peça aos estudantes que escrevam a nova regra de maneira compreensível e objetiva, de modo que os colegas consigam entendê-la, pois o representante terá de explicá-la a todos no final da atividade.

Glossário

Cunha: : objeto que vai diminuindo de grossura e é utilizado para rachar lenha, fender pedras etcétera; Voltar para o texto