Página 173

CAPÍTULO 8 Triângulo retângulo

Fotografia. Base com formato de bloco retangular e sobre ela um monumento de bronze de uma pessoa em pé com um dos braços para cima onde há uma haste presa a outra haste na diagonal. Ao fundo, barcos no mar. — Monumento a Pitágoras, ilha de Samos, Grécia. (Fotografia de 2019.)

Observe a imagem e responda às questões no caderno.

a) O monumento lembra que tipo de triângulo?

b) A parte sobre a qual a escultura de Pitágoras está apoiada lembra um cateto ou uma hipotenusa de um triângulo retângulo?

c) Pesquise outros monumentos e edificações com formatos que lembrem triângulos. Depois, compartilhe os resultados obtidos com os colegas da turma.

Na ilha de Samos, na Grécia, há um monumento de bronze construído em homenagem a Pitágoras, filósofo a quem se atribuem inúmeras contribuições à Matemática. No monumento edificado de modo a lembrar um triângulo retângulo, a escultura de Pitágoras compõe um dos catetos.

Respostas e comentários

a) Resposta esperada: triângulo retângulo.

b) Resposta esperada: um cateto.

c) Resposta pessoal.

Capítulo 8 – Triângulo retângulo

Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas da Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.

Neste capítulo, retomamos e ampliamos o estudo dos triângulos retângulos, tratando das relações métricas em um triângulo retângulo, com destaque para o teorema de Pitágoras e suas aplicações. Além disso, exploramos a medida da distância entre dois pontos no plano cartesiano e a representação gráfica de um relevo, que pode ser associada com as vistas ortogonais de um sólido geométrico.

Nesta abertura, apresentamos um monumento construído em homenagem a Pitágoras, que faz menção à figura de um triângulo retângulo. Explore um pouco mais essa fotografia pedindo que os estudantes identifiquem nela outras estruturas que lembram triângulos retângulos. Espera-se que eles reconheçam as fórmas triangulares formadas pelo mastro, pela retranca e pelo cabo da vela das embarcações.

Promova uma discussão e levante os conhecimentos prévios que os estudantes têm sobre esse matemático e sobre o triângulo retângulo. Espera-se que eles identifiquem o triângulo retângulo como aquele que tem um ângulo interno reto.

Página 174

1. Um pouco de História

Pitágoras é um matemático cuja história está bastante envolvida de algum misticismo e, por isso, pouco se sabe com certeza sobre ele. Pitágoras teria nascido na ilha de Samos por volta do ano 570 antes de Cristo, cêrca de cinquenta anos depois do nascimento de Tales de Mileto.

Fotografia. Escultura de cor clara do busto de um homem de turbante e barba longa. — Busto de Pitágoras, nos Museus Capitolinos em Roma, Itália. Escultura em mármore. (Fotografia de 2015.)

Filho de um rico comerciante, teria viajado pelo Egito, pela Babilônia e talvez tenha chegado até a Índia. Ao voltar para a Grécia, fixou-se em sua terra natal, mas, descontente com as arbitrariedades do governo de Samos, controlado pelo tirano Polícrates, mudou-se para a colônia grega Crotona, situada na Itália. Lá, fundou a escola pitagórica.

Nessa escola, havia aulas de Religião, Filosofia, Política, Música, Astronomia e Matemática. Os estudantes eram organizados em duas categorias: os dos três primeiros anos eram chamados de ouvintes, e os dos anos seguintes, de matemáticos, pois somente a estes eram revelados os segredos da Matemática.

O lema da escola era “Tudo é número”. Nela, procuravam explicar com números tudo o que existe na natureza.

Os pitagóricos tinham o conhecimento como única aspiração e formaram uma sociedade secreta cujo emblema era um pentágono estrelado — ou pentagrama.

Ilustração. Estrela pentagrama verde de cinco pontas. — Pentágono estrelado ou pentagrama.

Os estudos dos pitagóricos trouxeram grandes contribuições para a Matemática, principalmente para a Geometria. Entre essas contribuições, a de maior sucesso foi, sem dúvida, o conhecido teorema de Pitágoras.

Mesmo depois da morte de seu fundador, por volta de 490 antes de Cristo, a sociedade dos pitagóricos continuou a existir por pelo menos mais dois séculos.

2. Teorema de Pitágoras

Neste capítulo, vamos estudar várias relações entre as medidas de comprimento dos elementos de um triângulo retângulo. Por isso, convém recordar a nomenclatura a ser usada.

Elementos de um triângulo retângulo

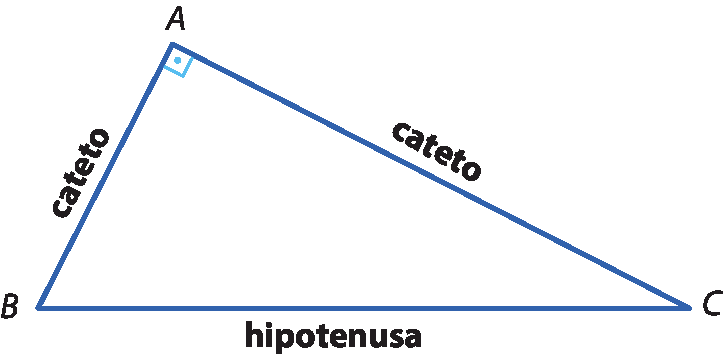
Já sabemos que um triângulo á bê cê é denominado triângulo retângulo em a quando o ângulo reto tem vértice a.

Chamamos catetos os lados perpendiculares entre si que formam o ângulo reto em um triângulo retângulo. E o lado oposto ao ângulo reto é chamado hipotenusa.

Ilustração. Triângulo ABC. Lado AC e AB nomeados como cateto. Lado BC nomeado como hipotenusa. Ângulo reto em A.

Respostas e comentários

1. Um pouco de História

Neste texto, como introdução, apresentamos a escola pitagórica, seu lema e sua contribuição na construção da Matemática, palavra cuja origem é atribuída a Pitágoras. Sugerimos o trabalho de leitura e exploração do texto com os estudantes dispostos em duplas ou trios. Se possível, para que desenvolvam a competência geral 1, pode-se propor aos estudantes que façam uma pesquisa sobre Pitágoras e os pitagóricos, listando algumas de suas contribuições na história da Matemática. dêsse modo, os estudantes podem perceber que o conhecimento científico se desenvolve com base na observação do mundo físico e para explicar a realidade.

2. Teorema de Pitágoras

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah um três e ê éfe zero nove ême ah um quatro.

Neste tópico, o estudante é levado a reconhecer as condições para dois triângulos serem semelhantes; a seguir os passos das demonstrações das relações métricas do triângulo retângulo, incluindo o teorema de Pitágoras; a resolver e elaborar problemas de aplicação do teorema de Pitágoras. Assim, são desenvolvidas as habilidades (ê éfe zero nove ême ah um três) e (EF09MA14).

Destaque os elementos de um triângulo retângulo, incluindo a determinação dos lados opostos a ângulos internos.

Se considerar necessário, recorde com os estudantes os casos de semelhança de triângulos: ângulo ângulo, lado ângulo lado e lado lado lado.

Página 175

Ilustração. Menina de cabelo castanho e blusa vermelha.
Ela fala: Observe o triângulo retângulo ABC.

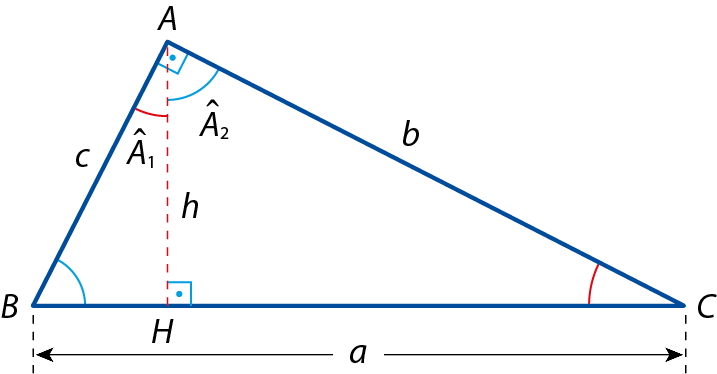
Ilustração. Triângulo ABC. De A, segmento de reta h até lado BC, ponto H e ângulo reto em H. Em A, ângulo A1 e A2. As medidas dos lados são: AB: c. AC: b e BC: a.

Nesse triângulo, destacamos as medidas:

• a, da hipotenusa

\overline{B C}

;

• c, do cateto

\overline{A B}

, oposto ao ângulo

\hat{C}

;

• b, do cateto

\overline{A C}

, oposto ao ângulo

\hat{B}

;

• h, da altura

\overline{A H}

, relativa à hipotenusa.

•

Um triângulo cujos lados medem 3 centímetros, 4 centímetros e 5 centímetros tem um ângulo interno reto. Com base nele, podemos obter que outros triângulos retângulos?

Em relação aos ângulos, sabemos que a soma das medidas dos ângulos internos de um triângulo é 180graus. Assim, nos triângulos retângulos, a soma das medidas dos dois ângulos agudos de cada triângulo é 90graus, ou seja, eles são complementares.

Esquema. Primeira linha: medida do ângulo A 1 mais medida do ângulo B é igual a 90°. Segunda linha: medida do ângulo B mais medida do ângulo C é igual a 90°. Fecha chaves. Medida do ângulo A 1 mais medida do ângulo B riscada é igual a medida do ângulo B riscada mais medida do ângulo C , então medida do ângulo A 1 é igual medida do ângulo C ou Ângulo A 1 é congruente ao ângulo C.

Esquema. Primeira linha: medida do ângulo A 2 mais medida do ângulo B é igual a 90°. Segunda linha: medida do ângulo B mais medida do ângulo C é igual a 90°. Fecha chaves. Medida do ângulo A 2 mais medida do ângulo C riscada é igual a medida do ângulo B mais medida do ângulo C riscada, então medida do ângulo A 2 é igual medida do ângulo B ou Ângulo A 2 é congruente ao ângulo B.

Observação

▶ Se dois triângulos têm dois pares de ângulos respectivamente congruentes, então eles são triângulos semelhantes. Chamamos esse fato de caso AA (ângulo-ângulo) de semelhança.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

1 Desenhe no caderno um triângulo retângulo cujos catetos meçam 8,4 centímetros e 11,2 centímetros.

a) Obtenha, com o auxílio de uma régua, a medida aproximada da hipotenusa dêsse triângulo.

b) Verifique se o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

2 Usando régua e compasso, construa no caderno triângulos cujos lados meçam:

• 2 centímetros, 4 centímetros e 5 centímetros;

• 3 centímetros, 3,5 centímetros e 4 centímetros;

• 4,2 centímetros, 5,6 centímetros e 7 centímetros.

(Ao usar o compasso, atenção para não se machucar com a ponta-seca.)

a) Classifique os triângulos construídos de acordo com as medidas dos ângulos internos.

b) Para cada triângulo, estabeleça uma relação entre o quadrado da medida do maior lado e a soma dos quadrados das medidas dos outros dois lados, utilizando os símbolos >, < ou =.

Respostas e comentários

Espera-se que os estudantes usem a semelhança de triângulos para obter triângulos retângulos com medidas de lados 3x, 4x e 5x, com x sendo um número tal que x > 0. Por exemplo, para x = 1,5, obtém-se o triângulo cujos lados medem 4,5 centímetros, 6 centímetros e 7,5 centímetros.

1. Construção de figura.

1. a) 14 centímetros

1. b) Sim.

2. Construção de figuras.

2. a) • obtusângulo

• acutângulo

• retângulo

2. b) • 25 > 20

• 16 < 21,25

• 49 = 49

Exercícios propostos

No exercício 1, os estudantes devem usar as medidas reais no desenho. Observe um desenho em escala menor, com medidas proporcionais.

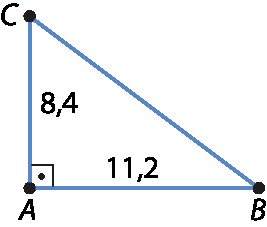
Ilustração. Triângulo ABC com ângulo reto em A. Medidas: AB: 11,2 e AC: 8,4.

Na escala real, os estudantes devem obter 14 centímetros.

No exercício 2, temos:

• 2 centímetros, 4 centímetros e 5 centímetros:

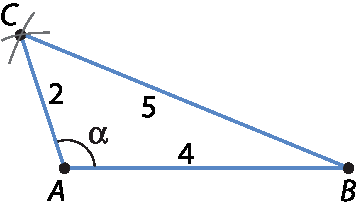
Ilustração. Triângulo ABC com ângulo alfa em A. Medidas: AB: 4, AC: 2 e BC: 5.

Verificamos que α > 90graus; assim, o triângulo á bê cê é obtusângulo.

Podemos também comparar o quadrado da medida do maior lado (25) com a soma dos quadrados das medidas dos outros dois lados (4 e 16). Assim, 4 + 16 < 25 indica que o ângulo oposto ao maior lado é obtuso.

• 3 centímetros, 3,5 centímetros e 4 centímetros:

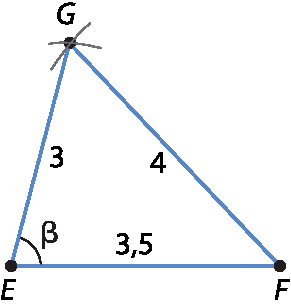
Ilustração. Triângulo EFG com ângulo beta em E. Medidas: EG: 3. EF: 3,5. FG: 4.

Analogamente ao anterior, verificamos que β < 90graus, assim como os demais ângulos internos. O triângulo é éfe gê é acutângulo.

Também verificamos

3elevado a 2 + (3,5)elevado a 2 > 4elevado a 2

9 + 12,25 > 16

Isso ocorre sempre que o ângulo oposto ao maior lado é agudo.

• 4,2 centímetros, 5,6 centímetros e 7 centímetros:

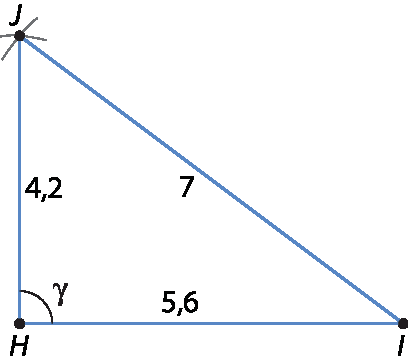
Ilustração. Triângulo HIJ com ângulo gama em H. Medidas: HJ: 4,2. HI: 5,6. IJ: 7.

Nesse caso, γ = 90graus e os demais ângulos internos são agudos, logo agá é jota é um triângulo retângulo.

Aqui vale a relação de Pitágoras (4,2)elevado a 2 + (5,6)elevado a 2 = 7elevado a 2, ou seja,

17,64 + 31,36 = 49. Isso indica que temos um triângulo retângulo.

Página 176

Enunciando o teorema de Pitágoras

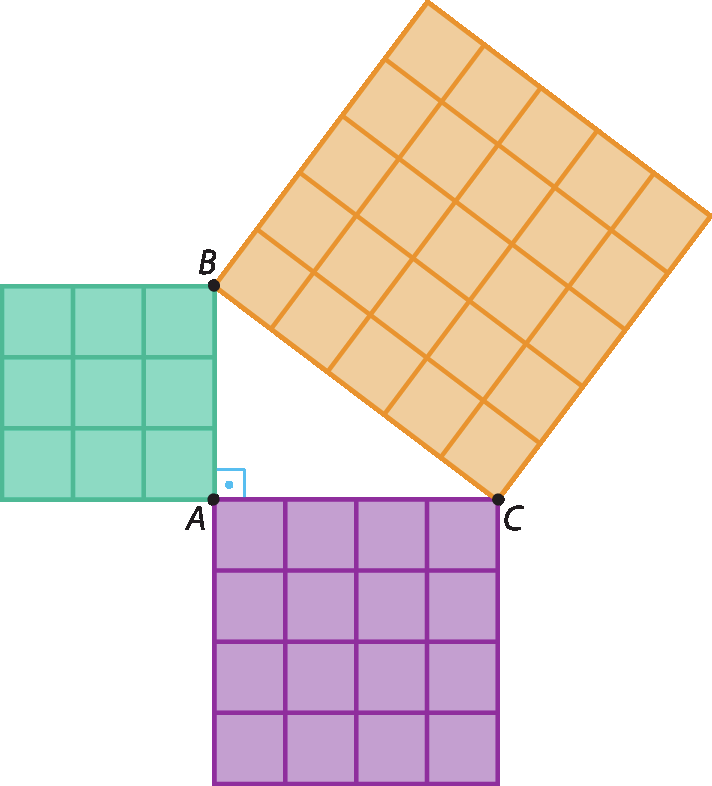
Ilustração. Triângulo retângulo ABC, com ângulo reto em A. Junto ao lado AB um quadrado verde dividido em 9 quadrados iguais. Junto ao lado AC um quadrado roxo dividido em 16 quadrados iguais. Junto ao lado BC quadrado laranja dividido em 25 quadrados iguais.

Considerando como unidade de medida a área de cada quadradinho que compõe os quadrados da figura, notamos que a medida da área do quadrado maior é igual à soma das medidas das áreas dos quadrados menores, ou seja:

25 = 9 + 16

Como 25 = 5elevado a 2, 9 = 3elevado a 2 e 16 = 4elevado a 2, podemos escrever essa igualdade da seguinte maneira:

5elevado a 2 = 3elevado a 2 + 4elevado a 2

Repare que 5, 3 e 4 são as medidas dos lados dos quadrados da figura e, consequentemente, as medidas dos respectivos lados do triângulo retângulo á bê cê.

A relação entre os quadrados das medidas dos lados dêsse triângulo retângulo é válida para todo triângulo retângulo e é conhecida como teorema de Pitágoras.

Em todo triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

Demonstrando o teorema de Pitágoras

Existem mais de trezentas demonstrações do teorema de Pitágoras. Vamos apresentar uma que faz uso da equivalência de medidas de áreas.

Ilustração. Homem loiro de barba, cabelo comprido e camiseta azul.
Ele fala: O livro A proposição de Pitágoras, de Elisha Scott Loomis, por exemplo, contém 370 demonstrações diferentes do teorema de Pitágoras.

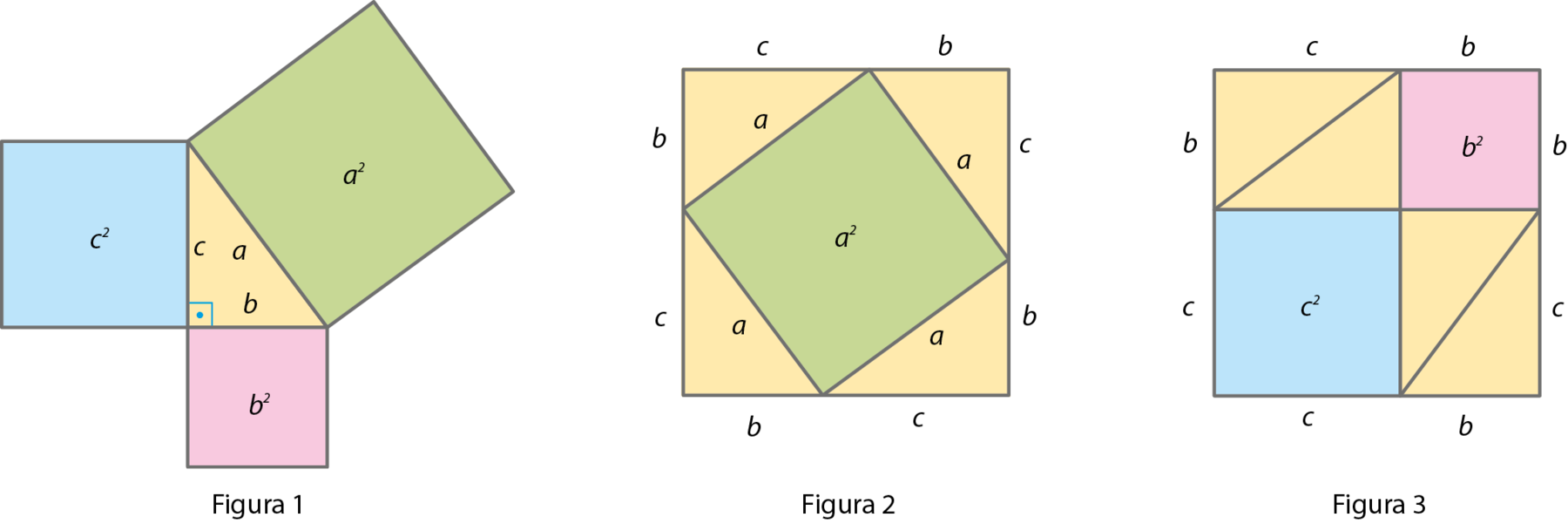
Considerando um triângulo retângulo, construímos quadrados sobre a hipotenusa de medida a e sobre os catetos de medidas b e c, como mostra a figura 1. Nas figuras 2 e 3, construímos quadrados de lados que medem (b + c).

Ilustração. Triângulo amarelo de lados a, b e c e ângulo reto entre b e c. Junto ao lado a, quadrado verde de medida de área a elevado ao quadrado. Um de seus lados é o próprio lado a do triângulo. Junto ao lado b, quadrado rosa de medida de área b elevado ao quadrado. Um de seus lados é o próprio lado b do triângulo. Junto ao lado c, quadrado azul de medida de área c elevado ao quadrado. Um de seus lados é o próprio lado c do triângulo.

Ilustração. Quadrado amarelo. Dentro, quadrado verde na diagonal com medida a elevado ao quadrado. Em cada lado entre o quadrado amarelo e o verde, um triângulo a por b por c.

Ilustração. Figura composta por dois triângulos amarelos formando um retângulo b por c. Ao lado, quadrado rosa b por b, com texto b elevado ao quadrado escrito ao centro. Abaixo dos triângulos quadrado azul c por c, com texto c elevado ao quadrado escrito ao centro, ao seu lado e abaixo do quadrado rosa, dois triângulos amarelos formando um retângulo b por c.

Respostas e comentários

Demonstrando o teorema de Pitágoras

Neste tópico, e em outros deste capítulo, a manipulação das figuras apresentadas é uma abordagem que pode enriquecer o aprendizado; ela pode ser aplicada paralelamente à leitura do texto ou à aula expositiva. Para isso, se possível, confeccione previamente em cartolina peças para compor as figuras 1, 2 e 3, replicando-as de modo que, em grupos, os estudantes montem as figuras como um quebra-cabeça.

Outra possibilidade é pedir aos estudantes que construam figuras semelhantes (ampliadas ou não) e recortem as figuras construídas. Em seguida, proponha a eles que manipulem essas partes recortadas de modo a compô-las de acordo com as figuras 1, 2 e 3, além de investigarem livremente outras composições.

Página 177

O quadrado da figura 2 é formado por quatro triângulos retângulos, congruentes ao triângulo da figura 1, e pelo quadrado verde. Assim, a medida da área do quadrado de lado medindo (b + c) é a soma das medidas das áreas dos quatro triângulos com a da área do quadrado verde.

O quadrado da figura 3 é formado por quatro triângulos retângulos, congruentes ao triângulo da figura 1, pelo quadrado azul e pelo quadrado rosa. Então, a medida da área do quadrado de lado de medida (b + c) é a soma das medidas das áreas dos quatro triângulos com as das áreas dos quadrados azul e rosa.

Logo, a medida da área do quadrado verde é a soma da medida da área do quadrado azul com a da área do quadrado rosa, ou seja:

a elevado a 2 = b elevado a 2 + c elevado a 2

Observe um exemplo de aplicação do teorema de Pitágoras.

Precisamos calcular a medida do comprimento x de uma escada que está apoiada em uma parede, conforme a figura a seguir. Para isso, vamos aplicar o teorema de Pitágoras:

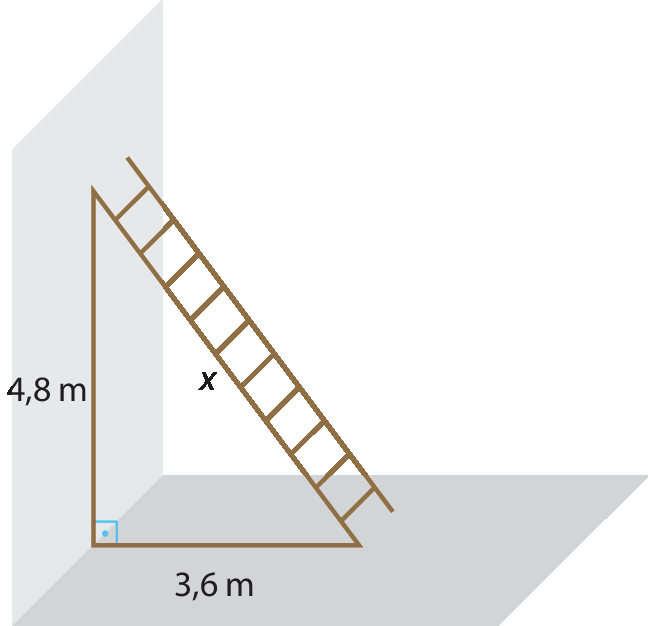
Ilustração. Parede com escada encostada sobre ela, formando um triângulo com o chão. A escada mede x. A altura da escada na parede até o chão é 4,8 metros. A distância da parede para a escada é 3,6 metros.

x elevado a 2 = (4,8)elevado a 2 + (3,6)elevado a 2

x elevado a 2 = 23,04 + 12,96

x elevado a 2 = 36

x = \pm \sqrt{36}

x = ±6

Como x é a medida do comprimento da escada, ele deve ser um número positivo. Portanto, o comprimento da escada mede 6 métros.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

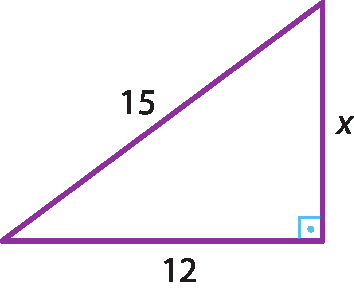
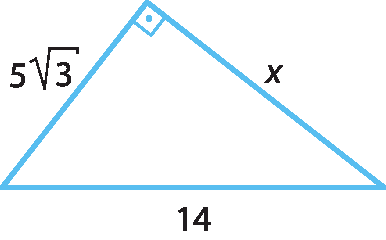
3 Calcule o valor de x aplicando o teorema de Pitágoras:

Ilustração. Triângulo roxo com as medidas dos lados: 15, 12 e x. Ângulo reto entre 12 e x.

Ilustração. Triângulo verde com as medidas dos lados: 10, x e x. Ângulo reto entre x e x.

Ilustração. Triângulo azul com as medidas dos lados: 14, x e 5 raiz quadrada de 3. Ângulo reto entre 5 raiz quadrada de 3 e x.

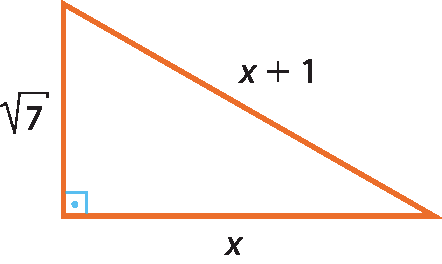
Ilustração. Triângulo laranja com as medidas dos lados: x, raiz quadrada de 7 e x + 1. Ângulo reto entre raiz quadrada de 7 e x.

4 Considere os quadrados á bê dê cê e dê é éfe gê representados na figura e, em seguida, faça o que se pede.

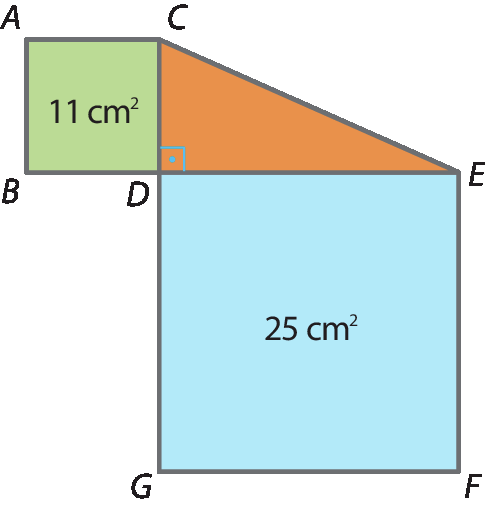
Ilustração. Quadrado verde ABCD com 11 centímetros quadrados. Ao lado, triângulo laranja CDE, com ângulo reto em D. Abaixo, quadrado azul DEFG com 25 metros quadrados.

a) Determine a medida da área do triângulo cê dê é.

b) Calcule a medida da hipotenusa dêsse triângulo.

Respostas e comentários

3. a) x = 9

3. b)

x = 5 \sqrt{2}

3. c) x = 11

3. d) x = 3

4. a)

2, 5 \sqrt{11} {cm}^{2}

4. b) 6 centímetros

Exercícios propostos

No exercício 3, devemos aplicar o teorema de Pitágoras para determinar x. Assim:

a) 15elevado a 2 = 12elevado a 2 + xelevado a 2 ⇒ ⇒ xelevado a 2 = 15elevado a 2 ‒ 12elevado a 2 ⇒ ⇒ xelevado a 2 = 81 ⇒ x =

\sqrt{81}

= 9

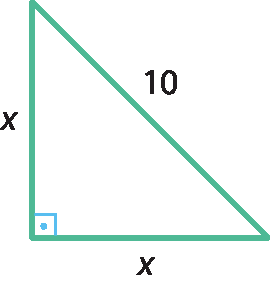
b) 10elevado a 2 = xelevado a 2 + xelevado a 2 ⇒ ⇒ 2xelevado a 2 = 100 ⇒ xelevado a 2 = 50 ⇒ ⇒ x =

\sqrt{50}

= 5

\sqrt{2}

c) 14elevado a 2 = xelevado a 2 +

{(5 \sqrt{3})}^{2}

⇒ ⇒ xelevado a 2 = 142 ‒

{(5 \sqrt{3})}^{2}

⇒ ⇒ xelevado a 2 = 196 ‒ 75 ⇒ ⇒ xelevado a 2 = 121 ⇒ x =

\sqrt{121}

= 11

d) (x + 1)elevado a 2 = xelevado a 2 + (

\sqrt{7}

)elevado a 2 ⇒ ⇒ xelevado a 2 + 2x + 1 ‒ xelevado a 2 = 7 ⇒ ⇒ 2x = 7 ‒ 1 ⇒ ⇒ 2x = 6 ⇒ x = 3

A seguir, uma possível resolução do exercício 4.

a) O lado do quadrado azul mede

\sqrt{11}

centímetros e o lado do quadrado verde mede

\sqrt{25}

centímetros, ou seja, 5 centímetros.

A medida A da área do triângulo laranja é dada por:

A = \frac{5 \cdot \sqrt{11}}{2} = 2, 5 \sqrt{11}

A área mede 2,5

\sqrt{11}

centímetros quadrados.

b) Seja x a medida da hipotenusa. xelevado a 2 = 11 + 25 = 36 ⇒

\Rightarrow x = \sqrt{36} = 6

A hipotenusa mede 6 centímetros.

Página 178

5 Em um esquadro, os lados perpendiculares medem 12 centímetros e

12 \sqrt{3}

centímetros. Quanto mede o lado oposto ao ângulo reto dêsse esquadro?

6 Aplicando o teorema de Pitágoras, determine, se possível, a medida x de cada uma das figuras.

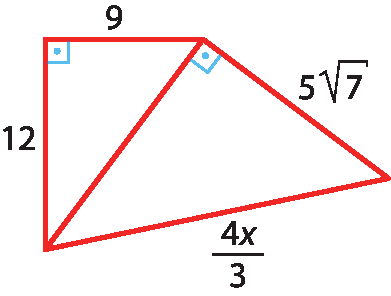
Ilustração. Dois triângulos unidos por um lado em comum entre eles. A medida do triângulo à esquerda é 12 e 9. Ângulo reto entre 12 e 9. A medida do triângulo à direita é fração, 4 x sobre 3, fim da fração e 5 raiz quadrada de 7. Ângulo reto entre lado comum dos triângulos e 5 raiz quadrada de 7.

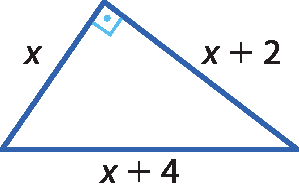
Ilustração. Triângulo azul. Lados medindo x, x mais 2 e x mais 4. Ângulo reto entre x e x mais 2.

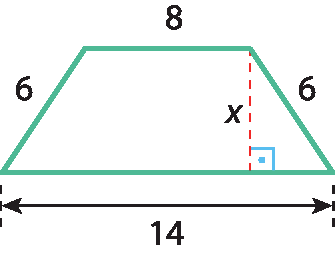
Ilustração. Trapézio com altura tracejada entre as bases medindo x. As medidas dos lados do trapézio são: 6, 6, 8 e 14.

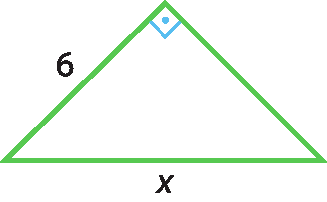
Ilustração. Triângulo verde Lados medindo 6 e x. Ângulo reto entre 6 e o outro lado sem medida indicada.

7 As diagonais de um losango medem 12 centímetros e 16 centímetros. O ângulo menor dêsse losango mede aproximadamente 74graus.

a) Determine a medida do lado dêsse losango.

b) Calcule a medida da área dêsse losango.

c) Para responder aos itens anteriores foi necessário usar todas as informações do enunciado? Justifique sua resposta.

8 Em um triângulo isósceles, um lado mede 12 centímetros e cada um dos lados congruentes mede 9 centímetros. Faça um esboço dêsse triângulo em seu caderno e calcule a medida da altura relativa ao lado de 12 centímetros dele.

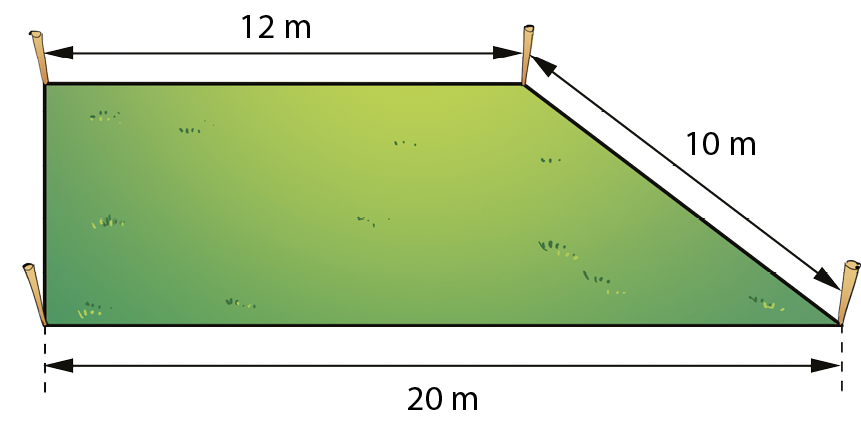
9 Quantos metros de arame são necessários para cercar, com 6 voltas, um terreno em formato de trapézio retângulo cujas bases medem 12 métros e 20 métros e cujo lado oblíquo mede 10 métros?

Ilustração. Terreno em formato de trapézio retângulo. As medidas são: base menor: 12 metros; um dos lados não paralelos: 10 metros; base maior 20 metros.

10 Em um triângulo retângulo, a hipotenusa mede

3 \sqrt{5}

métros e as medidas dos catetos são expressas por x e x + 3. Calcule a medida dos catetos.

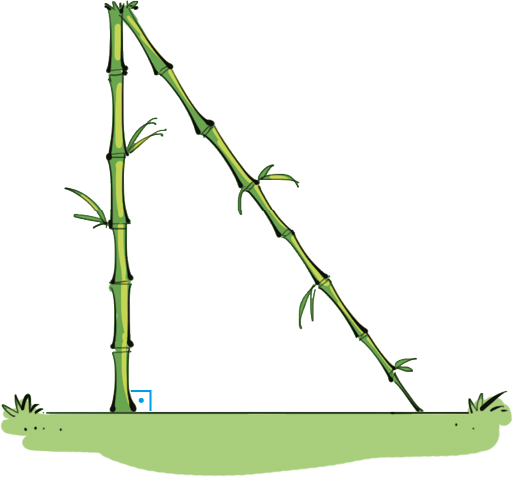
11 Um bambu foi quebrado pelo vento a uma altura de medida igual a 4,8 métros. Ele tombou de modo que sua ponta tocou o chão a 3,6 métros de sua base. Considerando que o bambu formou um ângulo reto com o solo, determine a medida da altura dêsse bambu.

Ilustração. Bambu na vertical e outro na diagonal formando triângulo junto ao chão. Ângulo reto entre o chão e o bambu na vertical.

12 Para reforçar a sustentação de uma placa de propaganda com formato retangular, que mede 2 métros de comprimento por 5 métros de largura, foram colocadas duas ripas de madeira no sentido das diagonais da placa. Qual é a medida aproximada do comprimento de cada ripa?

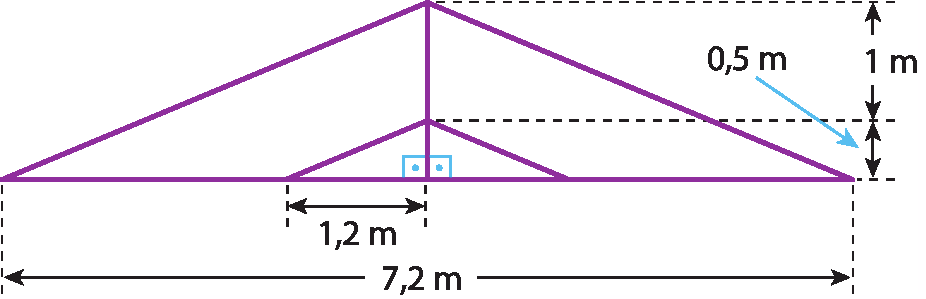
13 A figura a seguir representa parte da estrutura de madeira do telhado de uma residência. A base mede 7,2 métros e na metade dela é fixada, perpendicularmente, uma haste que mede 1,5 métro. Quantos metros de madeira são necessários para construir as outras partes dessa estrutura?

Ilustração. Triângulo maior com reta vertical tracejada no centro e um triângulo menor com dois ângulos retos. A medida da extremidade até o ângulo reto é 1,2 metros. A distância do topo do triângulo menor para o maior é 1 metro. A altura do triângulo menor é 0,5 metro. A medida do lado do triângulo maior é 7,2 metros.

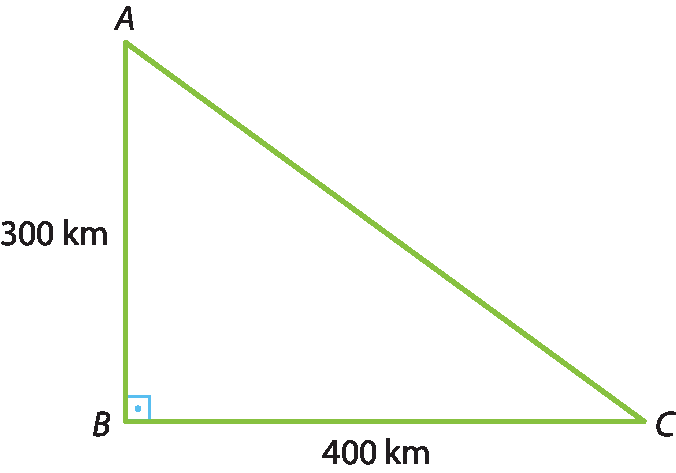
14 Um avião sai da cidade A e vai até a cidade B, que está à medida de distância de 300 km. Depois, decola em direção à cidade C, a 400 km. Se o avião fosse em linha reta da cidade a para a C, que distância percorreria?

Ilustração. Triângulo verde ABC. A medida AB é 300 quilômetros. A medida BC é 400 quilômetros. Ângulo reto em B.

Hora de criar – Em dupla com um colega, elaborem um problema cada um sobre medida de comprimento de lados de um triângulo retângulo. Troquem os problemas elaborados por vocês e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Respostas e comentários

5. 24 centímetros

6. a) x = 15

6. b) x = 6

6. c)

x = 3 \sqrt{3}

6. d) Faltam dados para calcular o valor de x.

7. a) 10 centímetros

7. b) 96 centímetros quadrados

7. c) Não, pois não foi necessário usar a medida do ângulo.

3 \sqrt{5} cm

9. 288 métros

10. 3 métros e 6 métros.

11. 10,8 métros

12. 5,38 métros

13. 10,4 métros

14. 500 quilômetros

15. Resposta pessoal.

Exercícios propostos

A seguir, a resolução do exercício 5. O contorno de um esquadro tem o formato de um triângulo retângulo.

É pedida a medida da hipotenusa, que representamos por x.

Aplicando o teorema de Pitágoras, obtemos:

xelevado a 2 = 12elevado a 2 +

{(12 \sqrt{3})}^{2}

xelevado a 2 = 12elevado a 2 + 3 · 12elevado a 2

xelevado a 2 = 4 · 12elevado a 2

xelevado a 2 = 576

x = 24

O lado oposto ao ângulo reto mede 24 centímetros.

As resoluções dos exercícios 6 a 12 e do exercício 14 estão no início deste Manual, nas orientações específicas do capítulo 8.

No exercício 6, se julgar conveniente, comente com os estudantes que no item a o valor de x pode ser obtido por meio da análise das medidas dos dois triângulos apresentados na figura. No item d, note que faltam dados para calcular o valor de x. Já no exercício 7, há dado a mais.

No exercício 13, observe uma representação sem escala da estrutura maior, cuja medidas são dadas em metro.

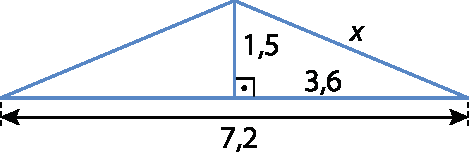
Ilustração. Triângulo com altura 1,5. Medida de um dos lados sendo x e da base 7,2. Da altura do triângulo até lado direito mede 3,6.

Observando essa figura:

xelevado a 2 = 1,5elevado a 2 + 3,6elevado a 2 ⇒ x = 3,9

Observe uma representação sem escala da estrutura menor, com medidas em metro.

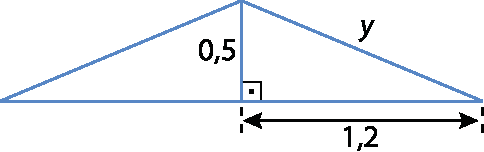
Ilustração. Triângulo com altura 0,5. Medida de um dos lados sendo y. Da altura do triângulo até lado direito mede 1,2.

yelevado a 2 = 0,5elevado a 2 + 1,2elevado a 2 ⇒ y = 1,3

Assim, com a base dela e a haste vertical já consideradas, ainda faltam 10,4 métros de madeira, pois:

2 · 3,9 + 2 · 1,3 = 7,8 + 2,6 = 10,4

Portanto, são necessários 10,4 métros de madeira.

A resposta ao exercício 15 é pessoal, mas sugerimos incentivar os estudantes a elaborar problemas com base em situações contextualizadas.

Sugestão de leitura

Para ampliar o trabalho com o teorema de Pitágoras, sugerimos:

SANTOS, M. C. Teorema de Pitágoras: suas diversas demonstrações, 2011. Monografia (Especialização em Educação Matemática para professores do Ensino Médio), Universidade Estadual da Paraíba, Campina Grande, 2011. Disponível em: https://oeds.link/scxFV4. Acesso em: 17 agosto 2022.

O autor apresenta diferentes demonstrações, geométricas e algébricas, do teorema.

Página 179

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

O tangram é formado por sete peças: cinco triângulos retângulos isósceles (sendo dois grandes e congruentes, dois pequenos e congruentes e um médio) e dois paralelogramos (sendo um deles um quadrado).

Com essas sete peças, é possível compor muitas figuras. Observe, por exemplo, este retângulo, feito com as peças do tangram.

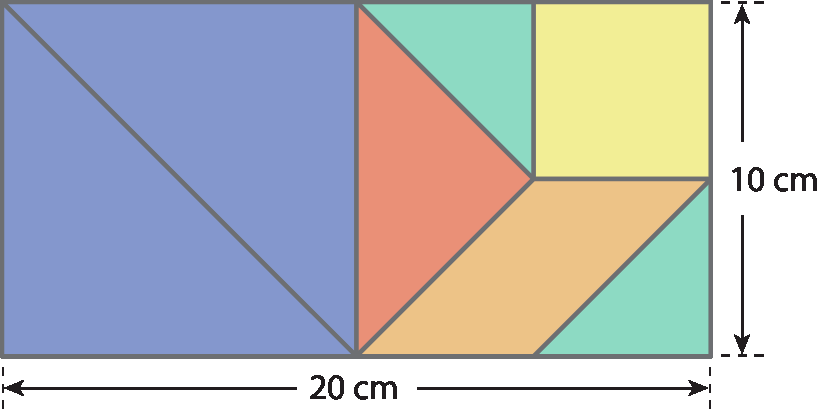
Ilustração. Figura composta por dois triângulos azuis grandes formando um quadrado. À direita, quadrado composto por um triângulo médio laranja, dois triângulos pequenos verdes, um quadrado amarelo e um paralelogramo laranja. Juntas todas as essas figuras compõem um retângulo de dimensões 10 cm por 20 cm.

Sabendo que a área do quadrado formado pelos dois triângulos maiores equivale à metade da área de todas as peças do tangram, determine a medida do perímetro aproximada de cada peça dêsse tangram. Use para

\sqrt{2}

o valor aproximado 1,41.

PARA SABER MAIS

Triângulos pitagóricos

Triângulos retângulos cujas medidas dos lados são expressas por números inteiros são chamados triângulos pitagóricos.

Entre eles, o mais conhecido é o triângulo cujas medidas dos lados são números inteiros e consecutivos: 3, 4 e 5.

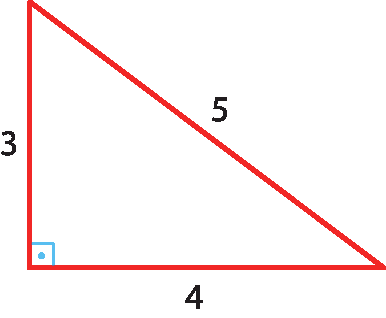
Ilustração. Triângulo com as medidas dos lados: 3, 4 e 5. Ângulo reto entre 3 e 4.

Pelo caso lado lado lado de semelhança, qualquer triângulo retângulo cujos lados sejam proporcionais aos números 3, 4 e 5 é um triângulo pitagórico.

Em outras palavras, os triângulos cujas medidas dos lados são dadas pelos ternos pitagóricos (6, 8, 10), (9, 12, 15), (12, 16, 20), reticências, (3k, 4k, 5k), sendo k um número inteiro positivo, são triângulos pitagóricos.

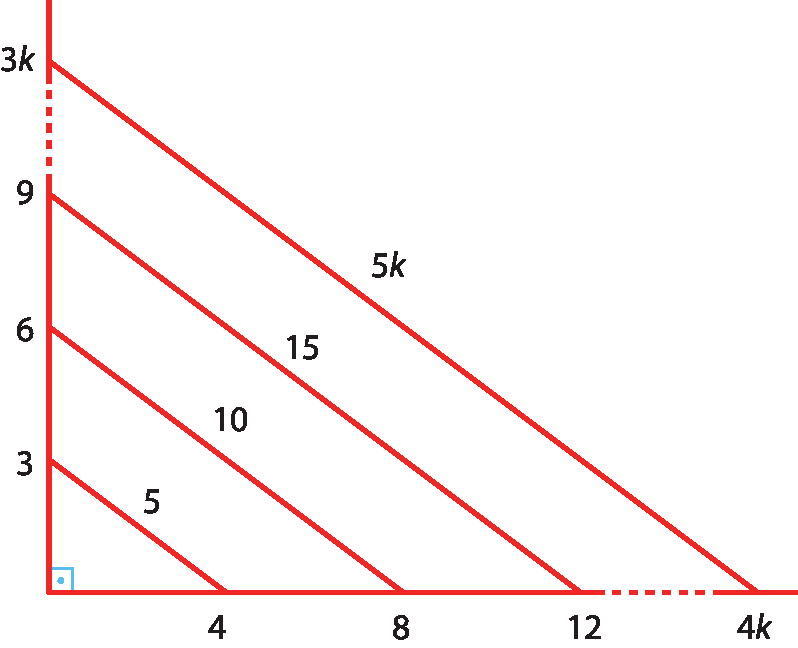
Esquema. Na parte inferior, reta horizontal com pontos: 4, 8, 12, 4k. À esquerda, reta vertical com pontos: 3, 6, 9 e 3k. Retas diagonais ligam pontos à esquerda e abaixo. Do ponto 4 a 3 mede 5. Do ponto 8 a 6 mede 10. Do ponto 12 a 9 mede 15. Do ponto 4k a 3k mede 5k.

Esse assunto inspirou diversos estudos que chegaram a resultados bastante curiosos.

Um desses estudos mostra como podemos obter determinado tipo de ternoglossário pitagórico e, por consequência, um triângulo pitagórico. Observe a figura.

Consideremos dois números ímpares consecutivos (ou dois números pares consecutivos) x e (x + 2).

• A medida de um cateto é a soma dos números: x + (x + 2).

• A medida do outro cateto é o produto dos números: x ⋅ (x + 2).

• A medida da hipotenusa é o produto dos números, mais 2.

Por exemplo, se x = 1, temos x + 2 = 3; então:

• um cateto mede 1 + 3 = 4;

• o outro cateto mede 1 ⋅ 3 = 3;

• a hipotenusa mede 1 ⋅ 3 + 2 = 5.

Então, esse triângulo é pitagórico, e tem lados de medidas 3, 4 e 5.

Observe outro exemplo, em que x = 8 e x + 2 = 10.

Os catetos medem 18 (8 + 10) e 80 (8 ⋅ 10), e a hipotenusa mede 82 (8 ⋅ 10 + 2), ou seja, respectivamente 18², 80² e 82².

Note que 822 = 182 + 802.

Respostas e comentários

Para saber mais:

A medida do perímetro de cada triângulo maior é 34,1 centímetros; de cada triângulo menor é 17,05 centímetros; do triângulo médio é 24,1 centímetros; do quadrado é 20 centímetros; do outro paralelogramo é 24,1 centímetros.

Pense mais um poucoreticências

Peça aos estudantes que construam o tangram.

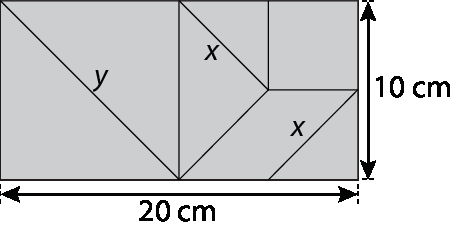
Ilustração. Figura composta por dois triângulos cinzas grandes formando um quadrado. À direita, quadrado composto por um triângulo médio cinza, dois triângulos pequenos cinza, um quadrado cinza e um paralelogramo cinza. Juntas todas essas figuras compõem um retângulo de dimensões 10 centímetros por 20 centímetros.

• Do triângulo maior, obtemos:

y^{2} = 10^{2} + 10^{2}

y = \sqrt{2 \cdot 10^{2}}

y =

10 \sqrt{2}

= 14,1

• Do triângulo menor, obtemos: xelevado a 2 = 5elevado a 2 + 5elevado a 2

x = \sqrt{2 \cdot 5^{2}}

x = 5 \sqrt{2} = 7, 05

A medida do perímetro de cada triângulo maior é 34,1 centímetros (10 + 10 + 14,1), e a de cada triângulo menor é 17,05 centímetros (5 + 5 + 7,05).

No triângulo médio, os catetos medem 7,05 centímetros, e a hipotenusa, 10 centímetros. Assim, a medida do perímetro do triângulo médio é 24,1 centímetros (7,05 + 7,05 + 10).

Os lados do quadrado menor medem 5 centímetros. Assim, o perímetro dêsse quadrado mede 20 centímetros (5 + 5 + 5 + 5).

No paralelogramo, dois dos lados medem 5 centímetros, e cada um dos outros dois lados mede 7,05 centímetros. O perímetro dêsse paralelogramo mede 24,1 centímetros (5 + 5 + 7,05 + 7,05).

Para saber mais

Esta seção oferece uma boa oportunidade de aplicar alguns conceitos, como semelhança de triângulos e proporcionalidade. Explore com os estudantes as diferentes estratégias de resolução dos exercícios propostos.

As resoluções das atividades 1 a 4 do Agora é com você! estão no início deste Manual, nas orientações específicas do capítulo 8.

Para ampliar a atividade 4, proponha aos estudantes que construam os triângulos cujas medidas obtiveram no quadro elaborado. Em seguida, peça a eles que verifiquem com um transferidor se esses triângulos construídos são triângulos retângulos.

Página 180

Agora é com você!

FAÇA AS ATIVIDADES NO CADERNO

Reúna-se com um colega, usem uma calculadora e façam o que se pede.

1 Um dos catetos de um triângulo pitagórico mede 15 centímetros. Determinem dois possíveis pares de medidas do outro cateto e da hipotenusa dêsse triângulo.

2 A hipotenusa de um triângulo pitagórico semelhante ao triângulo de lados 3 centímetros, 4 centímetros e 5 centímetros mede 35 centímetros. Determinem as medidas do perímetro e da área dêsse triângulo.

3 O perímetro de um triângulo pitagórico semelhante ao triângulo de lados 3 centímetros, 4 centímetros e 5 centímetros mede 108 centímetros. Determinem a medida dos catetos e da hipotenusa dêsse triângulo.

4 Construam no caderno um quadro como o do modelo a seguir e atribuam a x cinco números inteiros, completando-o. Depois, verifiquem que os ternos pitagóricos obtidos, ou seja, os números das três colunas da direita, satisfazem o teorema de Pitágoras.

x	x + 2	x + (x + 2)	x ⋅ (x + 2)	x ⋅ (x + 2) + 2

3. Aplicações do teorema de Pitágoras

Relacionando as medidas da diagonal e do lado de um quadrado

Considere o quadrado a bê cê dê, com lado medindo 𝓁 e diagonal d.

Aplicando o teorema de Pitágoras ao triângulo retângulo á bê cê, temos:

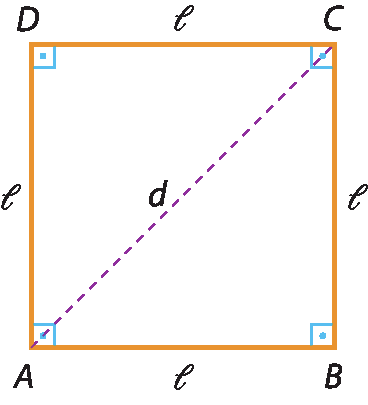
Ilustração. Quadrado ABCD com medida L cursivo em cada lado. Reta diagonal tracejada AC com medida d.

(AC)elevado a 2 = (AB)elevado a 2 + (BC)elevado a 2

d elevado a 2 = 𝓁 elevado a 2 + 𝓁 elevado a 2

d elevado a 2 = 2𝓁 elevado a 2

d = \sqrt{2 ℓ^{2}}

d = ℓ \sqrt{2}

Portanto, com a expressão

d = ℓ \sqrt{2}

é possível determinar a medida da diagonal de um quadrado quando se conhece a medida de seu lado, e vice-versa.

Acompanhe alguns exemplos.

a) Vamos calcular a medida da diagonal de um quadrado cujo perímetro mede 12 centímetros. Se P = 12 centímetros, então 𝓁 = 3 centímetros.

d = ℓ \sqrt{2}

d = 3 \sqrt{2}

Logo, a diagonal dêsse quadrado mede

3 \sqrt{2} cm .

b) Vamos calcular a medida do lado de um quadrado cuja diagonal mede

7 \sqrt{2} cm .

Substituímos d por

7 \sqrt{2}

d = ℓ \sqrt{2} .

ℓ \sqrt{2} = 7 \sqrt{2}

𝓁 = 7

Logo, o lado dêsse quadrado mede 7 centímetros.

Respostas e comentários

1. Respostas possíveis: 20 centímetros e 25 centímetros; 8 centímetros e 17 centímetros; 36 centímetros e 39 centímetros; 112 centímetros e 113 centímetros.

2. Medida do perímetro: 84 centímetros; medida da área: 294 centímetros².

3. 27 centímetros, 36 centímetros e 45 centímetros.

4. Construção de quadro.

3. Aplicações do teorema de Pitágoras

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah um três e ê éfe zero nove ême ah um quatro.

Neste tópico, os estudantes poderão compreender e demonstrar relações entre as medidas da altura e do lado de um triângulo equilátero aplicando o teorema de Pitágoras. Eles também vão descrever os passos para a construção, com régua e compasso, de um quadrado dada a medida do seu lado. Com isso, os estudantes poderão desenvolver as habilidades (ê éfe zero nove ême ah um três) e (ê éfe zero nove ême ah um quatro).

Uma das aplicações do teorema de Pitágoras é mostrar outras relações importantes em figuras geométricas, como na relação da diagonal e do lado de um quadrado qualquer: a medida (d) da diagonal pode ser dada em função da medida (ℓ) do lado.

Aproveite o momento e retome a ideia de que a diagonal do quadrado e seu lado estabelecem uma razão irracional.

Proponha aos estudantes que acompanhem a construção do quadrado apresentado no exemplo c. Depois, solicite que reproduzam essa construção no caderno. Em seguida, peça a eles que justifiquem por que AD =

u \sqrt{2}

. Espera-se que os estudantes percebam que é porque AD é a medida da diagonal do quadrado de lado medindo u.

Após reproduzirem a construção do quadrado do exemplo c, peça aos estudantes que verifiquem com o compasso que AG = 2u.

Página 181

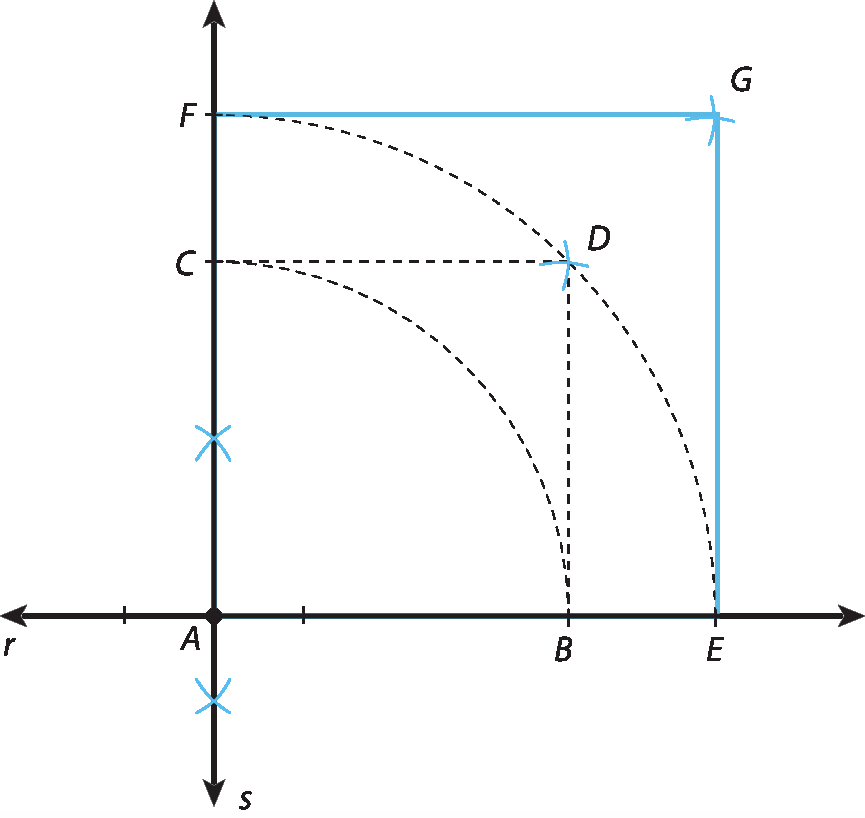
c) Dado o segmento

\overline{A B}

com medida u, vamos construir um quadrado cujo lado meça

\sqrt{2}

Ilustração. Segmento de reta AB com medida u.

Usando régua e compasso, podemos seguir estes passos:

• transportamos

\overline{A B}

para uma reta r ;

• por a, traçamos a reta s, perpendicular a r ;

• com abertura do compasso igual a u, traçamos três arcos: com centro em a, obtemos o ponto C em s; com centro em B e, depois, em C, obtemos o ponto D ;

• as medidas dos lados do quadrado a bê cê dê são iguais a u; portanto, suas diagonais

\overline{A D}

\overline{C B}

medem u

\sqrt{2}

\sqrt{2}

• com abertura do compasso igual a á dê (AD =

\sqrt{2}

u), traçamos três arcos: com centro em A, obtemos o ponto ê em r e o ponto F em s; com centro em ê e, depois, em F, obtemos o ponto G;

• traçamos

\overline{E G}

\overline{F G}

e obtemos o quadrado AEGF, com lado de medida

\sqrt{2}

(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)

Ilustração. Eixo horizontal r com pontos A, B e E. Eixo vertical s passa sobre ponto A, com pontos C e F. O ponto B liga com C formando ponto D na extremidade superior direita. E liga com G. Arco traçado sobre D em EF.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

16 Considere que o lado de um quadrado a bê cê dê mede 15 centímetros.

a) Determine a medida de sua diagonal.

b) Calcule a medida da área do quadrado cujo lado tem a mesma medida da diagonal do quadrado a bê cê dê.

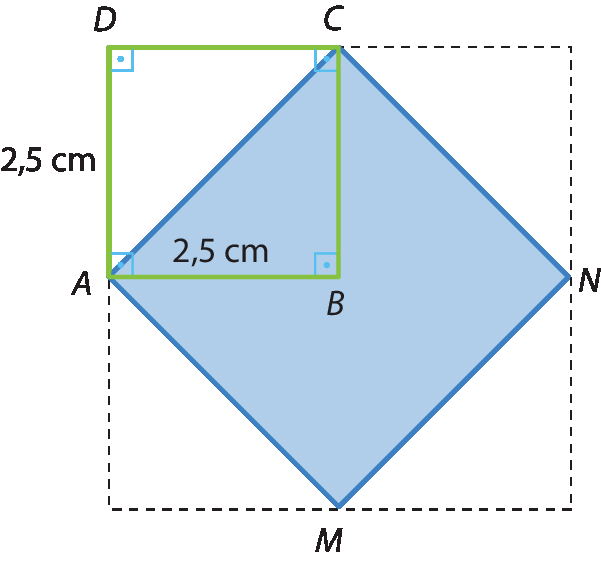
17 Calcule a medida da área do quadrado á ême êne cê, no qual B é ponto médio de uma de suas diagonais.

Ilustração. Losango ACNM. No centro, ponto B. Ao redor, quadrado tracejado. E parcialmente no losango e no quadrado tracejado, quadrado ABCD de lado 2,5 centímetros.

18 A diagonal de um quadrado mede

10 \sqrt{2} cm .

Três quadrados que têm diagonais com essa medida são colocados um ao lado do outro, de modo que formem um retângulo. Calcule a medida do perímetro dêsse retângulo.

19 Qual é a medida da diagonal do cubo a seguir, destacada em vermelho?

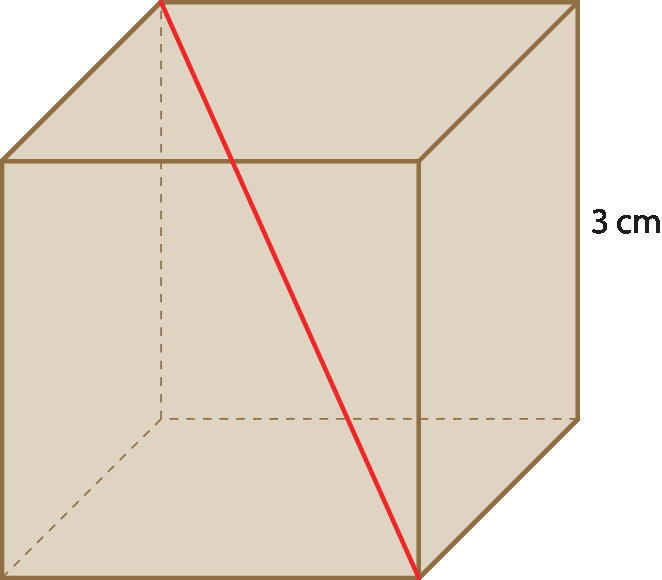
Ilustração. Cubo com lado de 3 centímetros. Dentro, diagonal vermelha.

Respostas e comentários

16. a) 15

\sqrt{2}

centímetros

16. b) 450 centímetros quadrados

17. 12,50 centímetros quadrados

18. 80 centímetros

19. 3

\sqrt{3}

centímetros

Exercícios propostos

No exercício 16, no item a, a diagonal é determinada pela relação com a medida do lado de um quadrado; como o lado mede 15 centímetros, a diagonal mede

15 \sqrt{2}

centímetros. O quadrado do item b tem lado medindo

15 \sqrt{2}

centímetros. Assim, a medida A da área desse quadrado, em centímetros quadrados, é:

A =

{(15 \sqrt{2})}^{2}

A = 2 · 15elevado a 2

A = 450

A área do quadrado mede 450 centímetros quadrados.

No exercício 17, observe que o segmento

\overline{A C}

, que é a diagonal do quadrado a bê cê dê, é também o lado do quadrado á ême êne cê. Assim:

•

A C = d_{A B C D} = 2, 5 \sqrt{2}

•

A_{A M N C} = (A C)^{2} = {(2, 5 \sqrt{2})}^{2}

A_AMNC = 2,5 · 2,5 · 2 = 12,5

Portanto, a área do quadrado á ême êne cê mede 12,5 centímetros quadrados.

No exercício 18, solicite aos estudantes que expliquem como calcular a medida do perímetro do retângulo formado, ou seja, de quais medidas necessitam para chegar a esse valor. Eles devem perceber que: basta conhecer a medida do lado de cada quadrado; o contorno dêsse retângulo tem medida dada pela adição da medida de 8 lados do quadrado. Como a medida do lado do quadrado é 10 centímetros (da relação da diagonal e da medida do lado de um quadrado), então o perímetro do retângulo mede 80 centímetros (8 · 10 = 80).

No exercício 19, vamos considerar a figura:

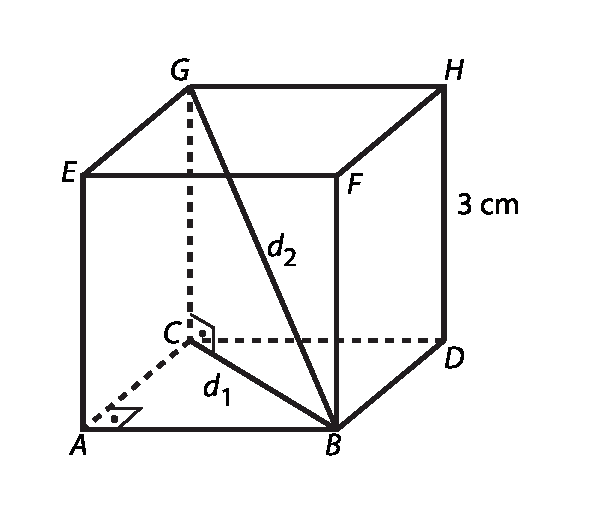
Ilustração. Cubo ABCDEFGH com lado de 3 centímetros. Dentro, diagonal d2 em BG e diagonal d1 em BC.

Calculamos a medida da diagonal da base do cubo (d₁). Como essa é uma região quadrada de lado 3 centímetros (medida da aresta do cubo),

d_{1} = 3 \sqrt{2}

centímetros.

A medida da diagonal procurada (d₂) é a hipotenusa do triângulo retângulo BCG, reto em C. Assim, em centímetro, essa diagonal é dada por:

(d₂)elevado a 2 = 3elevado a 2 +

{(3 \sqrt{2})}^{2}

(d₂)elevado a 2 = 9 + 18

(d₂)elevado a 2 = 27

d_{2} = \sqrt{27} = 3 \sqrt{3}

A diagonal mede

3 \sqrt{3}

centímetros.

Página 182

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e resolvam o exercício a seguir.

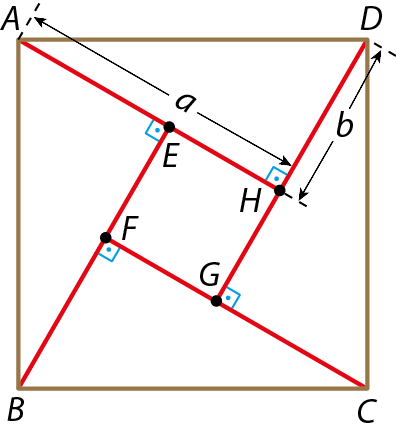
Ilustração. Quadrado ABCD. Dentro, no centro, quadrado EFGH. DE A até H, medida a e de D até H, medida b. Ao redor do quadrado EFGHG, triângulos: ABE, BCF, CDG e ADH.

Mostrem que, se a bê cê dê é um quadrado, a medida da área do quadrado ê éfe gê agá é igual a (a ‒ b)2.

Relacionando as medidas da altura e do lado de um triângulo equilátero

Considere o triângulo equilátero á bê cê, com lados medindo 𝓁 e altura h.

Aplicando o teorema de Pitágoras no triângulo agá cê á, temos:

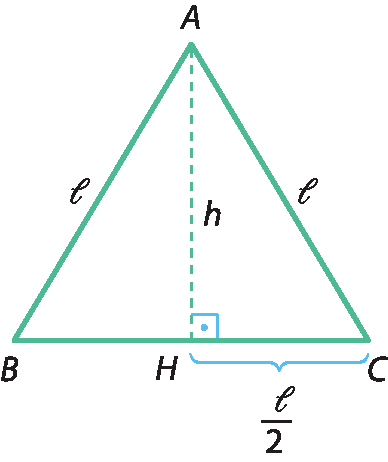
Ilustração. Triângulo ABC. Altura do triângulo tracejada medindo h e vai de A até lado BC, no ponto H. Cada lado do triângulo mede L cursivo. De H até C, medida fração, L cursivo sobre 2, fim da fração.

(AH)elevado a 2 + (HC)elevado a 2 = (AC)elevado a 2

h^{2} + {(\frac{ℓ}{2})}^{2} = ℓ^{2}

h^{2} + \frac{ℓ^{2}}{4} = ℓ^{2}

h^{2} = ℓ^{2} ‒ \frac{ℓ^{2}}{4}

h^{2} = \frac{3 ℓ^{2}}{4}

h = \sqrt{\frac{3 ℓ^{2}}{4}}

h = \frac{ℓ \sqrt{3}}{2}

A igualdade

h = \frac{ℓ \sqrt{3}}{2}

possibilita determinar a medida da altura do triângulo equilátero quando se conhece a medida dos lados dêsse triângulo, e vice-versa.

Acompanhe os exemplos a seguir.

a) Vamos calcular a medida da altura de um triângulo equilátero cujo perímetro mede 18 centímetros. Se P = 18 centímetros, então 𝓁 = 6 centímetros.

h = \frac{ℓ \sqrt{3}}{2}

h = \frac{6 \sqrt{3}}{2}

h = 3 \sqrt{3}

Logo, a altura dêsse triângulo mede

3 \sqrt{3}

centímetros.

b) Vamos calcular a medida do lado de um triângulo equilátero cuja altura mede

6 \sqrt{3} cm.

S e h = 6 \sqrt{3}

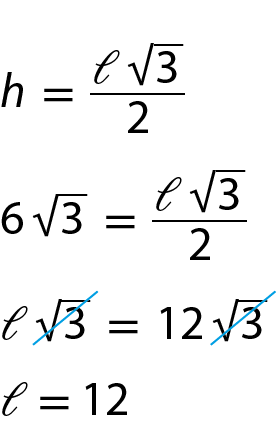
h é igual a fração, L cursivo raiz quadrada de 3 sobre 2.

Abaixo, 6 raiz quadrada de 3 é igual a fração, L cursivo raiz quadrada de 3 sobre 2.
Abaixo, L cursivo raiz quadrada de 3 riscada é igual a 12 raiz quadrada de 3 riscada.
Abaixo, L cursivo é igual 12.

Logo, o lado dêsse triângulo mede 12 centímetros.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

20 O lado de um triângulo equilátero mede 3 centímetros. Calcule a medida da altura dêsse triângulo.

21 Determine a medida da área de um triângulo equilátero cuja altura mede

12 \sqrt{3}

centímetros.

Respostas e comentários

Pense mais um pouco...: Demonstração.

20.

\frac{3 \sqrt{3}}{2} cm

21.

144 \sqrt{3} {cm}^{2}

Pense mais um poucoreticências

Apresentamos uma possível solução para esta atividade.

Aplicando o teorema de Pitágoras no triângulo á agá dê, obtemos:

AD2 = a2 + b2

Da figura podemos dizer que:

AEFGH = AABCD ‒ 4 · AAHD

AEFGH =

A D^{2} ‒ 4 \cdot \frac{a b}{2}

AEFGH = a2 + b2 ‒ 2ab

AEFGH = (a ‒ b)2

Relacionando as medidas da altura e do lado de um triângulo equilátero

Outra relação que obtemos como aplicação do teorema de Pitágoras é a que expressa a medida h da altura de um triângulo equilátero em relação à medida ℓ de seu lado (nesse caso, as três alturas são congruentes).

h = \frac{ℓ \sqrt{3}}{2}

Note que, desse modo, temos uma relação para a medida a da área de um triângulo equilátero de lados de medida ℓ.

A = \frac{ℓ \cdot h}{2}

A = \frac{ℓ \cdot \frac{ℓ \sqrt{3}}{2}}{2} = \frac{\frac{ℓ^{2} \sqrt{3}}{2}}{2}

A = \frac{ℓ^{2} \sqrt{3}}{2} \cdot \frac{1}{2}

A = \frac{ℓ^{2} \sqrt{3}}{4}

Exercícios propostos

As resoluções dos exercícios 20 e 21 estão no início deste Manual, nas orientações específicas do capítulo 8.

Página 183

22 Com um barbante que mede 48 centímetros, contorna-se exatamente a figura de um triângulo equilátero. Qual é a medida da altura dêsse triângulo?

23 O lado de um triângulo equilátero tem a mesma medida da diagonal de um quadrado de lado medindo 25 centímetros. Calcule a medida da altura dêsse triângulo.

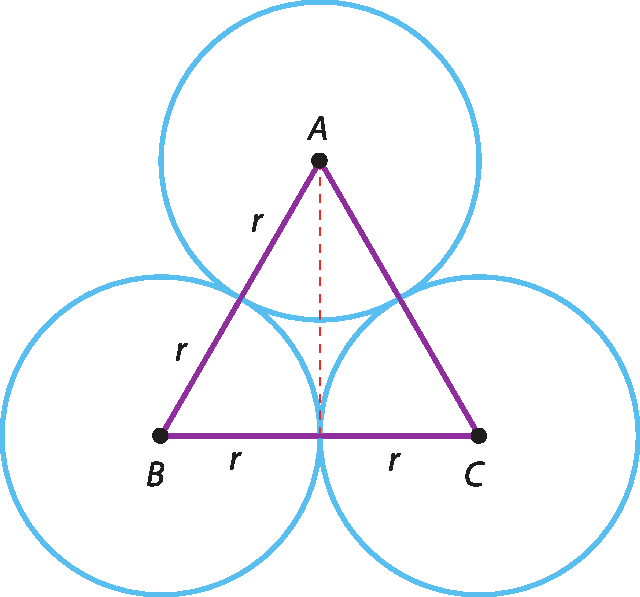
24 Na figura a seguir, o raio de cada circunferência mede 1,5 centímetro.

Determine a medida da área do triângulo á bê cê.

Ilustração. Três circunferências. Acima, circunferência com centro A. Abaixo, circunferência com centro B e ao lado, com centro C. Triângulo ABC é formado com os pontos ABC. A medida de cada centro até a extremidade da circunferência é r.

Pense mais um poucoreticências

FAÇA A ATIVIDADE NO CADERNO

Reúna-se com um colega e façam o que se pede.

Ilustração. Um menino branco de cabelo castanho e camiseta branca de gola verde, sentado numa cadeira cortando um triângulo vermelho com uma tesoura em cima de uma mesa cinza. Do lado dele, um menino negro de cabelo castanho e camiseta branca de gola verde, sentado numa cadeira mexendo em pequenos triângulos vermelhos em cima da mesma mesa cinza.

Em papel quadriculado, recortem 20 triângulos retângulos congruentes de modo que a medida de um cateto (x centímetro) seja o dobro da medida do outro cateto (2x centímetros). Disponham os triângulos lado a lado sobre a carteira formando um quadrado.

Qual é a medida do lado dêsse quadrado?

(Usem tesouras com pontas arredondadas e as manuseiem com cuidado!)

4. Relações métricas em um triângulo retângulo

Além do teorema de Pitágoras, há outras relações métricas no triângulo retângulo. Porém, antes de estudá-las, vamos conhecer alguns conceitos para entender melhor os termos que serão usados.

Projeções ortogonais

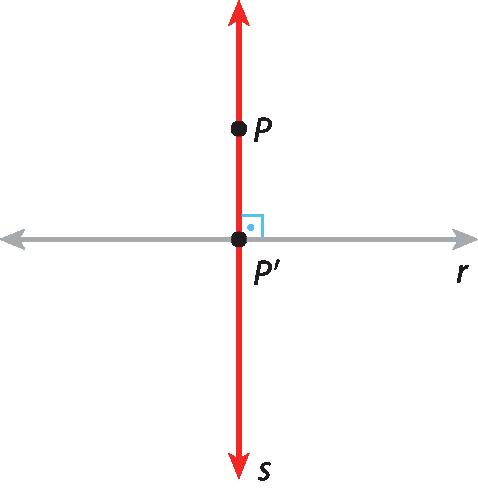
Considere uma reta r e um ponto P externo a ela.

Vamos traçar por P a reta s, perpendicular à reta r. No cruzamento das retas r e s obtemos o ponto pê ', que é chamado projeção ortogonal de P sobre r.

Ilustração. Eixo horizontal r e eixo vertical s. No centro, ponto P linha. Na parte superior do eixo s, ponto P.

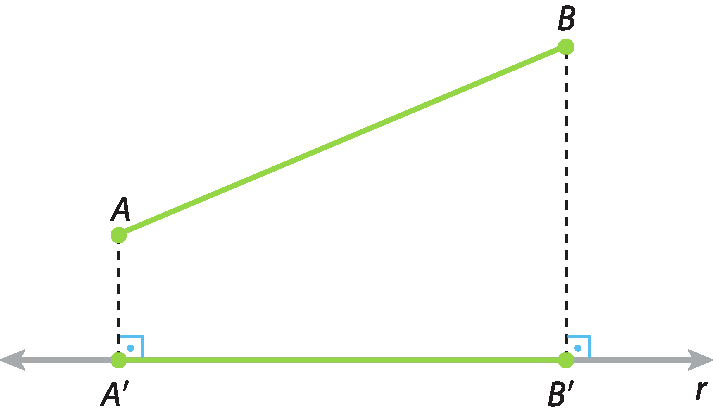
Considere agora a reta r e o segmento

\overline{A B}

da figura a seguir.

Projetando ortogonalmente as extremidades do segmento

\overline{A B}

sobre r, obtemos os pontos á ' e bit'.

O segmento

\overline{A ʹ B ʹ}

é chamado projeção ortogonal de

\overline{A B}

sobre r.

Ilustração. Eixo horizontal r e sobre ele segmento de reta A linha B linha.
Acima do eixo r, sem pontos em comum, segmento de reta AB. Os ponto A e A linha estão alinhados verticalmente, assim como os pontos B e B linha.

Respostas e comentários

22.

8 \sqrt{3} cm

23.

\frac{25 \sqrt{6}}{2} cm

24.

2, 25 \sqrt{3} {cm}^{2}

Pense mais um poucoreticências:

2 x \sqrt{5} cm

Resposta possível:

Ilustração. Quadrado composto por 20 triângulos em posições diferentes.

Exercícios propostos

As resoluções e comentários dos exercícios 22 a 24 estão no início deste Manual, nas orientações específicas do capítulo 8.

Pense mais um poucoreticências

Oriente os estudantes a fazer a resolução, inicialmente, por tentativa e erro. Depois, questione como compor, com dois dos triângulos recortados, um ângulo reto, que forme um “canto do quadrado” a ser obtido. Esse questionamento (ou dica) estimulará uma reflexão, motivando o redirecionamento de novas tentativas, e será um incentivo àqueles que ainda não chegaram à resposta.

Se julgar necessário passar outra dica, sugira aos estudantes que tentem construir um triângulo retângulo justapondo 5 dos triângulos recortados.

Observando a figura indicada como resposta, verificamos que o lado do quadrado obtido mede o dobro da medida h da hipotenusa dos triângulos considerados. Obtemos, então:

helevado a 2 = xelevado a 2 + (2x)elevado a 2 = 5xelevado a 2 ⇒ h = x

\sqrt{5}

Assim, o lado do quadrado mede 2x

\sqrt{5}

centímetros.

Página 184

Também podemos projetar ortogonalmente um ponto ou um segmento sobre um segmento.

Observe os exemplos.

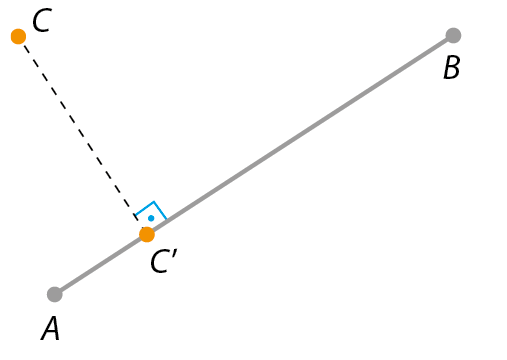
Ilustração. Segmento AB na diagonal com ponto C linha. Acima de C linha, reta tracejada com ponto C, perpendicular a AB.

Dizemos que centésimo' é a projeção ortogonal do ponto C sobre o segmento

\overline{A B} .

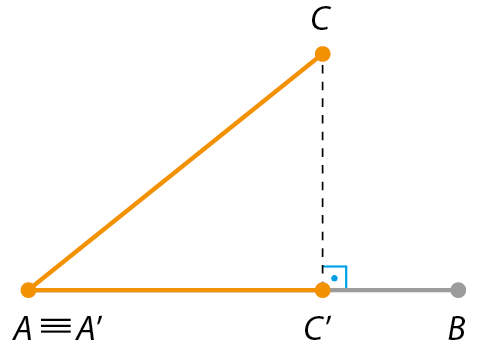
Ilustração. Segmento de reta AB com ponto C linha entre A e B e segmento de reta AC. Os pontos C e C linha estão alinhados verticalmente. A é coincidente a A linha.

Dizemos que

\overline{A ʹ C ʹ}

é a projeção ortogonal do segmento

\overline{A C}

sobre o segmento

\overline{A B} .

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

25 Observe as figuras. Depois, classifique cada sentença em verdadeira ou falsa.

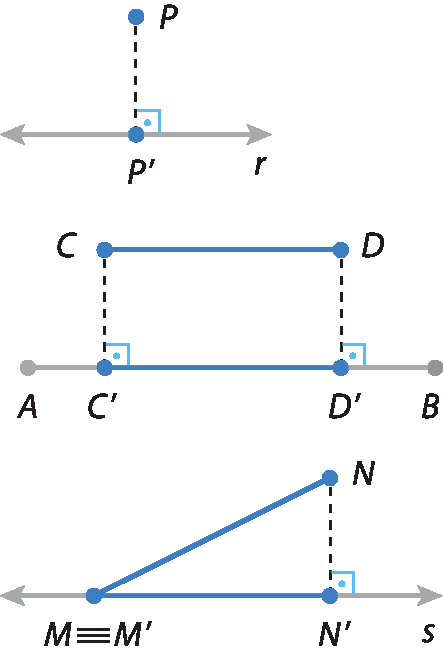
Ilustração. Eixo horizontal r. No centro, ponto P linha. Segmento de reta vertical tracejado do ponto P linha ao ponto P. Ilustração. Segmento AB na horizontal com ponto C linha e D linha sobre ele. Acima, segmento CD na horizontal. Segmento de reta tracejado vertical de C para C linha e do ponto D para D linha. Ilustração. reta s na horizontal com ponto N linha à direita. Segmento de reta tracejado vertical de N linha para cima em N. Segmento de reta diagonal de N até eixo s, no ponto M. M é coincidente a M linha.

a) P é a projeção ortogonal do ponto pê' sobre a reta r.

\overline{C ʹ D ʹ}

é a projeção ortogonal do segmento

\overline{C D}

sobre o segmento

\overline{A B}

c) N ' é a projeção ortogonal do ponto N sobre a reta s.

\overline{M ʹ N ʹ}

é a projeção ortogonal do segmento

\overline{M N}

sobre a reta s.

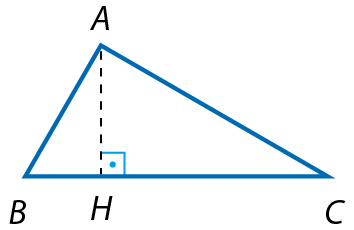
26 Quais são as projeções ortogonais dos lados

\overline{A B}

\overline{A C}

sobre o lado

\overline{B C}

em cada triângulo?

Ilustração. Triângulo ABC com segmento de reta de A até lado BC, no ponto H.

Ilustração. Triângulo ABC com segmento de reta de A até lado BC, no ponto M.

Relações métricas

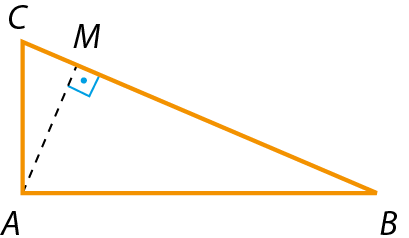
Observe o triângulo á bê cê com hipotenusa de medida a e catetos de medidas b e c.

Ilustração. Triângulo ABC. De A, segmento de reta h até lado BC, no ponto H e ângulo reto em H. Em A, ângulo A1 e A2. As medidas dos lados são: AB: c. AC: b e BC: a. De B até H, medida n e de H até c, medida m.

Considerando a altura

\overline{A H}

, de medida h, relativa à hipotenusa, temos:

•

\overline{B H}

, de medida n, é a projeção ortogonal do cateto

\overline{A B}

sobre a hipotenusa

\overline{B C}

;

•

\overline{H C}

, de medida m, é a projeção ortogonal do cateto

\overline{A C}

sobre a hipotenusa

\overline{B C}

Respostas e comentários

25. a) Falsa.

25. b) Verdadeira.

25. c) Verdadeira.

25. d) Verdadeira.

26. a) Respectivamente

\overline{B H}

\overline{H C}

26. b) Respectivamente

\overline{B M}

\overline{C M}

4. Relações métricas em um triângulo retângulo

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah um três e ê éfe zero nove ême ah um quatro.

Neste tópico, além de aplicar a semelhança de triângulos ao demonstrar relações métricas no triângulo retângulo e resolver problemas que envolvem o teorema de Pitágoras, abordamos as projeções ortogonais, propiciando, assim, o desenvolvimento das habilidades (ê éfe zero nove ême ah um três) e (ê éfe zero nove ême ah um quatro).

O teorema de Pitágoras é uma relação métrica importante a ser considerada em um triângulo retângulo, mas há outras que envolvem as medidas da hipotenusa e da altura relativa a ela, além das medidas das projeções dos catetos sobre a hipotenusa.

Explore com os estudantes a noção de projeção ortogonal de um ponto e de um segmento sobre uma reta (e sobre outro segmento), conceitos necessários para a compreensão de algumas das relações métricas que serão apresentadas.

Ao tratar da projeção ortogonal de um segmento de reta sobre uma reta, proponha à turma esta pergunta: No caso de um segmento

\overline{C D}

ser perpendicular a uma reta r, que figura corresponde à projeção ortogonal dêsse segmento sobre essa reta? Espera-se que os estudantes respondam que a figura correspondente à projeção ortogonal do segmento

\overline{C D}

sobre a reta r, nesse caso, é apenas um ponto.

Exercícios propostos

No exercício 25, verifique se os estudantes invertem a ordem de referência entre o objeto a ser projetado (representado apenas pelas letras) e a sua projeção (representada pelas letras com apóstrofo). Espera-se que eles considerem falsa apenas a afirmação do item a.

No exercício 26, aplicando as projeções dos lados

\overline{A B}

\overline{A C}

sobre

\overline{B C}

, respectivamente, obtemos:

\overline{B H}

\overline{H C}

;

\overline{B M}

\overline{C M}

Sugestão de leitura

Para ampliar o trabalho com projeções ortogonais, sugerimos:

LAMAS, R. C. P.; MAURI, J. O teorema de Pitágoras e as relações métricas no triângulo retângulo com material emborrachado. IBILCE/Unésp, São José do Rio Preto, 2006. Publicação na página da Pró-Reitoria de Graduação – Núcleos de Ensino. Disponível em: https://oeds.link/GFhwO0. Acesso em: 22 julho 2022.

As autoras apresentam uma situação didática para trabalhar as relações métricas no triângulo retângulo.

Página 185

Considerando os triângulos retângulos á bê cê, agá bê á e agá á cê, por meio da semelhança de triângulos, podemos estabelecer relações entre as medidas de seus lados.

1ª relação

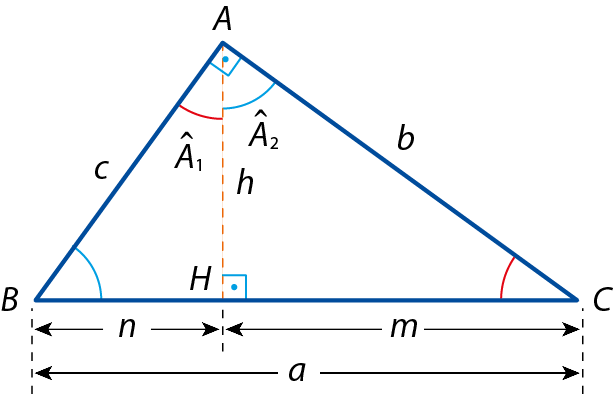
Considere o triângulo á bê cê da figura. Traçando a altura relativa à hipotenusa, obtemos alguns pares de triângulos semelhantes.

Ilustração. Triângulo ABC. De A, segmento de reta h até lado BC, no ponto H e ângulo reto em H. As medidas dos lados são: AB: c. AC: b e BC: a. Em H, ângulo H1 e H2. De B até H, medida n e de H até c, medida m.

1. Comparando os triângulos á bê cê e agá bê á, temos:

•

\hat{A} ≅ \hat{H}

1 (ângulos retos)

•

\hat{B} ≅ \hat{B}

(ângulo comum)

Logo, pelo caso ângulo ângulo, os triângulos á bê cê e agá bê á são semelhantes; portanto, os lados dêsses triângulos são proporcionais. Então, podemos escrever a proporção:

\frac{a}{c} = \frac{c}{n}

, ou seja, c elevado a 2 = an

2. Comparando os triângulos á bê cê e agá á cê, temos:

•

\hat{A} ≅ {\hat{H}}_{2}

(ângulos retos)

•

\hat{C} ≅ \hat{C}

(ângulo comum)

Do mesmo modo, pelo caso ângulo ângulo, os triângulos á bê cê e agá á cê são semelhantes. Portanto:

\frac{a}{b} = \frac{b}{m}

, ou seja, b elevado a 2 = am

O quadrado da medida de cada cateto é igual ao produto da medida da hipotenusa pela medida da projeção ortogonal dêsse cateto sobre ela.

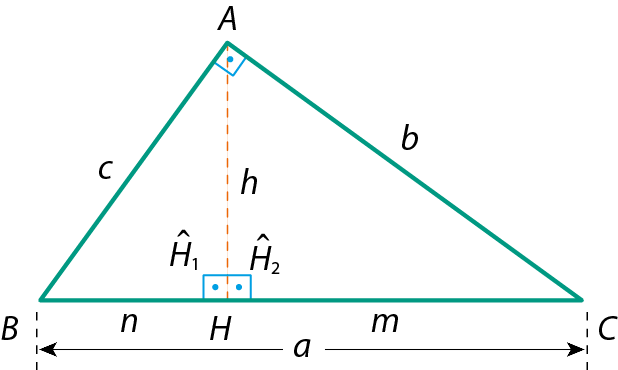
2ª relação

Comparando os triângulos á bê agá e cê á agá, temos:

•

\hat{H} ≅ \hat{H}

2 (ângulos retos)

•

\hat{A} ≅ \hat{C}

(ambos têm por complemento o ângulo

\hat{B}

)

Ilustração. Triângulo ABC. De A, segmento de reta h até lado BC, no ponto H e ângulo reto em H. As medidas dos lados são: AB: c. AC: b e BC: a. Em H, ângulo H1 e H2. Em A, ângulo A 1. De B até H, medida n e de H até c, medida m.

Logo, pelo caso ângulo ângulo, os triângulos á bê agá e cê á agá são semelhantes. Portanto:

\frac{h}{m} = \frac{n}{h}

, ou seja, h elevado a 2 = mn

O quadrado da medida da altura relativa à hipotenusa é igual ao produto das medidas das projeções ortogonais dos catetos sobre a hipotenusa.

Respostas e comentários

Relações métricas

Se julgar necessário, retome o conceito de semelhança de triângulos e explore os casos de semelhança, pois as demonstrações apresentadas tomam por base esse conceito.

Para cada relação métrica demonstrada, peça aos estudantes que desenhem triângulos retângulos (com auxílio de régua, transferidor ou compasso), meçam com a régua as medidas dos elementos envolvidos e verifiquem (utilizando uma calculadora) a respectiva relação métrica para os triângulos construídos.

Para traçar a altura relativa à hipotenusa, eles devem traçar a perpendicular a esse segmento que passa pelo vértice oposto.

Página 186

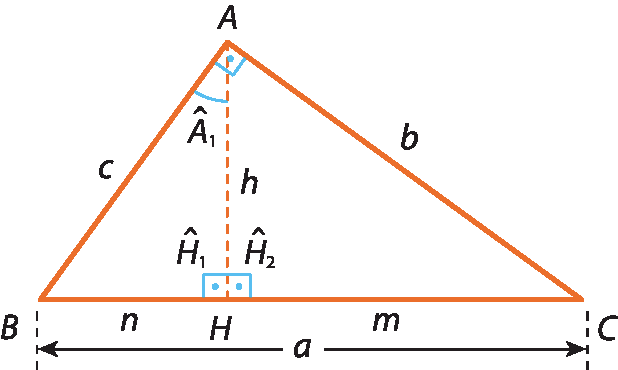
3ª relação

Comparando os triângulos á bê cê e agá á cê, temos:

•

\hat{A} ≅ \hat{H}

2 (ângulos retos)

•

\hat{C} ≅ \hat{C}

(ângulo comum)

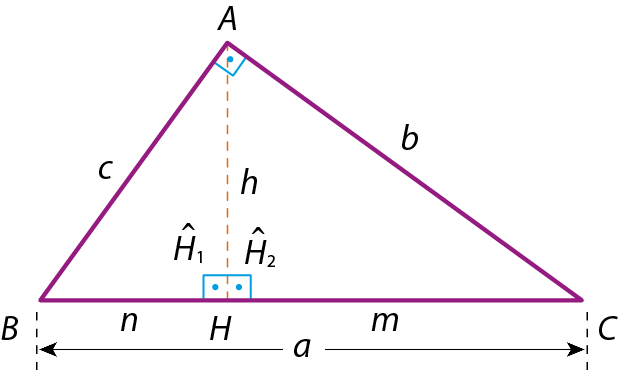
Logo, pelo caso ângulo ângulo, os triângulos á bê cê e agá á cê são semelhantes. Portanto:

\frac{a}{b} = \frac{c}{h}

, ou seja, bc = ah

O produto das medidas dos catetos é igual ao produto da medida da hipotenusa pela medida da altura relativa à hipotenusa.

Outra demonstração do teorema de Pitágoras

Dado um triângulo retângulo á bê cê, vamos provar que o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

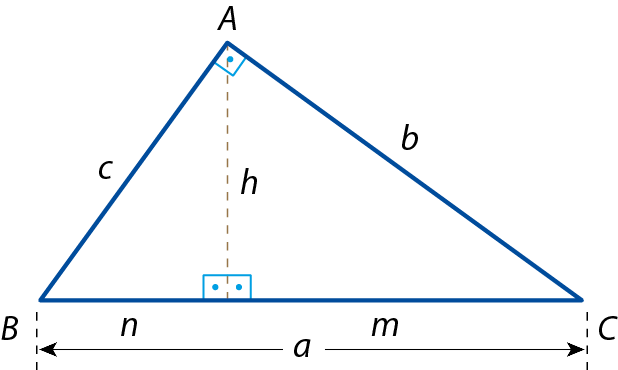
Ilustração. Triângulo ABC. De A, segmento de reta h até lado BC, no ponto H e ângulo reto em H. As medidas dos lados são: AB: c. AC: b e BC: a. De B até H, medida n e de H até c, medida m.

Hipótese: △á bê cê é um triângulo retângulo em a.

Tese: b elevado a 2 + c elevado a 2 = a elevado a 2

• Demonstração Como o quadrado da medida de cada cateto é igual ao produto da medida da hipotenusa pela medida da projeção ortogonal dêsse cateto sobre ela, temos:

b elevado a 2 = am e c elevado a 2 = an

Adicionando membro a membro essas duas igualdades, temos:

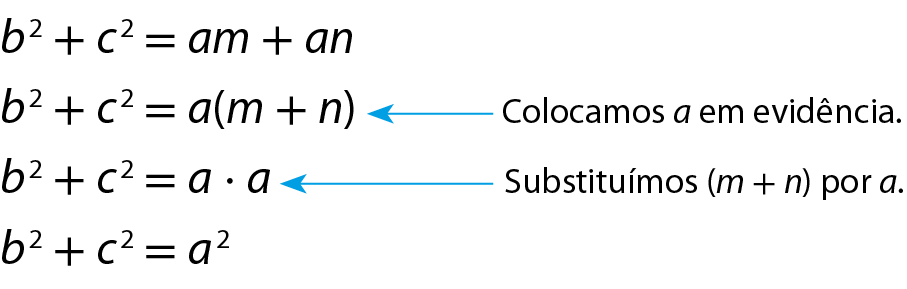
Esquema. b elevado ao quadrado mais c elevado ao quadrado é igual a am mais an. b elevado ao quadrado mais c elevado ao quadrado é igual a a, abre parênteses, m mais n, fecha parênteses. Colocamos a em evidência. b elevado ao quadrado mais c elevado ao quadrado é igual a a vezes a. Substituímos abre parênteses, m mais n, fecha parênteses, por a. b elevado ao quadrado mais c elevado ao quadrado é igual a a elevado ao quadrado.

dêsse modo, também provamos o teorema de Pitágoras.

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

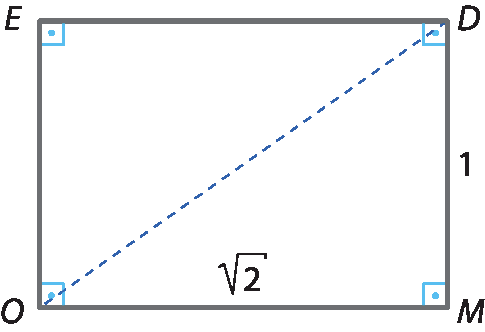
27 Considere a figura e responda às questões.

a) Qual é a medida do perímetro do △ó dê ême ?

b) Considere um quadrado de lado de medida ó dê. Qual é a medida da área dêsse quadrado?

Ilustração. Retângulo EDMO com medida DM: 1 e OM: raiz quadrada de 2. Diagonal tracejada de O até D.

Respostas e comentários

27. a)

1 + \sqrt{2} + \sqrt{3}

27. b) 3

Outra demonstração do teorema de Pitágoras

Observe aos estudantes que esta é uma demonstração algébrica do teorema de Pitágoras, agora fazendo uso das relações recém-estudadas.

Exercícios propostos

Para o exercício 27, verifique se os estudantes obtêm a medida ó dê utilizando conhecimentos construídos anteriormente (no capítulo 1, quando estudaram a localização de números irracionais na reta real) ou se aplicam novamente o teorema de Pitágoras. Ressalte essa ligação com conhecimentos anteriores. Aplicando o teorema de Pitágoras, obtemos:

ODelevado a 2 = 1elevado a 2 +

{(\sqrt{2})}^{2}

= 1 + 2 = 3

Então, OD =

\sqrt{3}

. Assim, o perímetro do triângulo mede 1 +

\sqrt{2}

\sqrt{3}

Um quadrado cujo lado mede ó dê terá a medida de área dada por OD2, ou seja: OD2 = 3

Página 187

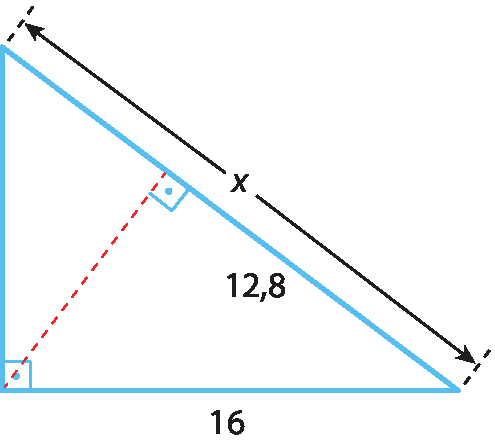
28 Aplicando as relações métricas dos triângulos retângulos, calcule o valor de x.

Ilustração. Triângulo com segmento de reta tracejado do topo até o lado maior. As medidas dos lados são: 16, x. Da extremidade até segmento de reta tracejado, medida 12,8.

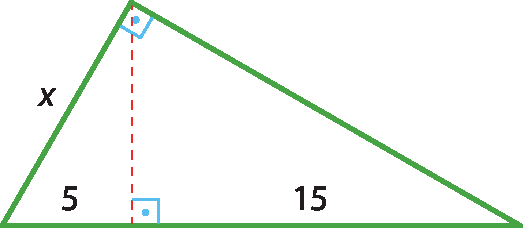
Ilustração. Triângulo com segmento de reta tracejado do topo até o lado maior. Da extremidade até segmento de reta tracejado, medida 5 e do segmento de reta tracejado até extremidade direita, medida 15. Um dos lados do triângulo mede x.

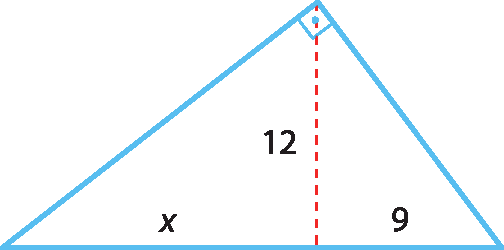
Ilustração. Triângulo com segmento de reta tracejado com medida 12 do topo até o lado maior. Da extremidade até segmento de reta tracejado, medida x e do segmento de reta tracejado até extremidade direita, medida 9.

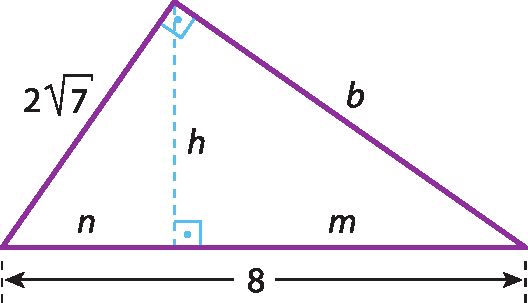
29 Calcule as medidas h, n, m e b do triângulo retângulo a seguir.

Ilustração. Triângulo com segmento de reta tracejado com medida h do topo até o lado maior. Da extremidade até o segmento de reta tracejado, medida n e do segmento de reta tracejado até extremidade direita, medida m. As medidas dos lados são: 2 raiz quadrada de 7, b e 8.

30 As projeções dos catetos de um triângulo retângulo sobre a hipotenusa medem 1,8 centímetro e 3,2 centímetros. Determine a medida dos catetos dêsse triângulo.

31 (unifór-Ceará) Na figura a seguir, tem-se um retângulo cujos lados medem 8 centímetros e 6 centímetros. Os pontos M, N, P e Q são pontos médios dos lados.

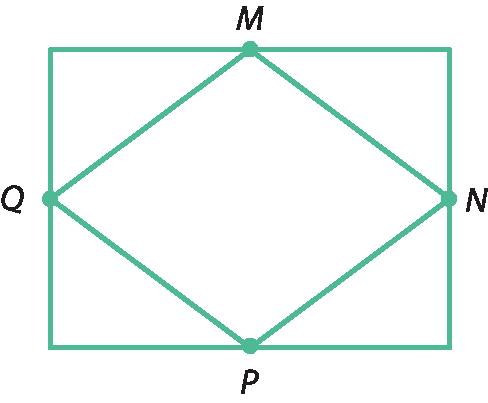
Ilustração. Losango MNPQ. Ao redor, retângulo.

O perímetro do quadrilátero ême êne pê quê é:

a) 20 centímetros.

b) 24 centímetros.

c) 32 centímetros.

d) 36 centímetros.

e) 52 centímetros.

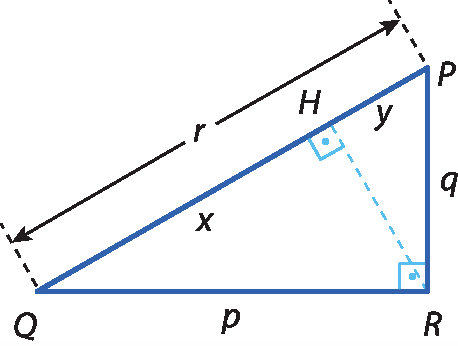
32 Aplique os casos de semelhança entre triângulos para provar que:

a) p 2 = rx

Ilustração. Triângulo PQR. De R, segmento de reta até lado PQ, no ponto H e ângulo reto em H. As medidas dos lados são: PQ: r. PR: q. QP: P. De P até H: y. De H até Q: x.

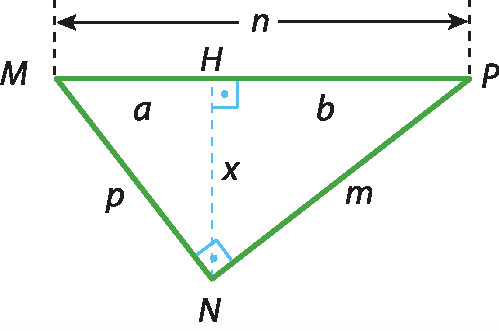
b) x 2 = ab

Ilustração. Triângulo MNP. De N, segmento de reta x até lado MP, no ponto H e ângulo reto em H. As medidas dos lados são: MP: n. MN: P. PN: m. De M até H: a. De H até P: b.

33 (ú éfe pê é) Quanto mede, em centímetro, a altura relativa à hipotenusa de um triângulo retângulo cujos catetos medem 15 centímetros e 20 centímetros?

34 A medida da área do triângulo retângulo érre ésse tê é 36 centímetros quadrados. Determine o produto da medida da hipotenusa pela medida da altura referente à hipotenusa.

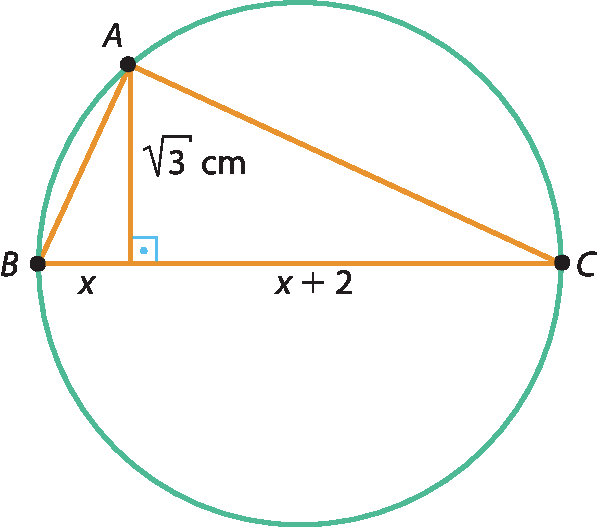
35 Determine a medida do diâmetro

\overline{B C}

da circunferência da figura.

Ilustração. Circunferência com triângulo ABC. Segmento de reta de A até lado BC com medida de raiz quadrada de 3 centímetros. De B até o segmento de reta, medida x e do segmento de reta até C, medida x mais 2.

Hora de criar – Em dupla com um colega, elaborem um problema cada um sobre relações métricas no triângulo retângulo. Troquem os problemas elaborados por vocês e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.

Respostas e comentários

28. a) x = 20

28. b) x = 10

28. c) x = 16

29.

h = \frac{3 \sqrt{7}}{2}

n = 3,5

m = 4,5

b = 6

30. 3 centímetros e 4 centímetros.

31. Alternativa a.

32. Demonstração.

33. 12 centímetros

34. 72 centímetros quadrados

35. BC = 4 centímetros

36. Resposta pessoal.

Exercícios propostos

As resoluções dos exercícios 28 a 30 e dos exercícios 33 e 34 estão no início deste Manual, nas orientações específicas do capítulo 8.

Apresentamos uma possível resolução do exercício 31.

Cada lado do quadrilátero ême êne pê quê é hipotenusa de um triângulo retângulo de catetos medindo 4 centímetros e 3 centímetros.

Representando por x a medida desses lados, obtemos, pelo teorema de Pitágoras:

xelevado a 2 = 3elevado a 2 + 4elevado a 2 = 25 ⇒ x = 5

A medida do perímetro é dada por:

5 + 5 + 5 + 5 = 20

Logo, a medida do perímetro é 20 centímetros.

Para o exercício 32, seguem as demonstrações.

a) Comparando os triângulos pê quê érre e érre quê agá, temos:

P \hat{R} Q ≅ R \hat{H} Q

(ângulos retos)

R \hat{Q} P ≅ R \hat{Q} H

(ângulo comum).

Logo, pelo caso ângulo ângulo, os triângulos retângulos pê quê érre e érre quê agá são semelhantes. Assim:

\frac{R Q}{H Q} = \frac{P Q}{R Q}

⇒

\Rightarrow \frac{p}{x} = \frac{r}{p} \Rightarrow p^{2} = r x

b) Comparando os triângulos ême agá êne e êne agá pê, temos:

M \hat{H} N ≅ N \hat{H} P

(ângulos retos)

H \hat{M} N ≅ H \hat{N} P

(ambos têm por complemento o ângulo

\hat{P}

(ambos têm por complemento o ângulo

Logo, pelo caso ângulo ângulo, os triângulos retângulos ême agá êne e êne agá pê são semelhantes. Assim:

\frac{H N}{H P} = \frac{H M}{H N} ⇒ \frac{x}{b} = \frac{a}{x}

⇒

⇒ x2 = ab

Para o exercício 35, apresentamos uma possível resolução a seguir.

{(\sqrt{3})}^{2}

= x · (x + 2)

x2 + 2x ‒ 3 = 0

Δ = (2)2 ‒ 4 · 1 · (‒3) = 16

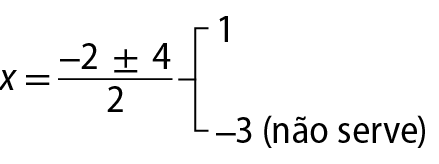
Esquema. x é igual a fração, menos 2 mais ou menos 4 sobre 2. X é igual a 1 ou x é igual a menos 3, não serve.

d = x + x + 2

d = 1 + 1 + 2 = 4

Portanto, o diâmetro

\overline{B C}

mede 4 centímetros.

No exercício 36, embora a resposta seja pessoal, incentive os estudantes a elaborar problemas envolvendo situações contextualizadas.

Página 188

TRABALHANDO A INFORMAÇÃO

A representação de um relevo

O estudo topográfico de uma região consiste na descrição exata e pormenorizada de um terreno com todos os seus acidentes geográficos. Com base em estudos topográficos, são construídos os chamados perfis topográficos, como o do conjunto Pão de Açúcar e morro da Urca, no Rio de Janeiro (Rio de Janeiro), na figura cinco.

Para entender como esses perfis são construídos, imagine os morros sendo cortados por planos horizontais paralelos ao nível do mar em altitudes de medidas 50 métros, 100 métros, 150 métros, reticências, 350 métros. Agora imagine linhas conectando todos os pontos sobre a superfície dos morros pertencentes aos planos de mesma altitude. Essas linhas imaginárias, como as linhas brancas nas figuras um e dois, são chamadas de curvas de nível.

Fotografia I. CURVAS DE NÍVEL – PÃO DE AÇÚCAR E MORRO DA URCA. Vista frontal de Pão de açúcar e ao lado, um morro. Ao redor, águia e barcos. Linhas brancas horizontais ao redor da imagem.

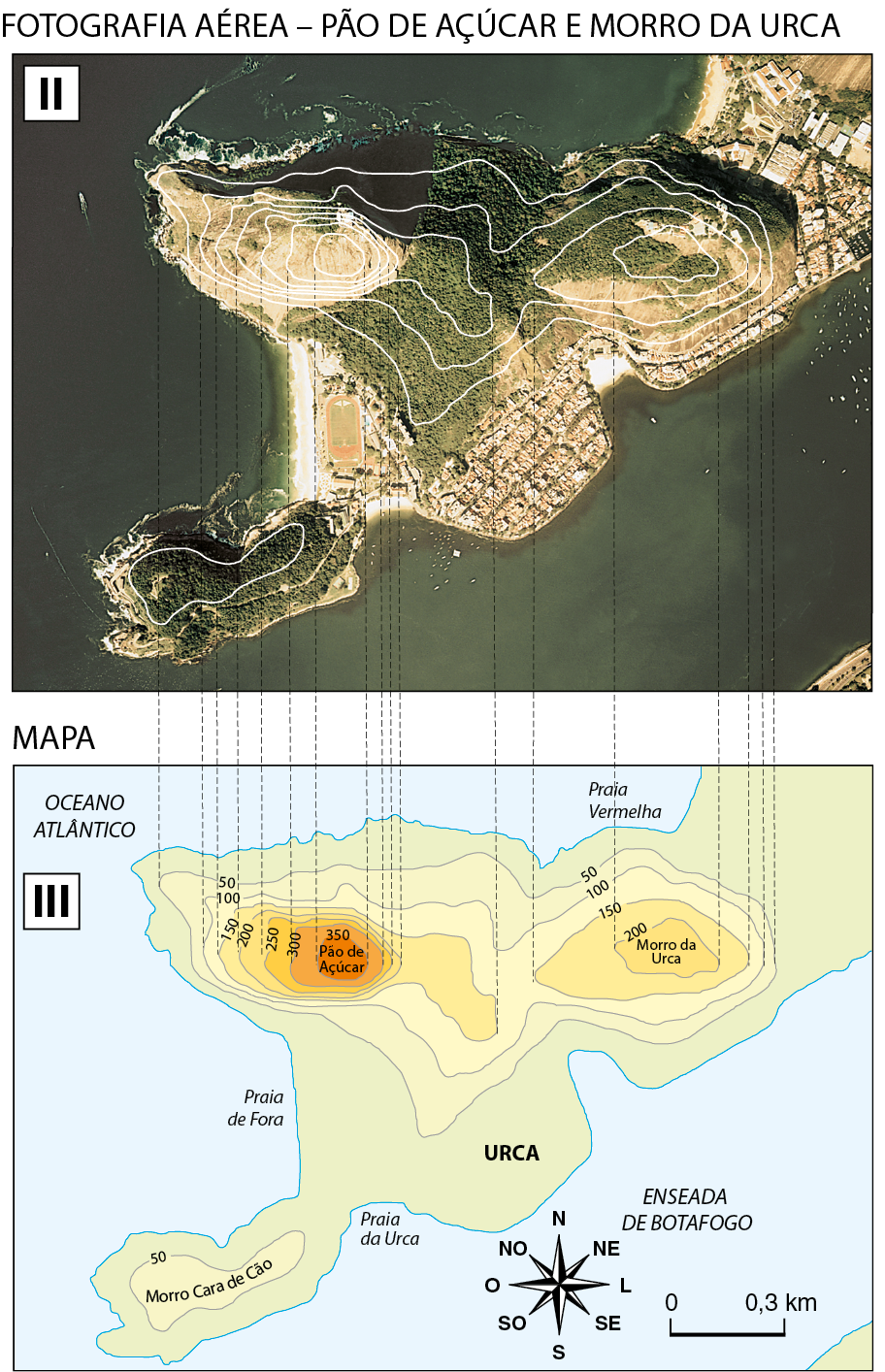
Fotografia II. FOTOGRAFIA AÉREA – PÃO DE AÇÚCAR E MORRO DA URCA. Vista aérea de região com de Pão de açúcar e um morro. Linhas onduladas ao redor da região. Abaixo, mapa III. Na parte superior. Pão de Açúcar e à direita, morro da Urca. Ao redor do pão de açúcar, linhas ao redor. De fora para dentro: 50, 100, 150, 200, 250, 300 e 350. Ao redor do Morro da Urca, linhas ao redor. De fora para dentro: 50, 100, 150, 200. Acima, Praia Vermelha. Na parte inferior, morro Cara de Cão e À direita, Praia da Urca e Enseada de Botafogo. No canto inferior direito, rosa dos ventos e escala de 0 a 0,3 quilômetros.

Na figura dois, note que as curvas de nível aparecem vistas de cima.

A figura três é um desenho do contorno da fotografia aérea da figura dois, identificando as curvas de nível e suas altitudes correspondentes, em metro.

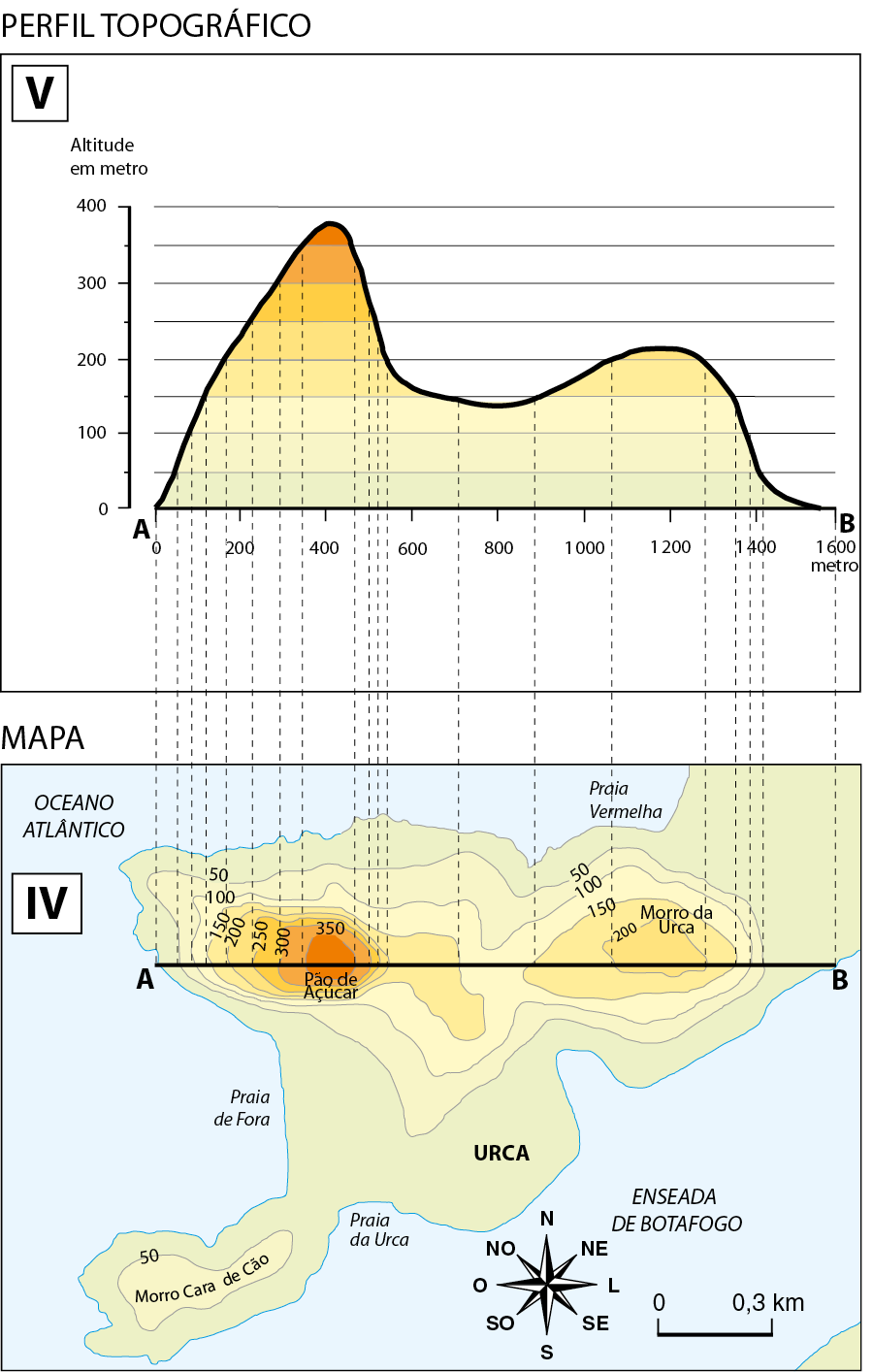
Para construir o perfil topográfico dessa região, traçamos uma semirreta de origem a, que passa pelo cume dos morros, e as perpendiculares a ela, pelos pontos de intersecção com as curvas de nível (figura quatro). As perpendiculares são prolongadas para obter a figura cinco, que representa o perfil topográfico do Pão de Açúcar e do morro da Urca.

Mapa IV. Na parte superior. Pão de Açúcar e à direita, morro da Urca. Ao redor do pão de açúcar, linhas ao redor. De fora para dentro: 50, 100, 150, 200, 250, 300 e 350. Ao redor do Morro da Urca, linhas ao redor. De fora para dentro: 50, 100, 150, 200. Segmento AB vai da extremidade esquerda até a extremidade direita da região. Acima, Praia Vermelha. Na parte inferior, morro Cara de Cão e À direita, Praia da Urca e Enseada de Botafogo. No canto inferior direito, rosa dos ventos e escala de 0 a 0,3 quilômetros. Acima, gráfico V. PERFIL TOPOGRÁFICO. Eixo x, AB com pontos de 0 a 1600 metros. Eixo y, amplitude em metro de 0 a 400. Linha ondulada sai de 0, sobe até 400, 400, desce em 700, 150. Sobe em 1200, 200 e desce em 1400, 0. — Fonte: FERREIRA, G. M. L. Atlas geográfico: espaço mundial. quarta edição revista e atual. São Paulo: Moderna, 2013. página 15.

Respostas e comentários

Trabalhando a informação

Habilidade da Bê êne cê cê: ê éfe zero nove ême ah um sete.

Nesta seção, apresentamos a construção de perfis topográficos utilizados para descrever terrenos e seus acidentes geográficos e analisamos a construção do perfil topográfico do Pão de Açúcar e do morro da Urca. Para a construção do perfil apresentado, aplicamos o conceito de projeção ortogonal a objetos tridimensionais, desenvolvendo, assim a habilidade (ê éfe zero nove ême ah um sete).

Amplie a discussão do assunto da seção levando material de consulta para os estudantes ou solicitando-lhes que levem material pesquisado por eles para o desenvolvimento em sala de aula. Se possível, pode-se propor atividade interdisciplinar com Geografia.

Solicite aos estudantes a leitura em duplas com registro próprio de cada etapa do procedimento para a construção de um perfil topográfico, estimulando-os a aplicar conhecimentos de diferentes linguagens (verbal, visual, matemática e científica) para expressar opiniões e partilhar informações, desenvolvendo, assim, a competência geral 4.

Página 189

Agora quem trabalha é você!

FAÇA AS ATIVIDADES NO CADERNO

1 Analise o perfil topográfico da figura cinco e dê a medida da altitude aproximada do Pão de Açúcar e do morro da Urca.

2 (saréspi) A figura indica seis rádios e o desenho de suas vistas superior e lateral.

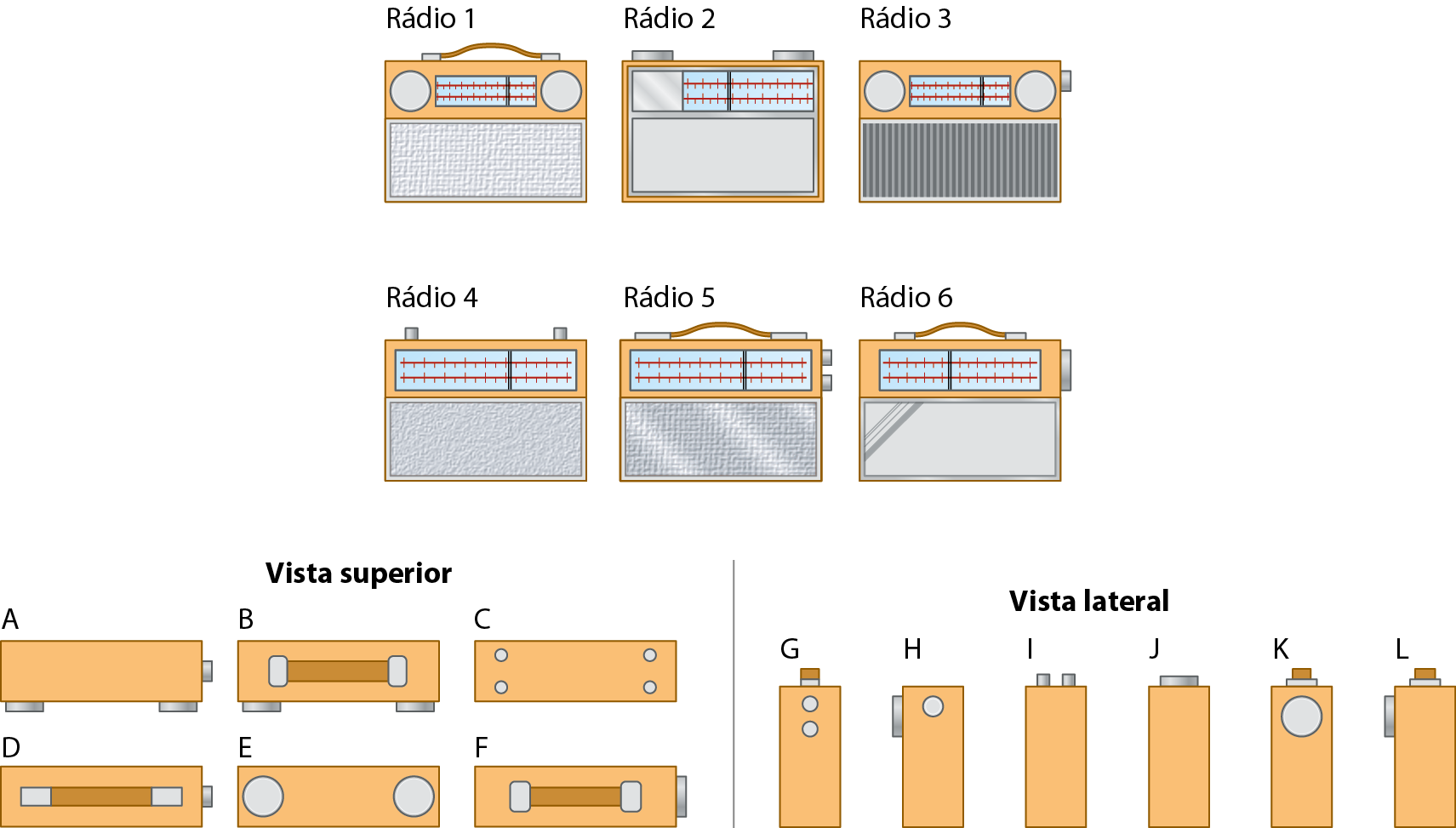
Ilustração. Rádio 1. Rádio em formato retangular com alça na parte superior. Abaixo, dois botões e painel retangular. Abaixo, região cinza com quadrados. Rádio 2. Rádio em formato retangular com dois botões redondos na parte superior. Abaixo, visor retangular e painel ao lado. Abaixo, região cinza. Rádio 3. Rádio em formato retangular e botão redondo na parte superior lateral direita. Abaixo, dois botões e painel retangular. Abaixo, região cinza com faixas verticais. Rádio 4. Rádio em formato retangular com dois botões redondos pequenos na parte superior. Abaixo, visor retangular e painel ao lado. Abaixo, região cinza. Rádio 5. Rádio em formato retangular com alça na parte superior e dois botões laterais. Abaixo, painel retangular e região cinza. Rádio 6. Rádio em formato retangular com alça na parte superior e botão à direita. Abaixo, painel retangular. Abaixo, região cinza com faixas diagonal. Ilustração. Vista superior. A. Retângulo com dois botões abaixo e um na lateral. B. Retângulo com alça ao centro e dois botões abaixo. C. Retângulo com quatro botões dentro do retângulo. D. Retângulo com alça ao centro e botão pequeno à direita. E. Retângulo com dois botões dentro dele. F. Retângulo com alça ao centro e botão à direita. Ilustração. Vista lateral. G. Retângulo vertical com dois botões pequenos dentro dele e retângulo pequeno marrom na parte de cima. H. Retângulo vertical com um botão na parte superior e um à direita. I. Retângulo vertical com dois botões pequenos na parte superior. J. Retângulo vertical com botão na parte superior. K. Retângulo vertical com botão grande na lateral e um pequeno na parte superior além de um retângulo pequeno marrom na parte superior. L. Retângulo vertical com botão grande à esquerda e um pequeno na parte superior, além de um retângulo pequeno marrom na parte superior.

A tabela correta que relaciona cada rádio com suas vistas é:

Rádio	Vista superior	Vista lateral
1	B	L
2	E	J
3	A	K
4	C	G
5	F	H
6	D	I

Rádio	Vista superior	Vista lateral
1	D	I
2	C	L
3	F	H
4	E	G
5	A	J
6	B	K

Rádio	Vista superior	Vista lateral
1	B	L
2	E	J
3	A	H
4	C	I
5	D	G
6	F	K

Rádio	Vista superior	Vista lateral
1	F	L
2	E	J
3	A	H
4	C	I
5	D	G
6	B	K

Respostas e comentários

1. Pão de açúcar: aproximadamente 380 métros; morro da Urca: aproximadamente 210 métros.

2. Alternativa c.

Agora quem trabalha é você!

A atividade 1 pode ser resolvida considerando que as altitudes estão indicadas no perfil topográfico da figura cinco. A altitude do Pão de Açúcar está entre 350 métros e 400 métros, aproximadamente 380 métros; já a do morro da Urca é pouco mais do que 200 métros e menor do que 250 métros, aproximadamente 210 métros.

A resolução da atividade 2 está no início deste Manual, nas orientações específicas do capítulo 8.

Página 190

5. O teorema de Pitágoras no plano cartesiano

O técnico de um time de futebol é muito exigente nos treinos de cobrança de escanteio. Ele quer saber a medida exata da distância entre o ponto de esquina do campo de onde se cobra o escanteio e o ponto da marca do pênalti, lugar onde se posiciona um atacante para cabecear a bola ao gol. Sabendo que a marca do pênalti fica a 11 métros da linha de fundo e a 34 métros da linha lateral do campo, vamos ajudar o técnico a calcular a medida da distância pretendida.

Fotografia. Mulher uniformizada em campo de futebol. Ela cobra escanteio onde há uma bandeira. Ao fundo, pessoas na frente do gol. — Cobrança de escanteio durante uma partida de futebol, na Califórnia, Estados Unidos, em 2022.

Vamos imaginar a figura do campo em um plano cartesiano com a origem na esquina de escanteio (ponto ê), com o eixo vertical sobre a linha de fundo e o eixo horizontal sobre a linha lateral.

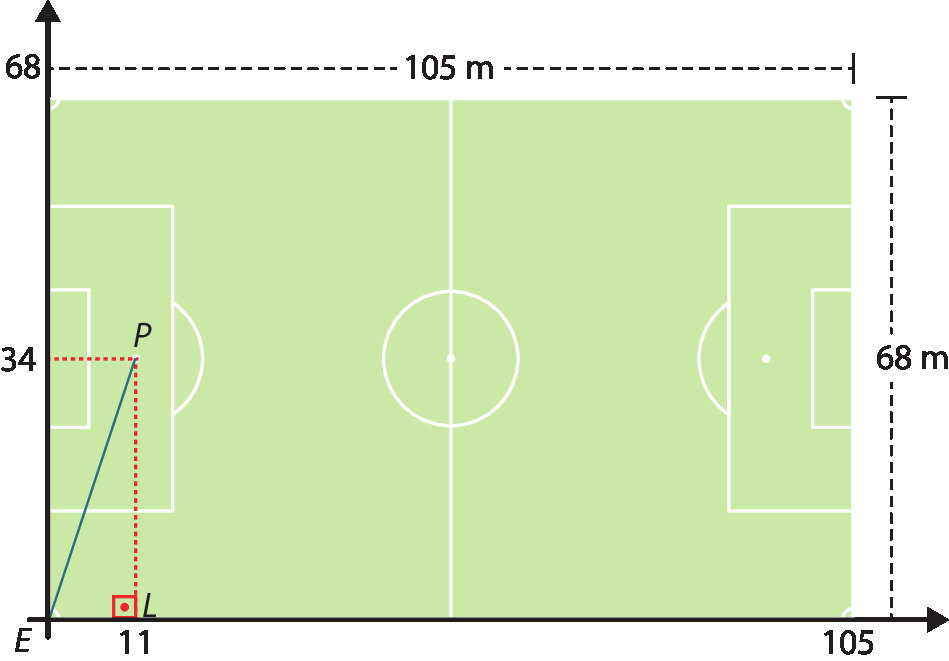
Ilustração. Campo de futebol com medida 68 metros por 105 metros sobre eixo horizontal e vertical. No canto inferior esquerdo, ponto E. Segmento de reta de 11 (L) à direita da área do escanteio até marca do pênalti, ponto P. Segmento de reta da marca do pênalti até centro do gol, 34. Segmento de reta diagonal de E até P. Segmento de reta vertical no centro do campo QR sendo 52,5 em R. Segmento de reta horizontal no centro do campo cruza com reta vertical em C. Segmento de reta diagonal de E até E linha na extremidade superior direita.

Observe, na ilustração, que o técnico quer calcular a medida da distância de ê a P, e também que é éle = 11 e LP = 34.

No triângulo retângulo é éle pê, com catetos medindo 11 e 34, aplicamos o teorema de Pitágoras:

(EP)elevado a 2 = (EL)elevado a 2 + (LP)elevado a 2

(EP)elevado a 2 = (11)elevado a 2 + (34)elevado a 2

E P = \sqrt{11^{2} + 34^{2}}

E P = \sqrt{121 + 1156} ≃ 35, 74

Portanto, a distância de ê a P mede, aproximadamente, 35,74 metros.

Note que, no plano cartesiano, temos ê = (0, 0) e P = (11, 34), e que a medida é éle é dada pela diferença das abscissas:

é éle = 11 ‒ 0 = 11

Note também que a medida LP é dada pela diferença das ordenadas:

LP = 34 ‒ 0 = 34

Ilustração. Mulher de cabelo preto e camiseta branca. Ela fala: Não obtivemos a medida da distância exata, mas talvez o técnico a considere uma boa aproximação.

Respostas e comentários

5. O teorema de Pitágoras no plano cartesiano

Habilidades da Bê êne cê cê: ê éfe zero nove ême ah um quatro e ê éfe zero nove ême ah um seis.

Neste tópico, serão apresentadas algumas aplicações do teorema de Pitágoras no plano cartesiano, como a determinação da distância entre dois pontos do plano, favorecendo o desenvolvimento das habilidades (EF09MA14) e (EF09MA16).

Se julgar necessário, retome com os estudantes a localização de pontos no plano cartesiano dadas as suas coordenadas e a identificação das coordenadas de pontos demarcados em um plano cartesiano. Verifique se eles reconhecem a indicação (x, y) como as coordenadas cartesianas associadas a um ponto do plano e se identificam o 1º elemento (x) do par ordenado (a abscissa do ponto) como a coordenada relativa ao eixo horizontal, e o 2º elemento (y) do par (a ordenada do ponto) como a coordenada relativa ao eixo vertical.

Explore a situação apresentada e sua representação no plano cartesiano, perguntando aos estudantes quais são as coordenadas do ponto ê, origem do sistema de coordenadas cartesianas, e do ponto P. Espera‑se que eles reconheçam que a origem do sistema é dada pelas coordenadas (0, 0) e, assim, temos ê = (0, 0). Além disso, para identificar as coordenadas de P, eles precisam observar as linhas tracejadas que partem do 11 e do 34, e que o cruzamento dessas linhas é o ponto P, ou seja, temos P = (11, 34).

Assim, os estudantes devem perceber que, nesse caso, a medida da distância de ê a P corresponde à medida da hipotenusa de um triângulo retângulo (é éle pê) cujos catetos medem 34 e 11.

Página 191

Assim, o cálculo anterior fica:

E P = \sqrt{{(11 ‒ 0)}^{2} + {(34 ‒ 0)}^{2}}

E P = \sqrt{121 + 1156}

EP ≃ 35,74

Agora, vamos explorar outras distâncias no campo de futebol colocado no plano cartesiano.

Observe na figura os pontos P = (11, 34), Q = (52,5; 68), C = (52,5; 34) e E' = (105, 68).

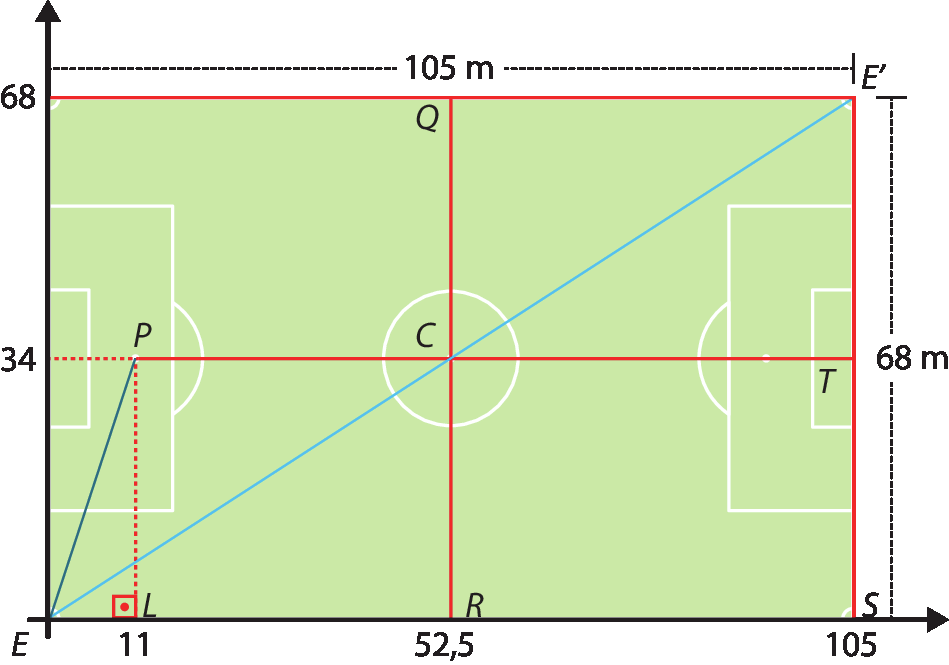
1. Para determinar a medida da distância entre os pontos ê e E', podemos:

• aplicar o teorema de Pitágoras no △ESE ', considerando catetos cujas medidas são 105 e 68: (EE ')elevado a 2 = (ES)2 + (ésse minúsculoE ')2 (EE ')elevado a 2 = (105)2 + (68)2 EE ' =

\sqrt{105^{2} + 68^{2}}

EE ' =

\sqrt{11 025^{2} + 4624}

≃ 125,1

A distância da esquina ê à esquina E' mede aproximadamente 125,1 metros.

• aplicar o teorema de Pitágoras no △ESE', considerando as coordenadas dos pontos ê = (0, 0) e E ' = (105, 68): (EE ')2 = (ES)2 + (SE ')2 (EE ')2 = (105 ‒ 0)2 + (68 ‒ 0)2 EE '

= \sqrt{{(105 ‒ 0)}^{2} + {(68 ‒ 0)}^{2}}

EE '

= \sqrt{11025 + 4624} ≃ 125, 1

A distância da esquina ê à esquina E' mede aproximadamente 125,1 metros.

2. Para calcular a distância entre os pontos C e E ', podemos:

• aplicar o teorema de Pitágoras no △CTE, considerando catetos cujas medidas são 52,5 e 34: (CE ')2 = (CT)2 + (TE')2 (CE ‘)2 = (52,5)2 + (34)2 CE '

= \sqrt{{(52, 5)}^{2} + {(34)}^{2}}

CE '

= \sqrt{2756, 25 + 1156} ≃ 62, 55

A distância do centro C à esquina E' mede aproximadamente 62,55 metros.

• aplicar o teorema de Pitágoras no △CTE, considerando as coordenadas dos pontos C = (52,5; 34) e E ' = (105, 68). (CE' )2 = (CT)2 + (TE‘)2 (CE' )2 = (105 ‒ 52,5)2 + (68 ‒ 34)2 CE'

= \sqrt{{(105 ‒ 52, 5)}^{2} + {(68 ‒ 34)}^{2}}

CE'

= \sqrt{{(52, 5)}^{2} + {(34)}^{2}}

CE'

= \sqrt{2 756, 25 + 1 156} ≃ 62, 55

3. Quando os pontos estão em um segmento horizontal:

P T = \sqrt{{(105 ‒ 11)}^{2} + {(34 ‒ 34)}^{2}} = \sqrt{{(105 ‒ 11)}^{2}} = |105 ‒ 11| = 94

4. Quando os pontos estão em um segmento vertical:

TE'

= \sqrt{{(105 ‒ 105)}^{2} + {(68 ‒ 34)}^{2}} = \sqrt{{(68 ‒ 34)}^{2}} = |68 ‒ 34| = 34

Respostas e comentários

O teorema de Pitágoras no plano cartesiano

Na ilustração do campo de futebol sobre o plano cartesiano, explore cada par de pontos e os segmentos que têm esses pontos como extremidades.

Reproduza na lousa esse plano cartesiano e peça a alguns estudantes que demarquem nele pares de pontos para que outros colegas determinem as medidas das distâncias entre eles, com a colaboração de toda a turma.

O objetivo desta abordagem mais aritmética do que algébrica é trabalhar as ideias em um contexto específico, por meio da resolução de um problema com dados numéricos. Consideramos aqui uma abordagem inicial que fornecerá aos estudantes pré-requisitos necessários para o estudo de Geometria Analítica no Ensino Médio.

Página 192

Observações

▶ Ainda na ilustração da página 191, temos o ponto C como ponto médio do segmento

\overline{E E ʹ}

Note que:

x_{c} = \frac{105 + 0}{2} = 52, 5,

ou seja,

x_{c} = \frac{x_{E} + x_{E ʹ}}{2}

y_{c} = \frac{68 + 0}{2} = 34,

ou seja,

y_{c} = \frac{y_{E} + y_{E ʹ}}{2}

▶ A medida da distância entre pontos com mesma ordenada, isto é, pontos de um segmento horizontal, é dada pela diferença de abscissas em módulo.

P Q = \sqrt{{(x_{P} ‒ x_{Q})}^{2}} = |x_{P} ‒ x_{Q}|

▶ A medida da distância entre pontos com mesma abscissa, isto é, pontos de um segmento vertical, é dada pela diferença de ordenadas em módulo.

P Q = \sqrt{{(y_{P} ‒ y_{Q})}^{2}} = |y_{P} ‒ y_{Q}|

▶ A medida da distância entre dois pontos quaisquer P(xP , yP) e Q(xQ , yQ) no plano cartesiano é dada por:

P Q = \sqrt{{(x_{P} ‒ x_{Q})}^{2} + {(y_{P} ‒ y_{Q})}^{2}}

EXERCÍCIOS PROPOSTOS

FAÇA AS ATIVIDADES NO CADERNO

37 Considere a ilustração do campo de futebol da página 191 e, usando as coordenadas dos pontos na figura, calcule a medida da distância entre os seguintes pontos:

a) ê e T;

b) ê e Q;

c) P e C;

d) C e T;

e) C e Q.

38 Represente em um plano cartesiano o losango de vértices a(0, 0), B(6, 2), C(8, 8) e D(2, 6). Depois, calcule:

a) as medidas das diagonais dêsse losango;

b) a medida dos lados dêsse losango.

39 Dados os pontos destacados no plano cartesiano e sabendo que a = (3, 2), calcule a medida da distância entre cinco pares desses pontos.

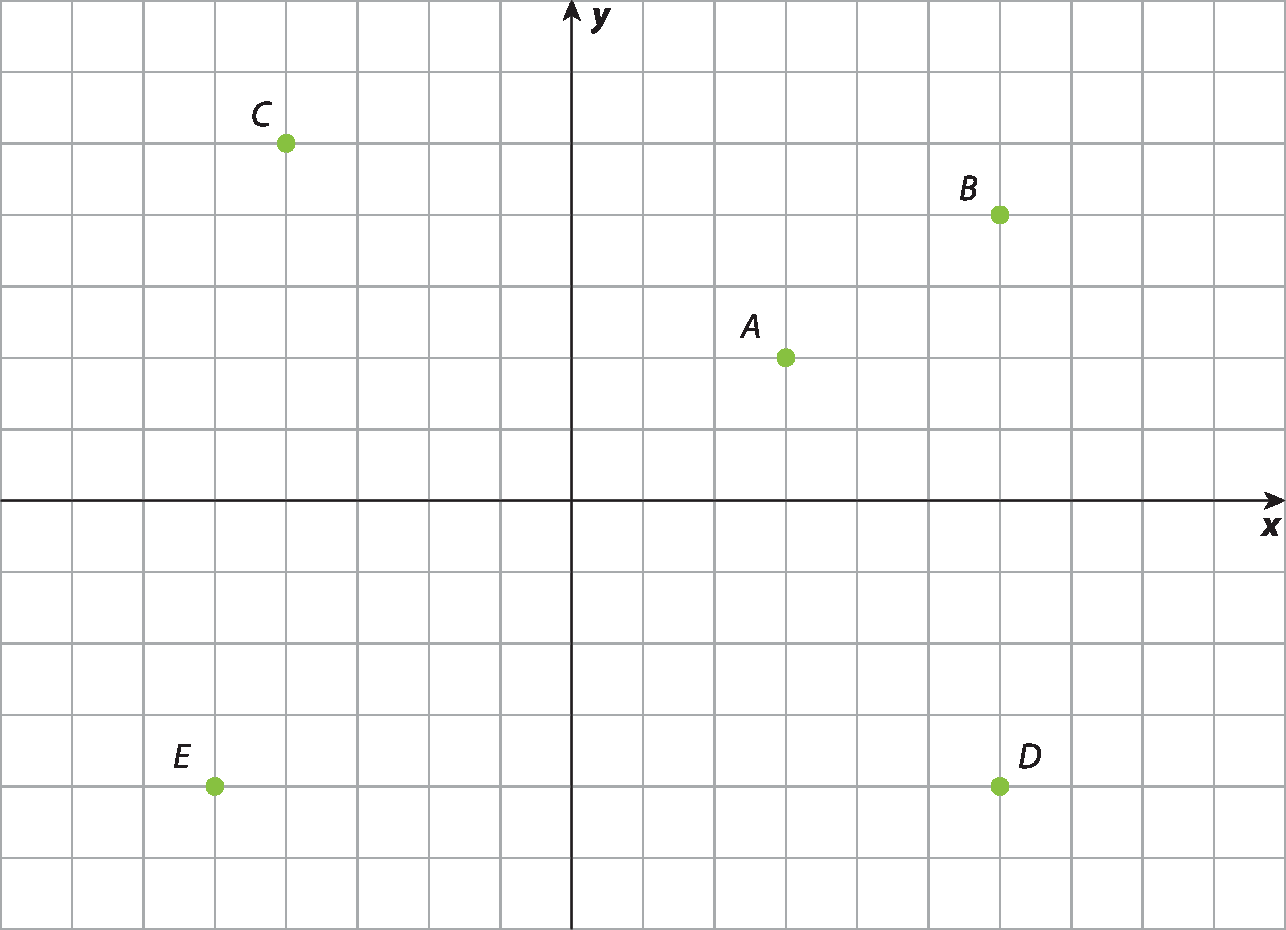
Ilustração. Malha quadriculada com eixo x e eixo y. Pontos A, B, C, D e E dispostos pela malha quadriculada com as coordenadas: A(3, 2), B(6, 4), C(menos 4, 6), D(menos 6, menos 4), E(menos 5, menos 4).

Respostas e comentários

37. a) 110,4

37. b) 85,9

37. c) 41,5

37. d) 52,5

37. e) 34

38. a)

4 \sqrt{2}; 8 \sqrt{2}

38. b)

2 \sqrt{10}

39.

A B = \sqrt{13}

A C = \sqrt{58},

A D = 3 \sqrt{5}

, A Ê = 10,

B C = \sqrt{101}

, bê dê = 8,

B E = \sqrt{185}

C D = \sqrt{181}

C E = \sqrt{82}

, dê ê = 11

Exercícios propostos

As resoluções dos exercícios 37 a 39 estão no início deste Manual, nas orientações específicas do capítulo 8.

Amplie o exercício 38 pedindo aos estudantes que determinem as medidas do perímetro e da área do losango. Espera-se que eles reconheçam que:

• a medida do perímetro P do losango, em unidade de comprimento, é dada por:

P = 4 \cdot 2 \sqrt{10} = 8 \sqrt{10} ≃ 25, 3

• a medida da área A do losango, em unidade de área, é dada por:

A = \frac{4 \sqrt{2} \cdot 8 \sqrt{2}}{2} = 32

No exercício 39, proponha aos estudantes que reproduzam a figura em papel quadriculado e sugira a eles que determinem a projeção ortogonal de cada um desses pontos sobre cada eixo coordenado.

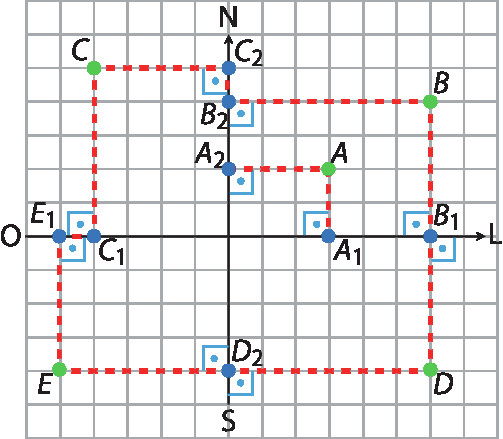
Ilustração. Malha quadriculada com eixo OL na horizontal e eixo NS na vertical. Pares ordenados: A (3, 2); B (6, 4); C (menos 4, 5); D (6, menos 4); E (menos 5, menos 4); A1 (3, 0); B1 (6, 0); C1 (menos 4, 0); D1 (6, 0); E1 (menos 5, 0), A2 (0, 2); B2 (0, 4); C2 (0, 5); D2 (0, menos 4); E2 (0, menos 4).

Peça-lhes que, considerando o lado de cada quadradinho como a unidade de medida de comprimento, determinem as coordenadas dos pontos que são essas projeções ortogonais.

• A1 = (3, 0); B1 = (6, 0); C1 = (‒4, 0); D1 = (6, 0); E1 = (‒5, 0).

• A2 = (0, 2); B2 = (0, 4); C2 = (0, 5); D2 = (0, ‒4); E2 = (0, ‒4).

Página 193

EXERCÍCIOS COMPLEMENTARES

FAÇA AS ATIVIDADES NO CADERNO

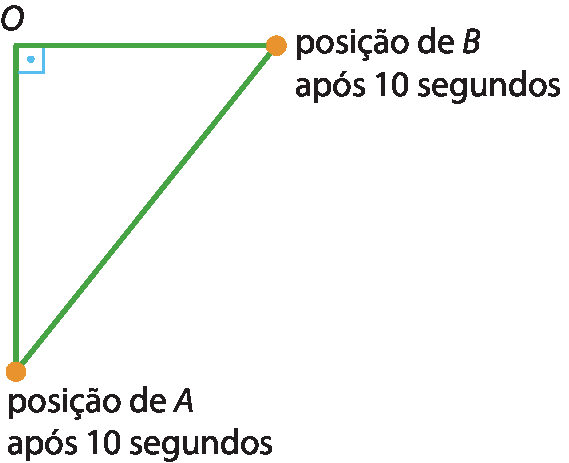
1 Dois ciclistas, a e B, partem de um ponto O e movem-se perpendicularmente um em direção ao outro, à medida de velocidades de 16 metros por segundo e 12 metros por segundo, respectivamente. Que medida de distância os separará após 10 segundos?

Ilustração. Triângulo retângulo com com ângulo reto em O e vértices O, posição de A após 10 segundos e posição de B após 10 segundos.

2 Uma balsa está fazendo a travessia de veículos e transeuntes, pois a ponte sobre o rio foi interditada. Ela parte do ponto a, que, por segurança, fica a 50 metros da ponte, e chega ao ponto B.

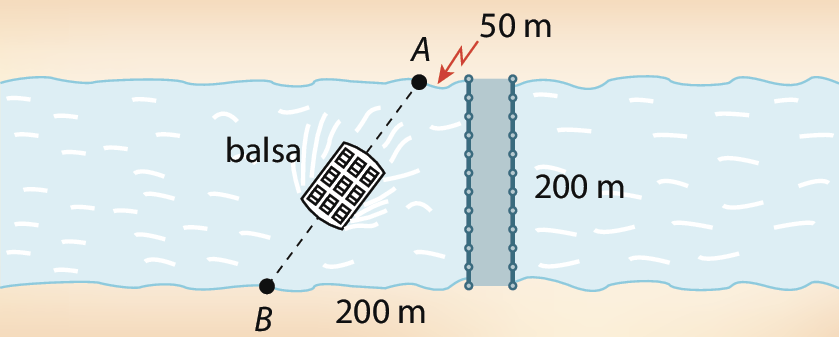
Ilustração. Rio com uma ponte de 200 metros. À esquerda, ponto A com distância de 50 metros da ponte. Na outra margem ponto B com distância de 200 metros da ponte. entre os pontos, balsa dentro do rio.

a) Quantos metros a balsa percorre nessa travessia?

b) Se a balsa demorar 5 minutos para fazer a travessia, qual será a medida da velocidade média em quilômetro por hora?

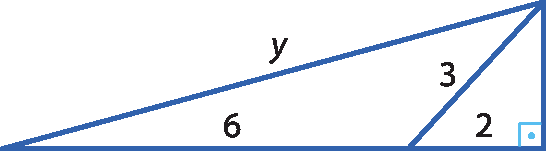
3 Determine o valor de y na figura.

Ilustração. Dois triângulos, lado a lado. Triângulo formado à esquerda tem medidas 6, y e 3. No triângulo à direita, medidas 3 e 2.

4 Em um trapézio retângulo a bê cê dê, a altura

\overline{A D}

mede 6 centímetros, a base menor

\overline{D C}

mede 3,5 centímetros e a diagonal maior

\overline{B D}

mede 10 centímetros. Determine:

a) a medida da base maior;

b) a medida do lado oblíquo;

c) a medida do perímetro dêsse trapézio;

d) a medida da área dêsse trapézio.

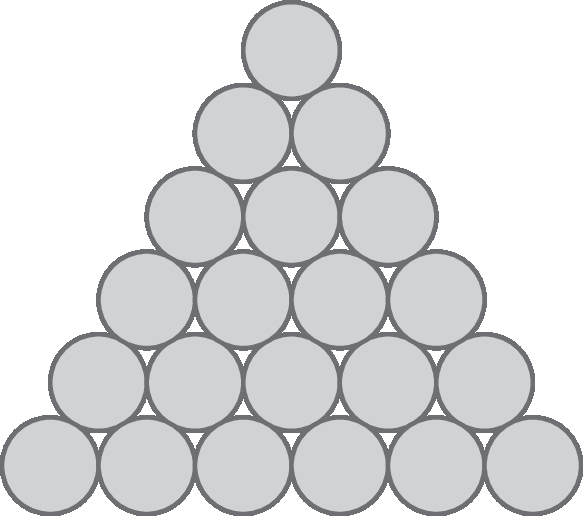
5 A figura representa a vista frontal de uma pilha de latas de leite em pó deitadas. Determine a medida da altura da pilha, sabendo que o raio de cada lata mede 4,5 centímetros.

Ilustração. Vista frontal de pilha de latas. De baixo para cima: 6 latas, 5 latas, 4 latas, 3 latas, duas latas, uma lata.

6 Em um triângulo isósceles, cada lado congruente mede 15 centímetros. Determine a medida da área dêsse triângulo, sabendo que sua base mede 24 centímetros.

7 É possível colocar um lápis de 18 centímetros em um estojo retangular de 12 centímetros por 15 centímetros? Justifique sua resposta.

8 Observe a figura e faça o que se pede.

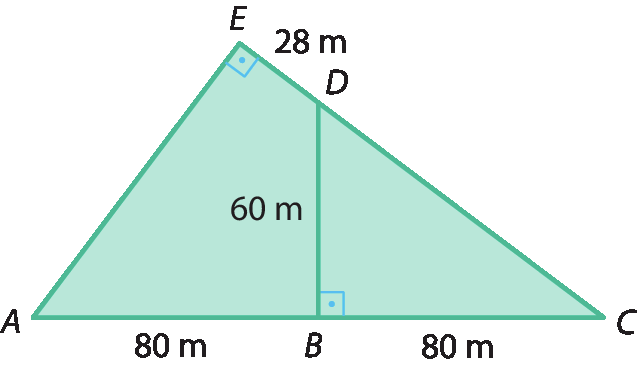
Ilustração. Figura composta por triângulo BCD à direita com medidas: BC: 80 metros. BD: 60 metros. À esquerda, quadrilátero ABDE com as medidas: AB: 80 metros. BD: 60 metros e DE: 28 metros.

a) Determine as medidas CD, ê cê e A Ê.

b) Determine as medidas de área dos △á cê ê e △BCD.

c) Calcule a medida da área do quadrilátero á bê dê é.

9 Um losango tem 60 centímetros de perímetro. Sabendo que a diagonal maior dêsse losango mede 26 centímetros, calcule a medida da diagonal menor.

10 As dimensões de um retângulo são expressas por x + 1 e x ‒ 2. Sabendo que a medida da área é 18 centímetros quadrados, determine a medida da diagonal dêsse retângulo.

11 (Fuvésti-São Paulo) Um trapézio retângulo tem bases 5 e 2 e altura 4. O perímetro dêsse trapézio é:

a) 13.

b) 14.

c) 15.

d) 16.

e) 17.

Respostas e comentários

1. 200 métros

2. a) 250 métros

2. b) 3 quilômetros por hora

y = \sqrt{69}

4. a) 8 centímetros

4. b) 7,5 centímetros

4. c) 25 centímetros

4. d) 34,5 centímetros quadrados

(\frac{45 \sqrt{3}}{2} + 9) cm

6. 108 centímetros quadrados

7. Sim, se o lápis for acomodado no sentido da diagonal, que mede 19,2 centímetros.

8. a) CD = 100 métros, EC = 128 métros e AE = 96 métros.

8. b) .6144 métros quadrados e .2400 métros quadrados.

8. c) .3744 métros quadrados

4 \sqrt{14} cm

10.

3 \sqrt{5} cm

11. Alternativa d.

Exercícios complementares

Neste bloco de exercícios, os estudantes têm a oportunidade de retomar os principais conceitos tratados no capítulo e verificar possíveis dificuldades que ainda apresentem. Sugerimos que as atividades sejam desenvolvidas em duplas, o que ampliará e enriquecerá o repertório de estratégias que eles já têm e consolidará os conhecimentos construídos.

Incentive-os a reproduzir um esquema das figuras dadas nos enunciados ou a fazer desenhos que representem uma situação exposta para aplicar as informações importantes e completar com outras que forem relevantes para a resolução dos exercícios.

Estimule a troca das respostas obtidas, de modo que o debate não se restrinja à resposta final, mas também à resolução dos exercícios.

As resoluções do exercício 1 e dos exercícios 3 a 11 estão no início deste Manual, nas orientações específicas do capítulo 8.

No exercício 2, analisando a figura, podemos desenhar o seguinte triângulo retângulo:

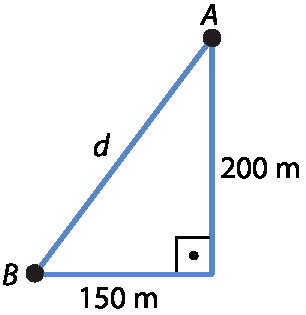
Ilustração. Triângulo retângulo. A medida AB é d. As outras medidas são: 150 metros e 200 metros.

a) Aplicando o teorema de Pitágoras, obtemos a medida da distância d percorrida pela balsa: d elevado a 2 = 150elevado a 2 + 200elevado a 2 d elevado a 2 = .62500

Portanto, d = 250 métros.

b) d = 250 métros e t = 5 minutos

v_{m é d i a} = \frac{250 m}{5 min} = 50

metros por minuto

v_{m é d i a} = \frac{50 \cdot 1 m}{1 min} =

= \frac{50 \cdot \frac{1}{1000} km}{\frac{1}{60} h}

v_{m é d i a} = 50 \cdot \frac{1}{1000} \cdot \frac{60}{1}

quilômetros por hora vmédia = 3 quilômetros por hora

Página 194

12 (ó ême-á bê cê) No triângulo á bê cê, a medida do ângulo

\hat{A}

é 90graus e

\overline{A D}

é a medida da altura relativa ao lado

\overline{B C} .

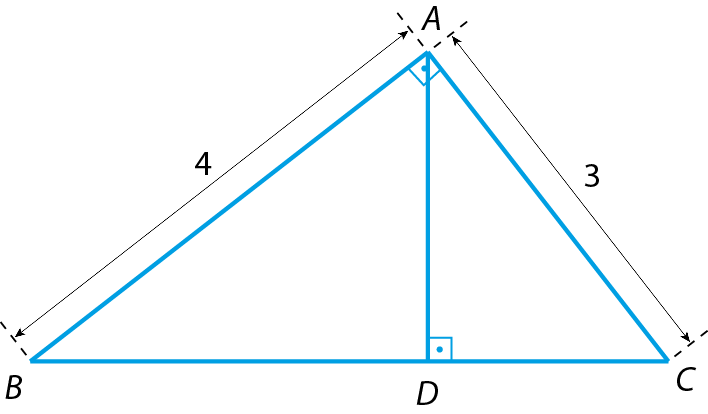
Ilustração. Triângulo ABC. Em A, reta vertical até lado BC, ponto D. A medida AB é 4 e AC: 3.

Se m = BD, n = DC e L = 25 ⋅ m ⋅ n, então L é igual a:

a) 100.

b) 121.

c) 169.

d) 144.

e) 225.

13 Qual é medida da área da figura a seguir?

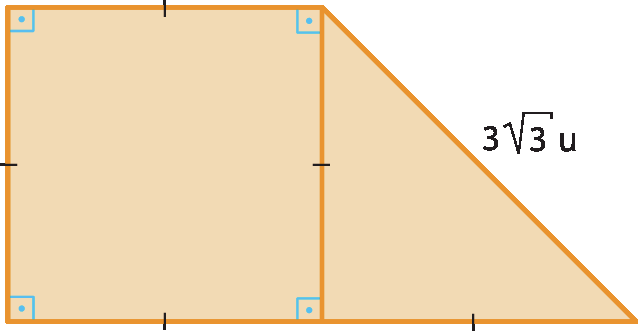
Ilustração. Quadrado. À direita, triângulo com um dos lados medindo 3 raiz quadrada de 3 u.

14 (uél-Paraná) As medidas, em centímetro, dos três lados de um triângulo retângulo são expressas por (x ‒ 2), x e (x + 2). A medida, em centímetro, da hipotenusa dêsse triângulo é:

a) 5.

b) 8.

c) 10.

d) 12.

e) 14.

15 A medida da altura relativa à hipotenusa de um triângulo retângulo é 12 centímetros, e um dos segmentos determinados por essa altura sobre a hipotenusa mede 9 centímetros. Calcule a medida dos catetos desse triângulo.

16 O cateto de um triângulo retângulo e a projeção desse cateto sobre a hipotenusa medem 1 centímetro e

\frac{\sqrt{5}}{5}

centímetros, respectivamente. Determine a medida da hipotenusa dêsse triângulo.

17 A figura mostra o esquema do roteiro de uma prova de ciclismo.

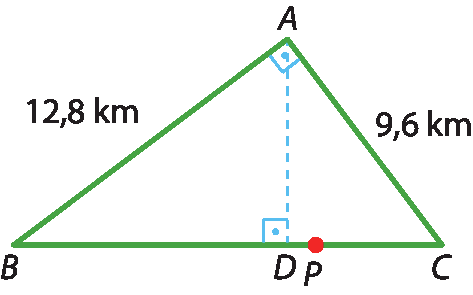
Ilustração. Triângulo ABC. Em A, segmento de reta vertical até lado BC, no ponto D. A medida AB é 12,8 quilômetros. AC: 9,6 quilômetros. À direita do ponto D, ponto P.

A sequência do percurso é:

O ponto P está a 80 metros do ponto D. Quantos quilômetros tem esse percurso?

18 (FEI-São Paulo) Se em um triângulo os lados medem 9, 12 e 15 centímetros, então a altura relativa ao maior lado mede:

a) 8,0 centímetros.

b) 7,2 centímetros.

c) 6,0 centímetros.

d) 5,6 centímetros.

e) 4,3 centímetros.

19 (FEI-São Paulo) Em um triângulo retângulo, a altura relativa à hipotenusa mede 12 centímetros e a diferença entre as medidas das projeções dos catetos sobre a hipotenusa é 7 centímetros. A hipotenusa desse triângulo mede:

a) 10 centímetros.

b) 15 centímetros.

c) 20 centímetros.

d) 25 centímetros.

e) 30 centímetros.

20 (ulbra-Rio Grande do Sul) A área do triângulo a seguir mede 6 métros². O valor do perímetro desse triângulo é:

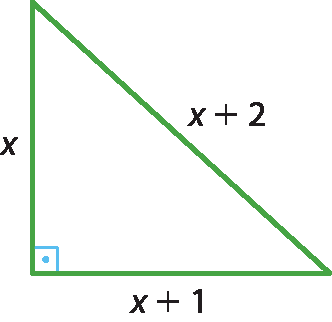
Ilustração. Triângulo retângulo com as medidas: x, x + 1 e x + 2

a) 6 métros.

b) 9 métros.

c) 10 métros.

d) 12 métros.

e) 20 métros.

21 (ú éfe pê é) Um barco navegou 10 quilômetros para o oeste, depois 5 quilômetros para o sul, depois 13 quilômetros para o leste e finalmente 9 quilômetros para o norte. Onde o barco parou relativamente ao ponto de partida?

a) 5 quilômetros ao norte

b) 3 quilômetros a sudeste

c) 4 quilômetros ao sul

d) 3 quilômetros a sudoeste

e) 5 quilômetros a nordeste

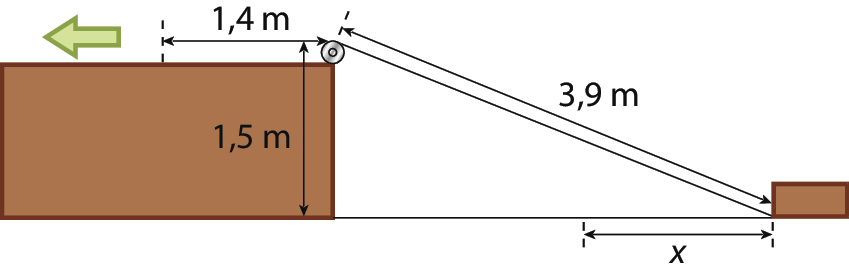
22 (ú éfe pê érre) Uma corda de 3,9 métros de comprimento conecta um ponto na base de um bloco de madeira a uma polia localizada no alto de uma elevação, conforme o esquema a seguir. Observe que o ponto mais alto dessa polia está 1,5 métro acima do plano em que esse bloco desliza. Caso a corda seja puxada 1,4 métro, na direção indicada, a distância x que o bloco deslizará será de:

a) 1,0 métro.

b) 1,3 métro.

c) 1,6 métro.

d) 1,9 métro.

e) 2,1 métros.

Ilustração. À esquerda, bloco retangular com seta para esquerda e da metade do bloco até a polia na extremidade direita, 1,4 metros. A altura do bloco é 1,5 metros. À direita, bloco com corda de 3,9 centímetros até a polia. Parte da distância da polia até o bloco é x.

Respostas e comentários

12. Alternativa d.

13. 20,25 u2

14. Alternativa c.

15. 15 centímetros e 20 centímetros.

16.

\sqrt{5} cm

17. 46 quilômetros

18. Alternativa b.

19. Alternativa d.

20. Alternativa d.

21. Alternativa ê.

22. Alternativa c.

Exercícios complementares

As resoluções dos exercícios 12 a 14, do exercício 16 e dos exercícios 18 a 22 estão no início deste Manual, nas orientações específicas do capítulo 8.

No exercício 15, para facilitar a resolução, peça aos estudantes que representem essa situação por um desenho e só então apliquem as relações métricas necessárias.

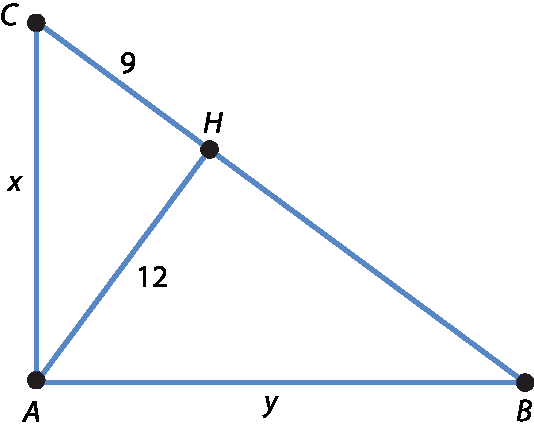
Ilustração. Triângulo ABC. Com lados medindo: AB: y, AC: x. Segmento de reta de A até lado BC, no ponto H. De C até H mede 9.

Pelo teorema de Pitágoras, aplicado ao triângulo á agá cê:

x elevado a 2 = 9elevado a 2 + 12elevado a 2 ⇒ x = 15

Pela 2ª relação métrica:

12elevado a 2 = 9 · HB ⇒ HB = 16

Empregando o teorema de Pitágoras no triângulo a agá bê:

y elevado a 2 = 12elevado a 2 + 16elevado a 2 ⇒ y = 20

Logo, os catetos dêsse triângulo medem 15 centímetros e 20 centímetros.

No exercício 17, verifique se os estudantes interpretam e relacionam as informações do enunciado. Proponha a resolução com o auxílio de calculadora.

Utilizando o teorema de Pitágoras, obtemos a medida BC:

(BC)elevado a 2 = 12,8elevado a 2 + 9,6elevado a 2

B C = \sqrt{163, 84 + 92, 16}

BC = 16

Pela 3ª relação métrica, obtemos a medida AD:

12,8 · 9,6 = 16 · AD

A D = \frac{12,8 \cdot 9,6}{16}

AD = 7,68

Pela 1ª relação métrica, determinamos a medida BD:

(12,8)elevado a 2 = 16 · BD

B D = \frac{163,84}{16}

BD = 10,24

Com a informação de que P está a 80 metros de D:

DP = 80 métros = 0,08 quilômetro

Sendo assim:

• BP = BD + DP = 10,24 quilômetros + 0,08 quilômetro = 10,32 quilômetros

• PC = BC ‒ BP = 16 quilômetros ‒ 10,32 quilômetros = 5,68 quilômetros

Adicionamos todas as medidas das distâncias percorridas, considerando a sequência do percurso:

A → D → B → A → C → P

AD + DB + BA + AC + CP = 7,68 quilômetros + 10,24 quilômetros + 12,8 quilômetros + 9,6 quilômetros + 5,68 quilômetros = 46 quilômetros

Página 195

VERIFICANDO

FAÇA AS ATIVIDADES NO CADERNO

1 Se uma escada de 5 metros for apoiada em uma parede, com distância da base à parede medindo 3 metros, a que medida de altura a escada deve ser apoiada na parede?

a) 3 metros

b) 4 metros

c) 5 metros

d) 6 metros

2 O teorema de Pitágoras enuncia que:

a) um triângulo retângulo tem dois catetos e uma hipotenusa.

b) a soma da medida dos catetos ao quadrado é igual à da medida da hipotenusa.

c) a soma da medida dos catetos é sempre menor que a da medida da hipotenusa.

d) a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.

3 Entre as alternativas a seguir, dadas em metro, quais medidas correspondem às medidas dos catetos do triângulo ilustrado?

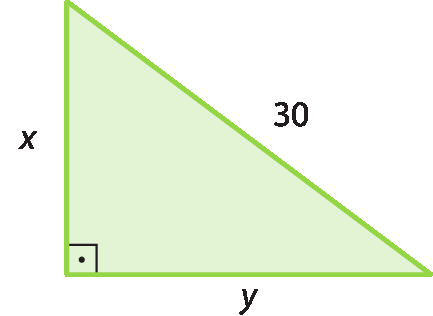
Ilustração. Triângulo verde com as medidas dos lados: x, y e 30. Ângulo reto entre x e y.

a) 15 métros e 15 métros

b) 10 métros e 20 métros

c) 18 métros e 24 métros

d) 6 métros e 29 métros

4 Com base nas informações da figura, qual é a medida da hipotenusa do triângulo?

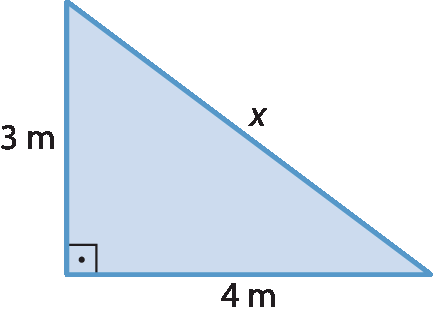
Ilustração. Triângulo azul com as medidas dos lados: x, 3 metros, 4 metros. Ângulo reto entre 3 metros e 4 metros.

a) 5 métros

b) 7 métros

c) 12 métros

d) 25 métros

5 Sem utilizar o teorema de Pitágoras, calcule o valor de x.

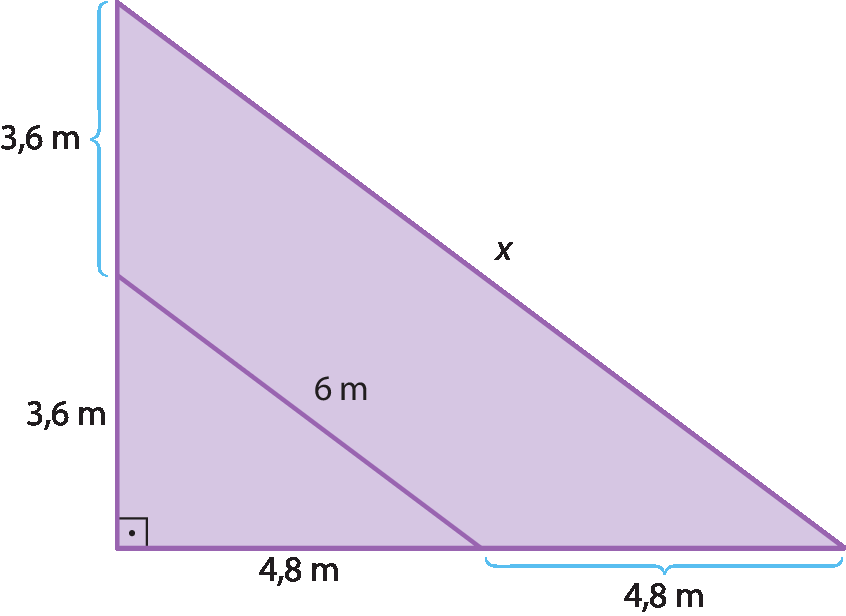
Ilustração. Triângulo com as medidas: 3,6 metros, 4,8 metros e 6 metros. Acima, na diagonal, quadrilátero com 6 metros, 4,8 metros, 3,6 metros e x.

a) 36 métros

b) 24 métros

c) 12 métros

d) 6 métros

6 Qual é a medida do comprimento da diagonal de um retângulo de lados medindo 8 métros e 6 métros?

a) 6 métros

b) 8 métros

8 \sqrt{2}

métros

d) 10 métros

7 Qual é a medida do comprimento da diagonal de um quadrado de lado medindo 10 centímetros?

10 \sqrt{2}

centímetros

10 \sqrt{3}

centímetros

c) 10 centímetros

d) 5 centímetros

8 Qual é a medida da área de um quadrado que tem o lado de mesma medida que a da diagonal de um quadrado de lado de medida 5 métros?

a) 25 métros quadrados

b) 50 métros quadrados

c) 125 métros quadrados

d) 12,5 métros quadrados

Organizando

Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.

a) Quais são os elementos principais de um triângulo retângulo?

b) Como o teorema de Pitágoras relaciona esses elementos?

c) O que são os triângulos pitagóricos?

Respostas e comentários

1. Alternativa b.

2. Alternativa d.

3. Alternativa c.

4. Alternativa a.

5. Alternativa c.

6. Alternativa d.

7. Alternativa a.

8. Alternativa b.

Organizando:

a) Os dois catetos, que formam o ângulo reto, e a hipotenusa, que é o lado que se opõe ao ângulo reto.

b) A soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.

c) São triângulos retângulos cujas medidas dos lados são expressas por números inteiros positivos.

Verificando

Nesta seção, apresentamos testes que abrangem todo o capítulo, sendo uma oportunidade para os estudantes validarem o entendimento do conteúdo estudado. Caso eles apresentem dúvidas em relação a alguma das atividades propostas, oriente-os a rever os conceitos apresentados no capítulo, assim também desenvolverão a autonomia no estudo.

As resoluções e comentários dos testes 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 8.

Organizando

a) O elemento que caracteriza o triângulo retângulo é o ângulo reto. Quanto aos lados, devem ser destacados os catetos e a hipotenusa.

b) Espera-se que os estudantes enunciem o teorema de Pitágoras: a soma dos quadrados das medidas dos catetos é igual ao quadrado da medida da hipotenusa.

c) Espera-se que os estudantes associem o nome triângulo pitagórico com o teorema de Pitágoras. Assim, devemos enunciar: triângulos pitagóricos são triângulos cujas medidas são números naturais não nulos que satisfazem o teorema de Pitágoras; logo, são triângulos retângulos cujas medidas dos lados são números inteiros positivos.

Página 196

DIVERSIFICANDO

Uma “quase” circunferência!

Aninha ficou admirada quando a professora de Arte disse que, naquela aula, com paciência, os estudantes fariam uma “quase” circunferência usando triângulos retângulos.

Ilustração. Sala de aula com professora a frente da lousa, um menino olhando para ela e atrás dele uma menina olhando para trás. Menina de cabelo castanho, faixa azul e camiseta branca. Ela pensa: Como assim, linha reta fazendo curva?

A professora pediu a eles que, primeiramente, desenhassem no caderno, com régua e esquadro, um quadrado de 12 centímetros de medida de lado. Na sequência, eles deveriam:

• em cada lado do quadrado, marcar pontos de 0,5 centímetro em 0,5 centímetro, a partir do vértice;

• construir 8 triângulos retângulos com catetos nos lados do quadrado, sendo um cateto medindo 0,5 centímetro e o outro, 6 centímetros;

• construir grupos de 8 triângulos retângulos com catetos nos lados do quadrado, sendo que, em cada um, a soma das medidas dos catetos seja sempre igual a 6,5 centímetros.

Observe como Aninha começou o desenho no caderno dela.

Ilustração. Modelo. Quadrado com pontos pretos ao redor e linhas vermelhas curvadas nas laterais. Dentro, 49 pontos de interrogações na cor cinza distribuídos em fileiras.

Agora é com você!

FAÇA A ATIVIDADE NO CADERNO

Em um papel quadriculado, para facilitar, desenhe um quadrado cujos lados tenham 24 quadradinhos e siga as indicações da professora de Aninha para obter uma “quase” circunferência. O que poderia ser feito para obter uma figura mais próxima de uma circunferência?

Respostas e comentários

Dividir os lados em um número maior de quadradinhos.

Diversificando

A seção apresenta um procedimento usando triângulos retângulos e papel quadriculado para fazer uma composição que lembra uma circunferência.

Na atividade do Agora é com você!, os estudantes devem obter a seguinte figura:

Ilustração. Malha quadriculada com linhas sobrepostas formando uma circunferência dentro de um quadrado vermelho.

Glossário

Terno: : conjunto de três elementos; trio.; Voltar para o texto