
CAPÍTULO 11 Circunferência, arcos e relações métricas

Revelada pela lente fotográfica do artista, uma circunferência imaginária, espelhada na água tranquila do lago, pode surgir da simetria do arco da ponte.
Observe a imagem e responda às questões no caderno.
a) Você conhecia ou já tinha ouvido falar dessa ponte? Comente sua resposta.
b) Sabendo que a altura da ponte da fotografia mede 15 métros, o diâmetro da circunferência imaginária que ela fórma, ao ser refletida na água, mede quantos metros?
c) Reúna-se com alguns colegas e pesquisem fotografias de outros lugares, objetos ou obras de arte que contenham formatos que possam ser associados a uma circunferência. Depois, compartilhe com os demais colegas e o professor os resultados que vocês obtiveram.
Respostas e comentários
a) Resposta pessoal.
b) 30 métros
c) Resposta pessoal.
Capítulo 11 – Circunferência, arcos e relações métricas
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas de Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, tratamos da circunferência e da determinação da medida de seu comprimento, das medidas de arcos e das relações métricas em uma circunferência. O conceito de proporcionalidade, frequente no desenvolvimento de vários conteúdos abordados ao longo do Ensino Fundamental e já estudado neste volume, também é utilizado para determinar a medida de arcos de circunferência. Além disso, ampliamos o trabalho com gráficos explorando os formados por semicoroas circulares.
A abertura do capítulo traz uma imagem que pode ser associada a uma circunferência. Em uma roda de conversa, aproveite para estimular os estudantes a expor o que sabem sobre essa figura geométrica, quais são seus principais elementos, mobilizando conhecimentos construídos anteriormente.
Para responder à questão proposta no item b é necessário considerar que a medida do raio é igual à metade da medida do diâmetro.
Incentive os estudantes a pesquisar fotografias de outras situações em que se observam elementos que possam ser associados à circunferência ou ao círculo e aproveite o momento para discutir com eles o que essas figuras geométricas planas têm em comum e o que elas têm de diferente, conduzindo os estudantes a perceber que o círculo é a região interna delimitada por uma circunferência.
1. Circunferência e arcos de circunferência
Em muitas culturas agrícolas é empregado um sistema de irrigação chamado pivô central. Nesse sistema, a água é distribuída de maneira controlada, com economia e eficiência, por meio de uma tubulação que, apoiada em torres sobre rodas, dá voltas completas em torno de um dispositivo central.




Respostas e comentários
1. Circunferência e arcos de circunferência
Habilidade da Bê êne cê cê: ê éfe zero nove ême ah um um.
Peça aos estudantes que citem exemplos de elementos do cotidiano que possam ser associados à circunferência ou ao círculo. Espera‑se que sejam citados: tampos de mesas, dê vê dês, pneus, ventiladores, moedas, anéis e alianças, pizzas etcétera
Solicite aos estudantes que façam composições envolvendo circunferências. Depois, faça uma exposição na sala para divulgar os trabalhos elaborados por eles.
É interessante que os estudantes pesquisem na internet outras obras de arte em que os elementos utilizados para compor a obra dão ideia de circunferência. Ao final da pesquisa, peça a eles que compartilhem com os colegas as obras encontradas. Esse trabalho pode ser feito de maneira interdisciplinar com Arte e favorece o desenvolvimento da competência geral 3, pois os estudantes podem fruir diferentes manifestações artísticas.

Circunferência é a linha formada por todos os pontos de um plano que estão à mesma medida de distância de um ponto fixo dêsse plano.
Na circunferência a seguir:
• O é o centro;
•
ABé uma corda;
•
segmento O Cé um dos raios;
•
segmento D Eé um dos diâmetros.
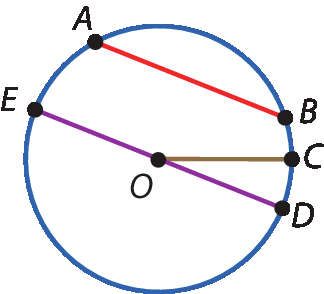
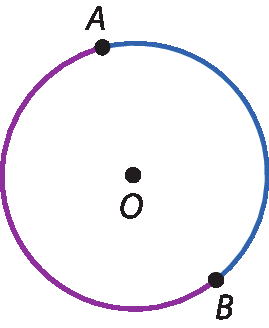
Considere dois pontos distintos de uma circunferência. Esses pontos a dividem em duas partes chamadas de arco.

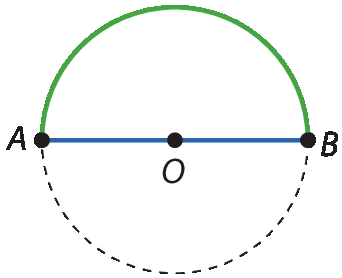
Quando os dois pontos coincidem com os extremos de um diâmetro, cada um dos arcos é chamado de semicircunferência.
Medida do comprimento de uma circunferência
Acompanhe a situação a seguir.
Aline é arquiteta e está desenhando a planta de uma quadra poliesportiva.

Qual deverá ser a medida do comprimento da circunferência central dessa quadra, sabendo que o raio deve medir 1,8 metro?
Já sabemos que a razão entre a medida do comprimento (C ) de uma circunferência e a medida de seu diâmetro (d ) é constante e aproximadamente igual a 3,14. Essa constante é representada pela letra grega π (lemos: “pi”). Ou seja, dada uma circunferência de raio medindo r, verificamos:
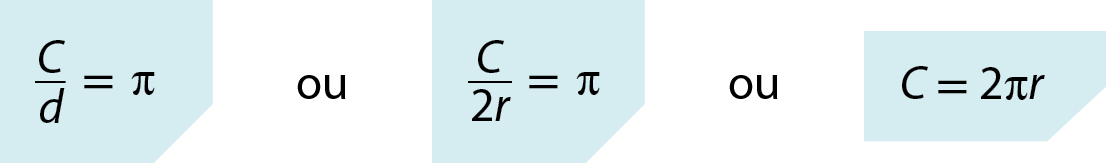
Respostas e comentários
Circunferência e arcos de circunferência
Inicialmente, reproduza as figuras na lousa para que os estudantes as identifiquem. Depois, peça a eles que leiam o texto desta página e verifiquem os elementos que não foram reconhecidos. Em seguida, desenhe na lousa outras circunferências para que os estudantes tracem raios, cordas, diâmetros e destaquem nelas dois arcos de medidas diferentes.
Na situação anterior, como o raio da circunferência central da quadra mede 1,8 métro, podemos calcular a medida do comprimento dessa circunferência, em metro, da seguinte maneira:
C = 2πr ≃ 2 ⋅ 3,14 ⋅ 1,8
C ≃ 11,3
Portanto, o comprimento da circunferência do círculo central da quadra poliesportiva mede, aproximadamente, 11,3 métros.
Convém lembrar que o número π, que indica a razão entre a medida do comprimento de uma circunferência e a medida do seu diâmetro, é um número irracional, isto é, não pode ser representado na fórma decimal exata nem por uma dízima periódica.
π = 3,141592653reticências
Acompanhe alguns exemplos de aplicação.

a) Vamos calcular a medida do comprimento de uma circunferência, cujo diâmetro mede 16 centímetros, considerando π = 3,14.
É dado d = 16 centímetros e sabemos que C = πd.
Assim, obtemos:
C = 3,14 ⋅ 16 = 50,24
Logo, o comprimento da circunferência mede 50,24 centímetros.
b) Vamos calcular a medida do raio de uma circunferência, cujo comprimento mede 37,68 centímetros, considerando π = 3,14.
É dado: C = 37,68 centímetros e sabemos que C = 2πr.
Assim, obtemos:
2πr = 37,68
2 ⋅ 3,14 ⋅ r = 37,68
6,28 ⋅ r = 37,68
r = 6
Logo, a medida do raio da circunferência é 6 centímetros.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
Para os exercícios a seguir, adote π = 3,14.
1 Um ciclista deu quinhentas pedaladas completas. O raio da roda da bicicleta dêsse ciclista mede 25 centímetros. Determine quantos metros ele percorreu aproximadamente, supondo que cada pedalada corresponde a uma volta completa da roda da bicicleta.
2 Construa uma circunferência de raio medindo r. Trace dois diâmetros,
ACe
segmento B D, perpendiculares entre si. Determine a diferença entre as medidas do comprimento da circunferência e do perímetro do quadrado a bê cê dê em função de r. (Use
raiz quadrada de 2= 1,41.)
3 Um marceneiro construiu uma porta com as características da figura a seguir.
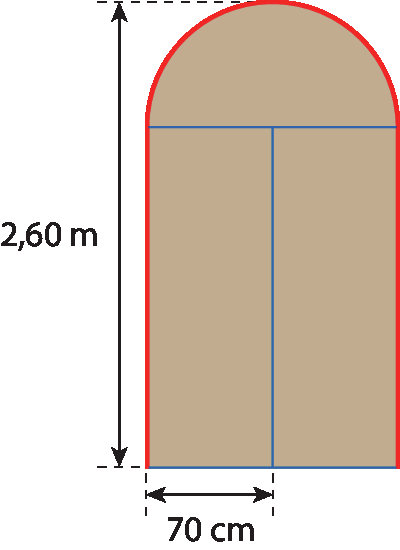
Determine a medida do comprimento do acabamento em madeira destacado em vermelho na figura.
Respostas e comentários
1. 785 métros
2. 0,64r
3. 5,998 métros
Medida do comprimento de uma circunferência
Leia a situação dada no livro e apresente a expressão do cálculo da medida do comprimento de uma circunferência. Peça aos estudantes que utilizem essa expressão para calcular a medida do comprimento da circunferência central da quadra da situação. Só depois siga para a resolução apresentada no livro.
Explore com os estudantes os exemplos apresentados. Comente que em geral usamos a aproximação 3,14 para o valor de π, mas que podem ser solicitadas outras aproximações, como 3,1416.
Se julgar conveniente, proponha uma pesquisa sobre o número π.

Sugestão de leitura
Para aprofundar o tema da pesquisa, sugerimos:
KELLER, F. A. L. Descobrindo o número π. Dissertação (Mestrado Profissional em Matemática). Programa de Pós-Graduação em Ensino de Ciências Exatas, Universidade Federal de São Carlos, São Carlos, 2013. Disponível em: https://oeds.link/vq6R4O. Acesso em: 23 julho 2022.
Nesse trabalho, é apresentada uma sequência didática com base na Engenharia didática como metodologia de investigação a fim de explorar a relação entre a medida de comprimento de uma circunferência e a medida de seu diâmetro.
Exercícios propostos
As resoluções dos exercícios 1 e 2 estão no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 3, os estudantes devem perceber, por meio da ilustração, que a parte de cima da porta é uma semicircunferência de raio medindo 70 centímetros. Assim, podem chegar à conclusão de que a medida do comprimento dessa semicircunferência, em metro, será:
As laterais da porta correspondem a dois segmentos de reta, e cada um deles tem comprimento de medida igual a 2,60 métros ‒ 0,7 métro, ou seja, o comprimento de cada um deles mede 1,90 métro. Logo, o comprimento dessas duas laterais juntas mede 3,8 métros.
Dessa maneira, o comprimento do acabamento em vermelho mede 5,998 métros, pois:
2,198 + 3,8 = 5,998
4 Uma polegada equivale a cêrca de 2,5 centímetros. A medida do diâmetro de um cano é de
fração três quartosde polegada. A quantos centímetros essa medida equivale, aproximadamente?

5 O diâmetro da roda de uma moto mede 70 centímetros. Se ela der 10 voltas completas por segundo, qual será a velocidade aproximada, em quilômetro por hora, dessa roda?

6 O diâmetro de uma praça circular mede 118 métros. Edu e Ari, partindo de um mesmo ponto, correm em torno dela em sentido contrário e param ao se encontrar. Nesse instante, Edu havia percorrido 192,52 métros. Qual dos dois é mais rápido?
7 Em outra praça circular, Teca e Lia fizeram o mesmo que Edu e Ari. Quando elas se encontraram, Teca havia percorrido 180 métros, e Lia, 196,8 métros. Qual é a medida aproximada do raio dessa praça?
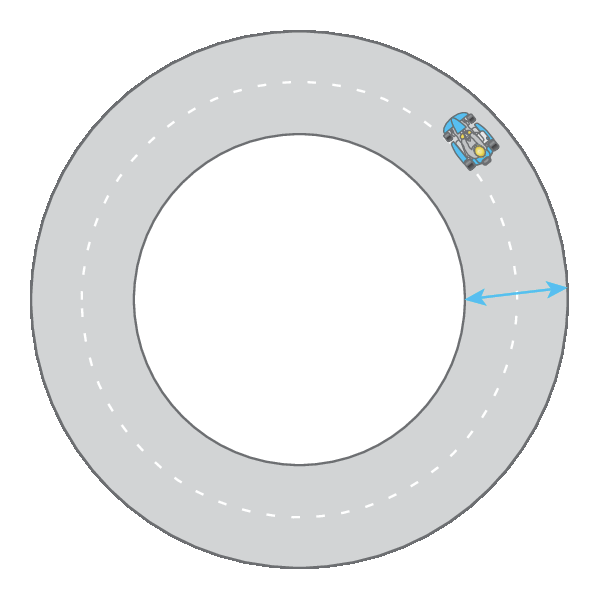
8 Uma pista circular de corrida de kart foi construída a partir de duas circunferências concêntricas cujos comprimentos têm medidas .1500 métros e .1200 métros. Determine a medida aproximada da largura dessa pista.
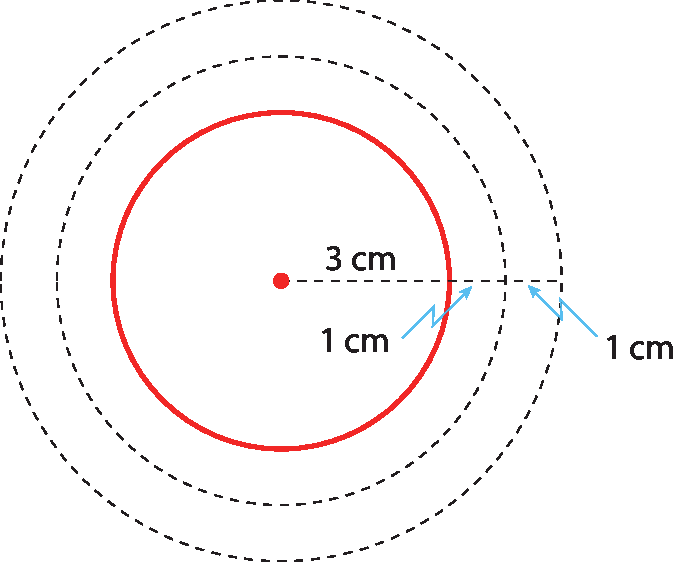
9 Lucila traçou uma circunferência de 3 centímetros de raio. Depois traçou outras circunferências, concêntricas à primeira, aumentando a medida do raio de 1 em 1 centímetro. Quantas circunferências ela deverá traçar até encontrar aquela que tenha o triplo da medida do comprimento da primeira?
10

Hora de criar – Em dupla, cada um cria um problema sobre medida de comprimento de uma circunferência. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
A figura representa uma lata de formato cilíndrico.
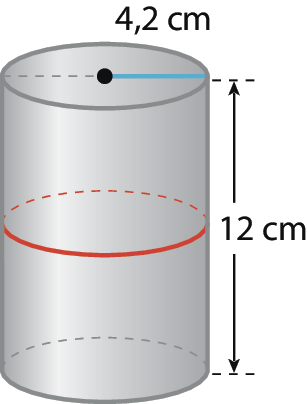
Calcule, aproximadamente, a medida de comprimento em centímetro de fita adesiva que é necessária para contornar a linha vermelha sobre a lata.
Respostas e comentários
4. Equivale a 1,875 centímetro.
5. 79,128 quilômetros por hora
6. Edu, pois Ari percorreu 178 métros a menos do que Edu.
7. 60 métros
8. 47,77 métros
9. 6 circunferências.
10. Resposta pessoal.
Pense mais um pouco...: 26,4 centímetros
Exercícios propostos
As resoluções dos exercícios 4, 6, 7 e 8 estão no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 4, peça aos estudantes que levem para a sala de aula régua ou trena com escalas em polegada e em centímetro. Providencie pedaços de canos plásticos, com diâmetros diferentes, para que sejam medidos. Também podem ser medidas as telas (na diagonal) de aparelhos celulares, de monitores de computador, de televisores. Explique que é essa medida que determina as polegadas da tela desses aparelhos.
No exercício 5, se os estudantes fizerem os cálculos sem as transformações necessárias das unidades de medida, faça intervenções para perceberem que o exercício solicita a velocidade em quilômetro por hora e que nenhum dado original foi dado em quilômetro ou em hora, mas em centímetro e em segundo.
Se o diâmetro da roda da moto mede 70 centímetros, podemos calcular a medida C, em centímetro, do seu comprimento:
C = π · d ⇒ C = 3,14 · 70 ⇒ C = 219,8
Logo, em 10 voltas, ela percorrerá um total de .2198 centímetros, que é equivalente a 21,98 métros ou a 0,02198 quilômetros. Com essa informação, podemos determinar a velocidade, lembrando que 1 segundo é equivalente a
1, 3600 avoshora e que a relação entre as grandezas envolvidas é de proporcionalidade direta; assim, obtemos que a medida da velocidade é x, em quilômetro por hora, tal que:
⇒
⇒ x = 0,02198 · .3600 ⇒
⇒ x = 79,128
Explore as diferentes estratégias de resolução do exercício 9. Como a circunferência de raio 3 centímetros tem medida de comprimento (cê₁) dada por: C₁ = 2 · π · 3 e queremos determinar uma circunferência cuja medida do comprimento seja o triplo de C₁, obtemos: Cf = 2 · π · 3 · 3 ⇒ Cf = 9 · 2 · π
Logo, o raio da última circunferência deve medir 9 centímetros e, portanto, é necessário traçar 6 circunferências (pois 3 + 6 = 9).
Na resolução do exercício 10, incentive os estudantes a considerar objetos que apresentem elementos que possam ser associados a circunferências.
Pense mais um poucoreticências
Os estudantes devem atentar a que não é necessária a informação sobre a altura da lata, uma vez que não influencia na quantidade de fita adesiva passando pela linha vermelha; o que importa, nesse caso, é o raio da base dessa lata. Assim, com π = 3,14, temos que a medida do comprimento de fita é: C = 4,2 · 2 · π = 26,376, ou seja, aproximadamente 26,4 centímetros.
Arco de circunferência
Ana Paula faz projetos de lustres e luminárias. Ela precisa projetar um lustre com 12 lâmpadas igualmente espaçadas entre si e à mesma distância do centro do lustre. Para isso, ela desenhou um esquema: uma circunferência dividida em 12 arcos de mesma medida angular.

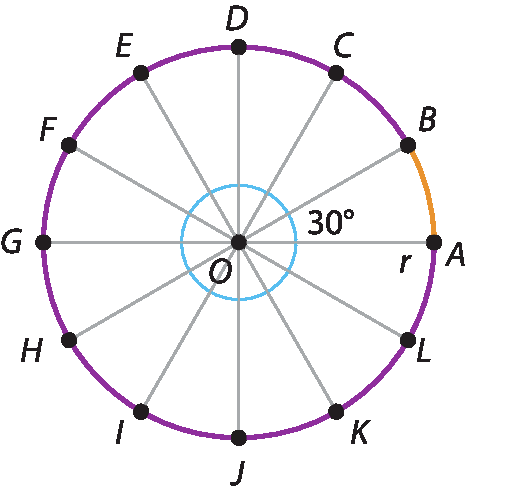
Ana Paula percebeu que a soma de todas as medidas angulares desses arcos é igual à medida angular de uma circunferência (360graus) e, portanto, cada um deles mede 30graus (pois 360graus : 12).
Na circunferência, Ana Paula destacou o arco
Arco AB, correspondente ao ângulo central
A O B.

Indicamos a medida angular do arco
Arco ABpor m(
Arco AB) = 30graus.
O arco
Arco ABda figura é
1 12 avosda circunferência, então podemos dizer que a medida do comprimento dêsse arco, na mesma unidade de medida da circunferência, é igual a
Fração. Numerador 2 vezes pi vezes r, denominador 12.
Observe algumas relações que podemos estabelecer entre a medida angular e a medida do comprimento de arcos de uma mesma circunferência.
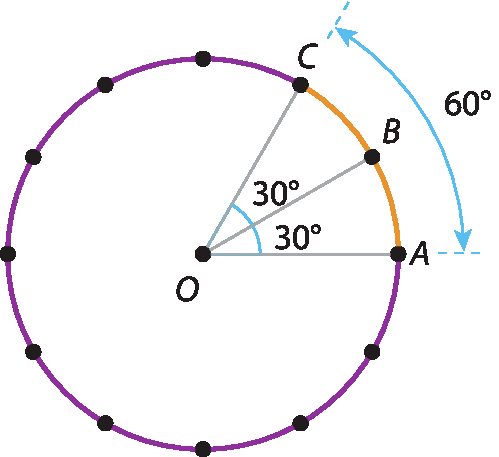
• Um arco de medida angular de 60graus tem o dobro da medida do comprimento de um arco de 30graus, ou seja,
2 vezes, fração, Numerador 2 vezes pi vezes r, denominador 12.
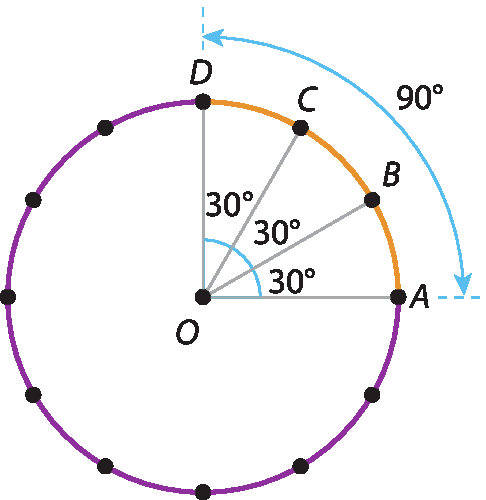
• Um arco de medida angular de 90graus tem o triplo da medida do comprimento de um arco de 30graus, ou seja,
3 vezes, fração, Numerador 2 vezes pi vezes r, denominador 12.
Respostas e comentários
Arco de circunferência
Em duplas, peça aos estudantes que leiam o texto apresentado e elaborem uma ficha com os principais conceitos, ilustrando-a com figuras. Depois, proponha a cada dupla que exponha seu fichamento. Registre na lousa uma ficha correspondente às anotações da turma.
Apresente novos exemplos e destaque sempre a medida angular dos arcos envolvidos. Considere arcos que correspondem a divisões da circunferência em partes iguais:
• medida de um arco que corresponde a um sexto da circunferência: 60graus
• medida de um arco que corresponde a um terço da circunferência: 120graus
• medida de um arco que corresponde a um oitavo da circunferência: 45graus
• medida de um arco que corresponde a um quarto da circunferência: 90graus
• medida de um arco que corresponde à metade da circunferência: 180graus
• medida de um arco que corresponde a três quartos de uma circunferência: 270graus
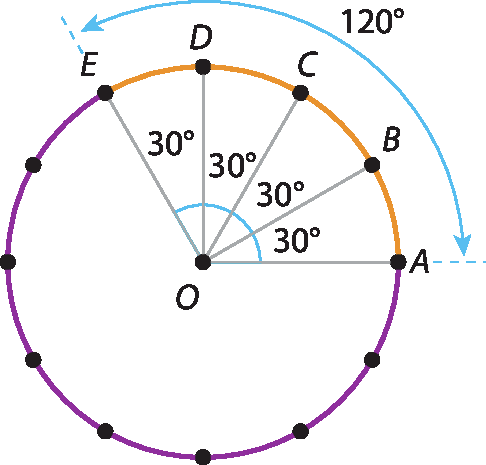
• Um arco de medida angular de 120graus tem o quádruplo da medida do comprimento de um arco de 30graus, ou seja, 4 ⋅
Fração. Numerador 2 vezes pi vezes r, denominador 12.

Vamos considerar a seguinte terminologia:
• ℓ: medida do comprimento de um arco da circunferência (medido em determinada unidade de comprimento);
• α: medida angular do mesmo arco em grau;
• r : medida do raio da circunferência (medido na mesma unidade de comprimento de ℓ).
Lembrando que o arco de uma circunferência mede 360graus, podemos, por meio da regra de três, organizar o seguinte quadro:
|
Medida do comprimento do arco |
Medida angular do arco |
|---|---|
|
2πr |
360° |
|
ℓ |
α |
Assim, obtemos a proporção:
Fração. Numerador 2 pi r, denominador l, igual, fração, Numerador 360 graus, denominador alfaAcompanhe dois exemplos.
a) Vamos calcular a medida do comprimento de um arco de 20graus em uma circunferência com raio de medida 10 centímetros.
|
Medida do comprimento do arco (cm) |
Medida angular do arco (grau) |
|---|---|
|
2π ⋅ (10) |
360° |
|
ℓ |
20° |
9ℓ = 10π
Considerando π ≃ 3,14, obtemos:
Portanto, o arco mede, aproximadamente, 3,49 centímetros.
b) Vamos calcular a medida em grau de um arco que mede 6π centímetros de comprimento em uma circunferência com raio de medida 15 centímetros.
|
Medida do comprimento do arco (cm) |
Medida angular do arco (grau) |
|---|---|
|
2π ⋅ (15) |
360° |
|
6π |
α |
5α = 360
α = 72
Portanto, o arco mede 72graus.
Clique no play e acompanhe as informações do vídeo.
Respostas e comentários
Arco de circunferência
Explore com os estudantes a medida linear de um arco de circunferência, ou seja, a medida do seu comprimento. Depois, peça a eles que a comparem com a medida angular, observando o que essas medidas têm de diferente.
Se julgar necessário, retome a noção de grandezas diretamente proporcionais para a realização dos exemplos do livro do estudante. Amplie, propondo na lousa outros exemplos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
11 Uma circunferência tem raio de medida 12 centímetros. Calcule a medida aproximada, em centímetro, de um arco dessa circunferência correspondente a um ângulo central de 40°.
12 Construa uma circunferência com raio de medida 3 centímetros. Trace dois diâmetros perpendiculares entre si. Quantos centímetros mede aproximadamente cada um dos quatro arcos em que a circunferência ficou dividida?
13 Uma circunferência é dividida em 12 arcos congruentes de medida 3π centímetros de comprimento. Determine:
a) a medida do comprimento da circunferência;
b) a medida do raio dessa circunferência.
14 Calcule a medida aproximada do comprimento dos arcos
Arco AB,
Arco BCe
Arco CDda circunferência.
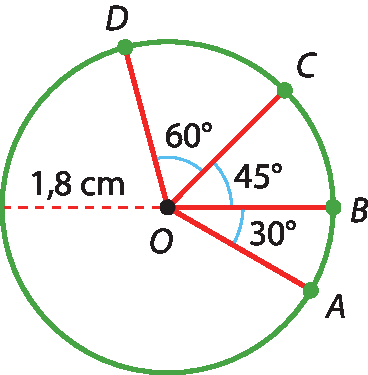
15 Calcule a medida aproximada do comprimento da linha representada pela figura a seguir. Utilize uma régua para obter a medida dos segmentos necessários para o cálculo.

16 Construa uma circunferência cujo raio meça 4 centímetros. Trace um de seus diâmetros e apague metade da circunferência traçada. A figura obtida tem medida de perímetro de quantos centímetros, aproximadamente?
17 Na figura, considere que o comprimento do arco
Arco ABmede 6,28 centímetros.
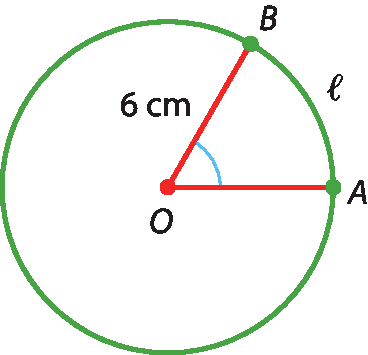
Calcule a medida aproximada do ângulo
ângulo AOB.
18 Calcule em grau a medida de um arco de circunferência de 9,42 centímetros, sabendo que o raio dessa circunferência mede 15 centímetros.
19 Uma circunferência tem a medida do raio igual a 18 centímetros. Calcule a medida aproximada do comprimento do arco de 40graus contido nessa circunferência.
20 O pêndulo de um relógio de parede tem 30 centímetros de comprimento.

A cada movimento, o pêndulo descreve um arco de 20graus.
Determine a medida aproximada do percurso realizado pelo peso dêsse pêndulo.
21 Calcule a medida em grau de um arco de 7,85 centímetros em uma circunferência de 10 centímetros de raio.
22 Alguns adereços das fantasias de Carnaval são apreciados por sua beleza e pompa.

Observe, no esquema a seguir, a estrutura de um desses adereços feita com arame grosso.
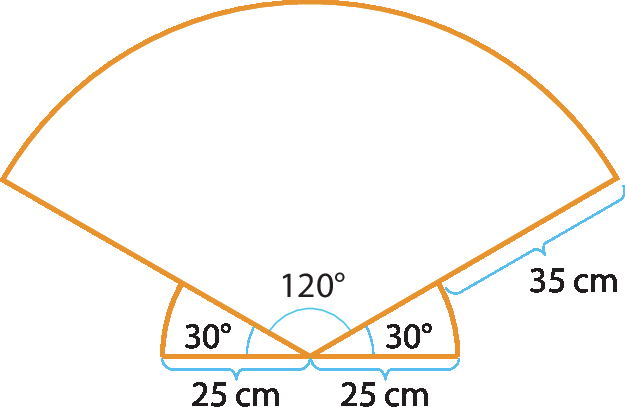
Quantos metros de arame, aproximadamente, são necessários para construir esse adereço?
23

Hora de criar – Em dupla, cada um cria um problema sobre medida do comprimento de arco de circunferência. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Respostas e comentários
11. 8,4 centímetros
12. 4,71 centímetros
13. a) 36π centímetros
13. b) 18 centímetros
14. arco
Arco AB: 0,9 centímetro; arco
Arco BC: 1,4 centímetro; arco
Arco CD: 1,9 centímetro.
15. Aproximadamente 8,95 centímetros.
16. 20,56 centímetros
17. 60graus
18. 36graus
19. 12,56 centímetros
20. 10,5 centímetros
21. 45graus
22. 3,22 métros
23. Resposta pessoal.
Exercícios propostos
As resoluções dos exercícios 11 a 21 estão no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 15, peça aos estudantes que discutam com os colegas o procedimento utilizado para chegar à resposta. É importante que eles percebam que o “caminho sinuoso” entre dois pontos é sempre mais longo que o “caminho em linha reta”. dêsse modo, será possível saber que o comprimento da linha é maior que a distância em linha reta das duas extremidades da linha traçada. Verifique se eles percebem que podem colocar o número π em evidência, multiplicando-o pela soma das medidas dos três raios.
No exercício 22, podemos verificar pelo esboço que o raio do setor menor mede 25 centímetros e o raio do setor maior mede 60 centímetros (25 centímetros + 35 centímetros).
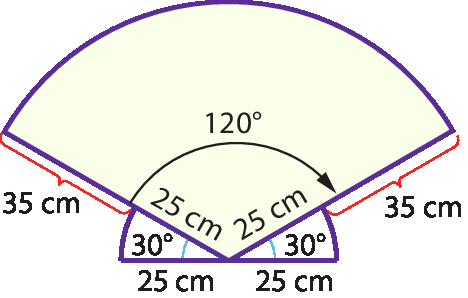
Assim, podemos determinar a medida do comprimento dos arcos de 30graus e de 120graus, em centímetro:
|
Medida do comprimento do arco (em cm) |
Medida angular do arco |
|---|---|
|
2 ⋅ π ⋅ 25 |
360° |
|
x |
30° |
x ≃ 13,08
|
Medida do comprimento do arco (em cm) |
Medida angular do arco |
|---|---|
|
2 ⋅ π ⋅ 60 |
360° |
|
y |
120° |
y ≃ 125,6
Adicionando todas as partes do arame, obtemos aproximadamente 321,76 centímetros, ou seja, cerca de 322 centímetros ou 3,22 métros.
Para elaborar o problema no exercício 23, incentive os estudantes a utilizar diferentes contextos em que percebem que há elementos que podem ser associados ao arco de circunferência. Caso tenham dificuldades, eles podem aproveitar, por exemplo, a fotografia da abertura deste capítulo ou as pesquisas que realizaram durante o desenvolvimento dos conteúdos já estudados para criar situações com base neles.
Propriedades entre arcos e cordas de uma circunferência
1ª propriedade
Considere a figura a seguir, em que
Arco ABe
Arco CDsão arcos congruentes de uma circunferência.
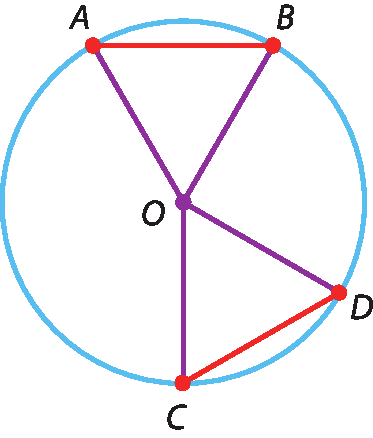
Vamos mostrar que as cordas
ABe
CDtambém são congruentes.
Hipótese:
Arco AB≅
Arco CDTese:
AB≅
CDObserve que:
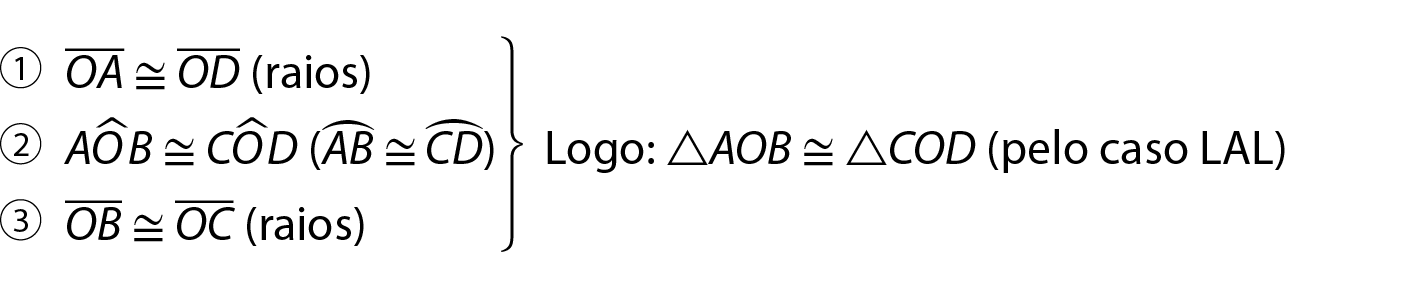
Portanto, os lados correspondentes são congruentes, isto é,
segmento a b congruente segmento c d.
Em toda circunferência, se dois arcos têm a mesma medida, então as cordas compreendidas por esses arcos são congruentes.

2ª propriedade
Considere a figura a seguir, em que o diâmetro
ABé perpendicular à corda
CD.
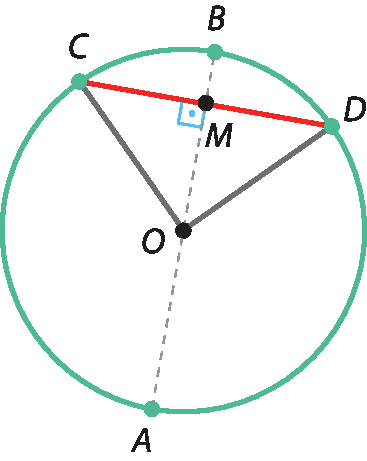
Observe que
segmento o c congruente segmento o d(raios) e, portanto, △cê ó dê é um triângulo isósceles cuja altura é
OM.
Como em um triângulo isósceles a altura relativa à base coincide com a mediana, então M é ponto médio de
CD. Logo,
segmento m c congruente segmento m d.
Com isso, mostramos que:
Em uma circunferência, todo diâmetro perpendicular a uma corda divide-a ao meio.
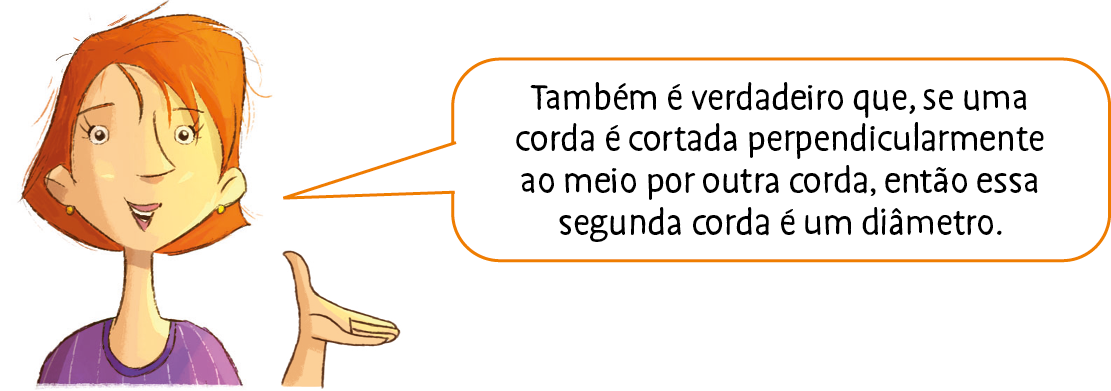
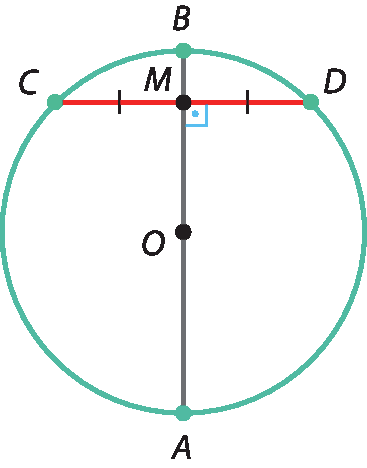
Se
segmento c m congruente segmento m be
segmento a b perpendicular segmento c d, então
ABé diâmetro.
Respostas e comentários
Propriedades entre arcos e cordas de uma circunferência
Apresente cada propriedade e peça aos estudantes que elaborem exemplos de situações envolvendo a respectiva propriedade estudada.
Se julgar conveniente, discuta com eles a demonstração da recíproca da 1ª propriedade:
A recíproca é verdadeira, ou seja, se
ABe
CDsão cordas congruentes, então os arcos correspondentes a cada uma delas são também congruentes.
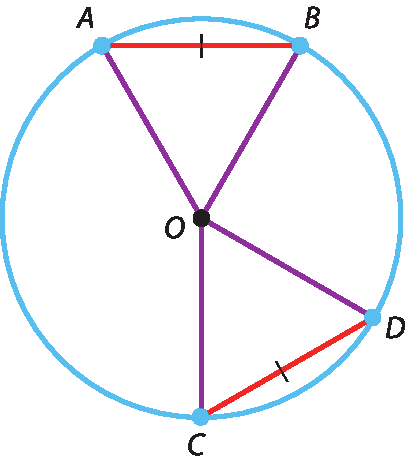
Hipótese:
segmento a b congruente segmento c dTese:
arco a b congruente arco c dDemonstração
Considerando os triângulos á ó bê e COD, temos:
•
segmento o a congruente segmento o c(raios)
•
segmento o b congruente segmento o d(raios)
•
arco a b congruente arco c d(por hipótese)
Logo, o triângulo á ó bê e cê ó dê são congruentes pelo caso lado lado lado. Assim, concluímos que
ângulo a o b congruente ângulo c o d.
Portanto,
arco ab congruente arco c d.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
24 Na figura, A bê = 1,2 centímetro e
medida de ângulo a o b é igual a 45 graus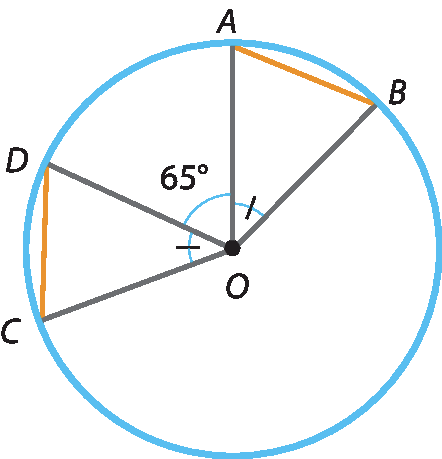
Calcule:
a) a medida da corda
CD;
b) a medida do ângulo
ângulo BOC.
25 Considere um ponto P comum ao diâmetro
XYde uma circunferência (de centro óh) e a uma corda
AB. Determine a medida do raio dessa circunferência, sabendo que
XYé perpendicular a
AB, ó pê = 5 centímetros e AB = 24 centímetros.
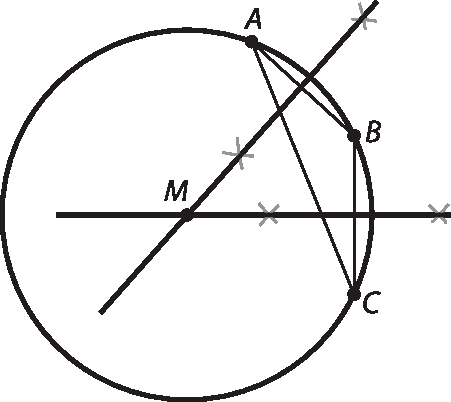
26 Marque sobre uma folha do caderno três pontos: a, B e C, não alinhados. Trace o segmento
ABe o segmento
BC. Trace a mediatriz de cada um desses segmentos. Chame de M o ponto de encontro dessas mediatrizes. Com centro em M e abertura ei ém, trace uma circunferência. Qual é a posição dos pontos a, B e C em relação à circunferência?
(Ao usar o compasso, atenção para não se machucar com a ponta-seca!)
27 Construa um triângulo á bê cê, em que A bê = 4 centímetros, BC = 3,6 centímetros e AC = 7 centímetros. Trace uma circunferência que passe pelos vértices dêsse triângulo.
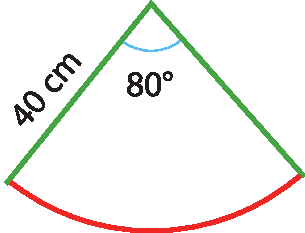
28 Para confeccionar um chapéu de palhaço, Aline seguiu o modelo indicado na figura. Determine a medida aproximada do arco de circunferência dêsse modelo.
2. Triângulo retângulo inscrito em uma circunferência
Considere a figura a seguir.
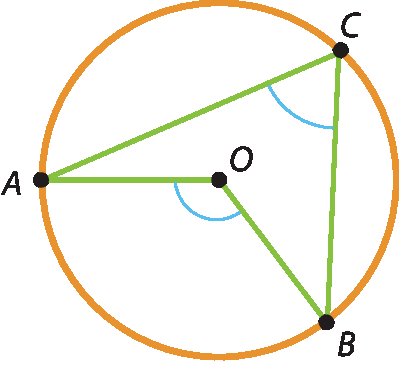
Nela, destacamos o ângulo inscrito
ACB, ou seja, um ângulo cujo vértice está sobre a circunferência.
Sabemos que um ângulo inscrito em uma circunferência tem por medida a metade da medida do ângulo central correspondente e, portanto, a metade da medida do arco compreendido por seus lados, ou seja:
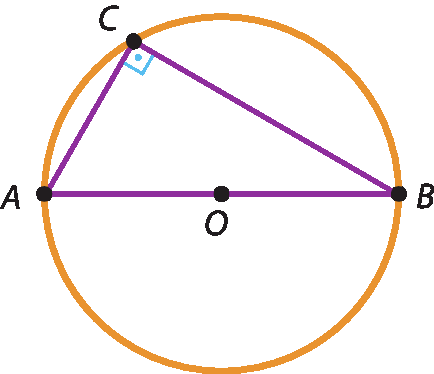
Esta outra figura mostra um triângulo em que um dos lados é um diâmetro da circunferência. Esse triângulo é retângulo, pois:
90graus
Respostas e comentários
24. a) 1,2 centímetro
24. b) 155graus
25. 13 centímetros
26. Estão situados sobre a circunferência.
27. Construção de figura.
28. 55,8 centímetros
Exercícios propostos
As resoluções dos exercícios 24, 25 e 28 estão no início deste Manual, nas orientações específicas do capítulo 11.
Incentive os estudantes a fazer um esboço das situações propostas neste bloco de exercícios.
No exercício 26, um possível esboço é o que segue. Por meio dele, os estudantes podem verificar que os pontos a, B e C, nesse caso, estão sobre a circunferência.
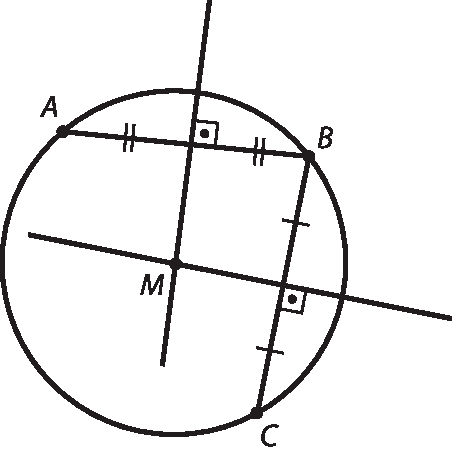
Após a resolução do exercício 26, questione os estudantes sobre qual posição teriam as mediatrizes de
ABe de
BCcaso os pontos a, B e C estivessem alinhados. Existiria o ponto M? Existiria uma circunferência passando por a, B e C? Fazendo um novo esboço, eles podem verificar que as mediatrizes desses segmentos seriam paralelas e, portanto, não teriam ponto em comum.
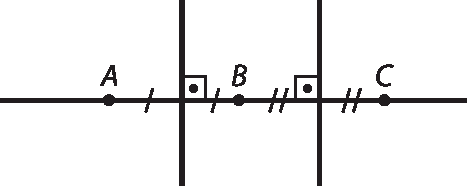
Assim, não existiria o ponto M nem uma circunferência que passasse por esses três pontos simultaneamente.
Para o exercício 27, com régua e compasso, construímos o triângulo com lados com as medidas indicadas. Como dois lados dêsse triângulo serão cordas da circunferência, cada mediatriz desses dois lados passará pelo centro da circunferência (os diâmetros perpendiculares às cordas dividem essas cordas ao meio). Logo, essas duas mediatrizes determinarão o ponto M, centro da circunferência.
2. Triângulo retângulo inscrito em uma circunferência
Habilidade da Bê êne cê cê: ê éfe zero nove ême ah um um.
Para comprovar a definição apresentada neste tópico, peça aos estudantes que, usando régua, transferidor e compasso, desenhem um triângulo retângulo qualquer com uma circunferência o circunscrevendo.
De modo geral, todo triângulo inscrito em uma semicircunferência é retângulo e, reciprocamente, todo triângulo retângulo pode ser inscrito em uma semicircunferência.

Clique no play e acompanhe as informações do vídeo.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
29 Determine a medida da mediana, relativa à hipotenusa, de um triângulo retângulo cujos catetos medem
raiz de 20centímetros e 4 centímetros.
30 A mediana de um triângulo retângulo relativa à hipotenusa mede 4 centímetros, e um dos catetos mede
raiz de 15centímetros. Qual é a medida do outro cateto?
31 A mediana relativa à hipotenusa de um triângulo retângulo mede 12 centímetros. Calcule quantos centímetros mede o comprimento da circunferência que o circunscreve.
32 O comprimento de uma circunferência mede 10π centímetros. Determine:
a) a medida do cateto maior de um triângulo retângulo inscrito nessa circunferência, sabendo que o menor cateto tem a mesma medida da mediana relativa à hipotenusa;
b) a medida da área dêsse triângulo.
33 Considere o triângulo á bê cê inscrito em uma circunferência de raio de medida 3 centímetros.
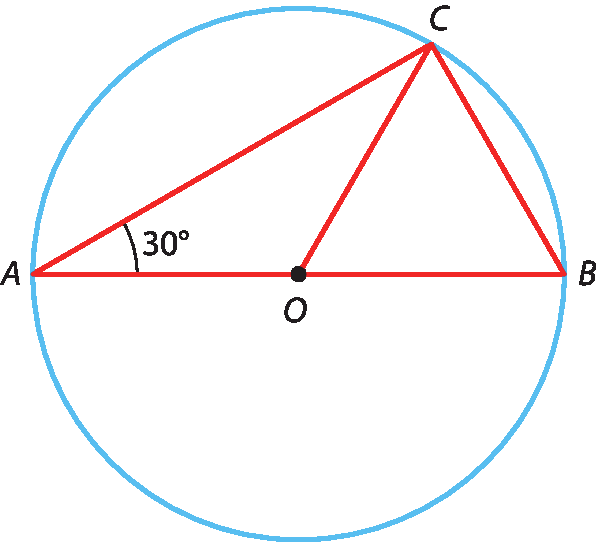
a) Quais são as medidas de
ângulo A C B,
ângulo ABC,
ângulo BOC,
ângulo BCOe
ângulo AOC?
b) Quais são as medidas de
O B,
O C,
BC,
ABe
ACc) Classifique, quanto às medidas dos ângulos e às medidas dos lados, os triângulos á bê cê, á ó cê e ó bê cê.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Deseja-se cortar, de um toco de árvore cujo raio mede 20 centímetros, uma coluna de base quadrada em formato como o de um bloco retangular.
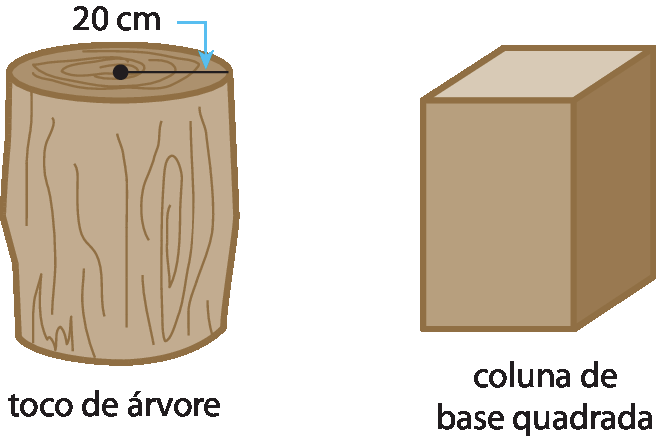
1 Determine a medida máxima do lado da base que se pode obter.
2 Calcule a medida da área da base quadrada da coluna em centímetro quadrado.
Respostas e comentários
29. 3 centímetros
30. 7 centímetros
31. Aproximadamente 75,36 centímetros.
32. a)
5 raiz quadrada de 3 centímetros32. b)
25 raiz quadrada de 3, tudo sobre 2 centímetros quadrados33. a) 90graus, 60graus, 60graus, 60graus e 120graus.
33. b) 3 centímetros, 3 centímetros, 3 centímetros, 6 centímetros e
3 raiz de 3centímetros.
33. c) Triângulo retângulo e escaleno, triângulo obtusângulo e isósceles, triângulo acutângulo e equilátero.
Pense mais um poucoreticências:
1.
20 raiz de 2centímetros
2. 800 centímetros quadrados
Exercícios propostos
As resoluções dos exercícios 29 a 31 e 33 estão no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 32, os estudantes deverão perceber que, se a circunferência tem 10π centímetros de comprimento, então ela tem raio de medida igual a 5 centímetros, pois:
Fração. 10 vezes pi sobre 2 vezes pi é igual a 5..
Como o triângulo está inscrito na circunferência, a hipotenusa tem medida igual à do diâmetro dessa circunferência, que é 10 centímetros. Note que a mediana dêsse triângulo relativa à hipotenusa é um raio dessa circunferência e, portanto, mede 5 centímetros. Assim, o menor cateto também mede 5 centímetros. Segue um esboço da situação:
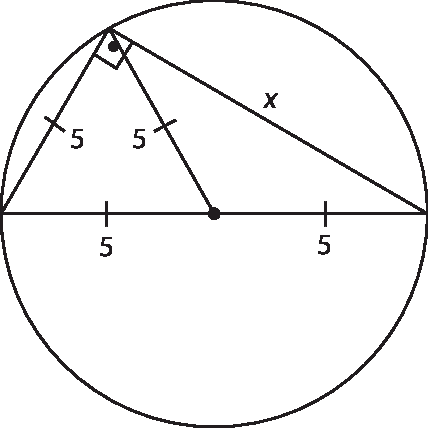
dêsse modo, uma possível resolução para os itens a e b dêsse exercício é:
a) Considerando x, em centímetro, a medida do cateto procurado, basta utilizar o teorema de Pitágoras para determinar seu valor: 10duas = 5duas + xduas ⇒ xduas = 75 ⇒
Sentença matemática. ou x é igual a 5 raiz de 3b) Como o triângulo é retângulo, considerando um dos catetos como base, a altura relativa a essa base é o outro cateto. Logo, a área dêsse triângulo, em centímetros quadrados, mede:
A igual, fração, numerador 5 raiz de 3 vezes 5, denominador 2
A igual, numerador 25 raiz de 3, denominador 2
Pense mais um poucoreticências
Peça aos estudantes que deixem registrada toda a resolução da atividade proposta, incluindo explicações e cálculos, para que possam comparar e discutir com os colegas.
Na atividade 1, se a medida da diagonal do quadrado coincide com a do diâmetro da circunferência (40 centímetros) e ℓ é a medida do lado dêsse quadrado, em centímetro, temos, pelo teorema de Pitágoras:
Na atividade 2, se a base quadrada tem lado de medida igual a
l igual 20 raiz de 2centímetros, então a área dessa base, em centímetros quadrados, mede:
Proponha aos estudantes que calculem também a medida do volume da coluna em formato de paralelepípedo. Nesse caso, eles poderão atribuir valores para a medida de altura dessa coluna ou apenas representá-la por uma letra.
3. Relações métricas em uma circunferência
1ª relação
Considerando a figura a seguir, vamos demonstrar que:
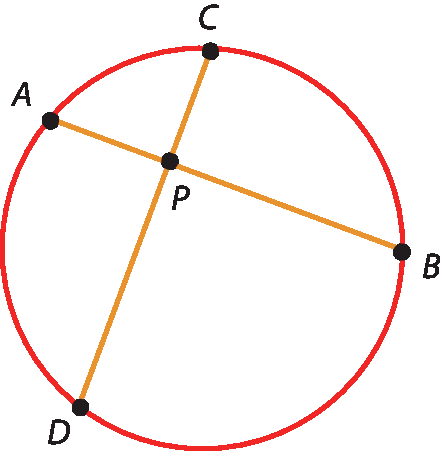
Se duas cordas se intersectam em um ponto interior a uma circunferência, então o produto das medidas dos dois segmentos de uma delas é igual ao produto das medidas dos segmentos da outra.
Hipótese: as cordas
ABe
CDse intersectam em um ponto P, interior à circunferência.
Tese: pê á ⋅ PB = PC ⋅ PD
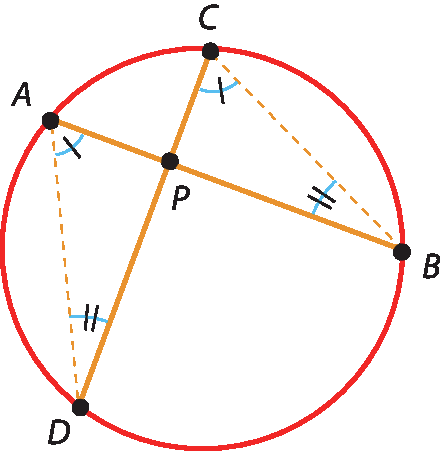
Traçando os segmentos
ADe
CB, obtemos os triângulos á pê dê e CPB. Nesses triângulos:
• os ângulos
Ae
Csão congruentes, pois são ângulos inscritos e determinam na circunferência o mesmo arco
Arco BD;
• os ângulos
Be
Dsão congruentes, pois são ângulos inscritos e determinam na circunferência o mesmo arco
Arco AC.
Logo, pelo caso ângulo-ângulo de semelhança de triângulos, os triângulos á pê dê e CPB são semelhantes.
Portanto,
fração, numerador P A, denominador P C, igual, fração, numerador P D, denominador P B, ou seja:
pê á ⋅ PB = PC ⋅ PD
Acompanhe alguns exemplos.
Vamos calcular o valor de x em cada figura.
a)
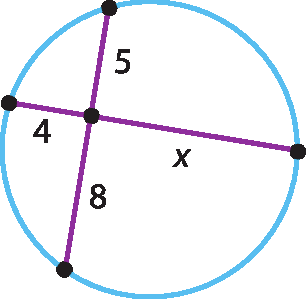
4 ⋅ x = 8 ⋅ 5
4x = 40
x =
40 quartosx = 10
b)
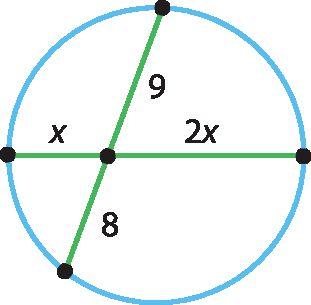
2x ⋅ x = 8 ⋅ 9
2x duas = 72
x duas = 36
x = ±6
Como xis é um número positivo, xis = 6.
Respostas e comentários
3. Relações métricas em uma circunferência
Habilidade da Bê êne cê cê: ê éfe zero nove ême ah um um.
Iniciamos o estudo das relações métricas em uma circunferência. A 1ª relação é a que envolve duas cordas que se cruzam em um ponto interno à circunferência.
Peça aos estudantes que mostrem situações (com representação de esquemas) em que duas cordas podem ter um único ponto em comum. Espera-se que surja esta situação também:

Discuta com eles por que ela não está nas condições da hipótese da 1ª relação. Espera-se que percebam que o ponto comum às duas cordas não é um ponto interior à circunferência, mas um ponto pertencente à circunferência. Destaque que não são formados 4 segmentos.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
34 Calcule o valor de x em cada uma das figuras.
a)
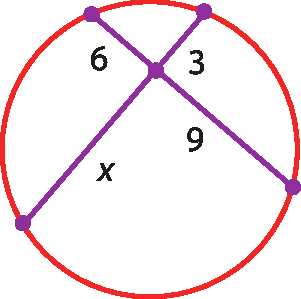
b)
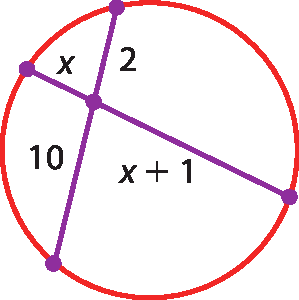
c)
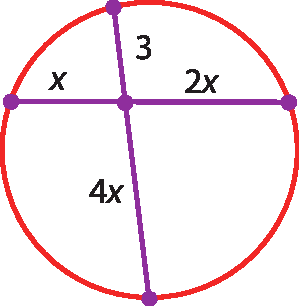
d)
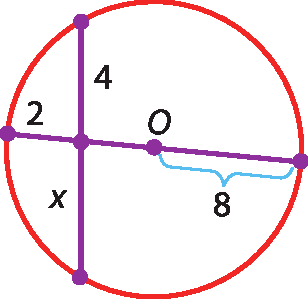
35 Determine a medida da área do △ABC a seguir.
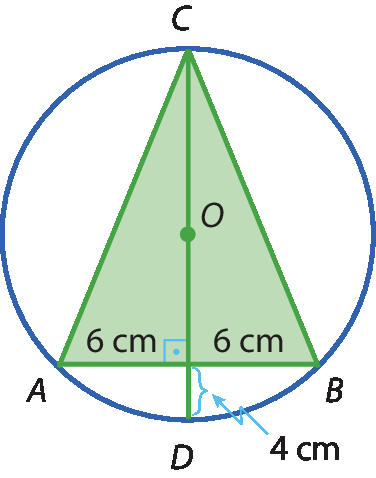
36 Uma praça circular é cortada por duas ruas, como mostra a figura a seguir.
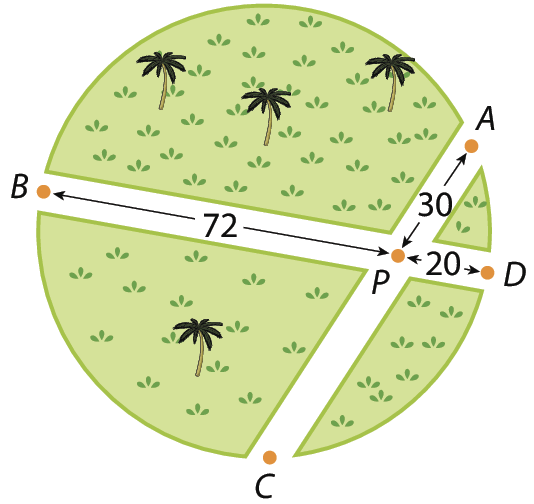
Para ir de a até P, Rita dá 30 passos. Luísa dá 72 passos para ir de B a P e 20 passos para ir de P a D. Calcule quantos passos Rita deve dar para chegar até C, admitindo que os passos das duas garotas tenham mesma medida de comprimento.
37 Uma corda de 6 centímetros corta perpendicularmente um diâmetro a 4 centímetros do centro de uma circunferência. Calcule a medida da área do círculo determinada por essa circunferência.
2ª relação
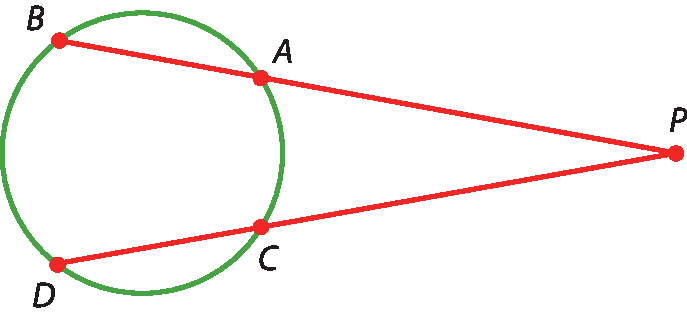
Considerando a figura apresentada, vamos provar que:
Se, de um ponto exterior a uma circunferência, traçamos dois segmentos secantes, então o produto das medidas de um segmento secante e de sua parte externa é igual ao produto das medidas do outro segmento secante e de sua parte externa.
Hipótese:
PBe
PDsão segmentos secantes à circunferência, com P no exterior.
Tese: pê á ⋅ PB = PC ⋅ PD
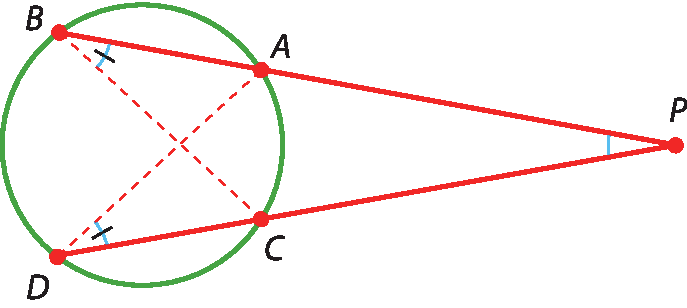
Traçando os segmentos
ADe
BC, obtemos os triângulos pê á dê e PCB. Nesses triângulos:
• os ângulos
D e Bsão congruentes, pois são ângulos inscritos e determinam na circunferência o mesmo arco
Arco AC;
• o ângulo
Pé comum.
Respostas e comentários
34. a) x = 18
34. b) x = 4
34. c) x = 6
34. d) x = 7
35. 54 centímetros quadrados
36. 48 passos.
37. 25π centímetros quadrados
Exercícios propostos
As resoluções dos exercícios 34 a 37 estão no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 36, questione os estudantes a respeito da necessidade da informação de que “os passos das duas garotas têm o mesmo comprimento”. Espera-se que eles observem que sem essa afirmação não seria possível estabelecer essas relações, pois não teríamos a garantia de tal proporcionalidade, visto que cada medida estaria em uma unidade diferente.
2ª relação
Converse com os estudantes sobre essa relação métrica e incentive-os a compor alguns exemplos com circunferência e duas retas secantes a ela e anotar as medidas dos segmentos obtidos, verificando essa relação. Se possível, os estudantes podem utilizar softwares de geometria dinâmica para explorar essa sugestão de atividade e, assim, desenvolver a competência geral 5.
Logo, pelo caso ângulo-ângulo de semelhança de triângulos, os triângulos á pê dê e CPB são semelhantes.
Portanto,
fração, numerador P A, denominador P C, igual, fração, numerador P D, denominador P B, ou seja:
pê á ⋅ PB = PC ⋅ PD
Acompanhe alguns exemplos.
Vamos calcular o valor de x em cada figura.
a)
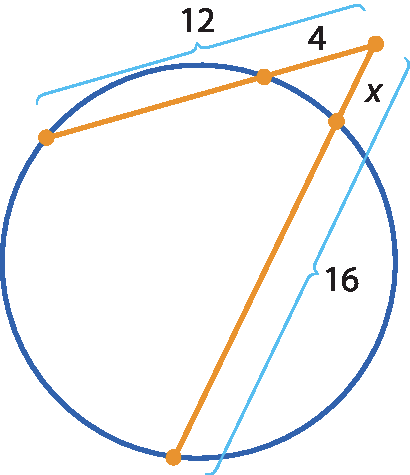
16 ⋅ x = 4 ⋅ 12
16x = 48
x =
48 16 avosx = 3
b)
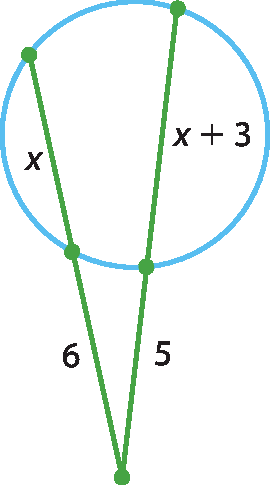
6 ⋅ (6 + x) = 5 ⋅ (x + 8)
36 + 6x = 5x + 40
6x ‒ 5x = 40 ‒ 36
x = 4
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
38 Calcule o valor de x em cada uma das figuras.
a)
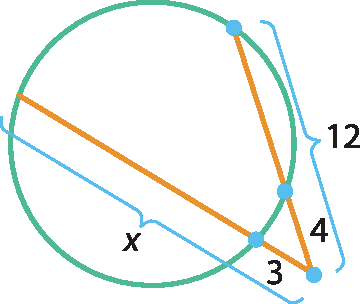
b)
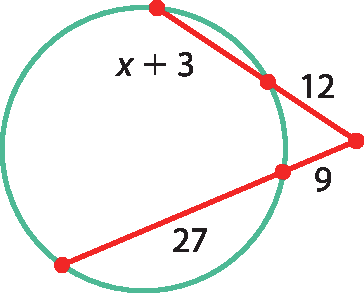
c)
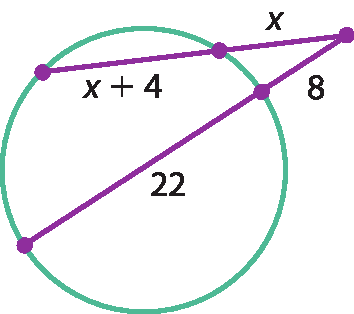
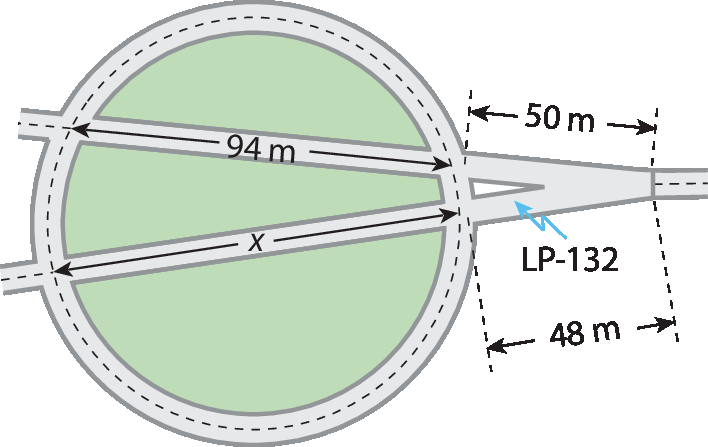
39 O canteiro circular de uma rotatória é cortado por duas estradas, como mostra a figura a seguir. A medida do comprimento da parte da estrada LP-132 que corta o canteiro está indicada por x. Calcule o valor de x.
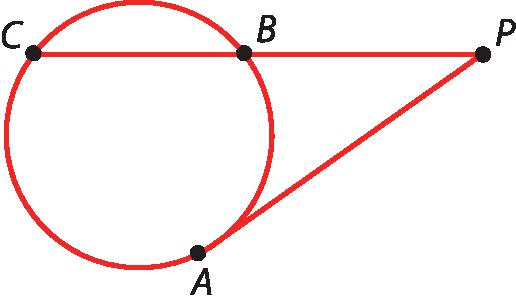
3ª relação
Na figura a seguir,
Segmento de reta P Aé tangente à circunferência.
Vamos provar que:
Se, de um ponto exterior a uma circunferência, traçamos um segmento tangente e um segmento secante a essa circunferência, então o quadrado da medida do segmento tangente é igual ao produto das medidas do segmento secante e de sua parte externa.
Respostas e comentários
38. a) x = 16
38. b) x = 12
38. c) x = 10
39. 102 métros
Exercícios propostos
As resoluções dos exercícios 38 e 39 estão no início deste Manual, nas orientações específicas do capítulo 11.
3ª relação
Após trabalhar a 3ª relação, se julgar conveniente, explore a situação indicada a seguir.
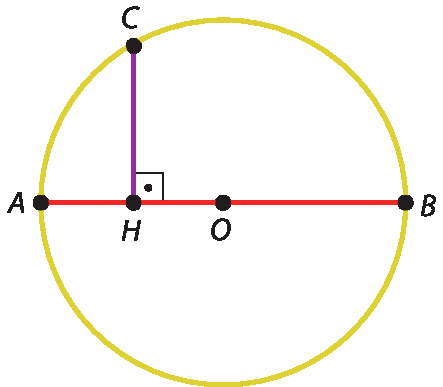
Na circunferência desta figura, temos que óh é o centro,
ABé um diâmetro e
Segmento CHé um segmento perpendicular a
AB. Vamos provar que (HC)duas = AH · HB
Hipótese:
Segmento CHé perpendicular a
AB
Tese: (HC)duas = AH · HB
Demonstração
Unindo C com a e C com B, obtemos o triângulo á bê cê, que é retângulo (inscrito em uma semicircunferência).
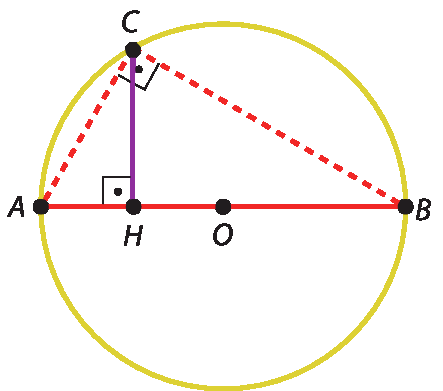
Em um triângulo retângulo, o quadrado da medida da altura (relativa à hipotenusa) é igual ao produto das medidas das projeções dos catetos (sobre a hipotenusa), isto é: (HC)duas = á agá · HB
Segue um exemplo de aplicação dessa relação para representar geometricamente
raiz quadrada de sete. Traçamos uma circunferência cujo diâmetro mede 8. Marcamos sobre um dos diâmetros um ponto M, distante 7 unidades de um dos extremos. Traçamos por esse ponto uma perpendicular que encontrará a circunferência no ponto C.
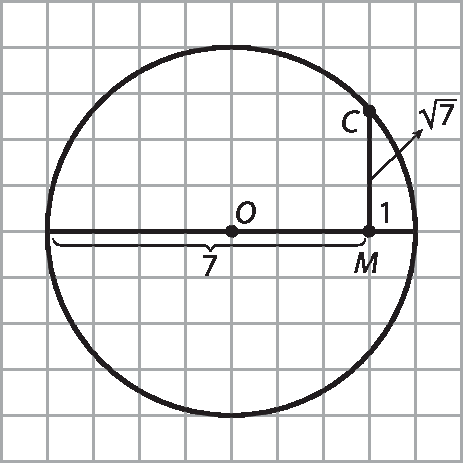
(CM)duas = 7 · 1 = 7 ⇒ CM =
raiz de 7Hipótese:
PAe
PCsão segmentos tangente e secante à circunferência, respectivamente.
Tese: (pê á)duas = PB ⋅ PC
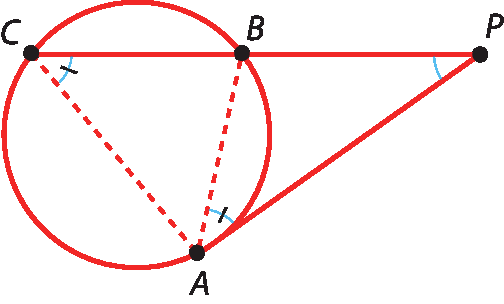
Traçando os segmentos
ABe
AC, obtemos os triângulos pê bê a e pê á cê. Nesses triângulos:
• os ângulos
Ce
Asão congruentes, pois são ângulos com vértice na circunferência e determinam nela o mesmo arco
Arco AB;
• o ângulo
Pé comum.
Logo, pelo caso ângulo-ângulo de semelhança de triângulos, os triângulos PBA e PAC são semelhantes.
Portanto,
fração, numerador P A, denominador P C, igual, fração, numerador P B, denominador P A, ou seja:
(pê á)duas = PB ⋅ PC
Acompanhe os exemplos.
Vamos calcular o valor de x em cada figura, sabendo que
Segmento MNé tangente à circunferência.
a)
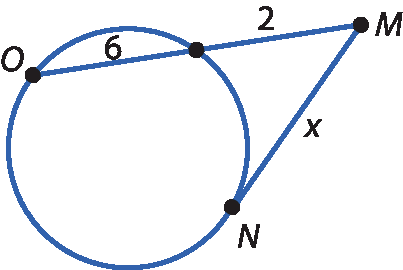
x duas = 8 ⋅ 2
x duas = 16
x = ±4
Como x é um número positivo, x = 4.
b)
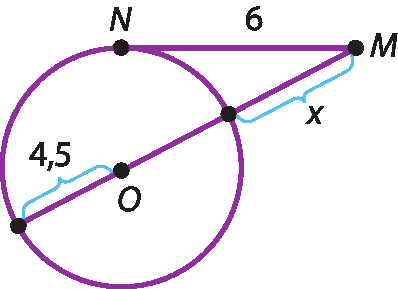
6duas = x ⋅ (x + 9)
xduas + 9x ‒ 36 = 0
Como x é um número positivo, x = 3.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
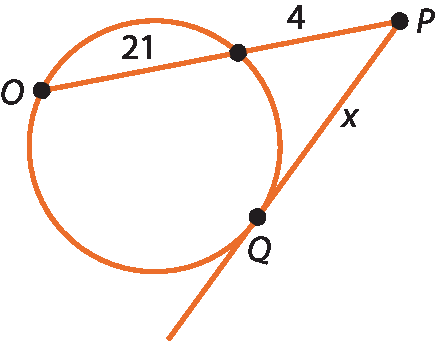
40 Calcule o valor de x nas figuras a seguir, sendo
Segmento P Qtangente à circunferência.
a)
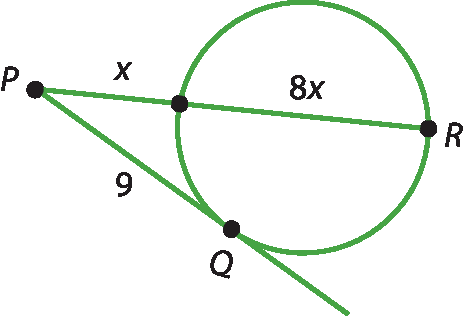
b)
41 Um fotógrafo assistia a uma apresentação circense na qual um acrobata, durante toda sua apresentação, descreveu um movimento circular em torno do picadeiro. Em três momentos distintos, o fotógrafo tirou fotografias conforme o esquema a seguir.
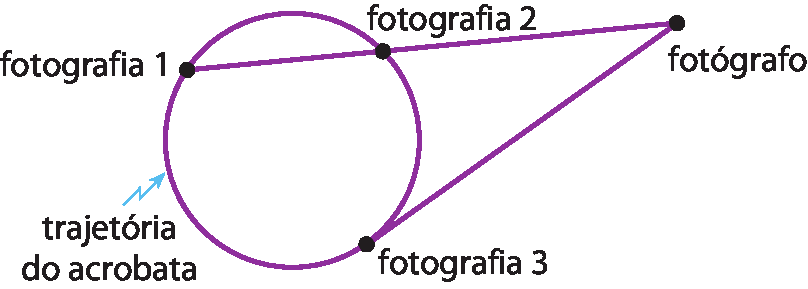
Estime valores para as medida das distâncias entre o acrobata e o fotógrafo, nos momentos das fotografias, de modo que atendam à 3ª relação estudada.
42

Hora de criar – Em dupla, cada um cria um problema sobre uma das três propriedades estudadas. Troquem de caderno e, depois de cada um resolver o problema elaborado pelo outro, destroquem para corrigi-los.
Respostas e comentários
40. a) x = 10
40. b) x = 3
41. Resposta pessoal.
42. Resposta pessoal.
Exercícios propostos
A resolução do exercício 40 está no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 41, sugira aos estudantes que nomeiem os pontos nos quais se encontram o fotógrafo e o acrobata em cada fotografia. Por exemplo, F para a posição do fotógrafo e a₁, a₂ e a₃ para as posições do acrobata nas fotografias 1, 2 e 3, respectivamente. Assim, é necessário que eles percebam que os valores escolhidos devem satisfazer a relação:
(FA3)duas = (FA2) · (FA1)
Uma possível resposta:
FA3 = 6 métros, FA2 = 4 métros e FA1 = 9 métros.
Note que: 4 · 9 = 36 = 6duas
Para o exercício 42, incentive os estudantes a elaborar problemas envolvendo cada uma das relações trabalhadas neste tópico; para isso, eles podem ser organizados em três grupos e os participantes de cada grupo elaboram um problema para uma relação. Depois, apresentam alguns dos problemas elaborados aos colegas dos demais grupos.
TRABALHANDO A INFORMAÇÃO

Semicoroa circular
Nesta reportagem, observe um tipo de gráfico, diferente dos que já estudamos até aqui, muito usado em jornais e revistas.
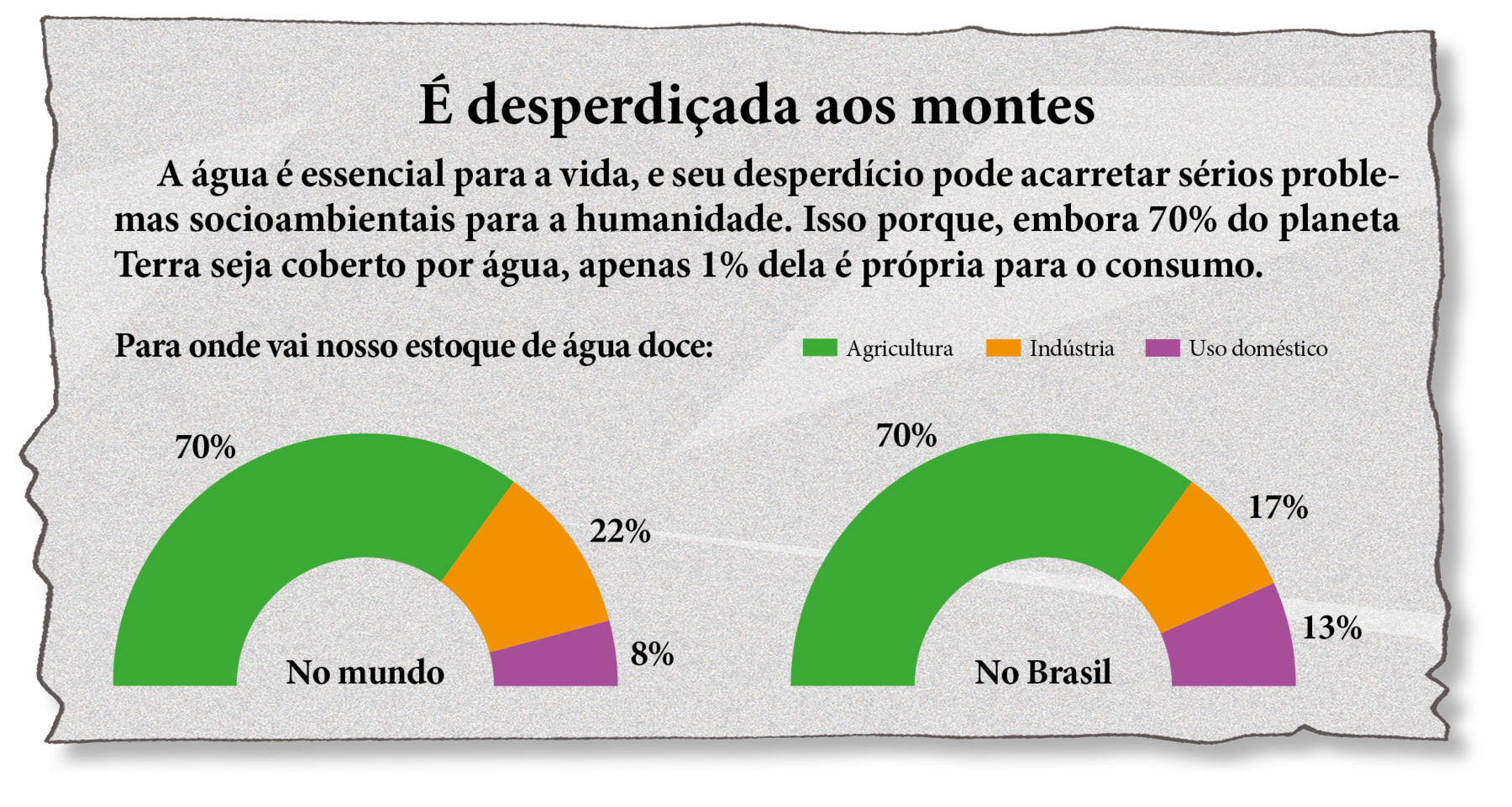
Podemos considerar o gráfico usado na reportagem como uma variação de um gráfico de setores. Porém, em vez de ser composto de setores circulares cujo total fórma um círculo, suas partes compõem uma semicoroa circular, ou seja, uma região limitada por duas semicircunferências concêntricas.
Para construir um gráfico com semicoroa circular, uma vez construída a tabela com as frequências relativas dos dados pesquisados, basta multiplicar as porcentagens por 180graus (no gráfico de setores multiplicamos por 360graus) e construir, com um transferidor, setores circulares adjacentes, de mesmo raio e centro, cujas medidas angulares são os produtos obtidos. A soma desses setores resulta em um semicírculo do qual retiramos outro semicírculo concêntrico de raio menor.
No exemplo da reportagem, 70% da água doce é destinada à agricultura (tanto no Brasil como no mundo). Então, o setor que inicialmente devemos representar para esse dado deve medir 0,7 ⋅ 180graus, isto é, 126graus.
Agora quem trabalha é você!
FAÇA A ATIVIDADE NO CADERNO
Faça uma pesquisa com os colegas de turma sobre a quantidade de água que eles bebem, em média, por dia. Em seguida, construa uma tabela e um gráfico como o da reportagem apresentada.
Considere na pesquisa as seguintes quantidades (e que 1 copo = 200 mililitros):
• 1 copo;
• 2 copos;
• 3 copos;
• 4 copos;
• 5 copos;
• 6 ou mais copos.
Respostas e comentários
Construção de tabela e de gráfico.
Trabalhando a informação
Habilidade da Bê êne cê cê: ê éfe zero nove ême ah dois três.
Esta seção aborda gráficos formados por semicoroa circular. Explique aos estudantes que coroa circular é a região do plano delimitada por duas circunferências concêntricas (que têm mesmo centro) de raios medindo R e r.
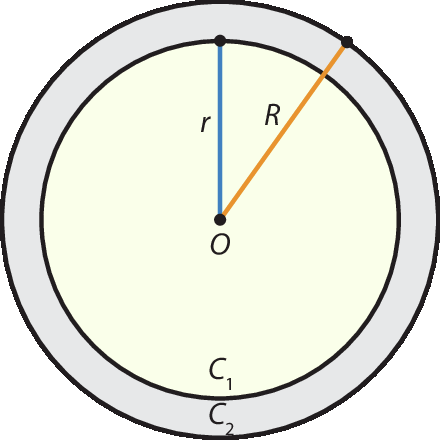
Explore o formato e os elementos do gráfico dado por uma semicoroa (metade de uma coroa) circular.
Para a construção do gráfico solicitado na questão do Agora quem trabalha é você!, organize os estudantes em duplas. Os dois estudantes da dupla devem fazer juntos a organização da tabela e a construção do gráfico relativo à pesquisa de cada um deles.
Em seguida, promova uma apresentação dos gráficos de cada dupla.
O trabalho com a atividade de pesquisa, construção de tabela e gráfico favorece o desenvolvimento da habilidade (ê éfe zero nove ême ah dois três).
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 Um autorama circular tem duas pistas, A e B, conforme esquema a seguir.
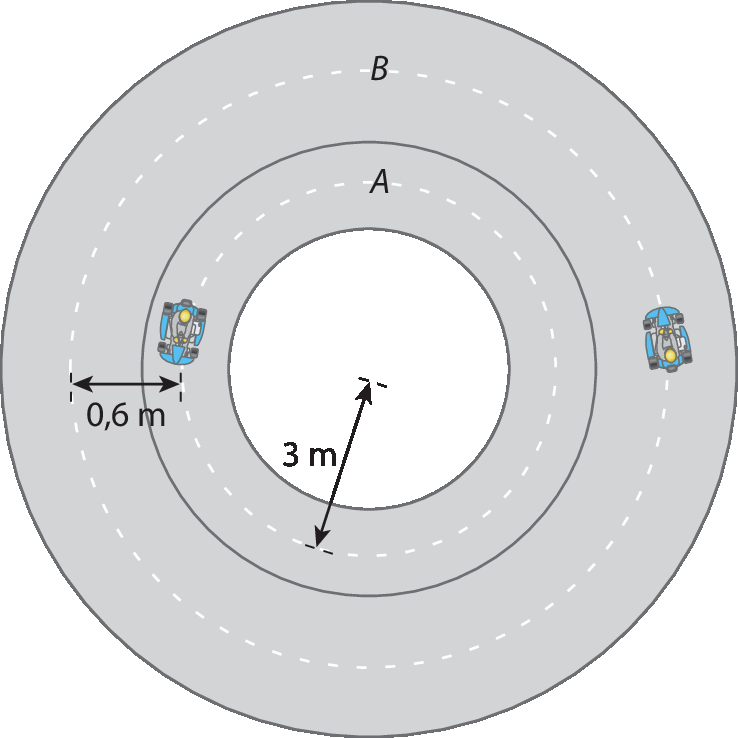
a) Depois que um carro der 36 voltas na pista a, quantos metros terá andado?
b) Quantos metros terá andado um carro que der 24 voltas na pista B?
2 O ponteiro dos minutos de um relógio de parede mede 9 centímetros. Determine a medida da distância, em centímetro, que o extremo dêsse ponteiro percorre em 20 minutos.
3 Um ciclista, em uma pista circular de 24 métros de raio, dá 15 voltas em 160 segundos. Qual é medida da velocidade média dele nesse trajeto?
4 Observe a circunferência a seguir em que as cordas,
ABe
CD, concorrem no ponto M.
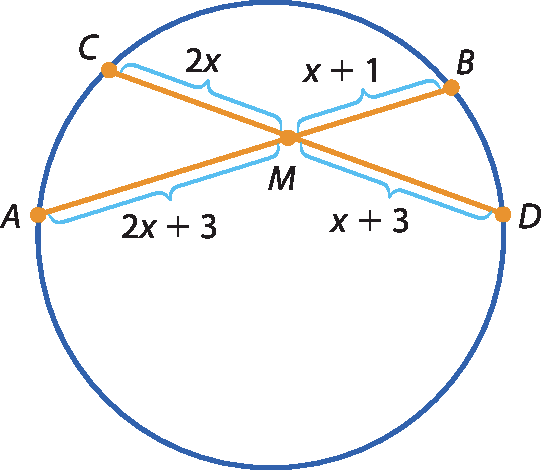
Sejam ei ém, MB, CM e MD dadas em centímetro. Quanto vale AB?
a) 36.
b) 18.
c) 14.
d) 13.
5 (u ésse éfe-São Paulo) Na circunferência a seguir, de centro óh e raio r = 4, a corda
CDcorta o diâmetro
ABno ponto P de tal fórma que P é o ponto médio do raio
OAe PC = 2 ⋅ PD.
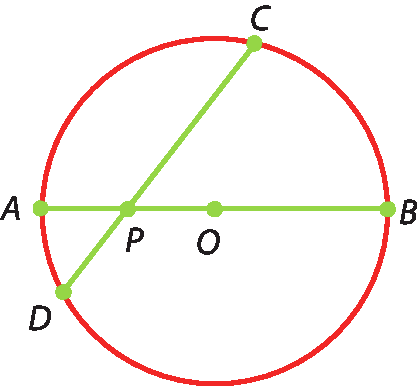
Então:
a) CD =
2 raiz quadrada de 6b) CD =
3 raiz quadrada de 6c) CD =
6 raiz quadrada de 6d) CD =
raiz de 6e) CD = 6
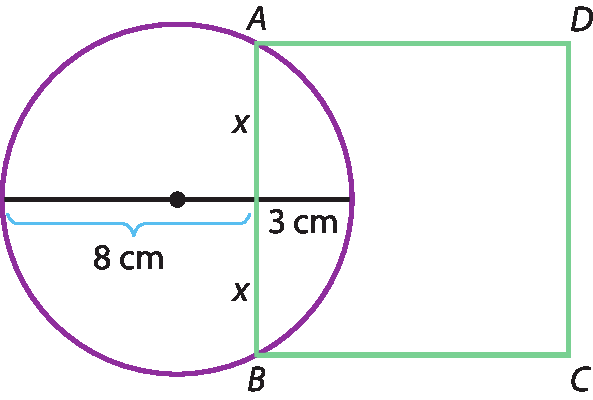
6 Considerando a figura, determine a medida da área do quadrado a bê cê dê.
7 Em uma circunferência, uma corda é intersectada por um diâmetro que fica dividido em dois segmentos, um de 7 centímetros e um de 2 centímetros. Se essa intersecção é feita a 2,5 centímetros do centro da circunferência, quanto mede o raio da circunferência?
8 Construa uma circunferência de 12 centímetros de diâmetro e trace um diâmetro
AB. Marque sobre ele, distante 11 centímetros de a, um ponto M. Trace, por esse ponto, uma perpendicular que intersecte a circunferência em um ponto P. O segmento
PMé a representação geométrica de qual número?
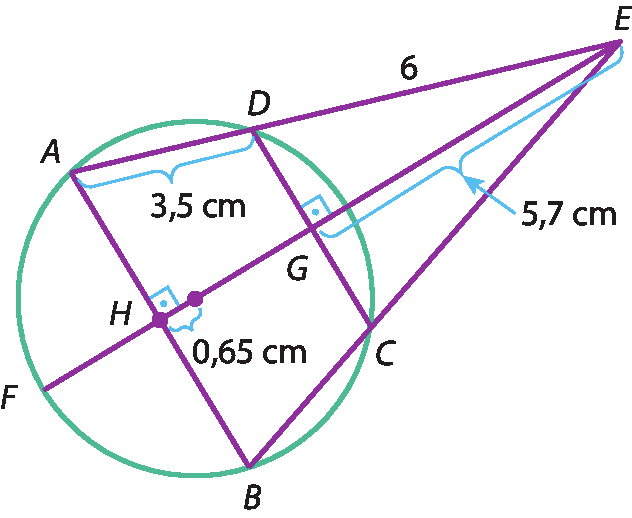
9 Determine a medida da altura
EHdo triângulo ABE na figura.
Respostas e comentários
1. a) Aproximadamente 678,24 métros.
1. b) Aproximadamente 542,59 métros.
2. 6π centímetros
3. 14,13 métros por segundo
4. Alternativa d.
5. Alternativa b.
6. 96 centímetros2
7. 4,5 centímetros
8. PM =
raiz de 119. 9,025 centímetros
Exercícios complementares
Este bloco de exercícios é mais uma oportunidade de os estudantes revisitarem os principais conceitos tratados e mobilizarem os conhecimentos construídos ao longo do capítulo, identificando possíveis dúvidas.
As resoluções do exercício 2 e dos exercícios 4 a 9 estão no início deste Manual, nas orientações específicas do capítulo 11.
No exercício 1, a pista a tem a medida do raio médio igual a 3 métros e a pista B, 3,6 métros. Assim:
a) A medida da distância percorrida, em metro, é dada por 36 · 2 · π · 3, ou seja, 216π métros. Com π = 3,14, temos que essa distância mede 678,24 métros, pois: 216 · 3,14 = 678,24
b) A medida da distância percorrida, em metro, é dada por 24 · 2 · π · 3,6, ou seja, 172,8π métros. Com π = 3,14, temos que essa distância mede cêrca de 542,59 métros, pois: 172,8 · 3,14 = 542,592
No exercício 3, temos que o raio r mede 24 métros. Assim, a medida do comprimento da pista é:
C = 2π · 24 = 48π
Como são realizadas 15 voltas, a medida da distância percorrida é igual a 15 · 48π, ou seja, 720π. Considerando π = 3,14, a medida da distância percorrida é .2260,8 métros. Dessa maneira, como o tempo do percurso foi igual a 160 segundos, a velocidade, em métro por segundo, é:
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
1 Um corredor treina em uma pista circular de comprimento de medida 31,4 quilômetros. Qual é a medida do raio da circunferência da pista?
a) 197,19 quilômetros
b) 98,6 quilômetros
c) 10 quilômetros
d) 5 quilômetros
2 Um automóvel é fabricado com rodas aro 17”. Sabendo que 1” equivale a 2,54 centímetros, qual é a medida aproximada do comprimento da circunferência dessa roda?
a) 15,95 centímetros
b) 106,8 centímetros
c) 135,6 centímetros
d) 271,2 centímetros
3 Qual é, aproximadamente, a medida do comprimento de arco compreendido por um ângulo de 45graus em uma circunferência de raio de medida 4,5 métros?
a) 14,13 métros
b) 28,26 métros
c) 3,53 métros
d) 1,18 métro
4 Qual é a medida do comprimento da hipotenusa de um triângulo retângulo inscrito em uma circunferência de raio de medida 15 centímetros?
a) 30 centímetros
b) 15π centímetros
c) 60 centímetros
d) 30π centímetros
5 Qual é o valor de x na figura?
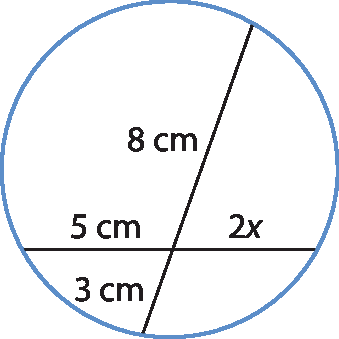
a) 0,417 centímetro
b) 2,4 centímetros
c) 4,2 centímetros
d) 20 centímetros
6 Sendo x, em centímetro, a medida da corda indicada na figura, qual é, aproximadamente, a medida do comprimento de uma circunferência cujo raio mede x?
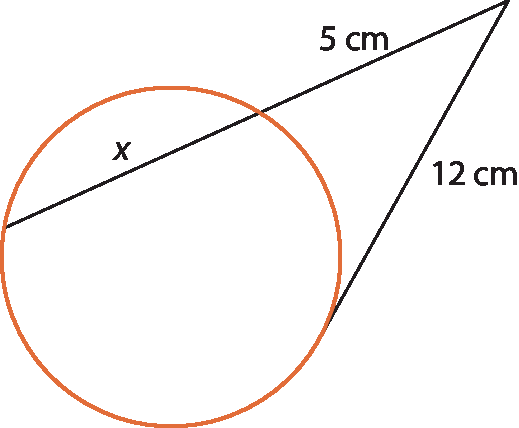
a) 18,09 centímetros
b) 21,42 centímetros
c) 33,18 centímetros
d) 149,46 centímetros
7 Sendo x a medida, em centímetro, da corda indicada na figura, aproximadamente, qual é a medida da área de um quadrado cujos lados medem x?
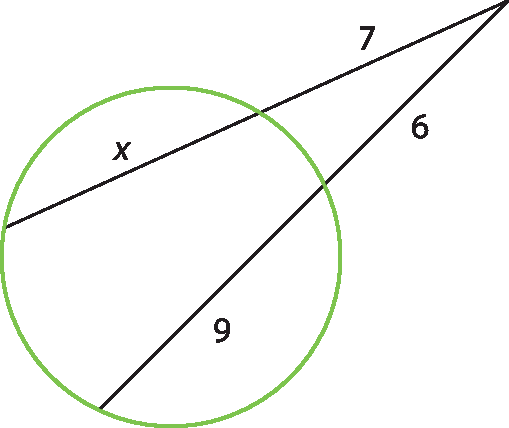
a) 165,38 centímetros
b) 64
c) 34,31 centímetros
d) 22 centímetros
8 Qual é a medida do ângulo correspondente a um índice de 50% em um gráfico de semicoroa circular?
a) 90graus
b) 45graus
c) 180graus
d) 120graus
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir.
a) O que é um arco de circunferência?
b) A razão entre a medida do comprimento de uma circunferência e a medida de seu diâmetro é sempre o mesmo valor. Qual é esse valor?
c) Como podemos determinar a medida do comprimento de uma circunferência qualquer? Sabendo a medida do comprimento de uma circunferência, é possível determinar a medida de seu diâmetro?
d) Explique as três relações métricas em uma circunferência que você aprendeu neste capítulo.
Respostas e comentários
1. Alternativa d.
2. Alternativa c.
3. Alternativa c.
4. Alternativa a.
5. Alternativa b.
6. Alternativa d.
7. Alternativa c.
8. Alternativa a.
Organizando:
a) É cada uma das partes em que uma circunferência fica dividida por dois de seus pontos distintos.
b) O valor é sempre igual a pi (π), aproximadamente 3,14.
c) Sabendo a medida do raio r de uma circunferência, a medida de seu comprimento é dada por 2πr. A medida do diâmetro D é dada por
d igual a c sobre pi.
d) Espera-se que os estudantes enunciem, com suas palavras, as relações métricas estudadas.
Verificando
Os testes desta seção são mais uma oportunidade para o estudante validar o entendimento do conteúdo estudado neste capítulo.
As resoluções dos testes 1 a 8 estão no início deste Manual, nas orientações específicas do capítulo 11.
Organizando
Incentive os estudantes a organizar seu aprendizado no caderno, fazendo resumos e mapas conceituais ou aplicando destaques em conceitos importantes.
As questões propostas têm como objetivo fazer com que os estudantes retomem os conteúdos aprendidos no capítulo e que reflitam sobre algumas temáticas.