
CAPÍTULO 12 Polígonos regulares e áreas


Tradicional no Pará, o carimbó reúne elementos de culturas indígenas, ibéricas e africanas. Em suas músicas, nos instrumentos e nas danças, expressa características das populações tradicionais da região e a relação delas com o ambiente. Em tupi, curimbó significa “pau oco” e é o nome do instrumento de percussão indígena de onde deriva carimbó. Essa manifestação artística e cultural tem sido preservada pela oralidade dos mestres populares e, em 2014, tornou-se um Patrimônio Cultural Imaterial do Brasil.
Observe, leia e responda no caderno.
a) Junte-se a outros três colegas e pesquisem o carimbó e outras manifestações artísticas e culturais de diferentes regiões do Brasil. Conversem sobre a importância de reconhecer e valorizar o multiculturalismo nas matrizes históricas e culturais brasileiras.
b) Com base na pesquisa que realizaram, que elementos da obra Dançando carimbó, de Thais Gomez, vocês acreditam que mais representam o carimbó?
c) Que tipo de instrumento musical é o curimbó? Qual é o formato dele? Que elemento geométrico foi utilizado na tela Dançando carimbó para o representar?
Respostas e comentários
a) Resposta pessoal.
b) Resposta pessoal.
c) O curimbó é um instrumento de percussão, um tambor; ele pode ser associado a um cilindro reto; na tela Dançando carimbó ele foi representado por meio de uma figura que lembra um círculo.
Capítulo 12 – Polígonos regulares e áreas
Os objetivos deste capítulo e suas justificativas, as indicações das habilidades e competências específicas de Matemática (Bê êne cê cê), além de outras informações, estão no início deste Manual, nas orientações específicas.
Neste capítulo, ampliamos o trabalho sobre polígonos regulares e seus elementos ao apresentar as relações métricas entre elementos de um polígono regular e a circunferência a que ele está inscrito.
Desenvolvemos o estudo de polígonos regulares, com o uso da linguagem algébrica, e de questões de construção geométrica de figuras. Nas demonstrações mostramos a aplicação do teorema de Pitágoras e da proporcionalidade.
Tratamos da medida da área de um polígono regular, de um círculo e de suas partes; e da medida do volume de alguns sólidos geométricos.
O contexto da abertura deste capítulo possibilita desenvolver o Tema Contemporâneo Transversal educação para valorização do multiculturalismo nas matrizes históricas e culturais brasileiras, pois os estudantes podem pesquisar e debater sobre o carimbó, que é uma manifestação artística que pode representar o multiculturalismo brasileiro, visto que reúne elementos de diferentes culturas.
Associado a isso, podem-se desenvolver atividades interdisciplinares com Arte, solicitando aos estudantes que pesquisem e analisem diferentes fórmas de expressão, representação e encenação da dança, em diferentes regiões do Brasil. Também é possível explorar a pintura Dançando carimbó e outras que retratem o multiculturalismo nas matrizes históricas brasileiras, orientando os estudantes a analisar aspectos históricos, sociais e políticos da produção artística. Dessa maneira, os estudantes desenvolvem a competência geral 3, pois poderão fruir e valorizar diferentes manifestações artísticas.

Sugestão de leitura
Para enriquecer o trabalho, sugerimos:
HUERTAS, B. M. O carimbó: cultura tradicional paraense, patrimônio imaterial do Brasil. Revista CPC, [sem local], número 18, página 81 a 105, 2014. Disponível em: https://oeds.link/LE71Uz. Acesso em: 23 julho 2022.
Nesse artigo, a autora apresenta um breve histórico sobre o carimbó e explora a relação dessa manifestação artística com o modo de vida de comunidades tradicionais.
1. Relações métricas nos polígonos regulares
Retomando o estudo dos polígonos regulares
Ao elaborar um projeto para a construção de mostradores de relógios de parede feitos com chapas de madeira, Edgard precisa efetuar cálculos das medidas de um dodecágono regular com base na medida do raio da circunferência circunscrita a ele. Em particular, para saber quanto material comprar, ele precisará calcular a medida da área dêsse polígono.

Situações como a de Edgard requerem um estudo sobre as relações métricas em polígonos regulares, o que faremos neste capítulo.

Por exemplo:
• Um polígono é regular quando todos os seus lados são congruentes entre si e todos os seus ângulos são congruentes entre si.
• Todo polígono regular é inscritível e circunscritível em uma circunferência.
Também vimos que, se uma circunferência é dividida em três ou mais arcos congruentes:
• as cordas determinadas pelos pontos consecutivos de divisão formam um polígono regular inscrito na circunferência;
• as tangentes aos pontos consecutivos de divisão formam um polígono regular circunscrito à circunferência. Observe os exemplos a seguir.
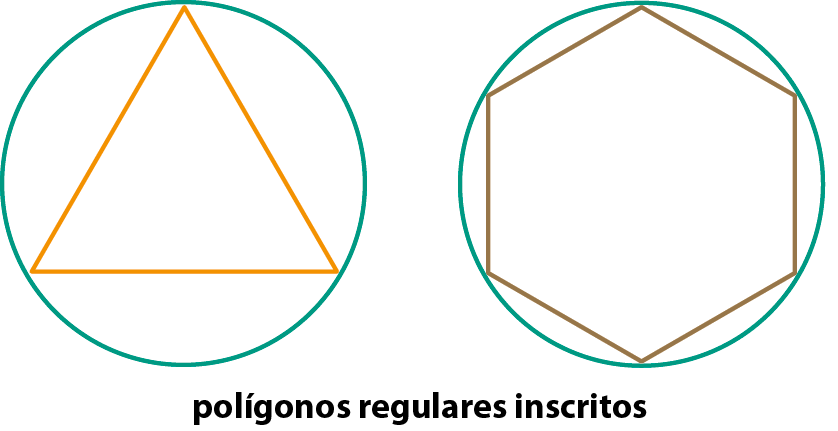
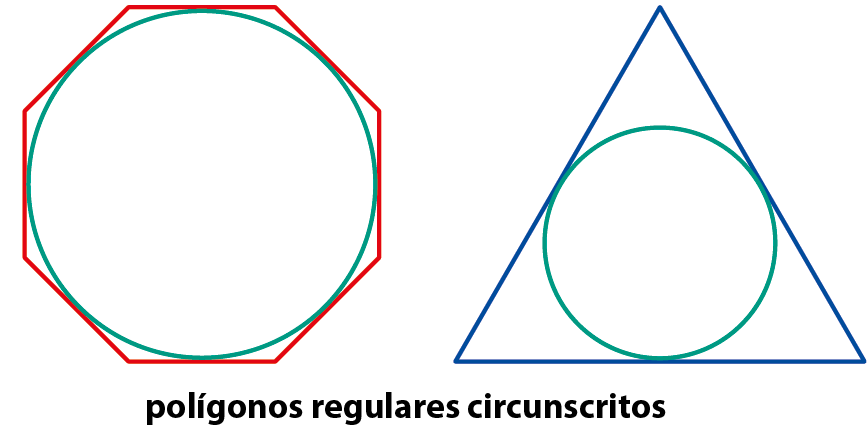
Em um polígono regular, consideramos:
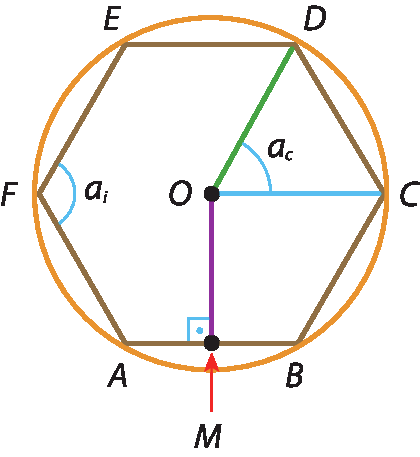
• centro do polígono: centro da circunferência circunscrita a ele (ponto óh);
• raio do polígono: raio da circunferência circunscrita a ele (
Segmento OC.);
• apótema do polígono: segmento que une o centro do polígono ao ponto médio de um de seus lados (
Segmento OM.);
• ângulo central: aquele cujo vértice é o centro do polígono e cujos lados são semirretas que contêm dois vértices consecutivos do polígono (
ângulo COD.);
•
a índice c igual a 360 graus sobre n.e
a índice i igual a, fração de numerador S índice i, e de denominador n, igual a, fração de numerador: abre parênteses n menos 2, fecha parênteses, vezes 180 graus, e de denominador n., em que n é o número de lados.
Respostas e comentários
Orientação: A situação descrita será explorada no exercício 36, na página 291.
1. Relações métricas nos polígonos regulares
Habilidades da Bê êne cê cê: EF09MA11 e ê éfe zero nove ême ah um quatro.
Neste tópico, ao estudar os polígonos regulares inscritos em uma circunferência, os estudantes mobilizam as habilidades (ê éfe zero nove ême ah um um) e (ê éfe zero nove ême ah um quatro), pois precisam compreender os conceitos de ângulo central e de ângulo inscrito e aplicar o teorema de Pitágoras para resolver problemas. Pergunte aos estudantes em que situações observam formatos de objetos que podem associar a polígonos regulares. Espera-se que identifiquem os favos hexagonais de uma colmeia ou os pentágonos em uma bola de futebol, por exemplo.
Aproveite o momento e verifique que conhecimentos eles já têm sobre polígonos regulares. Peça que deem exemplos dêsse tipo de polígono: quadrado, triângulo equilátero, hexágono regular etcétera
Desenhe na lousa um polígono regular com alguns de seus elementos e peça aos estudantes que os identifiquem.

Quadrado inscrito
Considere uma circunferência de centro óh e raio de medida r.
Para construir um quadrado a bê cê dê inscrito nessa circunferência, podemos traçar dois diâmetros perpendiculares entre si (
segmento AC.e
segmento BD.), determinando os vértices do quadrado.
Vamos calcular as medidas do lado e do apótema dêsse quadrado em função de r.
Cálculo da medida do lado (𝓁)

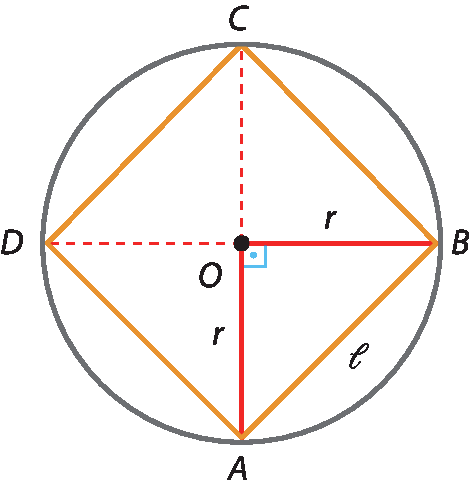
No △á ó bê, pelo teorema de Pitágoras, obtemos:
(AB )elevado a 2 = (AO )elevado a 2 + (BO )elevado a 2
𝓁elevado a 2 = r elevado a 2 + r elevado a 2
𝓁elevado a 2 = 2r elevado a 2 (r > 0)
L igual a mais ou menos, raiz quadrada de 2 r elevado ao quadrado.
L igual a mais ou menos, r vezes raiz quadrada de 2.
Como 𝓁 é um número positivo, pois é a medida do lado do quadrado, obtemos:
Cálculo da medida do apótema (a)
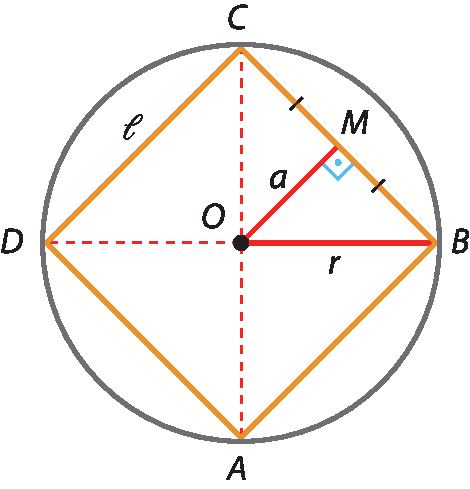
No △ô ême bê, pelo teorema de Pitágoras, obtemos:
(OM )elevado a 2 + (BM )elevado a 2 = (BO )elevado a 2
a elevado ao quadrado, fim do expoente, mais, abre parênteses, L sobre 2, fecha parênteses, elevado ao quadrado, igual a, r elevado ao quadrado.
a elevado ao quadrado, fim do expoente, mais, fração de numerador 2 vezes r elevado ao quadrado, e de denominador 4, fim da fração, igual a, r elevado ao quadrado.
a elevado ao quadrado, igual a, r elevado ao quadrado, fim do expoente, menos, fração de numerador 2 vezes r elevado ao quadrado, e de denominador 4, igual a, fração de numerador 2 vezes r elevado ao quadrado, e de denominador 4, abre parênteses, r maior que zero, fecha parênteses.
a igual a, mais ou menos, raiz quadrada de fração de numerador 2 vezes r elevado ao quadrado, e de denominador 4.
a igual a mais ou menos fração de numerador r vezes raiz quadrada de 2, e de denominador 2.
Como a é um número positivo, pois é a medida do apótema do quadrado, obtemos:
Respostas e comentários
Quadrado inscrito
Explore o quadrado inscrito em uma circunferência de raio medindo r. Peça aos estudantes que identifiquem os elementos do quadrado em relação aos elementos da circunferência. Espera-se que eles percebam que:
• as diagonais do quadrado são diâmetros da circunferência e, portanto, que a medida d da diagonal é dada por: d = 2r
• como o ângulo central do quadrado mede 90graus
abre parênteses, 360 graus sobre 4, fecha parênteses, cada triângulo retângulo cuja hipotenusa é o lado do quadrado (de medida ℓ) é um triângulo isósceles cujos catetos medem r. Assim, pelo teorema de Pitágoras, determinamos que:
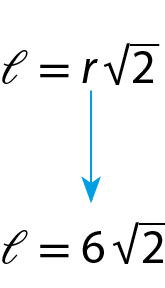
L igual r vezes raiz quadrada de 2Note que essa relação poderia ter sido obtida por
d igual a l raiz quadrada de 2, pois:
Acompanhe os exemplos a seguir.
a) Vamos calcular as medidas do lado e do apótema de um quadrado inscrito em uma circunferência com raio medindo 6 centímetros. Observe a figura a seguir.
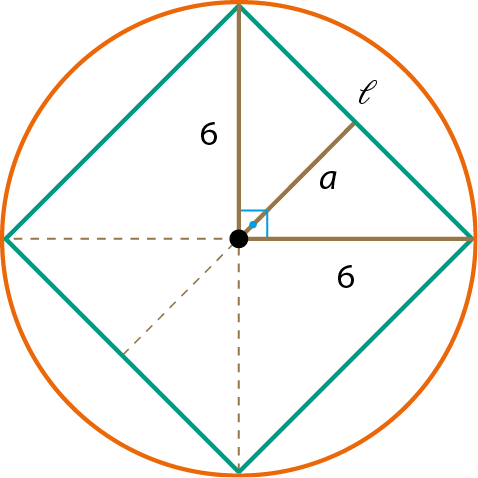
Pelo teorema de Pitágoras, obtemos:
𝓁elevado a 2 = 6elevado a 2 + 6elevado a 2
𝓁elevado a 2 = 72
L igual a, mais ou menos raiz quadrada de 72
L igual a mais ou menos 6 vezes raiz quadrada de 2.
Como 𝓁 é um número positivo,
L igual a 6 vezes raiz quadrada de 2.centímetros.
a igual a L sobre 2
a igual a fração de numerador 6 vezes raiz quadrada de 2, e de denominador 2
a igual a 3 vezes raiz quadrada de 2
Portanto,
a igual a 3 vezes raiz quadrada de 2.centímetros.

Sim; do enunciado, sabemos que r = 6 centímetros. Então:
Portanto,
L igual a 6 vezes raiz quadrada de 2.centímetros e
a igual a 3 vezes raiz quadrada de 2.centímetros.
b) Vamos calcular a medida do raio de uma circunferência na qual está inscrito um quadrado cujo lado mede
5 raiz quadrada de 2.centímetros. Observe a figura a seguir.
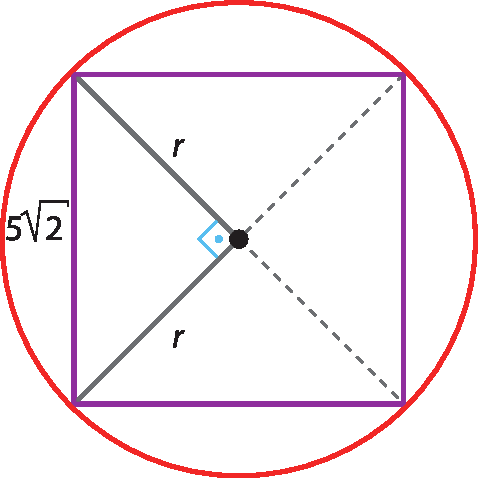
Pelo teorema de Pitágoras, obtemos:
2r elevado a 2 = 25 ⋅ 2
r elevado a 2 = 25
r = ±5
Como r é um número positivo, r = 5 centímetros.

Sim; do enunciado, sabemos que
L igual a 5 vezes raiz quadrada de 2centímetros. Então:
r = 5
Portanto, r = 5 centímetros.
Respostas e comentários
Quadrado inscrito
Verifique se os estudantes percebem que o apótema do quadrado é a altura de um desses triângulos retângulos isósceles relativa à hipotenusa. Há vários caminhos para determinar a medida dessa altura, ou seja, do apótema do quadrado. Os estudantes devem mobilizar seus conhecimentos prévios para usar o fato de que a altura relativa à base de um triângulo isósceles coincide com a mediana relativa a essa mesma base (que no caso é a hipotenusa).
dêsse modo, um dos caminhos para determinar a medida a do apótema do quadrado é aplicar o teorema de Pitágoras no triângulo ô ême bê, como feito no desenvolvimento na página anterior.
Outra maneira é usar a relação métrica no triângulo retângulo cê ó bê: o produto da medida da hipotenusa pela medida da altura relativa a ela é igual ao produto das medidas dos catetos. Assim, temos:
Ao utilizar o teorema de Pitágoras para calcular a medida do lado e do apótema do quadrado, os estudantes mobilizam e aprofundam o desenvolvimento da habilidade (ê éfe zero nove ême ah um quatro).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)
1 Construa um quadrado inscrito em uma circunferência de raio medindo 3 centímetros.
a) Que número irracional representa a medida do lado dêsse quadrado? A representação decimal dêsse número tem infinitas casas decimais e não é periódica. Determine essa representação decimal com uma casa decimal.
b) Que número irracional representa a medida do apótema?
2 O apótema de um quadrado inscrito em uma circunferência mede
6 raiz de 2.centímetros. Calcule a medida da diagonal dêsse quadrado.
3 A diagonal de um quadrado mede
5 raiz de 2.centímetros. Calcule a medida da distância do centro dêsse quadrado a um de seus lados.
4 O lado de um quadrado circunscrito a uma circunferência mede 8 centímetros.
a) Calcule a medida do lado de um quadrado inscrito nessa circunferência.
b) Calcule a medida da diagonal do quadrado inscrito nessa circunferência.
5 Construa um quadrado circunscrito e um quadrado inscrito em uma mesma circunferência. Determine a diferença entre as medidas dos perímetros desses quadrados em função da medida r do raio da circunferência.
6 Uma fábrica de chocolates lançou no mercado a nova caixa de bombons decorada. O desenho da tampa da caixa foi elaborado com base em dois quadrados, como se vê na figura a seguir.

A medida do lado do quadrado menor é 10 centímetros. E os seus vértices são os pontos médios dos lados do quadrado maior. Determine:
a) a medida do lado do quadrado maior;
b) a medida do comprimento da faixa vermelha que cobre os lados dos dois quadrados;
c) a soma das medidas das áreas dos quatro triângulos da tampa.
Hexágono regular inscrito
Considere uma circunferência de centro óh e raio de medida r.
Como o ângulo central do hexágono regular mede
360 graus sobre 6= 60graus, podemos construir na circunferência um ângulo central com essa medida, obtendo um arco
AB. Com a abertura do compasso igual a
segmento AB, marcamos os outros vértices do hexágono.
Vamos calcular as medidas do lado e do apótema dêsse hexágono em função de r.
(Ao usar o compasso, atenção para não se machucar com a ponta-sêca.)
Cálculo da medida do lado (𝓁)
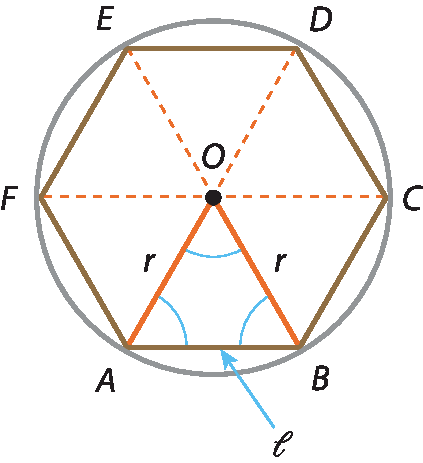
O △á ó bê é equiângulo, logo é equilátero, ou seja: A bê = ó á = ó bê.
Portanto:
ℓ = érre
Respostas e comentários
1. a)
3 vezes raiz quadrada de 2, aproximadamente igual a, 4,21. b)
fração de numerador 3 vezes raiz quadrada de 2, e de denominador 22. 24 centímetros
3. 2,5 centímetros
4. a)
4 vezes raiz quadrada de 2, fim da raiz, centímetros.4 b) 8 centímetros
5.
abre parênteses, 8 menos 4 vezes raiz de 2, fecha parênteses, vezes r6. a)
10 vezes raiz quadrada de 2, fim da raiz, centímetros6. b)
abre parênteses, 40 mais 40 vezes raiz quadrada de 2, fecha parênteses, centímetro.6. c) 100 centímetros quadrados
Exercícios propostos
A seguir, apresentamos uma possível resolução do exercício 1.
Obtemos o quadrado dividindo a circunferência em quatro arcos de mesma medida. Traçando duas retas perpendiculares que passam pelo centro, obtemos os arcos desejados.
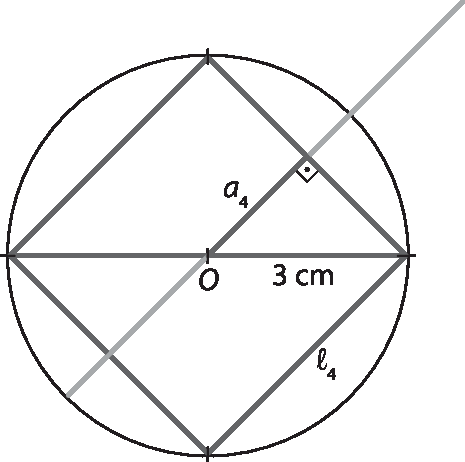
a) O raio mede 3 centímetros. Assim, indicando por ℓ, em centímetro, a medida do lado dêsse quadrado, temos:
L igual a r vezes raiz quadrada de 2, implica, L igual a, 3 vezes raiz quadrada de 2, implicaℓ ≃ 4,2
b) Indicando a medida do apótema do quadrado por a, em centímetro, temos:
a igual a fração de numerador r vezes raiz quadrada de 2, e de denominador 2, implica, a igual a fração de numerador 3 vezes raiz quadrada de 2, e de denominador 2,Ressalte aos estudantes que, no caso do quadrado inscrito, a diagonal é um diâmetro.
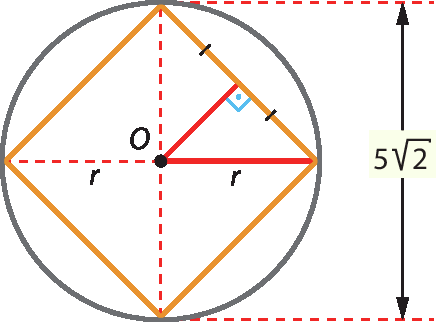
Para o exercício 3, de acordo com o enunciado, um possível esquema da situação é apresentado a seguir, em que destacamos a circunferência circunscrita ao quadrado, cujo centro O é o centro dessa circunferência.
No exercício 5, uma possível resolução é a que segue.
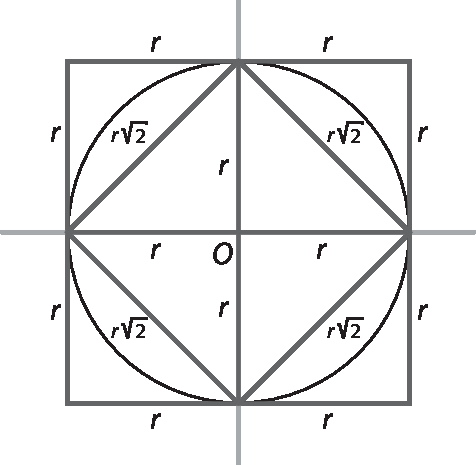
Como a diagonal do quadrado inscrito é um diâmetro, a medida da diagonal é 2r; assim, a medida do lado do quadrado inscrito é
r vezes raiz quadrada de 2. O lado do quadrado circunscrito é um diâmetro, então mede 2r. dêsse modo:
• perímetro pê₁ do quadrado circunscrito: P1 = 4 · 2r = 8r
• perímetro pê₂ do quadrado inscrito:
P índice 2, igual a, 4 vezes r, raiz quadrada de 2, igual a, 4r, raiz quadrada de 2.Portanto, a diferença entre esses perímetros é:
As resoluções dos exercícios 2 a 4 e 6 estão no início deste Manual, nas orientações específicas do capítulo 12.
Cálculo da medida do apótema (a)
No △OMB, pelo teorema de Pitágoras, obtemos:
(ó ême )2 + (MB )2 = (bê ó )2
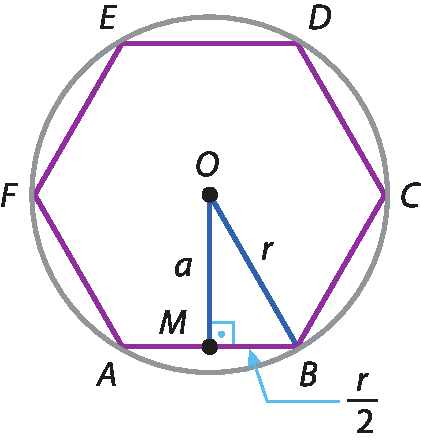
Como a é um número positivo, pois é a medida do apótema, obtemos:
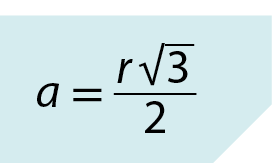
Acompanhe os exemplos a seguir.
a) Vamos calcular a medida do raio de uma circunferência na qual o apótema do hexágono regular inscrito mede
12 vezes raiz quadrada de 3centímetros.
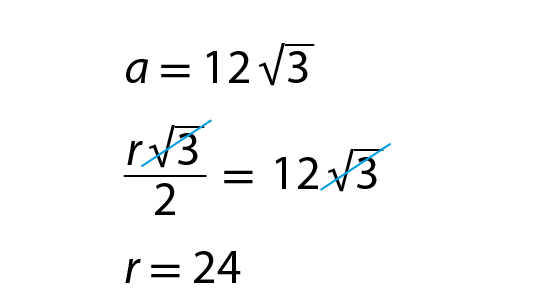
Portanto, o raio mede 24 centímetros.
b) Vamos calcular a medida do perímetro do hexágono regular a seguir, sendo A Ê =
10 raiz quadrada de 3.centímetros.
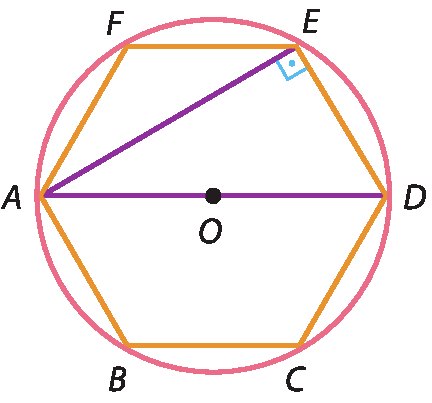
• ê de = r;
• á dê = 2r;
• A Ê =
10 raiz quadrada de 3.centímetros;
• △á dê é é retângulo.
Pelo teorema de Pitágoras no △á dê é, obtemos:
(A Ê )2 + (ê de )2 = (á dê)2
+ r elevado a 2 = (2r)elevado a 2
300 = 4r elevado a 2 ‒ r elevado a 2
300 = 3relevado a 2
relevado a 2 = 100
r = ±10
Como r é um número positivo, pois é medida de raio, obtemos r = 10 centímetros. Logo, 𝓁 = 10 centímetros. Portanto, a medida do perímetro é 60 centímetros.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
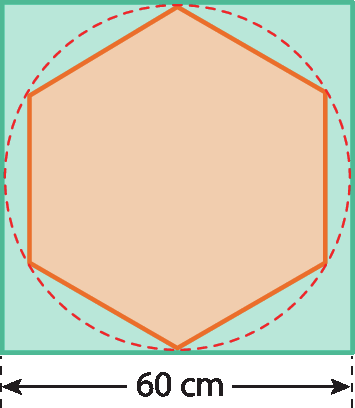
7 Marina é projetista em uma fábrica de lustres. Ela criou um lustre formado por quatro placas quadradas de polipropileno translúcido (um tipo de plástico que deixa passar a luz) com 60 centímetros de lado cada uma. A figura central dessas placas é um hexágono regular, desenhado com base em uma circunferência tangente aos lados das placas. Determine as medidas do lado e da área dêsse polígono.
Respostas e comentários
7. Medida do lado: 30 centímetros; medida da área: .1350
raiz quadrada de 3.centímetros quadrados.
Hexágono regular inscrito
No caso do hexágono regular inscrito, os estudantes devem perceber que o lado do hexágono tem a mesma medida do raio (ℓ = r) e que o apótema é a altura de cada um dos 6 triângulos equiláteros que compõem esse hexágono (e que também têm lado medindo ℓ). dêsse modo, a medida a do apótema do hexágono regular pode também ser obtida pela relação da medida h da altura em função da medida ℓ do lado de um desses triângulos equiláteros. Assim, temos:
No exemplo b, retome com os estudantes que todo triângulo inscrito em uma semicircunferência é um triângulo retângulo.
Exercícios propostos
No exercício 7, o lado do quadrado circunscrito à circunferência mede 60 centímetros. Logo, o raio da circunferência mede 30 centímetros. Temos um hexágono regular inscrito nessa mesma circunferência; então, o lado dêsse hexágono mede 30 centímetros, ou seja, ℓ = 30 centímetros.
A medida da área do hexágono regular é igual à medida da área de 6 triângulos equiláteros de lado medindo r. A altura de cada um desses triângulos equiláteros é o apótema a do hexágono.
A altura de medida h de um triângulo equilátero de lado medindo ℓ3 é dada por:
h igual a, fração de numerador L índice 3, vezes raiz quadrada de 3, e de denominador 2,Peça aos estudantes que determinem a medida da área de um triângulo equilátero nessas condições, em função da medida ℓ3 de seu lado. A medida dessa área, em centímetros quadrados, é dada por:
Assim, temos que a medida da área do hexágono regular, em centímetros quadrados, é
8 Um hexágono regular é inscrito em uma circunferência de raio medindo 3,2 centímetros. Calcule:
a) a medida dos lados dêsse hexágono;
b) a medida do perímetro dêsse hexágono;
c) a medida do apótema.
9 O apótema de um hexágono regular inscrito em uma circunferência mede
9 raiz quadrada de 3.centímetros. Calcule a medida do lado do quadrado inscrito nessa circunferência.
10 A menor diagonal de um hexágono regular mede
12 raiz quadrada de 3.centímetros. Calcule a medida do perímetro dêsse hexágono.
11 Divide-se uma circunferência de diâmetro medindo 10 centímetros em seis partes iguais. Escolhem-se três pontos alternados dessa divisão, os quais são unidos com segmentos de reta. Determine a medida de cada um desses segmentos.
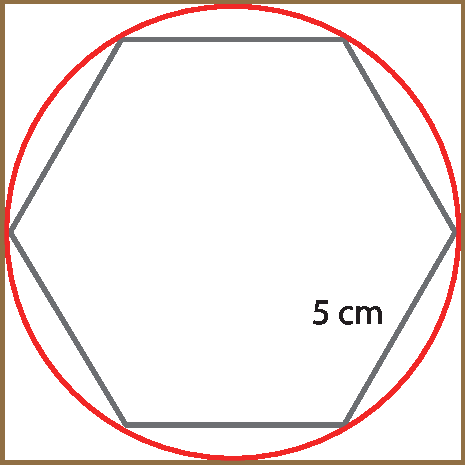
12 Considerando a figura a seguir, determine a medida do perímetro do quadrado circunscrito à circunferência.
13

Hora de criar – Junto com um colega, elaborem um tabuleiro de jogo (por exemplo, dama ou uma trilha a ser percorrida por peões, tampinhas etcétera) em formato de hexágono regular. Estabeleçam as regras do jogo e, em dia a ser agendado pelo ou pela professor ou professora, joguem uma partida para apresentar à turma.
Triângulo equilátero inscrito
Para construir um triângulo equilátero á bê cê inscrito em uma circunferência, dividimos a circunferência em seis arcos congruentes e unimos, alternadamente, os pontos de divisão por meio de segmentos.
Vamos calcular a medida do lado e do apótema dêsse triângulo em função de r.
Cálculo da medida do lado (𝓁)
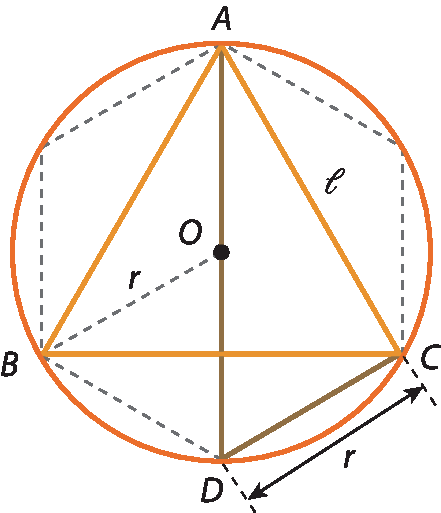
Observe que:
• o △á dê cê é retângulo (inscrito na semicircunferência);
• DC = r, pois
segmento DCé lado de um hexágono regular inscrito na circunferência.
No △á dê cê, pelo teorema de Pitágoras, obtemos:
(á cê )2 + (DC )2 = (á dê )2
(𝓁)2 + (r)2 = (2r)2
𝓁2 + r2 = 4r2
𝓁2 = 3r2 (r > 0)
L igual a mais ou menos raiz quadrada de 3 vezes r elevado ao quadrado.
Como 𝓁 é um número positivo, pois é a medida do lado do triângulo, obtemos:
Cálculo da medida do apótema (a)
No △ó ême cê, pelo teorema de Pitágoras, obtemos:
(OM)elevado a 2 + (MC)elevado a 2 = (OC)elevado a 2
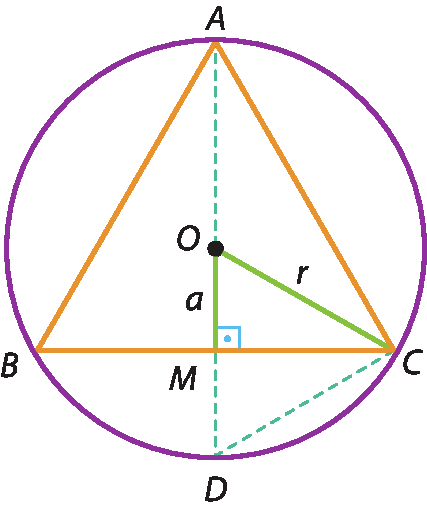
Como a é um número positivo, pois é a medida do apótema, obtemos:
a =
fração r sobre 2.Respostas e comentários
8. a) 3,2 centímetros
8. b) 19,2 centímetros
8. c)
1,6 vezes raiz quadrada de 3, fim da raiz, centímetros9.
18 vezes raiz quadrada de 2, fim da raiz, centímetros.10. 72 centímetros
11.
5 vezes raiz quadrada de 3, fim da raiz, centímetros.12. 40 centímetros
13. Resposta pessoal.
Exercícios propostos
No exercício 10, espera-se que os estudantes percebam que a medida da menor diagonal é o dobro da medida a do apótema. Assim, temos:
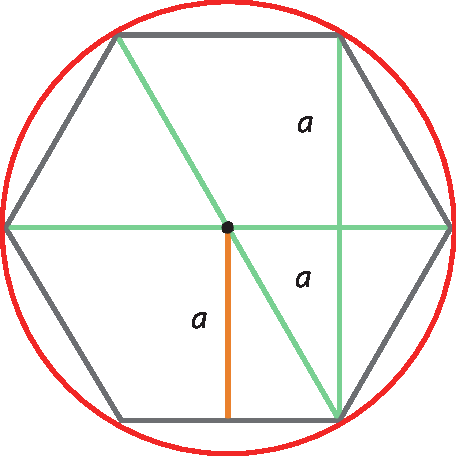
Com
a igual a fração de numerador r vezes raiz quadrada de 3 e de denominador 2, e 2a igual a, 12 vezes raiz quadrada de 3., obtemos:
⇒ r = 12
Como no hexágono regular a medida do lado é igual à medida do raio da circunferência que o circunscreve, o lado mede 12 centímetros e o perímetro mede 72 centímetros (6 · 12).
No exercício 13, oriente os estudantes a pesquisar jogos de tabuleiro e agende um dia para que apresentem a pesquisa e as produções aos demais colegas.
As resoluções dos exercícios 8, 9, 11 e 12 estão no início deste Manual, nas orientações específicas do capítulo 12.
Triângulo equilátero inscrito
Apresentamos outra maneira de calcular a medida (ℓ) do lado e a medida (a) do apótema de um triângulo equilátero inscrito em uma circunferência de raio medindo r.
O ângulo central de um triângulo equilátero mede 120graus.
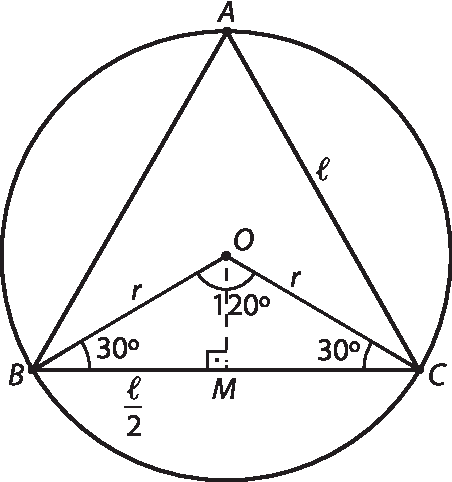
O triângulo bê ó cê é isósceles e, portanto, os ângulos da base são congruentes e medem 30graus(pois: 30graus + 30graus + 120graus = 180graus).
O segmento
OMé o apótema do triângulo equilátero ABC. Assim, é perpendicular à base
BCe, portanto,
segmento OMé a altura relativa a essa base do triângulo bê ó cê. Logo,
segmento OMé também mediana e M é ponto médio de
Segmento BCe o triângulo bê ó ême é retângulo em M.
• Cálculo da medida ℓ do lado:
cos 30graus
igual fração, BM sobre BO.• Cálculo da medida a do apótema:
sen 30graus
igual fração, OM sobre BO.2a = r
Acompanhe a aplicação dêsse cálculo no exemplo a seguir.
O lado de um triângulo equilátero inscrito em uma circunferência mede
9 raiz quadrada de 3.centímetros. Vamos calcular a medida do raio dessa circunferência.
Observe a figura geométrica a seguir.
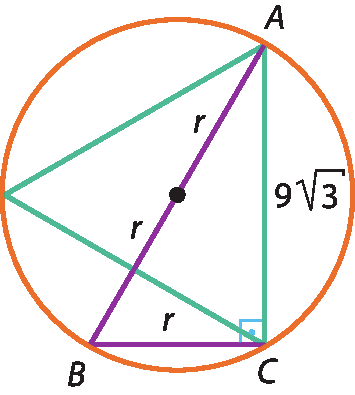
No △á bê cê, pelo teorema de Pitágoras, obtemos:
(á cê )2 + (BC )2 = (A bê)2
81 ⋅ 3 + relevado a 2 = 4relevado a 2
81 ⋅ 3 = 3relevado a 2
relevado a 2 = 81
r = ±9

Como r é um número positivo, pois é a medida do raio, obtemos r = 9 centímetros.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
(Ao usar o compasso, atenção para não se machucar com a ponta-seca.)
14 Trace uma circunferência de raio medindo 3 centímetros e um triângulo equilátero inscrito nela. Calcule:
a) a medida do lado do triângulo;
b) a medida do apótema.
15 Se o apótema de um triângulo equilátero mede
raiz quadrada de 12.centímetros, determine:
a) a medida do lado do triângulo;
b) a medida da altura do triângulo.
16 Um triângulo equilátero é inscrito em uma circunferência de raio medindo 8 centímetros.
a) Calcule a medida do apótema.
b) Adicione a medida do raio com a medida do apótema.
c) Calcule a medida da altura do triângulo aplicando a fórmula
h igual a fração de numerador L vezes raiz quadrada de 3, e de denominador 2.d) Considerando um triângulo equilátero em que o lado tem medida 𝓁, o raio tem medida r, e o apótema, medida a, e tendo em vista os resultados dos itens b e c, podemos dizer que
fração de numerador L vezes raiz quadrada de 3, e de denominador 2, fim da fração, igual a, r mais a.?
17 Um colégio está divulgando uma campanha contra o tabagismo. Para isso, promoveu um concurso entre os estudantes para a escolha de um cartaz para a campanha. O cartaz a seguir foi o vencedor.

Sabendo que o raio da circunferência que circunscreve o triângulo equilátero mede 30 centímetros, determine a medida da área dêsse triângulo.
18 Em uma mesma circunferência, são inscritos um quadrado e um triângulo equilátero. O apótema do quadrado mede
3,5 raiz quadrada de 2.centímetros. Calcule a medida do apótema do triângulo.
Respostas e comentários
14. a)
3 vezes raiz quadrada de 3, fim da raiz, centímetros.14. b) 1,5 centímetro
15. a) 12 centímetros
15. b)
6 vezes raiz quadrada de 3, fim da raiz, centímetros.16. a) 4 centímetros
16. b) 12 centímetros
16. c) 12 centímetros
16. d) Sim.
17.
675 vezes raiz quadrada de 3, fim da raiz, centímetros quadrados.18. 3,5 centímetros
Exercícios propostos
Apresentamos a seguir uma possível resolução para o exercício 14.
Indicando a medida do lado do triângulo equilátero por ℓ e a de seu apótema por a, temos:
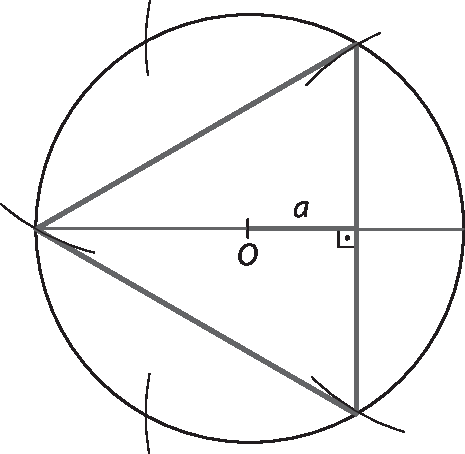
a)
L igual a, r vezes raiz quadrada de 3, igual a, 3 vezes raiz quadrada de 3.Logo, o lado do triângulo equilátero inscrito nessa circunferência mede
3 raiz quadrada de 3.centímetros.
b)
a, igual a, r sobre 2, igual a, 3 sobre 2, igual a 1 vírgula 5
Logo, o apótema dêsse triângulo mede 1,5 centímetro.
No exercício 17, a medida do raio da circunferência circunscrita a esse triângulo é r = 30 centímetros. Assim, podemos obter um esquema da situação:
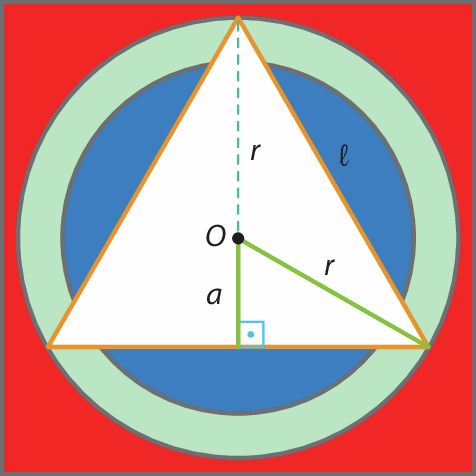
A medida ℓ do lado é dada por:
centímetros
Logo, a medida A da área dêsse triângulo equilátero, em centímetros quadrados, é igual a:
Como atividade complementar, pode-se pedir aos estudantes que pesquisem os malefícios do cigarro. Ao trabalhar esse tema, contribui-se para desenvolver a competência geral 8, pois os estudantes podem perceber e discutir a importância de cuidar da saúde.
As resoluções dos exercícios 15, 16 e 18 estão no início deste Manual, nas orientações específicas do capítulo 12.
19 Em uma circunferência, é inscrito um triângulo equilátero cujo lado mede
15 vezes raiz quadrada de 3.centímetros. Calcule a medida do lado do hexágono regular inscrito nessa circunferência.
20

Hora de criar – Junte-se a três colegas para discutirem e determinarem um tema para uma campanha em prol da melhora da vida da sua comunidade. Criem, usando polígonos e circunferências, um logotipo para essa campanha.
2. Medida da área de um polígono regular
Considere um polígono regular de n lados.
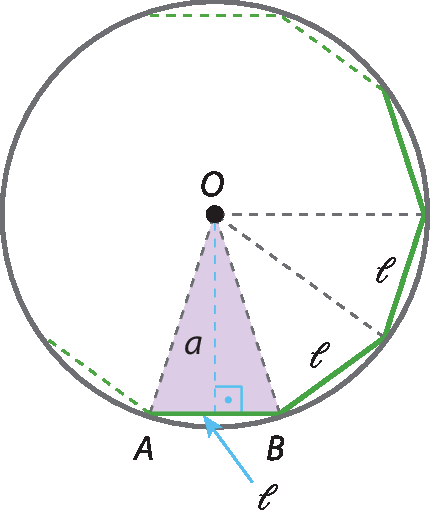
Indicando por 𝓁 a medida do lado do polígono e por a a medida de seu apótema, a medida da área do △á ó bê é dada por:
Como o polígono tem n lados congruentes, terá também n triângulos de mesma medida de área do △á ó bê.
Portanto, a medida da área A do polígono é dada por:
, ou seja,
A igual a, fração de numerador n vezes L vezes a, e de denominador 2.A medida do perímetro do polígono é n ⋅ 𝓁. Indicando essa medida por 2p, obtemos:

A = p ⋅ a

A medida p é chamada de medida do semiperímetro.
Acompanhe o exemplo a seguir.
Vamos calcular a medida da área de um decágono regular de lado medindo 12 centímetros. Considere tangente de 18graus = 0,32.
• Cálculo da medida do semiperímetro, em centímetro:
p igual a, fração de numerador 10 vezes 12, e de denominador 2, igual a, 60., ou seja, p = 60 centímetros
• Cálculo da medida do ângulo central:
a índice c, igual a, 360 graus sobre 10, igual.36graus
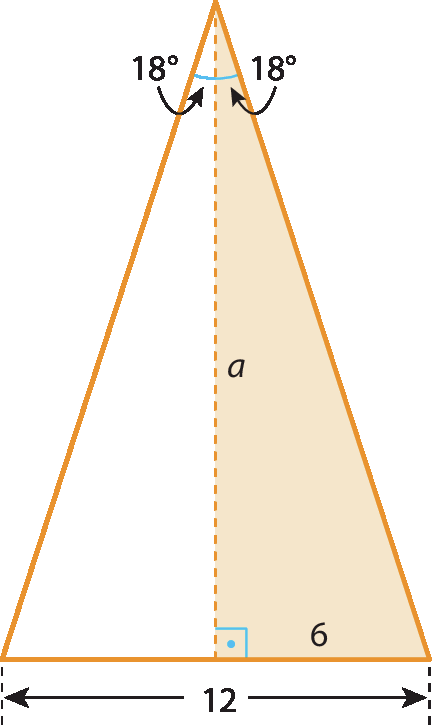
• Cálculo da medida a do apótema, em centímetro: tangente de 18graus =
fração 6 sobre a.a ⋅ 0,32 = 6
fração de numerador: a vezes 0,32 e de denominador 0,32, igual a, 6 sobre 0,32.
a = 18,75, ou seja, o apótema mede 18,75 centímetros.
Respostas e comentários
19. 15 centímetros
20. Resposta pessoal.
Exercícios propostos
Na resolução do exercício 19, indicando a medida do lado do triângulo equilátero por ℓ3 e a medida do lado do hexágono regular por ℓ6, temos:
=
15 vezes raiz quadrada de 3.Logo, r = 15 centímetros e ℓ6 = 15 centímetros.
O exercício 20 tem como objetivo fazer com que os estudantes utilizem polígonos e circunferências para criar um logotipo para uma campanha que eles irão determinar. É importante que todos os integrantes dos grupos participem das discussões. Ao final, peça aos grupos que apresentem os logotipos criados e que falem um pouco sobre o tema que pensaram.
2. Medida da área de um polígono regular
Habilidades da Bê êne cê cê: ê éfe zero nove ême ah um um e ê éfe zero nove ême ah um quatro.
Explore a figura inicial com os estudantes, reproduzindo-a na lousa. Amplie o triângulo destacado de modo que eles percebam que esse triângulo é isósceles, cuja base é o lado do polígono regular considerado (de medida ℓ), a altura é o apótema do polígono (de medida a) e os lados congruentes são raios da circunferência (de medida r).
Aproveite o momento e retome as propriedades válidas para um triângulo isósceles, indicando, principalmente, que nesse triângulo a altura relativa à base coincide com a bissetriz e a mediana relativas à mesma base.
• Cálculo da medida da área do polígono, em centímetro quadrado: A = p ⋅ a A = 60 ⋅ 18,75 A = .1125
Logo, a área do decágono regular mede .1125 centímetros quadrados.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
21 O professor de Matemática de uma escola promoveu um campeonato de pipas entre os estudantes. Para isso, passou a seguinte especificação: a pipa deverá ter a fórma de um hexágono regular de lados medindo 20 centímetros. Calcule as medidas do apótema e da área da pipa.

22 O lado de um pentágono regular mede 20 centímetros. Calcule a medida da sua área. (Dado: tangente de 36graus ≃ 0,73.)
23 Um eneágono regular é inscrito em uma circunferência de raio medindo 18 centímetros. Calcule a medida da sua área, sabendo que sen 20graus ≃ 0,34 e cos 20graus ≃ 0,93.
24 Esta figura faz parte de um anúncio publicitário.

Sabendo que o diâmetro da circunferência da figura mede 3,6 centímetros, determine a medida da área do triângulo equilátero impresso nesse anúncio.
25 Determine a medida da área das bases e a medida da área de superfície lateral de um cubo que tem uma das faces inscrita em uma circunferência de raio medindo 3 centímetros.
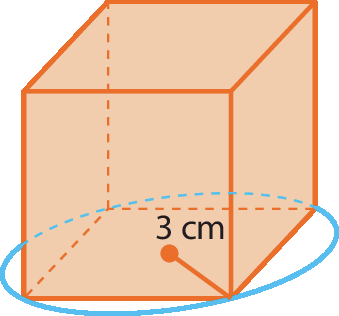
26 Observe as figuras a seguir.
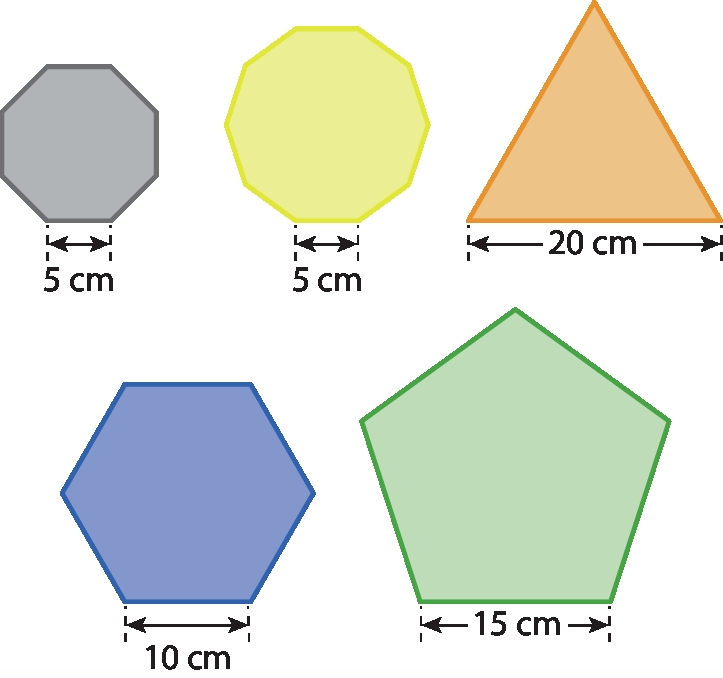
a) Represente em um gráfico de colunas as medidas das áreas dos polígonos regulares. (Considere:
Raiz quadrada de 3.= 1,73; tangente de 30graus = 0,58; tangente de 36graus = 0,73; tangente de 22,5graus = 0,41; tangente de 18graus = 0,32.)
b) Calcule a média das medidas das áreas desses polígonos (área média).
27

Hora de criar – Em dupla com um colega separem algumas revistas que possam ser recortadas. Após cada um escolher uma imagem (paisagem, flores, um rosto etcétera), colem as duas imagens em dois pedaços de cartolina ou papelão. Usando lápis e régua, tracem polígonos cobrindo toda a imagem. Depois, cada um de vocês deve recortar os polígonos traçados sobre suas imagens, fazendo um quebra-cabeça. Troque seu quebra-cabeça com o do colega para cada um montar o quebra-cabeça do outro.
(Usem tesouras com pontas arredondadas e as manuseiem com cuidado!)
Respostas e comentários
21. Medida do apótema:
10 raiz quadrada de 3.centímetros; medida da área:
600 raiz quadrada de 3, fim da raiz, centímetros quadrados..
22. Aproximadamente 395 centímetros quadrados.
23. Aproximadamente 922 centímetros quadrados.
24.
2,43 raiz quadrada de 3, fim da raiz, centímetros quadrados.25. Área das bases: 18 centímetros quadrados; área da superfície lateral: 72 centímetros quadrados.
26. a) Construção de gráfico.
26. b) 226,89 centímetros quadrados
27. Resposta pessoal.
Exercícios propostos
No exercício 21, o raio da circunferência que circunscreve o hexágono mede r = ℓ = 20 centímetros. Então, a medida a do apótema do hexágono é dada por:
Logo,
a igual 10 raiz quadrada de 3.centímetros.
A medida da área A dêsse hexágono é dada por:
Assim,
A igual 600 raiz quadrada de 3.centímetros quadrados.
No exercício 26, apresentamos o cálculo da medida da área do decágono regular. As demais medidas de áreas são obtidas de maneira análoga.
Cálculo da medida do ângulo central do decágono:
a índice c, igual a, 360 sobre 10, implica, a índice c, igual.
36graus
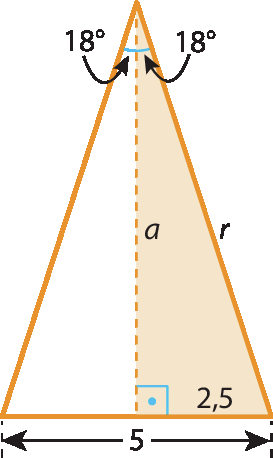
tg 18graus =
fração 2,5 sobre a.a igual a, 2,5 sobre 0,32 igual a 7,8125.
Assim, obtemos:
Área do decágono regular igual a p vezes a, igual. fração de numerador 10 vezes 5, e de denominador 2, fim da fração, vezes 7,8125
Portanto, Adecágono (regular) ≃ 195,31 centímetros quadrados.
dêsse modo, os estudantes devem obter as seguintes medidas de áreas:
• octógono regular: 121,95 centímetros quadrados;
• triângulo equilátero: 173 centímetros quadrados;
• hexágono regular: 259,5 centímetros quadrados;
• pentágono regular: 385,27 centímetros quadrados.
As resoluções dos exercícios 22 a 25 e dos demais itens do exercício 26 estão no início deste Manual, nas orientações específicas do capítulo 12.
No exercício 27, incentive os estudantes a compor diferentes quebra-cabeças com base nos conceitos já estudados neste capítulo. Proponha a eles que apresentem aos demais colegas as produções.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Ângela é proprietária de uma loja de artesanato. No final do ano, ela pretende oferecer como brinde aos clientes da loja um enfeite confeccionado em madeira. O enfeite será uma flor estilizada, formada por polígonos regulares: um hexágono e seis pentágonos.
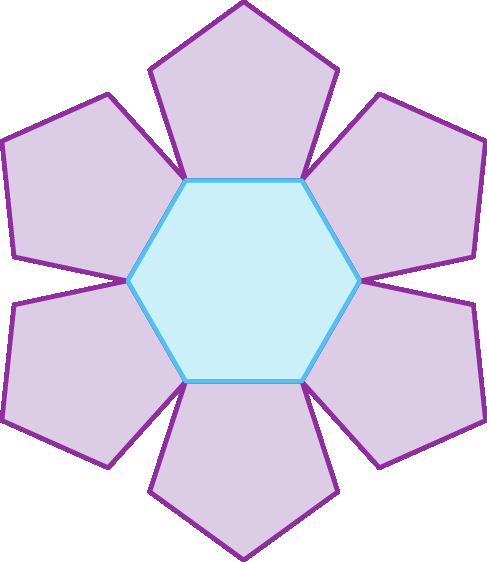
Sabendo que o hexágono tem lado de medida igual a 2,0 centímetros, determine a medida da área aproximada de madeira que Ângela utilizará para produzir cada enfeite. Considere tangente de 36º = 0,73.
3. Medida da área de um círculo
Considere um círculo de centro óh e raio de medida r.
Vamos inscrever nesse círculo um polígono regular de n lados, sendo a a medida do apótema do polígono.
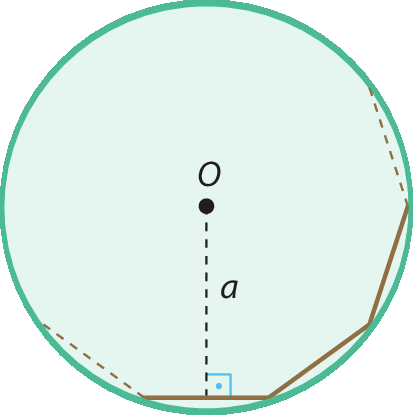
Supondo que o número de lados (n ) cresça indefinidamente, acontecerá o seguinte:
• a medida do perímetro 2p do polígono regular vai se aproximar da medida do comprimento 2πr da circunferência e, portanto, a medida do semiperímetro p se aproximará de πr ;
• a medida do apótema do polígono regular vai se aproximar da medida do raio do círculo;
• a medida da área do polígono regular vai se aproximar da medida da área do círculo.
Então, vamos encontrar uma fórmula que forneça a medida da área de um círculo:
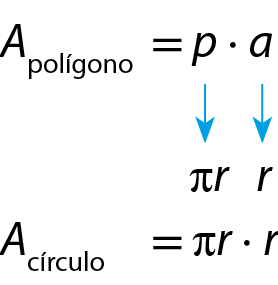
Acírculo = πr 2
Observe um exemplo.
Vamos calcular, em metro quadrado, a medida da área de uma praça circular que tem raio medindo 35 métros. Considere π ≃ 3,14.
Acírculo = π ⋅ r 2
Acírculo ≃ 3,14 ⋅ (35)2
Acírculo ≃ 3,14 ⋅ .1225
Acírculo ≃ .3846,50
Logo, a área da praça mede aproximadamente .3846,50 métros quadrados.
Respostas e comentários
Pense mais um poucoreticências: Aproximadamente 51,48 centímetros quadrados.
Pense mais um poucoreticências
Vamos indicar por a6 e por a5 as medidas dos apótemas do hexágono regular e do pentágono regular, respectivamente.
Para o hexágono regular, temos:
ℓ = r = 2 centímetros
Portanto,
a 6, igual, raiz quadrada de 3.centímetros.
centímetros
Para o pentágono regular, pela figura do enunciado, verificamos que o lado de cada pentágono regular mede ℓ = 2 centímetros (mesma medida do lado do hexágono). Então:
p 5, igual, fração 5 vezes 2 sobre 2, implica, p 5 igual a 5.centímetros
O ângulo central do pentágono regular mede:
Assim, cada triângulo isósceles que compõe cada um desses pentágonos regulares tem base medindo 2 centímetros e ângulo do vértice de 72graus:
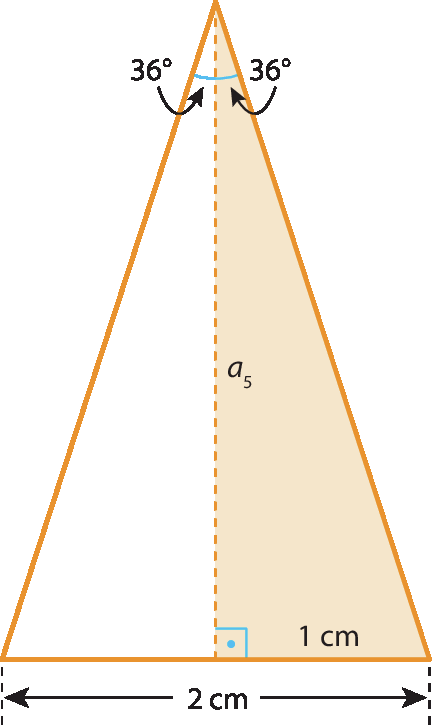
tangente de 36graus =
fração 1 sobre a 5.0,73 igual a, 1 sobre a índice 5, implica, a índice 5, igual a, 1 sobre 0,73.
Então, a5 ≃ 1,37 centímetro.
Apentágono(regular) ≃ 5 · 1,37
Logo, Apentágono(regular) ≃ 6,85 centímetros quadrados.
Medida aproximada da área de madeira utilizada em cada enfeite:
Amadeira ≃ 10,38 + 6 · 6,85
Assim, Amadeira ≃ 51,48 centímetros quadrados.
3. Medida da área de um círculo
Habilidades da Bê êne cê cê: ê éfe zero nove ême ah um um e ê éfe zero nove ême ah um quatro.
Explore com os estudantes a determinação da medida da área do círculo. Sugira a eles que desenhem polígonos regulares inscritos em uma mesma circunferência, cada vez com maior número de lados, para que percebam a ideia de limite que pode ser associada à comparação da medida da área do círculo com a de um polígono regular de n lados, com n tendendo ao infinito (quanto maior o número n, melhor é a aproximação da medida dessas áreas).
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
28 (saréspi) Juliana colocou um copo molhado sobre a mesa, onde ficou a marca da base circular do copo. A área da marca mede 16π centímetros quadrados.

O diâmetro da base do copo mede:
a) 4 centímetros.
b) 8 centímetros.
c) 16 centímetros.
d) ≃ 5,7 centímetros.
29 (Fuvésti-São Paulo) O triângulo á bê cê é inscrito em uma circunferência de raio medindo 5 centímetros. Sabe-se que a e B são extremidades de um diâmetro e que a corda
BCmede 6 centímetros. Então a área do triângulo á bê cê, em centímetros quadrados, mede:
a) 24.
b) 12.
c)
fração de numerador 5 vezes raiz quadrada de 3, e de denominador 2.
d)
6 vezes raiz quadrada de 3..
e)
2 vezes raiz quadrada de 3..
30 (unifór-Ceará) Um triângulo está inscrito em uma circunferência de centro óh, como mostra a figura a seguir.
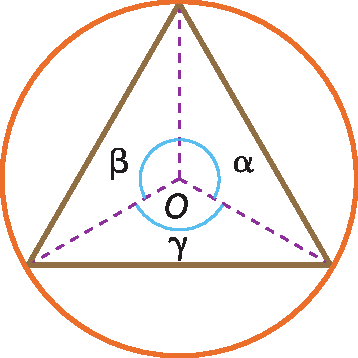
Se o raio da circunferência mede 1 centímetro e os ângulos α, β e γ são congruentes, então o lado do triângulo mede:
a) 1,2 centímetro.
b) 1,3 centímetro.
c)
raiz quadrada de 2.centímetros.
d) 1,5 centímetro.
e)
raiz quadrada de 3.centímetros.
31 Junte algumas moedas de diferentes valores. Com uma régua, meça cada diâmetro em milímetro, e calcule a medida da área aproximada da face de cada uma delas. Em seguida, construa uma tabela com essas medidas.
32 Calcule a medida da área da parte pintada de lilás, considerando
raiz quadrada de 3.= 1,73 e π = 3,14.
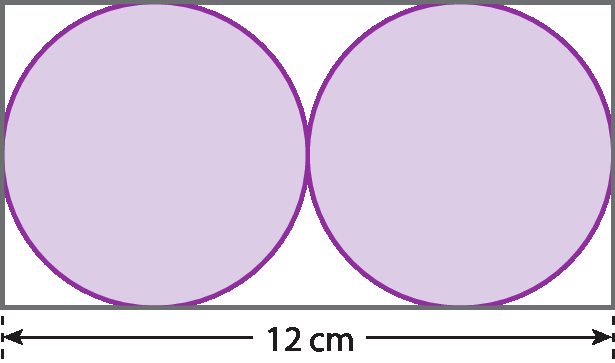
33 Calcule a medida da área aproximada da parte pintada de verde, sabendo que A bê = 4 centímetros.

34 Durante uma aula de Arte, Pedro elaborou um painel, conforme a figura a seguir.

Esse painel foi feito em um papel quadriculado cujo quadradinho mede 3 centímetros de lado. Determine a medida da área da parte pintada de verde.
35 Na figura, r é a medida do raio da circunferência em uma unidade u, e
Arco AB congruente arco BC congruente arco CD congruente arco DE congruente arco EF congruente arco FA.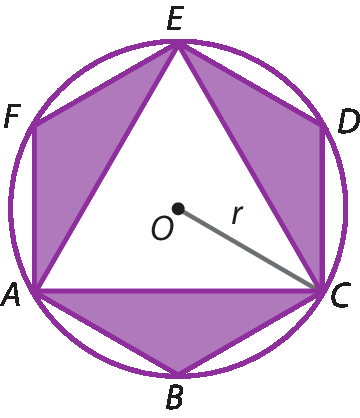
Calcule a medida da área da região pintada de roxo.
36 Retomando a situação de Edgard sobre o projeto de construção de mostradores de relógios de parede, descrita no início do capítulo, considere um polígono regular de 12 lados inscrito em uma circunferência de raio medindo 10 centímetros.
a) Quanto mede o ângulo central do polígono?
b) Use o quadro de razões trigonométricas da página 204, com duas casas decimais, para determinar as medidas do apótema e do lado dêsse polígono.
c) Qual é a diferença entre as medidas do comprimento da circunferência e do perímetro dêsse polígono?
d) Qual é a medida da área dêsse polígono?
Respostas e comentários
28. Alternativa b.
29. Alternativa a.
30. Alternativa e.
31. Construção de tabela.
32. 56,52 centímetros quadrados
33. 6,28 centímetros quadrados
34. 36 centímetros quadrados
35.
Fração de numerador 3 r elevado ao quadrado, fim do expoente, vezes raiz quadrada de 3, e de numerador 4, fim da fração, u elevado ao quadrado.36. a) 30graus
36. b) Medida do apótema: 9,70 centímetros; medida do lado: 5,20 centímetros.
36. c) 0,4 centímetro
36. d) 302,64 centímetros quadrados
Exercícios propostos
No exercício 31, uma coleção de moedas pode ser formada pelas que estão em circulação no Sistema Monetário Brasileiro. Fazendo as medições dos diâmetros e usando π = 3,14, podemos montar a seguinte tabela:
|
Valor da moeda |
Medida do diâmetro (em mm) |
Medida da área (em mm2) |
|---|---|---|
|
R$ 0,05 |
22 |
379,94 |
|
R$ 0,10 |
20 |
314 |
|
R$ 0,25 |
25 |
490,625 |
|
R$ 0,50 |
23 |
415,265 |
|
R$ 1,00 |
27 |
572,625 |
Dados obtidos na coleção de moedas considerada.
No exercício 34, vamos analisar um dos conjuntos de quadradinhos que formam uma parte da área pintada de verde:

Nesse conjunto, a área destacada em amarelo nos quadradinhos 1 e 3 juntos é igual à área em verde nos quadradinhos 2 e 4 juntos. Trocando nesse conjunto a parte em amarelo com essas partes em verde, temos:
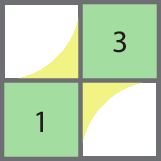
A área em verde corresponde à área de 2 quadradinhos. Como no painel há dois conjuntos com regiões idênticas pintadas de verde, temos que nele toda a área pintada de verde corresponde à área de 4 quadradinhos (3 centímetros de lado). Ou seja:
Averde = 4 · 32
Portanto, Averde = 36 centímetros quadrados.
As resoluções dos exercícios 28 a 30 e dos exercícios 32, 33, 35 e 36 estão no início deste Manual, nas orientações específicas do capítulo 12.
PARA SABER MAIS
Construção de polígono regular de êne lados
Lizandra precisa programar um tear eletrônico para compor contornos de polígonos regulares na fabricação de tecidos.

Acompanhe as etapas do programa que ela elaborou para a máquina seguir, também descritas no fluxograma.
1. Definir a medida do comprimento 𝓁 centímetro do lado do polígono.
2. Definir o número n de lados do polígono, n ⩾ 3.
3. Definir o número k = 1.
4. Calcular a medida
a índice e, igual a, 360 graus sobre n.do ângulo externo.
5. Bordar em linha reta caminho com 𝓁 centímetro.
6. Fazer k = k + 1.
7. Se k > n, desligar a máquina.
8. Girar no sentido horário ae graus e voltar para o item 5.
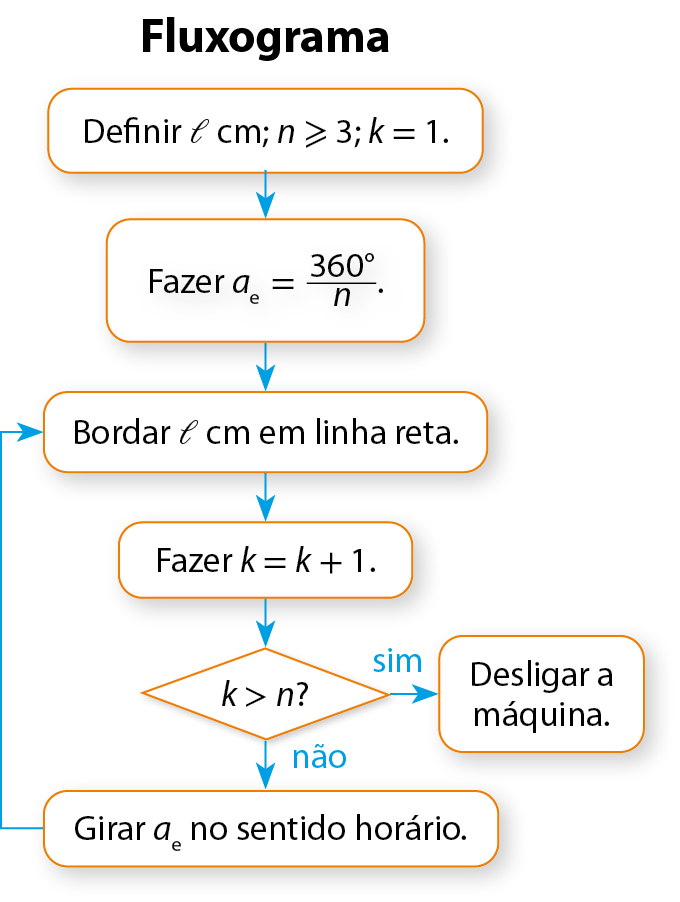
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Seguindo as etapas descritas por Lizandra, escolha um número n de lados e construa em uma folha avulsa um polígono regular de lados medindo 6 centímetros.
2 Construa novamente o polígono da atividade 1 mudando o item 8 para “Girar no sentido anti-horário ae graus e voltar para o item 5”.
Respostas e comentários
1. Construção de figura.
2. Construção de figura.
Para saber mais
Nessa seção, ao trabalhar com fluxogramas, contribui-se para o desenvolvimento da habilidade (ê éfe zero nove ême ah um cinco).
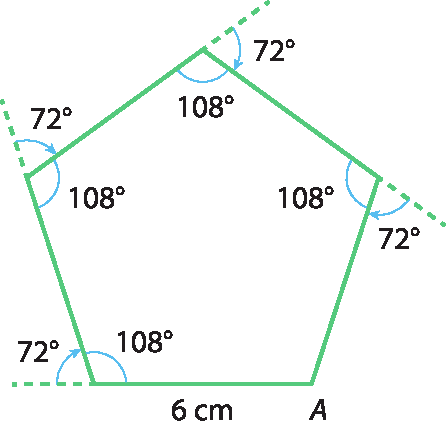
Na atividade 1 do Agora é com você!, escolhendo n = 5, por exemplo, o procedimento será:
Com ae = 72graus (pois 360graus : 5 = 72graus) e iniciando no ponto A, traçamos um segmento de 6 centímetros (“bordar 6 centímetros em linha reta”), que é o primeiro lado; para k = 2, com n = 5, obtemos 2 < 5, ou seja, k não é maior do que n; seguimos o fluxograma e giramos 72graus no sentido horário; traçamos outro segmento de 6 centímetros (segundo lado); para k = 3, temos k < n, então giramos 72graus no sentido horário; traçamos outro segmento de 6 centímetros (terceiro lado); para k = 4, temos k < n, portanto, giramos 72graus no sentido horário; traçamos outro segmento de 6 cm (quarto lado); para k = 5, com n = 5, temos k < n e giramos 72graus no sentido horário; traçamos outro segmento de 6 centímetros (quinto lado) e voltamos ao ponto A; para k = 6, temos k > n, então desligamos a máquina e o pentágono está construído.
A resolução da atividade 2 está no início deste Manual, nas orientações específicas do capítulo 12.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Todas as figuras a seguir são formadas por duas circunferências concêntricas cujos raios medem 2 centímetros e 3 centímetros, mas apenas duas delas podem ser sobrepostas de modo que toda a região contida nas circunferências esteja pintada de verde. Descubra que figuras são essas e determine a medida da área da região pintada de verde em cada uma dessas figuras.
a)
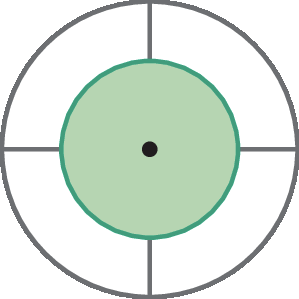
b)
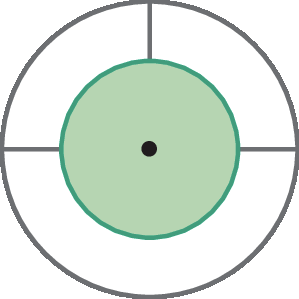
c)
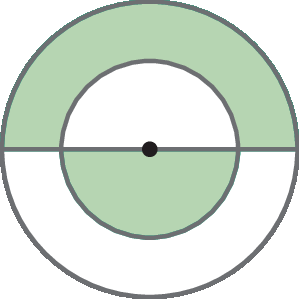
d)
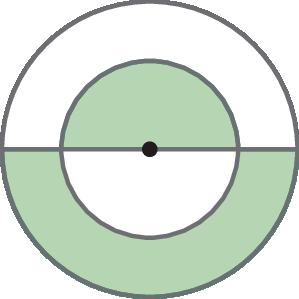
e)
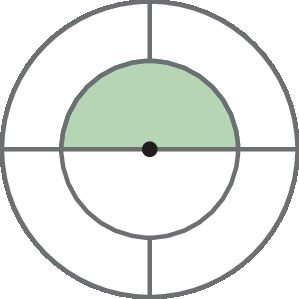
f)
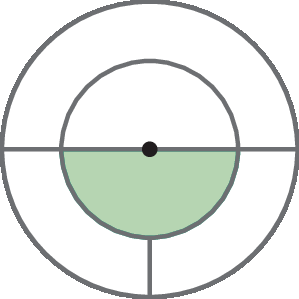
Medida da área de uma coroa circular
A figura a seguir mostra dois círculos concêntricos. O círculo menor tem raio de medida r, e o círculo maior, raio de medida R.
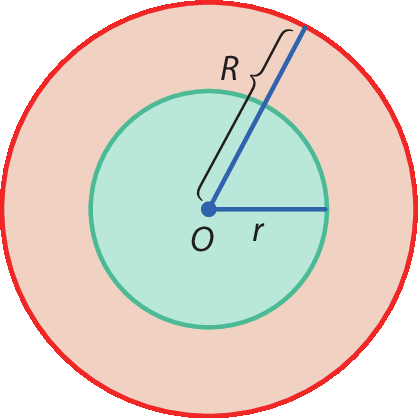
A parte da figura pintada de vermelho é chamada de coroa circular.
Observe que a medida da área da coroa circular é igual à diferença entre as medidas das áreas dos dois círculos, ou seja:
Acoroa circular = πR 2 ‒ πr 2
Acoroa circular = π(R 2 ‒ r 2)
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
37 Calcule a medida aproximada da área pintada de azul em cada uma das figuras a seguir.
a)
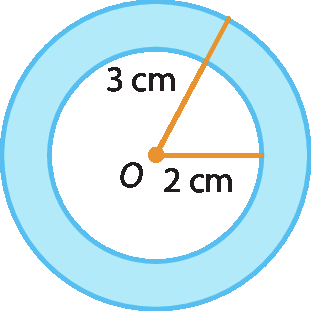
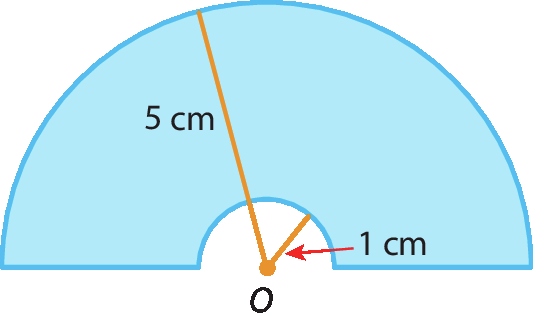
b)
38 Dois círculos concêntricos de raios medindo 6 centímetros e 2 centímetros formam uma coroa circular.
Calcule a medida da área dessa coroa.
Respostas e comentários
Pense mais um poucoreticências: Alternativas c, d; medida da área:
fração 9 pi sobre 2.centímetros quadrados.
37. a) Aproximadamente 15,70 centímetros quadrados.
37. b) Aproximadamente 37,68 centímetros quadrados.
38. 100,48 centímetros quadrados
Pense mais um poucoreticências
As únicas duas figuras que podem ser sobrepostas são as das alternativas c e d, pois rotacionando uma delas 180graus em torno do centro, pode-se perceber que são idênticas. Observe o cálculo da medida da área (A) pintada de verde nesse caso.
Logo,
A igual a 9pi sobre 2.centímetros quadrados.
Alternativamente, pode-se perceber que a medida da área verde de cada figura é igual à metade da medida da área de um círculo de medida do raio igual a 3 centímetros.
Medida da área de uma coroa circular
Pergunte aos estudantes se eles se lembram da definição de coroa circular:
Coroa circular é a região do plano limitada por duas circunferências concêntricas.
Depois, diga que a medida da área de uma coroa circular é obtida por meio da medida de área do círculo de raio maior subtraída da medida de área do círculo de raio menor.
As resoluções dos exercícios 37 e 38 estão no início deste Manual, nas orientações específicas do capítulo 12.
Pense mais um poucoreticências
FAÇA A ATIVIDADE NO CADERNO
Adotando π = 3,14, calcule:
• a medida da área total da parte verde do alvo;
• a medida da área total da parte amarela do alvo.
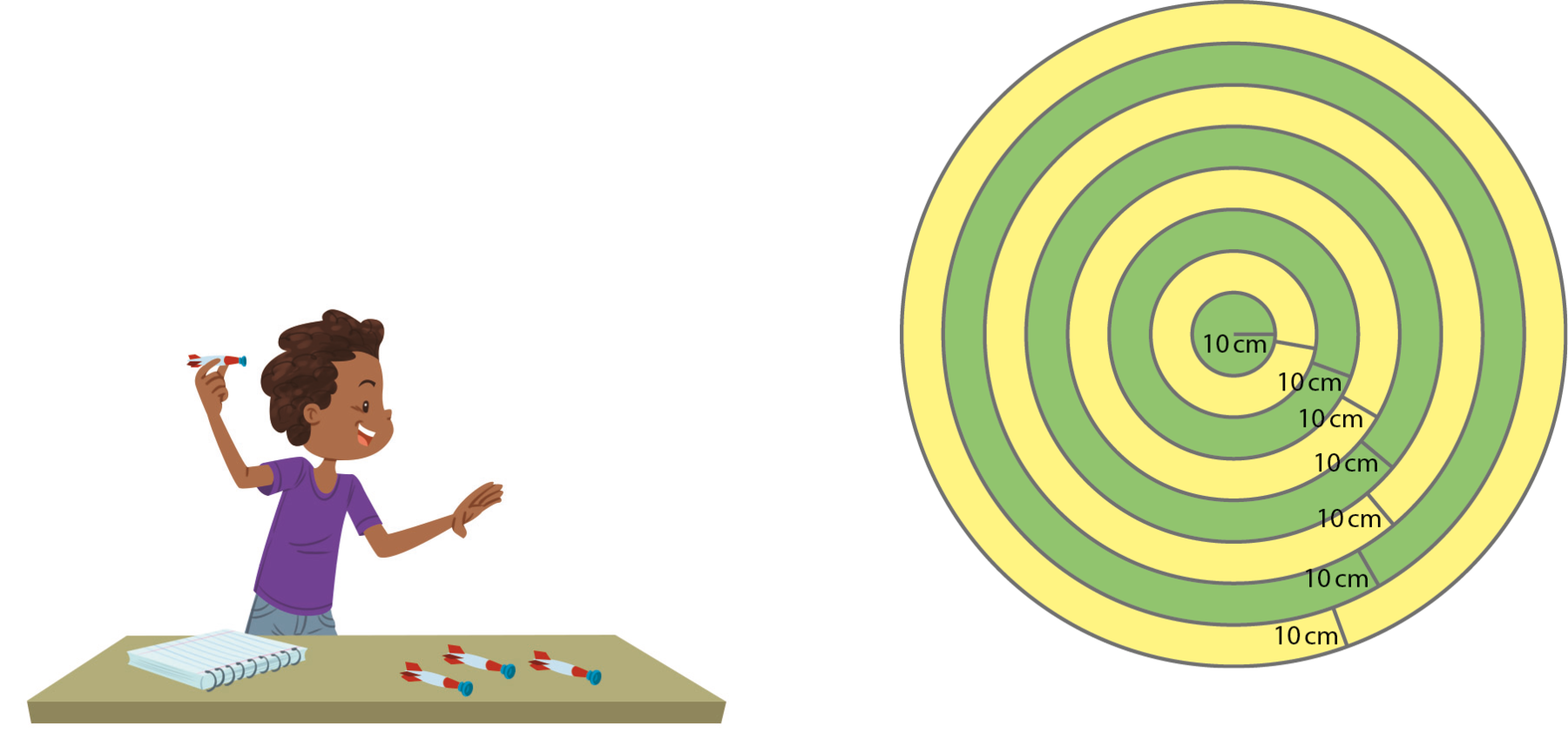
(As imagens não respeitam as proporções reais entre os objetos.)
Medida da área de um setor circular
Todo ângulo central determina em um círculo uma região chamada de setor circular.
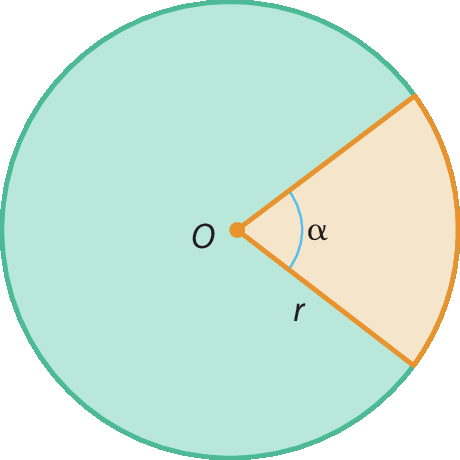
Considerando o setor circular em que a medida do ângulo central, em grau, é α, podemos calcular a medida da área dêsse setor estabelecendo uma proporção. Observe.

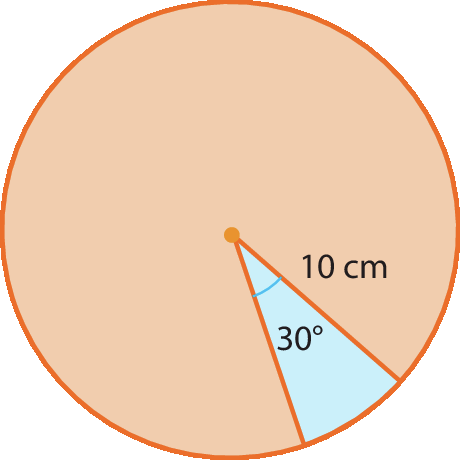
Acompanhe um exemplo.
Vamos calcular a medida da área do setor circular cujo ângulo central mede 30graus e cujo raio mede 10 centímetros.
Pelo enunciado, temos: α = 30graus e r = 10 centímetros.
Assim:
12 ⋅ Asetor circular = 100π
Portanto, a medida da área do setor circular é
fração 25 pi sobre 3.centímetros quadrados.
Respostas e comentários
Pense mais um poucoreticências: Parte verde: .8792 centímetros quadrados; parte amarela: .11304 centímetros quadrados.
Pense mais um poucoreticências
Sejam Cn os círculos de raio medindo 10n centímetros no esquema dado, com n = 1, 2, reticências, 7. Assim, C₁ é o círculo central de raio medindo 10 centímetros e C₇ é o círculo de raio medindo 70 centímetros, por exemplo. A área da região verde é dada pela relação entre as áreas desses círculos:
Averde = (AC7 ‒ AC6) + (AC5 ‒ AC4) + (AC3 ‒ AC2) + AC1
Cálculo da medida da área de cada círculo, em centímetros quadrados:
AC7 = π · 702 ⇒ AC7 = .15386
AC6 = π · 602 ⇒ AC6 = .11304
AC5 = π · 502 ⇒ AC5 = .7850
AC4 = π · 402 ⇒ AC4 = .5024
AC3 = π · 302 ⇒ AC3 = .2826
AC2 = π · 202 ⇒ AC2 = .1256
AC1 = π · 102 ⇒ AC1 = 314
Cálculo da medida da área verde, em centímetros quadrados:
A = (.15386 ‒ .11304) + (.7850 ‒ .5024) + (.2826 ‒ .1256) + 314
A = .4082 + .2826 + .1570 + 314
A = .8792
Como AC8 = π · 802 = .20096 centímetros quadrados, temos:
Aamarela = AC8 ‒ Averde = .20096 ‒ .8792
Portanto, Aamarela = .11304 centímetros quadrados.
Medida da área de um setor circular
Pergunte aos estudantes se eles se lembram da definição de setor circular:
Setor circular é uma região do círculo delimitada por dois de seus raios e um arco.
Explore a noção de proporcionalidade envolvida no cálculo da medida da área de um setor circular. Comente com os estudantes que esse cálculo pode ser usado para determinar a medida da área dos setores circulares de um gráfico de setores e, assim, construir gráficos dêsse tipo.
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
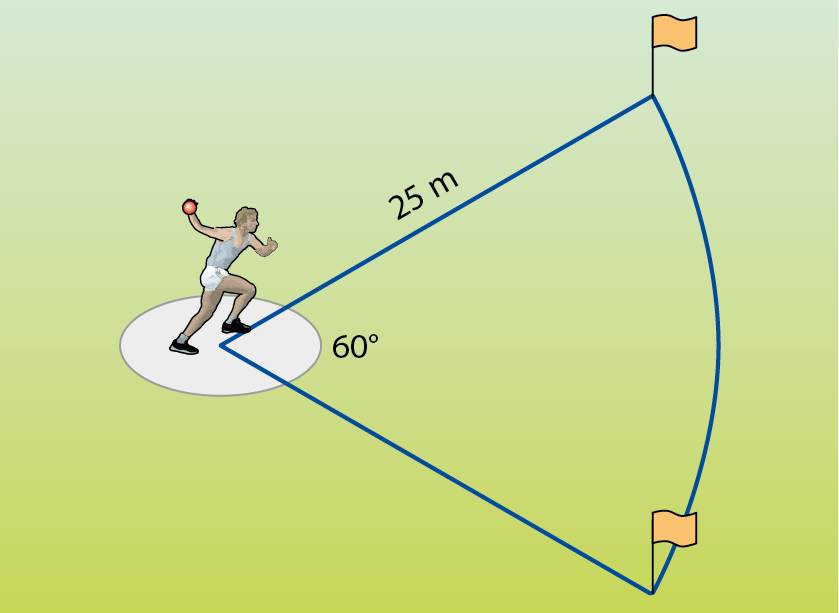
39 Em uma pista de atletismo, o campo de arremesso de peso tem a fórma de um setor circular com 60º de abertura e raio medindo 25 métros. Calcule a medida da área dêsse campo.
40 Para fazer um molde, Clarice desenhou a figura a seguir.
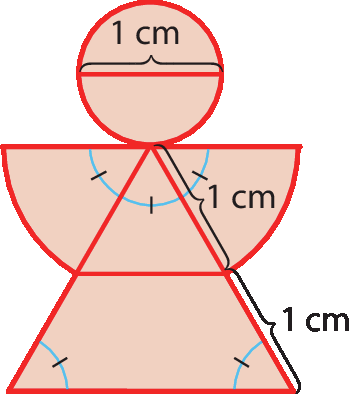
Calcule a medida da área aproximada da figura desenhada por Clarice.
41 Em uma circunferência cujo raio mede 15 centímetros, o arco de um setor circular mede 10π centímetros. Determine:
a) a medida do ângulo central dêsse setor;
b) a medida da área dêsse setor.
42 (púqui-Rio de Janeiro) Triplicando-se o raio de uma circunferência:
a) a medida da área é multiplicada por 9π.
b) a medida do comprimento é multiplicada por 3π.
c) a medida da área é multiplicada por 9, e a do comprimento, por 3.
d) as medidas da área e do comprimento são ambas multiplicadas por 3.
e) a medida da área é multiplicada por 3, e a do comprimento, por 9.
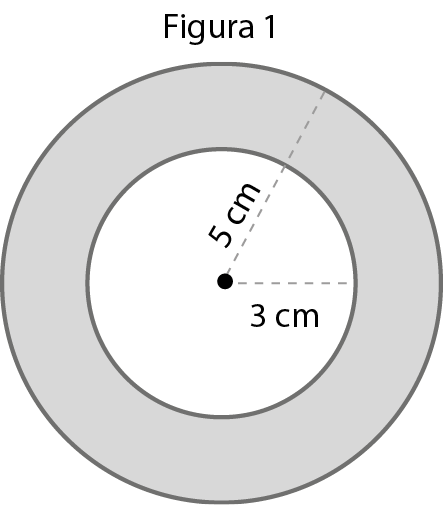
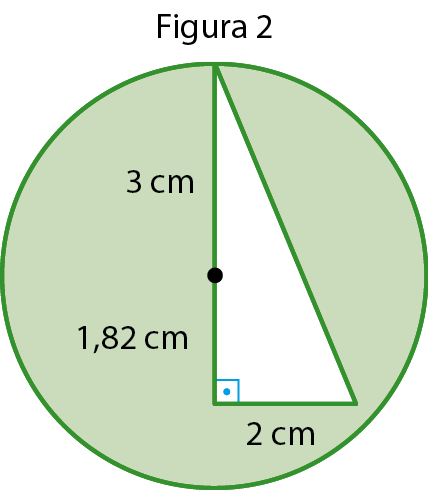
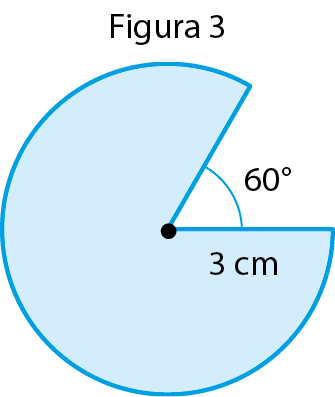
43 Em cada figura, calcule a medida da área da parte colorida. Em seguida, verifique se existem figuras equivalentes. (Adote π = 3,14.)

44 (Fuvésti-São Paulo) Um comício político lotou uma praça semicircular cujo raio mede 130 métros. Admitindo uma ocupação média de quatro pessoas por métro quadrado, qual é a melhor estimativa do número de pessoas presentes?
a) dez mil
b) cem mil
c) meio milhão
d) um milhão
e) muito mais de um milhão
45 (Vunéspi) Um cavalo se encontra preso em um cercado de pastagem cuja forma é um quadrado, com lado medindo 50 métros. Ele está amarrado a uma corda de 40 métros que está fixada em um dos cantos do quadrado. Considerando π = 3,14, calcule a medida da área, em metro quadrado, da região do cercado que o cavalo não conseguirá alcançar, porque está amarrado.
a) .1244
b) .1256
c) .1422
d) .1424
e) .1444
Respostas e comentários
39.
fração 625 pi sobre 6.métros quadrados ≃ 327 métros quadrados
40. 3,56 centímetros quadrados
41. a) 120graus
41. b) 75π centímetros quadrados
42. Alternativa c.
43. Figura 1: 50,24 centímetros quadrados; figura 2: 23,44 centímetros quadrados; figura 3: 23,55 centímetros quadrados; figura 4: 23,44 centímetros quadrados. As figuras 2 e 4 são equivalentes.
44. Alternativa b.
45. Alternativa a.
Exercícios propostos
Para a resolução do exercício 39, vamos considerar π ≃ 3,14. Assim, a medida A da área do setor circular é dada por:
Logo,
A igual a 625 pi sobre 6, implica, A aproximadamente igual a 327.métros quadrados.
No exercício 40, vamos considerar π = 3,14 e
raiz quadrada de 3.= 1,73. Na figura, todos os ângulos demarcados medem 60graus, pois são ângulos internos de um triângulo equilátero cujo lado mede ℓ = 2 centímetros.
Assim, a figura é composta de um círculo de raio medindo 0,5 centímetro, dois setores circulares de 60graus e raio de 1 centímetro e uma região determinada por um triângulo equilátero de lado medindo 2 centímetros.
• Cálculo da medida da área do círculo, em centímetro quadrado: πr2 = 3,14 · (0,5)2 Ac = 0,785
• Cálculo da medida da área de cada setor circular, em centímetro quadrado:
As ≃ 0,523
• Cálculo da medida da área do triângulo equilátero, em centímetro quadrado:
A medida da área da figura, em centímetro quadrado, é dada pela soma das medidas das áreas dos elementos que a compõem:
Afigura ≃ (0,785 + 2 · 0,523 + 1,73) ≃ 3,56
No exercício 44, a medida a da área, em métro quadrado, de um semicírculo de raio medindo 130 métros é dada por:
A = .8450π
Como admitimos uma ocupação média de 4 pessoas por metro quadrado, fazendo π = 3,14, temos:
4 · .8450 · 3,14 ≃ .106132
Logo, a melhor estimativa, entre as alternativas, é cem mil pessoas.
As resoluções dos exercícios 41 a 43 e 45 estão no início deste Manual, nas orientações específicas do capítulo 12.
TRABALHANDO A INFORMAÇÃO
Atenção ao ler gráficos
Ler um texto ou assistir a um filme requer atenção, assim como acontece com a leitura de um gráfico, especialmente gráficos duplos em que compará-los é inevitável e desejado.
Há gráficos que apresentam erros em sua construção, e outros que apresentam inadequações.
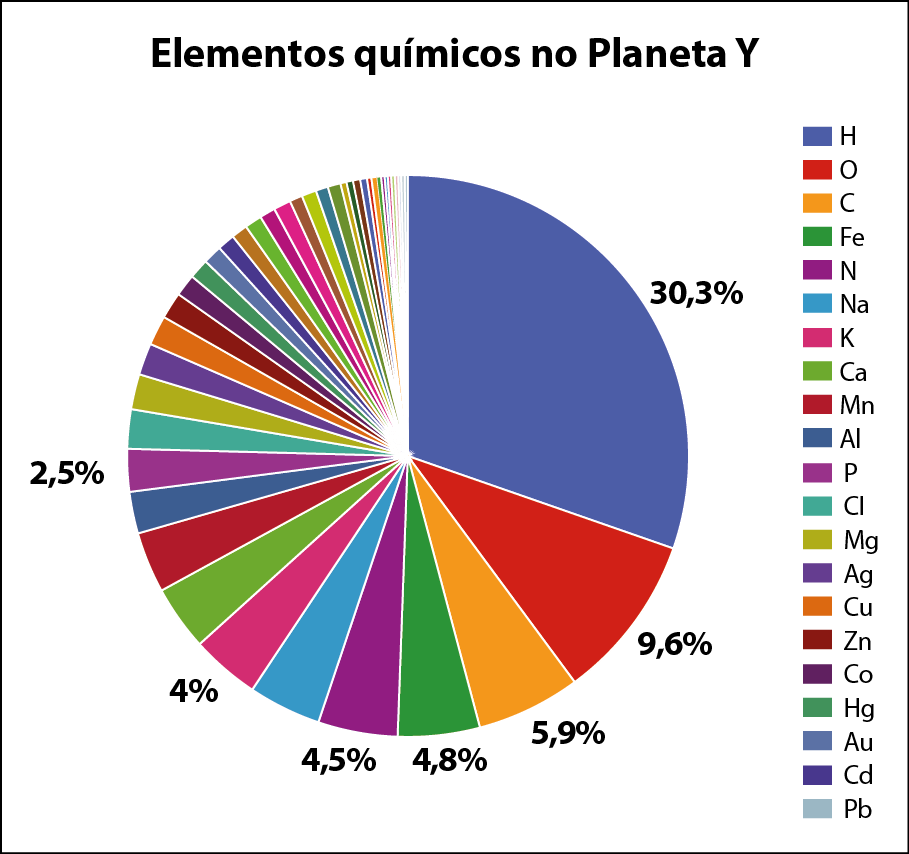
• Em um gráfico de setores, por exemplo, um erro banal é quando a soma das porcentagens dos setores, exceto nos casos de arredondamento, difere de 100% (ver gráfico 1). Já uma inadequação é haver uma quantidade muito grande de setores e de cores muito parecidas, tornando as legendas incompreensíveis (ver gráfico 2).
Gráfico 1
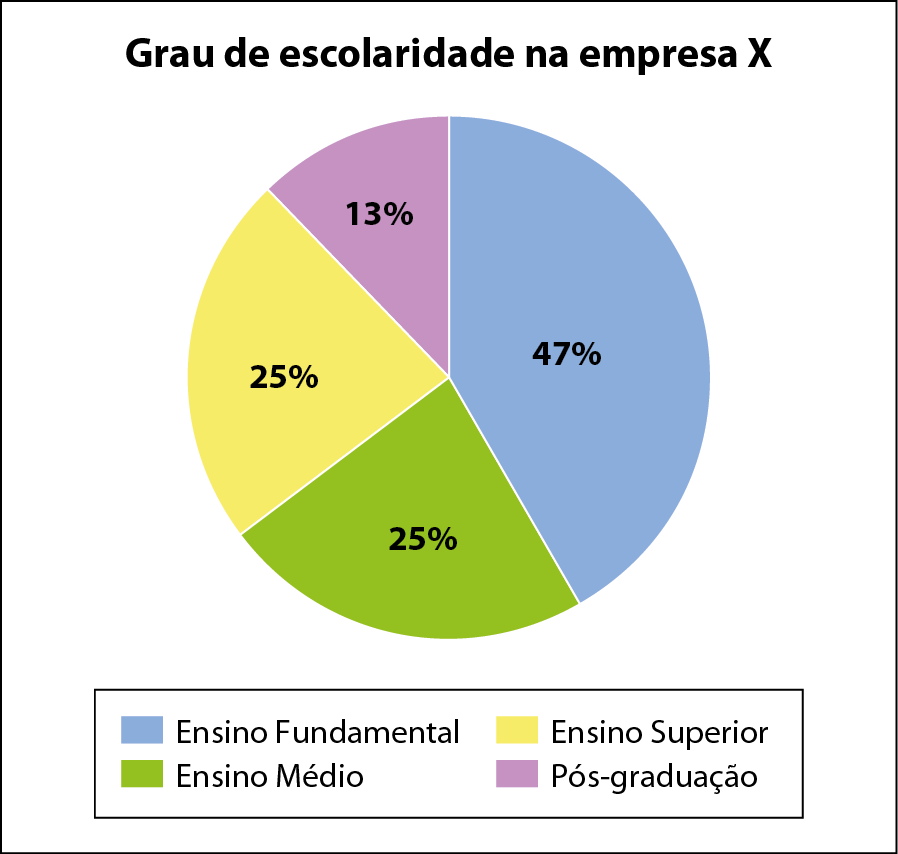
Gráfico 2
• Em gráficos de colunas ou gráficos de barras, os erros mais comuns ocorrem por não contemplarem a proporcionalidade entre os comprimentos das colunas/barras e os valores que elas representam.
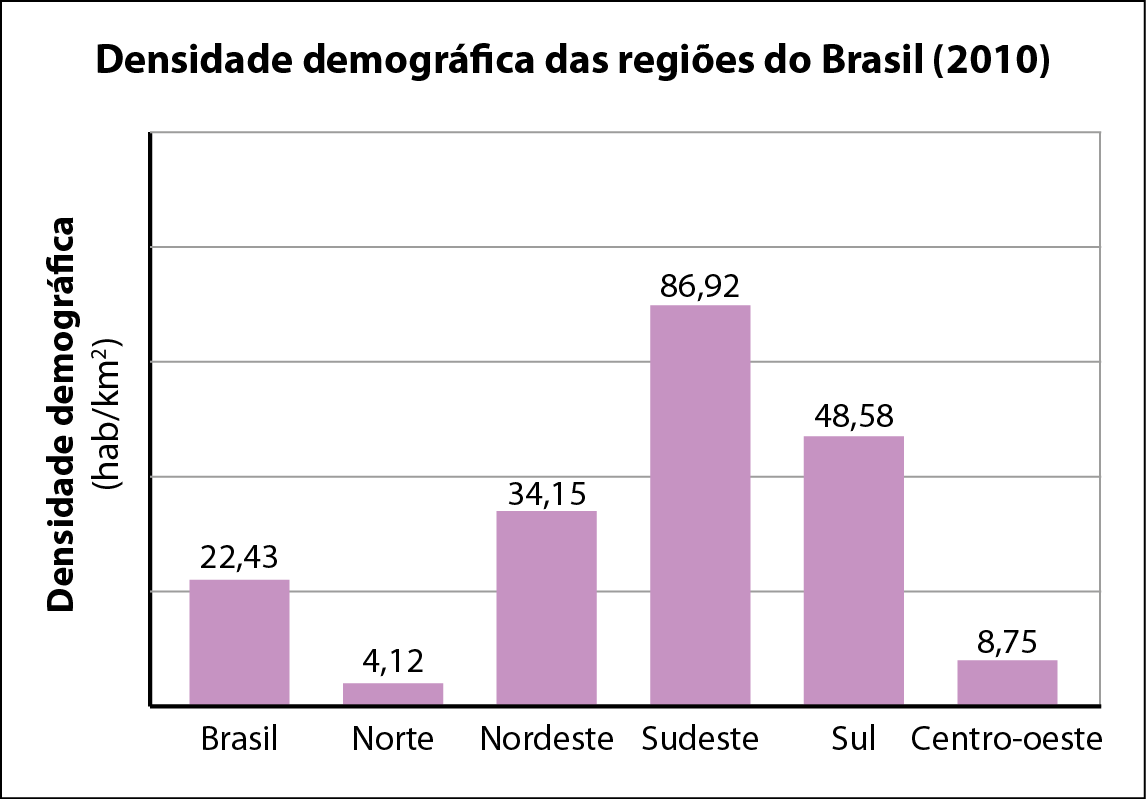
Observe que a coluna referente à região Sudeste não é proporcional às demais colunas. Por exemplo, com o compasso no gráfico, se adicionarmos a altura da coluna Brasil e a da coluna Sul, veremos que uma sobre a outra resulta quase na altura da coluna Sudeste. No entanto, a soma dos valores 22,43 + 48,58 = 71,01 é diferente do valor da coluna Sudeste (86,92). Se o eixo vertical fosse graduado (não graduá-lo é um erro), a falta de proporcionalidade dificilmente ocorreria.
(Ao usar o compasso, atenção para não se machucar com a ponta-seca.)
Respostas e comentários
Trabalhando a informação
Habilidade da Bê êne cê cê: ê éfe zero nove ême ah dois um.
Nesta seção, trabalhamos com gráficos cujos elementos induzem a erros de leitura e interpretação, desenvolvendo, assim, a habilidade (EF09MA21).
Antes de trabalhar o texto desta seção apresente apenas os gráficos em cópia ampliada, fixando-os na lousa, para que os estudantes explorem cada gráfico. Verifique, por exemplo, se eles percebem que no gráfico 1, de maneira equivocada, o total é 110% e não 100%. Eles podem observar esse fato na própria figura (sem efetuar a soma das porcentagens), pois os dois setores de 25% deveriam corresponder à metade do círculo, mas não é o que acontece.
Para ampliar a discussão, apresente outros gráficos de setores.
Analise com eles o gráfico de colunas apresentado, sobre a densidade demográfica das regiões do Brasil, e verifique se percebem que nem todas as colunas têm a altura proporcional às demais. Espera-se que os estudantes percebam que a coluna referente à região Sudeste não é proporcional às demais, pois sua altura deveria ser quase o dobro da altura da coluna referente à região Sul.
• Uma inadequação que por vezes ocorre tanto em gráficos de colunas quanto em gráficos de linhas duplas é quando a graduação do eixo vertical não inicia do zero. No gráfico de linhas duplas, por exemplo, esse fato pode induzir o leitor a erros ao comparar os valores de cada linha em uma mesma vertical. Acompanhe no gráfico a seguir.
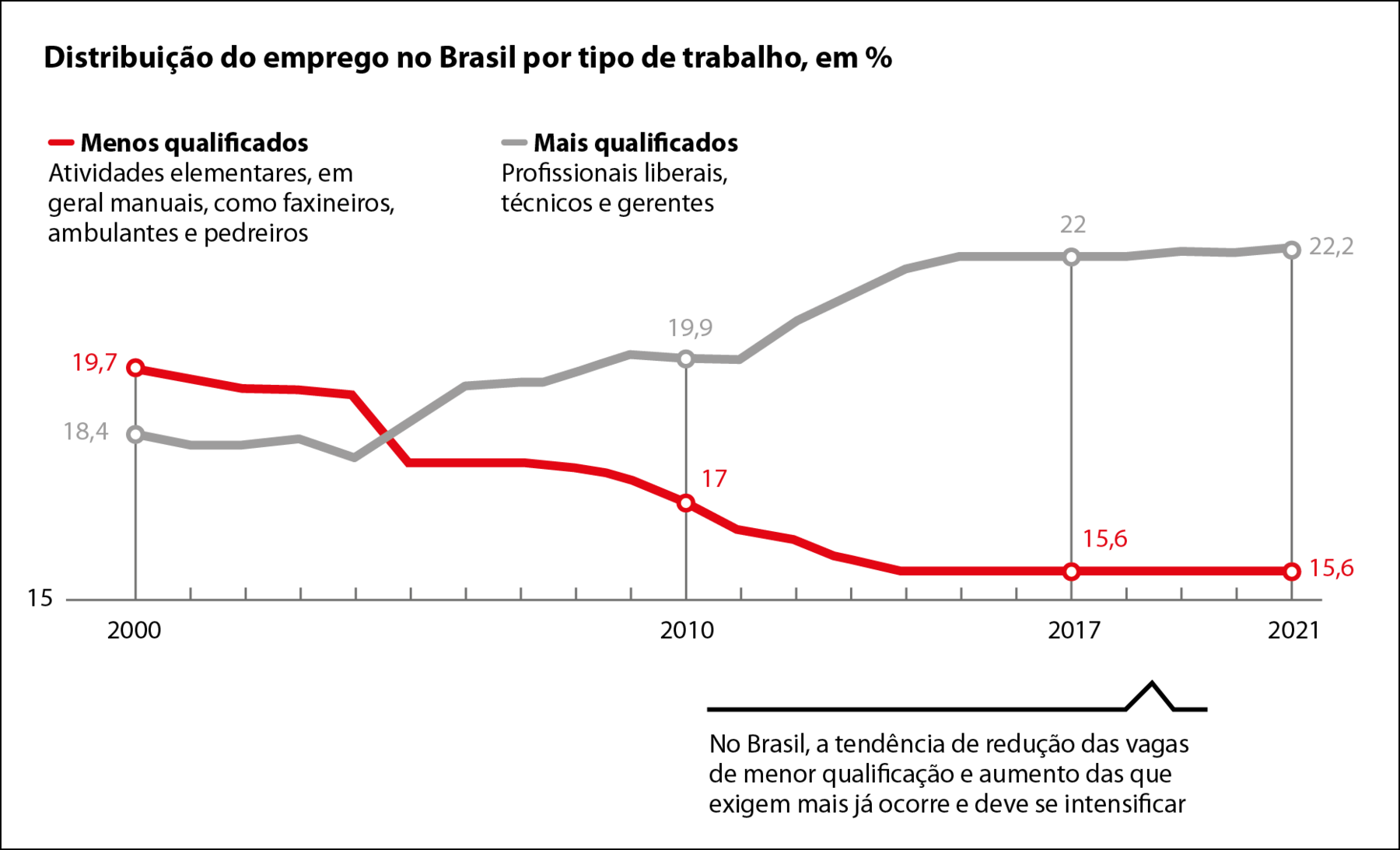
Observe que os valores do eixo vertical não começam no zero, mas no 15. O fato de a escala vertical iniciar no valor 15 faz com que em 2010, por exemplo, tenhamos a impressão de que a porcentagem de empregos mais qualificados (19,9) seja pouco mais do que o dobro (ou seja, 100%) da porcentagem de empregos menos qualificados (17). Mas isso não é verdade: 19,9 é apenas 17% maior do que 17, pois 19,9 : 17 ≃ 1,17.
Agora observe os valores de 2021. Calculando 22,2 : 15,6 ≃ 1,42. Isso significa que 22,2 é aproximadamente 42% maior do que 15,6. No entanto, no gráfico, a altura de 22,2 é 10 vezes maior do que a altura de 15,6, ou seja, .1000% maior.
A compreensão da leitura que obtemos em um gráfico como esse pode nos induzir a conclusões equivocadas. Por isso, é preciso muita atenção na leitura.
Agora quem trabalha é você!
FAÇA A ATIVIDADE NO CADERNO
Considerando o gráfico “Distribuição do emprego no Brasil por tipo de trabalho, em porcentagem” responda:
a) Em que ano os dois tipos de emprego representavam a mesma porcentagem?
b) Em 2000, o emprego menos qualificado era aproximadamente quantos por cento maior do que o emprego mais qualificado?
Respostas e comentários
a) Em 2004.
b) 7%
Agora quem trabalha é você!
As atividades propostas podem ser respondidas em duplas, pois a discussão enriquece o aprendizado e amplia o repertório de estratégias de resolução dos estudantes.
No item a, os estudantes devem observar no gráfico de linhas o ano em que as linhas se cruzam, pois isso indica quando a distribuição dos tipos de empregos foi igual; isso ocorreu em 2004 (quatro marcações após 2000 e antes da quinta marcação).
No item b, considerando que no ano 2000 as porcentagens indicadas são 19,7% e 18,4%, temos que 19,7 é cêrca de 7% maior do que 18,4 (pois 19,7 : 18,4 ≃ 1,07).
4. Estudando alguns sólidos

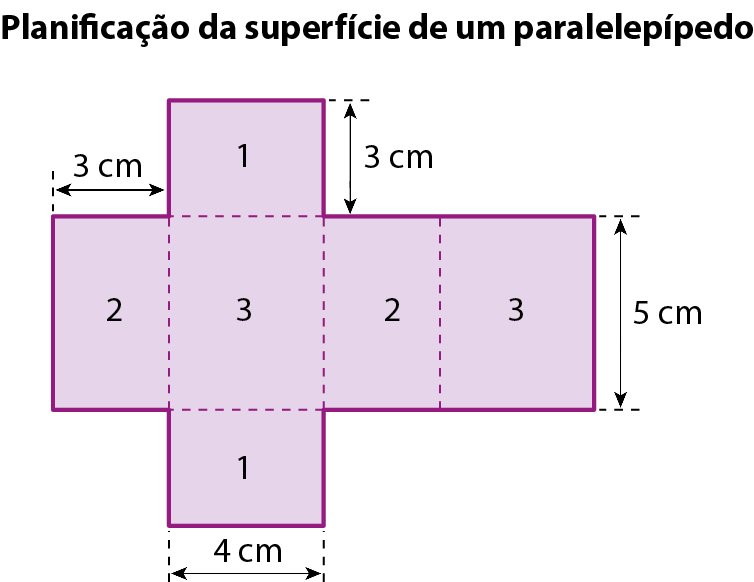
Cálculo da medida A da área em centímetro quadrado:
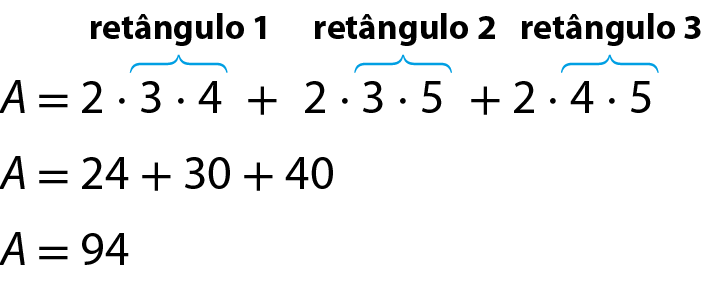
A área total da superfície do paralelepípedo mede 94 centímetros quadrados.
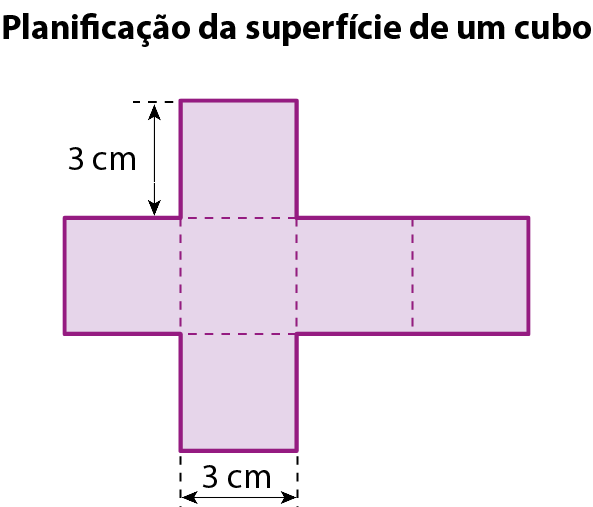
Cálculo da medida a da área em centímetro quadrado:

A área total da superfície do cubo mede 54 centímetros quadrados.
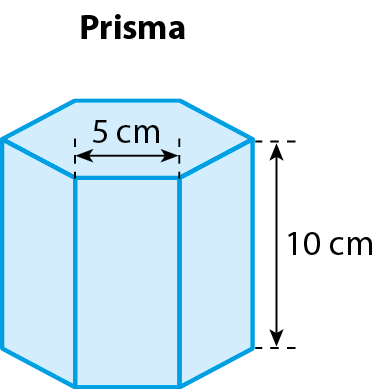
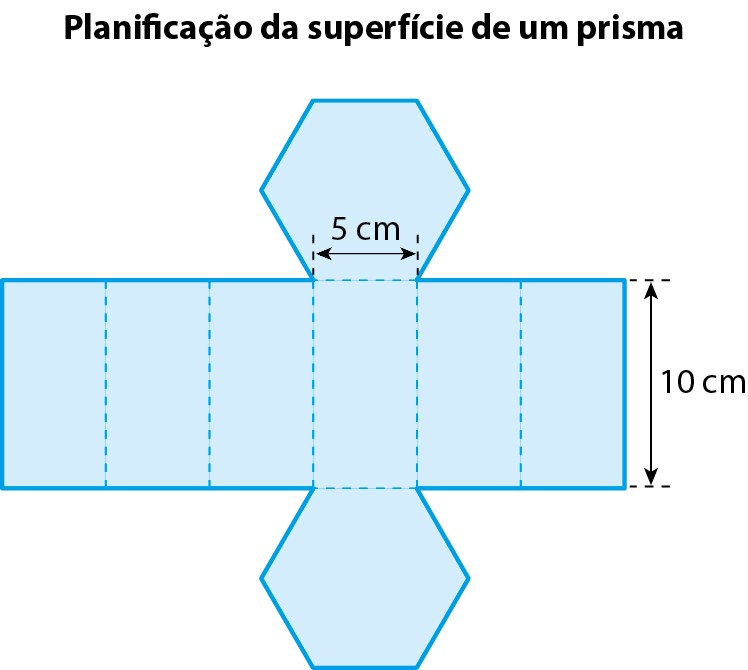
Do mesmo modo, podemos determinar a medida da área total da superfície de um prisma fazendo sua planificação. Observe.
Respostas e comentários
4. Estudando alguns sólidos
Habilidade da Bê êne cê cê: ê éfe zero nove ême ah um nove.
Esse tópico desenvolve a habilidade (ê éfe zero nove ême ah um nove), pois trata de expressões de cálculo da medida de volume de prismas retos e de cilindros retos.
Ao explorar as planificações indicadas, reforce a ideia do que é base dos prismas apresentados e como determinar a medida da altura deles.
Amplie esse tema explorando outros exemplos, como um prisma reto de base pentagonal (considerando que a base é um pentágono regular) e sua planificação:
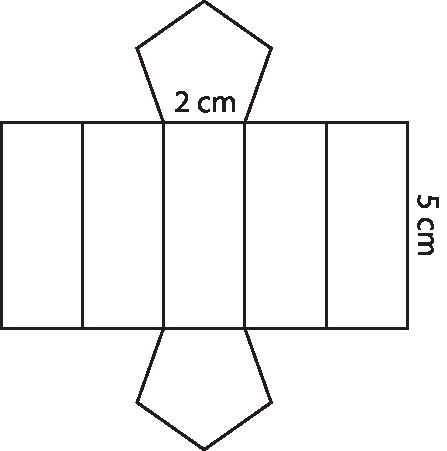
Cálculo da medida da área de uma das bases (pentágono regular):
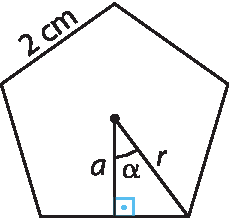
• Medida α do ângulo central:
72graus
• Cálculo da medida do apótema:
tangente de 72graus
igual a, 1 sobre a, implica, 3,0777 igual a 1 sobre a.a ≃ 0,32 centímetro
• Cálculo da medida de área:
Abase = Apentágono (regular) = p · a
Abase ≃ 1,6 centímetros quadrados
A medida da área lateral corresponde à medida da área de 5 retângulos congruentes de lados medindo 2 centímetros por 5 centímetros.
Alateral = 5 · 2 · 5
Alateral = 50 centímetros quadrados
A medida da área total corresponde à medida da área da superfície do prisma pentagonal, ou seja, é a soma das medidas das áreas das duas bases com a medida da área lateral.
Atotal = 2 · 1,6 centímetros quadrados + 50 centímetros quadrados = 53,2 centímetros quadrados
Cálculo da medida a da área em centímetro quadrado:
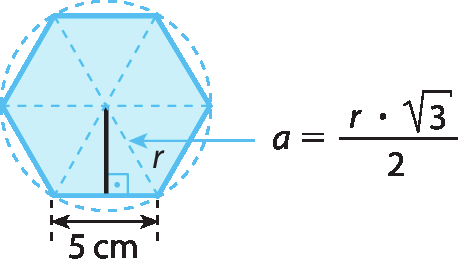
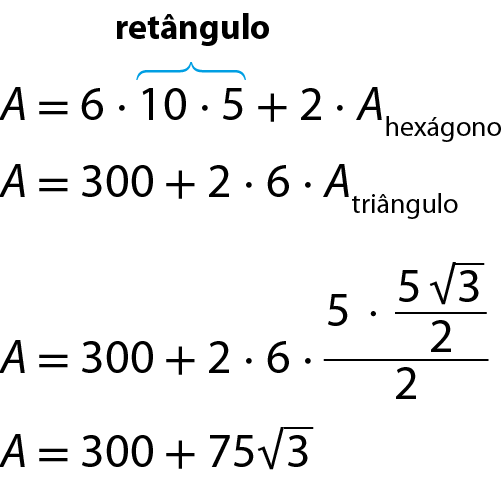
A área total da superfície do prisma mede
abre parêntese, 300 mais 75 vezes raiz quadrada de 3, fecha parêntese.centímetros quadrados.
Vamos recorrer à planificação da superfície de um cilindro para determinar a medida da área total de sua superfície.

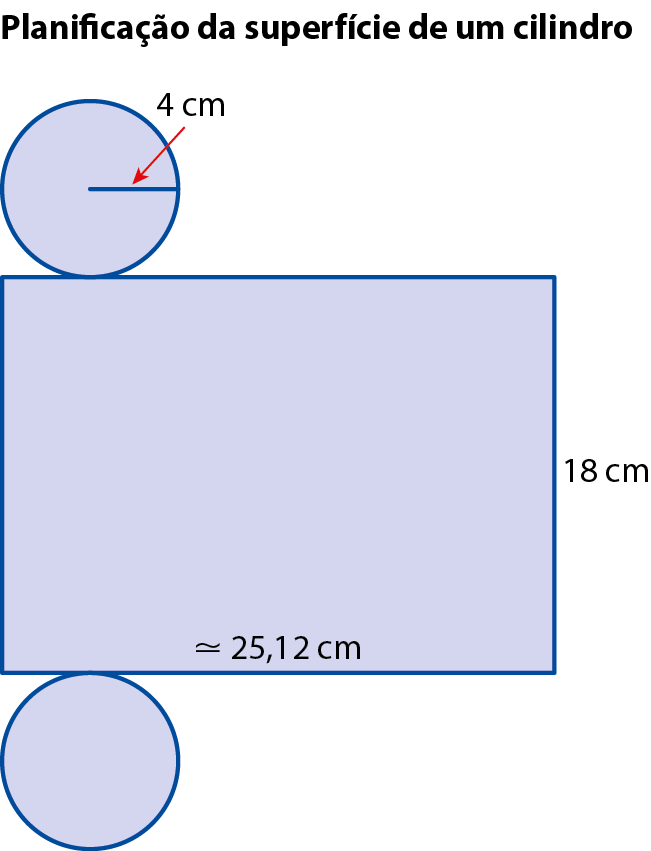
Cálculo da medida A da área em centímetro quadrado:

A área total da superfície do cilindro mede aproximadamente 552,64 centímetros quadrados.
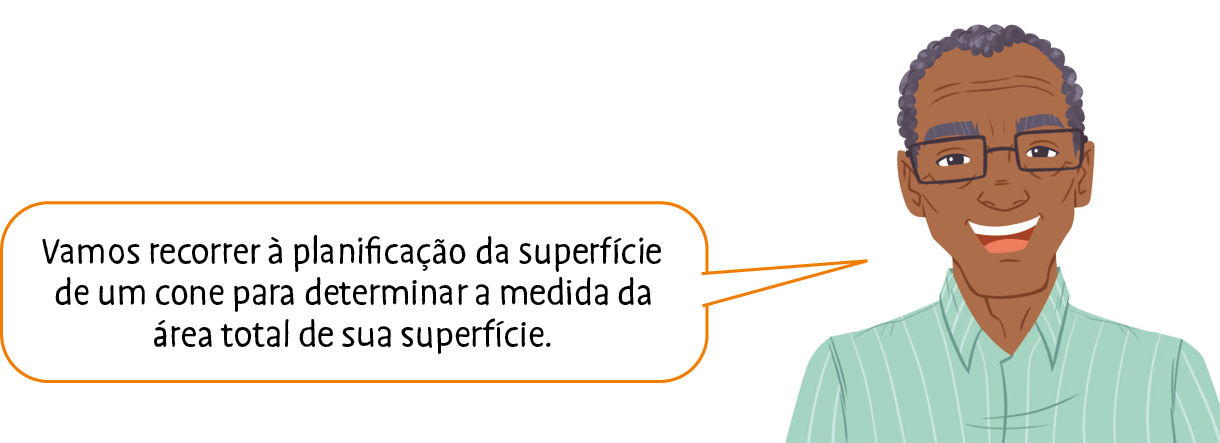

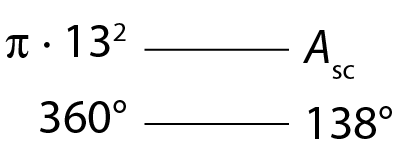
Medida da área do setor circular (Asc)
Aplicando regra de três:
Respostas e comentários
Estudando alguns sólidos
Se possível, leve para a sala de aula modelos de cilindros e de cones (retos) que possam ser desmontados e remontados para que os estudantes percebam os elementos da planificação de sua superfície.
Espera-se que eles percebam que a planificação da superfície de um cilindro reto é composta de dois círculos congruentes e de um retângulo de dimensões de medidas h (altura do cilindro) e 2πr (comprimento da circunferência da base).
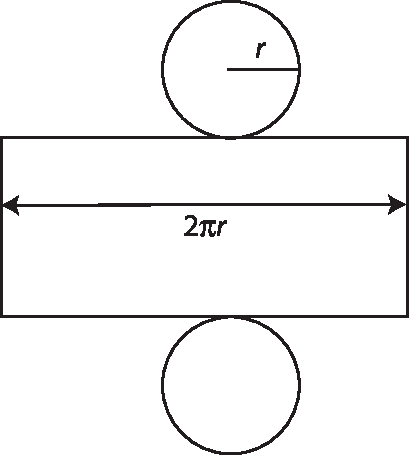
Do mesmo modo, espera-se que observem que a planificação da superfície de um cone circular reto é composta do círculo da base e de um setor circular de raio de medida g (medida da geratriz do cone) e comprimento do arco de medida 2πr (medida do comprimento da circunferência da base).
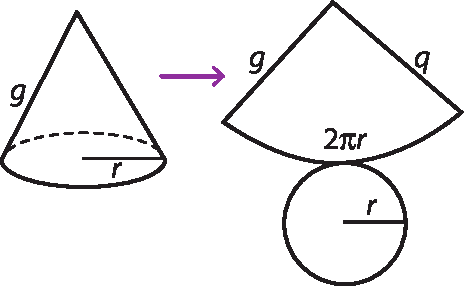
Questione os estudantes sobre como seria a planificação da superfície esférica. Espera-se que eles compreendam que a superfície de uma esfera não pode ser planificada.
Cálculo da medida a da área em centímetro quadrado:
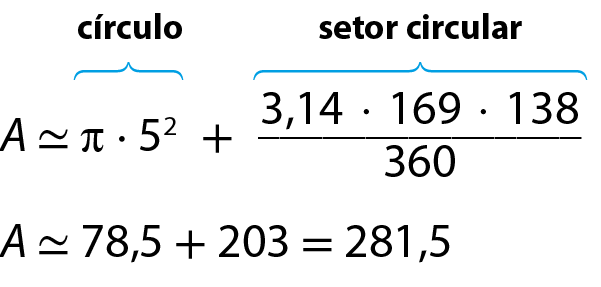
A área total da superfície do cone mede aproximadamente 281,5 centímetros quadrados.
A medida do volume de prismas e cilindros retos

Situação 1
Em acrílico, construímos um modelo de prisma de base retangular e um modelo de prisma de base triangular, cujas dimensões internas estão indicadas nas figuras. Observe que eliminamos uma das faces, pois nesses modelos de prisma despejaremos areia até a borda.
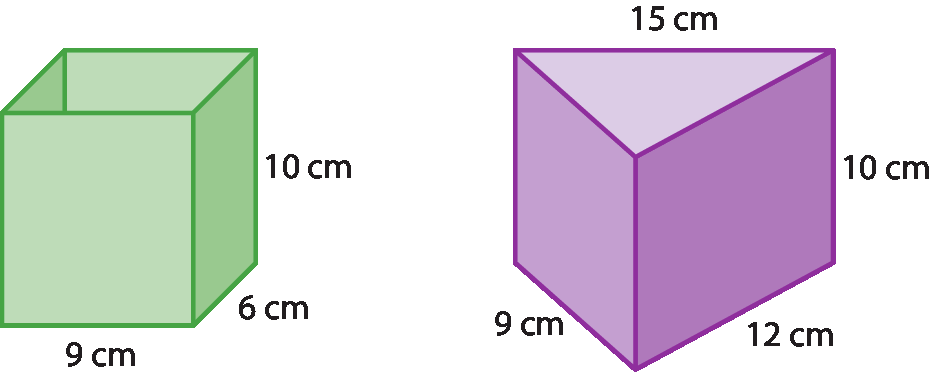
Observe que os dois prismas têm as mesmas medidas de altura (10 centímetros) e de área da base (54 centímetros quadrados).
Enchemos o prisma de base retangular com areia. Ao despejar totalmente a areia do prisma de base retangular no prisma de base triangular, verificamos que os dois têm a mesma medida de volume. Como já sabemos calcular a medida do volume do primeiro prisma (V = 9 ⋅ 6 ⋅ 10), concluímos que o volume do segundo prisma também mede 540 centímetros cúbicos.

Vprisma reto = (medida da área da base) ⋅ (medida da altura)
Respostas e comentários
A medida do volume de prismas e cilindros retos
Explore a situação 1 com os estudantes incentivando-os a indicar uma expressão para o cálculo da medida do volume do prisma. Em seguida, explore o fato de o prisma de base triangular apresentado ter um triângulo retângulo como base (pois 152 = 92 + 122). Assim, a medida do volume dêsse prisma de base triangular é dada por:
Logo, VPrisma = 540 centímetros quadrados.
Situação 2
Para determinar a medida do volume de um cilindro reto, Emanuele fez o seguinte experimento. Ela providenciou dois recipientes de acrílico (sem as faces superiores), cujas dimensões internas estão representadas nas figuras a seguir, e encheu um deles com água. Depois, despejou completamente a água dêsse recipiente no outro e percebeu que a medida de volume de ambos são equivalentes.
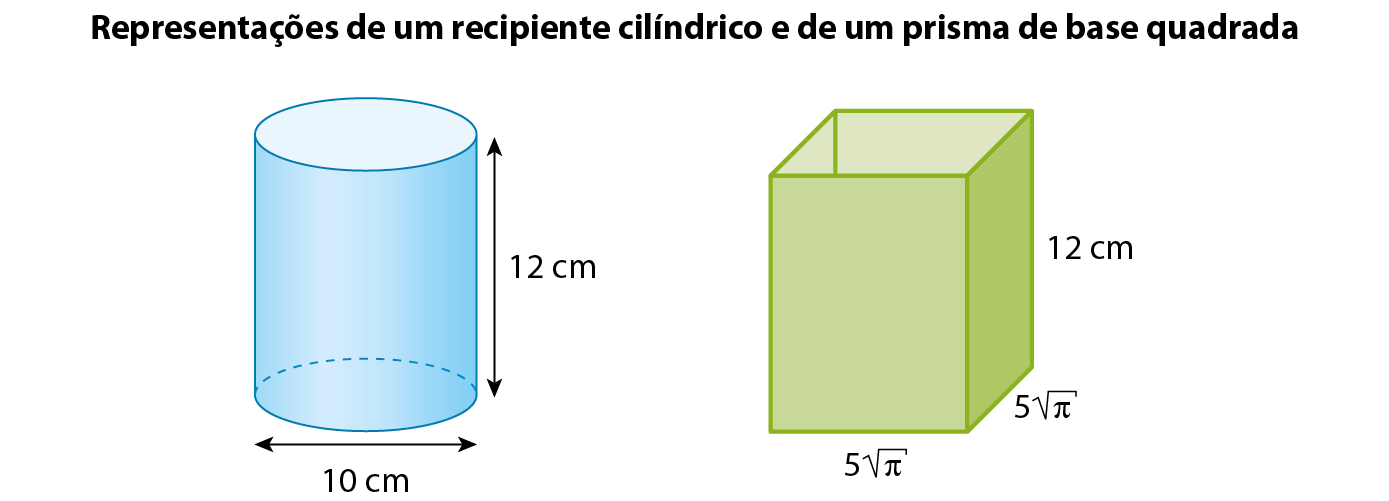
Seja vêp a medida do volume do prisma utilizado por Emanuele. Como já estudamos, essa medida de volume é dada por:
Vp = (medida da área da base) ⋅ (medida da altura)
Vp = (5
raiz quadrada de pi.⋅ 5
raiz quadrada de pi.) ⋅ (12)
Vp = (52π) ⋅ (12)
Como o volume do cilindro reto e do prisma reto utilizados por Emanuele têm a mesma medida de volume, podemos dizer que a medida vêc do volume do cilindro é:
Vc = Vp
Vc = (52π) ⋅ (12)
Observando essa última expressão, podemos perceber que a medida do volume do cilindro utilizado por Emanuele é obtida por meio do produto da medida da área de sua base (52π) pela medida de sua altura (12).

Vcilindro = (medida da área da base) ⋅ (medida da altura)
Se considerarmos um cilindro de raio cuja medida é érre e cuja medida da altura é agá, então, a medida do volume dêsse cilindro será dada por:
Vcilindro = (πr2) ⋅ (agá) ou Vcilindro = π ⋅ r 2 ⋅ agá
Respostas e comentários
A medida do volume de prismas e cilindros retos
Na situação 2, incentive os estudantes a comparar a medida do volume do cilindro com a do prisma de base quadrada; destaque que ambos têm a altura de mesma medida.
Se possível, podem ser confeccionados um prisma e um cilindro, ambos retos e com apenas uma das bases (de maneira que fiquem “abertos”), por meio da planificação deles e de maneira que tenham a mesma medida de altura e as figuras das bases sejam equivalentes. Com um material como confetes de papel, os estudantes podem repetir o experimento dessa situação a fim de verificar se a quantidade de confetes que cabe no cilindro é a mesma que cabe no prisma construído. Ressalte que as medidas empíricas são aproximadas e, portanto, deve-se considerar que poderão ocorrer erros de aproximação.
Alternativamente, pode-se utilizar as expressões do cálculo da medida de volumes para verificar a medida de volume de alguns recipientes. Por exemplo, com um recipiente cilíndrico, os estudantes medem o diâmetro do círculo da base dele e calculam a medida de sua área; depois, medem a altura e calculam a medida do volume do recipiente, em centímetro cúbico. Sabendo que .1000 centímetros cúbicos = 1 litro, eles podem preencher o recipiente com água e, depois, utilizar um medidor graduado de volume para conferir se a medida de volume dada em centímetro cúbico equivale, de fato, à medida, em litro. Novamente, destaque que as medições realizadas podem decorrer de aproximações e dependem da precisão dos instrumentos utilizados, bem como de sua correta aferição.
PARA SABER MAIS
Calculando a medida do volume de uma pirâmide
Em acrílico, construímos um modelo de pirâmide de base quadrada e um modelo de prisma de base quadrada, com base nas planificações das suas superfícies, cujas dimensões internas estão indicadas nas figuras a seguir. Observe que eliminamos uma das faces de cada um dos modelos para enchê-los com areia.
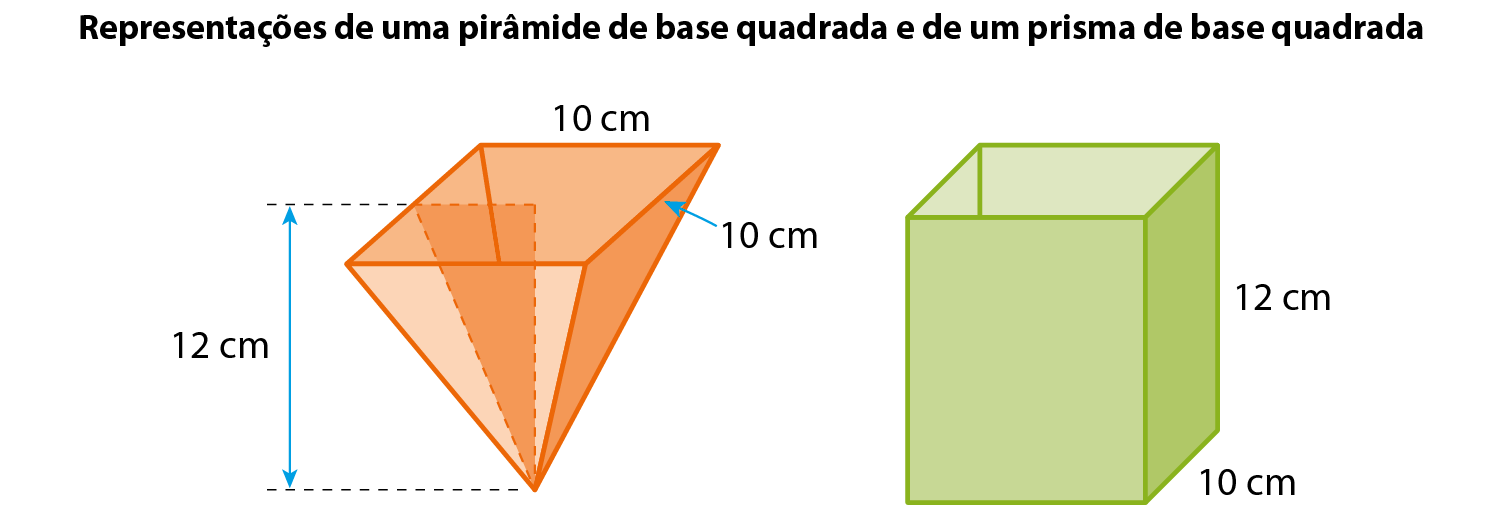
Observe que o prisma e a pirâmide têm as mesmas medidas de área da base e, ainda, têm as mesmas medidas de altura.
Enchendo a pirâmide de areia e despejando seu conteúdo no prisma, é possível repetir o procedimento exatamente três vezes, ou seja, para encher um prisma, precisamos do conteúdo de três pirâmides cujas medidas da área da base e da altura sejam as mesmas das respectivas medidas do prisma.
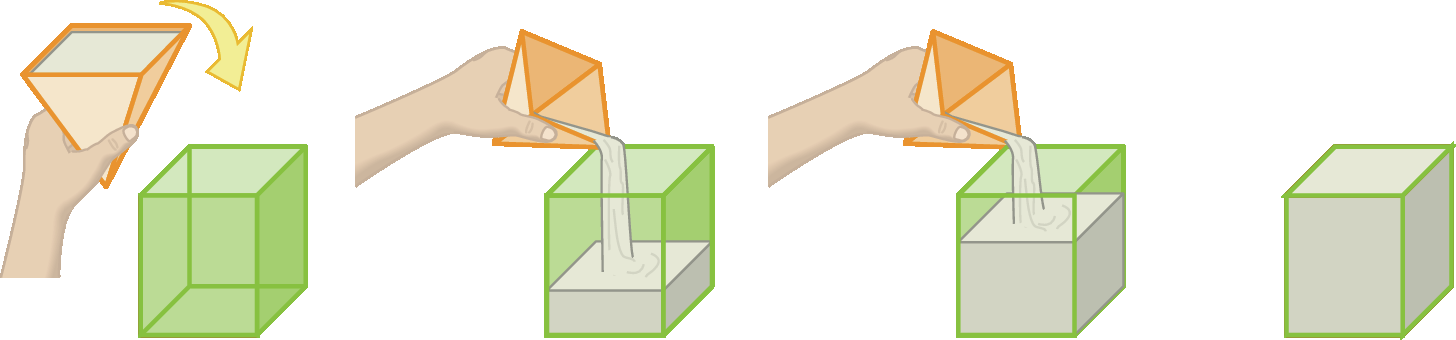
O volume da pirâmide corresponde, portanto, a um terço do volume do prisma. Assim, a medida V do volume da pirâmide é dada por:
Logo, a medida do volume da pirâmide é 400 centímetros cúbicos.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Se a medida do volume de um prisma é .1500 centímetros cúbicos, qual é a medida do volume de uma pirâmide cujo polígono da base é equivalente ao polígono da base dêsse prisma e cuja medida da altura é igual à medida da altura do prisma?
2 Com base no resultado do experimento, que relaciona a medida do volume da pirâmide e a medida do volume do prisma, escreva no caderno uma expressão para determinar a medida do volume de uma pirâmide qualquer.
Respostas e comentários
1. 500 centímetros cúbicos
2. Vpirâmide =
fração 1 sobre 3.⋅ (medida da área da base) ⋅ (medida da altura)
Para saber mais
Verifique se os estudantes conseguem mobilizar os conhecimentos sobre o cálculo da medida do volume de prismas retos e de cilindros retos, transpondo esses conhecimentos para a situação apresentada nessa situação.
Para resolver a atividade 1 do Agora é com você!, deve-se considerar que a medida do volume da pirâmide será igual a um terço da medida do prisma considerado. Assim, como .1500 : 3 = 500, a medida do volume procurado é 500 centímetros cúbicos.
A atividade 2 resume a relação entre a medida do volume do prisma e a da pirâmide (ambas as figuras têm a mesma medida da altura e a mesma medida da área):
EXERCÍCIOS PROPOSTOS
FAÇA AS ATIVIDADES NO CADERNO
46 Um recipiente cilíndrico tem raio que mede 5 centímetros e altura que mede 12 centímetros. Fábio possui um recipiente em fórma de cone e cujas medidas do raio da base e da altura são respectivamente iguais às do recipiente cilíndrico. Fábio enche de água esse recipiente em fórma de cone e, depois, despeja todo o conteúdo no recipiente cilíndrico, fazendo esse processo 3 vezes, como indica a figura.

Qual é a medida aproximada do volume do recipiente que tem fórma de cone?
47 (Urca-Ceará) Suponha que um grão de feijão ocupe, aproximadamente, o espaço de um prisma quadrangular regular de altura 1 centímetro e aresta da base 0,4 centímetro. Quantos grãos de feijão cabem, aproximadamente, num depósito do formato de um prisma quadrangular de altura 1 métro e aresta da base 40 centímetros?
a) .1000
b) .10000
c) .100000
d) ..1000000
e) ..10000000
48 Um marceneiro vai produzir peças de madeira em formato de prisma de base triangular. Os lados da base do polígono medem 5 centímetros, 5 centímetros e 6 centímetros. A altura de cada peça mede 12 centímetros. Qual é a menor medida do volume de madeira necessária para produzir 10 dessas peças?
49 Os Aparai e os Wayana são povos indígenas de língua karib que habitam a região de fronteira entre o Brasil, o Suriname e a Guiana Francesa. Em seu processo de cestaria eles produzem recipientes como os da fotografia.

Considerando que um desses cestos possa ser associado a um cilindro cujo raio da base mede 21 centímetros e cuja altura mede 45 centímetros, determine a medida:
a) da área total da superfície dêsse cesto;
b) do volume de um desses cestos.
50

Em grupo de três colegas, reproduzam em uma cartolina os sólidos como os das situações 1 e 2 e da seção Para saber mais três experiências anteriores. Em seguida, usando confete de papel ou material similar, verifiquem as relações entre as medidas dos volumes.
(Usem tesouras com pontas arredondadas e as manuseiem com cuidado!)
EXERCÍCIOS COMPLEMENTARES
FAÇA AS ATIVIDADES NO CADERNO
1 A medida do lado de um quadrado inscrito em uma circunferência é
8 vezes raiz quadrada de 2.centímetros. Calcule a medida do apótema do triângulo equilátero inscrito nessa circunferência.
2 A medida do perímetro de um hexágono regular inscrito em uma circunferência é 42 métros. Calcule a medida do perímetro do quadrado inscrito nessa circunferência.
Respostas e comentários
46. V = 314 centímetros cúbicos
47. Alternativa d.
48. No mínimo .1440 centímetros cúbicos.
49. a) Aproximadamente .7319 centímetros quadrados.
49. b) Aproximadamente .62313 centímetros cúbicos.
50. Montagem de sólidos.
1. 4
raiz quadrada de 2.centímetros
2.
28 vezes raiz quadrada de 2, fim da raiz, metros.Exercícios propostos
As resoluções dos exercícios 46 a 49 estão no início deste Manual, nas orientações específicas do capítulo 12.
Reserve uma aula para desenvolver o exercício 50 ou instrua os estudantes a confeccionar em casa os sólidos geométricos que serão utilizados.
Exercícios complementares
Este bloco de exercícios explora os principais conceitos estudados no capítulo. Espera-se que os estudantes mobilizem os conhecimentos construídos, percebendo se ainda têm alguma dificuldade.
As resoluções dos exercícios 1 e 2 estão no início deste Manual, nas orientações específicas do capítulo 12.
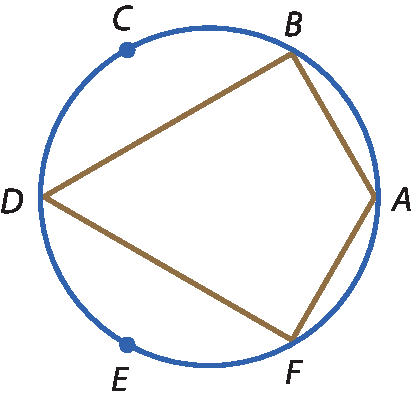
3 A circunferência a seguir, cujo raio mede
7 vezes raiz quadrada de 2.centímetros, está dividida em seis arcos congruentes. Calcule a medida do perímetro do polígono á bê dê éfe.
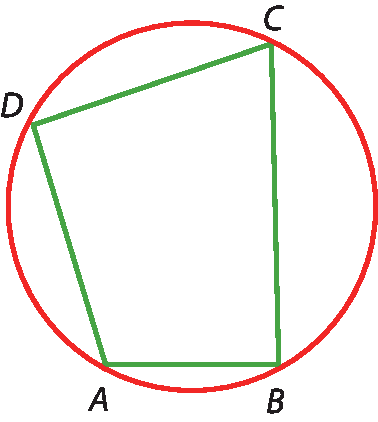
4 Na figura,
segmento AD.e
segmento DC.são lados de um quadrado inscrito,
segmento AB.é lado de um hexágono regular inscrito,
segmento BC.é lado de um triângulo equilátero inscrito. Sabe-se que bê cê =
4 raiz quadrada de 3.. Calcule A bê e á dê.
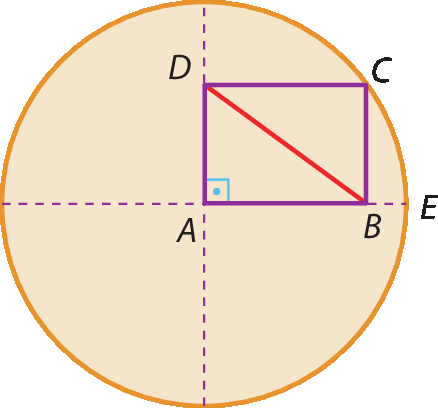
5 Na figura a seguir, a bê cê dê é um retângulo inscrito em um quadrante de um círculo. Calcule a medida de
segmento BD., sendo cedê = 8 centímetros e bê ê = 2 centímetros.
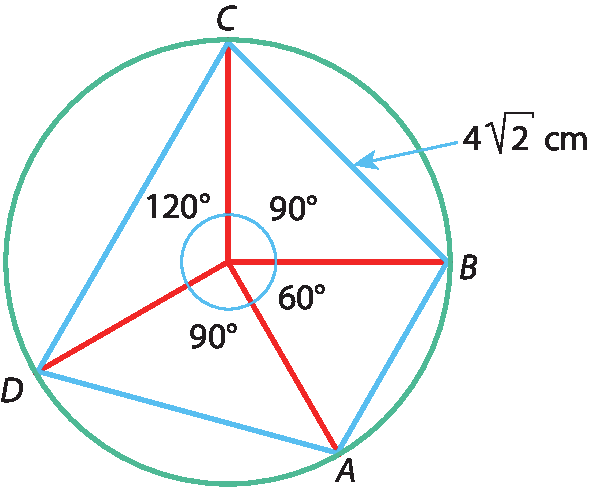
6 Considerando a figura a seguir, calcule:
a) a medida do raio da circunferência;
b) a medida de
segmento AB.;
c) a medida de
segmento CD..
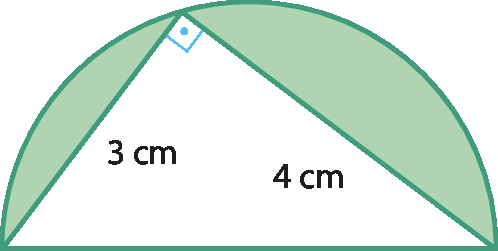
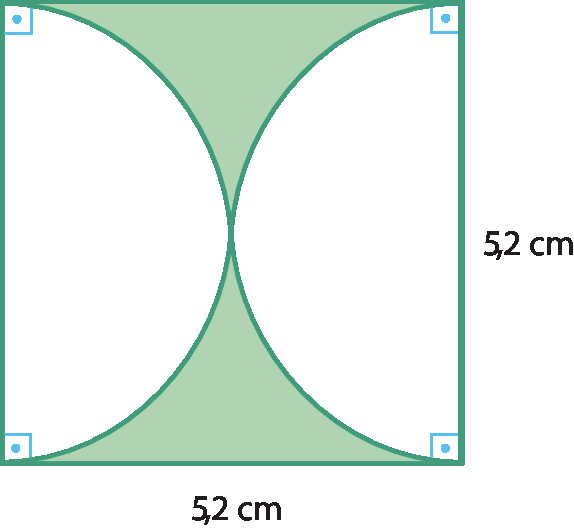
7 Considerando π = 3,14, determine a medida da área da figura pintada de verde. No item b, O é o centro da circunferência.
a)
b)
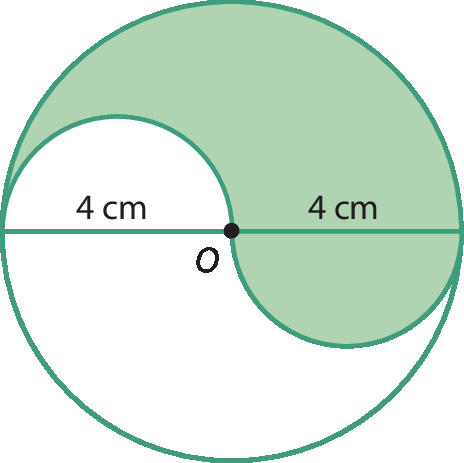
c)
8 Qual é a diferença entre as medidas dos perímetros de dois quadrados, um circunscrito e outro inscrito em uma mesma circunferência cujo raio mede
raiz quadrada de 2.centímetros?
9 Raul deu de presente à sua mãe um relógio de parede com formato de hexágono regular, como na figura a seguir.
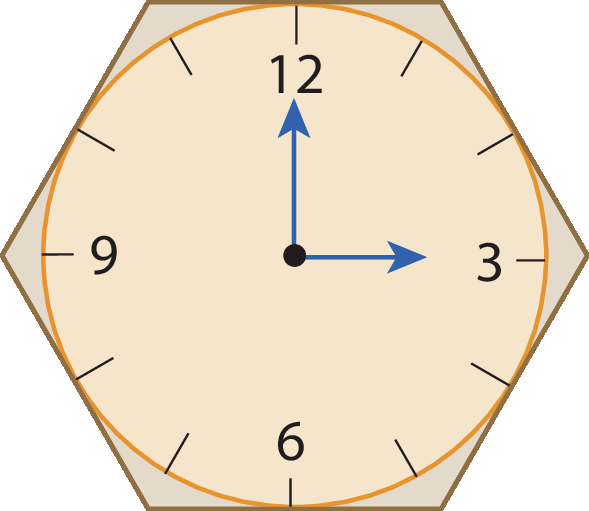
Determine a medida da área do mostrador circular dêsse relógio, sabendo que o hexágono regular circunscrito tem lado medindo 12 centímetros.
Respostas e comentários
3.
14 vezes raiz quadrada de 2, vezes, abre parênteses, 1 mais raiz quadrada de 3, fecha parênteses, centímetros.4. AB = 4 e AD =
4 raiz quadrada de 2..
5. BD = 10 centímetros
6. a) 4 centímetros
6. b) AB = 4 centímetros
6. c) CD =
4 vezes raiz quadrada de 3, fim da raiz, centímetros.7. a) 3,8125 centímetros quadrados
7. b) 25,12 centímetros quadrados
7. c) 5,8136 centímetros quadrados
8.
8, abre parêntese, raiz quadrada de 2 menos 1, fecha parêntese, centímetros.9. 108π centímetros quadrados
Exercícios complementares
As resoluções dos exercícios 3 a 6 e dos exercícios 8 e 9 estão no início deste Manual, nas orientações específicas do capítulo 12.
Acompanhe uma possível resolução para o exercício 7.
a) O triângulo em branco é um triângulo retângulo de lados medindo 3 centímetros, 4 centímetros e 5 centímetros. Assim, a medida da área da região verde, em centímetro quadrado, é dada por:
A verde, igual, A quadrado, menos, A círculo.b) As regiões destacadas em branco e em verde são idênticas, ou seja, se sobrepõem. Assim, a parte verde completa um semicírculo de raio medindo 4 centímetros.
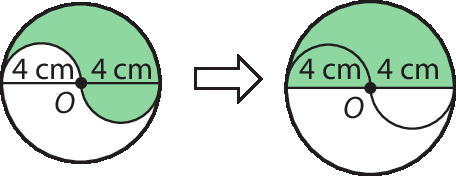
Logo, a medida da área verde, em centímetro quadrado, é dada por:
c) As duas partes brancas juntas formam um círculo cujo diâmetro mede 5,2 centímetros (raio 2,6 centímetros). Assim, a medida da área da parte verde, em centímetro quadrado, é dada por:
10 Ao quadricular uma ilustração do calçadão de uma praia, Lucas notou que a área ocupada pelas pedras azul-escuras era maior que a ocupada pelas pedras azul-claras.
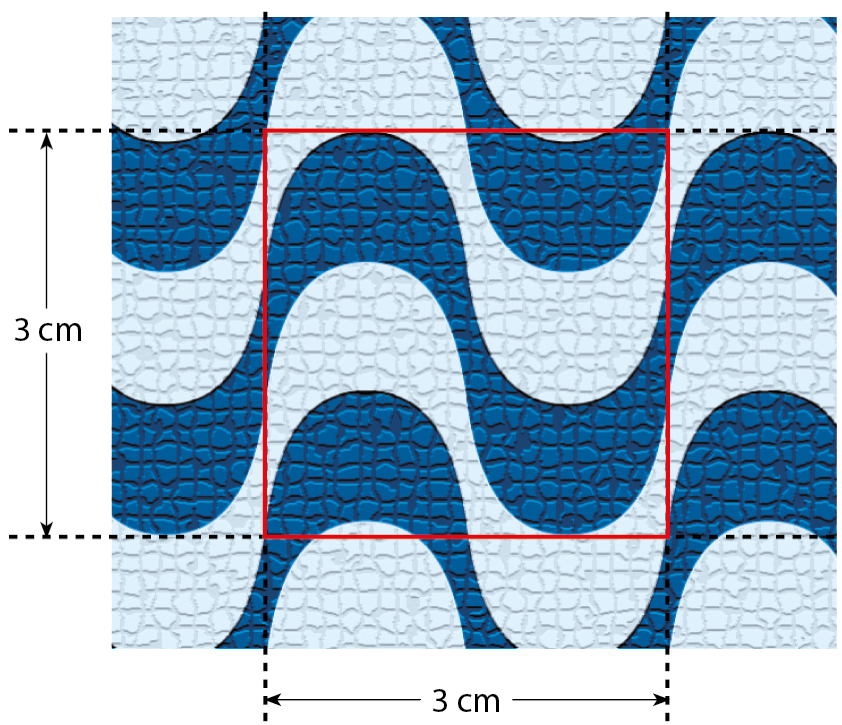
a) Faça a estimativa da medida da área, em centímetro quadrado, ocupada pelas pedras azul-escuras do quadrado em destaque na ilustração do calçadão.
b) Considerando que a área estimada da parte azul-escura no quadrado seja igual à área de um círculo, faça um desenho de como ficaria um novo revestimento para esse calçadão com círculos azul-escuros. Indique as medidas em seu desenho.
11 Calcule a medida da área aproximada da parte da figura pintada de vermelho, sabendo que o lado do quadradinho do quadriculado mede 0,5 centímetro.
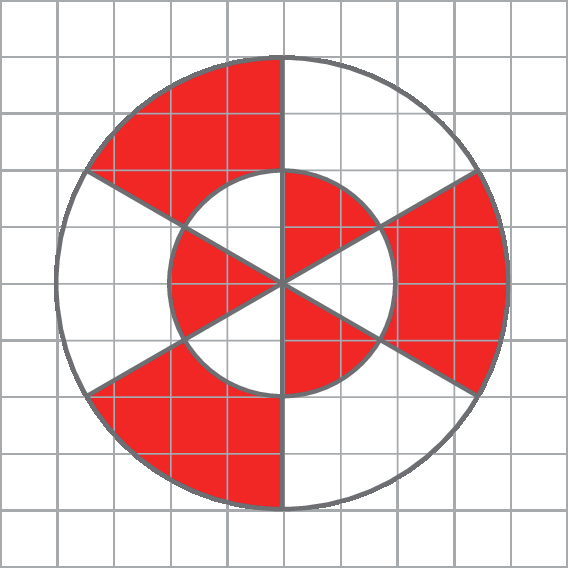
12 Uma folha de papel tem medidas 18 centímetros por 12 centímetros.
a) Qual é o maior número de círculos tangentes entre si com raio medindo 3 centímetros que é possível desenhar nessa folha?
b) Se esses círculos forem recortados, qual é a quantidade de aparas de papel, em centímetro quadrado, que restará? (Adote π = 3,14.)
13 (unifór-Ceará) Uma indústria utiliza as placas retangulares de alumínio mostradas na figura, nas quais toda a região sombreada, que está fóra dos círculos, é desperdiçada.
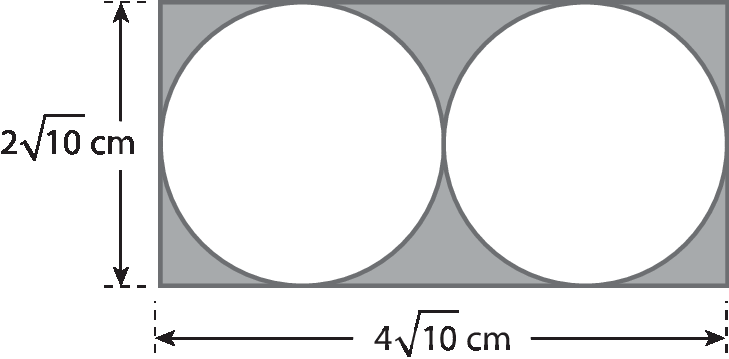
Qual é a medida da área desperdiçada, em centímetro quadrado? (Considere π = 3,1.)
14 A situação ilustrada de uma caixa de biscoitos sugere um quadrado circunscrito a uma circunferência. Sabendo que o lado do quadrado mede 3,6 centímetros e que o comprimento da caixa mede 20 centímetros, efetue os cálculos pedidos a seguir.
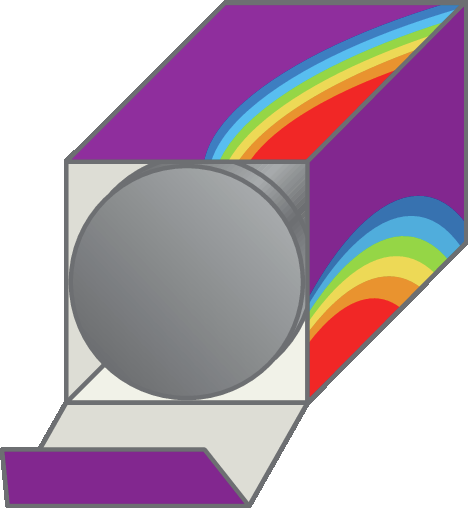
a) a medida do raio dessa circunferência;
b) a medida do volume da caixa de biscoitos;
c) a medida do volume aproximado da pilha de biscoitos dessa caixa.
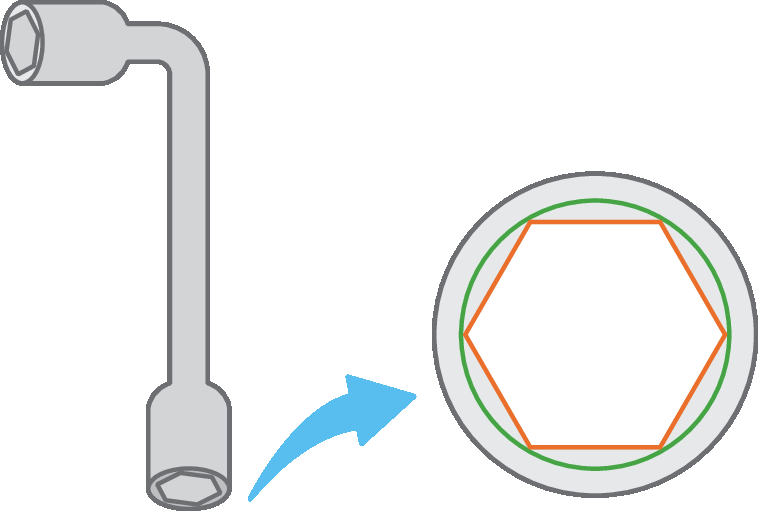
15 A ferramenta representada na figura é uma chave L número 10. Sabendo que a circunferência destacada em verde tem, na realidade, raio medindo 5 centímetros, calcule a medida do lado e do apótema do hexágono destacado na cor laranja. Explique por que essa ferramenta tem esse nome.
Respostas e comentários
10. a) 6 centímetros quadrados
10. b) Resposta pessoal; o círculo terá 1,38 cm de raio.
11. 6,28 centímetros quadrados
12. a) 6 círculos.
12. b) 46,44 centímetros quadrados
13. 17 centímetros quadrados
14. a) 1,8 centímetros
14. b) 259,2 centímetros cúbicos
14. c) 203,5 centímetros cúbicos
15. Medida do lado: = 5 centímetros; medida do apótema:
igual, fração 5 raiz quadrada de 3 sobre 2.centímetros. A chave L número 10 tem esse nome porque tem o formato da letra L, e o número 10 corresponde à medida aproximada do diâmetro da circunferência, em milímetro.
Exercícios complementares
Acompanhe uma possível resolução do exercício 10.
a) Considerando que, aproximadamente,
dois terços.do quadrado é composto de pedras azul-escuras e
um terço.de pedras azul-claras, temos, em centímetro quadrado: Aquadrado = 3 · 3 = 9
Assim, a medida da área das pedras azul-escuras é 6 centímetros quadrados, pois:
dois terços, vezes, 9 igual a 6.
A medida estimada da área ocupada pelas pedras azul-escuras no quadrado é de 6 centímetros quadrados.
b) Acírculo = π · rduas ⇒ 6 = 3,14 · rduas ⇒ rduas = 1,91 ⇒ r = 1,38
Assim, com r = 1,38 centímetro, uma representação possível é:
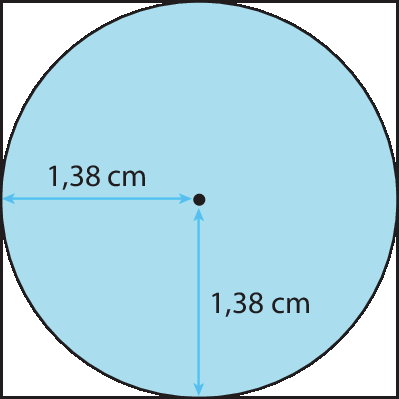
No exercício 11, assim como em outros que pedem o cálculo da medida da área de parte de um mosaico, discuta com os estudantes a possibilidade de, mentalmente, reunirem as porções que constituem essa parte e, feito isso, compararem a parte composta com o todo. Nesse exercício, tal procedimento os leva a perceber que a área da superfície pintada de vermelho corresponde à metade do círculo. A medida da área do círculo, com π = 3,14, em centímetros quadrados, é: 2duas · 3,14 = 12,56
Portanto, temos que a área em vermelho tem medida de 6,28 centímetros quadrados (pois 12,56 : 2 = 6,28).
As resoluções dos exercícios 12 a 15 estão no início deste Manual, nas orientações específicas do capítulo 12.
No exercício 14, basta os estudantes visualizarem que a medida do raio da circunferência é, de fato, metade da medida do lado dêsse quadrado. Amplie as discussões para questões de aumento ou diminuição da medida da área dêsse quadrado e dessa circunferência à medida que variamos as medidas do lado e do raio, respectivamente.
VERIFICANDO
FAÇA AS ATIVIDADES NO CADERNO
Para a resolução dos testes, considere π = 3,14.
1 Qual é a medida da área de um quadrado inscrito em uma circunferência de raio medindo 12 centímetros?
a) 144 centímetros quadrados
b) 288 centímetros quadrados
c) 452,16 centímetros quadrados
d) 904,32 centímetros quadrados
2 Um triângulo regular está inscrito em uma circunferência com 157 métros de medida de comprimento. Qual é a medida do apótema dêsse triângulo?
a) 25 métros
b) 17,5 métros
c) 12,5 métros
d) 10 métros
3 Qual é a medida do lado de um hexágono regular inscrito em uma circunferência que determina um círculo de medida da área igual a 113,04 métros quadrados?
a) 6 métros
b) 12 métros
c) 36 métros
d) 113,04 métros
4 Qual é a diferença entre a medida do lado de um hexágono regular e a do apótema de um triângulo regular, ambos inscritos na mesma circunferência de raio de medida r?
a) r
b)
fração r sobre 2.c)
fração r sobre 4.d) 0
5 Qual é a medida da área de uma coroa circular de raios maior e menor, respectivamente, medindo 5 métros e 3 métros?
a) 25,12 métros quadrados
b) 28,26 métros quadrados
c) 50,24 métros quadrados
d) 78,5 métros quadrados
6 Quanto mede a área de um hexágono regular inscrito em uma circunferência de raio medindo r?
a)
fração de numerador 3 vezes r elevado ao quadrado, fim do expoente, vezes raiz quadrada de 3, e de denominador 2, fim da fraçãob) 3r duas
raiz quadrada de 3.c)
fração de numerador 3 vezes r elevado ao quadrado, fim do expoente, vezes raiz quadrada de 2, e de denominador 2, fim da fraçãod) 3r
raiz quadrada de 3.7 Qual é a medida do volume de uma pirâmide de altura que mede 9 métros cuja base é um quadrado inscrito em uma circunferência de raio com medida igual a 4 métros?
a) 10,7 métros cúbicos
b) 12 métros cúbicos
c) 48 métros cúbicos
d) 96 métros cúbicos
8 A pirâmide de Quéops, no Egito, mede 146 metros de altura, e cada lado da sua base mede 230 metros de comprimento. Qual é, aproximadamente, a medida do volume ocupado pela pirâmide?
a) 11,1 mil metros cúbicos
b) 17,6 mil metros cúbicos
c) 1,6 milhão de metros cúbicos
d) 2,5 milhões de metros cúbicos
9 Quantos centímetros cúbicos de água cabem em uma taça cônica de altura medindo 10 centímetros e raio da circunferência na parte aberta medindo 3 centímetros?
a) 31,4 centímetros cúbicos
b) 94,2 centímetros cúbicos
c) 282,6 centímetros cúbicos
d) 314 centímetros cúbicos
Organizando
Vamos organizar o que você aprendeu neste capítulo? Para isso, responda às questões a seguir:
a) Quais são as relações algébricas das respectivas medidas dos lados, apótemas e raios da circunferência nos polígonos regulares inscritos destacados no capítulo?
b) Em quais situações do dia a dia podemos observar alguns polígonos regulares?
c) Há alguma sentença algébrica que relaciona a medida da área de qualquer polígono regular com as medidas do apótema e do perímetro? Qual?
d) Supondo uma sequência de polígonos regulares em que o número de lados cresça indefinidamente, quais aproximações (tendências) podemos fazer, com base na resposta da questão anterior, para obter a fórmula da medida da área de um círculo?
e) Dados um cone e um cilindro, ambos com as respectivas medidas da base e da altura iguais, qual é a razão entre as medidas de seus volumes?
Respostas e comentários
1. Alternativa b.
2. Alternativa c.
3. Alternativa a.
4. Alternativa b.
5. Alternativa c.
6. Alternativa a.
7. Alternativa d.
8. Alternativa d.
9. Alternativa b.
Organizando: a) Para os polígonos regulares destacados, inscritos em uma circunferência com raio de medida r, podemos calcular as medidas do lado (𝓁) e do apótema (a) em função de r.
Quadrado:
L igual a r vezes raiz quadrada de 2, a igual a, fração de numerador r vezes raiz quadrada e 2, e de denominador 2.;
Hexágono regular:
L igual a r, a igual a, fração de numerador r vezes raiz quadrada de 3, e de denominador 2;;
Triângulo regular:
L igual a r vezes raiz quadrada de 3, a igual a, r sobre 2..
b) Resposta pessoal. Espera-se que o estudante cite situações que envolvam objetos como espelhos, revestimentos cerâmicos, bandeiras, painéis, placas de sinais de trânsito etcétera
c) Sim. A = p ⋅ a, em que p é a medida do semiperímetro e a é a medida do apótema.
d) A medida do semiperímetro aproxima-se de πr, a medida do apótema aproxima-se de r e a medida da área do polígono aproxima-se de πr 2. Assim, concluímos que a medida da área de um círculo é dada por A = πr 2.
e)
V do cone sobre V do cilindro, igual a, 1 terço.Verificando
Os testes desta seção são mais uma oportunidade para o estudante validar o entendimento do conteúdo estudado neste capítulo.
As resoluções dos testes 1 a 9 estão no início deste Manual, nas orientações específicas do capítulo 12.
Organizando
Incentive os estudantes a organizar seu aprendizado no caderno, fazendo resumos e mapas conceituais ou aplicando destaques em conceitos importantes.
As questões propostas têm como objetivo fazer com que eles retomem os conteúdos aprendidos no capítulo e que reflitam sobre algumas temáticas.
DIVERSIFICANDO
Jogo do desenhe ou responda
Número de participantes: 2 jogadores
Material
• 20 cartas com figuras geométricas (polígono e seus elementos; circunferência e seus elementos – ângulo, mediatriz, bissetriz etcétera), com ênfase em figuras estudadas nos capítulos 11 e 12 deste livro. As figuras devem estar identificadas corretamente.
• Um saquinho não transparente para guardar as cartas confeccionadas.
• Papel e lápis para esboçar as figuras e marcar os pontos.
Regras
• Após o sorteio, o primeiro a jogar retira uma carta do saquinho, sem mostrá-la.
• O jogador que tira a carta deve dizer ao outro uma característica da figura para que ele tente adivinhá-la com um desenho ou uma resposta oral. Para cada carta, podem ser dadas até três dicas, uma a cada tentativa. Por exemplo, se a carta tiver um quadrado, o jogador poderá dar as seguintes dicas: “é um quadrilátero”, “tem ângulos opostos congruentes” e “tem todos os lados com medidas iguais”.
• Se um jogador der uma dica errada, perderá 2 pontos.
• Pontuação: ao acertar o nome ou o desenho na 1ª tentativa, o jogador ganha 3 pontos; na 2ª tentativa, ganha 2 pontos; e na 3ª, ganha 1 ponto.
• Após o acerto ou erro na 3ª tentativa, passa-se a vez.
• Vence aquele que completar primeiro 15 pontos. Caso nenhum jogador consiga atingir os 15 pontos, vence aquele que conseguir a maior pontuação.
Agora é com você!
FAÇA AS ATIVIDADES NO CADERNO
1 Observe o diálogo entre Rafael e Karina. De acordo com as regras, o que deverá acontecer com a pontuação de Rafael?

2 Se um jogador tirasse uma carta com um hexágono regular, que dica ele poderia dar sobre essa figura?
Respostas e comentários
1. Rafael deu uma dica errada e, segundo as regras, deve perder 2 pontos.
2. Respostas possíveis: “Você pode encontrar um formato parecido na colmeia de abelhas”, ou “A soma das medidas dos ângulos internos é 720graus ”, ou “Minha figura tem seis lados de mesma medida”.
Diversificando
Organize os estudantes em duplas e estimule-os a jogar. Depois de algumas partidas, proponha às duplas que troquem de elementos para novas partidas. Então, sugira às duplas formadas que discutam as questões apresentadas no Agora é com você!.
Ao final, faça uma roda de conversa para que os estudantes exponham suas respostas, dúvidas, observações e conclusões.
Pode-se aproveitar o momento para discutir sobre ética, honestidade e espírito colaborativo.