Página 272
CAPÍTULO
9 Movimento e força
Em nosso cotidiano, realizamos várias atividades relacionadas ao movimento, como atravessar ruas, ir à padaria, ir à escola e brincar com os amigos. Que tal realizarmos e analisarmos alguns movimentos em sala de aula? Para isso, realize a atividade a seguir.
Vamos praticar
Material
cadeira
A. Junte-se a um colega. Enquanto ele realiza os movimentos de se levantar da cadeira e dar cinco passos pela sala de aula, você deve ficar em repouso, analisando-o.
B. Em seguida, realize os mesmos movimentos do seu colega, enquanto ele o analisa.
Agora, responda à questão a seguir no caderno.
a) Enquanto você caminha e o seu colega o analisa, apenas você está em movimento? Justifique sua resposta.
Resposta e instruções nas orientações ao professor.
Movimento
Com base na atividade realizada na seção Vamos praticar, podemos estudar alguns conceitos relacionados ao movimento. Na Física, a determinação de movimento depende do que chamamos de referencial, que é estudado pela Mecânica, uma área da Física.
Para verificarmos se um corpo está em repouso ou em movimento, precisamos adotar um referencial, a fim de conferir se o objeto mudou de posição em relação a esse referencial no decorrer do tempo.
Considere a situação a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.
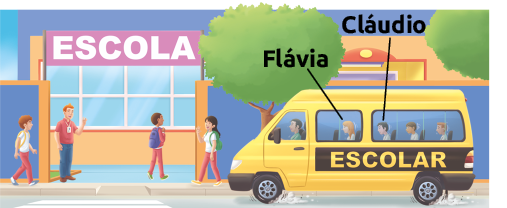
Questão 1. Considerando a situação
representada na imagem, cite quais são
os corpos em movimento e os corpos em repouso em relação ao motorista do
veículo escolar.
Resposta: As árvores, o muro da escola e as pessoas na calçada e na escola estão em movimento em relação ao motorista. No entanto, o veículo escolar e os respectivos passageiros estão em repouso em relação ao motorista.
Página 273
Como pudemos verificar na situação representada, Flávia e Cláudio estão sentados no veículo escolar, portanto a posição de um em comparação ao outro não se altera, nem em relação aos outros passageiros.
Com base nisso, podemos afirmar que eles estão em repouso entre si e em relação aos passageiros do veículo escolar. No entanto, como esse veículo está em movimento em relação ao chão, Flávia, Cláudio e os outros passageiros também estão em movimento em relação ao chão.
Professor, professora: Os conceitos de grandezas escalares e vetoriais serão abordadas nas páginas 284 e 285.
Deslocamento
Muitas atividades do nosso cotidiano estão relacionadas ao conceito de deslocamento. Para estudá-lo, é importante definir a posição inicial (representada por ) e a posição final (representada por ) do corpo.
Observe a situação a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Como você deve ter observado na imagem, a posição inicial do professor mostra o ponto em que ele inicia o seu movimento (em frente à quadra esportiva). Já a posição final mostra o ponto em que o professor termina o movimento (no prédio da escola).
O deslocamento está relacionado à variação da posição de um determinado corpo. Ele é dado pela diferença entre a posição final e a posição inicial . Dessa maneira, temos:
em que:
- é o deslocamento;
- é a posição final;
- é a posição inicial.
No Sistema Internacional de Unidades (SI), a unidade-padrão usada para medir o deslocamento é o metro .
Página 274
Observe a seguir algumas conversões do metro que também podem ser usadas.
O deslocamento é uma grandeza que tem direção e sentido, e seu valor é dado pela diferença entre a posição final e a posição inicial de um corpo. Além disso, no deslocamento, não importa o quanto se percorreu, mas sim a distância em linha reta entre a posição final e a posição inicial do movimento.
A distância total percorrida é uma grandeza que representa quanto um corpo percorreu em um trajeto, sem levar em consideração a direção e o sentido do movimento.
Velocidade média e velocidade instantânea
Considere a situação a seguir.
João tem 14 anos e quer ser um ciclista profissional. Para atingir o seu objetivo, ele participa de um projeto social que oferece treinamento de ciclismo.
Duas vezes por semana, João pedala durante uma hora e pretende melhorar o seu desempenho, aumentando a distância do percurso e a velocidade.
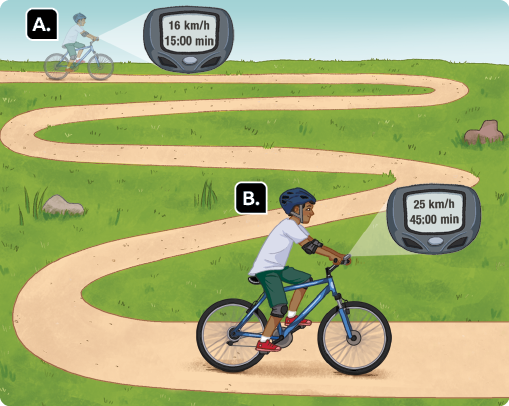
Representação com elementos não proporcionais entre si. Cores-fantasia.
A persistência é uma competência que diz respeito à capacidade de se manter determinado, com foco e responsabilidade para atingir um objetivo em determinada tarefa. O indivíduo persistente se esforça, busca estratégias, supera obstáculos, independentemente das adversidades, desconfortos e desafios. Seja persistente em busca de seus objetivos.
Questão 2. Observe o velocímetro da
bicicleta de João nos momentos A e B. A
velocidade atingida por ele foi a mesma ao longo de todo o
percurso?
Resposta: A velocidade atingida por João durante a realização do percurso não foi constante, ela variou.
Como observamos no velocímetro da bicicleta de João, durante um percurso, raramente um corpo mantém uma velocidade constante. Dessa forma, ao estudarmos uma situação envolvendo movimento, geralmente usamos a velocidade média . Essa grandeza estabelece uma relação entre o deslocamento e o intervalo de tempo gasto em todo o percurso.
Página 275
Podemos calcular a velocidade média dividindo o deslocamento pelo intervalo de tempo gasto nesse deslocamento. Observe a seguir.
ou
em que:
- é a velocidade média do corpo;
- é o deslocamento do corpo;
- é o intervalo de tempo.
No SI, a unidade da velocidade é o metro/segundo , lê-se "metro por segundo".
Durante um percurso, a velocidade pode, por exemplo, diminuir, se houver obstáculos, e aumentar em locais sem obstáculos.
A velocidade de um corpo em determinado instante é chamada velocidade instantânea. Os valores indicados nos velocímetros da bicicleta de João são exemplos dessa grandeza.
Considere o outro exemplo a seguir.
Um automóvel passa pelo marco do e, após 1,5 hora, ele passa pelo marco do . Com base nas informações fornecidas, determine a velocidade média do automóvel.
Dados:
Resolução:
Primeiro, calculamos o deslocamento do automóvel.
Agora, transforma-se a unidade de medida da grandeza deslocamento de quilômetro para metro.
Também deve ser transformada a unidade de medida da grandeza tempo de hora para segundo.
Página 276
Utilizando a equação de velocidade média, tem-se:
Conclusão:
A velocidade média do automóvel no trecho mencionado na questão é de , isto é, a cada segundo, o automóvel se desloca .
Sugestões complementares
O livro Física do dia a dia: 105 perguntas e respostas sobre física fora da sala de aula aborda questionamentos relacionados a fenômenos que ocorrem no cotidiano das pessoas. O livro tem respostas de fácil compreensão a qualquer leitor.

Capa do livro Física do dia a dia: 105 perguntas e respostas sobre física fora da sala de aula, de Regina Pinto de Carvalho (org.), 2011.
Movimento retilíneo uniforme
Considere um carro que se movimenta em uma trajetória retilínea e em velocidade constante durante todo o percurso. Observe a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Em Física, dizemos que esse corpo realiza um movimento retilíneo uniforme (MRU). Nesse tipo de situação, a velocidade média do corpo durante o percurso tem o mesmo valor que a instantânea. No entanto, situações como essa dificilmente ocorrem no cotidiano.
Nesse tipo de movimento, é possível determinar a posição (s) de um corpo em qualquer instante (t) por meio da função horária da posição de um corpo no MRU.
Página 277
Observe a seguir como podemos deduzir essa função horária da posição no MRU, considerando a situação do carro se movimentando em uma trajetória retilínea e em velocidade constante.
Dados:
Resolução:
Substituindo os dados da situação na equação, temos:
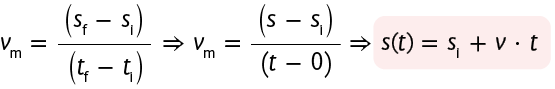
em que:
é a posição do corpo no instante t;
é a posição do corpo no instante inicial ;
v é a velocidade do corpo;
t é o instante no qual o corpo está na posição s.
A função horária da posição no MRU pode fornecer a posição de um corpo em movimento em qualquer instante, desde que se saiba a posição inicial e a velocidade.
Aceleração média
Podemos perceber no dia a dia que a velocidade de um corpo em movimento varia no decorrer de sua trajetória, podendo aumentar ou diminuir. Quando um corpo está em movimento e sua velocidade varia no decorrer do tempo, podemos dizer que esse corpo está em aceleração.
A aceleração é uma grandeza física relacionada à variação da velocidade de um corpo, seja aumentando ou diminuindo seu valor. Já a aceleração média fornece a taxa de variação de velocidade de um corpo em determinado intervalo de tempo. Observe a situação a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.
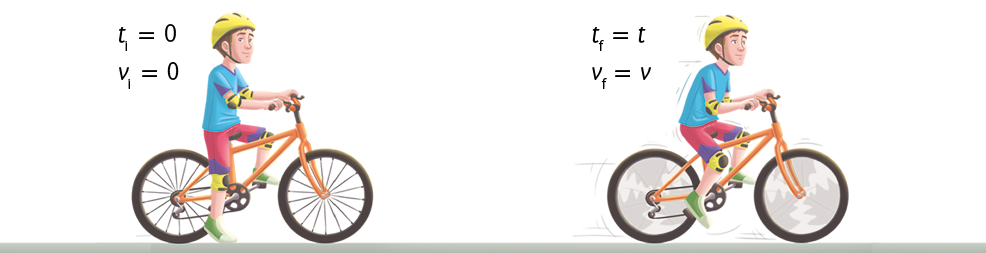
Página 278
Podemos calcular a aceleração média dividindo a variação da velocidade pelo intervalo de tempo gasto nesse deslocamento. Observe a seguir.
ou
em que:
- é a aceleração média;
- é a velocidade final;
- é a velocidade inicial;
- é o tempo final;
- é o tempo inicial.
No SI, a unidade da aceleração é o (lê-se "metro por segundo ao quadrado"). Outra unidade de medida de aceleração muito utilizada em vários países é o quilômetro por hora ao quadrado .
Dica!
Lembre-se de que não podemos realizar cálculos com valores expressos em unidades de medida diferentes.
Comumente, quando a velocidade de um corpo está aumentando, dizemos que ele está "acelerando" e, quando a velocidade está diminuindo, dizemos que o corpo está "desacelerando". Na Física, essas duas situações caracterizam dois tipos de movimentos — o movimento acelerado e o movimento retardado, respectivamente.
Considere que um motorista esteja dirigindo um veículo por uma avenida retilínea que apresenta alguns semáforos. Observe a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.


Representação de um carro em movimento: acelerado (imagem A) e retardado (imagem B).
pA. Logo que a luz verde do semáforo acende, o veículo inicia seu movimento, aumentando a sua velocidade. Temos, assim, um movimento acelerado.
B. Ao identificar a luz amarela de um semáforo acesa, o motorista precisou frear o veículo, diminuindo a sua velocidade. Temos, assim, um movimento retardado.
Página 279
Movimento retilíneo uniformemente variado
Considere a situação a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Questão 3. Qual é a variação de velocidade
do avião a cada intervalo de
tempo indicado?
Resposta: A cada intervalo de tempo, a variação de velocidade é de .
Questão 4. O que você concluiu quanto à
aceleração do avião?
Resposta pessoal. Espera-se que os alunos respondam que a aceleração é constante, ou seja, sempre com a mesma intensidade.
Como pudemos perceber, durante o percurso, a velocidade do avião não se manteve constante, aumentando gradativamente. A cada intervalo de tempo indicado, houve uma variação de na velocidade, como mostra o quadro a seguir.
|
Deslocamento |
Intervalo de tempo |
|
|---|---|---|
|
AB |
0 a 4 |
14 |
|
BC |
4 a 8 |
14 |
|
CD |
8 a 12 |
14 |
|
DE |
12 a 16 |
14 |
|
EF |
16 a 20 |
14 |
Agora, verificaremos a aceleração média desse avião em dois dos intervalos de tempo.
|
Intervalo AB |
Intervalo BC |
||
|---|---|---|---|
|
Dados: |
Resolução: |
Dados: |
Resolução: |
|
|
|||
Ao verificarmos os valores de e de para os outros intervalos de tempo, podemos concluir que, para cada intervalo de tempo, a aceleração média desse avião é . Assim, a velocidade do avião aumentou uniformemente (de em para cada intervalo de tempo), mantendo sua aceleração constante em todo o percurso. Esse tipo de movimento é chamado movimento retilíneo uniformemente variado (MRUV).
Questão 5. Qual será a velocidade desse avião em , considerando que ele continue realizando o movimento retilíneo uniformemente variado? Faça os cálculos no caderno.
Resposta: Considere e . Substituindo os valores na equação temos:
Página 280
O tema é ...
Educação para o trânsito
Pedestre, respeite as leis de trânsito!
Quando pensamos em trânsito seguro, geralmente imaginamos um trânsito solidário, com todos respeitando as leis de trânsito, os pedestres e os motoristas. De fato, como prevê o Código Nacional de Trânsito, os motoristas precisam ser responsáveis, pois suas atitudes têm consequências em sua vida e na de outras pessoas.
Os pedestres, assim como os ciclistas, os motociclistas e os motoristas, também fazem parte do sistema de trânsito, por isso, eles também têm responsabilidades no trânsito.
a) Junte-se a um colega e analisem a imagem a seguir. Em seguida, identifiquem e conversem sobre as atitudes de responsabilidade dos pedestres em relação ao trânsito que estão representadas na imagem.
Resposta nas orientações ao professor.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Página 281
Agora, leia sobre cada uma das atitudes relacionadas à segurança dos pedestres, representadas na imagem.
O pedestre deve atravessar a rua na faixa de segurança quando o sinal de pedestres estiver verde para ele e o semáforo estiver vermelho para os veículos. O pedestre deve olhar para os dois lados antes de atravessar, aguardar a passagem ou frenagem do veículo e, aí sim, atravessar em linha reta, sem correr.
Em locais onde não houver semáforo para pedestres, mas existir faixa de segurança, o pedestre deve sempre atravessar a rua nessa faixa, de maneira segura.
Onde não houver faixa de pedestre, deve-se verificar se não há automóveis passando na rua e seguir o percurso sem diminuir o ritmo ou parar no meio da rua. Além disso, deve-se seguir em linha reta, de forma a reduzir ao máximo o percurso.
Crianças devem estar sempre acompanhadas de um adulto para atravessar ruas e outras vias públicas.
Não é prudente atravessar a rua usando o celular ou observando a paisagem. Também não se deve andar com fones de ouvido, pois o sentido da audição nos alerta de muitos perigos no trânsito.
Deve-se olhar atentamente para os lados ao descer de um carro ou ônibus. Depois, esperar que o veículo saia para, então, atravessar a via.
Ao caminhar nas calçadas, o pedestre precisa ter cuidado com automóveis que podem sair ou entrar na garagem de um prédio ou residência. Algumas portas de garagem têm luz de alerta e alarme sonoro, mas outras não. É preciso estar atento.
Agora, responda às questões a seguir em seu caderno.
1. Onde há faixa de segurança, você sempre atravessa a rua caminhando por ela ou prefere encurtar o caminho?
2. Em sua opinião, deveriam existir multas de trânsito para pedestres que não respeitam as sinalizações? Justifique sua resposta.
3. Ao redor da sua escola, há segurança para o trânsito
de pedestres, como faixa de segurança, semáforos e guardas de trânsito?
Reúna-se com seus colegas e elaborem um texto coletivo sobre o
assunto, incluindo, se necessário,
possíveis melhorias para o trânsito de pedestres ao redor
da
escola.
4. Entreviste
um guarda de trânsito sobre os
comportamentos dos pedestres nas proximidades da escola onde você estuda ou de
outras escolas. Anote os dados da entrevista e depois faça com seus colegas de
grupo um cartaz alertando sobre os perigos
identificados após a análise da entrevista.
Respostas e instruções nas orientações ao professor.
Página 282
Atividades
Faça as atividades no caderno.
1. Reescreva a frase a seguir em seu caderno, substituindo o ▲ pelo trecho que a completa corretamente, apresentado nas alternativas.
Quando a velocidade de um corpo varia no tempo, é possível afirmar que ▲.
a) o corpo desenvolve um MRU.
b) o corpo pode estar acelerando ou freando.
c) a aceleração do corpo em movimento é nula.
d) a velocidade do corpo é zero.
Resposta: Alternativa b.
2. Um veículo movimenta-se sobre uma rodovia, que pode ser representada pela reta orientada a seguir.

Supondo que o veículo inicia seu movimento na posição B, indo até a posição C e retornando ao ponto A, determine o que se pede a seguir.
a) A distância percorrida.
Resposta nas orientações ao professor.
b) O deslocamento.
Resposta nas orientações ao professor.
c) Qual é o significado do resultado obtido no item b? Explique sua resposta.
Resposta nas orientações ao professor.
3. Dois veículos se deslocam por uma via pública retilínea no mesmo sentido. O veículo da pista lenta (A) se move a em relação à rodovia. O veículo da pista rápida (B), que está à frente, se afasta com velocidade de em relação ao veículo da pista lenta. Uma criança e sua mãe estão em repouso em relação à pista.
Representação com elementos não proporcionais entre si. Cores-fantasia.
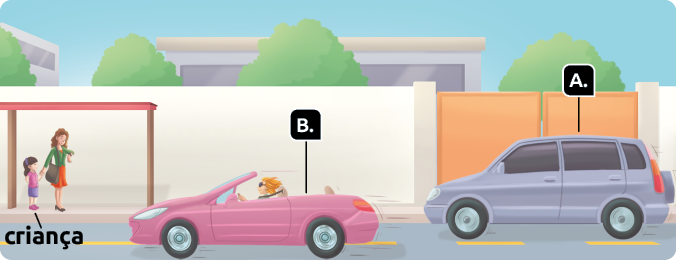
a) Qual é a velocidade da criança em relação ao veículo da pista lenta e em relação ao veículo da pista rápida? Qual é a velocidade de (B) em relação a (A)?
Resposta: A velocidade da criança em relação ao veículo da pista lenta é . A velocidade da criança em relação ao veículo da pista rápida é . A velocidade do veículo B em relação ao veículo A é , pois os dois veículos se movem para o mesmo sentido.
Página 283
4. Uma das principais atrações turísticas do estado do Paraná é o passeio de trem que liga as cidades de Curitiba e Morretes. Considerando que a distância entre as duas cidades é de , o trem percorre todo o trajeto em três diferentes momentos.
Metade do trajeto é percorrido com uma velocidade de .
Os próximos são percorridos com uma velocidade de .
O restante do trajeto é percorrido com uma velocidade de .
Com base nessas informações, julgue as afirmativas a seguir como verdadeiras ou falsas, justificando as falsas em seu caderno.
a) O tempo gasto na primeira etapa da viagem de trem é de .
b) O tempo gasto na terceira etapa da viagem é de .
c) O tempo total gasto na viagem de trem de Curitiba a Morretes é de .
d) A velocidade média do trem durante todo o percurso da viagem é de .
e) Por todo o trajeto da viagem, o trem não apresenta aceleração.
Resposta nas orientações ao professor.
5. Um voo durou , com a velocidade média da aeronave de . Aproximadamente 30 minutos após a aterrissagem do avião, e a da pista de pouso, um dos passageiros deslocou-se em direção a um hotel por meio de um automóvel, que manteve a velocidade média de , durante 15 minutos. Considere que o passageiro não ficou em repouso em relação ao chão durante todo o tempo indicado.
a) Qual foi a duração da viagem, em minutos, desde o momento da decolagem do avião até a chegada do passageiro no hotel?
Resposta: A duração da viagem foi de . Sabendo que , somando todos os tempos, temos: .
b) Determine a velocidade média do passageiro, em , a partir da decolagem do avião até a chegada ao hotel, considerando que todo o trajeto tenha sido feito em linha reta.
Resposta nas orientações ao professor.
6. Daniel avistou um semáforo e diminuiu a velocidade da motocicleta de para em 3 segundos.
Dica!
Os valores de aceleração que estiverem acompanhados do sinal negativo indicam que ocorreu uma aceleração negativa, caracterizando o movimento retardado. Já os valores acompanhados de sinal positivo indicam que ocorreu aceleração positiva – movimento acelerado.
a) Calcule a aceleração da motocicleta nesse intervalo de tempo.
Resposta nas orientações ao professor.
b) Nessa situação, Daniel e sua motocicleta realizaram um movimento acelerado ou retardado? Justifique sua resposta.
Resposta: Daniel e sua motocicleta realizaram um movimento retardado, pois sua velocidade diminuiu durante o intervalo de tempo, ou seja, sofreu uma desaceleração. Além disso, o valor da aceleração foi negativo.
Página 284
Força
Observe a foto a seguir.

Questão 6. O que provoca a
movimentação e a sustentação
da pessoa acima da superfície da água?
Resposta: Os jatos de água impulsionam o equipamento e, consequentemente, movimentam a pessoa presa ao flyboard, suspendendo-a acima da superfície da água.
Nos tópicos anteriores, abordamos a Cinemática, área da Mecânica que estuda os movimentos, sem levar em consideração os fatores que possam influenciá-los ou gerá-los. A descrição do movimento é realizada com base em grandezas, como a posição, a velocidade e a aceleração do corpo.
Como você deve ter percebido, existe alguma força que faz a pessoa se movimentar utilizando o flyboard. A força é uma grandeza que influencia diretamente o movimento dos corpos. Essa grandeza é objeto de estudo da Dinâmica, área da Mecânica que trata das causas dos movimentos.
Para compreender melhor os conceitos de força e sua influência em nossas vidas, é importante conhecer os conceitos de grandeza escalar e de grandeza vetorial. Estudaremos elas a seguir.
Grandezas escalares e grandezas vetoriais
Considere que Júlia foi ao médico e que, durante a consulta, foram verificadas a temperatura de seu corpo, , e a massa de seu corpo, . Note que as grandezas citadas, temperatura e massa, foram representadas pelos seus valores numéricos, acompanhados de suas respectivas unidades de medida. Não são necessárias outras informações para o médico interpretar essas grandezas ou indicá-las em seu prontuário✚.
- Prontuário:
- ficha que contém os dados de um paciente. ↰
As grandezas que são suficientemente representadas por seu valor numérico e sua unidade de medida, não sendo necessárias outras informações para que sejam compreendidas, são denominadas grandezas escalares.
Página 285
Assim como a temperatura e a massa, o volume, o tempo e o comprimento são exemplos de grandezas escalares comuns em nosso cotidiano.
Entretanto, existem grandezas cujo valor numérico e cuja unidade de medida não são suficientes para caracterizá-las.
Observe a situação a seguir.

Para indicar a localização do supermercado, além da distância que a pessoa deve percorrer, é necessário que a pessoa informante forneça outras informações, como as direções e os sentidos que ela deve seguir. De forma geral, a pessoa informante precisa descrever, detalhadamente, a trajetória que a pessoa deve realizar para chegar ao seu destino final: o supermercado.
Nessa situação, estão envolvidas as grandezas vetoriais, que são representadas por um valor numérico (intensidade), uma unidade de medida, uma direção e um sentido. Uma grandeza vetorial é representada por um vetor, ou seja, um segmento de reta orientado, e seu símbolo vem acompanhado de uma pequena seta sobre ele. Por exemplo, indica o vetor deslocamento; , o vetor velocidade de um corpo; e , o vetor aceleração.
A força também é uma grandeza vetorial e é indicada por . No Sistema Internacional de Unidades, a unidade de medida de força é (Newton). Analise o exemplo a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Considere que Rafael esteja aplicando uma força de em um armário para mudá-lo de posição. Podemos notar que essa informação é insuficiente para sabermos de que maneira Rafael está movimentando o armário. Para caracterizar o vetor força que Rafael está aplicando no armário, devemos considerar as informações a seguir.
Valor numérico: .
Direção: horizontal.
Sentido da força: da direita para a esquerda.
Página 286
Em nosso dia a dia, são comuns situações em que várias forças atuam sobre um corpo. Nesses casos, há um sistema de forças atuando sobre esse corpo e cada uma delas pode ser representada por um vetor.
Os vetores de um sistema podem atuar sobre um corpo de diversas maneiras. Para compreender como isso ocorre em cada um desses casos, podemos efetuar uma soma de vetores, que permite substituir o conjunto de vetores por um único vetor, que representa a força resultante desse sistema.
Verifique, na cena a seguir, dois exemplos de sistemas de força.
Representação com elementos não proporcionais entre si. Cores-fantasia.

A. Luís chamou Cíntia para brincar de empurrar uma bola inflável. Se Cíntia e Luís aplicarem força na bola, na direção horizontal e no sentido da esquerda para a direita, os dois colegas aplicarão forças com mesma direção e mesmo sentido.
Nesse caso, a intensidade do vetor força resultante é obtida pela soma da intensidade das forças aplicadas à bola, isto é, . A força resultante tem direção horizontal e sentido da esquerda para a direita.
B. André e Larissa estão aplicando sua força na mesma direção, porém em sentido contrário à força aplicada por Rafael e Júlia.
Nesse caso, a intensidade do vetor força resultante é obtida pela diferença da intensidade das forças aplicadas à corda. Adotando o sentido da esquerda para direita como positivo, o vetor da força resultante aplicada sobre a corda pode ser obtido da seguinte maneira: como a força de tem o mesmo sentido do referencial adotado, ela tem sinal positivo; e a força de tem sentido contrário ao referencial e seu sinal é negativo.
Página 287
Agora, representaremos os vetores por meio de um vetor resultante. Observe, a seguir, as informações referentes à soma dos vetores das forças aplicadas por Luís e Cíntia.
Informação |
Vetor |
Intensidade |
|---|---|---|
|
Vetor da força aplicada por Luís. |

|
Intensidade |
|
Vetor da força aplicada por Cíntia. |

|
Intensidade |
|
Posicione o início do segundo vetor no final do primeiro . |

|
Intensidade do vetor da força resultante
|
|
O vetor da força resultante é o que se estende do início do primeiro vetor ao final do segundo vetor. |

|
Agora, verifique a seguir as informações referentes à soma dos vetores das forças aplicadas por André, Larissa, Rafael e Júlia.
Informação |
Vetor |
Intensidade |
|---|---|---|
|
Vetor da força aplicada por André e Larissa. |

|
Intensidade |
|
Vetor da força aplicada por Rafael e Júlia. |

|
Intensidade |
|
Posicione o início do vetor no final do primeiro . |
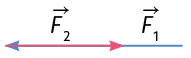
|
Intensidade do vetor da força resultante
|
|
O vetor da força resultante é o que vai do início do primeiro vetor ao final do segundo vetor. |
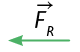
|
As leis de Newton
O estudo do movimento dos corpos teve grandes avanços graças a uma concepção filosófica surgida na Europa, no século XV, chamada filosofia mecanicista. Os adeptos dessa concepção filosófica buscavam explicar alguns fenômenos naturais, entre eles, o movimento dos corpos e o movimento dos astros no Universo.
Página 288
Influenciado pelos trabalhos publicados de filósofos mecanicistas, o cientista inglês Isaac Newton (1643-1727) apresentou, em seu trabalho denominado Principia – os princípios matemáticos da filosofia natural, um conjunto de leis que formaram a base para entendermos o movimento dos corpos, suas causas e suas interações.
Com base nessas leis, podemos descrever os movimentos, que podem incluir desde o simples caminhar de uma pessoa até o lançamento de foguetes espaciais.
As leis de Newton não se aplicam em casos de corpos que se movimentam com velocidades próximas à velocidade da luz (cerca de ) nem para descrever o movimento de partículas, como os átomos.

Primeira lei de Newton ou princípio da inércia
Que tal investigar de forma prática o princípio da inércia? Para isso, realize a atividade a seguir.
Vamos praticar
Materiais
- carteira escolar
- caderno escolar
A. Afaste-se alguns centímetros de sua carteira e observe seu caderno.
B. Empurre levemente seu caderno na direção horizontal.
Agora, responda às questões a seguir no caderno.
a) Na etapa A, seu caderno estava em repouso ou em movimento em relação à carteira?
b) De acordo com o que foi estudado até agora, o que é necessário aplicar no caderno para que ele entre em movimento sobre a carteira?
c) Enquanto você empurrava o seu caderno na etapa B, ele estava em repouso ou em movimento em relação à carteira?
Respostas e instruções nas orientações ao professor.
Como observamos ao realizar a atividade da seção Vamos praticar, o caderno estava em repouso sobre a carteira. Se a força resultante aplicada sobre o caderno for nula, ou seja, igual a zero, ele permanecerá em repouso. Mas, se for aplicada uma força na direção horizontal sobre o caderno, a força resultante deixará de ser nula, e ele iniciará um movimento em relação à carteira.
Página 289
A situação em que o caderno permanece em repouso em relação a um referencial exemplifica ideias anteriores de físicos e filósofos aprimoradas por Newton no chamado princípio da inércia.
A tendência natural dos corpos de permanecer em seu estado de repouso ou em movimento retilíneo com velocidade constante é chamada inércia.
Leia a seguir o que afirma a primeira lei de Newton, ou princípio da inércia.
Todo corpo em repouso ou em movimento retilíneo com velocidade constante tende a permanecer em seu estado de movimento, indefinidamente, se a força resultante que atua sobre ele for nula.
Segunda lei de Newton ou princípio fundamental da dinâmica
Quando você aplicou uma força para empurrar o caderno, na atividade da seção Vamos praticar, ele iniciou um movimento e sua velocidade variou, ou seja, naquele momento, houve uma aceleração. Com isso, uma força resultante aplicada a um corpo de massa m produziu uma aceleração nesse corpo, dada pela relação apresentada a seguir.
em que:
é o valor da força resultante aplicada no corpo;
m é o valor da massa do corpo;
é o valor da aceleração adquirida pelo corpo.
A relação anterior é definida vetorialmente, o que significa que a grandeza força resultante tem a mesma direção e o mesmo sentido da aceleração. Para o cálculo da intensidade desses vetores, assim como a grandeza massa, podemos escrever a expressão como apresentado a seguir.
A unidade de medida da força é o (lê-se "quilograma-metro por segundo ao quadrado"). Essa unidade é conhecida como newton . O newton é definido como a força necessária para produzir a aceleração de em uma massa de .
A aceleração do corpo é proporcional à força aplicada sobre ele, ou seja, se aumentarmos a intensidade da força, o corpo adquire maior aceleração; e, se diminuirmos a intensidade da força, o corpo adquire menor aceleração. No entanto, uma força de mesma intensidade produz efeitos diferentes em corpos diferentes.
Página 290
Por exemplo, ao empurrar uma caixa vazia e uma caixa com limões com forças de mesma intensidade, percebe-se que a aceleração adquirida pela caixa vazia é maior do que a adquirida pela caixa com limões. Isso ocorre, porque existe uma relação entre a massa de um corpo e a inércia: quanto maior a massa de um corpo, maior será sua resistência a mudar seu estado de movimento.
Assim, podemos enunciar a segunda lei de Newton, como apresentado a seguir.
Quando uma força resultante não nula atua em um corpo, este sofre uma aceleração na mesma direção da força. Essa aceleração é diretamente proporcional à força e inversamente proporcional à massa desse corpo.
Terceira lei de Newton ou princípio da ação e reação
Em seus estudos sobre o movimento e as interações que existem entre os corpos, Newton percebeu que, para toda força de ação aplicada a um corpo, existe uma força de reação do corpo no sentido oposto àquela que está recebendo.
Por exemplo, para deslocar o skate, a pessoa empurra o chão com o pé e o chão empurra o pé da pessoa. Essas duas forças atuam aos pares, ou seja, para toda força de ação existe uma de reação. Apesar de atuarem aos pares, as forças de ação e de reação exercem influência em corpos diferentes.

Com base nisso, podemos enunciar a terceira lei de Newton, como apresentado a seguir.
Se um corpo A aplica uma força sobre o corpo B, esse corpo B aplica uma força de mesmo valor, mesma direção, porém em sentido oposto, sobre o corpo A.
Tipos de força
Como estudamos, as leis de Newton descrevem e explicam as causas dos movimentos dos corpos. Esses movimentos são influenciados por diferentes tipos de forças, como atrito e peso.
Estudaremos cada uma dessas forças a seguir.
Página 291
Força de atrito
Para redecorar a própria casa, Carla precisou empurrar um armário de um cômodo, que tem piso liso, até o quintal, que tem um piso áspero de concreto.
Observe a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.


Representação de Carla empurrando o armário em piso liso (situação A) e em piso áspero (situação B).
Questão 7. Em qual das
situações (A ou B) Carla teve de
aplicar uma força de maior intensidade para
movimentar o armário? Justifique sua resposta.
Resposta: Carla teve de aplicar uma força de maior intensidade na situação B. Espera-se que os alunos relacionem a intensidade da força aplicada à diferença de atrito entre os dois pisos.
A força de atrito está presente em muitas situações de nosso cotidiano, como quando empurramos objetos, escovamos os dentes, escrevemos ou andamos. Elas são inevitáveis e também necessárias, pois sem elas não seria possível caminhar ou andar de bicicleta, nem segurar um lápis, por exemplo.
A força de atrito atua quando existe contato entre dois ou mais corpos. Uma de suas características é ser contrária ao movimento.
Nas situações A e B, o atrito ocorre nos pontos de contato entre a base do armário e o chão. Essa força de atrito é contrária à força aplicada no armário e, consequentemente, é contrária ao seu movimento.
Alguns fatores influenciam o atrito entre dois corpos, por exemplo, as características das superfícies em contato, como seu grau de polimento e a presença de substâncias lubrificantes.
Força peso
Com os estudos sobre movimentos, tanto dos corpos na Terra quanto dos astros no Universo, Isaac Newton concluiu que a força que faz um objeto cair em direção à superfície da Terra é da mesma natureza da força que age nos astros do Universo, como a força que mantém a Lua em órbita ao redor da Terra. Essa força de atração entre os corpos que têm massa é chamada força da gravidade.
Página 292
Com essas observações, Newton descreveu o comportamento dos astros elaborando a lei da gravitação universal, enunciada a seguir.
Todos os corpos no Universo se atraem mutuamente. Essa atração é proporcional às suas massas e inversamente proporcional ao quadrado da distância entre eles.
Isso significa dizer que quaisquer corpos com massa, por menor que sejam, se atraem, e, quanto maior a massa dos corpos, maior será a atração gravitacional. Por outro lado, quanto maior for a distância entre esses corpos, menor será essa força.
Considere um fruto que acabou de se desprender de uma árvore. Existe uma força de atração entre ele e a Terra que é sentida por ambos os corpos. Por ter menor massa, no entanto, o fruto cairá em direção à superfície terrestre.
A força gravitacional é também chamada peso . Ela é um vetor vertical com direção orientada do espaço para o centro da Terra.
Representação com elementos não proporcionais entre si. Cores-fantasia.

De acordo com a segunda lei de Newton, a força peso provoca uma aceleração nos corpos, chamada aceleração da gravidade , que também é direcionada do espaço para a Terra. Todos os corpos submetidos somente à ação da força peso caem com a mesma aceleração da gravidade. Por isso, o valor do peso dos corpos é dado pela relação apresentada a seguir.
em que:
P é o valor do peso do corpo;
m é o valor da massa do corpo;
g é o valor da aceleração da gravidade local.
Como o peso é uma força, sua unidade de medida, no Sistema Internacional de Unidades (SI), é o newton .
De acordo com a relação anterior, podemos notar que o peso de um corpo depende da aceleração da gravidade local.
Página 293
Trabalho
Observe a seguir a situação vivida por Eduardo.
Representação com elementos não proporcionais entre si. Cores-fantasia.


Representação de uma pessoa empurrando o carro até uma oficina mecânica: do ponto de partida (imagem A) ao ponto de chegada (imagem B).
Como podemos observar na imagem, o carro de Eduardo apresentou um problema mecânico e parou de funcionar (imagem A). Diego, funcionário de uma oficina mecânica próxima ao local no qual ocorreu o defeito no carro de Eduardo, empurrou o veículo até a porta da oficina (imagem B).
Para empurrar o veículo, Diego precisou aplicar uma força suficiente para deslocá-lo até a posição desejada: a oficina. Nesse caso, a força aplicada realizou um trabalho, grandeza escalar relacionada com a transferência de energia de um corpo para outro. O trabalho realizado pela força é dado pela relação a seguir.
em que:
é o trabalho realizado pela força;
F é a força aplicada ao corpo;
é o deslocamento realizado durante a ação da força.
Estudamos que no SI a unidade de medida da força é o newton e a unidade de medida do deslocamento é o metro . Observe, a seguir, a determinação da unidade de medida do trabalho no SI.

A unidade de medida do trabalho é o (lê-se "newton vezes metro"). Essa unidade é conhecida como joule , em homenagem ao físico experimental inglês James Prescott Joule (1818-1889).
Página 294
Energia mecânica
A energia se manifesta no Universo de diversas formas. Entre elas, podemos destacar a energia mecânica, que está relacionada à capacidade de um corpo realizar trabalho.
Entre as várias formas de energia que conhecemos, existe uma que está associada ao movimento dos corpos em relação a um referencial, a chamada energia cinética. Por exemplo, um veículo em movimento, uma pessoa correndo ou nadando e um fruto caindo de uma árvore são corpos que têm energia cinética.
Quanto maior a velocidade de um corpo, maior é a sua energia cinética. Além disso, se compararmos dois corpos à mesma velocidade, aquele que apresentar maior massa tem maior energia cinética.
Agora, considere um fruto pendurado em uma árvore, como os abacates em um abacateiro.
Nessa situação, podemos dizer que duas forças estão agindo sobre o abacate: o peso e a força de tração exercida pelo ramo da árvore.
Quando o abacate está em repouso, as duas forças se equilibram e não realizam trabalho. Contudo, se em algum momento a força de tração deixar de existir (o abacate se soltar do ramo), a força peso fará o abacate cair, realizando trabalho sobre ele.

Quando empurramos um objeto, por exemplo, transformamos a energia do nosso corpo em energia cinética do objeto, que se move. No caso do abacate caindo, ocorre o mesmo: sua energia cinética se altera durante a queda. Isso significa que, antes de cair, o abacate tinha um tipo de energia armazenada, chamada energia potencial.
Existem alguns tipos de energia potencial. No caso do abacate, como a energia armazenada depende da posição desse fruto no campo gravitacional da Terra, ela é denominada energia potencial gravitacional .
Essa energia depende da massa do corpo, do valor da aceleração da gravidade no local e da altura em que esse corpo se encontra em relação à superfície do planeta Terra.
Página 295
Máquinas simples
Muitas tarefas do dia a dia, como trocar um pneu furado, abrir uma porta ou uma torneira, podem ser facilitadas se usarmos determinados objetos ou instrumentos criados pelo ser humano, como as máquinas simples.
A construção e o desenvolvimento de máquinas proporcionam vantagens ao ser humano para a realização das atividades do cotidiano. Utilizar a criatividade proporciona a originalidade e a criação de novas ferramentas para facilitar sua aplicação.
Alguns exemplos dessas máquinas são a alavanca, o plano inclinado e a roldana. Estudaremos cada uma delas a seguir.
Alavanca
A alavanca é uma máquina simples formada por uma haste ou barra rígida, apoiada em um ponto fixo. Dependendo da localização do ponto de apoio e do corpo a ser movido, a alavanca permite ampliar ou diminuir a intensidade da força aplicada em uma de suas extremidades.
Esse tipo de máquina simples é encontrado, por exemplo, em alicates, chaves de rodas, torneiras e maçanetas das portas.
Analise a alavanca a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Fonte de pesquisa: TREFIL, James; HAZEN, Robert Miller. Física viva: uma introdução à física conceitual. Tradução: Ronaldo Sérgio de Biasi. Rio de Janeiro: LTC, 2006. v. 1. p. 147.
A força potente é a força que aplicamos na alavanca.
A força resistente é a força exercida pelo objeto a ser levantado, nesse caso, é o peso do objeto.
O braço de potência é a distância entre o ponto de apoio e o local de aplicação da força potente.
O braço de resistência é a distância entre o ponto de apoio e o local de aplicação da força resistente.
Página 296
Com base na imagem da alavanca, podemos compreender que, quanto maior for o braço de potência, em relação ao braço de resistência, menor será a força potente necessária para levantar o objeto em questão. Nesse caso, a alavanca aumenta o efeito da força potente aplicada em uma das extremidades.
O alicate é um objeto utilizado para prender e cortar determinados materiais. Essa ferramenta apresenta uma junção de duas alavancas.
Ao utilizar o alicate, a pessoa aplica a força no cabo dessa ferramenta. A intensidade da força que o alicate exerce sobre o objeto a ser cortado é maior do que a intensidade da força que a pessoa aplica no cabo da ferramenta.
Observe, a seguir, a configuração das grandezas físicas aplicadas no uso do alicate.
Questão 8. Por que os
braços de resistência em alicates
são menores que os braços de potência?
Resposta: Porque dessa maneira aumenta-se o efeito da força potente aplicada, pois quanto maior o braço de potência, menor a força que aplicamos na alavanca.
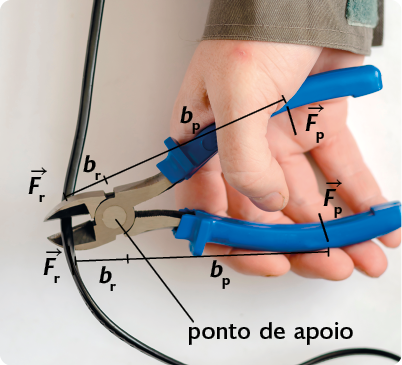
As alavancas podem ser classificadas em interfixa, inter-resistente e interpotente.
A alavanca é classificada como interfixa quando o ponto de apoio está localizado entre a força potente e a força resistente. A tesoura, o alicate e a gangorra são exemplos desse tipo de alavanca.

Página 297
Na alavanca inter-resistente, o ponto de apoio se localiza em uma das extremidades da barra, próximo do local onde é aplicada a força resistente. O abridor de garrafas e o quebra-nozes são exemplos desse tipo de alavanca.
Imagens não proporcionais entre si.

Na alavanca interpotente, o ponto de apoio se localiza em uma das extremidades da barra, próximo de onde se aplica a força potente. A pinça e o cortador de unha são exemplos desse tipo de alavanca.

Plano inclinado
Para colocar um sofá dentro de um caminhão de mudanças, o funcionário da transportadora tem duas opções. Confira cada uma delas a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.


Questão 9. Qual opção
(A
ou B) exige menor esforço
físico do funcionário? Para responder a essa questão, analise somente a força aplicada para elevar o sofá, e desconsidere
a força de atrito entre o sofá e a
superfície da rampa.
Resposta: Espera-se que os alunos respondam que o funcionário fará um menor esforço físico se empurrar o sofá pela rampa (opção A).
Página 298
Quando elevamos um objeto sem usar um plano inclinado, a força aplicada deve ter, no mínimo, a mesma intensidade do peso do objeto. Se usarmos um plano inclinado, a força necessária para elevar o objeto será menor se comparada à força utilizada em um deslocamento somente vertical. Isso é possível porque o plano inclinado sustenta parte do peso do objeto. No entanto, o deslocamento nesse caso é maior que o deslocamento vertical. É importante notar que, em ambos os casos, o trabalho realizado será o mesmo, pois o trabalho não depende da trajetória do deslocamento.
De todas as máquinas simples, é possível que o plano inclinado seja a mais antiga utilizada pelo ser humano.
Antigas civilizações perceberam que, ao arrastar objetos por rampas, empregavam menor esforço físico do que se os carregassem. Essa constatação levou essas civilizações a construir rampas com toras e varas, facilitando a execução de tarefas cotidianas.
Há uma hipótese que relaciona o plano inclinado à construção das pirâmides no Egito Antigo, por exemplo. Nesse caso, os planos inclinados eram construídos com toras, cascalhos e lama retirada do rio Nilo. Cada bloco era colocado em uma espécie de trenó de madeira e puxado, com o auxílio de cordas, por uma equipe de trabalhadores. Para facilitar o transporte dos blocos, eles molhavam constantemente as toras para diminuir a força de atrito entre elas e o trenó.

Conforme a pirâmide se tornava mais alta, o plano inclinado aumentava, tanto na altura como no comprimento, para manter a inclinação adequada.
Observe as imagens a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.
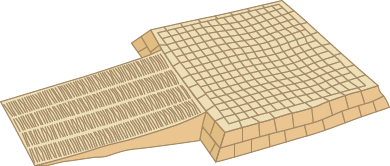
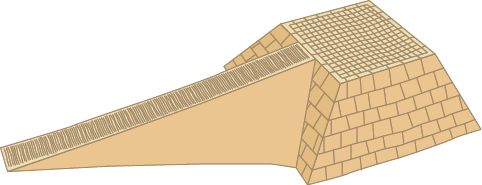
Representação esquemática da construção de uma pirâmide no Egito Antigo.
Página 299
Outra máquina simples relacionada ao plano inclinado é a rosca, presente em instrumentos como a prensa. Observe a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.

As roscas consistem em filetes salientes, ao longo de superfícies cilíndricas, que podem estar na parte externa do cilindro, como nos parafusos, ou na parte interna, como nas porcas. As roscas são caracterizadas pelo diâmetro do cilindro, pela espessura e pelo número de filetes, normalmente medido em milímetros ou polegadas.


Roldanas
Observe a foto a seguir.
Questão 10. Para elevar as
massas no aparelho de musculação, em que direção e sentido o
homem mostrado na foto aplica força?
Resposta: A direção da força aplicada pelo homem é vertical, e o sentido é para baixo.
Questão 11. Como a força
que ele faz é transferida para as massas?
Resposta: A força é transferida por meio de cabos de aço e roldanas.

Página 300
As roldanas são máquinas simples que facilitam a realização de tarefas, como elevar ou transportar objetos utilizando cordas. Elas estão presentes, por exemplo, nos guindastes.
Imagens não proporcionais entre si.


A roldana é composta basicamente de um disco rígido, que tem um sulco em sua parte central. Geralmente, nesse sulco, é colocada uma corda ou cabo, em que é aplicada a força potente para erguer o objeto. Uma roldana simples gira livremente em torno de um eixo.
As roldanas podem mudar a direção e/ou o sentido da força aplicada para mover o objeto, ou, em alguns casos, diminuir a intensidade da força necessária para movimentar certos objetos.
Existem dois tipos básicos de roldana: a fixa e a móvel.
A roldana fixa tem o suporte de seu eixo fixo a um ponto ou a uma superfície. Esse tipo de roldana somente altera a direção e/ou o sentido da força aplicada, ou seja, não altera a intensidade da força aplicada. Além disso, a rotação da roldana evita o desgaste da corda e facilita a execução da tarefa.
Observe um exemplo de roldana fixa, utilizada para hastear uma bandeira do Brasil.


Mastro com bandeira hasteada (foto A) com destaque para a roldana fixa (foto B).
No mastro de uma bandeira existem duas roldanas, uma superior e outra inferior. Nessa situação, abordaremos o funcionamento da roldana superior, destacada na foto B.
Página 301
No hasteamento de uma bandeira, a pessoa aplica uma força no sentido contrário ao deslocamento da bandeira. Essa situação é vantajosa, pois permite à pessoa hastear a bandeira permanecendo no solo, ou seja, ela não precisa subir até o topo do mastro para puxar a bandeira.
Nas roldanas móveis, o corpo a ser puxado encontra-se preso ao suporte do eixo da roldana, e todo esse conjunto é móvel. Isso significa que a força resistente é aplicada no eixo da roldana.
Analise o funcionamento de uma roldana móvel.
Representação com elementos não proporcionais entre si. Cores-fantasia.

Na roldana móvel, a força de resistência, nesse caso o peso do corpo, é sustentada por duas partes da corda, uma fixada em uma haste e outra sendo puxada por uma pessoa. Dessa forma, a força necessária para realizar o trabalho é reduzida pela metade.
Esse tipo de roldana costuma ser usado para aplicar forças de grande intensidade, como é o caso dos guindastes.
Fonte de pesquisa: HEWITT, Paul G. Física conceitual. Tradução: Trieste Freire Ricci. 12. ed. Porto Alegre: Bookman, 2015. p. 120-121.
Em muitas situações, é necessária a associação de diversas roldanas, pois, assim, é possível combinar mudanças de direção e sentido e alterar a intensidade da força aplicada para realizar um trabalho.
Observe a seguir.
O guindaste é um exemplo de associação entre uma roldana fixa e uma roldana móvel. A roldana fixa direciona a força potente até a roldana móvel. Enquanto a roldana fixa não altera a força potente, a roldana móvel atua reduzindo a força necessária para levantar o objeto.
Representação com elementos não proporcionais entre si. Cores-fantasia.
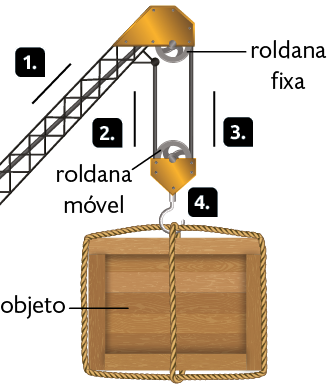
1.
2.
3.
4.
Página 302
Hora de investigar
A força de atrito está presente em várias situações do cotidiano. Sem a presença dela, não seria possível caminhar, andar de carro ou segurar um objeto.
a) Quais características de uma superfície influenciam na força de atrito entre dois corpos? Registre sua resposta no caderno.
b) A massa do corpo interfere na força de atrito? Justifique sua resposta. Registre sua resposta no caderno.
Respostas nas orientações ao professor.
Materiais
- caixa de sapatos
- copo plástico de
- pedaço de barbante de de comprimento
- tesoura com pontas arredondadas
- pequenas rochas
- superfície horizontal, plana e áspera (um piso de concreto, por exemplo)
- superfície horizontal, plana e lisa (um piso de madeira lixado e polido, por exemplo)
- régua
Como proceder
A. Peça a um adulto que, utilizando a tesoura, faça dois furos, um ao lado do outro, em uma das laterais menores da caixa de sapatos, mantendo uma distância de, aproximadamente, entre os furos.
B. Passe o pedaço de barbante pelos furos feitos na lateral da caixa, de modo que as extremidades fiquem do lado de fora da caixa.
C. Faça um nó no barbante, para fixá-lo na caixa de sapatos.
D. Encha o copo plástico com pequenas rochas e despeje-as no interior da caixa de sapatos. Repita esse procedimento outras duas vezes, totalizando a adição de três copos com rochas. Em seguida, coloque a caixa de sapatos sobre a superfície plana e lisa.
Cuidado!
Somente um adulto poderá manusear a tesoura.

Página 303
E. Puxe lentamente a caixa de sapatos pelo barbante, aplicando uma força horizontal.

Dica!
Aplique sempre a força horizontal para puxar a caixa.
F. Em seguida, coloque a caixa de sapatos sobre a superfície plana e áspera. Puxe o barbante lentamente, aplicando uma força horizontal.
G. Por fim, despeje no interior da caixa de sapatos mais dois copos contendo rochas. Repita os procedimentos descritos na etapas E e F.
Minhas observações
1. Em qual superfície houve maior resistência para mover a caixa de sapatos? Justifique sua resposta.
2. O que influenciou no resultado obtido nessa atividade?
3. Quando você colocou mais rochas no interior da caixa de sapatos, como foi orientado na etapa G, o que aconteceu ao tentar movê-la? Como você explica esse resultado?
4. Faça um desenho representando a etapa E dessa atividade e, em seguida, indique nele as principais forças que atuaram nessa situação.
Respostas e instruções nas orientações ao professor.
Elaborando nossas conclusões
1. Junte-se
a um colega e conversem sobre a dificuldade
de movimentar a caixa em pisos mais ásperos, bem como sobre
a
relação dessa dificuldade com a quantidade
de rochas em seu interior. Em uma folha avulsa, escrevam um texto acerca da conclusão a que chegaram após a
conversa. Troquem seus textos com os demais colegas, comparando suas
conclusões, e, em seguida, complementem o texto de vocês, se julgarem
necessário.
Resposta e instruções nas orientações ao professor.
Vamos ampliar a investigação!
1. Você
já ouviu falar na importância dos lubrificantes no funcionamento dos motores
dos automóveis? Para que eles servem?
Junte-se a três colegas e elaborem uma atividade prática para investigar a
importância dos lubrificantes. Para isso, descrevam o passo a passo dessa
atividade prática, listando os materiais necessários. Em seguida, realizem a
atividade e registrem os resultados obtidos, apresentando-os aos colegas da
turma.
Resposta e instruções nas orientações ao professor.
Página 304
Atividades
Faça as atividades no caderno.
1. Ao empurrar uma estante de , vê-se que ela se deslocou na horizontal, para a esquerda, adquirindo uma aceleração horizontal de . Sabendo disso, calcule a intensidade, a direção e o sentido da força resultante sobre a estante.
Resposta: A força resultante tem intensidade de e tem a mesma direção e o mesmo sentido que a aceleração horizontal, ou seja, para a esquerda.
.
2. Em sua casa, Márcia aplica uma força de em um cubo de gelo de , que passa a deslizar sobre uma bancada de mármore. Desconsiderando o atrito entre o gelo e a bancada, calcule o valor numérico da aceleração do gelo.
Resposta:
3. O Artigo 65 do Código de Trânsito Brasileiro torna obrigatório o uso do cinto de segurança, tanto para o condutor como para os passageiros. Com base na primeira lei de Newton, justifique o motivo pelo qual esse equipamento de segurança sempre deve ser utilizado.
Resposta nas orientações ao professor.

4. De acordo com seus conhecimentos sobre as leis de Newton, julgue as afirmativas a seguir como verdadeiras ou falsas, justificando as falsas em seu caderno.
a) A tendência natural de um corpo em repouso para um determinado referencial é que esse corpo sofra uma aceleração, de mesma direção e mesmo sentido que a força resultante.
b) Quanto maior a intensidade da força resultante, maior é a intensidade da aceleração imposta para um corpo cuja massa permaneça constante.
c) As forças de ação e reação se anulam, já que contêm a mesma intensidade, mas sentidos opostos.
d) O atrito é uma força de contato entre dois ou mais corpos. Ela é uma força de resistência à tentativa de movimento ou ao movimento relativo entre as superfícies em contato.
a) Resposta: Falsa. De acordo com a primeira lei de Newton ou lei da inércia, a tendência de um corpo que esteja em repouso é que ele permaneça em repouso. b) Resposta: Verdadeira. c) Resposta: Falsa. Apesar de o par de ação e reação ter a mesma intensidade e direção, mas sentidos opostos, não significa que elas se anulam, pois são forças aplicadas em corpos distintos. d) Resposta: Verdadeira.
Página 305
5. Em um edifício residencial de pequeno porte, um elevador demora para sair do térreo e subir até o 4º andar. Sabendo que a distância entre dois pavimentos é de e que a força que atua no elevador para elevá-lo tem intensidade de , calcule o trabalho realizado pelo motor do elevador durante essa subida.
Resposta: .
6. Há muito tempo que as máquinas são utilizadas na realização de atividades humanas. Elas possibilitam, por exemplo, que poucas pessoas executem atividades que necessitariam de várias pessoas para serem realizadas. Analise as situações a seguir.
Professor, professora: As legendas das imagens não foram inseridas para não comprometer a realização da atividade.
Representação com elementos não proporcionais entre si. Cores-fantasia.



a) De que maneira cada uma das máquinas simples representadas em cada situação (A, B e C) contribui para facilitar o trabalho de quem as manuseia? Justifique sua resposta.
Resposta nas orientações ao professor.
b) De que forma as situações representadas podem nos ajudar a explicar a hipótese da construção das pirâmides do Egito?
Resposta nas orientações ao professor.
7. Com o mesmo pedaço de madeira, é possível construir diversas configurações de alavancas para erguer um objeto de , como podemos observar nas imagens a seguir.
Representação com elementos não proporcionais entre si. Cores-fantasia.


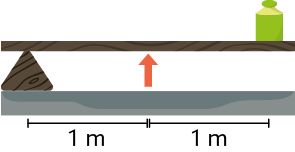
Representação de diferentes configurações (A, B e C) de alavancas.
a) Indique, para cada uma das configurações de alavanca apresentadas, o valor de sua força resistente, de seu braço de potência e de seu braço de resistência.
Resposta: A - ; ; ; B - ; ; ; C - ; ; .
b) Qual das alavancas apresentadas exige aplicação de força de menor intensidade para equilibrá-la? Justifique sua resposta.
Resposta: A alavanca na configuração B é a que necessita de menor força. Comparando o comprimento dos braços de potência e de resistência, tem-se que o braço de potência é maior nessa alavanca, portanto, a força potente é menor que a resistente.
Página 306
8. Para retirar os parafusos da roda de um caminhão, Sílvio usou uma chave de roda. No entanto, após algumas tentativas, ele percebeu que a força que estava aplicando era insuficiente para retirar os parafusos. A solução que ele encontrou foi a de inserir o cabo da chave de roda em um cano de ferro. Aplicando sua força próximo à extremidade do cano, ele conseguiu retirar os parafusos. Observe.
Representação com elementos não proporcionais entre si. Cores-fantasia.
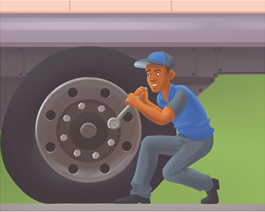
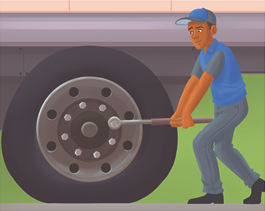
a) O que aconteceu com o braço potente dessa alavanca quando Sílvio colocou o cano de ferro?
Resposta nas orientações ao professor.
b) Explique, com suas palavras, por que Sílvio conseguiu retirar os parafusos depois de colocar o cano de ferro no cabo da chave de roda.
Resposta nas orientações ao professor.
9. A imagem a seguir mostra o movimento executado por um atleta durante a prova olímpica de salto em distância.

Durante o salto, o atleta manifesta diferentes formas de energia mecânica. Com relação às posições A, B e C, escreva em seu caderno a letra da alternativa que corresponde às formas de energia mecânica para cada momento do salto.
a) A: energia potencial gravitacional; B: energia cinética e potencial gravitacional; C: energia potencial gravitacional.
b) A: energia cinética; B: energia cinética; C: energia cinética.
c) A: energia cinética e potencial gravitacional; B: energia potencial gravitacional; C: energia nula.
d) A: energia cinética; B: energia cinética e potencial gravitacional; C: energia nula.
Resposta: Alternativa d.
Página 307
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Com as informações que você estudou no capítulo 8 (Calor e temperatura), como você explica que a frase "estou com calor" está fisicamente errada?
2. Considere as afirmativas listadas a seguir.
A maior parte das panelas é constituída de metais.
Durante a fervura de determinada quantidade de água sobre a chama de um fogão, verifica-se a movimentação de água de baixo para cima.
O principal responsável pelo aquecimento da Terra é o Sol.
Com base em seus conhecimentos adquiridos no estudo dos processos de transmissão de calor, elabore uma explicação relacionando as três afirmativas apresentadas anteriormente.
3. O desenvolvimento da automação nos meios de produção causou grandes mudanças na sociedade. Elabore um texto em uma folha de papel avulsa expondo sua opinião e confrontando a sociedade e o consumo, bem como a produção e o descarte dos bens materiais no ambiente.
4. Em uma folha de papel avulsa, explique a afirmação a seguir e, em seguida, elabore um desenho que represente sua explicação.
"Determinado objeto se move em relação a um referencial. Esse objeto percorre certa distância, no entanto, seu deslocamento é nulo".
Versão adaptada acessível
4. Explique oralmente a afirmação a seguir.
"Determinado objeto se move em relação a um referencial. Esse objeto percorre certa distância, no entanto, seu deslocamento é nulo".
Resposta: Espera-se que os alunos mencionem que a distância percorrida depende da trajetória descrita pelo objeto que se move. O deslocamento depende apenas das posições inicial e final. Sendo assim, se um objeto percorre determinada distância, mas sua posição final coincide com sua posição inicial, seu deslocamento é nulo.
5. No início do capítulo 9 (Movimento e força), você estudou sobre o movimento retilíneo uniforme (MRU) e o movimento retilíneo uniformemente variado (MRUV). Explique o que é cada tipo de movimento, destacando suas características e citando exemplos de seu cotidiano.
6. Suponha que, uma pessoa esteja em pé no interior de um ônibus. Com base nos conceitos estudados nas leis de Newton, explique o que aconteceria com essa pessoa nas situações apresentadas a seguir.
Se o ônibus estivesse em movimento e executasse uma frenagem brusca.
Se o ônibus estivesse em repouso e entrasse em movimento por meio de uma grande intensidade de aceleração.
7. Durante a realização de uma tarefa diária, uma pessoa é submetida ao levantamento de um objeto que tem grande quantidade de massa e, consequentemente, grande peso. De acordo com os estudos sobre as máquinas simples e seu desenvolvimento, explique o que essa pessoa poderá fazer para exercer menor força possível.
Respostas nas orientações ao professor.