Página 13
UNIDADE
1
Sistemas de numeração e números naturais

Agora vamos estudar...
- alguns sistemas de numeração: egípcio, romano e decimal;
- os números naturais;
- a reta numérica;
- os números pares e os números ímpares;
- comparação de números naturais;
- arredondamento.
Página 14
Alguns sistemas de numeração
Com a evolução das sociedades, contar tornou-se inevitável. Era necessário, por exemplo, conhecer a quantidade de animais no controle do rebanho, registrar a quantidade de dias e trocar mercadorias. Para representar quantidades, acredita-se que os pastores contavam o rebanho utilizando pedras, ou seja, uma pedra para cada animal.
Dada a necessidade de contagens extensas, algumas civilizações começaram a criar símbolos e sistemas de numeração próprios.
Sistema de numeração egípcio
A civilização egípcia surgiu na Antiguidade há aproximadamente 6.000 anos. Os egípcios criaram um dos primeiros sistemas de numeração, que atualmente não é mais usado. Os numerais egípcios eram representados por figuras da fauna e da flora do rio Nilo, utensílios, pessoas e partes do corpo humano, chamados de hieróglifos✚.
| Hieróglifo | Número | Significado |
|---|---|---|
|
|
1 |
Traço vertical |
|
|
10 |
Asa |
|
|
100 |
Corda enrolada |
|
|
1.000 |
Flor de lótus |
|
|
10.000 |
Dedo levantado, ligeiramente inclinado |
|
|
100.000 |
Girino |
|
|
1.000.000 |
Homem ajoelhado levantando os braços |
Fonte de pesquisa: IFRAH, Georges. História universal dos algarismos: a inteligência dos homens contada pelos números e pelo cálculo. Tradução: Alberto Muñoz e Ana Beatriz Katinsky. Rio de Janeiro: Nova Fronteira, 1997. v. 1.
- Hieróglifo:
- notação simbólica criada pelos egípcios para representar números e letras.↰
Atenção!
No sistema de numeração egípcio, não há um símbolo para representar o zero.
Para escrever outros números nesse sistema, há algumas regras, descritas a seguir.
Cada símbolo podia ser repetido até 9 vezes.
![]()
![]()
Os numerais egípcios podiam ser escritos em qualquer posição.
![]()
![]()
![]()
Página 15
Para determinar o valor de um número representado, adicionavam-se os valores dos símbolos utilizados.
![]()
![]()
![]()
Atividades
Faça as atividades no caderno.
1. Utilizando o sistema de numeração atual, escreva no caderno o número representado em cada item.






2. Utilizando os numerais egípcios, escreva no caderno um número que expresse:
a) a quantidade de estudantes que há em sua turma.
b) o ano atual.
c) o dia, o mês e o ano em que você nasceu.
3. Quantos símbolos que representam o zero são utilizados ao escrever o número quatrocentos mil:
a) no sistema de numeração atual?
b) no sistema de numeração egípcio?
4. No sistema de numeração egípcio, uma das regras é:
Cada símbolo pode ser repetido até nove vezes.
Nos itens a seguir, agrupe símbolos egípcios e realize as trocas necessárias para que os números sejam representados respeitando as regras desse sistema de numeração.




5. Utilizando uma única vez cada hieróglifo indicado responda às questões.

a) Quantos números podem ser formados com esses hieróglifos no sistema de numeração egípcio? Justifique sua resposta.
b) Qual número pode ser formado com esses hieróglifos no sistema de numeração atual?
Página 16
Sistema de numeração romano
A civilização romana desenvolveu-se na península Itálica há aproximadamente 2.500 anos, onde está atualmente localizada a Itália. Os romanos criaram um sistema de numeração que foi amplamente utilizado na Europa até por volta do século XIV. Esse sistema ainda é utilizado em diversas situações.
No sistema de numeração romano, são usadas apenas sete letras do alfabeto latino.

|
I |
X |
C |
M |
V |
L |
D |
|---|---|---|---|---|---|---|
|
1 |
10 |
100 |
1.000 |
5 |
50 |
500 |
Atenção!
No sistema de numeração romano, não há um símbolo para representar o zero.
Para escrever outros números nesse sistema, há algumas regras, descritas a seguir.
- I, X, C e M são símbolos que podem aparecer até três vezes seguidas. Já os símbolos V, L e D não podem ser repetidos na representação de um número.
- Quando um símbolo da numeração romana está à direita de outro numeral com valor maior ou igual ao dele, adicionam-se os valores dos símbolos para representar o número.
Quando, em um número escrito com símbolos romanos, temos I à esquerda de V ou X, X à esquerda de L ou C e C à esquerda de D ou M, devemos subtrair o menor valor do maior.
Atenção!
As regras apresentadas nesta página são utilizadas para a escrita de números de 1 a 3.999.
Atividades
Faça as atividades no caderno.
6. Utilizando o sistema de numeração atual, escreva no caderno o número representado em cada item.
a) XLIII
b) LXVII
c) CDLXXXI
d) DVI
e) CMXIX
f) MDCL
g) MMXL
h) MMMCDXLIV
Página 17
7. No caderno, escreva os números a seguir usando o sistema de numeração romano.
a) 61
b) 302
c) 1.236
d) 2.001
8. Em 2014, a matemática iraniana Maryam Mirzakhani (1977-2017) foi a primeira mulher no mundo a ser premiada com a Medalha Fields. Esse prêmio é concedido a matemáticos que se destacam com sua pesquisa, como uma maneira de reconhecer suas realizações para a Matemática.

a) Utilizando símbolos da numeração romana, escreva em seu caderno o ano de nascimento e o de morte de Maryam e o ano em que ela ganhou a Medalha Fields.
b) Realize uma pesquisa e obtenha mais informações a respeito de Maryam Mirzakhani. Depois, compartilhe as informações que você obteve com os colegas e o professor.
Atenção!
A pesquisa proposta no item b pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
9. Utilizando símbolos da numeração romana, represente no caderno:
a) a quantidade de estudantes de sua turma.
b) a sua idade em anos.
c) o número do seu calçado.
d) o dia do mês em que você nasceu.
e) o ano em que você nasceu.
f) o ano em que estamos.
10. Escreva em seu caderno o número três mil utilizando:
a notação atual.
numerais romanos.
a) Quantas vezes você usou um símbolo específico para o zero na escrita com a notação atual? E com os símbolos da numeração romana?
b) O que você pode concluir com relação à escrita do zero na numeração romana?
11. A partir do número , traços horizontais são indicados acima de um símbolo da numeração romana ou conjunto de símbolos. Utiliza-se um traço para representar os milhares e dois traços para representar os milhões, conforme indicado nos exemplos.
a) Escreva no caderno os números a seguir em notação atual.
b) Escreva no caderno os números a seguir com símbolos romanos.
215.023
9.107.000
Página 18
Sistema de numeração decimal
O sistema de numeração que usamos hoje é chamado sistema de numeração decimal e foi criado pelos hindus há aproximadamente 1.500 anos. Nesse sistema, os elementos são agrupados de 10 em 10, ou seja, um sistema de base 10.
10 unidades equivalem a 1 dezena.

10 dezenas equivalem a 1 centena.

10 centenas equivalem a 1 unidade de milhar.

Também podemos representar o agrupamento de 10 unidades e a troca por 1 dezena utilizando um ábaco.
Como não podemos colocar 10 contas na haste das unidades, elas são retiradas e trocadas por 1 conta na haste das dezenas.
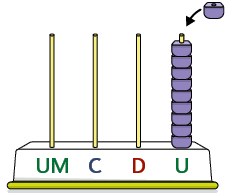
O número registrado é 10.
Atenção!
Lembre-se:
U – Unidade
D – Dezena
C – Centena
UM – Unidade de milhar
O sistema de numeração decimal também é chamado sistema de numeração indo-arábico, pois ele foi inventado pelos hindus e aperfeiçoado pelos árabes. Os símbolos utilizados para representar qualquer número nesse sistema recebem o nome de algarismos. São eles:
0, 1, 2, 3, 4, 5, 6, 7, 8 e 9
Atenção!
O termo algarismo tem origem em al-Khowarizmi, parte do nome do matemático, astrônomo e geógrafo árabe Mohammed Ibn Mussa al-Khowarizmi (c. 780-850), um dos responsáveis pela propagação do sistema de numeração indo-arábico na Europa e em outras partes do mundo.
Página 19
O sistema de numeração decimal é posicional, ou seja, um algarismo pode assumir valores diferentes de acordo com a posição que ele ocupa na representação de um número. Considere, por exemplo, os números 178, 1.283 e 8.647 representados nos ábacos.
178
O algarismo 8 representa 8 unidades.
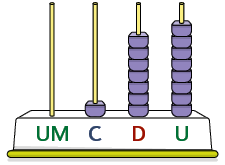
1.283
O algarismo 8 representa 8 dezenas.

8.647
O algarismo 8 representa 8 unidades de milhar.

Podemos concluir que o algarismo 8 assume valores diferentes em cada um desses números.
- No número 178, o valor posicional do algarismo 8 é 8.
- No número 1.283, o valor posicional do algarismo 8 é 80.
- No número 8.647, o valor posicional do algarismo 8 é 8.000.
O sistema de numeração decimal tem o algarismo zero (0), que representa a ausência de quantidade. Esse algarismo estrutura todo o sistema de numeração decimal.
Relação entre alguns sistemas de numeração
Estudamos algumas características dos sistemas de numeração egípcio, romano e decimal. O quadro a seguir resume algumas semelhanças e diferenças entre esses sistemas de numeração.
|
Sistema de numeração |
Base 10 |
Posicional |
Símbolo para representar o zero |
|---|---|---|---|
|
Decimal |

|

|

|
|
Romano |

|

|

|
|
Egípcio |

|

|

|
Página 20
Ordens e classes
No sistema de numeração decimal, a posição de cada algarismo, contada da direita para a esquerda, indica uma ordem. Cada grupo de três ordens recebe o nome de classe.
O quadro a seguir é chamado quadro de ordens e classes. Nele, está representado o número 2.502.293.
|
Classe dos milhões |
Classe dos milhares |
Classe das unidades simples |
||||||
|---|---|---|---|---|---|---|---|---|
|
9ª ordem |
8ª ordem |
7ª ordem |
6ª ordem |
5ª ordem |
4ª ordem |
3ª ordem |
2ª ordem |
1ª ordem |
|
Centena de milhão |
Dezena de milhão |
Unidade de milhão |
Centena de milhar |
Dezena de milhar |
Unidade de milhar |
Centena |
Dezena |
Unidade |
|
2 |
5 |
0 |
2 |
2 |
9 |
3 |
||
Lê-se: dois milhões, quinhentos e dois mil, duzentos e noventa e três.
Atenção!
Logo à esquerda da classe dos milhões, há a classe dos bilhões, seguida pela classe dos trilhões, depois pela classe dos quatrilhões, e assim por diante.
O número 2.502.293 tem sete ordens. O esquema a seguir apresenta o valor posicional de cada algarismo de acordo com a ordem que ele ocupa.
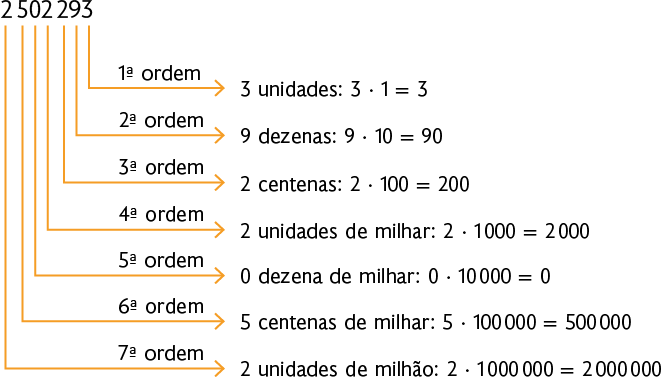
Podemos decompor o número de várias maneiras. Analise duas delas.
Questão 1. Decomponha no caderno os números apresentados em cada item.
a) 1.346.809
b) 96.855.190
Página 21
Atividades
Faça as atividades no caderno.
12. Escreva no caderno, com algarismos e por extenso, os números representados nos ábacos.
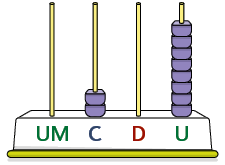
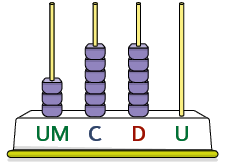
13. Resolva os itens.
a) Escreva no caderno o valor posicional de cada algarismo dos números destacados nas informações a seguir.
Uiramutã é o único município do estado de Roraima que faz fronteira com mais de um país. De acordo com o IBGE, em 2021 a população estimada desse município era 11.014 habitantes.
Município de Uiramutã (RR)
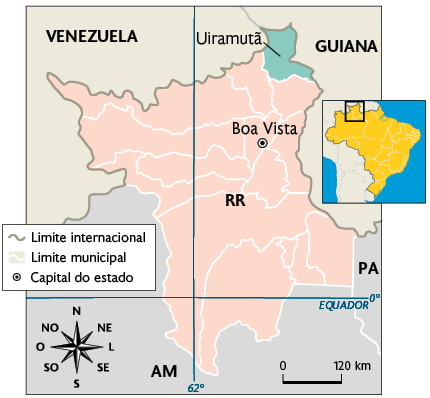
Fonte de pesquisa: IBGE. Atlas geográfico escolar. 8. ed. Rio de Janeiro, 2018.
A primeira medalha olímpica de ouro na história da ginástica artística feminina do Brasil foi conquistada por Rebeca Andrade, nos jogos Olímpicos de Tóquio, em 2021, no Japão.

b) Analise o mapa do item anterior e determine quantos e quais são os países que fazem fronteira com Uiramutã.
14. Junte-se a um colega e escrevam no caderno, para cada item, um número de 4 algarismos diferentes em que o algarismo 7 tenha valor posicional:
a) 70
b) 7
c) 7.000
d) 700
15. No número a seguir, A e B representam algarismos diferentes:
7A5B4
Quais devem ser os algarismos representados por A e B para que esse número:
a) seja o maior possível?
b) seja o menor possível?
c) tenha o algarismo 2 com valor posicional 2.000 e o algarismo 1 com valor posicional 10?
d) esteja entre 72.510 e 72.550?
Página 22
16. Resolva no caderno cada item utilizando os algarismos apresentados a seguir.
- 5
- 6
- 7
- 2
- 8
- 3
- 9
a) Escreva um número de 6 algarismos diferentes em que o valor posicional do algarismo 3 seja 3.000.
b) Escreva um número de 7 algarismos diferentes em que o valor posicional do algarismo 5 seja 500.000.
c) Escreva um número de 5 algarismos diferentes em que o valor posicional do algarismo 2 seja 20.
d) Escolha um dos números que você escreveu nos itens anteriores e o decomponha.
17. A professora de Ricardo escreveu dois números:

a) Quantas ordens tem cada número?
b) Qual é o valor posicional do algarismo 7 em cada número?
c) Em qual dos números o valor posicional do algarismo 3 é 30.000?
d) No caderno, escreva por extenso cada número.
18. Junte-se a um colega e, utilizando os algarismos apresentados a seguir, façam o que se pede.
- 5
- 1
- 6
- 2
- 7
- 3
- 8
- 4
- 9
a) Utilizando uma única vez cada algarismo, formem:
o maior número de 5 ordens;
o menor número de 7 ordens;
um número de 6 ordens maior do que 652.187.
b) Escrevam no caderno, por extenso, cada número que vocês formaram no item anterior.
c) Qual é o maior número que podemos formar utilizando uma única vez cada um desses algarismos? Quantas ordens tem esse número?
19. Em cada item, efetue as adições necessárias e componha os números.
a)
b)
c)
20. Copie no caderno e complete a decomposição dos números, substituindo cada letra pelo número adequado.
a)
b)
c)
d)
Página 23
Números naturais
Considere a sequência dos números naturais.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, ...
Nessa sequência, a partir do 0, o próximo número natural é obtido adicionando uma unidade ao número anterior.
- O número 1 é igual ao anterior (0) mais 1:
- O número 2 é igual ao anterior (1) mais 1:
- O número 3 é igual ao anterior (2) mais 1:
e assim por diante.

As reticências (...) indicam que há infinitos números nessa sequência, pois sempre é possível escrever o próximo número adicionando uma unidade ao número natural anterior.
Cada número natural, com exceção do zero, tem um antecessor, que é o número natural que vem imediatamente antes dele na sequência numérica. Além disso, cada número natural tem um sucessor, que é o número natural que vem imediatamente depois dele na sequência numérica.
A seguir é apresentado o antecessor e o sucessor do número 12.
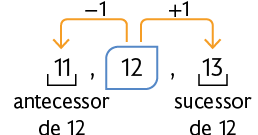
Dois ou mais números naturais são consecutivos se um vem imediatamente após o outro na ordem em que aparecem na sequência dos números naturais. No exemplo anterior, podemos dizer que 11, 12 e 13 são números consecutivos.
Questão 2. Escreva no caderno três números naturais consecutivos, sendo um deles:
a) 25.
b) 99.
c) 141.
d) 999.
Reta numérica
Podemos representar cada número natural por um ponto em uma reta, chamada reta numérica.
Para fazer essa representação, escrevemos os números naturais do menor para o maior, da esquerda para a direita, iniciando pelo ponto que corresponde ao número zero, chamado origem. Além disso, em uma reta numérica, os pontos são igualmente espaçados.
Página 24
Na reta numérica a seguir, estão representados os primeiros 15 números consecutivos da sequência dos números naturais.
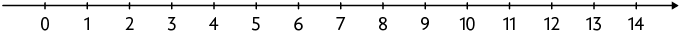
Assim, na sequência dos números naturais representados na reta numérica, um número que está à direita do outro será sempre maior do que ele. Portanto:
- vem antes do , então ;
- vem depois do , então .
Números pares e números ímpares
A professora de Fernanda escreveu na lousa duas sequências com números naturais: uma de números pares e outra de números ímpares.

Analise o que a professora está dizendo.


Página 25
A seguir, é apresentado um algoritmo✚ que possibilita verificar se um número é par ou ímpar.
- Algoritmo:
- sequência de comandos, regras ou tarefas que possibilita solucionar um problema.↰
Início
1º. Escolha um número natural.
2º. O número termina em 1, 3, 5, 7 ou 9?
3º. Se sim, o número é ímpar. Caso contrário, o número é par.
Fim
Podemos representar um algoritmo por meio de um fluxograma✚. Considere, por exemplo, o algoritmo anterior representado dessa maneira.
- Fluxograma:
- representação gráfica de uma sequência de comandos, regras ou tarefas que possibilita solucionar um problema.↰
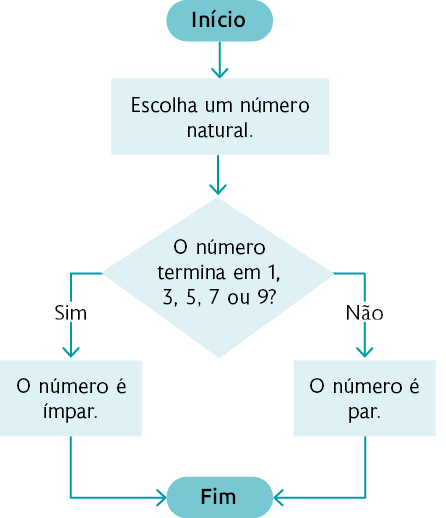
Atenção!
Em um fluxograma, cada tipo de figura tem um significado.



Além disso, as figuras são conectadas por setas. Quando as setas partem de uma figura que indica um questionamento para tomada de decisão, elas são acompanhadas das palavras Sim e Não. A cada resposta, o fluxograma segue determinando o caminho.
Questão 3. Escreva, em seu caderno, um algoritmo semelhante ao apresentado nesta página. Porém, troque a pergunta do passo 2 e faça os ajustes necessários.
Questão 4. Em seu caderno, represente o algoritmo que você escreveu na questão anterior em um fluxograma.
Questão 5. Utilizando o algoritmo apresentado nesta página ou o escrito por você na questão 3, verifique no caderno se os números apresentados nos itens são pares ou ímpares.
a) 423
b) 13.572
c) 9.274.361
d) 864.135.210
Página 26
Atividades
Faça as atividades no caderno.
21. Determine o antecessor e o sucessor de cada número natural a seguir.
a) 929
b) 500
c) 1.347
d) 3.568
e) 12.009
f) 18.701
g) 508.000
h) 746.800
22. Considere os seguintes algarismos.
- 7
- 1
- 5
- 3
- 4
- 0
- 9
- 8
Utilizando esses algarismos, escreva no caderno:
a) o maior número natural com três algarismos diferentes.
b) o menor número natural com quatro algarismos diferentes.
c) Dois números naturais consecutivos de dois algarismos que adicionados resultem em 79.
23. Sabendo que A, B e C representam números naturais, copie os itens a seguir no caderno substituindo cada pelo símbolo ou , de acordo com a reta numérica apresentada.
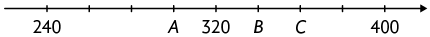
a)
b)
c)
d)
e)
f)
24. Para aguardar o atendimento em algumas agências bancárias, o cliente recebe uma senha. Ao chegar em uma dessas agências, Cláudia recebeu a seguinte senha.

Escreva no caderno a sequência de números naturais consecutivos que representa as senhas das:
a) 7 pessoas que chegaram depois de Cláudia;
b) 5 pessoas que chegaram antes de Cláudia.
25. Na reta numérica a seguir, os pontos destacados correspondem a números naturais.

De acordo com as informações a seguir, determine o número natural correspondente a cada letra.
Os pontos correspondem a números naturais consecutivos.
A letra E corresponde a 372 unidades a mais do que o menor número natural de três algarismos.
26. No cálculo indicado a seguir, cada figura representa um número natural.
Determine o número natural referente a cada figura, sabendo que eles são consecutivos.
Atenção!
Esses números podem ser de 0 a 10.
Página 27
27. O sistema braile é um código universal de leitura tátil e escrita com símbolos em alto-relevo. Esse sistema é formado por símbolos compostos de pontos. Com base nesses pontos, podem ser formados 63 símbolos, que representam não somente as letras do alfabeto, mas também os sinais de pontuação e os números. Os algarismos de 1 a 9 e o algarismo 0 são representados por um símbolo seguido de outro. O primeiro símbolo indica que será representado um número; o segundo símbolo é o mesmo que também representa as letras de A até J, respectivamente.
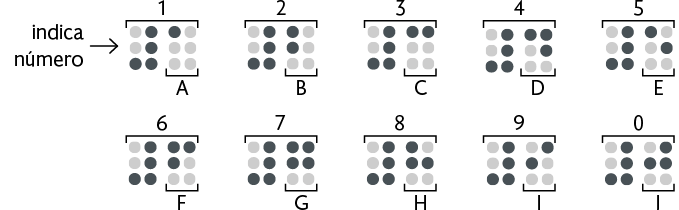
Em um número formado por dois ou mais algarismos, apenas o primeiro
é precedido pelo símbolo
![]() . Analise a seguir a representação do número 143.
. Analise a seguir a representação do número 143.

a) Represente no caderno os maiores números naturais de dois e três algarismos distintos usando o sistema braile.
b) Faça uma pesquisa e obtenha mais informações a respeito de outro sistema de símbolos ou sinais utilizado na comunicação entre pessoas com deficiência. Em seguida, liste-os.
c) Entreviste uma pessoa com deficiência visual de sua comunidade ou realize uma pesquisa em sites e livros para obter mais informações a respeito do sistema braile.
d) Após a entrevista ou pesquisa realizada no item anterior, qual é sua opinião a respeito do sistema braile? Apresente-a aos colegas e argumente com o objetivo de defender suas ideias.
e) Sua opinião a respeito do sistema braile mudou após a entrevista ou pesquisa realizada no item c? Converse com os colegas e professor.
f) Mariana estuda o sistema braile e recebeu a seguinte mensagem em uma de suas redes sociais.

Você acha que Mariana concorda com essa mensagem? E você, concorda? Justifique sua resposta.
Página 28
28. Algumas invenções e descobertas importantes que ocorreram ao longo da História estão apresentadas a seguir.
Imagens não proporcionais entre si.



Na reta numérica a seguir, cada letra está associada a um dos anos citados. Escreva no caderno o ano representado em cada letra.

29. Analise os números nas fichas e os envelopes em que elas serão guardadas.
- 143
- 92
- 80
- 95
- 2
- 129
- 64
- 47
- 158
- 71
- 15
- 81
- 24
- 56




a) Escreva no caderno os números das fichas que devem ser guardadas em cada envelope de acordo com as indicações.
b) Há fichas que não foram guardadas em nenhum envelope. Quais são os números representados nessas fichas?
30. Considere a sequência de figuras representadas por palitos.

Sabendo que a regularidade na quantidade de palitos utilizada para representar cada figura da sequência será mantida, ou seja, cada figura, a partir da 2ª, será representada com 2 palitos a mais do que a anterior, responda às questões.
a) Quantos palitos são necessários para representar a 5ª figura dessa sequência?
b) O número que representa a quantidade de palitos utilizados para representar a 5ª figura dessa sequência é par ou ímpar?
Página 29
Arredondamento
No gráfico está representada a população estimada dos cinco estados mais populosos do Brasil em 2021.
Estados brasileiros mais populosos em 2021
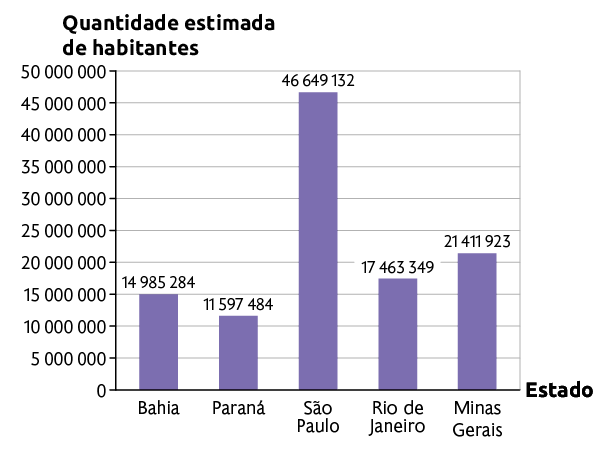
Fonte de pesquisa: IBGE Cidades. Disponível em: https://oeds.link/JOX77t. Acesso em: 10 fev. 2022.
Para facilitar a leitura e a interpretação desses números com muitos algarismos, fazemos um arredondamento de cada número para a unidade de milhão mais próxima.
Assim, podemos dizer que a população do estado da Bahia era de aproximadamente 15.000.000 de habitantes em 2021. Já o Rio de Janeiro tinha uma população de aproximadamente 17.000.000 de habitantes nesse mesmo ano.
A quantidade de habitantes na Bahia foi arredondada para 15.000.000, pois 14.985.284 está mais próximo desse número do que de 14.000.000.

De modo geral, para fazer arredondamentos, observamos o algarismo à direita da ordem que queremos arredondar. Se ele for 0, 1, 2, 3 ou 4, mantemos a ordem; se ele for 5, 6, 7, 8 ou 9, adicionamos uma ordem.
Atividades
Faça as atividades no caderno.
31. Copie o quadro em seu caderno e, em seguida, complete a segunda e a terceira coluna fazendo arredondamentos para a centena e para a unidade de milhar mais próximas.
|
Número |
Número arredondado para a centena mais próxima |
Número arredondado para a unidade de milhar mais próxima |
|---|---|---|
|
1.617 |
||
|
4.950 |
||
|
2.198 |
||
|
6.243 |
||
|
3.444 |
Página 30
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Escreva em uma folha de papel avulsa, utilizando numerais egípcios e romanos, os números indicados a seguir.
a) 38
b) 507
c) 2.003
d) 4.262
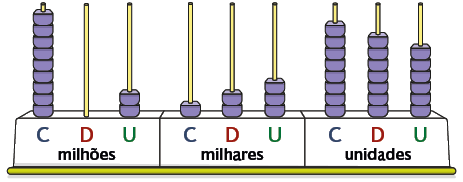
2. Escreva em uma folha de papel avulsa, com algarismos e por extenso, o número representado em cada ábaco.
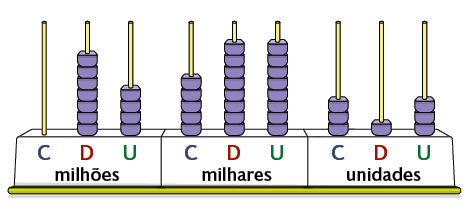
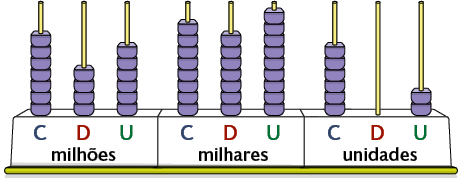
3. Determine o valor posicional de cada algarismo dos números a seguir.
a) 134
b) 3.201
c) 7.220
d) 91.050
e) 709.055
f) 4.381.896
4. Associe cada número apresentado a uma ou mais informações a seguir.
- 246.088
- 1.356.152
- 96.294.000
- 24.955
- 4.886.002
A . É composto de 7 ordens.
B . Tem o algarismo 6 na classe dos milhares.
C . O valor posicional do algarismo 4 é 4.000.
D . Está entre 100.000 e 1.000.000.
E . Seu antecessor é um número ímpar.
5. Em cada item, determine o valor das letras A e B, sabendo que A é o menor número natural possível com algarismos diferentes e B é o maior número natural possível com algarismos diferentes.
a)
b)
c)
d)
6. Em uma folha de papel avulsa, escreva quatro números de seis algarismos diferentes. Depois, arredonde cada um dos números que você escreveu para:
a) a dezena mais próxima.
b) a centena mais próxima.
c) a dezena de milhar mais próxima.