Página 69
UNIDADE
3
Múltiplos e divisores

Agora vamos estudar...
- os múltiplos de um número natural;
- os divisores de um número natural;
- os critérios de divisibilidade;
- os números primos e os números compostos;
- a decomposição de números compostos em fatores primos.
Página 70
Múltiplos
As receitas culinárias geralmente apresentam os ingredientes e o modo de preparo de um alimento para determinada quantidade de porções. Analise os ingredientes e o rendimento de uma receita de tapioca que Ana está preparando.

Se desejar uma quantidade maior de tapiocas, Ana terá de preparar mais de uma receita. No preparo de:
- 2 receitas, obtêm-se 24 tapiocas, pois ;
- 3 receitas, obtêm-se 36 tapiocas, pois ;
- 4 receitas, obtêm-se 48 tapiocas, pois ;
- 5 receitas, obtêm-se 60 tapiocas, pois .
Os números 24, 36, 48 e 60 são múltiplos de 12, pois podem ser representados pela multiplicação de um número natural por 12. Por exemplo:
24 é múltiplo de 12.
24 também é múltiplo de 2, pois podemos escrever .
60 é múltiplo de 12.
60 também é múltiplo de 5, pois podemos escrever .
Atenção!
Todo número natural é múltiplo dele mesmo.
O número zero é múltiplo de qualquer número natural.
Página 71
Atividades
Faça as atividades no caderno.
1. Entre os números a seguir, quais são múltiplos de 8? Em seu caderno, represente esses números com uma multiplicação de um número natural por 8.
-
88
-
162
-
94
-
160
-
100
-
247
-
120
-
96
-
240
2. Em seu caderno, escreva multiplicações para representar a quantidade total de objetos em cada item.


3. Determine o número natural que substitui corretamente as letras em cada item.
a) 18 é múltiplo de A e de B, pois .
b) 20 é múltiplo de A e de B, pois .
4. Descubra o que há em comum nos números de cada conjunto a seguir.
Conjunto 1
-
2
-
4
-
8
-
14
-
22
-
28
-
34
Conjunto 2
-
3
-
9
-
27
Conjunto 3
-
5
-
25
5. Considere o padrão nos números de cada conjunto da atividade anterior.
a) Mantendo esse padrão, escreva em seu caderno mais 2 números que poderiam estar em cada conjunto.
b) O número 100 pode estar em quais conjuntos?
6. Considere os 6 primeiros múltiplos do número 12.
0, 12, 24, 36, 48 e 60
Agora, escreva no caderno os 10 primeiros múltiplos de cada número indicado.
a) Múltiplos de 2.
b) Múltiplos de 3.
c) Múltiplos de 5.
d) Múltiplos de 7.
Página 72
7. Escreva no caderno, quando possível, uma multiplicação com 2 fatores naturais, sendo um deles o número 6 e cujo resultado seja:
a) 42
b) 18
c) 24
d) 54
e) 16
f) 72
8. Quais dos números indicados nos itens da atividade anterior são múltiplos de 6?
9. Elabore um problema envolvendo três entre os múltiplos de 7 a seguir e peça a um colega que o resolva. Depois, verifique se a resolução está correta.
-
14
-
21
-
28
-
35
-
42
10. Junte-se a um colega e leiam a tirinha a seguir.

SOUSA, Mauricio de. Magali. São Paulo: Globo, n. 235, jun. 1998.
a) Qual é o assunto de cada livro que as mães estão lendo?
b) Qual é o ingrediente citado na tirinha? Qual é a quantidade desse ingrediente?
c) Suponha que a receita da tirinha rendesse 3 porções. Se fossem utilizadas 8 colheres de açúcar mascavo, a receita renderia quantas porções?
11. Responda às questões de acordo com os números indicados a seguir.
-
20
-
24
-
64
-
16
-
10
-
48
-
30
-
50
-
60
-
36
-
28
-
72
a) Quais desses números são múltiplos de 4?
b) Quais deles são múltiplos de 5?
c) Quais são múltiplos de 4 e também de 5?
Página 73
12. Considere a sequência dos 12 primeiros múltiplos de 2.
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22
Agora, considere a sequência dos 10 primeiros múltiplos de 3.
0, 3, 6, 9, 12, 15, 18, 21, 24, 27
Em seu caderno, escreva os números que aparecem tanto na sequência dos 12 primeiros múltiplos de 2 como na dos 12 primeiros múltiplos de 3.
Atenção!
Os números que você escreveu são alguns dos múltiplos comuns de 2 e 3.
O menor múltiplo comum de 2 e 3, diferente de zero, é o 6. Esse número é chamado mínimo múltiplo comum de 2 e 3 e pode ser indicado da seguinte maneira:
13. Nos quadros a seguir estão representadas as sequências dos 12 primeiros múltiplos de 4, de 6 e de 9.
Múltiplos de 4
0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44
Múltiplos de 6
0, 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66
Múltiplos de 9
0, 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99
a) Entre esses números, quais são os múltiplos comuns de 4 e 6?
b) Qual é o mínimo múltiplo comum de:
4 e 6?
4 e 9?
6 e 9?
14. Heitor está fazendo um tratamento médico no qual deve tomar dois medicamentos, sendo um de 8 em 8 horas e outro de 6 em 6 horas. Ele tomou os medicamentos juntos às 8h da manhã. Após quantas horas Heitor tomará novamente os dois medicamentos juntos?
Atenção!
Nunca tome medicamentos sem orientação médica, pois isso pode causar graves danos à saúde.
15. (OBMEP–2019)
No Planeta Pemob as semanas têm 5
dias: Aba, Eba, Iba, Oba e Uba, nessa ordem. Os anos são divididos em 6 meses com 27 dias cada um.
Se o primeiro dia de um certo ano foi Eba, qual foi o
último dia desse ano?

a) Aba.
b) Eba.
c) Iba.
d) Oba.
e) Uba.
Página 74
Divisores
Bianca fez 16 bombons para vender. Ela pode embalar esses bombons de diferentes maneiras, de modo que todas as embalagens fiquem completas, com a mesma quantidade de bombons, e nenhum bombom fique sem ser embalado.
Embalar cada bombom separadamente.
Serão necessárias 16 embalagens para embalar todos os bombons.
Embalar em caixas em que caibam 2 bombons em cada uma.
Nesse caso, serão necessárias 8 caixas para embalar todos os bombons.

Embalar em caixas em que caibam 4 bombons em cada uma.
Utilizando 4 caixas, será possível embalar todos os bombons.

Embalar em caixas em que caibam 8 bombons em cada uma.
Serão necessárias 2 caixas para embalar todos os bombons.

Embalar em uma caixa em que caibam 16 bombons.
Nesse caso, 1 caixa será suficiente para embalar todos os bombons.

Página 75
Na página anterior, vimos que 16 bombons podem ser embalados em caixas com 1, 2, 4, 8 ou 16 bombons em cada uma, de modo que nenhum bombom fique sem ser embalado.
Como as divisões de 16 por 1, 2, 4, 8 e 16 são divisões exatas, podemos dizer que:
16 é divisível por 1, por 2, por 4, por 8 e por 16.
Assim:
1, 2, 4, 8 e 16 são os divisores naturais de 16.
Questão 1. É possível embalar 16 bombons
em caixas com 5
unidades em cada uma sem que fiquem bombons sem ser embalados? Por quê?
Atividades
Faça as atividades no caderno.
16. Arnaldo empilhou 24 livros de modo que todas as pilhas ficassem com a mesma quantidade de livros.

Escreva em seu caderno outras 3 maneiras de empilhar esses livros de modo que as pilhas fiquem com a mesma quantidade de livros.
17. Analise as divisões a seguir.


a) 168 é divisível por 5? Por quê?
b) Por que 3 é divisor de 156?
18. Junte-se a um colega, efetuem os cálculos e verifiquem se as seguintes afirmações são verdadeiras ou falsas. Depois, reescrevam as afirmações falsas no caderno, tornando-as verdadeiras.
a) 3 é divisor de 42.
b) 8 é divisor de 26.
19. Nas imagens a seguir, aparecem algumas pilhas de blocos numerados.




a) Em seu caderno, escreva todos os divisores naturais do maior número da pilha B.
b) Em qual pilha há dois números que têm o 4 e o 6 como seus divisores?
Página 76
Critérios de divisibilidade
Para embalar uma produção de de uva, Paulo pode utilizar embalagens de ou de . Que tipo de embalagem ele deverá utilizar para que todas tenham a mesma medida de massa?
Podemos determinar o tipo de embalagem que Paulo vai utilizar verificando se 987 é divisível por 2 e por 3.
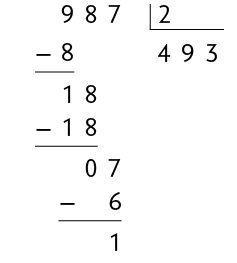
Se Paulo utilizar embalagens de , uma delas terá massa diferente das demais, pois é uma divisão não exata. Ou seja, 987 não é divisível por 2.
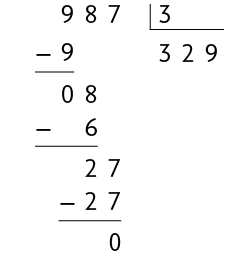
Se utilizar embalagens com , todas as embalagens terão a mesma massa, pois é uma divisão exata. Ou seja, 987 é divisível por 3.
Para verificar se um número natural é divisível por outro, podemos utilizar os critérios de divisibilidade.
Divisibilidade por 2
Considere as sequências de números a seguir.
A. 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, ...
B. 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, ...
Questão 2. Os números da sequência
A são
pares ou ímpares? E os da sequência B?
Questão 3. Ao dividir os números da sequência A e da sequência B por 2, o que podemos perceber com relação aos restos das divisões? Faça os cálculos no caderno.
Questão 4. O que os números divisíveis por
2 têm em comum?
Questão 5. Copie a frase a seguir no caderno substituindo as letras A, B, C, D e E pelos algarismos corretos.
Um número natural é divisível por 2 quando é par. Desse modo, um número divisível por 2 tem o algarismo da unidade igual a A, B, C, D ou E.
Página 77
Divisibilidade por 3
Considere as divisões de alguns números naturais por 3.
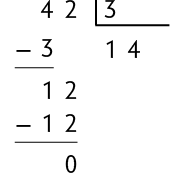
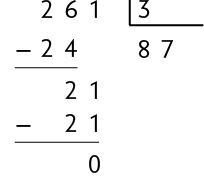
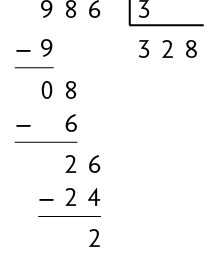
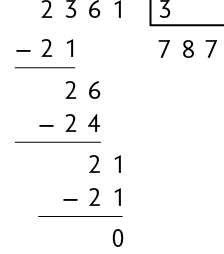
Questão 6. Os números 42, 261, 986 e
2.361
são divisíveis por 3? Justifique sua resposta.
Questão 7. No caderno, adicione os valores correspondentes aos algarismos dos números divisíveis por 3 da questão anterior. O que essas somas têm em comum?
Questão 8. A característica dos números da questão anterior é uma condição necessária para que um número seja divisível por 3. Agora, copie no caderno a frase a seguir substituindo a letra A pelos números adequados.
Um número natural é divisível por 3 quando a soma dos valores correspondentes de seus algarismos for um número divisível por A.
Divisibilidade por 6
Considere os números das fichas a seguir.
-
84
-
92
-
108
-
423
-
132
-
378
Atenção!
Utilize os critérios de divisibilidade já estudados para verificar se esses números são divisíveis por 2 e por 3.
Questão 9. Quais desses números são
divisíveis por 2? E por 3?
Questão 10. Quais desses números são
divisíveis, simultaneamente, por 2 e por 3?
Questão 11. Com auxílio de uma calculadora, verifique se esses números são divisíveis também por 6.
Página 78
Questão 12. O que podemos perceber com
relação aos números que são
divisíveis simultaneamente por 2 e por 3 e os que são divisíveis por 6?
Questão 13. Copie no caderno a frase a seguir substituindo as letras A e B pelos algarismos corretos.
Um número natural é divisível por 6 quando for divisível, simultaneamente, por A e por B.
Divisibilidade por 9
Considere os números a seguir.
-
72
-
417
-
684
-
243
-
3.987
Questão 14. Com auxílio de uma calculadora, verifique quais desses números são divisíveis por 9 e anote-os no
caderno.
Questão 15. No caderno, adicione os valores correspondentes aos algarismos dos números divisíveis por 9. O que podemos perceber com relação ao resultado obtido?
Questão 16. No caderno, adicione os valores correspondentes aos algarismos do número 417. A soma obtida tem as mesmas características da questão anterior? Justifique sua resposta.
Questão 17. Agora, copie no caderno e complete a frase a seguir substituindo a letra A pelo número adequado.
Um número natural é divisível por 9 quando a soma dos valores correspondentes aos seus algarismos for um número divisível por A.
Divisibilidade por 5
Considere a sequência a seguir dos múltiplos naturais de 5.
0, 5, 10, 15, 20, 25, 30, 35, 40, 45, …
Questão 18. Escreva no caderno os próximos três números dessa sequência.
Questão 19. Os números 95 e 100 pertencem a
essa sequência? E o número
108? Justifique sua resposta.
Questão 20. O que podemos perceber em
relação ao algarismo das unidades
dos números dessa sequência?
Questão 21. Copie no caderno e complete a frase a seguir substituindo as letras A e B pelos algarismos corretos.
Um número natural é divisível por 5 quando o algarismo da unidade for A ou B.
Página 79
Divisibilidade por 10
Considere a sequência numérica a seguir dos múltiplos naturais de 10.
0, 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, …
Questão 22. Qual é o próximo número dessa
sequência?
Questão 23. Escreva no caderno um número que pertence a essa sequência e outro que não pertence a ela.
Questão 24. Escreva no caderno algumas multiplicações de um número natural por 10.
Questão 25. Todos os resultados dessas
multiplicações são divisíveis por
um mesmo número natural. Que número é esse?
Questão 26. O que podemos perceber em
relação ao algarismo das unidades
dos múltiplos de 10?
Questão 27. Copie no caderno a frase a seguir substituindo a letra A pelo algarismo correto.
Um número natural é divisível por 10 quando o algarismo da unidade for A.
Divisibilidade por 100
Considere a sequência dos múltiplos de 100 entre 1 e 1.000.
100, 200, 300, 400, 500, 600, 700, 800, 900
Questão 28. Escreva no caderno a sequência dos múltiplos de 100 entre 900 e 1.500.
Questão 29. O número 3.200 é um múltiplo de
100? E 3.250?
Questão 30. O que podemos perceber em
relação aos algarismos da dezena e
da unidade de um múltiplo de 100 maior do que 1?
Questão 31. Copie no caderno a frase a seguir substituindo a letra A pelo algarismo correto.
Um número natural é divisível por 100 quando os algarismos da dezena e da unidade forem, simultaneamente, A.
Divisibilidade por 1.000
Considere a sequência numérica dos múltiplos naturais de 1.000.
0, 1.000, 2.000, 3.000, 4.000, 5.000, …
Questão 32. Escreva no caderno o próximo número dessa sequência.
Questão 33. O número 10.000 pertence a essa
sequência? E o número 10.200? Justifique sua
resposta.
Questão 34. O que podemos perceber em
relação aos algarismos da centena, da
dezena e da unidade dos números dessa sequência?
Página 80
Questão 35. Agora, copie no caderno a frase a seguir substituindo a letra A pelo algarismo correto.
Um número natural é divisível por 1.000 quando seus três últimos algarismos forem, simultaneamente, A.
Divisibilidade por 4
Considere os números apresentados a seguir.
-
320
-
501
-
316
-
2.000
-
2.048
-
4.225
Questão 36. Faça os cálculos no caderno e escreva quais desses números são divisíveis por 4.
Questão 37. Entre os números divisíveis por 4 apresentados, escreva no caderno aqueles cujos números formados pelos algarismos da dezena e da unidade também sejam divisíveis por 4.
Questão 38. Entre os números divisíveis por
4 apresentados, há também
múltiplos de 10? E de 100?
Questão 39. Todo número divisível por 10
também é divisível por 4? E todo
número divisível por 100? Justifique sua resposta com exemplos.
Questão 40. O número formado pelos dois
últimos algarismos de 316 é um
múltiplo de 4 e é par. Ser par é condição suficiente para que um número seja
divisível por 4? Justifique sua resposta com um exemplo.
Questão 41. Copie no caderno a frase a seguir substituindo as letras A e B pelos números adequados.
Um número natural com mais de dois algarismos é divisível por 4 quando seus dois últimos algarismos forem, simultaneamente, A ou formarem, na ordem em que aparecem, um número divisível por B.
Divisibilidade por 8
Considere os números a seguir.
-
4.984
-
3.256
-
1.152
Agora, analise as decomposições desses números.
Atenção!
Todo número natural múltiplo de 1.000 é também múltiplo de 8, pois .
Todo número natural com mais de três algarismos pode ser decomposto em uma adição de duas parcelas em que uma delas é um múltiplo de 1.000.
Página 81
Questão 42. Os números 4.000, 3.000 e 1.000 são divisíveis
por 8? Por quê?
Questão 43. Se 4.000, 3.000
e 1.000 são divisíveis por 8, qual é a condição
para que os números 4.984, 3.256
e 1.152 também sejam divisíveis por 8?
Questão 44. Utilize o algoritmo da divisão no caderno para verificar se os números 984, 256 e 152 são divisíveis por 8.
Questão 45. Com o auxílio de uma calculadora, verifique se os números 4.984, 3.256 e 1.152 são divisíveis por 8.
Questão 46. Agora, copie no caderno a frase a seguir substituindo as letras A e B pelos números adequados.
Um número natural com mais de três algarismos é divisível por 8 quando seus três últimos algarismos forem, simultaneamente, A ou formarem, na ordem em que aparecem, um número divisível por B.
Atividades
Faça as atividades no caderno.
20. Verifique se os seguintes números são divisíveis, simultaneamente, por 2, por 3, por 6 e por 9.
a) 193
b) 252
c) 276
d) 567
e) 386
f) 795
g) 541
h) 2.968
i) 978
21. Um algarismo do número a seguir está oculto.
2 3 ⬤
a) Se esse número for divisível por 3, então qual pode ser esse algarismo oculto?
b) Qual algarismo pode estar oculto para o número ser divisível por 2?
c) Para que esse número seja divisível por 6, qual algarismo está oculto?
d) Se esse número for divisível por 9, então qual algarismo está oculto?
22. Uma turma tem 32 estudantes. É possível formar grupos com 3 estudantes, sem que nenhum deles fique sem grupo? Justifique sua resposta.
23. Determine o maior número de três algarismos divisível por:
a) 2
b) 3
c) 6
d) 9
Página 82
24. Considere os seguintes números.
-
40
-
36
-
42
-
60
-
80
-
35
a) Quais desses números são divisíveis por 4?
b) Quais não são divisíveis por 3?
c) Quais são divisíveis por 4 e 5, simultaneamente?
d) Quais são divisíveis por 20?
25. Considere os números a seguir.
-
1.734
-
3.627
-
1.224
-
1.412
-
2.518
Quais deles são divisíveis:
a) por 4?
b) por 6?
c) por 8?
d) por 9?
e) por 4, 6, 8 e 9, simultaneamente?
f) por nenhum deles?
26. Utilizando o fluxograma apesentado a seguir, podemos verificar se um número natural é divisível por 2.
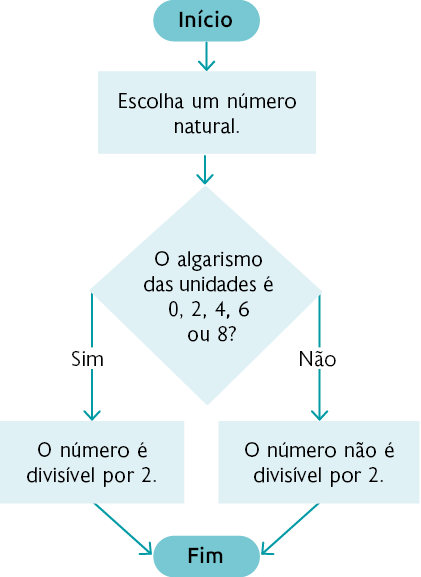
Agora, construa no caderno um fluxograma que possibilite verificar se um número natural é divisível por 100.
Página 83
Números primos e números compostos
Considere a sequência dos números naturais de 1 a 10.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Agora, vamos escrever os divisores de cada um desses números.
- Divisores de 1: 1
- Divisores de 2: 1 e 2
- Divisores de 3: 1 e 3
- Divisores de 4: 1, 2 e 4
- Divisores de 5: 1 e 5
- Divisores de 6: 1, 2, 3 e 6
- Divisores de 7: 1 e 7
- Divisores de 8: 1, 2, 4 e 8
- Divisores de 9: 1, 3 e 9
- Divisores de 10: 1, 2, 5 e 10
Os números que estão em destaque na sequência dos números naturais de 1 a 10 têm apenas 2 divisores naturais: o número 1 e o próprio número. Esses números são chamados números primos.
Os outros números dessa sequência, com exceção do 1, têm mais de 2 divisores. Esses números são chamados números compostos.
Atenção!
Números primos são os números naturais que têm apenas 2 divisores naturais, o número 1 e o próprio número.
Números compostos são os números naturais maiores do que 1 que têm mais de 2 divisores.
Os números primos sempre despertaram grande interesse entre os matemáticos. Entre eles, podemos destacar o matemático grego Eratóstenes (276 a.C.-194 a.C.), que criou um método para determinar se um número era primo ou não. Esse método ficou conhecido como crivo de Eratóstenes.
Questão 47. Junte-se a um colega e façam uma pesquisa sobre Eratóstenes e outras de suas contribuições para a Matemática anotando no caderno.
Atenção!
A pesquisa proposta na questão 47 pode ser feita em livros, revistas e sites. Mas cuidado!
Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
A seguir é apresentado como determinar os números primos da sequência dos números naturais de 1 a 50, utilizando o crivo de Eratóstenes.
Escrevemos a sequência dos números naturais de 1 a 50 e riscamos o número 1, pois esse número não é primo. Em seguida, contornamos o número 2, que é o próximo da sequência e é o primeiro número primo. Depois, riscamos os múltiplos de 2, pois esses não são primos.

Página 84
- Agora contornamos o próximo número da sequência que não foi riscado, o 3, pois ele é um número primo. Em seguida, riscamos os múltiplos de 3, pois esses números não são primos.
- Esse procedimento deve ser seguido com os próximos números da sequência que não foram riscados, até não existir mais números a serem contornados ou riscados.

Ao final, podemos verificar que os números contornados são os números primos da sequência dos números naturais de 1 a 50.
Podemos também verificar se um número é primo realizando algumas divisões. Por exemplo: O número 127 é primo?
Para resolver esta questão, podemos dividir esse número pelos números primos menores do que ele, em ordem crescente, até obter um quociente menor do que o divisor ou igual a ele.
Se alguma das divisões for uma divisão exata, então o número não é primo, pois tem mais de 2 divisores.
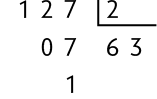
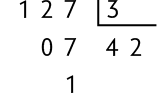
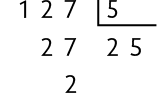
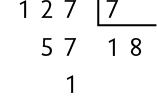
Atenção!
Essas divisões não são exatas e os quocientes são maiores do que os divisores. Portanto, devemos continuar efetuando divisões até obter um quociente menor do que o divisor ou igual a ele.
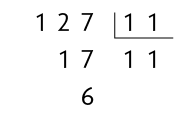
Essa foi a última divisão realizada, pois obtivemos um quociente igual ao divisor.
Caso continuássemos as divisões, os quocientes seriam cada vez menores. Porém, já testamos os primos menores do que 11 e não obtivemos uma divisão exata. Portanto, 127 é um número primo.
Atividades
Faça as atividades no caderno.
27. Quais são os números primos entre 1 e 50?
28. Quais são os números primos entre 51 e 100?
29. Classifique os números a seguir em primo ou composto.
a) 159
b) 247
c) 269
d) 301
e) 331
f) 541
Página 85
30. Junte-se a um colega e respondam às questões.
a) Por que o número 1 não é primo?
b) Qual é o único número natural par que é primo? Por que ele é primo?
c) Qual é o menor número ímpar que seja primo?
d) O número 112 é primo? Por quê?
e) Quantos números primos há entre 1 e 100?
f) O número 17 é primo? Por quê?
g) Qual é o maior número primo de dois algarismos?
31. (OBMEP–2015)
Um quadro com linhas e colunas numeradas de 1 a 100 foi preenchido da seguinte forma:
na linha 1, todas as casas foram preenchidas com 1;
na linha 2, as casas pertencentes a colunas de número par foram preenchidas com 1 e as demais, com 0;
na linha 3, as casas pertencentes a colunas múltiplas de três foram preenchidas com 1 e as demais, com 0;
continuando, cada uma das demais linhas do quadro foi preenchida com o algarismo 1 nas casas de colunas múltiplas do número correspondente à linha, e com 0 nas demais.
|
COLUNAS/LINHAS |
1 |
2 |
3 |
4 |
5 |
6 |
… |
99 |
100 |
|---|---|---|---|---|---|---|---|---|---|
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
… |
1 |
1 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
… |
0 |
1 |
|
3 |
0 |
0 |
1 |
0 |
0 |
1 |
… |
1 |
0 |
|
4 |
0 |
0 |
0 |
1 |
0 |
0 |
… |
0 |
1 |
|
5 |
0 |
0 |
0 |
0 |
1 |
0 |
… |
0 |
1 |
|
6 |
0 |
0 |
0 |
0 |
0 |
1 |
… |
0 |
0 |
|
99 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
1 |
0 |
|
100 |
0 |
0 |
0 |
0 |
0 |
0 |
… |
0 |
1 |
a) Qual é o algarismo que foi escrito na linha 7 e coluna 21?
b) Qual é a soma dos algarismos da linha 23? Por quê?
32. Utilizando as informações da atividade anterior, responda: qual é a soma dos algarismos da coluna 29?
33. Escreva no caderno todos os divisores naturais do número 72 e, em seguida, contorne os que são números primos.
Página 86
Decomposição em fatores primos
Decompor um número em fatores primos significa escrever esse número como um produto de números primos.
A seguir são apresentadas 3 maneiras diferentes de decompor o número 40 em um produto de fatores primos.



Atenção!
A decomposição de um número composto, diferente de zero, em fatores primos é única, diferenciando-se apenas pela ordem dos fatores.
Para qualquer uma das decomposições, obtemos o mesmo produto de fatores primos.
A.
B.
C.
Assim, é a decomposição em fatores primos do número 40. Também podemos decompor um número em fatores primos usando uma regra prática. Analise a decomposição do número 40.
Inicialmente dividimos o número 40 por um de seus divisores primos. Nesse caso, vamos começar pelo menor número primo possível, o 2. O resultado 20 da divisão é escrito logo abaixo do 40.
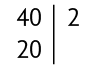
Dividimos o quociente obtido (20) por um de seus divisores primos, e assim sucessivamente, até obtermos o quociente 1.
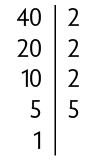
Assim: .
Página 87
Também poderíamos decompor o número 40 em fatores primos das seguintes maneiras.

ou
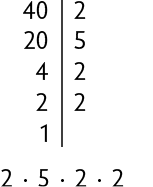
ou
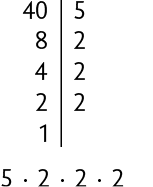
Note que o resultado final é o mesmo em todas as maneiras.
Atividades
Faça as atividades no caderno.
34. Decomponha no caderno os seguintes números em fatores primos sem usar a regra prática.
a) 12
b) 20
c) 55
d) 150
e) 196
f) 210
35. Agora, decomponha no caderno os seguintes números em fatores primos usando a regra prática.
a) 200
b) 315
c) 550
d) 676
e) 430
f) 720
36. Em cada item, determine o número representado pelo produto de fatores primos.
a)
b)
c)
d)
e)
f)
g)
h)
37. Qual é o
número cuja decomposição em fatores primos é o produto de todos os números
primos de um algarismo?
38. A idade atual de meu avô é um número entre 70 e 80. Descubra a idade dele, sabendo que ela pode ser representada pelo produto de 2 números primos consecutivos.
39. Junte-se a um colega, leiam as afirmações a seguir e copiem no caderno apenas as verdadeiras. Depois, reescrevam as afirmações falsas, tornando-as verdadeiras.
a) A decomposição em fatores primos de 180 é .
b) A decomposição em fatores primos de 50 é .
c) A decomposição em fatores primos de 44 é .
d) A decomposição em fatores primos de 350 é .
Página 88
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Considere as medidas das dimensões da embalagem de leite e das caixas A e B a seguir.

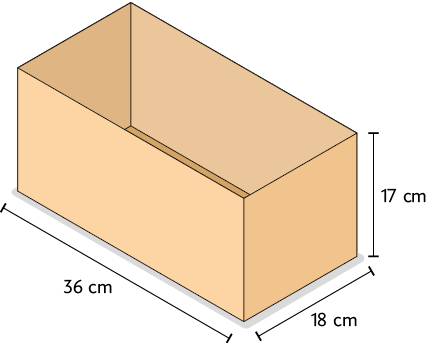
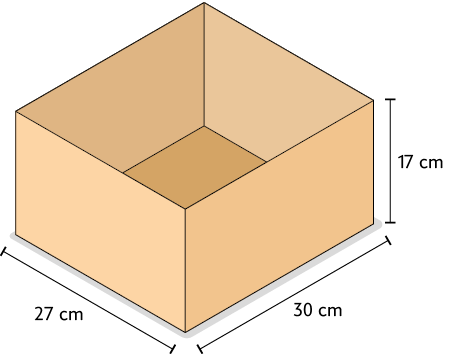
Atenção!
As medidas indicadas correspondem às dimensões internas das caixas.
a) Colocando as embalagens de leite em pé dentro das caixas, no máximo quantas embalagens cabem em cada caixa?
b) Em alguma das caixas sobra espaço ao colocar a maior quantidade possível de embalagens de leite?
2. Em uma folha de papel avulsa, escreva os 10 primeiros múltiplos de:
a) 3
b) 7
c) 10
3. Com os algarismos 2, 3, 4 e 5, forme um número natural com quatro algarismos, sem repeti-los, divisível por:
a) 2
b) 4
c) 5
d) 8
4. Utilizando os algarismos da atividade anterior, sem repetir, é possível formar um número natural com quatro algarismos que seja divisível por 6? Justifique sua resposta.
5. Cada letra representa um fator primo da decomposição de um número. Copie as sentenças em uma folha de papel avulsa substituindo cada letra pelo fator primo adequado.
a)
b)
c)
d)
6. Verifique se os números a seguir são divisíveis por 9 e por 10.
a) 4.708
b) 11.260
c) 3.591
d) 96.480
7. Um número de 5 algarismos é ímpar. É possível que ele seja divisível por 100? Justifique sua resposta.