Página 189

UNIDADE

Polígonos

Fotografia. Vitral composto de pedaços de vidros coloridos em diferentes tons de azul e em formatos quadrangulares. — Vitral do Santuário Dom Bosco, em Brasília, em 2013, composto de placas de vidro com formatos quadrangulares.

Agora vamos estudar...

os polígonos;
os triângulos;
os quadriláteros.

Página 190

Os polígonos

Com certeza você já percebeu como a Matemática está presente em nosso cotidiano, não é? Muitas construções apresentam formato parecido com figuras geométricas, seus contornos poderiam ser associados a algumas linhas estudadas na Geometria e, nesse ramo da Matemática, os polígonos são conceitos de grande importância. Por isso, vamos estudar suas características.

Antes, porém, analisaremos as figuras apresentadas a seguir.

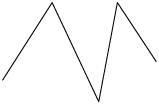
Ilustração de uma figura formada por 4 segmentos de reta sendo semelhante a letra M.

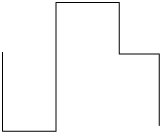
Ilustração de 7 segmentos de reta colocados um seguido do outro, perpendicularmente, de maneira a formar um caminho.

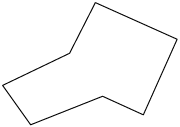
Ilustração de 7 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura de 7 lados.

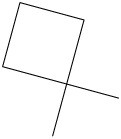
Ilustração de 4 segmentos de reta com cada ponto de suas extremidades em comum com outro, exceto um deles. Há dois segmentos que se cruzam.

Ilustração de 8 segmentos de reta colocados um seguido do outro, como se fosse parte de uma estrela, mas sem estar completa, apenas com 3 pontas.

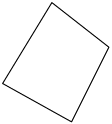
Ilustração de 4 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura de 4 lados.

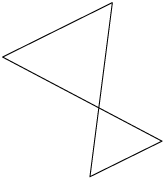
Ilustração de 4 segmentos de reta com cada ponto de suas extremidades em comum com outro. Há dois segmentos que se cruzam.

Ilustração de uma estrela com 5 pontas formada por 10 segmentos de reta..

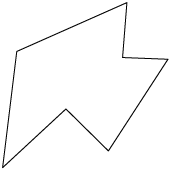
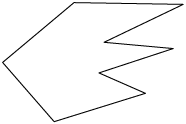
Essas figuras são formadas por sequências de segmentos de reta, de maneira que dois segmentos consecutivos não são parte de uma mesma reta. Além disso, a extremidade final do primeiro segmento é a extremidade inicial do segundo; a extremidade final do segundo é a extremidade inicial do terceiro; e assim sucessivamente.

Figuras com essas características são chamadas linhas poligonais, as quais podem ser simples e abertas, não simples e abertas, simples e fechadas e não simples e fechadas.

Considerando as imagens apresentadas, temos:

Características das figuras apresentadas
Linha poligonal	Simples	Não simples
Aberta	A, B e E	D
Fechada	C, F e H	G

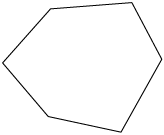
Um polígono é uma linha poligonal simples e fechada.

Atenção!

A palavra polígono deriva do grego poli (muitos) e gono (ângulos).

Página 191

A seguir são representados exemplos de polígonos e de não polígonos.

Polígonos

Ilustração de 7 segmentos de reta formando uma figura com 7 lados, com 5 pontas para fora e duas para dentro.

Ilustração de 8 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura de 8 lados, com um dos lados formando 3 pontas .

Ilustração de 6 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura de 6 lados.

Não polígonos

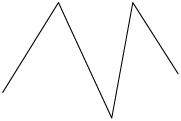
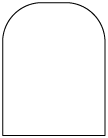
Ilustração de uma figura formada por 3 segmentos de reta consecutivos, como se fosse parte de um quadrado e um arco unido dois segmentos. — Não é polígono, pois não é uma linha poligonal.

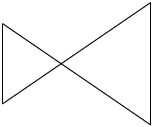
Atenção!

A parte interna de um polígono é a região plana delimitada por ele. Um polígono e sua parte interna determinam uma região poligonal. No entanto, exceto quando for dito o contrário, também nomearemos de polígono a região poligonal correspondente, ou seja, a figura geométrica plana formada por seus lados (contorno) e sua parte interna.

Ilustração de um polígono de 4 lados, com sua região interna colorida. — Região poligonal que poderá ser chamada de polígono.

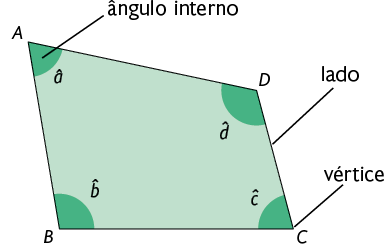
No polígono a seguir foram destacados alguns de seus elementos.

Esse polígono tem:

3 lados;
3 vértices;
3 ângulos internos.

Ilustração de um polígono com 3 lados. Na região poligonal há a demarcação de um ângulo interno. As extremidades são indicadas como vértice. Cada segmento que liga dois vértices é denominado 'lado'.

Note que a quantidade de lados, de vértices e de ângulos internos é igual. Isso ocorre em qualquer polígono.

Página 192

Os polígonos são nomeados de acordo com a quantidade de lados. A seguir são representados alguns exemplos.

Características de alguns polígonos
Quantidade de lados	Quantidade de vértices	Quantidade de ângulos internos	Nomenclatura
3	3	3	Triângulo
4	4	4	Quadrilátero
5	5	5	Pentágono
6	6	6	Hexágono
7	7	7	Heptágono
8	8	8	Octógono
9	9	9	Eneágono
10	10	10	Decágono

Questão 1. Você percebeu que, a partir dos polígonos de 5 lados, a nomenclatura de todos finaliza com "gono"? Em sua opinião, qual é o nome de um polígono de:

11 lados?
16 lados?
21 lados?

Polígonos convexos e polígonos não convexos

Os polígonos podem ser classificados como convexos ou não convexos.

Se qualquer reta cortar (separar em, pelo menos, duas partes) o polígono, determinando exatamente 2 pontos de interseção, ele é convexo.

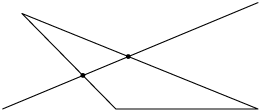
Ilustração de um triângulo com uma reta passando por ele e marcando dois pontos, um em cada lado do polígono.

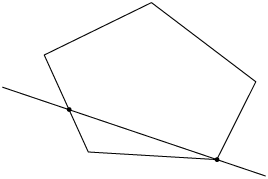
Ilustração de um polígono de 5 lados com uma reta passando por ele e marcando dois pontos, um em cada lado do polígono.

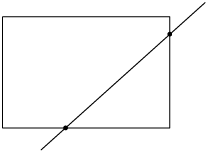
Ilustração de um retângulo com uma reta passando pela figura e marcando dois pontos, um em cada lado do polígono.

A seguir, veremos alguns exemplos de polígonos não convexos. Note que é possível traçar pelo menos uma reta que corta o polígono, determinando mais de 2 pontos de interseção.

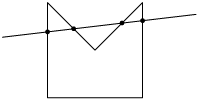
Ilustração de um polígono de 5 lados, formando duas pontas. Há uma reta passando por esse polígono e marcando 4 pontos sobre ele.

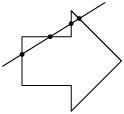
Ilustração de um polígono de 7 lados, formando uma figura semelhante a uma seta. Há uma reta passando por esse polígono e marcando 4 pontos sobre ele.

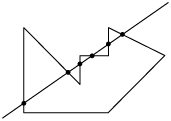
Ilustração de um polígono de 8 lados. Há uma reta passando por ele e marcando 6 pontos sobre ele.

Página 193

Atividades

Faça as atividades no caderno.

1. De acordo com as figuras, responda às questões.

Ilustração de uma figura semelhante a um semicírculo, com a região interna colorida.

Ilustração de 9 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura de 9 lados, com a região interna colorida.

Ilustração de 4 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura de 4 lados, com a região interna colorida.

Ilustração de 5 segmentos de reta com cada ponto de suas extremidades em comum com outro, formando uma figura com 5 lados iguais, com a região interna colorida.

a) Quais dessas figuras são polígonos?

b) Quais não são polígonos?

c) Em seu caderno, represente um polígono e um não polígono.

2. Em seu caderno, copie o quadro a seguir e complete-o com os números que faltam.

Características de alguns polígonos
Nome	Quantidade de lados	Quantidade de vértices
Quadrilátero
Octógono
Decágono

3. Classifique os polígonos a seguir de acordo com a quantidade de lados.

Ilustração de um polígono com 5 lados iguais.

Ilustração de um polígono com 3 lados iguais.

Ilustração de um polígono com 6 lados iguais.

Ilustração de um polígono com 7 lados iguais.

Ilustração de um polígono com 9 lados iguais.

4. O tangram é um quebra-cabeça chinês composto de 7 peças cuja origem envolve muitas lendas. Uma delas diz que seu surgimento ocorreu casualmente, quando um artista chinês derrubou uma prancha de formato quadrado, quebrando-a em 7 partes. Ao tentar juntá-las, o artista verificou que era possível representar diversas outras figuras além do quadrado original da prancha.

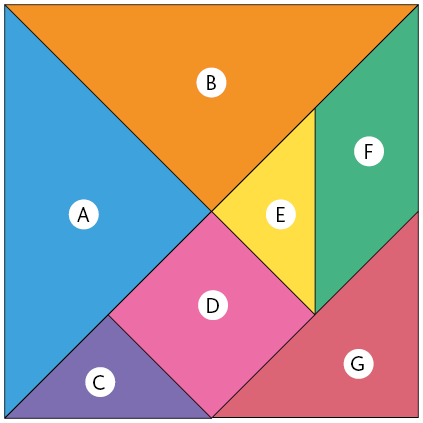
Ilustração de um quadrado formado por peças do Tangram. Dentre as peças, há 5 triângulos indicados por A, B, C, E, G com tamanhos e cores diferentes, mas cada um tem dois lados de mesma medida e um ângulo interno reto; 2 quadriláteros D e F: um paralelogramo que possui os quatro ângulos internos retos e o outro com os quatro lados com a mesma medida de comprimento. — Tangram.

a) Em relação às peças do tangram, quantas têm formato de:

triângulo?
pentágono?

b) Classifique as afirmações em verdadeira ou falsa.

Com as peças C e E, é possível representar um polígono com 3 ângulos internos.
Com as peças B, C e D é possível representar um pentágono.
Com as peças B e D é possível representar um pentágono.

Página 194

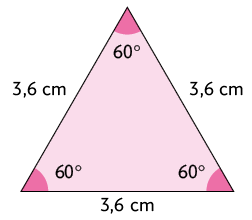
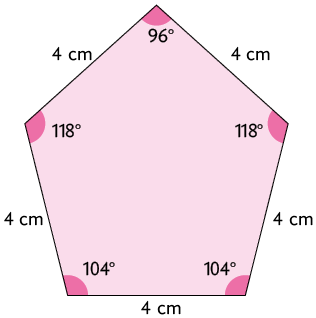
5. Você sabe o que é um polígono regular? Trata-se de um polígono com todos os lados medindo o mesmo comprimento e todos os ângulos internos congruentes. A seguir temos as representações de um polígono regular e de um polígono não regular.

Ilustração de um polígono de 5 lados com medidas de comprimento todas iguais. Os ângulos internos estão destacados: 108 graus. — Polígono regular

Ilustração de um polígono de 6 lados, sendo 4 lados com mesma medida de comprimento e os outros 2 com outra medida de comprimento. Os ângulos internos estão destacados: 120 graus. — Polígono não regular

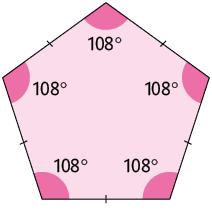
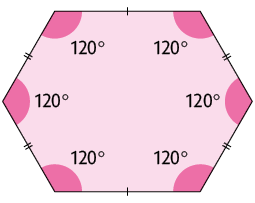
Embora todos os seus ângulos internos sejam congruentes, seus lados não têm a mesma medida de comprimento.

Atenção!

Nas figuras, os lados com a mesma medida de comprimento estão indicados com a mesma quantidade de risquinhos.

De acordo com as medidas indicadas, classifique os polígonos a seguir em regular ou não regular.

Ilustração de um triângulo com medidas de comprimento todas iguais a '3,6 centímetros'. Os ângulos internos estão destacados: 60 graus.

Ilustração de um polígono de 5 lados com medidas de comprimento iguais a 4 centímetros. Os ângulos internos estão destacados sendo eles: 118 graus, 104 graus, 104 graus, 118 graus e 96 graus.

Ilustração de um retângulo. Estão indicadas as medidas de comprimento de seus lados, que são: 3,2 centímetros e 5,4 centímetros.

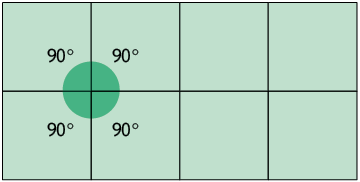
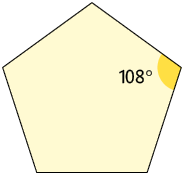
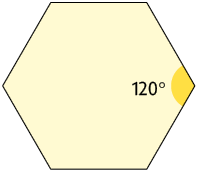
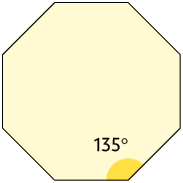
6. Os mosaicos são utilizados, por exemplo, para revestir paredes e fachadas de construções. Eles são compostos de pequenas peças fixadas sobre a superfície, de modo que elas não se sobreponham e que não sobrem espaços descobertos. Utilizando apenas quadrados é possível formar um mosaico. Note que a soma das medidas dos ângulos indicados no mosaico é $360 graus$ .

Ilustração de 8 quadrados, organizados de maneira a formar um retângulo com 4 quadrados em cima e 4 embaixo. Os 4 primeiros quadrados possuem dois de seus lados em comum, há uma demarcação no ângulo interno de cada quadrado que está no vértice em comum e mede 90 graus.

$90 graus mais 90 graus mais 90 graus mais 90 graus igual a 360 graus$

Escreva no caderno com quais polígonos regulares a seguir não é possível formar um mosaico usando apenas um tipo.

Ilustração de um triângulo equilátero com um de seus ângulos internos demarcado e medida correspondente a 60 graus.

Ilustração de um pentágono regular com um de seus ângulos internos destacados: 108 graus.

Ilustração de um hexágono regular com um de seus ângulos internos destacados: 120 graus.

Ilustração de um octógono regular com um de seus destacados ângulos internos: 135 graus.

Página 195

7. Analise as malhas quadriculadas.

Ilustração de parte de uma malha quadriculada com um retângulo formado por 5 quadradinhos de base e 3 quadradinhos de altura.

Ilustração de parte de uma malha quadriculada com uma figura formada por um retângulo ao lado de um trapézio. O retângulo é formado por 3 quadradinhos de base e 2 quadradinhos de altura; e o trapézio é formado por 5 quadradinhos na base maior e 3 quadradinhos na base menor.

Ilustração de parte de uma malha quadriculada com um retângulo formado por 5 quadradinhos de base e 2 quadradinhos de altura.

Ilustração de parte de uma malha quadriculada com um triângulo, formado por 4 quadradinhos de base e 5 quadradinhos de altura.

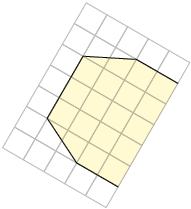
Ilustração parte de uma malha quadriculada, com uma figura formada por um retângulo: base medindo 5 quadradinhos e altura, medindo 2 quadradinhos; e um trapézio: base medindo 5 quadradinhos e altura, 2 quadradinhos.

Ilustração de parte de triângulo com três lados de medidas diferentes, formado por 5 quadradinhos de base e 4 quadradinhos de altura.

Juntando a malha A com a E, obtemos o seguinte polígono. Classifique-o de acordo com a quantidade de lados.

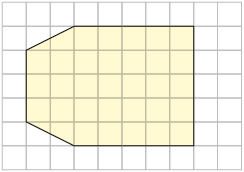
Ilustração de uma figura em malha quadriculada, formada por um quadrado e um trapézio. Quadrado com 5 quadradinhos de lado e um de seus lados é a base de um trapézio com base medindo 5 quadradinhos e altura, 2 quadradinhos.

8. Considerando as malhas quadriculadas da atividade anterior, responda às questões.

a) Que polígono podemos obter ao juntar adequadamente as malhas:

A e B?
D e F?
E e F?
B e D?

b) Em apenas um caso podemos unir duas malhas e obter um polígono regular. Quais são essas malhas? Qual é o nome do polígono formado?

9. Analise as figuras geométricas espaciais.

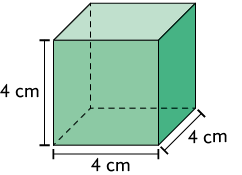
Ilustração de um cubo com medida de comprimento de cada uma de suas faces, iguais a '4 centímetros'. — Cubo.

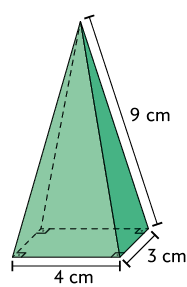
Ilustração de uma pirâmide de base retangular, com medida de comprimento das bases, iguais a '4 centímetros' e '3 centímetros'. Na lateral de uma das faces, a medida do lado do triângulo da pirâmide está indicado: '9 centímetros'. — Pirâmide.

a) Quanto à quantidade de lados, nomeie, em seu caderno, as faces de cada uma dessas figuras geométricas espaciais.

b) A face de alguma dessas figuras é um polígono regular? Se sim, qual seria?

10. A medida do perímetro de um polígono é a medida do comprimento de seu contorno. Sabendo disso, determine a medida do comprimento do lado de um:

a) heptágono regular cujo perímetro mede $749 centímetros$ .

b) decágono regular cujo perímetro mede $873 centímetros$ .

c) octógono regular cujo perímetro mede $524 centímetros$ .

d) dodecágono regular cujo perímetro mede $483 centímetros$ .

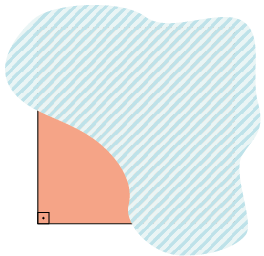
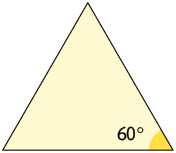
11. Parte de um polígono regular foi coberta por uma mancha, como representado a seguir. Qual é a medida de cada um de seus outros ângulos internos?

Ilustração de parte de um polígono regular coberto por uma mancha. Na parte visível do polígono aparece um ângulo reto formado por dois lados desse polígono.

Página 196

Os triângulos

Olhando ao seu redor, você consegue identificar elementos que se pareçam com um triângulo? Muitos objetos têm esse formato ou se assemelham a esse polígono, como é caso das bandeirinhas apresentadas na imagem.

Ilustração de dois fios, um acima do outro, cheios de bandeirinhas triangulares de várias cores e estampas.

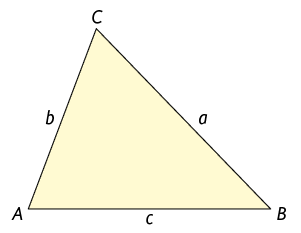
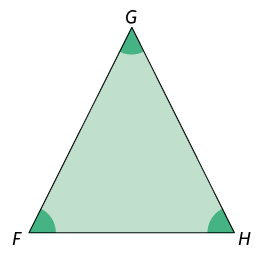
O triângulo é um polígono com 3 lados e, consequentemente, 3 vértices e 3 ângulos internos. A seguir estão representados um triângulo e alguns de seus elementos.

Para indicar a medida do comprimento de cada lado, podemos usar a letra minúscula do vértice oposto. E quanto à medida de cada ângulo interno, também podemos usar com a letra minúscula do vértice, porém com circunflexo.

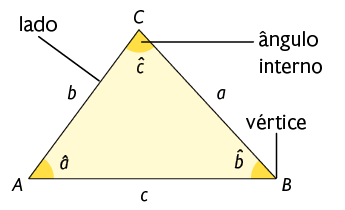
Ilustração de um triângulo A B C. Os ângulos internos estão indicados: ângulo a referente ao vértice A, ângulo b referente ao vértice B, nesse vértice está indicado 'vértice' e ângulo c referente ao vértice C, está indicado 'ângulo interno'. O lado A B tem medida de comprimento c. O lado B C tem medida de comprimento a. E o lado A C tem medida de comprimento b, e está indicado 'lado'.

Atenção!

Podemos nomear um triângulo pelas 3 letras maiúsculas de seus vértices. Por exemplo, o triângulo apresentado pode ser chamado triângulo ABC ou simplesmente $△ A B C$ .

Os triângulos podem ser classificados de acordo com as medidas do comprimento de seus lados.

Equilátero: triângulo cujos lados têm medidas de comprimento iguais.

Ilustração de um triângulo A B C. A medida de comprimento de seus lados são iguais. A medida de comprimento do lado A C é b; do lado A B é c e do lado B C é a.

$a = b = c$

Isósceles: triângulo em que pelo menos 2 de seus lados têm medidas de comprimento iguais.

Ilustração de um triângulo A B C. Dois de seus lados têm medidas de comprimento iguais: A C e B C. A medida de comprimento do lado A C é b; do lado A B é c e do lado B C é a.

$a = b$

Escaleno: triângulo em que todos os lados apresentam diferentes medidas de comprimento.

Ilustração de um triângulo A B C com as medidas de comprimento diferentes. A medida de comprimento do lado A C é b; do lado A B é c e do lado B C é a.

$a \neq b$ ; $b \neq c$ ; $c \neq a$

Página 197

Os triângulos também podem ser classificados conforme a medida de seus ângulos internos.

Triângulo retângulo: tem um ângulo reto, ou seja, cuja medida é igual a $90 graus$ .

Ilustração de um triângulo. Dois lados desse triângulo apresentam seus segmentos perpendiculares entre si, formando um ângulo interno, reto.

Triângulo obtusângulo: tem um ângulo obtuso, ou seja, cuja medida é maior do que $90 graus$ .

Ilustração de um triângulo. Dois lados desse triângulo formam um ângulo interno maior do que 90 graus (obtuso).

Triângulo acutângulo: tem todos os ângulos com medidas menores do que $90 graus$ .

Ilustração de um triângulo. Todos os lados desse triângulo formam ângulos internos menores do que 90 graus (agudos).

Questão 2. Em sua opinião, é possível um triângulo:

a) acutângulo ser classificado como triângulo retângulo? Justifique sua resposta.

b) obtusângulo ser classificado como triângulo retângulo? Justifique sua resposta.

Atividades

Faça as atividades no caderno.

12. Quantos triângulos podemos identificar em cada item?

Ilustração de um quadrilátero com suas duas diagonais traçadas.

Ilustração de um triângulo equilátero com vários outros triângulos na sua região interna. No centro, há um triângulo grande com seus vértices na metade de cada um dos lados do triângulo maior, que divide-o em 4 triângulos de mesmo tamanho. Em 3 desses, há novamente a divisão do triângulo em 4 triângulos menores, formados a partir da metade de cada um dos lados do triângulo e novamente há a divisão do triângulo em 4 triângulos menores.

13. No caderno, nomeie os triângulos e identifique os vértices, os lados e os ângulos internos de cada um deles.

Ilustração de um triângulo A B C. Os lados A B e A C são perpendiculares entre si. Os três ângulos estão destacados.

Ilustração de um triângulo F G H com todos os lados iguais. Os três ângulos estão destacados.

Página 198

14. Com uma régua, meça o comprimento dos lados de cada triângulo e classifique-o em equilátero, isósceles ou escaleno.

Ilustração de um triângulo retângulo A B C com três medidas de comprimento diferentes.

Ilustração de um triângulo J K L. Todos os ângulos internos têm a mesma medida.

Ilustração de um triângulo D E F. Dois dos ângulos de suas bases são iguais.

Ilustração de um triângulo G H I. Todos os ângulos internos têm a mesma medida.

Ilustração de um triângulo Q R S. Todos os ângulos internos têm medidas diferentes.

15. Em cada item, estão indicadas as medidas dos três ângulos internos de um triângulo. Com base nisso, classifique cada triângulo em retângulo, obtusângulo ou acutângulo.

a) $120 graus$ , $40 graus$ e $20 graus$ .

b) $45 graus$ , $90 graus$ e $45 graus$ .

c) $60 graus$ , $60 graus$ e $60 graus$ .

d) $75 graus$ , $45 graus$ e $60 graus$ .

16. Paulo dobrou uma folha de papel ao meio e desenhou parte de um triângulo.

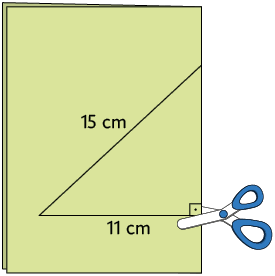
Ilustração de uma folha de papel dobrada ao meio, coincidindo com um dos lados do triângulo retângulo que está sob ela desenhado. Os outros dois lados medem '11 centímetros' e '15 centímetros'. Há uma tesoura encaixada no papel.

Em seguida, recortou a folha e obteve a representação de um triângulo.

Ilustração de um triângulo com dois lados de mesma medida de comprimento. Há um segmento tracejado, perpendicular à base desse triângulo, representado a sua altura.

a) Qual é a medida do comprimento de cada lado do triângulo que Paulo representou?

b) Com base na medida do comprimento dos lados, classifique o triângulo que Paulo representou.

c) É possível construir um triângulo equilátero com o mesmo procedimento de Paulo? E um triângulo escaleno?

Página 199

Os quadriláteros

Denise representou alguns polígonos em uma folha de papel. Em seguida, ela recortou essas representações e montou um mosaico.

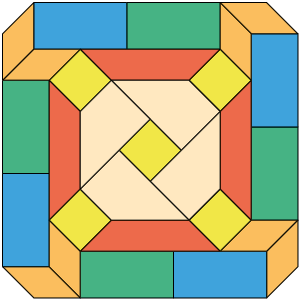
Ilustração de um mosaico colorido, formado só por quadriláteros de diferentes formas e tamanhos. — Mosaico montado por Denise.

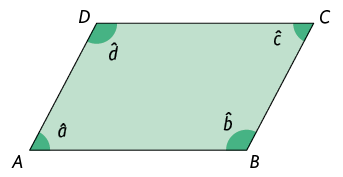
As figuras que compõem esse mosaico são quadriláteros, ou seja, têm 4 lados, 4 vértices e 4 ângulos internos.

Assim como no triângulo, para indicar a medida de cada ângulo interno de um quadrilátero, podemos usar a letra do vértice, porém minúscula e com circunflexo.

Ilustração de um quadrilátero A B C D. Os ângulos internos estão indicados: ângulo a referente ao vértice A, está indicado 'ângulo interno', ângulo b referente ao vértice B, ângulo c referente ao vértice C e ângulo d referente ao vértice D. No lado C D está indicado 'lado' e no vértice C está indicado 'vértice'.

Atenção!

Podemos nomear um quadrilátero pelas 4 letras maiúsculas de seus vértices. Por exemplo, a figura a seguir pode ser chamada quadrilátero $A B C D$ .

De acordo com a medida do comprimento de seus lados, alguns quadriláteros recebem nomes especiais.

Paralelogramo: quadrilátero com 2 pares de lados paralelos.

Ilustração de um quadrilátero A B C D. O lado A B é paralelo ao lado D C; e o lado A D é paralelo ao lado B C. Os ângulos internos estão indicados: ângulo a referente ao vértice A, ângulo b referente ao vértice B, ângulo c referente ao vértice C e ângulo d referente ao vértice D. — Em um paralelogramo, as medidas dos ângulos internos opostos são iguais:

$\hat{a} = \hat{c}$ ; $\hat{b} = \hat{d}$

Além disso, os lados opostos têm a mesma medida de comprimento:

$A B = D C$ ; $A D = B C$

Nesse paralelogramo os lados $\overline{A B}$ e $\overline{D C}$ são paralelos, assim como os lados $\overline{A D}$ e $\overline{B C}$ .

Trapézio: quadrilátero com apenas 1 par de lados paralelos.

Ilustração de um quadrilátero B C D E. Apenas os lados B C e D E são paralelos. — Nesse trapézio os lados $\overline{B C}$ e $\overline{E D}$ são paralelos.

Contudo, alguns quadriláteros não são paralelogramos nem trapézios.

Questão 3. Junte-se a um colega e desenhem, cada um em seu caderno, dois quadriláteros que não sejam paralelogramo nem trapézio.

Página 200

De acordo com suas características, alguns paralelogramos recebem nomes especiais.

Retângulo: paralelogramo com os 4 ângulos internos retos.

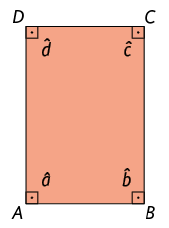
Ilustração de um quadrilátero A B C D, com todos os ângulos internos medindo 90 graus. Os ângulos internos estão indicados: ângulo a referente ao vértice A, ângulo b referente ao vértice B, ângulo c referente ao vértice C e ângulo d referente ao vértice D.

$ângulo a igual a ângulo b igual a ângulo c igual a ângulo d igual a 90 graus$

Quadrado: paralelogramo com os 4 ângulos internos retos e os 4 lados com medidas de comprimento iguais.

Ilustração de um quadrilátero E F G H, cuja medida do comprimento de seus lados são iguais e com todos os ângulos internos medindo 90 graus: ângulo e referente ao vértice E, ângulo f referente ao vértice F, ângulo g referente ao vértice G e ângulo h referente ao vértice H.

$ângulo e igual a ângulo f igual a ângulo g igual a ângulo h igual a 90 graus$

$E F = F G = G H = E H$

Losango: paralelogramo com os 4 lados com medidas de comprimento iguais.

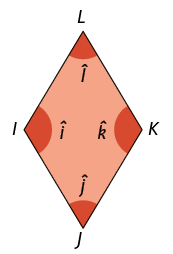
Ilustração de um quadrilátero I J K L, com dois pares de lados paralelos, e medida de altura diferente da medida da largura. Ângulo i referente ao vértice I, ângulo j referente ao vértice J, ângulo k referente ao vértice K e ângulo l referente ao vértice L.

$I J = J K = K L = I L$

Questão 4. Todo quadrado pode ser classificado como:

a) retângulo? Justifique sua resposta.

b) losango? Justifique sua resposta.

Instrumentos e softwares

Construindo quadriláteros no GeoGebra

Siga as orientações do professor e estes passos para construir um quadrilátero qualquer e um paralelogramo no GeoGebra.

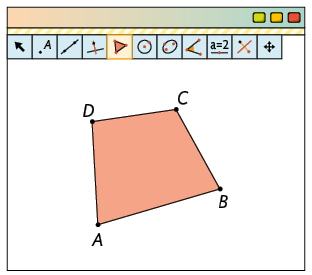
Quadrilátero qualquer

1º. Com a ferramenta Ponto, marque 4 pontos quaisquer A, B, C e D, de modo que os quatro não estejam alinhados.

2º. Com a ferramenta Polígono, clique sobre os pontos A, B, C, D e A, nessa ordem.

Ilustração da tela de um software com diversos ícones de ferramentas, com ícone de polígono, selecionado. Há um quadrilátero com vértices A, B, C, D.

Página 201

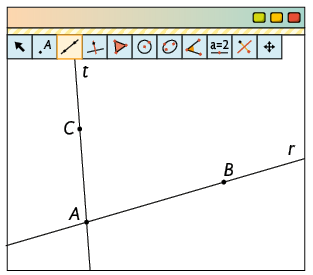
Paralelogramo

1º. Clique com a ferramenta Ponto marcando 3 pontos quaisquer $A$ , $B$ e $C$ , de modo que os três não estejam alinhados.

2º. Com a ferramenta Reta, trace as retas r e t que passam por $A$ e $B$ , e por $A$ e $C$ , respectivamente.

Ilustração da tela de um software com diversos ícones de ferramentas, com ícone de reta, selecionado. Há uma reta t passando pelos pontos A e C, e há também uma reta r, que cruza com a reta t no ponto A passando pelo ponto B.

3º. Trace uma reta p, paralela à r, passando por $C$ , e uma reta q, paralela à t, passando por $B$ , conforme vimos na página 186.

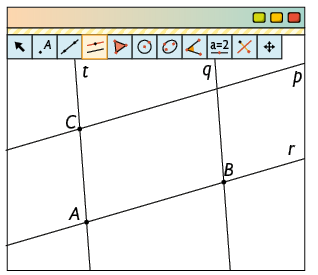
Ilustração da tela de um software com diversos ícones de ferramentas e com ícone de reta paralela, selecionado. Há uma reta t, paralela à reta q, que cruza com a reta p no ponto C e que cruza com a reta r no ponto A. As retas p e r também são paralelas. As retas q e r se cruzam no ponto B. Com o cruzamento dessas retas forma-se um quadrilátero.

4º. Com a ferramenta Interseção de dois objetos, clique sobre a reta p e, depois, sobre a reta q para marcar o ponto $D$ .

5º. Com a ferramenta Polígono, construa o paralelogramo ABDC.

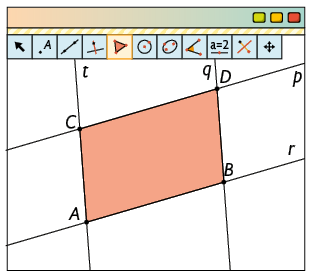
Ilustração da tela de um software com diversos ícones de ferramentas, com ícone de polígono, selecionado. Há uma reta t, paralela à reta q, que cruza com a reta p no ponto C e que cruza com a reta r no ponto A. As retas p e r também são paralelas. As retas q e r se cruzam no ponto B e as retas p e q se cruzam no ponto D. Com essas retas forma-se um quadrilátero de vértices C A B D, no qual a sua região interna está destacada.

Faça o teste: Com a ferramenta Ângulo, meça os ângulos internos do paralelogramo construído e verifique se as medidas dos ângulos opostos são iguais. Além disso, usando a ferramenta Mover, arraste os pontos $A$ , $B$ ou $C$ para verificar se o quadrilátero ABDC continua sendo um paralelogramo.

Página 202

Atividades

Faça as atividades no caderno.

17. Com os instrumentos de medida adequados, verifique se entre os quadriláteros a seguir há algum retângulo, losango ou quadrado. Depois, classifique-os.

Ilustração de um quadrilátero com todas as medidas de comprimento de seus lados diferentes.

Ilustração de um quadrilátero com dois pares de lados paralelos, e medida de altura diferente da medida da largura.

Ilustração de um quadrilátero com todas as medidas de comprimento de seus lados iguais e perpendiculares entre si.

Ilustração de um quadrilátero com suas medidas de comprimento iguais, duas a duas e com lados perpendiculares entre si.

Ilustração de um quadrilátero com 2 pares de lados paralelos.

18. Considere os quadriláteros representados nas malhas quadriculadas a seguir.

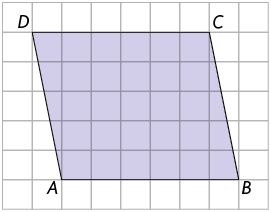
Ilustração de malha quadriculada com um quadrilátero A B C D formado por 2 pares de lados paralelos.

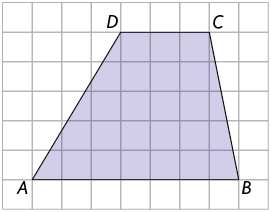
Ilustração de malha quadriculada com um quadrilátero A B C D formado por 1 par de lados paralelos.

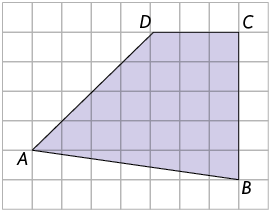
Ilustração de malha quadriculada com um quadrilátero A B C D com nenhum par de lados paralelos.

Associe no caderno cada quadrilátero a uma das informações a seguir, escrevendo a letra e o número correspondentes.

1. Quadrilátero sem pares de lados paralelos, ou seja, não é paralelogramo nem trapézio.

2. Quadrilátero apenas com os lados $\overline{A B}$ e $\overline{C D}$ paralelos, ou seja, é um trapézio.

3. Paralelogramo com lado $\overline{A D}$ paralelo ao lado $\overline{B C}$ e lado $\overline{A B}$ paralelo ao lado $\overline{C D}$ .

Página 203

19. Nomeie os quadriláteros que podemos identificar na figura. Em seguida, classifique cada um deles em paralelogramo ou trapézio.

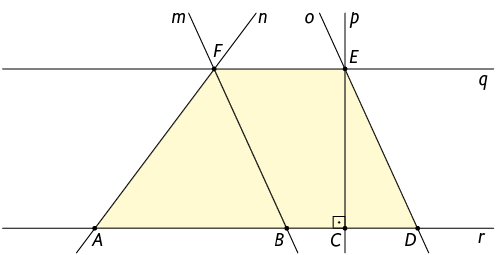
Ilustração de duas retas paralelas na horizontal, q, r, cortadas por outras quatro retas m, n, o, p. A reta n cruza com a reta r formando o ponto A. A reta m, cruza com a reta r, formando o ponto B. As retas m, n cruzam com a reta paralela q, formando o ponto F. A reta p cruza perpendicularmente com a reta r formando o ponto C. A reta o, cruza com a reta r, formando o ponto D. As retas o, p cruzam com a reta paralela q, formando o ponto E. A região formada pelos pontos A D E F, está colorida.

Atenção!

As retas m e o são paralelas, assim como as retas q e r.

20. No caderno, associe cada quadrilátero representado na malha quadriculada a um único nome. Para isso, escreva a letra e o número correspondentes.

A. Quadrado

B. Retângulo

C. Losango

D. Trapézio

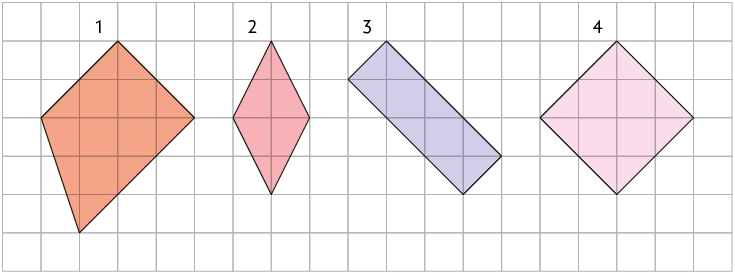
Ilustração de uma malha quadriculada com 4 quadriláteros indicados por: 1, 2, 3, 4. Quadrilátero 1: tem um par de lados paralelos. Quadrilátero 2: tem dois pares de lados paralelos, e medida de altura diferente da medida da largura. Quadrilátero 3: tem dois pares de lados paralelos, sendo que cada par tem a mesma medida de comprimento. Quadrilátero 4: tem dois pares de lados paralelos e com medida de altura igual a da largura.

21. Classifique as afirmações em verdadeira ou falsa. Em seguida, reescreva as falsas em seu caderno corrigindo-as.

a) Todo retângulo é um quadrado, mas nem todo quadrado é um retângulo.

b) Existem losangos que são retângulos.

c) Alguns trapézios podem ser classificados como paralelogramos.

d) Todo quadrado é um losango, mas nem todo losango é um quadrado.

e) Existem retângulos que são losangos.

f) Alguns paralelogramos podem ser classificados como trapézios.

22. Utilizando o GeoGebra, construa:

a) um quadrilátero qualquer.

b) um paralelogramo.

c) um trapézio.

Página 204

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

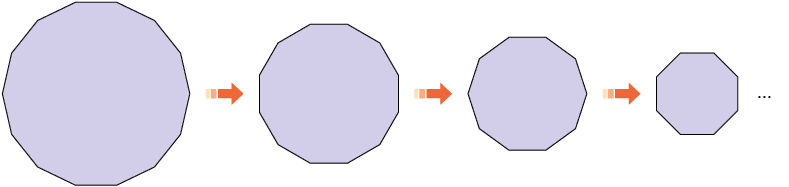
1. Descubra o padrão da sequência e, em uma folha de papel avulsa, escreva os nomes dos dois polígonos seguintes.

Ilustração de 4 polígonos regulares alinhados e separados por uma seta da esquerda para direita. Os polígonos regulares têm, nessa ordem: 14 lados, 12 lados, 10 lados e 8 lados. Ao lado, reticências.

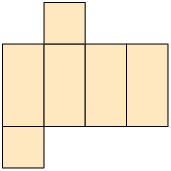
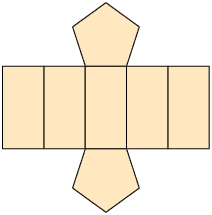
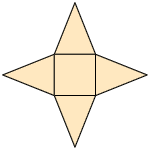
2. De acordo com a quantidade de lados, classifique os polígonos que formam cada planificação a seguir.

Ilustração de uma planificação composta por dois triângulos e três retângulos, que estão lado a lado e alinhados. Os dois triângulos estão nos lados opostos do retângulo central.

Ilustração de uma planificação composta por dois quadrados e quatro retângulos, que estão lado a lado e alinhados. Um dos quadrados está abaixo do primeiro retângulo e o outro está acima do segundo retângulo.

Ilustração de uma planificação composta por dois pentágonos e cinco retângulos, que estão lado a lado e alinhados. Os dois pentágonos estão nos lados opostos do retângulo central.

Ilustração de uma figura plana composta por um quadrado no centro e 4 triângulos ao redor. Cada triângulo tem um lado em comum com um lado do quadrado.

3. Usando os instrumentos que julgar necessário, classifique os triângulos da malha triangular a seguir conforme a medida do comprimento de seus lados e a medida de seus ângulos internos.

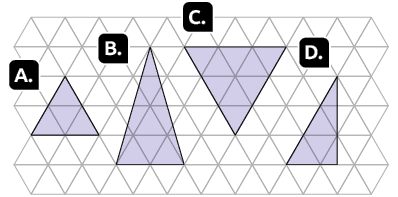
Ilustração de malha triangular com 4 triângulos. Triângulo A: ocupa 4 triângulos da malha. Triângulo B: tem a medida do comprimento da base formada por 2 triângulos e sua altura ocupa 4 linhas da malha. Triângulo C: ocupa 9 triângulos da malha. Triângulo D: tem a medida do comprimento da base formada por 1 triângulo e meio e sua altura ocupa 3 linhas da malha.

Atenção!

A malha é formada apenas por triângulos equiláteros.

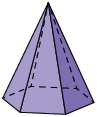
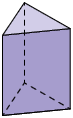
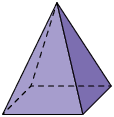
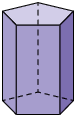
4. Em uma folha de papel avulsa, escreva quantos triângulos e quantos quadriláteros há na planificação de cada figura geométrica espacial representada a seguir.

Ilustração de uma pirâmide de base hexagonal.

Ilustração de um prisma de base triangular.

Ilustração de uma pirâmide de base quadrangular.

Ilustração de um prisma de base pentagonal.

5. Classifique as afirmações a seguir em verdadeira ou falsa. Depois, em uma folha de papel avulsa, reescreva as falsas corrigindo-as.

a) O paralelogramo é um quadrilátero com apenas 1 par de lados paralelos.

b) O trapézio é um quadrilátero com apenas 1 par de lados paralelos.

c) Todo quadrado é também losango.

d) O retângulo é um paralelogramo que tem os 4 lados com as medidas de comprimento iguais.