1. Em uma folha de papel avulsa, escreva os números por extenso.

a) 4.690

Resposta: Quatro mil, seiscentos e noventa.

b) 15.783

Resposta: Quinze mil, setecentos e oitenta e três.

c) 76.254

Resposta: Setenta e seis mil, duzentos e cinquenta e quatro.

d) 158.391

Resposta: Cento e cinquenta e oito mil, trezentos e noventa e um.

2. Escreva em uma folha de papel avulsa, com algarismos e por extenso, os números representados nos ábacos.

A.

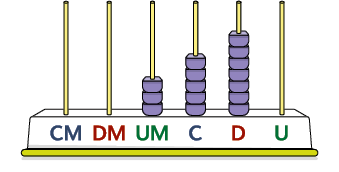
Respostas: 3.570; três mil, quinhentos e setenta.

B.

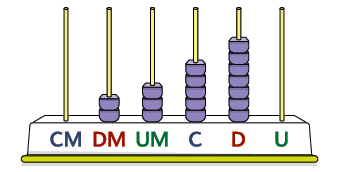
Respostas: 23.570; vinte e três mil, quinhentos e setenta.

C.

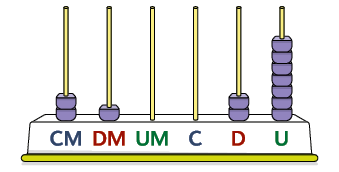
Respostas: 210.027; duzentos e dez mil e vinte e sete.

3. Em uma folha de papel avulsa, escreva os números representados nos ábacos da atividade 2 em ordem crescente.

Resposta: 3.570, 23.570, 210.027.

4. Determine:

a) o maior número com 5 algarismos diferentes.

Resposta: 98.765.

b) o menor número de 4 ordens.

Resposta: 1.000.

c) o maior número de 5 ordens menor do que 25.100.

Resposta: 25.099.

d) um número de 8 ordens em que o algarismo 5 ocupe a ordem das unidades simples.

Resposta pessoal. Sugestões de resposta: 10.326.185; 86.932.145.

5. Determine o valor posicional de cada algarismo dos números a seguir.

a) 154

b) 3.208

c) 7.250

d) 36.954

e) 78.521

f) 91.057

Respostas na seção Respostas e na seção Resoluções.

6. Decomponha, de duas maneiras diferentes, os números apresentados a seguir.

a) 13.642

b) 36.980

c) 49.015

d) 1,459

e) 3,657

f) 9,274

Respostas na seção Respostas e na seção Resoluções.

7. Raquel e três amigas estão brincando com um jogo no qual uma partida é composta de 4 etapas. Verifique na tabela a quantidade de pontos de cada participante em uma partida desse jogo.

Fonte de pesquisa: registros de Raquel.

Determine o nome do vencedor dessa partida, ou seja, quem fez mais pontos. Depois, calcule a diferença entre a quantidade de pontos do vencedor e a quantidade de quem marcou menos pontos.

Respostas: Lúcia; 7 pontos.

8. Em cada item, arredonde os números à unidade de milhar mais próxima e efetue os cálculos mentalmente. Depois, efetue os cálculos exatos da maneira que preferir e compare os resultados obtidos.

a) $24.800+11.045$

b) $4.902+2.299$

c) $35.247+9.867$

d) $8.276-6.305$

e) $49.872-39.755$

f) $57.912-39.804$

Respostas: a) 36.000 e 35.845; b) 7.000 e 7.201; c) 45.000 e 45.114; d) 2.000 e 1.971; e) 10.000 e 10.117; f) 18.000 e 18.108.

9. Considere os números a seguir.

• 333
• 127
• 829
• 499
• 468
• 256

Utilizando dois desses números, determine, quando possível, uma adição e uma subtração cujo resultado seja:

a) menor do que 600.

b) maior do que 1.200.

c) um número entre 300 e 500.

d) par.

e) ímpar.

f) ímpar e maior do que 800.

Respostas na seção Respostas e na seção Resoluções.

10. Nos cálculos a seguir, cada letra representa um algarismo. Efetue os cálculos e determine o algarismo correspondente a cada letra.

Respostas: A: 5; B: 3; C: 9; D: 6.

11. Em uma folha de papel avulsa, escreva uma subtração em que o minuendo seja o triplo do subtraendo.

Resposta pessoal. Sugestão de resposta: $53.688-17.896=35.792$.

12. Lucas e quatro amigos foram a uma lanchonete. O gráfico a seguir apresenta a quantia em reais gasta individualmente por eles.

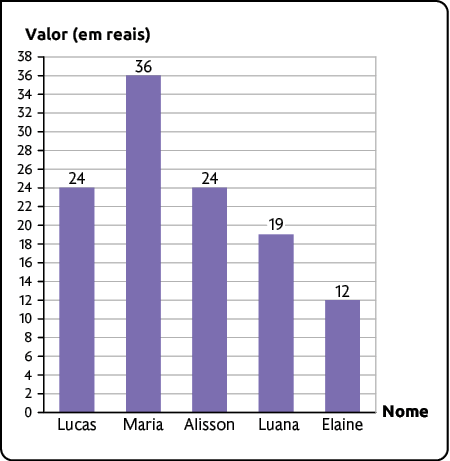
Fonte de pesquisa: registros de Lucas.

a) Quem gastou a maior quantia? E a menor?

Respostas: Maria; Elaine.

b) Se a conta fosse dividida igualmente entre eles, quantos reais cada um pagaria?

Resposta: R$ 23,00.

13. Relacione cada fração a seguir à letra correspondente na reta numérica.

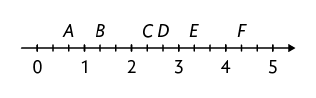
Respostas: A: $\frac{2}{3}$; B: $\frac{4}{3}$; C: $\frac{7}{3}$; D: $\frac{8}{3}$; E: $\frac{10}{3}$; F: $\frac{13}{3}$.

14. Considere um dado de 6 faces, numeradas de 1 a 6.

a) Ao lançar esse dado, quais são os possíveis resultados?

Resposta: 1, 2, 3, 4, 5 ou 6.

b) Os resultados desse experimento são igualmente prováveis? Justifique sua resposta.

Resposta: Sim, pois a probabilidade de sair qualquer um dos resultados é a mesma.

c) Nesse experimento, qual é a probabilidade de sortear um número ímpar? E de sortear um número igual ou maior do que 5?

Respostas: $\frac{3}{6}$ ou $\frac{1}{2}$; $\frac{2}{6}$ ou $\frac{1}{3}$.

15. Faça as transformações necessárias e, em uma folha de papel avulsa, escreva:

a) $59\text{cm}$ em metros.

b) $20\text{m}$ em quilômetros.

c) $0,26\text{m}$ em milímetros.

d) $0,954\text{km}$ em metros.

Respostas: a) $0,59\text{m}$; b) $0,020\text{km}$; c) $260\text{mm}$; d) $954\text{m}$.

16. As frações a seguir representam partes de um mesmo todo. Em uma folha de papel avulsa, copie as que apresentam frações equivalentes a $\frac{2}{8}$.

• $\frac{1}{4}$
• $\frac{2}{4}$
• $\frac{4}{24}$
• $\frac{6}{24}$
• $\frac{4}{16}$
• $\frac{6}{18}$
• $\frac{8}{32}$

Resposta: $\frac{1}{4}$, $\frac{6}{24}$, $\frac{4}{16}$ e $\frac{8}{32}$.

17. Em uma folha de papel avulsa, determine o nome de cada polígono com relação à quantidade de lados de cada um.

Qual é a quantidade de lados, vértices e ângulos internos de cada um deles?

Respostas na seção Respostas e na seção Resoluções.

18. Escreva em uma folha de papel avulsa o nome de cada figura geométrica espacial apresentada.

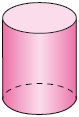
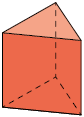
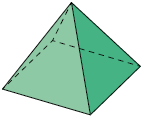
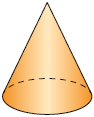
a) Quais figuras geométricas espaciais têm apenas faces planas?

b) Determine a quantidade de faces, vértices e arestas das figuras que você citou no item anterior.

Respostas na seção Respostas e na seção Resoluções.

19. Para cada item, escreva em uma folha de papel avulsa o nome da figura geométrica espacial correspondente à planificação.

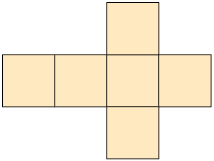
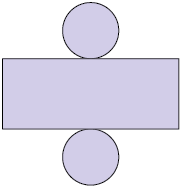
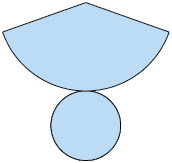
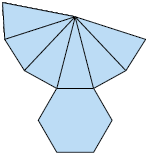
A: cubo; B: cilindro; C: cone; D: pirâmide de base hexagonal.

a) Entre as planificações apresentadas, quais são compostas apenas de polígonos?

Resposta: Planificações: A e D.

b) Quais figuras geométricas planas você identificou nessas planificações?

Resposta: A: quadrado; B: círculo e retângulo; C: círculo; D: hexágono e triângulo.