Página XLII
Resoluções
O que eu já sei?
1. a) 4.690: quatro mil, seiscentos e noventa.
b) 15.783: quinze mil, setecentos e oitenta e três.
c) 76.254: setenta e seis mil, duzentos e cinquenta e quatro.
d) 158.391: cento e cinquenta e oito mil, trezentos e noventa e um.
2. De acordo com a quantidade de contas apresentadas em cada haste dos ábacos, temos:
A. 3.570; três mil, quinhentos e setenta.
B. 23.570; vinte e três mil, quinhentos e setenta.
C. 210.027; duzentos e dez mil e vinte e sete.
3. Para escrever os números em ordem crescente, devemos ordená-los do menor para o maior. Assim: , , .
4. a) Para determinar o maior número de 5 algarismos, devemos escrever em ordem decrescente os cinco maiores algarismos, ou seja, 98.765.
b) Um número de 4 ordens é formado por 4 algarismos. Assim, o menor número de quatro ordens é o primeiro número com quatro ordens, ou seja, 1.000.
c) Sabemos que 25.100 tem cinco ordens. Para escrever o maior número de 5 ordens menor do que 25.100, subtraímos uma unidade dele, ou seja, . Assim, 25.099 é o maior número de cinco ordens menor do que 25.100.
d) A resposta será correta se o número tiver oito ordens e o algarismos 5 estiver na ordem das unidades simples.
Sugestões de resposta: 10.326.185; 86.932.145.
5. a) 154
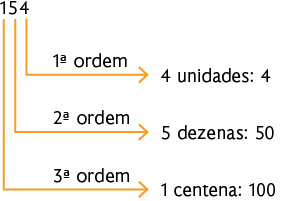
b) 3.208
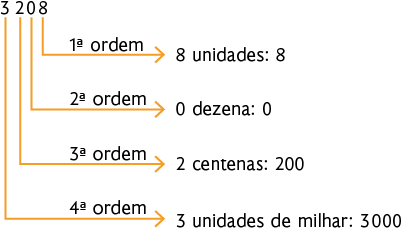
c) 7.250
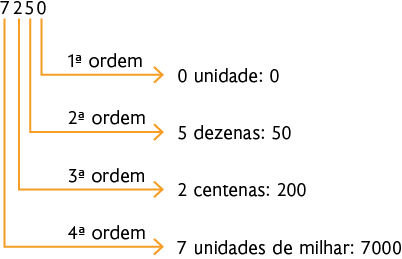
d) 36.954
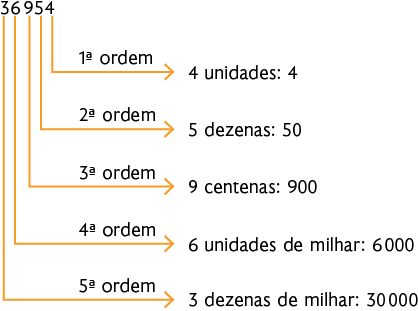
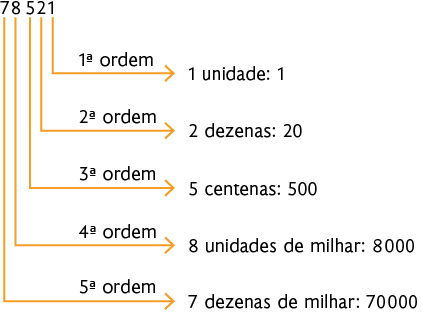
e) 78.521
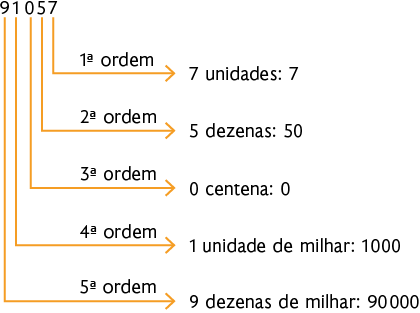
f) 91.057
Página XLIII
6. Sugestões de respostas:
a)
b)
c)
d)
e)
f)
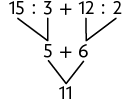
7. Devemos adicionar a quantidade de pontos que cada jogadora marcou em cada etapa. Assim:
Raquel: , ou seja, 131 pontos;
Ivone: , ou seja, 132 pontos;
Carla: , ou seja, 127 pontos;
Lúcia: , ou seja, 134 pontos.
Portanto, Lúcia foi a vencedora.
Como Lúcia marcou mais pontos (134) e Carla marcou menos pontos (127), para determinar a diferença entre a pontuação das duas calculamos .
8.a) Arredondando o número 24.800 para a unidade de milhar mais próxima, obtemos 25.000.

Arredondando o número 11.045 para a unidade de milhar mais próxima, obtemos 11.000.

A soma dos números arredondados é ;
A soma exata é .
b) Arredondando o número 4.902 para a unidade de milhar mais próxima, obtemos 5.000.

Arredondando o número 2.299 para unidade de milhar mais próxima, obtemos 2.000.

A soma dos números arredondados é ;
A soma exata é .
c) Arredondando o número 35.247 para a unidade de milhar mais próxima, obtemos 35.000.

Arredondando o número 9.867 para a unidade de milhar mais próxima, obtemos 10.000.

A soma dos números arredondados é ;
A soma exata é .
d) Arredondando o número 8.276 para a unidade de milhar mais próxima, obtemos 8.000.

Arredondando o número 6.305 para a unidade de milhar mais próxima, obtemos 6.000.

A subtração dos números arredondados é ;
A subtração exata é .
e) Arredondando o número 49.872 para a unidade de milhar mais próxima, obtemos 50.000.

Arredondando o número 39.755 para unidade de milhar mais próxima, obtemos 40.000.

A subtração dos números arredondados é ;
A subtração exata é .
f) Arredondando o número 57.912 para a unidade de milhar mais próxima, obtemos 58.000.

Arredondando o número 39.804 para a unidade de milhar mais próxima, obtemos 40.000.

A subtração dos números arredondados é ;
A subtração exata é .
Página XLIV
9. Há várias respostas para esta atividade. Algumas sugestões são:
a) Adição: e ;
Subtração: e .
b) Adição: e ;
Nesse caso, não há subtração cujo resultado seja maior do que 1.200.
c) Adição: e ;
Subtração: e .
d) Adição: e ;
Subtração: e .
e) Adição: e ;
Subtração: e .
f) Adição: e ;
Nesse caso, não há subtração cujo resultado seja ímpar e maior do que 800.
10. Realizando a operação inversa no primeiro cálculo, fazemos , e assim obtemos o algarismo correspondente a cada letra. Portanto, e .
Para determinar o algarismo que corresponde à letra C, realizamos a operação inversa entre os algarismos 6 e 3, pois ocupam a mesma ordem no subtraendo e na diferença, assim , logo . Como , para determinar o valor de D fazemos , portanto .
11. Existem várias respostas para essa atividade. O minuendo pode ser qualquer número, desde que o subtraendo seja o seu triplo, ou seja, 3 vezes o minuendo. Possível resposta: .
12.a) Maria, pois a barra que representa a quantia gasta por ela é a maior; Elaine, pois a barra que representa a quantia gasta por ela é a menor.
b) Juntando os valores gastos por Lucas e seus quatro amigos, obtemos . Dividindo esse total pela quantidade pessoas, obtemos . Portanto, se a conta fosse dividida igualmente entre todos eles, cada um pagaria R$ 23,00.
13. Cada inteiro na reta está dividido em 3 partes iguais. Assim, basta substituir cada letra pela fração correspondente em ordem crescente.
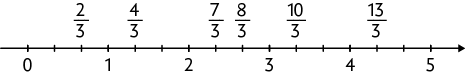
14.a) De acordo com enunciado da atividade, os possíveis resultados ao lançar esse dado são: 1, 2, 3, 4, 5 ou 6.
b) Sim, pois como há um número diferente em cada face, todos os resultados têm a mesma chance de ocorrer.
c) O dado contém seis faces numeradas de 1 a 6. Como há 3 números ímpares entre esses números (1, 3 e 5), a chance de sortear um número ímpar é 3 em 6, ou seja, . Entre esses números, a probabilidade de sortear um número igual ou maior do que 5 é 2 em 6, ou seja, .
15.a) Como , para transformar em uma medida em , fazemos .
Portanto, .
b) Como , para transformar em uma medida em , fazemos . Portanto, .
c) Como , para transformar em uma medida em , fazemos . Portanto, .
d) Como , para transformar em uma medida em , fazemos . Portanto, .
16. Para determinar as frações equivalentes a , multiplicamos ou dividimos o numerador e o denominador da fração pelo mesmo número.
Dividindo por 2, obtemos a fração .
Multiplicando por 2, 3 e 4, respectivamente, obtemos , e .
17. Resposta no final da seção Resoluções.
18. Figura A: cilindro; Figura B: prisma de base triangular; Figura C: pirâmide de base quadrada; Figura D: cone.
a) As figuras B e C são formadas apenas por faces planas.
b) Figura B: 5 faces, 6 vértices e 9 arestas; Figura C: 5 faces, 5 vértices e 8 arestas.
19. Figura A: cubo; Figura B: cilindro; Figura C: cone; Figura D: pirâmide de base hexagonal.
a) As planificações A e D são formadas apenas por polígonos.
b) Podemos identificar o quadrado na figura A, o círculo e o retângulo na figura B, o círculo na figura C, e o hexágono e o triângulo na figura D.
Unidade 1
Sistemas de numeração e números naturais
Atividades
1. Considerando os símbolos em cada item e as regras para utilizá-los, temos:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
f) ![]()
Página XLV
2.a) Resposta pessoal: A resposta depende da quantidade de estudantes na sala de aula. Considerando que são 42 estudantes, temos:
![]()
b) Resposta pessoal: A resposta depende do ano vigente. Considerando que o ano seja 2024, temos:
![]()
c) Resposta pessoal: A resposta depende do dia, mês e ano em que o estudante nasceu. Considerando que tenha nascido em 12 de maio de 2013, temos:
![]()
![]()
![]()
3.a) 5 símbolos, pois quatrocentos mil é representado como 400.000 no sistema de numeração atual.
b) Nenhum, pois não há um símbolo para representar o zero no sistema de numeração egípcio.
4.a) Como são 10 símbolos equivalentes a 10
unidades cada um, temos um agrupamento
de 100, que é representado por: ![]()
b) Como são 15 símbolos
equivalentes a 10.000 unidades cada um, temos um
agrupamento de 150.000, representado por: ![]()
c) Como são 10 símbolos
equivalentes a 1.000 unidades cada um e 2 símbolos equivalentes
a 100 unidades cada um, temos um agrupamento de 1.200,
representado por: ![]()
d) Como são 10 símbolos
equivalentes a 100.000 unidades cada um, 1
equivalente a 10.000 unidades e 1 equivalente a 1.000 unidades, temos um agrupamento de 1.011.000, representado por: ![]()
e) Como são 10 símbolos
equivalentes a 1.000 unidades cada um e 10
equivalentes a 100 unidades, temos um agrupamento de 11.000,
representado por: ![]()
5.a) Um número. Espera-se que os estudantes digam que, independentemente da ordem dos hieróglifos no sistema de numeração egípcio, o número obtido será sempre o mesmo.
b) ![]()
6. De acordo com valor de cada símbolo, temos:
a)
b)
c)
d)
e)
f)
g)
h)
7. Decompondo cada número para obter os símbolos correspondentes ao sistema de numeração romano.
a)
b)
c)
d)
8.a) • Ano de nascimento:
Ano de morte: .
Ano em que Maryam Mirzakhan ganhou a Medalha Fields: .
b) Resposta pessoal. Espera-se que os estudantes obtenham algumas informações a respeito de Maryam Mirzakhani, como o fato de que ela, ainda no Ensino Médio, foi a primeira mulher a participar da Olímpiada Internacional de Matemática de Hong Kong, ganhando medalha de ouro.
9.a) Resposta pessoal: A resposta depende da quantidade de estudantes na sala de aula. Considerando 35 estudantes, temos: .
b) Resposta pessoal: A resposta depende da idade do estudante. Caso ele tenha 11 anos, temos: .
c) Resposta pessoal: A resposta depende do número do calçado do estudante. Considerando que ele calce 36, temos: .
d) Resposta pessoal: A resposta depende do dia e do mês em que o estudante nasceu. Considerando a data de nascimento em 29 de abril, ou seja, 29/04, temos: .
e) Resposta pessoal: A resposta depende do ano em que o estudante nasceu. Considerando que ele tenha nascido em 2013, temos: .
f) Resposta pessoal: A resposta depende do ano vigente. Considerando o ano 2024, temos: .
10. • 3.000
Como e , representamos o número três mil por MMM.
a) Três vezes. Nenhuma.
b) Resposta pessoal. Espera-se que os estudantes respondam que não há símbolos para representar o zero no sistema de numeração romano.
11. a) •
b) •
Página XLVI
Questão 1.
a) Existem várias respostas para este item. Uma delas é:
b) Existem várias respostas para este item. Uma delas é:
Atividades
12. A. ; duzentos e oito.
B. ; três mil, seiscentos e sessenta.
13. a) •
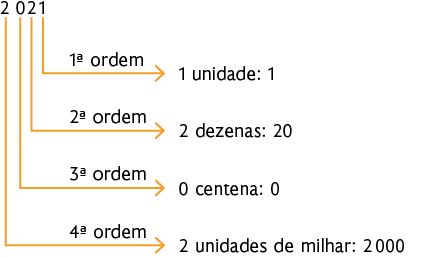
b) Dois; Venezuela e Guiana.
14. Para que o algarismo 7 tenha valor posicional:
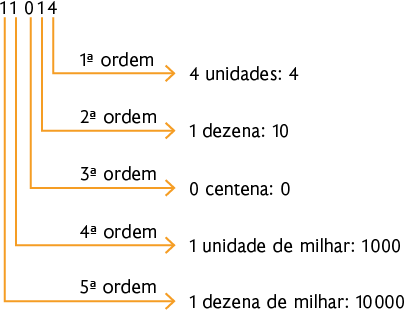
a) 70, ele deve ocupar a ordem das dezenas. Sugestão de resposta: 2.571.
b) 7, ele deve ocupar a ordem das unidades. Sugestão de resposta: 3.527.
c) 7.000, ele deve ocupar a ordem das unidades de milhar. Sugestão de resposta: 7.541.
d) 700, ele deve ocupar a ordem das centenas. Sugestão de resposta: 1.722.
15.a) Nesse item, os algarismos devem ser os maiores possíveis, tal que . Assim, e .
b) Nesse item, os algarismos devem ser os menores possíveis, tal que . Assim, e .
c) Para que o algarismo:
2 tenha valor posicional 2.000, ele deve ocupar a ordem das unidades de milhar;
1 tenha valor posicional 10, ele deve ocupar a ordem das dezenas.
Como A ocupa a ordem das unidades de milhar e B, a ordem das dezenas, então e .
d) O algarismo A deve ser igual a 2, pois todos os números que estão entre 72.510 e 72.550 têm como algarismo das dezenas de milhar, unidades de milhar e centenas 7, 2 e 5, respectivamente. O algarismo B deve satisfazer a seguinte condição: B e o algarismo das unidades formam, na ordem em que aparecem, um número entre 10 e 50. Como o algarismo das unidades é 4, então B pode ser 1, 2, 3 ou 4. Porém, como , então B deve ser 1, 3 ou 4.
16. Para auxiliar os itens a, b e c desta atividade, podemos construir no caderno um quadro de ordens.
|
UM |
CM |
DM |
UM |
C |
D |
U |
|---|---|---|---|---|---|---|
a) Para que o valor posicional do algarismo 3 seja 3.000, ele deve ocupar a ordem das unidades de milhar. Qualquer número de 6 algarismos diferentes em que o valor posicional do algarismo 3 seja 3.000 no quadro de ordens é uma resposta válida. Nesse caso, duas sugestões são: 563.728 e 673.289.
b) Para que o valor posicional do algarismo 5 seja 500.000, ele deve ocupar a ordem das centenas de milhar. Qualquer número de 7 algarismos diferentes em que o valor posicional do algarismo 5 seja 500.000 no quadro de ordens é uma resposta válida. Nesse caso, duas sugestões são: 9.576.382 e 6.573.289.
c) Para que o valor posicional do algarismo 2 seja 20, ele deve ocupar a ordem das dezenas. Qualquer número de 5 algarismos diferentes em que o valor posicional do algarismo 2 seja 20 no quadro de ordens é uma resposta válida. Nesse caso, duas sugestões são: 65.728 e 73.928.
d) Sugestões de resposta:
;
17.a) Cada um dos números apresentados tem 7 ordens.
b) No número 7.386.792, o algarismo 7 tem valor posicional 7.000.000, pois ocupa a ordem das unidades de milhão. Já no número 8.432.176, o algarismo 7 tem valor posicional 70, pois ocupa a ordem das dezenas nele.
c) Para que o algarismo 3 tenha valor posicional 30.000, ele deve ocupar a ordem das dezenas de milhar, o que ocorre no número 8.432.176.
d) 7.386.492: sete milhões, trezentos e oitenta e seis mil, quatrocentos e noventa e dois;
8.432.176: oito milhões, quatrocentos e trinta e dois mil, cento e setenta e seis.
18. a) • Para que o número com 5 ordens seja o maior possível sem que nenhum algarismo se repita, devemos escrever os cinco maiores algarismos apresentados em ordem decrescente. Assim, o maior número possível é 98.765.
Página XLVII
Para que o número com 7 ordens seja o menor possível e sem que nenhum algarismo se repita, devemos escrever os sete menores algarismos apresentados em ordem crescente. Sendo assim, o menor número possível é 1.234.567
Qualquer número de 6 ordens que seja possível escrever com os algarismos apresentados e maior do que 652.187 é uma resposta válida. Uma sugestão de resposta é 678.521.
b) Considerando as sugestões de resposta no item anterior, temos:
98.765: noventa e oito mil, setecentos e sessenta e cinco;
1.234.567: um milhão, duzentos e trinta e quatro mil, quinhentos e sessenta e sete;
678.521: seiscentos e setenta e oito mil, quinhentos e vinte e um.
c) Para que o número seja o maior possível, sem repetição de nenhum algarismo, devemos escrever os algarismos apresentados em ordem decrescente. Assim, obtemos o número 987.654.321. Portanto, obtemos um número de 9 ordens.
19.a)
b)
c)
20.a) Sugestão de resposta:
b)
c) Sugestão de resposta:
d) Sugestão de resposta:
Questão 2.
a) Entre os três números naturais consecutivos, sendo o 25 um deles, há três possibilidades:
1º) ser o maior deles, isto é, .
2º) estar entre os outros dois, isto é, .
3º) ser o menor deles, isto é, .
b) Entre os três números naturais consecutivos, sendo o 99 um deles, há três possibilidades:
1º) ser o maior deles, isto é, .
2º) estar entre os outros dois, isto é, .
3º) ser o menor deles, isto é, .
c) Entre os três números naturais consecutivos, sendo o 141 um deles, há três possibilidades:
1º) ser o maior deles, isto é, .
2º) estar entre os outros dois, isto é, .
3º) ser o menor deles, isto é, .
d) Entre os três números naturais consecutivos, sendo o 999 um deles, há três possibilidades:
1º) ser o maior deles, isto é, .
2º) estar entre os outros dois, isto é, .
3º) ser o menor deles, isto é, .
Questão 3. Uma sugestão de resposta é trocar o passo 2 para verificar se o número termina em 0, 2, 4, 6 ou 8. Assim, temos o seguinte algoritmo:
Início
1º. Escolha um número natural.
2º. O número termina em 0, 2, 4, 6 ou 8?
3º. Se sim, o número é par. Caso contrário, o número é ímpar.
Fim.
Questão 4. Considerando a possível resposta na questão anterior, temos o seguinte fluxograma.
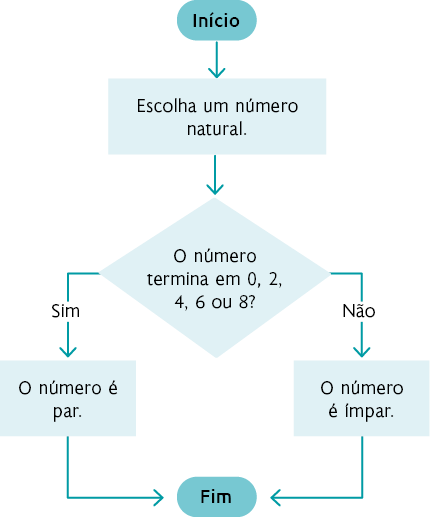
Questão 5.
a) Ímpar, pois o número termina em 3.
b) Par, pois o número termina em 2.
c) Ímpar, pois o número termina em 1.
d) Par, pois o número termina em 0.
Atividades
21.a) Antecessor: ; sucessor: .
b) Antecessor: ; sucessor: .
c) Antecessor: ; sucessor: .
Página XLVIII
d) Antecessor: ; sucessor: .
e) Antecessor: ; sucessor: .
f) Antecessor: ; sucessor: .
g) Antecessor: ; sucessor: .
h) Antecessor: ; sucessor: .
22. a) Para formar o maior número natural possível com três algarismos diferentes, devemos escrever em ordem decrescente os três maiores algarismos apresentados. Assim, o número formado é o 987.
b) Para formar o menor número natural possível com quatro algarismos diferentes, devemos escrever os quatro maiores algarismos que foram apresentados em ordem crescente, de modo que 0 não seja o primeiro algarismo. Portanto, o número formado é o 1.034.
c) Precisamos compor dois números consecutivos menores do que 79, de modo que a soma deles resulte em 79. Considerando os algarismos possíveis, esses números devem estar entre 30 e 41 e ser consecutivos. Com isso, obtemos os números 39 e 40, pois .
23. a) Como A está à direita do 240 na reta numérica, então .
b) Como A está à esquerda de C na reta numérica, então .
c) Como 400 está à direita de B na reta numérica, então .
d) Como 320 está à direita de A na reta numérica, então .
e) Como 240 está à esquerda do 320 e 320 está à esquerda de B na reta numérica, então .
f) Como B está a esquerda de C e C está a esquerda de 400 na reta numérica, então .
24. a) Escrevendo a sequência dos 7 números naturais consecutivos a 127, temos:
b) Escrevendo a sequência dos 5 números naturais consecutivos que antecedem o 127, temos:
25. Sabendo que o menor número natural de três algarismos é 100 e que o ponto E corresponde a 372 unidades a mais do que 10, temos .
Como os pontos correspondem a números naturais consecutivos, temos:
.
26. Devemos encontrar 3 números naturais consecutivos entre 0 e 10 que ao serem adicionados resultem em 27. Considerando a adição de três números consecutivos cuja soma seja maior do que 20, temos:
6, 7 e 8:
7, 8 e 9:
8, 9 e 10:
Assim, concluímos que ⬛: 8, ▲: 9 e ⬤: 10.
27. a) O maior número natural de dois algarismos distintos é o 98 e de três algarismos é o 987.
98

987

b) Sugestões de respostas: Língua Brasileira de Sinais (Libras); Língua de Sinais Kaapor Brasileira; Sistema de Símbolos Bliss; Sistema Rebus; Pictogram Ideogram Communication System (PIC); Picture Communication Symbols (PCS); LMBrain.
c) Resposta pessoal.
d) Resposta pessoal.
e) Resposta pessoal.
f) Resposta pessoal.
28. A letra A representa 1.624, pois 1.624 está à direita de 1.600 e à esquerda de 1.700. Além disso, 1.876 está à direita de 1.800 e é menor do que 1.888, por isso B representa 1.876. Por fim, como 1.888 está à esquerda de 1.900 e é maior do que 1.876, concluímos que C representa 1.888.
29. a) Como os números ímpares terminam em 1, 3, 5, 7 ou 9 e os pares em 0, 2, 4, 6 ou 8, no envelope:
A: serão guardadas as fichas com os números 2, 24 e 56, pois eles são pares e menores do que 60.
B: serão guardadas as fichas com os números 15, 47 e 71, pois eles são ímpares e menores do que 80.
C: serão guardadas as fichas com os números 64, 80 e 92, pois eles são pares e estão entre 60 e 100.
D: serão guardadas as fichas com os números 81, 95 e 129, pois eles são ímpares e estão entre 80 e 130.
b) Os números 143 e 158, pois ambos não estão entre 60 e 130.
30. a) Nessa sequência, a partir da segunda figura, cada uma é obtida adicionando dois palitos à figura anterior. Assim, a 5ª figura terá 11 palitos.
b) O número que representa a quantidade de palitos dessa figura é ímpar, pois o algarismo das unidades dele é 1.
31. Utilizando a reta numérica como suporte, verificamos que:
Página XLIX
o número 1.617 é arredondado para 1.600 e 2.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.

o número 4.950 é arredondado para 5.000, pois esse número é a centena e a unidade de milhar mais próximas.

o número 2.198 é arredondado para 2.200 e 2.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.

o número 6.243 é arredondado para 6.200 e 6.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.
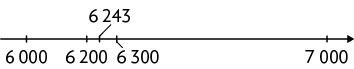
o número 3.444 é arredondado para 3.400 e 3.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.
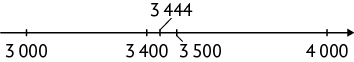
o número 5.771 é arredondado para 5.800 e 6.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.

o número 7.428 é arredondado para 7.400 e 7.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.
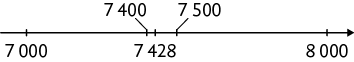
o número 4.581 é arredondado para 4.600 e 5.000, pois esses números são, respectivamente, a centena e a unidade de milhar mais próximas.

|
Número |
Número arredondado para a centena mais próxima |
Número arredondado para a unidade de milhar mais próxima |
|---|---|---|
|
1.617 |
1.600 |
2.000 |
|
4.950 |
5.000 |
5.000 |
|
2.198 |
2.200 |
2.000 |
|
6.243 |
6.200 |
6.000 |
|
3.444 |
3.400 |
3.000 |
O que eu estudei?
1. Considerando o valor de cada símbolo egípcio e romano, podemos escrever:
a)
![]()
b)
![]()
c) ![]()
d)
![]()
2. De acordo com a quantidade de contas em cada haste dos ábacos, temos:
A. 74.588.313: setenta e quatro milhões, quinhentos e oitenta e oito mil, trezentos e treze.
B. 746.879.602: setecentos e quarenta e seis milhões, oitocentos e setenta e nove mil, seiscentos e dois.
C. 902.123.876; novecentos e dois milhões, cento e vinte e três mil, oitocentos e setenta e seis.
3.a)
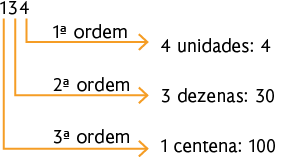
b)
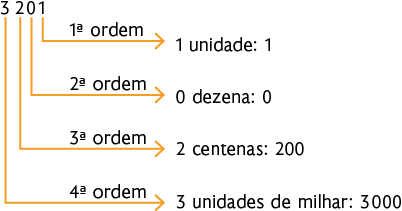
c)
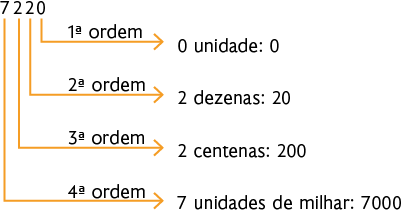
Página L
d)
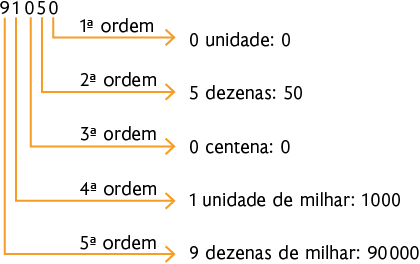
e)
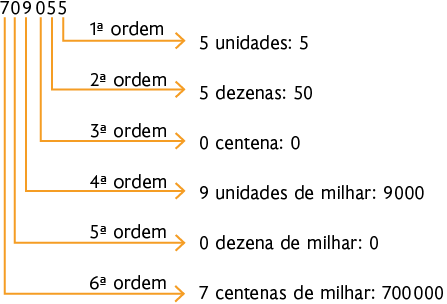
f)
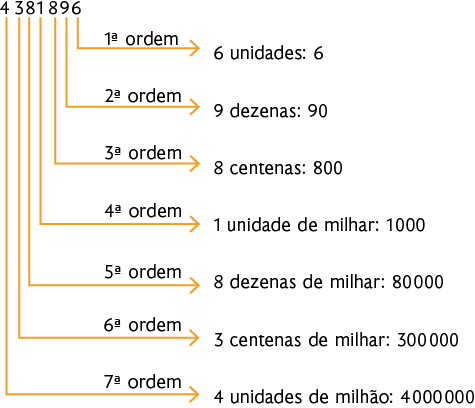
4. Os números que estão associados à informação A são formados por sete ordens, a saber: 1.356.152 e 4.886.002. Os números 246.088, 1.356.152 e 4.886.002 estão relacionados à informação B, pois em todos eles o algarismo 6 está na classe dos milhares. Já os números cujo algarismo 4 tem valor posicional 4.000, ou seja, que correspondem à informação C, são 96.294.000 e 24.955. A informação de D pede o número que está entre 100.000 e 1.000.000 e, dos números apresentados, o 246.088 é o único que pode ser associado. A informação E considera os números cujos respectivos antecessores sejam ímpares. Como todo número natural par tem um número natural ímpar como seu antecessor, devemos associar os números que terminem em 0, 2, 4, 6 ou 8. São eles: 246.088, 1.356.152, 96.294.000 e 4.886.002.
5. Considerando as regras para A e B, temos:
a)
b)
c)
d)
6. Respostas pessoais. As respostas dependem dos números escritos pelos estudantes. Considerando, por exemplo, os números 652.145, 711.423, 900.138 e 578.005, temos os seguintes casos:
a) Arredondando-os para a dezena mais próxima, obtemos: 652.150, 711.420, 900.140 e 578.010.
b) Arredondando-os para a centena mais próxima, obtemos: 652.100, 711.400, 900.100 e 578.000.
c) Arredondando-os para a unidade de milhar mais próxima, obtemos: 652.000, 711.000, 900.000 e 578.000.
Unidade 2
Operações com números naturais e igualdades
Questão 1. Como para obter o total de medalhas é necessário juntar todas as quantidades em uma adição, espera-se que os estudantes respondam adição.
Atividades
1. Realizando os cálculos, temos:
a)
b)
c)
2. As possíveis adições de duas parcelas diferentes, em que essas parcelas são os números apresentados:
3. a) Para verificar qual é a constante mágica, adicionamos os números de qualquer linha, coluna ou diagonal. As adições dos números que estão nas linhas são:
As adições dos números que estão nas colunas são:
As adições dos números que estão nas diagonais são:
A constante mágica é 207.
Página LI
b) Se adicionarmos 45 unidades a cada número do quadrado mágico, cada parcela das adições de qualquer linha, coluna ou diagonal ficará acrescida de 45 unidades, ou seja, em cada soma serão adicionadas 135 unidades . Desse modo, as adições dos números que estão nas linhas, nas colunas e nas diagonais resultarão em 342 unidades, pois . Logo, o quadrado continuará sendo mágico com constante mágica igual a 342.
c) Resposta pessoal. Espera-se que os estudantes concluam que há diversas versões entre os historiadores para a origem dos quadrados mágicos, mas que possivelmente eles tenham surgido na China e na Índia há cerca de 3.000 anos.
4.a) 1º dia de viagem: Elias saiu de Fortaleza (CE) e foi até Recife (PE), passando por Natal (RN). A distância de Fortaleza até Natal mede e de Natal até Recife é de . Desse modo, Elias percorreu, no 1º dia de viagem, a medida da distância total de , pois .
2º dia de viagem: Elias saiu de Recife (PE) e foi até Aracaju (SE) passando por Maceió (AL). A distância de Recife até Maceió mede e de Maceió até Aracaju mede . Portanto, a medida da distância total percorrida por Elias no 1º dia de viagem é , pois .
b) Do item anterior, sabemos que Elias percorreu de Fortaleza até Recife e de Recife até Aracaju, . Como a distância de Aracaju até Salvador mede , a medida da distância total percorrida por Elias de Fortaleza até Salvador foi , pois .
5.a) O arredondamento à unidade de milhar dos números 20.582 e 36.418 são 21.000 e 36.000, respectivamente. Realizando a adição, temos
b) O arredondamento à unidade de milhar dos números 19.602 e 15.903 são 20.000 e 16.000, respectivamente. Realizando a adição, temos
c) O arredondamento à unidade de milhar dos números 179.389 e 51.164 são 179.000 e 51.000, respectivamente. Realizando a adição, temos
6. Realizando os cálculos com os números exatos, apresentados na atividade anterior, temos:
a)
O resultado do cálculo com arredondamento é igual ao resultado do cálculo exato.
b)
O resultado do cálculo feito com arredondamento é diferente do resultado do cálculo exato.
c)
O resultado do cálculo feito com arredondamento é diferente do resultado do cálculo exato.
Questão 2. Com base no preço de cada objeto, podemos escrever as seguintes adições.
a) televisão e smartphone: e
b) videogame e notebook: e
c) notebook e smartphone: e
d) smartphone e videogame: e
Questão 3. Podemos associar os pontos feitos pelos jogadores em cada rodada da seguinte maneira.
Pontos de Ivo:
Pontos de Gilberto:
Atividades
7. Realizando os cálculos apresentados nas fichas, temos:
Ficha A:
Ficha B:
Ficha C:
Ficha D:
Ficha E:
Ficha F:
Ficha G:
Ficha H:
As fichas que possuem os resultados dos cálculos iguais são A e G, B e E, C e H e, D e F.
8. Pelos cálculos apresentados na atividade anterior, as fichas que possuem os resultados iguais são A e G, B e E, C e H e, D e F.
9.a) Como a bolsa custa R$ 67,00 e o cinto custa R$ 54,00, o valor total da compra desses produtos será R$ 121,00, pois .
b) Como o cinto custa R$ 54,00 e os sapatos custam R$ 86,00, o valor total da compra desses produtos será R$ 140,00, pois .
10.a)
b)
c)
d)
e)
f)
11. Resposta pessoal. Sugestão de resposta: Lucas trabalha em uma papelaria. Seu chefe pediu que contasse a quantidade de canetas que havia no estoque. Lucas contou 101 canetas azuis, 213 canetas pretas e 329 canetas vermelhas. Quantas canetas, ao todo, havia no estoque? Resposta: 643 canetas.
12.a)
b)
c)
Página LII
d) Como , o pode ser substituído por qualquer número. Uma sugestão de resposta é
e)
f)
13. As medias de extensão dos circuitos de Mônaco, Interlagos, Monza e Suzuka são , , e , respectivamente. Calculando a diferença entre as medidas de extensão dos circuitos de:
a) Suzuka e Mônaco, temos , ou seja, .
b) Monza e Interlagos, temos , ou seja, .
c) Monza e Mônaco, temos , ou seja, .
d) Suzuka e Interlagos, temos , ou seja, .
14. Considerando uma subtração em que o minuendo seja o maior número de 3 algarismos diferentes e o subtraendo seja o menor número de 3 algarismos iguais, uma sugestão de resposta é .
15. a) A quantidade de museus construídos de 2014 a 2021 é igual à diferença entre a quantidades de museus que havia em 2021 e a quantidade que havia em 2014, ou seja, .
b) Resposta pessoal.
c) Resposta pessoal. Espera-se que os estudantes concluam que os museus são espaços de valorização da história, cultura, arte, ciência etc., além de serem locais de pesquisa para desenvolvimento individual ou coletivo. Os estudantes podem citar o Museu Imperial, o Museu Inhotim e o Museu Oscar Niemeyer como alguns dos principais museus do Brasil.
d) Resposta pessoal.
e) Resposta pessoal.
16. Como o quadrado é mágico, podemos calcular sua constante mágica adicionando os números de uma linha, coluna ou diagonal. Efetuando a adição na diagonal que não tem letras, temos: . Portanto, sua constante mágica é 130.
Na primeira coluna, temos . Assim, , pois .
Na quarta coluna, temos . Assim, , pois .
Na segunda linha, como , temos . Assim, , pois .
Na terceira linha, como , temos . Assim, , pois .
Na quarta linha, temos . Assim, , pois .
Como , na segunda coluna, temos . Logo, , pois .
Além disso, , pois e .
17. a) Para obter o número apresentado no visor usando os algarismos e símbolos, devemos escrever a seguinte subtração:
.
b) Para obter o número apresentado no visor, há duas possibilidades com os números e sinais propostos: ou .
18. a) No início do dia 2 de janeiro, o hodômetro do caminhão de Carlos estava marcando e ao final do dia 12 de janeiro marcava . A quantidade de quilômetros percorrida do início do dia 2 até o fim do dia 12 de janeiro é dada por: .
Portanto, ele percorreu com seu caminhão nesse período.
b) No início do dia 2 de janeiro, o hodômetro do caminhão de Carlos estava marcando e ao final do dia 23 de janeiro marcava . A quantidade de quilômetros percorrida do início do dia 2 até o fim do dia 23 de janeiro é dada por:
Portanto, ele percorreu com seu caminhão nesse período.
c) No início do dia 24 de janeiro o hodômetro do caminhão de Carlos estava marcando . Como ele percorreu do início do dia 24 de janeiro até o fim do dia 31 de janeiro, a quilometragem de seu caminhão ao final do dia 31 de janeiro marcava , pois .
19. a)
b)
c)
d)
e)
f)
20. Realizando as subtrações, temos:
a) Resposta pessoal. Espera-se que os estudantes percebam que o minuendo é um número formado por algarismos consecutivos, da esquerda para a direita, começando com o algarismo 1. O subtraendo é obtido do minuendo retirando-se o algarismo que está na última posição, da esquerda para a direita. O resultado de cada cálculo é um número formado por algarismos todos iguais a 1 com a quantidade de algarismos igual à quantidade de algarismos do minuendo.
b) Os cálculos são diferenças entre números que satisfazem as características observadas no item anterior, logo:
Página LIII
21.a) Jair comprou 280 latas de suco, vendeu 82 latas no sábado e 120 latas no domingo. Logo, a expressão numérica que representa esse problema é , ou seja, a Expressão 2.
Resolvendo-a, temos: . Portanto, sobraram 78 latas.
b) Maria tem 120 cartões-postais de cidades do Brasil e 280 de outros países, dos quais 82 são repetidos. Logo, a expressão numérica que representa esse problema é , ou seja, a Expressão 1. Resolvendo-a, temos:
Portanto, Maria tem 318 cartões-postais em sua coleção, sem contar os repetidos.
22.a) Na resolução da expressão, da primeira para a segunda linha, temos:
, desse modo , pois .
Da segunda para a terceira linha, temos:
, desse modo , pois .
Da terceira para a quarta linha, temos:
, desse modo , pois .
b) Na resolução da expressão, da primeira para a segunda linha, temos:
, desse modo , pois .
Ainda da primeira para a segunda linha, substituindo as letras E e F, pelos números correspondentes da primeira linha, obtemos e .
Da segunda para a terceira linha, temos:
como , segue que , pois .
Da terceira para a quarta linha, temos:
e, sendo , , pois .
23. Resolvendo primeiro o cálculo dos parênteses, quando ocorrem, e, em seguida, as operações na ordem em que aparecem, temos:
a)
b)
c)
d)
.
24. Considerando a quantidade total de estudantes e a quantidade de cada turma, a expressão que determina a quantidade de estudantes do 6º ano B é dada por: .
Resolvendo essa expressão, temos:
Portanto, a quantidade de estudantes do 6º ano B é 29.
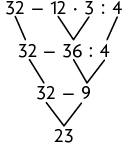
25. A expressão numérica que representa os cálculos que Mário fez na calculadora é:
Resolvendo essa expressão, temos:
Portanto, o número que Mário visualizou na calculadora ao final dessas operações foi 625.
26. Há duas possibilidades para substituir o de modo que o resultado seja 110. Substituindo os números e resolvendo a expressão, temos:
27. O esquema que representa o problema de Nair é:
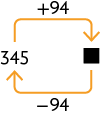
Logo, Nair tinha R$ 439,00 antes da compra, pois e .
28. A. O deve ser substituído por 235, pois .
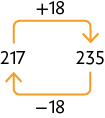
B. O deve ser substituído por 29 e o deve ser substituído por 122, pois e .
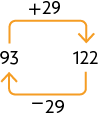
C. O deve ser substituído por 148, pois .
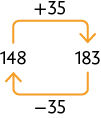
D. O deve ser substituído por 21 e o deve ser substituído por 128, pois e .
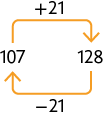
29.a) O número que substitui adequadamente é 405, pois . Além disso, e .
b) O número que substitui adequadamente é 782, pois . Além disso, e .
Página LIV
30.a) Em 2010, o município de Bonito (MS) tinha 19.587 habitantes, dos quais 9.878 eram homens. Assim, em Bonito havia 9.709 mulheres em 2010, pois .
b) Resposta pessoal. Espera-se que os estudantes respondam, entre outras possíveis respostas, a destinação correta dos resíduos.
31.a) Agnaldo é 27 anos mais novo que seu pai, que tem 56 anos. Portanto, Agnaldo tem 29 anos, pois .
b) Após dar 48 figurinhas para seu irmão, Rubens ficou com 237 figurinhas. Assim, Rubens tinha inicialmente 285 figurinhas, pois .
32.a) Aline pensou em um número do qual ela subtraiu 57 e obteve o número 143. Assim, para determinar o número que Aline pensou, basta realizar a operação inversa da subtração, ou seja, adicionar 143 com 57, desse modo: . Portanto, Aline pensou no número 200.
b) Para determinar o número do qual Mário subtraiu 85 unidades, realizamos a operação inversa da subtração, adicionando 381 com 85, ou seja, efetuamos . Portanto, o número é 466.
c) Para determinar o número ao qual Lara adicionou 242 unidades, realizamos a operação inversa da adição, subtraindo 242 de 489, ou seja, efetuamos . Portanto, o número é 247.
33. Resposta pessoal. Sugestão de resposta: Lúcio ganhou de sua avó R$ 25,00. Ao juntar com a quantia que ele já tinha, ele ficou com R$ 52,00. Quantos reais Lúcio tinha antes de ganhar dinheiro de sua avó?
Resposta: Antes de ganhar dinheiro de sua avó, Lúcio tinha R$ 27,00, pois .
34. Como um adulto em repouso tem frequência cardíaca aproximada de 70 batimentos por minuto, então:
a) em , o coração de uma pessoa adulta em repouso bate, em média, 630 vezes, pois .
b) em , o coração de uma pessoa adulta em repouso bate, em média, 2.870 vezes, pois .
c) em , o coração de uma pessoa adulta em repouso bate, em média, 700 vezes, pois .
d) em , o coração de uma pessoa adulta em repouso bate, em média, 1.540 vezes, pois .
35.a) Temos uma adição de 3 parcelas iguais a 412. Assim:
.
b) Temos uma adição de 4 parcelas iguais a 78. Assim:
.
c) Temos uma adição de 5 parcelas iguais a 101. Assim:
.
d) Temos uma adição de 6 parcelas iguais a 508. Assim:
.
36.a)
b)
c)
d)
37.a) Como a letra E representa o algarismo das unidades, então e obtemos . A multiplicação deve ter como resultado um número em que o algarismo das unidades seja igual a 5. Isso ocorre somente quando , pois . Além disso, deve ter como resultado um número cujo algarismo das unidades seja igual a 9, o que implica em ou . Mas, não podemos ter , pois como , , deve ser um número cujo algarismo das unidades seja 3. Assim, e, desse resultado, concluímos que e . Substituindo A, B, C, D e E, obtemos:
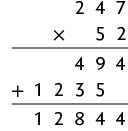
b) Como , teremos , pois representa o algarismo das unidades. Além disso, , e como , segue que , pois representa o algarismo das unidades. Além disso, , pois . A multiplicação deve ter como resultado um número cujo algarismo das unidades seja 4. Isso implica , ou , mas não podemos ter , visto que , logo . Por fim, deve ser igual a 6, então . Substituindo as letras F, G, H, I, J e K no algoritmo, temos:
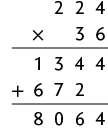
38.a) Como nessa empresa há 62 funcionários e foram servidas 2 frutas para cada um deles, temos: . Portanto, foram servidas, diariamente, 124 frutas aos funcionários.
b) Com base no item anterior, serão servidas por dia 124 frutas no horário do almoço. Desse modo, em 12 dias serão servidas 1.488 frutas, pois , e, em 20 dias, serão servidas 2.480, pois .
39. Como o time de Gustavo fez o triplo de pontos do time de Pedro e os dois times fizeram juntos 32 pontos, basta dividir o total de pontos por 4, ou seja, . Portanto, o time de Pedro fez 8 pontos e o time de Gustavo fez 24 pontos, pois e .
40. Resposta pessoal. Sugestão de resposta: José tem um álbum de figurinhas. A fim de completar seu álbum o mais rápido possível, José comprou 25 pacotes de figurinhas. Sabendo que em cada pacote contém 4 figurinhas, quantas figurinhas José comprou?
Resposta: José comprou 100 figurinhas, pois .
41. A medida da altura do hotel JW Marriott Marquis equivale a nove vezes a altura do Cristo Redentor, que é de . Assim, fazemos: .
Logo, a altura do hotel mede aproximadamente 342 metros.
Página LV
42.a)
b)
c)
Resposta pessoal. Sugestão de resposta: Observando os cálculos, vemos que os resultados são números formados, em sequência, da esquerda para a direita, pelo primeiro fator da multiplicação, o algarismo 0 e o primeiro fator da multiplicação novamente.
43. Considerando o que foi observado na atividade anterior, com relação ao resultado de uma multiplicação em que um dos fatores é um número de dois algarismos e o outro é 1.001, temos:
a)
b)
c)
d)
e)
f)
44. Efetuando os cálculos, temos:
a)
b)
c)
d)
45.a) Arredondando 51 e 103 à dezena mais próxima, obtemos 50 e 100, respectivamente. Com isso, temos:
cálculo aproximado: ;
cálculo exato: .
b) Arredondando 139 e 197 à dezena mais próxima, obtemos 140 e 200, respectivamente. Com isso, temos:
cálculo aproximado: ;
cálculo exato: .
c) Arredondando 77 e 302 à dezena mais próxima, obtemos 80 e 300, respectivamente. Com isso, temos:
cálculo aproximado: ;
cálculo exato: .
d) Arredondando 34 e 151 à dezena mais próxima, obtemos 30 e 150, respectivamente. Com isso, temos:
cálculo aproximado: ;
cálculo exato: .
e) Arredondando 182 e 41 à dezena mais próxima, obtemos 180 e 40, respectivamente. Com isso, temos:
cálculo aproximado: ;
cálculo exato: .
f) Arredondando 219 e 401 à dezena mais próxima, obtemos 220 e 400, respectivamente. Com isso, temos:
cálculo aproximado: ;
cálculo exato: .
Questão 4. Podemos efetuar os cálculos multiplicando o valor de cada embalagem pela adição das quantidades de embalagens de suco de laranja e de uva, isto é, .
Também podemos multiplicar o valor de cada embalagem pela quantidade de embalagens de suco de laranja e pela quantidade de embalagens de suco de uva para, depois, adicionamos os resultados, isto é, .
Portanto, Murilo gastou R$ 504,00 na compra dos sucos.
Atividades
46. Realizando os cálculos, associando os fatores de maneiras diferentes, temos:
a)
b)
c)
d)
e)
f)
47. Podemos calcular quantos quadradinhos foram pintados de amarelo na malha multiplicando o número que representa a quantidade de linhas pelo número que representa a quantidade de colunas, isto é, . Outra maneira é multiplicar o número que representa a quantidade de colunas pelo número que representa a quantidade de linhas, isto é, .
Portanto, há 60 quadradinhos pintados de amarelo na malha quadriculada.
48. Vamos associar fatores que multiplicados resultam em número terminado em zero. Assim:
a)
b) temos duas possibilidades:
c) temos três possibilidades:
d) temos três possibilidades:
e) temos duas possibilidades:
f) temos três possibilidades:
Página LVI
49.a) Para cada um dos 3 planos de internet, podemos escolher um plano de telefone entre 4 opções. Logo, o total de possibilidades é dado por . Portanto, cada deve ser substituído por 4 e 12, respectivamente.
b) Para cada um dos 4 planos de internet, podemos escolher um plano de telefone entre 5 opções. Logo, teriam 20 possibilidades de escolha, pois .
50. Na vitrine, estão 5 camisetas, 3 bermudas e 2 bonés. Se uma pessoa comprar 1 item de cada, teremos . Logo, uma pessoa que deseja comprar uma camiseta, uma bermuda e um boné terá 30 possibilidades de compra.
51. Usando a propriedade distributiva da multiplicação, a substituição de cada nos itens ocorre da seguinte maneira:
a)
b)
c)
52.a) Como são usados 26 parafusos na montagem de cada bicicleta e, por dia, são montadas 53 bicicletas, temos: . Portanto, são usados 1.378 parafusos diariamente.
b) Como são usados 26 parafusos na montagem de cada bicicleta, considerando que serão montadas 76 bicicletas, temos . Assim, serão utilizados 1.976 parafusos. Como para montar 53 bicicletas são utilizados 1.378 parafusos, fazemos . Portanto, serão utilizados 598 parafusos a mais.
Questão 5. Como há 315 cadeiras e foram vendidos todos os ingressos, então foram vendidos 315 ingressos. Desse total, 35 foram vendidos a R$ 20,00 e o restante a R$ 34,00. Então, a quantidade de reais arrecadados dessa vez é dada pela expressão . Resolvendo-a, temos:
Portanto, dessa vez foram arrecadados R$ 10.220,00.
Atividades
53. Resolvendo as expressões numéricas, temos:
a)
b)
c)
d)
e)
f)
54. • Fernando comprou 3 camisetas por R$ 28,00 cada, 2 bermudas por R$ 33,00 cada e 1 boné por R$ 19,00. Assim, a quantia que Fernando gastou é representada pela expressão . Resolvendo-a, temos:
.
Portanto, nessa compra Fernando gastou R$ 169,00.
55. As substituições adequadas de cada por , ou , de modo que o resultado não se altere em cada item, são:
a)
b)
c)
d)
56. Para obter de alumínio, é necessário cerca de 75 latas de alumínio. Assim, para determinar quantos quilogramas aproximadamente é possível obter com a quantidade de latas dada em cada item, basta dividir a quantidade de latas por 75. Realizando as divisões, temos:
a)
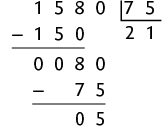
Assim, com 1.580 latas é possível obter aproximadamente de alumínio.
b)
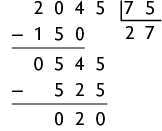
Assim, com 2.045 latas é possível obter aproximadamente de alumínio.
c)
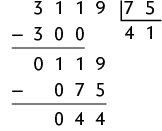
Assim, com 3.119 latas é possível obter aproximadamente de alumínio.
d)
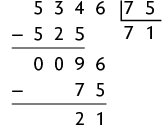
Assim, com 5.346 latas é possível obter aproximadamente de alumínio.
e)
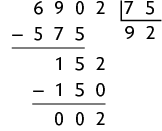
Assim, com 6.902 latas é possível obter aproximadamente de alumínio.
f)
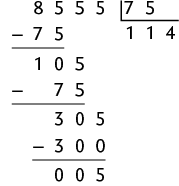
Assim, com 8.555 latas é possível obter aproximadamente de alumínio.
Página LVII
g)
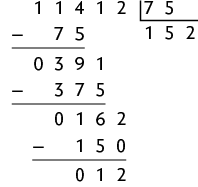
Assim, com 11.412 latas é possível obter aproximadamente de alumínio.
h)
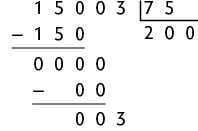
Assim, com 15.003 latas é possível obter aproximadamente de alumínio.
57. Efetuando os cálculos, temos:
a)
b)
c)
d)
58. a) Em uma divisão, o dividendo é igual ao quociente multiplicado pelo divisor mais o resto. Nesse caso, temos: . Portanto, o dividendo é 3.415.
b) Como o dividendo é igual a 242 e o divisor é a metade do dividendo, o divisor será igual a 121, pois . Realizando a divisão, temos: . Portanto, o quociente é igual a 2.
59. a) Resposta pessoal. Sugestão de resposta: Escolhendo o dividendo igual a 252 e o divisor igual a 12, temos ; e escolhendo o dividendo igual a 375 e o divisor igual a 25, temos .
b) Resposta pessoal. Sugestão de resposta: Escolhendo o dividendo igual a 1.200 e o divisor igual a 2, temos ; e escolhendo o dividendo igual a 1.400 e o divisor igual a 20, temos .
60. a) De acordo com valores da tabela, temos , pois , , e , pois . Substituindo cada letra no esquema, obtemos:
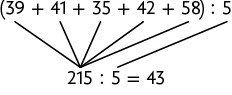
b) Com base no item anterior, Eliane vendeu de segunda-feira a sexta-feira 43 sanduíches naturais em média. Como no sábado ela vendeu 30 sanduíches naturais a mais do que essa quantidade, fazemos: . Portanto, Eliane vendeu 73 sanduíches naturais no sábado.
c) A média de sanduíches vendidos diariamente de segunda-feira a sábado é calculada adicionando a quantidade de sanduíches vendidos em cada dia dividida pela quantidade de dias. Desse modo, temos:
Portanto, a média de sanduíches vendidos diariamente de segunda-feira até sábado foi 48 sanduíches.
61. a) Jandira usou a metade dos de fita que comprou para confeccionar os laços, ou seja, ela usou de fita, pois .
b) Jandira usou metade da quantidade que tinha para fazer os laços e o restante para enfeitar as caixas. Como o restante representa a outra metade, ou seja, de fita, e ela enfeitou 7 caixas de presente com pedaços de fita de mesma medida de comprimento, temos: . Portanto, ela usou de fita para enfeitar cada caixa.
62. a) Como a máquina produz 8.200 peças em 2 horas, para saber a quantidade de peças que essa máquina produz em 1 hora, fazemos . Portanto, o número que substitui o é 4.100.
b) Como o valor da compra de 3 computadores iguais foi R$ 9.900,00, para saber o valor de cada computador, fazemos . Portanto, o número que substitui o R$ 3.300,00.
63. a) A média dos gastos com alimentação de Adriane e Diego na viagem, nos 5 primeiros dias, é dada por:
Portanto, em média, Adriane e Diego gastaram R$ 100,00 diariamente com alimentação.
b) Com R$ 270,00 para serem gastos com alimentação nos próximos 3 dias de viagem, de modo que o gasto por dia seja o mesmo, Adriane e Diego podem gastar R$ 90,00 por dia, pois .
64. a) Adicionando os preços de cada item comprado, temos . Portanto, o valor da compra foi de R$ 270,00.
Dividindo essa quantia pela quantidade de parcelas, obtemos: . Assim, concluímos que o valor de cada parcela será R$ 90,00.
b) Caso André dividisse a compra em 5 parcelas iguais, teríamos o seguinte o fluxograma.
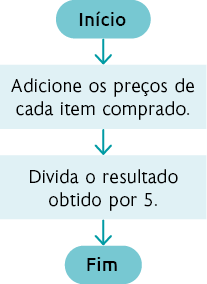
65. a) O símbolo deve ser substituído por 960, pois e .
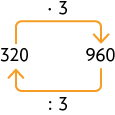
Página LVIII
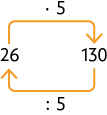
b) O deve ser substituído por 26, pois e .
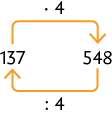
c) O deve ser substituído por 548 e o deve ser substituído por 4, pois e .
66. a) O número que substitui o adequadamente é 625, pois , e .
b) O número que substitui o adequadamente é 768, pois , e .
67. a) Se um número dividido por 8 é igual a 64, então realizando a operação inversa, temos .
O número pensado é o 512.
b) Se um número multiplicado por 23 é igual a 1.104, então realizando a operação inversa, temos .
O número é o 48.
Questão 6. Efetuando os cálculos, cada letra é substituída de maneira adequada como segue:
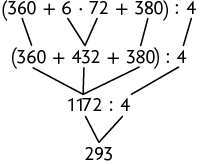
Logo, o valor de cada prestação será R$ 293,00.
Questão 7. Lurdes comprou 1 sofá, 2 poltronas e 4 cadeiras e deu uma entrada de R$ 499,00, que deve ser subtraída do valor total da compra, a ser paga em 5 parcelas iguais. Assim, a expressão numérica que representa o valor de cada prestação é dada por .
Resolvendo essa expressão numérica, temos:
Logo, Lurdes vai pagar R$ 323,00 em cada prestação.
Atividades
68. a)
b)
c)
69. Efetuando os cálculos, temos:
a)
b)
c)
d)
70. De acordo com a atividade anterior, o dividendo obtido é um número de três algarismos, sendo que dois algarismos são iguais a 1 e o outro é zero, que está sempre na ordem das dezenas. O divisor obtido é formado por um algarismo igual ao que aparece no dividendo. Considerando o dividendo e o divisor, o resultado de cada item será o mesmo, ou seja, 101.
71. Efetuando os cálculos, temos:
a)
b)
c)
d)
72. Subtraindo o valor da bolsa que Jaqueline comprou do total da compra, vamos obter o valor dos 5 cadernos. Dividindo esse valor por 5, obtemos o valor de cada caderno. Logo, a expressão que permite calcular o preço de um caderno é dada por . Resolvendo-a, obtemos . Portanto, cada caderno custa R$ 7,00.
73. A expressão numérica que representa os gastos divididos entre Flávio e seus amigos e o que ele gastou sozinho é dada por . Resolvendo-a, temos .
Portanto, Flávio gastou R$ 212,00 nessa viagem.
74. a) Como , e , substituindo cada , temos:
b) Como , e substituindo cada , temos:
75. a) Dividindo por R$ 20,00 o total economizado por Marcela e João, obtemos . Logo, a quantia economizada pode ser dividida por 9 partes iguais de R$ 20,00. Como Marcela economizou R$ 20,00 a mais do que João, ela economizou 5 partes e João, 4 partes, o que corresponde a R$ 100,00 e R$ 80,00, respectivamente, pois e .
b) Dos 200 pontos que Thaís e Gustavo fizeram juntos, Gustavo fez o triplo de pontos de Thaís, ou seja, Thais fez uma parte do total e Gustavo fez três partes. Dividindo o total de pontos em 4 partes iguais, temos . Portanto, Thaís fez 50 pontos, o que corresponde a uma parte, , e Gustavo fez 150 pontos, o que corresponde a 3 partes, pois .
Página LIX
76. Resposta pessoal. Sugestões de resposta:
Mário e Pedro compraram o mesmo quebra-cabeça em lojas diferentes. Os dois quebra-cabeças juntos custam R$ 70,00. Sabendo que Mário pagou R$ 10,00 a mais pelo seu quebra-cabeça, quantos reais cada um deles gastou?
Resposta: R$ 40,00 e R$ 30,00.
Caroline foi visitar um sítio que ficava a de sua casa. O trajeto percorrido até o sítio tinha uma parte de estrada de terra e outra de asfalto. O trajeto percorrido no asfalto foi 7 vezes maior do que o trajeto percorrido na estrada de terra. Quantos quilômetros foram percorridos em cada tipo de estrada?
Resposta: de asfalto e de estrada de terra.
Questão 8. O número da figura e a quantidade de fatores iguais nas multiplicações são iguais.
Questão 9. A multiplicação de fatores iguais que representa a quantidade de quadradinhos na figura 5 é dada por .
A potência correspondente a essa quantidade de quadradinhos é dada por .
Atividades
77. Efetuando os cálculos, temos:
a)
b)
c)
d)
e)
f)
g)
h)
78.a) Na multiplicação há 2 fatores iguais a 8. Escrevendo-a como uma potência, temos .
b) Na multiplicação há 3 fatores iguais a 5. Escrevendo-a como uma potência, temos .
c) Na multiplicação , há 4 fatores iguais a 6. Escrevendo-a como uma potência, temos:
d) Na multiplicação há 3 fatores iguais a 10. Escrevendo-a como uma potência, temos:
79. Com base nas informações das colunas, a letra A deve ser substituída pela potência e a letra B pelo produto de fatores iguais . A letra C deve ser substituída pela potência e a letra D deve ser substituída pelo produto de fatores iguais . A letra E deve ser substituída pela potência e a letra F deve ser substituída pelo produto de fatores iguais . A letra G deve ser substituída pela potência e a letra H deve ser substituída pelo produto de fatores iguais . Substituindo as letras, no quadro, temos:
|
Base |
Expoente |
Potência |
Produto de fatores iguais |
|---|---|---|---|
|
3 |
2 |
||
|
5 |
7 |
||
|
7 |
5 |
||
|
28 |
4 |
||
|
12 |
3 |
80. Para obter a quantidade de quadradinhos, devemos multiplicar a quantidade de linhas pela quantidade de quadradinhos em cada linha ou multiplicar a quantidade de colunas pela quantidade de quadradinhos em cada coluna.
a) A figura possui 2 linhas e 2 colunas, ambas com 2 quadradinhos. Assim, calculamos .
b) A figura possui 5 linhas e 5 colunas, ambas com 5 quadradinhos. Assim, calculamos .
c) A figura possui 3 linhas e 3 colunas, ambas com 3 quadradinhos. Assim, calculamos .
d) A figura possui 4 linhas e 4 colunas, ambas com 4 quadradinhos. Assim, calculamos .
e) A figura possui 6 linhas e 6 colunas, ambas com 6 quadradinhos. Assim, calculamos .
81. Considerando a quantidade de cubos, em cada dimensão da pilha, temos:
a)

Portanto, a quantidade de cubos da pilha é .
b)

Portanto, a quantidade de cubos da pilha é .
c)

Portanto, a quantidade de cubos na pilha é .
Página LX
82. A próxima potência será . Logo, a quantidade de cubos da próxima pilha é dada por , ou seja, 216 cubos.
83. A quantidade de opções que Gilberto tem para compor o uniforme de seu time é dada por , ou seja, há 64 maneiras diferentes.
84. a) De acordo com o organograma, 2 funcionários são subordinados a cada gerente.
b) Se cada um dos 4 funcionários dessa empresa tiver 2 assistentes, ao todo serão . Como , a quantidade de assistentes escrita em forma de potência é dada por .
85. a) Como Mariana enviou 3 cartas com a letra A no envelope para três estudantes e cada destinatário enviou uma carta para outros 3 estudantes com a letra B, concluímos que foram enviadas cartas com a letra B. Cada um dos 9 destinatários enviou 3 cartas para outros estudantes com a letra C no envelope. Desse modo, a quantidade de cartas enviadas com a letra C é dada por .
b) Com base no item anterior, 27 estudantes receberam uma carta com a letra C no envelope. Repetindo o procedimento, cada um dos 27 destinatários enviou 3 cartas com a letra D para outros estudante. Desse modo, . Logo, foram enviados 81 envelopes com a letra D.
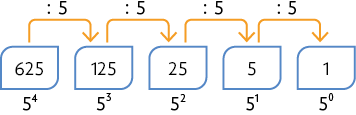
Questão 10. Na sequência o número que ocupa cada posição, a partir da segunda, foi obtido dividindo-se o número da posição anterior por 5. Cada número dessa sequência pode ser escrito na forma de potência como segue:
A regra dessa sequência e cada número dela escrito na forma de potência podem ser representados pelo esquema.
Atividades
86. Efetuando os cálculos, temos:
a)
b)
c)
d)
87. a) Como e , temos .
b) Como e , temos .
c) Como e , temos .
d) Como e , temos .
e) Como e , temos . Além disso, e . Desse modo, .
f) Há várias possibilidades para o . Entre elas, temos , pois e .
88. a) Como e , então .
b) Como e , então .
89. Em cada item, colocando, após o algarismo 1, a quantidade de zeros correspondente ao expoente da potência de 10, temos:
a)
b)
c)
d)
e)
f)
90. a) Como e , então .
b) Como e , então .
c) Como e , então .
d) Como e , então .
e) Como e , então .
f) Como e , então .
91. • Como , o valor correspondente à letra A é 10.000.
Como , o valor correspondente à letra B é 5.
Como , o valor correspondente à letra C é 3.
Como , o valor correspondente à letra D é 100.000.000.000.
Completando o quadro com os valores correspondentes a cada letra, temos:
|
Base |
Expoente |
Resultado da potenciação |
|---|---|---|
|
10 |
4 |
10.000 |
|
10 |
5 |
100.000 |
|
10 |
3 |
1.000 |
|
10 |
11 |
100.000.000.000 |
92. a) O número 987.000 possui 3 zeros à direita do algarismo 7. Logo, a potência de base 10 que substitui corretamente o é e, assim, temos .
b) O número 40.000 possui 4 zeros à direita do algarismo 4. Logo, a potência de base 10 que substitui corretamente o é e, assim, temos .
c) O número 312.000.000 possui 6 zeros à direita do algarismo 2. Logo, a potência de base 10 que substitui corretamente o é e, assim, temos .
d) O número 2.500.000 possui 5 zeros à direita do algarismo 5. Logo, a potência de base 10 que substitui corretamente o é e, assim, temos .
Página LXI
e) O número 140.000.000 possui 7 zeros à direita do algarismo 4. Logo, a potência de base 10 que substitui corretamente o é e, assim, temos .
f) O número 700.000.000 possui 8 zeros à direita do algarismo 7. Logo, a potência de base 10 que substitui corretamente o é e, assim, temos .
93. a) A representação de cem mil no sistema de numeração decimal é 100.000, a qual tem 5 zeros à direita do algarismo 1. Portanto, podemos representá-lo como .
b) O número 1.000.000 possui 6 zeros à direita do algarismo 1. Então, podemos representá-lo como .
c) O número 100.000.000.000 possui 11 zeros à direita do algarismo 1. Então, podemos representá-lo como .
d) A representação de 10 milhões no sistema de numeração decimal é 10.000.000, a qual tem 7 zeros à direita do algarismo 1. Portanto, podemos representá-lo como .
e) A representação do número um bilhão no sistema de numeração decimal é 1.000.000.000, a qual tem 9 zeros à direita do algarismo 1. Portanto, podemos representá-lo como .
f) 10.000 possui 4 zeros à direita do algarismo 1. Portanto, podemos representá-lo como .
g) A representação de cem milhões no sistema de numeração decimal é 100.000.000, a qual tem 8 zeros à direita do algarismo 1. Portanto, podemos representá-lo como .
h) 1.000.000.000.000 possui 12 zeros à direita do algarismo 1. Então, podemos representá-lo como .
i) A representação de dez bilhões no sistema de numeração decimal é , a qual tem 10 zeros à direita do algarismo 1. Portanto, podemos representá-lo como .
94. a)
b)
c)
d)
95. • Terra: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 150.000.000 tem 7 zeros à direita do algarismo 5, então .
Marte: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 228.000.000 tem 6 zeros à direita do algarismo 8, então .
Urano: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 2.871.000.000 tem 6 zeros à direita do algarismo 1, então .
Mercúrio: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 58.000.000 tem 6 zeros à direita do algarismo 8, então .
Vênus: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 108.000.000 tem 6 zeros à direita do algarismo 8, então .
Júpiter: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 778.000.000 tem 6 zeros à direita do algarismo 8, então .
Saturno: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 1.427.000.000 tem 6 zeros à direita do algarismo 7, tem .
Netuno: A medida de distância arredondada à unidade de milhão mais próxima é igual a . Como o número 4.500.000.000 tem 8 zeros à direita do algarismo 5, tem .
96. Podemos resolver essa atividade de duas maneiras diferentes.
Efetuamos a adição das medidas das distâncias da cidade A para a cidade C e da cidade C para a cidade D, que equivale à diferença entre as medidas das distâncias da cidade B à cidade D e a da cidade B à cidade C , ou seja, . Como , segue que , pois . Portanto, a distância da cidade A para a cidade D mede . Representando em potência de base 10, temos .
Efetuamos a adição da medida da distância da cidade A para a cidade B, que equivale à diferença entre as medidas das distâncias da cidade A à cidade C e da cidade B à cidade C , com a medida da distância da cidade B para a cidade D , isto é, . Como , segue que , pois . Portanto, a distância da cidade A para a cidade D mede . Representando em potência de base 10, temos .
Logo, a resposta correta é a alternativa c.
97. Na adição , cada parcela é uma potência de base 10. Então, o resultado de cada potenciação será um número formado por um algarismo 1 seguido de alguns zeros. Assim, a soma dos algarismos de cada parcela da adição é 1 e como essa adição possui 5 parcelas, temos: .
Portanto, a soma dos algarismos do número é 5 e a resposta correta é a alternativa b.
Questão 11. Ao adicionarmos um número aos dois membros de uma igualdade, a relação de igualdade se mantém. Assim, adicionando o número 4 ao 1º membro de uma igualdade, para que permaneça uma relação de igualdade, devemos adicioná-lo também ao 2º membro.
Página LXII
Questão 12. Ao dividirmos os dois membros de uma igualdade por um mesmo número diferente de zero, a relação de igualdade se mantém. Assim, dividindo o primeiro membro de uma igualdade por 5, para que permaneça uma relação de igualdade, devemos dividir o 2º membro por 5.
Atividades
98.a) Como a balança está em equilíbrio, a soma das medidas das massas que estão no prato à esquerda é igual à soma das que estão no prato à direita. Usando o para representar a medida da massa da caixa laranja, a igualdade que representa o equilíbrio da balança é dada por:
b) Para calcular a medida da massa da caixa laranja, na igualdade obtida no item anterior, adicionamos os números que estão no primeiro membro e, depois, subtraímos o número 10 dos dois membros da igualdade.
Portanto, a massa da caixa laranja mede .
c) Resposta pessoal. Sugestão de resposta: Considere a seguinte balança em equilíbrio.
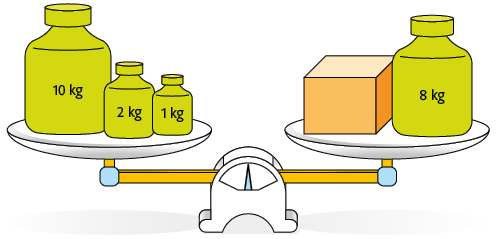
Como a balança está em equilíbrio, usando o para representar a medida da massa da caixa laranja, a igualdade que representa o equilíbrio da balança é dada por:
Calculando a medida da massa da caixa laranja, temos:
Portanto, a massa da caixa laranja mede .
99.a) Efetuando a subtração no primeiro membro da igualdade, temos . Subtraindo o número 2 dos dois membros da igualdade, obtemos .
b) Subtraindo o número 9 em ambos os membros da igualdade, temos .
c) Subtraindo o número 4 em ambos os membros da igualdade, temos . Dividindo ambos os membros por 2, temos .
d) Efetuando os cálculos no primeiro membro da igualdade, obtemos:
Subtraindo o número 20 em ambos os membros da igualdade, obtemos:
.
e) Efetuado as operações no segundo membro da igualdade, temos:
Subtraindo 5 em ambos os membros da igualdade, obtemos . Por fim, dividindo ambos os membros por 3, temos: .
f) Efetuando as operações em ambos os membros da igualdade, temos:
Somando o número 10 em ambos os membros, temos .
100.a) Se colocarmos em um dos pratos da balança 3 caixas com massa medindo , estaremos adicionando , pois . Para manter a balança em equilíbrio, devemos adicionar no outro prato.
b) Ao dobrar a medida de massa em um dos pratos, para manter a balança em equilíbrio, também devemos dobrar a medida da massa do outro prato.
c) A massa total que está no prato da direita mede , pois . Quando Renata trocou a peça de por uma peça de , o prato da direita passou a ter de medida de massa, pois . Assim, a quantidade de medida de massa nesse prato passou de para , ou seja, teve um aumento de . Portanto, para manter a balança em equilíbrio, Renata deve adicionar uma peça medindo de massa no prato da esquerda.
101. Vamos determinar o valor de na expressão que Daniela escreveu. Subtraindo o número 12 em ambos os membros da expressão, temos:
Portanto, Daniela tinha 13 reais.
102. Em um dos pratos, há um total de de medida de massa, pois . Para Gabriel deixar a balança em equilíbrio, dispondo somente de peças medindo de massa, ele deve colocar 6 peças no outro prato da balança, pois .
Página LXIII
103. Resposta pessoal. Sugestão de resposta: Certo dia, Mariana viu que havia 347 seguidores em determinada rede social. No dia seguinte, ao checar novamente a quantidade de seguidores, ela viu que estava com 403 seguidores. Quantos novos seguidores Mariana obteve entre essas duas vezes que visualizou seu perfil?
Resposta: Representando a quantidade de novos seguidores que Mariana obteve por , podemos escrever a igualdade . Subtraindo o número 347 de ambos os membros da igualdade, temos:
Portanto, Mariana obteve 56 novos seguidores.
O que eu estudei?
1. Efetuando os cálculos, temos:
a)
b)
c)
d)
2.a) Para determinar o quanto Carla economizou ao final do 3º mês, adicionamos os valores, em reais, economizados em cada mês.
Portanto, ao final do 3º mês, Carla economizou R$ 996,00.
b) Como Amanda também economizou R$ 966,00, sendo a mesma quantia todo mês, concluímos que Amanda economizou R$ 322,00 por mês, pois .
3. Efetuando os cálculos, temos:
a)
b)
c)
d)
e)
f)
4.a) Como e a soma possui a propriedade comutativa, então .
b) Como e a soma possui a propriedade comutativa, então .
c) Se o representa o número 90 e o representa o número 30, obtemos a igualdade . Realizando os cálculos, temos:
5.a) Arredondando à centena de milhar mais próxima a população estimada:
da Região Norte , obtemos .
da Região Nordeste , obtemos .
da Região Sudeste , obtemos .
da Região Sul , obtemos .
da Região Centro-Oeste , obtemos .
b) Os arredondamentos obtidos no item anterior, escritos utilizando potência de base 10, são:
c) A população brasileira estimada em 2021 é igual à adição da população estimada das regiões do Brasil, isto é:
Portanto, em 2021 o Brasil tinha uma população estimada de 213.317.639 habitantes.
6.a) Subtraindo o número 15 na igualdade , temos:
b) Efetuando os cálculos nos dois membros da igualdade, temos:
Adicionando em ambos os membros da igualdade, e subtraindo 30 em ambos os membros dessa igualdade, obtemos:
c) Adicionando o número 12 em ambos os lados da igualdade, , temos:
Dividindo ambos os membros dessa última igualdade por 5, temos:
d) Efetuando a divisão no segundo membro da igualdade , temos:
Adicionando o número 32 em ambos os lados dessa igualdade, temos:
Agora, dividindo ambos os membros da última igualdade por 3, temos:
e) Efetuando os cálculos nos dois membros da igualdade , temos:
Dividindo ambos os membros dessa igualdade por 7, temos .