Página LXIV
Unidade 3
Múltiplos e divisores
Atividades
1. Os múltiplos de 8 são os números que podem ser representados pela multiplicação de um número natural por 8. Dos números apresentados, os múltiplos de 8 são:
88, pois
160, pois
120, pois
96, pois
240, pois
2. Para determinar a quantidade total de objetos em cada item, podemos multiplicar o número que representa a quantidade de objetos em uma linha pelo número que representa a quantidade de objetos em uma coluna, e vice-versa.
A. Como há 18 bolas de futebol agrupadas em 3 linhas e 6 colunas, as multiplicações que representam essa quantidade são e .
B. Como há 20 lápis agrupados em duas linhas e 10 colunas, as multiplicações que representam essa quantidade são e .
3. a) O número 18 é múltiplo de 1, 2, 3, 6, 9 e 18. Assim:
Se , então , pois .
Se , então , pois .
Se , então , pois .
Se , então , pois .
Se , então , pois .
Se , então , pois .
b) O número 20 é múltiplo de 1, 2, 4, 5, 10 e 20. Assim:
Se , então , pois .
Se , então , pois .
Se , então , pois .
Se , então , pois .
Se , então , pois .
Se , então , pois .
4. Os números do conjunto 1 são múltiplos de 2, os do conjunto 2 são múltiplos de 3 e os do conjunto 3 são múltiplos de 5. Sendo assim, podemos escrevê-los da seguinte maneira:
Conjunto 1: ; ; ; ; ; ; .
Conjunto 2: ; ; .
Conjunto 3: ; .
5. a) São respostas válidas para cada conjunto qualquer número que seja múltiplo de 2 no conjunto 1, seja múltiplo de 3 no conjunto 2 e seja múltiplo de 5 no conjunto 3. Assim:
Conjunto 1: 38 e 44, pois e .
Conjunto 2: 33 e 39, pois e .
Conjunto 3: 35 e 55, pois e .
b) Como o número 100 é múltiplo de 2 e de 5 , ele pode pertencer ao conjunto 1 e ao conjunto 3.
6. a) Os 10 primeiros múltiplos de 2 são: , , , , , , , , e .
b) Os 10 primeiros múltiplos de 3 são: , , , , , , , , e .
c) Os 10 primeiros múltiplos de 5 são: , , , , , , , , e .
d) Os 10 primeiros múltiplos de 7 são: , , , , , , , , e .
7. a) ou
b) ou
c) ou
d) ou
e) 16 não é múltiplo de 6, pois não pode ser representado pela multiplicação de um número natural por 6.
f) ou
8. Os números 42, 18, 24, 54 e 72 são múltiplos de 6, pois podem ser representados pela multiplicação de um número natural por 6.
9. Resposta pessoal. Veja uma sugestão de elaboração a seguir.
Escreva, em seu caderno, três múltiplos de 7 menores e três múltiplos de 7 maiores do que os números apresentados a seguir.
-
21
-
28
-
35
10. a) As histórias "Os três porquinhos" e "Chapeuzinho Vermelho" e um livro de receitas.
b) Açúcar mascavo; 2 colheres.
c) Supondo que 2 colheres rendem 3 porções, então 8 colheres renderão 12 porções, pois e .
11. a) Um número é múltiplo de 4 se pode ser representado pela multiplicação de um número natural por 4. Assim, os números 20, 60, 24, 48, 36, 64, 28, 16 e 72 são múltiplos de 4, pois , , , , , , , e .
b) Um número é múltiplo de 5 se pode ser representado pela multiplicação de um número natural por 5. Assim, os números 20, 10, 60, 30 e 50 são múltiplos de 5, pois , , , e .
c) Os múltiplos de 4 e também de 5 são os números que podem ser escritos como a multiplicação de um número natural por 4 e por 5. Assim, os números 20 e 60 são múltiplos de 4 e de 5, pois e ; e .
12. Os números que aparecem em comum nas sequências dos múltiplos de 2 e de 3 são 0, 6, 12 e 18.
Página LXV
13. a) Os múltiplos comuns de 4 e 6 pertencem à sequência dos múltiplos de 4 e também à sequência dos múltiplos de 6. Esses números são 0, 12, 24 e 36.
b) Sabemos que o mínimo múltiplo comum de dois ou mais números é o menor múltiplo comum deles diferente de zero. Os múltiplos comuns de 4 e 6 são 0, 12, 24 e 36; então, o menor múltiplo comum é 12, ou seja, . Os múltiplos comuns de 4 e 9 são 0 e 36; então, menor múltiplo comum é 36, ou seja, . Os múltiplos comuns de 6 e 9 são 0, 18, 36 e 54; então, o menor múltiplo comum é 18, ou seja, .
14. Para determinar o próximo horário em que Heitor tomará os dois remédios juntos novamente, devemos encontrar o mínimo múltiplo comum entre 6 e 8. Escrevendo alguns múltiplos de 6 e alguns múltiplos de 8, temos:
Múltiplos de 6: 0, 6, 12, 18, 24, 30.
Múltiplos de 8: 0, 8, 16, 24, 32, 40.
Nesse caso, o menor múltiplo comum entre 6 e 8 é o 24, ou seja, . Portanto, Heitor voltará a tomar os dois remédios juntos novamente após 24 horas.
15. Considerando 6 meses de 27 dias, calculamos . Portanto, o ano no Planeta Pemob tem 162 dias. Como a semana completa tem 5 dias, precisamos determinar qual é o múltiplo de 5 mais próximo de 162.
Múltiplos de 5: 0, 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 115, 120, 125, 130, 135, 140, 145, 150, 155, 160 e 165.
Como 162 não é múltiplo de 5, concluímos que esse ano teve 32 semanas completas com cinco dias e mais dois dias da 33ª semana, pois .
A ordem dos dias da semana é Aba, Eba, Iba, Oba e Uba. Como Eba foi o primeiro dia do ano, após cinco dias Aba foi o último dia da semana de certo ano. Nessas condições, considerando a ordem dos dias da semana, o último dia do ano foi Iba. Portanto, a alternativa c é a correta.
Questão 1. Não, pois a divisão de 16 por 5 não é exata, ou seja, 5 não é um divisor natural de 16.
Atividades
16. Para obter outras maneiras de empilhar 24 livros de modo que todas as pilhas tenham a mesma quantidade de livros, podemos determinar os divisores exatos de 24, que são: 1, 2, 3, 4, 6, 8, 12 e 24. Desse modo, podemos formar 1 pilha com 24 livros; 2 pilhas com 12 livros cada uma; 3 pilhas com 8 livros cada uma; 4 pilhas com 6 livros cada uma; 6 pilhas com 4 livros cada uma; 8 pilhas com 3 livros cada uma; 12 pilhas com 2 livros cada uma; ou 24 pilhas com 1 livro cada uma. A possibilidade de 3 pilhas com 8 livros cada uma é a distribuição apresentada por Arnaldo.
17. a) Não, pois a divisão de 168 por 5 não é exata, ou seja, o resto da divisão não é zero.
b) Porque a divisão de 156 por 3 é exata, ou seja, o resto da divisão é zero.
18. a) Verdadeira, pois essa divisão é exata, ou seja, o resto da divisão é zero.
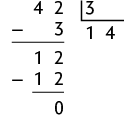
b) Falsa, pois a divisão de 26 por 8 não é exata, ou seja, o resto da divisão é diferente de zero. Sugestão de resposta: 26 não é divisível por 8 porque a divisão de 26 por 8 não é exata.
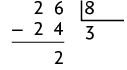
19. a) O maior número da pilha B é 90 e seus divisores são: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45 e 90.
b) Dos números da pilha A, o 6 é divisor apenas do número 42. Na pilha B, o 6 é o divisor do número 90. Na pilha C, o 4 é divisor do número 36. Na pilha D, o 4 é divisor dos números 16 e 32 e o 6 é divisor dos números 18 e 54. Portanto, na pilha D há dois números divisíveis por 4 e dois divisíveis por 6.
Questão 2. Os números da sequência A são pares, pois o algarismo das unidades é 0, 2, 4, 6 ou 8. Os números da sequência B são ímpares, pois os algarismos das unidades são 1, 3, 5, 7 ou 9.
Questão 3. Resposta pessoal. Espera-se que os estudantes respondam que o resto da divisão dos números da sequência A por 2 é 0, pois os números apresentados nessa sequência são múltiplos de 2. O resto da divisão dos números da sequência B por 2 é 1, pois os números dessa sequência são ímpares.
Questão 4. Resposta pessoal. Espera-se que os estudantes respondam que são números pares, ou seja, o algarismo das unidades é 0, 2, 4, 6 ou 8.
Questão 5. Um número natural é divisível por 2 quando é par. Desse modo, um número divisível por 2 tem o algarismo da unidade igual a 0, 2, 4, 6 ou 8.
Questão 6. Os números 42, 261 e 2.361 são divisíveis por 3, pois as divisões são exatas, ou seja, o resto da divisão deles por 3 é zero. Já o número 986 não é divisível por 3, pois a divisão não é exata, ou seja, o resto da divisão dele por 3 é diferente de zero.
Questão 7. Ao somarmos os algarismos dos números divisíveis por 3, temos:
42:
261:
2.361:
Espera-se que os estudantes respondam que os números 6, 9 e 12 são múltiplos de 3, pois , e .
Questão 8. Um número será divisível por 3 quando a soma dos valores correspondentes de seus algarismos for um número divisível por 3.
Página LXVI
Questão 9. Sabemos que um número é divisível por 2 quando o algarismo das unidades termina em 0, 2, 4, 6 ou 8, ou seja, se é par. Além disso, um número é divisível por 3 se a soma de seus algarismos for um número divisível por 3. Dos números apresentados, os números pares são 84, 92, 108, 132 e 378, logo são divisíveis por 2. Para verificar quais são divisíveis por 3, fazemos:
84: . Como 12 é divisível por 3, então 84 também é divisível por 3.
92: . Como 11 não é divisível por 3, então 92 não é divisível por 3.
108: . Como 9 é divisível por 3, então 108 também é divisível por 3.
423: . Como 9 é divisível por 3, então 423 também é divisível por 3.
132: . Como 6 é divisível por 3, então 132 também é divisível por 3.
378: . Como 18 é divisível por 3, então 378 também é divisível por 3.
Portanto, os números 84, 108, 423, 132 e 378 são divisíveis por 3.
Questão 10. Os números que são divisíveis, simultaneamente, por 2 e 3 são 84, 108, 132 e 378.
Questão 11. Os números 84, 108, 132 e 378 são divisíveis por 6, pois são, ao mesmo tempo, divisíveis por 2 e por 3 e .
Questão 12. Resposta pessoal. Espera-se que os estudantes respondam que os mesmos números que são divisíveis por 2 e por 3 também são divisíveis por 6.
Questão 13. Um número natural é divisível por 6 quando for divisível, simultaneamente, por 2 e por 3.
Questão 14. Os números 72, 684, 243 e 3.987 são divisíveis por 9, pois o resto da divisão é zero, ou seja, a divisão é exata.
Questão 15. Ao somarmos os algarismos dos números divisíveis por 9, temos:
72:
684:
243:
3.987:
Espera-se que os estudantes respondam que os números que correspondem às somas dos algarismos são divisíveis por 9.
Questão 16. A soma dos algarismos do número 417 é . Como a soma é 12, esse valor não tem as mesmas características de 417, pois 12 é múltiplo de 3, mas não é múltiplo de 9.
Questão 17. Um número natural é divisível por 9 quando a soma dos valores correspondentes aos seus algarismos também for um número divisível por 9.
Questão 18. Os números que aparecem na sequência são os múltiplos de 5. Os próximos 3 números dessa sequência são: 50, 55 e 60.
Questão 19. Sim, pois as divisões e são exatas. Não, pois a divisão de 108 por 5 não é exata, ou seja, o resto é diferente de zero.
Questão 20. Resposta pessoal. Espera-se que os estudantes respondam que o algarismo das unidades, nos números dessa sequência, é sempre 0 ou 5.
Questão 21. Um número natural é divisível por 5 quando o algarismo das unidades for 0 ou 5.
Questão 22. A sequência apresentada é a dos múltiplos de 10. O próximo número dessa sequência é o 110.
Questão 23. Pertence a essa sequência qualquer número múltiplo de 10. Sugestão de resposta: 120 pertence à sequência; 131 não pertence à sequência.
Questão 24. Sugestões de resposta: , e .
Questão 25. Como todos os números são múltiplos de 10, podemos afirmar que esses números são divisíveis por 10.
Questão 26. Resposta pessoal. Espera-se que os estudantes respondam que o algarismo das unidades dos números múltiplos de 10 é sempre 0.
Questão 27. Um número natural será divisível por 10 quando o algarismo das unidades for 0.
Questão 28. Os múltiplos de 100 entre 900 e 1.500 são 1.000, 1.100, 1.200, 1.400.
Questão 29. O número 3.200 é múltiplo de 100, pois . Já o 3.250 não é múltiplo de 100, pois não pode ser escrito como uma multiplicação entre dois números naturais em que um dos fatores é o 100.
Questão 30. Resposta pessoal. Espera-se que os estudantes respondam que, em um número múltiplo de 100 maior do que 1, os algarismos da unidade e da dezena são 0.
Questão 31. Um número natural será divisível por 100 quando os algarismos da dezena e da unidade forem, simultaneamente, 0.
Questão 32. A sequência apresentada é dos múltiplos de 1.000. Assim, o próximo número dessa sequência será 6.000.
Questão 33. Sim, pois 10.000 é múltiplo de 1.000. Não, pois 10.200 não é múltiplo de 1.000.
Questão 34. Resposta pessoal. Espera-se que os estudantes respondam que os algarismos da centena, da dezena e da unidade são todos iguais a 0 nos números da sequência apresentada.
Questão 35. Um número natural é divisível por 1.000 quando seus três últimos algarismos forem, simultaneamente, 0.
Questão 36. Dos números apresentados, os divisíveis por 4 são 320, 316, 2.000 e 2.048, pois a divisão é exata, ou seja, tem resto igual a zero.
Questão 37. Entre os números divisíveis por 4, os algarismos da dezena e da unidade de 320, 316 e 2.048 formam, respectivamente, os números 20, 16 e 48, e esses números são divisíveis por 4, pois a divisão deles por 4 é exata, ou seja, o resto da divisão por 4 é igual a zero.
Página LXVII
Questão 38. Entre os números divisíveis por 4, os números 320 e 2.000 são múltiplos de 10, pois e . Além disso, 2.000 também é múltiplo de 100, pois .
Questão 39. Nem todo número divisível por 10 também é divisível por 4. Por exemplo, o número 110 é divisível por 10, mas não é divisível por 4, já que não é uma divisão exata. Com relação aos números divisíveis por 100, todos também são divisíveis por 4, pois é uma divisão exata e, portanto, todo número divisível por 100 pode ser escrito como um produto em que um dos fatores é 4.
Questão 40. O número 314, por exemplo, é par e não é divisível por 4, pois a divisão dele por 4 não é exata. Portanto, ser par não é uma condição suficiente para que um número seja divisível por 4.
Questão 41. Um número natural com mais de dois algarismos é divisível por 4 quando seus dois últimos algarismos forem, simultaneamente, 0 ou formarem, na ordem em que aparecem, um número divisível por 4.
Questão 42. Os números 4.000, 3.000, e 1.000 são divisíveis por 8, pois todo número natural múltiplo de 1.000 também é múltiplo de 8.
Questão 43. Como os números 4.000, 3.000 e 1.000 são divisíveis por 8, para que 4.984, 3.256 e 1.152 também sejam divisíveis por 8, os números 984, 256 e 152 devem ser, pois:
Questão 44. Realizando o algoritmo da divisão, temos:
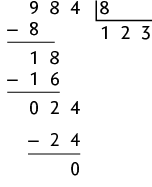
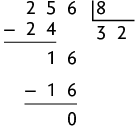
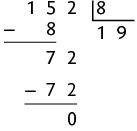
Portanto, os números 984, 256 e 152 são divisíveis por 8.
Questão 45. Os números 4.984, 3.256 e 1.152 são divisíveis por 8, pois as divisões são exatas, ou seja, o resto da divisão por 8 é igual a zero.
Questão 46. Um número natural com mais de três algarismos é divisível por 8 quando seus três últimos algarismos forem, simultaneamente, 0 ou formarem, na ordem em que aparecem, um número divisível por 8.
Atividades
20. a) 193: é ímpar e a soma de seus algarismos é igual a 13, que não é divisível por 3 nem por 9. Assim, 193 não é divisível pelos números 2, 3, 6 e 9.
b) 252: é par e a soma de seus algarismos é 9, que é divisível por 3 e 9. Portanto, 252 é divisível por 2, 3, 6 e 9.
c) 276: é par e a soma de seus algarismos é 15, que é divisível por 3. Portanto, ele é divisível por 2, 3 e 6.
d) 567: é ímpar e a soma dos algarismos é 18, que é divisível por 3 e por 9, assim 567 não é divisível por 2 nem por 6, mas é divisível por 3 e 9.
e) 386: é par, mas a soma de seus algarismos é 17, que não é divisível por 3 nem por 9. Assim, 386 é divisível apenas por 2.
f) 795: é ímpar e a soma de seus algarismos é 21, que é divisível por 3, mas não é divisível por 9. Portanto, 795 é divisível apenas por 3.
g) 541: é ímpar e a soma de seus algarismos é 10, que não é divisível por 3 nem por 9. Portanto, 541 não é divisível pelos números 2, 3, 6 e 9.
h) 2.968: é par, mas a soma de seus algarismos é 25, que não é divisível por 3 nem por 9. Portanto, 2.968 é divisível apenas por 2.
i) 978: é par e a soma de seus algarismos é 24, que é divisível por 3, mas não é divisível por 9. Portanto, 978 é divisível por 2, 3 e 6.
21. a) Para que o número seja divisível por 3, a soma dos seus algarismos deve ser um número divisível por 3. Como , as opções para que a soma seja divisível por 6 são 231, (pois ), 234 (pois ) e 237 (pois ).
b) Para que o número seja divisível por 2, o número deve ser par, ou seja, o algarismo das unidades deve ser 0, 2, 4, 6 ou 8. Então, as opções serão 230, 232, 234, 236 e 238.
c) Para que o número seja divisível por 6, deve ser divisível por 2 e por 3 ao mesmo tempo. Com base nos itens a e b, a única possibilidade para completar a ordem das unidades no número é o algarismo 4, pois o número 234, que é par, também é divisível por 3.
d) Para que o número seja divisível por 9, a soma de seus algarismos deve ser divisível por 9. Nesse caso, a única possibilidade para completar a ordem das unidades no número é o algarismo 4, pois formará o número 234, cuja soma de seus algarismos é divisível por 9.
22. O número 32 não é divisível por 3, pois , que não é divisível por 3. Portanto, não é possível formar grupos com 3 estudantes sem que nenhum deles fique sem grupo.
23. a) Para ser divisível por 2, o número deve ser par. Então, o maior número de três algarismos divisível por 2 formado é 998.
b) Para ser divisível por 3, a soma dos algarismos do número deve ser divisível por 3. Logo, o maior número de três algarismos divisível por 3 é 999, cuja soma de seus algarismos é divisível por 3.
c) Para ser divisível por 6, o número deve ser divisível por 2 e 3 ao mesmo tempo. Nesse caso, o maior número de três algarismos possível é 996, pois é par e a soma de seus algarismos é divisível por 3.
d) Para ser divisível por 9, a soma dos algarismos do número deve ser divisível por 9. Então, o maior número de três algarismos possível é 999, cuja soma de seus algarismos é divisível por 9.
Página LXVIII
24. a) Como os números apresentados são formados por 2 algarismos, basta realizar a divisão dos que são pares por 4. Assim, os números 40, 36, 60 e 80 são divisíveis por 4, pois as divisões deles por 4 são exatas.
b) Para que um número não seja divisível por 3, a soma dos algarismos não deve ser um número divisível por 3. Os números com essa característica são 40, 80 e 35.
c) Para que um número seja divisível por 5, o algarismo da unidade deve ser 0 ou 5. Considerando os números divisíveis por 4 apresentados no item a, os números divisíveis por 4 e 5 ao mesmo tempo são 40, 60 e 80.
d) Como , os números divisíveis por 20 são os mesmos divisíveis por 4 e por 5. Portanto, 40, 60 e 80 são divisíveis por 20, pois , e .
25. a) Os números apresentados não terminam em zero. Então, devemos analisar se os dois últimos algarismos formam, na ordem em que aparecem, um número divisível por 4. Como 34 não é divisível por 4, então 1.734 não é divisível por 4. Como 27 não é divisível por 4, então 3.627 não é divisível por 4. Como 24 é divisível por 4, então 1.224 é divisível por 4. Como 12 é divisível por 4, então 1.412 é divisível por 4. Como 18 não é divisível por 4, então 2.518 não é divisível por 4.
b) Para um número ser divisível por 6, ele deve ser divisível por 2 e 3 ao mesmo tempo.
Um número será divisível por 2 se ele for par, ou seja, se o algarismo da unidade for 0, 2, 4, 6 ou 8. Então, 3.627 não será divisível por 6 porque não é par.
Um número será divisível por 3 se a soma dos algarismos dele for divisível por 3.
A soma dos algarismos de 1.734 é divisível por 3. Portanto, ele é divisível por 6. A soma dos algarismos de 1.224 é divisível por 3. Portanto, ele é divisível por 6. A soma dos algarismos de 1.412 não é divisível por 3. Portanto, ele não é divisível por 6. A soma dos algarismos de 2.518 não é divisível por 3. Portanto, ele não é divisível por 6.
c) Os números apresentados não são terminados em 000. Então, devemos analisar se os três últimos algarismos formam, na ordem em que aparecem, um número par divisível por 8. Como 734 não é divisível por 8, então 1.734 não é divisível por 8. Como 627 não é par, então 3.627 não é divisível por 8.
Como 224 é divisível por 8, então 1.224 é divisível por 8. Como 412 não é divisível por 8, então 1.412 não é divisível por 8. Como 518 não é divisível por 8, então 2.518 não é divisível por 8.
d) A soma dos algarismos deve ser divisível por 9 para que um número seja divisível por 9. Como a soma dos algarismos de 1.734 não é divisível por 9 , então 1.734 não é divisível por 9. Como a soma dos algarismos de 3.627 é divisível por 9 , então 3.627 é divisível por 9. Como a soma dos algarismos de 1.224 é divisível por 9 , então 1.224 é divisível por 9. Como a soma dos algarismos de 1.412 não é divisível por 9 , então 1.412 não é divisível por 9. Como a soma dos algarismos de 2.518 não é divisível por 9, , então 2.518 não é divisível por 9.
e) Analisando os itens anteriores, verificamos que apenas o número 1.224 é divisível por 4, 6, 8 e 9 simultaneamente.
f) Com base nos itens anteriores, verificamos que apenas o 2.518 não é divisível por 4, 6, 8 ou 9.
26. Para que um número natural seja divisível por 100, os algarismos da dezena e da unidade precisam ser zero.
Questão 47. Resposta pessoal. Espera-se que os estudantes verifiquem em sua pesquisa que, além da contribuição nos estudos dos números primos, Eratóstenes usou conceitos matemáticos importantes e calculou a medida da circunferência da Terra e também seu eixo de inclinação.
27. Os números que só têm dois divisores, o 1 e o próprio número, são chamados números primos. Assim, conforme o crivo de Eratóstenes, os números primos entre 1 e 50 são 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47.

Página LXIX
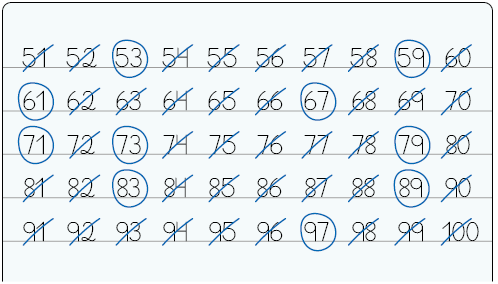
28. Com base no crivo de Eratóstenes, os números primos entre 51 e 100 são: 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.
29. a) 159 é divisível por 3, logo é um número composto.
b) 247 é divisível por 13, logo é um número composto.
c) 269 é primo, pois é divisível por 1 e por ele mesmo.
d) 301 é divisível por 7, logo é um número composto.
e) 331 é primo, pois é divisível por 1 e por ele mesmo.
f) 541 é primo, pois é divisível por 1 e por ele mesmo.
30. a) O número 1 não é primo, pois tem apenas um divisor, que é ele mesmo.
b) O número 2 é o único número natural par que é primo, pois tem apenas dois divisores, que são o 1 e ele mesmo.
c) O 3 é o menor número natural primo ímpar, pois tem apenas dois divisores, que são o 1 e ele mesmo.
d) O número 112 não é primo, porque é par, ou seja, é divisível por 2. Além disso, ele tem outros divisores, o que faz dele um número composto. Os divisores de 112 são: 1, 2, 4, 7, 8, 14, 16, 28, 56 e 112.
e) Contando os números contornados no crivo de Eratóstenes, obtemos 25 números primos entre 1 e 100.
f) O número 17 é primo, pois tem apenas dois divisores, que são o 1 e ele mesmo.
g) Analisando em ordem decrescente os números de 2 algarismos, verificamos que 99 é um número composto, pois além de 1 e dele mesmo, é divisível por 3, 9 e 11. O número 98 também é composto e, além do 1 e dele mesmo, é divisível por 2, 7, 14 e 49. Sendo assim, o número 97 é o maior número natural primo de dois algarismos, pois é divisível apenas por 1 e por ele mesmo.
31. a) A casa correspondente à linha 7 e à coluna 21 deve ter sido preenchida com o algarismo 1, porque essa casa corresponde ao número 21, que é múltiplo de 7, ou seja, .
b) Entre 1 e 100 existem 4 múltiplos de 23, que são 23, 46, 69 e 92, pois , , e . Como as casas de colunas múltiplas do número correspondente à linha foram preenchidas com o algarismo 1, a soma dos algarismos dessa linha é 4.
32. O número 29 é primo e, por isso, tem apenas dois divisores, que são o 1 e ele mesmo. Logo, há apenas dois algarismos iguais a 1 na coluna 29. Portanto, a soma dos algarismos dessa coluna é 2.
33. Os divisores naturais do número 72 são 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 e 72, dos quais apenas o 2 e o 3 são números primos.
34. Decompondo os números dos itens em fatores primos sem usar a regra prática, temos:
a)
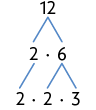
Portanto, .
b)

Portanto, .
c)

Portanto, .
d)

Portanto, .
e)

Portanto, .
f)

Portanto, .
35. Utilizando a regra prática para a decomposição dos números apresentados, temos:
a)
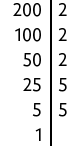
Portanto, .
Página LXX
b)
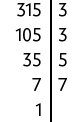
Portanto, .
c)
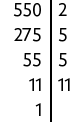
Portanto, .
d)

Portanto, .
e)
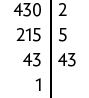
Portanto, .
f)
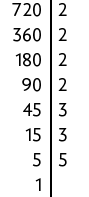
Portanto, .
36. a)
b)
c)
d)
e)
f)
g)
h)
37. Os números primos de 1 algarismo são 2, 3, 5 e 7. Realizando a multiplicação entre esses números, obtemos .
38. Devemos identificar dois números primos consecutivos tais que a multiplicação resulte em um número entre 70 e 80. Os 6 primeiros números primos são 2, 3, 5, 7, 11 e 13. Efetuando a multiplicação entre dois números consecutivos, temos:
A idade atual do avô é 77 anos, pois o único produto obtido entre 70 e 80 resulta da multiplicação dos números 7 e 11, ou seja, .
39. a) Verdadeira. Realizando a decomposição em fatores primos de 180, temos:
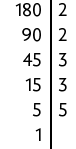
Portanto, .
b) Falsa. Realizando a decomposição em fatores primos de 50, obtemos:
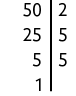
Portanto, uma sugestão de resposta é: A decomposição de 50 em fatores primos é .
c) Falsa. Realizando uma possível decomposição em fatores primos de 44, obtemos:
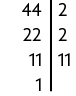
Portanto, uma sugestão de resposta é: A decomposição de 44 em fatores primos é .
d) Verdadeira. Realizando a decomposição em fatores primos de 350, temos:
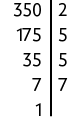
Portanto, .
O que eu estudei?
1. As caixas A e B têm a mesma medida de altura da embalagem de leite, ou seja, .
a) Vamos analisar a caixa A, cujas arestas têm comprimento e largura medindo e , respectivamente. Já as arestas referentes ao comprimento e à largura da embalagem de leite medem, respectivamente, e . Como 18 e 36 são múltiplos de 9 e 6, podemos organizar as embalagens de leite dentro da caixa A de duas maneiras.
Página LXXI
1ª maneira: dispor 4 embalagens de leite no comprimento e 3 na largura, pois e .
2ª maneira: dispor 6 embalagens de leite no comprimento e 2 na largura, pois e .
Nas duas maneiras, a quantidade de embalagens de leite na caixa A será a mesma, pois e .
Analisando a caixa B, verificamos que o comprimento e a largura de suas arestas medem e , respectivamente. Como 27 é múltiplo de 9 e 30 é múltiplo de 6, podemos organizar as embalagens de leite dentro da caixa B de uma maneira, que é dispor 3 embalagens de leite no comprimento e 6 na largura, pois e . Então, a quantidade de embalagens de leite na caixa B seria 15, pois .
Portanto, na caixa A cabem 12 embalagens de leite e na caixa B, 15 embalagens de leite.
b) Não sobra espaço, pois é possível ocupar todo o interior das caixas com a maior quantidade possível de embalagens de leite.
2. Considerando os 10 primeiros múltiplos de cada número, temos:
a) múltiplos de 3: 0, 3, 6, 9, 12, 15, 18, 21, 24 e 27, pois , , , , , , , , e .
b) múltiplos de 7: 0, 7, 14, 21, 28, 35, 42, 49, 56 e 63, pois , , , , , , , , e .
c) múltiplos de 10: 0, 10, 20, 30, 40, 50, 60, 70, 80 e 90, pois , , , , , , , , e .
3. a) Para que o número seja divisível por 2, ele deve ser par, isto é, o algarismo da unidade deve ser 0, 2, 4, 6 ou 8. De acordo com os algarismos apresentados, o número a ser formado só pode ter 2 ou 4 como algarismo da unidade, ou seja, ⬛ ⬛ ⬛ 2 ou ⬛ ⬛ ⬛ 4. Sugestões de resposta: 3.452 e 2.534.
b) Como não há o algarismo zero, a única opção para que o número seja divisível por 4, nesse caso, é que os dois últimos algarismos (da dezena e da unidade) na ordem em que aparecem devem formar um número divisível por 4. Sugestões de resposta: 3.524 e 4.352.
c) Para que o número seja divisível por 5, o algarismo da unidade deve ser 0 ou 5, ou seja, ⬛ ⬛ ⬛ 5. Sugestões de resposta: 2.435 e 3.425.
d) Para que um número formado com esses algarismos seja divisível por 8, os três últimos algarismos (centena, dezena e unidade) na ordem em que aparecem devem formar um número divisível por 8. Sugestões de resposta: 4.352 e 5.432.
4. Não, pois um número divisível por 6 deve ser divisível por 2 e por 3 também. Com esses algarismos é possível formar um número divisível por 2 (como 3.452 ou 5.342), porém ele não será divisível por 3, porque a soma desses algarismos não é divisível por 3 .
5. Utilizando a regra prática para decompor os números a seguir em fatores primos, temos:
a)
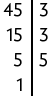
Portanto, .
b)
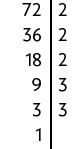
Portanto, .
c)
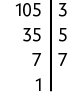
Portanto, .
d)
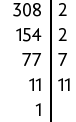
Portanto, .
6. Para que um número seja divisível por 10, o algarismo da unidade deve ser zero, e para que ele seja divisível por 9, a soma de seus algarismos deve ser um número divisível por 9.
a) 4.708 não é divisível por 9, pois , que não é divisível por 9, e não é divisível por 10, pois não termina em zero.
b) 11.260 não é divisível por 9, pois , que não é divisível por 9, e é divisível por 10, pois termina em zero.
c) 3.591 é divisível por 9, pois , que é divisível por 9, e não é divisível por 10, pois não termina em zero.
d) 96.480 é divisível por 9, pois , que é divisível por 9, e é divisível por 10, pois termina em 0.
7. Não, pois, se o número é ímpar, o algarismo das unidades termina em 1, 3, 5, 7 ou 9, mas para que um número seja divisível por 100, os algarismos da dezena e da unidade devem ser, simultaneamente, 0, ou seja, ele deve ser par.
Página LXXII
Unidade 4
Figuras geométricas espaciais
Questão 1. Das figuras apresentadas, B, C, D, G e H são formadas apenas por superfícies planas.
Questão 2. A figura geométrica espacial da imagem C representa um cubo. Dos objetos apresentados, o dado é o que se parece com essa figura. A imagem F representa uma esfera. O objeto que se parece com essa figura é a bola de futebol.
Questão 3. Sabendo que um cubo tem 12 arestas e todas as arestas têm a mesma medida de comprimento, calculamos , pois todas as arestas juntas medem de comprimento. Portanto, cada aresta desse cubo mede .
Atividades
1. Como Roberto está desmontando uma caixa com formato de paralelepípedo reto retângulo, que tem 6 faces retangulares, a imagem apresentada no item B representa a caixa totalmente desmontada, pois é formada por 6 retângulos, sendo os dois menores em lados opostos de um mesmo retângulo maior. Essa disposição permite que a caixa feche sem faltar, sobrar ou sobrepor nenhuma face, o que não ocorre nas outras imagens.
2. Sabendo que as faces com o mesmo tamanho, ou seja, aquelas que estão em posições opostas, contêm a mesma letra, concluímos que:
a) existem duas faces opostas iguais com a letra A.
b) existem duas faces opostas iguais com a letra B.
3. a) Falsa; Sugestão de resposta: Todo paralelepípedo reto retângulo tem 6 faces.
b) Falsa; Sugestão de resposta: Um paralelepípedo reto retângulo tem 8 vértices.
c) Verdadeira, pois todo paralelepípedo reto retângulo tem 12 vértices.
d) Falsa; Sugestão de resposta: Nem todo paralelepípedo reto retângulo tem faces quadradas e retangulares.
e) Verdadeira, pois o cubo é um paralelepípedo reto retângulo cujas faces são quadrados.
f) Falsa; Sugestão de resposta: Um paralelepípedo reto retângulo pode ter duas faces quadradas.
4. A. Para que a pilha tenha formato de um cubo, todas as arestas devem ter medidas iguais.
Comparando os 11 cubos que já estão na pilha do item A, verificamos que o comprimento da aresta do cubo a ser formado deve medir três arestas dos cubos que compõem a pilha. Assim, para completar a pilha devemos acrescentar, no mínimo, 16 cubos, sendo 7 na segunda fileira e 9 na terceira fileira. Com isso, teremos 3 cubos de medida de comprimento em todas as arestas da montagem final, conforme mostra a figura.

B. Com base nos 4 cubos que já estão na pilha do item B, verificamos que o comprimento da aresta do cubo a ser formado deve medir duas arestas dos cubos que compõem a pilha. Então, para completar a pilha, devemos acrescentar, no mínimo, 4 cubos, sendo 1 na primeira fileira e 3 na segunda fileira. Com isso, teremos 2 cubos de medida de comprimento em todas as arestas da montagem final, conforme mostra a imagem.

C. Verificando os 7 cubos que já estão na pilha do item C, notamos que o comprimento da aresta do cubo a ser formado deve medir três arestas dos cubos que compõem a pilha. Para completar essa pilha, então, devemos acrescentar, no mínimo, 20 cubos, sendo 4 na primeira fileira, 8 na segunda fileira e 8 na terceira fileira. Assim, teremos 3 cubos de medida de comprimento em todas as arestas da montagem final, conforme mostra a imagem.

D. Com base nos 5 cubos que já estão na pilha D, podemos verificar que o comprimento das arestas do cubo a ser formado deve medir três arestas dos cubos que compõem a pilha. Para completar a pilha, devemos acrescentar, no mínimo, 22 cubos, sendo 5 na primeira fileira, 8 na segunda fileira e 9 na terceira fileira. Assim, teremos 3 cubos de medida de comprimento em todas as arestas da montagem final, conforme mostra a imagem.

5. Como o comprimento das arestas em cada cubo mede , na caixa:
A podem ser colocados 4 cubos na medida do comprimento, pois , 2 cubos na medida da largura, pois , e 3 cubos na medida da altura, pois . Assim, cabem 24 cubos no máximo, pois .
Página LXXIII
B podem ser colocados 5 cubos na medida do comprimento, pois , 4 cubos na medida da largura, pois , e 4 cubos na medida da altura, pois . Assim, cabem 80 cubos no máximo, pois .
C podem ser colocados 9 cubos na medida do comprimento, pois , 4 cubos na medida da largura, pois , e 3 cubos na medida da altura, pois . Assim, cabem 108 cubos no máximo, pois .
6. Numerando cada face da planificação, temos:
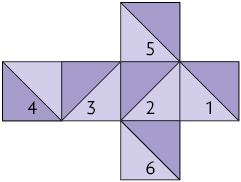
Dobrando as arestas para montar o cubo, as faces com os números 6 e 4 se unem por uma mesma aresta, assim como as faces numeradas como 6 e 3, como é possível perceber na imagem a seguir.
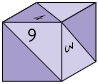
Portanto, a imagem apresentada no item B representa o cubo construído por Luísa.
7. Devemos juntar as peças de modo que todas as partes se encaixem, formando um cubo, e não sobre espaço entre as peças. De acordo com o formato de cada peça, será possível formar um cubo ao juntar as peças A e F; B e E; C e D.
8. Podemos verificar que a pilha tem 3 caixas de medida de comprimento. Como cada caixa mede de comprimento, o comprimento da pilha mede , pois . Verificamos também que a pilha tem 5 caixas de medida de largura. Como a largura de cada caixa mede , a pilha mede de largura, pois . Por fim, constatamos que a pilha tem 4 caixas de medida de altura, e a altura de cada caixa mede . Assim, a altura dessa pilha mede , pois .
9. Podemos verificar que a pilha de paralelepípedos é formada por 5 paralelepípedos de mesma medida de comprimento. Como o comprimento dessa pilha mede , fazemos . Logo, o comprimento de cada paralelepípedo mede . Verificamos também que a largura dessa pilha mede e é formada por 2 paralelepípedos de mesma medida de largura. Calculando , obtemos a medida da largura de cada paralelepípedo, que é . Como a altura da pilha de paralelepípedos mede e tem 5 paralelepípedos com a mesma medida de altura, calculamos . Portanto, cada paralelepípedo tem de medida de altura.
Questão 4. Sugestão de resposta: Os prismas têm duas bases e as pirâmides têm apenas uma base.
Atividades
10. Sabendo que os prismas têm duas bases paralelas e idênticas entre si, concluímos que as figuras dos itens B, D e F são prismas e as figuras apresentadas nos itens A, C e E, que apresentam uma única base, são pirâmides.
11. A figura geométrica espacial do item A é um prisma cujas bases são triângulos e as faces laterais são retângulos. Com base nas planificações, verificamos que a planificação do item 3 é a que apresenta essas características.
A figura geométrica espacial do item B é uma pirâmide cuja base é um quadrado e as faces laterais são triângulos. A planificação que tem essas características é a do item 2.
A figura geométrica espacial do item C é uma pirâmide cuja base é um pentágono e as faces laterais são triângulos. A planificação do item 1 é a que tem essas características.
12. A planificação de uma pirâmide de base triangular é formada por 4 triângulos. Analisando as planificações, notamos que as figuras dos itens A e C são as que permitem construir a pirâmide de base triangular de modo que não falte nenhuma face ou nenhuma fique sobreposta.
13. De acordo com as figuras apresentadas, podemos montar um quadro.
|
Figura |
Faces |
Vértices |
Arestas |
|---|---|---|---|
|
A |
6 |
8 |
12 |
|
B |
8 |
8 |
14 |
|
C |
9 |
9 |
16 |
|
D |
10 |
16 |
24 |
14. Resposta no final da seção Resoluções.
15. Uma pirâmide de base quadrada possui 5 faces e 5 vértices, portanto a quantidade de faces dessa pirâmide é igual à quantidade de vértices.
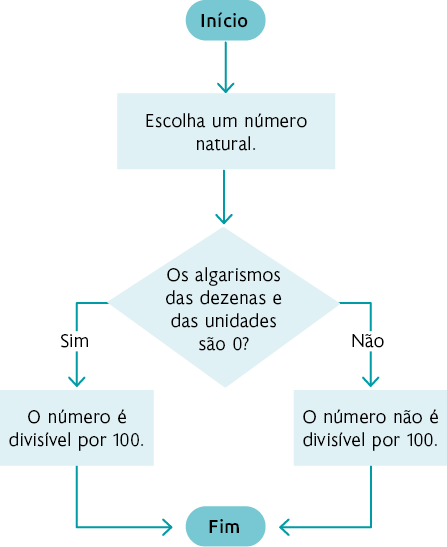
16. O objetivo do fluxograma apresentado é identificar características em relação à quantidade de lados do polígono da base de um prisma ou de uma pirâmide e a quantidade de arestas dessas figuras. Nesse sentido, relacionando as letras às informações apresentadas, obtemos o seguinte fluxograma.
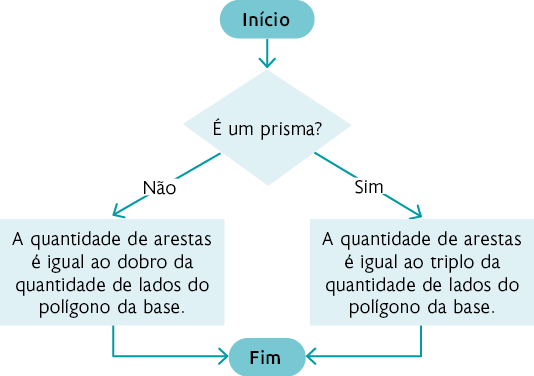
Página LXXIV
a) Sendo uma pirâmide, de acordo com o fluxograma, a quantidade de arestas do poliedro será igual ao dobro da quantidade de lados do polígono da sua base. Nesse caso, como o polígono da base tem 20 lados, então a pirâmide tem 40 arestas, pois .
b) Sendo um prisma, de acordo com o fluxograma, a quantidade de arestas do poliedro é igual ao triplo da quantidade de lados do polígono da base. Nesse caso, como o polígono da base tem 16 lados, então o prisma tem 48 arestas, pois .
17. Como o prisma que será construído terá 9 faces e em um prisma temos duas faces que são bases e as demais são faces laterais, calculamos e concluímos que o polígono da base terá 7 lados, ou seja, é um heptágono. Nas pirâmides, uma face é base e as demais são faces laterais, então o polígono da base terá 10 lados, pois a pirâmide que será construída terá 11 faces e . Portanto, o polígono da base da pirâmide é um decágono e a alternativa b corresponde à resposta correta.
O que eu estudei?
1. Identificando com letras as faces da figura desenhada por Pedro, temos:
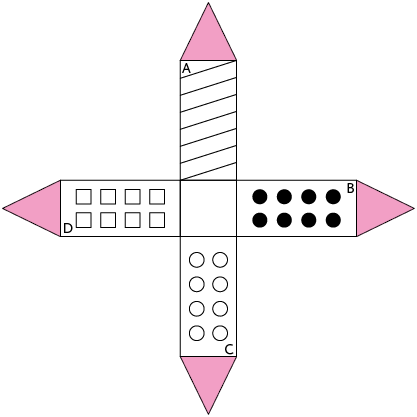
Analisando essa figura e imaginando sua montagem, verificamos que as faces nomeadas por A e C serão opostas, assim como as faces nomeadas com B e D. Então, a imagem 2 não representa uma possível montagem, pois apresenta as faces A e C adjacentes. Além disso, a imagem 4 apresenta as faces A e B em posições opostas. Portanto, as imagens 1, 3 e 5 representam a torre montada por Pedro, ou seja, a alternativa a é a correta.
2. A figura apresentada na alternativa D não representa uma planificação do cubo, pois duas faces estão do mesmo lado na imagem e, em uma tentativa de montagem, essas faces vão ficar sobrepostas e a figura não vai fechar.
3. a) O prisma tem 8 faces laterais, pois a figura A, que representa sua base, é um polígono de 8 lados. A pirâmide tem 6 faces laterais, pois a figura B, que representa sua base, é um polígono de 6 lados.
b) Como os nomes estão relacionados com a quantidade de lados do polígono da base, temos um prisma de base octogonal e uma pirâmide de base hexagonal, respectivamente.
Unidade 5
Frações
Questão 1. Como há 5 partes verdes, então restam 4 partes, pois . Assim, a fração da figura que indica as partes não pintadas de verde é .
Questão 2. Como a figura está dividida em 9 partes e todas estariam pintadas, a fração da figura que poderia corresponder às partes pintadas é .
Questão 3. Como 5 dos 12 estudantes são homens, a fração que representa a razão entre a quantidade de homens e o total de estudantes é .
Questão 4. Como dos mangás será lidos na viagem, então e . Ou, ainda, sabendo que Rosana vai organizar na estante 20 dos 24 mangás, basta realizarmos a subtração para obter a quantidade que Rosana levará na viagem, que é 4 mangás.
Questão 5. Os egípcios conheciam apenas frações unitárias. Os escribas egípcios representavam as frações colocando sobre a notação de um número inteiro um sinal oval alongado. Exemplos:
|
Escrita egípcia |
Nossa escrita |
|---|---|

|
|

|
|

|
Atividades
1. Figura A: , pois a figura foi dividida em 5 partes iguais e 4 estão pintadas.
Figura B: , pois a figura foi dividida em 8 partes iguais e 5 estão pintadas.
Figura C: , pois a figura foi dividida em 8 partes iguais e 6 estão pintadas.
Figura D: , pois a figura foi dividida em 7 partes iguais e 4 estão pintadas.
2. Sabemos que os triângulos são todos iguais. Como a medida da área branca corresponde a 15 triângulos e a medida da área cinza corresponde a 17 triângulos e , a região que tem maior medida de área é a cinza. Nesse caso, a fração do quadrado que representa a região cinza é e a que representa a região branca é .
3. a) A figura A foi dividida em 10 partes iguais. A figura B foi dividida em 100 partes iguais.
Página LXXV
b) • Como há 4 das 10 partes pintadas de roxo, a fração da figura A que representa as partes pintadas de roxo é .
Como há 1 das 10 partes pintada de verde, a fração da figura A que representa as partes pintadas de verde é .
Como há 2 das 10 partes pintadas de laranja, a fração da figura A que representa as partes pintadas de laranja é .
c) • A fração da figura B que representa as partes pintadas de roxo é , pois há 25 das 100 partes da figura B pintadas de roxo.
A fração da figura B que representa as partes pintadas de verde é , pois há 31 das 100 partes da figura B pintadas de verde.
A fração da figura B que representa as partes pintadas de laranja é , pois há 18 das 100 partes da figura B pintadas de laranja.
4. Como o retângulo foi dividido em 18 partes iguais, das quais 11 foram pintadas em azul, a fração que representa as partes pintadas em azul é .
5. a) Quatro quintos: .
b) Sete nonos: .
c) Oito treze avos: .
d) Quatorze centésimos: .
e) Trinta e três milésimos: .
6. a) : três nonos;
b) : oitenta e seis centésimos;
c) : dezenove quatrocentos e um avos;
d) : trinta e cinco trinta e seis avos;
e) : seiscentos e vinte e três milésimos;
f) : vinte e dois centésimos;
g) : quarenta e nove décimos;
h) : quarenta e sete centésimos.
7. a) Subtraindo as questões de Ciências e de Matemática do total de questões, obtemos . Portanto, 10 questões eram de Língua Portuguesa.
b) Como 10 das 60 questões eram de Língua Portuguesa, podemos representar essa situação com a razão .
c) Como havia 20 questões de Ciências e 30 questões de Matemática, podemos representar essa situação com a razão .
8. Primeiramente, devemos determinar a quantidade de meninos e meninas nessa turma do 6º ano. Sabemos que a quantidade de meninas é igual ao dobro da quantidade de meninos. Como há 36 estudantes nessa turma, listamos os divisores de 36, que são 2, 3, 4, 6, 9, 12, 18 e 36. O dobro de cada número é 4, 6, 8, 12, 18, 24, 36 e 72. Somando cada divisor de 36 com o seu respectivo dobro, a única adição que resulta 36 é , ou seja, são 12 meninos e 24 meninas na turma.
a) A quantidade de meninas em relação ao total de estudantes é 24 em 36, ou seja, .
b) A quantidade de meninos em relação ao total de estudantes é 12 em 36, ou seja, .
9. a) A razão entre a quantidade de estudantes de francês e a quantidade de estudantes de inglês é .
b) Não, pois nessa escola, a cada 100 estudantes de inglês, há 40 de francês.
10. Primeiramente dividimos o número aproximado de municípios da Região Nordeste pelo denominador da fração, ou seja, . Em seguida, multiplicamos o resultado obtido pelo numerador, isto é, . Portanto, no estado da Bahia, há aproximadamente 420 municípios.
11. Para determinar a quantidade de blusas vermelhas, primeiramente dividimos a quantidade total de blusas que Érica comprou para sua loja pelo denominador da fração, isto é, . Em seguida, multiplicamos esse resultado pelo numerador da fração, ou seja, . Portanto, 40 blusas eram vermelhas. Sendo assim, 20 blusas não eram vermelhas, pois .
12. Sabemos que . Assim:
a) em de há , pois e .
b) em de há , pois e .
c) em de há , pois e .
d) em de há , pois e .
13. a) Em de há , pois e .
b) Em de há , pois e .
c) Em de há , pois e .
d) Em de há , pois e .
e) Em de há , pois e .
f) Em de há , pois e .
g) Em de há , pois e .
Página LXXVI
h) Em de há , pois e .
14. Devemos determinar quantas figurinhas cada neto de Marcela recebeu, com base nas frações indicadas. Assim, Hugo recebeu de 36 figurinhas, ou seja, 18 figurinhas, pois e ; Igor recebeu de 36 figurinhas, ou seja, 12 figurinhas, pois e ; Júlio recebeu de 36 figurinhas, ou seja, 6 figurinhas, pois e .
Portanto, Hugo recebeu 18 figurinhas, Igor recebeu 12 figurinhas e Júlio recebeu 6 figurinhas.
15. Sabemos que 1 dia tem 24 horas e que 2 dias inteiros tem 48 horas. Como de 24 horas equivale a 8 horas, pois e , uma pessoa dorme em média por dia. Dividindo as horas de 2 dias inteiros pelo tempo em que um adulto dorme , concluímos que são necessários 6 dias para dormir o equivalente às horas de 2 dias inteiros.
16. Como correspondem a 40 gibis, então representa 20 gibis, pois . Além disso, como representa uma parte de cinco partes e equivale a 20 gibis, concluímos que Anderson tem 100 gibis, pois .
17. Resposta pessoal. Sugestão de resposta: Sabendo que metade das figurinhas que André vai distribuir serão dadas ao colega mais velho, metade do restante caberá ao colega mais novo e o que sobrar será distribuído aos outros 2 colegas, quantas figurinhas o colega mais velho vai receber? E quantas serão dadas a cada um dos outros 3 colegas? Respostas: O colega mais velho receberá 40 figurinhas. O colega mais novo receberá 20 figurinhas e cada um dos outros dois receberá 10 figurinhas.
18. a) ;
b) ;
c) ;
d) ;
e) ;
f) .
19. a) As frações próprias, ou seja, aquelas em que o numerador é menor do que o denominador, são frações menores do que um inteiro. Das frações indicadas, e são menores do que um inteiro.
b) As frações e correspondem a 1.
c) As frações , e são impróprias, pois o denominador é menor do que o numerador.
20. a) : fração própria, pois o numerador é menor do que o denominador.
b) : fração imprópria, pois o numerador é maior do que o denominador.
c) : fração imprópria e aparente, pois é caso particular de fração imprópria, cujo numerador é múltiplo do denominador.
d) : fração própria, pois o numerador é menor do que o denominador.
e) : fração imprópria, pois o numerador é maior do que o denominador.
f) : fração imprópria e aparente, pois é caso particular de fração imprópria, cujo numerador é múltiplo do denominador.
21. a) : cinco meios. Representando com figuras, temos:

O número na forma mista correspondente é , que se lê dois inteiros e um meio.
b) : quatro terços. Representando com figuras, temos:
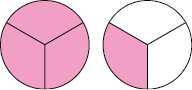
O número na forma mista correspondente é , que se lê um inteiro e um terço.
c) : seis quartos. Representando com figuras, temos:

O número na forma mista correspondente é , que se lê um inteiro e dois quartos.
d) : sete quintos. Representando com figura, temos:
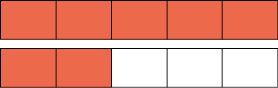
O número na forma mista correspondente é , que se lê um inteiro e dois quintos.
e) : nove sextos. Representando com figura, temos:
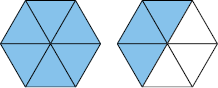
O número na forma mista correspondente é , que se lê um inteiro e três sextos.
f) : doze oitavos. Representando com figura, temos:

O número na forma mista correspondente é , que se lê um inteiro e quatro oitavos.
Página LXXVII
22. Os múltiplos de 9 maiores do que 10 são: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99. Para escrever frações aparentes que sejam equivalentes a 9, basta escrevermos no numerador os múltiplos de 9 e, no denominador, os divisores desses números tal que o quociente seja 9. Algumas sugestões de resposta são: , , , , , , e .
23. Figura A: e ; Figura B: e ; Figura C: e ; Figura D: e .
24. a)
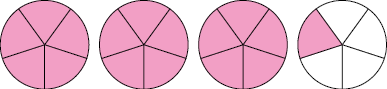
A fração correspondente é .
b)

A fração correspondente é .
c)

A fração correspondente é .
d)

A fração correspondente é .
25. Figura A: ; uma sugestão de fração equivalente é .
Figura B: ; uma sugestão de fração equivalente é .
Figura C: ; uma sugestão de fração equivalente é .
26. A.
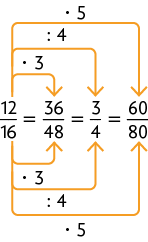
B.
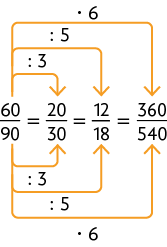
As frações dos itens A e B são equivalentes, pois representam a mesma parte de uma unidade, ou seja, se multiplicarmos ou dividirmos o numerador e o denominador de uma fração por um mesmo número diferente de zero, obtemos uma fração equivalente à inicial.
27. Sabemos que frações equivalentes representam a mesma parte de uma unidade, uma quantidade ou de um inteiro. Assim, se multiplicarmos ou dividirmos o numerador e o denominador de uma fração por um mesmo número diferente de zero, obtemos uma fração equivalente à inicial. Portanto, existem infinitas respostas para esta atividade. Algumas sugestões são:
a)
b)
c)
d)
e)
f)
28. Com base no conceito de equivalência de frações:
a) a fração não é equivalente às demais, pois e nenhuma das três frações é equivalente a .
b) a fração não é equivalente às demais, pois e nenhuma das três frações é equivalente a .
c) a fração não é equivalente às demais, pois e nenhuma das três frações é equivalente a .
29. Observando a primeira e a última fração, verificamos que . Então, para os denominadores A e D devemos ter . Considerando os números apresentados, constatamos que e , pois . Desse modo, , pois , e , pois . Portanto, .
30. a) Como , então , pois . Assim, .
b) Como , então , pois . Além disso, como , então , pois . Portanto, .
c) Como , então , pois . Além disso, como , então , pois . Portanto, .
d) Como , então , pois . Além disso, como , então , pois . Portanto, .
Página LXXVIII
31. a) . Assim, esse item deve ser associado ao número 2.
b) . Assim, esse item deve ser associado ao número 4.
c) . Assim, esse item deve ser associado ao número 3.
d) . Assim, esse item deve ser associado ao número 1.
32. Como equivale a , temos:
a) de , isto é, .
b) de , isto é, .
c) de , isto é, .
d) de , isto é, .
e) de , isto é, .
f) de , isto é, .
Os pares de frações equivalentes entre si são e ; e ; e .
33. a) Como , a quantidade de cartas de Evandro e Ulisses é a mesma. Assim, para determinar a quantidade de cartas de cada um, fazemos . Portanto, Evandro e Ulisses têm 12 cartas cada um e a alternativa correta é a V.
b) Sim, pois elas representam a mesma quantidade do total de cartas.
34. Como 210 de um total de 280 poltronas ficaram ocupadas, a fração que representa a quantidade de poltronas ocupadas é . Entre as frações apresentadas, é a única fração equivalente a , pois .
35. Comparando as quantidades representadas pelas frações, verificamos que . Com isso, constatamos que Sandro e Hugo colaram a mesma quantidade de figurinhas no álbum.
36. a) Como , temos:
tinta azul: de , isto é, .
tinta verde: de , isto é, .
tinta vermelha: de , isto é, .
b) As frações e são equivalentes, pois ao multiplicarmos o numerador e o denominador de por 2 obtemos , e se dividirmos por 3 o numerador e o denominador de obtemos .
37. As frações equivalentes a são: e .
38. Figura A: ; .
Figura B: ; .
Figura C: ; .
Figura D: ; .
39. a)
b)
c)
d)
40. A. Como e , então . Além disso, . Assim, e, portanto, , pois .
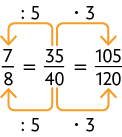
B. Como , então , logo , pois . Além disso, , pois e .
Questão 6. Como Natália percorreu de 40 km, calculamos e . Já Rúbia percorreu , então calculamos e . Portanto, Natália percorreu aproximadamente e Rúbia percorreu, aproximadamente, .
Questão 7. Como nenhuma das frações tem denominador igual, devemos obter as frações equivalentes com o mesmo denominador e, em seguida, compará-las.
a) Obtendo a fração equivalente a e a com denominadores iguais, temos e . Como , a maior fração é .
b) Obtendo a fração equivalente a e a com denominadores iguais, temos e . Como , a maior fração é .
Página LXXIX
c) Obtendo a fração equivalente a e com denominadores iguais, temos e . Como , a maior fração é .
Atividades
41. Como os denominadores das frações são iguais, basta compararmos os numeradores.
a) Como , a maior fração é .
b) Como , a maior fração é .
c) Como , a maior fração é .
d) Como , a maior fração é .
e) Como , a maior fração é .
f) Como , a maior fração é .
42. a) O total de quadradinhos pode ser obtido multiplicando a quantidade de linhas pela quantidade de colunas, assim , isto é, 140 quadradinhos.
14 quadradinhos são pintados de amarelo, logo a fração correspondente é .
42 quadradinhos são pintados de azul, logo a fração correspondente é .
56 quadradinhos são pintados de rosa, logo a fração correspondente é .
28 quadradinhos são pintados de vermelho, logo a fração correspondente é .
b) Como o denominador é o mesmo, basta compararmos os numeradores de cada fração.
Portanto, escrevendo em ordem crescente, temos: , ou, de maneira simplificada, .
43. Como o denominador é o mesmo, basta compararmos os numeradores de cada fração. Escrevendo-as em ordem decrescente, temos . Como cada unidade está dividida em 5 partes iguais, associando cada fração à letra adequada na reta numérica, temos:

44. a) A equipe laranja, pois .
b) Como os denominadores são iguais, para escrever em ordem crescente comparamos os numeradores: , , , .
45. Para determinar qual dos dois estava mais próximo de Juiz de Fora, devemos obter as frações equivalentes cujos denominadores são iguais.
Ronaldo:
Mário:
Como , concluímos que Ronaldo percorreu o maior trajeto.
46. a) Como os denominadores são iguais, ordenamos as frações comparando os numeradores. Assim, temos , e .
b) Obtemos frações com denominadores iguais e comparamos os numeradores.
Como , as frações em ordem crescente são , , .
c) Obtemos frações com denominadores iguais e comparamos os numeradores.
Como , as frações em ordem crescente são , , .
d) Obtemos frações com denominadores iguais e comparamos os numeradores.
Como , as frações em ordem crescente são , , 1.
47. Comparando as frações em cada item, temos:
a)
b)
c) Como e , então .
d) Como , então .
e) Como , então .
f) Como e , então .
g) Como e , então .
h) Como , e , então .
Página LXXX
48. Sim, pois as frações , e são equivalentes, ou seja, .
49. a) Como as frações possuem denominadores diferentes, obtemos frações equivalentes com mesmo denominador para compará-las.
Sílvio: .
Isadora: .
Como , então . Portanto, Sílvio leu a maior quantidade de páginas.
b) Em ambos os casos, basta dividir a quantidade de páginas pelo denominador e multiplicar pelo numerador. Assim, temos:
Sílvio: e . Portanto, Sílvio leu 42 páginas.
Isadora: e . Portanto, Isadora leu 36 páginas.
50. Para compararmos as frações, primeiramente devemos obter frações equivalentes com denominador comum.
Azul: .
Vermelho: .
Amarelo: .
a) Como a maior fração é , concluímos que a maior parte dos balões era vermelha.
b) Como a menor fração é , concluímos que a menor parte dos balões era azul.
51. a) Primeiramente, devemos encontrar frações equivalentes com denominador comum entre e .
Adriana: .
Michele: .
Como , então . Portanto, Michele foi quem acertou mais questões.
b) Como o denominador comum entre 10 e 4 é 20, sabemos que Adriana acertou 15 das 20 questões da prova de Matemática e Michele acertou 16 das 20 questões dessa mesma prova.
52. a) Para representarmos a menor quantidade, devemos escrever o menor número apresentado no numerador e o maior número no denominador. Assim, a fração que representa a menor quantidade é .
b) Para representarmos a maior quantidade, devemos escrever o maior número apresentado no numerador e o menor número no denominador. Assim, a fração que representa a maior quantidade é .
Questão 8. Devemos verificar no gráfico quantos estudantes preferem cada gênero literário e, em seguida, escrever a fração decimal correspondente.
a) Gênero policial: , ou seja, 14%.
b) Gênero romance: , ou seja, 19%.
c) Gênero suspense: , ou seja, 16%.
d) Gênero outros: , ou seja, 13%.
Questão 9. Resposta pessoal.
Questão 10.
a) Como a bicicleta custa R$ 400,00 e o valor do desconto é R$ 60,00, calculamos . Portanto, o valor da bicicleta com desconto é R$ 340,00.
b) Para calcular 10% de R$ 400,00, como , fazemos e . Então, , ou seja, a bicicleta custaria R$ 360,00 com 10% de desconto.
Atividades
53. a)
b)
c)
d)
e)
f)
54. Como as figuras são formadas por 100 quadradinhos, temos, na figura A, 22 quadradinhos coloridos de 100, ou seja, , e na figura B, 82 quadradinhos coloridos de 100, ou seja, .
55. a)
b)
c)
d)
e)
f)
56. a)
b)
c)
d)
Página LXXXI
e)
f)
57. a) Das figurinhas que Paulo tem, calculamos as seguintes porcentagens, que representam a quantidade de figurinhas de:
animais: .
plantas: .
carros: .
b) Adicionando as porcentagens referentes às quantidades do item anterior, temos . Subtraindo de 100%, temos . Portanto, a porcentagem correspondente é 5% e a fração decimal é .
58. a) Devemos determinar a fração correspondente a cujo denominador seja 100, isto é, . Portanto, César já economizou 25% do preço do violão.
b) Realizando os cálculos, temos: . Portanto, César já economizou R$ 125,00.
59. a) Como 10% de R$ 300,00 é 30, então 20% é R$ 60,00.
b) Como 10% de R$ 500,00 é 50, então 30% é R$ 150,00.
c) Como 10% de R$ 200,00 é 20, então 40% é R$ 80,00.
d) Como 10% de R$ 700,00 é 70, então 50% é R$ 350,00.
e) Como 10% de R$ 600,00 é 60, então 60% é R$ 360,00.
f) Como 10% de R$ 100,00 é 10, então 70% é R$ 70,00.
60. Resposta pessoal. Sugestão de resposta: Quantos reais Pedro vai pagar de entrada? Qual será o valor de cada parcela?
Respostas: R$ 116,00; R$ 116,00.
61. a) Realizando os cálculos, temos: 55% de , pois e .
Portanto, 660 mulheres trabalham nessa empresa.
b) Subtraindo a porcentagem de mulheres que trabalham nessa empresa de 100%, temos , ou seja, 45% dos funcionários são homens.
Como 660 dos 1.200 funcionários são mulheres, fazemos , ou seja, 540 funcionários são homens.
c) Como 45% dos funcionários dessa empresa são homens e 55% são mulheres, a fração decimal que representa a quantidade de homens é e a de mulheres é .
62. a) Foram gastos com o chuveiro elétrico, aproximadamente, R$ 60,00, pois calculando 30% de R$ 200,00, temos e .
b) Como a porcentagem gasta com a geladeira é a mesma gasta com o chuveiro elétrico, o valor gasto em reais é o mesmo, ou seja, R$ 60,00.
c) Foram gastos com as lâmpadas, aproximadamente, R$ 30,00, pois calculando 15% de R$ 200,00, temos e .
d) Foram gastos com a lavadora, aproximadamente, R$ 20,00, pois calculando 15% de R$ 200,00, temos e .
e) Como a porcentagem gasta com os outros aparelhos é a mesma gasta com as lâmpadas, o valor gasto em reais é o mesmo, ou seja, R$ 30,00.
63. a) ;
b) ;
c) ;
d) ;
e) ;
f) .
64. a) Adicionando as frações, temos . Portanto, da parede foi azulejada por Rafael nesse dia.
b) Como a fração representa a parede totalmente coberta, fazemos . Portanto, falta azulejar das paredes.
65. a) Nesse caso, podemos substituir o por qualquer número. Sugestão de resposta: .
b) Podemos substituir o por qualquer número de 1 a 7, de modo que a soma dos numeradores seja 8. Sugestão de resposta: .
c) No numerador, podemos substituir o por qualquer número desde que a diferença entre os numeradores seja o número 9. No denominador, . Sugestão de resposta: .
d) Podemos substituir o por qualquer número desde que a diferença entre os numeradores seja um número maior do que 9. Sugestão de resposta: .
e) Podemos substituir o por qualquer número desde que a soma entre os numeradores seja um número menor do que 18. Sugestão de resposta: .
f) No numerador, podemos substituir o por qualquer número desde que a diferença entre os numeradores seja 6. No denominador, . Sugestão de resposta: .
Página LXXXII
66. Existem várias possibilidades de respostas para esta atividade.
a) A soma entre os numeradores deve ser igual a 6 e o denominador deve ser 8. Sugestão de resposta: .
b) A diferença entre os numeradores deve ser 2 e o denominador deve ser 12. Sugestão de resposta: .
c) Sugestão de resposta: .
d) Sugestão de resposta: .
67. a) O recipiente da figura A está dividido em 4 marcações e o líquido contido nele alcança a 3ª marcação. Portanto, a fração é . O recipiente da figura B está dividido em 6 marcações e o líquido contido nele alcança a 1ª marcação. Portanto, a fração que representa a quantidade de líquido é . O recipiente da figura C está dividido em 5 marcações e o líquido contido nele alcança a 2ª marcação. Portanto, a fração é . O recipiente da figura D está dividido em 7 marcações e o líquido contido nele alcança a 4ª marcação. Portanto, a fração é .
b) Na figura A, 1 das 4 marcações não foi preenchida com líquido, logo a fração que representa a parte não preenchida é . Na figura B, 5 das 6 marcações não foram preenchidas com o líquido, logo a fração é . Na figura C, 3 das 5 marcações não foram preenchidas com o líquido, logo a fração é . Na figura D, 3 das 7 marcações não foram preenchidas com o líquido, logo a fração é .
68. Resposta pessoal. Sugestão de resposta: Qual será a medida de área ocupada pelo jardim e pela praça? Qual é a medida de área ocupada pelo estacionamento?
Respostas: ; .
69. a)
b)
c)
d)
e)
f)
g)
h)
70. Para facilitar a organização na reta numérica, vamos obter os resultados com mesmo denominador.
a)
b)
c)
d)
Organizando os resultados obtidos na reta numérica, temos:

71. a) Devemos juntar a quantidade de etanol abastecida com a quantidade de gasolina abastecida. Assim:
, ou seja, a fração que representa a parte abastecida é .
b) O tanque totalmente abastecido pode ser representado por . Desse modo, calculamos . Portanto, faltou abastecer .
72. a) Adicionando a quantidade de quibes e coxinhas, temos:
Logo, a fração que representa a parte da encomenda que já está pronta é .
b) Para determinar a fração que representa a quantidade de empadas, calculamos:
Portanto, a fração da encomenda que representa a quantidade de empadas é .
c) A quantidade de empadas é dada por:
de , pois e .
Nessa encomenda, devem ter 200 empadas.
73. Adicionando as quantidades de fatias que os três amigos comeram, temos:
Como a fração que representa o total de pedaços é , fazemos: . Portanto, a fração que representa os pedaços que sobraram de pizza é .
Página LXXXIII
74. Subtraindo da quantidade de água que foi colocada no aquário a quantidade retirada, obtemos:
a) A fração da medida de capacidade do recipiente que tem água é .
b) Para determinarmos a capacidade do aquário que não tem água, calculamos . Portanto, da capacidade do aquário estão sem água.
75. Resposta pessoal. Sugestão de respostas:
Situação 1: Quantos ingressos inteiros foram vendidos? E quantas meias-entradas foram vendidas?
Respostas: 252 ingressos; 147 ingressos.
Situação 2: Que fração representa a quantidade de estudantes que votou no candidato C? Qual dos candidatos ganhou a presidência? E a vice-presidência?
Respostas: A fração representa a quantidade de estudantes que votou no candidato C; O estudante A ganhou a presidência e o estudante C, a vice-presidência.
O que eu estudei?
1. Como o total de triângulos é 66, a fração que representa a quantidade de triângulos pintados de:
a) roxo, em relação ao total de triângulos, é .
b) verde, em relação ao total de triângulos, é .
c) amarelo, em relação ao total de triângulos, é .
2. Como 28 dos 32 estudantes jogaram futebol, a fração que representa essa quantidade é , ou de maneira simplificada, , isto é, da turma jogaram futebol.
3. Realizando os cálculos, temos de , pois e . Portanto, nessa viagem foram consumidos de combustível.
4. Sabendo que é equivalente a , fazemos os cálculos a seguir.
a) de , isto é, .
b) Como , então de , isto é, .
c) Como , então de , isto é, .
d) Como , então de , isto é, .
5. a)
b)
c)
d)
6. a) Determinando as frações equivalentes com denominador comum para a quantidade de questões que Paulo e Laís acertaram, temos:
Paulo:
Laís:
Portanto, Laís acertou mais questões, pois .
b) Para ser aprovado na 1ª fase do concurso, os candidatos devem acertar das questões, pois . Sendo assim, Paulo não foi aprovado na primeira fase do concurso, pois .
c) Laís foi aprovada na 1ª fase, pois , ou seja, ela acertou uma quantidade maior do que o mínimo necessário de questões.
d) Como o denominador das frações equivalentes é 90, basta subtrairmos do mínimo de questões necessárias para passar para a próxima fase a quantidade de acertos de Paulo, ou seja, . Logo Paulo deveria ter acertado 4 questões a mais.
7. Como Ricardo tem 60% da quantidade de selos de Renata, ou seja, de 500, calculamos e . Assim, ele tem 300 selos. Como José tem 30% da quantidade de selos de Ricardo, ou seja, de 300, calculamos e . Portanto, José tem 90 selos.
8. a)
b)
c)
d)
e)
f)
g)