Página LXXXIV
Unidade 6
Números decimais
Questão 1. Considerando a quantidade de zeros do denominador de cada fração, temos:
a)
b)
c)
d)
e)
Questão 2. Os estudantes podem representar com diferentes tipos de figuras. Sugestão de resposta:

Fração decimal: .
Número na forma mista: .
Questão 3. Como o algarismo 8 ocupa a ordem das unidades no número 8,9, seu valor posicional é 8. Já no número 4,68, o algarismo 8 ocupa a ordem dos centésimos, então seu valor posicional é 0,08. Por fim, o algarismo 8 ocupa a ordem dos décimos no número 17,851, logo seu valor posicional é 0,8.
Questão 4. Há várias maneiras de decompor os números apresentados. Apresentamos uma delas.
• 72,08: .
• 5,115: .
Atividades
1. De acordo com a quantidade de partes em que cada cubo foi dividido, as partes amarelas podem ser representadas por:
A . ou .
B . ou .
C . ou .
2. Completando o quadro com a fração decimal ou o número decimal que falta, temos:
| Fração decimal | Número decimal |
|---|---|
|
1,76 |
|
|
58,221 |
|
|
4.710,8 |
|
|
1,008 |
3. De acordo com as frações decimais apresentadas, temos:
Morango: . Lê-se: noventa centésimos.
Pera: . Lê-se: oitenta e cinco centésimos.
Banana: . Lê-se: setenta e dois centésimos.
Melancia: . Lê-se: noventa e quatro centésimos.
4. Cada recipiente foi dividido em 10 partes iguais. Assim, as frações que representam a quantidade de água em cada um deles pode ser representada por:
A . ou .
B . ou .
5. Cada retângulo representa uma unidade. Considerando o retângulo totalmente pintado dividido em 4 partes iguais como no outro retângulo, temos , ou seja, . A fração que representa as partes pintadas de verde é e o número decimal é 1,75. Além disso, como , o número decimal que corresponde às partes pintadas de verde é 1,75.
6. Utilizando a régua para medir os segmentos, obtemos as seguintes medidas de comprimento: segmento CD: ; segmento EF: ; segmento GH: ; segmento IJ: .
7. a) De acordo com a imagem, a medida da temperatura é .
b) Uma sugestão de resposta para a decomposição do número 38,3 é .
8. Fazendo a correspondência entre a fração decimal e o número decimal, temos:
a)
b)
c)
9. Sabemos que , ou seja, . Como o golpe da tamburutaca leva aproximadamente , fazemos: . Portanto, a alternativa E é a correta.
10. Como 1 centavo é igual a do real, 5 centavos podem ser representados por , ou ainda, 0,05; 10 centavos podem ser representados por , ou ainda, 0,10; 25 centavos podem ser representados por , ou ainda, 0,25; 50 centavos podem ser representados por , ou ainda, 0,50. Portanto, escrevemos: no item A, ou 0,05; no item B, ou 0,10; no item C, ou 0,25; no item D, ou 0,50.
11. Representando os números de cada balança no quadro de ordens, temos:
|
Parte inteira |
Parte decimal |
||||
|---|---|---|---|---|---|
|
D Dezena |
U Unidade |
, |
d Décimo |
c Centésimo |
m Milésimo |
|
1 |
, |
4 |
8 |
6 |
|
|
0 |
, |
6 |
7 |
4 |
|
|
2 |
, |
5 |
0 |
8 |
|
|
0 |
, |
9 |
9 |
5 |
|
Escrevendo esses números por extenso.
A. 1,486: um inteiro e quatrocentos e oitenta e seis milésimos;
B. 0,674: seiscentos e setenta e quatro milésimos;
C. 2,508: dois inteiros e quinhentos e oito milésimos;
D. 0,955: novecentos e noventa e cinco milésimos.
12. Relacionando o número decimal à fração irredutível equivalente, temos:
a)
b)
c)
d)
e)
f)
Página LXXXV
13. Fazendo a decomposição dos números decimais de duas maneiras diferentes, temos:
a) ;
b) ;
c) ;
d) ;
14. Compondo os números indicados, temos:
a)
b)
c)
d)
15. Escrevendo o número decimal correspondente a cada fração e por extenso, temos:
a) ; oito décimos.
b) ; dois inteiros e quinze centésimos.
c) ; seis inteiros e quatro milésimos.
d) ; três inteiros e noventa e cinco centésimos.
e) ; um inteiro e quatro décimos.
f) ; cinco inteiros e sessenta e seis centésimos.
16. Para determinar a quantia economizada, efetuamos uma adição, ou seja, . Portanto, Josemar economizou R$ 788,80.
17. Resposta pessoal. Sugestão de resposta: Mariana quer economizar R$ 50,00 a fim de comprar um presente de aniversário para sua amiga. Ela já tem a quantia representada pela cédula e as moedas. Quanto falta para Mariana obter a quantia necessária? Resposta: Faltam R$ 25,45.
18. Comparando os números indicados, temos:
a) O número 3,3 é maior do que 3 e menor do que 4, pois 3,3 está à direita do 3 na reta numérica e antes do 4.
b) O número 5,55 é maior do que 4 e maior do que 5, pois 5,55 está à direita do 4 e do 5 na reta numérica.
c) A fração é menor do que 1 e menor do que 2, pois e está à esquerda do 1 e do 2 na reta numérica.
d) A fração é maior do que 8 e menor do que 9, pois .
19. Relacionando os números apresentados com as letras indicadas na reta numérica, temos:
A: 1,375; B: 1,8; C: 2,50; D: 3,7; E: ; F: 4,75.
Substituindo na reta numérica, obtemos:
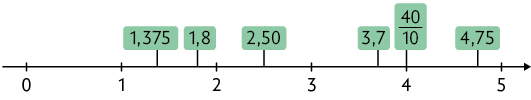
20. Substituindo os números que estão na posição correta, temos:
A.
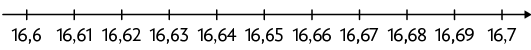
B.
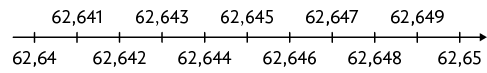
21. Fazendo comparação em cada quadro, verificamos que os números de mesmo valor em cada item são:
a) 7,00 e 7.
b) 0,01 e 0,010.
c) 5,03 e 5,030.
d) 3,100 e 3,10.
22. a) Na loja A, a lata de tinta custa R$ 399,90; na loja B, custa R$ 340,00; na loja C, custa R$ 335,99. Comparando os preços, verificamos que o preço da lata de tinta é maior na loja B e menor na loja C.
b) O rolo para pintura custa R$ 12,94 na loja A, R$ 15,50 na loja B e R$ 18,81 na loja C. Portanto, o maior preço é na loja C e o menor preço na loja A.
c) Ana vai comprar a lata de tinta na loja C e o rolo para pintura na loja A, pois são os produtos de menor preço.
23. Resposta no final da seção Resoluções.
24. Comparando as medidas de massa indicadas nas balanças, verificamos que Marina comprou de batata, Renata comprou e Paulo comprou . Portanto, Renata comprou mais quilogramas de batata e Marina comprou menos.
25. Comparando os números apresentados, temos:
a)
b)
c)
d)
e)
f)
g)
h)
i)
26. Observando o quadro, podemos verificar que:
a) Maria pode ser classificada com obesidade grau II, pois seu IMC (36,3) está entre 35 e 35,9.
b) Laís pode ser classificada com peso normal, pois seu IMC (24,2) está entre 18,5 e 24,9.
c) Raul pode ser classificado com obesidade grau II, pois seu IMC (38,9) está entre 35 e 35,9.
d) Felipe pode ser classificado com obesidade grau III, pois seu IMC (42,5) está acima de 40.
e) Thaís pode ser classificada com sobrepeso, pois seu IMC (27,5) está entre 25 e 29,9.
f) João pode ser classificado com obesidade grau III, pois seu IMC (43,2) está acima de 40.
27. De acordo com a posição das letras na reta numérica, podemos verificar que:
a) W não é maior do que X, pois W está à esquerda de X.
b) U é maior do que 4 e menor do que 5, pois U está entre 4 e 5.
c) Y não é maior do que K, pois Y está à esquerda de K.
d) X não é maior do que Z, pois X está à esquerda de Z.
e) Z é menor do que Y, pois Z está à esquerda de Y.
f) K não é menor do que 9, pois K está à direita de 9.
Página LXXXVI
28. Utilizando uma única vez cada algarismo e a vírgula, verificamos que:
a) 0,158 é o menor número possível de ser formado.
b) 1,580 é o único número possível de ser formado que esteja entre 1,55 e 1,8.
c) os possíveis números que podem ser formados de modo que o 5 tenha valor posicional 0,005 são: 0,185; 0,815; 1,085; 1,805; 8,015 e 8,105. Escrevendo esses números em ordem crescente, obtemos:
29. Resposta no final da seção Resoluções.
O que eu estudei?
1. De acordo com as medidas de temperaturas indicadas, temos:
1º dia:
2º dia:
3º dia:
2. Como , temos:
a)
b)
c)
d)
e)
3. Escrevendo a fração decimal e o número decimal correspondente a cada fração, temos:
a)
b)
c)
d)
e)
f)
4. Fazendo a equivalência entre as duas retas, constatamos que:
a) , pois representam o mesmo número.
b) C não é igual a D, pois representam números diferentes.
c) E não é menor do que F, pois representam o mesmo número.
d) A não é maior do que B, pois representam o mesmo número.
e) D não é menor do que C, pois D está à direita de C.
5. Adicionando as quantias representadas pelas cédulas e pelas moedas, concluímos que Gabriela poupou R$ 121,55, Rose poupou R$ 125,50 e Bárbara poupou R$ 112,25. Escrevendo as quantias em ordem crescente, obtemos
Unidade 7
Operações com números decimais
Questão 1. Para obter o valor do desconto, precisamos subtrair o valor da lapiseira com desconto do valor sem desconto.
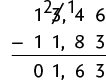
Portanto, o desconto sobre o preço da lapiseira é R$ 1,63.
Atividades
1. Vamos efetuar os cálculos de cada item utilizando o algoritmo usual da adição e o da subtração.
a)
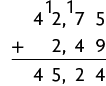
Ou seja, .
b)
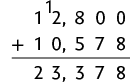
Ou seja, .
c)
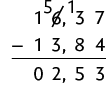
Ou seja, .
d)
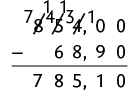
Ou seja, .
e)
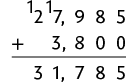
Ou seja, .
f)
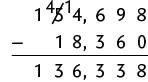
Ou seja, .
2. Para obter a soma exata, efetuamos os cálculos com o algoritmo usual da adição.
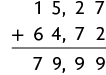
A diferença entre o resultado exato e o aproximado é 0,01.
Página LXXXVII
3. Devemos arredondar as parcelas para a unidade mais próxima, como fez Leonardo.
a) Arredondando os números 4,85 e 7,15 para a unidade mais próxima, obtemos 5 e 7, respectivamente. A soma dos números arredondados é . A soma exata é .
b) Arredondando os números 10,79 e 9,4 para a unidade mais próxima, obtemos 11 e 9, respectivamente. A soma dos números arredondados é . A soma exata é .
c) Arredondando os números 0,94 e 2,09 para a unidade mais próxima, obtemos 1 e 2, respectivamente. A soma dos números arredondados é . A soma exata é .
d) Arredondando os números 14,23 e 50,59 para a unidade mais próxima, obtemos 14 e 51, respectivamente. A soma dos números arredondados é . A soma exata é .
e) Arredondando os números 26,34 e 3,64 para a unidade mais próxima, obtemos 26 e 4, respectivamente. A soma dos números arredondados é . A soma exata é .
f) Arredondando os números 1,25 e 5,95 para a unidade mais próxima, obtemos 1 e 6, respectivamente. A soma dos números arredondados é . A soma exata é .
4. Para determinar a medida do perímetro das figuras, devemos adicionar a medida de cada um de seus lados. Com isso, o perímetro da figura A mede , pois ; o perímetro da figura B mede , pois ; o perímetro da figura C mede , pois .
5. a) Comparando as medidas dos perímetros, constatamos que a figura B é a que tem a menor medida.
b) As figuras A e C apresentam medidas de perímetro iguais a .
6. a) Como cada número, do segundo em diante, é obtido adicionando 2,5 ao número anterior, os próximos três números da sequência são: 15,9; 18,4; 20,9.
b) Como cada número, do segundo em diante, é obtido subtraindo 4,5 do número anterior, os próximos três números da sequência são: 59,7; 55,2; 50,7.
c) Como cada número, do segundo em diante, é obtido adicionando 1,321 ao número anterior, os próximos três números da sequência são: 6,748; 8,069; 9,39.
d) Como cada número, do segundo em diante, é obtido subtraindo 6,48 ao número anterior, os próximos três números da sequência são: 67,8; 61,32; 54,84.
e) Como cada número, do segundo em diante, é obtido adicionando 1,85 ao número anterior, os próximos três números da sequência são: 148,15; 150; 151,85.
f) Como cada número, do segundo em diante, é obtido subtraindo 1,987 ao número anterior, os próximos três números da sequência são: 4,824; 2,837; 0,85.
7. a) Arredondando os números 3,17 e 1,42 para a unidade mais próxima, obtemos 3 e 1, respectivamente. A soma dos números arredondados é .
b) Arredondando os números 5,83 e 2,35 para a unidade mais próxima, obtemos 6 e 2, respectivamente. A soma dos números arredondados é .
c) Arredondando os números 2,78 e 4,19 para a unidade mais próxima, obtemos 3 e 4, respectivamente. A soma dos números arredondados é .
d) Arredondando os números 0,89 e 1,26 para a unidade mais próxima, obtemos 1 e 1, respectivamente. A soma dos números arredondados é .
e) Arredondando os números 8,9 e 1,38 para a unidade mais próxima, obtemos 9 e 1, respectivamente. A soma dos números arredondados é .
f) Arredondando os números 4,56 e 0,48 para a unidade mais próxima, obtemos 5 e 0, respectivamente. A soma dos números arredondados é .
8. Para sabermos se Neide poderá comprar a camiseta e a saia, precisamos primeiramente adicionar os dois itens, ou seja, . Como R$ 86,30 R$ 87,00, concluímos que Neide poderá comprar a camiseta e a saia. Além disso, ela receberá R$ 0,70 de troco, pois .
9. a) Arredondando para a unidade mais próxima o preço do pacote de macarrão, obtemos 4, e arredondando o preço do pacote de sal, obtemos 16. Como os preços de uma dúzia de ovos e um pacote de farinha de trigo já foram arredondados por Catarina, basta somarmos todos os preços arredondados, ou seja, . Assim, Catarina vai gastar, aproximadamente, R$ 23,00.
b) Efetuando a adição dos preços exatos, obtemos R$ 23,23, pois . A diferença entre a soma com os valores exatos e a dos preços arredondados é dada por: . Logo, a diferença entre os valores é R$ 0,23.
10. Para determinar a medida da massa da caixa C, subtraímos a medida da massa indicada na balança com as caixas A e B da medida indicada na balança com as caixas A, B e C , ou seja, . Assim, a massa da caixa C mede .
Para determinar a medida da massa da caixa A, subtraímos a medida da massa da caixa C da medida indicada na balança com as caixas A e C , ou seja, . Assim, a massa da caixa A mede .
Para determinar a medida da massa da caixa B, uma possibilidade é subtrair a medida de massa da caixa A da medida de massa indicada na balança com as caixas A e B , ou seja, . Assim, a massa da caixa B mede .
11. Resposta pessoal. Sugestão de resposta: Em seu caderno, determine quantos reais uma pessoa gastaria ao comprar uma unidade de cada produto do quadro no supermercado A.
Resposta: Gastaria R$ 40,90.
Página LXXXVIII
12. a) Para determinar quantos reais Rute pagou pelos 3 buquês, fazemos:
. Portanto, Rute pagou R$ 394,66 na compra dos 3 buquês.
b) Para determinar o troco que Rute recebeu, calculamos . Portanto, Rute recebeu de troco R$ 5,34.
13. a) Devemos subtrair o valor da calça jeans em promoção do preço dela sem desconto, ou seja, . De modo semelhante, calculamos o desconto no preço do macacão, que é dado por . Portanto, a loja está dando R$ 12,99 de desconto no preço da calça jeans e R$ 11,15 de desconto no preço do macacão.
b) Primeiramente, devemos determinar, separadamente, quanto Lilian gastaria se os produtos não estivessem com desconto e, em seguida, qual seria o gasto com desconto. Para isso, calculamos e . Em seguida, efetuamos uma subtração com os resultados obtidos, ou seja, . Portanto, Lilian gastaria R$ 35,44 a mais se não tivesse comprado os produtos na promoção.
c) Resposta pessoal. Sugestão de resposta: Se todos os produtos fossem comprados na promoção, quantos reais seriam gastos? Resposta: Seriam gastos R$ 252,95.
14. a) Comparando as medidas indicadas, constatamos que Erika de Souza é a jogadora mais alta, pois mede de altura, e Débora da Costa é a mais baixa, pois mede de altura.
b) Efetuando uma subtração com as medidas de altura de Erika de Souza e Débora da Costa, temos: , ou seja, a diferença é .
c) Organizando em ordem crescente o nome das jogadoras da seleção brasileira de basquetebol em 2019, de acordo com a medidas de suas alturas, temos: Débora da Costa, com ; Tainá Paixão, com ; Patrícia Teixeira, com ; Rapha Monteiro, com ; Clarissa dos Santos, com ; Erika de Souza, com .
Questão 2. O item A utiliza a sequência da calculadora para efetuar ; o item B utiliza a sequência da calculadora para efetuar ; o item C utiliza a sequência da calculadora para efetuar ; o item D utiliza a sequência da calculadora para efetuar . Assim, a alternativa correta é a C.
Questão 3. Para efetuar , devemos digitar a seguinte sequência de teclas na calculadora:
Para efetuar , devemos digitar a seguinte sequência na calculadora:
Atividades
15. a)
b)
c)
d)
e)
f)
16. Devemos multiplicar por 1.000 as medidas em quilograma de cada item para obter as medidas em grama.
a) , isto é, .
b) , isto é, .
c) , isto é, .
d) , isto é, .
e) , isto é, .
f) , isto é, .
17. Devemos substituir cada símbolo pelo fator correspondente e, em seguida, efetuar as multiplicações para obter o valor de cada letra. Fazendo as substituições adequadas, obtemos:
a) . Portanto, .
b) . Portanto, .
c) . Portanto, .
d) Sabendo que , obtemos . Portanto, .
e) Sabendo que , obtemos . Portanto, .
18. a) 1,1 milhão corresponde a
b) 214,3 milhões correspondem a
c) 5,01 milhões correspondem a
Questão 4. O item A utiliza a sequência de teclas da calculadora para efetuar ; o item B utiliza a sequência de teclas da calculadora para efetuar ; o item C utiliza a sequência de teclas da calculadora para efetuar ; o item D utiliza a sequência de teclas da calculadora para efetuar . Assim, a alternativa correta é D.
Questão 5. Para efetuar , devemos digitar a seguinte sequência de teclas na calculadora:
Para efetuar , devemos digitar a seguinte sequência na calculadora:
Atividades
19. Sabemos que na divisão de um número decimal por uma potência de 10 (10, 100, 1.000, ...), a vírgula desloca-se para a esquerda conforme a quantidade de zeros do divisor. Então:
a) , pois o divisor tem um zero.
b) , pois o divisor tem dois zeros.
c) , pois o divisor tem dois zeros.
d) , pois o divisor tem três zeros.
e) , pois o divisor tem três zeros.
f) , pois o divisor tem três zeros.
Página LXXXIX
20. Realizando os cálculos apresentados em cada item, temos:
A:
B:
C:
D:
1:
2:
3:
4:
Portanto, os itens que apresentam os mesmos resultados são A e 2; B e 1; C e 3; D e 4.
21. Para obter o valor de cada letra na segunda coluna, devemos dividir por 1.000 os valores da primeira coluna. Efetuando os cálculos e substituindo cada letra pelo número decimal correspondente, temos:
|
Quilogramas (kg) |
Toneladas (t) |
|---|---|
|
350 |
0,35 |
|
625 |
|
|
979 |
|
|
1.502 |
|
|
3.450 |
|
|
5.600 |
|
|
10.238 |
|
|
15.500 |
|
|
15.890 |
22. a)
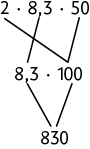
b)
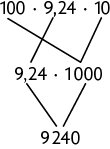
c)
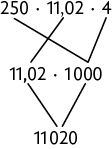
d)
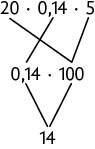
23.
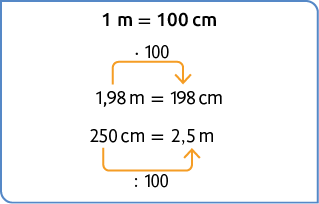
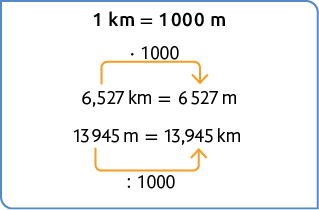
24. a) Para obter o número que, multiplicado por 10, resulte em 123,58, calculamos .
b) Para obter o número que, dividido por 1.000, resulte em 47,654, calculamos .
c) Para obter o número que, multiplicado por 100, resulte em 0,0392, calculamos .
Questão 6. Usando o algoritmo, vamos aplicar a multiplicação desconsiderando a vírgula e, em seguida, acrescentamos a vírgula ao resultado para que a quantidade de casas decimais seja igual à quantidade de casa decimais do fator decimal. Realizando as multiplicações, temos:
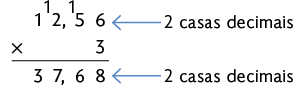
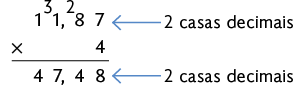
Portanto, Simone gastou R$ 37,68 na compra de de brim e R$ 47,48 na compra de de voal.
Página XC
Atividades
25. Efetuando os cálculos com o algoritmo usual da multiplicação, temos:
a)
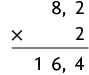
b)
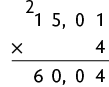
c)
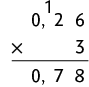
d)

e)
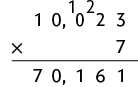
f)
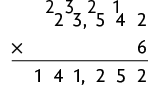
26. a) Multiplicando por 15 segundos a medida da distância percorrida em 1 segundo, obtemos . Portanto, uma pessoa percorre, aproximadamente, 15 segundos.
b) Como 1 hora tem 3.600 segundos, calculamos . Portanto, ao caminhar por 1 hora uma pessoa percorre, aproximadamente, de medida de distância.
Como , então . Portanto, ao caminhar durante 1 hora, uma pessoa percorre, aproximadamente, .
27. a) Devemos multiplicar por R$ 0,61 o consumo de Ronaldo em cada mês para obter o total da fatura. Assim, efetuamos para obter o total da fatura de maio, que é R$ 100,65, e efetuamos para obter o total da fatura de abril, que é R$ 105,53.
b) Calculando a diferença entre os dois valores, obtemos , ou seja, R$ 4,88.
c) Primeiramente, devemos determinar o consumo de Ronaldo em março, ou seja, . Em seguida, adicionamos as notas que ele usou para pagar, isto é, . Por fim, calculando , concluímos que Ronaldo recebeu R$ 18,13 de troco.
d) Como já sabemos quanto Ronaldo gastou com energia nos meses de março, abril e maio, vamos calcular o gasto de Ronaldo em fevereiro. Como ele consumiu , efetuamos , ou seja, R$ 88,45. Assim, o gasto total de Ronaldo de fevereiro até maio de 2024 é dado por:
, isto é, R$ 396,50.
e) Como duas cédulas de R$ 200,00 equivalem a R$ 400,00 e , que foi o valor calculado no item d, seria possível pagar o valor que Ronaldo gastou com as faturas de fevereiro até maio de 2024. Além disso, calculando , concluímos que ele receberia R$ 3,50 de troco.
28. a) De acordo com a promoção, se Renata imprimir 20 fotos, ela vai pagar 0,85 centavos por foto. Assim: . Portanto, Renata vai pagar R$ 17,00 para imprimir 20 fotos.
b) Se Renata imprimir 155 fotos, ela vai pagar 0,73 centavos por foto. Assim: . Portanto, Renata vai pagar R$ 113,15 para imprimir 155 fotos.
c) Se Renata imprimir 1.010 fotos, ela vai pagar 0,62 centavos por cada foto. Então, . Portanto, Renata pagará R$ 626,20 para imprimir 1.010 fotos.
29. a) Devemos multiplicar a quantidade de quilômetros de uma volta pela quantidade de voltas percorridas. Assim, para 5 voltas, a medida da distância percorrida será , pois ; para 10 voltas, a medida da distância percorrida será , pois ; para 15 voltas, a medida da distância percorrida será , pois .
b) Multiplicando a quantidade de voltas percorridas pela medida da pista, em quilômetro, obtemos . Portanto, em 52 voltas nessa pista a medida da distância percorrida será .
30. a) A quantia que Beatriz tem é dada por:
Isto é, R$ 9,55. Como , então Beatriz poderá comprar a revista.
b) Sobrarão R$ 0,40, pois .
31. Primeiramente, devemos determinar o valor arrecadado em cada sessão. Como na quinta-feira o ingresso custa R$ 6,50, calculamos:
primeira sessão:
segunda sessão:
Em seguida, adicionamos os dois valores obtidos, isto é, .
Portanto, foram arrecadados pela bilheteria desse cinema R$ 5.219,50 nessas duas sessões.
Página XCI
32. a)
b)
c)
d)
e)
f)
33. Resposta pessoal. Sugestão de resposta: Joel pretende comprar o smartphone da promoção apresentada. Qual será o valor do desconto se ele pagar o valor à vista? Resposta: O desconto será R$ 185,91.
34. Realizando os cálculos, temos:
a)
b)
c)
d)
e)
f)
g)
h)
35. De acordo com a multiplicação , temos:
a)
b)
c)
d)
e)
f)
g)
h)
36. A medida da área do retângulo é dada por , isto é, . Portanto, a medida da área do retângulo é maior do que .
37. a) Arredondando para a unidade mais próxima, verificamos que Eva abasteceu seu automóvel com aproximadamente de gasolina, Antônio abasteceu seu caminhão com aproximadamente de diesel e Rodrigo abasteceu seu veículo com aproximadamente de etanol.
Arredondando o preço do litro da gasolina, que é R$ 6,61, para a unidade mais próxima, obtemos R$ 7,00. Arredondando o preço do litro do óleo diesel, que é R$ 5,84, para a unidade mais próxima, obtemos R$ 6,00. Arredondando o preço do litro do etanol, que é R$ 4,89, para a unidade mais próxima, obtemos R$ 5,00.
b) Considerando os arredondamentos, Eva gastou aproximadamente R$ 182,00, pois ; Antônio gastou aproximadamente R$ 744,00, pois ; e Rodrigo gastou aproximadamente R$ 180,00, pois .
c) Considerando os valores exatos, Eva gastou R$ 168,56, pois ; Antônio gastou R$ 722,99, pois ; e Rodrigo gastou R$ 177,02, pois .
38. a) A medida da área do piso da sala é dada por , isto é, .
b) Serão necessárias, no mínimo, 40 caixas para revestir o piso da sala, pois 40 é o número mais próximo de 39,75, e com essa quantidade todo o piso da sala será coberto sem que nenhuma parte fique sem revestimento.
39. Realizando os cálculos com os números exatos, obtemos . O resultado exato está próximo do resultado de Fabrícia.
40. Arredondando os números como Fabrícia fez e efetuando os cálculos, temos:
a) , pois 2 é o número natural mais próximo de 2,43 e 3 é o número natural mais próximo de 3,21.
b) , pois 5 é o número natural mais próximo de 5,01 e 9 é o número natural mais próximo de 8,70.
c) , pois 10 é o número natural mais próximo de 10,27 e 6 é o número natural mais próximo de 6,49.
d) , pois 1 é o número natural mais próximo de 0,87 e 12 é o número natural mais próximo de 12,43.
41. a) Realizando os cálculos, temos:
muçarela:
mortadela:
Adicionando os valores, obtemos , ou seja, aproximadamente R$ 13,94.
b) Realizando os cálculos, temos:
apresuntado:
muçarela:
Adicionando os valores, obtemos , isto é, aproximadamente, R$ 9,87. Calculando quantos reais Paola recebeu de troco, fazemos , ou seja, Paola recebeu de troco, aproximadamente, R$ 10,13.
42. a) O desconto é R$ 3,40, pois .
b) Marina gastou R$ 93,81, pois .
43. Como , então ; como , então ; como , então ; como e , então , pois ; como , pois , então .
44. Resposta pessoal. Sugestão de resposta: Qual é medida da área total das portas de um guarda-roupa de 4 portas? Resposta: .
45. Realizando os cálculos, temos:
a)
b)
c)
d)
e)
f)
46. Para determinar a medida da distância de uma volta nessa pista de caminhada, em quilômetro, basta dividir o total percorrido pela quantidade de voltas. Assim, , ou seja, . Para determinar quantos metros tem uma volta nessa pista de caminhada, basta multiplicar o resultado por 1.000. Desse modo, , ou seja, .
Página XCII
47. a)
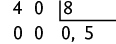
b)
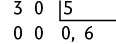
c)
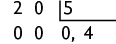
d)
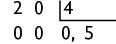
e)
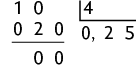
f)
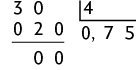
g)
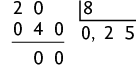
h)
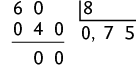
48. a) Como e , então pode ser qualquer número entre 3,25 e 3,75.
Sugestão de resposta: .
b) Como e , então pode ser qualquer número entre 38,5 e 42,8.
Sugestão de resposta: .
c) Como e , então pode ser qualquer número entre 113,5 e 114,2.
Sugestão de resposta: .
d) Como e , então pode ser qualquer número entre 58,5 e 60,375.
Sugestão de resposta: .
e) Como e , então pode ser qualquer número entre 57,75 e 61.
Sugestão de resposta: .
f) Dividindo e , então pode ser qualquer número entre 163,25 e 165,5.
Sugestão de resposta: .
g) Dividindo e , então pode ser qualquer número entre 182,2 e 182,5.
Sugestão de resposta: .
49. a) Para determinar quanto custa de laranja, fazemos . Portanto, de laranja custa R$ 3,75.
b) Realizando os cálculos, verificamos que Daniela gastaria R$ 9,38 para comprar de laranja, pois . Como , ela poderia pagar essa compra com uma cédula de R$ 10,00.
50. De acordo com o esquema, e . Então, e . Para obter C, calculamos . Como sabemos que , então . Do cálculo , obtemos . Por fim, para obter A calculamos . Como sabemos que , então .
Resposta pessoal. Sugestão de resposta:
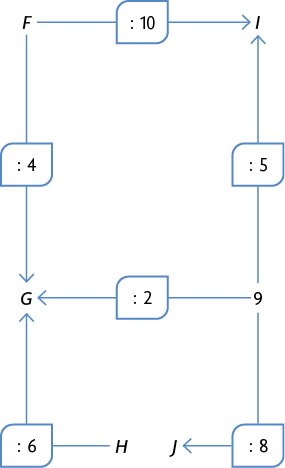
Resposta: , , , , .
51. a) Para determinar a quantidade de litros de leite produzidos de segunda-feira a sexta-feira, fazemos
, isto é, .
b) A média diária da quantidade produzida de litros é dada por . Portanto, foram produzidos por dia, em média, .
Página XCIII
52. • Opção 1: Primeiramente, subtraímos o valor da entrada do valor total. Assim, . Em seguida, dividimos o resultado pela quantidade de parcelas, ou seja, . Portanto, o valor da parcela será R$ 333,75.
Opção 2: Primeiramente, subtraímos o valor da entrada. Assim, . Em seguida, dividimos o resultado pela quantidade de parcelas, ou seja, . Portanto, o valor da parcela será R$ 332,00.
53. a) Um veículo bicombustível consome, em média, de etanol por quilômetro rodado, pois .
b) Um veículo bicombustível consome, em média, de gasolina por quilômetro rodado, pois .
54. a) Como um quadrado tem 4 lados e a medida do perímetro é a soma das medidas de todos os lados, a medida do lado de um quadrado cujo perímetro mede é dado por , ou seja, .
b) Para obter a medida da área de um quadrado, multiplicamos a medida de seu comprimento pela medida de sua largura. Sendo assim, efetuamos . Portanto, a área desse quadrado mede .
55. Sugestão de resposta: Qual será a despesa mensal de cada uma das ocupantes desse apartamento nesse mês? Resposta: A despesa mensal de cada uma das ocupantes será R$ 622,25.
Questão 7. O valor total da compra de Vitor é R$ 50,24, pois .
Como de batata custaram R$ 10,78, fazemos .
Como de abóbora custaram R$ 25,50, fazemos .
Como de maçã custaram R$ 13,96, fazemos .
Portanto, o quilograma da batata custou R$5,39, o da abóbora custou R$ 8,50 e o da maçã custou R$ 3,49.
Atividades
56. a)
b)
c)
d)
e)
f)
g)
h)
57. Primeiramente, subtraímos o valor da entrada pago por Solange e, em seguida, dividimos pela quantidade de parcelas. Assim, e . Portanto, o valor de cada parcela será R$ 115,50.
58. Como a medida do perímetro é dada pela soma das medidas dos lados de um polígono e os polígonos representados em cada figura têm os lados com mesma medida, calculamos:
Figura A: . Portanto, cada lado do pentágono mede ;
Figura B: . Portanto, cada lado do octógono mede .
59. Cada uniforme custa R$ 53,65, pois .
60. Para obter o número que Heitor pensou, vamos efetuar as operações inversas das que ele efetuou. Assim, e . Portanto, o número que Heitor pensou foi o 5,3.
61. a) De acordo com o pedido feito pelas amigas e o preço de cada produto, temos:
Portanto, elas gastaram R$ 47,55.
b) Dividindo o valor gasto igualmente entre elas, obtemos . Portanto, cada uma delas gastou R$ 15,85.
62. Para obter a medida da massa da bola de basquetebol, basta dividir por 3 a medida indicada na balança com três bolas de basquetebol. Assim, , ou seja, cada bola de basquetebol mede de massa. Para obter a medida da massa das outras bolas, analisamos primeiro a balança que tem os três tipos de bolas, subtraindo a medida da massa da bola de basquetebol, ou seja, . Logo, a soma da medida de massa da bola de voleibol com a bola de futebol é . Como a soma das medidas de massa de uma bola de voleibol com duas bolas de futebol é , subtraímos dessa medida de massa o resultado anterior, ou seja: . Logo, a massa de uma bola de futebol mede . Por fim, fazendo , obtemos a medida da massa da bola de voleibol, que é .
63. a) Como o número seguinte é o produto obtido da multiplicação do número anterior com o 3, os próximos três números da sequência são: 515,16; 1.545,48; 4.636,44.
b) Como o número seguinte é o quociente da divisão entre o número anterior e o 2, os próximos três números da sequência são: 6,275; 3,1375; 1,56875.
c) Como o número seguinte é o produto obtido da multiplicação do número anterior com o 5, os próximos três número da sequência são: 406,25; 2.031,25; 10.156,25.
d) Como o número seguinte é o quociente da divisão entre o número anterior e o 10, os próximos três números da sequência são: 1,23987; 0,123987; 0,0123987.
64. Primeiramente, subtraímos da medida da massa bruta a medida da massa da embalagem, ou seja, . Em seguida, dividimos o resultado obtido pela quantidade de tomates, isto é, . Portanto, a medida da massa aproximada de cada tomate é .
65. a) . Arredondando para o décimo mais próximo, obtemos 0,6.
b) . Arredondando para o décimo mais próximo, obtemos 0,4.
c) . Arredondando para o décimo mais próximo, obtemos 1,6.
d) . Arredondando para o décimo mais próximo, obtemos 3,8.
Página XCIV
e) . Arredondando para o décimo mais próximo, obtemos 0,6.
f) . Arredondando para o décimo mais próximo, obtemos 3,2.
g) . Arredondando para o décimo mais próximo, obtemos 4,1.
h) . Arredondando para o décimo mais próximo, obtemos 15,6.
Questão 8. Para determinar quantos quilogramas de uva Catarina comprou, primeiro multiplicamos o dividendo 62,9 e o divisor 12,58 por 100 e, em seguida, efetuamos a divisão. Assim, , ou seja, Catarina comprou de uva.
Para determinar quantos quilogramas de chuchu Catarina comprou, primeiro multiplicamos o dividendo 12,76 e o divisor 5,8 por 100 e, em seguida, efetuamos a divisão. Assim, , ou seja, Catarina comprou de chuchu.
Para determinar quantos quilogramas de cenoura Catarina comprou, primeiro multiplicamos o dividendo 27,71 e o divisor 8,15 por 100 e, em seguida, efetuamos a divisão. Assim, , ou seja, Catarina comprou de cenoura.
Atividades
66. a)
b)
c)
d)
e)
f)
67. a) Devemos aproximar cada número à unidade mais próxima para efetuar a divisão como Carolina fez.
b) •
68. a) Em cada caso, dividindo o preço que Miriam pagou pela respectiva medida de massa do produto, temos:
. Portanto, o preço do quilograma da laranja é R$ 5,34.
. Portanto, o preço do quilograma da maçã é R$ 7,60.
. Portanto, o preço do quilograma da pera é R$ 14,90.
b) Primeiro, calculamos o gasto de Miriam na feira, ou seja, . Depois, adicionamos a quantia que ela vai usar para pagar os produtos, isto é, . Por fim, efetuamos para obter o troco. Assim, Miriam receberá R$ 9,28 de troco.
c) Resposta pessoal. Sugestão de resposta: Sabendo que Miriam comprou de acerola por R$ 4,92, quanto custa um quilograma da acerola? Resposta: Um quilograma da acerola custa R$ 9,84.
69. Sugestões de resposta: Sabendo que Carlos comprou carne de todos os tipos que estavam em promoção nesse açougue, quantos reais ele pagou no quilograma de cada uma delas?
Resposta: Carlos pagou R$ 35,90 no quilograma da alcatra, R$ 22,24 no quilograma do acém, R$ 6,98 no quilograma da coxa de frango desossada e R$ 34,70 no quilograma de patinho.
70. Primeiro, calculamos o custo da quantidade de amendoim e do açúcar para fazer uma receita.
Amendoim: , ou seja, R$ 8,00.
Açúcar: , ou seja, R$ 0,40.
Adicionando os dois valores, obtemos , isto é, R$ 8,40.
Calculando os novos preços de custo com o aumento, obtemos:
açúcar:
, ou seja, R$ 0,44.
amendoim:
, isto é, R$ 7,96.
Para determinar quantos reais ela deve pagar no amendoim para manter o mesmo custo, dividimos o preço de custo atual pela quantidade de amendoim utilizada na receita. Assim:
, isto é, R$ 9,95.
Portanto, a alternativa correta é a letra e.
71. a) ;
b) ;
c) ;
d) ;
e) ;
f) .
72. a) ;
b) ;
c) ;
d) .
73. Como 3,6 está entre 3 e 4, calculamos e . Além disso, 3,6 está mais próximo de 4, por isso estima-se que será um valor próximo de 64. Como 5,1 está entre 5 e 6, calculamos e . Além disso, como 5,1 está mais próximo de 5, estima-se que será um valor próximo de 625.
Os cálculos exatos são e .
74. Resposta pessoal. Sugestão de resposta: O comprimento do lado do quarto de Cláudia mede . Sabendo que esse quarto tem formato quadrado, escreva uma potência para representar a medida da área desse quarto e calcule-a.
Resposta: .
Página XCV
O que eu estudei?
1. a)
b)
c)
d)
e)
f)
2. a) Como o liquidificador e o ferro mais baratos custam, respectivamente, R$ 89,98 e R$ 73,86, Camila vai gastar R$ 163,84, pois .
b) Como o liquidificador e o ferro mais caros custam, respectivamente, R$ 99,00 e R$ 79,37, Camila vai gastar R$ 178,37, pois .
c) Como o liquidificador e o ferro na loja B custam, respectivamente, R$ 89,98 e R$ 79,37, Camila vai gastar R$ 169,35, pois .
3. O quadrado é mágico, pois a soma dos números de cada linha, coluna ou diagonal é sempre o mesmo, ou seja, 13,8.
4. Para o primeiro quadrado mágico, determinamos a constante mágica adicionando os números da diagonal secundária, ou seja, .
Como , então ; como , então ; como , então ;
como , então ; como , então .
Para o segundo quadrado mágico, determinamos a constante mágica adicionando os números da diagonal principal, ou seja, . Como , então ; como , então ; como , então ; como , então .
5. a) Adicionando as medidas de cada lado indicadas na figura, temos:
Portanto, serão necessários, no mínimo, de tela para cercar o terreno.
b) Como Paulo já tem , fazemos . Portanto, faltam de tela para cercar todo o terreno.
6. a)
b) Como , então .
c)
d) Como , então .
e)
7. Como a medida do comprimento perímetro é a soma das medidas de todos os lados, na figura A temos , pois , e na figura B temos , pois .
8. O item A e o item 2 têm o mesmo resultado, pois e . O item B e o item 3 têm o mesmo resultado, pois e . O item C e o item 1 têm o mesmo resultado, pois e . O item D e o item 4 têm o mesmo resultado, pois e . O item E e o item 6 têm o mesmo resultado, pois e . O item F e o item 5 têm o mesmo resultado, pois e .
9. Sabendo que , temos as seguintes equivalências:
a) equivalem a , pois , assim como equivalem a , pois .
b) equivalem a , pois , assim como equivalem a , pois .
c) equivalem a , pois , assim como equivalem a , pois .
d) equivalem a , pois , assim como equivalem a , pois .
e) equivalem a , pois , assim como equivalem a , pois .
f) equivalem a , pois , assim como equivalem a , pois .
10. Realizando os cálculos, temos:
|
Despesas |
Quantidade |
Preço unitário |
Total |
|---|---|---|---|
|
Hospedagem |
4 diárias |
R$ 120,00 |
R$ 480,00 |
|
Alimentação |
12 refeições |
R$ 45,50 |
R$ 546,00 |
|
Combustível |
R$ 6,92 |
R$ 4.432,50 |
|
|
Pedágio |
2 |
R$ 9,35 |
R$ 18,70 |
|
Passeio |
3 |
R$ 39,90 |
R$ 119,70 |
|
Total |
R$ 1.596,90 |
11. a) A diferença entre o total a prazo e o preço à vista é R$ 329,63, pois .
b) O valor de cada parcela será R$ 870,12, pois .
Página XCVI
Unidade 8
Retas e ângulos
Atividades
1. a) Como os pontos A, E e F pertencem à reta s, então a reta que passa pelos pontos A, E e F é a s.
b) As retas r e s passam pelo ponto D; logo, o ponto D pertence às retas r e s.
c) Os pontos B, C e D pertencem à reta r; logo, a reta r passa pelos pontos B, C e D.
2. a) O ponto A pertence à reta r e à reta t, portanto a frase é verdadeira.
b) O ponto C não pertence às retas r, s e u, portanto a afirmação é falsa. Para tornar essa frase verdadeira, podemos reescrevê-la da seguinte maneira: As retas r, s e u não passam pelo ponto C.
c) O ponto B pertence às retas s e t, portanto a frase é verdadeira.
d) O ponto C pertence à reta t, portanto a afirmação é falsa. Para tornar essa frase verdadeira, podemos reescrevê-la da seguinte maneira: O ponto C pertence à reta t.
3. Respostas pessoais. Espera-se que os estudantes percebam a diferença entre os comprimentos dos segmentos e atribuam-lhes medidas de comprimento de acordo com a diferença observada.
4. Com base nas medições, obtemos que: , e .
5. A. A figura geométrica é um triângulo, cujo contorno é formado pelos 3 segmentos , , e .
B. A figura geométrica é um pentágono, cujo contorno é formado pelos 5 segmentos , , , , e .
C. A figura geométrica é um hexágono, cujo contorno é formado pelos 6 segmentos , , , , e .
D. A figura geométrica é um heptágono, cujo contorno é formado pelos 7 segmentos , , , , , e .
6. a) No intervalo de tempo de 30 segundos, o ponteiro gira 15 segundos (um quarto de volta) e, em seguida, gira 15 segundos novamente (mais um quarto de volta). Portanto, em 30 segundos o ponteiro gira meia-volta.
b) Do item anterior, sabemos que o ponteiro gira meia-volta em 30 segundos. Como 1 minuto possui 60 segundos, então em 1 minuto o ponteiro gira 30 segundos (meia-volta) e, em seguida, gira mais 30 segundos (mais meia-volta). Portanto, em 1 minuto, o ponteiro gira uma volta completa.
c) No intervalo de tempo de 45 segundos, o ponteiro realiza 3 giros de 15 segundos cada (3 giros de um quarto de volta), consecutivamente, pois . Portanto, em 45 segundos o ponteiro gira três quartos de volta.
d) Como, em 1 minuto, o ponteiro gira uma volta e, em 30 segundos, meia-volta, então em 1 minuto e 30 segundos o ponteiro gira uma volta e meia.
7. Do momento 1 para o 2, o skate gira meia-volta; do momento 2 para o 3, gira um quarto de volta; do momento 3 para o 4, gira mais um quarto de volta. Assim, do momento 1 para o 2 o skate gira meia-volta e do momento 2 ao 4, mais meia-volta. Portanto, do momento 1 ao 4 o skate girou uma volta completa.
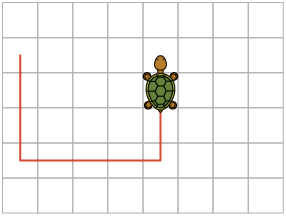
8. a) Ao executar os comandos, Armando fez a tartaruga percorrer o caminho conforme a figura.
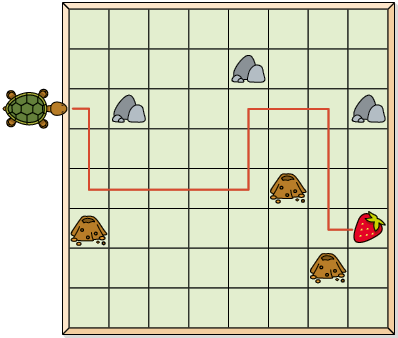
Portanto, Armando levou a tartaruga até o morango.
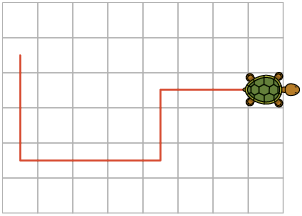
b) Executando os comandos de Armando em cada figura, obtemos:
A.
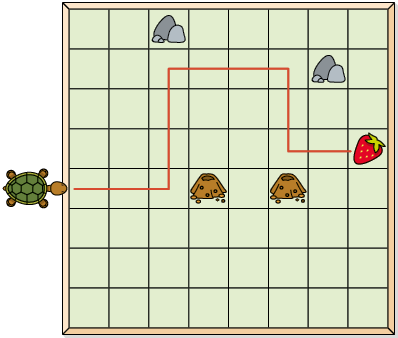
Portanto, é possível levar a tartaruga até o morango.
B.
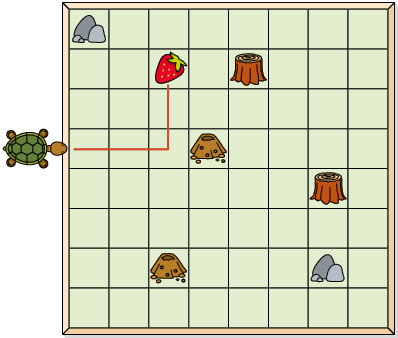
Página XCVII
Portanto, é possível levar a tartaruga até o morango.
C.
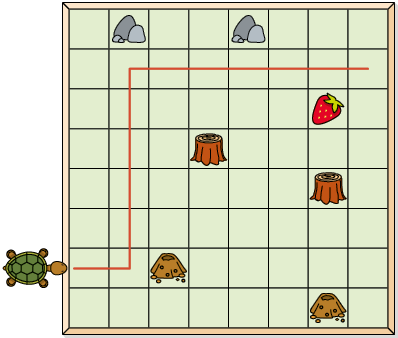
Portanto, não é possível levar a tartaruga até o morango.
D.
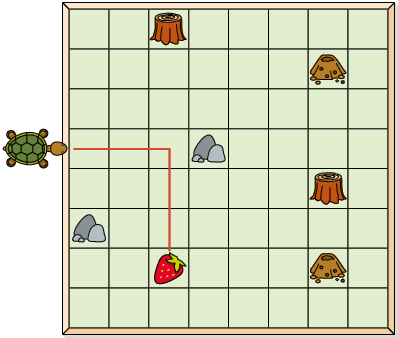
Portanto, é possível levar a tartaruga até o morango.
9. a) Resposta pessoal. Espera-se que os estudantes percebam que a medida do ângulo é menor do que e, portanto, o ângulo é agudo.
b) Resposta pessoal. Espera-se que os estudantes percebam que a medida da abertura do ângulo é maior do que e, portanto, o ângulo é obtuso.
Usando um transferidor, temos e . Portanto, o ângulo é agudo e o ângulo é obtuso.
10. a) O ângulo destacado na figura A mede . Portanto, é um ângulo reto.
b) O ângulo destacado na figura B mede . Portanto, é um ângulo reto.
c) O ângulo destacado na figura C mede . Portanto, é um ângulo agudo.
d) O ângulo destacado na figura D mede . Portanto, é um ângulo obtuso.
11. a) O ângulo de visão do torcedor T1 mede e o ângulo de visão do torcedor T2 mede .
b) O ângulo de visão do torcedor T1 é obtuso, pois é maior do que e menor do que . Já o ângulo de visão do torcedor T2 é agudo, pois é menor do que .
12. A. As retas r e s estão em um mesmo plano e não se cruzam, portanto são paralelas.
B. As retas y e z estão em um mesmo plano e não se cruzam, portanto são paralelas.
C. As retas t e u estão em um mesmo plano e se cruzam em um único ponto, portanto são concorrentes.
D. As retas a e b estão em um mesmo plano e se cruzam em um único ponto, portanto são concorrentes.
13. a) As ruas Arara, Pardal e Tucano são concorrentes à avenida das Maritacas pois cada uma delas cruza a avenida das Maritacas em um único ponto.
b) As ruas Pardal e Arara são perpendiculares à avenida Papagaio, pois cada uma delas forma um ângulo reto com a avenida Papagaio.
14. Resposta pessoal. Sugestão de resposta:
Marcando 3 pontos A, B e C que não estejam alinhados, temos:

a) Com o auxílio de uma régua, traçamos uma reta que passa pelos pontos A e B.
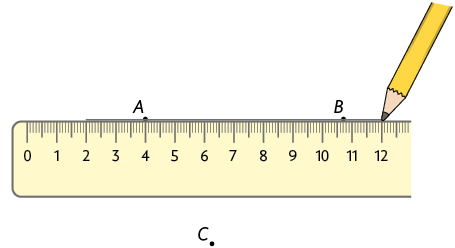
Desse modo, obtemos a reta .

b) Para construir uma reta paralela à reta passando por C, posicionamos um dos lados do esquadro sobre e a régua sobre o outro lado do esquadro. Mantendo a régua fixa, deslizamos o esquadro até alcançar ponto C.
Em seguida, traçamos uma reta passando pelo ponto C.
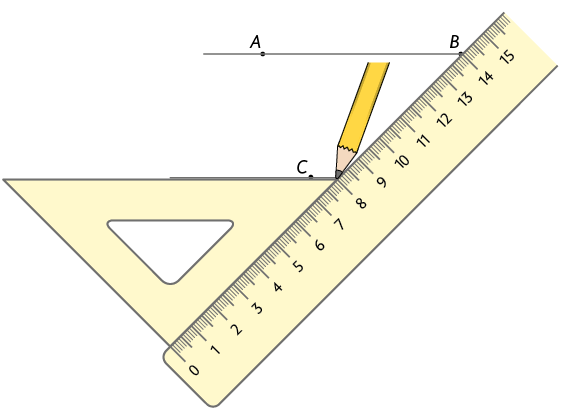
Página XCVIII
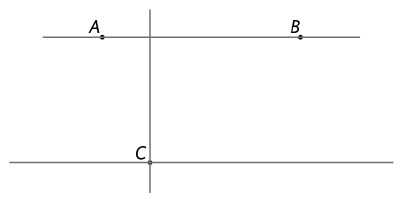
Com o auxílio de uma régua, prolongando a reta que passa por C, obtemos a reta paralela à reta que passa por C.

c) Para traçar uma reta perpendicular à reta passando pelo ponto C, posicionamos a régua e um dos lados do esquadro que formam um ângulo reto sobre a reta . Depois, deslizamos o esquadro até alcançar o ponto C e traçamos a reta que passa por esse ponto.
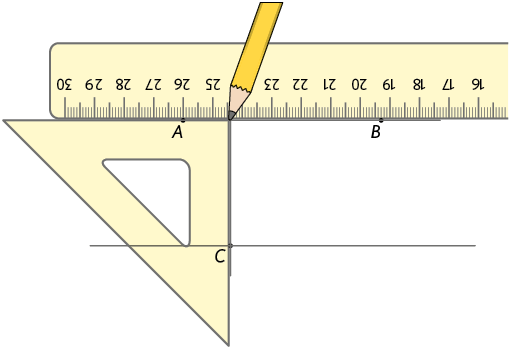
Com o auxílio de uma régua, prolongamos esta última reta traçada e assim obtemos a reta perpendicular à reta que passa por C.
No GeoGebra, podemos fazer as mesmas construções da seguinte maneira:
Usando a ferramenta Ponto, marcamos 3 pontos A, B e C que não estejam alinhados.
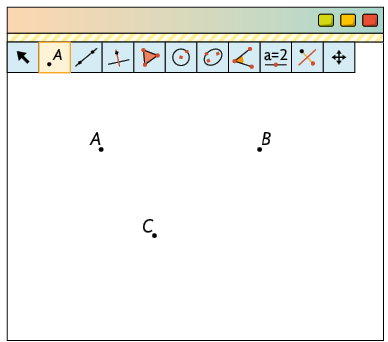
Para traçar a reta , com a ferramenta Reta selecionada, clicamos nos pontos A e B.
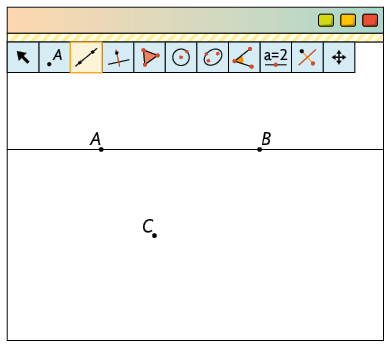
Para traçar uma reta paralela à reta passando por C, com a ferramenta Reta Paralela selecionada, clicamos no ponto C e na reta .
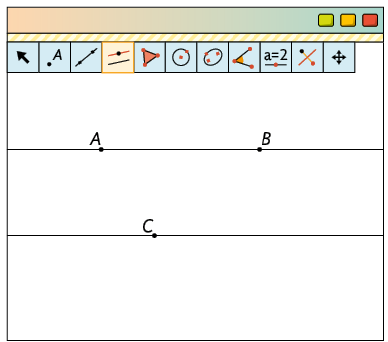
Para traçar uma reta perpendicular à reta passando por C, com a ferramenta Reta Perpendicular selecionada, clicamos no ponto C e depois sobre a reta .
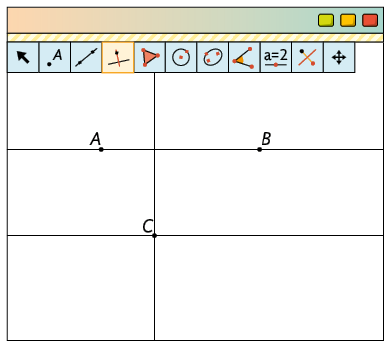
15. a) As retas h e r são perpendiculares, pois formam um ângulo reto.
b) As retas r e g são oblíquas, pois formam um ângulo cuja medida é menor do que .
Página XCIX
c) As retas s e t são oblíquas, pois formam um ângulo cuja medida é menor do que .
d) As retas h e s são perpendiculares, pois formam um ângulo reto.
16. a) As retas s e u são oblíquas, pois o ângulo formado entre elas não é reto.
b) As retas t e r são perpendiculares, pois formam um ângulo reto.
c) As retas r e u são oblíquas, pois o ângulo formado entre elas não é reto.
d) As retas v e r são perpendiculares, pois formam um ângulo reto.
O que eu estudei?
1. Considerando os comandos apresentados na atividade, prosseguimos da seguinte maneira.
Avance um quadradinho para frente.

Gire um quarto de volta para a direita e avance 3 quadradinhos.

Gire um quarto de volta para a esquerda e avance 4 quadradinhos.
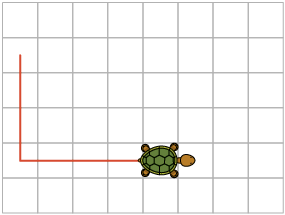
Gire três quartos de volta para a direita e avance 2 quadradinhos.
Gire um quarto de volta para a direita e avance 3 quadradinhos.
2. Espera-se que, em cada item, os estudantes estimem, visualmente, quais ângulos têm medidas maiores, menores ou iguais a .
A. O ângulo é reto, pois mede .
B. O ângulo é obtuso e mede .
C. O ângulo é reto, pois mede .
D. O ângulo é agudo e mede .
3. a) • As retas paralelas à reta r são as retas v e x, pois não cruzam a reta r.
A reta paralela à reta s é a reta t, pois não cruza a reta s.
As retas paralelas à reta x são r e v, pois não cruzam a reta x.
A reta paralela à reta t é a reta s, pois não cruza a reta t.
b) • As retas concorrentes à reta v são s, t e u, pois cada uma delas cruza a reta v em um ponto.
As retas concorrentes à reta s são r, u, v e x, pois cada uma delas cruza a reta s em um ponto.
As retas concorrentes à reta t são r, u, v e x, pois cada uma delas cruza a reta t em um ponto.
As retas concorrentes à reta u são r, s, t, v e x, pois cada uma delas cruza a reta u em um ponto.
4. a) As retas r e s formam ângulos retos ao se cruzarem. Portanto, elas são perpendiculares. Desse modo, substituindo o pela palavra adequada, temos: As retas r e s são perpendiculares.
b) As retas t e u se cruzam em um único ponto formando ângulos que não são retos. Portanto, elas são oblíquas. Desse modo, substituindo o pela palavra adequada, temos: As retas t e u são oblíquas.
c) As retas u e v não se cruzam, portanto são paralelas. Portanto, substituindo o pela palavra adequada, temos: As retas u e v são paralelas.
Página C
Unidade 9
Polígonos
Questão 1. Considerando a quantidade de lados dos polígonos, temos:
• 11 lados: undecágono;
• 16 lados: hexadecágono;
• 21 lados: hendecoságono.
Atividades
1. a) As figuras B, C e D são polígonos, pois são linhas poligonais simples e fechadas.
b) A figura A não é um polígono, pois não é uma linha poligonal.
c) Resposta pessoal. Sugestão de resposta:


2.
|
Nome |
Quantidade de lados |
Quantidade de vértices |
|---|---|---|
|
Quadrilátero |
4 |
4 |
|
Octógono |
8 |
8 |
|
Decágono |
10 |
10 |
3. Considerando a quantidade de lados dos polígonos, temos:
A. quadrilátero; B. pentágono; C. triângulo; D. hexágono; E. heptágono; F. eneágono.
4. a) De acordo com a quantidade de lados de cada peça do tangram, verificamos que:
as peças A, B, C, E e G são triângulos, ou seja, 5 peças têm 3 lados, 3 vértices e 3 ângulos internos;
nenhuma peça tem 5 lados, então não há pentágono.
b) De acordo com as afirmações dadas:
As peças C e E juntas formam um triângulo, que tem 3 ângulos internos. Assim, a afirmação é verdadeira.
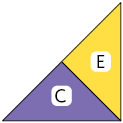
A afirmação é verdadeira, pois juntando as peças B, C e D forma-se uma figura cujo contorno tem 5 lados.
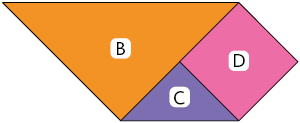
A afirmação é verdadeira, pois juntando as peças B e D forma-se uma figura cujo contorno tem 5 lados.
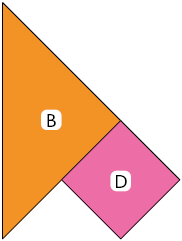
5. Considerando a medida dos lados e dos ângulos internos de cada imagem, verificamos que o polígono A é regular, pois todos os lados têm a mesma medida de comprimento e todos os ângulos internos são congruentes. Verificamos também que o polígono B é não regular, pois todos os lados têm a mesma medida de comprimento, mas os ângulos internos não são congruentes. Por fim, verificamos que o polígono C é não regular, pois, apesar de todos os ângulos internos serem congruentes, as medidas de comprimento dos lados são diferentes.
6. Não é possível fazer um mosaico usando apenas o pentágono e o octógono, pois como 360 não é divisível por 108 e nem por 135, os ângulos das peças não se encaixarão perfeitamente sem sobra ou falta.
7. O polígono obtido é um hexágono, pois tem 6 lados.
8. a) Juntando adequadamente as malhas A e B, obtemos um octógono, pois a figura formada terá 8 lados; juntando as malhas D e F, obtemos um quadrilátero, pois a figura formada terá 4 lados; juntando as malhas E e F, obtemos um heptágono, pois a figura formada terá 7 lados; juntando as malhas B e D, obtemos um heptágono, pois a figura formada terá 7 lados.
b) Considerando que o polígono regular tem medidas iguais para o comprimento dos lados e os ângulos internos são congruentes, as malhas a serem unidas são A e C. Será formado um polígono de 4 lados, ou seja, um quadrilátero ou quadrado.
9. a) Cada face do cubo tem o formato de quadrilátero, que é um polígono de 4 lados. As faces laterais da pirâmide têm o formato de triângulos, que são polígonos de 3 lados, e a sua base tem formato de um quadrilátero, que é um polígono de 4 lados.
b) Sim. Considerando que o polígono regular tem medidas iguais para o comprimento dos lados e os ângulos internos são congruentes, o quadrado é o polígono regular.
Página CI
10. Dividindo a medida do perímetro pelo número que representa a quantidade de lados do polígono, temos:
a) , ou seja, o comprimento de cada lado do heptágono regular mede .
b) , ou seja, o comprimento de cada lado do decágono regular mede .
c) , ou seja, o comprimento de cada lado do octógono regular mede .
d) , ou seja, o comprimento de cada lado do dodecágono regular mede .
11. Considerando que os ângulos internos de um polígono regular são congruentes, os outros ângulos internos desse polígono medem .
Questão 2.
a) Um triângulo acutângulo não pode ser classificado como triângulo retângulo, pois todos os seus ângulos internos são menores do que , enquanto o triângulo retângulo deve ter obrigatoriamente um ângulo interno medindo .
b) Como um dos ângulos internos do triângulo obtusângulo é maior do que , é impossível que outro ângulo dele meça , pois a soma das medidas dos ângulos internos de um triângulo é .
Atividades
12. Contando os triângulos e fazendo as devidas sobreposições, podemos identificar, na figura A, 4 triângulos mais 4 triângulos fazendo sobreposição dois a dois, totalizando 8 triângulos. Já na figura B, podemos identificar 53 triângulos no total, sendo 27 triângulos verdes pequenos, 13 triângulos brancos, 9 triângulos fazendo sobreposição com 4 triângulos pequenos (3 triângulos verdes e 1 triângulo branco), 3 triângulos fazendo sobreposição com 13 triângulos (9 triângulos verdes pequenos, 3 triângulos brancos pequenos e 1 triângulo branco médio) e 1 triângulo de contorno.
13. A . Nome: triângulo ;
Vértices: A, B e C;
Lados: , e ;
Ângulos internos: , e .
B . Nome: triângulo ;
Vértices: F, G e H;
Lados: , e ;
Ângulos internos: ; ; .
14. Utilizando a régua para medir os lados de cada triângulo, podemos identificar que:
o triângulo é escaleno, pois os três lados têm medidas de comprimento diferentes.
o triângulo é equilátero, pois os três lados têm a mesma medida de comprimento.
o triângulo é isósceles, pois o lado tem medida de comprimento diferente dos outros dois que têm a mesma medida de comprimento.
o triângulo é equilátero, pois todos os lados têm a mesma medida de comprimento.
o triângulo é escaleno, pois os três lados têm medidas de comprimento diferentes.
15. a) O triângulo é obtusângulo, pois .
b) O triângulo é retângulo, pois um dos ângulos tem medida igual a .
c) O triângulo é acutângulo, pois todos os ângulos têm medida menor do que .
d) O triângulo é acutângulo, pois todos os ângulos têm medida menor do que .
16. De acordo com a medida dos lados apresentada na imagem, temos:
a) As medidas dos lados são , e .
b) O triângulo formado é isósceles, pois dois lados têm medidas de comprimento iguais.
c) Sim, é possível construir um triângulo equilátero com o mesmo procedimento de Paulo. Para isso, a medida do comprimento de um dos lados a ser cortado deve ter metade da medida do outro lado.
Não é possível construir um triângulo escaleno.
Questão 3. Resposta pessoal. Sugestão de resposta:
Questão 4. Considerando as características do quadrado, do retângulo e do losango, verificamos que:
a) um quadrado pode ser classificado como retângulo, pois para ser retângulo é necessário ser um paralelogramo com os 4 ângulos internos retos, o que corresponde às características dos quadrados.
b) um quadrado pode ser classificado como losango, pois para ser losango é necessário ser um paralelogramo com os 4 lados de medidas iguais, o que corresponde às características dos quadrados.
Atividades
17. Utilizando a régua para medir o comprimento dos lados de cada quadrilátero e o transferidor para medir seus ângulos internos, verificamos que a figura A é um quadrilátero sem nome especial, pois possui 4 lados; a figura B é um losango, pois é um paralelogramo (tem 2 pares de lados paralelos) com os 4 lados com medidas de comprimento iguais; a figura C é um quadrado, pois é um paralelogramo (tem 2 pares de lados paralelos) com os 4 ângulos internos retos e os 4 lados com medidas de comprimento iguais; consequentemente, é um retângulo e um losango; a figura D é um retângulo, pois é um paralelogramo (possui 2 pares de lados paralelos) com os 4 ângulos internos retos; a figura E é um paralelogramo, pois possui 2 pares de lados paralelos; a figura F é um paralelogramo, pois possui 2 pares de lados paralelos.
Página CII
18. O quadrilátero desenhado na malha A deve ser associado às informações do item 3. O quadrilátero desenhado na malha B deve ser associado às informações do item 2. O quadrilátero desenhado na malha C deve ser associado às informações do item 1.
19. De acordo com a figura, os quadriláteros , e são trapézios, pois têm apenas 1 par de lados paralelos. Já o quadrilátero é um paralelogramo, pois possui 2 pares de lados paralelos.
20. O quadrilátero 1 é trapézio, pois tem apenas um par de lados paralelos. Portanto, deve ser associado ao item D. O quadrilátero 2 é um losango, pois é um paralelogramo cujos 4 lados têm medidas de comprimentos iguais. Assim, deve ser associado ao item C. O quadrilátero 3 é um retângulo, pois é um paralelogramo cujos 4 ângulos internos são retos. Então, deve ser associado ao item B. O quadrilátero 4 é um quadrado, pois é um paralelogramo com os 4 ângulos internos retos e cujos 4 lados têm medidas de comprimentos iguais. Assim, deve ser associado ao item A.
21. a) A afirmação é falsa, pois nem todo retângulo tem todos os lados com mesma medida de comprimento. Sugestão de correção: Todo quadrado é um retângulo, mas nem todo retângulo é um quadrado.
b) A afirmação é verdadeira, pois losangos são paralelogramos cujos 4 lados têm medidas de comprimentos iguais, assim como os quadrados, que são retângulos. Logo, os retângulos que são quadrados também podem ser classificados como losangos.
c) A afirmação é falsa, pois os trapézios têm apenas um par de lados paralelos e os paralelogramos têm dois pares. Sugestão de correção: Os trapézios não podem ser classificados como paralelogramos.
d) A afirmação é verdadeira, pois os quadrados são paralelogramos cujos 4 lados têm medidas de comprimentos iguais, o que os classifica como losangos, mas o losango nem sempre tem os 4 ângulos internos retos, que é uma característica dos quadrados.
e) A afirmação é verdadeira, pois os quadrados podem ser retângulos os quais podem ter os 4 lados com medidas de comprimentos iguais, o que classifica alguns retângulos como losangos.
f) A afirmação é falsa, pois os paralelogramos possuem dois pares de lados paralelos e os trapézios somente um. Sugestão de correção: Os paralelogramos não podem ser classificados como trapézios.
22. Respostas pessoais.
a) Procedimentos para construção de um quadrilátero qualquer:
1º) Com a ferramenta Ponto, marque 4 pontos quaisquer E, F, G e H, de modo que os quatro não estejam alinhados.
2º) Com a fermenta Polígono, clique sobre os pontos E, F, G, H e E, nessa ordem.
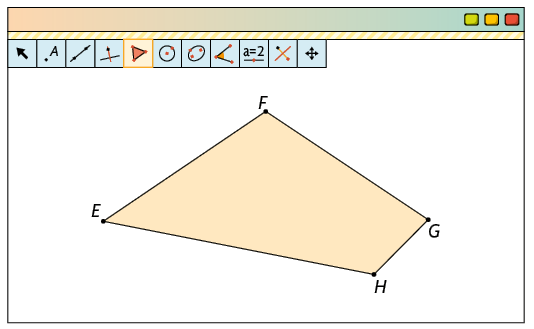
b) Procedimentos para construção de um paralelogramo:
1º) Com a ferramenta Ponto selecionada, marque 3 pontos quaisquer E, F e G, de modo que não estejam alinhados.
2º) Com a ferramenta Reta, trace as retas r e t que passam por E e F, por E e G, respectivamente.
3º) Trace uma reta p, paralela à r, passando por G. Para isso, com a ferramenta Reta paralela, clique sobre o ponto G e a reta r. Repita esse procedimento para traçar uma reta q, paralela à t, passando por F.
4º) Com a ferramenta Interseção de dois objetos, clique sobre a reta p e, depois, sobre a reta q para marcar o ponto H.
5º) Com a ferramenta Polígono, construa o paralelogramo .
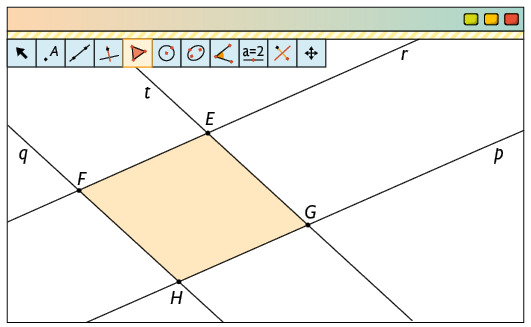
c) Procedimentos para construção de um trapézio:
1º) Com a ferramenta Ponto selecionada, marque 3 pontos quaisquer E, F e G, de modo que não estejam alinhados.
2º) Com a ferramenta Reta, trace a reta r que passa por E e F.
3º) Com a ferramenta Reta Paralela, trace uma reta s paralela à t e passando por C.
4º) Com a ferramenta Ponto, marque sobre a reta r dois pontos H e I, de modo que G fique entre eles.
5º) Com a ferramenta Polígono, construa um trapézio .
Página CIII
O que eu estudei?
1. Cada polígono, do segundo em diante, tem dois lados a menos do que o anterior. Sendo assim, os próximos dois polígonos terão 6 e 4 lados, respectivamente. Portanto, os próximos polígonos serão um hexágono e um quadrilátero.
2. De acordo com a quantidade de lados dos polígonos que formam cada planificação, temos, no item A, triângulos e quadriláteros; no item B, quadriláteros; no item C, pentágonos e quadriláteros; no item D, triângulos e um quadrilátero.
3. Utilizando a régua para medir o comprimento dos lados de cada quadrilátero e o transferidor para medir seus ângulos internos, verificamos que: a figura A é um triângulo equilátero e acutângulo, pois tem os 3 lados com medidas iguais e todos os seus ângulos internos são menores do que ; a figura B é um triângulo isósceles e acutângulo, pois tem pelo menos 2 de seus lados com medidas iguais e todos os seus ângulos internos são menores do que ; a figura C é um triângulo equilátero e acutângulo, pois tem os 3 lados com medidas iguais e todos os seus ângulos internos são menores do que ; a figura D é um triângulo escaleno e retângulo, pois os 3 lados apresentam diferentes medidas de comprimento e têm um ângulo reto, ou seja, igual a .
4. De acordo com as figuras geométricas espaciais apresentadas, há 6 triângulos e nenhum quadrilátero na planificação da figura A; há 2 triângulos e 3 quadriláteros na planificação da figura B; 4 triângulos e 1 quadrilátero na planificação da figura C;d há 5 quadriláteros e nenhum triângulo na planificação da figura D.
5. a) Falsa, pois o paralelogramo é um quadrilátero com 2 pares de lados paralelos. Sugestão de correção: O paralelogramo é um quadrilátero com 2 pares de lados paralelos.
b) Verdadeira.
c) Verdadeira.
d) Falsa, pois o retângulo é um paralelogramo com os 4 ângulos internos retos. Sugestão de correção: O retângulo é um paralelogramo com os 4 ângulos internos retos.
Unidade 10
Grandezas e medidas
Questão 1. Resposta pessoal. Sugestão de resposta: Podemos usar o centímetro como unidade para medir o comprimento de uma caneta e o metro para medir o comprimento de um campo de futebol.
Atividades
1. Resposta pessoal. Sugestão de respostas: A unidade de medida de comprimento mais adequada para expressar:
a) a medida da altura de uma árvore é o metro .
b) a medida da distância entre duas cidades é o quilômetro .
c) a medida da espessura de uma grafite de lapiseira é o milímetro .
d) a medida da altura de uma pessoa pode ser o centímetro ou o metro .
e) a medida da altura de um prédio é o metro .
2. Resposta pessoal. A resposta depende da medida do palmo de cada estudante.
3. Resposta pessoal. Espera-se que os estudantes analisem os comprimentos de cada segmento de reta e estimem que o segmento de reta mede de comprimento.
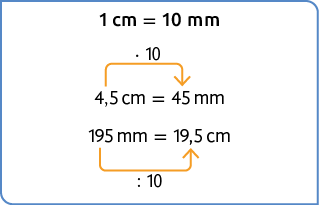
4. Realizando as conversões necessárias, obtemos:
a) , pois .
b) , pois .
c) , pois .
d) , pois .
e) , pois .
f) , pois .
5. Sugestão de respostas:
a) O comprimento de uma sala pode ser medido usando uma trena ou metro articulado.
b) A cintura de uma pessoa pode ser medida usando uma fita métrica.
c) A espessura de um parafuso pode ser medida usando um micrômetro ou paquímetro.
d) O comprimento de um segmento de reta pode ser medido usando uma régua.
e) A altura de uma porta pode ser medida usando uma trena ou metro articulado.
f) A espessura de um vidro pode ser medida usando um micrômetro ou paquímetro.
6. Como , realizando a conversão de 8 quilômetros em metro, obtemos . Adicionando essa quantidade aos outros 250 metros, fazemos . Portanto, Clarice correu
7. Como , para a conversão da medida de comprimento de cada colar em milímetro, calculamos . Assim, cada colar mede de comprimento. Dividindo essa medida pela medida do diâmetro de cada conta, obtemos 80 contas azuis, pois , e 50 contas vermelhas, pois