Página CIV
8. Como serão emendados 4 pedaços de cano e serão feitas 3 emendas, fazemos:
e
Portanto, o comprimento dos 4 pedaços de cano emendados mede aproximadamente .
9. Para obter a medida de distância, em quilômetro, que o corredor precisa percorrer para cumprir a corrida, inicialmente convertemos em quilômetro. Como , fazemos . Subtraindo esse resultado do percurso total, obtemos . Portanto, faltam para o corredor cumprir a prova.
10. Como , então , ou seja, o comprimento do papel kraft mede . Dividindo esse resultado pela medida do comprimento de cada tira, obtemos . Portanto, Felipe vai cortar 20 tiras.
11. a) O Pico da Neblina é o ponto mais alto do Brasil.
b) O Pico da Bandeira mede de altitude.
c) O Pico das Agulhas Negras mede de altitude e a da Pedra da Mina mede .
d) Como , o Pico da Neblina é o que mais se aproxima dessa medida, pois mede .
e) Resposta pessoal. Sugestão de resposta: Entre os pontos apresentados no gráfico, qual tem a menor medida de altitude? Qual é essa medida? Resposta: Pico do Cristal; .
12. a) Os estudantes podem identificar vários elementos na planta baixa apresentada. Algumas sugestões de respostas são: sofá, camas, mesa de jantar e fogão.
b) De acordo com a planta baixa, há duas portas na cozinha, uma porta no dormitório 1, uma porta no dormitório 2, uma porta no dormitório 3, uma porta no banheiro 1, uma porta no banheiro 2 e uma porta na sala de estar, totalizando 8 portas.
c) De acordo com a planta baixa, as medidas de comprimento e de largura do dormitório 1 são e , respectivamente.
d) A resposta deste item depende da estrutura da casa de cada estudante.
13. a) Como as dimensões do dormitório medem e , para determinar a medida do comprimento do dormitório fazemos inicialmente a conversão da espessura da parede, que equivale a , em metros, calculando . Com isso, obtemos que a espessura da parede mede . Em seguida, subtraímos a medida da espessura das duas paredes que estão sendo consideradas na medida indicada, ou seja, . Assim, verificamos que o comprimento do dormitório mede . Já a medida da largura é , conforme está indicado na imagem, pois nesse caso as paredes não estão consideradas.
b) Para determinar a medida da largura do banheiro, devemos subtrair da medida da largura do apartamento a medida da largura de todos os outros cômodos e das paredes. Assim: , ou seja, a largura do banheiro mede .
14. A resposta para esta atividade depende da sala de aula dos estudantes. Espera-se que eles indiquem as medidas na planta baixa corretamente. Por exemplo, se as dimensões medirem, respectivamente, e , eles devem construir uma planta baixa com e .
15. A resposta para esta atividade depende da escola do estudante.
16. De acordo com o esquema:
a) A medida da distância entre as cidades A e D é dada pela soma das medidas da distância entre as cidades A e C com C e D. Assim, , ou seja, essa medida é .
b) A medida da distância entre as cidades B e C é dada pela diferença entre as medidas da distância entre as cidades B e D com C e D. Assim: , ou seja, essa medida é .
Questão 2. Utilizando uma régua, verificamos que as dimensões do retângulo são e .
Questão 3. A adição é dada por , ou seja, a soma é .
Questão 4. A resposta para esta questão depende do triângulo e do quadrilátero que o estudante vai desenhar. Sugestão de resposta:

Medida do perímetro: .

Medida do perímetro: .
Atividades
17. Como a medida de cada lado do triângulo do item A mede , a medida do seu perímetro é dada por , ou seja, . Como a largura e o comprimento do retângulo do item B medem, respectivamente, e , a medida do perímetro é dada por , ou seja, . Como a medida dos lados do quadrado do item C medem , a medida do perímetro é dada por , ou seja, .
Página CV
18. a) Não, pois como um lado do retângulo coincide com um lado do triângulo e o outro lado do retângulo também coincide com um lado do quadrado, as medidas dos comprimentos desses lados não são consideradas ao decompor essa figura.
b) Como a figura apresentada é uma composição dos polígonos da atividade anterior, conhecemos as dimensões de cada polígono usado nela. Assim, a medida do perímetro dessa figura é dada por: , ou seja, .
19. a) Utilizando uma régua, verificamos que a imagem mede de comprimento e de largura. Logo, as dimensões da obra original são .
b) Adicionando as medidas do comprimento dos lados da obra original, temos: , ou seja, o perímetro da obra original mede .
20. A. De acordo com a figura, a soma das medidas dos lados é dada por: . Subtraindo esse resultado da medida do perímetro, obtemos , ou seja, o comprimento lado indicado por x mede .
B. De acordo com a figura, a soma das medidas dos lados é dada por: . Subtraindo esse resultado da medida do perímetro, obtemos , ou seja, o comprimento do lado indicado por x mede .
21. a) Como a largura do campo mede 35 m a menos do que o comprimento, calculamos . Assim, a medida da largura do campo é .
b) O perímetro do campo mede , pois .
22. De acordo com a medida dos lados das figuras 1, 2 e 3:
a) a medida do perímetro da figura A é dada por , ou seja, é .
b) a medida do perímetro da figura B é dada por , ou seja, é .
23. Sugestão de respostas: A unidade mais indicada para expressar a medida da massa de:
a) uma pessoa é o quilograma ().
b) um caminhão é a tonelada ().
c) um cachorro adulto é o quilograma ().
d) uma bicicleta é o quilograma ().
e) um comprimido pode ser o grama () ou miligrama ().
f) um elefante adulto é a tonelada ().
24. Utilizando o método apresentado por Amanda e sabendo que , temos as seguintes equivalências:
a) equivalem a . Então:
Assim, equivalem a .
b) equivalem a . Então:
Assim, equivalem a .
c) equivalem a . Então:
Assim, equivalem a .
d) equivalem a .Então,
.
Assim, equivalem a .
25. Utilizando o método apresentado por Tobias, temos:
a) .
Assim, equivalem a .
b) .
Assim, equivalem a .
c) .
Assim, equivalem a .
d) .
Assim, equivalem a .
26. Como , realizando as transformações necessárias, temos:
a)
b)
c)
d)
27. Realizando a conversão de quilograma em grama, temos: , ou seja,
Dividindo a quantidade total de geleia pela quantidade que ela vai armazenar em cada pote, obtemos
. Portanto, ela vai armazenar a geleia em 16 potes.
28. a) , isto é , .
b) , isto é, .
c) , isto é, .
d) , isto é, .
29. a) , ou seja, .
b) ou seja, .
c) ou seja, .
d) , ou seja, .
e) ou seja, .
f) ou seja, .
g) ou seja, .
h) ou seja, .
30. Para converter em miligrama, fazemos . Assim, esse morcego tem aproximadamente, de medida de massa.
31. Resposta pessoal. Sugestão de resposta: Quantos miligramas de vitamina C uma pessoa terá ingerido ao todo após tomar os 10 comprimidos da embalagem?
Resposta: .
32. Como as balanças estão em equilíbrio, a medida de massa da caixa A é dada pela soma das medidas de massa de cada peça do outro prato, ou seja, , pois . A medida de massa da caixa B é dada pela soma das medidas de massa das peças do outro prato menos a medida da massa da peça que está sobre o prato com a caixa B, ou seja, , pois
Página CVI
33. Como a medida da massa de cada recipiente com açúcar deve ser a mesma, precisamos determinar qual será a medida da massa correspondente a cada recipiente ocupado. Como , fazemos: e . Assim, a medida da massa de cada recipiente após Flávia distribuir o açúcar será .
Para calcular a quantidade de açúcar que ela deve colocar no recipiente A, fazemos , ou seja, ela deve colocar de açúcar no recipiente A.
Para calcular a quantidade de açúcar que ela deve colocar no recipiente B, fazemos , ou seja, ela deve colocar de açúcar no recipiente B.
34. a) Considerando que um ano tem 365 dias, fazemos . Portanto, em 2020, cada brasileiro produziu, aproximadamente, de lixo por dia.
b) Como uma pessoa produz aproximadamente de lixo por dia, uma família com 6 pessoas produz diariamente de lixo, pois . Em 7 dias, haverá uma produção de de lixo, pois . Em um ano, será produzido de lixo, pois . Transformando esse último resultado em tonelada, obtemos: , ou seja, são aproximadamente de lixo.
35. Inicialmente, calculamos a medida de massa total de soja produzida, que é , pois . Dividindo o total de soja produzida pela medida da massa de cada saca, obtemos , isto é, o sítio de Márcio produziu 1.125 sacas de soja.
36. a) A resposta para este item depende do ano vigente. Caso o ano seja 2024 ele será bissexto, pois 2024 é divisível por 4.
b) Devemos adicionar um dia no mês de fevereiro, que é o 29, pois fevereiro normalmente tem 28 dias.
c) Analisando cada ano apresentado, verificamos que:
2400 termina em 00 e é divisível por 400. Logo, 2400 é um ano bissexto.
2300 termina em 00, mas não é divisível por 400. Logo, 2300 não é um ano bissexto.
2008 não termina em 00 e é divisível por 4. Logo, 2008 é um ano bissexto.
2009 não termina em 00 e não é divisível por 4. Logo, 2009 não é um ano bissexto.
2800 termina em 00 e é divisível por 400. Logo, 2800 é um ano bissexto.
Portanto, os anos bissextos são 2400, 2008 e 2800.
37. a) Uma semana tem 7 dias.
b) Um ano tem 12 meses.
c) Como um ano tem 6 bimestres, fazemos . Assim, um bimestre tem 2 meses. Além disso, como um ano tem 2 semestres, calculamos , ou seja, um semestre tem 6 meses.
d) Um ano tem 365 dias ou 366 dias em anos bissextos.
38. De acordo com as informações apresentadas no enunciado, temos:
1º domingo: dia 6 de novembro;
2º domingo: dia 13 de novembro ;
3º domingo: dia 20 de novembro ;
4º e último domingo: dia 27 de novembro .
Portanto, o último domingo desse mês será dia 27.
39. a) Para determinar que dia da semana foi anteontem, considerando que daqui cinco dias será quinta-feira, contamos 7 dias antes de quinta-feira, ou seja, uma semana. Portanto, se daqui a 5 dias for quinta-feira, anteontem deve ter sido quinta-feira.
b) Contando 8 dias a partir de sábado, ou seja, uma semana mais um dia, verificamos que o dia de hoje é um domingo. Logo, o dia de ontem foi sábado.
c) Contando 4 dias a partir de quarta-feira, concluímos que hoje é um domingo. Assim, depois de amanhã será terça-feira.
Questão 5. Como , e , realizando as conversões necessárias, verificamos que:
a) 1 hora equivale a , pois .
b) 37 minutos equivalem a , pois .
c) 1 dia equivale a , pois como , então e .
d) 7 horas equivalem a , pois e .
Questão 6. A resposta para esta questão depende da rotina de cada estudante.
Questão 7. Espera-se que os estudantes obtenham informações a respeito do relógio do sol, da clepsidra, do relógio de vela, da ampulheta, do relógio de pêndulo etc.
Atividades
40. Realizando as conversões necessárias, temos:
a)
b)
c)
d)
e)
f)
41. De acordo com os horários indicados em cada relógio, os relógios A e H estão marcando ; os relógios B e E estão marcando ; os relógios C e G estão marcando ; os relógios D e F estão marcando .
42. a) De acordo com as imagens, no momento A, o relógio está indicando ; no momento B, o relógio está indicando .
b) Convertendo em minutos os horários registrados nos relógios, temos:
Momento A: . Assim,
, ou seja,
Página CVII
Momento B: . Assim,
, ou seja,
Assim: .
Logo, entre os momentos A e B, foram decorridos ou , pois .
c) Como, no momento B, o relógio está indicando , fazemos:
Como , após a partir do momento B, o horário indicado no relógio será .

43. Para determinar a quantidade de horas necessárias para a produção de 126 garrafas, fazemos . Transformando em minutos, obtemos , ou seja, serão necessários para produzir 126 garrafas.
44. a) Fazendo a conversão necessária, temos:
, ou seja, .
b) Medida do tempo de Daniel Ferreira do Nascimento para concluir a corrida: . Assim:
Subtraindo esse resultado do tempo do primeiro colocado, temos . Portanto, o atleta Daniel Ferreira do Nascimento cruzou a linha de chegada após o 1º colocado.
c) Resposta pessoal. Sugestão de resposta: Quantos segundos a mais o 3º colocado levou para concluir a corrida em relação ao 1º colocado? Resposta:
45. a) Calculando a diferença entre os horários apresentados nos relógios, temos:
1º e 2º relógios: ;
2º e 3º relógios: .
Portanto, os ônibus dessa linha partem do terminal rodoviário após 25 minutos.
b) Como os ônibus partem de 25 em 25 minutos, adicionando essa medida de tempo a partir do último horário apresentado, obtemos os horários , e .
46. Se a cada hora o relógio atrasa , após um dia, ou seja, após , ele terá atrasado , pois . Assim, em 7 dias, haverá um atraso de , pois . Convertendo 840 segundos em minutos, temos: . Portanto, em 7 dias, será necessário adiantar o relógio em 14 minutos.
47. a) Horário de saída: . Assim,
, ou seja, .
Horário de chegada: . Assim,, ou seja, .
Desse modo: , ou seja, , que equivalem a .
Portanto, o voo realizado por Roberto e sua esposa durou
b) Contabilizando as noites hospedadas, temos:
1ª noite: 28 de junho;
2ª noite: 29 de junho;
3ª noite: 30 de junho;
4ª noite: 1 de julho;
5ª noite: 2 de julho;
6ª noite: 3 de julho;
7ª noite: 4 de julho;
Portanto, Roberto e sua esposa saíram do hotel dia 5 de julho.
48. Calculando a diferença entre a maior e a menor temperatura, temos: , ou seja, a diferença entre as temperaturas é .
49. a) A maior medida de temperatura máxima prevista foi em Caçapava do Sul.
b) Calculando a variação de temperatura de cada município, obtemos:
Itaqui: , ou seja, ;
Bagé: , ou seja, ;
Caçapava do Sul: , ou seja, ;
Cachoeira do Sul: , ou seja, ;
Porto Alegre: , ou seja, ;
Gramado: , ou seja, ;
Gravataí: , ou seja, ;
Torres: , ou seja, .
Logo:
• Menor variação: Itaqui, Porto Alegre, Gravataí e Torres.
• Maior variação: Caçapava do Sul.
50. a) Calculando 75% de , ou seja, de 20, obtemos: e . Portanto, houve um aumento de
b) Ao meio-dia, o termômetro estava marcando , pois .
51. a) Resposta pessoal.
b) Neste caso, a variação de temperatura será , pois .
52. Calculando as variações de temperatura em cada dia, temos:
10/01: , ou seja, ;
11/01: , ou seja, ;
12/01: , ou seja, ;
13/01: , ou seja, ;
14/01: , ou seja, ;
15/01: , ou seja, ;
Página CVIII
16/01: , ou seja, ;
17/01: , ou seja, ;
18/01: , ou seja, ;
19/01: , ou seja, ;
20/01: , ou seja, ;
21/01: , ou seja, ;
22/01: , ou seja, ;
23/01: , ou seja, ;
24/01: , ou seja, ;
25/01: , ou seja, ;
26/01: , ou seja, ;
27/01: , ou seja, ;
28/01: , ou seja, ;
29/01: , ou seja, ;
30/01: , ou seja, ;
31/01: , ou seja, .
a) A maior variação ocorreu no dia 25/01. A variação foi de .
b) A menor variação ocorreu nos dias 14/01 e 19/01.
c) Resposta pessoal. Sugestão de resposta: No período de 10/01/2022 a 31/01/2022, qual foi a maior medida de temperatura registrada em São Joaquim? E qual foi a menor medida de temperatura registrada? Respostas: ; .
Questão 8.
As figuras B e D têm a
mesma medida de área, pois ambas são formadas pela
mesma quantidade de ![]() .
.
Atividades
53. De acordo com as figuras apresentadas, a figura A mede 32 unidades de área; a figura B mede 32 unidades de área; a figura C mede 33 unidades de área; a figura D mede 38 unidades de área; a figura E mede 44 unidades de área; a figura F mede 24 unidades de área.
a) As figuras que têm medida
de área maior do que 32 ![]() são
C, D e E.
são
C, D e E.
b) A figura B tem medida de área igual à da figura A.
c) A figura F é a figura com menor medida de área. Logo, não há nenhuma figura com medida de área menor do que ela.
54. Como a unidade de medida de área é duas vezes maior do que a obtida na atividade anterior, as medidas obtidas nesse caso são metade das calculadas na atividade anterior. Assim, a figura A mede 16 unidades de área, pois ; a figura B mede 16 unidades de área, pois ; a figura C mede 16,5 unidades de área, pois ; a figura D mede 19 unidades de área, pois ; a figura E mede 22 unidades de área, pois ; a figura F mede 12 unidades de área, pois .
55. A figura C é composta por duas unidades da figura B e quatro unidades da figura A. Assim, Edson utilizou , ou seja, 40 unidades da figura C e , ou seja, 20 unidades da figura B para cobrir a figura que ele mediu.
56. A figura laranja é formada por cinco figuras verdes de medida de largura e de comprimento. Logo, a figura laranja é composta por 25 unidades da figura verde, pois .
57. a) Na malha A, foram coloridos 97 quadradinhos.
b) Na malha B, foram coloridos 137 quadradinhos.
c) Como a quantidade de quadradinhos pintados na malha A é menor do que a medida de área do círculo e na malha B ultrapassa a medida de área, concluímos que e . Calculando a média entre essas medidas de área, obtemos: .
Reescrevendo a frase e substituindo as respectivas letras, temos: Com esse procedimento, Paula concluiu que a medida de área do círculo é maior do que 97 quadradinhos e menor do que 137 quadradinhos. Então, ela calculou a média desses números para obter a medida de área aproximada do círculo. Portanto, a área do círculo mede aproximadamente 117 quadradinhos.
58. Aplicando uma estratégia semelhante à da atividade 57, temos:
Nesta malha quadriculada, colorimos a maior quantidade de quadradinhos limitados pela circunferência, ou seja, 61 quadradinhos.

Nesta malha quadriculada, colorimos a menor quantidade de quadradinhos limitados pela circunferência, ou seja, 97 quadradinhos.
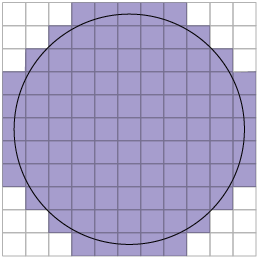
Fazendo a média das duas quantidades de quadradinhos pintados, obtemos . Portanto, a área aproximada do círculo mede 79 quadradinhos.
59. De acordo com as figuras apresentadas, temos:
Medida de área da figura A: , ou seja, .
Medida de área da figura B: , ou seja, .
Página CIX
Medida de área da figura C:
.
Medida de área da figura D:
.
60. O comprimento dos lados de cada quadradinho mede . Desse modo, a área de cada quadradinho mede . Como são 38 quadradinhos, ao todo, a área da figura formada pelos quadradinhos coloridos mede .
Adicionando as medidas de comprimento dos lados de cada quadradinho que compõem o contorno da figura, verificamos que o perímetro dessa figura mede .
61. A área que não é destinada ao palco mede , pois . Como 4 pessoas ocupam aproximadamente 1 metro quadrado, calculamos . Portanto, aproximadamente, 1.096 pessoas estavam nesse show.
62. a) De acordo com o gráfico, o ano em que houve o maior desmatamento na Amazônia foi 2021, totalizando de área desmatada.
b) Em 2010, a área desmatada era de .
c) De acordo com o gráfico, fazemos . Portanto, em 2019 e 2020 foram desmatados na Amazônia.
d) De acordo com o gráfico, o ano em que ocorreu o menor desmatamento foi em 2012.
63. Como , realizando a conversão, fazemos . Portanto, um terreno de 30 hectares mede .
64. Como , realizando a conversão, fazemos . Portanto, um terreno de 125 hectares mede de área.
65. a) Realizando cálculos, temos os seguintes resultados.
• A área da propriedade mede , pois .
• A área destinada ao plantio de café mede , pois .
• A área destinada à criação de gado mede , pois .
b) Como , realizando a conversão, obtemos: . Portanto, a área da propriedade destinada à criação de gado mede .
66. Realizando as conversões, temos e . Portanto, a área do terreno mede
67. Realizando as medições com uma régua, verificamos que os lados do quadrado A medem de comprimento e os lados do retângulo B medem, respectivamente, e . Assim, temos:
Medida do perímetro do quadrado A: , ou seja,
Medida da área do quadrado A: , ou seja, .
Medida do perímetro do retângulo B: , ou seja, .
Medida da área do retângulo B: , ou seja, .
68. a) Como o comprimento do lado de cada quadrado que compõe a planificação mede , a área de cada quadrado mede , pois . Como a planificação é formada por 6 quadrados iguais, a área da planificação mede , pois .
b) A planificação apresentada é de um cubo.
69. a) A largura do retângulo mede , pois .
b) A largura do retângulo mede , pois .
70. A medida de área do quadrado é obtida multiplicando a medida de comprimento pela medida da largura. Como essas medidas são iguais e a área desse quadrado mede , calculamos , pois . Portanto, a medida de comprimento do lado do quadrado é .
71. De acordo com os anúncios dos terrenos, a área do terreno A mede , pois , e a área do terreno B mede , pois .
72. De acordo com a imagem, verificamos que a medida do comprimento equivale ao dobro da medida da largura de cada um dos seis retângulos que a compõem. Como a soma dessas medidas é , concluímos que o comprimento e a largura medem, respectivamente, e , pois é a única adição que resulta em 21, de modo que umas das parcelas seja o dobro da outra. Assim, o comprimento do retângulo maior deve medir , pois essa dimensão é a soma do comprimento de dois retângulos menores, ou seja, . Logo, a área do retângulo maior mede , pois e, portanto, a alternativa correta é a e.
73. Resposta pessoal. Sugestão de resposta: O perímetro de um retângulo mede . Sabendo que o comprimento de um dos seus lados mede , qual é medida de área desse retângulo? Resposta: .
74. Resposta no final da seção Resoluções.
75. a) Sim, pois ao dobrarmos a medida do comprimento do lado, a medida do perímetro também dobra; ao triplicarmos a medida do comprimento do lado, a medida do perímetro também triplica; e assim por diante.
b) Não, pois, ao dobrarmos a medida do comprimento do lado, a medida da área quadruplica, por exemplo.
76. Calculando a medida da área de cada triângulo, verificamos que a área do triângulo A mede , pois ; a área do triângulo B mede , pois ; a área do triângulo C mede , pois ; a área do triângulo D mede , pois ; a área do triângulo E mede , pois .
77. Calculando a medida da área de cada triângulo, verificamos que a área do triângulo A mede , pois ; a área do triângulo B mede , pois ; a área do triângulo C mede , pois .
Página CX
78. Considerando que as figuras são formadas por retângulos e triângulos retângulos, basta calcular a área de cada polígono separadamente e juntar as medidas obtidas. Assim, a área da figura A mede , pois ; a área da figura B mede , pois ; a área da figura C mede , pois .
79. a) De acordo com a imagem, o comprimento do lado do jardim mede , pois .
b) Utilizando a fórmula da área do triângulo retângulo, verificamos que a área do jardim mede , pois .
80. Subtraindo as medidas conhecidas, com base na imagem, da medida do perímetro do triângulo, obtemos a medida do comprimento do lado menor. Assim, , ou seja, o comprimento do lado menor do triângulo mede . Usando essa medida na fórmula, verificamos que a área do triângulo retângulo mede , pois .
81. Resposta pessoal. Sugestão de resposta: Qual é a medida da área do triângulo apresentado?
Resposta: .
Questão 9. Como foram acrescentadas duas camadas com 8 caixas cada, então temos um acréscimo de 16 caixas. Sabendo que a pilha inicial tinha um volume de 32 caixas, então . Portanto, a nova pilha terá 48 caixas de medida de volume.
Atividades
82. De acordo com a imagem das pilhas de cubos, o volume da pilha A mede 45 cubos, pois , e o volume da pilha B mede 31 cubos, pois .
83. Como a medida de comprimento da aresta de cada cubo equivale a , então a medida de volume de cada cubo é . Como a pilha tem 7 cubos, então o volume da pilha mede . Logo, para que a pilha tenha medida de volume igual a , fazemos . Portanto, faltam 8 cubos.
84. Calculando a medida do volume dos paralelepípedos retos retângulos, verificamos que o volume do paralelepípedo A mede , pois , e o volume do paralelepípedo B mede , pois .
85. A medida do volume da figura é dada por , ou seja, .
86. O volume de cada cubo mede , pois , e o volume da caixa mede , pois . Portanto, cabem, no máximo, 12 cubos na caixa, ou seja, .
87. Resposta pessoal. Sugestão de resposta: Qual é a medida de volume da figura apresentada? Resposta: .
88. A unidade mais adequada para expressar a medida de capacidade de:
a) um copo é o mililitro.
b) um balde é o litro.
c) uma piscina é o litro.
d) um frasco de perfume é o mililitro.
e) uma caixa-d'água é o litro.
f) uma xícara de café é o mililitro.
89. Realizando as conversões, temos:
a)
b)
c)
d)
e)
f)
g)
h)
90. Realizando as conversões, temos:
a)
b)
c)
d)
e)
f)
g)
h)
91. Resposta no final da seção Resoluções.
92. De acordo com os dados do enunciado, Raul levou , ou seja, de água.
Como sobraram 5 litros de água, então a quantidade de litros de água consumida foi , ou seja, . Convertendo em mililitros, temos , ou seja, .
93. a) Como foram produzidos de suco, fazendo a con- versão obtemos , ou seja, . A quantidade de garrafas de que foram produzidas pode ser calculada da seguinte maneira: . Portanto, foram produzidas 50 garrafas de suco de laranja de .
b) Temos que . Portanto, o valor arrecadado com a venda de 50 garrafas de suco foi de R$ 450,00.
c) A quantidade de garrafas de que são necessárias pode ser calculada da seguinte maneira: . Portanto, seriam necessárias 100 garrafas.
d) Resposta pessoal. Sugestão de resposta: Escreva uma possibilidade de armazenamento do suco produzido usando apenas garrafas de e .
Resposta: 30 garrafas de e 35 garrafas de .
Página CXI
94. a) Se a torneira ficar aberta por 150 minutos, a piscina terá , pois . Como , a piscina não ficará cheia em 150 minutos.
b) Para encher a piscina, são necessários 200 minutos, pois . Convertendo 200 minutos em horas e minutos, obtemos:
Portanto, para encher a piscina serão necessárias .
O que eu estudei?
1. A quantidade de carros na fila é dada por . Portanto, nessa fila há, aproximadamente, 714 carros.
2. a) A baleia-azul pode atingir 28 metros a mais do que a baleia-branca, pois .
b) De acordo com a tabela, a medida de comprimento mais próxima de é , que corresponde à medida de comprimento da baleia-cinzenta.
c) De acordo com a medida do comprimento da baleia-azul e da baleia-cinzenta, temos . Portanto, a medida de comprimento da baleia-azul é, aproximadamente, 2 vezes maior do que a medida de comprimento da baleia-cinzenta.
d) Comparando a medida de comprimento das baleias apresentadas, verificamos que a medida de comprimento da baleia-azul excede em mais de qualquer das outras três medidas. Além disso, a medida de comprimento da baleia-branca é mais do que a metade a menos do que as outras três. Sendo assim, as espécies referidas são a baleia-corcunda e a baleia-cinzenta, pois calculando a diferença entre as medidas de comprimento delas obtemos , ou seja, .
3. De acordo com o enunciado, o perímetro com maior medida tem , pois , e o perímetro com menor medida tem , pois .
4. A resposta para esta atividade depende do ano vigente. Caso o ano seja 2024:
a) o mês de fevereiro tem 29 dias.
b) o primeiro dia do ano será segunda-feira.
c) o último dia do ano será terça-feira.
d) no primeiro semestre desse ano há 182 dias.
5. a) Como não existem anos terminados em 00 entre os anos 2017 e 2027, devemos procurar os anos bissextos compreendidos neste período que sejam divisíveis por 4. Nesse caso, os anos possíveis são 2020 e 2024.
b) Para serem bissextos, os anos terminados em 00 também são divisíveis por 400. Com isso, os anos 2000 e 2400 são anos bissextos e, além disso, obedecem à restrição de serem menores do que 2500.
6. a) Fazendo as conversões necessárias, obtemos:
, ou seja, .
b) Medida da área destinada ao plantio de frutas: 30% de , ou seja, , isto é, ou .
Medida da área destinada ao plantio de arroz: 20% de , ou seja, , isto é, ou .
Medida da área destinada ao plantio de milho: 50% de , ou seja, , isto é, ou .
c) Como a área destinada ao plantio de frutas mede e o alqueire paulista equivale a , temos: . Portanto, a área destinada ao plantio de frutas mede aproximadamente 7,4 alqueires.
7. Com base nas medidas de área indicadas nos quadrados, verificamos que o comprimento dos lados do quadrado maior medem e o comprimento dos lados do quadrado médio medem . Desse modo, concluímos que os lados do quadrado menor medem , pois . Logo, o perímetro dessa figura mede , pois
. Portanto, a alternativa correta é a d.
8. Cada um dos quadrados mede de área e cada quadrado cobre do quadrado justaposto. Como o primeiro quadrado não é coberto por nenhum outro quadrado, então . Portanto, a área da figura mede e a alternativa correta é a b.
9. Realizando a conversão de miligrama em grama, temos: , ou seja, . Como a caixa contém 30 comprimidos, fazemos . Portanto, a massa do componente principal em uma embalagem com 30 comprimidos mede .
10. Convertendo em gramas, temos , ou seja, . Desse modo, . Portanto, no primeiro mês de vida, a medida de massa de Flávia aumentou .
11. Contando a quantidade de cubinhos da pilha, de cima para baixo, temos 4 cubos na primeira camada, 7 cubos na segunda camada e 11 cubos na terceira camada. Logo, . Como uma unidade de medida é formada por dois cubos, a pilha mede 11 unidades, pois .
12. Calculando primeiramente a medida de comprimento da aresta do cubo pequeno, temos: , ou seja, . Assim, a largura do empilhamento mede , pois e a altura do empilhamento mede , pois . Calculando a medida do volume , verificamos que a pilha tem de medida de volume.
13. Multiplicando as 5 garrafas pela medida da capacidade de cada uma, obtemos , pois . Para converter em mililitros, calculamos , ou seja, há de suco. Como precisamos saber a quantidade de garrafas de necessárias ao armazenamento, calculamos . Portanto, serão necessárias 25 garrafas para armazenar esse suco.
14. Para dissolver o conteúdo de 3 envelopes de gelatina, são necessários de água, pois . Convertendo em litros, temos: . Portanto, para dissolver o conteúdo de 3 envelopes de gelatina, são necessários de água.
Página CXII
Unidade 11
Estatística e probabilidade
Questão 1. O título do gráfico é Quantidade de atletas em cinco edições dos Jogos Olímpicos de verão e a fonte de pesquisa é o site do COB (Comitê Olímpico Brasileiro).
Atividades
1. a) A maior medida de temperatura está prevista para quinta-feira. Está prevista a medida de temperatura de .
b) Estão previstas medidas de temperatura abaixo de na terça-feira e na sexta-feira.
2. a) Adicionando a quantidade de livros de cada tipo vendidos durante a semana, obtemos:
96 dicionários, pois .
78 livros infantis, pois .
66 livros de literatura, pois .
90 livros de culinária, pois .
66 livros técnicos, pois .
84 livros de outros tipos, pois .
b) Para calcular a média de livros vendidos por dia, é necessário calcular a quantidade de livros vendidos em cada dia, juntar essas quantidades e, depois, dividir pela quantidade de dias. Assim, na segunda-feira, foram vendidos 51 livros, pois ; na terça-feira, foram vendidos 17 livros, pois ; na quarta-feira, foram vendidos 86 livros, pois ; na quinta-feira, foram vendidos 90 livros, pois ; na sexta-feira, foram vendidos 107 livros, pois 46 no sábado, foram vendidos 70 livros, pois . Juntando esses resultados, temos , e dividindo a soma por 6 obtemos . Portanto, em média, foram vendidos 80 livros.
c) Resposta pessoal. Sugestão de resposta: O tipo de livro mais vendido foi o dicionário e os menos vendidos foram os livros de literatura e os técnicos. O dia da semana que mais vendeu livros foi sexta-feira e o dia que menos vendeu livros foi segunda-feira.
3. a) O texto aborda a quantidade de casos de COVID-19 registrados nas diferentes regiões do Brasil desde seu primeiro registro, no dia 26 de fevereiro de 2020, até o dia 21 de fevereiro de 2022.
b) Até 21 de fevereiro de 2022, foram registrados 2.992.934 casos da COVID-19 na Região Centro-Oeste.
c) Organizando os dados em uma tabela, temos:
|
Região |
Quantidade de casos |
|---|---|
|
Sudeste |
11.019.303 |
|
Norte |
2.359.747 |
|
Sul |
5.962.950 |
|
Nordeste |
5.910.617 |
|
Centro-Oeste |
2.992.934 |
Fonte de pesquisa: BRASIL. Ministério da Saúde. Painel Coronavírus. Disponível em: https://oeds.link/mH7eJZ. Acesso em: 5 maio 2022.
4. a) O título do gráfico é Quantidade de casos mensais de dengue – 2023 e a fonte de pesquisa é a direção do posto de saúde.
b) A variável pesquisada é a quantidade de casos de dengue. A frequência para o mês de agosto é 10 casos.
c) A maior quantidade de casos de dengue foi registrada em março e a menor, em setembro.
d) Foram registrados mais de 10 casos de dengue em janeiro, fevereiro, março, abril, maio, junho, julho e dezembro, ou seja, em 8 meses.
e) Resposta pessoal. Sugestão de resposta: A dengue é uma doença que pode levar à morte. A pessoa que a contrai fica incapacitada de trabalhar por um período de, pelo menos, uma semana, e pode apresentar, em muitos casos, sintomas graves. A falta de limpeza de locais onde o mosquito pode procriar é a maior causa do aumento da população desse transmissor e, com isso, os casos de dengue podem aumentar muito, sobrecarregando o sistema de saúde.
5. a) A atividade física de maior gasto calórico em é o caminhar acelerado.
b) Como uma pessoa de gasta ao nadar por , então ela gastará aproximadamente ao nadar por , pois .
c) Uma porção de de abacate tem e uma porção de de banana prata tem . Logo, a fruta mais calórica é a banana prata.
6. a) O 2º material mais reciclado no Brasil em 2019, em porcentagem, foi o papel .
b) O material menos reciclado no Brasil em 2019, em porcentagem, foi o plástico .
7. a) O título do gráfico é Pessoas de 5 anos ou mais de idade alfabetizadas e não alfabetizadas no Brasil – 2015, a fonte de pesquisa foi o IBGE (Instituto Brasileiro de Geografia e Estatística) e as informações do gráfico foram obtidas em 20 de fevereiro de 2022.
b) As variáveis pesquisadas são a quantidade de pessoas com 5 anos ou mais de idade alfabetizadas e não alfabetizadas.
c) A informação indicada no eixo horizontal é região brasileira.
Página CXIII
d) O Nordeste é a região com a maior quantidade de pessoas não alfabetizadas em 2015, apresentando 8.726.000 pessoas não alfabetizadas.
e) O Sudeste é a região com mais pessoas alfabetizadas em 2015, e o Centro-Oeste é a região com o menos pessoas alfabetizadas em 2015.
f) Efetuando os cálculos, verificamos que a quantidade de pessoas com 5 anos ou mais de idade:
alfabetizadas
no Brasil em 2015 é dada por:
não
alfabetizadas no Brasil em 2015 é dada por:
g) Resposta pessoal. Sugestão de resposta: De modo geral, o analfabetismo afeta o desenvolvimento social de um país. Entre os vários problemas decorrentes do analfabetismo, podemos citar a exclusão social, a falta de capacitação profissional e o aumento da taxa de criminalidade.
h) Resposta pessoal. Sugestão de resposta: A Região Sudeste tinha a maior quantidade de pessoas de 5 anos ou mais alfabetizadas em 2015, e a Região Centro-Oeste tinha a menor quantidade. A Região Nordeste tinha a maior quantidade de pessoas com 5 anos ou mais de idade não alfabetizadas em 2015, e a Região Centro-Oeste tinha a menor quantidade.
8. a) O título do gráfico é Meio de transporte utilizado pelos estudantes para irem à escola – março de 2023 e a fonte de pesquisa é a direção da escola.
b) A variável da pesquisa é o meio de transporte utilizado pelos estudantes.
c) Em porcentagem, 10% dos estudantes utilizam bicicleta para irem à escola. Para obter a quantidade de estudantes, calculamos de 820, ou seja, . Portanto, 82 estudantes utilizam bicicleta para irem à escola.
9. Em um gráfico de setores, a medida da área de cada setor é proporcional ao valor representado por ela. Sendo assim, o esporte que a maioria dos estudantes prefere será representado pelo setor com a maior área, e assim por diante. Com isso, temos as seguintes considerações:
O futebol, que é o esporte com a maior porcentagem, deve estar indicado na legenda com a cor azul do maior setor do gráfico. Com isso, excluímos a alternativa A, pois nela a parte azul está indicando o voleibol. Como o voleibol é o esporte com a segunda maior porcentagem, deve estar indicado na legenda com a cor alaranjada. Como o basquetebol é o terceiro esporte com maior porcentagem, deve estar indicado na legenda com a cor roxa. Já a categoria "Outros" deve estar indicado na legenda com a cor amarela, pois apresenta a quarta preferência, e o handebol é o esporte com menor porcentagem, logo deve ser representado pela cor verde. Portanto, excluímos a alternativa C, e a resposta correta é a alternativa B.
10. a) O título do gráfico é Despesas da família de Bernardo – outubro de 2023 e a fonte de pesquisa são os registros da família de Bernardo.
b) A variável da pesquisa são os valores das despesas por grupo da família de Bernardo.
c) A despesa que representa o maior gasto em outubro de 2023 é a alimentação.
d) A porcentagem da renda familiar gasta com saúde foi 10%.
e) Em porcentagem, a família de Bernardo gasta 30% com moradia. O gasto com saúde e transporte juntos é dado por . Portanto, a quantia gasta com moradia é maior do que a quantia gasta com saúde e transporte juntos.
f) Em outubro de 2023, a família de Bernardo gastou R$ 1.080,00 reais com moradia, pois , e R$ 1.440,00 com alimentação, pois .
g) Sugestões de resposta: Lazer e educação.
i) Resposta pessoal. Sugestão de resposta: Em outubro de 2023, a família de Bernardo teve o maior gasto com alimentação, usando 40% da renda familiar. O segundo maior gasto foi com moradia, com 30% da renda familiar. Juntas, as despesas com alimentação e moradia totalizaram 70% da renda. Desconsiderando as outras despesas, o menor gasto foi com saúde, com apenas 10% do total da renda familiar.
11. a) O título do gráfico é Percentual de animais adotados na feira de adoção – 21/03/2023 e a fonte de pesquisa é a direção da ONG.
b) A variável de pesquisa é a quantidade de cada grupo de animais adotados.
c) O percentual de gatos adotados foi 35%.
d) Em porcentagem, foram adotados 5% de peixes. Calculando 5% do total de 40 animais adotados, obtemos . Portanto, foram adotados 2 peixes.
e) Com base nas informações, 45% dos animais adotados foram cachorros. Calculando 45% de 40, temos , ou seja, foram adotados 18 cachorros.
Dos animais adotados, 15% foram pássaros. Calculando 15% de 40, temos , ou seja, foram adotados 6 pássaros. Efetuando , obtemos a diferença entre a quantidade de cachorros e pássaros adotados, que é 12 animais.
12. Do total de turistas que a Região Sul recebeu, 53,2% visitaram o Rio Grande do Sul (RS), 15,1% visitaram Santa Catarina (SC) e 31,7% visitaram o Paraná (PR). Desse modo, o gráfico que representa as informações indicadas no mapa é o gráfico apresentado na alternativa B.
Página CXIV
13. a) O título do gráfico é Produção aproximada de feijão no Brasil – 2014 a 2020.
b) A informação expressa no eixo vertical é produção de feijão (em milhões de toneladas) e no eixo horizontal é o ano da produção.
c) Em 2020 foram produzidas, aproximadamente, 3 milhões de toneladas de feijão.
d) Adicionando a produção de feijão, em milhões, em cada ano representado no gráfico, temos , ou seja, foram produzidas 20,8 milhões de toneladas de feijão ao todo nos anos representados no gráfico.
e) Em 2016, foram produzidas aproximadamente 2,6 toneladas de feijão e em 2017, aproximadamente 3,0 toneladas de feijão. Como , houve uma diferença de aproximadamente 0,4 milhão de toneladas na produção de feijão entre esses dois anos.
f) Resposta pessoal. Sugestão de resposta: Entre os anos apresentados no gráfico, o ano em que houve a maior produção de feijão foi em 2014, com, aproximadamente, 3,3 milhões de toneladas e o ano em que houve a menor produção foi em 2016, com, aproximadamente, 2,6 milhões de toneladas. A produção de feijão diminuiu de 3,3 milhões de toneladas no ano de 2014 para 2,6 milhões de toneladas em 2016. Por outro lado, de 2016 para 2017 a produção aumentou para 3,0 milhões de toneladas, voltando a diminuir em 2018 e se mantendo em 2019. Por fim, aumentou novamente para 3,0 milhões de toneladas em 2020.
14. a) O título do gráfico é Medidas de temperaturas diárias (máxima e mínima) registradas em Campina Grande nos últimos 7 dias de janeiro de 2022 e a fonte de pesquisa é o site do Inmet (Instituto Nacional de Meteorologia).
b) As variáveis pesquisadas foram as medidas das temperaturas diárias máxima e mínima, registradas em Campina Grande (PB).
c) A informação expressa no eixo vertical é a medida de temperatura em e no eixo horizontal o dia em que a temperatura foi medida.
d) No dia 25, a medida da temperatura máxima registrada foi .
e) Somente no dia 29 a medida da temperatura mínima foi menor do que .
f) No dia 30, a medida da temperatura máxima foi e a mínima, . Como , houve de variação entre as medidas das temperaturas máxima e mínima no dia 30. Já no dia 26, a medida da temperatura máxima foi e a mínima, . Como , houve de variação entre as medidas das temperaturas máxima e mínima no dia 26.
g) No dia 29, a medida da temperatura máxima foi .
15. a) • Em 30/10/2021, o computador custava R$ 2.350,00.
Em 12/12/2021, o computador custava R$ 3.200,00.
b) Como o computador custava R$ 2.700,00 em 29/11/2021 e , a diferença entre os dois preços é R$ 810,00.
c) No dia 15/10/2021, o computador custava R$ 2.500,00, e no dia 29/11/2021 ele custava 2.700,00. Assim, houve um aumento de preço de R$ 200,00 entre essas datas, pois . Como o computador custava R$ 3.200,00 em 12/12/2021, houve o aumento de R$ 530,00 de 29/11/2021 a 12/12/2021, pois . Portanto, o maior aumento do preço do computador ocorreu no intervalo de 29/11/2021 a 12/12/2021.
d) Resposta pessoal.
e) Resposta pessoal. Sugestão de resposta: De acordo com os dados apresentados no gráfico, o menor preço do computador ocorreu em 30/10/2021, e o maior preço ocorreu em 12/12/2021. De 15/10/2021 a 30/10/2021 o preço do computador diminuiu R$ 150,00. Porém, de 30/10/2021 a 12/12/2021 o preço do computador sofreu aumentos sucessivos, chegando ao valor de R$ 3.200,00.
16. a) • Em 2014, foram produzidos aproximadamente 2.296.800 automóveis bicombustíveis.
Em 2019, foram produzidos aproximadamente 2.048.900 automóveis bicombustíveis.
b) Comparando as informações do gráfico, verificamos que, de 2014 a 2016, houve uma queda na produção de automóveis bicombustíveis no Brasil. Entre os fatores que contribuíram para a redução da produção de carros nesse período, o mais importante foi a crise econômica no país.
c) Calculando o aumento em cada um dos anos, verificamos que em 2017 houve aumento de 351.200 unidades de automóveis biocombustíveis produzidas, pois ; em 2018 houve aumento de 29.800 automóveis, pois ; em 2019, houve aumento de 62.000 automóveis, pois . Comparando as quantidades, concluímos que o maior aumento na produção de automóveis bicombustíveis foi em 2017.
d) Resposta pessoal. Sugestão de resposta: A maior produção de automóveis bicombustíveis ocorreu em 2014, com um total de, aproximadamente, 2.296.800 unidades produzidas, e a menor produção foi no ano 2016 com, aproximadamente, 1.605.900 unidades produzidas. De 2014 a 2016 houve reduções sucessivas na produção de automóveis, chegando a 1.605.900 automóveis produzidos em 2016. De 2016 a 2019 houve aumentos sucessivos na produção e, em 2019, foram produzidos 2.048.900 automóveis bicombustíveis.
17. a) O estado que produziu a maior quantidade de cana-de-açúcar na safra 2020/2021 foi São Paulo, com .
b) Em 2017 o Brasil produziu de soja, e em 2020 produziu de soja. Como , a diferença entre as quantidades produzidas em 2020 e em 2017 foi .
c) A maior produção de mandioca ocorreu em 2020. Foram produzidas de mandioca.
18. a) O mês em que houve o maior consumo de energia elétrica foi fevereiro de 2022. Nesse mês, foram consumidos .
Página CXV
b) Como em julho de 2021 foram consumidos de energia elétrica, efetuamos , obtendo assim o total gasto, ou seja, R$ 87,74. Já no mês de agosto, como foram consumidos de energia elétrica, então o total gasto é dado por , ou seja, R$ 104,96.
19. a) Alguns dos gases existentes na atmosfera retêm parte do calor do Sol, aquecendo a superfície terrestre e provocando o efeito estufa.
b) Essas atividades provocam um aumento na concentração de certos gases na atmosfera.
c) Possíveis respostas: Entre os vários problemas causados pelo aquecimento global, podemos citar o derretimento das geleiras, o qual provoca a elevação do nível dos oceanos, a maior ocorrência de tempestades e as mudanças no regime de chuvas e de ventos.
d) Entre 1911 e 1920, a temperatura média aproximada do planeta era . Entre os anos de 2011 e 2020 era .
20. a) A taxa de incidência de COVID-19 para o estado de São Paulo foi 10.754,2 e para o estado do Espírito Santo foi 25.109,2.
b) A taxa indica que, até 22/2/2022, a cada 100 mil habitantes desse estado, 11.370,1 foram infectados por COVID-19.
c) O estado de São Paulo apresentou o menor número de casos notificados por 100 mil habitantes, com taxa de 10.754,2.
d) Registre os dados do texto no Calc formando uma tabela. Para isso, digite "Estados" na coluna A e "Taxa de incidência da COVID-19" na coluna B, digitando as respectivas taxas de cada estado, conforme mostra a imagem.
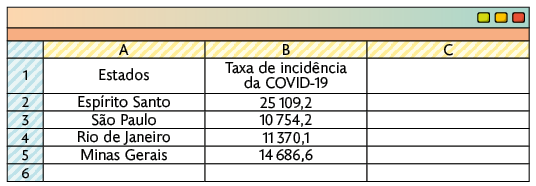
Selecione as células com os dados. Para isso, clique na célula A1 e, mantendo o botão pressionado, arraste até a célula B5.
Em seguida, clique no menu Inserir e selecione a opção Gráfico, ou clique diretamente no botão Inserir gráfico. Na janela Assistente de gráficos, selecione Tipo de gráfico e escolha Coluna.
Ainda na janela Assistente de gráficos, selecione Elementos do gráfico e preencha os campos Título com Taxa de Incidência da COVID-19 nos estados da Região Sudeste do Brasil até 22/2/2022, Eixo X com Estados e Eixo Y com Taxa de incidência da COVID-19. Ao final, desmarque a opção Exibir legenda e clique em Finalizar. A fonte de pesquisa pode ser colocada em uma célula abaixo do gráfico.
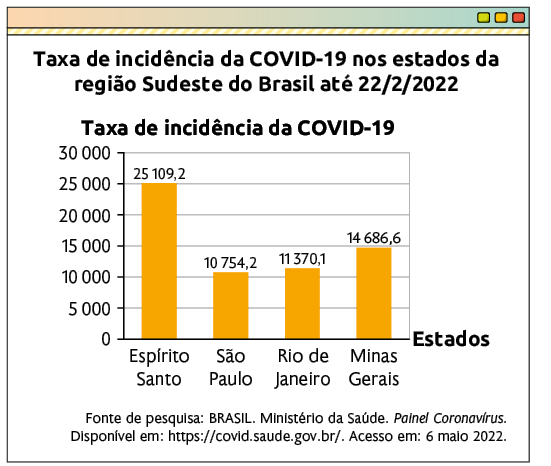
e) Resposta pessoal. Espera-se que os estudantes escolham o gráfico de colunas, pois com ele é possível fazer a comparação dos dados.
f) Resposta pessoal. Sugestão de reposta: A maior taxa de incidência da COVID-19 ocorreu no estado do Espírito Santo, com 25.109,2 pessoas infectadas a cada 100 mil habitantes. A menor taxa de incidência da COVID-19 ocorreu no estado de São Paulo, com 10.745,2 pessoas infectadas a cada 100 mil habitantes.
g) Resposta pessoal. Espera-se que os estudantes concluam que as vacinas são importantes, pois é um método eficaz e seguro na prevenção de doenças, eliminando ou reduzindo o risco de contágio.
21. Resposta pessoal. Espera-se que os estudantes definam o assunto a ser pesquisado, sigam as etapas de coleta e organização dos dados em tabelas e gráficos e apresentem os resultados da pesquisa com suas conclusões.
22. No total, há 15 pedaços de papel, com um número em cada um deles.
a) Os números terminados em zero são 180, 190 e 30. Portanto, a probabilidade de o papel sorteado conter um número terminado em zero é ou .
b) Os números pares são 192, 180, 152, 130, 72, 190, 30 e 108. Portanto, a probabilidade de o papel sorteado conter um número par é .
c) Os números maiores do que 100 são 192, 205, 180, 152, 136, 117, 241, 190, 147 e 108. Portanto, a probabilidade de o papel sorteado conter um número maior do que 100 é ou .
d) Os números menores do que 125 são 117, 72, 51, 30, 85, 67 e 108. Portanto, a probabilidade de o papel sorteado conter um número menor do que 125 é .
e) Os números ímpares são 205, 117, 241, 51, 85, 147 e 67. Portanto, a probabilidade de o papel sorteado conter um número ímpar é .
Página CXVI
f) Os números maiores do que 77 e menores do que 151 são 136, 117, 85, 147 e 108. Portanto, a probabilidade de o papel sorteado conter um número maior do que 77 e menor do que 151 é ou .
23. a) Como a cada 120 calças 5 apresentam defeito na costura, a probabilidade é ou .
b) Dobrando a quantidade de calças, a quantidade de calças com defeito na costura também dobra. Logo, em um lote de 240 calças poderá haver 10 calças com defeito na costura. Desse modo, a probabilidade é . Essa probabilidade será a mesma de retirar, ao acaso, uma calça com defeito na costura de um lote de 120 calças, pois .
24. a) Foram realizados 30 lançamentos.
b) O resultado foi cara em 13 lançamentos e coroa em 17 lançamentos.
c) A razão entre o número de lançamentos cujo resultado foi cara e o total de lançamentos é . Escrevendo esse número na forma percentual, temos e , ou seja, aproximadamente, 43%.
d) Uma moeda tem duas faces, sendo elas cara e coroa. Portanto, a probabilidade de sair cara na face voltada para cima é , ou, na forma percentual, .
e) Resposta pessoal. Espera-se que os estudantes percebam que a razão obtida no item c é menor do que a obtida no item anterior.
f) Resposta pessoal. Espera-se que os estudantes lancem a moeda, registrem os dados em uma tabela e, com isso, percebam que a razão obtida é um número próximo da probabilidade obtida no item d.
25. a) • Nessa atividade, cada um dos 5 integrantes do grupo deverá retirar 4 cartas do monte. Como , foram retiradas 20 cartas.
Resposta pessoal. A quantidade de vezes em que foram retiradas cartas de copas depende de cada retirada.
b) Resposta pessoal. Espera-se que os estudantes escrevam a razão formada pelo número de vezes em que saiu a carta de copas e o número 20 (total de retiradas) e, depois, representem esse número nas formas decimal e percentual.
c) Um jogo de baralho tem 52 cartas com 13 cartas de cada naipe, ou seja, um jogo de baralho tem 13 cartas com o naipe de copas. Portanto, a probabilidade de retirar, ao acaso, uma carta de copas de um jogo de baralho é ou . Na forma percentual, temos .
d) Resposta pessoal. Espera-se que os estudantes comparem a probabilidade do item anterior com a razão obtida no item b, verificando se é maior, menor ou igual.
O que eu estudei?
1. Resposta pessoal. Sugestão de resposta: A região do Brasil que possui a maior quantidade de municípios é a Região Nordeste, com 1.794 municípios, e a região do Brasil que possui a menor quantidade de municípios é a Região Norte, com 450 municípios.
2. a) A descarga de banheiro é a modalidade com o maior consumo de água. Esse gasto corresponde a 33% do consumo médio diário de água por família.
b) Como o consumo médio diário de água é , há um gasto de 33% de com descarga de banheiro, que representam de água, pois . Para cozinhar e beber, há um gasto de 27% de , que representam de água, pois . Com higiene pessoal, há um gasto de 25% de , que representam de água, pois . Para a lavagem de roupas, há um gasto de 12% de , que representam de água, pois . Outros gastos compreendem 3% de , que representam de água, pois .
3. a) Em apenas 4 das 28 peças de dominó, os pontos somados resultam em 6. Assim, a probabilidade é ou .
b) • Das 28 peças de dominó, temos 16 peças cujos pontos somados resultam em um número par. Portanto, a probabilidade é ou .
Em 9 das 28 peças de dominó, os pontos somados são maiores do que 7. Portanto, a probabilidade é .
4. Quando são lançados 2 dados, há um total de 36 combinações diferentes das faces que ficam para cima, pois .
a) As quantidades de pontos obtidas serão iguais em ambos os dados quando as faces que ficarem para cima forem 1, 2, 3 , 4, 5 ou 6 em ambos os dados. Portanto, a probabilidade é ou .
b) • Para que a soma dos pontos obtidos seja igual a 2, as faces dos dois dados viradas para cima devem ser iguais a 1. Portanto, a probabilidade é .
A soma dos pontos será igual a 7 quando as faces dos 2 dados voltadas para cima forem 1 e 6, 2 e 5, 3 e 4, 6 e 1, 5 e 2 ou 4 e 3. Assim há 6 possibilidades da soma dos pontos ser igual a 7. Portanto, a probabilidade de a soma ser igual a 7 é ou .
A soma dos pontos será igual a 5 quando as faces dos 2 dados voltadas para cima forem 1 e 4, 2 e 3, 3 e 2 ou 4 e 1. Portanto, a probabilidade de a soma ser igual a 5 é ou .
A soma dos pontos será igual a 11 quando as faces dos 2 dados voltadas para cima forem 5 e 6 ou 6 e 5. Portanto, a probabilidade de a soma ser igual a 11 é ou .
Unidade 12
Coordenadas, ampliação e redução de figuras
Questão 1.
a) As vagas ocupadas pelos carros azuis são , , , e .
Página CXVII
b) As vagas ocupadas pelos carros amarelos são , e .
c) As vagas ocupadas pelos carros verdes são , , , , e .
Questão 2. As vagas desocupadas são , , , , , , , , , , , , , , , e .
Atividades
1. As letras que ocupam as posições indicadas em cada item formam as seguintes palavras.
a) QUADRADO.
b) PENTÁGONO.
c) HEXÁGONO.
d) TRIÂNGULO.
2. De acordo com o quadro da atividade anterior, temos:
a)
b)
c)
d)
e)
f)
g)
h)
3. Além das posições apresentadas, o cavalo pode se descolocar para as casas , , , , e .
4. a) Devemos representar as coordenadas dos vértices de cada figura.
Figura 1: , , e .
Figura 2: , , , , , , e .
b) Cada quadradinho mede de comprimento de lado. Adicionando essas medidas em cada lado da figura, de acordo com a quantidade de quadradinhos, temos:
figura 1: . Assim, o perímetro mede .
figura 2: . Assim, o perímetro mede .
5. a) Camila acertou os dardos , e . Essas posições estão, respectivamente, nas regiões vermelha, branca e verde. Realizando a adição da pontuação, temos . Logo, Camila marcou 125 pontos.
b) Daniela acertou os dardos , e . Essas posições estão todas na região amarela. Realizando a adição da pontuação, temos . Logo, Daniela marcou 150 pontos.
Questão 3. Espera-se que o estudante encontre em sua pesquisa que René Descartes propôs a criação do plano cartesiano e relacionou a Geometria, a Aritmética e a Álgebra, sendo fundamental para estudos de Geometria analítica. Além disso, deu uma solução ao problema de quadratura do círculo e criou a notação de expoentes. Descartes também teve grande influência no desenvolvimento do método científico.
Questão 4. O primeiro número indica o eixo horizontal e o segundo número indica o eixo vertical. Assim, as coordenadas dos outros pontos são: , , , , , e .
Questão 5. Não, pois a ordem dos números em um par ordenado é muito importante. Ao invertermos essa ordem, obtemos a localização de pontos diferentes. Assim, indica o ponto D e indica o ponto H.
Atividades
6. a)
b)
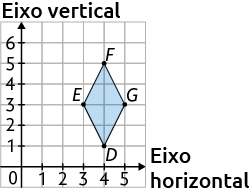
7. As coordenadas dos pontos dos vértices do pentágono são , , , e .
8. a) No plano cartesiano 1 as coordenadas são e .
b) Para deslocar do ponto C para o ponto D no plano cartesiano 2, Lucas seguiu o seguinte deslocamento:
avançar 6 unidades para cima;
avançar 2 unidades para a direita;
avançar 2 unidades para baixo;
avançar 3 unidades para a direita;
avançar 3 unidades para cima;
avançar 2 unidades para a direita;
avançar 8 unidades para baixo;
avançar 4 unidades para a esquerda;
avançar 2 unidades para cima.
c) No plano cartesiano 2, as coordenadas são e .
9. Resposta no final da seção Resoluções.
10. Os pontos F, G e K estão localizados na região da mancha no plano cartesiano.
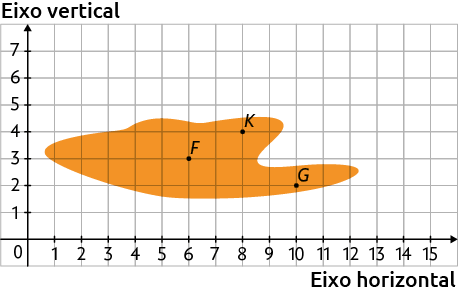
11. De acordo com o plano cartesiano, as coordenadas dos pontos são: , , , e .
12. a) Verdadeira, pois as medidas dos ângulos não se alteraram e a medida de cada lado do polígono 2 aumentou um quadradinho.
b) Falsa, pois o polígono 4 é uma redução do polígono 1.
c) Verdadeira, pois é possível obter a medida do comprimento de cada lado do polígono 4 dividindo a medida do comprimento de cada lado do polígono 5 por 4.
d) Verdadeira, pois é possível obter a medida do comprimento de cada lado do polígono 3 multiplicando a medida do comprimento de cada lado do polígono 4 por 2.
e) Verdadeira, pois, de acordo com os itens anteriores, o polígono 4 é uma redução do polígono 5 e o polígono 3 é uma ampliação do polígono 4.
Página CXVIII
13. Sugestão de resposta:
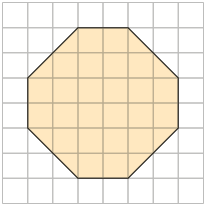
a) Ampliando esse polígono na razão , obtemos:
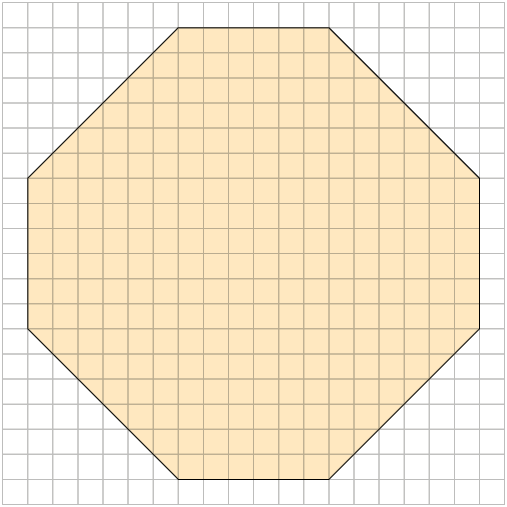
b) Reduzindo esse polígono na razão , obtemos:

14. a) A figura B é uma redução da figura A.
b) As medidas do comprimento dos lados da figura B representam a metade da medida do comprimento dos lados da figura A, desse modo a figura B foi reduzida na razão .
c) As medidas do comprimento dos lados da figura A representam o dobro da medida do comprimento dos lados da figura B, desse modo a figura A foi ampliada na razão .
15. Resposta no final da seção Resoluções.
16. a) Sabendo que as dimensões da redução aplicada na página do livro medem de comprimento e de largura, multiplicamos cada uma dessas medidas por 29 para determinar as medidas aproximadas da obra. Assim e . Portanto, as medidas aproximadas do comprimento e da largura são e , respectivamente.
17. Resposta no final da seção Resoluções.
O que eu estudei?
1. a) A posição das figuras que formam um quadrado ao serem encaixadas são e ; e ; e ; e .
b) Sugestão de resposta: Quatro posições quaisquer que não estejam ocupadas por figuras no quadro, sendo duas posições para a primeira figura e duas posições para a segunda figura. e ; e ; e .
2. a) • Na coordenada está o ponto A.
Na coordenada está o ponto D.
Na coordenada está o ponto F.
b) • O ponto B possui coordenada .
O ponto C possui coordenada .
O ponto E possui coordenada .
3. As coordenadas dos vértices desse polígono são , , , , , e .
4. De acordo com a imagem a seguir, a coordenada do vértice que falta para completar o quadrado é .
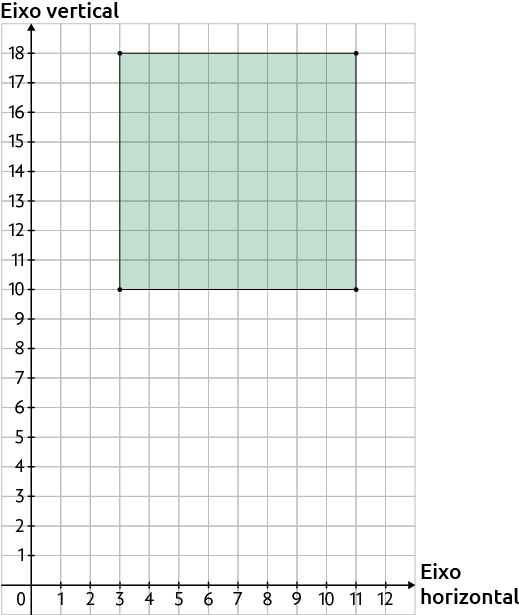
O que eu aprendi?
1. a) • Duzentos e oitenta e cinco mil, quatrocentos e noventa e dois: 285.492.
Cento e setenta e seis mil, trezentos e quarenta e cinco: 176.345.
Novecentos e cinquenta e quatro mil, duzentos e trinta e dois: 954.232.
Setecentos e vinte e cinco mil, quatrocentos e dezoito: 725.418.
Página CXIX
b) Escrevendo esses números em ordem crescente, temos: 176.345, 285.492, 725.418, 954.232.
c) O maior número apresentado no quadro é o 954.232. Realizando as decomposições, temos:
d) O menor número apresentado é 176.345 e, nesse número, o algarismo 6 corresponde a 6 unidades de milhar, ou seja, 6.000.
2. a) Como há 3 níveis com 20 fases em cada um deles, devemos multiplicar o número de níveis pelo número de fases para descobrirmos quantas fases ao todo tem o jogo, ou seja, . Para determinar quantos pontos um jogador precisa fazer para concluir o jogo precisamos multiplicar a quantidade de fases pela quantidade de pontos necessários em cada fase. Assim: .
Portanto, para concluir esse jogo é necessário obter 599.940 pontos.
b) Como Murilo passou 5 fases, a quantidade de pontos feitos por ele é dada por: .
Para determinar quantos pontos ele ainda precisa obter, fazemos: .
Portanto, Murilo ainda precisa obter 549.995 pontos.
3. a) Observando a figura A, de acordo com o formato de cada face, podemos verificar que sua planificação é a 2, pois apresenta 2 faces triangulares e 3 retangulares; A figura B é uma pirâmide e sua planificação é a 3, pois tem 5 faces triangulares e uma face pentagonal; A planificação da figura C é a 1, pois é um prisma, logo suas faces laterais são retângulos.
b) Figura A: prisma de base triangular; Figura B: pirâmide de base pentagonal; Figura C: prisma de base pentagonal.
c) O prisma de base triangular tem 6 vértices e 6 arestas; a pirâmide de base pentagonal tem 6 vértices e 10 arestas; o prisma de base pentagonal tem 10 vértices e 15 arestas. Portanto, entre essas figuras, o prisma de base pentagonal é a figura com a maior quantidade de vértices e o prisma de base triangular é a figura com a menor quantidade de arestas.
4. a) , pois multiplicando o numerador e denominador de por 2 obtemos . Analisando as frações com denominadores iguais, verificamos que .
b) , pois multiplicando o numerador e o denominador de por 2, obtemos . Analisando as frações com denominadores iguais, verificamos que .
c) , pois multiplicando o numerador e o denominador de por 3 e de por 5, obtemos e . Analisando as frações com denominadores iguais, verificamos que .
5. a) ;
b) ;
c) .
6. a) Para determinar quantos reais Marcos gastou, fazemos:
Portanto, Marcos gastou R$ 6,55.
b) Como Marcos gastou no total R$ 6,55 e o picolé custou R$ 2,35, fazemos:
Portanto, Marcos pagou R$ 4,20 na garrafa de água mineral.
7. Como a medida de uma volta completa é , para determinar a medida de distância percorrida por um carro ao dar 9 voltas completas, fazemos: .
Portanto, o carro percorrerá .
8. Maria economizou 75% do valor total da bicicleta, assim devemos calcular 75% de R$ 1.258,00. Como , fazemos:
Logo, Maria economizou R$ 943,50.
Para determinar quantos reais ela ainda precisa economizar, realizamos: .
Portanto, Maria ainda precisa economizar R$ 314,50.
9. Triângulo A: Isósceles, pois tem dois lados com mesma medida de comprimento. Triângulo B: Escaleno, pois seus três lados têm medidas de comprimento diferentes.
10. Como o triângulo apresentado é retângulo, podemos determinar a medida de sua área calculando a medida da área do retângulo e dividindo essa medida por dois, ou seja, . Portanto, a área do triângulo mede .
Para calcular a medida da área do retângulo, basta multiplicar a medida do comprimento pela medida da largura. Assim, .
Logo, a área do retângulo mede .
11. a) O polígono com 5 lados é chamado de pentágono.
b) O polígono com 4 lados é chamado de quadrilátero.
c) O polígono com 6 lados é chamado de hexágono.
12. Sabemos que a quantidade de arestas de um prisma é igual ao triplo da quantidade de lados do polígono da base. Para determinar a quantidade de lados do polígono da base, conhecendo a quantidade de arestas do prisma, fazemos . Portanto, o polígono da base desse prisma tem 6 lados.
13. a) , pois e .
b) Para sabermos quantos reais Jorge gasta mensalmente com aluguel e alimentação juntos, basta multiplicar a fração obtida no item anterior pelo salário de Jorge. Assim, . Portanto, Jorge gasta R$ 1.050,00 com aluguel e alimentação juntos.
Página CXX
Resolução referente à seção O que eu já sei.
17. Podemos montar um quadro com o nome e quantidade de lados, vértices e ângulos de cada figura.
|
Figura |
Nome da figura com relação à quantidade de lados |
Quantidade de lados |
Quantidade de vértices |
Quantidade de ângulos internos |
|---|---|---|---|---|
|
A |
Hexágono |
6 |
6 |
6 |
|
B |
Triângulo |
3 |
3 |
3 |
|
C |
Quadrilátero |
4 |
4 |
4 |
|
D |
Pentágono |
5 |
5 |
5 |
|
E |
Quadrilátero |
4 |
4 |
4 |
|
F |
Heptágono |
7 |
7 |
7 |
Resolução referente à unidade 4.
14. Completando o quadro com os números que representam as letras, temos:
|
Prisma |
Quantidade de lados do polígono da base |
Quantidade de faces |
Quantidade de arestas |
Quantidade de vértices |
|---|---|---|---|---|
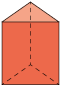
|
3 |
5 |
|
6 |
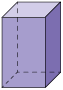
|
|
|
12 |
|
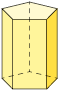
|
|
7 |
|
|
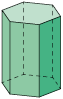
|
6 |
|
|
|
|
Pirâmide |
Quantidade de lados do polígono da base |
Quantidade de faces |
Quantidade de arestas |
Quantidade de vértices |
|---|---|---|---|---|
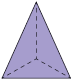
|
3 |
|
6 |
4 |
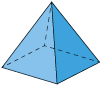
|
|
|
8 |
|
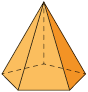
|
5 |
6 |
|
|
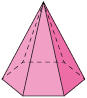
|
|
7 |
12 |
|
Página CXXI
a) A quantidade de arestas de um prisma é igual ao triplo da quantidade de lados do polígono da base. Então, podemos obter a quantidade de arestas de um prisma multiplicando o número que representa a quantidade de lados do polígono da base por 3. Em relação às pirâmides, a quantidade de arestas equivale ao dobro da quantidade de lados do polígono da base. Assim, podemos obter a quantidade de arestas de uma pirâmide multiplicando o número que representa a quantidade de lados do polígono da base por 2.
b) De acordo com o quadro, a quantidade de vértices dos prismas é igual ao dobro da quantidade de lados do polígono da base. Já a quantidade de vértices das pirâmides é igual a 1 unidade a mais do que a quantidade de lados do polígono da base. Como o dodecágono é um polígono de 12 lados, um prisma cuja base é um dodecágono terá 24 vértices, pois , e uma pirâmide cuja base é um dodecágono terá 13 vértices, pois .
Resolução referente à unidade 6.
23. a) Comparando as medidas das alturas apresentadas, concluímos que a jogadora mais alta do time é Manuela, com , e a mais baixa é Nicole, com .
b) Escrevendo as medidas de altura em ordem crescente, ou seja, da menor para a maior, temos:
.
29. Relacionando as letras indicadas no fluxograma com os números das informações, temos o seguinte fluxograma.
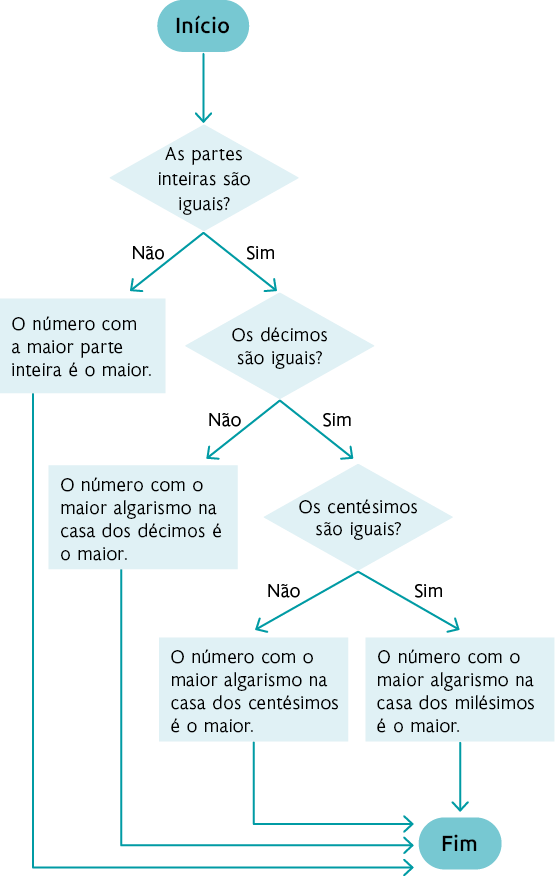
Resposta pessoal. Sugestão de resposta: 2,478 e 2,445. O número 2,478 é maior, pois o algarismo da casa do centésimo é o maior.
Página CXXII
Resolução referente à unidade 10.
74. a) De acordo com os desenhos feitos por Beto, temos as seguintes considerações.
A afirmação é verdadeira, pois o comprimento do lado do quadrado B mede , que é o dobro de ;
A afirmação é falsa, pois o perímetro do quadrado A mede . Já o perímetro do quadrado B mede . Assim, a medida do perímetro do quadrado A equivale à metade da medida do perímetro do quadrado B.
A afirmação é falsa, pois a área do quadrado B mede e a área do quadrado A mede . Assim, a medida de área do quadrado B equivale ao quádruplo da medida de área do quadrado A.
A afirmação é verdadeira, pois o perímetro do quadrado B mede e o perímetro do quadrado A mede . Assim, a medida do perímetro do quadrado B é o dobro da medida do perímetro do quadrado A.
b)


c) Respostas pessoais. Espera-se que os estudantes respondam que de acordo com os quadrados representados no item b:
a medida de comprimento do lado do quadrado 2 é o triplo da medida de comprimento do lado do quadrado 1, pois .
a medida do perímetro do quadrado 2 equivale ao triplo da medida do perímetro do quadrado 1, pois como o perímetro do quadrado 1 mede e o do quadrado 2 mede , temos .
a medida de área do quadrado 2 equivale a nove vezes a medida de área do quadrado 1, pois como a área do quadrado 1 mede e a área do quadrado 2 mede , então .
91. Escrevendo as medidas apresentadas em ordem crescente, temos:
Resolução referente à unidade 12.
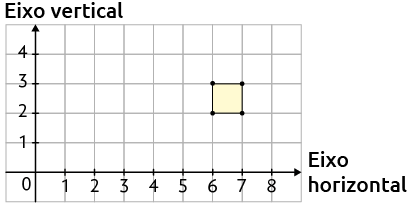
9. a) A coordenada que completa o quadrado é .
Página CXXIII
b) A coordenada que completa o quadrado é .
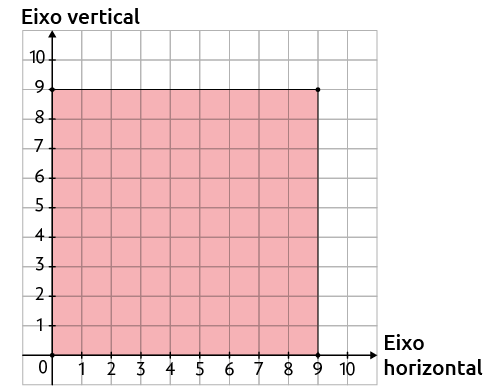
c) A coordenada que completa o quadrado é .
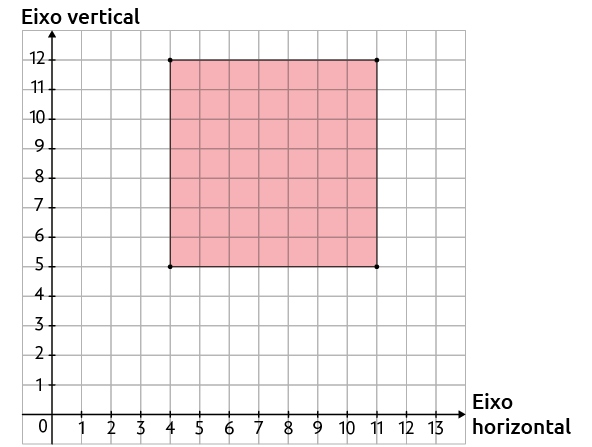
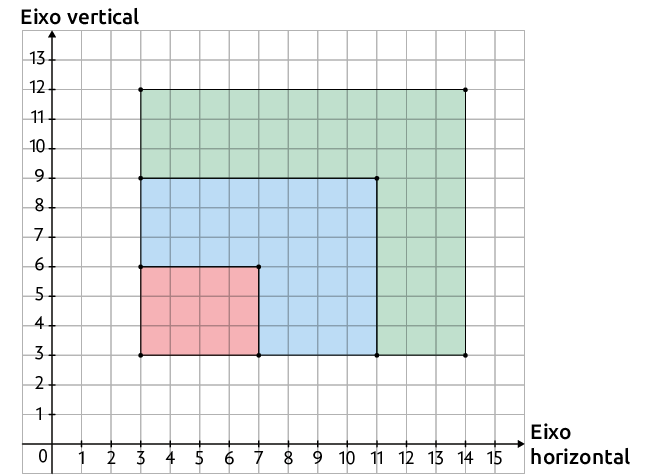
15. Os vértices do quadrilátero maior azul são , , e . A partir desse quadrilátero, construímos:
a) uma redução cujos vértices são , , e , conforme o quadrilátero vermelho na imagem a seguir.
b) uma ampliação cujos vértices são , , e , conforme o quadrilátero verde na imagem a seguir.
Página CXXIV
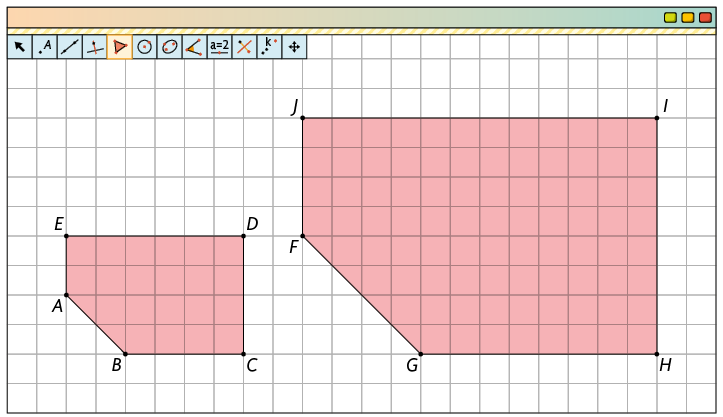
17. a) Utilizando a ferramenta Polígono, construa o polígono e , de modo que a medida do comprimento dos lados do polígono seja o dobro da medida do comprimento dos lados do polígono .
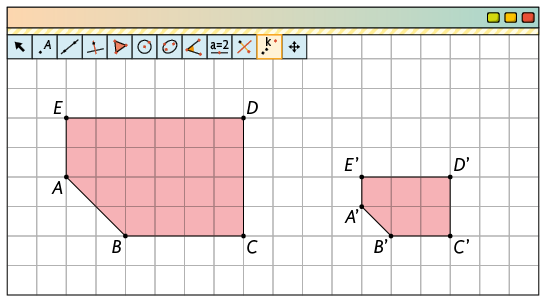
b) Utilizando a ferramenta Polígono, construa o polígono . Em seguida, com a ferramenta Homotetia selecionada, clique sobre um ponto na malha quadriculada e sobre o polígono . O polígono construído é uma redução cujos lados medem metade do comprimento dos lados do polígono .
c) Apenas o polígono continua semelhante ao polígono , pois ele foi construído com a ferramenta Homotetia, que é própria do GeoGebra para realizar ampliação e redução. Desse modo, ao alterar um dos vértices do polígono o respectivo vértice do polígono também será alterado mantendo as proporções.