Página 31
UNIDADE
2
Operações com números naturais e igualdades

Agora vamos estudar...
- adição;
- subtração;
- multiplicação;
- divisão;
- potenciação;
- expressões numéricas;
- igualdades.
Página 32
Adição
Os Jogos Olímpicos são competições poliesportivas✚ que ocorrem de 4 em 4 anos desde 1896. Nesses jogos, participam atletas de vários países. Na edição de 2012, o Brasil conquistou 17 medalhas, na edição de 2016, 19 medalhas e na edição de 2020, que ocorreu em 2021, 21 medalhas.

- Poliesportivo
- : que envolve várias práticas esportivas.↰
Questão 1.
Que cálculo você faria para obter o total de medalhas conquistadas
pelo Brasil nas edições de
2012, 2016 e 2020?
Professor, professora: Espera-se que os estudantes respondam adição.
Para obter o total de medalhas conquistadas pelo Brasil nessas edições, adicionamos as quantidades de medalhas conquistadas em cada uma delas.
ou
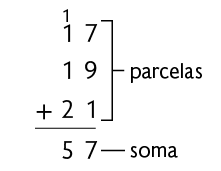
Portanto, o Brasil conquistou, ao todo, 57 medalhas nessas três edições.
Instrumentos e softwares
Utilizando a calculadora para obter somas
Efetuar cálculos, realizar medições e desenhar figuras são atividades que realizamos em outros componentes curriculares além da Matemática e em diversas situações, como no trabalho, em casa e no supermercado. Existem alguns instrumentos que podem nos auxiliar na realização dessas tarefas. Entre eles, podemos destacar a calculadora, que é um instrumento utilizado para efetuar cálculos. Analise como podemos efetuar utilizando esse instrumento.
1º.
Com a calculadora ligada, digite as teclas
e, em seguida, a tecla
.
2º.
Digite as teclas
.
3º.
Por fim, digite a tecla
. Deste modo, obtém-se o
resultado da adição.

Para efetuar essa adição com o aplicativo calculadora do smartphone, realizamos os mesmos procedimentos anteriores.
Página 33
Atividades
Faça as atividades no caderno.
1.
Efetue os cálculos usando uma calculadora.
a)
b)
c)
Respostas: a) 82.742; b) 999.820; c) 8.683.456.
2. Junte-se a um colega e, utilizando os números apresentados, escrevam no caderno todas as adições possíveis com duas parcelas diferentes. Em seguida, resolvam-nas.
-
1.228
-
3.090
-
4.281
-
998
Respostas: ; ; ; ; ; .
3. Um quadrado mágico recebe esse nome porque a soma dos números de cada linha, coluna ou diagonal é sempre a mesma. Essa soma é chamada constante mágica. Analise um exemplo.
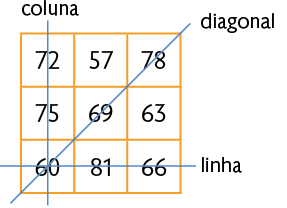
a) Efetue os cálculos e verifique qual é a constante mágica desse quadrado mágico.
Resposta: 207.
b) Se adicionarmos 45 unidades a cada número do quadrado mágico mostrado anteriormente, ele continuará sendo mágico? Se sim, determine sua constante mágica.
Respostas: Sim. A constante mágica do novo quadrado é 342.
c) Realize uma pesquisa a respeito da origem dos quadrados mágicos.
Resposta nas orientações ao professor.
Atenção!
A pesquisa proposta no item c pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
4. Elias mora em Fortaleza (CE) e decidiu fazer uma viagem. O esquema a seguir apresenta o trajeto que ele fez e as medidas das distâncias que percorreu.
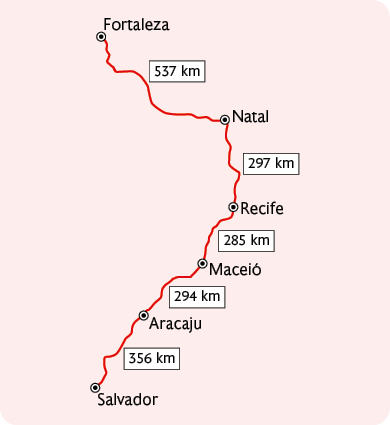
No 1º dia de viagem, Elias saiu de Fortaleza (CE) e foi até Recife (PE), passando por Natal (RN). No 2º dia, saindo de Recife, ele passou por Maceió (AL) e foi até Aracaju (SE). Por fim, no 3º dia de viagem, Elias foi até Salvador (BA).
a) Quantos quilômetros Elias percorreu no 1º dia de viagem? E no 2º dia?
b) Qual é, em quilômetros, a medida da distância percorrida por Elias de Fortaleza até Salvador?
Respostas: a) ; ; b) .
5. Arredonde cada número à unidade de milhar mais próxima. Depois, efetue os cálculos mentalmente.
a)
Resposta: .
b)
Resposta: .
c)
Resposta: .
6. Efetue os cálculos exatos da atividade anterior da maneira que preferir e compare-os com os resultados aproximados.
Respostas: a) 57.000; b) 35.505; c) 230.553.
Página 34
Propriedades da adição
Agora, vamos estudar as propriedades da adição. Essas propriedades nos auxiliarão em alguns cálculos.
Propriedade comutativa
Henrique e Luciana pesquisaram o preço de alguns produtos em um site.
Imagens não proporcionais entre si.




Em seguida, eles calcularam a quantia que vão gastar caso comprem o videogame e a televisão.
-
Henrique
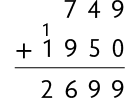
-
Luciana
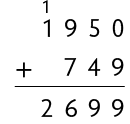
Como a adição tem a propriedade comutativa, ao trocar a ordem das parcelas, a soma não se altera.
Em uma adição, ao trocar a ordem das parcelas, o resultado permanece o mesmo. Essa é a propriedade comutativa da adição.
Questão 2. Escreva no caderno duas adições que possibilitem determinar o preço total dos seguintes produtos. Depois, efetue-as.
a) Televisão e smartphone.
Resposta: R$ 3.200,00 (; ).
b) Videogame e notebook.
Resposta: R$ 3.439,00 (; ).
c) Notebook e smartphone.
Resposta: R$ 3.940,00 (; ).
d) Smartphone e videogame.
Resposta: R$ 1.999,00 (; ).
Propriedade associativa
No quadro a seguir está indicada a quantidade de pontos que Fernando e seus amigos fizeram em três rodadas de um jogo.
|
Rodada/Jogador |
1ª |
2ª |
3ª |
|---|---|---|---|
|
Fernando |
70 |
35 |
42 |
|
Ivo |
48 |
80 |
30 |
|
Gilberto |
60 |
47 |
18 |
Página 35
A seguir são apresentadas três maneiras diferentes de calcular o total de pontos de Fernando.
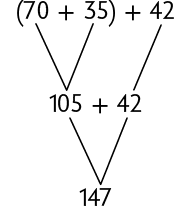

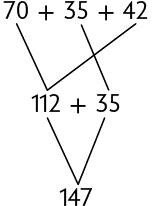
Como a adição tem a propriedade associativa, ao associar as parcelas de maneiras diferentes, a soma não se altera.
Em uma adição de três ou mais parcelas, ao associá-las de maneiras diferentes, o resultado permanece o mesmo. Essa é a propriedade associativa da adição.
Questão 3. Calcule em seu caderno a quantidade total de pontos de Ivo e de Gilberto associando as parcelas de duas maneiras diferentes.
Respostas: Ivo: 158 pontos; Gilberto: 125 pontos.
Propriedade do elemento neutro
Janaina efetuou as seguintes adições.
Como a adição tem a propriedade do elemento neutro, quando uma das parcelas é igual a zero, a soma é igual à outra parcela.
Ao adicionar um número a zero, o resultado é igual ao próprio número. Por isso, dizemos que o zero é o elemento neutro da adição.
Atividades
Faça as atividades no caderno.
7. Efetue os cálculos mentalmente e associe as fichas cujos cálculos têm resultados iguais. Para isso, escreva os pares de letras correspondentes.
A.
B.
C.
D.
E.
F.
G.
H.
Resposta: A-G; B-E; C-H; D-F.
8. Efetue os cálculos da atividade anterior da maneira que preferir e verifique se suas associações estão corretas.
Respostas: A. 69; B. 133; C. 34; D. 47; E. 133; F. 47; G. 69; H. 34.
Página 36
9. Analise o preço de alguns itens em uma loja.
Imagens não proporcionais entre si.



Marilda comprou a bolsa e o par de sapatos, e calculou mentalmente o valor total de sua compra.
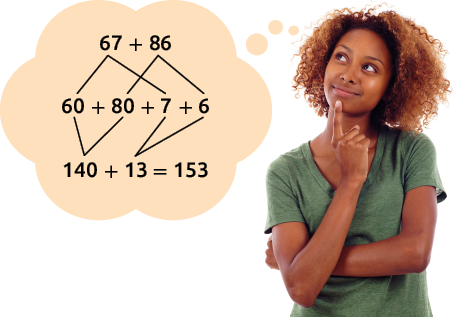
Assim como Marilda calcule mentalmente quantos reais uma pessoa vai gastar se comprar os produtos mostrados em cada item.
Imagens não proporcionais entre si.




Respostas A. R$ 121,00; B. R$ 140,00.
10. Roberta calculou mentalmente .

De maneira semelhante ao pensamento de Roberta, calcule as adições.
a)
b)
c)
d)
e)
f)
Respostas: a) 130; b) 150; c) 80; d) 170; e) 160; f) 100.
11. Elabore e escreva em seu caderno o enunciado de um problema cuja solução pode ser obtida pelo cálculo a seguir. Depois, mostre a um colega o problema que você escreveu para que ele o resolva. Verifique se a resposta obtida está correta.
Resposta pessoal.
12. Copie as adições a seguir no caderno e substitua cada pelo número adequado.
a)
Resposta: .
b)
Resposta: .
c)
Resposta: .
d)
Sugestão de resposta: .
e)
Resposta: .
f)
Resposta: .
Página 37
Subtração
Entre os esportes automobilísticos, a Fórmula 1 é uma das modalidades mais conhecidas e tradicionais.
Em 2021, foram realizadas 22 corridas pelo Grande Prêmio (GP), e o piloto neerlandês Max Verstappen conquistou o Campeonato mundial nesse ano.


Fonte de pesquisa: LEWIS, Neil. The Grand Prix Cookbook: Cook The World Of Grand Prix Racing. Lulu, 2018. Disponível em: https://oeds.link/a9RVQq. Acesso em: 4 fev. 2022.
Qual é a diferença, em metros, entre a medida de extensão do circuito de Interlagos e a do circuito de Mônaco?
Para responder a esta pergunta, precisamos calcular .
ou
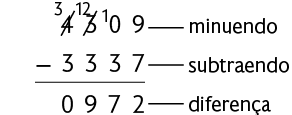
Portanto, a diferença entre as medidas de extensão desses circuitos é .
Página 38
Atividades
Faça as atividades no caderno.
13. De acordo com as informações da página anterior, determine a diferença, em metros, entre as medidas de extensão dos seguintes circuitos.
a) Suzuka e Mônaco.
b) Monza e Interlagos.
c) Monza e Mônaco.
d) Suzuka e Interlagos.
Respostas: a) ; b) ; c) ; d) .
14. No caderno, escreva e calcule o resultado de uma subtração em que o minuendo seja o maior número de três algarismos diferentes e o subtraendo seja o menor número de três algarismos iguais.
Resposta: .
15. Os museus são fundamentais no processo de preservação e conexão entre diferentes períodos históricos e culturais. De acordo com o Instituto Brasileiro de Museus (Ibram), em 2021 havia 3.891 museus no Brasil.
a) Sabendo que em 2014 havia 3.118 museus no Brasil, quantos foram construídos de 2014 a 2021?
Resposta: 773 museus.
b) Em sua opinião é importante visitar museus?
Resposta pessoal.
c) Faça uma pesquisa sobre a importância dos museus e quais são os principais do Brasil.
Resposta nas orientações ao professor.
d) Após a pesquisa no item c sua opinião sobre a importância dos museus mudou? Justifique sua resposta.
Resposta pessoal.
e) Você sabia que é possível visitar um museu de maneira virtual? Sim, é possível! Visite um museu virtualmente e compartilhe essa experiência com os colegas e o professor.
Resposta pessoal.
Atenção!
A visita virtual pode ser feita por meio do site Vila360. Disponível em: https://oeds.link/SJEK11. Acesso em: 27 abr. 2022.
16. Determine o número referente a cada letra no quadrado mágico a seguir.
Atenção!
Inicialmente, determine a constante mágica do quadrado.
19
A
B
55
C
28
D
13
52
E
37
F
10
43
G
46
Respostas: A: 34; B: 22; C: 49; D: 40; E: 25; F: 16; G: 31.
17.
Usando apenas uma vez os números e sinais matemáticos representados
em cada item, obtenha o número indicado no visor da calculadora em
cada um.
Atenção!
Para efetuar subtrações em uma calculadora, repita os
procedimentos da seção
Instrumentos e softwares da
página 32, porém utilizando a tecla
em vez da tecla
.

Resposta:

Resposta: ou
Página 39
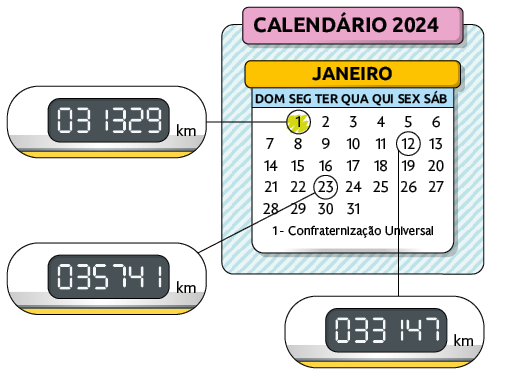
18. Carlos faz fretes✚ em seu caminhão. As imagens a seguir apresentam a quilometragem que o hodômetro✚ do caminhão estava marcando ao fim de três dias de trabalho.
- Frete:
- carregamento ou carga transportada, mediante pagamento, em qualquer meio de transporte.↰
- Hodômetro:
- instrumento que indica medidas de distâncias percorridas por pedestres ou por veículos.↰
a) Quantos quilômetros Carlos percorreu com seu caminhão do início do dia 2 até o fim do dia 12 de janeiro?
b) Quantos quilômetros Carlos percorreu ao todo do início do dia 2 até o fim do dia 23 de janeiro?
c) Carlos percorreu mais 1.645 km desde o início do dia 24 até o fim do dia 31 de janeiro. Que quilometragem seu caminhão estava marcando ao fim do dia 31 de janeiro?
Respostas: a) ; b) ; c) .
19. Lúcio calculou mentalmente o resultado de .
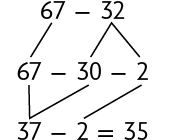
De maneira semelhante, calcule mentalmente os resultados dos cálculos a seguir.
a)
b)
c)
d)
e)
f)
Respostas: a) 65; b) 71; c) 52; d) 26; e) 61; f) 64.
20. Junte-se a um colega e obtenham, da maneira que preferirem, os resultados dos seguintes cálculos.
Respostas: ; ; ; .
a) O que podemos perceber em relação ao minuendo, ao subtraendo e ao resultado de cada cálculo?
Resposta pessoal. Espera-se que os estudantes percebam que os valores absolutos dos algarismos do minuendo e do subtraendo são números consecutivos, em ordem crescente, da esquerda para a direita, sempre começando do 1. O minuendo tem sempre um algarismo a mais do que o subtraendo, e o resultado é formado apenas por algarismos 1.
b) Agora, sem efetuar os cálculos por escrito ou em uma calculadora, determinem os resultados a seguir.
Respostas: e .
Expressões numéricas envolvendo adição e subtração
Márcio saiu de sua casa com R$ 168,00. Dessa quantia, ele gastou R$ 68,00 na compra de uma calça e R$ 14,00 em um restaurante. Quando estava voltando para casa, Márcio encontrou um amigo que lhe pagou R$ 25,00 que havia emprestado dele anteriormente.
Após comprar a calça, pagar o restaurante e receber o dinheiro emprestado, com quantos reais Márcio ficou?
Podemos responder a esta questão resolvendo a expressão numérica a seguir.
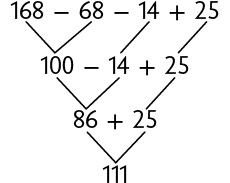
Portanto, Márcio ficou com R$ 111,00.
Página 40
Atividades
Faça as atividades no caderno.
21. No caderno, associe os problemas a seguir à expressão numérica que os representa. Depois, resolva as expressões e determine a resposta.
a) Jair comprou 280 latas de suco para vender em sua lanchonete. Ele vendeu 82 dessas latas no sábado e 120 no domingo. Quantas latas sobraram?
Resposta: 78 latas.
b) Em sua coleção, Maria tem 120 cartões-postais de cidades do Brasil e 280 de cidades de outros países. Do total de seus cartões-postais, 82 são repetidos. Sem contar os cartões repetidos, quantos cartões-postais Maria tem em sua coleção?
Resposta: 318 cartões-postais.
-
Expressão 1
-
Expressão 2
Resposta: a - Expressão 2; b - Expressão 1.
22. Efetue os cálculos e determine o número natural correspondente a cada letra.
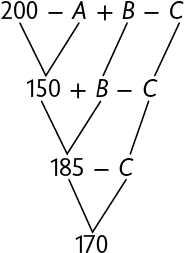
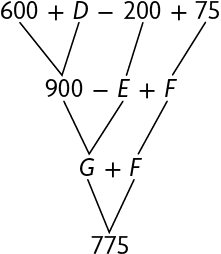
Respostas: a) A: 50; B: 35; C: 15; b) D: 300; E: 200; F: 75; G: 700.
23. Resolva no caderno as expressões numéricas a seguir.
Atenção!
Nas expressões numéricas com parênteses, efetuamos primeiro os cálculos que estão entre eles.
a)
b)
c)
d)
Respostas: a) 210; b) 502; c) 276; d) 1.189.
24. Na escola em que Silas estuda, os 115 estudantes matriculados no 6º ano estão distribuídos em 4 turmas e o quadro a seguir apresenta a quantidade de estudantes de 3 dessas turmas.
|
6º ano |
A |
B |
C |
D |
|---|---|---|---|---|
|
Quantidade de estudantes |
25 |
29 |
32 |
Escreva e resolva uma expressão numérica que possibilita determinar a quantidade de estudantes do 6º ano B.
Resposta: ou .
25. Junte-se a um colega e escrevam no caderno uma expressão numérica para o problema a seguir. Depois, resolvam-na.
Mário registrou o número 725 em uma calculadora e subtraiu 456 dele. Por fim, adicionou 356 ao resultado obtido. Qual número Mário visualizou na calculadora ao final das operações?
Resposta: ; 625.
26.
Considere os seguintes números.
-
45
-
20
-
85
-
50
Junte-se a um colega e copiem no caderno a expressão numérica a seguir, substituindo cada ⬛ pelos números dessas fichas, de maneira que o resultado seja verdadeiro.
Resposta: ou .
Página 41
Operações inversas: adição e subtração
Tiago tinha certa quantidade de selos em sua coleção. Ele ganhou 32 selos de sua tia e ficou com 78. Quantos selos Tiago tinha inicialmente em sua coleção?
Vamos resolver este problema! Para isso, representamos a quantidade de selos que Tiago tinha por ⬛ e construímos um esquema.
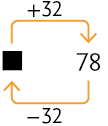
Subtraindo 32 de 78 obtemos o valor de ⬛.
ou
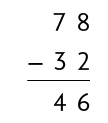
Logo, Tiago tinha inicialmente 46 selos em sua coleção.
Podemos perceber que ao adicionarmos 32 a 46 obtemos 78 e ao subtrair 32 de 78 obtemos 46, ou seja, a quantidade de selos que Tiago tinha inicialmente.
, ou seja,
Isso é possível porque a adição e a subtração são operações inversas.
Atividades
Faça as atividades no caderno.
27. De maneira semelhante à resolução do problema de Tiago, construa no caderno um esquema para resolver o problema a seguir.
Nair comprou um par de sapatos por R$ 94,00 e ainda ficou com R$ 345,00. Quantos reais Nair tinha antes dessa compra?
Resposta nas orientações ao professor.
28. Copie os esquemas no caderno e complete-os, substituindo cada ⬛ ou ◆ pelo número adequado.
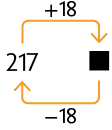
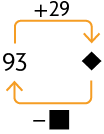
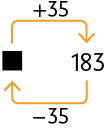

Respostas: A. ; B. e ; C. ; D. e .
Página 42
29. Determine nos esquemas o número que substitui cada ⬛ adequadamente.
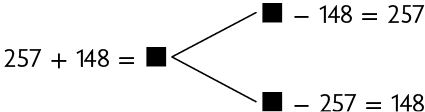
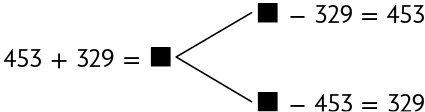
Respostas: A. ; B. .
30. O município de Bonito, no Mato Grosso do Sul, foi fundado em meados do século passado, em 1948. Em razão da beleza e da quantidade de pontos turísticos, Bonito é considerado um dos principais destinos de ecoturismo e turismo de aventura do Brasil.

a) De acordo com o Censo de 2010 do IBGE, o município de Bonito tinha 19.587 habitantes, entre os quais 9.878 eram homens. Qual era a quantidade de mulheres em Bonito nesse ano?
Resposta: 9.709 mulheres.
b) Em sua opinião, quais são as possíveis ações para ajudar na preservação ambiental de pontos turísticos, como o município de Bonito?
Resposta pessoal. Espera-se que os estudantes respondam, por exemplo, que podemos destinar os resíduos corretamente.
31. Resolva os problemas a seguir.
a) Agnaldo é 27 anos mais novo do que seu pai. Sabendo que seu pai tem 56 anos, qual é a idade de Agnaldo?
b) Do total de figurinhas que tinha, Rubens deu 48 para seu irmão e ficou com 237. Quantas figurinhas Rubens tinha inicialmente?
Respostas: a) 29 anos; b) 285 figurinhas.
32. Efetue os cálculos e responda.



Respostas: A. 200; B. 466; C. 247.
33. Em seu caderno, elabore um problema envolvendo cálculos com operações inversas. Depois, peça a um colega que o resolva. Ao final, verifique se ele resolveu corretamente.
Resposta pessoal.
Página 43
Multiplicação
O coração é o órgão responsável pelo bombeamento do sangue no corpo humano. Os primeiros batimentos do coração iniciam quando ainda somos fetos no útero da mãe, por volta da 4ª semana de gestação, e esse órgão continua a bater por toda nossa vida.
Imagens não proporcionais entre si. Cores-fantasia.
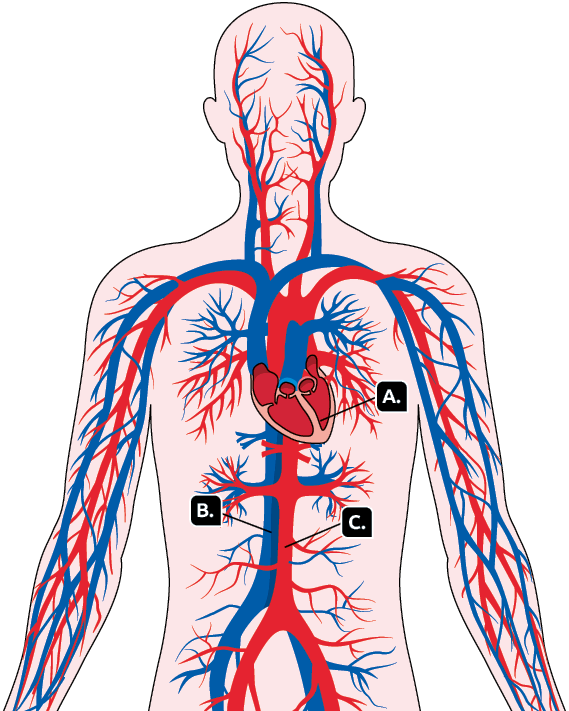
A. Ventrículo esquerdo
Possui a pressão sanguínea mais alta dentro do coração, pois é responsável pelo bombeamento do sangue arterial para todo o corpo.
B. Veia cava inferior
É a maior veia, cuja função é coletar sangue desoxigenado da parte inferior do corpo.
C. Artéria aorta
É a maior artéria, cuja função é levar sangue oxigenado para o corpo.
Atenção!
A frequência cardíaca de um adulto em repouso é aproximadamente 70 batimentos por minuto.
Em um intervalo de 15 minutos, aproximadamente quantas vezes bate o coração de um adulto em repouso?
Podemos responder a esta pergunta pelo resultado de uma adição de parcelas iguais.
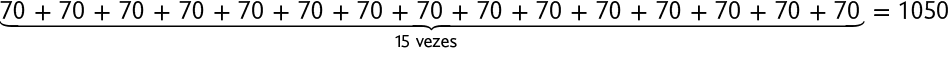
Essa adição tem 15 parcelas iguais a 70. Podemos indicá-la pela seguinte multiplicação.
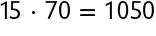
ou
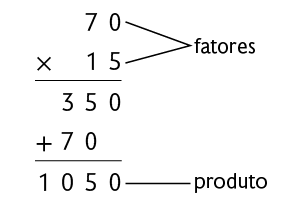
Logo, o coração de um adulto em repouso bate aproximadamente 1.050 vezes em 15 minutos.
Página 44
Atividades
Faça as atividades no caderno.
34. De acordo com a informação da página anterior, efetue uma multiplicação para calcular a quantidade aproximada de vezes que o coração de uma pessoa adulta em repouso bate em:
a) 9 minutos;
b) 41 minutos;
c) 10 minutos;
d) 22 minutos.
Respostas: a) 630 vezes; b) 2.870 vezes; c) 700 vezes; d) 1.540 vezes.
35. Copie as expressões numéricas no caderno e complete-as substituindo cada pelo número adequado.
a)
Resposta: .
b)
Resposta: .
c)
Resposta: .
36. Efetue os seguintes cálculos.
a)
b)
c)
d)
Respostas: a) 1.288; b) 1.095; c) 1.946; d) 3.048.
37. Copie os algoritmos no caderno e substitua cada uma das letras pelo algarismo adequado.


Respostas: a) A: 4; B: 5; C: 4; D: 8; E: 4; b) F: 2; G: 6; H: 2; I: 8; J: 0; K: 6.
38. Ter uma alimentação saudável contribui para fortalecer o coração e combater tanto o colesterol ruim quanto algumas doenças, como câncer e diabetes. Para incentivar os funcionários de uma empresa a adquirir bons hábitos alimentares, a diretoria da empresa decidiu servir, no horário do almoço, 2 frutas a cada um de seus 62 funcionários.
a) Diariamente, quantas frutas serão servidas aos funcionários dessa empresa?
b) Quantas frutas essa empresa vai servir a seus funcionários no horário do almoço durante 12 dias? E durante 20 dias?
Respostas: a) 124 frutas; b) 1.488 frutas; 2.480 frutas.
39. Em certo momento de um campeonato de futebol, o time de Gustavo fez o triplo dos pontos do time de Pedro. Considerando que os dois times juntos fizeram 32 pontos, qual foi a pontuação de cada um nesse momento?
Resposta: Nesse momento, o time de Gustavo fez 24 pontos e o time de Pedro fez 8 pontos.
40. Em seu caderno, elabore um problema que envolva uma multiplicação. Em seguida, entregue-o a um colega para que ele o resolva. Depois, confira se ele solucionou corretamente.
Resposta pessoal.
Página 45
41. O hotel JW Marriott Marquis, situado nos Emirados Árabes Unidos, é um dos mais altos do mundo. É composto de duas torres gêmeas e tem 72 andares e 1.608 quartos. Sua altura mede o equivalente a nove vezes a medida da altura do Cristo Redentor.

De acordo com a imagem, qual é a medida da altura aproximada desse hotel?
Resposta: .
42. Junte-se a um colega para efetuarem os cálculos a seguir da maneira que preferirem.
a)
b)
c)
O que vocês podem concluir em relação aos resultados dos cálculos?
Respostas nas orientações ao professor.
43. Considerando o que foi concluído na atividade anterior, determinem o resultado dos cálculos a seguir sem efetuá-los por escrito.
a)
b)
c)
d)
e)
f)
Respostas: a) 25.025; b) 68.068; c) 39.039; d) 51.051; e) 83.083; f) 94.094.
44.
Com uma calculadora, obtenha os resultados das seguintes
multiplicações.
Atenção!
Para efetuar multiplicações em uma calculadora, repita os
procedimentos da seção Instrumentos e
softwares da página 32,
porém utilizando a tecla
em vez da tecla
.
a)
b)
c)
d)
Respostas: a) 84.366; b) 180.000; c) 559.120; d) 129.042.
45. Para obter o resultado aproximado de e , podemos arredondar os fatores à dezena mais próxima.


De maneira semelhante, obtenha o resultado aproximado dos cálculos a seguir. Depois, efetue os cálculos exatos para conferir se os resultados realmente eram próximos deles.
a)
b)
c)
d)
e)
f)
Atenção!
Confira os cálculos usando uma calculadora.
Respostas: a) 5.000; 5.253; b) 28.000; 27.383; c) 24.000; 23.254; d) 4.500; 5.134; e) 7.200; 7.462; f) 88.000; 87.819.
Página 46
Propriedades da multiplicação
Agora, vamos estudar as propriedades da multiplicação, as quais nos auxiliarão em alguns cálculos.
Propriedade comutativa
Júlia pintou alguns quadradinhos na malha quadriculada representada a seguir.
Quantos quadradinhos Júlia pintou ao todo?
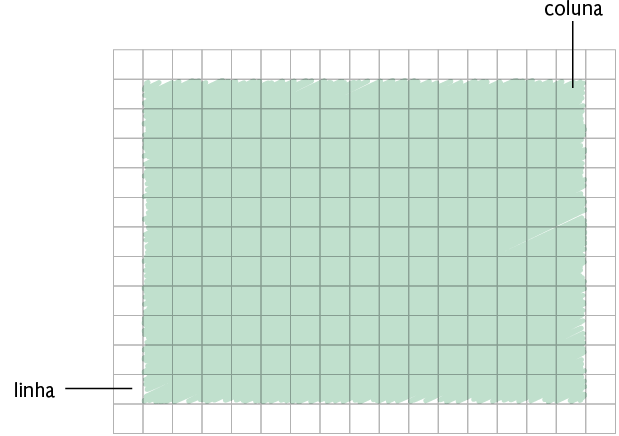
Podemos calcular a quantidade de quadradinhos de duas maneiras diferentes.
Multiplicando a quantidade de linhas pela quantidade de quadradinhos em cada uma delas.
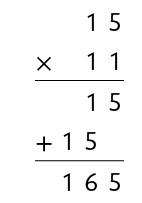
Multiplicando a quantidade de colunas pela quantidade de quadradinhos em cada uma delas.
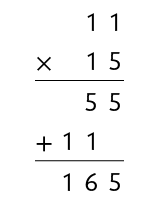
Logo, Júlia pintou 165 quadradinhos.
Como a multiplicação tem a propriedade comutativa, ao mudar a ordem dos fatores, o resultado não se altera.
Em uma multiplicação, ao mudar a ordem dos fatores, o resultado não se altera. Essa é a propriedade comutativa da multiplicação.
Propriedade do elemento neutro
Fernanda efetuou as seguintes multiplicações.
Ela percebeu que em todas as multiplicações um dos fatores era igual a 1.
Página 47
Como a multiplicação tem a propriedade do elemento neutro, se um dos fatores é igual a 1, o produto é igual ao outro fator.
Ao multiplicar um número por 1, o resultado é igual ao próprio número. Por isso, dizemos que o 1 é o elemento neutro da multiplicação.
Propriedade associativa
Marcos trabalha em uma sapataria e empilhou algumas caixas de sapato, conforme apresentado a seguir.

Para saber a quantidade de caixas de sapatos dessa pilha, sem contá-las uma a uma, podemos efetuar um dos três cálculos apresentados a seguir.
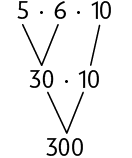
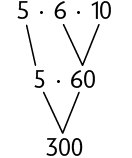
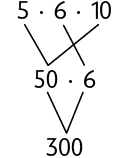
Como a multiplicação tem a propriedade associativa, ao associar os fatores de maneiras diferentes, o produto permanece o mesmo.
Em uma multiplicação de três ou mais fatores, ao associá-los de maneiras diferentes, o resultado permanece o mesmo. Essa é a propriedade associativa da multiplicação.
Propriedade distributiva
Murilo preparou uma festa de aniversário para seu filho. Para isso, ele comprou 15 embalagens com 6 latas de suco de uva em cada uma e 13 embalagens com 6 latas de suco de laranja em cada uma.

Podemos calcular de duas maneiras diferentes a quantidade de latas de suco que Murilo comprou ao todo.
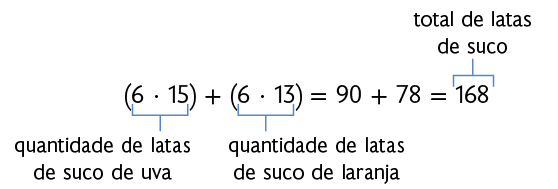
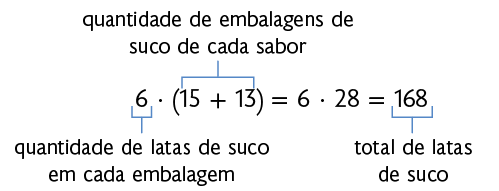
Portanto, Murilo comprou 168 latas de suco ao todo.
Página 48
Para multiplicar um número natural por uma adição (ou subtração) com dois ou mais termos, podemos multiplicar esse número pelos termos da adição (ou da subtração) e adicionar (ou subtrair) os resultados obtidos. Exemplos:
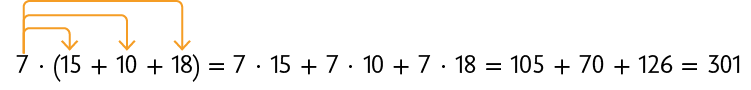
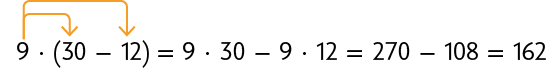
Essa é a propriedade distributiva da multiplicação.
Questão 4. Sabendo que Murilo pagou R$ 18,00 em cada embalagem, quantos reais ele gastou na compra dos sucos? Responda a esta pergunta efetuando os cálculos no caderno de duas maneiras diferentes.
Resposta: ; ; R$ 504,00.
Atividades
Faça as atividades no caderno.
46. Efetue os seguintes cálculos associando os fatores da maneira que preferir.
a)
b)
c)
d)
e)
f)
Respostas: a) 1.260; b) 720; c) 364; d) 980; e) 1.080; f) 992.
47. Usando duas multiplicações diferentes, calcule quantos quadradinhos foram pintados de amarelo na malha quadriculada a seguir.
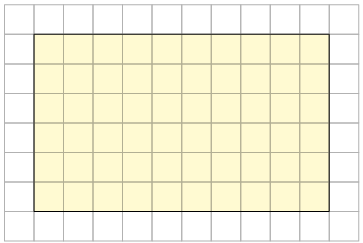
Resposta: e ; 60 quadradinhos.
48. Para calcular mentalmente o valor de , Estela escolheu a associação de dois dos fatores que resultavam em um número terminado em zero.
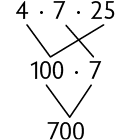
De maneira parecida, efetue mentalmente os seguintes cálculos.
a)
b)
c)
d)
e)
f)
Respostas: a) 1.100; b) 1.300; c) 800; d) 4.000; e) 2.700; f) 5.400.
Página 49
49. O quadro apresenta as diferentes opções de planos de internet e de quantidades de minutos para ligações que uma empresa de telefonia oferece.
|
Medida da velocidade de internet (em MB) |
Quantidade de minutos para ligações |
|||
|---|---|---|---|---|
|
1.500 |
2.000 |
4.500 |
7.000 |
|
|
10 |
/ |
/ |
/ |
/ |
|
100 |
/ |
/ |
/ |
/ |
|
200 |
/ |
/ |
/ |
/ |
a) Com 3 tipos de planos de internet e 4 de telefone, temos as possibilidades indicadas no quadro. Copie no caderno a multiplicação a seguir substituindo o pelo número adequado, de modo que represente o total de possibilidades indicadas.
b) Suponha que essa empresa passe a oferecer 4 planos de internet e 5 de telefone. Nesse caso, quantas possibilidades uma pessoa teria ao escolher 1 plano de internet e 1 de telefone?
Respostas: a) ; b) 20 possibilidades.
50. Certa loja expôs em sua vitrine as seguintes roupas.

Se uma pessoa deseja comprar dessa vitrine 1 camiseta, 1 bermuda e 1 boné, quantas possibilidades diferentes de compra ela teria?
Atenção!
Ao efetuar os cálculos, considere a quantidade de cada tipo de peça de roupa.
Resposta: 30 possibilidades.
51. Copie os itens no caderno e substitua cada pelo número adequado.
a)
Resposta: .
b)
Resposta: .
c)
Resposta: .
52. Uma fábrica utiliza 26 parafusos na montagem de uma bicicleta. Diariamente são montadas 53 bicicletas nessa fábrica.
a) Qual é a quantidade de parafusos utilizada diariamente na montagem de bicicletas?
Resposta: 1.378 parafusos.
b) Quantos parafusos a mais serão utilizados caso sejam produzidas diariamente 76 bicicletas?
Resposta: 598 parafusos.
Página 50
Expressões numéricas com multiplicação
Em certo teatro, as cadeiras estão dispostas como mostra a imagem a seguir.
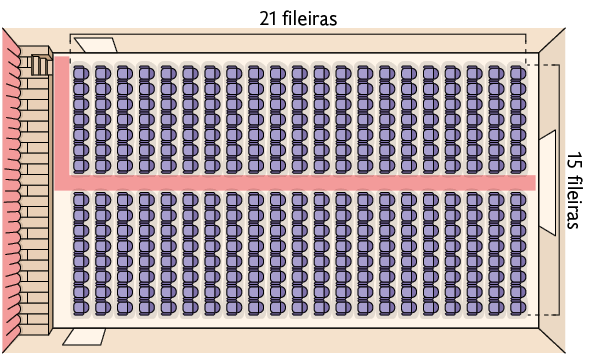
Nele foi apresentada uma peça teatral cujo ingresso custava R$ 34,00. Na 1ª apresentação foram vendidos 25 ingressos a menos do que a lotação máxima do teatro.
Quantos reais foram arrecadados nessa apresentação?
Podemos responder a esta pergunta resolvendo a seguinte expressão numérica.
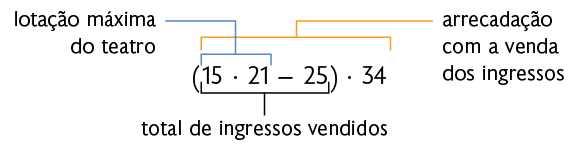
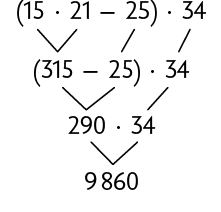
Atenção!
Essa expressão numérica envolve as operações de subtração e multiplicação. Em expressões desse tipo, efetuamos primeiro as multiplicações e, em seguida, as adições e as subtrações, na ordem em que aparecem. Se houver parênteses, as operações que estão dentro deles devem ser realizadas primeiro.
Logo, foram arrecadados R$ 9.860,00 na 1ª apresentação da peça.
Questão 5. Em outra apresentação foram vendidos todos os ingressos, dos quais 35 estavam em promoção a R$ 20,00 cada um deles. Quantos reais foram arrecadados dessa vez? Para responder a esta pergunta, escreva no caderno uma expressão numérica e resolva-a.
Resposta: ; R$ 10.220,00.
Atividades
Faça as atividades no caderno.
53. Obtenha os resultados das seguintes expressões numéricas.
a)
b)
c)
d)
e)
f)
Respostas: a) 3; b) 4; c) 9; d) 18; e) 7; f) 36.
54. Fernando comprou 3 camisetas, 2 bermudas e 1 boné.
Sabendo que ele pagou R$ 33,00 em cada bermuda, R$ 28,00 em cada camiseta e R$ 19,00 no boné, escreva no caderno uma expressão numérica que represente a quantia gasta por Fernando nessa compra. Quantos reais ele gastou?
Respostas: ; R$ 169,00.
55. Copie no caderno os itens a seguir, substituindo cada por , ou .
a) 8 3
Resposta: .
b) 9 2
Resposta: .
c) 2 6
Resposta: .
d) 35 3 7
Resposta: .
Página 51
Divisão
A reciclagem de materiais é uma atividade que gera muitos benefícios à sociedade. Uma das principais vantagens em reciclar metais, por exemplo, é a economia de energia.
Um dos metais recicláveis mais comuns é o alumínio, facilmente encontrado em latas de bebidas. Sabendo que é possível obter de alumínio reciclado com cerca de 75 latas, aproximadamente quantos quilogramas desse metal é possível obter com 1.695 latas?

Podemos responder a esta pergunta dividindo 1.695 (quantidade total de latas) por 75 (quantidade de latas para obter de alumínio reciclado).
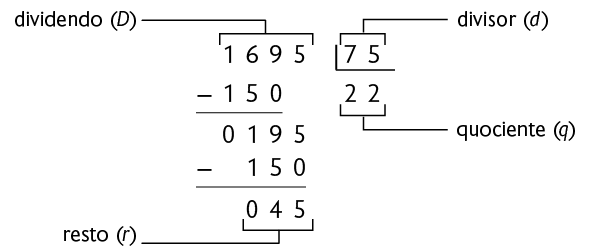
Portanto, com 1.695 latas é possível obter aproximadamente de alumínio reciclado.
Atividades
Faça as atividades no caderno.
56. De acordo com os dados do texto anterior, calcule aproximadamente quantos quilogramas de alumínio reciclado é possível obter com:
a) 1.580 latas;
b) 2.045 latas;
c) 3.119 latas;
d) 5.346 latas;
e) 6.902 latas;
f) 8.555 latas;
g) 11.412 latas;
h) 15.003 latas.
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
57. Com uma calculadora, efetue as divisões a seguir.
a)
b)
c)
d)
Atenção!
Para efetuar divisões em uma calculadora, repita os
procedimentos da seção
Instrumentos e softwares da
página 32, porém utilizando a tecla
em vez da tecla
.
Respostas: a) 123; b) 180; c) 625; d) 486.
Página 52
58. Responda às questões.
a) Em uma divisão, o quociente é 53, o divisor é 64 e o resto é 23. Qual é o dividendo?
b) Em uma divisão, o dividendo é 242 e o divisor é a metade do dividendo. Qual é o quociente?
Respostas: a) 3.415; b) 2.
59. Na divisão a seguir, o resto é zero. Com números naturais, quando isso ocorre, temos uma divisão exata.
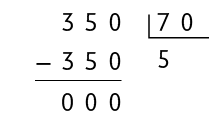
Escreva no caderno duas divisões exatas com números naturais em que:
a) o dividendo tenha três algarismos e o divisor, dois algarismos;
Sugestão de resposta: , .
b) o dividendo esteja entre 1.000 e 1.500 e o divisor seja um número par.
Sugestão de resposta: , .
60. Eliane é dona de um quiosque que vende sanduíches naturais. A tabela a seguir apresenta a quantidade de sanduíches que ela vendeu em 5 dias de uma semana em 2023.
|
Dia da semana |
Quantidade de sanduíches |
|---|---|
|
Segunda-feira |
39 |
|
Terça-feira |
41 |
|
Quarta-feira |
35 |
|
Quinta-feira |
42 |
|
Sexta-feira |
58 |
Fonte de pesquisa: anotações de Eliane.
a) Para calcular quantos sanduíches naturais Eliane vendeu em média por dia, da segunda à sexta-feira dessa semana, precisamos calcular a média aritmética da quantidade total vendida. Para isso, adicionamos as quantidades diárias que foram vendidas e dividimos o resultado pela quantidade de dias.
Determine o número correspondente a cada letra no esquema a seguir.
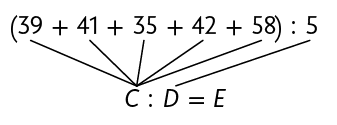
Atenção!
Eliane vendeu E sanduíches em média por dia.
Resposta: C: 215, D: 5, E: 43.
b) No sábado, Eliane vendeu 30 sanduíches naturais a mais do que a média desde a segunda à sexta-feira. Quantos sanduíches Eliane vendeu no sábado?
Resposta: 73 sanduíches.
c) Qual foi a média de sanduíches vendidos diariamente desde a segunda-feira até o sábado dessa semana?
Resposta: 48 sanduíches.
61. Jandira comprou de fita e usou a metade para confeccionar alguns laços. O restante foi usado para enfeitar 7 caixas de presente.
a) Com quantos metros de fita Jandira confeccionou os laços?
b) Sabendo que Jandira enfeitou cada caixa de presente com a mesma medida de comprimento de fita, quantos metros foram usados em cada uma?
Respostas: a) ; b) .
Página 53
62. Em cada item a seguir, somente um número natural substitui o corretamente. Efetue os cálculos mentalmente e copie no caderno os respectivos números.
a) Uma máquina produz 8.200 peças em 2 horas. Portanto, nesse ritmo ela produz peças em 1 hora.
-
3.600
-
4.200
-
4.100
-
3.500
b) Uma escola comprou 3 computadores iguais por R$ 9.900,00. O preço de cada computador foi .
-
R$ 3.300,00
-
R$ 2.600,00
-
R$ 2.100,00
-
R$ 2.200,00
Respostas: a) 4.100; b) R$ 3.300,00.
63. Adriane e Diego viajaram para conhecer o Marco Zero do Equador, construído exatamente onde passa a linha imaginária do Equador, dividindo o planeta em dois hemisférios, e onde há outras atrações turísticas de Macapá, no estado do Amapá.

O quadro apresenta a quantia que eles gastaram com alimentação nos cinco primeiros dias.
|
Dia |
Quarta-feira |
Quinta-feira |
Sexta-feira |
Sábado |
Domingo |
|---|---|---|---|---|---|
|
Quantia gasta (R$) |
85,00 |
97,00 |
107,00 |
131,00 |
80,00 |
a) Nesse período, quantos reais, em média, os dois gastaram diariamente com alimentação?
b) Sabendo que eles têm R$ 270,00 para os gastos com alimentação dos próximos três dias de viagem, e que pretendem gastar a mesma quantia diária, quanto eles podem gastar por dia?
Respostas: a) R$ 100,00; b) R$ 90,00.
64. Em uma loja, André comprou uma camiseta por R$ 63,00, uma calça por R$ 120,00 e uma bermuda por R$ 87,00, parcelando o total dessa compra em 3 vezes iguais.
Utilizando o fluxograma a seguir, ele determinou o valor de cada parcela dessa compra.
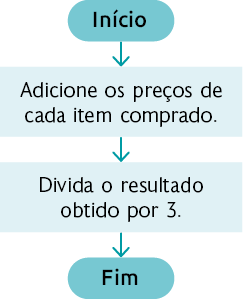
a) Qual é o valor de cada prestação dessa compra?
Resposta: R$ 90,00.
b) Construa um fluxograma para determinar o valor de cada prestação caso André dividisse a compra em 5 parcelas iguais.
Resposta nas orientações ao professor.
Página 54
Operações inversas: multiplicação e divisão
Juliana tem certa quantidade de fotos e vai distribuí-las igualmente em 4 álbuns, colando 38 fotos em cada um deles.
Quantas fotos Juliana tem?
Para resolver esse problema podemos representar a quantidade de fotos que Juliana tem por e construir o esquema a seguir.
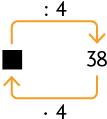
Então, para saber a quantidade de fotos que Juliana tem multiplicamos 38 por 4 e obtemos a resposta.
ou
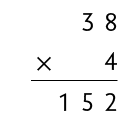
Podemos concluir que, ao multiplicar 38 por 4, obtemos 152 e que, ao dividir 152 por 4, obtemos 38, que se refere à quantidade de fotos em cada álbum.
e
Isso é possível porque a multiplicação e a divisão são operações inversas.
Atividades
Faça as atividades no caderno.
65. Determine nos esquemas o número que substitui cada ou adequadamente.
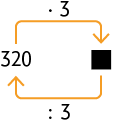
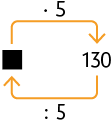
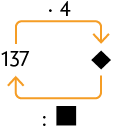
Respostas: A. ; B. ; C. e .
66. Determine nos esquemas o número que substitui cada adequadamente.
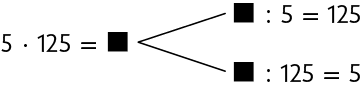
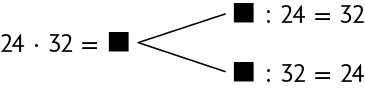
Respostas: A. ; B. .
67. Resolva os seguintes problemas.
a) Pensei em um número e o dividi por 8, obtendo 64 como resultado. Em que número pensei?
b) O produto de um número por 23 é igual a 1.104. Qual é esse número?
Respostas: a) 512; b) 48.
Página 55
Expressões numéricas com divisão
Jamil e Lurdes foram a uma loja comprar móveis e se depararam com os seguintes preços.
Imagens não proporcionais entre si.

R$ 360,00

R$ 72,00

R$ 380,00

R$ 426,00

R$ 974,00
Jamil comprou 1 cama, 6 cadeiras e 1 mesa. Sabendo que ele vai pagar a compra em 4 parcelas iguais, sem juro, qual será o valor de cada prestação?
Podemos responder a esta pergunta usando uma expressão numérica.
Questão 6. Efetue os cálculos necessários no caderno e determine o número que substitui cada letra corretamente.
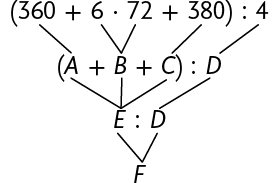
Atenção!
Em expressões desse tipo, efetuamos primeiro as multiplicações e as divisões na ordem em que aparecem e, depois, as adições e as subtrações, também na ordem em que aparecem. Se houver parênteses, as operações que estão dentro deles devem ser realizadas primeiro.
De acordo com os cálculos que você efetuou, qual é o valor de cada prestação?
Respostas: A: 360; B: 432; C: 380; D: 4; E: 1.172; F: 293; O valor de cada prestação é R$ 293,00.
Questão 7. Lurdes comprou 1 sofá, 2 poltronas e 4 cadeiras. Para pagar a compra, ela deu uma entrada de R$ 499,00 e pagará o restante em 5 parcelas iguais, sem juro. Calcule no caderno quantos reais Lurdes vai pagar em cada prestação.
Resposta: ; R$ 323,00
Atividades
Faça as atividades no caderno.
68. Resolva as expressões numéricas.
a)
b)
c)
Respostas: a) 81; b) 21; c) 29.
69. Efetue os cálculos a seguir da maneira que preferir.
a)
b)
c)
d)
Respostas: a) 101; b) 101; c) 101; d) 101.
70. De acordo com os resultados obtidos na atividade anterior, determine o resultado dos cálculos sem efetuá-los por escrito ou em uma calculadora.
a)
b)
c)
d)
Respostas: a) 101; b) 101; c) 101; d) 101.
71. Efetue os cálculos da atividade anterior da maneira que preferir, depois confira se as respostas estão corretas.
Resposta pessoal.
Página 56
72. Jaqueline gastou R$ 87,00 na compra de 5 cadernos iguais e 1 mochila. Sabendo que a mochila custou R$ 52,00, copie no caderno, entre as expressões numéricas a seguir, aquela que permite calcular o preço de 1 caderno. Depois resolva a expressão que você copiou e obtenha o preço de cada caderno.
Resposta: ; R$ 7,00.
73. Flávio fez uma viagem com três amigos e gastou R$ 376,00 com pedágio e combustível, R$ 55,00 com alimentação e R$ 63,00 com outras despesas. Sabendo que ele dividiu igualmente com seus amigos a despesa com pedágio e combustível, escreva uma expressão numérica e determine quantos reais Flávio gastou nessa viagem.
Resposta: ; R$ 212,00.
74.
Copie no caderno os itens a seguir, substituindo cada
por
,
,
ou
.


Respostas nas orientações ao professor.
75. Quando pensamos em divisão, imaginamos uma situação envolvendo a partilha de uma quantidade em partes iguais. Porém, há situações de partilha em partes desiguais. Vamos analisar e resolver o exemplo a seguir.
Para um show beneficente, Rafael e Ana venderam juntos 33 ingressos. Sabendo que Ana vendeu o dobro de ingressos de Rafael, quantos ingressos cada um deles vendeu?
Atenção!
Lembre-se: para calcular o dobro de uma quantidade, basta multiplicá-la por 2.
Resolução: Analisando essa situação, podemos afirmar que Rafael vendeu 1 parte do total de ingressos, enquanto Ana vendeu 2 partes. Dividindo o total de ingressos em 3 partes iguais, temos:
Portanto, Rafael vendeu 11 ingressos e Ana, 22, que corresponde a .
Agora é com você! As atividades a seguir envolvem a partilha de uma quantidade em duas partes desiguais. Junte-se a um colega e as resolvam.
a) Marcela e João economizaram dinheiro para comprar um presente a um familiar. Sabendo que ao todo eles economizaram R$ 180,00 e que Marcela economizou R$ 20,00 a mais que João, quantos reais cada um deles economizou?
Resposta: João economizou R$ 80,00 e Marcela, R$ 100,00.
b) Em um jogo de tabuleiro, Thaís e Gustavo fizeram 200 pontos ao todo. Sabendo que Gustavo fez o triplo da quantidade de pontos de Thaís, quantos pontos cada um deles fez nesse jogo?
Resposta: Gustavo fez 150 pontos e Thaís, 50.
76. Em seu caderno, elabore duas situações-problema envolvendo a partilha de uma quantidade em duas partes desiguais: uma semelhante ao item a e outra semelhante ao item b da atividade anterior. Em seguida, dê essas situações para um colega resolver e, ao final, confira se ele as solucionou corretamente.
Resposta pessoal.
Página 57
Potências
A cada figura a seguir, a quantidade de quadradinhos dobra.
-
Figura 1

-
Figura 2

-
Figura 3

ou
-
Figura 4

ou
A partir da Figura 2, a quantidade de quadradinhos pode ser calculada por uma multiplicação de fatores iguais, os quais podem ser representados por uma potência. Exemplos:
Figura 2
2 fatores iguais
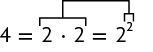
Potência:
(lê-se: dois elevado à segunda potência)
Figura 3
3 fatores iguais
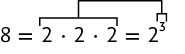
Potência:
(lê-se: dois elevado à terceira potência)
Figura 4
4 fatores iguais
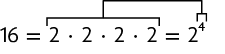
Potência:
(lê-se: dois elevado à quarta potência)
Atenção!
A potenciação é utilizada para representar uma multiplicação de fatores iguais, enquanto a multiplicação é usada para representar uma adição de parcelas iguais. Por exemplo:
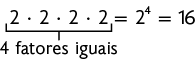
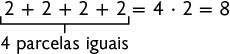
Questão 8.
Qual é a relação entre o número da figura e a quantidade de fatores
iguais nas multiplicações anteriores?
Resposta: São iguais.
Questão 9. Calcule no caderno a quantidade de quadradinhos da Figura 5 dessa sequência com uma multiplicação de fatores iguais. Depois escreva a potência correspondente.
Resposta: ; .
A operação que calcula o valor de uma potência é a potenciação. Por exemplo:
Página 58
Analise os nomes dos elementos de uma potenciação.
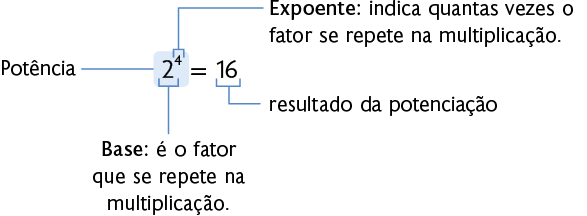
Atenção!
As potências de expoente 2 e de expoente 3 também podem ser lidas de outra maneira.
: três elevado ao quadrado.
: seis elevado ao cubo.
Instrumentos e softwares
Cálculo de potenciação na calculadora
Para calcular em uma calculadora, efetuamos uma multiplicação de fatores iguais, conforme as etapas apresentadas a seguir.
1º. Digite as teclas:






O número exibido é o resultado de .

Por outro lado, na maioria das calculadoras, a tecla
não serve apenas para exibir o resultado das operações, ela
também repete a última operação a cada vez que é digitada.
Utilizando esse recurso,
vamos obter, por exemplo, potências do número 7.
1º.
Digite as teclas
.
O número exibido é o resultado de .

2º.
Digite novamente a tecla
.
O número exibido é o resultado de .

Ao digitarmos mais vezes a tecla
,
obtemos
o resultado de
,
,
, ..., nessa ordem. Ou seja, para determinar a potência do
número, essa tecla deve ser digitada uma vez a menos que o valor
do expoente.
De modo geral, o procedimento para o cálculo pode ser diferente em algumas calculadoras, como a do aplicativo calculadora do smartphone.
Página 59
Atividades
Faça as atividades no caderno.
77.
Calcule as potências a seguir em uma calculadora.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) 256; b) 3.125; c) 729; d) 2.401; e) 20.736; f) 531.441; g) 3.375; h) 160.000.
78. No caderno, escreva os produtos de fatores iguais com uma potência, como no exemplo a seguir. Depois calcule seu valor.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
79. Determine a potência ou o produto de fatores iguais correspondente a cada letra.
|
Base |
Expoente |
Potência |
Produto de fatores iguais |
|---|---|---|---|
|
3 |
2 |
|
|
|
5 |
7 |
A |
B |
|
7 |
5 |
C |
D |
|
28 |
4 |
E |
F |
|
12 |
3 |
G |
H |
Respostas: A: ; B: ; C: ; D: ; E: ; F: ; G: ; H: .
80. No caderno, represente com uma potência a quantidade de quadradinhos de cada figura. Em seguida, calcule seu valor.




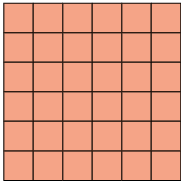
Respostas: A. ; B. ; C. ; D. ; E. .
81. Analise como podemos determinar a quantidade de cubos da pilha.

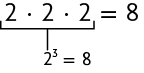
Utilizando uma potência, determine a quantidade de cubos em cada pilha a seguir.



Respostas: A. ; B. ; C. .
Página 60
82. As potências que você obteve nos itens A, B e C da atividade anterior formam uma sequência de potências de expoente 3. No caderno, escreva a próxima potência e calcule quantos cubos terá a pilha correspondente.
Resposta: .
83. Gilberto joga em um time de voleibol e, para compor o uniforme, dispõe das seguintes opções.

Usando 1 camiseta, 1 bermuda e 1 par de meias, de quantas maneiras diferentes Gilberto pode compor o uniforme de seu time?
Atenção!
Resolva esse problema utilizando uma potência.
Resposta: ; de 64 maneiras.
84. O esquema a seguir, chamado organograma, representa a hierarquia dos funcionários de uma empresa.
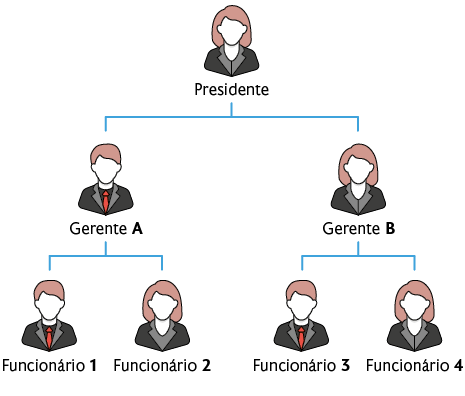
a) De acordo com esse organograma, quantos funcionários são subordinados a cada gerente?
Resposta: 2 funcionários.
b) Se nessa empresa houver 2 assistentes subordinados a cada funcionário, quantos assistentes haverá ao todo? Resolva este problema utilizando uma potência.
Resposta: ; 8 assistentes.
85. Na escola em que Mariana estuda foi feita uma dinâmica, na qual Mariana escreveu 3 cartas e enviou para 3 estudantes da mesma escola. Em cada envelope ela escreveu a letra A. Os estudantes que receberam essas cartas escreveram, cada um deles, 3 cartas semelhantes, registraram a letra B nos envelopes e encaminharam essas correspondências para outros 3 estudantes.
Esse procedimento se repetiu com todos que receberam uma carta, de modo que a letra registrada no envelope a ser enviado seguiu a ordem alfabética.
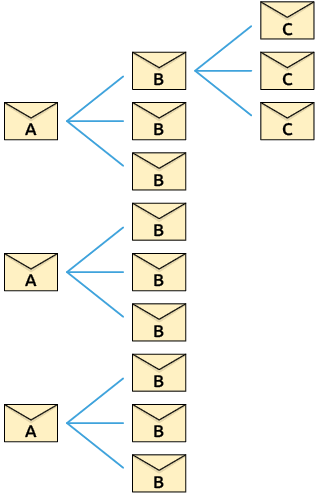
a) No caderno, escreva na forma de potência para calcular quantas cartas foram enviadas com a letra C registrada no envelope.
b) Faça o mesmo procedimento no caderno para descobrir quantas cartas foram enviadas com a letra D registrada no envelope.
Respostas: a) ; b) .
Página 61
Potências de expoente 1 e de expoente 0
Jonas escreveu as sequências A e B a seguir.
Na sequência A, o número que ocupa cada posição, a partir do segundo, foi obtido dividindo o número da posição anterior por 2.
Na sequência B, os números são obtidos de maneira semelhante, mas dividindo o número da posição anterior por 3.
Representando com potência os números dessas sequências, podemos escrever os seguintes esquemas.
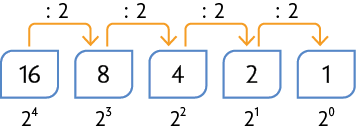
A. 16, 8, 4, 2, 1.
B. 81, 27, 9, 3, 1.
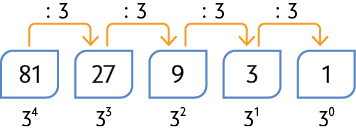
Na sequência A, note que e , e na sequência B, e .
Em potências cuja base é um número qualquer e expoente igual a 1, o resultado é igual ao próprio número.
Já as potências cuja base é um número diferente de zero e expoente igual a 0, o resultado é igual a 1.
Questão 10.
Descubra a regra da sequência a seguir. Depois, no caderno, represente com potências todos os termos dessa sequência.
625, 125, 25, 5, 1.
Resposta: Para obter um termo nessa sequência, a partir do segundo, dividimos o termo anterior por 5; , , , , .
Atividades
Faça as atividades no caderno.
86. Calcule o valor de cada potência a seguir.
a)
b)
c)
d)
Respostas: a) 8; b) 729; c) 2.401; d) 1.
87. Copie os itens no caderno substituindo cada pelo número adequado.
a)
Resposta: .
b)
Resposta: .
c)
Resposta: .
d)
Resposta: .
e)
Sugestão de resposta: .
f)
Sugestão de resposta: .
Página 62
Potências de base 10
Aline escreveu algumas potências em seu caderno.

Para calcular rapidamente uma potência de base 10, basta acrescentar à direita do algarismo 1 a quantidade de zeros correspondente ao expoente dessa potência. Por exemplo, para calcular , basta acrescentar 5 zeros à direita do algarismo 1.
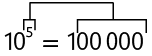
Do mesmo modo, podemos escrever um número com uma potência de base 10 simplificando sua escrita. Por exemplo:

Comumente, em informações com números "muito grandes", usamos essa forma de escrita. Por exemplo: a Terra tem aproximadamente 8.000.000.000 de habitantes em 2022.
Fonte de pesquisa: UNdata. Disponível em: https://oeds.link/A7l8Vn. Acesso em: 7 mar. 2022.
O dado numérico nessa informação pode ser representado da seguinte maneira.
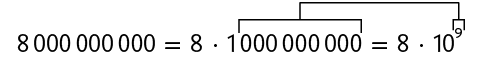
As potências de base 10 também podem ser usadas na decomposição dos números. Por isso, dizemos que nosso sistema de numeração é decimal, ou seja, de base 10.
Analise algumas maneiras de decompor, por exemplo, o número 243.781.
ou
ou
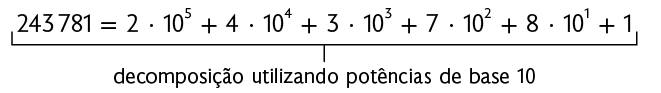
Página 63
Atividades
Faça as atividades no caderno.
88. Leia as informações a seguir e, usando potência de base 10, escreva no caderno o número apresentado em cada item.
Mapa do Brasil
Fonte de pesquisa: ATLAS geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.
A. A área do Brasil mede aproximadamente .
B. No Brasil havia cerca de 213.000.000 de habitantes em 2021.
Respostas: a) ; b) .
89. Calcule mentalmente.
a)
b)
c)
d)
e)
f)
Respostas: a) 100.000; b) 100.000.000; c) 10.000.000; d) 1.000.000; e) 10.000.000.000; f) 1.000.000.000.
90. Escreva os números a seguir no caderno usando potências de base 10.
a) 538.000
b) 2.300.000
c) 74.000.000
d) 957.000.000
e) 63.000.000.000
f) 12.500.000.000.000
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
91. Efetue os cálculos e registre no caderno o valor correspondente a cada letra.
|
Base |
Expoente |
Resultado da potenciação |
|---|---|---|
|
10 |
4 |
A |
|
10 |
B |
100.000 |
|
10 |
C |
1.000 |
|
10 |
11 |
D |
Respostas: A: 10.000; B: 5; C: 3; D: 100.000.000.000.
92. Determine nos itens a potência de base 10 que substitui cada ⬛ corretamente.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f)
Página 64
93. No caderno, escreva com uma potência de base 10 o número indicado em cada item.
a) Cem mil
b) 1.000.000
c) 100.000.000.000
d) Dez milhões
e) Um bilhão
f) 10.000
g) Cem milhões
h) 1.000.000.000.000
i) Dez bilhões
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) .
94. Decomponha os números utilizando potências de base 10.
a) 1.230
Resposta: .
b) 32.419
Resposta: .
c) 389.725
Resposta: .
d) 2.236.451
Resposta: .
95. Na tabela está indicada a medida da distância média entre cada planeta do Sistema Solar e o Sol.
|
Planeta |
Medida da distância média (em ) |
|---|---|
|
Terra |
149.600.000 |
|
Marte |
227.940.000 |
|
Urano |
2.870.990.000 |
|
Mercúrio |
57.910.000 |
|
Vênus |
108.210.000 |
|
Júpiter |
778.340.000 |
|
Saturno |
1.426.700.000 |
|
Netuno |
4.500.400.000 |
Fonte de pesquisa: NATIONAL AERONAUTICS AND SPACE ADMINISTRATION (NASA). Solar System Exploration. Disponível em: https://oeds.link/eUTf8h. Acesso em: 23 fev. 2022.
No caderno, arredonde essas medidas de distância à unidade de milhão mais próxima. Depois, escreva-as utilizando potências de base 10.
Resposta: Terra: ; Marte: ; Urano: ; Mercúrio: ; Vênus: ; Júpiter: ; Saturno: ; Netuno: .
96. O esquema a seguir apresenta a medida da distância entre algumas cidades.

Qual é a medida da distância, em metros, entre a cidade A e a cidade D?
a)
b)
c)
d)
e)
Resposta: Alternativa c.
97.
(OBMEP-2006) Qual é a soma dos
algarismos do número
?
a) 1
b) 5
c) 10
d) 1.889
e) 1.890
Resposta: Alternativa b.
Página 65
Igualdades
A balança de dois pratos representada a seguir está em equilíbrio.
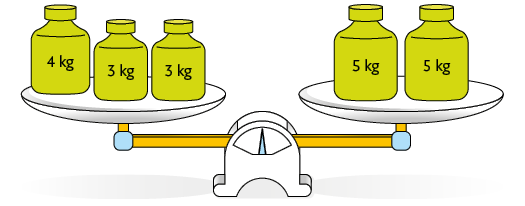
Atenção!
Uma balança de dois pratos está em equilíbrio quando as massas em cada um deles têm a mesma medida.
Podemos representar esse equilíbrio por meio da seguinte sentença matemática.
Dizemos que essa sentença é uma igualdade, pois temos o sinal de igual .
Uma sentença matemática que apresenta o sinal de igual é chamada igualdade. Em uma igualdade, chamamos a expressão à esquerda do sinal de 1º membro e a expressão à direita de 2º membro.
Em uma igualdade, o valor da expressão do 1º membro deve ser igual ao valor da expressão do 2º membro. Caso contrário, dizemos que a sentença matemática é falsa.
Agora, analise a situação a seguir e como Carol pensou para determinar a medida da massa da caixa azul.
Atenção!
A balança a seguir está em equilíbrio.
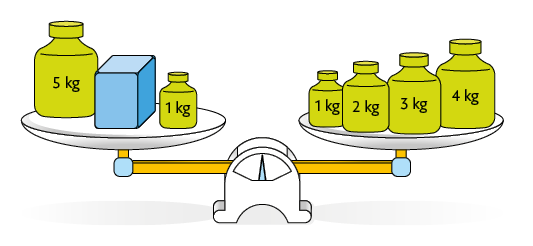

Página 66
Quando adicionamos ou subtraímos o mesmo número natural aos dois membros de uma igualdade, a relação de igualdade se mantém.
Ao adicionar 8 unidades em ambos os membros, a relação de igualdade se mantém.
Ao subtrair 5 unidades em ambos os membros, a relação de igualdade se mantém.
Quando multiplicamos os dois membros de uma igualdade por um mesmo número natural ou quando dividimos os dois membros de uma igualdade por um número natural diferente de zero, a relação de igualdade se mantém.
Ao multiplicar ambos os membros por 3, a relação de igualdade se mantém.
Ao dividir ambos os membros por 12, a relação de igualdade se mantém.
Questão 11.
Em uma igualdade, se adicionarmos o número 4 ao 1º
membro, quanto devemos adicionar ao 2º
membro para que permaneça uma relação de igualdade?
Resposta: 4.
Questão 12.
Em uma igualdade, se dividirmos o 1º
membro por 5, como devemos proceder com o 2º
membro para que permaneça uma relação de igualdade?
Resposta: Dividir por 5.
Atividades
Faça as atividades no caderno.
98. A balança a seguir está em equilíbrio.
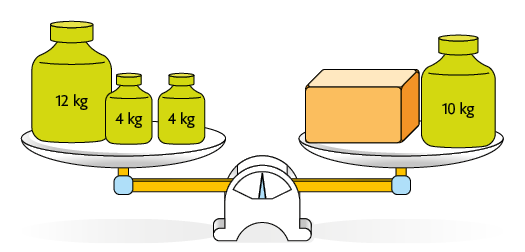
a) Usando um ⬛ para representar a medida da massa da caixa laranja escreva no caderno uma igualdade que represente o equilíbrio da balança.
Resposta: .
b) Calcule no caderno a medida da massa da caixa laranja.
Resposta: .
c) Em seu caderno, desenhe uma balança em equilíbrio parecida com a desta atividade, acrescentando uma caixa e peças com medidas de massa diferentes em cada um dos pratos. Em seguida, dê para um colega resolver e, ao final, confira se ele solucionou corretamente.
Resposta pessoal.
Versão adaptada acessível
c) Junte-se a um colega e desenhem uma balança em equilíbrio parecida com a retratada nesta atividade, acrescentando uma caixa e peças com medidas de massa diferentes em cada um dos pratos. Em seguida, entregue a atividade para uma dupla resolver e, ao final, confira se eles a solucionaram corretamente.
Resposta pessoal.
Página 67
99. Em cada expressão, determine o número que substitui o ⬛ para que a sentença seja uma igualdade.
Atenção!
Para determinar o valor do ⬛ no item c, subtraímos 4 aos dois membros da igualdade. Depois, dividimos ambos os membros por 2. Com isso, a igualdade não se altera.
a)
b)
c)
d)
e)
f)
Respostas: a) 8; b) 16; c) 8; d) 20; e) 5; f) 17.
100. A balança representada a seguir está em equilíbrio
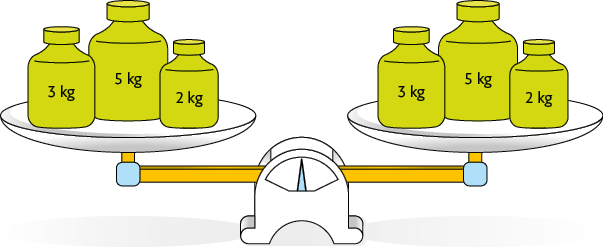
a) Para manter essa balança em equilíbrio, o que devemos fazer se colocarmos, em um dos seus pratos, 3 caixas com massa medindo cada uma?
Resposta: Devemos acrescentar a mesma medida de massa no outro prato, ou seja, .
b) Se dobrarmos a medida de massa em um dos pratos, o que devemos fazer para manter a balança em equilíbrio?
Resposta: Devemos dobrar a medida de massa do outro prato.
c) Renata trocou a peça de do prato da direita por uma peça de . O que ela deve fazer no prato da esquerda para manter o equilíbrio da balança?
Sugestão de resposta: Deve acrescentar uma peça com medida de massa de .
101. Após ganhar R$ 12,00 de seu pai, Daniela ficou com R$ 25,00.
Para calcular a quantia que tinha antes, ela escreveu a seguinte expressão.
Calcule no caderno a quantia que Daniela tinha antes de ganhar R$ 12,00 de seu pai.
Resposta: Daniela tinha 13 reais.
102. A balança a seguir não está em equilíbrio.
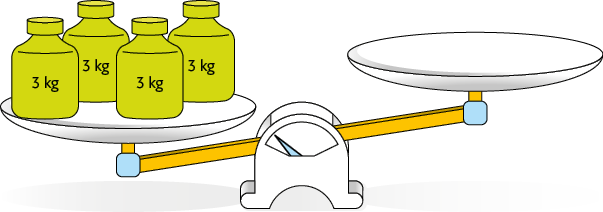
Gabriel quer deixar a balança em equilíbrio, mas só dispõe de peças com medida de massa igual a cada uma. Quantas dessas peças ele precisa colocar no outro prato para deixar a balança em equilíbrio?
Resposta: 6 peças.
103. Em seu caderno, elabore um problema envolvendo igualdade. Depois, entregue para um colega resolver. Ao final, verifique se ele solucionou corretamente.
Resposta pessoal.
Página 68
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Resolva as expressões numéricas em uma folha de papel avulsa.
a)
b)
c)
d)
Respostas: a) 30; b) 76; c) 93; d)1.066.
2.
Carla economizou dinheiro durante três meses. No 1º
mês, ela economizou R$ 182,00. No 2º
mês, o dobro da quantia que economizou no 1º
mês e, no 3º mês, R$ 56,00 a mais que
no 2º mês.
a) Qual foi a quantia total economizada por Carla ao final do 3º mês?
b) Amanda também economizou dinheiro durante três meses e obteve a mesma quantia de Carla. Porém, a quantia economizada por ela em cada um dos meses foi igual. Quantos reais Amanda economizou por mês?
Respostas: a) R$ 966,00; b) R$ 322,00.
3. Efetue as potenciações.
a)
b)
c)
d)
e)
f)
Respostas: a) 81; b) 1.000; c) 50.625; d) 400; e) 512; f) 1.
4. Na adição a seguir, cada figura representa um número natural.
a) Qual é o valor de ?
b) Qual é o valor de ?
c) Se ◆ representa o número 90 e ⬛ o número 30, então ▲ representa qual número?
Respostas: a) 180; b) 180; c) 60.
5. Na tabela está indicada a população estimada das cinco regiões do Brasil, em 2021.
|
Região |
População estimada |
|---|---|
|
Norte |
18.906.962 |
|
Nordeste |
57.667.842 |
|
Sudeste |
89.632.912 |
|
Sul |
30.402.587 |
|
Centro-Oeste |
16.707.336 |
Fonte de pesquisa: AGÊNCIA IBGE NOTÍCIAS. População estimada do país chega a 213,3 milhões de habitantes em 2021. Disponível em: https://oeds.link/Or44ZZ. Acesso em: 29 jun. 2022.
a) Arredonde a população estimada de cada região à centena de milhar mais próxima.
Resposta: Norte: 18.900.000; Nordeste: 57.700.000; Sudeste: 89.600.000; Sul: 30.400.000; Centro-Oeste: 16.700.000.
b) Agora, escreva em uma folha de papel avulsa os números obtidos no item anterior, utilizando potências de base 10.
Sugestão de resposta: Norte: ; Nordeste: ; Sudeste: ; Sul: ; Centro-Oeste: .
c)
Utilizando uma calculadora, determine qual era a população
brasileira estimada em 2021.
Resposta: 213.317.639 habitantes.
6. Determine o número que substitui cada adequadamente, de modo que as sentenças sejam uma igualdade.
a)
b)
c)
d)
e)
Respostas: a) 13; b) 5; c) 28; d) 12; e) 3.