Página 101
UNIDADE
5
Frações

Agora vamos estudar...
- as ideias de frações;
- frações próprias e frações impróprias;
- frações equivalentes;
- simplificação de frações;
- comparação de frações;
- frações decimais e porcentagens;
- adição e subtração de frações.
Página 102
Estudando frações
Fração como parte de um inteiro
A figura a seguir está dividida em 9 partes iguais, das quais João pintou 5 de verde. Considerando essa figura como o inteiro, podemos representar as partes pintadas de verde pela fração .
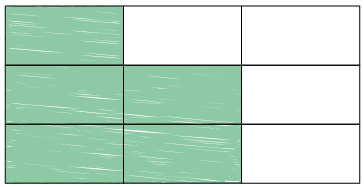
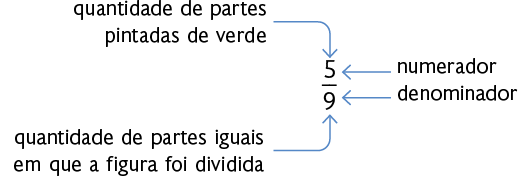
Nesse exemplo, a fração indica parte de um inteiro.
Questão 1. Escreva no caderno a fração da figura que indica as partes não pintadas de verde.
Resposta: .
Questão 2. Se toda a figura fosse pintada
de verde, que fração da figura
poderia corresponder à parte pintada?
Resposta: .
Leitura de fração
Na leitura de uma fração, lemos o numerador seguido do denominador. De acordo com o denominador, as frações recebem nomes específicos. Considere alguns exemplos.
Denominador menor do que 10
- : um meio
- : três quartos
- : quatro sétimos
- : dois terços
- : dois nonos
- : quatro quintos
Denominador igual a 10, 100, 1.000, ...
- : um décimo
- : oitenta e sete centésimos
- : quinhentos e dezessete milésimos
Atenção!
As frações com denominador igual a 10, 100, 1.000, ... são chamadas frações decimais.
Página 103
Denominador maior do que 10 e diferente de 100, 1.000, 10.000, ...
- : quatro doze avos
- : quinze setenta e um avos
- : dez vinte avos
- : quarenta e nove trezentos avos
Atenção!
O termo "avos" tem origem na palavra octavus (em latim, "oitavo"), que passou a ser escrito "oit'avos" para representar uma fração. Assim, a terminação "avo" passou a ser usada.
Fração como quociente de uma divisão
A fração também pode ser relacionada ao quociente de uma divisão. Vamos analisar um exemplo.
A figura apresentada a seguir está dividida em quatro partes iguais. Se pintarmos 4 dessas partes, então pintaremos a figura toda, ou seja, . Como , temos:
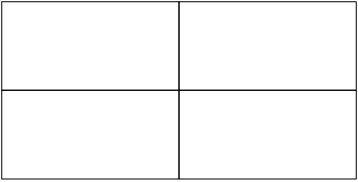
Atenção!
O traço da fração indica divisão.
Fração como razão
Em um curso de informática há 12 estudantes, dos quais 7 são mulheres.

Nesse caso, podemos dizer que 7 em 12 estudantes são mulheres ou que (sete doze avos) dos estudantes são mulheres.
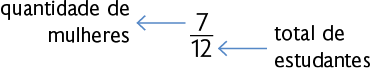
Nesse caso, a fração representa uma razão.
Questão 3. Escreva no caderno uma fração que represente a razão entre a quantidade de homens e o total de estudantes desse curso de informática.
Resposta: .
Página 104
Fração de uma quantidade
Rosana tem 24 mangás ✚ e vai organizar deles em uma estante. O restante será lido durante uma viagem. Para saber quantos mangás serão organizados na estante, precisamos calcular de 24. A seguir é apresentado como efetuar esse cálculo.
- Mangá:
- nome dado às histórias em quadrinhos de origem japonesa, em que a leitura é feita da direita para a esquerda. ↰
Inicialmente, separamos os 24 mangás em 6 grupos, cada um com a mesma quantidade, pois o denominador da fração é 6.

Em cada grupo há 4 mangás. Assim, de 24 é igual a 4.
Em seguida, para obter do total de mangás, consideramos 5 desses grupos.

de 24 é igual a 20.
Portanto, Rosana vai organizar 20 mangás na estante.
De maneira simplificada, podemos resolver esse problema de acordo com o procedimento apresentado a seguir.
Página 105
1º. Dividimos a quantidade de mangás (24) pelo denominador da fração (6).
2º. Multiplicamos o resultado obtido pelo numerador da fração (5).
Portanto, Rosana vai organizar na estante 20 dos 24 mangás.
Questão 4. Quantos
mangás
Rosana vai ler durante a viagem?
Resposta: 4 mangás.
Questão 5. Algumas civilizações antigas, como a egípcia, aplicam a ideia de fração em seu sistema de numeração. Baseado nessas civilizações, pesquise a respeito dos tipos de fração e de seus respectivos símbolos. Por fim, escreva no caderno algumas frações com esses símbolos.
Atenção!
A pesquisa proposta na questão 5 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Resposta nas orientações ao professor.
Versão adaptada acessível
Questão 5. Algumas civilizações antigas, como a egípcia, aplicam a ideia de fração em seu sistema de numeração. Com base nessas civilizações, junte-se a um colega e pesquisem os tipos de frações e seus respectivos símbolos. Por fim, escrevam algumas frações com esses símbolos.
Resposta nas orientações ao professor.
Instrumentos e softwares
Frações de uma quantidade na calculadora
Verifique como podemos calcular de 585, utilizando uma calculadora.
1º. Registre o número 585 digitando as teclas 5, 8 e 5, nessa ordem.
2º. Em seguida,
divida 585 pelo
denominador da fração (9). Para isso, digite as teclas
,
nessa ordem.
3º. Na
sequência, multiplique o resultado obtido pelo
numerador da fração (2). Para isso, digite as
teclas
,
nessa ordem.
4º. Por fim,
digite a tecla .

Atividades
Faça as atividades no caderno.
1. Cada figura foi dividida em partes iguais. Que fração de cada figura corresponde às partes pintadas de roxo?



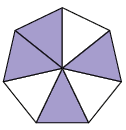
Respostas: A. ; B. ; C. ; D. .
Página 106
2. O quadrado a seguir foi dividido em triângulos iguais. Qual das regiões tem maior medida de área: a branca ou a cinza? Que fração do quadrado representa a região cinza? E a região branca?

Respostas: Cinza; região cinza: ; região branca: .
3. Cada figura a seguir foi dividida em partes iguais.
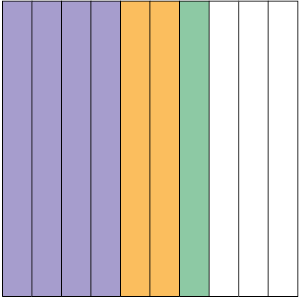
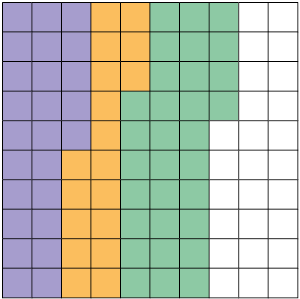
a) Em quantas partes iguais foi dividida a figura A? E a figura B?
Respostas: A: 10 partes iguais; B: 100 partes iguais.
b) Que fração da figura A representa as partes pintadas:
- de roxo?
- de verde?
- de laranja?
Respostas: Roxo: ; Verde: ; Laranja: .
c) Que fração da figura B representa as partes pintadas:
- de roxo?
- de verde?
- de laranja?
Respostas: Roxo: ; Verde: ; Laranja: .
4. O retângulo foi dividido em partes iguais.
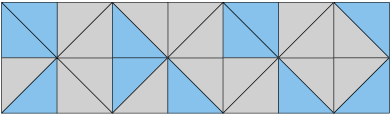
Que fração do retângulo representa as partes pintadas de azul?
Resposta: .
5. No caderno, escreva com algarismos cada uma das frações.
a) Quatro quintos.
b) Sete nonos.
c) Oito treze avos.
d) Quatorze centésimos.
e) Trinta e três milésimos.
Respostas: a) ; b) ; c) ; d) ; e) .
6. Escreva no caderno como se lê cada fração a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas nas orientações ao professor.
7. Em uma prova de concurso com 60 questões, havia 20 questões de Ciências, 30 de Matemática e o restante, de Língua Portuguesa.
a) Quantas eram as questões de Língua Portuguesa?
Resposta: 10 questões.
b) Escreva uma razão que represente a quantidade de questões de Língua Portuguesa em relação ao total de questões da prova.
Sugestão de resposta: .
c) Escreva uma razão que represente a quantidade de questões de Ciências em relação à quantidade de questões de Matemática.
Sugestão de resposta: .
Página 107
8. Em uma
turma de 6º ano há 36 estudantes. Nessa turma, a
quantidade de meninas é igual ao dobro da quantidade
de meninos. Escreva uma razão que represente a quantidade de:
a) meninas em relação à quantidade total de estudantes;
b) meninos em relação à quantidade total de estudantes.
Respostas: a) ; b) .
9. Certa
pesquisa realizada em uma escola mostrou que, para cada 5
estudantes de inglês, há 2 de francês.
a) Escreva a razão entre a quantidade de estudantes de francês e a quantidade de estudantes de inglês.
Resposta: .
b) Nessa escola, é possível que haja 20 estudantes de francês a cada 100 estudantes de inglês? Justifique sua resposta.
Resposta: Não, pois, separando os 100 estudantes em 5 partes iguais, cada parte terá 20 estudantes. Assim, tomando duas dessas partes, obtém-se 40, o que não se refere à quantidade dos que estudam francês.
10. A Região Nordeste do Brasil tem cerca de 1.800 municípios. Tendo quase deles, a Bahia é o estado com mais municípios dessa região. Quantos municípios aproximadamente tem o estado da Bahia?
Resposta: Aproximadamente 420 municípios.
11. Érica tem uma loja de roupas. Ela comprou um lote com 60 blusas, das quais eram vermelhas. Quantas blusas eram vermelhas? E quantas não eram vermelhas?
Respostas: 40 blusas; 20 blusas.
12. Quantos minutos há em:
a) de ?
b) de ?
c) de ?
d) de ?
Atenção!
Lembre-se de que equivale a .
Respostas: a) ; b) ; c) ; d) .
13. Com uma
calculadora, calcule os seguintes valores.
a) de
b) de
c) de
d) de
e) de
f) de
g) de
h) de
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
14. Marcela repartiu em partes desiguais 36 figurinhas entre os seus netos Hugo, Igor e Júlio. Nessa partilha, Hugo recebeu da quantidade total de figurinhas, Igor recebeu e Júlio, . Quantas figurinhas cada um dos netos de Marcela recebeu?
Resposta: Hugo: 18 figurinhas; Igor: 12 figurinhas; Júlio: 6 figurinhas.
15. Uma pessoa adulta dorme cerca de das horas de 1 dia. Quantos dias são necessários para dormir o equivalente às horas de 2 dias inteiros?
Resposta: 6 dias.
16. Anderson
tem uma coleção de gibis. Sabendo que de sua coleção correspondem a 40 gibis,
calcule quantos ele tem.
Atenção!
Determine inicialmente a quantidade de gibis que representa da coleção.
Resposta: 100 gibis.
17. André tem 140 figurinhas e vai distribuir delas entre seus 4 colegas.
De acordo com essa informação, elabore em seu caderno duas ou mais perguntas em relação à quantidade de figurinhas de André envolvendo a partilha delas em duas partes desiguais e a ideia de razão. Depois, dê as perguntas que elaborou para um colega resolver e, por fim, verifique se as respostas dele estão corretas.
Resposta pessoal.
Página 108
Frações próprias e frações impróprias
Até agora, estudamos frações que representam parte de uma unidade, de um inteiro ou de uma quantidade, ou seja, aquelas em que o numerador é menor do que o denominador, como . Frações com essa característica são chamadas frações próprias.
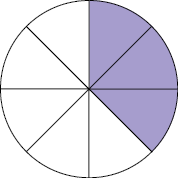
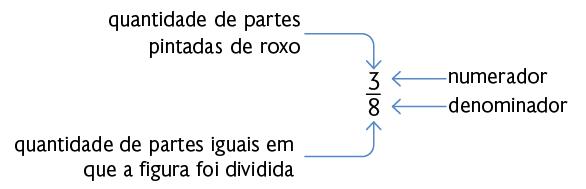
Uma fração própria representa parte de um inteiro, ou seja, uma quantidade maior do que zero e menor do que 1. Em frações com essa característica o numerador é menor do que o denominador.
Quanto às frações em que o numerador é maior do que o denominador ou igual a ele, como a chamamos? Por exemplo, a fração . Frações com essa característica são chamadas frações impróprias. Nesse caso, o numerador representa a quantidade de partes que estão sendo consideradas e o denominador indica em quantas partes iguais cada unidade foi dividida.
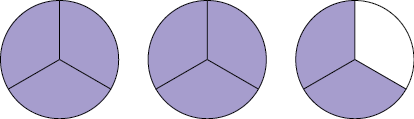
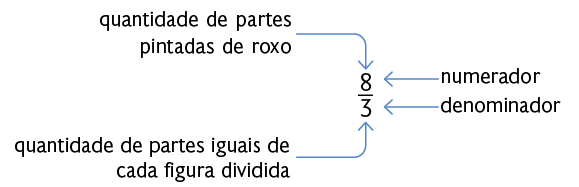
Uma fração imprópria representa uma quantidade igual ou maior do que 1 unidade. Em frações com essa característica, o numerador é maior ou igual ao denominador.
Página 109
Uma fração imprópria também pode ser escrita como um número na forma mista. Verifique, por exemplo, como representar a fração .
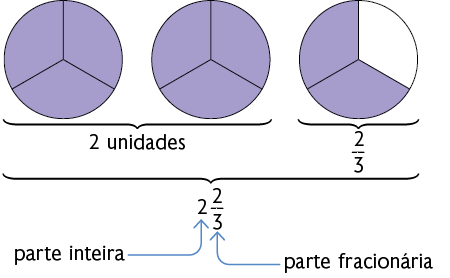
Portanto, as partes pintadas de roxo correspondem a ou .
O número é chamado número na forma mista. Lê-se: dois inteiros e dois terços.
Frações aparentes
A figura a seguir foi dividida em 6 partes iguais e todas foram pintadas.
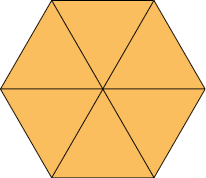
A fração corresponde às partes dessa figura pintadas de laranja, o que representa 1 unidade.
Frações impróprias que representam números naturais, e cujo numerador é múltiplo do denominador, são chamadas frações aparentes.
A fração aparente é um caso particular de fração imprópria.
Portanto, a fração é uma fração aparente.
Considere outros exemplos.

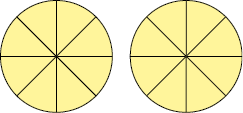
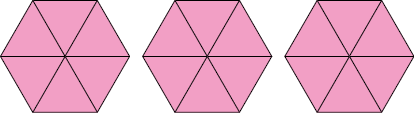
Página 110
Atividades
Faça as atividades no caderno.
18. Escreva no caderno a divisão e o número natural correspondentes a cada fração.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f)
19. Considere as seguintes frações.
a) Indique as frações menores do que 1.
b) Indique aquelas que correspondem ao número 1.
c) Indique as frações maiores do que 1.
Respostas: a) e ; b) e ; c) , e .
20. Classifique cada fração em própria, imprópria ou aparente.
a)
b)
c)
d)
e)
f)
Respostas: a) Própria; b) Imprópria; c) Imprópria e aparente; d) Própria; e) Imprópria; f) Imprópria e aparente.
21. No caderno, represente com figuras as frações impróprias a seguir. Depois, escreva o número na forma mista correspondente e como se lê cada um deles.
a)
b)
c)
d)
e)
f)
Respostas na seção Respostas e na seção Resoluções.
22. Escreva
três frações aparentes que representa o número 9, de modo que o numerador seja
maior do que 10 e menor do que 100.
Sugestões de resposta: , , , , , , e .
23. Em cada item, considere 1 figura como unidade e dividida em partes iguais. Represente no caderno as partes coloridas de laranja com uma fração e com um número na forma mista.
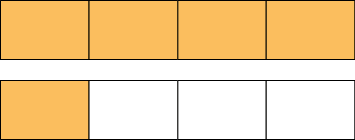
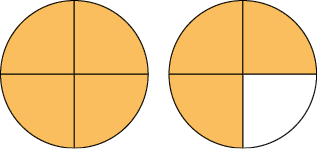
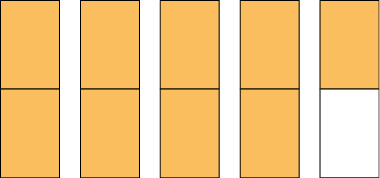
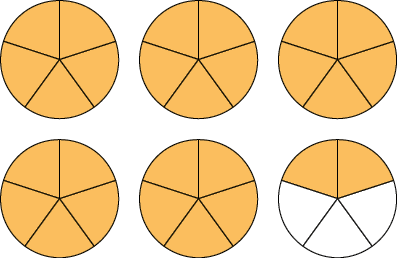
Respostas: A. , ; B. , ; C. , ; D. , .
24. No caderno, represente os números na forma mista a seguir utilizando figuras. Depois escreva a fração correspondente.
a)
b)
c)
d)
Respostas na seção Respostas e na seção Resoluções.
Página 111
Frações equivalentes
De maneiras diferentes, Danilo dividiu em partes iguais 3 tiras de papel com dimensões de mesmas medidas. Em seguida, ele as pintou de verde conforme as frações indicadas.
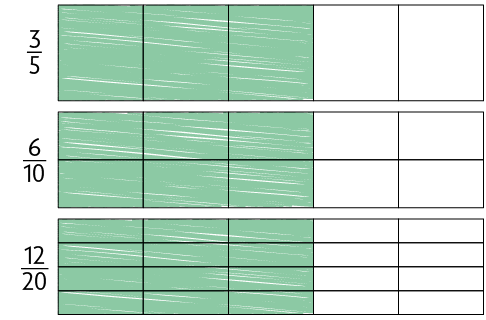
Em cada tira, as partes coloridas de verde representam a mesma parte da tira, ou seja, do todo. A parte pintada referente a corresponde a , que também se refere a . Então dizemos que as frações , e são equivalentes, isto é, .
Duas ou mais frações que representam a mesma parte de uma unidade, quantidade ou de um inteiro recebem o nome de frações equivalentes.
Agora, verifique como Soraia obteve duas frações equivalentes a .
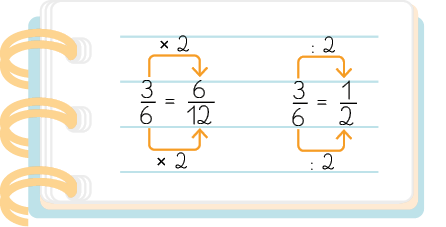
Para verificar se as frações que obteve eram equivalentes, Soraia desenhou 3 figuras iguais. Depois dividiu cada uma delas em partes iguais e as pintou de laranja, conforme as frações obtidas.
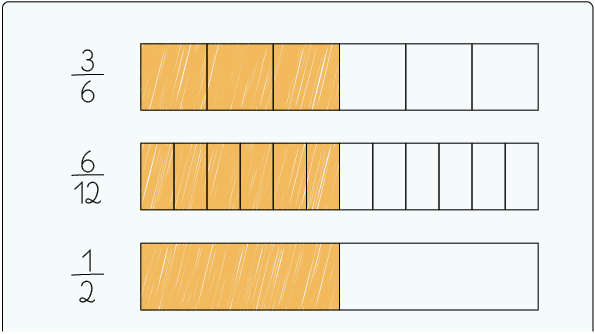
As partes coloridas de laranja de cada figura representam a mesma parte do todo. Portanto, as frações , e são equivalentes.
Ao multiplicar ou dividir o numerador e o denominador de uma fração por um mesmo número diferente de zero, obtemos uma fração equivalente à inicial.
Página 112
Atividades
Faça as atividades no caderno.
25. Cada figura a seguir foi dividida em partes iguais. Escreva duas frações equivalentes para representar as respectivas partes pintadas de roxo.
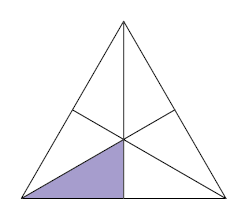
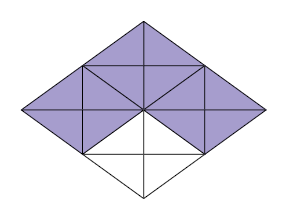
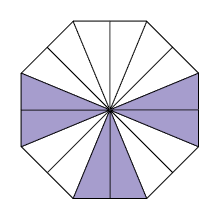
Sugestão de respostas: A. e ; B. e ; C. e .
26. Determine nos itens o número que substitui cada ⬛ adequadamente.
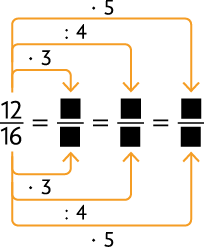
Resposta: .
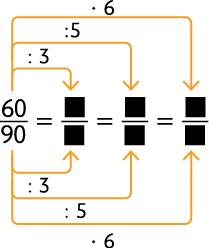
Resposta: .
Analisando as frações que você escreveu nos itens anteriores, as do item A são equivalentes? E as do item B?
Respostas: Sim; Sim.
27. Efetue os cálculos e escreva no caderno frações equivalentes à fração de cada item.
a)
b)
c)
d)
e)
f)
Sugestão de respostas: a) ; b) ; c) ; d) ; e) ; f) .
28. Em cada item qual fração não é equivalente às demais?
Respostas: a) ; b) ; c) .
29. Nas frações a seguir, substitua cada letra por um dos números apresentados, de modo que as frações sejam equivalentes.
-
12
-
36
-
8
-
3
Resposta: ; ; ; .
30. Copie os itens no caderno substituindo cada pelo número adequado, de maneira que as frações sejam equivalentes.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
Página 113
31. Associe as frações equivalentes. Para isso, escreva a letra e o número correspondentes.
a)
b)
c)
d)
1)
2)
3)
4)
Resposta: a-2; b-4; c-3; d-1.
32. Calcule quantos quilogramas há em:
Atenção!
Lembre-se de que equivale a .
a) de .
b) de .
c) de .
d) de .
e) de .
f) de .
Respostas: a) ; b) ; c) ; d) ; e) ; f) ;
Quais são os pares de frações equivalentes?
Questão: e ; e ; e .
33. Evandro, Cláudio e Ulisses colecionam cartas de jogo de tabuleiro.
Cláudio tem 96 cartas de jogo em sua coleção.
Evandro tem da quantidade de cartas de Cláudio.
Ulisses tem da quantidade de cartas de Cláudio.
a) Quantas cartas de jogo têm Evandro e Ulisses, respectivamente?
I) 12 e 36
II) 4 e 12
III) 12 e 4
IV) 36 e 12
V) 12 e 12
Resposta: Alternativa V.
b) As frações e são equivalentes? Justifique sua resposta.
Resposta: Sim, pois elas representam a mesma quantidade do total de cartas.
34. Em um cinema há 280 poltronas. Em certa sessão, 210 poltronas ficaram ocupadas. Entre as frações a seguir, qual representa a quantidade de poltronas ocupadas nessa sessão?
Resposta: .
35. Sandro, Bernardo e Hugo estão colecionando, cada um, figurinhas de um mesmo álbum. Verifique a fração das figurinhas já coladas no álbum de cada um.
Sandro: das figurinhas do álbum.
Bernardo: das figurinhas do álbum.
Hugo: das figurinhas do álbum.
Determine quais deles colaram a mesma quantidade de figurinhas no álbum.
Resposta: Sandro e Hugo.
36. Para obter de tinta de certa tonalidade, são misturados de tinta azul, de tinta verde e de tinta vermelha.
a) Sabendo que , quantos mililitros de tinta azul são usados nessa mistura? E de tinta verde? E vermelha?
Respostas: Azul: ; verde: ; vermelha: .
b) Quais das frações apresentadas no enunciado são equivalentes?
Resposta: e .
37. Quais das frações a seguir são equivalentes a ?
Resposta: e .
Página 114
Simplificação de frações
Diogo obteve algumas frações equivalentes à fração .
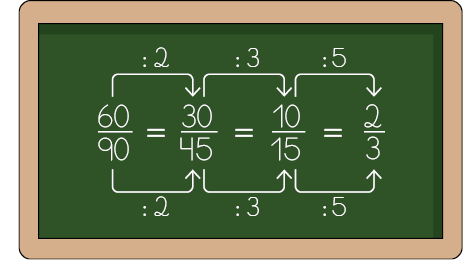
Atenção!
No dicionário, a palavra irredutível significa "aquilo que não pode ser reduzido ou simplificado".
O numerador e o denominador da fração não podem ser divididos por um mesmo número, pois não existe nenhum número natural que seja divisor de 2 e 3 simultaneamente. Nesse caso, dizemos que a fração é uma fração irredutível.
Para simplificar uma fração, dividimos o numerador e o denominador pelo mesmo número natural, diferente de 0 e de 1. Quando não é mais possível simplificar uma fração, torna-se uma fração irredutível.
Atividades
Faça as atividades no caderno.
38. Cada figura a seguir foi dividida em partes iguais. Escreva no caderno a fração correspondente às partes coloridas de roxo de cada figura. Em seguida, simplifique-as até obter frações irredutíveis.
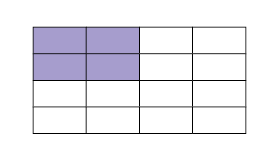

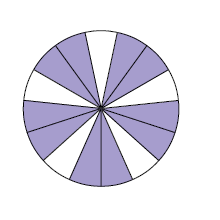
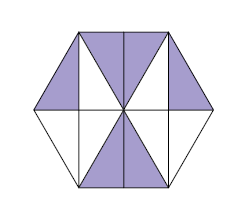
Respostas: A. , ; B. , ; C. , ; D. , .
39. Simplifique as frações a seguir até obter frações irredutíveis.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
40. Determine nos esquemas o número adequado que substitui cada uma das figuras.
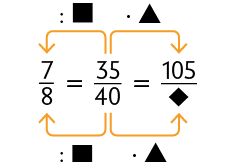
Resposta: , e .
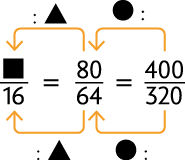
Resposta: , e .
Página 115
Comparação de frações
Comparação de frações com denominadores iguais
Natália e Rúbia participaram de uma maratona. Após 1 hora da largada, Natália havia percorrido do percurso e Rúbia, .
Qual das duas percorreu uma parte maior nessa 1 hora?
Para responder a esta questão, precisamos comparar as frações e , além de verificar qual das duas é maior.
Podemos representar, com um esquema, a parte do percurso que Natália e Rúbia haviam percorrido 1 hora após a largada.
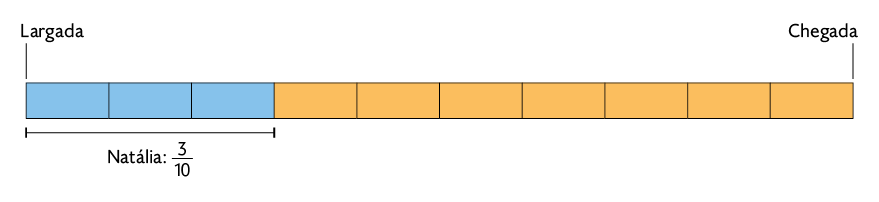
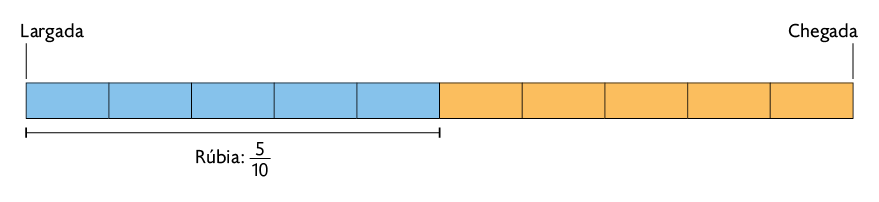
Podemos notar que a parte em azul, representando a fração , é maior do que a parte em azul representando a fração . Então, concluímos que .
Portanto, após 1 hora da largada, Rúbia havia percorrido uma parte maior do que Natália.
Ao compararmos frações com denominadores iguais, a maior fração é a que tiver o maior numerador.
Questão 6. Sabendo que o percurso de uma maratona tem cerca de , calcule no caderno aproximadamente quantos quilômetros Natália e Rúbia haviam percorrido após 1 hora.
Representando as frações e na reta numérica, temos:
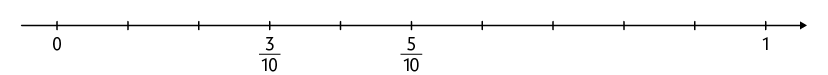
Resposta: Natália: aproximadamente ; Rúbia: aproximadamente .
Página 116
Verifique que está à direita de , pois .
Na reta numérica, ao comparar duas frações, a maior sempre estará à direita da menor.
Comparação de frações com denominadores diferentes
Luciano e Igor foram os candidatos a prefeito mais votados em uma eleição. Luciano recebeu dos votos válidos e Igor, . Qual dos dois candidatos recebeu mais votos?
Para responder a esta questão precisamos comparar as frações e , verificando qual das duas é maior. Note que essas frações têm denominadores diferentes.
Portanto, para comparar as frações e , devemos obter frações equivalentes a elas que tenham denominadores iguais.
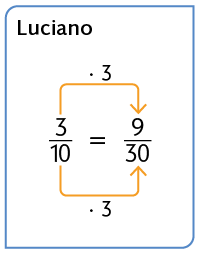
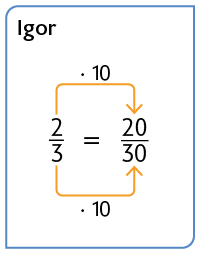
Atenção!
Como o número 30 é um múltiplo comum de 10 e 3, escrevemos as frações equivalentes às frações e com denominador 30.
Comparando as frações e , verificamos que . Então , portanto, Igor recebeu mais votos.
Na comparação de frações com denominadores diferentes, inicialmente obtemos frações equivalentes a elas com o mesmo denominador. Em seguida, comparamos as frações equivalentes.
Questão 7. Junte-se a um colega e, de maneira semelhante, compare cada par de frações, de um mesmo todo, e identifique a maior delas registrando em seu caderno.
a) e
b) e
c) e
Respostas: a) ; b) ; c)
Página 117
Atividades
Faça as atividades no caderno.
41. Compare cada par de frações, de um mesmo todo, e copie no caderno a maior delas.
a) e
b) e
c) e
d) e
e) e
f) e
Respostas: a) ; b) ; c) ; d) ; e) ; f)
42. O mosaico a seguir é formado por quadradinhos iguais.
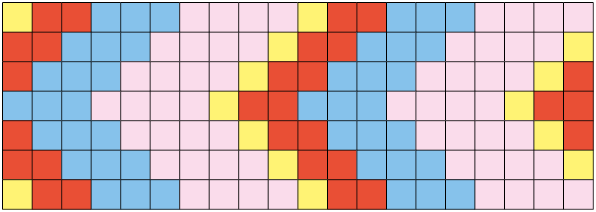
a) Escreva no caderno a fração do mosaico que corresponde às partes pintadas de:
- amarelo;
- azul;
- rosa;
- vermelho.
Respostas: Amarelo: ; azul: ; rosa: ; vermelho: .
b) Em ordem crescente, escreva no caderno as frações referentes às cores que formam o mosaico, colocando o símbolo entre elas.
Resposta: ou .
43. Escreva no caderno, em ordem decrescente, as frações apresentadas nas fichas. Para isso, utilize o símbolo entre elas.
Agora, associe cada fração à letra adequada na reta numérica a seguir.

Respostas: . B: ; D: ; E: ; H: ; J: ; L: .
44. Uma escola organizou uma gincana com os estudantes. A fração do total de pontos de cada equipe em uma das provas está indicada a seguir.
- Equipe amarela:
- Equipe azul:
- Equipa branca:
- Equipe laranja:
a) Sabendo que a pontuação máxima nessa gincana foi 20 pontos, qual das equipes pontuou mais?
Resposta: Equipe laranja.
b) Escreva no caderno, em ordem crescente, as frações que representam os pontos obtidos pelas equipes.
Resposta: .
Página 118
45. Ronaldo e Mário são caminhoneiros e saíram, cada um com seu caminhão, do município de Maceió, em Alagoas, com destino ao município de Juiz de Fora, em Minas Gerais.
Ronaldo percorreu do trajeto e parou para abastecer. Mário parou para abastecer após ter percorrido do mesmo trajeto. Ao abastecer os caminhões, qual dos dois estava mais próximo de Juiz de Fora?
Resposta: Ronaldo.
46. Em ordem crescente, escreva no caderno as frações de cada item.
a) , e .
b) , e .
c) , e .
d) , e 1.
Respostas: a) ; b) ; c) ; d)
47. Copie os itens em seu caderno substituindo cada ⬛ pelos símbolos , ou .
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
48. Entre seus 3 netos, Antônio dividiu certa quantia em reais da maneira indicada a seguir.

Essa quantia foi dividida igualmente entre os netos? Justifique sua resposta.
Resposta: Sim, pois as frações , e são equivalentes.
49. Sílvio e Isadora estão lendo o mesmo livro. Sílvio já leu das páginas do livro e Isadora, .
a) Quem já leu a maior quantidade de páginas desse livro?
Resposta: Sílvio.
b) Sabendo que o livro tem 90 páginas, quantas páginas cada um deles já leu?
Resposta: Sílvio: 42 páginas; Isadora: 36 páginas.
50. Uma festa de aniversário foi decorada com balões de diversas cores, dos quais eram azuis, eram vermelhos e eram amarelos.
a) Qual era a cor da maior parte dos balões?
b) Qual era a cor da menor parte dos balões?
Respostas: a) Vermelha. b) Azul.
51. Em uma prova de Matemática, Adriana acertou das questões, e Michele acertou .
a) Quem acertou mais questões na prova?
Resposta: Michele.
b) Sabendo que a prova tinha 20 questões, quantas Adriana acertou? E quantas Michele acertou?
Respostas: 15 questões; 16 questões.
52. Considere os números apresentados a seguir.
-
1
-
3
-
4
-
6
-
7
Usando uma única vez os números apresentados, escreva no caderno uma fração que representa:
a) a menor quantidade.
b) a maior quantidade.
Respostas: a) ; b) .
Página 119
Frações decimais e porcentagens
Na escola em que Priscila estuda, houve uma pesquisa com 100 estudantes sobre o gênero de livro preferido deles. No gráfico estão apresentados os dados coletados.
Gênero de livro preferido dos estudantes do 6º ano - 24/03/2023
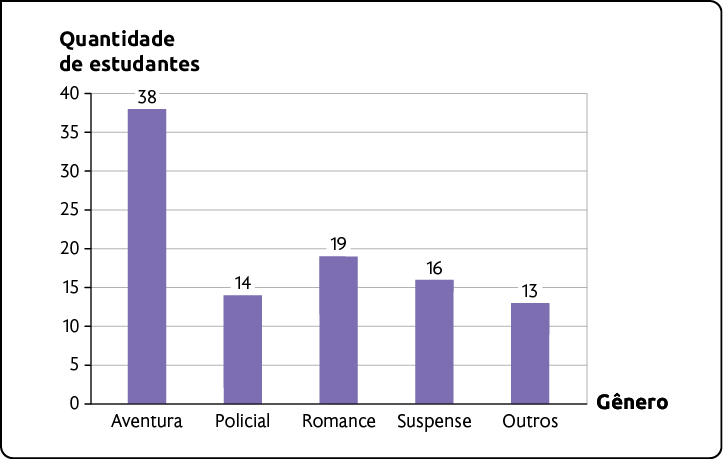
Fonte de pesquisa: registro dos estudantes do 6º ano.
De acordo com o gráfico, 38 estudantes preferem ler livros de aventura. Como 100 deles foram pesquisados, a fração corresponde a esses estudantes.
Para representar essa fração, podemos usar a porcentagem, que se refere a uma parte do total de 100 partes, representada pelo símbolo % (lê-se: "por cento").
No caso comentado, 38 dos 100 estudantes preferem ler livro de aventura, ou seja, 38 partes de um total de 100 partes. Assim, a fração decimal pode ser representada por 38%, lê-se: trinta e oito por cento.
A porcentagem, indicada pelo símbolo %, corresponde a uma fração com denominador 100. Se indicarmos 20%, por exemplo, significa que consideramos a fração .
Questão 8. Escreva no caderno a fração decimal e a porcentagem dos estudantes que preferem ler livros do gênero:
a) policial;
b) romance;
c) suspense;
d) outros.
Respostas: a) ; 14%. b) ; 19%. c) ; 16%. d) ; 13%.
Questão 9. Em sua opinião, quais outros
gêneros de livros poderiam ser
incluídos na opção "outros"?
Resposta pessoal.
Página 120
Verifique o preço de uma bicicleta.

Para obter o valor, em reais, do desconto para essa bicicleta, precisamos calcular 15% de R$ 400,00.
Sabemos que 100% corresponde ao total.
100% corresponde a R$ 400,00
Calculamos 1% dividindo o total (R$ 400,00) por 100.
Multiplicamos o resultado obtido (R$ 4,00) por 15, pois queremos calcular 15%.
Logo, 15% de 400 é igual a 60. Portanto, o valor do desconto é R$ 60,00.
Como calcular 15% de R$ 400,00 corresponde a calcular de 400, podemos esquematizar esse cálculo da seguinte maneira:
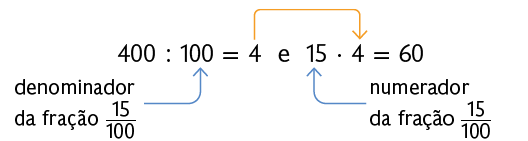
Questão 10. Junte-se a um colega e respondam às perguntas registrando no caderno.
a) Qual será o valor da bicicleta com o desconto?
b) Qual seria o valor da bicicleta se o desconto fosse de 10% no preço da etiqueta?
Respostas: a) R$ 340,00; b) R$ 360,00.
Instrumentos e softwares
Calculando porcentagens
Observe como podemos calcular 18% de 450.
1º. Registre o
número 450 e digite a tecla .
2º. Em seguida, registre o número 18, pois queremos calcular 18% do número.
3º. Digite a
tecla e
obtenha o resultado.

Página 121
Atividades
Faça as atividades no caderno.
53. Escreva cada fração na forma de porcentagem.
a)
b)
c)
d)
e)
f)
Respostas: a) 3%; b) 28%; c) 35%; d) 99%; e) 1%; f) 10%.
54. As figuras a seguir foram divididas em partes iguais. Escreva no caderno a fração decimal e a porcentagem que representam as partes coloridas de verde em cada figura.
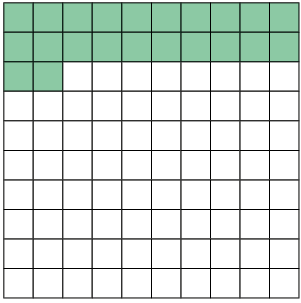
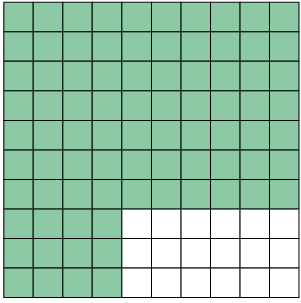
Respostas: A. ; 22%; B. ; 82%.
55. Com uma
calculadora, calcule as porcentagens a seguir.
a) 20% de 530.
b) 35% de 2.420.
c) 8% de 250.
d) 15% de 1.200.
e) 50% de 3.600.
f) 65% de 800.
Respostas: a) 106; b) 847; c) 20; d) 180; e) 1.800; f) 520.
56. Verifique como podemos escrever a fração na forma de porcentagem.
Escrevemos uma fração equivalente a que tenha denominador 100.
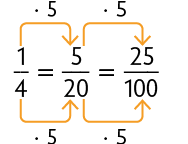
Como e , concluímos que .
Agora, escreva no caderno as frações na forma de porcentagem.
a)
b)
c)
d)
e)
f)
Respostas: a) 70%; b) 60%; c) 20%; d) 64%; e) 14%; f) 40%.
57. Paulo coleciona figurinhas, das quais são de animais, são de plantas, é de carros e o restante é de modalidades esportivas.
a) Das figurinhas que Paulo tem, quantos por cento são de:
- animais?
- plantas?
- carros?
Respostas: Animais: 40%; plantas: 30%; carros: 25%.
b) Escreva a fração decimal e a porcentagem das figurinhas de Paulo correspondentes a modalidades esportivas.
Resposta: ; 5%.
58. César está economizando dinheiro para comprar um violão que custa R$ 500,00. Ele já economizou uma quantia correspondente a do preço do violão.
a) Qual porcentagem corresponde à quantia que César já economizou?
b) Quantos reais César já economizou?
Respostas: a) 25%; b) R$ 125,00.
Página 122
59. Renato calculou mentalmente 30% de R$ 400,00.

Note que Renato calculou inicialmente 10% de 400. Mas como queria calcular 30% de 400, ele adicionou 3 vezes o resultado dos 10%. De maneira semelhante, calcule mentalmente:
a) 20% de R$ 300,00.
b) 30% de R$ 500,00.
c) 40% de R$ 200,00.
d) 50% de R$ 700,00.
e) 60% de R$ 600,00.
f) 70% de R$ 100,00.
Respostas: a) R$ 60,00; b) R$ 150,00; c) R$ 80,00; d) R$ 350,00; e) R$ 360,00; f) R$ 70,00.
60. Pedro comprou uma bicicleta no valor de R$ 580,00 com a seguinte condição de pagamento: entrada de 20% e o restante em 4 parcelas iguais.
Com essas informações, elabore duas ou mais questões para um colega resolver. Depois, verifique se as respostas dele estão corretas.
Resposta pessoal.
61. Certa empresa tem 1.200 funcionários, dos quais 55% são mulheres.
a) Quantas mulheres trabalham nessa empresa?
Resposta: 660 mulheres.
b) Qual é a porcentagem de homens que trabalha nessa empresa? Quantos homens trabalham nela?
Respostas: 45%; 540 homens.
c) Escreva as frações decimais que representam as porcentagens de homens e a de mulheres que trabalham nessa empresa.
Resposta: Homens: ; mulheres: .
62. Na tabela está indicada a porcentagem aproximada de energia elétrica consumida por alguns aparelhos, em relação ao valor da fatura, no mês de março na casa de Paula.
|
Aparelho elétrico |
Porcentagem de consumo |
|---|---|
|
Chuveiro elétrico |
30% |
|
Geladeira |
30% |
|
Lâmpadas |
15% |
|
Lavadora |
10% |
|
Outros |
15% |
Fonte de pesquisa: Anotações de Paula.
Sabendo que o valor da fatura desse mês foi R$ 200,00, calcule quantos reais, aproximadamente, foram gastos com:
a) chuveiro elétrico;
b) geladeira;
c) lâmpadas;
d) lavadora;
e) outros.
Respostas: a) R$ 60,00; b) R$ 60,00; c) R$ 30,00; d) R$ 20,00; e) R$ 30,00.
Página 123
Adição e subtração de frações
Frações com denominadores iguais
Gilberto fez uma viagem de carro com sua família. Ele partiu de Caxias do Sul (RS) em direção a Florianópolis (SC), parando duas vezes. Ao percorrer do trajeto, parou para abastecer. Depois, percorreu mais do trajeto e parou para almoçar.
Que fração representa o trajeto percorrido até a parada para o almoço?
Podemos responder a esta questão efetuando uma adição de frações.
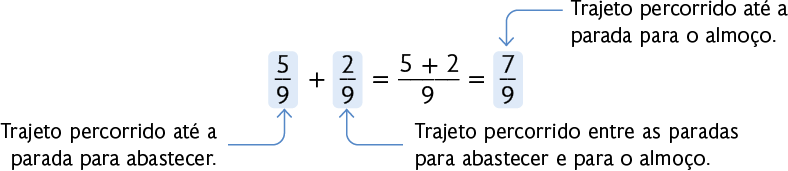
Representando essa situação por meio de uma figura dividida em partes iguais, temos:

Portanto, até a parada para o almoço Gilberto percorreu do trajeto.
Em uma adição de frações com denominadores iguais, adicionamos os numeradores e mantemos o denominador.
Que fração representa o trajeto a ser percorrido após a parada para o almoço?
Para responder a esta questão, escrevemos uma fração que represente o trajeto todo, ou seja, , e subtraímos , referente ao trajeto percorrido até parada para o almoço.

Portanto, após o almoço ainda faltava percorrer do trajeto.
Em uma subtração de frações com denominadores iguais, subtraímos os numeradores e mantemos o denominador.
Página 124
Frações com denominadores diferentes
Valquíria e Gabriela compraram um bolo e o dividiram em 12 partes iguais. Valquíria comeu do bolo e Gabriela, .
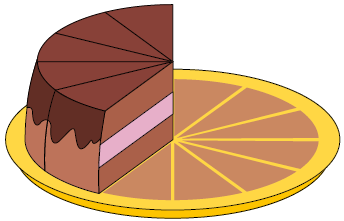
Para calcular a fração referente à parte do bolo que elas comeram juntas, precisamos calcular . Note que essas frações têm denominadores diferentes.
Para adicioná-las, podemos obter frações equivalentes com denominadores iguais.
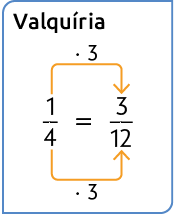
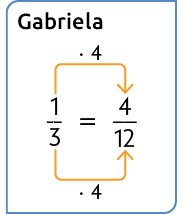
Em seguida, adicionamos as frações equivalentes.
Portanto, Valquíria e Gabriela comeram juntas do bolo.
Após as duas comerem, que fração representa o que sobrou do bolo todo?
Para responder a esta pergunta, precisamos calcular . Como 1 inteiro é equivalente a , temos:
Portanto, sobrou do bolo.
Atenção!
Nessa situação, 1 inteiro representa todo o bolo.
Em uma adição ou subtração de frações com denominadores diferentes, inicialmente fazemos a substituição por frações equivalentes com o mesmo denominador. Em seguida, adicionamos ou subtraímos as frações equivalentes.
Página 125
Instrumentos e softwares
Operações com frações em uma calculadora científica
As calculadoras científicas têm teclas que facilitam a obtenção de certos resultados. Entre essas teclas, algumas possibilitam efetuar operações com frações.
Verifique como calcular o valor de em uma calculadora científica.

1º passo
Para registrar a fração , digite as teclas
.

2º passo
Para adicionar a fração registrada no passo anterior e a fração , digite as teclas
.
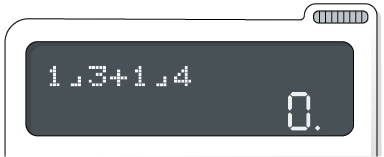
3º passo
Por fim, digite a tecla para obter o resultado.
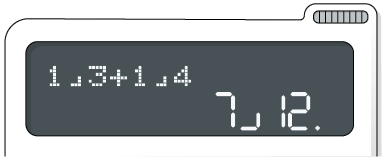
Em alguns casos, visualizamos no visor da calculadora o resultado de uma operação com frações em números na forma mista. Verifique, por exemplo, o cálculo de .
Seguindo os mesmos procedimentos apresentados anteriormente, obtemos o número na forma mista .
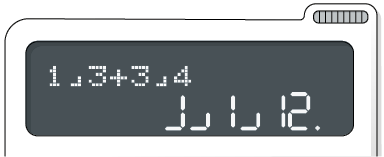
Para efetuar uma subtração, usamos os mesmos procedimentos
apresentados, porém digitamos a tecla em vez da
.
Página 126
Atividades
Faça as atividades no caderno.
63. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ou 1; d) ; e) ; f) .
64. Rafael está assentando azulejos na parede de uma cozinha.
Na parte da manhã, ele concluiu da parede.
Na parte da tarde, ele concluiu da parede.
a) Que fração da parede Rafael azulejou nesse dia?
b) Que fração da parede ainda falta azulejar?
Respostas: a) ; b)
65. Copie as frações no caderno e substitua cada ▲ pelo número que falta.
a)
b)
c)
d)
e)
f)
Sugestão de respostas: a) ; b) ; c) ; d) ; e) ; f) .
66. Em seu caderno, escreva duas frações cuja:
a) soma seja igual a .
b) diferença seja igual a .
c) soma esteja entre 0 e .
d) diferença seja maior do que .
Sugestão de respostas: a) ; . b) ; . c) ; . d) ; .
67. Os recipientes a seguir são iguais e as marcações indicadas são igualmente espaçadas, porém cada um deles está com uma quantidade diferente de líquido.




a) Que fração representa a quantidade de líquido de cada recipiente?
Resposta: A: ; B: ; C: ; D: .
b) Em cada recipiente, qual fração representa a quantidade de líquido que falta para encher?
Resposta: A: ; B: ; C: ; D: .
68. Leia o texto a seguir.
Um terreno terá de sua medida de área ocupada por um jardim, , por uma praça e o restante, por um estacionamento.
De acordo com o texto elabore questões envolvendo adição ou subtração de frações para um colega resolver. Em seguida, verifique se ele resolveu corretamente.
Resposta pessoal.
Página 127
69. Efetue os cálculos no caderno simplificando o resultado quando possível.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
70. Efetue
as operações em uma calculadora. Depois, desenhe em seu caderno uma reta
numérica, organizando nela os resultados obtidos.
a)
b)
c)
d)
Respostas nas orientações ao professor.
71. O tanque de combustível de um veículo flex estava vazio quando foi abastecido. Da capacidade total, foi abastecido com etanol e , com gasolina.
a) Considerando a capacidade total do tanque, que fração representa a parte abastecida?
b) Que fração da medida de capacidade total do tanque faltou abastecer?
Respostas: a) ; b) .
72. Joana faz salgados para vender. Ela recebeu uma encomenda de 450 salgados, dos quais são quibes, são coxinhas e o restante são empadas.
a) Sabendo que ela já fez os quibes e as coxinhas, que fração representa a parte da encomenda que já está pronta?
b) Que fração da encomenda representa a quantidade de empadas?
c) Essa encomenda deve ter quantas empadas?
Respostas: a) ; b) ; c) 200 empadas.
73. Três amigos, Júlio, Mateus e Ricardo, compraram uma pizza de 12 pedaços.
- Júlio comeu dela.
- Mateus comeu dela.
- Ricardo, dela.
Que fração representa os pedaços que sobraram da pizza?
Resposta: .
74. Em um
aquário despejaram certa quantidade de água, equivalente a de sua medida de
capacidade. Em seguida, desse mesmo aquário,
retirou-se o equivalente a de sua medida de capacidade. Que fração da
medida de capacidade do recipiente encontra-se:
a) com água?
b) sem água?
Respostas: a) ; b) .
75. Para cada situação, elabore algumas questões envolvendo adição ou subtração de frações para um colega resolver. Em seguida, verifique se ele resolveu corretamente.
Há 420 lugares em uma sala de cinema. Certo dia, todos os assentos foram ocupados em uma das sessões. Dos ingressos vendidos, eram inteiros e eram meias-entradas.
Na turma de Gustavo há 28 estudantes. Para participar de uma gincana eles devem eleger, por meio de uma votação, o presidente e o vice-presidente, entre os candidatos A, B e C. Entre os estudantes, votaram no candidato A e , no candidato B.
Resposta pessoal.
Página 128
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. O mosaico a seguir é composto de triângulos iguais.

Que fração desse mosaico corresponde às partes pintadas de:
a) roxo?
b) verde?
c) amarelo?
Respostas: a) ou ; b) ou ; c) ou .
2. Dos 32 estudantes de uma turma de 6º ano, 28 jogaram futebol na aula de Educação Física. Que fração representa a quantidade desses estudantes em relação à quantidade total da turma?
Resposta: .
3. O veículo de Paulo iniciou uma viagem com o tanque cheio e consumiu do combustível em todo o trajeto. Sabendo que a medida de capacidade desse tanque é , calcule quantos litros o veículo consumiu nessa viagem.
Resposta: .
4. Quantos quilogramas há em:
a) de ?
b) de ?
c) de ?
d) de ?
Professor, professora: Lembre os estudantes de que é a abreviatura de tonelada e de que .
Respostas: a) ; b) ; c) ; d) .
5. Em uma folha de papel avulsa, copie as igualdades substituindo cada ▲ pelo número adequado.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
6. Para ser aprovado na 1ª fase de um concurso, o candidato deve acertar das questões de uma prova. Paulo acertou delas e Laís, .
a) Quem acertou mais questões?
Resposta: Laís.
b) Paulo foi aprovado na 1ª fase do concurso? Justifique sua resposta.
Resposta: Não, pois .
c) Laís foi aprovada no concurso? Justifique sua resposta.
Resposta: Sim, pois .
d) Sabendo que a prova tinha 90 questões, quantas questões a mais Paulo deveria acertar para ser aprovado na 1ª fase do concurso?
Resposta: 4 questões.
7. José, Ricardo e Renata colecionam selos.
- Renata tem 500 selos.
- José tem 30% da quantidade de selos de Ricardo.
- Ricardo tem 60% da quantidade de selos de Renata.
Quantos selos cada um tem?
Resposta: Renata: 500 selos; Ricardo: 300 selos; José: 90 selos.
8. Em uma folha de papel avulsa, efetue os cálculos escrevendo os resultados com uma fração irredutível e com um número na forma mista.
a)
b)
c)
d)
e)
f)
g)
Respostas: a) ; . b) ; . c) ; . d) ; . e) ; . f) ; . g) ; .