Página 129
UNIDADE
6
Números decimais

Agora vamos estudar...
- os décimos, centésimos e milésimos;
- as transformações de números decimais em números fracionários;
- as transformações de números fracionários em números decimais;
- os números decimais na reta numérica;
- a comparação de números decimais.
Página 130
Décimo, centésimo e milésimo
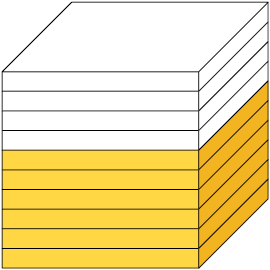
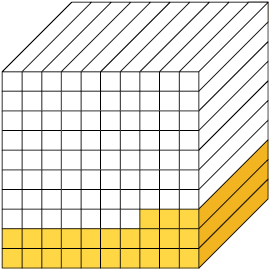
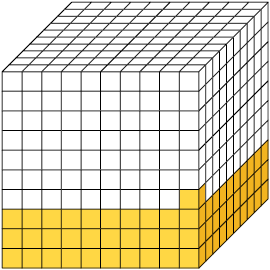
Considere o cubo como unidade. Cada parte obtida ao dividi-lo em 10, 100 ou 1.000 partes iguais corresponde, respectivamente, às frações decimais (um décimo), (um centésimo) e (um milésimo).
Todas as frações decimais podem ser representadas por um número na forma decimal ou, simplesmente, número decimal.
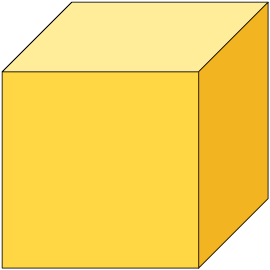
Unidade dividida em 10 partes iguais.
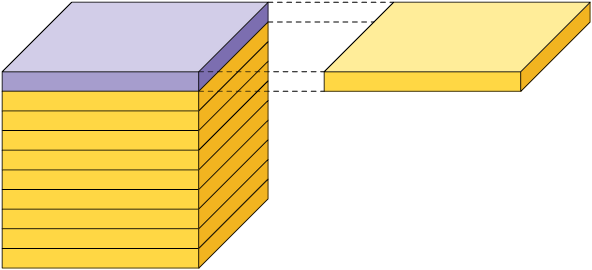
Unidade dividida em 100 partes iguais.
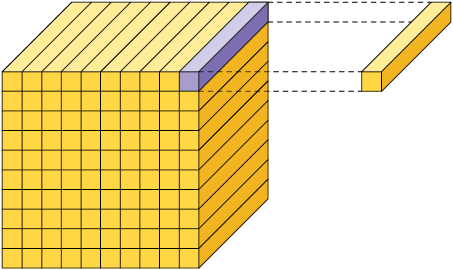
Unidade dividida em 1.000 partes iguais.
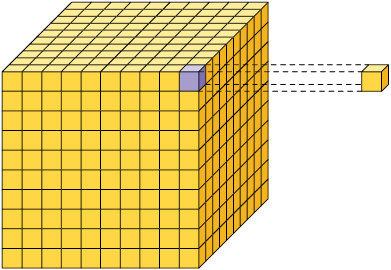
Página 131
Relação entre números decimais e frações decimais
Utilizando os conhecimentos apresentados no tópico anterior, podemos representar frações decimais na forma de números decimais. Vamos escrever as frações decimais , e na forma de números decimais.

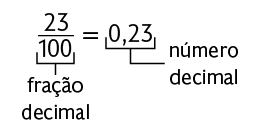
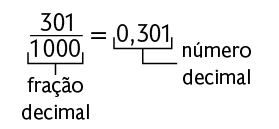
Uma estratégia prática para transformar frações decimais em números decimais é escrever o numerador da fração e usar vírgula para separar a parte inteira da parte decimal, de modo que a quantidade de algarismos da parte decimal seja igual à quantidade de zeros do denominador da fração. Considere alguns exemplos.
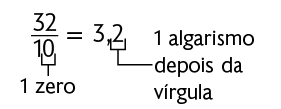
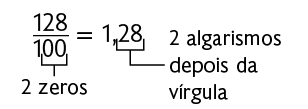
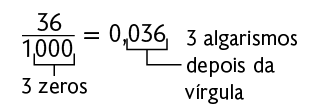
A seguir, verifique como é possível representar o número decimal 2,3 (lê-se 2 inteiros e 3 décimos) usando figuras. Nesse caso, vamos construir inicialmente 3 figuras com as mesmas dimensões. Cada uma delas corresponde a um inteiro, sendo uma delas dividida em 10 partes iguais. Em seguida, pintamos duas de verde e uma delas pintamos de verde apenas 3 partes.

Também podemos representar o número 2,3 pela fração decimal ou pelo número na forma mista .
Questão 1. Em seu caderno, escreva as frações decimais apresentadas a seguir na forma de número decimal.
a)
b)
c)
d)
e)
Respostas: a) 9,5; b) 4,23; c) 4,738; d) 0,75; e) 13,1.
Questão 2. Em seu caderno, represente o número 3,6 utilizando figuras. Depois, escreva a fração decimal e o número na forma mista correspondente a esse número.
Resposta nas orientações ao professor.
Versão adaptada acessível
Questão 2. Descreva a um colega como você representaria o número 3,6 com figuras. Depois, escreva a fração decimal e o número na forma mista correspondente a esse número.
Resposta: inicialmente, represento três figuras com as mesmas dimensões (cada uma delas corresponde a um inteiro) e pinto elas completamente. Em seguida, represento uma quarta figura, com a mesma dimensão das figuras anteriores, e a divido em dez partes iguais. Por fim, pinto seis dessas partes; Fração decimal: ; número na forma mista: .
Página 132
Números decimais no quadro de ordens
Podemos representar números decimais em um quadro de ordens. Verifique, por exemplo, como representamos nesse quadro os números 8,9 (oito inteiros e nove décimos); 4,68 (quatro inteiros e sessenta e oito centésimos); 17,851 (dezessete inteiros e oitocentos e cinquenta e um milésimos).
|
Parte inteira |
Parte decimal |
||||
|---|---|---|---|---|---|
|
D Dezena |
U Unidade |
, |
d Décimo |
c Centésimo |
m Milésimo |
|
8 |
, |
9 |
|||
|
4 |
, |
6 |
8 |
||
|
1 |
7 |
, |
8 |
5 |
1 |
Atenção!
No número 6,305, por exemplo, o algarismo:
- 6 tem valor posicional 6;
- 3 tem valor posicional 0,3;
- 0 tem valor posicional 0;
- 5 tem valor posicional 0,005.
A seguir, escrevemos uma possível decomposição dos números representados no quadro de ordens.
Questão 3. Qual é o valor posicional do
algarismo 8 em cada um dos
números representados no quadro de ordens?
Resposta: 8,9: o algarismo 8 tem valor posicional 8; 4,68: o algarismo 8 tem valor posicional 0,08; 17,851: o algarismo 8 tem valor posicional 0,8.
Questão 4. Decomponha em seu caderno os números apresentados a seguir.
a) 72,08
Sugestão de resposta: .
b) 5,115
Sugestão de resposta:
Transformação de números decimais em números fracionários
Agora, aprenderemos como transformar números decimais em números fracionários. Considere alguns exemplos.
Atenção!
Sempre que possível, simplifique as frações até sua forma irredutível.
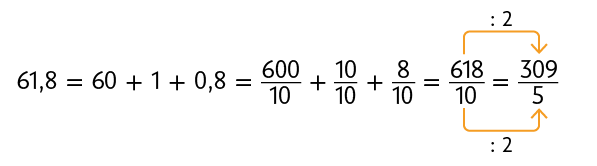
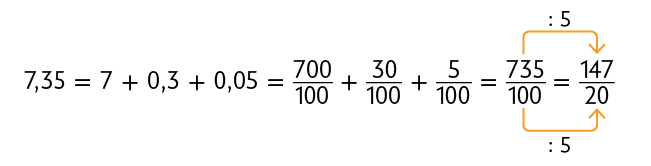
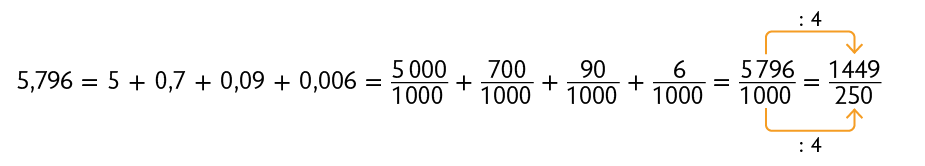
Página 133
Transformação de números fracionários em números decimais
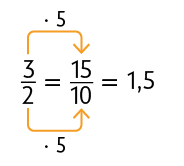
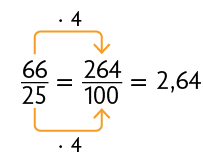
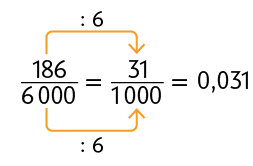
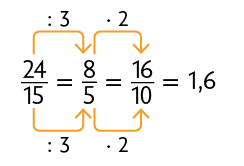
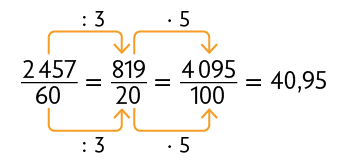
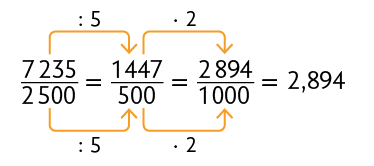
Vimos anteriormente que podemos transformar frações decimais em números decimais relacionando a quantidade de zeros do denominador com a quantidade de algarismos depois da vírgula. Agora, vamos analisar situações em que o denominador da fração, embora não seja 10, 100 ou 1.000, é múltiplo ou divisor desses números. Nessa situação, usamos frações equivalentes. Considere alguns exemplos.
Atividades
Faça as atividades no caderno.
1. Em cada item, os cubos estão divididos em partes iguais. Represente no caderno as partes amarelas da figura com uma fração decimal e com um número decimal.
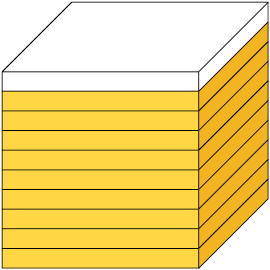
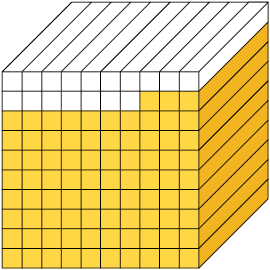
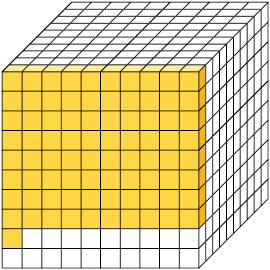
Respostas: A. ; 0,9. B. ; 0,83. C. ; 0,081.
2. Copie o quadro em seu caderno. Em seguida, complete-o com a fração decimal ou o número decimal que falta.
|
Fração decimal |
Número decimal |
|---|---|
|
58,221 |
|
|
|
|
|
1,008 |
Resposta na seção Respostas e na seção Resoluções.
Página 134
3. É importante ingerir água no decorrer do dia, seja ela obtida diretamente da ingestão de líquidos, seja pela ingestão de alimentos ricos em água, como frutas e verduras. A seguir está indicada a quantidade aproximada de água que algumas frutas têm em relação à medida de suas massas.
Imagens não proporcionais entre si.




No caderno, escreva as frações na forma de número decimal. Depois, escreva esses números por extenso.
Resposta: Morango: 0,90, noventa centésimos; Pera: 0,85, oitenta e cinco centésimos; Banana: 0,72, setenta e dois centésimos; Melancia: 0,94, noventa e quatro centésimos.
4. A capacidade de cada recipiente representado a seguir mede .


Atenção!
As marcações indicam a divisão de cada recipiente em partes iguais.
Escreva no caderno a quantidade de água de cada recipiente, em litro, com uma fração decimal e com um número decimal.
Respostas: A. , ; B. , .
5. Considerando cada retângulo a seguir como 1 unidade, escreva no caderno a fração e o número misto que representa as partes em verde. Depois, escreva o número decimal correspondente a essa fração.

Resposta: ; 1,75.
6. A régua
representada a seguir tem divisões em centímetros e milímetros. Cada centímetro
está dividido em 10 partes iguais, que correspondem a . Então cada
uma dessas partes corresponde a .
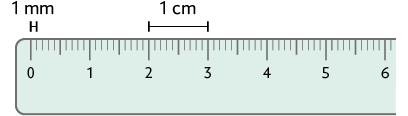
Como , temos:
Verifique o segmento de reta que Mariana traçou utilizando uma régua.
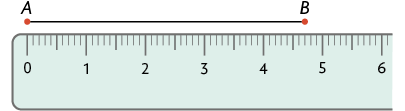
O comprimento desse segmento de reta mede . Podemos também representar essa medida da seguinte maneira:
Utilizando uma régua, determine a medida do comprimento de cada segmento de reta a seguir, em centímetros, e escreva-a no caderno.




Respostas: CD: ; EF: ; GH: ; IJ: .
Página 135
7. A medida de temperatura normal do corpo humano varia entre e . Raul mediu sua temperatura com o termômetro a seguir e confirmou que está com febre, ou seja, a medida da sua temperatura está maior do que a normal.
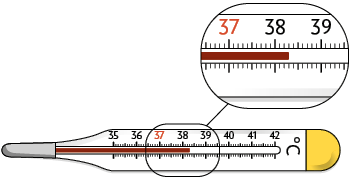
a) Qual medida de temperatura o termômetro está marcando?
Resposta: .
b) Decomponha o número decimal que expressa a medida que você escreveu no item a.
Sugestão de resposta: .
8. Na imagem a seguir está representada parte de uma fita métrica de .
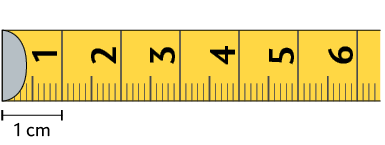
Nela, o metro está dividido em 100 partes iguais. Cada uma dessas partes corresponde a , então:
Copie no caderno os itens a seguir substituindo cada pelo número adequado.
a)
Resposta:
b)
Resposta: .
c)
Resposta: .
9. A tamburutaca é um animal marinho que consegue golpear suas presas em aproximadamente 3 milésimos de segundo.

Atenção!
Ao dividirmos um segundo em 1.000 partes iguais, cada uma delas corresponde a 1 milésimo de segundo (ms), ou seja:
.
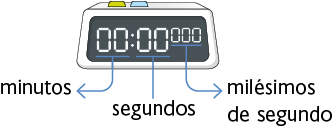
Determine qual dos cronômetros representados a seguir está indicando corretamente a medida do tempo do golpe da tamburutaca.





Resposta: Alternativa E.
Atenção!
Nos cronômetros apresentados, a indicação da medida do tempo decorrido está organizada da seguinte forma.
Página 136
10. A unidade monetária no Brasil é o Real. Um real equivale a 100 centavos, logo 1 centavo equivale a 1 centésimo de real.

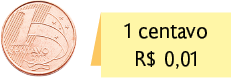
Atenção!
1 centavo é igual a de real ou 0,01 de 1 real.
Escreva no caderno a fração decimal e o número decimal que as moedas a seguir representam em relação a R$ 1,00.




Respostas: A. e 0,05; B. e 0,10; C. e 0,25; D. e 0,50.
11. Construa no caderno um quadro de ordens e escreva nele os números indicados no visor de cada balança representada a seguir. Depois escreva esses números por extenso.




Respostas nas orientações ao professor.
12. Em cada item, transforme o número decimal em uma fração. Por fim, escreva a fração em sua forma irredutível.
a) 2,8
b) 10,15
c) 7,109
d) 1,205
e) 25,1
f) 3,82
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
13. Estudamos anteriormente uma possível decomposição do número 17,851. Agora, considere outra maneira de decompor esse número.
Usando esse procedimento, decomponha os números apresentados de duas maneiras diferentes.
a) 18,9
b) 5,47
c) 93,858
d) 16,905
Sugestão de respostas: a) , ; b) , ; c) , ; d) ; .
14. Efetue os cálculos necessários e componha os números.
a)
b)
c)
d)
Respostas: a) 36,197; b) 64,802; c) 79,067; d) 1,514.
Página 137
15. Em cada item, transforme a fração em um número decimal. Depois, escreva como se lê esse número.
a)
Respostas: 0,8; oito décimos.
b)
Respostas: 2,15; dois inteiros e quinze centésimos.
c)
Respostas: 6,004; seis inteiros e 4 milésimos.
d)
Respostas: 3,95; três inteiros e noventa e cinco centésimos.
e)
Respostas: 1,4; um inteiro e 4 décimos.
f)
Respostas: 5,66; cinco inteiros e sessenta e seis centésimos.
16. O
dinheiro que Josemar economizou para comprar uma guitarra está representado a
seguir.
Imagens não proporcionais entre si.

Usando uma calculadora, determine o valor que Josemar economizou.
Resposta: R$ 788,80.
17. Com as cédulas e moedas apresentadas a seguir, elabore um problema envolvendo números decimais e dê a um colega para resolver. Por fim, verifique se a resposta dele está correta.
Imagens não proporcionais entre si.

Resposta pessoal.
Representando números decimais na reta numérica
Neste tópico, vamos estudar os números decimais na reta numérica. Inicialmente, representaremos o número 2,4 na reta. Para isso, acompanhe as explicações do professor Pedro.

Página 138


Agora, vamos representar o número 2,75 na reta numérica. Nesse caso, podemos usar a decomposição de números para facilitar a representação. O número 2,75 é maior do que 2 e menor do que 3 e, apesar de sua parte decimal estar na ordem dos centésimos, não é necessário dividir o intervalo em 100 partes iguais.
Inicialmente, realizamos a decomposição do número 2,75 (). Em seguida, transformamos 0,75 em uma fração e, por fim, obtemos sua forma irredutível.
Sendo assim, 2,75 é igual a 2 inteiros mais . Logo, podemos dividir o intervalo entre 2 e 3 em 4 partes iguais. Partindo do 2, contamos 3 dessas partes, da esquerda para a direita, e marcamos o número 2,75.
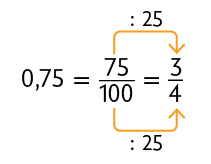

Atenção!
Nesse caso, cada parte equivale a ou 0,25.
Página 139
Verifique a seguir alguns números decimais representados na reta numérica.
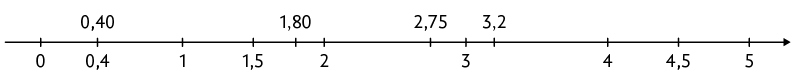
Os números que ocupam a mesma posição na reta numérica são equivalentes. Por exemplo, ao analisar essa reta, concluímos que 0,4 e 0,40 ocupam a mesma posição, logo .
Atividades
Faça as atividades no caderno.
18. Na reta numérica, quanto mais à direita um número estiver, maior ele será. Sabendo disso, analise a reta numérica a seguir e escreva no caderno qual termo substitui corretamente o em cada sentença: maior ou menor.
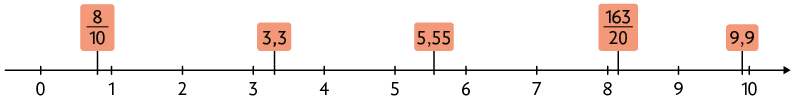
a) O número 3,3 é do que 3 e do que 4.
b) 5,55 é do que 4 e do que 5.
c) A fração é do que 1 e do que 2.
d) é do que 8 e do que 9.
Respostas: a) Maior, menor; b) Maior, maior; c) Menor, menor; d) Maior, menor.
19. Relacione os números apresentados a seguir com as letras indicadas na reta numérica.
-
2,50
-
1,8
-
3,7
-
-
1,375
-
4,75

Resposta: A: ; B: 1,8; C: ; D: ; E: ; F: .
20. O
intervalo apresentado em cada uma das retas numéricas está dividido em partes
iguais. Identifique o número que está na posição incorreta e, em seu caderno,
reconstrua a reta com os números corretos.
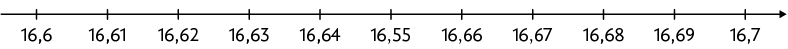
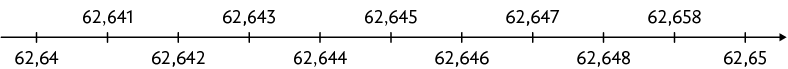
Respostas nas orientações ao professor.
Página 140
Comparação de números decimais
Vimos anteriormente que 0,4 é igual a 0,40. De fato, quando acrescentamos ou retiramos zeros à direita da parte decimal, o valor não se altera, logo .
Verifique como podemos comparar cubos de dimensão de mesma medida que evidenciem essa igualdade. Os cubos a seguir estão divididos em 10, 100 e 1.000 partes iguais.
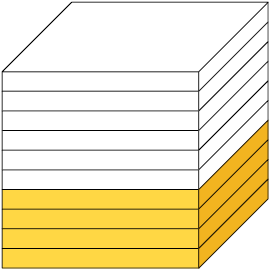
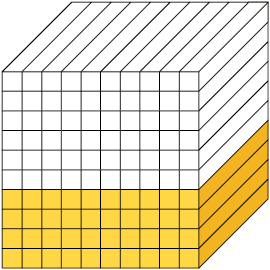
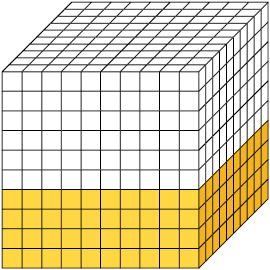
Note que as partes pintadas de amarelo em cada cubo representam a mesma parte do todo.
Agora, considere alguns exemplos de como podemos comparar dois números decimais.
- Inicialmente,
comparamos a parte inteira.
8,15 e 5,945
Como a parte inteira de 8,15 é maior do que a parte inteira de 5,945, segue que . Portanto, .
- Se as partes
inteiras forem iguais, comparamos os décimos.
2,45 e 2,61
Como as partes inteiras são iguais, comparamos os décimos: . Portanto, .
- Se a parte inteira e
os décimos forem iguais, comparamos os centésimos.
3,86 e 3,83
Como a parte inteira e os décimos são iguais, comparamos os centésimos: . Portanto, .
- Se a parte inteira,
os décimos e os centésimos forem iguais, comparamos os milésimos.
7,426 e 7,421
Como a parte inteira, os décimos e os centésimos são iguais, comparamos os milésimos: . Portanto, .
Atenção!
Lembre-se de que, na reta numérica, quanto mais à direita o número estiver, maior ele será.
Se a quantidade de casas depois da vírgula não for igual, podemos acrescentar ou retirar zeros à direita para igualar a quantidade de algarismos nas casas decimais. Vamos comparar 4,9 e 4,952, por exemplo. Nesse caso, temos que e, dessa forma, podemos comparar 4,900 e 4,952. Portanto, .
Página 141
Atividades
Faça as atividades no caderno.
21. Para cada quadro, copie em seu caderno os pares de números decimais que têm o mesmo valor.
- 7,00
- 7
- 0,07
- 0,007
- 0,700
- 7,777
- 0,1
- 0,01
- 0,001
- 0,010
- 1,00
- 10,000
- 503
- 5,30
- 5,003
- 5,030
- 5,03
- 53,03
- 0,310
- 3,010
- 3,100
- 31,0
- 3,001
- 3,10
Respostas: a) 7,00 e 7; b) 0,01 e 0,010; c) 5,03 e 5,030; d) 3,100 e 3,10.
22. Ana vai pintar sua casa e, para isso, precisa comprar 1 lata de tinta e um rolo para pintura. Ela fez uma pesquisa de preço dos mesmos produtos em 3 lojas diferentes. Verifique os preços que ela encontrou.
|
Loja |
Lata de tinta |
Rolo para pintura |
|---|---|---|
|
A |
339,90 |
12,94 |
|
B |
340,00 |
15,50 |
|
C |
335,99 |
18,81 |
Fonte de pesquisa: registros de Ana.
a) Em qual das lojas o preço da lata de tinta é maior? E em qual o preço é menor?
b) Em qual das lojas o rolo para pintura tem o maior preço? E em qual tem o menor preço?
c) Ana vai comprar os produtos nas lojas com o menor preço. Em quais lojas ela vai comprar a lata de tinta e o rolo para pintura?
Respostas: a) Loja B; Loja C. b) Loja C; Loja A. c) A lata de tinta na loja C e o rolo para pintura na loja A.
23. As medidas de altura, em metro, de algumas jogadoras de um time de basquetebol estão indicadas a seguir.
-
Paula
-
Maria
-
Mariana
-
Adriana
-
Júlia
-
Paola
-
Giovana
-
Nicole
-
Manuela
-
Ana Paula
-
Antônia
-
Patrícia
a) Qual é a jogadora mais alta do time? Qual é a mais baixa?
Respostas: Manuela; Nicole.
b) Em seu caderno, escreva as medidas de altura das jogadoras em ordem crescente colocando o símbolo entre elas.
Resposta: .
Página 142
24. Nas balanças estão indicadas as medidas de massa, em quilogramas, das batatas compradas por Marina, Renata e Paulo.



Quem comprou mais quilogramas de batatas? Quem comprou menos?
Respostas: Renata; Marina.
25. Determine, em cada item, qual símbolo substitui o ⬛ corretamente: (menor), (maior) ou (igual).
a) 0,23 ⬛ 0,32
b) 0,8 ⬛ 0,80
c) 2,00 ⬛ 20,0
d) 0,8 ⬛ 0,78
e) 14,500 ⬛ 14,5
f) 9,001 ⬛ 9,0001
g) 80,2 ⬛ 80,199
h) 5 ⬛ 0,500
i) 3,06 ⬛ 3,060
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) .
26. Na área da saúde são utilizados alguns índices internacionais para avaliar a obesidade de uma pessoa. Dois índices muito comuns são: o Índice de Massa Corporal (IMC), que relaciona a medida da massa em quilogramas e a medida da altura em metro da pessoa; e o Índice de Adiposidade Corporal (IAC), que relaciona medidas do quadril e da altura, ambas em metro.
No quadro estão indicadas as categorias de avaliação consideradas pelo IMC. Dependendo da categoria em que o paciente se encontra, o profissional da saúde pode solicitar outros testes e exames.
|
Categoria |
Valor do IMC |
|---|---|
|
Abaixo do peso |
Abaixo de 18,5 |
|
Peso normal |
de 18,5 a 24,9 |
|
Sobrepeso |
de 25 a 29,9 |
|
Obesidade grau I |
de 30 a 34,9 |
|
Obesidade grau II |
de 35 a 39,9 |
|
Obesidade grau III |
acima de 40 |
Para verificar o IMC dos funcionários, uma empresa realizou uma pesquisa, obtendo os resultados a seguir. Conforme o quadro do IMC, determine em qual categoria as respectivas pessoas podem ser classificadas.
a) Maria: 36,3
Resposta: Obesidade grau II.
b) Laís: 24,4
Resposta: Peso normal.
c) Raul: 38,9
Resposta: Obesidade grau II.
d) Felipe: 42,5
Resposta: Obesidade grau III.
e) Thaís: 27,5
Resposta: Sobrepeso.
f) João: 43,2
Resposta: Obesidade grau III.
Página 143
27. Na reta numérica a seguir, cada letra representa um número decimal em sua posição correta.
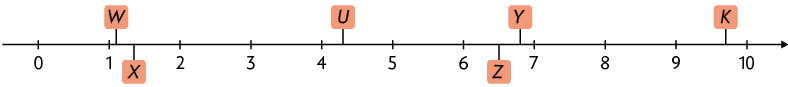
A seguir, identifique as afirmações verdadeiras.
a) W é maior do que X.
b) U é maior do que 4 e menor do que 5.
c) Y é maior do que K.
d) X é maior do que Z.
e) Z é menor do que Y.
f) K é menor do que 9.
Resposta: Alternativas b e e.
28. Considere os algarismos e a vírgula a seguir.
-
5
-
1
-
,
-
0
-
8
Utilizando uma única vez cada algarismo e a vírgula, escreva no caderno:
a) o menor número possível.
Resposta: 0,158.
b) o número entre 1,55 e 1,8.
Resposta: 1,580.
c) todos os números possíveis em que o 5 tenha valor posicional 0,005, em ordem crescente.
Resposta: .
29. O fluxograma a seguir pode ser usado para comparar dois números decimais até a ordem dos milésimos. Relacione o fluxograma e as informações indicadas nas fichas, escrevendo a letra e o número correspondentes.
Fluxograma
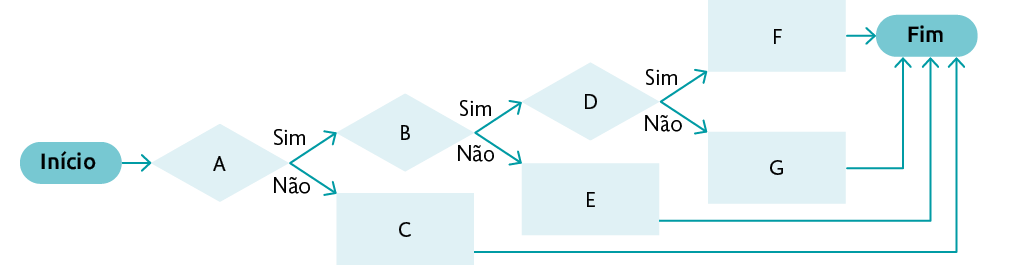
Informações
1. Os centésimos são iguais?
2. Os décimos são iguais?
3. As partes inteiras são iguais?
4. O número com o maior algarismo na casa dos milésimos é o maior.
5. O número com o maior algarismo na casa dos centésimos é o maior.
6. O número com o maior algarismo na casa dos décimos é o maior.
7. O número com a maior parte inteira é o maior.
Agora, escreva alguns pares de números decimais diferentes até a ordem dos milésimos e dê a um colega para compará-los usando esse fluxograma. Em seguida, verifique se as comparações estão corretas.
Resposta: A-3, B-2, C-7, D-1, E-6, F-4, G-5; Resposta pessoal.
Página 144
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Os termômetros a seguir apresentam as medidas de temperaturas máximas, em graus Celsius (), registradas em certa cidade em 3 dias.
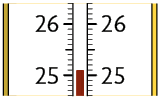
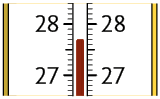
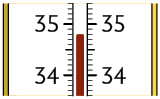
Em uma folha de papel avulsa, escreva em número decimal a medida da temperatura registrada a cada dia.
Respostas: 1º dia: ; 2º dia: ; 3º dia: .
2. Sabendo que , determine nos itens o número que substitui cada corretamente.
a)
b)
c)
d)
e)
Respostas: a) 0,007; b) , 0,035; c) 280, 0,28; d) 1.370, ; e) , 2,355.
3. Escreva a fração decimal e o número decimal correspondentes a cada fração a seguir.
a)
b)
c)
d)
e)
f)
Respostas: a) , 0,6; b) , 0,88; c) , 0,072; d) , 2,5; e) , 0,74; f) , 1,765.
4. Na primeira reta numérica, os intervalos entre os números 7 e 8 estão divididos em 10 partes iguais e na segunda, em 5 partes iguais.
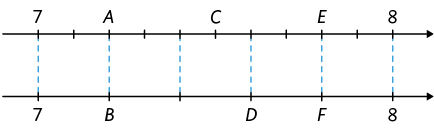
Sabendo que as letras representam números, identifique a afirmação verdadeira.
a)
b)
c)
d)
e)
Resposta: Alternativa a.
5. Jorge poupou R$ 118,75. Analise as quantias em reais que seus 3 amigos pouparam.
Imagens não proporcionais entre si.



Escreva, em ordem decrescente, as quantias em reais que os 3 amigos pouparam, colocando o símbolo entre elas.
Resposta: .