Página 175

UNIDADE

8

Retas e ângulos

Fotografia de um surfista fazendo uma manobra com sua prancha diante de uma onda, no mar.
Atleta de surf, executando um movimento aéreo de 360 ° , manobra em que o surfista efetua uma volta completa em torno de si mesmo.

Agora vamos estudar...

  • retas, semirretas e segmentos de reta;
  • ângulos;
  • medidas de ângulos;
  • como medir ângulos com o transferidor;
  • retas paralelas e retas concorrentes.

Página 176

Retas, semirretas e segmentos de reta

Podemos representar graficamente uma reta que passa pelos pontos A e B .

Ilustração de uma reta r com os pontos A e B em cima dela.

Nomeamos uma reta usando uma letra minúscula do nosso alfabeto ou relacionando dois pontos que pertencem a ela. No exemplo anterior, escrevemos: reta r , reta A B ou, simplesmente, A B ↔ .

Atenção!

Podemos dizer que a reta r passa pelos pontos A e B ou que os pontos A e B pertencem à reta r .

Ao representarmos graficamente uma reta, desenhamos apenas uma parte dela. Contudo, devemos sempre considerar a reta infinitamente prolongada nos dois sentidos, ou seja, ela não tem começo nem fim.

Em relação a uma reta, considera-se também uma semirreta e um segmento de reta.

A parte de uma reta com início em um de seus pontos e sem fim, é chamada semirreta. Esse ponto de início é a origem da semirreta.

Podemos representar graficamente uma semirreta com origem no ponto A e que passa pelo ponto B . Indicamos: semirreta A B ou A B → .

Ilustração de uma semirreta que inicia no ponto A e passa pelo ponto B.

A parte da reta compreendida entre dois de seus pontos, é chamada segmento de reta. Esses pontos são as extremidades do segmento de reta. Assim, um segmento de reta tem começo e fim e seu comprimento pode ser medido.

Podemos representar graficamente um segmento de reta com extremidades nos pontos C e D . Indicamos: segmento de reta C D ou C D ‾ .

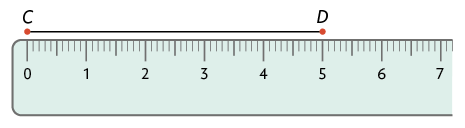
Ilustração de uma régua e, logo acima dela, o ponto C no marco 0 e o ponto D no marco 5, com um segmento de reta unindo esses pontos.

O comprimento desse segmento mede 5   cm .

Desse modo, escrevemos: C D = 5   cm .

Página 177

Atividades

Faça as atividades no caderno.

1. Em seu caderno, responda às questões sobre as retas e os pontos representados a seguir.

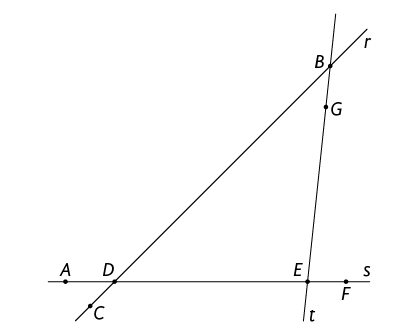
Esquema com retas. Há uma reta s na horizontal e, da esquerda para a direita, os pontos pertencentes a ela: A, D, E, F. No ponto D passa a reta r um pouco na diagonal e, de baixo para cima, há os pontos pertencentes a ela: C, D, B. No ponto B passa a reta t, na vertical e, de cima para baixo há os pontos pertencentes a ela: B, G, E.

a) Qual reta passa pelos pontos A , E e F?

Resposta: Reta s .

b) Qual ponto pertence à reta r e à reta s?

Resposta: Ponto D .

c) Por quais pontos passa a reta r ?

Resposta: Pontos B , C e D .

2. Analise a imagem e classifique cada frase em verdadeira ou falsa. Em seguida, reescreva as frases falsas em seu caderno, tornando-as verdadeiras.

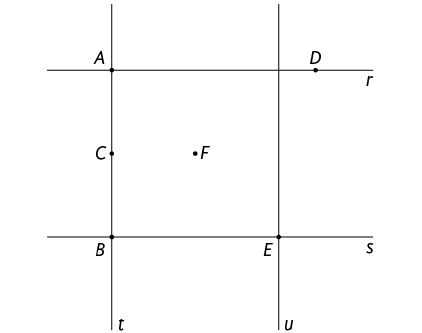
Esquema com as retas r e s, uma abaixo da outra, na horizontal e as retas t e u, lado a lado, na vertical. No cruzamento das retas t e r há o ponto A, no cruzamento das retas t e s há o ponto B e no cruzamento das retas u e s há o ponto E. Há o ponto F entre o cruzamento dessas retas, o ponto C na reta t entre os pontos A e B e o ponto D na reta r a direita, após os cruzamentos com as retas.

a) O ponto A pertence à reta r e à reta t .

Resposta: Verdadeira.

b) As retas r , s e u passam pelo ponto C .

Resposta: Falsa. Uma possível correção é: As retas r, s e u não passam pelo ponto C.

c) As retas s e t passam pelo ponto B .

Resposta: Verdadeira.

d) O ponto C não pertence a nenhuma das retas indicadas.

Resposta: Falsa. Uma possível correção é: O ponto C pertence à reta t .

3. Estime a medida do comprimento de cada segmento de reta a seguir e registre em seu caderno.

Ilustração de 3 segmentos de reta, um abaixo do outro. O primeiro, , indo do ponto A ao B, com 4 centímetros de medida de comprimento; o segundo de C a D com 3,5 centímetros de medida de comprimento e o terceiro de E a F com 6 centímetros de medida de comprimento.

Respostas pessoais.

Orientação para acessibilidade

Professor, professora: para que os estudantes estimem o comprimento dos segmentos na atividade 3, auxilie-os a, inicialmente, construir um segmento com o comprimento medindo 1 cm. Na sequência, auxilie-os na construção dos segmentos AB , CD e EF em uma folha de papel. Ao final de cada construção, solicite a eles que estimem o comprimento do segmento, considerando como referência o segmento cujo comprimento mede 1 cm.

4. Ícone uso de instrumentos Utilizando uma régua, meça o comprimento de cada segmento de reta da atividade anterior e compare com as medidas dos comprimentos que você estimou.

Resposta: A B = 4   cm ; C D = 3 , 5   cm ; E F = 6   cm .

5. O contorno do quadrado representado a seguir é formado por 4 segmentos de reta: A B ‾ , B C ‾ , C D ‾ e A D ‾ .

Ilustração de um quadrado com seus vértices nomeados de A, B, C, D.

Escreva em seu caderno o nome de cada figura geométrica plana representada a seguir. Depois, determine quantos segmentos de reta formam seu contorno e nomeie-os.

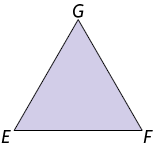
A. Ilustração de uma figura geométrica plana de 3 lados e seus vértices E, F, G.

Respostas: Triângulo; 3 segmentos de reta: E F ‾ , F G ‾ e G E ‾ .

B. Ilustração de uma figura geométrica plana de 5 lados e seus vértices H, I, J, K, L.

Respostas: Pentágono; 5 segmentos de reta: H I ‾ , I J ‾ , J K ‾ , K L ‾ e L H ‾ .

C. Ilustração de uma figura geométrica plana de 6 lados e seus vértices M, N, O, P, Q, R.

Respostas: Hexágono; 6 segmentos de reta: M N ‾ , N O ‾ , O P ‾ , P Q ‾ , Q R ‾ e R M ‾ .

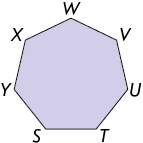
D. Ilustração de uma figura geométrica plana de 7 lados e seus vértices S, T, U, V, W, X, Y.

Respostas: Heptágono; 7 segmentos de reta: S T ‾ , T U ‾ , U V ‾ , V W ‾ , W X ‾ , X Y ‾ e Y S ‾ .

Página 178

Ângulos

Ícone Objeto digital

O professor de Caroline posicionou cinco estudantes no pátio da escola para realizarem uma atividade envolvendo giro. Inicialmente, Caroline estava posicionada de frente para Tatiane.

1º. O professor pediu a Caroline que girasse uma volta completa no sentido anti-horário. Após o giro, Caroline ficou novamente de frente para Tatiane.

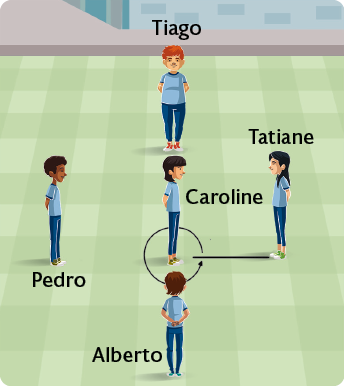
Ilustração de 5 crianças, Pedro, Tiago, Tatiane, Alberto e Caroline. Caroline está no meio, Tiago a sua esquerda, Alberto a sua direita, Pedro atrás dela e Tatiane na sua frente. No chão, em volta de Caroline, há a representação de uma volta completa, no sentido anti-horário.

2º. O professor pediu a Caroline que girasse meia-volta no sentido anti-horário. Após o giro, Caroline ficou de frente para Pedro.

Ilustração de 5 crianças, Pedro, Tiago, Tatiane, Alberto e Caroline. Caroline está no meio, Tatiane atrás dela, Pedro na sua frente, Tiago na sua direita e Alberto na sua esquerda. No chão, há a representação de rotação em sentido anti-horário entre a direção de Caroline em relação a Tatiane e depois em relação a Pedro.

3º. O professor pediu a Caroline que, da posição em que estava, de frente para Pedro, girasse um quarto de volta no sentido anti-horário. Após esse giro, Caroline ficou de frente para Alberto.

Ilustração de 5 crianças, Pedro, Tiago, Tatiane, Alberto e Caroline. Caroline está no meio, Tiago atrás dela, Alberto na sua frente, Pedro na sua direita e Tatiane na sua esquerda. No chão, há a representação de rotação em sentido anti-horário entre a direção de Caroline em relação a Pedro e depois em relação a Alberto.

4º. O professor pediu a Caroline que, da posição em que estava, de frente para Alberto, girasse três quartos de volta no sentido horário. Após esse giro, Caroline ficou de frente para Tatiane.

Ilustração de 5 crianças, Pedro, Tiago, Tatiane, Alberto e Caroline. Caroline está no meio, Tiago a sua esquerda, Alberto a sua direita, Pedro atrás dela e Tatiane na sua frente. No chão, há a representação de rotação em sentido horário entre a direção de Caroline em relação a Alberto e depois em relação a Tatiane.

Atenção!

Quando dizemos sentido horário estamos mencionando o giro no mesmo sentido dos ponteiros de um relógio e sentido anti-horário, o giro contrário aos dos ponteiros de um relógio.

Página 179

Podemos representar os giros citados na situação anterior da seguinte maneira.

Ilustração de um segmento de reta com a representação de um giro completo em torno do seu ponto fixo da extremidade.
Uma volta completa.
Ilustração de dois segmentos de reta, lado a lado, unidos por um ponto em comum, com a representação de meio giro em torno desse ponto.
Meia-volta.
Ilustração de dois segmentos de reta, formados como um vértice de um quadrado, unidos por um ponto em comum, com a representação de um quarto de giro em torno desse ponto.
Um quarto de volta.
Ilustração de dois segmentos de reta, formados como um vértice de um quadrado, unidos por um ponto em comum, com a representação de três quartos de giro na parte externa desse ponto.
Três quartos de volta.

Os giros em torno de um ponto fixo nos dão a ideia de ângulos.

Ângulo é uma figura geométrica formada por duas semirretas de mesma origem.

Na representação, as semirretas O A e O B são os lados do ângulo e o ponto O (origem das semirretas) é o vértice. Nomearemos esse ângulo por O ˆ , A O ˆ B ou B O ˆ A .

Ilustração de duas semirretas, denominados de 'lado', de mesma origem O, denominado vértice. Uma semirreta possui o ponto A e outra possui o ponto B, há um arco entre elas.

Atividades

Faça as atividades no caderno.

6. No relógio destaca-se o giro de 15 segundos do ponteiro. Portanto, esse ponteiro girou um quarto de volta.

Ilustração de um relógio com o ponteiro das horas apontando para um ponto entre os números 10 e 11, o ponteiro dos minutos apontando para o número 7 e o ponteiro dos segundos apontando para o número 3. Há uma seta representando o giro do ponteiro dos segundos de quando estava apontando para o 12 para a posição atual.

Escreva em seu caderno quanto gira esse ponteiro considerando cada intervalo de tempo a seguir.

a) 30 segundos.

Resposta: Meia-volta.

b) 1 minuto.

Resposta: Uma volta completa.

c) 45 segundos.

Resposta: Três quartos de volta.

d) 1 minuto e 30 segundos.

Resposta: Uma volta e meia.

7. O skate estreou como um esporte olímpico nos Jogos de Tóquio, em 2021. Analise nas imagens os movimentos do skate durante a manobra chamada flip.

Ilustração de um menino em cima de um skate, com todas as rodinhas rentes ao chão.
Momento 1
Ilustração de um menino fazendo manobra com skate. Ele está pulando, enquanto o skate também está no ar, com as rodas viradas para o lado.
Momento 2
Ilustração de um menino fazendo manobra com skate. Ele está pulando, enquanto o skate também está no ar, com as rodas viradas para cima.
Momento 3
Ilustração de um menino em cima de um skate, com todas as rodinhas rentes ao chão.
Momento 4

Nessa manobra, qual foi o giro do skate do momento 1 para o momento 4?

Resposta: Giro de uma volta completa.

Página 180

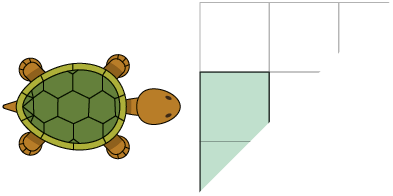
8. Para levar a tartaruga até o morango, Armando executou os seguintes comandos.

Comandos

1º. Siga um quadradinho em frente. Chegou no morango? Se sim, o objetivo foi concluído. Caso contrário, vá para o 2º comando.

2º. No próximo quadradinho há obstáculo? Se sim, vá para o 3º comando. Caso contrário, retorne ao 1º comando.

3º. O obstáculo é uma pedra? Se sim, gire um quarto de volta para a direita e retorne ao 1º comando. Caso contrário, gire um quarto de volta para a esquerda e retorne ao 1º comando.

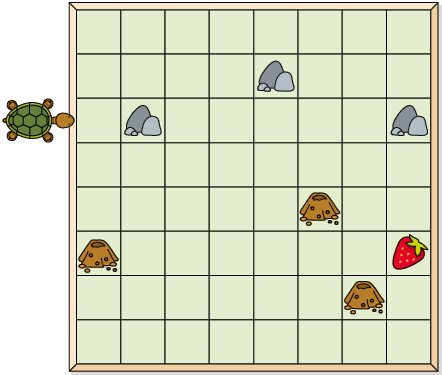
Ilustração, vista de cima, de uma tartaruga diante de um tabuleiro com 8 linhas e 8 colunas. A tartaruga está de frente para a terceira linha, do lado esquerdo do tabuleiro. Da esquerda para a direita e de cima para baixo, há pedras no quinto quadradinho da segunda linha, segundo quadradinho da terceira linha, último quadradinho da terceira linha, há formigueiros no sexto quadradinho da quinta linha, no primeiro quadradinho da sexta linha e no sétimo quadradinho da sétima linha. Há um morango no último quadradinho da sexta linha.

a) Ao executar esses comandos, Armando levou a tartaruga até o morango?

Resposta: Sim.

b) Executando os mesmos comandos de Armando, em quais das imagens é possível levar a tartaruga até o morango?

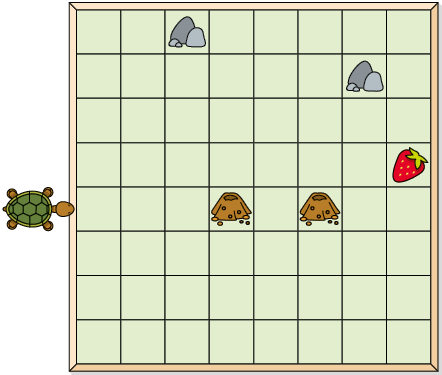
A. Ilustração, vista de cima, de uma tartaruga diante de um tabuleiro com 8 linhas e 8 colunas. A tartaruga está de frente para a quinta linha, do lado esquerdo do tabuleiro. Da esquerda para a direita e de cima para baixo, há pedras no terceiro quadradinho da primeira linha, sétimo quadradinho da segunda linha, há formigueiros no quarto quadradinho da quinta linha, no sexto quadradinho da quinta linha. Há um morango no último quadradinho da quarta linha.
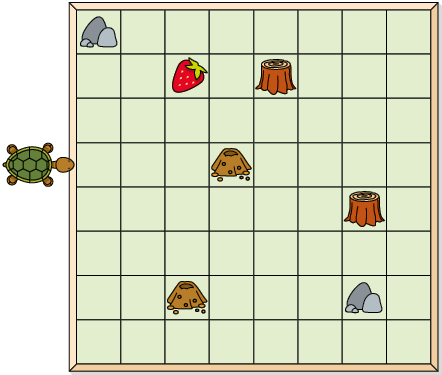
B. Ilustração, vista de cima, de uma tartaruga diante de um tabuleiro com 8 linhas e 8 colunas. A tartaruga está de frente para a quarta linha, do lado esquerdo do tabuleiro. Da esquerda para a direita e de cima para baixo, há pedras no primeiro quadradinho da primeira linha, sétimo quadradinho da sétima linha, há formigueiros no quarto quadradinho da quarta linha, no terceiro quadradinho da sétima linha. Há troncos no quinto quadradinho da segunda linha e no sétimo quadradinho da quinta linha e há um morango no terceiro quadradinho da segunda linha.
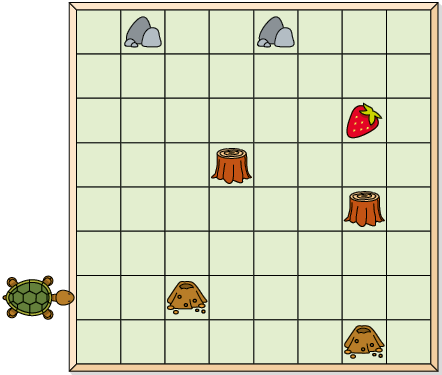
C. Ilustração, vista de cima, de uma tartaruga diante de um tabuleiro com 8 linhas e 8 colunas. A tartaruga está de frente para a sétima linha, do lado esquerdo do tabuleiro. Da esquerda para a direita e de cima para baixo, há pedras no segundo e quinto quadradinhos da primeira linha, há formigueiros no terceiro quadradinho da sétima linha, no sétimo quadradinho da oitava linha. Há troncos no quarto quadradinho da quarta linha e no sétimo quadradinho da quinta linha e há um morango no sétimo quadradinho da terceira linha.
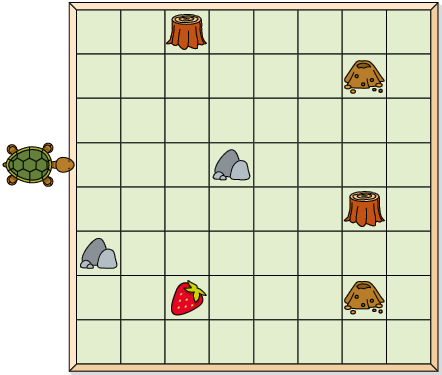
D. Ilustração, vista de cima, de uma tartaruga diante de um tabuleiro com 8 linhas e 8 colunas. A tartaruga está de frente para a quarta linha, do lado esquerdo do tabuleiro. Da esquerda para a direita e de cima para baixo, há pedras no quarto quadradinho da quarta linha, primeiro quadradinho da sexta linha, há formigueiros no sétimo quadradinho da segunda linha, no sétimo quadradinho da sétima linha. Há troncos no terceiro quadradinho da primeira linha e no sétimo quadradinho da quinta linha e há um morango no terceiro quadradinho da sétima linha.

Resposta: A, B e D.

Página 181

Medindo ângulos

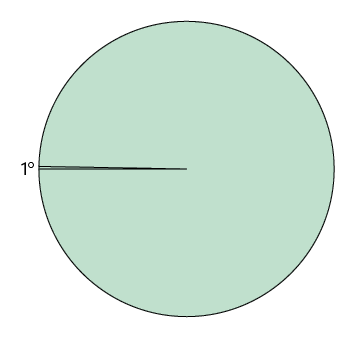
A medida da abertura de um ângulo, ou seja, a medida de um ângulo pode ser expressa na unidade de medida grau. O grau tem origem na divisão de um círculo em 360 partes iguais, sendo cada uma associada a um ângulo de 1 grau, que representamos por 1 ° (lê-se: um grau).

Ilustração de uma circunferência com dois segmentos de reta indo de sua extremidade até seu centro e, entre eles, demarcado o ângulo de 1 grau.
O giro de uma volta completa corresponde a um ângulo de 360 ° .

Um dos instrumentos utilizados para medir ângulos é o transferidor.

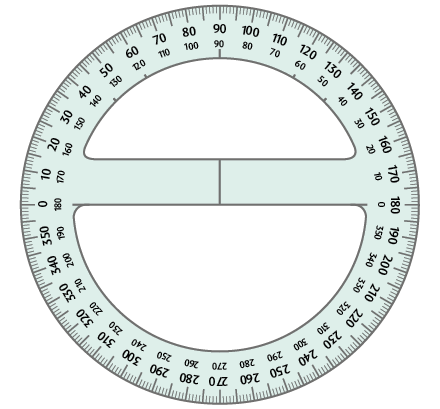
Ilustração de um transferidor circular, de volta inteira, com seus 360 graus demarcados.
Transferidor de volta inteira.
Ilustração de um transferidor de meia-volta, com seus 180 graus demarcados.
Transferidor de meia-volta.

Atenção!

Nesses transferidores, note que há duas graduações, uma no sentido horário e outra no anti-horário.

Para determinar qual medida do ângulo deve ser considerada em cada situação, devemos identificá-la usando um "arco". Verifique dois exemplos.

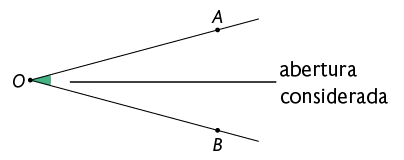
Ilustração de um arco interno entre duas semirretas de mesma origem O, uma possui o ponto A e outra possui o ponto B. Para esse ângulo está indicado que é a abertura considerada.
Ilustração de um arco externo entre duas semirretas de mesma origem O, uma possui o ponto A e outra possui o ponto B. Para esse ângulo está indicado que é a abertura considerada.

Em casos que não tenha indicação de arco, consideramos a menor medida.

Na próxima página estudaremos como medir um ângulo usando o transferidor.

Página 182

Instrumentos e softwares

Medindo ângulos com o transferidor

Medimos ângulos em graus com o transferidor.

1º. Posicione o centro do transferidor no vértice do ângulo, e a linha que indica o zero, isto é, a linha de fé, em um dos lados do ângulo.

2º. Leia a marca numérica do transferidor, indicada pelo outro lado do ângulo.

Nesse caso, o ângulo A O ˆ B mede 45 ° . Indicamos por med ( A O ˆ B ) = 45 ° .

Ilustração de um transferidor de meia-volta. Há a indicação do centro do transferidor, com o ponto O nele, uma semirreta que vai desse ponto e passa pelo ângulo de 0 graus, chegando ao ponto B, chamada de linha de fé. Há outra semirreta que vai do centro do transferidor e passa pelo ponto A. Destaque para a parte que essa semirreta passa pelo ângulo de 45 graus do transferidor e pelo ponto A.
Transferidor posicionado sobre um ângulo, com destaque para o centro do transferidor, a linha de fé e a marca numérica indicando a medida de 45 ° do ângulo.

Ângulos cuja medida seja menor ou igual a 180° podem ser classificados em reto, agudo, obtuso ou raso.

Ângulo reto: ângulo que corresponde a um quarto de volta, ou seja, 90 ° .

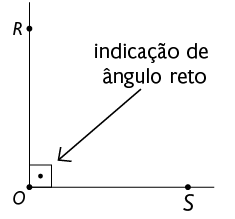
Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto R e outra possui o ponto S. Entre as duas semirretas há um pequeno quadrado com uma bolinha dentro que corresponde a 'indicação de um ângulo reto'.

Ângulo obtuso: ângulo cuja medida é maior do que 90 ° e menor do que 180 ° .

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto C e outra possui o ponto D. O ângulo tem medida maior do que 90 graus e menor do que 180 graus.

Ângulo agudo: ângulo cuja medida é maior do que 0 ° e menor do que 90 ° .

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto A e outra possui o ponto B. O ângulo tem medida maior do que 0 grau e menor do que 90 graus.

Ângulo raso: ângulo que corresponde a meia-volta, ou seja, 180 ° .

Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto E e outra possui o ponto F. O ângulo mede 180 graus.

Página 183

Atividades

Faça as atividades no caderno.

9. Ícone uso de instrumentos Junte-se a um colega e, fazendo estimativas, classifiquem cada ângulo em reto, agudo ou obtuso.

A. Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto A e outra possui o ponto B. O ângulo tem medida maior do que 0 grau e menor do que 90 graus.
B. Ilustração de um ângulo entre duas semirretas de mesma origem O, uma possui o ponto C e outra possui o ponto D. O ângulo tem medida maior do que 90 graus e menor do que 180 graus.

Agora, usando um transferidor, meçam os ângulos e verifiquem se a classificação feita por vocês está correta.

Respostas: A. Agudo; B. Obtuso; Resposta pessoal.

10. Ícone uso de instrumentos Com um transferidor, meça os ângulos destacados nas figuras. Em seguida, classifique-os em agudo, reto ou obtuso.

A. Ilustração de um retângulo com um de seus ângulos internos demarcados, medindo 90 graus.
B. Ilustração de um triângulo com um de seus ângulos internos demarcados, medindo 90 graus.
C. Ilustração de um trapézio retângulo com um de seus ângulos internos demarcados, medindo menos de 90 graus.
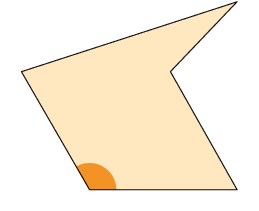
D. Ilustração de um pentágono irregular com um de seus ângulos internos demarcados, medindo mais de 90 graus.

Respostas: A. 90 ° , reto; B. 90 ° , reto; C. 45 ° , agudo; D. 120 ° , obtuso.

11. Dados os pontos A e B, o ângulo sob o qual o observador O vê esses dois pontos é o ângulo A O ˆ B . Esse é o ângulo de visão do observador O relativo aos pontos A e B. Na imagem, o ângulo A O ˆ B é o ângulo de visão do camelo para os pontos A e B.

Ilustração de um camelo e duas pirâmides ao fundo, cada uma de um lado do animal. Há um ponto O no olho do camelo, um ponto A no topo de uma pirâmide e um ponto B no topo da outra. Há dois segmentos de reta, um que une O com A e outro e une O com B. Entre os segmentos há a representação de um ângulo.

Agora, analise o ângulo de visão para os torcedores T1 e T2, localizados em diferentes partes da arquibancada de um campo de futebol.

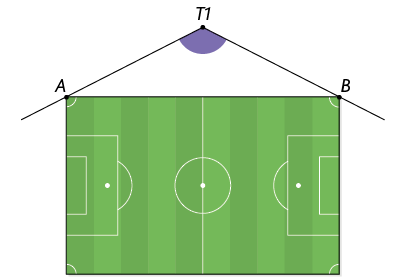
Ilustração de um campo de futebol, visto de cima com o ponto A em um e seus vértices o ponto B no vértice seguinte, seguindo o maior lado do campo. Do lado de fora do campo, ainda seguindo esse maior lado entre os pontos, há um ponto T 1. Há uma semirreta que liga os pontos T 1 e A e outra semirreta que liga os pontos T 1 e B, com um ângulo de aproximadamente 126 graus demarcado entre essas semirretas.
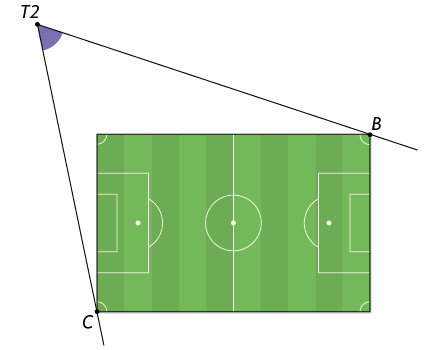
Ilustração de um campo de futebol, visto de cima com o ponto C em um e seus vértices o ponto B no vértice oposto. Do lado de fora do campo, perto do vértice que está entre esses dois demarcados, há um ponto T 2. Há uma semirreta que liga os pontos T 2 e B e outra semirreta que liga os pontos T 2 e C, com um ângulo de aproximadamente 60 graus demarcado entre essas semirretas.

a) Ícone uso de instrumentos Utilizando um transferidor, determine a medida do ângulo de visão para cada um desses torcedores.

Resposta: Torcedor T1: 126 ° ; torcedor T2: 60 ° .

b) O ângulo de visão para o torcedor T1 é agudo, obtuso ou raso? E o ângulo de visão para o torcedor T2?

Respostas: Obtuso; agudo.

Página 184

Retas paralelas e retas concorrentes

Alfredo estava na rua Paraná quando uma pessoa se aproximou e lhe fez a seguinte pergunta:

Ilustração de dois meninos conversando. Enquanto um deles pergunta: Por favor, esta é a rua Rio de Janeiro? O outro, responde: Não. A rua Rio de Janeiro é a próxima, paralela a esta.
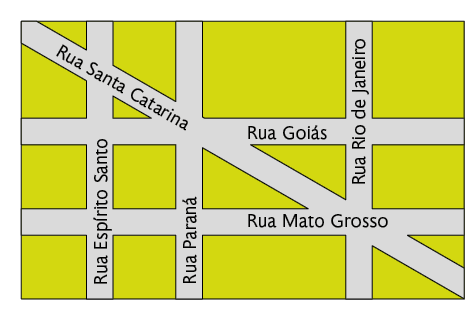
Ilustração. Vista de cima de duas ruas na horizontal, Rua Goiás e Rua Mato Grosso, representadas uma abaixo da outra e que não se cruzam. Há três ruas na vertical, Rua Espírito Santo, Rua Paraná e Rua Rio de Janeiro, lado a lado, que não se cruzam entre si mas cruzam com as duas anteriores. Há, na diagonal, a Rua Santa Catarina, que se cruza com todas as ruas anteriores.
Representação parcial da vista de cima do bairro, onde se localizam várias ruas, entre elas a Paraná e a Rio de Janeiro.

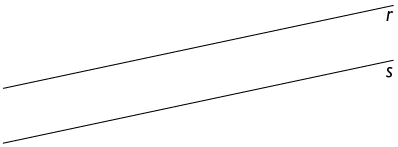
Vamos representar essas ruas por retas, como indicado na imagem. As retas s e r estão no mesmo plano, mas não se cruzam. Nesse caso, dizemos que essas retas são paralelas.

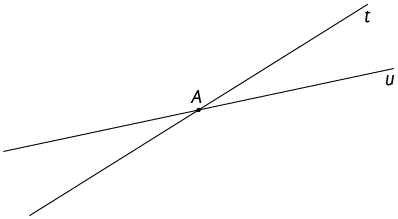
Já as retas t e m se cruzam em um único ponto no plano. Nesse caso, dizemos que as retas t e m são concorrentes.

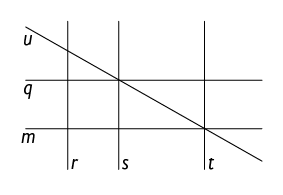
Ilustração de duas retas na horizontal, Q e M, que não se cruzam. Há três retas na vertical, R, S, T, lado a lado, que não se cruzam entre si mas cruzam com as duas anteriores. Há, na diagonal, a reta U, que se cruza com as retas Q, M, R, S, T.

Duas retas representadas no mesmo plano podem ser:

paralelas, quando não se cruzam.

Ilustração de duas retas, R e S, uma ao lado da outra, que não se cruzam.

concorrentes, quando se cruzam em um único ponto.

Ilustração de duas retas, T e U, se cruzando no ponto A.

Atenção!

Em particular, as retas concorrentes podem ser:

  • perpendiculares, quando formam ângulos retos.
  • oblíquas, quando não são perpendiculares.

Assim, ao responder à pergunta sobre a localização da rua Rio de Janeiro, paralela à rua em que estavam, Alfredo mentalmente associou essas ruas a retas paralelas.

Página 185

Instrumentos e softwares

Construindo retas paralelas e perpendiculares com régua e esquadro

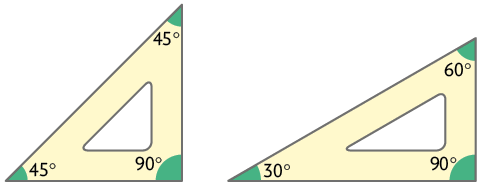
Os esquadros são instrumentos frequentemente utilizados para traçar ou verificar retas paralelas e perpendiculares. A seguir estão representados esquadros de dois tipos.

Ilustração de 2 esquadros, um ao lado do outro. No primeiro esquadro estão representados os ângulos de 90, 45 e 45 graus. No segundo esquadro estão representados os ângulos de 30, 90 e 60 graus.
esquadro de 45 ° ; esquadro de 6 0 °

Podemos usar uma régua e um esquadro para representar retas paralelas.

1º. Represente uma reta qualquer com a régua ou com o esquadro.

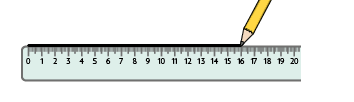
Ilustração de um lápis riscando uma reta, com o auxílio de uma régua.

2º. Posicione um dos lados do esquadro sobre a reta representada e a régua sobre outro lado do esquadro, para servir de apoio.

Ilustração de um esquadro com um de seus 3 lados para cima, onde está desenhada uma reta r. O lado direito do esquadro está apoiado sobre uma régua.

3º. Mantendo a régua fixa, como apoio, deslize o esquadro nos dois sentidos e represente a quantidade que desejar de retas paralelas à reta traçada inicialmente.

Ilustração de um esquadro com um de seus 3 lados para cima, onde há um lápis desenhando uma reta. O lado direito do esquadro está apoiado sobre uma régua e, no sentido dela, acima, há outras retas desenhadas, como a reta r.

Também podemos representar retas perpendiculares com uma régua e um esquadro.

1º. Represente uma reta qualquer com a régua ou com o esquadro.

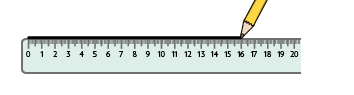
Ilustração de um lápis riscando uma reta, com o auxílio de uma régua.

2º. Posicione a régua e um dos lados do esquadro formando o ângulo reto sobre a reta traçada, como indicado.

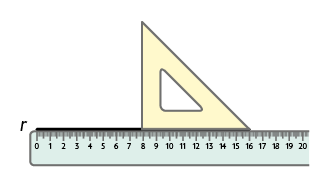
Ilustração de um esquadro com um de seus 3 lados sobre uma régua e há uma reta R desenhada acima da régua e à esquerda do esquadro.

3º. Mantendo a régua fixa, como apoio, deslize o esquadro nos dois sentidos e represente quantidade que desejar de retas perpendiculares à reta traçada inicialmente.

Ilustração de um esquadro com um de seus 3 lados sobre uma régua e há uma reta R desenhada acima da régua, com um lápis desenhando outras retas perpendiculares a essa.

4º. Depois, use a régua para prolongar a representação das retas.

Página 186

Construindo retas paralelas e perpendiculares com o GeoGebra

Existem alguns softwares de geometria dinâmica, como o GeoGebra, que podem ser úteis nas construções geométricas. A barra de ferramentas desse software traz diversos botões, os quais se referem a um conjunto de funções: marcar pontos, traçar retas, construir polígonos e circunferências, medir ângulos etc.

Siga as orientações do professor e estes passos para construir retas paralelas no GeoGebra.

Ícone Objeto digital

1º. Com a ferramenta Ponto, marque os pontos A e B . Em seguida, selecione a função Reta e trace a reta A B .

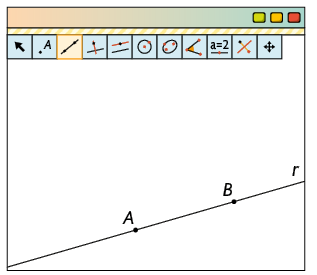
Ilustração de uma página de computador com o software Geogebra. Há vários botões de ferramentas e um com o desenho de uma reta está selecionado. Ainda na aba, está desenhada uma reta r com os pontos A e B contidos nela.

2º. Marque o ponto C não pertencente à reta A B . Com a função Reta paralela, selecione o ponto C e a reta A B . Desse modo, obtemos a reta s , paralela à reta A B .

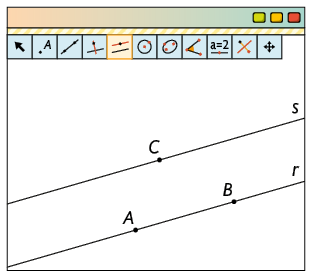
Ilustração de uma página de computador com o software Geogebra. Há vários botões de ferramentas e um com o desenho de duas retas paralelas está selecionado. Ainda na aba, estão desenhadas duas retas, s e r, paralelas. Na reta s há o ponto C e na reta r há os pontos A e B.

De maneira parecida, podemos construir retas perpendiculares no GeoGebra.

1º. Trace a reta A B , conforme descrito na construção anterior.

2º. Com a função Reta perpendicular, selecione o ponto A e a reta A B . Desse modo, obtemos a reta t , perpendicular à reta A B .

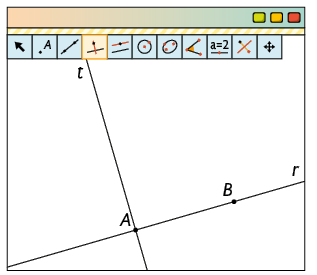
Ilustração de uma página de computador com o software Geogebra. Há vários botões de ferramentas e um com o desenho de duas retas perpendiculares está selecionado. Ainda na aba, estão desenhadas duas retas, t e r, perpendiculares e que tem o ponto A em comum. A reta r ainda tem o ponto B.

Faça o teste: com a função Mover selecionada, clique sobre a reta r ou sobre um dos pontos e arraste-o para outra posição. A maneira com que a construção foi realizada garante que as retas paralelas continuem paralelas e que as retas perpendiculares continuem perpendiculares.

Página 187

Atividades

Faça as atividades no caderno.

12. Classifique as retas representadas nas malhas quadriculadas a seguir em paralelas ou concorrentes.

A. Ilustração de uma malha quadriculada com duas retas na diagonal, R e S, lado a lado, que não se cruzam.
B. Ilustração de uma malha quadriculada com duas retas na vertical, Y e Z, lado a lado, que não se cruzam.
C. Ilustração de uma malha quadriculada com duas retas, T na horizontal e U na diagonal. As duas retas se cruzam.
D. Ilustração de uma malha quadriculada com duas retas, A e B, cada uma em uma direção da diagonal. As duas retas se cruzam.

Respostas: A. Paralelas; B. Paralelas; C. Concorrentes; D. Concorrentes.

13. O esquema a seguir representa a vista de cima de uma cidade, considerando as ruas como retas.

Esquema de várias retas representando ruas. No esquema, a avenida das Maritacas cruza com a Rua Pardal, com a Rua Arara e com a Rua Tucano. Um pouco mais acima, há a avenida Papagaio cruzando com a Rua Pardal com a representação de 90 graus, cruzando com a rua Arara também com a representação de 90 graus e a Avenida Papagaio também cruza com a Rua Tucano.

a) Das ruas que aparecem no esquema, quais são concorrentes à avenida das Maritacas?

Resposta: Rua Pardal, Rua Arara e Rua Tucano.

b) Quais ruas são perpendiculares à avenida Papagaio?

Resposta: Rua Pardal e Rua Arara.

14. Ícone uso de instrumentos Em seu caderno, marque três pontos quaisquer A, B e C, de modo que os três não estejam alinhados. Em seguida, usando régua e esquadro, construa:

Atenção!

Ao marcar os pontos, não deixe todos na mesma linha.

a) uma reta AB;

b) uma reta paralela à reta AB, passando por C;

c) uma reta perpendicular à reta AB, passando por C.

Agora, junte-se a um colega e, no GeoGebra, marque três pontos quaisquer A, B e C, de modo que os três não estejam alinhados. Em seguida, faça as mesmas construções sugeridas nos itens a, b e c.

Respostas pessoais.

Versão adaptada acessível

14. Ícone uso de instrumentos Junte-se a um colega e, em uma folha de papel, marquem três pontos quaisquer A, B e C, de modo que os três não estejam alinhados. Em seguida, usando régua e esquadro, construam:

Atenção!

Ao marcar os pontos, não deixe todos na mesma linha.

a) uma reta AB;

b) uma reta paralela à reta AB, passando por C;

c) uma reta perpendicular à reta AB, passando por C.

Agora, no GeoGebra, marquem três pontos quaisquer A, B e C, de modo que os três não estejam alinhados. Em seguida, façam as mesmas construções sugeridas nos itens a, b e c.

Respostas pessoais.

Orientação para acessibilidade

Professor, professora: instigue os estudantes a trocar ideias sobre os procedimentos necessários para construir as retas solicitadas nos itens a, b e c. Se julgar oportuno, ao final da atividade, solicite às duplas que compartilhem as estratégias utilizadas em suas construções.

15. De acordo com as medidas dos ângulos indicadas na imagem, classifique cada par de retas concorrentes em perpendiculares ou oblíquas.

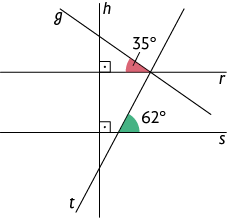
Ilustração com duas retas na horizontal, R e S, que não se cruzam. Há uma reta na vertical, H, que se cruza com as duas anteriores, com ângulos de 90 graus. Há uma reta G que se cruza com H e depois com a reta R com um ângulo de 35 graus, há uma reta T que se cruza com H e depois com a reta S e R, formando um ângulo de 62 graus com a reta S.

a) h e r

b) r e g

c) s e t

d) h e s

Respostas: a) Perpendiculares; b) Oblíquas; c) Oblíquas; d) Perpendiculares.

16. Escreva se as retas indicadas em cada item são perpendiculares ou oblíquas.

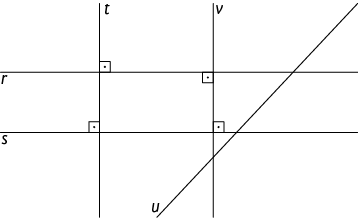
Ilustração com duas retas na horizontal, R e S, que não se cruzam. Há duas retas na vertical, T, V, lado a lado, que não se cruza entre si, mas cruzam com as 2 anteriores, com ângulos de 90 graus. Há, na diagonal, a reta U, que se cruza com as retas R, S, V.

a) s e u

b) t e r

c) r e u

d) v e r

Respostas: a) Oblíquas; b) Perpendiculares; c) Oblíquas; d) Perpendiculares.

Página 188

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Em uma malha quadriculada, trace o caminho da tartaruga conforme os comandos apresentados.

avance 1 quadradinho para a frente;

gire um quarto de volta para a direita e avance 3 quadradinhos;

gire um quarto de volta para a esquerda e avance 4 quadradinhos;

gire três quartos de volta para a direita e avance 2 quadradinhos;

gire um quarto de volta para a direita e avance 3 quadradinhos.

Ilustração, vista de cima, de uma tartaruga e, a sua frente, um pedaço de uma malha quadriculada, com alguns quadradinhos pintados.

Resposta:

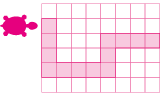
Ilustração de uma tartaruga em frente a uma malha quadriculada, na qual está representado um caminho formado por quadradinhos pintados de rosa. O caminho é: Começando pelo quadradinho em frente da tartaruga, o caminho segue por 3 quadradinhos para a direita, 4 quadradinhos para a esquerda, 2 para a esquerda, 3 para a direita.

2. Ícone uso de instrumentos Fazendo estimativas, classifique o ângulo destacado em cada figura geométrica plana a seguir em reto, agudo ou obtuso. Em seguida, use um transferidor para verificar se sua classificação está correta.

A. Ilustração de um retângulo com um de seus ângulos internos demarcados, medindo 90 graus.
B. Ilustração de um pentágono com um de seus ângulos internos demarcados, medindo mais de 90 graus.
C. Ilustração de um hexágono com um de seus ângulos internos demarcados, medindo 90 graus.
D. Ilustração de um pentágono com um de seus ângulos internos demarcados, medindo menos de 90 graus.

Respostas: A. Reto; B. Obtuso; C. Reto; D. Agudo.

Orientação para acessibilidade

Professor, professora: reproduza e disponibilize para os estudantes as figuras apresentadas na atividade 2. Em seguida, indique a localização dos ângulos destacados em cada uma. Na sequência, desafie a turma a realizar as estimativas solicitadas. Por fim, peça aos estudantes que compartilhem as estratégias utilizadas.

3. Analise as retas representadas em uma malha quadriculada.

Ilustração de uma malha quadriculada com três retas na horizontal, V, X e R, que não se cruzam. Há duas retas na vertical, S, T, lado a lado, que não se cruzam entre si, mas cruzam com as 3 anteriores. Há, na diagonal, a reta U, que se cruza com as retas V, X, R, S, T.

a) Quais retas são paralelas:

  • à reta r?
  • à reta s?
  • à reta x?
  • à reta t?

Respostas: Reta r: v e x; Reta s: t; Reta x: r e v; Reta t: s.

b) Quais retas são concorrentes:

  • à reta v?
  • à reta s?
  • à reta t?
  • à reta u?

Reta v: s, t e u; Reta s: r, u, v e x; Reta t: r, u, v e x; Reta u: r, s, t, v, e x.

4. A figura a seguir foi construída em uma malha quadriculada. De acordo com ela, copie as frases em uma folha de papel avulsa, substituindo cada ⬛ pela palavra paralelas, perpendiculares ou oblíquas.

Ilustração de uma malha quadriculada com duas retas na horizontal, R, T, que não se cruzam. Há duas retas na diagonal, U, V, lado a lado, que não se cruzam entre si, mas cruzam com as duas anteriores. Há, na vertical, a reta S, que se cruza com as retas R, T, U, V.

a) As retas r e s são ⬛.

b) As retas t e u são ⬛.

c) As retas u e v são ⬛.

Respostas: a) As retas r e s são perpendiculares; b) As retas t e u são oblíquas; c) As retas u e v são paralelas.