Página 205
UNIDADE
10
Grandezas e medidas

Agora vamos estudar...
- medidas de comprimento;
- medidas de massa;
- medidas de tempo;
- medidas de temperatura;
- medidas de área;
- medidas de capacidade;
- medidas de volume.
Página 206
Medidas de comprimento
Para medir, por exemplo, o comprimento de terrenos, a altura de pessoas ou a largura de construções, tem-se o metro como unidade de medida padronizada. Mas nem sempre foi assim! Antigamente, as unidades de medida eram baseadas em partes do corpo do rei, como o pé, o palmo, o passo e a jarda. Para um melhor entendimento, analise nas imagens as indicações dessas unidades no corpo de Henrique.

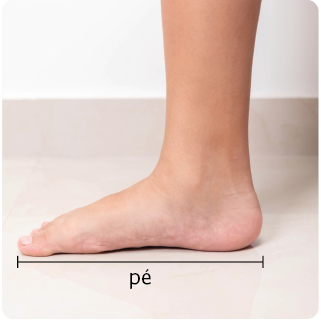



Imagens não proporcionais entre si.
Atenção!
Por volta do ano 1100, o rei Henrique determinou que a jarda correspondia à medida da distância que ia do seu nariz até a extremidade do seu polegar, com o braço estendido.
Porém, sem um padrão que fosse adotado por todos ou pela maioria dos países, havia confusão nas transações comerciais – imagine um país usando como referência as partes do corpo do rei rival. Por isso, atualmente existem unidades de medida padronizadas.
Além do metro, têm-se os submúltiplos, como o centímetro () e o milímetro (), e os múltiplos, como o quilômetro ().
Página 207
Conversão de unidades de medida de comprimento
O metro e suas unidades derivadas constituem o sistema métrico, com os quais medimos os comprimentos. No quadro estão representados os múltiplos e submúltiplos do metro.
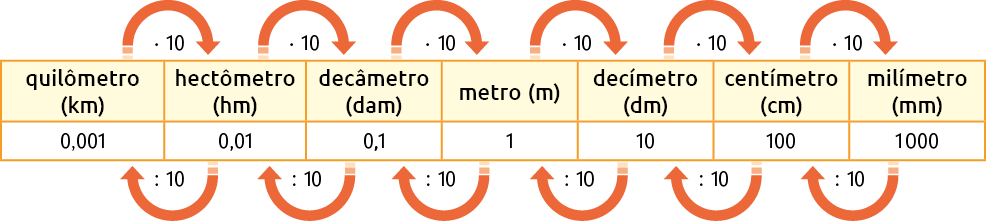
Esse quadro nos diz que , , , e assim por diante. Com base nessas informações, podemos converter uma unidade de medida em outra.
Converter em decímetro.
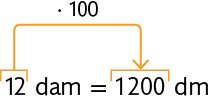
Converter em metro.
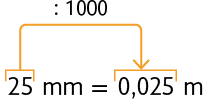
A escolha da unidade de medida mais adequada é feita de acordo com o comprimento a ser medido.
Questão 1. Qual unidade você usaria para
expressar a
medida do comprimento de uma caneta? E para expressar a medida do comprimento
de um campo de futebol?
Resposta pessoal. Sugestão de resposta: Centímetro. Metro.
Atividades
Faça as atividades no caderno.
1. Escreva no caderno a unidade de medida de comprimento mais adequada para expressar a medida da:
a) altura de uma árvore;
b) distância entre duas cidades;
c) espessura de uma grafite de lapiseira;
d) altura de uma pessoa;
e) altura de um prédio.
Sugestão de respostas: a) ; b) ; c) ; d) ou ; e) .
2. Em uma folha de papel sulfite ou no caderno, desenhe o contorno de uma de suas mãos aberta ao máximo. Em seguida, com uma régua, determine, em centímetro, a medida do comprimento de seu palmo.
Junte-se a um colega e comparem as medidas obtidas. O que puderam concluir?
Resposta pessoal.
Página 208
3. Entre os segmentos de reta a seguir, estime qual deles tem de comprimento.




Agora, use uma régua para conferir
se sua
estimativa está correta.
Sugestão de resposta: Segmento de reta ; Resposta pessoal.
Orientação para acessibilidade
Professor, professora: para que os estudantes realizem as estimativas na atividade 3, auxilie-os de maneira semelhante à sugerida para a atividade 3 da página 177 deste volume.
4. Copie e complete os itens substituindo cada pelo número adequado.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
5. A seguir estão representados alguns instrumentos utilizados para medir comprimentos.
Imagens não proporcionais entre si.






Atenção!
O paquímetro e o micrômetro são instrumentos utilizados para medir pequenos comprimentos que exigem precisão, com margens de erro menores do que .
Considerando os instrumentos apresentados, escreva no caderno qual é o mais adequado para medir:
a) o comprimento de uma sala;
b) a cintura de uma pessoa;
c) a espessura de um parafuso;
d) o comprimento de um segmento de reta;
e) a altura de uma porta;
f) a espessura de um vidro.
Sugestão de respostas: a) Trena ou metro articulado; b) Fita métrica; c) Micrômetro ou paquímetro; d) Régua; e) Trena ou metro articulado; f) Micrômetro ou paquímetro.
Página 209
6. Clarice é atleta e corre diariamente. Em um dia de treino ela correu uma distância cuja medida foi e de comprimento. Qual é a medida do comprimento dessa distância em metros?
Resposta: .
7. Patrícia vai usar as contas representadas a seguir para confeccionar dois colares cujos comprimentos medem, cada qual, .

Um dos colares terá apenas contas azuis, uma ao lado da outra, e o outro terá apenas contas vermelhas. Quantas contas azuis serão usadas na confecção de um dos colares? E quantas contas vermelhas são necessárias na confecção do outro colar?
Respostas: 80 contas azuis; 50 contas vermelhas.
8. Para determinado trabalho, um encanador precisa emendar 4 pedaços de cano, como o representado a seguir.

Atenção!
Ao resolver esta atividade, não se esqueça de descontar a medida do comprimento das emendas do cano, que nesse caso é .
Qual é a medida aproximada do comprimento dos 4 pedaços de cano emendados?
Resposta: Aproximadamente .
9. A corrida internacional de São Silvestre acontece todos os anos na cidade de São Paulo, desde 1925. Sabendo que a distância do percurso da prova mede e que um corredor já percorreu da prova, qual é a medida da distância, em quilômetros, que falta para ele cumprir a corrida?
Resposta: .
10. Felipe comprou um rolo de papel kraft cuja embalagem indica a medida de de comprimento. Se ele pretende cortar tiras medindo de comprimento, quantas tiras ele vai cortar?
Resposta: 20 tiras.
11. Considere as informações do gráfico a seguir.
Pontos mais altos do Brasil – 2022
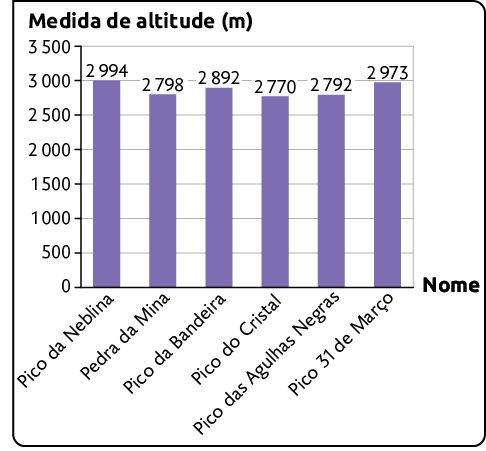
Fonte de consulta: BRASIL. Ministério do planejamento, orçamento e gestão. Anuário estatístico do Brasil. Rio de Janeiro: IBGE, 2013, v. 73. Disponível em: https://oeds.link/saTQlN. Acesso em: 11 jan. 2022.
Atenção!
A altitude é a medida da altura em relação ao nível do mar.
a) Qual é o ponto mais alto do Brasil?
b) Qual é a medida da altitude do Pico da Bandeira?
c) Qual é a medida da altitude do Pico das Agulhas Negras? E a da Pedra da Mina?
d) Entre os picos, qual deles apresenta a medida de altitude mais próxima de ?
e) De acordo com as informações do gráfico, elabore um problema. Depois, dê o problema que você fez para um colega resolver e, ao final, verifiquem se a resposta está correta.
Respostas: a) Pico da Neblina; b) ; c) ; ; d) Pico da Neblina; e) Resposta pessoal.
Página 210
12. A imagem representa a vista superior da casa de Cíntia, sem o telhado. Essa representação é conhecida como planta baixa✚.
- Planta baixa:
- vista superior de um corte horizontal de uma construção (considerando geralmente a medida de altura de do solo) com informações das respectivas dimensões.↰
Imagens não proporcionais entre si.
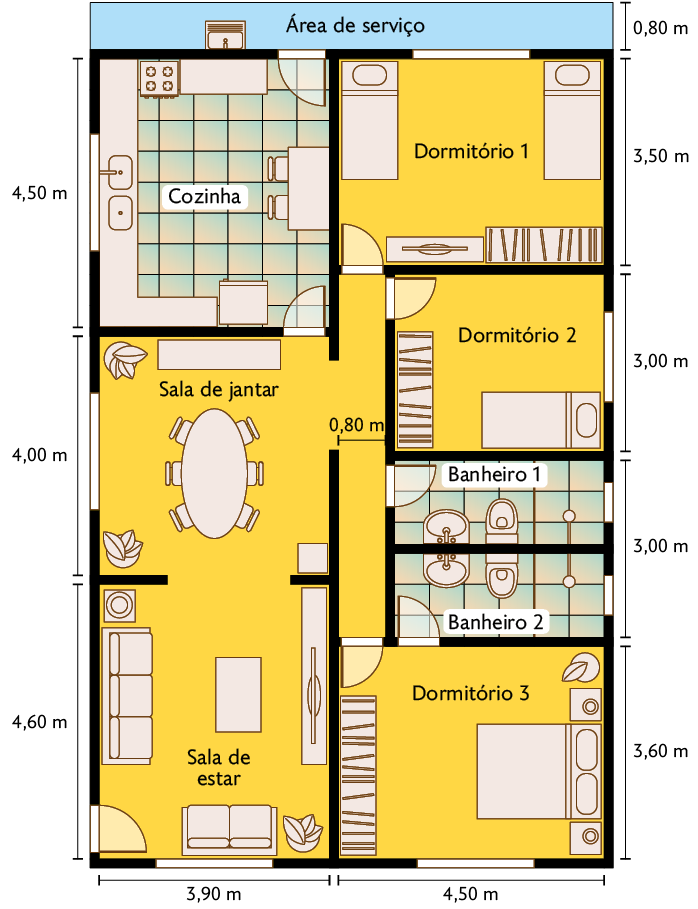

a) Junte-se a um colega para escreverem no caderno alguns dos elementos que vocês identificaram nessa planta baixa.
Sugestões de resposta: Sofá, camas, mesa de jantar, fogão etc.
b) De acordo com a planta baixa, há quantas portas na residência de Cíntia?
Resposta: 8 portas.
c) Quais são as medidas reais do comprimento e da largura do dormitório 1?
Respostas: ; .
d) Desenhe no caderno um esboço da planta baixa que representa a casa onde você mora.
Resposta pessoal.
Versão adaptada acessível
d) Descreva para um colega a planta baixa que representa a casa onde você mora.
Resposta pessoal.
Página 211
13. A imagem representa a planta baixa do apartamento de Abner.
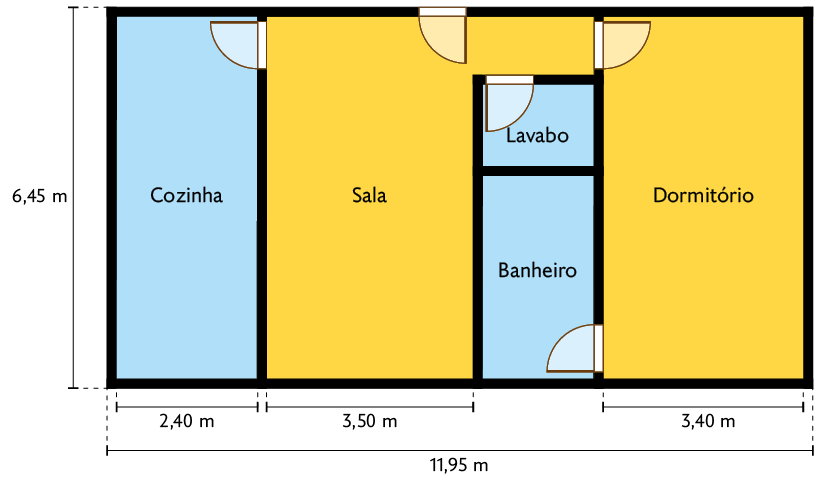
Sabendo que a espessura da parede mede , determine a medida:
a) das dimensões do dormitório;
b) da largura do banheiro.
Respostas: a) e ; b) .
14. Usando o
instrumento de medida adequado, meça o comprimento e a largura da sua sala de
aula. Em seguida, desenhe a respectiva planta baixa em seu caderno,
apresentando a disposição dos armários, carteiras, mesas, lousa, porta e
janelas. Considere do desenho para cada que você
mediu. Depois, compare seu desenho com o de um colega.
Resposta pessoal.
Professor, professora: Para auxiliar os estudantes a medir a sala de aula, providencie uma trena ou fita métrica e verifique como eles manuseiam essas ferramentas.
Versão adaptada acessível
14. Junte-se a quatro colegas e, usando o instrumento de medida adequado, meçam o comprimento e a largura da sala de aula de vocês. Em seguida, desenhem a respectiva planta baixa, apresentando a disposição de armários, carteiras, mesas, lousa, porta e janelas. Considerem do desenho para cada que vocês mediram. Depois, comparem seus desenhos com os de outros colegas.
Resposta pessoal.
15. Junte-se a um colega para imaginarem como é a vista aérea da escola. Em seguida, representem-na em um desenho, indicando todos os ambientes.
Resposta pessoal.
16. No esquema, as letras A, B, C e D representam quatro cidades.
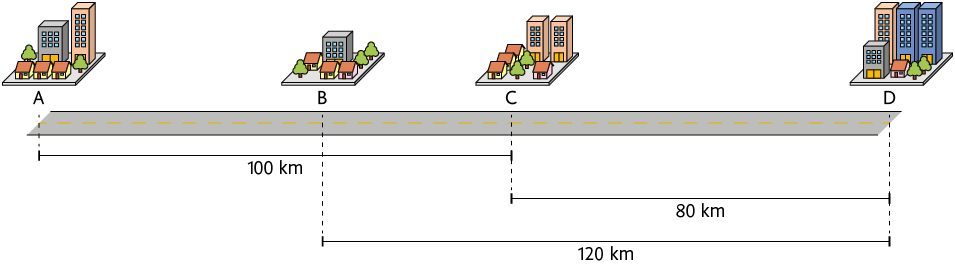
Calcule a medida da distância entre:
a) as cidades A e D;
b) as cidades B e C.
Respostas: a) ; b) .
Página 212
Perímetro
Jéssica desenhou o retângulo a seguir.

Questão 2. Com uma régua, determine as medidas das dimensões desse retângulo e anote-as em seu caderno.
Resposta: e .
Questão 3. Em seu caderno, adicione as medidas do comprimento dos lados desse retângulo e calcule a soma delas.
Resposta: .
O comprimento do contorno de uma figura geométrica plana é chamado perímetro. No caso de um polígono, a medida do perímetro é dada pela soma das medidas do comprimento de seus lados.
Questão 4. Com o auxílio de uma
régua, desenhe um
triângulo e um quadrilátero no caderno. Depois, calcule a medida do perímetro
de cada uma dessas figuras.
Resposta pessoal.
Atividades
Faça as atividades no caderno.
17. Determine
a medida do perímetro das figuras. Para isso, meça os comprimentos dos lados de
cada uma delas usando uma régua.
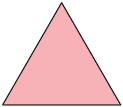


Respostas: A. ; B. ; C. .
18. Leia a afirmação de Rodolfo.

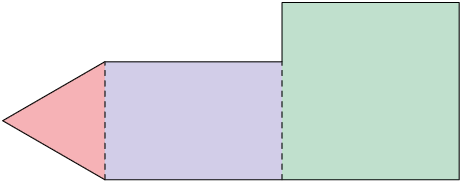
a) A afirmação de Rodolfo está correta? Justifique sua resposta.
Resposta: Não, pois um lado do retângulo coincide com um lado do triângulo, e o outro lado do retângulo também coincide com parte do lado do quadrado, assim as medidas desses comprimentos não são consideradas.
b) Se a resposta anterior for negativa, calcule no caderno a medida do perímetro da figura dada.
Resposta: .
Página 213
19. A obra de arte a seguir é de autoria de Andries Both (1612-1642), um pintor holandês que retratava cenas da vida cotidiana das classes mais baixas em Roma, no século XVII.
Nesta imagem, cada medida de da largura e do comprimento corresponde a das medidas da tela original.

Twee pelgrims op de weg, de Andries Both. Gravura, 1642.
a) Quais são as medidas das dimensões reais dessa obra?
Resposta: .
b) Qual é, em centímetros, a medida do perímetro real dessa obra de arte?
Resposta: .
20. A medida do perímetro do polígono A é e a do polígono B, . Calcule as medidas x e y indicadas nos lados desses polígonos.
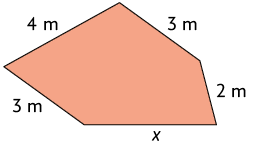
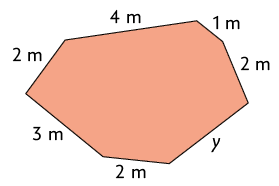
Respostas: A. ; B. .
21. A imagem representa um campo de futebol. Nela está indicada a medida do comprimento real do campo.
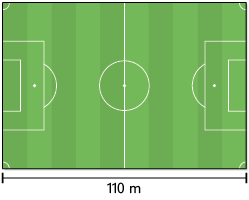
a) Sabendo que a largura desse campo mede a menos que o comprimento, determine a medida da largura do campo.
b) Qual é a medida do perímetro desse campo de futebol?
Respostas: a) ; b) .
22. As figuras A e B a seguir podem ser decompostas nos polígonos 1, 2 e 3.
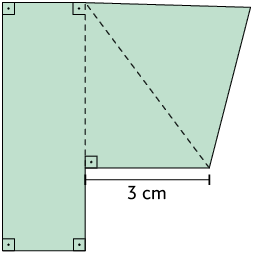
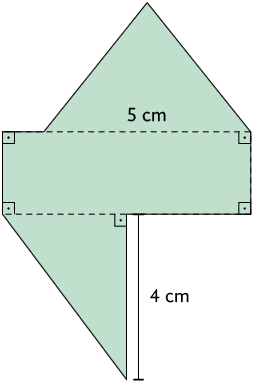
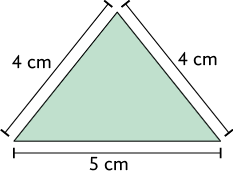
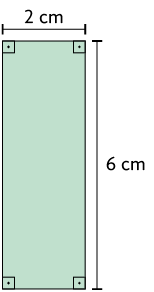
Qual é a medida do perímetro da:
a) figura A?
b) figura B?
22. Respostas: a) ; b) .
Página 214
Medidas de massa
Vimos que foi preciso criar uma unidade de medida padronizada para medir comprimentos. O mesmo ocorreu para medir a massa de um corpo. A unidade padrão de medida de massa é o quilograma .
O quilograma e seu submúltiplo grama são as unidades de medida de massa mais indicadas nas embalagens de produtos.
Imagens não proporcionais entre si.
Exemplos:



Além do grama e do quilograma, outras unidades de medida de massa muito utilizadas são o miligrama e a tonelada .
Atividades
Faça as atividades no caderno.
23. Escreva no caderno a unidade mais adequada para expressar a medida da massa de:
a) uma pessoa;
b) um caminhão;
c) um cachorro adulto;
d) uma bicicleta;
e) um comprimido;
f) um elefante adulto.
Sugestão de respostas: a) ; b) ; c) ; d) ; e) ou ; f) .
24. Amanda escreveu em gramas.
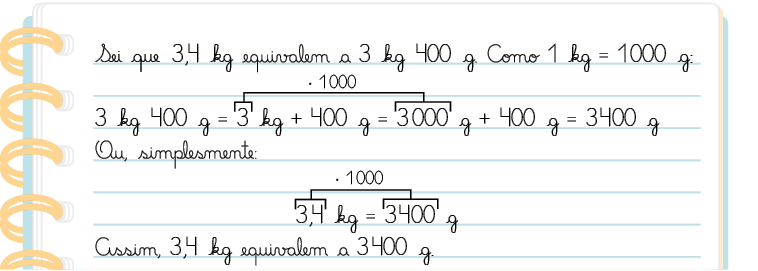
Agora, escreva em gramas as medidas a seguir.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
Página 215
25. Para escrever em quilogramas, Tobias procedeu da seguinte maneira.

De maneira semelhante, escreva em quilograma as medidas a seguir.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
26. Copie no caderno os itens substituindo cada pelo número adequado.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
27. Marta preparou de geleia de morango e precisa guardá-la em potes com de geleia em cada um. Quantos potes serão necessários para guardar toda a geleia?
Resposta: 16 potes.
28. Além das conversões de medidas das atividades 24 e 25, podemos converter uma medida em gramas em uma medida em miligramas. Por exemplo, vamos converter em miligramas. Como , segue que:

Escreva em miligramas as medidas a seguir.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d)
29. Também podemos converter uma medida em miligramas em uma medida em gramas. Para isso, dividimos a quantidade de miligramas por 1.000.

De maneira semelhante, escreva as medidas a seguir em gramas.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
30. O morcego-nariz-de-porco (Craseonycteris thonglongyai) é o menor mamífero voador do mundo, com massa medindo aproximadamente . Encontrado na Tailândia, esse mamífero pode viver em torno de 15 anos. Escreva a medida de massa aproximada desse morcego em miligramas.
Resposta: Aproximadamente .
31. O miligrama costuma ser uma unidade de medida de massa indicada nas embalagens de medicamentos. De acordo com a embalagem, a indicação informa a quantidade, em miligramas, de vitamina C em cada comprimido.

Com base nas informações apresentadas, elabore uma ou mais questões para um colega resolver. Depois, verifique se a resolução dele está correta.
Resposta pessoal.
Página 216
32. Cada balança a seguir está em equilíbrio, isto é, a medida da massa em cada prato é a mesma.
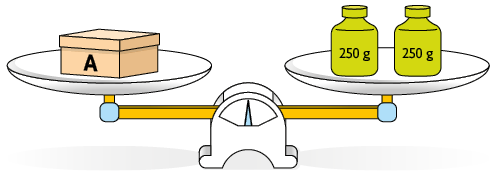
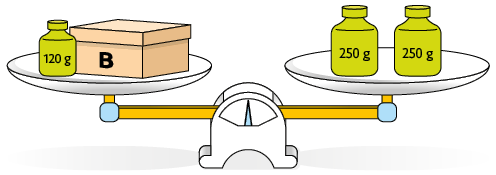
De acordo com essas balanças, qual é a medida da massa da caixa A? E a da caixa B?
Respostas: A: ; B: .
33. A seguir estão representados os dois recipientes e suas respectivas medidas de massas.
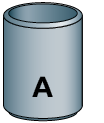
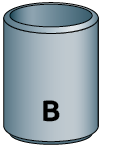
Flávia vai distribuir de açúcar nesses recipientes de modo que não sobre açúcar e os recipientes fiquem com a mesma medida de massa total. Determine a medida de massa de açúcar, em gramas, que Flávia vai colocar em cada recipiente.
Respostas: Recipiente A: ; Recipiente B: .
34. Com o crescimento da população e da urbanização, a produção de lixo no mundo vem aumentando a cada ano e, como a maioria do lixo produzido é depositada em lixões, os países estão enfrentando a contaminação do solo. Segundo estudos da Associação Brasileira de Empresas de Limpeza Pública e Resíduos Especiais (Abrelp), em 2020, os municípios brasileiros produziram aproximadamente milhões de toneladas de lixo, o que corresponde a aproximadamente de lixo produzido por habitante durante esse ano.
a) Qual é a medida da massa aproximada de lixo, em quilogramas, produzida diariamente por brasileiro em 2020?
Resposta: Aproximadamente .
b) Qual é a medida da massa aproximada de lixo, em quilogramas, produzida por uma família brasileira com pessoas durante uma semana de 2020? E qual é a medida da massa de lixo, em toneladas, produzida por essa família durante um ano?
Respostas: Aproximadamente ; Aproximadamente .
35. Márcio tem um sítio de hectares, no qual produziu, na última safra, de soja por hectare. Sabendo que a soja será comercializada em sacas com de medida da massa, determine o total de sacas de soja produzidas no sítio de Márcio nessa safra.
Resposta: 1.125 sacas.
Página 217
Medidas de tempo
O calendário
Tente imaginar como seria difícil realizar algumas atividades do dia a dia no momento correto ou registrar alguns fatos da história se o ser humano não tivesse desenvolvido maneiras de medir o tempo.
Antes de serem criadas as unidades de medida de tempo, como ano, semestre, bimestre, mês, dia, hora, minuto e segundo, antigas civilizações se baseavam em acontecimentos da natureza para identificar a melhor época para plantar, colher e caçar. Em resumo, o tempo era medido pela observação da natureza.
O calendário consiste em um instrumento de medida de tempo, no qual registramos e organizamos os dias, as semanas e os meses de um ano. Analise o calendário do ano de 2025.

Página 218
Atividades
Faça as atividades no caderno.
36. Um ano corresponde à medida do tempo que o planeta Terra leva para dar uma volta completa em torno do Sol (translação). Esse período de tempo mede aproximadamente 365 dias, 5 horas, 48 minutos e 46 segundos, ou seja, cerca de 365 dias e 6 horas.
Representação com elementos não proporcionais entre si. Cores-fantasia.
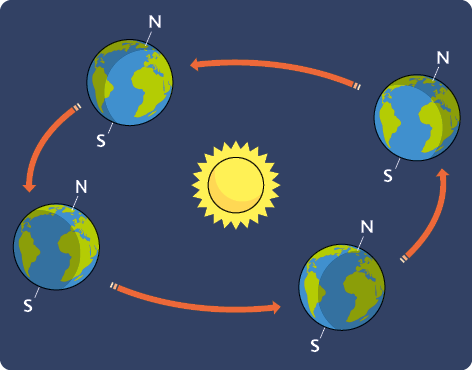
Considera-se o ano com 365 dias. A medida de tempo que excede esses 365 dias, ao final de 4 anos, corresponde a 1 dia quase completo. Assim, a cada 4 anos adiciona-se 1 dia ao ano, que passa a ter 366 dias. Esse ano é conhecido como ano bissexto, e o dia acrescentado é 29 de fevereiro. Além disso, para compensar a diferença entre 6 horas e 5 horas, 48 minutos e 46 segundos, estabeleceu-se que os anos terminados em 00 serão bissextos apenas se forem divisíveis por 400.
Portanto, podemos verificar se um ano é ou não bissexto da seguinte maneira.
Se o número referente ao ano não terminar em 00 e for divisível por 4, então o ano é bissexto.
Se o número referente ao ano terminar em 00, ele deve ser divisível por 400 para que seja bissexto.
a) O ano em que estamos é bissexto?
Resposta pessoal. A resposta depende do ano vigente.
b) A que mês de um ano bissexto é adicionado 1 dia? Que dia é esse?
Respostas: Fevereiro; dia 29.
c) Quais dos anos apresentados a seguir são bissextos?
- 2400
- 2300
- 2008
- 2009
- 2800
Respostas: 2400, 2008 e 2800.
37. Responda às seguintes perguntas.
a) Quantos dias tem 1 semana?
b) Quantos meses tem 1 ano?
c) Os meses do ano podem ser divididos igualmente em 6 bimestres ou em 2 semestres. Sendo assim, quantos meses tem 1 bimestre? E quantos meses tem 1 semestre?
d) Quantos dias tem 1 ano?
Respostas: a) 7 dias; b) 12 meses; c) 2 meses; 6 meses; d) 365 dias ou 366 dias em anos bissextos.
38. O 1º domingo de novembro de determinado ano é dia 6. Que dia será o último domingo desse mês?

Resposta: Dia 27.
39. Descubra a qual dia da semana se refere cada item.
a) Suponha que daqui a 5 dias seja quinta-feira. Que dia foi anteontem?
b) Se sábado foi há 8 dias, então que dia foi ontem?
c) Supondo que quarta-feira foi há 4 dias, que dia será depois de amanhã?
Respostas: a) Quinta-feira; b) Sábado; c) Terça-feira.
Página 219
O relógio
Algumas civilizações antigas baseavam-se na posição do Sol para se orientar quanto ao horário durante o dia. Para isso, era verificada, por exemplo, a medida da distância entre o Sol e a linha do horizonte.
Atualmente, para conferirmos o horário, durante o dia ou à noite, consultamos um relógio. Tanto nos relógios de ponteiros quanto nos digitais podemos identificar as horas , os minutos e os segundos.
Questão 5. Quantos segundos há em:
a) 1 hora?
Resposta: .
b) ?
Resposta: .
c) 1 dia?
Resposta: .
d) 7 horas?
Resposta: .
Analise os horários indicados nos relógios.


Atenção!
O relógio de ponteiros pode indicar dois horários, ou seja, , se for antes das do dia (meio-dia), ou , se for após as do dia.
Ao escrevermos horários, não podemos usar a notação para representar , por exemplo, pois o sistema de medida de tempo não é decimal. Verifique o horário correspondente a .
Assim, correspondem a .
Questão 6. Em qual horário você
costuma dormir?
Resposta pessoal.
Questão 7. Junte-se a um colega e pesquisem sobre instrumentos de medição de tempo que já foram utilizados no passado. Depois, compartilhe as informações obtidas com os demais colegas.
Resposta: Espera-se que os estudantes obtenham informações sobre o relógio do sol, a clepsidra, o relógio de vela, a ampulheta, o relógio de pêndulo etc.
Atenção!
A pesquisa proposta na questão 7 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Página 220
Atividades
Faça as atividades no caderno.
40. Copie no caderno os itens substituindo cada pelo número adequado. Para isso, realize as conversões necessárias.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
41. Associe os relógios que apresentam o mesmo horário. Para isso, escreva os pares de letras correspondentes.








Resposta: A–H; B–E; C–G; D–F.
42. Analise um relógio indicando dois horários diferentes de uma mesma tarde.


a) No momento A, que horário está indicado nesse relógio? E no momento B?
Respostas: A: ; B: .
b) Expresse no caderno a medida de tempo decorrido do momento A até o B em minutos e em segundos.
Respostas: ;
c) Que horário estará indicado nesse relógio quando, a partir do momento B, passarem ? Esboce um relógio no caderno e represente esse horário.
Resposta nas orientações ao professor.
Versão adaptada acessível
c) Que horário estará indicado nesse relógio quando, a partir do momento B, se passarem ? Represente em um relógio esse horário.
Resposta nas orientações ao professor.
43. Certa máquina produz 18 garrafas em 1 hora. Quantos minutos serão necessários para a produção de 126 garrafas?
Resposta:
Página 221
44. A corrida de São Silvestre é uma tradicional prova de atletismo realizada na cidade de São Paulo, todos os anos no dia 31 de dezembro. Essa prova reúne atletas de diversas partes do mundo, que percorrem uma distância que mede por algumas ruas da cidade.
A tabela apresenta as medidas do tempo que os 4 primeiros colocados da categoria masculina levaram para completar o trajeto da corrida em 2021.
|
Colocação |
Atleta |
País de origem |
Medida do tempo |
|---|---|---|---|
|
1ª |
Belay Tilahun Bezabh |
Etiópia |
|
|
2ª |
Daniel Ferreira do Nascimento |
Brasil |
|
|
3ª |
Hector Garibay Flores |
Bolívia |
|
|
4ª |
Elisha Kipchirchir Rotich |
Quênia |
Fonte de pesquisa: CORRIDA INTERNACIONAL DE SÃO SILVESTRE – Fundação Cásper Líbero. Gazeta esportiva. Disponível em: https://oeds.link/X8ugfN. Acesso em: 24 fev. 2022.
a) Escreva no caderno a medida do tempo em segundos que o 1º colocado da categoria masculina levou para concluir a corrida.
b) O atleta brasileiro Daniel Ferreira do Nascimento cruzou a linha de chegada quantos segundos após a chegada do 1º colocado?
c) De acordo com as informações apresentadas na tabela, elabore um problema envolvendo medidas de tempo. Depois, peça a um colega que o resolva.
Respostas: a) ; b) ; c) Resposta pessoal.
45. Os relógios a seguir apresentam uma sequência de horários nos quais os ônibus de certa linha partem de um terminal rodoviário.



a) Após quantos minutos, em média, os ônibus dessa linha partem do terminal rodoviário?
b) Considerando que os ônibus dessa linha sempre partem do terminal rodoviário com essa diferença entre os horários, escreva no caderno os próximos 3 horários em que os ônibus partem.
Respostas: a) ; b) ; ; .
46. Um
relógio está atrasando 5 segundos a cada hora. Considere o momento em que esse relógio está marcando o horário correto. Após
7 dias, quantos minutos será preciso adiantá-lo para
ajustar o horário correto?
Resposta:
47. Roberto e sua esposa fizeram uma viagem de férias para Belém, no estado do Pará.
O voo saiu de São Paulo no dia 28 de junho às da manhã e chegou a Belém às . Eles chegaram ao hotel às e ficaram hospedados nele por noites.
a) Quantas horas e minutos durou o voo de São Paulo a Belém?
b) Em que dia e mês Roberto e sua esposa saíram do hotel?
Respostas: a) ; b) 5 de julho.
Página 222
Medidas de temperatura
Outra grandeza a ser medida diariamente é a temperatura. Em certas situações, é preciso medir a temperatura corporal de uma pessoa, de um animal, do ambiente ou da água.
No Brasil, a referência para medir temperatura é a escala Celsius. Ela recebe esse nome porque foi desenvolvida em 1742 pelo sueco Anders Celsius. Para medir a temperatura, o instrumento utilizado é o termômetro, encontrado em diferentes modelos.
Analise as medidas de temperatura registradas nos termômetros a álcool a seguir.
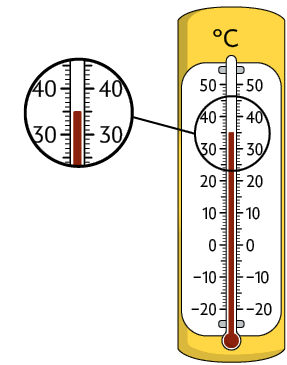
A medida da temperatura indicada no termômetro é acima de zero.
: trinta e cinco graus Celsius ou trinta e cinco graus positivos.
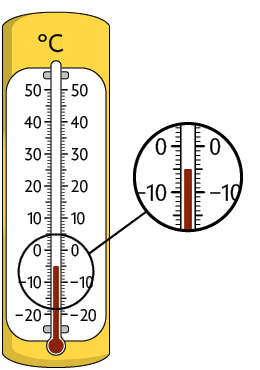
O termômetro está indicando a temperatura abaixo de zero.
: menos cinco graus Celsius ou cinco graus negativos.
Termômetros como esses são de álcool colorido, comumente utilizados para medir a temperatura de ambientes, a qual é indicada pelo número que o líquido alcança no marcador. Conforme a medida da temperatura aumenta, o líquido do termômetro expande, subindo pelo tubo.
Outros modelos de termômetros também usados para medir a temperatura de ambientes ou a temperatura do corpo humano são o termômetro digital e o infravermelho✚.
Imagens não proporcionais entre si.

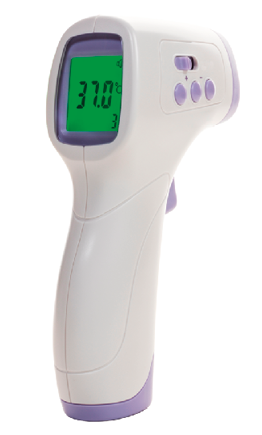
- Infravermelho:
- radiação eletromagnética invisível ao olho humano.↰
Página 223
Atividades
Faça as atividades no caderno.
48. Leia as informações a seguir.
-
Em 10 de julho de 1913 foi registrada a maior medida de temperatura ambiente no mundo com em Death Valley, na Califórnia.
-
Nos dias 4 e 5 de novembro de 2020 foi registrada a maior medida de temperatura ambiente no Brasil com no município de Nova Maringá, no Mato Grosso.
Qual é a diferença entre a maior medida de temperatura ambiente registrada no mundo e a maior registrada no Brasil?
Resposta: .
49. O mapa a seguir mostra a previsão das medidas de temperaturas máxima e mínima para alguns municípios do estado do Rio Grande do Sul em um mesmo dia.
Previsão das medidas de temperaturas máxima e mínima em alguns municípios do estado do Rio Grande do Sul
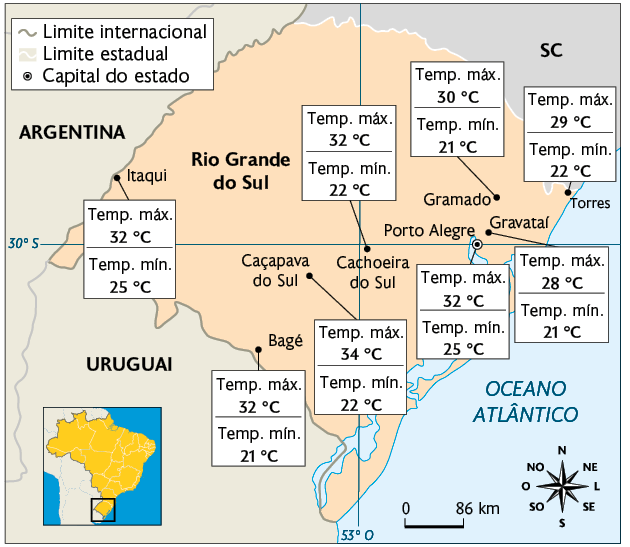
Fonte de pesquisa: PREVISÃO do tempo. Inmet.
Disponível em: https://oeds.link/fJlu3e. Acesso em: 25 fev. 2022.
ATLAS geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.
Subtraindo a medida de temperatura mínima da temperatura máxima prevista, obtém-se a variação de temperatura prevista para o dia.
a) Qual desses municípios teve a maior medida de temperatura máxima prevista?
b) Para qual desses municípios a variação de temperatura prevista:
foi menor?
foi maior?
Respostas: a) Caçapava do Sul; b) Menor: Itaqui, Porto Alegre, Gravataí e Torres; Maior: Caçapava do Sul.
50. No início da manhã, Sandra olhou o termômetro e verificou que ele marcava Ao meio-dia, ela olhou novamente o termômetro e verificou que a temperatura havia aumentado 75%.
a) De quantos graus foi o aumento na medida de temperatura entre os horários verificados?
b) Qual medida de temperatura o termômetro estava marcando ao meio-dia?
Respostas: a) ; b)
Página 224
51. Leia a tirinha.

MAURICIO DE SOUSA. Turma da Mônica. O Estado de S. Paulo, São Paulo, 23 maio 2002.
a) Em sua opinião, qual é a medida de temperatura em cada uma das cenas?
b) Na primeira cena, suponha que a medida de temperatura seja e, na segunda cena, . Nesse caso, qual é a variação de temperatura?
Respostas: a) Resposta pessoal; b)
52. Analise o gráfico e resolva os itens.
Medidas das temperaturas máxima e mínima registradas no município de São Joaquim (SC) – 10/01/2022 a 31/01/2022
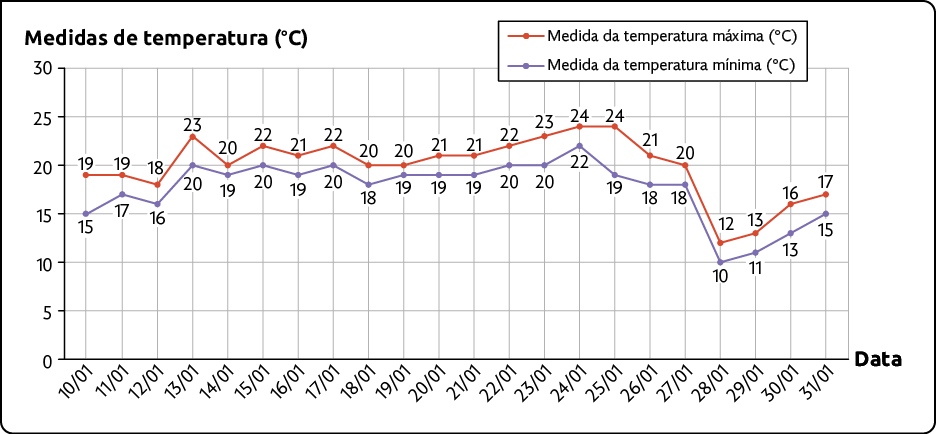
Fonte de pesquisa: DADOS Históricos Anuais. Inmet. Disponível em: https://oeds.link/fJlu3e. Acesso em: 25 fev. 2022.
a) Em que dia ocorreu a maior variação de temperatura? De quantos graus foi essa variação?
b) Em quais dias ocorreu a menor variação de temperatura? De quantos graus foi essa variação?
c) De acordo com as informações do gráfico, elabore duas ou mais questões para um colega resolver. Depois, verifique se a resposta dele está correta.
Respostas: a) Dia 25; ; b) Dias 14/01 e 19/01; ; c) Resposta pessoal.
Página 225
Medidas de área
Assim como podemos medir o comprimento ou a largura de uma sala, podemos também medir sua área. Vamos medir, por exemplo, a área das figuras representadas na malha.
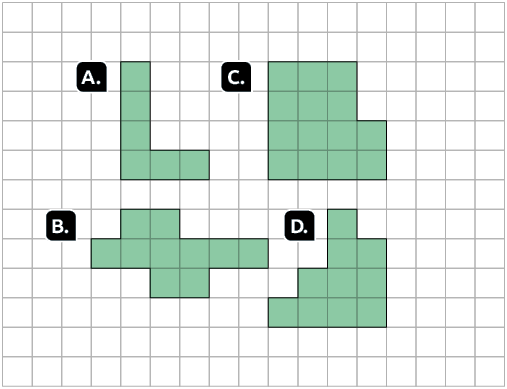
Para isso, inicialmente, escolhemos uma unidade de medida.
Considerando o ![]() como
unidade de medida de área, podemos construir o quadro a seguir, que indica a
medida da área de cada uma das figuras representadas na malha.
como
unidade de medida de área, podemos construir o quadro a seguir, que indica a
medida da área de cada uma das figuras representadas na malha.
|
Figura |
A |
B |
C |
D |
|---|---|---|---|---|
|
Medida da área |
6 |
10 |
14 |
10 |
Atenção!
Para medir
a área das figuras, considerando o ![]() como
unidade de medida de área, verificamos a quantidade de
como
unidade de medida de área, verificamos a quantidade de ![]() necessária
para cobrir cada figura.
necessária
para cobrir cada figura.
Agora, se considerarmos ![]() como
unidade de medida de área, obtemos as seguintes medidas.
como
unidade de medida de área, obtemos as seguintes medidas.
|
Figura |
A |
B |
C |
D |
|---|---|---|---|---|
|
Medida da área |
3 |
5 |
7 |
5 |
Note que, ao medirmos a mesma área utilizando diferentes
unidades de medida, nesse caso ![]() e
e
![]() ,
obtemos resultados diferentes.
,
obtemos resultados diferentes.
Questão 8. Quais das figuras representadas na malha
têm áreas com a mesma
medida?
Resposta: Figuras B e D.
Página 226
Atividades
Faça as atividades no caderno.
53. Utilizando
o ![]() como unidade de medida, determine a medida de
área de cada figura.
como unidade de medida, determine a medida de
área de cada figura.

a) Quais
figuras têm medida de área maior do que 32 ![]() ?
?
b) Qual figura tem medida de área igual à da figura A?
c) Quais figuras têm medida de área menor do que a da figura F?
Respostas: Figura A: 32 unidades de área; Figura B: 32 unidades de área; Figura C: 33 unidades de área; Figura D: 38 unidades de área; Figura E: 44 unidades de área; Figura F: 24 unidades de área; a) Figuras C, D e E; b) Figura B; c) Nenhuma.
54. Usando o ![]() como unidade de medida,
determine a medida de
área de cada figura da atividade anterior.
como unidade de medida,
determine a medida de
área de cada figura da atividade anterior.
Respostas: A. 16 unidades de área; B. 16 unidades de área; C. 16,5 unidades de área; D. 19 unidades de área; E. 22 unidades de área; F. 12 unidades de área.
55. Para medir a área de uma figura, Edson considerou as seguintes unidades de medida de área.
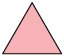
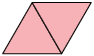
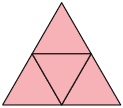
Se ele cobriu essa figura com 10 unidades do tipo C, então quantas unidades do tipo A ele utilizou? E quantas do tipo B?
Respostas: 40 unidades; 20 unidades.
56. Considerando a figura verde como unidade de medida, qual é a medida de área da figura laranja?
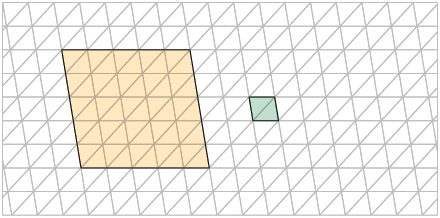
Resposta: 25 unidades.
Página 227
57. Junte-se a um colega para analisarem como Paula obteve a medida de área aproximada de um círculo.
Primeiro, com o auxílio de um compasso, ela traçou duas circunferências iguais, uma em cada malha quadriculada. Em seguida, ela pintou alguns quadradinhos da maneira apresentada a seguir.

Nesta malha quadriculada, Paula coloriu a maior quantidade de quadradinhos limitada pela circunferência.

Nesta outra malha quadriculada, Paula coloriu a maior quantidade de quadradinhos suficiente para cobrir totalmente a área do círculo.
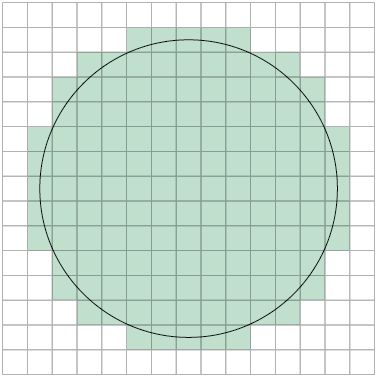
a) Quantos quadradinhos foram coloridos na malha A?
b) Quantos quadradinhos foram coloridos na malha B?
c) Determine o número que substitui as letras A, B e C no texto a seguir adequadamente. Depois faça os cálculos.
Com esse procedimento, Paula concluiu que a medida de área do círculo é maior do que A quadradinhos e menor do que B quadradinhos. Então, ela calculou a média desses números para obter a medida de área aproximada do círculo. Portanto, a área do círculo mede aproximadamente C quadradinhos.
Respostas: a) 97 quadradinhos; b) 137 quadradinhos; c) A: 97; B: 137; C: 117.
58. Junte-se a um colega para calcularem a medida de área aproximada do círculo representado na malha quadriculada. Para isso, usem o quadradinho da malha como unidade de medida de área.

Atenção!
Para determinar a medida da área aproximada do círculo, apliquem uma estratégia semelhante à apresentada na atividade 57.
Resposta: Aproximadamente 79 quadradinhos.
Página 228
Unidades de medidas de área
Estudamos nas páginas anteriores que, se utilizarmos unidades de medida diferentes para medir a área de uma mesma figura, os resultados também serão diferentes. Por isso, foi criada uma unidade de medida padronizada para medir superfícies, o metro quadrado , que corresponde à medida da área de um quadrado cujo comprimento do lado mede .
Usando folhas de jornal, André e Milena construíram um quadrado cuja área mede .

Atenção!
O metro quadrado é usado para expressar a medida da área de terrenos, de quadras esportivas, do piso de uma casa etc.
Dependendo da área a ser medida, também podemos usar submúltiplos e múltiplos do metro quadrado, como o centímetro quadrado e o quilômetro quadrado .
Um centímetro quadrado corresponde à medida da área de um quadrado cujo comprimento do lado mede . Em geral, o centímetro quadrado é usado para medir áreas menores. Na malha a seguir, estão representadas duas figuras e as medidas de suas áreas em centímetro quadrado.
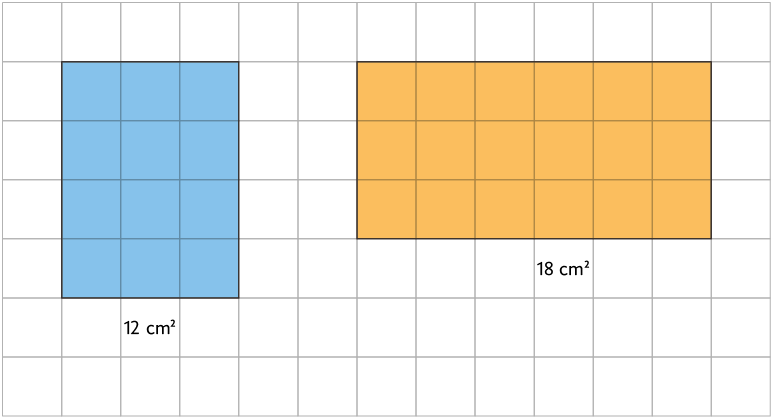
Já o quilômetro quadrado corresponde à medida da área de um quadrado cujo comprimento do lado mede . Em geral, o quilômetro quadrado é usado para medir áreas maiores, como a extensão territorial de um município ou de uma floresta.
Página 229
Atividades
Faça as atividades no caderno.
59. Sabendo que
a área de cada ![]() mede e de cada
mede e de cada ![]() mede , determine as medidas de área das figuras
representadas na malha quadriculada.
mede , determine as medidas de área das figuras
representadas na malha quadriculada.
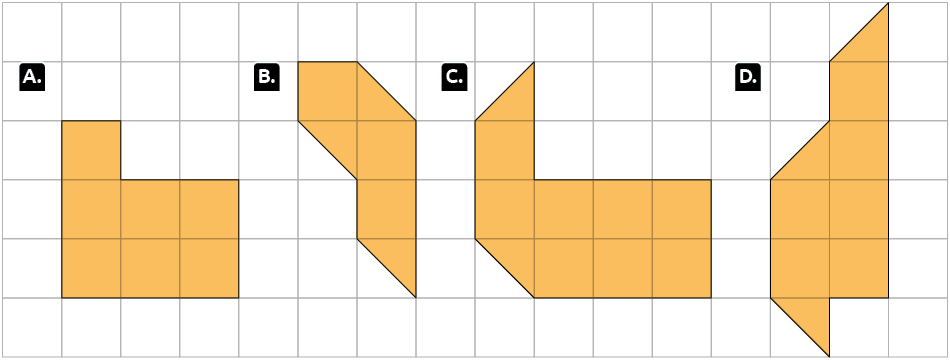
Respostas: A. ; B. ; C. ; D. .
60. Os lados dos quadradinhos da malha a seguir medem de comprimento. Sabendo disso, determine a medida da área e do perímetro da figura representada.
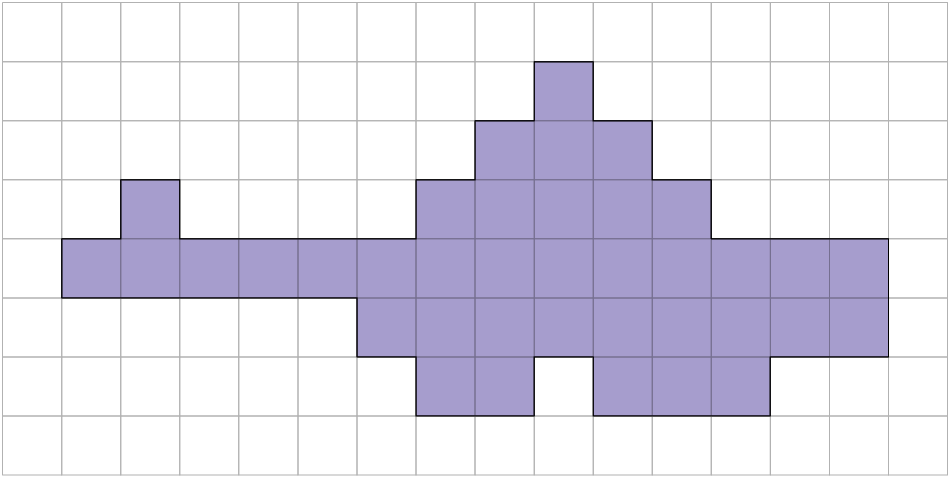
Resposta: A área mede e o perímetro, .
61. Para estimar a quantidade de espectadores em alguns eventos, estima-se que a cada metro quadrado estejam, em média, 4 pessoas. Com base nesse conhecimento, certo show foi realizado em uma região cuja área mede 324 metros quadrados. Sabendo que a área ocupada pelo palco mede e que o restante da região estava lotado, determine a quantidade aproximada de pessoas nesse show.
Resposta: Aproximadamente 1.096 pessoas.
Página 230
62. O gráfico apresenta as informações sobre a medida da área desmatada na Amazônia de 2010 a 2021.
Desmatamento da Amazônia – 2010 a 2021
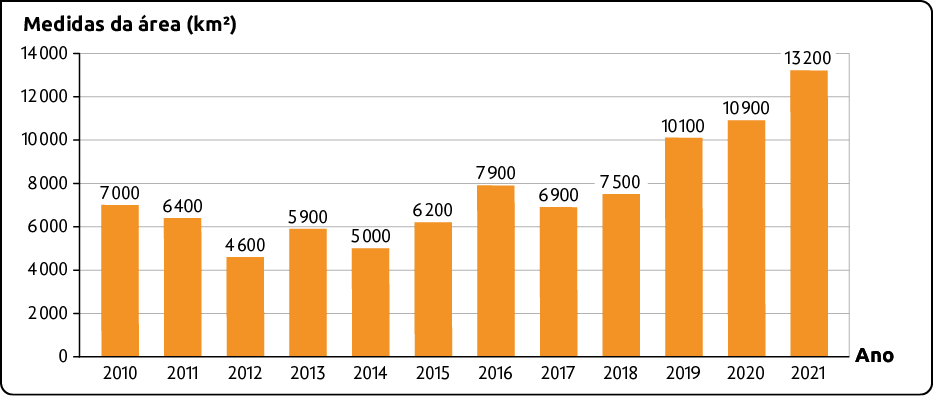
Fonte de pesquisa: TAXAS de desmatamento - Amazônia Legal. Terra Brasilis. Disponível em: https://oeds.link/2dtowM. Acesso em: 7 mar. 2022.
a) Em qual desses anos houve o maior desmatamento na Amazônia? Quanto mede a área desmatada?
b) Quanto mede a área desmatada em 2010?
c) Ao todo, quantos quilômetros quadrados foram desmatados na Amazônia em 2019 e 2020?
d) Em qual desses anos houve o menor desmatamento na Amazônia?
Respostas: a) 2021; ; b) ; c) ; d) 2012.
63. Outra unidade de medida muito usada para medir grandes áreas é o hectare . Comumente usada para expressar a medida da área de chácaras, florestas e fazendas, por exemplo, o hectare é uma unidade de medida agrária.
Qual é a medida da área, em metros quadrados, de uma propriedade de 30 hectares?
Resposta: .
64. Quantos metros quadrados tem um terreno de ?
Resposta: .
65. Além do hectare, no Brasil usa-se o alqueire como unidade de medida agrária não padronizada, que varia conforme a região do país.
alqueire paulista equivale a ;
alqueire mineiro equivale a ;
alqueire da Região Norte equivale a .
Metade de uma propriedade de alqueires mineiros foi reservada para o plantio de café. Da parte restante, metade foi destinada à criação de gado.
a) Qual é a medida da área, em metro quadrado:
dessa propriedade?
destinada ao plantio de café?
destinada à criação de gado?
b) A medida da área destinada à criação de gado corresponde a quantos hectares?
Respostas: a) ; ; ; b) .
66. Um fazendeiro comprou um terreno com 50 alqueires paulistas. Quantos hectares tem esse terreno?
Resposta: .
Página 231
Medida da área do retângulo e do quadrado
Uma professora de Matemática do 6º ano pediu a seus estudantes que calculassem a medida de área de um retângulo cujo comprimento mede e a largura, .
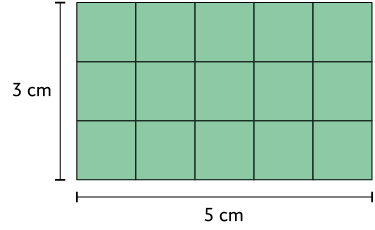
Atenção!
A área de
cada  que compõe esse
retângulo mede .
que compõe esse
retângulo mede .
Mateus e Flávia calcularam a medida da área desse retângulo.


De acordo com os cálculos de Mateus e Flávia, em um retângulo cujas dimensões medem e cabem 15 quadradinhos, cada um medindo . Portanto, a área do retângulo mede .
Para calcular a medida da área de um retângulo, multiplicamos a medida de seu comprimento pela medida de sua largura.
Como no quadrado as medidas dos lados são iguais, podemos calcular a medida da área multiplicando a medida do comprimento de seu lado por ela mesma.
Atenção!
O comprimento e a largura do retângulo (ou do quadrado) devem ser expressos na mesma unidade de medida. Se as medidas estão em , a medida da área será indicada em ; se estão em , a medida da área será indicada em ; e assim por diante.
Página 232
Atividades
Faça as atividades no caderno.
67. Determine
a medida da área e do perímetro do quadrado A e
do retângulo B. Para isso, meça o comprimento
dos lados com uma régua.

Resposta: O perímetro mede 12 cm e a área, .

Resposta: O perímetro mede 11 cm e a área, .
68. Analise a planificação de uma figura geométrica espacial.
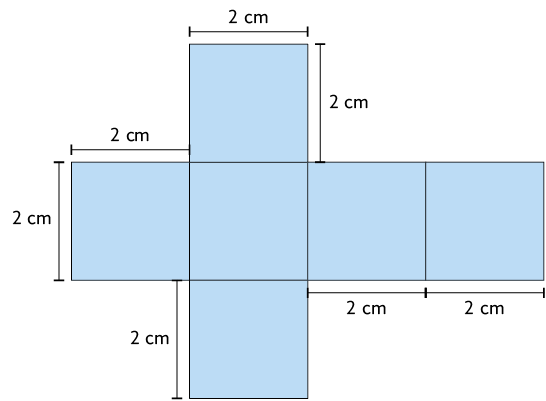
a) Qual é a medida da área dessa planificação?
b) Essa planificação é de qual figura geométrica espacial?
Respostas: a) ; b) Cubo.
69. Considerando as informações apresentadas, determine a medida da largura de cada retângulo.
a) Retângulo cujo comprimento mede e a área, .
b) Retângulo cujo comprimento mede e a área, .
Respostas: a) ; b) .
70. Qual é a medida do comprimento do lado de um quadrado cuja área mede ?
Resposta: .
71. Leia os seguintes anúncios e depois calcule a medida da área de cada terreno. Considere que esses terrenos tenham formato retangular.
A.
Vende-se terreno no Jardim Alvorada cujas dimensões medem e
B.
Terreno
Localizado na Rua das Hortênsias, Jardim Felicidade.
Respostas: A. ; B. .
72. (OBMEP-2010) Com seis retângulos idênticos formamos
um retângulo maior, com um dos lados medindo , como na figura.
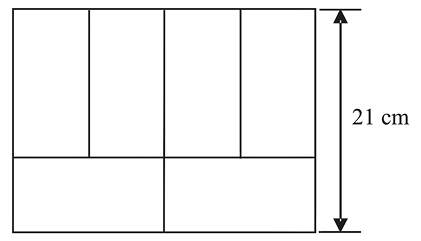
Qual é a área do retângulo maior, em ?
a) 210
b) 280
c) 430
d) 504
e) 588
Resposta: Alternativa e.
73. Elabore um problema envolvendo a medida da área de retângulos. Em seguida, peça a um colega que o resolva. Por fim, verifique se a resposta dele está correta.
Resposta pessoal.
Página 233
74. Analise
os quadrados que Beto desenhou.


Inicialmente, Beto desenhou o quadrado A cujo comprimento do lado mede . Em seguida, ele desenhou o quadrado B. Para isso, ele ampliou a medida do lado do quadrado A.
a) Classifique as afirmações em verdadeira ou falsa.
A medida do comprimento do lado do quadrado B é igual ao dobro da medida do lado do quadrado A.
A medida do perímetro do quadrado A é igual ao dobro da medida do perímetro do quadrado B.
A medida da área do quadrado B é igual ao dobro da medida da área do quadrado A.
A medida do perímetro do quadrado B é igual ao dobro da medida do perímetro do quadrado A.
Respostas: Verdadeira; Falsa; Falsa; Verdadeira.
b) De maneira semelhante à de Beto, construa dois quadrados: quadrado 1, com de comprimento no lado, e quadrado 2, com de comprimento no lado.
Resposta na seção Resoluções.
c) De acordo com o item b, responda às seguintes questões.
Quanto aos quadrados que você construiu, qual é a relação entre as medidas dos comprimentos dos lados?
Quando comparado com a medida do perímetro do quadrado 1, quais mudanças você percebe na medida do perímetro do quadrado 2?
Quando comparada com a medida da área do quadrado 1, quais mudanças você percebe na medida da área do quadrado 2?
Respostas na seção Resoluções.
75. Duas grandezas são diretamente proporcionais se, ao dobrarmos a medida de uma, a da outra também dobra; se, ao triplicarmos a medida de uma, a da outra também triplica; e assim por diante. Com essas informações, responda às questões.
a) A medida do perímetro do quadrado é diretamente proporcional à medida do comprimento de seu lado? Justifique sua resposta.
Resposta: Sim, pois ao dobrarmos a medida do comprimento do lado, a medida do perímetro também dobra; ao triplicarmos a medida do comprimento do lado, a medida do perímetro também triplica; e assim por diante.
b) A medida da área do quadrado é diretamente proporcional à medida do comprimento de seu lado? Justifique sua resposta.
Resposta: Não, pois, ao dobrarmos a medida do comprimento do lado, a medida da área quadruplica, por exemplo.
Página 234
Medida da área do triângulo retângulo
Em um trabalho escolar, Joaquim precisou medir a área de um triângulo retângulo desenhado em uma malha quadriculada. Nessa malha, o lado de cada quadradinho mede . Como não é possível determinar a medida da área desse triângulo contando os quadradinhos um a um, Joaquim desenhou outro triângulo igual, formando assim um retângulo cuja medida da área é igual ao dobro da medida da área do triângulo.
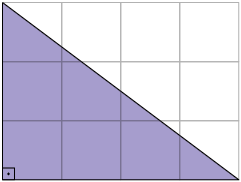
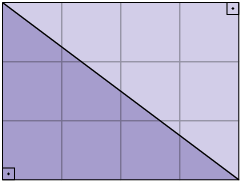
Desse modo, Joaquim concluiu que a medida da área desse triângulo é igual à metade da medida da área do retângulo, ou seja:
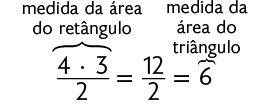
Portanto, a área desse triângulo mede .
Atividades
Faça as atividades no caderno.
76. Determine a medida da área de cada um dos triângulos retângulos a seguir.
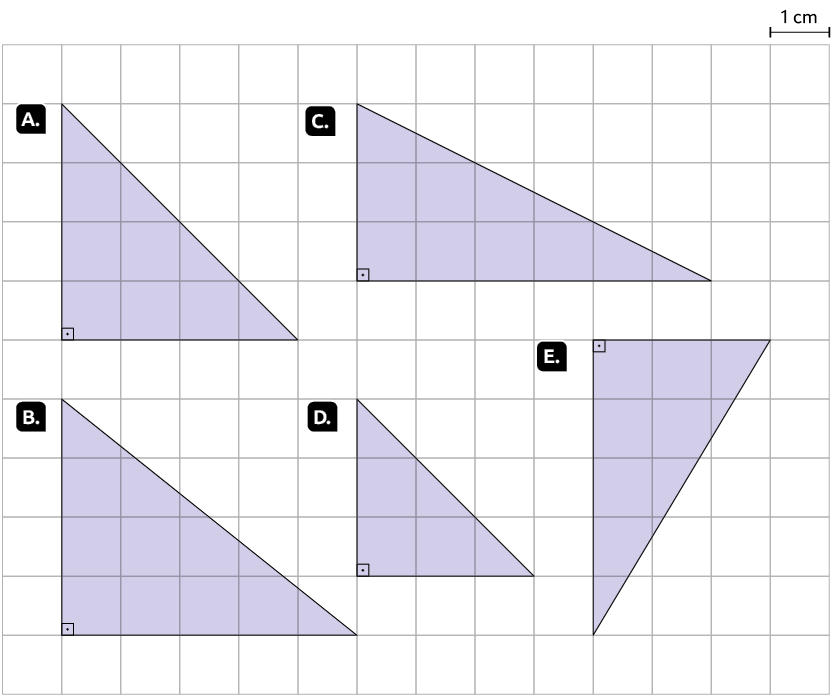
Respostas: A. ; B. ; C. ; D. ; E. .
Página 235
77. O retângulo a seguir foi dividido em 4 triângulos. Calcule a medida da área dos triângulos retângulos A, B e C.
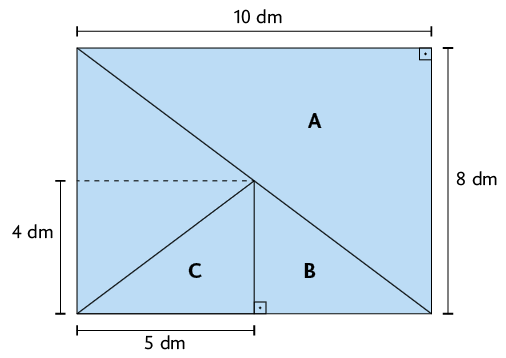
Respostas: A: ; B: ; C: .
78. Calcule a medida da área de cada figura.

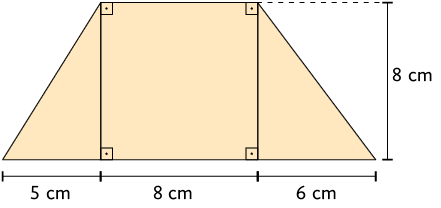

Respostas: A. ; B. ; C. .
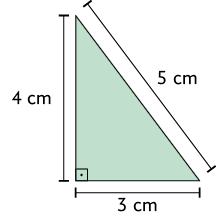
79. O esquema representa um jardim com o formato de um triângulo retângulo.

a) Sabendo que o perímetro desse jardim mede aproximadamente , determine a medida do comprimento do lado AB dele.
b) Qual é a medida da área desse jardim?
Respostas: a) ; b) .
80. Determine a medida da área do triângulo retângulo a seguir, sabendo que seu perímetro mede .
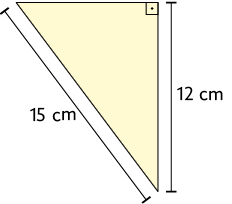
Resposta: .
81. De acordo com a imagem, elabore o enunciado de um problema envolvendo área de triângulos retângulos e, em seguida, dê para um colega resolver. Por fim, verifique se a resolução dele está correta.
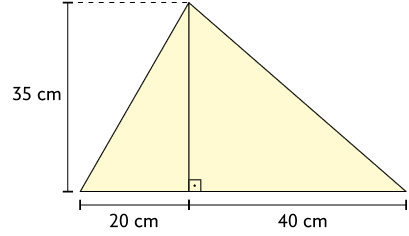
Resposta pessoal.
Página 236
Medidas de volume
Tadeu trabalha em uma loja de calçados e organizou certa quantidade de caixas em uma pilha, conforme apresentado a seguir.
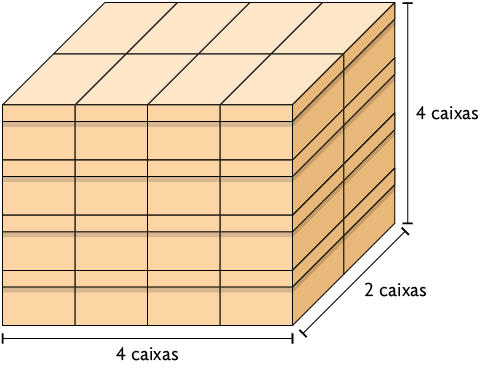
Qual é a medida do volume dessa pilha de caixas de calçados? Para responder a esta pergunta, vamos considerar cada caixa como unidade de medida de volume e determinar a quantidade delas nessa pilha.
1º. Calculamos a quantidade de caixas em cada camada.
2º. Como a pilha é composta de 4 camadas, temos:
Portanto, nessa pilha há 32 caixas de calçados. Assim, o volume dessa pilha mede 32 caixas.
Questão 9. Tadeu acrescentou mais duas camadas com 8 caixas cada uma. Considerando cada caixa como unidade de medida de volume, determine, em seu caderno, a medida do volume que essa pilha passou a ter.
Resposta: 48 caixas.
Para medir o volume de um objeto, foi criada uma unidade de medida padronizada, o metro cúbico . Um metro cúbico corresponde à medida do volume de um cubo cujo comprimento da aresta mede .
Além do metro cúbico, temos os seus múltiplos e submúltiplos para expressar a medida do volume de um objeto. Os submúltiplos mais utilizados são:
- o centímetro cúbico , que corresponde à medida do volume de um cubo cujo comprimento da aresta mede ;
- o decímetro cúbico , que corresponde à medida do volume de um cubo cujo comprimento da aresta mede , ou seja, .

Página 237
Medida do volume do paralelepípedo reto retângulo e do cubo
O paralelepípedo reto retângulo representado a seguir foi construído com cubos com medida de volume de cada.

A medida do volume do paralelepípedo reto retângulo é igual à soma das medidas dos volumes dos cubos. Porém, podemos obter a medida do volume desse paralelepípedo reto retângulo sem precisar contar os cubos um a um e, para isso, procedemos da seguinte maneira:
1º. Calculamos a quantidade de cubos em uma camada.
2º. Esse paralelepípedo reto retângulo é formado por 3 camadas de 20 cubos cada uma. Assim, para calcular a quantidade total de cubos, basta multiplicar o valor obtido anteriormente por 3.
Desse modo, um paralelepípedo reto retângulo, cujas medidas de comprimento, largura e altura são , e , respectivamente, tem a medida do volume igual a 60 cubos de de volume.
Portanto, o volume desse paralelepípedo reto retângulo mede .
Para obtermos a medida do volume de um paralelepípedo reto retângulo, multiplicamos a medida do comprimento, da largura e da altura dele.
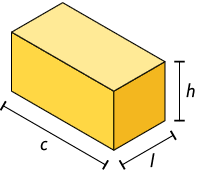
- c: medida do comprimento;
- l: medida da largura;
- h: medida da altura.
O cubo é um caso particular de paralelepípedo reto retângulo, em que o comprimento, a largura e a altura têm a mesma medida.
Para calcular a medida do volume de um cubo, basta calcular a medida do comprimento da aresta elevada ao cubo.
Atenção!
O comprimento, a largura e a altura do paralelepípedo reto retângulo (ou do cubo) devem ser expressos na mesma unidade de medida. Se as medidas estão em , a medida da área será indicada em ; se estão em , a medida da área será indicada em ; e assim por diante.
Página 238
Atividades
Faça as atividades no caderno.
Atenção!
Nas atividades 82 e 83, não há cubos atrás das pilhas.
82. Determine a medida do volume de cada pilha
usando o ![]() como unidade de medida.
como unidade de medida.

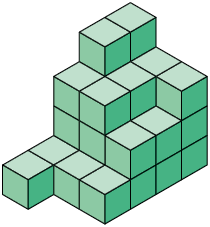
Respostas: A. 45 cubos; B. 31 cubos.
83. A medida do comprimento da aresta de cada cubo da pilha a seguir é .
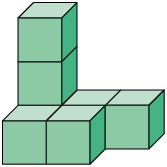
Quantos cubos iguais a esses faltam para que o volume total da pilha meça ?
Resposta: 8 cubos.
84. Determine a medida do volume dos paralelepípedos retos retângulos.
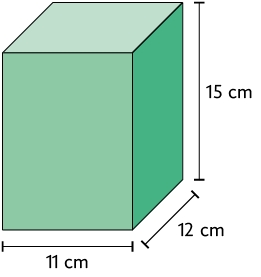

Respostas: A. ; B. .
85. A figura
é composta de paralelepípedos retos retângulos. Calcule, em metros cúbicos, a
medida de seu volume.
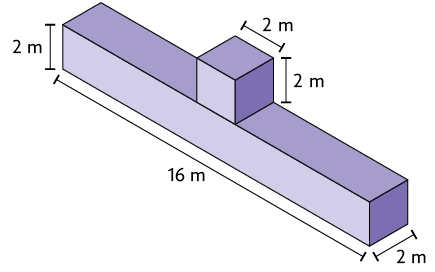
Resposta: .
86. As medidas indicadas na caixa azul correspondem às suas dimensões internas. No máximo, quantos cubos vermelhos cabem nessa caixa?

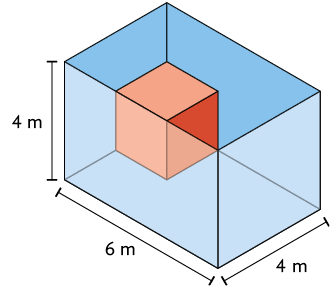
Resposta: 12 cubos.
87. Elabore o enunciado de um problema envolvendo volume e a figura apresentada a seguir, composta de paralelepípedos retos retângulos. Depois, dê para um colega resolver. Por fim, verifique se a resposta está correta.
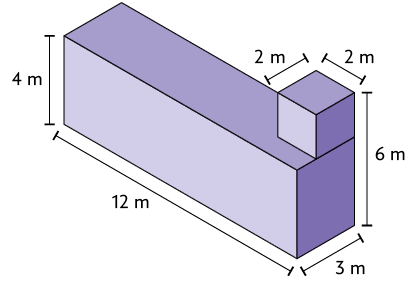
Resposta pessoal.
Página 239
Medidas de capacidade
Geralmente, as medidas de capacidade são usadas para indicar a quantidade de líquido ou gás que pode ser depositado em um recipiente, ou seja, a capacidade de um recipiente é igual a seu volume interno. As unidades de medida de capacidade mais utilizadas são o litro e o mililitro , o qual é um submúltiplo do litro.
A seguir estão representados alguns exemplos de produtos comercializados em litro e em mililitro.
Imagens não proporcionais entre si.




Podemos relacionar as unidades de medida de capacidade e de volume. Um recipiente cujo volume interno mede , por exemplo, tem capacidade de . Nesse caso, temos:
Conversão de unidades de medida de capacidade
Para escrever em mililitros, fazemos:
Portanto,
Podemos também converter uma medida em mililitros em uma medida em litros. Para isso, fazemos:
Portanto,
Também podemos expressar uma medida de capacidade em litros expressa com número decimal em uma medida em litros e mililitros, por exemplo:
Portanto,
Página 240
Atividades
Faça as atividades no caderno.
88. Escreva no caderno a unidade mais adequada, litro ou mililitro, para expressar a medida de capacidade de:
a) um copo de água;
b) um balde;
c) uma piscina;
d) um frasco de perfume;
e) uma caixa-d'água;
f) uma xícara de café.
Respostas: a) Mililitro; b) Litro; c) Litro; d) Mililitro; e) Litro; f) Mililitro.
89. Escreva as medidas indicadas em mililitros.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h)
90. Escreva as medidas indicadas em litros e mililitros.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
91. Considere as medidas de capacidade apresentadas a seguir.
Agora, copie a sequência em seu caderno substituindo cada por uma das medidas apresentadas, de maneira que a sequência fique em ordem crescente.
Resposta:
92. Raul e sua família foram acampar em um camping, localizado na cidade de Bonito, no estado do Mato Grosso do Sul. Ele levou, entre outros materiais, 3 recipientes com de água mineral cada um e 2 recipientes de cada um.
Sabendo que no final do acampamento sobrou 1 recipiente com , quantos litros de água foram consumidos? Escreva a medida que você obteve em mililitros.
Resposta: ; .
93. Uma casa de suco natural produziu de suco de laranja. Esse suco foi colocado em garrafas cuja capacidade mede
a) Quantas garrafas de suco de laranja foram produzidas?
b) Sabendo que a casa de suco vendeu todas as garrafas por R$ 9,00 cada uma, determine o valor arrecadado com essa venda.
c) Se o suco produzido fosse colocado em garrafas com capacidade de cada, quantas garrafas seriam necessárias?
d) Elabore um problema envolvendo os dados desse problema e dê para um colega resolver. Depois, verifique se ele resolveu corretamente.
Respostas: a) 50 garrafas; b) R$ 450,00; c) 100 garrafas; d) Resposta pessoal.
94. Renato começou a encher uma piscina de plástico cuja capacidade mede . A torneira da casa dele despeja de água por minuto.
a) Se ele deixar a torneira aberta por 150 minutos, a piscina vai ficar totalmente cheia? Caso contrário, quantos litros de água a piscina terá?
b) Quantas horas de torneira aberta é preciso para encher a piscina?
Respostas: a) Não; ; b) .
Página 241
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. O comprimento da fila de carros de certo congestionamento mede . Nessa fila, cada veículo ocupa uma medida de comprimento (considerando o distanciamento entre eles) de , em média. Quantos carros, aproximadamente, há nessa fila?
Resposta: Aproximadamente 714 carros.
2. As baleias são os maiores animais do planeta. Analise a medida do comprimento aproximada que algumas espécies de baleia atingem na fase adulta.
|
Espécies |
Medida do comprimento |
|---|---|
|
Baleia-azul |
33 |
|
Baleia-corcunda (jubarte) |
18 |
|
Baleia-cinzenta |
15 |
|
Baleia-branca (beluga) |
5 |
Fonte de pesquisa: NOAA Fisheries. Disponível em: https://oeds.link/gYHwL4. Acesso em: 10 mar. 2022.
a) Quantos metros a baleia-azul pode atingir a mais do que a baleia-branca?
b) Entre essas espécies de baleia, qual pode atingir a medida de comprimento mais próxima de ?
c) A medida de comprimento que a baleia-azul pode atingir é, aproximadamente, quantas vezes maior do que a da baleia-cinzenta?
d) Quais das espécies atingem medida de comprimento com de diferença uma da outra?
2. Respostas: a) ; b) Baleia-cinzenta; c) Aproximadamente 2 vezes; d) Baleia-corcunda e baleia-cinzenta.
3. As medidas das dimensões de um campo oficial de futebol podem variar da seguinte maneira:
comprimento: de a ;
largura: de a .
De acordo com essas informações, qual é a maior e a menor medida do perímetro que um campo de futebol pode ter?
Resposta: e .
4. Consulte um calendário do ano vigente e responda às questões.
a) Este ano tem o dia 29 de fevereiro?
b) Qual dia da semana corresponde ao 1º dia deste ano?
c) Qual dia da semana corresponde ao último dia deste ano?
d) Quantos dias há no 1º semestre deste ano?
Resposta: As respostas dependem do ano vigente.
5. Escreva em uma folha de papel avulsa dois anos bissextos:
a) entre os anos de 2017 e 2027;
b) terminados em 00 e anteriores ao ano 2500.
Respostas: a) 2020 e 2024; b) 2400 e 2000.
6. Renato comprou um sítio de 60 hectares no qual vai plantar frutas, arroz e milho.
a) Qual é a medida da área, em metro quadrado, do sítio de Renato?
b) Nesse sítio, o plantio de frutas vai ocupar 30% da área, o plantio de arroz, 20%, e o plantio de milho, 50%. Calcule, em hectares e em metros quadrados, a medida da área para cada tipo de plantio.
c) Quantos alqueires paulistas, aproximadamente, são destinados ao plantio de frutas?
Respostas: a) ; b) Fruta: ou ; arroz: ou ; milho: ou ; c) 7,4 alqueires paulistas.
Página 242
7. (OBMEP-2006) A figura é formada por três quadrados, um deles com área de e o outro com . Qual é o perímetro da figura?
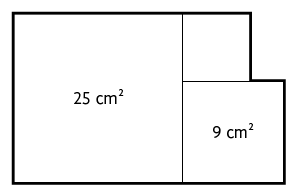
a)
b)
c)
d)
e)
Resposta: Alternativa d.
8. (OBMEP-2007) Nanci tem seis quadrados de cartolina iguais, como na figura I. Com essas cartolinas ela montou a figura II. Qual é a área dessa figura?
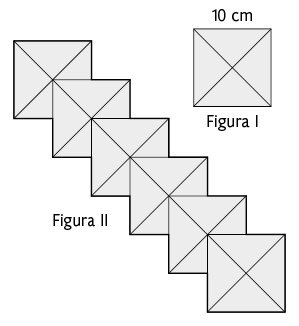
a)
b)
c)
d)
e)
Resposta: Alternativa b.
9. Em cada comprimido de certo medicamento a medida da massa do componente principal é . Qual é a medida da massa, em gramas, do componente principal desse medicamento em uma embalagem com 30 comprimidos?
Atenção!
Lembre-se:
Resposta:
10. Quando nasceu, a medida da massa de Flávia era . Com um mês de idade, sua massa media . Em seu primeiro mês de vida, quantos gramas a medida da massa de Flávia aumentou?
Resposta: .
Atenção!
Nas atividades 11 e 12, não há cubos atrás das pilhas.
11. Calcule a medida do volume do empilhamento
a seguir usando 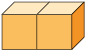 como unidade de
medida.
como unidade de
medida.
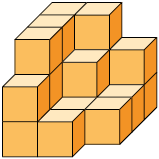
Resposta: 11 unidades.
12. Qual é a medida do volume, em centímetros cúbicos, do empilhamento de cubos a seguir?
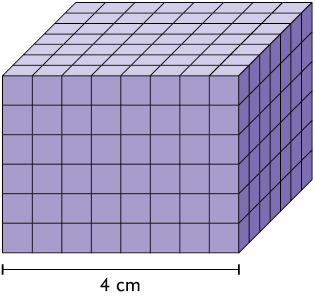
Resposta: .
13. Paulo comprou garrafas com de suco de uva cada. Ele deseja armazenar esse suco em garrafas com medida de capacidade de . Quantas garrafas serão necessárias para armazenar esse suco?
Resposta: 25 garrafas.
14. Ângela vai fazer gelatina de sobremesa para sua família. De acordo com o modo de preparo, para fazer cada envelope de gelatina, é necessário dissolver o conteúdo em de água.
Quantos litros de água serão necessários para Ângela dissolver o conteúdo de envelopes de gelatina?
Resposta: .