Página 187
UNIDADE
8
Grandezas e medidas

Agora vamos estudar...
- algumas grandezas e suas respectivas medidas;
- o Sistema Internacional de Unidades (SI);
- medidas de área;
- medidas de volume.
Página 188
Grandezas
Não é de hoje que situações envolvendo medidas de grandezas são essenciais no cotidiano das pessoas. A seguir são apresentadas algumas medidas necessárias em atividades diárias.
Medida de comprimento

Medida de capacidade

Medida de massa
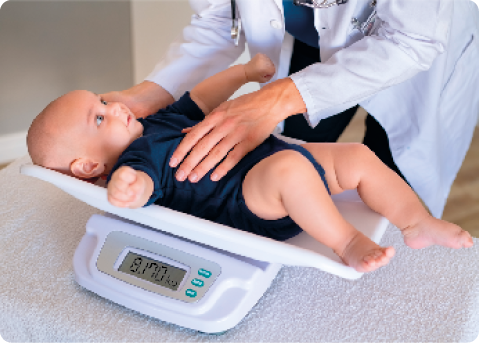
Medida de temperatura
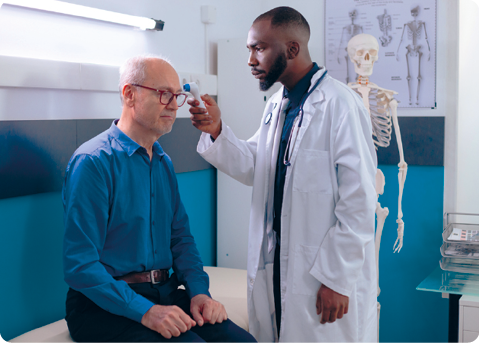
Questão 1. Escreva em seu caderno outras atividades cotidianas em que são usadas medidas.
Grandeza é tudo aquilo que pode ser medido, como comprimento, capacidade, massa, temperatura e velocidade.
Página 189
Questão 2. Escreva em seu caderno outros exemplos de grandezas.
Uma grandeza pode ser classificada em discreta ou contínua. A grandeza discreta é aquela cuja medida é sempre um número inteiro, como a quantidade de carros em um estacionamento e a quantidade de jogadores de um time de futebol.
A grandeza contínua é aquela que admite como medida um número qualquer, como a altura de uma pessoa e a duração de intervalo de tempo de uma corrida de atletismo.
Para representar a medida de uma grandeza, podemos usar um número seguido de uma unidade de medida. Nesse caso, esse número é resultante do processo de medição, ou seja, a medida da grandeza. Exemplos:
-
medida de comprimento
-
medida de massa
-
medida de capacidade
-
medida de tempo
Os números 300; 4,5; 250 e 24 são as medidas das grandezas, enquanto , , e são as unidades de medida utilizadas para expressar a medida dessas grandezas.
Entende-se por medir a ação de comparar uma grandeza com outra de mesma espécie, em que uma delas é escolhida como unidade de medida, como dois comprimentos ou duas massas.
Atenção!
Também é possível comparar duas grandezas de mesma espécie sem efetuar a medição delas. Por exemplo, para comparar a altura de duas pessoas sem realizar medições, podemos colocar uma de costas para a outra e analisar qual delas é a mais alta.
Lucas mediu o comprimento de um lápis, como representado na imagem.

Lucas escolheu o centímetro () como unidade de medida e comparou o comprimento do lápis com o da medida de . Nessa comparação, o comprimento cuja medida é cabe vezes no comprimento do lápis. Portanto, o comprimento do lápis de Lucas mede .
Em medições empíricas, a medida obtida é sempre um valor aproximado, em que a precisão do resultado depende do instrumento de medida utilizado.
Questão 3.
Determine, com uma régua em centímetro, a medida do
comprimento da linha apresentada a seguir.

Página 190
Sistema Internacional de Unidades (SI)
Em determinadas épocas, cada grupo social tinha o próprio sistema de unidades de medida, sendo algumas delas baseadas em partes do corpo do rei. Para compreender melhor, estão representadas nas imagens as indicações de algumas delas com base no corpo de Henrique.

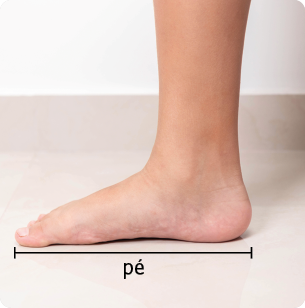


Imagens não proporcionais entre si.
Com a integração entre pessoas de diferentes regiões e países e por causa do avanço da ciência e do comércio, essas unidades acabaram tornando as relações de bases econômicas e científicas muito complexas, além da dificuldade pela imprecisão dos critérios.
Para resolver a situação, a França aprovou em 1790 a unificação dos pesos e das medidas, sendo o metro a unidade de base para comprimento e o quilograma, para a massa. Com o passar dos anos, esse sistema passou a ser adotado por outros países e novas unidades de base para outras grandezas foram acrescentadas, formando o atual Sistema Internacional de Unidades (SI). No quadro a seguir estão apresentadas unidades de medida de base utilizadas no SI.
|
Grandeza |
Unidades de base |
|
|---|---|---|
|
Nome |
Símbolo |
|
|
Comprimento |
metro |
|
|
Massa |
quilograma |
|
|
Tempo |
segundo |
|
|
Intensidade de corrente elétrica |
ampère |
|
|
Temperatura termodinâmica |
kelvin |
|
|
Quantidade de matéria |
mol |
|
|
Intensidade luminosa |
candela |
|
Página 191
Questão 4. Algumas unidades de medidas já tiveram sua definição modificada. Junte-se a um colega e faça uma pesquisa a respeito da necessidade da última mudança da definição do quilograma, ocorrida em 2019.
Atenção!
A pesquisa proposta na questão 4 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar de que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Além das unidades apresentadas, há as unidades derivadas, que são formadas pelas relações entre as unidades de base. Existem também as unidades de medidas suplementares, que têm unidades especiais.
Por exemplo, a unidade de medida da grandeza velocidade "metro por segundo" é derivada, pois é formada pela relação entre as unidades de base metro e segundo. Por esse motivo, o símbolo utilizado é . Já a unidade de medida de capacidade "mililitro", cujo símbolo é , é uma unidade suplementar, pois não é derivada das unidades de base.
Atividades
Faça as atividades no caderno.
1. Relacione uma grandeza (comprimento, massa, capacidade, temperatura, tempo e velocidade) com uma situação cotidiana indicada nos itens.






Página 192
2. Classifique as grandezas a seguir em discreta ou contínua.
a) Tempo de duração de uma partida de futebol.
b) Quantidade de convidados para uma festa.
c) Quantidade de animais de uma fazenda.
d) Salário mensal recebido por um trabalhador.
e) Quantidade de suco em uma jarra.
f) Massa de uma embalagem com café.
g) Capacidade de um copo.
h) Comprimento de uma mesa.
i) Quantidade de computadores em uma empresa.
3. Escreva em seu caderno o nome de um instrumento de medida utilizado para medir a grandeza:
a) tempo.
b) capacidade.
c) temperatura.
d) massa.
e) comprimento.
4. Analise a imagem a seguir e indique qual é a fruta com massa de maior medida: a melancia ou o melhão.

5. As informações a seguir mostram o resultado obtido por Ana, Fred e Lucas ao medir o comprimento da lousa com o palmo.
|
Estudante |
Resultado |
|---|---|
|
Ana |
7 palmos |
|
Fred |
8 palmos |
|
Lucas |
6 palmos |
Qual deles tem o palmo com maior medida de comprimento? Escreva uma justificativa em seu caderno.
6. Copie a ficha técnica a seguir em seu caderno. Depois, com os números apresentados e por meio de estimativas, complete-a.
-
25
-
60
-
350
-
1,7
|
Grandeza |
Medida |
Unidade de medida |
|---|---|---|
|
Altura |
||
|
Massa |
||
|
Tempo médio de vida |
anos |
|
|
Velocidade média de corrida |
7. Escreva em seu caderno as medidas apresentadas utilizando uma unidade de base do SI.
a)
b)
c)
d)
e)
f)
Atenção!
Página 193
Medidas de área
Em algumas situações cotidianas, é necessário medir áreas. Por exemplo, para determinar a quantidade de lajotas necessárias em um revestimento de piso, é preciso obter a medida da área desse piso.
Para medir áreas, devemos estabelecer uma unidade de medida de área.
Analise alguns exemplos.

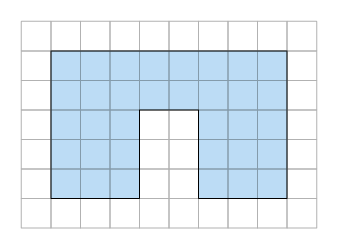




Para medir as áreas dessas figuras, foram usados ![]() ,
,
![]() e
e
![]() ,
que são unidades de medidas não padronizadas. No entanto, existe uma unidade de
medida padronizada para expressar medidas de área: o metro
quadrado .
,
que são unidades de medidas não padronizadas. No entanto, existe uma unidade de
medida padronizada para expressar medidas de área: o metro
quadrado .
Página 194
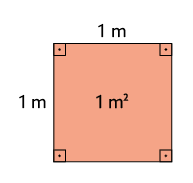
Um metro quadrado corresponde à medida da área de um quadrado cujo comprimento do lado mede .
Há ainda os múltiplos do metro quadrado, geralmente usados para expressar medidas de grandes áreas, como a de uma fazenda, e os submúltiplos do metro quadrado, que geralmente são utilizados para medir pequenas áreas, como a da superfície de um lenço de tecido.
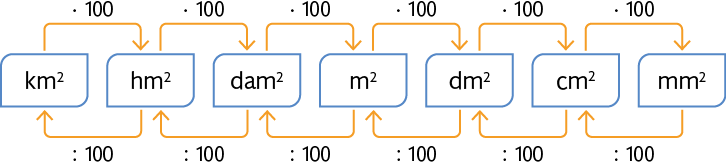
O esquema apresenta a relação entre o metro quadrado e seus múltiplos: decâmetro quadrado , hectômetro quadrado e quilômetro quadrado – e submúltiplos – decímetro quadrado , centímetro quadrado e milímetro quadrado .
Vamos usar duas maneiras de transformar a medida da área do quadrado apresentado no início desta página para centímetros quadrados.
Utilizando a relação .
Utilizando o esquema.
1º. Transformando metros quadrados em decímetros quadrados. Para isso, efetuamos uma multiplicação por 100.
2º. Transformando decímetros quadrados em centímetros quadrados. Para isso, efetuamos uma multiplicação por 100.
Atenção!
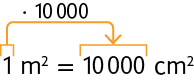
Para transformar metros quadrados em centímetros quadrados, basta multiplicar por duas vezes, ou seja, .
Portanto:
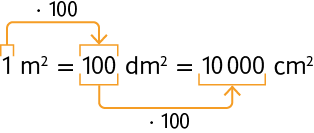
ou
Questão 5. Escreva em seu caderno em decâmetro quadrado.
Página 195
Atividades
Faça as atividades no caderno.
8. Considerando o quadradinho da malha como unidade, determine a medida de área de cada uma das figuras.

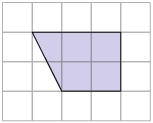

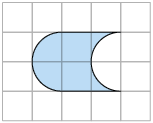
9. Algumas figuras foram representadas na malha triangular.

a) Considerando o triângulo da malha como unidade de medida, meça a área de cada uma das figuras.
b) Qual figura tem a menor medida de área? E qual tem a maior?
c) Quais figuras têm áreas de mesma medida?
10. Quantos decímetros quadrados cabem em um metro quadrado?
11. O hectare é uma unidade de medida de área utilizada para medir superfícies agrárias e equivale a . Qual é a medida em hectare da área de um sítio de ?
12. Qual múltiplo do metro quadrado apresentado no esquema da página anterior equivale a um hectare?
13. Indique qual unidade de medida de área é mais adequada para expressar a medida:
a) da área de um terreno residencial.
b) da extensão territorial de um país.
c) da área da tela de um smartphone.
d) da área da superfície de um botão de roupa.
e) da área de um campo de futebol profissional.
f) da área construída de um apartamento.
14. Em uma malha quadriculada, escreva uma medida de área utilizando o quadradinho da malha como unidade de medida. Em seguida, troque a malha com um colega e peça a ele que construa duas figuras geométricas planas diferentes cuja área tenha a medida indicada por você. Depois, verifique se as figuras desenhadas estão de acordo com o que você solicitou.
Página 196
Medida da área do retângulo
Roberto decidiu revestir o piso da sala de sua casa, que tem formato retangular, cujas medidas das dimensões são por , com lajotas de por . Como é possível determinar a quantidade necessária de lajotas? Uma das maneiras é representar o formato da sala em uma malha quadriculada e, em seguida, efetuar uma multiplicação.
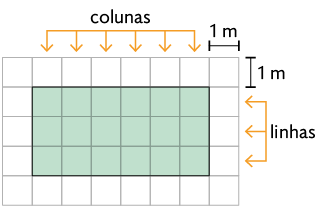
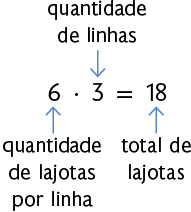
ou
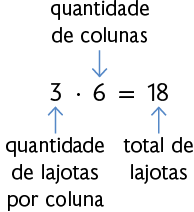
De acordo com esses cálculos, serão necessárias lajotas. Sabendo disso, podemos determinar a medida da área da sala da casa de Roberto. Como a área de cada lajota mede , concluímos que a área da sala mede .
Para calcular a medida da área A de um retângulo, basta multiplicar a medida de seu comprimento pela medida de sua largura.


Como o quadrado é um caso particular do retângulo, em que os lados têm comprimentos de mesma medida, obtemos:

Nesse caso, A e indicam, respectivamente, a medida da área e do comprimento do lado do quadrado.
Equivalência entre medidas de área
Existem figuras que podem ser decompostas em retângulos. Para calcular a medida da área de uma dessas figuras, podemos determinar a medida da área de cada um dos retângulos que a compõe e, em seguida, adicionar as medidas obtidas. Para compreender melhor, vamos mostrar como é possível calcular a medida da área da figura apresentada na próxima página.
Página 197
Figura inicial
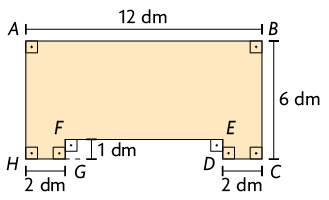
Figura decomposta em retângulos
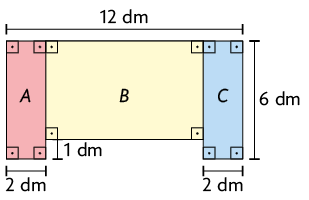
- Inicialmente, foi realizada a decomposição dessa figura em retângulos.
- Os retângulos A e C têm dimensões medindo e . Nesse caso, a medida da área de cada um deles é:
Já o retângulo B tem dimensões medindo e . Nesse caso, sua área mede:
Por fim, foram adicionadas as medidas obtidas.
Portanto, a área da figura mede .
Medida da área do paralelogramo
Vamos calcular a medida da área do paralelogramo , cujo comprimento da base mede b e cuja altura mede h. Para isso, inicialmente, realizamos a decomposição do paralelogramo para obter um triângulo retângulo. Em seguida, fazemos uma recomposição, sem perda e sobreposição, formando um retângulo.
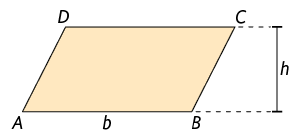
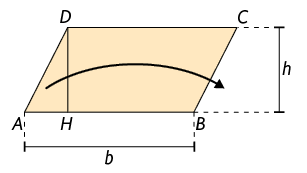
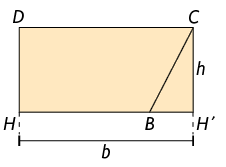
Assim, a medida da área do paralelogramo obtida é igual à medida da área do retângulo .
Para calcular a medida da área A de um paralelogramo em que o comprimento da base mede b e a altura mede h, fazemos:
Página 198
Vamos calcular, por exemplo, a medida da área de um paralelogramo cujo comprimento da base mede e cuja altura mede .
Portanto, a área desse paralelogramo mede .
Medida da área do triângulo
Considere o triângulo .
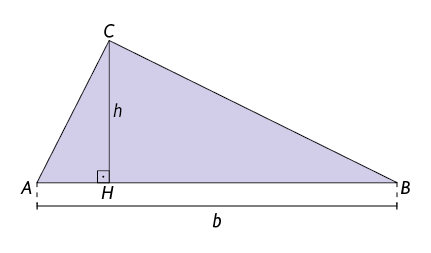
Atenção!
A altura de um triângulo é um segmento de reta que liga um vértice ao lado oposto (ou ao seu prolongamento), formando, assim, um ângulo reto. Nesse caso, esse lado oposto é chamado base do triângulo. Um triângulo tem três alturas, cada uma relativa a determinado lado.
Ao considerar que a base desse triângulo seja o lado , o comprimento da base do triângulo nesse caso mede b e o comprimento da altura mede h. Com isso, vamos determinar a medida da área desse triângulo.
Para isso, inicialmente, consideramos um novo triângulo igual ao e, consequentemente, com mesma medida de área. Em seguida, utilizando esses triângulos, sem perda e sobreposição, realizamos uma composição para obter o paralelogramo .
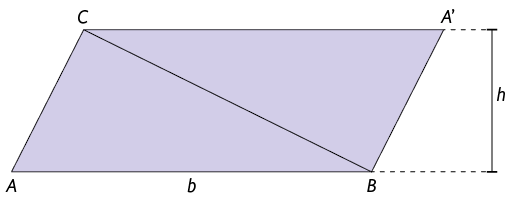
Atenção!
No paralelogramo , b é a medida do comprimento da base e h é a medida da altura.
Assim, a medida da área do triângulo é igual à metade da medida da área do paralelogramo .
Para calcular a medida da área A de um triângulo, em que o comprimento da base mede e o comprimento da altura mede , basta fazer:
Vamos calcular, por exemplo, a medida da área de um triângulo cujo comprimento da base mede e cuja altura mede .
Portanto, a área desse triângulo mede .
Página 199
Medida da área do trapézio
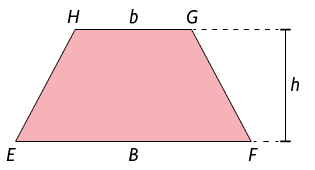
Considere o trapézio .
Atenção!
Os lados paralelos do trapézio são chamados bases, sendo um deles a base maior e o outro, a base menor.
Nesse trapézio, h é a medida da altura, B é a medida do comprimento da base maior e b é a medida do comprimento da base menor. Com isso, vamos determinar a medida da área dessa figura.
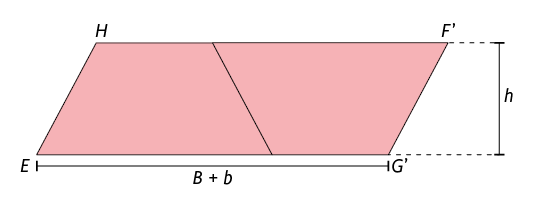
Para isso, inicialmente, consideramos um novo trapézio igual ao e, consequentemente, de mesma medida de área. Em seguida, utilizando essas figuras, sem perda e sobreposição, realizamos uma composição para obter o paralelogramo .
Atenção!
No paralelogramo , é a medida do comprimento da base e h é a medida da altura.
Assim, a medida da área do trapézio é igual à metade da medida da área do paralelogramo .
Para calcular a medida da área A de um trapézio cuja altura mede h, o comprimento da base maior mede B e o da base menor mede b, efetuamos:
Vamos calcular, agora, a medida da área do trapézio representado a seguir.

Atenção!
Nesse trapézio, a altura mede , a base menor, e a base maior, .
Portanto, a área desse trapézio mede .
Página 200
Atividades
Faça as atividades no caderno.
15. Calcule a medida da área de cada um dos retângulos representados a seguir.


16. O piso de uma piscina olímpica tem formato retangular cuja largura e comprimento medem, respectivamente, e . Quantos metros quadrados de azulejos serão necessários para revestir o piso dessa piscina?
17. Em uma malha quadriculada, construa um retângulo cuja área meça:
a) .
b) .
c) , em que o comprimento mede .
d) mais do que .
Versão adaptada acessível
17. Em um Geoplano, represente um retângulo cuja área meça:
a) .
b) .
c) , em que o comprimento mede .
d) mais do que .
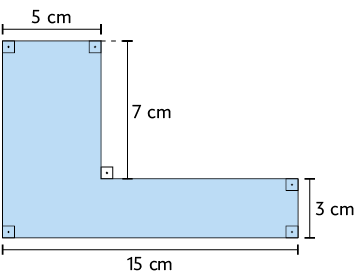
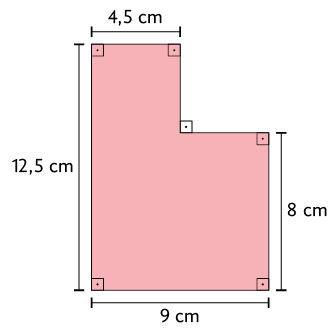
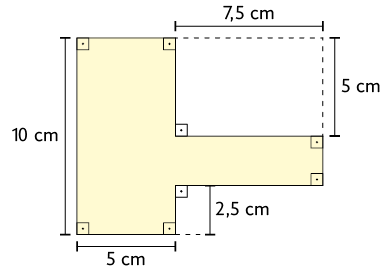
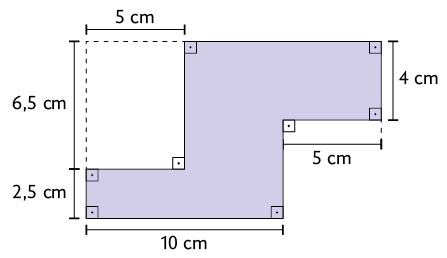
18. Os polígonos representados a seguir podem ser decompostos em retângulos. Calcule a medida da área de cada um desses polígonos.
Página 201
19. Para a construção de uma área de lazer em um terreno retangular, Marcela planejou uma divisão do terreno como representado a seguir.
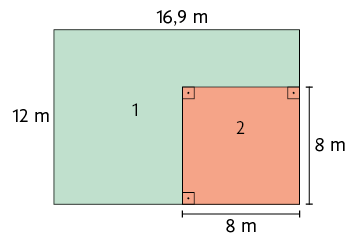
Qual é a medida da área da região 1? E da região 2?
20. Antônio vai revestir uma parede com lajotas, como a representada a seguir.
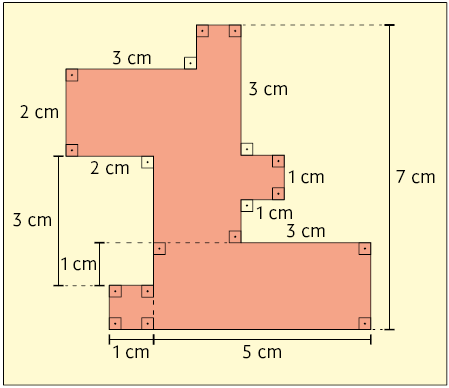
De acordo com as medidas em centímetros indicadas na imagem, determine a medida da área da figura presente em cada uma das lajotas.
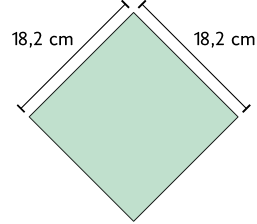
21. Qual figura tem a maior medida de área: um retângulo cujas dimensões medem e ou um quadrado cujo comprimento do lado mede ?
22. Determine a medida do comprimento da base de um paralelogramo cuja área mede e cuja altura mede .
23. Na
figura a seguir,
é um paralelogramo,
é um retângulo e é um ponto de . Determine a medida
da área da figura ,
sabendo que a área do retângulo mede .
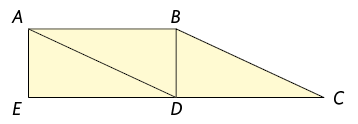
Na figura, .
24. Calcule a medida da área de cada paralelogramo.




Página 202
25. O paralelogramo e o retângulo representados a seguir têm alturas de mesma medida. Além disso, tem-se . O que é possível afirmar em relação às medidas das áreas dessas figuras? Justifique sua resposta.

26. Marta e Gilberto pretendem comprar um terreno cuja área mede no mínimo . A seguir estão representados dois terrenos em formato de paralelogramo que um corretor apresentou para eles.

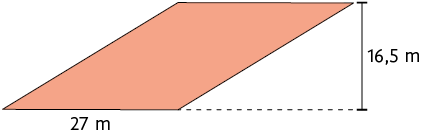
Entre os terrenos apresentados, qual Marta e Gilberto devem escolher? Justifique sua resposta.
27. Elabore um problema envolvendo a medida da área de um paralelogramo e o entregue para um colega resolver. Depois, verifique se o problema foi resolvido corretamente.
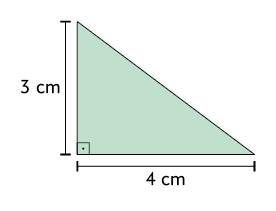
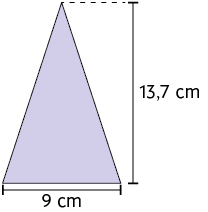
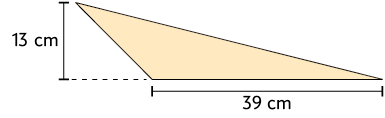
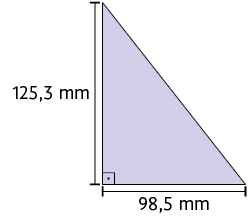
28. Calcule a medida da área de cada triângulo.

29. Elabore um problema envolvendo a medida da área de uma figura que pode ser decomposta em retângulos e triângulos. Em seguida, dê para um colega resolver e verifique se a resposta obtida está correta.
Página 203
30. A placa de sinalização representada a seguir é utilizada em edificações para indicar saídas de emergência.
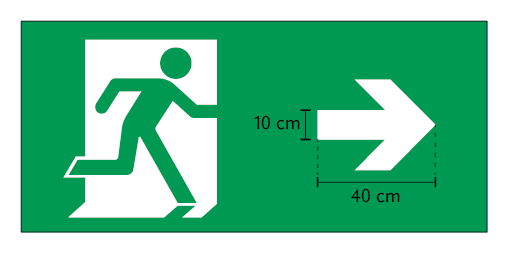
Com base nas medidas indicadas, é possível determinar a medida da área da seta? Justifique sua resposta.
31. Faça o cálculo da medida da área de cada trapézio.


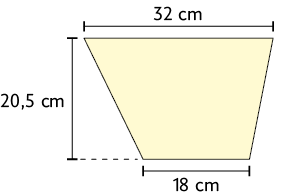
Compare os resultados que você obteve nos cálculos e responda aos itens.
a) Qual deles tem maior medida de área?
b) Quais deles têm medidas de áreas iguais?
32. Elabore um problema envolvendo a medida da área de um trapézio e peça a um colega que o resolva. Depois, verifique se ele foi resolvido corretamente.
33. (Enem–2015) O esquema I mostra a configuração de uma quadra de basquete. Os trapézios em cinza, chamados de garrafões, correspondem a áreas restritivas.

Visando atender às orientações do Comitê Central da Federação Internacional de Basquete (Fiba) em 2010, que unificou as marcações das diversas ligas, foi prevista uma modificação nos garrafões das quadras, que passaram a ser retângulos, como mostra o esquema II.

Após executadas as modificações previstas, houve uma alteração na área ocupada por cada garrafão, que corresponde a um(a):
a) aumento de .
b) aumento de .
c) aumento de .
d) diminuição de .
e) diminuição de .
Página 204
Noções de volume
Um tijolo, uma bola de futebol, um monte de areia e um livro são objetos tridimensionais que ocupam uma porção do espaço.




Aos objetos tridimensionais e às figuras geométricas espaciais, podemos associar o volume, que é uma grandeza, assim como comprimento, área, massa ou temperatura.
Logo, o volume de um objeto pode ser medido, o que depende de suas dimensões, e não da massa. Para medir a grandeza volume, é necessário estabelecer uma unidade de medida.
Considere as pilhas de cubo a seguir.
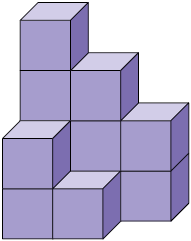
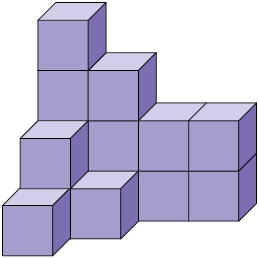
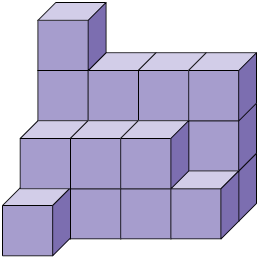
Questão 6. Sabendo que não há cubos ocultos atrás da pilha, escreva em seu caderno a quantidade de cubos que há em cada uma delas.
Considerando o cubo como unidade de medida, a quantidade de cubos que compõe cada pilha corresponde à medida de seu volume. Nesse caso, a unidade de medida adotada é não padronizada.
Página 205
Questão 7 Sabendo que não há cubos ocultos atrás da pilha, escreva em seu caderno a medida do volume da pilha a seguir, considerando o cubo como unidade de medida.
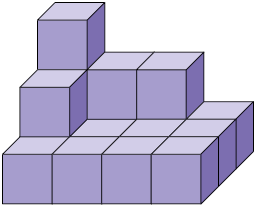
Também é possível usar unidades de medidas padronizadas para medir volumes, como o metro cúbico , o decímetro cúbico e o centímetro cúbico .
- Um metro cúbico corresponde à medida do volume de um cubo cujo comprimento das arestas mede .
- Um decímetro cúbico corresponde à medida do volume de um cubo cujo comprimento das arestas mede .
- Um centímetro cúbico corresponde à medida do volume de um cubo cujo comprimento das arestas mede .
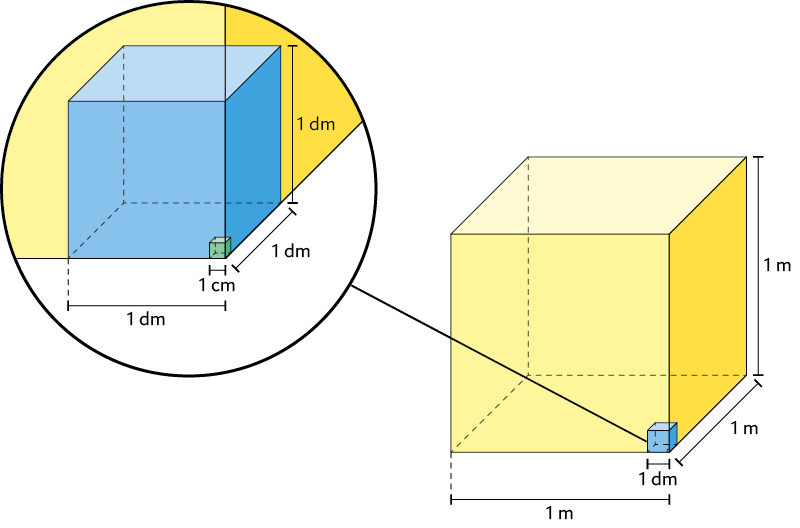
Questão 8. Responda às questões em seu caderno.
a) Imagine um recipiente cúbico cujas dimensões internas medem . Quantos cubos de cabem nesse recipiente?
b) Imagine um recipiente cúbico cujas dimensões internas medem . Quantos cubos de cabem nesse recipiente?
Página 206
Atividades
Faça as atividades no caderno.
34. Sabendo que não há cubos ocultos atrás da pilha, determine a medida de volume de cada uma delas considerando o cubo como unidade de medida.
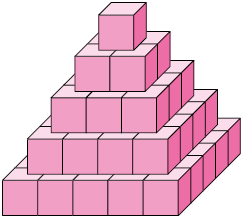
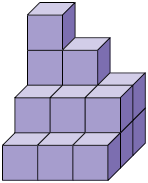
35. Sabendo que
o volume do ![]() mede e o do
mede e o do ![]() mede , determine a medida do volume de cada um dos
empilhamentos.
mede , determine a medida do volume de cada um dos
empilhamentos.
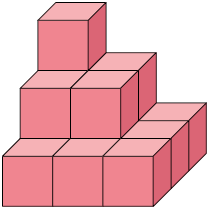
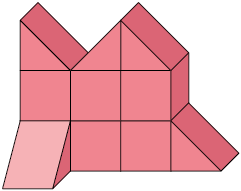
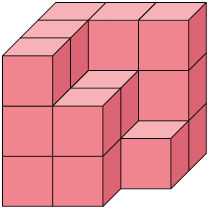
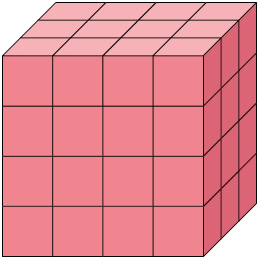
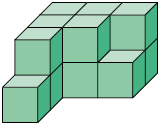
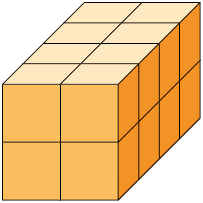
36. Bia organizou os pequenos cubos representados na imagem 1 e obteve o empilhamento apresentado na imagem 2.
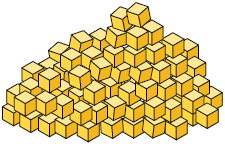

a) Quantos são os pequenos cubos organizados por Bia?
b) Bia reorganizou os cubos. Porém, dessa vez, ela os empilhou em camadas contendo 4 pequenos cubos. Quantas camadas há nesse novo empilhamento?
c) Os empilhamentos feitos por Bia têm a mesma medida de volume? Justifique sua resposta.
d) De acordo com os pequenos cubos usados por Bia, elabore uma questão e dê para um colega resolver. Depois, verifique se a resposta obtida por ele está correta.
Página 207
Medida do volume do paralelepípedo reto retângulo
O paralelepípedo reto retângulo a seguir foi representado com peças iguais de madeira.
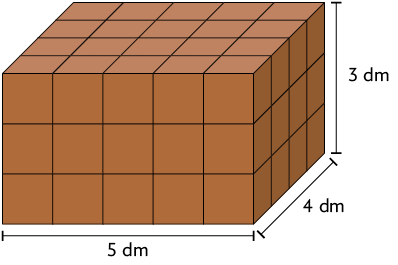
Atenção!
As peças de madeira têm formato de cubo cujo comprimento da aresta mede .
Questão 9. Qual é a medida do volume de
madeira em
decímetro cúbico utilizado na construção desse
paralelepípedo?
Para calcular a medida do volume desse paralelepípedo, podemos adicionar as medidas dos volumes das peças de madeira em formato cúbico. Para isso, inicialmente, determinamos a quantidade de peças usadas.
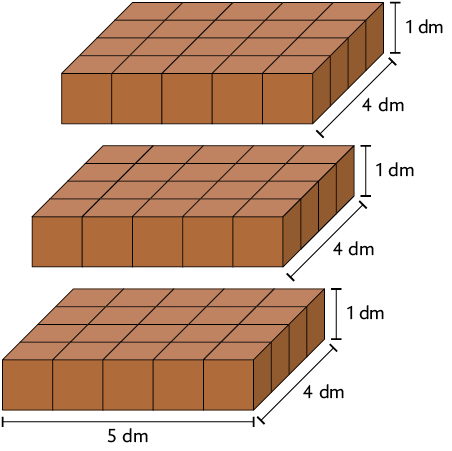
Em cada camada que compõe o paralelepípedo há 5 fileiras com 4 peças em cada uma. Como são 3 camadas, devemos fazer:
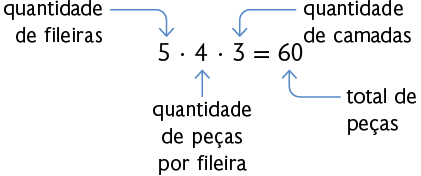
Como o volume de cada peça de madeira mede , para calcular a medida do volume do paralelepípedo, efetuamos:
Portanto, o volume desse paralelepípedo mede .
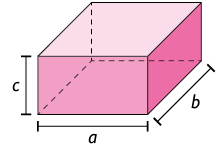
Para calcular a medida do volume V de um paralelepípedo reto retângulo em que as dimensões medem a, b e c, efetuamos:
Página 208
Nos casos apresentados, mostramos que a fórmula do volume do paralelepípedo reto retângulo é verdadeira quando a, b e c são números inteiros. Entretanto, essa fórmula também é válida quando as medidas são números racionais. Por exemplo, se as dimensões do paralelepípedo medem , e , temos:
O cubo é um caso particular de um paralelepípedo reto retângulo em que a medida do comprimento das arestas mede a.
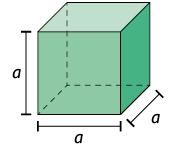
Assim, para calcular a medida do volume V de um cubo, efetuamos:
Atividades
Faça as atividades no caderno.
37. Calcule a medida de volume de cada paralelepípedo reto retângulo representado.
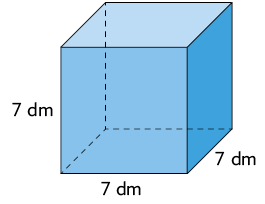
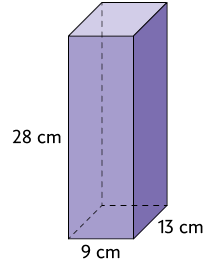
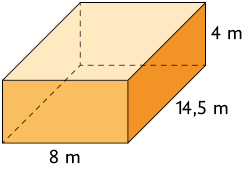

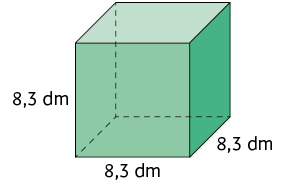
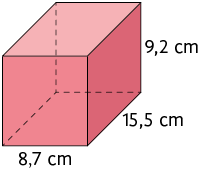
Imagens não proporcionais entre si.
38. O leite longa vida (UHT) é processado em temperatura ultra-alta para eliminar todos os microrganismos, a fim de que ele dure mais tempo após ser envasado em certo tipo de embalagem.

Analise um modelo de embalagem do leite longa vida cujo formato é de um paralelepípedo reto retângulo.
Qual é a medida do volume dessa embalagem?
Página 209
39. Faça uma estimativa de qual paralelepípedo reto retângulo tem a maior medida de volume. Depois, calcule a medida do volume de cada um e verifique se sua estimativa está correta.
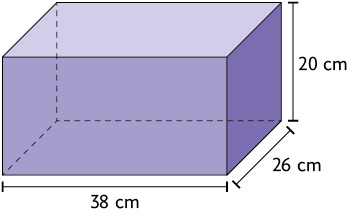
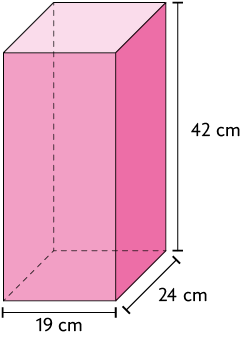
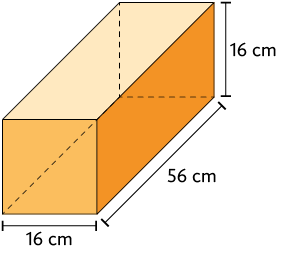
40. Para calcular o volume de areia em algumas regiões, é usado um recipiente de lata com formato de paralelepípedo reto retângulo, conforme representado a seguir.

Qual é a medida do volume desse recipiente?
41. Uma piscina olímpica tem formato de paralelepípedo reto retângulo cujas dimensões internas medem , e . Quantos litros de água serão necessários para encher completamente essa piscina?
Atenção!
42. Antônio e Jairo desenharam cubos usando um programa de computador. A medida do comprimento das arestas do cubo desenhado por Jairo é igual ao dobro da medida do comprimento das arestas do cubo desenhado por Antônio, que é . A medida do volume do cubo desenhado por Jairo é quantas vezes maior do que o do cubo desenhado por Antônio?
43. Ao multiplicar as medidas das três dimensões de um tijolo maciço com formato de paralelepípedo reto retângulo, obtém-se a medida:
a) do comprimento do tijolo.
b) da área do tijolo.
c) da massa do tijolo.
d) do volume do tijolo.
Página 210
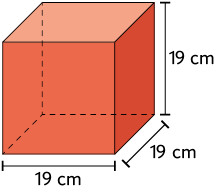
44. Considere os paralelepípedos reto retângulos.
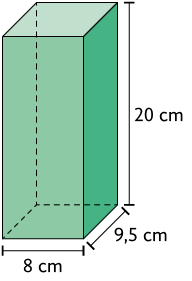
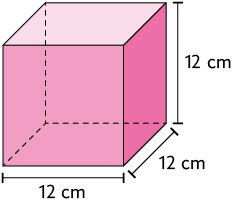
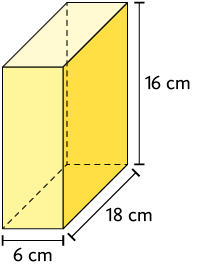
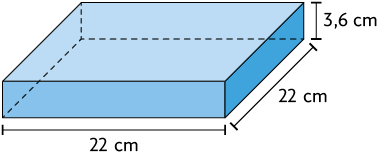
Efetue no caderno o cálculo da medida do volume de cada um desses paralelepípedos e, em seguida, responda às questões.
a) Qual deles tem a maior medida de volume? Qual tem a menor medida de volume?
b) Quais deles têm a mesma medida de volume?
45. (Enem–2017) Um casal realiza sua mudança de domicílio e necessita colocar numa caixa de papelão um objeto cúbico, de de aresta, que não pode ser desmontado. Eles têm à disposição cinco caixas, com diferentes dimensões, conforme descrito:
- Caixa 1: .
- Caixa 2: .
- Caixa 3: .
- Caixa 4: .
- Caixa 5: .
O casal precisa escolher uma caixa na qual o objeto caiba, de modo que sobre o menor espaço livre em seu interior.
A caixa escolhida pelo casal deve ser a de número:
a) 1.
b) 2.
c) 3.
d) 4.
e) 5.
46. Qual figura geométrica espacial tem volume de maior medida: um paralelepípedo reto retângulo cujas dimensões medem , e ou um cubo cujo comprimento das arestas mede ?
47. Elabore em seu caderno um problema envolvendo o volume do paralelepípedo reto retângulo representado a seguir.
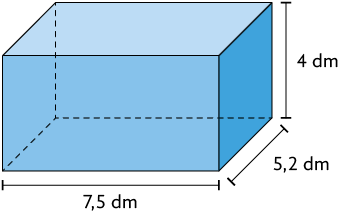
Depois, troque o problema que você elaborou com o de um colega. Você resolverá o dele, e ele, o seu. Por fim, verifique se o seu problema foi resolvido corretamente.
Página 211
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Escreva o nome da grandeza que pode ser medida por:
a) um recipiente de um litro graduado.
b) um cronômetro.
c) uma fita métrica.
d) uma balança digital.
e) um metro articulado.
f) uma balança de dois pratos.
g) uma trena.
2. Copie as sentenças a seguir substituindo cada pelo número adequado.
a) .
b) .
c) .
d) .
e) .
f) .
3. Durante a manhã de certo dia, o termômetro de uma cidade registrou uma medida de temperatura de . À tarde, nesse mesmo dia, esse termômetro registrou a medida de temperatura de .
a) Durante esse intervalo de tempo, a medida de temperatura aumentou ou diminuiu?
b) Qual é a unidade de medida de temperatura no SI? Ela foi utilizada para expressar as medidas de temperatura nesta atividade?
4. Calcule a medida da área de cada figura a seguir utilizando o quadrado da malha como unidade de medida.
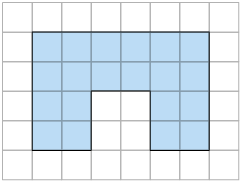
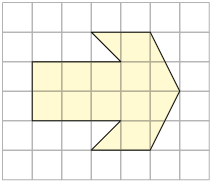
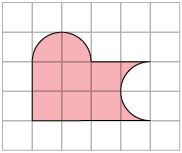
5. A figura geométrica plana a seguir foi construída em uma malha quadriculada cujo comprimento do lado de cada quadradinho mede . Em uma folha de papel avulsa, calcule a medida da área dessa figura em centímetros quadrados.

Página 212
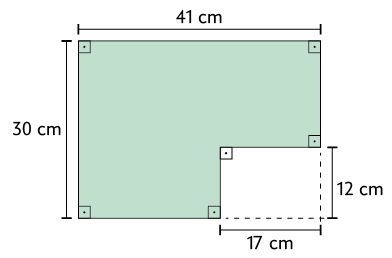
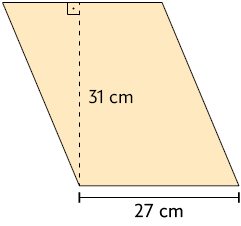
6. Calcule a medida da área das figuras representadas a seguir.
Atenção!
A figura C representa um paralelogramo.

7. Juliana confeccionou uma caixa em formato de prisma de base triangular. Analise o molde utilizado por ela.
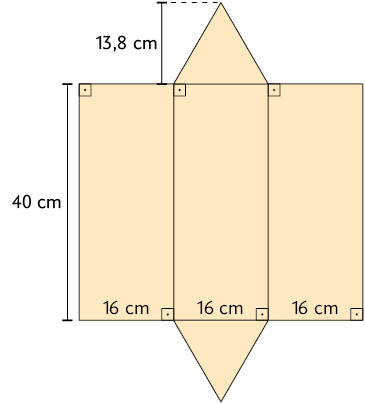
Quantos centímetros quadrados de cartolina ela utilizou?
8. A imagem a seguir representa um terreno em formato de trapézio.
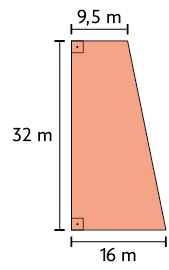
Qual é a medida da área desse terreno?
9. Pedro está empilhando pequenos cubos do material dourado. A seguir, estão representados os cubos que ele já empilhou.
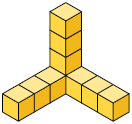
Pedro pretende obter um empilhamento em formato cúbico. No mínimo, quantos cubos ele ainda precisa colocar nesse empilhamento?
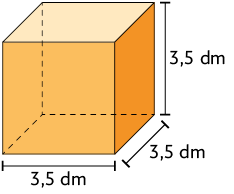
10. Determine a medida do volume do cubo a seguir.
11. Antônio planeja construir um reservatório de água com formato de paralelepípedo reto retângulo cujas dimensões internas medem , e . Qual é a medida do volume desse reservatório?