Página 257

UNIDADE

Transformações de figuras

Fotografia. Um bebê com a mão apoiada em um espelho vertical, olhando seu reflexo. — Bebê olhando sua imagem refletida no espelho.

Agora vamos estudar...

simetria axial;
transformação de reflexão;
transformação de rotação;
simetria de rotação;
transformação de translação;
plano cartesiano;
transformações no plano cartesiano.

Página 258

Simetria axial

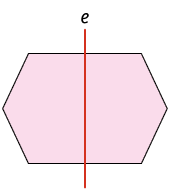
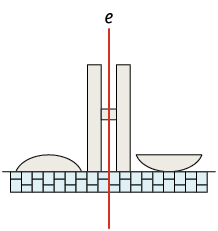
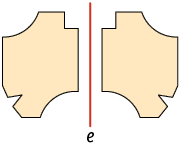
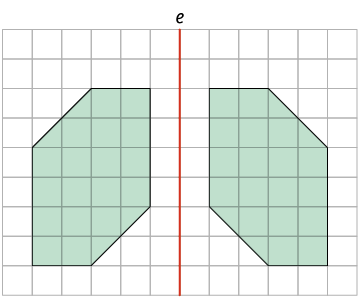
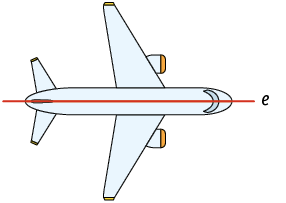
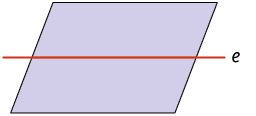
Você já estudou simetria? Para você, quando uma figura tem simetria? Neste tópico, vamos estudar a simetria axial. Considere as figuras a seguir.

Ilustração. Polígono de 12 lados. De cima para baixo, ele é constituído de um triângulo com base coincidente ao lado de um retângulo, que está apoiado em outro retângulo com base maior que a do retângulo acima, que está apoiada no lado de um triângulo, menor que a base do retângulo, posicionado abaixo.

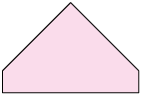
Ilustração. Polígono de 5 lados, semelhante a união de um triângulo e um retângulo com mesma medida da base do triângulo apoiado em sua base.

Ilustração. Polígono de 8 lados semelhante a união de 2 retângulos e um quadrado. Inicialmente um retângulo apoiado sobre um quadrado que estão sobre outro retângulo, formando uma figura que lembra a letra C.

Imagine uma reta vertical passando sobre cada uma das figuras consideradas.

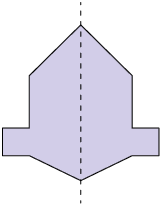
Ilustração do polígono anterior de 12 lados, dividido ao meio, por um eixo vertical tracejado, em duas figuras simétricas.

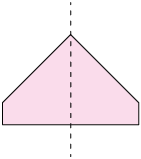
Ilustração do polígono anterior de 5 lados, dividido ao meio, por um eixo vertical tracejado, em duas figuras simétricas.

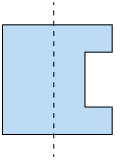
Ilustração do polígono anterior de 8 lados, dividido ao meio, por um eixo vertical tracejado, em duas figuras não simétricas.

Entre as figuras apresentadas, algumas delas – figuras A e B – apresentam o mesmo conjunto de pontos apenas refletidos em ambos os lados da reta, ou seja, as duas partes se sobrepõem se as "dobrarmos" ao longo da reta.

Dizemos que as figuras A e B têm simetria axial em relação à reta vertical que, nesse caso, recebe o nome de eixo de simetria.

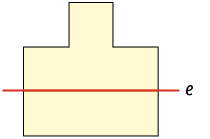
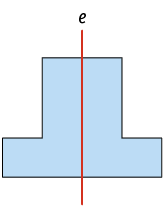
Outros exemplos de figuras que têm simetria axial em relação ao eixo traçado aparecem nas imagens a seguir.

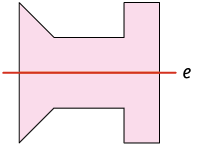
Ilustração. Polígono de 10 lados dividido ao meio, por um eixo indicado pela letra: e, na horizontal, em duas figuras simétricas.

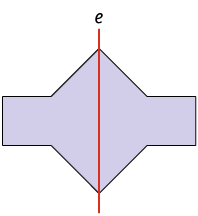
Ilustração. Polígono de dez lados dividido ao meio, por um eixo e, na vertical, em duas figuras semelhantes.

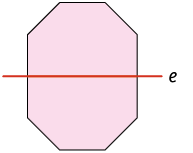
Ilustração. Polígono de 8 lados dividido ao meio, por um eixo e, na horizontal, em duas figuras semelhantes.

Questão 1. Quais das figuras a seguir têm simetria axial em relação ao eixo $e$ ?

Ilustração. Polígono de 6 lados dividido ao meio, por um eixo e, na vertical, em duas figuras semelhantes.

Ilustração. Polígono de 8 lados dividido por um eixo e, na horizontal, em duas figuras diferentes.

Ilustração. Polígono de 8 lados dividido ao meio, por um eixo e, na vertical, em duas figuras semelhantes.

Página 259

Transformação de reflexão

Com um programa de computador, Bernardo construiu a figura A e a reta $r$ . Em seguida, utilizando uma das ferramentas, ele construiu a figura B, refletindo a figura A em relação à reta $r$ .

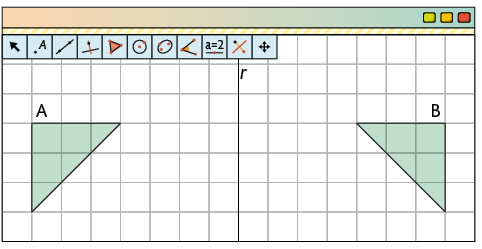
Ilustração. Tela do software de geometria dinâmica com a ferramenta Polígono, da barra de ferramentas, selecionada. Na tela há uma malha quadriculada com uma reta r ao centro na vertical, separando dois triângulos iguais. À esquerda da reta está um triângulo, figura A, com dois lados de mesmo comprimento, ambos com medidas de três unidades da malha, um posicionado em cima horizontalmente e outro do lado esquerdo verticalmente. À direita da reta está o outro triângulo, figura B, que é o espelhamento da figura A pela reta r.

Para construir a figura B, Bernardo aplicou na figura A uma transformação de reflexão em relação à reta $r$ (eixo). Nesse caso, dizemos que as figuras A e B são simétricas por reflexão em relação ao eixo $r$ .

Atenção!

A figura obtida ao aplicarmos uma transformação em dada figura chama-se imagem da figura inicial.

Analise outros exemplos.

A figura W é a imagem da figura E pela transformação de reflexão em relação ao eixo $s$ .

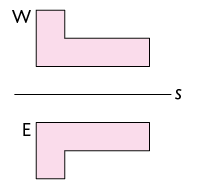
Ilustração. Há uma reta s, na horizontal, separando duas figuras iguais. Acima da reta está a figura W, um polígono de 6 lados semelhante a letra L. E abaixo da reta está a figura E. Ela é igual a figura W, e está em posição espelhada com relação a reta s, sendo semelhante a letra L voltada para baixo.

A figura R é a imagem da figura P pela transformação de reflexão em relação ao eixo $r$ .

Ilustração. Há uma reta r, na vertical, separando duas figuras iguais. À esquerda da reta está a figura P, um polígono de 7 lados semelhante a uma seta apontando para direita. E à direita da reta está a figura R. Ela é igual a figura P, mas está em posição espelhada com relação a reta r, sendo semelhante a uma seta apontando para esquerda.

Atenção!

A imagem de uma figura pela transformação de reflexão é idêntica à figura original.

Atividades

Faça as atividades no caderno.

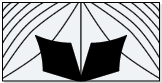
1. Em quais das figuras a linha e representa um eixo de simetria?

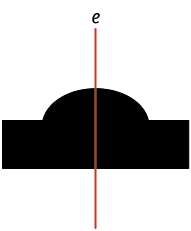
Ilustração. Uma figura formada por um retângulo, com medida da base maior que a medida da altura, e por uma figura que se assemelha a metade de um círculo, um pouco achatada, em forma oval, com sua parte reta apoiada na parte superior central do retângulo. A figura está dividida ao meio, por um eixo indicado por: e, na vertical, em duas figuras simétricas.

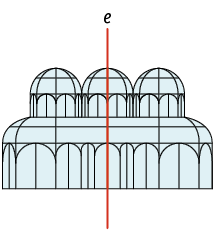
Ilustração. Figura representando a estufa do Jardim botânico da cidade de Curitiba, dividida por um eixo indicado por: e, na vertical, em duas figuras simétricas.

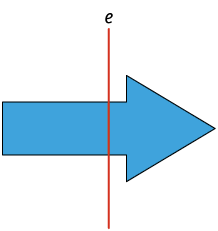
Ilustração. Polígono com 7 lados, que se assemelha a uma seta horizontal, apontando para a direita, dividido por um eixo indicado por: e, na vertical, em duas figuras diferentes.

Ilustração. Figura representando uma folha de árvore, dividida por um eixo indicado por: e, na vertical, em duas figuras simétricas.

Ilustração. Representação do congresso nacional. Figura composta por dois retângulos de mesmas dimensões, ambos com a medida da base menor que a altura, posicionados um ao lado do outro, com um retângulo de dimensões menores entre eles. No lado esquerdo há uma figura parecida com metade de um círculo, um pouco achatada em forma oval, com sua parte arredondada voltada para cima, e no lado direito há uma figura semelhante, com sua parte arredondada voltada para baixo. Os retângulos maiores e as figuras arredondadas estão apoiadas em um retângulo posicionado na parte inferior, com medida da base maior que a medida da altura, com seu interior composto por vários retângulos menores. Há um eixo indicado por: e, na vertical, separando a figura, ao centro, em duas partes.

Ilustração. Figura que se assemelha a um trevo de quatro folhas, separada por um eixo indicado por: e, na vertical, em duas figuras simétricas.

Página 260

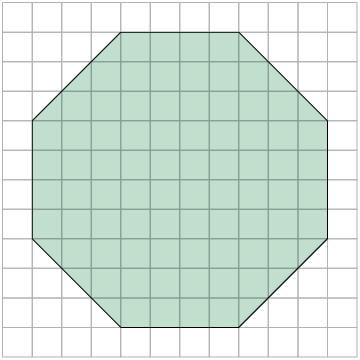
2. Junte-se a um colega, desenhem as figuras planas a seguir em uma malha quadriculada e tracem todos os eixos de simetria de cada uma delas.

Ilustração. Polígono de 16 lados em formato de uma estrela, cujas quatro pontas das diagonais são menores e de mesmo tamanho. As pontas posicionadas na horizontal e vertical são maiores e de mesmo tamanho.

Ilustração. Malha quadriculada com um polígono de 8 lados.

3. Considere as seguintes representações dos algarismos.

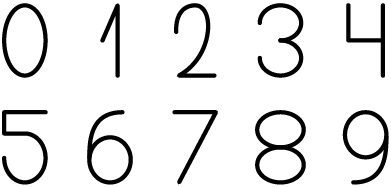
Ilustração dos números de 0 a 9 manuscritos, dispostos em duas linhas. Na primeira os números de 0 a 4 e na segunda linha os números de 5 a 9.

a) Quais têm eixo de simetria?

b) Quais têm mais de um eixo de simetria?

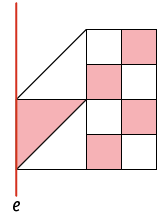
4. Analise a representação de parte de um mosaico. Em quais das alternativas a seguir, a imagem completa-o de modo que ele seja simétrico em relação ao eixo e?

Ilustração. Mosaico formado por três triângulos e oito quadrados da seguinte forma: À direita de um eixo e na vertical, encostado, na parte inferior, um quadrado formado por dois triângulos; acima do quadrado, outro triângulo. Ao lado direito dos triângulos, oito quadrados empilhados em duas colunas.

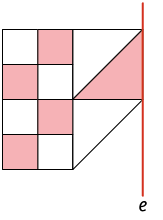
Ilustração. Mosaico formado por três triângulos e oito quadrados da seguinte forma: À esquerda de um eixo e na vertical, encostado, na parte superior, um quadrado formado por dois triângulos, abaixo do quadrado, outro triângulo. Ao lado esquerdo dos triângulos, oito quadrados empilhados em duas colunas.

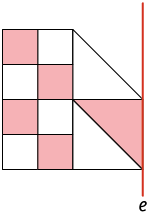
Ilustração. Mosaico formado por três triângulos e oito quadrados da seguinte forma: À esquerda de um eixo e na vertical, encostado, na parte inferior, um quadrado formado por dois triângulos, acima do quadrado, outro triângulo. Ao lado esquerdo dos triângulos, oito quadrados empilhados em duas colunas.

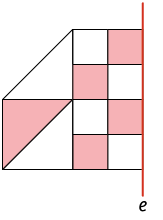
Ilustração. Mosaico formado por três triângulos e oito quadrados da seguinte forma: À esquerda de um eixo e na vertical, oito quadrados empilhados em duas colunas. Ao lado esquerdo dos quadrados, na parte inferior, um quadrado formado por dois triângulos e acima do quadrado, outro triângulo.

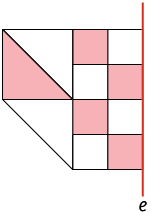
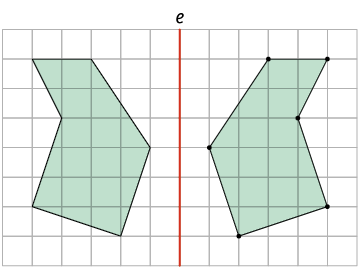
5. Em quais alternativas a seguir há figuras simétricas por reflexão em relação ao eixo e?

Ilustração. Há uma reta e, posicionada na diagonal, com uma figura posicionada acima e uma figura posicionada abaixo. Uma das figuras é obtida pela rotação de 180 graus da outra em torno em torno de um ponto da reta e.

Ilustração. Há uma reta e, posicionada na diagonal, com uma figura posicionada acima e uma figura posicionada abaixo. As duas figuras, juntamente com a reta e, formam uma figura simétrica.

Ilustração. Há uma reta e, posicionada na horizontal, com uma figura posicionada acima e uma figura posicionada abaixo. A de cima possui uma única estrela de cinco pontas em seu interior, enquanto a debaixo possui uma única estrela de seis pontas em seu interior.

Ilustração. Há uma reta e, posicionada na vertical, com uma figura posicionada à esquerda e outra à direita. As duas figuras, juntamente com a reta e, formam uma figura simétrica.

Página 261

6. A arte das mulheres do povo Sotho, em Lesoto e regiões vizinhas na África do Sul, pode ser vista em pinturas nas paredes de suas casas. Cada desenho usado como padrão tem, frequentemente, formatos geométricos, como o quadrado da figura 1. Os desenhos obtidos com esses padrões apresentam características de simetria axial. Com a figura simétrica a esse padrão em relação a um eixo vertical (figura 2) e depois a um eixo horizontal (figura 3), obtém-se um tema. Reproduzindo esse desenho, compõe-se o chamado litema, que formará a composição da pintura.

Ilustração. Figura quadrangular, representando uma pintura artística. — Figura 1: Padrão. Este é um dos mais populares.

Ilustração. Duas figuras quadrangulares iguais, representando uma pintura artística, uma ao lado da outra, de forma espelhada em relação ao eixo vertical, representando uma pintura artística. — Figura 2: Formada pelo padrão e sua figura simétrica por reflexão em relação a um eixo vertical.

Ilustração. Quatro figuras quadrangulares iguais, duas acima e duas abaixo. As duas acima estão uma ao lado da outra, de forma espelhada em relação ao eixo vertical. As de baixo estão uma ao lado da outra, ambas espelhadas com relação às figuras de cima com relação ao eixo horizontal. — Figura 3: Formada pela figura 2 e sua figura simétrica por reflexão em relação a um eixo horizontal. Este tema, obtido com o padrão da figura 1, é conhecido como Likhole.

Ilustração. Quatro figuras quadrangulares iguais, duas acima e duas abaixo. As duas acima estão uma ao lado da outra, de forma espelhada. As de baixo estão uma ao lado da outra, ambas espelhadas com relação às figuras de cima. Cada uma dessas quatro figuras é a composição de outras 4, duas acima, posicionadas de forma espelhada, e duas abaixo, espelhadas com relação às de cima. — Figura 4: Composição dos temas Likhole, formando um dos litemas mais populares.

a) Quantos eixos de simetria há no padrão representado na figura 1? E no padrão da figura 3?

b) Junte-se a um colega e criem o desenho de um litema com um padrão geométrico.

7. Verifique como Rui desenhou figuras simétricas em relação a um eixo em uma malha quadriculada.

1º. Na malha, ele desenhou uma figura e traçou um eixo e. Para cada vértice, ele obteve os pontos simétricos em relação a esse eixo.

2º. Por fim, Rui uniu os pontos e pintou a figura obtida.

Ilustração. Malha quadriculada com uma reta vertical indicada pela letra: e, separando dois polígonos iguais, de 6 lados, em posições espelhadas em relação à reta e.

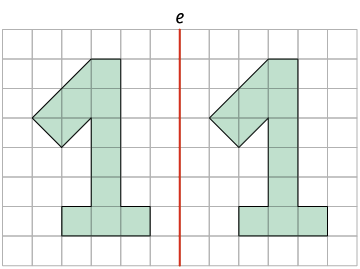
Utilizando o mesmo processo de Rui, Rogério desenhou figuras em duas malhas quadriculadas. Em qual delas ele cometeu algum erro ao tentar desenhar figuras simétricas por reflexão em relação ao eixo e?

Ilustração. Há um eixo indicado pela letra: e, na vertical, separando duas figuras iguais, cada uma é um polígono de 11 lados com o formato semelhante ao número um.

Ilustração. Malha quadriculada com eixo indicado pela letra: e, na vertical, separando dois polígonos iguais de 6 lados. Um está à esquerda e o outro está à direita em posição espelhada.

Página 262

Transformação de rotação

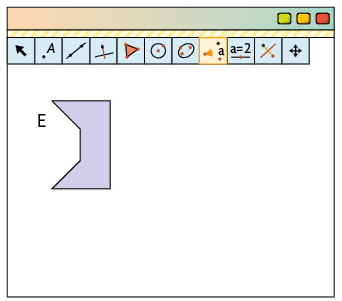
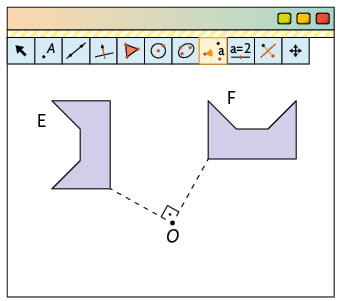
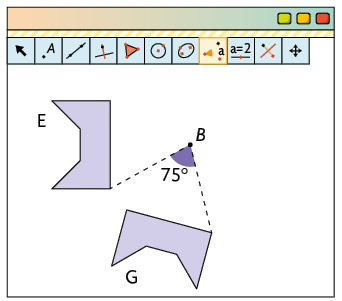
Você se lembra do programa utilizado por Bernardo no tópico Transformação de reflexão? Usando-o novamente, ele construiu a figura E. Em seguida, com uma das ferramentas do programa, produziu as figuras F e G rotacionando a figura E.

Ilustração. Tela do software de geometria dinâmica com a ferramenta rotação em torno de um Ponto, da barra de ferramentas, selecionada. Na tela há um polígono E, de 6 lados. Seus lados superior e inferior estão na horizontal, são de mesmo tamanho e estão alinhados. Seu lado à direita está na posição vertical. À esquerda há outros três lados, um acima e outro abaixo, posicionados na diagonal, inclinados para a direita, e de mesmo tamanho, conectados a um outro que está no meio e na vertical.

Ilustração. Na tela, à esquerda, a figura E, à direita, a imagem obtida por sua rotação em torno de um ponto O. Há um ângulo de medida 90 graus demarcado entre as figuras e com vértice no ponto O.

Ilustração. Tela do software de geometria dinâmica com a ferramenta Rotação em Torno de um Ponto, da barra de ferramentas, selecionada. À esquerda, a figura E, abaixo, a imagem obtida por sua rotação em torno de um ponto B, denotada por G. Há um ângulo de medida 75 graus demarcado entre as figuras e com vértice no ponto B.

Atenção!

A imagem de uma figura pela transformação de rotação é idêntica à figura original.

Para construir a figura F, Bernardo aplicou na figura E uma transformação de rotação de $90 graus$ , no sentido horário, em torno do ponto $O$ . Na construção da figura G, ele também aplicou uma transformação de rotação na figura E, porém de $75 graus$ no sentido anti-horário, em torno do ponto $B$ .

Nesse caso, dizemos que as figuras:

E e F são simétricas por rotação em torno do ponto $O$ .
E e G são simétricas por rotação em torno do ponto $B$ .

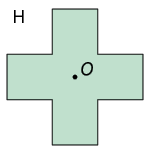
Simetria de rotação

Dizemos que uma figura tem simetria de rotação se ela permanecer a mesma após ser rotacionada em determinado ângulo e sentido em relação a um ponto.

A figura H, por exemplo, tem simetria de rotação, pois, ao ser rotacionada em $90 graus$ , no sentido anti-horário, em relação ao ponto $O$ , permanece a mesma.

Ilustração. Polígono com doze lados iguais, em formato de uma cruz, com um ponto O ao centro.

Página 263

Instrumentos e softwares

Transformação de reflexão e de rotação no GeoGebra

Com o GeoGebra, é possível construir figuras utilizando transformações de reflexão ou de rotação. Execute o passo a passo a seguir.

1º. Com a ferramenta Polígono, construa um polígono qualquer. Depois, com a ferramenta Reta, clique em dois pontos distintos para traçar uma reta.

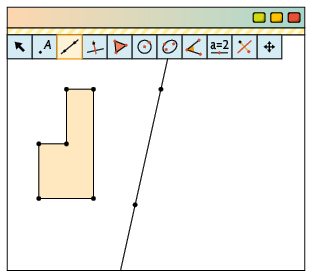
Ilustração. Tela do software de geometria dinâmica com a ferramenta reta, da barra de ferramentas, selecionada. Na tela há um polígono de seis lados à esquerda, com pontos em seus vértices, semelhante à letra L voltada para a esquerda, e uma reta posicionada diagonalmente a direita, com dois pontos sobre ela.

2º. Com a ferramenta Reflexão em Relação a uma Reta, clique no polígono e, depois, na reta.

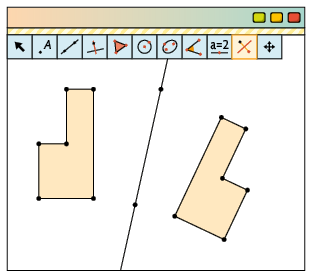
Ilustração. Tela do software de geometria dinâmica com a ferramenta Reflexão em relação à uma Reta, da barra de ferramentas, selecionada. Na tela há uma reta diagonal ao centro, inclinada para a direita, com dois pontos sobre ela, e duas figuras, uma à esquerda e outra à direita da reta, ambos polígonos iguais de 6 lados, mas espelhados em relação a reta.

Faça o teste: com a ferramenta Mover, mude a posição dos vértices do polígono e dos pontos da reta e verifique que a transformação é mantida.

Podemos obter uma figura simétrica por rotação em torno de um ponto com base nas seguintes instruções.

1º. Com a ferramenta Polígono, construa um polígono qualquer. Depois, com a ferramenta Ponto, clique e marque um ponto aleatório.

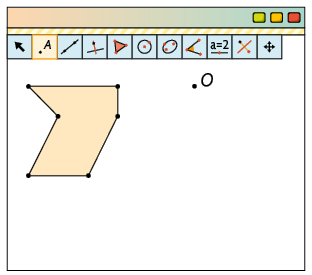
Ilustração. Tela do software de geometria dinâmica com a ferramenta Ponto, da barra de ferramentas, selecionada. Há um polígono de 6 lados à esquerda e um ponto O à direita.

2º. Com a ferramenta Rotação em Torno de um Ponto, clique no polígono e, depois, no ponto. No campo Ângulo da janela que será exibida, digite a medida do ângulo, em graus, e escolha o sentido – por exemplo, $90 graus$ no sentido anti-horário – e clique em OK.

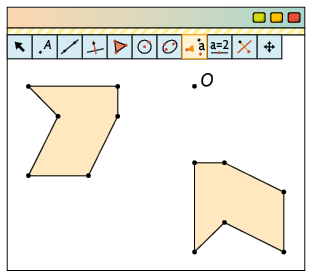
Ilustração. Tela do software de geometria dinâmica com a ferramenta Rotação em Torno de um Ponto, da barra de ferramentas, selecionada. Há um polígono de 6 lados à esquerda, ponto O à direita e um polígono abaixo do ponto O, resultante da rotação do polígono à esquerda, de um ângulo de 90 graus em torno do ponto O.

Faça o teste: com a ferramenta Mover, mude a posição do ponto O, feito no passo 1 da construção, e verifique que a transformação é mantida.

Página 264

Atividades

Faça as atividades no caderno.

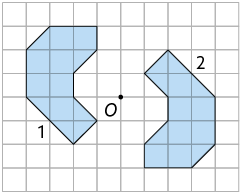
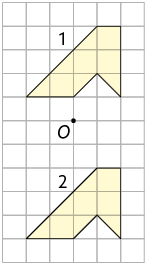
8. Em qual das malhas quadriculadas a figura 2 é simétrica à figura 1 por rotação em torno do ponto O?

Ilustração. Malha quadriculada. Nela, à esquerda, um polígono de 9 lados indicada pelo número: 1, à direita a imagem obtida por sua rotação, em torno de um ponto O, de 180 graus, indicada pelo número: 2.

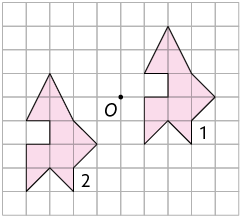
Ilustração. Malha quadriculada. Com um ponto O ao centro, um polígono de 11 lados, indicado pelo número 1, à direita e acima do ponto O e um polígono de 11 lados, indicado pelo número 2, à esquerda e abaixo do ponto O. Ambas são iguais e estão na mesma posição.

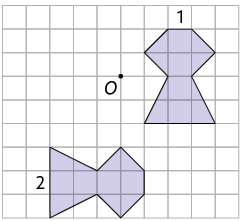
Ilustração. Malha quadriculada com um ponto O e, à direita, um polígono indicado pelo número: 1 e, abaixo, um polígono indicado pelo número: 2. Ambos os polígonos são iguais. O polígono 2 está rotacionado em relação ao ponto O 90 graus para a direita, quando comparado ao polígono 1.

Ilustração. Malha quadriculada com um ponto O ao centro, um polígono acima, indicado pelo número 1, e um polígono abaixo, transladado 6 unidades para baixo, indicado pelo número 2. Ambos são iguais, de 6 lados cada e estão em mesmas posições.

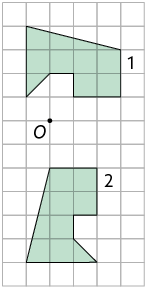
Ilustração. Malha quadriculada com um ponto O ao centro, um polígono acima, indicado pelo número 1, e um polígono abaixo, indicado pelo número 2. Ambos são semelhantes, de 7 lados cada e estão em posições diferentes, o polígono 1 está rotacionado em relação ao ponto O, 90 graus para a direita.

9. Com o auxílio de um transferidor, meça em cada item o ângulo de rotação que a figura 1 sofreu em relação ao ponto O, no sentido anti-horário.

Ilustração. À direita, a figura 1 à esquerda a imagem obtida por sua rotação em torno de um ponto O. Há um ângulo de medida 90 graus demarcado entre as figuras e com vértice no ponto O.

Ilustração. À direita, a figura 1 à esquerda a imagem obtida por sua rotação em torno de um ponto O. Há um ângulo de medida 100 graus demarcado entre as figuras e com vértice no ponto O.

10. Analise a figura apresentada.

Ilustração. Trapézio retângulo com base maior apoiada numa semirreta horizontal com origem no ponto O. A semirreta está abaixo do trapézio e o ponto O à direita.

Qual das figuras a seguir é simétrica por rotação a essa dada figura, após uma rotação de $90 graus$ , no sentido horário, em torno do ponto O?

Ilustração. Trapézio retângulo com base maior apoiada numa semirreta horizontal com origem no ponto O. A semirreta está acima do trapézio e o ponto O à esquerda.

Ilustração. Trapézio retângulo com base maior apoiada numa semirreta vertical com origem no ponto O. A semirreta está à direita do trapézio e o ponto O acima.

Ilustração. Trapézio retângulo com base maior apoiada numa semirreta vertical com origem no ponto O A semirreta está à esquerda do trapézio e o ponto O acima.

11. Utilizando o GeoGebra, construa um polígono qualquer, trace uma reta e marque um ponto exterior a ele. Depois, construa um polígono simétrico ao inicial por reflexão em relação à reta. Em seguida, obtenha um polígono simétrico ao inicial por rotação em torno do ponto marcado. Nesse caso, a rotação deve ser de $85 graus$ no sentido horário.

Página 265

12. Além de verificar a presença de simetria em fotos da natureza ou de lugares e objetos do dia a dia, podemos identificar também sua influência nas obras de arte de alguns artistas, como o caso do holandês Maurits Cornelis Escher (1898-1972).

Em uma viagem para a Espanha, ele visitou o Palácio de Alhambra, na cidade de Granada. Essa construção, de origem árabe, tem paredes cobertas por mosaicos geométricos, o que despertou o interesse de Escher pela arte das figuras geométricas que se repetem e se refletem.

Analise uma das criações do artista e verifique a presença de simetria nela.

Ilustração. Representação da obra de arte intitulada Serpentes, criada por Maurits Cornelis. Nela há três cobras de mesmo formato e dimensões, uma posicionada abaixo, uma superiormente à direita e outra superiormente à esquerda, se tocando entre si, todas ao entorno de uma escultura circular composta por várias coroas circulares se entrelaçando. — *Serpentes*, de Maurits Cornelis Escher. Xilogravura, $44 vírgula 7 centímetros por 49 vígula 8 centímetros$ , 1969.

a) O que despertou o interesse de Escher pela arte das figuras geométricas que se repetem e se refletem?

b) Que tipo de simetria está presente na criação de Escher apresentada?

c) Junte-se a um colega e pesquisem outras obras de Escher, anotando as informações que acharem mais interessantes e as que estiverem relacionadas à simetria. Com base nas informações coletadas, escrevam no caderno um texto a respeito do assunto, dando exemplos de suas obras.

d) No mínimo, em quantos graus em torno do centro a obra Serpentes pode ser rotacionada de modo que ela permaneça a mesma?

Página 266

Transformação de translação

Com o mesmo programa utilizado nos tópicos anteriores, Bernardo construiu, inicialmente, a figura P e, em seguida, a figura Q, transladando a primeira.

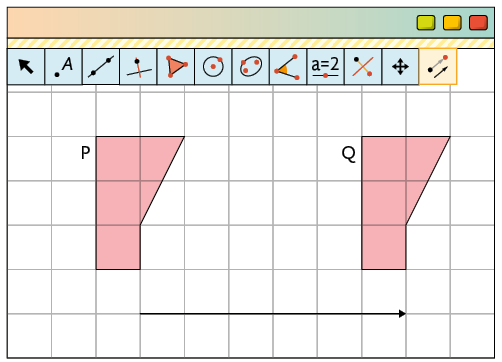
Para construir a figura Q, Bernardo aplicou na figura P uma transformação de translação na direção horizontal, 6 unidades para a direita. Nesse caso, dizemos que as figuras P e Q são simétricas por translação.

Atenção!

Na tela do programa que Bernardo está usando, a seta indica a direção, o sentido e a medida da distância em que a figura foi transladada.

Analise outros exemplos.

A figura K é a imagem da figura L pela transformação de translação na direção vertical, 2 unidades para baixo.

Ilustração. Malha quadriculada com dois triângulos iguais, um abaixo do outro, ambos de mesma medida, duas unidades da malha. O triângulo de cima está indicado pela letra L e o de baixo pela letra K. Ao lado do triângulo de cima há uma seta vertical apontando para baixo, com comprimento igual a duas unidades da malha.

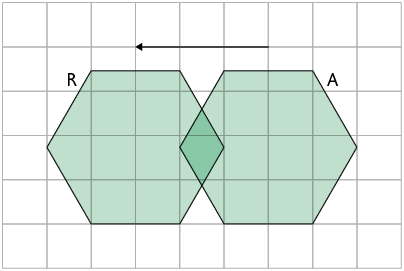
A figura R é a imagem da figura A pela transformação de translação na direção horizontal, 3 unidades para a esquerda.

Ilustração. Malha quadriculada com dois hexágonos. O da esquerda está indicado pela letra R, o da direita pela letra A. Acima há uma seta horizontal iniciando no meio do hexágono da direita apontando para a esquerda, com comprimento de três unidades da malha.

Atenção!

A imagem de uma figura pela transformação de translação é idêntica à figura original.

Página 267

Instrumentos e softwares

Transformação de translação no GeoGebra

Podemos construir figuras utilizando transformações de translação com o GeoGebra. Para isso, execute o passo a passo a seguir.

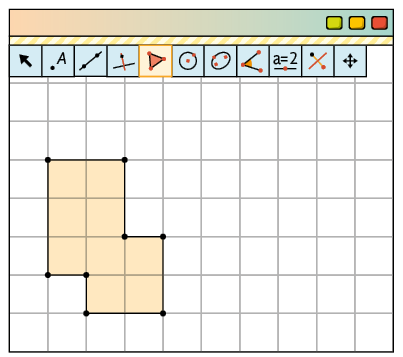
1º. Com a ferramenta Polígono, construa um polígono qualquer.

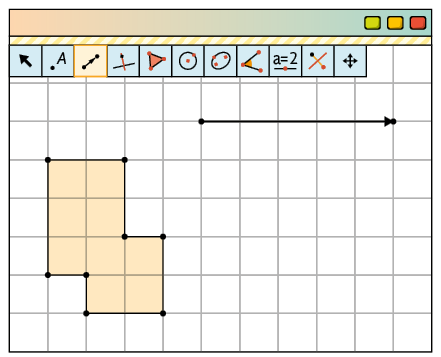
2º. Com a ferramenta Vetor, clique em dois pontos distintos para delimitar as extremidades da seta, que será a referência para a medida da distância, a direção e o sentido da translação, no exemplo, 5 unidades da malha, na horizontal e para a direita.

Ilustração. Tela do software de geometria dinâmica com a ferramenta Translação por um Vetor, da barra de ferramentas, selecionada. Malha quadriculada com um polígono de oito lados, composto por 9 quadradinhos de mesmo tamanho, formando uma coluna de 3 quadradinhos à esquerda, uma coluna de 4 quadradinhos ao centro, com o primeiro quadradinho de cima alinhado com o primeiro quadradinho de cima da coluna à esquerda, e uma coluna de dois quadradinhos à direita, alinhados com os últimos dois quadradinhos da coluna do meio. Acima e à direita há uma seta horizontal, com um ponto em cada uma de suas extremidades, apontando para a direita, com comprimento de cinco unidades da malha.

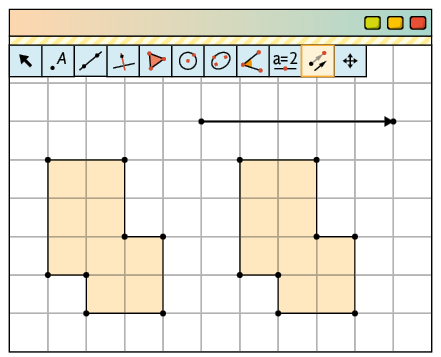
3º. Com a ferramenta Translação por um Vetor, clique no polígono e, depois, na seta.

Ilustração. Tela do software de geometria dinâmica com a ferramenta Translação por um Vetor, da barra de ferramentas, selecionada. Na tela há uma malha quadriculada com dois polígonos iguais, de oito lados, um ao lado do outro, e uma seta acima do polígono da direita, com um ponto em cada uma de suas extremidades e com comprimento de cinco unidades da malha.

Faça o teste: com a ferramenta Mover, mude a posição dos vértices do polígono ou das extremidades da seta construídos nos passos 1 e 2 para verificar que a transformação é mantida.

Página 268

Atividades

Faça as atividades no caderno.

13. Identifique em qual item a figura 2 é a imagem da figura 1 por translação.

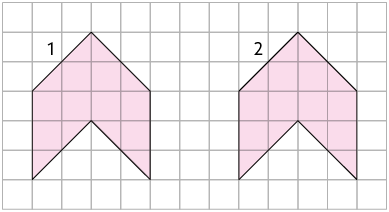
Ilustração. Duas dois polígonos de 6 lados semelhantes, indicados por 1 e 2, um ao lado do outro, separados por 3 fileiras da malha quadriculada. Ambos de assemelham a uma seta apontando para cima.

Ilustração. Malha quadriculada com dois polígonos de 6 lados, um ao lado do outro, separados por 2 fileiras da malha quadriculada. O polígono da esquerda está indicado pelo número 1, e o da direita pelo número 2. Os polígonos estão em posições refletidas verticalmente.

14. As figuras 2, 3 e 4 na malha quadriculada são imagens da figura 1 por translação. Associe cada uma delas à seta que indica a direção, o sentido e a medida da distância de cada figura transladada. Para isso, escreva o número e a letra correspondentes.

Ilustração. Malha quadriculada com 4 polígonos semelhantes, parecidos com a letra L maiúscula, de ponta cabeça, com suas extremidades pontudas. O polígono 1 está no meio, o polígono 2 está à direita, o polígono 4 está à esquerda e o polígono 3 está acima. Entre os polígonos 1 e 2, e entre os polígonos 1 e 3, há uma coluna de quadradinhos da malha, respectivamente. Entre os polígonos 1 e 4 há duas colunas de quadradinhos da malha. À esquerda, três setas verticais: A, B e C. A seta B está apontada para cima com 5 quadradinhos da malha de comprimento e a C para baixo também com 5 quadradinhos da malha de comprimento. A seta A tem comprimento igual a uma unidade da malha. Abaixo, três setas horizontais apontadas para a direita, E, G e H, de comprimentos cinco unidades, uma unidade e quatro unidades, respectivamente, e três apontadas para a esquerda, D, F e I, de comprimentos duas unidades, cinco unidades e quatro unidades.

15. Em uma malha quadriculada, copie a figura apresentada. Em seguida, obtenha as simétricas a ela por translação de acordo com as setas A e B, respectivamente.

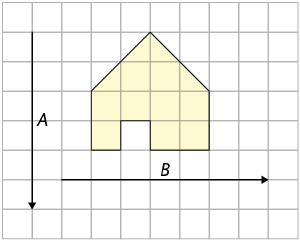
Ilustração. Malha quadriculada com um polígono de 9 lados, parecido com a figura de uma casa. À esquerda, há uma reta vertical A, com comprimento de seis unidades da malha, à direita, há uma reta horizontal B, com comprimento de 7 unidades da malha.

Versão adaptada acessível

15. Junte-se a um colega e, em uma malha quadriculada, copiem a figura apresentada. Em seguida, obtenham as simétricas a ela por translação, de acordo com as setas A e B, respectivamente.

16. Utilizando o GeoGebra, construa um polígono qualquer e seu simétrico por translação na direção, no sentido e na medida da distância que desejar.

17. No GeoGebra, construa um pentágono qualquer. Depois, obtenha uma figura simétrica a ele transladando-o 6 unidades da malha horizontalmente para a direita.

Página 269

Plano cartesiano

Neste tópico, vamos estudar o plano cartesiano, que recebe esse nome em homenagem ao matemático e filósofo francês René Descartes (1596-1650).

Fotografia. Pintura da imagem do matemático e filósofo francês René Descartes, com cabelos compridos vestindo um sobretudo. Ao fundo uma parede escura. — René Descartes, de Frans Hals. Óleo sobre tela, $77 vírgula 5 centímetros por 68 vírgula 5 centímetros$ , 1649.

O plano cartesiano é formado de duas retas numeradas e perpendiculares. A reta horizontal é o eixo das abscissas, e a vertical é o eixo das ordenadas. O ponto de interseção entre os eixos é denominado origem do plano cartesiano.

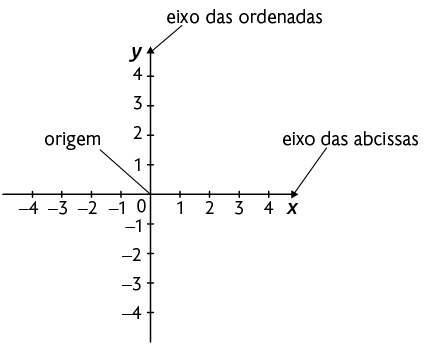
Ilustração de um plano cartesiano. Há dois eixos numerados, o eixo vertical, denominado y; e o eixo horizontal denominado x. Eles se cruzam na marcação de número 0. Está indicado que o cruzamento entre os eixos é a origem; o eixo vertical é eixo das ordenadas; e o eixo horizontal é eixo das abcissas.

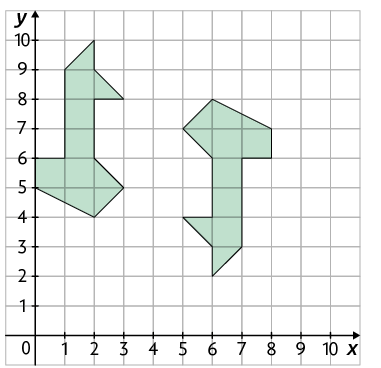
Podemos representar cada um dos pontos do plano como um par ordenado de números $A (x, y)$ . O primeiro valor indica a posição do ponto $A$ em relação ao eixo das abscissas, e o segundo indica a posição em relação ao eixo das ordenadas. Juntos, os valores $x$ e $y$ são chamados coordenadas do ponto $A$ .

No plano cartesiano representado na imagem, temos, por exemplo:

$ponto D com coordenadas 2 e 5$ .
$ponto E com coordenadas 5 e 2$ .
$ponto F com coordenadas 7 e menos 1$ .

Ilustração de um plano cartesiano sobre malha quadriculada com alguns pontos demarcados. Ponto D com coordenadas 2 e 5; ponto E com coordenadas 5 e 2; ponto F com coordenadas 7 e menos 1; ponto H com coordenadas menos 3 e 0; ponto W com coordenadas 0 e menos 1; e ponto O com coordenadas 0 e 0.

Questão 2. Escreva no caderno as coordenadas dos pontos $H$ , $O$ e $W$ .

Página 270

Atividades

Faça as atividades no caderno.

18. Patrícia construiu um plano cartesiano em uma malha quadriculada e explicou seu procedimento.

Ilustração. Pessoa ao lado direito e um balão de fala ao lado esquerdo, escrito: Tracei duas retas perpendiculares entre si, sendo a horizontal x e a vertical y.

Ilustração. Plano cartesiano sobre malha quadriculada

Ilustração. Plano cartesiano graduado sobre malha quadriculada

Em uma malha quadriculada, construa também um plano cartesiano e indique nele os pontos a seguir.

$ponto A maiúsculo com coordenadas 1 e 1$
$ponto B com coordenadas 2 e 0$
$ponto C com coordenadas 0 e menos 1$
$ponto D com coordenadas menos 2 e 2$

19. Na imagem, aparecem alguns pontos representados no plano cartesiano.

Ilustração. Plano cartesiano graduado sobre malha quadriculada contendo os seguintes pontos. Ponto A com coordenadas 0 e 3. Ponto B com coordenadas 4 e 0. Ponto C com coordenadas menos 3 e menos 1. Ponto D com coordenadas menos 1 e 1. Ponto E com coordenadas 3 e menos 2. Ponto F com coordenadas 3 e 2. Ponto G com coordenadas menos 3 e menos 4. Ponto H com coordenadas menos 3 e 4. Ponto I com coordenadas menos 3 e 2. Ponto J com coordenadas 2 e 4.E ponto K com coordenadas 1 e menos 2

a) Determine as coordenadas dos pontos indicados.

b) Quais pontos são simétricos por reflexão em relação ao eixo x? E em relação ao eixo y?

20. Leia as informações a seguir e determine as coordenadas dos pontos A, B, C e D.

O ponto A tem ordenada $8$ e abscissa $menos 6$ .

A abscissa do ponto B é igual à metade da abscissa de A, e a ordenada é igual a $menos 1$ .

O ponto C é simétrico ao ponto B por reflexão em relação ao eixo y.

O ponto D é simétrico ao ponto C por translação na direção vertical, $7$ unidades para cima.

Página 271

21. Analise o plano cartesiano com a representação do pentágono $A B C D E$ .

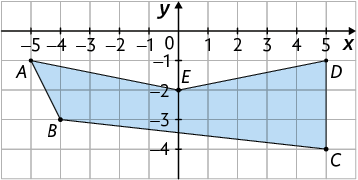
Ilustração. Plano cartesiano graduado sobre malha quadriculada com um polígono A B C D E. O vértice A tem coordenadas menos 5 e menos 1; vértice B tem coordenadas menos 4 e menos 3; vértice C tem coordenadas 5 e menos 4; vértice D tem coordenadas 5 e menos 1; e vértice E tem coordenadas 0 e menos 2.

a) Escreva as coordenadas dos vértices do pentágono.

b) Quais são as coordenadas dos vértices do pentágono simétrico ao pentágono $A B C D E$ por reflexão em relação ao eixo x?

22. Alguns polígonos estão representados no plano cartesiano a seguir.

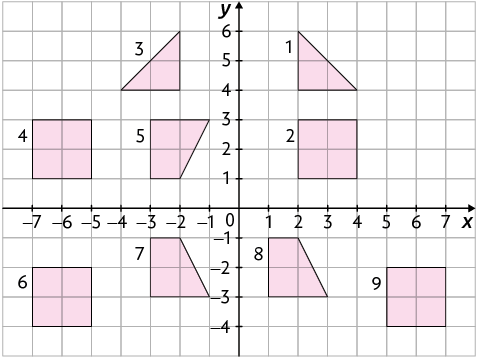
Ilustração. Plano cartesiano graduado sobre malha quadriculada com 9 polígonos. O polígono 1 é um triângulo com vértices de coordenadas 2 e 4; 2 e 6; 4 e 4. O polígono 2 é um quadrado com vértices de coordenadas 2 e 1; 4 e 1; 4 e 3; e 2 e 3. O polígono 3 é um triângulo com vértices de coordenadas menos 2 e 4; menos 2 e 6; menos 4 e 4. O polígono 4 é um quadrado com vértices de coordenadas menos 7 e 1; menos 5 e 1; menos 7 e 3; menos 5 e 3. O polígono 5 é um trapézio com vértices de coordenadas menos 3 e 1; menos 2 e 1; menos 1 e 3; e menos 3 e 3. O polígono 6 é um quadrado com vértices de coordenadas menos 7 e menos 2; menos 5 e menos 2; menos 5 e menos 4; menos 3 e 3. O polígono 7 é um trapézio com vértices de coordenadas menos 3 e menos 1; menos 2 e menos 1; menos 1 e menos 3; menos 3 e menos 3. O polígono 8 é um trapézio com vértices de coordenadas 1 e menos 1; 2 e menos 1; 3 e menos 3; 1 e menos 3. E o polígono 9 é um quadrado com vértices de coordenadas 5 e menos 2; 5 e menos 4; 7 e menos 4; 7 e menos 2.

Quais polígonos são simétricos por reflexão em relação ao eixo x? E em relação ao eixo y?

23. Com base nas imagens a seguir, elabore um problema. Depois, entregue-o a um colega para que ele o resolva. Por fim, verifique se o colega resolveu o problema corretamente.

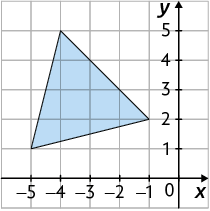
Ilustração. Plano cartesiano graduado sobre malha quadriculada com um triângulo cujos vértices estão posicionados nos pontos com coordenadas menos 5 e 1; menos 1 e 2; menos 4 e 5.

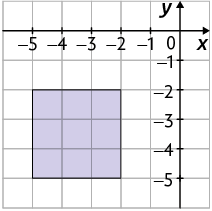
Ilustração. Plano cartesiano graduado sobre malha quadriculada com um quadrado cujos vértices estão posicionados nos pontos com coordenadas menos 2 e menos 2; menos 2 e menos 5; menos 5 e menos 5; menos 5 e menos 2.

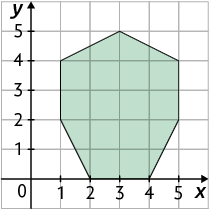
Ilustração. Plano cartesiano graduado sobre malha quadriculada com um polígono de 7 lados cujos vértices estão posicionados nos pontos com coordenadas 1 e 2; 2 e 0; 4 e 0; 5 e 2; 5 e 4; 3 e 5; 1 e 4.

Ilustração. Plano cartesiano graduado sobre malha quadriculada com um polígono de 5 lados cujos vértices estão posicionados nos pontos com coordenadas 1 e menos 5; 2 e menos 2; 3 e menos 3; 4 e menos 2; 5 e menos 5.

Página 272

Transformações no plano cartesiano

Considere o polígono $A B C D E$ no plano cartesiano.

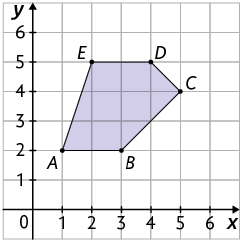
Ilustração. Plano cartesiano sobre malha quadriculada com um polígono A B C D E. O vértice A tem coordenadas 1 e 2; vértice B tem coordenadas 3 e 2; vértice C tem coordenadas 5 e 4; vértice D tem coordenadas 4 e 5; e vértice E tem coordenadas 2 e 5.

Questão 3. Escreva no caderno as coordenadas dos vértices do polígono $A B C D E$ .

Ao multiplicarmos as coordenadas de cada um dos vértices desse polígono por $menos 1$ , obtemos os seguintes pontos.

$ponto A linha com coordenadas menos 1 e menos 2$
$ponto B linha com coordenadas menos 3 e menos 2$
$ponto C linha com coordenadas menos 5 e menos 4$
$ponto D linha com coordenadas menos 4 e menos 5$
$ponto E linha com coordenadas menos 2 e menos 5$

Representando os polígonos $A B C D E$ e $A ’ B ’ C ’ D ’ E ’$ em um mesmo plano cartesiano, obtemos:

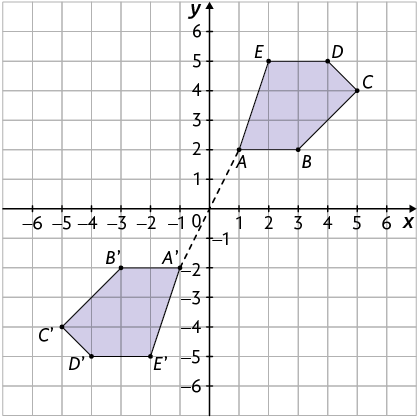
Ilustração. Plano cartesiano sobre malha quadriculada com dois polígonos semelhantes representados. Um deles tem vértices A B C D E, em que A tem coordenadas 1 e 2; B tem coordenadas 3 e 2; C tem coordenadas 5 e 4; D tem coordenadas 4 e 5; e o vértice E tem coordenadas 2 e 5. O outro polígono tem vértices nos pontos A linha B linha C linha D linha E linha. Há um segmento tracejado indo do vértice A de um polígono até o vértice A linha do outro e passando pela origem.

O polígono $A ’ B ’ C ’ D ’ E ’$ é a imagem do polígono $A B C D E$ pela transformação de rotação de $180 graus$ em relação à origem do plano cartesiano. Nesse caso, dizemos que os polígonos $A B C D E$ e $A ’ B ’ C ’ D ’ E ’$ são simétricos em relação à origem do plano cartesiano.

Para obter o simétrico de um polígono A em relação à origem do plano cartesiano, basta multiplicar as coordenadas dos vértices desse polígono por $menos 1$ .

Questão 4. Em um plano cartesiano, construa um pentágono A. Em seguida, construa o simétrico dele em relação à origem do plano cartesiano.

Questão 5. Quais são as coordenadas dos vértices do pentágono A que você construiu na questão 4? E do simétrico dele em relação à origem do plano cartesiano?

Página 273

Considere o retângulo $X Y Z W$ , cujas coordenadas dos vértices são $ponto X com coordenadas 1 e 2$ , $ponto Y com coordenadas 4 e 2$ , $ponto Z com coordenadas 4 e 4$ e $ponto W com coordenadas 1 e 4$ . Ao multiplicarmos as coordenadas dos vértices desse retângulo por 2, obtemos os seguintes pontos.

$ponto X linha com coordenadas 2 e 4$
$ponto Y linha com coordenadas 8 e 4$
$ponto Z linha com coordenadas 8 e 8$
$ponto W linha com coordenadas 2 e 8$

Os retângulos $X Y Z W$ e $X ’ Y ’ Z ’ W ’$ foram construídos em um mesmo plano cartesiano.

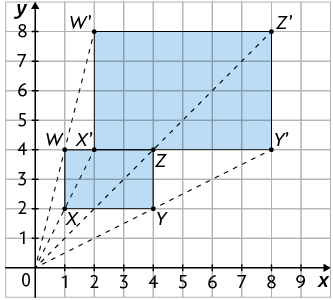
Ilustração. Plano cartesiano sobre malha quadriculada com dois retângulos. Um deles tem vértices X Y Z W, em que X tem coordenadas 1 e 2; Y tem coordenadas 4 e 2; Z tem coordenadas 4 e 4; e W tem coordenadas 1 e 4. O outro retângulo tem vértices nos pontos X linha Y linha Z linha W linha. Há 4 segmentos tracejados, um passa pelos vértices X e X linha; outro pelos vértices Y e Y linha; outro pelos vértices Z e Z linha; e o outro segmento passa pelos vértices W e W linha. .

Note que os retângulos $X Y Z W$ e $X ’ Y ’ Z ’ W ’$ apresentam o mesmo formato, ângulos cor- respondentes congruentes e lados correspondentes proporcionais – a medida do comprimento de cada lado do retângulo $X ’ Y ’ Z ’ W ’$ é igual ao dobro da medida do comprimento do lado correspondente no retângulo $X Y Z W$ . Nesse caso, o retângulo $X ’ Y ’ Z ’ W ’$ é uma ampliação do retângulo $X Y Z W$ .

Questão 6. Em um plano cartesiano, construa o polígono $E F G H I$ , cujas coordenadas dos vértices são $ponto E com coordenadas 1 e 2$ , $ponto F com coordenadas 3 e 4$ , $ponto g com coordenadas 4 e 3$ , $ponto h com coordenadas 4 e 1$ e $ponto I com coordenadas 1 e 1$ . Em seguida, multiplique cada coordenada por $menos 2$ , obtendo os pontos $E ’$ , $F ’$ , $G ’$ , $H ’$ e $I ’$ . Por fim, construa o polígono $E ’ F ’ G ’ H ’ I ’$ . O polígono construído é uma ampliação ou uma redução do polígono $E F G H I$ ? Justifique sua resposta em seu caderno.

Atividades

Faça as atividades no caderno.

24. Analise os polígonos no plano cartesiano a seguir.

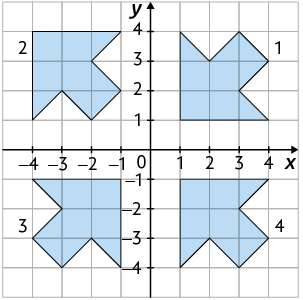
Ilustração. Plano cartesiano graduado sobre malha quadriculada com quatro polígonos que se assemelham a setas na diagonal. Polígono 1 com vértices de coordenadas: 1 e 1; 4 e 1; 3 e 2; 4 e 3; 3 e 4; 2 e 3; 1 e 4. Polígono 2 com vértices de coordenadas: menos 1 e 2; menos 1 e 4; menos 2 e 1; menos 2 e 3; menos 3 e 2; menos 4 e 1. Polígono 3 com vértices de coordenadas: menos 1 e menos 1; menos 1 e menos 4; menos 2 e menos 3; menos 3 e menos 2; menos 3 e menos 4; menos 4 e menos 1; menos 4 e menos 3. Polígono 4 com vértices de coordenadas: 1 e menos 1; 1 e menos 4; 2 e menos 3; 3 e menos 2; 3 e menos 4; 4 e menos 1; 4 e menos 3.

a) Qual polígono pode ser obtido multiplicando as coordenadas dos vértices do polígono 1 por $menos 1$ ?

b) Multiplicando por $menos 1$ as coordenadas dos vértices do polígono 4, podemos obter o polígono 2? Por quê?

Página 274

25. Em uma malha quadriculada, construa um plano cartesiano e represente o quadrilátero $A B C D$ .

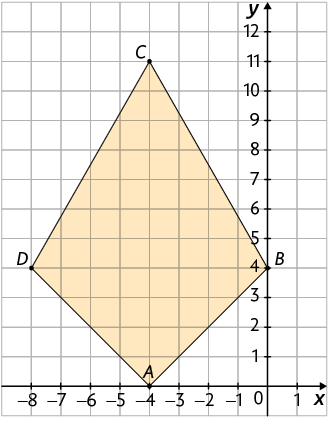
Ilustração. Plano cartesiano graduado sobre malha quadriculada com um quadrilátero A B C D, em que o vértice A tem coordenadas menos 4 e 0; vértice B tem coordenadas 0 e 4; vértice C tem coordenadas menos 4 e 11; e vértice D tem coordenadas menos 8 e 4.

Na sequência, multiplique as coordenadas dos vértices de $A B C D$ por $menos 2$ , obtendo os pontos $A ’$ , $B ’$ , $C ’$ e $D ’$ . Por fim, construa o polígono $A ’ B ’ C ’ D ’$ . O polígono $A B C D$ é uma ampliação ou uma redução do polígono $A ’ B ’ C ’ D ’$ ? Justifique sua resposta.

26. Em um plano cartesiano, Fátima representou um retângulo cujas coordenadas dos vértices são $coordenadas 5 e menos 5$ , $coordenadas 5 e menos 8$ , $coordenadas 13 e menos 8$ e $coordenadas 13 e menos 5$ .

a) Se as coordenadas dos pontos desse retângulo fossem multiplicadas por $menos 3$ , quais seriam as coordenadas dos vértices do novo retângulo? Ele seria uma ampliação ou uma redução da figura desenhada por Fátima?

b) Determine as coordenadas dos vértices do retângulo simétrico ao retângulo representado por Fátima em relação à origem do plano cartesiano.

27. Por qual número as coordenadas dos vértices do triângulo $A B C$ foram multiplicadas para obter o triângulo $D E F$ ?

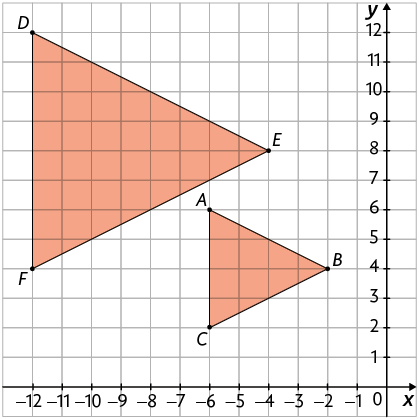
Ilustração. Plano cartesiano graduado sobre malha quadriculada com dois triângulos representados. O triângulo A B C tem o vértice A com coordenadas menos 6 e 6; vértice B com coordenadas menos 2 e 4; e vértice C com coordenadas menos 6 e 2. E o triângulo D E F tem o vértice D com coordenadas menos 12 e 12; vértice E com coordenadas menos 4 e 8; e vértice F com coordenadas 12 e 4.

Página 275

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Gabriela dobrou uma folha de papel ao meio, marcando bem o vinco. Com a folha ainda dobrada, ela fez o desenho apresentado a seguir.

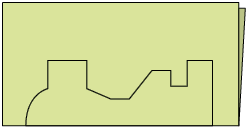
Ilustração. Folha de papel dobrada ao meio horizontalmente, com uma de suas metades voltada para frente, exibindo metade da figura que foi desenhada na folha encostada na parte dobrada. A figura apresenta 13 lados, o primeiro possui um formato curvo, o segundo adjacente a este lado curvo, está verticalmente com relação à base da folha de papel, o terceiro está horizontalmente, o quarto verticalmente, o quinto levemente diagonal quase horizontal, o sexto, pequeno traço horizontal, o sétimo um traço diagonal, o oitavo, um traço horizontal, o nono, um traço vertical, o décimo, um traço horizontal, o décimo primeiro um traço vertical, o décimo segundo, um traço horizontal e o décimo terceiro um traço vertical até a dobra do papel.

Com uma tesoura, Gabriela recortou sobre as linhas do desenho. Qual figura foi obtida ao desdobrar a folha de papel com o desenho?

Ilustração. De uma figura recortada na dobra de uma folha de papel que agora foi aberta reproduzindo a mesma figura do outro lado formando uma única figura simétrica com o eixo de simetria exatamente na dobra do papel que está indicado por uma linha pontilhada. A figura apresenta 12 lados, o primeiro possui um formato curvo, o segundo adjacente a este lado curvo, está verticalmente com relação à base da folha de papel, o terceiro está horizontalmente, o quarto verticalmente, o quinto está horizontal, o sexto, um traço diagonal, o sétimo, um traço horizontal, o oitavo, um traço vertical, o nono, um traço horizontal, o décimo um traço vertical, o décimo primeiro, um traço diagonal e o décimo segundo um traço vertical até a dobra do papel. A figura se repete simetricamente após a dobra do papel.

2. Em quais desenhos o eixo e não é eixo de simetria?

Imagens não proporcionais entre si.

Ilustração. Figura semelhante a um vaso com duas alças, uma na esquerda e outra na direita, há um eixo vertical indicado pela letra e representado exatamente no meio do vaso, representando a divisão em duas partes simétricas.

Ilustração. Figura semelhante a um avião visto de cima, com sua frente apontada para a direita, com um eixo indicado pela letra: e, na horizontal, representando dividir o avião em duas figuras simétricas.

Ilustração. Paralelogramo, com seus lados de cima e de baixo posicionados na horizontal. Os lados nas laterais estão posicionados diagonalmente, inclinados para a direita. Há um eixo indicado pela letra: e, na horizontal, indicando dividir o paralelogramo em duas figuras semelhantes.

Ilustração. Uma guitarra posicionada verticalmente, com seu braço voltado para cima, há um eixo indicado pela letra: e, na horizontal, representando dividir a figura em duas figuras não simétricas.

3. Quais letras a seguir não têm simetria axial?

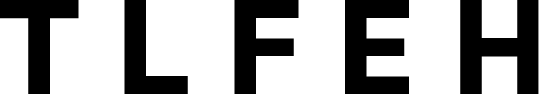
Ilustração. Cinco Polígonos, semelhantes às letras maiúsculas: T, L, F, E e H. Todas construídas com a utilização de retângulos.

4. Reproduza a figura a seguir em uma malha quadriculada. Depois, obtenha a simétrica a ela por reflexão em relação ao:

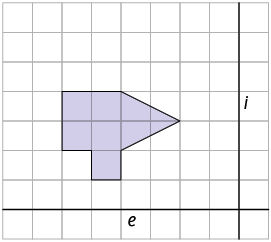
Ilustração. Malha quadriculada com eixo vertical denominado i. E eixo horizontal denominado e. Eles são perpendiculares entre si. Acima do eixo horizontal e à esquerda do eixo vertical há uma figura de 8 lados, composta por um quadrado que ocupa 4 quadradinhos da malha, com um triângulo alinhado à sua direita ocupando 2 quadradinhos de comprimento e 2 quadradinhos de base, e com um quadradinho abaixo do quadrado.

eixo i.

eixo e.

Versão adaptada acessível

4. Junte-se a um colega e reproduzam a figura apresentada em uma malha quadriculada. Depois, obtenham a simétrica a ela por reflexão em relação ao:

eixo i.

eixo e.

Página 276

5. Algumas figuras foram representadas na malha quadriculada.

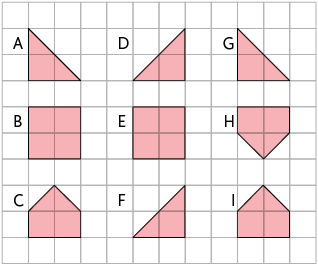
Ilustração de uma malha quadriculada com 9 polígonos. O polígono A é um triângulo retângulo, com dois quadradinhos de base e dois de altura. A altura está no lado esquerdo. O polígono B é um quadrado composto por 4 quadradinhos da malha. O polígono C é um pentágono formado por dois quadradinhos na base e um triângulo acima. O polígono D é um triângulo retângulo com dois quadradinhos de base e dois de altura. A altura está no lado direito. O polígono E é um quadrado composto por 4 quadradinhos da malha. O polígono F é um triângulo retângulo com dois quadradinhos de base e dois de altura. A altura está no lado direito. O polígono G é um triângulo retângulo com dois quadradinhos de base e dois de altura. A altura está no lado esquerdo. O polígono H é um pentágono formado por dois quadradinhos e abaixo deles um triângulo. E o polígono I é um pentágono formado por dois quadradinhos na base e um triângulo acima.

Quais pares de polígonos são simétricos por translação?

6. Em um programa de computador, Francisco construiu o pentágono $A B C D E$ . Depois, ele multiplicou as coordenadas dos vértices da figura por um número inteiro e obteve as coordenadas dos vértices do pentágono $F G H I J$ .

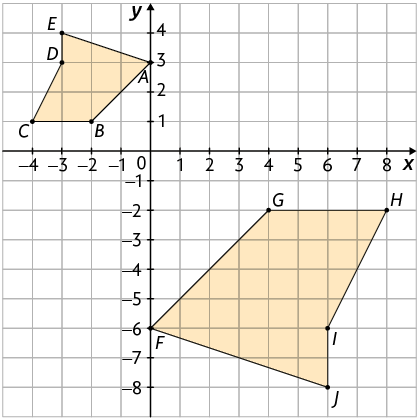
Ilustração. Plano cartesiano graduado sobre malha quadriculada com dois polígonos. O polígono A B C D E tem o vértice A com coordenadas 0 e 3; vértice B com coordenadas menos 2 e 1; vértice C com coordenadas menos 4 e 1; vértice D com coordenadas menos 3 e 3; e vértice E com coordenadas menos 3 e 4. E o polígono F G H I J tem o vértice F com coordenadas 0 e menos 6; vértice G com coordenadas 4 e menos 2; vértice H com coordenadas 8 e menos 2; vértice I com coordenadas 6 e menos 6; e vértice J com coordenadas 6 e menos 8.

a) Por qual número Francisco multiplicou as coordenadas dos vértices do pentágono $A B C D E$ para obter as coordenadas dos vértices do pentágono $F G H I J$ ?

b) O pentágono $F G H I J$ é uma redução ou ampliação do pentágono $A B C D E$ ?

c) Quais seriam as coordenadas dos vértices do novo pentágono se Francisco tivesse feito a multiplicação dos vértices do pentágono $A B C D E$ por 2?

7. Analise o polígono $A B C D E$ desenhado em um plano cartesiano.

Ilustração. Plano cartesiano graduado sobre malha quadriculada com um polígono A B C D. O vértice A tem coordenadas menos 2 e 0; vértice B tem coordenadas menos 1 e 1; vértice C tem coordenadas menos 1 e menos 3; vértice D tem coordenadas menos 3 e 3; e vértice E tem coordenadas menos 2 e menos 2.

a) Quais são as coordenadas dos vértices desse polígono?

b) Ao fazer uma rotação desse polígono de $180 graus$ em torno da origem do plano cartesiano, quais são as coordenadas dos vértices do polígono obtido?

8. As figuras representadas no plano cartesiano a seguir são simétricas por rotação em torno do ponto O, que não está indicado na imagem. Quais são as coordenadas do ponto O?

Ilustração. Plano cartesiano graduado sobre malha quadriculada dois polígonos. As coordenadas dos vértices de um dos polígonos são: 0 e 5; 0 e 6; 1 e 6; 1 e 9; 2 e 10; 2 e 9; 3 e 8; 2 e 8; 2 e 6; 3 e 5; 2 e 4. E as coordenadas dos vértices da outra figura são: 5 e 4; 6 e 4; 6 e 6; 5 e 7; 6 e 8; 8 e 7; 7 e 6; 7 e 3; 6 e 2; 6 e 3; 8 e 6.