Página XLII
Resoluções
O que eu já sei?
1. Considerando os números que já estão indicados na reta, verificamos que a letra A representa um número entre 0 e 1. Portanto, a letra A representa 0,61.
As letras B e C representam números entre 1 e 2, sendo . Assim, verificamos que a letra B representa 1,247 e a letra C representa 1,489.
As letras D, E, F e G representam números entre 2 e 3,5, sendo . Assim, verificamos que: a letra D representa 2,38; a letra E representa 2,92; a letra F representa 3 e a letra G representa 3,36.
a) Como os números são todos positivos, o maior número será o que estiver localizado mais distante do zero na reta, nesse caso, representado pela letra G. Já o menor número será o que estiver localizado mais próximo do zero na reta, nesse caso, associado à letra A. Portanto, o maior número será o 3,36 e o menor número será o 0,61.
b) • ;
;
.
2. a) Como o algarismo 6 ocupa a 3ª ordem (centenas simples) no número 12.657, seu valor posicional é 600.
b) Como o algarismo 6 ocupa a 5ª ordem (dezenas de milhar) no número 69.745, seu valor posicional é 60.000.
c) Como o algarismo 6 ocupa a 2ª ordem (dezenas simples) no número 32.561, seu valor posicional é 60.
d) Como o algarismo 6 ocupa a 1ª ordem (unidades simples) no número 98.456, seu valor posicional é 6.
3. a) Sim, pois o valor no 1º membro é igual ao do 2º membro.
b) Adicionando 50 ao 1º membro, teremos . Portanto, devemos acrescentar 50 ao 2º membro para que a igualdade se mantenha verdadeira.
c) Subtraindo 20 do 1º membro, teremos . Portanto, devemos subtrair 20 do 2º membro para que a igualdade se mantenha verdadeira.
4. a) , ou seja, R$ 780,00.
b) , ou seja, R$ 690,00.
c) , ou seja, R$ 740,00.
5. a) Os 10 primeiros múltiplos de:
4 são 0, 4, 8, 12, 16, 20, 24, 28, 32 e 36.
6 são 0, 6, 12, 18, 24, 30, 36, 42, 48 e 54.
8 são 0, 8, 16, 24, 32, 40, 48, 56, 64 e 72.
b) De acordo com os números listados no item anterior:
os múltiplos comuns de 4 e 6 são 0, 12, 24 e 36. Assim, .
os múltiplos comuns de 4 e 8 são 0, 8, 16, 24 e 32. Assim, .
os múltiplos comuns de 6 e 8 são 0, 24 e 48. Assim, .
6. a) As figuras A, C e E são prismas e as figuras B, D e F são pirâmides.
Figura A: Prisma de base triangular;
Figura B: Pirâmide de base pentagonal;
Figura C: Prisma de base quadrada;
Figura D: Pirâmide de base quadrada;
Figura E: Prisma de base pentagonal;
Figura F: Pirâmide de base triangular.
b) A figura E tem 7 faces, 10 vértices e 15 arestas.
c) Contando a quantidade de arestas em cada figura, temos:
figura A: 9 arestas; figura B: 10 arestas; figura C: 12 arestas; figura D: 8 arestas; figura E: 15 arestas; figura F: 6 arestas.
Portanto, a pirâmide de base triangular tem a menor quantidade de arestas e o prisma de base pentagonal tem a maior quantidade de arestas.
7. Como há 10 quadradinhos pintados de verde na figura A, a porcentagem que representa essa quantidade é 10%, que pode ser expressa pela fração e pelo número decimal 0,1.
A parte pintada de verde na figura B representa 50% dela. Essa quantidade pode ser expressa pela fração e pelo número decimal 0,5.
8. a) A diferença foi R$ 0,29, pois .
b) O aumento foi R$ 0,31, pois .
c) Vamos, inicialmente, identificar o maior e o menor preço ao longo deste ano. Nesse caso, os valores são, respectivamente, R$ 6,13 e R$ 4,10.
Portanto, R$ 2,03 foi a diferença entre o maior e o menor preço deste ano.
d) O aumento em reais do preço da gasolina é representado pela diferença entre os preços de dezembro e janeiro, ou seja, .
Portanto, houve R$ 1,94 de aumento.
9. a) Como R$ 45,00 corresponde a 10% de desconto, 20% de desconto corresponde ao dobro deste valor, isto é, R$ 90,00.
b) Sendo R$ 45,00 correspondente a 10% do preço original, o preço do produto sem desconto é , ou seja, R$ 450,00.
10. Figura A: quadrilátero; figura B: pentágono; figura C: triângulo; figura D: hexágono; figura E: quadrilátero; figura F: triângulo.
a) Nos polígonos, a quantidade de vértices corresponde à quantidade de lados. Portanto, o polígono que tem a maior quantidade de vértices é o hexágono.
b) A quantidade de ângulos internos corresponde à quantidade de vértices do polígono. Logo, o pentágono tem exatamente 5 ângulos internos.
c) O polígono com a menor quantidade de lados é o triângulo.
11. A figura A é formada por 19 quadrados e 4 triângulos. Como a medida da área de 2 triângulos corresponde à medida da área de 1 quadrado, a figura A é formada por 21 quadrados, isto é, sua área mede .
A figura B é formada por 9 quadrados e 5 triângulos, o que corresponde a 11 quadrados e 1 triângulo. Portanto, sua área mede .
Página XLIII
12. a) Os possíveis resultados são bolinha vermelha, azul, verde ou laranja.
b) A probabilidade de retirar uma determinada cor de bolinha é representada pela razão entre a quantidade de bolinhas de uma determinada cor e a quantidade total de bolinhas na urna. Portanto, a probabilidade de sortear uma bolinha:
azul é ou 0,2 ou 20%.
verde é ou 0,4 ou 40%.
laranja é ou 0,1 ou 10%.
13. a) Em 2017, a quantidade de embalagens recebidas foi a menor.
b) Em 2019, a quantidade de embalagens recebidas foi a maior.
c) Calculando a diferença entre a quantidade de embalagens recebidas e a quantidade de embalagens recicladas em cada ano, temos:
em 2017, pois .
em 2018, pois .
em 2019, pois .
em 2020, pois .
Comparando as quantidades, verificamos que em 2018 houve uma diferença de 206 toneladas. Essa foi a menor diferença entre a quantidade recebida e a reciclada de embalagens de óleo lubrificante.
Unidade 1
Múltiplos e divisores de um número
Questão 1. Um número é múltiplo de 4 quando pode ser escrito como uma multiplicação de números naturais em que um dos fatores é 4. Por exemplo, 12 é múltiplo de 4, pois . Analogamente, um número é múltiplo de 6 quando pode ser escrito como uma multiplicação de números naturais em que um dos fatores é 6. Por exemplo, 30 é múltiplo de 6, pois .
Questão 2. A quantidade de estudantes é maior do que 35 e menor do que 40. Sendo assim, a quantidade de estudantes da turma poderá ser 36, 37, 38 ou 39. Como ele está pensando em formar duplas ou trios, essa quantidade deve ser expressa por um número múltiplo de 2 e 3. Para ser múltiplo de 2, basta ser par, ou seja, poderá ser 36 ou 38. Porém, entre esses dois números, apenas 36 é múltiplo de 3. Portanto, há exatamente 36 estudantes.
Atividades
1. a) Um número será múltiplo de 2 quando puder ser escrito como uma multiplicação entre dois números naturais em que um dos fatores for 2. Nesse caso, os múltiplos de 2 são:
8, pois ;
12, pois ;
800, pois ;
122, pois .
b) Um número será múltiplo de 10 quando puder ser escrito como uma multiplicação em que um dos fatores for 10. Nesse caso, o único múltiplo de 10 é o 800, pois .
c) Um número será múltiplo de 5 quando puder ser escrito como uma multiplicação em que um dos fatores for 5. Nesse caso, os múltiplos de 5 são:
15, pois ;
95, pois ;
800, pois ;
45, pois .
2. Como Joana gostaria de distribuir em quantidades menores de bombons em cada caixa, temos entre os múltiplos de 24 as seguintes possibilidades:
2 caixas com 12 bombons em cada caixa: ;
3 caixas com 8 bombons em cada caixa: ;
4 caixas com 6 bombons em cada caixa: ;
6 caixas com 4 bombons em cada caixa: ;
8 caixas com 3 bombons em cada caixa: ;
12 caixas com 2 bombons em cada caixa: ;
24 caixas com 1 bombom em cada caixa: ;
Portanto, seria possível montar caixas com 1, 2, 3, 4, 6, 8 ou 12 bombons.
3. O número está entre 1.000 e 2.000. O algarismo das dezenas é o 7 e o das centenas é o 9. Como o número é um múltiplo de 5 e não é múltiplo de 10, o número que representa o ano indicado é 1975.
Questão 3.
|
Número natural |
É divisível por 2? |
|---|---|
|
20 |
Sim |
|
35 |
Não, pois 35 é ímpar. |
|
48 |
Sim, pois 48 é par. |
|
66 |
Sim, pois 66 é par. |
|
89 |
Não, pois 89 é ímpar. |
Questão 4. Para que um número seja divisível por 3, a soma dos valores correspondentes aos seus algarismos deve ser um número divisível por 3.
270: . Como 9 é divisível por 3, então 270 é um número divisível por 3.
202: . Como 4 não é divisível por 3, então 202 não é um número divisível por 3.
234: . Como 9 é divisível por 3, então 234 é um número divisível por 3.
613: . Como 10 não é divisível por 3, então 613 não é um número divisível por 3.
Questão 5. Resposta no final da seção Resoluções.
Página XLIV
Questão 6. Para que um número seja divisível por 9, a soma dos valores correspondentes ao seus algarismos deve ser um número divisível por 9.
270: . Como 9 é divisível por 9, então 270 é um número divisível por 9.
502: . Como 7 não é divisível por 9, então 502 não é um número divisível por 9.
738: . Como 18 é divisível por 9, então 738 é um número divisível por 9.
907: . Como 16 não é divisível por 9, então 907 não é um número divisível por 9.
Questão 7. Sim, pois todo número divisível por 100 tem os algarismos das unidades e das dezenas simultaneamente iguais a 0, o que satisfaz o critério de divisibilidade por 10.
Atividades
4. a) Um número será divisível por 2 se ele for par. Desse modo, o algarismo das unidades do número a ser formado pode ser substituído por 0, 2, 4, 6 ou 8.
b) Para um número ser divisível por 3, a soma dos valores correspondentes aos seus algarismos deve ser divisível por 3. Como , o valor de X pode ser:
2, pois e 27 é divisível por 3;
5, pois e 30 é divisível por 3;
8, pois e 33 é divisível por 3.
c) Um número será divisível por 5 quando o algarismo das unidades for 0 ou 5. Nesse caso, o algarismo das unidades do número deve ser substituído por 0 ou 5.
d) Um número será divisível por 10 se o algarismo das unidades for 0. Nesse caso, o algarismo das unidades deve ser substituído por 0.
e) Um número será divisível por 100 se os algarismos das unidades e dezenas forem simultaneamente 0. Nesse caso, não há algarismo para substituir X, de modo que o número formado seja divisível por 100, visto que o algarismo das dezenas é 7.
5. a) Apenas o número 1 divide qualquer número natural.
b) O maior divisor de um número é o próprio número.
c) Um número natural maior do que 1 pode ter no mínimo dois divisores, que são o 1 e o próprio número.
6. a) O número a ser substituído precisa ser par, ou seja, terminar em 2 ou 4.
Sugestões de resposta: 342, 754 e 254.
b) A soma dos algarismos do número a ser substituído precisa ser divisível por 3.
Sugestões de resposta: 234, 732 e 534.
c) O número a ser substituído precisa terminar em 0 ou 5 para ser divisível por 5.
Sugestões de resposta: 235, 725 e 345.
d) Um número natural é divisível por 6 quando também for divisível por 2 e 3, simultaneamente.
Sugestões de resposta: 42, 324 e 372.
e) O número a ser substituído precisa ser par, ou seja, terminar em 2 ou 4, e deve ser divisível por 8.
Sugestões de resposta: 24, 352 e 752.
f) Um número natural é divisível por 9 quando a soma dos valores correspondentes aos seus algarismos é um número também divisível por 9.
Sugestões de resposta: 27, 234 e 423.
7. a) Devemos encontrar os divisores de 40. Portanto, os grupos podem ter 2, 4, 5, 8, 10 ou 20 estudantes.
b) Devemos encontrar os divisores de 45. Portanto, os grupos podem ter 3, 5, 9 ou 15 estudantes.
c) Devemos encontrar os divisores de 50 estudantes. Portanto, os grupos podem ter 2, 5, 10 ou 25 estudantes.
8. Resposta no final da seção Resoluções.
9. a) Entre os números apresentados, os divisíveis por 3 são 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45 e 48.
b) Para que um número seja divisível por 5, o algarismo das unidades precisa ser 5 ou 0. Os divisores de 5 são 5, 10, 15, 20, 25, 30, 35, 40, 45 e 50.
c) Os números divisíveis por 8 são 8, 16, 24, 32, 40 e 48.
d) Para que um número seja divisível por 10, o algarismo das unidades precisa ser 0. Portanto, são divisíveis por 10 os números 10, 20, 30, 40 e 50.
10. Resposta pessoal. Sugestão de respostas:
Considere a sequência dos 10 primeiros múltiplos de 2. Qual é o número obtido pela diferença entre o sexto e o segundo número dessa sequência? Resposta: 8.
A idade de Pedro é dada pela soma dos divisores de 10. Qual é a idade de Pedro? Resposta: 50 anos.
Questão 8. Os outros números pares não são primos porque eles têm, no mínimo, três divisores (o 1, o 2 e eles próprios).
Questão 9. Primeiro, vamos listar todos os divisores de cada número.
Divisores do número 2: 1 e 2.
Divisores do número 6: 1, 2, 3 e 6.
Divisores do número 7: 1 e 7.
Divisores do número 15: 1, 3, 5 e 15.
Divisores do número 18: 1, 2, 3, 6, 9 e 18.
Divisores do número 26: 1, 2, 13 e 26.
Divisores do número 35: 1, 5, 7 e 35.
Assim, qualquer par de números que tenha apenas o número 1 como divisor serão primos entre si.
Sugestão de resposta: 2 e 15; 6 e 7; 6 e 35; 15 e 26.
Atividades
11. Inicialmente, riscamos todos os múltiplos de 2, ou seja, os números pares. Em seguida, os múltiplos de 3, 5 e 7. Por fim, riscamos os múltiplos de números primos que são maiores do que 10, como é o caso dos números 11, 13 e 17.
Página XLV
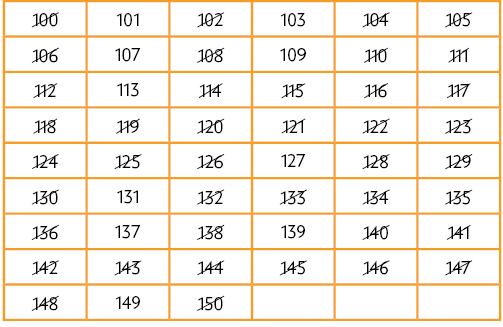
Portanto, os números primos entre 100 e 150 são: 101, 103, 107, 109, 113, 127, 131, 137, 139 e 149.
12. a) Falsa. Sugestão de correção: Nem todos os números primos são ímpares.
b) Falsa. Sugestão de correção: A decomposição em fatores primos do número é .
c) Verdadeira.
d) Verdadeira.
13. Decompondo os números em fatores primos, temos:
a)
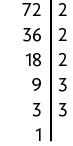
Assim, .
b)
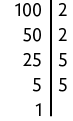
Assim, .
c)

Assim, .
14. a) Entre os números que aparecem como divisores, os primos são 2, 3, 5, 11, 13 e 23.
b) Os divisores primos do número 24 são os números 2 e 3.
15. Os números primos entre 1 e 31 são: 2, 3, 5, 7, 11, 13, 17, 19 e 23.
16. a) Neste caso, para ser múltiplo de 5 o algarismo das unidades deverá ser 5. Logo, o menor número natural formado será o 235.
b) Não é possível, pois , e esse resultado não é número múltiplo de 3.
c) Para ser múltiplo de 2, o número precisa ser par. Logo, o menor número par será o 352.
Para ser primo, o número não poderá ser par (pois, neste caso, seria múltiplo de 2) e nem ter o algarismo das unidades igual a 5 (pois seria múltiplo de 5). Assim, temos dois possíveis números: 253 e 523. Como o número 253 pode ser decomposto em fatores primos (), ele é um número composto. Sendo assim, concluímos que apenas o número 523 é primo.
Questão 10.
a) Divisores de 11: 1 e 11.
Divisores de 5: 1 e 5.
Portanto, .
b) Divisores de 12: 1, 2, 3, 4, 6 e 12.
Divisores de 36: 1, 2, 3, 4, 6, 9, 12, 18 e 36.
Portanto, .
c) Divisores de 4: 1, 2 e 4.
Divisores de 102: 1, 2, 3, 6, 17, 34, 51 e 102.
Portanto, .
d) Divisores de 123: 1, 3, 41 e 123.
Divisores de 13: 1 e 13.
Portanto, .
e) Divisores de 45: 1, 3, 5, 9, 15 e 45.
Divisores de 27: 1, 3, 9 e 27.
Portanto, .
f) Divisores de 37: 1 e 37.
Divisores de 100: 1, 2, 4, 5, 10, 20, 25, 50 e 100.
Portanto, .
Atividades
17. a) Os divisores de 30 são: 1, 2, 3, 5, 6, 10, 15 e 30.
b) Divisores de 18: 1, 2, 3, 6, 9 e 18.
Divisores de 50: 1, 2, 5, 10, 25 e 50.
Portanto, os divisores comuns são 1 e 2.
c) Divisores de 50: 1, 2, 5, 10, 25 e 50.
Divisores de 75: 1, 3, 5, 15, 25 e 75.
Divisores comum entre 50 e 75: 1, 5 e 25.
Portanto, o maior divisor comum é 25.
18. a) Os múltiplos positivos de 3 menores do que 50 são 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45 e 48.
b) Os múltiplos positivos de 5 menores do que 50 são 5, 10, 15, 20, 25, 30, 35, 40 e 45.
c) Os múltiplos positivos comuns de 3 e 5 são 15, 30 e 45.
d) O menor múltiplo comum de 3 e 5 é o 15.
19. a) Múltiplos de 10:
Múltiplos de 12:
Portanto, .
b) Múltiplos de 6:
Múltiplos de 9:
Portanto, .
c) Múltiplos de 12:
Múltiplos de 25:
Portanto, .
Página XLVI
d) Múltiplos de 18:
Múltiplos de 24:
Portanto, .
e) Múltiplos de 16:
Múltiplos de 48:
Portanto, .
f) Múltiplos de 18:
Múltiplos de 20:
Múltiplos de 24:
Portanto, .
g) Divisores de 15: 1, 3, 5 e 15.
Divisores de 18: 1, 2, 3, 6, 9 e 18.
Portanto, .
h) Divisores de 12: 1, 2, 3, 4, 6 e 12.
Divisores de 20: 1, 2, 4, 5, 10 e 20.
Portanto, .
i) Divisores de 7: 1 e 7.
Divisores de 11: 1 e 11.
Portanto, .
j) Divisores de 50: 1, 2, 5, 10, 25 e 50.
Divisores de 70: 1, 2, 5, 7, 10, 14, 35 e 70.
Portanto, .
k) Divisores de 22: 1, 2, 11 e 22.
Divisores de 30: 1, 2, 3, 5, 6, 10, 15 e 30.
Portanto, .
l) Divisores de 16: 1, 2, 4, 8 e 16.
Divisores de 32: 1, 2, 4, 8, 16 e 32.
Portanto, .
20. a) Múltiplos de 2:
Múltiplos de 3:
Portanto, .
b) Múltiplos de 3:
Múltiplos de 5:
Portanto, .
c) Múltiplos de 5:
Múltiplos de 13:
Portanto, .
d) Múltiplos de 2:
Múltiplos de 7:
Múltiplos de 11:
Portanto, .
e) Múltiplos de 5:
Múltiplos de 41:
Portanto, .
f) Múltiplos de 2:
Múltiplos de 7:
Portanto, .
g) Múltiplos de 11:
Múltiplos de 13:
Portanto, .
h) Múltiplos de 5:
Múltiplos de 11:
Portanto, .
i) Múltiplos de 7:
Múltiplos de 13:
Portanto, .
j) Múltiplos de 19:
Múltiplos de 37:
Portanto, .
21. Resposta pessoal. Espera-se que os estudantes digam que o de dois ou mais números primos é igual ao produto deles.
22. a) Múltiplos de 4:
Múltiplos de 5:
Portanto, .
b) Múltiplos de 6:
Múltiplos de 7:
Portanto, .
c) Múltiplos de 8:
Múltiplos de 9:
Portanto, .
d) Múltiplos de 10:
Múltiplos de 11:
Portanto, .
e) Múltiplos de 12:
Múltiplos de 13:
Portanto, .
f) Múltiplos de 14:
Múltiplos de 15:
Portanto, .
g) Múltiplos de 16:
Múltiplos de 17:
Portanto, .
h) Múltiplos de 18:
Múltiplos de 19:
Portanto, .
i) Múltiplos de 20:
Múltiplos de 21:
Portanto, .
j) Múltiplos de 22:
Múltiplos de 23:
Portanto, .
23. Resposta pessoal. Espera-se que os estudantes digam que o de dois números naturais consecutivos é igual ao produto deles.
Página XLVII
24. Nos itens apresentados, como o maior número é sempre o múltiplo dos demais, o será esse número. Então:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
25. Resposta pessoal. Espera-se que os estudantes digam que o de dois ou mais números diferentes de zero é igual ao maior deles, desde que ele seja múltiplo dos demais.
26. Como a professora quer dividir a turma em grupos de 3, 4, 6 ou 12 estudantes, precisamos determinar o múltiplo comum entre esses números que esteja entre 30 e 40.
Múltiplos de 3: 30, 33, 36 e 39
Múltiplos de 4: 32, 36 e 40
Múltiplos de 6: 30 e 36
Múltiplo de 12: 36
Dos números verificados, apenas o 36 é um múltiplo comum. Portanto, essa turma tem 36 estudantes.
27. Para resolver este problema, inicialmente, vamos determinar o entre 8 e 12.
Múltiplos de 8:
Múltiplos de 12:
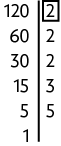
Logo, o . Portanto, João tomará os remédios juntos novamente depois de 24 horas.
28. Calculando o entre 8, 15 e 20, temos:
Múltiplos de 8:
Múltiplos de 15:
Múltiplos de 20:
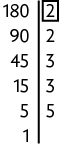
Logo, o . Portanto, os luminosos estarão acesos juntos novamente depois de 120 segundos.
29. a) Como um dos números é o triplo do outro, o será o maior deles, ou seja, um dos números será o próprio 45. Sabendo disso, verificamos que 45 é o triplo de 15. Portanto, os números procurados são 15 e 45.
b) Como o máximo divisor entre os números é 1, verificamos que os números devem ser primos entre si. Nesse caso, há mais de uma resposta correta.
Sugestão de resposta: 3 e 5.
30. Resposta pessoal. Sugestão de resposta:
Problema 1: Dois ônibus partem juntos de um mesmo terminal. O ônibus 1 realiza o trajeto em 25 minutos e o ônibus 2, em 35 minutos. Se eles saíram às da manhã, qual será o próximo horário de saída em que eles partirão juntos novamente? Resposta: O próximo horário de saída ocorrerá depois de 175 minutos, ou seja, às .
Problema 2: Giovana vai organizar os estudantes de sua turma em grupos com a mesma quantidade de pessoas em cada um. Sabendo que nessa turma há 15 meninas e 12 meninos, qual será a quantidade máxima de integrantes em cada grupo, sem misturar a quantidade de meninas e de meninos? Resposta: 3 integrantes.
31. Para dividir o número 216 e obter resto 6, o divisor deverá ser múltiplo de 210. Analogamente, para dividir o número 169 e obter resto 1, o divisor deverá ser múltiplo de 168. Sendo assim, precisamos determinar o mdc entre 210 e 168.
Divisores de 210: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70 e 210.
Divisores de 168: 1, 2, 3, 4, 6, 7, 8, 12, 14, 21, 24, 28, 42, 56, 84 e 168.
Logo, . Portanto, o maior número é 42.
32. Espera-se que os estudantes respondam que calcularam o mínimo múltiplo comum entre os números 8, 15 e 20. Utilizando esse procedimento, é possível resolver os problemas propostos nos itens desta atividade.
a) Para resolver este problema, precisamos calcular o entre 4, 5 e 10.
Múltiplos de 4:
Múltiplos de 5:
Múltiplos de 10:
Logo, o .
Portanto, os ônibus sairão juntos novamente depois de 20 horas.
b) Para resolver este problema, precisamos calcular o mdc entre 60 e 126.
Divisores de 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 e 60.
Divisores de 126: 1, 2, 3, 6, 7, 9, 14, 18, 21, 42, 63 e 126.
Logo, o . Portanto, ela deverá cortar os tecidos em pedaços cujo comprimento mede .
c) Para resolver este problema, precisamos calcular o entre 4, 6 e 8.
Múltiplos de 4:
Múltiplos de 6:
Múltiplos de 8:
Logo, o . Portanto, após 24 dias os três trabalharão juntos novamente, ou seja, no dia 27 de março.
Questão 11. Para obter o mdc entre 32 e 48, precisamos decompor, separadamente, cada número em fatores primos e, em seguida, identificar os fatores comuns.
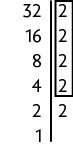
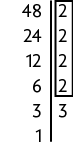
Efetuando o produto entre os fatores dos produtos comuns, obtemos . Portanto, .
Página XLVIII
Questão 12. Para obter o entre 32 e 48 precisamos decompor simultaneamente os dois números em fatores primos. Vamos efetuar esse procedimento no algoritmo.
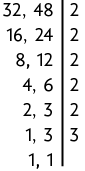
Efetuando o produto de todos os fatores obtidos no algoritmo, verificamos que:
Atividades
33. Para responder a essa questão, precisamos determinar o valor máximo para cada fone, que corresponde ao divisor de 180, 240 e 320, ou seja, o . Decompondo separadamente cada um destes números em fatores primos, temos:
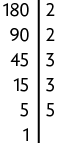
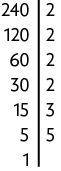

Como , concluímos que o valor máximo de cada fone é R$ 20,00.
Em seguida, dividimos o valor vendido em cada dia por esse resultado e adicionamos as quantidades obtidas.
Portanto, foram vendidos, ao todo, 37 fones.
34. Como o menor número é a metade do maior, então o maior número será o entre eles. Assim, 50 é o maior número e, como 50 é o dobro de 25, os números procurados são 25 e 50.
35. Para resolver este problema, precisamos calcular o entre 6 e 8. Decompondo simultaneamente esses números em fatores primos por meio do algoritmo, obtemos:
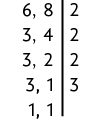
Assim, o . Portanto, após 24 horas, Carla vai ingerir as vitaminas ao mesmo tempo novamente.
36. Para resolver este problema, precisamos calcular o mdc entre 36 e 42. Então, vamos decompor, separadamente, cada número em fatores primos e, em seguida, identificar os fatores comuns.
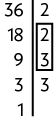
Assim, o . Portanto, Rafaela deve colocar 6 doces em cada prato.
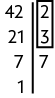
37. Para resolver este problema, precisamos encontrar o mdc entre 165, 220 e 275. Então, vamos decompor, separadamente, cada número em fatores primos e, em seguida, identificar os fatores comuns.
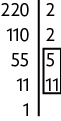
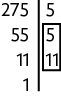
Assim, o . Portanto, Tobias deve colocar 55 ímãs em cada caixa.
38. De acordo com as informações do enunciado, formando agrupamentos de 2, 3, 4, 5 ou 6 bolinhas sobra 1 bolinha. Assim, a quantidade total de bolinhas menos 1 é representada por um múltiplo de 2, 3, 4, 5 e 6. Nesse caso, precisamos determinar o mínimo múltiplo comum entre 2, 3, 4, 5 e 6 simultaneamente.

Assim, o .
Analisando os múltiplos de 60, podemos listar alguns deles, como
Adicionando 1 unidade a esses múltiplos listados, verificamos que a quantidade total de bolinhas poderia ser . Porém, como a quantidade total de bolinhas deve ser múltiplo de 7, o menor múltiplo de 60 que atende a essa condição é 301. Portanto, concluímos que Rodrigo tem 301 bolinhas de gude.
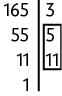
39. Para resolver esse problema, precisamos encontrar o mdc entre 48, 74 e 120. Então, vamos decompor, separadamente, cada número em fatores primos e, em seguida, identificar os fatores comuns.
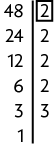
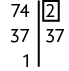
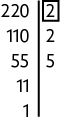
Logo, o . Portanto, T é igual a 2.
Página XLIX
40. Para resolver este problema, precisamos encontrar o entre 30, 20 e 15. Decompondo, simultaneamente, os três números em fatores primos, temos:

Logo, o . Portanto, após 60 minutos, ou seja, após 1 hora eles se encontrarão novamente nesse local.
41. Para que a quantidade de recipientes utilizados seja a menor possível, devemos ter a menor quantidade possível de bolinhas em cada recipiente. Sendo assim, precisamos calcular o mdc entre 180 e 220.
Logo, o . Portanto, Theo vai usar 20 caixas.
O que eu estudei?
1. a) Os números primos consecutivos menores do que 30 são 2, 3, 5, 7, 11, 13, 17, 19, 23 e 29. Deles, os dois números cuja adição resulta em 30 são 13 e 17.
b) Os números primos consecutivos menores do que 100 são 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97. Deles, os quatro números cuja adição resulta em 168 são 37, 41, 43 e 47.
c) Os números primos consecutivos menores do que 50 são 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 e 47. Deles, os dois números cujo produto resulta em 899 são 29 e 31.
2. a) Os números primos de apenas um algarismo são 2, 3, 5 e 7, dos quais o único número primo par é 2 e o maior número primo entre eles é 7. Portanto, o produto é igual a 14.
b) Os números primos de dois algarismos são 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97, dos quais o único número primo par é 2 e o maior número primo de dois algarismos é 97. Portanto, o produto é igual a 194.
3. Para que os números sejam primos entre si, o maior divisor comum entre eles deve ser o 1.
Divisores de 14: 1, 2, 7 e 14.
Divisores de 39: 1, 3, 13 e 39.
Divisores de 50: 1, 2, 5, 10, 25 e 50.
Para determinar outros três números, devemos escolher números que não tenham divisores comuns com os que já estão no quadro. Sugestão de resposta:
Divisores de 11: 1 e 11.
Divisores de 13: 1 e 13.
Divisores de 18: 1, 2, 3, 6 e 18.
Assim:
- 14
- 11
- 50
- 13
- 39
- 18
4. a) Os 15 primeiros múltiplos de 4 são 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52 e 56.
b) Os 10 primeiros múltiplos de 7 são 0, 7, 14, 21, 28, 35, 42, 49, 56 e 63.
c) Os três primeiros múltiplos comum de 4 e 7 são 0, 28 e 56.
d) De acordo com o item anterior, o .
e) Divisores de 4: 1, 2 e 4.
Divisores de 7: 1 e 7.
Logo, o .
f) Como o número 1 é o maior divisor comum entre eles, então 4 e 7 são números primos entre si.
5. Como o resto da divisão de um número por 2, 3, 4, 5, 6 ou 7 é 1, esse número não deve ser múltiplo de 2, 3, 4, 5, 6 e 7. Desse modo, o número que procuramos é 1 unidade maior do que o menor múltiplo dos números citados. Calculando o mínimo múltiplo comum entre esses números, temos:

Logo, o .
Portanto, o número procurado é 421, pois .
6. Para resolver este problema, precisamos calcular o mdc entre 162 e 90.
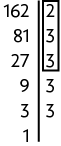
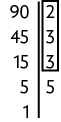
Como o e há 252 fichas no total , devemos dividir a quantidade de fichas pelo obtido. Assim, . Portanto, podem ser formadas 14 pilhas.
7. a) Calculando o entre 10 e 12, temos:

Logo, o .
Portanto, Maicon e Renata se encontram na casa da mãe a cada 60 dias.
Página L
b) Calculando o entre 10 e 18, temos:
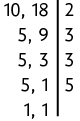
Logo, o .
Portanto, Maicon e Laura se encontram na casa da mãe a cada 90 dias.
c) Calculando o entre 10, 12 e 18, temos:

Logo, o .
Portanto, Maicon, Renata e Laura se encontram na casa da mãe a cada 180 dias.
d) Calculando o entre 12 e 18, temos:

Logo, o .
Portanto, Renata e Laura se encontram na casa da mãe a cada 36 dias.
8. Calculando o mdc entre 36 e 28, temos:
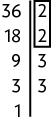
Como os fatores comuns são , o .
Portanto, podem ser formados no máximo 4 arranjos, cada um com 9 rosas e 7 margaridas .
Unidade 2
Os números inteiros
Questão 1. O município de Arcoverde está localizado em Pernambuco (PE). Esse estado faz fronteira com Alagoas (AL), Bahia (BA), Ceará (CE) Paraíba (PB) e Piauí (PI).
O município de Manaus está localizado no estado do Amazonas (AM). Esse estado faz fronteira com Acre (AC), Mato Grosso (MT), Pará (PA), Roraima (RR) e Rondônia (RO).
O município de Maringá está localizado no estado do Paraná (PR). Esse estado faz fronteira com Mato Grosso do Sul (MS), Santa Catarina (SC) e São Paulo (SP).
O município de Lajes está localizado no estado de Santa Catarina (SC). Esse estado faz fronteira com Rio Grande do Sul e Paraná.
O município de Vacaria está localizado no Rio Grande do Sul (RS). Esse estado faz fronteira apenas com Santa Catarina (SC).
Questão 2.
a) Os números negativos são , e .
b) Os números maiores do que o zero são e .
c) O número 0 (zero).
Atividades
1. O termômetro A está marcando e representa a medida da temperatura na cidade de Maringá (PR); O termômetro B está marcando e representa a medida da temperatura da cidade de Manaus (AM); O termômetro C está marcando e representa a medida da temperatura da cidade de Vacaria (RS).
2. a) O termômetro C está indicando a maior medida de temperatura. O termômetro A está indicando a menor medida de temperatura.
b) Verificamos que o termômetro A está indicando , o termômetro B está indicando , o termômetro C está indicando e o termômetro D está indicando .
3. a) Os termômetros B e F estão indicando uma temperatura com medida negativa.
b) A água estaria em estado líquido nos ambientes cujas medidas de temperatura estão indicadas nos termômetros A, C, D, e E, pois estão marcadas medidas de temperatura acima de zero.
A água estaria em estado sólido nos ambientes cujas medidas de temperatura estão indicadas nos termômetros abaixo de zero, ou seja, nos termômetros B e F.
c) Resposta Pessoal. Espera-se que os estudantes indiquem o termômetro A, pois apresenta uma medida de temperatura mais próxima da medida de temperatura do corpo humano.
4. a) A medida de temperatura média mensal esteve abaixo de zero em janeiro, fevereiro e dezembro.
b) A maior medida de temperatura média mensal foi registrada em agosto. Essa medida foi .
c) A medida de temperatura média foi maior do que em maio, junho, julho, agosto, setembro e outubro.
5. a) Espera-se que os estudantes respondam .
b) Espera-se que os estudantes respondam .
c) Espera-se que os estudantes respondam .
d) Espera-se que os estudantes respondam .
e) Espera-se que os estudantes respondam .
f) Espera-se que os estudantes respondam .
Página LI
6. a) O saldo estava positivo nos dias 25/09, 27/09 e 28/09. O saldo estava negativo nos dias 26/09 e 29/09.
b) Márcio fez a compra referida no dia 29/09, pois no extrato bancário há uma descrição de compra com cartão neste valor.
c) O histórico indica que a compra foi realizada com cartão de débito e podemos perceber que a compra foi efetuada em 27/09.
d) O saldo era positivo no valor de R$ 2,75.
e) Resposta pessoal.
Sugestão de resposta: Em qual dia Márcio depositou mais dinheiro do que ele retirou da conta? Resposta: No dia 27/09.
7. a) Como a Fossa das Marianas está abaixo do nível do mar, temos uma medida de altitude negativa, que representamos por .
b) Como a montanha K2 está acima do nível do mar, temos uma medida de altitude positiva, que representamos por .
c) Como o Mar Morto está abaixo do nível do mar, temos uma medida de altitude negativa, que representamos por .
d) Como o Pico da Neblina está acima do nível do mar, temos uma medida de altitude positiva, que representamos por .
e) Como a montanha Kilimanjaro está acima do nível do mar, temos uma medida de altitude positiva, que representamos por .
Questão 3. Resposta no final da seção Resoluções.
Atividades
8. a) Resposta no final da seção Resoluções.
b) O número está entre e .
O número 290 está entre 250 e 300.
O número 25 está entre 0 e 50.
O número está entre e .
O número está entre e .
9. Resposta no final da seção Resoluções.
10. a) Resposta no final da seção Resoluções.
b) O ponto A dista 9 unidades de medida do ponto O.
O ponto C dista 3 unidades de medida do ponto O.
O ponto D dista 3 unidades de medida do ponto O.
O ponto E dista 6 unidades de medida do ponto O.
O ponto F dista 10 unidades de medida do ponto O.
11. Para indicar a medida de altitude de um determinado local, geralmente utilizamos o nível do mar como referência. Quando a altitude indicada está acima do nível do mar, indicamos uma medida de altitude positiva e, quando está abaixo do nível do mar, indicamos uma medida de altitude negativa.
a) Os locais citados que ficam acima do nível do mar são o Monte Aconcágua, o Monte Elbrus, o Monte Everest e o Monte Branco.
b) Os locais que ficam abaixo da altitude de medida são o Mar Morto e o Lago Assal.
c) O local que tem maior medida de altitude é o Monte Everest. O local que tem menor medida de altitude é o Mar Morto.
12. a) Terra, Vênus e Mercúrio.
b) Em Marte, a temperatura média aproximada da superfície mede .
c) A temperatura média aproximada da superfície do planeta Netuno mede . Essa medida é negativa.
d) O planeta que tem maior medida de temperatura média aproximada é Vênus. Essa medida é .
e) Associando cada planeta à letra correspondente, temos:
Vênus: A; Mercúrio: B; Terra: C; Marte: D; Júpiter: E; Saturno: F; Urano: G e Netuno: H.
13. a) Resposta no final da seção Resoluções.
b) O número 4 é o mais próximo da origem. O número é o mais distante da origem.
c) Os números que estão a mais de sete unidades de distância da origem são , , , 9 e 11.
d) Resposta no final da seção Resoluções.
14. Como C e E estão situados à mesma medida de distância da origem e o ponto D está no ponto médio entre C e E, concluímos que D representa o zero (0) na reta numérica. Com base nesta informação, identificamos que E corresponde a 3 e, sendo simétrico a C, verificamos que C corresponde a . Como o ponto F está a 4 unidades à direita de E, então F corresponde a 7. Como B dista 6 unidades à esquerda do zero, verificamos que B corresponde a . Por fim, como A dista 9 unidades à esquerda de 0, então A corresponde a .
15. a)
b)
c)
d)
e)
f)
g)
16. a) Contando as unidades na reta, verificamos que a medida de distância entre C e D é igual a 6 unidades, pois C representa o número e D representa o número .
b) O ponto C está distante 8 unidades do ponto B.
c) Os pontos F e G distam 10 unidades um do outro.
d) O ponto D está distante 15 unidades do ponto F.
e) O ponto A é o mais distante do ponto E, com 30 unidades de medida de distância.
17. a) De acordo com a reta numérica apresentada, verificamos que as medidas de distância entre os pontos indicados e a origem são as seguintes:
Ponto A: 4 unidades.
Ponto B: 7 unidades.
Ponto C: 4 unidades.
Ponto D: 7 unidades.
b) O ponto A está à mesma medida de distância da origem que o ponto C. O ponto B está à mesma medida de distância da origem que o ponto D.
Página LII
18. a) Entre os números e 2, estão os números , , 0 e 1, cujos módulos são, respectivamente, 2, 1, 0 e 1.
b) Os números , , 0, 1 e 2 têm módulo menor do que 3.
19. Números simétricos são números que estão localizados à mesma distância da origem na reta numérica. Sendo assim, determinamos os simétricos dos números apresentados em cada item.
a) é simétrico de 3.
b) 2 é simétrico de .
c) 32 é simétrico de .
d) é simétrico de 9.
e) 15 é simétrico de .
f) é simétrico de 56.
g) 1 é simétrico de .
h) é simétrico de 10.
20. Existem várias respostas para os itens apresentados. Elencamos a seguir uma possível resposta para cada um deles.
a) Um possível número de três algarismos diferentes: 298. O oposto de 298 é .
b) Um possível número negativo de dois algarismos diferentes: . O oposto de é 98.
c) Um possível número múltiplo de 10: 70. O oposto de 70 é .
d) Um possível número par de três algarismos: 986. O oposto de 986 é .
21. Para completar o quadro substituindo as letras de cada coluna, devemos identificar o oposto do número apresentado em cada linha, seja na coluna da direita, seja na coluna da esquerda. Assim, temos o seguinte resultado.
|
Número |
Oposto do número |
|---|---|
|
26 |
|
|
7 |
|
|
19 |
|
|
31 |
|
22. a) O módulo de é 7.
b) O módulo de 3 é 3, e o módulo de é 3.
c) O módulo dos números e 5 é 5.
d) O módulo de é 15, e o módulo de é 9.
23. a) O simétrico de é 21 e o simétrico de 21 é .
b) Como , o oposto do módulo de é .
c) Como , o simétrico de é .
d) Como os números são simétricos, eles estão a mesma distância da origem, ou seja, o zero está exatamente no ponto médio da medida de distância desses números e um deles é negativo e o outro é positivo. Assim, . Portanto, os números são e 75.
24. Resposta no final da seção Resoluções.
25. Organizando as medidas de temperatura em ordem crescente, temos:
, , , , , , , .
26. a) De acordo com a posição das letras na reta numérica, verificamos que:
A: ; B: ; C: ; D: ; E: 5; F: 30; G: 38.
b) O maior número representado por uma dessas letras é o 38. O menor número é o .
c) Entre os números representados pelas letras:
são menores do que zero: , , e .
são maiores do que e menores do que 15: , e 5.
são maiores do que : , , , e .
27. a)
b)
c)
d)
e)
f)
g)
h)
28. Entre os números apresentados, verificamos que:
a) os maiores do que são , , e .
b) os que estão entre e 2 são e 1.
c) o menor do que é o .
29. a) O maior valor de x é 2 e o menor valor é .
b) O maior valor de x é e o menor valor é .
c) O maior valor de x é e o menor valor é .
d) O maior valor de x é 6 e o menor valor é .
e) O maior valor de x é e o menor valor é .
f) O maior valor de x é 4 e o menor valor é .
30. Escrevendo em ordem crescente todos os números inteiros, temos as seguintes sequências:
a) Números maiores do que e menores do que 4: , , , , , 0, 1, 2, 3.
b) Números maiores do que e menores do que : , , , , , .
c) Números diferentes de zero, cuja medida de distância em relação à origem é menor do que 4 unidades: , , , 1, 2, 3.
31. a) A maior medida de temperatura atmosférica registrada é . A menor medida é aproximadamente .
b) Na altitude indicada, o termômetro desse avião registrou de medida de temperatura atmosférica.
c) Uma medida de temperatura de pode ser registrada entre e de medida de altitude.
d) Em altitudes de medida acima de , a medida de temperatura atmosférica aproximada é negativa.
32. a) O saldo era o maior no dia 16/07. O saldo era o menor no dia 23/07.
b) O saldo era maior do que e menor do que R$ 10,00 no dia 25/07.
c) Resposta no final da seção Resoluções.
Página LIII
33. A equipe que obteve o menor saldo de gols nesse campeonato foi o Sport (PE). A equipe que obteve o maior saldo de gols nesse campeonato foi o Cuiabá (MT).
34. a) No período indicado, passaram-se 4 anos.
b) Escrevendo os anos em ordem crescente, temos:
9 a.C., 7 a.C., 3 a.C., 2 a.C., 1 a.C., 1 d.C., 2 d.C., 4 d.C.
Questão 4. Resposta no final da seção Resoluções.
Questão 5.
a)
b)
c)
d)
e)
f)
g)
h)
Questão 6. Sugestão de resposta: Ao adicionar um número inteiro a zero, o resultado é o próprio número inteiro.
Questão 7.
a)
b)
c)
d)
e)
f)
Questão 8. Independentemente do número inteiro que o estudante escolha, o resultado é zero. Caso ele escolha , a adição a ser efetuada é , cujo resultado é 0.
Questão 9. 0 (zero).
Atividades
35. a) Devemos substituir o por , pois a seta laranja indica que estamos deslocando 3 unidades para a esquerda (sentido negativo) a partir do número 8. Assim, .
b) Devemos substituir o por , pois a seta verde indica que estamos deslocando 9 unidades para a direita (sentido positivo) a partir do número . Assim, .
c) Devemos substituir o da parcela por , pois a seta laranja menor indica que estamos deslocando 5 unidades para a esquerda (sentido negativo) a partir do número 0. Com isso, substituímos o outro pelo resultado da adição indicada, ou seja, .
d) Devemos substituir os das parcelas, respectivamente, por e , pois a seta laranja indica que estamos deslocando 3 unidades para a esquerda (sentido negativo) a partir do número 0, e a seta verde indica que estamos deslocando 7 unidades para a direita (sentido positivo) a partir do número . Com isso, substituímos o último pelo resultado da adição indicada, ou seja, .
e) Devemos substituir os das parcelas, respectivamente, por e , pois a seta verde indica que estamos deslocando 3 unidades para a esquerda (sentido negativo) a partir do número 0, e a seta laranja indica que estamos deslocando 3 unidades para a direita (sentido positivo) a partir do número . Com isso, substituímos o último pelo resultado da adição indicada, ou seja, .
f) Devemos substituir os das parcelas, respectivamente, por e , pois a seta verde indica que estamos deslocando 7 unidades para a direita (sentido positivo) a partir do número 0, e a seta laranja indica que estamos deslocando 12 unidades para a esquerda (sentido negativo) a partir do número 7. Com isso, substituímos o último pelo resultado da adição indicada, ou seja, .
36. a) Raul deve depositar R$ 590,00, pois .
b) Raul deve depositar a mesma quantia em dinheiro para o saldo ficar igual a zero, ou seja, R$ 590,00. Para que o saldo fique igual a R$ 490,00, ele deve cobrir o valor correspondente ao saldo devedor e acrescentar a quantia de R$ 490,00, pois .
Portanto, Raul deverá depositar R$ 1.080,00.
37. Para descobrir o saldo da conta bancária de Fernanda, basta adicionarmos os valores do extrato, ou seja:
Portanto, o saldo após as movimentações é R$ 306,00.
38. a)
b)
c)
d)
e)
f)
g)
h)
39. Ao aplicar a propriedade comutativa da adição, a ordem das parcelas não altera o resultado da operação.
a) e .
b) e .
c) e .
d) e .
40. a)
b)
c)
d)
e)
f)
g)
h)
41. a) e .
b) e .
c) e .
d) e .
e) e .
f) e .
g) e .
h) e .
i) e .
Página LIV
42. Resposta no final da seção Resoluções.
a) A soma é maior do que 2 e menor do que 5 na pilha B.
b) A soma é um número entre e zero na pilha A.
c) Em nenhuma das pilhas a soma é menor do que .
d) A soma é maior do que zero e menor do que 2 na pilha C.
43. a) Calculando a pontuação obtida pelos respectivos jogadores, verificamos que:
Milena obteve pontos, pois .
Adriano obteve pontos, pois .
César obteve ponto, pois .
b) Adriano obteve a maior soma de pontos.
44. Adicionando os números da primeira coluna do quadrado A, obtemos 33, pois . Já na segunda coluna, obtemos 3, pois . Como as somas obtidas são diferentes, esse quadrado não é mágico.
Adicionando os números das linhas do quadrado B, obtemos os seguintes resultados:
; ; .
Adicionando os números das colunas, obtemos os seguintes resultados:
; ; .
Adicionando os números das diagonais, obtemos os seguintes resultados:
; .
Como a soma dos números das linhas, colunas e diagonais sempre é igual a 3, verificamos que os resultados são os mesmos. Portanto, o quadrado B é um quadrado mágico.
45. A resposta depende da criatividade dos estudantes. Apresentamos em cada item uma possível sugestão de resposta.
a) Pedro tinha R$ 7,00 em sua conta bancária e depositou R$ 32,00. Com quantos reais ele ficou em sua conta? Resposta: R$ 39,00.
b) Cássia perdeu 12 pontos na primeira rodada de um jogo e ganhou 13 pontos na segunda rodada. Com quantos pontos ela ficou ao final da segunda rodada? Resposta: 1 ponto.
c) Marcela tem R$ 9,00 e pagou R$ 3,00 por um bombom. Com quantos reais ela ficou? Resposta: R$ 6,00.
d) Joana deve R$ 25,00 para sua irmã e deve R$ 11,00 na cantina da escola. Quantos reais ela deve ao todo? Resposta: R$ 36,00.
46. a) Devemos substituir o por , pois a seta laranja indica um deslocamento de 3 unidades para a esquerda (sentido negativo) a partir do número 7. O deslocamento é feito para a esquerda porque é o oposto de . Assim, .
b) Devemos substituir o por , pois a seta laranja indica um deslocamento de 7 unidades para a esquerda (sentido negativo) a partir do número 9. O deslocamento é feito para a esquerda porque é o oposto de . Assim, .
c) Devemos substituir o por , pois a seta verde indica um deslocamento de 2 unidades para a direita (sentido positivo) a partir do número 0. Assim, .
d) Devemos substituir o , respectivamente, por e , pois a seta verde indica um deslocamento de 11 unidades para a esquerda (sentido positivo) a partir do número 11, e a seta laranja indica um deslocamento de 6 unidades para a esquerda (sentido negativo) a partir do número 11. O deslocamento é feito para a esquerda porque é o oposto de . Assim, .
47. Substituindo cada pelo número adequado, temos:
a)
b)
c)
d)
e)
f)
48. Efetuando os cálculos, temos:
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
49. Substituindo cada pelo sinal de ou adequado, temos:
a)
b)
c)
d)
e)
f)
50. a) A medida de temperatura máxima registrada nesse dia foi . A medida de temperatura mínima foi de .
b) A diferença entre as medidas de temperatura máxima e mínima é dada por , isto é, .
51. Na sequência A, cada número é obtido adicionando 9 unidades ao número anterior. Assim, os três próximos números dessa sequência são , e .
Na sequência B, cada número é obtido adicionando 12 unidades ao número anterior. Assim, os três próximos números dessa sequência são , e .
Na sequência C, cada número é obtido subtraindo 6 unidades do número anterior. Assim, os três próximos números dessa sequência são , e .
Página LV
Na sequência D, cada número é obtido subtraindo 7 unidades do número anterior. Assim, os três próximos números dessa sequência são , e .
52. a)
b)
c)
d)
e)
f)
53. a) Calculando o resultado de cada uma das expressões, temos:
Expressão A:
Expressão B:
Expressão C:
b) A expressão B tem o maior valor.
54. a) As medidas de altitudes aproximadas em ordem crescente são: , , , , , .
b)
Portanto, a diferença entre essas medidas é .
55. A medida de temperatura registrada pelo termômetro será , isto é, .
56. a)
Os possíveis valores de A e B são , ou . Substituindo esses valores na sentença, concluímos que e , pois
.
b)
Os possíveis valores de C e D são , ou . Substituindo esses valores na sentença, concluímos que e ou e , pois
e
.
c)
Os possíveis valores de E e F são , ou . Substituindo esses valores na sentença, concluímos que e ou e , pois
e
.
57. Saldo de gols marcados: .
Saldo de gols sofridos .
Saldo de gols: .
Portanto, o saldo de gols dessa equipe foi pontos.
58. Resposta pessoal. Sugestão de problema:
Em certo dia, a medida da temperatura máxima foi e a medida da temperatura mínima foi na cidade em que Daiane mora. Qual foi a variação média da medida da temperatura nesse dia? Resposta: .
Questão 10. Roberto acertou 15 pontos, pois , e errou 8 pontos, pois . Assim, o saldo de pontos de Roberto foi de , isto é, 7 pontos.
Questão 11.
a) Lúcia: quantidade de pontos das respostas corretas: .
Quantidade de pontos das respostas erradas: .
Saldo de pontos de Lúcia: .
b) Daniela: quantidade de pontos das respostas corretas: .
Quantidade de pontos das respostas erradas: .
Saldo de pontos de Daniela: .
c) Francisca: quantidade de pontos das respostas corretas: .
Quantidade de pontos das respostas erradas: .
Saldo de pontos de Francisca: .
Atividades
59. A multiplicação de 16 por 2 é dada por: e o triplo de é . Adicionando os dois resultados obtidos, obtemos .
60. a)
b)
c)
d)
e)
f)
g)
h)
61. Pela propriedade comutativa, as multiplicações A e H têm o mesmo resultado, bem como as multiplicações B e G e também F e K. Já pela propriedade associativa, as multiplicações C e I têm o mesmo resultado, assim como as multiplicações E e J. Por sua vez, a propriedade distributiva garante a equivalência entre as multiplicações D e L.
62. A. A: ; B: ; C: ;
D: ; E: ; F: .
B. A: ; B: ; C: ;
D: ; E: ; F: .
C. A: ; B: ; C: ;
D: ; E: ; F: .
63. Substituindo cada símbolo de acordo com a indicação, temos:
A:
B:
C:
D:
Página LVI
64. a) No termômetro B, pois , ou seja, .
b) Calculando a diferença entre as temperaturas, temos . Portanto, do 1º para o 2º momento a medida de temperatura diminuiu .
65. a) Sugestão de resposta:
e .
b) Sugestão de resposta:
e .
c) Sugestão de resposta:
e .
66.
Portanto, os destroços do Titanic estão a, aproximadamente, de medida de profundidade em relação ao nível do mar.
67. O menor número inteiro de dois algarismos é o e o menor número natural de dois algarismos é o 10. Substituindo esses valores em A e B, obtemos .
Portanto: A: ; B: 10; C: .
68. a) Sugestão de resposta: Escolhendo o número inteiro , temos .
b) Sugestão de resposta: Escolhendo o número inteiro , temos .
69. a) O deve ser substituído por , pois .
b) O deve ser substituído por 9, pois .
c) O deve ser substituído por , pois .
d) Os devem ser substituídos, respectivamente, por e , pois .
70. Em cada item, o pode ser substituído por um número que seja:
a) maior ou igual a . Sugestões de resposta:
b) menor do que 2. Sugestões de resposta: 1,
c) menor ou igual a . Sugestões de resposta:
d) maior ou igual a 2. Sugestões de resposta:
e) maior ou igual a 3. Sugestões de resposta:
f) menor ou igual a . Sugestões de resposta:
71. O saldo de Jonas antes dos depósitos era , pois . Para ficar com saldo de , Jonas depositou R$ 222,00, pois .
72. a)
b)
c)
d)
e)
f)
g)
73. Resposta pessoal. Sugestão de resposta:
A medida da temperatura interna de uma máquina de sorvete era em determinado momento. Após 5 minutos, essa medida ficou 3 vezes menor. Qual foi a medida da temperatura interna verificada nessa máquina após 5 minutos? Resposta: .
74. O número representado pelo no esquema A é 160, pois e . No esquema B, o deve ser substituído por , pois e . No esquema C, o deve ser substituído por , pois e .
75. a) Cada um dos deve ser substituído por , pois e .
b) Cada um dos deve ser substituído por , pois e .
c) Os devem ser substituídos, respectivamente, por , e , pois e .
d) Os devem ser substituídos, respectivamente, por , 8 e , pois e .
e) Os devem ser substituídos, respectivamente, por , 3, e , pois e .
f) Os podem ser substituídos por quaisquer números que satisfaçam a relação de igualdade. Sugestão de resposta: e .
76. a)
b)
c)
d)
e)
f)
g)
h)
77. a) O resultado da divisão de um número por seu oposto é sempre igual a .
b) O resultado da divisão de um número negativo por ele mesmo é sempre igual a 1.
c) Como , A deve ser , pois .
78. No item a, o número que substitui o é , pois e . No item b, o número que substitui o é , pois e . No item c, o número que substitui o é , pois e . Desse modo, as frases completas ficarão escritas da seguinte maneira:
a) Dividindo por e adicionado o resultado ao dobro de , obtemos .
b) Ao multiplicar por ele mesmo e subtrair 30 do resultado, obtemos 34.
c) Ao dividir pelo triplo de e subtrair do resultado, obtemos .
Página LVII
79. De acordo com o esquema, a letra A deve ser substituída por , pois e . Já a letra B deve ser substituída por 4, pois e .
80. Para calcular a média das medidas mínimas de temperatura, inicialmente, calculamos a soma das medidas de temperatura:
.
Em seguida, dividimos o resultado obtido pela quantidade de dias registrados, ou seja, . Portanto, a média das medidas mínimas de temperatura é .
81. Resposta pessoal. Sugestão de resposta:
Determine um número que ao ser multiplicado por 3 e adicionado 46 resulta em 10. Resposta: .
82. a)
b)
c)
d)
83. a) A potência é negativa, pois o expoente é ímpar.
b) A potência é positiva, pois o expoente é par.
c) A potência é positiva, pois o expoente é par.
84. a)
b)
c)
d)
e)
f)
85. a) , pois e
b) , pois e
c) , pois e
d) , pois e
86. A:
B:
C:
D:
E:
F:
Escrevendo esses números em ordem crescente, temos:
, , , , 1, 169.
87. Resposta pessoal. Sugestão de resposta:
Determine o número cuja potência ao quadrado resulta em seu oposto. Resposta: .
88. a)
b)
c)
d)
e)
f)
g)
89. O resultado de Júlia é o correto, pois ela efetuou , enquanto Fernando efetuou , ou seja, representam multiplicações diferentes e têm resultados diferentes. Isso aconteceu porque Fernando deixou de digitar os parênteses para indicar que a base da potência é , e não 5.
O que eu estudei?
1. a) São números naturais: 0 e 6.
b) São números positivos: e .
c) São números negativos: , e .
d) São números inteiros: , 0, 6.
e) É um número inteiro e não é natural: .
2. As letras D e E representam números positivos e as letras A, B e C representam números negativos. Portanto, temos:
A: ; E: 2; C:
3. a) Os números inteiros que têm módulo igual a 7 são e 7.
b) Apenas um número tem o módulo igual a zero. Esse número é o próprio 0 (zero).
c) Os números inteiros maiores do que e menores do que são , , e .
d) Entre e 21 existem 50 números inteiros.
e) O número simétrico de é 37. O simétrico de 12 é .
4. a) Para determinar qual foi a medida de temperatura máxima nesse dia, calculamos , ou seja, a medida da temperatura máxima nesse dia foi .
b) Realizando os cálculos, temos . Portanto, o saldo da conta de Gabriela passou a ser de R$ 395,00.
5. a) Como , devemos dividir 90 por para obter o resultado .
b) Realizando essa operação, obtemos: . Portanto, o resultado é .
c) Como o oposto de 2 é e , então . Portanto, o resultado é .
d) A base é positiva e o expoente também, mas a potência está multiplicada por um número negativo, ou seja, . Portanto, o resultado dessa potência é negativo.
6. Adicionando os valores do saldo da conta de Roberto dos meses de junho a setembro, temos:
e , ou seja, o saldo mensal médio da conta de Roberto nesse período foi .
Página LVIII
Unidade 3
Frações
Questão 1. Resposta pessoal. Espera-se que os estudantes concluam que as frações foram criadas com base na necessidade que os povos antigos tinham de fazer medições.
Questão 2. Considerando que o número de meninas dessa turma é 16 e o número de meninos é 12, a razão é dada pela fração .
Questão 3. Como a irmã de Célia leu do total de páginas, calculando, inicialmente, do total de páginas do livro, temos . Considerando que corresponde ao total de páginas, calculamos . Portanto, o livro tem 144 páginas.
Atividades
1. Considerando que o numerador indica a quantidade de partes coloridas de rosa e o denominador indica a quantidade de partes em que a figura está dividida, a parte pintada de rosa na figura A pode ser representada pela fração e, na figura B, pela fração .
2. a) Como há 32 assentos no total, a fração que representa um assento é .
b) Como há 16 fileiras de assentos com dois lugares cada, uma fileira pode ser representada por ou .
c) A quantidade de lugares ocupados pelas 28 crianças pode ser representada por ou .
3. a) A figura foi dividida em 9 partes iguais.
b) Como a figura foi dividida em 9 partes, então 3 partes dessa figura podem ser representadas por ou .
c) Como a figura foi dividida em 9 partes, então 6 partes dessa figura podem ser representadas por ou .
4. a) Adicionando a quantidade de carros, obtemos , ou seja, nesse estacionamento há 71 carros.
b) A quantidade de carros brancos pode ser representada por .
c) A razão entre a quantidade de carros pretos em relação à quantidade de carros prateados pode ser expressa pela fração ou .
5. a) Inicialmente, adicionamos a quantidade de balas de hortelã e morango e, em seguida, calculamos a diferença entre esse valor e o total. Assim: e , ou seja, 11 balas são de menta.
b) As balas de hortelã são representadas por .
c) A razão entre a quantidade de balas de menta em relação à quantidade de balas de morango é representada por .
6. A fração que representa a quantidade de comentários positivos corresponde a .
7. A razão entre a quantidade de livros de romance vendidos e o total de livros é dada pela fração ou .
8. A razão entre a medida de capacidade da tinta vermelha e a medida de capacidade da mistura pode ser expressa pela fração . Portanto, a alternativa correta é a d.
9. Como o paciente apresentou febre em 6 dias, essa quantidade corresponde a do total de dias. Além disso, como do total de dias equivale a 2 dias, ou seja, , a quantidade total de dias é 10, pois corresponde a e . Portanto, esse paciente ficou 10 dias no hospital.
10. a) Se o valor total da conta corresponde a R$ 85,00 e cada casal pagou desse valor, então o valor total da conta pode ser representado por . Como , cada parte dessa conta, ou seja, dela corresponde a R$ 17,00. Portanto, cada casal pagou R$ 34,00.
b) Gabriel pagou R$ 17,00, pois ele pagou da conta.
11. a) de correspondem a , pois e .
b) de correspondem a , pois e .
c) de 35 maçãs correspondem a 7 maçãs, pois e .
d) de correspondem a , pois e .
e) de 18 páginas correspondem a 6 páginas, pois e .
f) de R$ 42,00 correspondem a R$ 7,00, pois e .
12. Como o time A marcou do total de gols, o time B marcou . Além disso, sabemos do enunciado que foram marcados no total 60 gols. Assim, o time B marcou 28 gols, pois e .
13. a) Sabendo que o valor da entrada corresponde a do preço do videogame, calculamos e . Portanto, Lucimara vai pagar R$ 1.440,00 de entrada.
b) O restante do valor a pagar corresponde à diferença entre o valor total e a entrada, ou seja, . Portanto, Lucimara vai pagar R$ 960,00 após 30 dias.
14. Para determinar a quantidade de água que há na caixa d'água, calculamos de 1.000, ou seja, e . Portanto, há nessa caixa.
15. a) De acordo com o enunciado, 42 selos da coleção de Juliano correspondem a . Desse modo, para determinar o total de selos calculamos e . Portanto, Juliano tem 49 selos.
Página LIX
De modo semelhante, 54 selos da coleção de Fabrício correspondem a . Assim, para determinar o total de selos, calculamos e . Portanto, Fabrício tem 81 selos.
b) Calculando a diferença entre as quantidades obtidas no item anterior, obtemos 32 selos, pois .
c) Adicionando o total de selos de Juliano e Fabrício, obtemos . Portanto, Juliano e Fabrício têm juntos 130 selos.
16. a) Com base nas informações do enunciado, havia 360 camisas no estoque e corresponde às camisas vendidas. Para determinar a quantidade que essa fração representado total, calculamos e . Portanto, foram vendidas 285 camisas.
b) Considerando que foram arrecadados R$ 12.825,00 com a venda das 285 camisas, devemos dividir o total arrecadado pela quantidade de camisas vendidas para obter o valor de cada uma, ou seja, . Portanto, cada camisa custa R$ 45,00. Portanto, se todas as camisas fossem vendidas, a loja arrecadaria R$ 16.200,00, pois .
c) Efetuando os cálculos, verificamos que do estoque corresponde a 60 camisas, pois e . Multiplicando essa quantidade pelo preço de cada camisa, obtemos . Portanto, com essa venda a loja arrecadou R$ 2.700,00.
Verificamos também que do estoque corresponde a 90 camisas, pois e . Multiplicando essa quantidade pelo preço de cada camisa, obtemos R$ 4.050,00. Portanto, com essa venda a loja arrecadou .
17. Considerando que correspondem a 24 anos de vida da preguiça, calculamos e . Portanto, a preguiça vive, aproximadamente, 40 anos.
18. Resposta pessoal. Sugestão de resposta:
Carolina postou uma foto e obteve 13 curtidas e 8 comentários. Escreva uma razão entre a quantidade de curtidas e o total de comentários e curtidas. Resposta: .
Questão 4. Para que a fração seja equivalente, devemos substituir o em cada um dos itens por:
a) 15, pois e . Assim, .
b) 8, pois e . Assim, .
c) 5, pois e . Assim, .
Questão 5.
a) Como os denominadores das frações são iguais e , então .
b) Como as frações não têm o mesmo denominador, calculamos o e obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que . Sendo assim, .
c) Como as frações não têm o mesmo denominador, calculamos o e obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que . Sendo assim, .
Atividades
19. As frações que representam as partes pintadas de roxo nas figuras são:
figura A: .
figura B: .
figura C: .
figura D: .
20. Fazendo a simplificação, temos:
a)
b)
c)
d)
21. Realizando os cálculos, temos:
22. Sugestões de respostas:
a) , e .
b) , e .
c) , e .
d) , e .
e) , e .
f) , e .
23. Como as frações consideradas não têm o mesmo denominador, calculamos o e obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que . Sendo assim, . Portanto, Thiago caminhou por mais tempo.
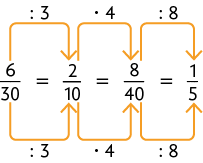
24. Seguindo o procedimento indicado no fluxograma, vamos efetuar os cálculos em cada um dos itens.
Página LX
a) Calculando o entre 8 e 16, temos:
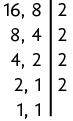
Logo, o . Com isso, obtemos as frações equivalentes e . Comparando-as, verificamos que . Sendo assim, .
b) Calculando o entre 9 e 3, temos:
Logo, o . Com isso, obtemos as frações equivalentes e . Comparando-as, verificamos que . Sendo assim, .
25. Como as frações consideradas não têm o mesmo denominador, calculamos primeiro o entre os números dos denominadores.

Logo, o . Com isso, obtemos as frações equivalentes ; ; e .
Comparando-as, verificamos que . Assim, organizamos em ordem crescente as frações iniciais, de modo que .
26. a) Não é possível determinar a quantidade de funcionários que vão ao trabalho de automóvel e quantos utilizam o transporte público, pois não foi informado o total de funcionários da empresa.
b) O meio de transporte mais utilizado é o transporte público.
c) Resposta pessoal. Sugestão de resposta:
Para determinar o meio de transporte mais usado que permite chegar ao trabalho nessa empresa é necessário comparar as frações.
d) Como as frações não têm o mesmo denominador, calculamos o entre eles.
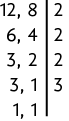
Logo, o . Com isso, obtemos as frações equivalentes e .
Como , concluímos que . Portanto, a maior fração é , logo, o meio de transporte mais usado para os funcionários chegarem à empresa é o transporte público.
27. a) Como as frações têm o mesmo denominador, comparamos os numeradores e verificamos que .
b) Como as frações não têm o mesmo denominador, primeiro calculamos o entre os números 30 e 24.
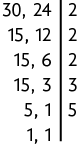
Logo, o . Com isso, obtemos as frações equivalentes e . Comparando-as, verificamos que . Sendo assim, .
Sugestão de resposta:
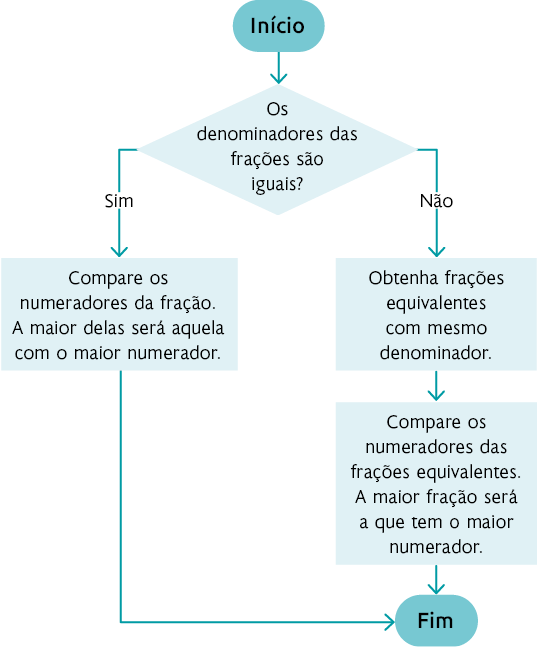
1º. Como os denominadores das frações são diferentes, calculamos o mmc entre os denominadores das frações.
2º. Encontramos as frações equivalentes, cujos denominadores são iguais ao mmc calculado.
3º. Comparamos os numeradores das frações.
4º. A maior fração será aquela cujo numerador apresenta o maior número.
Página LXI
O que eu estudei?
1. a) Como o dia tem 24 horas, a fração que representa a quantidade de horas que os recém-nascidos dormem é . Já as pessoas adultas dormem em média 8 horas por dia, o que podemos representar com a fração . Além disso, como os idosos dormem do tempo dos bebês, podemos obter a fração correspondente a essa medida de tempo dividindo 18 horas por 3 e escrevendo essa quantidade de horas na forma de fração, ou seja, . Simplificando essa fração, obtemos . Portanto, recém-nascidos dormem em média do dia, pessoas adultas dormem do dia e idosos dormem do dia.
b) Considerando as informações obtidas do item anterior, uma pessoa que necessita dormir em média 6 horas por dia é um idoso.
2. a) Calculando de 50, temos e . Portanto, Alice fez 35 gols.
b) Com base no item anterior, verificamos que 15 cobranças não resultaram em gols, pois . Nesse caso, podemos escrever e simplificar a fração que representa a razão entre as cobranças bem-sucedidas e as que não resultaram em gols, ou seja, . Portanto, obtemos a razão .
3. Considerando que o numerador indica a quantidade de partes coloridas e o denominador indica a quantidade de partes em que a figura está dividida, temos:
A .
B .
C .
D .
4. a) Como , obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que . Sendo assim, .
b) Como , obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que . Sendo assim, .
c) Como , concluímos que .
d) Como , obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que . Sendo assim, .
e) Como , obtemos as frações equivalentes e . Comparando as frações
equivalentes, verificamos que . Sendo assim, .
f) Como , obtemos as frações equivalentes e . Comparando as frações equivalentes, verificamos que .
5. a) Calculando de R$ 3.780,00, obtemos R$ 1.620,00, pois e . Portanto, Jorge usou R$ 1.620,00 para pagar suas contas.
b) Calculando de obtemos R$ 1.440,00, pois e . Portanto, Jorge investiu R$ 1.440,00 nesse mês.
6. De acordo com a figura, podemos verificar que a medida da área de um triângulo preto corresponde à metade da medida da área de cada quadradinho. Sendo assim, contamos 8 triângulos, que representam 4 quadradinhos. No total, há 16 quadradinhos, portanto, a medida da área em preto corresponde a do quadrado. A alternativa correta é a c.
7. a) Em relação às plantações, verificamos que são utilizados de água, pois e . Para a limpeza, verificamos que são utilizados de água, pois e .
b) Considerando que foram gastos , ou seja, de água para regar as plantações e para limpeza, efetuamos uma subtração para obter a quantidade de água utilizada para outras finalidades, ou seja, . Portanto, para as outras finalidades são utilizados de água.
8. Para determinar a quantidade de líquido contida em cada recipiente, devemos considerar a fração que representa a medida de sua capacidade ocupada.
Analisando as figuras, verificamos que o recipiente A contém de sua medida de capacidade ocupada com líquido, que representa , pois e . O recipiente B contém de sua medida de capacidade ocupados com líquido, que representa , pois e . O recipiente C contém de sua medida de capacidade ocupados com líquido, que representa , pois e .
Unidade 4
Os números racionais
Atividades
1. a) O número 1,4 está entre os números inteiros consecutivos 1 e 2.
b) O número 5,87 está entre os números inteiros consecutivos 5 e 6.
c) O número 0,3 está entre os números inteiros consecutivos 0 e 1.
Página LXII
d) O número está entre os números inteiros consecutivos e 0.
e) O número está entre os números inteiros consecutivos e .
f) O número 3,75 está entre os números inteiros consecutivos 3 e 4.
2. De acordo com a reta numérica apresentada, a letra A está associada ao menor número. Sendo assim, .
Como a letra B está associada a um número entre e , então .
Como a letra C está associada a um número entre e 0, então .
Como a letra D está associada a um número entre 0 e 1 e está mais próximo do 0, então .
Como a letra E está associada a um número entre 1 e 2 e está mais próximo do 1, então, .
Como a letra F está associada a um número entre 2 e 3, então .
Como a letra G está associada a um número entre 3 e 4, então .
3. Resposta pessoal. Sugestão de resposta:
Um número decimal que está entre os números:
a) 0 e 1 é o 0,5.
b) e é o .
c) 5 e 6 é o .
d) 2 e 3 é o .
4. O número 2,4 está localizado entre os números 2 e 3. De acordo com a reta numérica apresentada, a única letra que está representada entre 2 e 3 é a D.
5. Realizando as divisões necessárias, temos:
a)
b)
c)
d)
e)
f)
6. Sugestão de respostas: Fazendo as conversões necessárias, temos:
a)
b)
c)
d)
e)
f)
7. A alternativa correta é a c, pois é a única em que o numerador é menor do que o denominador. Além disso, .
8. Resposta pessoal. Sugestão de resposta:
Entre os números apresentados, quais estão na forma decimal? Escreva esses números na forma fracionária. Resposta: 0,2 e 3,5; e .
Questão 1. Calculando o módulo dos números apresentados, temos:
a)
b)
c)
d)
e)
f)
Atividades
9. Calculando os módulos dos números apresentados, temos:
Portanto, os números que têm módulos iguais são 7 e ; 2,8 e ; 1,2 e .
10. O oposto de:
a) é o 1.
b) 8 é o .
c) 3,4 é o .
d) é o 7,8.
e) é o .
f) é o .
11. a) Os números cujo módulo é igual a são e .
b) Os números cujo módulo é igual a são e .
c) Os números cujo módulo é igual a são e .
d) Os números cujo módulo é igual a são e .
12. a) O número que apresenta a maior medida de distância até a origem é .
b) Resposta pessoal. Espera-se que os estudantes digam que obtiveram a resposta verificando o número de maior módulo.
Página LXIII
13. De acordo com a fala das crianças, o número pensado por:
Armando é 2, pois é o oposto de .
Maria é 5, pois é um número positivo que tem módulo igual a 5.
Pedro é , pois é um número negativo que tem módulo igual a 25.
Questão 2. O maior número é . Sugestão de justificativa: é maior do que , pois e está à esquerda de na reta numérica.
Questão 3. Resposta pessoal. Uma possível resposta para essa questão é:
; ; ; ; ; .
Organizando esses números em ordem crescente, temos:
.
Atividades
14. a)
b)
c)
d)
e)
f)
15. Escrevendo os números em ordem crescente, temos:
.
16. a) Transformando em um número decimal, verificamos que . Representando os números 1,5 e 0,8 na reta numérica, temos:
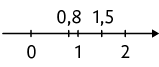
Assim, , pois 1,5 está à direita de 0,8.
b) Transformando em um número decimal, verificamos que . Representando os números 0,5 e 0,7 na reta numérica, temos:
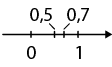
Portanto, , pois 0,5 está à esquerda de 0,7.
c) Transformando em um número decimal, verificamos que . Representando os números e na reta numérica, temos:
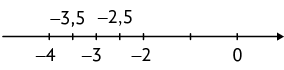
Assim, , pois está à direita de .
d) Transformando em um número decimal, verificamos que . Representando os números e na reta numérica, temos:
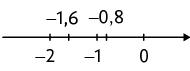
Portanto, , pois está à esquerda de .
17. Analisando a reta numérica apresentada, verificamos que: A: ; B: ; C: ; D: ; E:
Resposta pessoal. Este item tem várias respostas. Uma sugestão é: e 0,1.
18. Ordenando as medidas de tempo, temos . Logo, Guilherme foi o mais rápido, pois completou a última volta no menor intervalo de tempo.
19. a) Ordenando os valores do quadro em ordem crescente, temos:
R$ 49,00; R$ 58,00; R$ 78,90; R$ 100,00; R$ 135,50; R$ 148,00; R$ 148,90; R$ 237,00; R$ 269,00; R$ 364,30; R$ 378,10; R$ 405,50.
Portanto, o mês em que Marcela poupou a maior quantia foi dezembro. O mês em que Marcela poupou a menor quantia foi agosto.
b) A quantia poupada no mês de março foi menor do que a quantia poupada no mês de dezembro, pois .
c) R$ 405,50; R$ 378,10; R$ 364,30; R$ 269,00; R$ 237,00; R$ 148,90; R$ 148,00; R$ 135,50; R$ 100,00; R$ 78,90; R$ 58,00; R$ 49,00.
20. Inicialmente, transformamos as frações em números decimais. Assim, a equipe A venceu 0,4 das provas, pois e a equipe B venceu 0,6 das provas, pois . Comparando estes números, concluímos que . Portanto, quem ganhou mais provas foi a equipe B.
21. Primeiro, transformamos as frações em números decimais. Desse modo, verificamos que o cliente 1 pagou 0,4 do valor do automóvel como entrada, pois e o cliente 2 pagou 0,375 do valor do automóvel como entrada, pois . Comparando os dois números decimais, constatamos que . Portanto, quem pagou a maior quantia de entrada foi o cliente 1.
22. Efetuando os cálculos com base no enunciado, verificamos que o comprimento do barbante azul mede , pois .
Comparando as medidas de comprimento dos dois barbantes, constatamos que . Portanto, o pedaço de barbante azul terá a maior medida de comprimento.
O que eu estudei?
1. Resposta no final da seção Resoluções.
Página LXIV
2. Transformando as frações em números decimais, encontramos as seguintes igualdades:
; ; ; ; .
3. O oposto de:
a) é o 2.
b) é o 8,7.
c) 7,56 é o .
d) é o .
e) é o .
f) 2,7 é o .
4. a)
b)
c)
d)
e)
f)
g) Entre os números apresentados, o que tem o maior módulo é e o número que tem o menor módulo é .
h) Transformando as frações em números decimais, obtemos e . Organizando os números decimais em ordem decrescente, temos:
; ; ; ; ;
5. a)
b)
c)
d)
e)
f)
6. Resposta no final da seção Resoluções.
7. a) Falsa. Sugestão de correção: O número 10 é maior do que , pois, na reta numérica, 10 está à direita de .
b) Verdadeira.
c) Falsa. Sugestão de correção: O módulo de é , pois, na reta numérica, a distância entre o ponto correspondente ao número e a origem mede de unidade.
8. Resposta no final da seção Resoluções.
9. a) O barbante que tem a menor medida de comprimento é o 4.
b) Escrevendo as medidas dos barbantes em ordem decrescente, temos: ; ; ; .
10. De acordo com a primeira e a segunda dica, o número decimal é formado por três algarismos, de modo que o 3 ocupa a ordem dos décimos e o 1 a ordem das dezenas, pois o número é maior do que 10 e menor do que 16. Além disso, sabendo que os divisores de 36 são 1, 2, 3, 4, 6, 9, 12, 18 e 36 e o único número primo e ímpar é o 3, concluímos que o algarismo da unidade é o 3.
Portanto, o número desconhecido é 13,3.
11. Transformando as frações em números decimais, temos e . Como , concluímos que Tales economizou a maior quantia no mês de março.
Unidade 5
Operações com números racionais
Atividades
1. De acordo com o gráfico, temos as seguintes considerações.
a) No enunciado, é solicitada a fração de pessoas com sangue de um tipo ou de outro. Nesse caso, precisamos considerar a soma das duas populações. A população que tem grupo sanguíneo O é representada pela fração e a que tem grupo sanguíneo AB é representada pela fração . Como as frações têm denominadores diferentes, calculamos o e adicionamos as duas frações equivalentes, obtendo, assim, . Portanto, a fração que representa o total da população desses grupos é .
b) A população que tem grupo sanguíneo O é representada pela fração e a que tem grupo sanguíneo A é representada pela fração . Como as frações têm denominadores diferentes, calculamos o e efetuamos uma subtração com as frações equivalentes, obtendo, assim, . Portanto, a fração que representa a diferença entre a população desses grupos é .
c) A população que tem grupo sanguíneo B é representada pela fração e a que tem grupo sanguíneo AB é representada pela fração . Como as frações têm denominadores diferentes, calculamos o e efetuamos uma subtração com as frações equivalentes, obtendo, assim, . Portanto, a fração que representa a diferença entre a população desses grupos é .
d) No enunciado, é solicitada a fração de pessoas com sangue de um tipo ou de outro. Nesse caso, precisamos considerar a soma das duas populações. A população que tem grupo sanguíneo A é representada pela fração , a que tem grupo sanguíneo B é representada pela fração e a que tem grupo sanguíneo AB é representada pela fração . Como as frações têm denominadores diferentes, calculamos o e adicionamos as três frações equivalentes, obtendo, assim, . Portanto, a fração que representa a soma da população desses grupos é .
2. a) Como , temos .
b) Como , temos .
c) Como , temos .
Página LXV
d) Como , temos .
e) Como , temos .
f) Como , temos .
3. Neste mosaico, há 75 quadrados, sendo 6 pintados de verde, 20 pintados de amarelo, 22 pintados de laranja e 27 pintados de roxo. Assim:
a) as partes do mosaico pintadas de verde ou amarelo são representadas por .
b) as partes do mosaico pintadas de amarelo ou roxo são representadas por .
c) as partes do mosaico pintadas de verde, amarelo, roxo ou laranja são representadas por , ou seja, 1 inteiro.
d) as partes do mosaico pintadas de verde, laranja ou roxo são representadas por .
e) as partes do mosaico pintadas de amarelo, laranja ou roxo são representadas por .
f) Resposta pessoal. Os estudantes podem responder que, no item c, a fração representa todas as partes do mosaico e que, no item e, o cálculo pode ser feito subtraindo a fração de um inteiro, ou seja,
.
4. a) Como , então
.
b) Como , então
.
c) Como , então
.
d) Como , então
.
e) Como , então
.
5. Para resolver essa questão, precisamos obter a diferença entre as quantidades indicadas no marcador de combustível antes e depois de abastecer. Assim, calculamos . Portanto, a quantidade de combustível colocada ao abastecer corresponde a do tanque de combustível.
6. a) Para responder a essa pergunta, precisamos adicionar a fração que representa as medalhas de ouro com a que representa as medalhas de prata. Como as frações têm denominadores diferentes, calculamos o e, em seguida, efetuamos a adição com as frações equivalentes, ou seja, . Portanto, a fração representa a quantidade de medalhas de ouro e de prata conquistadas pelo Brasil nos jogos olímpicos nesse período.
b) Para obter a fração que representa as medalhas de bronze conquistadas, efetuamos uma subtração, retirando do total de medalhas as demais de outro tipo conquistadas. Como o total de medalhas pode ser representado por , calculamos e concluímos que a fração representa a quantidade de medalhas de bronze conquistadas.
c) Como as frações obtidas têm o mesmo denominador, basta verificar as quantidades indicadas no numerador para responder a esta pergunta. Portanto, o Brasil conquistou ao todo 150 medalhas, das quais 37 são de ouro, 42 são de medalhas de prata e 71 são de bronze.
7. Como as frações têm denominadores diferentes, calculamos o e, em seguida, adicionamos as frações equivalentes, ou seja, . Portanto, a fração representa os livros de Matemática e Geografia dessa biblioteca.
8. a) Se as máquinas demoram, respectivamente, e para produzir a mesma quantidade de peças, em a primeira vai produzir da quantidade de peças e a segunda, da quantidade de peças. Como , então . Neste caso, as duas máquinas fabricariam do total de encomendas.
b) Em elas vão produzir, respectivamente, e da quantidade de peças. Como , então . Portanto, neste caso, as duas máquinas produziriam do total de encomendas.
9. Efetuando-se cada um dos produtos, temos:
a)
b)
c)
d)
10. Fazendo a substituição, obtemos . Portanto, o caderno custou R$ 14,00.
11. a)
b)
c)
d)
e)
Página LXVI
12. a) Em um minuto, o atleta percorre, em média, do percurso. Calculando o trajeto percorrido em 17 minutos, temos . Portanto, após 17 minutos ele percorreu da medida de distância total.
b) Como , concluímos que, em 17 minutos, o atleta percorreu aproximadamente .
Questão 1. De acordo com as informações do texto, dos pastéis são de carne, então são de queijo. Assim, . Portanto, dos salgados são pastéis de queijo.
Questão 2. Para obter a quantidade de pastéis de carne, calculamos . Portanto, 180 pastéis eram de carne.
Para obter a quantidade de pastéis de queijo, calculamos . Portanto, 120 pastéis eram de queijo.
Atividades
13. a)
b)
c)
d)
e)
f)
14. Sugestão de respostas:
a) .
b) .
c) .
d) .
e) .
f) .
15. a) Como , devemos determinar que quantidade de pães doces essa fração do total de pães representa. Então, calculamos . Portanto, essa padaria produziu 35 pães do tipo doce.
b) Como , precisamos determinar que quantidade de pães de leite essa fração do total de pães representa. Então, calculamos . Portanto, essa padaria produziu 480 pães de leite.
16. a) Dividindo 12 e 27 por 3 e dividindo 14 e 35 por 7, temos:
b) Dividindo 64 e 88 por 8 e dividindo 39 e 65 por 5, temos:
c) Dividindo 81 e 45 por 9 e dividindo 7 e 91 por 7, temos:
Como , assim, podemos escrever . Dividindo 5 por 5, obtemos:
d) Dividindo 30 e 15 por 15 e dividindo 25 e 20 por 5, obtemos:
Dividindo 2 e 8 por 2, temos:
e) Dividindo 33 e 11 por 3, 40 e 100 por 20 e, 8 e 32 por 8, obtemos:
f) Dividindo 26 e 13 por 13 e dividindo 25 e 45 por 5, temos:
Dividindo 5 por 5, temos:
Questão 3. Para obter esta resposta, precisamos dividir a quantidade de suco pela medida de capacidade de cada garrafa. Assim, . Portanto, são necessárias 6 garrafas de .
Questão 4. Para obter esta resposta, devemos calcular a quantidade que a fração de pares de calçados masculinos representa do total de pares de calçados produzidos na semana. Nesse caso, verificamos que são 177 pares, pois . Para obter a quantidade de pares de calçados femininos, retiramos do total a quantidade de pares de calçados masculinos, ou seja, . Portanto, foram produzidos 708 pares de calçados femininos.
Página LXVII
Questão 5. Para obter a quantidade de calçados em cada lote, calculamos . Portanto, em cada lote, há 59 pares de calçados masculinos.
Questão 6. A quantidade de pares de calçados femininos de cada lote corresponde à diferença entre o total de pares de calçados por lote e a fração que representa um lote de pares de calçados masculinos, ou seja, . Como esses pares de calçados foram divididos em 2 lotes, calculamos a metade dessa fração, ou seja, . Portanto, a fração ou representa a quantidade de calçados femininos de cada lote.
Questão 7.
b)
c)
d)
Atividades
17. a) Sugestão de desenho:
b) Sugestão de desenho:
c) Sugestão de desenho:
d) Sugestão de desenho:
e) Sugestão de desenho:
f) Sugestão de desenho:

g) Sugestão de desenho:

h) Sugestão de desenho:

i) Sugestão de desenho:

18. Sugestão de resposta:
a)
b)
c)
19. a) cabe 3 vezes em , pois
b) cabe 4 vezes em , pois
20. a)
b)
c)
d)
e)
f)
Página LXVIII
21. Efetuando cada uma das divisões, temos:
A.
B.
C.
D.
Portanto, associando a letra ao número correspondente, temos A-3; B-1; C-4; D-2.
22. Para determinar a quantidade de peças necessárias, precisamos dividir a medida de massa do pacote de açúcar pela medida de massa da peça, ou seja, . Portanto são necessárias 4 peças de para que a balança fique em equilíbrio.
23. Precisamos dividir a medida de massa total da carne moída pela medida de massa de cada pacote para obter a resposta da pergunta. Assim, . Portanto, essa carne moída foi dividida em 12 pacotes.
24. Dividindo por 2 a fração que representa a quantidade de figurinhas, obtemos . Portanto, cada irmão de Renato recebeu do total de figurinhas.
25. a) Para preparar 6 porções, devemos utilizar metade dos ingredientes, pois:
Fazendo o cálculo de cada ingrediente, temos:
de farinha de milho amarela, pois .
de farinha de mandioca, pois .
4 ovos cozidos picados, pois .
de bacon picado em cubos, pois .
de linguiça, pois .
2 cebolas picadas, pois .
6 dentes de alho amassados, pois .
xícara de chá de azeitonas verdes picadas, pois .
xícara de chá de azeitonas pretas picadas, pois .
1 xícara de chá de salsinha picada, pois .
azeite.
b) Para preparar 3 porções, devemos utilizar um quarto dos ingredientes, pois:
Fazendo o cálculo de cada ingrediente, temos:
de farinha de milho amarela, pois .
de farinha de mandioca, pois .
2 ovos cozidos picados, pois .
de bacon picado em cubos, pois .
de linguiça, pois .
1 cebola picada, pois .
3 dentes de alho amassados, pois .
xícara de chá de azeitonas verdes picadas, pois .
xícara de chá de azeitonas pretas picadas, pois .
xícara de chá de salsinha picada, pois .
azeite.
26. a) Para obter a quantidade de copos de suco, devemos dividir a fração que representa o conteúdo do reservatório pela fração que representa a medida da capacidade de cada copo. Então, calculamos . Portanto, podem ser vendidos, no máximo, 30 copos de suco com da medida de capacidade do reservatório.
b) Se o reservatório da máquina estivesse completamente cheio, poderíamos representá-lo por . Assim, . Portanto, poderiam ser vendidos, no máximo, 50 copos de suco com o reservatório cheio.
c) Como cabem de suco nesse reservatório, calculamos . Portanto, no reservatório da máquina há, nesse momento, de suco.
d) A medida da capacidade de cada copo é dada por . Portanto, cada copo tem de medida de capacidade.
27. Efetuando-se cada um dos cálculos a seguir, temos:
a)
b)
c)
d)
e)
f)
g)
h)
Página LXIX
28. Como a adição e a subtração são operações inversas, temos:
a) , pois .
b) , pois .
c) , pois .
d) , pois .
e) , pois .
f) , pois .
29. Lembrando que a medida do perímetro é igual à soma da medida dos lados, então o perímetro da figura A mede , pois , e o perímetro da figura B mede , pois .
30. Verificamos que a medida de cada pilha é igual à soma das medidas de altura de cada peça que a compõe. Então:
a altura da peça A mede , pois .
a altura da peça B mede , pois .
a altura da peça C mede , pois .
a altura da peça D mede , pois .
31. Sugestões de resposta: ; .
32. a) Como , essa diferença foi .
b) Como , essa diferença foi .
c) Como , essa diferença foi .
33. Arredondando cada uma das parcelas das operações para a unidade mais próxima, obtemos:
a)
b)
c)
d)
e)
f)
34. Incialmente, calculamos o troco recebido por Alvimar, ou seja, . Portanto, Alvimar recebeu R$ 1,50 de troco.
Calculando quantas moedas de são necessárias para formar R$ 1,50, temos:
Nesse caso, Alvimar recebeu 6 moedas de R$ 0,25 de troco. Portanto, a alternativa c é a correta.
Questão 11. Sugestão de resposta: A quantidade de casas decimais do resultado (15,950) é igual à soma das quantidades de casas decimais dos fatores (6,38 e 2,5), que nesse caso é 3.
Atividades
35. a)
b)
c)
d)
e)
f)
g)
h)
36. a) Como cada número, a partir do segundo é obtido pela multiplicação do número anterior por 5, calculamos:
; ; .
Portanto, os três próximos números são: 32,5; 162,5; 812,5.
b) Como cada número, a partir do segundo é obtido pela multiplicação do número anterior por 4, calculamos:
; ; .
Portanto, os três próximos números são: 76,8; 307,2; 1.228,8.
37. A massa de uma moeda de R$ 0,25 mede . Como na pilha A existem 7 moedas, temos de medida da massa nessa pilha, pois .
Como na pilha B existem 13 moedas, temos de medida da massa nessa pilha, pois .
Como na pilha C existem 10 moedas, temos de medida da massa nessa pilha, pois .
Como na pilha D existem 15 moedas, temos de medida da massa nessa pilha, pois .
38. Multiplicando o valor de cada prestação pela quantidade dela, obtemos . Portanto, Odair vai pagar R$ 546,75.
39. De acordo com a imagem de cada retângulo, temos as seguintes medidas:
Retângulo A
Medida de comprimento e de largura: e , respectivamente.
Medida da área: , ou seja, .
Medida do perímetro: , ou seja, .
Retângulo B
Medida de comprimento e de largura: e , respectivamente.
Medida da área: , ou seja, .
Medida do perímetro: , ou seja, .
Retângulo C
Medida de comprimento e de largura: e , respectivamente.
Medida da área: , ou seja, .
Medida do perímetro: , ou seja, .
Retângulo D
Medida de comprimento e de largura: e , respectivamente.
Medida da área: , ou seja, .
Medida do perímetro: , ou seja, .
Página LXX
40. Sabendo que uma volta do percurso mede aproximadamente de distância, temos . Portanto, a medida da distância total percorrida por esses carros foi, aproximadamente, .
41. Cada litro de combustível custa R$ 4,78. Então, . Portanto, Mauro pagou R$ 121,89 para abastecer seu carro.
42. Inicialmente, calculamos a medida aproximada da área de cada estado, em .
Minas Gerais: ;
Espírito Santo:
Rio de Janeiro: ;
São Paulo:
Em seguida, para determinar a quantidade aproximada de habitantes de cada estado, multiplicamos densidade demográfica pela medida de área em .
Minas Gerais: ;
Espírito Santo: ;
Rio de Janeiro: ;
São Paulo: .
Portanto, obtemos, em valores aproximados, as seguintes populações.
Minas Gerais: 19.595.633 habitantes;
Espírito Santo: 3.515.125 habitantes;
Rio de Janeiro: 15.989.769 habitantes;
São Paulo: 41.261.611 habitantes.
43. Efetuando-se cada uma das divisões, temos:
a)
b)
c)
d)
e)
f)
g)
h)
44. Calculando o preço do arroz por quilograma para a embalagem de , verificamos que , ou seja, comprando um pacote de , cada quilograma custa R$ 3,79.
Calculando o preço do arroz por quilograma para a embalagem de , verificamos que , ou seja, comprando um pacote de , cada quilograma de arroz custa R$ 3,92.
Portanto, o preço do quilograma do arroz é menor na embalagem de .
45. Realizando os cálculos de maneira semelhante a de Anita, temos:
a)
b)
c)
d)
46. Dividindo a metragem pela quantidade de pedaços de madeira, obtemos , pois . Transformando essa medida em centímetros, obtemos . Assim, o comprimento de cada pedaço de madeira deve medir .
47. Com base no total gasto e o preço unitário dos produto, efetuamos os cálculos correspondentes.
lápis: . Portanto, A equivale a 7.
régua: . Portanto, B equivale a 3.
cola: . Portanto, C equivale a 4.
cartolina: . Portanto, D equivale a 11.
corretivo líquido: . Portanto, E equivale a 2.
48. Dividindo o valor total pelo valor de cada parcela, temos: . Portanto, Rafael parcelou sua compra em 11 prestações.
49. Realizando os cálculos, temos as seguintes potências:
a)
b)
c)
d)
e)
f)
50. Escrevendo a medida da área dos quadrados como potência e, em seguida, calculando-as, temos:
Quadrado A:
, ou seja, .
Quadrado B:
, ou seja, .
Quadrado C:
, ou seja, .
51. Resposta pessoal. Sugestão de problema:
Para fazer uma dobradura, Caio comprou uma folha de papel com formato quadrado cujo comprimento de cada lado mede . Escreva uma potência para representar a medida de área da folha e, em seguida, calcule-a.
Resposta: ; .
Página LXXI
O que eu estudei?
1. a) Para calcular essa quantidade, efetuamos . Portanto, Carlos vai precisar de de tinta.
b) Para calcular a quantidade de tinta necessária, efetuamos . Portanto, ele usaria de tinta.
2. Cada fatia de bolo corresponde a do bolo. Assim, 20 fatias representam de bolo ou, ainda, .
3. a) Como , verificamos que esta biblioteca tem 2.400 livros no total.
b) Para determinar a quantidade de livros de História, calculamos . Portanto, nesta biblioteca há 480 livros de História.
c) Inicialmente, calculamos a fração que corresponde aos livros de Biologia e História juntos, ou seja, . Assim, os livros que não são de História e nem de Biologia correspondem a , ou seja, do total de livros.
4. Calculando de 324, obtemos . Agora, calculamos a metade dessa quantidade, ou seja, . Portanto, para cobrir metade desse piso foram usadas 270 lajotas.
5. Calculando a quantidade de atletas que completaram cada etapa das modalidades, temos:
natação: , ou seja, 160 atletas continuaram na competição.
ciclismo: . Portanto, 120 atletas continuaram.
Como 20% dos atletas abandonaram a prova na última etapa, 80% deles continuaram na etapa da corrida, assim , ou seja, 96 pessoas concluíram a prova.
Logo, . Portanto, a soma dos algarismos de N é . Portanto, a alternativa correta é a d.
6. a) Para obter esta resposta, devemos subtrair do total a fração que representa o preço da camiseta, ou seja, . Portanto, a fração que corresponde ao preço da calça é .
b) Efetuando as multiplicações, verificamos que a camiseta custou R$ 40,00, pois e a calça custou R$ 72,00, pois .
7. Para comparar as frações correspondentes à quantidade de votos, vamos encontrar as frações equivalentes a cada uma das frações, calculando o . Assim, a fração que corresponde aos votos de João é , a de Rosa é , e a de Marcos é .
Comparando as frações equivalentes, concluímos que Rosa ganhou a eleição, pois .
8. Elias deve encher o primeiro recipiente com a água contida no segundo e depois encher o terceiro com o conteúdo do primeiro. Assim, o segundo e o terceiro recipientes terão a mesma quantidade de água.
9. a) Como a jarra está dividida em 5 partes e apenas uma delas está com água, a fração que corresponde à quantidade de água na jarra é .
b) Como já havia da medida de capacidade da jarra, calculamos . Portanto, a água no copo corresponde a da medida de capacidade da jarra.
c) Como há da medida de capacidade da jarra com água, faltam preencher da jarra, pois . Sabendo que um copo enche da medida da capacidade da jarra, dividimos a quantidade que falta preencher pela medida de capacidade correspondente ao copo, ou seja, . Portanto, são necessários 4 copos de água para encher a jarra.
10. Adicionando a medida da distância de cada etapa do percurso, temos:
Portanto, ao completar a prova, Felipe percorreu .
11. Convertendo em gramas, obtemos:
, ou seja,
Assim, . Portanto, foram embalados 5.000 pacotes de café.
12. a) Calculando a medida da distância total percorrida, temos , ou seja, . Portanto, para Márcia cumprir seu objetivo faltam , pois .
b) Como ela ainda tem 2 dias de treino, calculamos . Portanto, Márcia deverá percorrer por dia.
13. Calculando a medida do comprimento de cada pedaço, temos . Portanto, cada pedaço de fio vai ter .
14. a) Temos . Portanto, se Fernanda comprar a embalagem com 12 unidades, ela vai pagar R$ 3,98 em cada unidade.
b) Para responder a essa pergunta realizamos a seguinte operação:. Portanto, Fernanda vai economizar R$ 0,34 por unidade.