Página LXXII
Unidade 6
Cálculo algébrico
Questão 1.
a) Multiplicando o preço pela quantidade de livros, obtemos . Portanto, a pessoa vai pagar R$ 90,30 pelos livros.
b) Multiplicando o preço pela quantidade de livros, obtemos . Portanto, a pessoa vai pagar R$ 129,00 pelos livros.
c) Multiplicando o preço pela quantidade de livros, obtemos . Portanto, a pessoa vai pagar R$ 219,30 pelos livros.
Questão 2. Na compra de jogos, devem ser pagos reais.
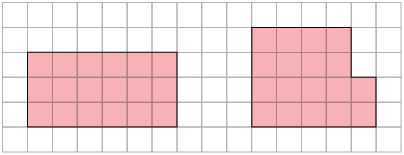
Questão 3. Como e , concluímos que a quantia paga na compra de 5 jogos é R$ 619,50 e a quantia paga na compra de 8 jogos é R$ 991,20.
Questão 4.
b)
c)
d)
e)
f)
g)
h)
Questão 5.
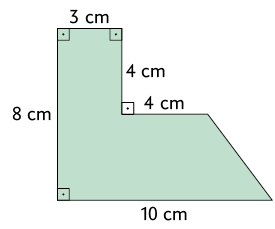
Atividades
1. a) Como 25% pode ser representado pela fração ou pelo número decimal 0,25, então as possíveis expressões são ou ou .
b)
c)
d) ou ou ou
e)
f)
g)
2. a) Analisando a situação, verificamos que os triângulos são formados por 3, 6 e 9 palitos, respectivamente. Ao adicionar 1 palito em cada lado do triângulo, 3 palitos serão adicionados no total. Assim, o 4º triângulo terá palitos e o 5º triângulo terá palitos.
b) Na primeira posição, o triângulo é formado por palitos, na segunda palitos e na terceira palitos. Portanto, o triângulo que está na posição será formado por .
c) Utilizando expressão obtida no item b, temos:
9º triângulo: . Portanto, serão 27 palitos.
21º triângulo: . Portanto, serão 63 palitos.
3. Sugestão de resposta:
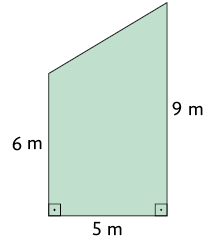
a) Sendo a expressão o primeiro termo da sequência e o segundo termo, cada um dos termos seguintes, do terceiro termo em diante, será a adição dos dois anteriores menos , ou seja:
3º termo:
4º termo:
5º termo:
Portanto, se essa regularidade continuar, os três próximos termos serão:
6º termo:
7º termo:
8º termo:
b) Sendo a expressão o primeiro termo da sequência, cada um dos termos seguintes, do segundo termo em diante, será o dobro do termo anterior menos , ou seja:
2º termo:
3º termo:
4º termo:
Portanto, seguindo essa regularidade, os três próximos termos serão:
5º termo:
6º termo:
7º termo:
c) Sendo o primeiro termo desta sequência, cada termo seguinte, do segundo em diante, é a adição do termo anterior com , ou seja:
2º termo:
3º termo:
Portanto, mantendo essa regularidade, os três próximos termos serão:
4º termo:
5º termo:
6º termo:
Página LXXIII
4. Esta atividade tem várias respostas. Apresentamos uma delas.
a) Escolhendo , obtemos a sequência .
b) Escolhendo , obtemos a sequência .
c) Escolhendo , obtemos a sequência .
5. a) Considerando como o preço de custo dessa peça e representando 28% na forma de número decimal 0,28, verificamos que o preço de venda pode ser representado pela expressão algébrica .
b) Utilizando a expressão obtida no item a, temos:
, ou seja, R$ 40,96.
, ou seja, R$ 32,96.
, ou seja, R$ 25,60.
, ou seja, R$ 30,08.
6. a) Sugestão de resposta:
, sendo o número natural que representa a posição da figura na sequência.
b) Utilizando a expressão obtida no item a, calculamos a quantidade de círculos referente a cada posição.
Como , precisamos calcular a quantidade para a 35ª posição. Então, , ou seja, nessa posição, a figura tem 1.225 círculos.
Como , precisamos calcular a quantidade para a 52ª posição. Então, , ou seja, nessa posição, a figura tem 2.704 círculos.
7. Para responder a cada um dos itens, vamos definir e como os números pensados por Daniele e Henrique, respectivamente.
a) A expressão algébrica que representa a fala de Daniele é:

A expressão algébrica que representa a fala de Henrique é:

b) Fazendo e , obtemos os seguintes valores:
Daniele:
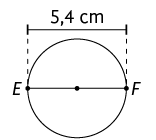
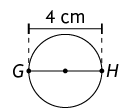
Henrique:
8. a) Identificando cada uma das quantias, temos: Lúcio: ; Alberto: ; Carla: ou ; Gilberto: ou ; Heloísa: ou .
b) Como Lúcio tem R$ 21,00, obtemos que , e fazendo as respectivas substituições, concluímos que:
Alberto tem R$ 41,00, pois .
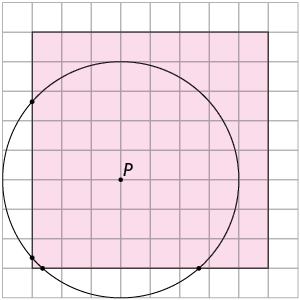
Carla tem R$ 34,00, pois .
Gilberto tem R$ 68,00, pois .
Heloísa tem R$ 34,00, pois .
9. É possível obter mais de uma expressão para representar os produtos citados. Apresentamos uma sugestão de resposta em cada item.
a) Sonho:
b) Pedaço de torta:
c) Fatia de bolo:
d) Biscoito:
10. Escrevendo de maneira simplificada cada um dos itens, obtemos:
a)
b)
c)
Associando as expressões equivalentes, temos a-3; b-1; c-2.
11. a) Escrevendo as representações em ordem crescente, temos ; ; .
b) Efetuando a adição dos três itens, obtemos .
Portanto, a expressão escrita na forma simplificada é igual a .
12. De acordo com as medidas apresentadas em cada uma das figuras, temos:
A.
B.
13. Simplificando cada uma das expressões, temos:
a)
b)
c)
d)
e)
f)
14. Esta atividade tem várias respostas. Apresentamos uma para cada item.
a)
b)
c)
d)
15. A fala de Camila pode ser expressa algebricamente como:
ou
A fala de Raí pode ser expressa algebricamente como:
ou
Questão 6.
a) Como , então .
b) Como , então .
c) Como , então .
d) Como , então .
Página LXXIV
Atividades
16. a) Se é o preço de etiqueta e é o valor de cada prestação, então:
Nesse caso, a fórmula representada na alternativa C é a que fornece o valor de cada prestação.
Portanto, a alternativa C é a correta.
b) Se , então . Portanto, quando o produto é vendido em 3 prestações, o valor de cada parcela é R$ 50,60.
17. Para , temos . Portanto, essa fábrica tem um lucro mensal de R$ 8.540,00.
18. Fazendo o mesmo procedimento apresentado na página 126, temos:
Assim:
a)
b)
c)
d)
19. a) De acordo com o enunciado, a fórmula utilizada por Amauri foi .
b) Executando o mesmo procedimento apresentado na página 126, temos:
Questão 7. O primeiro termo da sequência A é amarelo e o sexto termo da sequência B é 11.
Questão 8. Calculando cada um dos termos dessa sequência, temos:
Para ,
Para ,
Para ,
Para ,
Para ,
Assim, a sequência é .
Questão 9. Resposta pessoal. Espera-se que os estudantes usem com responsabilidade as ferramentas de pesquisa e que compartilhem os resultados obtidos com os colegas.
Atividades
20. a) Para , temos .
Para , temos .
Para , temos .
Para , temos .
Para , temos .
Assim, a sequência definida é .
b) Para , temos .
Para , temos .
Para , temos .
Para , temos .
Assim, a sequência definida é .
c) Para , temos .
Para , temos .
Para , temos .
Assim, a sequência definida é .
d) Para , temos .
Para , temos .
Para , temos .
Para , temos .
Assim, a sequência definida é .
e) Para , temos .
Para , temos .
Para , temos .
Assim, a sequência definida é .
f) Para , temos .
Para , temos .
Assim, a sequência definida é .
Entre as sequências definidas, as que foram descritas por uma lei de formação são a, b, d e f.
21. a) Os cinco primeiros termos da sequência são:
b) A sequência foi definida por recorrência, pois um termo sempre é definido em função do termo anterior.
c) Se , então . Consequentemente, todos os termos da sequência seriam iguais a 3 e, portanto, a sequência seria .
22. Calculando os termos de cada sequência, temos:
a)
b)
c)
d)
e)
Página LXXV
Logo, as expressões b e d podem descrever a sequência indicada.
Resposta pessoal. Espera-se que os estudantes respondam que duas ou mais definições aparentemente diferentes podem representar a mesma sequência.
23. a)
b)
24. a) Infinita.
b) Considerando os termos dessa sequência, temos:
Assim, a lei de formação dessa sequência é dada por para todo .
c)
25. a) Sugestão de resposta:
Podemos verificar que a sequência é formada pelos números naturais maiores do que 15. Portanto, uma definição que descreve a regularidade da sequência é , para todo , ou ainda, para todo , com .
b) Sugestão de resposta:
A partir do primeiro termo (), os próximos termos são obtidos adicionando 4 unidades ao termo anterior. Portanto, uma expressão que descreve a regularidade da sequência é para todo , com , ou, ainda, para todo .
26. a) São necessários 5 palitos para representar a 2ª figura e 9 palitos para representar a 4ª figura.
b) Como a quantidade de palitos que formam as figuras está relacionada com a posição da figura na sequência, podemos escrever:
1ª figura: 3 palitos.
2ª figura: 5 palitos ().
3ª figura: 7 palitos ().
4ª figura: 9 palitos ().
Ou seja, a partir da primeira figura, a próxima figura é formada por 2 palitos a mais do que a figura anterior. Portanto, uma possível resposta seria , para todo com ou , para todo , sendo n o número natural que representa a posição da figura na sequência.
c) Utilizando a expressão obtida no item b, concluímos que a 9ª figura é formada por 19 palitos, pois , e a 25ª figura é formada por 51 palitos, pois .
27. a) Calculando a medida da área do segundo retângulo, verificamos que a área do 2º retângulo mede , pois . Calculando a medida da área do quarto retângulo, verificamos que a área do 4º retângulo mede , pois .
b) Uma das medidas sempre é igual a e a outra aumenta conforme o número que representa a posição do termo aumenta. Sendo assim, a medida da área de um retângulo qualquer nessa sequência, mantendo a regularidade, pode ser descrita pela expressão , para todo , sendo n o número natural que representa a posição do retângulo nela.
c) Utilizando a expressão obtida no item b, verificamos que . Portanto, a área do 525º retângulo dessa sequência mede .
28. Ambos escreveram a lei de formação corretamente, pois as expressões escritas por Conceição e Jorge são equivalentes.
Questão 10. Resposta pessoal. Espera-se que os estudantes efetuem multiplicações para determinar as quantidades de livros lidos pelas personagens do problema.
Questão 11. Resposta pessoal. Esta questão tem várias respostas. Uma delas é:
Atividades
29. a) Essa sentença é uma equação.
b) Essa sentença não é uma equação, pois não há uma igualdade.
c) Essa sentença é uma equação.
d) Essa sentença é uma equação.
e) Essa sentença não é uma equação, pois não há uma incógnita.
f) Essa sentença não é uma equação, pois não há uma igualdade.
30. a)
b)
c)
d)
e)
Página LXXVI
f)
31. De acordo com os dados do problema, elaboramos a seguinte equação:
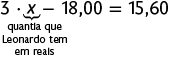
Resolvendo a equação, temos:
Portanto, Leonardo tem R$ 11,20.
32. a)
b)
c)
d)
e)
f)
g)
h)
33. Sabendo que a medida da área de um retângulo é igual ao produto obtido ao multiplicarmos a medida do comprimento pela medida de largura, temos:
Portanto, o comprimento do terreno mede .
34. a) Resolvendo a equação montada por Silas, temos:
Assim, .
b) Sugestão de respostas:
35. Seja a medida em quilogramas da massa corporal de Jéssica. Assim, de acordo com as informações da atividade, calculamos:
Portanto, a massa corporal de Jéssica mede .
36. Resolvendo a primeira equação, obtemos:
Resolvendo a segunda equação, obtemos:
37. a) Simplificando a equação, obtemos:
Resolvendo a equação, obtemos:
b) Simplificando a equação, obtemos:
Resolvendo a equação, obtemos:
c) Simplificando a equação, obtemos:
Resolvendo a equação, obtemos:
d) Simplificando a equação, obtemos:
Resolvendo a equação, obtemos:
Página LXXVII
38. a) De acordo com as informações da atividade, podemos escrever:
Portanto, a equação que permite obter solução para o problema está na alternativa C.
b) Resolvendo a equação, obtemos:
Portanto, Márcia tem R$ 35,00 e Nivaldo tem R$ 70,00.
39. Como temos um número representado por p, representamos seu sucessor por e a equação que representa essa situação é dada por . Resolvendo esta equação, obtemos:
Portanto, .
40. Como as idades são representadas por números consecutivos, vamos indicar por x a idade de Simone; por a idade de Jaqueline, que é mais velha; e por a idade de Mauro, por ser o mais novo entre eles. Assim:
Portanto, Jaqueline tem 14 anos, Simone tem 13 anos e Mauro tem 12 anos.
41. a) De acordo com as informações da atividade, devemos fazer as seguintes substituições:
Em seguida, resolvendo a equação, obtemos:
Portanto, esse prisma tem 8 faces.
Além disso, como , concluímos que esse prisma tem 12 vértices.
b) Em um prisma, a quantidade de arestas é igual ao triplo da quantidade de lados do polígono de sua base, Nesse caso, , sendo n o número de lados do polígono da base do prisma, ou seja, esse prisma tem 6 lados e recebe o nome de prisma de base hexagonal.
42. Resposta pessoal. Sugestão de problema:
Em um jogo de perguntas e respostas, Fábio acertou 6 perguntas e errou 1 pergunta. Sabendo que o jogador perde 2 pontos para cada erro e que Fábio tem 88 pontos, qual é o valor de cada acerto no jogo? Resposta: 15 pontos.
43. a) Nos cálculos a seguir, a incógnita representa a medida de massa de cada caixa em cada um dos itens.
Balança A.
Portanto, a situação da balança A pode ser descrita pela equação H.
Balança B.
Portanto, a situação da balança B pode ser descrita pela equação E.
Balança C.
Portanto, a situação da balança C pode ser descrita pela equação F.
Balança D.
Portanto, a situação da balança D pode ser descrita pela equação G.
b) Resolvendo cada uma das expressões determinadas no item anterior, temos:
Balança A:
Portanto, a massa da caixa verde mede .
Balança B:
Portanto, a massa da caixa amarela mede .
Balança C:
Portanto, a massa da caixa vermelha mede .
Página LXXVIII
Balança D:
Portanto, a massa da caixa roxa mede .
44. Considerando a medida da massa de cada caixa, em quilograma, a equação que descreve essa situação é .
Resolvendo a equação, obtemos:
Portanto, a massa de cada caixa mede .
45. Sendo a medida da massa de cada lata de achocolatado, em quilograma, a equação que descreve essa situação é .
Resolvendo a equação, temos:
Portanto, a massa de cada lata mede ou .
46. a)
b)
c)
d)
e)
f)
47. De acordo com as informações da atividade, temos:
A.
B.
C.
D.
Assim, obtemos as seguintes correspondências: A-3; B-1; C-2; D-4.
Resolvendo as equações em cada item, obtemos:
A.
Portanto, Josiane tem 18 anos.
B.
Portanto, eu tenho R$ 46,00.
Página LXXIX
C.
Portanto, Nair tem 6 canetas.
D.
Portanto, meu aquário tem 5 peixes.
48. Dos 453 minutos que Renato usou, 200 minutos estão inclusos no plano de ligações locais. Assim, Renato utilizou excedentes de seu plano telefônico, pois . Indicando por o valor pago por minuto excedente, temos:
Portanto, Renato pagou R$ 0,08 por minuto excedente.
49. De acordo com cada fala de Marisa, podemos escrever:
;
Resolvendo essa equação, obtemos:
Portanto, Marisa mede de altura.
De acordo com cada fala de Andrei, podemos escrever:
Resolvendo essa equação, obtemos:
Portanto, Andrei tem 31 figurinhas.
50. Utilizando o fato de que a soma das medidas dos ângulos internos de um triângulo é igual a , temos:
Portanto, as medidas dos ângulos internos são:
;
;
.
51. a) Na primeira rodada, o total de pontos de Júlia e de Isadora pode ser calculado da seguinte maneira:
Júlia:
Isadora:
Portanto, na primeira rodada Júlia fez 18 pontos e Isadora fez 6 pontos.
b) Na segunda rodada, o total de pontos de Júlia e Isadora pode ser calculado da seguinte maneira:
Júlia:
Isadora:
Portanto, na segunda rodada Júlia não pontuou e Isadora fez 12 pontos.
c) Como representa a quantidade de respostas certas e há 15 perguntas em cada rodada, podemos representar a quantidade de erros por . Assim, a expressão que determina a quantidade de pontos de um jogador em uma rodada é . Portanto, a expressão correta é a II.
d) Utilizando a expressão do item c, obtemos:
Júlia:
Isadora:
Portanto, Júlia teve 9 acertos e Isadora teve 11 acertos.
Página LXXX
52. De acordo com as informações da atividade, as vendas de sorvete em cada um dos três dias foi a seguinte:
sexta-feira: sorvetes;
sábado: sorvetes;
domingo: sorvetes.
Sabendo que nesses três dias foram vendidos 273 sorvetes, calculamos:
Portanto, na sexta-feira foram vendidos 57 sorvetes, no sábado, 72 sorvetes e no domingo, 144 sorvetes.
53. De acordo com as informações da atividade, escrevemos a equação a seguir.
.
Resolvendo-a, obtemos:
Com esse resultado, verificamos que o comprimento do retângulo mede , pois . Da mesma maneira, o comprimento de cada lado do quadrado mede , pois . Assim, obtemos:
Medida da área do retângulo A: , ou seja, .
Medida da área do quadrado B: , ou seja, .
54. Contando com Vanderlei, 5 pessoas iriam viajar. Porém, sabendo que 2 pessoas desistiram, apenas 3 pessoas tiveram que arcar com o custo do aluguel do veículo.
a) De acordo com as informações do problema, temos:
Resolvendo a equação, temos:
Portanto, cada pessoa pagaria inicialmente R$ 112,50.
b) Como , concluímos que o veículo foi alugado por R$ 562,50.
O que eu estudei?
1.
2. ou
3. a) ; ;
b)
4. Calculando primeiro a medida do perímetro do polígono, temos:
.
Como um triângulo equilátero tem todos os seus lados com a mesma medida, então cada lado deve medir .
5. a) . De acordo com o quadro, o IMC neste caso indica peso normal.
b) . De acordo com o quadro, o IMC neste caso indica abaixo do peso.
c) . De acordo com o quadro, o IMC neste caso indica peso normal.
d) . De acordo com o quadro, o IMC neste caso indica sobrepeso.
6. a) . Portanto, é equivalente a .
b) . Portanto, é equivalente a .
c) . Portanto, é equivalente a .
d) . Portanto, é equivalente a .
7. Utilizando as informações da atividade, podemos escrever a seguinte equação:
Resolvendo a equação, temos:
Portanto, o número em que Vânia pensou é 9.
Página LXXXI
8. A diferença entre as idades da mãe e da filha sempre será a mesma, ou seja, . Nesse caso, a mãe é 19 anos mais velha do que a filha. Com isso, considerando x a idade da filha, obtemos a seguinte equação:
Resolvendo a equação, obtemos:
Portanto, a mãe terá o dobro da idade da filha quando a filha tiver 19 anos. Isso representa uma diferença de 5 anos entre essa data e a idade da filha hoje, que é 14 anos. Portanto, a idade da mãe será o dobro da idade da filha daqui a 5 anos.
9. a) Açúcar: . Portanto, Marina pagou R$ 37,45 nos pacotes de açúcar.
b) Caixinha de leite: . Portanto, Marina pagou R$ 15,96 nas caixinhas de leite.
c) Garrafas de óleo: . Portanto, Marina pagou R$ 35,56 nas garrafas de óleo.
d) Cada garrafa de óleo: . Portanto, Marina pagou R$ 8,89 em cada garrafa de óleo.
10. Atribuindo valores consecutivos para , obtemos:
Logo, a sequência é . Esta sequência é definida por uma lei de formação.
11. Pela definição de perímetro de um polígono, temos:
Assim, e .
Portanto, os lados do triângulo medem , e .
12. Considerando a medida de uma das dimensões desconhecida do tijolo e de acordo com a fórmula da medida do volume de um paralelepípedo reto retângulo, obtemos a seguinte equação:
Portanto, a outra dimensão do tijolo mede .
13. Seja a quantidade de canetas que Débora tem. Assim:
Quantidade de canetas de Solange: .
Quantidade de canetas de Cíntia: .
Como elas têm 161 canetas juntas, podemos escrever e resolver a seguinte equação:
Assim, e . Portanto, Débora tem 52 canetas, Solange tem 56 canetas e Cíntia, 53 canetas.
14. De acordo com as informações de valor apresentadas na atividade, vamos representar com expressões algébricas os arremessos.
Arremessos que valem 1 ponto: .
Arremessos que valem 2 pontos: .
Arremessos que valem 3 pontos: .
Sabendo que ao todo foram 54 arremessos, obtemos a seguinte equação:
Assim, calculando a quantidade de pontos feitos pelo time nessa partida, obtemos:
Portanto, o time fez 112 pontos nessa partida.
Unidade 7
Figuras geométricas planas e ângulos
Atividades
1. a) O giro de meia-volta para a esquerda é o da Cena 4.
b) O giro de três quartos de volta para a esquerda é o da Cena 3.
c) O giro de uma volta completa para a esquerda é o da Cena 2.
2. Resposta pessoal. A resposta depende dos objetos que os estudantes vão sugerir. Sugestão de resposta:
Lousa, caderno, porta.
3. a) Jessé realizou um giro correspondente a de volta.
4. A. Nome do ângulo: , ou ; vértice: B; lados: e .
B. Nome do ângulo: , ou ; vértice: K; lados: e .
C. Nome do ângulo: , ou ; vértice: U; lados: e .
Página LXXXII
5. Resposta pessoal. Sugestão de resposta:

Questão 1.



Atividades
6. De acordo com os transferidores, a medida do ângulo indicado em A é , em B é , em C é , em D é , em E é e em F é .
7. O único ângulo reto, ou seja, que mede , está representado no item C.
Os ângulos representados nos itens A, E e F são agudos, pois suas medidas são maiores do que e menores do que ; Os ângulos B e D são obtusos, pois têm medidas entre e .
8. Caminho 3, pois todos os ângulos formados pelo caminho do robô medem .
9. ;
;
;
;
;
.
10. a) O ângulo reto é o .
b) Os ângulos agudos são , e .
c) O ângulo obtuso é .
d) O ângulo raso é .
11. a)
b)

c)
d)

12. a) Ambos correspondem a meia-volta.
13. O ângulo é congruente, pois tem a mesma medida do ângulo construído por Gabriel, ou seja, mede .
14. Ângulos adjacentes são aqueles que têm um lado em comum e as regiões formadas por eles não tem pontos em comum. Assim, são adjacentes e , e , e , e .
Questão 2. O ângulo:
complementar de mede , pois .
suplementar de mede , pois .
Questão 3. Resposta pessoal. Espera-se que os estudantes verifiquem que a medida do ângulo é 34° pois é um ângulo oposto pelo vértice ao ângulo , e por ser suplementar do ângulo .
Atividades
15. A. Como , a medida do seu ângulo complementar é , pois , e do seu suplementar é , pois .
B. Como , a medida do seu ângulo complementar é , pois , e do seu suplementar é , pois .
C. Como , a medida do seu ângulo complementar é , pois , e do seu suplementar é , pois .
Página LXXXIII
D. Como , a medida do seu ângulo complementar é , pois , e do seu suplementar é , pois .
E. Como , a medida do seu ângulo complementar é , pois , e do seu suplementar é , pois .
16. a) Como o pedaço de cartolina tem formato retangular, sabemos que o ângulo cortado pela linha tracejada mede . Além disso, ao desdobrar a folha, temos:
b) A medida do complementar de é , pois , e do suplementar é , pois .
17. Resposta no final da seção Resoluções.
18. Como são ângulos complementares, sabemos que . Como , ou seja, é o dobro de , então:
Logo, . Portanto, .
19. A. Como é oposto pelo vértice ao ângulo que mede , então, por definição, .
Sendo , então . Com isso, .
Como é oposto pelo vértice a , então, por definição, .
B. Como o ângulo é oposto pelo vértice ao ângulo que mede , temos .
Sendo um ângulo reto, então .
Como , então , isto é, .
Como , verificamos também que . Assim, .
Sendo oposto pelo vértice a , verificamos que .
20. Os ângulos de medidas e são opostos pelo vértice. Desse modo, as medidas desses ângulos são iguais. Como , temos . Além disso, . Com isso, fazemos os seguintes cálculos:
Portanto, .
21. A. Sabendo que , temos:
Portanto, os ângulos medem .
B. Sabendo que , temos:
Portanto, os ângulos medem .
22. a) • O ângulo de medida é oposto pelo vértice do ângulo de medida .
O ângulo de medida é oposto pelo vértice do ângulo de medida .
b) Resposta pessoal. Espera-se que os estudantes concluam que não, pois os ângulos de medidas e são suplementares, ou seja, a soma dessas medidas é sempre .
Questão 4.
a) e medem .
b) e medem .
c) e medem .
d) e medem .
Resposta pessoal. Espera-se que os estudantes respondam que os pares de medidas obtidos são iguais.
Questão 5. Resposta pessoal. Espera-se que os estudantes usem procedimentos semelhantes para concluir que os pares de ângulos colaterais são suplementares, como segue:
Os ângulos de medidas e são correspondentes. Assim, . Além disso, os ângulos de medidas e são suplementares, ou seja, . Portanto, concluímos que .
Os ângulos de medidas e são correspondentes. Assim, . Além disso, os ângulos de medida e são suplementares, ou seja, . Portanto, concluímos que .
Atividades
23. a) As letras que indicam as medidas de dois pares de ângulos correspondentes são:
e ; e ; e ; e .
b) As letras que indicam as medidas de dois pares de ângulos opostos pelo vértice são: e ; e ; e ; e .
c) As letras que indicam as medidas de dois pares de ângulos alternos internos são: e ; e .
d) As letras que indicam as medidas de dois pares de ângulos alternos externos são: e ; e .
Página LXXXIV
24. d) A alternativa d é falsa, pois, como as retas s e t são paralelas, mede . Sugestão de resposta:
A medida é .
25. Sabendo que o ângulo que mede é correspondente a e , verificamos que e . Como o ângulo que mede é alterno externo ao ângulo , obtemos . Além disso, . Sendo assim, temos:
Por fim, como é alterno interno a , desse modo .
26. A. Sabemos que os ângulos destacados são alternos internos. Assim:
Portanto, . Como , os ângulos indicados medem .
B. Sabemos que a medida do ângulo alterno externo a é dada por . Assim:
Portanto, . Como e , o ângulo agudo mede e o ângulo obtuso, .
C. Sabemos que a medida do ângulo alterno interno a é dada por . Assim:
Portanto, . Como e , os ângulos agudos medem e os ângulos obtusos medem .
27. a) Como são ângulos alternos internos, temos:
Portanto, .
b) Como são ângulos alternos internos, a medida do ângulo será a mesma. Assim, e, portanto, os ângulos medem .
28. Sabemos que, em um triângulo equilátero, cada um dos ângulos internos mede , ou seja, . Como é paralelo a , então . Logo, o triângulo cuja medida dos ângulos internos é representada por , e é equilátero. Consequentemente:
Portanto, a alternativa e está correta.
29. A. O ângulo de medida está dividido em duas partes pela reta tracejada. A menor parte dele mede , pois esse ângulo é alterno interno ao ângulo que mede .
A maior parte da medida do ângulo é dada por , pois esse ângulo é correspondente ao suplementar de .
Portanto, .
B. O ângulo de medida está dividido em duas partes pela reta tracejada. A maior parte dele mede , pois é correspondente ao suplementar de , ou seja, .
Para determinar a medida da menor parte do ângulo , devemos, primeiro, determinar a medida de cada parte em que o ângulo de medida foi dividido. Como o ângulo de medida é alterno interno à parte maior desse ângulo, então a medida da parte maior é dada por . Desse modo, a parte menor do ângulo mede .
Portanto, .
30. Traçando uma reta imaginária paralela às demais madeiras horizontais, de modo que divida o ângulo ao meio, verificamos que e são opostos pelo vértice. Assim , desse modo , ou seja, . Portanto, mede .
31. a) e .
b) A soma das medidas de cada par de ângulos colateral interno é .
c) e .
d) A soma das medidas de cada par de ângulos colaterais internos é .
Página LXXXV
e) Os ângulos colaterais internos e colaterais externos são suplementares, pois a soma entre cada par de ângulos é sempre .
32. O ângulo oposto pelo vértice ao ângulo de corresponde ao ângulo de medida . Assim, , e . Para determinarmos a medida de , devemos considerar que o maior triângulo apresentado é um triângulo retângulo, ou seja, um de seus ângulos mede . Desse modo, como a soma das medidas dos ângulos internos de um triângulo é , obtemos , isto é, .
33. Não.
Para que dois ângulos sejam suplementares, a soma de suas medidas deve ser . Como , que é diferente de , os ângulos indicados não são suplementares.
34. Os ângulos de medidas e são alternos internos. Logo, . Portanto, a alternativa c é a verdadeira.
35. Os ângulos de medidas e são alternos externos, ou seja, . Portanto, a alternativa a está correta.
36. A. Pentágono, pois tem 5 lados.
B. Heptágono, pois tem 7 lados.
C. Quadrilátero, pois tem 4 lados.
D. Octógono, pois tem 8 lados.
E. Triângulo, pois tem 3 lados.
F. Hexágono, pois tem 6 lados.
37. A: A obra de Luiz Sacilotto apresenta triângulos, quadriláteros, pentágonos e hexágonos.
B: A obra de Piet Mondrian apresenta quadriláteros.
38. A. Lados: , , , e ; vértices: A, B, C, D e E; ângulos internos: , , , e .
B. Lados: , , , , e ; vértices: F, G, H, I, J e K; ângulos internos: , , , , e .
C. Lados: , , e ; vértices: L, M, N e O; ângulos internos: , , e .
39. A. Convexo, pois as medidas de seus ângulos internos são menores do que 180° e qualquer reta que passa pelo seu interior corta seu contorno em somente dois pontos.
B. Não convexo, pois ao menos uma reta que passa pelo seu interior corta seu contorno em mais de dois pontos.
C. Não convexo, pois ao menos uma reta que passa pelo seu interior corta seu contorno em mais de dois pontos.
D. Convexo, pois as medidas de seus ângulos internos são menores do que 180° e qualquer reta que passa pelo seu interior corta seu contorno em somente dois pontos.
40. A menor quantidade de lados que um polígono pode ter é 3.
41. a) Heptágono, pois o polígono antes de ser dividido tem sete lados.
b) Pentágonos, pois após a divisão cada polígono tem 5 lados.
42. Os polígonos C e E são regulares, pois todos os lados têm a mesma medida de comprimento, assim como todos os ângulos internos.
43. a) Os triângulos e os quadriláteros são polígonos que formam as faces de um prisma de base triangular.
b) Os triângulos e um quadrilátero são polígonos que formam as faces de uma pirâmide de base quadrada.
44. O mosaico A é formado por hexágonos e triângulos.
O mosaico B é formado por quadriláteros e pentágonos.
45. A alternativa a é falsa, pois os polígonos que formam as faces e as bases do poliedro A podem ser nomeados quadriláteros e pentágono. A alternativa b é falsa, pois o poliedro B não tem faces ou base pentagonais. A alternativa c é falsa, pois a base do poliedro B é um hexágono. A alternativa d é verdadeira. A alternativa e é falsa, pois as faces e as bases do poliedro A são formadas por polígonos com quantidade de lados diferentes.
46. A. Vértices: C, D e F; medida dos ângulos internos: , e ; medida dos ângulos externos: , e .
B. Vértices: M, N e O; medida dos ângulos internos: , e ; medida dos ângulos externos: , e .
47. a) Em um triângulo, o ponto comum de cada dois lados é chamado vértice.
b) O triângulo é um polígono formado por três segmentos de reta.
c) Qualquer polígono de três lados é chamado triângulo.
d) Um triângulo tem três vértices.
48. a) Um triângulo é isósceles quando apresenta ao menos dois lados com medidas de comprimento iguais.
b) Os outros dois lados também medem de comprimento, pois em um triângulo equilátero todos os lados apresentam a mesma medida de comprimento.
c) Em um triângulo escaleno, as medidas do comprimento dos lados são diferentes. Nesse caso, essas medidas devem resultar em . Sugestão de resposta: , e .
d) Em relação às medidas de comprimento dos lados, o triângulo com , e é classificado como isósceles, pois tem dois lados com mesma medida de comprimento.
49. A. Isósceles, pois apresenta dois de seus lados com medidas de comprimento iguais.
B. Isósceles, pois apresenta dois de seus lados com medidas de comprimento iguais.
C. Equilátero, pois as medidas do comprimento de todos os lados são iguais.
D. Escaleno, pois as medidas do comprimento de todos os lados são diferentes.
50. A. Acutângulo, pois os três ângulos internos são agudos.
B. Obtusângulo, pois um ângulo interno é obtuso.
C. Retângulo, pois um de seus ângulos é reto.
D. Acutângulo, pois seus três ângulos são agudos.
Página LXXXVI
51.
Início
1º. Trace um segmento cuja medida do comprimento dos lados seja a maior.
2º. Com a ponta-seca do compasso em A e abertura com a medida do comprimento de um dos lados, trace um arco de circunferência.
3º. Com a ponta-seca do compasso em B e abertura com a medida de comprimento do terceiro lado, trace um arco de circunferência. O ponto em que os arcos se cruzam é o vértice C do triângulo.
4º. Com a régua, trace o segmento e e apague as marcas dos arcos.
Fim

52. Considere as medidas , e do comprimento dos lados para construir um triângulo .
1º. Trace um segmento cuja medida do comprimento seja .
2º. Com a ponta-seca do compasso em D e abertura medindo , trace um arco de circunferência.
3º. Com a ponta-seca do compasso em E e abertura medindo , trace um arco de circunferência. O ponto em que os arcos se cruzam é o vértice F do triângulo.
4º. Com a régua, trace o segmento e e apague as marcas dos arcos.


O triângulo é acutângulo, pois todos os ângulos são agudos.
53. Sugestão de resposta: A madeira colocada no portão formou alguns triângulos, que são figuras rígidas, por isso fortaleceu a estrutura do portão.
54. Sugestões de resposta:
, e ;
, e ;
, e ;
, e .
55. Não, pois a medida de comprimento de um dos lados do triângulo é igual à soma das medidas dos outros dois, isto é, .
56. Com as medidas de comprimento apresentadas no item A, não é possível construir um triângulo, pois .
Com as medidas de comprimento apresentadas no item B, não é possível construir um triângulo, pois .
Página LXXXVII
Com as medidas de comprimento apresentadas no item C, é possível construir um triângulo, pois ; e .
Com as medidas de comprimento apresentadas no item D, é possível construir um triângulo, pois ; e .
Com as medidas de comprimento apresentadas no item E, é possível construir um triângulo, pois ; e .
57. De acordo com as medidas já indicadas, considerando a condição de existência dos triângulos e sabendo que as medidas dos comprimentos devem ser números positivos, temos as considerações a seguir.
A menor medida de comprimento do lado do triângulo A é , pois se , temos . A maior medida de comprimento do lado do triângulo A é , pois se , temos .
A menor medida de comprimento do lado do triângulo B é , pois se , temos . A maior medida de comprimento do lado do triângulo B é , pois se , temos .
A menor medida de comprimento do lado do triângulo C é , pois se , temos . A maior medida de comprimento do lado do triângulo C é , pois se , temos .
Tanto a menor quanto a maior medida de comprimento do lado do triângulo D devem ser , pois se , temos , e se , temos .
58. Como a soma das medidas dos ângulos internos de um triângulo é , nos triângulos B e D temos , pois e .
59. A. A soma das medidas dos ângulos internos é .
B. A soma das medidas dos ângulos internos é .
C. A soma das medidas dos ângulos internos é .
D. A soma das medidas dos ângulos internos é .
60. Sabendo que e que , temos , isto é, . Assim:
Portanto, .
61. Douglas desenhou o polígono C, pois apresenta as medidas indicadas nos comandos seguidos por ele.
62. Os polígonos B e C, pois em cada um deles os lados têm a mesma medida de comprimento e todos os ângulos internos têm a mesma medida.
63. a) A vista de cima dos alvéolos construídos pelas abelhas lembra hexágonos.
b) Um hexágono pode ser decomposto em 4 triângulos. Assim, a soma das medidas dos ângulos internos de um hexágono é dada por .
c) Cada ângulo interno mede , pois .
64. As afirmações verdadeiras são b e d.
a) Os polígonos e não são regulares, pois a medida do comprimento dos lados e a medida dos ângulos internos são diferentes no polígono . Além disso, as medidas dos ângulos internos do polígono também são diferentes.
c) A soma das medidas do ângulos internos do polígono é igual a e a soma das medidas dos ângulos internos do polígono é igual a , ou seja, o triplo de .
65. a) Sugestão de resposta:
Os polígonos e não são regulares.
c) Sugestão de resposta:
A soma das medidas dos ângulos internos do polígono é três vezes a soma das medidas dos ângulos internos do polígono .
Questão 7. Podemos notar que a soma das medidas dos ângulos externos é sempre .
Atividades
66. Para obter as medidas desconhecidas, usamos as informações referentes à soma das medidas dos ângulos internos e à soma das medidas dos ângulos externos de um triângulo.
No triângulo A, temos:
;
;
;
.
No triângulo B, temos:
;
;
;
.
67. Para obter as medidas desconhecidas, usamos as informações referentes à soma dos ângulos internos e à soma dos ângulos externos de um triângulo.
No triângulo A, temos:
Como , então .
No triângulo B, temos:
Como , então .
No triângulo C, temos:
No triângulo D, temos:
Como e , obtemos .
Página LXXXVIII
68. A medida do ângulo alterno externo do ângulo de medida é , isto é, . Além disso, o suplementar do ângulo de medida é e o suplementar do ângulo de medida é . Desse modo:
Portanto, e .
69. Como um hexágono pode ser decomposto em quatro triângulos, a soma das medidas dos ângulos internos é dada por . Sendo ele um polígono regular, cada ângulo interno mede , pois . Como a adição do ângulo de medida com um ângulo interno desse hexágono equivale a , para obter o valor da medida do ângulo subtraímos a medida de um ângulo interno de , ou seja, . Além disso, como o ângulo de medida representa a metade da medida do ângulo externo de um hexágono regular , calculamos . Portanto, e .
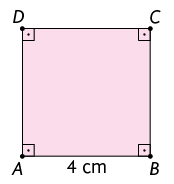
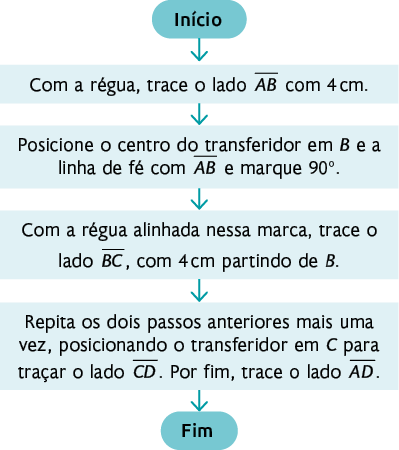
70. Para construir o quadrado, podemos considerar as seguintes etapas:
1º. Com a régua, trace o lado com .
2º. Posicione o centro do transferidor em B e a linha de fé com e marque .
3º. Com a régua alinhada nessa marca, trace o lado , com partindo de B.
4º. Repita os dois passos anteriores mais uma vez, posicionando o transferidor em C para traçar o lado . Por fim, trace o lado .
Sabendo que o ângulo interno de um pentágono regular mede , para construir o pentágono regular podemos seguir estas etapas:
1º. Com a régua, trace o lado com .
2º. Posicione o centro do transferidor em I e a linha de fé com e marque .
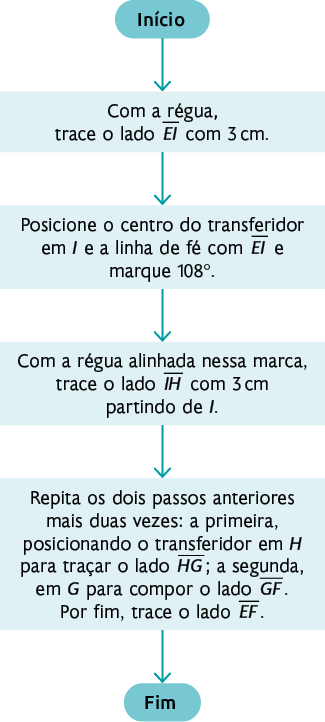
3º. Com a régua alinhada nessa marca, trace o lado com partindo de I.
4º. Repita os dois passos anteriores mais duas vezes: a primeira, posicionando o transferidor em H para traçar o lado ; a segunda, em G para compor o lado . Por fim, trace o lado .
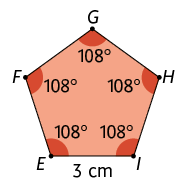
71. Como polígono é regular, os ângulos internos têm medidas iguais. Fazendo , deduzimos que o polígono foi dividido em 4 triângulos, ou seja, a figura é um hexágono. Logo, , isto é, cada um dos ângulos internos dessa figura mede .
72. Sabemos que e . Além disso, a soma das medidas dos ângulos externos de um triângulo é igual a .
Página LXXXIX
Assim, , isto é . Para obter as medidas dos ângulos , e , calculamos:
;
;
.
73. Sabemos que o suplementar de é , ou seja, . Como , verificamos que o triângulo é isósceles. Assim, . Logo, , pois .
Como , então . Além disso, e . Desse modo, , pois . Logo, a medida de é dada por , ou seja, . Portanto, a alternativa correta é a c.
74. O ângulo correspondente de é o ângulo de medida , assim . O suplementar do ângulo de medida é alterno interno ao ângulo de medida . Desse modo, é dado por , ou seja, .
75. A. Como é a medida de um ângulo interno de um polígono regular de 6 lados, temos , ou seja, .
B. Como é a medida de um ângulo interno de um polígono regular de 12 lados, temos , ou seja, .
C. Como o ângulo interno do polígono amarelo mede , pois , então . Logo, .
D. Como , então .
Questão 8. Como e , obtemos .
Atividades
76. A. Raios: , e ; cordas: e ; diâmetro: .
B. Raios: , , , e ; cordas: , e ; diâmetros: e .
C. Raios: , , e ; cordas: , e ; diâmetro: .
77. a) O comprimento do raio mede e o comprimento do diâmetro mede .
b) A medida de comprimento do diâmetro representa o dobro da medida de comprimento do raio.
c) Sim, pois em qualquer circunferência o diâmetro é uma corda que passa pelo centro. Como o raio é qualquer segmento de reta que une o centro da circunferência a um de seus pontos, a medida de comprimento do diâmetro é o dobro da medida de comprimento do raio.
78. a)
b)
c)
d)
79.
80. Traçando uma circunferência com centro em P, cujo raio mede , temos:
Portanto, há 4 pontos que estão sobre os lados do quadrado e distam de P.
81. Resposta pessoal. Espera-se que os estudantes escolham objetos diversos, como tampas de recipientes, aros de bordado, anéis e moedas.
Página XC
82. Como o comprimento da circunferência mede , temos:
Nesse caso, o raio da circunferência mede, aproximadamente, . Portanto, a alternativa correta é a b.
O que eu estudei?
1. a) O vértice do ângulo é O.
b) Os seus lados são as semirretas nomeadas por e .
c) A resposta depende da medida do ângulo desenhado pelo estudante. Caso seja uma medida entre e , o ângulo será agudo, se for será reto e se for maior do que e menor do que será obtuso.
2. As alternativas b, c e e são verdadeiras.
3. a) Sabemos que , assim:
Logo, o ângulo mede e o ângulo complementar de mede , pois .
b) Como , temos:
Assim, e .
c) Sabemos que , além disso .
Substituindo na primeira equação, temos:
A medida do ângulo suplementar de é , isto é, .
4. Como , o ângulo mede , pois .
5. a) Os ângulos com as mesmas medidas são e , e .
b) Sabemos que . Além disso, e, assim, .
6. A. Como a soma das medidas dos ângulos internos de um triângulo é , o ângulo destacado mede , pois .
B. Como a soma das medidas dos ângulos internos do hexágono é , a medida do ângulo indicado é .
C. Como a soma das medidas dos ângulos internos de um quadrilátero é , temos .
7. a) Como o eneágono pode ser decomposto em 7 triângulos, a soma das medidas dos ângulos internos do eneágono é dada por .
b) Como o eneágono é regular, cada ângulo interno mede .
c) Resposta pessoal. Sugestão de resposta:
No item a, decompus o eneágono em 7 triângulos não sobrepostos e multipliquei essa quantidade por . No item b, dividi a medida obtida no item a por 9, pois o eneágono é regular.
8. , isto é, a soma das medidas dos ângulos internos de dois triângulos é .
9. Como a soma das medidas dos ângulos externos de um polígono convexo é , de acordo com a quantidade de lados de cada polígono, temos:
A. ;
B. ;
C. ;
D. .
10. a) representa o raio.
b) representa a corda.
c) representa o diâmetro.
Unidade 8
Grandezas e medidas
Questão 1. Sugestões de resposta: Para medir a duração de intervalo de tempo de uma viagem, a medida de área de um terreno ou a medida do comprimento de um tecido.
Questão 2. Sugestão de resposta: Área; Volume; Tempo.
Questão 3. O comprimento da linha mede .
Questão 4. Resposta pessoal. Espera-se que os estudantes concluam que a massa do Protótipo Internacional do Quilograma, definição anterior dessa unidade de medida, sofria variações.
Atividades
1. A. Temperatura (mostrador digital de um forno).
B . Velocidade (radar eletrônico).
C . Capacidade (copo de medidas para receitas).
D . Massa (balança eletrônica).
E . Tempo (cronômetro digital).
F . Comprimento (fita métrica de costureira).
2. a) Contínua, pois a medida de um intervalo de tempo admite números não inteiros.
Página XCI
b) Discreta, pois a quantidade de pessoas é um número inteiro.
c) Discreta, pois a quantidade de animais é um número inteiro.
d) Contínua, pois o valor de um salário admite números não inteiros.
e) Contínua, pois a medida do volume de um suco admite números não inteiros.
f) Contínua, pois a quantidade de massa admite números não inteiros.
g) Contínua, pois a medida da capacidade de um copo admite números não inteiros.
h) Contínua, pois a medida de um comprimento admite números não inteiros.
i) Discreta, pois a quantidade de computadores é um número inteiro.
3. Sugestão de respostas:
a) Cronômetro.
b) Recipiente de .
c) Termômetro.
d) Balança de dois pratos.
e) Trena.
4. A melancia, pois seu prato está mais baixo.
5. Lucas tem o palmo com a maior medida de comprimento, pois ele utilizou uma quantidade menor de palmos para medir o comprimento da lousa.
6. Preenchendo o quadro, temos:
|
Grandeza |
Medida |
Unidade de medida |
|---|---|---|
|
Altura |
1,7 |
|
|
Massa |
350 |
|
|
Tempo médio de vida |
25 |
anos |
|
Velocidade média de corrida |
60 |
7. a) Como , então correspondem a , pois .
b) Como , então correspondem a , pois .
c) Como , então correspondem a , pois .
d) Como , então correspondem a , pois .
e) Como , então correspondem a , pois .
f) Como , então correspondem a , pois .
Questão 5. Como , temos que , pois .
Atividades
8. A figura A é formada por 5 quadradinhos completos. Logo, sua área mede 5 quadradinhos.
A figura B é formada por 4 quadradinhos completos e mais 2 partes de dois quadradinhos que, juntos, formam 1 quadradinho. Portanto, sua área mede 5 quadradinhos.
A figura C é formada por 2 quadradinhos completos, mais metade de 1 quadradinho e mais 2 partes de dois quadradinhos que, juntos, formam 1 quadradinho. Portanto, sua área mede 3,5 quadradinhos.
A figura D é formada por 2 quadradinhos completos e mais 4 partes de quatro quadradinhos que, juntos, formam 2 quadradinhos. Portanto, sua área mede 4 quadradinhos.
9. a) Considerando os triângulos que formam a malha como unidade de medida, verificamos as seguintes informações.
Como a figura A é formada por 14 triângulos, sua área mede 14 triângulos.
Como a figura B é formada por 14 triângulos, sua área mede 14 triângulos.
Como a figura C é formada por 13,5 triângulos, sua área mede 13,5 triângulos.
Como a figura D é formada por 22 triângulos, sua área mede 22 triângulos.
b) A figura com a menor medida de área é a C e a figura com a maior medida de área é a D.
c) As figuras com a mesma medida de área são A e B.
10. Em cabem , pois .
11. Como , temos que , ou seja, a área do sítio mede .
12. Hectômetro quadrado, pois .
13. a) (metro quadrado).
b) (quilômetro quadrado).
c) (centímetro quadrado).
d) (milímetro quadrado).
e) (decâmetro quadrado).
f) (metro quadrado).
14. Resposta pessoal. Sugestão de resposta: 18 quadradinhos de medida de área.
15. A. , ou seja, .
B. , ou seja, .
C. , ou seja, .
Página XCII
16. A quantidade necessária de metros quadrados de azulejos para cobrir o piso da piscina é dada por , ou seja, .
17. Resposta no final da seção Resoluções.
18. A. Decompondo a figura A, verificamos que a medida da sua área é dada por , ou seja, .
B. Decompondo a figura B, verificamos que a medida da sua área é dada por:
, ou seja, .
C. Decompondo a figura C, verificamos que a medida da sua área é dada por:
, ou seja, .
D. Decompondo a figura D, verificamos que a medida da sua área é dada por:
, ou seja, .
19. A medida de área da região 2 é dada por , ou seja, .
A medida de área da região 1 é dada pela diferença entre a medida de área total e a medida da área da região 2, ou seja, . Portanto, a área da região 1 mede .
20. Decompondo a figura, verificamos que a medida de área é dada por:
Portanto, a área da figura presente em cada lajota mede .
21. Um retângulo cujas dimensões medem e tem medida de área igual a , ou seja, . Um quadrado cujo comprimento do lado mede , tem medida de área igual a , ou seja, . Portanto, o quadrado tem a maior medida de área.
22. Para determinar a medida do comprimento da base do paralelogramo, precisamos dividir a medida da sua área pela medida da sua altura. Assim, a medida do comprimento da base é dada por , ou seja, .
23. A medida da área da figura é igual à soma das medidas das áreas do paralelogramo e do triângulo . O paralelogramo tem a mesma medida de área que o retângulo , pois as medidas do comprimento da base e da altura do paralelogramo são iguais às medidas do comprimento e da largura do retângulo. Sendo assim, a área do paralelogramo mede . Como o triângulo tem medida de área igual à metade da medida de área do retângulo , calculamos , obtendo a medida de para sua área. Assim, a área da figura é dada por , ou seja, mede .
24. A medida da área do paralelogramo A é , pois .
A medida da área do paralelogramo B é , pois .
A medida da área do paralelogramo C é , pois .
A medida da área do paralelogramo D é , pois .
25. As medidas das áreas são iguais. Indicando por e a medida da área do paralelogramo e do retângulo, respectivamente, e por h a medida da altura dessas figuras, temos:
Como , segue que .
26. A área do terreno A mede , pois .
A área do terreno B mede , pois .
Logo, eles devem escolher o terreno B, pois atende à condição estipulada, ou seja, a medida da área é maior do que .
27. Resposta pessoal. Sugestão de resposta:
Um paralelogramo tem medida da altura igual à metade da medida do comprimento da base. Determine a medida da área desse paralelogramo, sabendo que a altura mede . Resposta: .
28. A medida da área do triângulo:
A é dada por , ou seja, mede .
B é dada por , ou seja, mede .
C é dada por , ou seja, mede .
D é dada por , ou seja, mede .
E é dada por , ou seja, mede .
29. Resposta pessoal. Sugestão de resposta:
Determine a medida da área da figura a seguir.
Resposta: .
30. Não. Espera-se que os estudantes percebam a possibilidade de decompor a seta em retângulos, paralelogramos e triângulos, porém as medidas apresentadas não são suficientes para determinar, por exemplo, a medida do comprimento da base e a da altura dos paralelogramos que compõem a "ponta" da seta.
31. O trapézio A mede , pois .
O trapézio B mede , pois .
O trapézio C mede , pois .
Página XCIII
a) O trapézio C tem a maior medida de área.
b) Os trapézios A e B têm medidas de área iguais.
32. Resposta pessoal. Sugestão de resposta:
Determine a medida da área do trapézio da figura a seguir.
Resposta: .
33. Calculando , verificamos que, antes de 2010, a área do garrafão media . Depois de 2010, a área do garrafão passou a ter formato de retângulo. Assim, para determinar a atual medida de área, calculamos . Sendo assim, a medida de área do garrafão passou a ser igual a . Efetuando a subtração , concluímos que houve um aumento de . Portanto, a alternativa correta é a a.
Questão 6. A. 12 cubos; B. 15 cubos; C. 21 cubos.
Questão 7. A medida do volume da pilha é 17 cubos.
Questão 8.
a) Como , a quantidade de cubos é igual a , ou seja, cubos.
b) Como , a quantidade de cubos é igual a , ou seja, cubos.
Atividades
34. Contando a quantidade de cubos por camada e de baixo para cima, temos:
A. , ou seja, a pilha tem 14 cubos de medida de volume.
B. , ou seja, a pilha tem 16 cubos de medida de volume.
C. , ou seja, a pilha tem 55 cubos de medida de volume.
D. , ou seja, a pilha tem 18 cubos de medida de volume.
35.
A. A figura é formada por 14 ![]() . Portanto, seu volume mede .
. Portanto, seu volume mede .
B. A figura é formada por 6 ![]() e
5
e
5 ![]() . Portanto, seu volume mede .
. Portanto, seu volume mede .
C. A figura é formada por 20 ![]() . Portanto, seu volume mede .
. Portanto, seu volume mede .
D. A figura é formada por 48 ![]() .
. Portanto, seu volume mede .
.
. Portanto, seu volume mede .
36. a) A quantidade de pequenos cubos organizados por Bia é dada por , ou seja, 60 cubos.
b) Como , o novo empilhamento é formado por 15 camadas.
c) Sim, pois a quantidade de pequenos cubos utilizada é a mesma em ambos os empilhamentos.
d) Resposta pessoal. Sugestão de resposta:
Bia reorganizou os cubos. Porém, dessa vez, ela os empilhou em camadas contendo 10 pequenos cubos. Quantas camadas há nesse novo empilhamento?
Resposta: 6 camadas.
Questão 9. O volume desse paralelepípedo mede , ou seja, .
Atividades
37. Figura A: . Portanto, seu volume mede .
Figura B: . Portanto, seu volume mede .
Figura C: . Portanto, seu volume mede .
Figura D: . Portanto, seu volume mede .
Figura E: . Portanto, seu volume mede .
Figura F: . Portanto, seu volume mede .
38. O volume dessa embalagem mede , pois .
39. Figura A: . Portanto, seu volume mede .
Figura B: . Portanto, seu volume mede .
Figura C: . Portanto, seu volume mede .
Figura D: . Portanto, seu volume mede .
40. A medida do volume desse recipiente é dada por , ou seja, o volume desse recipiente mede .
41. A medida do volume dessa piscina é dada por , ou seja, o volume dessa piscina mede .
Como , serão necessários , ou seja, .
Página XCIV
42. A medida do volume do cubo desenhado por Antônio corresponde a , ou seja, . Como a aresta do cubo desenhado por Jairo mede , ou seja, , o volume do cubo mede , pois . Calculando , verificamos que a medida do volume do cubo desenhado por Jairo é 8 vezes maior do que a medida do volume do cubo desenhado por Antônio.
43. Ao multiplicar as medidas das três dimensões de um tijolo maciço com formato de paralelepípedo reto retângulo, obtém-se a medida do volume desse tijolo. Portanto, a alternativa correta é a d.
44. A medida do volume do paralelepípedo A é dada por , ou seja, . A medida do volume do paralelepípedo B é dada por , ou seja, . A medida do volume do paralelepípedo C é dada por , ou seja, . A medida do volume do paralelepípedo D é dada por , ou seja, .
a) O paralelepípedo D tem a maior medida de volume.
O paralelepípedo A tem a menor medida de volume.
b) Os paralelepípedos B e C têm a mesma medida de volume.
45. O volume do objeto cúbico mede , pois . Analisando a medida do volume das outras caixas, verificamos que uma das dimensões da caixa 2 mede , ela não pode ser usada para embalar o objeto. Então, de imediato, descartamos essa possibilidade.
Quanto às demais caixas possíveis, calculamos o volume e comparamos com o volume do objeto.
Caixa 1: , ou seja, .
Caixa 3: , ou seja, .
Caixa 4: , ou seja, .
Caixa 5: , ou seja, .
Nesse caso, a medida do volume da caixa 3 é a que mais se aproxima da medida do volume do objeto. Portanto, a alternativa correta é a c.
46. O volume do paralelepípedo reto retângulo mede , pois . Já o volume do cubo mede , pois . Em decímetro cúbico, essa medida corresponde a . Portanto, o paralelepípedo tem a maior medida de volume.
47. Resposta pessoal. Sugestão de resposta:
João ganhou de presente um aquário com o formato de um paralelepípedo reto retângulo como o apresentado na imagem. Qual é a medida do volume desse aquário? Resposta: A medida do volume desse aquário é igual a , ou seja, .
O que eu estudei?
1. a) Capacidade.
b) Tempo.
c) Comprimento.
d) Massa.
e) Comprimento.
f) Massa.
g) Comprimento.
2. a) Como , calculamos . Convertendo em decímetro quadrado, obtemos .
b) Como , calculamos . Convertendo em metro quadrado, obtemos .
c) Como , calculamos . Convertendo em hectômetro quadrado, obtemos .
d) Como , calculamos . Convertendo em metro quadrado, obtemos .
e) Como , calculamos . Convertendo em metro quadrado, obtemos .
f) Como , calculamos . Convertendo em milímetro quadrado, obtemos .
3. a) Como , a medida da temperatura aumentou durante esse intervalo de tempo.
b) A unidade de medida de temperatura no SI é o kelvin (K). Ela não foi utilizada nessa atividade.
4. A figura A é formada por 20 quadradinhos completos. Portanto, a área da figura A mede 20 quadradinhos.
A figura B é formada por 10 quadradinhos completos, 2 metades de um quadradinho e mais 4 pedaços que, juntos, formam 2 quadradinhos. Portanto, a área da figura B mede 13 quadradinhos.
A figura C é formada por 6 quadradinhos completos e mais 4 pedaços que, juntos, formam 2 quadradinhos. Portanto, a área da figura C mede 8 quadradinhos.
5. Como o comprimento do lado do quadradinho mede , a medida da área de cada quadradinho é . A figura desta atividade é formada por 15 quadradinhos completos mais 6 metades de quadradinho, ou seja, 3 quadradinhos. Portanto, a área dessa figura mede .
6. Como a figura A é um retângulo, a medida de sua área é dada por , ou seja, . A medida da área da figura B é igual a , ou seja, . Como a figura C é um paralelogramo, sua área mede , pois .
7. Analisando o molde, verificamos que ele é formado por 3 retângulos de dimensões e e 2 triângulos com medida do comprimento da base e medida de altura . Portanto, para confeccionar o molde, serão utilizados , ou seja, .
8. Como o terreno tem o formato de um trapézio com bases de medidas e e sua altura mede , a medida de sua área é dada por , ou seja, a área desse terreno mede .
Página XCV
9. Nesse empilhamento, Pedro já colocou 10 cubos, de modo que há 4 cubos em cada uma das dimensões. Assim, o menor formato cúbico que ele poderá obter será formado por uma pilha de 4 cubos de medida de aresta. Como , o empilhamento terá 64 cubos de medida de volume. Calculando , concluímos que ele precisa, no mínimo, de 54 cubos.
10. Como a aresta do cubo mede , a medida do volume será igual a , ou seja, .
11. A medida do volume do reservatório será , pois .
Unidade 9
Proporção
Questão 1. Sugestão de respostas:
A quantidade de pães comprados em uma padaria e o valor, em reais, a ser pago; a quantidade de calças produzidas em uma fábrica e a quantidade de funcionários para confeccioná-las.
Questão 2. Sugestão de respostas:
A medida da velocidade média de um automóvel e a medida do tempo para chegar ao destino desejado; a quantidade de costureiros para confeccionar determinada quantidade de roupas e a medida do tempo necessária para concluir a encomenda.
Atividades
1. a) • Como cada salgado custa R$ 4,30 e , o preço de 15 salgados será R$ 64,50.
Como cada salgado custa R$ 4,30 e , o preço de 28 salgados será R$ 120,40.
b) Sim. Sugestão de resposta:
Duplicando a quantidade de salgados, o preço também duplicará; triplicando a quantidade de salgados, o preço também triplicará; reduzindo a quantidade de salgados à metade, o preço também será reduzido à metade; e assim por diante.
2. A quantidade de calças produzidas por essa máquina e o tempo gasto na produção são grandezas diretamente proporcionais. Calculando , verificamos que, para produzir 1.500 calças, essa máquina gastará 6 vezes o tempo que leva para produzir 250 calças. Como essa máquina produz 250 calças por hora e , concluímos que a máquina produzirá 1.500 calças em 6 horas.
3. a) Não, pois essas grandezas não são proporcionais.
b) Não. Se as grandezas idade e medida de massa corporal fossem diretamente proporcionais, como a medida da massa corporal de Isabel era aos 2 anos de idade e , então a medida da massa corporal de Isabel deveria ser aos 10 anos, pois . Mas, em vez disso, Isabel tinha de medida da massa corporal aos 10 anos.
As grandezas idade e medida de massa corporal também não são inversamente proporcionais, pois a medida da massa de Isabel aumentou no decorrer dos anos, e não diminuiu.
4. A quantidade de colheitadeiras, mantendo o ritmo de trabalho, e o tempo gasto na colheita são grandezas inversamente proporcionais. Como e 3 colheitadeiras realizam a colheita em 8 dias, Juliano precisaria de 6 colheitadeiras para fazer a colheita em 4 dias, pois .
5. a) Havendo 350 candidatos inscritos no curso de Matemática e 50 vagas, a razão entre o número de candidatos e a quantidade de vagas será representada pela fração irredutível correspondente a . Dividindo o numerador e o denominador por 50, obtemos a fração , que está na forma irredutível. Logo, a razão entre o número de candidatos que fizeram a inscrição no curso de Matemática e a quantidade de vagas é ou ou, ainda, 7 está para 1.
b) Na turma de Cristina, a cada 10 estudantes, 5 são meninas. Assim, a razão entre a quantidade de meninas e a quantidade de estudantes nessa turma será representada pela fração irredutível correspondente a . Dividindo o numerador e o denominador por 5, obtemos a fração , que está na forma irredutível. Logo, a razão entre a quantidade de meninas e a quantidade de estudantes na turma de Cristina é ou ou, ainda, 1 está para 2.
c) A cada 10 pães vendidos, 8 são pães de leite. Assim, a razão entre a quantidade de pães de leite e a quantidade de pães vendidos será representada pela fração irredutível correspondente a . Dividindo o numerador e o denominador por 2, obtemos a fração , que está na forma irredutível. Logo, a razão entre a quantidade de pães de leite e a quantidade de pães vendidos é ou ou, ainda, 4 está para 5.
6. A quantidade de dias nos quais a torneira está pingando e a quantidade de água desperdiçada são grandezas diretamente proporcionais. Como em 1 dia são desperdiçados de água, em 30 dias serão desperdiçados de água, pois .
Questão 3. De acordo com a situação apresentada na página, as idades dos filhos somam 59 anos, o total da herança é R$ 64.900,00 e o filho mais novo tem 24 anos. Denominando x a herança do filho mais novo e organizando as informações, temos:
Filho mais novo
Idade (em anos)
59
24
Herança (em R$)
64.900
x
Assim, efetuando os cálculos, temos:
Portanto, o filho mais novo recebeu R$ 26.400,00 de herança.
Página XCVI
Atividades
7. a) Os números da coluna A serão diretamente proporcionais aos números da coluna B se . Fazendo os cálculos para determinar x, temos:
Portanto, .
b) Os números da coluna A serão diretamente proporcionais aos números da coluna B se . Fazendo os cálculos para determinar x, temos:
Portanto, .
8. Efetuando os cálculos, temos:
a)
Logo, .
b)
Logo, .
c)
Logo, .
d)
Logo, .
e)
Logo, .
f)
Logo, .
g)
Logo, .
h)
Logo, .
9. As quantidades de tinta branca e de tinta azul misturadas para obter uma mesma tonalidade são grandezas diretamente proporcionais. Com as informações organizadas, vamos efetuar os cálculos.
Portanto, ele deve misturar de tinta azul com de tinta branca para obter a mesma tonalidade da primeira mistura.
10. A quantidade de latas de leite condensado e a quantidade de docinhos que se pode fazer são grandezas diretamente proporcionais. Com as informações organizadas, vamos efetuar os cálculos.
Portanto, vai precisar de 15 latas de leite condensado para preparar 650 docinhos.
11. A quantidade de água que uma bomba puxa e a quantidade de tempo que ela leva pra fazer isso são grandezas diretamente proporcionais. Vamos denominar x a quantidade de litros de água que a bomba puxa em . Sabendo que e organizando as informações, temos:
Quantidade de água (em )
30
x
Tempo (em )
15
60
Página XCVII
Agora, efetuando os cálculos, temos:
Portanto, a bomba puxa de água em .
12. A quantidade de queijo e o seu preço são grandezas diretamente proporcionais. Vamos denominar x a quantidade de gramas de queijo que Fábio poderá comprar com R$ 26,00. Organizando as informações, temos:
Quantidade de queijo (em )
300
x
Preço (em R$)
6,5
26
Agora, efetuando os cálculos, temos:
Portanto, Fábio poderá comprar com R$ 26,00.
13. As idades dos amigos adicionadas é igual a 22, pois , o que corresponde ao número total de figurinhas, que é igual a 121. Como as figurinhas foram divididas em partes diretamente proporcionais a suas idades e queremos calcular quantas figurinhas o amigo mais novo recebeu, vamos denominar a quantidade de figurinhas que o amigo mais novo vai receber e organizar as informações. Assim,
Idade (em anos)
22
10
Quantidade de figurinhas
121
x
Agora, efetuando os cálculos, temos:
Portanto, o amigo mais novo vai receber 55 figurinhas.
14. A quantidade de café cru em grãos e a quantidade de café torrado obtida dos grãos crus são grandezas diretamente proporcionais. Vamos denominar x a quantidade de café cru em grãos necessária para obter de café torrado. Organizando as informações, temos:
Quantidade de café cru em grãos (em )
30
x
Quantidade de café torrado (em )
26
208
Agora, efetuando os cálculos, temos:
Portanto, para obter de café torrado são necessários de café cru em grãos.
15. O total investido por Carla, Sílvia e Gustavo na compra da empresa foi R$ 60.000,00, pois . Esse total investido corresponde ao lucro de R$ 12.000,00. Vamos organizar as informações e efetuar os cálculos para determinar qual parte do lucro coube a cada sócio.
Carla: Denomine x a parte do lucro que Carla recebeu. Assim, temos:
Quantidade investida (em R$)
60.000
10.000
Parte do lucro (em R$)
12.000
x
Agora, efetuando os cálculos, temos:
Portanto, Carla recebeu R$ 2.000,00 como parte do lucro da empresa.
Sílvia: Denomine y a parte do lucro que Sílvia recebeu. Assim, temos:
Quantidade investida (em R$)
60.000
20.000
Parte do lucro (em R$)
12.000
y
Agora, efetuando os cálculos, temos:
Portanto, Sílvia recebeu R$ 4.000,00 como parte do lucro da empresa.
Página XCVIII
Gustavo: Denomine z a parte do lucro que Gustavo recebeu. Assim, temos:
Quantidade investida (em R$)
60.000
30.000
Parte do lucro (em R$)
12.000
z
Agora, efetuando os cálculos, temos:
Portanto, Gustavo recebeu R$ 6.000,00 como parte do lucro da empresa.
16. Resposta pessoal. Sugestão de resposta:
Em uma fábrica, uma máquina produz 10.000 peças em . Quantas peças essa máquina vai produzir em ? Resposta: 25.000 peças.
17. a) Os números da coluna A serão inversamente proporcionais aos números da coluna B se . Desse modo, efetuando os cálculos, temos:
Portanto, .
b) Os números da coluna A serão inversamente proporcionais aos números da coluna B se . Desse modo, efetuando os cálculos, temos:
Portanto, .
18. a) A quantidade de páginas que Regina lê por dia e a quantidade de dias que ela gasta para ler o livro são grandezas inversamente proporcionais. Assim, com as informações organizadas, calculamos:
Portanto, para ler o livro em 16 dias, Regina deveria ler 21 páginas por dia.
b) Como Regina conseguiu ler o livro todo em 28 dias lendo 12 páginas por dia, o livro tem 336 páginas, pois . Outro modo de calcular quantas páginas o livro tem é usando as informações obtidas no item a. Para ter lido o livro em 16 dias, Regina deveria ler 21 páginas por dia; como , verificamos que o livro tem 336 páginas.
19. Mantendo a mesma quantidade de ração, as grandezas quantidade de cabeças de gado e a quantidade de dias que essas cabeças de gados podem ser alimentadas são inversamente proporcionais. Com as informações organizadas, calculamos:
Portanto, essa quantidade de ração será suficiente para alimentar 70 cabeças de gado por 4 dias.
20. O tempo gasto para percorrer a medida de distância entre duas cidades e a medida de velocidade média são grandezas inversamente proporcionais. Chamando x a medida de velocidade média para percorrer a distância entre duas cidades em 5 horas e organizando as informações, temos:
Tempo (em )
6
5
Velocidade média (em )
75
x
Efetuando os cálculos, obtemos:
Portanto, ele deveria manter uma medida de velocidade média de .
21. A capacidade do caminhão e o número de viagens que ele faz para retirar o entulho são grandezas inversamente proporcionais. Chamando x a quantidade de viagens que um caminhão de faria e organizando as informações, temos:
Capacidade do caminhão (em )
500
600
Quantidade de viagens
24
x
Efetuando os cálculos, obtemos:
Portanto, seriam necessárias 20 viagens.
Página XCIX
22. Dada uma quantidade de água em um acampamento, a quantidade de pessoas no acampamento e a quantidade de dias para os quais a quantidade de água é suficiente são grandezas inversamente proporcionais. Com mais 18 pessoas, o acampamento ficaria com 63 pessoas, pois . Considerando x a quantidade de dias nos quais a quantidade de água do acampamento seria suficiente para 63 pessoas e organizando as informações, temos:
Quantidade de pessoas
45
63
Quantidade de dias
7
x
Efetuando os cálculos, obtemos:
Portanto, essa quantidade de água seria suficiente para 5 dias.
23. Resposta pessoal. Sugestão de resposta:
Para fabricar certa quantidade de peças, uma empresa, utilizando 4 máquinas, demora 25 dias. Se mais 6 máquinas fossem adicionadas na fabricação dessas peças, elas seriam fabricadas em quantos dias? Resposta: 10 dias.
O que eu estudei?
1. Como o litro da gasolina custa R$ 7,26, para abastecer seu carro com de gasolina, Débora gastou R$ 283,14, pois . Sabendo que o litro do etanol custa R$ 5,14, vamos dividir 283,14 por 5,14 para calcular a quantidade aproximada de litros de etanol que Débora precisa para abastecer seu carro com o mesmo valor gasto de um abastecimento com gasolina. Como , verificamos que Débora abasteceria seu carro com, aproximadamente de etanol.
2. Para determinar a medida da área total aproximada de cada estado da Região Sul do Brasil, vamos dividir o número de habitantes pela densidade demográfica de cada região. Assim, temos:
Paraná:
Logo, o estado do Paraná possui aproximadamente de área total.
Santa Catarina:
Logo, o estado de Santa Catarina possui aproximadamente de área total.
Rio Grande do Sul:
Logo, o estado do Rio Grande do Sul tem aproximadamente de área total da Região Sul do Brasil.
3. a) Para que os números da coluna A sejam diretamente proporcionais aos números da coluna B, devemos ter . Fazendo os cálculos pra determinar o valor de x, temos:
Portanto, .
b) Para que os números da coluna A sejam inversamente proporcionais aos números da coluna B, devemos ter . Fazendo os cálculos pra determinar o valor de x, temos:
Portanto, .
4. O tempo gasto por Bruna nesse percurso e a velocidade média a que ela andou são grandezas inversamente proporcionais. Considerando x a velocidade média a que Bruna deveria ter andado para fazer o percurso em e organizando as informações, temos:
Tempo (em )
3
2
Velocidade média (em )
12
x
Efetuando os cálculos, obtemos:
Portanto, Bruna deveria ter andado a de velocidade média.
5. A quantidade de reais e a quantidade de dólares que pode ser comprada com essa quantidade de reais são grandezas diretamente proporcionais.
Página C
a) Considerando x a quantidade de reais que Guilherme vai gastar para comprar 2.500 dólares e organizando as informações, temos:
Dólares
1.800
2.500
Reais
9.072
x
Efetuando os cálculos, obtemos:
Portanto, Guilherme vai gastar R$ 12.600,00.
b) Seja x a quantidade de dólares que Guilherme compraria com R$ 14.112,00. Organizando as informações, temos:
Dólares
1.800
x
Reais
9.072
14.112
Efetuando os cálculos, obtemos:
Portanto, Guilherme compraria 2.800 dólares com essa quantia.
6. A quantidade de camisetas e a quantidade da peça de tecido usada para fazer essas camisetas são grandezas diretamente proporcionais. Como Jaqueline já fez 25 camisetas de tamanho M, sobrou da peça de tecido uma parte correspondente a 10 camisetas de tamanho M. Sabemos que 28 camisas de tamanho P correspondem a 35 de tamanho M. Considerando x a quantidade de camisetas de tamanho P que Jaqueline vai conseguir fazer com o restante do tecido, vamos calcular quantas camisetas P Jaqueline vai fazer com a quantidade de tecido que corresponde a 10 camisetas M.
Quantidade de camisetas de tamanho P longa
28
x
Quantidade de camisetas de tamanho M baby look
35
10
Efetuando os cálculos, obtemos:
Portanto, é possível fazer 8 camisetas de tamanho P longa com o que sobrou da peça de tecido.
Unidade 10
Porcentagem
Questão 1. Resposta pessoal. Espera-se que os estudantes respondam que a porcentagem surgiu em Roma, quando o imperador decretou um imposto sobre as mercadorias vendidas no mercado público, no qual dividiam-se o valor das mercadorias em 100 partes e retiravam-se uma para o imposto. Usavam as letras pc para indicar a porcentagem, por exemplo .
Questão 2. Para determinar a quantidade de votos que Paulo Fernandes recebeu, precisamos calcular 25% de 5.000. Nesta situação, 5.000 representa o total de eleitores que votaram, ou seja, corresponde a 100%. Logo, o cálculo de pode ser feito da seguinte maneira:
Portanto, Paulo Fernandes obteve 1.250 votos.
Questão 3. Para saber o preço do tablet à vista, inicialmente calculamos 30% de R$ 1.500,00 para obter o valor do desconto.
Desse modo, 30% de R$ 1.500,00 correspondem a R$ 450,00. Calculando o preço à vista, obtemos:
Portanto, o tablet custa R$ 1.050,00 à vista.
Para determinar o preço da máquina de lavar louças à vista, sabemos que, após o desconto, o valor passa a ser 70% do preço, ou seja, . Neste caso, podemos calcular 70% de 1.600.
Portanto, a máquina de lavar louças custa R$ 1.120,00 à vista.
Questão 4. Para determinar o novo salário de Edgar, calculamos o valor do acréscimo, que corresponde a 10,5% de R$ 1.890,00. Assim, temos:
, ou seja, houve um acréscimo de R$ 198,45.
Adicionando esse valor à quantia recebida em fevereiro, obtemos:
, ou seja, R$ 2.088,45
Logo, Edgar passou a receber R$ 2.088,45 de salário.
Atividades
1. A. Fração decimal: ; número decimal: 0,34;
porcentagem: 34%.
B. Fração decimal: ; número decimal: 0,58;
porcentagem: 58%.
2. Efetuando os cálculos em cada um dos itens, verificamos que:
a) 10% de correspondem a , pois .
b) 25% de correspondem a , pois .
c) 40% de correspondem a , pois .
Página CI
d) 60% de correspondem a , pois .
e) 75% de correspondem a , pois .
f) 90% de correspondem a , pois .
3. a) Considerando que e sabendo que , montamos e resolvemos a seguinte regra de três:
Número decimal
0,25
1
Porcentagem
x
100
Assim, . Portanto, .
b) De modo semelhante ao item anterior, considerando que , obtemos:
Número decimal
0,4
1
Porcentagem
x
100
Assim, . Portanto, .
c) Considerando que obtemos:
Número decimal
0,2
1
Porcentagem
x
100
Assim, . Portanto, .
d) Considerando que , obtemos:
Número decimal
0,5
1
Porcentagem
x
100
Assim, . Portanto, .
e) Considerando que , obtemos:
Número decimal
0,6
1
Porcentagem
x
100
Assim, . Portanto, .
4. a) Para saber quantos reais custa o smartphone à vista em cada loja, efetuamos os cálculos das referidas porcentagens e verificamos que:
na loja A,de R$ 960,00 correspondem a R$ 864,00, pois .
na loja B,de R$ 980,00 correspondem a R$ 833,00, pois .
Sendo assim, à vista, o smartphone custa R$ 864,00 na loja A e R$ 833,00 na loja B.
Portanto, o preço é menor na loja B.
b) Resposta pessoal. A resposta depende da análise crítica dos estudantes, de acordo com as expectativas deles.
c) Resposta pessoal. Espera-se que os estudantes concluam que o pagamento à vista pode gerar desconto e facilitar a organização financeira, evitando endividamento e o compromisso de pagamentos futuros. Por outro lado, o pagamento a prazo dá ao consumidor a oportunidade de comprar o produto sem necessariamente ter a quantia total e pode ser vantajoso para pessoas que se organizam melhor financeiramente.
d) Resposta pessoal. Espera-se que os estudantes estejam posicionados criticamente com relação às suas decisões e mudanças de opinião, quaisquer que sejam elas.
5. a) A 1ª opção oferece 20% de desconto, ou seja, do valor total de um caderno. Assim, o valor a ser pago na 1ª opção é dado por:
Portanto, o valor a ser pago é R$ 50,40.
Na 2ª opção, calculamos inicialmente o preço total de três cadernos e, em seguida, calculamos o desconto de 10% sobre este valor.
Portanto, o valor a ser pago é R$ 48,60.
Comparando as duas opções, verificamos que a 2ª opção oferece o menor preço na compra dos três cadernos.
b) Calculando a diferença entre os preços, obtemos:
, ou seja, R$ 1,80.
c) Resposta pessoal. Espera-se que os estudantes considerem importante analisar as opções antes de realizarem o pagamento.
Página CII
6. a) Calculando o valor da entrada a ser pago em cada moto, temos:
Moto A: 70% de R$ 13.430,00:
, ou seja, R$ 9.401,00.
Moto B: 50% de R$ 13.710,00:
, ou seja, R$ 6.855,00.
Portanto, o valor em reais da entrada da moto A é R$ 9.401,00 e da moto B é R$ 6.855,00.
b) Para calcular o valor de cada uma das prestações, inicialmente calculamos a quantia a ser paga após o pagamento da entrada para, em seguida, determinar o valor das prestações.
Moto A:
Assim, após a entrada restarão R$ 4.029,00 a serem pagos. Dividindo esse valor em 12 prestações, obteremos o valor de cada prestação da moto A.
, ou seja, R$ 335,75.
Moto B:
Assim, após a entrada restarão R$ 6.855,00 a serem pagos. Dividindo esse valor em 12 prestações, obteremos o valor de cada prestação da moto B.
, ou seja, R$ 342,75.
Comparando o valor das prestações nos dois casos, verificamos que Fernando vai pagar prestações de menor valor na moto A.
7. a) O total de estudantes da escola corresponde a 100%, dos quais 45% estudam no período da manhã e 15% no período da noite. Portanto, a quantidade de estudantes no período da tarde corresponde a.
b) A quantidade de estudantes no período da:
manhã corresponde a 45% de um total de 3.160 estudantes. , ou seja, 1.422 estudantes.
tarde corresponde a 40% de um total de 3.160 estudantes. , ou seja, 1.264 estudantes.
noite corresponde a 15% de um total de 3.160 estudantes. , ou seja, 474 estudantes.
8. Indicando por x a quantidade total de pessoas na festa, M a quantidade de mulheres e H a quantidade de homens, temos . Como havia 3 mulheres, escrevemos e, com isso, obtemos a seguinte igualdade que representa a quantidade de convidados homens na festa:
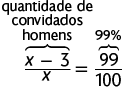
Para determinar o valor de x, resolvemos essa igualdade.
Logo, até o momento, havia 300 pessoas na festa, das quais 297 eram homens.
Indicando como y a quantidade de homens que devem deixar a festa para que a porcentagem de homens represente 98% do total de pessoas, temos:
Logo, 150 homens devem deixar a festa.
Portanto, a alternativa correta é a d.
9. a) Calculando a metade de R$ 48,00, que equivale a 50%, obtemos:
Como 25% é metade de 50%, calculamos:
Assim, adicionamos os dois descontos, ou seja, , obtendo um desconto total de R$ 36,00.
b) Calculando a metade de R$ 52,00, que equivale a 50%, obtemos:
Como 25% é metade de 50%, calculamos:
Assim, adicionamos os dois descontos, ou seja, , obtendo um desconto total de R$ 39,00.
c) Calculando a metade de R$ 84,00, que equivale a 50%, obtemos:
Como 25% é metade de 50%, efetuamos:
Assim, adicionamos os dois descontos, ou seja, , obtendo um desconto total de R$ 63,00.
d) Calculando a metade de R$ 30,00, que equivale a 50%, obtemos:
Como 25% é metade de 50%, efetuamos:
Assim, adicionamos os dois descontos, ou seja, , obtendo um desconto total de R$ 22,50.
Página CIII
10. Como o preço total à vista corresponde a 100%, o acréscimo de 14% neste valor corresponde a do valor à vista. Com isto, calculamos:
o preço a prazo do fogão: .
Portanto, o preço do fogão na venda a prazo é R$ 454,86.
o preço a prazo do micro-ondas: .
Portanto, o preço do micro-ondas na venda a prazo é R$ 535,80.
11. a) Como Pedro optou pelo pagamento à vista, ele pagou com um desconto de 25%, ou seja,do valor total. Assim:
.
Portanto, o valor pago por Pedro foi R$ 72,00.
b) Resposta pessoal. Espera-se que os estudantes usem corretamente a calculadora e validem os cálculos de modo adequado.
12. Resposta pessoal. Sugestão de problema:
Renato atrasou o pagamento de uma conta no valor de R$ 200,00. Com o atraso, haverá um acréscimo de 2%. Qual será a quantia, em reais, que será acrescida no valor total dessa compra? Resposta: R$ 4,00.
13. a) Inicialmente, calculamos o valor do desconto da batedeira.
, ou seja, de desconto.
Indicando por a porcentagem que corresponde ao desconto, temos:
Logo, a porcentagem de desconto no preço da batedeira é 10%.
b) Calculando o valor do desconto do fogão, temos:
, ou seja, de desconto.
Chamando de a porcentagem que corresponde ao desconto, obtemos:
Portanto, a porcentagem de desconto no preço do fogão é 20%.
14. Calculando inicialmente a quantidade de reprovados, temos:
.
Assim, foram reprovados candidatos.
Indicando como a porcentagem que corresponde à quantidade de reprovados, temos:
Logo, a porcentagem de reprovados é 91%.
15. a) Chamando de x a porcentagem que corresponde à comissão de Jáder, obtemos:
Portanto, a comissão em relação ao valor que Jáder vendeu é 2%.
b) Para determinar quantos reais Jáder recebeu ao todo em maio, vamos juntar seu salário fixo com a comissão que ele recebeu.
Portanto, Jáder recebeu, ao todo, em maio, R$ 1.780,76.
16. Resposta pessoal. Para responder a essa pergunta, os estudantes devem realizar a seguinte operação: Considerando x o valor que corresponde ado preço total, temos:
, ou seja, R$ 260,00.
Portanto, espera-se que os estudantes digam que não, pois o produto custaria R$ 260,00 com 35% de desconto na loja 2, ou seja, o mesmo preço da loja 1.
17. Como Lucas pagou R$ 33,00 com 20% de desconto, podemos concluir que R$ 33,00 correspondem a 80%.
Vamos denominar x o preço total do minicurso. Neste caso, temos a seguinte proporção:
, ou seja, R$ 41,25.
Logo, o valor do minicurso sem o desconto é R$ 41,25.
Portanto, alternativa correta é a d.
Página CIV
18. a) Indicando por x a porcentagem que 31 milhões corresponde do total de habitantes que residiam na zona rural, temos:
Portanto, a população brasileira que residia na zona rural correspondia a, aproximadamente, 15% da população do país.
b) Se aproximadamente 15% correspondem à quantidade de pessoas que residiam na zona rural, corresponde à porcentagem de habitantes que não residiam na zona rural.
.
Portanto, aproximadamente 174 milhões de habitantes não residiam na zona rural. Eles representam aproximadamente 85% da população brasileira.
19. a) Considerando x a quantidade total de estudantes nessa escola, temos a seguinte proporção:
, ou seja, 1.240 estudantes.
Portanto, nessa escola há, ao todo, 1.240 estudantes.
b) Se a escola tem 1.240 estudantes e 558 são meninos, então a quantidade de meninas é dada pela diferença entre essas quantidades, ou seja, .
Portanto, nessa escola estudam 682 meninas.
20. a) Como há 68 milhões de domicílios no Brasil, considere x a porcentagem correspondente à quantidade de casas com televisor, ou seja, 66,091 milhões. Assim:
Portanto, havia televisores em aproximadamente 97% dos domicílios.
b) O microcomputador é o bem que estava menos presente nos domicílios.
Considere x a porcentagem correspondente à quantidade de domicílios com microcomputador. Assim:
Portanto, havia microcomputador em, aproximadamente, 46% dos domicílios.
c) De acordo com o gráfico, havia máquina de lavar roupas em aproximadamente 41.601.000 domicílios. Considere x a porcentagem correspondente à quantidade de domicílios com máquina de lavar roupas. Temos a seguinte proporção:
Portanto, havia máquina de lavar roupas em, aproximadamente, 61% dos domicílios.
21. Considere x o preço do computador antes do acréscimo, ou seja, correspondente a 100% do preço. Temos:
Portanto, o computador custava R$ 1.600,00 antes do acréscimo.
Questão 5. Calculamos o desconto em reais subtraindo R$ 112,00 de R$ 140,00:
Portanto, o desconto foi R$ 28,00.
Questão 6. Para determinar a porcentagem do desconto, representamos a relação entre o valor do desconto e o preço sem o desconto pela fração . Transformando em um número decimal, temos:
Portanto, a porcentagem de desconto é 20%.
Atividades
22. a) . Portanto, correspondem a 30% de .
b) . Portanto, correspondem a 20% de .
23. a) Sendo R$ 209,85 o acréscimo em relação ao preço total de R$ 1.400,00, calculamos:
.
Portanto, o acréscimo foi, aproximadamente, 15%.
Página CV
b) Com o acréscimo de 15%, o valor do conjunto de sofás passou a ser , ou seja, R$ 1.609,85. Dado um desconto de 15% sobre este valor, o preço passará a ser 85% de 1.609,85:
Portanto, o preço passou a custar R$ 1.368,37.
24. Calculando a porcentagem para cada uma das despesas, temos:
transporte:
Portanto, o transporte corresponde a 8% do salário.
aluguel:
Portanto, o aluguel corresponde a 32% do salário.
alimentação:
Portanto, a alimentação corresponde a 18% do salário.
25. a) Do total de 5.570 municípios, 1.227 têm coleta seletiva. Isso representamunicípios sem coleta seletiva.
Portanto, aproximadamente 78% dos municípios brasileiros não tinham coleta seletiva.
b) Resposta pessoal. A resposta depende da amostra entrevistada.
c) Resposta pessoal. Espera-se que os estudantes opinem e demonstrem senso crítico em seu posicionamento ou mesmo na mudança de opinião após a contribuição e o compartilhamento de informações com os colegas.
26. Como 30 questões são de aritmética e 50 são de geometria, concluímos que o trabalho tem um total de 80 questões. Calculando quantas questões Júlia acertou em aritmética, temos:
Portanto, Júlia acertou 21 questões.
Para determinar quantas questões Júlia acertou na prova toda, calculamos:
A quantidade de questões que Júlia acertou apenas em geometria é dada por . Assim:
Logo, Júlia acertou 86% das questões de geometria.
Portanto, a alternativa correta é a e.
27. a) Sugestão de resposta:
Uma vantagem da produção de energia eólica é a diminuição da poluição atmosférica e uma desvantagem é a poluição sonora que afetará, principalmente, as pessoas que residem ao redor de onde for implementada a produção.
b) De um total de , a parte produzida por China, Estados Unidos, Alemanha, Índia e França equivale a . Assim:
Portanto, a produção realizada por China, Estados Unidos, Alemanha, Índia e França corresponde a, aproximadamente, 69,4% do total.
Para determinar a porcentagem que a produção do Brasil corresponde do total, calculamos:
Portanto, a produção realizada pelo Brasil corresponde a, aproximadamente, 2,4% do total.
c) Resposta pessoal. Espera-se que os estudantes produzam um texto relacionando o contexto da atividade e o conteúdo estudado, apresentando argumentos críticos e propositivos em relação ao assunto abordado.
O que eu estudei?
1. Realizando os cálculos, temos:
a) 15% de correspondem a , pois .
b) 20% de correspondem a , pois .
c) 35% de correspondem a , pois .
d) 42% de correspondem a , pois .
2. Na figura A, temos um total de 11 quadrados pintados por completo, que pode ser representado pela seguinte razão e porcentagem:
Portanto, nessa figura, 44% estão pintados de laranja.
Na figura B, temos um total de 5 quadrados pintados por completo, que pode ser representado pela seguinte razão e porcentagem:
Portanto, nessa figura, aproximadamente 31% estão pintados de laranja.
3. Se representam a medida da área construída de um total de , então, representam a medida da área não construída. Sendo assim, temos a seguinte razão e porcentagem:
Portanto, 62,5% da área do terreno não está construída.
Página CVI
4. Calculando a porcentagem correspondente a cada gasto, temos:
Aluguel:
Portanto, o valor do gasto com aluguel é R$ 810,00.
Alimentação:
Portanto, o valor do gasto com alimentação é R$ 675,00.
Saúde:
Portanto, o valor do gasto com saúde é R$ 324,00.
Transporte:
Portanto, o valor do gasto com transporte é R$ 405,00.
Outros:
Portanto, o valor do gasto com outras despesas é de R$ 486,00.
5. Denominando x a porcentagem que corresponde à quantidade de meninos, temos:
Portanto, 37,5% dessa turma são meninos.
6. Indicando como x a quantidade total de cálcio a ser ingerida em um dia, em miligramas, temos:
Sendo assim, a quantidade diária a ser ingerida é 800 miligramas.
Portanto, a alternativa correta é a c.
7. Considerarmos que o salário de Rubens corresponde a 100% e teve um aumento de 12%, a porcentagem que representa o novo salário de Rubens é .
, ou seja, R$ 1.680,00.
Portanto, Rubens passou a receber R$ 1.680,00 após o aumento.
8. Inicialmente, vamos calcular quanto é 60% de 80, ou seja, . Além disso, considerando x a porcentagem que 48 corresponde de 150, obtemos:
Portanto 60% de 80 corresponde a 32% de 150.
9. Sendo a quantidade total do pacote, calculamos a quantidade referente a cada componente:
Carboidratos:
Portanto, há de carboidratos.
Gorduras:
Logo, há de gorduras.
Proteínas:
Portanto, há de proteínas.
Outros:
Assim, há de outros componentes.
10. a) Calculando primeiro a quantidade em reais deste acréscimo, temos:
, ou seja, R$ 140,00.
Indicando por x a porcentagem correspondente ao acréscimo considerado, temos:
Portanto, o acréscimo foi 25%.
b) Como R$ 700,00 representam o valor total e R$ 140,00 representam o desconto para retornar o preço a R$ 560,00, considere x a porcentagem que corresponde ao desconto.
Portanto, deve ser dado desconto de 20% para que o valor retorne ao original.
11. O preço do televisor à vista corresponde ao preço total menos o desconto, ou seja, .
Sendo assim, calcular 87% de 1.100 equivale a efetuar . Com isso, verificamos que o preço do televisor à vista é R$ 957,00.
Analisando a situação e os resultados obtidos, verificamos que a quantia de R$ 965,00 é suficiente para comprar o televisor à vista e ainda vão sobrar R$ 8,00, pois .
12. Se a proporção é de 11 mulheres para cada 9 homens, então de cada 20 pessoas, 11 são mulheres. Sendo assim, temos a seguinte razão:
Portanto, há 55% de mulheres nesse congresso.
Página CVII
13. a) Calculando 30% de , obtemos:
Portanto, ele adicionou de etanol.
b) Considere x a quantidade de gasolina total para que sejam adicionados de etanol. Sendo assim, temos a seguinte proporção:
Portanto, ele abasteceu de gasolina em seu carro.
14. Como R$ 2.300,00 é a quantia total que Valdemar recebia antes do aumento, essa quantia representa 100%. Sendo x o novo salário com o aumento, temos:
Portanto, ele passou a receber R$ 2.415,00 de salário.
15. Indicando por x a quantidade total de associados e calculando 30% dos 50% que têm entre 18 e 30 anos, temos:
Como , a porcentagem dos associados entre 18 e 30 anos que praticam natação é 15%.
16. De acordo com o enunciado, 60% dos 40 estudantes praticam esportes, ou seja, . Assim, 24 estudantes praticam esportes. Considerando que todos os 22 meninos pratiquem esportes, pelo menos 2 meninas devem praticar algum esporte.
17. Considerando que a barra com 250 gramas corresponde a 100%, e denominando como x esta porcentagem, temos:
Sendo assim, 200 gramas correspondem a 80% de 250 gramas. Se o preço tivesse decrescido na mesma proporção, teríamos , ou seja, a barra com 200 gramas deveria custar R$ 4,00.
Sendo R$ 4,00 o preço total da barra de 200 gramas, vamos determinar o aumento percentual y para que seja cobrado R$ 5,00 por esta barra.
Assim, o aumento percentual foi.
Portanto, a alternativa correta é a d.
18. a) Sendo R$ 599,00 o preço pago, R$ 150,00 a entrada e p o valor da parcela, obtemos a equação .
Resolvendo-a, obtemos:
Portanto, o valor de cada parcela é R$ 89,80.
b) Pagando à vista, há um desconto de 15%, ou seja, do valor total. Assim:
.
Logo, o preço à vista dessa bicicleta é R$ 509,15. A diferença entre o preço a prazo e o preço à vista é R$ 89,85, pois .
Portanto, o valor pago a mais é de R$ 89,85.
19. a) Se Suzana realizar o pagamento no dia 2, então terá um desconto de 6,25%, isto é, pagará o correspondente a .
Assim: .
Portanto, o valor da taxa de condomínio no dia 2 será R$ 450,00.
b) Se Suzana realizar o pagamento no dia 5, será no valor de R$ 450,00.
c) Se Suzana realizar o pagamento no dia 6, significa que ela teve um atraso de 1 dia. Logo, deve pagar o valor total mais a multa de 2% mais 0,025% de R$ 480,00.
.
Portanto, o valor da taxa de condomínio no dia 6 será R$ 489,72.
d) Se Suzana realizar o pagamento no dia 10, significa que ela teve um atraso de 5 dias, ou seja, vai pagar o valor total mais a multa de 2% mais 5 vezes a multa diária de 0,025% de R$ 480,00.
Portanto, o valor da taxa de condomínio no dia 10 será R$ 490,20.