Página CVIII
Unidade 11
Estatística e probabilidade
Atividades
1. a) Sabendo que a tabela e o gráfico representam a mesma informação, verificamos que:
A: 18,7; B: 52,7; C: 13,3; D: 13.
b) A maior quantia em dólares foi gasta em Pequim no ano 2008. A menor quantia em dólares foi gasta no Rio de Janeiro no ano 2016.
c) Calculando a diferença entre estes valores obtemos , isto é, 34 bilhões de dólares.
2. a) A menor medida de temperatura ocorreu no dia 1º de julho. Essa medida foi .
b) Os dias 1 e 3 apresentaram a mesma medida de temperatura máxima, que é .
c) No dia 1, houve a maior diferença entre as medidas de temperatura máxima e mínima registradas. A diferença foi .
3. a) Para determinar a quantidade de medalhas conquistadas pelo Brasil, devemos adicionar a quantidade de medalhas de ouro, prata e bronze conquistadas:
Portanto, o Brasil conquistou 171 medalhas.
b) De acordo com o gráfico, verificamos que os Estados Unidos conquistaram mais medalhas. Calculando a quantidade de medalhas, obtemos 293 medalhas, ou seja, .
c) México e Canadá conquistaram entre 100 e 160 medalhas.
d) Como Canadá conquistou 35 medalhas de ouro e Cuba conquistou 33 medalhas de ouro, calculamos a diferença entre essas quantidades, que é dada por . Portanto, o Canadá conquistou 2 medalhas de ouro a mais do que Cuba.
e) Como os Estados Unidos conquistaram 85 medalhas de bronze e o México conquistou 63 medalhas de bronze, a diferença de medalhas de bronze é dada por . Portanto, o México conquistou 22 medalhas de bronze a menos do que os Estados Unidos.
4. a) No mês de fevereiro, houve o maior consumo de água. Essa quantidade foi .
b) Adicionando os valores desses 5 meses consecutivos, obtemos:
Portanto, foram consumidos .
c) O mês de menor consumo foi junho, com medida de , e o mês de maior consumo foi fevereiro, com medida de . Calculando a diferença entre esses meses, obtemos , isto é, foram registrados a menos no mês de menor consumo em relação ao mês de maior consumo.
5. a) De acordo com o gráfico, em 2017 houve a maior produção de maçãs. Como as informações estão apresentadas em 1.000 toneladas, calculamos .
Portanto, em 2007 houve uma produção de aproximadamente de maçãs.
b) A produção diminuiu. Calculando essa diferença, temos , que em toneladas representa , ou seja, aproximadamente .
c) Entre os anos de 2016 e 2017, houve o maior aumento de produção ocorrido de um ano para outro. Calculando a diferença entre essa produção, temos , que em toneladas representa uma diferença de , pois .
d) Entre os anos de 2018 e 2019, houve o menor aumento na produção ocorrido de um ano para outro.
e) A produção foi superior a de 2018 nos anos de 2015, 2017 e 2019.
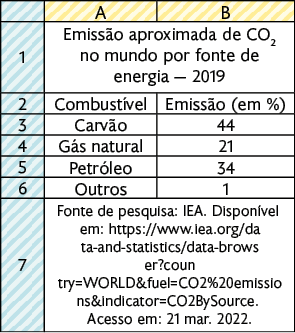
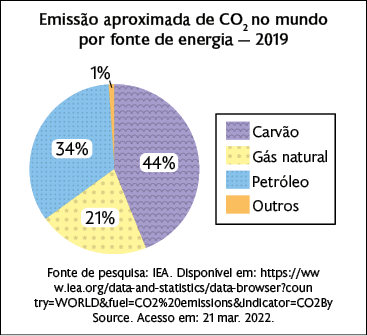
6. a) De acordo com as informações do gráfico, podemos observar que a maior porcentagem está relacionada ao consumo de petróleo e derivados.
b) O consumo de carvão mineral foi a fonte de energia para 27% da população mundial e o consumo de gás natural foi a fonte de energia para 23%. Calculando a diferença entre essas porcentagens, obtemos . Portanto, foram consumidos, aproximadamente, 4% a mais de carvão mineral do que de gás natural.
c) A porcentagem aproximada foi 19%, pois .
d) Resposta pessoal. Espera-se que os estudantes exercitem o senso crítico e a capacidade de argumentação para responderem e justificarem suas opiniões.
e) Resposta pessoal. Espera-se que os estudantes citem ações como apagar as luzes quando não houver pessoas nos ambientes, reduzir o tempo no banho, fazer uso da bicicleta como meio de transporte e preferir fontes de energia renováveis.
7. a) O carvão foi a fonte de energia que gerou a maior produção de .
b) A diferença entre as fontes de emissão de citadas é aproximadamente 13% .
c) Resposta pessoal. Sugestão de resposta: Qual foi, ao todo, a porcentagem aproximada de liberada por petróleo e gás natural? Resposta: 55%.
d) Ao construir a tabela no Calc, devemos lembrar de inserir um título, as informações correspondentes da tabela e a fonte das informações.
Para construir o gráfico, podemos proceder da seguinte maneira.
Página CIX
1º. Insira os dados no Calc, conforme apresentado a seguir. Selecione as células com os dados clicando em A1 e mantendo o botão pressionado para arrastar até a célula B5.
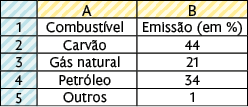
2º. Clique no menu Inserir e selecione a opção Gráfico ou, então, clique diretamente no botão Inserir gráfico. Na janela Assistente de gráficos, selecione Tipo de gráfico e escolha Pizza. Ainda nessa janela, selecione Elementos do gráfico, preencha o título "Emissão aproximada de no mundo por fonte de energia – 2019", deixe a opção Exibir legenda habilitada e clique em Finalizar.
3º. Para exibir os valores dos setores, dê um clique duplo no gráfico. Em seguida, clique com o botão direito sobre um setor e escolha Inserir rótulo de dados. Depois, clique com o botão direito, escolha Formatar rótulo de dados e altere os atributos de texto para Valor como porcentagem. Como não há um campo para inserir a fonte de pesquisa, digite a informação em uma célula abaixo do gráfico.
e) Resposta pessoal. Sugestão de resposta: É importante reduzirmos a emissão de , pois o excesso de dióxido de carbono na atmosfera é tóxico para os seres humanos, prejudicando a saúde e a qualidade de vida, principalmente de idosos e crianças.
f) Espera-se que os estudantes encontrem em sua pesquisa algumas consequências da emissão de gás carbônico em excesso na atmosfera, tais como o agravamento de doenças cardiopulmonares; o desequilíbrio climático; as médias de temperaturas máxima e mínimas mais extremas; o aumento da acidez na água do mar. Algumas atitudes que podem ser tomadas para diminuir a emissão de são: uso de energia renovável; redução de desmatamento e queimadas; uso de meios de transporte menos poluentes ou alternativos; incentivo ao reflorestamento; incentivo à agricultura sustentável.
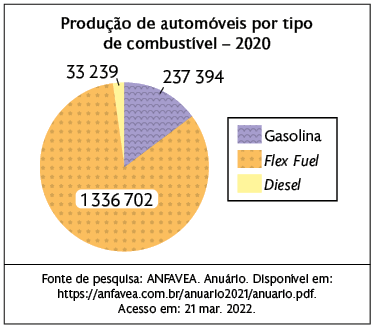
8. a) Adicionando as quantidades informadas de acordo com o tipo de combustível, temos:
Portanto, em 2020 foram produzidos 1.607.335 automóveis.
b) De acordo com o item a, sabemos que, em 2020, foram produzidos 1.607.335 automóveis. Deste modo, organizamos as informações no seguinte quadro.
|
Quantidade de automóveis |
Porcentagem |
|---|---|
|
1.607.335 |
100 |
|
33.239 |
x |
Utilizando regra de três, podemos obter o valor de x.
Portanto, aproximadamente 2% da produção de 2020 correspondem a automóveis movidos a diesel.
c) Para resolver esse item, efetuamos uma subtração entre as duas quantidades informadas.
Logo, a diferença é 1.099.308 automóveis.
Para obter a porcentagem referente a essa quantidade, novamente usamos a regra de três como estratégia.
|
Quantidade de automóveis |
Porcentagem |
|---|---|
|
1.607.335 |
100 |
|
1.099.308 |
x |
Portanto, aproximadamente 68% da produção de 2020 correspondem à diferença entre a produção de automóveis flex fuel e a de automóveis movidos a gasolina.
d) Para construirmos um gráfico de setores no Calc, fazemos:
1º. Insira os dados no Calc, conforme apresentado a seguir. Selecione as células com os dados clicando em A1 e mantendo o botão pressionado para arrastar até a célula B4.

2º. Clique no menu Inserir e selecione a opção Gráfico ou, então, clique diretamente no botão Inserir gráfico. Na janela Assistente de gráficos, selecione Tipo de gráfico e escolha Pizza. Ainda nessa janela, selecione Elementos do gráfico, preencha o título "Produção de automóveis por tipo de combustível – 2020", deixe a opção Exibir legenda habilitada e clique em Finalizar.
Página CX
3º. Para exibir os valores dos setores, dê um clique duplo no gráfico. Em seguida, clique com o botão direito sobre um setor e escolha Inserir rótulo de dados. Como não há um campo para inserir a fonte de pesquisa, digite a informação em uma célula abaixo do gráfico. Como não há campo para inserir a fonte de pesquisa, digite a informação em uma célula abaixo do gráfico.
Questão 1. Calculando a nova média, obtemos:
Portanto, a média permaneceria igual.
A amplitude mudaria, pois, como a maior nota é 9 e a menor nota é 6, a diferença passa a ser , isto é, a amplitude seria maior.
Questão 2. Sabemos que o peso da avaliação curricular é 4 e o peso da entrevista é 6. Assim, calculando a média ponderada, temos:
Portanto, a nota média de Ana foi 8,2.
Atividades
9. a) O mês de outubro apresentou o maior IPCA. O mês de dezembro apresentou o menor IPCA.
b) A média aritmética é dada por:
Portanto, a média aritmética mensal aproximada nesse quadrimestre foi 1,02%.
10. a) Inicialmente, vamos calcular a média e a amplitude das receitas da loja A.
Média: , ou seja, R$ 130,00.
Amplitude: , ou seja, R$ 85,00.
Calculando a média e a amplitude das receitas da loja B, temos:
média: , ou seja, aproximadamente, R$ 131,00.
Amplitude: , ou seja, R$ 72,00.
b) A loja B teve a receita mais homogênea nessa semana, pois as receitas dela têm uma menor amplitude quando comparada à das receitas da loja A.
11. a) Como , a média aritmética das notas de Rui foi 6,75.
b) Como , a média ponderada das notas de Rui foi 7,1.
c) Rui não seria aprovado com a média obtida no cálculo da média aritmética, pois obteve nota igual a 6,5. Rui seria aprovado se o resultado fosse obtido no cálculo da média ponderada, pois alcançou nota igual a 7,1.
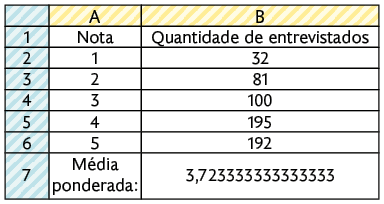
12. a) A nota 4 recebeu mais indicações. A nota 1 recebeu menos indicações.
b) Para calcularmos a média no Calc, procedemos da seguinte maneira.
1º. Copie as informações do quadro correspondentes à satisfação dos entrevistados com relação à empresa no intervalo A1:B6.
2º. Na célula A7, digite o texto "Média ponderada". Em seguida, na célula B7, digite a fórmula e pressione Enter.
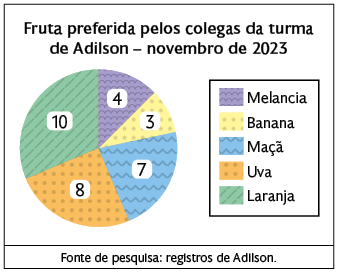
13. a) Sugestão de resposta: Uma pesquisa censitária é realizada com toda a população, enquanto uma pesquisa amostral é feita com uma parte da população.
b) Censitária, pois era possível entrevistar todos os colegas da turma.
c) Adilson utilizou gráfico e texto com dados estatísticos.
d) A banana foi a fruta que recebeu a menor quantidade de votos . Usando regra de três, calculamos a porcentagem correspondente a essa quantidade.
|
Porcentagem |
Quantidade de votos |
|---|---|
|
100 |
32 |
|
x |
3 |
Portanto, a banana recebeu, aproximadamente, 9,38% dos votos.
Página CXI
e) Para construir um gráfico de setores no Calc, realizamos os procedimentos indicados a seguir.
1º. Copie os valores da atividade no Calc e selecione todas as informações.
2º. Clique no menu Inserir e selecione a opção Gráfico ou, então, clique diretamente no botão Inserir gráfico. Na janela Assistente de gráficos, selecione Tipo de gráfico e escolha Pizza. Ainda nessa janela, selecione Elementos do gráfico, preencha o título "Fruta preferida pelos colegas da turma de Adilson – novembro de 2023", deixe a opção Exibir legenda habilitada e clique em Finalizar.
3º. Para exibir os valores dos setores, dê um clique duplo no gráfico. Em seguida, clique com o botão direito sobre um setor e escolha Inserir rótulo de dados. Como não há um campo para inserir a fonte de pesquisa, digite a informação em uma célula abaixo do gráfico.
14. a) A população desse tema de pesquisa são todos os eleitores desse estado, ou seja, 345.500 eleitores de um estado e a amostra, os 35.225 eleitores entrevistados.
b) A população desse tema de pesquisa são todos os estudantes da escola e a amostra, os 450 estudantes entrevistados.
c) A população desse tema de pesquisa são os ocupantes das poltronas e a amostra, os 85 ocupantes entrevistados.
15. a) Para os domicílios com acesso à internet, o tipo de pesquisa mais adequado é o censitário.
b) Para a preferência dos consumidores por determinada marca de produto, o tipo de pesquisa mais adequado é o amostral.
c) Para a população rural e urbana de um município, o tipo de pesquisa mais adequado é o censitário.
d) Para a aprovação do presidente de um país, o tipo de pesquisa mais adequado é o amostral.
16. Não, pois a população pesquisada são os funcionários da empresa que é dona da marca.
17. Tema: Satisfação dos moradores com o serviço de coleta de lixo no município.
Questionário: Já foi definido pela prefeitura.
Público-alvo: Adultos, moradores do município estudado.
a) Não, pois os adultos têm uma melhor percepção referente à qualidade do serviço de coleta de lixo.
b) Sugestão de resposta: Nas residências, por se tratar de um serviço público oferecido no bairro.
c) Não, pois pode demandar muito tempo entrevistar todos os moradores.
d) A pesquisa é amostral.
e) Resposta pessoal.
Questão 4. Adicionando a quantidade de lançamentos, obtemos . Portanto, Sara fez nesse experimento 70 lançamentos.
Atividades
18. Resposta pessoal. Espera-se que os estudantes compartilhem o resultado de suas pesquisas com os colegas, agregando conhecimento e validando as informações.
19. a) São 2 resultados possíveis: cara ou coroa.
b) A probabilidade é 1 em 2 ou, ainda, .
20. a) Como o espaço amostral é o conjunto de todos os resultados possíveis, temos:
b) A probabilidade de sair o número 12 é 1 em 20, ou seja, .
c) A probabilidade de um número sorteado ser ímpar é 10 em 20, ou seja, .
d) Como existem 11 números com dois algarismos, a probabilidade é 11 em 20, ou seja, .
e) Nesse espaço amostral, há 8 números primos, que são 2, 3, 5, 7, 11, 13, 17, 19.
Nesse caso, a probabilidade de um número sorteado ser primo é 8 em 20, ou seja, .
21. a) Cada estudante fará 10 lançamentos e o grupo será formado por 4 estudantes. Então, a quantidade de lançamentos do grupo deve ser igual a 40.
b) A resposta depende do resultado do experimento.
c) Cada um dos resultados tem a mesma chance de ocorrer e a probabilidade de aparecer determinada face é representada pela fração . Sendo assim, em 1.200 lançamentos, espera-se obter 200 pontos para determinada pontuação, pois .
Portanto, espera-se obter aproximadamente 200 resultados com pontuação 3 e 200 resultados com pontuação 5.
22. Inicialmente, vamos determinar o espaço amostral desse evento.
Desta maneira, verificamos que existem 9 possibilidades de somas e, dessas, 5 são resultados pares. Portanto, a alternativa correta é a b.
23. Resposta pessoal. Sugestão de resposta:
Para realizar 20 sorteios com números de 0 até 50, procedemos da seguinte maneira.
Na célula A1, digite e pressione Enter.
Página CXII
Clique na Alça de preenchimento automático, mantendo o botão pressionado, e arraste, por exemplo, até a célula A20. Os demais números sorteados serão exibidos.
Para descobrir a porcentagem de vezes que o número 7 foi sorteado, executamos os seguintes procedimentos.
Em uma célula vazia, digite a fórmula e pressione Enter.
Divida o resultado por 20, represente em forma de fração com denominador igual a 100 e anote a porcentagem.
O que eu estudei?
1. A menor porcentagem de estudantes com aprendizado adequado em Matemática ocorreu em 2013. A menor porcentagem de estudantes com aprendizado adequado em Língua Portuguesa ocorreu em 2011.
2. Calculando a média anterior, obtemos:
, ou seja, 14 pontos.
Para calcular a nova média, devemos descartar a maior e a menor nota atribuída.
, ou seja, 15 pontos.
Portanto, a nova média é 1 ponto maior em relação à media anterior. Logo, a alternativa correta é a b.
3. a) Calculando a porcentagem com relação à quantidade de votos, temos:
Portanto, a candidata eleita teve 4.284 votos.
b) A diferença em porcentagem na quantidade de votos obtida por esses dois candidatos foi .
Assim:
, ou seja, 476 votos.
c) Calculando a porcentagem, temos:
, ou seja, 952 votos foram brancos ou nulos.
4. a) O cargo é o de diretor de marketing. O cargo de maior salário na empresa A é o de diretor executivo.
b) Calculando a média salarial dos diretores da empresa A, obtemos:
, ou seja, aproximadamente R$ 9.433,33.
Calculando a média salarial dos diretores da empresa B, obtemos:
, ou seja, aproximadamente R$ 9.533,33.
Logo, a empresa B apresenta a maior média salarial.
c) Amplitude do salário na empresa A: , ou seja, R$ 1.700,00.
Amplitude do salário na empresa B: , ou seja, R$ 700,00.
5. a) A quantidade de resultados possíveis é , ou seja, são 36 os resultados possíveis.
b) Cada um dos resultados tem a mesma chance de acontecer e existem 3 chances de obter um número par e a letra C em um lançamento. Desse modo, calculamos:
Portanto, a probabilidade é, aproximadamente, 8%.
c) Cada um dos resultados tem a mesma chance de acontecer e existem 6 chances de obter um número ímpar e a letra ser uma vogal em um lançamento. Desse modo, calculamos:
. Portanto, a probabilidade é de, aproximadamente, 17%.
d) Contando inicialmente cada uma das quantidades, verificamos que 3 números são primos: 2, 3 e 5. Além disso, temos 4 consoantes: B, C, D e F. Logo, temos 12 em 36 chances, ou seja, . Portanto, a probabilidade é, aproximadamente, 33%.
Unidade 12
Transformações de figuras
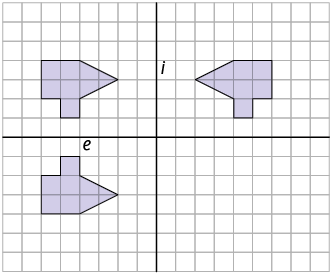
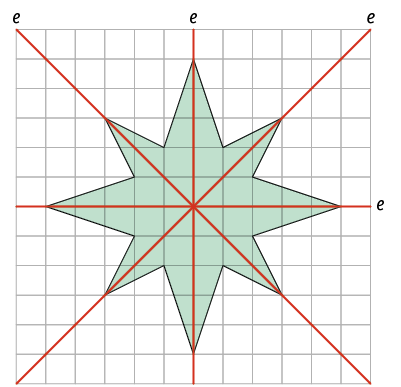
Questão 1. As figuras A e C têm simetria axial, pois são as únicas que apresentam duas partes que se sobrepõem se as "dobrarmos" ao longo da reta formada pelo eixo e.
Atividades
1. A linha e representa um eixo de simetria nas figuras A, B, D e F, pois elas apresentam duas partes opostas iguais, separadas pelo eixo e.
2. Traçando todos os eixos de simetria em cada uma das figuras, temos:
a)
Página CXIII
b)
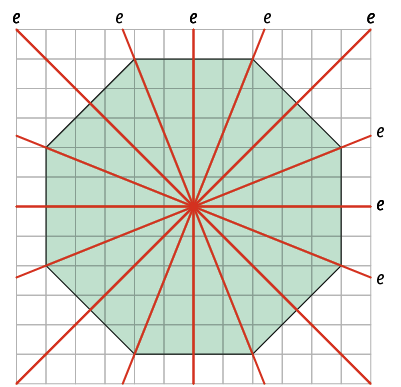
3. a) De acordo com os traçados apresentados, os algarismos que têm eixo de simetria são 0, 3 e 8. Esboçando a representação desses eixos, temos:



b) Os algarismos que têm mais de um eixo de simetria são 0 e 8, com dois eixos de simetria cada um.
4. A imagem que completa o mosaico adequadamente está representada na alternativa B.
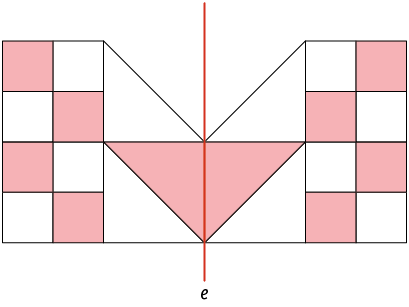
5. As alternativas são B e D, pois apresentam figuras iguais de modo espelhado. Na alternativa A, não há simetria por reflexão entre as figuras dos dois lados do eixo e, e sim por rotação. Já na alternativa C, as figuras não são simétricas.
6. a) No padrão representado na figura 1, há 1 eixo de simetria.

No padrão representado na figura 3, há 4 eixos de simetria.
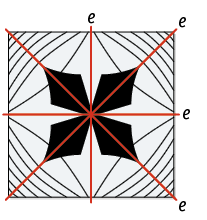
b) Resposta pessoal. O item a depende do desenho dos estudantes. Certifique-se de que eles utilizem padrões geométricos em suas criações.
7. Rogério cometeu um erro na figura A, pois, além de os pontos correspondentes aos vértices das duas figuras – uma de cada lado do eixo e – não terem a mesma distância até o eixo, eles não são simétricos por reflexão.
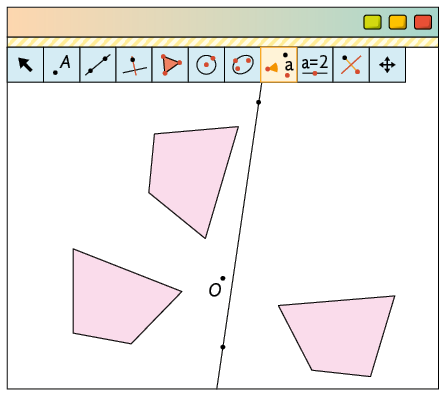
8. A figura 2 é simétrica à figura 1 por rotação na alternativa A, pois nessa alternativa a figura permanece a mesma após ser rotacionada em determinado ângulo em relação ao ponto O.
9. A. A figura 1 rotacionou em relação ao ponto O.
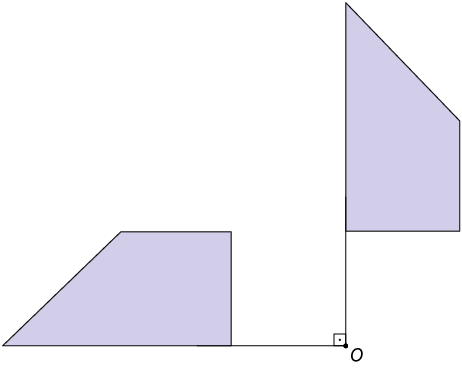
B. A figura 1 rotacionou em relação ao ponto O.
10. A figura apresentada na alternativa E é simétrica por rotação à figura dada, conforme as condições do enunciado.
11. Resposta pessoal. Sugestão de resposta:
Para realizar a construção no GeoGebra, executamos os procedimentos a seguir.
1º) Com a ferramenta Polígono, construa um polígono qualquer. Depois, com a ferramenta Reta, clique em dois pontos distintos para traçar uma reta e, com a ferramenta Ponto, clique e marque um ponto aleatório.
2º) Com a ferramenta Reflexão em Relação a uma Reta, clique no polígono e, depois, na reta.
3º) Com a ferramenta Rotação em Torno de um Ponto, clique no polígono inicial e, depois, no ponto. No campo Ângulo da janela que será exibida, digite a medida do ângulo, ou seja, , escolha o sentido horário e clique em OK.
Página CXIV
12. a) Sugestão de resposta: As paredes cobertas por mosaicos geométricos do Palácio na Alhambra, na cidade de Granada, na Espanha, foi o que despertou o interesse de Escher.
b) Nessa criação de Escher, está presente a simetria de rotação, pois ela apresenta três imagens idênticas e rotacionadas em torno de um ponto central.
c) Resposta pessoal. Espera-se que os estudantes apresentem um texto enriquecido com o resultado de suas pesquisas, usando sua capacidade de comunicação e desenvolvendo o senso estético, crítico e argumentativo em suas produções.
d) Para permanecer a mesma, a obra Serpentes deve ser rotacionada em .
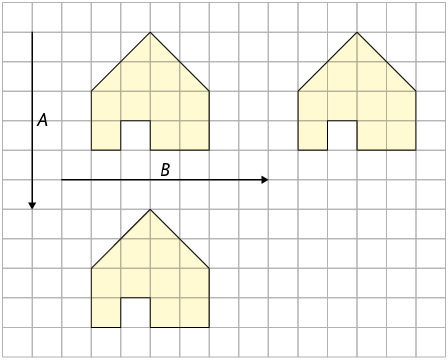
13. No item A, pois a figura 2 está transladada na direção horizontal, em 7 unidades para a direita.
14. A figura 2 está transladada na direção horizontal, 4 unidades à direita da figura 1, representada pela seta H.
A figura 3 está transladada 5 unidades para cima da figura 1, representada pela seta B.
A figura 4 está transladada na direção horizontal, 5 unidades à esquerda da figura 1, representada pela seta F.
15. As figuras que representam as imagens simétricas por translação, com sentido, direção e distância, de acordo com as setas A e B são:
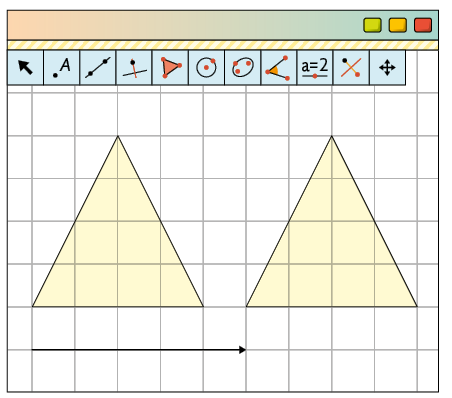
16. Resposta pessoal. Sugestão de resposta:
Para realizar a construção no GeoGebra, executamos os seguintes procedimentos.
1º) Com a ferramenta Polígono, construa um polígono qualquer.
2º) Com a ferramenta Vetor, clique em dois pontos distintos para delimitar as extremidades da seta, que será a referência para a medida da distância, a direção e o sentido da translação.
Resposta pessoal. Sugestão de resposta:
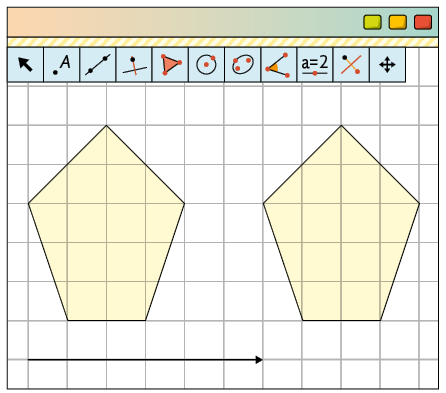
17. Resposta pessoal. Sugestão de resposta:
Para realizar a construção no GeoGebra, procedemos da seguinte maneira.
1º) Com a ferramenta Polígono, construa um polígono qualquer.
2º) Com a ferramenta Vetor, clique em dois pontos distintos para delimitar as extremidades da seta, que será a referência para a medida da distância, a direção e o sentido da translação.
Resposta pessoal. Sugestão de resposta:
Questão 2. As coordenadas dos pontos são , e .
Página CXV
Atividades
18. Indicando os pontos A, B, C e D no plano cartesiano construído na malha quadriculada, temos:

19. a) As coordenadas dos pontos indicados no plano cartesiano são:
, , , , , , , , , , .
b) Os pares de pontos G e H, E e F são simétricos por reflexão em relação ao eixo x. Os pares de pontos I e F são simétricos por reflexão em relação ao eixo y. Esses pontos são simétricos por reflexão, pois estão a uma mesma distância de cada um dos eixos mencionados, porém em lados opostos.
20. De acordo com as informações, as coordenadas dos pontos são:
, , , .
21. a) De acordo com o plano cartesiano apresentado, temos:
, , , , .
b) As coordenadas dos vértices do pentágono simétrico ao pentágono serão:
, , , , .
22. Em relação ao eixo x, são simétricos por reflexão os polígonos 5 e 7, pois os vértices do polígono 5 são , , , e os vértices do polígono 7 são , , , , respectivamente.
Em relação ao eixo y, são simétricos por reflexão os polígonos 3 e 1, pois os vértices do polígonos 3 são , , e os vértices do polígono 1 são , , , assim como os polígonos 6 e 9, pois o polígono 6 tem vértices , , , e os vértices do polígono 9 são , , , .
23. Resposta pessoal. Sugestão de resposta:
Quais são os vértices do polígono simétrico por reflexão ao eixo x do polígono cujos vértices são , , e ?
Resposta: Os vértices são , , e .
Questão 3. As coordenadas dos vértices do polígono apresentado são , , , e .
Questão 4. Resposta pessoal. Sugestão de resposta:
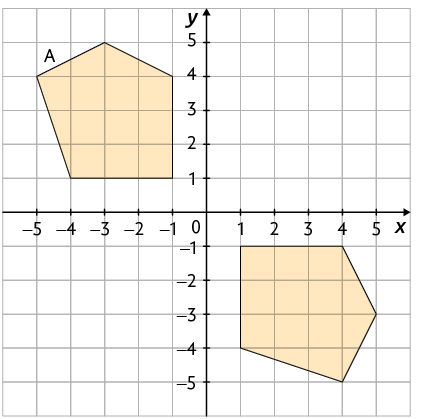
Questão 5. A resposta depende do polígono construído na questão anterior. De acordo com a sugestão apresentada, os vértices do pentágono A são , , , e . As coordenadas dos vértices do simétrico dele em relação à origem do plano cartesiano são , , , e .
Questão 6. Multiplicando as coordenadas do polígono por , obtemos , , , e .
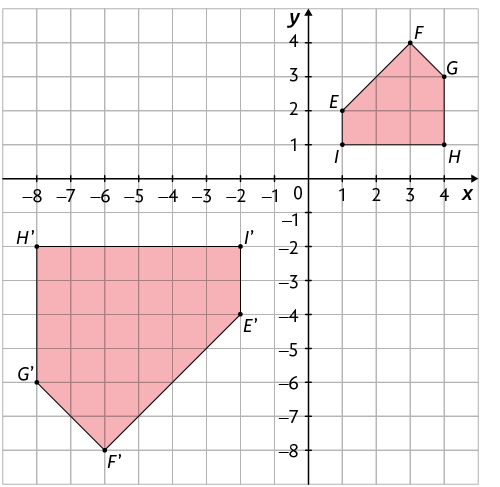
Portanto, o polígono é uma ampliação do polígono original .
Atividades
24. a) As coordenadas dos vértices do polígono 1 são:
, , , , , , .
Página CXVI
Multiplicando por essas coordenadas, obtemos o polígono cujas coordenadas do vértice são:
, , , , , , .
Portanto, com essa operação, podemos obter o polígono 3.
b) Não, pois, ao multiplicarmos as coordenadas dos vértices de um polígono por , obtemos seu simétrico em relação à origem do plano cartesiano e os polígonos 2 e 4 não têm essa característica.
25. Resposta no final da seção Resoluções.
26. a) Multiplicando por cada uma das coordenadas do vértice, obtemos:
, , e .
Essas coordenadas são referentes a uma ampliação da figura desenhada por Fátima.
b) Resposta no final da seção Resoluções.
27. As coordenadas dos vértices do triângulo são , e e as coordenadas do vértice do triângulo são , e , ou seja, as coordenadas do vértice foram multiplicadas por 2.
O que eu estudei?
1. A linha tracejada representa o eixo de simetria da figura, fazendo os desenhos ficarem simétricos após recortados. Analisando as duas partes da figura em relação a esse eixo, concluímos que a figura D representa a figura após o recorte e tendo o papel desdobrado. Portanto, a alternativa correta é a D.
2. Nos itens C e D, o eixo e não representa um eixo de simetria por reflexão, já que os dois lados do eixo não são iguais.
3. As letras F e L não têm simetria axial, pois não é possível traçar qualquer eixo que resulte em uma simetria axial.
4. Resposta no final da seção Resoluções.
5. Os pares de polígonos que são simétricos por translação são A e G; C e I; B e E; D e F, pois representam figuras iguais que foram apenas deslocadas.
6. a) As coordenadas dos vértices do pentágono são , , , e e as coordenadas do vértices do pentágono são , , , e , ou seja, as coordenadas foram multiplicadas por .
b) O pentágono é uma ampliação do pentágono .
c) As coordenadas dos vértices do novo pentágono seriam:
, , , e .
7. a) As coordenadas do vértice desse polígono são:
, , , , .
b) Fazendo uma rotação da figura apresentada de em torno da origem do plano cartesiano, as novas coordenadas serão:
, , , e .
8. Ao traçarmos retas ligando os vértices comuns das figuras, podemos verificar que todas elas passam pelo ponto cujas coordenadas são . Portanto, as coordenadas do ponto O são .
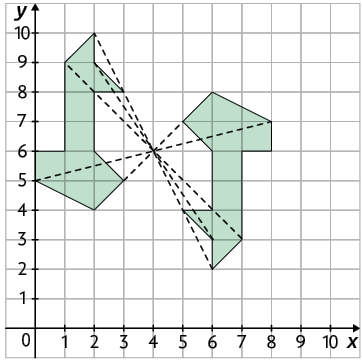
O que eu aprendi?
1. A. Como a soma dos ângulos internos de um triângulo é , podemos escrever e resolver a seguinte equação.
Portanto, o ângulo x mede . Esse triângulo é retângulo.
B. Como a soma dos ângulos internos de um triângulo é , podemos escrever e resolver a seguinte equação.
Portanto, os ângulos x medem . Esse triângulo é acutângulo.
2. O ponto que representa a metade da medida de distância entre os pontos B e D é a origem, ou seja, o ponto C é a origem e o associamos ao 0. Com isso, temos:
Portanto, , , , e .
3. a) Para determinar a quantidade da torta que foi comida, adicionamos as frações. Como os denominadores são diferentes, é necessário calcular . Assim, temos:
Portanto, é a fração que representa a quantidade de torta que foi comida.
Página CXVII
b) Para resolver esse problema, subtraímos a quantidade que Natália comeu da quantidade que Miguel comeu.
Portanto, a fração representa quanto Miguel comeu a mais do que Natália.
c) Para calcular quanto sobrou, realizamos a seguinte subtração:
Portanto sobrou da torta.
4. A. A medida do volume da figura geométrica espacial é a soma das medidas dos volumes de dois paralelepípedos reto retângulos. A medida do volume de cada um é dada por:
Adicionando os dois resultados, verificamos que o volume da figura geométrica espacial representado mede , pois .
B. A medida do volume da figura geométrica espacial é a soma das medidas dos volumes de dois paralelepípedos reto retângulos. Calculando a medida do volume de cada um deles, temos:
Adicionando os dois resultados, verificamos que o volume da figura geométrica espacial representado mede , pois .
C. A medida do volume do sólido geométrico espacial é a soma da medida dos volumes de três paralelepípedos reto retângulos. Calculando o volume de cada um deles, temos:
Adicionando os resultados, verificamos que o volume da figura geométrica espacial representado mede , pois .
5. Para determinar a medida da área da figura, vamos separá-la em dois retângulos e um triângulo.
Um retângulo tem dimensões e . Como , sua área mede .
O outro retângulo tem dimensões e . Como , sua área mede .
A base do triângulo mede e a altura mede . Como , sua área mede .
Desse modo, a medida da área dessa figura é , pois .
6. a) Calculando os primeiros termos da sequência, temos:
Portanto, temos a sequência .
b) Calculando os primeiros termos da sequência, temos:
Portanto, temos a sequência .
c) Calculando os primeiros termos da sequência, temos:
Portanto, temos a sequência .
7. a) A sequência foi definida por recorrência, pois, utilizando essa expressão, podemos calcular um termo da sequência com base nos termos anteriores.
b) Sendo , calculando os próximos termos da sequência, obtemos:
8. a) Contando os círculos da sequência, obtemos 3, 5 e 7 círculos.
b) Sugestão de resposta:
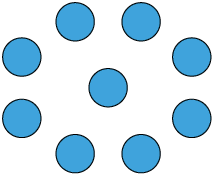
c) Como os termos da sequência são números ímpares, podemos expressá-la por , com , em que n indica a posição do termo na sequência.
d) • 9ª posição: . Assim, .
15ª posição: . Assim, .
17ª posição: . Assim, .
20ª posição: . Assim, .
9. De acordo com as informações, verificamos que as grandezas quantidade de convites comprados e convites sorteados são grandezas diretamente proporcionais. Considerando x a quantidade de convites sorteados quando 140 são comprados, temos:
Convite comprados
20
140
Convites sorteados
3
x
Página CXVIII
Com isso, efetuamos os cálculos.
Portanto, foram sorteados 21 convites.
10. Considere x o preço do guarda-roupa sem o acréscimo correspondendo a 100% do preço. Então R$ 649,60 corresponde a do preço. Desse modo, temos a seguinte proporção.
Portanto, o guarda-roupa, antes do acréscimo, custava R$ 580,00.
11. a) Calculando a média referente a cada colaborador, obtemos:
Matheus: , ou seja, .
Talita: , ou seja, .
Felipe: , ou seja, .
Portanto, Felipe apresentou a maior média de venda.
b) O colaborador que apresentou a maior média vendeu, aproximadamente, R$ 1.023,33.
12. a) A probabilidade de retirar um botão:
preto é dada por: , ou seja, 12,5%.
colorido é dada por: , ou seja, 87,5%.
b) Retirando 2 botões pretos, sobram 3 botões pretos. Retirando 8 botões coloridos, sobram 27 botões coloridos. Nesse caso, verificamos que a caixa terá 30 botões, sendo 3 pretos e 27 coloridos. Assim, a probabilidade de retirar um botão colorido nessa situação é dada por , ou 90%.
Resolução referente à unidade 1.
Questão 5.
|
Número natural |
Número formado pelos dois últimos algarismos da direita |
É divisível por 4? |
|---|---|---|
|
732 |
32 |
Sim, pois 32 é um número divisível por 4. |
|
500 |
00 |
Sim, pois os dois últimos algarismos da direita são simultaneamente 0. |
|
1.286 |
86 |
Não, pois 86 não é um número divisível por 4. |
|
756 |
56 |
Sim, pois 56 é um número divisível por 4. |
Espera-se que os estudantes digam que os dois últimos algarismos dos números que são divisíveis por 4 formam, na ordem em que aparecem, um número divisível por 4.
8.
|
Número |
Divisor |
|||
|---|---|---|---|---|
|
2 |
3 |
5 |
10 |
|
|
8.492 |
X (pois é um número par) |
|||
|
3.750 |
X (pois é um número par) |
X (pois a soma dos algarismos é divisível por 3) |
X (pois é um número terminado em 0) |
X (pois é um número terminado em 0) |
|
1.899 |
X (pois a soma dos algarismos é divisível por 3) |
|||
Resolução referente à unidade 2.
Questão 3.
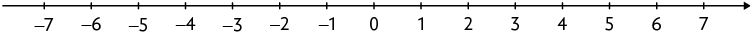
Página CXIX
8. a) Como a medida da distância entre dois pontos consecutivos é sempre igual a 50, temos:
A: 200; B: 300; C: 350; D: ; E: ; F: e G:
Reescrevendo a reta numérica, obtemos:
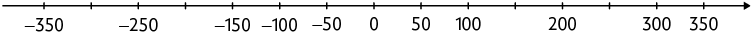
9. Como a letra A representa o maior número na reta numérica, A corresponde a 65. A letra B representa um número entre 10 e 20, ou seja, B corresponde a 18. As letras C, D e E são menores do que , de modo que . Assim, C: ; D: e E: . Substituindo as letras na reta numérica, obtemos:
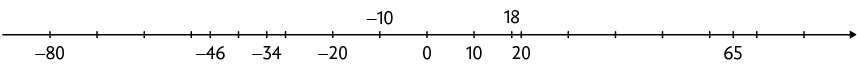
10. a) Como a medida da distância entre dois pontos consecutivos é sempre igual a uma unidade, temos:
D: 3; E: 6; F: 10; C: ; B: e A: .

13. a)
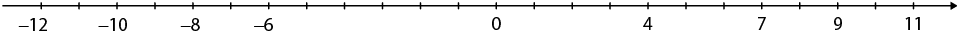
d) Números simétricos são dois números que estão à mesma distância da origem na reta numérica, mas localizados em sentidos contrários dela. Os números simétricos aos números da atividade são: 10, , , 12, , 6, 8 e . Localizando esses pontos na reta numérica, temos:

24. a)

b)

32. c) Escrevendo as quantias em ordem crescente, temos:
Questão 4. Como a rede de supermercados teve prejuízo de 5 milhões de reais ao final do mês de abril e lucro de 6 milhões de reais no mês de maio, ao final desse mês a empresa terá lucro de 1 milhão de reais.

42. Calculando a soma das faces visíveis de cada pilha, temos:
Pilha A:
Pilha B:
Pilha C:
Página CXX
Resolução referente à seção O que eu estudei? da unidade 4.
1. Realizando as transformações necessárias, temos:
; ; ; ; ; ;
; ; ; ; ; .
Completando o primeiro quadro:
|
Número decimal |
Número fracionário |
|---|---|
|
7,3 |
|
|
2,5 |
|
|
4,9 |
|
|
2,3 |
|
|
10,1 |
|
|
1,75 |
Completando o segundo quadro:
|
Número decimal |
Número fracionário |
|---|---|
|
0,2 |
|
|
0,4 |
|
|
7,9 |
|
|
123,05 |
|
|
0,12 |
|
|
0,9 |
Escrevendo-os em ordem decrescente, obtemos:
; ; ; ; ; ; ; ; ; ; ; .
6. Como , escrevendo os números em ordem crescente, temos:
.
8. Realizando as transformações das frações em números decimais, temos:
; ; .
Em seguida, escrevemos os números na reta numérica.

Resolução referente à unidade 7.
17.
|
Ângulo |
Complemento de |
Suplemento de |
|---|---|---|
Resolução referente à unidade 8.
17. Resposta pessoal. Sugestão de resposta:
Página CXXI
Resolução referente à unidade 12.
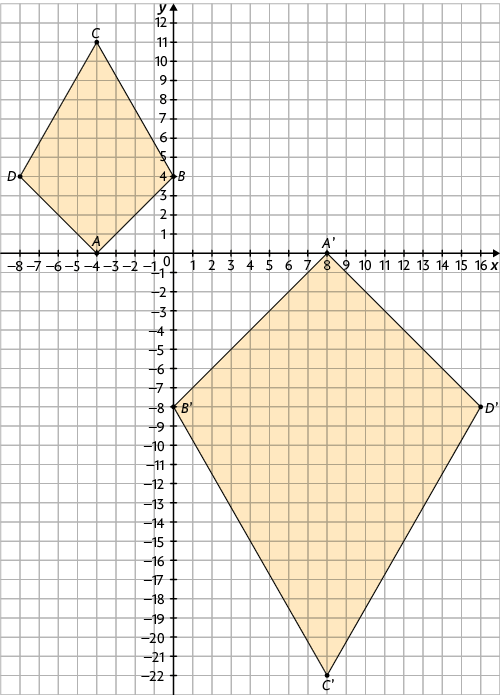
25. As coordenadas do vértice do polígono são , , e . Multiplicando por , obtemos os pontos , , e , que são coordenadas dos vértices do polígono .
Portanto, o polígono é uma ampliação do polígono original .
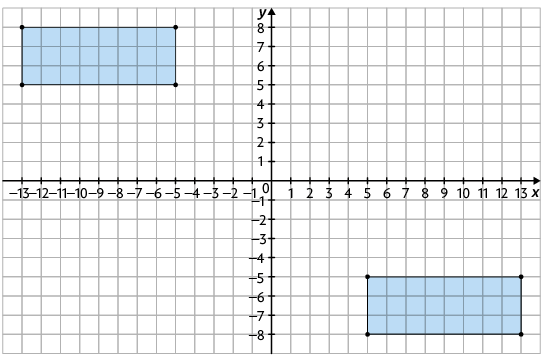
26. b) As coordenadas dos vértices do retângulo simétrico em relação à origem são , , e .
Resolução referente à seção O que eu estudei? da unidade 12.
4. As figuras simétricas por reflexão em relação aos eixos i e e são: