Página 13
UNIDADE
1
Múltiplos e divisores de um número

Agora vamos estudar...
- os múltiplos de um número natural;
- os divisores de um número natural;
- os números primos;
- a decomposição em fatores primos;
- o máximo divisor comum;
- o mínimo múltiplo comum.
Página 14
Múltiplos
O professor de Educação Física de Ana e seus colegas decidiram organizar um minitreino de basquetebol, mas não sabem se é melhor que eles formem duplas ou trios. Sabendo que todos vão participar do minitreino e que a quantidade de estudantes é maior do que 35 e menor do que 40, quantos há exatamente?
Para resolver esse problema, podemos utilizar o conceito de múltiplos de um número natural. Vamos lá?
A sequência representa os números que são múltiplos de 2.
Os números da sequência são ditos múltiplos de 2, pois todos podem ser escritos como uma multiplicação de números naturais em que um dos fatores é 2.
E o 13, é múltiplo de 2?
Para confirmar essa informação, devemos encontrar um número natural que, multiplicado por 2, resulta em 13. Como e , é possível perceber que ele não existe. Portanto, 13 não é um múltiplo de 2.
Questão 1. Quando um número é múltiplo de
4? E
de 6?
Respostas: Um número é múltiplo de 4 quando pode ser escrito como uma multiplicação de números naturais em que um dos fatores é 4. Um número é múltiplo de 6 quando pode ser escrito como uma multiplicação de números naturais em que um dos fatores é 6.
Questão 2. Qual é a solução do problema
proposto no início deste tópico?
Resposta: 36 estudantes.
Atividades
Faça as atividades no caderno.
1. Considere os números 8, 15, 17, 12, 51, 23, 95, 800, 45, 19, 122 e 91. Quais deles são:
a) múltiplos de 2?
b) múltiplos de 10?
c) múltiplos de 5?
Respostas: a) 8, 12, 800 e 122; b) 800; c) 15, 95, 800 e 45.
2. Para comemorar o aniversário de seu filho, Joana comprou 24 bombons de morango e decidiu dividi-los igualmente em caixas. Quais são as possibilidades para montá-las com quantidades menores de bombons sem que algum bombom fique fora delas?
Resposta: 1, 2, 3, 4, 6, 8, 12.
3. Determine o número que substitui o no texto a seguir, de acordo com as dicas apresentadas.
Dica!
- É menor do que 2.000 e maior do que 1.000.
- O algarismo das dezenas é o 7.
- Não é múltiplo de 10, mas é múltiplo de 5.
- O algarismo das centenas é o 9.
O Dia Internacional da Mulher é celebrado anualmente em 8 de março e foi instituído pela Organização das Nações Unidas (ONU) no ano .

Resposta: 1975.
Página 15
Divisores
Para um dia de feira, Marcos, que é feirante, vai dividir 192 maçãs em caixas com 8 frutas cada. Quantas caixas ele vai usar? Sobrarão maçãs fora delas?
Esse é um problema relativamente simples, pois, para saber de quantas caixas Marcos vai precisar, é necessário dividir o total de maçãs pela quantidade que haverá em cada uma, ou seja, efetuar .
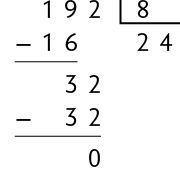
Atenção!
Como , verificamos que 8 é divisor de 192, mas 24 também o é.
Ao realizar a divisão, concluímos que Marcos vai usar 24 caixas e que não sobrarão maçãs fora delas. Nesse caso, podemos afirmar que 192 é divisível por 8 ou, ainda, que 8 é divisor de 192.
Vamos relembrar o conceito matemático de divisibilidade.
Um número natural é divisível por outro número natural não nulo quando a divisão do primeiro pelo segundo é exata, ou seja, tem resto igual a zero.
Levando em consideração o conceito apresentado, podemos relacionar as definições de múltiplos e divisores: se um número natural é divisível por outro, então o primeiro é múltiplo do segundo.
Relembrando alguns critérios de divisibilidade
Muitas vezes, é mais importante saber se um número é divisível por outro do que conhecer o resultado da divisão. Por isso, existem alguns critérios de divisibilidade que nos permitem saber essa resposta antes mesmo de efetuar divisões. Vamos relembrá-los?
Critério de divisibilidade por 2
Questão 3. Copie o quadro em seu caderno e complete-o.
Respostas nas orientações ao professor.
|
Número natural |
É divisível por 2? |
|---|---|
|
20 |
Sim |
|
35 |
Não |
|
48 |
|
|
66 |
|
|
89 |
Perceba que os números 35 e 89 não são múltiplos de 2 e que 20, 48 e 66 são. Há infinitos números que são divisíveis por 2, entre eles os apresentados anteriormente. Você sabe qual é a característica comum entre eles? Se respondeu que são pares, está correto!
Um número natural é divisível por 2 se for par.
Página 16
Critério de divisibilidade por 3
Para saber se um número é divisível por 3, basta adicionar os valores correspondentes aos algarismos dele. Se o resultado for divisível por 3, então o número também é. Vamos analisar dois exemplos.
17.846 é divisível por 3?
Adicionando os valores correspondentes aos algarismos, temos: . Como 26 não é divisível por 3, concluímos que 17.846 também não é.
7.194 é divisível por 3?
Adicionando os valores correspondentes aos algarismos, temos: . Como 21 é divisível por 3, concluímos que 7.194 também é.
Um número natural é divisível por 3 quando a soma dos valores correspondentes aos seus algarismos resulta em um número que também o é.
Questão 4. Considere os números 270, 202,
234 e 613. Quais são divisíveis
por 3?
Resposta: 270 e 234.
Critério de divisibilidade por 4
Questão 5. Copie o quadro em seu caderno e complete-o.
Resposta nas orientações ao professor.
|
Número natural |
Número formado pelos dois últimos algarismos da direita |
É divisível por 4? |
|---|---|---|
|
732 |
32 |
Sim |
|
500 |
00 |
Sim |
|
1.286 |
||
|
756 |
Você conseguiu perceber uma relação entre o número formado pelos dois últimos algarismos da direita e a divisibilidade por 4?
Um número natural com mais de dois algarismos é divisível por 4 se os dois últimos algarismos da direita formam, na ordem em que aparecem, um número divisível por 4 ou se são simultaneamente 0.
Vamos analisar alguns exemplos.
- 1.400 é divisível por 4, pois os dois últimos algarismos da direita são simultaneamente 0.
- 7.485 não é divisível por 4, pois os dois últimos algarismos da direita não são simultaneamente 0 nem formam um número (85) divisível por 4.
- 18.748 é divisível por 4, pois os dois últimos algarismos da direita formam um número (48) também divisível por 4.
Página 17
Critério de divisibilidade por 5
Analise o quadro. Você sabe qual é a característica comum entre os números divisíveis por 5? Se respondeu que é o fato de o algarismo das unidades ser 0 ou 5, você está correto.
|
Número natural |
Algarismo das unidades |
É divisível por 5? |
|---|---|---|
|
185 |
5 |
Sim |
|
244 |
4 |
Não |
|
750 |
0 |
Sim |
|
825 |
5 |
Sim |
|
888 |
8 |
Não |
Um número natural é divisível por 5 quando o algarismo das unidades é 0 ou 5.
Critério de divisibilidade por 6
Você já aprendeu e relembrou os critérios de divisibilidade por 2 e por 3. Agora, vamos aplicá-los para estabelecer a divisibilidade por 6.
Um número natural é divisível por 6 se o for por 2 e por 3 simultaneamente, ou seja, se for um número natural par e se a soma dos valores correspondentes aos seus algarismos for divisível por 3. Vamos analisar alguns exemplos.
1.848 é divisível por 6?
Como o número é par e , concluímos que sim, pois é divisível por 2 e por 3, simultaneamente.
179 é divisível por 6?
Não é par, logo não é divisível por 2. Portanto, também não é divisível por 6.
Um número natural é divisível por 6 quando também for divisível por 2 e 3, simultaneamente.
Critério de divisibilidade por 8
Para verificar se um número natural é divisível por 8, devemos analisar seus três últimos algarismos da direita.
Um número natural com mais de três algarismos é divisível por 8 se os três últimos algarismos da direita formam, na ordem em que aparecem, um número divisível por 8 ou se são simultaneamente 0.
Vamos analisar alguns exemplos.
- Os números 7.000, 12.000 e 13.000 são todos divisíveis por 8, pois os três últimos algarismos da direita são, simultaneamente, 0.
- O número 5.880 é divisível por 8, pois os últimos três algarismos da direita formam um número (880) também divisível por 8.
Página 18
Critério de divisibilidade por 9
Analise o quadro. Para saber se um número é divisível por 9, devemos analisar a soma dos valores correspondentes aos seus algarismos.
|
Número natural |
Soma dos valores correspondentes aos algarismos |
É divisível por 9? |
|---|---|---|
|
441 |
Sim |
|
|
321 |
Não |
|
|
741 |
Não |
|
|
2.302 |
Não |
|
|
3.870 |
Sim |
Um número natural é divisível por 9 quando a soma dos valores correspondentes aos seus algarismos é um número também divisível por 9.
Questão 6. Entre os números 270, 502, 738
e 907, quais são divisíveis por
9?
Resposta: 270 e 738.
Critério de divisibilidade por 10, 100 ou 1.000
Para saber se um número natural é divisível por 10, 100 ou 1.000, devemos analisar os seguintes critérios de divisibilidade.
Um número natural é divisível:
- por 10 se o algarismo das unidades for 0;
- por 100 se os algarismos das unidades e das dezenas forem simultaneamente 0;
- por 1.000 se os algarismos das unidades, dezenas e centenas forem simultaneamente 0.
Qualquer número cujo algarismo das unidades é diferente de 0 não é divisível por 10, 100 ou 1.000.
Questão 7. Todo número que é divisível por
100 é também divisível por 10?
Justifique sua resposta.
Resposta: Sim, pois todo número divisível por 100 tem os algarismos das unidades e das dezenas simultaneamente iguais a 0, o que satisfaz o critério de divisibilidade por 10.
Resumo dos critérios de divisibilidade
|
É divisível por... |
Quando? |
|---|---|
|
2 |
Se for um número par. |
|
3 |
Se a soma dos valores correspondentes aos seus algarismos for um número também divisível por 3. |
|
4 |
Se terminar com 00 ou se os dois últimos algarismos, na ordem em que aparecem, formarem um número divisível por 4. |
|
5 |
Se o algarismo das unidades for 0 ou 5. |
|
6 |
Se for divisível por 2 e por 3 simultaneamente. |
|
8 |
Se terminar com 000 ou se os três últimos algarismos, na ordem em que aparecem, formarem um número divisível por 8. |
|
9 |
Se a soma dos valores correspondentes aos seus algarismos for um número também divisível por 9. |
|
10 |
Se o algarismo das unidades for 0. |
|
100 |
Se os algarismos das unidades e dezenas forem simultaneamente 0. |
|
1.000 |
Se os algarismos das unidades, dezenas e centenas forem simultaneamente 0. |
Página 19
Atividades
Faça as atividades no caderno.
4. Considere , em que indica o algarismo das unidades. Por qual algarismo podemos substituir para que o número formado seja:
a) divisível por 2?
Resposta: 0, 2, 4, 6 ou 8.
b) divisível por 3?
Resposta: 2, 5 ou 8.
c) divisível por 5?
Resposta: 0 ou 5.
d) divisível por 10?
Resposta: 0.
e) divisível por 100?
Resposta: Não há valor para que torne o número divisível por 100.
5. Analise cada item e responda às questões em seu caderno.
a) Qual é o único número que é divisor de todos os números naturais?
Resposta: 1.
b) Qual é o maior divisor de um número natural?
Resposta: O próprio número.
c) Qual é a quantidade mínima de divisores que um número natural maior do que 1 pode ter?
Resposta: Dois.
6. Determine o número que substitui o adequadamente. Porém, ele deve ser menor do que 1.000 e formado pelos seguintes algarismos: 2, 3, 4, 5 ou 7.
a) é divisível por 2.
Sugestões de resposta: 342, 754 e 254.
b) é divisível por 3.
Sugestões de resposta: 234, 732 e 534.
c) é divisível por 5.
Sugestões de resposta: 235, 725 e 345.
d) é divisível por 6.
Sugestões de resposta: 42, 324 e 372.
e) é divisível por 8.
Sugestões de resposta: 24, 352 e 752.
f) é divisível por 9.
Sugestões de resposta: 27, 234 e 423.
7. Uma professora de Matemática decidiu realizar com o 7º ano um trabalho em grupo. Sabendo que todos os grupos devem ter a mesma quantidade de membros, quantos estudantes pode haver em cada grupo se a turma for composta de:
a) 40 estudantes?
Resposta: Os grupos podem ter 2, 4, 5, 8, 10 ou 20 estudantes.
b) 45 estudantes?
Resposta: Os grupos podem ter 3, 5, 9 ou 15 estudantes.
c) 50 estudantes?
Resposta: Os grupos podem ter 2, 5, 10 ou 25 estudantes.
8. Copie o quadro em seu caderno. Depois, complete-o marcando um X nas células que indicam os divisores dos números apresentados.
|
Número |
Divisor |
|||
|---|---|---|---|---|
|
2 |
3 |
5 |
10 |
|
|
8.492 |
||||
|
3.750 |
||||
|
1.899 |
||||
Respostas nas orientações ao professor.
9. O quadro apresenta os números de 1 a 50.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
Quais desses números são:
a) divisíveis por 3?
Resposta: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45 e 48.
b) divisíveis por 5?
Resposta: 5, 10, 15, 20, 25, 30, 35, 40, 45 e 50.
c) divisíveis por 8?
Resposta: 8, 16, 24, 32, 40 e 48.
d) divisíveis por 10?
Resposta: 10, 20, 30, 40 e 50.
10. Elabore dois problemas em seu caderno: um envolvendo múltiplos e outro compreendendo divisores, ambos de números naturais. Em seguida, peça a um colega que os resolva. Por fim, verifique se a resolução proposta por ele está correta.
Resposta pessoal.
Página 20
Números primos
Você lembra o que são números primos? Um número natural maior do que 1 é dito primo quando apresenta somente dois divisores: o 1 e ele próprio. Números naturais maiores do que 1 com mais de dois divisores são chamados números compostos.
O número 2 é o menor número natural primo e é o único par.
Questão 8. Por que não há, além do 2,
outros números primos pares?
Resposta: Os outros números pares não são primos porque eles têm, no mínimo, três divisores (o 1, o 2 e eles próprios).
Agora, vamos identificar quais são os números primos menores do que 100 utilizando o Crivo de Eratóstenes, criado pelo matemático grego Eratóstenes de Cirene (276 a.C.-194 a.C.). Para isso, executamos os seguintes passos.
1. Inicialmente, construímos um quadro com os números de 1 a 100.
2. Em seguida, riscamos o número 1.
3. Contornamos os números 2, 3, 5 e 7, que são primos, pois têm apenas dois divisores (o 1 e eles próprios).
4. Riscamos todos os múltiplos de 2, 3, 5 e 7, pois têm ao menos três divisores e, consequentemente, não são primos.
5. Por fim, contornamos todos os números que sobraram no quadro.


Página 21
Seguindo os passos apresentados na página anterior, obtemos os números primos menores do que 100. São eles:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89 e 97.
Você já ouviu falar em números primos entre si? São os números que têm como maior divisor comum entre eles o 1.
No quadro temos alguns exemplos de números que são primos entre si.
12
18
42
49
25
115
Perceba que, mesmo os números do quadro não sendo primos, pois têm mais de dois divisores, são primos entre si, já que o único divisor comum entre eles é o número 1.
Questão 9. Considere os números 2, 6, 7, 15, 18, 26 e 35. Agora, em seu caderno, forme 4 pares com esses números, de maneira que sejam primos entre si.
Sugestão de resposta: 2 e 15; 6 e 7; 6 e 35; 15 e 26.
Decomposição em fatores primos
Todos os números compostos podem ser decompostos. Há diversas maneiras de fazer isso. Analise, por exemplo, algumas possibilidades para o número 32.
Note que em os fatores da multiplicação são números primos. Assim, dizemos que essa é a decomposição em fatores primos do número 32.
Escrever um número composto por meio da multiplicação de outros números primos significa decompô-lo em fatores primos.
Para decompor um número em fatores primos, devemos realizar divisões por números primos, até que o resultado seja 1. Vamos decompor desse modo, por exemplo, o número 60. Nesse caso, vamos começar pelo menor número primo possível, o 2.
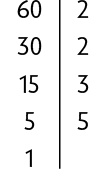
Assim, podemos escrever .
Página 22
Atividades
Faça as atividades no caderno.
11. Em seu caderno, escreva os números de 100 a 150 em um quadro. Em seguida, utilizando o Crivo de Eratóstenes, determine quais são primos.
Resposta: 101, 103, 107, 109, 113, 127, 131, 137, 139, 149.
12. Classifique as afirmações em verdadeiras ou falsas. Em seguida, em seu caderno, reescreva as falsas, corrigindo-as.
a) Todos os números primos são ímpares.
Resposta: Falsa. Sugestão de correção: Nem todos os números primos são ímpares.
b) A decomposição em fatores primos do número 342 é .
Resposta: Falsa. Sugestão de correção: A decomposição em fatores primos do número 342 é .
c) O menor número primo é o 2.
Resposta: Verdadeira.
d) O menor número primo maior do que 150 é 151.
Resposta: Verdadeira.
13. Decomponha os números em fatores primos.
a) 72
b) 100
c) 121
Respostas: a) ; b) ; c) .
14. Analise o quadro.
|
Número |
Divisores do número |
|---|---|
|
22 |
1, 2, 11, 22 |
|
23 |
1, 23 |
|
24 |
1, 2, 3, 4, 6, 8, 12, 24 |
|
25 |
1, 5, 25 |
|
26 |
1, 2, 13, 26 |
a) Quais números primos aparecem como divisores no quadro?
b) Quais são os divisores primos do número 24?
Respostas: a) 2, 3, 5, 11, 13 e 23; b) 2 e 3.
15. Na Antiguidade, as pessoas baseavam os calendários nos fenômenos que aconteciam regularmente, como posição do Sol, alteração das fases da Lua, época de plantio e colheita. Ao longo do tempo, diferentes civilizações desenvolveram calendários até chegar ao modelo que temos hoje, que é usado para marcar a passagem dos dias.
Analisando os dias de um calendário do mês de março, identifique quais dos números apresentados são primos.

Resposta: 2, 3, 5, 7, 11, 13, 17, 19 e 23.
16. Escreva, quando possível, o menor número natural formado pelos algarismos 2, 3 e 5, sem repeti-los, de modo que ele seja:
a) múltiplo de 5.
Resposta: 235.
b) múltiplo de 3.
Resposta: Não é possível, pois a soma dos algarismos não resulta em um número múltiplo de 3.
c) múltiplo de 2.
Resposta: 352.
Utilizando esses algarismos, sem repeti-los, é possível escrever um número primo de três algarismos? Se sim, apresente-o.
Resposta: Sim. 523 é primo.
Página 23
Máximo divisor comum
Para decorar a festa de aniversário de sua filha, Bianca comprou de fita branca e de fita rosa. Elas serão cortadas em pedaços iguais e com o comprimento de maior medida possível, sem que haja sobra de fita.
Vamos ajudar Bianca a verificar quanto deverá medir o comprimento de cada pedaço de fita. Para isso, procedemos da seguinte maneira.
1. Escrevemos a sequência dos divisores de 10, correspondente à medida do comprimento da fita branca.
1, 2, 5, 10.
2. Escrevemos a sequência dos divisores de 12, correspondente à medida do comprimento da fita rosa.
1, 2, 3, 4, 6, 12.
Os divisores comuns às duas sequências são 1 e 2. Nesse caso, o maior divisor comum de 10 e 12 é 2.
Assim, 2 é o máximo divisor comum de 10 e 12.
Indicamos esse fato por:
Portanto, o comprimento de cada pedaço de fita deve medir .
Vamos analisar outro caso. Considere as sequências.
- Divisores de 30: 1, 2, 3, 5, 6, 10, 15, 30.
- Divisores de 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80.
Ao analisarmos essas sequências, concluímos que os números 30 e 80 têm como divisores comuns: 1, 2, 5 e 10, sendo 10 o maior entre eles. Portanto, .
Dados dois ou mais números naturais não nulos, denomina-se máximo divisor comum (mdc) deles o maior de seus divisores comuns.
Questão 10. Calcule em seu caderno.
a)
b)
c)
d)
e)
f)
Respostas: a) 1; b) 12; c) 2; d) 1; e) 9; f) 1.
Página 24
Mínimo múltiplo comum
Em certo país, o presidente é eleito de 4 em 4 anos e os senadores de 6 em 6 anos. As eleições para esses dois cargos coincidiram em 2004.

Atenção!
O período para as eleições, em geral, muda de um país para outro. No Brasil, a votação para presidente e para senador ocorre de 4 em 4 anos. Na foto, temos a representação do Senado (prédio à esquerda) e da Câmara (prédio à direita), que formam o Congresso Nacional, um dos cartões-postais de Brasília, a capital do país.
Caso não ocorra nenhuma mudança política, depois de quantos anos elas coincidirão novamente?
Podemos resolver o problema proposto da seguinte maneira.
1. Escrevemos a sequência dos múltiplos de 4, correspondente às eleições para presidente.
2. Escrevemos a sequência dos múltiplos de 6, correspondente às eleições para senadores.
Os múltiplos comuns às duas sequências são Nesse caso, o menor múltiplo comum de 4 e 6 diferente de zero é 12.
Assim, 12 é o mínimo múltiplo comum de 4 e 6. Indicamos esse fato por:
Portanto, as eleições para esses dois cargos coincidirão novamente depois de 12 anos.
Dados dois ou mais números naturais não nulos, denomina-se mínimo múltiplo comum () deles o menor de seus múltiplos comuns diferente de zero.
Página 25
Atividades
Faça as atividades no caderno.
17. Resolva no caderno as questões a seguir.
a) Quais são os divisores do número 30?
b) Quais são os divisores comuns dos números 18 e 50?
c) Qual é o maior divisor comum dos números 50 e 75?
Respostas: a) 1, 2, 3, 5, 6, 10, 15 e 30; b) 1 e 2; c) 25.
18. Resolva no caderno o que se pede nos itens.
a) Quais são os múltiplos positivos de 3 menores do que 50?
Resposta: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45 e 48.
b) Quais são os múltiplos positivos de 5 menores do que 50?
Resposta: 5, 10, 15, 20, 25, 30, 35, 40 e 45.
c) Quais são os múltiplos positivos comuns de 3 e 5 menores do que 50?
Resposta: 15, 30 e 45.
d) Qual é o menor múltiplo comum de 3 e 5 diferente de zero?
Resposta: 15.
19. Em seu caderno, calcule:
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
i) .
j) .
k) .
l) .
Respostas: a) 60; b) 18; c) 300; d) 72; e) 48; f) 360; g) 3; h) 4; i) 1; j) 10; k) 2; l) 16.
20. Calcule o mmc dos seguintes números primos.
a) 2 e 3.
b) 3 e 5.
c) 5 e 13.
d) 2, 7 e 11.
e) 5 e 41.
f) 2 e 7.
g) 11 e 13.
h) 5 e 11.
i) 7 e 13.
j) 19 e 37.
Respostas: a) 6; b) 15; c) 65; d) 154; e) 205; f) 14; g) 143; h) 55; i) 91; j) 703.
21. O que você pôde verificar no resultado do mmc dos números primos da atividade anterior?
Resposta pessoal. Espera-se que os estudantes digam que o mmc de dois ou mais números primos é igual ao produto deles.
22. Determine o mmc dos seguintes números naturais consecutivos.
a) 4 e 5.
b) 6 e 7.
c) 8 e 9.
d) 10 e 11.
e) 12 e 13.
f) 14 e 15.
g) 16 e 17.
h) 18 e 19.
i) 20 e 21.
j) 22 e 23.
Respostas: a) 20; b) 42; c) 72; d) 110; e) 156; f) 210; g) 272; h) 342; i) 420; j) 506.
23. O que você pôde verificar no resultado do mmc dos números naturais consecutivos da atividade anterior?
Resposta pessoal. Espera-se que os estudantes digam que o mmc de dois números naturais consecutivos é igual ao produto deles.
24. Em cada item, o maior número é múltiplo dos menores. Calcule o mmc deles.
a) 3 e 9.
b) 5 e 35.
c) 2, 4 e 24.
d) 10 e 20.
e) 5 e 15.
f) 18 e 36.
g) 15 e 30.
h) 7, 21 e 42.
i) 20 e 40.
j) 12 e 48.
Respostas: a) 9; b) 35; c) 24; d) 20; e) 15; f) 36; g) 30; h) 42; i) 40; j) 48.
Página 26
25. O que você pôde verificar no resultado do mmc dos itens da atividade anterior?
Resposta pessoal. Espera-se que os estudantes digam que o mmc de dois ou mais números diferentes de zero é igual ao maior deles, desde que ele seja múltiplo dos demais.
26. A professora de uma turma do 8º ano quer separar os estudantes em grupos para realizar uma atividade. Ela verificou que é possível uma divisão em equipes com 3, 4, 6 ou 12 integrantes, sem que sobre alguém. Determine o total de estudantes dessa turma, sabendo que esse número está entre 30 e 40.
Resposta: 36 estudantes.
27. O médico de João receitou-lhe dois medicamentos: um deve ser tomado de 8 em 8 horas; o outro, de 12 em 12 horas. João ingeriu os dois remédios juntos às 6 horas da manhã. Depois de quantas horas ele os tomará juntos novamente?
Resposta: Depois de 24 horas.
28. Em uma decoração, há luminosos brancos, vermelhos e amarelos. Os brancos acendem a cada 8 segundos; os vermelhos, a cada 15 segundos; e os amarelos, a cada 20 segundos. Em determinado instante, os luminosos das três cores acenderam ao mesmo tempo. Depois de quantos segundos eles estarão acesos juntos novamente?
Resposta: Depois de 120 segundos.
29. Resolva
os itens em seu caderno.
a) O mínimo múltiplo comum de dois números é 45. Quais são eles, sabendo que um é o triplo do outro?
b) O máximo divisor comum de dois números é 1, e a diferença entre eles é 2. Cite dois números que tenham essas características.
Respostas: a) 15 e 45; b) Sugestão de resposta: 3 e 5.
30. Elabore dois problemas em seu caderno: um envolvendo o conceito de mínimo múltiplo comum e outro compreendendo a definição de máximo divisor comum. Depois, peça a um colega que os resolva.
Resposta pessoal.
31. Determine
o maior número possível pelo qual devemos
dividir 216 e 169 para obter os restos 6 e 1,
respectivamente.
Resposta: 42.
32. Que procedimentos você utilizou para resolver a atividade 28? Usando-os, é possível solucionar algum dos problemas propostos a seguir? Se sim, qual?
Resposta na seção Resoluções.
a) De uma rodoviária, saem todos os dias três ônibus que fazem rotas nacionais. O primeiro demora 4 horas para realizar seu percurso e retornar para a rodoviária; o outro leva 5 horas para isso; e o terceiro, 10 horas. Sabendo que hoje eles partiram juntos da rodoviária, depois de quantas horas sairão novamente ao mesmo tempo?
b) Para costurar peças de roupa, Larissa precisa dividir em pedaços menores, com a mesma medida de comprimento, dois tecidos: um azul e outro vermelho, cujos comprimentos medem e , respectivamente. Sabendo que ela pretende deixar esses pedaços com a maior medida de comprimento possível sem que haja sobra de tecido, determine a medida do comprimento de cada um.
c) Dois médicos e uma enfermeira fizeram plantão dia 3 de março. Os plantões dos médicos acontecem a cada 6 e 8 dias, respectivamente, enquanto os da enfermeira ocorrem a cada 4 dias. Qual será a próxima data em que os três trabalharão juntos novamente?
Agora, resolva os problemas propostos.
Respostas: a) 20 horas; b) 6 cm; c) 27 de março.
Página 27
Utilizando a decomposição em fatores primos para calcular o mmc e o mdc
Nesta unidade, estudamos a decomposição de números em fatores primos. Agora, vamos utilizá-la para nos auxiliar no cálculo do mmc e do mdc de dois ou mais números naturais.
Máximo divisor comum
Para determinar o mdc de dois números usando a decomposição em fatores primos, realizamos as seguintes etapas.
1. Decompomos os números em fatores primos.
2. Identificamos os fatores comuns.
3. Multiplicamos os fatores comuns às duas decomposições, obtendo, assim, o mdc.
Utilizando esse passo a passo, vamos calcular o .
1. Realizamos a decomposição dos números.
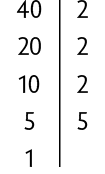
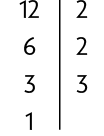
2.Os fatores comuns estão contornados.


3. Calculamos o produto dos fatores comuns.
Portanto, .
Questão 11. Utilizando a decomposição em fatores primos, calcule em seu caderno o .
Resposta: 16.
Página 28
Mínimo múltiplo comum
Você se lembra de como resolvemos o problema a respeito da eleição para presidência e senado? Como o presidente é eleito de 4 em 4 anos e os senadores de 6 em 6 anos, nós listamos múltiplos desses números e localizamos o menor não nulo, e assim determinamos o .
Agora, vamos calcular esse mmc utilizando a decomposição em fatores primos. Para isso, executamos as seguintes etapas.
1. Decompomos simultaneamente os números em fatores primos.
Etapa 1
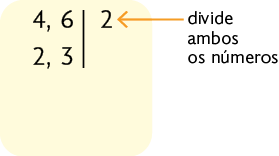
Etapa 2
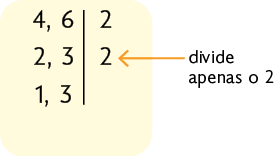
Etapa 3
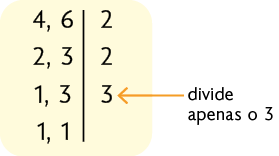
Atenção!
Em algumas etapas, note que o fator divide somente um dos números. Lembre-se também de que você deve utilizar sempre números primos.
2. Multiplicamos os fatores obtidos, calculando, assim, o mmc.
Agora, usando esse passo a passo, vamos calcular o .
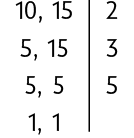
O é dado pelo produto dos fatores obtidos na decomposição, ou seja:
Questão 12. Utilizando a decomposição em fatores primos, calcule em seu caderno o .
Resposta: 96.
Questão 13.
Junte-se
a um colega e explique-lhe, com suas palavras, como você calcula o:
a) mínimo múltiplo comumss de dois números não nulos.
b) máximo divisor comum de dois números não nulos.
Respostas: a) Resposta pessoal; b) Resposta pessoal.
Página 29
Atividades
Faça as atividades no caderno.
33. Luciana vende fones de ouvido em uma loja. No primeiro dia, ela vendeu R$ 240,00; no segundo, R$ 180,00; e no terceiro, R$ 320,00. Sabendo que o preço é o maior possível, quantos fones Luciana vendeu ao todo nesses três dias?
Resposta: 37 fones.
34. O mínimo múltiplo comum de dois números é 50. Quais são eles, sabendo que o menor número é metade do maior?
Resposta: 25 e 50.
35. Carla está tomando algumas vitaminas por orientação médica. Uma deve ser ingerida de 8 em 8 horas; a outra, de 6 em 6 horas. Ela as tomou juntas às 8 horas da manhã. Após quantas horas Carla vai ingerir as vitaminas ao mesmo tempo novamente?
Resposta: 24 horas.
36. Rafaela está preparando pratos de doces para uma festa de aniversário. Ela tem 36 cajuzinhos e 42 casadinhos. Sabendo que ela deseja separá-los em pratos com a mesma quantidade, sem misturá-los, e utilizar o mínimo de recipientes possível, determine a quantidade de doces que Rafaela deverá colocar em cada prato.
Resposta: 6 doces.
37. Tobias coleciona ímãs de geladeira das viagens que realiza. Ele tem 165 ímãs que comprou em viagens ao Nordeste do país, 220 em passeios ao Norte, e 275 em idas ao Sul. Sabendo que ele deseja organizar sua coleção em caixas com igual quantidade de ímãs, cada uma com a maior quantia possível e apenas com objetos comprados na mesma região, determine quantos ímãs ele deve colocar em cada caixa.
Resposta: 55 ímãs.
38. Quando
Rodrigo junta suas bolinhas de gude em grupos com 2, 3, 4, 5 ou 6 bolinhas, sobra 1. Quando as
agrupa em 7,
não sobram bolinhas. Quantas bolinhas de gude ele
tem?
Resposta: 301 bolinhas.

39. é o maior divisor comum de 48, 74 e 120. Qual é esse número?
Resposta: 2.
40. Em uma pista de caminhada, Paulo, Aline e Tiago fazem seus exercícios diários. Paulo demora 30 minutos para dar uma volta completa, Aline leva 20 minutos, e Tiago, que anda mais rápido, faz o percurso em apenas 15 minutos. Os três partiram de certo ponto no mesmo instante. Depois de quantas horas, mantendo o mesmo ritmo de caminhada, eles se encontrarão novamente nesse local?
Resposta: 1 hora.
41. Theo tem uma coleção de bolinhas de gude, sendo 180 roxas e 220 azuis. Ele deseja organizá-las em caixas com a mesma quantidade de bolinhas, de modo que em cada uma tenha somente bolinhas de mesma cor e que a quantidade de recipientes utilizados seja a menor possível. Quantas caixas ele vai usar?
Resposta: 20 caixas.
Página 30
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Resolva os itens a seguir.
a) A soma de dois números naturais é 30. Quais são eles, sabendo que pertencem à sequência dos números primos e que, nessa sequência, são consecutivos.
b) A soma de quatro números naturais é 168. Quais são eles, sabendo que pertencem à sequência dos números primos e que, nessa sequência, são consecutivos.
c) O produto de dois números naturais é 899. Quais são eles, sabendo que são menores do que 50, pertencem à sequência dos números primos e que, nessa sequência, são consecutivos.
Respostas: a) 13 e 17; b) 37, 41, 43 e 47; c) 29 e 31.
2. Qual é o produto entre o único número primo par e o maior número primo de:
a) 1 algarismo?
b) 2 algarismos?
Respostas: a) 14; b) 194.
3. Copie o quadro e complete-o de maneira que todos os números do quadro sejam primos entre si.
14
50
39
Respostas na seção Respostas e na seção Resoluções.
4. Resolva os itens a seguir.
a) Quais são os 15 primeiros múltiplos de 4?
Resposta: 0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52 e 56.
b) Quais são os 10 primeiros múltiplos de 7?
Resposta: 0, 7, 14, 21, 28, 35, 42, 49, 56 e 63.
c) Quais são os 3 primeiros múltiplos comuns de 4 e 7?
Resposta: 0, 28 e 56.
d) Qual é o ?
Resposta: 28.
e) Qual é o ?
Resposta: 1.
f) Analisando a resposta ao item e, o que podemos afirmar a respeito dos números 4 e 7?
Resposta: São números primos entre si.
5. Qual é o menor número natural maior do que 1 que, dividido por 2, 3, 4, 5, 6 e 7, tem resto 1?
Resposta: 421.
6. Ana estava competindo com o seu pai em um jogo de tabuleiro. Nas instruções, ela descobriu que há 162 fichas azuis e 90 fichas laranjas nesse jogo, todas com dimensões de mesma medida. Eles decidiram empilhá-las de maneira que em cada agrupamento haja apenas fichas da mesma cor e que todos tenham a mesma medida de altura. Qual é a menor quantidade de pilhas que se pode formar?
Resposta: 14 pilhas de fichas.
7. Maicon, Renata e Laura são irmãos e não moram na mesma cidade que a mãe. Eles a visitam com a seguinte frequência: Maicon, a cada 10 dias, Renata, a cada 12 e Laura, a cada 18. Para cada item, calcule a frequência com que os filhos se encontram na casa da mãe.
a) Maicon e Renata.
b) Maicon e Laura.
c) Maicon, Renata e Laura.
d) Renata e Laura.
Respostas: a) A cada 60 dias; b) A cada 90 dias; c) A cada 180 dias; d) A cada 36 dias.
8. Beatriz comprou 36 rosas e 28 margaridas para fazer arranjos, todos com a mesma quantidade de flores de cada tipo. Sabendo que não podem sobrar rosas nem margaridas e que os arranjos devem ter a mesma quantidade de flores, determine a quantidade máxima de arranjos que Beatriz pode fazer.
Resposta: 4 arranjos.