Página 31
UNIDADE
2
Os números inteiros

Agora vamos estudar...
- os números inteiros;
- os números inteiros na reta numérica;
- a comparação entre números inteiros;
- adição com números inteiros;
- subtração com números inteiros;
- multiplicação com números inteiros;
- divisão com números inteiros;
- potenciação de números inteiros.
Página 32
Números positivos e números negativos
Em algumas situações do dia a dia, precisamos utilizar outros números, além dos números naturais.
No mapa, por exemplo, estão indicadas as medidas de temperaturas mínimas, em graus Celsius, registradas em algumas cidades brasileiras no dia 30 de julho de 2021.
Medidas de temperaturas mínimas registradas em algumas cidades brasileiras, em 30 de julho de 2021
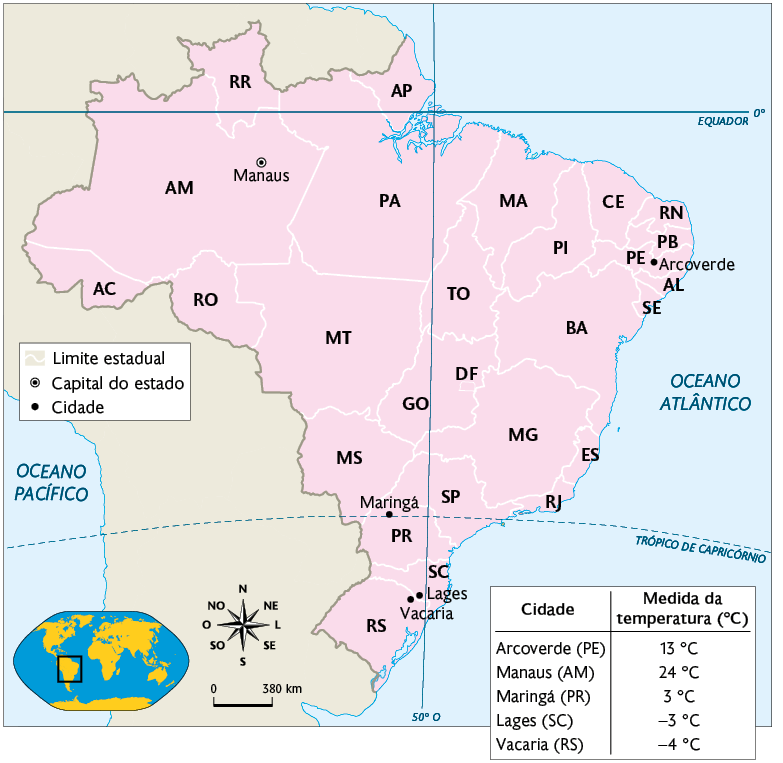
Fontes de pesquisa: INMET. Dados meteorológicos. Disponível em: https://oeds.link/CwKiZd. Acesso em: 12 jan. 2022.
ATLAS geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.
Questão 1. Os estados em que se localizam
as cidades destacadas no mapa
fazem fronteira com quais outros estados?
Resposta nas orientações ao professor.
Nesse dia, a medida de temperatura mínima registrada na cidade de Lages (SC) foi de , ou seja, uma temperatura com medida abaixo de zero. Para representar essa medida de temperatura, usamos o número , que é um número negativo.
Já na cidade de Arcoverde (PE), a medida de temperatura mínima registrada foi , ou seja, uma temperatura com medida acima de zero. O número 13, que representa essa medida de temperatura, é um número positivo.
Página 33
Os termômetros de álcool colorido estavam da seguinte forma ao registrarem as medidas de temperaturas mínimas nessas duas cidades no dia 30 de julho de 2021.
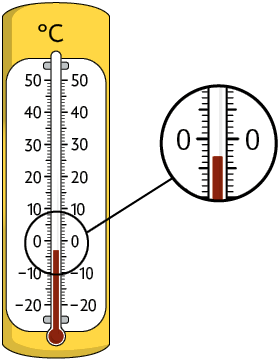
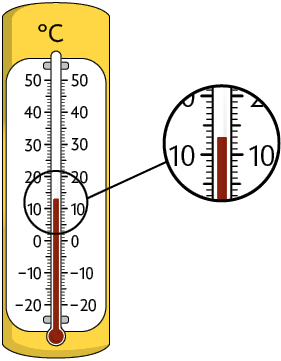
Para representar os números negativos, utilizamos o sinal . Esses números são menores do que 0 (zero).
Para representar os números positivos, utilizamos o sinal ou nenhum sinal. Esses números são maiores do que 0 (zero).
A seguir, alguns exemplos de números negativos e números positivos.
Números negativos
Números positivos
-
0,01
-
108,7
Atenção!
O número zero não é negativo nem positivo.
Questão 2. Analise os números
representados e responda às questões.
-
0
a) Quais números são negativos?
b) Quais números são maiores do que zero?
c) Que número não é negativo nem positivo?
Respostas: a) , e ; b) e ; c) 0 (zero).
Página 34
Atividades
Faça as atividades no caderno.
1. Em cada termômetro está registrada a medida de temperatura mínima de uma das cidades mostradas no mapa da página 32. Associe os termômetros às cidades citadas.
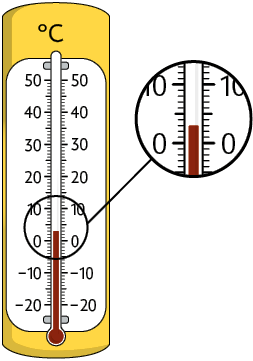
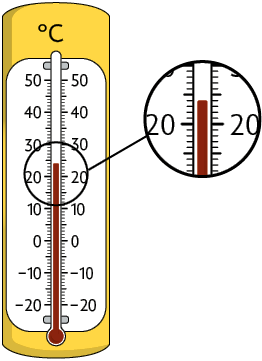
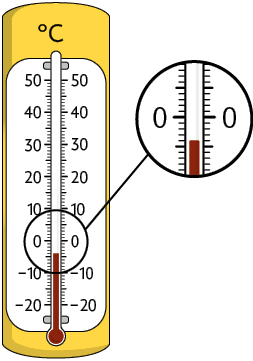
Respostas: A. Maringá (PR); B. Manaus (AM); C. Vacaria (RS).
2. Analise as medidas de temperaturas registradas nos termômetros.
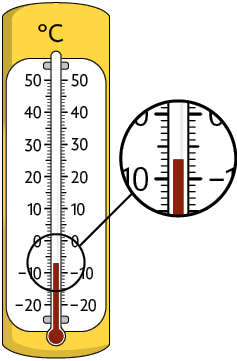
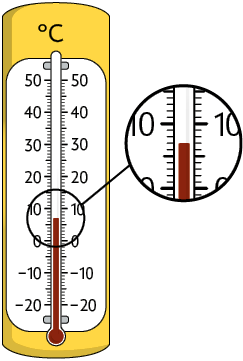
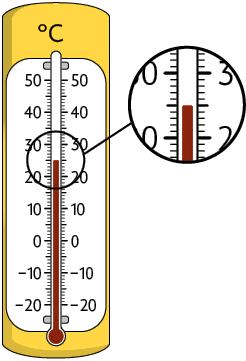
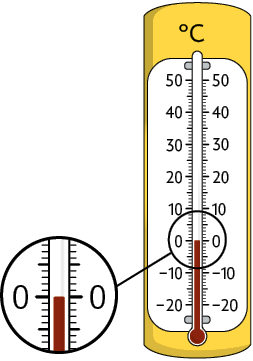
a) Qual deles está indicando a maior medida de temperatura? E qual está indicando a menor medida de temperatura?
b) Associe cada termômetro a uma das medidas de temperaturas indicadas a seguir.
Respostas: a) Termômetro C; termômetro A; b) Termômetro A e , termômetro B e , termômetro C e , termômetro D e .
Página 35
3. Além dos termômetros de álcool colorido, como os apresentados anteriormente, existem os termômetros digitais. Analise a medida de temperatura indicada no visor de cada termômetro digital a seguir.


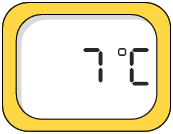
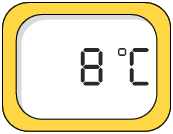
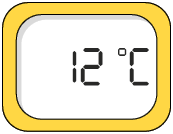
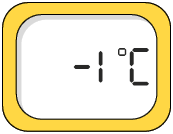
a) Quais termômetros estão indicando uma temperatura com medida negativa?
Resposta: Termômetros B e F.
b) Na escala Celsius, o zero corresponde à medida de temperatura em que, sob certas condições, ocorre a solidificação da água, ou seja, ela passa do estado líquido para o estado sólido. Em quais ambientes, cujas medidas de temperaturas estão indicadas nesses termômetros, a água estaria no estado líquido? E no estado sólido?
Respostas: A, C, D e E; B e F.
c) Qual dos termômetros está indicando uma medida de temperatura agradável para o corpo humano? Justifique sua resposta.
Resposta pessoal. Espera-se que os estudantes respondam que é o termômetro A, pois apresenta uma medida de temperatura mais próxima à medida de temperatura do corpo humano.
4. Analise o gráfico e responda às questões.
Medida de temperatura média mensal da cidade de Montreal, Canadá, em 2021
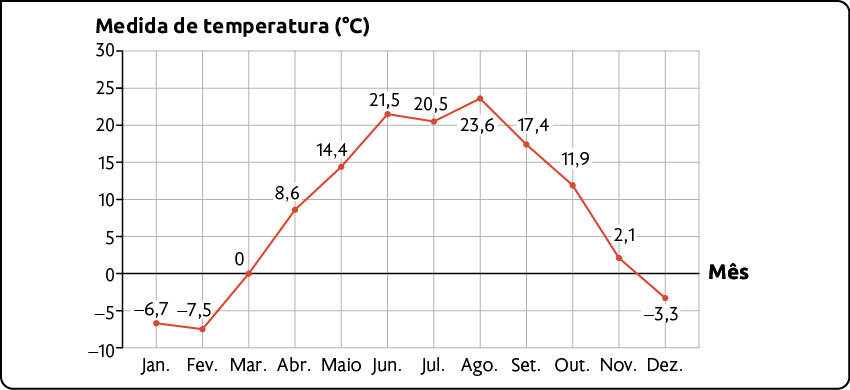
Fonte de pesquisa: CHARTS. Weather Dashboard for Montreal. Disponível em: https://oeds.link/ZGI5ar. Acesso em: 17 jan. 2022.
a) Em quais meses de 2021 a medida de temperatura média mensal esteve abaixo de zero?
Resposta: Janeiro, fevereiro e dezembro.
b) Nesse ano, em qual mês foi registrada a maior medida de temperatura média mensal? Qual foi essa medida?
Respostas: Agosto; .
c) Em quais meses a medida de temperatura média foi maior do que ?
Resposta: Maio, junho, julho, agosto, setembro e outubro.
Página 36
5. Em cada item, estime a medida de temperatura mais adequada à situação e registre-a no caderno.
a) Medida de temperatura normal do corpo humano.
Resposta pessoal. Espera-se que os estudantes respondam .
b) Medida de temperatura da água em ebulição.

Resposta pessoal. Espera-se que os estudantes respondam .
c) Medida de temperatura no interior do congelador de uma geladeira.

Resposta pessoal. Espera-se que os estudantes respondam .
d) Medida de temperatura do filamento de uma lâmpada incandescente quando acesa.

Resposta pessoal. Espera-se que os estudantes respondam .
e) Medida da temperatura ambiente da Antártida em certo dia do ano.

Resposta pessoal. Espera-se que os estudantes respondam .
f) Medida de temperatura de um forno pré-aquecido para assar pão.

Resposta pessoal. Espera-se que os estudantes respondam .
Página 37
6. Quando o saldo da conta bancária de um cliente é negativo, significa que ele deve dinheiro ao banco; quando é positivo, significa que ele tem dinheiro disponível em sua conta.
Considere o extrato bancário de Márcio.
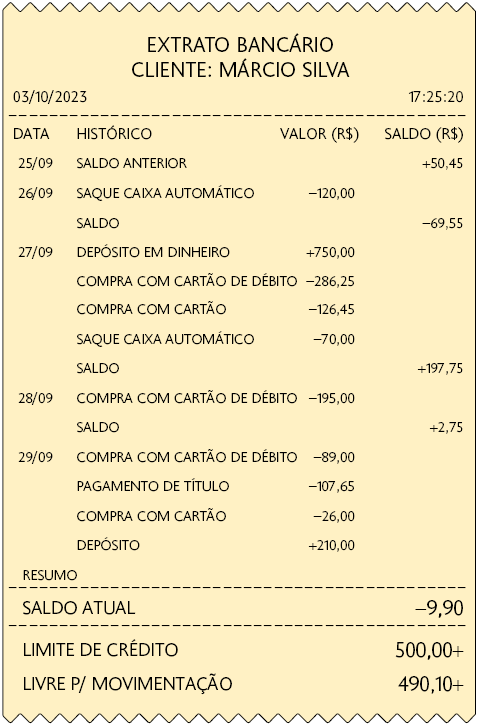
a) Em quais dias o saldo de Márcio estava positivo? E em quais dias estava negativo?
b) Em qual dia Márcio fez uma compra com cartão no valor de R$ 26,00?
c) O que está indicado no histórico do extrato quando ocorreu um débito de R$ 286,25?
d) Qual era o saldo de Márcio ao final do dia 28/09?
e) A partir das informações apresentadas no extrato bancário, elabore um problema e dê para um colega resolver. Depois, verifique se a resposta dele está correta.
Respostas: a) Positivo: 25/09, 27/09 e 28/09, negativo: 26/09 e 29/09; b) 29/09; c) Compra com cartão de débito; d) R$ 2,75; e) Resposta pessoal.
7. Para indicarmos altitudes, geralmente utilizamos o nível do mar como referência. Quando a altitude indicada está acima do nível do mar, temos uma medida de altitude positiva, e, quando está abaixo do nível do mar, temos uma medida de altitude negativa. Leia as informações a seguir e, usando números positivos ou números negativos, escreva no caderno as medidas de altitudes citadas.
a) A Fossa das Marianas, localizada no oceano Pacífico, tem de medida de profundidade em relação ao nível do mar. Esse é o ponto mais profundo do planeta Terra.
b) Localizada no norte do Paquistão, a montanha K2 é a segunda mais alta do mundo, com medida de altitude de aproximadamente .
c) Localizado na Ásia, entre Israel e Jordânia, o Mar Morto está abaixo do nível do mar. Devido à grande quantidade de sal em suas águas, é praticamente impossível a existência de seres vivos em suas águas ou nas proximidades.
d) Localizado no estado do Amazonas, o Pico da Neblina é a montanha mais alta do Brasil, com aproximadamente de medida de altitude.
e) Localizado no norte da Tanzânia, o Kilimanjaro é a montanha mais alta do continente africano, cuja altitude mede .
Respostas: a) ; b) Aproximadamente ; c) ; d) Aproximadamente ; e) .
Página 38
Os números inteiros na reta numérica
Neste tópico, vamos estudar como representar alguns números na reta numérica. Para isso, considere os números das fichas.
A. 5
B.
C.
D.
E. 2
F. 6
Para representá-los, traçamos inicialmente uma reta e nela indicamos a origem, indicada pelo ponto O, que corresponde ao número zero (0).

Em seguida, convencionamos que à direita de O o sentido é positivo e que à esquerda de O o sentido é negativo.
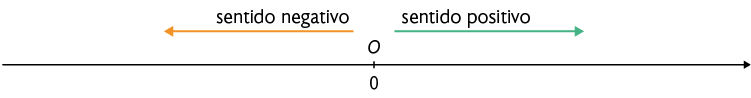
Na sequência, escolhemos um ponto U na reta à direita de O e adotamos a medida do comprimento do segmento de reta OU como unidade de medida.
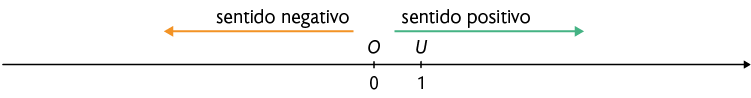
Depois, destacamos essa unidade nos dois sentidos da reta.
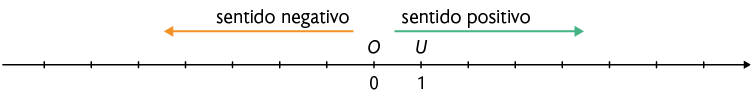
Em seguida, associamos cada unidade na reta numérica ao número positivo ou ao número negativo correspondente. Por último, registramos os números das fichas do início da página, indicando-os com letras.
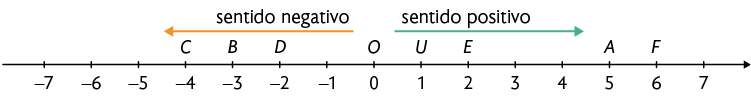
Página 39
Na reta numérica apresentada na página 38, aparecem números naturais e números inteiros negativos.
Números inteiros negativos
..., , , , , , ,
Números naturais
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...
Ao reunirmos os números naturais com os números inteiros negativos, obtemos os números inteiros.
Números inteiros
..., , , , , , 0, 1, 2, 3, 4, 5, ...
Atenção!
Os números naturais podem ou não vir acompanhados do sinal . Por exemplo, podemos escrever o número natural ou, simplesmente, 2.
Questão 3. Copie no caderno a reta numérica a seguir, substituindo as letras pelos números inteiros adequados.

Resposta: A: ; B: 7; C: 0; D: ; E: 2; F: .
Módulo ou valor absoluto
A medida da distância entre um ponto da reta numérica e a origem (0) é chamada módulo ou valor absoluto do número inteiro associado a esse ponto. Apresentamos a seguir alguns exemplos.
Na reta numérica, a medida da distância entre e a origem (0) são 2 unidades, ou seja, o módulo de é 2.

Na reta numérica, a medida da distância entre 3 e a origem (0) são 3 unidades, ou seja, o módulo de 3 é 3.

Página 40
Como o módulo de um número inteiro, diferente de zero, corresponde a uma medida de distância, o módulo é sempre um número positivo, no caso, um número natural.
Indicamos o módulo de um número por , como apresentado nos exemplos.
- (Lemos: módulo de é igual a 2)
- (Lemos: módulo de 3 é igual a 3)
Atenção!
O módulo do número 0 (zero) é 0.
O módulo de um número inteiro é sempre um número natural.
Quando dois números estão à mesma medida de distância da origem na reta numérica (ou seja, têm módulos iguais), mas estão localizados em sentidos contrários da reta, são chamados números opostos ou números simétricos. Nos exemplos anteriores, o número é o simétrico do número 2 e o número 3 é o simétrico do número .
Atenção!
O simétrico de um número positivo é sempre um número negativo, e o simétrico de um número negativo é sempre um número positivo.
Atividades
Faça as atividades no caderno.
8. Na reta numérica a seguir a medida da distância entre quaisquer dois pontos consecutivos é sempre a mesma.
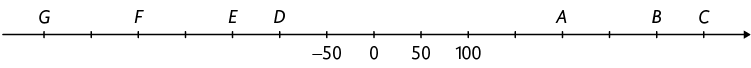
a) Associe um número inteiro a cada ponto da reta numérica indicado pelas letras.
Resposta: A: 200; B: 300; C: 350; D: ; E: ; F: ; G: .
b) Entre quais pontos marcados na reta numérica está localizado o número:
.
290.
25.
.
.
Resposta: : entre e ; 290: entre 250 e 300; 25: entre 0 e 50; : entre e ; : entre e .
9. Considere os números a seguir.
-
18
-
65
Cada letra indicada na reta numérica representa um desses números.
Que número cada letra representa?
Resposta: A: 65; B: 18; C: ; D: ; E: .
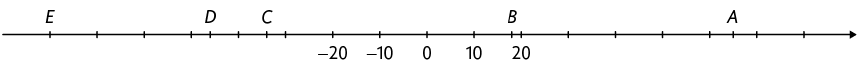
Página 41
10. Analise a reta numérica e resolva o que se pede.

Atenção!
A medida da distância entre quaisquer dois pontos consecutivos dessa reta numérica é sempre a mesma.
a) Determine os números inteiros associados aos pontos A, B, C, D, E e F.
Resposta: A: ; B: ; C: ; D: 3; E: 6; F: 10.
b) Nessa reta, o ponto B dista 7 unidades da origem, ou seja, está a uma medida de distância de 7 unidades do ponto O. A que medida de distância está cada um dos outros pontos indicados na reta?
Resposta: A dista 9 unidades de medida de O; C dista 3 unidades de medida de O; D dista 3 unidades de medida de O; E dista 6 unidades de medida de O; F dista 10 unidades de medida de O.
11. Analise a tabela a seguir, que indica a medida de altitude de alguns locais.
|
Local (país) |
Medida da altitude (m) |
|---|---|
|
Monte Aconcágua (Argentina) |
6.960 |
|
Monte Elbrus (Rússia) |
5.642 |
|
Mar Morto (Israel e Jordânia) |
|
|
Monte Everest (Nepal e República Popular da China) |
8.848 |
|
Vale da Morte (Estados Unidos) |
|
|
Lago Assal (República do Djibuti) |
|
|
Monte Branco (França e Itália) |
4.810 |
Fonte de pesquisa: GIRARDI, Gisele; ROSA, Jussara Vaz. Atlas geográfico do estudante. São Paulo: FTD, 2011.

De acordo com as informações da tabela, responda às questões a seguir.
a) Quais locais ficam acima do nível do mar?
Resposta: Monte Aconcágua, Monte Elbrus, Monte Everest e Monte Branco.
b) Quais locais ficam abaixo da altitude de medida ?
Resposta: Lago Assal e Mar Morto.
c) Qual desses locais tem maior medida de altitude? E qual tem menor medida de altitude?
Respostas: Monte Everest; Mar Morto.
Página 42
12. No esquema aparecem os 8 planetas do Sistema Solar e a medida da temperatura média aproximada da superfície de cada um deles.
Representações com elementos não proporcionais entre si e sem proporção de distância entre os astros. Cores-fantasia.
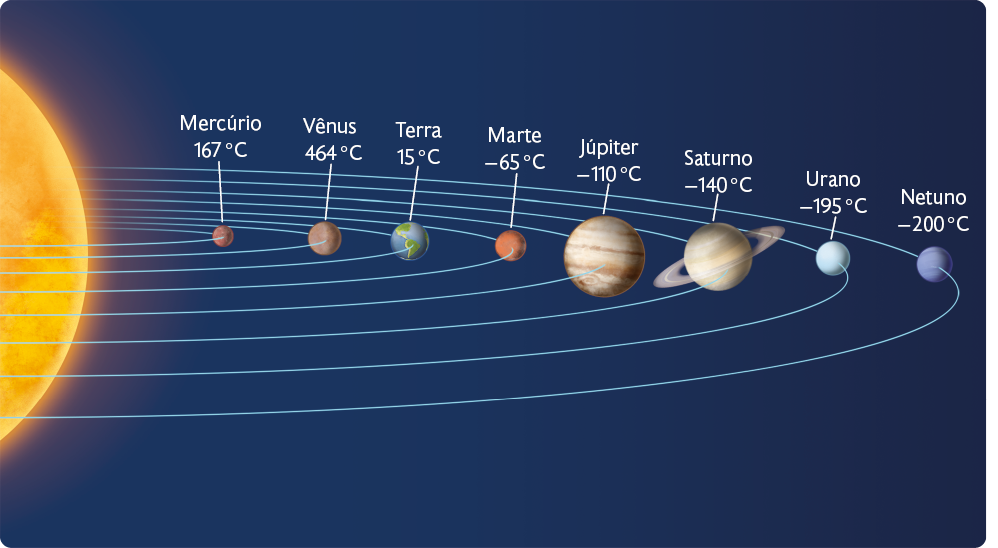
Fonte de pesquisa: NASA. Resources. Disponível em: https://oeds.link/Ov38ih. Acesso em: 29 jan. 2022.
Atenção!
Este esquema é apenas uma representação artística do Sistema Solar. As medidas dos planetas e das distâncias entre as órbitas de cada um deles não estão proporcionais às medidas reais.
a) Quais planetas têm a medida de temperatura média aproximada da superfície maior do que zero?
Resposta: Terra, Vênus e Mercúrio.
b) Em qual planeta a temperatura média aproximada da superfície mede ?
Resposta: Marte.
c) Qual é a medida da temperatura média aproximada da superfície do planeta Netuno? Essa medida é negativa ou positiva?
Respostas: ; negativa.
d) Qual planeta tem a maior medida de temperatura média aproximada do Sistema Solar? Qual é essa medida?
Respostas: Vênus; .
e) Na reta numérica, cada letra representa a medida da temperatura média aproximada da superfície dos planetas do Sistema Solar. Associe, no caderno, cada planeta à letra correspondente.

Resposta: Vênus: A; Mercúrio: B; Terra: C; Marte: D; Júpiter: E; Saturno: F; Urano: G; Netuno: H.
Página 43
13. Considere os seguintes números.
-
4
-
7
-
11
-
9
a) Desenhe no caderno uma reta numérica e localize nela esses números.
Resposta nas orientações ao professor.
b) Entre os números que você localizou, qual deles está mais próximo da origem da reta numérica? E qual está mais distante?
Respostas: 4; .
c) Quais números estão localizados a mais de 7 unidades de distância da origem?
Resposta: , , , 9 e 11.
d) Localize nessa reta numérica os números simétricos aos números dados. Quais são esses números?
Resposta: 10, , , 12, , 6, 8 e .
14. tecla Considere
a reta numérica a seguir.
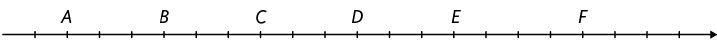
Leia as dicas apresentadas a seguir e determine o número associado a cada uma das letras indicadas na reta numérica.
Cada letra indicada na reta numérica representa um número inteiro.
A medida da distância entre dois pontos consecutivos da reta representa 1 unidade.
Os pontos C e E estão situados à mesma medida de distância da origem.
Resposta: A: ; B: ; C: ; D: 0; E: 3; F: 7.
15. Determine os módulos a seguir.
a)
b)
c)
d)
e)
f)
g)
Respostas: a) 5; b) 8; c) 11; d) 16; e) 2; f) 19; g) 33.
16. Considere os números representados por letras na reta numérica.
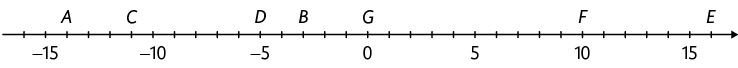
a) Qual é a medida da distância entre os pontos C e D?
b) Qual ponto está a uma distância de medida de 8 unidades do ponto B?
c) Quais pontos estão a uma distância de medida de 10 unidades um do outro?
d) Qual ponto está a uma distância de medida de 15 unidades do ponto F?
e) Qual é o ponto mais distante do ponto E? De quantas unidades é essa medida de distância?
Respostas: a) 6 unidades; b) C; c) F e G; d) D; e) A; 30 unidades.
17. Analise a reta numérica e resolva o que se pede nos itens.

a) Escreva no caderno a medida da distância da origem a cada ponto a seguir.
A
B
C
D
b) Quais pontos estão à mesma medida de distância da origem?
Respostas: a) A: 4 unidades; B: 7 unidades; C: 4 unidades; D: 7 unidades; b) A e C, B e D.
Página 44
18. Responda às questões a seguir.
a) Qual é o módulo de cada número inteiro que está entre e 2?
b) Quais números inteiros têm módulo menor do que 3?
Respostas: a) 2, 1, 0 e 1 b) , , 0, 1 e 2.
19. Determine, em seu caderno, o simétrico de cada número.
a) 3
b)
c)
d) 9
e)
f) 56
g)
h) 10
Respostas: a) ; b) 2; c) 32; d) ; e) 15; f) ; g) 1; h) .
20. Para cada item, escreva no caderno o número inteiro e, em seguida, seu oposto.
a) Um número de três algarismos diferentes.
b) Um número negativo de dois algarismos diferentes.
c) Um número múltiplo de 10.
d) Um número par de três algarismos.
Sugestões de respostas: a) 298 e ; b) e 98; c) 70 e ; d) 986 e .
21. Determine o número inteiro que as letras indicadas nos quadros representam.
|
Número |
Oposto do número |
|---|---|
|
26 |
|
|
A |
|
|
B |
7 |
|
19 |
C |
|
Número |
Oposto do número |
|---|---|
|
D |
|
|
E |
|
|
F |
31 |
|
G |
Respostas: A: 15; B: ; C: ; D: 79; E: 25; F: ; G: 44.
22. Para cada item, escreva no caderno o número que substitui o adequadamente.
a) O módulo de é .
b) O módulo de 3 é , e o módulo de é .
c) O módulo dos números e é 5.
d) O módulo de é , e o módulo de é .
Respostas: a) 7; b) 3 e 3; c) 5 e ; d) 15 e 9.
23. Responda aos itens a seguir no caderno.
a) Qual é o simétrico do simétrico de ?
b) Qual é o oposto do módulo de ?
c) Qual é o simétrico de ?
d) A medida da distância entre dois números simétricos é 150. Quais são esses números?
Respostas: a) ; b) ; c) ; d) e 75.
24. Desenhe em seu caderno a reta numérica a seguir.

a) Quais números estão representados pelas letras P, Q, R e S?
b) Na reta que você desenhou, localize os pontos , , e simétricos aos pontos P, Q, R e S, respectivamente, e escreva-os em seu caderno.
Respostas: a) P: 1, Q: 5, R: 7, S: 9; b) , , , .
Página 45
Comparação entre números inteiros
Leia a conversa entre Marilda e Jaime.

Nesses dois dias, os termômetros registraram as medidas de temperaturas apresentadas a seguir.
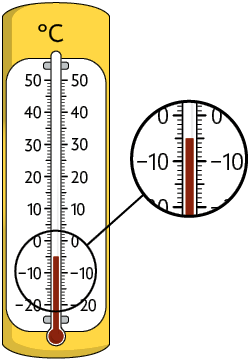
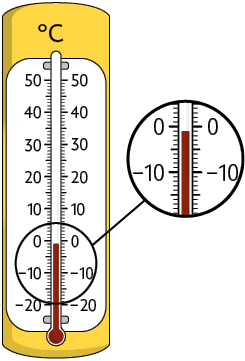
Note que a medida de temperatura é menor do que a medida de temperatura .
Representando essas medidas na reta numérica, temos:

Na reta, verificamos que está à esquerda de ; logo, é menor do que . Assim:
, ou seja, .
No domingo, a medida de temperatura registrada pelos termômetros foi de . Podemos representar as três medidas na reta numérica da seguinte maneira.

Na reta, está à esquerda de 2; logo, , ou seja, .
Página 46
Na reta numérica:
- os números que estão à esquerda de um número qualquer são menores do que esse número;
- os números que estão à direita de um número qualquer são maiores do que esse número.
Apresentamos alguns exemplos a seguir.
-
ou
-
ou
-
ou
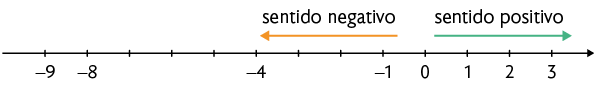
Atividades
Faça as atividades no caderno.
25. Organize as medidas de temperatura apresentadas em ordem crescente.
Resposta: , , , , , , , .
26. Os números a seguir foram representados por letras na reta numérica.
-
30
-
38
-
5
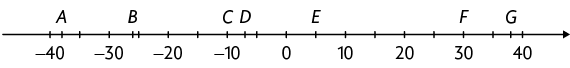
a) Determine a letra que representa cada número.
b) Qual dos números representados pelas letras é o maior? E o menor?
c) Quais dos números representados pelas letras são:
menores do que zero?
maiores do que e menores do que 15?
maiores do que ?
Respostas: a) A: , B: , C: , D: , E: 5, F: 30, G: 38; b) 38, ; c) menores do que zero: , , e ; maiores do que e menores do que 15: , e 5; maiores do que : , , 5, 30 e 38.
Página 47
27. Copie os itens no caderno e substitua cada pelo símbolo ou .
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
28. Considere os números a seguir.
Entre esses números:
a) quais são os números inteiros negativos maiores do que ?
b) quais números inteiros estão entre e 2?
c) qual é o maior número inteiro menor do que ?
Respostas: a) , , e ; b) e 1; c) .
29. Sabendo que x representa um número inteiro, determine o maior e o menor valor que x pode assumir em cada item.
a)
b)
c)
d)
e)
f)
Respostas: a) Maior valor: 2, menor valor: ; b) Maior valor: ; menor valor: ; c) Maior valor: ; menor valor: ; d) Maior valor: 6; menor valor: ; e) Maior valor: ; menor valor: ; f) Maior valor: 4; menor valor: .
30. Escreva no caderno, em ordem crescente, todos os números inteiros:
a) maiores do que e menores do que 4;
b) maiores do que e menores do que ;
c) diferentes de zero, cuja medida de distância em relação à origem é menor do que 4 unidades.
Respostas: a) , , , , , 0, 1, 2, 3; b) , , , , , ; c) , , , 1, 2, 3.
31. Durante o voo, os aviões atingem grandes altitudes. Um avião com capacidade para 225 passageiros, por exemplo, voa a aproximadamente de medida de altitude. No quadro apresentamos algumas medidas de altitudes e a medida da temperatura atmosférica aproximada registrada em cada uma delas.
|
Medida de altitude () |
Medida de temperatura () |
|---|---|
|
1.500 |
6 |
|
3.000 |
|
|
5.500 |
|
|
7.200 |
|
|
9.200 |
|
|
10.400 |
|
|
11.800 |
a) Qual é a maior medida de temperatura atmosférica registrada? E a menor?
b) Qual foi a medida de temperatura atmosférica aproximada registrada pelo termômetro desse avião à altitude de medida ?
c) De acordo com as informações do quadro, uma temperatura de medida pode ser registrada entre quais medidas de altitudes?
d) De acordo com as informações do quadro, em altitudes medindo acima de , a medida de temperatura atmosférica aproximada é positiva ou negativa?
Respostas: a) Aproximadamente , aproximadamente ; b) Aproximadamente ; c) Aproximadamente entre e ; d) Negativa.
Página 48
32. Sandro anotou na agenda o saldo de sua conta bancária em alguns dias.
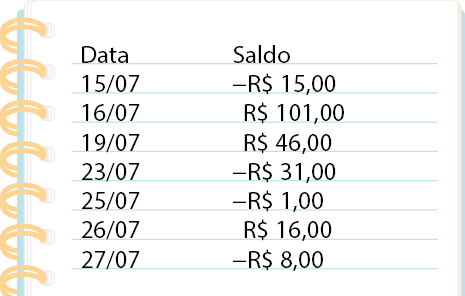
a) Em qual desses dias o saldo era maior? E em qual era menor?
Respostas: 16/07; 23/07.
b) Em qual dia o saldo era maior do que R$ 5,00 e menor do que R$ 10,00?
Resposta: 25/07.
c) Escreva no caderno em ordem crescente as quantias anotadas por Sandro usando o símbolo entre elas.
Resposta: .
33. Considere a tabela, que indica o saldo de gols de algumas equipes da série A do Campeonato Brasileiro de 2021.
|
Equipe |
Saldo de gols |
|---|---|
|
Bahia (BA) |
|
|
Cuiabá (MT) |
|
|
Grêmio (RS) |
|
|
Juventude (RS) |
|
|
São Paulo (SP) |
|
|
Sport (PE) |
Fonte de pesquisa: Confederação Brasileira de Futebol (CBF). Campeonato Brasileiro de Futebol – Série A – 2021. Disponível em: https://oeds.link/LApJb3. Acesso em: 25 fev. 2022.
Qual dessas equipes obteve o menor saldo de gols nesse campeonato? E o maior?
Respostas: Sport (PE); Cuiabá (MT).
34. Considera-se o ano 1 o início da Era Cristã, ou seja, o ano de nascimento de Jesus Cristo. Após esse ano, passou-se a usar as expressões "depois de Cristo" (d.C.) para fazer referência a determinado ano dessa era, e "antes de Cristo" (a.C.), ou o sinal para os anos que a antecederam. Nessa cronologia, não existe ano zero. Esse sistema de datação foi criado por Dionysius Exiguus, que recebeu a tarefa de criar um método de marcação do tempo que previsse a Páscoa. No entanto, não se sabe ao certo como ele determinou o ano de nascimento de Jesus. Atualmente, as terminologias d.C. e a.C. vêm sendo substituídas, respectivamente, por EC (Era Comum) e AEC (Antes da Era Comum), consideradas mais neutras e inclusivas para pessoas não cristãs.
Atenção!
O ano 1 d.C. foi imediatamente depois do ano 1 a.C.
A seguir, estão indicados alguns anos nesse sistema de datação.
-
7 a.C.
-
4 d.C.
-
2 d.C.
-
1 a.C.
-
2 a.C.
-
3 a.C.
-
1 d.C.
-
9 a.C.
a) Quantos anos se passaram do início do ano 2 a.C. ao fim do ano 2 d.C.?
b) Escreva no caderno os anos apresentados em ordem crescente.
Respostas: a) 4 anos; b) 9 a.C., 7 a.C., 3 a.C., 2 a.C., 1 a.C., 1 d.C., 2 d.C., 4 d.C.
Página 49
Adição com números inteiros
Vamos analisar algumas situações envolvendo movimentações mensais, em milhões de reais, de uma rede de supermercados durante alguns meses de 2023.
Em janeiro de 2023, essa rede obteve um lucro de 6 milhões de reais; já no mês de fevereiro, esse lucro ficou em 4 milhões de reais.
Para determinar o lucro obtido por essa rede de supermercados ao final de fevereiro, devemos adicionar o lucro de 6 milhões de reais com o lucro de 4 milhões de reais, ou seja, calcular . Para isso, vamos utilizar uma reta numérica.
A partir da origem, deslocamos 6 unidades para a direita, pois o sinal à frente do número 6 é .

Em seguida, deslocamos 4 unidades para a direita a partir do número 6, pois o sinal à frente do número 4 é .

Assim, .
Portanto, ao final desses 2 meses, a rede de supermercados obteve um lucro de 10 milhões de reais.
No mês seguinte, a rede sofreu um prejuízo de 12 milhões de reais.
Para saber de quantos reais foi o lucro ou prejuízo no fim do mês de março, devemos adicionar o lucro de 10 milhões de reais do mês anterior com o prejuízo de 12 milhões de reais, ou seja, calcular . Para isso, vamos utilizar uma reta numérica.
A partir da origem, deslocamos 10 unidades para a direita, pois o sinal à frente do número 10 é . Depois, deslocamos 12 unidades para a esquerda a partir do número 10, pois o sinal à frente do número 12 é .
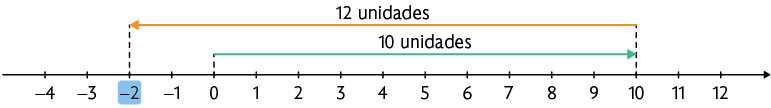
Assim, .
Portanto, a rede de supermercados obteve prejuízo de 2 milhões de reais ao final do mês de março.
Página 50
No mês de abril, a empresa obteve mais um prejuízo, dessa vez de 3 milhões de reais.
Para determinar de quantos reais foi o lucro ou prejuízo no fim do mês de abril, devemos adicionar o prejuízo de 2 milhões de reais com o prejuízo de 3 milhões de reais, ou seja, devemos calcular .

Assim, .
Portanto, a rede de supermercados obteve prejuízo de 5 milhões de reais ao final do mês de abril.
Questão 4. Se no mês de maio a rede de
supermercados teve
um lucro de 6 milhões de reais, qual foi o lucro ou prejuízo da empresa ao
final desse mês?
Resposta: Lucro de 1 milhão de reais.
Propriedades da adição
Propriedade comutativa
Apresentamos a seguir os cálculos realizados por Adriana e Inácio.


Como a adição possui a propriedade comutativa, ao trocar a ordem das parcelas, a soma não se altera.
Em uma adição de números inteiros, ao trocar a ordem das parcelas, a soma não se altera. Essa é a propriedade comutativa da adição de números inteiros.
Página 51
Propriedade do elemento neutro
Questão 5. Efetue os cálculos no caderno.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
Questão 6. No caderno, escreva suas observações com relação aos resultados obtidos na questão anterior.
Sugestão de resposta: Ao adicionar um número inteiro a zero, o resultado é o próprio número inteiro.
Como a adição tem a propriedade do elemento neutro, quando uma das parcelas é igual a zero, a soma é igual à outra parcela.
O resultado da adição de um número inteiro a zero é sempre igual ao próprio número. Por isso, dizemos que o zero é o elemento neutro da adição de números inteiros.
Propriedade associativa
Podemos calcular de duas maneiras diferentes.
Atenção!
Dependendo da maneira como as parcelas são associadas, os cálculos podem se tornar mais simples.
1ª maneira
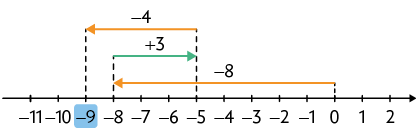
Calculamos . Depois, adicionamos ao resultado.
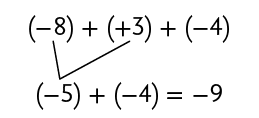
2ª maneira

Calculamos . Depois, adicionamos ao resultado.
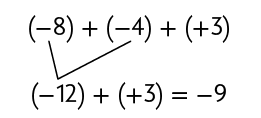
Como a adição tem a propriedade associativa, ao associar as parcelas de maneiras diferentes, a soma não se altera.
Em uma adição de três ou mais números inteiros, ao associar as parcelas de maneiras diferentes, a soma não se altera. Essa é a propriedade associativa da adição de números inteiros.
Página 52
Propriedade do elemento oposto
Questão 7. Efetue os cálculos no caderno.
Resposta: Em todos os itens, o resultado é 0.
a)
b)
c)
d)
e)
f)
Questão 8. Escolha um número inteiro qualquer. Em seguida, em seu caderno, adicione-o ao seu oposto. Qual foi o resultado obtido por você?
Resposta: 0.
Questão 9. Escreva no caderno o resultado da adição de dois números opostos.
Resposta: 0.
Em uma adição de dois números opostos, a soma é sempre zero. Essa é a propriedade do elemento oposto da adição de números inteiros.
Atividades
Faça as atividades no caderno.
35. Copie os cálculos em seu caderno, substituindo cada de acordo com as setas indicadas na reta numérica.
a)

b)
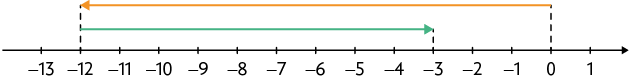
c)

d)

e)
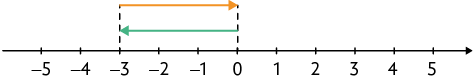
f)
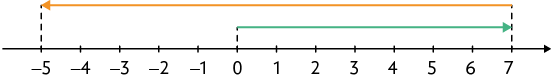
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
36. Raul tem um saldo bancário devedor de R$ 590,00. Quantos reais ele deve depositar para ficar:
a) com saldo igual a zero?
b) com saldo de R$ 490,00?
Respostas: a) R$ 590,00; b) R$ 1.080,00.
Página 53
37. Calcule o saldo da conta bancária de Fernanda após as movimentações indicadas no extrato a seguir.

Resposta: R$ 306,00.
38. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
39. Adicione os números de cada item trocando a ordem das parcelas e verifique a propriedade comutativa da adição de números inteiros.
a) e
b) e
c) e
d) e
Respostas: a) e ; b) e ; c) e ; d) e .
40. Copie cada cálculo substituindo o por um dos números a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
41. Efetue os cálculos de duas maneiras diferentes.
a)
b)
c)
d)
e)
f)
g)
h)
i)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) .
42. Adicione todos os números das faces visíveis dos dados de cada pilha. Depois, responda às questões.
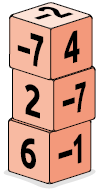
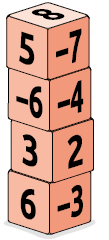
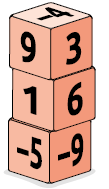
Em qual pilha a soma é:
a) maior do que 2 e menor do que 5?
b) um número entre e zero?
c) menor do que ?
d) maior do que zero e menor do que 2?
Respostas: a) B; b) A; c) Nenhuma das pilhas; d) C.
Página 54
43. Milena, Adriano e César estão disputando um jogo. Nesse jogo, os pontos ganhos são marcados por fichas com números positivos; os pontos perdidos, por fichas com números negativos. As fichas de cada um deles ao final de uma partida estão representadas a seguir.
Milena
Pontos ganhos:
-
5
Pontos perdidos:
Adriano
Pontos ganhos:
Pontos perdidos:
César
Pontos ganhos:
Pontos perdidos:
a) Ao final da partida, quantos pontos foram marcados por:
Milena?
Adriano?
César?
Respostas: Milena: ; Adriano: ; César: .
b) Qual jogador obteve a maior soma de pontos?
Resposta: Adriano.
44. Efetue os cálculos e verifique qual dos quadrados a seguir é um quadrado mágico.
Atenção!
Um quadrado é mágico quando a soma dos números de cada linha, coluna e diagonal é a mesma.
7
5
15
1
17
11
8
4
14
1
11
Resposta: Quadrado B.
45. Para cada item, elabore em seu caderno um problema envolvendo adição de números inteiros utilizando os números indicados e peça a um colega que o resolva. Depois, verifique se a resolução está correta.
a) e
b) e
c) e
d) e
Resposta pessoal.
Página 55
Subtração com números inteiros
São Joaquim, situada no sul do estado de Santa Catarina a uma medida de altitude de , é considerada a cidade mais fria do Brasil.

Considere o gráfico a seguir, indicando as medidas aproximadas das temperaturas diárias máxima e mínima registradas em São Joaquim no mês de julho de 2021.
Medidas aproximadas das temperaturas diárias máxima e mínima registradas em São Joaquim em julho de 2021
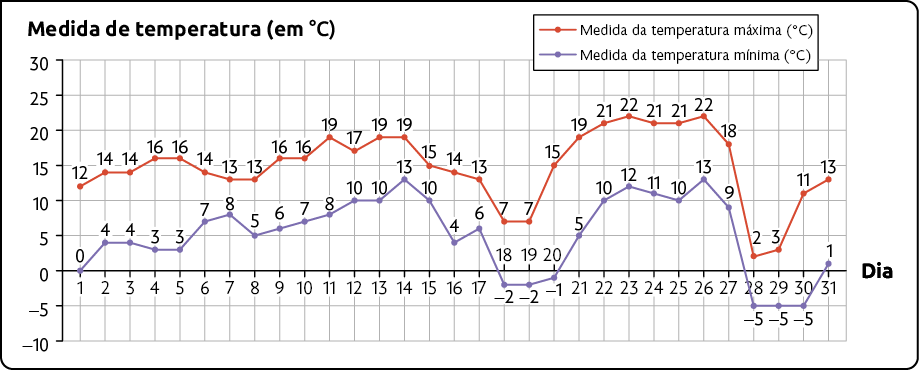
Fonte de pesquisa: INMET. Dados meteorológicos. Disponível em: https://oeds.link/CwKiZd. Acesso em: 12 jan. 2022.
Página 56
Podemos calcular a diferença entre as medidas de temperaturas máxima e mínima registradas em alguns dias do mês de julho de 2021 da seguinte maneira.
Dia 31
Medida de temperatura máxima: .
Medida de temperatura mínima: .
Como os dois números são positivos, basta efetuar a subtração a seguir.
Na subtração, um número menos outro significa a adição do primeiro com o oposto do segundo. Assim, subtrair de significa calcular a diferença , que é o mesmo que . Representamos esse cálculo na reta numérica da seguinte maneira.

Dia 20
Medida de temperatura máxima: .
Medida de temperatura mínima: .
Ao localizarmos os números e na reta numérica, notamos que a diferença entre eles é 16.

De outra maneira, corresponde à adição de ao oposto de , ou seja, 1. Indicando esse cálculo na reta numérica, temos:

Assim:

A seguir, alguns exemplos envolvendo subtração com números inteiros.
Atenção!
Subtrair um número de outro é o mesmo que adicionar o primeiro número ao oposto do segundo número.
Página 57
Atividades
Faça as atividades no caderno.
46. Em cada item, copie as expressões substituindo o pelo número adequado, de acordo com as setas indicadas na reta numérica correspondente.
a)
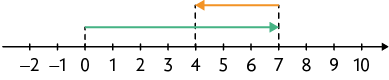
b)
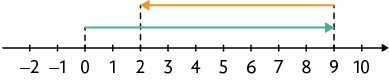
c)
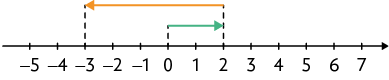
d)

Respostas: a) ; b) ; c) ; d) .
47. Para cada item, escreva no caderno o número que substitui o adequadamente.
a)
b)
c)
d)
e)
f)
Respostas: a) ; ; b) ; c) ; ; d) ; ; e) ; ; f) .
48. Efetue os cálculos no caderno.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) ; i) ; j) ; k) ; l) 0.
49. Copie as expressões e complete com o sinal ou de modo que o resultado seja verdadeiro.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
Página 58
50. Nos termômetros a seguir indicamos as medidas aproximadas de temperaturas mínima e máxima registradas na cidade de Inácio Martins, no Paraná, em 29 de julho de 2021.
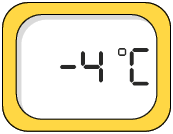
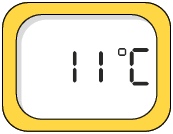
Fonte de pesquisa: INMET. Dados meteorológicos. Disponível em: https://oeds.link/CwKiZd. Acesso em: 11 mar. 2022.
a) Qual foi a medida de temperatura máxima registrada nesse dia? E a medida de temperatura mínima?
b) Qual é a diferença entre as medidas de temperaturas máxima e mínima registradas nesse dia?
Respostas: a) , ; b) .
51. Escreva no caderno os três próximos números de cada sequência.
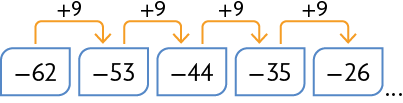
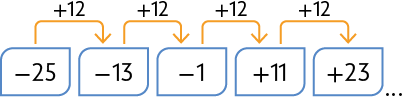
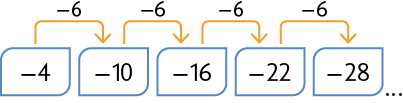
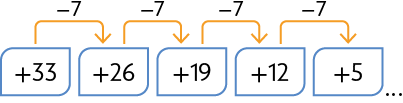
Respostas: A. , , ; B. , , ; C. , , ; D. , , .
52. Carla resolveu a expressão numérica da seguinte maneira.
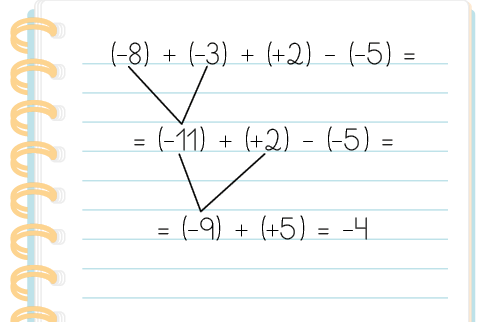
De maneira parecida, resolva no caderno as expressões numéricas a seguir.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
53. Estime o resultado das expressões numéricas.
A.
B.
C.
Resposta pessoal.
a) Agora, obtenha da maneira que preferir, o resultado exato delas.
Respostas: A. ; B. ; C. .
b) Qual expressão tem maior valor?
Resposta: Expressão B.
Página 59
54. A seguir estão representadas, com números inteiros, as medidas aproximadas de altitudes de diferentes locais do mundo.
A.Pico da Pedra da Mina, SP
B.Depressão de Danakil, Etiópia
C.Dhaulagiri, Nepal
D.Município de Triunfo, PE
E.Cidade de Apartaderos, Venezuela
F.Mar da Galileia, Israel
a) Escreva em ordem crescente as medidas de altitudes aproximadas desses locais.
Resposta: , , , , , .
b) Calcule a diferença, em metros, entre a maior e a menor medida aproximada de altitude dos locais indicados.
Resposta: .
55. Em certo dia, o termômetro registrava uma medida de temperatura de em uma cidade. Se diminuir , qual será a medida de temperatura que esse termômetro vai registrar?
Resposta: .
56. As
sentenças apresentadas em cada item devem ser compostas de exatamente três dos
números apresentados a seguir.
Copie-as em seu caderno substituindo as letras pelos números adequados.
a)
b)
c)
Respostas: a) ; b) ou ; c) ou .
57. Considere a tabela a seguir, que indica a quantidade de gols marcados e gols sofridos por uma equipe de futebol em quatro partidas.
|
Partida |
Número de gols marcados |
Número de gols sofridos |
|---|---|---|
|
1 |
2 |
4 |
|
2 |
3 |
2 |
|
3 |
0 |
2 |
|
4 |
3 |
5 |
Fonte de pesquisa: registros do técnico da equipe.
Qual foi o saldo de gols dessa equipe após as quatro partidas?
Resposta: .
58. Elabore no caderno um problema cujo contexto envolva números inteiros e que possa ser resolvido por uma subtração. Em seguida, troque-o com um colega. Depois, verifiquem as soluções.
Resposta pessoal.
Página 60
Multiplicação com números inteiros
Roberto, Lúcia, Daniela e Francisca estavam disputando em um jogo de perguntas e respostas. Nesse jogo, cada resposta correta valia pontos; cada resposta errada, pontos.
As anotações a seguir indicam a quantidade de acertos e erros de cada jogador ao final de uma partida.

Questão 10. Determine, em seu caderno, o saldo de pontos de Roberto nessa partida.
Resposta: 7.
Para responder a esta questão, precisamos calcular:
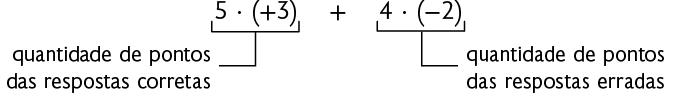
Inicialmente, calculamos quantos pontos Roberto obteve com as respostas corretas.

Agora, calculamos quantos pontos ele obteve com as respostas erradas.
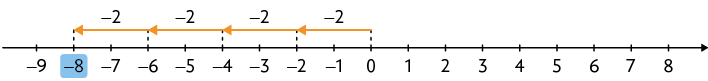
Atenção!
O produto tem o mesmo resultado de , ou seja:
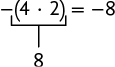
Realizando os cálculos, temos:
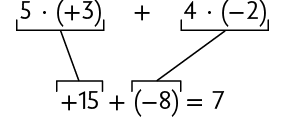
Portanto, o saldo de pontos obtidos por Roberto na partida é 7.
Página 61
Questão 11. De maneira semelhante, calcule em seu caderno o saldo de pontos obtidos por:
a) Lúcia.
b) Daniela.
c) Francisca.
Respostas: a) 12; b) 17; c) 2.
Atenção!
As propriedades da multiplicação de números naturais também são válidas nas multiplicações envolvendo números inteiros.
- Propriedade comutativa da multiplicação de números inteiros: em uma multiplicação, ao trocar a ordem dos fatores, o produto permanece o mesmo.
- Propriedade do elemento neutro da multiplicação de números inteiros: ao multiplicar um número por 1, o resultado é igual ao próprio número.
- Propriedade associativa da multiplicação de números inteiros: em uma multiplicação de três ou mais fatores, ao associá-los de maneiras diferentes, o produto permanece o mesmo.
- Propriedade distributiva da multiplicação de números inteiros: multiplicar um número pela soma de outros números é o mesmo que multiplicar por esse número cada parcela e, em seguida, adicionar os resultados. Isso também é válido quando multiplicamos um número pela diferença de dois números.
A seguir, vamos apresentar como calcular de duas maneiras.
1ª maneira
Para obtermos o resultado dessa multiplicação, substituímos por , pois é o simétrico de .
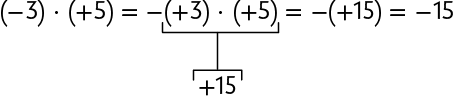
2ª maneira
Para obtermos o resultado, usamos a propriedade comutativa da multiplicação.
Portanto, .
No cálculo , podemos obter o resutado substituindo por , como indicado a seguir.
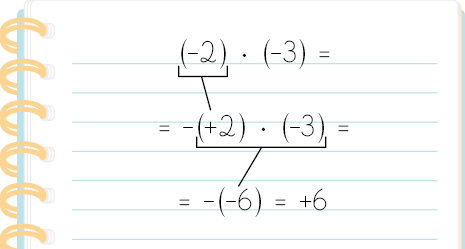
Página 62
- Em uma multiplicação de dois números com sinais diferentes (um positivo e um negativo), o produto é um número negativo.
- Em uma multiplicação de dois números com sinais iguais, o produto é um número positivo.
A seguir, apresentamos alguns exemplos.
Atividades
Faça as atividades no caderno.
59. Multiplique o número 16 por 2 e adicione o resultado ao triplo de . Que número você obteve?
Resposta: .
60. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
61. Sem
efetuar cálculos por escrito ou na calculadora, associe
no caderno as multiplicações que tenham o mesmo resultado.
A.
B.
C.
D.
E.
F.
G.
H.
I.
J.
K.
L.
Resposta: A e H; B e G; C e I; D e L; E e J; F e K.
62. Em cada item, determine o número correspondente às letras nos esquemas.
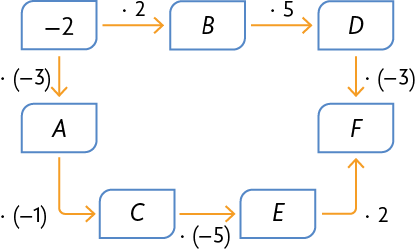
Resposta: A: 6, B: , C: , D: , E: 30, F: 60.
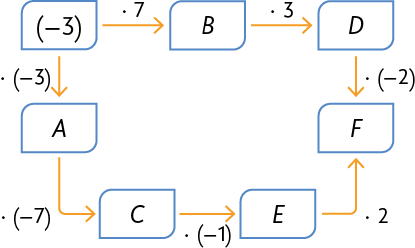
Resposta: A: 9, B: , C: , D: , E: 63, F: 126.
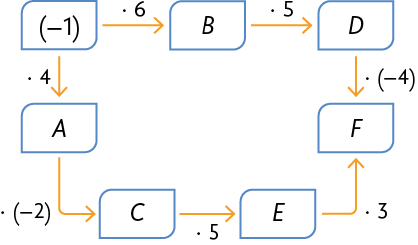
Resposta: A: , B: , C: 8, D: , E: 40, F: 120.
Página 63
63. De acordo com o significado dos símbolos, determine o número correspondente a cada letra.
significa: multiplicar por .
significa: multiplicar por .
significa: adicionar .
significa: adicionar .
Resposta: A: 15; B: 1; C: 9; D: 25.
64. Em um frigorífico, uma câmara fria estava registrando, em um 1º momento, . Após alguns minutos, em um 2º momento, a medida de temperatura da câmara estava registrando o equivalente a 4 vezes a medida de temperatura do 1º momento.
a) Em qual dos termômetros está registrada a medida de temperatura do 2º momento?




b) Em quantos graus diminuiu a medida de temperatura do 1º para o 2º momento?
Respostas: a) Termômetro B; b) .
65. Utilizando números inteiros positivos e negativos, escreva no caderno duas multiplicações cujo resultado seja:
a) .
b) .
c) .
Sugestão de respostas: a) e ; b) e ; c) e .
66. As embarcações são equipadas com radares e outras tecnologias que permitem evitar diversos acidentes. Contudo, antes do desenvolvimento desses equipamentos, muitos naufrágios ocorreram nos oceanos. A seguir, apresentamos algumas informações sobre dois naufrágios.
No litoral do estado do Maranhão, em uma região conhecida como parcel✚ Manoel Luiz, ocorreram muitos naufrágios. Um deles foi o do cargueiro inglês West Point, em 1943, que se chocou contra as colunas do parcel e afundou. Esse navio transportava cobre e bronze para serem utilizados na Segunda Guerra, na Europa. Seus destroços estão a em relação ao nível do mar.
- Parcel:
- recife de pouca profundidade, muito perigoso para a navegação.↰
Um dos naufrágios mais conhecidos do mundo é o do transatlântico de luxo Titanic, ocorrido em 14 de abril de 1912 no Atlântico Norte. Ele era o maior navio de sua época e muitos acreditavam que não poderia afundar. Porém, durante sua primeira viagem, depois de colidir com um iceberg, seu naufrágio foi inevitável. O Titanic transportava mais de 2.000 passageiros e tripulantes, dos quais apenas 706 sobreviveram ao desastre. Os destroços desse navio foram encontrados 73 anos após seu naufrágio e estão a uma profundidade aproximadamente 152 vezes maior do que os do navio West Point, naufragado no litoral brasileiro.
Fonte de pesquisa: COMO FOI o naufrágio e a redescoberta do Titanic. National Geographic, 27 ago. 2019. Disponível em: https://oeds.link/G65RQJ. Acesso em: 11 mar. 2022.
A aproximadamente quantos metros em relação ao nível do mar estão os destroços do Titanic?
Resposta: Aproximadamente .
Página 64
67. No
cálculo a seguir, a letra A representa o
menor número inteiro de dois algarismos; a letra B,
o menor número natural de dois algarismos. Com essas informações, determine os
valores das letras A, B e C.
Resposta: A: , B: 10, C: .
68. Para cada item, pense em um número inteiro, escreva no caderno um cálculo e determine o resultado.
a) Subtraia 13 do triplo do número que você pensou e multiplique por o resultado obtido.
Sugestão de resposta: Sendo o número inteiro pensado, .
b) Multiplique o número que você pensou por e adicione 10. Multiplique o resultado obtido por .
Sugestão de resposta: Sendo o número inteiro pensado, .
69. Entre os números indicados a seguir, escreva no caderno o que substitui o de maneira que as sentenças sejam verdadeiras.
-
9
Atenção!
Utilize somente uma vez cada número indicado nas fichas.
a)
b)
c)
d)
Respostas: a) ; b) 9; c) ; d) e .
70. Escreva no caderno um número inteiro que substitui o em cada item, de maneira que as sentenças sejam verdadeiras.
a)
b)
c)
d)
e)
f)
Sugestões de respostas: a) , , , 0, 1, ...; b) 0, 1, , , , ...; c) , , ,, ...; d) 2, 3, 4, 5, ...; e) 3, 4, 5, 6, ...; f) , , , , ...
71. Após
fazer um depósito em sua conta bancária, Jonas ficou com saldo de . Sabendo que
devia 4 vezes o valor do saldo atual, quantos reais ele
depositou?
Resposta: R$ 222,00.
72. Vagner e Renata obtiveram o resultado de de maneiras diferentes.
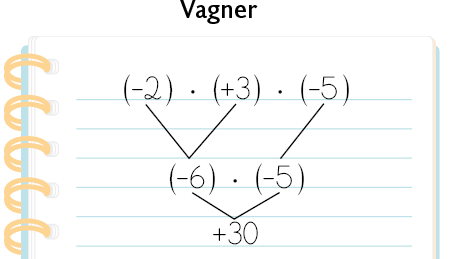
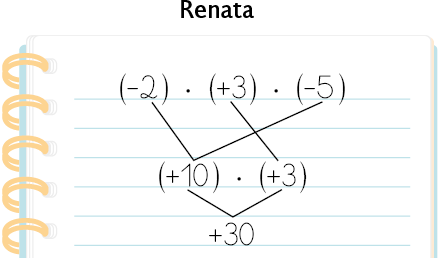
Agora, da maneira que achar mais conveniente, associe os fatores e obtenha o resultado de cada multiplicação a seguir.
a)
b)
c)
d)
e)
f)
g)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) .
73. Elabore um problema com um contexto envolvendo multiplicação de números inteiros. Em seguida, troque-o com um colega para que ele resolva o seu problema e você resolva o dele.
Resposta pessoal.
Página 65
Divisão com números inteiros
Uma professora escreveu os seguintes problemas na lousa.

Para resolver esses problemas, vamos construir um esquema para cada um deles.
Chamaremos o número desconhecido no problema 1 e ▲ o número desconhecido no problema 2.
Problema 1
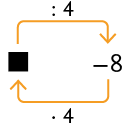
Se efetuarmos , então obteremos , que é o valor de ■.
Assim, , pois .
Problema 2
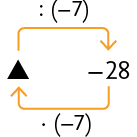
Se efetuarmos , então obteremos 196, que é o valor de ▲.
Assim, , pois .
Em uma divisão de dois números com sinais diferentes (um positivo e um negativo), o quociente é um número negativo. Exemplos:
Em uma divisão de dois números com sinais iguais, o quociente é um número positivo. Exemplos:
Atividades
Faça as atividades no caderno.
74. Em cada esquema, determine o número representado pelo ■.
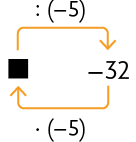
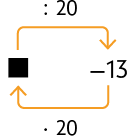
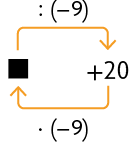
Respostas: A. 160; B. ; C. .
Página 66
75. Determine o número que substitui cada adequadamente.
Atenção!
No item f, você escolhe os números, porém pelo menos um deles deve ser negativo.
a) , pois
b) , pois
c) , pois
d) , pois
e) , pois
f) , pois
Respostas: a) , ; b) , ; c) , , ; d) , 8, ; e) , 3, , ; f) Sugestão de resposta: , 8, , , 8, .
76. Efetue os cálculos no caderno.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
77. Responda às questões a seguir.
a) Qual é o resultado da divisão de um número por seu oposto?
b) Qual é o resultado da divisão de um número negativo por ele mesmo?
c) Qual deve ser o valor de A para que a sentença seja verdadeira?
Respostas: a) ; b) 1; c) .
78. Efetue os cálculos necessários e escreva no caderno o número, entre os indicados nas fichas, que substitui o nas frases adequadamente.
a) Dividindo por e adicionando o resultado ao dobro de , obtemos .
b) Ao multiplicar por ele mesmo e subtrair 30 do resultado, obtemos 34.
c) Ao dividir pelo triplo de e subtrair do resultado, obtemos .
Respostas: a) ; b) ; c) .
79. Efetue os cálculos no caderno e determine o valor de cada letra nos esquemas.
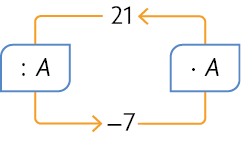
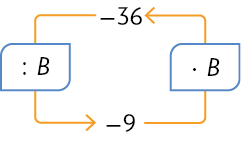
Respostas: A: ; B: 4.
80. Na tabela estão registradas as medidas das temperaturas mínimas na cidade de Nova York durante uma semana.
|
Dia |
Medida de temperatura mínima |
|---|---|
|
Domingo |
|
|
Segunda-feira |
1 |
|
Terça-feira |
|
|
Quarta-feira |
|
|
Quinta-feira |
|
|
Sexta-feira |
|
|
Sábado |
|
Fonte de pesquisa: ACCUWEATHER. Disponível em: https://oeds.link/2UWCub. Acesso em: 22 mar. 2022.
Determine a média das medidas mínimas de temperatura registradas em Nova York nessa semana.
Resposta: .
81. Elabore um problema envolvendo divisão de números inteiros e peça a um colega que o resolva. Depois, verifique se a resolução está correta.
Resposta pessoal.
Página 67
Potenciação de números inteiros
Assim como calculamos potências em que a base é um número positivo, também podemos calcular potências em que a base é um número negativo. A seguir, apresentamos dois exemplos.
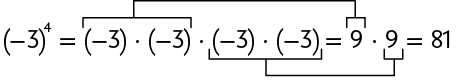
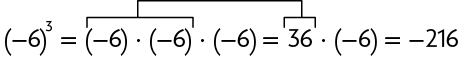
- Quando a base de uma potência é um número negativo e o expoente é par, a potência é positiva.
- Quando a base é um número negativo e o expoente é ímpar, a potência é negativa.
A seguir, apresentamos dois exemplos:
Agora, vamos apresentar as seguintes situações.
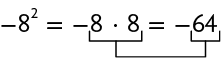
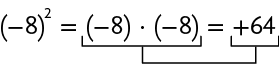
Note que as potências e representam multiplicações diferentes e têm resultados diferentes.
Atividades
Faça as atividades no caderno.
82. Efetue os cálculos.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) 1;
83. Apenas analisando as potências, verifique se elas são positivas ou negativas.
a)
b)
c)
Respostas: a) Negativa; b) Positiva; c) Positiva.
84. Determine o resultado dos cálculos a seguir.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) 36; c) ; d) ; e) 16; f) .
85. Sem efetuar cálculos, copie as sentenças substituindo cada pelo símbolo , ou , de modo que sejam verdadeiras.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
86. Calcule o valor de cada potência no caderno. Depois, escreva-os em ordem crescente.
A.
B.
C.
D.
E.
F.
Respostas: A. ; B. ; C. ; D. 169; E. ; F. 1; Em ordem crescente: , , , , 1, 169.
87. Elabore em seu caderno um problema com um contexto que envolva potências de números inteiros e, em seguida, peça a um colega que o resolva. Depois, verifique se a resposta está correta.
Resposta pessoal.
Página 68
Operações com números inteiros na calculadora científica
Neste tópico, vamos conhecer algumas funções da calculadora científica e usar essa ferramenta para adicionar, subtrair, multiplicar, dividir e até mesmo efetuar potenciações envolvendo números inteiros.
Instrumentos e softwares
A calculadora científica
Ao digitar uma tecla numérica da calculadora, digamos 3, ela sempre vai registrar um número inteiro positivo no visor. Uma maneira de registrarmos o número , por exemplo, é digitar a tecla com a operação de subtração antes do algarismo. No entanto, podemos encontrar outra tecla com um sinal de menos que é utilizada exclusivamente para fazer a mudança de sinal do número. Ela torna os cálculos envolvendo números inteiros negativos mais confiáveis e práticos do que o primeiro método, com a tecla da operação. Vamos usar essas e outras teclas nesta seção.
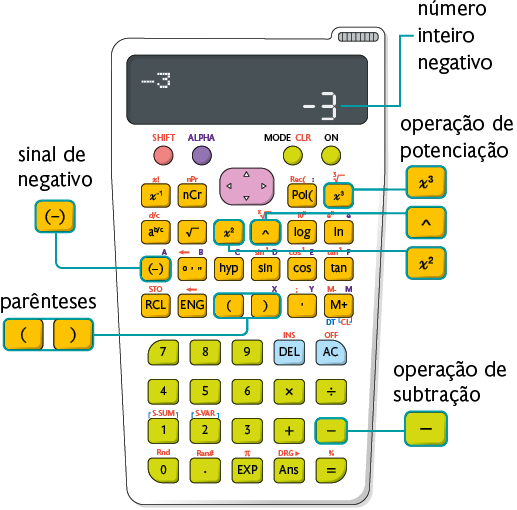
Os parênteses são necessários em alguns modelos de calculadoras científicas. Apresentamos a seguir alguns exemplos de cálculos com números inteiros.
Adição e subtração
Digite as teclas:
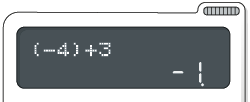
Digite as teclas:
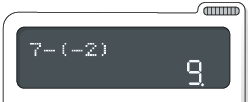
Página 69
Multiplicação e divisão
Digite as teclas:
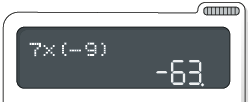
Digite as teclas:
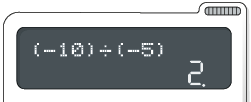
Potenciação
Digite as teclas:
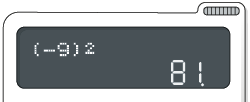
Digite as teclas:
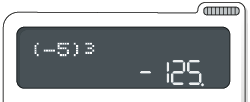
Digite as teclas:
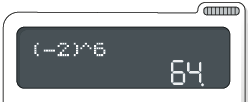
De modo geral, o procedimento para o cálculo pode ser diferente em algumas calculadoras, como a do aplicativo calculadora do smartphone.
Atividades
Faça as atividades no caderno.
88. Efetue
os cálculos com a calculadora científica.
a)
b)
c)
d)
e)
f)
g)
Respostas: a) ; b) ; c) ; d) 54; e) ; f) 49; g) 225.
89. Júlia e Fernando efetuaram na calculadora científica da seguinte maneira.
Júlia:
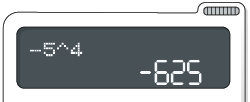
Fernando:
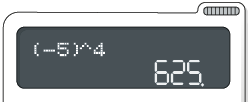
Note que o visor apresentou resultados com sinais opostos. Quem obteve o resultado correto de ? Explique por que isso aconteceu.
Resposta: O resultado de Júlia é o correto, pois ela efetuou , enquanto Fernando efetuou , ou seja, representam multiplicações diferentes e têm resultados diferentes. Isso aconteceu porque Fernando não digitou os parênteses para indicar que a base da potência é , e não 5.
Página 70
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Considere os números nas fichas.
-
0
-
6
Quais deles são números:
a) naturais?
b) positivos?
c) negativos?
d) inteiros?
e) inteiros e não são naturais?
Respostas: a) 0 e 6; b) e 6; c) , e ; d) , 0 e 6; e) .
2. Na reta numérica a seguir, quais letras indicam os números , 2 e , respectivamente?
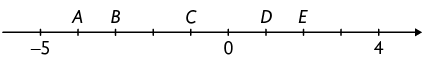
Resposta: A, E e C.
3. Resolva os itens a seguir.
a) Quais números inteiros têm módulo igual a 7?
b) Quantos números inteiros têm módulo igual a zero? Qual é esse número?
c) Quais números inteiros são maiores do que e menores do que ?
d) Quantos números inteiros existem entre e 21?
e) Qual é o número simétrico de ? E de 12?
Respostas: a) 7 e ; b) Um; 0; c) , , e ; d) 50; e) 37; .
4. Resolva
os problemas a seguir. Em seguida, utilizando uma calculadora científica,
verifique se os cálculos efetuados por você estão corretos.
a) Em certa cidade, a temperatura mínima em um dia mediu e a diferença entre as medidas máxima e mínima de temperaturas foi . Qual foi a medida máxima de temperatura nesse dia?
b) Gabriela foi ao banco, tirou um extrato de sua conta e verificou que tinha um saldo negativo de R$ 355,00. Após fazer um depósito de R$ 750,00, qual passou a ser o saldo da conta de Gabriela?
Respostas: a) ; b) R$ 395,00.
5. Em uma folha de papel avulsa, resolva os itens a seguir.
a) Deve-se dividir 90 por qual número para obter como resultado?
b) Subtraia 25 de . Qual é o resultado?
c) Qual é o resultado da divisão do oposto de 64 pelo quadrado do oposto de 2?
d) A potência é positiva ou negativa?
Respostas: a) ; b) ; c) ; d) Negativa.
6. O quadro mostra o saldo mensal da conta bancária de Roberto no último dia dos meses de junho a setembro de certo ano.
|
Mês |
Saldo (R$) |
|---|---|
|
Junho |
|
|
Julho |
|
|
Agosto |
|
|
Setembro |
110 |
Qual foi o saldo mensal médio da conta de Roberto nesse período?
Resposta: .