Página 71
UNIDADE
3
Frações

Agora vamos estudar...
- fração como parte de um todo;
- fração como resultado da divisão;
- fração como razão;
- fração de uma quantidade;
- frações equivalentes e simplificação de frações;
- comparação de frações.
Página 72
Ideia de fração
As frações podem ser usadas em diversWtuações. Mas você já pensou o que motivou a criação desses números?
Questão 1. Realize uma pesquisa
para determinar o que
motivou a criação das frações.
Resposta pessoal. Espera-se que os estudantes concluam que as frações foram criadas por causa da necessidade que os povos antigos tinham de fazer medições.
Atenção!
A pesquisa proposta na questão 1 pode ser feita em livros, revistas e sites. Mas cuidado! Devemos nos certificar que as informações sejam pesquisadas em fontes atuais e confiáveis. Para encerrar, uma dica: confira as informações obtidas comparando-as com outras fontes.
Aplicadas em nosso cotidiano, as frações podem representar diferentes ideias matemáticas. Nos tópicos a seguir, estudaremos as frações como parte de um inteiro, como razão, como quociente e calcularemos frações de uma quantidade.
Fração como parte de um inteiro
Marcelo dividiu uma figura em partes iguais e coloriu algumas delas de verde. A figura desenhada por ele corresponde a um inteiro, e a parte colorida de verde pode ser representada por meio de uma fração.
O denominador indica a quantidade de partes iguais em que a figura está dividida (18), e o numerador indica a quantidade de partes coloridas de verde (6), o que, nesse caso, representamos pela fração .
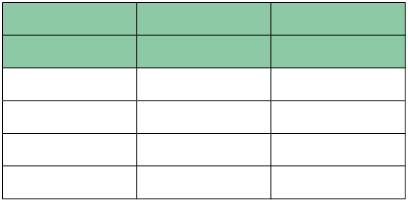
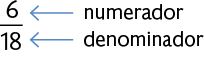
Nesse caso, a fração nos dá a ideia de parte de um inteiro.
Agora, considere cada uma das figuras A e B a seguir como um inteiro e divididas em partes iguais. Podemos representar a parte pintada de roxo de cada uma delas por meio de uma fração.
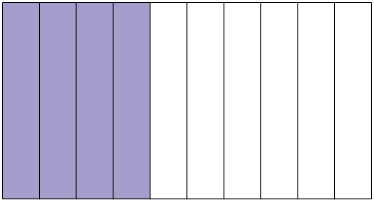
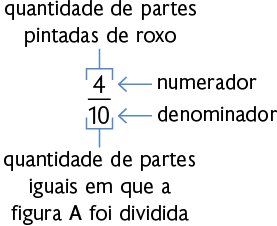
Página 73
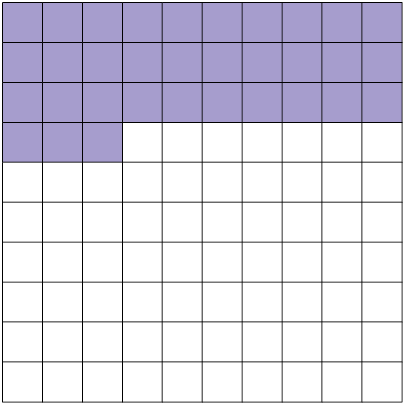
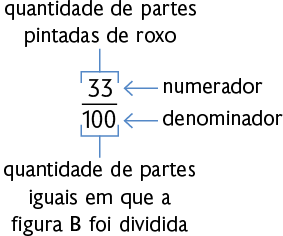
As frações e representam as partes pintadas de roxo das figuras A e B, respectivamente, e são chamadas frações decimais.
Frações cujo denominador é 10, 100, 1.000, ..., são chamadas frações decimais.
Fração como razão
A turma de Ana tem 28 estudantes, sendo 16 meninas e 12 meninos. Podemos representar a quantidade de meninos em relação ao total de estudantes da sala de aula por meio da fração , ou seja, na turma de Ana, a cada 28 estudantes, 12 são meninos. Dizemos que a razão entre a quantidade de meninos em relação ao total de estudantes da sala é .
Já a fração que representa a quantidade de meninas é , ou seja, nessa turma, a cada 28 estudantes, 16 são meninas. Assim, a razão entre a quantidade de meninas e o total de estudantes dessa sala de aula é dada pela fração .
Questão 2. Escreva em seu caderno uma fração que representa a razão entre a quantidade de meninas em relação à quantidade de meninos dessa turma.
Resposta: .
Fração como quociente de uma divisão
Podemos relacionar a fração a uma divisão, como apresentado no seguinte exemplo.
Eduardo é alfaiate e vai utilizar 48 botões para confeccionar 6 camisas. Nesse caso, dizemos que a quantidade de botões está relacionada à quantidade de camisas que ele vai confeccionar, o que representamos pela fração , ou seja, na razão de 48 para 6.
Página 74
A fração representa 8 inteiros, que corresponde à quantidade de botões que ele vai utilizar para confeccionar cada camisa. Nessa fração, o numerador corresponde ao dividendo e o denominador corresponde ao divisor.

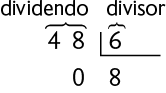
Portanto, Eduardo vai utilizar 8 botões para confeccionar cada camisa.
Toda fração pode ser escrita como uma divisão. Desse modo, o denominador da fração não pode ser zero.
Fração de uma quantidade
Célia leu 128 páginas de um livro, o que corresponde a do total de páginas. Quantas páginas tem esse livro?
Podemos calcular quantas páginas tem o livro que Célia está lendo da seguinte maneira.
Inicialmente, vamos considerar a figura a seguir dividida em 7 partes iguais, em que está representada a parte do livro que Célia leu.
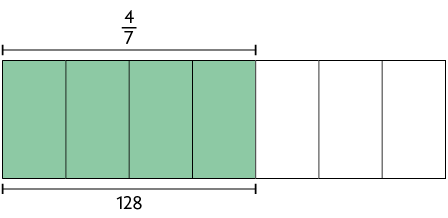
Cada parte da figura representa do total de páginas do livro. Assim, para determinar do total de páginas, basta dividir 128 por 4, obtendo 32, que representa 32 páginas.

Agora, calculamos a quantidade total de páginas do livro, que corresponde a , multiplicando 32 por 7.
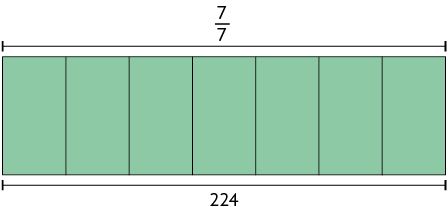
Portanto, o livro que Célia está lendo tem 224 páginas.
Questão 3. A irmã de Célia já leu 64 páginas de outro livro. Sabendo que essas páginas representam das páginas do livro, calcule no seu caderno quantas páginas ele tem.
Resposta: 144 páginas.
Página 75
Atividades
Faça as atividades no caderno.
1. Escreva no caderno uma fração para representar a parte pintada de rosa nas figuras a seguir, considerando que elas estão divididas em partes iguais.
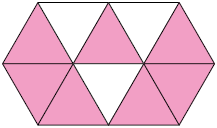
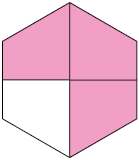
Respostas: A. ; B. .
2. Um ônibus escolar tem 16 fileiras de assentos com dois lugares cada.
a) Que fração representa um lugar desse ônibus?
b) Que fração representa uma fileira de assentos?
c) Sabendo que 28 crianças foram para a escola nesse ônibus, que fração representa a quantidade de lugares que foram ocupados?
Respostas: a) ; b) ou ; c) ou .
3. De acordo com a figura a seguir, responda às questões.
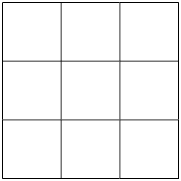
a) Em quantas partes iguais a figura foi dividida?
b) Que fração representa três partes dessa figura?
c) Que fração representa seis partes dessa figura?
Respostas: a) 9 partes iguais; b) ou ; c) ou .
4. Em um estacionamento há 32 carros prateados, 12 carros brancos, 18 carros pretos e 9 carros vermelhos.
a) Quantos carros há no estacionamento?
b) Que fração representa a quantidade de carros brancos nesse estacionamento?
c) Escreva uma razão para representar a quantidade de carros pretos em relação à quantidade de carros prateados nesse estacionamento.
Respostas: a) 71 carros; b) ; c) ou .
5. Um vendendor de doces tem 45 balas para vender, 19 de hortelã, 15 de morango e as demais de menta.
a) Quantas balas de menta o vendedor possui?
b) Do total de balas, que fração representa as de hortelã?
c) Escreva uma razão para representar a quantidade de balas de menta em relação à quantidade de balas de morango.
Respostas: a) 11 balas; b) ; c) .
6. Os diretores de uma empresa verificaram que 5 em cada 8 clientes deixaram comentários positivos no site dela. Que fração representa o total de comentários positivos feitos nesse site?
Resposta: .
7. Em uma livraria, a cada 50 livros vendidos, 15 são romances. Qual é a razão entre a quantidade de livros de romance vendidos e a quantidade total vendida?
Resposta: ou .
8. Para conseguir certa tonalidade de cor, um pintor precisa misturar de tinta vermelha com de tinta branca. Qual é a razão entre a medida de capacidade da tinta vermelha e a medida de capacidade da mistura?
a)
b)
c)
d)
Resposta: Alternativa d.
Página 76
9. Um paciente com suspeita de febre amarela ficou em observação em um hospital. Sua temperatura foi medida e ele apresentou febre em 6 dias, que correspondem a do tempo que ele ficou no hospital. Por quanto tempo esse paciente ficou no hospital?
Resposta: 10 dias.
10. No último sábado, Gabriel e dois casais foram a um restaurante. No momento de pagar a conta, eles fizeram a seguinte divisão: cada casal pagou da conta e Gabriel pagou da conta.
a) Sabendo que o valor total da conta foi de R$ 85,00, quantos reais cada casal pagou?
b) Quantos reais Gabriel pagou?
Respostas: a) R$ 34,00; b) R$ 17,00.
11. Calcule mentalmente as quantidades a seguir.
a) de
b) de
c) de 35 maçãs
d) de
e) de 18 páginas
f) de R$ 42,00
Respostas: a) ; b) ; c) 7 maçãs; d) ; e) 6 páginas; f) R$ 7,00.
12.No campeonato de handebol de uma escola, o time A venceu o time B, marcando do total de gols da partida. Sabendo que, ao todo, foram marcados 60 gols nessa partida, quantos gols o time B marcou?
Resposta: 28 gols.
13. Lucimara comprou o videogame indicado no cartaz.

Ela vai pagar do valor como entrada e o restante após 30 dias.
Quantos reais Lucimara vai pagar:
a) de entrada?
b) após 30 dias?
Respostas: a) R$ 1.440,00; b) R$ 960,00.
14. A caixa-d'água da casa de Ana comporta e, atualmente, está com dessa medida. Quantos litros de água há nessa caixa?
Resposta: .
15. Juliano e Fabrício colecionam selos. Da coleção de Juliano, correspondem a 42 selos, e da coleção de Fabrício, correspondem a 54 selos.
a) Quantos selos há na coleção de Juliano? E na coleção de Fabrício?
b) Qual é a diferença entre essas quantidades?
c) Quantos selos Juliano e Fabrício têm juntos?
Respostas: a) 49 selos; 81 selos; b) 32 selos; c) 130 selos.
Página 77
16. Durante uma liquidação em uma loja de roupas, foram vendidas das camisas do estoque pelo mesmo valor e foram arrecadados R$ 12.825,00. Antes da liquidação, havia 360 camisas iguais no estoque da loja.
a) Quantas camisas foram vendidas?
b) Se todas as camisas fossem vendidas, então quantos reais essa loja arrecadaria ao todo?
c) Quantos reais essa loja arrecadou quando vendeu do estoque? E do estoque?
Respostas: a) 285 camisas; b) R$ 16.200,00; c) R$ 2.700,00; R$ 4.050,00.
17. A preguiça é um animal muito comum no Brasil. Sobre as árvores, esse animal locomove-se lentamente, porém, na água, ele costuma se mover com mais velocidade. Seu alimento preferido são folhas de embaúba✚. Uma preguiça dorme cerca de do seu tempo de vida, o que corresponde a 24 anos.
- Embaúba:
- (Cecropia peltata) árvore nativa de regiões tropicais das Américas. Nasce em lugares sombrios, com folhas espessas e ásperas. É cultivada para a extração de polpa e como planta ornamental.↰
Aproximadamente quantos anos vive uma preguiça?

Resposta: Aproximadamente 40 anos.
18. Carolina postou uma foto em uma rede social.

Elabore uma questão envolvendo as informações da imagem e a relação entre razão e fração. Depois, peça a um colega que a resolva. Por fim, verifique se a resposta dele está correta.
Resposta pessoal.
Página 78
Frações equivalentes e simplificação de frações
As figuras foram divididas em partes iguais. Considerando as figuras A e B como o inteiro, podemos representar as partes pintadas de amarelo de cada uma delas com frações, como indicado a seguir.
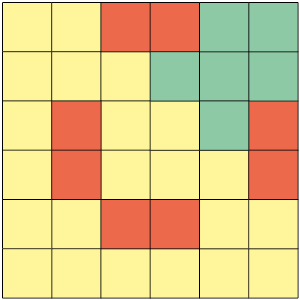
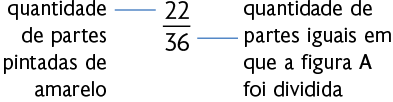
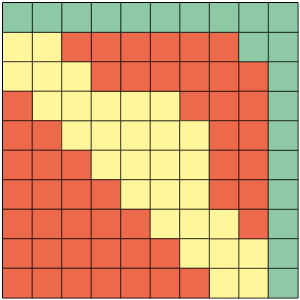

Cada fração indicada anteriormente pode ser simplificada até que se obtenha uma fração irredutível. Para simplificarmos uma fração, dividimos o numerador e o denominador pelo mesmo número natural, sendo ele diferente de 0 e de 1. Quando não podemos mais realizar as divisões, ou seja, simplificar essa fração, dizemos que ela é uma fração irredutível. Vamos executar esse processo da seguinte maneira:
Esquema I
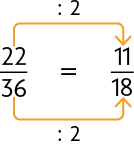
Esquema II
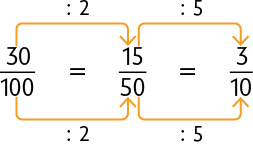
No esquema I, como as frações e representam a mesma parte do todo, dizemos que elas são equivalentes. O mesmo acontece no esquema II, com as frações e .
Atenção!
- Quando multiplicamos ou dividimos o numerador e o denominador de uma fração pelo mesmo número natural, diferente de 0 e 1, obtemos uma fração equivalente a ela.
- Quando o numerador e o denominador de uma fração não podem ser divididos por um mesmo número natural, diferente de 0 e 1, dizemos que essa é uma fração irredutível.
Questão 4. Copie em seu caderno os itens a seguir substituindo cada pelo número adequado, de maneira que as frações sejam equivalentes.
a)
b)
c)
Respostas: a) ; b) ; c) .
Página 79
Comparação de números positivos na forma de fração
Rafaela e Eduardo realizaram uma prova para concorrer a uma vaga de emprego. Rafaela acertou das questões dessa prova e Eduardo, . Qual deles acertou mais questões?
Para responder a essa pergunta, inicialmente é necessário efetuar a comparação das frações e a fim de verificar qual delas é a maior.
Inicialmente, vamos representar o número de questões que Rafaela e Eduardo acertaram por meio de figuras.
Atenção!
Cada uma dessas figuras tem dimensões com mesmas medidas e foram divididas em partes iguais.


De acordo com as figuras, podemos verificar que .
Portanto, Rafaela acertou mais questões na prova do que Eduardo.
Outra maneira de comparar as frações e é obtermos as frações equivalentes com denominadores iguais. Para determinar qual será esse denominador, calculamos inicialmente o mínimo múltiplo comum (mmc) dos denominadores. Nesse caso, vamos calcular o .
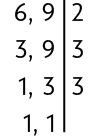
Atenção!
Na comparação de frações com denominadores diferentes, a obtenção de frações equivalentes com denominadores iguais é um método mais prático se comparado com a representação por meio de imagens ou figuras.
Logo, .
Agora, obtemos as frações equivalentes a e , porém com denominadores iguais a 18.
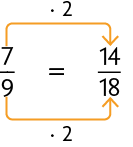
Atenção!
Multiplicamos o numerador e o denominador da fração por 2, pois .
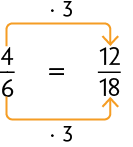
Atenção!
Multiplicamos o numerador e o denominador da fração por 3, pois .
Como , concluímos que .
Para comparar frações com denominadores diferentes, inicialmente, obtemos frações equivalentes a elas com o mesmo denominador. Em seguida, comparamos as frações equivalentes.
Página 80
Podemos representar as frações e na reta numérica. Nesse caso, dividimos um inteiro na reta numérica em 18 partes iguais, número que corresponde ao denominador das frações. Depois, a partir do zero, indicamos 12 e 14 dessas partes, para obter, respectivamente, as frações e , como indicado a seguir.

Questão 5.
Compare as frações de cada item usando o símbolo ou entre elas.
a) e
b) e
c) e
Respostas: a) ; b) ; c) .
Atividades
Faça as atividades no caderno.
19. Escreva uma fração para representar as partes pintadas de roxo em cada figura. Depois, se possível, simplifique-as e indique a fração irredutível correspondente.
Atenção!
Em cada item as figuras foram divididas em partes iguais.
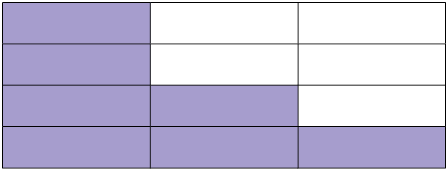

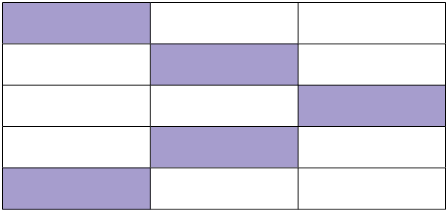
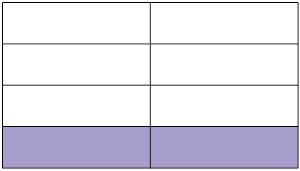
Respostas: A. ; B. ; C. ; D.
20. Em cada item, determine a fração irredutível.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) .
Página 81
21. Copie o esquema substituindo cada letra pelo número adequado.
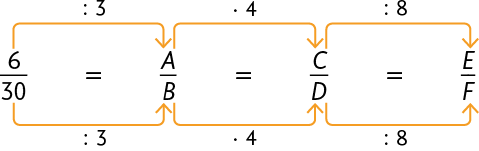
Resposta: .
22. Escreva no caderno uma fração:
a) cujo denominador seja 4;
b) cujo numerador seja 7;
c) que corresponda a 1 unidade;
d) que seja maior do que 2 e menor do que 5;
e) que, ao ser simplificada, seja igual a ;
f) que tenha quociente igual a 9.
Sugestões de respostas: a) ; b) ; c) ; d) ; e) ; f) .
23. Em uma academia, Pedro caminhou na esteira durante de uma hora. Já Thiago caminhou durante de uma hora. Qual deles caminhou por mais tempo na esteira?
Resposta: Thiago.
24. No fluxograma está indicado como comparar frações com denominadores diferentes.

Atenção!
Lembre-se de que, em um fluxograma, cada tipo de figura tem um significado e são conectadas por setas. O significado das figuras utilizadas neste fluxograma estão indicadas a seguir.


Seguindo os procedimentos indicados no fluxograma, compare as frações a seguir e reescreva-as usando o símbolo ou entre elas.
a) e
b) e
Respostas: a) ; b) .
25. No quadro está indicada a fração do total de pastéis de cada sabor que foram vendidos durante um dia em uma barraca.
| Sabor do pastel | Fração das vendas |
|---|---|
| Carne | |
| Queijo | |
| Frango | |
| Presunto e queijo |
Escreva em seu caderno as frações do quadro em ordem crescente.
Resposta: .
Página 82
26. Leia o texto e depois resolva os itens.
O gerente de uma empresa identificou que dos funcionários usam o transporte público para chegar ao trabalho, enquanto dos funcionários da mesma empresa usam automóvel.
a) É possível determinar a quantidade de funcionários que vão ao trabalho de automóvel e quantos utilizam o transporte público? Justifique sua resposta.
Resposta: Não é possível, pois não foi informado o total de funcionários da empresa.
b) Qual dos meios de transporte citados no texto é o mais usado para chegar ao trabalho nessa empresa?
Resposta: O transporte público.
c) Explique como podemos determinar a resposta da pergunta do item b.
Resposta pessoal: Sugestão de resposta: Para determinar o meio de transporte mais usado para chegar ao trabalho nessa empresa, é necessário comparar as frações.
d) Podemos comparar as frações citadas no texto usando as seguintes estratégias.
Resposta: A maior fração é . Portanto, o meio de transporte mais usado para os funcionários chegarem na empresa é o transporte público.
1º. Obtenha frações equivalentes às frações iniciais que tenham denominadores iguais.
2º. Compare os numeradores das frações equivalentes obtidas no passo anterior.
3º. A fração que tiver o maior numerador será a maior.
1º. Como os denominadores das frações são diferentes, calcule o mmc dos denominadores das frações.
2º. Obtenha as frações equivalentes com os denominadores iguais ao mmc calculado no passo anterior.
3º. Compare os numeradores das frações equivalentes.
4º. A fração que tiver o maior numerador será a maior.
Agora, escolha uma das estratégias apresentadas e compare as frações e para saber qual é o meio de transporte citado no texto mais usado para os funcionários chegarem na empresa.
e) Entre as estratégias apresentadas no item d, qual delas você considera mais prática ao comparar números positivos na forma de fração com denominadores diferentes? Justifique sua resposta.
Resposta pessoal.
f) Você conhece outra estratégia diferente das apresentadas para comparar frações com denominadores diferentes? Se sim, compartilhe a resposta com os colegas.
Resposta pessoal.
27. Compare as frações colocando o símbolo ou entre elas.
a) e
b) e
De maneira semelhante ao realizado no item d da atividade 26, escreva os procedimentos utilizados por você para comparar essas frações. Depois represente-os por meio de um fluxograma.
Respostas: a) ; b) ; • Resposta nas orientações ao professor.
Página 83
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Você já pensou no quanto uma noite mal dormida pode interferir no seu dia? Falta de concentração, ansiedade e bocejos frequentes são só alguns sintomas da privação de sono. Mas precisamos dormir por quanto tempo? A resposta para essa pergunta depende da sua idade. Recém-nascidos, por exemplo, dormem cerca de 18 horas por dia, enquanto adultos passam em média 8 horas dormindo. Idosos, por sua vez, chegam a dormir por volta de do tempo dos bebês.
a) Que fração do dia recém-nascidos passam dormindo? E pessoas adultas? E idosos? Em uma folha de papel avulsa, faça simplificações e responda a esta questão usando frações irredutíveis.
b) Considerando as informações apresentadas, uma pessoa que necessita dormir em média 6 horas por dia é um recém-nascido, um adulto ou um idoso?
Respostas: a) Recém-nascidos: ; Adultos ; Idosos: ; b) Idoso.
2. Em seu treino de futebol, Alice realizou 50 cobranças de pênalti. A fração que representa seus acertos é , ou seja, a cada 10 pênaltis cobrados, ela fez 7 gols.
a) Quantos gols Alice fez no total?
b) Qual é a razão entre as cobranças de pênalti que não resultaram em gols e as que marcaram gols?
Respostas: a) 35 gols; b) ou .
3. Escreva as frações que representam as partes pintadas de amarelo em cada uma das figuras, sabendo que elas estão divididas em partes iguais.
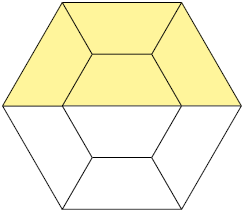
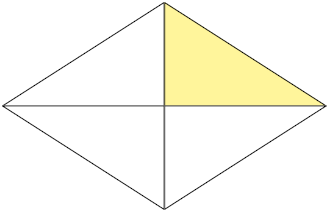
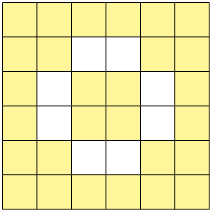
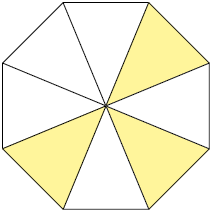
Respostas: A. ; B. ; C. ; D. .
Página 84
4. Copie os itens a seguir substituindo cada pelo símbolo , ou , de maneira que fiquem corretos.
a)
b)
c)
d)
e)
f)
Junte-se a um colega e conversem a respeito dos procedimentos que vocês utilizaram para concluir a atividade.
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
5. Este mês, Jorge tinha R$ 3.780,00. Ele gastou dessa quantia com o pagamento de contas e investiu do valor restante.
a) Qual foi o valor que Jorge usou para pagar contas?
b) Qual foi o valor investido por Jorge neste mês?
Respostas: a) R$ 1.620,00; b) R$ 1.440,00.
6. (Obmep-2010) A figura mostra um quadrado dividido em 16 quadradinhos iguais. A área em preto corresponde a que fração da área do quadrado?
a) .
b) .
c) .
d) .
e) .

Resposta: Alternativa c.
7. No sítio onde Rodrigo mora, há uma bomba que puxa de água por dia. Dessa água, utilizam-se diariamente para regar as plantações e para limpeza.
a) Quantos litros de água são utilizados diariamente para regar as plantações? E para a limpeza?
b) Quantos litros de água são utilizados diariamente para outras finalidades?
Respostas: a) e ; b) .
8. A seguir, estão representados 3 recipientes de mesma medida de capacidade de . Cada um deles está dividido em partes iguais e contém certa quantidade de líquido.



Determine, em mililitros, a quantidade de líquido contida em cada recipiente.
Respostas: A. ; B. ; C. .