Página 85
UNIDADE
4
Os números racionais

Agora vamos estudar...
- os números racionais;
- os números racionais na reta numérica;
- o módulo de um número racional;
- o oposto ou simétrico de um número racional;
- a comparação de números racionais.
Página 86
Números racionais
A professora Roberta escreveu alguns números na lousa.
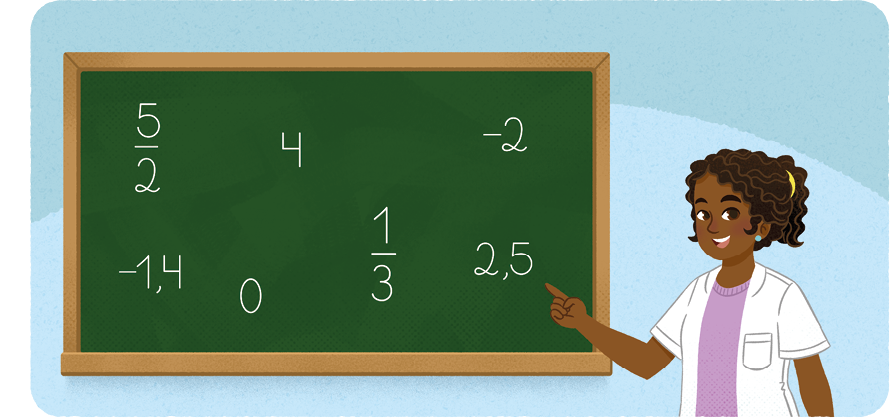
Eles são números racionais e podem ser escritos tanto na forma fracionária quanto na decimal.
Em seguida, a professora organizou esses números em uma reta numérica.
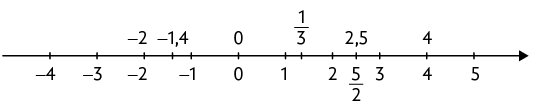
Atenção!
Todo número inteiro é racional.
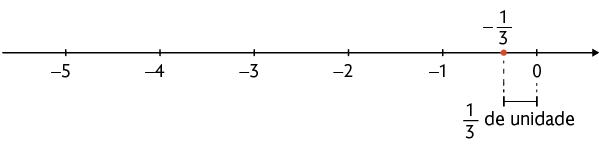
Analise como ela localizou, por exemplo, a fração nessa reta.

Página 87
Podemos transformar um número racional representado na forma decimal em fracionário. A seguir apresentamos alguns exemplos.
Também podemos fazer o inverso, como apresentado nos exemplos a seguir.
Atividades
Faça as atividades no caderno.
1. Analise o que Fernando está dizendo.

Entre quais números inteiros consecutivos estão os números indicados em cada item?
a) 1,4
b) 5,87
c) 0,3
d)
e)
f) 3,75
Respostas: a) 1 e 2; b) 5 e 6; c) 0 e 1; d) e 0; e) e ; f) 3 e 4.
2. Associe cada um dos números a uma letra na reta numérica.
-
0,2
-
2,6
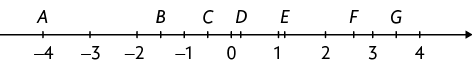
Respostas: A: ; B: ; C: ; D: 0,2; E: ; F: 2,6; G: .
3. Em cada item, escreva um número decimal que esteja entre os números:
a) 0 e 1.
b) e .
c) 5 e 6.
d) 2 e 3.
Resposta pessoal.
4. Analise a reta numérica a seguir.
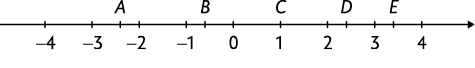
Determine a letra que corresponde ao número racional 2,4.
Resposta: D.
5. Em seu caderno, escreva os números fracionários na forma decimal.
a)
b)
c)
d)
e)
f)
Respostas: a) 0,1; b) ; c) 0,625; d) 1,75; e) 0,5625; f) .
6. Em seu caderno, escreva os números decimais na forma fracionária.
a) 0,2
b) 0,75
c) 1,5
d)
e)
f) 4,8
Sugestão de respostas: a) ; b) ; c) ; d) ; e) ; f) .
7. Em qual
item é apresentado o número 0,8 na forma
fracionária? Resolva a atividade mentalmente e
justifique sua resposta.
a)
b)
c)
d)
Resposta: Alternativa c, pois é a opção em que o numerador é menor do que o denominador e, além disso, .
8. Utilizando os números 0,2; ; 3,5 e , elabore uma questão envolvendo transformações entre números na forma decimal e na forma fracionária. Depois, troque com um colega e peça a ele que a responda.
Resposta pessoal.
Página 88
Módulo de um número racional
Já estudamos que a medida da distância entre um ponto da reta numérica e a origem (0) é chamada módulo ou valor absoluto do número associado a esse ponto. Na unidade 2, vimos alguns exemplos envolvendo números inteiros e, agora, vamos determinar o módulo dos números racionais. A seguir, apresentamos alguns exemplos.
, pois a distância entre o ponto correspondente ao número 2,6 e a origem da reta numérica mede 2,6 unidades.

, pois a distância entre o ponto correspondente ao número e a origem da reta numérica mede 5,1 unidades.

, pois a distância entre o ponto correspondente ao número e a origem da reta numérica mede de unidade.
Questão 1. Em seu caderno, calcule.
a)
b)
c)
d)
e)
f)
Respostas: a) 3,7; b) ; c) 7,8; d) ; e) 325,6; f) 458,2.
Quando dois números racionais estão a uma mesma medida de distância da origem na reta numérica (ou seja, têm módulos iguais), mas estão localizados em sentidos contrários, são chamados números opostos ou números simétricos.
- O número 2,3 é o oposto de , pois e eles estão localizados em sentidos contrários da reta numérica.
- O número é o oposto de , pois e eles estão localizados em sentidos contrários da reta numérica.
Página 89
Atividades
Faça as atividades no caderno.
9. Indique, entre os números apresentados, os que têm módulos iguais.
-
1
-
7
-
1,2
-
0
Resposta: 7 e ; 2,8 e ; 1,2 e .
10. Em cada item, determine o oposto do número.
a)
b) 8
c) 3,4
d)
e)
f)
Respostas: a) 1; b) ; c) ; d) 7,8; e) ; f) .
11. Determine os números cujo módulo é:
a) 0,5.
b) 2,1.
c) 5,9.
d) 7,3.
Respostas: a) e 0,5; b) e 2,1; c) e 5,9; d) e 7,3.
12. Analise os números indicados na reta numérica a seguir.

a) Entre os números destacados, qual apresenta a maior medida de distância até a origem?
Resposta: .
b) Explique para um colega como você obteve a resposta do item a.
Resposta pessoal. Espera-se que os estudantes digam que obtiveram a resposta analisando qual dos números tem maior módulo.
13. Armando e seus amigos estão brincando de adivinhar números. Verifique o que eles estão dizendo.



Determine o número que Armando e seus amigos estão pensando.
Resposta: Armando: 2; Maria: 5; Pedro: .
Página 90
Comparação de números racionais
Leonardo pesquisou na internet as medidas das temperaturas mínimas em algumas cidades em certo dia e as registrou em seu caderno.

Em seguida, ele organizou os valores obtidos em uma reta numérica.

Com o auxílio dela, podemos comparar as medidas de temperatura. Para isso, basta analisar a posição de um número em relação a outro. A seguir, apresentamos alguns exemplos.
- O número 23,5 está à direita de . Nesse caso, (lê-se: vinte e três vírgula cinco é maior do que menos quatro). Portanto, .
- O número 19 está à esquerda de 21. Nesse caso, (lê-se: dezenove é menor do que vinte e um). Portanto, .
- O número está à direita de . Nesse caso, (lê-se: menos um vírgula três é maior do que menos quatro). Portanto, .
- O número está à esquerda de 21. Nesse caso, (lê-se: menos um vírgula três é menor do que vinte e um). Portanto, .
Os números que estão à esquerda de um número qualquer na reta numérica são menores do que esse número. De maneira análoga, os números que estão à direita de um número qualquer na reta numérica são maiores do que esse número.
Questão 2. Qual número é maior: 2,3 ou
? Justifique
sua resposta.
Resposta: 2,3. Sugestão de justificativa: 2,3 é maior do que , pois , e 1,5 está à esquerda de 2,3 na reta numérica.
Questão 3. Em seu caderno, escreva alguns números racionais, tanto positivos quanto negativos, nas formas fracionária e decimal. Em seguida, organize-os em ordem crescente.
Resposta pessoal.
Página 91
Atividades
Faça as atividades no caderno.
14. Copie os itens no caderno, substituindo cada pelo símbolo ou .
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
15. Escreva os números apresentados a seguir em ordem crescente.
-
1
-
0
-
4,5
-
2,5
-
2
Resposta: .
16. Márcia comparou os números e 0,8 da seguinte maneira.

Atenção!
Você pode utilizar uma reta numérica para ajudar na comparação dos números.
Utilize o mesmo procedimento de Márcia e compare os números indicados em cada item.
a) e 0,8
b) e
c) e
d) e
Respostas: a) ; b) ; c) ; d) .
17. Em seu caderno, associe cada um dos números a uma letra da reta numérica.
-
5,9
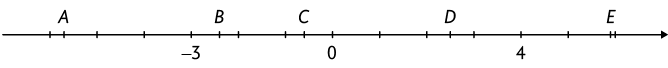
Resposta: A: ; B: ; C: ; D: ; E: 5,9.
Agora, escreva dois números racionais que estão entre B e D.
Resposta pessoal.
Página 92
18. Rodrigo, Guilherme e Tobias estão disputando um jogo de corrida em um videogame. A medida do tempo gasto por eles para completar a última volta em uma das partidas está indicada a seguir.
-
Rodrigo
-
Guilherme
-
Tobias
Qual dos amigos fez a volta mais rápida?
Resposta: Guilherme.
19. O quadro apresenta a quantia poupada por Marcela mensalmente durante o ano de 2023.
|
Mês |
Jan. |
Fev. |
Mar. |
Abr. |
Maio |
Jun. |
Jul. |
Ago. |
Set. |
Out. |
Nov. |
Dez. |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Quantia (R$) |
135,50 |
237,00 |
78,90 |
148,00 |
148,90 |
378,10 |
58,00 |
49,00 |
364,30 |
100,00 |
269,00 |
405,50 |
a) Em qual mês ela poupou a maior quantia? E em qual economizou a menor quantia?
Respostas: Em dezembro; em agosto.
b) A quantia poupada no mês de março foi maior, menor ou igual àquela economizada em dezembro?
Resposta: Menor.
c) Escreva as quantias poupadas por Marcela em ordem decrescente.
Resposta: R$ 405,50; R$ 378,10; R$ 364,30; R$ 269,00; R$ 237,00; R$ 148,90; R$ 148,00; R$ 135,50; R$ 100,00; R$ 78,90; R$ 58,00; R$ 49,00.
20. Duas equipes estão competindo em uma gincana escolar. A equipe A venceu das provas e a equipe B, venceu . Qual delas ganhou mais provas?
Resposta: Equipe B.
21. Marcelo é vendedor em uma concessionária. Em certo dia, ele vendeu dois carros. O cliente 1 pagou do valor total do automóvel como entrada; já o cliente 2 pagou do valor. Sabendo que os dois veículos vendidos têm o mesmo valor, qual dos clientes pagou a maior quantia de entrada?
Resposta: Cliente 1.
22. Para um trabalho escolar, Marcos vai usar dois pedaços de barbantes: um vermelho e um azul. Analise o que Marcos está dizendo.

Sabendo que o comprimento total do barbante azul mede , qual dos pedaços terá a maior medida de comprimento?
Resposta: Barbante azul.
Página 93
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Copie os quadros e complete-os com os números que faltam.
|
Número decimal |
7,3 |
4,9 |
2,3 |
10,1 |
||
|---|---|---|---|---|---|---|
|
Número fracionário |
|
|
Número decimal |
7,9 |
123,05 |
0,9 |
|||
|---|---|---|---|---|---|---|
|
Número fracionário |
|
|
Agora, escreva esses números em ordem decrescente.
Respostas na seção Resposta e na seção Resoluções.
2. Entre os números apresentados a seguir, identifique e anote aqueles que são iguais.
-
2,5
-
0,75
-
0,875
Resposta: ; ; ; ; .
3. Escreva o oposto do número apresentado em cada item.
a)
b)
c) 7,56
d)
e)
f) 2,7
Respostas: a) 2; b) 8,7; c) ; d) ; e) ; f) .
4. Calcule os módulos.
a)
b)
c)
d)
e)
f)
Respostas: a) 2,4; b) 3,83; c) 8,9; d) ; e) ; f) 12,7.
g) Qual dos números tem o maior módulo? E o menor?
Respostas: 12,7; .
h) Organize em ordem decrescente os resultados obtidos.
Resposta: 12,7; 8,9; 3,83; 3,5; 2,4; 0,4.
5. Copie os itens substituindo cada pelo símbolo , ou .
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
6. Escreva os números a seguir em ordem crescente.
-
1,582
-
0
-
11,45
-
4,8
Resposta: .
Página 94
7. Classifique as sentenças em verdadeiras ou falsas. Em seguida, copie as falsas em uma folha de papel avulsa, corrigindo-as.
a) O número 10 é maior do que 2,5, pois, na reta numérica, 10 está à esquerda de 2,5.
Resposta: Falsa. Sugestão de correção: O número 10 é maior do que 2,5, pois, na reta numérica, 10 está à direita de 2,5.
b) O oposto de é 10.
Resposta: Verdadeira.
c) O módulo de é 1, pois, na reta numérica, a distância entre 3 e 2 mede 1 unidade.
Resposta: Falsa. Sugestão de correção: O módulo de é , pois, na reta numérica, a distância entre o ponto correspondente ao número e a origem mede de unidade.
8. Copie a reta numérica apresentada.

Depois, represente nela os números a seguir.
-
2,1
-
4,9
Resposta na seção Resoluções.
9. Mariana e seus amigos vão construir 4 telefones de latas.
Confira a medida do comprimento dos quatro barbantes utilizados por eles.
Barbante 1: .
Barbante 2: .
Barbante 3: .
Barbante 4: .

Brinquedo telefone de latas.
a) Qual barbante tem a menor medida de comprimento?
Resposta: Barbante 4.
b) Escreva as medidas dos comprimentos dos barbantes em ordem decrescente.
Resposta: , , , .
10. Leia as dicas apresentadas a seguir.
O algarismo dos décimos é 3.
O número é maior do que 10 e menor do que 16.
O valor correspondente ao algarismo das unidades é um divisor de 36.
O algarismo das unidades é um número primo e ímpar.
Qual é o número desconhecido?
Resposta: 13,3.
11. Tales vai comprar um computador. Em fevereiro, ele poupou do valor do equipamento e em março, poupou . Em qual mês Tales economizou a maior quantia?
Resposta: Em março.