Página 95
UNIDADE
5
Operações com números racionais

Agora vamos estudar...
- adição e subtração de números racionais;
- multiplicação e divisão de números racionais;
- potenciação cuja base é um número racional.
Página 96
Adição e subtração de números racionais na forma de fração
Os tipos ou grupos sanguíneos dos seres humanos são A, B, AB e O. Verifique no gráfico a fração aproximada da população mundial que faz parte de cada um deles. Que fração da população corresponde ao grupo sanguíneo A ou B?
Ocorrência de cada grupo sanguíneo na população mundial
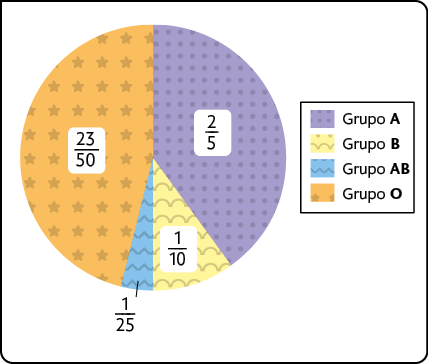
Fonte de pesquisa: HERLIHY, Barbara; MAEBIUS, Nancy K. Anatomia e Fisiologia do Corpo Humano Saudável e Enfermo. Tradução: Cíntia Bovi Binotti et al. Barueri: Manole, 2002. p. 278.
Podemos responder a essa questão com o resultado de uma adição de frações, assunto que provavelmente você já estudou em anos anteriores. Nesse caso, precisamos calcular .
Note que essas frações têm denominadores diferentes. Assim, para adicioná-las, determinamos frações equivalentes a elas, com o mesmo denominador.
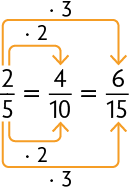
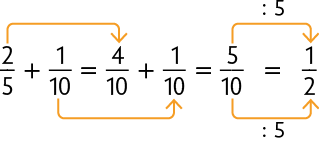
Nesse caso, não precisamos obter uma fração equivalente a , pois , que equivale a , tem denominador 10. Em seguida, adicionamos as frações com mesmo denominador e simplificamos o resultado, obtendo uma fração irredutível.
Também podemos realizar esse cálculo usando o mínimo múltiplo comum para obter frações equivalentes com o mesmo denominador. Nesse caso, o .
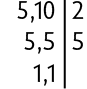
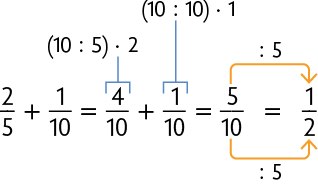
Atenção!
Dividimos o obtido pelo denominador de cada fração. Em seguida, multiplicamos o resultado dessa divisão pelo numerador de cada uma. Com isso, obtemos frações equivalentes às iniciais com denominador igual ao que, neste caso, é 10.
O resultado obtido, , representa a fração da população correspondente ao grupo sanguíneo A ou B.
Página 97
É possível efetuar cálculos envolvendo números inteiros e fracionários, e esse assunto provavelmente já foi visto por você em anos anteriores. Por exemplo, podemos obter o resultado de da seguinte maneira.
1. Escrevemos uma fração que representa o número 3.
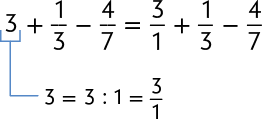
2. Calculamos o dos denominadores.
3. Usando o , realizamos o cálculo.
Portanto, o resultado obtido é .
Atenção!
Em uma adição ou subtração de frações com denominadores diferentes, inicialmente obtemos frações equivalentes a elas com o mesmo denominador. Em seguida, adicionamos ou subtraímos os numeradores delas.
Atividades
Faça as atividades no caderno.
1. Junte-se a um colega e, conforme os dados do gráfico da página anterior, respondam às questões a seguir.
a) Que fração representa a população que tem o grupo sanguíneo O ou AB?
b) Que fração representa a diferença entre a população que tem o grupo sanguíneo O e a que tem o A?
c) Que fração representa a diferença entre a população que tem o grupo sanguíneo B e a que tem o AB?
d) Que fração representa a população que tem o grupo sanguíneo A, B ou AB?
Respostas: a) ; b) ; c) ; d) .
Página 98
2. Efetue os cálculos em seu caderno.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ou ; f) .
3. O mosaico a seguir é formado por quadrados com as mesmas dimensões.
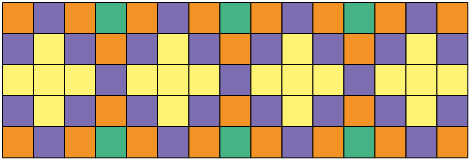
Que fração representa as partes do mosaico pintadas de:
a) verde ou amarelo?
b) amarelo ou roxo?
c) verde, amarelo, roxo ou laranja?
d) verde, laranja ou roxo?
e) amarelo, laranja ou roxo?
Respostas: a) ; b) ; c) ou 1; d) ; e) .
f) Junte-se a um colega e expliquem como vocês fizeram para resolver os itens c e e.
Resposta pessoal.
4. Efetue os cálculos a seguir.
a)
b)
c)
d)
e)
Respostas: a) ; b) ; c) ; d) ; e) .
5. Analise o marcador de combustível do automóvel de Arnaldo antes e depois de abastecê-lo.
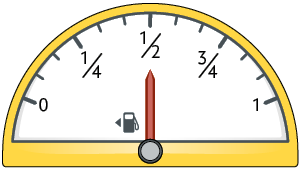
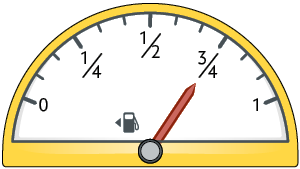
Que fração do tanque representa a quantidade de combustível colocada ao abastecer?
Resposta: .
6. De 1920 a 2021, o Brasil conquistou 150 medalhas, ao todo, nos jogos olímpicos, das quais foram de ouro, foram de prata e o restante, de bronze.
a) Que fração do total de medalhas representa as de ouro e as de prata conquistadas pelo Brasil nos jogos olímpicos?
Resposta: .
b) Que fração representa as medalhas de bronze conquistadas pelo Brasil?
Resposta: .
c) Quantas medalhas de ouro o Brasil conquistou ao todo nos jogos olímpicos no período de 1920 a 2021? E de prata? E de bronze?
Resposta: 37 medalhas de ouro; 42 medalhas de prata; 71 medalhas de bronze.
7. Na biblioteca de uma escola, há uma estante com diversos livros, dos quais são de Matemática e são de Geografia.
Que fração do total de livros dessa estante representa os de Matemática e os de Geografia juntos?
Resposta: .
8. Uma indústria recebeu uma encomenda para fabricar certa quantidade de peças. Para produzi-las, uma das máquinas demora e outra, mais moderna, .
Se as duas máquinas trabalharem juntas, que fração do total da encomenda elas fabricariam em:
a) ?
b) ?
Respostas: a) ; b) .
Página 99
Multiplicação de números racionais na forma de fração
Multiplicação de um número natural por uma fração
Joana comprou uma torta dividida em 10 pedaços iguais e comeu 3 deles. Que fração da torta Joana comeu?
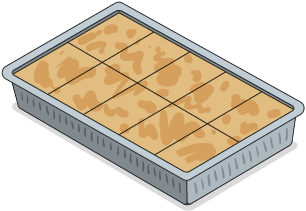
Podemos responder a essa pergunta resolvendo uma adição de frações.
Essa adição tem 3 parcelas iguais a . Então, podemos indicá-la pela seguinte multiplicação.
Portanto, Joana comeu da torta.
Atenção!
Para multiplicar um número natural por uma fração, efetuamos a multiplicação dele pelo numerador da fração e mantemos o denominador.
Atividades
Faça as atividades no caderno.
9. Efetue os cálculos.
a)
b)
c)
d)
Respostas: a) ; b) ; c) ; d) ou .
10. Heitor tinha R$ 56,00 e gastou dessa quantia na compra de um caderno. Quantos reais custou esse caderno?
Para obter o preço do caderno, precisamos calcular de 56, ou seja, .
Copie o cálculo a seguir no caderno substituindo ■ pelo número adequado.
Portanto, o caderno custou R$ ,00.
Resposta: ; R$ 14,00.
11. Em seu caderno, calcule e simplifique os resultados.
a)
b)
c)
d)
e)
Respostas: a) 7; b) 6; c) 21; d) 27; e) 45.
12. Em uma meia maratona o atleta percorre uma distância medindo . Em uma dessas provas, certo atleta percorreu em média do percurso a cada minuto.
a) Após , que fração do percurso ele percorreu?
b) A fração do percurso obtida no item a corresponde aproximadamente a uma medida de distância de quantos metros?
Respostas: a) ; b) Aproximadamente .
Página 100
Multiplicação de uma fração por outra fração
Do total de salgados que Tatiane preparou para uma festa de aniversário, representa a quantidade de pastéis, dos quais eram de carne e o restante era de queijo.
Que fração do total de salgados representa a quantidade de pastéis de carne?
Podemos responder a essa pergunta calculando de , ou seja, .
Podemos fazer esse cálculo utilizando figuras.
1º. Representamos pela figura a seguir o total de salgados que Tatiane preparou, e a dividimos em 4 partes iguais, indicando na cor amarela dos salgados, que corresponde aos pastéis.

2º. Dividimos em 5 partes iguais a parte indicada em amarelo e consideramos 3 delas, pois queremos calcular de .
Pela figura, percebemos que 3 partes de 20 foram consideradas.
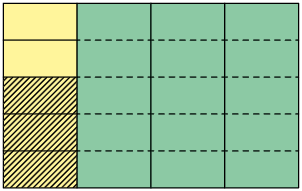
Portanto, corresponde a , ou seja, dos salgados eram pastéis de carne.
Questão 1. Que que fração dos salgados
representa a quantidade de pastéis
de queijo?
Resposta: ou .
Questão 2. Sabendo que Tatiane preparou 1.200 salgados ao todo, responda em seu caderno: Quantos pastéis eram de carne? E quantos eram de queijo?
Respostas: 180 pastéis eram de carne; 120 pastéis eram de queijo.
Atenção!
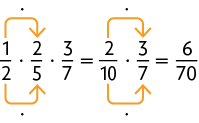
A maneira prática de multiplicar duas frações é multiplicando o numerador de uma pelo numerador da outra e o denominador de uma pelo denominador da outra.
Analise outros exemplos.
Página 101
Atividades
Faça as atividades no caderno.
13. Calcule:
a) o triplo de .
b) o quádruplo de .
c) o dobro de .
d) a metade de .
e) dois terços de .
f) cinco oitavos de .
Respostas: a) ; b) ou ; c) ou ; d) ou ; e) ou ; f) ou .
14. Copie no caderno os itens, substituindo as letras por números, de modo que as igualdades sejam verdadeiras.
a)
b)
c)
d)
e)
f)
Atenção!
Em cada item, letras iguais representam números iguais.
Sugestão de respostas: a) ; b) ; c) ; d) ; e) ; f) .
15. Uma padaria produz diariamente 2.240 pães, dos quais é do tipo doce e são de leite. Em certo dia, em consequência de um problema no forno, essa padaria produziu dos pães do tipo doce e dos pães de leite que normalmente prepara. No dia que ocorreu o problema no forno, essa padaria produziu quantos:
a) pães do tipo doce?
Resposta: 35 pães do tipo doce.
b) pães de leite?
Resposta: 480 pães de leite.
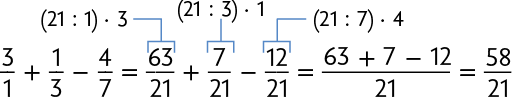
16. A professora de Camila escreveu o cálculo a seguir na lousa para os estudantes resolverem.

Camila resolveu esse cálculo simplificando as frações.


De maneira semelhante, simplifique em seu caderno as frações de cada item e determine o resultado dos cálculos.
a)
b)
c)
d)
e)
f)
Respostas: a) ; b) ; c) ; d) ; e) ; f) .
Página 102
Divisão de números racionais na forma de fração
Divisão de um número natural por uma fração
Fernando vai acampar em Ilhabela (SP) e vai levar, entre outros itens, de suco distribuídos em garrafas com capacidade para cada.
De quantas garrafas de ele vai precisar?
Podemos responder a essa pergunta obtendo o resultado da divisão a seguir.

Podemos efetuar esse cálculo usando figuras.
1º. Representamos de suco, ou seja, a unidade, por uma figura.

2º. Em seguida, dividimos essa figura em 2 partes iguais. Cada uma delas representa de suco.

3º. Como o conteúdo total de suco é , devemos representar 2 unidades e dividir cada uma em duas partes iguais.
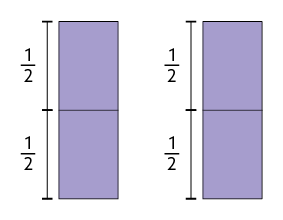
cabe 4 vezes em 2 unidades, ou seja, .
Portanto, Fernando vai precisar de 4 garrafas de para levar de suco.
Questão 3. Se Fernando fosse levar de suco, quantas garrafas de
seriam necessárias?
Resposta: 6 garrafas.
Atenção!
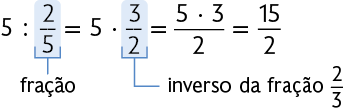
A maneira prática de dividir um número natural diferente de zero por uma fração é multiplicá-lo pelo inverso da fração.
Analise um exemplo.
Atenção!
O inverso de uma fração é outra que, multiplicada por ela mesma, resulta em 1. Por exemplo, o inverso de é , pois .
Página 103
Divisão de uma fração por um número natural
Uma fábrica produziu 885 pares de calçados em uma semana. Dessa produção, era de calçados masculinos e o restante, de calçados femininos. Os calçados masculinos foram entregues aos revendedores em três lotes, com a mesma quantidade de pares em cada um.
Que fração da produção total cada lote de calçados masculinos representa?
Podemos responder a essa pergunta obtendo o resultado da divisão a seguir.

Acompanhe como efetuar esse cálculo usando figuras.
1º. Representamos a produção total da fábrica por um retângulo. Em seguida, dividimos essa figura em 5 partes iguais e indicamos na cor amarela da produção, que corresponde aos calçados masculinos.

2º. Dividimos em 3 partes iguais a parte indicada em amarelo e consideramos 1 delas, pois queremos calcular .
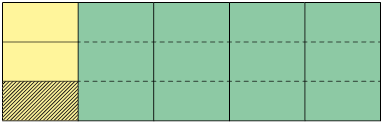
Na figura, percebemos que 1 parte de 15 foi considerada
Portanto, cada lote de calçados masculinos representa da produção total.
Questão 4. Quantos pares de calçados masculinos foram produzidos por essa fábrica nessa semana? E quantos pares de calçados femininos?
Respostas: 177 pares; 708 pares.
Questão 5. Quantos pares de calçados masculinos há em cada lote?
Resposta: 59 pares.
Questão 6. Os pares de calçados femininos foram divididos em dois lotes iguais. Que fração representa a quantidade de pares de calçados de cada lote em relação ao total produzido?
Resposta: ou .
Atenção!
A maneira prática de dividir uma fração por um número natural diferente de zero é multiplicá-la pelo inverso do número.
Analise um exemplo.
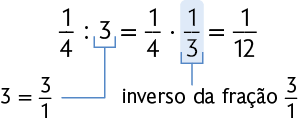
Atenção!
Podemos representar qualquer número natural diferente de zero usando uma fração. Por exemplo: .
Então, o inverso do número natural 3 é .
Página 104
Divisão de uma fração por outra fração
Um professor propôs aos estudantes a atividade indicada a seguir.
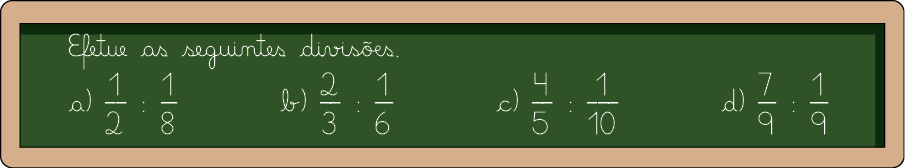
Para resolver o item a, precisamos saber quantas vezes cabe em . Para isso, vamos usar as figuras a seguir.

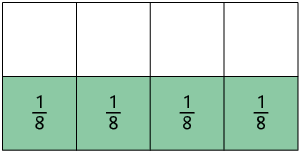
Analisando as figuras, percebemos que cabe 4 vezes em .
Portanto, .
Questão 7. De maneira semelhante, calcule em seu caderno o resultado dos itens b, c e d.
Respostas: b) 4; c) 8; d) 7.
Atenção!
A maneira prática de dividir uma fração por outra fração, diferente de zero, é multiplicar a primeira fração pelo inverso da segunda.
Analise um exemplo.

Atividades
Faça as atividades no caderno.
17. Junte-se a um colega, desenhem figuras no caderno e determinem o resultado de cada cálculo.
a)
b)
c)
d)
e)
f)
g)
h)
i)
Respostas: a) 12; b) 8; c) 6; d) 9; e) 20; f) 7; g) ; h) ; i) .
18. Escreva no caderno uma divisão de fração por fração cujo resultado seja:
a) 5
b) 8
c) 10
Sugestões de respostas: a) ; b) ; c) .
19. Analise as imagens e responda às questões.
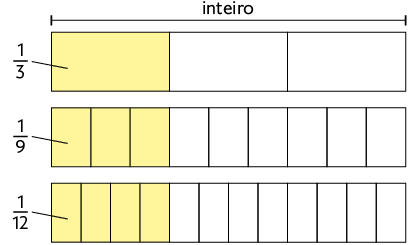
a) Quantas vezes cabe em ?
b) Quantas vezes cabe em ?
Respostas: a) 3 vezes; b) 4 vezes.
Página 105
20. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
Respostas: a) 12; b) ; c) ; d) ou ; e) ou ; f) ou .
21. Faça estimativas e associe cada cálculo a um resultado, escrevendo a letra e o número correspondentes.
A.
B.
C.
D.
1.6
2.
3.
4.
Agora, efetue as operações e verifique se sua resposta está correta.
Resposta: A-3; B-1; C-4; D-2.
22. Na imagem a seguir, a balança não está em equilíbrio.
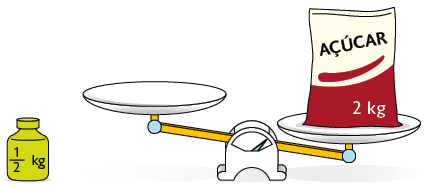
Quantas peças iguais a que está próxima à balança (de ) são necessárias para que ela fique em equilíbrio?
Resposta: 4 peças.
23. Simone dividiu de carne moída em pacotes de cada um. Em quantos pacotes essa carne foi dividida?
Resposta: 12 pacotes.
24. Renato repartiu igualmente das figurinhas que tinha entre seus dois irmãos. Que fração do total de figurinhas cada um deles recebeu?
Resposta: .
25. Leia a seguir uma receita.

Com base nas informações dessa receita, escreva no caderno a quantidade de cada ingrediente necessária para preparar:
a) 6 porções.
b) 3 porções.
Respostas nas orientações ao professor.
26. Na lanchonete de Pedro, há uma máquina de suco cujo reservatório está com de sua medida da capacidade. Sabendo que Pedro vende o suco em copos com da capacidade do reservatório da máquina, responda às questões.
a) No máximo, quantos copos de suco podem ser vendidos com o conteúdo que está no reservatório da máquina?
b) Se o reservatório da máquina estivesse completamente cheio, quantos copos de suco, no máximo, poderiam ser vendidos?
c) Sabendo que o reservatório da máquina tem medida de capacidade de , quantos litros de suco há no reservatório dela?
d) Qual é a medida da capacidade, em litros, de cada copo?
Respostas: a) 30 copos; b) 50 copos; c) ; d) ou .
Página 106
Adição e subtração de números racionais na forma de número decimal
No início desta unidade, vimos uma pessoa imprimindo um cupom fiscal, que, além de discriminar os produtos e seus valores, e caracteriza um documento que certifica o pagamento da compra realizada.
Veja a seguir parte do cupom fiscal que André recebeu ao comprar alguns produtos.

Para saber quantos reais ele gastou na compra desses produtos, calculamos .
No algoritmo usual da adição, escrevemos os números colocando vírgula abaixo de vírgula, como representado a seguir. Para efetuar os cálculos, adicionamos milésimos com milésimos, centésimos com centésimos, décimos com décimos, unidades com unidades, e assim por diante, realizando as trocas quando necessário.
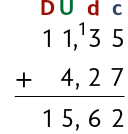
Portanto, André gastou R$ 15,62 na compra desses produtos.
Ele pagou a compra com uma cédula de R$ 20,00. Para saber quantos reais recebeu de troco, calculamos .
No algoritmo usual da subtração, representado a seguir, também escrevemos os números colocando vírgula abaixo de vírgula e, então, subtraímos milésimos de milésimos, centésimos de centésimos, décimos de décimos, unidades de unidades, e assim por diante, realizando as trocas quando necessário.
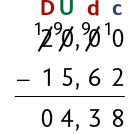
Portanto, André recebeu R$ 4,38 de troco.
Questão 8. Em sua opinião, por que devemos pedir cupom fiscal ao efetuar uma compra? Justifique sua resposta no caderno.
Resposta pessoal.
Questão 9. Faça uma pesquisa para saber quais informações um cupom fiscal deve apresentar e qual é a importância desse documento para os consumidores.
Resposta nas orientações ao professor.
Questão 10. Após a pesquisa realizada na
questão anterior, sua opinião em
relação à importância de solicitar o cupom fiscal ao realizar uma compra mudou?
Converse com os colegas e o professor sobre
isso.
Resposta pessoal.
Página 107
Atividades
Faça as atividades no caderno.
27. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) 58,345; b) 36,63; c) 160,944; d) 31,52; e) 19,142; f) 125,521; g) 247,703; h) 130,44.
28. Copie os itens no caderno e complete-os substituindo cada pelo número adequado.
a)
Resposta: .
b)
Resposta: .
c)
Resposta: .
d)
Resposta: .
e)
Resposta: .
f)
Resposta: .
29. Calcule a medida do perímetro de cada polígono.


Respostas: A. ; B. .
30. Em cada paralelepípedo reto retângulo a seguir estão indicadas as medidas de suas dimensões.


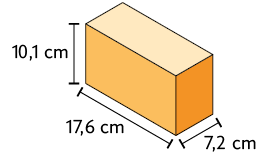

Sabendo que as pilhas representadas nos itens a seguir foram construídas com esses paralelepípedos, efetue os cálculos em seu caderno e determine a medida da altura de cada uma delas.
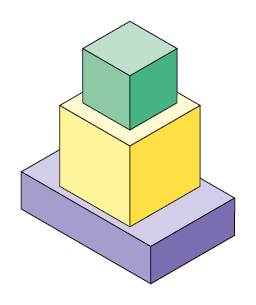
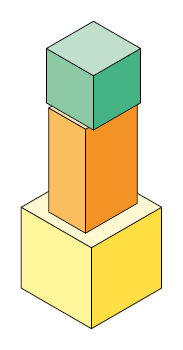
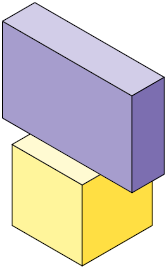
Respostas: A. ; B. ; C. ; D. .
Página 108
31. Escreva no caderno uma adição e uma subtração com números decimais, de modo que o resultado de cada uma seja o número apresentado a seguir.
17,245
Sugestões de resposta: ; .
32. O lançamento de dardo é uma modalidade esportiva em que o atleta deve arremessar um dardo com o objetivo de alcançar a maior medida de distância possível. Na tabela estão indicadas as marcas das três primeiras colocadas na final da prova feminina dessa modalidade nos Jogos Olímpicos de Tóquio, no Japão, em 2020.
|
Atleta |
Melhor lançamento (em metros) |
|---|---|
|
Shiying Liu (China) |
66,34 |
|
Maria Andrejczyk (Polônia) |
64,61 |
|
Kelsey-Lee Barber (Austrália) |
64,56 |
Fonte de pesquisa: Final Womens javelin throw Athletics Results: Tokyo 2020 Olympics. Marca. Disponível em: https://oeds.link/ujQ6pk. Acesso em: 23 mar. 2022.
Qual foi a diferença, em metro, entre os melhores lançamentos de:
a) Shiying Liu e Maria Andrejczyk?
b) Shiying Liu e Kelsey-Lee Barber?
c) Maria Andrejczyk e Kelsey-Lee Barber?
Respostas: a) ; b) ; c) .
33. Verifique como Luísa pensou para calcular mentalmente a diferença entre o preço à vista e o preço a prazo de um vestido.

Agora, arredonde os valores a seguir para a unidade mais próxima e efetue os cálculos mentalmente.
a)
b)
c)
d)
e)
f)
Respostas: a) 36; b) 51; c) 121; d) 13; e) 88; f) 16.
34. (Obmep-2017) Alvimar pagou uma compra de R$ 3,50 com uma [cédula] de R$ 5,00 e recebeu o troco em moedas de R$ 0,25. Quantas moedas ela recebeu?
a) 4
b) 5
c) 6
d) 7
e) 8
Resposta: Alternativa c.
Página 109
Multiplicação de números racionais na forma de número decimal
Multiplicação de um número natural por um número decimal
Clarice e Helena foram juntas à peixaria. Analise a cena.

Para saber quantos reais Clarice vai pagar por de sardinha, calculamos . Podemos realizar esse cálculo do seguinte modo.
Outro procedimento é desconsiderar a vírgula do número 6,38, fazer a multiplicação e, depois, acrescentar a vírgula ao resultado, como apresentado nos procedimentos a seguir.
Multiplicamos 6,38 por 100 e obtemos o número natural 638. Em seguida, calculamos .

Para compensar a multiplicação , dividimos o resultado por 100, pois a divisão é a operação inversa da multiplicação.
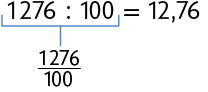
Portanto, Clarice vai pagar R$ 12,76 por de sardinha.
Atenção!
A maneira prática de multiplicar um número decimal por um número natural é inicialmente efetuar o cálculo desconsiderando a vírgula. Depois, a vírgula deve ser reposicionada ao resultado, de modo que a quantidade de casas decimais seja igual à quantidade de casas decimais do fator decimal.
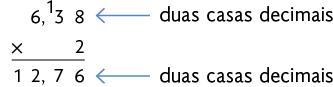
Página 110
Multiplicação de um número decimal por outro número decimal
Na página anterior, vimos que Helena pediu de sardinha. Para saber quantos reais ela vai pagar, calculamos . Esse cálculo pode ser realizado da seguinte maneira.
Outro procedimento é desconsiderar as vírgulas dos números 6,38 e 2,5, fazer a multiplicação e, depois, acrescentar a vírgula ao resultado, como apresentado nos procedimentos a seguir.
Multiplicamos 6,38 por 100 e 2,5 por 10 e obtemos os números naturais 638 e 25.
Em seguida, calculamos .
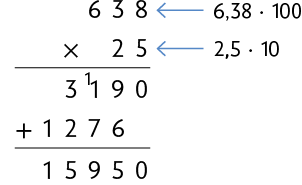
Para compensar as multiplicações e , dividimos o resultado por , ou seja, por 1.000, pois a divisão é a operação inversa da multiplicação.
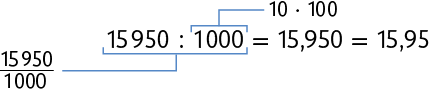
Portanto, Helena vai pagar R$ 15,95 por de sardinha.
Questão 11. No cálculo anterior, o que você
pôde perceber em relação à
quantidade de casas decimais do resultado e em relação às casas decimais dos
fatores? Responda a essa pergunta em seu caderno.
Sugestão de resposta: A quantidade de casas decimais do resultado (15,950) é igual à soma das quantidades de casas decimais dos fatores (6,38 e 2,5), nesse caso, 3.
Atividades
Faça as atividades no caderno.
35. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) 270,4; b) 55,08; c) 321,16; d) 274,056; e) 1,875; f) 70,56; g) 121,475; h) 1,605.
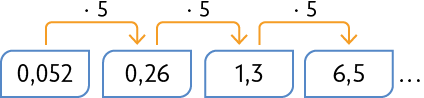
36. Efetue os cálculos e escreva no caderno os três próximos números de cada sequência.
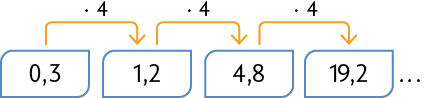
Resposta: 32,5; 162,5; 812,5.
Resposta: 76,8; 307,2; 1.228,8.
37. Uma moeda de 25 centavos tem de medida de massa.
Determine a medida da massa de cada pilha a seguir, sabendo que elas são formadas apenas por moedas de 25 centavos.




Respostas: A. ; B. ; C. ; D. .
Página 111
38. Odair comprou o eletrodoméstico a seguir em prestações iguais, como aparece no anúncio.


Calcule o valor total que Odair vai pagar por esse eletrodoméstico.
Resposta: R$ 546,75.
39. Determine a medida da área, em centímetros quadrados, e a medida do perímetro, em centímetros, de cada retângulo a seguir.
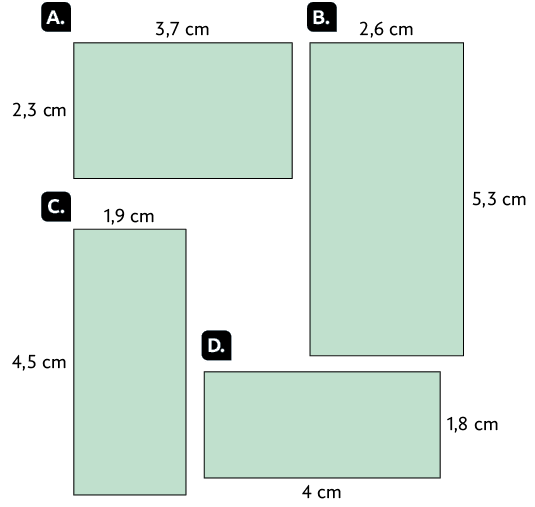
Respostas: A. e ; B. e ; C. e ; D. e .
40. O Autódromo de Interlagos, localizado na cidade de São Paulo, é usado em competições nacionais e internacionais de automobilismo. Uma volta completa nele corresponde a um percurso cuja medida da distância é de aproximadamente .
Em uma prova automobilística realizada nesse autódromo, os carros deveriam completar 71 voltas. Qual é a medida da distância total percorrida pelos carros que completaram essa prova?
Resposta: Aproximadamente .
41. Mauro abasteceu seu carro com de combustível. Quantos reais ele pagou, sabendo que de combustível custou R$ 4,78?
Resposta: R$ 121,89.
42. Dividindo
a quantidade de habitantes de um estado por sua medida da área (em ), obtemos a
quantidade média de habitantes por quilômetro quadrado desse
estado. A esse
quociente chamamos densidade demográfica.
O gráfico apresenta a densidade demográfica, em 2010, de cada estado da Região Sudeste, e a tabela traz a medida da área de cada um deles.
Densidade demográfica de cada estado da Região Sudeste (2010)
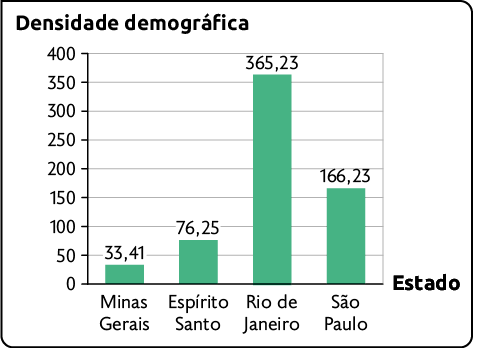
Fonte de pesquisa: IBGE. Cidades e Estados. Disponível em: https://oeds.link/PPUwHr.
Acesso em: 5 jan. 2022.
|
Estado |
Medida da área (em ) |
|---|---|
|
Minas Gerais |
586,52 |
|
Espírito Santo |
46,10 |
|
Rio de Janeiro |
43,78 |
|
São Paulo |
248,22 |
Fonte de pesquisa: IBGE. Cidades e Estados. Disponível em: https://oeds.link/PPUwHr. Acesso em: 5 jan. 2022.
Em seu caderno, efetue os cálculos e determine a quantidade aproximada de habitantes de cada estado.
Resposta: Valores aproximados: Minas Gerais: 19.595.633 habitantes; Espírito Santo: 3.515.125 habitantes; Rio de Janeiro: 15.989.769 habitantes; São Paulo: 41.261.611 habitantes.
Página 112
Divisão de números racionais na forma de número decimal
Divisão de números naturais com quociente decimal
Jair e Ângela são vendedores em uma mesma empresa. Eles viajam com seus carros para visitar os clientes em várias cidades. O carro de Jair percorre com de gasolina, enquanto o carro de Ângela percorre com de gasolina.
Qual vendedor tem o carro que percorre mais quilômetros com de gasolina?
Para responder a essa questão, precisamos determinar quantos quilômetros o carro de Jair percorre com de gasolina. Para isso, vamos calcular .
1º. Não podemos dividir 4 centenas por 32 e obter centenas inteiras como resultado, pois . Então, trocamos 4 centenas por 40 dezenas e adicionamos a 2 dezenas, obtendo 42 dezenas.

2º. Dividimos as 42 dezenas por 32. Obtemos 1 dezena e sobram 10 dezenas.
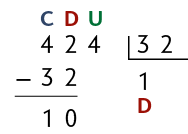
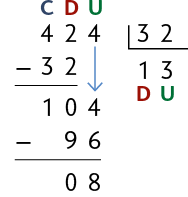
3º. Trocamos 10 dezenas por 100 unidades e adicionamos a 4 unidades. Dividimos as 104 unidades por 32. Obtemos 3 unidades e sobram 8 unidades.
4º. Trocamos 8 unidades por 80 décimos e colocamos uma vírgula no quociente para separar a parte inteira da parte decimal. Dividimos os 80 décimos por 32. Obtemos 2 décimos e sobram 16 décimos.
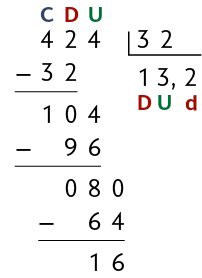
Página 113
5º. Trocamos 16 décimos por 160 centésimos e dividimos por 32, obtendo 5 centésimos.
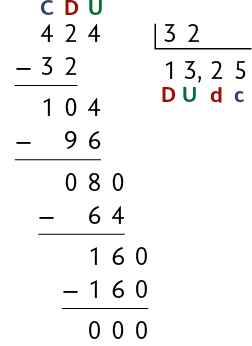
Portanto, o carro de Jair percorre com de gasolina e, assim, concluímos que o carro de Jair percorre mais quilômetros com de gasolina do que o carro de Ângela.
Em uma divisão cujo quociente é um número decimal e o resto é zero, dizemos que esse quociente está na forma de um número decimal exato.
Em alguns casos, não é possível obter unidades inteiras como quociente. O cálculo é um exemplo disso. Nesse caso, como a divisão de 1 por 2 não resulta em uma unidade inteira, trocamos 1 unidade por 10 décimos e colocamos um zero e uma vírgula no quociente. Em seguida, continuamos o cálculo normalmente.
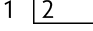
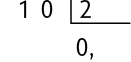
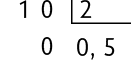
Em alguns casos, um ou mais algarismos da parte decimal do quociente se repetem indefinidamente. Chamamos esse tipo de quociente de dízima periódica, como no caso de .
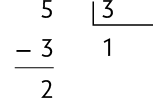
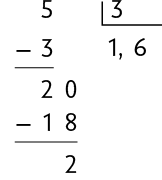
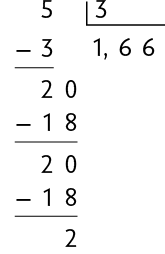
Ao continuar o cálculo, o resto da divisão sempre será 2. Por isso, não é possível chegar ao resto zero. Nesse caso, chamamos o algarismo que se repete de período da dízima periódica.
Atenção!
Podemos indicar uma dízima periódica de duas maneiras diferentes.
O período também pode ser formado por mais de um algarismo. Por exemplo:
Página 114
Divisão de um número decimal por um número natural
Cecília, ao comprar na promoção um pacote de lápis com 3 unidades por R$ 3,48, deparou-se com a seguinte dúvida: se um pacote contém 3 lápis, quantos reais vai custar cada lápis?
Para saber o preço de cada lápis, calculamos o valor de . Podemos realizar esse cálculo do seguinte modo.
1º. Multiplicamos o dividendo e o divisor por 100 para torná-los números naturais.
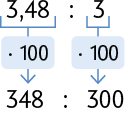
2º. Efetuamos .
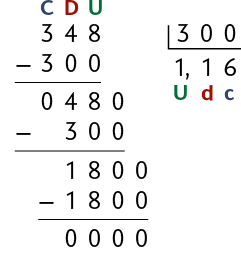
Atenção!
A divisão de 3,48 por 3 tem o mesmo resultado de 348 dividido por 300. Esse fato pode ser verificado em uma calculadora.
Portanto, cada lápis vai custar R$ 1,16.
Divisão de um número decimal por outro número decimal
Francisco abasteceu seu carro em um posto cujo preço de 1 litro de etanol é R$ 5,50. Quantos litros de etanol foram colocados no carro, sabendo que foi pago R$ 143,44 pelo abastecimento?
Para saber com quantos litros de etanol Francisco abasteceu seu carro, calculamos . Podemos efetuar esse cálculo do seguinte modo.
1º. Multiplicamos o dividendo e o divisor por 100 para torná-los números naturais.
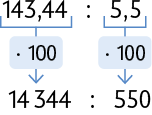
2º. Efetuamos .
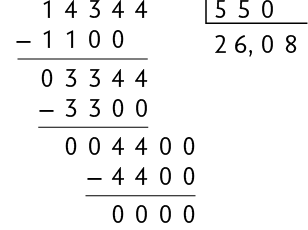
Atenção!
A divisão de 143,44 por 5,5 tem o mesmo resultado de 14.344 dividido por 550. Esse fato pode ser verificado em uma calculadora.
Portanto, Francisco abasteceu seu carro com de etanol.
Página 115
Atividades
Faça as atividades no caderno.
43. Efetue os cálculos.
a)
b)
c)
d)
e)
f)
g)
h)
Ao finalizar esta atividade, se possível,
utilize uma calculadora e verifique se os resultados dos cálculos estão
corretos.
Respostas: a) 2,4; b) 21,3; c) 8,47; d) 6,75; e) 14,13; f) 26,2; g) 1,5; h) 2,4.
44. Em um supermercado, uma mesma marca de arroz é vendida em 3 embalagens diferentes, como mostra o quadro.
|
Embalagem |
|||
|---|---|---|---|
|
Preço (R$) |
R$ 4,18 |
R$ 7,58 |
R$ 19,60 |
Em qual delas o preço do quilograma do arroz é menor?
Resposta: Na embalagem de .
45. Acompanhe como Anita fez para calcular mentalmente .

De maneira semelhante, resolva os cálculos a seguir.
a)
b)
c)
d)
Respostas: a) 4,3; b) 3,1; c) 8,1; d) 6,3.
46. João é marceneiro e recebeu uma encomenda para confeccionar algumas prateleiras de madeira. Para isso, ele comprou uma tábua com de medida de comprimento. Qual deve ser a medida do comprimento em centímetros de cada pedaço de madeira para que ele consiga fazer 5 prateleiras de mesma medida de comprimento, sem desperdiçar nenhum pedaço?
Resposta: .
47. Com base na nota fiscal representada a seguir, determine a quantidade de cada produto que Elaine comprou na papelaria.

Respostas: A: 7; B: 3; C: 4; D: 11; E: 2.
48. Rafael comprou um aparelho de som em prestações iguais. Sabendo que o valor de cada prestação é R$ 89,27 e que ele vai pagar R$ 981,97 ao todo, calcule em quantas prestações Rafael parcelou sua compra.
Resposta: 11 prestações.
Página 116
Potenciação cuja base é um número racional
Os números racionais podem ser utilizados como base na potenciação. Esses cálculos podem ser feitos de maneira parecida com a utilizada para os inteiros. A seguir, apresentamos alguns exemplos para números racionais na forma decimal.
Os números racionais escritos na forma de fração também podem ser base para potenciação.
Acompanhe o procedimento do professor Igor para calcular .
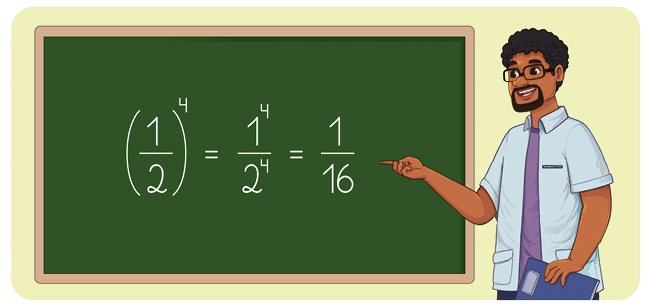
Atividades
Faça as atividades no caderno.
49. Calcule as potências.
a)
b)
c)
d)
e)
f)
Respostas: a) 0,0016; b) ; c) 0,49; d) ; e) 15,625; f) .
50. Para cada item, escreva uma potência para representar a medida da área do quadrado e calcule-a para obter essa medida.
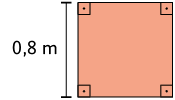


Respostas: A. , ; B. , ; C. , .
51. Em seu caderno, elabore um problema envolvendo o cálculo de uma potência com um número racional na base. Em seguida, troque com um colega para que ele o resolva.
Resposta pessoal.
Página 117
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Carlos precisa pintar de uma parede. Para isso, ele vai precisar de de uma lata de tinta de .
a) Quantos litros de tinta ele vai usar para pintar essa parede?
b) Quantos litros de tinta ele usaria se precisasse pintar a parede inteira?
Respostas: a) ; b) .
2. Em uma padaria, havia 4 bolos iguais, cada um dividido em 8 pedaços de mesma medida. Sabendo que José comprou 20 pedaços desses bolos, que número misto representa a quantidade de bolos comprados por ele?
Professor, professora: Diga aos estudantes que considerem o bolo dividido em partes exatamente iguais, o que, em geral, não ocorre com precisão na realidade.
Resposta: .
3. Na biblioteca de certa escola há 160 livros de Biologia, que correspondem a do total de livros.
a) Qual é a quantidade total de livros da biblioteca?
b) Qual é a quantidade de livros de História, sabendo que eles correspondem a do total?
c) Que fração do total de livros corresponde aos que não são de História nem de Biologia?
Respostas: a) 2.400 livros; b) 480 livros; c) .
4. Para cobrir do piso de um estabelecimento, foram utilizadas 324 lajotas. Quantas lajotas foram usadas para cobrir metade desse piso?
Atenção!
Para resolver esta atividade, obtenha frações equivalentes a e com denominador 10.
Resposta: 270 lajotas.
5. (UFMG-2006) Uma prova de triatlo compreende 3 etapas: natação, ciclismo e corrida.
Em uma dessas provas, dos 170 atletas que iniciaram a competição, 10 abandonaram na etapa de natação; dos que continuaram, desistiu ao longo da etapa de ciclismo; e dos que começaram a última etapa, 20% abandonaram a corrida.
Apenas N atletas completaram a prova. Então, é correto afirmar que a soma dos algarismos do número N é:
a) 16
b) 13
c) 14
d) 15
Resposta: Alternativa d.
6. Luan gastou R$ 112,00 comprando uma calça e uma camiseta.
Sabendo que dessa quantia correspondem ao preço da camiseta, responda às questões a seguir.
a) Que fração da quantia gasta por Luan representa o preço da calça?
b) Quantos reais Luan pagou pela camiseta? E pela calça?
Respostas: a) ; b) R$ 40,00; R$ 72,00.
7. (Obmep-2006) Três candidatos concorreram à eleição de representante de uma turma de escola: João, Rosa e Marcos. João obteve dos votos e Rosa, dos votos. Quem ganhou a eleição?
Resposta: Rosa.
8. Elias
tem 3 recipientes não graduados: o primeiro com da medida da capacidade do segundo e o
terceiro com
da capacidade do segundo.
Sabendo que o primeiro e o terceiro recipientes estão vazios e que o segundo está cheio de água, como Elias deve proceder para repartir o conteúdo de líquido do segundo recipiente de modo que dois deles fiquem com a mesma quantidade?
Resposta: Elias deve encher o primeiro recipiente com a água contida no segundo e depois encher o terceiro com o conteúdo do primeiro. Assim, o segundo e o terceiro recipientes terão a mesma quantidade de água.
Página 118
9. Em uma jarra dividida em 5 partes iguais, como mostra a imagem, foi colocada certa quantidade de água.

a) Que fração da medida da capacidade da jarra corresponde à quantidade de água nela?
b) Ao encher um copo com água e despejar nessa jarra, ela passa a ter de sua medida da capacidade. Que fração corresponde à quantidade de água do copo em relação à capacidade da jarra?
c) Quantos desses copos cheios de água são necessários para encher essa jarra, considerando a quantidade de água já colocada?
Respostas: a) ; b) ; c) 4 copos.
10. Felipe participou de uma competição de ciclismo que deveria ser realizada em 3 etapas. O esquema representa a medida da distância de cada uma.
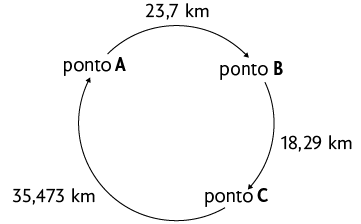
Sabendo que Felipe completou a prova, qual é a medida da distância em quilômetros que ele percorreu ao todo?
Resposta: .
11. Certa indústria embalou de café torrado e moído em pacotes cuja medida da massa é . Quantos pacotes de café foram embalados?
Resposta: 5.000 pacotes.
12. Márcia vai participar de uma maratona. Nos 3 primeiros dias de seu treino, as medidas das distâncias que ela correu foram, respectivamente, , e .
a) A medida da distância que Márcia estabeleceu como objetivo foi correr ao todo nos 5 primeiros dias. Qual é a medida da distância, em quilômetros, que ainda falta para ela cumprir esse objetivo?
b) Se Márcia percorrer a mesma medida da distância em cada dia de treino que resta, quantos quilômetros ela percorrerá por dia para cumprir seu objetivo?
Respostas: a) ; b) .
13. Bruno é eletricista e está instalando alguns postes de luz em uma praça. Para isso, vai precisar dividir um fio de de medida de comprimento em 6 partes iguais. Qual será a medida do comprimento, em metros, de cada pedaço de fio?
Resposta: .
14. Fernanda estava no supermercado no qual faz suas compras quinzenalmente, quando foi anunciada uma promoção no preço da caixa de leite, como representado a seguir.

a) Se Fernanda comprar a embalagem com 12 caixas de leite, quantos reais ela vai pagar em cada unidade?
b) Quantos reais ela vai economizar em cada unidade se, em vez de comprar as caixas unitárias, ela adquirir a embalagem com 12 unidades, oferecida nessa promoção?
Respostas: a) R$ 3,98; b) R$ 0,34.