Página 143

UNIDADE

Figuras geométricas planas e ângulos

Fotografia de uma mesa com uma figura sendo montada com pedaços de tecidos. Também sobre a mesa há uma xícara, rolos de linha, tesoura, prato com bolachas. — O *patchwork* (do inglês *patch*, que significa "peça ou remendo"; e *work*, "trabalho") é a arte de unir pedacinhos de tecidos com diferentes formatos, como triangulares e quadrangulares.

Agora vamos estudar...

ângulos;
algumas propriedades das retas paralelas cortadas por uma transversal;
polígonos;
triângulos;
circunferência.

ORIENTAÇÕES AO PROFESSOR

Ao desenvolver esta página de abertura, faça questionamentos como: Qual é a relação entre a foto apresentada e os conteúdos expostos no título da unidade? Vocês sabem o que é um patchwork? Os formatos dos pedaços de tecidos são parecidos com alguma figura geométrica que você conhece? Se sim, qual? Peça a eles que compartilhem suas respostas com a turma, intervindo se necessário. Em seguida, explique aos estudantes que patchwork é considerada uma das primeiras manifestações artísticas femininas e teve origem na necessidade de usar as sobras dos tecidos usados na confecção de roupas.

Metodologias ativas

Ao desenvolver esta página de abertura, avalie a possibilidade de usar a metodologia ativa Abordagem por pares. Para obter informações sobre essa metodologia no tópico Metodologias e estratégias ativas, consulte as orientações gerais deste manual.

Sugestão de avaliação

Para avaliar o conhecimento prévio dos estudantes sobre os conteúdos que serão trabalhados ao longo desta unidade, proponha a eles os seguintes problemas:

a) Qual é o nome de um polígono de três lados? Quantos ângulos internos esse polígono tem?

b) Um triângulo retângulo tem um dos ângulos internos medindo $45 graus$ . Classifique cada um dos ângulos internos desse triângulo de acordo com sua medida.

Resoluções e comentários

a) O polígono que tem três lados é o triângulo. Todo triângulo tem 3 ângulos internos.

b) Inicialmente, determinaremos as medidas dos ângulos desconhecidos. Como o triângulo é retângulo, um de seus ângulos internos mede $90 graus$ . Utilizando o fato de que a soma das medidas dos ângulos internos de um triângulo é $180 graus$ e indicando a medida do terceiro ângulo interno do triângulo por x, temos:

$x mais 90 graus mais 45 graus igual a 180 graus assim x igual a 45 graus$

Portanto, os ângulos internos desse triângulo medem $45 graus$ , $45 graus$ e $90 graus$ . Assim, os ângulos cuja medida é $45 graus$ são agudos, pois têm medida maior do que $0 grau$ e menor do que $90 graus$ . Já o ângulo cuja medida é $90 graus$ é reto.

Informações sobre avaliações diagnósticas podem ser encontradas no tópico Avaliação, nas orientações gerais deste manual.

Página 144

Ângulos

Utilizando duas tiras de papel, um pedaço de borracha e uma tachinha, uma professora de Matemática do 7º ano construiu um objeto e o levou para a sala de aula. Com esse objeto, ela realizou alguns movimentos e representou-os na lousa.

Objeto digital

Cena 1

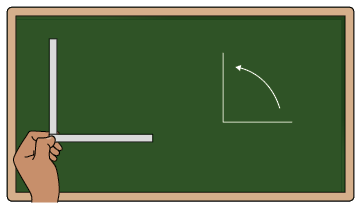
Ilustração de uma lousa com uma mão na frente segurando duas tiras de papel que se assemelham a letra L, de modo a formar um giro de um quarto de volta entre elas. Na lousa há o desenho de duas semirretas de mesma origem e formando um giro de um quarto de volta entre elas.

Cena 2

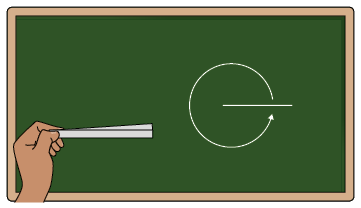
Ilustração de uma lousa com uma mão na frente segurando duas tiras de papel sobrepostas, de modo a formar um giro inteiro entre elas. Na lousa há o desenho de duas semirretas de mesma origem e formando um giro inteiro entre elas.

Cena 3

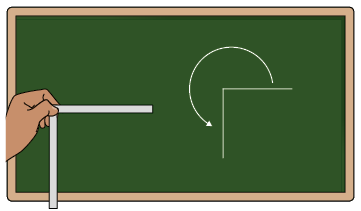
Ilustração de uma lousa com uma mão na frente segurando duas tiras de papel que se assemelham a uma letra L espelhada na horizontal, de modo a formar um giro de três quartos de volta entre elas. Na lousa há o desenho de duas semirretas de mesma origem e formando um giro de três quartos de volta entre elas.

Cena 4

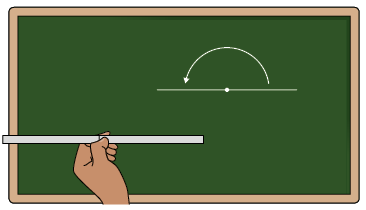
Ilustração de uma lousa com uma mão na frente segurando duas tiras de papel, alinhadas lado a lado, de modo a formar meio giro de volta entre elas. Na lousa há o desenho de duas semirretas de mesma origem e formando meio giro de volta entre elas.

Nessas cenas, cada registro que a professora fez na lousa para representar os movimentos corresponde a um ângulo.

Na cena 1, o ângulo que a professora representou corresponde a um giro de um quarto de volta para a esquerda.

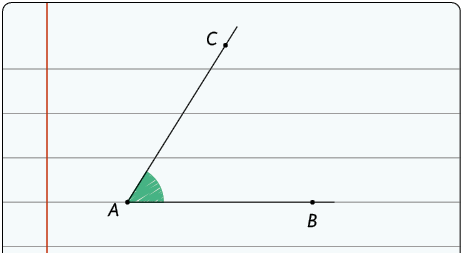
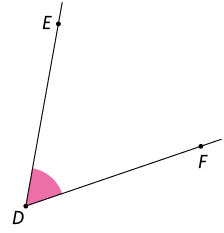
Ângulo é a figura geométrica formada por duas semirretas com a mesma origem. Como as semirretas formam dois ângulos e precisamos definir a qual ângulo estamos nos referindo, destacamos com um pequeno arco apenas uma das regiões.

Um ângulo pode ser representado da seguinte maneira.

Ilustração de duas semirretas, denominados de 'lado', de mesma origem O, denominado vértice. Uma semirreta possui o ponto A e outra possui o ponto B, há um arco entre elas e entre elas é a 'região determinada por A O B'.

Os lados desse ângulo são as semirretas $O A$ e $O B$ .
O vértice é o ponto O.
Esse ângulo pode ser nomeado por $\hat{O}$ , $A \hat{O} B$ ou $B \hat{O} A$ .

ORIENTAÇÕES AO PROFESSOR

Objetivos da unidade

Medir ângulos usando o transferidor.

Classificar um ângulo em reto, raso, obtuso ou agudo.

Determinar a medida do complementar e do suplementar de um ângulo.

Identificar ângulos opostos pelo vértice.

Identificar, em duas retas paralelas cortadas por uma transversal, pares de ângulos correspondentes, alternos internos, alternos externos e opostos pelo vértice.

Nomear um polígono de acordo com a quantidade de lados.

Classificar triângulos de acordo com a medida do comprimento dos lados e dos ângulos internos.

Determinar a soma das medidas dos ângulos internos de um polígono.

Reconhecer um polígono regular.

Identificar polígonos nas faces de uma figura geométrica espacial.

Construir polígono regular usando régua e transferidor.

Identificar raio, corda e diâmetro de uma circunferência.

Calcular a medida do comprimento de uma circunferência.

Identificar a relação entre raio e diâmetro de uma circunferência.

Construir circunferências usando régua e compasso.

Justificativas

Os conteúdos abordados ao longo desta unidade são ferramentas necessárias na descrição e na inter-relação humana com o espaço de vivência. Além disso, o estudo de alguns dos conteúdos propostos possibilitará o desenvolvimento do raciocínio lógico e da criatividade dos estudantes.

Antes de iniciar o conteúdo desta página, é necessário verificar os conhecimentos prévios que os estudantes têm a respeito de ângulos, assunto já estudado em anos anteriores. Permita a eles que compartilhem com a turma suas opiniões, tendo a oportunidade de resgatar esses conhecimentos e de tornar o estudo mais significativo.

Página 145

Atividades

Faça as atividades no caderno.

1. Volte à página 144 e identifique em qual cena a professora desenhou um ângulo que representa os seguintes giros para a esquerda.

a) Meia-volta.

b) Três quartos de volta.

c) Uma volta completa.

Respostas: a) Cena 4; b) Cena 3; c) Cena 2.

2. Os ângulos podem ser identificados em diversas situações do dia a dia. Analise na imagem apresentada dois ângulos indicados.

Esquema com a fotografia de uma bicicleta. Nela há dois ângulos demarcados entre partes do seu quadro.

Escreva no caderno quatro lugares ou objetos nos quais você pode identificar ângulos.

Resposta pessoal.

3. Um dos parafusos da placa que indica a localização do evento de Matemática da escola se soltou. Para que todos encontrem o local correto, Jessé colocou o parafuso novamente e ajustou a posição da placa.

Ilustração de um menino com a mão no queixo e olhando para uma placa em um poste. Na placa há uma seta apontando para baixo. Ela está presa por um parafuso, enquanto o outro está no chão.

Ilustração de um menino girando em sentido anti-horário a placa anterior, em um poste.

Ilustração de um menino com a mão sobre a mesma placa anterior, em um poste. A seta da placa agora aponta para direita e está presa por dois parafusos.

a) Para ajustar a posição da placa, Jessé realizou o menor giro possível. A que fração de uma volta corresponde esse giro?

Resposta: $início de fração, numerador: 1, denominador: 4, fim de fração.$ de volta.

b) Desenhe em seu caderno uma placa com uma seta semelhante à da cena apresentada, mas que esteja apontando para algum outro lado que não tenha aparecido nas cenas.

Resposta pessoal.

c) Considerando a posição da placa na 1ª cena como a posição inicial, o giro que a placa com a seta vai realizar, com base na placa que você desenhou, corresponde a que fração de uma volta?

Resposta pessoal.

Versão adaptada acessível

b) Imagine a posição de uma placa com uma seta semelhante à da cena, mas que esteja apontando para algum outro lado que não tenha aparecido nas cenas.

Resposta pessoal.

c) Considerando a posição da placa na 1ª cena como a posição inicial, o giro que a placa com a seta vai realizar, com base na placa que você imaginou, corresponde a que fração de uma volta?

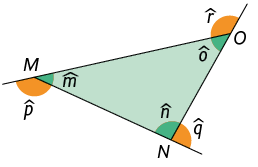
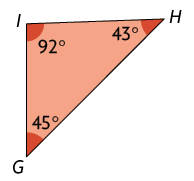
Resposta pessoal.

4. Escreva no caderno o nome, o vértice e os lados de cada ângulo.

Ilustração de um ângulo entre duas semirretas de mesma origem B, uma possui o ponto A e outra possui o ponto C. O ângulo tem medida maior do que 0 grau e menor do que 90 graus.

Resposta: Nome: $\hat{B}$ , $A \hat{B} C$ ou $C \hat{B} A$ ; vértice: $B$ ; lados: $\vec{B A}$ e $\vec{B C}$ .

Ilustração de um ângulo entre duas semirretas de mesma origem K, uma possui o ponto J e outra possui o ponto L. O ângulo tem medida maior do que 90 graus e menor do que 180 graus.

Resposta: Nome: $\hat{K}$ , $J \hat{K} L$ ou $L \hat{K} J$ ; vértice: $K$ ; lados: $\vec{K J}$ e $\vec{K L}$ .

Ilustração de um ângulo entre duas semirretas de mesma origem U, uma possui o ponto T e outra possui o ponto V. O ângulo tem medida maior do que 180 graus e menor do que 270 graus.

Resposta: Nome: $\hat{U}$ , $T \hat{U} V$ ou $V \hat{U} T$ ; vértice: $U$ ; lados: $\vec{U T}$ e $\vec{U V}$ .

5. Desenhe no caderno um ângulo $A \hat{O} B$ e um $B \hat{O} C$ .

Resposta pessoal.

ORIENTAÇÕES AO PROFESSOR

Metodologias ativas

Ao trabalhar com as atividades desta unidade, avalie a possibilidade de utilizar a metodologia ativa Pensar-conversar-compartilhar. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Ao realizar a atividade 1, proponha aos estudantes que confeccionem o instrumento utilizado pela professora. Nessa produção, alerte-os de eventuais riscos para garantir a integridade física deles, dos professores e das demais pessoas envolvidas no processo educacional. Se considerar o processo de construção arriscado em algum momento, ofereça ajuda a quem estiver com dificuldade, manipulando os objetos mais propensos a machucar, como as tachinhas. Com o instrumento em mãos, oriente-os a representar os ângulos correspondentes às cenas 2, 3 e 4, identificando qual deles representa os giros indicados na atividade.

A fim de complementar o trabalho com a atividade 2, peça aos estudantes que indiquem outros ângulos na foto da bicicleta.

Organize uma leitura conjunta da tirinha da atividade 3. Aproveite o momento para incentivar o desenvolvimento da leitura inferencial. É necessário verificar se eles compreendem o contexto, a sequência das imagens e como elas estão relacionadas. Por fim, possibilite que resolvam os itens propostos.

Na atividade 4, os estudantes devem nomear os ângulos indicados. Aproveite o momento para relembrá-los dos elementos que constituem um ângulo, a saber: lados e vértices. Em seguida, escolha alguns estudantes para escrever suas respostas na lousa. Nesse momento, é interessante que as diferentes maneiras de nomear o ângulo sejam apresentadas.

Se julgar oportuno, na atividade 5, oriente os estudantes a marcar os pontos A, B, C e O, e, em seguida, traçar as semirretas $\vec{O A}$ , $\vec{O B}$ e $\vec{O C}$ , obtendo, assim, a representação dos ângulos solicitados.

Página 146

Medindo ângulos

Para medirmos ângulos, utilizamos uma unidade de medida chamada grau, que indicamos pelo símbolo $°$ .

A ideia de medir ângulos surgiu na Mesopotâmia, região onde hoje se situa o Iraque, com base na divisão de um círculo em 360 partes iguais. Cada parte é associada ao ângulo de 1 grau ( $1 grau$ ).

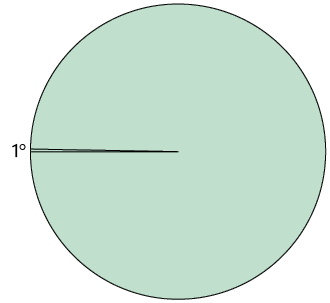
Ilustração de uma circunferência com dois segmentos de reta indo de sua extremidade até seu centro e, entre eles, demarcado o ângulo de 1 grau. — O giro de uma volta completa corresponde a um ângulo de $360 graus$ .

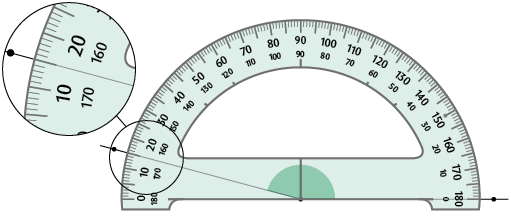
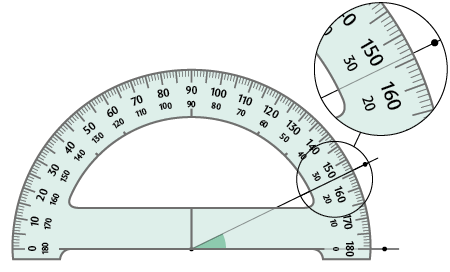
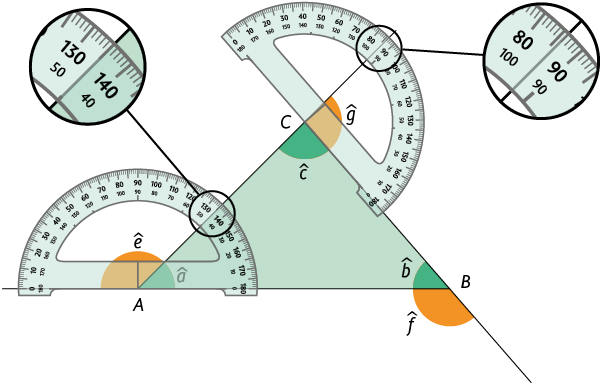
Um dos instrumentos utilizados para medir a abertura de um ângulo, isto é, determinar sua medida, é o transferidor.

A seguir estão representados dois modelos diferentes de transferidor.

Ilustração de um transferidor de meia volta. A linha onde está marcado o número 0 é chamada linha de fé, e é uma linha na horizontal. E a linha onde está marcado o número 90 é denominada centro do transferidor e é vertical. — Transferidor de $180 graus$ meia volta.

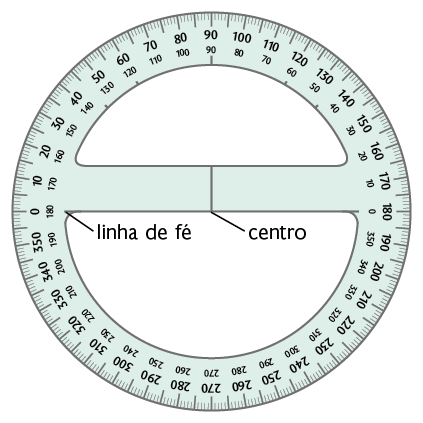
Ilustração de um transferidor de volta inteira. A linha onde está marcado o número 0 é chamada linha de fé, e é uma linha na horizontal. E a linha onde está marcado o número 90 é denominada centro do transferidor e é vertical. — Transferidor de $360 graus$ (volta inteira).

Na imagem está apresentado o procedimento de medição de um ângulo usando um transferidor.

Ilustração de um ângulo demarcado na menor abertura entre duas semirretas de mesma origem A, no centro do transferidor de meia volta. Uma semirreta está alinhada com a demarcação do 0 grau e passa pelo ponto B, à direita do transferidor, e a outra com a demarcação de 75 graus, no sentido anti-horário, passando pelo ponto C. Há a demarcação da linha que passa no ângulo 0 e para ela a seguinte indicação: linha de fé do transferidor coincide com um dos lados do ângulo. E a demarcação no centro do transferidor com a frase 'centro do transferidor coincide com o vértice do ângulo'.

Atenção!

Para determinar qual medida do ângulo estamos considerando em cada situação, fazemos um pequeno "arco" na abertura correspondente.

Exemplos:

Ilustração de um arco na menor distância entre duas semirretas de mesma origem O. Uma possui o ponto A e outra possui o ponto B. Está indicado que esse arco é a medida considerada.

Ilustração de um arco na maior distância entre duas semirretas de mesma origem O. Uma possui o ponto A e outra possui o ponto B. Está indicado que esse arco é a medida considerada.

O ângulo $B \hat{A} C$ mede $75 graus$ (lê-se: setenta e cinco graus). Essa medida pode ser indicada como $medida do ângulo b a c igual a 75 graus$ ou $medida do ângulo a igual a 75 graus$ .

ORIENTAÇÕES AO PROFESSOR

Antes de iniciar o conteúdo desta página, faça as seguintes perguntas aos estudantes: Como é possível medir um ângulo? Como é possível verificar se a medida de um ângulo é maior do que a de outro? Qual é a unidade utilizada para medir ângulos? Permita a eles que compartilhem com a turma suas explicações, tendo a oportunidade de resgatar o conhecimento prévio sobre o assunto e de tornar o estudo mais significativo.

Explique aos estudantes que em alguns transferidores há duas graduações, sendo uma no sentido horário e outra no anti-horário.

Aproveite o momento para conversar com os estudantes sobre fatos históricos envolvendo o sistema numérico usado na Mesopotâmia, relacionando-o com ângulo.

De acordo com os historiadores matemáticos Carl Boyer e Uta Merzbach, a Mesopotâmia adotou um sistema numérico de base 60, em lugar do Sistema Numérico Decimal. Segundo os pesquisadores, há algumas possíveis razões que levaram esses povos a utilizarem esse sistema numérico, como motivações astronômicas e a combinação dos sistemas mais antigos de base 10 e de base 6. No entanto, o motivo de maior aceitação, segundo eles, é que a base 60 foi voluntariamente adotada em estreita relação com a metrologia, em que uma grandeza de 60 unidades poderia ser facilmente subdividida em meios, terços, quartos, quintos, sextos, décimos, doze avos, quinze avos, vigésimos e trigésimos. Assim, presume-se que a divisão do círculo está relacionada ao sistema de base 60, visto que 360 é um múltiplo de 60. Essas informações encontram-se no livro História da Matemática, desses autores.

Página 147

Classificação dos ângulos

Podemos classificar os ângulos de acordo com sua medida.

Reto: ângulo cuja medida é $90 graus$ .
Agudo: ângulo cuja medida é maior do que $0 grau$ e menor do que $90 graus$ .
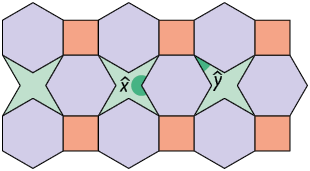
Raso: ângulo cuja medida é $180 graus$ .
Obtuso: ângulo cuja medida é maior do que $90 graus$ e menor do que $180 graus$ .

Analise alguns exemplos e suas classificações.

$medida do ângulo a b c igual a 90 graus$

$A \hat{B} C$ é reto.

$medida do ângulo k l m igual a 56 graus$

$K \hat{L} M$ é agudo.

$medida do ângulo r s t igual a 180 graus$

$R \hat{S} T$ é raso.

$medida do ângulo x y z igual a 110 graus$

$X \hat{Y} Z$ é obtuso.

Questão 1. No caderno, com o auxílio de um transferidor, construa os ângulos $A \hat{B} C$ , $K \hat{L} M$ , $R \hat{S} T$ e $X \hat{Y} Z$ citados anteriormente.

Respostas na seção Resoluções.

Ângulos congruentes

Ângulos com medidas iguais são chamados ângulos congruentes. Usamos o símbolo $≅$ para indicar a congruência dos ângulos, conforme está representado nas imagens.

Ilustração de um ângulo de 68 graus entre duas semirretas de mesma origem I, uma possui o ponto H e outra possui o ponto J. A abertura do ângulo está virada para cima.

Ilustração de um ângulo de 68 graus entre duas semirretas de mesma origem U, uma possui o ponto V e outra possui o ponto T. A abertura do ângulo está virada para baixo.

Nesse caso, $medida do ângulo h i j igual a medida do ângulo t u v igual a 68 graus$ , ou seja, os ângulos são congruentes. Assim, indicamos $H \hat{I} J ≅ T \hat{U} V$ .

Ângulos adjacentes

Quando dois ângulos têm um lado em comum e as regiões determinadas por eles não têm pontos em comum, dizemos que eles são adjacentes.

Na imagem apresentada, verificamos que $\vec{O C}$ é comum aos ângulos $A \hat{O} B$ e $B \hat{O} C$ , e nenhum ponto da região de $A \hat{O} B$ é comum à região $B \hat{O} C$ . Sendo assim, esses ângulos são adjacentes.

Nesse mesmo exemplo, $\vec{O B}$ é comum aos ângulos $A \hat{O} C$ e $B \hat{O} C$ , mas existe pelo menos um ponto na região determinada pelo ângulo $B \hat{O} C$ que também faz parte da região determinada pelo ângulo $A \hat{O} C$ . Portanto, eles não são adjacentes.

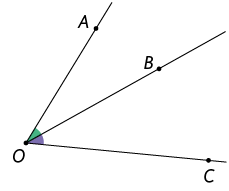
Ilustração de três semirretas com a mesma origem O. Em uma delas há o ponto A, em outra que está no meio há o ponto B e na outra, um ponto C. Está demarcado um ângulo entre as semirretas que têm o ponto A e B. E outro ângulo está demarcado entre as semirretas que têm o ponto B e C.

Página 148

Atividades

Faça as atividades no caderno.

6. De acordo com os transferidores, determine qual é a medida da abertura de cada um dos ângulos a seguir.

Ilustração de um ângulo demarcado na menor abertura entre duas semirretas de mesma origem, no centro do transferidor de meia volta. Uma semirreta está alinhada com a demarcação do 0 grau, à direita do transferidor, e a outra com a demarcação de 47 graus, no sentido anti-horário.

Resposta: A: $47 graus$ ; B: $132 vírgula 5 graus$ ; C: $90 graus$ ; D: $165 graus$ ; E: $26 graus$ ; F: $89 graus$ .

7. Classifique cada ângulo representado na atividade 6 em reto, agudo ou obtuso.

Respostas: A. Agudo; B. Obtuso; C. Reto; D. Obtuso; E. Agudo; F. Agudo.

8. Uma equipe de tecnologia projetou um robô e registrou seus movimentos com as representações a seguir, indicando a vista superior, em malha quadriculada, de alguns caminhos percorridos por ele.

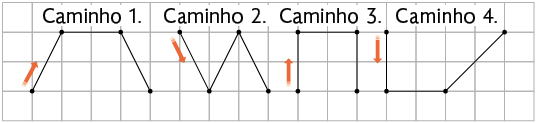
Ilustração de uma malha quadriculada com 4 caminhos desenhados. O caminho 1 é composto de 3 linhas que formam ângulos maiores que 90 graus entre si, o caminho 2 é composto de 4 linhas que que formam ângulos menores que 90 graus entre si, o caminho 3 é composto de 3 linhas que formam 90 graus entre si e o caminho 4 é composto de 3 linhas, onde apenas duas formam o ângulo de 90 graus entre elas.

Atenção!

As setas indicam o movimento inicial feito pelo robô.

Qual dos caminhos representados mostra que o robô mudou de direção apenas em ângulo reto?

Resposta: Caminho 3.

ORIENTAÇÕES AO PROFESSOR

A atividade 6 aborda medições de ângulos com o transferidor. Utilize-a para verificar se os estudantes compreenderam o uso desse instrumento. Caso necessário, elabore alguns ângulos na lousa e, com o auxílio dos estudantes, meça esses ângulos utilizando o transferidor.

Na atividade 7, os estudantes devem classificar os ângulos da atividade anterior em reto, agudo ou obtuso. Se necessário, oriente-os a consultar essas definições no tópico Classificação dos ângulos.

A atividade 8 possibilita retomar a ideia de ângulo enquanto giro. Após todos os estudantes finalizarem a atividade, converse com eles sobre as mudanças de direção do robô no caminho 3. Instigue-os a perceber que, para executar cada uma dessas mudanças de direção, o robô deu um giro de um quarto de volta. Por fim, desafie-os a classificar tanto os ângulos correspondentes às mudanças de direção do caminho 1 quanto suas medidas.

Página 149

9. Com o auxílio de um transferidor, meça os ângulos indicados na imagem.

Ilustração de vários segmentos de reta, contínuos, formando vários ângulos e passando, nessa ordem, pelos pontos: A, B, C, D, E, F, G, H. O ângulo b mede 30 graus, o c mede 45 graus, o d mede 90 graus, o e mede 110 graus, o f mede 60 graus e o ângulo g mede 180 graus.

Resposta: $medida do ângulo b igual a 30 graus$ , $medida do ângulo c igual a 45 graus$ , $medida do ângulo D igual a 90 graus$ , $medida do ângulo e igual a 110 graus$ , $medida do ângulo f igual a 60 graus$ e $medida do ângulo g cigual a 180 graus$ .

10. Considerando os ângulos indicados na atividade anterior, responda às questões.

a) Qual ângulo é reto?

b) Quais são agudos?

c) Qual é obtuso?

d) Qual é raso?

Respostas: a) $C \hat{D} E$ ; b) $A \hat{B} C$ , $B \hat{C} D$ e $E \hat{F} G$ ; c) $D \hat{E} F$ ; d) $F \hat{G} H$ .

11. Utilizando um transferidor, construa no caderno um ângulo:

a) de $62 graus$ .

b) de $112 graus$ .

c) reto.

d) raso.

Respostas na seção Resoluções.

12. Surfistas californianos, cansados de passar os dias esperando por boas ondas, colocaram rodinhas de patins em uma madeira que lembrava uma prancha. Foi aí que surgiu o skate, no final de 1950, na Califórnia, nos Estados Unidos.

Desde então, o esporte evoluiu, assim como as manobras que fazem parte dele, incluindo o Frontside $180 graus$ Flip. Nessa manobra, tanto o skatista quanto o skate dão um giro de $180 graus$ .

a) O giro realizado pelo skatista na manobra Frontside $180 graus$ Flip corresponde a que fração de uma volta? E o giro realizado pelo skate?

Resposta: Meia-volta; meia-volta.

b) Junte-se a um colega e realizem uma pesquisa sobre outras manobras realizadas por skatistas, anotando as informações que acharem mais interessantes e aquelas relacionadas a ângulos.

Resposta pessoal.

13. Gabriel construiu o ângulo a seguir em seu caderno.

Ilustração de uma folha de caderno com o desenho de um ângulo entre duas semirretas de mesma origem A, uma possui o ponto C e outra possui o ponto B. Esse ângulo tem medida aproximada de 58 graus.

Com um transferidor, identifique qual dos ângulos a seguir é congruente ao que Gabriel construiu.

Ilustração de um ângulo demarcado entre duas semirretas de mesma origem D, uma possui o ponto E e outra possui o ponto F. Esse ângulo tem medida aproximada de 46 graus.

Ilustração de um ângulo demarcado entre duas semirretas de mesma origem G, uma possui o ponto H e outra possui o ponto I. Esse ângulo tem medida aproximada de 58 graus.

Ilustração de um ângulo demarcado entre duas semirretas de mesma origem J, uma possui o ponto K e outra possui o ponto L. Esse ângulo tem medida aproximada de 55 graus.

Resposta: $H \hat{G} I$ .

14. Analise os três ângulos destacados a seguir.

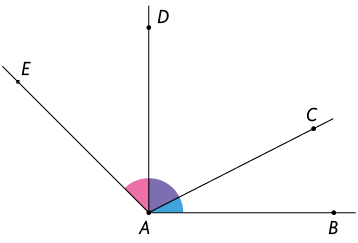
Ilustração de 4 semirretas com a mesma origem O. Em uma delas há o ponto E, em outra ao lado dessa há o ponto D, na próxima em sentido horário há o ponto C e na outra, o ponto B. Está demarcado um ângulo entre as semirretas que têm o ponto E e D, outro entre as semirretas com os pontos D e C e outro ângulo entre as semirretas que têm o ponto C e B.

Agora, determine os pares de ângulos adjacentes.

Resposta: $B \hat{A} C$ e $C \hat{A} D$ ; $C \hat{A} D$ e $D \hat{A} E$ ; $B \hat{A} D$ e $D \hat{A} E$ ; $C \hat{A} E$ e $B \hat{A} C$ .

ORIENTAÇÕES AO PROFESSOR

Ao realizar as atividades 9 e 10, peça aos estudantes que estimem as medidas dos ângulos e, de acordo com elas, classifiquem cada um desses ângulos em agudo, obtuso, reto ou raso. Após realizarem as medições, peça a eles que verifiquem se suas classificações estão corretas.

Durante o desenvolvimento da atividade 9 é necessário verificar se os estudantes posicionam o transferidor corretamente e conseguem ler a medida do ângulo.

Caso os estudantes apresentem dificuldades na atividade 11, retome as discussões propostas ao realizar a questão 1. Além disso, caso julgue pertinente, organize-os em trios para que compartilhem experiências. Caso deseje complementar essa atividade, questione-os sobre qual dos ângulos construídos é agudo e qual é obtuso.

Aproveite a atividade 12 para promover um bate-papo sobre a cultura juvenil do skate. Pergunte: Alguém da turma anda ou já andou de skate? Você conhece algum atleta de skate profissional? Que outros esportes de rua você conhece? Envolva a sala na discussão, buscando despertar o ânimo dos estudantes e, assim, promover uma conversa sobre o tema. Para obter informações sobre Culturas juvenis, consulte as orientações gerais deste manual. Com base nessa dinâmica é possível abordar o tema contemporâneo transversal Saúde, discutindo benefícios ao se praticar alguma atividade física.

Ao desenvolver o item b, explique aos estudantes a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Com isso, abordam-se aspectos das Competências gerais 1, 4 e 9 e da Competência específica de Matemática 8, ao promover discussões sobre questões de natureza social, valorizando a diversidade de opiniões. Se achar pertinente, converse com eles sobre o combate aos diversos tipos de violência, especialmente o bullying. Para obter informações a respeito desse assunto no tópico Cultura de paz e combate ao bullying, consulte as orientações gerais deste manual.

Metodologias ativas

Para desenvolver a atividade 12, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Ao realizar a atividade 13, se julgar pertinente, proponha aos estudantes que determinem os ângulos congruentes sem realizar medições. Na sequência, permita que resolvam a atividade e verifiquem suas estimativas.

A atividade 14 envolve a ideia de ângulo adjacente. Antes de iniciá-la, pergunte aos estudantes o que são ângulos adjacentes. Se achar pertinente, peça a eles que pesquisem a definição da palavra adjacente no dicionário e, em seguida, relacionem o resultado obtido ao conceito de ângulos adjacentes.

Página 150

Ângulos complementares e ângulos suplementares

Na imagem está representado o ângulo $A \hat{O} B$ . Com base na semirreta $O A$ , construímos um ângulo $A \hat{O} C$ medindo $90 graus$ .

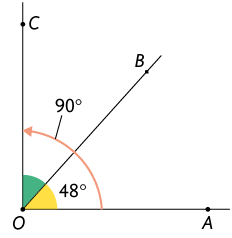
Ilustração de uma semirreta, com origem O, passando pelo ponto A e a demarcação de que faz 90 graus com a outra semirreta também de origem O e que passa por C. Entre essas duas semirretas, há outra de origem O que passa pelo ponto B e forma dois ângulos entre A O C. Um deles é o ângulo A O B com 48 graus.

Como a soma das medidas de $A \hat{O} B$ e $B \hat{O} C$ é $90 graus$ , dizemos que $A \hat{O} B$ e $B \hat{O} C$ são ângulos complementares. Dizemos também que $B \hat{O} C$ é o complemento de $A \hat{O} B$ ou que $B \hat{O} C$ é o complementar de $A \hat{O} B$ , e vice-versa.

Nesta outra imagem está representado o ângulo $D \hat{O} E$ . Partindo da semirreta $O D$ , construímos um ângulo $D \hat{O} F$ medindo $180 graus$ .

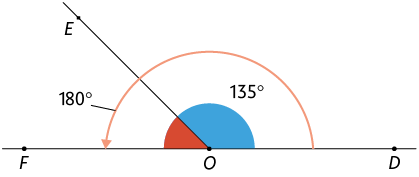
Ilustração de uma semirreta, com origem O, passando pelo ponto F e a demarcação de que faz 180 graus com a outra semirreta também de origem O e que passa por D. Entre essas duas semirretas, há outra de origem O que passa pelo ponto E e forma dois ângulos entre F O D. Um deles é o ângulo D O E com 135 graus.

Como a soma das medidas de $D \hat{O} E$ e $E \hat{O} F$ é $180 graus$ , dizemos que $D \hat{O} E$ e $E \hat{O} F$ são ângulos suplementares. Dizemos também que $E \hat{O} F$ é o suplemento de $D \hat{O} E$ ou que $E \hat{O} F$ é o suplementar de $D \hat{O} E$ , e vice-versa.

Podemos obter as medidas dos ângulos $B \hat{O} C$ e $E \hat{O} F$ realizando os cálculos a seguir.

$med (B \hat{O} C) = med (A \hat{O} C) -$ $medida do ângulo a o b igual a 90 graus menos 48 graus igual a 42 graus$
$med (E \hat{O} F) = med (D \hat{O} F) -$ $medida do ângulo d o e igual a 180 graus menos 135 graus igual a 45 graus$

Dois ângulos são:

complementares quando a soma de suas medidas é $90 graus$ ;
suplementares quando a soma de suas medidas é $180 graus$ .

Questão 2. Calcule mentalmente e registre no caderno a medida do ângulo:

a) complementar de $72 graus$ .

Resposta: $18 graus$ .

b) suplementar de $72 graus$ .

Resposta: $108 graus$ .

Página 151

Ângulos opostos pelo vértice

As retas r e t a seguir são concorrentes. Ao se cruzarem, elas formam quatro ângulos.

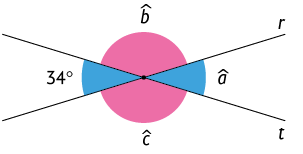
Ilustração de duas retas, r e t que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo com medida 34 graus e o ângulo a são opostos pelo vértice horizontalmente; e os ângulos b e c são opostos pelo vértice verticalmente.

Atenção!

Daqui em diante, indicaremos a medida de um ângulo com uma letra minúscula com circunflexo.

Podemos obter a medida $\hat{a}$ sem utilizar transferidor com os seguintes procedimentos.

Os ângulos de medidas $\hat{b}$ e $\hat{a}$ , nesse caso, são suplementares.

$medida do ângulo b mais a medida do ângulo a igual a 180 graus$

Ilustração de duas retas, r e t que se cruzam formando um X. 2 dos respectivos ângulos formados estão demarcados, em que o ângulo de cima da vertical é b e o ângulo da direita da horizontal é a.

Os ângulos de medidas $\hat{b}$ e $34 graus$ também são suplementares.

$medida do ângulo b mais 34 graus igual a 180 graus$

Dessas duas igualdades, temos que $\hat{b} + \hat{a}$ é igual a $medida do ângulo b mais 34 graus$ , então:

$medida do ângulo b mais a medida do ângulo a igual a medida do ângulo b mais 34 graus$

$medida do ângulo b mais medida do ângulo a menos medida do ângulo b igual a medida do ângulo b mais 34 graus menos medida do ângulo b$

$medida do ângulo a igual a 34 graus$

Portanto, $medida do ângulo a igual a 34 graus$ .

Questão 3. Converse com seus colegas a fim de obter uma maneira de determinar a medida $\hat{c}$ sem utilizar o transferidor.

Resposta pessoal.

Nesta imagem, os pares de ângulos de medidas $\hat{a}$ e $\hat{b}$ , $\hat{c}$ e $\hat{d}$ são chamados opostos pelo vértice.

Dois ângulos opostos pelo vértice têm medidas iguais. Assim, nesta imagem, temos $\hat{a} = \hat{b}$ e $\hat{c} = \hat{d}$ .

Ilustração de duas retas, r e t que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo a e o ângulo b são opostos pelo vértice horizontalmente; e os ângulos c e d que são opostos pelo vértice verticalmente.

ORIENTAÇÕES AO PROFESSOR

Antes de iniciar o conteúdo desta página, é necessário verificar o conhecimento prévio dos estudantes relacionado a ângulos opostos pelo vértice, assunto que já foi estudado em anos anteriores. Peça a eles que compartilhem com a turma suas explicações, tendo a oportunidade de resgatar o conhecimento prévio sobre o assunto e de sistematizar o que compartilharem.

Na questão 3, se necessário, chame a atenção dos estudantes para o fato de que $medida do ângulo a mais medida do ângulo b igual a 180 graus$ . Em seguida, instigue-os a perceber que os ângulos de medidas $\hat{c}$ e $\hat{b}$ são opostos pelo vértice. Por fim, possibilite que determinem a medida desejada.

Aproveite o fato de nessa questão ser proposto um diálogo entre os estudantes e explique a eles a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e limitações dos outros. Com isso, abordam-se aspectos da Competência geral 9 e da Competência específica de Matemática 8, ao promover discussões que levam à busca de soluções de problemas, valorizando a diversidade de opiniões.

Página 152

Atividades

Faça as atividades no caderno.

15. Utilizando um transferidor, meça os ângulos apresentados. Depois, para cada um deles, escreva a medida de seu complemento e a medida de seu suplemento.

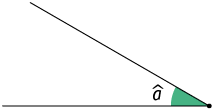
Ilustração de um ângulo a, equivalente a 30 graus, demarcado entre duas semirretas de mesma origem.

Resposta: $medida do ângulo a igual a 30 graus$ ; medida do complemento: $60 graus$ ; medida do suplemento: $150 graus$ .

Ilustração de um ângulo b, equivalente a 50 graus, demarcado entre duas semirretas de mesma origem.

Resposta: $medida do ângulo b igual a 50 graus$ ; medida do complemento: $40 graus$ ; medida do suplemento: $130 graus$ .

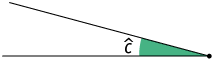
Ilustração de um ângulo c, equivalente a 15 graus, demarcado entre duas semirretas de mesma origem.

Resposta: $medida do ângulo c igual a 15 graus$ ; medida do complemento: $75 graus$ ; medida do suplemento: $165 graus$ .

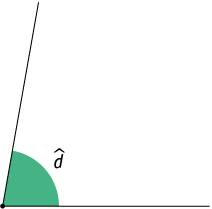
Ilustração de um ângulo d, equivalente a 80 graus, demarcado entre duas semirretas de mesma origem.

Resposta: $medida do ângulo d igual a 80 graus$ ; medida do complemento: $10 graus$ ; medida do suplemento: $100 graus$ .

Ilustração de um ângulo e, equivalente a 45 graus, demarcado entre duas semirretas de mesma origem.

Resposta: $medida do ângulo e igual a 45 graus$ ; medida do complemento: $45 graus$ ; medida do suplemento: $135 graus$ .

16. Carolina dobrou um pedaço de cartolina em formato de retângulo, conforme a imagem.

Ilustração de uma cartolina em formato retangular e uma linha tracejada que vai do vértice inferior esquerdo até um ponto do lado direito do retângulo. Há uma seta indicando a dobradura do lado formado pela linha tracejada diante da outra parte. — Etapa 1

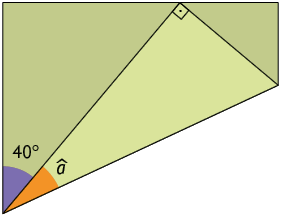
Ilustração de uma cartolina retangular dobrada, em que seu vértice inferior direito encosta no lado de cima. No vértice inferior esquerdo são formados os ângulos a e 40 graus. — Etapa 2

a) Determine a medida $\hat{a}$ do ângulo indicado.

Resposta: $medida do ângulo a igual a 25 graus$ .

b) Qual é a medida do complemento e a do suplemento do ângulo de medida $\hat{a}$ ?

Resposta: Medida do complemento: $65 graus$ ; medida do suplemento: $155 graus$ .

17. Copie o quadro no caderno substituindo as letras pelas medidas adequadas.

Ângulo complementar e ângulo suplementar
ângulo	$6 graus$	$31 graus$	E	G	$136 graus$
complemento	A	C	$18 graus$	H
suplemento	B	D	F	$91 graus$	I

Resposta na seção Respostas e na seção Resoluções.

18. Junte-se a um colega e resolvam esta atividade no caderno. Sabendo que os ângulos de medidas $\hat{a}$ e $\hat{b}$ são complementares e que $\hat{a} = 2 \hat{b}$ , obtenha a medida de cada um deles.

Resposta: $medida do ângulo a igual a 60 graus$ e $medida do ângulo b igual a 30 graus$ .

ORIENTAÇÕES AO PROFESSOR

Na atividade 15, caso não haja transferidor para todos os estudantes, reúna-os em grupos para que realizem esta atividade. Sempre que necessário, auxilie-os no posicionamento correto do transferidor para realizar as medições.

Caso os estudantes apresentem dificuldades na atividade 16, instigue-os, por meio de questionamentos, a perceber que, ao dobrar e desdobrar o pedaço de cartolina, marcam-se três ângulos: um de $40 graus$ e outros dois congruentes. Além disso, como a cartolina tem formato retangular, a soma das medidas desses três ângulos é $90 graus$ . Por fim, possibilite que resolvam a atividade.

Busca-se com a atividade 17 constatar se os estudantes compreenderam os conceitos de ângulo complementar e de ângulo suplementar. É necessário verificar também se eles efetuam os cálculos corretamente. Se necessário, complete algumas das células do quadro com eles.

A atividade 18 propõe a abordagem do conceito de ângulos complementares em um contexto algébrico. Se julgar conveniente, oriente os estudantes a escrever no caderno a expressão algébrica que relaciona $\hat{a}$ e $\hat{b}$ como dois ângulos complementares, ou seja, $medida do ângulo a mais medida do ângulo b igual a 90 graus$ . Durante o desenvolvimento dessa atividade, explique aos estudantes a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Com isso, abordam-se aspectos das Competências gerais 1, 4 e 9 e da Competência específica de Matemática 8. Se achar pertinente, converse com eles sobre o combate aos diversos tipos de violência, especialmente o bullying. Para obter informações a respeito desse assunto no tópico Cultura de paz e combate ao bullying, consulte as orientações gerais deste manual.

Metodologias ativas

Para desenvolver as atividades 16 e 18, avalie a possibilidade de utilizar a metodologia ativa Pensamento do design. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 153

19. Sem utilizar transferidor ou outro instrumento, determine as medidas indicadas nas imagens a seguir.

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo b e o ângulo c são opostos pelo vértice horizontalmente; e o ângulo de medida 74 graus e o ângulo a são opostos pelo vértice verticalmente.

Resposta: $medida do ângulo a igual a 74 graus$ , $medida do ângulo b igual a 106 graus$ e $medida do ângulo c igual a 106 graus$ .

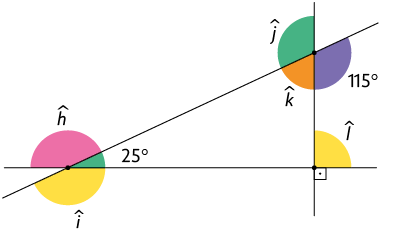
Ilustração de três retas que se cruzam formando um triângulo. No primeiro vértice, há o ângulo interno de 25 graus e os ângulos externos e opostos pelo vértice h e i. No segundo vértice, há o ângulo interno k e os ângulos externos e opostos pelo vértice j e 115 graus. No terceiro vértice, há os ângulos externos e suplementares i e 90 graus.

Resposta: $medida do ângulo h igual a 155 graus$ , $medida do ângulo i igual a 155 graus$ , $medida do ângulo j igual a 115 graus$ , $medida do ângulo k igual a 65 graus$ e $medida do ângulo l igual a 90 graus$ .

20. Na imagem apresentada, a soma das medidas $\hat{a}$ e $\hat{c}$ é $102 graus$ . Qual é a medida $\hat{b}$ ?

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo a e o ângulo c são opostos pelo vértice horizontalmente; e o ângulo b está na parte de cima.

Resposta: $medida do ângulo b igual a 129 graus$ .

21. Efetue os cálculos e determine o valor de x e as medidas dos ângulos.

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo x mais 18 graus e o ângulo 3 x são opostos pelo vértice horizontalmente;

Ilustração de duas retas que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo 4 x mais 9 graus e o ângulo 5 x menos 21 graus são opostos pelo vértice verticalmente.

Respostas: A. $x igual a 9 graus$ ; medidas dos ângulos: $27 graus$ ; B. $x igual a 30 graus$ ; medidas dos ângulos: $129 graus$ .

22. Utilizando dois palitos de sorvete e uma tachinha, Marcela construiu o seguinte instrumento.

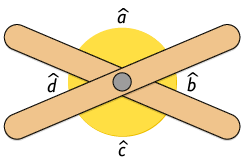
Ilustração de dois palitos de sorvete que se cruzam formando um X. Os respectivos ângulos formados estão demarcados, em que o ângulo d e o ângulo b são opostos pelo vértice horizontalmente; e os ângulos a e c que são opostos pelo vértice verticalmente.

a) Na imagem, podemos identificar dois pares de ângulos opostos pelo vértice. Considerando esses pares, copie as afirmações a seguir no caderno substituindo o $█$ pela medida adequada.

O ângulo de medida $\hat{a}$ é oposto pelo vértice do ângulo de medida $█$ .

O ângulo de medida $\hat{d}$ é oposto pelo vértice do ângulo de medida $█$ .

Resposta: $\hat{c}$ ; $\hat{b}$ .

b) De acordo com a abertura dos palitos, a soma das medidas $\hat{a}$ e $\hat{b}$ sofre variação? Converse com os colegas a respeito do motivo dessa ocorrência.

Resposta pessoal. Espera-se que os estudantes concluam que não, pois os ângulos de medidas $\hat{a}$ e $\hat{b}$ são suplementares, ou seja, a soma dessas medidas é sempre $180 graus$ .

ORIENTAÇÕES AO PROFESSOR

Ao realizar as atividades 19 e 20, se julgar necessário, lembre os estudantes de que dois ângulos são suplementares quando a soma de suas medidas é $180 graus$ .

Metodologias ativas

Ao desenvolver o trabalho com a atividade 20, avalie a possibilidade de utilizar a metodologia ativa Pensamento do design. Para obter informações sobre essa metodologia no tópico Metodologias e estratégias ativas, consulte as orientações gerais deste manual.

Para solucionar a atividade 21, os estudantes podem escrever equações de primeiro grau. Ao analisar a situação, obtém-se:

$medida do ângulo a mais a medida do ângulo c igual a 102 graus$ e $medida do ângulo a mais medida do ângulo b igual a 180 graus$

Como $\hat{a} = \hat{c}$ (ângulos opostos pelo vértice), obtemos o valor de $\hat{a}$ e, consequentemente, o valor de $\hat{b}$ , que é o desejado.

Verifique a possibilidade de providenciar palitos de sorvete e tachinhas para que os estudantes tenham em mãos o instrumento apresentado na atividade 22. Desse modo, espera-se auxiliá-los na obtenção das respostas dos itens propostos.

Aproveite o fato de o item b propor uma conversa entre colegas para orientá-los sobre a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Com isso, abordam-se aspectos das Competências gerais 1, 4 e 9 e da Competência específica de Matemática 8. Se achar pertinente, converse com eles sobre o combate aos diversos tipos de violência, especialmente o bullying. Obtenha informações a respeito desse assunto no tópico Cultura de paz e combate ao bullying, nas orientações gerais deste manual.

Página 154

Retas paralelas cortadas por uma transversal

Na imagem a seguir, as retas r e s são paralelas e são cruzadas por uma reta transversal, formando vários ângulos.

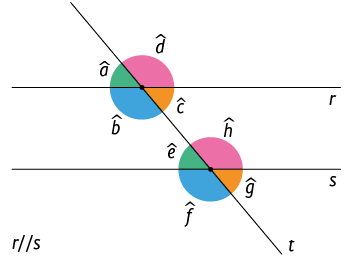
Ilustração de duas retas r e s, paralelas, cortadas por outra reta transversal t. Todos os ângulos estão demarcados. Entre t e r estão os seguintes ângulos: à direita de t e acima de r está o ângulo d; abaixo de r e à esquerda de t está o ângulo b. Acima de r e à esquerda de t está o ângulo a; e abaixo de r e à direita de t, o ângulo c. Entre t e s estão os seguintes ângulos: à direita de t e acima de s está o ângulo h; à esquerda de t e abaixo de s está o ângulo f; à esquerda de t e acima de s está o ângulo e; à direita de t e abaixo de s está o ângulo g. Abaixo dessa representação, há as letras r e s com duas barras entre elas.

Atenção!

A notação $r // s$ indica que as retas r e s são paralelas.

Os pares de ângulos indicados com a mesma cor nessa imagem são denominados ângulos correspondentes.

Questão 4. Utilizando um transferidor, faça as medições dos ângulos e escreva no caderno os seguintes pares de medidas.

a) $\hat{a}$ e $\hat{e}$

b) $\hat{b}$ e $\hat{f}$

c) $\hat{c}$ e $\hat{g}$

d) $\hat{d}$ e $\hat{h}$

Os pares de medidas que você obteve são iguais ou diferentes?

Respostas: a) $50 graus$ ; b) $130 graus$ ; c) $50 graus$ ; d) $130 graus$ ; Resposta pessoal. Espera-se que os estudantes respondam que os pares de medidas obtidos são iguais.

Na imagem anterior, os ângulos são formados por uma reta transversal que cruza retas paralelas. Nela, os pares de ângulos de medidas $\hat{a}$ e $\hat{e}$ , $\hat{b}$ e $\hat{f}$ , $\hat{c}$ e $\hat{g}$ , $\hat{d}$ e $\hat{h}$ são ângulos correspondentes.

Dois ângulos correspondentes têm medidas iguais quando são formados por retas paralelas e uma transversal. Assim, na imagem anterior, temos:

$\hat{a} = \hat{e}$

$\hat{b} = \hat{f}$

$\hat{c} = \hat{g}$

$\hat{d} = \hat{h}$

Quando as retas não são paralelas, não podemos estabelecer ângulos correspondentes com medidas iguais.

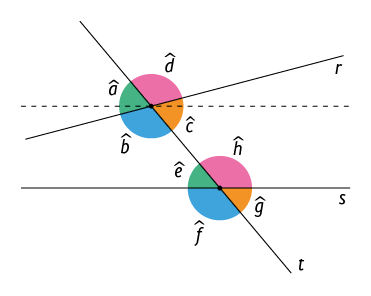
Ilustração de duas retas r e s, cortadas por outra reta transversal t. Todos os ângulos estão demarcados. Entre t e r estão os seguintes ângulos: à direita de t e acima de r está o ângulo d; abaixo de r e à esquerda de t está o ângulo b. Acima de r e à esquerda de t está o ângulo a; e abaixo de r e à direita de t, o ângulo c. Entre t e s estão os seguintes ângulos: à direita de t e acima de s está o ângulo h; à esquerda de t e abaixo de s está o ângulo f; à esquerda de t e acima de s está o ângulo e; à direita de t e abaixo de s está o ângulo g. Há uma projeção de reta paralela a s, passando na intersecção das retas r e t.

Atenção!

Na imagem por exemplo, as retas r e s não são paralelas. Assim:

$\hat{a} \neq \hat{e}$

$\hat{b} \neq \hat{f}$

$\hat{c} \neq \hat{g}$

$\hat{d} \neq \hat{h}$

ORIENTAÇÕES AO PROFESSOR

Antes de iniciar o conteúdo desta página, pergunte aos estudantes o que são retas paralelas. Pergunte também a respeito da palavra transversal, instigando-os a pensar em que contextos eles a utilizaram ou leram. Se necessário, consulte o significado desse termo em um dicionário, relacionando-o com a ideia de reta transversal.

Para complementar o trabalho com a questão 4, organize os estudantes em grupos e disponibilize, para cada um deles, uma malha quadriculada. Em seguida, peça aos grupos que representem, na malha, duas retas paralelas cortadas por uma transversal e destaquem os 8 ângulos formados, colorindo os correspondentes com uma mesma cor. Na sequência, oriente-os a medir os pares de ângulos correspondentes e a verificar se são ou não congruentes. Durante essa dinâmica, verifique como os estudantes manuseiam o transferidor, orientando-os se necessário.

Se necessário, explique aos estudantes que a linha tracejada na imagem representa uma reta imaginária que é paralela à reta s.

Página 155

Utilizando um transferidor, podemos verificar que a medida $\hat{a}$ na imagem a seguir é $47 graus$ .

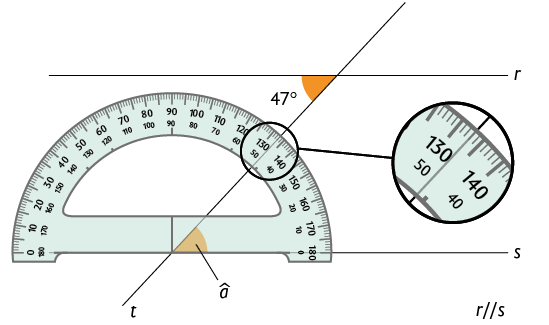
Ilustração de duas retas paralelas, r e s, cortadas por uma transversal, t. O cruzamento de t com r forma o ângulo de 47 graus à esquerda e abaixo do cruzamento. Do mesmo modo, o cruzamento de t com s forma o ângulo a à direita e acima do cruzamento. Há um transferidor de meia volta com a reta s em cima do marco 0 e o destaque para a reta t passando pelo marco de 47 graus.

Também podemos determinar a medida $\hat{a}$ sem fazer medições. Para isso, vamos indicar na imagem o ângulo de medida $\hat{c}$ . Temos $medida do ângulo c igual a 47 graus$ , pois $\hat{c}$ e $47 graus$ são medidas de ângulos opostos pelo vértice. Como os ângulos de medidas $\hat{c}$ e $\hat{a}$ são correspondentes, temos $medida do ângulo a igual a medida do ângulo c igual a 47 graus$ .

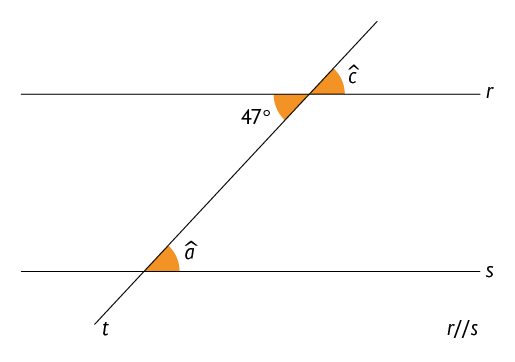
Ilustração de duas retas paralelas, r e s, cortadas por uma transversal, t. O cruzamento de t com r forma o ângulo: c à direita e acima do cruzamento e forma o ângulo de 47 graus à esquerda e abaixo do cruzamento. Do mesmo modo, o cruzamento de t com s forma o ângulo a à direita e acima do cruzamento.

Na imagem a seguir, os ângulos são formados por uma reta transversal que cruza retas paralelas. Nela, os pares de ângulos de medidas $\hat{b}$ e $\hat{h}$ , $\hat{c}$ e $\hat{e}$ são chamados ângulos alternos internos, e os ângulos de medidas $\hat{d}$ e $\hat{f}$ , $\hat{a}$ e $\hat{g}$ , ângulos alternos externos.

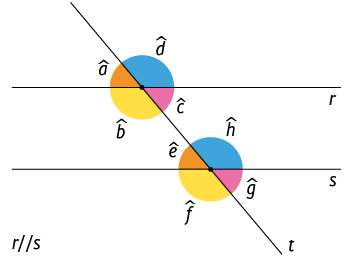
Atenção!

Os pares de ângulos alternos internos ou alternos externos têm medidas iguais quando são formados por retas paralelas e uma transversal. Assim, na imagem a seguir, temos:

• medida dos ângulos alternos internos:

$\hat{b} = \hat{h}$

$\hat{c} = \hat{e}$

• medida dos ângulos alternos externos:

$\hat{d} = \hat{f}$

$\hat{a} = \hat{g}$

Quando as retas não são paralelas, não podemos estabelecer ângulos alternos com medidas iguais.

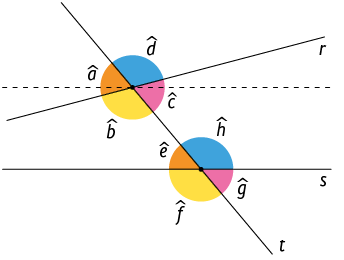
Atenção!

Nesta imagem, por exemplo, as retas r e s não são paralelas. Assim:

$\hat{b} \neq \hat{h}$

$\hat{c} \neq \hat{e}$

$\hat{d} \neq \hat{f}$

$\hat{a} \neq \hat{g}$

Página 156

Na imagem, os ângulos são formados por uma reta transversal que cruza as retas paralelas. Nela, os pares de ângulos de medidas $\hat{a}$ e $\hat{f}$ , por exemplo, são chamados ângulos colaterais externos, e os ângulos de medidas $\hat{c}$ e $\hat{h}$ , por exemplo, são chamados ângulos colaterais internos.

A seguir, vamos verificar a relação entre esses pares de ângulos.

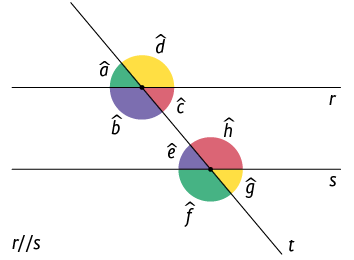
Os ângulos de medidas $\hat{a}$ e $\hat{e}$ são correspondentes assim $\hat{a} = \hat{e}$ . Além disso, os ângulos de medidas $\hat{e}$ e $\hat{f}$ são suplementares, ou seja, $medida do ângulo e mais medida do ângulo f igual a 180 graus$ . Portanto, concluímos que $medida do ângulo a mais a medida do ângulo f igual a 180 graus$ .
Os ângulos de medidas $\hat{d}$ e $\hat{h}$ são correspondentes assim $\hat{d} = \hat{h}$ . Além disso, os ângulos de medidas $\hat{d}$ e $\hat{c}$ são suplementares, ou seja, $medida do ângulo d mais medida do ângulo c igual a 180 graus$ . Portanto, concluímos que $medida do ângulo c mais a medida do ângulo h igual a 180 graus$ .

Assim, demonstramos que o par de ângulos colaterais externos de medidas $\hat{a}$ e $\hat{f}$ e o par de ângulos colaterais internos de medidas $\hat{c}$ e $\hat{h}$ são suplementares.

Questão 5. Em seu caderno, use procedimento semelhante ao apresentado para os demais pares de ângulos colaterais indicados na imagem e conclua que eles também são suplementares.

Resposta pessoal. Espera-se que os estudantes usem procedimentos semelhantes para concluir que os pares de ângulos colaterais são suplementares.

Os pares de ângulos colaterais internos ou colaterais externos são suplementares quando são formados por retas paralelas e uma transversal. Assim, na imagem anterior temos:

medidas dos ângulos colaterais internos:

$medida do ângulo b mais medida do ângulo e igual a 180 graus$

$medida do ângulo c mais a medida do ângulo h igual a 180 graus$

medidas dos ângulos colaterais externos:

$medida do ângulo a mais a medida do ângulo f igual a 180 graus$

$medida do ângulo d mais medida do ângulo g igual a 180 graus$

Quando as retas não são paralelas, não podemos estabelecer ângulos colaterais suplementares.

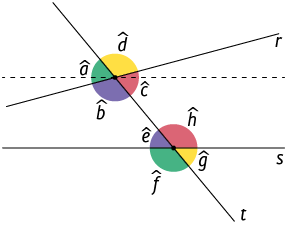
Atenção!

Nesta imagem, por exemplo, as retas r e s não são paralelas. Assim:

$medida do ângulo b mais medida do ângulo e diferente de 180 graus$

$medida do ângulo c mais medida do ângulo h diferente de 180 graus$

$medida do ângulo a mais medida do ângulo f diferente de 180 graus$

$medida do ângulo d mais medida do ângulo g diferente de 180 graus$

Página 157

Instrumentos e softwares

Ângulos formados por retas paralelas cortadas por uma transversal com o GeoGebra

Com as orientações do professor e o passo a passo a seguir, vamos verificar algumas relações entre as medidas dos ângulos formados por duas retas paralelas e uma transversal.

1º. Com a ferramenta Reta, marque dois pontos A e B para traçar a reta r. Depois, usando a ferramenta Reta Paralela, marque um ponto C não pertencente à reta r. Em seguida, clique na reta r para traçar a reta s. Por fim, novamente com a ferramenta Reta, clique em B e C para traçar uma reta t transversal à r e s.

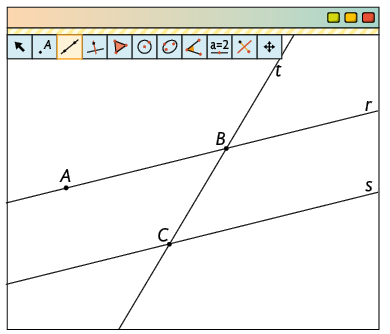
Ilustração de uma página de computador com software de geometria. Há vários botões de ferramentas e um com o desenho de uma reta está selecionado. Ainda na aba, há desenhado duas retas paralelas r e s, com r contendo os pontos A e B e s contendo o ponto C. Ainda, há uma reta transversal t que cruza s em C e cruza r em B.

2º. Com a ferramenta Ponto, clique sobre as retas e marque os pontos D, E, F, G e H, como na imagem.

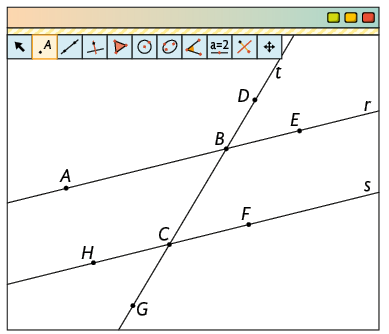
Ilustração de uma página de computador com software de geometria. Há vários botões de ferramentas e um com o desenho de ponto e a letra A ao lado está selecionado. Ainda na aba, há desenhado duas retas paralelas r e s, com r contendo os pontos A e B e s contendo o ponto C. Ainda, há uma reta transversal t que cruza s em C e cruza r em B. Ainda na reta r há o ponto E à direita de B e na reta s há o ponto H à esquerda e o ponto F à direita de C. Na reta t há o ponto d acima de B e G abaixo de C.

3º. Com a ferramenta Ângulo, clique em $E$ , $B$ e $D$ , nessa ordem, para medir o ângulo $E \hat{B} D$ . De maneira semelhante, meça os demais ângulos, como na imagem. Deixe ângulos correspondentes com mesma cor clicando com o botão direito, escolhendo a opção Configurações e selecionando a aba Cor.

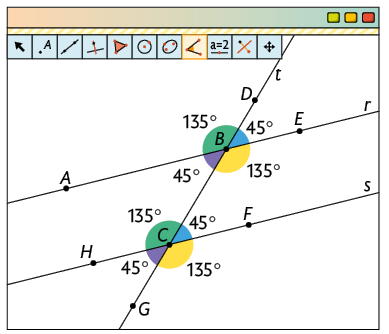
Ilustração de uma página de computador com software de geometria. Há vários botões de ferramentas e um com o desenho de ângulo está selecionado. Ainda na aba, há desenhado duas retas paralelas r e s, com r contendo os pontos A e B e s contendo o ponto C. Ainda, há uma reta transversal t que cruza s em C e cruza r em B. Ainda na reta r há o ponto E à direita de B e na reta s há o ponto H à esquerda e o ponto F à direita de C. Na reta t há o ponto d acima de B e G abaixo de C. Entre t e r estão os seguintes ângulos: à direita de t e acima de r está o ângulo 45 graus; abaixo de r e à esquerda de t está o ângulo 45 gruas. Acima de r e à esquerda de t está o ângulo 135 graus; e abaixo de r e à direita de t, o ângulo 135 graus. Entre t e s estão os seguintes ângulos: à direita de t e acima de s está o ângulo 45 graus; à esquerda de t e abaixo de s está o ângulo 45 graus; à esquerda de t e acima de s está o ângulo 135 graus; à direita de t e abaixo de s está o ângulo 135 graus.

Faça o teste: com a ferramenta Mover, clique e arraste os pontos A, B ou C e verifique se os ângulos correspondentes permanecem congruentes.

ORIENTAÇÕES AO PROFESSOR

Os passos apresentados nesta seção correspondem ao GeoGebra, software que representa conceitos de Geometria e Álgebra. Nele, é possível realizar diversas construções geométricas usando pontos, retas, circunferências e outras curvas, considerando relações entre os elementos envolvidos, como posição relativa, pertinência e interseção. Utilizado em escolas e universidades de diversos países, o software pode ser obtido gratuitamente e está disponível em vários idiomas, inclusive em português. O download pode ser feito no site indicado a seguir. Disponível em: https://oeds.link/GZJU80. Acesso em: 22 abr. 2022.

Caso essa seção seja realizada no laboratório de informática da escola, certifique-se de que todos os computadores estão com o software instalado. Uma alternativa é utilizar a versão on-line, disponível no mesmo site.

Explique aos estudantes que o GeoGebra considera o sentido anti-horário dos cliques para definir o ângulo e a sua medida.

O trabalho desenvolvido ao longo desta página contempla aspectos da habilidade EF07MA23, visto que possibilita a verificação de relações entre ângulos formados por retas paralelas cortadas por uma transversal.

Antes de realizar as construções, oriente os estudantes a ocultar os eixos e a malha. Diga que, para ocultar os eixos, é necessário clicar com o botão direito na Janela de Visualização e desmarcar a opção Exibir Eixos. Já para ocultar a malha, deve-se clicar com o botão direito na Janela de Visualização, clicar em Exibir Malha e selecionar a opção Sem Malha.

Caso os pontos fiquem em posições que dificultem as medições dos ângulos, oriente os estudantes a movê-los, clicando com a ferramenta Mover no ponto e arrastando sobre a reta.

Metodologias ativas

Ao desenvolver a seção Instrumentos e softwares, avalie a possibilidade de utilizar a metodologia ativa Tiras de classificação. Para obter informações sobre essa metodologia no tópico Metodologias e estratégias ativas, consulte as orientações gerais deste manual.

Página 158

Atividades

Faça as atividades no caderno.

23. De acordo com a figura geométrica a seguir, escreva no caderno as letras que indicam as medidas de dois pares de ângulos:

a) correspondentes.

Sugestões de respostas: $\hat{a}$ e $\hat{e}$ ; $\hat{b}$ e $\hat{f}$ ; $\hat{c}$ e $\hat{g}$ ; $\hat{d}$ e $\hat{h}$ .

b) opostos pelo vértice.

Sugestões de resposta: $\hat{a}$ e $\hat{c}$ ; $\hat{b}$ e $\hat{d}$ ; $\hat{e}$ e $\hat{g}$ ; $\hat{f}$ e $\hat{h}$ .

c) alternos internos.

Sugestões de resposta: $\hat{b}$ e $\hat{h}$ ; $\hat{c}$ e $\hat{e}$ .

d) alternos externos.

Sugestões de resposta: $\hat{a}$ e $\hat{g}$ ; $\hat{d}$ e $\hat{f}$ .

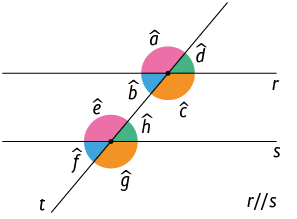
24. Em relação à figura geométrica a seguir, apenas uma das afirmações é falsa. Identifique-a e reescreva-a corrigida no caderno.

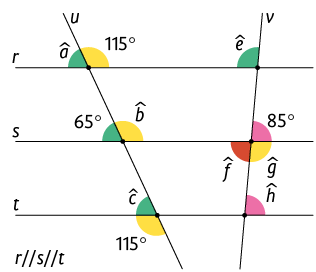
Ilustração de três retas paralelas, r, s e t, cortadas por duas transversais, u e v. Nos cruzamentos da reta u: formam com a reta r os ângulos de 115 graus à direita e acima do cruzamento e o ângulo a à esquerda e acima do cruzamento, forma com a reta s o ângulo b à direita e acima do cruzamento e o ângulo 65 graus à esquerda e acima do cruzamento e forma com a reta t o ângulo c à esquerda e acima do cruzamento e 115 graus à esquerda e abaixo do cruzamento. Do mesmo modo, nos cruzamentos da reta v: forma com a reta r o ângulo e à esquerda e acima do cruzamento, forma com a reta s o ângulo f à esquerda e abaixo do cruzamento, o ângulo g à direita e abaixo do cruzamento e 85 graus à direita e acima do cruzamento e forma com a reta t o ângulo h à direita e acima do cruzamento. Abaixo dessa representação, há as letras r, s e t com duas barras entre cada uma.

a) A medida $\hat{b}$ é $115 graus$ .

b) Os ângulos de medidas $\hat{e}$ e $\hat{h}$ são suplementares.

c) Os ângulos de medidas $\hat{a}$ e $\hat{c}$ são correspondentes.

d) A medida $\hat{c}$ é $60 graus$ .

e) Os ângulos de medidas $\hat{f}$ e $\hat{g}$ juntos formam um ângulo de $180 graus$ .

Resposta: Alternativa d; Sugestão de correção: A medida $\hat{c}$ é $65 graus$ .

25. Utilizando esquadros e um transferidor, Flávia construiu a figura geométrica a seguir.

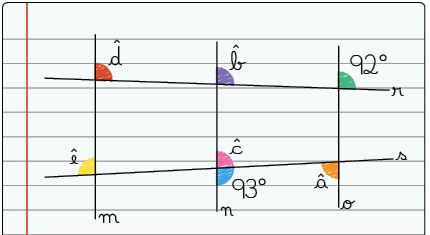
Ilustração de uma folha de papel com linhas desenhadas três retas m, n, o, paralelas e verticais, cortadas por duas retas transversais, r e s. Nos cruzamentos da reta r: forma com a reta m o ângulo d à direita e acima do cruzamento, forma com a reta n o ângulo b à direita e acima do cruzamento e forma com a reta, o, o ângulo 92 graus à direita e acima do cruzamento. Do mesmo modo, nos cruzamentos da reta s: forma com a reta m o ângulo e à esquerda e acima do cruzamento, forma com a reta n o ângulo c à direita e acima do cruzamento e 93 graus à direita e abaixo do cruzamento, forma com a reta, o, o ângulo 'a à esquerda e abaixo do cruzamento.

Determine as medidas $\hat{a}$ , $\hat{b}$ , $\hat{c}$ , $\hat{d}$ e $\hat{e}$ , sabendo que as retas m, n e o são paralelas.

Resposta: $medida do ângulo a igual a 87 graus$ , $medida do ângulo b igual a 92 graus$ , $medida do ângulo c igual a 87 graus$ , $medida do ângulo d igual a 92 graus$ e $medida do ângulo e igual a 93 graus$ .

26. Efetue os cálculos em seu caderno e obtenha o valor de x e as medidas dos ângulos indicados.

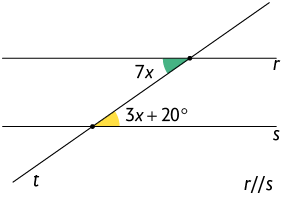
Ilustração de duas retas paralelas, r e s cortadas por uma reta transversal t. Há 2 ângulos demarcados. Um deles tem medida 7 x e está à esquerda de t e abaixo de r. Também está demarcado o ângulo 3 x mais 20 graus que está acima de s e à direita de t. Abaixo dessa representação, há as letras r e s com duas barras entre elas.

Resposta: $x igual a 5 graus$ , e os ângulos indicados medem $35 graus$ .

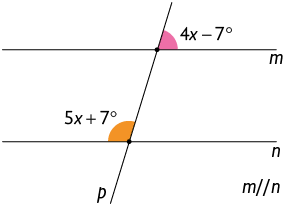
Ilustração de duas retas paralelas, m e n cortadas por uma reta transversal p. Há 2 ângulos demarcados. Um deles tem medida 4 x menos 7 graus e está à direita de p e acima de m. Também está demarcado o ângulo 5 x mais 7 graus que está acima de n e à esquerda de p. Abaixo dessa representação, há as letras m e n com duas barras entre elas.

Resposta: $x igual a 20 graus$ , o ângulo agudo mede $73 graus$ e o ângulo obtuso mede $107 graus$ .

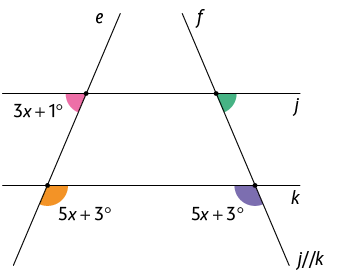
Ilustração de duas retas paralelas, k, j, cortadas por duas transversais, e, e f. Nos cruzamentos da reta e: forma com a reta j o ângulo '3 x mais 1 grau' à esquerda e abaixo do cruzamento, forma com a reta k o ângulo '5 x mais 3 graus' à direita e abaixo do cruzamento. Do mesmo modo, nos cruzamentos da reta f: forma com a reta j um ângulo não denominado, à direita e abaixo do cruzamento, forma com a reta k o ângulo '5 x mais 3' à esquerda e abaixo do cruzamento. Abaixo dessa representação, há as letras j e k com duas barras entre elas.

Resposta: $x igual a 22 graus$ , os ângulos agudos medem $67 graus$ e os ângulos obtusos $113 graus$ .

ORIENTAÇÕES AO PROFESSOR

Ao abordar a verificação de relações entre ângulos formados por retas paralelas cortadas por uma transversal, as atividades desta seção contemplam a habilidade EF07MA23.

Busca-se, com a atividade 23, verificar se os estudantes reconhecem pares de ângulos congruentes em retas paralelas cortadas por uma transversal. Se necessário, explique a eles que o termo "alterno" está relacionado à reta transversal e os termos "internos" e "externos" estão associados às retas paralelas.

Ao realizar a atividade 24 com os estudantes, questione a veracidade dos demais itens. Por exemplo, o item a é verdadeiro, pois os ângulos de medidas $\hat{b}$ e $115 graus$ são correspondentes. Dessa maneira, peça a eles que apresentem justificativas para os itens verdadeiros.

As retas paralelas e transversais da atividade 25 estão representadas de maneira não convencional. Com isso, alguns estudantes podem ter dificuldade durante a resolução. Nesse caso, oriente-os a escrever no caderno os pares de ângulos congruentes para, em seguida, determinar suas medidas.

Na atividade 26, verifique como os estudantes escrevem e resolvem as equações correspondentes. Se necessário, oriente-os a resolver a atividade em trios, para que troquem ideias e desenvolvam estratégias.

Página 159

27. Duas retas paralelas cortadas por uma transversal formam um par de ângulos alternos internos cujas medidas são $2 x mais 30 graus$ e $4 x menos 20 graus$ .

a) Qual é o valor de x?

b) Determine as medidas de cada ângulo.

Respostas: a) $25 graus$ ; b) $80 graus$ .

28. Na imagem, o triângulo $A B D$ é equilátero, e o segmento $A B$ é paralelo ao segmento $C E$ .

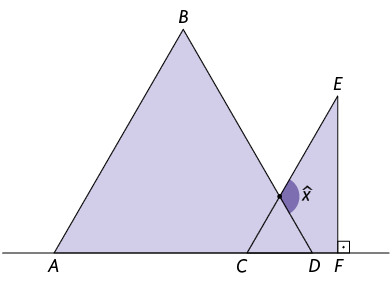
Ilustração de um triângulo A B D e ao lado há o triângulo C E F, ambos com suas bases sobre um mesmo segmento de reta, além disso o lado C E cruza o lado B D do triângulo anterior, formando um ângulo x, dentro do triângulo C E F, o qual também possui no vértice F um ângulo interno reto.

Qual é a medida $\hat{x}$ ?

a) $80 graus$

b) $90 graus$

c) $100 graus$

d) $110 graus$

e) $120 graus$

Resposta: Alternativa e.

29. Na imagem, as retas r e s são paralelas.

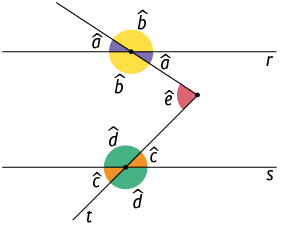
Ilustração de duas retas paralelas, r e s, cortadas cada uma por uma transversal, as quais se encontram entre as retas r e s, formando o ângulo e' no menor ângulo. A reta transversal que cruza a reta r forma o ângulo a, à esquerda e acima do cruzamento, a à direita e abaixo do cruzamento, b à direita e acima e b à esquerda e abaixo do cruzamento. A reta transversal que cruza a reta s forma o ângulo d, à esquerda e acima do cruzamento, d à direita e abaixo do cruzamento, c à direita e acima e c à esquerda e abaixo do cruzamento.

Podemos calcular a medida $\hat{e}$ sem usar o transferidor. Para isso, traçamos arbitrariamente uma reta v paralela à reta r e à reta s passando pelo vértice do ângulo. Assim, $\hat{e} = \hat{a} + \hat{c}$ .

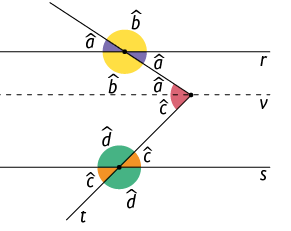
Ilustração de duas retas paralelas, r e s, cortadas cada uma por uma transversal, as quais se encontram na projeção de outra reta v paralela entre as retas r e s, formando o ângulo a' acima de v e ângulo c abaixo de v. A reta transversal que cruza a reta r forma o ângulo a, à esquerda e acima do cruzamento, ângulo a, à direita e abaixo do cruzamento, ângulo b à direita e acima e ângulo b à esquerda e abaixo do cruzamento. A reta transversal que cruza a reta s forma o ângulo d, à esquerda e acima do cruzamento, ângulo d à direita e abaixo do cruzamento, ângulo c à direita e acima e ângulo c à esquerda e abaixo do cruzamento.

Atenção!

A reta v é tracejada, pois representa uma reta imaginária.

Agora, determine, no caderno, a medida $\hat{x}$ para cada item.

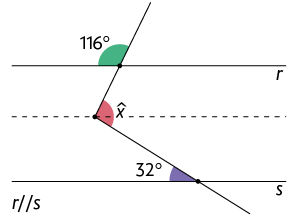
Ilustração de duas retas paralelas, r e s, cortadas cada uma por uma transversal, as quais se encontram na projeção de outra reta paralela entre as retas e r s, formando o ângulo x no menor ângulo. A reta transversal que cruza a reta r forma o ângulo de 116 graus, à esquerda e acima do cruzamento, enquanto a que cruza a reta s forma o ângulo de 32 graus, à esquerda e acima do cruzamento. Abaixo dessa representação, há as letras r, s e t com duas barras entre cada uma.

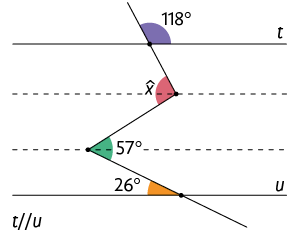
Ilustração de um esquema com duas retas horizontais paralelas, t, u e duas projeções de retas também paralelas a essas entre elas. Há três segmentos de retas transversais. A primeira está acima e cruza a reta t formando um ângulo 118 graus à direita da reta transversal e acima de t. A segunda transversal está abaixo, cruza com a transversal de cima, na projeção superior, formando um ângulo x no menor ângulo entre as retas. E a terceira transversal cruza com a segunda, na projeção inferior, formando um ângulo de 57 graus no menor ângulo entre as retas. Ela também encontra com a reta u, formando um ângulo de 26 graus acima de u e à esquerda da transversal. Abaixo dessa representação, há as letras t e u com duas barras entre elas.

Respostas: A. $medida do ângulo x igual a 96 graus$ ; B. $medida do ângulo x igual a 93 graus$ .

30. Amanda vai construir um portão de madeira semelhante à representação a seguir.

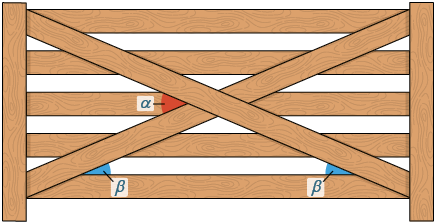
Ilustração de um portão de madeira com ripas na horizontal e duas se cruzando nas diagonais. Há a demarcação de um ângulo alfa entre o cruzamento das duas madeiras, à esquerda. Também há a demarcação que as madeiras das diagonais formam ângulo beta com linha horizontal.

Todas as madeiras horizontais do portão são paralelas. Sabendo que $β$ mede $23 graus$ , determine a medida de $α$ .

Resposta: $α$ mede $46 graus$ .

ORIENTAÇÕES AO PROFESSOR

Ao realizar a atividade 27, se necessário, auxilie os estudantes em relação aos procedimentos algébricos, visto que ela envolve conhecimentos da unidade temática Álgebra.

Na atividade 28, verifique se os estudantes sabem que um triângulo equilátero tem todos os ângulos internos congruentes. Depois, se necessário, peça a eles que construam o esquema apresentado a seguir em que $medida do ângulo A B D igual a 60 graus$ , pois é ângulo interno do triângulo equilátero.

Em seguida, aplicando as relações entre ângulos formados por retas paralelas cortadas por uma transversal, obtém-se a medida desejada.

Na atividade 29, enfatize que a reta tracejada é, por construção, paralela às demais. Desse modo, tem-se as relações entre ângulos formados por retas paralelas cortadas por uma transversal, possibilitando a obtenção da medida desconhecida.

Na atividade 30, sugira aos estudantes que representem o portão considerando as madeiras como retas. Além disso, caso julgue necessário, oriente-os a traçar uma reta imaginária paralela às horizontais passando pelo vértice do ângulo $α$ .

Página 160

31. A figura geométrica a seguir é formada por uma reta transversal que corta duas retas paralelas. Cada par de ângulos colaterais internos e de ângulos colaterais externos estão destacados com a mesma cor. Com base nessas informações, resolva o que se pede nos itens.

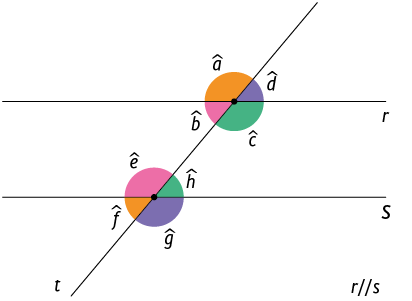
a) Calcule $\hat{b} + \hat{e}$ e $\hat{c} + \hat{h}$ .

b) Qual é a soma das medidas de cada par de ângulos colaterais internos?

c) Calcule $\hat{a} + \hat{f}$ e $\hat{d} + \hat{g}$ .

d) Qual é a soma das medidas de cada par de ângulos colaterais externos?

e) Os ângulos colaterais internos e colaterais externos são complementares ou suplementares?

Respostas: a) $180 graus$ ; $180 graus$ ; b) $180 graus$ ; c) $180 graus$ ; $180 graus$ ; d) $180 graus$ ; e) Suplementares.

32. Na imagem, as retas r e s são paralelas.

Ilustração de um triângulo com ângulos internos: a', b, 90 graus. Há uma reta s cruzando o lado entre os vértices com ângulos internos a e b, formando 120 graus à direita e acima desse cruzamento. Paralela à reta s, há a reta r, que passa pelo vértice que possui o ângulo interno a, formando 140 graus entre r e a continuidade do lado entre vértices com ângulos a e 90 graus.

Quais são as medidas $\hat{a}$ e $\hat{b}$ ?

Resposta: $medida do ângulo a igual a 20 graus$ e $medida do ângulo b igual a 70 graus$ .

33. As retas r e s na figura geométrica a seguir podem ser paralelas? Justifique sua resposta.

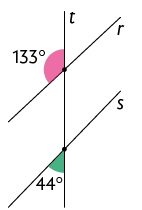
Ilustração de duas retas paralelas r e s cortadas por uma transversal t. O cruzamento com a reta r forma o ângulo: 133 graus à esquerda e acima do cruzamento. Do mesmo modo, o cruzamento com a reta s forma o ângulo: 44 graus à esquerda e abaixo do cruzamento.

Resposta: Não, pois os ângulos indicados não são suplementares.

34. A seguir, as retas j e k são paralelas cortadas pela transversal i.

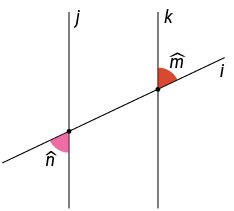
Ilustração de duas retas paralelas, j e k, cortadas por uma transversal, i. O cruzamento de i com j forma o ângulo: n à esquerda e abaixo do cruzamento. Do mesmo modo, o cruzamento de i com k forma o ângulo m à direita e acima do cruzamento.

Determine a afirmação verdadeira.

a) os ângulos de medidas $\hat{m}$ e $\hat{n}$ são complementares.

b) os ângulos de medidas $\hat{m}$ e $\hat{n}$ são suplementares.

c) os ângulos de medidas $\hat{m}$ e $\hat{n}$ são iguais.

d) os ângulos de medidas $\hat{m}$ e $\hat{n}$ são adjacentes.

Resposta: Alternativa c.

35. Na figura geométrica a seguir, as retas r e s são paralelas cortadas pelas transversais t e u.

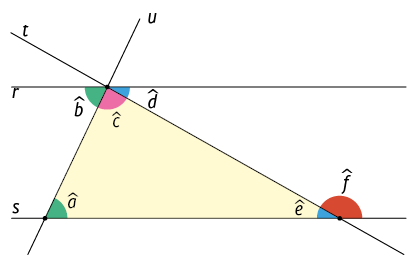
Ilustração de três retas, s, t, u que se cruzam formando um triângulo. No vértice formado pelo cruzamento das retas a e u, há o ângulo interno a. No vértice formado pelo cruzamento das retas s e t, há o ângulo interno e; e o ângulo externo e suplementar f. No vértice formado pelo cruzamento das retas u e t, há o ângulo interno c, há uma reta r paralela a reta s passando pelo vértice formando pelo cruzamento das retas u e t, nela há a representação dos ângulos externos e suplementares na reta r, ângulo b e, ângulo a.

Podemos afirmar que:

a) $\hat{f} = \hat{b} + \hat{c}$

b) $\hat{a} = \hat{e}$

c) $\hat{c} + \hat{d} = \hat{e} + \hat{f}$

d) $\hat{f} = \hat{d}$

Resposta: Alternativa a.

ORIENTAÇÕES AO PROFESSOR

A atividade 31 trabalha a ideia de ângulos colaterais. Se necessário, utilize a definição do termo "colateral" para enfatizar que os pares de ângulos colaterais estão em um mesmo lado da reta transversal. Explique aos estudantes que os termos "internos" e "externos" estão relacionados às retas paralelas. Ao final da atividade, sintetize para a turma que a soma das medidas de um par de ângulos colaterais é igual a $180 graus$ , ou seja, esses ângulos são suplementares.

Ao realizar a atividade 32, questione os estudantes a respeito da soma das medidas dos ângulos internos de um triângulo. Se julgar pertinente, organize-os em duplas para que solucionem o problema.

Na atividade 33, verifique se os estudantes percebem que se as retas fossem paralelas, os ângulos em destaque seriam colaterais externos, ou seja, a soma de suas medidas seria igual a $180 graus$ . Aproveite essa atividade para desenvolver com os estudantes a ideia de redução ao absurdo, quando se parte de uma premissa e se chega a uma contradição.

Na atividade 34, alguns estudantes podem argumentar que os ângulos são iguais levando em consideração apenas a representação geométrica. Se isso acontecer, explique a eles que a figura auxilia na compreensão da situação, mas é necessário usar os conceitos matemáticos para realizar as análises necessárias.

Na atividade 35, sugira aos estudantes que, por meio de desenhos, estabeleçam relações entre os pares de ângulos que estão sendo comparados em cada item, utilizando uma das retas transversais indicadas. Para ampliar o desenvolvimento com esta atividade, peça aos estudantes que justifiquem o porquê de os demais itens serem falsos.

Página 161

Polígonos

Você provavelmente já estudou polígonos, seus elementos e algumas de suas características. Neste momento, vamos estudar também os seus ângulos internos.

Considere algumas linhas em um plano. Tais linhas podem ser abertas ou fechadas, cruzando-se ou não.

Classificação para linhas em um plano
Linhas	Que se cruzam (não simples)	Que não se cruzam (simples)
Abertas
Fechadas

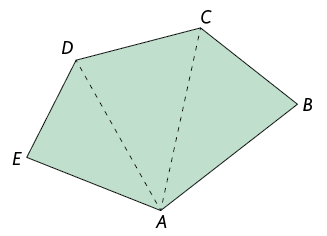
Uma linha do plano fechada, formada apenas por segmentos de reta que não se cruzam, de maneira que dois segmentos consecutivos não são parte de uma mesma reta, é chamada polígono. Cada segmento de reta é um lado do polígono.

A região interna a um polígono é a região plana delimitada por ele. Um polígono e sua região interna determinam uma região poligonal. No entanto, exceto quando dito o contrário, também vamos usar a palavra polígono para nos referir à região poligonal correspondente, ou seja, à figura geométrica plana formada por seus lados (contorno) e sua região interna.

A seguir, alguns elementos de um polígono foram destacados.

Ilustração de um quadrilátero A B C D, com a demarcação de vértice, lado e ângulo interno.

Vértices: A, B, C e D.
Lados: $\overline{A B}, \overline{B C}, \overline{C D}$ e $\overline{A D}$ .
Ângulos internos: $\hat{A}, \hat{B}, \hat{C}$ e $\hat{D}$ .

Página 162

Podemos nomear um polígono conforme a quantidade de lados que ele tem. Exemplos:

Polígonos
Quantidade de lados do polígono	Nome do polígono
3	triângulo
4	quadrilátero
5	pentágono
6	hexágono
7	heptágono
8	octógono
9	eneágono
10	decágono
11	undecágono
12	dodecágono

Ilustração de um polígono de 4 lados com seus ângulos internos demarcados. — Quadrilátero.

Ilustração de um polígono de 5 lados com seus ângulos internos demarcados. — Pentágono.

Ilustração de um polígono de 6 lados com seus ângulos internos demarcados. — Hexágono.

Ilustração de um polígono de 7 lados com seus ângulos internos demarcados. — Heptágono.

Ilustração de um polígono de 8 lados com seus ângulos internos demarcados. — Octógono.

Ilustração de um polígono de 9 lados com seus ângulos internos demarcados. — Eneágono.

Os polígonos que têm todos os lados com a mesma medida de comprimento e todos os ângulos internos com a mesma medida são denominados polígonos regulares.

Os polígonos também podem ser classificados em convexos ou não convexos.

Um polígono é convexo quando qualquer reta que passa por seu interior corta seus lados em somente dois pontos. Analise dois exemplos.

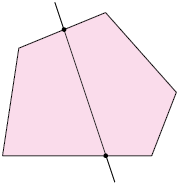
Ilustração de um polígono de 5 lados com uma reta o cruzando e cortando seus lados em dois pontos.

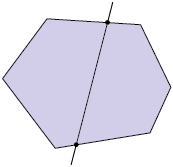
Ilustração de um polígono de 6 lados com uma reta o cruzando e cortando seus lados em dois pontos.

Um polígono é não convexo quando existe pelo menos uma reta que passa por seu interior cortando seus lados em mais de dois pontos. Analise dois exemplos.

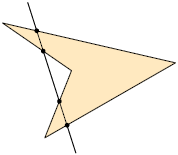
Ilustração de um polígono de 4 lados com uma reta que cruza seus 4 lados em 4 pontos.

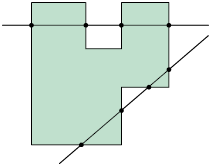
Ilustração de um polígono de 10 lados com duas reta, uma cruzando 4 de seus lados em 4 pontos e a outra também cruzando 4 de seus lados em 4 pontos.

ORIENTAÇÕES AO PROFESSOR

Atividade a mais

Copie as frases no caderno substituindo as letras maiúsculas em destaque por palavras ou números adequados.

a) O pentágono tem A lados, B vértices e C ângulos internos.

b) O D tem 7 lados, E vértices e F ângulos internos.

c) O G tem H lados, 10 vértices e I ângulos internos.

Resoluções e comentários

a) Neste item, espera-se que os estudantes associem o prefixo "penta" à quantidade de lados, de vértices e de ângulos internos do polígono. A frase correta é: O pentágono tem 5 lados, 5 vértices e 5 ângulos internos.

b) Neste item, espera-se que os estudantes identifiquem que as informações referem-se ao polígono de 7 lados, ou seja, ao heptágono. A frase correta é:

O heptágono tem 7 lados, 7 vértices e 7 ângulos internos.

c) Neste item, espera-se que os estudantes identifiquem que as informações referem-se ao polígono de 10 lados, ou seja, ao decágono. A frase correta é:

O decágono tem 10 lados, 10 vértices e 10 ângulos internos.

Página 163

Atividades

Faça as atividades no caderno.

36. Classifique os polígonos a seguir conforme a quantidade de lados.

Ilustração de um polígono irregular de 5 lados.

Ilustração de um polígono irregular de 7 lados.

Ilustração de um polígono irregular de 4 lados.

Ilustração de um polígono irregular de 6 lados.

Respostas: A. Pentágono; B. Heptágono; C. Quadrilátero; D. Octógono; E. Triângulo; F. Hexágono.

37. Muitos artistas utilizam figuras geométricas planas como fonte de inspiração para compor suas obras. Entre eles, podemos citar o holandês Piet Mondrian (1872-1944) e o brasileiro Luiz Sacilotto (1924-2003), um dos principais artistas do abstracionismo^✚ no Brasil.

Analise a seguir duas obras desses artistas. Depois, identifique polígonos em cada uma delas e classifique-os conforme a quantidade de lados.

Abstracionismo:: ou arte abstrata, é conhecido por não se preocupar em representar seres ou objetos com formatos reais. No abstracionismo geométrico, comumente usam-se figuras geométricas, linhas e cores para compor a obra.^↰

Fotografia de uma pintura com tons de vermelho, composta por polígonos de 3, 4, 5 e 6 lados. — Concreção 8601, de Luiz Sacilotto. Têmpera vinílica sobre tela, $90 centímetros por 90 centímetros$ , 1986.

Fotografia de uma pintura com polígonos de 4 lados, de vários tamanhos, branco, azul, vermelho e amarelo. — Composição II com vermelho, azul e amarelo, de Piet Mondrian. Óleo sobre tela, $46 centímetros por 46 centímetros$ , 1929.

Respostas: A. Triângulos, quadriláteros, pentágonos e hexágonos; B. Quadriláteros.

38. No caderno, nomeie os lados, vértices e ângulos internos dos polígonos a seguir.

Ilustração de um pentágono irregular de vértices, em sentido horário, B, A, E, D, C e com seus ângulos internos demarcados.

Resposta: Lados: $\overline{A B}, \overline{B C}, \overline{C D}, \overline{D E}$ e $\overline{A E}$ ; vértices: $A$ , $B$ , $C$ , $D$ e $E$ ; ângulos internos: $\hat{A}, \hat{B}, \hat{C}, \hat{D}$ e $\hat{E}$ .

Ilustração de um polígono irregular com 7 lados de vértices, em sentido horário, G, F, K, J, I, H e com seus ângulos internos demarcados.

Resposta: Lados: $\overline{F G}, \overline{G H}, \overline{H I}, \overline{I J}, \overline{J K}$ e $\overline{K F}$ ; vértices: $F$ , $G$ , $H$ , $I$ , $J$ e $K$ ; ângulos internos: $\hat{F}, \hat{G}, \hat{H}, \hat{I}, \hat{J}$ e $\hat{K}$ .

Ilustração de um quadrilátero irregular de vértices, em sentido horário, G, F, K, J, I, H e com seus ângulos internos demarcados.

Resposta: Lados: $\overline{L M}, \overline{M N}, \overline{N O}$ e $\overline{L O}$ ; vértices: $L$ , $M$ , $N$ , e $O$ ; ângulos internos: $\hat{L}, \hat{M}, \hat{N}$ e $\hat{O}$ .

ORIENTAÇÕES AO PROFESSOR

Ao realizar a atividade 36, chame a atenção dos estudantes para a relação entre o prefixo do nome de cada polígono e a sua quantidade de lados e de ângulos internos.

Na atividade 37, alguns estudantes podem incluir quadrados e retângulos na classificação. Caso isso aconteça, explique a eles que os quadriláteros são uma maneira mais ampla de classificar os polígonos que têm quatro lados. Utilize essa atividade também para desenvolver o tema contemporâneo transversal Diversidade cultural, abordando as diferentes culturas expressas por meio da arte. Para um estudo mais detalhado sobre as obras e os artistas apresentados, converse com o professor do componente curricular de Arte e, juntos, promovam um debate com a turma, evidenciando, por exemplo, as características de cada uma dessas obras. Com isso, abordam-se aspectos da Competência geral 3 e da Competência específica de Matemática 3.

Metodologias ativas

Para desenvolver a atividade 37, avalie a possibilidade de utilizar a metodologia ativa Caminhada na galeria. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Busca-se, com a atividade 38, evidenciar os elementos de um polígono e nomeá-los. Se necessário, lembre os estudantes de que já foi estudado como nomear ângulos em tópicos anteriores. Complemente essa atividade perguntando a eles quais polígonos apresentados não são convexos. Em caso de dificuldade, reproduza a figura B na lousa e mostre aos estudantes porque esse polígono não é convexo.

Página 164

39. Classifique os polígonos em convexos ou não convexos.

Ilustração de um polígono irregular de 7 lados em que todos os seus ângulos internos são maiores que 90 graus.

Ilustração de um polígono irregular de 8 lados em que alguns de seus ângulos internos medem 90 graus e outros medem mais que 90 graus.

Ilustração de um polígono irregular de 11 lados em que 5 lados do polígono estão dispostos em zig-zag o mesmo do outro lado com outros 5 lados, e um lado fecha a base do polígono.

Ilustração de um polígono de 4 lados, semelhante a uma trapézio retângulo.

Resposta: Convexos: polígonos A e D; Não convexos: polígonos B e C.

40. Qual é a menor quantidade de lados de um polígono?

Resposta: 3 lados.

41. O polígono a seguir foi dividido em outros dois.

Polígono original

Ilustração de um polígono de 7 lados com uma linha tracejada o cortando simetricamente ao meio.

Polígono dividido

Ilustração de dois polígonos de 5 lados, iguais, mas espelhados, lado a lado.

a) Classifique o polígono original, antes de ser dividido, de acordo com a quantidade de lados.

b) Agora, classifique os polígonos obtidos após a divisão de acordo com a quantidade de lados.

Respostas: a) Heptágono; b) Pentágonos.

42. Alguns polígonos foram desenhados em uma malha formada por triângulos regulares.

Ilustração de uma malha triangular com 5 polígonos pintados. O polígono A é um hexágono com lados com diferentes medidas; o polígono B é um losango com todos os lados iguais e ângulos internos com medidas diferentes; o polígono C é um triângulo com todos os lados e ângulos internos com medidas iguais; o polígono D é um paralelogramo com lados com diferentes medidas; e o polígono E é um hexágono com todos os lados e ângulos internos com medidas iguais.

Quais desses polígonos são regulares?

Resposta: Polígonos C e E.

43. Quais polígonos formam as faces de:

a) um prisma de base triangular?

b) uma pirâmide de base quadrada?

Respostas: a) Triângulos e quadriláteros; b) Triângulos e quadrilátero.

44. Classifique, em relação à quantidade de lados, os polígonos que formam os mosaicos a seguir.

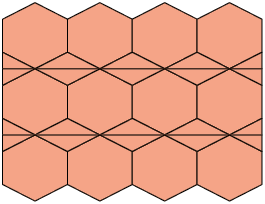
Ilustração de um mosaico formado por polígonos de 6 lados e de por polígonos de 3 lados.

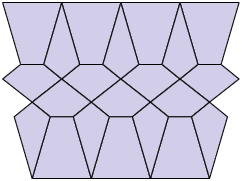
Ilustração de um mosaico formado por polígonos de 4 lados e por polígonos de 5 lados.

Respostas: A. Hexágonos e triângulos; B. Quadriláteros e pentágonos.

45. Analise o prisma A e a pirâmide B.

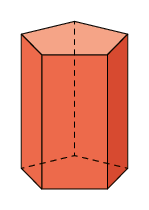
Ilustração de um prisma de base pentagonal.

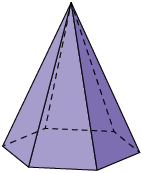
Ilustração de um prisma de base hexagonal.

Com base nas figuras que você analisou, indique a afirmação verdadeira.

a) As faces laterais do prisma A são pentágonos, e as bases, triângulos.

b) As duas figuras geométricas espaciais têm faces que são pentágonos.

c) Nenhuma das figuras geométricas espaciais tem faces hexagonais.

d) Podemos nomear os polígonos que formam as faces e a base da pirâmide B de triângulos e hexágono, respectivamente.

e) As faces e as bases do prisma A são polígonos com a mesma quantidade de lados.

Resposta: Alternativa d.

ORIENTAÇÕES AO PROFESSOR

Na atividade 39, se necessário, sugira aos estudantes que desenhem as figuras no caderno e tracem algumas retas cortando o contorno da figura. Em seguida, eles devem analisar se é possível traçar alguma reta que corte o contorno do polígono em mais de dois pontos.

Na atividade 40, espera-se que os estudantes percebam que a menor quantidade de lados para obter um polígono é 3. Se necessário, pergunte a eles se é possível desenhar um polígono com 1 lado, com 2 lados e com 3 lados.

Para complementar a atividade 41, organize os estudantes em grupos, confeccione a representação de alguns polígonos em folhas de papel e distribua para a turma. Feito isso, solicite aos estudantes que nomeiem os polígonos de acordo com a quantidade de lados. Em seguida, com uma tesoura de pontas arredondadas, peça a eles que dividam esse polígono em outros polígonos. Por fim, oriente-os a trocar os polígonos obtidos com os outros grupos para que sejam nomeados de acordo com a quantidade de lados.

Durante as divisões das representações, alerte os estudantes para os eventuais riscos, de modo a garantir a integridade física deles, dos professores e das demais pessoas envolvidas no processo educacional.

Na atividade 42, é possível que alguns estudantes classifiquem o polígono B como sendo regular. Se isso acontecer, peça a eles que analisem os ângulos desse polígono. Ao final da atividade, explique a eles que, em um polígono regular, os lados são congruentes e os ângulos internos são congruentes.

A atividade 43 envolve maior nível de abstração, visto que exige do estudante a mobilização de características de prismas e pirâmides sem o suporte de representações. Com isso, se julgar oportuno, leve para a sala de aula alguns objetos que lembram essas figuras geométricas espaciais para que, em caso de dificuldade, eles possam manipulá-las.

Ao realizar a atividade 44, se julgar necessário, faça uma análise conjunta das imagens. Em seguida, com os estudantes, represente na lousa os polígonos que formam cada um dos mosaicos. Por fim, deixe que eles os classifiquem.

Em caso de dificuldade na atividade 45, organize os estudantes em grupos para que analisem e conversem a respeito das afirmações expostas. Além disso, solicite a eles que justifiquem o motivo das afirmações serem falsas. Por fim, organize um bate-papo para que as conclusões sejam expostas.

Página 165

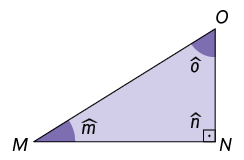
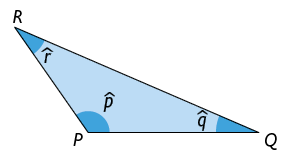
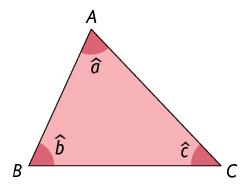
Triângulos

Você já deve ter estudado anteriormente que o triângulo é o polígono com a menor quantidade de lados. Agora, vamos conhecer outros elementos e propriedades a respeito dele.

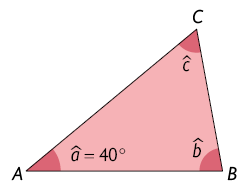
Triângulo é um polígono que tem 3 lados e, consequentemente, 3 vértices, 3 ângulos internos e 3 ângulos externos.

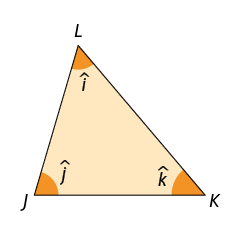
Na imagem, está representado um triângulo e alguns de seus elementos.

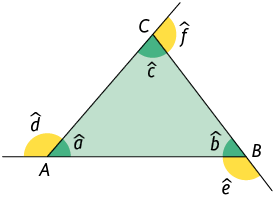
Ilustração de um triângulo A B C com ângulos internos a minúsculo, b minúsculo e c minúsculo. O ângulo externo e suplementar de a minúsculo é d minúsculo. O ângulo externo e suplementar de c minúsculo é f minúsculo. O ângulo externo e suplementar de b minúsculo é e minúsculo.

Nome: triângulo $A B C$ ou $△ A B C$ .
Lados: $\overline{A B}$ , $\overline{B C}$ e $\overline{A C}$ .
Vértices: $A$ , $B$ e $C$ .
Medidas dos ângulos internos: $\hat{a}$ , $\hat{b}$ e $\hat{c}$ .
Medidas dos ângulos externos: $\hat{d}$ , $\hat{e}$ e $\hat{f}$ .

Nesse triângulo, o lado $\overline{B C}$ é chamado lado oposto ao ângulo de medida $\hat{a}$ e, do mesmo modo, o ângulo de medida $\hat{a}$ é chamado ângulo oposto ao lado $\overline{B C}$ .

Os triângulos podem ser classificados conforme as medidas dos comprimentos dos lados e a medida dos seus ângulos internos.

Classificação de triângulos de acordo com as medidas dos lados.

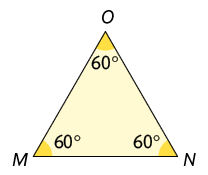
Equilátero

Triângulo que tem todos os lados com medidas de comprimento iguais.

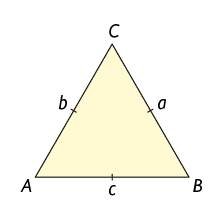
Ilustração de um triângulo A B C. As medidas de comprimentos dos lados são: lado A B é c minúsculo; lado B C é a minúsculo; e lado A C é b minúsculo. Há um risquinho cortando cada lado do triângulo indicando que todos possuem a mesma medida.

$a = b = c$ .

Isósceles

Triângulo que tem pelo menos 2 lados com medidas de comprimento iguais.

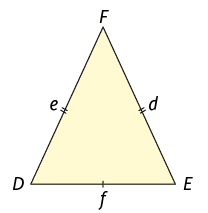
Ilustração de um triângulo D E F. As medidas de comprimentos dos lados são: lado D E é f minúsculo; lado E F é d minúsculo; e lado D F é e minúsculo. Há dois risquinhos cortando os lados D F e E F indicando que possuem a mesma medida. Há um risquinho cortando o lado D E.

$e = d$ .

Escaleno

Triângulo que tem os 3 lados com medidas de comprimento diferentes.

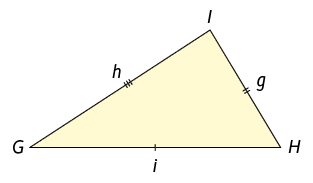
Ilustração de um triângulo G H I. As medidas de comprimentos dos lados são: lado G H é i minúsculo; lado H I é g minúsculo; e lado G I é h minúsculo. Há dois risquinhos cortando os lados G I e H I indicando que possuem a mesma medida. Há um risquinho cortando o lado G H.

$i \neq g$ , $g \neq h$ e $i \neq h$ .

ORIENTAÇÕES AO PROFESSOR

Sugestão de avaliação

Para avaliar como os estudantes estão lidando com os conteúdos estudados até o momento, faça na lousa um quadrilátero convexo não regular, um pentágono não convexo e um hexágono convexo não regular. Feito isso, peça a eles que:

a) classifiquem os polígonos de acordo com a sua quantidade de lados;

b) escrevam o nome do polígono não convexo.

Resoluções e comentários

a) Ao classificar os polígonos de acordo com a quantidade de lados, temos: quadrilátero, pentágono e hexágono.

b) Verifique se eles reconhecem quando um polígono é não convexo. Se necessário, na lousa, trace uma reta sobre o pentágono, de modo que ela corte o contorno desse polígono em mais de dois pontos.

Informações sobre avaliações podem ser encontradas no tópico Avaliação, nas orientações gerais deste manual.

Antes de apresentar o conteúdo desta página, verifique o conhecimento dos estudantes relacionados aos lados e aos ângulos de triângulos. Permita a eles que compartilhem com a turma suas explicações, tendo a oportunidade de resgatar o conhecimento prévio sobre o assunto e de tornar o estudo mais significativo.

Explique aos estudantes que o triângulo equilátero é também isósceles, pois tem 2 lados com mesma medida de comprimento.

Página 166

Classificação de triângulos conforme as medidas dos ângulos internos.

Acutângulo

Triângulo que tem os 3 ângulos internos agudos.

Ilustração de um triângulo de vértices J L K, com seus 3 ângulos internos demarcados: j minúsculo, i minúsculo, k minúsculo.

$0 grau menor do que medida do ângulo j menor do que 90 graus$ , $0 grau menor do que medida do ângulo k menor do que 90 graus$ e $0 grau menor do que medida do ângulo i menor do que 90 graus$

Retângulo

Triângulo que tem 1 ângulo interno reto.

$medida do ângulo n igual a 90 graus$

Obtusângulo

Triângulo que tem 1 ângulo interno obtuso.

Ilustração de um triângulo de vértices R Q P, com seus 3 ângulos internos demarcados: r minúsculo, q minúsculo, p minúsculo.

$90 graus menor do que medida do ângulo p menor do que 180 graus$

Analise, agora, algumas construções com palitos de sorvete e tachinhas.

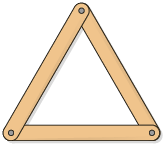
Ilustração de 3 palitos de sorvete ligados um ao outro por suas extremidades, com tachinhas, formando um triângulo.

Ilustração de 4 palitos de sorvete ligados um ao outro por suas extremidades, com tachinhas, formando um quadrado.

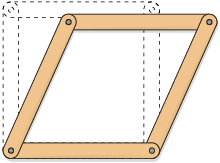
Ilustração de 4 palitos de sorvete ligados um ao outro por suas extremidades, com tachinhas, formando um paralelogramo com ângulos internos diferentes de 90 graus. Ao fundo há a projeção desses palitos formando um quadrilátero com ângulos internos de 90 graus.

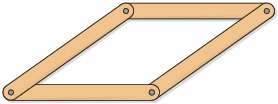
Ilustração de 4 palitos de sorvete ligados um ao outro por suas extremidades, com tachinhas, formando um losango.

A construção com formato triangular é a única que não permite ser deformada. Essa característica é conhecida como rigidez do triângulo.

Com os demais formatos, é possível obter outras construções mantendo a quantidade e as medidas do comprimento dos lados e variando as medidas dos ângulos internos.

Atenção!

A característica de rigidez do triângulo é motivo pelo qual as estruturas triangulares são usadas, por exemplo, em objetos do dia a dia e em construções.

Imagens não proporcionais entre si.

Fotografia de um triângulo de sinalização em uma via e ao fundo um carro parado. — Triângulo de sinalização.

Fotografia da vista de baixo de um telhado, com sua estrutura de madeira possuindo formato triangular. — Estrutura de madeira de uma cobertura.

ORIENTAÇÕES AO PROFESSOR

Se necessário, lembre os estudantes de que um ângulo é agudo quando sua medida é maior do que $0 grau$ e menor do que $90 graus$ ; é reto quando sua medida é $90 graus$ ; é obtuso quando sua medida é maior do que $90 graus$ e menor do que $180 graus$ .

Para ilustrar a rigidez dos triângulos apresentada nesta página, providencie palitos de sorvete e tachinhas e leve esses materiais para a sala de aula. Organize os estudantes em grupos e peça a eles que construam representações de triângulos e de quadriláteros. Em seguida, eles devem tentar deformar a construção em formato de triângulo e a construção em formato de quadrilátero para verificar a rigidez dos objetos representados. Desse modo, desenvolve-se aspectos da habilidade EF07MA25.

Página 167

Imagine três segmentos de reta com as suas respectivas medidas de comprimento. Será que podemos construir um triângulo usando as medidas de comprimento desses segmentos como medidas dos lados? A seguir, estudaremos a condição de existência dos triângulos para descobrir a resposta a essa pergunta.

Nas imagens, estão apresentados dois exemplos de construções impossíveis.

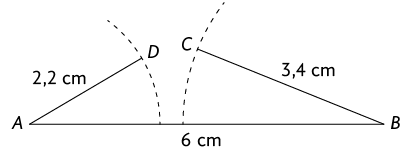
Ilustração de um segmento de reta, com seus pontos das extremidades A, B e sua medida comprimento indicada de 6 centímetros. Cada ponto A e B é centro de um arco pontilhado traçado cruzando o próprio segmento. O arco com centro em A possui um segmento de reta partindo de A ate um ponto D no arco, esse segmento mede 2,2 centímetros. O arco com centro em A possui um segmento de reta partindo de B até um ponto C no arco, esse segmento mede 3,4 centímetros. A figura final lembra um triângulo sem um de seus vértices.

$6 maior do que 2 vírgula 2 mais 3 vírgula 4. está indicado que 2 vírgula 2 mais 3 vírgula 4 corresponde a 5 vírgula 6$

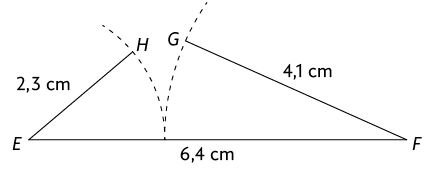
Ilustração de um segmento de reta, com seus pontos das extremidades E, F e sua medida comprimento indicada de 6,4 centímetros. Cada ponto E e F é centro de um arco pontilhado traçado cruzando o próprio segmento. O arco com centro em E possui um segmento de reta partindo de E ate um ponto H no arco, esse segmento mede 2,3 centímetros. O arco com centro em F possui um segmento de reta partindo de F até um ponto G no arco, esse segmento mede 4,1 centímetros. A figura final lembra um triângulo sem um de seus vértices.

$6 vírgula 4 igual a 2 vírgula 3 mais 4 vírgula 1 está indicado que 2 vírgula 3 mais 4 vírgula 1 corresponde a 6 vírgula 4$

Agora, a imagem mostra o exemplo de uma construção possível de triângulo.

Ilustração de um triângulo A B C. As medidas de comprimentos dos lados são: lado A B é 6,9 centímetros; lado B C é 5,3 centímetros; e lado A C é 3,7 centímetros.

$6 vírgula 9 menor do que 3 vírgula 7 mais 5 vírgula 3 está indicado que 3 vírgula 7 mais 5 vírgula 3 corresponde a 9$
$3 vírgula 7 menor do que 6 vírgula 9 mais 5 vírgula 3. está indicado que 6 vírgula 9 mais 5 vírgula 3 corresponde a 12 vírgula 2$
$5 vírgula 3 menor do que 6 vírgula 9 mais 3 vírgula 7. está indicado que 6 vírgula 9 mais 3 vírgula 7 corresponde a 10 vírgula 6$

Para a construção de um triângulo ser possível, a medida do comprimento de cada lado dele precisa ser menor do que a soma das medidas do comprimento dos outros dois. Assim, se considerarmos três segmentos de reta tais que um tem medida de comprimento maior do que a soma da medida do comprimento dos outros dois, não podemos formar um triângulo com essas medidas de comprimento de segmentos de reta.

Ilustração de um triângulo A B C. As medidas de comprimentos dos lados são: lado A B é c minúsculo; lado B C é a minúsculo; e lado A C é b minúsculo.

Em termos gerais, para ser possível a construção de um triângulo com seus lados medindo a, b e c de comprimento, a condição de existência precisa ser satisfeita.

$a < b + c$
$b < a + c$
$c < a + b$

Ou seja, se essas sentenças são verdadeiras, o triângulo pode ser construído com essas medidas.

Questão 6. Escreva no seu caderno um número representando uma medida de comprimento em centímetros. Depois, junte-se a dois colegas, reúnam a medida de cada um formando três medidas e, com uma calculadora, verifique se é possível construir um triângulo com elas.

Resposta pessoal.

ORIENTAÇÕES AO PROFESSOR

Na questão 6, é proposta uma questão para trabalhar a desigualdade triangular. Avalie a possibilidade de levar para a sala de aula régua, canudinhos e tesouras com pontas arredondadas, de modo que os estudantes possam verificar empiricamente essa propriedade, com base nas medidas que eles indicarem.

Aproveite que a questão 6 deve ser feita em grupo e explique aos estudantes a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Com isso, abordam-se aspectos das Competências gerais 1, 4 e 9 e da Competência específica de Matemática 8. Se julgar pertinente, converse com eles sobre o combate aos diversos tipos de violência, especialmente o bullying. Para obter informações a respeito desse assunto no tópico Cultura de paz e combate ao bullying, consulte as orientações gerais deste manual.

Página 168

Instrumentos e softwares

Construindo triângulo com régua e compasso

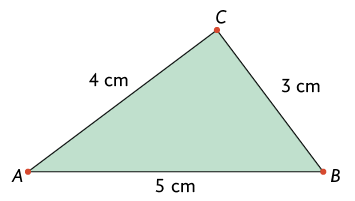
Com as orientações do professor e o passo a passo a seguir, construa um triângulo cujas medidas dos comprimentos dos lados são $5 centímetros$ , $4 centímetros$ e $3 centímetros$ .

1º. Trace um segmento de reta $A B$ com uma das medidas de comprimento, nesse caso, $5 centímetros$ .

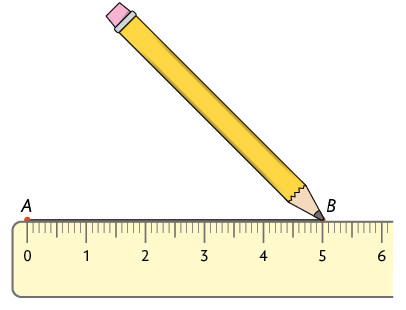
Ilustração de um lápis traçando uma reta que passa nos pontos A e B, com o auxílio de uma régua. O ponto A está no marco 0 e o ponto B está no marco 5.

2º. Com a ponta-seca do compasso em $A$ e abertura de $4 centímetros$ , trace um arco de circunferência.

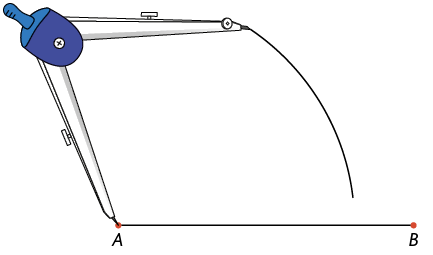
Ilustração de um compasso traçando um arco, com sua ponta seca no ponto A do segmento de reta que vai do ponto A ao ponto B.

3º. Com a ponta-seca do compasso em $B$ e abertura de $3 centímetros$ , trace um arco de circunferência. O ponto em que os arcos se cruzam é o vértice $C$ do triângulo.

Ilustração de um compasso traçando um arco, com sua ponta seca no ponto B do segmento de reta que vai de um ponto A ao ponto B. O arco traçado cruza com outro já desenhado.

4º. Com a régua, trace os segmentos $B C$ e $A C$ e obtenha o triângulo $A B C$ . Por fim, apague as marcas dos arcos.

Ilustração de um triângulo A B C. As medidas de comprimentos dos lados são: lado A B é 5 centímetros; lado B C é 3 centímetros; e lado A C é 4 centímetros.

ORIENTAÇÕES AO PROFESSOR

Se julgar necessário, explique aos estudantes que, para obter uma abertura de $4 centímetros$ no compasso, é necessário posicionar, na régua, uma das pontas na marca do zero, e a outra na marca do $4 centímetros$ .

Leve uma régua e um compasso para a sala de aula e faça na lousa diferentes triângulos.

Esta seção contempla aspectos da habilidade EF07MA24, ao trabalhar a construção de triângulos utilizando régua e compasso.

Metodologias ativas

Ao desenvolver a seção Instrumentos e softwares, avalie a possibilidade de utilizar a metodologia ativa Tiras de classificação. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Ao trabalhar com essa seção, alerte os estudantes para os eventuais riscos, de modo a garantir a integridade física de todos os envolvidos no processo educacional.

Página 169

Atividades

Faça as atividades no caderno.

46. Nomeie os vértices, as medidas dos ângulos internos e as dos ângulos externos de cada triângulo.

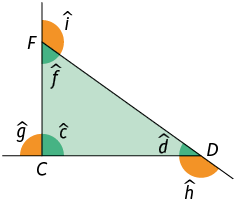
Ilustração de um triângulo C D F com ângulos internos c minúsculo, d minúsculo, f minúsculo. O ângulo externo e suplementar de c minúsculo é g minúsculo. O ângulo externo e suplementar de d minúsculo é h minúsculo. O ângulo externo e suplementar de f minúsculo é i minúsculo.

Ilustração de um triângulo M N O com ângulos internos m minúsculo, n minúsculo, o minúsculo. O ângulo externo e suplementar de m minúsculo é p minúsculo. O ângulo externo e suplementar de n minúsculo é q minúsculo. O ângulo externo e suplementar de o minúsculo é r minúsculo.

Respostas: A. Vértices: C, D, F; medida dos ângulos internos: $\hat{c}$ , $\hat{d}$ , $\hat{f}$ ; medida dos ângulos externos: $\hat{g}$ , $\hat{h}$ , $\hat{i}$ . B. Vértices: M, N, O; medida dos ângulos internos: $\hat{m}$ , $\hat{n}$ , $\hat{o}$ . medida dos ângulos externos: $\hat{p}$ , $\hat{q}$ , $\hat{r}$ .

47. Copie no caderno cada item substituindo o $█$ pela palavra adequada.

a) Em um triângulo, o ponto comum de cada 2 lados é chamado $█$ .

b) O triângulo é um polígono formado por $█$ segmentos de reta.

c) Qualquer polígono de 3 lados é chamado $█$ .

d) Um triângulo tem $█$ vértices.

Respostas: a) vértice; b) três; c) triângulo; d) três.

48. Junte-se a um colega e respondam às seguintes questões.

a) Quando um triângulo é chamado isósceles?

Resposta: Quando tem pelo menos dois lados com medidas iguais.

b) Quais são as medidas de comprimento dos outros dois lados de um triângulo equilátero, sabendo que um deles mede $5 centímetros$ de comprimento?

Resposta: $5 centímetros$ .

c) A soma das medidas dos comprimentos dos lados de um triângulo escaleno é $15 centímetros$ . Quais são as possíveis medidas de comprimento inteiras para os lados dele?

Sugestão de resposta: $6 centímetros$ , $5 centímetros$ e $4 centímetros$ .

d) Como é classificado, quanto às medidas dos lados, um triângulo com os lados medindo $3 centímetros$ , $5 centímetros$ e $5 centímetros$ de comprimento?

Resposta: Isósceles.

49. Classifique os triângulos representados a seguir conforme a medida do comprimento dos seus lados.

Ilustração de um triângulo G H I. As medidas de comprimentos dos lados são: lado G H é 4 metros; lado H I é 5,8 metros; e lado G I é 4 metros.

Ilustração de um triângulo A B C. As medidas de comprimentos dos lados são: lado A B é 3 metros; lado B C é 3 metros; e lado A C é 4 metros.

Ilustração de um triângulo M N O. As medidas de comprimentos dos lados são: lado M N é 3 metros; lado N O é 3 metros; e lado O M é 3 metros.

Ilustração de um triângulo D E F. As medidas de comprimentos dos lados são: lado D E é 6 metros; lado E F é 2,8 metros; e lado D F é 8,3 metros..

Respostas: A. Isósceles; B. Isósceles; C. Equilátero; D. Escaleno.

50. Classifique cada triângulo a seguir em acutângulo, retângulo ou obtusângulo.

Ilustração de um triângulo M N O com a indicação de todos os seus ângulos internos de 60 graus.

Ilustração de um triângulo G H I com as seguintes medidas de seus ângulos internos: 45 graus; 43 graus; e 92 graus.

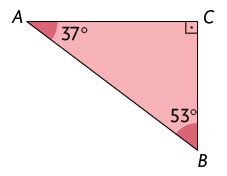
Ilustração de um triângulo A B C com as seguintes medidas de seus ângulos internos: 37 graus; 53 graus; e 90 graus.

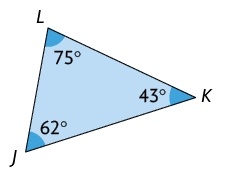
Ilustração de um triângulo J K L com as seguintes medidas de seus ângulos internos: 62 graus; 43 graus; e 75 graus.

Respostas: A. Acutângulo; B. Obtusângulo; C. Retângulo; D. Acutângulo.

ORIENTAÇÕES AO PROFESSOR

Caso os estudantes apresentem dificuldades na atividade 46, retome o trabalho com o tópico Triângulos, em especial com os elementos desta figura geométrica.

Após os estudantes realizarem as atividades 47, 48 e 49, organize um bate-papo buscando explorar as características e as propriedades de um triângulo e suas classificações quanto às medidas dos comprimentos de seus lados. Permita-lhes compartilhar suas opiniões com a turma, intervindo quando necessário.

Aproveite que a atividade 48 foi proposta para ser feita em duplas e enfatize a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Com isso, abordam-se aspectos das Competências gerais 1, 4 e 9 e da Competência específica de Matemática 8. Se considerar pertinente, converse com eles sobre o combate aos diversos tipos de violência, especialmente o bullying. Para obter informações a respeito desse assunto no tópico Cultura de paz e combate ao bullying, consulte as orientações gerais deste manual.

Caso os estudantes apresentem dificuldades na atividade 50, com questionamentos, lembre-os de que um triângulo é retângulo quando tem um ângulo reto, obtusângulo quando tem um ângulo obtuso e acutângulo quando tem os 3 ângulos internos agudos.

Página 170

51. Em seu caderno, escreva um algoritmo apresentando o passo a passo da construção de um triângulo qualquer, dada a medida de comprimento dos três lados, usando os mesmos procedimentos indicados na seção Instrumentos e softwares da página 168. Por último, represente-o por meio de um fluxograma.

Resposta na seção Respostas e na seção Resoluções.

52. Usando os mesmos passos da seção Instrumentos e softwares da página 168, construa um triângulo cujos comprimentos dos lados medem $7 centímetros$ , $6 centímetros$ e $5 centímetros$ . Em seguida, organize em um fluxograma os procedimentos que você realizou para fazer essa construção.

Agora, meça com um transferidor os ângulos internos do triângulo construído e verifique se ele é acutângulo, retângulo ou obtusângulo.

Resposta na seção Respostas e na seção Resoluções.

Versão adaptada acessível

52. Junte-se a um colega e, usando os mesmos passos da seção Instrumentos e softwares da página 168, construam um triângulo cujos comprimentos dos lados meçam 7 cm, 6 cm e 5 cm. Em seguida, organizem em um fluxograma os procedimentos que vocês realizaram para fazer essa construção.

Agora, meçam com um transferidor os ângulos internos do triângulo construído e verifiquem se ele é acutângulo, retângulo ou obtusângulo.

Resposta na seção Respostas e na seção Resoluções.

Orientação para acessibilidade

Professor, professora: aproveite esta atividade para que os estudantes troquem ideias a respeito dos procedimentos de construção do triângulo, bem como dos necessários para realizar as medições com um transferidor. Além disso, se julgar oportuno, oriente-os a escrever um algoritmo (passo a passo) antes de organizar os procedimentos realizados em um fluxograma.

53. Igor fortaleceu o portão de sua horta colocando uma madeira na transversal, como a representação a seguir.

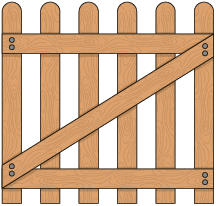
Ilustração de um portão de madeira com ripas de madeira na vertical. Na parte superior e na inferior do portão há uma ripa de madeira na horizontal, pregada nas verticais, e outra na diagonal das duas horizontais.

Por que a madeira colocada por Igor fortaleceu o portão?

Sugestão de resposta: A madeira colocada no portão formou alguns triângulos, que são figuras rígidas.

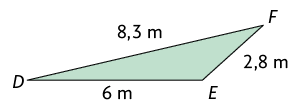
54. Considere um serralheiro que dispõe de várias barras de ferro cujas medidas são $9 metros$ , $12 metros$ e $3 metros$ de comprimento. Cite algumas combinações de três dessas barras que tornam possível construir um triângulo.

Sugestões de resposta: $9 metros$ , $9 metros$ , $9 metros$ ; $3 metros$ , $3 metros$ , $3 metros$ ; $12 metros$ , $12 metros$ , $12 metros$ ; $9 metros$ , $9 metros$ , $12 metros$ .

55. Para confeccionar uma maquete, Paula pretende montar a estrutura do telhado de uma casa em formato de triângulo. Para isso, ela dispõe de 3 palitos cujas medidas de comprimento são $7 centímetros$ , $5 centímetros$ e $2 centímetros$ , respectivamente. É possível usá-los para construir essa figura geométrica? Por quê?

Resposta: Não, pois a medida de um dos lados do triângulo é igual à soma das medidas dos outros dois $abre parênteses 7 igual a 5 mais 2 fecha parênteses$ .

56. Quais dos quadros a seguir apresentam 3 medidas de comprimento com as quais é possível construir um triângulo?

A. $8 centímetros$ , $3 centímetros$ e $5 centímetros$ .

B. $7 vírgula 2 centímetros$ , $2 vírgula 8 centímetros$ e $12 centímetros$ .

C. $6 centímetros$ , $4 vírgula 2 centímetros$ e $3 vírgula 5 centímetros$ .

D. $5 vírgula 5 centímetros$ , $2 centímetros$ e $4 vírgula 8 centímetros$ .

E. $6 vírgula 8 centímetros$ , $6 vírgula 2 centímetros$ e $12 centímetros$ .

Resposta: Alternativas C, D e E.

57. Escreva no caderno a menor e a maior medida de comprimento inteira possíveis para x em cada um dos triângulos a seguir.

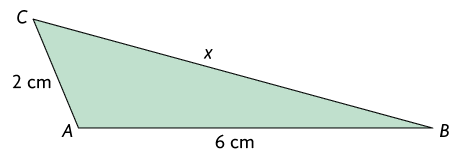
Ilustração de um triângulo A B C. As medidas de comprimentos dos lados são: lado A B é 6 centímetros; lado B C é x; e lado A C é 2 centímetros.

Ilustração de um triângulo D E F. As medidas de comprimentos dos lados são: lado D E é x; lado E F é 4 centímetros; e lado F D é 3 centímetros.

Ilustração de um triângulo G H I. As medidas de comprimentos dos lados são: lado G H é 5 centímetros; lado H I é 3 centímetros; e lado G I é x.

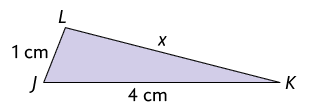
Ilustração de um triângulo J K L. As medidas de comprimentos dos lados são: lado J K é 4 centímetros; lado K L é x; e lado J L é 1 centímetros.

Respostas: A. $5 centímetros$ e $7 centímetros$ ; B. $2 centímetros$ e $6 centímetros$ ; C. $3 centímetros$ e $7 centímetros$ ; D. $4 centímetros$ e $4 centímetros$ .

ORIENTAÇÕES AO PROFESSOR

As atividades 51 e 52 contemplam a habilidade EF07MA26, visto que desafiam os estudantes a descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de um triângulo qualquer, sendo conhecidas as medidas de comprimento de seus lados. Essas atividades possibilitam o desenvolvimento com o pensamento computacional – obtenha informações a esse respeito no tópico Pensamento computacional, nas orientações gerais deste manual –, com as Competências gerais 1 e 5, ao fazer uso dos conhecimentos historicamente construídos sobre o mundo digital e por fazer uso de tecnologias digitais de forma crítica e reflexiva para resolver problema, e de aspectos da Competência específica de Matemática 6, por meio da exploração de situações-problema cujas respostas devem ser expressas em fluxogramas.

As atividades 53, 54 e 55 contemplam aspectos da habilidade EF07MA25, ao abordar o reconhecimento da rigidez de triângulos.

Ao realizar a atividade 53, verifique a possibilidade de representar o portão usando tarraxas e palitos de sorvete. Faça duas representações: uma com a madeira transversal adicionada e a outra, apenas com as madeiras horizontais e verticais. Em seguida, manipule-as a fim de verificar sua rigidez.

Nas atividades 54, 55 e 56, os estudantes devem verificar a condição de existência de um triângulo. Se julgar necessário, retome as desigualdades que devem ser satisfeitas e exponha alguns exemplos na lousa.

Na atividade 57, os estudantes devem analisar as medidas dos comprimentos indicadas, a fim de determinar a menor e a maior medida possíveis para x. Aproveite esta atividade para verificar se os estudantes compreenderam que a soma das medidas de dois lados de um triângulo é sempre maior do que a medida de comprimento do terceiro lado.

Página 171

Ângulos internos em polígonos convexos

Daniela desenhou um triângulo, marcou seus ângulos internos com cores diferentes e mediu cada um deles.

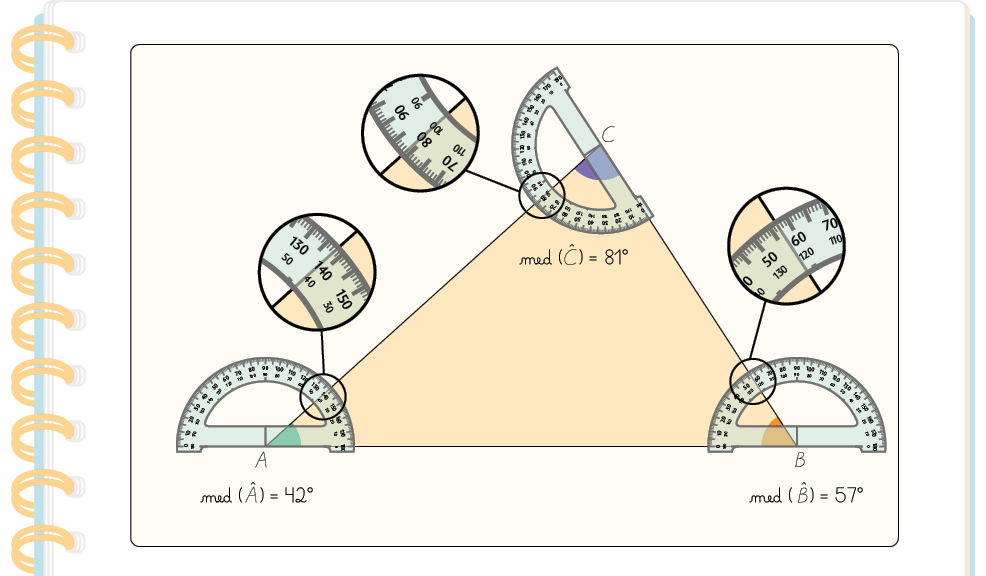
Ilustração de uma folha de caderno com um triângulo A B C desenhado. Há um transferidor medindo cada ângulo interno do triângulo e as informações: medida do ângulo A igual a 42 graus, medida do ângulo B igual a 57 graus e medida do ângulo C igual a 81 graus.

Em seguida, Daniela adicionou as medidas obtidas nesse triângulo.

$△ A B C$ : $medida do ângulo a mais medida do ângulo b mais medida do ângulo c igual a 42 graus mais 57 graus mais 81 graus igual a 180 graus$

Note que, ao adicionarmos as medidas dos ângulos internos do triângulo apresentado, obtemos $180 graus$ . Isso ocorre em qualquer triângulo.

Agora, vamos realizar a atividade a seguir.

Ilustração de um papel com um triângulo desenhado. Os ângulos internos do triângulo estão demarcados com as cores verde, laranja e roxa. — Primeiro, construímos um triângulo qualquer em uma folha de papel, destacamos seus ângulos internos e o recortamos.

Ilustração com o triângulo anterior recortado em 3 partes. O recorte separa cada ângulo interno. — Separamos o triângulo em 3 partes, cada uma com um de seus ângulos internos.

Ilustração com as 3 partes recortadas do triângulo anterior. Essas partes estão encaixadas lado a lado, com um vértice em comum e os três ângulos internos formando um ângulo de 180 graus. — Encaixamos essas partes lado a lado e concluímos que os três ângulos internos juntos formam um ângulo de $180 graus$ .

Portanto, concluímos na prática que a soma das medidas dos ângulos internos de um triângulo é $180 graus$ .

Página 172

Agora, vamos demonstrar que essa propriedade é válida para todos os triângulos.

Considere o triângulo $A B C$ a seguir e a medida de cada ângulo interno sendo $\hat{a}$ , $\hat{b}$ e $\hat{c}$ .

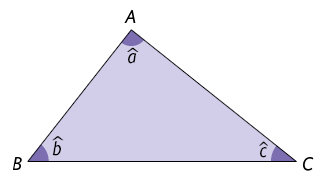
Ilustração de um triângulo A B C com ângulos internos a minúsculo, b minúsculo, c minúsculo, respectivamente.

Traçando uma reta paralela ao lado $\overline{B C}$ que passa pelo vértice $A$ , obtemos os ângulos de medida $\hat{x}$ e $\hat{y}$ , indicados a seguir.

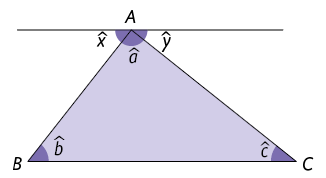
Ilustração de um triângulo A B C com ângulos internos a minúsculo, b minúsculo, c minúsculo, respectivamente. Há uma reta passando pelo vértice A paralela ao lado BA do triângulo. Os ângulos externos e suplementares de a são x e y.

Nesse caso, $\hat{x} = \hat{b}$ e $\hat{y} = \hat{c}$ , pois são as medidas dos ângulos alternos internos. Assim:

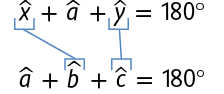
Esquema formado pelas equações: ângulo x mais ângulo a mais ângulo y, igual a 180 graus. Abaixo há a outra equação: ângulo a mais ângulo b mais ângulo c, igual a 180 graus. O ângulo x da primeira equação está relacionado com o ângulo b da segunda e o ângulo y da primeira equação está relacionado com o ângulo c da segunda.

Esse procedimento pode ser feito para qualquer triângulo e chegaremos à mesma conclusão. Assim, a propriedade vale sempre. Com isso, concluímos que a soma das medidas dos ângulos internos de qualquer triângulo é $180 graus$ .

Para obtermos a soma das medidas dos ângulos internos de um polígono convexo, podemos dividi-lo em triângulos não sobrepostos, ligando alguns de seus vértices não consecutivos. Depois, multiplicamos por $180 graus$ a quantidade de triângulos obtidos. Como exemplo, vamos aplicar esse procedimento no pentágono convexo a seguir.

Atenção!

Ao decompor um polígono convexo em triângulos, os vértices dos triângulos devem coincidir com os do polígono.

Ilustração de um pentágono irregular A B C D E.

Ilustração de um pentágono irregular A B C D E. Internamente há as os segmentos de reta tracejados indo de A. a D e de A. a C.

$3 vezes 180 graus igual a 540 graus$

3 triângulos.

Portanto, a soma das medidas dos ângulos internos de um pentágono é $540 graus$ .

Página 173

Atividades

Faça as atividades no caderno.

58. Calcule mentalmente e indique em quais dos triângulos a seguir o ângulo x mede $51 graus$ .

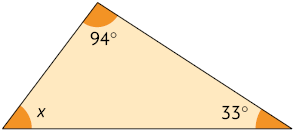
Ilustração de um triângulo com as seguintes medidas de seus ângulos internos: 94 graus; 33 graus; e x.

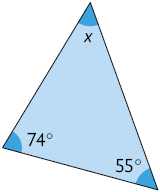
Ilustração de um triângulo com as seguintes medidas de seus ângulos internos: 74 graus; 55 graus; e x.

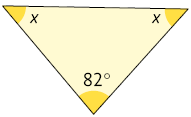
Ilustração de um triângulo com as seguintes medidas de seus ângulos internos: 82 graus; x; e x.

Ilustração de um triângulo com as seguintes medidas de seus ângulos internos: 22 graus; 107 graus; e x.

Resposta: Alternativas B e D.

59. Os polígonos a seguir estão divididos em triângulos. Calcule a soma das medidas dos ângulos internos de cada um deles.

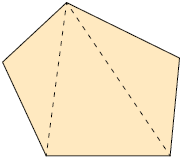
Ilustração de um pentágono irregular dividido em 3 triângulos.

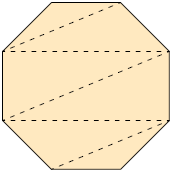
Ilustração de um octógono dividido em 6 triângulos.

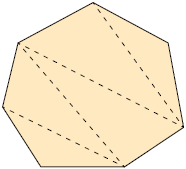
Ilustração de um heptágono irregular dividido em 5 triângulos.

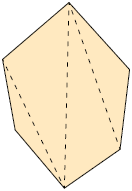
Ilustração de um hexágono irregular dividido em 4 triângulos.

Respostas: A. $540 graus$ ; B. $1.080 graus$ ; C. $900 graus$ ; D. $720 graus$ .

60. Determine as medidas de $\hat{b}$ e $\hat{c}$ no triângulo a seguir, sabendo que $\hat{b}$ é o dobro de $\hat{a}$ .

Ilustração de um triângulo com as seguintes medidas de seus ângulos internos: a minúsculo igual a 40 graus; b minúsculo; e c minúsculo.

Resposta: $medida do ângulo b igual a 80 graus$ e $medida do ângulo c igual a 60 graus$ .

61. Douglas desenhou um polígono de acordo com os seguintes comandos.

Trace um segmento de reta:

$A B$ de $3 vírgula 5 centímetros$ ;
$B C$ de $3 vírgula 3 centímetros$ formando um ângulo $A \hat{B} C$ de $60 graus$ ;
de $A$ até $C$ .

Realize as medições necessárias e verifique qual dos polígonos a seguir Douglas desenhou.

Ilustração de um triângulo A B C com a medida do ângulo B menor que 60 graus.

Ilustração de um triângulo A B C com A B medindo 3,5 centímetros, B C medindo 3,3 centímetros e o ângulo b medindo 60 graus.

Resposta: Polígono C.

ORIENTAÇÕES AO PROFESSOR

Na atividade 58, se julgar necessário, instigue os estudantes, por meio de questionamentos, a compreender que a soma das medidas dos ângulos internos de um triângulo é $180 graus$ . Caso apresentem dificuldades em escrever e resolver as equações, apresente a eles alguns exemplos na lousa, retomando as propriedades das igualdades já estudadas.

Ao realizar a atividade 59, verifique se os estudantes compreenderam que a soma das medidas dos ângulos internos é igual à quantidade de triângulos em que o polígono foi dividido multiplicado por $180 graus$ . Se necessário, organize-os em trios para que troquem ideias e desenvolvam estratégias.

Na atividade 60, se necessário, oriente os estudantes a obter, inicialmente, a medida de $\hat{b}$ , para em seguida calcular a medida de $\hat{c}$ .

Na atividade 61, os estudantes devem realizar medições para verificar qual polígono satisfaz aos comandos indicados. Oriente-os a utilizar régua e transferidor para medir, respectivamente, o comprimento de cada lado dos polígonos e o ângulo indicado.

Página 174

62. De acordo com as medidas indicadas em cada polígono, determine quais são os polígonos regulares.

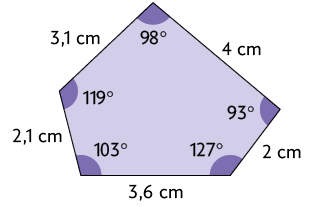
Ilustração de um pentágono com os lados demarcados medindo, em sentido horário, 2,1 centímetros, 3,1 centímetros, 4 centímetros, 2 centímetros e 3,6 centímetros. Os ângulos internos desse polígono medem, em sentido horário, 119 graus, 98 graus, 93 graus, 127 graus e 103 graus.

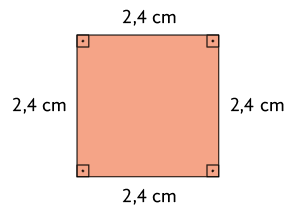
Ilustração de um quadrilátero com todos os lados demarcados e medindo 2,4 centímetros e os 4 ângulos internos medindo 90 graus.

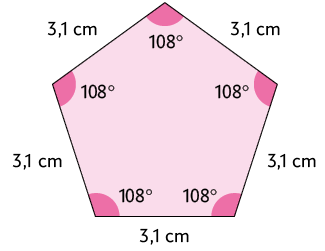
Ilustração de um pentágono com todos os lados demarcados e medindo 3,1 centímetros e os 5 ângulos internos medindo 108 graus.

Resposta: Alternativas B e C.

63. Existem elementos que lembram polígonos tanto nas construções como na natureza. Na natureza, um exemplo são os alvéolos construídos pelas abelhas.

Fotografia de dois favos de mel com destaque para um alvéolo visto de cima. Ele se assemelha a um polígono regular de 6 lados. — Favos de mel.

a) A vista de cima de cada alvéolo lembra um polígono regular. Qual é o nome dele?

b) Qual é a soma das medidas dos ângulos internos do polígono que você citou no item a?

c) Qual é a medida de cada ângulo interno dele?

Respostas: a) Hexágono; b) $720 graus$ ; c) $120 graus$ .

64. Junte-se a um colega e analisem as figuras a seguir.

Ilustração de um trapézio de vértices A B C D.

Ilustração de um paralelogramo de vértices M N O P. E com ângulos internos diferentes de 90 graus.

Ilustração de um triângulo de vértices E F G.

Ilustração de um pentágono de vértices Q R S T U.

Ilustração de um quadrilátero de vértices H I J K.

Quais das afirmações a seguir são verdadeiras?

a) Os polígonos $A B C D$ e $M N O P$ são regulares.

b) A soma das medidas dos ângulos internos do polígono $H I J K$ é igual à do $M N O P$ .

c) A soma das medidas dos ângulos internos do polígono $Q R S T U$ é quatro vezes a soma das medidas dos ângulos internos do polígono $E F G$ .

d) A soma das medidas dos ângulos internos do polígono $H I J K$ é $360 graus$ .

Resposta: Alternativas b e d.

65. Considerando as afirmações da atividade 64, reescrevam no caderno as falsas, corrigindo-as.

Sugestão de respostas: a) Os polígonos $A B C D$ e $M N O P$ não são regulares; c) A soma das medidas dos ângulos internos do polígono $Q R S T U$ é três vezes a soma das medidas dos ângulos internos do polígono $E F G$ .

ORIENTAÇÕES AO PROFESSOR

Antes de realizar a atividade 62, questione os estudantes sobre o conceito de polígonos regulares. Permita a eles que compartilhem com a turma seus conhecimentos e certifique-se de que todos identificam esse tipo de polígono.

Na atividade 63, espera-se que os estudantes percebam que a vista de cima de um alvéolo lembra um polígono regular de 6 lados, ou seja, um hexágono. Ao trabalhar com o item b, sugira, se necessário, aos estudantes que representem um hexágono no caderno e, em seguida, decomponha-o em triângulos não sobrepostos, de maneira que os vértices dos triângulos coincidam com os do hexágono.

Aproveite essa atividade para sugerir aos estudantes que pesquisem por que as abelhas constroem os alvéolos nesse formato para, então, compartilhar seus achados com a turma. Com isso, é possível relacionar Matemática com o componente curricular de Ciências.

Para que os estudantes realizem as análises necessárias à resolução das atividades 64 e 65, oriente-os a utilizar, quando julgarem necessário, instrumentos de medida.

Aproveite que a atividade 64 deve ser realizada em dupla para enfatizar a importância da empatia, do respeito, da boa convivência social, de não ter preconceitos e compreender e aceitar as necessidades e as limitações dos outros, de modo a promover a saúde mental e a cultura de paz. Com isso, abordam-se aspectos das Competências gerais 1, 4 e 9 e da Competência específica de Matemática 8. Se achar pertinente, converse com eles sobre o combate aos diversos tipos de violência, especialmente o bullying. Obtenha informações a respeito desse assunto no tópico Cultura de paz e combate ao bullying, nas orientações gerais deste manual.

Página 175

Ângulos externos em polígonos convexos

Analise experimentalmente a soma das medidas dos ângulos externos de um polígono convexo, conforme os procedimentos a seguir.

Nas imagens, estão representados os ângulos externos de cada polígono sendo recortados e, em seguida, encaixados.

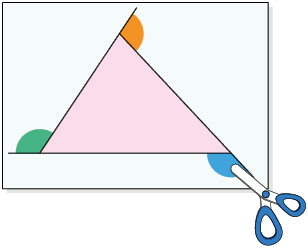
Ilustração de um papel com o desenho de um triângulo e seus 3 ângulos externos demarcados. Há uma tesoura começando a cortar o ângulo externo.

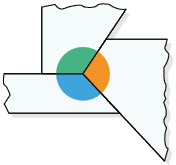
Ilustração com os 3 ângulos externos recortados do triângulo anterior. Essas partes estão encaixadas lado a lado, com um vértice em comum e os 3 ângulos formando um ângulo de 360 graus.

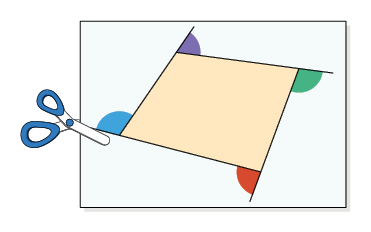
Ilustração de um papel com o desenho de um quadrilátero e seus 4 ângulos externos demarcados. Há uma tesoura começando a cortar o ângulo externo.

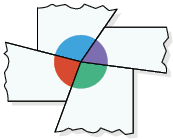
Ilustração com os 4 ângulos externos recortados do quadrilátero anterior. Essas partes estão encaixadas lado a lado, com um vértice em comum e os 4 ângulos formando um ângulo de 360 graus.

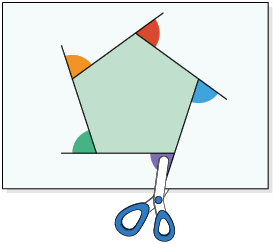
Ilustração de um papel com o desenho de um pentágono e seus 5 ângulos externos demarcados. Há uma tesoura começando a cortar o ângulo externo.

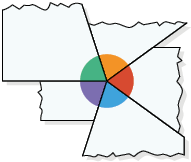
Ilustração com os 5 ângulos externos recortados do pentágono anterior. Essas partes estão encaixadas lado a lado, com um vértice em comum e os 5 ângulos formando um ângulo de 360 graus.

Questão 7. De acordo com as imagens, o que podemos notar em relação à soma das medidas dos ângulos externos de um polígono convexo?

Sugestão de resposta: A soma é $360 graus$ .

A soma das medidas dos ângulos externos de um polígono convexo é sempre $360 graus$ .

Agora, vamos estudar outra propriedade envolvendo os ângulos internos e externos em um triângulo. Para isso, considere um triângulo $A B C$ qualquer. Prolongando o lado $\overline{B C}$ , determinamos um ângulo externo cuja medida será indicada por $\hat{x}$ .

Ilustração de um triângulo de vértices A B C, com seus 3 ângulos internos demarcados: a, b, c. — Triângulo $A B C$ .

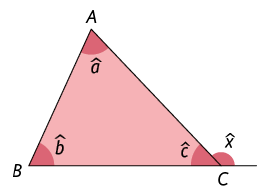
Ilustração de um triângulo de vértices A B C, com seus 3 ângulos internos demarcados: a, b, c. Há um prolongamento do lado B C e está demarcado o ângulo externo x, suplementar a c. — Lado $\overline{B C}$ prolongado e ângulo externo $\hat{x}$ .

Os ângulos de medida $\hat{c}$ e $\hat{x}$ são adjacentes, pois têm apenas o lado $\overline{A C}$ comum. Pela construção feita, esses ângulos são suplementares. Então, $medida do ângulo c mais medida do ângulo x igual a 180 graus$ ou, ainda, $medida do ângulo c igual a 180 graus menos medida do ângulo x$ .

ORIENTAÇÕES AO PROFESSOR

Antes de iniciar o conteúdo desta página, verifique o conhecimento dos estudantes relacionado aos ângulos externos de um polígono. Permita a eles que compartilhem suas explicações com a turma, tendo a oportunidade de resgatar o conhecimento prévio sobre o assunto e de tornar o estudo mais significativo.

Aproveite para distinguir ângulos externos e internos de um polígono, utilizando como base as imagens desta página.

A questão 7 instiga os estudantes a perceber que a soma das medidas dos ângulos externos de um polígono convexo é $360 graus$ . Avalie a possibilidade de mostrar essa propriedade empiricamente em sala de aula, conforme apresentado nesta página. Explique aos estudantes que essa apresentação não é uma demonstração matemática, mas serve de ilustração.

Página 176

Além disso, como a soma das medidas dos ângulos internos do triângulo é $180 graus$ , então $medida do ângulo a mais medida do ângulo b mais medida do ângulo c igual a 180 graus$ . Substituindo $\hat{c}$ por $180 graus menos a medida do ângulo x$ nessa igualdade, obtemos:

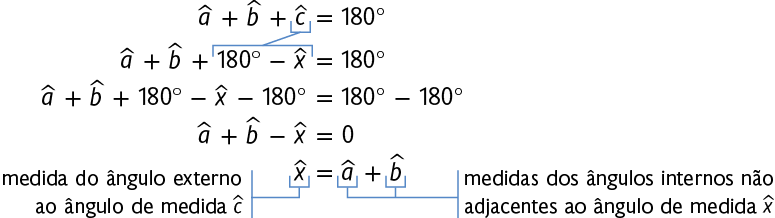
Esquema formado pelas equações: ângulo a mais ângulo b mais ângulo c, igual a 180 graus. Na segunda linha há a equação: ângulo a mais ângulo b mais 180 graus menos ângulo x, igual a 180 graus. O ângulo c da primeira equação está relacionado com o ângulo 180 gruas menos ângulo x da segunda. Na terceira linha: ângulo a mais ângulo b mais 180 graus menos ângulo x menos 180 graus, igual a 180 graus menos 180 graus. Na quarta linha: ângulo a mais ângulo b menos ângulo x, igual a 0. Na quinta linha: ângulo x, igual a ângulo a mais ângulo b, com a indicação que o ângulo x é a medida do ângulo externo ao ângulo de medida c; o ângulo a e o ângulo b são as medidas dos ângulos internos não adjacentes ao ângulo de medida x.

Esse procedimento pode ser feito com qualquer vértice do triângulo e chegaremos à mesma relação entre as medidas dos ângulos. Assim, mostramos a validade da propriedade a seguir.

Em um triângulo, a medida de um ângulo externo é igual à soma das medidas dos ângulos internos não adjacentes a ele.

Ângulos internos e ângulos externos em polígonos regulares

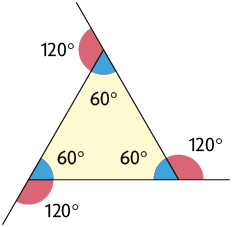
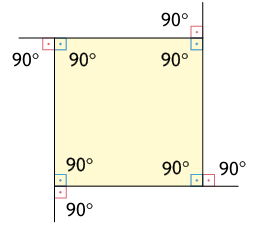
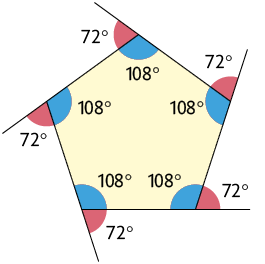
Como visto anteriormente, polígonos regulares têm lados com medidas iguais e ângulos internos congruentes. Como consequência, os ângulos externos de um polígono regular também são todos congruentes. Exemplos:

Ilustração de um triângulo com ângulos internos e externos demarcados. Os ângulos internos medem 60 graus e os ângulos externos medem 120 graus.

Ilustração de um quadrilátero com ângulos internos e externos demarcados. Os ângulos internos medem 90 graus e os ângulos externos medem 90 graus.

Ilustração de um pentágono com ângulos internos e externos demarcados. Os ângulos internos medem 108 graus e os ângulos externos medem 72 graus.

Atenção!

Cada ângulo interno e seu ângulo externo adjacente são suplementares.

Para calcular a medida do ângulo externo de um polígono, dividimos $360 graus$ pela quantidade de lados dele.

Para calcular a medida do ângulo interno, subtraímos a medida do ângulo externo de $180 graus$ .

Exemplos:

Cálculo da medida do ângulo externo do octógono regular.

Esquema com uma igualdade. Início de fração, numerador: 360 graus, denominador: 8, fim de fração, igual 45 graus. Está indicado que 360 graus corresponde a soma das medidas dos ângulos externos de um polígono. E 8 corresponde a quantidade de lados do octógono.

Portanto, cada ângulo externo do octógono regular mede $45 graus$ .

Cálculo da medida do ângulo interno do decágono regular.

Esquema com as igualdades: 180 graus, menos, abre parênteses, início de fração, numerador: 360 graus, denominador: 10, fim de fração, fecha parênteses, igual a 180 graus, menos 36 graus, igual a 144 graus. Está indicado que a fração é a medida de um ângulo externo do dodecágono regular.

Portanto, cada ângulo interno do decágono regular mede $144 graus$ .

Página 177

Instrumentos e softwares

Construindo polígono regular com régua e transferidor

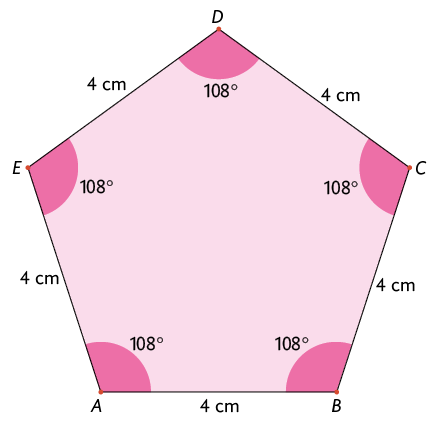
Com as orientações do professor e o passo a passo a seguir, podemos construir um pentágono regular $A B C D E$ cujos lados medem $4 centímetros$ de comprimento.

1º. Calcule a medida do ângulo interno do pentágono regular, nesse caso, $108 graus$ .

2º. Com a régua, trace o lado $\overline{A B}$ com $4 centímetros$ .

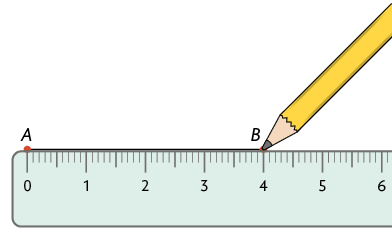
Ilustração de um lápis traçando uma reta que passa nos pontos A e B, com o auxílio de uma régua. O ponto A está no marco 0 e o ponto B está no marco 4.

3º. Posicione o centro do transferidor em $B$ e a linha de fé com $\overline{A B}$ e marque $108 graus$ .

Ilustração de um transferidor de meia volta, com o ponto B no centro, e ponto A ao lado de 0, de forma que a semirreta A B passa por 0 e mede 4 centímetros. Há um lápis fazendo um ponto em cima do marco 108 do transferidor.

4º. Com a régua alinhada nessa marca, trace o lado $\overline{B C}$ com $4 centímetros$ partindo de $B$ .

Ilustração de um segmento de reta A B, com 4 centímetros e há uma régua com o marco 0 posicionado no ponto B e marco 4 posicionado no ponto C, traçando um segmento de reta B C, que forma 108 graus com A B.

5º. Repita os dois passos anteriores mais duas vezes: a primeira posicionando o transferidor em $C$ para traçar o lado $\overline{C D}$ e a segunda em $D$ para compor o lado $\overline{D E}$ . Por fim, trace o lado $\overline{A E}$ .

Ilustração de um pentágono de vértices A B C D E com ângulos internos demarcados. Os ângulos internos medem 108 graus e os lados medem 4 centímetros.

Página 178

Atividades

Faça as atividades no caderno.

66. Determine a medida desconhecida de cada ângulo em destaque nos triângulos.

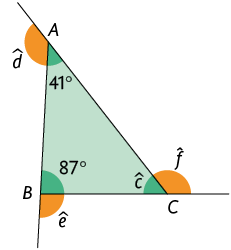
Ilustração de um triângulo A B C com ângulos internos 41 graus, 87 graus, c, respectivamente. O ângulo externo e suplementar ao de 41 graus é d. O ângulo externo e suplementar ao de 87 graus é e. O ângulo externo e suplementar ao de c é f.

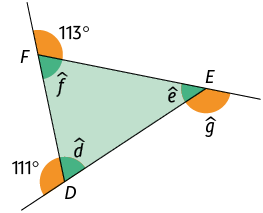
Ilustração de um triângulo D E F com ângulos internos d, e, f, respectivamente. O ângulo externo e suplementar ao d é 111 graus. O ângulo externo e suplementar ao e é g. O ângulo externo e suplementar ao f é 113 graus.

Respostas: A. $medida do ângulo c igual a 52 graus$ , $medida do ângulo d igual a 139 graus$ , $medida do ângulo e igual a 93 graus$ , $medida do ângulo f igual a 128 graus$ ; B. $medida do ângulo d igual a 69 graus$ , $medida do ângulo e igual a 44 graus$ , $medida do ângulo f igual a 67 graus$ , $medida do ângulo g igual a 136 graus$ .

67. Em cada triângulo, determine as medidas dos ângulos indicados por letras.

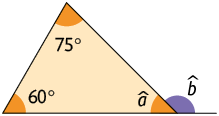
Ilustração de um triângulo com ângulos internos medindo a; 75 graus; e 60 graus. O ângulo externo e suplementar de a é b.

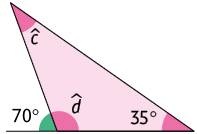
Ilustração de um triângulo com ângulos internos medindo c; d; 35 graus. O ângulo externo e suplementar ao d é 70 graus.

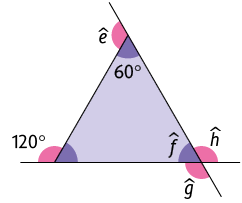
Ilustração de um triângulo com ângulos internos medindo um valor não descrito, 60 graus e f. O ângulo externo e suplementar do ângulo não descrito é 120 graus. O ângulo externo e suplementar de 60 graus é g. Os ângulos externos e suplementares de f são g e h.

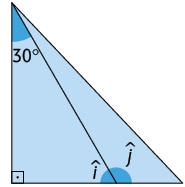
Ilustração de dois triângulos, com um lado em comum. O da esquerda possui os ângulos internos demarcados medindo 30 graus, 90 graus, i. O triângulo da direita possui só um dos ângulos internos demarcados, o j, que é suplementar ao i.

Respostas: A. $ângulo a igual a 45 graus$ ; $medida do ângulo b igual a 135 graus$ ; B. $medida do ângulo c igual a 35 graus$ , $medida do ângulo d igual a 110 graus$ ; C. $medida do ângulo e igual a 120 graus$ , $medida do ângulo f igual a 60 graus$ , $medida do ângulo g igual a 120 graus$ , $medida do ângulo h igual a 120 graus$ ; D. $medida do ângulo i igual a 60 graus$ , $medida do ângulo j igual a 120 graus$ .

68. Determine as medidas $\hat{a}$ e $\hat{b}$ , conforme as informações da imagem.

Ilustração de duas retas paralelas, r e s. Há uma reta transversal que cruza as retas r e s, formando o ângulo 65 graus, à esquerda e acima do cruzamento com s; ângulo a, estando à direita e acima do cruzamento com r. Há outra reta que cruza r, formando o ângulo 2 b menos 5 graus, à esquerda e acima do cruzamento com r e se cruza com a outra reta transversal acima de r, formando o ângulo b, abaixo do x do cruzamento.

Resposta: $medida do ângulo a igual a 115 graus$ e $medida do ângulo b igual a 70 graus$ .

69. No mosaico a seguir, os hexágonos e quadriláteros são regulares. Usando uma calculadora, determine as medidas $\hat{x}$ e $\hat{y}$ .

Ilustração de um mosaico formado por hexágonos regulares, octógonos e quadrados. Está demarcado um ângulo x que gira externamente todo o vértice do hexágono e um ângulo interno y do octógono. O ângulo y forma 360 graus com mais dois ângulos internos dos hexágonos que estão do lado e mais um ângulo interno do quadrado.

Resposta: $medida do ângulo x igual a 240 graus$ e $medida do ângulo y igual a 30 graus$ .

ORIENTAÇÕES AO PROFESSOR

Antes de iniciar as atividades 66 e 67, questione os estudantes sobre a soma das medidas dos ângulos internos de um triângulo. Aproveite o momento para verificar se todos concluem que essa soma é $180 graus$ .

A atividade 68 retoma as relações entre os ângulos definidos por retas paralelas cortadas por uma transversal, já estudadas anteriormente. Com base nessa atividade, acompanhe a aprendizagem dos estudantes a respeito desse assunto. Além disso, ela envolve conhecimentos algébricos, ao utilizar uma incógnita para representar a medida de um ângulo. Com isso, é possível relacionar as unidades temáticas Geometria e Álgebra.

Na atividade 69, os estudantes podem determinar as medidas $\hat{x}$ e $\hat{y}$ usando a medida do ângulo de uma volta. Inicialmente, oriente-os a determinar a medida de cada ângulo interno do hexágono regular e do quadrado. Ao explorar medidas de ângulos internos de polígonos regulares, sem o uso de fórmulas, vinculadas à construção de mosaicos, contempla-se a habilidade EF07MA27.

Página 179

70. Usando os mesmos procedimentos apresentados na seção Instrumentos e softwares da página 177 construa um quadrado $A B C D$ com comprimento dos lados medindo $4 centímetros$ e um pentágono regular $E F G H I$ com comprimento dos lados medindo $3 centímetros$ . Depois, descreva por escrito e por meio de um fluxograma, em seu caderno, os procedimentos que você utilizou nessa construção.

Resposta na seção Respostas e na seção Resoluções.

Versão adaptada acessível

70. Junte-se a um colega e, usando os mesmos procedimentos apresentados na seção Instrumentos e softwares da página 177, construam um quadrado ABCD com compimento dos lados medindo 4 cm e um pentágono regular EFGHI com comprimento dos lados medindo 3 cm. Depois, descrevam por escrito e por meio de um fluxograma os procedimentos que vocês utilizaram nessas construções.

Resposta na seção Respostas e na seção Resoluções.

Orientação para acessibilidade

Professor, professora: aproveite esta atividade para que os estudantes troquem ideias a respeitos dos procedimentos utilizados na construção do quadrado e do pentágono. Além disso, oriente-os a conversar sobre o posicionamento da régua e do transferidor em cada um dos passos que serão executados.

71. A soma das medidas dos ângulos internos de um polígono regular é $720 graus$ . Determine a medida de cada um desses ângulos.

Resposta: $120 graus$ .

72. Determine a medida de cada ângulo interno e de cada ângulo externo do triângulo.

Ilustração de um triângulo A B C, com ângulos internos a, b, c, respectivamente e ângulos externos e suplementar ao ângulo a; f, suplementar ao ângulo b; e g suplementar ao ângulo c,. Há um transferidor de meia volta medindo o ângulo interno a, equivalente a 45 graus, e um transferidor de meia volta medindo o ângulo externo g, equivalente a 94 graus.

Resposta: $ângulo a igual a 45 graus$ , $medida do ângulo b igual a 49 graus$ , $medida do ângulo c igual a 86 graus$ , $medida do ângulo e igual a 135 graus$ , $medida do ângulo f igual a 131 graus$ e $medida do ângulo g igual a 94 graus$ .

73. Na figura, $A B = A C$ , $B P = B R$ , $C Q = C R$ e a medida do ângulo $A \hat{Q} R$ é $123 graus$ .

Ilustração de um triângulo de vértices A B C. Entre os vértices B e C há o ponto R, entre os vértices A e B, há o ponto P e entre os vértices A e C, há o ponto Q. Estão também demarcados os triângulos B P R, R Q C e o ângulo P R Q.

Atenção!

Em um triângulo isósceles, os ângulos da base são congruentes.

O ângulo $P \hat{R} Q$ mede:

a) $48 graus$ .

b) $57 graus$ .

c) $66 graus$ .

d) $68 graus$ .

e) $123 graus$ .

Resposta: Alternativa c.

74. Calcule, em seu caderno, as medidas dos ângulos indicados por letras no paralelogramo.

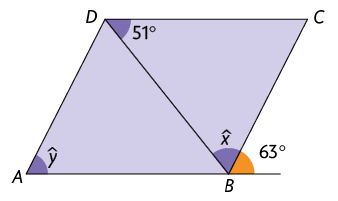
Ilustração de dois triângulos lado a lado, com um lado em comum, que juntos formam um paralelogramo. O da esquerda possui vértices A B D e o da direita, B C D. Do primeiro triângulo citado, está demarcado o ângulo D A B, equivalente à y, e do segundo triângulo está demarcado o ângulo C D B, equivalente a 51 graus e o ângulo D B C, equivalente a x. Há a demarcação de um ângulo externo no vértice B de 63 graus, de modo que esse ângulo, x e o ângulo A B D são suplementares.

Resposta: $medida do ângulo x igual a 66 graus$ e $medida do ângulo y igual a 63 graus$ .

ORIENTAÇÕES AO PROFESSOR

A atividade 70 contempla a habilidade EF07MA28, visto que desafia os estudantes a descrever, por escrito e por meio de um fluxograma, um algoritmo para a construção de polígonos regulares, sendo conhecidas as medidas dos comprimentos de seus lados. Essas atividades possibilitam o desenvolvimento com o pensamento computacional – cujas informações podem ser obtidas nas orientações gerais deste manual –, com as Competências gerais 1 e 5, ao fazer uso de conhecimentos historicamente construídos sobre o mundo digital e de tecnologias digitais de maneira crítica e reflexiva para, então, resolver problemas, e de aspectos da Competência específica de Matemática 6, ao explorar situações-problema cujas respostas devem ser expressas por meio de fluxogramas.

Ao realizar a atividade 71, se necessário, oriente os estudantes a, inicialmente, determinar qual polígono convexo tem a soma das medidas dos ângulos internos igual a $720 graus$ . Para isso, eles podem construir polígonos com base na composição de triângulos não sobrepostos, tais que os vértices dos triângulos coincidam com os do polígono.

Ao realizar a atividade 72, verifique se os estudantes realizam corretamente a leitura das medidas indicadas no transferidor. Se necessário, retome o trabalho com o uso desse instrumento.

Na atividade 73, sugira aos estudantes que reproduzam a figura no caderno dando destaque aos ângulos congruentes. Em seguida, eles devem usar essas informações para descobrir a medida dos ângulos internos dos triângulos CQR e BPR, que serão úteis para obter a medida do ângulo destacado.

Na atividade 74, lembre os estudantes de que, em um paralelogramo, os lados são dois a dois paralelos. Assim, a diagonal desse polígono é transversal a duas retas paralelas.

Metodologias ativas

Para desenvolver a atividade 74, avalie a possibilidade de utilizar a metodologia ativa Pensamento do design. Obtenha informações sobre essa metodologia no tópico Metodologias e estratégias ativas, nas orientações gerais deste manual.

Página 180

75. Um mosaico pode ser caracterizado como uma superfície composta de ladrilhos ou pequenas peças de diversas cores e formatos, colocadas lado a lado sem sobreposição. Eles podem ser encontrados em objetos artesanais, como bandejas, jarras, porta-retratos e espelhos, e em decorações de paredes e pisos.

Existem apenas três tipos de mosaicos regulares e uniformes, ou seja, tendo apenas peças com formato de polígonos regulares idênticos, combinados a cada vértice. As peças deles têm formato de triângulos equiláteros, quadrados ou hexágonos regulares. Nesses casos, as medidas dos ângulos internos compõem $360 graus$ .

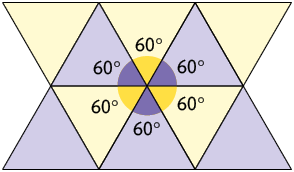
Ilustração de um mosaico formado por triângulos equiláteros. Há uma demarcação de que o encontro de 6 triângulos em um vértice em comum é composto por cada ângulo interno dos triângulos de 60 graus. — Triângulos equiláteros

$6 vezes 60 graus igual a 360 graus$

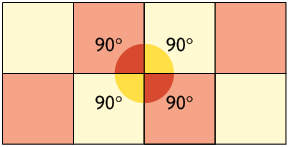
Ilustração de um mosaico formado por quadrados. Há uma demarcação de que o encontro de 4 quadrados em um vértice em comum é composto por cada ângulo interno dos quadrados de 90 graus. — Quadrados

$4 vezes 90 graus igual a 360 graus$

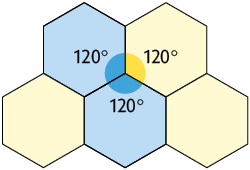
Ilustração de um mosaico formado por hexágonos regulares. Há uma demarcação de que o encontro de 3 hexágonos em um vértice em comum é composto por cada ângulo interno dos quadrados de 120 graus. — Hexágonos regulares

$3 vezes 120 graus igual a 360 graus$

Outro padrão de mosaico que pode ser criado são os chamados semirregulares, pois apresentam peças com formato de polígonos regulares, mas não necessariamente idênticas. A seguir são apresentados alguns mosaicos semirregulares.

Ilustração de um mosaico formado por hexágonos regulares e triângulos regulares.

Ilustração de um mosaico formado por quadrados e triângulos regulares, de forma que as figuras se organizam linearmente.

Ilustração de um mosaico formado por quadrados e triângulos regulares.

Ilustração de um mosaico formado por hexágonos, quadrados e triângulos regulares.

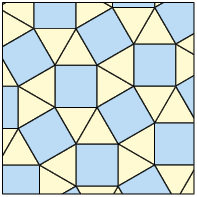
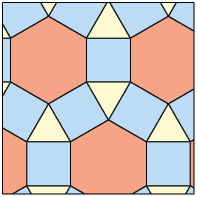
Agora, em seu caderno, determine a medida $\hat{a}$ nos próximos quatro tipos de mosaicos semirregulares apresentados.

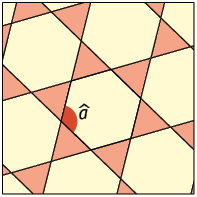
Ilustração de um mosaico formado por hexágonos e triângulos regulares. Está demarcado um ângulo interno, a, do hexágono.

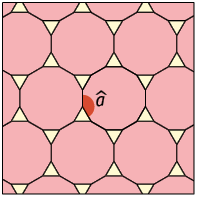
Ilustração de um mosaico formado por dodecágonos e triângulos regulares. Está demarcado um ângulo a, interno do dodecágono.

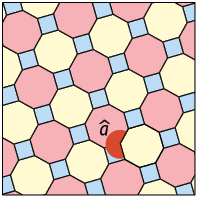
Ilustração de um mosaico formado por octógonos e quadrados regulares. Está demarcado um ângulo, a, que gira externamente todo o vértice do octógono.

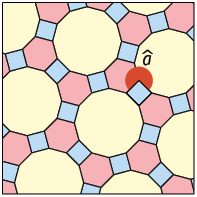
Ilustração de um mosaico formado por dodecágonos, hexágonos e quadrados regulares. Há demarcado um ângulo, a, que gira externamente todo o vértice do quadrado.

Respostas: A. $medida do ângulo a igual a 120 graus$ ; B. $medida do ângulo a igual a 150 graus$ ; C. $medida do ângulo a igual a 225 graus$ ; D. $medida do ângulo a igual a 270 graus$ .

Página 181

Circunferência

O aspecto visual e as características das formas circulares foram e ainda são fontes de inspiração para várias áreas, como Engenharia, Artes e Arquitetura.

Fotografia aérea de uma ponte que possui um formato circular em seu percurso. — Ponte Laguna Garzon, no Uruguai, em 2021.

Uma linha fechada, em um plano, formada por pontos equidistantes^✚ de um ponto fixo (centro) é chamada circunferência.

Atenção!

A circunferência é o lugar geométrico – conjunto de pontos do plano que têm uma mesma propriedade – de todos os pontos de um plano que estão localizados a uma mesma medida de distância de um ponto fixo.

Equidistante:: que apresenta a mesma distância.^↰

Na circunferência a seguir, podemos identificar:

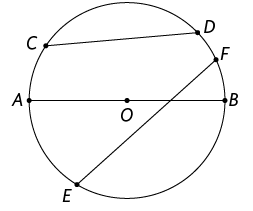
Ilustração de uma circunferência de centro O. Há um segmento de reta A B com os pontos A e B na circunferência, passando por O. Além disso, acima de A e B, na circunferência, há os pontos C, D e um segmento de reta entre eles. Também há na circunferência os pontos E e F e um segmento de reta entre eles, que cruza o segmento de reta A B.

o centro $O$ ;
os raios $\overline{O A}$ e $\overline{O B}$ ;
as cordas $\overline{A B}, \overline{C D}$ e $\overline{E F}$ ;
o diâmetro $\overline{A B}$ .

O raio da circunferência é qualquer segmento de reta que une o centro da circunferência a um de seus pontos.
A corda da circunferência é qualquer segmento de reta que une dois pontos distintos dela.
O diâmetro da circunferência é qualquer corda que passa pelo centro da circunferência.
A medida do comprimento do diâmetro é o dobro da medida do comprimento do raio.

Página 182

Comprimento da circunferência

A medida do comprimento de uma circunferência é a mesma de seu contorno. Assim, para medir o comprimento da borda de um objeto com formato circular, como uma lata em forma de cilindro, podemos usar uma fita métrica e obter a medida aproximada do comprimento da circunferência desse objeto.

Existe uma relação entre a medida do comprimento da circunferência e a medida do comprimento de seu diâmetro. A razão entre eles é um número próximo de 3,14, que é uma aproximação do número $π$ (lê-se pi).

Esquema com as igualdades: pi, igual a, início de fração, numerador: c, denominador: d, fim de fração, ou, C, igual a d, vezes pi. Está indicado que o C da primeira igualdade é a medida do comprimento da circunferência e o d da primeira igualdade é a medida do comprimento do diâmetro.

Ilustração de um menino tocando em uma lata em forma de cilindro em cima de um balcão.

Essa razão é a mesma para todas as circunferências. No quadro, estão apresentadas medidas aproximadas obtidas de alguns objetos.

Imagens não proporcionais entre si.

Medidas aproximadas de alguns objetos
Objeto	CD.	Prato.	Tampa de pote.
Medida aproximada do comprimento da circunferência ( $C$ )	$37 vírgula 7 centímetros$	$70 centímetros$	$30 centímetros$
Medida aproximada do comprimento do diâmetro ( $d$ )	$12 centímetros$	$22 centímetros$	$9 vírgula 6 centímetros$
Razão aproximada $\frac{C}{d}$	$3 vírgula 14$	$3 vírgula 18$	$3 vírgula 12$

Questão 8. Arquimedes (287 a.C. – 212 a.C.) foi um matemático, filósofo, físico, engenheiro, inventor e astrônomo grego. Em seus estudos, ele concluiu que o número $π$ estava entre $início de fração, numerador: 223, denominador: 71, fim de fração$ e $início de fração, numerador: 22, denominador: 7, fim de fração$ . Considerando a conclusão de Arquimedes, determine uma aproximação para $π$ com duas casas decimais.

Resposta: 3,14.

Temos que $pi igual a 3 vírgula 1 4 1 5 9 2 6 5...$ , porém utilizaremos apenas duas casas decimais e vamos considerar $pi igual a 3 vírgula 14$ .

Sendo $d igual a 2 vezes r$ , em que d é o diâmetro e r é o raio, podemos ter:

$C igual a d vezes pi. está indicado que d corresponde a 2 vezes r. Assim C igual a 2 vezes r vezes pi$

ORIENTAÇÕES AO PROFESSOR

Ao desenvolver esta página com os estudantes, eles têm a oportunidade de estabelecer o número $π$ como a razão entre a medida do comprimento da circunferência e a medida do comprimento de seu diâmetro, desenvolvendo, assim, a habilidade EF07MA33.

Complemente o trabalho com a questão 8 lendo para os estudantes o texto a seguir, que apresenta algumas informações históricas a respeito do descobrimento do número $π$ .

Um texto a mais

[...]

Na matemática, é a Arquimedes que devemos os primeiros grandes avanços na pista do número $π$ . Antes dele, outros haviam se interessado pelo círculo, mas muitas vezes seus esforços careciam de rigor. Basta lembrarmos de Os nove capítulos: lá encontrávamos campos circulares de 10 bu de diâmetro com circunferência de 30 bu. Dados dessa natureza redundam em afirmar que o número $π$ é igual a 3. No papiro de Ahmes, a resolução aproximada da quadratura do círculo equivale a considerar que $π$ tem valor de cerca de 3,16.

Já Arquimedes entende que é difícil e mesmo impossível calcular um valor exato de $π$ . Ele também terá, assim, de se contentar com estimativas, mas sua abordagem se distingue em dois pontos. Primeiro, ao passo que seus antecessores talvez considerassem dispor de um método exato, o cientista siciliano tem perfeita consciência de contar apenas com valores aproximados. Depois, ele vai calcular a diferença entre suas estimativas e o verdadeiro valor de $π$ , desenvolvendo em seguida métodos que permitiam reduzir cada vez mais essa defasagem.

Com seus cálculos, ele acaba concluindo que o valor buscado está compreendido entre dois números que, escritos no nosso atual sistema decimal, ficam aproximadamente entre 3,1408 e 3,1428...

[...]

LAUNAY, Mickaël. A fascinante história da matemática. Da pré-história aos dias de hoje. Rio de Janeiro: Bertrand Brasil, 2019. p. 85.

Algo a mais

Para fatos históricos sobre Geometria, consulte o livro indicado a seguir.

EVES, Howard. Tópicos de História da Matemática para uso em sala de aula: Geometria. São Paulo: Atual, 1994.

Página 183

Instrumentos e softwares

Construindo circunferência com régua e compasso

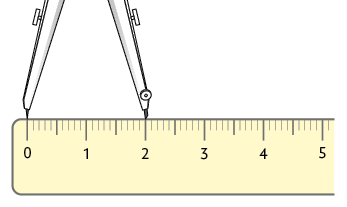
Com as orientações do professor e o passo a passo a seguir, vamos construir uma circunferência com $2 centímetros$ de medida de raio.

1º. Com o auxílio da régua, marque a abertura do compasso igual à medida do raio, nesse caso, $2 centímetros$ .

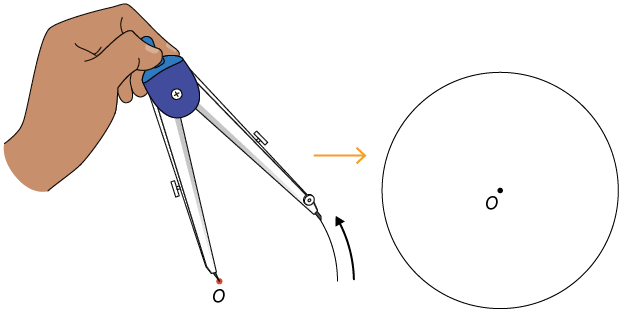
2º. Fixe a ponta-seca do compasso em um ponto O qualquer e, mantendo a abertura, gire-o uma volta completa.

Ilustração de uma régua e um compasso com abertura correspondente a 2 centímetros. A ponta-seca está posicionada no marco 0 da régua e a outra ponta no marco 2.

Ilustração de uma mão segurando um compasso com a ponta seca no ponto O e o girando em sentido anti-horário. Há uma seta apontando para um círculo de centro O.

Atividades

Faça as atividades no caderno.

76. Em cada item, estão traçados alguns segmentos de reta nas circunferências. Sabendo que em cada circunferência o ponto O é seu centro, identifique em seu caderno os raios, as cordas e os diâmetros traçados nelas.

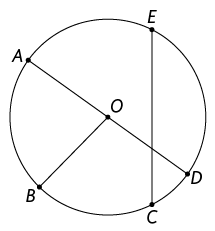
Ilustração de uma circunferência de centro O. Há um segmento de reta A D com os pontos A e D na circunferência, passando por O. Na circunferência também há um ponto B e um segmento de reta O B. Além disso, na circunferência há os pontos E e C e um segmento de reta entre eles, que cruza o segmento de reta A D.

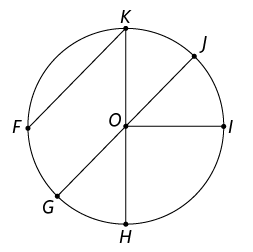
Ilustração de uma circunferência de centro O. Há um segmento de reta G J com os pontos G e J na circunferência, passando por O. Há um segmento de reta K H com os pontos K e H na circunferência, passando por O. Na circunferência também há um ponto I e um segmento de reta O I. Além disso, na circunferência há o ponto F e um segmento de reta F K.

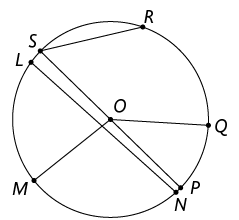
Ilustração de uma circunferência de centro O. Há um segmento de reta S P com os pontos S e P na circunferência, passando por O. Na circunferência também há um ponto Q e M e os segmentos de reta O Q e O M. Além disso, na circunferência há os pontos L, N e R e os segmentos de reta L N e S R.

Respostas. A. raios: $\overline{O A}$ , $\overline{O B}$ e $\overline{O D}$ ; cordas: $\overline{C E}$ e $\overline{A D}$ ; diâmetro: $\overline{A D}$ . B. raios: $\overline{O G}$ , $\overline{O H}$ , $\overline{O I}$ , $\overline{O J}$ e $\overline{O K}$ ; cordas: $\overline{F K}$ , $\overline{G J}$ e $\overline{H K}$ ; diâmetros: $\overline{H K}$ e $\overline{G J}$ . C. raios: $\overline{O M}$ , $\overline{O P}$ , $\overline{O Q}$ , e $\overline{O S}$ ; cordas: $\overline{S P}$ , $\overline{S R}$ e $\overline{L N}$ ; diâmetro: $\overline{S P}$ .

77. Analise a circunferência de centro O.

Ilustração de uma circunferência de centro O e raio de 3,5 centímetros.

a) Com o auxílio de uma régua, determine a medida do comprimento do raio e a medida do comprimento do diâmetro dessa circunferência.

Resposta: Medida do comprimento do raio: $1 vírgula 5 centímetro$ , medida do comprimento do diâmetro: $3 centímetros$ .

b) Qual é a relação entre essas medidas?

Resposta: A medida do diâmetro é o dobro da medida do raio.

c) Essa relação ocorre em qualquer circunferência? Justifique sua resposta.

Resposta: Sim, pois em qualquer circunferência o diâmetro é uma corda que passa pelo centro. Como o raio é qualquer segmento de reta que une o centro da circunferência a um de seus pontos, a medida do diâmetro é o dobro da medida do raio.

ORIENTAÇÕES AO PROFESSOR

Metodologias ativas

Busca-se, com a atividade 76, verificar se os estudantes identificam os elementos de uma circunferência. Se necessário, retome os conceitos de raio, diâmetro e corda. Ao final da atividade, é necessário verificar se eles compreenderam que o diâmetro é um caso particular de uma corda, visto que passa pelo centro da circunferência, sendo a corda com a maior medida de comprimento. Questione-os também sobre a relação entre diâmetro e raio.

Na atividade 77, oriente os estudantes a posicionar a régua corretamente, de modo que o zero coincida com uma das extremidades do segmento a ser medido. Para ampliar o desenvolvimento com a atividade do item c, sugira aos estudantes que desenhem diferentes circunferências e, em seguida, meçam o comprimento do raio e do diâmetro. Com isso, contemplam-se aspectos da habilidade EF07MA22. Com essa atividade, faça uma síntese da relação entre diâmetro e corda e entre raio e diâmetro.

Página 184

78. Construa no caderno uma circunferência com:

a) raio $\overline{O A}$ medindo $3 centímetros$ .

b) raio $\overline{B C}$ medindo $6 centímetros$ .

c) diâmetro $\overline{E F}$ medindo $5 vírgula 4 centímetros$ .

d) diâmetro $\overline{G H}$ medindo $4 centímetros$ .

Resposta na seção Resoluções.

79. Construa uma circunferência com diâmetro medindo $5 centímetros$ . Em seguida, usando o mesmo centro, construa outra circunferência com raio medindo $8 centímetros$ .

Resposta na seção Resoluções.

80. Considere o quadrado cujo comprimento do lado mede $4 centímetros$ e o ponto P em seu interior, ambos representados na malha quadriculada.

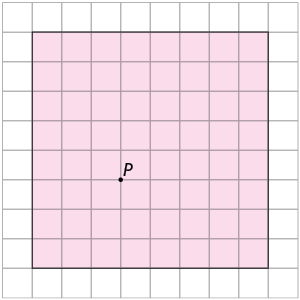
Ilustração de uma malha quadriculada com um quadro de 8 quadradinhos de lado. Há um ponto P que está há 3 quadrinhos da base e 3 da altura do quadrado.

Quantos pontos que estão sobre os lados desse quadrado estão a exatamente $2 centímetros$ do ponto P?

Resposta: 4 pontos.

81. Escolha 3 objetos circulares, meça o comprimento da circunferência e do diâmetro deles. Depois, com uma calculadora, determine a razão entre as medidas. Para realizar os registros, copie e complete o quadro a seguir no caderno, substituindo cada $█$ pelas informações que você coletou.

Medidas aproximadas de alguns objetos
Objeto	Medida do comprimento da circunferência ( $C$ )	Medida do diâmetro ( $d$ )	Razão $\frac{C}{d}$
$█$	$█$	$█$	$█$
$█$	$█$	$█$	$█$
$█$	$█$	$█$	$█$

As razões $\frac{C}{d}$ calculadas estão próximas do valor do número $π$ ?

Respostas pessoais.

82. O comprimento de uma circunferência mede $79 vírgula 76 centímetros$ . Podemos afirmar que o raio da circunferência mede aproximadamente:

a) $12 centímetros$ .

b) $12 vírgula 7 centímetros$ .

c) $13 centímetros$ .

d) $13 vírgula 22 centímetros$ .

e) $13 vírgula 5 centímetros$ .

Resposta: Alternativa b.

83. Utilizando um programa de computador, Rômulo fez uma composição artística utilizando circunferências.

Ilustração de várias circunferências com partes sobrepostas, cada uma com um tamanho e cor interna.

Agora é sua vez! Com o auxílio de um compasso, faça uma composição artística utilizando circunferências. Por fim, pinte-a.

Resposta pessoal.

Versão adaptada acessível

Agora, junte-se a um colega e conversem a respeito de como vocês fariam uma composição artística com circunferências. Depois, façam essa composição artística.

Resposta pessoal.

Orientação para acessibilidade

Professor, professora: se julgar conveniente, durante a conversa, oriente os estudantes a trocar ideias sobre a posição das circunferências e a medida do comprimento de seus diâmetros.

ORIENTAÇÕES AO PROFESSOR

Nas atividades 78 e 79, verifique como os estudantes manuseiam o compasso. Caso necessário, retome a seção Instrumentos e softwares: Construindo circunferências com régua e compasso.

Ao construir as circunferências solicitadas, os estudantes desenvolvem aspectos da habilidade EF07MA22.

A atividade 80 desafia os estudantes a resolver um problema que envolve objetos equidistantes, conforme indicado na habilidade EF07MA22. Para que eles resolvam a atividade, disponibilize malhas quadriculadas – aquelas cujo comprimento de lado dos quadradinhos mede $0 vírgula 5 centímetro$ – e peça a eles que reproduzam a figura e o ponto apresentado. Em seguida, converse com eles sobre a circunferência como lugar geométrico. Por fim, eles devem resolver o problema.

A atividade 81 aborda a relação entre a medida do comprimento da circunferência e de seu diâmetro, inclusive de maneira experimental, instigando os estudantes a perceber que essa relação se aproxima de $π$ . Ao fazer isso, contempla-se a habilidade EF07MA33. Ao realizar essa atividade, disponibilize barbante e régua em quantidade suficiente para que eles possam contornar o objeto circular utilizando o cordão e, em seguida, medir o comprimento do contorno utilizando a régua.

Ao trabalhar com a atividade 82, verifique se os estudantes aplicam corretamente a fórmula $C maiúsculo igual a 2 pi r$ . Caso apresentem dificuldade na atividade, retome o trabalho com o tópico Comprimento da circunferência.

Na atividade 83, os estudantes devem compor uma produção artística usando circunferências, como orienta a habilidade EF07MA22. Aproveite o momento para propor ao professor do componente curricular de Arte que converse com os estudantes sobre artistas que usavam figuras geométricas em suas obras.

Metodologias ativas

Ao final do trabalho com as atividades desta unidade, avalie a possibilidade de utilizar a metodologia ativa Escrita rápida. Para obter informações sobre essa metodologia no tópico Metodologias e estratégias ativas, consulte as orientações gerais deste manual.

Página 185

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Desenhe em uma folha de papel avulsa um ângulo $A \hat{O} B$ .

a) Qual é o vértice do ângulo $A \hat{O} B$ ?

b) Quais são os seus lados?

c) O ângulo $A \hat{O} B$ é agudo, reto, obtuso ou raso?

Respostas: a) $O$ ; b) Semirretas $O A$ e $O B$ ; c) Resposta pessoal.

2. Considerando os ângulos representados na figura, indique quais afirmações a seguir são verdadeiras.

a) A medida do ângulo $A \hat{O} B$ é maior do que o ângulo $A \hat{O} C$ .

b) A medida do ângulo $B \hat{O} C$ é menor do que o ângulo $A \hat{O} C$ .

c) O ângulo $A \hat{O} B$ é agudo.

d) A medida do ângulo $A \hat{O} C$ é maior do que $180 graus$ .

e) A medida do ângulo $B \hat{O} C$ é menor do que $90 graus$ .

Resposta: Alternativas b, c e e.

3. Junte-se a um colega e resolvam os itens a seguir.

a) Se o ângulo $\hat{A}$ mede x, e seu suplementar mede o triplo, qual é a medida de $\hat{A}$ e a de seu complementar?

b) O ângulo $\hat{B}$ é suplementar de $\hat{C}$ . Sabendo que $medida do ângulo b igual a x mais 32 graus$ e $medida do ângulo c igual a 3 x$ , qual é a medida dos ângulos $\hat{B}$ e $\hat{C}$ ?

c) Os ângulos $\hat{D}$ e $\hat{F}$ são complementares. A medida de $\hat{F}$ é cinco vezes a medida de $\hat{D}$ . Qual é a medida do ângulo suplementar de $\hat{D}$ ?

Respostas: a) $45 graus$ e $45 graus$ ; b) $69 graus$ e $111 graus$ ; c) $165 graus$ .

4. Pedro fez o desenho representado a seguir.

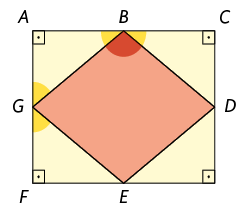
Ilustração de um retângulo A C, vértice não identificado, F. Internamente dentro do retângulo há um losango G B D E, com seus vértices nos lados do retângulo. O vértice G está entre F e A, o vértice B está entre A e C, o vértice D está entre C e o vértice não identificado, o vértice E está entre o ângulo não identificado e F. estão demarcados os ângulos G B D; A B G; C B D; B G A; F G E.

Sabendo que $medida do ângulo a g b igual a 50 graus$ e que $med (A \hat{B} G) = med (C \hat{B} D)$ , qual é a medida do ângulo $G \hat{B} D$ ?

Resposta: $100 graus$ .

5. Na imagem apresentada, as retas i e e são paralelas, assim como f e p.

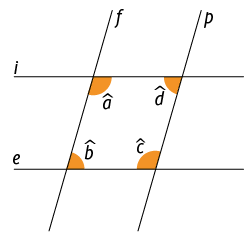
Ilustração das retas paralelas i, e. Há as retas transversais às anteriores e paralelas entre si, f, p. As retas formam entre si um quadrilátero com ângulos internos medindo a, b, c, d.

a) Indique quais são os ângulos da imagem com mesma medida.

b) Calcule as medidas dos ângulos $\hat{a}$ , $\hat{b}$ , $\hat{c}$ e $\hat{d}$ , sabendo que o maior ângulo entre as retas e e p mede $106 graus$ .

Respostas: a) $\hat{a}$ e $\hat{c}$ , $\hat{b}$ e $\hat{d}$ ; b) $medida do ângulo a igual a 106 graus$ , $medida do ângulo b igual a 74 graus$ , $medida do ângulo c igual a 106 graus$ , $medida do ângulo d igual a 74 graus$ .

ORIENTAÇÕES AO PROFESSOR

1. Objetivo

Avaliar se o estudante reconhece um ângulo e seus elementos.

Como proceder

Se necessário, desenhe na lousa um ângulo agudo, um reto, um obtuso e um raso e peça aos estudantes que classifiquem cada um e identifiquem vértice e lados.

2. Objetivo

Avaliar se os estudantes identificam corretamente, por meio de comparação, o ângulo de maior medida.

Como proceder

Em cada item, se necessário, evidencie a abertura dos ângulos que estão sendo comparados, para que o estudante perceba o que tem maior medida.

3 e 4. Objetivo

Avaliar se os estudantes compreenderam corretamente os conceitos de ângulos complementares e suplementares.

Como proceder

Caso os estudantes apresentem dificuldade, proponha a eles que consultem a página 150 para relembrar as definições de ângulos complementares e suplementares. Para determinar o ângulo requerido em cada item da atividade 3, oriente-os a escrever e a resolver uma equação. Na atividade 4, verifique se eles percebem que o ângulo requerido é suplementar à soma das medidas dos ângulos $A \hat{B} G$ e $C \hat{B} D$ .

5. Objetivo

Avaliar se os estudantes reconhecem pares de ângulos correspondentes em retas paralelas cortadas por uma reta transversal.

Como proceder

Caso os estudantes apresentem dificuldade, faça o desenho na lousa e mostre a eles que o ângulo medindo $\hat{d}$ é oposto pelo vértice ao ângulo correspondente ao de medida $\hat{b}$ , e que o ângulo medindo $\hat{a}$ é oposto pelo vértice ao ângulo correspondente ao de medida $\hat{c}$ . Em seguida, oriente-os a usar o conceito de ângulo suplementar para calcular a medida de cada um deles.

Página 186

6. Sem realizar medições, determine em cada polígono a medida do ângulo destacados em rosa.

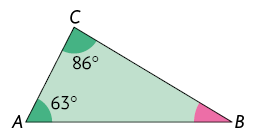
Ilustração de um triângulo de vértices A B C, com seus 3 ângulos internos demarcados: 63 graus, ângulo destacado em rosa e 86 graus.

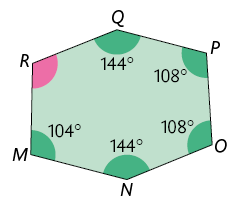
Ilustração de um hexágono de vértices M N O P Q R, com seus 6 ângulos internos demarcados: 104 graus, 144 graus, 108 graus, 108 graus, 144 graus e ângulo destacado em rosa.

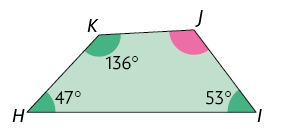
Ilustração de um trapézio de vértices H I J K, com seus 4 ângulos internos demarcados: 47 graus, 53 graus, ângulo destacado em rosa e 136 graus.

Respostas: A. $31 graus$ ; B. $112 graus$ ; C. $124 graus$ .

7. Considere o eneágono regular.

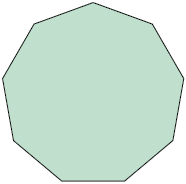
a) Qual é a soma das medidas dos ângulos internos desse eneágono?

Resposta: $1.260 graus$ .

b) Qual é a medida de cada ângulo interno desse eneágono?

Resposta: $140 graus$ .

c) Escreva em uma folha de papel avulsa as estratégias que você utilizou para responder aos itens a e b.

Resposta pessoal. Sugestão de resposta: No item a, decompus o eneágono em 7 triângulos não sobrepostos e multipliquei $180 graus$ por essa quantidade. No item b, dividi a medida obtida no item a por 9, pois o eneágono é regular.

8. Na figura a seguir, os pontos A, B e C estão na mesma reta.

Ilustração de uma reta com os pontos A B C. Há um triângulo com dois vértices sendo A e B e outro com dois dos vértices sendo os pontos B e C. Os dois triângulos possui os ângulos internos demarcados.

Determine a soma das medidas dos ângulos destacados.

Resposta: $360 graus$ .

9. Sem realizar medições, determine a medida do ângulo externo de cada polígono regular.

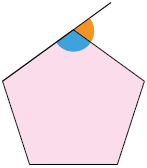
Ilustração de um pentágono regular com um de seus ângulos internos demarcados e seu respectivo ângulo externo também demarcado.

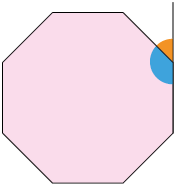
Ilustração de um octógono regular com um de seus ângulos internos demarcados e seu respectivo ângulo externo também demarcado.

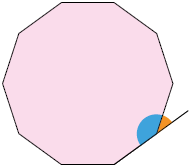
Ilustração de um decágono regular com um de seus ângulos internos demarcados e seu respectivo ângulo externo também demarcado.

Ilustração de um hexágono regular com um de seus ângulos internos demarcados e seu respectivo ângulo externo também demarcado.

Respostas: A. $72 graus$ ; B. $45 graus$ ; C. $36 graus$ ; D. $60 graus$ .

10. Considere a circunferência de centro O apresentada a seguir.

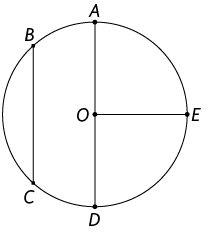
Ilustração de uma circunferência de centro O. Há um segmento de reta com os pontos A e D na circunferência, passando por O. Na circunferência também há um ponto E e um segmento de reta O E. Além disso, na circunferência há os pontos B e C e um segmento de reta entre eles.

Agora, classifique em raio, corda ou diâmetro o:

a) $\overline{O E}$ .

b) $\overline{B C}$ .

c) $\overline{A D}$ .

Respostas: a) Raio; b) Corda; c) Diâmetro.

ORIENTAÇÕES AO PROFESSOR

6, 7 e 8. Objetivo

Avaliar se o estudante consegue determinar as medidas dos ângulos internos de um polígono.

Como proceder

Se necessário, lembre os estudantes de que a soma das medidas dos ângulos internos de um triângulo é $180 graus$ . Caso apresentem dificuldade nos itens B e C da atividade 6, oriente-os a decompor cada polígono em triângulos não sobrepostos, cujos vértices coincidem com os do polígono, para, em seguida, relacionar a quantidade de triângulos com a soma das medidas dos ângulos internos. Essa mesma estratégia pode ser utilizada na atividade 7. Se necessário, explique a eles que em um polígono regular os ângulos internos têm mesma medida.

9. Objetivos

Constatar se o estudante compreendeu como calcular a medida de um ângulo externo.

Como proceder

Verifique se os estudantes calculam corretamente a medida de cada ângulo interno de um polígono regular. Caso eles apresentem dificuldade, retome na lousa os procedimentos indicados para a atividade 7. Para calcular a medida do ângulo externo em cada item, mostre a eles, quando necessário, que a soma da medida de um ângulo interno com seu externo é $180 graus$ , ou seja, esses ângulos são suplementares.

10. Objetivo

Acompanhar se o estudante compreendeu a distinção entre diâmetro, raio e corda de uma circunferência.

Como proceder

Caso os estudantes apresentem dificuldade, oriente-os a consultar as definições desses elementos na página 181. Explique a eles que, por definição, o diâmetro é um caso particular de uma corda, por conter o centro da circunferência.