Página 213
UNIDADE
9
Proporção

Agora vamos estudar...
- grandezas diretamente e inversamente proporcionais;
- regra de três e grandezas diretamente proporcionais;
- regra de três e grandezas inversamente proporcionais.
Página 214
Grandezas diretamente proporcionais
Jorge foi almoçar em um restaurante que cobra R$ 4,80 a cada de alimento vendido. Sabendo que ele colocou em seu prato exatamente de alimento, quantos reais ele pagou por essa quantidade?

Para obter o preço que Jorge pagou, podemos organizar as informações da seguinte maneira:
Quantidade de alimento (em )
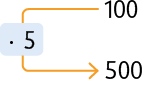
Preço (em R$)
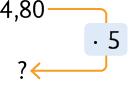
Como o preço está relacionado diretamente à quantidade de alimento, e de alimento correspondem a vezes , o valor a ser pago também deve ser multiplicado por , ou seja:
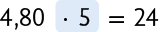
Assim, Jorge pagou R$ 24,00 por essa quantidade de alimento.
Nessa situação, podemos observar que o preço a ser pago varia de acordo com a quantidade de alimento: se a quantidade aumentar 5 vezes, então o preço a ser pago também aumentará 5 vezes; se diminuir pela metade, então o preço a ser pago também vai diminuir pela metade; e assim por diante. Assim, podemos dizer que a quantidade de alimento e o preço a ser pago são grandezas diretamente proporcionais.
Atenção!
Na situação apresentada, as grandezas envolvidas são quantidade de alimento (em ) e preço (em R$).
Existem casos, porém, em que duas grandezas não são proporcionais entre si.
Por exemplo, as grandezas idade e altura de uma pessoa não são proporcionais entre si: uma pessoa cuja medida da altura é com anos de idade não terá altura medindo quando tiver anos de idade.
Questão 1. Cite oralmente, com a ajuda
dos
colegas, outros exemplos de duas grandezas que são diretamente
proporcionais entre si.
Sugestão de resposta: A quantidade de pães comprados em uma padaria e o valor, em reais, a ser pago; a quantidade de calças produzidas em uma fábrica e a quantidade de funcionários para confeccioná-las, entre outras.
Página 215
Grandezas inversamente proporcionais
Mateus contratou 4 operários para construir sua casa. Esses operários levarão 210 dias para terminar a construção.
Mantendo o mesmo ritmo de trabalho, quantos dias 8 operários levariam para construir a mesma casa?
Para responder a essa pergunta, podemos organizar os dados da seguinte maneira:
Quantidade de operários
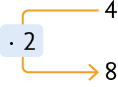
Medida de tempo (em dias)
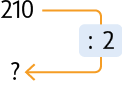
A quantidade de operários dobrou, ou seja, foi multiplicada por 2. Nesse caso, se eles mantiverem o mesmo ritmo de trabalho, a medida de tempo gasta para terminar a construção será reduzida pela metade, ou seja, será dividida por 2.
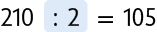
Assim, 8 operários levarão 105 dias para terminar essa construção.
Nessa situação, podemos observar que a medida do tempo gasta para terminar a construção depende da quantidade de operários: se a quantidade de operários triplicar, a medida de tempo gasta para a construção diminuirá pela terça parte; se a quantidade de operários diminuir pela metade, a medida de tempo gasta para a construção será o dobro; e assim por diante. Portanto, podemos dizer que a quantidade de operários e a medida de tempo gasta para construir a casa são grandezas inversamente proporcionais.
Questão 2. Cite oralmente, com a ajuda
dos
colegas, outros exemplos de duas grandezas que são inversamente
proporcionais entre si.
Sugestão de resposta: A medida da velocidade média de um automóvel () e a medida do tempo () para chegar ao destino desejado; a quantidade de costureiros para confeccionar determinada quantidade de roupas e a medida do tempo () necessária para concluir a encomenda, entre outras.
Atividades
Faça as atividades no caderno.
1. O dono de uma lanchonete organizou o preço de venda de 1 a 5 salgados.
|
Quantidade de salgados |
Preço (em R$) |
|---|---|
|
1 |
4,30 |
|
2 |
8,60 |
|
3 |
12,90 |
|
4 |
17,20 |
|
5 |
21,50 |
a) Calcule o preço de:
- 15 salgados.
- 28 salgados.
Resposta: a) R$ 64,50; R$ 120,40.
b) O preço e a quantidade de salgados são grandezas diretamente proporcionais? Por quê?
Resposta: Sim. Sugestão de resposta: Duplicando a quantidade de salgados, o preço também duplicará; triplicando a quantidade de salgados, o preço também triplicará; reduzindo a quantidade de salgados à metade, o preço também será reduzido à metade; e assim por diante.
Página 216
2. Em uma indústria, certa máquina produz 250 peças por hora. Em quantas horas essa mesma máquina vai produzir 1.500 peças?
Resposta: 6 horas.
3. A seguir está indicada a medida da massa corporal de Isabel em algumas idades.
|
Idade (em anos) |
Medida da massa corporal (em ) |
|---|---|
|
2 |
13 |
|
10 |
30 |
|
12 |
40 |
|
14 |
52 |
a) Com base nas informações, é possível saber a medida da massa corporal que Isabel terá aos 16 anos?
b) As grandezas idade e medida da massa corporal são proporcionais?
Respostas: a) Não; b) Não.
4. Para colher o trigo que plantou, Juliano alugou 3 colheitadeiras que, juntas, vão concluir toda a colheita em 8 dias. Quantas colheitadeiras Juliano precisaria alugar para realizar a mesma colheita em 4 dias, mantendo o mesmo ritmo de trabalho?
Resposta: 6 colheitadeiras.
5. Para obter de carne de marisco, é necessário recolher cerca de de mariscos. De acordo com essa informação, temos:
|
Carne (em ) |
Mariscos (em ) |
|---|---|
|
1 |
15 |
|
2 |
30 |
|
3 |
45 |
|
4 |
60 |
|
5 |
75 |
|
6 |
90 |
|
7 |
105 |
|
8 |
120 |
Nessa situação, a medida de massa de carne obtida varia de acordo com a medida da massa de mariscos recolhida: obtém-se de carne a cada de mariscos, de carne a cada de mariscos, e assim por diante.
Com base nas informações, podemos escrever as seguintes frações e simplificá-las.
Note que a fração irredutível obtida nas simplificações é a mesma em todos os casos.
Dizemos que ou é a razão entre as duas grandezas apresentadas. Uma das maneiras de ler essa razão é 1 está para 15.
Leia as informações a seguir e obtenha a razão entre as grandezas apresentadas em cada item.
a) Em um vestibular, 350 candidatos fizeram inscrição para o curso de Matemática, que oferece 50 vagas. Obtenha a razão entre a quantidade de candidatos e a quantidade de vagas.
b) Na turma de Cristina, a cada 10 estudantes, 5 são meninas. Obtenha a razão entre a quantidade de meninas e a quantidade de estudantes dessa turma.
c) Em uma padaria, a cada 10 pães vendidos, 8 são pães de leite. Obtenha a razão entre a quantidade de pães de leite e a quantidade de pães vendidos.
Sugestões de respostas: a) ou ou ou ; b) ou ou ou ; c) ou ou ou .
6. Certa torneira pingando desperdiça de água por dia. Em 30 dias, quantos litros de água serão desperdiçados por essa torneira?
Resposta: .
Página 217
Regra de três e grandezas diretamente proporcionais
A regra de três é outra maneira de resolver situações-problema que envolvem grandezas proporcionais. A seguir, vamos apresentar uma situação e como resolvê-la usando a regra de três.
O carro de Joana percorre, em média, com de combustível. Para percorrer , esse mesmo carro gasta, em média, de combustível.
De acordo com essas informações, temos:
Medida da distância (em )

Quantidade de combustível (em )
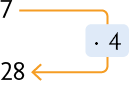
Nessa situação, quadruplicando a medida da distância percorrida, a quantidade de combustível também quadruplicará; triplicando a medida da distância percorrida, a quantidade de combustível também triplicará; reduzindo a medida da distância percorrida à metade, a quantidade de combustível também será reduzida à metade; e assim por diante. Dessa maneira, a medida da distância percorrida e a quantidade de combustível gasta são grandezas diretamente proporcionais.
Como são grandezas diretamente proporcionais, temos:
e
A fração irredutível obtida nas simplificações é a mesma, então as frações são equivalentes e, assim, podemos escrever a seguinte proporção:
Proporção é uma igualdade entre duas razões.
Uma das maneiras de ler essa proporção é: 100 está para 400 assim como 7 está para 28.
Podemos multiplicar os dois membros da proporção inicialmente por 28 e, em seguida, por 400, sem ela se alterar.
1º.
2º.
3º.
De maneira prática, essas multiplicações equivalem a multiplicar o numerador de uma fração pelo denominador da outra.
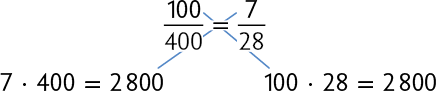
Assim, .
Página 218
Podemos calcular quantos quilômetros o carro de Joana percorre, em média, com de combustível. Para isso, vamos denominar x a medida da distância que o carro percorre com de combustível. Assim, temos:
Medida da distância (em )
100
x
Quantidade de combustível (em )
7
42
Como a distância percorrida e a quantidade de combustível gasta são grandezas diretamente proporcionais, podemos escrever a seguinte proporção:
Resolvemos essa proporção e obtemos o valor de x.
Atenção!
Na proporção a seguir, o produto de x e 7 é igual ao produto de 100 e 42.
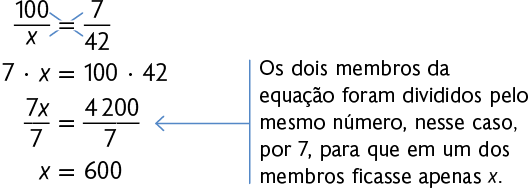
Assim, o carro de Joana percorre, em média, com de combustível.
Agora, analise outra situação.
Um pai dividiu uma herança de R$ 64.900,00 entre seus dois filhos de 35 e 24 anos de idade. A herança foi dividida em partes diretamente proporcionais às suas idades. Sabendo disso, quantos reais cada filho recebeu?
Como a herança foi dividida em partes diretamente proporcionais às idades, adicionamos as idades dos filhos , que corresponde ao total da herança, em reais. Depois, organizamos as informações para calcular quantos reais o filho mais velho recebeu.
Filho mais velho
Idade (em anos)
59
35
Herança (em R$)
64.900
x
Portanto, o filho mais velho recebeu R$ 38.500,00 de herança.
Questão 3. Agora, em seu caderno, de maneira semelhante, calcule quantos reais o filho mais novo recebeu.
Resposta: R$ 26.400,00.
Página 219
Atividades
Faça as atividades no caderno.
7. Determine o valor de x de modo que os números da coluna A sejam diretamente proporcionais aos números da coluna B.
a)
|
A |
B |
|---|---|
|
3 |
2 |
|
x |
8 |
b)
|
A |
B |
|---|---|
|
5 |
x |
|
3 |
6 |
Respostas: a) ; b)
8. Efetue os cálculos e determine o valor de x nas proporções a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
Respostas: a) ; b) ; c) ; d) ; e) ; f) ; g) ; h) .
9. Misturando de tinta branca com de tinta azul, Renato obteve determinada tonalidade de tinta. Quantos litros de tinta azul ele deve misturar a de tinta branca para obter a mesma tonalidade da primeira mistura?
Atenção!
Tinta branca (em )
5
30
Tinta azul (em )
4
x
Resposta: .
10. Com 3 latas de leite condensado, Camila prepara 130 docinhos. Quantas latas de leite condensado ela vai precisar para fazer uma encomenda de 650 docinhos iguais a esse?
Atenção!
Quantidade de latas de leite condensado
3
x
Quantidade de docinhos
130
650
Resposta: 15 latas de leite condensado.
11. Uma bomba puxa de água a cada . Quantos litros de água essa mesma bomba puxa em ?
Resposta: .
12. Fábio comprou um pedaço de queijo com e pagou R$ 6,50. Quantos gramas desse mesmo queijo ele poderá comprar com R$ 26,00?
Resposta: .
13. Dois amigos, de 10 e 12 anos de idade, repartirão entre si 121 figurinhas em partes diretamente proporcionais a suas idades. Quantas figurinhas o amigo mais novo vai receber?
Resposta: 55 figurinhas.
14. O café é uma fruta originária da Etiópia, na África. Porém foram os árabes que propagaram a cultura do café pelo mundo. A palavra "café" originou-se do termo árabe qahwa, que significa vinho, por isso, na Europa, o café era conhecido como "vinho da Arábia".
Sabendo que de café cru em grãos rendem de café torrado, quantos quilogramas de café cru serão necessários para obter de café torrado?
Resposta: .
15. Carla, Sílvia e Gustavo compraram uma empresa em sociedade. Cada um participou, respectivamente, com as seguintes quantias em dinheiro: R$ 10.000,00, R$ 20.000,00 e R$ 30.000,00. No balanço do final do ano, foi verificado que a empresa teve lucro de R$ 12.000,00, o qual foi repartido entre os sócios em partes diretamente proporcionais às quantias investidas. Quantos reais cada sócio recebeu?
Resposta: Carla: R$ 2.000,00; Silvia: R$ 4.000,00; Gustavo: R$ 6.000,00.
16. Leia a frase a seguir.
Uma máquina produz peças em .
De acordo com essa frase, elabore uma pergunta em que seja possível resolver uma situação-problema por meio de grandezas diretamente proporcionais. Depois, apresente sua pergunta a um colega e verifique se ele a responde corretamente.
Resposta pessoal.
Página 220
Regra de três e grandezas inversamente proporcionais
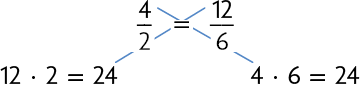
Para fazer determinado serviço, 2 pintores levam 12 dias. Trabalhando no mesmo ritmo, 4 pintores levam 6 dias para fazer o mesmo serviço. Assim, temos:
Quantidade de pintores
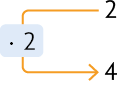
Medida de tempo (em dias)
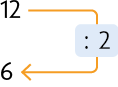
Essas grandezas são inversamente proporcionais, pois, quando dobramos a quantidade de pintores (de 2 para 4), a quantidade de dias reduz-se pela metade (de 12 para 6). Nessa situação, temos:
e
Como a fração irredutível obtida nas simplificações não é a mesma, concluímos que as frações não são equivalentes. De fato, essas frações não poderiam ser equivalentes, pois, se fossem, as grandezas seriam diretamente proporcionais.
Contudo, se invertemos uma das frações, obtemos uma proporção.
, pois e ou , pois e
Desse modo, obtemos uma proporção tal que, multiplicando o numerador de uma fração pelo denominador da outra, obtemos o mesmo resultado.
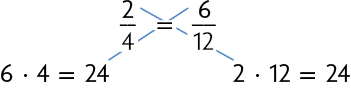
ou
É possível calcular quantos pintores deveriam ser contratados para realizar o mesmo serviço em 3 dias, mantendo o mesmo ritmo de trabalho, usando procedimento semelhante.
Para resolvermos essa situação, vamos chamar de x a quantidade de pintores que deveria ser contratada.
Quantidade de pintores
2
x
Medida de tempo (em dias)
12
3
Como a quantidade de pintores e a medida de tempo gasto para fazer o serviço são grandezas inversamente proporcionais, invertemos uma das frações e escrevemos a proporção.
Página 221
Resolvemos, então, usando a regra de três e obtemos o valor de x.
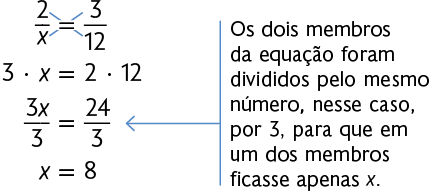
Assim, deveriam ser contratados 8 pintores para realizar o mesmo serviço em 3 dias.
Atividades
Faça as atividades no caderno.
17. Determine o valor de x de modo que os números da coluna A sejam inversamente proporcionais aos números da coluna B.
a)
|
A |
B |
|---|---|
|
x |
12 |
|
6 |
8 |
b)
|
A |
B |
|---|---|
|
9 |
8 |
|
24 |
x |
Respostas: a) ; b) .
18. Lendo 12 páginas por dia, Regina conseguiu terminar de ler um livro em 28 dias.
a) Mantendo o mesmo ritmo de leitura, quantas páginas Regina deveria ter lido por dia, para que tivesse concluído a leitura do livro em 16 dias?
b) Quantas páginas esse livro tem?
Atenção!
Quantidade de páginas lidas por dia
12
x
Medida de tempo (em dias)
28
16
Respostas: a) 21 páginas; b) 336 páginas.
19. Com certa quantidade de ração, Joaquim alimenta 40 cabeças de gado durante 7 dias. Durante quantos dias essa mesma quantidade de ração será suficiente para alimentar 70 cabeças de gado?
Atenção!
Quantidade de cabeças de gado
40
70
Quantidade de dias
7
x
Resposta: 4 dias.
20. Cléber fez o percurso entre duas cidades em , com medida de velocidade média de . Que medida da velocidade média ele deveria manter para fazer o mesmo percurso em ?
Resposta: .
21. Para retirar o entulho de uma construção, um caminhão com medida de capacidade de fez viagens. Se fosse utilizado um caminhão com medida de capacidade de , quantas viagens seriam necessárias?
Resposta: 20 viagens.
22. A água potável levada a um acampamento com 45 pessoas é suficiente para 7 dias. Caso fossem 18 pessoas a mais no acampamento, essa mesma quantidade de água seria suficiente para quantos dias?
Resposta: 5 dias.
23. Elabore uma atividade cujas grandezas estejam no quadro a seguir. Em seguida, dê para um colega resolver. Por fim, verifique se a resposta está correta.
Atenção!
Quantidade de máquinas
4
10
Quantidade de dias
25
x
Resposta pessoal.
Página 222
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Débora abasteceu seu carro bicombustível com de gasolina a R$ 7,26 o litro. O litro do etanol custava R$ 5,14.
Com o mesmo valor gasto para abastecer o carro com gasolina, Débora abasteceria seu carro com aproximadamente quantos litros de etanol?
Resposta: Aproximadamente .
2. Densidade demográfica é a quantidade média de habitantes de um lugar por quilômetro quadrado. Se dissermos, por exemplo, que a densidade demográfica de um lugar é , queremos dizer que nesse local há, em média, habitantes para cada quilômetro quadrado.
A tabela a seguir registra dados sobre a população e a densidade demográfica dos estados da Região Sul do Brasil, de acordo com a projeção estimada pelo IBGE em 2021.
|
Estado |
População |
Densidade demográfica (em ) |
|---|---|---|
|
Paraná |
11.597.484 |
58,19 |
|
Santa Catarina |
7.338.473 |
76,66 |
|
Rio Grande do Sul |
11.466.630 |
40,7 |
Fonte de pesquisa: IBGE. Cidades e Estados. Disponível em: https://oeds.link/2Q3MtT. Acesso em: 17 mar. 2022.
De acordo com essas informações, determine a medida da área total aproximada dos estados da Região Sul, em 2021.
Resposta: Paraná: , Santa Catarina: ; Rio Grande do Sul: .
3. Determine um valor para x de modo que os números da coluna A sejam, em relação aos números da coluna B:
a) diretamente proporcionais.
b) inversamente proporcionais.
|
A |
B |
|---|---|
|
6 |
10 |
|
x |
12 |
Respostas: a) ; b) .
4. Seja para passeio, exercícios físicos ou locomoção, andar de bicicleta pode ser um modo muito prazeroso de prevenir problemas de saúde, manter o bem-estar, a qualidade de vida e ainda preservar o meio ambiente.
Pensando nesses benefícios, Bruna anda frequentemente de bicicleta. Certo dia, ela fez um percurso em com uma medida de velocidade média de . Para fazer o mesmo percurso em , Bruna deve andar com qual velocidade média?
Resposta: .
5. Para comprar 1.800 dólares em certo dia, Guilherme gastou R$ 9.072,00. Considerando o mesmo dia, quantos:
a) reais ele gastará para comprar 2.500 dólares?
b) dólares ele compraria com R$ 14.112,00?
Respostas: a) R$ 12.600,00; b) 2.800 dólares.
6. Com uma
peça de tecido Jaqueline faz 28 camisetas P longa ou 35 de tamanho M de modelo baby look.
Sabendo que Jaqueline já fez 25 das camisetas de tamanho M, determine a quantidade de camisetas de tamanho P que é possível produzir com o que sobrou da peça de tecido.
Resposta: Jaqueline conseguirá fazer 8 camisetas de tamanho P.