1. O mosaico apresentado a seguir é formado por polígonos regulares.

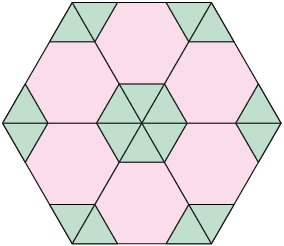
a) Em uma folha de papel avulsa, escreva o nome dos polígonos regulares usados para formar esse mosaico.

b) Na imagem, está indicado o ângulo externo de um polígono idêntico ao usado no mosaico. Qual é a medida desse ângulo externo?

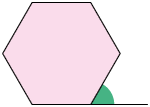
c) O que podemos afirmar em relação à medida do ângulo externo do polígono rosa e à medida do ângulo interno do polígono verde?

2. Em cada item, verifique se é possível construir um triângulo com base nas medidas dos comprimentos dos segmentos dados. Justifique sua resposta.

a) $2\text{cm}$, $5\text{cm}$ e $2\text{cm}$.

b) $3\text{cm}$, $5\text{cm}$ e $6\text{cm}$.

c) $6\text{cm}$, $8\text{cm}$ e $10\text{cm}$.

d) $15\text{cm}$, $9\text{cm}$ e $5\text{cm}$.

3. Em cada item, compare os números substituindo cada ■ pelo símbolo $>$ ou $<$.

a) $-5\text{█}-4$

b) $-10\text{█}10$

c) $-7\text{█}-8$

d) $0\text{█}6$

e) $-6\text{█}0$

f) $9\text{█}-9$

4. Eduarda tem em seu estojo 60 lápis de cor. Ela verificou que $\frac{1}{5}$ desses lápis são em tons de verde, sendo metade deles em tons claros de verde.

a) Determine a quantidade de lápis de cor em tons de verde que Eduarda tem.

b) Que fração do total de lápis de cor representa a quantidade de tons claros de verde? Quantos são esses lápis?

5. Em uma folha de papel avulsa, escreva o número correspondente a cada uma das letras apresentadas na reta numérica.

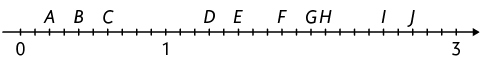
6. Para preparar $2\text{L}$ de tinta, são necessários $60\text{mL}$ de água. Sabendo que as grandezas são diretamente proporcionais, quantos mililitros de água são necessários para preparar $4,5\text{L}$ de tinta?

7. Certo carro custava R$ 32.500,00 no mês de janeiro. Para aumentar as vendas, no mês de fevereiro, o lojista ofereceu um desconto de 5% sobre o preço de janeiro. Em decorrência da valorização dos automóveis, foi aplicado em março um acréscimo de 10% sobre o preço de fevereiro. Sendo assim, qual foi o preço desse carro em março?

8. A empresa onde Cláudia é gerente fez uma pesquisa para verificar se todas as caixas com formato de paralelepípedo reto retângulo produzidas têm volume interno máximo medindo $500{\text{dm}}^3$. A seguir estão indicadas as medidas das dimensões internas de cada modelo.

Dimensões internas de diferentes modelos de caixas

Modelo	Medida da altura ($\mathrm{d}\mathrm{m}$)	Medida do comprimento ($\mathrm{d}\mathrm{m}$)	Medida da largura ($\mathrm{d}\mathrm{m}$)
A	7	8	6,5
B	7,5	6,5	8
C	9	8	7
D	6	7,5	9
E	8,5	9	8

a ) Determine a medida do volume interno, em decímetros cúbicos, de cada um dos modelos de caixa.

b ) Dos modelos de caixa, algum tem volume interno com medida maior do que a estipulada? Se sim, cite os que você identificar.

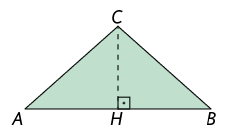
9. Leia as informações e classifique os triângulos de acordo com a medida do comprimento de seus lados. Em seguida, calcule a medida da área de cada um deles.

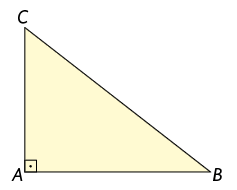
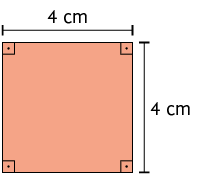
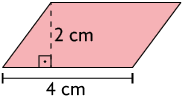
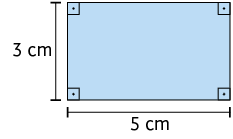
10. Em uma folha de papel avulsa, calcule a medida da área dos quadriláteros.

11. Para representar cada figura da sequência a seguir, adiciona-se um palito em cada lado do quadrado representado, a partir do segundo.

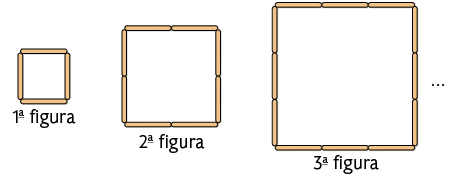
a) Quantos palitos terá a 4ª figura dessa sequência?

b) Escreva, em uma folha de papel avulsa, uma expressão algébrica que expresse a quantidade de palitos de cada figura dessa sequência. Use n para indicar a posição da figura.

c) Utilizando a expressão algébrica que você escreveu no item anterior, determine quantos palitos terá a sétima e a décima quinta figura dessa sequência.

12. Cláudio é técnico de basquetebol e fez uma pesquisa entre seus jogadores para saber a medida da altura de cada um deles. Com os dados coletados, ele construiu o gráfico a seguir.

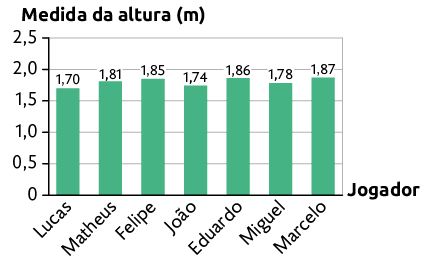
Fonte de pesquisa: anotações do técnico Cláudio.

a) Qual é a média das medidas de altura desses jogadores?

b) Determine a amplitude do conjunto de dados coletados pelo técnico Cláudio.

13. As balanças representadas a seguir estão em equilíbrio e as caixas indicadas com mesma letra têm medidas de massa iguais.

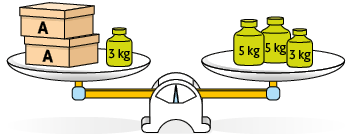
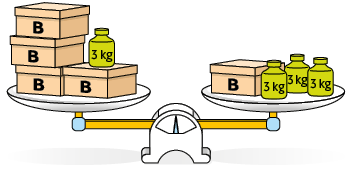
Qual é a medida da massa de cada caixa?

14. De dezembro a março é inverno no hemisfério Norte e verão no hemisfério Sul. As estações do ano ocorrem por causa da inclinação da Terra em relação ao Sol. Por isso, há regiões no mundo com medidas de temperatura muito diferentes umas das outras. Analise a seguir um exemplo de termômetro que indica a medida de temperatura no mesmo horário e no mesmo dia em duas cidades em hemisférios diferentes.

Qual é a diferença entre essas medidas de temperatura?

15. Sofia confeccionou algumas fichas com números e cores diferentes, como representado na imagem, e vai colocá-las em uma urna para fazer sorteios.

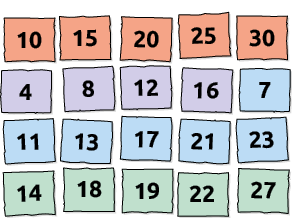
a) A chance de Sofia retirar aleatoriamente uma ficha roxa é igualmente provável à de retirar uma ficha azul? Justifique sua resposta.

b) Qual é a probabilidade de Sofia retirar aleatoriamente uma ficha com um número par? E com um número menor do que 22?