Página 29
UNIDADE
2
Conjuntos

Agora vamos estudar...
- a ideia de conjunto;
- relações entre conjuntos;
- alguns conjuntos numéricos, como o dos números naturais, o dos números inteiros e o dos números racionais;
- dízima periódica.
Página 30
Estudando conjuntos
Em muitas das atividades que realizamos no dia a dia, é preciso classificar e separar objetos em grupos ou classes, ou seja, formar coleções deles. Nesses casos, estamos formando conjuntos.
Analise na imagem alguns itens que foram dispostos em cima de uma mesa.

Os objetos foram separados em dois conjuntos, de acordo com as características da superfície de cada um deles.
Cada objeto de um conjunto é chamado elemento. Geralmente, os conjuntos são nomeados por letras maiúsculas e seus elementos são dispostos entre chaves, separados por vírgula. Acompanhe alguns exemplos.
Denominamos A o conjunto dos divisores positivos de 24.
Denominamos B o conjunto dos divisores positivos de 40.
Denominamos C o conjunto dos divisores positivos de 12.
O conjunto que não tem elementos é chamado conjunto vazio e pode ser indicado por ou . Por exemplo, o conjunto dos divisores pares de 15 é vazio, pois 15 não tem divisor par. Assim, nomeando esse conjunto por D, temos ou .
Os conjuntos A, B e C, representados anteriormente, são denominados conjuntos finitos, pois seus elementos podem ser contados, ou seja, podemos associá-los aos números naturais de 1 até certo número n.
Já o conjunto dos números ímpares maiores do que 19 é um conjunto infinito, pois não é finito. Para o representarmos, escrevemos alguns de seus elementos seguidos de reticências. Nomeando esse conjunto por E, temos:
Página 31
Quando um objeto é elemento de um conjunto, dizemos que ele pertence ao conjunto. Vamos analisar alguns exemplos.
- 3 é divisor de 24, então ele pertence ao conjunto A dos divisores positivos de 24. Indicamos esse fato por (lê-se: 3 pertence a A).
- 8 é divisor de 40, então ele pertence ao conjunto B dos divisores positivos de 40. Indicamos esse fato por .
Do mesmo modo, dizemos que um objeto não pertence a um conjunto quando ele não é elemento do conjunto. Analisaremos alguns exemplos.
- 3 não é divisor de 40, então ele não pertence ao conjunto B dos divisores positivos de 40. Indicamos esse fato por: (lê-se: 3 não pertence a B).
- 8 não é divisor de 12, então ele não pertence ao conjunto C dos divisores positivos de 12. Indicamos esse fato por: .
Podemos representar os conjuntos A, B e C por meio do diagrama de Venn.
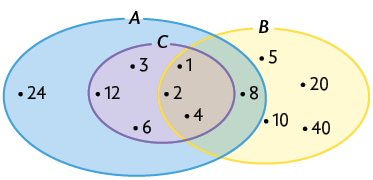
Analisando o diagrama, percebemos que todos os elementos de C também são elementos de A. Então, dizemos que o conjunto C está contido no conjunto A e indicamos da seguinte maneira: (lê-se: C está contido em A).
Atenção!
O conjunto vazio está contido em qualquer conjunto.
Além disso, embora o conjunto C tenha elementos comuns com B, nem todos os elementos de C pertencem a B. Então, dizemos que C não está contido em B e indicamos do seguinte modo: (lê-se: C não está contido em B).
Atenção!
Os símbolos e são utilizados para indicar pertinência ou não de um elemento a um conjunto. E os símbolos e indicam a inclusão ou não de um conjunto em outro.
O conjunto formado por todos os elementos comuns a dois ou mais conjuntos é denominado conjunto interseção. Por exemplo, os números 1, 2, 4 e 8 estão tanto no conjunto A como no conjunto B, ou seja, 1, 2, 4 e 8 são todos os números que pertencem aos conjuntos A e B simultaneamente. Podemos indicar esse conjunto interseção da seguinte maneira:
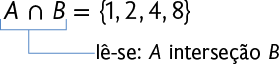
Considerando todos os elementos de A e todos os elementos de B, podemos formar o conjunto união de A e B, o qual pode ser representado do seguinte modo:

Questão 1. Em seu caderno, escreva os elementos dos conjuntos e .
Página 32
Atividades
Faça as atividades no caderno.
1. Junte-se a um colega para realizar esta atividade.
Uma professora de Matemática levou alguns objetos para a sala de aula: colher, régua, tesoura, sabonete, revista, frasco de xampu, tubo de creme dental, moeda, jornal e garrafa de suco. Ela os colocou em cima de uma mesa, como representado a seguir, e pediu a Ricardo que escolhesse alguns objetos com características comuns e formasse um conjunto.

Ao final, Ricardo fez anotações no caderno a respeito do conjunto formado.

Assim como Ricardo, formem outros três conjuntos com alguns dos objetos apresentados. Em seguida, descrevam o critério de classificação usado e indiquem a quantidade de elementos contida em cada conjunto formado.
Imagens não proporcionais entre si.
2. Escreva no caderno os conjuntos a seguir, explicitando seus elementos entre chaves.
a) Múltiplos positivos de 3 menores do que 40.
b) Divisores positivos de 55 maiores do que 10.
c) Múltiplos positivos de 7 maiores do que 20 e menores do que 38.
d) Divisores positivos de 80 menores do que 60.
3. Considerando os elementos dos conjuntos A, B, C e D, copie no caderno os itens, substituindo cada pelo símbolo ou .
a)
b)
c)
d)
e)
f)
g)
h)
4. A relação entre os conjuntos A, B, C e D está representada pelo diagrama a seguir.
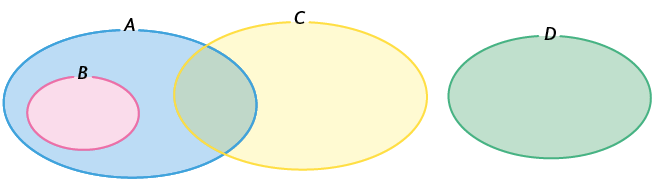
Verifique se as afirmações são verdadeiras ou falsas.
a)
b)
c)
d)
e)
f)
Página 33
5. No esquema a seguir, foram contornados alguns números para obter os conjuntos A, B, C e D.
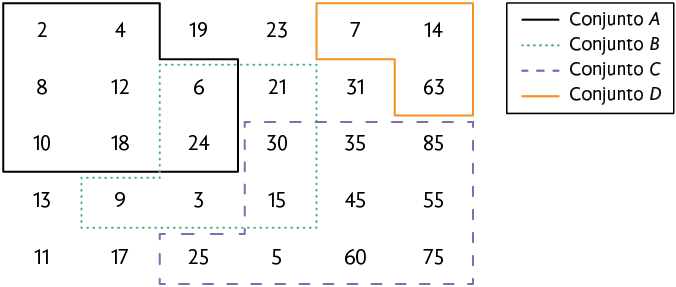
Podemos representar o conjunto A como: .
Usando a notação entre chaves, represente no caderno o conjunto:
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
i) .
6. Escreva no caderno:
a) o conjunto A formado pelos números naturais pares maiores do que 7 e menores do que 20.
b) o conjunto B formado pelos números naturais ímpares maiores do que 7 e menores do que 20.
c) o conjunto interseção de A e B.
7. Copie no caderno os itens a seguir e, com base no diagrama de Venn apresentado, substitua cada pelo símbolo , , ou .
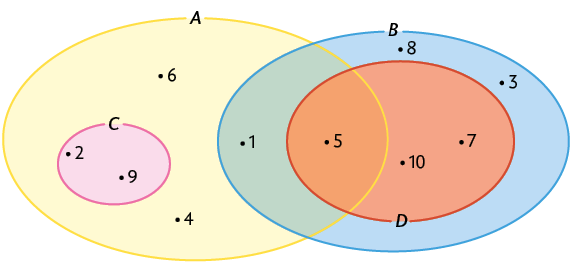
a)
b)
c)
d)
e)
f)
8. O diagrama a seguir mostra o resultado de uma pesquisa relacionada à leitura de dois jornais produzidos em uma escola. Nele, os números indicam as quantidades de leitores.
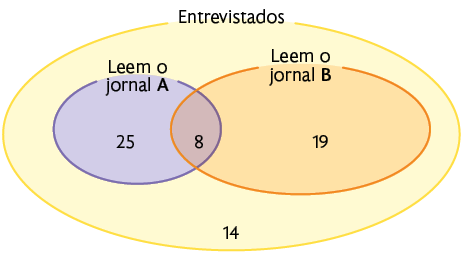
a) Quantos entrevistados leem pelo menos um dos jornais?
b) Quantos entrevistados não leem nenhum dos jornais?
c) Quantos entrevistados leem apenas o jornal A? E quantos leem apenas o jornal B?
d) Quantos entrevistados leem ambos os jornais?
e) Ao todo, quantas pessoas foram entrevistadas?
Página 34
Conjuntos numéricos
Conjunto dos números naturais e conjunto dos números inteiros
Ao longo da história, o ser humano precisou quantificar o rebanho, os objetos, os membros de sua comunidade etc.
Por essa necessidade, foram criados os números 1, 2, 3, 4, e assim por diante, usados atualmente para representar contagens. Acrescidos do zero, eles formam o conjunto dos números naturais, que indicamos por , representado a seguir.
Podemos destacar algumas características do conjunto dos números naturais.
- Todo número natural tem um sucessor e, com exceção do zero, todo número natural tem um antecessor.
- A soma de dois números naturais é um número natural.
- O produto de dois números naturais é um número natural.
- O conjunto é infinito e não há um número natural maior do que todos os outros, pois todo número natural tem um sucessor.
Os números naturais, no entanto, não foram suficientes para dar conta de novas necessidades que surgiram com o passar dos anos, como a situação de representar uma dívida. Por isso, foram criados os números inteiros negativos, que, reunidos aos números naturais, formam o conjunto dos números inteiros, representado por .
Qualquer número natural também é inteiro. Podemos representar a relação entre o conjunto dos números naturais e o conjunto dos números inteiros em um diagrama de Venn.
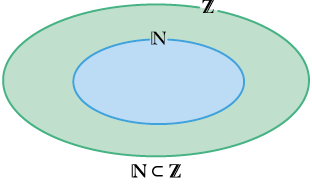
O conjunto dos números naturais está contido no conjunto dos números inteiros.
Página 35
Existem infinitos números inteiros. Alguns desses números foram representados por meio de pontos na reta numérica a seguir.
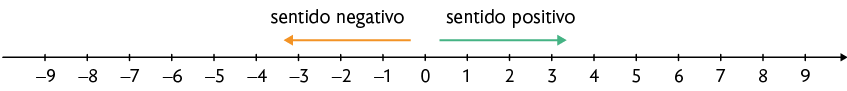
Podemos destacar as seguintes características do conjunto dos números inteiros.
- Cada número inteiro tem um antecessor e um sucessor. Por exemplo, em relação ao número , o antecessor é e o sucessor é .
- A soma e a diferença entre dois números inteiros também é um número inteiro.
- O produto de dois números inteiros também é um número inteiro.
Questão 2. Em seu caderno, escreva o antecessor e o sucessor dos números a seguir.
a) 25
b)
c)
Conjunto dos números racionais
Além dos conjuntos mencionados ( e ), há também o conjunto dos números racionais, que indicamos por , cujos elementos são obtidos da divisão de dois números inteiros em que o divisor é diferente de zero.
Os números racionais podem ser expressos tanto por fração como por um número na forma decimal. Acompanhe alguns exemplos.
Os números inteiros também são racionais, pois qualquer inteiro pode ser representado por uma fração. Podemos indicar os números inteiros e 4, por exemplo, obtendo frações equivalentes a eles.
Os números racionais são aqueles que podem ser representados na forma , sendo a e b números inteiros, com .
Página 36
No diagrama de Venn, está representada a relação entre os conjuntos dos números naturais , dos inteiros e dos racionais .
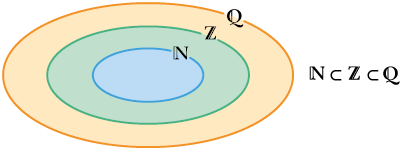
O conjunto dos números naturais está contido no conjunto dos inteiros, que, por sua vez, está contido no conjunto dos racionais.
Questão 3. Em seu caderno, escreva o número na forma , sendo a e b números inteiros, com .
Ao dividirmos dois números inteiros, podemos ter três opções para o quociente.
- Um número inteiro, quando a divisão for exata. Por exemplo, .
- Um número decimal com quantidade finita de casas decimais. Por exemplo:
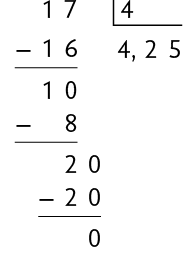
Um número decimal com infinitas casas decimais com algarismos que se repetem obedecendo a um padrão. Por exemplo:
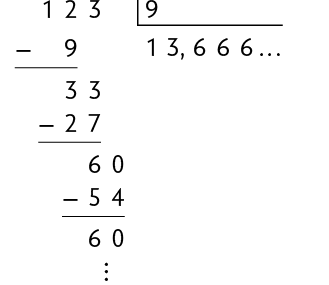
Na divisão de 123 por 9, o algarismo 6 repete-se infinitamente no quociente. Quando isso ocorre, chamamos o número racional obtido no quociente de dízima periódica. O padrão de repetição infinita de um ou mais algarismos define o período da dízima.
Podemos representar uma dízima periódica escrevendo a fração associada a ela. Também podemos indicar o número na forma decimal com reticências ou, ainda, com um traço sobre o período. Por exemplo, ou ou .
O padrão de repetição de uma dízima periódica pode ocorrer de diferentes maneiras. Acompanhe alguns exemplos.
- ou
- ou
- ou
- ou
Página 37
Podemos representar números racionais por meio de pontos em uma reta numérica.

Com relação ao conjunto dos números racionais, podemos destacar as características a seguir.
- A soma e a diferença entre dois números racionais também é um número racional.
- O produto de dois números racionais é um número racional.
- O quociente da divisão de um número racional por outro racional, diferente de zero, é também um número racional.
Fração geratriz
As frações que geram as dízimas periódicas são chamadas frações geratrizes. Exemplos.
Acompanhe os cálculos para obter a fração geratriz da dízima periódica .
1º. Consideramos x a parte decimal da dízima periódica , ou seja, .
2º. Multiplicamos ambos os membros da equação por uma potência de base 10 cujo expoente seja igual à quantidade de casas decimais no período da dízima. Nesse caso, .
3º. Subtraímos x de ambos os membros da equação , o que resulta em:
4º. Por fim, adicionamos a parte inteira à parte decimal na forma fracionária.
Portanto, .
Página 38
Atividades
Faça as atividades no caderno.
9. Determine quais das situações a seguir apresentam números naturais, quais delas apresentam números inteiros e quais apresentam números racionais.




10. Considere os números a seguir.
Escreva no caderno quais deles pertencem ao conjunto dos números:
a) naturais.
b) inteiros.
c) racionais.
11. Copie os itens no caderno, substituindo cada pelo símbolo ou .
a) .
b) .
c) .
d) .
e)
f) .
g) .
h) .
12. Copie no caderno as afirmações, corrigindo as que estão incorretas.
a) Todo número natural é também um inteiro.
b) O conjunto dos números inteiros está contido no conjunto dos números naturais.
c) Todo número racional pode ser representado por uma fração.
d) Todos os números inteiros pertencem ao conjunto dos números naturais.
e) Todo número fracionário pertence ao conjunto dos números racionais.
13. Escreva no caderno:
a) dois números naturais maiores do que 20.
b) três números inteiros menores do que 0.
c) dois números racionais negativos.
d) quatro números racionais entre e 1.
14. Verifique se as afirmações a seguir são verdadeiras ou falsas, no caderno, copie e corrija as falsas.
a) .
b) .
c) .
d) .
e) .
f) .
g) .
h) .
Página 39
15. Analise os números a seguir e, no caderno, relacione em pares os números que têm o mesmo valor.
-
0,375
16. Escreva no caderno as frações a seguir na forma decimal.
a)
b)
c)
d)
e)
f)
17. Acompanhe o procedimento de Beatriz para escrever o número 0,8 na forma fracionária.
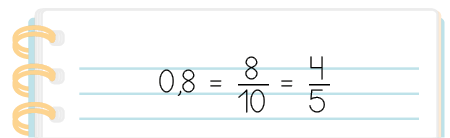
Escreva no caderno os números decimais a seguir na forma fracionária. Depois, assim como Beatriz, simplifique cada fração, tornando-a irredutível.
a)
b)
c)
d)
18. Considere os números a seguir.
Cada letra indicada na reta numérica a seguir representa um dos números apresentados.
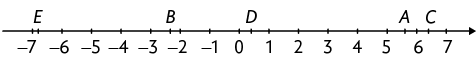
Qual número cada letra representa?
19. Determine os dois números inteiros consecutivos que substituem de maneira correta cada .
a) .
b) .
c) .
d) .
20. Escreva no caderno a fração geratriz da dízima periódica indicada em cada item.
a)
b)
c)
d)
21. Para obter a fração geratriz da dízima periódica , Lucas realizou alguns cálculos. Acompanhe o procedimento dele.

De maneira semelhante ao procedimento de Lucas, escreva no caderno a fração geratriz de cada dízima periódica a seguir.
a)
b)
c)
d)
Página 40
Conjunto dos números irracionais
Existem números racionais cujas infinitas casas decimais não são dízimas periódicas, pois os algarismos da parte decimal não estabelecem um padrão de repetição. Os números decimais com essa característica formam o conjunto dos números irracionais, que representamos por .
Verifique alguns exemplos de números irracionais.
Os números irracionais não podem ser representados por uma fração, ou seja, não é possível escrevê-los na forma , sendo a e b números inteiros, com .
No diagrama de Venn a seguir, está representada a relação entre os conjuntos dos números naturais , dos inteiros , dos racionais e dos irracionais .
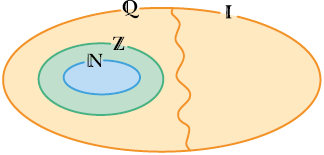
Atenção!
Convém destacar que todas as raízes quadradas não exatas de números naturais são números irracionais.
Ao realizar adições, subtrações, multiplicações e divisões envolvendo apenas números irracionais, o resultado pode ser tanto um número racional quanto um irracional, dependendo dos números com os quais se opera.
Conjunto dos números reais
Ao considerarmos a união do conjunto dos números racionais com o dos números irracionais, obtemos o conjunto dos números reais, que indicamos por .
Assim, todos os números estudados até agora também pertencem ao conjunto dos números reais.
e
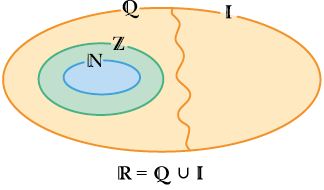
Podemos representar números reais em uma reta numérica.

Uma reta numérica que representa os números reais é chamada reta real.
Atenção!
Em algumas situações, é necessário excluir o zero dos conjuntos numéricos. Para representar um conjunto excluindo o zero, usamos o asterisco (*). Por exemplo:
Página 41
Atividades
Faça as atividades no caderno.
22. Escreva no caderno:
a) três números reais que pertençam ao conjunto dos números inteiros.
b) dois números que não pertençam ao conjunto dos números racionais.
c) quatro números que pertençam à união dos conjuntos dos números racionais e dos números irracionais.
d) cinco números reais entre e .
e) três números reais entre e .
f) dois números racionais entre 0 e 1.
23. Determine o símbolo que substitui corretamente cada ■, usando , , ou .
a)
b)
c)
d)
e)
f)
g)
h)
i)
24. Cada número a seguir pertence a mais de um conjunto numérico. Escreva no caderno a que conjuntos (, , , e ) pertence cada um deles.
a)
b)
c)
d)
e)
f)
25.No caderno, associe cada número apresentado a uma das letras indicadas na reta numérica.
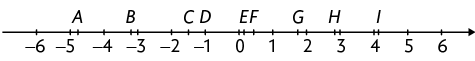
26. Analise os números do quadro.
- 20
- 0
Escreva no caderno quais dos números apresentados pertencem ao conjunto dos números:
a) naturais.
b) inteiros.
c) racionais.
d) irracionais.
e) reais.
27. Com base na reta numérica apresentada, substitua cada por ou para indicar se o número representado pela letra pertence ou não ao conjunto.
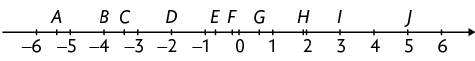
28. Junte-se a um colega, desenhem no caderno uma reta numérica e, nela, representem os seguintes números.
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
Página 42
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Os conjuntos A, B, C e D estão representados por meio dos diagramas a seguir. Escreva, em uma folha de papel avulsa, o conjunto indicado em cada item, apresentando os elementos entre chaves.
a)
b)
c)
d)
e)
f)
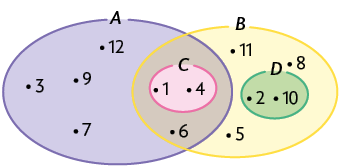
2. Sabendo que , e , escreva em uma folha de papel avulsa os elementos do conjunto A.
3. Quais dos números a seguir são naturais?
-
7
-
5
-
8
-
0,8
-
2
4. Em uma folha de papel avulsa, escreva em ordem crescente os números a seguir.
-
1
-
0
-
16
5. Escreva em uma folha de papel avulsa:
a) um número racional entre e .
b) dois números racionais entre e .
c) três números racionais entre e .
6. Determine, em uma folha de papel avulsa, um número racional que substitua cada de modo que as sentenças se tornem verdadeiras.
a)
b)
c)
d)
7. Junte-se a um colega e verifiquem se as afirmações a seguir são verdadeiras ou falsas.
a) O conjunto dos números reais corresponde à união dos conjuntos dos racionais e dos irracionais.
b) Todo número real é racional, mas nem todo número racional é real.
c) Todo número natural é um inteiro.
d) é um número racional.
8. (Saresp-2005) A parte decimal da representação de um número segue o padrão de regularidade indicado:
Este número é:
a) racional não inteiro.
c) irracional negativo.
b) inteiro negativo.
d) irracional positivo.
9. Copie, em uma folha de papel avulsa, somente as sentenças verdadeiras.
A.
B.
C.
D.
E.
F.
10.
Sabendo
que o produto de dois números irracionais pode ser um número racional, escreva,
em uma folha de papel avulsa, um exemplo dessa situação.