Página 115

UNIDADE

Transformações geométricas

Fotografia. Representação do espaço, em que há o planeta Terra e o Sol. A Terra está mais à frente com parte dela iluminada pelo Sol, que está um pouco mais ao fundo e é menor. — Representação do planeta Terra, durante execução do movimento em torno de si mesmo, conhecido como rotação, e do movimento ao redor do Sol, denominado translação.

Agora vamos estudar...

transformação de reflexão;
transformação de rotação;
transformação de translação;
composição de transformações.

Página 116

Estudando transformações geométricas

Você estudou algumas transformações geométricas no 7º ano. Vamos relembrá-las?

Transformação de reflexão

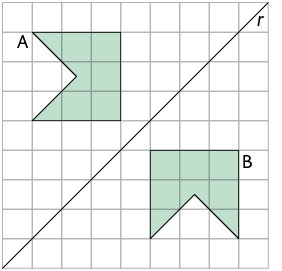
A figura B foi construída refletindo a figura A em relação à reta $r$ (eixo). Nesse caso, para construir a figura B, aplicou-se uma transformação de reflexão na figura A em relação ao eixo r.

Ilustração de uma malha quadriculada com duas figuras iguais, em formato de bandeirinha, com uma reta r entre elas. À esquerda, indicada por A, a figura está de lado, com as pontas viradas para a esquerda. À direita, indicada por B, está a outra figura, com as pontas viradas para baixo.

Atenção!

A figura obtida ao aplicarmos uma transformação em uma dada figura chama-se imagem da figura inicial. No exemplo apresentado, B é a imagem da figura A pela transformação de reflexão em relação ao eixo r.

Dizemos que as figuras A e B são simétricas por reflexão em relação ao eixo r.

A imagem de uma figura pela transformação de reflexão é idêntica à figura original.

Transformação de rotação

A figura D foi construída rotacionando a figura C em torno do ponto O. Nesse caso, para construir a figura D, aplicou-se uma transformação de rotação de $90 graus$ na figura C, no sentido horário, em torno do ponto O.

Dizemos que as figuras C e D são simétricas por rotação em torno do ponto O.

Ilustração de uma malha quadriculada com dois polígonos iguais de 6 lados. Há duas linhas tracejadas, perpendiculares entre si, que as unem por um ponto O. Abaixo, a figura C semelhante a uma letra L virada pra baixo e para esquerda. Acima, está a figura D, semelhante a uma letra L feita de forma espelhada.

A imagem de uma figura pela transformação por rotação é idêntica à figura original.

Página 117

Transformação de translação

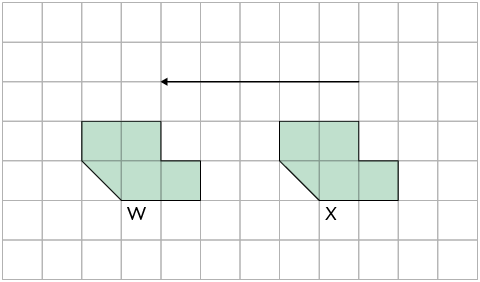
A figura W foi construída transladando a figura X.

Ilustração de uma malha quadriculada com duas figuras iguais lado a lado. A da esquerda é a figura W e a da direita a figura X. Acima, há uma seta da direita para a esquerda, ocupando 5 quadradinhos. Ela indica que cada quadradinho da figura W está a uma distância de 5 unidades do respectivo quadradinho da figura X.

Atenção!

A seta apresentada indica a direção, o sentido e a medida da distância em que a figura deve ser transladada.

Nesse caso, para construir a figura W, foi aplicada na figura X uma transformação de translação na direção horizontal 5 unidades para a esquerda. Dizemos que as figuras W e X são simétricas por translação.

A imagem de uma figura pela transformação de translação é idêntica à figura original.

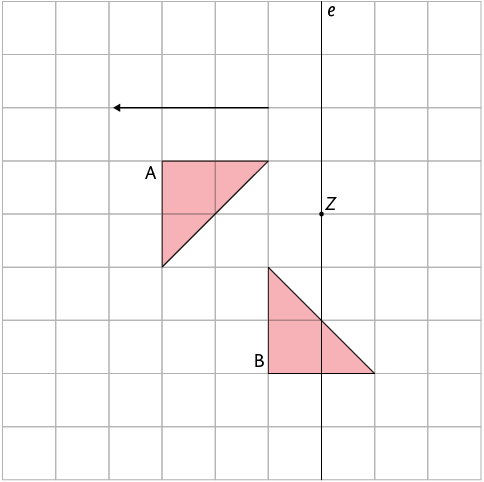
Questão 1. Entre as afirmações a seguir, determine aquela que é verdadeira.

a) A figura B é a imagem da figura A pela transformação de reflexão em relação ao eixo e.

b) A figura B é a imagem da figura A pela rotação de $90 graus$ , no sentido anti-horário, em torno do ponto Z.

c) A figura B é a imagem da figura A pela transformação de translação na direção vertical, 3 unidades para baixo.

d) A figura A é a imagem da figura B pela rotação de $90 graus$ , no sentido anti-horário, em torno do ponto Z.

Ilustração de uma malha quadriculada com duas figuras, uma acima à esquerda da outra. A da esquerda é a figura A que tem acima, uma seta, da esquerda para a direita, ocupando 3 quadradinhos. Há ainda, a uma distância de dois quadradinhos do meio figura A, uma reta indicada por e, que passa pelo ponto z, que também está a uma distância de dois quadradinhos do meio figura B.

Página 118

Instrumentos e softwares

Transformações no plano cartesiano com o GeoGebra

Com o GeoGebra, é possível construir figuras geométricas no plano cartesiano usando transformações de reflexão, rotação ou translação. Execute o passo a passo a seguir.

1º. Clique com o botão direito sobre a Janela de Visualização, habilite a opção Exibir Eixos e, na aba Exibir Malha, escolha a opção Malha Principal.

2º. Para construir os vértices do polígono, digite suas coordenadas no campo Entrada... (por exemplo, $ponto A com coordenadas 1 e 1$ , $ponto B com coordenadas 1 e 3$ , $ponto C com coordenadas 2 e 3$ e $ponto D com coordenadas 2 e 1$ ) e pressione Enter. Com a ferramenta Polígono, clique nos pontos A, B, C, D criados e novamente em A, para construir o quadrilátero $A B C D$ . Construa também dois pontos distintos, como $coordenada 3 e 1$ e $coordenada 4 e 3$ , e trace por eles a reta que será a referência da reflexão.

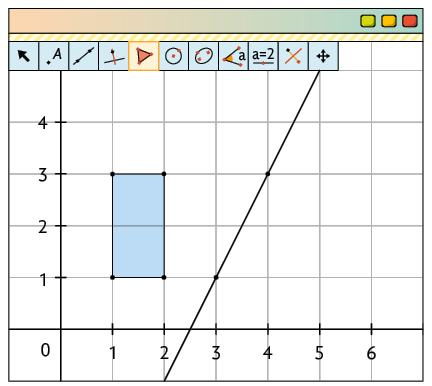
Ilustração. Tela de um software de geometria com um plano cartesiano em uma malha quadriculada. Nele há um quadrilátero desenhado paralelo ao eixo vertical e com vértices com coordenadas 1 e 1; 1 e 3; 2 e 1; 2 e 3. Também há uma reta traçada passando pelo ponto de coordenadas 3 e 1; e pelo ponto de coordenadas 4 e 3. Há ícones de seleção e o ícone de polígono está selecionado.

3º. Com a ferramenta Reflexão em Relação a uma Reta, clique no polígono e, depois, na reta que passa por $coordenada 3 e 1$ e $coordenada 4 e 3$ .

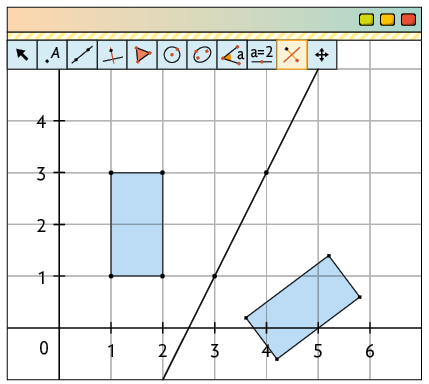
Ilustração. Tela de um software de geometria comum plano cartesiano em malha quadriculada com dois polígonos desenhados. Eles são iguais mas posicionados de maneiras distintas em torno de uma reta entre eles, com dois pontos distintos sobre ela. Um polígono está paralelo ao eixo vertical e o polígono refletido, está inclinado e em cima do eixo horizontal. Há ícones de seleção e o ícone de reflexão está selecionado.

Página 119

Para obter uma figura simétrica por rotação em torno de um ponto, execute os passos a seguir.

1º. Construa o polígono e o ponto que será a referência para a rotação. Para isso, use procedimento semelhante ao 2º passo da construção anterior.

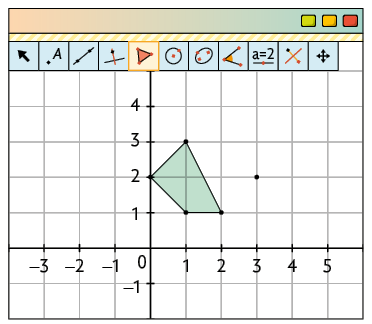
Ilustração. Tela de um software de geometria com um plano cartesiano em uma malha quadriculada. Nela há um polígono desenhado com vértices de coordenadas 0 e 2; 1 e 1; 2 e 1; 1 e 3. Também há um ponto marcado nas coordenadas 3 e 2. Há ícones de seleção e o ícone de polígono está selecionado.

2º. Com a ferramenta Rotação em Torno de um Ponto, clique no polígono e, depois, no ponto. No campo Ângulo da janela que será exibida, digite a medida do ângulo em grau, escolha o sentido – por exemplo, $90 graus$ e anti-horário – e clique em OK.

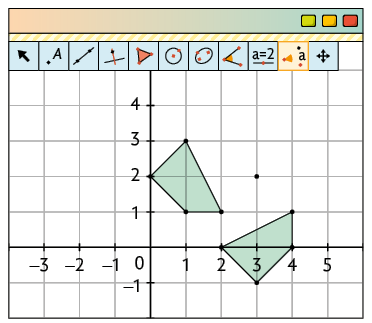
Ilustração. Tela de um software de geometria com um plano cartesiano em uma malha quadriculada. Nela há dois polígonos desenhados. Eles são iguais, mas rotacionados de maneiras distintas em torno de um ponto marcado nas coordenadas 3 e 2. O ícone de rotação em torno de um ponto está selecionado.

Já para a transformação de translação, execute os passos a seguir.

1º. Construa o polígono e dois pontos distintos para delimitar as extremidades da seta, que será a referência para a medida da distância, a direção e o sentido da translação. Com a ferramenta Vetor, clique nesses dois pontos, primeiro na extremidade inicial, depois na final.

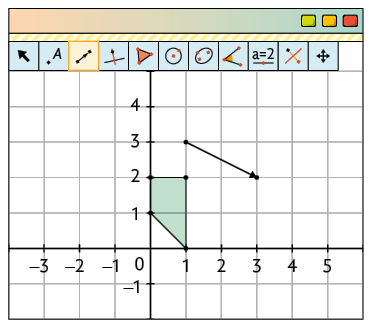
2º. Com a ferramenta Translação por um Vetor, clique no polígono e, depois, na seta.

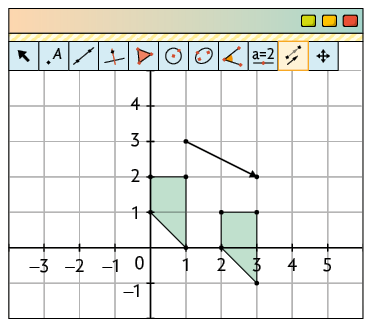
Ilustração. Tela de um software de geometria com um plano cartesiano em uma malha quadriculada. Nela há duas figuras iguais, uma transladada da outra para direita e para baixo e acima há uma seta inclinada com essa indicação. Há ícones de seleção e o ícone translação por um vetor, está selecionado.

Página 120

Atividades

Faça as atividades no caderno.

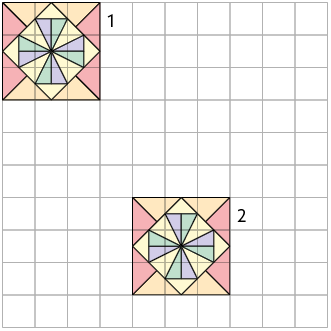
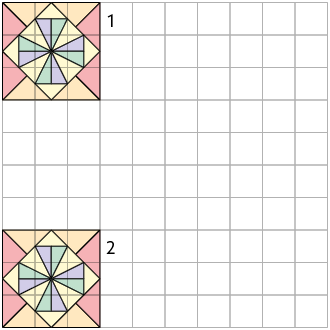
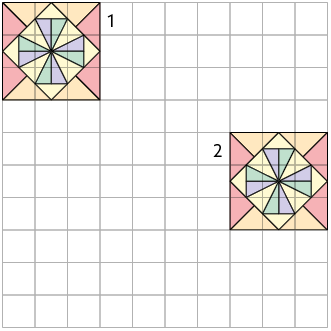
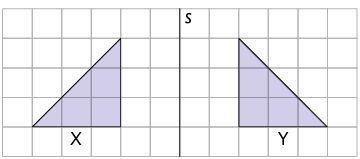
1. Determine em qual das malhas quadriculadas as figuras X e Y são simétricas por reflexão em relação ao eixo s.

Ilustração de uma malha quadriculada com dois triângulos iguais: o triângulo X à esquerda e o Y à direita. Entre eles há um eixo s, na vertical. Os triângulos estão alinhados, porém espelhados.

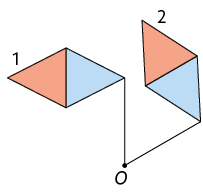
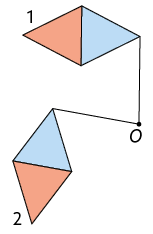
2. Em cada item, para construir a figura 2, aplicou-se uma transformação de rotação na figura 1 em torno do ponto O. Dado o ângulo de rotação em cada item, escreva no caderno se ela foi aplicada no sentido horário ou no anti-horário.

a) Ângulo de rotação: $60 graus$ .

Ilustração de duas figuras em formato de losango. Ambas apresentam um fio, que as unem pelo ponto O. A figura 1 aparece horizontalmente, à esquerda, a figura 2 é obtida por sua rotação em torno de um ponto O. Ela aparece no lado direito da figura 1, um pouco inclinada para a esquerda.

b) Ângulo de rotação: $280 graus$ .

Ilustração de duas figuras em formato de losango. Ambas apresentam um fio, que as unem pelo ponto O. Acima, a figura 1 aparece horizontalmente, abaixo, a figura 2 é obtida por sua rotação em torno de um ponto O. Ela aparece verticalmente, um pouco inclinada para a direita, em relação à figura 1.

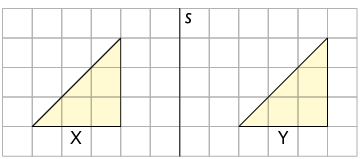
3. Em qual das malhas quadriculadas a figura 2 é simétrica à figura 1 por rotação em torno do ponto O?

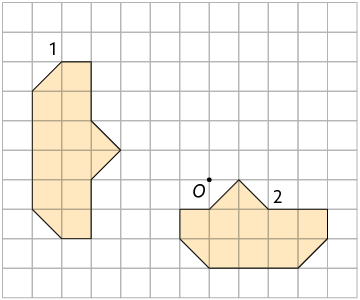
Ilustração de uma malha quadriculada com dois polígonos semelhantes a um barquinho. Na figura 1 o barquinho está em pé e a figura é simétrica. Na figura 2 o barquinho está na horizontal com a vela mais próxima do lado direito e próxima a um ponto O.

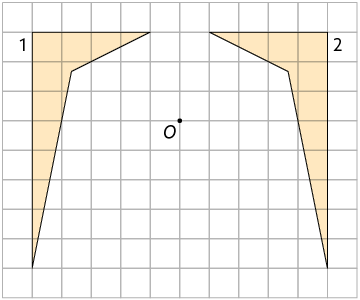
Ilustração de uma malha quadriculada com dois polígonos iguais, que são semelhantes a um bumerangue. Na figura 1, as pontas estão voltadas para a direita e alinhado com a figura 1. A figura 2 aparece com as pontas voltadas para a esquerda e, entre elas, está o ponto O.

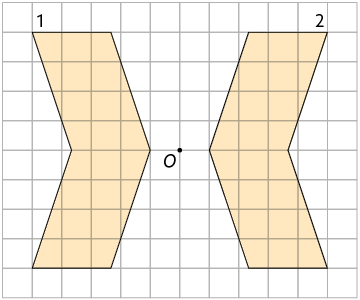
Ilustração de uma malha quadriculada com dois polígonos iguais, com 6 lados, no formato de uma ponta de seta. Na figura 1, a ponta da seta esta voltada para direita e alinhada com o ponto O. Na figura 2 a ponta da seta está voltada para esquerda e, alinhada com o ponto O.

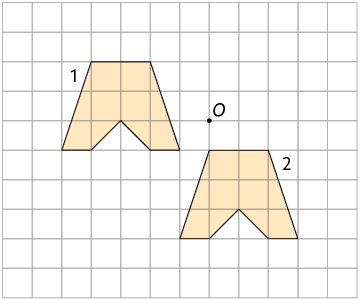
Ilustração de uma malha quadriculada com dois polígonos iguais. Na figura 1 o polígono está acima e à esquerda. Na figura 2 o polígono está mais abaixo e à direita, próximo a um ponto O.

Página 121

4. No nordeste de Angola, país localizado na África, existe um povo chamado Quioco. Uma de suas tradições é, enquanto contam suas histórias, fazer desenhos na areia, os quais, no idioma local, são conhecidos por sona. Alguns exemplos estão representados a seguir.

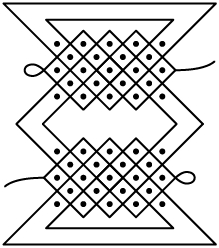
Ilustração de uma figura formada por um losango central e duas figuras semelhantes a um triângulo, um em cima e o outro embaixo. Entre os vértices em comum do losango e do triângulo, há vários losangos menores com pontos dentro. — Casal de animais.

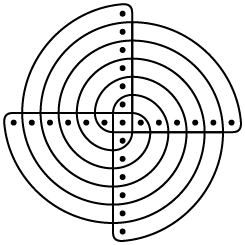
Ilustração de um círculo formado por 4 partes iguais. Nas partes que se encontram tem vários pontos, como se essas, conectasse a figura em suas partes. — Teia de aranha.

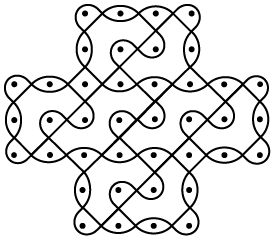
Ilustração de uma figura que lembra uma cruz, porém com a parte que está na vertical, um pouco mais larga que a horizontal. Cada parte da cruz é formada por peças que se sobrepõem, com um ponto dentro delas. — Caminho percorrido pela galinha.

a) Considere um ponto no centro de cada um dos desenhos. Ao aplicarmos uma transformação de rotação no sentido horário em torno desse ponto, qual será o ângulo de rotação para que sua imagem coincida com a figura inicial?

b) Em sua opinião, é importante conhecer e respeitar os diferentes costumes de um povo? Converse com os colegas e professor, argumentando para defender suas ideias.

c) Realize uma pesquisa sobre a importância de respeitar a diversidade cultural. Em seguida, apresente os resultados obtidos para a turma.

5. A figura apresentada a seguir é uma reprodução de um trabalho do artista holandês Maurits Cornelis Escher (1898-1972). Considere um ponto no centro dessa figura. Ao aplicar uma transformação de rotação em torno dele no sentido anti-horário, qual é o menor ângulo de rotação para que sua imagem coincida com a figura inicial?

Ilustração de uma figura simétrica em formato circular, reprodução do artista Maurits Cornelis Escher. No centro, há 3 desenhos semelhantes a uma ave, com seus bicos encostados pela ponta, as aves possuem a mesma distância entre si. Ao redor, há ainda várias dessas aves, todas simétricas, uma em relação a outra, que se repetem infinitamente. Essa composição se repete outras 3 vezes em diferentes rotações. — *Limite circular* I, de Maurits Cornelis Escher. Xilogravura, $41 vírgula 8 centímetros por 41 vírgula 8 centímetros$ , 1958.

Página 122

6. Em uma malha quadriculada, reproduza e obtenha a imagem das figuras por meio da translação determinada pela seta.

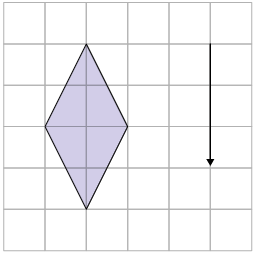
Ilustração de uma malha quadriculada com um losango e uma seta ao lado que aponta para baixo, que indica a translação de 3 quadradinhos para baixo.

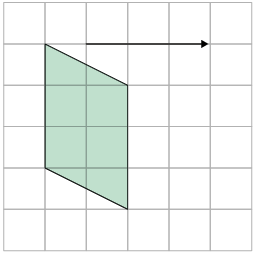
Ilustração de uma malha quadriculada com um paralelogramo e uma seta acima que aponta para o lado direito, que indica a translação de 3 quadradinhos para o lado.

Versão adaptada acessível

6. Junte-se a um colega e, em uma malha quadriculada, reproduzam e obtenham a imagem das figuras por meio da translação determinada pela seta.

7. Em quais malhas quadriculadas a figura 2 é simétrica à figura 1 por translação?

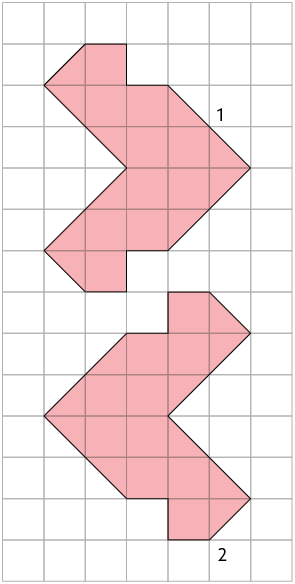
Ilustração de uma malha quadriculada com dois polígonos iguais de 12 lados, um acima do outro, indicados por 1 e 2. Polígono 1: tem suas partes simétricas, com uma ponta voltada para a direita. Polígono 2: tem suas partes simétricas, com uma ponta voltada para a esquerda.

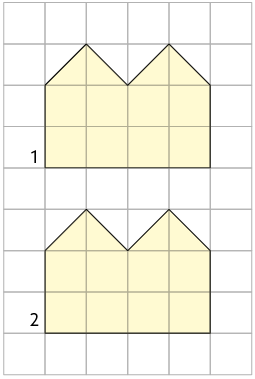
Ilustração de uma malha quadriculada com dois polígonos iguais de 7 lados, indicados por 1 e 2. Ambos estão na mesma posição, porém um acima do outro: polígono 1 acima e polígono 2, abaixo.

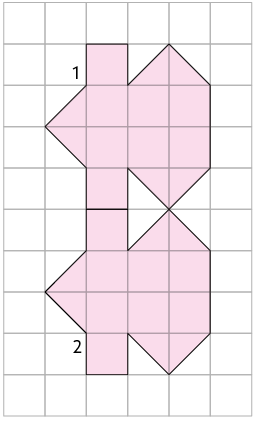
Ilustração de uma malha quadriculada com dois polígonos iguais, indicados por 1 e 2. Ambos estão na mesma posição, porém um acima do outro: polígono 1 acima e polígono 2, abaixo.

8. Utilizando o GeoGebra, construa:

a) o polígono $A B C D$ cujas coordenadas dos vértices são $ponto A com coordenadas 2 e 3$ , $ponto B maiúsculo com coordenadas 5 e 3$ , $ponto C com coordenadas menos 2 e 0$ e $ponto D com coordenadas menos 1 e 2$ .

b) a reta r que passa pelos pontos $ponto E com coordenadas 1 e 2$ e $ponto F com coordenadas 0 e 0$ .

c) a imagem do polígono $A B C D$ pela transformação de reflexão em relação a reta r.

d) a imagem do polígono $A B C D$ pela transformação de rotação de $75 graus$ , no sentido anti-horário, em torno do ponto $ponto O com coordenadas 3 e 5$ .

e) a imagem do polígono $A B C D$ pela transformação de translação na direção vertical, 3 unidades para baixo.

Página 123

Composição de transformações

No tópico anterior, relembramos certas transformações geométricas. Agora, vamos analisar algumas combinações delas.

Reflexão e rotação

Considere o triângulo $A B C$ e a reta r. Ao aplicarmos, no triângulo $A B C$ , uma reflexão em relação à reta r seguida de uma rotação de $90 graus$ em torno do ponto O, no sentido anti-horário, obtemos o triângulo $A com índice 2 B com índice 2 C com índice 2$ .

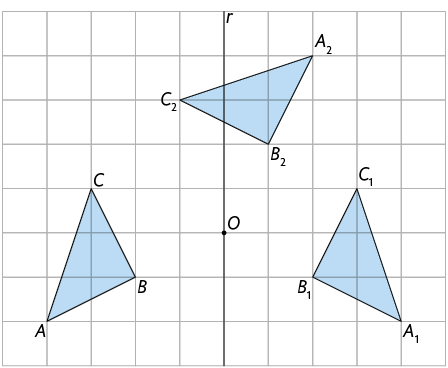
Ilustração de uma malha quadriculada com três triângulos iguais e uma reta r, posicionada verticalmente, bem ao meio da ilustração, contendo um ponto O. À esquerda da reta e do ponto O, triângulo A B C; ao lado e à direita da reta e do ponto O, triângulo A 1 B 1 C 1, refletido em relação à reta r; e o triângulo A 2 B 2 C 2, obtido por sua rotação em torno do ponto O em 90 graus. Ele está acima e à direita do triângulo ABC.

Ao aplicarmos no triângulo $A B C$ a transformação de reflexão em relação à reta r, obtemos o triângulo $A com índice 1 B com índice 1 C com índice 1$ . Já ao aplicarmos nele a transformação de rotação em torno do ponto O, obtemos o triângulo $A com índice 2 B com índice 2 C com índice 2$ .

A imagem de uma figura pela composição de transformações de reflexão e rotação é idêntica à figura original.

Reflexão e translação

Considere o triângulo $E F G$ e a reta r. Ao aplicarmos no triângulo $E F G$ uma reflexão em relação à reta r seguida de uma translação na direção horizontal, 2 unidades para a esquerda, obtemos o triângulo $E com índice 2 F com índice 2 G com índice 2$ .

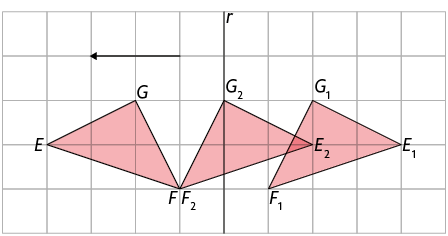
Ilustração de uma malha quadriculada com três triângulos iguais, alinhados horizontalmente e uma reta r, posicionada verticalmente, bem ao meio da ilustração. À esquerda, triângulo EFG, que tem uma seta acima, apontando para à esquerda com tamanho de 2 quadradinhos. Refletido à direita em relação à reta r, está o triângulo E2 F2 G2, que tem seu vértice F1, junto ao vértice F. à frente, transladado em dois quadradinhos para a direita, está o triângulo E1 F1 G1.

Ao aplicarmos no triângulo $E F G$ a transformação de reflexão em relação à reta r, obtemos o triângulo $E com índice 1 F com índice 1 G com índice 1$ . Aplicando nele a transformação de translação na direção horizontal, 2 unidades para a esquerda, obtemos o triângulo $E com índice 2 F com índice 2 G com índice 2$ .

A imagem de uma figura pela composição de transformações de reflexão e translação é idêntica à figura original.

Página 124

Rotação e translação

Considere o triângulo $X Y Z$ e o ponto A. Ao aplicarmos no triângulo $X Y Z$ uma rotação de $60 graus$ em torno do ponto A, no sentido horário, seguida de uma translação na direção vertical, 2 unidades para baixo, obtemos o triângulo $X com índice 2 Y com índice 2 Z com índice 2$ .

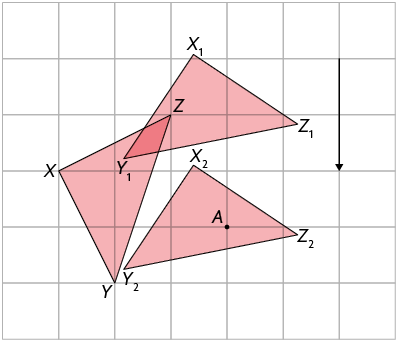
Ilustração de uma malha quadriculada com três triângulos iguais e um ponto A que indica o ponto de rotação dos triângulos X1 Y1 Z1 e X2 Y2 Z2, em relação ao triângulo X Y Z. À esquerda, triângulo X Y Z, seguido pelo triângulo X1 Y1 Z1, obtido por sua rotação em torno de um ponto A em 90 graus. Ele está acima e à direita do triângulo X Y Z. E transladado, em relação ao triângulo X1 Y1 Z1 em dois quadradinhos para baixo, está o triângulo X2 Y2 Z2.

Ao aplicarmos no triângulo $X Y Z$ a transformação de rotação em torno do ponto A, obtemos o triângulo $X com índice 1 Y com índice 1 Z com índice 1$ . Aplicando nele a transformação de translação na direção vertical, 2 unidades para baixo, obtemos o triângulo $X com índice 2 Y com índice 2 Z com índice 2$ .

A imagem de uma figura pela composição de transformações de rotação e translação é idêntica à figura original.

Agora, vamos construir uma figura utilizando a composição de transformações. Para isso, realizamos os seguintes passos.

1º. Inicialmente, construímos a figura a seguir.

Ilustração de um polígono de 6 lados com formato de letra L de ponta cabeça.

2º. Na sequência, aplicamos nela três rotações em torno do ponto A, no sentido anti-horário: uma de $90 graus$ , outra de $180 graus$ e, por fim, uma de $270 graus$ .

3º. Por fim, aplicamos na figura obtida no 2º passo uma transformação de reflexão em relação à reta r.

Ilustração de um quadrado com um buraco quadrado no meio e o ponto A ao centro. Ele é formado pela junção de 4 polígonos de 6 lados como o polígono anterior. Cada polígono forma um canto do quadrado. — Figura obtida ao final do 2º passo.

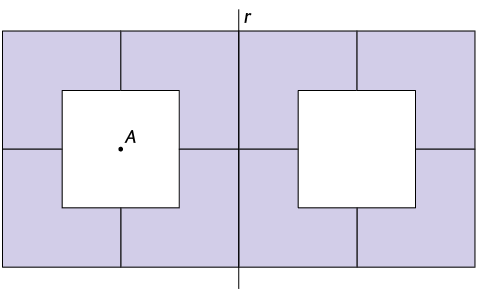
Ilustração de dois quadrados como os da figura anterior. Eles estão alinhados um ao lado do outro de modo a formar um retângulo. Apenas o primeiro quadrado tem um ponto A no centro. — Figura obtida ao final do 3º passo.

Atenção!

Em geral, trocando a ordem das transformações, o resultado é diferente.

Página 125

Instrumentos e softwares

Composição de transformações com o GeoGebra

As etapas apresentadas nesta seção possibilitam construir no GeoGebra a figura obtida ao final do 3º passo, explicado na página anterior, utilizando o plano cartesiano e uma ordem diferente da indicada para a composição de transformações.

1º. Com a ferramenta Polígono, construa o polígono a seguir.

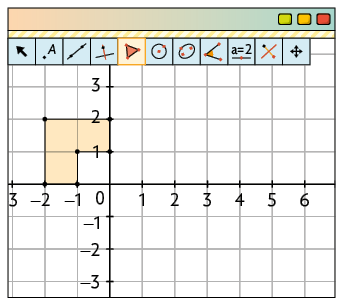
Ilustração. Tela de um software de geometria com um plano cartesiano em uma malha quadriculada. Nela há um polígono de 6 lados, no formato da letra L de ponta cabeça, como a da página anterior, cujos vértices têm coordenadas menos 2 e zero; menos 2 e 2; zero e 2; zero e 1; menos 1 e 1; menos 1 e zero.

2º. Com a ferramenta Reflexão em Relação a uma Reta, clique no polígono e depois no eixo horizontal.

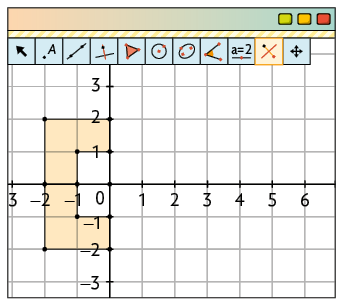
Ilustração. Tela de um software de geometria com malha quadriculada e dois polígonos de 6 lados, desenhado no plano cartesiano. Um polígono é o mesmo da ilustração anterior, com o outro polígono refletido no eixo horizontal, cujos vértices têm coordenadas menos 2 e zero; menos 2 e menos 2; zero e menos 2; zero e menos 1; menos 1 e menos 1; menos 1 e zero.

3º. Marque o ponto O na origem. Com a ferramenta Rotação em Torno de um Ponto, aplique na figura obtida no passo anterior duas rotações em torno do ponto O, no sentido anti-horário: uma de $90 graus$ e outra de $180 graus$ .

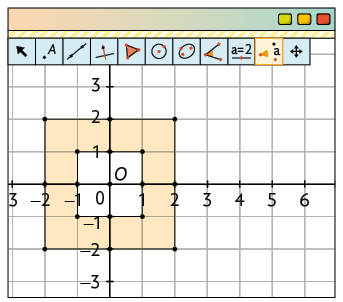
Ilustração. Tela de um software de geometria com malha quadriculada e quatro polígonos de 6 lados, desenhado no plano cartesiano. Dois polígonos são os mesmos da ilustração anterior, sendo refletidos no eixo vertical de modo a formar um quadrado com um buraco no formato de um outro quadrado no meio. Os vértices do quadrado maior, ou de fora, têm coordenadas menos 2 e 2; 2 e 2; 2 e menos 2; menos 2 e menos 2. Quadrado menor, ou de dentro, com coordenadas: menos 1 e 1; 1 e 1; 1 e menos 1; menos 1 e menos 1.

4º. Com a ferramenta Vetor, construa uma seta medindo 4 unidades de malha, na direção e no sentido da translação. Usando a ferramenta Translação por um Vetor, clique em uma figura e, depois, na seta. Repita essa ação para as demais figuras.

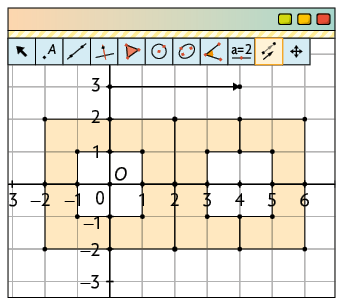
Ilustração. Tela de um software de geometria com malha quadriculada e dois quadrados como os da ilustração anterior. Um deles é o mesmo da ilustração anterior e com as mesmas coordenadas e o outro tem coordenadas: quadrado de fora: 2 e 2; 6 e 2; 6 e menos 2; 2 e menos 2. quadrado de dentro: 3 e 1; 5 e 1; 5 e menos 1; 3 e menos 1.

Página 126

Atividades

Faça as atividades no caderno.

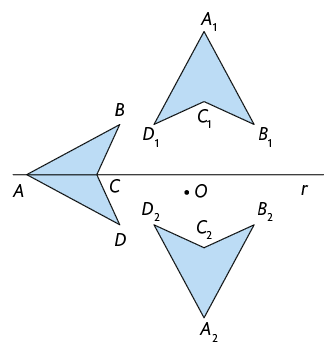
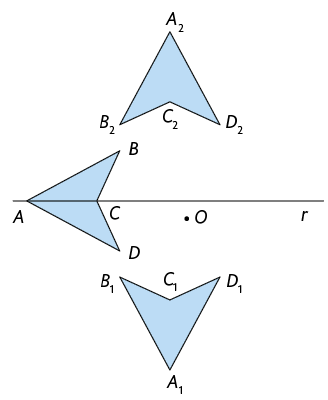
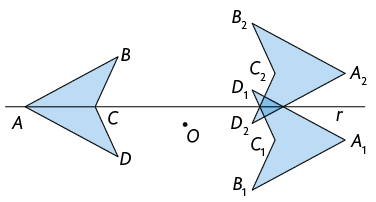
9. Antônio aplicou no quadrilátero $A B C D$ uma transformação de rotação de $90 graus$ em torno do ponto O, no sentido horário, seguida de uma reflexão em relação à reta r, obtendo o quadrilátero $A com índice 2 B com índice 2 C com índice 2 D com índice 2$ . Qual dos itens apresenta corretamente o resultado obtido por Antônio?

Ilustração de três quadriláteros iguais e uma reta r, posicionada horizontalmente, bem ao meio da ilustração e com o ponto O abaixo dela. À esquerda, está o quadrilátero: A B C D, o quadrilátero: A1 B1 C1 D1, está acima e à direita do quadrilátero A B C D e, o quadrilátero A2 B2 C2 D2, está refletido, em relação à reta r.

10. O triângulo $A com índice 2 B com índice 2 C com índice 2$ foi obtido aplicando no triângulo $A B C$ uma translação seguida de uma reflexão em relação à reta r.

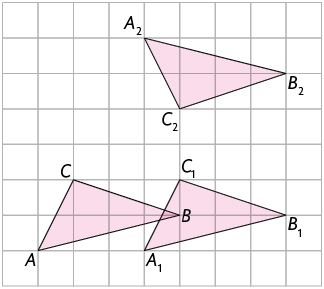
Ilustração de uma malha quadriculada com três triângulos iguais. À esquerda, está o triângulo A B C, à frente, transladado em 3 quadradinhos para a direita, está o triângulo A1 B1 C1. E acima, refletido em relação ao triângulo A1 B1 C1, está o triângulo A2 B2 C2.

Copie os triângulos em uma malha quadriculada e desenhe:

a seta que indica a direção, o sentido e a medida da distância em que o triângulo $A B C$ foi transladado.

a reta r.

Versão adaptada acessível

Junte-se a um colega e copiem os triângulos em uma malha quadriculada. Depois, desenhem:

a seta que indica a direção, o sentido e a medida da distância em que o triângulo $A B C$ foi transladado.

a reta r.

11. A foto a seguir apresenta três exemplos de cerâmica marajoara, considerada a arte em cerâmica mais antiga do Brasil.

Ilustração de três cerâmicas marajoara, vistas de frente. São semelhantes a alguns pratos, e todas decoradas com traços gráficos simétricos. Os traços também apresentam simetria de reflexão e rotação. A borda das cerâmicas é mais escura e apresenta alguns traços que estão em relevo. — Cerâmica marajoara, típica da região amazônica.

Que transformações geométricas você identifica nas cerâmicas apresentadas?

Página 127

12. Utilizando um software de Geometria dinâmica, Maria construiu uma figura usando composição de transformações. A seguir, está representada a figura inicial e o resultado obtido por ela.

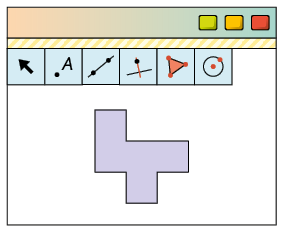
Ilustração. Tela de um software de geometria com um polígono de 10 lados, no formato de T com uma ponta acima e na extremidade superior do T. Há ícones de seleção e nenhum ícone está selecionado. — Figura inicial.

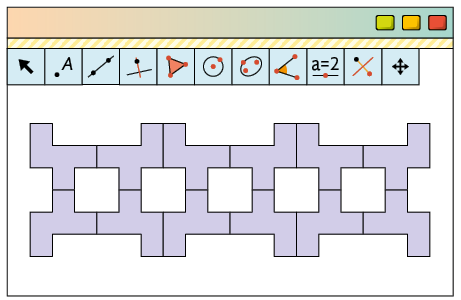
Ilustração. Tela de um software de geometria com 12 polígonos como os da ilustração anterior. Eles estão separados em 3 grupos com 4 desses polígonos, que formam um quadrado ao centro. Há ícones de seleção e o ícone de polígono está selecionado. — Resultado obtido por Maria.

a) Entre os itens a seguir, quais indicam, na ordem em que aparecem, uma composição de transformações que pode ter sido usada por Maria?

A. Reflexão, rotação e translação, translação e reflexão.

B. Reflexão, reflexão, reflexão, translação e translação.

C. Rotação, reflexão, rotação, translação e translação.

D. Translação, translação, translação, reflexão, translação.

b) No GeoGebra, construa uma figura usando composição de transformações.

13. A imagem apresentada foi obtida utilizando composição de transformação.

Ilustração formada por 42 polígonos iguais, distribuídos em 7 linhas e 6 colunas. Cada polígono tem formato de um peixe. Esses polígonos estão agrupados em pares, com os peixes conectados por sua cauda .

a) Qual é o menor elemento utilizado para compor essa imagem? Dê sua resposta fazendo um desenho em seu caderno.

b) Quais transformações foram usadas nessa construção?

Página 128

O que eu estudei?

Faça as atividades em uma folha de papel avulsa.

1. Analise a imagem.

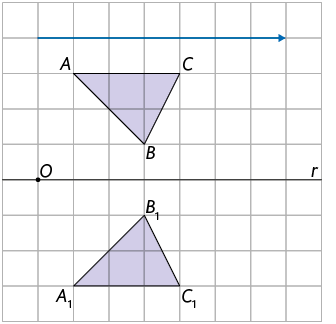
Ilustração de uma malha quadriculada com dois triângulos iguais e uma reta horizontal passando entre os triângulos e com um ponto O pertencente a ela, e na esquerda da ilustração. O triângulo A B C está acima da reta e acima dele há uma seta que aponta para a direita e tem tamanho de 7 quadradinhos e abaixo da reta está o triângulo A1 B1 C1. Os triângulos estão alinhados, porém espelhados.

Agora, copie a frase a seguir em uma folha de papel avulsa, substituindo o $█$ por "reflexão em relação à reta r"; "rotação em torno do ponto O" ou "translação indicada pela seta azul".

O triângulo $A com índice 1 B com índice 1 C com índice 1$ é a imagem do triângulo $A B C$ pela transformação de $█$ .

2. Em uma malha quadriculada, reproduza a figura a seguir. Depois, desenhe a imagem da figura construída por rotação de $90 graus$ em torno do ponto O no sentido anti-horário.

Ilustração de uma malha quadriculada com uma figura de 10 lados que tem a sua base desenhada sobre uma reta com o ponto O pertencente à reta e distante 2 quadradinhos da figura. A figura se assemelha a representação de uma escada com 3 degraus de um quadradinho e ao final, um degrau com 2 quadradinhos de altura.

Versão adaptada acessível

2. Junte-se a um colega e, em uma malha quadriculada, reproduzam a figura a seguir. Depois, desenhem a imagem da figura construída por rotação de 90° em torno do ponto O no sentido anti-horário.

3. Em qual malha quadriculada a figura 2 é a imagem da figura 1 pela transformação de translação na direção horizontal, 7 unidades para a direita, seguida de uma translação na direção vertical, 4 unidades para baixo?

Ilustração de uma malha quadriculada com duas figuras formada pela simetria vertical e horizontal. A figura 1 está no canto superior da malha e a figura 2 está 4 quadrinhos à direita, seguida pela localização de três quadradinhos abaixo da figura 1.