Página 129
UNIDADE
7
Cálculo algébrico

Agora vamos estudar...
- expressões algébricas;
- valor numérico de expressões algébricas;
- monômios e polinômios;
- operações com monômios e com polinômios.
Página 130
Expressões algébricas
Em algumas situações, a inclusão de letras para generalizar uma situação foi importante para o desenvolvimento da Matemática e, consequentemente, de suas aplicações na resolução de problemas de todas as áreas de conhecimento.
Em Matemática, a área que estuda a representação de letras no lugar de números é chamada álgebra. Esse nome surgiu da expressão al-jabr, do livro Al-Jabr wa'l mugabalah, publicado pelo matemático árabe Al-Khowarizmi por volta de 830.
As letras podem aparecer em expressões algébricas, fórmulas e equações.
No livro Al-Jabr wa'l mugabalah, Al-Khowarizmi utilizava um método de resolução de equações parecido com o que utilizamos hoje; a diferença é que em seu método todos os números e símbolos eram expressos por palavras.

Questão 1. Faça uma pesquisa sobre as
contribuições de Al-Khowarizmi
para a Matemática.
A seguir, apresentamos um exemplo em que podemos usar letras para representar números.
João tem certa quantia em reais, Fernando tem R$ 7,00 a mais do que João e Amanda tem o dobro da quantia de Fernando. Para representar a quantia que cada um deles tem, vamos escrever expressões algébricas. Para isso, vamos chamar de a quantia que João tem.
João:
Fernando:
Amanda:
No exemplo, a letra x pode assumir valores como R$ 10,00 e R$ 15,00, entre outros.
Expressões que apresentam letras e números são chamadas expressões algébricas. As letras que aparecem nas expressões algébricas são chamadas variáveis, pois podem assumir diversos valores. A seguir, apresentamos alguns exemplos de expressões algébricas.
2
Atenção!
Em geral, para representar uma expressão algébrica, não utilizamos o símbolo ou entre o número e as variáveis.
Questão 2. Uma caneta custa x reais, e um caderno, y reais. Em seu caderno, escreva uma expressão algébrica para representar o valor a ser pago ao se comprar duas canetas e três cadernos.
Página 131
Valor numérico de uma expressão algébrica
Em algumas situações é necessário obter o valor numérico de uma expressão algébrica. Nesse caso, substituímos as letras, ou seja, as variáveis da expressão, por números.
A seguir, apresentamos um exemplo de como obter o valor numérico de uma expressão algébrica.
A fileira a seguir foi construída utilizando dois modelos de cubos, cuja medida do comprimento das arestas é diferente.
Atenção!
Os cubos de mesma cor têm arestas de mesma medida de comprimento. A variável x representa uma medida em metros.
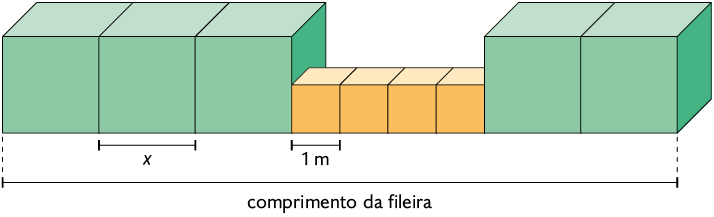
Para representar a medida do comprimento dessa fileira, em metros, podemos escrever uma expressão algébrica e, em seguida, simplificá-la.
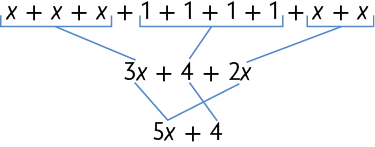
Assim, a expressão algébrica que representa a medida do comprimento da fileira de cubos, em metros, é .
Se o comprimento da aresta do cubo verde medisse , ou seja, se , qual seria a medida do comprimento dessa fileira, em metros?
Para responder a essa pergunta, podemos realizar o seguinte cálculo:
Portanto, a medida do comprimento dessa fileira seria .
Atenção!
Quando simplificamos uma expressão algébrica, escrevemos uma expressão algébrica equivalente, mas de maneira mais simples.
Página 132
Atividades
Faça as atividades no caderno.
1. No caderno, associe cada frase a uma das expressões algébricas. Para isso, escreva a letra e o número correspondentes.
A. A metade de x mais 2.
B. O dobro de x mais o quadrado de x.
C. O triplo de x menos 7, mais a quinta parte do dobro de x.
1.
2.
3.
2. Escreva no caderno uma expressão algébrica para representar cada frase.
a) O triplo do número mais 4.
b) O quadrado do número mais o dobro desse número.
c) A metade do número menos 5.
d) O quíntuplo do número mais a oitava parte desse número menos 3.
e) A quarta parte do número menos 4, mais o quadrado de .
Em seu caderno, elabore e escreva duas frases semelhantes às apresentadas. Depois, solicite a um colega que escreva as expressões algébricas de variável x para representar as frases escritas. Por último, peça a ele que calcule o valor numérico de cada expressão, dado um valor estipulado por você para a variável. Por fim, verifiquem se as respostas estão corretas.
3. Analise a expressão algébrica a seguir, a qual foi associada a uma frase.
O dobro de um número menos sua terça parte.
Escreva no caderno uma frase associada a cada expressão algébrica a seguir.
a)
b)
c)
d)
4. Uma sequência de figuras foi desenhada na malha quadriculada a seguir. A partir da 2ª, cada figura tem 1 quadradinho a mais do que a figura anterior.
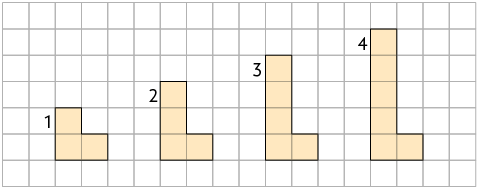
a) Quantos quadradinhos tem a figura 2? E a figura 4?
b) Ao continuar essa sequência, quantos quadradinhos terá a figura 6?
c) Escreva no caderno uma expressão algébrica que, de acordo com a sequência, represente a quantidade de quadradinhos para uma figura na posição .
d) De acordo com a expressão algébrica que você escreveu, efetue os cálculos e determine quantos quadradinhos terá:
- a figura 10;
- a figura 16;
- a figura 27.
5. Simplifique
as expressões algébricas.
a)
b)
c)
d)
e)
f)
Página 133
Monômios
Um professor de Matemática do 8º ano pediu aos estudantes que escrevessem uma expressão algébrica para cada problema a seguir.

Podemos escrever expressões algébricas para cada problema apresentado.
1.
2.
3.
A essas expressões algébricas dá-se o nome de monômio.
Monômio é toda expressão algébrica formada por um único termo. Esse termo pode ser constituído de um número ou variável apenas ou do produto de um número por uma ou mais variáveis, que apresentam somente expoentes naturais. A seguir, apresentamos alguns exemplos.
Em um monômio, o número é chamado coeficiente, e as variáveis, parte literal, como apresentado nos exemplos a seguir.
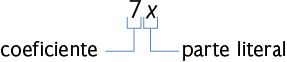
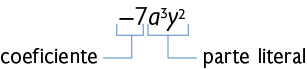
Quando o coeficiente de um monômio é 1, indicamos apenas as variáveis. No caso de ser , indicamos o sinal de menos seguido das variáveis. Já nos monômios formados apenas por um número, podemos escolher uma letra para representar a variável, e sua parte literal é essa variável com expoente zero. A seguir, apresentamos alguns exemplos.

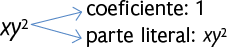

Página 134
Monômios que apresentam a mesma parte literal são chamados monômios semelhantes. Apresentamos a seguir alguns exemplos.
- Monômios semelhantes
- e
- e
- e
- e
- Monômios não semelhantes
- e
- e
- e
- e
Indicamos o grau de um monômio adicionando os expoentes das variáveis. O monômio , por exemplo, tem grau 6, pois . Analise mais dois exemplos.
Monômio de grau 3 ou de 3º grau, pois .
Monômio de grau 4 ou de 4º grau, pois .
O grau de um monômio de coeficientes não nulos é dado pela soma dos expoentes das variáveis. Um monômio representado apenas por um número não nulo tem grau zero.
Questão 3. Escreva em seu caderno um monômio de 5º grau com três variáveis.
Atividades
Faça as atividades no caderno.
6. Escreva no caderno o coeficiente e a parte literal do monômio indicado em cada item.
a)
b)
c)
d)
e)
f)
g)
h)
i) 18
7. Em seu caderno, escreva o grau de cada monômio da atividade anterior.
8. Escreva no caderno o monômio:
a) de coeficiente e parte literal ;
b) de coeficiente e parte literal ;
c) de coeficiente e parte literal .
9. Separe no caderno os monômios a seguir em grupos, de modo que em cada grupo tenha somente monômios semelhantes.
10. Escreva no caderno três monômios semelhantes ao monômio .
Página 135
11. Em seu caderno, elabore um problema envolvendo o valor numérico de uma expressão algébrica, identificação de monômios, bem como seu grau, área e perímetro. Para essa produção, considere o retângulo apresentado a seguir.

Agora, peça a um colega que resolva o problema e, depois, verifiquem se as respostas estão corretas.
12. Os gregos já empregavam letras para designar números e até mesmo objetos. Os gregos também deixaram os primeiros vestígios do cálculo aritmético efetuado sobre letras. Diofanto de Alexandria (300 a.C.) empregava as letras com abreviação. Em geral, os gregos representavam as quantidades por linhas, determinadas por uma ou duas letras, e raciocinavam como em geometria.
Os cálculos sobre letras são mais numerosos nos autores hindus do que nos gregos. Os árabes do Oriente empregavam símbolos algébricos a partir da publicação da Aljebr walmukâbala de Alkarismí (século IX), e os árabes do Ocidente, a partir do século XII; no século XV, Alcalsâdi introduziu novos símbolos.
A álgebra moderna só adquiriu caráter próprio, independente da aritmética, a partir de Viète, que sistematicamente substituiu a álgebra numérica pela álgebra dos símbolos. Viète não empregava o termo álgebra, e sim análise, para designar essa parte da ciência Matemática em que brilha seu nome.
Outrora, atribuía-se à origem da palavra álgebra ao nome do matemático árabe Geber; na realidade, essa origem estava presente na operação que os árabes denominavam aljebr.

Fonte de pesquisa: LISBOA, Almeida. O emprego das letras no cálculo. In: SOUZA, Júlio César de Mello e. Matemática divertida e curiosa. 2. ed. Rio de Janeiro: Record, 1991. p. 48-49.
a) De que maneira Diofanto de Alexandria expressava seus cálculos aritméticos?
b) Como os gregos expressavam seus cálculos aritméticos?
c) Com base nas informações apresentadas, qual foi a contribuição de Viète para a álgebra?
d) Em seu caderno, escreva um texto expressando sua opinião a respeito da importância de atribuir letras e números para representar expressões, equações e fórmulas.
Página 136
Operações com monômios
Adição e subtração de monômios
A seguir estão representados três paralelepípedos retos retângulos.
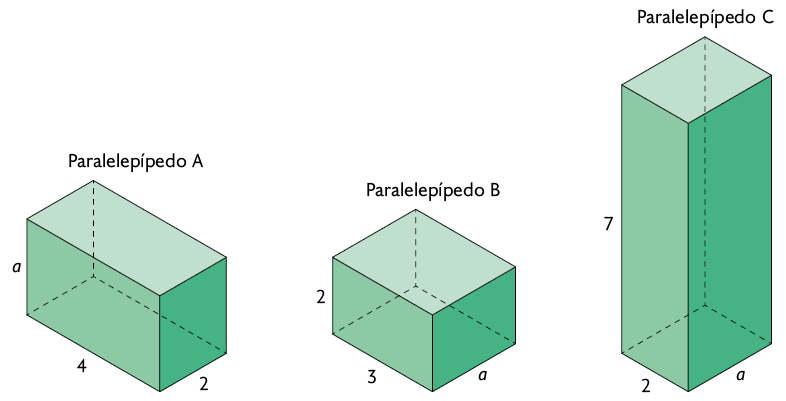
Com base nas medidas indicadas, qual é a medida do volume dos três paralelepípedos retos retângulos juntos?
Para responder a essa pergunta, vamos determinar inicialmente a medida do volume de cada paralelepípedo reto retângulo.
Em seguida, adicionamos as medidas dos volumes obtidos.
Utilizando a propriedade distributiva da multiplicação em relação à adição, simplificamos a expressão algébrica obtida.
Portanto, a soma das medidas dos volumes dos três paralelepípedos retos retângulos é .
Quando uma expressão algébrica apresenta monômios semelhantes, podemos simplificá-la, adicionando ou subtraindo os coeficientes dos monômios e mantendo a parte literal. Exemplos:
Página 137
Atividades
Faça as atividades no caderno.
13. Simplifique a expressão algébrica em cada item para obter um monômio.
a)
b)
c)
d)
e)
14. Escreva no caderno um monômio para representar a medida do perímetro de cada figura.
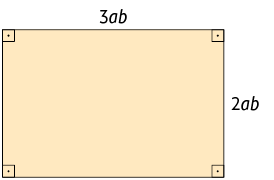
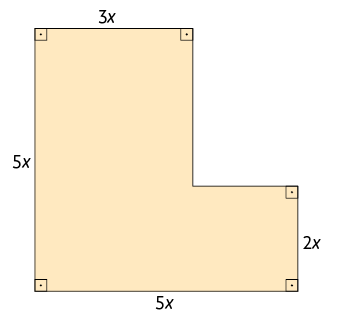
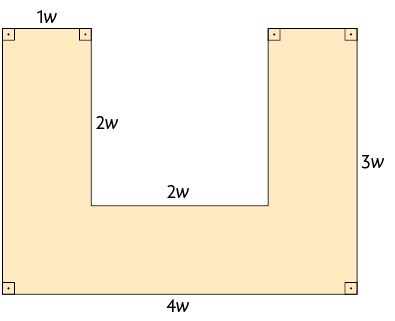
15. Copie no caderno as sentenças substituindo cada pelo monômio adequado.
a)
b)
c)
d)
16. Junte-se a um colega e determinem o monômio que representa a medida da área total das figuras em cada item, sabendo que os monômios indicados representam a medida da área das partes dessas figuras.
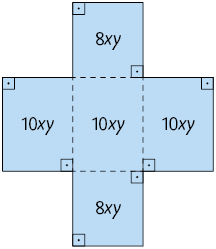
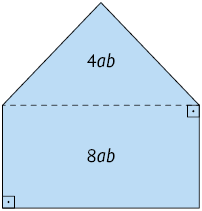
17. Junte-se a um colega e escrevam no caderno o que se pede em cada item.
a) Uma adição de monômios cujo resultado seja .
b) Uma subtração de monômios cujo resultado seja .
c) Uma adição de 3 monômios cujo resultado seja .
Página 138
Multiplicação de monômios
Antônio comprou um terreno com formato retangular cuja medida do comprimento é o dobro da medida da largura. Na figura estão indicadas as medidas das dimensões dele.

De acordo com a figura, qual é a medida da área do terreno que Antônio comprou?
Para responder a essa pergunta, precisamos multiplicar os monômios que representam as medidas do comprimento e da largura do terreno.
Portanto, a medida da área do terreno que Antônio comprou é .
Em uma multiplicação de monômios, calculamos o produto dos coeficientes e o produto das partes literais. A seguir, apresentamos alguns exemplos.
Atenção!
Simplificamos as expressões usando a propriedade comutativa da multiplicação e a propriedade da multiplicação de potências de mesma base.
Divisão de monômios
Aurélio fez a seguinte pergunta para Paula.

Página 139
Será que a resposta de Paula está correta?
Para verificar, vamos utilizar a operação inversa da multiplicação, ou seja, a divisão.

O monômio que satisfaz as condições mencionadas é . Portanto, a resposta de Paula está correta.
Em uma divisão de monômios, dividimos os coeficientes e dividimos as partes literais. A seguir, apresentamos um exemplo.
Esse cálculo também pode ser representado da seguinte maneira.
Atenção!
Simplificamos a expressão usando a propriedade da divisão de potências de mesma base.
Atividades
Faça as atividades no caderno.
18. Efetue no caderno as multiplicações dos monômios de cada item. Depois, simplifique os produtos obtidos.
a)
b)
c)
d)
e)
f)
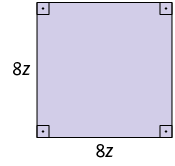
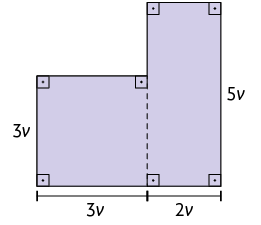
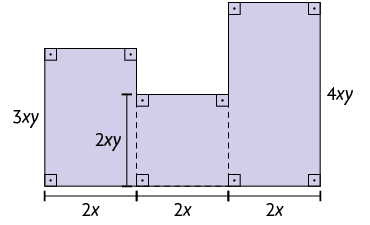
19. Escreva no caderno o monômio que representa a medida da área de cada figura.
Página 140
20. Determine o valor das letras p, q, r, s, t, w e v indicadas nos expoentes, de modo que os resultados dos cálculos estejam corretos.
a)
b)
c)
d)
21. Efetue as divisões de cada item. Em seguida, simplifique os resultados obtidos.
a)
b)
c)
d)
e)
f)
22. Com base nas medidas dos comprimentos dos lados dos retângulos apresentados, calcule quantas vezes a medida da área do retângulo verde corresponde à medida da área do retângulo laranja.

23. Junte-se a um colega e respondam às questões a seguir.
a) Que monômio multiplicado por resulta em ?
b) Que monômio dividido por resulta em ?
c) Que monômio multiplicado por resulta em ?
d) Que monômio dividido por resulta em ?
24. A imagem representa um retângulo cuja área mede . Que monômio representa a medida A?

25. Copie no caderno as sentenças a seguir, substituindo cada pelo monômio adequado.
a)
b)
c)
d)
e)
f)
26. Nos
cálculos a seguir, as letras A, B, C e D representam monômios.
Sabendo que as letras
iguais indicam o mesmo monômio, determine o monômio correspondente a cada
letra.
Página 141
Polinômios
Juliano separou algumas partes de sua chácara, com formato de retângulo, para o plantio de hortaliças orgânicas.
No esquema estão representadas as medidas das dimensões de cada uma dessas partes.
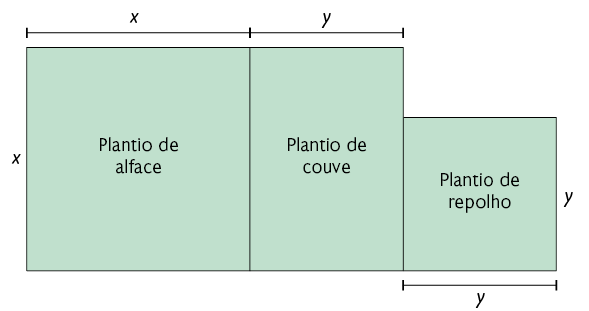
Com base nas indicações do esquema, qual expressão algébrica representa a medida da área total que Juliano reservou para o plantio de hortaliças orgânicas?
Para responder a essa pergunta, vamos determinar inicialmente a medida da área de cada parte.
Agora, adicionamos as medidas das áreas e obtemos a expressão algébrica que representa a medida da área dos três plantios.
A expressão algébrica que representa a medida da área total reservada para o plantio de hortaliças orgânicas é chamada polinômio.
Polinômio é uma adição algébrica de monômios. Cada monômio que o compõe é chamado termo do polinômio. Acompanhe alguns exemplos.
Quando um polinômio tem termos que são monômios semelhantes, podemos simplificá-lo. Para exemplificar, vamos simplificar o polinômio a seguir, que apresenta essas características.
Página 142
Primeiro, eliminamos os parênteses, aplicando a propriedade distributiva da multiplicação em relação à adição.
Em seguida, organizamos os monômios semelhantes lado a lado e efetuamos as adições e subtrações entre eles.

Dizemos que o polinômio está na forma reduzida.
Podemos classificar um polinômio escrito na forma reduzida de acordo com a quantidade de termos.
São chamados binômios os polinômios que têm 2 termos.
Por exemplo: e .
São chamados trinômios os polinômios que têm 3 termos.
Por exemplo: e .
Os monômios também são polinômios, porém com um único termo.
Os polinômios com quatro termos ou mais não recebem nomes particulares.
Também podemos definir o grau de um polinômio. Para definir, por exemplo, o grau do polinômio reduzido , determinamos inicialmente o grau de cada um de seus termos.
4º grau
3º grau, pois
6º grau, pois
Em seguida, verificamos o termo com maior grau. Nesse caso, o termo é o de maior grau. Portanto, esse polinômio é do 6º grau ou de grau 6.
O grau de um polinômio de coeficientes não nulos escrito na forma reduzida é dado pelo termo de maior grau. Dizemos que um polinômio é nulo quando todos os seus coeficientes forem iguais a zero. O grau do polinômio nulo não é definido.
Atividades
Faça as atividades no caderno.
27. Os polinômios a seguir estão na forma reduzida. Separe-os em 3 grupos: no grupo 1, os monômios; no grupo 2, os binômios; e no grupo 3, os trinômios.
A.
B.
C.
D.
E.
F.
G.
H.
I.
J.
Página 143
28. Volte à atividade anterior e determine o grau do polinômio de cada item.
29. De acordo com os valores de e , calcule o valor numérico de cada polinômio.
A.
;
B.
;
30. Simplifique cada polinômio deixando-o na forma reduzida.
a)
b)
c)
31. Escreva no caderno um polinômio na forma reduzida que represente a medida do perímetro da figura a seguir.

32. Em uma partida de basquetebol, é usado o jargão "cestinha" para o jogador que fez mais pontos. Carlos foi o "cestinha" em uma partida de basquetebol da escola. Ele acertou cestas de 1 ponto, cestas de 2 pontos e cestas de 3 pontos.
a) Escreva no caderno o polinômio que representa a quantidade total de pontos que Carlos fez nessa partida.
b) Sabendo que Carlos fez 15 pontos nessa partida, atribua valores para , e e determine 3 possibilidades diferentes de cestas que ele pode ter feito nessa partida.
c) No caderno, elabore um problema envolvendo polinômios, semelhante ao apresentado anteriormente, e peça a um colega que o resolva. Depois, verifiquem se as respostas estão corretas.
33. Para realizar um trabalho escolar, Ana recortou de uma cartolina com formato retangular 2 pedaços também retangulares, como mostra a figura.
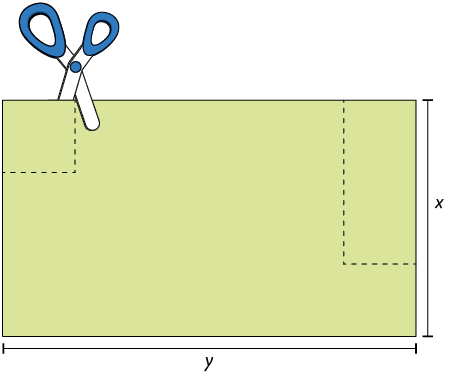

a) Com base nas imagens e nas suas indicações de medida, escreva um polinômio na forma reduzida que represente a medida da área do pedaço de cartolina que sobrou.
b) Qual é o grau do polinômio que você escreveu no item a?
Página 144
Operações com polinômios
Adição de polinômios
Analise os polinômios indicados nas fichas a seguir.
A.
B.
C.
Podemos calcular a adição dos polinômios A e B da seguinte maneira.
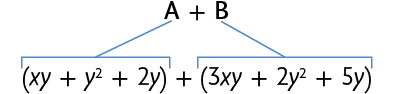
Inicialmente, eliminamos os parênteses e organizamos os termos semelhantes lado a lado. Depois, efetuamos as adições.
Portanto, o resultado da adição dos polinômios A e B é o polinômio .
Questão 4. Determine no caderno o resultado da adição dos polinômios B e C.
Ao adicionar um polinômio ao outro e obter o polinômio nulo como resultado, chamamos esses polinômios de opostos. Para obter um polinômio oposto a outro, reescrevemos ele trocando o sinal de cada um de seus termos. O oposto do polinômio , por exemplo, é , pois:
Ao adicionarmos a seu oposto, obtemos o polinômio nulo.
Questão 5. Escreva no caderno o polinômio oposto ao obtido na questão 4.
Página 145
Subtração de polinômios
Para calcular a subtração , adicionamos o 1º polinômio ao oposto do 2º polinômio.
Agora, finalizamos o cálculo.
Portanto, o resultado da subtração é o polinômio .
Atividades
Faça as atividades no caderno.
34. Copie no caderno as expressões dos quadros A, B, C e D, substituindo cada figura pelo polinômio correspondente. Depois, simplifique o polinômio.
A.
B.
C.
D.
35. Em seu caderno, determine o polinômio que, ao ser adicionado ao indicado em cada item, resulta no polinômio nulo.
a)
b)
c)
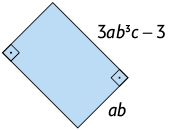
36. Escreva no caderno o polinômio reduzido que representa a diferença entre as medidas dos perímetros dos retângulos I e II indicados em cada item.
A. Retângulo I
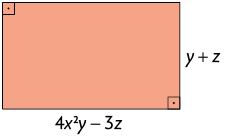
Retângulo II
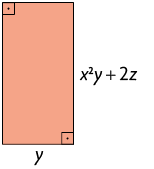
B. Retângulo I
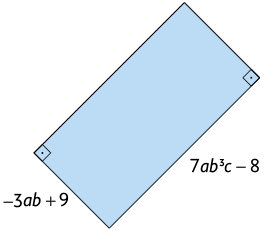
Retângulo II
Página 146
37. A seguir, estão representados alguns paralelepípedos retos retângulos, cujas medidas das dimensões estão indicadas em metro.
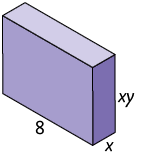
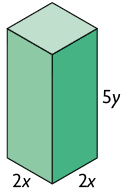
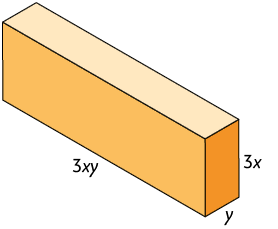
Foram montadas as seguintes pilhas utilizando alguns paralelepípedos retos retângulos como esses.
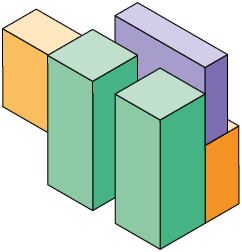
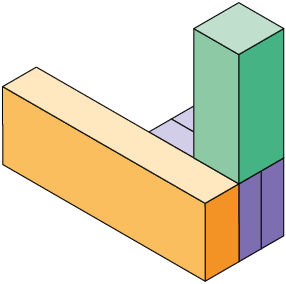
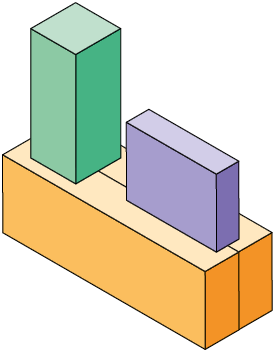
a) Qual polinômio representa a medida do volume total de cada pilha montada?
b) Supondo e , calcule a medida do volume total de cada pilha.
38. Em seu caderno, desenhe a representação de um polígono com até seis lados e indique a medida do comprimento de cada um de seus lados por meio de monômios e binômios. Depois, elabore um problema envolvendo essa figura, polinômios e valor numérico de polinômios. Por fim, peça a um colega que o resolva.
Versão adaptada acessível
38. Junte-se a um colega, desenhem a representação de um polígono com até seis lados e indiquem a medida do comprimento de cada um de seus lados por meio de monômios e binômios. Depois, elaborem um problema envolvendo essa figura, polinômios e valor numérico de um polinômio. Por fim, peçam a outra dupla que o resolva.
Página 147
Multiplicação de polinômios
Usando resina, a artesã Rosana confeccionou uma peça com formato que lembra um paralelepípedo reto retângulo, cujas medidas das dimensões estão indicadas na imagem.
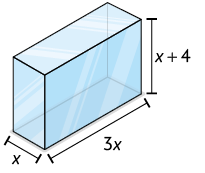
Qual polinômio representa a medida do volume da peça que Rosana confeccionou?
Podemos responder a essa pergunta multiplicando as medidas do comprimento, da largura e da altura da caixa.

Portanto, o polinômio que representa a medida do volume dessa peça é .
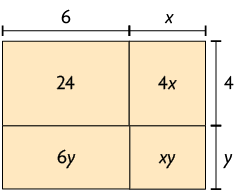
Agora, analise as medidas dos lados do retângulo a seguir. Podemos obter a medida da área total desse retângulo de duas maneiras diferentes.

1ª maneira
Dividimos o retângulo em outros quatro retângulos menores. Em seguida, obtemos a medida da área de cada um deles e as adicionamos.
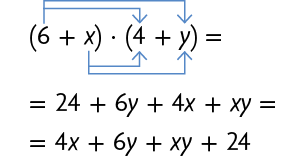
2ª maneira
Multiplicamos a medida do comprimento pela medida da largura do retângulo. Depois, utilizamos a propriedade distributiva da multiplicação em relação à adição e obtemos a medida da área total.

Página 148
Atividades
Faça as atividades no caderno.
39. Efetue os cálculos no caderno e determine o polinômio que representa a medida do volume do paralelepípedo reto retângulo a seguir.
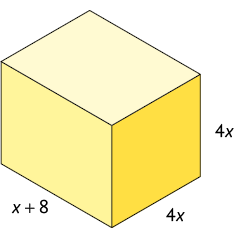
40. Supondo , calcule a medida do volume do paralelepípedo reto retângulo da atividade anterior.
41. Efetue os cálculos a seguir no caderno e obtenha um polinômio na forma reduzida.
a)
b)
c)
d)
e)
f)
42. Escreva no caderno um polinômio na forma reduzida para representar a medida da área de cada retângulo.


43. Escreva
no caderno o produto de um monômio pelo
polinômio
cujo resultado seja:
a)
b)
c)
d)
44. Copie as sentenças a seguir no caderno, substituindo cada pelo termo adequado.

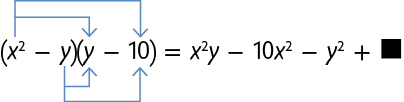
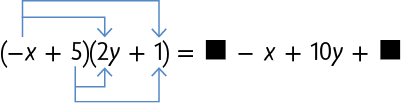
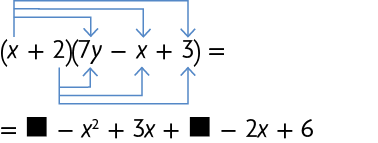
45. Entre os
polinômios a seguir, qual é o único que não representa a medida da área do
retângulo?

A.
B.
C.
D.
Página 149
Divisão de polinômio por monômio
Assim como dividimos monômio por monômio, dividimos polinômio por monômio. Acompanhe, por exemplo, como podemos resolver , com .
Atenção!
Nos exemplos e atividades envolvendo divisão nesta página e nas seguintes, estamos considerando o denominador diferente de zero, pois não existe divisão por zero.
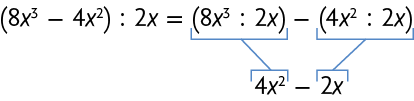
Também podemos realizar esse cálculo escrevendo a expressão em forma de fração e dividir cada termo pelo monômio.
Portanto, o resultado de é o polinômio .
Em uma divisão de um polinômio por um monômio não nulo, dividimos cada termo do polinômio pelo monômio. Acompanhe um exemplo.

O cálculo anterior também pode ser representado da seguinte maneira.
Questão 6. Em seu caderno, escreva uma divisão de um polinômio por um monômio não nulo cujo quociente seja igual a .
Questão 7. Qual é o grau do polinômio e do
monômio que você escreveu no
item anterior?
Atividades
Faça as atividades no caderno.
46. Efetue no caderno a divisão de polinômio por monômio em cada item e obtenha um polinômio na forma reduzida.
a)
b)
c)
d)
Página 150
47. Nos itens a seguir, cada figura corresponde a um dos polinômios indicados nas fichas. Efetue os cálculos no caderno e determine qual polinômio cada figura representa.
a)
b)
c)
Atenção!
Nas divisões indicadas, os divisores são monômios não nulos.
48. Em cada retângulo está indicada a medida do comprimento de um de seus lados e a medida de sua área A. Efetue os cálculos no caderno e determine a medida do comprimento do outro lado.
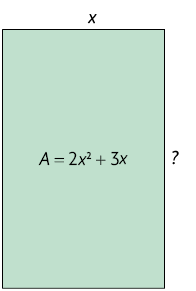
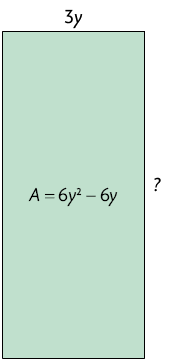
Atenção!
Nesta atividade, utilize a operação inversa da multiplicação, ou seja, a divisão.
49. Copie no caderno as sentenças a seguir substituindo cada pelo polinômio adequado.
a)
b)
c)
d)
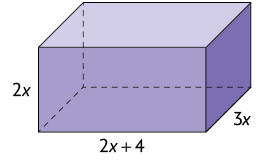
50. Analise os paralelepípedos retos retângulos representados e resolva o que se pede.
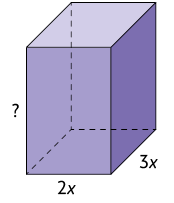
a) Sabendo que a medida do volume do paralelepípedo reto retângulo 1 é , qual polinômio representa a medida de sua altura?
b) De acordo com as medidas indicadas no paralelepípedo reto retângulo 2 e sabendo que , calcule a medida de seu volume.
Página 151
Fatoração de polinômios
Vamos estudar uma maneira de fatorar um polinômio, ou seja, escrevê-lo como um produto de polinômios. Essa maneira consiste em colocar um fator comum em evidência.
Atenção!
Existem outras maneiras de fatorar um polinômio. Elas serão estudadas no próximo volume.
Considere, por exemplo, o polinômio . Para fatorar esse polinômio, inicialmente decompomos cada um de seus termos em um produto de fatores.
No exemplo, o fator y é comum aos dois termos do polinômio. Por isso, podemos escrever esse fator multiplicando os outros fatores que não são comuns. Nesse caso, dizemos que y foi colocado em evidência.
Portanto, a forma fatorada de é .
Mínimo múltiplo comum de polinômios
Neste tópico, vamos aprender a calcular o mínimo múltiplo comum () de polinômios.
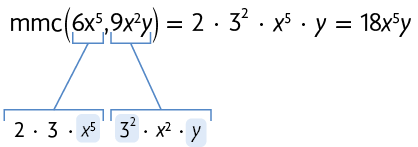
Vamos calcular, por exemplo, o de e .
Inicialmente, fatoramos os coeficientes dos monômios.
Depois, efetuamos o produto de todos os fatores de e considerando apenas os de maior expoente. O é o produto desses fatores:
De maneira semelhante à apresentada, vamos determinar o de e .
Inicialmente, fatoramos os coeficientes dos polinômios.
Efetuamos o produto de todos os fatores dos polinômios, considerando apenas os de maior expoente. O é o produto desses fatores:
Página 152
Para obter o de dois ou mais polinômios, fatoramos inicialmente os coeficientes dos polinômios. Depois, multiplicamos todos os fatores dos polinômios fatorados, considerando apenas os de maior expoente.
A seguir, apresentamos alguns exemplos.

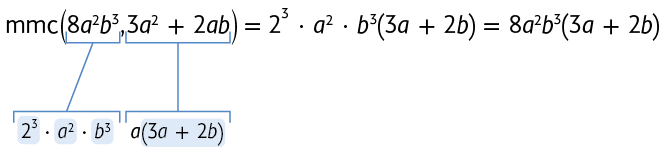
Atividades
Faça as atividades no caderno.
51. Desenvolva os cálculos para obter o dos polinômios.
a)
b)
c)
d)
e)
f)
52. Efetue os cálculos mentalmente e determine qual deve ser o valor de cada figura para que o esteja correto.
a)
b)
c)
d)
53. No caderno, associe os polinômios ao correspondente.
A.
B.
C.
D.
E.
F.
1.
2.
3.
Página 153
Frações algébricas
Em uma fábrica, uma máquina A produz 1.840 peças em t minutos. Que expressão algébrica representa a produção dessa máquina em 1 minuto?
Para responder a essa pergunta, podemos escrever a expressão algébrica a seguir.
, ou ,
Essa expressão é chamada fração algébrica.
Fração algébrica é uma expressão algébrica escrita em forma de fração e que apresenta variáveis no denominador.
Em uma fração algébrica, o denominador representa um número diferente de zero.
Acompanhe alguns exemplos.
Atividades
Faça as atividades no caderno.
54. Entre as expressões algébricas a seguir, quais são frações algébricas?
A.
B.
C.
D.
E.
F.
55. Com base nas informações apresentadas no início desta página, responda às questões a seguir.
a) Nessa mesma fábrica, uma máquina B demora a mais para produzir a mesma quantidade de peças da máquina A. Que fração algébrica representa a produção da máquina B em ?
b) Sabendo que a máquina A produz as 1.840 peças em , qual é a quantidade de peças que ela produz por minuto? E qual é a quantidade de peças que a máquina B produz por minuto?
Página 154
56. Para cada frase, escreva no caderno uma fração algébrica.
a) A adição de um número a com 3 dividido por um número b.
b) O produto entre e dividido pela adição de x e y.
c) A diferença entre os números e dividido por .
d) Um número y dividido pelo produto entre 2 e .
e) A diferença entre o quadrado de e 5, dividido pelo triplo de y.
f) A quinta parte de x adicionada a y, dividido pelo dobro de z.
57. Silas tem x revistas em quadrinhos em sua coleção. Dessa coleção, y revistas são repetidas. Sabendo que Silas distribuiu igualmente as revistas não repetidas em z prateleiras, que fração algébrica representa a quantidade de revistas que ele vai colocar em cada prateleira?
58. Junte-se a um colega e, utilizando as sentenças apresentadas a seguir, escrevam no caderno 3 frações algébricas diferentes. Depois determinem o valor numérico de cada fração algébrica que vocês escreveram considerando e .
59. Considere a frase apresentada a seguir.

Escreva no caderno uma fração algébrica para representar essa frase.
60. As despesas da festa de final de ano em uma empresa foram de R$ 1.350,00. Esse total seria dividido entre todos os funcionários, porém, na última hora, 3 deles desistiram de ir à festa.
Considere p a quantidade de funcionários da empresa e resolva os itens a seguir.
a) Escreva no caderno a fração algébrica que representa a quantia que cada funcionário pagaria se não houvesse a desistência dos 3 funcionários.
b) Que expressão algébrica representa a quantidade de funcionários que de fato pagaram a festa?
c) Que fração algébrica representa a quantia que cada funcionário pagou?
d) Calcule a quantia que cada funcionário deveria pagar, antes e depois de 3 deles desistirem, para , ou seja, considerando que a empresa tem 30 funcionários.
Página 155
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. Escreva em uma folha de papel avulsa as expressões algébricas que representam as situações a seguir.
a) A medida da área de um quadrado cujo comprimento do lado mede x.
b) A quantidade de figurinhas de José, sabendo que Paulo tem n figurinhas e José tem 5 figurinhas a mais do que Paulo.
c) O preço de x quilogramas de tomate, sabendo que o preço por quilograma é R$ 5,48.
2. (Obmep-2006) A figura representa parte de uma régua graduada de meio em meio centímetro, onde estão marcados alguns pontos. Qual deles melhor representa o número ?

a) R
b) S
c) T
d) U
e) V
3. Em uma balança foram colocadas uma penca de bananas e três maçãs, como representado na imagem a seguir.

a) Se a medida da massa da penca de bananas é , escreva a expressão algébrica que representa a medida da massa das 3 maçãs, em quilogramas.
b) Escreva a expressão algébrica que representa a medida da massa aproximada de uma maçã.
4. Em certo plano telefônico é cobrada uma taxa fixa de R$ 69,90 por mês mais R$ 0,17 por minuto em ligações locais.
a) Representando a medida do tempo em minutos por , escreva em uma folha de papel avulsa uma expressão algébrica que permita calcular o gasto mensal de um cliente que usa esse plano e faz somente ligações locais.
b) Quantos reais esse cliente gastou em um mês em que utilizou 200 minutos em ligações locais?
5. Certa funcionária recebe um salário fixo de R$ 1.255,00 e mais 3% do valor de todas as vendas que efetuar no mês.
a) Qual será o salário da funcionária no mês em que ela vender R$ 20.000,00 em produtos? E se ela vender R$ 30.000,00?
b) Sendo o valor das vendas realizadas no mês, escreva em uma folha de papel avulsa uma expressão algébrica que represente o salário da funcionária.
6. Larissa tem livros. Eduarda tem livros, que são 6 livros a mais do que Larissa, e Bruno tem livros, que é o triplo da quantidade de Eduarda.
a) Qual é a quantidade de livros de Eduarda? E a de Bruno?
b) Qual é a quantidade de livros de Larissa? E a de Eduarda?
c) Se Eduarda tem 14 livros, qual é a quantidade de livros de Larissa? E a de Bruno?
Página 156
7. (Enem-2010) Uma professora realizou uma atividade com seus estudantes utilizando canudos de refrigerantes para montar figuras, em que cada lado foi representado por um canudo. A quantidade de canudos de cada figura depende da quantidade de quadrados que formam cada figura. A estrutura de formação das figuras está representada a seguir.



Que expressão fornece a quantidade de canudos em função da quantidade de quadrados de cada figura?
a)
b)
c)
d)
e)
8. Qual é a medida do volume de um cubo cuja aresta mede ?
9. Certo retângulo cujas medidas do comprimento e da largura são c e l, respectivamente, tem seu perímetro medindo .
a) A expressão algébrica que representa a medida do perímetro é um monômio?
b) É possível expressar a medida do perímetro de um quadrado, cujo comprimento do lado mede , por um monômio? Em caso afirmativo, escreva em uma folha de papel avulsa esse monômio.
10. Escreva em uma folha de papel avulsa os polinômios na forma reduzida de cada item. Depois, classifique-os em monômio, binômio ou trinômio.
a)
b)
c)
11. O polinômio assume maior valor numérico para e ou para e ? Qual é esse valor?
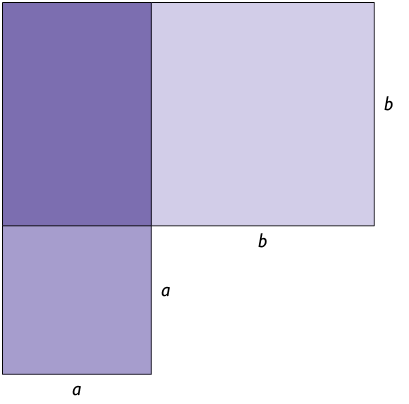
12. A figura a seguir é formada por dois quadrados e um retângulo. Escreva em uma folha de papel avulsa um polinômio que represente a medida da área dessa figura. Depois, calcule a medida da área para e .
13. Que fração algébrica representa um número x dividido pela adição de um número y com 4?