Página 157
UNIDADE
8
Equações e sistemas de equações

Agora vamos estudar...
- equação do 1º grau com uma incógnita;
- equação fracionária;
- equação do 1º grau com duas incógnitas;
- sistemas de equação do 1º grau com duas incógnitas;
- equação do 2º grau do tipo .
Página 158
Equação do 1º grau com uma incógnita
Na unidade anterior, estudamos expressões algébricas, fórmulas e equações. Nesta unidade, vamos retomar o conceito de equações e aprofundá-lo. Relembre o que é uma equação.
Equação é uma sentença matemática expressa por uma igualdade em que há pelo menos uma letra que representa um número desconhecido. Cada letra é uma incógnita da equação.
Analise a seguinte situação.
O dobro da idade de Tiago mais 10 anos é igual a 38 anos. Qual é a idade de Tiago?
Para responder a essa pergunta, podemos escrever uma equação e resolvê-la. Indicando por x a idade em anos de Tiago, escrevemos a equação a seguir.

Atenção!
Em uma equação, cada lado em relação ao sinal de igual é chamado membro.
Essa equação é um exemplo de equação do 1º grau com uma incógnita.
Uma equação do 1º grau com uma incógnita x é uma sentença matemática que pode ser escrita na forma , sendo a e b números reais, com a não nulo.
Vamos resolver a equação , ou seja, obter o valor desconhecido da incógnita.
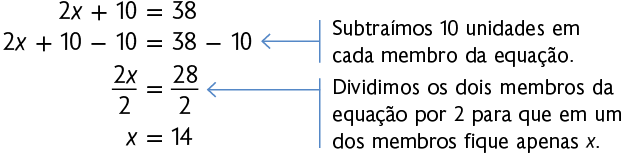
Assim, . Portanto, Tiago tem 14 anos.

Página 159
Acompanhe outra situação.
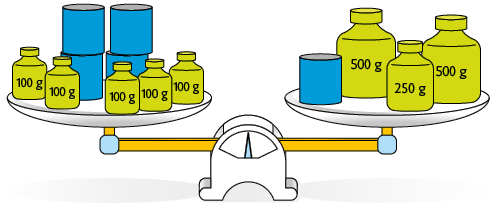
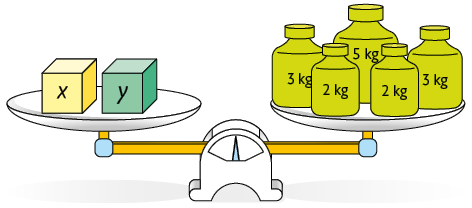
Os pratos da balança representada a seguir estão em equilíbrio. Sabendo que todas as latas de leite em pó têm a mesma medida de massa, podemos obter a medida da massa de cada lata escrevendo e resolvendo uma equação.
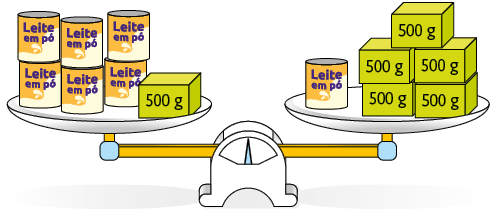
Atenção!
Como a balança está em equilíbrio, a medida da massa em um prato é igual à medida da massa em outro prato.
Indicando por x a medida da massa, em quilogramas, de uma lata de leite em pó, temos:
Resolvendo a equação, obtemos:
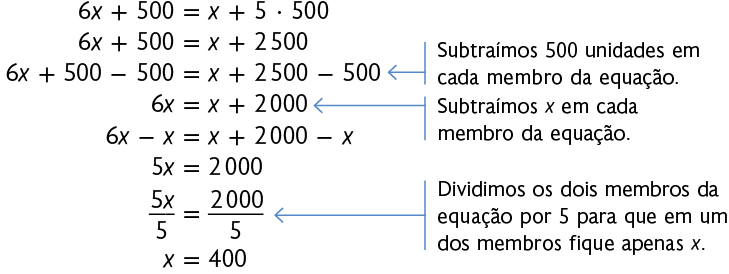
Portanto, a massa de cada lata de leite em pó mede .
Questão 1. As balanças representadas em cada item estão em equilíbrio. Em seu caderno escreva e resolva uma equação que possibilite determinar a medida da massa da:
A. Lata vermelha.
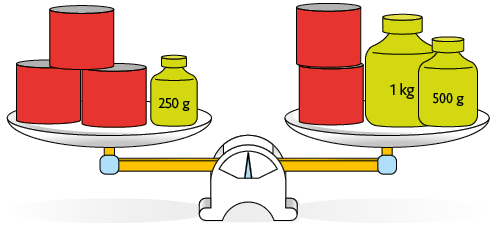
B. Lata azul.
Página 160
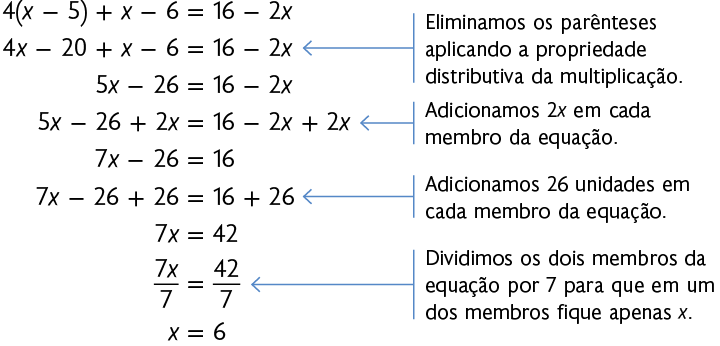
Podemos simplificar e resolver a equação , procedendo da seguinte maneira:
Atividades
Faça as atividades no caderno.
1. Júlia comprou um vestido e uma saia por R$ 149,95. Sabendo que a saia custou R$ 60,00, qual das equações a seguir permite obter o preço do vestido?
a)
b)
c)
d)
2. Resolva a equação da atividade anterior e obtenha o preço do vestido.
3. Resolva no caderno as equações a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
4. Bruna expressou um procedimento matemático.

a) Qual das equações a seguir permite obter o número pensado por Bruna?
I)
II)
III)
IV)
b) Determine o número pensado por Bruna.
Página 161
5. No caderno, associe cada situação a seguir a uma das equações.
A.
Letícia pensou em um número, multiplicou-o por 5, adicionou 17 unidades ao produto e obteve 82 como resultado. Em que número Letícia pensou?
B.
O triplo da idade de Gustavo é igual a 78 anos. Qual é a idade de Gustavo?
C.
O dobro da quantia em reais que eu tenho menos R$ 63,00 é igual a R$ 153,00. Quantos reais eu tenho?
1.
2.
3.
6. Resolva no caderno as equações da atividade anterior e determine a resposta de cada situação.
7. Geraldo tem um jardim com formato retangular cujo perímetro mede . A medida do comprimento desse jardim é maior do que a medida de sua largura.

a) Calcule, em metro, a medida da largura e do comprimento desse jardim.
b) Calcule a medida da área desse jardim.
8. Junte-se a um colega e escrevam no caderno uma equação para representar a situação a seguir. Em seguida, resolvam essa equação e deem a resposta da situação.
A sequoia é considerada a espécie de árvore mais alta do mundo. Ao multiplicarmos a medida da altura que uma sequoia pode atingir por 2 e adicionarmos ao resultado, obtemos . Qual é a medida da altura que essa árvore pode atingir?
9. Escreva no caderno a equação correspondente a cada situação. Depois, resolva as equações e dê a resposta de cada situação.
a) Paguei a conta da lanchonete com uma cédula de R$ 50,00 e recebi R$ 22,00 de troco. Qual foi o valor da conta?
b) O dobro da quantia que recebi, adicionado a R$ 69,00, resulta em R$ 195,00. Qual foi a quantia que recebi?
c) O triplo da idade de André mais 18 anos é igual a 108 anos. Qual é a idade de André?
d) Pensei em um número e multipliquei-o por 6. Ao resultado adicionei 32 e obtive 116. Em que número pensei?
Página 162
Equações fracionárias
Na unidade anterior, você estudou frações algébricas, ou seja, expressões algébricas escritas na forma de fração, que têm variáveis no denominador. Usando frações algébricas, podemos escrever equações fracionárias.
Equação fracionária é uma equação que tem pelo menos uma fração com letras no denominador. Essas letras são as incógnitas da equação.
Considere o problema a seguir.
Agnaldo produz de queijo com certa quantidade de litros de leite. Utilizando a mesma receita, para produzir de queijo ele precisa acrescentar de leite. Quantos litros de leite ele usa para fazer de queijo? E para fazer de queijo?
Para resolver o problema apresentado, escrevemos, inicialmente, uma equação que o represente, indicando por x a quantidade de litros de leite necessária para produzir de queijo.
Atenção!
Na equação escrita, indica a quantidade de litros de leite necessária para produzir de queijo.
Para que essa equação seja possível, o denominador de cada fração deve ser diferente de zero. Nesse caso, tem-se e .
Acompanhe a resolução dessa equação fracionária.
Inicialmente, determinamos o , que é . Depois, multiplicamos cada membro da equação pelo para eliminar os denominadores.
Em seguida, eliminamos os parênteses aplicando a propriedade distributiva da multiplicação.
Página 163
Na sequência, resolvemos a equação e obtemos o valor de .
Por último, verificamos se o valor obtido para a incógnita não anula algum dos denominadores da equação e se mantém verdadeira a igualdade.
Nesse caso, o valor obtido para a incógnita não anulou os denominadores das frações e manteve verdadeira a igualdade. Assim, é a solução dessa equação fracionária.
Portanto, para fazer de queijo Agnaldo utiliza de leite , e para fazer ele utiliza de leite .
Agora, acompanhe a resolução da seguinte equação fracionária.
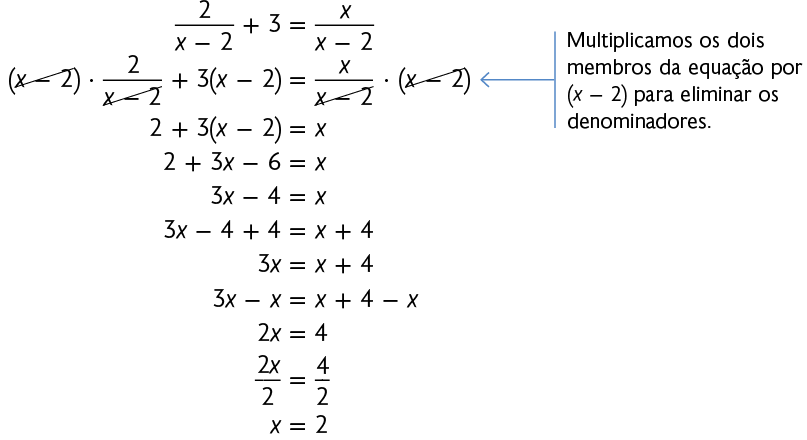
Atenção!
Para tornar possível a equação anterior, devemos considerar o denominador de cada fração diferente de zero, ou seja, .
Como vimos anteriormente, ao resolver uma equação fracionária, é preciso garantir que o valor obtido para a incógnita não anule algum dos denominadores da equação e que ele mantenha verdadeira a igualdade. Quando uma dessas situações não ocorre, a equação não tem solução.
Página 164
Verificamos então o valor na equação fracionária:
Assim, não pode ser solução dessa equação, pois esse valor anula o denominador e não existe divisão por zero.
Logo, essa equação não tem solução.
Atividades
Faça as atividades no caderno.
10. Resolva as equações quando possível.
a) , com .
b) , com .
c) , com .
d) , com e .
e) , com e .
f) , com .
11. Escreva no caderno uma equação que possibilite resolver cada um dos problemas apresentados. Depois, resolva a equação e obtenha a solução do problema.
A.
Um automóvel, a certa medida de velocidade média, percorre em horas. Para percorrer mantendo a mesma medida de velocidade média, esse automóvel gasta 1 hora a mais. Quanto tempo esse automóvel leva para percorrer os ?
B.
Em uma indústria, diariamente certa quantidade de funcionários produzia 300 peças. A produção diária dessa indústria passou para 420 peças após a contratação de mais 30 funcionários. Considerando que os funcionários têm a mesma produtividade, quantos funcionários trabalhavam nessa indústria antes da contratação? E após a contratação?
Atenção!
Indique por x a quantidade de funcionários e por a quantidade de funcionários depois da contratação.
12. Marta
pagou R$ 150,00 na compra de x cadernos e R$
225,00 na compra de livros. Todos os cadernos que Marta comprou
têm o mesmo preço e todos os livros também têm o mesmo preço. Sabendo
que cada livro custa o dobro de cada caderno, calcule quantos cadernos e quantos livros Marta
comprou.
Página 165
Equações do 1º grau com duas incógnitas
Sabrina fez uma pergunta a Lucas.


Indicando um dos números por e o outro por , podemos escrever a equação para representar o que Sabrina está perguntando.
Vamos calcular alguns dos possíveis valores de e .
|
|
||
|---|---|---|
Os valores de e em cada linha são alguns dos possíveis valores que satisfazem a equação, ou seja, são alguns dos possíveis números em que Sabrina pensou.
A equação escrita que representa o questionamento de Sabrina é um exemplo de equação do 1º grau com duas incógnitas.
Uma equação do 1º grau com duas incógnitas, x e y, é uma sentença matemática que pode ser escrita na forma , sendo a, b e c números reais, com a e b não nulos.
Acompanhe outros exemplos de equações do 1º grau com duas incógnitas.
As soluções de uma equação do 1º grau com duas incógnitas são pares ordenados . Algumas soluções da equação são , , e .
Página 166
Representação geométrica de uma equação do 1º grau com duas incógnitas
É possível demonstrar que a representação geométrica de uma equação do 1º grau com duas incógnitas é uma reta.
Acompanhe a seguir as etapas necessárias para realizar essa representação no plano cartesiano.
1. Atribua valores para x e calcule o valor correspondente para y, a fim de obter algumas soluções da equação.
2. Em seguida, represente esses pontos (soluções) no plano cartesiano.
3. Por fim, trace a reta que passa por esses pontos.
Agora, utilizando as etapas indicadas, vamos representar a equação no plano cartesiano.
1.
|
x |
y |
Solução |
|---|---|---|
|
0 |
||
|
1 |
||
|
2 |
||
|
3 |
Atenção!
Como a representação gráfica de uma equação do 1º grau com duas incógnitas é uma reta, basta determinar duas soluções da equação.
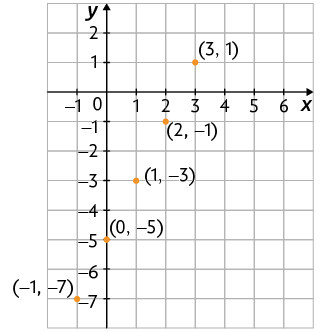
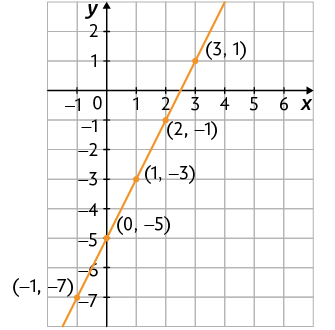
Questão 2. Construa um plano cartesiano em uma malha quadriculada. Em seguida, obtenha a representação geométrica das equações a seguir.
a)
b)
Página 167
Atividades
Faça as atividades no caderno.
13. Em quais itens estão apresentadas equações do 1º grau com duas incógnitas?
A.
B.
C.
D.
E.
F.
G.
H.
I.
J.
K.
L.
14. Escreva no caderno uma equação para representar cada situação a seguir.
a) O dobro da minha idade mais o triplo da idade do meu filho é igual a 84 anos.
b) Paguei R$ 6,50 por 2 salgados e 1 suco.
c) A diferença entre o preço de 1 par de tênis e de 1 par de sapatos é R$ 48,00.
d) Comprei 3 kg de tomate e 4 kg de batata por R$ 16,53.
Atenção!
Utilize as letras e para representar as incógnitas.
15. Mariana pensou em dois números cuja diferença é 12. Sabendo que um dos números é maior do que 20 e menor do que 23, determine todos os possíveis pares de números em que Mariana pode ter pensado.
16. Em qual dos itens é indicada a representação geométrica da equação ?
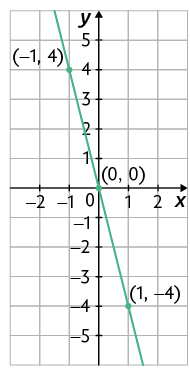
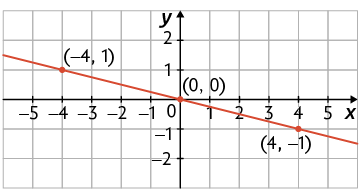
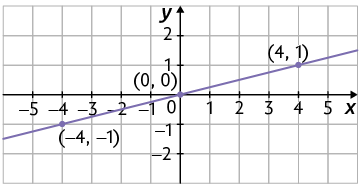
17. Represente geometricamente as equações de cada item. Para isso, use uma malha quadriculada.
a)
b)
c)
d)
Página 168
Sistemas de duas equações do 1º grau com duas incógnitas
Em um final de semana, foi realizada uma partida entre os times do 8º ano A e 8º ano B pelo campeonato de futebol da escola.
Durante a partida, foram marcados 8 gols. A diferença entre a quantidade de gols marcados pelo time do 8º ano A e a de gols marcados pelo time do 8º ano B foi 2 gols.
De acordo com essas informações, quantos gols marcou cada time nessa partida?
Para responder a essa pergunta, podemos escrever duas equações, uma para representar o total de gols marcados durante a partida e outra para representar a diferença entre a quantidade de gols marcados na partida pelos dois times.
Vamos indicar por a quantidade de gols marcados pelo 8º ano A e por a quantidade de gols marcados pelo 8º ano B. Assim:


Para representar essa situação, temos duas equações com duas incógnitas em cada uma delas.
Nesse caso, temos o seguinte sistema de duas equações do 1º grau com duas incógnitas.
Atividades
Faça as atividades no caderno.
18. Represente cada uma das situações apresentadas nos itens a seguir por meio de um sistema de equações.
a) Em uma caixa, foram colocadas bolinhas vermelhas e amarelas, chegando a um total de 12 bolinhas. A caixa tem 2 bolinhas vermelhas a mais do que amarelas.
b) Certo tipo de doce é vendido em embalagens do tipo x e y. Duas embalagens do tipo x e três embalagens do tipo y totalizam 19 doces. Já três embalagens do tipo x e duas embalagens do tipo y totalizam 21 doces.
c) Em uma sala de aula há 31 estudantes, entre meninos e meninas. Nela, há 5 meninas a mais do que meninos.
Atenção!
Utilize as letras e para representar as incógnitas.
Página 169
Solução de um sistema de duas equações do 1º grau com duas incógnitas
Neste tópico, vamos estudar alguns métodos para obter a solução de um sistema de duas equações do 1º grau com duas incógnitas. Antes disso, devemos saber que:
Uma solução de um sistema de duas equações do 1º grau com duas incógnitas é um par ordenado que é solução das duas equações simultaneamente.
Método da substituição
Raul gastou R$ 220,00 na compra de 2 calças e 1 camisa.

Quantos reais custou cada peça de roupa, sabendo que as calças custaram o mesmo preço e a camisa custou R$ 26,00 a menos que a calça?
Nesse caso, indicando por o preço de cada calça e por o preço da camisa escrevemos as seguintes equações:


Assim, temos o seguinte sistema de equações: .
Acompanhe como podemos resolvê-lo utilizando o método da substituição.
Inicialmente, escolhemos uma das equações e isolamos uma das incógnitas. Nesse caso, escolhemos a 2ª equação e isolamos no 1º membro.
Depois, substituímos por na outra equação e resolvemos a equação obtida.
Página 170
Para obter o valor de , basta substituir por 56 na equação .
Portanto, uma calça custou R$ 82,00, e uma camiseta, R$ 56,00.
Agora, vamos resolver o sistema .
Efetuando os cálculos, obtemos:
Sendo assim, o sistema inicial é equivalente ao sistema .
Substituindo em , obtemos:
Sabendo que , calculamos o valor de x.
Portanto, a solução do sistema é .
Atividades
Faça as atividades no caderno.
19. Use o método de substituição para resolver, em seu caderno, os sistemas de equações apresentados nos itens a seguir.
a)
b)
c)
d)
e)
f)
Página 171
20. Marcos e Otávio são pintores. Ao todo, eles receberam R$ 980,00 por um trabalho que realizaram. Sabendo que Marcos recebeu R$ 228,00 a menos do que Otávio, calcule quantos reais cada um deles recebeu.
Atenção!
Indique por a quantia, em reais, recebida por Marcos e por a quantia recebida por Otávio. Em seguida, escreva no caderno um sistema de equações e resolva-o.
21. Os Jogos Olímpicos de Tóquio 2020 foram realizados de 23 de julho de 2021 a 8 de agosto de 2021.

O Brasil participou dessa edição em 35 modalidades esportivas, com 302 atletas ao todo. O número de homens participantes foi maior do que o de mulheres, com diferença de 22 atletas.
Fonte de consulta: COMITÊ OLÍMPICO DO BRASIL (COB). Time Brasil. Disponível em: https://oeds.link/2fLqW5. Acesso em: 2 maio 2022.
Quantos homens e quantas mulheres compuseram a delegação de atletas do Brasil nessa edição?
22. Junte-se a um colega para resolver esta atividade.
a) Relacionem no caderno cada problema a seguir ao sistema de equações que permite resolvê-lo.
A.
Solange e Gabriel têm juntos R$ 776,00. A quantia que Solange tem é o triplo da quantia de Gabriel. Quantos reais cada um deles tem?
B.
O dobro da quantidade de figurinhas que Marcos tem adicionado ao quíntuplo da quantidade de figurinhas que Renata tem é igual a 125 figurinhas. A diferença entre as quantidades de figurinhas que eles têm é igual a 10 figurinhas. Quantas figurinhas cada um deles tem, sabendo que Marcos tem mais figurinhas do que Renata?
C.
Em um estacionamento há carros e motos, totalizando 250 veículos. Quantos carros e quantas motos há nesse estacionamento, sabendo que o dobro da quantidade de carros é igual ao triplo da quantidade de motos?
D.
A soma da idade de Carlos com o dobro da idade de Lúcia é igual a 125 anos. Qual é a idade de Carlos e a de Lúcia, sabendo que Lúcia tem o dobro da idade de Carlos?
I.
II.
III.
IV.
b) Resolvam no caderno os sistemas e determinem a resposta de cada problema.
Página 172
23. Em certa escola estudam meninos e meninas, totalizando 2.500 estudantes. Quantos meninos e quantas meninas estudam nessa escola, sabendo que o triplo da quantidade de meninos é igual ao dobro da quantidade de meninas?
24. A
diferença entre a idade de Marcela e a de Augusto é igual a
28 anos. Há 6 anos, a idade de Marcela era o triplo da
idade de Augusto. Qual é a idade atual de cada um deles?
25. Certa marca vende suco em embalagens do tipo x e do tipo y. Juntas, 4 embalagens do tipo x e 2 do tipo y contêm . Já 1 embalagem do tipo x e 6 do tipo y contêm . Qual é a medida da capacidade de cada tipo de embalagem?
26. Em uma sessão de cinema foram arrecadados R$ 2.720,00 com a venda das entradas. Cada uma custa R$ 16,00 e estudantes pagam meia-entrada. Com a venda das entradas inteiras, arrecadou-se R$ 800,00 a mais do que o triplo do valor arrecadado com a venda das meias-entradas. Quantas pessoas ao todo pagaram para assistir a essa sessão?
27. No último fim de semana, Adriana fez uma viagem com seu carro. Ela partiu de Londrina com destino a Maringá, ambas cidades no Paraná. Porém, no caminho, Adriana resolveu passar por Astorga, também no Paraná, antes de ir a Maringá, o que aumentou o trajeto em .
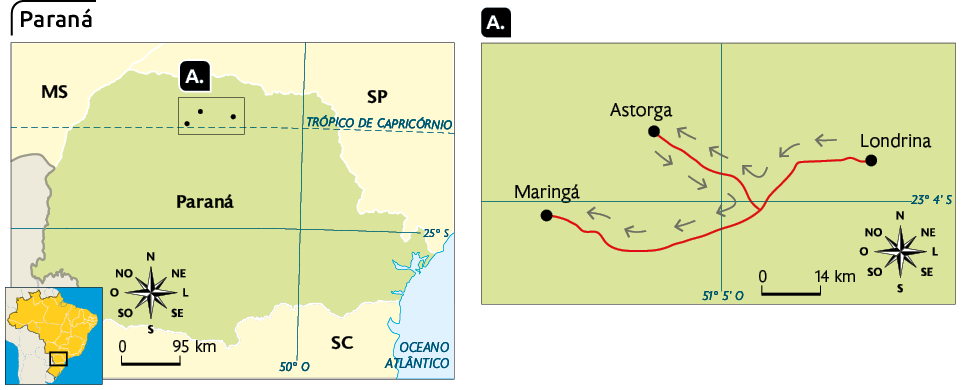
Fonte de consulta: ATLAS geográfico escolar. 8. ed. Rio de Janeiro: IBGE, 2018.
Atenção!
Indique por a medida da distância entre Londrina e Astorga e por a medida da distância entre Astorga e Maringá.
a) Sabendo que Adriana percorreu um total de , qual é a medida da distância entre Londrina e Maringá, sem passar por Astorga?
b) A distância entre Londrina e Astorga mede a menos do que a distância entre Astorga e Maringá. Sabendo disso, calcule a medida da distância entre:
Londrina e Astorga;
Astorga e Maringá.
28. Com exatamente R$ 120,00 e sem receber troco, Raquel pode comprar 4 bolas de futebol e 1 de voleibol ou 2 bolas de futebol e 2 de voleibol. Qual é o preço unitário de cada bola?
Página 173
Método da adição
Em uma sala de aula, há 36 estudantes entre meninos e meninas. A diferença entre a quantidade de meninos e de meninas é 6 estudantes. Quantos meninos e quantas meninas há nessa turma, sabendo que há mais meninos do que meninas?

Indicando por a quantidade de meninos e por a quantidade de meninas, podemos escrever as seguintes equações:


Assim, temos o seguinte sistema de equações: .
Acompanhe como podemos resolvê-lo utilizando o método da adição.
As duas equações apresentam termos opostos ( na 1ª equação e na 2ª equação). Nesse caso, vamos adicioná-las.
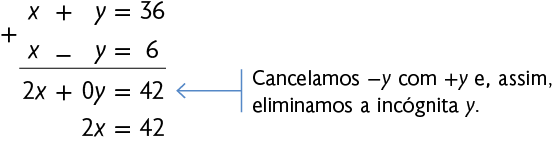
Agora, resolvemos a equação e obtemos o valor de .
Por fim, obtemos o valor de . Para isso, substituímos por 21 em uma das equações do sistema, por exemplo, na 1ª equação.

Portanto, nessa sala de aula há 21 meninos e 15 meninas.
Página 174
Considere o sistema de equações . Vamos resolvê-lo utilizando o método da adição.
Note que as duas equações desse sistema não têm termos opostos. Assim, não podemos eliminar uma das incógnitas apenas adicionando as duas equações. Em casos semelhantes a esse, com o objetivo de obter termos opostos nas equações, multiplicamos uma ou as duas por números escolhidos convenientemente.
Agora, vamos resolver o sistema.
1º. A 1ª equação tem o termo e a 2ª equação tem o termo . Assim, basta multiplicar todos os termos da 1ª equação por para obter uma equação equivalente e com o termo , oposto ao termo .
2º. Adicionamos as duas equações.
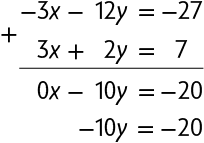
3º. Resolvemos a equação obtida e calculamos o valor de .
4º. Obtemos o valor de x. Para isso, substituímos por 2 em uma das equações do sistema, por exemplo, na 1ª equação.

Portanto, a solução do sistema é .
Questão 3. No sistema , as equações também não têm termos opostos. Utilizando o método apresentado nesta página, resolva esse sistema em seu caderno.
Página 175
Atividades
Faça as atividades no caderno.
29. Resolva em seu caderno os sistemas de equações a seguir por meio do método da adição.
a)
b)
c)
d)
e)
f)
30. A soma de dois números é igual a 12 e a diferença entre eles é igual ao único número primo que é par. Quais são esses números?
31. A soma das idades de Júlia e André é igual a 34 anos. A diferença entre as idades deles é igual a 8 anos. Qual é a idade de Júlia e a de André, sabendo que André é mais novo do que Júlia?
32. Participaram de uma excursão homens e mulheres, sendo a maioria homens. A soma das quantidades de homens e de mulheres é igual a 130 pessoas e a diferença entre a quantidade de homens e a de mulheres é igual a 12 pessoas. Quantos homens e quantas mulheres participaram dessa excursão?
33. Acompanhe o que Rafael e Fábio estão dizendo.


Calcule a medida da massa de cada um deles.
34. Elabore um problema envolvendo um sistema de duas equações do 1º grau com duas incógnitas. Em seguida, peça a um colega que o resolva. Por fim, verifique se a resposta obtida está correta.
Página 176
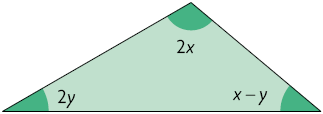
35. Com base nas informações apresentadas em cada item, determine x e y, em graus.
a) A diferença entre x e y é igual a .
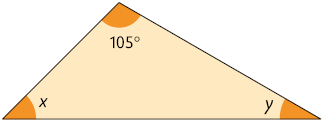
b) y é o dobro de x.
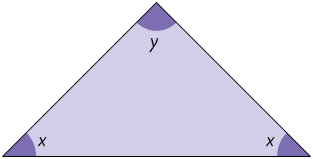
c) A adição de x e y é igual a .
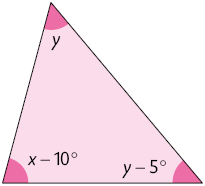
d) A diferença entre x e y é igual a .
Atenção!
A soma das medidas dos ângulos internos de um triângulo é .
36. Use o método da adição para resolver, em seu caderno, os sistemas de equação a seguir.
a)
b)
c)
d)
e)
f)
g)
h)
37. (Unifor-CE-2005) Em uma barraca na praia, um grupo de turistas pagou R$ 23,40 pelo consumo de 6 cocos verdes e 12 pastéis, enquanto outro grupo pagou R$ 21,30 por 7 cocos verdes e 9 pastéis.
Nessa barraca, 1 coco verde e 1 pastel custam, juntos:
a) R$ 2,10
b) R$ 2,30
c) R$ 2,50
d) R$ 2,70
e) R$ 2,90
38. (Obmep-2007) Juliana tem 8 cartões de papel retangulares iguais. Se ela enfileirar todos os cartões juntando lados de mesma medida, ela pode obter um retângulo de perímetro ou um retângulo de perímetro .
Qual é a área de cada cartão?
a)
b)
c)
d)
e)
Página 177
Análise da solução de um sistema de equações por meio da representação geométrica
Neste tópico, vamos representar geometricamente alguns sistemas de equações. Para isso, representaremos em um mesmo plano cartesiano cada uma das equações que os compõem.
• Considere o sistema .
As retas que representam as equações são concorrentes, ou seja, cruzam-se em um único ponto, nesse caso, em . Portanto, é a solução desse sistema.
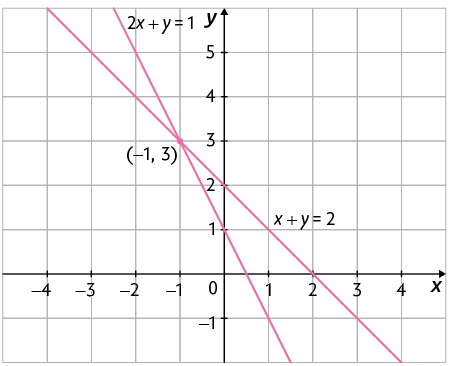
Questão 4. Utilizando qualquer um dos métodos apresentados anteriormente, resolva em seu caderno o sistema e verifique se, de fato, sua solução é .
O sistema estudado é um exemplo de sistema possível e determinado.
Um sistema de equações é possível e determinado quando tem uma única solução. As retas que representam as equações de um sistema possível e determinado são concorrentes.
• Considere o sistema .
Como não existem números que adicionados resultem em 2 e 3, simultaneamente, tal sistema não tem solução. Além disso, como não há pontos que satisfazem as duas equações simultaneamente, as retas que as representam são paralelas, ou seja, estão em um mesmo plano e não se cruzam.
Página 178
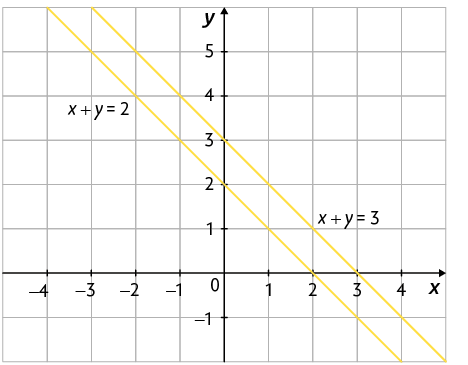
O sistema estudado é um exemplo de sistema impossível.
Um sistema de equações é impossível quando não tem solução. As retas que representam as equações de um sistema impossível são paralelas.
• Considere o sistema .
Note que as equações são equivalentes, pois ao multiplicarmos cada termo da primeira equação por 2 obtemos a segunda equação. Nesse caso, as equações têm as mesmas soluções e, consequentemente, o sistema apresenta infinitas soluções. As retas que representam as equações são coincidentes, ou seja, estão sobrepostas.
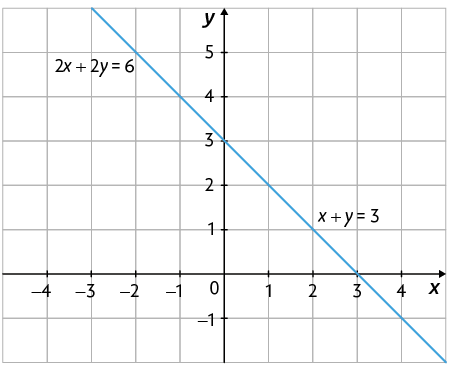
O sistema estudado é um exemplo de sistema possível e indeterminado.
Um sistema de equações é possível e indeterminado quando tem infinitas soluções. As retas que representam as equações de um sistema possível e indeterminado são coincidentes.
Página 179
Instrumentos e softwares
Equações do primeiro grau com o GeoGebra
Com o GeoGebra, é possível representar graficamente equações do 1º grau e analisar a solução de um sistema. Execute o passo a passo a seguir.
1º. Clique com o botão direito sobre a Janela de visualização, habilite a opção Mostrar Eixos e, na aba Malha, escolha a opção Malha principal.
2º. Represente graficamente cada equação digitando-a no campo Entrada... e pressionando Enter, uma por vez, por exemplo, e .
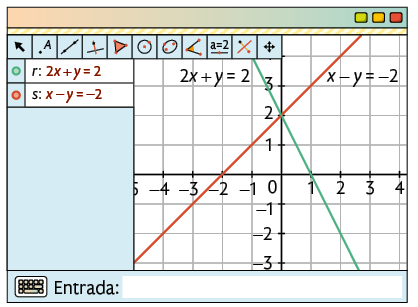
3º. Selecione a ferramenta Interseção de Dois Objetos e clique nas duas retas para verificar se elas são concorrentes, coincidentes ou paralelas.
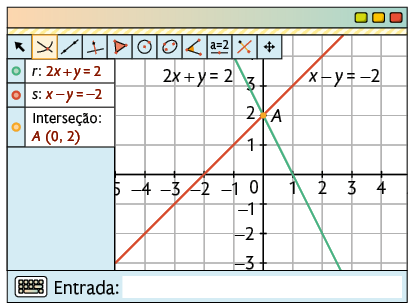
Atenção!
Para mostrar a equação que a reta representa, clique sobre ela com o botão direito e, em Exibir Rótulo, habilite a opção Valor.
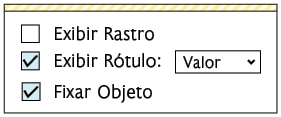
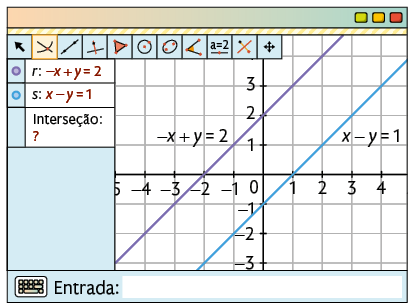
Nesse exemplo, como a interseção entre as retas é um ponto, elas são concorrentes, então o sistema é possível e determinado.
Página 180
Analise outros exemplos:
•
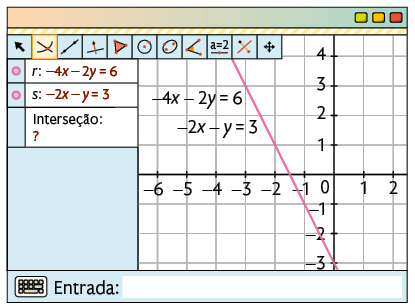
Como as retas são paralelas, não existe interseção entre elas. Assim, o sistema é impossível. Para esse tipo de sistema, o GeoGebra indica a interseção com uma interrogação (?).
•
Note que, como as retas são coincidentes, elas estão sobrepostas. Assim, o sistema é possível e indeterminado. Note que para esse tipo de sistema, o GeoGebra também indica a interseção com uma interrogação (?).
Atividades
Faça as atividades no caderno.
39. Represente cada um dos sistemas geometricamente.
a)
b)
c)
d)
Página 181
40. A imagem mostra a representação geométrica do sistema .
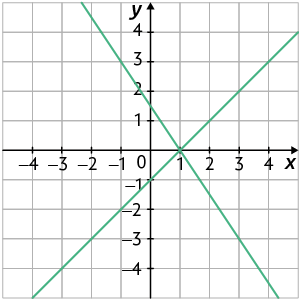
a) O sistema apresentado é possível e determinado, impossível ou possível e indeterminado? Justifique sua resposta.
b) Caso a resposta do item a seja possível e determinado, determine a solução do sistema.
41. A imagem mostra a representação geométrica de um sistema de equações.
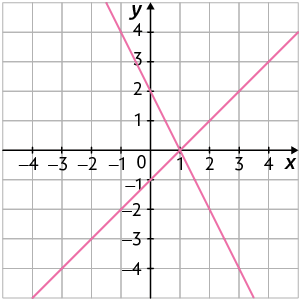
Entre os sistemas de equações a seguir, determine aquele que está representado geometricamente.
a)
b)
c)
d)
42. Classifique cada uma das afirmações em verdadeira ou falsa. Depois, reescreva as falsas em seu caderno, corrigindo-as.
a) As retas que representam um sistema possível e determinado são paralelas.
b) As retas que representam as equações de um sistema possível e indeterminado são coincidentes.
c) Um sistema de equações é possível e determinado quando tem uma única solução.
43. Artur é 8 anos mais velho do que sua irmã Isadora. Adicionando suas idades, obtemos 26 anos.
a) Escreva um sistema de equações que possibilite determinar a idade de cada um dos irmãos.
b) Ao representar geometricamente o sistema escrito por você no item a, obteremos retas concorrentes, paralelas ou coincidentes?
c) Qual é a idade de cada um dos irmãos?
44. Escreva
um sistema de duas equações do 1º grau com duas
incógnitas. Em seguida, peça a um colega que represente esse
sistema utilizando o GeoGebra. Por fim,
desafie-o a classificar as retas obtidas em concorrentes, paralelas ou
coincidentes.
45. Elabore um problema envolvendo o sistema apresentado a seguir.
Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Página 182
Equação do 2º grau do tipo
Antônio foi desafiado a determinar a medida do comprimento do lado de um quadrado com área medindo . Analise o que ele está dizendo.

A equação escrita por Antônio está apresentada a seguir.
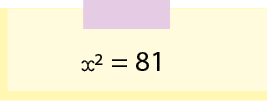
Atenção!
Note que essa equação pode ser escrita na forma , em que e .
No caso apresentado, temos um exemplo de equação do 2º grau com uma incógnita.
Para resolver essa equação, Antônio precisava descobrir quais são os números que, elevados ao quadrado, resultam em 81. Como resposta, ele obteve os seguintes valores para x.
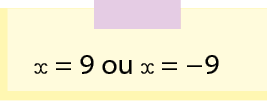

Portanto, Antônio concluiu que a medida do comprimento do lado do quadrado deve ser .
Utilizando uma calculadora, é possível determinar o número positivo que, elevado ao quadrado, resulte em 81. Para isso, basta digitar a seguinte sequência de teclas:

Questão 5. Utilizando
uma calculadora, determine o número positivo que,
elevado ao quadrado, resulte aproximadamente em:
a) 125.
b) 69.
c) 42,25.
d) 5,76.
Página 183
Instrumentos e softwares
Equações do tipo com o GeoGebra
Com o GeoGebra, é possível resolver equações do tipo , com a diferente de zero. Vamos resolver, por exemplo, a equação . Para isso, execute o passo a passo a seguir.
1º. No campo Entrada..., da Janela Álgebra, digite a equação .
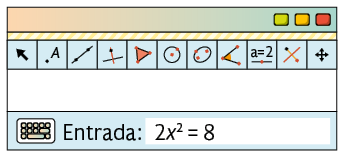
Atenção!
Para escrever o , digite .
Após realizar o 1º passo, a equação fica armazenada na Janela Álgebra, conforme apresentado a seguir.
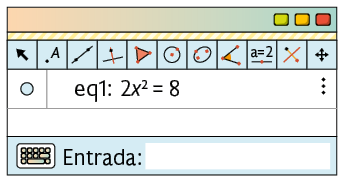
2º. Na linha correspondente a eq1, clique com o botão esquerdo do mouse em . Em seguida, selecione a opção Resolver.
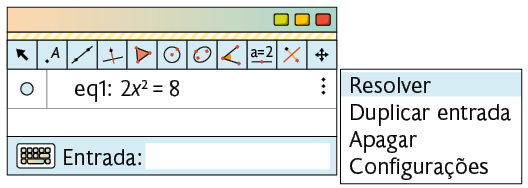
Na Janela Álgebra, serão exibidas as soluções da equação (l1=Resolver(eq1)).

Página 184
Atividades
Faça as atividades no caderno.
46. Em quais itens as equações apresentadas são do 2º grau do tipo ?
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
47. Em cada item, escreva uma equação que possibilite resolver o problema. Em seguida, resolva a equação e determine a solução do problema.
a) O quadrado de um número é igual a 9. Que número é esse?
b) O dobro do quadrado de um número é igual a 800. Que número é esse?
c) O triplo do quadrado de um número é igual a 1.875. Que número é esse?
d) O dobro do quadrado de um número é igual a 392. Que número é esse?
e) O triplo do quadrado de um número é igual a 3.675. Que número é esse?
48. Calcule a medida da área de cada quadrado.


49. Leia o problema a seguir.
Roberto comprou 40 placas de vidro em formato quadrado para instalar em sua casa. A medida da área total que ele comprou foi de . Qual é a medida do comprimento do lado de cada placa?
a) Escreva uma equação do tipo que represente a situação.
b) Utilizando
o GeoGebra,
resolva o problema apresentado.
50. Utilizando
pedaços de retalhos com formato de quadrado de dimensões de mesma medida,
Marcos confeccionou o tapete apresentado a seguir.

Sabendo que a área desse tapete mede, determine a medida de comprimento do lado de cada um dos pedaços de retalho. Resolva esse problema utilizando uma calculadora.
51. Elabore um problema envolvendo equações do 2º grau do tipo e a imagem apresentada a seguir.
Depois, peça a um colega que o resolva. Por fim, verifique se a resposta obtida por ele está correta.
Atenção!
Se considerar necessário, utilize uma calculadora ou o GeoGebra para resolver o problema proposto.
Página 185
O que eu estudei?
Faça as atividades em uma folha de papel avulsa.
1. As balanças a seguir estão em equilíbrio. Nelas, caixas de mesma cor têm a mesma medida de massa.
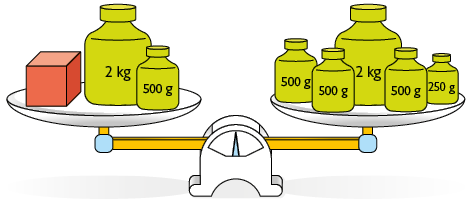
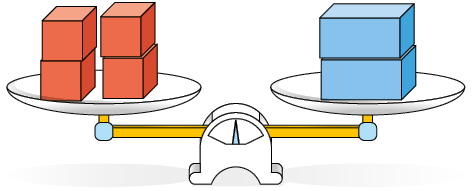
Qual é a medida da massa de uma caixa vermelha, em gramas? E de uma caixa azul?
2. Qual é o número cujo quádruplo adicionado a 46 resulta em 118?
3. Lauro comprou 2 caixinhas de leite a R$ 3,50 cada uma delas e 5 pães. Pagou a compra com a cédula a seguir e recebeu R$ 5,50 de troco.

Quanto custou cada pão?
4. Carla nasceu 4 anos antes de seu irmão. Em certo momento, ela tinha o triplo da idade do irmão. Qual era a idade do irmão nesse momento?
5. Em uma folha de papel avulsa, associe cada informação a uma equação.
A. A divisão de por é igual a .
B. A divisão de por é igual à divisão de por .
C. A divisão de por é igual a dividido por .
1.
2.
3.
6. Resolva as equações da atividade anterior em uma folha de papel avulsa.
7. Em uma marcenaria eram produzidas 2 estantes por dia. Essa produção aumentou para 3 estantes por dia após a contratação de 3 funcionários.
Quantos passaram a ser os funcionários dessa marcenaria após as contratações, sabendo que todos mantiveram o mesmo ritmo de trabalho?
8. Resolva os sistemas de equações a seguir.
a)
b)
c)
d)
e)
f)
Página 186
9. Em cada item a seguir, é apresentada a mesma balança em equilíbrio em momentos diferentes. Em uma folha de papel avulsa, escreva e resolva um sistema que possibilite determinar os valores de x e y.
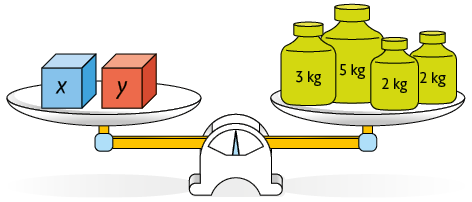
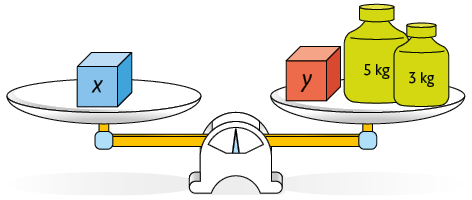
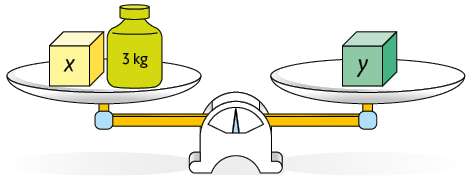
10. Em uma sala de aula há 42 estudantes. Sabendo que há mais meninas do que meninos na turma e que a diferença entre a quantidade de meninas e a de meninos é 4, quantas meninas e quantos meninos há nessa sala de aula?
11. Ao serem distribuídas 40 balas entre certo número de crianças, cada uma delas recebe a mesma quantidade de balas que receberia se fossem distribuídas 50 balas entre esse número de crianças mais 1 criança. Quantas balas cada criança recebe?
12. Leandro pagou R$ 119,00 na compra de 1 calça e 1 camiseta. Sabendo que a camiseta custou R$ 25,00 a menos do que a calça, qual é o preço da calça?
13. Para um espetáculo de teatro, foram colocados à venda ingressos com dois preços distintos. Esses ingressos, dependendo do preço, apresentavam cores diferentes: azul e branco. Observando duas pessoas na fila da bilheteria, constatou-se o seguinte: a primeira comprou 2 ingressos azuis e 2 brancos e gastou R$ 140,00; a segunda comprou 2 ingressos azuis e 3 brancos e gastou R$ 180,00. Qual era o preço de cada ingresso?
14. Um mosaico é formado por 700 quadrados de mesma medida de área. Se a medida da área total desse mosaico é de , qual é a medida do comprimento do lado de cada quadrado?